《三角函数》单元测试2
必修4三角函数单元测试题(含答案)

必修4三角函数单元测试题(含答案) 三角函数单元测试1.sin210的值是多少?A。
3/2B。
-3/2C。
1/2D。
-1/22.终边相同的角是哪一组?A。
π或kπB。
(2k+1)π或(4k±1)π(k∈Z)C。
kπ±π/3或π/3k(k∈Z)D。
kπ±π/6或kπ±π/6(k∈Z)3.已知cosθ·tanθ<0,那么角θ在哪两个象限之间?A。
第一或第二象限角B。
第二或第三象限角C。
第三或第四象限角D。
第一或第四象限角4.已知弧度数为2的圆心角所对的弦长是2,则这个圆心角所对的弧长是多少?A。
2sin1B。
sin2C。
2D。
π5.要得到函数y=2sin(xπ/36),x∈R的图像,只需把函数y=2sinx,x∈R的图像上所有的点:A。
向左平移π/36个单位长度,再把所得各点的横坐标不变,纵坐标伸长到原来的3倍B。
向右平移π/36个单位长度,再把所得各点的横坐标不变,纵坐标伸长到原来的3倍C。
向左平移π/36个单位长度,再把所得各点的横坐标不变,纵坐标缩短到原来的1/3D。
向右平移π/36个单位长度,再把所得各点的横坐标不变,纵坐标缩短到原来的1/36.设函数f(x)=sin((x+π/3)/3)(x∈R),则f(x)在区间:A。
(2π/7,2π/3)上是增函数B。
(-π,2π/3)上是减函数C。
(π,8π/4)上是增函数D。
(-π,2π/3)上是增函数7.函数y=Asin(ωx+φ)(ω>0,φ<π)的部分图象如图所示,则函数表达式是:A。
y=-4sin(x+π/4)B。
y=4sin(x-π/4)C。
y=-4sin(x-π/4)D。
y=4sin(x+π/4)8.函数y=sin(3x-π/4)的图象是中心对称图形,其中它的一个对称中心是:A。
(-π/4,0)B。
(-π,0)C。
(π,0)D。
(11π/12,0)9.已知f(1+cosx)=cos2x,则f(x)的图象是下图的:(删除明显有问题的段落)4.A5.D6.C7.B8.A9.C10.B二、填空题11.012.513.1/214.-sin(15π/4)三、解答题15.cosα=√(1-sin²α)=√(1-1/4)=√(3/4)=±√3/216.M={θ|θ∈[0,π/4]},N={θ|θ∈[π/4,π]}17.(1)sin²θ+cos²θ+sinθ+cosθ+2sinθcosθ=1+sinθ+cosθsinθ+cosθ+2sinθcosθ=sinθ+cosθ2sinθcosθ=0sinθ=0或cosθ=0θ=kπ或θ=kπ±π/2 (k∈Z)2)将sinθ和cosθ代入原方程得m=1/218.(1)f(x)=sin(3x-π/2)2)a=2,b=419.最大值为1/√3,最小值为-120.(I)π/2II)g(x)=2cos(2x-π/2)-sin(2x)二、填空题11.412.013.414.20三、解答题15.已知 $A(-2,a)$ 是角 $\alpha$ 终边上的一点,且$\sin\alpha=-\dfrac{a}{\sqrt{a^2+16}}$,求 $\cos\alpha$ 的值。
第七章《三角函数》单元测试
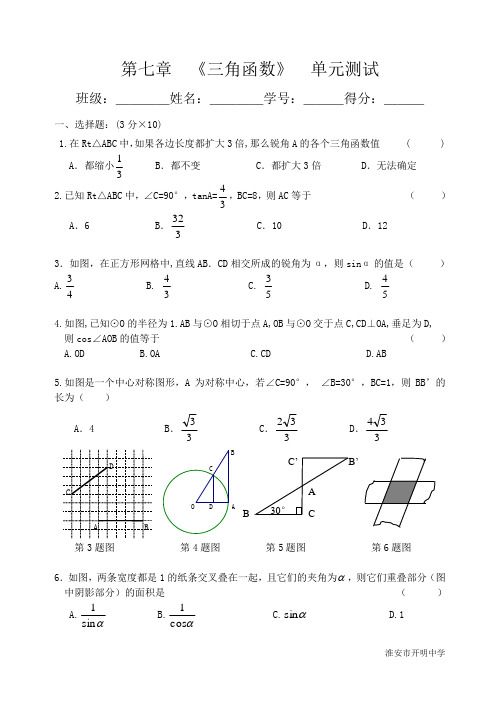
第七章 《三角函数》 单元测试班级:____姓名:____学号:___得分:___一、选择题:(3分×10)1.在Rt △ABC 中,如果各边长度都扩大3倍,那么锐角A 的各个三角函数值 ( )A .都缩小31B .都不变C .都扩大3倍D .无法确定 2.已知Rt △ABC 中,∠C=90°,tanA=43,BC=8,则AC 等于 ( )A .6B .323C .10D .123.如图,在正方形网格中,直线AB .CD 相交所成的锐角为α,则sin α的值是( ) A.34 B. 43 C. 35 D. 454.如图,已知⊙O 的半径为1.AB 与⊙O 相切于点A,OB 与⊙O 交于点C,CD ⊥OA,垂足为D, 则cos ∠AOB 的值等于 ( ) A.OD B.OA C.CD D.AB5.如图是一个中心对称图形,A 为对称中心,若∠C=90°, ∠B=30°,BC=1,则BB ’的长为( )A .4B .33 C .332 D .334第3题图 第4题图 第5题图 第6题图6.如图,两条宽度都是1的纸条交叉叠在一起,且它们的夹角为α,则它们重叠部分(图中阴影部分)的面积是 ( ) A.αsin 1 B.αcos 1 C.αsin D.1O DCA BC DF EDBA7.如图,AC 是电杆AB 的一根拉线,测得BC=6米,∠ACB=52°,则拉线AC 的长为 ( ) A.︒526sin 米 B. ︒526tan 米 C. 6·cos52°米 D. ︒526cos 米8.直角三角形纸片的两直角边长分别为6,8,现将ABC △如图那样折叠,使点A 与点B 重合,折痕为DE ,则t a nC B E ∠的值是 ( )A .247BC .724D .13第7题图 第8题图二、填空题:(3分×8) 9. 在Rt △ABC 中,∠ACB=900,sinB=27则cosB= . 10.21θ=,则θ= ,11.在△ABC 中,若2|tan 1|cos )0A B -+=,则∠C 的度数为 . 12.如图,△ABC 中,AB=AC=5,BC =8,则tanB= .13.用不等号“>”或“<”连接:sin50°________cos50°。
高一年级数学三角函数单元测试题二

三角函数单元测试题二一、选择题:本大题共12小题:每小题5分:共60分在每小题给出的四个选项中:只有一项是符合题目要求的.(1)的值为().A. B. C. D.(2)函数的定义域是().(A)(B)(C)取(D)(3)已知:是第二象限角:且:则等于().A. B.C.-7 D.7(4)函数的最小正周期是().A. B. C. D.(5)(文)当时:函数的最大值为().(A)0 (B)5 (C)(D)3(理)函数的值域为().A. B.C. D.(6)若:则的值为().A. B. C. D.(7)设:则、、的大小是().A. B. C. D.((8).函数的单调递增区间是().(A)(B)(C)(D)(9)函数的图象可由函数的图象向右平移()个单位而得到.(A)(B)(C)(D)(10)设:那么是函数为奇函数的().A.充分非必要条件B.必要非充分条件C.充分必要条件D.既非充分也非必要条件(11)如果:那么的值为().A. B.- C. D.-(12)函数的图象与函数的图象在闭区间上().A.可能没有公共点 B.只有一个公共点C.一定有两个公共点 D.至少有一个公点二、填空题:本大题共4小题:每小题4分:共16分把答案填在题中横线上(13)中::那么这个三角形的最大角的度数为.(14)已知,那么的值等于.(15)函数的图象的两条相邻的对称轴之间的距离为:则.(16)是定义在R上的奇函数:且对任意成立:则的值= .三、解答题:本大题共6小题:共74分解答应写出文字说明:证明过程和演算步骤(17)(本小题满分12分).已知:求的值.(18)(本小题满分12分)设函数满足(Ⅰ)求、的值:(Ⅱ)求使成立的的取值集合.(19)(本小题满分12分)求函数的最大值和最小值.(20)(本小题满分12分)在:角A、B、C的对边分别为、、:若:且:求的值.(21)(本小题满分12分)在中:于D:作:交AC于F:BC于E.求当x 取什么值时:的面积最大:并求这面积的最大值.(22)(本小题满分14分)已知:求的最大值.单元测试题答案一、选择题(1)B (2)C (3)D (4)C (5)(文)B、(理)A (6)A (7)A (8)A (9)B (10)C (11)D (12)D提示:(3)由得:又(4)经变形:得(5)(理)由:根据反余弦函数的图象:可得函数的值域为.(6)由已知可得且(7)(10)必要性显然:若:即:则∴是奇函数.(11)令:则(12)取特例作研究:设:则结合图象作分析时:注意两函数相邻两个公共点间距离为:区间的长度也为.二、填空题:(13)(14)(15)3 (16)0提示:(13)本题即:求角C:可用余弦定理.(15)本题即的最小正周期之半为(16)易有:又:故三、解答题(17)∵:故∴:∴∴(18)(Ⅰ)由:即:故又:即:故(Ⅱ)∴:即∴∴∴所求的取值集合为(19)设:则由可得到.又.故:可得时:的最大值为:时:的最小值为.(20)由,得:∴:∴又:依正弦定理有∴:即由此可得(21)如图:设:(均定值):则在:中:分别可得:于是因此当即时:的最大面积为.。
第五章三角函数单元测试卷及参考答案

第五章 三角函数单元测试卷一、单选题(每题只有一个选项为正确答案,每题5分,共40分) 1.已知角α的终边经过点(,3)P x -,且3tan 4α=-,则cos α=( ) A .35±B .45±C .45-D .452.已知3cos 4x =,则cos2x =( ) A .14-B .14C .18-D .183.如果函数y =3cos (2x +φ)的图象关于点(43π,0)中心对称,那么|φ|的最小值为( ) A .6πB .4π C .3π D .2π4.已知函数()sin 3f x x x =,则在下列区间使函数()f x 单调递减的是( )A .3,24ππ⎛⎫⎪⎝⎭B .0,4π⎛⎫⎪⎝⎭C .5,4ππ⎛⎫ ⎪⎝⎭D .,24ππ⎛⎫-- ⎪⎝⎭5.若,αβ为锐角,45sin ,cos()513ααβ=+=,则sin β等于( ) A .1665B .5665C .865D .47656.函数()sin()(0,0)f x A x A ωϕω=+>>的部分图象如图所示,则下列说法中错误的是( )A .()f x 的最小正周期是2πB .()f x 在1931,1212ππ⎡⎤⎢⎥⎣⎦上单调递增 C .()f x 在175,1212ππ⎡⎤--⎢⎥⎣⎦上单调递增D .直线1712x π=-是曲线()y f x =的一条对称轴7.已知7sin 6πα⎛⎫+=⎪⎝⎭2cos 23πα⎛⎫- ⎪⎝⎭=( ) A .23-B .13-C .23D .138.将函数()2sin 2cos 2cos sin sin 22f x x x ππθθθθ⎛⎫=+--<< ⎪⎝⎭的图象向右平移()0ϕϕ>个单位长度后得到函数()g x 的图象,若()f x ,()g x 的图象都经过点P ⎛ ⎝⎭,则ϕ的值可以是( ) A .53πB .56π C .2π D .6π 二、多选题(每题有多个选项为正确答案,每题5分,共20分) 9.设函数()sin 23f x x π⎛⎫=+⎪⎝⎭,给出下列命题,不正确的是( ). A .()f x 的图象关于直线3x π=对称B .()f x 的图象关于点,012π⎛⎫⎪⎝⎭对称 C .把()f x 的图象向左平移12π个单位长度,得到一个偶函数的图象D .()f x 的最小正周期为π,且在06,π⎡⎤⎢⎥⎣⎦上为增函数10.设函数()sin 2cos 244f x x x ππ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭,则()f x ( ) A .是偶函数 B .在区间0,2π⎛⎫⎪⎝⎭上单调递增 C .最大值为2 D .其图象关于点,04π⎛⎫⎪⎝⎭对称 11.如图是函数sin()()y A x x R ωϕ=+∈在区间5,66ππ⎡⎤-⎢⎥⎣⎦上的图象.为了得到这个函数的图象,只要将sin ()y x x R =∈的图象上所有的点( ).A .向左平移3π个单位长度,再把所得各点的横坐标缩短到原来的12,纵坐标不变 B .向左平移6π个单位长度,再把所得各点的横坐标仲长到原来的12,纵坐标不变C .把所得各点的横坐标缩短到原来的12,纵坐标不变,再向左平移6π个单位长度D .向左平移3π个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变12.函数()sin()0,0,||2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图像如图所示,将函数()f x 的图像向左平移3π个单位长度后得到()y g x =的图像,则下列说法正确的是( )A .函数()g x 为奇函数B .函数()g x 的最小正周期为πC .函数()g x 的图像的对称轴为直线()6x k k ππ=+∈ZD .函数()g x 的单调递增区间为5,()1212k k k ππππ⎡⎤-++∈⎢⎥⎣⎦Z三、填空题(每题5分,共20分)13.已知点P(tan α,cos α)在第三象限,则角α的终边在第________象限. 14.函数()f x =sin 6x π⎛⎫-⎪⎝⎭cos x 的最小值为_________.15.已知1sin 34πα⎛⎫+=⎪⎝⎭,则cos 6πα⎛⎫-= ⎪⎝⎭______.16.已知函数()tan(),(0,0)2f x x πωϕωϕ=+><<的相邻两个对称中心距离为32π,且()f π=,将其上所有点的再向右平移3π个单位,纵坐标不变,横坐标变为原来的13,得()g x 的图像,则()g x 的表达式为_______四、解答题(17题10分,其余每题12分,共70分) 17.已知1tan 42πα⎛⎫+=⎪⎝⎭. (Ⅰ)求tan α的值;(Ⅱ)求()()22sin 22sin 21cos 2sin παπαπαα⎛⎫+-- ⎪⎝⎭--+的值.18.已知函数()24f x x π⎛⎫- ⎝=⎪⎭.(1)求函数()f x 的最小值和最大值及相应自变量x 的集合; (2)求函数()f x 的单调递增区间;(3)画出函数()y f x =区间[]0,π内的图象.19.已知()2sin cos cos 44f x x x x x ππ⎛⎫⎛⎫=+-+ ⎪ ⎪⎝⎭⎝⎭ (1)求函数()f x 的单调递减区间;(2)若关于x 的函数()()()22sin 2g x f x k x =-+在区间,122ππ⎡⎤⎢⎥⎣⎦上有唯一零点,求实数k 的取值范围.20.一半径为2米的水轮如图所示,水轮圆心O 距离水面1米;已知水轮按逆时针做匀速转动,每3秒转一圈,如果当水轮上点P 从水中浮现时(图中点0P )开始计算时间. (1)以水轮所在平面与水面的交线为x 轴,以过点O 且与水面垂直的直线为y 轴,建立如图所示的直角坐标系,试将点P 距离水面的高度h (单位:米)表示为时间t (单位:秒)的函数;(2)在水轮转动的任意一圈内,有多长时间点P 距水面的高度超过2米?21.已知函数()()sin 0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的图象在y 轴右侧的第一个最高点和第一个最低点的坐标分别为()02x ,和()0,2x +π-.若将函数()f x 的图象向左平移3π个单位长度后得到的图象关于原点对称. (1)求函数()f x 的解析式;(2)若函数()()10y f kx k =+>的周期为23π,当0,3x π⎡⎤∈⎢⎥⎣⎦时,方程()1f kx m +=恰有两个不同的解,求实数m 的取值范围.22.已知函数()()sin 0,0,2f x A x A πωϕωϕ⎛⎫=+>>≤⎪⎝⎭的图象如图所示.(1)求函数()f x 的单调递增区间; (2)将函数()y f x =的图象向右平移6π个单位长度得到曲线C ,把C 上各点的横坐标伸长到原来的2倍,纵坐标不变,得到的曲线对应的函数记作()y g x =. (i )求函数()()2x h x f g x ⎛⎫=⎪⎝⎭的最大值; (ii )若函数()2()()2F x g x mg x m R π⎛⎫=-+∈ ⎪⎝⎭在()()0,n n N π+∈内恰有2015个零点,求m 、n 的值.参考答案: 一、单选题 1.【答案】D【解析】角α的终边经过点(),3P x -,由3tan 4α=-,可得334x -=-,所以4x =. 所以4cos 5α==.故选D.2.【答案】D【解析】由3cos 4x =得2231cos 22cos 12148x x ⎛⎫=-=⨯-= ⎪⎝⎭,故选D .. 3.【答案】A【解析】∵函数y =3cos (2x +φ)的图象关于点4,03π⎛⎫⎪⎝⎭中心对称. ∴4232k ππϕπ⋅+=+∴13()6πϕπ=-∈k k Z 当2k =时,有min ||6πϕ=.故选:A. 4.【答案】C【解析】依题意,函数()2sin(3)3f x x π=-,令3232,232k x k k Z πππππ+≤-≤+∈, 解得52211,183318k k x k Z ππππ+≤≤+∈, 所以函数 在3,24ππ⎛⎫⎪⎝⎭ 上先增后减,在0,4π⎛⎫ ⎪⎝⎭ 上单调递增,在5,4ππ⎛⎫⎪⎝⎭上单调递减, 在,24ππ⎛⎫-- ⎪⎝⎭ 上先增后减.故选C . 5.【答案】A【解析】由角的关系可知根据同角三角函数关系式,可得()312cos ,sin 513ααβ=+= ()sin sin βαβα=+-⎡⎤⎣⎦ ()()sin cos cos sin αβααβα=+-+ 12354135135=⨯-⨯ 1665=所以选A 6.【答案】C【解析】由图可知,2A =,该三角函数的最小正周期7233T πππ=-=,故A 项正确; 所以21Tπω==,则()2sin()f x x ϕ=+. 因为563f f ππ⎛⎫⎛⎫= ⎪⎝ ⎝⎭⎭⎪,所以该函数的一条对称轴为5736212x πππ+==, 将7,212π⎛⎫⎪⎝⎭代入2sin()y x ϕ=+,则72()122k k ππϕπ+=+∈Z ,解得2()12k k πϕπ=-+∈Z ,故()2sin 22sin 1212f x x k x πππ⎛⎫⎛⎫=-+=- ⎪ ⎪⎝⎭⎝⎭.令22()2122k x k k πππππ--+∈Z ,得5722()1212k x k k ππππ-≤≤+∈Z , 令1k =,则1931,1212x ππ⎡⎤∈⎢⎥⎣⎦故函数()f x 在1931,1212ππ⎡⎤⎢⎥⎣⎦上单调递增.故B 项正确; 令322()2122k x k k πππππ+≤-≤+∈Z , 得71922()1212k x k k ππππ+≤≤+∈Z , 令1k =-,175,1212x ππ⎡⎤∈--⎢⎥⎣⎦ 故函数()f x 在175,1212ππ⎡⎤--⎢⎥⎣⎦上单调递减.故C 项错误; 令()122x k k πππ-=+∈Z ,得7()12x k k ππ=+∈Z ,令2k =-,1712x π=-故直线1712x π=-是()f x 的一条对称轴.故D 项正确.故选C. 7.【答案】B【解析】由题意7sin sin sin 666πππαπαα⎛⎫⎛⎫⎛⎫+=++=-+⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,所以sin 63πα⎛⎫+=⎪⎝⎭, 所以2cos 2cos 2cos 2cos 23336ππππαπααα⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫-=-+=-+=-+⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦ 2212sin 121633πα⎛⎛⎫=+-=⨯--=- ⎪ ⎝⎭⎝⎭. 故选B . 8.【答案】B 【解析】易得()()2sin 2cos 2cos sin sin sin 2cos cos2sin sin 2f x x x x x x θθθθθθ=+-=+=+.因为函数()f x 的图象过点P ⎛ ⎝⎭,22ππθ-<<,所以代入函数解析式得3πθ=. 所以()sin 23f x x π⎛⎫=+⎪⎝⎭.根据题意,得()()sin 23g x x πϕ⎡⎤=-+⎢⎥⎣⎦,又因为()g x 的图象也经过点P ⎛ ⎝⎭,所以代入得sin 23πϕ⎛⎫-=⎪⎝⎭将53πϕ=、56π、2π或6π代入sin 23πϕ⎛⎫-=⎪⎝⎭只有56π成立. 故选B. 二、多选题 9.【答案】ABD【解析】因为sin 03f ππ⎛⎫== ⎪⎝⎭,所以A 不正确; 因为sin 1122f ππ⎛⎫==⎪⎝⎭,所以B 不正确;因为函数()f x 的最小正周期为π,但sin 112226f f πππ⎛⎫⎛⎫==>=⎪ ⎪⎝⎭⎝⎭,所以D 不正确;把函数()f x 的图象向左平移12π个单位长度,得到函数sin 2sin 2cos21232y x x x πππ⎡⎤⎛⎫⎛⎫=++=+= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦的图象,函数cos 2y x =为偶函数,所以C 正确. 故选:ABD. 10.【答案】AD【解析】()sin 2cos 2224444f x x x x x ππππ⎛⎫⎛⎫⎛⎫=+++=++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ .选项A :()2))()f x x x f x -=-== ,它是偶函数,正确;选项B :0,2x π⎛⎫∈ ⎪⎝⎭,所以()20,x π∈,因此()f x 是单调递减,错误;选项C :()2f x x =,错误;选项D :函数的对称中心为(,0)24k ππ+ ,k Z ∈,当0k =,图象关于点,04π⎛⎫⎪⎝⎭对称, 错误. 故选:AD 11.【答案】AC【解析】由图象知,A=1,T=π,所以ω=2,y=sin (2x+ϕ),将(6π-,0)代入得:sin(ϕ3π-)=0,所以ϕ3π-=kπ,k z ∈,取ϕ=3π,得y=sin (2x+3π),sin y x =向左平移3π,得sin 3y x π⎛⎫=+ ⎪⎝⎭.然后各点的横坐标缩短到原来的12,得sin 23y x π⎛⎫=+ ⎪⎝⎭.故A 正确.sin y x =各点的横坐标缩短到原来的12,得sin 2y x =.然后向左平移6π个单位,得sin 26y x π⎛⎫=+ ⎪⎝⎭sin 23x π⎛⎫=+ ⎪⎝⎭.故C 正确.故选:AC 12.【答案】BD 【解析】由图象可知3A =,33253441234ππππω⎛⎫=⋅=--= ⎪⎝⎭T , ∴2ω=,则()3sin(2)f x x ϕ=+.将点5,312π⎛⎫ ⎪⎝⎭的坐标代入()3sin(2)f x x ϕ=+中,整理得5sin 2112πϕ⎛⎫⨯+= ⎪⎝⎭, ∴522,Z 122k k ππϕπ⨯+=+∈,即2,Z 3k k πϕπ=-∈.||2ϕπ<,∴3πϕ=-,∴()3sin 23f x x π⎛⎫=-⎪⎝⎭. ∵将函数()f x 的图象向左平移3π个单位长度后得到()y g x =的图象, ∴()3sin 23sin 2,333πππ⎡⎤⎛⎫⎛⎫=+-=+∈ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦g x x x x R . ∴()g x 既不是奇函数也不是偶函数,故A 错误; ∴()g x 的最小正周期22T ππ==,故B 正确. 令2,32x k k πππ+=+∈Z ,解得,122k x k ππ=+∈Z .则函数()g x 图像的对称轴为直线,122k x k ππ=+∈Z .故C 错误; 由222,232k x k k πππππ-++∈Z ,可得5,1212k x k k ππππ-+∈Z ,∴函数()g x 的单调递增区间为5,,1212k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦.故D 正确. 故选:BD.三、填空题 13.【答案】二【解析】因为点P (tanα,cosα)在第三象限,所以tanα<0,cosα<0, 则角α的终边在第二象限,故答案为二. 14.【答案】34-【解析】由函数()211sin()cos (sin cos )cos cos cos 62222f x x x x x x x x x π=-=-=-1112(1cos 2)sin(2)44264x x x π=-+=--, 当sin(2)16x π-=-时,即,6x k k Z ππ=-+∈时,函数取得最小值34-. 15.【答案】14【解析】因为1sin()34πα+=,则1cos()sin(())sin()62634ππππααα-=--=+=. 16.【答案】2()tan()9g x x π=+. 【解析】由题意,函数()tan()f x x ωϕ=+的相邻两个对称中心距离为1322w ππ⋅=,解得13w =,且()f π=,即tan()3πϕ+=,因为02πϕ<<,解得3πϕ=,所以1()tan()33f x x π=+,将()f x 图象上的点向右平移3π个单位,可得112()tan[()]tan()33339f x x x πππ=-+=+, 再把所得图象的纵坐标不变,横坐标变为原来的13,可得2()tan()9f x x π=+的图象, 即函数()g x 的解析式为2()tan()9f x x π=+. 故答案为:2()tan()9f x x π=+. 四、解答题17.【答案】(Ⅰ)1tan =-3α;(Ⅱ)15-19.【解析】解:(Ⅰ)tantan 1tan 14tan()41tan 21tantan 4παπααπαα+++===--,解得;(Ⅱ)22sin(22)sin ()21cos(2)sin παπαπαα+----+=22sin 2cos 1cos 2sin αααα-++ 2222sin cos cos 2cos sin ααααα-=+22tan 1152tan 19αα-==-+. 18.【答案】(1,取得最大值时相应x 的集合为3,8x x k k Z ππ⎧⎫=+∈⎨⎬⎩⎭; 最小值为,取得最小值时相应x 的集合为,8x x k k Z ππ⎧⎫=-+∈⎨⎬⎩⎭; (2)3,88k k ππππ⎡⎤-++⎢⎥⎣⎦,k Z ∈;(3)图象见解析. 【解析】(1)()f x ,当2242x k πππ-=+,即38x k ππ=+时,等号成立, ∴()f x 取得最大值时相应x 的集合为3,8x x k k Z ππ⎧⎫=+∈⎨⎬⎩⎭()f x 的最小值为,当2242x k πππ-=-+,即8x k ππ=-+时,等号成立,∴()f x 取得最大值时相应x 的集合为,8x x k k Z ππ⎧⎫=-+∈⎨⎬⎩⎭(2)由222242k x k πππππ-+≤-≤+求得388k x k ππππ-+≤≤+, ∴()f x 的单调递增区间是3,88k k ππππ⎡⎤-++⎢⎥⎣⎦,k Z ∈(3)列表:()f x 图像如图所示:19.【答案】(1)()7,1212k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦;(2)14k k ⎧⎪<≤⎨⎪⎩或12k ⎫=-⎬⎭. 【解析】(1)()2sin cos cos 44f x x x x x ππ⎛⎫⎛⎫=+-+ ⎪ ⎪⎝⎭⎝⎭sin 222sin 23x x x π⎛⎫=+=+ ⎪⎝⎭令3222232k x k πππππ+++,k Z ∈,解得71212k xk ππππ++,k Z ∈, ∴()f x 的单调递减区间()7,1212k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦(2)由(1)知,函数()2sin 23f x x π⎛⎫=+⎪⎝⎭()g x 在,122ππ⎡⎤⎢⎥⎣⎦有零点等价于()()2sin 2f x k x =+在,122ππ⎡⎤⎢⎥⎣⎦有唯一根,∴可得2sin 2sin 23k x x π⎛⎫=+- ⎪⎝⎭1sin 22cos 226x x x π⎛⎫=-+=+ ⎪⎝⎭设()cos 26h x x π⎛⎫=+⎪⎝⎭,,122x ππ⎡⎤∈⎢⎥⎣⎦则72,636x πππ⎡⎤+∈⎢⎥⎣⎦ 根据函数()h x 在,122x ππ⎡⎤∈⎢⎥⎣⎦上的图象, ∵2y k =与()y h x =有唯一交点,∴实数k 应满足1222k -<≤或21k =- ∴144k -<≤或12k =-.故实数k 的取值范围1{|4k k<或1}2k =-.20.【答案】(1)()22sin 1036t h t ππ⎛⎫=-+≥⎪⎝⎭;(2)有1s 时间点P 距水面的高度超过2米. 【解析】(1)设水轮上圆心O 正右侧点为A ,y 轴与水面交点为B ,如图所示:设()sin h a t b ωϕ=++,由1OB =,2OP =,可得03BOP π∠=,所以06AOP π∠=.2a ∴=,1b =,6πϕ=-,由题意可知,函数2sin 16h t πω⎛⎫=-+ ⎪⎝⎭的最小正周期为3T =,223T ππω∴==, 所以点P 距离水面的高度h 关于时间t 的函数为()22sin 1036t h t ππ⎛⎫=-+≥⎪⎝⎭;(2)由22sin 1236t h ππ⎛⎫=-+>⎪⎝⎭,得21sin 362t ππ⎛⎫->⎪⎝⎭, 令[]0,3t ∈,则211,3666t ππππ⎡⎤-∈-⎢⎥⎣⎦, 由256366t ππππ<-<,解得1322<<t ,又31122-=, 所以在水轮转动的任意一圈内,有1s 时间点P 距水面的高度超过2米. 21.【答案】(1)()2sin 3f x x π⎛⎫=-⎪⎝⎭;(2))1,3 【解析】(1)由题意可知函数()f x 的周期2T π=,且2A =,所以21Tπω==,故()()2sin f x x ϕ=+.将函数()f x 的图象向左平移3π个单位长度后得到的图象对应的函数解析式为2sin 3y x ϕπ⎛⎫=++ ⎪⎝⎭,因为函数2sin 3y x ϕπ⎛⎫=++ ⎪⎝⎭的图象关于原点对称,所以()3k k ϕπ+=π∈Z ,即()3k k ϕπ=π-∈Z . 又2πϕ<,所以3πϕ=-,故()2sin 3f x x π⎛⎫=- ⎪⎝⎭.(2)由(1)得函数()12sin 13y f kx kx π⎛⎫=+=-+ ⎪⎝⎭,其周期为23π, 又0k >,所以2323k π==π.令33t x π=-,因为0,3x π⎡⎤∈⎢⎥⎣⎦,所以2,33t ππ⎡⎤∈-⎢⎥⎣⎦, 若sin t s =在2,33ππ⎡⎤⎢⎥⎣⎦-上有两个不同的解,则s ⎫∈⎪⎪⎣⎭,所以当)1,3m ∈时,方程()1f kx m +=在0,3x π⎡⎤∈⎢⎥⎣⎦上恰有两个不同的解,即实数m的取值范围是)1,3.22.【答案】(1)5,1212k k ππππ⎡⎤-++⎢⎥⎣⎦,k Z ∈;(2)(i )34;(ii )1m =-,1343n =. 【解析】(1)由图象可得1A =,最小正周期721212T πππ⎛⎫=⨯-=⎪⎝⎭,则22T πω==,由77sin 211212f ππϕ⎛⎫⎛⎫=⨯+=-⎪ ⎪⎝⎭⎝⎭,所以523k πϕπ=-+,k Z ∈,又2πϕ≤,则易求得3πϕ=,所以()sin 23f x x π⎛⎫=+ ⎪⎝⎭,由222232k x k πππππ-+≤+≤+,k Z ∈,得51212k x k ππππ-+≤≤+,k Z ∈, 所以单调递增区间为5,1212k k ππππ⎡⎤-++⎢⎥⎣⎦,k Z ∈.(2)(i )由题意得()sin g x x =,()()sin sin 23x h x f g x x x π⎛⎫⎛⎫==+ ⎪ ⎪⎝⎭⎝⎭112cos 2444x x =-+ 11sin 2264x π⎛⎫=-+ ⎪⎝⎭, 所以()()2x h x f g x ⎛⎫=⎪⎝⎭的最大值为34; (ii )令()0F x =,可得22sin sin 10x m x --=,令[]sin 1,1t x =∈-, 得2210t mt --=,易知>0∆,方程必有两个不同的实数根1t 、2t , 由1212t t =-,则1t 、2t 异号, ①当11t >且210t -<<或者101t <<且21t <-时,则方程1sin x t =和2sin x t =在区间()0,n π均有偶数个根,不合题意,舍去;②当101t <<且0201t <<时,则方程1sin x t =和2sin x t =在区间()0,n π均有偶数个根,不合题意,舍去; ③当11t =且212t =-,当()0,2x π∈时,1sin x t =,只有一根,2sin x t =有两根, 所以,关于x 的方程22sin sin 1x m x --在()0,2x π∈上有三个根,由于201536712=⨯+,则方程22sin sin 10x m x --=在()0,1342π上有2013个根,由于方程1sin x t =在区间()1342,1343ππ上只有一个根,方程2sin x t =在区间()1343,1344ππ上两个根,因此,不合题意,舍去;④当11t =-时,则212t =,当()0,2x π∈时,1sin x t =只有一根,2sin x t =有两根, 所以,关于x 的方程22sin sin 10x m x --=在()0,2x π∈上有三个根,由于201536712=⨯+,则方程22sin sin 10x m x --=在()0,1342π上有2013个根,由于方程2sin x t =在区间()1342,1343ππ上有两个根,方程1sin x t =在区间()1343,1344ππ上有一个根,此时,满足题意;因此,1343n =,21121022m ⎛⎫⎛⎫⨯-⨯-= ⎪ ⎪⎝⎭⎝⎭, 得1m =-,综上,1m =-,1343n =.。
高中一年级下册数学 三角函数第一章单元测试题2

三角函数单元测试题(1)
一、选择题
1、若sin cos 0θθθ>,则在( )
A 、第一、二象限
B 、第一、三象限
C 、第一、四象限
D 、第二、四象限
2、给出的下列函数中在2
ππ(,)上是增函数的是( ) A 、sin y x = B 、cos y x = C 、sin 2y x = D 、cos 2y x =
3、若θ是第四象限的角,则-2
πθ是( ) A 、第一象限 B 、第二象限 C 、第三象限 D 、第四象限
4、下列关于函数2()log cos()f x x π=-的说法中正确的是( )
A 、是偶函数,但不是周期函数
B 、是周期函数,但不是偶函数
C 、是偶函数,也是周期函数
D 、不是偶函数,也不是周期函数
5.设M 和m 分别表示函数1cos 31-=
x y 的最大值和最小值,则m M +等于 ( ) A .32 B .32- C .3
4- D .2- 6、函数3sin(2)13y x π
=-+的对称中心是( )
A 、03π(,)
B 、13π
(,) C 、213π(,) D 、06
π(,) 7、已知α是第二象限的角,1tan(2),cos 2
παα+=-=则 tan 2x
姓名:
7.
8. 9.
三、解答题
10、函数sin() (0,0)y A x b A ωϕω=++>>在其一个周期内,的图象上有一个最高点312π(,)和一个最低点712
π(,-5)。
(1)求函数解析式;
(2)作出这个函数在一个周期内的简图。
11
、求函数lg(2cos 1)y x =-+。
人教版数学九年级第二十八章锐角三角函数单元测试精选(含答案)2

)
2
5
21
A.
2
B.12
C.14
D.21
19.如图,AB 是一垂直于水平面的建筑物,某同学从建筑物底端 B 出发,先沿水平方
向向右行走 20 米到达点 C,再经过一段坡度(或坡比)为 i=1:0.75、坡长为 10 米的
斜坡 CD 到达点 D,然后再沿水平方向向右行走 40 米到达点 E(A,B,C,D,E 均在
人教版数学九年级第二十八章锐角三角函数单元测试精选
(含答案)
学校:___________姓名:___________班级:___________考号:___________
评卷人 得分
一、单选题
1. cos 60 的值等于( )
1
A.
2
B. 2 2
C. 3 2
D. 3 3
2.如图,点 A 为∠α边上任意一点,作 AC⊥BC 于点 C,CD⊥AB 于点 D,下列用线 段比表示 sinα的值,错误的是( )
已知红军亭高度为 12 米,请根据测量数据求出凤凰山与中心广场的相对高度 AB.( 3
取 1.732,结果保留整数)
评卷人 得分
三、填空题
2
39.在 Rt△ABC 中,∠C=90°,AB=6,cosB= ,则 BC 的长为_____.
3 40.如图,在菱形 ABCD 中, AB 2 , B 是锐角, AE BC 于点 E,M 是 AB 的
C.10 3
D. 8 3
22.图 1 是一个地铁站入口的双翼闸机.如图 2,它的双翼展开时,双翼边缘的端点 A 与 B 之间的距离为 10cm,双翼的边缘 AC=BD=54cm,且与闸机侧立面夹角∠PCA= ∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )
人教版数学高二第一章三角函数单元测试精选(含答案)2

6
,
5 6
上单调递增
B.最小正周期是π
C.图象关于点
4
,
0
成中心对称
D.图象关于直线 x= 成轴对称
6
【来源】高中数学人教 A 版必修 4 第一章 三角函数 1.4.3 正切函数的性质与图象
【答案】B
9.已知函数
f(x)=3sin
ωx-
π 4
(0<ω<1),且
f
π 2
=0,则函数
)
A. 8
B. 8
C. 6
D. 6
【来源】福建省福州格致中学 2017-2018 学年高一下学期第四学段质量检测数学试题
【答案】C
23.如图,在棱长为 a 的正方体 ABCD A1B1C1D1 中,P 为 A1D1 的中点,Q 为 A1B1 上 任意一点, E , F 为 CD 上任意两点,且 EF 的长为定值,则下面的四个值中不为定
【来源】广东省揭阳市第三中学 2017-2018 学年高二上学期数学试题 1(必修 5 第一章)
【答案】D
16.若θ∈[ , ],sin2θ= 3 7 ,则 cosθ= ( )
42
8
3
A.
5
4
B.-
5
C. 7 4
3
D.
4
【来源】2017 秋人教 A 版高中数学必修四:学业质量标准检测 3
【答案】C
sin
பைடு நூலகம்
π 2
2 2cos2 (π θ) cos(-θ)
θ
-3
,则
f
17π 3
=_____.
【来源】2018-2019 学年高中数学(人教 A 版,必修 4)第一章《三角函数》测试题
2023最新人教版高中数学必修一第五章《三角函数》单元测试(附答案解析)

试卷第 4 页,共 4 页
1.C
参考答案:
【解析】运用诱导公式,结合特殊角的三角函数值即可化简求解..
【详解】 cos
150
cos150 cos(1800 300 ) cos 300
3, 2
故选:C.
【点睛】关键点点睛:该题考查的是有关三角函数化简求值问题,正确解题的关键是熟练应 用诱导公式以及熟记特殊角三角函数值. 2.A
答案第 2 页,共 12 页
【详解】 f (x) sin x cos
2
sin( x
π 4
)
,因为
x
a
,
b
,所以
x
π 4
a
π 4
,
b
π 4
,因
为 1
2
sin( x
π 4
)
2 ,所以
2 2
sin( x
π 4
)
1.
正弦函数
y
sin
x
在一个周期
π 2
,
3π 2
内,要满足上式,则
x
π 4
π 4
f
x
sin x
的图象过点
1 3
,1
,若
f
x 在2, a 内有
5
个
零点,则 a 的取值范围为______.
四、解答题
17.在① sin
6 3
,②
tan 2
2 tan 4 0 这两个条件中任选一个,补充到下面的
问题中,并解答.
已知角 a 是第一象限角,且___________.
(1)求 tan 的值;
S1 S2
2
1 2
可求得
第一章 三角函数(含解析)——高一数学北师大版必修二单元测试

第一章 三角函数——2024-2025学年高一数学北师大版必修二单元测试一、选择题1.若角的终边上有一点,且,则( )A.4B. C.-C.-1 D.2.要得到函数的图象,只需要将函数的图象( )A.向左平移个单位长度 B.向左平移个单位长度C.向右平移个单位长度 D.向右平移个单位长度3.函数在区间上的最小值为,则m 的最大值为( )A.B.C.D.4.已知一样本数据(如茎叶图所示)的中位数为12,若x,y 均小于4,则该样本的方差最小时,的值分别为( )A.1,3B.11,13C.2,2D.12,125.为了得到函数的图象,只需将函数的图象( )A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度 D.向右平移个单位长度6.设函数在的图象大致如图,则的最小正周期为( )α()2,P m -sin α=m =4±1±3πsin 34y x ⎛⎫=+ ⎪⎝⎭sin 3y x =3π4π43π4π4()πsin 26f x x ⎛⎫=- ⎪⎝⎭[]0,m 12-π6π32π3π,x y ()πsin 24f x x ⎛⎫=- ⎪⎝⎭()cos2g x x =3π83π8π8π8()πsin (0)3f x x ωω⎛⎫=-> ⎪⎝⎭[]π,π-()f xA.B.C.D.7.函数的定义域是( )A. B.C. D.8.已知函数在上的大致图象如下所示,则的解析式可能为( )A. B.C. D.二、多项选择题9.要得到函数的图象,只要将函数图象上所有的点( )A.横坐标缩短到原来的(纵坐标不变),再将所得图象向左平移个单位B.横坐标缩短到原来的(纵坐标不变),再将所得图象向左平移个单位C.向左平移个单位,再将所得图象每一点的横坐标缩短到原来的(纵坐标不变)D.向左平移个单位,再将所得图象每一点的横坐标缩短到原来的(纵坐标不变)10π932π274π325π18()π3tan 24x f x ⎛⎫=-+ ⎪⎝⎭π4x x ⎧⎫≠⎨⎬⎩⎭π2x x ⎧⎫≠⎨⎬⎩⎭π2π,2x x k k ⎧⎫≠+∈⎨⎬⎩⎭Z ππ,4x x k k ⎧⎫≠+∈⎨⎬⎩⎭Z ()f x []4,4-()f x ()π31cos 42x x f x ⎛⎫⋅+ ⎪⎝⎭=()()21610x x f x ⋅-=()()4f x x x =⋅-()πsin4x f x x =⋅πsin 23y x ⎛⎫=+ ⎪⎝⎭sin y x =12π312π6π312π61210.要得到的图象,可以将函数的图象上所有的点( )A.向右平行移动个单位长度,再把所得各点的横坐标缩短到原来的倍B.向右平行移动个单位长度,再把所得各点的横坐标缩短到原来的倍C.横坐标缩短到原来的倍,再把所得各点向右平行移动个单位长度D.横坐标缩短到原来的倍,再把所得各点向右平行移动个单位长度12.已知则________.13.筒车是我国古代发明的一种水利灌溉工具.因其经济又环保,至今还在农业生产中使用(如图).假设在水流稳定的情况下,筒车上的每一个盛水筒都做匀速圆周运动.现有一半径为2米的筒车,在匀速转动过程中,筒车上一盛水筒M 距离水面的高度H(单位:米)与转动时间t (单位:秒)满足函数关系式,,且时,盛水筒M 与水面距离为2.25米,当筒车转动20秒后,盛水筒M 与水面距离为______米.sin 25y x π⎛⎫=- ⎪⎝⎭sin y x =5π1210π12125π1210π1sin ,3α=cos 2απ⎛⎫+= ⎪⎝⎭52sin 6π04H t ϕ⎛⎫=++ ⎪⎝⎭,ππ2ϕ⎛⎫∈ ⎪⎝⎭0t =14.已知,则__________.四、解答题15.已知函数(1)若,,求的值域;(2)若,,都有恒成立,求a 的取值范围.16.已知函数.(1)若为偶函数,求函数的定义域;(2)若过点,设,若对任意的,,都有,求实数的取值范围.17.某同学用“五点法”画函数在某一个周期内的图像时,列表并填入了部分数据,如表:x0200(1)请将上表数据补充完整,函数的解析式为______(直接写出结果即可);(2)求函数在区间上的最大值和最小值.()sin f x a x =0a =[]0,πx ∈()f x 0a >[]0,2x ∈π()1122f x a ≥+31cos π45α⎛⎫-= ⎪⎝⎭πcos 4α⎛⎫+= ⎪⎝⎭()sin(2)(0π)f x x ϕϕ=+<<()f x π1()lg 62g x fx ⎡⎤⎛⎫=-+ ⎪⎢⎥⎝⎭⎣⎦()f x π,16⎛⎫ ⎪⎝⎭2()cos 2sin h x x a x =+1ππ,22x ⎡⎤∈-⎢⎥⎣⎦2π0,2x ⎡⎤∈⎢⎥⎣⎦()()123h x f x <+a ()()πsin 0,0,2f x A x A ωϕωϕ⎛⎫=+>>< ⎪⎝⎭x ωϕ+π2π3π22ππ62π3()()sin f x A x ωϕ=+()f x ()f x =()f x π,02⎡⎤-⎢⎥⎣⎦18.已知函数.(1)求函数的单调增区间;(2)将的图像向左平移个单位得到函数,求在上的值域.19.已知函数(,且)为偶函数.(1)求a 的值;(2)若,使成立,求实数m 的取值范围.()2sin 26f x x π⎛⎫=+ ⎪⎝⎭()f x ()f x 6π()g x ()g x 0,3π⎡⎤⎢⎥⎣⎦()()2log 1x f x a x =+-0a >1a ≠[][]120,π,1,1x x ∀∈∃∈-()2112π11sin cos 24x m x f x m⎛⎫+-+-≥⎪⎝⎭参考答案1.答案:C解析:由已知,得,解得.因为所以,则.故选:C.2.答案:B解析:因为,所以要得到函数的图象,只需要将函数的图象向左平移个单位长度.3.答案:C 解析:令,,解得,,故的图象在y 轴右侧的第一条对称轴为,而,而在上的最小值为,故m 的最大值为,故选:C.4.答案:C解析:因为x,y 均小于4,由茎叶图可知,中位数为,所以,样本的平均值为,要使样本的方差最小,即使最小,又,当且仅当“”时,等号成立,所以x,y 均为2,选C.5.答案:Bsin α===1m =±sin α=0y <1m =-3ππsin 3sin 344y x x ⎡⎤⎛⎫⎛⎫=+=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦3πsin 34y x ⎛⎫=+ ⎪⎝⎭sin 3y x =π4ππ2π62x k -=+k ∈Z ππ23k x =+k ∈Z ()f x π3x =()102f =-()f x []0,m 12-π2π2033⨯-=1010122x y+++=4x y +=12351010141516201010x y +++++++++++=2S 22x y +222()82x y x y ++≥=2x y ==解析:因为,所以,故为了得到的图象,只需将的图象向右平移个单位长度.故选:B.6.答案:C解析:由函数的图象,函数的最小正周期且,可排除A,D;又由,即,,若选B,则,此时,此时k 不为整数,排除B 项;若选C,则,此时,此时,排除C 项.故选:C.7.答案:C解析:由正切函数的定义域,令,,即,所以函数的定义域为.故选:C.8.答案:B解析:函数图象关于y 轴对称,函数为偶函数,选项D 中函数满足,为奇函数,排除D ;又选项C 中函数满足,与图象不符,排除C ;()3πcos 24f x x ⎛⎫=- ⎪⎝⎭()f x ()g x 3π8(2)4f =3ππ3πsin 2sin 2cos 24424πx x x ⎛⎫⎛⎫⎛⎫-=-+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭()πsin (0)3f x x ωω⎛⎫=-> ⎪⎝⎭()f x 4π13ππ()99T <--=4π10π2(π99T <-=4π4ππ()sin()0993f ω-=--=4πππ93k ω--=k ∈Z 32π272π2716ω==4π27ππ9163k -⨯-=2π34π23ω==4π3ππ923k -⨯-=1k =-πππ242x k +≠+k ∈Z ()π2π2x k k ≠+∈Z ()π3tan 24x f x ⎛⎫=-+ ⎪⎝⎭π2π,2x x k k ⎧⎫≠+∈⎨⎬⎩⎭Z ππ()sin(sin ()44x xf x x x f x --=-=-=-选项A 中函数满足,与图象不符,排除A ,只有B 可选.故选:B.9.答案:BC解析:要得到函数的图象,只要将函数图象上所有的点横坐标缩短到原来的(纵坐标不变),再将所得图象向左平移个单位;或者向左平移个单位,再将所得图象每一点的横坐标缩短到原来的(纵坐标不变).10.答案:AD解析:将函数的图象上所有的点向右平行移动个单位长度得到,再把所得各点的横坐标缩短到原来的倍得到.也可以将函数的图象上所有的点横坐标缩短到原来的倍得到,再把所得各点向右平行移动个单位长度得到.故选:AD.sin y x =5πn 5si y x π-⎛⎫= ⎪⎝⎭1225sin y x π-⎛⎫= ⎪⎝⎭sin y x =2π32(1cos)4(2)32f ⨯⨯⨯+==πsin 23y x ⎛⎫=+ ⎪⎝⎭sin y x =12π6π31212sin2y x =10πsin210y x π⎛⎫=- ⎪⎝⎭5sin 2x π=-⎛⎫ ⎪⎝⎭12.答案:解析:由诱导公式可得:,故答案为:.13.答案:解析:因为时,盛水筒M 与水面距离为2.25米,所以,即,又,则,当时,.故答案为:.14.答案:解析:,故答案为:.15.答案:(1);(2)13-1cos sin 23ααπ⎛⎫+=-=- ⎪⎝⎭13-140t =52.252sin 4ϕ=+1sin 2ϕ=π,π2ϕ⎛⎫∈ ⎪⎝⎭5π6ϕ=t 20=5π512sin 2060644πH ⎛⎫=⨯++= ⎪⎝⎭1415-π331cos cos ππcos π4445ααα⎡⎤⎛⎫⎛⎫⎛⎫+=--=--=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦15-2⎤⎦01a <≤解析:(1)当时,,令,则,由,则,故,又,故,即的值域为;(2)令,则,当时,,,则,由,即,化简得,令,,由,故,故在上单调递增,故,解得;当时,,,故,则有,即,由,故有,,解得,综0a =()f x=t =>21cos 1cos 222sin t x xx =++-+=+=+[]0,πx ∈[]sin 0,1x∈[]22,4t ∈0t >2t ⎤∈⎦()f x 2⎤⎦0t =≥222sin t x =+[)0,πx ∈2t ⎤∈⎦22sin 2t x -=()22sin 2t f x a x a t ⎛⎫-==+ ⎪⎝⎭()1122f x a ≥+2211222t a t a ⎛⎫-+≥+ ⎪⎝⎭2310222a t t a +--≥()231222a t t g t a +--=2t ⎤∈⎦0a >10a-<()g t 2⎤⎦3120222aga ⨯-≥=1a ≤[]π,2πx ∈2t ⎤∈⎦22sin 2t x -=()22sin 2t f x a x a t ⎛⎫-==+ ⎪⎝⎭2211222t a t a ⎛⎫-+≥+ ⎪⎝⎭2110222a t t a -++-≥0a >2110222aa --≥()211220222a a -⨯++-≥1a ≤上所述,.16.答案:(1)(2)解析:(1)因为为偶函数,所以,即,因为,所以,解得:,,所以,,所以的定义域为.(2)因为过点,所以,因为,所以,所以,因为,所以,所以,又因为对任意的,,都有成立,所以,,,因为,所以,01a <≤ππππ,62x k x k k ⎧⎫-<<+∈⎨⎬⎩⎭Z 5544⎛⎫-⎪⎝⎭,()sin(2)(0π)f x x ϕϕ=+<<π2ϕ=()cos2f x x =π1062f x ⎛⎫-+> ⎪⎝⎭π1cos 232x ⎛⎫->- ⎪⎝⎭2ππ2π2π22π333k x k -<-<+k ∈Z ππππ62k x k -<<+k ∈Z ()g x ππππ,62x k x k k ⎧⎫-<<+∈⎨⎬⎩⎭Z ()f x π,16⎛⎫ ⎪⎝⎭πsin 13ϕ⎛⎫+= ⎪⎝⎭0πϕ<<π6ϕ=π()sin 26f x x ⎛⎫=+ ⎪⎝⎭2π0,2x ⎡⎤∈⎢⎥⎣⎦2ππ7π2666x ⎡⎤+∈⎢⎥⎣⎦,22π1()sin 2,162f x x ⎛⎫⎡⎤=+∈- ⎪⎢⎥⎝⎭⎣⎦1ππ,22x ⎡⎤∈-⎢⎥⎣⎦2π0,2x ⎡⎤∈⎢⎥⎣⎦()()123h x f x <+()()12max min 3h x f x <+()1max15322h x <-+=()2222()cos 2sin sin 2sin 1sin 1h x x a x x a x x a a =+=-++=--++1ππ,22x ⎡⎤∈-⎢⎥⎣⎦[]1sin 1,1x ∈-设,则有图象开口向下,对称轴为的抛物线,当时,在上单调递增,所以,所以,解得,所以;当时,在上单调递减,所以,所以,解得,故;当时,,故,解得所以,综上所述:实数a 的取值范围为.17.答案:(1)答案见解析;(2)最大值为1,最小值为.解析:(1)表格如下0200根据表格可得,,再根据五点法作图可得,,故解析式为:.[]sin ,1,1t x t =∈-()()221g t a t a =+--t a =1a ≥()g t [1,1]t ∈-()()max 12g t g a ==522a <54a <514a ≤<1a ≤-()g t [1,1]t ∈-()()max 12g t g a =-=-522a -<54a >-514a -<≤-11a -<<()()2max 1g t g a a ==+2512a +<a <<11a -<<5544⎛⎫-⎪⎝⎭,2-x ωϕ+π2π3π22πxπ12-π65π122π311π12()sin y A x ωϕ=+2-12π2ππ236ω⋅=-2ω∴=ππ262ϕ⨯+=π6ϕ∴=()π2sin 26f x x ⎛⎫=+ ⎪⎝⎭(2)因为,所以,得,所以,当即时,在区间上的最小值为,当即时,在区间上的最大值为1.18.答案:(1)(2)解析:(1)令,由的单调性可知,当时,即时此函数单调递增.所以函数的单调增区间为.(2)由题可得:,时,有,所以的值域为.19.答案:(1)(2)解析:(1)因为函数为偶函数,则,即,整理得,可得,结合x 的任意性可得,π02x -≤≤5πππ2666x -≤+≤π11sin 262x ⎛⎫-≤+≤ ⎪⎝⎭ππ262x +=-π3x =-()f x π,02⎡⎤-⎢⎥⎣⎦2-ππ266x +=0x =()f x π,02⎡⎤-⎢⎥⎣⎦,36k k ⎡⎤-++πππ⎢⎣π⎥⎦()k ∈Z 1,12⎡⎤-⎢⎥⎣⎦26z x π=+2sin y z =()2222k z k k -+≤≤+ππππ∈Z 36k x k ππ-+≤≤+ππ()k ∈Z ()f x ,36k k ⎡⎤-++πππ⎢⎣π⎥⎦()k ∈Z ()2sin 22sin 22cos 2662g x x x x ⎡⎤⎛⎫⎡⎤=++=+= ⎪⎢⎥⎢⎥⎝⎭⎣⎦⎣⎦πππ0,3x ⎡π⎤∈⎢⎥⎣⎦2023x π≤≤()g x 1,12⎡⎤-⎢⎥⎣⎦4a =[)1,0-()f x ()()0f x f x --=()()22log 1log 10x x a x a x -⎡⎤⎡⎤+--++=⎣⎦⎣⎦222221log log log 2log 0142xxx x x x a a a a -+⎛⎫-== ⎪+⎝⎭-=14xa ⎛⎫= ⎪⎝⎭4a =此时,可得的定义域为R,符合题意,综上所述:.(2)因为,则,则,当且仅当,即时,等号成立,所以,由题意可得:,即,因为,令,则,设,可得,解得,若,可知的图象开口向上,对称轴,由题意可得,整理得,又因为,则,解得,所以实数m 的取值范围.()()()()2222log 41log 41log 2log 22x x x x x f x x -=+-=+-=+()f x 4a =[]21,1x ∈-212,22x ⎡⎤∈⎢⎥⎣⎦22222x x -+≥=2222x x -=20x =()()22222log 22log 21x x f x -=+≥=211π11sin cos 124x m x m⎛⎫+-+-≥⎪⎝⎭2111sin sin 043x m x m +--≥[]10,πx ∀∈[]1sin 0,1t x =∈23104t mt m +--≥()[]21,0,143h t t mt t m =+--∈()10043h m =--≥403m -≤<403m -≤<()h t ()0,12mt =-∈223144304m m m m ⎛⎫∆=---=++≤ ⎪⎝⎭()()2140m m m +-+≥221154024m m m ⎛⎫-+=-+> ⎪⎝⎭10m +≥10m -≤<[)1,0-。
人教A新版必修1《第5章 三角函数》单元测试卷(二).docx

人教A新版必修1《第5章三角函数》单元测试卷(二)一、解答题(本大题共27小题,共324.0分)1.写出与;终边相同的角的集合S,并把S中适合不等式-2TT <<4TT的元素月写出来.2.已知一扇形的中心角为。
,所在圆的半径为R.(1)若a = 60°, R = 6cm,求该扇形的弧长;(2)若扇形的周长为12cm,问当Q多大时,该扇形有最大面积?并求出这个最大面积.3.已知tan© =-龙,求sin©,cos©的值.(2)sina • cosa. 5. (1)已知切Tia = 3,求sin (7r — Q )COS (2TT —。
)的值;(2)已知sina • cosa = 0 < a < -,求sizwr — cos 。
的值.6. 已知函数,3) =tan(x + S ).(1)求函数『3)的最小正周期与定义域;(2)设月是锐角,且/(幻= 2sin(/?+:),求乃的值.4. 已知tana = 3,计算:(1)4sina-2cosa 5cosa+3sina'7.已知函数y = 1 - 3cos2x, x E R,求出函数的最大值、最小值,并且求使函数取得最大值、最小值的x的集合.8.已知函数y = 2sin(-x + -) (% e R)2 4列表:(1)利用“五点法”画出该函数在长度为一个周期上的简图;作图:(2)说明该函数的图象可由y = sinx^x E R)的图象经过怎样的变换得到.9.已知函数f(x) = sin(2x€ [。
,丸].(1)用“五点法"在所给的直角坐标系中画出函数f(x)的图象;(2)写出y = f(x)的图象是由y = sinx的图象经过怎样的变换得到的.10.振动量y = 4sin(o)x +(p)(o> > 0)的初相和频率分别是-n■和求该振动量的解析式.11. (10分)已知sina = |, cos/? =-j, a E (:,"), /?是第三象限角,求cos(a + Q), sin(a-幻的值.12. 已知tan(a + Q) = 5, tan(a —幻=3,求tan2a f tan2/3, tan(2a + j)的值.sin(27r-a)tan(a+7r)-tan(-a)cos (7r-a)tan(37r-a)/c 、、[ A ,A - 25TT . 25TT , / 25TT 、 . . 5TT(2)计算cos ------ F cos ------ F tan( ------- ) + sin —. 6 3 4 6(1)化简, 13.2 ,14.B知sin。
三角函数》单元测试卷含答案

三角函数》单元测试卷含答案三角函数》单元测试卷一、选择题(本大题共10小题,每小题5分,共50分)1.已知点P(tanα,cosα)在第三象限,则角α的终边在(。
)A.第一象限B.第二象限C.第三象限D.第四象限2.集合M={x|x=kπ/2±π/4,k∈Z}与N={x|x=kπ/4,k∈Z}之间的关系是(。
)A.M∩NB.M∪NC.M=ND.M∩N=∅3.若将分针拨慢十分钟,则分针所转过的角度是(。
)A.60°B.-60°C.30°D.-30°4.已知下列各角(1)787°,(2)-957°,(3)-289°,(4)1711°,其中在第一象限的角是(。
)A.(1)(2)B.(2)(3)C.(1)(3)D.(2)(4)5.设a>0,角α的终边经过点P(-3a,4a),那么sinα+2cosα的值等于(。
)A.5/21B.-1/55C.-5/13D.-2/56.若cos(π+α)=-3/22,π<α<2π,则sin(2π-α)等于(。
)A.-2/3B.3/2C.-2/5D.3/47.若是第四象限角,则απ-α是(。
)A.第一象限角B.第二象限角C.第三象限角D.第四象限角8.已知弧度数为2的圆心角所对的弦长也是2,则这个圆心角所对的弧长是(。
)A.2B.2sin1C.2cos1D.sin29.如果sinx+cosx=4/3,且π/4<x<π/2,那么cotx的值是(。
)A.-3/4B.-4/3或-3/4C.-4/3D.3/4或-3/410.若实数x满足log2x=2+sinθ,则|x+1|+|x-10|的值等于(。
)A.2x-9B.9-2xC.11D.9二、填空题(本大题共6小题,每小题5分,共30分)11.tan300°+cot765°的值是_____________.12.若sinα+cosα=2,则sinαcosα的值是_____________.13.不等式(lg20)2cosx>1,(x∈(0,π))的解集为_____________.14.若θ满足cosθ>-1/2,则角θ的取值集合是_____________.15.若cos130°=a,则tan50°=_____________.16.已知f(x)=sin2x+cosx,则f(π/6)为_____________.sinα=√(1-cos^2α)=√(1-(2x^2/(x^2+5^2)))=√((25-x^2)/(x^2+25)),tanα=sinα/cosα=(25-x^2)/(2x)。
(12)三角函数 单元测试题

三角单元测试题一、选择题:(每小题5分,计50分)1.(2006 (A )关于x 轴对称 (B )关于y 轴对称 (C )关于原点对称(D )关于直线x =2π对称2. (2008全国Ⅱ卷文).若sin 0α<且tan 0α>是,则α是( ) A .第一象限角 B . 第二象限角 C . 第三象限角 D . 第四象限角3.(2008北京文)已知△ABC 中,a =2,b =3,B =60°,那么角A 等于( ) (A )135° (B)90° (C)45° (D)30°4.(2006江西文)函数4sin 21y x π⎛⎫=++ ⎪3⎝⎭的最小正周期为( ) A.π2B.π C.2πD.4π5.(2008福建文)函数cos ()y x x R =∈的图像向左平移2π个单位后,得到()y g x =的图像, 则()g x 的解析式为( )A.sin x - B.sin x C.cos x - D.cos x6.(2008全国Ⅱ卷文)函数x x x f cos sin )(-=的最大值为( ) A .1B .2 C .3D .27.(2003全国文)函数sin()(0)y x R ϕϕπϕ=+≤≤=是上的偶函数,则( ) (A )0 (B )4π (C )2π(D )π8.( 2007广东文)已知简谐运动()2sin()(||)32f x x ππϕϕ=+<的图象经过点(0,1),则该简谐运动的最小正周期T 和初相ϕ分别为( )9.(2004辽宁)若函数)sin()(ϕω+=x x f 的图象(部分)如图所示,则ϕω和的取值是( )A .3,1πϕω==B .3,1πϕω-==C .6,2ϕω==D .6,2ϕω-==10.(2007江西文)若tan α=3,tan β=34,则tan(α-β)等于( ) A .-3 B .-31 C .3 D .31二.填空题: (每小题5分,计20分)11.(2006重庆文)已知sin 5α=,2παπ≤≤,则tan α= 。
北师大版数学八年级上第一章三角函数单元检测题含答案

北师大版数学八年级上第一章三角函数单
元检测题含答案
一、选择题
1. 下面那个角不是锐角?
A. 40°
B. 75°
C. 120°
D. 160°
答案:D
2. 在一个三角形中,如果一个角是直角,则其余两个角的和是多少度?
A. 45°
B. 90°
C. 120°
D. 180°
答案:C
二、填空题
1. 在单位圆上,角θ对应的弧长为$\frac{\pi}{6}$,则$\sinθ$的值是\_\_\_\_\_\_\_。
答案:0.5
2. 若$\cosθ = -0.8$,则角θ的终边位于哪个象限?
答案:第二象限
三、解答题
1. 已知直角三角形的一条直角边的长度为5cm,斜边的长度为13cm,求另一个直角边的长度。
答案:12cm
2. 已知$\sinθ = \frac{3}{5}$,求$\cosθ$和$\tanθ$的值。
答案:$\cosθ = \frac{4}{5}$,$\tanθ = \frac{3}{4}$
四、计算题
1. $\sin30° + \cos45°$的值等于\_\_\_\_\_\_\_。
答案:$\frac{\sqrt{2} + 1}{2}$
2. $\sin(30° + 45°)$的值等于\_\_\_\_\_\_\_。
答案:$\frac{\sqrt{6} + \sqrt{2}}{4}$
以上是北师大版数学八年级上第一章三角函数单元检测题的内容和答案。
希望对你有帮助!。
人教版高中数学必修第一册第五单元《三角函数》测试(答案解析)(2)

一、选择题1.将函数sin 4y x π⎛⎫=- ⎪⎝⎭的图像上所有点的横坐标变为原来的2倍(纵坐标不变),再将所得的图像向左平移π6个单位,则所得图像对应的解析式为( ) A .sin 212y x π⎛⎫=+ ⎪⎝⎭B .sin 212y x π⎛⎫=- ⎪⎝⎭C .sin 26x y π⎛⎫=-⎪⎝⎭ D .sin 212x y π⎛⎫=-⎪⎝⎭ 2.若函数()()sin 06f x x πωω⎛⎫=+> ⎪⎝⎭的图象的相邻两条对称轴之间的距离为2π,且该函数图象关于点()0,0x 成中心对称,00,2x π⎡⎤∈⎢⎥⎣⎦,则0x 等于( ) A .512π B .4π C .3π D .6π3.已知()0,πα∈,2sin cos 1αα+=,则cos 21sin 2αα=-( ) A .2425-B .725-C .7-D .17-4.已知3sin 5α=-,则cos2=α( ) A .15-B .15C .725-D .7255.已知函数()()2sin ,0,2f x x x x π=∈⎛⎫⎡⎤ ⎪⎢⎥⎣⎦⎝⎭,则()f x 的单调递增区间是( ) A .06,π⎡⎤⎢⎥⎣⎦B .0,4⎡⎤⎢⎥⎣⎦πC .0,3π⎡⎤⎢⎥⎣⎦D .0,2π⎡⎤⎢⎥⎣⎦6.已知函数()()sin 20,2f x A x A πϕϕ⎛⎫=+>< ⎪⎝⎭满足03f π⎛⎫=⎪⎝⎭,则()f x 图象的一条对称轴是( ) A .6x π=B .56x π=C .512x π=D .712x π=7.已知函数()cos 2cos sin(2)sin f x x x ϕπϕ=⋅-+⋅在3x π=处取得最小值,则函数()f x 的一个单调递减区间为( )A .4,33ππ⎛⎫⎪⎝⎭B .2,33ππ⎛⎫-⎪⎝⎭ C .5,36ππ⎛⎫⎪⎝⎭D .,63ππ⎛⎫-⎪⎝⎭ 8.sin15cos15+=( ) A .12B .22C .32D .629.已知函数()()ππ36sin 0f x A x A ⎛⎫=> ⎪⎝⎭+在它的一个最小正周期内的图像上,最高点与最低点的距离是5,则A 等于( ). A .1B .2C .2.5D .410.()()sin f x A x =+ωϕ0,0,2A πωϕ⎛⎫>>< ⎪⎝⎭的部分图象如图所示,若将函数()f x 的图象向右平移2π个单位长度,得到函数()g x 的图象,则( )A .()12sin 212g x x π⎛⎫=- ⎪⎝⎭ B .()12sin 212g x x π⎛⎫=+⎪⎝⎭ C .()2sin 212g x x π⎛⎫=- ⎪⎝⎭ D .()2sin 212g x x π⎛⎫=+⎪⎝⎭11.已知函数()y f x =的图象如图所示,则此函数可能是( )A .sin 6()22x x x f x -=- B .sin 6()22x x x f x -=- C .cos6()22x xx f x -=- D .cos6()22x x xf x -=-12.已知某扇形的弧长为32π,圆心角为2π,则该扇形的面积为( ) A .4π B .6π C .2π D .94π 二、填空题13.已知()0,απ∈且tan 3α=,则cos α=______. 14.已知()tan 3πα+=,则2tan 2sin αα-的值为_______.15.已知α、β均为锐角,且sin 10α=,()cos 5αβ+=,则cos 2β=_______________16.下列函数中,以π2为周期且在区间ππ,42⎛⎫⎪⎝⎭单调递增的是______.①()cos2f x x =;②()sin 2f x x =;③()cos f x x =;④()sin f x x = 17.若函数()|2cos |f x a x =+的最小正周期为π,则实数a 的值为____.18.方程21sin cos 2x x x =在[0,]4π上的解为___________19.已知函数()cos 2f x x =,若12,x x 满足12|()()|2f x f x -=,则12||x x -的一个取值为________. 20.若0,2x π⎛⎫∀∈ ⎪⎝⎭,sin cos m x x ≥+恒成立,则m 的取值范围为_______________. 三、解答题21.已知函数()()0,22f x x ππωϕωϕ⎛⎫=+>-≤<⎪⎝⎭的图象关于直线3x π=对称,且图象上相邻两个最高点的距离为π. (1)求ω和ϕ的值;(2)当0,2x π⎡⎤∈⎢⎥⎣⎦时,求函数()y f x =的最大值和最小值. 22.已知向量2(cos ,sin )m x a x =,(3,cos )n x =-,函数3()f x m n =⋅-. (1)若1a =,当[0,]2x π∈时,求()f x 的值域; (2)若()f x 为偶函数,求方程3()4f x =-在区间[,]-ππ上的解.23.已知 3sin 5α=,12cos 13,,2παπ⎛⎫∈ ⎪⎝⎭,3,2πβπ⎛⎫∈ ⎪⎝⎭求sin()αβ+,cos()αβ-,tan2α的值. 24.已知函数25()23sin cos()2cos (0)32f x wx wx wx w π=+-+>的图像上相邻的两个最低点的距离为π. (1)求w 的值;(2)求函数()f x 的单调递增区间.25.在①函数()()sin 20,2f x x πωϕωϕ⎛⎫=+><⎪⎝⎭的图象向右平移6π个单位长度得到()g x 的图像,()g x 图像关于,012π⎛⎫⎪⎝⎭对称;②函数()()12cos sin 062f x x x πωωω⎛⎫=+-> ⎪⎝⎭这两个条件中任选一个,补充在下而问题中,并解答.已知______,函数()f x 的图象相邻两条对称轴之间的距离为2π. (1)若()f x 在[]0,α上的值域为1,12⎡⎤⎢⎥⎣⎦,求a 的取值范围; (2)求函数()f x 在[]0,2π上的单调递增区间.26.如图,扇形ABC 是一块半径为2千米,圆心角为60的风景区,P 点在弧BC 上,现欲在风景区中规划三条商业街道,要求街道PQ 与AB 垂直,街道PR 与AC 垂直,线段RQ 表示第三条街道.(1)如果P 位于弧BC 的中点,求三条街道的总长度;(2)由于环境的原因,三条街道PQ 、PR 、RQ 每年能产生的经济效益分别为每千米300万元、200万元及400万元,问:这三条街道每年能产生的经济总效益最高为多少?【参考答案】***试卷处理标记,请不要删除一、选择题1.C 解析:C 【分析】根据正弦型函数的图像的变换规律进行求解即可. 【详解】 将函数sin 4y x π⎛⎫=-⎪⎝⎭的图像上所有点的横坐标变为原来的2倍(纵坐标不变),所得到的函数的解析式为:sin 24x y π⎛⎫=-⎪⎝⎭,将sin 24x y π⎛⎫=- ⎪⎝⎭的图像向左平移π6个单位,得到的函数的解析式为:1sin[]264y x ππ⎛⎫=+- ⎪⎝⎭,化简得:sin 26x y π⎛⎫=- ⎪⎝⎭. 故选:C2.A解析:A 【分析】由已知条件求得函数()f x 的最小正周期T ,可求得ω的值,再由已知可得()026x k k Z ππ+=∈,结合00,2x π⎡⎤∈⎢⎥⎣⎦可求得0x 的值. 【详解】由题意可知,函数()f x 的最小正周期T 满足22T π=,T π∴=,22T πω∴==,()sin 26f x x π⎛⎫∴=+ ⎪⎝⎭,由于函数()f x 的图象关于点()0,0x 成中心对称,则()026x k k Z ππ+=∈,解得()0212k x k Z ππ=-∈, 由于00,2x π⎡⎤∈⎢⎥⎣⎦,解得0512x π=. 故选:A. 【点睛】结论点睛:利用正弦型函数的对称性求参数,可利用以下原则来进行: (1)函数()()sin f x A x =+ωϕ关于直线0x x =对称()02x k k Z πωϕπ⇔+=+∈;(2)函数()()sin f x A x =+ωϕ关于点()0,0x 对称()0x k k Z ωϕπ⇔+=∈.3.D解析:D 【分析】利用22sin cos 1αα+=以及2sin cos 1αα+=解出sin α,cos α的值,再利用二倍角公式化简即可求解. 【详解】因为2sin cos 1αα+=,所以cos 12sin αα=-, 代入22sin cos 1αα+=得()22sin 12sin 1αα+-=, 因为()0,πα∈,所以4sin 5α,所以43cos 12sin 1255αα=-=-⨯=-,所以4324sin 22sin cos 25525ααα⎛⎫==⨯⨯-=- ⎪⎝⎭, 2247cos 212sin 12525αα⎛⎫=-=-⨯=- ⎪⎝⎭cos 211sin 2717252425αα-==--⎛⎫- ⎪⎭-⎝, 故选:D 【点睛】关键点点睛:本题的关键点是熟记同角三角函数基本关系,以及三角函数值在每个象限内的符号,熟记正余弦的二倍角公式,计算仔细.4.D解析:D 【分析】由题中条件,根据二倍角的余弦公式,可直接得出结果. 【详解】 因为3sin 5α=-, 所以297cos 212sin 122525αα=-=-⨯=. 故选:D.5.A解析:A 【分析】根据三角恒等变换公式化简()f x ,结合x 的范围,可得选项. 【详解】因为()()2sin ,0,2f x x x x π=+∈⎛⎫⎡⎤ ⎪⎢⎥⎣⎦⎝⎭,所以 ()()222sin sin cos +3cos f x x xx x x x +==222cos +12cos 2+22sin 2+26x x x x x π⎛⎫=+=+=+ ⎪⎝⎭,因为0,2x π⎡⎤∈⎢⎥⎣⎦,所以72+,666x πππ∈⎡⎤⎢⎥⎣⎦,所以由2+662x πππ≤≤,解得06x π≤≤, 所以()f x 的单调递增区间是06,π⎡⎤⎢⎥⎣⎦,故选:A.6.D解析:D 【分析】利用三角函数的性质,2()sin()033f A ππϕ=+=,求ϕ,然后,令()f x A =,即可求解 【详解】根据题意得,2()sin()033f A ππϕ=+=,得23k πϕπ+=,k z ∈又因为2πϕ<,进而求得,3πϕ=,所以,()sin(2)3f x A x π=+,令()f x A =,所以,sin(2)13x π+=,所以,2,32x k k z πππ+=+∈,解得,k x k z 122ππ=+∈,当1k =时,712x π=,所以,()f x 图象的一条对称轴是712x π= 故选D 【点睛】关键点睛:求出ϕ后,令()f x A =,所以,sin(2)13x π+=,进而求解,属于中档题7.D解析:D 【分析】先化简()f x 并根据已知条件确定出ϕ的一个可取值,然后根据余弦函数的单调递减区间求解出()f x 的一个单调递减区间. 【详解】 因为()()()cos2cos sin 2sin cos2cos sin 2sin cos 2f x x x x x x ϕπϕϕϕϕ=⋅-+⋅=⋅+⋅=-,且()f x 在3x π=处有最小值,所以2cos 133f ππϕ⎛⎫⎛⎫=-=-⎪ ⎪⎝⎭⎝⎭,所以22,3k k Z πϕππ-=+∈, 所以2,3k k Z πϕπ=--∈,取ϕ的一个值为3π-, 所以()cos 23f x x π⎛⎫=+ ⎪⎝⎭,令222,3k x k k Z ππππ≤+≤+∈,所以,63k x k k Z ππππ-≤≤+∈,令0k =,所以此时单调递减区间为,63ππ⎡⎤-⎢⎥⎣⎦, 故选:D. 【点睛】思路点睛:求解形如()()cos f x A x ωϕ=+的函数的单调递减区间的步骤如下: (1)先令[]2,2+,k k k x Z ωϕπππ+∈∈;(2)解上述不等式求解出x 的取值范围即为()f x 的单调递减区间.8.D解析:D 【分析】由辅助角公式可直接计算得到结果. 【详解】()6sin15cos152sin 15452sin 60+=+==. 故选:D.9.B解析:B【分析】根据正弦型函数图象性质确定函数()f x 的最小正周期T ,再根据最高点与最低点的距离是55=,从而解得A 的值. 【详解】解:函数()()ππ36sin 0f x A x A ⎛⎫=> ⎪⎝⎭+的最小正周期2263T πππω=== 函数()()ππ36sin 0f x A x A ⎛⎫=>⎪⎝⎭+在它的一个最小正周期内的图像上,最高点与最低点的距离是5,5=,解得2A =.故选:B. 【点睛】对于三角函数,求最小正周期和最值时可先把所给三角函数式化为()sin y A ωx φ=+或()cos y A x ωϕ=+的形式,则最小正周期为2T ωπ=,最大值为A ,最小值为A -;奇偶性的判断关键是解析式是否为sin y A x ω=或cos y A x ω=的形式.10.A解析:A 【分析】根据图象易得2A =,最小正周期T 2433ππ⎛⎫=-- ⎪⎝⎭,进而求得ω,再由图象过点2,23π⎛⎫⎪⎝⎭求得函数()f x ,然后再根据平移变换得到()g x 即可. 【详解】由图象可知2A =,最小正周期2T 4433πππ⎡⎤⎛⎫=--= ⎪⎢⎥⎝⎭⎣⎦, ∴212T πω==,1()2sin 2f x x ϕ⎛⎫=+ ⎪⎝⎭, 又22sin 233f ππϕ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭,∴232k ππϕπ+=+,26k πϕπ=+,∵||2ϕπ<,∴6π=ϕ,1()2sin 26f x x π⎛⎫=+ ⎪⎝⎭,将其图象向右平移2π个单位长度得 11()2sin 2sin 226212g x x x πππ⎡⎤⎛⎫⎛⎫=-+=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,故选:A 11.D解析:D 【分析】由函数图象可得()y f x =是奇函数,且当x 从右趋近于0时,()0f x >,依次判断每个函数即可得出.【详解】由函数图象可得()y f x =是奇函数,且当x 从右趋近于0时,()0f x >,对于A ,当x 从右趋近于0时,sin60x >,22x x -<,故()0f x <,不符合题意,故A 错误; 对于B ,()()sin 6sin 6()2222x x x xx xf x f x ----===--,()f x ∴是偶函数,不符合题意,故B 错误; 对于C ,()()cos 6cos 6()2222x x x xx xf x f x ----===--,()f x ∴是偶函数,不符合题意,故C 错误; 对于D ,()()cos 6cos 6()2222x x x xx xf x f x ----===---,()f x ∴是奇函数,当x 从右趋近于0时,cos60x >,22x x ->,()0f x ∴>,符合题意,故D 正确. 故选:D. 【点睛】思路点睛:函数图象的辨识可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置. (2)从函数的单调性,判断图象的变化趋势; (3)从函数的奇偶性,判断图象的对称性; (4)从函数的特征点,排除不合要求的图象.12.D解析:D 【分析】由弧长公式求出3r =,再由扇形的面积公式求出答案. 【详解】扇形的圆心角322l r r ππθ===,所以3r =,则扇形的面积113932224S lr ππ==⨯⨯=. 故选:D. 二、填空题13.【分析】本题考查同角三角函数及其关系借助公式求解即可求解时需要判定符号的正负【详解】解:法一:由可得代入解得因为所以所以法二:由且可取终边上的一点坐标为根据三角函数终边定义公式故答案为:【点睛】方法解析:10【分析】本题考查同角三角函数及其关系,借助公式sin tan cos ααα=,22sin +cos =1αα求解即可,求解时需要判定符号的正负. 【详解】解:法一:由sin tan =3cos ααα=可得sin =3cos αα,代入22sin +cos =1αα解得cos α= 因为()0,tan 30απα∈=>,,所以0,2πα⎛⎫∈ ⎪⎝⎭,所以cos α=. 法二:由()0,απ∈且tan 3α=可取α终边上的一点坐标为(1,3),根据三角函数终边定义公式cos 10α===.【点睛】方法点睛:同角三角函数基本关系的3个应用技巧: (1)弦切互化利用公式sin tan ()cos 2k απααπα=≠+实现角α的弦切互化; (2)和(差)积转换利用2(sin cos )=1sin 2ααα±±进行变形、转化;(3)巧用“1”的变换22222211sin+cos =cos (tan 1)sin (1)tan αααααα=+=+. 14.【分析】利用诱导公式求出再利用二倍角公式求出以及同角三角函数的基本关系求出即可得解;【详解】解:由题意所以所以所以故答案为: 解析:3320-【分析】利用诱导公式求出tan α,再利用二倍角公式求出tan2α,以及同角三角函数的基本关系求出2sin α,即可得解; 【详解】解:由题意()tan 3πα+=,所以tan 3α=,所以22tan 3tan 21tan 4ααα==--,222222sin tan 9sin sin cos tan 110αααααα===++,所以23933tan 2sin 41020αα-=--=-.故答案为:3320-15.【分析】先由题意得到求出根据由两角差的余弦公式求出再由二倍角公式即可求出结果【详解】因为均为锐角所以又所以所以则故答案为:解析:45【分析】先由题意得到,0,2πα⎛⎫∈ ⎪⎝⎭,0,2πβ⎛⎫∈ ⎪⎝⎭,()0,αβπ+∈,求出sin 10α=,()cos 5αβ+=,根据()cos cos βαβα=+-,由两角差的余弦公式,求出cos β,再由二倍角公式,即可求出结果. 【详解】因为α、β均为锐角,所以0,2πα⎛⎫∈ ⎪⎝⎭,0,2πβ⎛⎫∈ ⎪⎝⎭,()0,αβπ+∈,又sin 10α=,()cos 5αβ+=,所以cos 10α==,()sin 5αβ+==, 所以()()()cos cos cos cos sin sin βαβααβααβα=+-=+++==, 则294cos 22cos 1155ββ=-=-=. 故答案为:45. 16.①【分析】利用与的关系确定①②的周期在给定区间上去掉绝对值符号后确定单调性化简和后可得其性质从而判断③④【详解】周期是时是增函数①满足题意;周期是时是减函数②不满足题意;周期是③不满足题意;不是周期解析:① 【分析】利用()f x 与()f x 的关系确定①②的周期,在给定区间上去掉绝对值符号后确定单调性,化简cos x 和sin x 后可得其性质,从而判断③④【详解】()cos2f x x =周期是2π,,42x ππ⎛⎫∈ ⎪⎝⎭时,()cos2cos2f x x x ==-是增函数,①满足题意;()sin 2f x x =周期是2π,,42x ππ⎛⎫∈ ⎪⎝⎭时,()sin 2sin 2f x x x ==是减函数,②不满足题意;()cos cos f x x x ==,周期是2π,③不满足题意; sin ,0()sin sin ,0x x f x x x x ≥⎧==⎨-<⎩不是周期函数,④不满足题意.故答案为:①. 【点睛】结论点睛:本题考查三角函数的周期性与单调性,解题时可利用如下结论:①()sin()f x A x ωϕ=+(或cos()A x ωϕ+,函数()y f x =的周期是函数()y f x =周期的一半;②sin y x ω=不是周期函数.17.【分析】利用来求解【详解】因为函数的最小正周期为所以都有成立故则故答案为: 解析:0【分析】利用()()f x f x π=+来求解. 【详解】因为函数()f x 的最小正周期为π,所以x R ∀∈,都有()()f x f x π=+成立, 故()2cos 2cos 2cos a x a x a x π+=++=-,则0a =. 故答案为:0.18.【分析】由二倍角公式和两角差的正弦公式化简变形后由正弦函数性质得出结论【详解】由得得∴又∴故答案为:【点睛】方法点睛:本题考查求解三角方程解题方法:(1)利用三角函数的恒等变换公式化方程为的形式然后解析:12π 【分析】 由二倍角公式和两角差的正弦公式化简变形后由正弦函数性质得出结论. 【详解】由21sin cos 2x x x =得1cos 21222x x -+=,得sin 206x π⎛⎫-= ⎪⎝⎭,∴26x k ππ-=,,212k x k Z ππ=+∈,又0,4x π⎡⎤∈⎢⎥⎣⎦,∴12x π=. 故答案为:12π.【点睛】方法点睛:本题考查求解三角方程,解题方法:(1)利用三角函数的恒等变换公式化方程为sin()x k ωϕ+=的形式,然后由正弦函数的定义得出结论.(2)用换元法,如设sin x t =,先求得方程()0f t =的解0t ,然后再解方程0sin x t =.19.(答案不唯一)【分析】根据的值域为可知若满足则必有的值分别为再根据三角函数的性质分析即可【详解】因为的值域为故若满足则必有的值分别为故的最小值当且仅当为相邻的两个最值点取得此时为的半个周期即故答案为解析:π2(答案不唯一) 【分析】根据()cos2f x x =的值域为[]1,1-可知若12,x x 满足()()122f x f x -=则必有()()12,f x f x 的值分别为±1,再根据三角函数的性质分析即可.【详解】因为()cos2f x x =的值域为[]1,1-,故若12,x x 满足()()122f x f x -=则必有()()12,f x f x 的值分别为±1,故12x x -的最小值当且仅当12,x x 为()cos2f x x =相邻的两个最值点取得.此时12x x -为()cos2f x x =的半个周期,即12222ππ⨯=. 故答案为:2π【点睛】关键点点睛:相邻的两个最值点的横坐标的距离为半个周期是解题的突破点.20.【分析】根据三角函数的性质求得的最大值进而可求出结果【详解】因为由可得所以则因为恒成立所以只需故答案为:解析:)+∞【分析】根据三角函数的性质,求得sin cos x x +的最大值,进而可求出结果. 【详解】因为sin cos 4x x x π⎛⎫+=+ ⎪⎝⎭,由0,2x π⎛⎫∈ ⎪⎝⎭可得3,444x πππ⎛⎫+∈ ⎪⎝⎭,所以sin 42x π⎛⎤⎛⎫+∈ ⎥ ⎪ ⎝⎭⎝⎦,则(sin cos 4x x x π⎛⎫+=+∈ ⎪⎝⎭,因为0,2x π⎛⎫∀∈ ⎪⎝⎭,sin cos m x x ≥+恒成立,所以只需m ≥故答案为:)+∞.三、解答题21.(1)2ω=,6πϕ=-;(2)max ()f x =min ()2f x =-. 【分析】(1)由图象上相邻两个最高点的距离为π得()f x 的最小正周期T π=,故2ω=,由函数图象关于直线3x π=对称得232k ππϕπ⨯+=+,k Z ∈,再结合范围得6πϕ=-;(2)由(1)得()26f x x π⎛⎫=- ⎪⎝⎭,进而得52666x πππ-≤-≤,再结合正弦函数的性质即可得答案. 【详解】(1)因为()f x 的图象上相邻两个最高点的距离为π, 所以()f x 的最小正周期T π=,从而22Tπω==. 又因为()f x 的图象关于直线3x π=对称,所以232k ππϕπ⨯+=+,k Z ∈,又22ππϕ-≤<,所以2236ππϕπ=-=-. 综上,2ω=,6πϕ=-.(2)由(1)知()26f x x π⎛⎫=- ⎪⎝⎭.当0,2x π⎡⎤∈⎢⎥⎣⎦时,可知52666x πππ-≤-≤.故当226x ππ-=,即3x π=时,max ()f x =当266x ππ-=-,即0x =时,min ()f x =. 【点睛】本题解题的关键在于先根据0,2x π⎡⎤∈⎢⎥⎣⎦得52666x πππ-≤-≤,进而结合正弦函数的性质,采用整体思想求解,考查运算求解能力,是中档题.22.(1)[-;(2)75,1212x ππ=±±. 【分析】(1)将()f x 化为()cos(2)6f x x π=+,然后可得答案; (2)由()f x 为偶函数可求出0a =,然后可得答案. 【详解】(1)2()sin cos 2sin 2222a f x x a x x x x =--=-当1a =,1()cos 2sin 2cos(2)226f x x x x π=-=+由7[0,],2[,],cos(2)[1,266662x x x πππππ∈∴+∈∴+∈-所以()f x 的值域为[-(2)若()f x 为偶函数,则()()f x f x -=恒成立2sin 22sin 222a a x x x x +=-成立,整理得sin 20,0a x a =∴=所以由3()24f x x ==-得cos 22x =-又752[2,2],,1212x x ππππ∈-∴=±± 23.1665-;3365;247- 【分析】由已知条件,利用同角三角函数基本关系结合角所在的象限求出cos α,sin β,以及tan α的值,再利用两角和的正弦公式,两角差的余弦公式,正切的二倍角公式即可求解.【详解】 因为,2παπ⎛⎫∈⎪⎝⎭,3sin 5α=,所以4cos 5α===-,因为3,2πβπ⎛⎫∈ ⎪⎝⎭,12cos 13,所以5sin13β===-,所以3124516 sin()sin cos cos sin51351365αβαβαβ⎛⎫⎛⎫⎛⎫+=+=⨯-+-⨯-=-⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,4123533cos()cos cos sin sin51351365αβαβαβ⎛⎫⎛⎫⎛⎫-=+=-⨯-+⨯-=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭因为sin3tancos4ααα==-,所以22322tan244tan21tan7314ααα⎛⎫⨯-⎪⎝⎭===--⎛⎫-- ⎪⎝⎭,综上所述:16sin()65αβ+=-,33cos()65αβ-=,24tan27α=-.24.(1)1;(2)()36k k k Zππππ⎡⎤-++∈⎢⎥⎣⎦,.【分析】本题考查三角函数的图像和性质、三角恒等变换,根据三角恒等变换公式()f x化简函数解析式,根据图像和性质求单调递增区间.【详解】(1)5()(cos cos sin sin)(1cos2)332f x wx wx wx wxππ=--++23sin23sin cos222wx wx wx=--+1cos2323cos222wxwx wx-=-⨯-+12cos22wx wx=+sin(2)6wxπ=+又因为()f x图象上相邻的两个最低点间的距离为π,0w>,所以22w,解得1w=.(2)据(1)求解知,()sin(2)6f x xπ=+令222()262k x k k Zπππππ-+≤+≤+∈,所以()36k x k k Zππππ-+≤≤+∈,所以所求的单调递增区间是()36k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦,.【点睛】思路点睛:三角恒等变换综合应用的解题思路:(1)利用降幂、升幂公式将()f x 化为sin cos a x b x 的形式;(2)构造())f x x x +;(3)和差公式逆用,得())f x x ϕ=+ (其中ϕ为辅助角,tan b aϕ=);(4)利用())f x x ϕ=+研究三角函数的性质; (5)反思回顾,查看关键点、易错点和答题规范. 25.(1),63ππ⎡⎤⎢⎥⎣⎦;(2)06,π⎡⎤⎢⎥⎣⎦,27,36ππ⎡⎤⎢⎥⎣⎦,5,23ππ⎡⎤⎢⎥⎣⎦.【分析】先选条件①或条件②,结合函数的性质及图像变换,求得函数()sin 26f x x π⎛⎫+ ⎝=⎪⎭,(1)由[]0,x α∈,得到2,2666x πππα⎡⎤+∈+⎢⎥⎣⎦,根据由正弦函数图像,即可求解; (2)根据函数正弦函数的形式,求得36k x k ππππ-+≤≤+,k Z ∈,进而得出函数的单调递增区间. 【详解】 方案一:选条件①由函数()f x 的图象相邻两条对称轴之间的距离为2π,可得22T ππω==,解得1ω=, 所以()()sin 2f x x ϕ=+,又由函数()f x 的图象向右平移6π个单位长度得到πsin 2φ3g x x, 又函数()g x 图象关于,012π⎛⎫⎪⎝⎭对称,可得6k πϕπ=+,k Z ∈,因为2πϕ<,所以6π=ϕ,所以()sin 26f x x π⎛⎫+ ⎝=⎪⎭.(1)由[]0,x α∈,可得2,2666x πππα⎡⎤+∈+⎢⎥⎣⎦, 因为函数()f x 在[]0,α上的值域为1,12⎡⎤⎢⎥⎣⎦,根据由正弦函数图像,可得52266ππαπ≤+≤,解得63ππα≤≤,所以α的取值范围为,63ππ⎡⎤⎢⎥⎣⎦.(2)由222262k x k πππππ-+≤+≤+,k Z ∈,可得36k x k ππππ-+≤≤+,k Z ∈,当0k =时,可得66x ππ-≤≤;当1k =时,可得2736x ππ≤≤; 当2k =时,可得51336x ππ≤≤, 所以函数()f x 在[]0,2π上的单调递增区间为06,π⎡⎤⎢⎥⎣⎦,27,36ππ⎡⎤⎢⎥⎣⎦,5,23ππ⎡⎤⎢⎥⎣⎦. 方案二:选条件②: 由()12cos sin 62f x x x πωω⎛⎫=+- ⎪⎝⎭12cos sin cos cos sin 662x x x ππωωω⎛⎫=+- ⎪⎝⎭211cos cos 2cos 2222x x x x x ωωωωω=+-=+sin 26x πω⎛⎫=+ ⎪⎝⎭,因为函数()f x 的图象相邻两条对称轴之间的距离为2π,可得22T ππω==,所以1ω=, 可得()()sin 2f x x ϕ=+, 又由函数()f x 的图象向右平移6π个单位长度得到πsin 2φ3g x x, 又函数()g x 图象关于,012π⎛⎫⎪⎝⎭对称,可得6k πϕπ=+,k Z ∈,因为2πϕ<,所以6π=ϕ,所以()sin 26f x x π⎛⎫+ ⎝=⎪⎭.(1)由[]0,x α∈,可得2,2666x πππα⎡⎤+∈+⎢⎥⎣⎦, 因为函数()f x 在[]0,α上的值域为1,12⎡⎤⎢⎥⎣⎦, 根据由正弦函数图像,可得52266ππαπ≤+≤,解得63ππα≤≤,所以α的取值范围为,63ππ⎡⎤⎢⎥⎣⎦.(2)由222262k x k πππππ-+≤+≤+,k Z ∈,可得36k x k ππππ-+≤≤+,k Z ∈,当0k =时,可得66x ππ-≤≤;当1k =时,可得2736x ππ≤≤; 当2k =时,可得51336x ππ≤≤, 所以函数()f x 在[]0,2π上的单调递增区间为06,π⎡⎤⎢⎥⎣⎦,27,36ππ⎡⎤⎢⎥⎣⎦,5,23ππ⎡⎤⎢⎥⎣⎦. 【点睛】解答三角函数图象与性质的综合问题的关键是首先将已知条件化为()sin()f x A wx ϕ=+或()cos()f x A wx ϕ=+的形式,然后再根据三角函数的基本性质,结合数形结合法的思想研究函数的性质(如:单调性、奇偶性、对称性、周期性与最值等),进而加深理解函数的极值点、最值点、零点及有界性等概念与性质.26.(1)2+(千米);(2). 【分析】(1)根据P 位于弧BC 的中点,则P 位于BAC ∠的角平分线上,然后分别在,,Rt APQ Rt APR 正AQR 中求解.(2)设PAB θ∠=,060θ<<︒,然后分别在,Rt APQ Rt APR 表示 PQ ,PR ,在AQR 中由余弦定理表RQ ,再由300200400W PQ PR RQ =⨯+⨯+⨯求解.【详解】(1)由P 位于弧BC 的中点,在P 位于BAC ∠的角平分线上, 则1||||||sin 2sin30212PQ PR PA PAB ==∠=⨯︒=⨯=,||cos 22AQ PA PAB =∠=⨯= 由60BAC ∠=︒,且AQ AR =,∴QAR 为等边三角形,则||RQ AQ ==三条街道的总长||||||112l PQ PR RQ =++=++ ; (2)设PAB θ∠=,060θ︒<<︒, 则sin 2sin PQ AP θθ==,PR AP =()()sin 602sin 603cos sin θθθθ-=-=-, cos 2cos AQ AP θθ==,||||cos(60)2cos(60)cos AR AP θθθθ=-=-=+,由余弦定理可知:2222cos60RQ AQ AR AQ AR =+-,22(2cos )(cos )22cos (cos )cos 603θθθθθθ=+-⨯+=,则|RQ =设三条街道每年能产生的经济总效益W , 300200400W PQ PR RQ =⨯+⨯+⨯,3002sin sin )200θθθ=⨯+-⨯+,400sin θθ=++200(2sin )θθ=++)θϕ=++tan 2ϕ=,当()sin 1θϕ+=时,W 取最大值,最大值为【点睛】方法点睛:解三角形应用题的两种情形:(1)实际问题经抽象概括后,已知量与未知量全部集中在一个三角形中,可用正弦定理或余弦定理求解;(2)实际问题经抽象概括后,已知量与未知量涉及到两个或两个以上的三角形,这时需作出这些三角形,先解够条件的三角形,然后逐步求解其他三角形,有时需设出未知量,从几个三角形中列出方程(组),解方程(组)得出所要求的解.。
人教版高中数学必修第一册第五单元《三角函数》测试题(有答案解析)(2)

一、选择题1.已知5π2sin 63α⎛⎫+= ⎪⎝⎭,则πcos 23α⎛⎫-= ⎪⎝⎭( )A .B .19-C .3D .192.已知α为第二象限角,且π3cos 25α⎛⎫-= ⎪⎝⎭,则tan α=( ). A .34-B .43-C .53-D .45-3.已知函数()sin()(0)f x x ωω=>在区间,123ππ⎛⎤- ⎥⎝⎦上单调递增,在区间5,312ππ⎡⎫⎪⎢⎣⎭上单调递减,则ω=( )A .362k -,k ∈N B .362k +,k ∈N C .32D .34.计算cos 20cos80sin160cos10+=( ).A .12B C .12-D . 5.已知3sin 7a π=,4cos 7b π=,3tan()7c π=-,则a ,b ,c 的大小关系为( ) A .a b c <<B .b c a <<C .c b a <<D .c a b <<6.把函数sin y x =的图象上所有的点向左平行移动6π个单位长度,再把所得图象上所有点的横坐标缩短到原来的12倍(纵坐标不变),得到的图象所表示的函数解析式是( ) A .sin 23y x π⎛⎫=- ⎪⎝⎭B .sin 26x y π⎛⎫=+⎪⎝⎭ C .sin 26y x π⎛⎫=-⎪⎝⎭D .sin 26y x π⎛⎫=+⎪⎝⎭7.sin 20cos10cos160sin10-=( )A .B .12C .12-D .28.若1sin 63πα⎛⎫-= ⎪⎝⎭,则2cos 23πα⎛⎫+ ⎪⎝⎭等于( ).A .79-B .13-C .13D .799.若将函数3sin(2)3y x π=+的图象向左平移6π个单位长度,则平移后图象的一个对称中心是( ) A .,06π⎛⎫ ⎪⎝⎭B .,06π⎛⎫-⎪⎝⎭C .,012π⎛⎫⎪⎝⎭D .,03π⎛⎫⎪⎝⎭10.刘徽是中国魏晋时期杰出的数学家,他提出“割圆求周”方法:当n 很大时,用圆内接正n 边形的周长近似等于圆周长,并计算出精确度很高的圆周率 3.1416π≈.在《九章算术注》中总结出“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”的极限思想,可以说他是中国古代极限思想的杰出代表.运用此思想,当π取3.1416时可得cos89︒的近似值为( ) A .0.00873B .0.01745C .0.02618D .0.0349111.已知tan 2α=,则sin sin 44ππαα⎛⎫⎛⎫-+= ⎪ ⎪⎝⎭⎝⎭( ) A .310-B .310 C .35D .3512.已知2cos 432θπ⎛⎫= ⎪⎝⎭-,则sin θ=( ) A .79 B .19C .-19D .-79二、填空题13.已知()sin()cos()1f x a x b x παπβ=++-+,其中α,β,a ,b 均为非零实数,若()20202f =,则()2021f =________.14.已知函数sin cos y x x =-,其图象的对称轴中距离y 轴最近的一条对称轴方程为x =________.15.已知锐角α满足1cos()35πα+=,则sin α=______. 16.若()()2sin 03f x x πωω⎛⎫=+> ⎪⎝⎭的最小正周期为4π,则()()tan 06g x x πωω⎛⎫=+> ⎪⎝⎭的最小正周期为______.17.已知1tan()3πα+=-,则sin 2cos 5cos sin αααα+=-______. 18.已知tan 2α=,则cos2=α__. 19.已知tan 2α=,则cos 22πα⎛⎫-= ⎪⎝⎭___________.20.若2sin 63πα⎛⎫+= ⎪⎝⎭,则sin 26πα⎛⎫-= ⎪⎝⎭________. 三、解答题21.已知函数2()2sin 23sin cos 1f x x x x =++.求: (1)()f x 的最小正周期; (2)()f x 在0,2π⎡⎤⎢⎥⎣⎦上的最值. 22.已知函数()cos f x x =.(1)已知α,β为锐角,()5f αβ+=-,4tan 3α=,求cos2α及()tan βα-的值;(2)函数()()321g x f x =+,若关于x 的不等式()()()2133g x a g x a ≥+++有解,求实数a 的最大值.23.如图为一个观览车示意图,该观览车圆半径为4.8m ,圆上最低点与地面距离为0.8m ,60秒转动一圈.图中OA 与地面垂直,以OA 为始边,逆时针转动θ到OB .设B 点与地面的距离为h .(1)求h 与θ的函数关系式;(2)设从OA 开始转动,经过10秒到达OB ,求h . 24.已知函数25()23cos()2cos (0)32f x wx wx wx w π=+-+>的图像上相邻的两个最低点的距离为π. (1)求w 的值;(2)求函数()f x 的单调递增区间. 25.已知函数2()sin(2)2cos 1(0)6f x x x πωωω=-+->的最小正周期为π,(1)求ω的值 (2)求()f x 在区间70,12π⎡⎤⎢⎥⎣⎦上的最大值和最小值.26.已知α∈(0,)2π,tan α=12,求tan 2α和sin ()4πα-的值.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【分析】先用诱导公式化为5cos 2cos 233ππαα⎛⎫⎛⎫-=+⎪ ⎪⎝⎭⎝⎭,再用二倍角公式计算. 【详解】225521cos 2cos 212sin 1233639a a πππα⎛⎫⎛⎫⎛⎫⎛⎫-=+=-+--⨯= ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.故选:D 2.A解析:A 【分析】 由已知求出3sin 5α=,即可得cos α,进而求出所求. 【详解】 ∵π3cos 25α⎛⎫-=⎪⎝⎭,∴3sin 5α=,∵α为第二象限角,∴4cos 5α==-, ∴sin 3tan cos 4ααα==-. 故选:A .3.C解析:C 【分析】 由题意知,当3x π=时,函数()f x 取得最大值,可求得362k ω=+,k ∈N .再由函数的单调区间得出不等式组,解之可得选项. 【详解】由题意知,当3x π=时,函数()f x 取得最大值,所以232k ππωπ⋅=+,k Z ∈.得362k ω=+,k ∈N .因为()f x 在区间,123ππ⎛⎤-⎥⎝⎦上递增,在5,312ππ⎡⎫⎪⎢⎣⎭上递减,所以312πππω≥+且5123πππω≥-, 解得1205ω<≤.因此32ω=.故选:C.4.A解析:A 【分析】将160化为20,10化为80后,利用两角差的余弦公式可求得结果. 【详解】cos 20cos80sin160cos10+cos 20cos80sin 20sin80=+()cos 8020=-cos60=12=. 故选:A .5.C解析:C 【分析】3sin07a π=>,4cos 07b π=<,a b >且均属于()1,1-,而1c <-,大小关系即可确定. 【详解】 解:3sin7a π=>;427πππ<<, 4cos coscos 72πππ∴<<,即10b -<<. 又正切函数在(0,)2π上单调递增,347ππ<; 3tantan 174ππ∴>=;33tan()tan 177c ππ∴=-=-<-, 01a b c ∴>>>->,故选:C. 6.D解析:D 【分析】根据三角函数的图象变换规律可得解析式. 【详解】函数sin y x =的图象上所有的点向左平行移动6π个单位长度,得sin 6y x π⎛⎫=+ ⎪⎝⎭,再把所得图象上所有点的横坐标缩短到原来的12倍(纵坐标不变),可得sin 26y x π⎛⎫=+ ⎪⎝⎭. 故选:D .7.B解析:B 【分析】利用诱导公式cos160cos 20=-,再利用两角和的正弦公式即可求解. 【详解】sin 20cos10cos160sin10-()sin 20cos10cos 18020sin10=-- sin 20cos10cos 20sin10=+()sin 2010=+sin30=12=故选:B8.A解析:A 【分析】 根据1sin 63πα⎛⎫-=⎪⎝⎭,利用诱导公式得到cos 3πα⎛⎫+ ⎪⎝⎭,再由2cos 2cos 233ππαα⎛⎫⎛⎫⎛⎫+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,利用二倍角公式求解. 【详解】 因为1sin sin 6233πππαα⎛⎫⎛⎫⎛⎫-=-+=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,所以1cos 33πα⎛⎫+=⎪⎝⎭, 所以227cos 2cos 22cos 13339πππααα⎛⎫⎛⎫⎛⎫⎛⎫+=+=+-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,故选:A9.A解析:A 【分析】先求出平移后的解析式为23sin 23y x π⎛⎫=+ ⎪⎝⎭,令()223x k k Z ππ+=∈解方程即可求解. 【详解】将函数3sin(2)3y x π=+的图象向左平移6π个单位长度得:23sin 23sin 2633y x x πππ⎡⎤⎛⎫⎛⎫=++=+⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, 令()223x k k Z ππ+=∈,解得:()32kx k Z ππ=-+∈, 当1k =时,326x πππ=-+=,所以平移后图象的一个对称中心为,06π⎛⎫⎪⎝⎭,故选:A10.B解析:B 【分析】根据cos89sin1︒=,将一个单位圆分成360个扇形,由这360个扇形的面积之和近似为单位圆的面积求解. 【详解】因为()cos89cos 901sin1︒=-=,所以将一个单位圆分成360个扇形,则每一个扇形的圆心角为1︒, 所以这360个扇形的面积之和近似为单位圆的面积,即2136011sin112π⨯⨯⨯⨯≈,所以 3.1416sin10.01745180180π≈≈≈, 故选:B11.B解析:B【分析】利用两角和与差的正弦公式、同角三角函数的基本关系式化简所求表达式,由此求得所求表达式的值. 【详解】sin sin sin cos cos sin sin cos cos sin 444444ππππππαααααα⎛⎫⎛⎫⎛⎫⎛⎫-+=-⋅+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭()22222211sin cos sin cos 22sin cos αααααα-=-=⨯+ 221tan 114132tan 124110αα--=⨯=⨯=++. 故选:B12.C解析:C 【分析】根据题中条件,由诱导公式,以及二倍角公式,即可求出结果. 【详解】 因为2cos 432θπ⎛⎫=⎪⎝⎭-, 所以241sin cos 2cos 12124299ππθθθ⎛⎫⎛⎫=-=--=⨯-=- ⎪ ⎪⎝⎭⎝⎭.故选:C二、填空题13.0【分析】由题设条件结合周期性及诱导公式运算即可得解【详解】由题意所以所以故答案为:0解析:0 【分析】由题设条件结合周期性及诱导公式运算即可得解. 【详解】由题意,()sin(2020)cos(2020)1sin cos()12020a b a b f παπβαβ++-++-=+=sin cos 12a b αβ=++=,所以sin cos 1αβ+=a b ,所以()sin(2021)cos(202)201211f a b παπβ++-+=sin()cos()1sin cos 1110a b a b παπβαβ==++-+-+=-+=-.故答案为:0.14.【分析】函数令求解【详解】已知函数令解得所以其图象的对称轴中距离轴最近的一条对称轴方程为故答案为:解析:4π-【分析】函数4y x π⎛⎫=- ⎪⎝⎭,令42x k πππ-=+求解.【详解】已知函数sin cos 4y x x x π⎛⎫=-=- ⎪⎝⎭,令,42x k k Z πππ-=+∈,解得 3,4x k k Z ππ=+∈, 所以其图象的对称轴中距离y 轴最近的一条对称轴方程为x =4π-. 故答案为:4π-15.【分析】利用余弦的两角和公式展开结合代入计算即可【详解】解得根据代入计算解得故答案为:【分析】利用余弦的两角和公式展开,结合22sin cos 1αα+=,代入计算即可. 【详解】1cos cos 2513πααα⎛⎫+=⋅= ⎪⎝⎭,解得2cos 5αα=+,根据22sin cos 1αα+=,代入计算,解得sin α=. 16.【分析】先由的最小正周期求出的值再由的最小正周期公式求的最小正周期【详解】的最小正周期为即则所以的最小正周期为故答案为:解析:8π 【分析】 先由()f x 的最小正周期,求出ω的值,再由()tan y x ωϕ=+的最小正周期公式求()g x的最小正周期. 【详解】()()2sin 03f x x πωω⎛⎫=+> ⎪⎝⎭的最小正周期为4π,即24ππω=,则8ω=所以()tan 86g x x π⎛⎫=+ ⎪⎝⎭的最小正周期为8T π=故答案为:8π 17.【分析】由已知条件求出再根据同角公式弦化切可解得结果【详解】故答案为:【点睛】关键点点睛:弦化切求解是解题关键 解析:516【分析】由已知条件求出1tan 3α=-,再根据同角公式弦化切可解得结果. 【详解】1tan()3πα+=-,1tan 3α∴=-,sin 2cos tan 25cos sin 5tan αααααα++∴=--123153-+=⎛⎫-- ⎪⎝⎭516=. 故答案为:516【点睛】关键点点睛:弦化切求解是解题关键.18.【分析】利用余弦的倍角公式和三角函数的基本关系式即可求解【详解】由又由故答案为: 解析:35【分析】利用余弦的倍角公式和三角函数的基本关系式,即可求解. 【详解】由tan 2α=,又由22222222cos sin cos 2cos sin cos sin 1tan 1431tan 145ααααααααα--===-++-=-==+. 故答案为:35. 19.【分析】本题首先可通过三角恒等变换将转化为然后代入即可得出结果【详解】因为所以故答案为:【点睛】关键点点睛:本题考查给值求值问题能否合理利用同角三角函数关系诱导公式二倍角公式是解决本题的关键考查计算解析:45【分析】本题首先可通过三角恒等变换将cos 22πα⎛⎫- ⎪⎝⎭转化为22tan tan 1αα+,然后代入tan 2α=即可得出结果. 【详解】 因为tan 2α=, 所以2222sin cos 2tan 4cos 2sin 22sin cos tan 15παααααααα⎛⎫-==== ⎪++⎝⎭, 故答案为:45. 【点睛】关键点点睛:本题考查给值求值问题,能否合理利用同角三角函数关系、诱导公式、二倍角公式是解决本题的关键,考查计算能力,是中档题.20.【分析】由结合诱导公式和二倍角公式得出答案【详解】故答案为:解析:19-【分析】 由sin 2sin 2632πππαα⎡⎤⎛⎫⎛⎫-=+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,结合诱导公式和二倍角公式得出答案. 【详解】2sin 63πα⎛⎫+= ⎪⎝⎭,21cos 212sin 369ππαα⎛⎫⎛⎫∴+=-+= ⎪ ⎪⎝⎭⎝⎭.22326πππαα⎛⎫+=+- ⎪⎝⎭, 1sin 2sin 2cos 263239ππππααα⎡⎤⎛⎫⎛⎫⎛⎫∴-=+-=-+=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦.故答案为:19-三、解答题21.(1)π;(2)最小值为1,最大值为4. 【分析】(1)由二倍角降幂,由两角差的正弦公式化函数为一个角的一个三角函数形式,然后结合正弦函数性质可求得最小正周期; (2)求出26x π-的范围,然后由正弦函数性质得最值.【详解】(1)因为2()2sin cos 1f x x x x =++1cos2cos 1x x x =-++2cos 22x x =-+2sin 226x π⎛⎫=-+ ⎪⎝⎭,所以()f x 的最小正周期22T ππ==. (2)因为02x π≤≤,所以52666x πππ-≤-≤. 所以1sin 2126x π⎛⎫-≤-≤ ⎪⎝⎭. 所以()2sin 22[1,4]6f x x π⎛⎫=-+∈ ⎪⎝⎭.即()f x 的最小值为1,最大值为4. 【点睛】方法点睛:本题考查两角差的正弦公式,二倍角公式,考查正弦函数的性质.此类问题的解题方法是:利用二倍角公式降幂,利用诱导公式、两角和与差的正弦(余弦)公式展开与合并,最终把函数化为()sin()f x A x m ωϕ=++形式,然后结合正弦函数性质求解. 22.(1)7cos 225α=-,()2tan 11βα-=;(2)a 的最大值为3. 【分析】(1)利用二倍角公式,求出cos2α,然后分别求出()cos αβ+,sin()αβ+,进而求出()tan αβ+,最后,利用()()tan tan 2βααβα-=+-求解即可(2)由()()[]3213cos212,4g x f x x =+=+∈-,得关于x 的不等式()()()2133g x a g x a ≥+++有解,化简得,即()()()213g x a g x ≥++⎡⎤⎣⎦有解,令()3t g x =+,然后,利用对勾函数的性质求解即可【详解】解:(1)∵4tan 3α=,∴222222cos sin cos 2cos sin cos sin ααααααα-=-=+2222411tan 73251tan 413αα⎛⎫- ⎪-⎝⎭===-+⎛⎫+ ⎪⎝⎭,∵α,β为锐角,即α,0,2πβ⎛⎫∈ ⎪⎝⎭, ∴()20,απ∈,()0,αβπ+∈.22422tan 243tan 21tan 7413ααα⨯===--⎛⎫- ⎪⎝⎭, ∵()cos f x x =,∴()()cos 5f αβαβ+=+=-, ∴()sin αβ+==,∴()()()sin tan 2cos αβαβαβ++==-+, ∴()()()()242tan tan 227tan tan 2241tan tan 211127αβαβααβααβα-++--=+-===+++⨯. 综上,7cos 225α=-,()2tan 11βα-=. (2)()()[]3213cos212,4g x f x x =+=+∈-, 关于x 的不等式()()()2133g x a g x a ≥+++有解,即()()()213gx a g x ≥++⎡⎤⎣⎦有解,令()3t g x =+,则[]1,7t ∈,()()231t a t -≥+有解,即916a t t+≤+-有解, max97a t t ⎛⎫+≤+ ⎪⎝⎭,设()9h t t t =+,则()h x 在[)1,3上单调递减,在(]3,7上单调递增,则()(){}max9max 1,710t h h t ⎛⎫+== ⎪⎝⎭, ∴3a ≤,故实数a 的最大值为3. 【点睛】关键点睛:(1)利用二倍角公式,以及正切函数的两角和差公式求解; (2)通过化简,把问题转化为()()()213gx a g x ≥++⎡⎤⎣⎦有解,令()3t g x =+,然后,利用对勾函数的性质求解;主要考查学生的转化化归思想以及运算能力,属于中档题 23.(1) 5.6 4.8cos h θ=-;(2)3.2m. 【分析】(1)建立平面直角坐标系,结合条件求出点B 的坐标后可得h 与θ间的函数关系式; (2)由60秒转动一圈,易得点A 在圆上转动的角速度是/30rad s π,再计算出经过10秒后转过的弧度数为3π,然后代入(1)中所求函数解析式计算即可得到答案. 【详解】(1)以圆心O 原点,建立如图所示的坐标系,如下图所示,则以Ox 为始边,OB 为终边的角为2πθ-,故点B 坐标为 4.8cos ,4.8sin 22ππθθ⎛⎫⎛⎫⎛⎫-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, ∴ 5.6 4.8sin 5.6 4.8cos 2h πθθ⎛⎫=+-=- ⎪⎝⎭; (2)点A 在圆O 上逆时针运动的角速度是/30rad s π,∴经过t 秒后转过的角度30t πθ=,则经过10秒后转过的角度为3πθ=,∴ 5.6 4.8cos 5.6 2.4 3.23h π=-=-=(m ).【点睛】关键点点睛:本题考查的知识点是在实际问题中建立三角函数模型,在建立函数模型的过程中,以圆心O 为原点,以水平方向为x 轴方向,以竖直方向为y 轴方向建立平面直角坐标系,是解决本题的关键. 24.(1)1;(2)()36k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦,.【分析】本题考查三角函数的图像和性质、三角恒等变换,根据三角恒等变换公式()f x 化简函数解析式,根据图像和性质求单调递增区间. 【详解】(1)5()23(cos cossin sin )(1cos 2)332f x wx wx wx wx ππ=--++23sin 23sin cos 222wx wx wx =--+1cos 2323cos 222wx wx wx -=-⨯-+12cos 22wx wx =+ sin(2)6wx π=+又因为()f x 图象上相邻的两个最低点间的距离为π,0w >, 所以22w,解得1w =.(2)据(1)求解知,()sin(2)6f x x π=+令222()262k x k k Z πππππ-+≤+≤+∈,所以()36k x k k Z ππππ-+≤≤+∈,所以所求的单调递增区间是()36k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦,.【点睛】思路点睛:三角恒等变换综合应用的解题思路:(1)利用降幂、升幂公式将()f x 化为sin cos a x b x 的形式;(2)构造())f x x x +;(3)和差公式逆用,得())f x x ϕ=+ (其中ϕ为辅助角,tan b aϕ=);(4)利用())f x x ϕ=+研究三角函数的性质; (5)反思回顾,查看关键点、易错点和答题规范.25.(1)1ω=;(2)最大值为1;最小值为. 【分析】(1)根据三角函数的倍角公式以及辅助角公式将函数进行化简即可. (2)求出角的取值范围,结合三角函数的最值性质进行判断求解即可. 【详解】解:(1)因为2π()sin(2)(2cos 1)6f x x x ωω=-+-ππ(sin 2cos cos 2sin )cos 266x x x ωωω=-+12cos22x x ωω=+ πsin(2)6x ω=+,所以()f x 的最小正周期2ππ2T ω==,0>ω, 解得1ω=.(2)由(1)得π()sin(2)6f x x =+. 因为7π12x ≤≤0,所以ππ4π2663x +≤≤. 所以,当ππ262x +=,即π6x =时,()f x 取得最大值为1; 当π4π263x +=,即7π12x =时,()f x取得最小值为. 26.an 2α=43,sin ()4πα-=. 【分析】 先由tan α=12可得tan 2α=43,再由sin cos αα=12,结合角的范围可得sin α和cos α的值,再由in ()4πα-的展开求解即可.【详解】∵tan α=12,∴tan 2α=22tan 1tan a a -=122114⨯-=43. 且sin cos αα=12,即cos α=2sin α. 又sin 2α+cos 2α=1,∴5sin 2α=1.而α∈(0,)2π,∴sin α,cos α. ∴sin ()4πα-=sin αcos4π-cos αsin 4π。
三角函数____第二单元_和差倍角公式测试题

和差倍角1.在△ABC 中,已知2sinAcosB =sinC ,则△ABC 一定是 ( ) A .直角三角形 B .等腰三角形 C .等腰直角三角形 D .正三角形2.2cos10°-sin20°sin70°的值是( ) A .12B .32C . 3D . 23.f(x)=sinx cosx1+sinx +cosx 的值域为( )A .(―3―1,―1) ∪(―1, 3―1)B .[-2-12,―1] ∪(―1, 2-12)C .(-3-12,3-12)D .[-2-12,2-12]4.已知x ∈(-π2,0),cosx =45,则tan2x 等于( ) A .724B .-724C .247D .-2475.已知sin(θ+π)<0,cos(θ-π)>0,则下列不等关系中必定成立的是( )A .tan θ2<cot θ2,B .tan θ2>cot θ2,C .sin θ2<cos θ2,D .sin θ2>cos θ2.6.已知0<α<π2,tan α2+cot α2=52,则sin(α-π3)的值为( )A .4+3310B .4-3310C .33-410D .-4+33107.等式sin α+3cos α=4m -64-m 有意义,则m 的取值范围是( )A .(-1,73)B .[-1,73]C .[-1,73]D .[―73,―1]8.在△ABC 中,tanA tanB >1是△ABC 为锐角三角形的 ( ) A .充要条件B .仅充分条件 C .仅必要条件D .非充分非必要条件 9.已知α.β是锐角,sin α=x ,cos β=y ,cos(α+β)=-35,则y 与x 的函数关系式为( )A .y =―351―x 2+45x (35<x <1) B .y =―351―x 2+45x (0<x <1) C .y =―351―x 2―45x (0<x <35= D .y =―351―x 2―45x (0<x <1=10.已知α∈(0,π),且sin α+cos α=15,则tan α的值为( )A .-43B .-43 或-34C .-34D .43 或-3411.在△ABC 中,已知tan A +B2=sinC ,则以下四个命题中正确的是( )(1)tanA ·cotB =1.(2)1<sinA +sinB ≤2.(3)sin 2A +cos 2B =1.(4)cos 2A +cos 2B =sin 2C . A .①③ B .②④ C .①④ D .②③二、填空题:13.若x =π3是方程2cos(x +α)=1的解,α∈(0,2π),则α=___________14.已知cos θ+cos 2θ=1,则sin 2θ+sin 6θ+sin 8θ=___________ 15.函数y =5sin(x +20°)-5sin(x +80°)的最大值是___________16.若圆内接四边形的四个顶点A 、B 、C 、D 把圆周分成AB ︵∶BC ︵∶CD ︵∶DA ︵=4∶3∶8∶5,则四边形四个内角A 、B 、C 、D 的弧度数为___________三、解答题17.设cos(α-β2)=-19,sin(α2-β)=23,且π2<α<π,0<β<π2,求cos (α+β).18.已知f(x)=2asin 2x -22asinx +a +b 的定义域是[0, π2],值域是[-5,1],求a 、b 的值.19.已知6sin 2α+sin αcos α-2cos 2α=0,α∈[π2,π],求sin(2α+π3)的值.20.在△ABC 中,sinA +cosA =22,AC =2,AB =3,求tanA 的值和△ABC 的面积.21.在矩形ABCD 中,AB =a ,BC =2a ,在BC 上取一点P ,使得AB +BP =PD ,求tan ∠APD 的值.22.是否存在锐角α和β,使α+2β=2π3①,且tan α2tan β=2-3②,同时成立?若存在,求出α和β的值;若不存在,请说明理由.参考答案:1.B 由2sinAcosB =sin(A +B)⇒sin(B -A)=0⇒B =A .2.C 原式=2cos(30°―20°)―sin20°cos20°=3cos20°cos20°=3.3.B 令t =sin x +cos x =2sin(x +π4)∈[―2,―1]∪(―1, 2).则f(x)=t 2-121+t=t -12∈[-2-12,―1]∪(―1, 2-12).4.D .5.B ∵sin θ>0,cos θ<0,tan θ2-cot θ2=sinθ2cos θ2-cos θ2sinθ2=-2cos θsin θ>0.∴tanθ2>cot θ2.6.B tanα2+cot α2=2sin α=52.∴sin α=45.cos α=35. sin(α-π3)=12sin α-32cos α=4-3310. 7.C 8.A9.A y =cos β=cos[(α+β)-α]=cos(α+β)cos α+sin(α+β)sin α =―351―x 2+45x >0⇒4x >31―x 2⇒35<x <1.10.A 解:当α∈(0,π2)时,sin α+cos α=2sin(α+π4)>1.故α∈(π2,π). ∴sin α>0,cos α<0.且|sin α|>|cos α|∴|tan α|>1. 由(sin α+cos α)2=125⇒sin2α=-2425⇒2tan α1+tan 2α=-2425⇒tan α=-43或tan α=-34(舍). 11.B 解:由tan A +B 2=1-cos(A +B)sin(A +B)=1+cosC sinC =sinC 。
完整版)高中三角函数测试题及答案

完整版)高中三角函数测试题及答案高一数学必修4第一章三角函数单元测试班级:__________ 姓名:__________ 座号:__________评分:__________一、选择题:共12小题,在每小题给出的四个选项中,只有一项是符合题目要求的。
(48分)1、已知$A=\{\text{第一象限角}\}$,$B=\{\text{锐角}\}$,$C=\{\text{小于90°的角}\}$,那么$A$、$B$、$C$ 关系是()A.$B=A\cap C$B.$B\cup C=C$C.$A\cap D$D.$A=B=C$2、将分针拨慢5分钟,则分钟转过的弧度数是A。
$\frac{\pi}{3}\sin\alpha-\frac{2}{3}\cos\alpha$ B。
$-\frac{\pi}{3}$C。
$\frac{\pi}{6}$D。
$-\frac{\pi}{6}$3、已知 $\tan\alpha=-5$,那么 $\tan\alpha$ 的值为A。
2B。
$\frac{1}{6164}$C。
$-\frac{1}{6164}$D。
$-\frac{2}{3}$4、已知角 $\alpha$ 的余弦线是单位长度的有向线段,那么角 $\alpha$ 的终边()A。
在 $x$ 轴上B。
在直线 $y=x$ 上C。
在 $y$ 轴上D。
在直线 $y=x$ 或 $y=-x$ 上5、若 $f(\cos x)=\cos 2x$,则 $f(\sin 15^\circ)$ 等于()A。
$-\frac{2}{3}$B。
$\frac{3}{2}$C。
$\frac{1}{2}$D。
$-\frac{1}{2}$6、要得到 $y=3\sin(2x+\frac{\pi}{4})$ 的图象只需将$y=3\sin 2x$ 的图象A。
向左平移 $\frac{\pi}{4}$ 个单位B。
向右平移 $\frac{\pi}{4}$ 个单位C。
高一数学必修第一二章测试题及答案

高一数学必修第一二章测试题及答案The Standardization Office was revised on the afternoon of December 13, 2020第一.二章《三角函数》单元检测试卷一、选择题:(本答题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.在平行四边形ABCD 中,BD CD AB +-等于()A .B .C .D .2.若|a |=2,|b |=5,|a +b |=4,则|a -b |的值()A .13B .3C .42D .73.函数sin(2)3y x π=+图像的对称轴方程可能是()A .6x π=-B .12x π=-C .6x π=D .12x π=5.点A(x,y)是300°角终边上异于原点的一点,则xy值为() 333333函数)32sin(π-=x y 的单调递增区间是()A .⎥⎦⎤⎢⎣⎡+-125,12ππππk k Z k ∈ B .⎥⎦⎤⎢⎣⎡+-1252,122ππππk k Z k ∈C .⎥⎦⎤⎢⎣⎡+-65,6ππππk k Z k ∈ D .⎥⎦⎤⎢⎣⎡+-652,62ππππk k Z k ∈ 7.sin(-310π)的值等于() A .21B .-21C .23D .-238.在△ABC 中,若)sin()sin(C B A C B A +-=-+,则△ABC 必是() A .等腰三角形B .直角三角形C .等腰或直角三角形D .等腰直角三角9.函数x x y sin sin -=的值域是()A .0B .[]1,1-C .[]1,0D .[]0,2-10.函数x x y sin sin -=的值域是()A .[]1,1-B .[]2,0C .[]2,2-D .[]0,2-11.函数x x y tan sin +=的奇偶性是()A .奇函数B .偶函数C .既奇又偶函数D .非奇非偶函数 12.比较大小,正确的是() A .5sin 3sin )5sin(<<- B .5sin 3sin )5sin(>>-C .5sin )5sin(3sin <-<D .5sin )5sin(3sin >->二、填空题(每小题5分,共20分)13.终边在坐标轴上的角的集合为_________.14.已知扇形的周长等于它所在圆的周长的一半,则这个扇形的圆心角是________________. 15.已知角α的终边经过点P(-5,12),则sin α+2cos α的值为______.16.一个扇形的周长是6厘米,该扇形的中心角是1弧度,该扇形的面积是________________. 三、解答题:(本大题共6小题,共70分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
oy1 1211π x《三角函数》单元测试班级 姓名 学号一、选择题(共大题共12小题,每小题5分,共60分) 1、函数x y 2sin 3=的图象可以看成是将函数)3x 2sin(3y π-=的图象-------------( ) (A )向左平移个6π单位 (B )向右平移个6π单位 (C )向左平移个3π单位 (D )向右平移个3π单位2、已知542cos ,532sin -=θ=θ,则角θ终边所在象限是--------------------------------( )(A ) 第三象限 (B )第四象限 (C )第三或第四象限 (D )以上都不对3、已知α是锐角,则下列各式成立的是------------------------------------------------------( ) (A )21cos sin =α+α(B )1cos sin =α+α(C )34cos sin =α+α(D )35cos sin =α+α 4、函数)2x lg(xcos lg x sin y 2++=的定义域为----------------------------------------------------( ) (A )2k 2x k 2π+π<≤π )z k (∈ (B ) 2k 2x k 2π+π<<π )z k (∈ (C ) π+<<π)1k 2(x k 2 )z k (∈ (D ) 2k 2x 2k 2π+π<<π-π )z k (∈5、右图是函数)2|)(|x sin(2y π<φφ+ω=的图象,那么--------------------------------- ( )(A )6,1110π=φ=ω (B )6,1110π-=φ=ω (C )6,2π=φ=ω (D )6,2π-=φ=ω 6、已知)(x f 是奇函数,且0<x 时,x x x f 2sin co s )(+=,则当0>x 时,)(x f 的表达式是------------------------------------------------------------------------------------------------------( )(A )x 2sin x cos +(B )x 2sin x cos +-(C )x 2sin x cos -(D )x 2sin x cos --7、若43π=β+α,则)tan 1)(tan 1(β-α-的值是------------------------------------------( ) (A ) 21 (B ) 1 (C ) 23(D ) 28、函数x x y 66cos sin +=的最小正周期为--------------------------------------------------( ) (A ) π2 (B ) π (C )2π(D ) π+πk 2 )Z k (∈9、ABC ∆中,若C B A sin cos cos =+,则ABC ∆的形状是-----------------------------( )(A )等腰三角形 (B )等边三角形 (C )等腰直角三角形 (D )直角三角形10、已知锐角θ满足a 2sin =θ,则θ+θcos sin 的值是---------------------------------( ) (A )a a a -++21 (B )1+a (C )1+±a (D )a a a --+21 11、已知x 2sin )x (tan f =,则)1(-f 的值是-----------------------------------------------( ) (A ) 1 (B ) 1- (C )21(D ) 0 12、已知2a x cos x sin b x cos a )x (f 2--=的最大值是21,且43)3(f =π,则=π-)3(f -------------------------------------------------------------------------------------- ( )(A )21 (B ) 43- (C ) 4321或- (D ) 430-或 一、填空题(每小题4分,共16分)13、函数xcos x sin 1xcos x sin y -+=的最大值为_______________.14、函数)4x 3sin(y π+=的图象沿向量a =_______________平移得到)4x 3cos(y π+=.15、函数)x 3cos(y ϕ+=关于原点对称的充要条件是_________________________. 16、关于x 的函数)x sin()x (f ϕ+=有以下命题: (1) 对任意的ϕ,)(x f 都是非奇非偶函数. (2) 不存在ϕ,使)(x f 既是奇函数,又是偶函数. (3) 存在ϕ,使)(x f 是奇函数. (4) 对任意的ϕ,)(x f 都不是偶函数.其中一个假命题的序号是_________________.因为当=ϕ_______________时,该命题的结论不成立.三、解答题(本大题共6小题,共74分)17.(12分)在△ABC 中,,,a b c 分别是,,A B C 的对边,且cos ,cos 2B bC a c=-+(1)求角B 的大小;(2)若13,4b a c =+=,求a 的值;18.(12分)已知△ABC 的面积22()S a b c =--且8,b c +=求△ABC 面积的最大值.19.(12分)已知090,αβ<<<且sin ,sin αβ是方程221(2cos40)cos 4002x x -+-=的两个根,求cos(2)αβ-的值.20.(13分)是否存在实数a ,使得函数23a 85x cos a x sin y 2-++=在闭区间]2,0[π上的最大值是1?若存在,求对应的a 值?若不存在,试说明理由.21.(12分)已知函数)2||,0,0A )(x sin(A )x (f π<φ>ω>φ+ω=的图象在y 轴上的截距为1,它在y 轴右侧的第一个最大值点和最小值点分别为)2,(0x 和)2,3(0-+πx . (1)试求)x (f 的解析式;(2)将)x (f y =图象上所有点的横坐标缩短到原来的31(纵坐标不变),然后再将新的图象向x 轴正方向平移3π个单位,得到函数)x (g y =的图象.写出函数)x (g y =的解析式并用列表作图的方法画出)x (g y =在长度为一个周期的闭区间上的图象.22.(13分)某港口水的深度y (米)是时间t (240≤≤t ,单位:时)的函数,记作y=f(t), 下面是某日水深的数据:t/h 0 3 6 9 12 15 18 21 24 y/m10.013.09.97.010.013.010.17.010.0经常期观察,y=f(t)的曲线可以近似得看成函数b t A y +=ωsin 的图象,(1)试根据以上的数据,求出函数y=f(t)的近似表达式;(2)一般情况下,船舶航行时,船底离海底的距离为5m 或5m 以上时认为是安全的,某船吃水深度(船底离水面的距离)为6.5m ,试求一天内船舶安全进出港的时间.参考答案一、选择题 1. A 2. B 3. C 4. A 5. C 6. B 7. D 8. C 9. C 10. B. 11. B 12. D 二、填空题 13.212+ 14. )(0,63k 2π-π, Z k ∈ 15. 2k π+π=ϕ ,Z k ∈ 16.(1),0=ϕ;(或 (4),2π=ϕ)三、解答题 17. 解:(1)由cos ,cos 2B b C a c =-+得cos sin ,cos 2sin sin B BC A C=-+ 即:2sin cos sin cos cos sin 0,A B C B C B ++=∴2sin cos sin()0,A B B C ++= 而sin()sin ,2sin cos sin 0,B C A A B A +=∴+=又1sin 0,cos ,2A B ≠∴=- 而20,.3B B ππ<<∴=(2)利用余弦定理可解得:1a =或 3.a =18、解:.22222()(2cos )()2(1cos )s a b c b c bc A b c bc A =--=+---=-,又11sin ,2(1cos )sin ,22s bc A bc A bc A =∴-=1cos 1sin ,4A A ∴=- 代入22cos sin 1A A +=,解得8sin .17A = ∵8,b c +=2144640,0,sin ().21717217b c b c s bc A bc +>>∴==≤= 当4b c ==时,△ABC 的面积取得最大值6417.19、解:由已知得,sin sin ,αβ<22212cos 404(cos 40)2sin 40,2∆=--=由求根公式得,2sin (cos40sin40)sin52α=-=, 2sin (cos40sin40)sin852β=+=,又∵090,αβ<<< ∴5,85,αβ==62cos(2)cos(75)4αβ-∴-=-= 20. 解:原函数整理为 2185c o s c o s 2-++-=a x a x y , 令t=cosx , 则 21854)2(2185)(222-++--=-++-=a a a t a at t t f ]1,0[∈t (1)时当02<a , 12185)0()(max =-==a f t f , 512=∴a (舍);(2)时当120≤≤a , 121854)2()(2max =-+==a a a f t f ,4-=∴a 或 23=a ,23=∴a ; (3)时当12>a , 123813)1()(max =-==a f t f , 1320=a (舍),综上所述可得 23=a .21.解:(1)由题意可得: π6=T , 2=A , )31s i n (2)(ϕ+=∴x x f ,函数图像过(0,1), 21sin =∴ϕ, 2πϕ< ,6πϕ=∴ , )63sin(2)(π+=∴x x f ;(2))6sin(2)(π-=x x g ;图象略:略.22. 解:(1) 106sin3+=t y π.; (2) 1时至5时,13时至17时.。
