习题课1
07 11.2 习题课(1)

边为角的邻边 找夹边的另一角(ASA)
找任一角 (AAS)
找夹边
已知两角
(ASA)
找任一边(AAS)
全等三角形,是证明两条线段或两个角 相等的重要方法之一,证明时应注意:
①要观察待证的线段或角,在哪两个可能全等的三 角形中; ②分析要证两个三角形全等,已有什么条件,还缺 什么条件; ③有公共边的,公共边一定是对应边;有公共角的, 公共角一定是对应角;有对顶角,对顶角也是对 应角。
已知一边一角
。
找任一角(AAS)
找夹角的另一边(SAS)
边为角的邻边 找夹边的另一角(ASA)
找任一角 (AAS)
B
E
A
C
5、(2007年山西模拟)下列各组条件,能
D
F
判定△ABC≌△DEF的是(
A、AB=DE,BC=EF,∠A=∠D
)
B、∠A=∠D,∠C=∠F,AC=EF
C、AB=DE,BC=EF,△ABC的周长=△DEF的周长 D、∠A=∠D,∠B=∠E,∠C=∠F
C
看谁方法多?
如图,已知AB= A′B′, 要说明
△ABC≌△A′B′C′,还需增加两个什么 条件?
A A′
B
C B′
C′
巩固练习
1、(2007年河北模拟)下列说法中:
①如果两个三角形可以依据“AAS”来判定全等,那么
一定也可以依据“ASA”来判定它们全等;
②如果两个三角形都和第三个三角形不全等,那么这
找夹边
已知两角
(ASA)
找任一边(AAS)
3、(2007沈阳)如图,AC、BD相交于点O,
∠A=∠D,请你再补充一个条件,使得
△AOB≌△DOC,你补充的条件是 。 D O
第5章 习题课 (1)

3、按酸碱质子理论,Na2HPO4 是 (D)
A. 中性物质
B. 酸性物质
C. 碱性物质
D. 两性物质
20
4、共轭酸碱对的Ka和Kb的关系是 (C)
A. Ka=Kb
B. Ka·Kb =1
C. Ka·Kb= KW D. Kb/Ka = KW
5、H2PO4-的共轭碱是 (B)
A. H3PO4
B. HPO42-
18
质子理论
19
1、提出酸碱质子理论的科学家是 (A)
A. Bronsted-Lowry
B. Arrhennius
C. Debye Huckel
D. Lewis
2、按酸碱质子理论,下面哪个物质是酸?(A)
A. Fe(H2O)63+ C. NaAc
B. (CH2)6N4 D. H2NCH2COO-
H2SO4的两个H+全部被滴定,H3PO4被滴定3/2个H+
pH=9.78,H3PO4被滴定2个H+
cH3PO4 50.00 (30.00 26.00) 1.000 2
2cH
2
SO4
3 2 cH 3PO4
50.00
26.00 1.000
cH3PO4 0.16mol L1 cH2SO4 0.14mol L1
C. PO43-
D. OH-
6、已知H3PO4的pKa1 - pKa3分别 为2.12、
7.20、12.36,则PO43-的pKb1为 (C)
A. 11.88
B. 6.80
C. 1.64
D. 2.12
21
7、下列阴离子的水溶液,若浓度相同, 则何者碱度最强?(B)
高二物理习题课一 电场的力的性质

答案:(3)2
gL
高中·物理
达标测评
随堂演练·检测效果
1.(2017·青岛质检)一个带正电的粒子,在xOy平面内以速度v0从O点进 入一个匀强电场,重力不计.粒子只在静电力作用下继续在xOy平面内沿 图中的虚线轨迹运动到A点,且在A点时的速度方向与y轴平行,则电场强 度的方向可能是( A.沿x轴正方向 B )
mg q sin
,
故选项A正确,B错误.在B处剪断细线,小球受重力和静电力两个力,两
个力的合力与绳子的拉力方向相反,大小恒定,则小球沿水平方向做
初速度为零的匀加速直线运动,静电力做正功,选项C,D错误.
高中·物理
方法总结 解决带电体在电场中受力问题的基本思路 对处于平衡状态的带电体先进行受力分析,画出受力图,然后用力的合成或
C.带电粒子所受静电力的方向向左
D.带电粒子做匀变速运动 解析:由运动轨迹的弯曲特点可知,带电粒子受水平向左的静电力作用,
故粒子带负电;由于粒子在匀强电场中运动,则粒子受静电力保持恒定,
可知粒子运动的加速度不变而做匀变速ቤተ መጻሕፍቲ ባይዱ动,选项A,C,D正确.
高中·物理
3.(2016·合肥一中检测)如图所示,上端固定在天花板上的绝缘轻绳连接带
应水平向左,则静电力、重力的合力方向与速度相反,如图所示,
故微粒做加速度大小为 20 m/s 的匀减速直线运动;
2
答案:(1)见解析
高中·物理
(2)电场强度的大小和方向; (3)要使微粒从A点沿直线运动到B点,微粒射入电场时的最小速度vA是 多大?
解析:(2)由 qE=
mg E= = q tan 30
1 m v12 2
8-习题课-1

五、设 z f ( x 2 y 2 , e xy ), (其中f具 有一阶连续偏数),求 z z , x y
x 六、设 z f ( x , ) ,(其中f具 有二阶连续偏导数),求 y 2z 2z 2z , , 2. 2 x xy y
七、填空题 y dy y 2 arctan ,则 ______. 1、设 ln x x dx z z x z _______. 2、设 z y ,则 _______, x y
x
二、求下列各极限: 1、 lim 2 xy 4 ; x 0 xy y0 1 cos( x 2 y 2 ) 3、 lim 2 x 0 ( x y 2 ) x 2 y 2 y0 2、 lim sin xy ; x 0 x y0
. 11 xy 三、 证明极限 lim 不存在 . x 0 y x y 0
习题课--1
第八章
多元函数微分法
一、 基本概念 二、多元函数微分法 三、多元函数微分法的应用
练Hale Waihona Puke 题一、 填空题:1、函数 z
y 的定义域是______________. y 2、函数 z arcsin 的定义域是_______________. x y2 2x 3、函数 z 2 的间断点是________________. y 2x
2
八、设2 sin( x 2 y 3 z ) x 2 y 3 z , z z 1. 证明: x y
2z . 九、设 z 3 xyz a , 求 xy
3 3
十、求由下列方程组所确定的函数的导数或偏导数: z x 2 y 2 dy dz 1、设 2 ,求 , . dx dx x 2 y 2 3 z 2 20
热力学第一定律习题课 (1)全

= 1.3%
(5)
P
qm ws
220 t/h103 kg/t 3600 s/h
1.1361 03
kJ/kg
=
6.94 104
kW
讨论
(1)本题的数据有实际意义,从计算中可以看到,忽略进出 口的动、位能差,对输轴功影响很小,均不超过3%,因此在实 际计算中可以忽略。 (2)蒸汽轮机散热损失相对于其他项很小,因此可以认为一 般叶轮机械是绝热系统。
m2u2 m1u1 m2 m1 h 0
u2
m2
m1 h
m2
m1u1
方法三 取充入气罐的m2-m1空气为闭口系
Q U W
Q 0 ? W ? U ?
U m2 m1 u2 u
W W1 W2 m2 m1 pv W2
2
则 Q23 U23 W23 U3 U2 87.5 kJ175 kJ 87.5 kJ
U1 U3 U123 87.5 kJ (77.5 kJ) 165 kJ
讨论
热力学能是状态参数,其变化只决定于初 终状态,于变化所经历的途径无关。
而热与功则不同,它们都是过程量,其变 化不仅与初终态有关,而且还决定于变化所 经历的途径。
1 2
(cf23
c22 )
ws
因为w3 0,所以
燃烧室 压 气 机
cf 3' 2 q (h3' h2 ) cf22
2 670103 J/kg- (800 - 580) 103 J/kg + (20 m/s)2 = 949 m/s
( 4 ) 燃气轮机的效率
取燃气轮机作为热力系,因为燃气在
( 5 ) 燃气轮机装置的总功率 装置的总功率=燃气轮机产生的功率-压气机消耗的功率
有机化学习题课(1-3章)

➢若环上连有支链时,支链作为取代基,其所在位次即 是环上碳原子的位次号,最后将取代基的位次和名称放 在“螺”之前。
16
桥环烷烃的命名:
和螺环烷烃的相似。
不同之处:
✓环上的编号是从一个桥头碳原子开始,沿最 长的桥到另一个桥头碳原子,再沿次长的桥编 回到开始的桥头碳原子,最短桥上的碳原子最 后编号。 ✓各桥的碳原子数由大到小分别用数字表示。
其中,CH3OCH3的C-O-C键角不是180°。
5
九、化合物按碳架和官能团分类(P23)
(1)脂肪族 卤代烷 (2)脂肪族 羧酸
(3)杂环族,四氢吡咯 (4)脂环族,酮
(5)芳香族,醚
(6)芳香族,醛
(7)脂肪族,胺
(8)脂肪族,炔
(9)脂环族,醇
例如: 呋喃
呋喃甲醛 (糠醛)
吡啶
(参见第十七章)
24
1、烯炔的命名——特别注意两点
① 所有烯炔的名称中主链的碳数必须放在烯前。 ② 若双键和三键处于相同的位次供选择时,优先给 双键最低编号。 例如:
1-戊烯-4-炔
25
习题 3.1 命名下列化合物(P73)
(1)
(2)
2,5-二甲基-3-己烯
2,6-二甲基-4-辛烯
(3)
3-己炔 (二乙基乙炔)
(1)E>A>B>C>D
(2)F>G>E>H>D>C>B>A
(3)D>B>C>A 14
第二章 脂环烃
命名规则不清
15
螺环烷烃命名:
➢两个碳环共有的碳原子称为螺原子,以螺作为词头, 按成环的碳原子总数称为“某烷”。
物理第7章习题课 (1)

I
20 I (B) 2R
( D) 0
a
[ D ]
o
I b
3.有一边长为 l 电阻均匀分布的正三角形导线框 abc,与电源相连的长直导线1和2彼此平行并分 别与导线框在 a 点和 b 点相接,如图所示。导线 1 和 2 的电流为 I,令长直导线 1、2 和导线框 b 2 在线框中心点 o 产生的磁感应 I 强度分别为 B1、B2 和 B3,则点 o o的磁感应强度大小: 1 I a c
BNM 0 R t NM
B 0R t
4.图示一通以电流 I1 的无限长直导线 一侧放置一通 有电流 I2 的等腰直角 三角 形线圈,且与直导线共面,已 知一直角边与导线平行,相距为b, 直角边长为a,求线圈中各导线受力
I1
A
I2
B I 2dx
o
b
x
C
x
dF a
AC导线处于不均匀磁场中
(C) B沿闭合回路L的线积分改变, L上各点的B不变.
(D) B沿闭合回路L的线积分不变 , L上各点的B改变.
[ D ]
6.一半径为a的无限长直载流导线,沿轴向均匀 地流有电流 I,若作一个半径为R=5a、高为l 的 圆柱曲面,已知此柱面的轴与载流直导线的轴平 行相距3a(如图)则B在圆柱侧面S 的积分为: 3a (A) s B dS >0 2a (B) s B dS <0 5a (C) s B dS =0 l (D) B dS 无法确定。 s
L1
L2
B dl
2 0 I
L3
B dl B dl
2 I
0
L3
高中数学《求数列的通项习题课一》专题突破含解析

习题课一 求数列的通项题型一 利用累加、累乘法求数列的通项公式【例1】 (1)数列{a n }满足a 1=1,对任意的n ∈N *都有a n +1=a 1+a n +n ,求数列{a n }的通项公式;(2)已知数列{a n }满足a 1=23,a n +1=nn +1a n ,求a n .解 (1)∵a n +1=a n +n +1,∴a n +1-a n =n +1,即a 2-a 1=2,a 3-a 2=3,…,a n -a n -1=n (n ≥2).等式两边同时相加得a n -a 1=2+3+4+…+n (n ≥2),即a n =a 1+2+3+4+…+n =1+2+3+4+…+n =n (n +1)2,n ≥2.又a 1=1也适合上式,∴a n =n (n +1)2,n ∈N *.(2)由条件知a n +1a n =nn +1,分别令n =1,2,3,…,n -1,代入上式得(n -1)个等式,累乘,即a 2a 1·a 3a 2·a 4a 3·…·a n a n -1=12×23×34×…·n -1n (n ≥2).∴a na 1=1n ,又∵a 1=23,∴a n =23n ,n ≥2.又a 1=23也适合上式,∴a n =23n ,n ∈N *.规律方法 (1)求形如a n +1=a n +f (n )的通项公式.将原来的递推公式转化为a n +1-a n =f (n ),再用累加法(逐差相加法)求解,即a n =a 1+(a 2-a 1)+(a 3-a 2)+…+(a n -a n -1)=a 1+f (1)+f (2)+f (3)+…+f (n -1).(2)求形如a n +1=f (n )a n 的通项公式.将原递推公式转化为a n +1a n=f (n ),再利用累乘法(逐商相乘法)求解,即由a 2a 1=f (1),a 3a2=f (2),…,a na n -1=f (n -1),累乘可得a na1=f (1)f (2)…f (n -1).【训练1】 数列{a n }中,a 1=2,a n +1-a n =2n ,求{a n }的通项公式.解 因为a 1=2,a n +1-a n =2n ,所以a 2-a 1=2,a 3-a 2=22,a 4-a 3=23,…,a n -a n -1=2n -1,n ≥2,以上各式累加得,a n -a 1=2+22+23+…+2n -1,故a n=2(1-2n-1)1-2+2=2n,当n=1时,a1也符合上式,所以a n=2n.题型二 构造等差(比)数列求通项公式【例2】 (1)在数列{a n}中,a1=13,6a n a n-1+a n-a n-1=0(n≥2,n∈N*).①证明:数列{1a n}是等差数列;②求数列{a n}的通项公式.(2)已知数列{a n}中,a1=2,a n+1=2a n-3,求a n.(1)①证明 由6a n a n-1+a n-a n+1=0,整理得1a n-1a n-1=6(n≥2),故数列{1a n}是以3为首项,6为公差的等差数列.②解 由①可得1a n=3+(n-1)×6=6n-3,所以a n=16n-3,n∈N*.(2)解 由a n+1=2a n-3得a n+1-3=2(a n-3),所以数列{a n-3}是首项为a1-3=-1,公比为2的等比数列,则a n-3=(-1)·2n-1,即a n=-2n-1+3.规律方法 (1)课程标准对递推公式要求不高,故对递推公式的考查也比较简单,一般先构造好等差(比)数列让学生证明,再在此基础上求出通项公式,故同学们不必在此处挖掘过深. (2)形如a n+1=pa n+q(其中p,q为常数,且pq(p-1)≠0)可用待定系数法求得通项公式,步骤如下:第一步 假设递推公式可改写为a n+1+t=p(a n+t);第二步 由待定系数法,解得t=qp-1;第三步 写出数列{a n+q p-1}的通项公式;第四步 写出数列{a n}的通项公式.【训练2】 已知各项均为正数的数列{b n}的首项为1,且前n项和S n满足S n-S n-1=S n+S n-1(n≥2).试求数列{b n}的通项公式.解 ∵S n-S n-1=S n+S n-1(n≥2),∴(S n+S n-1)(S n-S n-1)=S n+S n-1(n≥2).又S n >0,∴S n -S n -1=1.又S 1=1,∴数列{S n }是首项为1,公差为1 的等差数列,∴S n =1+(n -1)×1=n ,故S n =n 2.当n ≥2时,b n =S n -S n -1=n 2-(n -1)2=2n -1.当n =1时,b 1=1符合上式.∴b n =2n -1.题型三 利用前n 项和S n 与a n 的关系求通项公式【例3】 (1)已知数列{a n }的前n 项和为S n ,若S n =2a n -4,n ∈N *,则a n 等于( )A.2n +1 B.2n C.2n -1D.2n -2(2)已知数列{a n }中,前n 项和为S n ,且S n =n +23·a n ,则a n a n -1的最大值为( )A.-3B.-1C.3D.1解析 (1)因为S n =2a n -4,所以n ≥2时,S n -1=2a n -1-4,两式相减可得S n -S n -1=2a n -2a n -1,即a n =2a n -2a n -1,整理得a n =2a n -1,所以a n a n -1=2.因为S 1=a 1=2a 1-4,即a 1=4,所以数列{a n }是首项为4,公比为2的等比数列,则a n =4×2n -1=2n +1,故选A.(2)由S n =n +23a n 得,当n ≥2时,S n -1=n +13a n -1,两式作差可得:a n =S n -S n -1=n +23a n -n +13a n -1,整理得a n a n -1=n +1n -1=1+2n -1,由此可得,当n =2时,a n a n -1取得最大值,其最大值为3.答案 (1)A (2)C规律方法 已知S n =f (a n )或S n =f (n )的解题步骤:第一步 利用S n 满足条件p ,写出当n ≥2时,S n -1的表达式;第二步 利用a n =S n -S n -1(n ≥2),求出a n 或者转化为a n 的递推公式的形式;第三步 若求出n ≥2时的{a n }的通项公式,则根据a 1=S 1求出a 1,并代入n ≥2时的{a n }的通项公式进行验证,若成立,则合并;若不成立,则写出分段形式.如果求出的是{a n }的递推公式,则问题化归为例2形式的问题.【训练3】 在数列{a n }中,a 1=1,a 1+2a 2+3a 3+…+na n =n +12a n +1(n ∈N *),求数列{a n }的通项公式a n .解 由a 1+2a 2+3a 3+…+na n =n +12a n +1,得当n ≥2时,a 1+2a 2+3a 3+…+(n -1)a n -1=n2a n ,两式作差得na n =n +12a n +1-n 2a n ,得(n +1)a n +1=3na n (n ≥2),即数列{na n }从第二项起是公比为3的等比数列,且a 1=1,a 2=1,于是2a 2=2,故当n ≥2时,na n =2×3n -2.于是a n ={1,n =1,2×3n -2n,n ≥2,n ∈N *.一、素养落地1.通过学习数列通项公式的求法,提升数学运算与逻辑推理素养.2.求数列通项的方法有:(1)公式法,(2)累加、累乘法,(3)构造法等,但总的思想是转化为特殊的数列(一般是等差或等比数列)求解.二、素养训练1.数列1,3,6,10,15,…的递推公式可能是( )A.a n ={1(n =1)a n +1+n -1(n ∈N *,n ≥2)B.a n={1(n =1)a n -1+n (n ∈N *,n ≥2)C.a n={1(n =1)a n -1+n -1(n ∈N *,n ≥2)D.a n={1(n =1)a n -1+n +1(n ∈N *,n ≥2)解析 由题意可得,a 1=1,a 2-a 1=2,a 3-a 2=3,a 4-a 3=4,a 5-a 4=5,……∴a n -a n -1=n (n ≥2),故数列的递推公式为a n ={1(n =1)a n -1+n (n ∈N *,n ≥2)故选B.答案 B2.数列{a n }中,a 1=1,且a n +1=a n +2n ,则a 9=( )A.1 024B.1 023C.510D.511解析 由题意可得a n +1-a n =2n ,则a 9=a 1+(a 2-a 1)+(a 3-a 2)+…+(a 9-a 8)=1+21+22+…+28=29-1=511.故选D.答案 D3.已知数列{a n }的各项均为正数,且a 2n -a n -n 2-n =0,则a n=________.解析 由a 2n -a n -n (n +1)=0,得[a n -(n +1)](a n +n )=0.又a n >0,所以a n=n +1.答案 n +14.已知数列{a n }中,a 1=1,对于任意的n ≥2,n ∈N *,都有a 1a 2a 3…a n =n 2,则a 10=________.解析 由a 1a 2a 3…a n =n 2,得a 1a 2a 3…a n -1=(n -1)2(n ≥2),所以a n =n 2(n -1)2(n ≥2),所以a 10=10081.答案 100815.已知数列{a n }满足a 1=1,a n +1=a n a n +2(n ∈N *),求数列{a n }的通项公式.解 由a n +1=a n a n +2,得1a n +1=2an +1,所以1an +1+1=2(1a n+1).又a 1=1,所以1a 1+1=2,所以数列{1a n+1}是以2为首项,2为公比的等比数列,所以1a n +1=2×2n -1=2n ,所以a n =12n -1.基础达标一、选择题1.已知数列{a n }中,a 1=2,a n +1=a n +2n (n ∈N *),则a 100的值是( )A.9 900 B.9 902 C.9 904D.11 000解析 a 100=(a 100-a 99)+(a 99-a 98)+…+(a 2-a 1)+a 1=2(99+98+…+2+1)+2=2×99×(99+1)2+2=9 902.答案 B2.已知数列{a n }中,a 1=1,a n +1=a n1+2a n,则这个数列的第n 项为( )A.2n -1B.2n +1C.12n -1D.12n +1解析 ∵a n +1=a n 1+2an,a 1=1,∴1a n +1-1a n =2.∴{1a n}为等差数列,公差为2,首项1a1=1.∴1a n =1+(n -1)×2=2n -1,∴a n =12n -1.答案 C3.若数列{a n }中,a 1=3,a n +a n -1=4(n ≥2),则a 2 021的值为( )A.1 B.2 C.3D.4解析 ∵a 1=3,a n +a n -1=4(n ≥2),∴a n +1+a n =4,∴a n +1=a n -1,∴a n =a n +2,即奇数项、偶数项构成的数列均为常数列,又∵a 1=3,∴a 2 021=3.答案 C4.已知数列{a n }的首项为a 1=1,且满足a n +1=12a n +12n ,则此数列的通项公式a n 等于( )A.2nB.n (n +1)C.n2n -1D.n (n +1)2n解析 ∵a n +1=12a n +12n ,∴2n +1a n +1=2n a n +2,即2n +1a n +1-2n a n =2.又21a 1=2,∴数列{2n a n }是以2为首项,2为公差的等差数列,∴2n a n =2+(n -1)×2=2n ,∴a n =n 2n -1.答案 C5.已知数列{a n }的前n 项和为S n ,且a 1=2,S n +1=4a n +2,则a 12=( )A.20 480B.49 152C.60 152D.89 150解析 由题意得S 2=4a 1+2,所以a 1+a 2=4a 1+2,解得a 2=8,故a 2-2a 1=4,又a n +2=S n +2-S n +1=4a n +1-4a n ,于是a n +2-2a n +1=2(a n +1-2a n ),因此数列{a n +1-2a n }是以a 2-2a 1=4为首项,2为公比的等比数列,即a n +1-2a n =4×2n -1=2n +1,于是a n +12n +1-a n2n =1,因此数列{a n2n}是以1为首项,1为公差的等差数列,得a n2n =1+(n -1)=n ,即a n =n ·2n .所以a 12=12×212=49 152,故选B.答案 B 二、填空题6.在等比数列{a n }中,a 1,a 2,a 3分别是下表第一、二、三行中的某一个数,且a 1,a 2,a 3中的任何两个数不在下表的同一列.第一列第二列第三列第一行3210第二行6414第三行9818则数列{a n }的通项公式为________.解析 当a 1=3时,不合题意;当a 1=2时,当且仅当a 2=6,a 3=18时,符合题意;当a 1=10时,不合题意.因此a 1=2,a 2=6,a 3=18,所以公比q =3,故a n =2×3n -1.答案 a n =2×3n -17.在数列{a n }中,a 1=1,a n +1=n +1na n ,则数列{a n }的通项公式a n =________.解析 当n ≥2时,a n =a n a n -1·a n -1a n -2·…·a 3a 2·a 2a 1·a 1=nn -1·n -1n -2·…·32·21=n ,当n =1时,a 1=1也符合此式,∴a n =n .答案 n8.已知数列{a n }满足ln a 13·ln a 26·ln a 39·…·ln a n 3n =3n 2(n ∈N *),则a 10=________.解析 ∵ln a 13·ln a 26·ln a 39·…·ln a n 3n =3n2(n ∈N *),∴ln a 13·ln a 26·ln a 39·…·ln a n -13(n -1)=3(n -1)2(n ≥2),∴ln a n =3n 2n -1(n ≥2),∴a n =e 3n 2n -1(n ≥2),∴a 10=e 1003.答案 e1003三、解答题9.设f (x )=log 2x -log x 4(0<x <1),数列{a n }的通项a n 满足f (2a n )=2n ,求数列{a n }的通项公式.解 ∵f (x )=log 2x -log x 4(0<x <1),f (2an )=2n ,∴log 22an -log 2an 4=2n ,由换底公式得log 22an -log 24log 22an =2n ,即a n -2a n =2n ,∴a 2n -2na n -2=0,解得a n =n ±n 2+2.又0<x <1,∴0<2an <1,∴a n <0,∴a n =n -n 2+2,∴数列{a n }的通项公式是a n =n -n 2+2.10.设数列{a n }的前n 项和为S n ,数列{S n }的前n 项和为T n ,满足T n =2S n -n 2,n ∈N *.(1)求a 1的值;(2)求数列{a n }的通项公式.解 (1)当n =1时,T 1=2S 1-1,因为T 1=S 1=a 1,所以a 1=2a 1-1,所以a 1=1.(2)当n ≥2时,T n -1=2S n -1-(n -1)2,则S n =T n -T n -1=2S n -n 2-[2S n -1-(n -1)2]=2(S n -S n -1)-2n +1=2a n -2n +1,因为当n =1时,a 1=S 1=1也满足上式,所以S n =2a n -2n +1(n ≥1),①当n ≥2时,S n -1=2a n -1-2(n -1)+1,②①-②,得a n =2a n -2a n -1-2,所以a n =2a n -1+2(n ≥2),所以a n +2=2·(a n -1+2),因为a 1+2=3≠0,所以数列{a n +2}是以3为首项,2为公比的等比数列,所以a n +2=3×2n -1,所以a n =3×2n -1-2.能力提升11.已知数列{a n }满足a 1=1,a 2=13,若a n (a n -1+2a n +1)=3a n -1·a n +1(n ≥2,n ∈N *),则数列{a n }的通项公式a n =________.解析 由题意知a n a n -1+2a n a n +1=3a n -1a n +1,∴1a n +1+2a n -1=3a n ,∴1a n +1-1a n =2(1a n -1a n -1),即1a n +1-1a n1a n -1a n -1=2,∴数列{1an +1-1a n}是首项为2,公比为2的等比数列,∴1a n +1-1a n =2×2n -1=2n .利用累加法,得1a 1+(1a 2-1a 1)+(1a 3-1a 2)+…+(1a n -1a n -1)=1+2+22+…+2n -1,即1a n =2n -12-1=2n -1,∴a n =12n -1.答案 12n -112.已知数列{a n }的前n 项和为S n ,且满足a 1=1,nS n +1-(n +1)S n =n (n +1)2,n ∈N *.(1)求数列{a n }的通项公式.(2)是否存在正整数k ,使a k ,S 2k ,a 4k 成等比数列?若存在,求k 的值;若不存在,请说明理由.解 (1)法一 由nS n +1-(n +1)S n =n (n +1)2,得S n +1n +1-S nn =12,∴数列{S nn}是首项为S 11=1,公差为12的等差数列,∴S nn =1+12(n -1)=12(n +1),∴S n =n (n +1)2.当n ≥2时,a n =S n -S n -1=n (n +1)2-(n -1)n2=n .而a 1=1适合上式,∴a n =n .法二 由nS n +1-(n +1)S n =n (n +1)2,得n (S n +1-S n )-S n =n (n +1)2,∴na n +1-S n =n (n +1)2.①当n ≥2时,(n -1)a n -S n -1=n (n -1)2,②①-②,得na n +1-(n -1)a n -a n =n (n +1)2-n (n -1)2,∴na n +1-na n =n ,∴a n +1-a n =1,∴数列{a n }是从第2项起的等差数列,且首项为a 2=2,公差为1,∴a n =2+(n -2)×1=n (n ≥2).而a 1=1适合上式,∴a n =n .(2)由(1),知a n =n ,S n =n (n +1)2.假设存在正整数k ,使a k ,S 2k ,a 4k 成等比数列,则S 22k =a k ·a 4k ,即[2k (2k +1)2]2=k ·4k .∵k 为正整数,∴(2k +1)2=4.得2k +1=2或2k +1=-2,解得k =12或k =-32,与k 为正整数矛盾.∴不存在正整数k ,使a k ,S 2k ,a 4k 成等比数列.创新猜想13.(多选题)已知数列{a n }的前n 项和为S n ,a 1=1,a 2=2,且对于任意n >1,n ∈N *,满足S n +1+S n -1=2(S n +1),则( )A.a 9=17 B.a 10=18C.S 9=81D.S 10=91解析 ∵对于任意n >1,n ∈N *,满足S n +1+S n -1=2(S n +1),∴S n +1-S n =S n -S n -1+2,∴a n +1-a n =2.∴数列{a n }在n ≥2时是等差数列,公差为2.又a 1=1,a 2=2,则a 9=2+7×2=16,a 10=2+8×2=18,S 9=1+8×2+8×72×2=73,S 10=1+9×2+9×82×2=91.故选BD.答案 BD14.(多空题)设S n是数列{a n}的前n项和,且满足a2n+1=2a n S n,且a n>0,则S n=________,a100=________.解析 由S n是数列{a n}的前n项和,且满足a2n+1=2a n S n,则当n=1时,a21+1=2a1S1,即S21=1;当n≥2时,(S n-S n-1)2+1=2(S n-S n-1)S n,整理得S 2n-S2n-1=1.所以数列{S2n}是以1为首项,1为公差的等差数列,则S2n=n.由于a n>0,所以S n=n,故a100=S100-S99=100-99=10-311.答案 n 10-311。
25 12.3.1 习题课(1)

D B H G C E
A
B
D
F
E
C
11、已知:如图, 11、已知:如图,在△ABC中,AB=AC,O ABC中 AB=AC, ABC内一点 内一点, OB=OC。求证: 是△ABC内一点,且OB=OC。求证:AO⊥BC A
O B C
12、如图,已知在△ABC中 AB=AC, 12、如图,已知在△ABC中,AB=AC, BD⊥AC于 CE⊥AB于 BD与CE相交于 相交于M BD⊥AC于D,CE⊥AB于E,BD与CE相交于M 求证:BM=CM。 点。求证:BM=CM。
第十二章 轴对称
12.3.1 习题课
义务教育课程标准实验教科书——人教版——八年级上册
回顾: 回顾:
图形 概 念 性 质
性质 判定
判 定
性质1: 性质1 等边对等角 判定: 判定: 等角对等边
A
B
C
有两边 相等的 三角形 是等腰 三角形
∵AB=CD ∴∠B = ∠C
∠B ∵ ∠B = ∠C ∴ AB=CD
等腰三角形性质与判定的应用: 等腰三角形性质与判定的应用:
(1)计算角的度数 利用等腰三角形的性质, 利用等腰三角形的性质,结合三角形 内角和定理及推论计算角的度数,是等腰 内角和定理及推论计算角的度数, 三角形性质的重要应用。 三角形性质的重要应用。 已知角的度数,求其它角的度数; ①已知角的度数,求其它角的度数; 已知条件中有较多的等腰三角形( ②已知条件中有较多的等腰三角形(此时 往往设法用未知数表示图中的角, 往往设法用未知数表示图中的角,从中得 到含这些未知数的方程或方程组); 到含这些未知数的方程或方程组); (2)证明线段或角相等
练习: 练习:
1.等腰三角形顶角为36° 底角为_______。 1.等腰三角形顶角为36°,底角为_______。 等腰三角形顶角为36 _______ 2.等腰三角形顶角和一个底角之和为100° 2.等腰三角形顶角和一个底角之和为100°, 等腰三角形顶角和一个底角之和为100 则顶角度数为_____________。 则顶角度数为_____________。 _____________ 3.等腰三角形两个角之比为4:1, 3.等腰三角形两个角之比为4:1,则顶角为 等腰三角形两个角之比为4:1 __________,底角为___________ ___________。 __________,底角为___________。 4.等腰三角形两边长为4 4.等腰三角形两边长为4、6,这个三角形周 等腰三角形两边长为 长为_____________。 长为_____________。 _____________
静力学习题课(1)

F4=8 ( N ), F5=10 ( N ), 则 该 力 系 简 化 的 最 后 结 果
为
。
答案:-40N·m,顺时针方向
受力分析题
1、请画出 横梁AB、立柱AE、整体的受力分析图
受力分析题
2、请画出物体D、轮O、杆AB的受力图
计算题
图示电动机用螺栓A,B固定在角架上,自重不计。角架用螺 栓C,D固定在墙上。若M=20kN·m,a=0.3m,b=0.6m,求螺 栓A,B,件、活动铰支座;柔索约束,光滑接触面约束;固定铰支座, 固定端约束
2、平面任意力系向一点的简化,需要将力系中各力都
到
作用面内任意选定的一点上,该点称为
。
答案:平行移动;简化中心
填空题
3、
是作用在刚体平面内上的两个力偶等效的充分
必要条件。
答案:力偶矩相同
4、对于给定的任意力系,其主矢与简化
。但在一
般情况下,简化中心的位置不同时,对应的力系的
。
答案:中心位置无关;主矩则不同
填空题
图示结构受矩为 M=10KN.m 的力偶作用。若 a=1m,各杆自重不计。则固定铰支座 D 的反
力的大小为
,方向
。
答案:10KN;水平向右
已知平面平行力系的五个力分别为 F1=10(N),F2=4(N),F3=8(N),
1、解锯弓
(1)取梁锯弓画受力图如图所示。(2)建直角坐标系,列平衡方程:
解得:
FBA=5.18kN FD=-2.44kN(↓) FC=-1.18kN(↑)
2、解锯床转盘
(1)取锯床转盘画受力图如图所示。(2)建直角坐标系,列平衡方程:
解得 :
FOX=5kN (→)FOy=1.34kN(↑) M=500N·m( )
物理化学下学期习题课(1)

7)Ag + 2 Cl AgCl 反应在25℃,101.325kPa下进行放热127.07 kJ·mol-1,若布置成可逆电池,在可逆电池中进行,则放热32.998 O O kJ·mol-1。该反应的 ∆r H(298K)=______, ∆r S m (298K)=_____。 m
θ θ ∆ r H m = Q p, m ⇒ ∆ r H m = −127.02kJ ⋅ mol −1
物 理 化 学
习 题 课
填
空
题
相
变
热
力
学
6)在0℃到100℃的范围内液态的水的蒸气压与温度的关系可近似地表示为如下关 系: lg (p/kPa) = -2265/ (T/K) +8.0187 某地区的气压只有60.0kPa,那么这个地区水的沸点为___89.8___℃。 lg60=-2265/T +8.0187 T=89.8℃
8)在相图中总可以利用杠杆规则计算两相平衡时两相的相对 的量。
对。
物 理 化 学
习 题 课
思
考
题
相
变
热
力
学
9)在简单低共熔物的相图中,三相线上的任何一个系统点的 液相组成都相同。
对,在三相线上,自由度数为零,为无变量系统,所以在此线上液相组成不变。
10)三组分系统最多同时存在5个相。
对,F=3-P+2。
物
理
化
学
习
题
课
思
考
题
电
化
学
4)无限稀电解质溶液的摩尔电导率可以看成是正、负离子无限稀 摩尔电导率之和,这一规律只适用于强电解质。 错,弱电解质也适用。 5)电解质的无限稀释摩尔电导率 得到。 错,只适用于强电解质。 6)德拜-休克尔公式适用于强电解质。 错,只适用于强电解质稀溶液。 7)恒温、恒压下∆G>0的反应不能自发进行。 错,恒T、P,W’=0时, ∆G>0 的过程不能自发进行。
电路习题课(1-4)

Uoc= U1+ U2
U1= 456/9-45 2/10
b a
=30 - 9 = 21V
+
4
15A 4 2
U2 -
U2= (15 4/10) 2=12V Uoc= U1+ U2= 21+12 = 33V
b
3 6 4
a
求内阻Ri :
Ri 2 4
Ri=2+1.6=3.6
b
a
12V
U5
1
二、求电路中所有 的电压U 和 I 。
U1 a
U2
2 c
2 8V
d
40V
4
2
U3
I
1
U7 U6
b
2 U4
4 8 12 = = 0 .4 A I = 2 + 2 + 2 + 2 + 1 + 1 10 U 1 = U = 0.8V , U3 = U 4 = 0.8V , 2 = 0V U = 0.4V , U6 = 0.4V , U 7 5 Uab = U2 + 8 + U6 U4 = 0.8 + 8 + 0.4 + 0.8 = 10V
3
二、 求电流 I。
解: 用戴维南定理: 4
+ - 45V Is 15A 4 6 2 + 6 2
I
6.4
3 + - 45V Is 15A 4
a
Ri
a
4
Uoc -
+
Uoc -
b
b
3 + 4 - 45V 6 2 4 3 6
a 采用迭加定理求开路电压Uoc +
大一高数课件第十章 10-习题课-1

半圆周 ( x − a ) 2 + y 2 = a 2 , y ≥ 0 ,沿逆时针方向 .
三、证明: 证明:
xdx + ydy 在整个 xoy 平面除去 y 的负半轴及 2 2 x +y
内是某个二元函数的全微分, 原点的开区域 G 内是某个二元函数的全微分,并 求出一个这样的二元函数 .
测验题答案
(2) I2 = ∫ ( x2 − y+ y2)d x + ( y2 − x)d y L
= ∫ ( x2 − y)d x + ( y2 − x)dy + ∫ y2 dx
L L
L: x = acost, y = asint ,
t : 0 →π
= I − ∫ a sin3 t d t = −2a3
0
π 3
非闭
I = ∫ Pdx + Qdy =0
L
闭合
∂P ∂Q ∂P = ≠ ∂y ∂x ∂y ∂x非闭 补充曲线或用公式
∂Q ∂P 闭合 I = ∫∫ ( − )dxdy ∂x ∂y ∂Q D
解
由 I = ∫ ( x2 + 2xy)dx + ( x2 + y4 )dy
1
y
A
∂P ∂ 2 知 = ( x + 2 xy ) = 2 x ∂ y ∂y ∂Q ∂ 2 = ( x + y4 ) = 2 x x ∂x ∂x o 1 ∂P ∂Q 1 2 1 , 即 = 故原式 = ∫ x dx + ∫ (1 + y 4 )dy = 23 . ∂y ∂x 0 0
λ→0 i=1
n
∫ P( x, y)dx+ Q( x, y)dy
哈工程通信原理习题课(第5讲)_1

A
t -Ts/2 0 Ts/2
图P5-3
解答:(1)由图P5-3可以得到: 2 A(1 t ) Ts g (t ) 0
Ts t 2 其他
又 P(0) P(1) P
1 ,而且 g1 (t ) g (t ), g 2 (t ) 0 2
ATs 2 G( f ) S a ( fTs ) 2 2
该频率分量的功率为:
A2 4 A2 4 A2 A2 2 A2 Pv ( ) Sa ( ) Sa ( ) 4 4 4 16 2 16 2
5.5 设某二进制数字基带信号中,数字信息“1”和“0”分 g (t ) g (t ) 表示,且“1”与“0”出现的概率相等, g (t ) 及 别由 是升余弦频谱脉冲,即
0
t Ts/2
-Ts/2
-Ts/4
0
Ts/4
Ts/2
t
图P5-2(a)
图P5-2(b)
解答:(1)由随机基带序列的功率谱密度公式:
P ( ) P ( ) P ( ) s u v 2 f P(1 P) G1( f )G2 ( f ) f s PG1(mf s ) (1 P)G2 (mf s ) ( f mf ) s s m 2
将
P 带入上式整理得:
1 1 P ( ) f G ( mf ) (1 ) G ( mf ) v s g (t ) 1 s 2 s g ( t ) m 1 1 1 1 g (t ) g2 (t ) 2 因为 g1 ( t ) P 1 G1 ( mf s ) P 1 g2 ( t ) P G2 ( mf s ) P 得Pv ( ) 0 代入上式
习题课1答案
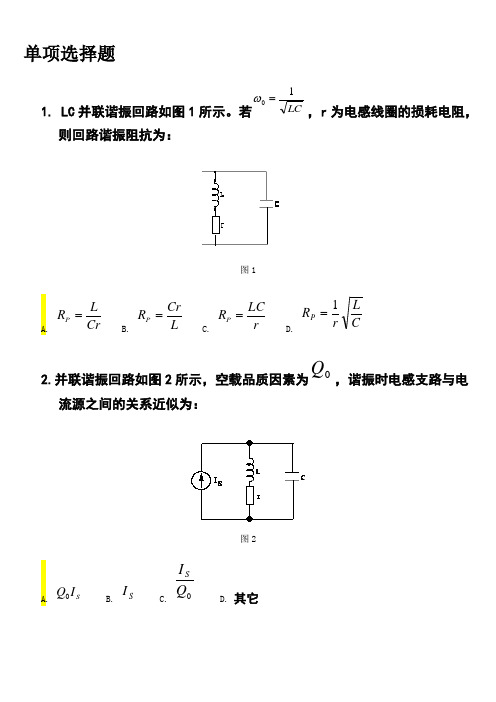
单项选择题1. LC 并联谐振回路如图1所示。
若LC 10=ω,r 为电感线圈的损耗电阻,则回路谐振阻抗为:图1 A. Cr L R P = B. L Cr R P = C. r LC R P = D. C L r R P 1=2.并联谐振回路如图2所示,空载品质因素为0Q ,谐振时电感支路与电流源之间的关系近似为:图2A. S I Q 0B. S IC. 0Q I SD. 其它3.串并联阻抗等效互换两支路(如图3所示)的品质因数分别为1L Q 、2L Q ,它们之间的关系为:图3A. 21L L Q Q >B. 21L L Q Q <C. 21L L Q Q =D. 不定4.回路抽头如图4所示,接入系数P 为:图4 A. 21N N B. 211N N N + C. 12N N D. 212N N N +5.非线性电路的重要特性之一是:A. 满足叠加原理;B. 不满足叠加原理;C.用传递函数描述;D.用线性微分方程描述;6. 并联谐振回路外加信号频率等于回路谐振频率时回路呈()A感性 B容性 C阻性 D容性或感性7. 小信号调谐放大器主要用于无线通信系统的()A.发送设备 B.接收设备 C.发送设备、接收设备8.LC单振荡回路的矩形系数值与电路参数的大小()A、有关B、成正比C、成反比D、无关9.高频小信号调谐放大器的级数愈多,其总的通频带()。
A、愈宽B、愈窄C、不变10.对于高频小信号放大,我们通常采用()和()相结合的方式来实现。
A、非线性放大器,集中选频放大器B、非线性放大器,LC谐振回路C、集成线性放大器,集中选频放大器D、集成线性放大器,LC谐振回路11.高频小信号谐振放大器不稳定的主要原因是:()A、增益太大B、通频带太宽C、晶体管集电结电容的反馈作用D、谐振曲线太尖锐12.在调谐放大器的 LC 回路两端并上一个电阻 R ,可以()A .提高回路的 Q 值。
B .加宽放大器的通频带。
高等数学习题课(1)函数极限与连续性

连续,
证明 f (x) 对一切 x 都连续 .
提示:
lim f (x x) lim [ f (x) f (x)]
x0
x0
f (x) f (0)
f (x 0) f (x)
P73 题5. 证明: 若 f (x) 在 (, )内连续, lim f (x)
x
存在, 则 f (x) 必在 (, )内有界.
III.课堂训练题 1. 求数列极限
1 lim[ n n n n ] n
2 lim 1 a1 a2 1 a2n ,( a 1) n
2. 求下列极限
1 lim x0
1 tan x 1 sin x sin3 x
2 lim sin x 1 sin x x
公式:sin A sin B 2cos A B sin A B
xx0
f (x)
f
(x0 )
6. 连续函数的性质
1) 有限个连续函数的和、差、积、商(分母不为 零),仍为连续函数;
2) 单值单调连续函数的反函数在对应区间上也为 单值单调的连续函数;
3) 连续函数的复合函数也是连续函数; 4) 一切初等函数在其定义区间内都是连续函数。
7. 闭区间上连续函数的性质
有 y f (x0 x) f (x0 )
如 果 lim y 0
①
x0
或
lim
x0
f
( x0
x)
f
(x0 )
②
或
lim
x x0
f (x)
f (x0 )
③
则 称 函 数y f (x) 在 点 x0 处 连 续 。
命题:lim xx0
f
(x)
f
期中习题课 (1)

已知Ka(HCOOH ) = 2.0×10-4, Kb(HCOO-) = 5.0×10-11 [OH-]计= 5.0 10-11 0.0800 = 2.0×10-6 (mol/L) pOH计= 5.70 pH计= 8.30
(C) Zn的含量
(D) Mg的含量
9.在配合滴定中, 用回滴法测定Al3+时, 若在
pH=5~6时以某金属离子标准溶液回滴过量的 EDTA, 金属离子标准溶液应选( )
(A) Mg2+ ( )
(B) Zn2+
(C) Ag+
(D) Bi3+
10.Fe3+ 与 Sn2+反应的平衡常数对数值(lgK)为 ----((Fe3+/Fe2+)= 0.77 V, (Sn4+/Sn2+)= 0.15 V)
酸碱滴定
§.1. 酸碱平衡的理论基础 一、酸碱质子理论:(给出H+,酸;接受H+,碱) 二、酸碱离解平衡: 共轭酸碱对之间Ka、Kb的相互转化(多元酸)。 三、水溶液中弱酸(碱)存在形式的分布: 1、平衡浓度;分析浓度;分布系数,分布曲线 2、一元、二元、三元酸的分布系数 3、一元、二元、三元酸分布曲线(会看图)
滴定体系 化学计量点前 0.1% Ce4+滴定 Fe2+ Fe3+滴定 Sn2+ 0.86
(V)
化学计量点 1.06 0.32
化学计量点后 0.1
0.23
1.26
0.50
Ce4++Fe2+ 2Fe3+ +Sn2+
Ce3++Fe3+ 2Fe2+ +Sn4+
微分方程习题课(1)-10

一、一阶微分方程求解 二、解微分方程应用问题
机动
目录
上页
下页
返回
结束
一、一阶微分方程求解
1. 一阶标准类型方程求解 四个标准类型: 可分离变量方程, 齐次方程, 线性方程, 贝努里方程 关键: 关键 辨别方程类型 , 掌握求解步骤 2. 一阶非标准类型方程求解 变量代换法 —— 代换自变量 自变量 代换因变量 因变量 代换某组合式 某组合式
y − y′x = x 1 y′ − y = −1 即 x 定解条件为 y x=1 =1.
思考: 思考 能否根据草图列方程?
y
M(x, y)
x tanα = xy′
o
机动
x
目录
x
上页 下页 返回 结束
第七章 习题课 (二) 二阶微分方程的 解法及应用
一、两类二阶微分方程的解法 二、微分方程的应用
机动
思考 若问题改为求解 y x=0 = 0 ,
则求解过程中得 问开方时正负号如何确定 正负号如何确定? 正负号如何确定
机动 目录 上页 下页 返回 结束
例7.
且满足方程
f (x) = sin x − ∫
求 f (x) .
x (x − t) f (t) dt 0
x x f (t) dt + t 0 0
通解
2 − y3
1 − y3 e = ex + C 3
机动
目录
上页
下页
返回
结束
′ = x2 − y2 + y (2) xy
方程两边同除以 x 即为齐次方程 , 令 y = u x ,化为分 离变量方程.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6.解 : (1)公司现有的资本结构是负债和普通股权益各 占50%,需新增普通股权益额为3 000*50%=1 500(万元)。 (2)普通股权益包括内部留存收益300万元,以 及外部新发行普通股1 200万元(1 500-300)。 留存收益资本成本= 新发行普通股成本=
3012% 40% 8% 12.8% 30 3012% 40% 8% 13.33% 27
经营期某年净现金 该年 该年 该年 该年 该年 流量(NCF t ) 净利润 折旧 摊销 利息 回收额 15
投资决策
习题课
NCF2=10+100+50+110+0=270(万元) NCF3=110+100+0+110+0=320(万元) NCF4=160+100+0+110+0=370(万元) NCF5=210+100+0+110+0=420(万元) NCF6=260+100+0+0+0=360(万元) NCF7=300+100+0+0+0=400(万元) NCF8=350+100+0+0+0=450(万元) NCF9=400+100+0+0+0=500(万元) NCF10=450+100+0+0+0=550(万元) NCF11=500+100+0+0+(100+200) =900(万元)
投资决策
习题课
5. 解:计算以下相关指标: 项目寿命期=1+10=11(年) 固定资产原值=1000+100=1100(万元) 年折旧=(1100-100)/10=100(万元) 因此,建设期净现金流量为: NCF0=-(1000+50)=-1050(万元) NCF1=-200(万元) 按简化公式计算的经营期净现金流量为:
2
投资决策
习题课
2.已知宏达公司拟于2000年初用自有资金购置设 备一台,需一次性投资100万元,经测算,该设 备使用寿命为5年,设备投入运营后每年可新增 净利润20万元,假定该设备按直线法折旧,预计 净残值率为5%,不考虑建设安装期。 请计算: (1)使用期内各年净现金流量; (2)该设备的投资回收期; (3)若以10%为折现率,计算其净现值。
投资决策
习题课
3.假设华达公司拟投资一项目,需购入一台新设备,现有 A、B两种方案可供选择,预计有关资料如下: (1)A方案需投资250万元,使用寿命5年,5年后 无残值。5年中每年销售收入为160万元,每年的付现 成本为50万元。 (2)B方案需投资300万元,使用寿命也是5年,5 年后残值收入为50万元。5年中每年销售收入为200万 元,第一年付现成本为50万元,以后随着设备陈旧将逐 年增加修理费用10万元,另需垫支流动资本80万元。 假设销售货款均于当年收现,采用直线法计提折旧 ,公司所得税税率为40%,使计算两个方案的现金流量 。
经营期某年净现金 该年 该年 该年 该年 该年 流量(NCF t ) 净利润 折旧 摊销 利息 回收额
按简化公式计算的经营期净现金流量为: NCF2~8=168+100+110=378(万元) NCF9~10=168+100=268(万元) NCF11=168+100+100=368(万元)
16
6.芬利公司年初的市场价值资本结构被认为是目标资本结 构,资料如下(单位:元): 债务(无短期负债) 30 000 000 普通股权益 30 000 000 总计 60 000 000 公司计划筹资3 000万元投资新项目。将按面值发 行公司债,利率为8%;发行普通股,发行价格为30元 ,公司每股净得资金27元,股东要求报酬率为12%;股 利支付率为40%,预期持续增长率为8%;公司当年的 留存收益预计为300万元;边际税率为40%。 要求: (1)维持现有资本结构,需新增多少普通股权益额? (2)计算普通股权益中各部分的资本成本。 17 (3)计算公司的加权平均资本成本。
5
投资决策
3. 解:
习题课
(1)先计算两个方案每年的折旧额。 A方案每年折旧额=250/5=50(万元)
B方案每年折旧额=(300-50)/5=50(万元)
(2)分别表格计算两个方案每年营业现金净流量 和现金流量,如表1和表2。
6
7
8
投资决策
习题课
4.某固定资产项目需要一次投入价款1000万元,资金来源 为银行借款,年利息率10%,建设期为1年。该固定资 产可使用10年,按直线法折旧,期满有净残值100万元 。投入使用后,可使经营期第1~7年每年产品销售收入 (不含增值税)增加804万元,第8~10年每年产品销 售收入(不含增值税)增加694万元,同时使第1~10 年每年的经营成本增加370万元。该企业所得税率为 25%,不享受减免税待遇。投产后第7年末,用税后利 润归还借款的本金,在还本之前的经营期内每年末支付 借款利息110万元,连续归还7年。 要求:计算该项目净现金流量和NPV;设定折现率 10%。(中间结果保留一位小数)。
9
投资决策
习题课
4. 解:计算以下相关指标: 项目寿命期=1+10=11(年) 建设期资本化利息=1000×10%×1 =100(万元) 固定资产原值=1000+100=1100(万元) 年折旧=(1100-100)/10=100(万元) 经营期第1~7年每年总成本增加额 =370+100+110=580(万元) 经营期第8~10年每年总成本增加额 =370+100=470(万元)
投资决策
习题课
5.某工业项目需要原始投资1250万元,其中固定资产投资 1000万元,开办费投资50万元,流动资金投资200万元 。建设期为1年,建设期发生与购建固定资产有关的资 本化利息100万元。固定资产投资和开办费投资于建设 起点投入,流动资金于完工时,即第1年末投入。该项 目寿命期10年,固定资产按直线法折旧,期满有100万 元净残值;开办费于投产当年一次摊销完毕。从经营期 第1年起连续4年每年归还借款利息110万元,流动资金 于终结点一次回收。投产后每年获净利润分别为10万元 、110万元、160万元、210万元、260万元、300万元 、350万元、400万元、450万元和500万元。 要求:计算项目各年净现金流量。设定折现率10% 。 14
3
投资决策
习题课
2. 解: (1)该设备各年净现金流量测算: NCF0=-100(万元) NCF1-4=20+(100-5)/5=39(万元) NCF5 =39+5= 44(万元) (2)静态投资回收期= 100/39= 2.56(年) (3)该投资项目的净现值 = 39× 3.7908+100×5%×0.6209-100 = 147.842+3.1045-100 4 = 50. 95(万元)
投资决策
习题课
1.某公司因业务发展需要购入一套设备,需要投 资22万元,使用寿命5年,采用直线法折旧,5 年后设备净残值为2万元。5年中每年销售收入为 8万元,每年付现成本为3万元。假设所得税率为 40%,公司资本成本率为10%。 要求: (1)计算该项目的净现金流量; (2)用净现值法计算该项目的净现值,并评价 项目的可行性。[(P/A, 10%, 5)=3.7908; (P/F, 10%, 5)= 0.6209]
1
投资决策
习题课
1. 解: (1)NCF0=-22(万元) NCF1-4=8-3-[8-3-(22-2)÷5]×40% = 4.6(万元) NCF5=4.6+2=6.6(万元) (2)NPV=-22+4.6×(P/A,10%, 5) +2×(P/F, 10%, 5) = -22+17.44+1.24=-3.32(万元) 因为项目的净现值小于0,所以该项目不可行。
7.解答: (1)银行借款成本=10%×(1-30%)=7% (2)债券成本=〔1×10%×(1-30%)〕/ 〔0.85×( 1- 2%)〕 =8.4% (3)普通股成本=(D1/P0)+g =〔5×(1+5%)/100〕 +5% =10.25% (4)加权平均资本成本 =7%×100/1000+8.4%×100/1000 +10.25%×800/1000 21 =9.74%
10
投资决策
习题课
4. 解: 经营期第1~7年每年营业利润增加额 =804-580=224(万元) 经营期第8~10年每年营业利润增加额 =694-470=224(万元) 每年应缴所得税增加额 =224×25%=56(万元) 每年净利润增加额=224-56=168万元
11
投资决策
习题课
4. 解: 因此,该项目净现金流量为: NCF0=-1000(万元Байду номын сангаас NCF1=0
18
6.解 : (3)公司的加权平均资本成本=
1,200 300 8% (1 40%) 50% 13.33% 12.8% 9.012% 3,000 3,000
19
7.某企业所得税率为30%,目前拥有资本1000万 元,其结构为:(1)债务资本20%。其中长期 借款100万元,利率10%;公司债券100万元, 债券面值1元,票面利率10%,期限10年,分期 付款,当前市价0.85元,如果按当前市价发行新 债券,发行费用为市价的2%;(2)普通股权益 资本80%。发行普通股10万股,每股面值80元 ,当前市价100元,本年派发股利每股5元,预 计以后年度股利以5%稳定增长。 (1)计算长期借款的资本成本。 (2)计算债券的资本成本。 (3)计算普通股的资本成本。 20 (4)计算该企业的综合资本成本。
