中国地图投影总结
中国常用的地图投影

中国常用的地图投影举例第三节中国常用的地图投影举例科学事业的发展同社会制度和经济基础是密切相联系的,旧中国是一个半封建半殖民地的国家,测绘事业也濒于停顿,编制出版的少量地图质量也很差,更少考虑到采用自己设计及计算的地图投影。
在解放前出版的几种地图中曾采用过的几种地图投影,也多半是因循国外陈旧的地图投影,很少自行设计新投影。
解放后,在党和政府的领导下,非常重视测绘科学事业的发展,我国测绘工作者不仅在地图投影的理论上有了研究,同时结合我国具体情况,设计了一些适合于我国情况的新的地图投影。
下面介绍我国出版的地图中常用的一些地图投影。
世界地图的投影等差分纬线多圆锥投影正切差分纬线多圆锥投影(1976年方案)任意伪圆柱投影:a=0.87740,6=0.85当φ=65°时P=1.20正轴等角割圆柱投影半球地图的投影东半球图横轴等面积方位投影φ0=0°,λ0=+70°横轴等角方位投影φ0=0°,λ0=+70°西半球图横轴等面积方位投影φ0=0°,λ0=-110°横轴等角方位投影φ0=0°,λ0=-110°南、北半球地图正轴等距离方位投影正轴等角方位投影正轴等面积方位投影亚洲地图的投影斜轴等面积方位投影φ0=+40°,λ0=+90°φ0=+40°,λ0=+90°彭纳投影标准纬线φ0=+40°,中央经线λ0=+80°标准纬线φ0=+40°,中央经线λ0=+80°欧洲地图的投影斜轴等面积方位投影φ0=52°30′,λ0=20°正轴等角圆锥投影φ1=40°30′,λ0=65°30′北美洲地图的投影斜轴等面积方位投影φ0=+45°,λ0=-100°彭纳投影南美洲地图的投影斜轴等面积方位投影φ0=0°,λ0=+20°桑逊投影λ0=+20°澳洲地图的投影斜轴等面积方位投影φ0=-25°,λ0=+135°正轴等角圆锥投影φ1=34°30′,φ2=-15°20′拉丁美洲地图的投影斜轴等面积方位投影φ0=-10°,λ0=-60°中国地图的投影中国全图斜轴等面积方位投影φ0=-27°30′λ0=+105°或φ0=30°00′λ0=+105°或φ0=35°00′λ0=+105°斜轴等角方位投影(中心点位置同上)彭纳投影伪方位投影中国全图(南海诸岛作插图)正轴等面积割圆锥投影两条标准纬线曾采用φ1=24°00′,φ2=48°00′或φ1=25°00′,φ2=45°00′或φ1=23°30′,φ2=48°30′目前常采用φ1=25°00′,φ2=47°00′正轴等角割圆锥投影中国分省(区)地图的投影正轴等角割圆锥投影正轴等面积割圆锥投影正轴等角圆柱投影高斯-克吕格投影(宽带)中国大比例尺地图的投影多面体投影(北洋军阀时期)等角割圆锥投影(兰勃特投影) (解放前)高斯-克吕格投影(中华人民共和国成立以后)。
(地图学课件)第2讲链接(第三章我国地形图采用的地图投影)
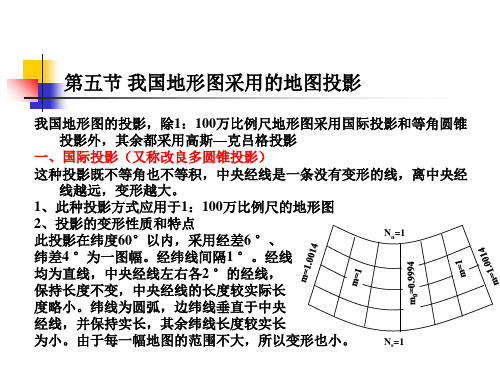
此投影在纬度60°以内,采用经差6 °、
Nn=1
纬差4 °为一图幅。经纬线间隔1 °。经线
均为直线,中央经线左右各2 °的经线,
保持长度不变,中央经线的长度较实际长
度略小。纬线为圆弧,边纬线垂直于中央
经线,并保持实长,其余纬线长度较实长
为小。由于每一幅地图的范围不大,所以变形也小。 Ns=1
第五节 我国地形图采用的地图投影
第五节 我国地形图采用的地图投影
我国地形图的投影,除1:100万比例尺地形图采用国际投影和等角圆锥 投影外,其余都采用高斯—克吕格投影
一、国际投影(又称改良多圆锥投影) 5、对多圆锥投影原理的解释 多圆锥投影,中央经线投影为直线且保持长度不变,其余经线投影为对
称于中央经线的曲线;赤道投影为直线,其余纬线投影为同轴圆弧, 圆心位于中央经线上,各纬线投影后保持长度不变且与中央经线正 交。
我国地形图的投影,除1:100万比例尺地形图采用国际投影和等角圆锥 投影外,其余都采用高斯—克吕格投影
一、国际投影(又称改良多圆锥投影) 3、拼接时产生的后果 由于各幅地图均系单独投影,虽然同一列与同一行图幅可以密切拼接,
但上下左右四幅拼接在一起,则发生裂隙。如果九幅或更多幅地图 拼接在一起,则变形更大,但仍可有效的进行研究地区的阅读。 4、七十年代以前,我国1/100万地图一直采用国际投影,现在改用等角 圆锥投影。
第五节 我国地形图采用的地图投影
我国地形图的投影,除1:100万比例尺地形图采用国际投影和等角圆锥
投影外,其余都采用高斯—克吕格投影
一、国际投影(又称改良多圆锥投影)
这种投影既不等角也不等积,中央经线是一条没有变形的线,离中央经
线越远,变形越大。
1、此种投影方式应用于1:100万比例尺的地形图
地图投影知识点总结

地图投影知识点总结地图投影是将三维地球表面映射到二维平面上的过程。
由于地球是一个三维的球体,而地图是一个二维平面,因此无法完美地将地球表面映射到地图上。
地图投影是一项复杂的工程,需要考虑到地球的形状、尺寸、方向和角度等因素,以及地球表面的曲率和变形等问题。
地图投影有很多种类,每种投影方法都有其优点和局限性。
以下是地图投影的一些基本知识点总结:地图投影的分类:地图投影可分为等距投影、等角投影和等面积投影。
等距投影是指保持地球表面上任意两点之间的距离比例不变,但方向可能会发生变化。
等角投影是指保持地球表面上任意两点之间的夹角不变,但距离和面积可能会发生变化。
等面积投影是指保持地球表面上任意两个区域的面积比例不变,但方向和角度可能会发生变化。
根据投影面的形状,地图投影可分为圆柱投影、圆锥投影和平面投影。
地图投影的选择:选择适合的地图投影方法需要考虑到所要表达的地理信息、地图的使用目的和范围等因素。
例如,对于航海、航空和导航等领域,需要选用等角投影;而对于地图的变形要求较小的地理信息分析和遥感影像处理等领域,适合使用等面积投影。
地图投影的变形:地图投影会造成三种类型的变形:形状变形、大小变形和方向变形。
形状变形是指地球表面上的形状在地图上可能发生拉伸或压缩;大小变形是指地球表面上的面积在地图上可能会发生增加或减小;方向变形是指地球表面上的方向在地图上可能会发生偏差。
地图投影方法的选择要考虑到这些变形问题,以减小变形的影响。
常见的地图投影方法:1. 麦卡托投影:是一种圆柱形等距投影,常用于世界地图,保持了纬线和经线的直角,但是南北两极地区的变形严重。
2. 鲍尔投影:是一种圆柱形等面积投影,保持了地区间的面积比例,但是形状变形较大。
3. 兰伯特等角投影:是一种圆锥形等角投影,保持了地区间的角度比例,但是大小和形状变形较大。
4. 鲁宾逊投影:是一种混合投影,综合了以上投影方法的优点,常用于世界地图,尽量减小了地图的变形。
常用的几种地图投影

常用的几种地图投影常用的几种地图投影转自#从世界范围看,各国大中比例尺地形图所使用的投影很不统一,据不完全统计有十几种之多,最常用的有横轴等角椭圆柱投影等。
中华人民共和国成立后,我国大中比例尺地形图一律规定采用以克拉索夫斯基椭球体元素计算的高斯-克吕格投影。
我国新编1:100万地形图,采用的则是边纬与中纬变形绝对值相等的正轴等角圆锥投影。
一、高斯-克吕格投影高斯-克吕格投影是一种等角横切椭圆柱投影,见图6-1所示。
我国现行的大于1:50万地形图都采用高斯-克吕格投影。
其中大于1:1万及更大比例尺地形图采用按经差3o分带,1: 2.5万~1:50万比例尺的地形图采用经差6o分带。
图6-1 高斯-克吕格投影示意图高斯-克吕格投影,欧美一些国家称之为横轴等角墨卡托投影。
美国及其它一些国家地形图使用的UTM投影(Universal Transverse Mercatol Projection,即通用横轴墨卡托投影),亦属横轴等角椭圆柱投影的系列。
UTM投影与高斯-克吕格投影的区别在于,该投影是横轴等角割椭圆柱投影。
UTM投影,在投影带内有两条长度比等于1的标准经线,而中央经线的长度比为0.9996。
因而使投影带内变形差异更小,其最大长度变形不超过0.04%。
坐标网的规定:坐标网是地图上地理坐标网(经纬网)和直角坐标网(方里网)的总称。
编绘地图时,坐标网是绘制地图图形的控制网。
使用地图时可以根据它确定地面点的位置和进行各种量算。
一般的地图只绘经纬网,在高斯-克吕格投影的地图上,为了迅速而准确地确定方向、距离、面积等,还绘有方里网,具体规定为:1.经纬网经纬网是由经线和纬线组成的坐标网。
它标示制图物体在地图上的地理位置,故又称为地理坐标网。
在1:1万~1:10万的地形图上,内图廓即是经纬线。
为了在使用时能够加密成网,在内外图廓间绘有分度带,需要时将对应点连线就构成经纬线网。
在1:20万~1:100万地形图上,图廓本身是经纬线,图面上直接绘出经纬线网,并在内图廓和图内经纬线网格上绘有按规定间隔供加密的分割线。
我国分省地图投影标准纬线

我国分省地图投影标准纬线正轴圆锥投影和圆柱投影最适宜于沿纬线伸展的地区,特别是正轴圆锥投影适宜于中纬度地区,正轴圆柱投影最适宜于低纬度和赤道地区。
对于沿经线伸展的地区,宜采用横轴圆柱投影。
xx分省(区)地图投影的选择:(1)从制图区域的形状和位置来看:我国绝大多数省(区)处于中纬度地区,因此最适宜采用圆锥投影;对于个别省区,如广东省包括南海诸岛及南中国海域,它位于赤道附近地区,可采用正轴圆柱投影;对于经差较小的地区,亦可采用高斯—克吕格投影。
即正轴等角圆锥投影;正轴等角割圆柱投影;宽带高斯—克吕格投影。
我国目前各省(区)按制图区域单幅地图选择投影时,所采用的两条标准纬线如下:注:北京市、天津市标准纬线同河北省,上海市标准纬线同江苏省。
xx采用正圆柱投影。
另一种情况,是采用分带投影的方法,即把相近的同纬度省(区)合用一个投影,把全国各省(区)分别采用若干个正轴等角圆锥投影,下表是将全国各省(区)分为10个投影带,计算得采用正轴等角圆锥投影时长度变形小于0.5%,xx常用的地图投影举例(1)世界地图的投影:正轴等角割圆柱投影(2)半球地图的投影:东半球图:横轴等积方位投影φ0=0,λ0=±70横轴等角方位投影φ0=0,λ0=±70西半球图:横轴等积方位投影φ0=0,λ0=-110横轴等角方位投影φ0=0,λ0=-110xxxx地图:正轴等距离方位投影、正轴等角方位投影、正轴等面积方位投影(3)xx地图的投影:斜轴等面积方位投影φ0=+40,λ0=+90;φ0=+40,λ0=+85彭纳投影φ0=+40,λ0=+80;φ0=+30,λ0=+80(4)xx全图(xx作插图)正轴等面积割圆锥投影:两条标准纬线曾采用φ1=2400,φ2=4800或φ1=2500,φ2=45 00或φ1=23 30,φ2=48 30.目前常采用φ1=25 00,φ2=47 00。
地图投影

一、我国的大地坐标系1954年北京坐标系(1980年前)基础:克拉索夫斯基参考椭球体坐标原点:前苏联波尔科夫天文台1980年西安坐标系或国家大地坐标系基础:1975年国家大地测量与地球物理联合会推荐的参考椭球体坐标原点:西安泾阳县永乐镇石际寺村二、水准原点:1956年黄海高程系(高程:72.2897米)1985年国家高程系(高程:72.2604米)三、地图投影1、地图投影的定义地图投影,Map Projection.把地球表面的任意点,利用一定数学法则,转换到地图平面上的理论和方法。
书面概念化定义:地图投影就是指建立地球表面(或其他星球表面或天球面)上的点与投影平面(即地图平面)上点之间的一一对应关系的方法。
即建立之间的数学转换公式。
它将作为一个不可展平的曲面即地球表面投影到一个平面的基本方法,保证了空间信息在区域上的联系与完整。
这个投影过程将产生投影变形,而且不同的投影方法具有不同性质和大小的投影变形。
2、地图投影的基本方法地图投影的基本方法主要包括几何透视法(主要绘制小比例尺地图)和数学分析法3、地图投影的分类几何投影中根据投影面与地球表面的关系分切投影和割投影。
①、按地图投影的构成方法分类1、几何投影A、方位投影B、圆柱投影C、圆锥投影2、非几何投影A、伪方位投影B、伪圆柱投影C、伪圆锥投影D、多圆锥投影②、按地图投影的变形性质分类1、等角投影2、等积投影3、任意投影4、各种投影的经纬线形状各种投影的经纬线形状5、各种投影的变形规律及应用6、高斯——克吕格投影(等角横切椭圆柱投影)假想用一个圆柱横切于地球椭球体的某一经线上,这条与圆柱面相切的经线,称中央经线。
以中央经线为投影的对称轴,将东西各3°或1°30′的两条子午线所夹经差6°或3°的带状地区按数学法则、投影法则投影到圆柱面上,再展开成平面,即高斯-克吕格投影,简称高斯投影。
这个狭长的带状的经纬线网叫做高斯-克吕格投影带。
地 图 投 影

• 我国地图比例尺分级系统: 大比例尺:1:500—1:10万
中比例尺:1:10万—1:100万 小比例尺:〈1:100万
• 在我国,1:100万采用兰勃投影(正轴 等积割圆锥投影),大部分分省图、大 多数同级比例尺都采用此投影;
• 1:50万、1:25万、1:10万、1:5万、 1:2.5万、1:1万、1:5000采用高斯—克 吕格投影。
11
地图投影变形的图解示例
(摩尔维特投影-等积伪圆柱投影)
长度变形 角度变形
12
地图投影变形的图解示例
(UTM-横轴等角割圆柱投影)
面积变形和长度变形
13
地图投影:投影分类
变形分类: 等角投影:投影前后角度不变 等面积投影:投影前后面积不变; 任意投影:角度、面积、长度均变形
14
等积投影、等角投影、等距投影
16
17
18
19
(2)非几何投影 不借助几何面,根据某些条件用数学解析
法确定球面与平面之间点与点的函数关系。
20
二、按照投影面的位置分类
– 正轴投影:投影面中心轴与地轴相互重合 – 斜轴投影:投影面中心轴与地轴斜向相交 – 横轴投影:投影面中心轴与地轴相互垂直
– 相切投影:投影面与椭球体相切 – 相割投影:投影面与椭球体相割
形状不变
15
地图投影:投影分类
一、按构成方法分类
– (1)几何投影:
(1.1)方位投影:投影面是一个与地球相切或相割的平面。 (1.2)圆柱投影:投影面是一个与地球相切或相割的圆柱。 (1.3)圆锥投影:投影面是一个与地球相切或相割的圆锥。
– (2)非几何投影
伪方位投影 伪圆柱投影 伪圆锥投影 多圆锥投影
中国有多大?地图投影骗了你,我国一城市向西飞到欧洲非洲,向东还没有出国境

中国有多⼤?地图投影骗了你,我国⼀城市向西飞到欧洲⾮洲,向东还没有出国境我国陆地⾯积960万平⽅千⽶,陆上边界2万多千⽶。
内海和边海的⽔域⾯积约470万平⽅千⽶。
34个省级⾏政区中新疆维吾尔⾃治区的⾯积最⼤,⾯积166万平⽅公⾥,占中国国⼟总⾯积六分之⼀。
新疆的⾯积⽐河南 + ⼭东 + 河北 + 北京 + 天津 + ⼭西 + 陕西 + 湖北 + 安徽 + 江苏 + 上海 +浙江+ 湖南这13 个省市加⼀起还要⼤⼀点。
在如此辽阔的疆域上,要出个省是真的不容易。
由于地图投影的问题,地图上直观看到的距离往往与真实距离相差甚远,我们以新疆最西端的喀什市为例,来直观感受⼀下新疆到底有多⼤,中国到底有⼤多。
喀什地区,是新疆维吾尔⾃治区的5个地区之⼀,驻地喀什市。
三⾯环⼭,⼀⾯敞开,总⾯积16.2万平⽅千⽶,辖1个市和11个县。
喀什是南疆的政治、经济、⽂化、交通中⼼。
1、1100公⾥以内喀什市距离⾸府乌鲁⽊齐约1100公⾥,⽽这个距离,可以到印度北部,可以到巴基斯坦⾸都伊斯兰堡,可以到阿富汗⾸都喀布尔,可以到塔吉克斯坦⾸都杜尚别,可以到乌兹别克斯坦⾸都塔什⼲,可以到吉尔吉斯斯坦⾸都⽐什凯克,可以到哈萨克斯坦原⾸都阿拉⽊图,可以到达⼟库曼斯坦西部地区。
但是,这个距离除了能到西藏外,其他省份⼀个都到不了。
最近的⼀个青海省,距离也有1200多公⾥。
总结⼀下,喀什到乌鲁⽊齐的距离⽐到达四个国家的⾸都还要远,可是这个距离还不能到达除了西藏外的其他省份。
2、1100-1750公⾥1750公⾥,是喀什市距离新疆最东端最远的距离。
⽽这个距离,⾜以让你到达蒙古国、俄罗斯、伊朗、印度⾸都新德⾥、尼泊尔⾸都加德满都,已经接近了⾥海。
但是,这个距离却到不了拉萨(已经很接近了),到不了我们除西藏、青海、⽢肃外的其他省份。
3、1750-3500公⾥3500公⾥,是喀什市距离祖国⾸都北京的⼤致距离。
这个距离,向北可以跨越俄罗斯到达北冰洋,向西可以到达乌克兰、⼟⽿其,西南可以到达阿拉伯半岛,向南可以跨越印度全境到达斯⾥兰卡、东南可以到达泰国。
3.5我国常用的地图投影选择3.5.1高斯-克吕格投影

3.5我国常用的地图投影选择我国基本比例尺地图常用的投影系统主要有两类,即比例尺小于或等于1:100万时采用正轴等角割圆锥投影,1:1万至1:50万的地形图全部采用高斯-克吕格投影。
1:2.5万至1:50万的地形图,采用6°分带方案,全球共分为60个投影带;我国位于东经72°到136°之间,共含11个投影带。
1:1万比例尺地图采用3°分带方案,全球共120个投影带。
3.5.1高斯-克吕格投影1.高斯-克吕格投影的概念以椭圆柱面作为投影面,并与椭球体面相切于一条经线上,该经线即为投影带的中央经线,按等角条件将中央经线东西一定范围内的区域投影到椭圆柱表面上,再展开成平面,便构成了横轴等角切椭圆柱投影(如图3-22所示)。
该投影早在19世纪20年代由德国的数学家、物理学家、天文学家高斯(C.F.Gauss,1777—1855)最先设计,后又于1912年经德国的克吕格(J.Kruger,1857—1923)对投影公式加以补充完善,故后人称该投影为高斯-克吕格投影。
高斯-克吕格投影满足的基本条件如下: .在中央经线(椭圆筒和地球椭球体的切线)和赤道投影成垂直相交的直线。
投影后没有角度变形(即经纬线投影后仍正交)。
中央经线上没有长度变形,等变形线为平行于中央经线的直线。
根据上述3个条件,即可导出高斯投影的直角坐标基本公式:式中:X、Y为平面直角坐标系的纵、横坐标;φ,λ为椭球面上地理坐标系的经纬度(分别自赤道和投影带中央经线起算),以弧度计;S为从赤道至纬度φ的子午线弧长;N为纬度φ处的卯酉圈曲率半径(可据纬度由制图用表查取);n即n2=e'2cos2φ,其中e'2=(a2-b2)/b2,为地球的第二偏心率,a、b分别为地球椭球体的长短半轴。
2.投影的变形分析与投影带的划分高斯投影没有角度变形,面积变形是通过长度变形来表达,其长度变形的基本公式为:高斯-克吕格投影的中央经线和赤道为互相垂直的直线,其他经线均为凹向并对称于中央经线的曲线,其他纬线均为以赤道为对称的向两极弯曲的曲线,经纬线成直角相交。
3第三章地图投影

(3)角度变形
(3)角度变形
(3)角度变形
' (180 2 ') (180 2 )
X A
2( ')
即: ( ')
Y
2
将上式代入(2-14)式得:
sin sin( ')= a b
2
ab
若已知经线长度比m,纬线长度比n,以及经
纬线夹角q,则角度最大变形公式可写成:
❖ 因此,通过对地图与地球仪上经纬网的比较, 可以发现,地图投影变形表现在长度、面积和 角度三方面。
地球仪与地图上经纬网比较
a
b
纬线长度a 经线长度b、c 同一纬线上,经差相同的纬线弧长c
c 同一经线上,纬差相同的经线弧长 同纬度带,同经差构成球形梯面b、 c 经纬线正交否b、c
1.变形概念
❖ 地图投影变形是球面转化成平面的必然结果, 没有变形的投影是不存在的。
若投影后,经纬线不正交,则:
P = a·b= m ·n ·sinq (q ≠ 90)
面积比和面积变形因位置不同而异
(3)角度变形
❖ 地面上任意两条方向线的夹角а,与经过投影后的相应 两方向线夹角а′之差值,称为角度变形
❖ 投影面上经纬线夹角变形ε为: ε=θ′-90°
❖ 过地面上一点可以引无数的方向线,由两条方向线组 成的角度有无数个。
❖ 利用变形椭圆的图解和理论,我们就能更为科 学和准确地阐述地图投影的概念、变形的性质 及变形大小
微分圆何以投影后为椭圆
❖ 经线CD和纬线AB为直角坐标系X、Y,圆心 0为直角坐标系原点
x' x
m 为经线长度比;
y' y
n
地图制图中的投影变换与校正

地图制图中的投影变换与校正地图是人们认识和理解地球的重要工具,而要制作准确的地图就需要进行投影变换与校正的处理。
投影变换是将地球的曲面投影到平面上的过程,而校正则是通过修正投影变换中的误差,使得地图更贴近真实地球的形貌和尺度。
一、投影变换在地图制图中,由于地球是一个凹凸不平的曲面,无法直接用平面表示,因此需要进行投影变换。
投影变换的目的是将地球的表面投影到平面上,并保持地面上的角度、形状和面积等特性。
不同的投影方法会导致地图上的形状、大小和方向产生变化。
常见的投影方法有圆柱投影、圆锥投影和平面投影。
圆柱投影是将地球的表面投影在圆柱体上,再展开成平面图,适用于赤道附近的地区;圆锥投影是将地球的表面投影在圆锥体上,再展开成平面图,适用于高纬度地区;平面投影则是将地球的表面直接投影到平面上,适用于局部地区的制图。
不同的投影方法有不同的优势和局限性。
比如,圆柱投影能够保持地面上的角度和形状特性,但在极地地区会出现严重的形变;圆锥投影则能够较好地保持地球的形状和面积特性,但在赤道附近会有较大的形变;平面投影具有保持局部地区地面特性的优势,但在远离中心点的地方会产生较大的形变。
二、校正由于投影变换会导致地图上的形状、大小和方向等产生变化,因此需要进行校正,使地图更符合实际地球的形貌和尺度。
校正的方法主要有拓扑校正和尺度校正。
拓扑校正是指通过修正地图上的形状和角度,使之与现实地球的形貌一致。
拓扑校正主要包括平移、旋转和形变等操作。
平移是将地图上的点移动到正确的位置,以修正地图的位置偏差;旋转则是将地图旋转到正确的方向,以修正地图的旋转偏差;形变是通过缩放地图上的特定区域,使其更符合真实地球的形貌。
尺度校正是指通过修正地图上的比例尺,使之与实际地球的尺度一致。
尺度校正主要包括线性校正和面积校正。
线性校正是通过拉伸或压缩地图上的线段,使其长度与实际距离一致;面积校正则是通过拉伸或压缩地图上的面积,使其面积与实际区域一致。
地图学投影总结

关于地图学中几种投影的总结类型一、方位投影方位投影是以平面作为投影面,使平面与地球表面相切或相割,并将球面上的经纬线投影到平面上所得到的图形。
方位投影可分为透视方位投影类和非透视方位投影两。
根据投影面和地球球面相切位置的不同,透视投影可分为三种①当投影面切于地球极点时,称为正轴方位投影。
②当投影面切于赤道时,称为横轴方位投影。
③当投影面切于既不在极点也不在赤道时,称为斜轴方位投影。
一、正轴方位投影投影中心为极点,纬线为同心圆,经线为同心圆的半径,两条经线间的夹角与实地相等。
等变形线都是以投影中心为圆心的同心圆。
包括等角、等距变形性质,主要用于制作两极地区图。
1.正轴等角方位投影平射正轴方位投影又叫等角方位投影或球面投影。
投影条件:视点位于球面上,投影面切于极点。
特点:①纬线投影为以极点为圆心的同心圆,纬线方向上的长度比大于1。
赤道上的长度变形比原来扩大1倍。
②经线投影为以极点为圆心的放射性直线束,经线夹角等于相应的经差,沿经线方向上的长度比大于1,赤道上各点沿经线方向上的长度变形比原来扩大1倍。
③这种投影的误差分布规律是,由投影中心向外逐渐增大。
④经纬线投影后,仍保持正交,所以经纬线方向就是主方向,又因为m = n,即主方向长度比相等,⑤没有角度变形,但面积变形较大,在投影边缘面积变形是中心的四倍。
2.正轴等距方位投影等距方位投影属于任意投影,它既不等积也不等角。
投影后经线保持正长,经线上纬距保持相等。
角度、面积等变形线为以投影中心为圆心的同心圆。
在此投影中,球面上的微圆投影为椭圆,且误差椭圆的长半径和纬线方向一致,短半径与经线方向一致,并且等于微圆半径r 又由于自投影中心,纬线扩大的程度越来越大,所以变形椭圆的长半径也越来越长,椭圆就越来越扁了。
等距正轴方位投影常用来做两极的投影。
二.横轴方位投影平面与球面相切,其切点位于赤道上的任意点。
特点:通过投影中心的中央经线和赤道投影为直线,其他经纬线投影后都是对称于中央经线和赤道的曲线1.横轴等距方位投影其特点是在中央经线上从中心向南向北,纬线间隔相等;在赤道上,自投影中心向西,向东,经线间隔是逐渐扩大的。
我国常用的地图投影参数

我国常用的地图投影世界地图1、正切差分纬线多圆锥投影(1976年方案)2、任意伪圆柱投影a=0.87740,b=0.85当P=1.203、正轴等角割圆柱投影4、组合圆柱投影(在纬度以内是正轴等角圆柱投影、纬度以外是任意圆柱投影)半球地图东半球地图横轴等面积方位投影,横轴等角方位投影,西半球地图横轴等面积方位投影,横轴等角方位投影,水陆半球地图斜轴等面积方位投影,和,南、北半球地图正轴等距离方位投影正轴等面积方位投影份洲和各大洋地图亚洲地图斜轴等面积方位投影,或,彭纳投影标准纬线,中央经线标准纬线,中央经线欧洲地图斜轴等面积方位投影 ',或,正轴等角圆锥投影 ', '拉丁美洲地图斜轴等面积方位投影,彭纳投影标准纬线,中央经线大洋洲地图斜轴等面积方位投影,澳洲地图斜轴等积方位投影,正轴等角圆锥投影 ', '拉丁美洲地图斜轴等面积方位投影,南美洲地图斜轴等面积方位投影,彭纳投影太平洋地图斜轴等面积(或任意)方位投影,或,乌尔马耶夫正弦任意伪圆柱投影大西洋地图斜轴任意伪方位投影,斜轴等面积方位投影,横轴等面积方位投影,印度洋斜轴等面积方位投影,墨卡托投影太平洋与印度洋地图乌尔马耶夫正弦任意伪圆柱投影墨卡托投影中国地图中国全图斜轴等面积方位投影 ',或 ',或 ',斜轴等角方位投影(中心点位置同上)彭纳投影伪方位投影双重方位(任意性质),中国全图(南海诸岛作插图)正轴等面积割圆锥投影 ', '或 ', '或 ', '正轴等角割圆锥投影 ', '中国分省(区)地图正轴等角割圆锥投影正轴等面积割圆锥投影正轴等角圆柱投影高斯-克吕格投影(宽带)分带方案的正轴等角圆锥投影Welcome To Download !!!欢迎您的下载,资料仅供参考!。
我国常用的三种地图投影

椭球体参数我国常用的3个椭球体参数如下(源自“全球定位系统测量规范GB/T 18314-2001”)Krassovsky (北京54采用)(长轴a: 6378245, 短轴b: 6356863.0188)IAG 75(西安80采用)(长轴a: 6378140, 短轴b: 6356755.2882)WGS 84(长轴a: 6378137, 短轴b: 6356752.3142)墨卡托(Mercator)投影墨卡托(Mercator)投影,是一种"等角正切圆柱投影”,荷兰地图学家墨卡托(Gerhardus Mercator 1512-1594)在1569年拟定, 假设地球被围在一中空的圆柱里,其标准纬线与圆柱相切接触,然后再假想地球中心有一盏灯,把球面上的图形投影到圆柱体上,再把圆柱体展开,这就是一幅选定标准纬线上的“墨卡托投影”绘制出的地图。
墨卡托投影没有角度变形,由每一点向各方向的长度比相等,它的经纬线都是平行直线,且相交成直角,经线间隔相等,纬线间隔从标准纬线向两极逐渐增大。
墨卡托投影的地图上长度和面积变形明显,但标准纬线无变形,从标准纬线向两极变形逐渐增大,但因为它具有各个方向均等扩大的特性,保持了方向和相互位置关系的正确。
在地图上保持方向和角度的正确是墨卡托投影的优点,墨卡托投影地图常用作航海图和航空图,如果循着墨卡托投影图上两点间的直线航行,方向不变可以一直到达目的地,因此它对船舰在航行中定位、确定航向都具有有利条件,给航海者带来很大方便。
“海底地形图编绘规范”(GB/T 17834-1999,海军航保部起草)中规定1:25万及更小比例尺的海图采用墨卡托投影,其中基本比例尺海底地形图(1:5万,1:25万,1:100万)采用统一基准纬线30°,非基本比例尺图以制图区域中纬为基准纬线。
基准纬线取至整度或整分。
墨卡托投影坐标系取零子午线或自定义原点经线(L0)与赤道交点的投影为原点,零子午线或自定义原点经线的投影为纵坐标X轴,赤道的投影为横坐标Y轴,构成墨卡托平面直角坐标系。
掌握测绘技术中的地图投影知识

掌握测绘技术中的地图投影知识地图投影是测绘技术中的一个重要环节,它对于地理信息的准确表达和传播具有至关重要的作用。
在测绘工作中,地图投影的选择和使用将直接影响地图的形状、大小、比例尺和形变程度等方面。
因此,掌握地图投影知识是每一位测绘人员都应具备的基本技能之一。
一、什么是地图投影?地图投影是指将三维空间中的地球表面投影到一个平面上的过程。
由于地球是一个椭球体,将其投影到平面上必然会引发形变。
投影的目的是为了将地球表面的特征以尽可能准确和可读的方式展示在二维地图上。
地图投影常用的方法有圆锥投影、圆柱投影和平面投影等。
二、地图投影的原理不同的地图投影方法,采用不同的原理来处理地球表面的形变问题。
圆锥投影是将一个圆锥体展开,并与地球的表面相切,然后将切点处的经纬线形成的网格投射到一个平面上。
这种投影方法在大面积纬度地区较为常用。
圆柱投影是将一个柱体展开,并与地球的表面相切。
圆柱体的纬度线将形成一系列的平行线,并将地球表面投影到一个平面上。
这种投影方法常用于赤道附近地区。
平面投影是将地球表面投影到一个平面上,这种投影方法在小范围地图中较常见。
三、地图投影的适用性不同的地图投影方法在适用范围上有所差异。
圆锥投影适用于大范围纬度地区,特别是靠近两极的地区。
圆柱投影适用于赤道附近的地区,其形变程度相对较小。
平面投影则适用于较小范围的地图,其形变程度相对较小。
四、地图投影的选择在实际工作中,选择合适的地图投影方法是十分重要的。
首先,需要根据地图的使用需求和所在区域的地理特点来进行选择。
其次,还需要考虑地图的比例尺。
较小比例尺的地图形变程度相对较小,而较大比例尺的地图形变程度较大,这需要在选择投影方法时予以考虑。
此外,还需对地图投影的计算方法和相关软件进行学习和掌握,以便能够准确地进行地图的投影和制作。
五、地图投影的应用地图投影技术广泛应用于测绘、地理信息系统、导航、军事等领域。
在测绘中,地图投影是制作地图的基础。
1地图投影

3
地球的大小
2021/2/5
广东水电学院水利系测量教研室
4
摊开在平面上的地球
2021/2/5
广东水电学院水利系测量教研室
5
地球椭球体
2021/2/5
广东水电学院水利系测量教研室
6
地球椭球体
2021/2/5
广东水电学院水利系测量教研室
7
2021/2/5
广东水电学院水利系测量教研室
8
2021/2/5
地图投影和高斯投影
2021/2/5
广东水电学院水利系测量教研室
1
如今我在什么地方?我不知道那是什么地方。 我猜不着。到底这里是哪里?映入我眼帘的只是不 知何处去的人蔓,行色匆匆地从我身边走过去。
村上春树
2021/2/5
广东水电学院水利系测量教研室
2
地球的形状
2021/2/5
广东水电学院水利系测量教研室
自1952年起,我国将其作为国家大地测量和地形图的基本投影, 亦称为主投影。
2021/2/5
广东水电学院水利系测量教研室
47
高斯—克吕格投影
2021/2/5
广东水电学院水利系测量教研室
48
高斯—克吕格投影
2021/2/5
广东水电学院水利系测量教研室
49
带号计算
6° 带带号: n6=L/6°(取商的整数+1)
2021/2/5
广东水电学院水利系测量教研室
31
Map projection
Locations are expressed as latitude and longitude on the globe and as x,y coordinates on a map.
地图投影第三章方位投影

横轴方位投影
平面与球面相切,其切点位于赤道上的任意点。特点:通 过投影中心的中央经线和赤道投影为直线,其他经纬线都 是对称于中央经线和赤道的曲线。
横轴方位投影
横轴等距方位投影:中央经线上 从中心向南北,纬线间隔相等; 赤道上,自投影中心向东西, 经线间隔逐渐扩大。
横轴等积方位投影:中央经线上 从中心向南北,纬线间隔逐渐 缩小;赤道上,自投影中心向 东西,经线间隔也是逐渐缩小 的。
角度、面积等变形线为以投影中心为圆线的同心圆。 球面上的微圆投影为椭圆,且误差椭圆的
长半径和纬线方向一致,短半径与经线方 向一致,且等于微圆半径r,又因自投影中 心,纬线扩大程度越来越大,所以变形 椭圆的长半径也越来越长,椭圆越来越扁。 常用来做两极的投影。
横轴方位投影 ——等距
经纬线形状
中央经线为直线,其它经线是对 称于中央经线的曲线。中央纬线 为直线,其它纬线是对称于中央 纬线的曲线。在中央经线上纬线 间隔相等。在中央纬线上经线间 隔相等。
4
3 21
最大角度变形公式为:
五. 正射投影
对于正射投影而言,D=∞,因此
直角坐标公式为 投影变形公式为:
3 21
六. 球面投影(等角方位投影)
对于等角方位投影而言,D=R,L=2R,因此有:
4
3 21
七. 球心投影(日晷投影)
对于等角方位投影而言,D=0,L=R,因此有:
投影变形公式为:
4
斜轴方位投影
投影面切于两极和赤道间的任意一点上。中央经线投影为 直线,其他经线投影为对称于中央经线的曲线,纬线投影 为曲线。
斜轴方位投影
斜轴等距方位投影:中央经线上 的纬线间隔相等。
斜轴等积方位投影:中央经线上 自投影中心向上、向下纬线间隔 是逐渐缩小的。
