七年级数学上册 第5章 相交线与平行线单元综合试题(含解析)(新版)华东师大版
七年级上册数学单元测试卷-第5章 相交线与平行线-华师大版(含答案)

七年级上册数学单元测试卷-第5章相交线与平行线-华师大版(含答案)一、单选题(共15题,共计45分)1、在面积为15的平行四边形ABCD中,过点A作AE垂直于直线BC于点E,作AF垂直于直线CD于点F,若AB=5,BC=6,则CE+CF的值为( )A.11+B.11-C.11+或11-D.11+ 或1+2、如图,直线m∥n,直角三角板ABC的顶点A在直线m上,则∠α的余角等于()A.19°B.38°C.42°D.52°3、如图,由AB∥CD可以得到()A.∠1=∠2B.∠2=∠3C.∠1=∠4D.∠3=∠44、如图,点在直线上移动,是直线上的两个定点,且直线.对于下列各值:①点到直线的距离;②的周长;③的面积;④的大小.其中不会随点的移动而变化的是()A.①②B.①③C.②④D.③④5、如图,下列说法中错误的是()A.∠GBD和∠HCE是同位角B.∠ABD和∠ACE是同位角C.∠FBC和∠ACE是内错角D.∠GBC和∠BCE是同旁内角6、图中,∠1与∠2是对顶角的是()A. B. C. D.7、下列命题中,真命题的个数是()①同位角相等;②a,b,c是三条直线,若a⊥b,b⊥c,则a⊥c;③a,b,c是三条直线,若a∥b,b∥c,则a∥c;④过一点有且只有一条直线与已知直线平行.A.1个B.2个C.3个D.4个8、已知∠1和∠2是同旁内角,∠1=40°,∠2等于()A.160°B.140°C.40°D.无法确定9、下列说法中:①在同一平面内,不相交的两条直线必平行;②同旁内角互补;③相等的角是对顶角;④从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离;⑤经过一点,有且只有一条直线与已知直线垂直.其中说法正确的个数有()A.1个B.2个C.3个D.4个10、如图,如果∠AFE+∠FED=180°,那么()A.AC∥DEB.AB∥FEC.ED⊥ABD.EF⊥AC11、如图,货船A与港口B相距35海里,我们用有序数对(南偏西40°,35海里)来描述货船B相对港口A的位置,那么港口A相对货船B的位置可描述为()A.(南偏西50°,35海里)B.(北偏西40°,35海里)C.(北偏东50°,35海里)D.(北偏东40°,35海里)12、如图,△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论:①△BDF和△CEF都是等腰三角形;②DE=BD+CE;③△ADE 的周长等于AB与AC的和;④BF=CF.其中正确的有()A.①②③B.①②③④C.①②D.①13、如图,于点C,点D是线段上任意一点.若,则的长不可能是()A.4B.5C.6D.714、如图,已知BE平分∠ABC,且BE∥DC,若∠ABC=50°,则∠C的度数是( )A.20°B.25°C.30°D.50°15、如图,AB∥CD,EF⊥AB于E,EF交CD于F,已知∠2=30°,则∠1是()A.20°B.60°C.30°D.45°二、填空题(共10题,共计30分)16、一个正方体中有一条棱是a,与a平行棱长有________ 条,与a垂直并相交的棱长有________ 条.17、(问题探究)如图1,,直线,垂足为,交于点,点到直线的距离为2,点到的距离为1,,,则的最小值是________;(提示:将线段沿方向平移1个单位长度即可解决,如图2所示.)(关联运用)如图3,在等腰和等腰中,,在直线上,,连接、,则的最小值是________.18、如图,直线被直线c所截,.那么________ .19、已知直线,a与b之间的距离为5,a与b之间有一点P,点P到a的距离是2,则点P到b的距离是________.20、如图,有一个长方形纸片,减去相邻的两个角,使∠ABC=90°,如果∠1=152°,那么∠2=________°.21、如图,AB∥CD,∠A=45゜,∠C=35゜,则∠D=________,∠1=________.22、如图,直线AB∥CD,BC平分∠ABD,∠1=55°,图中∠2=________23、如图,AB∥CD,∠A=45°,∠C=∠E,则∠C=________度.24、如图,DE//BC,BE平分∠ABC,若∠1=70°,则∠CBE的度数为________。
七年级数学上册 第5章 相交线与平行线单元综合试题(含解析)(新版)华东师大版

相交线与平行线一、选择题(共19小题)A.50° B.120°C.130°D.150°A.40° B.60° C.80° D.100°A.40° B.65° C.115°D.25°A.30° B.45° C.60° D.65°A.30° B.35° C.40° D.45°A.25° B.35° C.50° D.65°A.30° B.45° C.60° D.90°A.80° B.75° C.70° D.65°A.20° B.30° C.40° D.70°A.70° B.80° C.110°D.120°A.152°B.118°C.28° D.62°A.30° B.40° C.50° D.70°A.50° B.40° C.30° D.25°A.26° B.36° C.46° D.56°A.110°B.90° C.70° D.50°A.100°B.90° C.80° D.70°A.64° B.63° C.60° D.54°二、填空题(共10小题)三、解答题(共1小题)华师大新版七年级(上)近3年中考题单元试卷:第5章相交线与平行线参考答案与试题解析一、选择题(共19小题)A.50° B.120°C.130°D.150°【考点】平行线的性质.【分析】由平行线的性质可得出∠2,根据对顶角相得出∠1.【解答】解:如图:∵AB∥CD,∴∠A+∠2=180°,∴∠2=130°,∴∠1=∠2=130°.故选C.【点评】本题考查了平行线的性质,关键是根据两直线平行同旁内角互补和对顶角相等分析.A.40° B.60° C.80° D.100°【考点】平行线的性质.【分析】根据对顶角相等和利用三角形的内角和定理列式计算即可得解.【解答】解:如图:∵∠4=∠2=40°,∠5=∠1=60°,∴∠3=180°﹣60°﹣40°=80°,故选C.【点评】本题考查了平行线的性质,三角形的内角和定理,熟记性质并准确识图理清各角度之间的关系是解题的关键.A.40° B.65° C.115°D.25°【考点】平行线的性质.【分析】由平行线的性质可求得∠EFB=∠C,在△AEF中由三角形外角的性质可求得∠EFB,可求得答案【解答】解:∵∠EFB是△AEF的一个外角,∴∠EFB=∠A+∠E=25°+40°=65°,∵AB∥CD,∴∠C=∠EFB=65°,故选B.【点评】本题主要考查平行线的性质,掌握平行线的性质是解题的关键,即①两直线平行⇔同位角相等,②两直线平行⇔内错角相等,③两直线平行⇔同旁内角互补.A.30° B.45° C.60° D.65°【考点】平行线的性质.【分析】先根据两角互余的性质求出∠3的度数,再由平行线的性质即可得出结论.【解答】解:∵∠1+∠3=90°,∠1=30°,∴∠3=60°.∵直尺的两边互相平行,∴∠2=∠3=60°.故选C.【点评】本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等.A.30° B.35° C.40° D.45°【考点】平行线的性质.【专题】计算题.【分析】先根据平行线的性质得∠BEF=∠C=70°,然后根据三角形外角性质计算∠A的度数.【解答】解:∵AB∥CD,∴∠BEF=∠C=70°,∵∠BEF=∠A+∠F,∴∠A=70°﹣30°=40°.故选C.【点评】本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.A.25° B.35° C.50° D.65°【考点】平行线的性质;垂线.【分析】先根据三角形内角和定理求出∠C的度数,然后根据两直线平行内错角相等即可求出∠ABC 的大小.【解答】解:∵CB⊥DB,∴∠CBD=90°,∴∠C+∠D=90°,∵∠D=65°,∴∠C=25°,∵AB∥CD,∴∠BAC=∠C=25°.故选A.【点评】此题考查了平行线的性质,解题的关键是:熟记两直线平行同位角相等;两直线平行内错角相等;两直线平行同旁内角互补.A.30° B.45° C.60° D.90°【考点】平行线的性质.【分析】由直角三角板的特点可得:∠C=30°,然后根据两直线平行内错角相等,即可求∠CAE的度数.【解答】解:∵∠C=30°,BC∥DE,∴∠CAE=∠C=30°.故选A.【点评】此题考查了平行线的性质,解题的关键是:熟记两直线平行同位角相等;两直线平行内错角相等;两直线平行同旁内角互补.A.80° B.75° C.70° D.65°【考点】平行线的性质.【分析】根据EF∥AC,求出∠EFB=∠C=60°,再根据DF∥AB,求出∠DFC=∠B=45°,从而求出∠EFD=180°﹣60°﹣45°=75°.【解答】解:∵EF∥AC,∴∠EFB=∠C=60°,∵DF∥AB,∴∠DFC=∠B=45°,∴∠EFD=180°﹣60°﹣45°=75°,故选B.【点评】本题考查了平行线的性质,找到平行线、得到相应的同位角或内错角是解题的关键.A.20° B.30° C.40° D.70°【考点】平行线的性质.【分析】延长ED交BC于F,根据平行线的性质求出∠MFC=∠B=70°,求出∠FDC=40°,根据三角形外角性质得出∠C=∠MFC﹣∠MDC,代入求出即可.【解答】解:延长ED交BC于F,∵AB∥DE,∠ABC=70°,∴∠MFC=∠B=70°,∵∠CDE=140°,∴∠FDC=180°﹣140°=40°,∴∠C=∠MFC﹣∠MDC=70°﹣40°=30°,故选B.【点评】本题考查了三角形外角性质,平行线的性质的应用,解此题的关键是求出∠MFC的度数,注意:两直线平行,同位角相等.A.70° B.80° C.110°D.120°【考点】平行线的性质.【分析】根据平行线的性质求出∠3=∠1=70°,即可求出答案.【解答】解:∵直线l1∥l2,∠1=70°,∴∠3=∠1=70°,∴∠2=180°﹣∠3=110°,故选C.【点评】本题考查了平行线的性质,邻补角定义的应用,解此题的关键是求出∠3的度数,注意:两直线平行,同位角相等.A.70 B.65 C.60 D.55【考点】平行线的性质.【分析】先由垂直的定义,求出∠PEF=90°,然后由∠BEP=50°,进而可求∠BEF=140°,然后根据两直线平行同旁内角互补,求出∠EFD的度数,然后根据角平分线的定义可求∠EFP的度数,然后根据三角形内角和定理即可求出∠EPF的度数.【解答】解:如图所示,∵EP⊥EF,∴∠PEF=90°,∵∠BEP=50°,∴∠BEF=∠BEP+∠PEF=140°,∵AB∥CD,∴∠BEF+∠EFD=180°,∴∠EFD=40°,∵FP平分∠EFD,∴=20°,∵∠PEF+∠EFP+∠EPF=180°,∴∠EPF=70°.故选:A.【点评】此题考查了平行线的性质,解题的关键是:熟记两直线平行同位角相等;两直线平行内错角相等;两直线平行同旁内角互补.A.152°B.118°C.28° D.62°【考点】平行线的性质.【分析】根据两直线平行,同位角相等求出∠1的同位角,再根据对顶角相等求解.【解答】解:∵如图,l1∥l2,∠1=62°,∴∠3=∠1=62°,∴∠2=∠3=62°(对顶角相等),故选D.【点评】本题考查了平行线的性质,是基础题,熟记性质是解题的关键.A.30° B.40° C.50°D.70°【考点】平行线的性质.【分析】根据平行线的性质求出∠C,根据等腰三角形的性质得出∠B=∠C=70°,根据三角形内角和定理求出即可.【解答】解:∵AB=AC,∴∠B=∠C,∵AD∥BC,∠1=70°,∴∠C=∠1=70°,∴∠B=70°,∴∠BAC=180°﹣∠B﹣∠C=180°﹣70°﹣70°=40°,故选B.【点评】本题考查了三角形内角和定理,等腰三角形的性质,平行线的性质的应用,解此题的关键是求出∠C的度数和得出∠B=∠C,注意:三角形内角和等于180°,两直线平行,内错角相等.A.50° B.40° C.30° D.25°【考点】平行线的性质.【分析】由两直线平行,同位角相等,可求得∠3的度数,然后求得∠2的度数.【解答】解:如图,,∵∠1=50°,∴∠3=∠1=50°,∴∠2=90°﹣50°=40°.故选B.【点评】此题考查了平行线的性质.注意两直线平行,同位角相等定理的应用是解此题的关键.A.26° B.36° C.46° D.56°【考点】平行线的性质.【分析】如图,首先运用平行线的性质求出∠AOB的大小,然后借助平角的定义求出∠3即可解决问题.【解答】解:如图,∵直线l4∥l1,∴∠1+∠AOB=180°,而∠1=124°,∴∠AOB=56°,∴∠3=180°﹣∠2﹣∠AOB=180°﹣88°﹣56°=36°,故选B.【点评】该题主要考查了平行线的性质及其应用问题;应牢固掌握平行线的性质,这是灵活运用、解题的基础和关键.A.50° B.30° C.20° D.15°【考点】平行线的性质;三角形的外角性质.【分析】如图,首先运用平行线的性质求出∠4,然后借助三角形的外角性质求出∠3,即可解决问题.【解答】解:由题意得:∠4=∠2=40°;由外角定理得:∠4=∠1+∠3,∴∠3=∠4﹣∠1=40°﹣20°=20°,故选C.【点评】该题主要考查了三角形外角的性质、平行线的性质等几何知识点及其应用问题;解题的关键是牢固掌握三角形外角的性质、平行线的性质等几何知识点,这也是灵活运用、解题的基础.A.110°B.90° C.70° D.50°【考点】平行线的性质.【分析】根据平行线的性质得出∠2=∠3,然后根据对顶角相等得出∠3=∠1=70°,即可求出答案.【解答】解:∵∠3=∠1=70°,∵直线l1∥l2,∴∠3=∠2,∵∠3=∠1=70°,∴∠2=70°,故选C.【点评】本题考查了平行线的性质的应用,注意:两直线平行,同位角相等.A.100°B.90° C.80° D.70°【考点】平行线的性质;三角形内角和定理.【分析】先根据平行线的性质求出∠C的度数,再根据三角形内角和定理求出∠A的度数即可.【解答】解:∵DE∥BC,∠AED=40°,∵∠B=40°,∴∠A=180°﹣∠C﹣∠B=180°﹣40°﹣60°=80°.【点评】本题考查的是平行线的性质及三角形内角和定理,先根据平行线的性质求出∠C的度数是解答此题的关键.A.64° B.63° C.60° D.54°【考点】平行线的性质.【分析】先根据平行线的性质求出∠BEN的度数,再由角平分线的定义得出∠BEF的度数,根据平行线的性质即可得出∠2的度数.【解答】解:∵AB∥CD,∠1=63°,∴∠BEN=∠1=63°.∵EN平分∠BEF,∴∠BEF=2∠BEN=126°,∴∠2=180°﹣∠BEF=180°﹣126°=54°.故选D.【点评】本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等;两直线平行,同旁内角互补.也考查了角平分线定义.二、填空题(共10小题)【考点】平行线的性质.【专题】计算题.【分析】先根据平行线的性质得∠2=∠1=120°,然后根据三角形外角性质计算∠ACB的大小.【解答】解:∵l∥m,∴∠2=∠1=120°,∴∠ACB=120°﹣55°=65°.故答案为65°.【点评】本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.【考点】平行线的性质;垂线.【分析】先根据a⊥c得出∠1=90°,再由直线a∥b可得出∠1=∠2=90°,由此可得出结论.【解答】解:如图所示,∵a⊥c,∴∠1=90°.∵a∥b,∴∠1=∠2=90°,∴b⊥c.故答案为:⊥.【点评】本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等.【考点】平行线的性质.【分析】由平行线的性质可求得∠B,在△ABC中利用三角形外角的性质可求得∠2.【解答】解:∵l1∥l2,∴∠B=∠1=60°,∵∠2为△ABC的一个外角,∴∠2=∠B+∠A=60°+40°=100°,故答案为:100°.【点评】本题主要考查平行线的性质,掌握平行线的性质是解题的关键,即①两直线平行⇔同位角相等,②两直线平行⇔内错角相等,③两直线平行⇔同旁内角互补【考点】平行线的性质.【专题】计算题.【分析】先根据平行线的性质,由l1∥l2得∠3=∠1=40°,再根据平行线的判定,由∠α=∠β得AB∥CD,然后根据平行线的性质得∠2+∠3=180°,再把∠1=40°代入计算即可.【解答】解:如图,∵l1∥l2,∴∠3=∠1=40°,∵∠α=∠β,∴AB∥CD,∴∠2+∠3=180°,∴∠2=180°﹣∠3=180°﹣40°=140°.故答案为140°.【点评】本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.【考点】平行线的性质;三角形的外角性质.【分析】根据AB∥CD,求出∠DFE=56°,再根据三角形外角的定义性质求出∠E的度数.【解答】解:∵AB∥CD,∴∠DFE=∠A=56°,又∵∠C=27°,∴∠E=56°﹣27°=29°,故答案为29°.【点评】本题考查了平行线的性质、三角形的外角的性质,找到相应的平行线是解题的关键.【考点】平行线的性质.【分析】根据邻补角定义求出∠3的度数,再根据平行线的性质求出∠2的度数即可.【解答】解:如图,∵∠1=100°,∴∠3=180°﹣100°=80°,∵m∥n,∴∠2=∠3=80°.故答案为80°.【点评】本题考查了平行线的性质,找到相应的同位角是解题的关键.【考点】平行线的性质.【分析】先根据对顶角相等,∠1=65°,求出∠3的度数,再由两直线平行,同旁内角互补得出∠2的度数.【解答】解:解:∵∠1=125°,∴∠3=∠1=125°,∵a∥b,∴∠2=180°﹣∠3=180°﹣125°=55°.故答案为:55°.【点评】本题考查了平行线的性质,对顶角的性质,熟记定理是解题的关键.【考点】平行线的性质;三角形的外角性质.【分析】首先由平行线的性质可求得∠4的度数,然后再根据三角形的外角的性质即可求得∠3的度数.【解答】解:如图:∵a∥b,∴∠4=∠1=50°.由三角形的外角的性质可知:∠4=∠2+∠3,∴∠3=∠4﹣∠2=50°﹣30°=20°.故答案为:20°.【点评】本题主要考查的是三角形的外角的性质和平行线的性质,熟练掌握三角形的外角的性质和平行线的性质是解题的关键.【考点】平行线的性质.【分析】两直线平行,同旁内角互补,据此进行解答.【解答】解:∵a∥b,∠1=120°,∴∠2=180°﹣∠1=180°﹣120°=60°,故答案为:60°【点评】本题考查了平行线的性质.注意两直线平行,同旁内角互补.【考点】平行线的性质.【分析】根据FG∥CD得出∠GFB=∠DCF,再由互补和角平分线得出∠DCF=(180°﹣α),解答即可.【解答】解:∵点A,C,F,B在同一直线上,∠ECA为α,∴∠ECB=180°﹣α,∵CD平分∠ECB,∴∠DCB=(180°﹣α),∵FG∥CD,∴∠GFB=∠DCB=90﹣.【点评】此题考查平行线的性质,关键是根据平行线得出∠GFB=∠DCF和利用角平分线解答.三、解答题(共1小题)【考点】平行线的性质.【分析】由平行线的性质得到∠ABC=∠1=65°,∠ABD+∠BDC=180°,由BC平分∠ABD,得到∠ABD=2∠ABC=130°,于是得到结论.【解答】解:∵AB∥CD,∴∠ABC=∠1=65°,∠ABD+∠BDC=180°,∵BC平分∠ABD,∴∠ABD=2∠ABC=130°,∴∠BDC=180°﹣∠ABD=50°,∴∠2=∠BDC=50°.【点评】本题考查了平行线的性质和角平分线定义等知识点,解此题的关键是求出∠ABD的度数,题目较好,难度不大.。
华东师大版七年级上册第5章《相交线与平行线》训练卷(解析版)
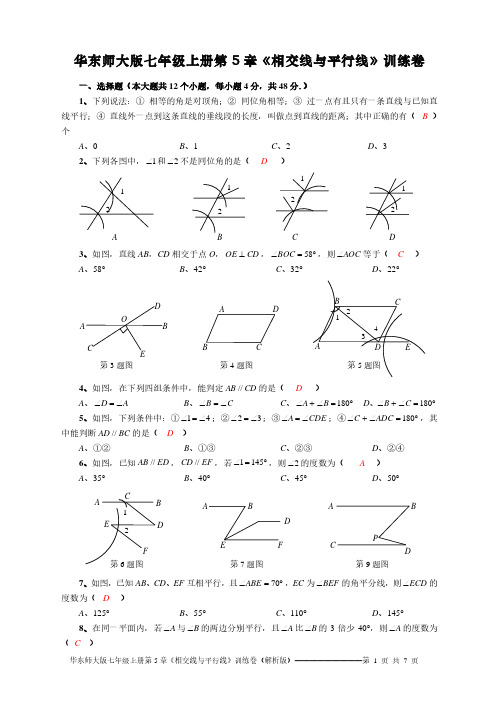
华东师大版七年级上册第5章《相交线与平行线》训练卷一、选择题(本大题共12个小题,每小题4分,共48分.)1、下列说法:① 相等的角是对顶角;② 同位角相等;③ 过一点有且只有一条直线与已知直线平行;④ 直线外一点到这条直线的垂线段的长度,叫做点到直线的距离;其中正确的有( B )个A 、0B 、1C 、2D 、32、下列各图中,1∠和2∠不是同位角的是( D )3、如图,直线AB ,CD 相交于点O ,CD OE ⊥,︒=∠58BOC ,则AOC ∠等于( C ) A 、58° B 、42°C 、32°D 、22°4、如图,在下列四组条件中,能判定CD AB //的是( D )A 、A D ∠=∠B 、C B ∠=∠ C 、︒=∠+∠180B AD 、︒=∠+∠180C B 5、如图,下列条件中:①41∠=∠;②32∠=∠;③CDE A ∠=∠;④︒=∠+∠180ADC C ,其中能判断BC AD //的是( D )A 、①②B 、①③C 、②③D 、②④ 6、如图,已知ED AB //,EF CD //,若︒=∠1451,则2∠的度数为( A )A 、35°B 、40°C 、45°D 、50°7、如图,已知AB 、CD 、EF 互相平行,且︒=∠70ABE ,EC 为BEF ∠的角平分线,则ECD ∠的度数为( D )A 、125°B 、55°C 、110°D 、145°8、在同一平面内,若A ∠与B ∠的两边分别平行,且A ∠比B ∠的3倍少40°,则A ∠的度数为( C )1 F第7题图ED ABPC第9题图DABF第6题图EDA C B2第3题图DA CBO第4题图DA C B1 234第5题图EDA CB 1 2 A12 B12C12 DA 、20°B 、125°C 、20°或125°D 、无法确定 9、如图,CD AB //,︒=∠︒=∠1545D B ,,则P ∠的度数是( D ) A 、15°B 、30°C 、45°D 、60°10、如图,CD AB //,将一副直角三角板作如下摆放,︒=∠60GEF ,︒=∠45MNP .下列结论:①MP GE //;②︒=∠150EFN ;③︒=∠65BEF ;④︒=∠35AEG .其中正确的个数是( B )A 、1B 、2C 、3D 、411、如图,如果EF AB //,CD EF //,下列各式正确的是( D ) A 、︒=∠−∠+∠90321 B 、︒=∠+∠−∠90321 C 、︒=∠+∠+∠90321 D 、︒=∠−∠+∠9013212、如图,BC AB ⊥,AE 平分BAD ∠交BC 于E ,DE AE ⊥,︒=∠+∠9021,M 、N 分别是BA ,CD 延长线上的点,点E 在BC 上,下列结论:①CD AB //;②DEC EAD ∠=∠;③︒=∠+∠180ADC AEB ;④DE 平分ADC ∠,其中正确的有( C )A 、1个B 、2个C 、3个D 、4个二、填空题(本大题共4个小题,每小题4分,共16分)13、如图所示,已知直线AB ,CD 相交于O ,OA 平分EOC ∠,︒=∠70EOC ,则____=∠BOD ; 【答案】︒3514、如图,直线AB 与CD 相交于点O ,射线OE 平分BOD ∠,若︒=∠20DOE ,则____=∠BOC ; 【答案】140°15、如图所示,CD AB //,若︒=∠120ABE ,︒=∠40ECD ,则____=∠BEC ;【答案】100度 16、如图,已知AE 平分BAC ∠,AE BE ⊥于E ,AC ED //,若︒=∠32BAE ,则____=∠BED ; 【答案】︒122三、解答题(本大题6个小题,共56分。
最新华东师大版七年级数学上册《相交线与平行线》单元测试题解析版

《第5章相交线与平行线》一、选择题1.如图,点P是直线a外的一点,点A、B、C在直线a上,且PB⊥a,垂足是B,PA⊥PC,则下列不正确的语句是()A.线段PB的长是点P到直线a的距离B.PA、PB、PC三条线段中,PB最短C.线段AC的长是点A到直线PC的距离D.线段PC的长是点C到直线PA的距离2.在一个平面内,任意四条直线相交,交点的个数最多有()A.7个B.6个C.5个D.4个3.如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=35°,则∠2的度数为()A.10° B.20° C.25° D.30°4.如图,直线a,b被直线c所截,∠1与∠2的位置关系是()A.同位角B.内错角C.同旁内角 D.对顶角5.如图,AB∥EF,CD⊥EF,∠BAC=50°,则∠ACD=()A.120°B.130°C.140°D.150°6.如图,是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是()A.同位角相等,两直线平行B.内错角相等,两直线平行C.两直线平行,同位角相等D.两直线平行,内错角相等7.如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,则∠AED=()A.65° B.115°C.125°D.130°8.某商品的商标可以抽象为如图所示的三条线段,其中AB∥CD,∠EAB=45°,则∠FDC的度数是()A.30° B.45° C.60° D.75°9.如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是()A.60° B.50° C.40° D.30°10.下列说法正确的是()(1)如果∠1+∠2+∠3=180°,那么∠1与∠2与∠3互为补角;(2)如果∠A+∠B=90°,那么∠A是余角;(3)互为补角的两个角的平分线互相垂直;(4)有公共顶点且又相等的角是对顶角;(5)如果两个角相等,那么它们的余角也相等.A.1个B.2个C.3个D.4个二、填空题11.已知a,b,c为平面内三条不同直线,若a⊥b,c⊥b,则a与c的位置关系是.12.将一副直角三角板ABC和EDF如图放置(其中∠A=60°,∠F=45°).使点E落在AC边上,且ED∥BC,则∠CEF的度数为.13.如图△ABC中,∠A=90°,点D在AC边上,DE∥BC,若∠1=155°,则∠B的度数为.14.如图,与∠1构成同位角的是,与∠2构成内错角的是.15.如图,已知∠1=∠2,∠B=40°,则∠3= .16.如图,已知AB∥CD,BC∥DE.若∠A=20°,∠C=120°,则∠AED的度数是.17.上午九点时分针与时针互相垂直,再经过分钟后分针与时针第一次成一条直线.18.如图,AB∥CD,直线EF分别交AB、CD于M,N两点,将一个含有45°角的直角三角尺按如图所示的方式摆放,若∠EMB=75°,则∠PNM等于度.三、解答题(共46分)19.)如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,求∠ADE的度数.20.小明到工厂去进行社会实践活动时,发现工人师傅生产了一种如图所示的零件,工人师傅告诉他:AB∥CD,∠BAE=45°,∠1=60°,小明马上运用已学的数学知识得出∠ECD的度数.你能求出∠ECD的度数吗?如果能,请写出理由.21.如图,要测量两堵墙所形成的∠AOB的度数,但人不能进入围墙,如何测量请你写出两种不同的测量方法,并说明几何道理.22.如图所示,直线AB、CD相交于O,OE平分∠AOD,∠FOC=90°,∠1=40°,求∠2和∠3的度数.23.如图,∠1和∠2是哪两条直线被哪一条直线所截形成的?它们是什么角?∠1和∠3是哪两条直线被哪一条直线所截形成的?它们是什么角?24.将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.(1)求证:CF∥AB;(2)求∠DFC的度数.25.如图,直线AB∥CD,直线EF分别交AB、CD于点M、N,∠EMB=50°,MG平分∠BMF,MG交CD 于G,求∠1的度数.《第5章相交线与平行线》参考答案与试题解析一、选择题1.如图,点P是直线a外的一点,点A、B、C在直线a上,且PB⊥a,垂足是B,PA⊥PC,则下列不正确的语句是()A.线段PB的长是点P到直线a的距离B.PA、PB、PC三条线段中,PB最短C.线段AC的长是点A到直线PC的距离D.线段PC的长是点C到直线PA的距离【考点】点到直线的距离.【分析】利用点到直线的距离的定义、垂线段最短分析.【解答】解:A、根据点到直线的距离的定义:即点到这一直线的垂线段的长度.故此选项正确;B、根据垂线段最短可知此选项正确;C、线段AP的长是点A到直线PC的距离,故选项错误;D、根据点到直线的距离即点到这一直线的垂线段的长度.故此选项正确.故选C.【点评】本题主要考查了点到直线的距离的定义,及垂线段最短的性质.2.在一个平面内,任意四条直线相交,交点的个数最多有()A.7个B.6个C.5个D.4个【考点】相交线.【专题】分类讨论.【分析】在平面上画出4条直线,当这4条直线经过同一个点时,有1个交点;当3条直线经过同一个点,第4条不经过该点时,有4个交点;当4条直线不经过同一点时,有6个交点.故可得出答案.【解答】解:如图所示:①当4条直线经过同一个点时,有1个交点;②当3条直线经过同一个点,第4条不经过该点时,有4个交点;③当4条直线不经过同一点时,有6个交点.综上所述,4条直线相交最多有6个交点.故选B.【点评】此题在相交线的基础上,着重培养学生的观察、实验能力.3.如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=35°,则∠2的度数为()A.10° B.20° C.25° D.30°【考点】平行线的性质.【分析】延长AB交CF于E,求出∠ABC,根据三角形外角性质求出∠AEC,根据平行线性质得出∠2=∠AEC,代入求出即可.【解答】解:如图,延长AB交CF于E,∵∠ACB=90°,∠A=30°,∴∠ABC=60°,∵∠1=35°,∴∠AEC=∠ABC﹣∠1=25°,∵GH∥EF,∴∠2=∠AEC=25°,故选C.【点评】本题考查了三角形的内角和定理,三角形外角性质,平行线性质的应用,主要考查学生的推理能力.4.如图,直线a,b被直线c所截,∠1与∠2的位置关系是()A.同位角B.内错角C.同旁内角 D.对顶角【考点】同位角、内错角、同旁内角;对顶角、邻补角.【分析】根据内错角的定义求解.【解答】解:直线a,b被直线c所截,∠1与∠2是内错角.故选B.【点评】本题考查了同位角、内错角、同位角:三线八角中的某两个角是不是同位角、内错角或同旁内角,完全由那两个角在图形中的相对位置决定.在复杂的图形中判别三类角时,应从角的两边入手,具有上述关系的角必有两边在同一直线上,此直线即为截线,而另外不在同一直线上的两边,它们所在的直线即为被截的线.5.如图,AB∥EF,CD⊥EF,∠BAC=50°,则∠ACD=()A.120°B.130°C.140°D.150°【考点】平行线的性质;垂线.【分析】如图,作辅助线;首先运用平行线的性质求出∠DGC的度数,借助三角形外角的性质求出∠ACD即可解决问题.【解答】解:如图,延长AC交EF于点G;∵AB∥EF,∴∠DGC=∠BAC=50°;∵CD⊥EF,∴∠CDG=90°,∴∠ACD=90°+50°=140°,故选C.【点评】该题主要考查了垂线的定义、平行线的性质、三角形的外角性质等几何知识点及其应用问题;解题的方法是作辅助线,将分散的条件集中;解题的关键是灵活运用平行线的性质、三角形的外角性质等几何知识点来分析、判断、解答.6.如图,是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是()A.同位角相等,两直线平行B.内错角相等,两直线平行C.两直线平行,同位角相等D.两直线平行,内错角相等【考点】作图—基本作图;平行线的判定.【分析】由已知可知∠DPF=∠BAF,从而得出同位角相等,两直线平行.【解答】解:∵∠DPF=∠BAF,∴AB∥PD(同位角相等,两直线平行).故选:A.【点评】此题主要考查了基本作图与平行线的判定,正确理解题目的含义是解决本题的关键.7.如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,则∠AED=()A.65° B.115°C.125°D.130°【考点】平行线的性质.【分析】根据平行线性质求出∠CAB的度数,根据角平分线求出∠EAB的度数,根据平行线性质求出∠AED的度数即可.【解答】解:∵AB∥CD,∴∠C+∠CAB=180°,∵∠C=50°,∴∠CAB=180°﹣50°=130°,∵AE平分∠CAB,∴∠EAB=65°,∵AB∥CD,∴∠EAB+∠AED=180°,∴∠AED=180°﹣65°=115°,故选B.【点评】本题考查了角平分线定义和平行线性质的应用,注意:平行线的性质有:①两条平行线被第三条直线所截,同位角相等,②两条平行线被第三条直线所截,内错角相等,③两条平行线被第三条直线所截,同旁内角互补.8.某商品的商标可以抽象为如图所示的三条线段,其中AB∥CD,∠EAB=45°,则∠FDC的度数是()A.30° B.45° C.60° D.75°【考点】平行线的性质.【专题】几何图形问题.【分析】由邻补角的定义即可求得∠BAD的度数,又由AB∥CD,即可求得∠ADC的度数,则问题得解.【解答】解:∵∠EAB=45°,∴∠BAD=180°﹣∠EAB=180°﹣45°=135°,∵AB∥CD,∴∠ADC=∠BAD=135°,∴∠FDC=180°﹣∠ADC=45°.故选B.【点评】此题考查了平行线的性质.注意两直线平行,内错角相等.9.如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是()A.60° B.50° C.40° D.30°【考点】平行线的性质;垂线.【分析】根据直角三角形的两锐角互余,求出∠D=40°,再根据平行线的性质即可解答.【解答】解:如图所示,∵FE⊥BD,∴∠FED=90°,∴∠1+∠D=90°,∵∠1=50°,∴∠D=40°,∵AB∥CD,∴∠2=∠D=40°.故选C.【点评】本题主要考查平行线的性质、垂线及直角三角形的性质,解决此题时,根据直角三角形的性质求出∠D的度数是解决此题的关键.10.下列说法正确的是()(1)如果∠1+∠2+∠3=180°,那么∠1与∠2与∠3互为补角;(2)如果∠A+∠B=90°,那么∠A是余角;(3)互为补角的两个角的平分线互相垂直;(4)有公共顶点且又相等的角是对顶角;(5)如果两个角相等,那么它们的余角也相等.A.1个B.2个C.3个D.4个【考点】对顶角、邻补角;余角和补角.【分析】根据定义及定理分别判断各命题,即可得出答案.【解答】解:(1)互为补角的应是两个角而不是三个,故错误;(2)没说明∠A是∠B的余角,故错误;(3)互为邻补角的两个角的平分线互相垂直,故错误;(4)根据对顶角的定义可判断此命题错误.(5)相等角的余角相等,故正确.综上可得(5)正确.故选A.【点评】本题考查对顶角及邻补角的知识,难度不大,注意熟练掌握各定义定理.二、填空题11.已知a,b,c为平面内三条不同直线,若a⊥b,c⊥b,则a与c的位置关系是平行.【考点】平行线的判定;垂线.【分析】根据在同一平面内,如果两条直线同时垂直于同一条直线,那么这两条直线平行可得答案.【解答】解:∵a⊥b,c⊥b,∴a∥c,故答案为:平行.【点评】此题主要考查了平行线的判定,关键是掌握在同一平面内,如果两条直线同时垂直于同一条直线,那么这两条直线平行.12.将一副直角三角板ABC和EDF如图放置(其中∠A=60°,∠F=45°).使点E落在AC边上,且ED∥BC,则∠CEF的度数为15°.【考点】平行线的性质.【分析】根据直角三角形两锐角互余求出∠1,再根据两直线平行,内错角相等求出∠2,然后根据∠CEF=45°﹣∠2计算即可得解.【解答】解:∵∠A=60°,∠F=45°,∴∠1=90°﹣60°=30°,∠DEF=90°﹣45°=45°,∵ED∥BC,∴∠2=∠1=30°,∠CEF=∠DEF﹣∠2=45°﹣30°=15°.故答案为:15°.【点评】本题考查了平行线的性质,直角三角形两锐角互余的性质是基础题,熟记性质是解题的关键.13.如图△ABC中,∠A=90°,点D在AC边上,DE∥BC,若∠1=155°,则∠B的度数为65°.【考点】平行线的性质;直角三角形的性质.【专题】探究型.【分析】先根据平角的定义求出∠EDC的度数,再由平行线的性质得出∠C的度数,根据三角形内角和定理即可求出∠B的度数.【解答】解:∵∠1=155°,∴∠EDC=180°﹣155°=25°,∵DE∥BC,∴∠C=∠EDC=25°,∵△ABC中,∠A=90°,∠C=25°,∴∠B=180°﹣90°﹣25°=65°.故答案为:65°.【点评】本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等.14.如图,与∠1构成同位角的是∠B ,与∠2构成内错角的是∠BDE .【考点】同位角、内错角、同旁内角.【分析】两个角分别在被截线的同一方,并且都在截线的同侧,具有这种位置关系的两个角叫做同位角,与∠1构成同位角的是∠B;两个角都在被截线之间,并且都在截线的两侧,具有这种位置关系的两个角,叫做内错角,与∠2构成内错角的是∠BDE.【解答】解;根据同位角、内错角的定义,与∠1构成同位角的是∠B,与∠2构成内错角的是∠BDE.【点评】正确记忆同位角以及内错角的定义是解决本题的关键.15.如图,已知∠1=∠2,∠B=40°,则∠3= 40°.【考点】平行线的判定与性质.【专题】计算题.【分析】由∠1=∠2,根据“内错角相等,两直线平行”得AB∥CE,再根据两直线平行,同位角相等即可得到∠3=∠B=40°.【解答】解:∵∠1=∠2,∴AB∥CE,∴∠3=∠B,而∠B=40°,∴∠3=40°.故答案为40°.【点评】本题考查了平行线的判定与性质:内错角相等,两直线平行;两直线平行,同位角相等.16.如图,已知AB∥CD,BC∥DE.若∠A=20°,∠C=120°,则∠AED的度数是80°.【考点】平行线的性质.【分析】延长DE交AB于F,根据平行线的性质得到∠AFE=∠B,∠B+∠C=180°,根据三角形的外角的性质即可得到结论.【解答】解:延长DE交AB于F,∵AB∥CD,BC∥DE,∴∠AFE=∠B,∠B+∠C=180°,∴∠AFE=∠B=60°,∴∠AED=∠A+∠AFE=80°,故答案为:80°.【点评】本题考查了平行线的性质,三角形的外角的性质,熟练掌握平行线的性质是解题的关键.17.上午九点时分针与时针互相垂直,再经过16分钟后分针与时针第一次成一条直线.【考点】钟面角.【专题】计算题.【分析】9点后分针与时针第一次成一条直线,则分针再3与4之间,时针在9与10之间,设9点时x分时,分针与时针第一次成一条直线,根据分针每分钟转动6°,时针每分钟转动0.5°,则x•6°﹣3×30°=x•0.5°,然后解方程即可.【解答】解:9点时x分时,分针与时针第一次成一条直线,根据题意得x•6°﹣3×30°=x•0.5°,解得x=16,即9时16分钟时分针与时针第一次成一条直线.故答案为.【点评】本题考查了钟面角:钟面被分成12大格,每大格为30°;分针每分钟转动6°,时针每分钟转动0.5°.18.如图,AB∥CD,直线EF分别交AB、CD于M,N两点,将一个含有45°角的直角三角尺按如图所示的方式摆放,若∠EMB=75°,则∠PNM等于30 度.【考点】平行线的性质.【分析】根据平行线的性质得到∠DNM=∠BME=75°,由等腰直角三角形的性质得到∠PND=45°,即可得到结论.【解答】解:∵AB∥CD,∴∠DNM=∠BME=75°,∵∠PND=45°,∴∠PNM=∠DNM﹣∠DNP=30°,故答案为:30.【点评】本题考查了平行线的性质,等腰直角三角形的性质,熟练掌握平行线的性质是解题的关键.三、解答题(共46分)19.如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,求∠ADE的度数.【考点】平行线的性质;三角形内角和定理.【分析】先根据三角形内角和定理求出∠BAC的度数,再由角平分线的性质求出∠BAD的度数,根据平行线的性质即可得出结论.【解答】解:∵在△ABC中,∠B=46°,∠C=54°,∴∠BAC=180°﹣46°﹣54°=80°.∵AD平分∠BAC,∴∠BAD=∠BAC=40°.∵DE∥AB,∴∠ADE=∠BAD=40°.【点评】本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等.20.(8分)小明到工厂去进行社会实践活动时,发现工人师傅生产了一种如图所示的零件,工人师傅告诉他:AB∥CD,∠BAE=45°,∠1=60°,小明马上运用已学的数学知识得出∠ECD的度数.你能求出∠ECD的度数吗?如果能,请写出理由.【考点】平行线的性质.【分析】首先过点E作EF∥AB,又由AB∥CD,可得EF∥AB∥CD,然后由两直线平行,内错角相等,求得∠FEA的度数与∠C=∠FEC,又由∠AEC=60°,即可求得∠C的度数.【解答】解:∠ECD=15°.理由:如图,过点E作EF∥AB,∵AB∥CD,∴EF∥AB∥CD,∴∠BAE=∠AEF=45°,∠ECD=∠FEC,∴∠CEF=∠AEC﹣∠AEF=60°﹣45°=15°,∴∠ECD=15°.【点评】此题主要考查了平行线的性质,注意掌握两直线平行,内错角相等与辅助线的添加方法是解此题的关键.21.如图,要测量两堵墙所形成的∠AOB的度数,但人不能进入围墙,如何测量请你写出两种不同的测量方法,并说明几何道理.【考点】对顶角、邻补角.【专题】应用题.【分析】根据平角的定义以及对顶角相等的性质进行设计方案.【解答】解:方法一:延长AO到C,测量∠BOC,利用邻补角的数量关系求∠AOB.∵∠AOB=180°﹣∠BOC.方法二:延长AO到C,延长BO到D,测量∠DOC,利用对顶角相等求∠AOB.∴∠AOB=∠DOC.【点评】能够运用数学知识解决生活中的问题,提高数学知识的应用能力.22.如图所示,直线AB、CD相交于O,OE平分∠AOD,∠FOC=90°,∠1=40°,求∠2和∠3的度数.【考点】对顶角、邻补角;角平分线的定义.【专题】计算题.【分析】由已知∠FOC=90°,∠1=40°结合平角的定义,可得∠3的度数,又因为∠3与∠AOD互为邻补角,可求出∠AOD的度数,又由OE平分∠AOD可求出∠2.【解答】解:∵∠FOC=90°,∠1=40°,AB为直线,∴∠3+∠FOC+∠1=180°,∴∠3=180°﹣90°﹣40°=50°.∠3与∠AOD互补,∴∠AOD=180°﹣∠3=130°,∵OE平分∠AOD,∴∠2=∠AOD=65°.【点评】本题主要考查邻补角的概念以及角平分线的定义.23.如图,∠1和∠2是哪两条直线被哪一条直线所截形成的?它们是什么角?∠1和∠3是哪两条直线被哪一条直线所截形成的?它们是什么角?【考点】同位角、内错角、同旁内角.【分析】根据同位角的概念作答.准确识别同位角、内错角、同旁内角的关键,是弄清哪两条直线被哪一条线所截.也就是说,在辨别这些角之前,要弄清哪一条直线是截线,哪两条直线是被截线.【解答】解:∠1和∠2是直线EF、DC被直线AB所截形成的同位角,∠1和∠3是直线AB、CD被直线EF所截形成的同位角.【点评】同位角,即位置相同,两个角都在第三条直线的同旁,同在被截两条直线的上方或下方.在截线的同旁找同位角和同旁内角,在截线的两旁找内错角.要结合图形,熟记同位角、内错角、同旁内角的位置特点,比较它们的区别与联系.24.将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.(1)求证:CF∥AB;(2)求∠DFC的度数.【考点】平行线的判定;角平分线的定义;三角形内角和定理.【专题】证明题.【分析】(1)首先根据角平分线的性质可得∠1=45°,再有∠3=45°,再根据内错角相等两直线平行可判定出AB∥CF;(2)利用三角形内角和定理进行计算即可.【解答】(1)证明:∵CF平分∠DCE,∴∠1=∠2=∠DCE,∵∠DCE=90°,∴∠1=45°,∵∠3=45°,∴∠1=∠3,∴AB∥CF(内错角相等,两直线平行);(2)∵∠D=30°,∠1=45°,∴∠DFC=180°﹣30°﹣45°=105°.【点评】此题主要考查了平行线的判定,以及三角形内角和定理,关键是掌握内错角相等,两直线平行.25.如图,直线AB∥CD,直线EF分别交AB、CD于点M、N,∠EMB=50°,MG平分∠BMF,MG交CD 于G,求∠1的度数.【考点】平行线的性质;角平分线的定义;对顶角、邻补角.【专题】计算题.【分析】根据角平分线的定义,两直线平行内错角相等的性质解答即可.【解答】解:∵∠EMB=50°,∴∠BMF=180°﹣∠EMB=130°.∵MG平分∠BMF,∴∠BMG=∠BMF=65°,∵AB∥CD,∴∠1=∠BMG=65°.【点评】主要考查了角平分线的定义及平行线的性质,比较简单.。
第5章 相交线与平行线数学七年级上册-单元测试卷-华师大版(含答案)

第5章相交线与平行线数学七年级上册-单元测试卷-华师大版(含答案)一、单选题(共15题,共计45分)1、若∠A与∠B是对顶角且互补,则它们两边所在的直线()A.互相垂直B.互相平行C.既不垂直也不平行D.不能确定2、如图,,、、分别平分、和。
以下结论:①;②;③;④. 其中正确的结论是()A.①②③B.②③④C.①③④D.①②④3、下列说法正确的个数是()①同一平面内,过一点有且只有一条直线与已知直线垂直;②同一平面内,过一点有且只有一条直线与已知直线平行;③若三条直线a⊥c,b⊥c,则a∥b;④9的平方根是3;⑤﹣2是4的平方根;⑥平方根等于本身的数是0和1.A.1个B.2个C.3个D.4个4、如下图,在下列条件中,能判定AB//CD的是()A.∠1=∠3B.∠2=∠3C.∠1=∠4D.∠3=∠45、把一块直尺与一块三角板如图放置,若∠1=40°,则∠2的度数为()A.130°B.140°C.120°D.125°6、过一点画已知直线的平行线,则( )A.有且只有一条B.有两条C.不存在D.不存在或只有一条7、如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=15°,那么∠2的度数是()A.30°B.25°C.20°D.15°8、如图,若乙、丙都在甲的北偏东70°方向上,乙在丁的正北方向上,且乙到丙、丁的距离相同.则α的度数是()A.25°B.30°C.35°D.40°9、如图,已知直线,,,则的度数为()A.115°B.95°C.90°D.65°10、如图,直线a∥b,直线c分别与a,b相交,∠1=50°,则∠2的度数为()A.150°B.130°C.100°D.50°11、如图,将三角板的直角顶点放在直角尺的一边上,∠1=30°,∠2=50°,则∠3的度数为( )A.80°B.50°C.30°D.20°12、下列四个命题是真命题的是()A.内错角相等B.如果两个角的和是180°,那么这两个角是邻补角 C.在同一平面内,平行于同一条直线的两条直线互相平行 D.在同一平面内,垂直于同一条直线的两条直线互相垂直13、直线a、b、c、d位置如图,∠1=58°,∠2=58°,∠3=70°,则∠4=()A.58°B.70°C.110°D.116°14、下列定理中,没有逆定理的是()A.两直线平行,同旁内角互补B.线段垂直平分线上的点到线段两端点距离相等C.两个全等三角形的对应角相等D.在角的平分线上的点到这个角的两边的距离相等15、如图,下列条件中:(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.其中能判定AB∥CD的条件个数有()A.4B.3C.2D.1二、填空题(共10题,共计30分)16、如图,将一张长方形纸条折叠,若,则的度数为________.17、把一张长方形纸片沿折叠后与的交点为,、分别折到、的位置上,若,则________.18、如图,若要,需增加条件________.(填一个即可)19、如图,直线AB,CD相交于点O,OE⊥AB,O为垂足,∠EOD=26°,则∠AOC=________,∠COB=________.20、如图,现给出下列条件:①∠1=∠B,②∠2=∠5,③∠3=∠4,④∠BCD+∠D=180°,⑤∠B+∠BCD=180°,其中能够得到AB∥CD的条件有________.(填序号)21、平面上有10条直线,其中有4条直线是互相平行,那么这10条直线最多将平面分成________ 个部分.22、如图,在中,角是边上的一点,作垂直, 垂直,垂足分别为,则的最小值是________.23、如图,EF∥AD,∠1=∠2.说明:∠DGA+∠BAC=180°.请将说明过程填写完成.解:∵EF∥AD,(已知)∴∠2=________.(________)又∵∠1=∠2,(________)∴∠1=∠3,(________)∴AB∥________,(________)∴∠DGA+∠BAC=180°.(________)24、按图填空,并注明理由.已知:如图,∠1=∠2,∠3=∠E.求证:AD∥BE.证明:∵∠1=∠2 (已知)∴________∥________(________ )∴∠E=∠________(________ )又∵∠E=∠3 (已知)∴∠3=∠________(________ )∴AD∥BE.(________ )25、完成下列证明:如图,已知AD BC,EF BC,1= 2.求证:DG//BA.证明:因为AD BC.EF BC(已知).所以EFB= ADB= ________,所以EFB= ADB(等量代换),所以EF//AD________,所以1= BAD________,又因为1= 2(已知),所以________= ________(等量代换),所以DG//BA________.三、解答题(共5题,共计25分)26、如图,直线a∥b,△DCB中,AB与DC垂直,点A在线段BC上,直线b经过点C.若∠1=73°﹣∠B,求∠2的度数.27、如图,∠1=121°,∠2=120°,∠3=120°,试写出其中的平行线,并说明理由.28、如图,DF∥AB,∠B=∠EFD,且∠AFE=65°,求∠C的度数.29、如图,∠E=∠1,∠3+∠ABC=180°,BE是∠ABC的角平分线.你能判断DF与AB的位置关系吗?请说明理由.30、如图,CD⊥AB于D,点F是BC上任意一点,FE⊥AB于E,且∠1=∠2.求证:∠3=∠ACB.下面给出了部分证明过程和理由,请补全所有内容.证明:∵CD⊥AB,FE⊥AB∴∠BDC=∠BEF=90°(__▲__)∴EF∥DC(__▲__)∴∠2=__▲__(_▲__)又∵∠2=∠1(已知)∴∠1=__▲_(等量代换)∴DG∥BC(_▲_)∴∠3=∠ACB(两直线平行,同位角相等)参考答案一、单选题(共15题,共计45分)1、A2、D3、B4、C5、A6、D7、A8、C9、A10、B11、D12、C13、C14、C15、B二、填空题(共10题,共计30分)16、17、18、20、21、22、23、24、25、三、解答题(共5题,共计25分)27、29、。
第5章 相交线与平行线数学七年级上册-单元测试卷-华师大版(含答案)

第5章相交线与平行线数学七年级上册-单元测试卷-华师大版(含答案)一、单选题(共15题,共计45分)1、如图所示,由已知条件推出结论正确的是( )A.由∠1=∠5,可以推出AB∥CDB.由∠3=∠7,可以推出AD∥BCC.由∠2=∠6,可以推出AD∥BCD.由∠4=∠8,可以推出AD∥BC2、如图,其中能判定的是( )A. B. C. D..3、下面是投影屏上出示的解答题,需要回答横线上符号代表的内容.如图,直线直线,在中,,顶点在上,顶点在上,且平分,若,求的度数.解:∵,,∴_______①_______,∵直线直线,∴_____②______ ,∵平分,∴_____③_____= ,∵直线直线,∴___④_____= ,下列选项错误的是()A.①代表64°B.②代表C.③代表D.④代表4、如图,下列说法中,正确的是()A.因为∠A+∠D=180°,所以AB∥CDB.因为∠C+∠D=180°,所以AB∥CDC.因为∠A+∠D=180°,所以AD∥BCD.因为∠A+∠C=180°,所以AB∥CD5、如图,0M⊥NP,ON⊥NP,所以ON与OM重合,理由是()A.两点确定一条直线B.同一平面内,经过一点有且只有一条直线与已知直线垂直C.过一点只能作一直线D.垂线段最短6、如图,直线,则的度数为()A.150°B.140°C.130°D.120°7、下列语句不正确的是()A.在同一平面内,过直线外一点有且只有一条直线与已知直线平行.B.两直线被第三直线所截,如果同位角相等,那么两直线平行C.两点确定一条直线D.内错角相等8、如图,直线AB,CD相交于点O,OE⊥CD于点O,∠BOC=140°,则∠AOE的度数等于()A.40°B.50°C.60°D.70°9、下列说法中,正确的是()A.在同一平面内,不相交的两条直线必平行B.过任意一点可作一条已知直线的平行线C.两条直线被第三条直线所截,所得到同位角相等D.两条直线的交点叫做垂足10、如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=32°,那么∠2的度数是()A.32 °B.58 °C.68 °D.60 °11、如图所示,l1∥l2,图中与直线l垂直的直线是()A.直线aB.直线lC.直线a,bD.直线a,b,c12、如图,AB∥CD,∠1=70°,∠AEF=90°,则∠A的度数为( )A.70°B.60°C.40°D.20°13、如图,在一张长方形纸片上画一条线段AB,将右侧部分纸片四边形ABCD沿线段AB翻折至四边形ABC'D',若∠ABC=58°,则∠1=()A.60°B.64°C.42°D.52°14、如图,AF是∠BAC的平分线,EF∥AC交AB于点E,若∠1=155°,则∠BEF的度数为( )A.50°B.12.5°C.25°D.15°15、如图,点E在AD延长线上,下列条件中不能判定BC∥AD的是()A. B. C. D.二、填空题(共10题,共计30分)16、如图,抛物线y= (p>0),点F(0,p),直线l:y=-p.已知抛物线上的点到点F的距离与到直线l的距离相等,过点F的直线与抛物线交于A,B两点,AA1⊥l,BB1⊥l,垂足分别为A1、B1,连接A1F,B1F,A1O,B1O。
华东师大版七年级数学上册第五章相交线与平行线单元测试题(含答案)

华东师大版七年级数学上册第五章相交线与平行线单元测试题一.选择题(每小题4分,共40分)1 •下列图形可以由一个图形经过平移变换得到的是( )3•对于命题“若a 2>b\则a>b\下而四组关于g 方的值中,能说明这个命题是假命题的是()A.B.D.A ・ “=3, b=2 B. a — - 3, b=2C ・“=3, b= - 1 D. a=・ 1, b=34•如图,下列判断中错误的是( )A.ZA 与Z1是同位角 C. Z4与Z1是内错角5. 如图,ZBAC=9O% AD 丄BC 于点 D, A.点C 到AB 的垂线段是线段ACC.线段AB 的长度是点B 到AC 的距离B.ZA 与ZB 是同旁内角 D.Z1与Z3是同位角则下列结论中错误的是()B.点A 到BC 的距离是线段AD 的长度 D •线段AB 是点B 到的距离D.B DCB第4题图6. 如图,给岀了过直线外一点作已知直线的平行线的方法,英依据是() A.同位角相等,两直线平行 B.内错角相等,两直线平行 C.同旁内角互补,两直线平行 D.两直线平行,同位角相等7. 下列说法正确的个数是()①同位角相等;②过一点有且只有一条直线与已知直线垂直:③过一点有且只有一条直线与已知直线平行:④三条直线两两相交,总有三个交点; ⑤若 a//b> b//c> 则 a//c.A ・1个 B.2个 C.3个 D.4个8. 如图,ABCD 为一长方形纸带,AB//CD.将ABCD 沿EF 折,爪D 两点分别与从 D 对应,若Z1 = 2Z2,则ZAEF 的度数为()9. 如图,Zl=68。
,直线“平移后得到直线6则Z2- Z3的度数为()10. 如图,AB//CD,则下列各式中正确的是() A.Zl = 180°-Z3二.填空题(每小题4分,共24分)11. 直线,松、CD 相交于点O,若ZJOC= 50% 12. 如图,测量运动员跳远成绩选取的是AB 的长度,其依据是.A .60°B.65°C. 72°D. 75°B.Z1 = Z3-Z2C.Z2+Z3=180°-ZlD. Z2+Z3 = 180°+Zl则 ZBOD= 第12題图13 •若直线a丄S b丄g则直线。
第5章 相交线与平行线数学七年级上册-单元测试卷-华师大版(含答案)

第5章相交线与平行线数学七年级上册-单元测试卷-华师大版(含答案)一、单选题(共15题,共计45分)1、在同-平面内,若∠A与∠B的两边分别垂直,且∠A比∠B的3倍少40°,则∠A的度数为()A.20°B.55°C.20°或 125°D.20°或55°2、如图,已知直线a∥b,将一块含有30°角的三角板ABC的一锐角顶点B放在直线a 上,直角顶点C放在直线b上,一直角边AC与直线a交于点D.若∠1=45°,那么∠ABD的度数是()A.10°B.15°C.30°D.45°3、如图,AB∥CD,EC分别交AB,CD于点F,C,连结DF,点G是线段CD上的点,连结FG.若∠1=∠3,∠2=∠4,则结论①∠C=∠D;②FG⊥CD;③EC⊥FD中,正确的是()A.①②B.②③C.①③D.①②③4、如图,直线a、b被直线c所截,下列条件能使a∥b的是()A.∠1=∠6B.∠2=∠6C.∠1=∠3D.∠5=∠75、如图,直线a∥b,∠1=60°,∠2=40°,则∠3等于()A.40°B.60°C.80°D.100°6、如图,AB//CD,∠A=50°,则∠1的度数是()A.40°B.50°C.130°D.150°7、如图,在下列给出的条件中,不能判定AB∥DF的是()A.∠1=∠AB.∠A=∠3C.∠1=∠4D.∠A+∠2=180°8、如图所示,已知AC⊥BC,CD⊥AB,垂足分别是C,D,那么以下线段大小的比较必定成立的是()A.CD>ADB.AC<BCC.BC>BDD.CD<BD9、下列说法正确的是()A.垂线段最短B.线段最短C.过A、B两点作直线AB垂直于直线 D.过A、B两点作直线AB平行于直线10、如图,直线,,则c与b相交所形成的度数为()A. B. C. D.11、如图,在中,,,是的平分线,经过A,D两点的圆的圆心O恰好落在上,分别与、相交于点E、F.若圆半径为2.则阴影部分面积().A. B. C. D.12、如图,A处在B处的北偏东45°方向,A处在C处的北南偏西15°方向,则∠BAC等于()A.30°B.45°C.50°D.60°13、如图①,一张四边形纸片ABCD,∠A=50°,∠C=150°.若将其按照图②所示方式折叠后,恰好MD′∥AB,ND′∥BC,则∠D的度数为().A.70°B.75°C.80°D.85°14、将一直角三角板与两边平行的纸条如图放置.若∠1=50°,则∠2的度数为()A.30°B.40°C.50°D.60°15、如图,点A的坐标为(-3,-2),⊙A的半径为1,P为坐标轴上一动点,PQ切⊙A 于点Q,在所有P点中,使得PQ长最小时,点P的坐标为()A.(0,-2)B.(0,-3)C.(-3,0)或(0,-2)D.(-3,0)二、填空题(共10题,共计30分)16、如图,∠A=70°,O是AB上一点,直线OD与AB所夹的∠AOD=100°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转________.17、经过一点________一条直线垂直于已知直线.18、将一块木板与一块含30°的直角三角板如图放置,若AD∥BC,∠DEG=34°,则∠BFE 的度数为________.19、如图,O是⊙O的圆心,点A、B、C在⊙O上,AO∥BC,∠AOB=38º,则∠OAC的度数是________.20、如图所示,若∠1+∠2=180°,∠3=75°,则∠4=________度.21、数一数下面的图形中有多少组互相平行的线段,有多少组互相垂直相交的线段.(1)图1:互相平行:________ 组;互相垂直:________ 组.(2)图2:互相平行:________ 组;互相垂直:________ 组.22、下列说法中:①同位角相等;②过一个点有且只有一条直线与已知直线垂直;③两直线相交成的四个角中相邻两角的角平分线互相垂直;④三条直线两两相交,总有三个交点;⑤若a∥b,b∥c,则a∥c;⑥若a⊥b,b⊥c,则a⊥c.其中正确的说法是________23、若直线a∥b,a⊥c,则直线b ________c.24、如图,a∥b,点在直线a上,且AB⊥BC,∠1=30°,那么∠2=________.25、如图,填空①如果∠1=∠2,那么根据________,可得________∥________;②如果∠DAB+∠ABC=180°,那么根据________,可得________∥________.③当________∥________时,根据________,得∠3=∠C.三、解答题(共5题,共计25分)26、已知:如图,,求证:.27、完成下面的证明:已知,如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD 求证:∠EGF=90°证明:∵HG∥AB(已知)∴∠1=∠3________又∵HG∥CD(已知)∴∠2=∠4∵AB∥CD(已知)∴∠BEF+________=180°________又∵EG平分∠BEF(已知)∴∠1= ∠________又∵FG平分∠EFD(已知)∴∠2= ∠________∴∠1+∠2= (________)∴∠1+∠2=90°∴∠3+∠4=90°________即∠EGF=90°.28、如图,△ABC中BD、CD平分∠ABC、∠ACB,过D作直线平行于BC,交AB,AC于E,F,求证:EF=BE+CF.29、已知:如图,∠ABC=∠ADC,DE是∠ADC的平分线,BF是∠ABC的平分线,且DE//BF.求证:∠1=∠3.30、如图,四边形ABCD中,AD∥BC,F为AB边上一点,且∠ADF=∠CDB,射线DF、CB 相交于点E,∠BFE=∠CBD.求证:AB∥CD.参考答案一、单选题(共15题,共计45分)1、C2、B4、B5、C6、C7、A8、C9、A10、C11、C12、D13、C14、B15、D二、填空题(共10题,共计30分)16、17、18、19、21、22、23、24、25、三、解答题(共5题,共计25分)26、27、28、29、30、。
第5章 相交线与平行线数学七年级上册-单元测试卷-华师大版(含答案)

第5章相交线与平行线数学七年级上册-单元测试卷-华师大版(含答案)一、单选题(共15题,共计45分)1、如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E,若∠E=35°,则∠BAC的度数为()A.40°B.45°C.50°D.55°2、点A为直线l外一点,点B在直线l上,若AB=5厘米,则点A到直线l的距离为()A.就是5厘米B.大于5厘米C.小于5厘米D.最多为5厘米3、在同一平面内有三条直线,若其中有两条且只有两条直线平行,则它们交点的个数为( )A.0个B.1个C.2个D.3个4、如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过F作DE∥BC,交AB于点D,交AC于点E.若BD=3,DE=5,则线段EC的长为( )A.3B.4C.2D.2.55、如图,将一副三角板按如图放置,∠BAC=∠DAE=90°,∠B=45°,∠E=60°,则下列结论正确的有()个.①∠1=∠3;②∠CAD+∠2=180°;③如果∠2=30°,则有AC∥DE;④如果∠2=30°,则有BC∥AD.A.4B.3C.2D.16、如图,直线l1∥l2,等腰Rt△ABC的直角顶点C在l1上,顶点A在l2上,若∠β=14°,则∠α=()A.31°B.45°C.30°D.59°7、如图,六边形ABCDEF的内角都相等,∠DAB=60°,AB=DE,则下列结论成立的个数是()①AB∥DE;②EF∥AD∥BC;③AF=CD;④四边形ACDF是平行四边形;⑤六边形ABCDEF既是中心对称图形,又是轴对称图形.A.2B.3C.4D.58、如图,△ABC中,∠C=90°,点D在AC边上,DE∥AB,若∠ADE=46°,则∠B的度数是()A.34°B.44°C.46°D.54°9、如图,下列结论中不正确的是()A.若AD∥BC,则∠1=∠BB.若∠1=∠2,则AD∥BCC.若∠2=∠C,则AE∥CDD.若AE∥CD,则∠1+∠3=180°10、如图所示,因为AB⊥l,BC⊥l,B为垂足,所以AB和BC重合,其理由是()A.两点确定一条直线B.在同一平面内,过一点有且只有一条直线与已知直线垂直C.过一点能作一条垂线D.垂线段最短11、如图,在四边形ABCD中,点E在BC上,连接AE,DE,∠BAE=∠EDC=47°,若AE∥CD,∠B=65°,则下列说法中不正确的是()A.∠C=∠AEBB.AB∥DEC.∠DEC=65°D.∠AEB=58°12、下列说法中正确的是()A.过一点有且只有一条直线平行于已知直线B.两条直线被第三直线所截,同位角相等C.两条直线有两种位置关系:平行、相交D.同一平面内,垂直于同一条直线的两条直线平行13、如图,若∠A+∠D=180°,∠B=60°,则∠1等于()A.120°B.80°C.60°D.40°14、如图,把矩形 ABCD 沿 EF 对折后使两部分重合,若∠1=50°,则∠AEF=()A.110°B.115°C.65°D.130°15、如图AB∥CD,则∠1=()A.75°B.80°C.85°D.95°二、填空题(共10题,共计30分)16、如图,在梯形ABCD中,AD平行于BC,AC⊥AB,AD=CD,cos∠DCA=0.8,BC=10,边AB的长为________.17、用一张正方形纸片折成一个“小蝌蚪”图案(如图1)。
第5章 相交线与平行线数学七年级上册-单元测试卷-华师大版(含答案)

第5章相交线与平行线数学七年级上册-单元测试卷-华师大版(含答案)一、单选题(共15题,共计45分)1、如图,,点在上,,若,则()A.70°B.145°C.110°D.140°2、下列命题中,真命题有()(1)直线外一点与直线上各点连接的所有线段中,垂线段最短;(2)两条直线被第三条直线所截,内错角相等;(3)经过两点有一条直线,并且只有一条直线;(4)如果一条直线和两条直线中的一条垂直,那么这条直线也和另一条垂直.A.1个B.2个C.3个D.4个3、如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐的角∠A是120°,第二次拐的角∠B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是( ).A.120°B.130°C.140°D.150°4、如图,AB∥CD.BC⊥CD于点C,EC平分∠BEF,若∠1=35°,则∠2的度数()A.110°B.115°C.120°D.130°5、如图,已知,,,则的度数是()A. B. C. D.6、图中,∠1与∠2是对顶角的是()A. B. C. D.7、在同一平面内,两条直线的位置关系可能是()A.相交、平行B.相交、垂直C.平行、垂直D.平行、相交、垂直8、如图,直线l1∥l2, AB=BC,CD⊥AB于点D,若∠DCA=20°,则∠1的度数为()A.80°B.70°C.60°D.50°9、如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF,以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°﹣∠ABD;④∠BDC=∠BAC.其中正确的结论有()A.4个B.3个C.2个D.1个10、已知直线a∥b,将一块含45°角的直角三角板(∠C=90°)按如图所示的位置摆放,若∠1=60°,则∠2的度数是()A.70°B.75°C.80°D.85°11、如图,在纸片中,,将绕着点A按逆时针方向旋转到的位置(点B’、C’分别为点B、C的对应点),连接,若' ,则的度数为()A. B. C. D.12、如图,直线AB,CD相交于点O,OE⊥AB于O,若∠BOD=40°,则不正确的结论是()A.∠AOC=40°B.∠COE=130°C.∠EOD=40°D.∠BOE=90°13、如图,直线,被直线所截,下列条件一定能判定直线的是()A. B. C. D.14、如图,直线a∥b,直线c与a、b均相交.如果∠1=50°,那么∠2的度数是()A.50°B.100°C.130°D.150°15、如图,AB平行CD,如果∠B=20°,那么∠C为( )A.40°B.20°C.60°D.70°二、填空题(共10题,共计30分)16、如图,一把直尺沿直线断开并错位,点E、D、B、F在同一直线上,若∠ADE=145°,则∠DBC的度数为________.17、以下四个命题:①在同一平面内,过一点有且只有一条直线与已知直线垂直;②两条直线被第三条直线所截,同旁内角互补;③数轴上的每一个点都表示一个实数;④如果点的坐标满足,那么点一定在第二象限.其中正确命题的序号为________.18、如图,已知,,,则________.19、如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠A=∠CDE;④∠ABC+∠C=180∘.其中,能推出AB∥CD 的条件是________(填序号)20、如图所示,AB⊥l1, AC⊥l2,则点A到直线l1的距离是线段________的长度.21、如图,已知AB∥CD,点E,F分别在直线AB,CD上点P在AB,CD之间且在EF的左侧.若将射线EA沿EP折叠,射线FC沿FP折叠,折叠后的两条射线互相垂直,则∠EPF的度数为________.22、如图,,平分,的度数是 ________.23、如图,a∥b,∠1=110°,∠3=40°,则∠2=________°24、如图,△ABC中,∠C=90°,AD平分∠BAC,CD=3cm,点P是边AB上的动点,则DP长的最小值为________ cm.25、如图,a∥b,∠1=40°,∠2=80°,则∠3=________ 度.三、解答题(共5题,共计25分)26、如图,将△ABC绕点C顺时针旋转90°后得△DEC,若BC∥DE,求∠B的度数.27、在平面上有三条直线a,b,c,它们之间有哪几种可能的位置关系?你能画出来吗?28、如图有下面三个判断:①∠A=∠F,②∠C=∠D,③∠1=∠2,请你用其中两个作为条件,余下一个作为结论,编一道证明题并写出证明过程.29、如图,AB∥CD,∠CED=90°,∠BED=40°,求∠C的度数.30、如图,已知AB⊥CD,EF⊥AB,∠DGC=105°,∠BCA=75°,请说明∠CEF+∠CDG=180°的理由.参考答案一、单选题(共15题,共计45分)1、A2、B3、D4、A5、C6、C7、A8、B9、A10、B11、C12、C13、C14、C15、B二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)26、28、29、。
第5章 相交线与平行线数学七年级上册-单元测试卷-华师大版(含答案)

第5章相交线与平行线数学七年级上册-单元测试卷-华师大版(含答案)一、单选题(共15题,共计45分)1、以下四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是()A.如图1,展开后测得∠1=∠2B.如图2,展开后测得∠1=∠2且∠3=∠4 C.如图3,测得∠1=∠2 D.如图4,展开后再沿CD折叠,两条折痕的交点为O,测得OA=OB,OC=OD2、若A,B,C是直线l上的三点,P是直线l外一点,且PA=5cm,PB=4cm,PC=3cm,则点P到直线l的距离 ( )A.等于3 cmB.大于3 cm而小于4 cm ;C.不大于3cm D.小于3 cm3、如图,直线l1∥l2,若∠1=140°,∠2=70°,则∠3的度数是( )A.60°B.65°C.70°D.80°4、如图,直线AB∥EF,点C是直线AB上一点,点D是直线AB外一点,若∠BCD=95°,∠CDE=25°,则∠DEF的度数是()A.110°B.115°C.120°D.125°5、如图BD∥AC, , BE 平分∠ABD ,交AC于点E. 若∠A=30º,则∠1的度数为()A.65°B.60°C.75°D.70°6、下列命题真命题的个数有()①经过一点有且只有一条直线与已知直线平行;②直线外一点与直线上各点连接的所有线段中,垂线段最短;③若a b,则c﹣a c﹣b ;④同位角相等;A.3个B.2个C.1个D.0个7、如图,矩形ABCD沿AE折叠,使D点落在BC边上的F点处,如果∠BFA=30°,那么∠CEF等于()A.20°B.30°C.45°D.60°8、如图,AB//CD,∠CDE=140°,则∠A的度数为()A.140°B.60°C.50°D.40 °9、如图,AB∥CD,点E在BC上,DE⊥BC,∠B=40°,则∠D的度数为()A.40°B.50°C.38°D.60°10、△ABC中AB=AC,AB的垂直平分线交AB于点D,交直线AC于点E,∠AEB=70°,那么∠BAC等于()A.55°或125°B.65°C.55°D.125°11、如图,∠A=35°,∠B=∠C=90°,则∠D的度数是()A.35°B.45°C. 55°D.65°12、如图所示,CD⊥AB,垂足为D,点F是BC上任意一点,FE⊥AB,垂足为E,且∠CDG=∠BFE,∠AGD=80°,∠ACB的度数为().A.50°B.55°C.80°D.60°13、一辆汽车在公路上行驶,两次拐弯后,仍在原来的方向上平行行驶,那么两个拐弯的角度可能为()A.先右转30°,后右转40°B.先右转50°,后左转100°C.先右转50°,后左转130°D.先右转50°,后左转50°14、如图,直线a、b被直线c所截,若a∥b,则∠1与∠2满足的关系式()A.∠1=∠2B.∠1>∠2C.∠1+∠2=180°D.∠1<∠215、如图,AB∥CD∥EF,则下列式子正确的是( )A.∠1+∠2-∠3=180°B.∠1+∠2+∠3=180°C.∠2+∠3-∠1=180°D.∠1-∠2+∠3=180°二、填空题(共10题,共计30分)16、如图,直线a∥b,∠1=110°,∠2=55°,则∠3的度数为________.17、把一块直尺与一块三角板如图放置,若∠1=40°,则∠2的度数为________18、如图,△ABC中,D,E分别在边AB,AC上,DE∥BC.若∠A=60°,∠B=70°,则∠AED的度数为________.19、如图把三角板的直角顶点放在直线b上,若∠1=40°,则当∠2=________ 度时,a∥b.20、如图,直线,的顶点在直线上,边与直线相交于点.若是等边三角形,,则=________°21、如图,在△ABC中,BC=8cm,BP、CP分别是∠ABC和∠ACB的平分线,且PD∥AB,PE ∥AC,则△PDE的周长是________ cm.22、已知:AB、CD相交于点O,∠1=80°,如果DE∥AB,求∠D的度数为________.23、如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并证明你的结论.解:∠C与∠AED相等,理由如下:∵∠1+∠2=180°(已知),∠1+∠DFE=180°(邻补角定义)∴∠2=________.(________.),∴AB∥EF(________.)∴∠3=________.(________.)又∠B=∠3(已知)∴∠B=________.(等量代换)∴DE∥BC(________.)∴∠C=∠AED(________.).24、如图,AB∥CD,直线EF分别交AB,CD于M,N两点,将一把含有45°角的直角三角尺按如图所示的方式摆放.若∠EMB=75°,则∠PNM=________25、如图,把一张长方形纸条按图中那样折叠后,若得到∠AOB′=70°,则∠OGC=________.三、解答题(共5题,共计25分)26、如图,直线a∥b,△DCB中,AB与DC垂直,点A在线段BC上,直线b经过点C.若∠1=73°﹣∠B,求∠2的度数.27、如图,直线AB,CD相交于点O.射线OF⊥CD于点O,∠BOF=30°,求∠BOD,∠AOD的度数.28、如图,为了加固房屋,要在屋架上加一根横梁DE,使DE∥BC.如果∠ABC=31°,∠ADE应为多少度?29、如图,点E在DF上,点B在AC上,,.求证:∥.30、如图,DE⊥AB,垂足为D,EF∥AC,∠A=30°,(1)求∠DEF的度数;(2)连接BE,若BE同时平分∠ABC和∠DEF,问EF与BF垂直吗?为什么?参考答案一、单选题(共15题,共计45分)1、C2、C3、C4、C5、C6、C7、B8、D9、B10、A11、A12、C13、D14、A二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)27、29、。
第5章 相交线与平行线数学七年级上册-单元测试卷-华师大版(含答案)

第5章相交线与平行线数学七年级上册-单元测试卷-华师大版(含答案)一、单选题(共15题,共计45分)1、如图,∠1与∠2是()A.对顶角B.同位角C.内错角D.同旁内角2、如图,AB∥CD,∠EFD=64°,∠FEB的角平分线EG交CD于点G,则∠GEB的度数为()A.66°B.56°C.68°D.58°3、如图,已知直线a,b平行,又被直线c所截,那么∠1的同位角是()A.∠5B.∠4C.∠3D.∠24、如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上,若∠1=20°,则∠2的度数是()A.15°B.20°C.25°D.30°5、一副直角三角板如图叠放在一起,点D在AC上,点F在BA上,BC∥FD,∠A=∠FDE=90°,则∠BFE的度数为()A.60°B.65°C.70°D.75°6、如图,将矩形纸带ABCD,沿EF折叠后,C、D两点分别落在C′、D′的位置,经测量得∠EFB=65°,则∠AED′的度数是()A.65°B.55°C.50°D.25°7、如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是()A.∠3=∠4B.∠A=∠DCEC.∠D=∠DCED.∠D+∠ACD=180°8、如图,下列条件:①∠1=∠3,②∠2+∠4=180°,③∠4=∠5,④∠2=∠3,⑤∠6=∠2+∠3中能判断直线l1∥l2的有()A.5个B.4个C.3个D.2个9、如图,能判定EB∥AC的条件是()A.∠1=∠2B.∠3=∠4C.∠5=∠6D.∠2=∠310、将一个直角三角板和一把直尺如图放置,如果∠α=44°,则∠β的度数是()A.44°B.45°C.46°D.54°11、如图,,,,则()A. B. C. D.12、如图,直线a∥b,∠1=85°,∠2=30°,则∠3=()A.85°B.60°C.55°D.35°13、如图,已知a∥b,∠1=50°,∠3=10°,则∠2等于()A.30°B.40°C.50°D.60°14、下列说法中:①不相交的两条直线叫做平行线;②对顶角的角平分线在同一直线上;③过一点有且只有一条直线与已知直线平行;④几个实数相乘,积的符号由负因数的个数确定。
第5章 相交线与平行线数学七年级上册-单元测试卷-华师大版(含答案)

第5章相交线与平行线数学七年级上册-单元测试卷-华师大版(含答案)一、单选题(共15题,共计45分)1、下列说法中,正确的个数是()(1)同角的余角相等(2)相等的角是对顶角(3)在同一平面内,不相交的两条直线叫平行线(4)直线外一点与直线上各点连接的所有线段中,垂线段最短.A.1B.2C.3D.42、如图:在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=5,则CE2+CF2等于()A.75B.100C.120D.1253、如图,直线AB∥CD,AF交CD于点E,∠CEF=140°,则∠A等于()A.50°B.45°C.40°D.35°4、如图,直线,将含有角的三角板的直角顶点C放在直线n上,则等于()A. B. C. D.5、下列结论正确的是()A.两直线被第三条直线所截,同位角相等B.三角形的一个外角等于两个内角的和C.多边形最多有三个外角是钝角D.连接平面上三点构成的图形是三角形6、已知:如图,直线a∥b,∠1=50°.∠2=∠3,则∠2的度数为()A.50°B.60°C.65°D.75°7、如图,下列给定的条件中,不能判定的是()A. B. C. D.8、如图,将一块含30°的三角板叠放在直尺上.若∠1=40°,则∠2=()A.45°B.50°C.60°D.70°9、如图,△ABC是一块直角三角板,∠C=90°,∠A=30°,现将三角板叠放在一把直尺上,AC与直尺的两边分别交于点D、E,AB与直尺的两边分别交于点F、G,若∠1=40°,则∠2的度数为()A.40°B.50°C.60°D.70°10、如图,AB是⊙O的直径,点C,D在⊙O上,且点C,D在AB的异侧,连接AD,BD,OD,OC,若∠ABD=15°,且AD∥OC,则∠BOC的度数为()A.120°B.105°C.100°D.110°11、如图,AE∥DB,∠1=85°,∠2=28°,则∠C的度数为()A.55°B.56°C.57°D.60°12、如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=()A.30°B.35°C.40°D.50°13、如图,直线a,b被c所截,a∥b,若∠1=35°,则∠2的大小为()A.35°B.145°C.55°D.125°14、如图,在△ABC中,点D,E,F分别是AB,AC,BC的中点,已知∠ADE=65°,则∠CFE的度数为()A.60°B.65°C.70°D.75°15、如图,下列说法中错误的是()A.∠GBD和∠HCE是同位角B.∠ABD和∠ACE是同位角C.∠FBC和∠ACE是内错角 D.∠GBC和∠BCE是同旁内角二、填空题(共10题,共计30分)16、如图,要在渠岸AB上找一点D,在点D处开沟,把水渠中的水引到C点,要使沟最短,线段CD与渠岸AB的位置关系应是________,理由是________.17、在菱形ABCD中,∠C=∠EDF=60°,AB=1,现将∠EDF绕点D任意旋转,分别交边AB、BC于点E、F(不与菱形的顶点重合),连接EF,则△BEF的周长最小值是________.18、如图,AB∥CD,EP平分∠BEF,FP平分∠DFE,则∠P=________ 。
第5章 相交线与平行线数学七年级上册-单元测试卷-华师大版(含答案)

第5章相交线与平行线数学七年级上册-单元测试卷-华师大版(含答案)一、单选题(共15题,共计45分)1、下列命题是假命题的是()A.垂线段最短B.过一点有且只有一条直线与已知直线垂直C.两点确定一条直线D.过一点有且只有一条直线与已知直线平行2、如图,直线m∥n,∠1=70°,∠2=30°,则∠A等于()A.40°B.45°C.50°D.55°3、下列命题是真命题的是()A.同角的补角相等B.一条直线截另外两条直线所得到的同位角相等 C.有公共顶点且相等的两个角是对顶角 D.两个无理数的和仍是无理数4、如图,OP∥QR∥ST,则下列等式中正确的是()A.∠1+∠2-∠3=90°B.∠2+∠3-∠1=180°C.∠1-∠2+∠3=180°D.∠1+∠2+∠3=180°5、如图,直线l1∥l2, CD⊥AB于点D,∠1=50°,则∠BCD的度数为()A.50°B.45°C.40°D.30°6、下列说法:①两点之间的所有连线中,线段最短;②相等的角是对顶角;③过直线外一点有且仅有一条直线与己知直线平行;④两点之间的距离是两点间的线段.其中正确的个数是()A.1个B.2个C.3个D.4个7、如图,AB∥CD,点E在CB的延长线上,若∠ABE=60°,则∠ECD的度数为()A.120°B.100°C.60°D.20°8、如图,已知点为内一点,,,交于点,若,则的度数为()A. B. C. D.9、如图,直线AB∥CD,AF交CD于点E,∠CEF=140°,则∠A等于()A.35°B.40°C.45D.50°10、如图,AB∥CD,BE平分∠ABC,∠C=36°,那么∠ABE的大小是()A.18°B.24°C.36°D.54°.11、如图,a∥b,则下列结论中正确的是()A.∠1=∠2B.∠2+∠3=180°C.∠1=∠4D.∠2=412、点P为直线l外一点,点A、B、C为直线上三点,PA=2cm,PB=3cm,PC=4cm,则点P 到直线l的距离为()A.等于2cmB.小于2cmC.大于2cmD.不大于2cm13、如图,在△ABC中,∠C=90°。
第5章 相交线与平行线数学七年级上册-单元测试卷-华师大版(含答案)

第5章相交线与平行线数学七年级上册-单元测试卷-华师大版(含答案)一、单选题(共15题,共计45分)1、下列命题: (1)两直线平行,同旁内角互补(2) 同角的补角相等. (3) 直角三角形的两个锐角互余. (4) 同位角相等。
其中真命题的个数()A.1个B.2个C.3个D.4个2、如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是()A.∠3=∠4B.∠D=∠DCEC.∠1=∠2D.∠A BD=∠23、如图,七年级(下)教材第6页给出了利用三角尺和直尺画平行线的一种方法,能说明AB∥DE的条件是()A.∠CAB=∠FDEB.∠ACB=∠DFEC.∠ABC=∠DEFD.∠BCD=∠EFG4、如图,已知直线c与a,b分别交于点A,B,且1=120º,当2=()时,直线a b.A.60ºB.120ºC.30ºD.150º5、体育课上,老师测量某同学的跳远成绩的依据是()A.经过直线外一点,有且只有一条直线与这条直线平行B.两点之间线段最短C.垂线段最短D.两点之间确定一条直线6、下列说法:①两点之间,线段最短;②同旁内角互补;③若AC=BC,则点C是线段AB 的中点;④经过一点有且只有一条直线与这条直线平行,其中正确的说法有()A.1个B.2个C.3个D.4个7、如图,直线a,b被直线c所截,且a∥b,下列结论不正确的是()A.∠1=∠3B.∠2+∠4=180°C.∠1=∠4D.∠2=∠38、如图,把三角板的直角顶点放在直尺的一边上,若,则的度数为()A.30°B.40°C.50°D.60°9、如图,AD∥BE,∠GBE的平分线BF的反向延长线交AD的反向延长线于M点,若∠BAD=70°,则∠M的度数为()A.20°B.35°C.45°D.70°10、如图, 已知直线AB∥CD,∠C=115°,∠A=25°,则∠E的度数是( )A.70°B.80°C.90°D.100°11、如果与的两边分别平行,比的3倍少,则的度数是()A. B. C. 或 D.以上都不对12、如图,在△ABC中,∠BAC=90°,BD平分∠ABC,CD∥AB交BD于点D,已知∠ACB=34°,则∠D的度数为()A.30°B.28°C.26°D.34°13、如图,小章利用一张左、右两边已经破损的长方形纸片ABCD做折纸游戏,他将纸片沿EF折叠后,D,C两点分别落在点D′,C′的位置,∠DEF=∠D′EF,并利用量角器量得∠EFB=66°,则∠AED′的度数为( )A.66°B.132°C.48°D.38°14、如图,直线a∥b,∠1=70°,那么∠2的度数是()A.50°B.60°C.70°D.80°15、如图所示,BD平分∠ABC,DE∥BC,且∠D=30°,则∠AED的度数为()A.50°B.60°C.70°D.80°二、填空题(共10题,共计30分)16、如图,已知,,,则________.17、如图,∠AOB的一边OA为平面镜,∠AOB=37°36′,在OB上有一点E,从E点射出一束光线经OA上一点D反射,反射光线DC恰好与OB平行,则∠DEB的度数是________°.18、△ABC中,BO平分∠ABC,CO平分∠ACB,MN过点O,交AB于M,交AC于N,且MN∥BC,若AB=12cm,AC=18cm,则△AMN周长为________.19、如图,已知,∠1=∠2,CF⊥AB,DE⊥AB,说明:FG∥BC.解:∵CF⊥AB,DE⊥AB(已知)∴∠BED=90°,∠BFC=90°∴∠BED=∠BFC∴ ________∥________( ________)∴∠1=∠__ ________(________ )又∵∠1=∠2(已知)∴∠2=∠BCF∴FG∥BC(________ )20、如图,所示直线AB、CD被直线EF所截,请添加一个条件________ ,使AB∥CD.21、如图,已知AD∥BC,BE平分∠CBD,∠D=110°,那∠EBC的度数是________.22、如图,四边形ABCD中,点M、N分别在AB、BC上,将∆BMN沿MN翻折,得∆FMN,若MF∥AD,FN∥DC,则∠D的度数为________º23、如图,AB∥CD,BE平分∠ABD,DE平分∠BDC,且BE与DE相交于点E,求证∠E=90°证明:∵AB∥CD(________)∴∠ABD+∠BDC=180°(________)∵BE平分∠ABD(________)∴∠EBD= ________(________)又∵DE平分∠BDC∴∠BDE= ________(________)∴∠EBD+∠EDB= ∠ABD+ ∠BDC(________)= (∠ABD+∠BDC)=90°∴∠E=90°.24、如图,∠ADB=90°,则AD________BD;用“<”连接AB,AC,AD,结果是________.25、如图,BC⊥AC,BC=12,AC=9,AB=15,则点C 到线段AB 的距离是________.三、解答题(共5题,共计25分)26、如图,直线a∥b,△DCB中,AB与DC垂直,点A在线段BC上,直线b经过点C.若∠1=73°﹣∠B,求∠2的度数.27、如图,己知∠A=∠1,∠C=∠F,请问BC与EF平行吗?请说明理由.28、如图,AC⊥BC于C,CD⊥AB于D,DE⊥BC于E,试比较四条线段DE、DC、AC、AB的大小.29、如图,直线AB、CD相交于点O,且OE为∠BOC的平分线,DF∥OE,若∠AOC=36°,求∠D的度数.30、如图,直线AB,CD相交于点O,OD平分∠EOB,OF平分∠AOE,GH⊥CD,垂足为H,求证:GH∥FO.参考答案一、单选题(共15题,共计45分)1、C2、C3、A4、B5、C6、A7、D8、D9、B10、C11、C12、B13、C14、C15、B二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)27、29、。
第5章 相交线与平行线数学七年级上册-单元测试卷-华师大版(含答案)

第5章相交线与平行线数学七年级上册-单元测试卷-华师大版(含答案)一、单选题(共15题,共计45分)1、在同一平面内有直线a1, a2, a3, a4,…,a100,若a1⊥a2, a2∥a3, a3⊥a4, a4∥a5,…,按此规律进行下去,则a1与a100的位置关系是()A.平行B.相交C.重合D.无法判断2、如图所示,CD∥AB,OE平分∠AOD,OF⊥OE,∠D=50°,则∠BOF为( )A.35°B.30°C.25°D.20°3、如图,直线AB、CD相交于点E,EF⊥AB于E,若∠CEF=59°,则∠AED的度数为()A.149°B.121°C.95°D.31°4、如下图,已知a⊥b.垂足为O.直线c经过点O,则∠1与∠2的关系一定成立的是( )A.相等B.互余C.互补D.对顶角5、如图,把含30°角的直角三角板的直角顶点C放在直线a上,其中∠A=30°,直角边AC和斜边AB分别与直线b相交,如果a∥b,且∠1=25°,则∠2的度数为()A.20°B.25°C.30°D.35°6、如图,矩形ABCD的顶点A、C分别在直线a、b上,且a//b,∠1=60°,则∠2的度数为()A.30°B.45°C.60°D.75°7、如图,直线AB∥CD,BC平分∠ABD,∠1=65°,则∠2的度数为()A.65°B.50°C.45°D.40°8、如图,下列条件能判定的是 ( )A. B. C. D.9、如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC 于F,M为EF中点,则AM的最小值为( )A. B. C. D.10、如图,将矩形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=32°,则∠GHC等于()A.112°B.110°C.108°D.106°11、为防止森林火灾的发生,会在森林中设置多个观测点.如图.若起火点在观测台的南偏东的方向上.点表示另一处观测台,若那么起火点在观测台的()A.南偏东B.南偏西C.北偏东D.北偏西12、如图,直线为直角,则等于()A. B. C. D.13、如图,在△ABC中,D、E、F分别在AB、BC、AC上,且EF∥AB,要使DF∥BC,只需满足下列条件中的()A.∠1=∠2B.∠2=∠AFDC.∠1=∠AFDD.∠1=∠DFE14、如图,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2的度数是( )A.20°B.25°C.30°D.70°15、已知a∥b,某学生将一直角三角板放置如图所示,如果∠1=35°,那么∠2的度数为()A.35°B.55°C.56°D.65°二、填空题(共10题,共计30分)16、a如图,矩形OABC中,点A、C分别在x轴,y轴的正半轴上,且,点P为线段OA上一动点,则最小值为________.17、在中,点是两边的中点,点是边上的一个动点,如,则________。
第5章 相交线与平行线数学七年级上册-单元测试卷-华师大版(含答案)

第5章相交线与平行线数学七年级上册-单元测试卷-华师大版(含答案)一、单选题(共15题,共计45分)1、如图,直线l与直线a、b分别相交,且a∥b,∠1=110°,则∠2的度数是()A.20°B.70°C.90°D.110°2、下列图形中,∠1与∠2是对顶角的是()A. B. C. D.3、如图,已知D、E在△ABC的边上,DE∥BC,∠B=60°,∠AED=40°,则∠A的度数为()A.100°B.90°C.80°D.70°4、如图,下列说法正确的是()A.若AB∥DC,则∠1=∠2B.若AD∥BC,则∠3=∠4C.若∠1=∠2,则AB∥DCD.若∠2+∠3+∠A=180°,则AB∥DC5、以下四种沿折叠的方法中,由相应条件不一定能判定纸带两条边线a、b互相平行的是()A.展开后测得B.展开后测得且C.测得D.测得6、如图,直线a∥b,,,则的度数是()A. B. C. D.7、如图所示,三角形ABC的面积为1cm2。
AP垂直∠ABC的平分线BP于P。
则与三角形PBC 的面积相等的长方形是( )。
A. B. C. D.8、如图,下列条件中,①;②;③;④,能判断直线的有()A.1个B.2个C.3个D.4个9、如图,直线 a,b 被直线 m 所截,若 a∥b,∠2=72°,则∠1=()A.72°B.98°C.108°D.118°10、如图所示,点在的延长线上,下列条件中能判断的是()A. B. C. D.11、如图,小明课间把老师的三角板的直角顶点放在黑板的两条平行线a、b上,已知∠1=55°,则∠2的度数为()A.45°B.35°C.55°D.125°12、如图,直线a∥b,射线DC与直线a相交于点C,过点D作DE⊥b于点E,已知∠1=25°,则∠2的度数为()A.115°B.125°C.155°D.165°13、如图,AB∥CD,∠A+∠E=75°,则∠C为A.60 °B.65°C.75°D.80°14、如图,下面推理中,正确的是()A.∵∠A+∠D=180°∴AD∥BCB.∵∠C+∠D=180°∴AB∥CDC.∵∠A+∠D=180°∴AB∥CDD.∵∠B+∠C=180°∴AD∥BC15、如图,将三角尺的直角顶点放在直尺的一边上,己知,,则的度数等于().A.50°B.30°C.20°D.15°二、填空题(共10题,共计30分)16、如图,∠1=15°,AO⊥OC,点B、O、D在同一直线上,则∠2=________°.17、如图1是长方形纸带, ∠DEF=17°,将纸带沿EF折叠成图2,再沿BF折叠成图3,则图3中的∠CFE的度数是________.18、如图,直线AB、CD相交于点O,OE⊥AB,O为垂足,如果∠EOD=38°,则∠AOC=________度,∠COB=________度.19、探究:如图①,点A在直线MN上,点B在直线MN外,连结AB,过线段AB的中点P 作PC∥MN,交∠MAB的平分线AD于点C,连结BC,求证:BC⊥AD.应用:如图②,点B在∠MAN内部,连结AB,过线段AB的中点P作PC∥AM,交∠MAB的平分线AD于点C;作PE∥AN,交∠NAB的平分线AF于点E,连结BC、BE.若∠MAN=150°,则∠CBE的大小为________ 度.20、如图,在平面直角坐标系中,一次函数的图象与轴和轴分别相交于、两点.动点从点出发,在线段上以每秒3个单位长度的速度向点作匀速运动,到达点停止运动,点关于点的对称点为点,以线段为边向上作正方形.设运动时间为秒.若正方形对角线的交点为,则的最小值为________ .21、在半径为5的中,弦AB=8,弦CD=6,且AB||CD,则AB与CD间的距离为________.22、如图,三角形中,.三条边中最长的边是________.23、如图,直线,则________.24、如图,矩形ABCD中,点M是CD的中点,点P是AB上的一动点,若AD=1,AB=2,则PA+PB+PM的最小值是________.25、一张纸条的上下边缘,将它折叠成如图所示的形状,若,则的度数是________.三、解答题(共5题,共计25分)26、如图,直线a∥b,△DCB中,AB与DC垂直,点A在线段BC上,直线b经过点C.若∠1=73°﹣∠B,求∠2的度数.27、如图,,,,试探索与有怎样的数量关系,并说明理由.28、如图,点D是△ABC的边AB上一点,点E为AC的中点,过点C作CF∥AB交DE延长线于点F.求证:点E平分DF.29、如图,EG⊥BC于点G,AD⊥BC于点D,∠1=∠E,请证明AD平分∠BAC.30、如图,AC与BD交于点O,AD=CB,点E,F是BD上两点,且AE=CF,DE=BF.证明AE∥CF。
第5章 相交线与平行线数学七年级上册-单元测试卷-华师大版(含答案)

第5章相交线与平行线数学七年级上册-单元测试卷-华师大版(含答案)一、单选题(共15题,共计45分)1、下列说法正确的是()A.同位角相等B.有一个角为60º的等腰三角形一定是等边三角形C.同旁内角相等,两直线平行D.垂直于同一条直线的两条直线平行2、如图,把河中的水引到村庄C拟修水渠中最短的是()A. B. C. D.3、如图,已知AB∥CD,直线EF分别交AB,CD于点E、F,EG平分∠AEF,若∠2=50°,则∠1的度数是()A.70°B.65°C.60°D.50°4、给出下列说法:1. 两条直线被第三条直线所截,同位角相等;2. 平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交;3. 相等的两个角是对顶角;4. 从直线外一点到这条直线的垂线段,叫做这点到直线的距离;其中正确的有()A.0个B.1个C.2个D.3个5、如图,直线c与直线a、b相交,且a∥b,则下列结论:①∠1=∠2;②∠1=∠3;③∠3=∠2中正确的个数为()A.0B.1C.2D.36、如图,直线a∥b,三角板的直角顶点在直线a上,已知∠1=25°,则∠2的度数是A.25°B.55°C.65°D.155°7、如图,要得到AB∥CD,下列结论正确的是()A.∠A=∠EBCB.∠ABC=∠DCFC.∠B=∠DD.∠A+∠ABC=180°8、下列命题:①两直线平行,内错角相等;②如果m是无理数,那么m是无限小数;③64的立方根是8;④同旁内角相等,两直线平行;⑤如果a是实数,那么是无理数.其中正确的有()A.1个B.2个C.3个D.4个9、如图,a∥b,将一块三角板的直角顶点放在直线a上,∠1=42°,则∠2的度数为( )A.46°B.48°C.56°D.72°10、如图,△CEF中,∠E=70°,∠F=50°,且AB∥CF ,AD∥CE,连接BC,CD,则∠A的度数是()A.40°B.45°C.50°D.60°11、如图,AB∥CD,AD=CD,∠1=70°30',则∠2的度数是()A.40°30'B.39°30'C.40°D.39°12、下列说法错误的是().A.过直线外一点有且仅有一条直线与它平行B.相交的两条直线只有一个交点C.经过一点有且只有一条直线与已知直线垂直D.经过两点有且只有一条直线13、如果线段AB与线段CD没有交点,则()A.线段AB与线段CD一定平行B.线段AB与线段CD一定不平行C.线段AB与线段CD可能平行D.以上说法都不正确14、下面四个图形中,∠1=∠2一定成立的是()A. B. C. D.15、下列说法错误的是()A.对顶角一定相等B.在同一平面内,有且只有一条直线和已知直线垂直 C.同位角相等,两直线平行 D.如果两个角的和是90°,那么称这两个角互为余角二、填空题(共10题,共计30分)16、如图两平行线a、b被直线l所截,且∠1=60°,则∠2的度数为________.17、如图,在△ABC中,ED∥BC,∠ABC和∠ACB的平分线分别交ED于点G、F,若BE=3,CD=4,ED=5,则FG的长为________.18、如图,CD平分∠ACB,交AB于点D,DE∥BC,交AC于点E,EF平分∠AED,交AB于点F,连接CF,下列四个结论:①∠CDE=∠DCE;② CD∥EF;③∠CDE=∠CFE;④ S△=S△ADE,其中正确的结论有________ACF19、如图,在△ABC中,高AD与中线CE相交于点F,AD=CE=6,FD=1,则AB=________.20、如图,若,,则________.21、以下五个条件中,能得到互相垂直关系的有________.(填写序号)①对顶角的平分线;②邻补角的平分线;③平行线截得的一组同位角的平分线;④平行线截得的一组内错角的平分线;⑤平行线截得的一组同旁内角的平分线.22、如图,已知CD平分∠ACB,DE∥BC,∠AED=70°,则∠EDC=________.23、如图,五边形ABCDE是正五边形,若l1∥l2,∠1=47°,则∠2=________°.24、已知与的两边分别平行,其中为,的为,则________度.25、如图,已知a∥b,AC⊥AB,AC交直线b于点C,∠1=65°,那么∠2的度数为________.三、解答题(共5题,共计25分)26、如图,已知,∠,求、、的度数.27、如图,已知△ABC中,AD⊥BC于点D,E为AB边上任意一点,EF⊥BC于点F,∠1=∠2.求证:DG∥AB.请把证明的过程填写完整.证明:∵AD⊥BC,EF⊥BC(),∴∠EFB=∠ADB=90°(垂直的定义)∴EF∥▲()∴∠1= ▲()又∵∠1=∠2(已知)∴▲()∴DG∥AB()28、如图,∠AOE与∠BOF互余,那么AO与BO是否垂直?试说明理由.29、如图,己知,,,求的度数.30、如图,点A、B、C、D在一条直线上,CE与BF交于点G,∠A=∠1,CE∥DF,求证:∠E=∠F参考答案一、单选题(共15题,共计45分)1、B2、C4、B5、D6、C7、B8、B9、B10、D11、D12、C13、C14、B15、B二、填空题(共10题,共计30分)16、17、18、19、21、22、23、24、25、三、解答题(共5题,共计25分)26、28、29、30、。
第5章 相交线与平行线数学七年级上册-单元测试卷-华师大版(含答案)

第5章相交线与平行线数学七年级上册-单元测试卷-华师大版(含答案)一、单选题(共15题,共计45分)1、如图,AB∥CD,AD与BC相交于点O,∠B=30°,∠D=40°,则∠AOC的度数为()A.60°B.70°C.80°D.90°2、某城市有四条直线型主干道分别为l1, l2, l3, l4, l3和l4相交,l1和l2相互平行且与l3、l4相交成如图所示的图形,则共可得同旁内角()对.A.4B.8C.12D.163、如图,已知∠1 = 70º,如果CD∥BE,那么∠B的度数为()A.70ºB.100ºC.110ºD.120º4、如图,己知AB∥CD,DB⊥BC,∠1=40°,则∠2的度数为( )A.30°B.40°C.50°D.60°5、将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边在同一条直线上,则∠1的度数为()A.75°B.65°C.45°D.30°6、如图,ABCD为一长方形纸带,AB∥CD,将ABCD沿EF折,A,D两点分别与对应,若∠1=2∠2,则∠AEF的度数为()A.60°B.65°C.72°D.75°7、如图,直线AB∥CD,∠CGF=130°,则∠BFE的度数是()A.30°B.40°C.50°D.60°8、如图,有一条直的宽纸带,按图折叠,则∠α的度数等于()A.50 oB.60 oC.75 oD.85 o9、如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E,若∠E=35°,则∠BAC的度数为()A.40°B.45°C.50°D.55°10、如图,在四边形ABCD中,下列条件中可以判定AD∥BC的是()A.∠1=∠3B.∠2=∠4C.∠B=∠DD.∠B+∠BCD=180°11、如图,在ABCD中,∠BAC=78°,∠ACB=38°,则∠D的度数是()A.52°B.64°C.78°D.38°12、如图,下列说法中,正确的是()A.因为∠A+∠D=180°,所以AD∥BCB.因为∠C+∠D=180°,所以AB∥CDC.因为∠A+∠D=180°,所以AB∥CDD.因为∠A+∠C=180°,所以AB∥CD13、如图,a∥b,若∠1=50°,则∠2的度数为()A.50°B.120°C.130°D.140°14、如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=38°时,∠1=()A.52°B.38°C.42°D.60°15、如图为平面上五条直线L1, L2, L3, L4, L5相交的情形,根据图中标示的角度,判断下列叙述何者正确()A.L1和L3平行,L2和L3平行 B.L1和L3平行,L2和L3不平行 C.L1和L3不平行,L2和L3平行 D.L1和L3不平行,L2和L3不平行二、填空题(共10题,共计30分)16、如图,CD⊥AB,垂足为C,∠1=130°,则∠2=________度.17、如图,△ABC中,IB,IC分别平分∠ABC,∠ACB,过I点作DE∥BC,分别交AB于D,交AC于E,给出下列结论:①△DBI是等腰三角形;②△ACI是等腰三角形;③AI平分∠BAC;④△ADE周长等于AB+AC,其中正确的是: ________(只需填写序号)。
第5章 相交线与平行线数学七年级上册-单元测试卷-华师大版(含答案)
第5章相交线与平行线数学七年级上册-单元测试卷-华师大版(含答案)一、单选题(共15题,共计45分)1、如图,已知∠3=∠4,要得到AB∥CD,需要添加的条件是()A.∠1=∠4B.∠3=∠2C.∠1=∠2D.∠1与∠2互补2、如图是郝老师的某次行车路线,总共拐了三次弯,最后行车路线与开始的路线是平行的,已知第一次转过的角度,第三次转过的角度,则第二次转过的角度是()A. B. C. D.无法确定3、若一副三角板按如图所示放置,则∠EGA的度数为()A.30°B.45°C.60°D.75°4、如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上,若∠1=20°,则∠2的度数是()A.15°B.20°C.25°D.30°5、如图所示,直线a,b被直线c所截,现给出下列四个条件:①∠1=∠5;②∠1=∠7;③∠2+∠3=180°;④∠4=∠7.其中能说明a∥b的条件序号为( )A.①②B.①③C.①④D.③④6、如图,直线 l1∥l2,∠α=∠β,∠1=50°,则∠2的度数为()A.130°B.120°C.115°D.100°7、在同一平面内,直线a、b相交于O,b∥c,则a与c的位置关系是()A.平行B.相交C.重合D.平行或重合8、如图,直线∥,∠1=100°,∠2=125°,则∠A的度数为()A.25°B.30°C.35°D.45°9、如图,在ABCD中,DB=DC,∠C=70°,AE⊥BD于E,则∠DAE等于()A.35°B.30°C.25°D.20°10、如图,AB∥CD,DE⊥CE,∠1=34°,则∠DCE的度数为()A.34°B.56°C.66°D.54°11、如图所示,点E在AC的延长线上,下列条件中不能判断BD∥AE的是()A.∠1=∠2B.∠D+∠ACD=180°C.∠D=∠DCED.∠3=∠412、如图,直线a,b被直线c所截,那么∠1的同位角是()A.∠2B.∠3C.∠4D.∠513、如图,a∥b,则∠A的度数是()A.22°B.32°C.68°D.78°14、如图,AB∥EF∥CD,∠ABC=46°,∠CEF=154°,则∠BCE 等于()A.16°B.20°C.23°D.26°15、如图,BD∥AC,BE平分∠ABD,交AC于点E.若∠A 40°,则∠1的度数为()A.80°B.70°C.60°D.40°二、填空题(共10题,共计30分)16、如图:BE平分∠ABC,DE∥BC.如果∠2=22°,那么∠ADE=________.17、如图已知BE平分∠ABC,E点在线段AD上,∠ABE=∠AEB,AD与BC平行吗?为什么?解:因为BE平分∠ABC(已知)所以∠ABE=∠EBC(________)因为∠ABE=∠AEB(________)所以∠________ =∠________ ( ________)所以AD∥BC(________ )18、如图,若使,需要添加一个条件,则这个条件是________(填一个即可)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相交线与平行线一、选择题(共19小题)1.(2015•随州)如图,AB∥CD,∠A=50°,则∠1的大小是()A.50° B.120°C.130°D.150°2.(2015•临沂)如图,直线a∥b,∠1=60°,∠2=40°,则∠3等于()A.40° B.60° C.80° D.100°3.(2015•通辽)如图,已知AB∥CD,若∠A=25°,∠E=40°,则∠C等于()A.40° B.65° C.115°D.25°4.(2015•邵阳)将直尺和直角三角板按如图方式摆放,已知∠1=30°,则∠2的大小是()A.30° B.45° C.60° D.65°5.(2015•资阳)如图,已知AB∥CD,∠C=70°,∠F=30°,则∠A的度数为()A.30° B.35° C.40° D.45°6.(2015•河池)如图,AB∥CD,CB⊥DB,∠D=65°,则∠ABC的大小是()A.25° B.35° C.50° D.65°7.(2015•南宁)如图,一块含30°角的直角三角板ABC的直角顶点A在直线DE上,且B C∥DE,则∠CAE等于()A.30° B.45° C.60° D.90°8.(2015•佛山)如图,在△ABC中,点D、E、F分别是三条边上的点,EF∥AC,DF∥AB,∠B=45°,∠C=60°.则∠EFD=()A.80° B.75° C.70° D.65°9.(2015•恩施州)如图,已知AB∥DE,∠ABC=70°,∠CDE=140°,则∠BCD的值为()A.20° B.30° C.40° D.70°10.(2015•荆州)如图,直线l1∥l2,直线l3与l1,l2分别交于A,B两点,若∠1=70°,则∠2=()A.70° B.80° C.110°D.120°11.(2015•鄂州)如图,AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,与∠EFD的平分线FP 相交于点P,且∠BEP=50°,则∠EPF=()度.A.70 B.65C.60 D.5512.(2015•遵义)如图,直线l1∥l2,∠1=62°,则∠2的度数为()A.152°B.118°C.28° D.62°13.(2015•长春)如图,在△ABC中,AB=AC,过点A作AD∥BC.若∠1=70°,则∠BAC的大小为()A.30° B.40° C.50° D.70°14.(2015•咸宁)如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=50°,则∠2的度数为()A.50° B.40° C.30° D.25°15.(2015•北京)如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=124°,∠2=88°,则∠3的度数为()A.26° B.36° C.46° D.56°16.(2015•东营)如图,将三角形纸板的直角顶点放在直尺的一边上,∠1=20°,∠2=40°,则∠3等于()A.50° B.30° C.20° D.15°17.(2015•六盘水)如图,直线l1和直线l2被直线l所截,已知l1∥l2,∠1=70°,则∠2=()A.110°B.90° C.70° D.50°18.(2015•沈阳)如图,在△ABC中,点D是边AB上一点,点E是边AC上一点,且DE∥BC,∠B=40°,∠AED=60°,则∠A的度数是()A.100°B.90° C.80° D.70°19.(2015•贵港)如图,直线AB∥CD,直线EF与AB,CD相交于点E,F,∠BEF的平分线与CD相交于点N.若∠1=63°,则∠2=()A.64° B.63° C.60° D.54°二、填空题(共10小题)20.(2015•株洲)如图,l∥m,∠1=120°,∠A=55°,则∠ACB的大小是.21.(2015•崇左)若直线a∥b,a⊥c,则直线b c.22.(2015•锦州)如图,已知l1∥l2,∠A=40°,∠1=60°,∠2=.23.(2015•泰州)如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=.24.(2015•大连)如图,AB∥CD,∠A=56°,∠C=27°,则∠E的度数为.25.(2015•郴州)如图,已知直线m∥n,∠1=100°,则∠2的度数为.26.(2015•苏州)如图,直线a∥b,∠1=125°,则∠2的度数为.27.(2015•岳阳)如图,直线a∥b,∠1=50°,∠2=30°,则∠3=.28.(2015•衡阳)如图,已知直线a∥b,∠1=120°,则∠2的度数是.29.(2015•杭州)如图,点A,C,F,B在同一直线上,CD平分∠ECB,FG∥CD.若∠ECA为α度,则∠GFB为度(用关于α的代数式表示).三、解答题(共1小题)30.(2015•益阳)如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.华师大新版七年级(上)近3年中考题单元试卷:第5章相交线与平行线参考答案与试题解析一、选择题(共19小题)1.(2015•随州)如图,AB∥CD,∠A=50°,则∠1的大小是()A.50° B.120°C.130°D.150°【考点】平行线的性质.【分析】由平行线的性质可得出∠2,根据对顶角相得出∠1.【解答】解:如图:∵AB∥CD,∴∠A+∠2=180°,∴∠2=130°,∴∠1=∠2=130°.故选C.【点评】本题考查了平行线的性质,关键是根据两直线平行同旁内角互补和对顶角相等分析.2.(2015•临沂)如图,直线a∥b,∠1=60°,∠2=40°,则∠3等于()A.40° B.60° C.80° D.100°【考点】平行线的性质.【分析】根据对顶角相等和利用三角形的内角和定理列式计算即可得解.【解答】解:如图:∵∠4=∠2=40°,∠5=∠1=60°,∴∠3=180°﹣60°﹣40°=80°,故选C.【点评】本题考查了平行线的性质,三角形的内角和定理,熟记性质并准确识图理清各角度之间的关系是解题的关键.3.(2015•通辽)如图,已知AB∥CD,若∠A=25°,∠E=40°,则∠C等于()A.40° B.65° C.115°D.25°【考点】平行线的性质.【分析】由平行线的性质可求得∠EFB=∠C,在△AEF中由三角形外角的性质可求得∠EFB,可求得答案【解答】解:∵∠EFB是△AEF的一个外角,∴∠EFB=∠A+∠E=25°+40°=65°,∵AB∥CD,∴∠C=∠EFB=65°,故选B.【点评】本题主要考查平行线的性质,掌握平行线的性质是解题的关键,即①两直线平行⇔同位角相等,②两直线平行⇔内错角相等,③两直线平行⇔同旁内角互补.4.(2015•邵阳)将直尺和直角三角板按如图方式摆放,已知∠1=30°,则∠2的大小是()A.30° B.45° C.60° D.65°【考点】平行线的性质.【分析】先根据两角互余的性质求出∠3的度数,再由平行线的性质即可得出结论.【解答】解:∵∠1+∠3=90°,∠1=30°,∴∠3=60°.∵直尺的两边互相平行,∴∠2=∠3=60°.故选C.【点评】本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等.5.(2015•资阳)如图,已知AB∥CD,∠C=70°,∠F=30°,则∠A的度数为()A.30° B.35° C.40° D.45°【考点】平行线的性质.【专题】计算题.【分析】先根据平行线的性质得∠BEF=∠C=70°,然后根据三角形外角性质计算∠A的度数.【解答】解:∵AB∥CD,∴∠BEF=∠C=70°,∵∠BEF=∠A+∠F,∴∠A=70°﹣30°=40°.故选C.【点评】本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.6.(2015•河池)如图,A B∥CD,CB⊥DB,∠D=65°,则∠ABC的大小是()A.25° B.35° C.50° D.65°【考点】平行线的性质;垂线.【分析】先根据三角形内角和定理求出∠C的度数,然后根据两直线平行内错角相等即可求出∠ABC 的大小.【解答】解:∵CB⊥DB,∴∠CBD=90°,∴∠C+∠D=90°,∵∠D=65°,∴∠C=25°,∵AB∥CD,∴∠BAC=∠C=25°.故选A.【点评】此题考查了平行线的性质,解题的关键是:熟记两直线平行同位角相等;两直线平行内错角相等;两直线平行同旁内角互补.7.(2015•南宁)如图,一块含30°角的直角三角板ABC的直角顶点A在直线DE上,且BC∥DE,则∠CAE等于()A.30° B.45° C.60° D.90°【考点】平行线的性质.【分析】由直角三角板的特点可得:∠C=30°,然后根据两直线平行内错角相等,即可求∠CAE的度数.【解答】解:∵∠C=30°,BC∥DE,∴∠CAE=∠C=30°.故选A.【点评】此题考查了平行线的性质,解题的关键是:熟记两直线平行同位角相等;两直线平行内错角相等;两直线平行同旁内角互补.8.(2015•佛山)如图,在△ABC中,点D、E、F分别是三条边上的点,EF∥AC,DF∥AB,∠B=45°,∠C=60°.则∠EFD=()A.80° B.75° C.70° D.65°【考点】平行线的性质.【分析】根据EF∥AC,求出∠EFB=∠C=60°,再根据DF∥AB,求出∠DFC=∠B=45°,从而求出∠EFD=180°﹣60°﹣45°=75°.【解答】解:∵EF∥AC,∴∠EFB=∠C=60°,∵DF∥AB,∴∠DFC=∠B=45°,∴∠EFD=180°﹣60°﹣45°=75°,故选B.【点评】本题考查了平行线的性质,找到平行线、得到相应的同位角或内错角是解题的关键.9.(2015•恩施州)如图,已知AB∥DE,∠ABC=70°,∠CDE=140°,则∠BCD的值为()A.20° B.30° C.40° D.70°【考点】平行线的性质.【分析】延长ED交BC于F,根据平行线的性质求出∠MFC=∠B=70°,求出∠FDC=40°,根据三角形外角性质得出∠C=∠MFC﹣∠MDC,代入求出即可.【解答】解:延长ED交BC于F,∵AB∥DE,∠ABC=70°,∴∠MFC=∠B=70°,∵∠CDE=140°,∴∠FDC=180°﹣140°=40°,∴∠C=∠MFC﹣∠MDC=70°﹣40°=30°,故选B.【点评】本题考查了三角形外角性质,平行线的性质的应用,解此题的关键是求出∠MFC的度数,注意:两直线平行,同位角相等.10.(2015•荆州)如图,直线l1∥l2,直线l3与l1,l2分别交于A,B两点,若∠1=70°,则∠2=()A.70° B.80° C.110°D.120°【考点】平行线的性质.【分析】根据平行线的性质求出∠3=∠1=70°,即可求出答案.【解答】解:∵直线l1∥l2,∠1=70°,∴∠3=∠1=70°,∴∠2=180°﹣∠3=110°,故选C.【点评】本题考查了平行线的性质,邻补角定义的应用,解此题的关键是求出∠3的度数,注意:两直线平行,同位角相等.11.(2015•鄂州)如图,AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,与∠EFD的平分线FP 相交于点P,且∠BEP=50°,则∠EPF=()度.A.70 B.65 C.60 D.55【考点】平行线的性质.【分析】先由垂直的定义,求出∠PEF=90°,然后由∠BEP=50°,进而可求∠BEF=140°,然后根据两直线平行同旁内角互补,求出∠EFD的度数,然后根据角平分线的定义可求∠EFP的度数,然后根据三角形内角和定理即可求出∠EPF的度数.【解答】解:如图所示,∵EP⊥EF,∴∠PEF=90°,∵∠BEP=50°,∴∠BEF=∠BEP+∠PEF=140°,∵AB∥CD,∴∠BEF+∠EFD=180°,∴∠EFD=40°,∵FP平分∠EFD,∴=20°,∵∠PEF+∠EFP+∠EPF=180°,∴∠EPF=70°.故选:A.【点评】此题考查了平行线的性质,解题的关键是:熟记两直线平行同位角相等;两直线平行内错角相等;两直线平行同旁内角互补.12.(2015•遵义)如图,直线l1∥l2,∠1=62°,则∠2的度数为()A.152°B.118°C.28° D.62°【考点】平行线的性质.【分析】根据两直线平行,同位角相等求出∠1的同位角,再根据对顶角相等求解.【解答】解:∵如图,l1∥l2,∠1=62°,∴∠3=∠1=62°,∴∠2=∠3=62°(对顶角相等),故选D.【点评】本题考查了平行线的性质,是基础题,熟记性质是解题的关键.13.(2015•长春)如图,在△ABC中,AB=AC,过点A作AD∥BC.若∠1=70°,则∠BAC的大小为()A.30° B.40° C.50°D.70°【考点】平行线的性质.【分析】根据平行线的性质求出∠C,根据等腰三角形的性质得出∠B=∠C=70°,根据三角形内角和定理求出即可.【解答】解:∵AB=AC,∴∠B=∠C,∵AD∥BC,∠1=70°,∴∠C=∠1=70°,∴∠B=70°,∴∠BAC=180°﹣∠B﹣∠C=180°﹣70°﹣70°=40°,故选B.【点评】本题考查了三角形内角和定理,等腰三角形的性质,平行线的性质的应用,解此题的关键是求出∠C的度数和得出∠B=∠C,注意:三角形内角和等于180°,两直线平行,内错角相等.14.(2015•咸宁)如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=50°,则∠2的度数为()A.50° B.40° C.30° D.25°【考点】平行线的性质.【分析】由两直线平行,同位角相等,可求得∠3的度数,然后求得∠2的度数.【解答】解:如图,,∵∠1=50°,∴∠3=∠1=50°,∴∠2=90°﹣50°=40°.故选B.【点评】此题考查了平行线的性质.注意两直线平行,同位角相等定理的应用是解此题的关键.15.(2015•北京)如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=124°,∠2=88°,则∠3的度数为()A.26° B.36° C.46° D.56°【考点】平行线的性质.【分析】如图,首先运用平行线的性质求出∠AOB的大小,然后借助平角的定义求出∠3即可解决问题.【解答】解:如图,∵直线l4∥l1,∴∠1+∠AOB=180°,而∠1=124°,∴∠AOB=56°,∴∠3=180°﹣∠2﹣∠AOB=180°﹣88°﹣56°=36°,故选B.【点评】该题主要考查了平行线的性质及其应用问题;应牢固掌握平行线的性质,这是灵活运用、解题的基础和关键.16.(2015•东营)如图,将三角形纸板的直角顶点放在直尺的一边上,∠1=20°,∠2=40°,则∠3等于()A.50° B.30° C.20° D.15°【考点】平行线的性质;三角形的外角性质.【分析】如图,首先运用平行线的性质求出∠4,然后借助三角形的外角性质求出∠3,即可解决问题.【解答】解:由题意得:∠4=∠2=40°;由外角定理得:∠4=∠1+∠3,∴∠3=∠4﹣∠1=40°﹣20°=20°,故选C.【点评】该题主要考查了三角形外角的性质、平行线的性质等几何知识点及其应用问题;解题的关键是牢固掌握三角形外角的性质、平行线的性质等几何知识点,这也是灵活运用、解题的基础.17.(2015•六盘水)如图,直线l1和直线l2被直线l所截,已知l1∥l2,∠1=70°,则∠2=()A.110°B.90° C.70° D.50°【考点】平行线的性质.【分析】根据平行线的性质得出∠2=∠3,然后根据对顶角相等得出∠3=∠1=70°,即可求出答案.【解答】解:∵∠3=∠1=70°,∵直线l1∥l2,∴∠3=∠2,∵∠3=∠1=70°,∴∠2=70°,故选C.【点评】本题考查了平行线的性质的应用,注意:两直线平行,同位角相等.18.(2015•沈阳)如图,在△ABC中,点D是边AB上一点,点E是边AC上一点,且DE∥BC,∠B=40°,∠AED=60°,则∠A的度数是()A.100°B.90° C.80° D.70°【考点】平行线的性质;三角形内角和定理.【分析】先根据平行线的性质求出∠C的度数,再根据三角形内角和定理求出∠A的度数即可.【解答】解:∵DE∥BC,∠AED=40°,∴∠C=∠AED=60°,∵∠B=40°,∴∠A=180°﹣∠C﹣∠B=180°﹣40°﹣60°=80°.【点评】本题考查的是平行线的性质及三角形内角和定理,先根据平行线的性质求出∠C的度数是解答此题的关键.19.(2015•贵港)如图,直线AB∥CD,直线EF与AB,CD相交于点E,F,∠BEF的平分线与CD相交于点N.若∠1=63°,则∠2=()A.64° B.63° C.60° D.54°【考点】平行线的性质.【分析】先根据平行线的性质求出∠BEN的度数,再由角平分线的定义得出∠BEF的度数,根据平行线的性质即可得出∠2的度数.【解答】解:∵AB∥CD,∠1=63°,∴∠BEN=∠1=63°.∵EN平分∠BEF,∴∠BEF=2∠BEN=126°,∴∠2=180°﹣∠BEF=180°﹣126°=54°.故选D.【点评】本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等;两直线平行,同旁内角互补.也考查了角平分线定义.二、填空题(共10小题)20.(2015•株洲)如图,l∥m,∠1=120°,∠A=55°,则∠ACB的大小是65°.【考点】平行线的性质.【专题】计算题.【分析】先根据平行线的性质得∠2=∠1=120°,然后根据三角形外角性质计算∠ACB的大小.【解答】解:∵l∥m,∴∠2=∠1=120°,∵∠2=∠ACB+∠A,∴∠ACB=120°﹣55°=65°.故答案为65°.【点评】本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.21.(2015•崇左)若直线a∥b,a⊥c,则直线b ⊥c.【考点】平行线的性质;垂线.【分析】先根据a⊥c得出∠1=90°,再由直线a∥b可得出∠1=∠2=90°,由此可得出结论.【解答】解:如图所示,∵a⊥c,∴∠1=90°.∵a∥b,∴∠1=∠2=90°,∴b⊥c.故答案为:⊥.【点评】本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等.22.(2015•锦州)如图,已知l1∥l2,∠A=40°,∠1=60°,∠2=100°.【考点】平行线的性质.【分析】由平行线的性质可求得∠B,在△ABC中利用三角形外角的性质可求得∠2.【解答】解:∵l1∥l2,∴∠B=∠1=60°,∵∠2为△ABC的一个外角,∴∠2=∠B+∠A=60°+40°=100°,故答案为:100°.【点评】本题主要考查平行线的性质,掌握平行线的性质是解题的关键,即①两直线平行⇔同位角相等,②两直线平行⇔内错角相等,③两直线平行⇔同旁内角互补23.(2015•泰州)如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=140°.【考点】平行线的性质.【专题】计算题.【分析】先根据平行线的性质,由l1∥l2得∠3=∠1=40°,再根据平行线的判定,由∠α=∠β得AB∥CD,然后根据平行线的性质得∠2+∠3=180°,再把∠1=40°代入计算即可.【解答】解:如图,∵l1∥l2,∴∠3=∠1=40°,∵∠α=∠β,∴AB∥CD,∴∠2+∠3=180°,∴∠2=180°﹣∠3=180°﹣40°=140°.故答案为140°.【点评】本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.24.(2015•大连)如图,AB∥CD,∠A=56°,∠C=27°,则∠E的度数为29°.【考点】平行线的性质;三角形的外角性质.【分析】根据AB∥CD,求出∠DFE=56°,再根据三角形外角的定义性质求出∠E的度数.【解答】解:∵AB∥CD,∴∠DFE=∠A=56°,又∵∠C=27°,∴∠E=56°﹣27°=29°,故答案为29°.【点评】本题考查了平行线的性质、三角形的外角的性质,找到相应的平行线是解题的关键.25.(2015•郴州)如图,已知直线m∥n,∠1=100°,则∠2的度数为80°.【考点】平行线的性质.【分析】根据邻补角定义求出∠3的度数,再根据平行线的性质求出∠2的度数即可.【解答】解:如图,∵∠1=100°,∴∠3=180°﹣100°=80°,∵m∥n,∴∠2=∠3=80°.故答案为80°.【点评】本题考查了平行线的性质,找到相应的同位角是解题的关键.26.(2015•苏州)如图,直线a∥b,∠1=125°,则∠2的度数为55°.【考点】平行线的性质.【分析】先根据对顶角相等,∠1=65°,求出∠3的度数,再由两直线平行,同旁内角互补得出∠2的度数.【解答】解:解:∵∠1=125°,∴∠3=∠1=125°,∵a∥b,∴∠2=180°﹣∠3=180°﹣125°=55°.故答案为:55°.【点评】本题考查了平行线的性质,对顶角的性质,熟记定理是解题的关键.27.(2015•岳阳)如图,直线a∥b,∠1=50°,∠2=30°,则∠3=20°.【考点】平行线的性质;三角形的外角性质.【分析】首先由平行线的性质可求得∠4的度数,然后再根据三角形的外角的性质即可求得∠3的度数.【解答】解:如图:∵a∥b,∴∠4=∠1=50°.由三角形的外角的性质可知:∠4=∠2+∠3,∴∠3=∠4﹣∠2=50°﹣30°=20°.故答案为:20°.【点评】本题主要考查的是三角形的外角的性质和平行线的性质,熟练掌握三角形的外角的性质和平行线的性质是解题的关键.28.(2015•衡阳)如图,已知直线a∥b,∠1=120°,则∠2的度数是60°.【考点】平行线的性质.【分析】两直线平行,同旁内角互补,据此进行解答.【解答】解:∵a∥b,∠1=120°,∴∠2=180°﹣∠1=180°﹣120°=60°,故答案为:60°【点评】本题考查了平行线的性质.注意两直线平行,同旁内角互补.29.(2015•杭州)如图,点A,C,F,B在同一直线上,CD平分∠ECB,FG∥CD.若∠ECA为α度,则∠GFB为90﹣度(用关于α的代数式表示).【考点】平行线的性质.【分析】根据FG∥CD 得出∠GFB=∠DCF,再由互补和角平分线得出∠DCF=(180°﹣α),解答即可.【解答】解:∵点A,C,F,B在同一直线上,∠ECA为α,∴∠ECB=180°﹣α,∵CD平分∠ECB,∴∠DCB=(180°﹣α),∵FG∥CD,∴∠GFB=∠DCB=90﹣.【点评】此题考查平行线的性质,关键是根据平行线得出∠GFB=∠DCF和利用角平分线解答.三、解答题(共1小题)30.(2015•益阳)如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.【考点】平行线的性质.【分析】由平行线的性质得到∠ABC=∠1=65°,∠ABD+∠BDC=180°,由BC平分∠ABD,得到∠ABD=2∠ABC=130°,于是得到结论.【解答】解:∵AB∥CD,∴∠ABC=∠1=65°,∠ABD+∠BDC=180°,∵BC平分∠ABD,∴∠ABD=2∠ABC=130°,∴∠BDC=180°﹣∠ABD=50°,∴∠2=∠BDC=50°.【点评】本题考查了平行线的性质和角平分线定义等知识点,解此题的关键是求出∠ABD的度数,题目较好,难度不大.21。
