(完整版)七年级数学下册《相交线与平行线》证明题
(完整版)七年级数学下册《相交线与平行线》证明题

①2121②12③12④优学教育------七年级数学下五六单元测试题一、选择题:(每题2.5分,共35分)1.下列所示的四个图形中,1∠和2∠是同位角...的是( )A. ②③B. ①②③C. ①②④D. ①④2.如右图所示,点E 在AC 的延长线上,下列条件中能判断...CD AB //( ) A. 43∠=∠ B. 21∠=∠ C. DCE D ∠=∠ D.180=∠+∠ACD D3.一学员练习驾驶汽车,两次拐弯后,行驶的方向与原来的方向相同,这两次拐弯的角度可能是( )A. 第一次向左拐 30,第二次向右拐 30B. 第一次向右拐 50,第二次向左拐 130C. 第一次向右拐 50,第二次向右拐 130D. 第一次向左拐 50,第二次向左拐 1304.两条平行直线被第三条直线所截,下列命题中正确..的是( ) A. 同位角相等,但内错角不相等 B. 同位角不相等,但同旁内角互补 C. 内错角相等,且同旁内角不互补 D. 同位角相等,且同旁内角互补 5.下列说法中错误..的个数是( ) (1)过一点有且只有一条直线与已知直线平行。
(2)过一点有且只有一条直线与已知直线垂直。
(3)在同一平面内,两条直线的位置关系只有相交、平行两种。
(4)不相交的两条直线叫做平行线。
(5)有公共顶点且有一条公共边的两个角互为邻补角。
A. 1个 B. 2个 C. 3个 D. 4个 6.下列说法中,正确..的是( ) A. 图形的平移是指把图形沿水平方向移动。
B. 平移前后图形的形状和大小都没有发生改变。
C. “相等的角是对顶角”是一个真命题。
D. “直角都相等”是一个假命题。
EDC BA4321ba3图④212图⑤cba 31图⑥A’C ’B ’AB C三、填空题:(每题2.5分,共40分)1.把命题“等角的余角相等”写成“如果……,那么……。
”的形式 为 。
2.如图④,若 22021=∠+∠ ,则=3∠ 。
人教版七年级数学下册第五章相交线与平行线:几何计算和证明综合练习试题(含答案)

人教版七年级数学下册第五章相交线与平行线:几何计算和证明综合练习试题1、如图,已知∠2=∠3,∠C=∠D,求证:∠A=∠F.证明:∵∠2=∠3,∠1=∠2,∴∠1=∠3.∴DB∥CE.∴∠DBA=∠C.∵∠D=∠C,∴∠D=∠DBA.∴DF∥AC.∴∠A=∠F.2、如图,已知EF∥AD,∠1=∠2,∠BAC=80°,求∠AGD的度数.解:∵EF∥AD,∴∠2=∠3(两直线平行,同位角相等).∵∠1=∠2,∴∠1=∠3(等量代换).∴AB∥DG(内错角相等,两直线平行).∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补).3、如图,∠1=115°,∠2=50°,∠3=65°,EG为∠NEF的平分线.求证:AB∥CD,EG∥FH.证明:∵∠1=115°,∴∠FCD=180°-∠1=180°-115°=65°.∵∠3=65°,∴∠FCD=∠3.∴AB∥CD.∵∠2=50°,∴∠NEF=180°-∠2=180°-50°=130°.∵EG为∠NEF的平分线,∴∠GEF=12∠NEF=65°.∴∠GEF=∠3.∴EG∥FH.4、如图,已知∠B=∠D,∠E=∠F,判断BC与AD的位置关系,并说明理由.解:BC∥AD,理由:∴BE∥FD.∴∠B=∠BCF.又∵∠B=∠D,∴∠BCF=∠D.∴BC∥AD.5、如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠1.求证:AD平分∠BAC.证明:∵AD⊥BC,EG⊥BC,∴∠ADC=∠EGC=90°.∴AD∥EG.∴∠1=∠2,∠E=∠3.∵∠E=∠1,∴∠2=∠3.∴AD平分∠BAC.6、如图,B,C,E三点在一条直线上,A,F,E三点在一条直线上,AB∥CD,∠1=∠2,∠3=∠4.求证:AD∥BE.证明:∵AB∥CD,∴∠4=∠BAE.∴∠3=∠BAE.∵∠1=∠2,∴∠1+∠CAF=∠2+∠CAF,即∠BAE=∠CAD.∴∠3=∠CAD.∴AD∥BE.7、如图,已知AB∥CD,试判断∠B,∠BED和∠D之间的关系,并说明理由.解:∠BED=∠B+∠D.理由如下:过点E作EF∥AB,则∠B=∠BEF.∵AB∥CD,∴EF∥CD.∴∠DEF=∠D.∵∠BED=∠BEF+∠DEF,∴∠BED=∠B+∠D.8、如图,∠AEF+∠CFE=180°,∠1=∠2,EG与HF平行吗?为什么?解:平行.理由:∵∠AEF+∠CFE=180°,∴AB∥CD.∴∠AEF=∠EFD.∴∠AEF -∠1=∠EFD -∠2,即∠GEF =∠HFE.∴EG ∥HF.9、如图,A ,B ,C 三点在同一直线上,∠1=∠2,∠3=∠D ,试判断BD 与CF 的位置关系,并说明理由.解:BD ∥CF.理由如下:∵∠1=∠2,∴AD ∥BF.∴∠D =∠DBF.∵∠3=∠D ,∴∠3=∠DBF.∴BD ∥CF.10、如图,∠ABC =∠ADC ,BF ,DE 分别是∠ABC ,∠ADC 的平分线,∠1=∠2,试说明:DC ∥AB.解:∵BF ,DE 分别是∠ABC ,∠ADC 的平分线,∴∠3=12∠ADC ,∠2=12∠ABC. ∵∠ABC =∠ADC ,∴∠3=∠2.∵∠1=∠2,∴∠1=∠3.∴DC∥AB.11、如图,AD平分∠BAC,AD⊥BC于D,点E,A,C共线,∠DAC=∠EFA,延长EF 交BC于点G.求证:EG⊥BC.证明:∵AD平分∠BAC,∴∠DAC=∠DAB.又∵∠DAC=∠EFA,∴∠DAB=∠EFA.∴AD∥EG.∴∠ADC=∠EGD.∵AD⊥BC,∴∠ADC=90°.∴∠EGD=90°.∴EG⊥BC.12、已知AB∥CD,点E为AB,CD之外任意一点.(1)如图1,探究∠BED与∠B,∠D的数量关系,并说明理由;(2)如图2,探究∠CDE与∠B,∠BED的数量关系,并说明理由.解:(1)∠B=∠BED+∠D.理由如下:过点E作EF∥AB.又∵AB∥CD,∴EF∥AB∥CD.∴∠BEF=∠B,∠D=∠DEF.∵∠BEF=∠BED+∠DEF,∴∠B=∠BED+∠D.(2)∠CDE=∠B+∠BED.理由如下:过点E作EF∥AB.又∵AB∥CD,∴EF∥AB∥CD.∴∠B+∠BEF=180°,∠CDE+∠DEF=180°.又∵∠DEF=∠BEF-∠BED,∴∠CDE+∠BEF-∠BED=∠B+∠BEF,即∠CDE=∠B+∠BED.13、如图,把一张长方形纸片ABCD沿EF折叠后,D,C分别落在D′和C′的位置上,ED′与BC的交点为G.若∠EFG=50°,求∠1,∠2,∠3的度数.解:根据折叠的性质可知,∠DEF=∠D′EF,∠EFC=∠EFC′.∵∠EFG=50°,∴∠EFC=180°-50°=130°.∴∠EFC′=∠EFC=130°.∴∠3=∠EFC′-∠EFG=130°-50°=80°.∵AD∥BC,∴∠DEF=∠EFG=50°.∴∠DED′=2∠DEF=100°.∴∠1=180°-∠DED′=180°-100°=80°.∵AD∥BC,∴∠1+∠2=180°.∴∠2=180°-∠1=100°.故∠1=80°,∠2=100°,∠3=80°.14、如图,AE⊥BC,FG⊥BC,∠1=∠2,∠D=∠3+60°,∠CBD=70°.(1)求证:AB∥CD;(2)求∠C的度数.解:(1)证明:∵AE⊥BC,FG⊥BC,∴AE∥GF.∴∠2=∠A.∵∠1=∠2,∴∠1=∠A.∴AB∥CD.(2)∵AB∥CD,∴∠D+∠CBD+∠3=180°.∵∠D =∠3+60°,∠CBD =70°,∴∠3=25°.∵AB ∥CD ,∴∠C =∠3=25°.15、(1)如图1,AB ∥CD ,则∠E +∠G 与∠B +∠F +∠D 有何关系?(2)如图2,若AB ∥CD ,又能得到什么结论?请直接写出结论.解:(1)过点E 作EM ∥AB ,过点F 作FN ∥AB ,过点G 作GH ∥CD. ∵AB ∥CD ,∴AB ∥EM ∥FN ∥GH ∥CD.∴∠1=∠B ,∠2=∠3,∠4=∠5,∠6=∠D.∴∠1+∠2+∠5+∠6=∠B +∠3+∠4+∠D ,即∠BEF +∠FGD =∠B +∠EFG +∠D.(2)∠B +∠F 1+∠F 2+…+∠F n -1+∠D =∠E 1+∠E 2+…+∠E n .16、已知E ,F 分别是AB ,CD 上的动点,P 也为一动点.(1)如图1,若AB ∥CD ,求证:∠P =∠BEP +∠PFD ;(2)如图2,若∠P =∠PFD -∠BEP ,求证:AB ∥CD ;(3)如图3,AB ∥CD ,移动E ,F ,使∠EPF =90°,作∠PEG =∠BEP ,则∠AEG∠PFD =2.证明:(1)过点P作PG∥AB,则∠EPG=∠BEP.∵AB∥CD,∴PG∥CD.∴∠GPF=∠PFD.∴∠EPF=∠EPG+∠FPG=∠BEP+∠PFD.(2)过点P作PQ∥AB,则∠QPE=∠BEP.∵∠EPF=∠PFD-∠BEP,∴∠PFD=∠EPF+∠BEP=∠EPF+∠QPE=∠FPQ. ∴DC∥PQ.∴AB∥CD.。
第五章相交线与平行线证明题专题一

相交线与平行线证明题专题训练一、两组平行线1、已知:如图,∠A=∠ACE,∠B=∠BDF,且∠A=∠B,求证:EC∥DF。
2、如图∠A=∠1,∠C=∠2,求证:AB3、已知CD证:ABC DFEBA12GFEDCBA217、如图,BD丄AC 于D,EF丄AC 于F.∠AMD=∠AGF.∠1=∠2=35°。
求证:DM∥BC.8、已知:如图,EF⊥AB,∠1=∠2,∠3=∠B.求证:CD⊥AB.693DGA EBHCF10、已知:如图,DG ⊥BC ,AC ⊥BC ,EF ⊥AB ,∠1=∠2 求证:CD ⊥AB 。
二、求特殊角1、、已知,如图,AB ∥CD ∥GH ,EG 平分∠BEF ,FG 平分∠EFD 求证:∠EGF=90°2、如图,已知∠ABC=90°,∠1=∠2,∠DCA=∠CAB .求证:(1)CD ⊥CB ;(2)CD 平分∠ACE .求证:AB7、如图,点E在直线DF上,点B在直线AC上,DB、EC分别交AF于点G、H,若∠AGB=∠EHF,21FEDCBA3、∠C=∠D,请你判断∠A和∠F的大小关系,并说明你的理由.8、如图,已知AB//CD,∠1=∠2,∠3=∠4,试证明AD//BE。
9、如图,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.证明:(1)AE//FC(2)BC平分∠DBE四、寻找角之间的关系1、将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE,交DE于点F.(1)求证:CF∥AB;(2)求∠DFC的度数。
2、如图,已知∠1=∠2,∠3=∠4,∠5=∠6,求证:AD//BC。
3、如图,BCE、AFE是直线,AB//CD,∠1=∠2,∠3=∠4,求证:AD//BE。
4、如图,∠ABD和∠BDC的平分线交于一点E,BE交CD于点F,∠1+∠2=90°。
求证:(1)AB//CD;(2)∠2+∠3=90°。
___版七年级下第二章平行线与相交线证明题

___版七年级下第二章平行线与相交线证明题.1.如图,已知直线EF与AB、CD都相交,且AB∥CD,求证:AD∥BE。
证明:由___可得∠1=∠2,又因为BCE、AFE是直线,所以∠2=∠3,因此∠1=∠3.根据平行线内角相等可知AD∥BE。
2.如图,已知∠A=∠F,∠C=∠D,求证:BD∥CE。
证明:由∠A=∠F可得AC∥DF,又因为∠C=∠D,所以∠1=∠C。
根据平行线内角相等可知BD∥CE。
3.已知∠B=∠BGD,∠DGF=∠F,求证∠B+∠F=180°。
证明:由∠B=∠BGD可得AB∥CD,又因为∠DGF=∠F,所以CD∥EF。
由AB∥CD和CD∥EF可得AB//EF,所以∠B+∠F=180°。
4.已知:如图、BE//CF,BE、CF分别平分∠ABC和∠BCD,求证:___。
证明:由BE、CF分别平分∠___和∠BCD可得∠1=∠2,又因为BE//CF,所以∠1=∠2.根据平行线内角相等可知∠ABC=∠BCD,所以___。
5.如图,已知:∠___∠B+∠F。
求证:AB//EF。
证明:经过点C作CD//AB,可得∠BCD=∠B。
因为∠___∠B+∠F,所以∠___∠BCD+∠F,即∠3=∠4.又因为∠1=∠2,所以∠1+∠___∠2+∠CAF,即∠1=∠2.根据平行线内角相等可知AB//EF。
7、已知:DE⊥AO于E,BO⊥AO,∠CFB=∠EDO,试证明:CF∥DO。
证明:由DE⊥___和BO⊥AO可得∠DEA=∠BOA=90°。
由∠___∠EDO可得∠EDO=∠DOF,又因为∠DOF=∠CFB,所以CF∥DO。
8、已知:如图2-82,DE∥BC,∠ADE=∠___,求证:∠1=∠2.证明:根据题目条件,DE∥BC,所以∠ADE=180°-∠A,又∠ADE=∠___,所以∠EFC=180°-∠A。
根据平行线内角相等的性质,可得∠1=∠ADE=180°-∠A,∠2=∠EFC=180°-∠A,所以∠1=∠2.9、如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE。
word完整版北师大版七年级下第二章平行线与相交线证明题

B CD 4FECD) ) )z Ez )A B z DCz )))))又) 180°)( )又)())ABA BFE和zABC BE DE// 2-82 ))())试说明 z C= z D )) )) 求证AB//EF ))AFD) )BCE)AB// CF ) )z Fz DOF= z CFB EFC 求证CFB= z EDO CF // DO()) ))BD //CE. 匸仁z 2,z_ ( (已知), 等量代换))即 z ABC= z BCD z (z 1=z CDE // BO ( z EDO= z DOF ( (求证:BD// CE 5•如图,已知:z BCF= z B+ z F 证明:经过点C 作CD//AB••• BD// CE (3.已知z B =z 证明:•••/ • AB// CD •••/ DGF=z • CD// EF •/ AB// EF • z B + zBC, z ADE=z z BCD= z B 。
(z BCF= z B+ z F ,(已知))=z F o ( 8、已知:如图 z 1 = z 2 证明:••• DE // • z ADE= _ •••/ ADE=z \G D-------- D分别平分z ) ) ) ) )4.已知:如图、BE//CF BCD 求证:AB//CD证明:••• BE 、平分z ABC (已CD//EF o ( AB//EF (证明:••• DE 丄AO , BO 丄AO (已知)z DEA= z BOA=90 0(( 又•••/ C= z D(已知) • z 1 = z C(等量代换)• BD // CE()F 求证z B +已知) BGD z DGF=z B =z BGD(F ;(已知 ((F = 180 °z 2= - z2 —BE//CF (已知)z 1 = z 2 ( z 仁-z _________2CF 平分z BCD ( 1 1z ABC= z BCD ( 2 2 AB//CD (• DB// EF ( • z 1 = z 2 (9、如图,已知z A= z F 证明:•••/ A= z F(已知)• AC // DF( • z D= z 北师大版七年级下第二章平行线与相交线1.如图,已知直线 EF 与AB CD 都相交,且 AB// CD 说 明z 仁z 2的理由.理由:••• EF 与AB 相交(已知)• z 仁 z 3( )•/ AB// CD (已知)• z 2=z 3( • z 仁z 2(AC// DF (z D=z洞z A =z F ,z C =z D, A =z F (已知)• z 3=z ______ (• AD// BE (7、已知:DE 丄 AO 于 E , BO 丄 AO ,/ CFB= z EDO 试 说明:CF // DO1 2 :B6.已知,如图,BCE AFE 是直线 3=z 4 o 求证:AD// BE= 证明:••• AB// CD (已知)• z 4=z ______ ( 3=z 4 (已知) 3=z _____ ( 1 = z 2 (已知) 1 + z CAF=/ 2+z CAF ( 即z = z BC( —( EFC( ____ (10、如图,已知/ B+ / BCD=180 °,/ B= / D.求证:/ E= / DFE.证明:T/ B+ / BCD=180 ° (已知),• AB // CD().• / B= / DCE ( ).又•••/ B= / D (已知),• / DCE= / D ().• AD // BE().• / E= / DFE ( ).11、如图,已知:/ 1 = / 2,当DE// FH时,(1)证明/ EDA= / HFB ( 2) CD 与FG 有何关系?证明:(1)v DE // FH (已知),•••/ EDF= / DFH ( ),•••/ EDA= / HFB ( ). (2) I / EDF= / DFH ( ),且/ CDF= / EDF- / 1,/ DFG= / DFH- / 2 , 又•••/仁/ 2 (已知)• CD // FG( 14、如图所示,已知直线EF和, AB,CD 分别相交于K,H,且EG 丄AB, / CHF=60 0,/E=30。
人教版七年级数学下册:平行线与相交线证明题过程(含答案与解析)

人教版七年级数学下册:平行线与相交线证明一.解答题(共8小题)1.如图,已知DF∥AC,∠C=∠D,要证∠AMB=∠2,请完善证明过程:∵DF∥AC(_________)∴∠D=∠1(_________)∵∠C=∠D(_________)∴∠1=∠C(_________)∴DB∥EC(_________)∴∠ABM=∠2(_________)2.已知:如图,EF⊥AB,CD⊥AB,AC⊥BC,∠1=∠2,求证:DG⊥BC证明:∵EF⊥AB CD⊥AB_________∴∠EFA=∠CDA=90°(垂直定义)∠1=∠_________∴EF∥CD_________∴∠1=∠2(已知)∴∠2=∠ACD(等量代换)∴DG∥AC_________∴∠DGB=∠ACB_________∵AC⊥BC(已知)∴∠ACB=90°(垂直定义)∴∠DGB=90°即DG⊥BC.3.请填空完成下面的证明:如图,点D、E、F分别是三角形ABC的边BC、CA、AB上的点,DE∥BA,∠A=∠FDE.求证:DF∥AC.证明:∵DE∥BA∴∠A=_________(_________)∵∠A=∠FDE∴∠FDE=_________∴DF∥AC(_________)4.推理填空:如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.因为EF∥AD,所以∠2=_________.(_________)又因为∠1=∠2,所以∠1=∠3.(_________)所以AB∥_________.(_________)所以∠BAC+_________=180°(_________)又因为∠BAC=70°,所以∠AGD=_________.5.如图:∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,∠DBF=∠F,那么EC与DF平行吗?为什么?请完成下面的解题过程解:∵BD平分∠ABC,CE平分∠ACB (已知)∴∠DBC=∠_________,∠ECB=∠_________∵∠ABC=∠ACB (已知)∴∠_________=∠_________.∠_________=∠_________(已知)∴∠F=∠_________∴EF∥AD_________.6.补全下列推理过程:如图,EF∥AD,∠1=∠2,∠BAC=80°.求∠AGD的度数.因为EF∥AD (已知)所以∠2=_________(_________)又因为∠1=∠2 (已知)所以∠1=∠3(等量代换)所以AB∥_________(_________)所以∠BAC+_________=180°(两直线平行,同旁内角互补)因为∠BAC=80°(已知)所以∠AGD=_________(等量代换)7.完成下面的证明:(1)如图1,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DE∥BA,DF∥CA.求证:∠FDE=∠A.证明:∵DE∥BA,∴∠FDE=_________(_________),∵DF∥CA,∴∠A=_________(_________),∴∠FDE=∠A;(2)如图2,AB和CD相交于点O,∠C=∠COA,∠D=∠BOD,求证:AC∥BD;证明:∵∠C=∠COA,∠D=∠BOD,∵∠COA=∠BOD(_________),∴∠C=_________,∴AC∥BD(_________).参考答案与试题解析一.解答题(共8小题)1.如图,已知DF∥AC,∠C=∠D,要证∠AMB=∠2,请完善证明过程:∵DF∥AC(已知)∴∠D=∠1(两直线平行,内错角相等)∵∠C=∠D(已知)∴∠1=∠C(等量代换)∴DB∥EC(同位角相等,两直线平行)∴∠ABM=∠2(两直线平行,同位角相等)考点:平行线的判定与性质.专题:推理填空题.分析:先根据平行线的性质由DF∥AC得到∠D=∠1,再根据等量代换得到∠1=∠C,于是可根据平行线的判定方法得到DB∥EC,然后根据平行线的性质得到∠AMB=∠2.解答:证明:∵DF∥AC(已知),∴∠D=∠1(两直线平行,内错角相等),∵∠C=∠D(已知),∴∠1=∠C(等量代换),∴DB∥EC(同位角相等,两直线平行),∴∠AMB=∠2(两直线平行,同位角相等).故答案为:已知,两直线平行,内错角相等,已知,等量代换,同位角相等,两直线平行,两直线平行,同位角相等.点评:本题考查了平行线的判定与性质:同位角相等,两直线平行;内错角相等,两直线平行;两直线平行,同位角相等;两直线平行,内错角相等.2.已知:如图,EF⊥AB,CD⊥AB,AC⊥BC,∠1=∠2,求证:DG⊥BC 证明:∵EF⊥AB CD⊥AB已知∴∠EFA=∠CDA=90°(垂直定义)∠1=∠ACD∴EF∥CD(两直线平行,同位角相等)∴∠1=∠2(已知)∴∠2=∠ACD(等量代换)∴DG∥AC(内错角相等,两直线平行)∴∠DGB=∠ACB(两直线平行,同位角相等)∵AC⊥BC(已知)∴∠ACB=90°(垂直定义)∴∠DGB=90°即DG⊥BC.考点:平行线的判定与性质;垂线.专题:推理填空题.分析:根据垂直定义求出∠EFA=∠CDA=90°,求出∠1=∠ACD,推出EF∥CD,根据平行线的性质得出∠2=∠ACD,推出DG∥AC,根据平行线的性质推出∠ACB=∠DGB即可.解答:证明:∵EF⊥AB,CD⊥AB(已知),∴∠EFA=∠CDA=90°(垂直定义),∴EF∥CD(同位角相等,两直线平行),∴∠1=∠ACD(两直线平行,同位角相等),∵∠1=∠2(已知),∴∠2=∠ACD(等量代换),∴DG∥AC(内错角相等,两直线平行),∴∠DGB=∠ACB(两直线平行,同位角相等),∵AC⊥CB,∴∠ACB=90°,∴∠DGB=90°,即DG⊥BC,故答案为:已知,ACD,(两直线平行,同位角相等),(内错角相等,两直线平行),(两直线平行,同位角相等).点评:本题考查了平行线的判定和性质,三角形内角和定理,垂直定义的应用,主要考查学生的推理能力.3.请填空完成下面的证明:如图,点D、E、F分别是三角形ABC的边BC、CA、AB上的点,DE∥BA,∠A=∠FDE.求证:DF∥AC.证明:∵DE∥BA∴∠A=∠DEC(两直线平行,同位角相等)∵∠A=∠FDE∴∠FDE=∠DEC∴DF∥AC(内错角相等,两直线平行)考点:平行线的判定与性质.专题:推理填空题.分析:根据平行线的性质得出∠A=∠DEC,求出∠FDE=∠DEC,根据平行线的判定推出即可.解答:证明:∵DE∥BA,∴∠A=∠DEC(两直线平行,同位角相等),∵∠A=∠FDE(已知),∴∠FDE=∠DEC(等量代换),∴DF∥AC(内错角相等,两直线平行),故答案为:∠DEC,两直线平行,同位角相等;∠DEC,内错角相等,两直线平行.点评:本题考查了平行线的性质和判定的应用,注意:①两直线平行,同位角相等,②内错角相等,两直线平行.4.推理填空:如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.因为EF∥AD,所以∠2=∠3.(两直线平行,同位角相等)又因为∠1=∠2,所以∠1=∠3.(等量代换)所以AB∥DG.(内错角相等,两直线平行)所以∠BAC+∠AGD=180°(两直线平行,同旁内角互补)又因为∠BAC=70°,所以∠AGD=110°.考点:平行线的判定与性质.专题:推理填空题.分析:根据平行线的性质推出∠1=∠2=∠3,推出AB∥DG,根据平行线的性质得出∠BAC+∠DGA=180°,代入求出即可.解答:解:∵EF∥AD,∴∠2=∠3(两直线平行,同位角相等),∵∠1=∠2,∴∠1=∠3(等量代换),∴AB∥DG(内错角相等,两直线平行),∴∠BAC+∠DGA=180°(两直线平行,同旁内角互补),∵∠BAC=70°,∴∠AGD=110°,故答案为:∠3,两直线平行,同位角相等,等量代换,DG,内错角相等,两直线平行,∠AGD,两直线平行,同旁内角互补,110°.点评:本题考查了平行线的性质和判定的应用,注意:平行线的性质是①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.5.如图:∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,∠DBF=∠F,那么EC与DF 平行吗?为什么?请完成下面的解题过程解:∵BD平分∠ABC,CE平分∠ACB (已知)∴∠DBC=∠ABC,∠ECB=∠ACB∵∠ABC=∠ACB (已知)∴∠DBC=∠ECB.∠F=∠DBF(已知)∴∠F=∠ECB∴EF∥AD(同位角相等,两直线平行).考点:平行线的判定.专题:推理填空题.分析:利用角平分线的性质得出∠DBC=∠ABC,∠ECB=∠ACB,进而求出∠F=∠ECB,得出答案即可.解答:解:∵BD平分∠ABC,CE平分∠ACB(已知)∴∠DBC=∠ABC,∠ECB=∠ACB,∵∠ABC=∠ACB (已知)∴∠DBC=∠ECB.∵∠DBF=∠F,(已知)∴∠F=∠ECB,∴EF∥AD(同位角相等,两直线平行).点评:此题主要考查了平行线的判定以及角平分线的性质,得出∠F=∠ECB是解题关键.6.补全下列推理过程:如图,EF∥AD,∠1=∠2,∠BAC=80°.求∠AGD的度数.因为EF∥AD (已知)所以∠2=∠3(两直线平行,同位角相等)又因为∠1=∠2 (已知)所以∠1=∠3(等量代换)所以AB∥DG(内错角相等,两直线平行)所以∠BAC+∠AGD=180°(两直线平行,同旁内角互补)因为∠BAC=80°(已知)所以∠AGD=100°(等量代换)考点:平行线的判定与性质.专题:推理填空题.分析:根据平行线性质推出∠2=∠3,推出∠1=∠3,根据平行线的判定推出AB∥DG,根据平行线的性质得出∠BAC+∠AGD=180°,代入求出即可.解答:解:∵EF∥AD,∴∠2=∠3(两直线平行,同位角相等),∵∠1=∠2,∴∠1=∠3,∴AB∥DG(内错角相等,两直线平行),∴∠BAC+∠AGD=180°,∵∠BAC=80°,∴∠AGD=100°,故答案为:∠3,两直线平行,同位角相等,DG,内错角相等,两直线平行,∠AGD,100°.点评:本题考查了平行线的性质和判定的应用,注意:平行线的性质是:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.7.完成下面的证明:(1)如图1,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DE∥BA,DF∥CA.求证:∠FDE=∠A.证明:∵DE∥BA,∴∠FDE=∠BFD(两直线平行,内错角相等),∵DF∥CA,∴∠A=∠BFD(两直线平行,同位角相等),∴∠FDE=∠A;(2)如图2,AB和CD相交于点O,∠C=∠COA,∠D=∠BOD,求证:AC∥BD;证明:∵∠C=∠COA,∠D=∠BOD,∵∠COA=∠BOD(对顶角相等),∴∠C=∠D,∴AC∥BD(内错角相等,两直线平行).考点:平行线的判定与性质.专题:推理填空题.分析:(1)根据平行线的性质得出∠FDE=∠BFD,∠A=∠BFD,推出即可;(2)根据对顶角相等和已知求出∠C=∠D,根据平行线的判定推出即可.解答:(1)证明:∵DE∥BA,∴∠FDE=∠BFD(两直线平行,内错角相等),∵DF∥CA,∴∠A=∠BFD(两直线平行,同位角相等),∴∠FDE=∠A,故答案为:∠BFD,两直线平行,内错角相等,∠BFD,两直线平行,同位角相等;(2)证明:∵∠C=∠COA,∠D=∠BOD,又∵∠COA=∠BOD(对顶角相等),∴∠C=∠D,∴AC∥BD(内错角相等,两直线平行),故答案为:对顶角相等,∠D,内错角相等,两直线平行.点评:本题考查了平行线的性质和判定的应用,注意:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然,题目比较好,难度适中.8.如图,在△ABC中,DE∥BC,连结DC,点F是边BC上一点,GF⊥AB,垂足为G,∠1=∠2,求证:CD⊥AB.考点:平行线的判定与性质;垂线.专题:证明题.分析:求出∠BGF=90°,根据平行线的性质和已知求出∠2=∠BCD,推出FG∥CD,根据平行线的性质得出∠CDB=∠BGF=90°即可.解答:证明:∵FG⊥AB,∴∠BGF=90°,∵DE∥BC,∴∠1=∠BCD,∵∠1=∠2,∴∠2=∠BCD,∴FG∥CD,∴∠CDB=∠BGF=90°,∴CD⊥AB.点评:本题考查了平行线的性质和判定,垂直的定义的应用,主要考查学生的推理能力.。
word完整版北师大版七年级下第二章平行线与相交线证明题

B CD 4FECD) ) )z Ez )A B z DCz )))))又) 180°)( )又)())ABA BFE和zABC BE DE// 2-82 ))())试说明 z C= z D )) )) 求证AB//EF ))AFD) )BCE)AB// CF ) )z Fz DOF= z CFB EFC 求证CFB= z EDO CF // DO()) ))BD //CE. 匸仁z 2,z_ ( (已知), 等量代换))即 z ABC= z BCD z (z 1=z CDE // BO ( z EDO= z DOF ( (求证:BD// CE 5•如图,已知:z BCF= z B+ z F 证明:经过点C 作CD//AB••• BD// CE (3.已知z B =z 证明:•••/ • AB// CD •••/ DGF=z • CD// EF •/ AB// EF • z B + zBC, z ADE=z z BCD= z B 。
(z BCF= z B+ z F ,(已知))=z F o ( 8、已知:如图 z 1 = z 2 证明:••• DE // • z ADE= _ •••/ ADE=z \G D-------- D分别平分z ) ) ) ) )4.已知:如图、BE//CF BCD 求证:AB//CD证明:••• BE 、平分z ABC (已CD//EF o ( AB//EF (证明:••• DE 丄AO , BO 丄AO (已知)z DEA= z BOA=90 0(( 又•••/ C= z D(已知) • z 1 = z C(等量代换)• BD // CE()F 求证z B +已知) BGD z DGF=z B =z BGD(F ;(已知 ((F = 180 °z 2= - z2 —BE//CF (已知)z 1 = z 2 ( z 仁-z _________2CF 平分z BCD ( 1 1z ABC= z BCD ( 2 2 AB//CD (• DB// EF ( • z 1 = z 2 (9、如图,已知z A= z F 证明:•••/ A= z F(已知)• AC // DF( • z D= z 北师大版七年级下第二章平行线与相交线1.如图,已知直线 EF 与AB CD 都相交,且 AB// CD 说 明z 仁z 2的理由.理由:••• EF 与AB 相交(已知)• z 仁 z 3( )•/ AB// CD (已知)• z 2=z 3( • z 仁z 2(AC// DF (z D=z洞z A =z F ,z C =z D, A =z F (已知)• z 3=z ______ (• AD// BE (7、已知:DE 丄 AO 于 E , BO 丄 AO ,/ CFB= z EDO 试 说明:CF // DO1 2 :B6.已知,如图,BCE AFE 是直线 3=z 4 o 求证:AD// BE= 证明:••• AB// CD (已知)• z 4=z ______ ( 3=z 4 (已知) 3=z _____ ( 1 = z 2 (已知) 1 + z CAF=/ 2+z CAF ( 即z = z BC( —( EFC( ____ (10、如图,已知/ B+ / BCD=180 °,/ B= / D.求证:/ E= / DFE.证明:T/ B+ / BCD=180 ° (已知),• AB // CD().• / B= / DCE ( ).又•••/ B= / D (已知),• / DCE= / D ().• AD // BE().• / E= / DFE ( ).11、如图,已知:/ 1 = / 2,当DE// FH时,(1)证明/ EDA= / HFB ( 2) CD 与FG 有何关系?证明:(1)v DE // FH (已知),•••/ EDF= / DFH ( ),•••/ EDA= / HFB ( ). (2) I / EDF= / DFH ( ),且/ CDF= / EDF- / 1,/ DFG= / DFH- / 2 , 又•••/仁/ 2 (已知)• CD // FG( 14、如图所示,已知直线EF和, AB,CD 分别相交于K,H,且EG 丄AB, / CHF=60 0,/E=30。
(完整)七年级相交线与平行线证明题

七年级下册订交线与平行线证明题 A1判断正误:(1)三条直线两两订交有三个交点(2)两条直线订交不行能有两个交点.(3)在同一平面内的三条直线的交点个数可能为 0 , 1, 2 , 3 .(4) 同一平面内的n条直线两两订交,此中无三线共点,则可得 1 n n 1 个交点.2(5)同一平面内的 n 条直线经过同一点可得 2n n 1 个角(平角除外).2、已知,如图,AEC A C ,证明AB∥CD.A BEC D3 以下图,已知A1,C 2 ,求证:AB∥CD.4、如图,已知 ABBC , BC CD , 1 2 .试判断 BE 与 CF 的关系,并说明你的原因。
解: BE ∥ CF .原因:∵ AB BC ,BCCD ,(已知)∴90 (垂直的定义)∵ 1 2 ()∴ ABC 1BCD2 ,即EBCBCF ,∴ ∥()5 如图:已知 12 , A C ,求证:① AB ∥ DC② AD ∥BC证明:∵ 1 2 ()∵∥().∴ CCBE (两直线平行,内错角相等. )DC又∵ A C ()1∴ A()A2E∴∥().B图6 如图,直线 AB 、 CD 被 EF 所截, 12 , 34, 13 90 ,那么AB 与 CD 平行吗?为何?7 如图,已知AOE BEF 180 ,AOE CDE180 ,求证:CD∥BE.8 如图,已知,1 2 ,23,求证:AB∥EF.证明:∵1 2 (已知),∴∥.()∵23(已知),∴∥.()∴∥.()9请将以下证明过程中的原因或步骤增补完好:如图 , EF ∥ AD ,12,BAC 70 ,求AGD 的度数.请将解题过程填写完好.解:∵ EF ∥ AD ,(已知)∴2.()又∵1 2 ,(已知)∴13.()∴AB∥,∴BAC180 .()又∵BAC 70(已知),∴AGD.11 已知:如图, AD 、 BC 交于点 O ,ABC BCD ,BE均分ABC ,CF平分 BCD ,那么BE与CF平行吗?为何?A BEO FC D图 112 以下右图所示,①已知: AB ∥ CD ,1 2 ,求证:BE∥CF②已知: AB ∥ CD , BE ∥ CF ,求证: 1 2 AB1E FC 2 D图 313 已知:如图,∠A=∠F,∠C=∠D.求证: BD∥CE.。
证明题七年级下册

证明题七年级下册一、相交线与平行线证明题。
1. 如图,已知直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE,∠2 : ∠1 = 4:1,求∠AOF的度数。
证明:设∠1 = x,因为∠2:∠1 = 4:1,则∠2 = 4x。
因为OE平分∠BOD,所以∠DOE=∠1 = x。
又因为∠2+∠DOE = 180°(邻补角之和为180°),即4x + x=180°,5x = 180°,解得x = 36°。
所以∠COE=180° - ∠1=180° - 36° = 144°。
因为OF平分∠COE,所以∠COF=(1)/(2)∠COE=(1)/(2)×144° = 72°。
∠AOC = ∠1 = 36°(对顶角相等)所以∠AOF=∠AOC + ∠COF = 36°+72° = 108°。
2. 已知:如图,AB∥CD,∠1 = ∠2,求证:AM∥CN。
证明:因为AB∥CD,所以∠EAB = ∠ACD(两直线平行,同位角相等)。
又因为∠1 = ∠2,所以∠EAB - ∠1=∠ACD - ∠2,即∠MAC = ∠NCA。
所以AM∥CN(内错角相等,两直线平行)3. 如图,已知∠1 = ∠2,∠C = ∠D,求证:∠A = ∠F。
证明:因为∠1 = ∠2,∠1 = ∠3(对顶角相等),所以∠2 = ∠3。
所以DB∥EC(同位角相等,两直线平行)。
所以∠D = ∠4(两直线平行,同位角相等)。
又因为∠C = ∠D,所以∠C = ∠4。
所以DF∥AC(内错角相等,两直线平行)。
所以∠A = ∠F(两直线平行,内错角相等)二、三角形证明题。
4. 在△ABC中,AD是BC边上的中线,E是AD的中点,BE的延长线交AC于F。
求证:AF=(1)/(3)AC。
证明:过点D作DG∥BF交AC于G。
七年级下册相交线与平行线练习题及答案

七年级下册相交线与平行线练习题及答案第五章相交线与平行线一、典型例题例1.如图1,直线a与b平行,∠1=(3x+70)°,∠2=(5x+22)°,求∠3的度数。
图1例2.已知:如图2,AB∥EF∥CD,EG平分∠XXX,∠B+∠BED+∠D=192°,求∠EGD的度数。
图2例3.如图3,已知AB∥CD,且∠B=40°,∠D=70°,求∠DEB的度数。
图3例4.平面上n条直线两两相交且无3条或3条以上直线共点,有多少个不同交点?例5.6个不同的点,其中只有3点在同一条直线上,2点确定一条直线,问能确定多少条直线?例6.10条直线两两相交,最多将平面分成多少块不同的区域?例7.两条直线相交于一点,所形成的角中有2对对顶角,4对邻补角,那么,三条直线相交于一点时,有多少对对顶角,多少对邻补角?四条直线相交于一点时,有多少对对顶角,多少对邻补角?n条直线相交于一点时,有多少对对顶角,多少对邻补角?二、巩固练1.平面上有5个点,其中仅有3点在同一直线上,过每2点作一条直线,一共可以作直线()条。
A。
6B。
7C。
8D。
92.平面上三条直线相互间的交点个数是()。
A。
3B。
1或3C。
1或2或3D。
不一定是1,2,33.平面上6条直线两两相交,其中仅有3条直线过一点,则截得不重叠线段共有()。
A。
36条B。
33条C。
24条D。
21条4.已知平面中有n个点,A、B、C三个点在一条直线上,A、D、F、E四个点也在一条直线上,除这些之外,再没有三点共线或四点共线,以这n个点作一条直线,一共可以画出38条不同的直线,这时n等于()。
A。
9B。
10C。
11D。
125.若平行直线AB、CD与相交直线EF、GH相交成如图所示的图形,则共得同旁内角()。
A。
4对B。
8对C。
12对D。
16对6.如图,已知FD∥BE,则∠1+∠2-∠3=()。
图4A。
90°B。
135°C。
人教版七年级下册数学第5章相交线与平行线证明题专题训练
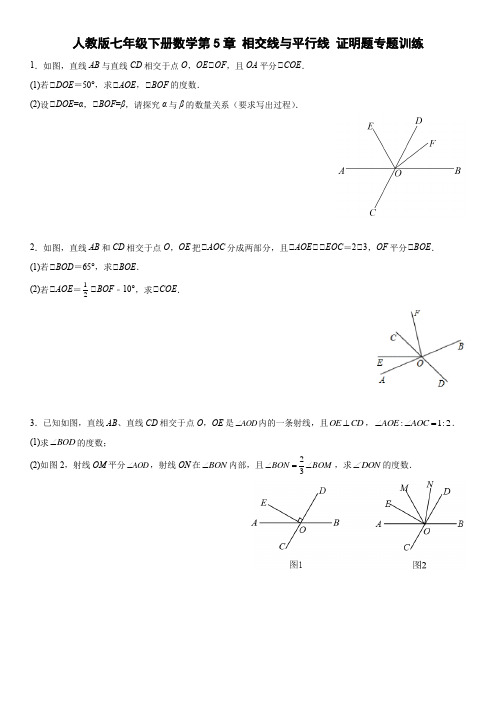
人教版七年级下册数学第5章 相交线与平行线 证明题专题训练1.如图,直线AB 与直线CD 相交于点O ,OE ⊥OF ,且OA 平分⊥COE . (1)若⊥DOE =50°,求⊥AOE ,⊥BOF 的度数.(2)设⊥DOE =α,⊥BOF =β,请探究α与β的数量关系(要求写出过程).2.如图,直线AB 和CD 相交于点O ,OE 把⊥AOC 分成两部分,且⊥AOE ⊥⊥EOC =2⊥3,OF 平分⊥BOE . (1)若⊥BOD =65°,求⊥BOE .(2)若⊥AOE =12⊥BOF ﹣10°,求⊥COE .3.已知如图,直线AB 、直线CD 相交于点O ,OE 是AOD ∠内的一条射线,且OE CD ⊥,:1:2AOE AOC ∠∠=. (1)求BOD ∠的度数;(2)如图2,射线OM 平分AOD ∠,射线ON 在BON ∠内部,且23BON BOM ∠=∠,求DON ∠的度数.4.如图,⊥1+⊥2=180°,⊥C =⊥D .求证:AD ⊥BC .5.如图,FCG B ∠=∠,180DEF D +=︒∠∠,则AB 与EF 平行吗?为什么?6.已知,如图,ABC ADC ∠=∠,BF 、DE 分别平分ABC ∠与ADC ∠,且13∠=∠.求证://AB DC .7.如图,点A 在CF 上,46BAF ∠=︒,136ACE ∠=︒,CE DG ⊥于点C .问 //DG AB 吗?为什么?8.如图,//AB CD ,//CD EF ,//BC ED ,70B ∠=︒,求C ∠,D ∠和E ∠的度数.9.将一副直角三角板按如图所示的方式放置,60B ∠=︒,45E ∠=︒,75AFD ∠=︒.求证://AE BC .10.如图,已知180BAD ADC ∠+∠=︒,AE 平分BAD ∠,交CD 于点F ,交BC 的延长线于点E ,DG 交BC 的延长线于点G ,CFE AEB ∠=∠. (1)若87B ∠=︒,求DCG ∠的度数;(2)AD 与BC 是什么位置关系?请说明理由;(3)若DAB α∠=,DGC β∠=,直接写出α,β满足什么数量关系时AE DG ∥.11.如图,已知射线AM ⊥BN ,连结AB ,点C 是射线BN 上的一个动点(与点B 不重合),AD ,AE 分别平分⊥BAC 和⊥CAM ,交射线BN 于点D ,E . (1)试说明:⊥ACB =2⊥AEB ;(2)若⊥ADB ﹣⊥BAD =45°,求⊥AEB 的度数.12.如图所示,点B 、E 分别在AC 、DF 上,BD 、CE 均与AF 相交,A F ∠=∠,C D ∠=∠,求证:12∠=∠.13.如图,⊥ENC +⊥CMG =180°,AB ⊥CD . (1)求证:⊥2=⊥3.(2)若⊥A =⊥1+70°,⊥ACB =42°,则⊥B 的大小为______.14.已知:如图,ABC 中,点D 、E 分别在AB 、AC 上,EF 交DC 于点F ,32180∠+∠=︒ ,1B ∠=∠. (1)求证:∥DE BC ;(2)若DE 平分ADC ∠,33B ∠=∠,求2∠的度数.15.如图,点D ,E 分别在AB 和AC 上,DE BC ∥,30DBE ∠=︒,25EBC ∠=︒,求BDE ∠的度数.16.如图,已知,A ADE C E ∠=∠∠=∠. (1)若3,EDC C ∠=∠求C ∠的度数; (2)求证://BE CD .17.已知:如图,CDG B ∠=∠,AD BC ⊥于点D ,EF BC ⊥于点F ,试判断1∠与2∠的关系,并说明理由.(写出推理依据)18.已知:如图,⊥BAP+⊥APD =180°,⊥1 =⊥2.求证:AE⊥PF.19.如图,AE⊥BC,FG⊥BC,⊥1=⊥2,求证:AB⊥CD.20.如图,AB⊥DE,C为BD上一点,⊥A=⊥BCA,⊥E=⊥ECD,求证:CE⊥CA.21.如图,AB⊥BC于点B,DC⊥BC于点C,DE平分⊥ADC交BC于点E,点F为线段CD延长线上一点,⊥BAF=⊥EDF(1)求证:⊥DAF=⊥F;(2)在不添加任何辅助线的情况下,请直接写出所有与⊥CED互余的角.22.已知AB⊥CD,点E为AB,CD之外任意一点.(1)如图1,探究⊥BED与⊥B,⊥D的数量关系,并说明理由;(2)如图2,探究⊥CDE与⊥B,⊥E的数量关系,并说明理由.参考答案:1.解:⊥⊥DOE=50°,⊥⊥COE=180°-⊥DOE=180°-50°=130°,⊥OA平分⊥COE,⊥⊥AOE=12⊥COE=12×130°=65°,⊥OE⊥OF,⊥⊥EOF=90°,⊥⊥BOF=180°-⊥AOE-⊥EOF=180°-65°-90°=25°;(2)解:⊥⊥DOE=α,⊥⊥COE=180°-⊥DOE=180°-α,⊥OA平分⊥COE,⊥⊥AOE=12⊥COE=12(180°-α)=90°-12α,⊥OE⊥OF,⊥⊥EOF=90°,⊥⊥BOF=β=180°-⊥AOE-⊥EOF=180°-(90°-12α)-90°=12α,即α=2β.2.解:⊥⊥AOC与⊥BOD是对顶角,⊥⊥AOC=⊥BOD=65°.⊥⊥AOE:⊥EOC=2:3,⊥⊥AOE=25⊥AOC=26°.⊥⊥BOE=180°-⊥AOE=180°-26°=154°;(2)解:设⊥AOE=2x,⊥EOC=3x.⊥⊥AOE=12⊥BOF-10°,⊥⊥BOF=4x+20°.⊥OF平分⊥BOE,⊥⊥BOE=2⊥BOF=8x+40°.⊥⊥AOE +⊥BOE =2x +8x +40°=180°. ⊥x =14°. ⊥⊥COE =3x =42°. 3.解:⊥OE ⊥CD , ⊥⊥COE =90°, ⊥⊥AOE :⊥AOC =1:2, ⊥⊥AOC =90°×23=60°,⊥⊥BOD =⊥AOC =60°; (2)由(1)可知:⊥BOD =60°,⊥⊥AOD =180°-⊥BOD =180°-60°=120°, ⊥OM 平分⊥AOD , ⊥⊥AOM =12 ×120°=60°,⊥⊥BOM =180°-⊥AOM =180°-60°=120°, ⊥⊥BON =23 ⊥BOM =23×120°=80°,⊥⊥DON =⊥BON -⊥BOD =80°-60°=20°. 4.证明:⊥⊥1+⊥2=180°,⊥2+⊥AED =180°, ⊥⊥1=⊥AED , ⊥DE ⊥AC , ⊥⊥D =⊥DAF , ⊥⊥C =⊥D , ⊥⊥DAF =⊥C , ⊥AD ⊥BC . 5.解:AB 与EF 平行, 理由:⊥FCG B ∠=∠, ⊥//AB DC ,⊥180DEF D +=︒∠∠, ⊥//EF DC ,6.证明:BF ,DE 分别平分ABC ∠与ADC ∠21ABC ∴∠=∠,22ADC ∠=∠ ABC ADC ∠=∠ 12∠∠∴=13∠=∠23∴∠=∠//AB CD ∴.7.解://DG AB ,理由如下. ⊥CE CD ⊥, ⊥90DCE ∠=︒, ⊥136ACE ∠=︒,⊥36013690134ACD ∠=︒-︒-︒=︒, ⊥46BAF ∠=︒,⊥180********BAC BAF ∠=︒-∠=︒-︒=︒, ⊥ACD BAC ∠=∠, ⊥//DG AB . 8.//AB CD ,//CD EF ,////AB CD EF ∴,70C B ∴∠=∠=︒,E D ∠=∠,又//BC DE , 180C D ∴∠+∠=︒,⊥⊥D =110°,110E ∴∠=︒.答:C ∠,D ∠和E ∠的度数分别是70︒、110︒、110︒. 9.解:由直角三角板的性质可得: ⊥C=30°,⊥⊥AFD=⊥C+⊥CDF=75°,⊥⊥CDF=⊥E , ⊥AE⊥BC . 10.解:⊥180BAD ADC ∠+∠=︒, ⊥AB CD ∥, ⊥87B DCG ∠=∠=︒. (2)解:AD 与BC 是的位置关系为:AD BC ∥,理由如下: ⊥AE 平分BAD ∠, ⊥BAE DAE ∠=∠, ⊥180BAD ADC ∠+∠=︒, ⊥AB CD ∥, ⊥BAE CFE ∠=∠, ⊥AEB CFE ∠=∠, ⊥⊥AEB =⊥BAE =⊥DAE , ⊥AD BC ∥. (3)解:α与β的数量关系为:12αβ=,理由如下:当AE DG ∥时,AEB DGC β∠=∠=,由(2)中推导可知,1122AEB EAD BAD α∠=∠=∠=,⊥12αβ=. 11.解:⊥AE 平分⊥CAM2.CAM EAM ∴∠=∠,AM BN ∥,.CAM ACB EAM AEB ∴∠=∠∠=∠2.ACB AEB ∴∠=∠(2) 解:,AM BN ∥,.CAM ACB ADB DAM ∴∠=∠∠=∠⊥AD 平分⊥BAC.BAD CAD ∴∠=∠45,ADB BAD ︒∠-∠=45.DAM CAD ︒∴∠-∠= 45.CAM ACB ︒∴∠=∠= 由(1)知,2,ACB AEB ∠=∠22.5.AEB ︒∴∠= 12.证明:⊥A F ∠=∠, ⊥AC DF ∥, ⊥ABD D ∠=∠, 又⊥C D ∠=∠, ⊥ABD C ∠=∠, ⊥DB CE ∥, ⊥13∠=∠, ⊥23∠∠=, ⊥12∠=∠. 13.(1)证明:⊥⊥ENC +⊥CMG =180°,⊥CMG =⊥FMN , ⊥⊥ENC +⊥FMN =180°, ⊥FG ⊥ED , ⊥⊥2=⊥D , ⊥AB ⊥CD , ⊥⊥3=⊥D , ⊥⊥2=⊥3;(2)解:⊥AB ⊥CD ,⊥⊥A +⊥ACD =180°,⊥⊥A =⊥1+70°,⊥ACB =42°,⊥⊥1+70°+⊥1+42°=180°,⊥⊥1=34°,⊥AB ⊥CD ,⊥⊥B =⊥1=34°.故答案为:34°.14.解:(1)⊥32180∠+∠=︒,⊥2+⊥DFE =180°, ⊥⊥3=⊥DFE ,⊥EF //AB ,⊥⊥ADE =⊥1,又⊥1B ∠=∠,⊥⊥ADE =⊥B ,⊥DE //BC ,(2)⊥DE 平分ADC ∠,⊥⊥ADE =⊥EDC ,⊥DE //BC ,⊥⊥ADE =⊥B ,⊥33B ∠=∠⊥⊥5+⊥ADE +⊥EDC =3B B B ∠+∠+∠=180°, 解得:36B ∠=︒,⊥⊥ADC =2⊥B =72°,⊥EF //AB ,⊥⊥2=⊥ADC =180°-108°=72°,15.解:⊥30DBE ∠=︒,25EBC ∠=︒,⊥⊥ABC =⊥DBE +⊥EBC =55°,⊥DE ⊥BC ,⊥⊥BDE +⊥ABC =180°,⊥⊥BDE =180°-⊥ABC =125°.16.(1)A ADE ∠=∠,//ED AC ∴,180EDC C ∴∠+∠=︒.3EDC C ∠=∠ ,3180C C ∴∠+∠=︒,45C ∴∠=︒ ;(2)A ADE ∠=∠,//ED AC ∴,ABE E ∴∠=∠.C E ∠=∠,ABE C ∴∠=∠,//BE CD ∴ .17.CDG B ∠=∠DG AB ∴1DAB ∴∠=∠ 又AD BC ⊥于点D ,EF BC ⊥于点FAD EF ∴2DAB ∴∠=∠12∠∠∴=18.证明:⊥⊥BAP +⊥APD =180°⊥AB⊥CD⊥⊥BAP=⊥CPA⊥⊥1 =⊥2⊥⊥BAP-⊥1=⊥CPA-⊥2,即⊥EAP=⊥FPA ⊥AE⊥PF19.证明:如图,设BC 与AE 、GF 分别交于点M 、N.⊥AE⊥BC,FG⊥BC,⊥⊥AMB=⊥GNB=90°,⊥AE⊥FG,⊥⊥A=⊥1;又⊥⊥2=⊥1,⊥⊥A=⊥2,⊥AB⊥CD.20.证明⊥AB⊥DE,⊥⊥B+⊥D=180°,⊥⊥A=⊥BCA,⊥E=⊥ECD,⊥⊥B=180°-2⊥BCA,⊥D=180°-2⊥ECD,⊥(180°-2⊥BCA)+(180°-2⊥ECD)=180°,⊥⊥BCA+⊥ECD=90°,⊥⊥ACE=90°,⊥CE⊥CA.21.解:(1)⊥AB⊥BC于点B,DC⊥BC于点C,⊥⊥B+⊥C=180°,⊥AB⊥CF,⊥⊥BAF+⊥F=180°,又⊥⊥BAF=⊥EDF,⊥⊥EDF+⊥F=180°,⊥ED⊥AF,⊥⊥ADE=⊥DAF,⊥EDC=⊥F,⊥DE平分⊥ADC,⊥⊥ADE=⊥CDE,⊥⊥DAF=⊥F;(2)⊥⊥C=90°,⊥⊥CED+⊥CDE=90°,⊥⊥CED与⊥CDE互余,又⊥⊥ADE=⊥DAF=⊥EDC=⊥F,⊥与⊥CED互余的角有⊥ADE,⊥CDE,⊥F,⊥FAD.22.解:(1)⊥B=⊥BED+⊥D.理由如下:过点E作EF⊥AB.又⊥AB⊥CD,⊥EF⊥AB⊥CD.⊥⊥BEF=⊥B,⊥D=⊥DEF.⊥⊥BEF=⊥BED+⊥DEF,⊥⊥B=⊥BED+⊥D.(2)⊥CDE=⊥B+⊥BED.理由如下:过点E作EF⊥AB.又⊥AB⊥CD,⊥EF⊥AB⊥CD.⊥⊥B+⊥BEF=180°,⊥CDE+⊥DEF=180°.又⊥⊥DEF=⊥BEF-⊥BED,⊥⊥CDE+⊥BEF-⊥BED=⊥B+⊥BEF,即⊥CDE=⊥B+⊥BED.。
七年级下数学平行线相交线必背证明题
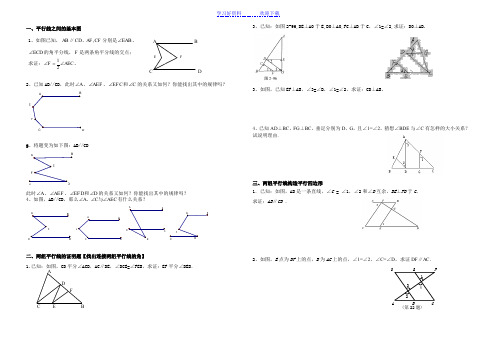
一、平行线之间的基本图1、如图已知,AB ∥CD .,AF CF 分别是EAB ∠、ECD ∠的角平分线,F 是两条角平分线的交点;求证:12F AEC ∠=∠.2、已知AB//CD ,此时A ∠、AEF ∠、EFC ∠和C ∠的关系又如何?你能找出其中的规律吗?ED3、将题变为如下图:AB//CDDC此时A ∠、AEF ∠、EFD ∠和D ∠的关系又如何?你能找出其中的规律吗? 4、如图,AB//CD ,那么AEC C A ∠∠∠与、有什么关系?DEEC二、两组平行线的证明题【找出连接两组平行线的角】1.已知:如图,CD 平分∠ACB ,AC ∥DE ,∠DCE=∠FEB ,求证:EF 平分∠DEB .3、已知:如图2-96,DE ⊥AO 于E,BO ⊥AO,FC⊥AB 于C ,∠1=∠2,求证:DO ⊥AB.3、如图,已知EF ⊥AB ,∠3=∠B ,∠1=∠2,求证:CD ⊥AB 。
4、已知AD ⊥BC ,FG ⊥BC ,垂足分别为D 、G ,且∠1=∠2,猜想∠BDE 与∠C 有怎样的大小关系?试说明理由.三、两组平行线构造平行四边形1.已知:如图,AB 是一条直线,∠C = ∠1,∠2和∠D 互余,BE ⊥FD 于G . 求证:AB ∥CD .2、如图,E 点为DF 上的点,B 为AC 上的点,∠1=∠2,∠C =∠D ,求证DF ∥AC .DB C AFEADFBE CAB CDEF1 423 (第22题)3、如图,M 、N 、T 和A 、B 、C 分别在同一直线上, 且∠1=∠3,∠P=∠T ,求证:∠M=∠R 。
四、证特殊角1、AB ∥CD ,∠BAC 的平分线和∠ACD 的平分线交于点E ,则∠AEC 的度数是 .2、AB CD ∥,直线EF 与AB 、CD 分别相交于E 、F 两点,EP 平分∠AEF ,过点F 作PF EP 垂足为P ,若∠PEF =300,则∠PFC =_____.3.已知:如图,AB ∥DE ,CM 平分∠BCE ,CN ⊥CM .求证:∠B =2∠DCN .4.如图已知直线a ∥b ,AB 平分∠MAD ,AC 平分∠NAD ,DE ⊥AC 于E ,求证:∠1=∠2.五、寻找角之间的关系1、如图2-97,已知:∠1=∠2,∠3=∠4,∠5=∠6.求证:AD ∥BC.2、已知,如图,BCE 、AFE 是直线,AB ∥CD ,∠1=∠2,∠3=∠4。
完整版北师大版七年级下第二章平行线与相交线证明题.2808

北师大版七年级下第二章平行线与相交线1. 如图,已知直线 EF 与 AB、CD都相交,且 AB∥CD,说明∠1=∠2 的理由 .理由:∵ EF 与 AB相交 (已知 )∴∠1=∠3( )ABA D21C DF4E F 3B C E6. 已知,如图, BCE、AFE是直线, AB∥C D,∠1=∠2,∠∵A B∥CD(已知) 3=∠4。
求证:AD∥BE。
∴∠2=∠3( ) 证明:∵ AB∥C D(已知)∴∠1=∠2( ) ∴∠4=∠()∵∠3=∠4(已知)E1 ∴∠3=∠()A B3DC2F2. 如图:已知∠ A=∠F,∠C=∠D,求证:BD∥CE 。
∵∠1=∠2(已知)∴∠1+∠CAF=∠2+∠CAF()即∠∠ =证明:∵∠ A=∠F (已知)∴∠3=∠()∴A C∥DF ()∴AD∥BE()∴∠D=∠() 7、已知:DE ⊥AO 于 E, BO⊥AO ,∠CFB= ∠EDO 试又∵∠ C=∠D (已知),说明: CF∥DO∴∠1=∠ C (等量代换)证明:∵ DE⊥AO, BO⊥AO(已知)∴B D∥CE()。
∴∠DEA= ∠BOA=90 0 ()3. 已知∠ B=∠BGD∠DGF=∠F 求证∠ B +∠F =180°∵DE∥BO ())证明:∵∠ B=∠BGD (已知)∴∠EDO= ∠DOF ()∴A B∥CD ()∵∠DGF=∠F;(已知)∴CD∥EF ()∵A B∥EF ()∴∠+∠=°()。
B F 180A B又∵∠ CFB=∠EDO()∴∠DOF= ∠CFB()∴CF∥DO ())1EF2C D4.已知:如图、 BE//CF ,BE 、CF 分别平分∠ ABC 和∠8、已知:如图 2-82 ,DE∥BC,∠ADE=∠EFC,求证:BCD 求证: AB//CD∠1=∠2 证明:∵ BE、平分∠ ABC (已知)1∴∠1=∠2∵CF 平分∠ BCD ( )证明:∵ DE ∥BC ( ) ∴∠ADE =______( ) ∵∠ADE =∠EFC ( ) ∴______=______( ) ∴∠2= 1 2∠ ( )∴DB ∥EF ( ) ∴∠1=∠2( )∵BE//CF (已知) 9、如图,已知∠ A=∠F ,∠C=∠D ,试说明 BD ∥CE.∴∠1=∠2( ) 证明:∵∠ A=∠F(已知) ∴ 1 2 ∠ABC=1 2∠BCD ( )即∠ABC= ∠BCD ∴AC ∥DF( ) ∴∠D=∠ ( )∴AB//CD ( ) 又∵∠ C=∠D(已知 )∴∠1=∠C(等量代换 )5.如图,已知:∠ BCF= ∠B+∠F 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
①
2
1
21
②12
③1
2
④
优学教育------七年级数学下五六单元测试题
一、选择题:(每题2.5分,共35分)
1.下列所示的四个图形中,1∠和2∠是同位角...的是( )
A. ②③
B. ①②③
C. ①②④
D. ①④
2.如右图所示,点E 在AC 的延长线上,下列条件中能判断...CD AB //( ) A. 43∠=∠ B. 21∠=∠ C. DCE D ∠=∠ D.
180=∠+∠ACD D
3.一学员练习驾驶汽车,两次拐弯后,行驶的方向与原来的方向相同,这两次拐弯的角度可能是( )
A. 第一次向左拐 30,第二次向右拐 30
B. 第一次向右拐 50,第二次向左拐 130
C. 第一次向右拐 50,第二次向右拐 130
D. 第一次向左拐 50,第二次向左拐 130 4.两条平行直线被第三条直线所截,下列命题中正确..
的是( ) A. 同位角相等,但内错角不相等 B. 同位角不相等,但同旁内角互补 C. 内错角相等,且同旁内角不互补 D. 同位角相等,且同旁内角互补 5.下列说法中错误..
的个数是( ) (1)过一点有且只有一条直线与已知直线平行。
(2)过一点有且只有一条直线与已知直线垂直。
(3)在同一平面内,两条直线的位置关系只有相交、平行两种。
(4)不相交的两条直线叫做平行线。
(5)有公共顶点且有一条公共边的两个角互为邻补角。
A. 1个 B. 2个 C. 3个 D. 4个 6.下列说法中,正确..
的是( ) A. 图形的平移是指把图形沿水平方向移动。
B. 平移前后图形的形状和大小都没有发生改变。
C. “相等的角是对顶角”是一个真命题。
D. “直角都相等”是一个假命题。
E
D
C B
A
432
1
b
a
3
图④
212
图⑤c
b
a 3
1图⑥
A’
C ’
B ’
A
B C
三、填空题:(每题2.5分,共40分)
1.把命题“等角的余角相等”写成“如果……,那么……。
”的形式 为 。
2.如图④,若 22021=∠+∠ ,则=3∠ 。
3.如图⑤,已知b a //,若 501=∠,则=∠2 ; 若
1003=
∠,则=∠2 。
4.如图⑥,为了把ABC ∆平移得到‘
’‘C B A
∆,可以先将ABC ∆向右平移 格,再向上平移 格。
四、解答题。
(每题4分,共40分)
1、如图,已知:21∠∠=, 50=D ∠,求B ∠的度数。
2、如图,CD AB //,AE 平分BAD ∠,CD 与AE 相交于F ,E CFE ∠=∠。
求证:BC AD //。
3、如图,已知CD AB //, 40=∠B ,CN 是BCE ∠的平分线,CN CM ⊥,求BCM ∠的度数。
H
G 2
1
E
D
C
B
A
2
1
F
E
D
C
B
A
N
M
E
D
C
B
A
4、如图,AB∥CD∥PN,∠ABC=50°,∠CPN=150°.求∠BCP的度数.
5、如图,∠CAB=100°,∠ABF=110°,AC∥PD,BF∥PE,求∠DPE的度数.
6、如图,DB∥FG∥EC,∠ABD=60°,∠ACE=36°,AP平分∠BAC.
求∠P AG的度数.
7、如图,AB∥CD,∠1=115°,∠2=140°,求∠3的度数.
8、已知:如图,AC∥DE,DC∥EF,CD平分∠BCA.
求证:EF平分∠BED.
22.(12分)求下列各式中的x 的值:
(1) ()9-242
=x ; (2)()25122
=-x ;
(3)()375433
-=-x ; (4)()08123
=+-x ;
23.(6分)已知实数a 、b 、c 在数轴上的对应点如图所示,化简:
c b a c b a a -+-+--
24.(7分)若a 、b 、c 是有理数,且满足等式332232+-=++c b a ,试计算 ()20112010
b c a +-
的值。
二、填空题(每小题3分,共30分)
11. 3-绝对值是 ,3- 的相反数是 .
12. 81的平方根是 ,364 的平方根是 ,-343的立方根是 ,256的平方根是 . 13. 比较大小:
(1)10 π;(2)
3
3 2;(3)
10
1
101;(4)14.当 时,33
4
5223+
-+++-x x x 有意义。
15.已知212+++b a =0,则
a
b
= . 16.最大的负整数是 ,最小的正整数是 ,绝对值最小的实数是 ,不超过380-的最大整数是 . 17.已知 ,3,3
1
2==
b a 且0 ab ,则 b a +的值为 。
18.已知一个正数x 的两个平方根是1+a 和3-a ,则a = ,x = .
19.设a 是大于1的实数,若 3
1
2,32,
++a a a 在数轴上对应的点分别记作A 、B 、C ,则A 、B 、C 三点在数轴上从左至右的顺序是 .
20.若无理数m 满足14 m ,请写出两个符合条件的无理数。
