【浙教版】九年级数学下册第1章解直角三角形练习题(含答案)
(精练)浙教版九年级下册数学第一章 解直角三角形含答案

浙教版九年级下册数学第一章解直角三角形含答案一、单选题(共15题,共计45分)1、已知一个坡的坡比为i,坡角为α,则下列等式成立的是()A.i=sinαB.i=cosαC.i=tanαD.i=cotα2、如图,在笔直的海岸线l上有A,B两个观测站,AB=2 km,从A处测得船C在北偏东45°的方向,从B处测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为()A.4 kmB. kmC.2 kmD. km3、如图,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60米到达C点,测得点B在点C的北偏东60°方向,则这段河的宽度为()A.60(+1)米B.30(+1)米C.(90-30 )米D.30(-1)米4、在△ABC中,(tanA﹣)2+|﹣cosB|=0,则∠C的度数为()A.30°B.45°C.60°D.75°5、如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF交于点O.下列结论:①∠DOC=90°,②OC=OE,③tan∠OCD=,④S△ODC =S四边形BEOF中,正确的有()A.1个B.2个C.3个D.4个6、在正方形网格中,∠α的位置如图所示,则tanα的值是()A. B. C. D.27、已知:△ABC中,∠C=90°,cosB=, AB=15,则BC的长是()A.3B.3C.6D.8、如图,一座厂房屋顶人字架的跨度AC=12m,上弦AB=BC,∠BAC=25°.若用科学计算器求上弦AB的长,则下列按键顺序正确的是()A. B. C.D.9、我国的“蛟龙号”创造了世界同类潜水器最大下潜深度纪录7062米.如图,在某次任务中,“蛟龙号”在点A处测得正前方海底沉船C的俯角为45°,然后在同一深度向正前方直线航行600米到点B,此时测得海底沉船C 的俯角为60°,那么“蛟龙号”在点B下潜到沉船C处,下潜的垂直深度是()米.A.600﹣600B.600+600C.900﹣300D.900+30010、如图,在四边形ABCD中,E、F分別是AB、AD的中点,若EF=2,BC=5,CD=3,则tanC等于()A. B. C. D.11、的值等于()A. B. C.1 D.12、如图,正方形ABCD中,对角线AC,BD交于点O,点M,N分别为OB,OC 的中点,则cos∠OMN的值为( )A. B. C. D.113、如图,在边长为1的小正方形组成的网格中,点A、B、O为格点,则tan∠AOB=()A. B. C. D.14、如图,是河堤横断面的迎水坡,堤高,水平距离,则斜坡的坡度为()A. B. C. D.15、△ABC 在网格中的位置如图所示(每个小正方形的边长均为 1), AD ^ BC 于 D .下列选项中,错误的是()A.sina=cosaB.tanC=2C.tana =1D.sin =cos二、填空题(共10题,共计30分)16、若cosα= ,α为锐角,则sinα=________.17、若a为锐角,且sin a= ,则cos a=________.18、如图,在矩形ABCD中,把∠A沿DF折叠,点A恰好落在矩形的对称中心E 处,则tan∠ADF=________19、已知△ABC中,AB=10,AC=2 ,∠B=30°,则△ABC的面积等于________.20、计算(﹣)﹣1+(2 ﹣1)0﹣|tan45°﹣2 |=________.21、如图,在四边形ABCD中,E、F分别是AB、AD的中点,若EF=4,BC=10,CD=6,则tanC=________22、计算:________.23、如图,小颖利用有一个锐角是的三角板测量一棵树的高度,已知她与树之间的水平距离BE为5m,AB为即小颖的眼睛距地面的距离,那么这棵树高是________24、若sinα= ,α是锐角,则α=________度.25、点A是反比例函数y=(x>0)图象上的一点,点B在x轴上,点C是坐标平面上的一点,O为坐标原点,若以点A,B,C,O为顶点的四边形是有一个角为60°的菱形,则点C的坐标是________.三、解答题(共5题,共计25分)26、计算:.27、如图,地面上小山的两侧有A、B两地,为了测量A、B两地的距离,让一热气球从小山两侧A地出发沿与AB成30°角的方向,以每分钟50m的速度直线飞行,8分钟后到达C处,此时热气球上的人测得CB与AB成70°角,请你用测得的数据求A,B两地的距离AB长.(取1.7,sin20°取0.3,cos20°取0.9,tan20°取0.4,sin70°取0.9,cos70°取0.3,tan70°取2.7.)28、为积极宣传国家相关政策,某村在一山坡的顶端的平地上竖立一块宣传牌.小明为测得宣传牌的高度,他站在山脚C处测得宣传牌的顶端的仰角为,已知山坡的坡度,山坡的长度为米,山坡顶端与宣传牌底端的水平距离为2米,求宣传牌的高度(精确到1米)(参考数据:,,,)29、观察与思考:阅读下列材料,并解决后面的问题.在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,过A作AD⊥BC于D(如图),则sinB=, sinC=,即AD=csinB,AD=bsinC,于是csinB=bsinC,即=.同理有:=,=,所以==即:在一个三角形中,各边和它所对角的正弦的比相等.在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.根据上述材料,完成下列各题.(1)如图,△ABC中,∠B=450,∠C=750, BC=60,则∠A=;AC= ;(2)如图,一货轮在C处测得灯塔A在货轮的北偏西30°的方向上,随后货轮以60海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得灯塔A在货轮的北偏西75°的方向上(如图),求此时货轮距灯塔A的距离AB.30、如图示一架水平飞行的无人机AB的尾端点A测得正前方的桥的左端点P的俯角为α其中tanα=2 ,无人机的飞行高度AH为500 米,桥的长度为1255米.①求点H到桥左端点P的距离;②若无人机前端点B测得正前方的桥的右端点Q的俯角为30°,求这架无人机的长度AB.参考答案一、单选题(共15题,共计45分)1、C2、B3、B4、B5、C6、D7、C8、B9、D10、B11、A12、B13、A14、A15、D二、填空题(共10题,共计30分)16、17、18、19、21、22、23、24、25、三、解答题(共5题,共计25分)26、30、。
浙教版九年级下册数学第一章 解直角三角形 含答案

浙教版九年级下册数学第一章解直角三角形含答案一、单选题(共15题,共计45分)1、已知在Rt△ABC中,∠C=90°,AC=6,BC=8,那么cosA的值为()A. B. C. D.2、已知∠A是锐角,且sinA=,那么∠A等于()A.30°B.45°C.60°D.75°3、如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF交于点O.下列结论:①∠DOC=90°, ②OC=OE,③tan∠OCD = ,④中,正确的有()A.1个B.2个C.3个D.4个4、如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3.5cm,则此光盘的直径是()cm.A.7B.7C.18D.125、若二次函数y=ax2+bx+c的图象与x轴有两个交点A和B,顶点为C,且b2﹣4ac=4,则∠ACB的度数为( )A.30°B.45°C.60°D.90°6、如果三角形满足一个角是另一个角的4倍,那么我们称这个三角形为“实验三角形”,下列各组数据中,能作为一个“实验三角形”三边长的一组是()A.1,1,B.1,1,C.1,2,D.1,2,37、如图,菱形ABCD和菱形ECGF的边长分别为2和3,∠A=120°,则图中阴影部分的面积是( )A. B.2 C.3 D.8、某滑雪场举办冰雪嘉年华活动,采用直升机航拍技术拍摄活动盛况.如图,通过直升机的镜头C观测到水平雪道一端A处的俯角为30°,另一端B处的俯角为45°.若直升机镜头C处的高度CD为300米,点A、D、B在同一直线上,则雪道AB的长度为()A.300米B.150 米C.900米D.(300 +300)米9、在中,,则的值为()A. B. C. D.10、如图,在坡角为α的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树的坡面上的距离AB为()米。
(典型题)浙教版九年级下册数学第一章 解直角三角形含答案

浙教版九年级下册数学第一章解直角三角形含答案一、单选题(共15题,共计45分)1、比较tan46°,cos29°,sin59°的大小关系是()A.tan46°<cos29°<sin59°B.tan46°<sin59°<cos29° C.sin59°<tan46°<cos29° D.sin59°<cos29°<tan46°2、某班的同学想测量一教楼AB的高度.如图,大楼前有一段斜坡BC,已知BC 的长为16米,它的坡度.在离C点45米的D处,测得一教楼顶端的仰角为,则一教楼AB的高度约()米(结果精确到0.1米)(参考数据:,,,)A.44.1B.39.8C.36.1D.25.93、sin45°的值等于()A. B. C. D.14、如图,Rt△ABC中,∠C=90°,AB=7,∠B=35°,则AC的长为()A.7cos35°B.7tan35°C.7sin35°D.7sin55°5、在数学活动课上,老师出示两张等腰三角形纸片,如图所示.图1的三角形边长分别为4,4,2;图2的三角形的腰长也为4,底角等于图1中三角形的顶角;某学习小组将这两张纸片在同一平面内拼成如图3的四边形OABC,连结AC.该学习小组经探究得到以下四个结论,其中错误的是()A.∠OCB=2∠ACBB.∠OAB+∠OAC=90°C.AC=2D.BC=46、如图,在△ABC中,∠A=90°,AB=6,AC=8,以点B为圆心,小于AB的长为半径画弧,分别交AB,BC于D,E两点,再分别以点D和点E为圆心,大于DE的长为半径画弧,两弧交于点F,射线BF交AC于点G,则tan∠CBG=()A. B. C. D.7、如图,已知l1∥l2∥l3∥l4,相邻两条平行直线间的距离相等.若等腰直角的三个顶点分别在三条平行直线上,则∠α的正弦值是()A. B. C. D.8、是()A. B. C. D.9、在Rt△ABC中,∠C=90°,各边都扩大2倍,则锐角A的正弦值()A.扩大2倍B.缩小C.不变D.无法确定10、α是锐角,且sinα>,则α()A.小于30°B.大于30°C.小于60°D.大于60°11、如图,在6×6的正方形网格中,△ABC的顶点都在小正方形的顶点上,则tan∠BAC的值是()A. B. C. D.12、数学实践探究课中,老师布置同学们测量学校旗杆的高度.如图所示,小明所在的学习小组在距离旗杆底部10米的地方,用测角仪测得旗杆顶端的仰角为60°,则旗杆的高度是()米.A. 10B.20C.D.1013、如图,已知△ABC的三个顶点均在格点上,则cosA的值为()A. B. C. D.14、如图,在菱形ABCD中,DE⊥AB,cosA=,则tan∠DBE()A. B.2 C. D.15、如图,在菱形ABCD中,DE⊥AB,cosA= ,AE=6,则tan∠BDE的值是( )A. B. C. D.二、填空题(共10题,共计30分)16、若为一锐角,且,则=________ .17、若等腰三角形一腰上的高与腰长之比为1∶2,则该等腰三角形顶角的度数为________.18、如图,在5×5的正方形网格中,每个小正方形的边长均为1,点A、B、C 都在格点上,则cos∠BAC的值为________.19、如图,在四边形中,,交于F,使得且.若在线段上取一点G,满足:平分且,则的值为________.20、如图,为测量一座大厦AB的高度,当小明在C处时测得楼顶A的仰角为60°,接着沿BC方向行走30m至D处时测得楼顶A的仰角为30°,则大厦AB 的高度是________.21、若α是锐角,且sinα=1﹣3m,则m的取值范围是________ ;将cos21°,cos37°,sin41°,cos46°的值,按由小到大的顺序排列是________ .22、如图,在矩形中,,,将矩形沿折叠,点落在处,若的延长线恰好过点,则的值为________.23、活动楼梯如图所示,∠B=90°,斜坡AC的坡度为1:1,斜坡AC的坡面长度为8m,则走这个活动楼梯从A点到C点上升的高度BC为________.24、若sinA= ,则cos(90°﹣A)=________.25、如图,点P在正方形ABCD的BC边上,连接AP,作AP的垂直平分线,交AD延长线于点E,连接PE,交CD于点F.若点F是CD的中点,则tan∠BAP=________.三、解答题(共5题,共计25分)26、计算:27、图1是放置在水平地面上的落地式话筒架实物图,图2是其示意图.支撑杆AB垂直于地面l,活动杆CD固定在支撑杆上的点E处.若∠AED=48°,BE=110cm,DE=80cm,求活动杆端点D离地面的高度DF.(结果精确到1cm,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11)28、底我市新湖一路贯通工程圆满竣工,若要在宽为40米的道路AD两边安装路灯,灯柱AB高10米,路灯的灯臂BC与灯柱AB成130°角,路灯采用圆锥形灯罩,灯罩的轴线CO与灯臂BC垂直,当灯罩的轴线CO通过公路的中心线时照明效果最好,此时路灯的灯臂BC应为多少米?(结果精确到0.01)(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).29、已知不等臂跷跷板AB长为4米,如图1,当AB的一端A碰到地面时,AB 与地面的夹角为α,如图2,当AB的另一端B碰到地面时,AB与地面的夹角为β,已知α=30°,β=37°,求跷跷板AB的支撑点O到地面的高度OH (sin37°=0.6,cos37°=0.8,tan37°=0.75).30、如图,内接于⊙ .若⊙ 的半径为6,,求的长.参考答案一、单选题(共15题,共计45分)1、D2、C3、B4、C5、D7、A8、A9、C10、D11、C12、D13、D14、B15、C二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、三、解答题(共5题,共计25分)26、27、29、30、。
浙教版九年级下册数学第一章 解直角三角形含答案【有解析】

浙教版九年级下册数学第一章解直角三角形含答案一、单选题(共15题,共计45分)1、下列运算正确的是()A.sin60°=B.a 6÷a 2=a 3C.(﹣2)0=2D.(2a 2b)3=8a 6b 32、在Rt△ABC中,∠C=90°,若cosA=,则sinB的值是()A. B. C. D.3、如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的三个顶点分别在这三条平行直线上,则sinα的值是()A. B. C. D.4、如图,直径为10的⊙A经过点C(0,5)和点O(0,0),B是y轴右侧⊙A 优弧上一点,则∠OBC的余弦值为()A. B. C. D.5、如图,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内),已知AB=a,AD=b,∠BCO=x,则点A到OC的距离等于()A.asinx+bsinxB.acosx+bsinxC.asinx+bcosxD.acosx+bcos x6、如图,在ABCD中,∠DAB=60°,AB=8,AD=6.⊙O分别切边AB,AD于点E,F,且圆心O好落在DE上.现将⊙O沿AB方向滚动到与BC边相切(点O在ABCD的内部),则圆心O移动的路径长为()A.2B.4C.5﹣D.8﹣27、sin30°的相反数()A. B.﹣ C. D.8、一个矩形按如图1的方式分割成三个直角三角形,把较大两个直角三角形纸片按图2中①、②两种方式放置,设①中的阴影部分面积为,②中的阴影部分面积为,当时,则矩形的两边之比为()A. B. C. D.9、当锐角时,的值是()A.大于B.小于C.大于D.小于10、在Rt△ABC,∠C=90°,AC=12,BC=5,则sinA的值为( )A. B. C. D.11、数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A、B的距离,他们设计了如图所示的测量方案:从树A沿着垂直于AB的方向走到E,再从E沿着垂直于AE的方向走到F,C为AE上一点,其中3位同学分别测得三组数据:①AC,∠ACB;②EF、DE、AD;③CD,∠ACB,∠ADB.其中能根据所测数据求得A、B两树距离的有()A.0组B.一组C.二组D.三组12、如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,则∠CDE的正切值为()A. B.2 C.3 D.413、如图,在△ABC中,∠B=90°,tan∠C= ,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是()A.18cm 2B.12cm 2C.9cm 2D.3cm 214、的值等于()A.1B.C.D.15、如图,在正方形中,对角线相交于点O,点E在BC边上,且,连接AE交BD于点G,过点B作于点F,连接OF 并延长,交BC于点M,过点O作交DC于占N,,现给出下列结论:① ;② ;③ ;④ ;其中正确的结论有()A.①②③B.②③④C.①②④D.①③④二、填空题(共10题,共计30分)16、如图,已知菱形的面积为,,对角线、交于点,若点为对角线上一点,则的最小值是________.17、已知,在△ABC中,∠A=45°,AC=, AB=+1,则边BC的长为________ .18、若是锐角,且,则________.19、如图,已知在平行四边形ABCD中,AB=8 ,BC=20,∠A=60°,P是边AD上一动点,连结PB,将线段PB绕着点P逆时针旋转90°得到线段PQ,若点Q恰好落在平行四边形ABCD的边上,那么AP的值是________.20、在中,,,,则________.21、如图,在扇形OAB中,∠AOB=90°,半径OB=2.∠BOC=60°,连接AB,AB、OC交于点D,则图中阴影部分的面积为________.22、在由边长为1的小正方形所组成的网格中,如图放置,则________.23、运用科学计算器计算:2 cos72°=________.(结果精确到0.1)24、已知asinθ+cosθ=1,且bsinθ﹣cosθ=1,(其中θ是锐角),则ab=________.25、如图,点BEC在一直线上,△ BEA,△CED在直线BC同侧,BE=BA=4,CE=CD=6,∠B=∠C=a,当tan 时,△ADE外接圆的半径为________。
第一章 解直角三角形数学九年级下册-单元测试卷-浙教版(含答案)

第一章解直角三角形数学九年级下册-单元测试卷-浙教版(含答案)一、单选题(共15题,共计45分)1、如图,四边形ABCD是矩形,BC=4,AB=2,点N在对角线BD上(不与点B,D重合),EF,GH过点N,GH∥BC交AB于点G,交DC于点H,EF∥AB交AD于点E,交BC于点F,AH交EF于点M.设BF=x,MN=y,则y关于x的函数图象是()A. B. C. D.2、2sin60°的值等于()A.1B.C.D.3、如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行40分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是()A.20海里B.40海里C. 海里D. 海里4、如图,某飞机于空中处探测到正下方的地面目标,此时飞机高度,从飞机上看地面控制点的俯角为,则处到控制点的距离可表示为()A. B. C. D.5、如图,沿AE折叠矩形纸片ABCD,使点D落在BC边的点F处已知AB=8,BC=10,则tan ∠EFC的值为()A. B. C. D.6、位于重庆西部的融创文旅城是集商场、室内乐园、室外飞天项目、渝乐小镇于一体的大型文娱项目,小明为了测量室外飞天项目中摩天轮最高处点距离地面的高度,他先是在处测得顶点的仰角为,然后沿水平向摩天轮方向前行了50米到达处,再沿着坡比为的小山坡走到点,测得米,此时点到的水平距离为70米,与地面垂直,则摩天轮最高处点距离地面的高度约为(参考数据:)()米A.90.2B.91.3C.93.4D.95.427、如图,点A、B、O是正方形网格上的三个格点,⊙O的半径为OA,点P是优上的一点,则cos∠APB的值是()A.45°B.1C.D.无法确定8、在△ABC中,(2cosA-)2+| -tanB|=0,则△ABC一定是()A.直角三角形B.钝角三角形C.等腰三角形D.锐角三角形9、河堤横断面如图所示,迎水坡米,迎水坡的坡比为(坡比是坡面的铅直高度与水平度之比),则的长是()A. 米B. 米C.15米D.10米10、如图,在A、B 两地之间要修一条笔直的公路,从A地测得公路走向是北偏东48°,A,B两地同时开工,若干天后公路准确接通,若公路AB长8千米,另一条公路BC长是6千米,且BC的走向是北偏西42°,则A地到公路BC的距离是()A.6千米B.8千米C.10千米D.14千米11、如图,在△ABC中,∠A=45°,∠C=90°,点D在线段AC上,∠BDC=60°,AD=1,则BD等于( )A. B. +1 C. -1 D.12、在中,,,,则的值为()A. B. C. D.13、按键,使科学记算器显示回后,求sin90°的值,以下按键顺序正确的是()A. B. C.D.14、如图,△ABC内接于⊙O,连接OA、OC,⊙O的半径为3,且sinB= ,则弦AC的长为()A. B.5 C. D.15、如图,已知AE与BF相交于点D,AB⊥AE,垂足为点A,EF⊥AE,垂足为点E,点C在AD上,连接BC,要计算A、B两地的距离,甲、乙、丙、丁四组同学分别测量了部分线段的长度和角的度数,各组分别得到以下数据:甲:AC、∠ACB;乙:EF、DE、AD;丙:AD、DE和∠DCB;丁:CD、∠ABC、∠ADB.其中能求得A、B两地距离的数据有()A.甲、乙两组B.丙、丁两组C.甲、乙、丙三组D.甲、乙、丁三组二、填空题(共10题,共计30分)16、矩形ABCD中,AB=4,BC=6,点E为BC的中点,沿AE将△AEB翻折得到△AFE,sin ∠FCE=________.17、计算:–2cos60°=________.18、用一副如图-1所示的七巧板,拼出如图-2所示中间有一个空白正方形的“风车图”,则图2中tan∠ABC=________19、计算=________ .20、在Rt△ABC中,∠C=90°,sinA= ,那么cosA=________.21、如图所示,已知⊙O的半径为5cm,弦AB的长为8cm,P是AB延长线上一点,BP=2cm,则tan∠OPA等于________.22、计算:=________.23、在平面直角坐标系中,点A的坐标为(1,),以原点为中心,将点A逆时针旋转30°得到A′,则点A′的坐标为________.24、如图,点A是反比例函数y=(x>0)图象上一点,过点A作AB⊥x轴于点B,连接OA,OB,tan∠OAB=.点C是反比例函数y=(x>0)图象上一动点,连接AC,OC,若△AOC的面积为,则点C的坐标为________.25、已知锐角满足,则锐角的度数是________度三、解答题(共5题,共计25分)26、计算:()﹣1﹣20150+|﹣|﹣2sin60°27、如图,禁渔期间,我渔政船在A处发现正北方向B处有一艘可疑船只,测得A、B两处距离为99海里,可疑船只正沿南偏东53°方向航行.我渔政船迅速沿北偏东27°方向前去拦截,2小时后刚好在C处将可疑船只拦截.求该可疑船只航行的速度.(参考数据:sin27°≈, cos27°≈, tan27°≈, sin53°≈,cos53°≈, tan53°≈)28、某海域有A,B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C 处,求该船与B港口之间的距离即CB的长(结果保留根号).29、如图,某商店营业大厅自动扶梯AB的倾斜角为31°,AB的长为12米,求大厅两层之间的距离BC的长.(结果精确到0.1米)(参考数据:sin31°=0.515,cos31°=0.857,tan31°=0.60)30、如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角α=43°.求飞机A与指挥台B的距离(结果取整数).【参考数据:sin43°=0.68,cos43°=0.73,tan43°=0.93】参考答案一、单选题(共15题,共计45分)1、B2、C3、D4、D6、C7、C8、D9、A10、B11、B12、A13、A14、B15、D二、填空题(共10题,共计30分)16、17、18、19、20、22、23、24、25、三、解答题(共5题,共计25分)26、29、30、。
浙教版九年级数学下《第一章解直角三角形》单元测试题含答案
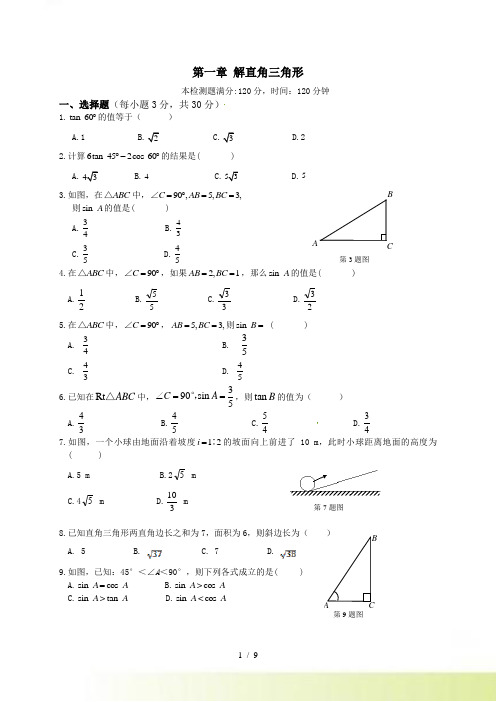
第一章 解直角三角形本检测题满分:120分,时间:120分钟一、选择题(每小题3分,共30分)1.tan 60︒ 的值等于( )A.1B.2C.3D.2 2.计算6tan 452cos 60︒-︒ 的结果是( ) A.43 B.4C.53D.53.如图,在ABC △中,90,5,3,∠C AB BC =︒== 则sin A 的值是( ) A.34B.34C.35D.454.在ABC △中,90C =︒∠,如果2,1AB BC ==,那么sin A 的值是( ) A.21 B.55C.33D.23 5.在ABC △中,90C =︒∠,5,3,AB BC ==则sin B = ( ) A. 34 B. 53 C.43 D. 456.已知在Rt ABC △中,390sin 5C A ∠==°,,则tan B 的值为( ) A.43 B.45C.54D.347.如图,一个小球由地面沿着坡度12∶i =的坡面向上前进了10 m ,此时小球距离地面的高度为( )A.5 mB.25 mC.45 mD.310 m 8.已知直角三角形两直角边长之和为7,面积为6,则斜边长为( ) A. 5 B.C. 7D.9.如图,已知:45°<∠A <90°,则下列各式成立的是( ) A.sin cos A A = B.sin cos A>A C.sin tan A>A D.sin cos A<A第7题图AC第9题图第3题图ACB10.如图,在菱形ABCD 中,⊥DE AB ,3cos 5A =, 2BE =,则tan ∠DBE 的值是( ) A .12B .2C .52 D .55二、填空题(每小题3分,共24分)11.在Rt △ABC 中,90,3,4=︒==ABC AB BC ∠,则sin A =______.12.比较大小:8cos 31︒ 35.(填“>”“=”或“<”) 13.如图,小兰想测量南塔的高度,她在A 处仰望塔顶,测得仰角为30°,再往塔的方向前进50 m 至B 处,测得仰角为60°,那么塔高约为 _________ m.(小兰身高忽略不计,31732.≈) 14.已知等腰三角形的腰长为2,腰上的高为1,则它的底角等于________.15.大坝的横断面是梯形,坝内斜坡的坡度,坝外斜坡的坡度,则两个坡角的和为 .16.如图,△ABC 的顶点都在方格纸的格点上,则sin A =_ .17.如图,在四边形ABCD 中,609069=︒==︒==A B D BC ,CD ∠,∠∠,,则AB =__________.18.如图,在△ABC 中,已知324530,∠,∠AB B C ==︒=︒,则AC =________. 三、解答题(共66分) 19.(8分)计算下列各题: (1)()42460sin 45cos 22+- ;(2)2330tan 3)2(0-+--.20.(8分)在数学活动课上,九年级(1)班数学兴趣小组的同学们测量校园内一棵大树的高度,设计的方案及测量数据如下:(1)在大树前的平地上选择一点A ,测得由点A 看大树顶端C 的仰角为35°;A CB 第18题图(2)在点A 和大树之间选择一点B (A,B,D 在同一条直线上),测得由点B 看大树顶端C 的仰角恰好为45°;(3)量出A,B 两点间的距离为45 m ..请你根据以上数据求出大树CD 的高度.(结果保留3个有效数字)21.(8分)每年的5月15日是“世界助残日”.某商场门前的台阶共高出地面1.2米,为帮助残疾人便于轮椅行走,准备拆除台阶换成斜坡,又考虑安全,轮椅行走斜坡的坡角不得超过9︒,已知此商场门前的人行道距商场门的水平距离为8米(斜坡不能修在人行道上),问此商场能否把台阶换成斜坡? (参考数据:)22.(8分)如图,为了测量某建筑物CD 的高度,先在地面上用测角仪自A 处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100 m ,此时自B 处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5 m ,请你计算出该建筑物的高度.(取3≈ 1.732,结果精确到1 m ) 23.(8分)如图,在梯形ABCD 中,∥AD BC ,AB CD AD ==,⊥BD CD .(1)求sin ∠DBC 的值;(2)若BC 的长度为4cm ,求梯形ABCD 的面积. 24.(8分)如图,在ABC Rt △中,290,10,sin 5C AB A =︒==∠ ,求BC 的长和tan B 的值.25.(9分)如图,小明家住在32 m 高的A 楼里,小丽家住在B 楼里,B 楼坐落在A 楼的正北面,已知当地冬至12时太阳光线与水平面的夹角为30︒.(1)如果,A B 两楼相距203 m ,那么A 楼落在B 楼上的影子有多长?CA B第24题图(2)如果A 楼的影子刚好不落在B 楼上,那么两楼的距离应是多少?(结果保留根号)26.(9分)在△ABC 中,BC a,AC b,AB c ===.若90C ∠=︒,如图①,根据勾股定理,则222a b c +=.若△ABC 不是直角三角形,如图②和图③,请你类比勾股定理,试猜想22a b +与2c 的关系,并证明你的结论.ABCABABC①②③第26题图第一章 解直角三角形检测题参考答案1.C2.D 解析:16tan 452cos 6061252︒-︒=⨯-⨯= .3.C 解析:3sin 5BC A AB == . 4.A 解析:5.D 解析:由勾股定理知,所以所以sin.54=AB AC 6.A 解析:如图,设则由勾股定理知,所以tan B7.B 解析:设小球距离地面的高度为则小球水平移动的距离为所以解得8.A 解析:设直角三角形的两直角边长分别为则所以斜边长9.B 解析:在锐角三角函数中仅当∠45°时,,所以选项错误;因为45°<∠A <90°,所以∠B <45°,即∠A >∠B ,所以BC >AC , 所以AB BC >AB AC,即sin cos A>A ,所以选项正确,选项错误; tan A = ACBC>1,<1,所以选项错误. 10.B 解析:设又因为在菱形中,所以所以所以由勾股定理知所以211.45解析:在ABC Rt △中,90ABC =︒∠,由勾股定理,得222AC AB BC =+, ABC第6题答图所以2222345AC AB BC =+=+=,所以4sin 5==BC A AC . 12.> 解析:因为8cos 31 6.86,35 5.92︒≈≈ ,所以∠8cos 3135︒> . 13.43.3 解析:因为,所以所以所以()3502532517324332=⨯=≈⨯=DC ..m . 14.15°或75° 解析:如图,.在图①中,,所以∠∠;在图②中,,所以∠∠.15. 解析:设两个坡角分别为,,则tan ,tan ,所以,所以两个坡角的和为.16.55解析:利用网格,过点向所在直线作垂线,设网格中小正方形的边长为1,则利用勾股定理得,所以sin A =55. 17. 解析:如图,延长,交于点.∵ ∠,∴ .∵,∴,则.∵ ,∴.第14题答图18.6 解析:如图,过点作于点.∵ ,∠,∴.∴.19.解:(1)()24232622cos 45sin 60224224 ⎛⎫-+=⨯-+ ⎪ ⎪⎝⎭366622222222.⎛⎫=-+=-+= ⎪ ⎪⎝⎭(2)()023tan 30321323323 --+-=-+-=-. 20.解:∵ ∠90°, ∠45°,∴∵,∴设高CD 为m x ,则 m ,()45m AD x .=+.∵ ∠35°,∴ tan ∠tan 35°5.4+x x. 整理,得 4.5tan 351tan 35⨯=-x ≈10.5.故大树的高度约为10.521.解:因为所以斜坡的坡角小于,故此商场能把台阶换成斜坡.22.解:设,则由题意可知,m .在Rt △AEC 中,tan ∠CAE =AE CE,即tan 30°=100+x x , ∴33100=+x x ,即3x 3(x +100),解得x 50+503.经检验50+503是原方程的解.∴故该建筑物的高度约为23.解:(1)∵ ,∴ ∠∠. ∵∥,∴ ∠∠∠. 在梯形中,∵,∴ ∠∠∠∠∵ ,∴ 3∠ ,∴ ∠30° ,∴(2)如图,过点作于点. 在Rt △中,•∠,• ∠,∴在Rt △中,,∴ 梯形ABCD 的面积为24.解:∵ 2sin ,10,5===BC A AB AB ∴ 4=BC . 又∵ 22221,=-=AC AB BC ∴ 21tan 2==AC B BC . 25.解:(1)如图,过点作于点,∵,,∴ .故.∴ 楼落在楼上的影子有12 m 长. (2)若楼的影子刚好不落在楼上,,∴ 两楼的距离应是m.26.解:如图①,若△是锐角三角形,则222a b c +>.证明如下:过点作,垂足为,设为x ,则a x -.根据勾股定理,得22222()b x AD c a x -==--, 即222222b x c a ax x -=-+-.∴ 2222a b c ax +=+. ∵ 0,0a x >>,∴ 20ax >,∴ 222a b c +>.如图②,若△是钝角三角形,C ∠为钝角,则222a b c +<.证明如下: 过点作,交的延长线于点.设=x ,则222BD a x =-.根据勾股定理,得2222()b x a x c ++-=.即2222a b bx c ++=.∵ 0,0b x >>,∴ 20bx >,∴ 222a b c +<.。
浙教版九年级下册数学第一章 解直角三角形含答案(必考题)

浙教版九年级下册数学第一章解直角三角形含答案一、单选题(共15题,共计45分)1、小明在学完《解直角三角形》一章后,利用测角仪和校园旗杆的拉绳测量校园旗杆的高度,如图,旗杆的高度与拉绳的长度相等,小明先将拉到的位置,测得为水平线),测角仪的高度为米,则旗杆的高度为()A. 米B. 米C. 米D. 米2、构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图.在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB使BD=AB,连接AD,得∠D=15°,所以tan15°====2﹣.类比这种方法,计算tan22.5°的值为()A. +1B. ﹣1C.D.3、如图,在直径为4的⊙O中,弦AC=,则劣弧AC所对的圆周角∠ABC的余弦值是:()A. B. C. D.4、如图,AB为半圆O的直径,现将一块等腰直角三角板如图放置,锐角顶点P 在半圆上,斜边过点B,一条直角边交该半圆于点Q.若AB=2,则线段BQ的长为()A. B. C. D.15、如图,在Rt△ABC中,斜边AB的长为m,∠A=35°,则直角边BC的长是()A.msin35°B.mcos35°C.D.6、如图,Rt△ABC中,∠A=90°,AD⊥BC于点D,若BD:CD=3:2,则tanB=()A. B. C. D.7、已知∠A是锐角,且sinA=,那么∠A等于()A.30°B.45°C.60°D.75°8、小明沿着坡度为1:2的山坡向上走了1000m,则他升高了( )A.200 mB.500mC.500 mD.1000m9、如图,下列说法中错误的是()A.OA的方向是东北方向B.OB的方向是北偏西30°C.OC的方向是南偏西60°D.OD的方向是南偏东30°10、李红同学遇到了这样一道题:tan(α+20°)=1,你猜想锐角α的度数应是()A.40°B.30°C.20°D.10°11、在Rt△ABC中,,AC=3,BC=4,则sinA的值为()A. B. C. D.12、如图,在中,,,为边上的一个动点(不与、重合),连接,则的最小值是()A. B. C. D.213、2sin60°的值等于()A. B.2 C.1 D.14、如图,点P(x,y)(x>0,y>0)在半径为1的圆上,则cosα=()A.xB.yC.D.15、在Rt△ABC中,∠C=90°,AB=10,sin∠B=,则BC=()A.15B.6C.9D.8二、填空题(共10题,共计30分)16、计算:=________.17、如图,在Rt△ABC中,CD是斜边AB上的中线,已知CD=2,AC=3,则sinB的值是________.18、如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设OP=x(x≥0),则x的取值范围是________.19、计算“2sin30°-(π- )0+| -1|+()-1”的结果是 ________.20、若cosA=0.6753,则锐角A=________ (用度、分、秒表示).21、如图,建筑物BC的屋顶有一根旗杆AB,从地面上点D处观测旗杆顶点A的仰角为50°,观测旗杆底部点B的仰角为45°。
浙教版九年级下册数学第一章 解直角三角形 含答案

浙教版九年级下册数学第一章解直角三角形含答案一、单选题(共15题,共计45分)1、如图,击打台球时小球反弹前后的运动路线遵循对称原理,即小球反弹前后的运动路线与台球案边缘的夹角相等(α=β),在一次击打台球时,把位于点P处的小球沿所示方向击出,小球经过5次反弹后正好回到点P,若台球案的边AD的长度为4,则小球从P点被击出到回到点P,运动的总路程为()A.16B.16C.20D.202、如图,铁路MN和公路PQ在点O处交汇,∠QON=30°.公路PQ上A处距O 点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路MN上沿ON方向以20米/秒的速度行驶时,A处受噪音影响的时间为()A.16秒B. 20秒 D.22秒3、如图,一艘轮船在B处观测灯塔A位于南偏东50°方向上,相距40海里,轮船从B处沿南偏东20°方向匀速航行至C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是()A.20海里B.40海里C.20 海里D.40 海里4、某人沿坡度i=1:的坡面向上走50米,则此人离地面的高度为()A.25米B.50米C.25 米D.50 米5、如图,在△ABC中,AC=6,∠BAC=60°,AM为△ABC的角平分线,若,则AM长为()A.6B.C.D.6、如图,在5×4的正方形网格中,每个小正方形的边长均是1,△ABC的顶点均在小正方形的顶点上,则tanA的值为()A. B. C. D.7、如图,△ABC内接于⊙O,若sin∠BAC= ,BC=2 ,则⊙O的半径为()A.3B.6C.4D.28、斜坡的倾斜角为α,一辆汽车沿这个斜坡前进了500米,则它上升的高度是()A.500•sinα米B. 米C.500•cosα米D. 米9、如图,平行四边形 ABCD 中,AD∥BC,AB=BC=CD=AD=4,∠A=∠C=60°,连接 BD,将△BCD 绕点 B 旋转,当 BD(即 BD′)与 AD 交于一点 E,BC(即BC′)同时与 CD 交于一点 F 时,下列结论正确的是()①AE=DF;②∠BEF=60°;③∠DEB=∠DFB;④△DEF 的周长的最小值是4+2A.①②B.②③C.①②④D.①②③④10、如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠BED的正切值等于()A. B. C.2 D.11、在Rt△ABC中,∠C=90°,sinA=,则cosB的值等于()A. B. C. D.12、如图,C.D分别是一个湖的南、北两端A和B正东方向的两个村庄,CD=6km,且D位于C的北偏东30°方向上,则AB的长为()A.2 kmB.3 kmC. kmD.3km13、如图,在ABCD中,∠ABC=45°,BC=4,点F是CD上一个动点,以FA、FB为邻边作另一个AEBF,当F点由D点向C点运动时,下列说法正确的选项是()①AEBF的面积先由小变大,再由大变小;②AEBF的面积始终不变;③线段EF最小值为A.①B.②C.①③D.②③14、图1是一张圆形纸片,直径AB=4,现将点A折叠至圆心O形成折痕CD,再把点C,D都折叠至圆心O处,最后将图形打开铺平(如图2所示),则弧EF的长为( )A. πB. πC. πD. π15、如图,在中,,D从A出发沿方向以向终点C匀速运动,过点D作交于点E,过点E 作交于点F,当四边形为菱形时,点D运动的时间为()A. B. C. D.二、填空题(共10题,共计30分)16、如图,A是半径为1的⊙O的外一点,OA=2,AB是⊙O的切线,B是切点,弦BC∥AO,连结AC,则图中的阴影部分的面积等于________.17、若α是锐角,且sinα=1﹣3m,则m的取值范围是________ ;将cos21°,cos37°,sin41°,cos46°的值,按由小到大的顺序排列是________ .18、如图,点D(0,3),O(0,0),C(4,0),B在⊙A上,BD是⊙A的一条弦.则sin∠OBD=________.19、一个小球由地面沿着坡度1:2的坡面向上前进了10米,此时小球距离地面的高度为________米.20、计算:cos30°﹣sin60°=________.21、如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,那么山高AD为________ 米(结果保留整数,测角仪忽略不计,≈1.414,≈1.732).22、如图,从与旗杆AB相距27m的点C处,用测角仪CD测得旗杆顶端A的仰角为30°,已知测角仪CD的高为1.5米,则旗杆AB的高约为________m(精确到0.1m,参考数据≈1.73)23、计算:sin45°+6tan30°﹣2cos30°=________.24、如图,在矩形ABCD中,CD是⊙O直径,E是BC的中点,P是直线AE上任意一点,AB=4,BC=6,PM、PN相切于点M、N,当∠MPN最大时,PM的长为________.25、计算:________.三、解答题(共5题,共计25分)26、计算:.27、随着人们经济收入的不断提高,汽车已越来越多地进入到各个家庭.某大型超市为缓解停车难问题,建筑设计师提供了楼顶停车场的设计示意图.按规定,停车场坡道口上坡要张贴限高标志,以便告知车辆能否安全驶入.如图,地面所在的直线ME与楼顶所在的直线AC是平行的,CD的厚度为0.5m,求出汽车通过坡道口的限高DF的长(结果精确到0.1m,sin28°≈0.47,cos28°≈0.88,tan28°≈0.53).28、乌鞘岭隧道群是连霍国道主干线上隧道最密集、路线最长、海拔最高、地质条件最复杂、施工难度最大的咽喉工程.乌鞘岭特长公路隧道群的全部贯通,将使连霍国道主干线在甘肃境内1608公里路段全部实现高速化,同时也使甘肃河西五市与省会兰州及东南沿海省、市实现全线高速连接.如图,在建设中为确定某隧道AB的长度,测量人员在离地面2700米高度C处的飞机上,测得正前方A、B两点处的俯角分别是60°和30°,求隧道AB的长(结果保留根号)29、钓鱼岛自古就是中国的领土,中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视监测.一日,中国一艘海监船从A点沿正北方向巡航,其航线距钓鱼岛(设M,N为该岛的东西两端点)最近距离为14.4km(即MC=14.4km).在A点测得岛屿的西端点M在点A的北偏东42°方向;航行4km后到达B点,测得岛屿的东端点N在点B的北偏东56°方向,(其中N,M,C在同一条直线上),求钓鱼岛东西两端点MN之间的距离(结果精确到0.1km).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,sin56°≈0.83,cos56°≈0.56,tan56°≈1.48)30、已知:如图,为了躲避台风,一轮船一直由西向东航行,上午点,在处测得小岛的方向是北偏东,以每小时海里的速度继续向东航行,中午点到达处,并测得小岛的方向是北偏东,若小岛周围海里内有暗礁,问该轮船是否能一直向东航行?参考答案一、单选题(共15题,共计45分)1、B2、A3、B4、A5、C6、D7、A8、A9、C10、D11、B12、B13、D14、C15、D二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)26、28、30、。
浙教版九年级下册数学第一章 解直角三角形 含答案

浙教版九年级下册数学第一章解直角三角形含答案一、单选题(共15题,共计45分)1、如图,一个小球由地面沿着坡度的坡面向上前进了10m,此时小球距离地面的高度为()A.2 mB.2mC.4 mD. m2、的值等于()A. B. C. D.3、如图1是一个手机的支架,由底座、连杆和托架组成(连杆始终在同一平面内),垂直于底座且长度为的长度为的长度可以伸缩调整.如图2,保持不变,转动,使得,假如时为最佳视线状态,则此时的长度为(参考数据:)()A. B. C. D.4、在Rt△ABC中,∠C=90°,AB=2BC,则cosA的值是( )A. B.2 C. D.5、如果Rt△ABC中各边的长度都扩大到原来的2倍,那么锐角∠A的三角比的值()A.都扩大到原来的2倍B.都缩小到原来的一半C.没有变化D.不能确定6、如图,已知AD是等腰△ABC底边上的高,且tan∠B=,AC上有一点E满足AE∶CE= 2∶3,则tan∠ADE的值是()A. B. C. D.7、在Rt△ABC中,∠C=90°,AB=13,AC=12,则cosA=()A. B. C. D.8、cos30o=()A. B. C. D.9、某人在坡角为的山坡上种树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为()A.5cosB.C.5sinD.10、在△ABC中,AC=6,BC=5,sinA= ,∠A、∠B为锐角,则tanB=()A. B. C. D.11、如图,△ABC中,AB=AC=10,tanA=2,BE⊥AC于点E,D是线段BE上的一个动点,则的最小值是( )A. B. C. D.1012、为测量如图所示上山坡道的倾斜度,小明测得图中所示的数据,则该坡道倾斜角α的正切值是()A. B. C. D.13、如图,是的内接三角形,,是直径,,则的长为()A.4B.C.D.14、点M(-sin 60°,cos 60°)关于x轴对称的点的坐标是( )A. B. C. D.15、如图:为了测楼房BC的高,在距离楼房10米的A处,测得楼顶B的仰角为,那么楼房BC的高为()A.10tana(米)B. (米)C. (米)D.(米)二、填空题(共10题,共计30分)16、已知方程x2-4x+3=0的两根为直角三角形的两直角边长,则其最小角的余弦值为________.17、已知△ABC,AB=AC,BC=8,点D、E分别在边BC、AB上,将△ABC沿着直线DE翻折,点B落在边AC上的点M处,且AC=4AM,设BD=m,那么∠ACB的正切值是________.(用含m的代数式表示)18、如图,已知等腰,,以为直径的圆交于点,过点的的切线交于点,若,,则的半径是________.19、在以O为坐标原点的直角坐标平面内有一点A(4,2),如果AO与x轴正半轴的夹角为α,那么cosα=________.20、若α为锐角,且tanα=1,则α=________度21、计算:2﹣1×+2cos30°=________.22、如图,我市在建高铁的某段路基横断面为梯形,∥,长为6米,坡角为45°,的坡角为30°,则的长为 ________ 米(结果保留根号)23、计算:﹣tan60°=________.24、如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A、C两点测得该塔顶端F的仰角分别为∠α=48°和∠β=65°,矩形建筑物宽度AD=20m,高度CD=30m,则信号发射塔顶端到地面的高度FG为________米(结果精确到1m).参考数据:sin48°=0.7,cos48°=0.7,tan48°=1.1,cos65°=0.4,tan65°=2.125、已知∠A=60°,则cosA=________.三、解答题(共5题,共计25分)26、计算:2sin60°+|3﹣|﹣()﹣1+(π﹣2018)027、如图,大海中某岛C的周围25km范围内有暗礁.一艘海轮向正东方向航行,在A处望见C在北偏东60°处,前进20km后到达点B,测得C在北偏东45°处.如果该海轮继续向正东方向航行,有无触礁危险?请说明理由.(参考数据:≈1.41,≈1.73)28、计算:| -2|+2cos45°- + .29、为提升城市品味、改善居民生活环境,我省某市拟对某条河沿线十余个地块进行片区改造,其中道路改造是难度较大的工程如图是某段河道坡路的横截面,从点A到点B,从点B到点C是两段不同坡度的坡路,CM是一段水平路段,CM与水平地面AN的距离为12米.已知山坡路AB的路面长10米,坡角BAN=15°,山坡路BC与水平面的夹角为30°,为了降低坡度,方便通行,决定降低坡路BC的坡度,得到新的山坡AD,降低后BD与CM相交于点D,点D,A,B在同一条直线上,即∠DAN=15°.为确定施工点D的位置,求整个山坡路AD的长和CD的长度(sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,sin30°=0.50,cos30°≈0.87,tan30°≈0.58结果精确到0.1米)30、停车难已成为合肥城市病之一,主要表现在居住停车位不足,停车资源结构性失衡,中心城区供需差距大等等.如图是张老师的车与墙平行停放的平面示意图,汽车靠墙一侧OB与墙MN平行且距离为0.8米,已知小汽车车门宽AO为1.2 米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?请说明理由.(参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)参考答案一、单选题(共15题,共计45分)1、A2、A3、C4、D6、B7、C8、C9、B10、D11、B12、B13、B14、B15、A二、填空题(共10题,共计30分)16、17、18、19、21、22、23、24、25、三、解答题(共5题,共计25分)26、28、。
浙教版九年级下册数学第一章 解直角三角形含答案

浙教版九年级下册数学第一章解直角三角形含答案一、单选题(共15题,共计45分)1、如图,在中,,沿的中线,将折叠,使点A落在点D处,若恰好与垂直,则的值为( )A. B. C. D.2、已知2cosA=1,则锐角A的度数是( )A.30°B.45°C.60°D.75°3、如图,在正方形中,边长,是为中点,连接,,把沿着翻折,得到,则点到的距离为()A. B.4 C. D.4、如图,在△ABC中,∠C=90o, AC=3,BC=4,则sinB的值是()A. B. C. D.5、如图,在中,,,,则()A. B. C. D.6、如图,要拧开一个边长为a=6mm的正六边形螺帽,扳手张开的开口b至少为( )A.6 mmB.12mmC.6 mmD. 4mm7、在△ABC中,∠C=90°,且两条直角边a,b满足a2﹣5ab+6b2=0,则tanA的值为()A.5或6B.2C.3D.2或38、在Rt△ABC中,∠C=90°,BC=3cm,AC=4cm,那么sinA为()A. B. C. D.9、“折竹抵地”问题源自《九章算术》中,即:今有竹高一丈,末折抵地,去本四尺,问折者高几何?意思是:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远(如图),则折断后的竹子高度为多少尺?(1丈=10尺)( )A.3B.5C.D.410、已知sinα•cosα=, 45°<α<90°,则cosα﹣sinα=()A. B.- C. D.±11、公元3世纪,刘徽发现可以用圆内接正多边形的周长近似地表示圆的周长.如图所示,他首先在圆内画一个内接正六边形,再不断地增加正多边形的边数;当边数越多时,正多边形的周长就越接近于圆的周长.刘徽在《九章算术》中写道:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣.”我们称这种方法为刘徽割圆术,它开启了研究圆周率的新纪元.小牧通过圆内接正边形,使用刘徽割圆术,得到π的近似值为()A. B. C. D.12、已知α,β是△ABC的两个角,且sinα,tanβ是方程2x2﹣3x+1=0的两根,则△ABC是()A.锐角三角形B.直角三角形或钝角三角形C.钝角三角形D.等边三角形13、如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径r=5,AC=5 ,则∠B的度数是()A.30°B.45°C.50°D.60°14、如图,在中,平分,交于点E,交于点F,且交于点O,若,则的值为()A. B. C. D.15、如图,小明站在某广场一看台C处,测得广场中心F的俯角为21°,若小明身高CD=1.7米,BC=1.9米,BC平行于地面FA,台阶AB的坡度为i=3:4,坡长AB=10.5米,则看台底端A点距离广场中心F点的距离约为()米.(参考数据:sin21°≈0.36,cos21°≈0.93,tan21°≈0.38)A.8.9B.9.7C.10.8D.11.9二、填空题(共10题,共计30分)16、先用计算器求:tan20°≈________,tan40°≈________,tan60°≈________,tan80°≈________,再按从小到大的顺序用“<”把tan20°,tan40°,tan60°,tan80°连接起来:________.归纳:正切值,角大值________.17、如图所示,在四边形中,,分别是的中点,,则的长是________.18、如图,在四边形中,,交于F,使得且.若在线段上取一点G,满足:平分且,则的值为________.19、阅读理解:已知∠A、∠B是Rt△ABC的两个锐角,锐角∠A的邻边与对边的比值叫做锐角∠A的余切,记作cotA,记cotA= ,已知tanB=,则cotB的值等于________.20、如图,有一斜坡,坡顶B离地面的高度为,斜坡的倾斜角是,若,则此斜坡的为________m.21、如图,在△ABC中,∠BAC=90°,AB=AC=5,将△ABC折叠,使点B落在AC边上的点D处,EF为折痕,若sin∠CFD的值为,则BE=________.22、如图,点A、B、C在正方形网格的格点上,则的值为________.23、一段公路的坡度为1∶3,某人沿这段公路路面前进100米,他上升的最大高度为________.24、河堤横断面如图所示,堤高BC=6米,迎水坡AB的坡比是1:,则AC 的长是________米.25、在△ABC中,若+ ,则∠C的度数为________.三、解答题(共5题,共计25分)26、计算:.27、居家学习期间,小睛同学运用所学知识在自家阳台测对面大楼的高度如图,她利用自制的测角仪测得该大楼顶部的仰角为,底部的俯角为:又用绳子测得测角仪距地面的高度为.求该大棱的高度(结果精确到)(参考数据:,,)28、钓鱼岛是我国的神圣领土,中国人民维护国家领土完整的决心是坚定的,多年来,我国的海监、渔政等执法船定期开赴钓鱼岛巡视.某日,我海监船(A 处)测得钓鱼岛(B处)距离为20海里,海监船继续向东航行,在C处测得钓鱼岛在北偏东45°的方向上,距离为10海里,求AC的距离.(结果保留根号)29、如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向的B处,求此时轮船所在的B处与灯塔P的距离.(参考数据:≈2.449,结果保留整数)30、如图,已知OB的方向是南偏东60°,OA、OC分别平分∠NOB和∠NOE,(1)请直接写出OA的方向是,OC的方向是(2)求∠AOC的度数.参考答案一、单选题(共15题,共计45分)1、B2、C3、A4、C5、C6、C7、D8、C9、C10、B11、A12、B13、D14、C15、C二、填空题(共10题,共计30分)16、17、18、20、21、22、23、24、25、三、解答题(共5题,共计25分)26、29、。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1章解直角三角形1.2017·金华在Rt△ABC中,∠C=90°,AB=5,BC=3,则tan A的值是( )A.34B.43C.35D.452.2017·兰州如图1-BZ-1,一个斜坡长为130 m,坡顶到水平地面的距离为50 m,那么这个斜坡与水平地面夹角的正切值等于( )A.513B.1213C.512D.13121-BZ-11-BZ-23.2017·绥化某楼梯的侧面如图1-BZ-2所示,已测得BC的长约为3.5米,∠BCA 约为29°,则该楼梯的高度AB可表示为( )A.3.5sin29°米B.3.5cos29°米C.3.5tan29°米D.3.5cos29°米4.2017·绍兴如图1-BZ-3,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,若保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( )A.0.7米B.1.5米C.2.2米D.2.4米5.2017·泰州小明沿着坡度i为1∶3的直路向上走了50 m,则小明沿垂直方向升高了________m.1-BZ-31-BZ -46.2016·上海如图1-BZ -4,在矩形ABCD 中,BC =2.将矩形ABCD 绕点D 顺时针旋转90°,点A ,C 分别落在点A ′,C ′处,如果点A ′,C ′,B 在同一条直线上,那么tan ∠ABA ′的值为________.7.2017·大连如图1-BZ -5,一艘海轮位于灯塔P 的北偏东60°方向,距离灯塔86 nmile 的A 处,它沿正南方向航行一段时间后,到达位于灯塔P 的南偏东45°方向上的B 处.此时,B 处与灯塔P 之间的距离为________n mile .(结果取整数,参考数据:3≈1.7,2≈1.4)1-BZ -51-BZ -68.2017·东营一数学兴趣小组来到某公园,准备测量一座塔的高度.如图1-BZ -6,在A 处测得塔顶的仰角为α,在B 处测得塔顶的仰角为β,又测量出A ,B 两点间的距离为s 米,则塔高为______米.9.2017·义乌以Rt △ABC 的锐角顶点A 为圆心,适当长为半径作弧,与边AB ,AC 各相交于一点,再分别以这两个交点为圆心,适当长为半径作弧,过两弧的交点与点A 作直线,与边BC 交于点D, 若∠ADB =60°,点D 到AC 的距离为2,则AB 的长为__________.10.2017·舟山如图1-BZ -7,把n 个边长为1的正方形拼接成一排,求得tan ∠BA 1C =1,tan ∠BA 2C =13,tan ∠BA 3C =17,计算tan ∠BA 4C =__________……按此规律,写出tan∠BA n C =__________(用含n 的代数式表示).图1-BZ -711.2016·台州计算:tan 45°-sin 30°+()2+20.12.2017·包头如图1-BZ -8,在△ABC 中,∠C =90°,∠B =30°,AD 是△ABC 的角平分线,DE ∥BA 交AC 于点E ,DF ∥CA 交AB 于点F ,已知CD =3.(1)求AD 的长;(2)求四边形AEDF 的周长.(注意:本题中的计算过程和结果均保留根号)图1-BZ -813.2017·丽水如图1-BZ -9是某小区的一个健身器材示意图,已知BC =0.15 m ,AB =2.70 m ,∠BOD =70°,求端点A 到地面CD 的距离(精确到0.1 m ).(参考数据:sin 70°≈0.94,cos 70°≈0.34,tan 70°≈2.75)图1-BZ -914.2017·台州如图1-BZ-10是一辆小汽车与墙平行停放的平面示意图,汽车靠墙一侧OB与墙MN平行且距离为0.8米.已知小汽车车门宽AO为1.2米,当车门打开角度∠AOB 为40°时,车门是否会碰到墙?请说明理由.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)图1-BZ-1015.2017·赤峰王浩同学用木板制作一个带有卡槽的三角形手机架,如图1-BZ-11所示.已知AC=20 cm,BC=18 cm,∠ACB=50°,王浩的手机长度为17 cm,宽为8 cm,王浩同学能否将手机放入卡槽AB内?请说明你的理由.(提示:sin50°≈0.8,cos50°≈0.6,tan50°≈1.2)图1-BZ-1116.2017·舟山如图1-BZ-12是小强洗漱时的侧面示意图,洗漱台(矩形ABCD)靠墙摆放,高AD=80 cm,宽AB=48 cm,小强身高166 cm,下半身FG=100 cm,洗漱时下半身与地面成80°(∠FGK=80°),身体前倾成125°(∠EFG=125°),脚与洗漱台的距离GC=15 cm(点D,C,G,K在同一直线上).(1)此时小强头部E点与地面DK相距多少?(2)小强希望他的头部E点恰好在洗漱盆AB的中点O的正上方,他应向前或后退多少?(参考数据:sin80°≈0.98,cos80°≈0.17,2≈1.41,结果精确到0.1 cm)图1-BZ-121.A [解析] 在Rt △ABC 中,根据勾股定理,得AC =AB 2-BC 2=52-32=4,再根据正切的定义,得tan A =BC AC =34.2.C [解析] 在直角三角形中,根据勾股定理可知水平的直角边长为120 m ,正切值为对边与邻边的比值,故斜坡与水平地面夹角的正切值等于50120=512,故选C.3.A [解析] 在直角三角形ABC 中,已知斜边BC 和锐角,求锐角的对边,故用正弦,ABBC=sin29°,所以AB =3.5sin29°米,故选A.4.C [解析] 在Rt △ACB 中,根据勾股定理求出AB =2.5米,则A ′B =AB =2.5米,在Rt △A ′BD 中,根据勾股定理求出BD =1.5米,则CD =BC +BD =0.7+1.5=2.2(米),故选C.5.25 [解析] 如图,过点B 作BE ⊥AC 于点E ,∵坡度i =1∶3,∴tan A =1∶3=33, ∴∠A =30°. ∵AB =50 m , ∴BE =12AB =25 m.∴小明沿垂直方向升高了25 m. 6.5-12[解析] 设AB =x ,则CD =x ,A ′C =x +2. ∵AD ∥BC ,∴C ′D BC =A ′D A ′C ,即x 2=2x +2,解得x 1=5-1,x 2=-5-1(舍去). ∵AB ∥CD ,∴∠ABA ′=∠BA ′C .∵tan ∠BA ′C =BC A ′C =25-1+2=5-12, ∴tan ∠ABA ′=5-12.7.102 [解析] 过点P 作AB 的垂线,垂足为C ,在Rt △APC 中,∠APC =90°-60°=30°,∴PC =PA ·cos ∠APC =86×cos30°=86×32=43 3(n mile).在Rt △BPC 中,∠B =45°,∴PB =PC ÷sin45°=433÷22=433×2≈102(n mile),故答案为:102. 8.tan α·tan βtan β-tan α·s[解析] 在Rt △CBD 中,BD =CD tan β,∴AD =CDtan β+s .在Rt △CAD 中,CD =AD tan α=(CDtan β+s )tan α,化简,得CD =tan α·tan βtan β-tan α·s (米).9.2 3 [解析] 如图,由题意可知AD 是∠BAC 的平分线.过点D 作DE ⊥AC ,垂足为E ,则DE =2,所以DB =DE =2,在Rt △ABD 中,tan ∠ADB =ABBD,所以AB =2×3=2 3.10.113 1n 2-n +1[解析] 根据所给的三角函数值进行分析可以得到如下规律:tan ∠BA 1C =11=112-(1-1),tan ∠BA 2C =13=122-(2-1),tan ∠BA 3C =17=132-(3-1),tan ∠BA 4C =142-(4-1)=113……按此规律,tan ∠BA n C =1n 2-(n -1)=1n 2-n +1.11.解:原式=1-12+1=32.12.解:(1)在△ABC 中, ∵∠C =90°,∠B =30°, ∴∠BAC =60°.∵AD 是△ABC 的角平分线, ∴∠CAD =∠BAD =12∠BAC =30°.在Rt △ACD 中,∵∠CAD =30°,CD =3, ∴AD =2CD =6. (2)∵DE ∥BA, DF ∥CA ,∴四边形AEDF 为平行四边形,∠BAD =∠EDA . ∵∠CAD =∠BAD , ∴∠CAD =∠EDA , ∴AE =DE ,∴四边形AEDF 为菱形. ∵DE ∥BA ,∴∠CDE =∠B =30°. 在Rt △CDE 中,∠C =90°, ∴cos ∠CDE =CD DE,∴DE =3cos30°=2 3.∴四边形AEDF 的周长为4DE =4×23=8 3.13.解:如图,过点A 作AE ⊥CD 于点E ,过点B 作BF ⊥AE 于点F ,∵OD ⊥CD ,∴AE ∥OD ,∴∠A =∠BOD =70°.在Rt △ABF 中,AB =2.7 m ,∴AF =2.7×cos70°≈2.7×0.34=0.918(m),∴AE =AF +BC ≈0.918+0.15=1.068≈1.1(m).答:端点A 到地面CD 的距离约是1.1 m.14.解:如图,过点A 作AC ⊥OB 于点C .在Rt △AOC 中,∠AOC =40°, ∴sin40°=AC AO. 又∵AO =1.2米,∴AC =1.2×sin40°≈1.2×0.64=0.768(米). ∵0.768<0.8, ∴车门不会碰到墙.15.解:王浩同学能将手机放入卡槽AB 内. 理由:过点A 作AD ⊥BC 于点D ,∵∠C =50°,AC =20 cm ,∴AD =AC ·sin50°≈20×0.8=16(cm),CD =AC ·cos50°≈20×0.6=12(cm).∵BC =18 cm ,∴BD =BC -CD =18-12=6(cm), ∴AB =AD 2+BD 2=162+62=292(cm). ∵17=289<292,∴王浩同学能将手机放入卡槽AB内.16.解:(1)过点F作FN⊥KD于点N,过点E作EM⊥FN于点M. ∵EF+FG=166 cm,FG=100 cm,∴EF=66 cm.∵∠FGK=80°,∴∠GFN=10°,FN=100×sin80°≈98(cm).又∵∠EFG=125°,∴∠EFM=180°-125°-10°=45°,∴FM=66×cos45°=33 2≈46.53(cm),∴MN=FN+FM≈144.5(cm).即小强头部E点与地面DK相距约144.5 cm.(2)过点E作EP⊥AB于点P,延长OB交MN于点H.∵AB=48 cm,O为AB的中点,∴AO=BO=24 cm.∵EM=FM≈46.53 cm,∴PH≈46.53 cm.∵GN=100×cos80°≈17(cm),CG=15 cm,∴OH≈24+15+17=56(cm),∴OP=OH-PH≈56-46.53=9.47≈9.5(cm).即他应向前约9.5 cm.。
