浙教版数学九年级下册全册优质课件
合集下载
浙教版九年级下册数学《相交两圆的性质定理》PPT课件
RT
r
O1
O2
r
R
T O2 O1
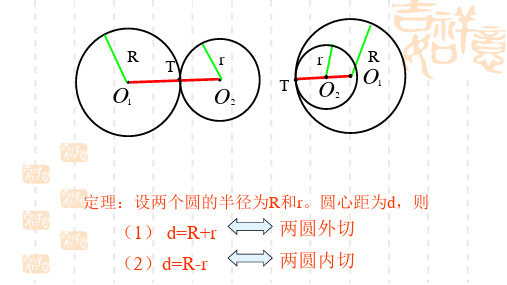
定理:设两个圆的半径为R和r。圆心距为d,则
(1) d=R+r
两圆外切
(2)d=R-r
两圆内切
T. . . 01 02
. T. .
01
02
A
A
定理:相切两圆的连心线必经过切点。
定理:如果两圆相切,那么其中任一个圆的过 两圆切点的切线,也必是另一个圆的切线。
两圆相切添两圆的公共切线
圆和圆的 五种位置关系
Rr
O1
O2
外离
O1O2>R+r
Rr
O1
O2
外切
O1O2=R+r
Rr O1 O2
相交
R-r<O1O2<R+r
R
O1
r
O2
内切
O1O2=R-r
R
O1
r
O2
内含
0≤O1O2<R-r
R r
O1O2
同心圆 (一种特殊的内含)
O1O2=0
相交两圆的性质定理
相交两圆的连心线垂直平分公共弦
已知:⊙01、⊙02 的半径分别为 r 和 R,( R>r ) 0102 >R+r,
两圆的内公线长 d 2 (R r)2
A
O1
O2
B E
公切线与连心线的夹角为∠ 0201E,再 用三角函数计算
BM C
O1 .
A . O2
如图 ,⊙O1与⊙O2 外切于A ,它们的半
径分别为
R 和r ,直线BC是⊙O1与⊙O2
A
O
O
2
1
r
O1
O2
r
R
T O2 O1
定理:设两个圆的半径为R和r。圆心距为d,则
(1) d=R+r
两圆外切
(2)d=R-r
两圆内切
T. . . 01 02
. T. .
01
02
A
A
定理:相切两圆的连心线必经过切点。
定理:如果两圆相切,那么其中任一个圆的过 两圆切点的切线,也必是另一个圆的切线。
两圆相切添两圆的公共切线
圆和圆的 五种位置关系
Rr
O1
O2
外离
O1O2>R+r
Rr
O1
O2
外切
O1O2=R+r
Rr O1 O2
相交
R-r<O1O2<R+r
R
O1
r
O2
内切
O1O2=R-r
R
O1
r
O2
内含
0≤O1O2<R-r
R r
O1O2
同心圆 (一种特殊的内含)
O1O2=0
相交两圆的性质定理
相交两圆的连心线垂直平分公共弦
已知:⊙01、⊙02 的半径分别为 r 和 R,( R>r ) 0102 >R+r,
两圆的内公线长 d 2 (R r)2
A
O1
O2
B E
公切线与连心线的夹角为∠ 0201E,再 用三角函数计算
BM C
O1 .
A . O2
如图 ,⊙O1与⊙O2 外切于A ,它们的半
径分别为
R 和r ,直线BC是⊙O1与⊙O2
A
O
O
2
1
浙教版数学九年级下册全册优质课件【完整版】

若AC=5呢?
A
C
取宝物比赛
10m
10m
(1)
1m
5m
(2)
B
∠A的对边
sinA
斜边
斜边
∠A的对边 cosA
∠A的邻边 斜边
A
∠A的邻边
C
tanA
∠A的对边 ∠A的邻边
下课了!
锐角三角函数
B
∠A的对边
sinA
斜边
斜边
∠A的对边 cosA
∠A的邻边 斜边
A
∠A的邻边
C
tanA
∠A的对边 ∠A的邻边
水平宽度
梯子在上升变陡的过程中,倾 斜角,铅直高度与梯子的比,水 平宽度与梯子的比,铅直高度与 水平宽度的比,都发生了什么变 化?
铅 直 高 度
水平宽度
梯子在上升变陡的过程中,倾 斜角,铅直高度与梯子的比,水 平宽度与梯子的比,铅直高度与 水平宽度的比,都发生了什么变 化?
铅 直 高 度
水平宽度
cos 60 a 1
2a 2
60°
tan 60 3a 3 a
设两条直角边长为a,则斜边长= a2 a2 2a
sin 45 a 2 2a 2
cos 45 a 2
45°
2a 2
tan 45 a 1 a
仔细观察,说说你发现 30°、45°、60°角的正弦值、余这弦值张和表正有切哪值些如下规表律:?
你想知道小明怎样 算出的吗?
?
1.65米
30°
10米
例3 (1)如图,在Rt△ABC中, ∠C=90°,AB= 6 ,BC= 3 。求∠A的度 数。
(2)如图,已3知圆锥的高AO等于圆锥的底面半
新浙教版九年级数学下册第一章《解直角三角形》优质公开课课件.ppt

1.3.1解直角三角形
第1课时 解直角三角形
1.(4分)△ABC中,a,b,c分别是∠A,∠B,∠C的对边,如
果a2+b2=c2,那么下列结论正确的是 (A )
A.c sinA=a B.b cosB=c C.a tanA=b D.c tanB=b
2.(4分)如图是教学用的直角三角形,边AC=30 cm,∠C=90°,
10 ,则
6.(4分)在△ABC中,∠C=90°,a=35,c=35 2 ,则∠A=
_4_5__°,b=_3__5_.
7.(4分)如图所示,AB是伸缩式的遮阳棚,CD是窗户,要想在 夏至的正午时刻阳光刚好不能射入窗户,则AB的长度是__3__ 米.(假设夏至的正午时刻阳光与地平面的夹角为60°)
8.(12分)在Rt△ABC中,∠C=90°. (1)已知a=4,b=8,求c的长; (2)已知b=10,∠B=60°,求a,c的长; (3)已知c=20,∠A=60°,求a,b的长.
=4,∴AC
=BC·sinB=4×sin60°=2 3 ,∴△ABC的周长=AB+AC +BC=6+2 3
14.(10分)一副直角三角板如图放置,点C在FD的延长线上, AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,AC= 12 2,试求CD的长.
解:过点B作BM⊥FD于点M.在△ACB中,∠ACB=90°,∠A= 45°,AC=12 2,∴BC=AC=12 2.
tan∠BAC= 33,则边BC的长为 ( C)
A.30 3 cm C.10 3 cm
B.20 3 cm D.5 3 cm
,第2题图)
3.(4分)已知:在△ABC中,AB=AC,∠BAC=120°,AD为
BC边上的高,则下列结论中,正确的是 ( B )
第1课时 解直角三角形
1.(4分)△ABC中,a,b,c分别是∠A,∠B,∠C的对边,如
果a2+b2=c2,那么下列结论正确的是 (A )
A.c sinA=a B.b cosB=c C.a tanA=b D.c tanB=b
2.(4分)如图是教学用的直角三角形,边AC=30 cm,∠C=90°,
10 ,则
6.(4分)在△ABC中,∠C=90°,a=35,c=35 2 ,则∠A=
_4_5__°,b=_3__5_.
7.(4分)如图所示,AB是伸缩式的遮阳棚,CD是窗户,要想在 夏至的正午时刻阳光刚好不能射入窗户,则AB的长度是__3__ 米.(假设夏至的正午时刻阳光与地平面的夹角为60°)
8.(12分)在Rt△ABC中,∠C=90°. (1)已知a=4,b=8,求c的长; (2)已知b=10,∠B=60°,求a,c的长; (3)已知c=20,∠A=60°,求a,b的长.
=4,∴AC
=BC·sinB=4×sin60°=2 3 ,∴△ABC的周长=AB+AC +BC=6+2 3
14.(10分)一副直角三角板如图放置,点C在FD的延长线上, AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,AC= 12 2,试求CD的长.
解:过点B作BM⊥FD于点M.在△ACB中,∠ACB=90°,∠A= 45°,AC=12 2,∴BC=AC=12 2.
tan∠BAC= 33,则边BC的长为 ( C)
A.30 3 cm C.10 3 cm
B.20 3 cm D.5 3 cm
,第2题图)
3.(4分)已知:在△ABC中,AB=AC,∠BAC=120°,AD为
BC边上的高,则下列结论中,正确的是 ( B )
浙教版九年级数学下册课件 2.3 三角形的内切圆

2 如图,点O是△ABC的内心,若∠ACB=70°,则 ∠AOB=( ) A.140° B.135° C.125° D.110°
(来自《典中点》)
知2-练
3 下列说法错误的是( ) A.三角形有且只有一个内切圆 B.等腰三角形的内心一定在它的底边的高上 C.三角形的内心不一定都在三角形的内部 D.若I是△ABC的内心,则AI平分∠BAC
(来自《典中点》)
总结
知2-讲
因为三角形的内心是三角形三条角平分线的交 点,所以三角形的内心与任一顶点的连线平分三角 形的内角.
(来自《点拨》)
13 三角形内切圆的圆心是( ) A.三个内角平分线的交点 B.三边中垂线的交点 C.三条中线的交点 D.三条高线的交点
知2-练
(来自《典中点》)
知2-练
知1-讲
见切点,连半径,结合等腰三角形、等边三角形的 性质求出半径长.
(来自《点拨》)
知1-讲
例2 已知:如图, ⊙O是△ABC的内切圆,切点分别为D, E,F.设△ABC的周长为l,求证: AE+BC= 1 l. 2
证明:∵⊙O是△ABC的内切圆,E,F为切点,
∴AE=AF(根据什么?).
A
同理,BD=BF,CD=CE.
理解三角形内切圆的概念要注意以下三点: ①与各边相切; ②在三角形内部; ③圆心叫做三角形的内心.
知1-讲
例1 如图,等边三角形ABC的边长为3 cm,求△ABC
的内切圆⊙O的半径.
解:如图,设⊙O切AB于点D,连结OA,OB,OD.
∵ ⊙O是△ABC的内切圆,
∴AO,BO 是∠BAC, ∠ABC,
(来自《典中点》)
1. 三角形的内切圆中“切”是指三角形的三边与圆的 位置关系.
(来自《典中点》)
知2-练
3 下列说法错误的是( ) A.三角形有且只有一个内切圆 B.等腰三角形的内心一定在它的底边的高上 C.三角形的内心不一定都在三角形的内部 D.若I是△ABC的内心,则AI平分∠BAC
(来自《典中点》)
总结
知2-讲
因为三角形的内心是三角形三条角平分线的交 点,所以三角形的内心与任一顶点的连线平分三角 形的内角.
(来自《点拨》)
13 三角形内切圆的圆心是( ) A.三个内角平分线的交点 B.三边中垂线的交点 C.三条中线的交点 D.三条高线的交点
知2-练
(来自《典中点》)
知2-练
知1-讲
见切点,连半径,结合等腰三角形、等边三角形的 性质求出半径长.
(来自《点拨》)
知1-讲
例2 已知:如图, ⊙O是△ABC的内切圆,切点分别为D, E,F.设△ABC的周长为l,求证: AE+BC= 1 l. 2
证明:∵⊙O是△ABC的内切圆,E,F为切点,
∴AE=AF(根据什么?).
A
同理,BD=BF,CD=CE.
理解三角形内切圆的概念要注意以下三点: ①与各边相切; ②在三角形内部; ③圆心叫做三角形的内心.
知1-讲
例1 如图,等边三角形ABC的边长为3 cm,求△ABC
的内切圆⊙O的半径.
解:如图,设⊙O切AB于点D,连结OA,OB,OD.
∵ ⊙O是△ABC的内切圆,
∴AO,BO 是∠BAC, ∠ABC,
(来自《典中点》)
1. 三角形的内切圆中“切”是指三角形的三边与圆的 位置关系.
新浙教版九年级数学下册第一章《锐角三角函数(1)》精品课件1.ppt
• 10、人的志向通常和他们的能力成正比例。2021/1/142021/1/142021/1/141/14/2021 6:41:13 PM • 11、夫学须志也,才须学也,非学无以广才,非志无以成学。2021/1/142021/1/142021/1/14Jan-2114-Jan-21 • 12、越是无能的人,越喜欢挑剔别人的错儿。2021/1/142021/1/142021/1/14Thursday, January 14, 2021 • 13、志不立,天下无可成之事。2021/1/142021/1/142021/1/142021/1/141/14/2021
• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
边之比 定义 表示 公式
B
∠A的对边a 正弦函数
斜边c
∠A的
对边 ∠A的邻边b
a
斜边c
余弦函数
sinA cosA
sssiiinnn
AAA
===
aaa ccc
cccooosss
AAA
===
bbb ccc
A
∠ A的邻边b
C
∠A的对边a ∠A的邻边b
正切函数
• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
边之比 定义 表示 公式
B
∠A的对边a 正弦函数
斜边c
∠A的
对边 ∠A的邻边b
a
斜边c
余弦函数
sinA cosA
sssiiinnn
AAA
===
aaa ccc
cccooosss
AAA
===
bbb ccc
A
∠ A的邻边b
C
∠A的对边a ∠A的邻边b
正切函数
浙教版数学九年级(下)PPT资料优秀版

观察上表,你获得什么启示? 实验次数越多,频率越接近概率
120° 17202°° 120°
P=1/10000000
如我果们某 知让运道动,如任员意图投抛一一的次枚篮转均投匀盘中的的硬自概币率由,”正为面转0.朝动上”一的概次率,是停0.止转动后,指针落在红
观(1)察该上运色表动,区员你投获域5得次什的篮么,必概启有示率4?次是投中1. /3,以下是实验的方法:
80
25
160
58
240
78
320
110
400
130
频率
(4)根据上面的表格,在下图中画出频率分布折线图
0 80 160 240 320 400
(5)议一议:频率与概率有什么区别和联系?随着重复实验 次数的不断增加,频率的变化趋势如何?
通过大量重复的实验,用一个事件发生的频率来估 计这一事件发生的概率
计如约果需 某麦运色种动多员的少投一k小g次? 篮奶投中牛的概,据率为统0. 计,平均出生1千万头牛才会有1头是白色的, 如果某运由动员此投一估次篮计投中出的概生率为一0. 头奶牛为白色的概率为多少?
P=1/10000000
例1.在同样条件下对某种小麦种子进行发芽实验,统计发芽 种子数,获得如下频数分布表:
(3)若要销售这批西装2000件,为了方便购买次品西装的顾客前
来调换,至少应该进多少件西装?
概率是理论性的东西,频率是实践性的 东西,理论应该联系实际,因此我们可 以通过大量重复的实验,用一个事件发 生的频率来估计这一事件发生的概率
概率是理论性的东西,频率是实践性的 东西,理论应该联系实际,因此我们可 以通过大量重复的实验,用一个事件发 生的频率来估计这一事件发生的概率
浙教版九年级数学(全一册)课件第2章 直线与圆的位置关系 切线的性质与判定

★应用格式 OA为⊙O的半径 BC ⊥ OA于A
BC为⊙O的切线
新课讲解
B
O
A
C
新课讲解 判一判: 下列各直线是不是圆的切线?如果不是,请说明为什么?
O.
A l
(1)
(1)不是,因为没
有垂直.
O.
O
A
l
B
(2)
A
l
(3)
(2),(3)不是,因为没有经过半径的
外端点A.
注意:在此定理中,“经过半径的外端”和“垂直于 这条半径”,两个条件缺一不可,否则就不是圆的切线.
分析:根据切线的判定定理,要 证明AC是⊙O的切线,只要证明
A
E
F
由点O向AC所作的垂线段OF是
⊙O的半径就可以了,而OE是 B
O
C
⊙O的半径,因此只需要证明
OF=OE.
新课讲解
证明:连结OE ,OA, 过O 作OF ⊥AC.
∵⊙O 与AB 相切于E , ∴OE ⊥ AB.
又∵△ABC 中,AB =AC ,
的直径为6. 求证:直线AB是⊙O的切线.
作垂直 O
AC B
AC B
对比思考
新课讲解
2 切线的性质定理
思考:如图,如果直线l是⊙O 的切线,点A为切点,那么OA 与l垂直吗?
★切线性质 圆的切线垂直于经过切点的半径.
★应用格式 ∵直线l是⊙O 的切线,A是切点, ∴直线l ⊥OA.
O
A
l
新课讲解
性 质 有1个公共点
有切线时常用辅助线 添加方法: 见切线,连切点,得垂直.
d=r
情景引入
砂轮上打磨工件时飞出的火星
1 切线的判定定理
浙教版初中数学九年级下册(1.1 锐角三角函数2)课件(共25张PPT)
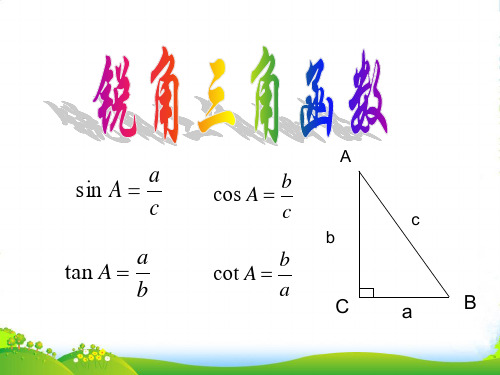
B
A
∠ A的邻边b
∠A的对边a 正弦函数
斜边c
∠A的
对边 a
∠A的邻边b 斜边c
余弦函数
C
∠A的对边a ∠A的邻边b
正切函数
sinA cosA tanA
ssssiiiinnnn ccccoooossss ttttaaaannnn
AAAA AAAA AAAA
==== ==== ====
aaaaccccbbbaaaabbbbcccc
BC
比值 A B 是一个确定的值.
与点B在角的边上的位置无关.
Do you know
三角函数的由来
“三角学”一词,是由希腊文三角形与测量二字构成 的,原意是三角形的测量,也就是解三角形.后来范围 逐渐扩大,成为研究三角函数及其应用的一个数学分支.
三角测量在我国出现的很早.据记载,早在公元前 两千年,大禹就利用三角形的边角关系,来进行对山川 地势的测量.
sin A a c
tan A a b
A
cos A b c
b
cot A b a
C
c
a
B
从最简单的做起---波利亚
探索园地
•
【量一量】你的那块不 等腰的三角尺中,
30°角所对的直角边
与斜边的长分别是多少?
它们的比等于多少?
如果改成是测量 这块等腰的三角 尺呢?还有刚才
的结论吗?
• 【想一想】老师上课时 用的那块不等腰的三角
∠A的邻边b ∠A的对边a 余切函数
cotA
ccccooootttt AAAA ==== bbbbaaaa
这四个函数统称为锐角A的三角函数.
例:求出如图所示的Rt△ABC 中你会求∠A的四个三角函数值 A 吗?∠B的呢?
新浙教版九年级数学下册第一章《 有关三角函数的计算》课件

D
ห้องสมุดไป่ตู้太阳光
25° A
住
宅
新
楼
楼
B
C
某居民小区有一朝向为正南方向的居民楼,该居民楼的一楼是 高6米的小区超市,超市以上是居民住房.在该楼的前面要盖一栋高20米的 新楼.当冬季正午的阳光与水平线的夹角为25°时.
问:若新楼的影子恰好落在超市1米高的窗台处,两楼应相距多少米?
D
太阳光
25° A
F
住 宅
新
楼
w如图,在Rt△ABC中,∠C=90°, BC=ABsin16° .
w你知道sin16°等于多少吗?
对于不是30°,45°,60°这些特殊角的三角函 数值,可以利用计算器来求
w怎样用科学计算器求锐角的三角函数值呢?
动手实践
知识在于积累
驶向胜利 的彼岸
w用科学计算器求锐角的三角函数值,要用到三个键: w例如,求sin16°、cos42°、tan85° 和sin72°38′25″的按键盘顺序如下: sin cos tan
A
B
变式:在△ABC中,已知AB=12cm,AC=10cm
∠ A=35 °,求△ABC 的周长和面积(周长精确到 0.1cm,面积保留3个是效数字).
模型: △ABC 的面积=1/2AC・AB ・sin ∠ A
随堂练习
行家看“门道”
驶向胜利 的彼岸
w1 用计算器求下列各式的值: w(1)sin56°,(2) sin15°49′,(3)cos20°,(4)tan29°, w(5)tan44°59′59″,(6)sin15°+cos61°+tan76°.
按键的顺序
显示结果
sin16° sin 1 6 °′″ =
ห้องสมุดไป่ตู้太阳光
25° A
住
宅
新
楼
楼
B
C
某居民小区有一朝向为正南方向的居民楼,该居民楼的一楼是 高6米的小区超市,超市以上是居民住房.在该楼的前面要盖一栋高20米的 新楼.当冬季正午的阳光与水平线的夹角为25°时.
问:若新楼的影子恰好落在超市1米高的窗台处,两楼应相距多少米?
D
太阳光
25° A
F
住 宅
新
楼
w如图,在Rt△ABC中,∠C=90°, BC=ABsin16° .
w你知道sin16°等于多少吗?
对于不是30°,45°,60°这些特殊角的三角函 数值,可以利用计算器来求
w怎样用科学计算器求锐角的三角函数值呢?
动手实践
知识在于积累
驶向胜利 的彼岸
w用科学计算器求锐角的三角函数值,要用到三个键: w例如,求sin16°、cos42°、tan85° 和sin72°38′25″的按键盘顺序如下: sin cos tan
A
B
变式:在△ABC中,已知AB=12cm,AC=10cm
∠ A=35 °,求△ABC 的周长和面积(周长精确到 0.1cm,面积保留3个是效数字).
模型: △ABC 的面积=1/2AC・AB ・sin ∠ A
随堂练习
行家看“门道”
驶向胜利 的彼岸
w1 用计算器求下列各式的值: w(1)sin56°,(2) sin15°49′,(3)cos20°,(4)tan29°, w(5)tan44°59′59″,(6)sin15°+cos61°+tan76°.
按键的顺序
显示结果
sin16° sin 1 6 °′″ =
浙教版九年级数学下册第一章教学课件全套

这几个比值都是锐角∠A的函数,记作sin A、cos A、 tan A,即
A的对边 sin A= 斜边 A的对边 tan A= A的邻边
A的邻边 cos A= 斜边
图 19.3.1
分别叫做锐角∠A的正弦、余弦、正切,统称为锐角∠A的 三角函数.
1、sinA 不是一个角 2、sinA不是 sin与A的乘积 3、 sinA 是一个比值 4、sinA 没有单位
建立数学模型
C
5.5米
引例:山坡上种树,要求株距(相临两树间的水平
距离)是5.5米,测得斜坡倾斜角是24º,求斜坡上相
邻两树间的坡面距离是多少米?第二棵树离开地面的高度是 B 多少米?(精确到0.1米)
解:在Rt△ABC中,∠C=90°
AC cos A AB
24º
C
≈6.0(米)
5.5米
A
B c
a
A b ┌ C
练习:
1、下图中∠ACB=90° ,CD⊥AB 指出∠A的对边、邻边。 B D
A
C
2、1题中如果CD=5,AC=10,则sin∠ACD= sin ∠DCB=
如图:在等腰△ABC 中,AB=AC=5,BC=6. 求: sinB,cosB,tanB
A
5 B 5
┌ 6 D
C
提示:过点A作AD垂直于BC于D.
C
A
12cm
B
课堂小结
我学会了……
1.3 解直角三角形
数学家华罗庚曾经说:“宇宙之 大,粒子之微,火箭之速,化工之 巧,地球之变,日月之繁,无处不 用数学。”这是对数学与生活的精 彩描述。在我们周围处处有数学, 时时会碰到数学问题。
生活中的数学问题
引例:在山坡上种树(从低处往高处种),测得斜坡倾斜角 是24º,要求株距(相邻两树间的水平距离)是5.5米,求斜 坡上相邻两树间的坡面距离是多少米?第二棵树离开地面的 高度是多少米?(精确到0.1米) B 24º 5.5米 A
浙教版九年级数学下册教学课件全册

案例分析
案例总结
总结案例中的数学知识点和解题方法 ,加深学生对数学知识的理解和掌握 。
通过案例分析,帮助学生理解数学概 念、定理和公式在实践中的应用。
教学方法2:启发式教学
01
02
03
问题导入
通过设置问题情境,引导 学生主动思考和探索数学 问题。
启发思考
引导学生逐步深入思考问 题,激发他们的思维能力 和创造力。
考试分析
对考试成绩进行分析,找出学 生在学习中存在的问题和薄弱 环节,以便进行有针对性的辅
导和加强。
学生反馈与评价
学生意见收集
通过问卷调查、座谈会等方式, 收集学生对教学的意见和建议,
了解学生的学习需求和期望。
学生作业分析
分析学生作业中的常见错误和问题 ,找出学生在学习中存在的困难和 不足,以便进行有针对性的指导和 帮助。
浙教版九年级数学下册教科书
包含了本学期需要学习的所有知识点和例题,是教学的主要依据。
浙教版九年级数学下册教学参考书
提供了详细的教学建议、课程内容的解析和例题的解答,有助于教师更好地备 课和教学。
网络资源
浙教版九年级数学下册课件
可以在网络上找到一些教师分享的课件,这些课件通常包含了详细的教学内容和 练习题,可以作为教学辅助材料。
05
教学评价与反馈
作业与考试
作业布置
根据教学内容和学生实际情况 ,布置有针对性的作业,以巩 固所学知识和提高解题能力。
作业批改
认真批改学生的作业,及时发 现和纠正学生在学习中存在的 问题,并给予必要的指导和帮 助。
考试安排
定期组织考试,检测学生对所 学知识的掌握程度和应用能力 ,及时调整教学策略。
学生发展的关注
新浙教版九年级数学下册第二章《切线长定理》精品课件.ppt

B
P O
C
小结:切线是直线,不可以度量;切 线长是指切线上的一条线段的长,可 以度量。
想一想:
(1)切线长 PA、 PB之间的关 系,同时观察∠1,∠2的关系。
(2)请根据你的观察尝试总结它们之 间的关系。
A
O
1
2
p
B
切线长定理 从圆外一点引圆的两条切线, 它们的切线长相等,圆心和这一点的连线 平分两条切线的夹角。
2.2切 线 长 定 理
复习旧知
(1)和圆有唯一公共点的直 线叫 圆的切线
(2)圆的切线 垂直于 过切点的 半径。
探索新知:
• 想一想:过圆外一点, 可以画圆的几条切线? 画出图形并观察,可以 得出那些结论?
切线长:在经过圆外一点的圆的切线上, 这点和切点之间的线段的长。 思考:切线
长和切线的 区别和联系?
请你们结合图形
A
用数学语言表达
定理
O
p
B
PA、PB分别切⊙O于A、 B,连结PO
PA = PB ∠OPA=∠OPB
• 例1:如图,一个圆柱形钢材
放在“V”型的支架中(图
1),图2是它的截面示意
图,CA和C2 B3 都是⊙O的 切线,切点分别是A、B。
ห้องสมุดไป่ตู้⊙O的半径为
cm,A
B=6cm,求∠ACB的度
数。
)
(2)从圆外一点引圆的两条切线,它们的长相等。
(
)
练习2:填空选择
(1)如图:PA,PB切圆于A,B两点,
∠APB=50度,连结PO,
则∠APO= 25度
A O
P
B
练习3、如图,已知⊙O的半
径为3厘米,PO=6厘米,
P O
C
小结:切线是直线,不可以度量;切 线长是指切线上的一条线段的长,可 以度量。
想一想:
(1)切线长 PA、 PB之间的关 系,同时观察∠1,∠2的关系。
(2)请根据你的观察尝试总结它们之 间的关系。
A
O
1
2
p
B
切线长定理 从圆外一点引圆的两条切线, 它们的切线长相等,圆心和这一点的连线 平分两条切线的夹角。
2.2切 线 长 定 理
复习旧知
(1)和圆有唯一公共点的直 线叫 圆的切线
(2)圆的切线 垂直于 过切点的 半径。
探索新知:
• 想一想:过圆外一点, 可以画圆的几条切线? 画出图形并观察,可以 得出那些结论?
切线长:在经过圆外一点的圆的切线上, 这点和切点之间的线段的长。 思考:切线
长和切线的 区别和联系?
请你们结合图形
A
用数学语言表达
定理
O
p
B
PA、PB分别切⊙O于A、 B,连结PO
PA = PB ∠OPA=∠OPB
• 例1:如图,一个圆柱形钢材
放在“V”型的支架中(图
1),图2是它的截面示意
图,CA和C2 B3 都是⊙O的 切线,切点分别是A、B。
ห้องสมุดไป่ตู้⊙O的半径为
cm,A
B=6cm,求∠ACB的度
数。
)
(2)从圆外一点引圆的两条切线,它们的长相等。
(
)
练习2:填空选择
(1)如图:PA,PB切圆于A,B两点,
∠APB=50度,连结PO,
则∠APO= 25度
A O
P
B
练习3、如图,已知⊙O的半
径为3厘米,PO=6厘米,
浙教版九年级数学下册电子课本课件【全册】

浙教版九年级数学下册电子课本课 件【全册】
1.1锐角三角函数
浙教版九年级数Biblioteka 下册电子课本课 件【全册】1.2锐角三角函数的计算
浙教版九年级数学下册电子课本课 件【全册】
1.3解直角三角形
浙教版九年级数学下册电子课本课 件【全册】
第2章 直线与圆的位置关系
浙教版九年级数学下册电子课本课 件【全册】
浙教版九年级数学下册电子课本 课件【全册】目录
0002页 0042页 0118页 0137页 0213页 0258页 0324页
第1章 解直角三角形 1.2锐角三角函数的计算 第2章 直线与圆的位置关系 2.2切线长定理 第3章 投影与三视图 3.2简单几何体的三视图 3.4简单几何体的表面展开图
第1章 解直角三角形
1.1锐角三角函数
浙教版九年级数Biblioteka 下册电子课本课 件【全册】1.2锐角三角函数的计算
浙教版九年级数学下册电子课本课 件【全册】
1.3解直角三角形
浙教版九年级数学下册电子课本课 件【全册】
第2章 直线与圆的位置关系
浙教版九年级数学下册电子课本课 件【全册】
浙教版九年级数学下册电子课本 课件【全册】目录
0002页 0042页 0118页 0137页 0213页 0258页 0324页
第1章 解直角三角形 1.2锐角三角函数的计算 第2章 直线与圆的位置关系 2.2切线长定理 第3章 投影与三视图 3.2简单几何体的三视图 3.4简单几何体的表面展开图
第1章 解直角三角形
浙教版数学九年级下册 1.1 锐角三角函数 课件(共25张PPT)

观察以上计算结果,你发现了什么?
sinA=cosB ,cosA=sinB (∠A+∠B=90)
tanA·tanB=1
(∠A+∠B=90)
B
c
a
┌
A
b
C
sin A a cos A b tan A a
c
c
b
sin B b cos B a
c
c
tan B b a
如图,在△ABC中,若AB=5,BC=3,则下列结论正确
锐角A,A′的余弦值的关系为( ) A
A.cosA=cosA′ B.cosA=3cosA′ C.3cosA=cosA′ D.不能确定 2.如图,已知P是射线OB上的任意一点,PM⊥OA于M,
且PM:OM=3:4,则cosα的值等于( C)
3 A.4
4 B.3
C.4 5
3
D.
5
3.在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,
是关于锐角α的三角函数。
AB AB AC
B
A
C
锐角α的正弦,余弦和正切统称∠α的三角函数.
比值 BC 叫做∠α的正弦(sine),记做sinα.
AB
BC
比值 AC
即sinα= AB
叫做∠α的余弦(cosine) ,记做cosα.
AB
即cosα= AC
AB 比值 叫做∠α的正切(tangent) ,记做tanα.
b,c,则下列各项中正确的是( ) B
A.a=c·sinB B.a=c·cosB C.a=c·tanB D.以上均不正确
4.在Rt△ABC中,∠C=90°,cosA= 2 ,则tanB等于( )
C
最新浙教版九年级数学下册教学课件全册

最新浙教版九年级数学下册 教学课件全册
第1章 解直角三角形 1.1 锐角三角函数
1.1 锐角三角函数(1)
锐角三角函数的定义
直角三角形ABC可以简记为Rt△ABC,你能 说出各条边的名称吗?
B
斜边 c
对边 a
┓┓
A
C
邻边 b
实际问题
某商场有一自动扶梯,其倾斜角为30°,高为7m, 扶梯的长度是多少?
作业
1.计算:(1)tan450-sin300; (2)cos600+sin450-tan300;
36 tan2 300 3 sin 600 2 cos 450.
2.如图,河岸AD,BC互相平行,桥AB垂直 于两岸.桥长12m,在C处看桥两端A,B,夹 角∠BCA=600. 求B,C间的距离(结果精确到1m).
提示
1.sinA,cosA,tanA 是在直角三角形中定义的, ∠A是锐角(注意数形结合,构造直角三角形).
2.sinA, cosA,tanA 是一个比值(数值). 3.sinA, cosA, tanA 的大小只与∠A的大小有 关,而与直角三角形的边长无关.
小练习
1、如图1,在Rt△MNP中,∠N=90゜. ∠P的对边是_________,∠P的邻边是___________; ∠M的对边是________,∠M的邻边是___________;
1 2
(C) 小于 3
2
(B)大于
1 2
(D)大于 3
2
☆ 应用练习 1.已知角,求值 2.已知值,求角 3. 确定值的范围 4. 确定角的范围
确定角的范围
3. 当∠A为锐角,且tan A的 值大于 3 时,∠A( B )
3
(A)小于30° (B)大于30°
第1章 解直角三角形 1.1 锐角三角函数
1.1 锐角三角函数(1)
锐角三角函数的定义
直角三角形ABC可以简记为Rt△ABC,你能 说出各条边的名称吗?
B
斜边 c
对边 a
┓┓
A
C
邻边 b
实际问题
某商场有一自动扶梯,其倾斜角为30°,高为7m, 扶梯的长度是多少?
作业
1.计算:(1)tan450-sin300; (2)cos600+sin450-tan300;
36 tan2 300 3 sin 600 2 cos 450.
2.如图,河岸AD,BC互相平行,桥AB垂直 于两岸.桥长12m,在C处看桥两端A,B,夹 角∠BCA=600. 求B,C间的距离(结果精确到1m).
提示
1.sinA,cosA,tanA 是在直角三角形中定义的, ∠A是锐角(注意数形结合,构造直角三角形).
2.sinA, cosA,tanA 是一个比值(数值). 3.sinA, cosA, tanA 的大小只与∠A的大小有 关,而与直角三角形的边长无关.
小练习
1、如图1,在Rt△MNP中,∠N=90゜. ∠P的对边是_________,∠P的邻边是___________; ∠M的对边是________,∠M的邻边是___________;
1 2
(C) 小于 3
2
(B)大于
1 2
(D)大于 3
2
☆ 应用练习 1.已知角,求值 2.已知值,求角 3. 确定值的范围 4. 确定角的范围
确定角的范围
3. 当∠A为锐角,且tan A的 值大于 3 时,∠A( B )
3
(A)小于30° (B)大于30°
1.1锐角三角函数(第一课时)课件(共17张PPT)浙教版数学九年级下册

cosA=
=
∠的邻边
温馨提醒:以正弦为例
sinA(省去角的符号),
30°的正弦表示为sin30°,比值 叫做∠A的正切值,记做tanA,即
斜边
∠BAC的正弦表示为sin∠BAC
,∠1的正弦表示为:sin∠1.
tanA=
∠的对边
∠的邻边
=
概念运用
①BC=8,AC=6
概念
cosA=
= ,
tanA=
4
3
sinA=
4
5
3
= ,
5
= .
解后反思:在直角三角
形中,已知什么条件可
以求三角函数值?
课堂练习
1.如图,在Rt△ABC中,∠ACB=90°,作CD⊥AB于
点D,若BC=5,BD=4,求sin∠A.
C
A
B
思路1:求AB的长
思路2:等角转化
△BCD∽△BAC
B"
P
C" Q
图(1)
图(2)
角为30°
’’ 1
""
=
= =
’’ 2
"
’’
3 "
=
=
=
’’
2
"
’’
3 ""
=
=
=
’’
3
"
请先按暂停键!
思考完成后
再按回播放键!
边的比值为定值
探索规律
当∠PAQ发生改变时,刚才所获得的发现是否还成立呢?
解:设AB=5k,AC=3k,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
铅 直 高 度
水平宽度
梯子在上升变陡的过程中,倾斜 角,铅直高度与梯子的比,水平 宽度与梯子的比,铅直高度与水 平宽度的比,都发生了什么变化?
铅 直 高 度
水平宽度
梯子在上升变陡的过程中,倾 斜角,铅直高度与梯子的比,水 平宽度与梯子的比,铅直高度与 水平宽度的比,都发生了什么变 化?
铅 直 高 度
水平宽度
梯子在上升变陡的过程中,倾 斜角,铅直高度与梯子的比,水 平宽度与梯子的比,铅直高度与 水平宽度的比,都发生了什么变 化?
铅 直 高 度
水平宽度
越大 梯子越陡——倾斜角_____ 越大 倾斜角越大——铅直高度与梯子的比_____ 越小 倾斜角越大——水平宽度与梯子的比_____
倾斜角越大——铅直高度与水平宽度
A
C
取宝物比赛
10m
10m
(1)
1m
5m
(2)
B
∠A的对边
sinA 斜边
斜边 ∠A的对边
cosA
∠A的邻边 斜边
A
∠A的邻边
C
tanA
∠A的对边 ∠A的邻边
下课了!
锐角三角函数
B
∠A的对边
sinA 斜边
斜边 ∠A的对边
cosA
∠A的邻边 斜边
A
∠A的邻边
C
tanA
∠A的对边 ∠A的邻边
活 动 1
B
AC 1 BC 和 AB1 , AC
B1C 1 和 有什么关系? AC 1
A C C1
(3)如果改变B在梯子上的位置 呢?
想一想
B
B1 (1)直角三角形AB1C1和直角三
角形ABC有什么关系? (2)
BC AB B1C 1 AC 和 AB1 , AB
AC 1 和 AB1 ,
BC AC
B1C 1 和 AC 1 有什么关系?
浙教版九年级下册
数 学
全册优质课件
取宝物比赛10m来自10m(1)1m
5m
(2)
梯子在上升变陡的过程中,倾斜 角,铅直高度与梯子的比,水平宽 度与梯子的比,铅直高度与水平宽 度的比,都发生了什么变化?
铅 直 高 度
倾斜角
水平宽度
梯子在上升变陡的过程中,倾斜 角,铅直高度与梯子的比,水平宽 度与梯子的比,铅直高度与水平宽 度的比,都发生了什么变化?
A C C1
(3)如果改变B在梯子上的位置 呢?
B
∠A的对边
sinA 斜边
斜边 ∠A的对边
cosA
∠A的邻边 斜边
A
∠A的邻边
C
tanA
∠A的对边 ∠A的邻边
牛 刀 小 试
B
例1 如图,在Rt△ABC中,∠C=90° AB=5,BC=3, 求∠A, ∠B的正弦, 余弦和正切. 观察以上计算结果,你发现了什么? 若AC=5,BC=3呢? 若AC=5呢?
cos 60
tan 60
a 1 2a 2
3a 3 a
60°
设两条直角边长为a,则斜边长= a2 a2 2a
a sin 45 2a a cos 45 2a
2 2 2 2
45°
a tan 45 1 a
仔细观察,说说你发现 这张表有哪些规律? 30°、45°、60°角的正弦值、余弦值和正切值如下表: 锐角a 30° 三角函数 sin a
两块三角尺中有几个不同的锐 角?分别求出这几个锐角的正 弦值、余弦值和正切值. 60° 30° 45° 45°
设30°所对的直角边长为a,那么斜边长为2a 另一条直角边长=
sin 30
a 1 2a 2
30°
cos30
tan 30
3a 3 2a 2
a 3 3 3a
3a 3 sin 60 2a 2
BC B1C 1 AC (2) AB 和 AB1 , AB
B
和
AC 1 AB1
,
BC AC
B1C 1 和 AC 1有什么关系?
A C C1
(3)如果改变B在梯子上的位置 呢?
想一想
B1 (1)直角三角形AB1C1和直角三
角形ABC有什么关系? (2)
BC AB B1C 1 AC 和 AB1 , AB
你想知道小明怎样 算出的吗?
?
30°
1.65米
10米
例3 (1)如图,在Rt△ABC中, ∠C=90°,AB=6 ,BC=3 。求∠A的度 数。 (2)如图,已知圆锥的高 AO等于圆锥的底面半 3 径OB的 倍,求α. A
B
6 3
(2)
O
A
C
B
(1)
例4 如图,在Rt△ABC中,∠ACB=90度,CD⊥AB于D , 已知∠B=30度,计算 tan ACD sin BCD的值。
B1 (1)直角三角形AB1C1和直角三
角形ABC有什么关系? (2)
BC AB B1C 1 和 AB1
,
AC AB
和
AC 1 BC AB1 , AC
B
B1C 1 和 AC 1有什么关系?
A C C1
(3)如果改变B在梯子上的位置 呢?
想一想
B1 (1)直角三角形AB1C1和直角三
角形ABC有什么关系?
越大 的比_____
铅 直 高 度 水平宽度
想一想
B1 (1)直角三角形AB1C1和直角三
角形ABC有什么关系?
BC B1C 1 AB和 AB1
(2)
B
,
B1C 1 和 有什么关系? AC 1
AC AC 1 BC 和 , AB AB1 AC
A C C1
(3)如果改变B在梯子上的位置 呢?
想一想
A
D
B
C
例5
3 , AC 2 3, 如图,在△ABC中,∠A=30度, tanB 2
C
AC 2 3
求AB。 解:过点C作CD⊥AB于点D ∠A=30度,
1 CD 1 CD 2 3 3 sin A 2 AC 2
A
3 AD 3 AD 2 3 3 cos A 2 AC 2 CD 3 BD 3 2 2 tan B 3 BD 2
3 1 2 2
2
2
cos45 tan 45 ( 2) sin 45
2 2 1 2 2
=0
=1
例2 操场里有一个旗杆,老师让小明去测量旗杆
高度,小明站在离旗杆底部10米远处,目测旗杆的顶 部,视线与水平线的夹角为30度,并已知目高为1.65 米.然后他很快就算出旗杆的高度了。
1 2
45°
2 2
60°
3 2
cos a
tan a
3 2
3 3
2 2
1 2
1
3
例1 求下列各式的值:
(1)cos260°+sin260°
(3)tan450.sin450-4sin300.cos450+cos2300
cos45 tan 45 ( 2) sin 45
解: (1) cos260°+sin260°
水平宽度
梯子在上升变陡的过程中,倾斜 角,铅直高度与梯子的比,水平 宽度与梯子的比,铅直高度与水 平宽度的比,都发生了什么变化?
铅 直 高 度
水平宽度
梯子在上升变陡的过程中,倾 斜角,铅直高度与梯子的比,水 平宽度与梯子的比,铅直高度与 水平宽度的比,都发生了什么变 化?
铅 直 高 度
水平宽度
梯子在上升变陡的过程中,倾 斜角,铅直高度与梯子的比,水 平宽度与梯子的比,铅直高度与 水平宽度的比,都发生了什么变 化?
铅 直 高 度
水平宽度
越大 梯子越陡——倾斜角_____ 越大 倾斜角越大——铅直高度与梯子的比_____ 越小 倾斜角越大——水平宽度与梯子的比_____
倾斜角越大——铅直高度与水平宽度
A
C
取宝物比赛
10m
10m
(1)
1m
5m
(2)
B
∠A的对边
sinA 斜边
斜边 ∠A的对边
cosA
∠A的邻边 斜边
A
∠A的邻边
C
tanA
∠A的对边 ∠A的邻边
下课了!
锐角三角函数
B
∠A的对边
sinA 斜边
斜边 ∠A的对边
cosA
∠A的邻边 斜边
A
∠A的邻边
C
tanA
∠A的对边 ∠A的邻边
活 动 1
B
AC 1 BC 和 AB1 , AC
B1C 1 和 有什么关系? AC 1
A C C1
(3)如果改变B在梯子上的位置 呢?
想一想
B
B1 (1)直角三角形AB1C1和直角三
角形ABC有什么关系? (2)
BC AB B1C 1 AC 和 AB1 , AB
AC 1 和 AB1 ,
BC AC
B1C 1 和 AC 1 有什么关系?
浙教版九年级下册
数 学
全册优质课件
取宝物比赛10m来自10m(1)1m
5m
(2)
梯子在上升变陡的过程中,倾斜 角,铅直高度与梯子的比,水平宽 度与梯子的比,铅直高度与水平宽 度的比,都发生了什么变化?
铅 直 高 度
倾斜角
水平宽度
梯子在上升变陡的过程中,倾斜 角,铅直高度与梯子的比,水平宽 度与梯子的比,铅直高度与水平宽 度的比,都发生了什么变化?
A C C1
(3)如果改变B在梯子上的位置 呢?
B
∠A的对边
sinA 斜边
斜边 ∠A的对边
cosA
∠A的邻边 斜边
A
∠A的邻边
C
tanA
∠A的对边 ∠A的邻边
牛 刀 小 试
B
例1 如图,在Rt△ABC中,∠C=90° AB=5,BC=3, 求∠A, ∠B的正弦, 余弦和正切. 观察以上计算结果,你发现了什么? 若AC=5,BC=3呢? 若AC=5呢?
cos 60
tan 60
a 1 2a 2
3a 3 a
60°
设两条直角边长为a,则斜边长= a2 a2 2a
a sin 45 2a a cos 45 2a
2 2 2 2
45°
a tan 45 1 a
仔细观察,说说你发现 这张表有哪些规律? 30°、45°、60°角的正弦值、余弦值和正切值如下表: 锐角a 30° 三角函数 sin a
两块三角尺中有几个不同的锐 角?分别求出这几个锐角的正 弦值、余弦值和正切值. 60° 30° 45° 45°
设30°所对的直角边长为a,那么斜边长为2a 另一条直角边长=
sin 30
a 1 2a 2
30°
cos30
tan 30
3a 3 2a 2
a 3 3 3a
3a 3 sin 60 2a 2
BC B1C 1 AC (2) AB 和 AB1 , AB
B
和
AC 1 AB1
,
BC AC
B1C 1 和 AC 1有什么关系?
A C C1
(3)如果改变B在梯子上的位置 呢?
想一想
B1 (1)直角三角形AB1C1和直角三
角形ABC有什么关系? (2)
BC AB B1C 1 AC 和 AB1 , AB
你想知道小明怎样 算出的吗?
?
30°
1.65米
10米
例3 (1)如图,在Rt△ABC中, ∠C=90°,AB=6 ,BC=3 。求∠A的度 数。 (2)如图,已知圆锥的高 AO等于圆锥的底面半 3 径OB的 倍,求α. A
B
6 3
(2)
O
A
C
B
(1)
例4 如图,在Rt△ABC中,∠ACB=90度,CD⊥AB于D , 已知∠B=30度,计算 tan ACD sin BCD的值。
B1 (1)直角三角形AB1C1和直角三
角形ABC有什么关系? (2)
BC AB B1C 1 和 AB1
,
AC AB
和
AC 1 BC AB1 , AC
B
B1C 1 和 AC 1有什么关系?
A C C1
(3)如果改变B在梯子上的位置 呢?
想一想
B1 (1)直角三角形AB1C1和直角三
角形ABC有什么关系?
越大 的比_____
铅 直 高 度 水平宽度
想一想
B1 (1)直角三角形AB1C1和直角三
角形ABC有什么关系?
BC B1C 1 AB和 AB1
(2)
B
,
B1C 1 和 有什么关系? AC 1
AC AC 1 BC 和 , AB AB1 AC
A C C1
(3)如果改变B在梯子上的位置 呢?
想一想
A
D
B
C
例5
3 , AC 2 3, 如图,在△ABC中,∠A=30度, tanB 2
C
AC 2 3
求AB。 解:过点C作CD⊥AB于点D ∠A=30度,
1 CD 1 CD 2 3 3 sin A 2 AC 2
A
3 AD 3 AD 2 3 3 cos A 2 AC 2 CD 3 BD 3 2 2 tan B 3 BD 2
3 1 2 2
2
2
cos45 tan 45 ( 2) sin 45
2 2 1 2 2
=0
=1
例2 操场里有一个旗杆,老师让小明去测量旗杆
高度,小明站在离旗杆底部10米远处,目测旗杆的顶 部,视线与水平线的夹角为30度,并已知目高为1.65 米.然后他很快就算出旗杆的高度了。
1 2
45°
2 2
60°
3 2
cos a
tan a
3 2
3 3
2 2
1 2
1
3
例1 求下列各式的值:
(1)cos260°+sin260°
(3)tan450.sin450-4sin300.cos450+cos2300
cos45 tan 45 ( 2) sin 45
解: (1) cos260°+sin260°
