苏教版四年级下册数学解决问题的策略-画图PPT课件(一)
合集下载
四年级数学下册课件解决问题的策略苏教版13(共30张PPT)

时货车共行多少千米?
想:围成的长方形的面积都是多少平方厘米?
你发现在什么情况下长方形的周长最大?
两地相距多少千米?相遇时离中点多少千米?
相遇后,两车继续行驶了3小时,甲车正好到达B地,这时乙车离A地还有多少千米?
3、两地相距360千米,甲、乙两车同时从两地相向而行,经过两车4小时相遇。
3盆 24个 4、甲、乙两车从A、B两地相向而行,甲车每小时行90千米,乙车每小时行80千米,甲车开出1小时20分后,乙车才开出,又经过2小
你发现在什么情况下长方形的周长最大?
答:租( )条大船,( )小船,一共需要
学校
用48个1平方厘米的正方形拼成长方形,有多少种不同的拼法?它们的周长各是多少?你发现了什么?
2、运动方向是相对(相向)
2、两地相距360千米,甲、乙两车同时从两地相向而行,甲车每小时行50千米,乙车每小时行40千米。
3小时后,两船相距多少千米?如果此时乙船提速20%,那么还要多少小时才能追上甲船?
2、一种圆珠笔有3支装和5支装两种不同规格的包装。
学校栽了一些盆花。如果每个教室放3盆, 相遇时间=总路程÷速度和
学校栽了一些盆花。 1、某校三年级有3个班,四年级有2个班。
可以放24个教室;如果每个教室放4盆,可 1、多多有5元和2元的人民币各若干张,他要取出37元,有多少种不同的取法?(用什么策略解决问题)
2、一种圆珠笔有3支装和5支装两种不同规格的包 装。张老师要购买38支圆珠笔,可以分别购买3枝 装和5枝装的各几盒?一共有几种不同的选择方法? 如果要购买30支呢?
3、小红从家到少年宫,如果只是向东、向北
走,一共有多少种不同的路线可走?
相遇后,两车继续行驶了3小时,甲车正好到达B地,这时乙车离A地还有多少千米?
四年级数学下册五解决问题的策略教学课件苏教版.ppt

直观、清楚、方便分析
12
72
思路1:两人邮票的总数加12枚,等于小春邮票枚数的 2倍,可以先求小春的枚数,再求小宁的枚数。 思路2:两人邮票的总数减12枚,等于小宁邮票枚数的 2倍,可以先求小宁的枚数,再求小春的枚数。
从图上直观、清楚地看清了数量间的关系,大家
找到了解决问题的两种思路,请你选择一种思路,
12
72
思路2:两人邮票的总数减12枚,等于小宁邮票枚数的
2倍,可以先求小宁的枚数,再求小春的枚数。
(72-12)÷2 =60÷2
30+12=42(枚)
=30(本)
咱们已经做完题了,但是要检验上面 的解答对不对,有哪些方法?
用“把得数带入原题”的方法检验, 要分几步检验呢?你是怎样检验的,把你 的方法填在课本上。
典题精讲
两个小队的少先队员去植树,一共植了34棵。其中 第二小队比第一小队多植4棵。两个小队各植树多少 棵?(先根据题意把线段图补充完整,在解答。)
(34+4)÷2
=38÷2
=19(棵) 19-4=15(棵)
(34-4)÷2
=30÷2
=15(棵) 15+4=19(棵)
答Hale Waihona Puke 第一小队植15棵,第二小队植19棵。
从三年级起,我们学会了从条件想起、从问 题想起,还有灵活运用两种策略,以及列表、画 图整理的策略。大家已经感受到,运用策略能帮 助我们分析数量关系,找到解决问题的思路和方 法。为了提高分析问题和解决问题的能力,我们 今天学习新的解决问题的策略。
探究新知
小宁和小春共有72枚邮票,小春比小 宁多12枚。两人各有邮票多少枚?
小宁和小春共有72枚邮票,小春比 小宁多12枚。两人各有邮票多少枚?
12
72
思路1:两人邮票的总数加12枚,等于小春邮票枚数的 2倍,可以先求小春的枚数,再求小宁的枚数。 思路2:两人邮票的总数减12枚,等于小宁邮票枚数的 2倍,可以先求小宁的枚数,再求小春的枚数。
从图上直观、清楚地看清了数量间的关系,大家
找到了解决问题的两种思路,请你选择一种思路,
12
72
思路2:两人邮票的总数减12枚,等于小宁邮票枚数的
2倍,可以先求小宁的枚数,再求小春的枚数。
(72-12)÷2 =60÷2
30+12=42(枚)
=30(本)
咱们已经做完题了,但是要检验上面 的解答对不对,有哪些方法?
用“把得数带入原题”的方法检验, 要分几步检验呢?你是怎样检验的,把你 的方法填在课本上。
典题精讲
两个小队的少先队员去植树,一共植了34棵。其中 第二小队比第一小队多植4棵。两个小队各植树多少 棵?(先根据题意把线段图补充完整,在解答。)
(34+4)÷2
=38÷2
=19(棵) 19-4=15(棵)
(34-4)÷2
=30÷2
=15(棵) 15+4=19(棵)
答Hale Waihona Puke 第一小队植15棵,第二小队植19棵。
从三年级起,我们学会了从条件想起、从问 题想起,还有灵活运用两种策略,以及列表、画 图整理的策略。大家已经感受到,运用策略能帮 助我们分析数量关系,找到解决问题的思路和方 法。为了提高分析问题和解决问题的能力,我们 今天学习新的解决问题的策略。
探究新知
小宁和小春共有72枚邮票,小春比小 宁多12枚。两人各有邮票多少枚?
小宁和小春共有72枚邮票,小春比 小宁多12枚。两人各有邮票多少枚?
苏教版数学四年级下册解决问题的策略PPT课件

长兴小学原有一个长方形操场,长50米、宽40米。扩建后,长
增加10米,宽增加8米,那么操场的面积扩大了多少呢?先画图,
再解答。
50米
10米
40米
8 米
方法1
(50+10)×(40+8)-50 ×40 =60 ×48-2000 =2880-2000 = 880(平方米)
答:操场的面积增加了880平方米。
【重点】掌控画图分析数量关系的策略。
【难点】能知道并分析不同方法是怎样分别处理条件之间的联系。
策略1 回想起来了吗?谁能说一说?
在解决谁比谁多多少、少多少的简单情境中,我们习惯于用线段 来描写“多少”,所以也就有了“线段图”。 在知道两个人(乃至是两类量)的一共,又知道谁比谁多多少的 情境下,我们可以通过画线段图,明晰关系,分析解题。
策略2 回想起来了吗?谁能说一说?
在解决“面积”类型的问题上,我们习惯于用长方形图、正方形 图这样的示意图来出现数量之间的关系。 及时在示意图的边上标好数据,那么增减变化、关系情形也就一 目了然了。与之类似的,还有点子图,含义相通。要学会公道挑 选需要的示意图。
一边算,一边看看你能联想到什么解决问题的策略。
李辉和张强一共有画片86张,张强给李辉8张后,两人就一样多了。 两人本来各有画片多少张?(先画图,再解答。)
8×2=16(张)
(86-16)÷2 =70÷2 =35(张)
李辉
方法1
张强
35+16=51(张)
16张
(86)张
答:李辉本来有画片35张,张强本来有画片51张。
方法2
8×2=16(张) (86+16)÷2
12×34+12×26 =408+312 =720
苏教版四年级下册数学解决问题的策略ppt课件

原来花圃的面积 增加的
?平方米
面积18
平方米
8米
3米
1、在刚才解题过程中,经历了哪些步 骤?你觉得哪些步骤很重要?
2、画示意图时,你认为要注意些什么?
严格执行突发事件上报制度、校外活 动报批 制度等 相关规 章制度 。做到 及时发 现、制 止、汇 报并处 理各类 违纪行 为或突 发事件 。
❖题目中的条件和问题是否都作了 准确的标注
面 积
3米
严格执行突发事件上报制度、校外活 动报批 制度等 相关规 章制度 。做到 及时发 现、制 止、汇 报并处 理各类 违纪行 为或突 发事件 。
剩下的面积
6米
减少的面积
8米
3米
严格执行突发事件上报制度、校外活 动报批 制度等 相关规 章制度 。做到 及时发 现、制 止、汇 报并处 理各类 违纪行 为或突 发事件 。
原来鱼池的面积 5米
20米
减少的部分是多少平方米呢? 它对解题是很有帮助的!
严格执行突发事件上报制度、校外活 动报批 制度等 相关规 章制度 。做到 及时发 现、制 止、汇 报并处 理各类 违纪行 为或突 发事件 。
?
现在鱼池的面积 原来鱼池的面积 ?平方米
5米 减少的面积31050平方
米
20米
长:150÷5=30(米) 面积:30×(20-5)=450
1、先画什么ቤተ መጻሕፍቲ ባይዱ要标出什么? 2、增加的长是3米,它和原来的8米比应该 画多长? 3、条件和问题要不要填在示意图中。
严格执行突发事件上报制度、校外活 动报批 制度等 相关规 章制度 。做到 及时发 现、制 止、汇 报并处 理各类 违纪行 为或突 发事件 。
原来花圃的面积 ?平方米
四年级下册数学课件5.1用画图策略解决和差问题∣苏教版(秋) (共21张PPT)
拓展提高
6. 小明和爸爸现在年龄的和是34岁,4年后爸爸比小明大24岁, 小明今年多少岁?
【答案】(34—24)÷2=5(岁)
【解析】4年后爸爸比小明大24岁,也就是爸爸比小明大24岁,这个差是永远不变的。所以 归根结底,这还是和差问题。
发散思维
7. 爸爸今年48岁,儿子今年21岁,多少年前爸爸的年龄正好是儿子 的4倍?
【答案】48—21=27(岁) 27÷(4—1)=9(岁) 21—9=12(岁)
【解析】根据题意,爸爸和儿子的年龄差是27岁,这是一个不变量。那么,可以求出几年 前儿子的年龄,即27÷(4—1)=9(岁),再用21减去9 得到12年前。
方法1:两人邮票的总数减去12枚,等于小宁邮标枚数的2倍, 可以先求小宁有多少枚。
小宁(72—12)÷2=30(枚),小春30+12=42(枚) 或72—30=42(枚)
课题引入
【解析】
方法2:两人邮票的总数加上12枚,等于小春邮标枚数的2倍, 可以先求小春有多少枚。
小春(72+12)÷2=42(枚),小宁42—12=30(枚) 或72—42=30(枚)。
知识梳理
【例】张宁和王晓星一共有卡片74张。王晓星给张宁5张后,两人 画片的张数同样多。两人原来各有卡片多少张?(先把已知 条件在线段图上表示出来,再解答)
5×2=10(张) 74
知识梳理
【解析】从图中可知,王晓星减去10张就和张宁一样多,张宁加上10张就和王晓星一样多。 因此,从74张里面减去10张就是张宁张数的2倍,从74张里面加上10张就是王晓星张数的2 倍。因此,可以这样解答: 方法一: 5×2=10(张),(74—10)÷2=32(张),74—32=42(张),答张宁有32 张,王晓星有42张; 方法二:5×2=10(张),(74﹢10)÷2=42(张),74—42=32(张),答张宁有32张, 王晓星有42张。(求出第一个人的张数后,第二个人的张数有多种方法计算,不一一列举)
苏教版四年级下册数学解决问题的策略画图课件(共19张PPT)

苏教版四年级下册
小刚有16枚邮票
相差6枚
小红有10枚邮票
小刚有160枚邮票
多的6枚
小红有10枚邮票
小刚有16枚邮票
小红有160 枚邮票
少的16枚
小刚有136枚邮票
3枚多的63枚枚
小红有103 枚邮票
小宁和小春共有72枚邮票,小春
比小宁多12枚。两人各有邮票多少
枚? ?枚
小宁 小春
多( 12)枚 (72)枚
少15
150本 =45(本)
本
45+15=60(本)
练一练 一个双层书架,上层书的本数是下层的3倍。
如果从上层搬60本书到下层,那么两层的本数正
好相等。原来上、下层各有多少本书?
(先根据题意画出线段图,再在图中表示出条件和问题) ?本
上层
下层
?本
60本
60本
回顾思考 我们之前已经学过哪些解决问题的策略?
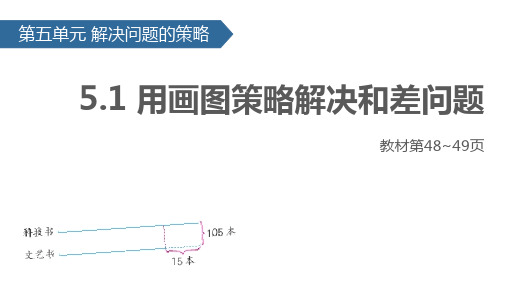
看图说出已知条件和问题,再解答。
科技书
文艺书
科故技事书书 和文艺 书各有多少本?
少15本
105本 150本
科技书、文艺 书和故事书各 有多少本?
பைடு நூலகம்一比
科技书 文艺书
科技书 文艺书 故事书
少15本
105本
(105-15)÷2 =90÷2 =45(本) 45+15=60(本)
(150-15)÷3
=135÷3
?枚
小宁 小春
?枚 ?枚
多( 12)枚 (72)枚
小宁 小春宁
多((127)2枚-1(2 )72枚)枚
这时的邮票总数等于 原来小宁邮票数的2倍
小宁春 小春
多( 12)枚((772+2)12)枚枚
小刚有16枚邮票
相差6枚
小红有10枚邮票
小刚有160枚邮票
多的6枚
小红有10枚邮票
小刚有16枚邮票
小红有160 枚邮票
少的16枚
小刚有136枚邮票
3枚多的63枚枚
小红有103 枚邮票
小宁和小春共有72枚邮票,小春
比小宁多12枚。两人各有邮票多少
枚? ?枚
小宁 小春
多( 12)枚 (72)枚
少15
150本 =45(本)
本
45+15=60(本)
练一练 一个双层书架,上层书的本数是下层的3倍。
如果从上层搬60本书到下层,那么两层的本数正
好相等。原来上、下层各有多少本书?
(先根据题意画出线段图,再在图中表示出条件和问题) ?本
上层
下层
?本
60本
60本
回顾思考 我们之前已经学过哪些解决问题的策略?
看图说出已知条件和问题,再解答。
科技书
文艺书
科故技事书书 和文艺 书各有多少本?
少15本
105本 150本
科技书、文艺 书和故事书各 有多少本?
பைடு நூலகம்一比
科技书 文艺书
科技书 文艺书 故事书
少15本
105本
(105-15)÷2 =90÷2 =45(本) 45+15=60(本)
(150-15)÷3
=135÷3
?枚
小宁 小春
?枚 ?枚
多( 12)枚 (72)枚
小宁 小春宁
多((127)2枚-1(2 )72枚)枚
这时的邮票总数等于 原来小宁邮票数的2倍
小宁春 小春
多( 12)枚((772+2)12)枚枚
苏教版四年级数学下册5.1.画线段图解决问题课件

当堂检测
3.甲、乙两地相距495千米,一辆汽车从甲地开往乙地,已经行 了3小时,剩下的路程比已经行的多45千米。这辆汽车的平均速 度是多少千米/时?(教材P54 练习八 第11题)
你能先根据题意把线段 图补充完整,再解答吗?
(495-45)÷2=225(千米) 225÷3=75(千米/时) 答:这辆汽车的平均速度是75千米/时。
小宁和小春共有 72 枚邮票,小春比小宁多12枚。 两人各有邮票多少枚?
看图说出已知条件 和问题,再解答?
科技书 文艺书
少15本
105本
题型: 都是已知两个数量的和与差,求这两个数量。(和差问题)
思路: 借助线段图分析数量关系,想办法把两个不相等的数量转化 为相等的数量。
归纳: (和+差)÷2=较大数 (和-差)÷2=较小数
小春
添12枚 多12枚
共72 +枚12=84( )
2 给小宁添上12枚,变成和小春一样多。
72+12=84(枚) 小春:84÷2=42(枚) 小宁:72-42=30(枚)或 42-12=30(枚)
探索新知
比较这两种解法,它们在思路上有什么相同点和不同点呢?
去多法
补少法
都是先设法使两个人的邮票枚数变得同样多,使两个不相等
每条短花边长多少 厘米?长花边呢?
方法一:(90-10)÷4=20(cm) 方法二:(90+10×3)÷4=30(cm)
20+10=30(cm)
30-10=20(cm)
答:每条短花边长20厘米,长花边长30厘米。
随堂小练
3. 一个双层书架,上层书架的本数是下层的3倍。如果从上层搬60本 到下层,那么两层书的本数正好相等。原来上、下层各有图书多少
科技书和文 艺书各有多 少本?
苏教版四年级数学下册解决问题的策略2画示意图解决问题ppt课件

苏教版四年级数学下册 解决问题的策略2画 示意图解决问题ppt课件
2020/9/25
导学单
1.大声读题,讨论如何画图。 2.画完图后,说说增加的面积是哪部分? 3.自己列式计算并检验。
8米
3米
原来花圃的面积 增加的
?平方米
面积18
平方米
小营村原来有一个宽20米的长方形鱼池。因扩 建公路,鱼池的宽减少了5米,这样鱼池的面积 就减少了150平方米。现在鱼池的面积是多少 平方米?(先在图中画出减少的部分,再解答)
现在鱼池的面积?平方米
20米
5米 减少的面积150平方米
创编题
王大爷家有一块边长为6米的正方形菜地,在菜 地的四周有一条2米宽的空地。王大爷准备在空 地中栽月季花,每棵月季花占地1平方米,一共 可栽多少棵月季花?
2020/9/25
导学单
1.大声读题,讨论如何画图。 2.画完图后,说说增加的面积是哪部分? 3.自己列式计算并检验。
8米
3米
原来花圃的面积 增加的
?平方米
面积18
平方米
小营村原来有一个宽20米的长方形鱼池。因扩 建公路,鱼池的宽减少了5米,这样鱼池的面积 就减少了150平方米。现在鱼池的面积是多少 平方米?(先在图中画出减少的部分,再解答)
现在鱼池的面积?平方米
20米
5米 减少的面积150平方米
创编题
王大爷家有一块边长为6米的正方形菜地,在菜 地的四周有一条2米宽的空地。王大爷准备在空 地中栽月季花,每棵月季花占地1平方米,一共 可栽多少棵月季花?
苏教版四年级下册数学解决问题的策略-画图PPT课件(一)

18÷3 × 8
= 6 ×8
= 48(平方米) 答:原来花圃的面积是48平方米。
A
10
原来鱼池的面积 5米
20米
减少的部分的面积怎么
画呢?
A
11
?
现在鱼池的面积 原来鱼池的面积 ?平方米
20米
5米 减少的面积31050平方
分步式:
米
综合式:
(1)150÷5=30(米)
150 ÷5×(20—5)
(2)30 ×(20—5)
增加24平方米
4米 增加24平方米
4、如果草坪的面积增加了24平方米,那么可以把 长 ( 增加8米) 把宽 ( 增加4米 ) .我还可以( 把长和宽同时增加 )。
A
20
原来试验田的面积 ?平方米
原来试验田的面积 ?平方米
如果这块试验田的长增加6米,面积就比原 来增加48平方米。如果这块试验田的宽增加4米,面 积也比原来增加48平方米。
增加的 面积为 18平方 米
3米
要求出原来的宽
A
7
原来花圃的面积 增加的
?平方米
面积18
平方米
8米
3米
A
8
原来花圃的面积 ?平方米
增加的 面积18 平方米
8米
3米
18÷3=6(米)
A
9
原来花圃的面积 增加的
?平方米
面积18
平方米
分步式:
8米
3米
综合式:
(1)18÷3=6(米)
(2)8×6=48(平方米) 答:原来花圃的面积是48平方米。
= 880(平方米)
答:操场的面积增加了880平方米。
A
27
50米
四年级数学下册课件-5.3解决问题策略 苏教版(共8张PPT)

如果要求“买一件上衣比买一条裤子多 多少元?”,应该怎样解答?
48元
裤子:
上衣:
?元
48×3=144(元) 144-48= 96(元)
48元
裤子:
上衣:
?元 48×3=144(元) 144+48=192(元)
48元
裤子:
上衣:
?元
48×3=144(元) 144-48= 96(元)
比一比:两道题有什么相同,有什么 不同?解答过程呢?
新苏教版三年级数学下册
解决问题的策略(二) ——画线段图
48元
裤子:
上衣:
?元
48元
裤子: 上衣:
?元
导学单: 1.想一想:你能根据线段图说出数量之间的关系吗?先
么?再求什么? 2.算一算:在课堂探究本上列式解答; 3.说一说:在小组里交流自己的解题过程,看是否有不
的解题方法;
4.比一比:如果要求“买一件上衣比买一条裤子多用多少 元?”,应该怎样解答?
1.基础题:完成想想做做第3、4题。 2.提高题:爸爸的年龄比小红大24岁,爸爸今 年的岁数是小红的4倍,爸爸、小红今年各几岁?
四年级下册数学-第五单元 解决问题的策略 第2课时 画示意图解决问题|苏教版 ppt课件

,这样鱼池的面积 就减少了150平方米。如今鱼池的面积是多少 平方米?〔先在图中画出减少的部分,再解答〕
如今鱼池的面积 ?平方米
20米
5米 减少的面积150平方米
根据左图可知:原来的长度并没有改动。 原长:150÷5=30〔米〕 如今鱼池的面积: 30×〔20-5〕=450〔平方米〕 答:如今鱼池的面积为450平方米。
四年级下册数学第五单元解决问题的策略第2课时画示意图解决问题
第 五 单元 处理问题的战略
第 2 课时 画表示图处理问题
1.大声读题,讨论如何画图。 2.画完图后,说说添加的面积是哪部分? 3.本人列式计算并检验。
8米
3米
原来花圃的面积 ?平方米
添加的 面积18 平方米
根据左图我们可看出原来的宽没有改动 原宽=18÷3=6〔米〕 原花圃面积:6×8=48〔平方米〕 答:原来花圃的面积是48平方米。
如今鱼池的面积 ?平方米
20米
5米 减少的面积150平方米
根据左图可知:原来的长度并没有改动。 原长:150÷5=30〔米〕 如今鱼池的面积: 30×〔20-5〕=450〔平方米〕 答:如今鱼池的面积为450平方米。
四年级下册数学第五单元解决问题的策略第2课时画示意图解决问题
第 五 单元 处理问题的战略
第 2 课时 画表示图处理问题
1.大声读题,讨论如何画图。 2.画完图后,说说添加的面积是哪部分? 3.本人列式计算并检验。
8米
3米
原来花圃的面积 ?平方米
添加的 面积18 平方米
根据左图我们可看出原来的宽没有改动 原宽=18÷3=6〔米〕 原花圃面积:6×8=48〔平方米〕 答:原来花圃的面积是48平方米。
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
21
图1
图2
原来试验田的 面积?平方米
6米
增加的面积 48平方米
A
图2 22
原来试验田的 面积?平方米
4
增加的面积
米
48平方米
图1
A
23
分步式:
(1)48÷4=12(米)
6米
增加的
原来试验田的面积 面积48
?平方米
8 平方米
12
4米 增加的面积48平方米
(2) 48÷6=8(米) (3)12×8=96(平方米)
增加的 面积为 18平方 米
3米
要求出原来的宽
A
7
原来花圃的面积 增加的
?平方米
面积18
平方米
8米
3米
A
8
原来花圃的面积 ?平方米
增加的 面积18 平方米
8米
3米
18÷3=6(米)
A
9
原来花圃的面积 增加的
?平方米
面积18
平方米
分步式:
8米
3米
综合式:
(1)18÷3=6(米)
(2)8×6=48(平方米) 答:原来花圃的面积是48平方米。
18÷3 × 8
= 6 ×8
= 48(平方米) 答:原来花圃的面积是48平方米。
A
10
原来鱼池的面积 5米
20米
减少的部分的面积怎么
画呢?
A
11
?
现在鱼池的面积 原来鱼池的面积 ?平方米
20米
5米 减少的面积31050平方
分步式:
米
综合式:
(1)150÷5=30(米)
150 ÷5×(20—5)
(2)30 ×(20—5)
增加24平方米
4米 增加24平方米
4、如果草坪的面积增加了24平方米,那么可以把 长 ( 增加8米) 把宽 ( 增加4米 ) .我还可以( 把长和宽同时增加 )。
A
20
原来试验田的面积 ?平方米
原来试验田的面积 ?平方米
如果这块试验田的长增加6米,面积就比原 来增加48平方米。如果这块试验田的宽增加4米,面 积也比原来增加48平方米。
A
14
挑战一:难度两星级
我们学校有一块长方形的草坪,长是6米,宽是3 米。
6米
3米 原来草坪的面积
2米 增加了?平方米
2、如果草坪的宽增加2米,面积增加( 12平方米 )
A
15
挑战一:难度三星级
我们学校有一块长方形的草坪,长是6米, 宽是3米。
6米
?米
3米 原来草坪的面积
增加24平方米
3、如果草坪的面积增加了24平方米,
=480+400
= 880(平方米)
答:操场的面积增加了880平方米。
A
29
50米
10米
40米
10×40
+
8米
50×8 + 8×10
50×8+8×10+10×40
=400+80+400
=480+400
= 880(平方米)
答:操场的面积增加了880平方米。
A
30
A
31
答:原来试验田的面积是96平方米。
综合式: 48÷4×(48÷6) =12×8
=96(平方米)
答:原来试验田的面积是96平方米。
A
24
50米
10米
40米
8米
A
25
50米
10米
40米
8米
A
26
50米
10米
40米
8米
(50+10)×(40+8)-50 ×40
=60 ×48-2000
=2880-2000
那么(
)?。
A
16
挑战一:难度三星级
我们学校有一块长方形的草坪,长是6米, 宽是3米。
6米
8米
3米 原来草坪的面积
增加24平方米
3、如果草坪的面积增加了24平方米,那么(可以 把 长增加8米 )。
A
17
挑战一:难度三星级
我们学校有一块长方形的草坪,长是6米, 宽是3米。
6米
3米 原来草坪的面积
?米 增加24平方米
3、如果草坪的面积增加了24平方米,那么
(
)?。
A
18
我们学校有一块长方形的草坪,长是6米,宽 是3米。
6米
3米 原来草坪的面积
4米 增加24平方米
3、如果草坪的面积增加了24平方米,那么 (可以把宽增加4米 )。
A
19
我们学校有一块长方形的草坪,长是6米,宽是
3米。
6米
8米
3米 原来草坪的面积
=30 ×15
=30 ×15
=450(平方米)
=450(平方米) 答:现在鱼池的面积是450平方米。 答:现在鱼池的面积是450平方米。
A
12
A
13
挑战一:难度一星级
我们学校有一块长方形的草坪,长是6米, 宽是3米。
6米
3米
方减 米少
了 ? 平
2米
1、如果草坪的长减少了2米,面积减少 ( 6平方米 )?
= 880(平方米)
答:操场的面积增加了880平方米。
A
27
50米10米40米源自10×408米(50+10)×8
(50+10)×8+ 10×40 =60×8+400
=480+400
=880(平方米)
答:操场的面积增加了880平方米。
A
28
50米
10米
40米
(40+8)×10
8米
50×8
(40+8)×10+50×8
苏教版四年级数学下册
A
1
面积为?平方米
6米
8米
面积=长×宽
A
2
面积为48平方米
6米
? 米
长=面积÷宽
A
3
面积为48平方米
?米
8米
宽=面积÷长
A
4
6米
8米
如果我们想增加这块 长方形花圃的面积可 以怎么办呢?
A
5
A.增加它的长 B.增加它的宽
C.把长和宽同时增加
A
6
原来花圃的面积 ?平方米
8米
