高三数学一轮复习专题题库：立体几何(16)

合集下载

高三数学一轮复习【立体几何】练习题

高三数学一轮复习【立体几何】练习题1.空间中，用a，b，c表示三条不同的直线，γ表示平面，则下列说法正确的有()A.若a∥b，b∥c，则a∥cB.若a⊥γ，b⊥γ，则a∥bC.若a∥γ，b∥γ，则a∥bD.若a⊥b，b⊥c，则a⊥c答案AB解析根据空间平行直线的传递性可知A正确；由直线与平面垂直的性质定理知B正确；若a∥γ，b∥γ，则a，b可能平行、相交或异面，故C错误；若a⊥b，b⊥c，则a，c可能相交、平行或异面，故D错误.2.对于两条不同直线m，n和两个不同平面α，β，下列选项正确的为()A.若m⊥α，n⊥β，α⊥β，则m⊥nB.若m∥α，n∥β，α⊥β，则m⊥n或m∥nC.若m∥α，α∥β，则m∥β或m⊂βD.若m⊥α，m⊥n，则n∥α或n⊂α答案ACD解析对A，令m，n分别为直线m，n的方向向量，因为m⊥α，n⊥β，所以m⊥α，n⊥β，又α⊥β，所以m⊥n，即m⊥n，所以选项A正确；对B，如图所示，在正方体ABCD-A1B1C1D1中，令平面ABCD为平面α，平面ABB1A1为平面β，直线A1C1为m，直线C1D为n，满足α⊥β，m∥α，n∥β，但m与n既不平行也不垂直，所以选项B错误；对C，若m⊄β，过m作一平面γ分别与平面α和平面β相交，且交线分别为a，b，则m∥a，a∥b，所以m∥b，所以m∥β；若m⊂β，符合题意，所以选项C 正确；对D，若n⊂α，符合题意；若n⊄α，过直线n作一平面β与平面α相交，设交线为b，因为b⊂α，m⊥α，所以m⊥b，又m⊥n，且n，b在同一平面内，所以n∥b，所以n∥α，所以选项D正确.综上，选ACD.3.如图是一个正方体的平面展开图，则在该正方体中()A.AE∥CDB.CH∥BEC.DG⊥BHD.BG⊥DE答案BCD解析由正方体的平面展开图还原正方体如图，连接AH，DE，BG，BH，DG，HC.由图形可知，AE⊥CD，故A错误；因为HE∥BC，HE＝BC，所以四边形BCHE为平行四边形，所以CH∥BE，故B正确；因为DG⊥HC，DG⊥BC，HC∩BC＝C，HC，BC⊂平面BHC，所以DG⊥平面BHC，又BH⊂平面BHC，所以DG⊥BH，故C正确；因为BG∥AH，而DE⊥AH，所以BG⊥DE，故D正确.故选BCD.4.用一个平面截正方体，所得的截面不可能是()A.锐角三角形B.直角梯形C.有一个内角为75°的菱形D.正五边形答案BCD解析对于A，如图1，截面的形状可能是正三角形，故A可能；图1图2对于B，首先考虑平面截正方体得到的截面为梯形，且QR与AA1不平行，如图2所示，不妨假设PQ⊥QR，因为AA1⊥平面A1B1C1D1，PQ⊂平面A1B1C1D1，所以AA1⊥PQ，从而有PQ⊥平面A1ABB1，这是不可能的，故B不可能；对于C，当平面截正方体得到的截面为菱形(非正方形)时，只有如下情形，如图3，其中P，R为所在棱的中点，易知当菱形为PBRD1时，菱形中的锐角取得最小值，即∠PD1R最小.设正方体的棱长为2，则PD1＝RD1＝5，PR＝22，则由余弦定理，得cos∠PD1R＝PD21＋RD21－PR22PD1·RD1＝5＋5－82×5×5＝15<6－24＝cos 75°，所以∠PD1R>75°，故C不可能；图3对于D，假设截面是正五边形，则截面中的截线必然分别在5个面内，由于正方体有6个面，分成两两平行的三对，故必然有一对平行面中有两条截线，而根据面面平行的性质可知这两条截线互相平行，但正五边形的边中是不可能有平行的边的，故截面的形状不可能是正五边形，故D不可能.综上所述，选BCD.5.已知正方体ABCD-A1B1C1D1的棱长为2，M为AA1的中点，平面α过点D1且与CM垂直，则()A.CM⊥BDB.BD∥平面αC.平面C1BD∥平面αD.平面α截正方体所得的截面图形的面积为9 2答案ABD解析如图，连接AC，则BD⊥AC.因为BD⊥AM，AM∩AC＝A，AM，AC⊂平面AMC，所以BD⊥平面AMC，又CM⊂平面AMC，所以BD⊥CM，故A正确；取AD的中点E，连接D1E，DM，由平面几何知识可得D1E⊥DM，又CD⊥D1E，DM∩CD＝D，DM，CD⊂平面CDM，所以D1E⊥平面CDM，又CM⊂平面CDM，所以D1E⊥CM.连接B1D1，过点E作EF∥BD，交AB于F，连接B1F，所以CM⊥EF，又D1E∩EF＝E，D1E，EF⊂平面D1EFB1，所以CM⊥平面D1EFB1，所以平面α截正方体所得的截面图形即梯形D1EFB1.由EF∥BD，BD⊄平面α，EF⊂平面α，得BD∥平面α，故B正确；连接AB1，AD1，易知平面AB1D1∥平面C1BD，而平面AB1D1∩平面α＝B1D1，所以平面C1BD与平面α不平行，故C不正确；截面图形为等腰梯形D1EFB1，EF＝2，B1D1＝22，D1E＝B1F＝5，所以截面图形的面积S＝12×(2＋22)×（5）2－⎝⎛⎭⎪⎫22－222＝92，故D正确.6.在正方体ABCD-A1B1C1D1中，N为底面ABCD的中心，P为线段A1D1上的动点(不包括两个端点)，M为线段AP的中点，则()A.CM与PN是异面直线B.CM>PNC.平面PAN⊥平面BDD1B1D.过P，A，C三点的正方体的截面一定是等腰梯形答案BCD解析对于选项A，如图，连接NC，PC，则A，N，C三点共线.又M为AP的中点，N为AC的中点，所以CM与PN共面，故A错误；对于选项B，因为P为线段A1D1上的动点(不包括两个端点)，所以AC>AP.在△MAC中，CM2＝AC2＋AM2－2AC·AM cos∠MAC＝AC2＋14AP2－AC·AP·cos∠MAC.在△PAN中，PN2＝AP2＋AN2－2AP·AN cos∠PAN＝AP2＋1 4AC 2－AP ·AC cos ∠PAN ，则CM 2－PN 2＝34(AC 2－AP 2)>0，所以CM >PN ，故B 正确；对于选项C ，在正方体ABCD-A 1B 1C 1D 1中，易知AC ⊥平面BDD 1B 1，即AN ⊥平面BDD 1B 1，又AN ⊂平面PAN ，所以平面PAN ⊥平面BDD 1B 1，故C 正确；对于选项D ，连接A 1C 1，在平面A 1B 1C 1D 1内作PK ∥A 1C 1，交C 1D 1于K ，连接KC .在正方体中，A 1C 1∥AC ，所以PK ∥AC ，PK ，AC 共面，所以四边形PKCA 就是过P ，A ，C 三点的正方体的截面，AA 1＝CC 1，A 1P ＝C 1K ，所以AP ＝CK ，即梯形PKCA 为等腰梯形，故D 正确.故选BCD.7.如图，在正四棱柱ABCD-A 1B 1C 1D 1中，AA 1＝2AB ＝2，点P 为线段AD 1上一动点，则下列说法正确的是( )A.直线PB 1∥平面BC 1DB.三棱锥P-BC 1D 的体积为13C.三棱锥D 1-BC 1D 外接球的表面积为3π2D.直线PB 1与平面BCC 1B 1所成角的正弦值的最大值为53 答案 ABD解析对于A 选项，连接B 1D 1，AB 1，根据正四棱柱的性质可知AD 1∥BC 1，BD ∥B 1D 1，因为BC 1⊄平面AB 1D 1，AD 1⊂平面AB 1D 1，所以BC 1∥平面AB 1D 1，同理得BD ∥平面AB 1D 1，又BC 1∩BD ＝B ，所以平面AB 1D 1∥平面BC 1D ，又PB 1⊂平面AB 1D 1，所以PB 1∥平面BC 1D ，所以A 选项正确；对于B 选项，易知AD 1∥平面BC 1D ，所以V P-BC 1D ＝V A-BC 1D ＝V C 1-ABD ＝13×12×1×1×2＝13，所以B 选项正确；对于C 选项，三棱锥D 1-BC 1D 的外接球即正四棱柱ABCD-A 1B 1C 1D 1的外接球.设外接球的半径为R ，则4R 2＝12＋12＋22＝6，所以外接球的表面积为4πR 2＝6π，所以C 选项错误；对于D 选项，过P 作PE ∥AB ，交BC 1于点E ，则PE ⊥平面BCC 1B 1，连接B 1E ，则∠PB 1E 即直线PB 1与平面BCC 1B 1所成的角，当B 1E 最小时，∠PB 1E 最大，此时B 1E ⊥BC 1，由等面积法得S △BB 1C 1＝12BC 1·B 1E ＝12BB 1·B 1C 1，解得B 1E ＝25，在Rt △PB 1E 中，PE ＝AB ＝1，所以PB 1＝12＋⎝ ⎛⎭⎪⎫252＝35，所以∠PB 1E 的正弦值的最大值为PE PB 1＝53，所以D 选项正确.故选ABD.8.如图，已知正方体ABCD-A 1B 1C 1D 1的棱长为2，E ，F ，G 分别为BC ，CC 1，BB 1的中点，则( )A.直线D1D与直线AF垂直B.直线A1G与平面AEF平行C.平面AEF截正方体ABCD-A1B1C1D1所得的截面的面积为9 2D.点A1和点D到平面AEF的距离相等答案BCD解析对于选项A，假设AF与D1D垂直，又D1D⊥AE，AE∩AF＝A，AE，AF⊂平面AEF，所以D1D⊥平面AEF.因为EF⊂平面AEF，所以D1D⊥EF，这显然是错误的，所以假设不成立，故A错误；图1对于选项B，取B1C1的中点N，连接A1N，GN，如图1所示，易知A1N∥AE，又AE⊂平面AEF，A1N⊄平面AEF，所以A1N∥平面AEF.因为GN∥EF，EF⊂平面AEF，GN⊄平面AEF，所以GN∥平面AEF.又A1N，GN⊂平面A1GN，A1N∩GN＝N，所以平面A1GN∥平面AEF.因为A1G⊂平面A1GN，所以A1G∥平面AEF，故B正确；对于选项C，连接AD1，FD1，如图2所示，因为AD1∥EF，所以四边形AD1FE 为平面AEF截正方体ABCD-A1B1C1D1所得的截面，又AD1＝22＋22＝22，图2EF ＝12＋12＝2，D 1F ＝AE ＝12＋22＝5，所以四边形AD 1FE 为等腰梯形，高为（5）2－⎝ ⎛⎭⎪⎫222＝322，则S 梯形AD 1FE ＝12×(2＋22)×322＝92，故C 正确；对于选项D ，连接A 1D ，如图2所示，由选项C 可知A 1D 与平面AEF 相交且交点为A 1D 的中点，所以点A 1和点D 到平面AEF 的距离相等，故D 正确.综上，选BCD.9.已知棱长为a 的正方体ABCD-A 1B 1C 1D 1中，M 是B 1C 1的中点，点P 在正方体的表面上运动，且总满足MP ⊥MC ，则下列结论中正确的是( ) A.点P 的轨迹中包含AA 1的中点B.点P 在侧面AA 1D 1D 内的轨迹的长为5a4 C.MP 长度的最大值为21a4D.直线CC 1与直线MP 所成角的余弦值的最大值为55 答案 BCD解析如图，取A 1D 1的中点E ，分别取A 1A ，B 1B 上靠近A 1，B 1的四等分点F ，G ，连接EM ，EF ，FG ，MG ，易知EM ∥FG 且EM ＝FG ，所以E ，M ，F ，G 四点共面.连接GC ，因为MG 2＝⎝ ⎛⎭⎪⎫a 22＋⎝ ⎛⎭⎪⎫a 42＝5a 216，MC 2＝⎝ ⎛⎭⎪⎫a 22＋a 2＝5a 24，GC 2＝⎝ ⎛⎭⎪⎫3a 42＋a 2＝25a 216，因此MG 2＋MC 2＝GC 2，所以MG ⊥MC ，易知ME ⊥MC ，又MG ∩ME ＝M ，MG ，ME ⊂平面MEFG ，所以MC ⊥平面MEFG ，即点P 的轨迹为四边形MEFG (不含点M )，易知点P 在侧面AA 1D 1D 内的轨迹为EF ，且EF ＝MG ＝5a4，所以A 选项错误，B 选项正确；根据点P 的轨迹可知，当P 与F 重合时，MP 最长，易知FG ⊥平面BB 1C 1C ，则FG ⊥MG ，连接MF ，所以MF ＝a 2＋5a 216＝21a4，故C 选项正确；由于点P 的轨迹为四边形MEFG (不含点M )，所以直线CC 1与直线MP 所成的最小角就是直线CC 1与平面MEFG 所成的角，又向量CC 1→与平面MEFG 的法向量CM →的夹角等于∠C 1CM ，且sin ∠C 1CM ＝a25a 2＝55，所以直线CC 1与平面MEFG 所成角的余弦值为55，即直线CC 1与直线MP 所成角的余弦值的最大值等于55，故D 选项正确.10.如图，长方体ABCD-A 1B 1C 1D 1中，AB ＝BC ＝1，AA 1＝2，M 为AA 1的中点，过B 1M 作长方体的截面α交棱CC 1于N ，则( )A.截面α可能为六边形B.存在点N，使得BN⊥截面αC.若截面α为平行四边形，则1≤CN≤2D.当N与C重合时，截面图形的面积为36 4答案CD解析设N0为棱CC1的中点，当N从C1移动到C时，其过程中存在以下几种情况，如图1，当点N在线段C1N0上时，截面α为平行四边形；当点N在线段N0C上(不包括点N0，C)时，截面α为五边形；当点N与点C重合时，截面α为梯形.图1图2由以上分析可知，对于A，截面α不可能为六边形，所以A错误；对于B，假设BN⊥截面α，因为B1M⊂α，所以BN⊥B1M，所以必有点N，C重合，而BC与平面B1CQM不垂直，所以B错误；对于C，当截面α为平行四边形时，点N在线段C1N0上，则1≤CN≤2，所以C 正确；对于D，当点N与点C重合时，截面α为梯形，如图2，过M作MM′⊥B1C，垂足为M′.设梯形的高为h，B1M′＝x，则在Rt△B1MM′中，由勾股定理，得h2＝(2)2－x2，①同理h 2＝⎝ ⎛⎭⎪⎫522－⎝ ⎛⎭⎪⎫52－x 2，② 由①②，解得x ＝255，h ＝65，所以截面α的面积等于12×⎝⎛⎭⎪⎫5＋52·h ＝12×352×65＝364，所以D 正确. 综上可知，选CD.。

高三数学复习专题目录.docx

高三数学复习专题目录专题一、数列与不等式数列（1）数列（2）专题二、三角函数三角函数（1）三角函数（2）专题三、立体几何立体几何（1）立体几何（2）专题一、数列与不等式一.基础知识梳理数列：1. 了解数列的概念和几种简单的表示方法（列表、图像、通项公式）2.了解数列是自变量为正整数的一类函数.3.了解递推公式是给出数列的一种方法，能据递推公式写出前几项，同时求出通项公式.4,理解等差、等比数列的概念，掌握等差数列的通项公式与前n项公式，并能解决简单实际问题.5.体会等差数列、等比数列与一次函数，指数函数，二次函数的关系.不等式：（必修部分）1.一元二次不等式^2+^ + c>0（cz>0）与相应的函数y = ax2+bx+c（a>0\相应的方程ax2+bx +c = 0（«〉。

）之间的关系2.一元二次不等式恒成立情况小结：J G >0 [a<0 ax2 + bx + c>0（a/0）恒成立 o。

，ax2 +bx + c <0（a/0）恒成立o。

3.二元一次不等式表示的平面区域：直线I: ax + by + c = 0把直角坐标平面分成了三个部分：（1）直线/上的点（x, y）的坐标满足ax +by+ c = 0（2）直线Z一侧的平面区域内的点（x, y）^^ax + by + oO（3）直线Z另一侧的平面区域内的点（x,y）满足ox + /<y + c<0所以，只需要在直线Z的某一侧的平面区域内，任取一特殊点（将，光），从ax0+by0+c值的正负，即可判断不等式表示的平面区域。

4.线性规划：如果两个变量x,y满足一组一次不等式，求这两个变量的一个线性函数的最大值或最小值，称这个线性函数为目标函数，称一次不等式组为约束条件，像这样的问题叫作二元线性规划问题.其中，满足约束条件的解（x,y）称为可行解，由所有可行解组成的集合称为可行域，使目标函数取得最大值和最小值的可行解称为这个问题的最优解.5.基本不等式：⑴如果"eR,那么/+〃 2 2沥，（当且仅当“=。

【精品】2019届高三数学年复习专题--立体几何专题训练附参考答案

1 【精品】2019届高三数学年复习专题--立体几何专题训练附参考答案一、解答题 1.如图所示，在四棱锥P-ABCD 中，底面ABCD 是棱长为2的正方形，侧面PAD 为正三角形，且面PAD ⊥面ABCD ，E 、F 分别为棱AB 、PC 的中点．（1）求证：EF ∥平面PAD ；（2）求三棱锥B-EFC 的体积；（3）求二面角P-EC-D 的正切值．2.如图，三棱柱ABF-DCE 中，∠ABC=120°，BC=2CD ，AD=AF ，AF ⊥平面ABCD ．（Ⅰ）求证：BD ⊥EC ；（Ⅱ）若AB=1，求四棱锥B-ADEF 的体积．3.正方体ABCD-A 1B 1C 1D 1，AA 1=2，E 为棱CC 1的中点．（1）求证：B 1D 1⊥AE ；（2）求三棱锥A-BDE 的体积．4.如图，四棱锥P-ABCD 中，底面ABCD 是矩形，平面PAD ⊥底面ABCD ，且△PAD 是边长为2的等边三角形，PC= ，M 在PC 上，且PA ∥面MBD ．（1）求证：M 是PC 的中点；（2）求多面体PABMD 的体积．25.已知四棱锥P-ABCD ，底面ABCD 为菱形，∠ABC=60°，△PAB 是等边三角形，AB=2，PC= ，AB 的中点为E.（1）证明：PE ⊥平面ABCD ；（2）求三棱锥D-PBC 的体积．6.一块边长为10cm 的正方形铁块按如图所示的阴影部分裁下，然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器．（1）试把容器的容积V 表示为x 的函数.（2）若x =6，求图2的主视图的面积.7.如图，矩形ABCD 中，BC=2，AB=1，PA ⊥平面ABCD ，BE ∥PA ，BE=PA ，F 为PA 的中点．（1）求证：PC ∥平面BDF ．（2）记四棱锥C-PABE 的体积为V 1，三棱锥P-ACD 的体积为V 2，求的值．8.如图，直三棱柱ABC-A 1B 1C 1中，D ，E 分别是AB ，BB 1的中点，AA 1=AC=CB=2，AB=2 ．（Ⅰ）证明：BC 1∥平面A 1CD ；（Ⅱ）求锐二面角D-A 1C-E 的余弦值．9.如图，在四棱锥P-ABCD中，底面ABCD是菱形，∠DAB=60°，PD⊥平面ABCD，PD=AD=1，点E、F分别为AB和PC的中点，连接EF、BF．（1）求证：直线EF∥平面PAD；（2）求三棱锥F-PBE的体积．10.如图，梯形FDCG，DC∥FG，过点D，C作DA⊥FG，CB⊥FG，垂足分别为A，B，且DA=AB=2．现将△DAF沿DA，△CBG沿CB翻折，使得点F，G重合，记为E，且点B在面AEC的射影在线段EC上．（Ⅰ）求证：AE⊥EB；（Ⅱ）设=λ，是否存在λ，使二面角B-AC-E的余弦值为？若存在，求λ的值；若不存在，说明理由．11.在四边形ABCD中，对角线AC，BD垂直相交于点O，且OA=OB=OD=4，OC=3．将△BCD沿BD折到△BED的位置，使得二面角E-BD-A的大小为90°（如图）．已知Q为EO的中点，点P在线段AB 上，且．（Ⅰ）证明：直线PQ∥平面ADE；（Ⅱ）求直线BD与平面ADE所成角θ的正弦值．12.如图，四棱锥P-ABCD是底面边长为1的正方形，PD⊥BC，PD=1，PC=．（Ⅰ）求证：PD⊥面ABCD；（Ⅱ）求二面角A-PB-D的大小．3413.如图在三棱锥A-BCD 中，侧面ABD 、ACD 是全等的直角三角形，AD 是公共的斜边，且AD= ，BD=CD=1，另一个侧面是正三角形. （1）求证：AD ⊥BC ；（2）求二面角B-AC-D 的余弦值；（3）点E 在直线AC 上，当直线ED 与平面BCD 成30°角若时，求点C 到平面BDE 的距离．14.如图所示，在边长为的正方形ABCD 中，以A 为圆心画一个扇形，以O 为圆心画一个圆，M ，N ，K 为切点，以扇形为圆锥的侧面，以圆O 为圆锥底面，围成一个圆锥，求圆锥的全面积与体积．15.如图，在四棱锥P-ABCD 中，PA ⊥平面ABCD ，∠ABC=∠BAD=90°，AD=AP=4，AB=BC=2，M 为PC 的中点，点N 在线段AD 上．（I ）点N 为线段AD 的中点时，求证：直线PA ∥BMN ；（II ）若直线MN 与平面PBC 所成角的正弦值为，求平面PBC 与平面BMN 所成角θ的余弦值．16.如图，在正方体ABCD-A 1B 1C 1D 1中，E 是CC 1的中点，求证：（1）AC 1⊥BD ；（2）AC 1∥平面BDE ．17.如图，棱长为1的正方体ABCD-A 1B 1C 1D 1中，（1）求证：AC ⊥平面B 1D 1DB ；（2）求三棱锥B-CD 1B 1的体积．18.在四棱锥P-ABCD中，平面PAD⊥平面ABCD，∠APD=90°，PA=PD=AB=a，ABCD是矩形，E是PD的中点．（1）求证：PB∥平面AEC（2）求证：PB⊥AC．19.如图，已知平面ADC∥平面A1B1C1，B为线段AD的中点，△ABC≈△A1B1C1，四边形ABB1A1为正方形，平面AA1C1C丄平面ADB1A1，A1C1=A1A，∠C1A1A=，M为棱A1C1的中点．（I）若N为线段DC1上的点，且直线MN∥平面ADB1A1，试确定点N的位置；（Ⅱ）求平面MAD与平面CC1D所成的锐二面角的余弦值．20.如图，三棱柱ABC-A1B1C1中，D为AA1的中点，E为BC的中点．（1）求证：直线AE∥平面BDC1；（2）若三棱柱 ABC-A1B1C1是正三棱柱，AB=2，AA1=4，求平面BDC1与平面ABC所成二面角的正弦值．21.如图所示，已知长方体ABCD中，AB=4，AD=2，M为DC的中点．将△ADM沿AM折起，使得AD⊥BM．（1）求证：平面ADM⊥平面ABCM；（2）若点E为线段DB的中点，求点E到平面DMC的距离．5622.如图所示，在正方体ABCD-A 1B 1C 1D 1中，E 是棱DD 1的中点．（1）若正方体的棱长为1，求三棱锥B 1-A 1BE 的体积；（2）在棱C 1D 1上是否存在一点F ，使B 1F ∥面A 1BE ？若存在，试确定点F 的位置，并证明你的结论．23.如图，三棱柱ABC-A 1B 1C 1中，BC ⊥平面AA 1C 1C ，BC=CA=AA 1=2，∠CAA 1=60°．（1）求证：AC 1⊥A 1B ；（2）求直线A 1B 与平面BAC 1所成角的正弦值．24.在图所示的几何体中，底面ABCD 为正方形，PD ⊥平面ABCD ，EC ∥PD ，且PD=AD=2EC=2，N 为线段PB 的中点．（1）证明：NE ⊥平面PBD ；（2）求四棱锥B-CEPD 的体积．25.已知梯形ABCD 中AD ∥BC ，∠ABC=∠BAD=，AB=BC=2AD=4，E 、F 分别是AB 、CD 上的点，EF ∥BC ，AE=x ．沿EF 将梯形AEFD 翻折，使平面AEFD ⊥平面EBCF （如图）．G 是BC 的中点．（1）当x =2时，求证：BD ⊥EG ；（2）当x 变化时，求三棱锥D-BCF 体积的最大值．26.如图，长方体ABCD-A 1B 1C 1D 1中，AB=16，BC=10，AA 1=8，点E ，F 分别在A 1B 1，D 1C 1上，A 1E=D 1F=4，过点E ，F 的平面α与此长方体的面相交，交线围成一个正方形．（1）在图中画出这个正方形（不必说明画法和理由）；（2）求直线AF 与平面α所成角的正弦值．727.在如图所示的多面体ABCDEF 中，四边形ABCD 为正方形，底面ABFE 为直角梯形，∠ABF 为直角，，，平面ABCD ⊥平面ABFE ．（1）求证：DB ⊥EC ；（2）若AE=AB ，求二面角C-EF-B 的余弦值．28.如图，四棱锥P-ABCD 中，AD ⊥平面PAB ，AP ⊥AB ．（1）求证：CD ⊥AP ；（2）若CD ⊥PD ，求证：CD ∥平面PAB ．29.如图所示，四棱锥P-ABCD 的侧面PAD 是边长为2的正三角形，底面ABCD 是∠ABC=60°的菱形，M 为PC 的中点，PC= ．（Ⅰ）求证：PC ⊥AD ；（Ⅱ）求三棱锥M-PAB 的体积．30.如图，在四棱锥P-ABCD 中，底面ABCD 是平行四边形，∠ADC=45°，AD=AC=2，O 为AC 的中点，PO ⊥平面ABCD 且PO=6，M 为BD的中点．（1）证明：AD ⊥平面PAC ；（2）求直线AM 与平面ABCD 所成角的正切值．31.如图，多面体EF-ABCD 中，ABCD 是正方形，AC 、BD 相交于O ，EF ∥AC ，点E 在AC 上的射影恰好是线段AO 的中点．（Ⅰ）求证：BD ⊥平面ACF ；（Ⅱ）若直线AE 与平面ABCD 所成的角为60°，求平面DEF 与平面ABCD 所成角的正弦值．32.如图，三棱锥P-ABC 中，平面PAC ⊥平面ABC ，∠BCA=90°，且BC=CA=2，PC=PA ．（1）求证：PA ⊥BC ；8 （2）当PC 的值为多少时，满足PA ⊥平面PBC ？并求出此时该三棱锥P-ABC 的体积．33.如图，直三棱柱ABC-A 1B 1C 1中，AA 1=AB ，AB ⊥BC ，且N 是A 1B 的中点．（1）求证：直线AN ⊥平面A 1BC ；（2）若M 在线段BC 1上，且MN ∥平面A 1B 1C 1，求证：M 是BC 1的中点．34.．如图所示，在长方体ABCD-A 1B 1C 1D 1中，AB=AD=1，AA 1=2，点P 为DD 1的中点．（1）求证：直线BD 1∥平面PAC （2）求证：平面PAC ⊥平面BDD 1B 1．35.如图，在四棱锥P-ABCD 中，底面ABCD 为直角梯形，AD ∥BC ，∠ADC=90°，平面PAD ⊥底面ABCD ，Q 为AD 的中点，M 是棱PC 上的点，PA=PD=2，BC=AD=1，CD= ．（1）求证：平面MQB ⊥平面PAD ；（2）若二面角M-BQ-C 大小的为60°，求QM 的长．36.如图，正方体ABCD-A 1B 1C 1D 1的棱长为2，E 、F 、G 分别为 AB 、BB 1、B 1C 1 的中点．（1）求证：A 1D ⊥FG ；（2）求二面角 A 1-DE-A 的正切值．37.四棱锥P-ABCD 的直观图与三视图如图，PC ⊥面ABCD（1）画出四棱锥P-ABCD 的侧视图（标注长度）（2）求三棱锥A-PBD的9 体积．38.如图，长方体ABCD-A 1B 1C 1D 1中，AB=AD=1，AA 1=2，点P 为棱DD 1上一点．（1）求证：平面PAC ⊥平面BDD 1B 1；（2）若P 是棱DD 1的中点，求CP 与平面BDD 1B 1所成的角大小．39.如图，四棱锥P-ABCD 中，PA ⊥底面ABCD ，AB ∥CD ，AD=CD=1，∠BAD=120°，PA= ，∠ACB=90°，M 是线段PD 上的一点（不包括端点）．（Ⅰ）求证：BC ⊥平面PAC ；（Ⅱ）求二面角D-PC-A 的正切值；（Ⅲ）试确定点M 的位置，使直线MA 与平面PCD 所成角θ的正弦值为．40.已知四棱锥P-ABCD 中，AD=2BC ，且AD ∥BC ，点M ，N 分别是PB ，PD 中点，平面MNC 交PA 于Q ．（1）证明：NC ∥平面PAB（2）试确定Q 点的位置，并证明你的结论．41.一个正三棱柱的三视图如图所示，求这个三棱柱的表面积和体10 积．42.如图，四棱锥P-ABCD 的底面是正方形，侧棱PA ⊥底面ABCD ，E 是PA 的中点．（Ⅰ）求证：PC ∥平面BDE ；（Ⅱ）证明：BD ⊥CE ．43.如图所示，在正方体ABCD-A 1B 1C 1D 1中，E 、G 、H 分别是BC 、C 1D 1、AA 1、的中点．（Ⅰ）求异面直线D 1H 与A 1B 所成角的余弦值（Ⅱ）求证：EG ∥平面BB 1D 1D ．44.如图所示，在四棱锥P-ABCD 中，AB ∥CD ，AB ⊥AD ，AB=AD=AP=2CD=2，M 是棱PB 上一点．（Ⅰ）若BM=2MP ，求证：PD ∥平面MAC ；（Ⅱ）若平面PAB ⊥平面ABCD ，平面PAD ⊥平面ABCD ，求证：PA ⊥平面ABCD ；（Ⅲ）在（Ⅱ）的条件下，若二面角B-AC-M 的余弦值为，求的值．45.如图，已知在侧棱垂直于底面的三棱柱ABC-A 1B 1C 1中，AC=3，AB=5，BC=4，AA 1=4点D 是AB 的中点．（1）求证：AC 1∥平面B 1DC ；11 （2）求三棱锥A 1-B 1CD 的体积．46.如图，以正四棱锥V-ABCD 的底面中心O 为坐标原点建立空间直角坐标系O-xyz ，其中O x ∥BC ，O y ∥AB ，E 为VC 中点，正四棱锥的底面边长为2a ，高为h ，且有cos ＜，＞=-．（1）求的值；（2）求二面角B-VC-D 的余弦值．47.如图1，四边形ABCD 为直角梯形，AD ∥BC ，AD ⊥AB ，AD=1，BC=2，E 为CD 上一点，F 为BE 的中点，且DE=1，EC=2，现将梯形沿BE 折叠（如图2），使平面BCE ⊥ABED ．（1）求证：平面ACE ⊥平面BCE ；（2）能否在边AB 上找到一点P （端点除外）使平面ACE 与平面PCF 所成角的余弦值为？若存在，试确定点P 的位置，若不存在，请说明理由．48.如图，三棱柱ABC-A 1B 1C 1中，侧面ACC 1A 1⊥侧面ABB 1A 1，∠B 1A 1A=∠C 1A 1A=60°，AA 1=AC=4，AB=1．（Ⅰ）求证：A 1B 1⊥B 1C 1；（Ⅱ）求三棱锥ABC-A 1B 1C 1的侧面积．49.在四棱锥中P-ABCD ，底面ABCD 是正方形，侧面PAD ⊥底面ABCD ，且PA=PD=AD 、E 、F ，分别为PC 、BD 的中点．（1）求证：EF ∥平面PAD ；（2）若AB=2，求三棱锥E-DFC 的体积．1250.如图，四棱锥P-ABCD 中，△PAD 为正三角形，AB ∥CD ，AB=2CD ，∠BAD=90°，PA ⊥CD ，E 为棱PB 的中点（Ⅰ）求证：平面PAB ⊥平面CDE ；（Ⅱ）若直线PC 与平面PAD 所成角为45°，求二面角A-DE-C 的余弦值．51.如图，在边长为2的正方形ABCD 中，点E ，F 分别是AB ，BC 的中点，将△AED ，△DCF 分别沿DE ，DF 折起，使A ，C 两点重合于P ．（Ⅰ）求证：平面PBD ⊥平面BFDE ；（Ⅱ）求四棱锥P-BFDE 的体积．【答案】1.（1）证明：取PD 中点G ，连结GF 、AG ，∵GF 为△PDC 的中位线，∴GF ∥CD 且，又AE ∥CD 且，∴GF ∥AE 且GF=AE ，13 ∴EFGA 是平行四边形，则EF ∥AG ，又EF ⊄面PAD ，AG ⊂面PAD ， ∴EF ∥面PAD ；（2）解：取AD 中点O ，连结PO ，∵面PAD ⊥面ABCD ，△PAD 为正三角形，∴PO ⊥面ABCD ，且，又PC 为面ABCD 斜线，F 为PC 中点，∴F 到面ABCD 距离，故；（3）解：连OB 交CE 于M ，可得R t △EBC ≌R t △OAB ， ∴∠MEB=∠AOB ，则∠MEB+∠MBE=90°，即OM ⊥EC ．连PM ，又由（2）知PO ⊥EC ，可得EC ⊥平面POM ，则PM ⊥EC ，即∠PMO 是二面角P-EC-D 的平面角，在R t △EBC 中，，∴， ∴，即二面角P-EC-D的正切值为．2.（Ⅰ）证明：三棱柱ABF-DCE 中，AF ⊥平面ABCD ．∴DE ∥AF ，ED ⊥平面ABCD ，∵BD ⊂平面ABCD ，∴ED ⊥BD ，又ABCD 是平行四边形，∠ABC=120°，故∠BCD=60°． ∵BC=2CD ，故∠BDC=90°．故BD ⊥CD ． ∵ED∩CD=D ，∴BD ⊥平面ECD ． ∵EC ⊂平面ECD ， ∴BD ⊥EC ；（Ⅱ）解：由BC=2CD ，可得AD=2AB ，∵AB=1，∴AD=2，作BH ⊥AD于H ，∵AF ⊥平面ABCD ，∴BH ⊥平面ADEF ，又∠ABC=120°， ∴BH=，∴．3.解：（1）证明：连接BD ，则BD ∥B 1D 1， ∵ABCD 是正方形，∴AC ⊥BD ． ∵CE ⊥面ABCD ， ∴CE ⊥BD ．又AC∩CE=C ， ∴BD ⊥面ACE ． ∵AE ⊂面ACE ， ∴BD ⊥AE ，∴B 1D 1⊥AE ．-----------（6分）（2）S △ABD =2 △．-----------（12分） 4.证明：（1）连AC 交BD 于E ，连ME ．14∵ABCD 是矩形，∴E 是AC 中点．又PA ∥面MBD ，且ME 是面PAC 与面MDB 的交线， ∴PA ∥ME ，∴M 是PC 的中点．解：（2）取AD 中点O ，连OC ．则PO ⊥AD ，由平面PAD ⊥底面ABCD ，得PO ⊥面ABCD ，∴ ，，∴ ， ∴ ，，∴．5.证明：（1）由题可知PE ⊥AB ，CE ⊥AB ． ∵AB=2，∴PE=CE= ．又∵PC= ，∴PE 2+EC 2=PC 2， ∴∠PEC=90°，即PE ⊥CE ．又∵AB ，CE ⊂平面ABCD ， ∴PE ⊥平面ABCD ；解：（2）S △BCD =×22×sin 120°= ，PE= ．由（1）知：PE ⊥平面ABCD ，V P-BCD =•S △BCD •PE=1．∵V D-PBC =V P-BCD ，∴三棱锥D-PBC 的体积为1． 6.解：（1）设所截等腰三角形的底边边长为x cm ．在R t △EOF 中，EF=5cm ，OF=x cm ，所以EO=．于是V=x 2（cm 3）．依题意函数的定义域为{x |0＜x ＜10}．（2）主视图为等腰三角形，腰长为斜高，底边长=AB=6，底边上的高为四棱锥的高=EO==4，S==12（cm 2）7.（1）证明：连结BF ，连接BD 交AC 与点O ，连OF ，依题得O 为AC 中点，又F 为PA 的中点，所以OF 为△PAC 中位线，所以OF ∥PC因为OF ⊂平面BDF ，PC ⊄平面BDF 所以PC ∥平面BDF ． ∴V 1=梯形 =（2）解：设BE=a ，则PA=2BE=2a ， V 2=△ =（a +2a ）×1×2=a ． =． ∴．8.解：（Ⅰ）连结AC 1，交A 1C 于点O ，连结DO ，则O 为AC 1的中点，因为D 为AB 的中点，所以OD ∥BC 1，又因为OD ⊂平面A 1CD ，BC 1⊄平面A 1CD ，∴BC 1∥平面A 1CD…（4分）（Ⅱ）由，，可知AC ⊥BC ，以C 为坐标原点，方向为x 轴正方向，方向为y轴正。

2016届高三数学一轮阶段性测试题9《立体几何》(含解析)新人教A版

阶段性测试题九(立体几何)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。

满分150分。

考试时间120分钟。

第Ⅰ卷(选择题共60分)一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．)1．(文)(2014·辽宁师大附中期中)已知两个不同的平面α、β和两条不重合的直线m、n，有下列四个命题①若m∥n，m⊥α，则n⊥α②若m⊥α，m⊥β，则α∥β③若m⊥α，m∥n，n⊂β，则α⊥β④若m∥α，α∩β＝n，则m∥n其中正确命题的个数是()A．0个B．1个C．2个D．3个[答案] D[解析]由线面垂直的性质知①正确；垂直于同一条直线的两个平面平行，∴②正确；由m⊥α，m∥n知n⊥α，又n⊂β，∴α⊥β，∴③正确；如图，正方体ABCD－A1B1C1D1中，平面ABCD与平面ADD1A1分别为α、β，CC1为m，则m∥α，α∩β＝n，但m与n不平行，∴④错，故选D．(理)(2014·浙江台州中学期中)设a、b是两条不同的直线，α、β是两个不同的平面，则下列四个命题①若a⊥b，a⊥α，则b∥α②若a∥α，α⊥β，则a⊥β③a⊥β，α⊥β，则a∥α④若a⊥b，a⊥α，b⊥β，则α⊥β其中正确的命题的个数是()A．0个B．1个C．2个D．3个[答案] B[解析]①中可能有b⊂α；②中a⊂β，或a∥β，a与β斜交，a⊥β，都有可能；③中可能有a⊂α；若a⊥b，a⊥α，则b∥α或b⊂α，又b⊥β，∴α⊥β，∴④正确，故选B．2．(2014·山东省博兴二中质检)设m、n是两条不同直线，α、β是两个不同的平面，下列命题正确的是()A．m∥α，n∥β且α∥β，则m∥nB．m⊥α，n⊥β且α⊥β，则m⊥nC．m⊥α，n⊂β，m⊥n，则α⊥βD ．m ⊂α，n ⊂α，m ∥β，n ∥β，则α∥β[答案] B[解析] 设m 与n 相交，m 、n 都在平面γ内，γ∥α，γ∥β时，满足A 的条件，∴A 错；若m ⊥α，α⊥β，则m ⊂β或m ∥β，又n ⊥β，∴n ⊥m ，∴B 正确；若m ⊥α，m ⊥n ，则n ∥α或n ⊂α，结合n ⊂β得不出α⊥β，故C 错；当m ∥n 且满足D 的条件时，得不出α∥β，故D 错．3．(2015·河南八校联考)一个几何体的三视图如图所示，其中正视图是一个正三角形，则这个几何体的外接球的表面积为( )A ．16π3B ．8π3C ．43D ．23π[答案] A [解析] 由三视图知该几何体为三棱锥，底面是等腰三角形，其底长为2，高为1，棱锥高为3，顶点在底面射影为等腰直角三角形底边的中点D ，直观图如图，BD ⊥AC ，PD ⊥平面ABC ，DA＝DB ＝DC ＝1，故球心O 在PD 上，设OP ＝R ，则(3－R)2＋12＝R2，∴R ＝233.∴S 球＝4πR2＝16π3.4．(文)(2014·吉林市摸底)下图是某四棱锥的三视图，则该几何体的表面积等于( )A ．17＋65B ．34＋6 5C ．6＋65＋43D ．6＋63＋413[答案] B[解析] 由三视图知，这是一个底面是矩形的四棱锥，矩形的长和宽分别是6,2，四棱锥的高是4，其直观图如图，作PE ⊥平面ABCD ，则垂足E 为AD 的中点，PE ＝4，作EF ⊥BC ，垂足为F ，则PF ⊥BC ，∵EF ＝2，∴PF ＝25，∵AB ⊥AD ，∴AB ⊥PA ，PA ＝PE2＋AE2＝5，∴S ＝6×2＋12×6×4＋12×6×25＋2×(12×2×5)＝34＋65，故选B ．(理)(2015·豫南九校联考)已知四棱锥的三视图如图所示，则四棱锥的四个侧面中面积最大的是( )A ．3B ．25C ．6D ．8 [答案]C [解析] 由三视图知，该几何体是四棱锥，其直观图如图，其四个侧面中面积最大的是△PBC ，由图中数据知AB ＝2，BC ＝4，PA ＝PD ＝3，∴PE ＝5，取BC 中点F ，则EF ⊥BC ，∴PF ⊥BC ，PF ＝PE2＋EF2＝3，∴S △PBC ＝12BC·PF ＝6.5．(2014·云南景洪市一中期末)一个几何体的三视图如图所示，其中俯视图与左视图均为半径是1的圆，则这个几何体的体积是( )A ．4π3B ．πC ．2π3D ．π3[答案] B[解析] 由三视图知，这是一个半径为1的球，截去14，故其体积为V ＝34·(4π3·13)＝π.6．(2015·江西三县联考)平面α与平面β平行的条件可以是( )A ．α内有无穷多条直线与β平行B ．直线a ∥α，a ∥βC ．直线a ⊂α，直线b ⊂β，且a ∥β，b ∥αD ．α内的任何直线都与β平行[答案] D[解析] 当α∩β＝l 时，α内与l 平行的直线都与β平行，故A 错；当α∩β＝l ，a ∥l ，a ⊄α，a ⊄β时，满足B 的条件，∴B 错；当α∩β＝l ，a ⊂α，a ∥l ，b ⊂β，b ∥l 时，有a ∥β，b ∥α，∴C 错，故选D ．7．(2014·长春市一调)某几何体的三视图如图(其中俯视图中的圆弧是半圆)，则该几何体的表面积为( )A ．92＋14πB ．82＋14πC ．92＋24πD ．82＋24π[答案] A[解析] 由三视图知，该几何体是一个组合体，下部是长宽分别为5、4，高为4的长方体，上部为底半径为2，高为5的半圆柱，故其表面积S ＝5×4＋(5＋4)×2×4＋π·22＋12(2π×2×5)＝92＋14π，故选A ．8．(2015·许昌、平顶山、新乡调研)一个几何体的三视图如图所示，则该几何体的体积为( )A ．103B ．10C ．30D ．24＋2 5[答案] B[解析] 由三视图可知，该几何体为直四棱柱，底面为直角梯形，S 底＝12×(2＋3)×2＝5，棱柱高为2，V ＝5×2＝10.9．(2015·广东揭阳一中期中)下列命题中，错误的是( )A ．一条直线与两个平行平面中的一个相交，则必与另一个平面相交B ．平行于同一平面的两个不同平面平行C ．如果平面α不垂直平面β，那么平面α内一定不存在直线垂直于平面βD ．若直线l 不平行平面α，则在平面α内不存在与l 平行的直线[答案] D[解析] 当直线l 在平面α内时可知D 错误．10．(文)(2015·广东执信中学期中)将正方体(如图1所示)截去两个三棱锥，得到如图2所示的几何体，则该几何体的左视图为( )[答案] B[解析] 其左视图可考虑在原正方体中，将该几何体投射到平面BCC1B1上，则A 点射影为B ，D 点射影为C ，D1点射影为C1，AD1的射影为BC1，应为实线，DD1的射影CC1为实线，B1C 应为虚线(左下到右上)，故应选B ．(理)(2015·甘肃天水一中段测)在正方体ABCD －A1B1C1D1中，点E1，F1分别是线段A1B1，A1C1的中点，则直线BE1与AF1所成角的余弦值是( )A ．3010B ．12C ．3015D ．1510[答案] A[解析] 以A 为原点，直线AB 、AD 、AA1分别为x 轴、y 轴、z 轴建立空间直角坐标系A －xyz ，设棱长为1，则B(1,0,0)，E1(12，0,1)，F1(12，12，1)，∴AF1→＝(12，12，1)，BE1→＝(－12，0,1)．cos 〈AF1→，BE1→〉＝AF1→·BE1→|AF1→||BE1→|＝3452×62＝3010，故选A ． 11．(2015·深圳市五校联考)一个多面体的三视图如图所示，则该多面体的体积为( )A ．233B ．223C ．6D ．7[答案] A[解析] 由三视图可知，该多面体是由正方体截去两个正三棱锥所成的几何体，如图，正方体棱长为2，正三棱锥侧棱互相垂直，侧棱长为1，故几何体的体积为：V ＝V 正方体－2V 三棱锥＝2×2×2－2×(13×12×1×1×1)＝233.12．(2014·长沙市重点中学月考)某几何体的三视图如图所示，则它的表面积为( )A ．2＋1＋52πB ．2＋1＋252πC ．2＋(1＋5)πD ．2＋2＋52π[答案] A[解析] 由三视图知，该几何体是倒立的半个圆锥，圆锥的底半径为1，高为2，故其表面积为S ＝12π·12＋12×2×2＋12π·1·22＋12＝2＋1＋52π，故选A ．第Ⅱ卷(非选择题共90分)二、填空题(本大题共4个小题，每小题4分，共16分，把正确答案填在题中横线上．)13．(2015·甘肃天水一中段测)若某几何体的三视图如下，该几何体的体积为2，则俯视图中的x ＝________.[答案] 2[解析] 由三视图可知，该几何体为四棱锥，高为2，底面为直角梯形，面积S ＝12(1＋x)×2＝1＋x ，因此V ＝13Sh ＝13·(1＋x)·2＝2，解得x ＝2.14．(2014·成都七中模拟)已知正方体ABCD －A1B1C1D1的棱长为1，点M 是BC1的中点，P 是BB1一动点，则(AP ＋MP)2的最小值为________．[答案] 52[解析] 将平面ABB1A1展开到与平面CBB1C1共面，如下图，易知当A 、P 、M 三点共线时(AP ＋MP)2最小．AM2＝AB2＋BM2－2AB×BMcos135°＝12＋(22)2－2×1×22×(－22)＝52.15．(2014·海南省文昌市检测)边长是22的正三角形ABC 内接于体积是43π的球O ，则球面上的点到平面ABC 的最大距离为________．[答案] 433[解析] 设球半径为R ，则由条件知43πR3＝43π，∴R ＝3，正三角形ABC 所在平面截球得截面如图，OO1⊥平面ABC(O1为△ABC 的中心)，OA ＝3，O1A ＝23×32×22＝263，∴OO1＝OA2－O1A2＝33，∴球面上的点到平面ABC 的最大距离为PO1＝PO ＋OO1＝433.16．一个几何体的三视图如图所示，则这个几何体的体积为________．[答案] 9[解析] 由三视图可得该几何体是一个三棱锥，底面是等腰三角形，底边长为6，高为3，三棱锥的高为3，所以V ＝13×(12×6×3)×3＝9.三、解答题(本大题共6个小题，共74分，解答应写出文字说明，证明过程或演算步骤．)17．(本小题满分12分)(2015·石光中学月考)如图所示，在四棱锥P －ABCD 中，底面ABCD 是边长为a 的正方形，侧面PAD ⊥底面ABCD ，且PA ＝PD ＝22AD ，若E ，F 分别为PC ，BD 的中点．(1)求证：EF ∥平面PAD ；(2)求证：平面PDC ⊥平面PAD ；(3)求四棱锥P －ABCD 的体积．[解析] (1)连接EF ，AC ，∵四棱锥P －ABCD 中，底面ABCD 是边长为a 的正方形且点F 为对角线BD 的中点， ∴对角线AC 经过F 点，又点E 为PC 的中点，∴EF 为△PAC 的中位线，∴EF ∥PA ．又PA ⊂平面PAD ，EF ⊄平面PAD ，∴EF ∥平面PAD ．(2)∵底面ABCD 是边长为a 的正方形，∴CD ⊥AD ，又侧面PAD ⊥底面ABCD ，侧面PAD ∩底面ABCD ＝AD ，∴CD ⊥平面PAD ．又CD ⊂平面PCD ，∴平面PDC ⊥平面PAD ．(3)过点P 作AD 的垂线PG ，垂足为点G ，∵侧面PAD ⊥底面ABCD ，PG ⊂平面PAD ，侧面PAD ∩底面ABCD ＝AD ，∴PG ⊥平面ABCD ，即PG 为四棱锥P －ABCD 的高，又PA ＝PD ＝22AD 且AD ＝a ，∴PG ＝a 2.∴V 四棱锥P －ABCD ＝13S 正方形ABCD·PG ＝13×a2×a 2＝16a3.18．(本小题满分12分)(文)(2014·合肥市质检)如图，在多面体ABCDFE中，底面ABCD 是梯形，且AD ＝DC ＝CB ＝12AB ．直角梯形ACEF 中，EF 綊12AC ，∠ECA 是直角，且平面ACEF ⊥平面ABCD ．(1)求证：BC ⊥AF ；(2)试判断直线DF 与平面BCE 的位置关系，并证明你的结论．[解析] (1)证明：取AB 的中点H ，连接CH ，∵底面ABCD 是梯形，且AD ＝DC ＝CB ＝12AB ，易证四边形AHCD 为菱形，∴AD ＝HC ＝12AB ，∴∠ACB ＝90°，∴BC ⊥AC ．∵平面ACEF ⊥平面ABCD ，且平面ACEF ∩平面ABCD ＝AC ，∴BC ⊥平面ACEF ，而AF ⊂平面ACEF ，故BC ⊥AF.(2)DF ∥平面BCE.证明如下：连接DH 交AC 于点M ，易知M 为AC 的中点，连接FM.在菱形AHCD 中，DM ⊥AC ，由第一问知BC ⊥AC ，故DM ∥BC ．在直角梯形ACEF 中，EF 綊CM ，四边形EFMC 是平行四边形，故FM ∥EC ．而BC ，CE ⊂平面BCE ，BC ∩CE ＝C ，而DM ，MF ⊂平面DMF ，DM ∩MF ＝M ，故平面BCE ∥平面DMF ，DF ⊂平面DMF ，从而，DF ∥平面BCE.(理)(2014·天津南开中学月考)如图，三棱柱ABC －A1B1C1的底面为边长为2的等边三角形，侧棱长为3，且侧棱与底面垂直，D 为B1C1的中点．(1)求证AC1∥平面A1BD ；(2)求异面直线AC1与BD 所成角的余弦值；(3)求二面角B1－A1B －D 的平面角的正弦值．[解析] 因为三棱柱的侧棱垂直于底面，所以平面BB1C1C ⊥平面A1B1C1.在等腰三角形A1B1C1中，D 为B1C1中点，∴A1D ⊥B1C1，∴A1D ⊥平面BB1C1C ．取BC 的中点E ，连接DE ，则直线ED ，B1C1，A1D 两两垂直．如图，以D 为坐标原点建立空间直角坐标系，在等边三角形A1B1C1中，边长为2，所以A1D ＝3，所以D(0,0,0)，B1(1,0,0)，C1(－1,0,0)，A1(0,0，3)，B(1，－3，0)，C(－1，－3，0)，A(0，－3，3)．(1)证明：DA1→＝(0,0，3)，DB →＝(1，－3，0)．设平面A1BD 的一个法向量为m ＝(x1，y1，z1)，则⎩⎨⎧ 3z ＝0，x1－3y1＝0.令y1＝3，则x1＝3，z1＝0. 所以m ＝(3，3，0)．又AC1→＝(－1，3，－3)，AC1→·m ＝0，∴AC1→⊥m ，又∵AC1⊄平面BDA1，∴AC1∥平面BDA1.(2)AC1→＝(－1，3，－3)，DB →＝(1，－3，0)，cos 〈AC1→，DB →〉＝AC1→·DB →|AC1→|·|DB →|＝－1－37·2＝－277. 异面直线AC1与BD 所成角的余弦值为277.(3)B1B →＝(0，－3，0)，B1A1→＝(－1,0，3)，设平面B1BA1的一个法向量为n ＝(x2，y2，z2)，则⎩⎨⎧ －3y2＝0，－x2＋3z2＝0.令z2＝3，则x2＝3. 所以n ＝(3,0，3)．cos 〈m ，n 〉＝m·n |m|·|n|＝912＝34.∴二面角B1－A1B －D 的平面角的正弦值为74.19．(本小题满分12分)(文)(2015·江西三县联考)如图，四边形ABEF 是等腰梯形，AB ∥EF ，AF ＝BE ＝2，EF ＝42，AB ＝22，ABCD 是矩形．AD ⊥平面ABEF ，其中Q ，M 分别是AC ，EF 的中点，P 是BM 中点．(1)求证：PQ ∥平面BCE ；(2)求证：AM ⊥平面BCM ；(3)求点F 到平面BCE 的距离．[解析] (1)因为AB ∥EM ，且AB ＝EM ，所以四边形ABEM 为平行四边形．连接AE ，则AE 过点P ，且P 为AE 中点，又Q 为AC 中点，所以PQ 是△ACE 的中位线，于是PQ ∥CE.∵CE ⊂平面BCE ，PQ ⊄平面BCE ，∴PQ ∥平面BCE.(2)AD ⊥平面ABEF ⇒BC ⊥平面ABEF ⇒BC ⊥AM.在等腰梯形ABEF 中，由AF ＝BE ＝2，EF ＝42，AB ＝22，可得∠BEF ＝45°，BM ＝AM ＝2，∴AB2＝AM2＋BM2，∴AM ⊥BM.又BC ∩BM ＝B ，∴AM ⊥平面BCM.(3)解法一：点F 到平面BCE 的距离是M 到平面BCE 的距离的2倍，∵EM2＝BE2＋BM2，∴MB ⊥BE ，∵MB ⊥BC ，BC ∩BE ＝B ，∴MB ⊥平面BCE ，∴d ＝2MB ＝4.解法二：VC －BEF ＝13S △BEF·BC ＝43BC ，VF －BCE ＝13S △BCE·d ＝d 3BC ．∵VC －BEF ＝VF －BCE ，∴d ＝4.(理)(2014·成都七中模拟)如图，四棱锥P －ABCD 中，底面ABCD 是平行四边形，PG ⊥平面ABCD ，垂足为G ，G 在AD 上且AG ＝13GD ，GB ⊥GC ，GB ＝GC ＝2，E 是BC 的中点，四面体P －BCG 的体积为83.(1)求过P 、C 、B 、G 四点的球的表面积；(2)求直线DP 与平面PBG 所成角的正弦值；(3)在棱PC 上是否存在一点F ，使DF ⊥GC ，若存在，确定点F 的位置，若不存在，说明理由．[解析] (1)∵四面体P －BCG 的体积为83，GB ⊥GC ，GB ＝GC ＝2，PG ⊥平面ABCD ，∴PG ＝4，以GP ，GB ，GC 为棱构造长方体，外接球的直径为长方体的对角线．∴(2R)2＝16＋4＋4，∴R ＝6，∴S ＝4π×6＝24π.(2)∵GB ＝GC ＝2，∠BGC ＝π2，E 为BC 的中点，∴GE ＝2，BGsin ∠AGB ＝2，∴∠AGB ＝π4，作DK ⊥BG 交BG 的延长线于K ，∴DK ⊥平面BPG ，∵BC ＝BG2＋CG2＝22，∴DG ＝34BC ＝322，∴DK ＝GK ＝32，PD ＝412. 设直线DP 与平面PBG 所成角为α，∴sinα＝DK DP ＝38282.(3)假设F 存在，过F 作FF ′⊥GC 交GC 于F ′，则必有DF ′⊥GC ．因为AG ＝13GD ，且AD ＝22，所以GD ＝322，又∠DGF ′＝45°，∴GF ′＝32＝34GC ，∴PF ＝34PC ．∴当CF CP ＝14时满足条件．20．(本小题满分12分)(2015·大连市二十中期中)如图，四边形ABCD 中，AB ⊥AD ，AD ∥BC ，AD ＝6，BC ＝4，AB ＝2，E 、F 分别在BC 、AD 上，EF ∥AB ．现将四边形ABEF 沿EF 折起，使得平面ABEF ⊥平面EFDC ．(1)当BE ＝1时，是否在折叠后的AD 上存在一点P ，使得CP ∥平面ABEF ？若存在，指出P 点位置，若不存在，说明理由；(2)设BE ＝x ，问当x 为何值时，三棱锥A －CDF 的体积有最大值？并求出这个最大值．[解析] (1)存在点P 使得满足条件CP ∥平面ABEF ，且此时AP AD ＝35.证明如下：AP AD ＝35，过点P 作MP ∥FD ，与AF 交于点M ，则有MP FD ＝35，又FD ＝5，故MP ＝3，又因为EC ＝3，MP ∥FD ∥EC ，故有MP 綊EC ，故四边形MPCE 为平行四边形，所以PC ∥ME ，又CP ⊄平面ABEF ，ME ⊂平面ABEF ，故有CP ∥平面ABEF 成立．(2)因为平面ABEF ⊥平面EFDC ，平面ABEF ∩平面EFDC ＝EF ，又AF ⊥EF ，所以AF ⊥平面EFDC ．由已知BE ＝x ，所以AF ＝x(0<x<4)，FD ＝6－x.故VA －CDF ＝13·(12DF·EF)·AF ＝13·12·2·(6－x)·x ＝13(6x －x2)＝13[－(x －3)2＋9]＝－13(x －3)2＋3.所以，当x ＝3时，VA －CDF 有最大值，最大值为3.21．(本小题满分12分)(文)如图，在直三棱柱ABC －A1B1C1中，BC ＝2，AB ＝AC ＝AA1＝1，D 是棱CC1上的一点，P 是AD 的延长线与A1C1的延长线的交点，且PB1∥平面BDA1.(2)求证：CD ＝C1D ；(2)求点C 到平面B1DP 的距离．[解析] (1)证明：连接B1A 交BA1于O ，∵PB1∥平面BDA1，B1P ⊂平面AB1P ，平面AB1P ∩平面BA1D ＝OD ，∴B1P ∥OD ．又∵O 为B1A 的中点，∴D 为AP 的中点，∴C1为A1P 的中点，∴△ACD ≌△PC1D ，∴CD ＝C1D ；(2)因为VC －B1PD ＝VB1－PCD所以13h·S △B1PD ＝13A1B1·S △PCD ，∵A1B1＝1，S △PCD ＝12CD·PC1＝14，在△B1PD 中，B1D ＝32，B1P ＝5，PD ＝52，∴cos ∠DB1P ＝255，sin ∠DB1P ＝55.∴S △B1PD ＝12×32×5×55＝34，∴h ＝13.(理) (2014·康杰中学、临汾一中、忻州一中、长治二中四校联考)如图，四边形ABCD 与BDEF 均为菱形，设AC 与BD 相交于点O ，若∠DAB ＝∠DBF ＝60°，且FA ＝FC ．(1)求证：FC ∥平面EAD ；(2)求二面角A －FC －B 的余弦值．[解析] (1)证明：∵四边形ABCD 与BDEF 均为菱形，∴AD ∥BC ，DE ∥BF.∵AD ⊄平面FBC ，DE ⊄平面FBC ，∴AD ∥平面FBC ，DE ∥平面FBC ，又AD ∩DE ＝D ，AD ⊂平面EAD ，DE ⊂平面EAD ，∴平面FBC ∥平面EAD ，又FC ⊂平面FBC ，∴FC ∥平面EAD ．(2)连接FO 、FD ，∵四边形BDEF 为菱形，且∠DBF ＝60°，∴△DBF 为等边三角形， ∵O 为BD 中点．所以FO ⊥BD ，O 为AC 中点，且FA ＝FC ，∴AC ⊥FO ，又AC ∩BD ＝O ，∴FO ⊥平面ABCD ，∴OA 、OB 、OF 两两垂直，建立如图所示的空间直角坐标系O －xyz ，设AB ＝2，因为四边形ABCD 为菱形，∠DAB ＝60°，则BD ＝2，OB ＝1，OA ＝OF ＝3，∴O(0,0,0)，A(3，0,0)，B(0,1,0)，C(－3，0,0)，F(0,0，3)，∴CF →＝(3，0，3)，CB →＝(3，1,0)，设平面BFC 的一个法向量为n ＝(x ，y ，z)，则有⎩⎪⎨⎪⎧ n·CF →＝0，n·CB →＝0，∴⎩⎨⎧3x ＋3z ＝0，3x ＋y ＝0，令x ＝1，则n ＝(1，－3，－1)，∵BD ⊥平面AFC ，∴平面AFC 的一个法向量为OB →＝(0,1,0)．∵二面角A －FC －B 为锐二面角，设二面角的平面角为θ，∴cosθ＝|cos 〈n ，OB →〉|＝|n·OB →||n|·|OB →|＝⎪⎪⎪⎪⎪⎪－35＝155， ∴二面角A －FC －B 的余弦值为155.22．(本小题满分14分)(文)(2014·黄石二中检测)如图，在直三棱柱ABC －A1B1C1中，AA1＝AC ＝2AB ＝2，且BC1⊥A1C ．(1)求证：平面ABC1⊥平面A1ACC1；(2)设D 是A1C1的中点，判断并证明在线段BB1上是否存在点E ，使DE ∥平面ABC1；若存在，求三棱锥E －ABC1的体积．[解析] (1)证明：在直三棱柱ABC －A1B1C1中，有A1A ⊥平面ABC ．∴A1A ⊥AC ，又A1A ＝AC ，∴A1C ⊥AC1.又BC1⊥A1C ，∴A1C ⊥平面ABC1，∵A1C ⊂平面A1ACC1，∴平面ABC1⊥平面A1CC1.(2)存在，E 为BB1的中点．取A1A 的中点F ，连EF ，FD ，当E 为B1B 的中点时，EF ∥AB ，DF ∥AC1，∴平面EFD ∥平面ABC1，则有ED ∥平面ABC1.当E 为BB1的中点时，VE －ABC1＝VC1－ABE ＝13×2×12×1×1＝13.(理)(2014·浙北名校联盟联考)已知在长方体ABCD －A ′B ′C ′D ′中，点E 为棱CC ′上任意一点，AB ＝BC ＝2，CC ′＝1.(1)求证：平面ACC ′A ′⊥平面BDE ；(2)若点P 为棱C ′D ′的中点，点E 为棱CC ′的中点，求二面角P －BD －E 的余弦值．[解析] (1)∵ABCD 为正方形，∴AC ⊥BD ，∵CC ′⊥平面ABCD ，∴BD ⊥CC ′，又CC ′∩AC ＝C ，∴BD ⊥平面ACC ′A ′，∴平面BDE ⊥平面ACC ′A ′.(2)以DA 为x 轴，以DC 为y 轴，以DD ′为z 轴建立空间直角坐标系，则D(0,0,0)，B(2,2,0)，E(0,2，12)，P(0,1,1)，设平面BDE 的法向量为m ＝(x ，y ，z)，∵DB →＝(2,2,0)，DE →＝(0,2，12)，∴⎩⎪⎨⎪⎧ m·DB →＝2x ＋2y ＝0，m·DE →＝2y ＋12z ＝0，令x ＝1，则y ＝－1，z ＝4，∴m ＝(1，－1,4)，设平面PBD 的法向量为n ＝(x ，y ，z)， ∵DP →＝(0,1,1)，∴⎩⎪⎨⎪⎧ n·DB →＝2x ＋2y ＝0，n·DP →＝y ＋z ＝0，令x ＝1，则y ＝－1，z ＝1，∴n ＝(1，－1,1)，∴cos 〈m ，n 〉＝m·n |m|·|n|＝63，∴二面角P －BD －E 的余弦值为63.。

江西省2015届高三数学理一轮复习备考试题：立体几何

江西省2015届高三数学一轮复习备考试题立体几何一、选择题 1、（2014年江西高考）一几何体的直观图如右图，下列给出的四个俯视图中正确的是2、（2013年江西高考）如图，正方体的底面与正四面体的底面在同一平面α上，且AB CD ，正方体的六个面所在的平面与直线CE ，EF 相交的平面个数分别记为,m n ，那么m n +=A.8B.9C.10D.11 3、（2012年江西高考）如图，已知正四棱锥S-ABCD 所有棱长都为1，点E 是侧棱SC 上一动点，过点E 垂直于SC 的截面将正四棱锥分成上、下两部分。

记SE=x （0＜x ＜1），截面下面部分的体积为V （x ），则函数y=V （x ）的图像大致为4、（红色六校2015届高三第一次联考）已知正方体被过一面对角线和它对面两棱中点的平面截去一个三棱台后的几何体的主（正）视图和俯视图如下，则它的左（侧）视图是( )5、（2014届江西省高三4月模拟）已知某几何体的三视图如图所示，则该几何体的体积为A.233B.223C.203D.1436、（吉安一中2014届高三下学期第一次模拟）如图，正四面体ABCD 的顶点A ，B ，C 分别在两两垂直的三条射线,,Ox Oy Oz 上，则在下列命题中，错误．．的为（）A. O-ABC 是正三棱B. 直线OB ∥平面ACDC. 直线AD 与OB 所成的角是45°D. 二面角D-OB-A 为45°7、（南昌三中2014届高三第七次考试）M 是正方体1111ABCD A B C D -的棱1DD 的中点，给出下列命题：①过M 点有且只有一条直线与直线AB 、11B C 都相交； ②过M 点有且只有一条直线与直线AB 、11B C 都垂直； ③过M 点有且只有一个平面与直线AB 、11B C 都相交；④过M 点有且只有一个平面与直线AB 、11B C 都平行.其中真命题是（） A ．②③④ B ．①③④ C ．①②④ D ．①②③ 8、设a ，b 是不同的直线，α，β是不同的平面，则下列命题：①若a ⊥b ，a ⊥α，则b ∥α； ②若a ∥α，α⊥β则a ⊥β； ③若a ⊥β，α⊥β，则a ∥α；④若a ⊥b ，a ⊥α，b ⊥β则a ⊥β．其中正确命题的个数是A ．0B ．1C ．2D ．39、将正方体(如图(a)所示)截去两个三棱锥，得到图(b)所示的几何体，则该几何体的侧视图为10、设m 、n 是两条不同的直线，α、β是两个不同的平面，考查下列命题，其中正确的命题是A 、n n αβαβ⊥,⇒⊥∥,m ∥mB 、,,m n m n αβαβ⊥⊂⊥⇒⊥C 、,,m n m n αβαββ⊥=⊥⇒⊥ D 、,,m n n αβαβ⊥⊥⇒⊥∥m11、平面四边形ABCD 中，1===CD AD AB ，CD BD BD ⊥=,2，将其沿对角线BD 折成四面体BCD A -'，使平面⊥BD A '平面BCD ，若四面体BCD A -'顶点在同一个球面上，则该球的体积为( )A.π23 B. π3 C. π32 D. π2 12、如右图所示是一个几何体的三视图，则该几何体的体积为( )A ．1B ．12C ．34D ．32二、解答题1、（2014年江西高考）如图，四棱锥ABCD P -中，ABCD 为矩形，平面⊥PAD 平面ABCD .（1）求证：;PD AB ⊥ （2）若,2,2,90===∠PC PB BPC 问AB 为何值时，四棱锥ABCD P -的体积最大？并求此时平面PBC 与平面DPC 夹角的余弦值.2、（2013年江西高考）如图，四棱锥P ABCD -中，PA ,ABCD E BD ⊥平面为的中点，G PD 为的中点，3,12DAB DCB EA EB AB PA ∆≅∆====，，连接CE 并延长交AD 于F .(1) 求证：AD CFG ⊥平面；(2)求平面BCP 与平面DCP 的夹角的余弦值.3、（2012年江西高考）在三棱柱ABC-A 1B 1C 1中，已知AB=AC=AA 1BC=4，在A 1在底面ABC 的投影是线段BC 的中点O 。

立体几何大题-2023届高三数学一轮复习

立体几何复习1.（多选）如图，四棱锥P ABCD -中，平面PAD ⊥底面ABCD ，PAD △是等边三角形，底面ABCD 是菱形，且60BAD ∠=︒，M 为棱PD 的中点，N 为菱形ABCD 的中心，下列结论正确的有（） A ．直线PB 与平面AMC 平行 B ．直线PB 与直线AD 垂直C ．线段AM 与线段CM 长度相等D ．PB 与AM 所成角的余弦值为24 2.（多选）如图，在长方体ABCD —A 1B 1C 1D 1中，AB ＝4，BC ＝BB 1＝2，E 、F 分别为棱AB 、A 1D 1的中点，则下列说法中正确的有（）A ．DB 1⊥CEB ．三棱锥D —CEF 的体积为83C ．若P 是棱C 1D 1上一点，且D 1P ＝1，则E 、C 、P 、F 四点共面D ．平面CEF 截该长方体所得的截面为五边形3.（多选）已知菱形ABCD 的边长为2, ∠ABC=3π,将ΔDAC 沿着对角线AC 折起至ΔD'AC,连接BD'.设二面角D'-AC-B 的大小为θ,则下列说法正确的是（）A.若四面体D'ABC 为正四面体，则θ=3π B.四面体D'ABC 的体积最大值为1 C.四面体D'ABC 的表面积最大值为2(3+2) D.当θ=23π时，四面体D'ABC 的外接球的半径为2134.如图，四棱锥P -ABCD 的底面为正方形，PD ⊥底面ABCD ．设平面PAD 与平面PBC 的交线为l ．（1）证明：l ⊥平面PDC ；（2）已知PD =AD =1，Q 为l 上的点，求PB 与平面QCD 所成角的正弦值的最大值．5.如图，点C 是以AB 为直径的圆上的动点（异于,A B ），已知2AB =，2AC =，AE =BEDC 为矩形，平面ABC ⊥平面BEDC .设平面EAD 与平面ABC 的交线为l .（1）证明：l BC ；（2）求平面ADE 与平面ABC 所成的锐二面角的余弦值.6.7. 在如图所示的几何体中，四边形ABCD 为正方形，PA ⊥平面ABCD ，//PA BE ，2BE =，4AB PA ==.（1）求证：//CE 平面PAD ；（2）在棱AB 上是否存在一点F ，使得二面角E PC F --的大小为60︒？如果存在，确定点F 的位置；如果不存在，说明理由.8.如图,四棱锥P -ABCD 中,底面ABCD 是直角梯形,AB ∥DC ,∠BAD =90°,PD =DC =BC =2PA =2AB =2,PD ⊥DC .(1)求证：PA ⊥平面ABCD ；(2)设BM =BD λ(0<λ<1),当二面角A-PM-B 的余弦值为77时,求λ的值.9.如图，四棱锥P ABCD -中，四边形ABCD 是菱形，PA PC =，BD PA ⊥，E 是BC 上一点，且3EC BE =，设AC BD O =.（1）证明：PO ⊥平面ABCD ；（2）若60BAD ∠=︒，PA PE ⊥，求二面角A PE C --的余弦值.10.如图，在四棱锥P ABCD -中，底面ABCD 是菱形，PA ⊥平面ABCD .（1）求证：平面PAC ⊥平面PBD ；（2）若2AP AB ==，60BAD ∠=︒，求二面角A PB D --的余弦值.11.如图，在三棱柱ABC-A 1B 1C 1中，ΔABC 是边长为2的等边三角形，平面ABC ⊥平面AA 1B 1B,A 1A=A 1B,∠A 1AB=60°,O 为AB 的中点，M 为A 1C 1的中点．（1)求证：OM//平面BB 1C 1C;（2)求二面角C 1-BA 1-C 的正弦值．12.如图，在五面体ABCDEF 中，四边形ABEF 为正方形，平面ABEF ⊥平面CDFE ，CD ∥EF ，DF ⊥EF ， EF ＝2CD ＝2．（1）若DF ＝2，求二面角A －CE －F 的正弦值；（2）若平面ACF ⊥平面BCE ，求DF 的长．13.如图，在斜三棱柱111ABC A B C -中，底面是边长为3的等边三角形，12A A =，点1A 在下底面上的射影是ABC ∆的中心O .（1）求证：平面1A AO ⊥平面11BCC B ；（2）求二面角1C AB C --的余弦值.14.如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，AD CD ⊥，//AD BC ，2PA AD CD ===，3BC =．E为PD的中点，点F在PC上，且13 PFPC=．（Ⅰ）求证：CD⊥平面PAD；（Ⅱ）求二面角F AE P--的余弦值；（Ⅲ）设点G在PB上，且23PGPB=．判断直线AG是否在平面AEF内，说明理由．15.如图，在三棱锥A－BCD中，△ABD与△BCD都为等边三角形，平面ABD⊥平面BCD，M，O分别为AB，BD 的中点，AO∩DM＝G，N在棱CD上且满足2CN＝ND，连接MC，GN．（1）证明：GN∥平面ABC；（2）求直线AC和平面GND所成角的正弦值．16.在多面体ABCDE中，平面ACDE⊥平面ABC，四边形ACDE为直角梯形，CD∥AE，AC⊥AE，AB⊥BC，CD＝1，AE＝AC＝2，F为DE的中点，且点E满足EB4EG=．（1）证明：GF∥平面ABC；（2）当多面体ABCDE的体积最大时，求二面角A—BE—D的余弦值．17一副标准的三角板(图1)中,∠ABC为直角,∠A=60°,∠DEF为直角,DE=EF,BC=DF.把BC与DF重合,拼成一个三棱锥(图2)｡设M是AC的中点,N是BC的中点｡(1)求证:平面ABC⊥平面EMN;(2)若AC=4,二面角E-BC-A为直二面角,求直线EM与平面ABE所成的正弦18.如图四边形ABCD为梯形，AD∥BC，BM⊥AD于M，CN⊥AD于N，∠A=45°，AD=4BC=4，AB=2，现沿CN将△CDN折起，使△ADN为正三角形，且平面AND⊥平面ABCN，过BM的平面与线段DN、DC分别交于E、F．(1)求证：EF⊥DA；(2)在棱DN上(不含端点)是否存在点E，使得直线DB与平面BMEF所成角的正弦值为34，若存在，请确定E点的位置；若不存在，说明理由．19.如图，在四棱锥P—ABCD中，底面ABCD为正方形，PD⊥底面ABCD，M为线段PC的中点，PD＝AD，N为线段BC上的动点．（1）证明：平面MND⊥平面PBC；（2）当点N在线段BC的何位置时，平面MND与平面PAB所成锐二面角的大小为30°？指出点N的位置，并说明理由．。

四川省2022届高三数学理一轮复习典型题专项训练立体几何

四川省2022届高三数学理一轮复习典型题专项训练立体几何一、选择、填空题1、〔2022全国III 卷高考〕中国古建筑借助榫卯将木构件连接起来，构件的凸出局部叫棒头，凹进局部叫卯眼，图中木构件右边的小长方体是棒头．假设如图摆放的木构件与某一带卯眼的木构件咬合成长方体，那么咬合时带卯眼的木构件的俯视图可以是〔〕2、〔2022全国III 卷高考〕圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，那么该圆柱的体积为〔〕A ．πB ．3π4C ．π２D ．π43、〔2022全国III 卷高考〕如图，网格纸上小正方形的边长为1，粗实现画出的是某多面体的三视图，那么该多面体的外表积为〔A 〕18+〔B 〕54+〔C 〕90 〔D 〕814、〔成都市2022届高三第二次诊断〕m ，是空间中两条不同的直线，α，β为空间中两个互相垂直的平面，那么以下命题正确的选项是〔〕A ．假设m α⊂，那么m β⊥B ．假设m α⊂，n β⊂，那么m n ⊥C ．假设m α⊄，m β⊥，那么//m αD ．假设m αβ=，n m ⊥，那么n α⊥5、〔成都市2022届高三第三次诊断〕在正三棱柱111ABC A B C - (底面是正三角形,侧棱垂直于底面的棱柱)中，所有棱长之和为定值a .假设正三棱柱111ABC A B C -的顶点都在球O 的外表上，那么当正三棱柱侧面积获得最大值24时，该球的外表积为〔〕A ．B ．323π C ．12π D ．643π6、〔达州市2022届高三第一次诊断〕如图某几何体的三视图是直角边长为1的三个等腰直角三角形，那么该几何体的外接球的外表积为〔〕A ．32π B C D ．3π 7、〔德阳市2022届高三二诊考试〕如下图的三视图表示的几何体的体积为323，那么该几何体的外接球的外表积为〔〕A ．12πB ．24πC ．36πD ．48π8、〔广元市2022届高三第一次高考适应性统考〕设,m n 是两条不同的直线，,αβ是两个不同的平面，且,m n αβ⊂⊂，以下命题中正确的选项是〔〕A ．假设αβ⊥，那么m n ⊥B ．假设//αβ，那么//m nC ．假设m n ⊥，那么αβ⊥D ．假设n α⊥，那么αβ⊥ 9、〔泸州市2022届高三第二次教学质量诊断〕设a ，b 是两条不同的直线，α、β是不重合的两个平面，那么以下命题中正确的选项是A ．假设a b ⊥，a α⊥，那么//b αB ．假设//a α，αβ⊥，那么//a βC ．假设//a α，//a β，那么//αβD ．假设//a b ，a α⊥，b β⊥，那么//αβ10、〔南充市2022届高三第二次高考适应性考试〕某三棱锥的三视图如下图，那么该三棱锥的外表积为( )A ．23472++B ．1072+ C. 710+ D ．3412+11、〔仁寿县2022届高三上学期零诊〕如图，正方体ABCD ﹣A 1B 1C 1D 1的棱长为1，E 为棱DD 1上的点，F 为AB 的中点，那么三棱锥B 1﹣BFE 的体积为12、〔遂宁市2022届高三三诊考试〕在一圆柱中挖去一圆锥所得的机械部件的三视图如下图，那么此机械部件的外表积为A ．π)27(-B ．π)27(+C ．π)26(+D ．π)37(-13、〔雅安市2022届高三下学期三诊〕某几何体的三视图如下图，其中，正视图、俯视图都是矩形，侧视图是直角三角形，那么该几何体的体积等于〔〕A ．1B ．2C ．3D ．414、〔资阳市2022届高三4月模拟考试〔三诊〕〕如图，二面角BC αβ--的大小为6π，AB CD αβ⊂⊂，，且AB 243BC CD ABC BCD ππ==∠=∠=，，，那么AD 与β所成角的大小为A ．π4B ．π3 C.π6D ．π1215、〔成都市石室中学高2022届高三下期二诊模拟〕一个底面为正方形的四棱锥，其三视图如下图，假设这个四棱锥的体积为2 ，那么此四棱锥最长的侧棱长为16、〔成都市2022届高三第二次诊断〕?九章算术?中将底面为长方形，且有一条侧棱与底面垂直的四棱锥称之为“阳马〞.现有一阳马，其正视图和侧视图是如下图的直角三角形.假设该阳马的顶点都在同一个球面上，那么该球的体积为〔〕A ．3B ．CD ．24π17、〔2022全国III 卷高考〕在封闭的直三棱柱111ABC A B C -内有一个体积为V 的球，假设AB BC ⊥，6AB =，8BC =，13AA =，那么V 的最大值是〔A 〕4π 〔B 〕92π〔C 〕6π 〔D 〕323π二、解答题1、〔2022全国III 卷高考〕如图，边长为2的正方形ABCD 所在平面与半圆弧CD 所在平面垂直，M是CD 上异于C ，D 的点．⑴证明：平面AM D ⊥平面BMC ；⑵当三棱锥M ABC -体积最大时，求面MAB 与面MCD 所成二面角的正弦值．2、〔2022全国III 卷高考〕如图，四面体ABCD 中，△ABC 是正三角形，△ACD 是直角三角形．ABDCBD ，AB BD ．〔1〕证明：平面ACD 平面ABC ；〔2〕过AC 的平面交BD 于点E ，假设平面AEC 把四面体ABCD 分成体积相等的两局部．求二面角D AE C 的余弦值． 3、〔2022全国III 卷高考〕如图，四棱锥P ABC -中，PA ⊥地面ABCD ，AD BC ，3AB AD AC ===，4PA BC ==，M 为线段AD 上一点，2AM MD =，N 为PC 的中点．〔I 〕证明MN平面PAB ；〔II 〕求直线AN 与平面PMN 所成角的正弦值.4、〔成都市2022届高三第二次诊断〕如图，D 是AC 的中点，四边形BDEF 是菱形，平面BDEF ⊥平面ABC ，60FBD ∠=，AB BC ⊥，AB BC ==〔1〕假设点M 是线段BF 的中点，证明：BF ⊥平面AMC ；〔2〕求平面AEF 与平面BCF 所成的锐二面角的余弦值.5、〔成都市2022届高三第三次诊断〕如图①,在等腰梯形ABCD 中，AB ∥CD ，60ABC ∠=，2CD =，4AB =，点E 为AB 的中点；现将三角形BEC 沿线段EC 折起，形成直二面角P EC A --,如图②，连接,PA PD 得四棱锥P AECD -，如图③.〔I 〕求证：PD EC ⊥；〔Ⅱ〕求平面PEC 与平面PAD 所成的锐二面角的余弦值.6、〔达州市2022届高三第一次诊断〕如图在棱锥P ABCD -中，ABCD 为矩形，PD ⊥面ABCD ，2PB =，PB 与面PCD 成045角，PB 与面ABD 成030角.〔1〕在PB 上是否存在一点E ，使PC ⊥面ADE ，假设存在确定E 点位置，假设不存在，请说明理由；〔2〕当E 为PB 中点时，求二面角P AE D --的余弦值.7、〔德阳市2022届高三二诊考试〕如图，在四棱锥P ABCD -中，底面ABCD 为边长为2的菱形，60DAB ∠=，90ADP ∠=，面ADP ⊥面ABCD ，点F 为棱PD 的中点.〔1〕在棱AB 上是否存在一点E ，使得//AF 面PCE ，并说明理由；〔2〕当二面角D FC B --的余弦值为14时，求直线PB 与平面ABCD 所成的角. 8、〔广元市2022届高三第一次高考适应性统考〕如图，ABC ∆是以ABC ∠为直角的三角形，SA ⊥平面,2,4,,ABC SA BC AB M N ===分别是,SC AB 的中点. 〔1〕求证：MN AB ⊥；〔2〕D 为线段BC 上的点，当二面角S ND A --时，求三棱锥D SNC -的体积. 9、〔泸州市2022届高三第二次教学质量诊断〕如图，三棱锥A BCD -的侧面ABD △是等腰直角三角形，90BAD ∠=，BD DC =，120BDC ∠=，且2AC AB =．〔I 〕求证：平面ABD ⊥平面BCD ；〔II 〕求二面角B AC D --的余弦值．10、〔南充市2022届高三第二次高考适应性考试〕如图，四棱锥ABCD P -中，底面ABCD 是边长为2的菱形，PB PA ABC ⊥︒=∠，660,2=PC . (Ⅰ)求证：平面⊥PAB 平面 ABCD ；(Ⅱ)假设PB PA =,求二面角D PC A --的余弦值.11、〔仁寿县2022届高三上学期零诊〕如图，直角梯形ABCD 与等腰直角三角形ABE 所在的平面互相垂直，AB ∥CD ，AB ⊥BC ，AB=2CD=2BC ，EA ⊥EB 〔1〕求证：EA ⊥平面EBC ；〔2〕求二面角C ﹣BE ﹣D 的余弦值．12、〔遂宁市2022届高三三诊考试〕如下图的几何体中，111C B A ABC -为三棱柱，且⊥1AA 平面ABC ，四边形ABCD 为平行四边形，︒=∠=60,2ADC CD AD ．〔1〕假设AC AA =1，求证：1AC ⊥平面CD B A 11；〔2〕假设12,CD AA AC λ==，二面角11C A D C --11C ACD -的体积． 13、〔雅安市2022届高三下学期三诊〕如图，在四棱锥S ABCD -中，SD ⊥底面ABCD ，M 为SD 的中点，底面ABCD 为直角梯形，AB AD ⊥，//AB CD ，且222CD AB AD ===. 〔1〕求证：//AM 平面SBC ，平面SBC ⊥平面SDB ；〔2〕假设SB 与平面SDC ，求二面角A SB C --的余弦值.14、〔资阳市2022届高三4月模拟考试〔三诊〕〕如图，三棱柱111ABC A B C -的各棱长均相等，1AA ⊥底面ABC ，E ，F 分别为棱1AA BC ，的中点．〔1〕过1FA 作平面α，使得直线BE //平面α，假设平面α与直线1BB 交于点H ，指出点H 所在的位置，并说明理由；〔2〕求二面角1B FH A --的余弦值．15、〔成都市石室中学高2022届高三下期二诊模拟〕如图，在多面体ABCDEF 中，矩形BDEF 所在平面与正方形ABC D 所在平面垂直，点M 为AE 的中点. 〔1〕求证：BM //平面EFC〔2〕假设DE AB =，求直线AE 与平面BDM 所成角的正弦值. 参考答案：一、选择、填空题 1、A2、【答案】B【解析】由题可知球心在圆柱体中心，圆柱体上下底面圆半径r那么圆柱体体积23ππ4V r h ==，应选B.3、B4、C5、【答案】D【解析】设正三棱柱111ABC A B C -底面边长为x ，侧棱为y ，那么63x y a +=，三棱柱111ABC A B C -侧面积3S xy =.所以2216336224x y a S xy +⎛⎫=≤= ⎪⎝⎭，当且仅当632a x y ==，即,126a ax y ==时，等号成立，所以24a =，2x =，4y =.所以正三棱柱111ABC A B C -的外接球的球心O 到顶点A 的间隔 4=，所以该球的外表积为643π.应选D. 6、D 7、C 8、D 9、D 10、B 11、11212、B 13、B 14、C 15、C 16、C 17、【答案】B 【解析】试题分析：要使球的体积V 最大，必须球的半径R 最大．由题意知球的与直三棱柱的上下底面都相切时，球的半径获得最大值32，此时球的体积为334439()3322R πππ==，应选B ．二、解答题1、解答：〔1〕∵正方形ABCD ⊥半圆面CMD ，∴AD ⊥半圆面CMD ，∴AD ⊥平面MCD .∵CM 在平面MCD 内，∴AD CM ⊥，又∵M 是半圆弧CD 上异于,C D 的点，∴CM MD ⊥.又∵AD DM D =，∴CM ⊥平面ADM ，∵CM 在平面BCM 内，∴平面BCM ⊥平面ADM .〔2〕如图建立坐标系： ∵ABC S ∆面积恒定，∴MO CD ⊥，M ABC V -最大.(0,0,1)M ，(2,1,0)A -，(2,1,0)B ，(0,1,0)C ，(0,1,0)D -,设面MAB 的法向量为111(,,)m x y z =，设面MCD 的法向量为222(,,)n x y z =，(2,1,1)MA =--，(2,1,1)MB =-，(0,1,1)MC =-，(0,1,1)MD =--，11111120(1,0,2)20x y z m x y z --=⎧⇒=⎨+-=⎩，同理(1,0,0)n =，，∴cos θ==，∴ sin θ=. 2、【解析】⑴取AC 中点为O ，连接BO ，DO ；ABC ∆为等边三角形 ∴BO AC ⊥ ∴AB BC = AB BC BD BDABD DBC =⎧⎪=⎨⎪∠=∠⎩ABD CBD ∴∆≅∆. ∴AD CD =,即ACD ∆为等腰直角三角形，ADC ∠ 为直角又O 为底边AC 中点 ∴DO AC ⊥令AB a =，那么AB AC BC BD a ====易得：OD =，OB = ∴222OD OB BD +=由勾股定理的逆定理可得2DOB π∠=即OD OB ⊥ 又∵OD ADC ⊂平面由面面垂直的断定定理可得ADC ABC ⊥平面平面 ⑵由题意可知V V D ACE B ACE --= 即B ,D 到平面ACE 的间隔相等即E 为BD 中点以O 为原点，OA 为x 轴正方向，OB 为y 轴正方向，OD 为z 轴正方向，设AC a =，建立空间直角坐标系，DABCEO那么()0,0,0O ，,0,02a A ⎛⎫ ⎪⎝⎭，0,0,2a D ⎛⎫ ⎪⎝⎭，,0B ⎛⎫ ⎪ ⎪⎝⎭，,4a E ⎛⎫ ⎪ ⎪⎝⎭易得：,24a a AE ⎛⎫=- ⎪ ⎪⎝⎭，,0,22a a AD ⎛⎫=- ⎪⎝⎭，,0,02a OA ⎛⎫= ⎪⎝⎭ 设平面AED 的法向量为1n ，平面AEC 的法向量为2n ，那么1100AE n AD n ⎧⋅=⎪⎨⋅=⎪⎩，解得(13,1,n =220AE n OA n ⎧⋅=⎪⎨⋅=⎪⎩，解得(20,1,n = 假设二面角D AE C --为θ，易知θ为锐角，那么12127cos 7n n n n θ⋅==⋅3、设),,(z y x n =为平面PMN 的法向量，那么⎪⎩⎪⎨⎧=⋅=⋅00PN n PM n ，即⎪⎩⎪⎨⎧=-+=-0225042z y x z x ，可取)1,2,0(=n ，于是2558|||||,cos |==><AN n AN n AN n . 4、解：〔1〕连接MD ，FD .∵四边形BDEF 为菱形，且60FBD ∠=， ∴DBF ∆为等边三角形.∵M 为BF 的中点，∴DM BF ⊥.∵AB BC ⊥，AB BC ==D 是AC 的中点， ∴BD AC ⊥. ∵平面BDEF平面ABC BD =，平面ABC ⊥平面BDEF ，AC ⊂平面ABC ，∴AC ⊥平面BDEF .又BF ⊂平面BDEF ，∴AC BF ⊥. 由DM BF ⊥，AC BF ⊥，DM AC D =，∴BF ⊥平面AMC .〔2〕设线段EF 的中点为N ，连接DN .易证DN ⊥平面ABC .以D 为坐标原点，DB ，DC ，DN 所在直线分别为轴，y 轴，轴建立如下图的空间直角坐标系.那么(0,1,0)A -，1(,0,)22E -，1(2F ，(1,0,0)B ，(0,1,0)C .∴1(2AE =-，(1,0,0)EF =，1(2BF =-，(1,1,0)BC =-.设平面AEF ，平面BCF 的法向量分别为111(,,)m x y z =，222(,,)n x y z =.由00AE m EF m ⎧⋅=⎪⎨⋅=⎪⎩1111102102x y z x ⎧-+=⎪⎪⇒⎨⎪=⎪⎩.解得11y z =. 取12z =-，∴(0,3,2)m =-.又由00BC n BF n ⎧⋅=⎪⎨⋅=⎪⎩22220102x y x z -+=⎧⎪⇒⎨-=⎪⎩解得22y . 取21z =，∴(3,3,1)n =. ∵cos ,m n <>m n m n⋅=17==.∴平面AEF 与平面BCF 所成的锐二面角的余弦值为17. 5、【解析】6、1)法一：要证明PC ⊥面ADE ，易知AD ⊥面PDC ，即得AD ⊥PC ，故只需0DE PC ⋅=即可，所以由()00||1DP PE PC DP PC PE PC PE +⋅=⇒⋅+⋅=⇒=,即存在点E 为PC 中点 …6分法二：建立如下图的空间直角坐标系D －XYZ ，由题意知PD ＝CD ＝1， CE PE PB λ=， (,1)PE PB λλ∴==-，(0,1,1)PC =-由()(0,1,1),,1)0PC DE PC DP PE λλ⋅=⋅+=-⋅-=，得12λ=，即存在点E 为PC 中点。

高三一轮复习-立体几何常见问题(带答案)

个性化辅导授课教案学员姓名：辅导类型（1对1、小班）：年级：辅导科目：学科教师：课题课型 □ 预习课 □ 同步课 □ 复习课 □ 习题课授课日期及时段年月日时间段教学内容多面体与球组合问题纵观近几年高考对于组合体的考查，重点放在与球相关的外接与内切问题上.要求学生有较强的空间想象能力和准确的计算能力，才能顺利解答.从实际教学来看，这部分知识是学生掌握最为模糊，看到就头疼的题目.分析原因，除了这类题目的入手确实不易之外，主要是学生没有形成解题的模式和套路，以至于遇到类似的题目便产生畏惧心理.本文就高中阶段出现这类问题加以类型的总结和方法的探讨.一、球与柱体的组合体规则的柱体，如正方体、长方体、正棱柱等能够和球进行充分的组合，以外接和内切两种形态进行结合，通过球的半径和棱柱的棱产生联系，然后考查几何体的体积或者表面积等相关问题. 1.1 球与正方体如图1所示，正方体1111ABCD A B C D -，设正方体的棱长为a ，,,,E F H G 为棱的中点，O 为球的球心.常见组合方式有三类：一是球为正方体的内切球，截面图为正方形EFGH 和其内切圆，则2aOJ r ==；二是与正方体各棱相切的球，截面图为正方形EFGH 和其外接圆，则22GO R a ==；三是球为正方体的外接球，截面图为长方形11ACA C 和其外接圆，则132A O R a '==.通过这三种类型可以发现，解决正方体与球的组合问题，常用工具是截面图，即根据组合的形式找到两个几何体的轴截面，通过两个截面图的位置关系，确定好正方体的棱与球的半径的关系，进而将空间问题转化为平面问题.例 1 棱长为1的正方体1111ABCD A B C D -的8个顶点都在球O 的表面上，E F ，分别是棱1AA ，1DD 的中点，则直线EF 被球O 截得的线段长为（）A ．22B ．1C ．212+D ．2解：由题意可知，球为正方体的外接球.平面11AA DD 截面所得圆面的半径12,22AD R ==11EF AA DD ⊂面，∴直线EF 被球O 截得的线段为球的截面圆的直径22R =.【牛刀小试】将棱长为2的正方体木块削成一个体积最大的球，则这个球的表面积为（） A ．2πB ．4πC ．8πD ．16π【答案】B【解析】体积最大的球是其内切球，即球半径为1，所以表面积为ππ4142=⋅=S .1.2 球与长方体长方体各顶点可在一个球面上，故长方体存在外切球.但是不一定存在内切球.设长方体的棱长为,,,a b c 其体对角线为l .当球为长方体的外接球时，截面图为长方体的对角面和其外接圆，和正方体的外接球的道理是一样的，故球的半径222.22l a b c R ++==例 2 在长、宽、高分别为2，2，4的长方体内有一个半径为1的球，任意摆动此长方体，则球经过的空间部分的体积为( ) A.10π3B.4πC.8π3D.7π3【牛刀小试】已知正四棱柱的底边和侧棱长均为32，则该正四棱锥的外接球的表面积为 .1.3 球与正棱柱球与一般的正棱柱的组合体，常以外接形态居多.下面以正三棱柱为例，介绍本类题目的解法构造直角三角形法.设正三棱柱111ABC A B C -的高为,h 底面边长为a ，如图2所示，D 和1D 分别为上下底面的中心.根据几何体的特点，球心必落在高1DD 的中点O ，3,,,23h OD AO R AD a ===借助直角三角形AOD 的勾股定理，可求223()()23hR a =+.例3 正四棱柱1111ABCD A B C D -的各顶点都在半径为R 的球面上，则正四棱柱的侧面积有最值，为 .【牛刀小试】直三棱柱111ABC A B C -的六个顶点都在球O 的球面上，若1AB BC ==，0120ABC ∠=，123AA =，则球O 的表面积为（）A ．4πB ．8πC ．16πD ．24π二、球与锥体的组合体规则的锥体，如正四面体、正棱锥、特殊的一些棱锥等能够和球进行充分的组合，以外接和内切两种形态进行结合，通过球的半径和棱锥的棱和高产生联系，然后考查几何体的体积或者表面积等相关问题.2.1 球与正四面体正四面体作为一个规则的几何体，它既存在外接球，也存在内切球，并且两心合一，利用这点可顺利解决球的半径与正四面体的棱长的关系.如图4，设正四面体S ABC -的棱长为a ，内切球半径为r ，外接球的半径为R ,取AB 的中点为D ，E 为S 在底面的射影，连接,,CD SD SE 为正四面体的高.在截面三角形SDC ,作一个与边SD 和DC 相切，圆心在高SE 上的圆,即为内切球的截面.因为正四面体本身的对称性可知，外接球和内切球的球心同为O .此时，,CO OS R OE r ===,23,,33SE a CE a ==则有2222233a R r a R r CE +=-=，=，解得：66,.412R a r a ==这个解法是通过利用两心合一的思路，建立含有两个球的半径的等量关系进行求解.同时我们可以发现，球心O 为正四面体高的四等分点.如果我们牢记这些数量关系，可为解题带来极大的方便.2.2 球与三条侧棱互相垂直的三棱锥球与三条侧棱互相垂直的三棱锥组合问题，主要是体现在球为三棱锥的外接球.解决的基本方法是补形法，即把三棱锥补形成正方体或者长方体.常见两种形式：一是三棱锥的三条侧棱互相垂直并且相等，则可以补形为一个正方体，它的外接球的球心就是三棱锥的外接球的球心.如图5，三棱锥111A AB D -的外接球的球心和正方体1111ABCD A B C D -的外接球的球心重合.设1AA a =，则32R a =.二是如果三棱锥的三条侧棱互相垂直并且不相等，则可以补形为一个长方体，它的外接球的球心就是三棱锥的外接球的球心.2222244a b c l R ++==(l 为长方体的体对角线长). CB ADSOE 图4例5 在正三棱锥S ABC -中，M N 、分别是棱SC BC 、的中点，且AM MN ⊥,若侧棱23SA =,则正三棱锥S ABC -外接球的表面积是 .【牛刀小试】一个几何体的三视图如图所示，其中主视图和左视图是腰长为1的两个全等的等腰直角三角形，则该几何体的外接球的表面积为( )A ．12πB ．43πC ．3πD ．123π2.3 球与正棱锥球与正棱锥的组合，常见的有两类，一是球为三棱锥的外接球，此时三棱锥的各个顶点在球面上，根据截面图的特点，可以构造直角三角形进行求解.二是球为正棱锥的内切球，例如正三棱锥的内切球，球与正三棱锥四个面相切，球心到四个面的距离相等，都为球半径R ．这样求球的半径可转化为球球心到三棱锥面的距离，故可采用等体积法解决，即四个小三棱锥的体积和为正三棱锥的体积.例6 在三棱锥P －ABC 中，PA ＝PB=PC=3,侧棱PA 与底面ABC 所成的角为60°，则该三棱锥外接球的体积为（） A ．π B.3π C. 4π D.43π【牛刀小试】已知正三棱锥P -ABC ,点P ,A ,B ,C 都在半径为3的球面上,若PA,PB,PC 两两互相垂直,则球心到截面ABC 的距离为____________.2.4 球与特殊的棱锥球与一些特殊的棱锥进行组合，一定要抓住棱锥的几何性质，可综合利用截面法、补形法等进行求解.例如，四个面都是直角三角形的三棱锥，可利用直角三角形斜边中点几何特征，巧定球心位置.如图8，三棱锥S ABC -,满足,,SA ABC AB BC ⊥⊥面取SC 的中点为O ,由直角三角形的性质可得：,OA OS OB OC ===所以O 点为三棱锥S ABC -的外接球的球心,则2SCR =. 例7 矩形ABCD 中，4,3,AB BC ==沿AC 将矩形ABCD 折成一个直二面角B ACD --,则四面体ABCD 的外接球的体积是( )A.π12125 B.π9125 C.π6125 D.π3125解：由题意分析可知，四面体ABCD 的外接球的球心落在AC 的中点，此时满足,OA OD OB OC ===522AC R ∴==,343V R π=1256π=. 五、与三视图相结合的组合体问题本类问题一般首先给出三视图，然后考查其直观图的相关的组合体问题.解答的一般思路是根据三视图还CBASO原几何体，根据几何体的特征选择以上介绍的方法进行求解.例9 【河北省唐山市2014－2015学年度高三年级摸底考试】某几何体的三视图如图所示，则该几何体的外接球的球面面积为（） A .5πB .12πC .20πD .8π【牛刀小试】若一个底面是正三角形的三棱柱的正视图如图所示，其顶点都在一个球面上，则该球的表面积为( )A.163 πB.193 πC.1912 πD.43π综合上面的五种类型，解决与球的外切问题主要是指球外切多面体与旋转体，解答时首先要找准切点，通过作截面来解决.如果外切的是多面体，则作截面时主要抓住多面体过球心的对角面来作；把一个多面体的几个顶点放在球面上即为球的内接问题．解决这类问题的关键是抓住内接的特点，即球心到多面体的顶点的距离等于球的半径．发挥好空间想象力，借助于数形结合进行转化，问题即可得解．如果是一些特殊的几何体，如正方体、正四面体等可以借助结论直接求解,此时结论的记忆必须准确.问题二：立体几何中的折叠问题立体几何中的折叠问题主要包含两大问题：平面图形的折叠与几何体的表面展开。

高三数学第一轮复习立体几何的综合问题知识精讲

高三数学第一轮复习：立体几何的综合问题【本讲主要内容】立体几何的综合问题立体几何知识的综合应用及立体几何与其它知识点的综合问题【知识掌握】【知识点精析】1. 立体几何的综合问题融直线和平面的位置关系于平面与几何体中，有计算也有论证。

解决这类问题需要系统地掌握线线、线面、面面的位置关系，特别是平行与垂直的判定与性质．深刻理解异面直线所成的角、斜线与平面所成的角、二面角的平面角的概念，理解点到面的距离、异面直线的距离的概念．2. 立体几何横向可与向量、代数、三角、解析几何等综合．3. 应用性问题、探索性问题需综合运用所学知识去分析解决．【解题方法指导】例1. 如图所示，在正方体ABCD—A1B1C1D1的侧面AB1内有一动点P到直线A1B1与直线BC的距离相等，则动点P所在曲线的形状为（）解析：P到直线BC的距离等于P到B的距离，动点P的轨迹满足抛物线定义．故选C.例2. 如图，四棱锥P－ABCD的底面是边长为a的正方形，PB⊥平面ABCD，（Ⅰ）若面PAD与面ABCD所成的二面角为60°，求这个四棱锥的体积；（Ⅱ）证明不论四棱锥的高怎样变化，面PAD与面PCD所成的二面角恒大于90°．（Ⅰ）解：∵PB⊥面ABCD，∴BA是PA在面ABCD上的射影，又DA⊥AB ∴PA⊥DA∴∠PAB是面PAD与面ABCD所成的二面角的平面角∴∠PAB＝60°，PB＝AB·tan60°＝3a ,∴ V 锥＝3233·3·31a a a =（Ⅱ）证明：不论棱锥的高怎样变化，棱锥侧面PAD 与PCD 恒为等腰三角形，作AE ⊥PD ，垂足为E ，连结CE ，则△ADE ≌△CDE ，因为AE ＝CE ，∠CED ＝90o，故∠CEA 是面PAD 与面PCD 所成的二面角的平面角．设AC 与BD 交于点O ，连结EO ，则EO ⊥AC ，所以a AD AE OA a =<<=22，22a AE <，在△AEC 中，02222cos 222222222<-=-=∙-+=∠AE a AE AE a AE EC AE AC EC AE CEA 所以面PAD 与面PCD 所成的二面角恒大于90o。

高三数学--立体几何专题

侧（左）视图正（主）视图俯视图高三数学(理)一轮复习资料-- 立体几何一、选择题1 、某几何体的正视图和侧视图均如图1所示，则该几何体的俯视图不可能是 ( )2、已知某空间几何体的主视图、侧视图、俯视图均为如图所示的等腰直角三角形，如果直角三角形的直角边长为1，那么这个几何体的表面积为( )A 、22 B 、3＋22 C 、32 D 、3＋323、已知a 、b 为两条不同的直线，α、β为两个不同的平面，且a ⊥α，b ⊥β，则下列命题中为假命题的是( )A 、若a ∥b ，则α∥βB 、若α⊥β，则a ⊥bC 、若a ，b 相交，则α，β相交D 、若α，β相交，则a ，b 相交4、设平面α与平面β相交于直线m ，直线a 在平面α内，直线b 在平面β内，且b m ⊥，则“αβ⊥” 是“a b ⊥”的（）A 、充分不必要条件B 、必要不充分条件C 、充要条件D 、即不充分不必要条件5、一个几何体的三视图如图所示，则这个几何体的体积等于（）A 、12B 、3 C 、563D 、46、某三棱锥的三视图如图所示，该三梭锥的表面积是（）A 、28+65B 、 30+65C 、 56+ 125D 、 60+1257、下列命题正确的是（）A 、若两条直线和同一个平面所成的角相等，则这两条直线平行B 、若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行C 、若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行D 、若两个平面都垂直于第三个平面，则这两个平面平行8、已知直二面角l αβ--，点,A A C l α∈⊥,C 为垂足，,,B BD l D β∈⊥为垂足．若AB=2，AC=BD=1，则D 到平面ABC 的距离等于（）A、3 B、3 C、3D 、 1 9、已知三棱锥的三个侧面两两垂直，三条侧棱长分别为4、4、7，若此三棱锥的各个顶点都在同一个球面上，则此球的表面积是( )A 、81πB 、36πC 、81π4D 、144π10 、如图，在正三棱柱ABC -A 1B 1C 1中，已知AB =1，D 在棱BB 1上，且BD =1，则AD 与平面AA 1C 1C 所成角的正弦值为 ( )A 、64B 、34C 、62D 、72二、填空题11、已知某三棱锥的三视图(单位：cm)如图所示，则该三棱锥的体积等于 ___________cm 3．12、如图，在正方体1111ABCD A B C D -中，M 、N 分别是CD 、1CC 的中点，则异面直线1A M 与DN 所成角的大小是____________。

高考数学一轮复习立体几何多选题知识点总结及解析

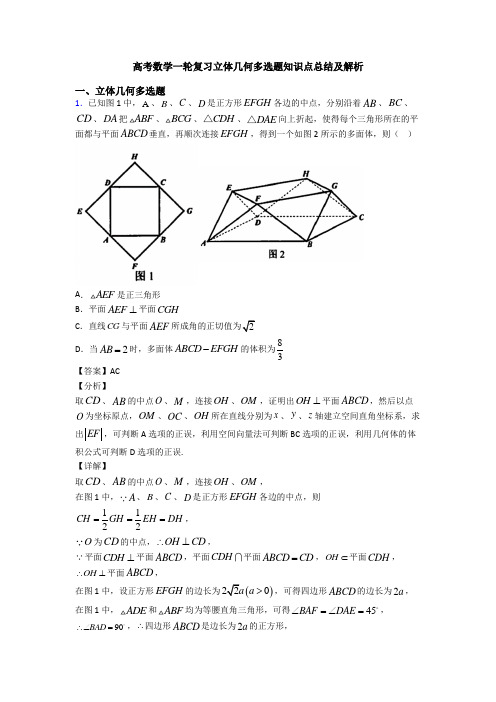
高考数学一轮复习立体几何多选题知识点总结及解析一、立体几何多选题1．已知图1中，A 、B 、C 、D 是正方形EFGH 各边的中点，分别沿着AB 、BC 、CD 、DA 把ABF 、BCG 、CDH △、DAE △向上折起，使得每个三角形所在的平面都与平面ABCD 垂直，再顺次连接EFGH ，得到一个如图2所示的多面体，则（）A ．AEF 是正三角形B ．平面AEF ⊥平面CGHC ．直线CG 与平面AEF 2D ．当2AB =时，多面体ABCD EFGH -的体积为83【答案】AC 【分析】取CD 、AB 的中点O 、M ，连接OH 、OM ，证明出OH ⊥平面ABCD ，然后以点O 为坐标原点，OM 、OC 、OH 所在直线分别为x 、y 、z 轴建立空间直角坐标系，求出EF ，可判断A 选项的正误，利用空间向量法可判断BC 选项的正误，利用几何体的体积公式可判断D 选项的正误. 【详解】取CD 、AB 的中点O 、M ，连接OH 、OM ，在图1中，A 、B 、C 、D 是正方形EFGH 各边的中点，则1122CH GH EH DH ===，O 为CD 的中点，OH CD ∴⊥，平面CDH ⊥平面ABCD ，平面CDH 平面ABCD CD =，OH ⊂平面CDH ，OH ∴⊥平面ABCD ，在图1中，设正方形EFGH 的边长为()220a a >，可得四边形ABCD 的边长为2a ，在图1中，ADE 和ABF 均为等腰直角三角形，可得45BAF DAE ∠=∠=， 90BAD ∴∠=，∴四边形ABCD 是边长为2a 的正方形，O 、M 分别为CD 、AB 的中点，则//OC BM 且OC BM =，且90OCB ∠=，所以，四边形OCBM 为矩形，所以，OM CD ⊥，以点O 为坐标原点，OM 、OC 、OH 所在直线分别为x 、y 、z 轴建立空间直角坐标系，则()2,,0A a a -、()2,,0B a a 、()0,,0C a 、()0,,0D a -、(),,E a a a -、()2,0,F a a 、(),,G a a a 、()0,0,H a .对于A 选项，由空间中两点间的距离公式可得2AE AF EF a ===，所以，AEF 是正三角形，A 选项正确；对于B 选项，设平面AEF 的法向量为()111,,m x y z =，(),0,AE a a =-，()0,,AF a a =，由11110m AE ax az m AF ay az ⎧⋅=-+=⎪⎨⋅=+=⎪⎩，取11z =，则11x =，11y =-，则()1,1,1m =-，设平面CGH 的法向量为()222,,n x y z =，(),0,CG a a =，()0,,CH a a =-，由222200n CG ax az n CH ay az ⎧⋅=+=⎪⎨⋅=-+=⎪⎩，取21z =-，可得21x =，21y =-，则()1,1,1n =--，()22111110m n ⋅=+--⨯=≠，所以，平面AEF 与平面CGH 不垂直，B 选项错误；对于C 选项，6cos ,23CG m CG m a CG m⋅<>===⨯⋅，设直线CG 与平面AEF 所成角为θ，则sin 6θ=，23cos 1sin θθ=-=，所以，sin tan 2cos θθθ==，C 选项正确；对于D 选项，以ABCD 为底面，以OH 为高将几何体ABCD EFGH -补成长方体1111ABCD A B C D -，则E 、F 、G 、H 分别为11A D 、11A B 、11B C 、11C D 的中点，因为2AB =，即1a =，则1OH =，长方体1111ABCD A B C D -的体积为2214V =⨯=，11211111113326A A EF A EF V S AA -=⋅=⨯⨯⨯=△，因此，多面体ABCD EFGH -的体积为111044463ABCD EFGH A A EF V V V --=-=-⨯=， D 选项错误. 故选：AC. 【点睛】方法点睛：计算线面角，一般有如下几种方法：（1）利用面面垂直的性质定理，得到线面垂直，进而确定线面角的垂足，明确斜线在平面内的射影，即可确定线面角；（2）在构成线面角的直角三角形中，可利用等体积法求解垂线段的长度h ，从而不必作出线面角，则线面角θ满足sin hlθ=（l 为斜线段长），进而可求得线面角；（3）建立空间直角坐标系，利用向量法求解，设a 为直线l 的方向向量，n 为平面的法向量，则线面角θ的正弦值为sin cos ,a n θ=<>.2．已知三棱锥A BCD -的三条侧棱AB ，AC ，AD 两两垂直，其长度分别为a ，b ，c ．点A 在底面BCD 内的射影为O ，点A ，B ，C ，D 所对面的面积分别为A S ，B S ，C S ，D S ．在下列所给的命题中，正确的有（） A ．2A BCO D S SS ⋅=； B ．3333A B C D S S S S <++；C ．若三条侧棱与底面所成的角分别为1α，1β，1γ，则222111sin sin sin 1αβγ++=；D ．若点M 是面BCD 内一个动点，且AM 与三条侧棱所成的角分别为2α，2β，2γ，则22cos α+2222cos cos 1βγ+=．【答案】ACD 【分析】由Rt O OA '与Rt O AD '相似，得边长关系，进而判断A 正确；当M 与O 重合时，注意线面角与线线角的关系，即可得C 正确；构造长方体，建立直角坐标系，代入夹角公式计算可得D 正确；代入特殊值，可得B 错误. 【详解】由三棱锥A BCD -的三条侧棱AB ，AC ，AD 两两垂直，则将三棱锥A BCD -补成长方体ABFC DGHE -，连接DO 并延长交BC 于O '，则AO BC ⊥．对A ：由Rt O OA '与Rt O AD '相似，则2O A O O O D '''=⨯又12A S BC O D '=⋅，12BCOS BC O O '=⋅， 22221124DS BC O A BC O A ⎛⎫''=⋅=⋅ ⎪⎝⎭所以2A BCOD S SS ⋅=，故A 正确．对B ：当1a b c ===时，33318B C D S S S ===，则33338B C D S S S ++=，而332333322288A S ⎛⎫=⨯⨯=> ⎪ ⎪⎝⎭，此时3333A B C D S S S S >++，故B 不正确．对D ：分别以AB ，AC ，AD 为x ，y ，z 轴，建立空间直角坐标系．设(),,M x y z ，则(),,AM x y z =，222AM x y z =++，(),0,0AB a =，()0,,0AC b =，()0,0,AD c =所以222222222cos cos cos AM AB AM AC AM AD AM ABAM ACAM ADαβγ⎛⎫⎛⎫⎛⎫⋅⋅⋅++=++ ⎪ ⎪ ⎪ ⎪⎪⎪⋅⋅⋅⎝⎭⎝⎭⎝⎭2222221x y z AMAMAM=++=，所以D 正确．对C ：当M 与O 重合时，AO ⊥面BCD ，由D 有222222cos cos cos 1αβγ++=，由各侧棱与底面所成角与侧棱与所AO 成角互为余角，可得C 正确．故选：ACD.【点睛】关键点睛：本题考查空间线面角、线线角、面积关系的问题，计算角的问题关键是建立空间直角坐标系，写出点的坐标，利用数量积的公式代入计算，解决这道题目还要结合线面角与线线角的关系判断.3．如图所示，正三角形ABC中，D，E分别为边AB，AC的中点，其中AB＝8，把△ADE 沿着DE翻折至A'DE位置，使得二面角A'-DE-B为60°，则下列选项中正确的是（）A．点A'到平面BCED的距离为3B．直线A'D与直线CE所成的角的余弦值为5 8C．A'D⊥BDD．四棱锥A'-BCED237【答案】ABD【分析】作AM⊥DE，交DE于M,延长AM交BC于N,连接A'M,A'N.利用线面垂直的判定定理判定CD⊥平面A'MN,利用面面垂直的判定定理与性质定理得到'A到平面面BCED的高A'H,并根据二面角的平面角，在直角三角形中计算求得A'H的值，从而判定A;根据异面直线所成角的定义找到∠A'DN就是直线A'D与CE所成的角，利用余弦定理计算即可判定B;利用勾股定理检验可以否定C;先证明底面的外接圆的圆心为N,在利用外接球的球心的性质进行得到四棱锥A'-BCED的外接球的球心为O,则ON⊥平面BCED,且OA'=OC,经过计算求解可得半径从而判定D.【详解】如图所示，作AM⊥DE，交DE于M,延长AM交BC于N,连接A'M,A'N.则A'M⊥DE,MN⊥DE, ,∵'A M∩MN=M,∴CD⊥平面A'MN,又∵CD⊂平面ABDC,∴平面A'MN⊥平面ABDC,在平面A'MN中作A'H⊥MN,则A'H⊥平面BCED,∵二面角A'-DE-B为60°，∴∠A'EF=60°，∵正三角形ABC中，AB=8,∴AN=43∴A'M3,∴A'H=A'M sin60°=3，故A正确；连接DN,易得DN‖EC,DN=EC=4,∠A'DN就是直线A'D与CE所成的角，DN=DA'=4,A'N=A'M3,cos∠A'DN=22441252448+-=⨯⨯,故B正确；A'D =DB =4,A'B=22121627A N BN +=+=',∴222A D DB A B '≠'+,∴A'D 与BD 不垂直，故C 错误’ 易得NB =NC =ND =NG =4，∴N 为底面梯形BCED 的外接圆的圆心，设四棱锥A'-BCED 的外接球的球心为O ,则ON ⊥平面BCED ,且OA'=OC , 若O 在平面BCED 上方，入图①所示：设ON =x ,外接球的半径为R ,过O 作A'H 的垂线，垂足为P ,则HP =x ,易得()()22222433x x R +=-+=,解得23x =-,舍去；故O 在平面BCED 下方，如图②所示：设ON =x ,外接球的半径为R ,过O 作A'H 的垂线，垂足为P , 则HP =x ,易得()()22222433x x R +=++=, 解得23x =, ∴244371699R ⨯=+=,237R ∴=,故D 正确. 故选:ABD .【点睛】本题考查立体几何中的折叠问题，涉及二面角问题，异面直线所成的角，用到线面、面面垂直的判定与性质及外接球的球心的性质和有关计算，余弦定理等，属综合性较强的题目，关键是利用线面垂直，面面垂直的判定和性质进行空间关系和结构的判定，注意球心在四棱锥的底面上方和下方的讨论与验证.4．在棱长为1的正方体1111ABCD A B C D -中，P 为底面ABCD 内（含边界）一点．（） A ．若13A P P 点有且只有一个 B ．若12A P ，则点P 的轨迹是一段圆弧 C ．若1//A P 平面11B D C ，则1A P 2D ．若12A P 且1//A P 平面11B DC ，则平面11A PC 截正方体外接球所得截面的面积为23π【答案】ABD 【分析】选项A ，B 可利用球的截面小圆的半径来判断；由平面1//A BD 平面11B D C ，知满足1//A P 平面11B D C 的点P 在BD 上，1A P 2P 与B 或D 重合，利用12sin 60A P r =︒，求出6r =，进而求出面积. 【详解】对A 选项，如下图：由13A P =P 在以1A 3的球上，又因为P 在底面ABCD 内（含边界），底面截球可得一个小圆，由1A A ⊥底面ABCD ，知点P 的轨迹是在底面上以A 为圆心的小圆圆弧，半径为22112r A P A A =-=C满足，故A 正确；对B 选项，同理可得点P 在以A 为圆心，半径为22111r A P A A =-=的小圆圆弧上，在底面ABCD 内（含边界）中，可得点P 轨迹为四分之一圆弧BD .故B 正确；对C 选项，移动点P 可得两相交的动直线与平面11B D C 平行，则点P 必在过1A 且与平面11B D C 平行的平面内，由平面1//A BD 平面11B D C ，知满足1//A P 平面11B D C 的点P 在BD上，则1A P 长的最大值为12A B =，则C 不正确；对选项D ，由以上推理可知，点P 既在以A 为圆心，半径为1的小圆圆弧上，又在线段BD 上，即与B 或D 重合，不妨取点B ，则平面11A PC 截正方体外接球所得截面为11A BC 的外接圆，利用2126622,,sin 60333A B r r S r ππ==∴=∴==︒.故D 正确.故选：ABD 【点睛】（1）平面截球所得截面为圆面，且满足222=R r d +（其中R 为球半径，r 为小圆半径，d 为球心到小圆距离）；（2）过定点A 的动直线平行一平面α，则这些动直线都在过A 且与α平行的平面内.5．已知四面体ABCD 的所有棱长均为2，则下列结论正确的是（） A ．异面直线AC 与BD 所成角为60︒B ．点A 到平面BCD 的距离为3C ．四面体ABCDD ．动点P 在平面BCD 上，且AP 与AC 所成角为60︒，则点P 的轨迹是椭圆【答案】BC 【分析】在正四面体中通过线面垂直可证得AC ⊥BD ，通过计算可验证BC,通过轨迹法可求得P 的轨迹为双曲线方程即可得D 错误. 【详解】取BD 中点E ,连接,AE CE ,可得BD ⊥面ACE ,则AC ⊥BD ,故A 错误；在四面体ABCD 中，过点A 作AF ⊥面BCD 于点F ,则F 为为底面正三角形BCD 的重心，因为所有棱长均为2,AF ==即点A 到平面BCD ,故B 正确；设O 为正四面体的中心则OF 为内切球的半径，OA 我外接球的半径，因为11433A BCD BCD BCD V S AF S OF -=⋅=⨯⋅△△，所以4AF OF =，即OF AO =所以四面体ABCD 的外接球体积334433V R OA ππ===,故C 正确；建系如图：0,0,,0,,033A C ⎛⎛⎫⎪ ⎪⎝⎭⎝⎭,设(,,0)P x y ，则,,AP x y AC →→⎛⎛== ⎝⎭⎝⎭，因为cos 60AP AC AP AC →→→→⋅=24192y +=，即833y +，平方化简可得：2240039y x y ---，可知点P 的轨迹为双曲线,故D 错误. 故选：BC ．【点睛】方法点睛：立体几何中动点轨迹的求解问题，解决此类问题可采用空间向量法，利用空间向量法表示出已知的角度或距离的等量关系，从而得到轨迹方程.6．如图，已知四棱锥P ABCD -所有棱长均为4，点M 是侧棱PC 上的一个动点（不与点,P C 重合），若过点M 且垂直于PC 的截面将该四棱锥分成两部分，则下列结论正确的是（）A ．截面的形状可能为三角形、四边形、五边形B ．截面和底面ABCD 所成的锐二面角为4π C ．当1PM =时，截面的面积为52D ．当2PM =时，记被截面分成的两个几何体的体积分别为()1212,>V V V V ，则123=V V 【答案】BCD 【分析】点M 是侧棱PC 上的一个动点，根据其不同位置，对选项逐一进行判断即可. 【详解】A 选项中，如图，连接BD ，当M 是PC 中点时，2MC =，由题意知三角形PDC 与三角形PBC 都是边长为4的正三角形，所以DM PC ⊥,BM BC ⊥，又DM ，BM 在面MBD 内，且相交，所以PC ⊥平面PBD ，三角形MBD 即为过点M 且垂直于PC 的截面，此时是三角形，点M 向下移动时，2MC <，如图，仍是三角形；若点M 由中点位置向上移动，2MC >，在平面PDC 内作EM PC ⊥，交PD 于E ，在平面PBC 内作FM PC ⊥交PB 于F ，平面MEF 交平面PAD 于EG ，交PAB 于FH ，即交平面ABCD 于GH ，则五边形MEGHF 即为过点M 且垂直于PC 的截面，此时是五边形；故截面的形状可能为三角形、五边形，A 错误；B 选项中，因为截面总与PC 垂直，所以不同位置的截面均平行，截面与平面ABCD 所成的锐角为定值，不妨取M 是中点，连接AC ，BD ，MB ，MD ，设AC ，BD 交点是N ，连接PN ，由题意知，四边形ABCD 是边长为4的菱形，BD AC ⊥，因为MB =MD ，所以MN BD ⊥，故MNC ∠是截面与平面ABCD 所成的锐角，过点M 作MQ AC ⊥，垂足Q.在三角形PAC中，MN =2，NQ=2，故在直角三角形MNQ 中，2cos 2NQ MNC MN ∠==，故4MNC π∠=，故B 正确；C 选项中，当PM =1时，M 是PC 中点，如图，五边形MEGHF 即为过点M 且垂直于PC 的截面，依题意，直角三角形PME 中，2cos PMPE EPM==∠，故E 为PD 的中点，同理，F是PB 的中点，则EF 是三角形PBD 的中位线，1222EF BD ==，G ，H 分别在,AD AB 的中点上，证明如下，当G ，H ，也是中点时，1//,2GH BD GH BD =，有//,22GH EF GH EF ==，四边形EFHG 是平行四边形.依题意，三角形PAC 中4,42PA PC AC ===，故PA PC ⊥，故PC GE ⊥，易见，正四棱锥中BD ⊥平面PAC ，故BD PC ⊥，GH PC ∴⊥，因为 ,GE GH 均在平面EFHG 内，且相交，所以PC ⊥平面EFHG ，故此时平面EFHG 和平面MEF 即同一平面.又BD ⊥平面PAC ，有GH ⊥面平面PAC ，GH GM ⊥，根据对称性有GH GE ⊥，四边形EFHG 是矩形. 即五边形MEGHF 即为过点M 且垂直于PC 的截面，平面图如下:依题意，22GH EF ==2EG FG ==，三角形高为()()22321h =-=，面积是122122⨯=，四边形面积是22242=，故截面面积是52 故C 正确；D 选项中，若PM =2，看B 选项中的图可知，21124M BCD P BCD P ABCD V V V V ---===，故剩余部分134P ABCD V V -=，所以123=V V ，故D 正确.故选：BCD. 【点睛】本题考查了棱锥的截面问题，考查了二面角、体积等计算问题，属于难题.7．已知棱长为1的正方体1111ABCD A B C D -，过对角线1BD 作平面α交棱1AA 于点E ，交棱1CC 于点F ，以下结论正确的是（） A ．四边形1BFD E 不一定是平行四边形 B ．平面α分正方体所得两部分的体积相等 C ．平面α与平面1DBB 不可能垂直 D ．四边形1BFD E 面积的最大值为2 【答案】BD 【分析】由平行平面的性质可判断A 错误;利用正方体的对称性可判断B 正确;当E ､F 为棱中点时,通过线面垂直可得面面垂直,可判断C 错误;当E 与A 重合,F 与1C 重合时,四边形1BFD E 的面积最大,且最大值为2,可判断D 正确. 【详解】如图所示,对于选项A,因为平面1111//ABB A CC D D ,平面1BFD E 平面11ABB A BE =,平面1BFD E平面111CC D D D F =,所以1//BE D F ,同理可证1//D E BF ,所以四边形1BFD E 是平行四边形,故A 错误; 对于选项B,由正方体的对称性可知,平面α分正方体所得两部分的体积相等,故B 正确; 对于选项C,在正方体1111ABCD A B C D -中,有1,AC BD AC BB ⊥⊥, 又1BD BB B ⋂=,所以AC ⊥平面1BB D , 当E ､F 分别为棱11,AA CC 的中点时, 有//AC EF ,则EF ⊥平面1BB D , 又因为EF ⊂平面1BFD E ,所以平面1BFD E ⊥平面1BB D ,故C 错误;对于选项D,四边形1BFD E 在平面ABCD 内的投影是正方形ABCD , 当E 与A 重合,F 与1C 重合时,四边形1BFD E 的面积有最大值,此时1212S D E BE =⋅=⋅=,故D 正确; 故选:BD. 【点睛】本题考查了正方体的几何性质与应用问题,也考查了点线面的位置关系应用问题,属于中档题.8．如图，矩形ABCD 中，M 为BC 的中点，将ABM 沿直线AM 翻折成1AB M ，连结1B D ，N 为1B D 的中点，则在翻折过程中，下列说法中所有正确的是（）A ．存在某个位置，使得CN AB ⊥ B ．翻折过程中，CN 的长是定值C ．若AB BM =，则1AM BD ⊥D ．若1AB BM ==，当三棱锥1B AMD -的体积最大时，三棱锥1B AMD -的外接球的表面积是4π 【答案】BD 【分析】对于选项A ，取AD 中点E ，取1AB 中点K ，连结KN ，BK ，通过假设CN AB ⊥，推出AB ⊥平面BCNK ，得到AB BK ⊥，则22AK AB BK AB =+>，即可判断；对于选项B ，在判断A 的图基础上，连结EC 交MD 于点F ，连结NF ，易得1NEC MAB ∠=∠，由余弦定理，求得CN 为定值即可；对于选项C ，取AM 中点O ，1B O ，DO ，由线面平行的性质定理导出矛盾，即可判断；对于选项D ，易知当平面1AB M 与平面AMD 垂直时，三棱锥1B AMD -的体积最大，说明此时AD 中点E 为外接球球心即可. 【详解】如图1，取AD 中点E ，取1AB 中点K ，连结EC 交MD 于点F ，连结NF ，KN ，BK ,则易知1//NE AB ，1//NF B M ，//EF AM ，//KN AD ，112NE AB =，EC AM = 由翻折可知，1MAB MAB ∠=∠，1AB AB =，对于选项A ，易得//KN BC ，则K 、N 、C 、B 四点共面，由题可知AB BC ⊥，若CN AB ⊥，可得AB ⊥平面BCNK ，故AB BK ⊥，则22AK AB BK AB =+>，不可能，故A 错误；对于选项B ，易得1NEC MAB ∠=∠，在NEC 中，由余弦定理得222cos CN CE NE NE CE NEC =+-⋅⋅∠，整理得222212422AB AB AB CN AM AM BC AB AM =+-⋅⋅=+，故CN 为定值，故B 正确；如图2，取AD 中点E ，取AM 中点O ，连结1B E ，OE ，1B O ，DO ，，对于选项C ，由AB BM =得1B O AM ⊥，若1AM B D ⊥，易得AM ⊥平面1B OD ，故有AM OD ⊥，从而AD MD =，显然不可能，故C 错误；对于选项D ，由题易知当平面1AB M 与平面AMD 垂直时，三棱锥B 1﹣AMD 的体积最大，此时1B O ⊥平面AMD ，则1B O OE ⊥，由1AB BM ==，易求得122BO =，2DM =22221122122B E OB OE ⎛⎫⎛⎫=+=+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，因此1EB EA ED EM ===，E 为三棱锥1B AMD -的外接球球心，此外接球半径为1，表面积为4π，故D 正确. 故选：BD. 【点睛】本题主要考查了立体几何中的翻折问题以及空间图形的位置关系，考查了空间想象能力，属于较难题.9．已知正四棱柱1111ABCD A B C D -的底面边长为2，侧棱11AA =，P 为上底面1111D C B A 上的动点，给出下列四个结论中正确结论为（）A ．若3PD =，则满足条件的P 点有且只有一个B ．若3PD =，则点P 的轨迹是一段圆弧C ．若PD ∥平面1ACB ，则DP 长的最小值为2D ．若PD ∥平面1ACB ，且3PD =，则平面BDP 截正四棱柱1111ABCD A B C D -的外接球所得平面图形的面积为94π 【答案】ABD 【分析】若3PD =，由于P 与1B 重合时3PD =，此时P 点唯一；()313PD =∈，，则12PD =，即点P 的轨迹是一段圆弧；当P 为11A C 中点时，DP 有最小值为3=，可判断C ；平面BDP 截正四棱柱1111ABCD A B C D -的外接球所得平面图形为外接球的大圆，其半径为32=，可得D . 【详解】如图：∵正四棱柱1111ABCD A B C D -的底面边长为2， ∴1122B D =11AA =， ∴()2212213DB =+=，则P 与1B 重合时3PD =，此时P 点唯一，故A 正确；∵()313PD =∈，，11DD =，则12PD =，即点P 的轨迹是一段圆弧，故B 正确；连接1DA ，1DC ，可得平面11//A DC 平面1ACB ，则当P 为11A C 中点时，DP 有最小值为()22213+=，故C 错误；由C 知，平面BDP 即为平面11BDD B ，平面BDP 截正四棱柱1111ABCD A B C D -的外接球所得平面图形为外接球的大圆，其半径为2221322122++=，面积为94π，故D 正确．故选：ABD ．【点睛】本题考查了立体几何综合，考查了学生空间想象，逻辑推理，转化划归，数学运算的能力，属于较难题.10．如图，1111ABCD A B C D -为正方体，下列结论中正确的是（）A ．11A C ⊥平面11BB D D B ．1BD ⊥平面1ACBC ．1BD 与底面11BCC B 2 D ．过点1A 与异面直线AD 与1CB 成60角的直线有2条【答案】ABD 【分析】由直线与平面垂直的判定判断A 与B ；求解1BD 与底面11BCC B 所成角的正切值判断C ；利用空间向量法可判断D ．【详解】对于A 选项，如图，在正方体1111ABCD A B C D -中，1BB ⊥平面1111D C B A ，11A C ⊂平面1111D C B A ，则111BB A C ⊥，由于四边形1111D C B A 为正方形，则1111AC B D ⊥， 1111BB B D B =，因此，11A C ⊥平面11BB D D ，故A 正确；对于B 选项，在正方体1111ABCD A B C D -中，1DD ⊥平面ABCD ，AC ⊂平面ABCD ，1AC DD ∴⊥，因为四边形ABCD 为正方形，所以，AC BD ⊥，1D DD BD =，AC ∴⊥平面11BB D D ， 1BD ⊂平面11BB D D ，1AC BD ∴⊥，同理可得11BD B C ⊥，1ACB C C =，1BD ∴⊥平面1ACB ，故B 正确；对于C 选项，由11C D ⊥平面11BCC B ，得11C BD ∠为1BD 与平面11BCC B 所成角，且111112tan 2C D C BD BC ∠==，故C 错误；对于D 选项，以点D 为坐标原点，DA 、DC 、1DD 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系，设正方体的棱长为1，则()1,0,0A 、()0,0,0D 、()0,1,0C 、()11,1,1B ，()1,0,0DA =，()11,0,1CB =，设过点1A 且与直线DA 、1CB 所成角的直线的方向向量为()1,,m y z =，则221cos ,21DA m DA m DA my z ⋅<>===⋅++， 1122111cos ,221CB m zCB m CB my z ⋅+<>===⋅⋅++，整理可得2222341y z y z z ⎧+=⎨=++⎩，消去y 并整理得2210z z +-=，解得12z =-12z =-由已知可得3z ≤，所以，12z =-+22y =± 因此，过点1A 与异面直线AD 与1CB 成60角的直线有2条，D 选项正确. 故选：ABD. 【点睛】方法点睛：证明线面垂直的方法：一是线面垂直的判定定理；二是利用面面垂直的性质定理；三是平行线法（若两条平行线中一条垂直于这个平面，则另一条也垂直于这个平面），解题时，注意线线、线面与面面关系的相互转化；另外，在证明线线垂直时，要注意题中隐含的垂直关系，如等腰三角形的底边上的高、中线和顶角的角平分线三线合一、矩形的内角、直径所对的圆周角、菱形的对角线互相垂直、直角三角形（或给出线段长度，经计算满足勾股定理）、直角梯形等等．。

湖南省2020届高三数学理一轮复习典型题专项训练：立体几何

湖南省2020届高三数学理一轮复习典型题专项训练立体几何一、选择、填空题1、（常德市2019届高三上学期检测）如图，网格线上小正方形的边长为1，粗实线画出的是某几何体的三视图，其正视图，侧视图均为等边三角形，则该几何体的体积为 A ．83(1)3π+ B ．43(2)π+ C ．43(2)3π+ D ．83(1)π+2、（衡阳八中2019届高三上学期第二次月考）某几何体的三视图如图所示，其中俯视图中六边形ABCDEF 是边长为1的正六边形，点G 为AF 的中点，则该几何体的外接球的表面积是（ C ）A.316π B. 318π C. 48164πD. 313148π3、（怀化市2019届高三统一模拟（二））某组合体的三视图如图所示.则该组合体的体积为 A. 4 B. 8 C.43 D. 834、（三湘名校教育联盟2019届高三第一次大联考）如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的体积为A.8B.16C.24D.485、（邵阳市2019届高三10月大联考）已知三棱锥P ABCA B C在球O的同一个-底面的3个顶点,,大圆上，且ABC-体积的最大值为23，则球△为正三角形，P为该球面上的点，若三棱锥P ABCO的表面积为( )A.12πB.16πC.32πD.64π6、（五市十校教研教改共同体2019届高三12月联考）已知E，F分别是三棱锥P ABC-的棱AP，EF=，则异面直线AB与PC所成的角为（）PC=，33BC的中点，6AB=，6A.120︒B.45︒C.30︒D.60︒7、（湘潭市2019届高三下学期第二次模拟）某几何体的三视图如图所示，则该几何体的体积为（）A. B. C. D.8、（益阳市2019届高三上学期期末考试）如图，—个圆柱从上部挖去半球得到几何体的正视图、侧28，则x =视图都是图1，俯视图是图2，若得到的几何体表面积为A.3B. 4C.5D.69、（永州市2019届高三上学期第二次模拟）如图，在正方体中，点在线段上运动，则下列判断中正确的是（）①平面平面；②直线平面；③异面直线与所成角的取值范围是；④三棱锥的体积不变.A. ① ②B. ①②④C. ③④D. ①④10、（岳阳市2019届高三教学质量检测（一模））个几何体的三视图如右图所示，已知这个几何10，则h为体的体积为3A. 23B.3 C. 33 D. 3511、（长郡中学2019届高三第六次月考）在三棱锥 P —ABC 中，PA 丄平面 ABC ，∠BAC =32π，AP=3，AB =32, Q 是边BC 上的一动点，且直线PQ 与平面ABC 所成角的最大值为3π，则三棱锥P —ABC 的外接球的表面积为A.π45B.π57C. π63D. π8412、（雅礼中学2019届高三第五次月考）如图1所示，是一个棱长为2的正方体被削去一个角后所得到的几何体的直观图，其中DD 1＝1，若此几何体的俯视图如图2所示，则可以作为其正视图的是13、（株洲市2019届高三教学质量统一检测（一））已知正方体1111ABCD A B C D -的棱长为2，M 为CC 1的中点．若AM ⊥平面α，且B ∈平面α，则平面α截正方体所得截面的周长为（）A ．32+25B ． 4+42C ． 22+25D ．6214、（湖南师大附中2019届高三月考试卷（六））正四棱锥S －ABCD 的侧棱长与底面边长相等，E 为SC 的中点，则BE 与SA 所成角的余弦值为(C)A.13B.12C.33D.3215、（湖南湖北八市十二校（湖南师范大学附属中学、衡阳八中等）2019届高三第二次调研联考）已知三棱锥的四个顶点都在半径为3的球面上，，则该三棱锥体积的最大值是A ．B ．C ．D ． 6416、（湖南师大附中2019届高三月考试卷（六））已知三棱锥P －ABC 的四个顶点均在某球面上，PC 为该球的直径，△ABC 是边长为4的等边三角形，三棱锥P －ABC 的体积为163，则此三棱锥的外接球的表面积为__80π3__．参考答案：1、C2、C3、D4、B5、B6、D7、A8、B9、B 10、B 11、12、C 13、A 14、【解析】如图，设AC ∩BD ＝O ，连接OE ，因为OE 是△SAC 的中位线，故EO ∥SA ，则∠BEO 为BE 与SA 所成的角．设SA ＝AB ＝2a ，则OE ＝12SA ＝a ，BE ＝32SA ＝3a ，OB ＝22SA ＝2a ，所以△EOB 为直角三角形，所以cos ∠BEO ＝OE BE ＝a 3a ＝33，故选C.15、A 16、【解析】依题意，记三棱锥P －ABC 的外接球的球心为O ，半径为R ，点P 到平面ABC 的距离为h ，则由V P －ABC ＝13S △ABC h ＝13×⎝⎛⎭⎫34×42×h ＝163得h ＝433.又PC 为球O 的直径，因此球心O 到平面ABC 的距离等于12h ＝233.又正△ABC 的外接圆半径为r ＝AB 2sin 60°＝433，因此R 2＝r 2＋⎝⎛⎭⎫2332＝203，所以三棱锥P －ABC 的外接球的表面积为4πR 2＝80π3.二、解答题1、（常德市2019届高三上学期检测）如图，在直三棱柱111C B A ABC -中，21111==C A B A ，321=CC ， ︒=∠120BAC ，O 为线段11C B 的中点，P 为线段1CC 上一动点（异于点1C C 、），Q 为线段BC 上一动点，且OP QP ⊥；（Ⅰ）求证：平面1A PQ ^平面1A OP ；（Ⅱ）若PQ BO //，求直线OP 与平面PQ A 1所成角的正弦值.2、（衡阳八中2019届高三上学期第二次月考）如图，已知AB ⊥平面ACD ，DE ⊥平面ACD ，△ACD 为等边三角形，AD ＝DE ＝2AB ，F 为CD 的中点. (1)求证：AF ∥平面BCE ；(2)求二面角C －BE －D 的余弦值的大小.3、（怀化市2019届高三统一模拟（二））如图，在四棱锥P-ABCD 中，PC ⊥底面A BCD ，底面ABCD 是直角梯形，AB ⊥AD ，AB //CD ，AB=2AD=2CD=4，PC=4. (1)证明：当点E 在PB 上运动时，始终有平面EAC ⊥平面PBC (2)求锐二而角A- PB-C 的余弦值.4、（三湘名校教育联盟2019届高三第一次大联考）如图，四棱锥P-ABCD 中，底面ABCD 为正方形，PA 丄底面ABCD,且PA=2AB ，F 是AB 的中点，点E 在线段PC 上，且PE ＝PC 31. （1）证明：平面DEF 丄平面ABCD; （2）求二面角B-AE-D 的余弦值.5、（邵阳市2019届高三10月大联考）如图，菱形ABCD 的边长为4，60DAB =∠°，矩形BDFE 的面积为8，且平面BDFE ⊥平面ABCD .(1)证明：AC BE ⊥；(2)求二面角E AF D --的正弦值.6、（五市十校教研教改共同体2019届高三12月联考）如图，四棱锥P ABCD -中，PA ⊥底面ABCD ，底面ABCD 为直角梯形，90CDA BAD ∠=∠=︒，222AB AD DC ===E ，F 分别为PD ，PB 的中点.（1）求证：//CF 平面PAD ；（2）若截面CEF 与底面ABCD 所成锐二面角为4，求PA 的长度.7、（湘潭市2019届高三下学期第二次模拟）如图，四棱锥的底面是直角梯形，，，和是两个边长为2的正三角形，，为的中点，为的中点.（1）证明：平面.（2）在线段上是否存在一点，使直线与平面所成角的正弦值为？若存在，求出点的位置；若不存在，说明理由.8、（益阳市2019届高三上学期期末考试）五面体ABCDEF 中，ADEF 是等腰梯形,AD = 2,AB=2,AF=FE = ED=BC = 1，∠SAD=900，平面 BAF 丄平面 ADEF 。

高三数学训练：立体几何(附答案)

四川省2019届高三数学理一轮复习典型题专项训练立体几何一、选择、填空题1、（2018全国III 卷高考）中国古建筑借助榫卯将木构件连接起来，构件的凸出部分叫棒头，凹进部分叫卯眼，图中木构件右边的小长方体是棒头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是（）2、（2017全国III 卷高考）已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为（） A ．πB ．3π4C ．π２D ．π43、（2016全国III 卷高考）如图，网格纸上小正方形的边长为1，粗实现画出的是某多面体的三视图，则该多面体的表面积为（A ）18365+ （B ）54185+ （C ）90 （D ）814、（成都市2018届高三第二次诊断）已知m ，是空间中两条不同的直线，α，β为空间中两个互相垂直的平面，则下列命题正确的是（）A ．若m α⊂，则m β⊥B ．若m α⊂，n β⊂，则m n ⊥C ．若m α⊄，m β⊥，则//m αD ．若m αβ=，n m ⊥，则n α⊥5、（成都市2018届高三第三次诊断）在正三棱柱111ABC A B C - (底面是正三角形,侧棱垂直于底面的棱柱)中，所有棱长之和为定值a .若正三棱柱111ABC A B C -的顶点都在球O 的表面上，则当正三棱柱侧面积取得最大值24时，该球的表面积为（） A ．43π B ．323π C ．12π D ．643π6、（达州市2017届高三第一次诊断）如图某几何体的三视图是直角边长为1的三个等腰直角三角形，则该几何体的外接球的表面积为（） A ．32π B ．3π C ．32π D ．3π7、（德阳市2018届高三二诊考试）如图所示的三视图表示的几何体的体积为323，则该几何体的外接球的表面积为（）A ．12πB ．24πC ．36πD ．48π8、（广元市2018届高三第一次高考适应性统考）设,m n 是两条不同的直线，,αβ是两个不同的平面，且,m n αβ⊂⊂，下列命题中正确的是（）A ．若αβ⊥，则m n ⊥B ．若//αβ，则//m nC ．若m n ⊥，则αβ⊥D ．若n α⊥，则αβ⊥9、（泸州市2018届高三第二次教学质量诊断）设a ，b 是两条不同的直线，α、β是不重合的两个平面，则下列命题中正确的是A ．若a b ⊥，a α⊥，则//b αB ．若//a α，αβ⊥，则//a βC ．若//a α，//a β，则//αβD ．若//a b ，a α⊥，b β⊥，则//αβ10、（南充市2018届高三第二次高考适应性考试）某三棱锥的三视图如图所示，则该三棱锥的表面积为( )A ．23472++B ．1072+ C. 710+ D ．3412+11、（仁寿县2018届高三上学期零诊）如图，正方体ABCD ﹣A 1B 1C 1D 1的棱长为1，E 为棱DD 1上的点，F 为AB 的中点，则三棱锥B 1﹣BFE 的体积为12、（遂宁市2018届高三三诊考试）在一圆柱中挖去一圆锥所得的机械部件的三视图如图所示，则此机械部件的表面积为A ．π)27(-B ．π)27(+C ．π)26(+D ．π)37(-13、（雅安市2018届高三下学期三诊）某几何体的三视图如图所示，其中，正视图、俯视图都是矩形，侧视图是直角三角形，则该几何体的体积等于（）A ．1B ．2C ．3D ．414、（资阳市2018届高三4月模拟考试（三诊））如图，二面角BC αβ--的大小为6π，AB CD αβ⊂⊂，，且2AB =，243BC CD ABC BCD ππ==∠=∠=，，，则AD 与β所成角的大小为A ．π4B ．π3 C.π6D ．π1215、（成都市石室中学高2018届高三下期二诊模拟）一个底面为正方形的四棱锥，其三视图如图所示，若这个四棱锥的体积为2 ，则此四棱锥最长的侧棱长为 .23A.11B .13C .10D16、（成都市2018届高三第二次诊断）《九章算术》中将底面为长方形，且有一条侧棱与底面垂直的四棱锥称之为“阳马”.现有一阳马，其正视图和侧视图是如图所示的直角三角形.若该阳马的顶点都在同一个球面上，则该球的体积为（）A ．863π B ．86π C ．6π D ．24π 17、（2016全国III 卷高考）在封闭的直三棱柱111ABC A B C -内有一个体积为V 的球，若AB BC ⊥，6AB =，8BC =，13AA =，则V 的最大值是（A ）4π （B ）92π（C ）6π （D ）323π二、解答题1、（2018全国III 卷高考）如图，边长为2的正方形ABCD 所在平面与半圆弧CD 所在平面垂直，M是CD 上异于C ，D 的点．⑴证明：平面AM D ⊥平面BMC ；⑵当三棱锥M ABC -体积最大时，求面MAB 与面MCD 所成二面角的正弦值．2、（2017全国III 卷高考）如图，四面体ABCD 中，△ABC 是正三角形，△ACD 是直角三角形．ABDCBD ??，AB BD =．（1）证明：平面ACD ^平面ABC ；（2）过AC 的平面交BD 于点E ，若平面AEC 把四面体ABCD 分成体积相等的两部分．求二面角D AE C --的余弦值．DABCE3、（2016全国III 卷高考）如图，四棱锥P ABC -中，PA ⊥地面A B C D ，ADBC ，3AB AD AC ===，4PA BC ==，M 为线段AD 上一点，2AM MD =，N 为PC 的中点．（I ）证明MN平面PAB ；（II ）求直线AN 与平面PMN 所成角的正弦值.4、（成都市2018届高三第二次诊断）如图，D 是AC 的中点，四边形BDEF 是菱形，平面BDEF ⊥平面ABC ，60FBD ∠=，AB BC ⊥，2AB BC ==.（1）若点M 是线段BF 的中点，证明：BF ⊥平面AMC ；（2）求平面AEF 与平面BCF 所成的锐二面角的余弦值.5、（成都市2018届高三第三次诊断）如图①,在等腰梯形ABCD 中，已知AB ∥CD ，60ABC ∠=，2CD =，4AB =，点E 为AB 的中点；现将三角形BEC 沿线段EC 折起，形成直二面角P EC A --,如图②，连接,PA PD 得四棱锥P AECD -，如图③.（I ）求证：PD EC ⊥；（Ⅱ）求平面PEC 与平面PAD 所成的锐二面角的余弦值.6、（达州市2017届高三第一次诊断）如图在棱锥P ABCD -中，ABCD 为矩形，PD ⊥面ABCD ，2PB =，PB 与面PCD 成045角，PB 与面ABD 成030角.（1）在PB 上是否存在一点E ，使PC ⊥面ADE ，若存在确定E 点位置，若不存在，请说明理由；（2）当E 为PB 中点时，求二面角P AE D --的余弦值.7、（德阳市2018届高三二诊考试）如图，在四棱锥P ABCD -中，底面ABCD 为边长为2的菱形，60DAB ∠=，90ADP ∠=，面ADP ⊥面ABCD ，点F 为棱PD 的中点.（1）在棱AB 上是否存在一点E ，使得//AF 面PCE ，并说明理由；（2）当二面角D FC B --的余弦值为14时，求直线PB 与平面ABCD 所成的角.8、（广元市2018届高三第一次高考适应性统考）如图，ABC ∆是以ABC ∠为直角的三角形，SA ⊥平面,2,4,,ABC SA BC AB M N ===分别是,SC AB 的中点. （1）求证：MN AB ⊥；（2）D 为线段BC 上的点，当二面角S ND A --的余弦值为66时，求三棱锥D SNC -的体积.9、（泸州市2018届高三第二次教学质量诊断）如图，三棱锥A BCD -的侧面ABD △是等腰直角三角形，90BAD ∠=，BD DC =，120BDC ∠=，且2AC AB =．（I ）求证：平面ABD ⊥平面BCD ；（II ）求二面角B AC D --的余弦值．DCBA10、（南充市2018届高三第二次高考适应性考试）如图，四棱锥ABCD P -中，底面ABCD 是边长为2的菱形，PB PA ABC ⊥︒=∠，660,2=PC . (Ⅰ)求证：平面⊥PAB 平面 ABCD ；(Ⅱ)若PB PA =,求二面角D PC A --的余弦值.11、（仁寿县2018届高三上学期零诊）如图，直角梯形ABCD 与等腰直角三角形ABE 所在的平面互相垂直，AB ∥CD ，AB ⊥BC ，AB=2CD=2BC ，EA ⊥EB （1）求证：EA ⊥平面EBC ；（2）求二面角C ﹣BE ﹣D 的余弦值．12、（遂宁市2018届高三三诊考试）如图所示的几何体中，111C B A ABC -为三棱柱，且⊥1AA 平面ABC ，四边形ABCD 为平行四边形，︒=∠=60,2ADC CD AD ．（1）若AC AA =1，求证：1AC ⊥平面CD B A 11；（2）若12,CD AA AC λ==，二面角11C A D C --的余弦值为24，求三棱锥11C ACD -的体积．13、（雅安市2018届高三下学期三诊）如图，在四棱锥S ABCD -中，SD ⊥底面ABCD ，M 为SD 的中点，底面ABCD 为直角梯形，AB AD ⊥，//AB CD ，且222CD AB AD ===.（1）求证：//AM 平面SBC ，平面SBC ⊥平面SDB ；（2）若SB 与平面SDC 所成角的正弦值为33，求二面角A SB C --的余弦值.14、（资阳市2018届高三4月模拟考试（三诊））如图，三棱柱111ABC A B C -的各棱长均相等，1AA ⊥底面ABC ，E ，F 分别为棱1AA BC ，的中点．（1）过1FA 作平面α，使得直线BE //平面α，若平面α与直线1BB 交于点H ，指出点H 所在的位置，并说明理由；（2）求二面角1B FH A --的余弦值．15、（成都市石室中学高2018届高三下期二诊模拟）如图，在多面体ABCDEF 中，矩形BDEF 所在平面与正方形ABC D 所在平面垂直，点M 为AE 的中点. （1）求证：BM //平面EFC（2）若DE AB =，求直线AE 与平面BDM 所成角的正弦值.参考答案：一、选择、填空题 1、A 2、【答案】B【解析】由题可知球心在圆柱体中心，圆柱体上下底面圆半径2213122r ⎛⎫=-= ⎪⎝⎭，则圆柱体体积23ππ4V r h ==，故选B.3、B4、C5、【答案】D【解析】设正三棱柱111ABC A B C -底面边长为x ，侧棱为y ，则63x y a +=，三棱柱111ABC A B C -侧面积3S xy =.所以2216336224x y a S xy +⎛⎫=≤= ⎪⎝⎭，当且仅当632a x y ==，即,126a a x y ==时，等号成立，所以24a =，2x =，4y =.所以正三棱柱111ABC A B C -的外接球的球心O 到顶点A 的距离为443434+=，所以该球的表面积为643π.故选D.6、D7、C8、D9、D 10、B 11、11212、B 13、B 14、C 15、C 16、C 17、【答案】B 【解析】试题分析：要使球的体积V 最大，必须球的半径R 最大．由题意知球的与直三棱柱的上下底面都相切时，球的半径取得最大值32，此时球的体积为334439()3322R πππ==，故选B ．二、解答题1、解答：（1）∵正方形ABCD ⊥半圆面CMD ，∴AD ⊥半圆面CMD ，∴AD ⊥平面MCD .∵CM 在平面MCD 内，∴AD CM ⊥，又∵M 是半圆弧CD 上异于,C D 的点，∴CM MD ⊥.又∵AD DM D =I ，∴CM ⊥平面ADM ，∵CM 在平面BCM 内，∴平面BCM ⊥平面ADM .（2）如图建立坐标系： ∵ABC S ∆面积恒定，∴MO CD ⊥，M ABC V -最大.(0,0,1)M ，(2,1,0)A -，(2,1,0)B ，(0,1,0)C ，(0,1,0)D -,设面MAB 的法向量为111(,,)m x y z =u r ，设面MCD 的法向量为222(,,)n x y z =r， (2,1,1)MA =--，(2,1,1)MB =-，(0,1,1)MC =-，(0,1,1)MD =--，11111120(1,0,2)20x y z m x y z --=⎧⇒=⎨+-=⎩，同理(1,0,0)n =，， ∴15cos 55θ==，∴ 25sin 5θ=.2、【解析】⑴取AC 中点为O ，连接BO ，DO ；ABC ∆为等边三角形∴BO AC ⊥∴AB BC =AB BC BD BDABD DBC =⎧⎪=⎨⎪∠=∠⎩ABD CBD ∴∆≅∆. ∴AD CD =,即ACD ∆为等腰直角三角形，ADC ∠ 为直角又O 为底边AC 中点 ∴DO AC ⊥令AB a =，则AB AC BC BD a ==== 易得：22OD a =，32OB a = ∴222OD OB BD +=由勾股定理的逆定理可得2DOB π∠=即OD OB ⊥OD ACOD OB AC OB O AC ABC OB ABC⊥⎧⎪⊥⎪⎪=⎨⎪⊂⎪⊂⎪⎩平面平面OD ABC ∴⊥平面又∵OD ADC ⊂平面由面面垂直的判定定理可得ADC ABC ⊥平面平面 ⑵由题意可知V V D ACE B ACE --= 即B ,D 到平面ACE 的距离相等即E 为BD 中点以O 为原点，OA 为x 轴正方向，OB 为y 轴正方向，OD 为z 轴正方向，设AC a =，建立空间直角坐标系，则()0,0,0O ，,0,02a A ⎛⎫ ⎪⎝⎭，0,0,2a D ⎛⎫ ⎪⎝⎭，30,,02B a ⎛⎫ ⎪ ⎪⎝⎭，30,,44a E a ⎛⎫ ⎪ ⎪⎝⎭ 易得：3,,244a a AE a ⎛⎫=- ⎪ ⎪⎝⎭，,0,22a a AD ⎛⎫=- ⎪⎝⎭，,0,02a OA ⎛⎫= ⎪⎝⎭ 设平面AED 的法向量为1n ，平面AEC 的法向量为2n ，则110AE n AD n ⎧⋅=⎪⎨⋅=⎪⎩，解得()13,1,3n =DABC EODABCEyxOz220AE n OA n ⎧⋅=⎪⎨⋅=⎪⎩，解得()20,1,3n =- 若二面角D AE C --为θ，易知θ为锐角，则12127cos 7n n n n θ⋅==⋅ 3、设),,(z y x n =为平面PMN 的法向量，则⎪⎩⎪⎨⎧=⋅=⋅00PN n PM n ，即⎪⎩⎪⎨⎧=-+=-0225042z y x z x ，可取)1,2,0(=n ，于是2558|||||||,cos |=⋅=><AN n AN n AN n .4、解：（1）连接MD ，FD .∵四边形BDEF 为菱形，且60FBD ∠=，∴DBF ∆为等边三角形.∵M 为BF 的中点，∴DM BF ⊥.∵AB BC ⊥，2AB BC ==，又D 是AC 的中点， ∴BD AC ⊥. ∵平面BDEF平面ABC BD =，平面ABC ⊥平面BDEF ，AC ⊂平面ABC ，∴AC ⊥平面BDEF .又BF ⊂平面BDEF ，∴AC BF ⊥. 由DM BF ⊥，AC BF ⊥，DM AC D =，∴BF ⊥平面AMC.（2）设线段EF 的中点为N ，连接DN .易证DN ⊥平面ABC .以D 为坐标原点，DB ，DC ，DN 所在直线分别为轴，y 轴，轴建立如图所示的空间直角坐标系.则(0,1,0)A -，13(,0,)22E -，13(,0,)22F ，(1,0,0)B ，(0,1,0)C . ∴13(,1,)22AE =-，(1,0,0)EF =，13(,0,)22BF =-，(1,1,0)BC =-.设平面AEF ，平面BCF 的法向量分别为111(,,)m x y z =，222(,,)n x y z =.由00AE m EF m ⎧⋅=⎪⎨⋅=⎪⎩111113022102x y z x ⎧-++=⎪⎪⇒⎨⎪=⎪⎩.解得1132y z =-.取12z =-，∴(0,3,2)m =-.又由00BC n BF n ⎧⋅=⎪⎨⋅=⎪⎩2222013022x y x z -+=⎧⎪⇒⎨-+=⎪⎩解得223y z =. 取21z =，∴(3,3,1)n =. ∵cos ,m n <>m n m n⋅=11777==⋅.∴平面AEF 与平面BCF 所成的锐二面角的余弦值为17.5、【解析】6、1)法一：要证明PC ⊥面ADE ，易知AD ⊥面PDC ，即得AD ⊥PC ，故只需0DE PC ⋅=即可，所以由()00||1DP PE PC DP PC PE PC PE +⋅=⇒⋅+⋅=⇒=,即存在点E 为PC 中点 …6分法二：建立如图所示的空间直角坐标系D －XYZ ，由题意知PD ＝CD ＝1， 2CE =，设PE PB λ=， (2,1,1)PE PB λλ∴==-，(0,1,1)PC =-由()(0,1,1)(2,,1)0PC DE PC DP PE λλλ⋅=⋅+=-⋅-=，得12λ=，即存在点E 为PC 中点。

高考数学一轮复习立体几何知识点

高考数学一轮复习立体几何知识点数学上，立体几何是3维欧氏空间的几何的传统名称，查字典数学网小编整理了2021年高考数学一轮复习立体几何知识点，期望对考生复习有关心。

1.平面的差不多性质：把握三个公理及推论，会说明共点、共线、共面问题。

能够用斜二测法作图。

2.空间两条直线的位置关系：平行、相交、异面的概念;会求异面直线所成的角和异面直线间的距离;证明两条直线是异面直线一样用反证法。

3.直线与平面①位置关系：平行、直线在平面内、直线与平面相交。

②直线与平面平行的判定方法及性质,判定定理是证明平行问题的依据。

③直线与平面垂直的证明方法有哪些?④直线与平面所成的角：关键是找它在平面内的射影，范畴是⑤三垂线定理及其逆定理：每年高考试题都要考查那个定理. 三垂线定理及其逆定理要紧用于证明垂直关系与空间图形的度量.如：证明异面直线垂直，确定二面角的平面角，确定点到直线的垂线.4.平面与平面(1)位置关系：平行、相交，(垂直是相交的一种专门情形)(2)把握平面与平面平行的证明方法和性质。

(3)把握平面与平面垂直的证明方法和性质定理。

专门是已知两平面垂直，一样是依据性质定理，能够证明线面垂直。

(4)两平面间的距离问题点到面的距离问题(5)二面角。

二面角的平面交的作法及求法：①定义法，一样要利用图形的对称性;一样在运算时要解斜三角形;要练说，得练看。

看与说是统一的，看不准就难以说得好。

练看，确实是训练幼儿的观看能力，扩大幼儿的认知范畴，让幼儿在观看事物、观看生活、观看自然的活动中，积存词汇、明白得词义、进展语言。

在运用观看法组织活动时，我着眼观看于观看对象的选择，着力于观看过程的指导，着重于幼儿观看能力和语言表达能力的提高。

②垂线、斜线、射影法，一样要求平面的垂线好找，一样在运算时要解一个直角三角形。

那个工作可让学生分组负责收集整理,登在小黑板上,每周一换。

要求学生抽空抄录同时阅读成诵。

其目的在于扩大学生的知识面,引导学生关注社会,热爱生活,因此内容要尽量广泛一些,能够分为人一辈子、价值、理想、学习、成长、责任、友谊、爱心、探究、环保等多方面。

高考数学一轮复习《空间几何体》练习题(含答案)

高考数学一轮复习《空间几何体》练习题（含答案）一、单选题1．降水量（precipitation[amount]）：从天空降落到地面上的液态或固态（经融化后）水，未经蒸发､渗透､流失，而在水平面上积聚的深度.降水量以mm 为单位，气象观测中一般取一位小数，现某地10分钟的降雨量为13.1mm ，小王在此地此时间段内用口径为10cm 的圆柱型量筒收集的雨水体积约为（）（其中π 3.14≈）A ．331.0210mm ⨯B ．331.0310mm ⨯C ．531.0210mm ⨯D ．531.0310mm ⨯2．某几何体的三视图如图所示(单位：cm )，则该几何体的表面积(单位：2cm )是（）A ．()256122cm +B ．()248162cm + C ．()280122cm + D ．()272162cm + 3．阿基米德（Archimedes ，公元前287年-公元前212年）是古希腊伟大的数学家，物理学家和天文学家，在他墓碑上刻着的一个圆柱容器里放了一个球，该球与圆柱的两个底面及侧面均相切，如图所示，则在该几何体中，圆柱表面积与球表面积的比值为（）A ．32B ．43C ．32或23D ．234．已知一个几何体的三视图如图所示，则这个几何体的表面积为（）A ．33πB ．2πC ．3πD ．4π5．某圆锥的母线长为2，高为423，其三视图如下图所示，圆锥表面上的点M 在正视图上的对应点为A ，圆锥表面上的点N 在侧视图上的对应点为B ，则在此圆锥侧面上，从M 到N 的路径中，最短路径的长度为A ．2B ．22C ．823+D ．223- 6．已知某空间几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：3cm ）是（）A ．323B ．163C ．4D ．87．已知正方体的六个面的中心可构成一个正八面体,现从正方体内部任取一个点,则该点落在这个正八面体内部的概率为（）A ．12B ．13C ．16D ．1128．某几何体的三视图如图所示，则该几何体的表面积为（）A ．810+16B ．40C ．810++24D ．489．棱长为1的正方体1111ABCD A B C D -中，点E 是侧面11CC B B 上的一个动点（包含边界），则下面结论正确的有（）①若点E 满足1AE B C ⊥，则动点E 的轨迹是线段；②若点E 满足130EA C ∠=，则动点E 的轨迹是椭圆的一部分；③在线段1BC 上存在点E ，使直线1A E 与CD ．所成的角为30；④当E 在棱1BB 上移动时，1EC ED +的最小值是352+． A ．1个 B ．2个 C ．3个 D ．4个10．某锥体的正视图和侧视图均为如图所示的等腰三角形，则该几何体的体积最小值为A ．4πB ．12C ．1D ．211．已知四棱锥S ABCD -的所有顶点都在同一球面上，底面ABCD 是正方形且和球心O 在同一平面内，当此四棱锥体积取得最大值时，其表面积等于443+，则球O 的体积等于（）A ．3223πB ．1623πC ．823πD ．423π 12．一个长方体被一平面截去一部分后，所剩几何体的三视图如图所示，则该几何体的体积为A ．36B ．48C ．64D ．72二、填空题13．如果用半径为r 的半圆形铁皮卷成一个圆锥筒，那么这个圆锥筒的高等于____． 14．点A ，B ，C ，D 在同一个球的球面上，3AB BC AC ==，若四面体ABCD 体积的3________.15．“方锥”，在《九章算术》卷商功中解释为正四棱锥.现有“方锥”S ABCD -，其中4AB =，SA 与平面ABCD 32，则此“方锥”的外接球表面积为________. 16．棱长为6的正方体内有一个棱长为x 的正四面体，正四面体的中心（正四面体的中心就是该四面体外接球的球心）与正方体的中心重合，且该四面体可以在正方体内任意转动，则x 的最大值为______．三、解答题17．如图，已知直三棱柱111ABC A B C ，其底面是等腰直角三角形，且22AB BC ==14AC AA ==.(1)求该几何体的表面积；(2)若把两个这样的直三棱柱拼成一个大棱柱，求拼得的棱柱表面积的最小值.18．如图是一个以111A B C为底面的直三棱柱被一平面所截得到的几何体，截面为ABC，已知11112A B B C==，11190A B C∠=︒，14AA=，13BB=，12CC=，求该几何体的体积．19．如图是某几何体的三视图，请你指出这个几何体的结构特征，并求出它的表面积与体积．（单位：cm）20．如图所示，在四棱锥P -ABCD 中，P A ⊥平面ABCD ，底面ABCD 是矩形，2PA AB ==，2AD =，过点B 作BE ⊥AC ，交AD 于点E ，点F ，G 分别为线段PD ，DC 的中点．(1)证明：AC ⊥平面BEF ；(2)求三棱锥F -BGE 的体积．21．如图，多面体ABCDEF 中，四边形ABCD 是边长为2的菱形，AC =23，△ADE 为等腰直角三角形，∠AED =90°，平面ADE ⊥平面ABCD ，且EF //AB ，EF =1.（1）证明：AC ⊥平面BDF ；（2）若G 为棱BF 的中点，求三棱锥G —DEF 的体积.22．如图，在三棱锥-P ABC 中，2AB BC ==，22PA PB PC AC ====，O 为AC 的中点．(1)证明：PO ⊥平面ABC ；(2)若点M 在棱BC 上，且MC ＝2MB ，求点C 到平面POM 的距离．23．如图，在三棱锥S －ABC 中，SA ＝SC ，D 为AC 的中点，SD ⊥AB ．(1)证明：平面SAC ⊥平面ABC ；(2)若△BCD 是边长为3的等边三角形，点P 在棱SC 上，PC ＝2SP ，且932S ABC V -=，求三棱锥A －PBC 的体积．24．如图，在四棱锥P ABCD -中，底面ABCD 是边长为4的菱形，60DAB ∠=︒，7PA PD ==，O F 、分别为AD AB 、的中点，PF AC ⊥.（1）求证：面POF ⊥面ABCD ；（2）求三棱锥B PCF -的体积。

【高考数学专题】立体几何中的翻折问题与最值问题专题高三一轮复习备考

立体几何中的翻折问题与最值问题一知识点导学1.解决折叠问题注意什么？折叠问题是立体几何的一个重要内容，是空间几何问题与平面几何问题相互转化的集中体现，处理这类问题的关键就是抓住折叠前后图形的特征关系。

解答折叠问题在于画好折叠前后的平面图形和立体图形，并弄清折叠前后哪些量和位置关系发生了变化，哪些量和位置关系没有发生变化，这些未发生变化的已知条件就是我们分析问题和解决问题的依据。

2立体几何常见的最值问题有哪些？如何解决？空间图形最值问题有线段、角、距离、面积、体积等最值问题，通常应注意分析题目中所有的条件，首先应该在充分理解题意的基础上，分析是否能用公理与定义直接解决题中问题;如果不能，再看是否可将问题条件转化为函数，若能写出确定的表意函数，则可用建立函数法求解;再不能，则要考虑其中是否存在不等关系，看是否能运用解等不式法求解;还不行则应考虑是否可将其体图展开成平面，这样依次顺序思考，基本可以找到解题的途径．3如何解决涉及几何体切接问题最值计算？求解与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径等.通过作截面，把空间问题转化为平面图形与圆的接、切问题，再利用平面几何知识寻找几何中元素间的关系求解．这样才能进一步将空间问题转化为平面内的问题；4解决折叠问题的步骤有哪些？二．考点典例考点一：面积、体积最值问题空间几何体的侧面积、表面积、截面面积、体积等最值问题，往往是几何体中有关几何元素如顶点、侧棱、侧面、截面等在运动变化过程中，达到某个特殊位置时所具有的度量性质。

因此，在解决此类问题时，要注意分析这些几何元素运动变化与所求量的联系，建立两者之间的数量关系。

实例演练1（2021•湖南模拟）如图所示，圆形纸片的圆心为O，半径为6cm，该纸片上的等边三角形ABC的中心为O，D，E，F为圆O上的点，DBC∆分别是∆，FAB∆，ECA以BC，CA，AB为底边的等腰三角形．沿虚线剪开后，分别以BC，CA，AB为折痕折起DBC ∆，ECA ∆，FAB ∆，使得D ，E ，F 重合，得到三棱锥．则当ABC ∆的边长变化时，三棱锥的表面积S 的取值范围是( )A ．(0,36)πB ．(0，C ．(0,45-D ．(0，解：设三棱锥的底面边长为a ，则0a <<连接OD ，交BC 于点G ，则6OD =，OG ，6DG =，∴2，侧面积为213(6)92S a a =⨯⨯=，∴三棱锥的表面积9S a =，0a <<9(0S a ∴=∈，，∴当ABC ∆的边长变化时，三棱锥的表面积S 的取值范围是(0，．故选：D ．实例演练2（2021•宜宾模拟）已知三棱锥A BCD -的各个顶点都在球O 的表面上，AD ⊥平面BCD ，BD CD ⊥，3BD =，CD =E 是线段CD 上一点，且3CD CE =．若球O 的表面积为40π，则过点E 作球O 的截面，所得截面圆面积的最小值为( )A ．4πB ．6πC ．8πD ．10π解：依题意，AD ，BD ，CD 两两互相垂直，取BC 中点M ，连接MD ，由对称性可知，球心O 在M 点正上方，且OM ⊥平面BCD ，OA OB OC OD R ====，3BD =，CD =6BC ∴=，则3BM CM DM ===，设球O 的半径为R ，则2440R ππ=，解得R由22222222()OM BM R OB AD OM DM R OA⎧+==⎨-+==⎩，解得12OM AD =⎧⎨=⎩，OM ⊥平面BCD ，OM ME ∴⊥，又13CE CD =cos CD BCD BC ∠==，∴在CEM ∆中，由余弦定理有2222cos 3ME CE MC CE MC BCD =+-⋅⋅∠=，故ME =，在OME ∆中，2OE =，要使过E 作圆O 的截面面积最小，则此时截面与OE垂直，设此时截面圆半径为r ，则r ==∴26min S r ππ==．故选：B ．实例演练3．（2021•河南模拟）现有一批大小不同的球体原材料，某工厂要加工出一个四棱锥零件，要求零件底面ABCD 为正方形，2AB =，侧面PAD ∆为等边三角形，线段BC 的中点为E ，若1PE =，则所需球体原材料的最小体积为( )A B ．283π C ．9π D 解：所需原材料体积最小的球体即为四棱锥P ABCD -的外接球，如图，设F 为AD 中点，G 为正方形ABCD 中心，PAD ∆为边长为2的等边三角形，PF ∴，又1PE =，2EF =，60PEF ∴∠=︒1PE EB EC ===，E ∴是PBC ∆的外心，过E 作面PBC 的垂线与过G 与面ABCD 的垂线交于O ，则O 为四棱锥P ABCD -外接球的球心．906030OEG OEP FEP ∠=∠-∠=︒-︒=︒，又1GE =，∴在直角三角形OGE 中求出OG =，又直角OAG ∆中，AG ，OA ∴=，即球半径R =，得343V R π==球．由于此时四棱锥P ABCD -在球心同侧，不是最小球，可让四棱锥下移到面ABCD 过球心时，即球半径12R AC =时，原材料最省，此时343V π=⨯=球．故选：A ．实例演练4（20211，O 为底面圆心，OA ，OB 为底面半径，且23AOB π∠=，M 是母线PA 的中点．则在此圆锥侧面上，从M 到B 的路径中，最短路径的长度为( )A B 1 C D 1解：由题意，在底面半径为1O 是底面圆心，P 为圆锥顶点，圆锥的侧面展开图是半圆，如图，A ，B 是底面圆周上的两点，23AOB π∠=，所以在展开图中，3APB π∠=2=，M 为母线PA 的中点，所以1PM =，所以从B 到M 的最短路径的长是BM A ．考点2：角的最值问题立体几何中的角有异面直线所成角、线面角和二面角的平面角三种。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

211. 下列说法中正确的是（）：
A. 直线l 平行于平面α内的无数条直线，则l //α
B. 若直线a 在平面α外，则a//α
C. 若直线a//b ，直线b ⊂α，则a//α
D. 若直线a//b ，b ⊂α，那么a 就平行于平面α内的无数条直线解析：画出图形，根据直线与平面平行的定义和判定定理进行分析。

解答: 由直线l 虽与平面α内无数条直线平行，但l 有可能在平面α内，知l 不一定平行于α，从而排除A
直线a 在平面α外，包括两种情况：a//α或a 与α相交，故a 与α不一定平行，从而排除B
直线a//b ，b ⊂α只能说明a 和b 无公共点，但a 可能在平面α内，故a 不一定平行于α，从而排除C
a//b ，b ⊂α，那么a ⊂α或a//α，故a 可能与平面α内的无数条直线平行，从而选择D
点评: 判定直线与平面平行时，要注意直线与平面平行的判定定理中的三个条件，缺一不可。

。

212.如图2－20，两个全等的正方形ABCD 和ABEF 所在平面相交于AB ，M ∈AC ，N ∈FB ，且AM ＝FN ，求证：MN//平面BCE 。

解析：要证MN //平面BCE ，就是要在平面BCE 上找一条直线，证明它与MN 平行即可。

证明: 连结AN 并延长，交BE 延长张于G ，连结CG 。

由AF//BG ，知
MC
AM
NB FN NG AN ==，故MN//CG ，MN ⊄平面BCE ，CG ⊂平面BCE ，于是MN//平面BCE 。

点评:证线面平行，通常转化为证线线平行，关键是在平面内找到所需的线。

213. 如图2－21，正方体ABCD －A 1B 1C 1D 1的棱长为2，E 为DD 1的中点，
（1）判断BD 1和过A 、C 、E 三点的平面的位置关系，并证明你的结论。

（2）求∆ACE 的面积。

证明（1）：连结BD ，令BD ∩AC ＝F 。

∵BD 1和过A 、C 、E 三点的平面平行，则F 是DB 的中点，又E 是DD 1的中点， ∴EF ∥BD 1
又EF ⊂平面ACE ，BD 1⊄平面ACE ， ∴BD 1∥平面ACE
D A F G
N
M B C
E
图2－
C B
A D A D
C B
E D
C
（2）在正方形ABCD 中，AB ＝2，AC ＝22，∴AF ＝2 在直角△ADE 中，AD ＝2，DE ＝1，∴AE ＝5
在Rt △EAF 中，EF ＝22AF EA -＝25-＝3 ∴63222
1
=⨯⨯=
∆ACE s 214. 直线a//直线b ，直线a 与平面α相交，判定直线b 与平面α的位置关系，并证明你的结论
证明：假设直线b 与α不相交，则b ⊂α或b//α
(1)若b ⊂α，由a//b ，b ⊂α，a ⊄α⇒a//α，与a 与平面α相交矛盾，故b ⊂α不可能。

(2)若b//α，又a// b ，a ，b 可以确定平面β，设α∩β＝c ，由c ⊂α,知b 与c 没有公共点，又b 、c 同在平面β内，故b//c ，又a//b ，故a//c ，c ⊂α，a ⊄α⇒a//α，这与a 与平面α相交矛盾。

故b 不平行α。

综上所述，b 与α必相交。

215. 如图2－22：在长方体AC 1中，（1）求证：BC 1//平行平面AB 1D 1
（2）若E 、F 分别是D 1C ，BD 的中点，则EF//ADD 1A 1
解析：（1）∵D 1C 1=
//DC =//AB ∴ABC 1D 1是平行四边形
BC 1//AD 1
又BC 1⊄平面AB 1D 1，又AD 1⊂平面AB 1D 1
BC 1//平面AB 1D 1
（2）证明：连结AF 、CF 、AD 1，
∵ABCD 是正方形，且F 是BD 的中点，知A 、F 、C 三点共线，且F 是AC 的中点，又E 是CD 1的中点
∴EF//AD ，又EF ⊄平面ADD 1A 1，AD ⊂平面ADD 1A 1， ∴EF//平面ADD 1A 1
216.在正方体木块ABCD －A 1B 1C 1D 1的表面上有一动点P 由顶点A 出发按下列规则向点C 1移动；
⑴点P 只能沿着正方体木块的棱或表面对角线移动； ⑵点P 每一变化位置，都使P 点到C 1点的距离缩短。

动点P 共有_________种不同的运行路线。

解析：通过画图逐一计数，共得12种不同路线（从B 到C 1，就有3种不同路线）经过一条边，一条对角线的情况有6种，
C B A D
F E A
D C
图2－
B
1C B A →→，11C A A →→，1C D A →→
11C B A →→，1C C A →→，11C D A →→
经过三条边的情况有6种：
11C B B A →→→，1C C B A →→→，1C C D A →→→
11C D D A →→→，111C B A A →→→，111C D A A →→→
217. 判定下列命题的真假
（1）两个平面垂直，过其中一个平面内一点作与它们的交线垂直的直线，必垂直于另一个平面；
（2）两个平面垂直，分别在这两个平面内且互相垂直的两直线，一定分别与另一平面垂直；
（3）两平面垂直，分别在这两个平面内的两直线互相垂直。

解析：（1）若该点在两个平面的交线上，则命题是错误的，
如图2－55，正方体AC 1中，平面AC ⊥平面AD 1，平面AC ∩平面AD 1＝AD ，在AD 上取点A ，连结AB 1，则AB 1⊥AD ，即过棱上一点A 的直线AB 1
与棱垂直，但AB 1与平面ABCD 不垂直，其错误的原因是AB 1没有
保证在平面ADD 1A 1内，可以看出：线在面内这一条件的重要性；
（2）该命题注意了直线在平面内，但不能保证这两条直线都与棱垂直，如图2－56，在正方体AC 1中，平面AD 1⊥平面AC ，AD 1⊂平面ADD 1A 1，AB ⊂平面ABCD ，且AB ⊥AD 1，即AB 与AD 1相互垂直，但AD 1与平面ABCD 不垂直；（3）如图2－56：正方体AC 1中，平面ADD 1A 1⊥平面ABCD ，AD 1⊂平面ADD 1A 1，AC ⊂平面ABCD ，AD 1与AC 所成的角为60，即AD 1
与AC 不垂直
解：由上面的分析知，命题⑴、⑵、⑶都是假命题。

点评:在利用两个平面垂直的性质定理时，要注意下列的三个条
件缺一不可：①两个平面垂直；②直线必须在其中一个面内；③直线必须垂直它们的交线。

218.已知平面α⊥平面β，平面α⊥平面γ，且β∩γ＝a ，求证：a ⊥α。

解析：此题需要作出辅助线，可有多种证明方法。

A B C D A 1
D 1 C 1 B 1 图2－ A B C
D
A 1 D 1 C 1
B 1 图2－56
证法1:如图2－57：在α内取一点P ，作PA ⊥β于A ，PB ⊥γ于B ，则PA ⊥a ，PB ⊥a ，又PA ⊂α，PB ⊂α，PA ∩PB ＝P ，∴ a ⊥α。

证法2：如图2－58，在a 上任取一点Q ，作QC ⊥α于C ，∵β∩γ＝a ，∴Q ∈β，又β⊥α，∴QC ⊂β，同理可证QC ⊂γ，∴QC 为β与γ的交线a ，∴ a ⊥α。

证法3：如图2－59，在a 上取点R ，在β内作RD 垂直于α、β的交线l 于D ， ∴RD ⊥α，同法在γ内，作RE 垂直于α，交α与γ的交线m 于E ，则RE ⊥α，过平面外一点，作这个平面的垂线是惟一的，∴RD 、RE 重合，则它既包含于β，又包含于γ， ∴ a ⊥α。

证法4：如图2－60，在β、γ内分别取M 、N 分别作α、β的交线l 和α、γ的交线m 的垂线c ，d ，则c ⊥α，d ⊥α，c//d ，c//a ，∴ a ⊥α。

点评: 此题是线线，线面，面面垂直转化典型题，多解题，对沟通知识和方法，开拓解题思路是有益的。

219. 下列四个平面图形中，每个小四边形皆为正方形，其中可以沿两个正方形的相邻边折叠围成一个立方体的图形是
（
）
解析：C
220. 如图，将锐角A 为60°，边长为a
的菱形ABCD 沿BD 折成60°的二面角，则A 与C 之间的距离为___________。

解析：
2
3a
A B P a γ β α 图2－
M N a γ β α l
m 图2－60
c
d
C
a γ
β α
图2－
Q
E a γ
β α 图2－
R D m l A. B. C. D.
A B
C
A
B
C
D
E
D。