2018年高中数学必修五达标练习:第2章 §1-1.1 正弦定理
2018版高中数学北师大版必修五学案:第二章 1.1 正弦定理二 精品

1.1 正弦定理(二)学习目标 1.熟记并能应用正弦定理的有关变形公式解决三角形中的问题.2.能根据条件,判断三角形解的个数.3.能利用两边夹角求三角形面积.知识点一 正弦定理的常见变形 1.sin A ∶sin B ∶sin C =____________; 2.a sin A =b sin B =csin C =a +b +c sin A +sin B +sin C=________; 3.a =________,b =________,c =________; 4.sin A =________,sin B =________,sin C =________. 知识点二 判断三角形解的个数思考1 在△ABC 中,a =9,b =10,A =60°,判断三角形解的个数. 梳理 已知三角形的两边及其中一边的对角,三角形解的个数并不一定唯一. 例如在△ABC 中,已知a ,b 及A 的值.由正弦定理a sin A =b sin B ,可求得sin B =b sin Aa.在由sin B 求B 时,如果a >b ,则有A >B ,所以B 为锐角,此时B 的值唯一;如果a <b ,则有A <B ,所以B 为锐角或钝角,此时B 的值有两个.思考2 已知三角形的两边及其夹角,为什么不必考虑解的个数? 梳理 解三角形4个基本类型:①已知三边;②已知两边及其夹角;③已知两边及其一边对角;④已知一边两角. 其中只有类型③解的个数不确定. 知识点三 三角形面积公式的拓展思考 如果已知底边和底边上的高,可以求三角形面积.那么如果知道三角形两边及夹角,有没有办法求三角形面积?梳理 △ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,则△ABC 的面积S =12ab sin C =12bc sinA =12ac sin B .类型一 判断三角形解的个数 引申探究例1中b =28 cm ,A =40°不变,当边a 在什么范围内取值时,△ABC 有两解(范围中保留sin 40°)?例1 在△ABC 中,已知a =20 cm ,b =28 cm ,A =40°,解三角形.(角度精确到1°,边长精确到1 cm)反思与感悟 已知两边和其中一边的对角解三角形时,首先求出另一边的对角的正弦值,根据该正弦值求角时,要根据已知两边的大小情况来确定该角有一个值还是两个值.或者根据该正弦值(不等于1时)在0°~180°范围内求角,一个锐角,一个钝角,只要不与三角形内角和定理矛盾,就是所求.跟踪训练1 已知三角形中a =23,b =6,A =30°,判断三角形是否有解,若有解,解该三角形.类型二 利用正弦定理求最值或取值范围例2 在锐角△ABC 中,角A ,B ,C 分别对应边a ,b ,c ,a =2b sin A ,求cos A +sin C 的取值范围.反思与感悟 解决三角形中的取值范围或最值问题:(1)先利用正弦定理理清三角形中元素间的关系或求出某些元素.(2)将所求最值或取值范围的量表示成某一变量的函数(三角函数),从而转化为函数的值域或最值问题. 跟踪训练2 在△ABC 中,若C =2B ,求cb 的取值范围.类型三 三角形面积公式的应用 命题角度1 已知边角求面积例3 在△ABC 中,AB =3,AC =1,B =30°,求△ABC 的面积.反思与感悟 三角形面积公式S =12ab sin C ,S =12bc sin A ,S =12ac sin B 中含有三角形的边角关系.因此求三角形的面积,与解三角形有密切的关系.首先根据已知,求出所需,然后求出三角形的面积.跟踪训练3 在△ABC 中,a =1,A =30°,C =45°,则△ABC 的面积为( ) A.22 B.24 C.32 D.3+14命题角度2 给出面积求边角例4 在△ABC 中,A =60°,AB =2,且△ABC 的面积为32,则AC 的长为________. 反思与感悟 利用三角形两边夹角表示的三角形面积公式有3个,到底选择哪一个,要看题目给出的条件和解题目标.跟踪训练4 已知锐角三角形ABC 的面积为33,BC =4,CA =3,则角C 的大小为( ) A .75° B .60° C .45° D .30°1.在△ABC 中,AC =6,BC =2,B =60°,则角C 的值为( ) A .45° B .30° C .75°D .90°2.在△ABC 中,若a cos A =b cos B =c cos C ,则△ABC 是( )A .直角三角形B .等边三角形C .钝角三角形D .等腰直角三角形3.已知△ABC 的面积为32,且b =2,c =3,则sin A =________.1.已知两边和其中一边的对角,求第三边和其他两个角,这时三角形解的情况可能无解,也可能一解或两解.首先求出另一边的对角的正弦值,当正弦值大于1或小于0时,这时三角形解的情况为无解;当正弦值大于0小于1时,再根据已知两边的大小情况来确定该角有一个值还是两个值.2.判断三角形的形状,最终目的是判断三角形是不是特殊三角形,当所给条件含有边和角时,应利用正弦定理将条件统一为“边”之间的关系式或“角”之间的关系式.答案精析问题导学 知识点一1.a ∶b ∶c 2.2R 3.2R sin A 2R sin B 2R sin C 4.a 2R b 2R c2R知识点二思考1 解 sin B =b a sin A =109×32=539,而32<539<1,所以当B 为锐角时,满足sin B =539的角有60°<B <90°,故对应的钝角B 有90°<B <120°, 也满足A +B <180°,故三角形有两解.思考2 如果两个三角形有两边及其夹角分别相等,则这两个三角形全等.即三角形的两边及其夹角确定时,三角形的六个元素即可完全确定,故不必考虑解的个数的问题. 知识点三思考 △ABC 中,如果已知边AB 、BC 和角B ,边BC 上的高记为h a ,则h a =AB sin B .从而可求面积. 题型探究例1 解 根据正弦定理,sin B =b sin A a =28sin 40°20≈0.899 9.因为0°<B <180°,且b >a ,B >A , (1)当B ≈64°时,C =180°-(A +B )≈180°-(40°+64°)=76°, c =a sin C sin A =20sin 76°sin 40°≈30(cm).(2)当B ≈116°时,C =180°-(A +B )≈180°-(40°+116°)=24°, c =a sin C sin A =20sin 24°sin 40°≈13(cm).综上,B ≈64°,C ≈76°,c ≈30 cm 或B ≈116°,C ≈24°,c ≈13 cm. 引申探究解 如图,∠A =40°,CD ⊥AD .AC =28 cm ,以C 为圆心,a 为半径画圆弧, 当CD <a <AC ,即b sin A <a <b , 28sin 40°<a <28时,△ABC 有两解(△AB 1C ,△AB 2C 均满足题设). 跟踪训练1 解 a =23,b =6,a <b ,A =30°<90°. 又因为b sin A =6sin 30°=3,b sin A <a <b , 所以本题有解,且有两解,由正弦定理,得 sin B =b sin A a =6sin 30°23=32,因为b >a ,B >A ,B ∈(0°,180°), 所以B =60°或120°.当B =60°时,C =90°,c =a 2+b 2= 43;当B =120°时,C =30°,c =a =2 3. 所以B =60°,C =90°,c =4 3 或B =120°,C =30°,c =2 3. 例2 解 ∵a =2b sin A ,∴由正弦定理,得sin A =2sin B sin A , 又∵A ∈(0,π2),sin A ≠0,∴sin B =12.∵B 为锐角,∴B =π6.令y =cos A +sin C =cos A +sin []π-(B +A ) =cos A +sin ⎝⎛⎭⎫π6+A=cos A +sin π6cos A +cos π6sin A=32cos A +32sin A =3sin ⎝⎛⎭⎫A +π3. 由锐角△ABC 知, π2-B <A <π2,∴π3<A <π2. ∵2π3<A +π3<5π6,∴12<sin ⎝⎛⎭⎫A +π3<32, ∴32<3sin ⎝⎛⎭⎫A +π3<32, 即32<y <32. ∴cos A +sin C 的取值范围是⎝⎛⎭⎫32,32.跟踪训练2 解 因为A +B +C =π,C =2B , 所以A =π-3B >0,所以0<B <π3,所以12<cos B <1,所以1<2cos B <2,又c b =sin C sin B =sin 2B sin B =2cos B , 所以1<cb<2.例3 解 由正弦定理,得1sin 30°=3sin C ,∴sin C =32. ∵0°<C <180°,AB >AC ,∴C >B , ∴C =60°或120°. ①当C =60°时,A =90°, ∴S △ABC =12×3×1=32;②当C =120°时,A =30°, S △ABC =12×3×1×sin 30°=34.跟踪训练3 D [B =180°-A -C =180°-30°-45°=105°, 由正弦定理,得b =a sin B sin A =112×6+24=6+22,∴S △ABC =12ab sin C =12×1×6+22×sin 45°=3+14.]例4 1 跟踪训练4 B 当堂训练 1.C 2.B 3.32。
新高中数学(北师大版)必修五同步练习:2-1-1正弦定理(含答案解析)

1.1正弦定理双基达标限时20 分钟1.以下对三角形解的状况的判断中,正确的选项是().A . a= 4, b= 5, A = 30°,有一解B.a= 5, b=4, A = 60°,有两解C.a=3, b=2, B= 120 °,有一解D. a=3, b=6, A = 60°,无解分析关于 A , bsin A<a<b ,故有两解;关于 B , b<a,故有一解;关于C, B= 120°且a>b,故无解;关于D, a<bsin A ,故无解.答案D2.相关正弦定理的表达:①正弦定理只合用于锐角三角形;②正弦定理不合用于直角三角形;③在某一确立的三角形中,各边与它所对角的正弦的比是必定值;④在△ABC中,sin A ∶ sin B ∶ sin C= a∶b∶ c.此中正确的个数是().A . 1B. 2C. 3D. 4分析正弦定理合用于随意三角形,故①②均不正确;由正弦定理可知,三角形一旦确定,则各边与其所对角的正弦的比就确立了,故③正确;由比率性质和正弦定理可推知④正确.答案B3.已知锐角△ABC的面积为 33,BC=4,CA=3,则角 C的大小为().A.75°B.60°C. 45°D. 30°分析由 S△ABC= 33=1BC·CA·sin C =1×3×4sin C 得 sin C=3,又 C 为锐角.故 C=22260°.答案B4.在△ ABC 中,由“ a>b ”推出“ sin A>sin B ;由”“ sin A>sin B ”推出“ a>b.”(填“能够”或“不能够”)分析在△ ABC 中,必有 sin B>0 ,由正弦定理得a=sin A,于是,若 a>b,则a>1,则sin A>1.b sin B b sin B由 sin B>0 ,可得 sin A>sin B ;反之,若sin A>sin B ,由 sin B>0 ,可得sin Aasin B >1,则 b >1, a>b.答案能够 能够5.已知 a ,b ,c 分别是△ ABC 的三个内角所对的边,若 a = 1,b = 3,A + C =2B ,则 sin A= ________.分析π∵ A + C =2B ,A + B + C =π,∴ B = ,3∴由正弦定理,a =b , 1 =3.∴ sin A =1.sin Asin Bsin A π2sin 3答案126.在△ ABC 中,已知 a =10, B =75°, C = 60°,试求 c 及△ ABC 的外接圆半径 R.解∵A +B + C = 180°,∴ A = 180°- 75°- 60°= 45°.3由正弦定理,得a = c = 2R ,∴ c = a ·sin C=10×2 = 5 6,∴ 2R = a= 10=sin A sin Csin A2sin A 222 102,∴ R = 5 2.综合提升(限时 25 分钟)7.在△ ABC 中,AB = 3,A = 45°,C = 75°,则 BC =().A .3- 3B. 2C . 2D .3+ 3分析 ∵AB = 3, A = 45°, C = 75°,由正弦定理得:BC = AB BC = AB =3 ,sin A sin C ?sin 45°sin 75 °6+ 24∴ BC =3- 3.答案 A8.已知△ ABC 中, A ,B ,C 的对边分别为a ,b , c.若 a =c = 6+ 2且 A = 75°,则 b 等于() .A . 2B . 4+2 3C .4- 2 3D.6- 2分析 sin A = sin 75 =°sin(30 °+45°)= sin 30 cos ° 45 °+ sin 45 cos ° 30 °=2+6,4由 a = c = 6+2可知, C = 75°,因此1B =30°, sin B = .2由正弦定理得 b =a ·sin B = 2+ 6 1sin A × =2,应选 A.2+ 6 24答案 A9.在△ ABC 中, a = 3 2, cos C = 1, S △ABC = 4 3,则 b = ______. 3分析1 sin C = 221 12 2 = 4 3? b = 2 3.cos C = ?; S ABC = absin C? ·32·b ·33△223答案2 310.已知△ ABC 中, a =x ,b =2,∠B = 45°,若三角形有两解, 则 x 的取值范围是 ________.分析 由正弦定理,得 x =bsin A= 2 2sin A ,sin B∵ 45°<A<90°或 90°<A<135°,∴ 2<x<2 2.答案2<x<2 2111.在△ ABC 中,已知 tan B = 3, cos C = 3,AC = 3 6,求△ ABC 的面积.解设 AB 、 BC 、 CA 的长分别为 c 、 a 、 b.由 tan B = 3,得 B = 60°,∴ sin B =3 1 2, cos B = .2又 sin C = 1- cos2C = 2 3 2,2 2由正弦定理,得c = bsin C =3 6× 3 = 8.sin B32 又∵ A + B + C = 180°,∴ sin A =sin(B +C)= sin Bcos C + cos Bsin C= 3 1 1 2 2 = 322 × + ×3 6+.3 2 3∴所求面积 S △ABC =1bcsin A =6 2+ 8 3.212.( 创新拓展 )在△ ABC 中,已知b + a sin B,且 2sin A ·sin B = 2sin2=C ,试判断其形asin B - sin A状.解 由正弦定理可得 b + a = sin B = b ,a sin B - sin Ab - a∴ b 2- a 2= ab ,① 又∵ 2sin Asin B = 2sin 2C ,∴由正弦定理,得 2ab = 2c 2.②由①、②得b2- a2= c2,即 b2= a2+ c2.∴该三角形为以 B 为直角极点的直角三角形.。
2018年高中数学北师大版必修五达标练习第2章 §1-1.3 正弦定理和余弦定理习题课 Word版含解析

[基础达标].在△中,=,=,=°,则等于( )..-.-解析:选.因为=,=,=°,所以在△中,由正弦定理可得=)==,又由>可得>,即得为锐角,则==..在△中,,,分别是角,,的对边,且=,则△是( ).直角三角形.等腰三角形或直角三角形.等边三角形.等腰直角三角形解析:选.因为=及-=,所以=,即=,所以+=,则△是直角三角形.故选..在△中,已知=,=,△的面积为,则·=( ).±.±..解析:选.因为=,=,△的面积为,所以△=···=×××=.所以=,所以=±=±.所以·=··=××=±,故选..在△中,=,且最大边长和最小边长是方程-+=的两个根,则第三边的长为( )....解析:选.已知=,且最大边长和最小边长是方程-+=的两个根,则第三边为,+=,=,所以=)=(π))===..△的内角、、的对边分别为、、.已知+ ( - )=,=,=,则=( )..解析:选.因为+(-)=,所以(+)+·-·=,所以++-=,整理得( +)=,因为≠,所以+=,所以=-,因为∈(,π),所以=,由正弦定理得=)==,又<<,所以=.故选..△中,=°,=,则++ )=.解析:由题知,设△外接圆半径,则=)=)=)==,则++)=++)++)==.答案:.在△中,已知∶=∶,=+,则三内角、、的度数依次是.解析:由题意知=,=+-,即=+-,又=+,所以=,得=°,=,=°,所以=°.答案:°,°,°.在△中,=°,=,则+的最大值为.解析:由正弦定理知)=°)=),所以=,=.又+=°,所以+=+(°-)=( +°-°)=( ++)=( +)=(+α),其中α=,α是第一象限角.由于°<<°,且α是第一象限角,因此+有最大值.答案:.在△中,内角,,的对边分别为,,,已知=(-) .()求角的大小;()若=,试确定△的形状.解:()由已知及正弦定理,有=( -) ,即+=.所以(+)=.因为(+)=≠,所以=,即=,所以=°.()由题设及余弦定理=+-得,=+-°,即+-=.所以(-)=.从而=.由第一问知=°,所以===°.所以△为正三角形..在△中,+=+.()求的大小;()求+的最大值.。
2018高中数学北师大版高二必修5_第二章1.1_正弦定理_作业_word版含解析

[学业水平训练]1.在△ABC 中,下列关系一定成立的是( ) A .a <b sin A B .a =b sin A C .a ≤b sin AD .a ≥b sin A解析:选D.由正弦定理,得asin A =bsin B,∴sin B =b a sin A ,在△ABC 中,∵0<sin B ≤1,∴0<b asin A ≤1,∴a ≥b sin A .2.在△ABC 中,已知a =8,B =60°,C =75°,则b 等于( ) A .4 2 B .4 3 C .4 6D.322 解析:选C.在△ABC 中,A =180°-(B +C )=45°,由正弦定理asin A =b sin B ,得b =a sin Bsin A=4 6. 3.在△ABC 中,根据下列条件解三角形,其中有两解的是( ) A .b =10,∠A =45°,∠C =70° B .a =30,b =25,∠A =150° C .a =7,b =8,∠A =98° D .a =14,b =16,∠A =45°解析:选D.对于A 项,∠B =180°-∠A -∠C =65°,由正弦定理知只有一解; 对于B 项,∵a >b ,∴A >B ,又A =150°, ∴只有一解;对于C 项,∵a <b ,∴A <B ,而A =98°,∴无解; 对于D 项,sin B =b sin A a =16×sin 45°14=427<1,且b sin A <a <b , ∴有两解.4.在△ABC 中,已知(b +c )∶(c +a )∶(a +b )=4∶5∶6,则sin A ∶sin B ∶sin C 等于( ) A .6∶5∶4 B .7∶5∶3 C .3∶5∶7D .4∶5∶6解析:选B.设b +c =4k ,c +a =5k ,a +b =6k (k >0),从而解出a =72k ,b =52k ,c =32k .∴a ∶b ∶c=7∶5∶3,∴sin A ∶sin B ∶sin C =7∶5∶3.5.在△ABC 中,A =π3,BC =3,则△ABC 的两边AC +AB 的取值范围是( )A .[33,6]B .(2,43)C .(33,43]D .(3,6]解析:选D.由正弦定理,得AC =BC ·sin B sin A =23sin B ,AB =BC ·sin Csin A=23sin C ,∴AC +AB =23(sin B +sin C ) =23⎣⎢⎡⎦⎥⎤sin B +sin ⎝ ⎛⎭⎪⎫2π3-B=23⎝⎛⎭⎪⎫sin B +32cos B +12sin B =6sin ⎝ ⎛⎭⎪⎫B +π6.∵0<B <2π3,∴π6<B +π6<5π6,∴12<sin ⎝⎛⎭⎪⎫B +π6≤1,∴3<6sin ⎝⎛⎭⎪⎫B +π6≤6. 6.已知△ABC 中,A =60°,a =3,则a +b +csin A +sin B +sin C =________.解析:由已知得a sin A =3sin 60°=2,所以由正弦定理知a +b +c sin A +sin B +sin C =asin A=2.答案:27.在△ABC 中,角A 、B 、C 的对边分别是a 、b 、c ,已知A =π3,b =1,△ABC 的外接圆半径为1,则S △ABC =________.解析:由正弦定理a sin A =b sin B =2R ,∴a =3,sin B =12,∵a >b ,∴A >B ,∴B =π6,C =π2.∴S△ABC=32. 答案:328.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .若a =2,b =2,sin B +cos B =2,则角A 的大小为________.解析:∵sin B +cos B =2sin ⎝ ⎛⎭⎪⎫π4+B =2, ∴sin ⎝ ⎛⎭⎪⎫π4+B =1.又0<B <π,∴B =π4.由正弦定理,得sin A =a sin Bb=2×222=12. 又a <b ,∴A <B .故A =π6.答案:π69.在△ABC 中,a =3,b =1,B =30°,解三角形. 解:由正弦定理,得a sin A =bsin B .∴sin A =a sin Bb =3sin 30°=32. ∴A =60°或A =120°.当A =60°时,C =90°,c =a 2+b 2=2. 当A =120°时,C =30°,c =b =1.10.在△ABC 中,(a 2+b 2)sin(A -B )=(a 2-b 2)sin(A +B ),试判断△ABC 的形状. 解:由(a 2+b 2)sin(A -B )=(a 2-b 2)sin(A +B ),得a 2[sin(A +B )-sin(A -B )]=b 2[sin(A +B )+sin(A -B )],∴a 2·cos A sin B =b 2sin A cos B .由正弦定理,得sin 2A cos A sinB =sin 2B sin A cos B .∵0<A <π,0<B <π,∴sin A >0,sin B >0,0<2A <2π,0<2B <2π,∴sin A cos A =sin B cos B ,即sin 2A =sin 2B . ∴2A =2B 或2A +2B =π,即A =B 或A +B =π2.∴△ABC 为等腰三角形或直角三角形.[高考水平训练]1.已知a 、b 、c 为△ABC 的三个内角A 、B 、C 的对边,向量m =(3,-1),n =(cos A ,sin A ),若m⊥n ,且a cos B +b cos A =c sin C ,则A 、B 的大小分别为( )A.π6,π3B.2π3,π6C.π3,π6D.π3,π3解析:选C.∵m⊥n ,∴3cos A -sin A =0,∴tan A = 3.∵A 为△ABC 的内角,∴A =π3.∵a cos B +b cos A =c sin C ,由正弦定理,有sin A cos B +sin B cos A =sin 2C ,∴sin(A +B )=sin 2C .∴sin C =sin 2C .∴sin C =1.∴C =π2.∴B =π6.2.在△ABC 中,A =π3,BC =3,则△ABC 的周长可以用角B 表示为________.解析:设周长为x ,则BCsin A =AB +BC +CA sin A +sin B +sin C =xsin A +sin B +sin C. ∴332=x32+sin B +sin C .∴x =3+23⎝ ⎛⎭⎪⎫sin B +12sin B +32cos B=3+6sin ⎝ ⎛⎭⎪⎫B +π6.答案:6sin ⎝⎛⎭⎪⎫B +π6+3 3.在△ABC 中,a =1,b =2,求角A 的取值范围.解:由a sin A =b sin B ,可得sin A =12sin B ,又因为0<sin B ≤1,所以0<sin A ≤12.所以0°<A ≤30°或150°≤A <180°. 又因为a <b ,所以只有0°<A ≤30°. 故角A 的取值范围为0°<A ≤30°.4.在△ABC 中,已知ln(sin A +sin B )=ln sin A +ln sin B -ln(sin B -sin A ),且cos(A -B )+cos C =1-cos 2C .(1)确定△ABC 的形状; (2)求a +cb的取值范围. 解:(1)∵ln(sin A +sin B )=ln sin A +ln sin B -ln(sin B -sin A ), ∴ln(sin 2B -sin 2A )=ln(sin A ·sinB ), ∴sin 2B -sin 2A =sin A ·sinB . 由正弦定理,得b 2-a 2=ab .① 又∵cos(A -B )+cos C =1-cos 2C , ∴cos(A -B )-cos(A +B )=2sin 2C , ∴2sin A sin B =2sin 2C . 由正弦定理,得ab =c 2.② 由①②,得b 2-a 2=c 2,∴b 2=a 2+c 2,∴△ABC 是以B 为直角的直角三角形. (2)由正弦定理,得a +cb =sin A +sin Csin B=sin A +sin C =sin A +sin ⎝ ⎛⎭⎪⎫π2-A =2sin ⎝⎛⎭⎪⎫A +π4.∵0<A <π2,∴π4<A +π4<3π4,∴22<sin ⎝ ⎛⎭⎪⎫A +π4≤1,∴1<2sin ⎝⎛⎭⎪⎫A +π4≤2,故a +cb的取值范围是(1,2].。
2018版高中数学北师大版必修五学案:第二章 解三角形 1.1 正弦定理(一) Word版含答案

1.1 正弦定理(一)[学习目标] 1.通过对任意三角形边长和角度的关系的探索,掌握正弦定理的内容及其证明方法.2.能运用正弦定理与三角形的内角和定理解决简单的解三角形问题.知识点一 正弦定理1.正弦定理的表示 文字 语言 在一个三角形中,各边和它所对角的正弦的比都相等,该比值为三角形外接圆的直径符号 语言在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,则a sin A =b sin B =c sin C =2R 2.正弦定理的常见变形(1)a =2R sin A ,b =2R sin B ,c =2R sin C ,其中R 为△ABC 外接圆的半径.(2)sin A =a 2R ,sin B =b 2R ,sin C =c 2R(R 为△ABC 外接圆的半径). (3)三角形的边长之比等于对应角的正弦比,即a ∶b ∶c =sin A ∶sin B ∶sin C .(4)a +b +c sin A +sin B +sin C =a sin A =b sin B =c sin C. (5)a sin B =b sin A ,a sin C =c sin A ,b sin C =c sin B .3.正弦定理的证明(1)在Rt △ABC 中,设C 为直角,如图,由三角函数的定义:sin A =a c ,sin B =b c,∴c=asin A=bsin B=csin 90°=csin C,∴asin A=bsin B=csin C.(2)在锐角三角形ABC中,设AB边上的高为CD,如图,CD=a sin_B=b sin_A,∴asin A=bsin B,同理,作AC边上的高BE,可得asin A=csin C,∴asin A=bsin B=csin C.(3)在钝角三角形ABC中,C为钝角,如图,过B作BD⊥AC于D,则BD=a sin(π-C)=a sin_C,BD=c sin_A,故有a sin C=c sin_A,∴asin A=csin C,同理,asin A=bsin B,∴asin A=bsin B=csin C.思考下列有关正弦定理的叙述:①正弦定理只适用于锐角三角形;②正弦定理不适用于直角三角形;③在某一确定的三角形中,各边与它所对角的正弦的比是一定值;④在△ABC中,sin A∶sin B∶sin C=BC∶AC∶AB.其中正确的个数有()A.1 B.2 C.3 D.4答案 B解析正弦定理适用于任意三角形,故①②均不正确;由正弦定理可知,三角形一旦确定,则各边与其所对角的正弦的比值也就确定了,所以③正确;由正弦定理可知④正确.故选B. 知识点二解三角形一般地,把三角形的三个角A,B,C和它们的对边a,b,c叫做三角形的元素.已知三角形的几个元素求其他元素的过程叫做解三角形.思考正弦定理能解决哪些问题?答案利用正弦定理可以解决以下两类有关三角形的问题:①已知两角和任意一边,求其他两边和第三个角;②已知两边和其中一边的对角,求另一边的对角,从而求出其他的边和角.。
人教A版高中数学必修五《1.1.1正弦定理》练习题.docx

& 鑫达捷致力于精品文档 精心制作仅供参考 &鑫达捷 §1.1.1 正弦定理一.知识与技能目标1. 掌握正弦定理的内容;2. 掌握正弦定理的证明方法;3. 会运用正弦定理解斜三角形的两类基本问题.二.课内检测1. 在ABC ∆中,若cos cos A b B a=,则ABC ∆是( ). A .等腰三角形 B .等腰三角形或直角三角形C .直角三角形D .等边三角形2. 已知△ABC 中,A ∶B ∶C =1∶1∶4,则a ∶b ∶c 等于( ). A .1∶1∶4 B .1∶1∶2 C .1∶1D .2∶23. 在△ABC 中,若sin sin A B >,则A 与B 的大小关系为( ).A. A B >B. A B <C. A ≥BD. A 、B 的大小关系不能确定4. 已知∆ABC 中,sin :sin :sin 1:2:3A B C =,则::a b c = .5. 已知∆ABC 中,∠A 60=︒,a =sin sin sin a b c A B C++++= . 6(选作)在45,2,,ABC c A a b B C ∆===o 中,求和.三.课外作业1. 已知△ABC 中,AB =6,∠A =30°,∠B =120︒,解此三角形.2. 已知△ABC 中,sin A ∶sin B ∶sin C =k ∶(k +1)∶2k (k ≠0),求实数k 的取值范围为.3. 在ABC ∆中,已知45A =o ,60B =o ,42a =cm ,解三角形.4. 在ABC ∆中,已知45B =o ,60C =o ,12a =cm ,解三角形.5.在60,1,,ABC b B c a A C ∆===o 中,求和.6(选作)在ABC ∆中,已知045,2,===B cm b xcm a ,如果利用正弦定理解三角形有两解,则x 的取值范围是_____.7.(选作)在ABC ∆中,已知B c b sin 2=,求C ∠的度数答案:6(选作) 2<x<22 7.(选作) 300 或1500。
18-19 第2章 §1 1.1 正弦定理

比值的 含义
)
课 时 分 层 作 业
返 首 页
自 主 预 习 • 探 新 知
(1)a= 2Rsin A ,b= 2Rsin B 变形
,c= 2Rsin C
合 作 探 究 • 攻 重 难
c a b (2)sin A= 2R ,sin B= 2R ,sin C=2R (3)a∶b∶c= sin A∶sin B∶sin C
2.三角形面积公式
自 主 预 习 • 探 新 知
阅读教材 P47~P48 问题 3,完成下列问题. 1 1 1 三角形 ABC 的面积:S= 2absin C= 2acsin B = 2bcsin A
.
当 堂 达 标 • 固 双 基
思考:(1)在△ABC 中,若已知边 a,b 和角 B,能否确定△ABC 的面积?
合 作 探 究 • 攻 重 难
asin B 2sin 60° 3 [解析] 由正弦定理得sin A= b = 3 = 3 . [答案] 3 3
当 堂 达 标 • 固 双 基
课 时 分 层 作 业
返 首 页
自 主 预 习 • 探 新 知
[合 作 探 究· 攻 重 难]
利用正弦定理解三角形
在△ABC中, (1)若A=45° ,B=30° ,a=2,求b,c与C;
第二章
解三角形
§1 正弦定理与余弦定理 1.1 正弦定理
自 主 预 习 • 探 新 知
学习目标:1.通过对任意三角形边长和角度关系的探索,掌握正弦定理的内 容及其证明方法.(重点)2.能运用正弦定理与三角形内角和定理解决简单的三角
当 堂 达 标 • 固 双 基
2018版高中数学人教版A版必修五学案§1.1.1 正弦定理(二)

.正弦定理(二)
[学习目标].熟记并能应用正弦定理的有关变形公式解决三角形中的问题.能根据条件,判断三角形解的个数.能利用正弦定理、三角恒等变换、三角形面积公式解决较为复杂的三角形问题.
知识点一正弦定理及其变形
.定理内容:===.
.正弦定理的常见变形:
()∶∶=∶∶;
()====;
()=,=,=;
()=,=,=.
知识点二对三角形解的个数的判断
已知三角形的两角和任意一边,求另两边和另一角,此时有唯一解,三角形被唯一确定.已知两边和其中一边的对角,求其他的边和角,此时可能出现一解、两解或无解的情况,三角形不能被唯一确定,现以已知,和解三角形为例,从两个角度予以说明:
()代数角度
由正弦定理得=,
①若>,则满足条件的三角形个数为,即无解.
②若=,则满足条件的三角形个数为,即一解.
③若<,则满足条件的三角形个数为或,即一解或两解.
()几何角度
图形
关系式
解的
个数
为锐角
①=;②≥
一解
<<
两解
<
无解
为
钝 角 或 直 角
>
一解
≤
无解
知识点三三角形面积公式 任意三角形的面积公式为:
()△===,即任意三角形的面积等于任意两边与它们夹角的正弦的乘积的一半. ()△=,其中为△的一边长,而为该边上的高的长. ()△=(++)=,其中,分别为△的内切圆半径及△的周长.。
2018版高中数学人教版A版必修五学案§1.1.1 正弦定理(一)

. 正弦定理(一)
[学习目标].通过对任意三角形边长和角度的关系的探索,掌握正弦定理的内容及其证明方法.能运用正弦定理与三角形的内角和定理解决简单的解三角形问题.
知识点一正弦定理
.正弦定理的表示
文字
语言 在一个三角形中,各边和它所对角的正弦的比都相等,该比值为三角形外接圆的直径
符号
语言
在△中,角,,所对的边分别为,,,则===
.正弦定理的常见变形
()=,=,=,其中为△外接圆的半径.
()=,=,=(为△外接圆的半径).
()三角形的边长之比等于对应角的正弦比,即∶∶=∶∶.
()===.
()=,=,=
.
.正弦定理的证明
()在△中,设为直角,如图,由三角函数的定义:
=,=,
∴====,
∴==.
()在锐角三角形中,设边上的高为,如图,
==,
∴=,
同理,作边上的高,可得=,
∴==.
()在钝角三角形中,为钝角,如图,
过作⊥于,则
=(π-)=,
=,故有=,
∴=,
同理,=,∴==.
思考下列有关正弦定理的叙述:①正弦定理只适用于锐角三角形;②正弦定理不适用于直角三角形;③在某一确定的三角形中,各边与它所对角的正弦的比是一定值;④在△中,∶∶=∶∶.其中正确的个数有()
....
答案。
2018版高中数学北师大版必修五学案:第二章 解三角形

[学习目标] 1.进一步熟练掌握正弦、余弦定理在解各类三角形中的应用.2.提高对正弦、余弦定理应用范围的认识.3.初步应用正弦、余弦定理解决一些和三角函数、向量有关的综合问题.知识点一 正弦定理及其变形 1.a sin A =b sin B =csin C=2R . 2.a =2R sin_A ,b =2R sin_B ,c =2R sin_C .(化角为边) 3.sin A =a 2R ,sin B =b 2R ,sin C =c2R .(化边为角)知识点二 余弦定理及其推论1.a 2=b 2+c 2-2bc cos_A ,cos A =b 2+c 2-a 22bc.(边角互化)2.在△ABC 中,c 2=a 2+b 2⇔C 为直角,c 2>a 2+b 2⇔C 为钝角;c 2<a 2+b 2⇔C 为锐角. 知识点三 解三角形的几类问题和解法在△ABC 中,边a 、b 、c 所对的角分别为A 、B 、C ,则有 (1)sin(A +B )=sin_C ,cos(A +B )=-cos_C , tan(A +B )=-tan_C ,(2)sin A +B 2=cos C 2,cos A +B 2=sin C 2.题型一 利用正弦、余弦定理解三角形或求值例1 如图,在△ABC 中,B =π3,AB =8,点D 在BC 边上,且CD =2,cos ∠ADC=17. (1)求sin ∠BAD ; (2)求BD ,AC 的长. 解 (1)在△ADC 中,因为cos ∠ADC =17,∠ADC ∈(0,π2),所以sin ∠ADC =437,所以sin ∠BAD =sin(∠ADC -∠B ) =sin ∠ADC ·cos B -cos ∠ADC ·sin B =437×12-17×32=3314. (2)在△ABD 中,由正弦定理得 BD =AB ·sin ∠BADsin ∠ADB =8×3314437 =3.在△ABC 中,由余弦定理得 AC 2=AB 2+BC 2-2AB ·BC ·cos B =82+52-2×8×5×12=49,所以AC =7.反思与感悟 应用正弦、余弦定理解三角形时,要注意结合题目中的条件,选择适当的定理.当题目中出现多个三角形时,应注意弄清每一个三角形中的边角关系,并分析这几个三角形中的边角之间的联系.跟踪训练1 如图,在△ABC 中,已知点D 在BC 边上,AD ⊥AC ,sin ∠BAC=223,AB =32,AD =3,则BD 的长为________. 答案3解析 ∵sin ∠BAC =sin(90°+∠BAD )=cos ∠BAD =223,∴在△ABD 中,有BD 2=AB 2+AD 2-2AB ·AD ·cos ∠BAD =18+9-2·32·3·223=3.∴BD = 3.题型二 判断三角形的形状例2 在△ABC 中,b =a sin C ,c =a cos B ,试判断△ABC 的形状. 解 由余弦定理知cos B =a 2+c 2-b 22ac ,代入c =a cos B ,得c =a ·a 2+c 2-b 22ac ,所以c 2+b 2=a 2,所以△ABC 是以A 为直角的直角三角形. 又因为b =a sin C ,所以b =a ·ca ,所以b =c ,所以△ABC 也是等腰三角形. 综上所述,△ABC 是等腰直角三角形.反思与感悟 (1)判断三角形形状时,要灵活应用正弦、余弦定理进行边角转化.但究竟是化边为角还是化角为边,应视具体情况而定. (2)常用的几种转化形式:①若cos A =0,则A =90°,△ABC 为直角三角形; ②若cos A <0,则△ABC 为钝角三角形;③若cos A >0且 cos B >0且cos C >0,则△ABC 为锐角三角形; ④若sin 2A +sin 2B =sin 2C ,则C =90°,△ABC 为直角三角形; ⑤若sin A =sin B 或sin(A -B )=0,则A =B ,△ABC 为等腰三角形;⑥若sin 2A =sin 2B ,则A =B 或A +B =90°,△ABC 为等腰三角形或直角三角形.跟踪训练2 在△ABC 中,cos A =45,且(a -2)∶b ∶(c +2)=1∶2∶3,试判断三角形的形状.解 由已知设a -2=x ,则b =2x ,c +2=3x , 所以a =2+x ,c =3x -2,由余弦定理得cos A =4x 2+(3x -2)2-(x +2)24x (3x -2)=45.解得x =4,所以a =6,b =8,c =10, 所以a 2+b 2=c 2,所以三角形为直角三角形. 题型三 正弦、余弦定理与三角变换的综合应用例3 在△ABC 中,a 、b 、c 分别为角A 、B 、C 的对边,且4sin 2B +C 2-cos 2A =72.(1)求A 的度数.(2)若a =3,b +c =3,求b 和c 的值.解 (1)由4sin 2B +C 2-cos 2A =72及A +B +C =180°,得2[1-cos(B +C )]-2cos 2 A +1=72,4(1+cos A )-4cos 2 A =5,即4cos 2A -4cos A +1=0, ∴(2cos A -1)2=0, 解得cos A =12.∵0°<A <180°,∴A =60°.(2)由余弦定理,得cos A =b 2+c 2-a 22bc .∵cos A =12,∴b 2+c 2-a 22bc =12,化简并整理,得(b +c )2-a 2=3bc ,所以32-(3)2=3bc ,则由⎩⎪⎨⎪⎧ b +c =3,bc =2.解得⎩⎪⎨⎪⎧ b =1,c =2.或⎩⎪⎨⎪⎧b =2,c =1.反思与感悟 本题解题关键是通过三角恒等变换借助于A +B +C =180°,求出A ,并利用余弦定理列出关于b 、c 的方程组.跟踪训练3 在△ABC 中,角A ,B ,C 所对的边分别是a ,b ,c ,且a 2+c 2-b 2=65ac .求2sin 2A +C 2+sin 2B 的值.解 由已知a 2+c 2-b 22ac =35,所以cos B =35,sin B =1-cos 2B =45,所以2sin 2A +C 2+sin 2B =2cos 2B 2+sin 2B =1+cos B +2sin B cos B =1+35+2×35×45=6425.题型四 有关创新型问题例4 已知x >0,y >0,且x 2-xy +y 2=1,求x 2-y 2的最大值与最小值. 解 构造△ABC ,使AB =1,BC =x ,AC =y ,C =60°, 由余弦定理知AB 2=AC 2+BC 2-2AC ·BC cos C , ∴1=x 2+y 2-xy ,即x ,y 满足已知条件, 由正弦定理得x sin A =y sin B =1sin 60°=233.∴x =233sin A ,y =233sin B ,x 2-y 2=43(sin 2A -sin 2B )=23(1-cos 2A -1+cos 2B ) =23(cos 2B -cos 2A ) =23[cos(240°-2A )-cos 2A ] =23(-32cos 2A -32sin 2A ) =-233sin(2A +60°).∵0°<A <120°,∴60°<2A +60°<300°, 当2A +60°=90°时,x 2-y 2有最小值-233.当2A +60°=270°时,x 2-y 2有最大值233.反思与感悟 解答此类题目,我们可以根据条件,构造三角形,利用正弦、余弦定理将问题予以转化.如本题中将x 2-y 2转化为三角恒等变换及y =A sin(ωx +φ)的值域的问题. 跟踪训练4 已知x 、y 均为正实数,且x 2+y 2-3=xy ,求x +y 的最大值.解 构造△ABC ,角A ,B ,C 的对边分别为x ,y ,3,C =60°,由余弦定理知x 2+y 2-3=xy ,即x 、y 满足已知条件. ∵x sin A =y sin B =3sin 60°=2, ∴x =2sin A ,y =2sin B , ∴x +y =2(sin A +sin B ) =2[sin A +sin(120°-A )] =2(sin A +32cos A +12sin A ) =23(32sin A +12cos A ) =23sin(A +30°).∵0°<A <120°,∴当A =60°时,x +y 有最大值2 3.约分忽略因式为0的情况致误例5 在△ABC 中,已知a ,b ,c 分别是角A ,B ,C 的对边,若a +b a =cos B +cos Acos B ,试判断三角形的形状.错解 由已知得1+b a =1+cos Acos B ,即a cos A =b cos B .由cos A =b 2+c 2-a 22bc ,cos B =a 2+c 2-b 22ac ,得a ·b 2+c 2-a 22bc =b ·a 2+c 2-b 22ac,整理得c 2(a 2-b 2)=a 4-b 4=(a 2-b 2)(a 2+b 2), ∴c 2=a 2+b 2,∴△ABC 为直角三角形.错因分析 利用余弦定理把角转化成边之间的关系,其思路是正确的,但在结果的判断上出现了严重的失误,由(a 2-b 2)(a 2+b 2-c 2)=0得a =b 或a 2+b 2=c 2,而不是a =b 且a 2+b 2=c 2. 正解 由已知得1+b a =1+cos Acos B ,即a cos A =b cos B .由cos A =b 2+c 2-a 22bc ,cos B =a 2+c 2-b 22ac ,得a ·b 2+c 2-a 22bc =b ·a 2+c 2-b 22ac ,整理得(a 2-b 2)(a 2+b 2-c 2)=0, 所以a 2-b 2=0或a 2+b 2-c 2=0, 即a =b 或a 2+b 2=c 2.故△ABC 为等腰三角形或直角三角形.误区警示 在转化的过程中,一定要注意转化的合理性与等价性.跟踪训练5 在△ABC 中,a ,b ,c 分别为内角A ,B ,C 的对边,且2a sin A =(2b +c )sin B +(2c +b )sin C . (1)求A 的大小;(2)若sin B +sin C =1,试判断△ABC 的形状. 解 (1)由2a sin A =(2b +c )sin B +(2c +b )sin C 得 2a 2=(2b +c )b +(2c +b )c , 即 a 2=b 2+c 2+bc ,由余弦定理得cos A =b 2+c 2-a 22bc =-bc 2bc =-12,∵A ∈(0°,180°),∴A =120°.(2)由(1)得a 2=b 2+c 2+bc ,由正弦定理得 sin 2A =sin 2B +sin 2C +sin B sin C . ∴sin 2B +sin 2C +sin B sin C =34,又sin B +sin C =1,∴sin B =sin C =12,∵B 、C ∈(0°,90°),∴B =C =30°, ∴△ABC 为等腰三角形.1.在钝角△ABC 中,a =1,b =2,则最大边c 的取值范围是( ) A .1<c <3 B .2<c <3 C.5<c <3 D .22<c <3答案 C解析 在钝角△ABC 中,由于最大边为c ,所以角C 为钝角.所以c 2>a 2+b 2=1+4=5,即c >5,又因c <a +b =1+2=3,所以5<c <3.2.在△ABC 中,若c =2a cos B ,则△ABC 的形状一定是( ) A.等腰直角三角形 B .直角三角形 C .等腰三角形 D .等边三角形 答案 C解析 ∵c =2a cos B ,由正弦定理得 2cos B sin A =sin C =sin(A +B ),∴sin A cos B -cos A sin B =0,即sin(A -B )=0, 又∵-π<A -B <π,∴A -B =0,∴A =B . ∴△ABC 是等腰三角形.3.已知△ABC 的三边长分别为AB =7,BC =5,AC =6.则AB →·BC →的值为( ) A .19 B .14 C .-18 D .-19 答案 D解析 由余弦定理的推论知: cos B =AB 2+BC 2-AC 22AB ·BC =1935.所以AB →·BC →=|AB →|·|BC →|·cos(π-B ) =7×5×(-1935)=-19,故选D.4.△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,已知b =c ,a 2=2b 2(1-sin A ),则A =( ) A.3π4 B.π3 C.π4 D.π6 答案 C解析 在△ABC 中,由余弦定理得a 2=b 2+c 2-2bc cos A , ∵b =c ,∴a 2=2b 2(1-cos A ), 又∵a 2=2b 2(1-sin A ), ∴cos A =sin A ,∴tan A =1, ∵A ∈(0,π),∴A =π4,故选C.5.在△ABC 中,若a cos A =b cos B =ccos C ,则△ABC 是________三角形.答案 等边解析 ∵a cos A =bcos B ,∴sin A cos B -sin B cos A =0, ∴sin(A -B )=0,∵A ,B ∈(0,π),∴A -B ∈(-π,π), ∴A -B =0,∴A =B . 同理B =C ,∴A =B =C , ∴△ABC 为等边三角形.1.判断三角形的形状是看该三角形是否为某些特殊的三角形(如锐角、直角、钝角、等腰、等边三角形等).对于给出条件是边角关系混合在一起的问题,一般地,应运用正弦定理和余弦定理,要么把它统一为边的关系,要么把它统一为角的关系,再利用三角形的有关知识、三角恒等变形方法、代数恒等变形方法等进行转化、化简,从而得出结论.2.解决正弦定理与余弦定理的综合应用问题,应注意根据具体情况引入未知数,运用方程思想来解决问题;平面向量与解三角形的交汇问题,应注意准确运用向量知识转化为解三角形问题,再利用正弦、余弦定理求解.。
2018年春高中数学必修五课后提升作业 一 1.1.1 正弦定理 含解析

温馨提示:此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
关闭Word文档返回原板块。
课后提升作业一正弦定理(45分钟70分)一、选择题(每小题5分,共40分)1.(2016·广州高二检测)在△ABC中,sinA=sinB,则必有( )A.A=BB.A≠BC.A=B或A=C-BD.A+B=错误!未找到引用源。
【解析】选A.因为错误!未找到引用源。
=错误!未找到引用源。
, sinA=sinB,所以a=b,故A=B.2.满足a=4,b=3和A=45°的△ABC的个数为( )A.0B.1C.2D.无数多个【解析】选B.因为A=45°<90°,a=4>3=b,所以△ABC的个数为1.3.在△ABC中,sinA=sinC,则△ABC一定是( )A.直角三角形B.等腰三角形C.锐角三角形D.钝角三角形【解析】选 B.设错误!未找到引用源。
=错误!未找到引用源。
=错误!未找到引用源。
=k,又sinA=sinC,即错误!未找到引用源。
=错误!未找到引用源。
,所以a=c,所以△ABC一定是等腰三角形.4.(2016·聊城高二检测)在△ABC中,a=15,b=10,A=60°,则cosB= ( )A.±错误!未找到引用源。
B.错误!未找到引用源。
C.错误!未找到引用源。
D.±错误!未找到引用源。
【解析】选C.由正弦定理可知错误!未找到引用源。
=错误!未找到引用源。
,即错误!未找到引用源。
=错误!未找到引用源。
,解得sinB=错误!未找到引用源。
,因为b<a,A=60°,所以B为锐角,故cosB=错误!未找到引用源。
=错误!未找到引用源。
.【误区警示】解答本题易出现选D的错误答案,导致出现这种错误的原因是忽略了b<a的条件.5.在△ABC中,若c=2acosB,则△ABC的形状为( )A.直角三角形B.等腰三角形C.等边三角形D.不等边三角形【解析】选B.由正弦定理知c=2RsinC,a=2RsinA,故sinC=2sinAcosB=sin(A+B)=sinAcosB+cosAsinB.所以sinAcosB=cosAsinB,即sin(A-B)=0,所以A=B.所以△ABC为等腰三角形.6.(2016·包头高二检测)在△ABC中,A,B,C所对的边分别为a,b,c,若a=8,B=60°,C=75°,则b等于( )A.4错误!未找到引用源。
高中数学必修5单元配套练习试题1.1.1 正弦定理及参考答案解析
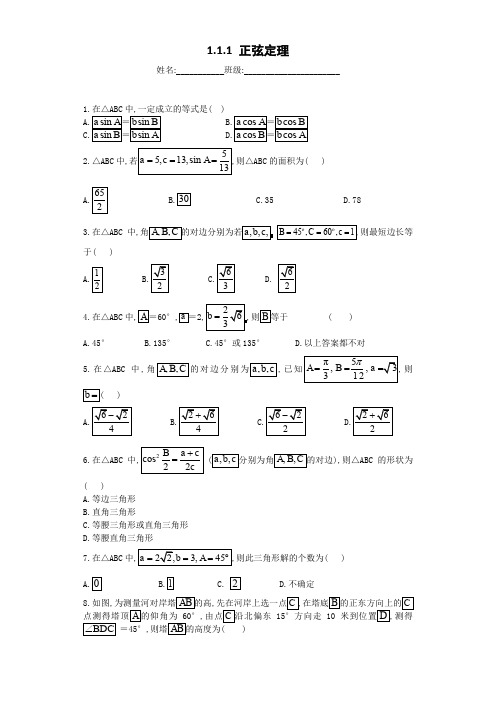
1.1.1 正弦定理姓名:___________班级:______________________1.在△ABC中,一定成立的等式是( )2.△ABC中,则△ABC的面积为( )3.在△ABC中,则最短边长等于( )4.在△ABC中 ( )A.45°B.135°C.45°或135°D.以上答案都不对5.在△ABC中,对边分别已则6.在△ABC中),则△ABC的形状为( )A.等边三角形B.直角三角形C.等腰三角形或直角三角形D.等腰直角三角形7.在△ABC中则此三角形解的个数为( )不确定8.如图,,,15°方向走10测得=45°,( )A.10 米9.在△ABC中,角所对的边分别为,且,则10.在△ABC中,角A,B,C所对的边分别是a,b,c,别在中12.在△ABC中,若C=2B,.13.在△ABC中,A=30°,C=45°,c求a、b及cos B.14.某社区拟建一个活动广场,老年活动区,路(不考虑宽度),饮区.(1);(2).参考答案1.C故选C. 考点:正弦定理.2.B所以三角形为直角三角形,其中c 为斜边,所以故选B.考点:正弦定理解三角形.3.C【解析】在△ABC 中因为大边对大角,所以△ABC 中,.在△ABC 中,考点:大边对大角,正弦定理解三角形.4.A263< 考点:正弦定理解三角形.5.D【解析】在△ABC 中,由正弦定理可得故选D. 考点:正弦定理的应用.6.B三角形为直角三角形. 考点:正弦定理边角互化的应用.7.C34=,,也可能是钝角,所以此三角形有两解,故选C.考点:正弦定理判定三角形解的个数.8.D【解析】在△BCD中,米..故选D.考点:利用正弦定理解三角形.考点:正弦定理解三角形.【解析】由,及,得,由正弦定理得即,考点:正弦定理解三角形.【解析】如图,,))同理,中)))θ+考点:正弦定理解三角形.12.(1,2) 【解析】因为A +B +C =π,C =2B,所以A =π-3B >0,所以0<B cos B <故1 2. 考点:正弦定理在解三角形中的应用.13.a =1,b【解析】因为A =30°,C =45°,c所以由正弦定理,得a 又B =180°-(30°+45°)=105°,所以cos B =cos 10b=2sin(45°+30°) 考点:正弦定理在解三角形中的应用.【解析】(1)由正弦定理,(2)在△A DC 中,设则,由正弦定理得i n D C ,,考点:正弦定理解三角形,三角恒等变换,函数的最值.。
2018年高中数学必修五达标练习:第2章 §1-1.1 正弦定理

[A 基础达标]1.在△ABC 中,若3a =2b sin A ,则B =( )A.π3B .π6 C.π3或2π3 D .π6或5π6解析:选C.由正弦定理,得3sin A =2sin B sin A ,所以sin A (2sin B -3)=0.因为0<A <π,0<B <π,所以sin A ≠0,sin B =32,所以B =π3或2π3. 2.已知△ABC 的三个内角之比为A ∶B ∶C =3∶2∶1,那么,对应的三边之比a ∶b ∶c 等于( )A .3∶2∶1B .3∶2∶1 C.3∶2∶1 D .2∶3∶1解析:选D.因为A ∶B ∶C =3∶2∶1,A +B +C =180°,所以A =90°,B =60°,C =30°,所以a ∶b ∶c =sin 90°∶sin 60°∶sin 30°=1∶32∶12=2∶3∶1. 3.符合下列条件的△ABC 有且只有一个的是( )A .a =1,b =2,A =30°B .a =1,b =2,c =3C .b =c =1,B =45°D .a =1,b =2,A =100° 解析:选C.对于A ,由正弦定理得1sin 30°=2sin B,所以sin B =22.又a <b ,所以B =45°或135°,所以满足条件的三角形有两个.对于B ,a +b =c ,构不成三角形.对于C ,b =c =1,所以B =C =45°,A =90°,所以满足条件的三角形只有一个.对于D ,a <b ,所以A <B ,而A =100°,所以没有满足条件的三角形.4.在△ABC 中,已知a 2tan B =b 2tan A ,则△ABC 的形状是( )A .锐角三角形B .直角三角形C .钝角三角形D .等腰三角形或直角三角形解析:选D.将a =2R sin A ,b =2R sin B (R 为△ABC 外接圆的半径)代入已知条件,得sin 2A tanB =sin 2B tan A ,则sin 2A sin B cos B =sin A sin 2B cos A . 因为sin A sin B ≠0,所以sin A cos B =sin B cos A, 所以sin 2A =sin 2B ,所以2A =2B 或2A =π-2B ,所以A =B 或A +B =π2,故△ABC 为等腰三角形或直角三角形. 5.△ABC 的三个内角A ,B ,C 所对的边分别为a ,b ,c ,若a sin A sin B +b cos 2A =2a ,则b a的值为( ) A .2 3B .2 2 C. 3D . 2 解析:选D.由正弦定理,得sin 2A sin B +sin B cos 2A =2sin A ,即sin B ·(sin 2A +cos 2A )=2sin A .所以sin B =2sin A .所以b a =sin B sin A = 2. 6.在△ABC 中,B =45°,C =60°,c =1,则最短边的边长等于__________.解析:由三角形内角和定理知:A =75°,由边角关系知B 所对的边b 为最小边,由正弦定理b sin B =c sin C 得b =c sin B sin C =1×2232=63. 答案:637.已知△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若a =52b ,A =2B ,则cos B =________. 解析:在△ABC 中,因为⎩⎪⎨⎪⎧a =52b ,A =2B ,所以⎩⎪⎨⎪⎧sin A =52sin B ,sin A =sin 2B =2sin B cos B ,所以cos B =54. 答案:54 8.△ABC 中,a ,b ,c 分别是内角A ,B ,C 所对的边,且cos 2B +3cos(A +C )+2=0,b =3,则c ∶sin C 等于________.解析:由题意得cos 2B -3cos B +2=0,即2cos 2B -3cos B +1=0,解得cos B =12或cos B =1(舍去),所以sin B =32,由正弦定理得c sin C =b sin B =332=2.答案:29.△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知cos(A -C )+cos B =1,a =2c ,求C 的大小.解:由B =π-(A +C ),得cos B =-cos(A +C ).于是cos(A -C )+cos B =cos(A -C )-cos(A +C )=2sin A sin C .所以sin A sin C =12.① 由a =2c 及正弦定理得sin A =2sin C .②由①②得sin 2C =14, 于是sin C =-12(舍去)或sin C =12. 又a =2c ,所以C =π6. 10.在△ABC 中,(a 2+b 2)sin(A -B )=(a 2-b 2)sin(A +B ),试判断△ABC 的形状.解:由(a 2+b 2)sin(A -B )=(a 2-b 2)sin(A +B ),得a 2[sin(A +B )-sin(A -B )]=b 2[sin(A +B )+sin(A -B )],所以a 2·cos A sin B =b 2sin A cos B .由正弦定理,得sin 2A cos A sin B =sin 2B sin A cos B .因为0<A <π,0<B <π,所以sin A >0,sin B >0,0<2A <2π,0<2B <2π,所以sin A cos A =sin B cos B ,即sin 2A =sin 2B .所以2A =2B 或2A +2B =π,即A =B 或A +B =π2. 所以△ABC 为等腰三角形或直角三角形.[B 能力提升]11.满足B =60°,AC =12,BC =k 的△ABC 恰有一个,则k 的取值范围是( )A .k =8 3B .0<k ≤12C .k ≥12D .0<k ≤12或k =8 3解析:选D.已知两边和其中一边的对角解三角形时,首先求出另一边的对角的正弦值,由正弦值求角时,需对角的情况进行讨论:当AC <BC sin B ,即12<k sin 60°,即k >83时,三角形无解;当AC =BC sin B ,即12=k sin 60°,即k =83时,三角形有一解;当BC sin B <AC <BC ,即32k <12<k ,即12<k <83时,三角形有两解; 当0<BC ≤AC ,即0<k ≤12时,三角形有一解.综上,0<k ≤12或k =83时,三角形有一解.12.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若1+tan A tan B =2c b,则角A 的大小为__________.解析:由1+tan A tan B =2c b可得 1+sin A cos B cos A sin B =2c b, 由正弦定理可得1+sin A cos B cos A sin B =2sin C sin B整理得sin A cos B +cos A sin B cos A sin B =2sin C sin B, 所以sin(A +B )=2sin C cos A ,所以cos A =12,又因为0<A <π, 所以A =π3. 答案:π313.在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知a sin 2B =3b sin A .(1)求B ;(2)若cos A =13,求sin C 的值. 解:(1)在△ABC 中,由a sin A =b sin B,可得a sin B =b sin A , 又由a sin 2B =3b sin A ,得2a sin B cos B =3b sin A =3a sin B ,所以cos B =32,得B =π6. (2)由cos A =13,可得sin A =223,则 sin C =sin[π-(A +B )]=sin(A +B )=sin ⎝⎛⎭⎫A +π6=32sin A +12cos A =26+16. 14.(选做题)在△ABC 中,已知a +b a =sin B sin B -sin A,且cos(A -B )+cos C =1-cos 2C . (1)试确定△ABC 的形状;(2)求a +c b的取值范围. 解:(1)在△ABC 中,设其外接圆半径为R , 根据正弦定理得,sin A =a 2R ,sin B =b 2R,代入a +b a =sin B sin B -sin A ,得a +b a =b b -a, 所以b 2-a 2=ab .①因为cos(A -B )+cos C =1-cos 2C ,所以cos(A -B )-cos(A +B )=2sin 2C ,所以sin A sin B =sin 2C .由正弦定理,得a 2R ·b 2R=⎝⎛⎭⎫c 2R 2, 所以ab =c 2.②把②代入①得,b 2-a 2=c 2,即a 2+c 2=b 2.所以△ABC 是直角三角形.(2)由第一问知B =π2,所以A +C =π2, 所以C =π2-A . 所以sin C =sin ⎝⎛⎭⎫π2-A =cos A . 根据正弦定理,得a +cb =sin A +sin C sin B=sin A +cos A =2sin ⎝⎛⎭⎫A +π4. 因为ac <ab =c 2,所以a <c ,所以0<A <π4,所以π4<A +π4<π2. 所以22<sin ⎝⎛⎭⎫A +π4<1, 所以1<2sin ⎝⎛⎭⎫A +π4<2, 即a +c b的取值范围是(1, 2 ).。
2018年高中数学必修五达标练习:第2章 §1-1.2 余弦定理

[A 基础达标]1.在△ABC 中,已知a =4,b =6,C =120°,则边c 的值是( ) A .8 B .217 C .6 2D .219解析:选D.由余弦定理得:c 2=a 2+b 2-2ab cos C =16+36-2×4×6cos 120°=76,所以c =219,故选D.2.在△ABC 中,若a =8,b =7,cos C =1314,则最大角的余弦值是( )A .-15B .-16C .-17D .-18解析:选C.由余弦定理,得c 2=a 2+b 2-2ab cos C =82+72-2×8×7×1314=9,所以c =3,故a 最大,所以最大角的余弦值为cos A =b 2+c 2-a 22bc =72+32-822×7×3=-17.3.在△ABC 中,a ,b ,c 为角A 、B 、C 的对边,且b 2=ac ,则B 的取值范围是( ) A.⎝⎛⎦⎤0,π3B .⎣⎡⎭⎫π3,π C.⎝⎛⎦⎤0,π6D .⎣⎡⎭⎫π6,π解析:选 A.cos B =a 2+c 2-b 22ac =(a -c )2+ac 2ac =(a -c )22ac +12≥12,因为0<B <π,所以B ∈⎝⎛⎦⎤0,π3.4.在△ABC 中,若b cos A =a cos B ,则△ABC 是( ) A .等边三角形 B .等腰三角形 C .直角三角形D .锐角三角形解析:选B.因为b cos A =a cos B , 所以b ·b 2+c 2-a 22bc =a ·a 2+c 2-b 22ac .所以b 2+c 2-a 2=a 2+c 2-b 2. 所以a 2=b 2.所以a =b .故此三角形是等腰三角形.5.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若C =120°,c =2a ,则( ) A .a >bB .a <bC .a =bD .a 与b 的大小关系不能确定解析:选A.由余弦定理,知c 2=a 2+b 2-2ab cos C ,则2a 2=a 2+b 2+ab ,即a 2=b 2+ab ,则⎝⎛⎭⎫b a 2+b a -1=0,所以b a =5-12<1,所以a >b ,故选A. 6.△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若2b cos B =a cos C +c cos A ,则B =________. 解析:依题意得2b ×a 2+c 2-b 22ac =a ×a 2+b 2-c 22ab +c ×b 2+c 2-a 22bc ,即a 2+c 2-b 2=ac ,所以2ac cos B =ac >0,cos B =12.又0<B <π,所以B =π3.答案:π37.设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且a =2,cos C =-14,3sin A =2sin B ,则c =________.解析:因为3sin A =2sin B ,所以3a =2b .又a =2,所以b =3.由余弦定理可知c 2=a 2+b 2-2ab cos C ,所以c 2=22+32-2×2×3×⎝⎛⎭⎫-14=16,所以c =4. 答案:48.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .若a 2=b 2+14c 2,则a cos Bc 的值为________.解析:因为a 2=b 2+14c 2,所以b 2=a 2-14c 2.所以cos B =a 2+c 2-b 22ac=a 2+c 2-⎝⎛⎭⎫a 2-14c 22ac =5c 8a .所以a cos Bc =a ·5c8a c =58.答案:589.设锐角△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知a =2b sin A . (1)求B 的大小;(2)若a =33,c =5,求b 的值.解:(1)由a =2b sin A ,根据正弦定理,得sin A =2sin B sin A ,因为sin A ≠0,所以sin B =12.因为△ABC 为锐角三角形,所以B =π6.(2)根据余弦定理,b 2=a 2+c 2-2ac cos B=27+25-2×33×5×32=7. 所以b =7.10.在△ABC 中,若已知(a +b +c )(a +b -c )=3ab ,并且sin C =2sin B cos A ,试判断△ABC 的形状.解:由正弦定理,可得sin B =b 2R ,sin C =c2R .由余弦定理,得cos A =b 2+c 2-a 22bc .代入sin C =2sin B cos A , 得c =2b ·b 2+c 2-a 22bc .整理得a =b .又因为(a +b +c )(a +b -c )=3ab , 所以a 2+b 2-c 2=ab ,即cos C =a 2+b 2-c 22ab =12,故C =π3.又a =b ,所以△ABC 为等边三角形.[B 能力提升]11.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .若b 2+c 2-a 2=3bc ,且b =3a ,则下列关系一定不成立的是( ) A .a =c B .b =c C .2a =cD .a 2+b 2=c 2解析:选B.因为b 2+c 2-a 2=3bc , 所以cos A =b 2+c 2-a 22bc =32.又因为A ∈(0°,180°),所以A =30°.因为b =3a ,所以sin B =3sin A =32.又因为B ∈(0°,180°),所以B =60°或B =120°.当B =60°时,C =90°,此时△ABC 为直角三角形,得到a 2+b 2=c 2,2a =c .当B =120°时,C =30°,此时△ABC 为等腰三角形,得到a =c .综上可知,b =c 一定不成立.故选B.12.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且a =3,b =4,c =6,则bc cos A +ac cos B +ab cos C 的值是__________. 解析:因为cos A =b 2+c 2-a 22bc ,所以bc cos A =12(b 2+c 2-a 2).同理ac cos B =12(a 2+c 2-b 2),ab cos C =12(a 2+b 2-c 2),所以bc cos A +ac cos B +ab cos C =12(a 2+b 2+c 2)=612.答案:61213.在△ABC 中,a ,b ,c 分别是角A ,B ,C 所对的边,cos B =35,且AB →·BC →=-21.若a =7,求角C 的大小. 解:因为AB →·BC →=-21,所以BA →·BC →=21.所以BA →·BC →=|BA →|·|BC →|cos B =ac cos B =21. 又cos B =35,所以sin B =45,ac =35.又a =7,所以c =5.所以b 2=a 2+c 2-2ac cos B =32,所以b =4 2.由正弦定理c sin C =b sin B ,得sin C =c b sin B =542×45=22.因为cos B =35>0,所以B 是锐角.因为c <b ,所以C 一定是锐角,所以C =45°.14.(选做题)如图,△ABC 的顶点坐标分别为A (3,4),B (0,0),C (c ,0). (1)若c =5,求sin A 的值; (2)若A 为钝角,求c 的取值范围. 解:(1)因为A (3,4), B (0,0), 所以AB =5, 当c =5时,BC =5, 所以AC =(5-3)2+(0-4)2=2 5.由余弦定理,知cos A =AB 2+AC 2-BC 22AB ·AC =52+(25)2-522×5×25=55. 因为0<A <π,所以sin A =1-cos 2A =1-⎝⎛⎭⎫552=255.(2)因为A (3,4),B (0,0),C (c ,0), 所以AC 2=(c -3)2+42,BC 2=c 2,由余弦定理,得cos A =AB 2+AC 2-BC 22AB ·AC .因为A 为钝角,所以cos A <0, 即AB 2+AC 2-BC 2<0,所以52+(c -3)2+42-c 2=50-6c <0,所以c >253.故c 的取值范围为⎝⎛⎭⎫253,+∞.。
2018年高中数学北师大版必修五达标练习:第2章 §1-1.1 正弦定理 Word版含解析

[A 基础达标]1.在△ABC 中,若3a =2b sin A ,则B =( )A.π3B .π6 C.π3或2π3 D .π6或5π6解析:选C.由正弦定理,得3sin A =2sin B sin A ,所以sin A (2sin B -3)=0.因为0<A <π,0<B <π,所以sin A ≠0,sin B =32,所以B =π3或2π3. 2.已知△ABC 的三个内角之比为A ∶B ∶C =3∶2∶1,那么,对应的三边之比a ∶b ∶c 等于( )A .3∶2∶1B .3∶2∶1 C.3∶2∶1 D .2∶3∶1解析:选D.因为A ∶B ∶C =3∶2∶1,A +B +C =180°,所以A =90°,B =60°,C =30°,所以a ∶b ∶c =sin 90°∶sin 60°∶sin 30°=1∶32∶12=2∶3∶1. 3.符合下列条件的△ABC 有且只有一个的是( )A .a =1,b =2,A =30°B .a =1,b =2,c =3C .b =c =1,B =45°D .a =1,b =2,A =100° 解析:选C.对于A ,由正弦定理得1sin 30°=2sin B,所以sin B =22.又a <b ,所以B =45°或135°,所以满足条件的三角形有两个.对于B ,a +b =c ,构不成三角形.对于C ,b =c =1,所以B =C =45°,A =90°,所以满足条件的三角形只有一个.对于D ,a <b ,所以A <B ,而A =100°,所以没有满足条件的三角形.4.在△ABC 中,已知a 2tan B =b 2tan A ,则△ABC 的形状是( )A .锐角三角形B .直角三角形C .钝角三角形D .等腰三角形或直角三角形解析:选D.将a =2R sin A ,b =2R sin B (R 为△ABC 外接圆的半径)代入已知条件,得sin 2A tanB =sin 2B tan A ,则sin 2A sin B cos B =sin A sin 2B cos A . 因为sin A sin B ≠0,所以sin A cos B =sin B cos A, 所以sin 2A =sin 2B ,所以2A =2B 或2A =π-2B ,所以A =B 或A +B =π2,故△ABC 为等腰三角形或直角三角形. 5.△ABC 的三个内角A ,B ,C 所对的边分别为a ,b ,c ,若a sin A sin B +b cos 2A =2a ,则b a的值为( ) A .2 3B .2 2 C. 3D . 2 解析:选D.由正弦定理,得sin 2A sin B +sin B cos 2A =2sin A ,即sin B ·(sin 2A +cos 2A )=2sin A .所以sin B =2sin A .所以b a =sin B sin A = 2. 6.在△ABC 中,B =45°,C =60°,c =1,则最短边的边长等于__________.解析:由三角形内角和定理知:A =75°,由边角关系知B 所对的边b 为最小边,由正弦定理b sin B =c sin C 得b =c sin B sin C =1×2232=63. 答案:637.已知△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若a =52b ,A =2B ,则cos B =________. 解析:在△ABC 中,因为⎩⎪⎨⎪⎧a =52b ,A =2B ,所以⎩⎪⎨⎪⎧sin A =52sin B ,sin A =sin 2B =2sin B cos B ,所以cos B =54. 答案:54 8.△ABC 中,a ,b ,c 分别是内角A ,B ,C 所对的边,且cos 2B +3cos(A +C )+2=0,b =3,则c ∶sin C 等于________.解析:由题意得cos 2B -3cos B +2=0,即2cos 2B -3cos B +1=0,解得cos B =12或cos B =1(舍去),所以sin B =32,由正弦定理得c sin C =b sin B =332=2.答案:29.△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知cos(A -C )+cos B =1,a =2c ,求C 的大小.解:由B =π-(A +C ),得cos B =-cos(A +C ).于是cos(A -C )+cos B =cos(A -C )-cos(A +C )=2sin A sin C .所以sin A sin C =12.① 由a =2c 及正弦定理得sin A =2sin C .②由①②得sin 2C =14, 于是sin C =-12(舍去)或sin C =12. 又a =2c ,所以C =π6. 10.在△ABC 中,(a 2+b 2)sin(A -B )=(a 2-b 2)sin(A +B ),试判断△ABC 的形状.解:由(a 2+b 2)sin(A -B )=(a 2-b 2)sin(A +B ),得a 2[sin(A +B )-sin(A -B )]=b 2[sin(A +B )+sin(A -B )],所以a 2·cos A sin B =b 2sin A cos B .由正弦定理,得sin 2A cos A sin B =sin 2B sin A cos B .因为0<A <π,0<B <π,所以sin A >0,sin B >0,0<2A <2π,0<2B <2π,所以sin A cos A =sin B cos B ,即sin 2A =sin 2B .所以2A =2B 或2A +2B =π,即A =B 或A +B =π2. 所以△ABC 为等腰三角形或直角三角形.[B 能力提升]11.满足B =60°,AC =12,BC =k 的△ABC 恰有一个,则k 的取值范围是( )A .k =8 3B .0<k ≤12C .k ≥12D .0<k ≤12或k =8 3解析:选D.已知两边和其中一边的对角解三角形时,首先求出另一边的对角的正弦值,由正弦值求角时,需对角的情况进行讨论:当AC <BC sin B ,即12<k sin 60°,即k >83时,三角形无解;当AC =BC sin B ,即12=k sin 60°,即k =83时,三角形有一解;当BC sin B <AC <BC ,即32k <12<k ,即12<k <83时,三角形有两解; 当0<BC ≤AC ,即0<k ≤12时,三角形有一解.综上,0<k ≤12或k =83时,三角形有一解.12.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若1+tan A tan B =2c b,则角A 的大小为__________.解析:由1+tan A tan B =2c b可得 1+sin A cos B cos A sin B =2c b, 由正弦定理可得1+sin A cos B cos A sin B =2sin C sin B整理得sin A cos B +cos A sin B cos A sin B =2sin C sin B, 所以sin(A +B )=2sin C cos A ,所以cos A =12,又因为0<A <π, 所以A =π3. 答案:π313.在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知a sin 2B =3b sin A .(1)求B ;(2)若cos A =13,求sin C 的值. 解:(1)在△ABC 中,由a sin A =b sin B,可得a sin B =b sin A , 又由a sin 2B =3b sin A ,得2a sin B cos B =3b sin A =3a sin B ,所以cos B =32,得B =π6. (2)由cos A =13,可得sin A =223,则 sin C =sin[π-(A +B )]=sin(A +B )=sin ⎝⎛⎭⎫A +π6=32sin A +12cos A =26+16. 14.(选做题)在△ABC 中,已知a +b a =sin B sin B -sin A,且cos(A -B )+cos C =1-cos 2C . (1)试确定△ABC 的形状;(2)求a +c b的取值范围. 解:(1)在△ABC 中,设其外接圆半径为R , 根据正弦定理得,sin A =a 2R ,sin B =b 2R,代入a +b a =sin B sin B -sin A ,得a +b a =b b -a, 所以b 2-a 2=ab .①因为cos(A -B )+cos C =1-cos 2C ,所以cos(A -B )-cos(A +B )=2sin 2C ,所以sin A sin B =sin 2C .由正弦定理,得a 2R ·b 2R=⎝⎛⎭⎫c 2R 2, 所以ab =c 2.②把②代入①得,b 2-a 2=c 2,即a 2+c 2=b 2.所以△ABC 是直角三角形.(2)由第一问知B =π2,所以A +C =π2, 所以C =π2-A . 所以sin C =sin ⎝⎛⎭⎫π2-A =cos A . 根据正弦定理,得a +cb =sin A +sin C sin B=sin A +cos A =2sin ⎝⎛⎭⎫A +π4. 因为ac <ab =c 2,所以a <c ,所以0<A <π4,所以π4<A +π4<π2. 所以22<sin ⎝⎛⎭⎫A +π4<1, 所以1<2sin ⎝⎛⎭⎫A +π4<2, 即a +c b的取值范围是(1, 2 ).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[A 基础达标]1.在△ABC 中,若3a =2b sin A ,则B =( )A.π3B .π6 C.π3或2π3 D .π6或5π6解析:选C.由正弦定理,得3sin A =2sin B sin A ,所以sin A (2sin B -3)=0.因为0<A <π,0<B <π,所以sin A ≠0,sin B =32,所以B =π3或2π3. 2.已知△ABC 的三个内角之比为A ∶B ∶C =3∶2∶1,那么,对应的三边之比a ∶b ∶c 等于( )A .3∶2∶1B .3∶2∶1 C.3∶2∶1 D .2∶3∶1解析:选D.因为A ∶B ∶C =3∶2∶1,A +B +C =180°,所以A =90°,B =60°,C =30°,所以a ∶b ∶c =sin 90°∶sin 60°∶sin 30°=1∶32∶12=2∶3∶1. 3.符合下列条件的△ABC 有且只有一个的是( )A .a =1,b =2,A =30°B .a =1,b =2,c =3C .b =c =1,B =45°D .a =1,b =2,A =100° 解析:选C.对于A ,由正弦定理得1sin 30°=2sin B,所以sin B =22.又a <b ,所以B =45°或135°,所以满足条件的三角形有两个.对于B ,a +b =c ,构不成三角形.对于C ,b =c =1,所以B =C =45°,A =90°,所以满足条件的三角形只有一个.对于D ,a <b ,所以A <B ,而A =100°,所以没有满足条件的三角形.4.在△ABC 中,已知a 2tan B =b 2tan A ,则△ABC 的形状是( )A .锐角三角形B .直角三角形C .钝角三角形D .等腰三角形或直角三角形解析:选D.将a =2R sin A ,b =2R sin B (R 为△ABC 外接圆的半径)代入已知条件,得sin 2A tanB =sin 2B tan A ,则sin 2A sin B cos B =sin A sin 2B cos A . 因为sin A sin B ≠0,所以sin A cos B =sin B cos A,所以sin 2A =sin 2B ,所以2A =2B 或2A =π-2B ,所以A =B 或A +B =π2,故△ABC 为等腰三角形或直角三角形. 5.△ABC 的三个内角A ,B ,C 所对的边分别为a ,b ,c ,若a sin A sin B +b cos 2A =2a ,则b a的值为( ) A .2 3B .2 2 C. 3D . 2 解析:选D.由正弦定理,得sin 2A sin B +sin B cos 2A =2sin A ,即sin B ·(sin 2A +cos 2A )=2sin A .所以sin B =2sin A .所以b a =sin B sin A = 2. 6.在△ABC 中,B =45°,C =60°,c =1,则最短边的边长等于__________.解析:由三角形内角和定理知:A =75°,由边角关系知B 所对的边b 为最小边,由正弦定理b sin B =c sin C 得b =c sin B sin C =1×2232=63. 答案:637.已知△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若a =52b ,A =2B ,则cos B =________. 解析:在△ABC 中,因为⎩⎪⎨⎪⎧a =52b ,A =2B ,所以⎩⎪⎨⎪⎧sin A =52sin B ,sin A =sin 2B =2sin B cos B ,所以cos B =54. 答案:54 8.△ABC 中,a ,b ,c 分别是内角A ,B ,C 所对的边,且cos 2B +3cos(A +C )+2=0,b =3,则c ∶sin C 等于________.解析:由题意得cos 2B -3cos B +2=0,即2cos 2B -3cos B +1=0,解得cos B =12或cos B =答案:29.△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知cos(A -C )+cos B =1,a =2c ,求C 的大小.解:由B =π-(A +C ),得cos B =-cos(A +C ).于是cos(A -C )+cos B =cos(A -C )-cos(A +C )=2sin A sin C .所以sin A sin C =12.① 由a =2c 及正弦定理得sin A =2sin C .②由①②得sin 2C =14, 于是sin C =-12(舍去)或sin C =12. 又a =2c ,所以C =π6. 10.在△ABC 中,(a 2+b 2)sin(A -B )=(a 2-b 2)sin(A +B ),试判断△ABC 的形状.解:由(a 2+b 2)sin(A -B )=(a 2-b 2)sin(A +B ),得a 2[sin(A +B )-sin(A -B )]=b 2[sin(A +B )+sin(A -B )],所以a 2·cos A sin B =b 2sin A cos B .由正弦定理,得sin 2A cos A sin B =sin 2B sin A cos B .因为0<A <π,0<B <π,所以sin A >0,sin B >0,0<2A <2π,0<2B <2π,所以sin A cos A =sin B cos B ,即sin 2A =sin 2B .所以2A =2B 或2A +2B =π,即A =B 或A +B =π2. 所以△ABC 为等腰三角形或直角三角形.[B 能力提升]11.满足B =60°,AC =12,BC =k 的△ABC 恰有一个,则k 的取值范围是( )A .k =8 3B .0<k ≤12C .k ≥12D .0<k ≤12或k =8 3解析:选D.已知两边和其中一边的对角解三角形时,首先求出另一边的对角的正弦值,由正弦值求角时,需对角的情况进行讨论:当AC <BC sin B ,即12<k sin 60°,即k >83时,三角形无解;当AC =BC sin B ,即12=k sin 60°,即k =83时,三角形有一解;当0<BC ≤AC ,即0<k ≤12时,三角形有一解.综上,0<k ≤12或k =83时,三角形有一解.12.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若1+tan A tan B =2c b,则角A 的大小为__________. 解析:由1+tan A tan B =2c b可得 1+sin A cos B cos A sin B =2c b, 由正弦定理可得1+sin A cos B cos A sin B =2sin C sin B整理得sin A cos B +cos A sin B cos A sin B =2sin C sin B, 所以sin(A +B )=2sin C cos A , 所以cos A =12,又因为0<A <π, 所以A =π3. 答案:π313.在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知a sin 2B =3b sin A .(1)求B ;(2)若cos A =13,求sin C 的值. 解:(1)在△ABC 中,由a sin A =b sin B,可得a sin B =b sin A , 又由a sin 2B =3b sin A ,得2a sin B cos B =3b sin A =3a sin B ,所以cos B =32,得B =π6. (2)由cos A =13,可得sin A =223,则 sin C =sin[π-(A +B )]=sin(A +B )=sin ⎝⎛⎭⎫A +π6=32sin A +12cos A =26+16. 14.(选做题)在△ABC 中,已知a +b a =sin B sin B -sin A,且cos(A -B )+cos C =1-cos 2C . (1)试确定△ABC 的形状;(2)求a +c b的取值范围. 解:(1)在△ABC 中,设其外接圆半径为R ,根据正弦定理得,sin A =a 2R ,sin B =b 2R, 代入a +b a =sin B sin B -sin A ,得a +b a =b b -a, 所以b 2-a 2=ab .①因为cos(A -B )+cos C =1-cos 2C ,所以cos(A -B )-cos(A +B )=2sin 2C ,所以sin A sin B =sin 2C .由正弦定理,得a 2R ·b 2R=⎝⎛⎭⎫c 2R 2, 所以ab =c 2.②把②代入①得,b 2-a 2=c 2,即a 2+c 2=b 2.所以△ABC 是直角三角形.(2)由第一问知B =π2,所以A +C =π2, 所以C =π2-A . 所以sin C =sin ⎝⎛⎭⎫π2-A =cos A . 根据正弦定理,得a +cb =sin A +sin C sin B=sin A +cos A =2sin ⎝⎛⎭⎫A +π4. 因为ac <ab =c 2,所以a <c ,所以0<A <π4,所以π4<A +π4<π2. 所以22<sin ⎝⎛⎭⎫A +π4<1, 所以1<2sin ⎝⎛⎭⎫A +π4<2, 即a +c b的取值范围是(1, 2 ).。
