忠县民族中学2012年秋季九年级第三次月考数学试卷
九年级数学第三次月考.doc

【本文由书林工作坊整理发布,谢谢你的关注!】1九年级数学第三次月考数 学 试 卷考生须知:1. 本卷共三大题,24小题. 全卷满分为150分,考试时间为120分钟.2. 答题前,请用蓝、黑墨水的钢笔或圆珠笔将学校、姓名、学号分别填在密封线内相应的位置上,不要遗漏.3. 本卷不另设答题卡和答题卷,请在本卷相应的位置上直接答题.答题必须用蓝、黑墨水的钢笔或圆珠笔(画图请用铅笔),答题 时允许使用计算器.参考公式:二次函数2(0)y ax bx c a =++≠图象的顶点坐标是24(,)24b ac b a a-- 一.选择题(本题共10小题,每小题4分,共40分)请选出各题中一个符合题意的正确选项填在相应的答案栏内,不选、 多选、错选均不给分.1. 若反比例函数(0)ky k x=≠的图象经过点(2,-3),则图象必经过另一点 A.(2,3)B.(-2,3)C.(3,2)D.(-2,-3)2. 已知圆锥的底面半径为3,母线长为5,则圆锥的侧面积是 A.15πB.15C.8πD.83. 将抛物线2y x =先向左平移1个单位,再向上平移1上个单位,得到的抛物线为 A.2(1)1y x =-- B.2(1)1y x =-+C.2(1)1y x =++D.2(1)1y x =+-4. 已知23a b =,则aa b +的值是 A.25 B.52C.35D.535. 如图,A 、B 、C 三点在⊙O 上,且∠AOB=80°,则∠C=A.100°B.80°C.50°D.40°6. 在同一坐标系中函数y kx =和ky x=的大致图象是(A)(B)(C)(D)7. 对于下列命题中,正确的是 A.所有的直角三角形都相似 B.所有的等边三角形都相似 C.所有的等腰三角形都相似D.所有的矩形都相似8. 如果α是锐角,且cos α=45,那么sin α的值是()A.45B.35C.34D.439. 已知二次函数2y ax bx c =++的图象如图所示,则一次函数y ax bc =+的图象不经过 A.第一象限B.第二象限C.第三象限D.第四象限10.探索以下规律,如图:…,根据以上规律,从2006到2008的箭头方向正确的是A. B.C.D.学校_________ 班级____________ 姓名_____________ 学号__________………………………………装………………………………订………………………………线…………………………………………用心思考,细心答题,相信你是最棒的!(第6题)ABOC(第9题)0 13 10【本文由书林工作坊整理发布,谢谢你的关注!】2二.填空题(本题共6小题,每小题5分,共30分)11.在Rt △ABC 中,已知∠C =900,AC =3,AB =5,则cosA = . 12.已知半径为6cm 的圆中,600的圆心角所对的弧长为cm.13.请写出一个顶点在x 轴上,且开口方向向下的二次函数:.14.已知△ABC ∽△A 1B 1C 1,且它们的相似比为23. 如果△ABC 的周长 为20cm ,那么△A 1B 1C 1的周长为cm.15.如图,已知⊙O 的直径为10,弦AB =6,点P 是弦AB 上的一个动 点,那么OP 的取值范围应该是 . 16.如图,将边长为1的正方形OAPB 沿x 轴正方向连续翻转 2007次,点P 依次落在点P 1,P 2,P 3,P 4,…,P 2007的位 置,则P 2007的横坐标x 2007=__________.三.解答题(本题共8小题,共80分. 请务必写出解答过程) 17.(本题8分)计算: 3(2)2tan 45(21)-+- .18.(本题8分)如图,在△ABC 中,AD 、CE 是两条高,连结DE ,如果BE=2,EA=3,CE=4,在不添加任何辅助线和字母的条件下,请写出 三个正确结论(要求:分别为边的关系,角的关系,三角形相似的关系),并对其中三角形相似的结论给予证明.19.(本题8分)如图,一渔船正以每小时30海里的速度由南向北航行,在A 处看见小岛P 在船的北偏东30°方向上.2小时后,渔船行至B 处,此时看见小岛P 在船的北偏东75°方向上.求此时渔船距小岛P 的距离BP.………………………………装………………………………订………………………………线………………………………………………OABP(第15题)A BCE D第19题图(第19题)APB北【本文由书林工作坊整理发布,谢谢你的关注!】320.(本题8分)现有9个相同的小正三角形拼成的大正三角形,将其部分涂黑.如图(1),(2)所示.图(1) 图(2)图(3) 图(4)观察图(1),图(2)中涂黑部分构成的图案.它们具有如下特征:①都是轴对称图形②涂黑部分都是三个小正三角形.请在图(3),图(4)内分别设计一个新图案,使图案具有上述两个特征.21. (本题10分)如图,已知AB 是⊙O 的直径,点C ,D 在⊙O 上,且AB =5,BC =3.(1)求sin ∠BAC 的值;(2)如果OE ⊥AC ,垂足为E ,求OE 的长; (3)求tan ∠ADC 的值(结果保留根号).22.(本题12分)某年级组织学生参加夏令营活动,本次夏令营分为甲、乙、丙三组进行活动. 下面两幅统计图反映了学生报名参加夏令营 的情况,请你根据图中的信息回答下列问题:报名人数分布直方图 报名人数扇形分布图(1)该年级报名参加丙组的人数为 ;(2)该年级报名参加本次活动的总人数 ,并补全频数分布直方图;(3)根据实际情况,需从甲组抽调部分同学到丙组,使丙组人数是甲组人数的3倍,应从甲组抽调多少名学生到丙组?………………………………装………………………………订………………………………线………………………………………………【本文由书林工作坊整理发布,谢谢你的关注!】423.(本题12分)初三(1)班数学兴趣小组在社会实践活动中,进行了如下的课题研究:用一定长度的铝合金材料,将它设计成 外观为长方形的三种框架,使长方形框架面积最大.小组讨论后,同学们做了以下三种试验:图案(1) 图案(2) 图案(3)请根据以上图案回答下列问题:(1)在图案(1)中,如果铝合金材料总长度(图中所有黑线的长度和)为6m ,当AB 为1m ,长方形框架ABCD 的面积是 m 2;(2)在图案(2)中,如果铝合金材料总长度为6m ,设AB 为x m ,长方形框架ABCD 的面积为S= (用含x 的代数式表示);当AB = m 时,框架ABCD 的面积S最大;在图案(3)中,如果铝合金材料总长度为l m, 设AB 为x m,当AB = m 时, 长方形框架ABCD 的面积S最大.(3)经过这三种情形的试验,他们发现对于图案(4)这样的情形也存在着一定的规律. … 探索: 如图案(4), 如果铝合金材料总长度为l m ,共有n条竖档时,那么当竖档AB 多少时,长方形框架ABCD 的面积最大. 图案(4)24.(本题14分)如图,平面直角坐标系中,直线AB 与x 轴,y 轴分别交于A (3,0),B (0,3)两点,点C 为线段AB 上的一动点,过点C 作CD ⊥x 轴于点D .(1)求直线AB 的解析式; (2)若S 梯形OBCD,求点C 的坐标; (3)在第一象限内是否存在点P ,使得以P ,O ,B 为顶点的三 角形与△OBA 相似.若存在,请求出所有符合条件的点P 的 坐标;若不存在,请说明理由.………………………………装………………………………订………………………………线………………………………………………。
初三第三次月考数学试卷.doc

初三第3次月考数学试卷一、单项选择题(每题3分,满分30分)1. 下列各式①. ®a 2-a 3=a 4 5 6 7® J (-2)2 = -2@( (-)-1 = 3 @ (^ -1)° = 1,其中止确的是()A.④⑤B.③④C.②③D.①④2. 卜•列图形既是轴对称图形,乂是中心对称图形的是(3. 如图是一种占代计时器——“漏壶”的示意图,在壶内盛有一定量的水,水从壶下的小孔漏出,壶 壁上画有刻度,人们可以根据壶中的水面的位置计算时间•现用x 表示时间,y 表示壶到水面的高 度,下列图象适合表示一小时内y 与/的函数关系的是(暂不考虑水量变化对压力的影响)()4 如图,在ZVIBC 中,BC=4,以点A 为圆心,2为半径的04与BC 相切丁•点Z ),交AB T 点、E,交 AC 于点F,点P 是0A 上的一点,且ZEPF=45°,图中阴影影部分的面积为(A. 4 一龙 8. 4—2龙 C 、8+兀 D. 8 —2龙 5 甲、乙、丙三个旅行团的游客人数都相等,且每个团游客的平均年龄都是35岁,这三个团游客年龄的方差S2甲=1.4, 52Z .=18.8, S?丙=2.5,导游小方最喜欢带游客年龄相近的团队,若在这三个I 才I 中选择一个,则他应选()^ DC A.rp 队 B.乙队 C.丙队 D.哪一个都可以 第4题图 6 假期到了,17名女教师去外地培训,住宿时人2人间和3人间可供租住,每个房间都要住满,她们 有儿种租住方案.()A.5种B.4种C.3种D.2种一 37 若 A (x“ yi ), B (X2, y?),C (x 3, y3)是反比例函数 y 二一图象上的点,K xi<x 2<0<x 3,则 y 】、y 2xy3的大小关系正确的是( )A. y 3>yi>y 2 B ・ yi>y 2>y3 C ・ y 2>yi>y 3 D ・ y 3>y 2>yi第3题图yD)&已知二次函数y = ax 2 + bx + c (a 丰0)和图象经过点(给,0)、(2, 0),且一2V“V —1,与 y 轴正半轴的交点在(0, 2)的下方,则下列结论:①日b c <0 ②方44日c ③2自+方+ 1<0④2臼+ c>0.则其中正确结论的序号是()A.①②B.②③C.①②④D.①②③④X 777 9•分式方程——- 1 =——-——有增根•则m 的值为() x — 1 (x — l )(x + 2)A.0和3 B ・1 C ・1和一2 D ・3 10. 如上图所示在锐角三角形ABC 中,AH 是BC 边上的高,分别以AB 、AC 为一边,向外作正方形 ABDE 和ACFG,连接CE 、BG 的EG, EG 与HA 的延长线交于点M,下列结论:①BG 二CE ②BG 丄CE ③AM 是Z1AEG 的中线 ④ZEAM=ZABC,其中正确结论的个数是()A.4个B.3个C.2个 D 」个二. 填空题(每题3分,满分30分)11. 2012年5月8日「最美教师”张丽莉为救学生身负重伤,张老师舍己救人的事迹受到全国人民的 极人关注,在住院期间,共有691万人以不同方式向她表示问候和祝福,将691万人川科学记数法 2 ]12._______________________________________________ 函数y^— + —中,口变量兀的取值范围是 ______________________________\J\ — x x13.___________________ 如图所示,E 、F 是矩形ABCD 对角线AC 上的两点,试添加一个条 件: ,使得△ ADF^/\CBE.14. 中国象棋红方棋子按兵种不同分布如下:1个帅,5个兵,“士、象、马、车、炮”各两个,将所有棋子反血朝上放在棋盘中,任取一个令疑士、彖、帅的概率是 ____________ .15._______________________________________________________________ 恻锥的母线长为6 cm,底面周长为55m 则圆锥的侧血积为 _______________________________________ .16.17.險若关5勺分式方程右=是-2有非负数解,则臼的取值范围是 ------------------------------19. Rt/XABC 11', Z>4 =90°,—个内介为 60°,点 P 是直线A3上不同于的一点,H.ZACP=30°,则PB 的长为 __________ .20. 如图,在平而直角坐标系中有—•边长为/的正方形OABC,边(M 、0C 分别在x 轴、y 轴上,如果表示为 ______________ 人.(结果保留两个有效数字)ED以对角线OB为边作第二个正方形O BBC,再以对角线为边作第三个正方形OB/B2C2,照此规律作下去,则点〃2012的坐标为____________________三、解答题(满份60分)2^7—11—ci21-(木小题满分5分)先化简:⑺一丁尸斗22.(本小题满分6分)每个小方格都是边长为1个单位长度的小止方形,菱形OABC在平血直角处标系中的位置如图所示.(1)将菱形OABC先向右平移4个单位,再向上平移2个单位,得到菱形OAQG,请画出菱形OA]QC],并直接写出点B]的坐标;(2)将菱形OABC绕原点O顺时针旋转90°,得到菱形OA2B2C2f请画出菱形OA2B2C2,并求出点B旋转到血的路径长.然后给。
2012年3月九年级月考数学试卷(含答案)

A DB CEA CB E DO(第5题) 2011-2012学年第二学期3月月考九年级数学试卷温馨提示:请认真审题,看清要求,仔细答题..............,祝你成功! 本试卷三大题,24小题,满分为120分。
全卷分试卷和答题卷两部分。
各题答案都必须写在答题卷上,直接写在试卷上无效。
一、选择题:(本题有10小题,每小题3分,共30分)1.-2的相反数是( ▲ )A .2B .2-C .12D .12-2.如下图,由几个小正方体组成的立体图形的俯视图是( ▲ )3.在一个不透明的口袋中,有大小、形状完全相同,颜色不同的球15个,从中摸出红球的概率为31,则袋中红球的个数为( ▲ )A .10B .15C .5D .3 4.2011年上半年某市累计实现自营进出口总值168000万美元,比2010年同期增长24.6%,把168000万美元用科学计数法表示为( ▲ ) A .16.8×104 美元 B .1.68×105 美元 C .0.168×109 美元 D .1.68×109美元 5.如图,直线AB 与直线CD 相交于点O ,E 是AOD ∠内一点,已知OE ⊥AB ,︒=∠45BOD ,则COE ∠的度数是( ▲ )A .︒125B .︒135C .︒145D .︒155(第8题)6.金华银泰百货一女装专柜对上周女装的销售情况进行了统计,销售情况如下表所示:经)颜色 黄色绿色白色紫色红色数量(件)100 180 220 80 550A.方差 B.众数 C.平均数 D.中位数 7.若两圆半径R =3,r =2,且圆心距为1,则这两圆的位置关系是( ▲ ) A .外切 B .内切 C .相交 D .内含8. 如图,已知DE ∥BC ,且ADDB =43,则△ADE 与△ABC 的周长之比为( ▲ )A .3∶7B .3∶4C .9∶16D .9∶499.如图,正方形ABCD、正方形A1B1C1D1、正方形A2B2C2D2均位于第一象限内,它们的边平行于x轴或y轴,其中点A、A1、A2在直线OM上,点C、C1、C2在直线ON上,O为坐标原点,已知点A的坐标为()3,3,正方形ABCD的边长为1.若正方形A2B2C2D2的边长为a,则点D2的坐标为(▲)A.(),2a aB.()2,3a aC.()3,4a aD.()4,5a a10. 如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连结DF交BE的延长线于点H,连结OH交DC于点G,连结HC.则以下四个结论中正确结论的个数为(▲)①OH=21BF;②∠CHF=45°;③GH=41BC;④DH2=HE·HBA. 1个B. 2个C. 3个D. 4个(第9题图)二、填空题:(本题有6小题,每小题4分,共24分)11.分解因式b2 -1=___▲_________12. 如图,将∠BAC沿DE向∠BAC内折叠,使AD与A’D重合,A’E与AE重合,若∠A=300,则∠1+∠2=_____▲____13. 如图,圆锥的底面半径为3cm,高为4cm,那么这个圆锥的侧面积是▲_cm2.14.随着近期国家抑制房价新政策的出台,某小区房价两次下跌,由原来的每平方米6000元降至每平方米4860元,设每次降价的百分率为x,则所列方程为▲_.15.如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为-3和1;④a-2b+c>0.其中正确的命题是▲.(只要求填写正确命题的序号)16.如图,梯形ABCD中,AD//BC,AB⊥AD,AB=4,AD=5.E为底边第15题(第10题图)ABCDFOGHEBC 上一动点,点F 在线段DE 上,始终保持BE =EF =x ,连结 AF ,BF .(1)当点E 运动到使∠DEC =45°时,则线段DF 的长为 ▲_ 。
重庆一中2012年3月九年级月考数学试题(含答案)

7题图重庆一中初2012级11-12学年度下期三月月考数 学 试 卷(全卷共五个大题,满分150分,考试时间120分钟)参考公式:抛物线)0(2≠++=a c bx ax y 的顶点坐标为)44,2(2ab ac a b --,对称轴公式为a b x 2-=.一、选择题:(本大题10个小题,每小题4分,共40分)在每个小题的下面,都给出了代号为A 、B 、C 、D 的四个答案,其中只有一个是正确的,请将正确答案的代号填入答题卷中对应的表格内.1.在2,0,-1,π这四个数中,最大的数是( )A .2B .0C .-1D .π 2.下列运算正确的是( )A .3362x x x += B .824x x x ÷= C .mnnmx x x =· D .()4520xx -=3.下面几何体的主视图是( )4.已知,如图,AB ∥CD ,∠DCE =80°,则∠BEF 的度数为( )A .120°B .110°C .100°D .80° 5.下列调查中,适合采用全面调查(普查)方式的是( )A .对某班50名同学视力情况的调查.B .对元宵节期间市场上汤圆质量情况的调查.C .对某类烟花爆竹燃放质量情况的调查.D .对重庆嘉陵江水质情况的调查.6.如图,⊙O 的弦AB =8,C 是AB 的中点,且OC =3,则⊙O 的半径等于( )A .8B .5C .10D .47.如图,函数2y x bx c =-++的部分图象与x 轴、y 轴的交点分别为A (1,0),B (0,3), 对称轴是x =-1.在下列结论中,错误的是( )A .顶点坐标为(-1,4)B .函数的解析式为223y x x =--+ C .当0x <时,y 随x 的增大而增大 D .抛物线与x 轴的另一个交点是(-3,0)A .B . D .C . 6题图CB A O · F A BC DE 4题图8.小桐家距学校1200米,某天小桐从家里出发骑自行车上学,开始她以每分钟a 米的速度匀速行驶了600米,遇到交通堵塞,耽搁了3分钟,然后以每分钟b 米的速度匀速前进一直到学校(a <b ),小桐离家的距离y 与时间x 之间的函数关系图象大致是( )9.下图是一组有规律的图案,第1个 图案由4个基础图形组成,第2个图案由7个基础图形组成,……,第9个图案中基础图形个数为( )A .27B .28C .3010.如图,正方形ABCD 的边长为2,E 为线段AB 上一点,点M 为边AD的中点,EM 的延长线与CD 的延长线交于点F ,MG ⊥EF ,交CD 于 N ,交BC 的延长线于G ,点P 是MG 的中点.连接EG 、FG .下列结论:①当点E 为边AB 的中点时,S △EFG =5;②MG =EF ;③当AE =3 时,FG =52;④若点E 从点A 运动到点B ,则此过程中点P 移动的 距离为2.其中正确的结论的个数为( )A . 1个B . 2个C . 3个D . 4个二、填空题:(本大题6个小题,每小题4分,共24分)在每小题中,请将答案直接填在答题卷中对应的横线上.11.重庆市2011年GDP 进入了“万亿俱乐部”,全年实现地区生产总值(GDP )10011亿元,同比增长16.4%,增速跃居全国第一.将10011亿用科学计数法表示为 亿. 12.若一个圆锥的底面圆的周长是4πcm ,母线长是6cm ,则该圆锥的侧面展开图的圆心角的度数是 . 13.在一次九年级学生视力检查中,随机检查了8个人的右眼视力,结果如下:4.0,4.2,4.5,4.0,4.4,4.5,4.0,4.8,则这组数据的中位数是_______________. 14.在□ABCD 中,点E 为AD 的中点,连接BE ,交AC 于点F ,则CA AF= . 15.在5个完全相同的小球上分别标上数字0、1、2、-3、-4,然后放进一个布袋内,先从布袋中任意摸出一个小球,记下小球上的数字作为点D 的横坐标,摸出的小球不放回,再任意摸出一个小球,记下小球上的数字作为点D 的纵坐标.则以点D 与点A (-1,1)、B (-2,-1)、C (1,-1)为顶点的四边形是平行四边形的概率是 .CBDEF14题图A E10题图(1)(2)(3)……16.因气候原因,某县城郊外山体引发滑坡,县城居民发现后立即从县城跑步前去救援,此时县政府紧急启动应急预案,一段时间后,公安干警、消防官兵、医疗人员分别乘坐甲、乙、丙三种速度各不相同的车,紧急从县城沿同一线路同时赶往事发地.已知公安、消防、医院分别用5分钟、6分钟、8分钟追上县城救援的居民,且甲车每小时走132km ,乙车每小时走112km ,则丙车每小时走 km .三、解答题:(本大题4个小题,每小题6分,共24分)解答时每小题必须给出必要的演算过程或推理步骤,请将解答书写在答题卷中对应的位置上.17.计算:202160cos 23643--+︒+-⨯--)()(π18.解方程:13-42+=-x x x19.如图,E F 、分别是□ABCD 的对角线AC 上的两点,且CE AF =,求证:DF BE =20.如图,四边形ABCD 为菱形,已知A (0,6),D (-8,0). (1)求点C 的坐标;(2)设菱形ABCD 对角线AC 、BD 相交于点E ,求经过点E 的反比例函数解析式.B19题图20题图四、解答题:(本大题4个小题,每小题10分,共40分)解答时每小题必须给出必要的演算过程或推理步骤,请将解答书写在答题卷中对应的位置上.21.先化简,再求值:3434421222--÷-+--+x x xx x x x ,其中x 满足x 2+2x-3=0.22.如图,已知抛物线c bx x y ++-=221经过A (2,0)、B (0,-6)两点,其对称轴与x 轴交于点C .(1)求该抛物线和直线BC 的解析式;(2)设抛物线与直线BC 相交于点D ,连结AB 、AD ,求△ABD 的面积.23.重庆一中综合实践活动艺体课程组为了解学生最喜欢的球类运动,对足球、乒乓球、篮球、排球四个项目进行了调查,并将调查的结果绘制成如下的两幅统计图(说明:每位同学只选一种自己最喜欢的球类),请你根据图中提供的信息解答下列问题: (1)求这次接受调查的学生人数,并补全条形统计图; (2)求扇形统计图中喜欢排球的圆心角度数; (3)若调查到爱好“乒乓球”的5名学生中有3名男生,2名女生,现从这5名学生中任意抽取2名学生,请用列表法或画树状图的方法,求出刚好抽到一男一女的概率.24.如图,梯形ABCD 中,AD ∥BC ,∠A =900, 点E 为CD 边的中点,BE ⊥CD ,且∠FBE =2∠EBC .在线段AD 上取一点F ,在线段BE 上取一点G ,使得BF =BG ,连接CG . (1)若AB =AF ,EG =2,求线段CG 的长; (2)求证:∠EBC +31∠ECG =30°.23题图A24题图BCDEFG五、解答题(本大题2个小题,25题10分,26题12分,共22分)解答时必须给出必要的演算过程或推理步骤,请将解答书写在答题卷中对应的位置上.25.重庆西永微电园入驻企业----方正集团开发了一种新型电子产品,是未来五年IT 行业倍受青睐的产品.在五年销售期限内,方正集团每年对该产品最多可投入100万元销售投资,该集团营销部门根据市场分析,对该产品的销售投资收益拟定了两种销售方案: 方案一:只在国内销售,每投入万元,每年可获得利润P 与x 关系如下表所示:方案二:五年销售期限内,每年均投入100万元销售投资。
2012年第三次质量检测(月考)数学试题
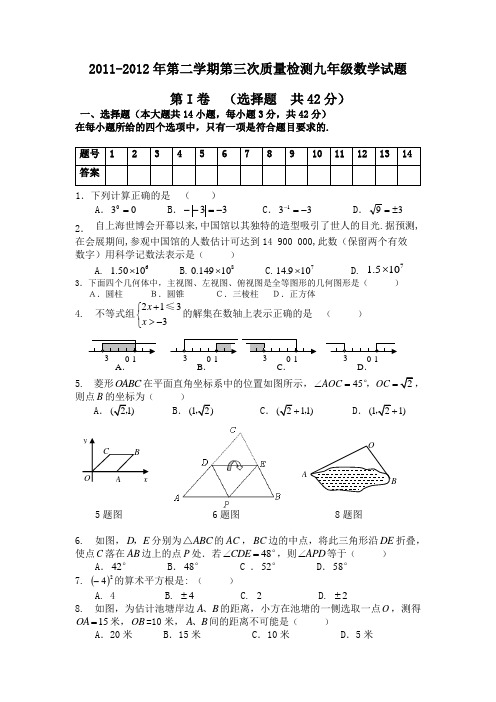
2011-2012年第二学期第三次质量检测九年级数学试题第I 卷 (选择题 共42分)一、选择题(本大题共14小题,每小题3分,共42分) 在每小题所给的四个选项中,只有一项是符合题目要求的.题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 答案1.下列计算正确的是 ( )A .030=B .33-=--C .331-=-D .39±= 2. 自上海世博会开幕以来,中国馆以其独特的造型吸引了世人的目光.据预测, 在会展期间,参观中国馆的人数估计可达到14 900 000,此数(保留两个有效 数字)用科学记数法表示是( )A. 61.5010⨯B.810149.0⨯C.7109.14⨯D. 71.510⨯3.下面四个几何体中,主视图、左视图、俯视图是全等图形的几何图形是( ) A.圆柱 B.圆锥 C.三棱柱 D.正方体4. 不等式组2133x x +⎧⎨>-⎩≤的解集在数轴上表示正确的是 ( )5. 菱形OABC 在平面直角坐标系中的位置如图所示,452AOC OC ∠==°,,则点B 的坐标为( )A .(21),B .(12),C .(211)+,D .(121)+,5题图 6题图 8题图6. 如图,D E ,分别为ABC △的AC ,BC 边的中点,将此三角形沿DE 折叠,使点C 落在AB 边上的点P 处.若48CDE ∠=°,则APD ∠等于( )A .42°B .48°C .52°D .58°7. ()24-的算术平方根是: ( )A. 4B. 4±C. 2D. 2±8. 如图,为估计池塘岸边A B 、的距离,小方在池塘的一侧选取一点O ,测得15OA =米,OB =10米,A B 、间的距离不可能是( )A .20米B .15米C .10米D .5米OABA .B .C .D .xyO C B A9. 如图,火车匀速通过隧道(隧道长大于火车长)时,火车进入隧道的时间x 与火车在隧道内的长度y 之间的关系用图象描述大致是( )A .B .C .D .10. 如图,PA 、PB 是⊙O 的切线,切点分别是A 、B ,如果∠P =60°, 那么∠AOB 等于( ) A. 60° B. 90° C. 120° D. 150°11. 如图,点A ,B 的坐标分别为(1, 4)和(4, 4),抛物线n m x a y +-=2)(的 顶点在线段AB 上运动,与x 轴交于C 、D 两点(C 在D 的左侧),点C 的横坐标 最小值为3-,则点D 的横坐标最大值为( ) A .-3 B .1 C .5 D .812. 把代数式322363x x y xy -+分解因式,结果正确的是( )A .(3)(3)x x y x y -B .223(2)x x xy y -+C .2(3)x x y -D .23()x x y -13. 为了解某班学生每天使用零花钱的情况,小红随机调查了15名同学,结果如下表:则这15A .3,14. 如图,△点C 原来的2倍,B 的横坐标是( )A .12a -B .1(1)2a -+C .1(1)2a --D .1(3)2a -+每天使用零花钱(单位:元)1 2 3 5 6 人 数 2 5 4 3 1火车隧道oyxoy xoy xoy xy xOD CB (4,4)A (1,4)第Ⅱ卷 (非选择题 共78分)二、填空题:(本大题共5个小题,每小题4分,共20分 把答案填写在题中的横线上.15. 已知圆锥的底面直径为4,母线长为6,则它的侧面展开图的圆心角为_____. 16. 有一组数据如下:2,3,a ,5,6,它们的平均数是4,则这组数据的方差是 .17. 如图,直角梯形ABCD 中,AD ∥BC ,AB ⊥BC ,AD = 2,将腰CD 以D 为中心逆 时针旋转90°至DE ,连接AE 、CE ,△ADE 的面积为3,则BC 的长为 . 18. 某校举行以“保护环境,从我做起”为主题的演讲比赛.经预赛,七、八年 级各有一名同学进入决赛,九年级有两名同学进入决赛.前两名都是九年级同学 的概率是 .19. 如图,正方形ABCD 边长为4,以BC 为直径的半圆O 交对角线BD 于E .则直线CD 与⊙O 的位置关系是 _____,阴影部分面积为(结果保留π) _______.三、解答题:(共58分)20. (本题7分)计算:(π-2011)0 +(sin60︒)-1-︱tan30︒-3︱+38.ABCDOE19题图21.(本题7分)化简: )212(112aa a a a a +-+÷--.22. (本题15分)如图,BD 为⊙O 的直径,点A 是弧BC 的中点,AD 交BC 于E 点,AE=2,ED=4. (1)求证: ABE ∆~ABD ∆;(2) 求tan ADB ∠的值;(3)延长BC 至F ,连接FD ,使BDF ∆的面积等于求EDF ∠的度数.23.(本题15分)某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:10500=-+.y x(1)设李明每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?(2)如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?(成本=进价×销售量)24.(本题14分)如图,二次函数c x y +-=221的图象经过点D ⎪⎭⎫ ⎝⎛-29,3,与x 轴交于A 、B 两点.⑴求c 的值;⑵如图①,设点C 为该二次函数的图象在x 轴上方的一点,直线AC 将四边形ABCD 的面积二等分,试证明线段BD 被直线AC 平分,并求此时直线AC 的函数解析式;⑶设点P 、Q 为该二次函数的图象在x 轴上方的两个动点,试猜想:是否存在这样的点P 、Q ,使△AQP ≌△ABP ?如果存在,请举例验证你的猜想;如果不存在,请说明理由.(图②供选用)。
重庆九年级(上)第三次月考数学试卷含答案

月考数学试卷
一
二
三
四
总分
一、选择题(本大题共 12 小题,共 48.0 分)
1. 下列各数中,绝对值最大的是( )
A. -6
B. -3
C. 0
D. 2
2.
如图是一个几何体的三视图,这个几何体是(
ABC...三 三 长棱 棱 方锥 柱 体
)
D.圆柱体
3. 计算(-x3y)2 的结果是( )
A. -x5y
第 2 页,共 20 页
于 x 的一次函数 y=2x+(m-1)图象经过第四象限,且使二次函数 y=x2+mx+ 的图象
与 x 轴最多有 1 个交点的概率是
.
17. “康河泛舟,问道剑桥”,甲乙两人相约泛舟康河,路线均为从 A 到 B 再返回 A,
且 AB 全长 2 千米,甲出发 2 分钟后,乙以另一速度出发,结果同时到达目的 B 地
6. 估计
的值在( )
A. 1 到 2 之间
B. 2 到 3 之间
C. 3 到 4 之间
D. 4 到 5 之间
7. 已知命题“如果 a2>4,那么 a>2”,能说明该命题是假命题的一个反例可以是(
)
A. a=10
B. a=-10
C. a=2
D. a=-2
8. 若 ห้องสมุดไป่ตู้+b=2,a-b=-1,则 a2-b2-1 的值是( )
生物学家费希尔,毕业于剑桥大学,长期在农业试验站做生物实验.费尔希在高等
植物基因性状研究实验中,从若干紫花与白花中各随机抽取 20 株测量高度(植株 正常高度 h 的取值范围为 35≤h≤43),过程如下:
收集数据(单位:cm): 紫花:42,42,28,54,29,52,44,36,39,49,33,40,35,52,29,32,51 ,55,42,38 白花植株高度为 35≤h≤43 的数据有:35,37,37,38,39,40,42,42 整理数据: 数据分为六组:25≤h<30,30≤h<35,35≤h<40,40≤h<45,45≤h<50,50≤h≤55
重庆初三初中数学月考试卷带答案解析

重庆初三初中数学月考试卷班级:___________ 姓名:___________ 分数:___________一、选择题1.在这四个数中,最小的数是()A.B.0C.4D.2.下列食品商标中不是轴对称图形的是()3.计算(xy2)3的结果是()A.B.C.D.4.在Rt△ABC中,∠C=90°,AB=10,cosA=,则的长是()A.8B.6C.4D.3 5.2013年9月某日,重庆部分区县的最高温度如下表所示:A、25℃B、26℃C、27℃D、28℃6.下列调查中,适宜采用抽样调查方式的是()A、调查初三某班同学对张伯苓校长的知晓情况B、调查我市中学生每天体育锻炼的时间C、调查乘坐轻轨的旅客是否携带了违禁物品7.抛物线y=-x2可由抛物线y=-(x-2)2+3如何平移得到()A.先向左平移2个单位,再向下平移3个单位B.先向右平移2个单位,再向下平移3个单位C.先向左平移2个单位,再向上平移3个单位D.先向右平移2个单位,再向上平移3个单位8.如图,将三角尺的直角顶点放在直尺的一边上,若,则的度数等于()A.68°B.64°C.58°D.52°9.已知抛物线y=x2+3x+c经过三点,则的大小关系为()A.B.C.D.10.某日,小明走路去学校,刚开始时,他比较悠闲地以较慢的速度匀速前进,突然发现时间可能来不及了,就加快步伐,越走越快,最后发现时间刚刚好,便以较快的速度匀速前进到达学校。
下列图象中能大概反映出小明走路速度和时间的函数关系的是()11.身高相等的四名同学甲乙丙丁一起参加风筝比较,四人放出风筝的线长、线与地面的夹角如右表所示(假设风筝线是拉直的),则四名同学所放的风筝中最高的是()放出风筝线长A、甲B、乙C、丙D、丁,0)和(2,12.如图,已知二次函数y=ax2+bx+c的图象与y轴正半轴的交点在(0,2)的下方,与轴的交点为(x1<-1,则下列结论正确的是()0),且-2<x1A.B.C.D.二、填空题1.函数的自变量的取值范围是。
重庆初三初中数学月考试卷带答案解析

重庆初三初中数学月考试卷班级:___________ 姓名:___________ 分数:___________一、选择题1.若实数a与-3互为相反数,则a的值为()A.B.0.3C.-3D.32.计算的结果是()A.B.C.D.3.右图是某个几何体的三视图,则这个几何体是()A.圆锥B.圆柱C.长方体D.三棱锥4.如图,AB∥CD,AD和BC相交于点O,∠A=30°,∠COD=80°,则()A.50°B.60°C.70°D.80°5.下列调查适合作普查的是()A.了解在校大学生的主要娱乐方式B.了解重庆市居民对废电池的处理情况C.日光灯管厂要检测一批灯管的使用寿命D.对甲型H7N9流感患者的同一车厢的乘客进行医学检查6.如图,在□ABCD中,AD = 6,点E在边AD上,且DE = 3,连接BE与对角线AC相交于点M,则的值为()A.B.C.D.7.已知,则的值是()A.3B.2C.1D.–18.如图,AB是的直径,点C是半圆的中点,动点P在弦BC上,则可能为()A.90°B.50°C.46°D.26°9.如图,反比例函数和上分别有两点B、C,且BC∥轴,点P是轴上一动点,则△BCP的面积是()A.5 B.5.5 C.6.5 D.1010.张老师骑自行车上班,最初以某一速度匀速行进,中途由于自行车发生故障,停下修车耽误了几分钟,为了按时到校,李老师加快了速度,仍保持匀速行进,如果准时到校.在课堂上,李老师请学生画出他行进的路程y(千米)与行进时间t(小时)的函数图象的示意图,同学们画出的图象如图所示,你认为正确的是()11.用棋子摆出下列一组“口”字,按照这种方法摆下去,则摆第13个“口”字需用棋子颗数为()A.52B.50C.48D.4612.如图二次函数的图象与轴交于(– 1,0),(3,0);下列说法正确的是()A.B.当时,y随x值的增大而增大C.D.当时,二、填空题1.春节假期,全国收费公路7座以下小型客车实行免费通行.据统计,春节期间,全国收费公路共免收通行费846000000元.846000000用科学记数法表示应为.2.分式方程的解为.3.、的半径分别为4和5,线段的长为3,则两圆的位置关系为.4.如图,在四边形中,、分别为、的中点,若,,,则.5.在平面直角坐标系中,已知A (1,0 )、B (1,1 ),现从0、、1、2四个数中选两个数分别作为点的横、纵坐标,则顺次连接、、三点能组成等腰三角形的概率为 .6.在一次知识竞赛中有两种评分规则,一种是从0分开始,答对一题给5分,弃权给2分,答错不给分;另一种是先给40分,然后答对一题给3分,弃权不给分,答错扣1分,某同学在这两种评分规则下都得81分,这次竞赛共有 题.三、解答题1.计算:.2.如图,在平面直角坐标系中,△ABC 的三个顶点的坐标分别为A (0,1),B (–1,1),C (–1,3).(1)画出△ABC 关于x 轴对称的△A 1B 1C 1; (2)画出△ABC 绕原点O 顺时针方向旋转90°后得到的△A 2B 2C 2;(3)C 1的坐标为 ,C 2的坐标为 ,在(2)中点A 旋转到A 2经过的路径长为 .3.先化简,再求值:,其中是不等式组的整数解.4.2012年秋冬北方干旱,光明社区出现饮用水紧张,每天需从社区外调运饮用水120吨.现从甲、乙两水厂调运饮用水到社区供水点,甲厂每天最多可调出80吨,乙厂每天最多可调出90吨.从两水厂运水到光明社区供水点的路程和运费如下表:到光明社区供水点的路程(千米)运费(元/吨千米)12(1)若某天调运水的总运费为26700元,则从甲、乙两水厂各调运了多少吨饮用水?(2)设某天从甲厂调运饮用水吨,总运费为元,试写出关于的函数关系式,并求出这天运费最少为多少元?5.某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B 、E 两组发言的人数比为,请结合图中相关数据回答下列问题:(1)A组有人,C组有人,E组有人,并补全直方图;(2)该年级共有学生600人,请估计全年级在这天发言次数不少于20的人数;(3)已知A组发言的学生中恰有一位女生,E组发言的学生中恰有两位男生,现从A组与E组中分别抽一位学生写报告,求所抽的两位学生至多有一位男生的概率.6.已知,矩形ABCD中,延长BC至E,使BE = BD,F为DE的中点,连结AF、CF.(1)若AB = 3,AD = 4,求CF的长;(2)求证:∠ADB = 2∠DAF.7.如图,一次函数分别交y轴、x轴于A、B两点,抛物线过A、B两点,作垂直x轴的直线,交x轴于H,交直线AB于M,交这个抛物线于N.(1)求这个抛物线的解析式;(2)若M在第一象限,求当t取何值时,MN有最大值?最大值是多少?(3)若∠ABO=∠BNH,求t的值.8.已知:如图,矩形ABCD,AB = 4,∠ACB = 30°.点E从点C出发,沿折线CA—AD以每秒一个单位长度的速度运动,过点E作EF∥CD交BC于点F,同时过点E作EG⊥AC交直线BC于点G,设运动的时间为t,△EFG与△ABC重叠部分的面积为S,当点E运动到点D时停止运动.(1)当点B与点G重合时,求此时t的值;(2)直接写出S与t之间的函数关系式和相应的自变量取值范围;(3)当t = 4时,将△EFG绕点E顺时针旋转一个角度(),∠GEF的两边分别交矩形的边于点M,点N.当△MEN为等腰三角形时,求此时△MEN的面积.重庆初三初中数学月考试卷答案及解析一、选择题1.若实数a与-3互为相反数,则a的值为()A.B.0.3C.-3D.3【答案】D【解析】相反数的定义:符合不同,绝对值相同的两个数互为相反数.若实数a与-3互为相反数,则a的值为3,故选D.【考点】相反数的定义点评:本题属于基础应用题,只需学生熟练掌握相反数的定义,即可完成.2.计算的结果是()A.B.C.D.【答案】B【解析】积的乘方法则:积的乘方,先把各个因式分别乘方,再把所得的幂相乘.,故选B.【考点】积的乘方法则点评:本题属于基础应用题,只需学生熟练掌握积的乘方法则,即可完成.3.右图是某个几何体的三视图,则这个几何体是()A.圆锥B.圆柱C.长方体D.三棱锥【答案】A【解析】根据图中几何体的三视图的特征即可作出判断.由图可得这个几何体是圆锥,故选A.【考点】由三视图判断几何体的形状点评:本题属于基础应用题,只需学生熟练掌握几何体的三视图,即可完成.4.如图,AB∥CD,AD和BC相交于点O,∠A=30°,∠COD=80°,则()A.50°B.60°C.70°D.80°【答案】C【解析】先根据三角形的内角和定理求得∠B的度数,再根据平行线的性质求解即可.∵∠A=30°,∠COD=80°∴∠B=180°-30°-80°=70°∵AB∥CD∴∠B=70°故选C.【考点】三角形的内角和定理,平行线的性质点评:平行线的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.5.下列调查适合作普查的是()A.了解在校大学生的主要娱乐方式B.了解重庆市居民对废电池的处理情况C.日光灯管厂要检测一批灯管的使用寿命D.对甲型H7N9流感患者的同一车厢的乘客进行医学检查【答案】D【解析】根据抽样调查与普查的特征依次分析各选项即可作出判断.A、B、调查对象太多,普查的意义不大,C、调查时具备破坏性,均应采用抽样调查;D、应采用普查,本选项正确.【考点】抽样调查与普查点评:本题属于基础应用题,只需学生熟练掌握抽样调查与普查的特征,即可完成.6.如图,在□ABCD中,AD = 6,点E在边AD上,且DE = 3,连接BE与对角线AC相交于点M,则的值为()A.B.C.D.【答案】A【解析】先根据平行四边形的性质证得△AEM∽△CBM,再根据相似三角形的性质求解即可.∵AD = 6,DE = 3∴AE = 3∵□ABCD∴AD =" BC" = 6,AD∥∴△AEM∽△CBM∴故选A.【考点】平行四边形的性质,相似三角形的判定和性质点评:平行四边形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.7.已知,则的值是()A.3B.2C.1D.–1【答案】C【解析】由题意把代入代数式,再化简求值即可.当时,故选C.【考点】代数式求值点评:计算题是中考必考题,一般难度不大,学生要特别慎重,尽量不在计算上失分.8.如图,AB是的直径,点C是半圆的中点,动点P在弦BC上,则可能为()A.90°B.50°C.46°D.26°【答案】D【解析】连接AC,根据圆周角定理可得∠ACB为直角,再由点C是半圆的中点可得△ABC为等腰直角三角形,根据等腰直角三角形的性质即可作出判断.连接AC则∠ACB=90°∵点C是半圆的中点∴AC=BC∴∠CAB=∠CBA=45°∴∠CAB∴可能为26°故选D.【考点】圆周角定理,等腰直角三角形的判定和性质点评:圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,均等于所对圆心角的一半.9.如图,反比例函数和上分别有两点B、C,且BC∥轴,点P是轴上一动点,则△BCP的面积是()A.5 B.5.5 C.6.5 D.10【答案】A【解析】连接BO、CO,由BC∥轴根据三角形的面积公式可得△BCP的面积等于△BOC的面积,再根据反比例函数中k的几何意义求解即可.连接BO、CO∵BC∥∴△BCP的面积等于△BOC的面积∵点B、C分别在反比例函数和上∴△BCP的面积故选A.【考点】反比例函数中k的几何意义点评:反比例函数中k的几何意义是初中数学的重点,是中考常见题,一般难度不大,需熟练掌握.10.张老师骑自行车上班,最初以某一速度匀速行进,中途由于自行车发生故障,停下修车耽误了几分钟,为了按时到校,李老师加快了速度,仍保持匀速行进,如果准时到校.在课堂上,李老师请学生画出他行进的路程y(千米)与行进时间t(小时)的函数图象的示意图,同学们画出的图象如图所示,你认为正确的是()【答案】C【解析】根据“最初以某一速度匀速行进,中途停下修车耽误了几分钟,为了按时到校,李老师加快了速度,仍保持匀速行进”即可作出判断.由题意符合条件的图象是第三个,故选C.【考点】实际问题的函数图象点评:解答此类问题的关键是读懂题意,正确理解各时间段的函数的函数变化特征.11.用棋子摆出下列一组“口”字,按照这种方法摆下去,则摆第13个“口”字需用棋子颗数为()A.52B.50C.48D.46【答案】A【解析】仔细分析所给图形的特征可得每一个图形均比上一个图形多4个“口”,即可求得结果.由图可得摆第13个“口”字需用棋子颗数,故选A.【考点】找规律-图形的变化点评:解答此类找规律的问题的关键是仔细分析所给图形的特征得到规律,再把这个规律应用于解题.12.如图二次函数的图象与轴交于(– 1,0),(3,0);下列说法正确的是()A.B.当时,y随x值的增大而增大C.D.当时,【答案】B【解析】根据抛物线的开口方向、对称轴位置、与坐标轴的交点坐标结合抛物线的对称性分析.由图可得,,,则,故A错误;当时,,故B正确;当时,y随x值的增大而增大,故C错误;当时,或,故D错误;故选B.【考点】二次函数的图象与系数的关系点评:此类问题是初中数学的重点,是中考必考题,一般出现在选择、填空题的最后一题,难度较大.二、填空题1.春节假期,全国收费公路7座以下小型客车实行免费通行.据统计,春节期间,全国收费公路共免收通行费846000000元.846000000用科学记数法表示应为.【答案】【解析】科学记数法的表示形式为,其中,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.846000000.【考点】科学记数法的表示方法点评:本题属于基础应用题,只需学生熟练掌握科学记数法的表示方法,即可完成.2.分式方程的解为.【答案】【解析】解分式方程的一般步骤:先去分母化分式方程为整式方程,再解这个整式方程即可,注意解分式方程最后一步要写检验.两边同乘得解这个方程得经检验是原方程的解.【考点】解分式方程点评:解方程是中考必考题,一般难度不大,学生要特别慎重,尽量不在计算上失分.3.、的半径分别为4和5,线段的长为3,则两圆的位置关系为.【答案】相交【解析】两圆的半径分别为R和r,且,圆心距为d:外离,则;外切,则;相交,则;内切,则;内含,则.∵∴两圆的位置关系为相交.【考点】圆与圆的位置关系点评:本题属于基础应用题,只需学生熟练掌握圆与圆的位置关系,即可完成.4.如图,在四边形中,、分别为、的中点,若,,,则.【答案】【解析】连接BD,根据三角形的中位线定理可求得BD的长,再根据勾股定理的逆定理可证得△BCD为直角三角形,最后根据锐角三角函数的定义求解即可.连接BD∵、分别为、的中点,∴∵,∴∴△BCD为直角三角形∴.【考点】三角形的中位线定理,勾股定理的逆定理,锐角三角函数的定义点评:解题的关键是熟熟记三角形的中位线定理:三角形的中位线平行于第三边,且等于第三边的一半.5.在平面直角坐标系中,已知A(1,0 )、B(1,1 ),现从0、、1、2四个数中选两个数分别作为点的横、纵坐标,则顺次连接、、三点能组成等腰三角形的概率为.【答案】【解析】根据等腰三角形的性质及概率公式求解即可.从0、、1、2四个数中选两个数共有12种组合,其中能组成等腰三角形的有(0,)、(0,1)、(2,0)、(2,)、(2,1)这5种情况,则概率为.【考点】等腰三角形的判断,概率公式点评:解题的关键是熟练掌握概率公式:概率=所求情况数与总情况数的比值.6.在一次知识竞赛中有两种评分规则,一种是从0分开始,答对一题给5分,弃权给2分,答错不给分;另一种是先给40分,然后答对一题给3分,弃权不给分,答错扣1分,某同学在这两种评分规则下都得81分,这次竞赛共有题.【答案】22【解析】设答对a题,未答b题,答错c题,根据题意可得5a+2b=81①,40+3a-c=81②,由①②推出a的取值范围,并确定处a的值,从而推出b、c的值,解决问题.设答对a题,未答b题,答错c题,可得:5a+2b=81①,40+3a-c=81②,由①知,a是奇数,且a≤16;由②知a ≥14,所以a=15, 由此求得b=3,c=4,故共有:15+3+4=22(题). 答:这张试卷共有22题.【考点】三元一次方程组的应用点评:解题的关键是读懂题意,找到等量关系,正确列出方程组,要注意未知数的取值的特征.三、解答题1.计算:.【答案】6【解析】根据有理数的乘方法则、立方根的性质、特殊角的锐角三角函数值计算即可. 原式. 【考点】实数的运算点评:实数的运算是中考必考题,一般难度不大,学生要特别慎重,尽量不在计算上失分.2.如图,在平面直角坐标系中,△ABC 的三个顶点的坐标分别为A (0,1),B (–1,1),C (–1,3).(1)画出△ABC 关于x 轴对称的△A 1B 1C 1; (2)画出△ABC 绕原点O 顺时针方向旋转90°后得到的△A 2B 2C 2;(3)C 1的坐标为 ,C 2的坐标为 ,在(2)中点A 旋转到A 2经过的路径长为 .【答案】(1) (2)如下图;(3)(–1,–3);(3,1);【解析】先根据轴对称变换、旋转变换的作图方法作出图形,再根据弧长公式求解即可.(1) (2)如下图(3)C 1的坐标为(–1,–3),C 2的坐标为(3,1),点A 旋转到A 2经过的路径长.【考点】基本作图,弧长公式点评:此类问题是初中数学的重点,是中考常见题,一般难度不大,熟练掌握各种几何变换的作图方法是解题的关键.3.先化简,再求值:,其中是不等式组的整数解.【答案】1【解析】先对小括号部分通分,同时把除化为乘,再根据分式的基本性质约分,然后求出不等式组的解集,最后选择一个适当的x的值代入求解即可.原式解得∵x为整数且∴,原式.【考点】分式的化简求值,解一元一次不等式组点评:计算题是中考必考题,一般难度不大,学生要特别慎重,尽量不在计算上失分.4.2012年秋冬北方干旱,光明社区出现饮用水紧张,每天需从社区外调运饮用水120吨.现从甲、乙两水厂调运饮用水到社区供水点,甲厂每天最多可调出80吨,乙厂每天最多可调出90吨.从两水厂运水到光明社区供水点的路程和运费如下表:运费(元/吨千米)12(1)若某天调运水的总运费为26700元,则从甲、乙两水厂各调运了多少吨饮用水?(2)设某天从甲厂调运饮用水吨,总运费为元,试写出关于的函数关系式,并求出这天运费最少为多少元?【答案】(1)50吨,70吨;(2),26100元【解析】(1)设从甲厂调运饮用水x吨,从乙厂调运饮用水y吨,根据“每天需从社区外调运饮用水120吨,调运水的总运费为26700元”即可列方程组求解;(2)设从甲厂调运饮用水x吨,则需从乙厂调运水(120-x)吨,根据“甲厂每天最多可调出80吨,乙厂每天最多可调出90吨”即可列不等式组求得x的范围,再根据题意列出关于的函数关系式,最后根据一次函数的性质求解即可.(1)设从甲厂调运饮用水x吨,从乙厂调运饮用水y吨,根据题意得解得∵5080,7090,∴符合条件故从甲、乙两水厂各调用了50吨、70吨饮用水;(2)设从甲厂调运饮用水x吨,则需从乙厂调运水(120-x)吨,根据题意可得解得.总运费,()∵W随x的增大而增大,故当时,元.∴每天从甲厂调运30吨,从乙厂调运90吨,每天的总运费最省,最少为26100元.【考点】二元一次方程组的应用,一元一次不等式组的应用,一次函数的应用点评:解题的关键是读懂题意,找到等量关系及不等关系,正确列方程组和不等式组求解.5.某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言的人数比为,请结合图中相关数据回答下列问题:(1)A组有人,C组有人,E组有人,并补全直方图;(2)该年级共有学生600人,请估计全年级在这天发言次数不少于20的人数;(3)已知A组发言的学生中恰有一位女生,E组发言的学生中恰有两位男生,现从A组与E组中分别抽一位学生写报告,求所抽的两位学生至多有一位男生的概率.【答案】(1)2,20,3,如下图;(2)60人;(3)【解析】(1)根据B、E两组发言的人数比为,即可求得B组发言人数的百分比,从而可以求得抽取的总人数,即可求得结果;(2)先求得发言次数不少于20的人数所占的百分比,再乘以600即可得到结果;(3)先列树状图表示出所有等可能的情况,再根据概率公式求解即可.(1)∵B、E两组发言的人数比为,E组发言人数的百分比为6%∴B组发言人数的百分比为20%∴B组发言的人数=10÷20%=50人∴A组有50×4%=2人,C组有50×40%=20人,E组有50×6%=3人(2)由题意得(人)答:全年级在这天发言次数不少于20的人数为60人;(3)列树状图:共有6六种等可能情况,符合至多有一位男生的情况有4种因此P(至多有一位男生).【考点】统计图的应用,概率的求法点评:统计图的应用初中数学的重点,是中考必考题,一般难度不大,需熟练掌握.6.已知,矩形ABCD中,延长BC至E,使BE = BD,F为DE的中点,连结AF、CF.(1)若AB = 3,AD = 4,求CF的长;(2)求证:∠ADB = 2∠DAF.【答案】(1);(2)连接BF,由BE=BD,EF=DF可证得∠DBF=∠EBF,再由CF=DE=DF即可证得∠DCF=∠FDC,从而可得∠ADF=BCF,再结合AD=BC即可证得△ADF≌△BCF,再根据全等三角形的性质即可作出判断.【解析】(1)根据矩形的性质可得,再根据个定理即可求的BD的长,从而可以求得BE、CE的长,再根据勾股定理即可求得DE的长,最后由F为DE的中点即可求得结果;(2)连接BF,由BE=BD,EF=DF可证得∠DBF=∠EBF,再由CF=DE=DF即可证得∠DCF=∠FDC,从而可得∠ADF=BCF,再结合AD=BC即可证得△ADF≌△BCF,再根据全等三角形的性质即可作出判断.(1)∵因为四边形ABCD是矩形∴在RT△ABD中,∴,∴∵F是DE的中点∴;(2)连接BF∵BE=BD,EF=DF∴∠DBF=∠EBF又∵CF=DE=DF∴∠DCF=∠FDC∠ADC+∠CDF=∠BCD+∠DCF即∠ADF=BCF又∵AD=BC∴△ADF≌△BCF∴∠DAF=∠FBC=∠DBE∵AD∥BC∴∠ADB=∠DBE∴∠ADB=2∠DAF.【考点】四边形的综合题点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.7.如图,一次函数分别交y轴、x轴于A、B两点,抛物线过A、B两点,作垂直x轴的直线,交x轴于H,交直线AB于M,交这个抛物线于N.(1)求这个抛物线的解析式;(2)若M在第一象限,求当t取何值时,MN有最大值?最大值是多少?(3)若∠ABO=∠BNH,求t的值.【答案】(1);(2)当时,最大值为4;(3)或【解析】(1)先求得一次函数于y轴、x轴的交点A、B的坐标,再由抛物线过A、B两点即可根据待定系数法求解;(2)先表示出MN的长与t的函数关系式,再根据二次函数的性质求解即可;(3)由∠ABO="∠BNH" 可得tan∠ABO=tan∠BNH,即,再分①时,②时,③时,三种情况求解即可.(1)在中,当时,;当时,∴将代入得,解得∴抛物线的解析式为;(2)∵,∴∵∴当时,最大值为4;(3)∵∠ABO="∠BNH"∴tan∠ABO=tan∠BNH即当时,;①时,,解得∴;②时,,解得∴;③时,,解得综上所述,当或时,∠ABO=∠BNH.【考点】二次函数的综合题点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.8.已知:如图,矩形ABCD,AB = 4,∠ACB = 30°.点E从点C出发,沿折线CA—AD以每秒一个单位长度的速度运动,过点E作EF∥CD交BC于点F,同时过点E作EG⊥AC交直线BC于点G,设运动的时间为t,△EFG与△ABC重叠部分的面积为S,当点E运动到点D时停止运动.(1)当点B与点G重合时,求此时t的值;(2)直接写出S与t之间的函数关系式和相应的自变量取值范围;(3)当t = 4时,将△EFG绕点E顺时针旋转一个角度(),∠GEF的两边分别交矩形的边于点M,点N.当△MEN为等腰三角形时,求此时△MEN的面积.【答案】(1)6或;(2);(3)或.【解析】(1)分当点B与点G第一次重合时,当点B与点G第二次重合时,两种情况结合图形特征求解;(2)分,,,,根据相似三角形的性质与三角形、梯形的面积公式求解即可;(3)分①当旋转角为30°时,②当旋转角为75°时,这两种情况,分别画出图形,根据勾股定理及三角形的面积公式求解即可.(1)当点B与点G第一次重合时,t=6当点B与点G第二次重合时,t=;(2)由题意得;(3)①当旋转角为30°时,∴;②当旋转角为75°时,作EH⊥AB于H,MG⊥AE于G,AH=2设则,又∵ GE=EH=∴∴解得:∴综上所述,△MNE的面积为或.【考点】动点问题的综合题点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.。
民族中学数学第三次月考试卷

民族中学九年级第三次月考数学试题一、精心选一选(每小题4分,共40分)1.在PMN Rt ∆中,°90=∠P ,=M sin ( )(A ) PMPN (B ) PN PM (C ) MN PN (D ) MN PM2. 与抛物线53212-+-=x x y 的形状大小开口方向相同,只有位置不同的抛物线是( )A .2523412-+-=x x yB .87212+--=x x yC .106212++=x x y D .532-+-=x x y3.在ABC Rt ∆中,︒=∠90C ,∠A 、∠B 、∠C 的对边分别为a 、b 、c ,则下列式子一定成立的是 ( )(A ) B c a sin ⋅= (B ) B c a cos ⋅= (C )B b a tan ⋅= (D ) Bab tan =4. 二次函数c bx x y ++=2的图象上有两点(3,-8)和(-5,-8),则此拋物线的对称轴是( ) A .直线x =4 B. 直线x =3 C. 直线x =-5 D. 直线x =-1 5.若︒<<︒900α,则下列说法不正确的是 ( ) (A) αsin 随α的增大而增大; (B )cos α随α的减小而减小; (C )tan α随α的增大而增大; (D )0<sin α<1.6.∠A 、∠B 、∠C 是ABC ∆的三个内角,下列各式成立的是 ( ) (A )2sin 2sinC B A =+(B )2cos 2cos AC B =+(C )2tan 2tan B C A =+(D )2cos2sin B C A += 7.如图,在ABC ∆中,AD 是BC 边上的高,︒=∠30C ,︒=∠105BAC ,322+=BC , 那么AD 的长是 ( )(A )21 (B ) 2 (C ) 2321+ (D ) 331+ 8.抛物线122+--=m mx x y 的图象过原点,则m 为( ) A .0B .1C .-1D .±19.把二次函数122--=x x y 配方成顶点式为( )A .2)1(-=x y B . 2)1(2--=x y C .1)1(2++=x y D .2)1(2-+=x y10.已知反比例函数xk y =的图象如右图所示,则二次函数222k x kx y +-=的图象大致为( )二、耐心填一填(每小题4分,共32分)11.如图,若CD 是RtΔABC 斜边上的高,AD =3,CD =4,则BC =_____. 12.当m 时,函数m x m x m m y +-+--=)2()32(22是二次函数. 13.右图是引拉线固定电线杆的示意图.已知:CD⊥AB,CD 33=m ,∠CAD=∠CBD=60°,则拉线AC 的长是____m. 14.在ABC Rt ∆,︒=∠90C ,b a 33=,则=A tan .15. 函数)0(2≠+=a c ax y 的图象的对称轴是 ;顶点坐标是 .16. 如图,已知正方形ABCD 的边长为2.如果将线段BD 绕着点B 旋转后,点D 落在CB 的延长线上的D′点处,那么tan BAD ∠′等于__________. 17. 要函数2mx y -=开口向上,则m .18. 抛物线2ax y =经过点(3,5),则a = . 三、细心做一做19.(8分)在ABC Rt ∆,︒=∠90C ,,53sin =A A A tan ,cos .20.(8分)︒∙︒+︒∙+︒∙︒60tan 60sin 45cos 245tan 30sin11题图A BCDA B C DDCBA13题图16题图21.(10分)如图,水库大坝的横断面积是梯形,坝顶宽是m 8,坝高为m 30,斜坡AD 的坡度为3:1=i ,斜坡CB 的坡度为i′=1:1,求斜坡AD 的坡角α,坝度宽AB 和斜坡AD 的长。
教育最新K12度秋期九年级数学上第三次月考题
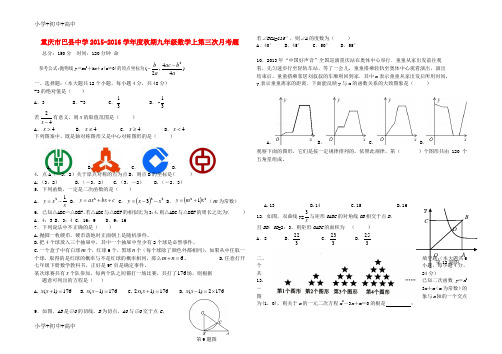
重庆市巴县中学2015-2016学年度秋期九年级数学上第三次月考题总分:150分 时间:120分钟 命参考公式:抛物线y =ax 2+bx +c (a ≠0)的顶点坐标为)44,2(2a b ac a b --一、选择题:(本大题共12个小题,每小题4分,共48分)-3的绝对值是( )A .3B .-3C .31 D .31- 若42-x 有意义,则x 的取值范围是( ) A .4>x B .4≠x C .4≥x D .4<x 下列图案中,既是轴对称图形又是中心对称图形的是( )A .B .C .D . 4. 点A (-3,2)关于原点对称的点为点B ,则点B 的坐标是( ) A.(3,2) B.(-3,2) C.(3,-2) D.(-2,3)5. 下列函数,一定是二次函数的是( ) A .xx y 12-= B .c bx ax y ++=2 C .()223x x y --= D .()221x m y +=(m 为常数) 6. 已知△ABC ∽△DEF ,若△ABC 与△DEF 的相似比为3:4,则△ABC 与△DEF 的周长之比为( ) A .4:3 B .3:4 C .16:9 D .9:16 7.下列说法中不正确的是( )A.抛掷一枚硬币,硬币落地时正面朝上是随机事件。
B.把4个球放入三个抽屉中,其中一个抽屉中至少有2个球是必然事件。
C.一个盒子中有白球m 个,红球6个,黑球n 个(每个球除了颜色外都相同),如果从中任取一个球,取得的是红球的概率与不是红球的概率相同,那么6=+n m 。
D.任意打开七年级下册数学教科书,正好是97页是确定事件。
某次球赛共有x 个队参加,每两个队之间都打一场比赛,共打了176场,则根据 题意可列出的方程是( )A.(1)176x x +=B.(1)176x x -=C.2(1)176x x +=D.(1)2176x x -=⨯9.如图,AB 是⊙O 的切线,B 为切点,AO 与⊙O 交于点C ,若∠BCA=115°,则∠A 的度数为( ) A .40° B .45° C .50° D .55°10.2013年“中国好声音”全国巡演重庆站在奥体中心举行.童童从家出发前往观 看,先匀速步行至轻轨车站,等了一会儿,童童搭乘轻轨至奥体中心观看演出,演出 结束后,童童搭乘邻居刘叔叔的车顺利回到家.其中x 表示童童从家出发后所用时间, y 表示童童离家的距离.下面能反映y 与x 的函数关系的大致图象是( )A .B .C .D .观察下面的图形,它们是按一定规律排列的,依照此规律,第( )个图形共由120 个五角星组成。
重庆市忠县中学高2013级2011-2012学年高二下学期三月月考数学试题(文)

重庆市忠县中学高2013级2011-2012学年高二下期三月考数学试题(文)一、选择题(本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.在复平面内,复数1ii z -=(i 是虚数单位)的共轭复数z 对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限2.右图是一个算法的程序框图,当输入的值x 为5时, 则其输出的结果是 ( );A. 0.5 ;B. 1 ;C. 2 ;D. 0.25 .3.已知集合{}{}23,1,,A x N x B a a =∈<=+.A B A ⋃=则a 的取值范围是:( ) {}.0,1;A B .{}1,0;- C .{}1,0,1;- D .{}1,1.- 4.已知,,a b R ∈则"00"a b <<且是"00"a b ab +<>且的什么条件?( ) A.充分不必要条件;B.充要条件;C.必要不充分条件;D.既不充分也不必要。
5.函数3(0)()(0,1)3(0)x x a x f x a a a x +<⎧=>≠⎨+≥⎩ 是R 上的增函数,则a 的取值范围是( )A .41,;3⎛⎤ ⎥⎝⎦B .()1,;+∞C .4,;3⎛⎫+∞ ⎪⎝⎭D . 41,.3⎛⎫⎪⎝⎭6.已知函数()2321,f x x x x =-++-则函数()()212f xg x x -=-的定义域是( )A .3,;2⎡⎫+∞⎪⎢⎣⎭B . ()3,22,;2⎡⎫⋃+∞⎪⎢⎣⎭C . (){}3,22,1;2⎡⎫⋃+∞⋃⎪⎢⎣⎭D .[)()1,22,.⋃+∞7.设函数()f x 是R 上以7为周期的奇函数,且()31,f <-()254,3a a f a --=+则a 的取值范围是:( ).A .[]()3,24,;--⋃+∞B .()()3,24,;--⋃+∞C .()(),32,4;-∞-⋃-D .(][),32,4.-∞-⋃-8.已知偶函数()()01x bf x aa a +=>≠且在(),0-∞上单调递增,则()3fb -与()2f a +的大小关系是:( )A .()()32;f b f a -=+B .()()32;f b f a -<+C .()()32;f b f a ->+D .()()32.f b f a -≥+9.已知定义在R 上的偶函数()f x 在[)0,+∞上递减,且()3 2.f =则不等式()3log 2f x <的解集是:( ) A .10,;27⎛⎫ ⎪⎝⎭ B .()27,;+∞ C .()10,27,;27⎛⎫⋃+∞ ⎪⎝⎭D .[)10,27,.27⎛⎤⋃+∞ ⎥⎝⎦ 10.设函数()55(0)log (0)x x f x x x ≤⎧=⎨>⎩ 若关于x 的方程()()220f x a f x -=恰有三个不同的实根,则实数a的取值范围是( )A.[)1,0;-B.(]0,1;C.[)(]1,00,1;-⋃D.()()1,00,1.-⋃二、填空题(本大题共5个小题,每小题5分,共25分.将正确答案填在题中横线上) 11.已知x 与y 之间的一组数据如下:()()()()()1,1,2,3,3,5,4,7,5,9.则y 与x 的线性回归方程y bx a =+必过点___________.12.观察:()()32'1,'3,sin 'cos .x x x x x ===由归纳推理可得:若定义在R 上的函数()f x 满足()(),f x f x -=-记()g x 为()f x 的导数,则()g x -与()g x 的关系是 . 13.定义两种运算:22,a b a b ⊕=-()2.a b a b =-试判断函数()222xf x x ⊕=-的奇偶性: .14.函数()253x y x A x -=∈-的值域是(][),04,.-∞⋃+∞,则集合____.A = 15.函数()y f x =是定义在R 上的增函数,且()()00,1 2.f f ≠=对任意实数,m n 恒有()()().f m n f m f n +=⋅集合()()(){}22,4,A x y f x f y =⋅≤()(){},21,.B x y f ax y a R =-+=∈若,A B ⋂=∅则a 的取值范围是 .三、解答题(本大题共6个小题,共75分.解答应写出文字说明、证明过程或演算步骤) 16.(本小题满分13分)已知集合31,1A x Zx ⎧⎫=∈≥⎨⎬-⎩⎭求函数()()32log 1x f x x x A =+-∈的值域。
忠县中考数学试卷

一、选择题(每小题3分,共30分)1. 若一个等腰三角形的底边长为10cm,腰长为12cm,则该三角形的面积是()A. 60cm²B. 64cm²C. 36cm²D. 50cm²2. 下列函数中,定义域为实数集R的是()A. y = √(-x)B. y = 1/xC. y = |x|D. y = x²3. 在平面直角坐标系中,点A(2,3)关于原点对称的点的坐标是()A.(-2,-3)B.(2,-3)C.(-2,3)D.(3,2)4. 若等差数列{an}的首项为2,公差为3,则第10项an是()A. 29B. 28C. 27D. 265. 下列不等式中,正确的是()A. |x| < 2B. x² < 1C. 2x > 4D. 3x ≤ 66. 在△ABC中,∠A=60°,∠B=45°,则∠C的度数是()A. 75°B. 90°C. 45°D. 30°7. 若sinθ = 1/2,且θ是第一象限的角,则cosθ的值是()A. √3/2B. 1/2C. -√3/2D. -1/28. 下列各式中,能化为分式的是()A. (x+1)/(x²-1)B. (x²+1)/(x²-1)C. (x²-1)/(x+1)D. (x²-1)/(x²+1)9. 若a,b,c是等比数列的前三项,且a+b+c=12,a²=bc,则b+c的值为()A. 6B. 8C. 10D. 1210. 在平面直角坐标系中,直线y=kx+b与x轴、y轴的交点分别为A、B,若OA=OB=2,则k²+b²的值为()A. 4B. 8C. 12D. 16二、填空题(每小题3分,共30分)11. 若a,b,c是等差数列,且a+b+c=18,则ac=______。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012年秋2013级第三阶段测试
数学试卷
(全卷共四个大题,满分150分,考试时间120分钟)
一、选择题:(本大题共10个小题,每小题4分,共40分)每小题只有一个答案是正确的,请将正确答案的代号填入题后的括号内。
1.3-的相反数是( )
A .3
B .3-
C .3±
D .13
- 2.第九届海峡交易会5月18日在榕城开幕,推出的重点招商项目总投资约450亿元人民币.将450亿元用科学记数法表示为( )
A .110.4510⨯元
B .94.5010⨯元
C .104.5010⨯元
D .845010⨯元
3.随机掷两枚硬币,落地后全部正面朝上的概率是( )
A .1
B .12
C .13
D .14
4.解集在数轴上表示为如图1所示的不等式组是(
A .32x x >-⎧⎨
⎩≥
B .32x x <-⎧⎨⎩≤
C .32x x <-⎧⎨⎩≥
D .32
x x >-⎧⎨⎩≤
5.如图,△ABC 是⊙O 的内接三角形,若∠ABC =70°,
则∠AOC 的度数等于( )
A .140°
B .130°
C .120°
D .110° 6.只用下列一种正多边形不能镶嵌成平面图案的是( )
A .正三角形
B .正方形
C .正五边形
D .正六边形
7.下列运算中,结果正确的是( )
A .444a a a +=
B .a 3·a 2=a 5
C .824a a a ÷=
D .236(2)6a a -=-
8.下列命题中,错误的是( )
A .矩形的对角线互相平分且相等
B .对角线互相垂直的四边形是菱形
C .等腰梯形的两条对角线相等
D .等腰三角形底边上的中点到两腰的距离相等
9.已知一次函数(1)y a x b =-+的图象如图3所示,那么的取值范围是( )
A .1a >
B .1a <
C .0a >
D .0a < 10.如图4所示,二次函数2(0)y ax bx c a =++≠的图象经过点(12)-,
,且与x 轴交图1 图3
5题图
点的横坐标分别为12x x ,,其中121x -<<-,201x <<
①420a b c -+<;
②20a b -<;
③1a <-;
④284b a ac +>.
其中正确的有( )
A .
1个 B .2个 C .3个 D .4个
二、填空题(本大题共6个小题,每小题4分,满分24分)
11.当x 时,二次根式
12.如图5,点D
E ,分别在线段AB AC ,上,BE CD ,相交
于点O AE AD =,,要使ABE ACD △≌△,需添加一个条
件是 (只要写一个条件).
13.等腰三角形的一个底角为030,则顶角的度数
是 度.
14.计算4133
m m m -+++= . 15.方程x 2+2x=0的解为
16.如图845AOB ∠= ,过OA 上到点O 的距离分别为
1357911 ,,,,,,的点作OA 的垂线与OB 相交,得到并标出 一组黑色梯形,它们的面积分别为1234S S S S ,,,,.
观察图中的规律,求出第10个黑色梯形的面积10S = .
三、解答题(本大题共4个小题,17、18小题各6分,19、20小题各7分共26分)
17.计算:22)12(301-+-+-.
18.用公式法求一元二次方程的解23510x x -+=
19.先化简,再求值)21(2
22222ab b a ab b a b a +-÷+-,其中32+=a ,32-=b 。
20. 如图,在△ABE 中,AB =AE,AD =AC,
∠BAD =∠EAC, BC 、DE 交于点 O.
求证:(1) △ABC ≌△AED ; (2) OB =OE .
图4 O C E A D B 图5
图8 E
四、解答题:(本大题共4个小题,每小题10分,共40分)解答时每小题必须给出必要的演算过程或推理步骤.
21.如图,在梯形ABCD 中,AD ∥BC,AB =AD =DC,
∠B =60º
(1)求证:AB ⊥AC ;
(2)若DC =6,求梯形ABCD 的面积 .
22. 已知:如图,在平面直角坐标系xOy 中,直线
AB 与x 轴交于点A (-2,0),与反比例函数在第一
象限内的图象的交于点B (2,n ),连结BO ,若S △AOB =4.
(1)求该反比例函数的解析式和直线AB 的解析式;
(2)若直线AB 与y 轴的交点为C ,求△OCB 的面积.
23.有两个可以自由转动的均匀转盘A B ,都被分成了3等份,并在每一份内均标有数字,如图所示,规则如下:
①分别转动转盘A B ,;②两个转盘停止后观察两个指针所指份内的数字(若指针停在等份线上,那么重转一次,直到指针指向某一份内为止).
(1) 用列表法(或树状图)分别求出“两个指针所
指的数字都是..
方程2560x x -+=的解”的概率和 “两个指针所指的数字都不是...方程2560x x -+= 的解”的概率;
(2)王磊和张浩想用这两个转盘作游戏,他们规定:若“两个指针所指的数字都.
是.2560x x -+= 的解”时,王磊得1分;若“两个指针所指的数字都不是...2560x x -+=的解”时,张浩得3分,这个游戏公平吗?若认为不公平,请修改得分规定,使游戏对双方公平.
24.已知:如图,在直角梯形ABCD 中,AD ∥BC ,
∠ABC =90°.点E 是DC 的中点,过点E 作DC
的垂线交AB 于点P ,交CB 的延长线于点M .点F 在
线段ME 上,且满足CF =AD ,MF =MA .
(1)若∠MFC =120°,求证:AM =2MB ;
(2)求证:∠MPB =90°- 1 2
∠FCM .
五、解答题(本大题共2个小题,每小题10分,共20分)
25.今年我国多个省市遭受严重干旱,受旱灾的影响,4月份,我市某蔬菜价格呈
A B
进入5月,由于本地蔬菜的上市,此种蔬菜的平均销售价格y (元/千克)从5月第1周的2.8元/千克下降至第2周的2.4元/千克,且y 与周数x 的变化情
况满足二次函数y =- 1 20
x 2+bx +c . (1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知
识直接写出4月份y 与x 的函数关系式,并求出5月份y 与x 的函数关系式;
(2)若4月份此种蔬菜的进价m (元/千克)与周数x 所满足的函数关系为m = 1 4
x +1.2,5月份此种蔬菜的进价m (元/千克)与周数x 所满足的函数关系为m =5
1 x +2.试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大?且最大利润分别是多少?
(3)若5月份的第2周共销售100吨此种蔬菜.从5月份的第3周起,由于受暴雨的影响,此种蔬菜的可供销量将在第2周销量的基础上每周减少a %,政府为稳定蔬菜价格,从外地调运2吨此种蔬菜,刚好满足本地市民的需要,且使此种蔬菜的销售价格比第2周仅上涨0.8 a %.若在这一举措下,此种蔬菜在第3周的总销售额与第2周刚好持平,请你参考以下数据,通过计算估算出a 的整数值.
(参考数据:372=1369,382=1444,392=1521,402=1600,412=1681)
26.已知:如图(1),在平面直角坐标xOy 中,边长为2的等边△OAB 的顶点B 在第一象限,顶点A 在x 轴的正半轴上.另一等腰△OCA 的顶点C 在第四象限,OC =AC ,∠C =120°.现有两动点P 、Q 分别从A 、O 两点同时出发,点Q 以每秒1个单位的速度沿OC 向点C 运动,点P 以每秒3个单位的速度沿A →O →B 运动,当其中一个点到达终点时,另一个点也随即停止.
(1)求在运动过程中形成的△OPQ 的面积S 与运动的时间t 之间的函数关系,并
写出自变量t 的取值范围;
(2)在等边△OAB 的边上(点A 除外)存在点D ,
使得△OCD 为等腰三角形,请直接写出所有符
合条件的点D 的坐标;
(3)如图(2),现有∠MCN =60°,其两边分别与
OB 、AB 交于点M 、N ,连接MN .将∠MCN 绕着
C 点旋转(0°<旋转角<60°),使得M 、N 始
终在边OB 和边AB 上.试判断在这一过程中,
△BMN 的周长是否发生变化?若没有变化,请
求出其周长;若发生变化,请说明理由.。
