信号与系统课件--卷积性质例3
北京邮电大学信号与系统-3.08 卷积特性(卷积定理)

f d
f ut d f t ut
ht
gt f t ht
G F H gt F 1 G
将时域求响应,转化为频域求响应
退出
,求 f t f1 t f1 t 的 例3-8-1 已知 f1 (t ) E Sa 2 频谱密度函数F . 2 2 2 解: F f t F1 F1 E Sa 2
退出
频谱结构
m时, F ( ) 0, C m
f C (t ) f (t ) cos C t
F ( )
f t
A
O
t
mO m
F cos C t
cos C t
( )
O
( )
t
C
O
C
FC ( )
1 FC ( ) F ( C ) F ( C ) 2 f t cos t
卷积 定义
f 1 f 2 t d
因此
e j t dt F f 1 t f 2 t f f t d 2 1 交换积分
f 1 f 2 t e jt dt d
证明
时域卷积对应频域频谱密度函数乘积
频域卷积定理
若
f 1 t F1 , f 2 t F2
1 则 f 1 t f 2 t F1 F2 2 时间函数的乘积 各频谱函数卷积的 1
应用
退出
信号与系统 梁风梅主编 电子工业出版社 ppt第三章答案

习题三3.1考虑一个连续时间LTI 系统,满足初始松弛条件,其输入)(t x 与输出)(t y 的关系由下列微分方程描述:d ()4()()d y t y t x t t+= (1)若输入(13)()()j t x t e u t -+=,求输出)(t y 。
(2)若输入()e cos(3)()t x t t u t -=,求输出)(t y 。
解:此系统的特征方程为40s += 所以4()t h y t Ae -= (1)(13)()()j tx t eu t -+=设(13)()e j t p y t Y -+= 则(13)(13)(13)(13j)e 4e e ,0j tj t j t Y Y t -+-+-+-++=>解得11336jY j -==+ 所以4(13)1()()()e e ()6t j t h p j y t y t y t A u t --+-⎛⎫=+=+ ⎪⎝⎭又因为初始松弛,所以106jA -+= 即16j A -=所以4(13)11()()()()()66t j th p j j y t y t y t e e u t --+--=+=+ (2)()cos(3)()t x t e t u t -=是(1)中(13)()()j tx t eu t -+=的实部,用2()x t 表示cos(3)()t e t u t -,用1()x t 表示(13)()j t e u t -+观察得{}21()Re ()x t x t =所以{}421111()Re ()cos(3)sin(3)()666t t t y t y t e e t e t u t ---⎛⎫==-++ ⎪⎝⎭3.2若离散时间LTI 系统的输入[]x n 与输出][n y 的关系由下述差分方程给出:][]1[25.0][n x n y n y =--求系统的单位冲激响应][n h 。
解:[]0.25[1][]h n h n n δ=-+因为该系统是因果的,所以0n <时,[]0h n =2231[0]0.25[1][0]01111[1]0.25[0][1]1044111[2]0.25[1][2]0444111[3]0.25[2][3]0444 (111)[]0.25[1][]0444n nh h h h h h h h h n h n n δδδδδ-=-+=+==+=⨯+==+=⨯+==+=⨯+==-+=⨯+=综上,1[][]4n h n u n = 3.3系统S 为两个系统1S 与2S 的级联:S1:因果LTI 系统,[]0.5[1][]w n w n x n =-+; S2: 因果LTI 系统,[][1][]y n ay n bw n =-+][n x 与][n y 的关系由下列差分方程给出:[]0.125[2]0.75[1][]y n y n y n x n +---=(1) 确定a 与b 。
清华大学信号与系统课件§3.8 时域 卷积定理

• 单脉冲的频谱 F0() 是连续谱, 它的大小是有限值;
• 周期信号的谱 F() 是离散谱,
含谱密度概念,它的大小用冲激 表示;
•
F0 ( )
是
F() 的包络的
1
1
。
2020/1/15
信号与系统
作业题
• 3-26,3-28,3-30,3-34*,3-36,3-38*, • 3-39,3-40,3-42*, 3-43*,3-44*, • 3-46*
2
T1 2
T
(t ).e
jn1t dt
1 T1
T
(t)
1 T1
e
n
jnt
2020/1/15
信号与系统
四、周期单位冲激序列的FT
T (t)
n
(t nT1)
Fn .e jn1t
n
1
e jnt
T1 n
FT [
F1()* F2()
2020/1/15
信号与系统
例:求余弦脉冲的频谱
1
c os t
FT
2
FT[cost ]
(
)
2
G(t)E NhomakorabeaFT
G( )
2
2
2
2
E f (t)
相 乘
卷 积
F ()
2
2
2020/1/15
信号与系统
f (t) G(t).cost
2020/1/15
信号与系统
卷积算子.ppt

2.3 卷积积分、算子
1.卷积积分概念
x(t)
系统 {x(0-)=0}
y(t)?
卷积与反卷积
已知x(t)和系统特性,求y(t) ——卷积运算 已知x(t)和y(t), 求系统特性——反卷积运算 已知系统特性和y(t), 求x(t)——反卷积运算
应用卷积运算对系统的要求
u(t t1
t1
t1 )
t1
e(t1) (t t1)dt1
任意信号可以分解为冲激信号的叠加
哈尔滨工业大学自动化测试与控制系
信号与系统—signals and systems
(t)
零状态LTI
h(t)
(t )
零状态LTI
h(t )
e( ) (t )
零状态LTI
e( ) h(t )
e( ) (t )d e(t)
零状态LTI
e( ) h(t )d r(t)
r(t) e( )h(t )d e(t) * h(t) 卷积积分
哈尔滨工业大学自动化测试与控制系
信号与系统—signals and systems
4.卷积积分(Convolution Integral) • 卷积积分的定义
信号与系统—signals and systems
6.卷积性质
①代数性质
i)交换律:f1(t ) f2 (t ) f2 (t ) f1(t )
证明:f1(t) f2 (t)
f1( ) f2 (t )d
信号与系统—signals and systems
f11(t))
例3 f1(t)、f2(t)如图所示,已知f(t) = f2(t) * f1(t) ,
《信号与系统教学课件》§2.6 卷积及其性质和计算

将卷积的微分性质和积分性质加以推广,可以得到
s
t
nm
f (n) 1
t
f (m) 2
t
f (m) 1
t
f (n) 2
t
X
二、卷积的性质
注意函数的积分和微分并不是一个严格的可逆关系, 因为函数加上任意常数后的微分与原函数的微分是相 同的。因此,对于等式
f1 t
f2 t
f1' t
k
d
k
f
3
t
d
令w k
f1
k
f2
w f3
t
k
w d w d k
令st f2t f3t
f1 k s t k d k
f1 t st
f1 t
f2 t
f3 t
f 1
t f2 t
f3 t
X
二、卷积的性质
一、代数性质 • 结合律
对于函数f1 t , f2 t , f3 t ,存在
h2 t
r(t)
h1 t
图2.6.2 卷积交换律的系统意义
X
二、卷积的性质
一、代数性质
• 结合律
对于函数f1 t , f2 t , f3 t ,存在
f1 t f2 t f3 t f1 t f2 t f3 t
根据卷积的定义
f1 t
f2
t
f3
t
f1
k
f2
X
三、卷积的计算
根据卷积的定义,卷积计算是由若干基本的信号运算组成的, 对于
s
t
f1
f2
t
d
第一步 反褶:将 f1 t 反褶运算,得到 f1
信号第二章3卷积

若将此信号作用到冲激信号为h(t)的线性时不 变系统,则系统的响应为
r (t ) H [e(t )] H [ e( ) (t )d ]
e( ) H [ (t )]d
e( )h(t )d
零状态响应:rzs (t ) e( )h(t )d h(t ) e(t )
def
2.算子符号基本规则
(1)算子多项式可以进行因式分解 ( p 2)( p 3) p 2 5 p 6 例如: (2)等式两端的算子符合因式不能相消 ( p 2) r (t ) ( p 1) e(t ) ( p 2)( p 3) r (t ) ( p 2 4 p 3) e(t ) 不能简化为: (3)算子的乘除顺序不能随意颠倒
(3)结合律: f1(t) f2 (t) f3 (t) f1(t) f2 (t) f3 (t)
e(t)
h1(t)
h2(t)
r(t)
串联系统 r (t ) e(t ) h1 (t ) h2 (t )
2.卷积的微分与积分
d f1 (t ) f 2 (t ) df 2 (t ) (4)微分性: f1 (t ) dt dt df1 (t ) (适于高阶微分) f 2 (t ) dt
r (t ) e( )h(t )d
1 (a) t 2
e(t ) * h(t ) 0
h(t )
e( )
1
1 2
t 2
(b)
0
1 t 1 2
相乘
t
1
1 t 1 2 t 1 e(t ) * h(t ) 1 1 (t )d 2 2 t2 t 1 4 4 16 (b)
信号与系统-第3章

第3章连续系统的时域分析本章内容LTI系统的时域分析方法线性微分方程的经典解法零输入-零状态微分算子与传输算子冲激响应和阶跃响应冲激响应阶跃响应卷积积分及其应用卷积积分的概念卷积积分的性质卷积积分在LTI系统分析中的应用LTI 连续系统的时域分析1)建立系统数学模型;2)求解线性微分方程。
由于在其分析过程涉及的函数变量均为时间t ,故称为时域分析法。
这种方法比较直观,物理概念清楚,是学习各种变换域分析法的基础。
其过程可以归结为:线性微分方程的经典解法)()()()()()()()(01)1(1)(01)1(1)(t f b t f b t f b t f b t y a t y a t ya t y m m m m n n n +′+++=+′+++−−−−L L 微分方程的经典解:y (t ) = y c (t ) + y p (t )(完全解)(齐次解)(特解)经典解法-齐次解不同特征根对应的齐次解的解。
y c (t )的函数形式由上述微分方程的特征根确定。
齐次解是齐次微分方程0)()()()(01)1(1)(=+′+++−−t y a t y a t y a t y n n n L经典解法-齐次解(续)=)(t y c 例如::则微分方程的齐次解为个根是单根,其余,即有重根,是特征方程的假设 - 211r n r r λλλλ===L ∑+=+nr j tj j e c 1λ∑=−r i t i r i i e t c 1λ经典解法-特解特解的函数形式与激励函数的形式有关。
表3-1 不同激励对应的特解A(常数)B(常数)线性微分方程的经典解法1)根据齐次方程的特征根求齐次解;2) 根据激励信号的函数形式求特解;3) 将特解代入原微分方程,根据方程两端对应项系数相等,求得特解中的待定系数;4) 将系统的n个初始条件代入全解中,确定齐次解中n个待定系数。
线性微分方程的经典解法(续)激励信号在t =0时刻接入系统:由于激励信号的作用,响应y (t )及其各阶导数有可能在t =0时刻发生跳变,为区分跳变前后的数值,我们用0-表示激励接入之前的瞬间,并称此时刻为“起始时刻”;而用0+表示激励接入之后的瞬间,并称此时刻为“初始时刻”。
《信号与系统》课程讲义3-4
t 2
1
§3.4卷积定理和相关定理
二、相关定理
1.能量信号与功率信号
①能量与能量信号
∫ i)能量 E =
+∞
|
f
(t) |2dt
−∞
ii)能量信号E<+ ∞,例 f (t) = EGτ (t)
∫ ②iii功))功功率率率与P信功=号率Tl→iPm信+<∞+号T1∞−T22T
f (t 例f
) 2 dt (t) =
) )
f f
2 2
(t (τ
−τ −t
)dt )dτ
③ ⇒ f1(t) * f2 (−t) = R12 (t)
§3.4卷积定理和相关定理
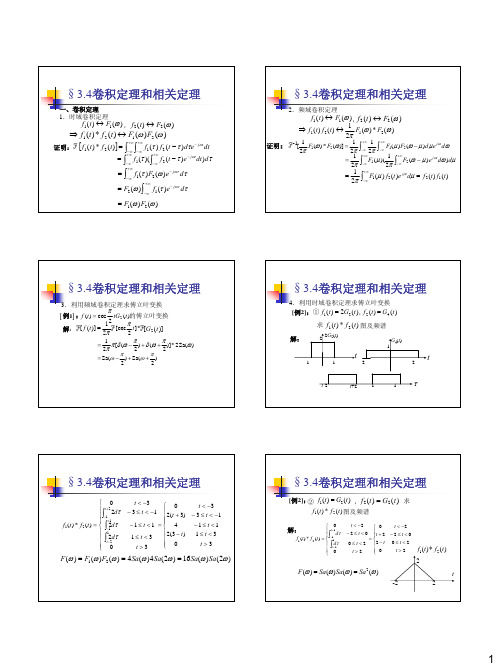
[例3]:已知 f1(t) = G2 (t),f2 (t) = (−t + 2)R2 (t) 求① f1(t) * f2 (t)
② R12 (t) = f1(t) * f2 (−t)
t+2 -1
1τ
§3.4卷积定理和相关定理
⎧0
∫⎪
⎪
t+2 2dτ
−1
∫ f1 (t )
*
f2 (t)
=
⎪ ⎨
⎪
∫⎪
⎪⎩
+21dτ
−1
12dτ
t−2
0
t < −3 ⎧ 0
− 3 ≤ t < −1 −1≤ t <1
=
⎪⎪⎪⎨2(t 4+
3)
1 ≤ t < 3 ⎪⎪2(3 − t)
t>3
⎪⎩ 0
t < −3 − 3 ≤ t < −1 −1≤ t <1
§3.4卷积定理和相关定理
3-4卷积定理和相关定理

1 2π
哈尔滨工业大学自动化测试与控制系
信号与系统— 信号与系统—signals and systems
3.利用频域卷积定理求傅立叶变换 . [例1]: f (t ) = G2 (t ) cos( t ) 的傅立叶变换 例 : 2 1 π 解:ℱ[ f (t )] = ℱ[cos t ] ∗ ℱ[G2 (t )] 2π 2 1 π π = π [δ (ω − ) + δ (ω + )] ∗ 2Sa(ω ) 2π 2 2
t < −2 0 −2 ≤ t < 0 t + 2 −2 ≤ t < 0 = 0 ≤ t < 2 2 − t 0 ≤ t < 2 0 t>2 t>2
2
f1 (t ) ∗ f 2 (t )
t < −2
F (ω ) = Sa(ω )Sa(ω ) = Sa 2 (ω )
-2 0 2
t
R12 (τ ) = ∫ f 1 (t ) f 2 (t − τ )dt = ∫ f 1 (t + τ ) f 2 (t )dt
−∞ −∞ +∞ +∞ +∞ +∞
R21 (τ ) = ∫ f 1 (t − τ ) f 2 (t )dt = ∫ f 1 (t ) f 2 (t + τ )dt
−∞ −∞
④复能量信号的相关函数: 复能量信号的相关函数:
R12 (τ ) = ∫
+∞ −∞
f1 (t ) f 2* (t − τ ) dt
⑤复功率信号的相关函数: 复功率信号的相关函数:
1 T R12 (τ ) = lim ∫ 2T f1 (t ) f 2* (t − τ )dt T →∞ T − 2
信号与系统课件

例1
0-和0+初始值举例 和 初始值举例1 初始值举例
例1:描述某系统的微分方程为 y”(t) + 3y’(t) + 2y(t) = 2f’(t) + 6f(t) 已知y(0-)=2,y’(0-)= 0,f(t)=ε(t),求y(0+)和y’(0+)。 已知 , , , 和 。 解:将输入f(t)=ε(t)代入上述微分方程得 将输入 代入上述微分方程得 y”(t) + 3y’(t) + 2y(t) = 2δ(t) + 6ε(t) 1) (1) 利用系数匹配法分析 上式对于t=0-也成立,在0-<t<0+ 分析: 也成立, 利用系数匹配法分析:上式对于 也成立 区间等号两端δ(t)项的系数应相等。 项的系数应相等。 区间等号两端 项的系数应相等 由于等号右端为2δ(t),故y”(t)应包含冲激函数,从而 应包含冲激函数, 由于等号右端为 , 应包含冲激函数 y’(t)在t= 0处将发生跃变,即y’(0+)≠y’(0-)。 在 处将发生跃变, 。 处将发生跃变 不含冲激函数, 将含有δ’(t)项。由于 但y’(t)不含冲激函数,否则 不含冲激函数 否则y”(t)将含有 将含有 项 y’(t)中不含 中不含δ(t),故y(t)在t=0处是连续的。 处是连续的。 中不含 , 在 处是连续的 ■ ▲ 第 24 页 y(0+) = y(0-) = 2 故 第 24 页
例1
例2
当微分方程右端含有冲激函数时,响应y(t)及其各阶导数中,有些在t=0处将发生跃变。 否则不会跃变。
三.零输入响应和零状态响应 零输入响应和零状态响应
y(t) = yzi(t) + yzs(t) ,也可以分别用经典法求解。 注意:对t=0时接入激励f(t)的系统,初始值 yzi(j)(0+), yzs(j)(0+) (j = 0,1,2,…,n-1)的计 算。 y(j)(0-)= yzi(j)(0-)+ yzs(j)(0-) y(j)(0+)= yzi(j)(0+)+ yzs(j)(0+) 对于零输入响应,由于激励为零,故有 yzi(j)(0+)= yzi(j)(0-) = y (j)(0-) 对于零状态响应,在t=0-时刻激励尚未接入,故应有 yzs(j)(0-)=0 yzs(j)(0+)的求法下面举例说明。
信号与系统卷积积分ppt课件

任意信号 f (t) 可表示为冲激信号加权和 f (t) f ( ) (t )d
若把它作用于冲激响应为h(t)的LTI系统,则响应为
r(t) H f (t)
H
f
(
)
(t
)
d
f ( )H (t )d
0
t
2 0 2 t u( 2) u(t ) t 0 t 2
i(t
)
e
t
t
e2
d
u(t
)
et
t
e2d u(t 2)
0
2
2
e
t 2
et
u(t)
e(t )
1
1 0 1 t 2
h(t) 1 t u(t) u(t 2)
2
h(t)
1
0
2t
卷积图解过程
解: 图解法
i)t
e( )
1
1 0 1 2
ii)h( ) h( )
h( )
1
2
0
h( )
1
0
2
iii)h( ) h(t )
h(t )
d
2
t
2
4
t 1
t2 t 1
4 24
卷积图解过程
1 t <2
f2
(t
1
)
f1(
信号与系统 卷积分析法46页PPT

21、要知道对好事的称颂过于夸大,也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
23、一切节省,归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰,决心到最后会全部推倒。——莎士比亚
25、学习是劳动,是充满思想的劳动。——乌申斯基
谢谢!
信号与系统 卷积分析法
67、有两种和平的暴力,那就是法律和礼节。——歌德
8、法律就是秩序,有好的法律才有好的秩序。——亚里士多德 9、上帝把法律和公平凑合在一起,可是人类却把它拆开。——查·科尔顿 10、一切法律都是无用的,因为好人用不着它们,而坏人又不会因为它们而变得规矩起来。——德谟耶克斯
信号与系统 郑君里§2.6 卷积

(t-)的响应
X
第 7 页
(3)卷积是系统分析中的重要方法,通过冲激响应h(t)建 立了响应r(t)与激励e(t)之间的关系。 一般数学表示: g(t ) f1 ( ) f 2 (t ) d
信号无起因时: g( t ) f ( )h(t ) d
e ht d
这就是系统的零状态响应。
rzs t et ht et ht
X
三.卷积的计算
由于系统的因果性或激励信号存在时间的局限性,卷 积的积分限会有所变化。卷积积分中积分限的确定是 非常关键的。 借助于阶跃函数u(t)确定积分限 利用图解说明确定积分限
第 4 页
X
第
卷积的图解说明
5 页
用图解法直观,尤其是函数式复杂时,用图形分段求 出定积分限尤为方便准确,用解析式作容易出错,最好将 两种方法结合起来。
f t
f1 f 2 t d
对 时延 t ( t ) t
积分结果为 t的函数
1. f1 (t ) f1 ( ), 积分变量改为
§2.6卷积
•卷积
•利用卷积积分求系统的零状态响应
•卷积图解说明
•卷积积分的几点认识
北京邮电大学电子工程学院 2003.1
一.卷积(Convolution)
设有两个函数 1 ( t )和f 2 ( t ), 积分 f
f t
第 2 页
f1 f 2 t d
(4)卷积是数学方法,也可运用于其他学科 。 (5)积分限由 f 1 (t ), f 2 (t ) 存在的区间决定,即由 f 1 ( ) f 2 ( t ) 0 的范围决定。
卷积的性质 ppt课件

f1 1 u(t 1)
f 2 e(t1)u(t 1)
s f1 f2 [1 u(t 1)] [e(t1)u(t 1)]
ppt课件
18
1* e (t1)u(t 1) u(t 1) e (t1)u(t 1)
e ( 1)u(
= r(t) r(t1) – r(t 2) + r(t-3)
ppt课件
4
一.卷积代数
mutative law f1 f2 f2 f1
f (t) h(t) f h
h(t )
h f
f(t)
2.distributive law f1 [ f2 f3 ] f1 f2 f1 f3
d 2r d 2t
h(t) (t) r(t) 2 (t 1) (t 2)
h3(t) r(t)
ppt课件
25
点评:本题是求反卷积的问题。 利用了sintu(t) 两次求导后出现冲激函数 和自身,具有这一特点的函数,求反卷积 用本例的方法比较简单。
ppt课件
26
16
4.P85.2-19(b) f1 1 1
解:方法一:t<0时:
f 2 e(t1)u(t 1)
-1
t 1
f1 f2
1 e(t 1)d
e(t1)
e
e0
0 1
t>0时:
1
t 1
2 e f1 f2 e(t 1)d 2e(t 1)d
y‘ zs
(t
)
f
’(t) h(t)
f '(t) (t) etu(t)带入上式,有
信号系统与卷积

信号系统与卷积在不少程序员眼中,卷积这个数学概念是很神秘很难懂的。
由于其在数学、物理学、电子工程、信号处理、计算机科学中极为重要,所以我试图在本文中讲解卷积的概念,力求易读易懂,让尽可能多的人理解卷积。
前几天见到VC知识库论坛上有人提问:“卷积是什么意思?”,似乎女友也问过类似问题,所以我想很有必要澄清这个既基础又重要的卷积概念。
如果您已经对此非常了解,那完全可以忽略本文了。
本文的目标读者是那些见了卷积这两个字就头大,又迫于工作需要,必须弄懂的人。
我假设您已经通过了大学一年级的高数考试,但现在已经忘得差不多了J。
很多教科书一上来就会给出卷积的定义,接着就是一串推导、证明、例子,如果你不太适应这种方式,那本文可能会非常适合你。
卷积在信号处理领域中尤为常用,就以此慢慢引入卷积概念吧。
日常生活中到处都是信号系统,它们接受一定的输入后,会给出一定的输出:手机受到对方来电的信号就会响铃或震动;电脑接到一串按键信号,屏幕就会输出一串对应的字符;女友在收到男友送的一束玫瑰后也许会送上一个热吻……现在,我们把这些信号系统抽象成“黑匣子”,不管它的内部构造,而只关注它对输入的响应。
数学化一点儿,将一个给定的信号系统记为S,设输入信号为x(t),输出信号为y(t),t可以代表时间,也可以是其它什么。
那么:y(t) = S{ x(t) }就表示系统S将x(t)这个输入信号转化为输出信号y(t)。
太一般化的信号系统不容易研究,那就加入一些“合理的”限制条件。
S是连续(continuous)的,如果t可以连续变化;特别的,x(t)和y(t)都是定义在实数域上的函数。
物理世界中的信号系统大多是连续的。
S是离散(discrete)的,如果t只能取一些分立的值;特别的,x(t)和y(t) 都是定义在整数域上的函数。
离散的信号系统可以比较方便的被计算机分析处理。
S是线性(linear)的,如果对任意两个输入信号x1、x2和任意的常数c1和c2有:S{ c1x1(t) + c2x2(t) } = c1S{ x1(t) } + c2S{ x2(t) }拿超市作比喻,我跟女友去买2斤萝卜和3斤白菜,即c1=2,c2=3,x1是萝卜,x2是白菜。
