高等数学经管类习题库上(2014版)梁景邦
经管类微积分(上)参考答案

经管类《微积分》(上)习题参考答案第一章 函数习题一一、1.否; 2.是; 3.是; 4.否.二、1.)[()5,33,2⋃; 2.()πππ+k k 2,2; 3. 2,24>-<<-x x 或;4.[]a a -1,; 5.[]2,0; 6.222+-x x . 三、1.奇函数;2.奇函数. 3.(略)四、1(略);2.212+x ; 3.11-+x x . 五、1.x v v u u y sin ,,ln 2===;2.x x u e y u ln ,==;3.1525++⋅x x .六、50500,,)50(8.050)(>≤<⎩⎨⎧-+=x x x a a ax x R .第二章极限与连续习题一一、 1.0,1,1,0; 2.e e e e ,,,231- 二、1.1; 2.0; 3.21; 4.4.三、1. (略); 2.证明(略),极限为2 四、()1lim 0=+→x f x ,()1lim 0-=-→x f x ,()x f x 0lim →不存在. 五、都不存在. 六、15832.5,32.4,221.3,1.2,0.1 1.8,3.7,.6e .七、2,1==b a 八、2.4,32.3,21.2,2.1-习题二 一、()().1,1.4,,22,1.3,2.2,.1+∞⋃第一类二、1.为可去间断点1=x ,为第二类间断点2=x ; 2.为跳跃间断点1=x . 三、2ln ,2==b a .四、0,0,10,00,1)(=⎪⎩⎪⎨⎧>=<-=x x x x x f 为()x f 的跳跃间断点。
五、()()+∞⋃∞-,00,. 六、左不连续;右连续. 七、,.4,.3,.2,2ln .1623e e e - 八、九、十 (略).第二章 测验题一、B A C A D .5,.4,.3,.2,.1.二、21.4,2.3,2.2,2.1-e .三、.31.4,3.3,1.2,61.1.四、x x x x p ++=232)(.五、为第二类间断点为可去间断点处连续21,1,2,,1===-=x x x x .六、.3,21==b a 七、(略). 八、a .第三章 导数与微分习题一一、),0(.2),(,)(2,)(.1000f x f x f x f '''')(),(1.3000000x x x y y x x x y y --=--=- 二、00,,2)(<>⎩⎨⎧='x x x e x f x 三、)0(2)(g a f ='. 四、处连续且可导0=x .五、()的有理数;互质与且)2(,201n m mna a ≠> ()互质)的有理数与且n m mna a 2(,1212-≠>. 习题二一、,ln 1.3,1.2,622ln 2.123x xx x x -++- )2(42,)2(42.422ππππππ-=---=-x y x y . )(4)(2.5222x f x x f ''+'二、2)1()sin 3(cos sin cos 2.1x x e x x e x x +-+-;x x x x x x x x cos sin ln cos 2sin .2+-+; 211arcsin 2.3xx -⋅; 21)ln (ln .4x x n x n --;a a x x x ax a a a 21211sec ln .5+⋅+-;6.x x exx 1tan 1sec 221sec 22⋅⋅⋅-; )(87略-.三、1.()x f x f '⋅)(2; 2.)()(222x x x x x e f e e e f xe '+.四、00,,11)12()(222=≠⎪⎪⎩⎪⎪⎨⎧+-='x x x e x x f x . 五、(略) 习题三一、()dx x x x 1ln .1+; ()dx e e f x x '.2;x e x e x x x ln ln ,arctan ),13sin(31,61,2.36+;4. ppQ -+2;252. 二、1.)sin ln (cos sin xxx x x x +⋅; 2.⎥⎦⎤⎢⎣⎡-----+-+------)5(51)4(54)3(53)2(5211)5()4()3()2()1(5432x x x x x x x x x x 三、1.()184-==p dpdQ,54.04-≈=P EP ED经济意义:当价格从4上升%1时,需求量从59下降%54.0;()246.04≈=P EP ER,价格从4上涨%1时总收益将从263增加%46.0.四、1.dx x x x x ⎥⎦⎤⎢⎣⎡--+-2222211cot )1(2)11ln(sin . 五、212x +. 第三章 测验题一、,1.3,1.2,)1(21.1arctan =⋅+--y dx e x x x π21)1()1(2.4xx f x f '-, 2ln 21.5-.二、..3,.2,.1C D D 三、1.yyxey e +-2; 2.0; 3.[]()0,,02121cos )(sin )()(),0(2=≠⎪⎪⎩⎪⎪⎨⎧''++-+'=''=x x g x xx g x x g x x f g a第四章 中值定理与导数的应用 习题一一、1.不满足,没有; 2.1; 3.满足,914; 4.4,1--.;5.不存在二、三、四、五(略)六、1.6,ln .5,21.4,21.3,0.2,21.1a -. 七、连续. 八、1.习题二一、1.单减,凹的; 2.)4,1(;3.0,0==x y ;4.29,23-;5. ac b 32≤.6.e p 1=二、单增区间为[]2,0;单减区间为]()[∞+⋃∞-,20,. 三、拐点为()7,1-;凹区间为)[∞+,1;凸区间为[]1,0.四、0,3,3,1==-==d c b a .五(略)六、为极大值3)3(,2==πf a .七、20000=Q ,最大利润()34000020000=L 元. 八、5.9元,购进140件时,最大利润490元. 九、十(略).第四章 测验题 一、..3;.2;.1A B B 二、()0.4;2,1.3;3.2;1.1=x三、.1.2;61.1-四、.1;0;3==-=c b a 五、获利最大时的销售量()t x -=425,当2=t 政府税收总额最大,其税收总额为10万元.六、()1证明略; ()254.06≈=P EP ER,经济意义:当价格从6上涨%1时,总收益从156增加%54.0.第五章 不定积分习题一一、1.dx x f )(,C x f +)(,)(x f ,C x f +)(; 2.C ; 3.C x +2; 4.32x. 二、1.C x x +-arctan ; 2.C x e x +-2;3.C x x +-sec tan ; 4.C x +tan 21. 三、1ln +=x y .四、12)(2+-=x x x G .习题二一、1.C e x x ++-tan tan ; 2.C x f +--)1(212; 3.C x F ++)12(; 4.C x f +--)2cos 3(31. 二、1.C x +|ln ln |ln ; 2.C x ++-|1cos |ln 2; 3.C e x +arctan ;4.C x +--21)32(312; 5.C x x x +---------999897)1(991)1(491)1(971;6.C e xx ++1; 7.C x x +-32)cos (sin 23; 8.C e x x ++-)1ln(; 9.C x x ++-)9ln(292122; 10.C x +)arctan(sin 212; 11.C x+-arcsin 1;12.C x x ++-+ln 12)ln 1(3223; 13.()()()C x x x +++++-+11ln 313123313132;14.C e x+-1arctan 2; 15.C xx ++61611ln; 16.C x x x +-+22211arccos 21. 习题三一、1.C x e x ++-)1(;2.C x xf +)(; 3.C x f x f x +'-'')()(; 4.C e xe x x +-2. 二、1.C x x x x +++-)1ln(6161arctan 31223; 2.C e xe x x +------11;3.C x x x x x ++-2ln 2ln 2; 4.C x x x x++++-)6ln 6ln 3(ln 123;5.C x x e x ++-)22(33323; 6.()()[]C x x x++ln sin ln cos 2;7.C x x x x x +--+2arcsin 12)(arcsin 22; 8.C x x x x ++-sin 4cos )24(; 9.C x x x +-+arctan )1(; 10.C x x x x x +++-+221ln 1ln .三、C x x x +-++21)arcsin 1(. 四、C x x x x ++-+arctan 22)1ln(2. 五、)1(21x x +.习题四1.C x x x x x x +--+-+++|1|ln 3|1|ln 4||ln 82131232.C x x x x +-+-+-arctan 21)1ln(41|1|ln 21||ln 2第六章 定积分及其应用习题一 一、a b a b -+-)(3331二、1.≥, 2.≥ 三、(提示:用定积分性质6证)四、1.412x x +; 2.81221213x x x x +-+; 3.3; 4.21; 5.28-x ; 6.]41,0(; 7.yx e y 2cos 22. 五、)(x f 在0=x 处有极小值0)0(=f .六、1.6π; 2.4; 3.38.七、1.1; 2.2八、4π.九、)1ln(e +十(略).习题二一、1.)(sin x f ; 2.)0(arctan )1(arctan f f -; 3.)]()([2122a F b F -; 4.3243π;5.0; 6.)()(a x f b x f +-+; 7.8; 8.0二、1.34-π; 2.32ln 22+; 3.a )13(-; 4.34; 5.22; 6.214-π; 7.)11(2e -; 8.)2(51-πe .三、四(略)五、(提示:令x t -=2π); 4π.六、()1,11=-=-a e x f x . 七、x x sin cos -. 八、x 2ln 21.习题三一、1.332; 2.2ln 23-; 3.67; 4.49.二、62221,21-=⎪⎭⎫ ⎝⎛=S a . 三、2ln 214+-x .四、1.π145; 2.24π; 3.ππ564,727. 五、10/100Q Qe -. 六、31666. 七、1.2; 2.2ln 21.。
2014成人高考专升本《高数二》经管类冲刺真题训练讲义1

2021成人高考专升本?高数二?经管类冲刺真题训练讲义1(微积分局部基此题型)说明:我们根据十多年来专升本考试内容及实体的分析与研究,按考试中出现的知识点及题型进展分类归纳,可以使大家一目了然地看出:哪些知识是必考的,考试题型是什么,此题型在十几年的试卷中考到的概率是多少。
备注【10-1】表示2021年试卷笫1题。
题目后的【A 】代表答案。
笫一章极限和连续常考知识点一、极限〔1〕函授在一点处的左极限与右极限以及函数在一点处极限存在的充分必要条件。
〔2〕极限的性质以及四那么运算。
〔3〕无穷小量的概念、性质及无穷小量阶的比较,等价无穷小量代换及其应用。
〔4〕两个重要的极限及其应用。
二、连续(1)函数在一点处连续与连续的概念及连续的判定。
〔2〕闭区间上连续函数的性质。
三、试卷内容比例本章内容约占试卷总分的15%共计22分。
真题训练及常用解题方法与技巧一. 求极限1. 代入法考试要点:lim ()()x af x f a →=,直接把x a =代入()f x 中,其依椐是初等函数连续性定理。
考察概率:50% 【10-1.】1ln(1)lim 1x x x →+=+A.ln 22B.0C.ln 2D.ln 2-[]【A 】【09-1.】2tan(1)lim1x x x →-=-A.0B.tan1C.4πD.2[]【B 】【06-11】2031lim 1x x x x →+-+【1-】【05-11】31lim(2)x x x →-+【2】【04-07】2limln(1)x x →+【0】2. 第一重要极限与等价无穷小替换法考察概率:70% 考试要点0sin (1)lim 1;(2)0~sin ~tan x xx x x x x→=→当时,【11-12】.2sin(2)lim_________.2x x x →-=-【1】【10-21】计算21sin(1)lim 1x x x →--.【12】 【10-12】当0x →时,()f x 与sin 2x 是等价无穷小量,那么0()lim _____.sin 2x f x x→=答案:【1】【08-12】____________0sin 2limx xx→=.【2】【07-12】____________21sin(1)lim 1x x x →-=-.【12】 【06-12】0tan 3lim x xx→=_________.【3】【05-1】设0sin 5lim x xx →等于〔〕A.0B.15C.1D.5【答案D 】【04-8】假设0x →时,函数()f x 与sin x 是等价无穷小,那么0()lim sin x f x x→=________.【答案1】 【04-2】设0sin lim 3x axx→=,那么a 的值为〔〕A.13B.1C.2D.3【答案D 】 【03-2】x xx 52sin lim 0→等于〔〕A.0B.52C.1D.25【答案B 】VIP 免费资料【02-7】xxx 2sin lim0→=__________.【答案2】【01-17】计算xx x sin )21ln(lim 0+→.【答案:2cos )21(2lim sin )21ln(lim0"0"0=+=+→→xx x x x x 】【01-2.】4)2sin(lim22--→x x x 等于〔〕 A.0B.41C.21D.1【答案B 】【00-6】65)1sin(lim21-+-→x x x x =____________.【答案71】3. 重要极限 考试要点〔1〕101lim(1);lim(1);xx x x e x e x→∞→+=+=〔2〕对于演算题,常用“添倒数辅助项方法〞;〔3〕推广公式0(1)lim(1);lim(1);bC bx C ab ab xx x a e ax e x++→∞→+=+= 考察概率40%【11-21.】计算20lim(1)xx x →+.【答案.2122lim(1)lim[(1)]x x x x x x e →→+=+=】【09-12.】1lim(1)_________.3xx x→∞-=【13e -】【06-1.】()20lim 1xx x →+=〔〕A.1B.eC.2eD.2e 【答案.D 】【05-12】3lim(1)x x x→∞-=________.【答案3e -】【04-16】计算2lim(1)x n x →∞+.【答案22222lim(1)lim(1)x x x x e x x →∞→∞⎡⎤+=+=⎢⎥⎣⎦】【03-6】xx x)211(lim -∞→=_________.【12e -】【01-18.】计算xx xx 3)2(lim -∞→_________. 【答案(2)3332221lim()lim(1)lim(1)()2xx x x x x x x x x x -⋅-⋅→∞→∞→∞-=-=+-6621lim[(1)]()2xx e x---→∞=+=-】 【01-1】以下各式中,正确的选项是[]A.e xxx =-∞→)11(lim ;B.e x x x =+∞→1)11(lim ;C.e x x x =+-→10)1(lim ;D.e x x x =+→10)1(lim【答案D 】【00-17】假设xx kx k x )2(lim -+∞→=8,求常数k .【答案:k k k xx xx x x x x x e ee xk x k x k x x k x k x k x 32)21(lim )1(lim )()(lim )2(lim ==-+=++=-+-∞→∞→∞→∞→】4. 用洛必达法那么求极限要点:对于00,∞∞型,直接用洛必达公式()'()lim lim ()'()=f x f x g x g x 洛,对于⋅∞∞-∞0,型,设法化为00,∞∞型后,再用洛必达方法. 考察概率:1993-2021年共考了20次,属于必考题,概率为100%。
高等数学(经管类专业适用)-第6章习题解答

第6章 概率统计练习6.1.11.观察一次打靶试验中击中的环数,若击中1环记为{1},并设A={奇数环}, B={小于9环},求Ω,A+B ,AB ,A +B .【解】Ω={0,1,2,3,4,5,6,7,8,9,10},A+B ={0,1,2,3,4,5,6,7,8,9} ,AB={1,3,5,7} ,A +B={0,1,2,3,4,5,6,7,8,10}.2.一位工人生产3件零件,设i A ={第i 个零件是不合格品}(1,2,3i =).请用诸i A 表示如下事件:(1) 全是合格品; (2) 全是不合格品;(3) 恰好有一个零件是不合格品; (4) 至少有一个零件是不合格品.【解】(1) 123A A A ;(2) 123A A A ;(3) 123123123A A A A A A A A A ++;(4) 123A A A ++. 练习6.1.21.一个小停车场有20个停车位,现在有6辆车需停在该停车场,有多少种不同的停放方法?【解】620P =20⨯19⨯18⨯17⨯16⨯15=27907200(种)2.学校举办一场十佳歌手赛,现从班上报名的15个同学中选取2个参加,共有多少种选法?【解】215151410521C ⨯==⨯(种) 3.10个螺丝钉中有3个是坏的,从中随机抽取4个,求: (1)恰好有两个是坏的概率; (2)4个全是好的概率.【解】设A ={恰好有两个是坏螺丝钉},B ={ 4个全是好螺丝钉}, (1)因4221037210,63,A n C m C C ====所以3()10A m P A n ==; (2)又4735B mC ==,故1()6B m P B n ==. 练习6.1.31.甲、乙两批种子发芽率分别是0.7和0.8,现从这两批种子中随机地各取一粒,求下列事件的概率:(1)两粒种子都发芽; (2)至少有一粒种子发芽.【解】设A ={甲的种子发芽},B={乙的种子发芽},由于两粒种子是独立地发芽,所以(1) ()()()P AB P A P B ==0.7⨯0.8=0.56;(2) ()()()()P A B P A P B P AB +=+-= 0.7+0.8-0.56=0.94.2.在200名学生中选修统计学的有137名,选修经济学的有50名,选修计算机的有124名.还知道,同时选修统计学与经济学的有33名,同时选修经济学与计算机的有29名同,同时选修统计学与计算机的有92名,三门课都选修的有18名.试求200名学生中在这三门课中至少选修一门的概率.【解】设A ={选修统计学},B ={选修经济学},C ={选修计算机},则 D ={至少选修一门}=A+B+C ,所以()()()()()()()()P D P A P B P C P AB P BC P AC P ABC =++---+ =137200+50200+124200-33200-29200-92200+18200=78(=0.875). 3.某射手的命中率为0.95,他独自重复向目标射击5次,求他恰好命中4次的概率以及至少命中3次的概率.【解】恰好命中4次的概率44155(4)(0.95)(0.05)0.2036P C =≈; 至少命中3次的概率555(3)(4)(5)P P P ++=33244155555(0.95)(0.05)(0.95)(0.05)(0.95)(0.05)C C C ++≈0.9987.习题6.11.在100件产品中,有2件次品,从中任取5件,问: (1)恰有1件次品的抽法有多少种? (2)没有次品的抽法有多少种? (3)至少有1件次品的抽法有多少种?【解】(1)14298236122807224560C C =⨯=;(2)59867910864C =; (3)142329829872245601520967376656C C C C +=+=.(本题的结果也可借助软件Excel 来求得)2.10个球中有3个红球7个绿球,随机抽取3个球分给3个小朋友,每人一球,求三个小朋友中恰有一个得到红球的概率.【解】用古典概型求解,设A ={三个小朋友恰有一个得到红球},因310n P =,123373m C C P =, 故 21()40m P A n ==. 3.在编号为1,2,…,100的奖券中,规定偶数号或三的倍数号中奖,现从中随机抽取一张,求中奖的概率.【解】设A ={偶数号奖券},B ={三的倍数号奖券},50()100P A =,33()100P B =,16()100P AB = 则C ={中奖奖券}=A +B ,故()()()()()P C P A B P A P B P AB =+=+- =503316100100100+-=670.67100=. 4.有10道判别对错的测验题,一人随意猜答,他答对7道题的概率是多少? 【解】由题意知,猜答10道测验题可看成10重伯努利试验,且0.5p =.所以答对7道题的概率是7731010(7)(0.5)(0.5)0.1172P C =≈. 5.长期统计资料表明,某地区在4月份下雨(设为事件A )的概率为14,刮风(设为事件B )的概率为13,既刮风又下雨的概率为18,求(),(),()P A B P B A P A B +. 【解】因111(),(),()438P A P B P AB ===,所以()3()1(),(),()8()2P AB P AB P A B P B A P B P A ==== 11()()()()24P A B P A P B P AB +=+-=. 练习6.2.11.已知随机变量X 只能取-1,0,1,2这四个值,其相应的概率依次为1232,,,2448c c c c,求常数c 的值.【解】 因11k k p ∞==∑,所以1232122448c c c c c+++=⇒=. 2.某银行举行有奖储蓄活动,现发行有奖储蓄券10万张,其中一等奖100张,二等奖500张,三等奖2000张,现任抽一张储蓄券,试求中奖等级X 的分布律.【解】若不中用{X =0}表示,其概率表示为{}00p P X ==, 根据题意X 为随机变量,其可能取值为0,1,2,3.{}1510010.00110p P X ====, {}2550020.00510p P X ====,{}35200030.0210p P X ====, {}001(0.0010.0050.02)0.974p P X ===-++=.则0k p ≥(0,1,23k =,),且301k k p ==∑.故随机变量X 的分布律为3.某观众拨打电视台热线电话参与活动,已知拨通电话的概率为0.4%,求观众拨打300次至少拨通1次电话的概率.【解】{至少拨通1次电话}的对立事件是{拨通0次电话}所求概率为1-00300300(0.004)(0.996)C 1≈.(本题的结果可借助软件Excel 来求得) 练习6.2.21.求0-1分布的分布函数.【解】由于0-1分布的分布律为:1{}(1)k k P X k p p -==-,0,1k =.当0x <时,(){}()0F x P X x P ==∅=≤;当01x <≤时,(){}{0}1F x P X x P X p ====-≤;当x ≥1时,(){}{0}{1}11F x P X x P X P X p p ===+==-+=….综合以上结果,则有00,()101,1 1.x F x p x x <⎧⎪=-<⎨⎪⎩,,≤,≥2.已知连续型随机变量X 的概率密度为()0kx x f x ≤≤⎧=⎨⎩,03, ,其它. 求(1)系数k ;(2){12}P X <≤.【解】(1) 由概率密度的性质,得3239()1022x kf x dx k xdx k +∞====-∞⎰⎰, 解得29k =, 所以2,03()90,x x f x ⎧≤≤⎪=⎨⎪⎩,其它.(2) 221{12}193P X xdx <≤==⎰. .3.设~(0,1)X N ,查表求 (1) {}2P X ≤;(2) {}1P X >-;(3){}0.5P X <. 【解】(1) {2}(2)0.9772P X ≤=Φ=;(2) {1}1(1)(1)0.8413P X >-=-Φ-=Φ=;(3) {}0.5(0.5)(0.5)2(0.5)120.691510.383P X <=Φ-Φ-=Φ-=⨯-=.4.设2~(1,2)X N ,查表求 (1) {}1P X ≤;(2) {}3P X <.【解】(1){}111()(0)0.52P X -≤=Φ=Φ=;(2){}3{33}P X P X <=-<<3131()()22---=Φ-Φ (1)1(2)=Φ-+Φ=0.8413-1+0.9772=0.8185.练习6.2.3某企业生产某种产品,生产出来后畅销的概率为0.7,滞销的概率为0.3.现有二种方案:(1)扩大工厂的规模,如果产品畅销可盈利700万元,滞销则亏损300万元;(2)不改变工厂规模,如果产品畅销可可盈利400万元,滞销则亏损100万元.试用决策矩阵表和决策树的方法选择一种最佳方案.【解】(1)用决策矩阵表的方法根据题意,建立如下损益矩阵表(单位:万元)从表可见,根据期望收益值最大的决策准则,选用扩大工厂规模的方案. (2)用决策树的方法由题意,画出对应的决策树如图所示.比较状态点B ,C ,显然扩大工厂规模的数学期望值大,即400>250,点B 和决策点R 之间的方案枝所代表的方案即为所选的最优方案,点B 的期望值即为决策的效益期望值.最后将状态点C 剪掉,采用扩大工厂规模的方案.习题6.21.现有产品10件,其中有3件次品,任意从中取出2件,求取出次品数X 的分布律. 【解】根据题意X 为随机变量,其可能取值为0,1,2.{}2712107015C p P X C ====,{}117322107115C C p P X C ====,{}2332101215C p P X C ====.则0k p ≥(1,23k =,),且317711151515k k p ==++=∑.故随机变量X 的分布律为2.设某射手每次射击击中目标的概率是0.8,现在连续射击30次,求击中目标次数X 的分布律.【解】由题意知(30,0.8)X B ,所以X 的分布律为3030{}(0.8)(0.2),0,1,2,,30.kk k P X k C k -===3.包裹的特快专递(EMS)规定:每包不得超过1公斤.令X 为任选一个包裹的重量,其密度函数为0.50()0k x x f x +<≤⎧=⎨⎩(), 1, ,其它. 求(1)系数k ;(2)这类包裹的重量X 至少3/4公斤的概率是多少? (3)这类包裹的重量X 最多1/2公斤的概率是多少? 【解】(1) 由概率密度的性质,得1201()(0.5)(0.50.5)10f x dx k x dx k x x k +∞=+=+==-∞⎰⎰, 所以0.5,01()0,x x f x +<≤⎧=⎨⎩,其它. (2) 1311{}(0.5)34324P X x dx ≥=+=⎰.(3)113{}(0.5)228P X x dx ≤=+=⎰4. 测量某目标距离的误差(单位:mm )2(20,40)X N ,求一次测量误差的绝对值不超过30mm 的概率.【解】{}3020302030()()4040P X ---≤=Φ-Φ (0.25)1(1.25)0.5987=Φ-+Φ=-+=5. 某企业计划推出一款新型产品,企业的备选方案有三种:(1)建立新型的生产线,投入的成本最大,但产量最高;(2)改造原来的生产线,投入的成本比新建生产线少,产量也会相应少些;(3)是继续使用原来的生产线,不会投入相应的成本,产量最少.根据市场需求分析和估计,产品畅销、一般、滞销的概率为0.5,0.3, 0.2.根据产量和销量的不同,企业的盈利情况如下表:(单位:万元)试通过决策分析,确定生产线方案.【解】由企业的盈利情况表,可以将不同方案的期望值计算出来1()500.5150.3100.227.5E A =⨯+⨯-⨯=, 2()300.5200.300.221E A =⨯+⨯+⨯=, 3()100.5100.300.28E A =⨯+⨯+⨯=,比较期望值,选择期望收益值最大的方案作为最优方案,即确定建立新型生产线的方案. 练习6.3.11、求满足{}0.05P U λ≥=的U 分布的临界值λ. 【解】由0.05α=得,()10.97520.05λΦ=-=,查标准正态分布表得 1.96λ=.2、求满足{}0.01,P T λ≥=10n =的t 分布的临界值λ. 【解】根据0.01α=,19n -=,查t 分布临界值表得 3.25λ=.3、求满足{}2120.95P λχλ<<=,15n =的2χ分布的临界值12,λλ. 【解】由已知114n -=,0.05α=.计算{}2110.9752P αχλ>=-=,查2χ分布临界值表得1 5.629λ=;计算{}220.0252P αχλ≥==,查2χ分布临界值表得226.119λ=.练习6.3.21.乳业有限公司生产的袋装牛奶是用自动包装机包装的.每袋牛奶净含量X 服从正态分布2(,)N μσ,今从一批装好的牛奶中随机地抽取8袋,测其牛奶的净含量(单位:ml )如下:499.5,500,498.5,501.5,500.5,500.5,499.5,500.5.试估计这批牛奶净含量的均值μ与方差2σ.【解】499.5+500+498.5+501.5+500.5+500.5+499.5+500.5500.06258x ==,82221111()(500.0625)0.8169617n i i i i s x x x n ===-=-≈-∑∑, 所以2ˆˆ500.0625,0.81696μσ==. (本题的结果可借助软件Excel 来求得)2.已知某种电子元件的寿命服从正态分布2(,)N μσ,现随机抽取10个,测得各电子元件的寿命(单位:小时)如下:3100 3480 2520 3700 2520 3200 2800 3800 3020 3260试估计这种电子元件寿命的均值μ与方差2σ.【解】3100+3480+2520+3700+2520+3200+2800+3800+3020+3260314010x ==,102221111()(3140)198133.333319n i i i i s x x x n ===-=-≈-∑∑, 所以2ˆˆ3140,198133.333μσ==. (可利用软件Excel 帮助计算) 练习6.3.31.设随机变量X 服从正态分布,即2~(,2.8)X N μ,已知一个容量为10的样本,其样本均值1500x =,求总体均值μ的置信区间(置信水平为0.95).【解】根据题意2~(,2.8)X N μ,总体方差2σ已知,求总体均值μ的置信区间, (1)因10.95α-=,则0.05α=,查标准正态分布表得 1.96λ=;(2)由已知,1500x =,10n =, 2.8σ=,计算得1501.7355x +=,1498.2645x =(3)所以μ的置信水平为95%的置信区间为(1498.2645,1501.7355).2.某保险公司要估计去年投保人的平均理赔额,随机地抽取25个投保人,得理赔均值为739.98元,标准差为312.70元,已知理赔额2~(,)X N μσ,试求总体均值μ的置信水平为0.95的置信区间.【解】根据题意知2~(,)X N μσ,总体方差2σ未知,求总体均值μ的置信区间, (1)因195%α-=,0.05α=,25n =,查t 分布临界值表得 2.064λ=; (2)由已知,739.98x =,312.70s =;计算区间端点值869.06256,x +=610.80744x -=(3)所以μ的置信水平为95%的置信区间为(610.80744,869.06256).3.某超市连续统计了十二个月的销售额(单位:万元),得方差20.305s =,如果销售额2~(,)X N μσ,试求方差2σ的置信水平为95%的置信区间.【解】根据题意2~(,)X N μσ,总体均值μ未知,求总体方差2σ的置信区间, (1)因195%α-=,0.05α=,111n -=,查2χ分布临界值表得1 3.816λ=,221.92λ=; (2)由已知,20.305s =,计算区间端点值21(1)n s λ-=0.8792,22(1)n s λ-=0.1531;(3)所以2σ的置信水平为95%的置信区间为(0.1531,0.8792).*练习6.3.41.据统计资料知,某地区家庭对食品月支出X 元服从正态分布,即2~(,20)X N μ,现随机抽取9个家庭,得知家庭对食品的平均月支出为780元.是否可以认为居民家庭对食品月支出均值为800元?(0.05α=)【解】由题意知,2~(,20)X N μ,方差2σ已知,要检验总体均值μ. (1)提出假设01:800,:800H H μμ=≠;(2)选取统计量~(0,1)X U N ;(3)对检验水平0.05α=,查标准正态分布表得 1.96λ=,故拒绝域为(,1.96)-∞- (1.96,+∞; (4)根据样本值计算出780x =,统计量的值为3u ==,落入拒绝域,所以拒绝接受0H ,不认为居民家庭对食品月支出均值为800元.2.已知某砖瓦厂生产机制砖的抗断强度2kg /cm X 服从正态分布2(,)N μσ,从一批机制砖中随机抽取6块,经测量计算出31.6x =,0.867s =.试在检验水平0.05α=下,检验这批机制砖的抗断强度均值μ是否为232.0kg /cm .【解】由题意知,总体2~(,)X N μσ,其中2σ未知. 要检验总体均值μ. (1)提出假设01:32.0,:32.0H H μμ=≠;(2)选取统计量~(1)X T t n -;(3)对显著性水平0.05α=,15n -=,查t 分布临界值表得 2.571λ=,因此,拒绝域为(, 2.571)(2.571,)-∞-+∞ ;(4)由样本31.6x =,s =0.867.得统计量的值为 1.13t =,不落入拒绝域,因此接受0H .即认为这批机制砖的抗断强度均值μ为232.0kg /cm .3.已知某厂生产的饮料中钙含量服从正态分布2(,2)N μ.现改进了加工工艺,随机抽取了9瓶100ml 加钙饮料,测得其钙含量(单位:mg )分别为:63.5 61.3 58.7 59.6 62.5 63.8 61.5 60.7 59.2 .问新工艺下饮料钙含量的方差是否为4?(0.01)α=【解】由题意知2~(,2)X N μ,均值μ未知,要检验总体方差2σ. (1)提出假设222201:2,:2H H σσ=≠;(2)选取统计量 22220(1)~(1)n S n χχσ-=-;(3)对显著性水平0.01α=,18n -=,查2χ分布临界值表得1 1.344λ=及221.955λ=,因此拒绝域为(0,1.344)(21.955,)+∞ ;(4)由样本值计算出61.2x =,2 3.3625s =,统计量的值为28 3.36256.7254χ⨯==,没有落入拒绝域,故接受0H .认为新工艺下饮料钙含量的方差是4.习题6.31.某百货公司准备在某地设置分店,为了确定分店的规模和商品的种类,需要知道该地区住户人均年收入情况,为此,在该地区随机抽查了10户居民,得人均年收入(单位:元)如下1213,1203,1106,1208,1307,1206,1101,1203,1216,1328.已知人均年收入服从2(,)N μσ,试估计该地区人均年收入的均值μ与方差2σ.【解】1213+1203+1106+1208+1307+1206+1101+1203+1216+13281209.110x ==,102221111()(1209.1)5131.6619n i i i i s x x x n ===-=-≈-∑∑, 故该地区人均年收入均值μ与方差2σ的估计值分别为:2ˆˆ1209.1,5131.66μσ==. (可利用软件Excel 帮助计算)2.测某型号螺丝钉的长度5次,数值(单位:mm )分别为108.5 109.0 110.0 110.5 112.0假设测量的长度服从正态分布2~(,0.5)X N μ,试求这批螺丝钉的长度均值μ的置信区间 (0.05α=).【解】根据题意2~(,0.5)X N μ,总体方差2σ已知,求总体均值μ的置信区间, (1)因0.05α=,查标准正态分布表得 1.96λ=; (2)由样本算得,110x =,5n =,0.5σ=,计算得110.44x +=,109.56x =(3)所以这批螺丝钉的长度均值μ的置信区间为(109.56,110.44).3.环保局人员从河流中取出15个水样,测定样本中的污染物的数量,计算得样本方差236.29s =.已知河流中的污染物的数量服从正态分布.求置信水平为95%的总体方差的置信区间.【解】根据题意2~(,)X N μσ,总体均值μ未知,求总体方差2σ的置信区间, (1)因195%α-=,0.05α=,114n -=,查2χ分布临界值表得1 5.629λ=,226.119λ=;(2)由已知,236.29s =,计算区间端点值21(1)n s λ-=90.258,22(1)n s λ-=10.452;(3)所以置信水平为95%的2σ的置信区间为(10.452,90.258).*4.某面粉厂用自动装袋机包装面粉,已知每袋面粉标准重量(单位:kg )2(25,0.1)X N ,长期实践表明方差2σ比较稳定, 从某日生产的袋装面粉中随机抽取10袋, 测得重量(单位:kg )分别为24.9,25.0,25.1,25.2,25.2,25.1,25.0,24.9,24.8,25.1试在检验水平0.05α=下,检验这批袋装面粉的重量均值μ是否合乎标准.【解】由题意知,2(25,0.1)X N ,方差2σ已知,要检验总体均值μ. (1)提出假设01:25,:25H H μμ=≠;(2)选取统计量~(0,1)X U N ;(3)对检验水平0.05α=,查标准正态分布表得 1.96λ=,故拒绝域为(,1.96)-∞- (1.96,+∞; (4)根据样本值计算出25.03x =,统计量的值为0.949u ==,没有落入拒绝域,所以接受0H ,即认为这批袋装面粉的重量均值μ是合乎标准的.复习题6一、选择题1. 某城市的汽车牌照号码由2个英文字母后接4个数字组成,其中4个数字互不相同的牌照号码共有( )个.A. 241026P ⋅;B. 242610P P ⋅;C. 242610⋅;D.242610P ⋅.2. 设事件A 与B 相互独立,如果11(),(),43P A P B ==则()P A B +=( ) A.712 B. 12 C. 512 D. 133. 若1(,)3X B n 且{2}{3}P X P X ===,则n 为( ). A. 2 B. 4 C. 6 D. 84.掷一颗骰子,用随机变量X 表示出现的点数,则{24}P X <≤的值为( ). A.16; B.13; C. 12; D. 23. 5. 设总体2~(,)X N μσ,且λ为临界值.若2σ未知,2,x s 分别为样本均值和样本方差,样本容量为n ,则总体均值μ的置信区间为( ).A. (,)x x nnλσλσ-+B. (,)ssx x nnλλ-+C .(x x +D .(x x -【答案】 二、填空题1. 口袋中有3个红球2个白球,从中任取2球,则取出的2球颜色相同的概率为______________.2. 一射手向指定目标射击4枪,各枪射中与否相互独立,且每枪射中的概率是0.2,则4枪中恰好射中1枪的概率为 .3. 设(1,4)X N , 则{1}P X ≤ = _________.4. 设{}0.1P T λ≥=,且10n =,则t 分布的临界值λ= .5. 设12,,,n X X X 是取自正态总体2(1,)N σ-的一个样本,X 为样本均值,X 服从的分布为 .【答案】1.223225C C C +=25;2.134(0.2)(0.8)0.4096C =;3.(0)0.5Φ=;4.1.833;5.标准正态分布. 三、解答题1. 在10件产品中有3件次品,现从中任取2件产品,求下列事件的概率: (1)两件都是正品;(2)恰有一件正品;(3)至少有1件正品.【解】设A ={两件都是正品};B={恰有一件正品},D={至少有1件正品},则A 与B 为互不相容事件,且D=A+B(1)P(A)=27210715C C =;(2)P(B)= 1173210715C C C =;(3)P(D)=P(A+B)=1415 . 2. 三人独立地去破译一份密码,已知各人能译出的概率分别为111,,543.问三人中至少有一人能将此密码译出的概率.【解】设i A ={第i 人破译密码},1,2,3i =,则123111(),(),()543P A P A P A ===,由题意,所求概率为1231231234323()1()1()()()15435P A A A P A A A P A P A P A ++=-++=-=-= 3. 设随机变量2(2,)X N σ ,且1{2}0.32P X <<=,求{0}P X <.【解】因1212232{2}()()0.5[1()]0.322P X σσσ--<<=Φ-Φ=--Φ=, 可得3()2σΦ=0.8,查表得30.842σ=,即σ=10.56, 所以02{0}()1(1.12)10.8686P X σ-<=Φ=-Φ=-=0.1314.4. 某工厂生产一种螺钉的长度服正态分布,为测量产品的长度(单位:mm ),现抽取10件,测得长度如下:32,33,30,36,38,39,35,37,36,34试估计这种产品的总体均值μ与总体方差2σ.【解】32+33+30+36+38+39+35+37+36+3410x ==35,10222111170()(35)7.778199n i ii i s x x x n ===-=-=≈-∑∑, 所以这种产品均值μ与方差2σ的估计值分别为:2ˆˆ35,7.778μσ==. 5.某果树场有一批红枣树,根据长期资料分析知,其每株产量服从正态分布,产量方差为4002kg .现随机抽9株,产量(单位:kg )分别为:112,131,98,105,115,121,90,110,125.求这批红枣树每株平均产量的置信水平为0.95的置信区间.【解】根据题意2~(,20)X N μ,总体方差2σ已知,求总体均值μ的置信区间, (1)因10.95α-=,即0.05α=,查标准正态分布表得 1.96λ=; (2)由样本算得,10079x =,9n =,20σ=,计算得124.96x =,98.82x -= (3)所以这批红枣树每株平均产量μ的置信区间为(98.82,124.96).。
【高级微观经济学】14年习题二

GS/ECON5010section“B”’Answers to Assignment2F2014Q1.For what values ofα,βandγwould the following pair of functions represent the Mar-shallian demand functions of a consumer with income y,facing prices(p1,p2)?x M1(p1,p2,y)=y2p1+p2p1x M2(p1,p2,y)=αyp2+βp1p2−γA1.Marshallian demand functions must obey the adding–up constraint,thatp1x M1(p1,p2,y)+p2x M2(p1,p2,y)=y(1−1)for every price–income combination(p1,p2,y).Herep1x M1(p1,p2,y)+p2x M2(p1,p2,y)=12y+p2+αy+βp1−γp2(1−2)The only way that the right hand expression in(1−2)can equal y exactly,for any values of p1,p2and y,is ifα=12(1−3)β=0(1−4)γ=1(1−5)So the“candidate”functionsx M1(p1,p2,y)=y2p1+p2p1(1−6)x M2(p1,p2,y)=y2p2−1(1−7)represent Marshallian demand functions if the2–by–2Slutsky matrix,with typical elementS ij≡∂x M i∂p j+x M j(p1,p2,y)∂x M i∂y(1−8)is symmetric,and negative semi–definite.From equations(1−6)–(1−8),that matrix isS= −y(p1)2−p22(p1)212p1+y4p1p212p1+y4p1p2−y4(p2)2−12p2(1−9)So the matrix is symmetric.The elements on the diagonal are negative.And the determinant of the matrix in equation(1−9)is:y216(p1)2(p2)2+y16(p1)2p2+1(p1)2−y216(p1)2(p2)2−y16(p1)2p2−1(p1)2=0so that the matrix is negative semi–definite,since the elements on the diagonal are negative and the determinant is0.Q2.The following table lists the prices of3goods,and the quantities a consumer chose of the goods,in3different years.For what values of A do these data satisfy the strong axiom of revealed preference?t p t1p t2p t3x t1x t2x t31511252025251125404031152530AA2.The costs of the three chosen bundles,in each of the three periods,can be represented by the matrix below,where element ij is the price of bundle j in year i:170205155+A170205155+A17026555+5ASince the bundle x1is not directly revealed preferred to the bundle x2,SARP can only be violated if the bundle x3is directly preferred to either of the other bundles.So if A<23,the third row of the matrix shows that x3is not revealed preferred to either of the other bundles.In that case there can be no violation of SARP.If23≤A<42then x3is revealed directly to be preferred to x1,but not to x2.In that case, the cost of bundle x3in year1falls between178and197,which is greater than the cost of the bundle x1,which was actually chosen in the year.So again,no possible violations of SARP:x1is not revealed directly to be preferred to anything,and x3is not revealed preferred to x2.If A≥42,then bundle x3is revealed preferred to bundle x2.So there is a violation of W ARP if bundle x2is revealed directly to be preferred to bundle x3.This will be the case if and only if A≤50.So violations of SARP can occur only if and only if42≤A≤50.Q3.Write down a von Neumann–Morgenstern expected utility function for a person who would be willing to choose each of the following actions if her initial wealth were W=200:(i)Pay more than$100for insurance against a disaster which would lose her all her wealth with probability0.5.(ii)Pay more than$100for an investment which would double her wealth with probability 0.5,and leave her wealth unchanged with probability0.5.A3.If the price were exactly$100in each case,the transactions in(i)and(ii)would both be fair bets:they would leave the expected value of the person’s wealth unchanged.So a person who would want to undertake both actions must be risk averse at lower levels of wealth,and risk–loving at higher levels.A utility–of–wealth function U(W)for such a person must have U (W)<0for some levels of wealth below$100,and U (W)<0for some levels of wealth above$100.For example,suppose thatU(W)=20000log W+W2(3−1)ThenU (W)=−20000W2+2(3−2)so that U (W)<0if and only if W>100.This person would get an expected utility level of−∞if some disaster could reduce her wealth W to0with positive probability.So she would certainly buy insurance against such a disaster at any price less than her whole wealth W=200.If the insurnce were ctuarially fair,then buying full insurance would leave her with certain wealth of$100.Buying the insurance gives her an expected utility ofU I=20000log100+(100)2≈102103(3−3) and going without insurance would leave her with expected utilityU NI=(0.5)[20000log200+(200)2]+(0.5)[20000log0+(0)2]=−∞(3−4)so she would buy the insurance in case(i).In case(ii),her expected utility if she did not undertake the investment would beU NRI=20000log200+(200)2≈145966(3−5)If she undertook the investment,and had to pay a price of$100,then she would have100if the investment failed,and2(200)−100=300if the investment succeeded,so that her expected utility would beU RI=(0.5)[20000log100+(100)2]+(0.5)[20000log300+(300)2≈153089(3−6) so that U RI>U NRI.Q4.(This is an example of the“St.Petersburg paradox”.)If a person were a von Neumann–Morgenstern expected utility maximizer,with a constant coefficient of relative risk aversion of2, what would be the certainty equivalent to the following compound lottery?A coin is tossed once.If it lands“heads”,she gets$1000000.If it lands“tails”,the coin is tossed again.If it lands“heads”on the second toss(after“tails”on thefirst),she gets$2000000.It it lands“tails”on both of thefirst two tosses,the coin is tossed again,and,if it lands“heads”on the third toss(after landing“tails”twice)she gets$4000000.The coin–tossing continues until thefirst“heads”,and her payoffwill be2t million dollars,where t is the number of times that the coin landed“tails”consecutively before thefirst“heads”.A4.With a CRR expected utility,her utility from a wealth level of W can be written U(W)= U1−β1−β,whereβis the coefficient of relative risk aversion.Withβ=2,this means that the utility of a wealth level W is−1/W.So if we measure wealth in millions of dollars,her expected utility from the gamble would beEU=−(0.5)11−(0.25)12−(0.125)14−···(4−1)since the probability of a head on thefirst toss is0.5,the probability that thefirst head is on the second toss is0.25,and so on.Expression(4−1)can be writtenEU=−12−18−132−···(4−2)orEU=−12∞t=014t(4−3)Now a general rule about infinite sums is that∞t=0x t=11−x(4−4)when x<1.[Proof:(1−x)[ ∞t=0x t]=(1−x)[1+x+x2+···]=(1+x+x2+···)−(x+x2+x3+···)=1]So,using this general rule,EU=−1211−0.25=−23(4−5)The certainty equivalent to this gamble is a certain amount of wealth CE such that U(CE) equals the expected utility of the gamble,or U(CE)=−23.So−1CE=−23(4−6)meaning that the certainty equivalent CE to the gamble is$1.5million.Q5.If a person were a von Neumann–Morgenstern expected utility maximizer,with a constant coefficient of relative risk aversion ofβ,with wealth W0and she faced a50%chance of losing all her wealth in some accident,for what values ofβand W0would she be willing to buy an insurance policy which provided full insurance against the accident,at a cost of a fractionα>0.5of her wealth?A5.If she did not buy the insurance,then her expected utility would beEU0=11−β[(0.5)(W0)1−β+(0.5)(0)1−β](5−1)whereas if she paidαW0for the insurance,her utility would be a certainEU1=11−β[(1−α)W0]1−β(5−2)First,note that the expression01−βis infinite ifβ>1.If her coefficient of relative risk aversion is greater than1,then she would be willing to pay anything for insurance against the loss of all of her wealth(whatever the probability of loss).Second,notice that whenβ<1,expression(5−2)is bigger than expression(5−1)if and only if[(1−α)W0]1−β>(0.5)(W0)1−β(5−3)So ifβ<1,her choice of whether to buy the insurance does not depend on her initial wealth W0 ;she will purchase the insurance if and only if(1−α)1−β>0.5(5−4) Taking logarithms of both sides of(5−4),it will hold if and only if(1−β)log(1−α)>log(0.5)=−log2(5−5)orβ>1−log(0.5)log(1−α)(5−6)。
工技大大一高数(经管类)历年试卷期末高等数学(一)经管类..

《高 等 数 学 (一)》试卷 经管类(本卷考试时间90分钟)大 题 一 二 三四 五 六 附加题 总 分小 题1 2 3 4 1 2 应得分 20 20 8 8 8 8 12 8 8 8 8 100+16 得 分一、填空题(每小题4分,共5×4=20分) 1. 设nn nx n x f )(lim )1(+=-¥® ,则=)(x f .2.已知函数xey x1arctan21+=+,则dy = . 3.设函数ïîïíì=¹=0,30,sin )(x x xkx x f 在点0=x 处连续,则常数=k . 4. 设某商品的需求函数为210475)(P P P D --=,则当5=P 时的需求价格弹性为 . 5.已知曲线方程为43ln 2x y y =+,则该曲线在点(1,1)处的切线方程为 .x1 1-sin+xx五、应用题五、应用题[8[8分]设某产品的需求函数为x P 1.080-=(P 为价格,x 为需求量),成本函数为,成本函数为x C 205000+=(元). (1) 试求边际利润函数)(x L ¢,并分别求出150=x 和400=x 时的边际利润. (2) 求需求量x 为多少时,其利润最大?最大利润为多少?六、证明题六、证明题[8[8分]设函数)(x f 在[]3,0上连续,在()3,0内可导,且3)2()1()0(=++f f f ,1)3(=f , 试证:必存在()3,0Îx ,使0)(=¢x f . 21+bx+ax。
14年真题大题版本

2014上海财经大学801经济学真题1. 张三的效用函数为U(X1,X2)=X1X2的根号,收入为100元,开始时X1的价格为1.,X2的价格为2(1)求张三初始时最优消费数量?征收从量税100%,张三的最优消费量?(2)对X1(3)征收总税额50元,张三的效用?(4)征收总额税还是征收从量税时的效用哪个效用要高?2. 两家厂商其成本函数都为C=10Y市场需求为Q=220-2P,(1)企业1为产量领导模型,求企业1和企业2的产量和利润?(2)企业1与企业2同时定价,求企业1的产量和利润?(3)企业1和企业2结成卡特尔的利润和产量?假定企业2一定不会背叛的情况下,企业1的最优产量与利润?3.政府为减少汽油的需求,征收从量税(1)画出预算线变动图,并指出消费者福利的变动。
(2)若政府将征税的税款全部退回,画出图并分析分析消费者福利的变动。
(3)若政府按初始消费量进行退税,画出图并分析消费者福利的变动。
(4)比较两种方案的退税额和税收收入的大小。
4.住房服务市场需求为S=Y-2R,实际房租为R,收入为Y,住房服务市场供给为S=2H,H为现存房子数量,Q为真实房价,m房产税,不用计提折旧,名义利率为i,房价变动率πH为通货膨胀率π和真实房价变动率⊿Q/Q(1)求住房服务市场均衡条件?(2) 求住房供给均衡条件,并求出真实房价的变动的影响?(3)政府增加房产税,和央行增加名义利率对真实房价的变动的影响?5. Y=K0.5,人口增长率为0.5%,折旧d=0.036,储蓄率为S=0.04,(1)稳态时人均资本存量?(2)最大消费量的储蓄率为多少?(3)储蓄率由0.04变动到0.36时,下一期的总产出和人均资本?(4)分别画出储蓄率由0.04变动到0.36总产出与人均资本达到稳态时的路径6.(1)政府减税时,用AD-AS曲线图分析在短期和中期的影响对价格和产出的影响?(2)政府减税时,用IS-LM曲线分析在短期和中期对利率的影响?。
高等数学经管类第一册习题答案

高等数学经管类第一册习题答案第一章答案§1.1.1 --§1.1.3函数、函数的性质、初等函数一、选择题1.C;2.D;3.D 二、填空题1. x -5x +11;2. 1;3. [0,1]2三、计算下列函数的定义域。
1. (-∞,2]⋃[3, +∞);2. (-∞,0)⋃(3, +∞);3. [2,3)⋃(3, +∞);4. [0,1] 四、(1)y =u 2, u =sin v , v =ln x . (2) y =u 2, u =ln t , t =arctan v , v =2x .⎧sin x +1, x ≥1⎧五、 f (x )=⎧sin x -1,0≤x⎧-sin x -3, x§1.2.1 数列的极限一、选择题1.C;2.D;3.D 二、填空题1.111;2. ;3. 22311三、计算下列极限1. . 2. . 3. 1. 4.23§1.2.2 函数的极限⎧2⎧⎧. 5. 10 ⎧3⎧4一、选择题1.C;2.D;3.D 二、填空题1. a =4, b =-2;2. 1;3.三、计算下列极限1. 2. 2. 6 . 3. 2x . 4.1. 5. 1 33α;3. ;4. 05β§1.2.3---§1.2.5 无穷小与无穷大; 极限的运算法则和极限存在准则;两个重要极限一、选择题1.AB;2.C;3. C 二、填空题1. -1;2.⎧3⎧6三、计算下列极限1. e . 2. ⎧ . 3. e .4.⎧2⎧-6205. e 2§1.2.5--§1.2.6 两个重要极限;无穷小的比较一、选择题1.C;2.B;3.A 二、填空题1.1;2. k >0;3. 高. 21-1-22三、计算下列极限1. 1. 2. . 3. e . 4. e 2. 5. e4§1.3.1 函数的连续性与间断点一、选择题1.B;2.C;3.A 二、填空题1. x =0, ±1;2. 三、求下列函数的不连续点并判别间断点的类型。
高等数学经济数学习题集含答案

《高等数学(经济数学1)》课程习题集西南科技大学成人、网络教育学院版权所有习题【说明】:本课程《高等数学(经济数学1)》(编号为01014)共有单选题,填空题1,计算题等多种试题类型,其中,本习题集中有[]等试题类型未进入。
一、单选题1.幂函数、指数函数、对数函数、三角函数和反三角函数统称()A 、函数B 、初等函数C 、基本初等函数D 、复合函数2.设,0,0,)(⎩⎨⎧≥+<=x x a x e x f x 当a=()时,)(x f 在),(+∞∞-上连续A 、0B 、1C 、2D 、33.由函数2x u e y u ==,复合而成的函数为()A 、2x e y =B 、2xe x =C 、2x xe y =D 、x e y =4.函数f(x)的定义域为[1,3],则函数f(lnx)的定义域为()A 、],[3e eB 、]3,[eC 、[1,3]D 、],1[3e5.函数x y x y z 2222-+=的间断点是()A 、{}02),(2=-x y y x B 、21=x C 、0=x D 、2=y6.不等式15<-x 的区间表示法是()A 、(-4,6)B 、(4,6)C 、(5,6)D 、(-4,8)7.求323lim 3x x x →-=-()A 、3B 、2C 、5D 、-58.求=++→43lim 20x x x ()A 、1B 、2C 、3D 、49.若f(x)的定义域为[0,1],则)(2x f 的定义域为()A 、[-1,1]B 、(-1,1)C 、[0,1]D 、[-1,0]10.求=+-→t e t t 1lim2()A 、21(1)e -+B 、211(1)2e +C 、)11(212+-e D 、11(1)2e-+ 11.求0sin limx xxω→=()A 、0B 、1C 、2ωD 、ω12.求=-∞→x x x )11(lim ()A 、e1B 、1C 、0D 、e13.求=-+→x x x 11lim()A 、1 B 、12C 、13D 、1414.已知xxx f +-=11)(,求)0(f =()A 、1 B 、2C 、3D 、4 15.求29)(x x f -=的定义域()A 、[-1,1]B 、(-1,1)C 、[-3,3]D 、(-3,3)16.求函数y =的定义域()A 、[1,2]B 、(1,2)C 、[-1,2]D 、(-1,2) 17.判断函数53)(2+=x x f 的奇偶性()A 、奇函数B 、偶函数C 、奇偶函数D 、非奇非偶函数18.求13+=x y 的反函数()A 、113y x =+B 、113y x =-C 、13x y +=D 、31-=x y19.求极限lim )x x →+∞的结果是()A 、0B 、12C 、∞D 、不存在20.极限01lim 23x x →+的结果是()。
线性代数(经管类)真题.docx

线性代数(经管类)试题一. 单项选择题(本大题共10小题,每小题2分,共20分)2. 设/I, B , C 均为〃阶方阵,AB = BA, AC = CA f 贝 ij ABC = ( D ) A. ACBB. CABC. CBAD. BCAABC = (AB)C = (BA)C = B(AC) = B(CA) = BCA .3. 设/为3阶方阵,〃为4阶方阵,且|A|=1, |B|=-2,则行列式\\B\A\之值为(A ) A. -8B. -2C. 2D. 8||B|AH-2A|=(-2)3|A|=-8.%1I a \2°13、<a\\ %]2a\3仃0 0、‘1 0 o'4. A = 。
21 ^22 。
23 ,B =Cl2\% 22 a 23,P 二 0 3 0 ,Q = 3 1 0,则B= ( B )卫31 °32 °33/Z 31彳皎 C/33丿<0 0 b<o o i 丿A. PAB. APC. Q/\D. AQ(a \\%如、<1 0 0、仙1 3如 a \3'AP = a 2\ a 22 a 230 3 0 = a 2\ 3^22 a 23 =B.\a 3\ a n 。
33 >0 bk^31 3畋 。
33丿5. 已知力是一个3x4矩阵,下列命题中正确的是(C )A. 若矩阵力中所有3阶子式都为0,则秩G4)二2B. 若〃中存在2阶子式不为0,则秩(力)二2C. 若秩04)二2,则/I 中所有3阶子式都为0D. 若秩U )=2,则M 中所有2阶子式都不为0 6. 下列命题中错误的是(C )• • A.只含有1个零向量的向量组线性相关 B.由3个2维向量组成的向量组线性相关 C.由1个非零向量组成的向量组线性相关D. 2个成比例的向量组成的向量组线性相关7・已知向量组a^a 2.a 3线性无关,0线性相关,则(D )1.已知2阶行列式 A. m — nb\ + C]“2 a 2 +c 2a \ a2S b 2 B. n — mb 2b\D. - (m + /?)b\a2b\C ]C. m + nb2a 2 + c 2A. 必能由a2,a3,f3线性表出B. a2必能由a x.a3.0线性表出注:0]心2,%3是4|,02,%3,0的一个极大无关组.8. 设/!为加XH 矩阵,则方程组月尸0只有零解的充分必要条件是力的秩(D ) A.小于刃B.等于刃C.小于刀D.等于刀注:方程组Ax=O 有n 个未知量.9. 设力为可逆矩阵,则与力必有相同特征值的矩阵为(A ) A. "B. A 2C. A _,D. A*| AE-A 7H (AE-A)T \=\AE-A\f 所以力与屮有相同的特征值. 10. 二次型/(x p x 2,x 3) = x^ +X2 +X3 +2x^2的正惯性指数为(C ) A. 0B. 1C. 2D. 3/(x 1,x 2,x 3) = (x l +x 2)2+X3 =yf + 迟,正惯性指数为 2.二、填空题(本大题共10小题,每小题2分,共20分)了 = 30 — 24 = (9,3,—3,12)' -(6-2,0,4) =(3,5-3,8)7 . 14.设力为〃阶可逆矩阵,且\A\=-~,则| | A'1 |= n15.设力为〃阶矩阵,B 为n 阶非零矩阵,若B 的每一个列向量都是齐次线性方程组Ax=0的解,则11 •行列式的值为 _____________13.设a = (3,—l,0,2)T, 0 = (3,1,-1,4)7',若向量了 满足2a + y = 30,则卩二 2007 2008 2009 201016. _________________________________________________________________ 齐次线性方程组+兀2 +兀3 =°的基础解系所含解向量的个数为 ________________________________________12X| - x 2 + 3兀3 = 0基础解系所含解向量的个数为« - r = 3 - 2 = 1.17. ___________________________________________________________________ 设〃阶可逆矩阵力的一个特征值是-3,则矩阵必有一个特征值为 __________________________________________-2、0的特征值为4,1,-2 ,则数兀二0」20.二次型 /(X ),x 2,x 3) = -4x }x 2 +2兀]£ + 6X 2X 3的矩阵是 _______________-2 r 0 33 0,三、计算题(本大题共6小题,每小题9分,共54分)ab c 21.计算行列式a 2b 2c 2的值. a + a 3h + b 3c + c 3甘町有特征畤"1 -2 18.设矩阵-2 x、一2 0 由第1. 2列正交, 即它们的内积(d + b) = 0 ,-21 b c 解:D =a2b2c2a + cdb + b3c + c31 1 1=abc0 b-a c-a0 b2-a2 c2-a2a b c 1 1 1 a2 b2 c2= abc a b c a3b3 c39 cr b2 c2= abc b-a c-b2-a2c2-•a■a2=abc(b 一 a)(c - a)(c — b) •(2)注意到CB T = (1,2,3) 1 =13,所以34A 2= (B rC)(B rC) = B r(CB T )C = \3B T C = \3A = \3 1 2线性无关组,并用该极人线性无关组表示向量组屮的其余向量•<2>‘2 4 6、 解:(1) A = B rC =1 (1,2,3)= 12 32丿<3 6 9,己知矩阵 B = (2,1,3), C = (123),22. "2 1-1 1、<1 10 r<1 1 0 1 、 1 2 1 1 T1 211T0 1103 0 -3 13 0 -3 10 -3 -3 -210 1J<2 1 -1 1丿k 0 -1 -1 一1丿解:A = (a|,(^2 9 oc^, )—<1 1 0 1、<1 1 0 1、<1 0 -1 n0 1 1 00 1 1 00 1 1 0 0 0 0-20 0 0 10 0 0 10 0 一1丿<0 0 0 0丿<0 00 0>,向量组的秩为 关组,旳=-Q| +a 2 •3, a }.a 2,a 4是一个极大无"12 3、<-14 ] 24.已知矩阵人=0 1 2 ,B = 25<0 ° bU 一3丿(1) 求A"1; (2)解矩阵方程AX = B.=abc(b 一 d)(c — a) 求(1) A = B T C ; (2)23. 设向量组內=(2」,3」几勺=(120」几&3=(—1」厂3,0八勺=(1」丄1卩求向量组的秩及一个极人2 31 0 0、2 0 1 0 -3、 解:(1)(A,E) = 0 1 20 1 00 1 0 0 1 -2<00 10 010 0 1 0 0 1」Z\ /<1 0 0 1 -21、1 -21、0 1 0 0 1 -2 /T0 1-2■ 9<0 0 1 0 01丿0 01 ZX] + 2 兀2 + 3 兀3 = 42X 2 4- ax 3 = 2有惟一解?有无穷多解?并在有解时求出其解(在有2x t + 2X 2 + 3X 3 = 6"2 3 4、"2 0 4、 工3时,r(A,ft) = r(A) = 3,有惟一解,此时(A,b)->0 2 a 20 2 0 2<0 0 10; \<0 0 10; \ /0、a 的三个特征值分别为1,2,5,求正的常数曰的值及可逆矩阵",使 3丿‘1 0 0、P'XAP= 0 2 00 0 5丿2 0 03 a解:由 |A|= 0 3 67 =2=2(9-/)= ix2x5,得宀 4, a = 2.a 30 a 3<1 -2 1、<-1 4>‘-4 - 9)X=A~}B = 0 1 -225 =0 11<0 ° 1 丿<1 一3丿、1 -3,(2)2 3 4、有无穷多解,此时0 2 3 2<o 0 0 o>G = 3 时,r(A,b) = r(A) = 2< /?,‘1 0 0 2>‘1 00 2、0 2 3 20 1 3/2 1 <0 0 0 0丿<0 0 0 0? Z〔2厂0、通解为 1 + k -3/2< 1 >其中R 为任意常数.25•问日为何值时,线性方程组解:<1 2 3 4、234、<1 234(必)= 0 2 a 20 2a 20 2a 2<2 2 3 6丿-2 -3 -2丿\ 0 ci _ 3 0 丿‘1 0 0 2>‘1 0 0 2、0 2 0 20 1 0 1,0 0 1 0丿,0 0 1 0丿‘2 0 26.设矩阵0 3 (0 a无穷多解时,要求用一个特解和导出组的基础解系表示全部解)./° = 1 ;兀3 = °2 0 0、AE-A= 0 2-3 -2 ..0 -2 2-3丿对于人=1,解(/IE —A)兀=0:"-1 0 0、"1 0 0、%! =0 <0、AE-A =0 -2 -2 0 1 1 9 v x2 =-x3 ,取门=-1<0 -2 一2丿<0 0 ° 丿无3 = 兀3对于兄2=2,解(/i£—A)兀=0:r0 0 0、‘0 1 0、x\ =x\TAE-A =0-1-2 T0 0 1 X2 = 0 ,取#2 = 0<0 -2 -1;0 0, 兀3 =0O对于几3=5,解(征一心=0:厂3 00、厂1 0X| =0 ◎九E —A =0 2-2 —> 0 1 -1 兀2 =兀3,P3 = 1,0-2 2 丿<0 0 0 ;\X3 = X3<1>'0 10、"0 0、令P =("|, “2 ' “3)= -1 0 1 ,则P是可逆矩阵,使P~'AP =0 2 0<10 1; <0 0 5丿四、证明题(本题6分)27.设昇,B, A+B均为〃阶正交矩阵,证明(4 + 3)7 =4一】+3".证:J, B, A + B均为/?阶正交阵,则A r=A-!, B T =B~\ (4+B)7 =(A + B)T,所以(A + B)T =(A + B)T = A1^ + B T = A~l + B~l・。
专升本《高等数学》考试题解(经管类)

专升本《高等数学》考试题(经管类)一、填空题(每题4分,共20分)1.设)(x f 的定义域是[0,1],则)(ln x f 的定义域是[1,e ] 。
2.函数⎪⎩⎪⎨⎧=+≠=0,20,1sin )(x a x xx x f 在0=x 处连续,则a = -2 。
3.由方程e xy e y =+所确定的隐函数)(x y y =在0=x 处的导数,='=0|x y e1-。
4.设固定成本为C 0,Q 为产量,F (Q )为可变成本,则总成本C=)(0Q F C +,平均成本=C QQ F C )(0+。
5.设矩阵⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫⎝⎛=8765,4321B A ,则=-B A 2⎪⎪⎭⎫⎝⎛---0123 二、单项选择题(每题4分,共20分)1.函数⎪⎩⎪⎨⎧=≠=000,1sin 2)(x x xx x f 在点0=x 处( D )A .无定义B .不连续C .可导D .连续但不可导2.设n n u ∑∞=1为任意项级数,且||1n n u ∑∞=发散,则( B )A .原级数收敛B .原级数敛散性不定C .原级数发散D .原级数条件收敛3.微分方程x y y x cos =+'的一个特解是( B )A .x sinB .x xsin 1C .x cosD .x xcos 14.极限3220sin limx dt t x x ⎰→等于( C ) A .41 B .34C .38D .43 5.已知矩阵⎪⎪⎪⎭⎫⎝⎛=323122211211a a a a a a A ,那么能左乘A 的矩阵是( D ) A .⎪⎪⎪⎭⎫ ⎝⎛323122211211b b b b b bB .),,(131211b b bC .⎪⎪⎪⎭⎫⎝⎛312111b b bD .⎪⎪⎭⎫ ⎝⎛22211211b bb b 三、解答题(每题5分,共20分)1.求极限11tan lim20-++→x x x x解:2121sec 2lim 11tan lim2020=++=-++→→xxx x xx x x 2.已知y x z arctan =,求yzx z ∂∂∂∂,解:222)(11y x y yx y xz +=+=∂∂2222)(1y x x yx y xyz +-=+-=∂∂3.设)0()(>+=x x x x f ,试求dx x f )(2'⎰ 解:xx f xx f 211)(211)(2+='+=' ∴C x x dx x dx x f ++=+='⎰⎰ln 21)211()(2 4.计算dxdy y x D22⎰⎰,其中D 是由直线x y y ==,2和双曲线1=xy 所围成的区域。
高等数学试卷:04-05经管(上)

共 4 页 第 1 页东 南 大 学 考 试 卷( A 卷) 课程名称 高等数学 考试学期 04-05-2 得分 适用专业 经管 考试形式 半开卷 考试时间长度 120分钟一. 选择题 (4分×5=20分) 1. 的是则设函数)(0,sin 12)(1x f x x x e x f x =++= ( B ) A. 连续点; B. 可去间断点; C. 第一类但非可去间断点; D. 第二类间断点. 2. 下列表达时则当都是无穷小时设当,),0)(()(),(,00x x x x x x x →≠→ββα 式中不一定为无穷小的是 ( A ) A.)()(2x x βα; B.x x x 1sin )()(22βα+; C. ))()(1ln(x x βα+; D.)()(x x βα+. 3. ⎰=-⎪⎩⎪⎨⎧≥<+=3 1 2)2(, 0 ,0 ,1)(dx x f x e x x x f x 则设 ( B ) A. 31-e ; B. 31+e ; C. 31; D. e 2. 4. ⎰='dx x f x x f x )(,)(2sin 则的一个原函数是已知 ( C ) A. C x x x +-2cos 2sin 2; B. C x x x ++2cos 2sin 2; C. C x x x +-2sin 2cos 2; D. C x x x +-2cos 2sin .5. 有极大值点函数 )1( 20 dt e t y x t ⎰-= ( D )A. 1=x ;B. 1-=x ;C. 1±=x ; D. 0=x .二. 填空题 (4分×5=20分)1. 11212lim -∞→=⎪⎭⎫ ⎝⎛+-e x x xx .共 4 页 第 2 页 2. 内向其图形在区间内单调增加在区间函数 ),( , (0,1) )ln(2)(+∞=e ex xx f 下凸. 3. .014sin cos 22=-+=⎪⎩⎪⎨⎧==x y t ty t x 程为所对应的点处的切线方在曲线π 4. )21(2)(111----=+⎰e dx e x x x .三. 求下列积分 (6分×3=18分)1. ⎰+dx x x )1ln(2. ⎰-dx x sin 11解: 原式=⎰+)2()1ln(2x d x (1分) 解: 原式=⎰+dx x x 2cos sin 1 (2分) =⎰+⋅-+dx xx x x 112)1ln(222 (1分) =⎰+dx x x x )cos sin (sec 22 =dx xx x x ⎰++--+11121)1ln(222 (2分) =⎰⎰-+x x d xdx 22cos )(cos sec (2分) =dx xx x x )111(21)1ln(22⎰++--+ =C x x ++cos 1tan (2分) =C x x x x x +++--+)1ln 2(21)1ln(222 (2分) 3. dx x x ⎰-1022解: 原式=tdt t dx x t x cos sin 1)1(1022sin 1102⎰⎰-=--=--π (2分)dt t ⎰-=022cos π dt t ⎰-+=0222cos 1π (2分) 42sin 41210202πππ=+=--t t . (2分) 四. 1. (6分).,1)(11 22=-=-=⎰x yt dx dy dt e x x y y 求所确定由方程设函数 解: 由题意,当1,1==y x 时. (1分)共 4 页 第 3 页 又 )2.(22 )3( 0211122分得分,由e xe dx dy dx dy e x y x yx y ===⋅-===-2. (7分)使得试补充定义设函数),0(],21,0(,1sin 1)(f x x x x f ∈-=ππ]21,0[)(在x f 上连续. 解: 由题意,)(lim )0(0x f f x +→=. 又xx x x x x x f x x x ππππππsin sin lim )1sin 1(lim )(lim 000-=-=+→+→+→ (1分) = )(1 sin lim 220分x x x x πππ-+→= )(1 2cos lim 20分x x x ππππ-+→ = )(2 0 )(1 2sin lim 220分分=+→πππx x 所以0)0(=f . (1分) 五. 1.(7分).arctan )1ln()1(,0:x x x x >++>时当证明解: 令.0)0(,arctan )1ln()1()(=-++=f x x x x f 则 (2分)又0111)1ln()(,02>+-++='>xx x f x 时当, (3分) 于是,)(,0单调增加时当x f x ≥从而有)0(0)0()(>=>x f x f即: ).0(arctan )1ln()1(>>++x x x x (2分) 2.(8分)最为何值时问内的驻点为在设)(, ).(),( )(,1a t a a t at a t f a t +∞-∞-=> 小? 并求最小值.解: .ln ln ln 1)(0ln )(a a a t a a a t f t -==-='得由 (2分) 0)(ln 1ln ln )(2e e a a a a a t ==-='得唯一驻点又由 (2分) .)(,0)(,;0)(,的极小值点为于是时当时当a t e a a t e a a t e a e e e =<'<>'> (2分)故.11ln 1)(,)(ee e e t a t e a e e -=-==最小值为的最小值点为 (2分)共 4 页 第 4 页 六.(8分),0423412所围成的平面图形与直线为曲线设=--=y x x y D 求: (1)D 的面积S ; (2)D 绕x 轴旋转一周所得的旋转体体积V .解: ).4,4()1,2(0423412和的交点为与直线曲线=--=y x x y (1分) (1) D =31)41243(4 2 2=--⎰dx x x ; (3分) (2) ππ58])41()243[(4 2 222=--=⎰dx x x V . (4分)七.(6分),0)1()0(,)1 ,0(,]1 ,0[)(==f f x f 且内可导在上连续在设函数证明至少存在 一点),1 ,0(∈ξ使得0)(2)(=+'ξξf f .证明: 设 ),()(2x f e x F x = (3分)条件上满足罗尔中值定理的在于是则]1,0[)(,0)1()0( x F F F ==,于是由罗尔中值定理得0)(),1 ,0(='∍∈∃ξξF ; (2分)即至少存在一点),1 ,0(∈ξ使得0)(2)(=+'ξξf f . (1分)。
高等数学上(经管类本科)第一章题目

高等数学上(经管类本科)第一章一、 选择题1. 下列各组函数中,【 】是相同的函数A. 2()ln f x x =和 ()2ln g x x =B. ()f x x =和()g x =C. ()f x x =和()2g x =D. ()x f x x=和()1g x = 2. 下列各组中,函数)(x f 与)(x g 一样的是【 】 A. 33)(,)(x x g x x f == B. x x x g x f 22tan sec )(,1)(-== C. 11)(,1)(2+-=-=x x x g x x f D. 2ln )(,ln 2)(x x g x x f == 3. 下列函数不相等的是【 】A. ()()==f x g x xB. ()()==f x g x xC. ()()22sin 31,sin 31=+=+y x u tD. ()()21,11-==+-x f x g x x x 4. 设函数1()f x x=,()1g x x =-, 则(())f g x =【 】 A. 11x - B. 11x + C. 11x- D. x 5. 设函数54)(2++=kx x x f ,若38)()1(+=-+x x f x f ,则=k 【 】 A. 1 B. -1 C. 2 D. -26. 设函数()1=+g x x ,当0≠x 时,()1-=⎡⎤⎣⎦x f g x x,则12⎛⎫= ⎪⎝⎭f 【 】 A .0 B. -3 C . 1 D. 1 7. 设函数()1=-g x x ,当0≠x 时,()1+=⎡⎤⎣⎦x f g x x ,则12⎛⎫-= ⎪⎝⎭f 【 】 A .0 B. 3 C . 1 D. 18. 反正切函数arctan y x =的定义域是【 】A. (,)22ππ-B. (0,)πC. (,)-∞+∞D. [1,1]- 9. 下列函数在定义域内,【 】是单调增加的奇函数A. 2y x =B. y x =C. sin y x =D. tan y x =10. 下列函数中,【 】不是奇函数 A. x x y +=tan B. 2x xe y = C. )1()1(-⋅+=x x y D. x xy 2sin 2⋅= 11. 设函数()()f x g x ,的定义域均为(,+)-∞∞,且()f x 为奇函数而()g x 为偶函数,则下列结论正确的是【 】A. ()()f x g x +为偶函数;B. ()()f x g x +为奇函数;C. ()()f x g x ⋅为偶函数;D. ()()f x g x ⋅为奇函数. 12. 下列函数中,在定义域内是单调增加、有界的函数是【 】 A. 2arctan y x x = B. cos y x x =C. arctan y x x =⋅D. arcsin y x x =+13. 下列函数中,在定义域内是单调增加、有界的函数是【 】A. arctan y x x =B. cos y x =C. sin y x x =⋅D. arcsin y x =14. 下列函数中,在定义域内是单调增加、有界的函数是【 】A. arcsin y x =B. cos y x =C. arctan y x x =D. sin y x =15. 设函数()()f x g x ,的定义域均为(,+)-∞∞中,则下列结论正确的是【 】 A. 若()f x 为奇函数,则()()f x g x +也为奇函数;B. 若()g x 为奇函数,则()()f x g x ⋅也为奇函数;C. 若()f x 和()g x 均为奇函数,则()()f x g x +也为奇函数;D. 若()f x 和()g x 均为奇函数,则()()f x g x ⋅也为奇函数.16. 设函数()()f x g x ,的定义域均为(,+)-∞∞,且()()()h x f x g x =+,则下列结论正确的是【 】A. 若()f x 为偶函数,则()h x 也为偶函数;B. 若()g x 为偶函数,则()h x 也为偶函数;C. 若()f x 和()g x 均为偶函数,则()h x 也为偶函数;D. 若()f x 为奇函数而()g x 为偶函数,则()h x 也为偶函数.17. 下列函数中,定义域是[1,1]-,且是单调递减的是【 】A. arcsin y x =B. arccos y x =C. arctan y x =D. arccot y x =18. 下列函数是奇函数的是【 】A. arcsin y x x =B. arccos y x x =C. arccot y x x =D. 2arctan y x x =二、填空题1. 函数log(2)log(2)y x x =++-的定义域为___________.2. 设)(x f 的定义域为)1,0(,则函数)12(-x f 的定义域为 ___________.3. 函数)2lg()(2x x x f +=的定义域为 ___________。
经济数学基础12历年真题

试卷代号:2006之青柳念文创作国家开放大学2013~2014学年度第二学期“开放专科”期末测验经济数学基础12 试题2014年7月一、单项选择题(每题3分,本题共15分)1.下列各函数中,( )不是基本初等函数.3.下列等式中正确的是( ).二、填空题(每题3分,共15分)6.函数()ln(1)f x x =-的定义域是. 7.函数()f x =2x =点的切线斜率是________________.8.若()()f x dx F x c =+⎰,则(3+5)f x dx =⎰.9.设矩阵1243A -⎡⎤=⎢⎥⎣⎦,I 为单位矩阵,则()T I A -=.10.若(,)4,()3r A b r A ==,则线性方程组AX b =.三、微积分计算题(每小题10分,共20分)11.设3cos ln y x x =+,求y '. 12.计算不定积分21sinx dx x ⎰.四、线性代数计算题(每小题15分,共30分)13.设矩阵231010010A -⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦,求-1A . 14.求下列线性方程组123412341234252302302146120x x x x x x x x x x x x -+-=⎧⎪+-+=⎨⎪-+-+=⎩的一般解. 五、应用题(本题20分)15.设生产某产品的总成本函数为()3C x x =+(万元),其中x 为产量(百吨),销售百吨时的边沿收入为()152R x x '=-(万元/百吨),求:(1)利润最大时的产量;(2)在利润最大时的产量的基础上再生产1百吨,利润会发生什么变更?参考答案一、单项选择属(每小题5分,共15分)1、B2、D3、A4、B5、B二、填空(每小题3分,共15分)三、微积分计算题(每小题10分,共20分)四、线性代数计算题(每小题15分,共30分)五、应用题(本题20分)试卷代号:2006国家开放大学2014~2015学年度第一学期“开放专科”期末测验经济数学基础12 试题2015年1月一、单项选择题(每题3分,本题共15分)1.下列各函数中为偶函数的是( ).2. 当x →+∞时,下列变量为无穷小量的是( )3.下列结论中正确的是( ).4.下列结论或等式正确的是( ).5. 线性方程组m n A X b ⨯=有无穷多解的充分需要条件是( )二、填空题(每题3分,共15分)6.函数()ln(1)f x x =+7.曲线y =(1,1)点的切线斜率是________________.8.若()()f x dx F x c =+⎰,则()x x e f e dx --=⎰.9.设方阵A 知足______________,则A 为对称矩阵.10.若线性方程组121200x x x x λ-=⎧⎨+=⎩有非零解,则λ=. 三、微积分计算题(每小题10分,共20分)四、线性代数计算题(每小题15分,共30分)五、应用题(本题20分)15.已知某产品的边沿成本为()43C x x '=-(万元/百台),其中x 为产量(百台),固定成本为18(万元),求最低平均成本. 参考答案一、单项选择属(每小题5分,共15分)1、C2、A3、D4、C5、B二、填空(每小题3分,共15分)三、微积分计算题(每小题10分,共20分)四、线性代数计算题(每小题15分,共30分)五、应用题(本题20分)试卷代号:2006中央广播电视大学2010~2011学年度第一学期“开放专科”期末测验经济数学基础 试题2011年1月一、单项选择题(每题3分,本题共15分)1.下列函数中为奇函数的是 ( ).A .2y x x =-B .x x y e e -=+C .1ln 1x y x -=+ D .sin y x x = 2.设需求量q 对价格p的函数为()3q p =-p E =( ).ABC. D3.下列无穷积分收敛的是 ( ).A .0x e dx +∞⎰B .211dx x +∞⎰C.1+∞⎰D .1ln xdx +∞⎰4.设A 为32⨯矩阵,B 为23⨯矩阵,则下列运算中()可以停止.A. ABB.A B +C.T ABD.T BA5.线性方程组121210x x x x +=⎧⎨+=⎩解的情况是().A .有唯一解B .只有0解C .有无穷多解D .无解二、填空题(每题3分,共15分)6.函数()f x =的定义域是.7.函数1()1x f x e =-的间断点是.8.若()()f x dx F x C =+⎰,则()x x e f e dx --=⎰.9.设10203231A a ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦,当a =时,A 是对称矩阵. 10.若线性方程组121200x x x x λ-=⎧⎨+=⎩有非零解,则λ=.三、微积分计算题(每小题10分,共20分)11.设53cos x y x =+,求dy .12.计算定积分1ln ex xdx ⎰.四、线性代数计算题(每小题15分,共30分)13.设矩阵100101,011212A B ⎡⎤⎡⎤⎢⎥⎢⎥=-=⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦,求1()T B A -. 14.求齐次线性方程组124123412342 23202530x x x x x x x x x x x +-=⎧⎪-+-+=⎨⎪-+-=⎩的一般解.五、应用题(本题20分)15.某厂生产某种产品的总成本为()3()C x x =+万元,其中x 为产量,单位:百吨.边沿收入为()152(/)R x x '=-万元百吨,求:(1)利润最大时的产量?(2)从利润最大时的产量再生产1百吨,利润有什么变更? 参考答案一、单项选择属(每小题5分,共15分)1、C2、D3、B4、A5、D二、填空(每小题3分,共15分)6.(,2](2,)-∞-+∞7.0x =8.()x F e c --+9.010.-1三、微积分计算题(每小题10分,共20分)四、线性代数计算题(每小题15分,共30分)五、应用题(本题20分)试卷代号:2006中央广播电视大学2010~2011学年度第二学期“开放专科”期末测验经济数学基础 试题2011年7月一、单项选择题(每题3分,本题共15分)1.函数lg(1)x y x =+的定义域是 ( ).A .1x >-B .0x >C .0x ≠D .10x x >-≠且2.下列函数在指定区间(,)-∞+∞上单调增加的是( ).A .sin xB .x eC .2xD .3x -3.下列定积分中积分值为0的是( ).A .112x xe e dx ---⎰B .112x x e e dx --+⎰ C .2(sin )x x dx ππ-+⎰D .3(cos )x x dx ππ-+⎰4.设AB 为同阶可逆矩阵,则下列等式成立的是( ).A. ()T T T AB A B =B.111()()T T AB A B ---=C.()T T T AB B A =D.111()()T T AB A B ---=5.若线性方程组的增广矩阵为12210A λ⎡⎤=⎢⎥⎣⎦,则当=λ()时线性方程组无解.A .12B .0C .1D .2二、填空题(每题3分,共15分)6.函数()2x xe ef x --=的图形关于对称. 7.已知sin ()1x f x x =-,当x →时,()f x 为无穷小量.8.若()()f x dx F x C =+⎰,则(23)f x dx -=⎰.9.设矩阵A 可逆,B 是A 的逆矩阵,则当1()T A -=.10.若n 元线性方程组0AX =知足()r A n <,则该线性方程组.三、微积分计算题(每小题10分,共20分)11.设3cos ln y x x =+,求y '.12.计算不定积分. 四、线性代数计算题(每小题15分,共30分)13.设矩阵01325227,0134830A B --⎡⎤⎡⎤⎢⎥⎢⎥=---=⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦,I是3阶单位矩阵,求1()I A B --.14.求线性方程组123412341234123432238402421262x x x x x x x x x x x x x x x x ---=⎧⎪---=⎪⎨-+-+=⎪⎪---+=⎩的一般解. 五、应用题(本题20分)15.已知某产品的边沿成本()2()C x '=元/件,固定成本为0,边沿收益()120.02R x x '=-,问产量为多少时利润最大?在最大利润产量的基础上再生产50件,利润将会发生什么变更? 参考答案一、单项选择属(每小题5分,共15分)1、D2、B3、A4、C5、A二、填空(每小题3分,共15分)6.原点7.08.1(23)2F x c -+ 9.T B10.有非零解三、微积分计算题(每小题10分,共20分)四、线性代数计算题(每小题15分,共30分)五、应用题(本题20分)试卷代号:2006中央广播电视大学2011~2012学年度第一学期“开放专科”期末测验经济数学基础 试题2012年1月一、单项选择题(每题3分,本题共15分)1.下列函数中为偶函数的是( ).A .3y x x =-B .1ln 1x y x -=+ C .2x x e e y -+= D .2sin y x x =2.设需求量q 对价格p的函数为()3q p =-p E =( ).ABC. D.3.下列无穷积分中收敛的是( ).A .0x e dx +∞⎰B.1+∞⎰ C .211dx x+∞⎰D .0sin xdx +∞⎰ 4.设A 为34⨯矩阵,B 为52⨯矩阵, 且乘积矩阵T T AC B 有意义,则C 为( )矩阵.A. 42⨯B.24⨯C.35⨯D.53⨯5.线性方程组12122123x x x x +=⎧⎨+=⎩的解的情况是(). A .无解B .只有0解C .有唯一解D .有无穷多解二、填空题(每题3分,共15分)6.函数1()ln(5)2f x x x =++-的定义域是. 7.函数1()1x f x e=-的间断点是. 8.若2()22x f x dx x c =++⎰,则()f x =.9.设111222333A ⎡⎤⎢⎥=---⎢⎥⎢⎥⎣⎦,则()r A =. 10.设齐次线性方程组35A X O ⨯=满,且()2r A =,则方程组一般解中自由未知量的个数为.三、微积分计算题(每小题10分,共20分)11.设ln cos x y e x =+,求dy .12.计算不定积分1ln e x xdx ⎰.四、线性代数计算题(每小题15分,共30分)13.设矩阵010100201,010341001A i ⎡⎤⎡⎤⎢⎥⎢⎥=-=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦,求1()I A -+. 14.求齐次线性方程组12341341234+203202530x x x x x x x x x x x +-=⎧⎪--+=⎨⎪++-=⎩的一般解. 五、应用题(本题20分)15.某厂生产某种产品q 件时的总成本函数为2()2040.01C q q q =++(元),单位销售价格为140.01p q =-(元/件),问产量为多少时可以使利润最大?最大利润是多少? 参考答案一、单项选择属(每小题5分,共15分)1、C2、D3、C4、B5、A二、填空(每小题3分,共15分)6.(5,2)(2,)-+∞ 7.0x =8.2ln 24x x +9.110.3三、微积分计算题(每小题10分,共20分)四、线性代数计算题(每小题15分,共30分)五、应用题(本题20分)试卷代号:2006中央广播电视大学2011~2012学年度第二学期“开放专科”期末测验经济数学基础 试题2012年7月一、单项选择题(每题3分,本题共15分)1.下列函数中为偶函数的是( ).A .3y x x =-B .x x y e e -=+C .1ln 1x y x -=+ D .sin y x x =2.设需求量q 对价格p 的函数为2()100pq p e -=,则需求弹性为p E =().A .2p -B .2pC .50p -D .50p3.下列函数中( )是2sin x x 的原函数.A .21cos 2xB .21cos 2x -C .22cos x -D .22cos x4.设121201320A -⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦,则()r A =( ) .5.线性方程组12111110x x ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦的解的情况是().A .无解B .有无穷多解C .只有0解D .有唯一解二、填空题(每题3分,共15分)6.设2(1)25f x x x -=-+,则()f x =.7.若函数1sin 2,0(),0x x f x x k x ⎧+≠⎪=⎨⎪=⎩在0x =处持续,则k=.8.若()()f x dx F x c =+⎰,则(23)f x dx -=⎰.9.若A 为n 阶可逆矩阵,则()r A =.10.齐次线性方程组AX O =的系数矩阵经初等行变换化为112301020000A -⎡⎤⎢⎥→-⎢⎥⎢⎥⎣⎦,则此方程组的一般解中自由未知量的个数为. 三、微积分计算题(每小题10分,共20分)11.设15x x y e =+,求dy .12.计算20cos x xdx π⎰.四、线性代数计算题(每小题15分,共30分)13.已知AX B =,其中1222110,11351A B ⎡⎤⎡⎤⎢⎥⎢⎥=--=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦,求X .14.讨论λ为何值时,齐次线性方程组1231231232+0250130x x x x x x x x x λ+=⎧⎪+-=⎨⎪++=⎩有非零解,并求其一般解.五、应用题(本题20分) 15.投产某产品的固定成本为36(万元),且产量x (百台)时的边沿成本为()260C x x '=+(万元/百台),试求产量由4百台增至6百台时总成本的增量,及产量为多少时,可以使平均成本达到最低.参考答案一、单项选择属(每小题5分,共15分)1、C2、A3、B4、C5、D二、填空(每小题3分,共15分)三、微积分计算题(每小题10分,共20分)四、线性代数计算题(每小题15分,共30分)五、应用题(本题20分)试卷代号:2006中央广播电视大学2012~2013学年度第一学期“开放专科”期末测验经济数学基础 试题2013年1月一、单项选择题(每题3分,本题共15分)1.下列各函数对中,( )中的两个函数相等.2.函数sin ,0(),0x x f x x k x ⎧≠⎪=⎨⎪=⎩在0x =处持续,则k =( ).A .-2B .-1C .1D .23.下列定积分中积分值为0的是( ).4.设120300132413A -⎡⎤⎢⎥=-⎢⎥⎢⎥--⎣⎦,则()r A =( ) . 5.若线性方程组的增广矩阵为120124A λλ⎡⎤=⎢⎥--⎣⎦,则当λ=( )时该线性方程组无解.A .1/2B .0C .1D .2二、填空题(每题3分,共15分)6.y = 7.设某商品的需求函数为2()10p q p e -=,则需求弹性p E =.8.若()()f x dx F x c =+⎰,则()x x e f e dx --=⎰.9.当a 时,矩阵13-1A a ⎡⎤=⎢⎥⎣⎦可逆. 10.已知齐次线性方程组AX O =中A 为35⨯矩阵,则()r A ≤.三、微积分计算题(每小题10分,共20分)11.设2cos ln y x x =+,求dy . 12.计算定积分ln320(1)x x e e dx +⎰.四、线性代数计算题(每小题15分,共30分)五、应用题(本题20分)15.设生产某种产品q 个单位时的成本函数为: 2()1000.256C q q q =++ (万元),求:(1)当q=10时的总成本、平均成本和边沿成本;(2)当产量q 为多少时,平均成本最小?参考答案一、单项选择属(每小题5分,共15分)1、D2、C3、A4、B5、A二、填空(每小题3分,共15分)三、微积分计算题(每小题10分,共20分)四、线性代数计算题(每小题15分,共30分)五、应用题(本题20分)试卷代号:2006中央广播电视大学2013~2014学年度第一学期“开放专科”期末测验经济数学基础12 试题2014年1月一、单项选择题(每题3分,本题共15分)1.下列各函数对中,( )中的两个函数相等.2.下列结论中正确的是( ).3.下列等式中正确的是( ).4.下列结论中正确的是( ).5.n 元线性方程组AX b =有解的充分需要条件是().二、填空题(每题3分,共15分)6.函数1()ln(2)f x x =+ 7.函数()f x =(1,1)点的切线斜率是________________.8.若cos x 是()f x 的一个原函数,则()f x =.9.设1312A ⎡⎤=⎢⎥--⎣⎦,则2I A -=. 10.若线性方程组121200x x x x λ-=⎧⎨+=⎩有非零解,则λ=. 三、微积分计算题(每小题10分,共20分)11.设5sin x y x e =+,求dy .12.计算不定积分. 四、线性代数计算题(每小题15分,共30分)13.设矩阵01010020-1,010341001A I ⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦,求-1I A +(). 14.求下列线性方程组13412341234203202530x x x x x x x x x x x +-=⎧⎪-+-+=⎨⎪-+-=⎩的一般解.五、应用题(本题20分)15.已知某产品的边沿成本为()43C x x '=-(万元/百台),x 为产量(百台),固定成本为18(万元),求最低平均成本.参考答案一、单项选择属(每小题5分,共15分)1、D2、D3、A4、B5、A二、填空(每小题3分,共15分)三、微积分计算题(每小题10分,共20分)四、线性代数计算题(每小题15分,共30分)五、应用题(本题20分)试卷代号:2441国家开放大学2013~2014学年度第二学期“开放专科”期末测验经济数学基础 1 试题2014年7月一、单项选择题(每题4分,本题共20分)1.函数()f x 的定义域为(,)-∞+∞,则函数()()f x f x +-的图形关于( )对称.A .y x =B .x 轴C .y 轴D .坐标原点2.当0x →时,变量( )是无穷小量.3.设()x f x e =,则0(1)(1)lim x f x f x∆→+∆-=∆ ( ). 4.若()cos f x x =,则()f x dx '=⎰( )A. sin x c +B.cos x c +C.sin x c -+D.cos x c -+5.下列无穷限积分收敛的是().二、填空题(每题4分,共20分)6.函数()ln(5)f x x =+的定义域是. 7.函数1,0sin ,0x x y x x ->⎧=⎨≤⎩的间断点是.8.若()f x 在(,)a b 内知足()0f x '<,则()f x 在(,)a b 内是.9.若()cos f x dx x c =+⎰,则()f x =.10.121(1)x dx x -=+⎰. 三、计算题(每小题11分,共44分)11.计算极限0sin 3lim sin 2x x x→. 12.设5ln x y x e -=+,求y '.13.计算不定积分. 14.计算定积分20sin x xdx π⎰.四、应用题(共16分)15.某厂生产某种产品q 件时的总成本函数为2()2040.01C q q q =++(元),单位销售价格为140.01p q =-(元/件),问产量为多少时可以使利润达到最大? 最大利润是多少?参考答案一、单项选择属(每小题4分,共20分)1-5 CCBBC二、填空(每小题4分,共20分)三、计算题(每小题11分,共44分)四、应用题(共16分)试卷代号:2441国家开放大学2014~2015学年度第一学期“开放专科”期末测验经济数学基础 1 试题2015年1月一、单项选择题(每题4分,本题共20分)1.下列函数中为奇函数的是( ).2.当0x →时,变量( )是无穷小量.3.函数226y x x =-+在区间(2,5)内知足( ).4.下列等式成立的是( )5.下列无穷限积分收敛的是().二、填空题(每题4分,共20分)6.函数1010()2x xf x -+=,则函数的图形关于对称.7.若函数,0(),0x x b x f x e x +≤⎧=⎨>⎩在点0x =处持续,则b =. 8.函数21y x =+的单调增加区间是.9.若()cos f x dx x c =+⎰,则()f x =.10.21ln(1)e d x dx dx+=⎰. 三、计算题(每小题11分,共44分)11.计算极限22023lim 6x x x x x →----.12.设3sin x y x e =+,求dy .13.计算不定积分.14.计算定积分21ln ex xdx ⎰.四、应用题(共16分)15.已知某产品的边沿成本为()2()C x '=元/件,固定成本为0,边沿收益()120.02R x x '=-,求:(1)产量为多少时利润最大? (2)在最大利润产量的基础上再生产50件,利润将会发生什么变更?参考答案一、单项选择属(每小题4分,共20分)1-5 CBDAD二、填空(每小题4分,共20分)三、计算题(每小题11分,共44分)四、应用题(共16分)。
全国2014年10月自考线性代数(经管类)试题和答案

a13 a 23 =2 ,若元素 aij 的代数余子公式为 Aij ( i,j=1,2,3) ,则 1
A31 A32 A33 【
A. 1 B.0 C.1 D.2 正确答案:D(2 分)
2.设 A 为 3 阶矩阵,将 A 的第 3 行乘以 则 A =【 A. 2 B. C. 】
A 表示方阵 A 的行列式, r A 表示矩阵 A 的秩。
一.单项选择题(本大题共 5 小题,每小题 2 分,共 10 分) 在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号 内。错选、多选或未选均无分。
a11 1.设 3 阶行列式 a 21 1
a12 a 22 1
正确答案: 解:
a3 2 a a 1
a2 a 1 0
a 1 1 0 0 0 1 1 0 0 1 0 0 a 2 a 0 0 0 0 1 0 3 0 0 0 0 0 1 a
0 1 a a2
0 0 0 0 0 1 0 0 0 0 1 0 ......2 分 1 0 0 1 0 0 a 1 1 0 0 0
1 得到单位矩阵 E , 2
1 2
1 2
D.2 正确答案:A(2 分) 3.设向量组 1 , 2 , 3 的秩为 2,则 1 , 2 , 3 中【 A.必有一个零向量 B.任意两个向量都线性无关 C.存在一个向量可由其余向量线性表出 D.每个向量均可由其余向量线性表出 正确答案:C(2 分) 】
正确答案:B(2 分)
2 2 2 5.二次型 f ( x1 , x2 , x3 ) x1 x2 x3 4x1 x2 的正惯性指数为【
】
A.0 B.1 C.2 D.3 正确答案:C(2 分) 二.填空题(本大题共 10 小题,每小题 2 分,共 20 分) 请在每小题的空格中填上正确答案。错误、不填均无分、 6.设 f ( x)
智慧树知到《高等数学上经管类》章节测试答案

智慧树知到《高等数学上经管类》章节测试答案智慧树知到《高等数学上经管类》章节测试答案第一章1、【单选题】(5 分)DA.B.C.D2、【单选题】(5 分)CA.无穷大量B.无界,但非无穷大量C.无穷小量D.有界,而未必是无穷小量3、【单选题】(5 分)CA.B.2C.3D.44、【单选题】(5 分)CA.B.C.D5、【单选题】(5 分)BA.0B.C.1D.不存在6、【单选题】(5 分)DA.1B.C.D.7、【单选题】(5 分)CA.B.C.D.8、【单选题】(5 分)BA.B.C.D.9、【单选题】(5 分)BA.B.C.D.10、【单选题】(5 分)BA.0B.C.1D.211、【单选题】(5 分)DA.B.C.D.12、【单选题】(5 分)BA.B.8C.1D.13、【单选题】(5 分)BA.1B.0C.D.-114、【单选题】(5 分)AA.1B.0C.D.15、【单选题】(5 分)CA.1B.0C.D.16、【单选题】(5 分)C 下列数列正确的是()A.有界数列一定有极限B.无界数列一定是无穷大量C.无穷大数列必为无界数列D.无界数列未必发散17、【单选题】(5 分)BA.0 个B.1 个C.2 个D.3 个18、【单选题】(5 分)CA.B.C.D.19、【单选题】(5 分)以下极限式正确的是()CA.B.C.D.20、【单选题】(5 分)BA.0B.-1C.1第二章1、【单选题】(5 分)BA.连续且可导B.连续而不可导C.既不连续也不可导D.可导而不连续2、【单选题】(5 分)AA.B.C.D.3、【单选题】(5 分)DA.-1B.-1000!C.1D.1000!4、【单选题】(5 分)CA.1B.0C.-1D.不能确定5、【单选题】(5 分)BA.B.C.D.6、【单选题】(5 分)CA.B.C.D.7、【单选题】(5 分)BA.B.C.D.8、【单选题】(5 分)AA.B.C.D.9、【单选题】(5 分)CA.B.C.D.10、【单选题】(5 分)DA.B.C.D.11、【单选题】(5 分)CA.B.C.D.12、【单选题】(5 分)AA.奇函数B.偶函数C.非奇函数非偶函数D.无法判断13、【单选题】(5 分)AA.B.C.D.14、【单选题】(5 分)DA.B.C.D.15、【单选题】(5 分)BA.B.C.D.16、【单选题】(5 分)AA.B.C.D.17、【单选题】(5 分)CA.B.C.D.18、【单选题】(5 分)AA.B.C.D.19、【单选题】(5 分)DA.B.C.D.20、【单选题】(5 分)BA.B.C.D.第三章1、【单选题】(5 分)AA.B.C.D.2、【单选题】(5 分)BA.B.C.D.3、【判断题】(5 分)BA.对B.错4、【单选题】(5 分)CA.B.C.D.15、【单选题】(5 分)BA.B.C.1D.-16、【单选题】(5 分)CA.B.C.D.7、【单选题】(5 分)BA.0B.1C.D.8、【单选题】(5 分)DA.B.C.不存在D.19、【单选题】(5 分)DA.B.C.D.10、【单选题】(5 分)CA.有三个实根B.无实根C.有唯一实根D.有两个实根11、【单选题】(5 分)AA.B.C.D.12、【单选题】(5 分)CA.B.C.D.13、【判断题】(5 分)BA.对B.错14、【单选题】(5 分)AA.2B.C.1D.015、【单选题】(5 分)BA.B.C.D.16、【单选题】(5 分)BA.B.C.D17、【单选题】(5 分)DA.x=2B.(2,-5)C.x=4D.(4,3)18、【单选题】(5 分)CA.B.C.D.19、【单选题】(5 分)BA.y=2B.y=-1C.y=0D.不存在20、【单选题】(5 分)CA.0B.1C.2D.3第四章1、【单选题】(5 分)DA.B.C.D.2、【单选题】(5 分)CA.B.C.D.3、【单选题】(5 分)BA.B.C.D.4、【单选题】(5 分)DA.B.C.D.5、【单选题】(5 分)下列等式中正确的是(D)A.B.C.D.6、【单选题】(5 分)CA.B.C.D.7、【单选题】(5 分)BA.B.C.D.8、【单选题】(5 分)BA.B.C.D.9、【单选题】(5 分)BA.B.C.D.10、【单选题】(5 分)CA.B.C.D.11、【单选题】(5 分)BA.B.C.D.12、【单选题】(5 分)BA.B.C.D.13、【单选题】(5 分)CA.B.C.D.14、【单选题】(5 分)CA.B.C.D.15、【单选题】(5 分)CA.B.C.D.16、【单选题】(5 分)AA.B.C.D.17、【单选题】(5 分)AA.B.C.D.18、【单选题】(5 分)CA.B.C.D.19、【单选题】(5 分)DA.B.C.D.20、【单选题】(5 分)CA.B.C.D.第五章1、【单选题】(5 分)CA.B.C.D.2、【单选题】(5 分)CA.B.C.D.没有任何关系3、【单选题】(5 分)AA.B.C.=0D.不能确定4、【单选题】(5 分) 下列积分最大的是(C)A.B.C.D.5、【单选题】(5 分)BA.B.C.D.6、【单选题】(5 分)AA.B.C.D.7、【单选题】(5 分)BA.B.C.D.8、【单选题】(5 分)CA.0B.-1C.1D.9、【单选题】(5 分)BA.B.C.D.10、【单选题】(5 分)DA.0B.C.D.211、【单选题】(5 分)DA.2B.-1C.1D.012、【单选题】(5 分)DA.B.C.D.213、【单选题】(5 分)AA.10B.8C.6D.414、【单选题】(5 分)DA.B.C.D.15、【单选题】(5 分)下列广义积分中,收敛的是(B)A.B.C.D.16、【单选题】(5 分)DA.B.C.D.17、【单选题】(5 分)BA.B.C.D.18、【单选题】(5 分)BA.B.C.D.19、【单选题】(5 分)CA.B.C.D.20、【单选题】(5 分)AA.B.C.D.第六章1、【单选题】(5 分)BA.B.C.D.2、【单选题】(5 分)AA.454B.400C.399D.4503、【单选题】(5 分)CA.4B.10C.5D.34、【单选题】(5 分)DA.增加约 0.33%B.减少约 0.33%C.增加约 0.66%D.减少约 0.66%5、【单选题】(5 分)AA.20B.1C.17.1D.10。
微积分(经管类)14-15-1期末试题答案2014.12

天津工业大学(2014—2015学年第一学期)《微积分(经管)》期末试卷(A 卷)(2015. 1理学院)特别提示:请考生在密封线左侧的指定位置按照要求填写个人信息,若写在其它处视为作弊。
本试卷共有八道大题,请认真核对后做答,若有疑问请与监考教师联系。
满分 21307888810总分 复核题目一 二 三 四 五 六 七 八得分评阅人一. 填空题(每空3分,请将答案写在空格处)1、 求极限311cos (1cos )limx x e x x →-=--4。
2、 设2cos2(1)xy x x π=- 的第一类间断点为:1x =。
3、 设0()0f x '≠存在,且当0x ∆→时,00()()f x x f x -∆-与A x ∆是等价无穷小,则常数A = 0()f x '-。
4、积分124215sin cos 1d x x x x x x -+-⎰=16π。
5、函数arcsin sin(tan )y x x x =+的微分=dy 22[arcsin sec cos tan ]1x x x x dx x ++-。
满分 21 得分 -------------------------------密封线----------------------------------------密封线----------------------------------------密封线---------------------------------------学院专业班学号姓名装订线装订线装订线6、函数(1)(2)x x y x x =--的水平渐近线为1y =±。
7、生产某产品的固定成本0C ,边际成本和边际收益分别为11114q MC 2+-=q , 2q -100MR =,求厂商利润表达式(只列式子不计算): ()()[]002111142100)(C dq q q q q L q-+---=⎰。
2014—2015学年第一学期14级经济管理基础A

2014—2015学年第⼀学期14级经济管理基础A课程编号:2014 — 2015学年第⼀学期上海中侨职业技术学院经济管理基础期末试卷(考试课程 A卷)(本试卷满分100分;考试时间:90分钟;考试⽅式:闭卷笔试出卷⼈:于建云出卷时间:)系年级专业班级姓名学号座位号得分统计表:⼀、单项选择题(每题1分,共15题,15分)1、下列不会引起⽜排需求发⽣变化的情况是():A.医⽣说多吃⽜⾁有损健康B.⽜的饲养者宣传⽜排中含有丰富的维⽣素C.⽜排价格从每千克3美元上升到每千克3.5美元D.汉堡包价格从每千克2美元跌到每千克1.5美元2、⽐萨和炸⽟⽶饼是替代品。
如果⽐萨价格上升,则():A.⽐萨的需求减少,炸⽟⽶饼的需求增加B.两种商品的需求都减少C.炸⽟⽶饼的需求量增加,⽐萨的需求量减少D.⽐萨的需求量减少,炸⽟⽶饼的需求增加3、长期供给弹性⽐短期供给弹性⼤是因为()A.在长期,机器和建筑物的存量可以调节B.在长期,新企业可以进⼊,现存企业可以退出C.在长期,顾客可以发现替代品D.a和b都对4、如果某⼀种商品的价格下跌10%,由此导致⼈们⽤于购买该商品的货币⽀出增加5%,则需求曲线在这⼀区域内的需求价格弹性为():A.富有弹性B.完全⽆弹性C.缺乏弹性,但不是完全⽆弹性D.具有单位弹性5、政府为了扶持农业,对农产品规定了⾼于其均衡价格的⽀持价格。
政府为了维持⽀持价格,应该采取的相应措施是()A.增加对农产品的税收B.实⾏农产品配给制C.收购过剩的农产品D.对农产品⽣产者予以补贴6、以下哪⼀种关于长期总供给曲线的表述是正确的?长期总供给曲线( )A.当⾃然失业率下降时向左移动。
B.是垂直的,因为所有物价与⼯资等的变动并不影响产量C.向右上⽅倾斜,因为价格预期和⼯资在长期中是固定的。
D.当政府提⾼最低⼯资时向右移动。
7、以下哪⼀个事件会使短期总供给曲线向右移动?()A.政府军备⽀出增加B.物价预期上升C.⽯油价格下降D.货币供给减少E.以上各项都不是8、以下不属于管理职能的是——。
《高等数学(经管类)》(上)勘误
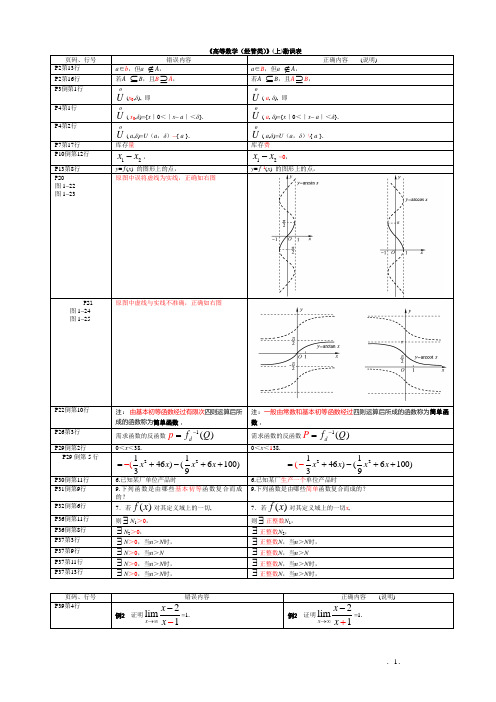
4.(1)-40
4.(1)-20
P208倒第8行
5.(2)减少13.9%
5.(2)增加13.9%
P208倒第7行
6.(1)
6.(1)
P208倒第6行
P208倒第5行
P208倒第4行
P208倒第2行
(2)-0.8,价格上涨1%,需求减少0.8%.
(2)-1,价格上涨1%,需求减少1%.
P208倒第1行
(3)增加0.2%;
(3)不变;
页码、行号
错误内容
正确内容(说明)
P209倒第4行
P209第6行
8.-3, 0,1
8.3, 3,2
P211第1行
P213倒第1行
2.(1)
2.(1)
P214第2行
(4)
(4)
P217倒第4行
(2)
(2)
P178第10行
P179倒第8行
P181第9行
例4设函数 在区间 上连续,
例4设函数 在区间 上连续,
P182倒第5行
牛顿-莱布尼茨公式
牛顿-莱布尼兹公式
P185倒第6行
上式(6-5)表明定积分
上式表明定积分
P187倒第4行
图6-7中:
图6-7中:
P193第2行
(7)
(7)
P194倒第2行
比如,对于例24有:
N>0,当n>N
正整数N,当n>N
P37第11行
N>0,当n>N时,
正整数N,当n>N时,
P37第13行
N>0,当n>N时,
正整数N,当n>N时,
页码、行号
错误内容
正确内容(说明)
P39第4行
高等数学经管类参考答案与提示

参考答案与提示习题1-21、7)0(=f ;27)4(=f ;9)21(=-f ;732)(2+-=a a a f ;62)1(2++=+x x x f2、1)2(-=-f ;0)1(=-f ;1)0(=f ;2)1(=f3、(1)[)(]1,00,1 -;(2)1>x (3)[]3,1- (4)()()()+∞∞-,22,11,4、(1)x y 2cos 2+=(2)23cot x arc y =习题1-31. (1)5;(2)1;(3)不存在;(4)不存在 2.(1)2;(2)25;(3)23;(4)32-;(5)12-;(6)1. 习题1-41. (1)无穷小;(2)无穷大;(3)无穷大(∞-);(4)-→0x 时是无穷小;+→0x 时是无穷大;2. (1)同阶无穷小;(2)高阶无穷小;(3)等价无穷小3. (1)1;(2)21;(3)23;(4)1 习题1-5(1).24;( 2).0;( 3).35;(4).∞;(5).503030532⋅;(6).21-;(7).0;(8).1259-;(9).24925+;(10).0 习题1-61.(1)35;(2)1x xsin lim x -=-→ππ;(3)4;(4)32(5)2;(6)2 2.(1)8e ;(2)1-e ;(3)32-e;(4)2-e (5)5e ;(6)e习题1-71.1=a ;1=b2.(1)1±=x 是第二类间断点中无穷间断点;(2)0x =是第二类间断点中的无穷间断点;(3)1=x 是第一类间断点中可去间断点;(4)1-=x 是第二类间断点中的无穷间断点,1=x 是第一类间断点中的跳跃间断点3.(1))1ln(+e ;(2)232;(3)e a log 3;(4)1 复习题一1、(1)1;(2)[]2,1)0,2(⋃-;(3)[)3,0;(4)3;(5)ke ;(6)23;(7)2;(8)第一类间断点且可去间断点2、(1)C ;(2C (A.1x y -=;1x y .C --=);(3)B ;(4)B ;(5)C ;(6)D ;(7)A ;(8)A3、(1)34;(2)312x x )1x sin(21x lim =-+-→;(3)2-e ;(4)1)x (sin x sin 330x lim =→;(5)31;(6)0)2x (sin xx 3x 2x lim=+-+∞→;(7)a cos ;(8)4π-4、1=a5、23=a 6、6b ,4a == 7、(1)21;(2)a 28、(1)11=x 是第一类间断点且是可去间断点,22=x 是第二类型无穷间断点;(2)01=x 是第一类间断点且是可去间断点,)(22Z k k x ∈+=ππ是第二类型无穷间断点;(3)0=x 是第一类间断点且是可去间断点;(4)0=x 是第一类间断点且是跳跃间断点 9、1=a习题2-11、(1) √ (2) × (3) × (4) × (5) × (6)、√2、2126()v t t =+∆+∆ 0.10.012|12.61|12.0601|12t t t v v v ∆=∆=====3、()2f x '=4、 (1) 在0x =处连续且可导(2) 在0x =处连续,但不可导5、切线方程:210x y --= 法线方程:230x y +-=6、t t d dtθ=7、dT dt习题2-21、 (1) × (2) × (3)、× (4)、√ (5)、×2、 (1) (0)0()2f f ππ''== (2) (0)1()1f f π''==- (3) (0)0(1)13f f ''== (4) 11(1)(4)418f f ''=-=-3、略4、 (1)2664x x ++ (2)212ln 2xx -(3)12632220xx x -----(4)1cos x x +(5)(ln sin cos )xa a x x ⋅+ (6)1cos ln sin x x x x⋅+(7)2983x x +- (8) 22(2tan 2sec )sec x x x x x ++(9) 31221122x x ---- (10)2sin 1cos x x x x ++-(11) 11222(1)x xx -+-- (12)22cos (sin 1)x x -- (13) cos 1sin x x x -+ (14) 22sin cos cos (1)x x x x x x +++(15)122ln 22xxx x --- (16)3cos 2sin 2x x xx- 5、切线方程:ln 210x y -+= 法线方程:ln 2ln 20x y +-= 6、切点坐标:(1,1)-- 切线方程:20x y ++= 法线方程:0x y -=习题2-31、(1)√ (2) × (3)× (4) ×2、(1) 2(41)xe x x ++(2) (3) tan x -(4) 23ln (1)+1x x + (5))1x ln n (nx 1n +- (6) 222sin 2sin 2sin cos x x x x x +(7)(8) (9) 24()x x e e ---(10)arcsin x(11)(12) 2242(1)16x x x -++ 3、()(1)(4)824f x f f '''===4、切线方程:20x y e --= 法线方程:230x y e +-= 5、30x y --习题2-41、(1)223(1)a y - (2)x ayax y+-+ (3)x y x y e y e x ---+ (4)21y xy - (5)y y e x -+ (6)cos()cos()x y x y e y xy e x xy +++-+2、 (1)232(2)31y y y x x x +-+-+ (2)cot 224(1)xxy y ye x x e +-- (3)(cos ln cos sin tan )y x x x x - (4) ln(5)5xyy x x -+-+ 3、(1)232te - (2) tan t 4、32t dydx π==-- 5、 (1)在0x =处切线方程:210x y +-= 法线方程:220x y -+=(2)在2t =处切线方程:43120x y a +-= 法线方程:3460x y a -+=习题2-51、 (1) 221(ln 3)3xx -(2) 22csc cot x x ⋅ (3)22(arctan )1x x x ++ (4) 2sec (tan sec )x x x + (5) -322(1)x x -+ (6) 21(ln 1)x x x x x-++2、(1) (1)7,(1)4,(1)0f f f ''''''=== (2)11(1),(0)2,(1)22f f f ''''''-==-= 3、 (1)0 (2) 3(ln3)xn(3)()11(2)!ln 1(1)(3)n n n n y x y y n xx--'''=+==-⋅≥ (4) ()xn x e + (5) 12cos(2)2n y x n π-=+⋅(6) 11(1)!5n ny n x +⎛⎫=- ⎪+⎝⎭4、略5、 (1)(4)4sin x ye x =-(2) (5)22sin cos 16cos y x x x x x =-- (3)(20)0y = 6、31cot 3,sin 3a θθ--。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
班级 会计1509 姓名 梁谢谢第一章 函数一、选择题1. 下列函数中,【 】不是奇函数A. x x y +=tanB. y x =C. )1()1(-⋅+=x x yD. x xy 2sin 2⋅=2. 下列各组中,函数)(x f 与)(x g 一样的是【 】A. 33)(,)(x x g x x f == B.x x x g x f 22tan sec )(,1)(-== C. 11)(,1)(2+-=-=x x x g x x f D. 2ln )(,ln 2)(x x g x x f ==3. 下列函数中,在定义域内是单调增加、有界的函数是【 】A. +arctan y x x =B. cos y x =C. arcsin y x =D. sin y x x =⋅4. 下列函数中,定义域是[,+]-∞∞,且是单调递增的是【 】A. arcsin y x =B. arccos y x =C. arctan y x =D. arccot y x = 5. 函数arctan y x =的定义域是【 】A. (0,)πB. (,)22ππ-C. [,]22ππ-D. (,+)-∞∞6. 下列函数中,定义域为[1,1]-,且是单调减少的函数是【 】A. arcsin y x =B. arccos y x =C. arctan y x =D. arccot y x = 7. 已知函数arcsin(1)y x =+,则函数的定义域是【 】A. (,)-∞+∞B. [1,1]-C. (,)ππ-D. [2,0]- 8. 已知函数arcsin(1)y x =+,则函数的定义域是【 】A. (,)-∞+∞B. [1,1]-C. (,)ππ-D. [2,0]-9. 下列各组函数中,【 】是相同的函数A. 2()ln f x x =和 ()2ln g x x =B. ()f x x =和()g x =C. ()f x x =和()2g x = D. ()sin f x x =和()arcsin g x x =10. 设下列函数在其定义域内是增函数的是【 】A. ()cos f x x =B. ()arccos f x x =C. ()tan f x x =D. ()arctan f x x = 11. 反正切函数arctan y x =的定义域是【 】A. (,)22ππ-B. (0,)πC. (,)-∞+∞D. [1,1]- 12. 下列函数是奇函数的是【 】A. arcsin y x x =B. arccos y x x =C. arccot y x x =D. 2arctan y x x = 13. 函数53sin ln x y =的复合过程为【 】A.x w w v v u u y sin ,,ln ,35====B.x u u y sin ln ,53== C.x u u y sin ,ln 53== D.x v v u u y sin ,ln ,35===二、填空题1. 函数5arctan 5arcsinxx y +=的定义域是___________.2. ()arcsin 3xf x =的定义域为 ___________.3. 函数1()arcsin3x f x +=的定义域为 ___________。
4. 设()3x f x =,()sin g x x x =,则(())g f x =___________.5. 设2()f x x =,()ln g x x x =,则(())f g x =___________.6.()2x f x =,()ln g x x x =,则(())f g x =___________.7. 设()arctan f x x =,则()f x 的值域为___________.8. 设2()arcsin f x x x =+,则定义域为 . 9. 函数ln(2)arcsin y x x =++的定义域为 .10. 函数2sin (31)y x =+是由_________________________复合而成。
第二章 极限与连续一、选择题1. 数列}{n x 有界是数列}{n x 收敛的【 】A. 充分必要条件B. 充分条件C. 必要条件D. 既非充分条件又非必要条件2. 函数)(x f 在点0x 处有定义是它在点0x 处有极限的【 】A. 充分而非必要条件B. 必要而非充分条件C. 充分必要条件D. 无关条件3. 极限2lim(1)k xx x e →+=,则=k 【 】A. 2B. 2-C. 2-eD. 2e4. 极限sin 2limx xx→∞=【 】A. 2B. ∞C. 不存在D.5. 极限=+→xx x 10)sin 1(lim 【 】A. 1B. ∞C. 不存在D. e6. 函数231)(22+--=x x x x f ,下列说法正确的是【 】.A. 1=x 为其第二类间断点B. 1=x 为其可去间断点C. 2=x 为其跳跃间断点D. 2=x 为其振荡间断点 7. 函数()sin xf x xπ=的可去间断点的个数为【 】.A. 0B. 1C. 2D. 38. 1=x 为函数231)(22+--=x x x x f 的【 】.A. 跳跃间断点B. 无穷间断点C. 连续点D. 可去间断点 9. 当0→x 时,2x 是2x x -的【 】A. 低阶无穷小B. 高阶无穷小C. 等价无穷小D. 同阶但非等价的的无穷小 10. 下列函数中,定义域是[1,1]-,且是单调递减的是【 】A. arcsin y x =B. arccos y x =C. arctan y x =D. arccot y x =11. 下列命题正确的是【 】A. 有界数列一定收敛B. 无界数列一定收敛C. 若数列收敛,则极限唯一D. 若函数()f x 在0x x =处的左右极限都存在,则()f x 在此点处的极限存在 12. 当变量0x →时,与2x 等价的无穷小量是【 】A . s i nx B. 1cos2x - C. ()2ln 1x + D. 21x e - 13. 1x =是函数22()1x f x x -=-的【 】.A. 无穷间断点B. 可去间断点C.跳跃间断点D. 连续点 14. 下列命题正确的是【 】A. 若0()f x A =,则0lim ()x x f x A →=B. 若0lim ()x x f x A →=,则0()f x A =C. 若0lim ()x x f x →存在,则极限唯一D. 以上说法都不正确15. 当变量0x →时,与2x 等价的无穷小量是【 】A. tan xB.1cos2x-C. ()2ln 1x+ D. 21xe-16. 0x =是函数2+1()1cos2x f x x=-的【 】.A. 无穷间断点B. 可去间断点C. 跳跃间断点D. 连续点17. 0(+0)f x 与0(0)f x -都存在是()f x 在0x 连续的【 】A. 必要条件B. 充分条件C. 充要条件D. 无关条件18. 当变量0x →时,与2x 等价的无穷小量是【 】A. arcsin x B . 1cos2x-C. ()2ln 1x + D. 21xe -19. 2x =是函数221()32x f x x x -=-+的【 】.A. 无穷间断点B. 可去间断点C. 跳跃间断点D. 连续点 20. {}n u 收敛是{}n u 有界的【 】A. 充分条件B. 必要条件C. 充要条件D. 无关条件21. 下面命题正确的是【 】A. 若{}n u 有界,则{}n u 发散B. 若{}n u 有界,则{}n u 收敛C. 若{}n u 单调,则{}n u 收敛D. 若{}n u 收敛,则{}n u 有界 22. 下面命题错误的是【 】A. 若{}n u 收敛,则{}n u 有界B. 若{}n u 无界,则{}n u 发散C. 若{}n u 有界,则{}n u 收敛D. 若{}n u 单调有界,则{}n u 收敛23. 极限10lim(13)x x →+=【 】A.∞B. 0C. 3e -D. 3e24. 极限1lim(13)x x x →-=【 】A.∞B. 0C. 3e -D. 3e25. 极限2lim(12)x x x →-=【 】A.4e B. 1C. 2e -D. 4e -26. 1x =是函数32()2x x f x x x -=+-的【 】A. 连续点B. 可去间断点C.无穷间断点D. 跳跃间断点27. 2x =-是函数32()2x x f x x x -=+-的【 】A. 连续点B. 可去间断点C.无穷间断点D. 跳跃间断点28. 2x =-是函数224()2x f x x x -=+-的【 】A. 连续点B. 可去间断点C.无穷间断点D. 跳跃间断点 29. 下列命题不正确的是【 】A. 收敛数列一定有界B. 无界数列一定发散C. 收敛数列的极限必唯一D. 有界数列一定收敛30. 极限211lim 1x x x →--的结果是【 】A. 2B. 2-C. 0D.不存在31. 当x →0时, 1sinx x是【 】 A. 无穷小量 B.无穷大量C. 无界变量D. 以上选项都不正确32. 0x =是函数sin ()xf x x=的【 】. A. 连续点 B. 可去间断点 C. 跳跃间断点 D.无穷间断点33. 设数列的通项(1)1nn x n-=+,则下列命题正确的是【 】A. {}n x 发散B. {}n x 无界C. {}n x 收敛D. {}n x 单调增加34. 极限21lim x x x x→-的值为【 】A. 1B. 1-C. 0D. 不存在 35. 当0x →时,sin x x -是x 的【 】A. 高阶无穷小B. 同阶无穷小,但不是等价无穷小C. 低阶无穷小D. 等价无穷小 36. 0x =是函数1()1xf x e =-的【 】. A. 连续点 B. 可去间断点 C. 跳跃间断点 D. 无穷间断点 37. 观察下列数列的变化趋势,其中极限是1的数列是【 】A. 1n nx n =+ B. 2(1)n n x =-- C. 13n x n =+ D. 211n x n =-38. 极限0lim x xx→的值为【 】A. 1B. 1-C. 0D. 不存在39. 下列极限计算错误的是【 】A. sin lim1x x x →∞= B. 0sin lim 1x xx→=C. 1lim(1)x x e x→∞+= D. 10lim(1)x x x e →+=40. 1x =是函数22()2x x f x x x -=+-的【 】.A. 连续点B. 可去间断点C. 无穷间断点D. 跳跃间断点 41. 当∞→x 时,arctanx 的极限【 】A.2π=B.2π-= C.∞= D.不存在42. 下列各式中极限不存在的是【 】A. ()327lim 1→∞-+-x x x x B. 2211lim 21→---x x x xC. sin 3lim→∞x x x D. ()201lim cos →+x x x x43. 无穷小量是【 】A.比0稍大一点的一个数B.一个很小很小的数C.以0为极限的一个变量D. 数0 44. 极限1lim(1)→-=x x x 【 】A.∞B. 1C. 1-e D. e45. 1=x 是函数21()1-=-x f x x 的【 】.A. 可去间断点B. 跳跃间断点C.无穷间断点D. 连续点46. 0=x 是函数1sin 0()10⎧<⎪=⎨⎪+≥⎩x x x f x xex 的【 】A. 连续点B. 可去间断点C.跳跃间断点D. 无穷间断点47. 01lim sinx x x→的值为【 】A. 1B. ∞C. 不存在D. 048. 当→∞x 时下列函数是无穷小量的是【 】A. cos -x x xB. sin x xC. 2sin -x xx D. 1(1)x x +49. 设210()210x x f x x x ⎧+<=⎨+≥⎩,则下列结论正确的是【 】A.()f x 在0x =处连续B.()f x 在0x =处不连续,但有极限C.()f x 在0x =处无极限D.()f x 在0x =处连续,但无极限二、填空题1. 当0→x 时,x cos 1-是2x 的_______________无穷小量.2. 0x =是函数xxx f sin )(=的___________间断点. 3.=-→x x x20)11(lim ___________。
