韩伯棠管理运筹学(第三版)_第十一章_图与网络模型
广东工业大学 管理运筹学第11章 图与网络模型2

初等圈
管
理
运
筹
学
27
连通图(3)
有向图
道路 回路
无向图
链(或道路) 圈(或回路)
道路(边的方向一致)
管 理 运 筹 学
不是道路
28
连通图(4)
定义10 一个图中任意两点间至少有一条链相 连,则称此图为连通图。任何一个不连通图 总可以分为若干个连通子图,每一个称为原 图的一个分图(连通分支)。
连通图
定义7 图G=(V, E), 若E'是E的子集,若V'是V 的子集,且E'中的边仅与V'中的顶点相关联, 则称G' = (V', E')为图G的一个子图,特别地, 若V' =V, 则称G'为G的一个生成子图(支撑子 图)。
子图 筹 管 理 运
学
生成子图
24
图与网络的基本概念(9)
有时需要用图来表示事物及事物之间的定量 的联系,这时图中除了顶点与边外,还有与 点或边有关的某些数量指标,常称它们为 “权”,权在图中可以表示距离、费用、通 过能力等。这种点或边带权的图称为网络 (或赋权图)
定理1 任何图中顶点次数的总和等于边数 的2倍。 定理2 任何图中次为奇数的顶点必有偶数 个。 定义6 在有向图中,以顶点v为始点的边数 称为顶点v的出次,记为d+(v);以v为终点 的边数称为v的入次,记为d-(v)。顶点v的 出次与入次的和称为点v的次。
管 理 运 筹 学
23
图与网络的基本概念(8)
管
理
运
筹
学
33
Dijkstra算法
原理:若(vs, v1, … , vn-1, vn)是vs到vn的最短路, 则(vs, v1, … , vn-1)是vs到vn-1的最短路。 思路:采用标号法。使用两种标号,T标号和P标号,
韩棠伯管理运筹学习题答案

韩棠伯管理运筹学习题答案韩棠伯管理运筹学习题答案韩棠伯是一位热爱学习的年轻人,对于管理运筹学这门课程也充满了兴趣。
每天晚上,他都会认真完成老师布置的学习题,以便更好地掌握这门学科的知识。
在这里,我们将为大家分享韩棠伯管理运筹学习题的答案。
第一题:线性规划韩棠伯在学习线性规划时,遇到了以下一道题目:某公司生产两种产品A和B,每个单位产品A的利润为10元,产品B的利润为15元。
产品A每个单位需要2个工时,产品B每个单位需要3个工时。
公司每天可用的总工时为60个。
问应该如何安排生产,才能获得最大利润?答案:设产品A的产量为x,产品B的产量为y。
根据题目中的条件,我们可以列出以下线性规划模型:目标函数:Maximize 10x + 15y约束条件:2x + 3y ≤ 60非负约束:x ≥ 0, y ≥ 0通过求解这个线性规划模型,我们可以得到最大利润的产量分配方案。
第二题:排队论在学习排队论时,韩棠伯碰到了以下一道题目:某家餐厅有一个服务台,平均每小时有30名顾客到达,服务员平均每小时能为25名顾客提供服务。
问在稳定状态下,平均顾客等待时间是多少?答案:根据排队论的基本原理,我们可以使用排队模型来解决这个问题。
根据题目中的条件,我们可以得到以下参数:顾客到达率(λ)= 30人/小时服务率(μ)= 25人/小时利用排队模型中的公式,我们可以计算出平均顾客等待时间(Wq):Wq = λ / (μ - λ)将具体数值代入公式,我们可以计算出平均顾客等待时间。
第三题:决策树在学习决策树时,韩棠伯遇到了以下一道题目:某公司要决定是否投资于一个新的项目。
如果投资成功,公司将获得300万元的利润;如果投资失败,公司将损失200万元。
根据市场分析,投资成功的概率为0.6,失败的概率为0.4。
问公司应该如何决策?答案:我们可以使用决策树来解决这个问题。
根据题目中的条件,我们可以绘制出以下的决策树:投资成功(0.6)/ \获得300万元损失200万元投资失败(0.4)/ \获得0万元损失200万元根据决策树,我们可以计算出投资的期望值,即投资成功的利润乘以成功的概率加上投资失败的利润乘以失败的概率。
韩伯棠教授《管理运筹学》第三版习题答案 高等教育出版社
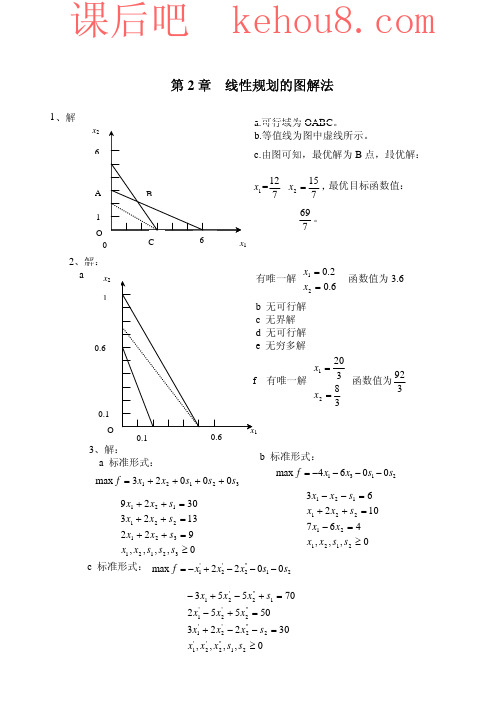
6 、解: b 1 ≤ c1 ≤ 3
c 2 ≤ c2 ≤ 6
d x1 = 6 x2 = 4
e x1 ∈ [4,8] x2 = 16 − 2x1
f 变化。原斜率从 − 2 变为 −1 3
7、解: 模型:
max z = 500x1 + 400x2
2x1 ≤ 300 3x2 ≤ 540 2x1 + 2x2 ≤ 440 1.2x1 +1.5x2 ≤ 300 x1, x2 ≥ 0
h 100×50=5000 对偶价格不变 i能 j 不发生变化 允许增加的百分比与允许减少的百分比之和没有超出 100% k 发生变化 2、解:
a 4000 10000 62000 b 约束条件 1:总投资额增加 1 个单位,风险系数则降低 0.057
约束条件 2:年回报额增加 1 个单位,风险系数升高 2.167 c 约束条件 1 的松弛变量是 0,约束条件 2 的剩余变量是 0
f 600000 + 300000 = 100% 故对偶价格不变 900000 900000
4、解:
a x1 = 8.5 x2 = 1.5 x3 = 0 x4 = 1 最优目标函数 18.5
b 约束条件 2 和 3
对偶价格为 2 和 3.5
c 选择约束条件 3,最优目标函数值 22
d 在负无穷到 5.5 的范围内变化,其最优解不变,但此时最优目标函数值变化
课后吧 kehou8.com
第 2 章 线性规划的图解法
1、解:
x2
6
a.可行域为 OABC。 b.等值线为图中虚线所示。
c.由图可知,最优解为 B 点,最优解:
A
B
12 x1 = 7
x2
《管理运筹学》第4版课后习题解析(韩伯棠)
《管理运筹学》第四版课后习题解析
韩伯棠
(2)模型变为 max z 5 xA 4 xB
50 xA 100 xB ≤ 1 200 000 100 xB ≥ 300 000 xA , xB ≥ 0
推导出 x1 18 000 , x2 3 000 ,故基金 A 投资 90 万元,基金 B 投资 30 万元。
第 2 章 线性规划的图解法
1.解: (1)可行域为 OABC。 (2)等值线为图中虚线部分。 (3)由图 2-1 可知,最优解为 B 点,最优解 x1 =
12 15 69 , x2 ;最优目标函数值 。 7 7 7
图 2-1 2.解: (1)如图 2-2 所示,由图解法可知有唯一解
8
《管理运筹学》第四版课后习题解析
韩伯棠
第 3 章 线性规划问题的计算机求解
1.解: ⑴甲、乙两种柜的日产量是分别是 4 和 8,这时最大利润是 2720 ⑵每多生产一件乙柜,可以使总利润提高 13.333 元 ⑶常数项的上下限是指常数项在指定的范围内变化时, 与其对应的约束条件的对偶价格不变。 比如油漆时间变为 100,因为 100 在 40 和 160 之间,所以其对偶价格不变仍为 13.333 ⑷不变,因为还在 120 和 480 之间。 2.解: ⑴不是,因为上面得到的最优解不为整数解,而本题需要的是整数解 ⑵最优解为 (4,8) 3 .解: ⑴农用车有 12 辆剩余 ⑵大于 300 ⑶每增加一辆大卡车,总运费降低 192 元 4.解: 计算机得出的解不为整数解,平移取点得整数最优解为(10,8) 5.解: 圆桌和衣柜的生产件数分别是 350 和 100 件,这时最大利润是 3100 元 相差值为 0 代表,不需要对相应的目标系数进行改进就可以生产该产品。 最优解不变,因为 C1 允许增加量 20-6=14;C2 允许减少量为 10-3=7,所有允许增加百分比 和允许减少百分比之和(7.5-6)/14+(10-9)/7〈100%,所以最优解不变。 6.解: (1) x1 150 , x2 70 ;目标函数最优值 103 000。 (2)1、3 车间的加工工时数已使用完;2、4 车间的加工工时数没用完;没用完的加工工时 数为 2 车间 330 小时,4 车间 15 小时。 (3)50,0,200,0。 含义:1 车间每增加 1 工时,总利润增加 50 元;3 车间每增加 1 工时,总利润增加 200 元; 2 车间与 4 车间每增加一个工时,总利润不增加。 (4)3 车间,因为增加的利润最大。 (5)在 400 到正无穷的范围内变化,最优产品的组合不变。 (6)不变,因为在 0,500 的范围内。 (7)所谓的上限和下限值指当约束条件的右边值在给定范围内变化时,约束条件 1 的右边 值在 200,440 变化,对偶价格仍为 50(同理解释其他约束条件) 。 (8)总利润增加了 100×50=5 000,最优产品组合不变。 (9)不能,因为对偶价格发生变化。
《管理运筹学》第三版习题答案(韩伯棠教授)

第 2 章 线性规划的图解法11a.可行域为 OABC 。
b.等值线为图中虚线所示。
12c.由图可知,最优解为 B 点,最优解: x 1 = 769 。
7 2、解:15 x 2 =7, 最优目标函数值:a x 210.60.1O1有唯一解x 1 = 0.2函数值为 3.6x 2 = 0.6b 无可行解c 无界解d 无可行解e 无穷多解1 2 2 1 2f 有唯一解20 x 1 =3 8函数值为 92 33、解:a 标准形式:b 标准形式:c 标准形式:x 2 = 3max fmax f= 3x 1 + 2 x 2 + 0s 1 + 0s 2 + 0s 3 9 x 1 + 2x 2 + s 1 = 303x 1 + 2 x 2 + s 2 = 13 2 x 1 + 2x 2 + s 3 = 9 x 1 , x 2 , s 1 , s 2 , s 3 ≥= −4 x 1 − 6x 3 − 0s 1 − 0s 23x 1 − x 2 − s 1 =6x 1 + 2x 2 + s 2 = 10 7 x 1 − 6 x 2 = 4x 1 , x 2 , s 1 , s 2 ≥max f = −x ' + 2x ' − 2 x ''− 0s − 0s'''− 3x 1 + 5x 2 − 5x 2 + s 1 = 70 2 x ' − 5x ' + 5x '' = 50122' ' ''3x 1 + 2 x 2 − 2x 2 − s 2 = 30'' ''4 、解:x 1 , x 2, x 2, s 1 , s 2 ≥ 0标准形式: max z = 10 x 1 + 5x 2 + 0s 1 + 0s 23x 1 + 4 x 2 + s 1 = 9 5x 1 + 2 x 2 + s 2 = 8 x 1 , x 2 , s 1 , s 2 ≥ 0s 1 = 2, s 2 = 0标准形式: min f = 11x 1 + 8x 2 + 0s 1 + 0s 2 + 0s 310 x 1 + 2x 2 − s 1 = 203x 1 + 3x 2 − s 2 = 18 4 x 1 + 9x 2 − s 3 = 36 x 1 , x 2 , s 1 , s 2 , s 3 ≥ 0s 1 = 0, s 2 = 0, s 3 = 136 、解:b 1 ≤c 1 ≤ 3c 2 ≤ c 2 ≤ 6d x 1 = 6 x 2 = 4e x 1 ∈ [4,8]x 2 = 16 − 2x 1f 变化。
《管理运筹学》第三版习题答案(韩伯棠教授)_khdaw

课后答案网
f
有唯一解
x1
=
20 3
函数值为 92
m x2
=
8 3
3
o 3、解: .c a 标准形式:
max f = 3x1 + 2x2 + 0s1 + 0s2 + 0s3
khdaw om b 标准形式:
9x1 + 2x2 + s1 = 30 3x1 + 2x2 + s2 = 13 2x1 + 2x2 + s3 = 9 x1, x2 , s1, s2 , s3 ≥ 0
30 − 9.189 111.25 −15
其对偶价格是否有变化
若侵犯了您的版权利益,敬请来信通知我们! ℡
课后答案网
第 4 章 线性规划在工商管理中的应用
m 1、解:为了用最少的原材料得到 10 台锅炉,需要混合使用 14 种下料方案
w o x1, x2,s1,s2 ≥ 0
khdaw.c s1 = 2,s2 =0
若侵犯了您的版权利益,敬请来信通知我们! ℡
课 后 答 案 网
课后答案网
5 、解: 标准形式: min f = 11x1 + 8x2 + 0s1 + 0s2 + 0s3 10x1 + 2x2 − s1 = 20
e x1 ∈ [4,8] x2 = 16 − 2x1
w f 变化。原斜率从 − 2 变为 −1 3
a 7、解: 模型: d max z = 500x1 + 400x2 h 2x1 ≤ 300 .k 3x2 ≤540 2x1 + 2x2 ≤ 440 1.2x1 +1.5x2 ≤ 300 wx1, x2 ≥ 0 a x1 = 150 x2 = 70 即目标函数最优值是 103000 w b 2,4 有剩余,分别是 330,15。均为松弛变量 m c 50, 0 ,200, 0 额外利润 250 w o d 在[0,500]变化,最优解不变。 .c e 在 400 到正无穷变化,最优解不变。 khdaw f 不变
管理运筹学--第11章 网络计划祥解

(4)工序a有紧后工序b与d,工序c有紧后工序d与e.
a b d c e
网络计划图是有向、有序的赋权图, 按项目 的工作流程自左向右的绘制. 在时序上反应完成各项工作的先后顺序. 节点编号必须按照箭尾节点的编号小于箭 头节点的编号 在网络图中只有一个起始节点,表示工程项 目的开始, 一个终点表示工程项目的完成。 线路:从起始节点开始沿箭线方向从左至 右到达终点的通路
i
实工序:需要时间的工序.可能不需要人力、物力.
虚工序:工时为的工序.不需要人力、物力, 不存在.
表明工序间的逻辑关系.
情况I:当多个工序都有一个共同的紧后(或紧 前)工序的同时,这多个工序中的一个或几个工 序还另有其他的紧后(或紧前)工序.
A C D
虚工序
B
情况II:当两工序有着共同的起始点和完成点.
网络计划
1956年美国杜邦公司制定了第一套网络计划 (Critical Path Method, CPM) 1958年美国海军武器部的“北极星”导弹计 划(Program Evaluation and Review Technique, PERT) 上海宝钢炼铁厂1号高炉土建施工、广州白 天鹅宾馆、软件开发、三峡工程等
A B A B
2. 事项
工序都有两个事项----开工事项、完工事项. tij j i (i ,j )
工序(i , j)的开 工事项
工序(i , j)的完 工事项
任一工序有且仅有两个事项;直接连结两个事项的箭杆 只能有一根.
a i a b j
i
b
j
×
i’
3. 工序间的基本逻辑关系
对工序(i, j):紧前工序、紧后工序、平行工序.
管理运筹学课件第11章 排队论

11.1.2 排队系统的三个特征
3.服务机构 从机构形式和工作情况来看有以下几种: (1)服务机构可以没有服务员,也可以有一个或多个服务员 (服务台、窗口)。如超市的货架可以没有服务员,但交款时可 能有多个服务员。 (2)多个服务台的情况中,可以是平行排列的(并联),也可 以是前后排列的(串联),也可以是混合的。 (3)服务方式可以对单个顾客进行,也可成批进行。我们只讨 S1 S1 论单个服务情况。 S S2 S2 (4)服务时间可分为确定型的和随机型的。如旅客列车对乘客 S3 S3 的服务是按列车时刻表进行位移服务的,是确定型的;因患者病 (a)单台单队 (b)多队多台并联 (c)单队多台并联 情不同,医生诊断的时间不是确定的,是随机型的。 S1 S4 (5)服务时间的分布总假定是平稳的,即分布的期望值、方差 S1 S2 S2 等参数不受时间的影响。
第11章 排队论
教学目标与要求
【教学目标】 1.理解下列基本概念:排队系统构成、特征、分类、主要性能指标及相互关系 2.掌握以下三种排队系统主要性能指标的计算:M/M/C/∞/∞;M/M/C/N/∞; M/M/C/∞/m。 3.了解M/G/1、M/D/1的主要指标计算公式 【知识结构】
基本概念 系统、特征、分类、指标、输入输出
2013-8-9
Ls Ws , 或Ws Ls
Lq Wq ,
Ws Wq 1
Ls Lq
Ls nPn
n 0
管理运筹学课件 n s 1
Lq
(n s ) P
n
12
11.1.5 排队系统的输入和输出
2013-8-9
模型的优化(目的) 管理运筹学课件
管理运筹学期末复习资料【韩伯棠】

运筹学(Operational Research)复习资料第一章绪论一、名词解释1.运筹学:运筹学是应用分析、试验、量化的方法,对经济管理系统中的人力、物力、财力等资源进行统筹安排,为决策者提供有依据的最优方案,以实现最有效的管理。
二、选择题1.运筹学的主要分支包括(ABDE )A图论B线性规划C非线性规划D整数规划E目标规划2. 最早运用运筹学理论的是( A )A . 二次世界大战期间,英国军事部门将运筹学运用到军事战略部署B . 美国最早将运筹学运用到农业和人口规划问题上C . 二次世界大战期间,英国政府将运筹学运用到政府制定计划D . 50年代,运筹学运用到研究人口,能源,粮食,第三世界经济发展等问题上第二章线性规划的图解法一、选择题/填空题1.线性规划标准式的特点:(1)目标函数最大化(2)约束条件为等式(3 决策变量为非负(4 ) 右端常数项为非负2. 在一定范围内,约束条件右边常数项增加一个单位:(1)如果对偶价格大于0,则其最优目标函数值得到改进,即求最大值时,最优目标函数值变得更大,求最小值时最优目标函数值变得更小。
(2)如果对偶价格小于0,则其最优目标函数值变坏,即求最大值时,最优目标函数值变小了;求最小值时,最优目标函数值变大了。
(3)如果对偶价格等于0,则其最优目标函数值不变。
3.LP模型(线性规划模型)三要素:(1)决策变量(2)约束条件(3)目标函数4. 数学模型中,“s·t”表示约束条件。
5. 将线性规划模型化成标准形式时,“≤”的约束条件要在不等式左端加上松弛变量。
6. 将线性规划模型化成标准形式时,“≥”的约束条件要在不等式左端减去剩余变量。
7.下列图形中阴影部分构成的集合是凸集的是A【解析】:如何判断是凸集?凸集:两点之间连线在图内凹集:两点之间连线在图外8. 线性规划问题有可行解且凸多边形无界,这时CA没有无界解 B 没有可行解 C 有无界解 D 有有限最优解9. 对于线性规划问题,下列说法正确的是( D )A. 线性规划问题可能没有可行解B. 在图解法上,线性规划问题的可行解区域都是“凸”区域C. 线性规划问题如有最优解,则最优解可在可行解区域顶点上到达D. 上述说法都正确第三章线性规划问题的计算机求解一、名词解释1.相差值:相应的决策变量的目标系数需要改进的数量,使得决策变量为正值。
运筹学答案_第_11_章__图与网络模型

习题 3
解:此题是一个求解最小生成树的问题,根据题意可知它要求出连接 v1 到 v8
的最小生成树。解此题可以得出结果为 18。也可以使用管理运筹学软件,得出 如下结果:
此问题的最小生成树如下:
*************************
管理运筹学软件,我们也可以得出结果如下:
从节点 1 到节点 6 的最大流
*************************
起点
终点
流量
费用
----
----
----
----
1
2
1
3
1
3
4
1
2
4
2
4
3
2
1
1
3
5
3
3
4
6
2
4
5
6
3
2
此问题的最大流为:5 此问题的最小费用为:39
起点
终点
距离
----
----
----
1
2
6
1
4
6
1
3
10
2
4
0
2
5
6
3
4
5
3
6
5
4
5
5
4
6
6
5
6
11
此问题的解为:22
即从 v1到v6 的最大流量为:22
习题 5 解:此题是一个求解最小费用最大流的问题,根据题意可知它要求出连接 v1
到 v6 的最小费用最大流量。解此问题可以得出最大流为 5,最小费用为 39。使用
运筹学课件第11章 网络计划

• 当用计算机网络计划软件编制网络计划 时,可在计算机上可进行网络计划图分 解与合并。网络计划图详细程度,可以 根据需要,将工作分解为更细的子工作; 也可以将几项工作合并为综合的工作。 以便显示不同粗细程度的网络计划。当 前的软件都实现这些操作。
第2节 网络计划图的时间参数计算。
• 网络计划的时间参数计算有几种类型:双代号网络 计划有工作计算法和节点计算法;单代号网络计划 有节点计算法。以下仅介绍工作计算法。其它的计 算法可参考[ 1]。
110 110 0
135 135 0
4 工装制造2 G 30
6 加工3 K 25
7
135 135 0 170 170 0
线路的组成
①→②→⑦→⑧ ①→②→③→⑦→⑧ ①→②→④→⑥→⑦→⑧
各工作的持续时间之和 (天) 60+45+35=140
60+10+18+35=123
60+20+30+25+35=170
①→②→④→⑤→⑦→⑧ 60+20+15+35=130
①→②→⑤→⑦→⑧
60+40+15+35=150
• (2) 按网络图的箭线的方向,从起始
2. 紧前工作和紧后工作
• 紧前工作是指紧排在本工作之前的工作;且开始或完成
后,才能开始本工作。紧后工作是指紧排在本工作之后
的工作;本工作开始或结束后,才能开始或结束的工作。
如图11-3中,只有工作A 完成后工作B,C,D,E 才能开始,
工作A 是B,C,D,E 的紧前工作;而工作 B,C,D,E 则是
况。按平均意义可用以下公式计算工作持续时 间值:
D a 4m b ;方差 2 b a 2
6
6
2.2 计算关系式
• 这些时间参数的关系可以用下图11-6表示工 作的关系状态。
《管理运筹学》第三版(韩伯棠 )课后习题答案 高等教育出版社
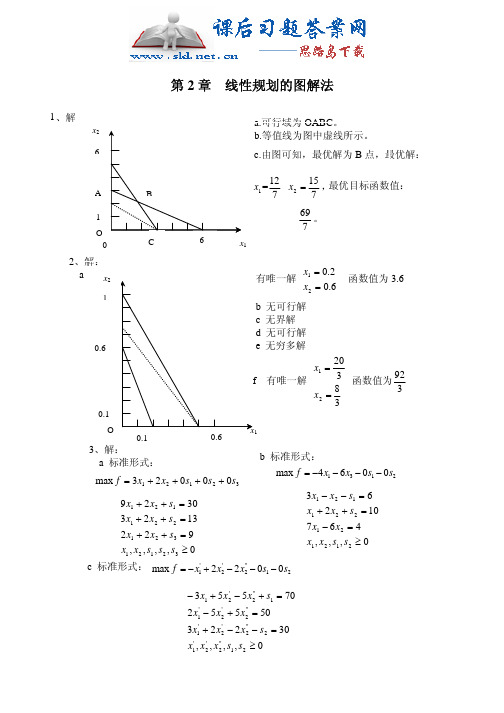
a、 在满足对职工需求的条件下,在 10 时安排 8 个临时工,12 时新安排 1 个临时工,13 时新安排 1 个临时工,15 时新安排 4 个临时工,17 时新 安排 6 个临时工可使临时工的总成本最小。
50xa + 100xb ≤ 1200000 5xa + 4xb ≥ 60000 100xb ≥ 300000 xa , xb ≥ 0 基金 a,b 分别为 4000,10000。 回报率:60000
b 模型变为: max z = 5xa + 4xb
50xa + 100xb ≤ 1200000 100xb ≥ 300000 xa , xb ≥ 0
xi ≥ 0, yi ≥ 0 i=1,2,…,11
稍微变形后,用管理运筹学软件求解可得:总成本最小为 264 元。 安排如下:y1=8( 即在此时间段安排 8 个 3 小时的班),y3=1,y5=1,y7=4,x8=6 这样能比第一问节省:320-264=56 元。
x2+x3+x4+x5+1 ≥ 3 x3+x4+x5+x6+2 ≥ 3 x4+x5+x6+x7+1 ≥ 6 x5+x6+x7+x8+2 ≥ 12 x6+x7+x8+x9+2 ≥ 12 x7+x8+x9+x10+1 ≥ 7 x8+x9+x10+x11+1 ≥ 7 x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11≥ 0 用管理运筹学软件我们可以求得此问题的解为:
b、 这时付给临时工的工资总额为 80 元,一共需要安排 20 个临时工的班 次。
约束 -------
1 2 3 4 5 6 7 8 9 10 11
管理运筹学 第三版韩伯棠 考点归纳

1.线性规划问题及其数学模型
2、约束条件不是等式的问题: 设约束条件为
ai1 x1+ai2 x2+ „ +ain xn ≤ bi 可以引进一个新的变量xs,使它等于约束右边与左边之差 xs=bi–(ai1 x1 + ai2 x2 + „ + ain xn ) 显然, xs也具有非负约束,即xs≥0,
A B B’
C’
C D x1
E
3.图解法的灵敏度分析
(二)约束条件中右边系数bi的灵敏度分析 可见,由于增加了10个台时数,使利润增加了500元,可见 每 个台时数可增加利润50元. 像这样在约束条件右边常量增加一个单位而使最优目标函数 值得到改进的数量称为这个约束条件的对偶价格。 本例中的设备对偶价格为50元/台时。 但不是每个约束条件右边常量的变化都会引起目标函数值的 变化的。 本例中,如果A原料的量增加10千克,也可以使可行域扩 大,但对最优解却没有影响,因此原料A的对偶价格为0。
3.图解法的灵敏度分析
(一)目标函数中的系数cj的灵敏度分析 由图可知,如果cj发生变化,则目标函数的等值线的斜率会 发生变化。如果要求最优解仍在B点,则会以B点为轴点而发 x 生转动。
2
z=27500=50x1+100x2
A B C
k=0
k=-c1/c2
E D x1
k=-2
k=-1
3.图解法的灵敏度分析
a11x1+a12x2+„+a1nxn≤( =, ≥ )b1 a21x1+a22x2+„+a2nxn≤( =, ≥ )b2
„„
am1x1+am2x2 +„+amnxn≤( =, ≥ )bm x1 ,x2 ,„ ,xn ≥ 0
管理运筹学课后答案-----韩伯裳
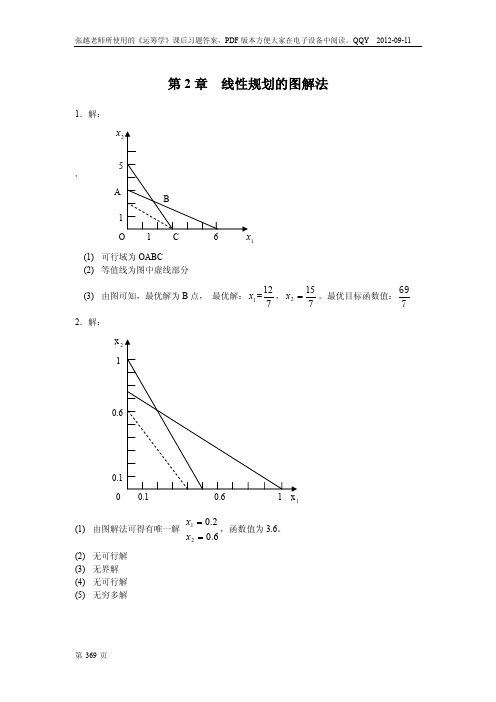
12 15 69 , x2 。最优目标函数值: 7 7 7
0.6
0.1 0 0.1 0.6 1 x1
(1) 由图解法可得有唯一解 (2) (3) (4) (5) 无可行解 无界解 无可行解 无穷多解
x1 0.2 x 2 0 .6
,函数值为 3.6。
第 369 页
张越老师所使用的《运筹学》课后习题答案,PDF 版本方便大家在电子设备中阅读。QQY 2012-09-11
从上午11时到下午10时分成11个班次设xi表示第i班次安排的临时工的人数模型如minf16x1x2x3x4x5x6x7x8x9x10x11x1x2x2x3x1x2x3x4x3x4x5x4x5x6x5x6x7x6x7x8x6x7x8x9x8x9x10x9x10x11在满足对职工需求的条件下在11时安排8个临时工13时新安排1个临时工14时新安排1个临时工16时新安排4个临时工18时新安排6个临时工可使临时工的总成本最小
' '' 3 x1 5 x 2 5x2 s1 70 ' '' 2 x1' 5 x 2 5x2 50 ' '' 3 x1' 2 x 2 2 x2 s 2 30 ' '' x1' , x 2 , x2 , s1 , s 2 0
4.解: 标准形式:
max z 10 x1 5 x2 0s1 0s 2
3 x1 4 x 2 s1 9 5 x1 2 x 2 s 2 8 x1 , x 2 , s1 , s 2 0
松弛变量(0,0) 最优解为 x1 =1,x 2 =3/2.
第 370 页
张越老师所使用的《运筹学》课后习题答案,PDF 版本方便大家在电子设备中阅读。QQY 2012-09-11
管理运筹学课后答案韩伯棠高等教育出版社第3版

管理运筹学高等教育出版社第三版韩伯棠管理运筹学作业第二章线性规划的图解法P23:Q2:(1)-(6);Q3:(2)Q2:用图解法求解下列线性规划问题,并指出哪个问题具有唯一最优解,无穷多最优解,无界解或无可行解。
(1)Min f=6X1+4X2约束条件:2X1+X2>=1,3X1+4X2>=3X1, X2>=0解题如下:如图1Min f=3.6X1=0.2, X2=0.6本题具有唯一最优解。
图1(2)Max z=4X1+8X2约束条件:2X1+2X2<=10-X1+X2>=8X1,X2>=0解题如下:如图2:Max Z 无可行解。
图2(3) Max z =X1+X2 约束条件 8X1+6X2>=24 4X1+6X2>=-12 2X2>=4 X1,X2>=0 解题如下:如图3: Max Z=有无界解。
图3(4) Max Z =3X1-2X2 约束条件:X1+X2<=1 2X1+2X2>=4 X1,X2>=0 解题如下:如图4: Max Z 无可行解。
图4(5)Max Z=3X1+9X2 约束条件:X1+3X2<=22-X1+X2<=4X2<=62X1-5X2<=0X1,X2>=0解题如下:如图5:Max Z =66;X1=4 X2=6本题有唯一最优解。
图5(6)Max Z=3X1+4X2 约束条件:-X1+2X2<=8X1+2X2<=122X1+X2<=162X1-5X2<=0X1,X2>=0解题如下:如图6Max Z =30.669X1=6.667 X2=2.667本题有唯一最优解。
图6Q3:将线性规划问题转化为标准形式(2)min f=4X1+6X2约束条件:3X1-2X2>=6X1+2X2>=107X1-6X2=4X1,X2>=0解题如下:1)目标函数求最小值化为求最大值:目标函数等式左边min改为max,等式右边各项均改变正负号。
管理运筹学--第11章 网络计划

5. 工时确定 单一时间确定法:以前多次执行过的、有可靠的生产 定额值的,可以一个确定的时间作为它的工时。
三种时间确定法:初次执行,无资料可循。
a=最乐观时间、b=最保守时间、m=最可能时间
估计
利用公式:
a 4m b 期望时间= 6
二、网络图
对承担的工程经过工序分解、工时确定, 根据生产工艺、 生产组织的制约确定出各工序间的逻辑关系后, 可以用 一张网络图把上述各点统一反映出来, 借以形象地表达 工程计划方案的编制. 绘制网络图:前进法、后退法、任意法. 草图 →逐步调整(尽量消除箭杆的交叉) (正确运用虚工序)
1.必须正确表达逻辑关系。
(2)A、B、C三项 工作同时开始
A B C
(3)A、B、C三项工作有 共同的后续工作或同 时结束
A B C
一、双代号网络图的绘制规则
1.必须正确表达逻辑关系.
(4) A、B、C三项工 作,A完成后, B、C开始
B A C
(5) A、B、C三项工 作, A、B完成后C 开始
一、双代号网络图的绘制规则
5. 绘制网络图时, 箭线不宜交叉;当交叉 不可避免时, 可用过桥法或指向法.
8 4 5 8
8
39 4 5
4
8 39 指向法
5
39
39 过桥法
×
√
√
一、双代号网络图的绘制规则
6. 双代号网络图中只有一个起始节点, 只有一个 终点节点.
3 7
1
2
5
8
4
6
×
一、双代号网络图的绘制规则
(2) 如果在其紧前工作中存在多项只作为本 工作紧前工作的工作,先将这些紧前工作的 结束节点合并,再从合并后的节点开始,画 出本工作;
韩伯棠管理运筹学(第三版)第十一章图与网络模型PPT课件
§1 图与网络的基本概念
e1
v1
e2
e3
e4 v2 e5 v3ee67ee98
e10
e11
v4
e12
v5 e13 e14
e15 v6 e16
e17
v7 e18
v8 e19
v10
v9 e20
• 链:由两两相邻的点及其相关联的边构成的点边序 列;如:
v1 , e1 , v2 , e4 , v5 , e7 , v3 , e9 , v7 , e18 , v9 ;
P=13
v2
17
15 P=0
V1 (甲地)
10
5
6 T=19
3
V4
4
2
4
V3
P=10
V5
T=14
T= ∞
V7 (乙地)
6
V6 T= ∞
38
§2 最短路问题
P=13
v2
17
15 P=0
V1 (甲地)
10
5
6 T=19
3
V4
4
2
4
V3
P=10
V5
T=14
T=30
V7 (乙地)
6
V6 T= ∞
39
§2 最短路问题
V7 (乙地)
17
v2
5
6
15
6 v4
V1
(甲地)
43
10
4
4
2
v5
v6
解 : 这 是 一 个v3求 无 向 图 的 最 短 路 的 问 题 。 可 以 把 无
向图的每一边(vi,vj)都用方向相反的两条弧(vi,vj) 和(vj,vi)代替,就化为有向图,即可用Dijkstra算 法来求解。也可直接在无向图中用Dijkstra算法来求
韩伯棠教授《管理运筹学》第三版习总复习

一、管理运筹学的定义运筹学(Operational Research,简称OR) ,英文直译为“运作研究”。
管理运筹学是应用分析、试验、量化的方法,对经济管理系统中的人力、物力、财力等资源进行统筹安排,为决策者提供有依据的最优方案,以实现最有效的管理。
——《中国企业管理百科全书》绪论二、管理运筹学Ⅰ的主要分支线性规划(Linear Programming,简称LP)整数规划(Integral Programming,简称IP)目标规划(Objective Programming,简称OP)动态规划(Dynamic Programming,简称DP)图与网络(Graph and Network)三、管理运筹学的工作步骤提出问题、分析问题建立模型求解解的检验、控制、实施四、运筹学方法的特点1. 最优化方法2. 定量的方法线性规划(LP)一、问题的提出1.生产计划安排问题:合理利用人力、物力、财力等,在资源有限的约束条件下,寻求使得获利最大的最优生产计划方案。
2.人力资源分配的问题:在满足工作的需要的条件下,寻求使用最少的劳动力的最优分配方案。
3.套裁下料问题:在保证正常生产,完成生产任务的条件下,寻求使用原料最省的最优下料方案。
4.投资问题:在投资额限制的条件下,从多个投资项目中选取使得投资回报最大的最优投资方案。
5.运输问题:寻求使得总运费最小的最优调运方案。
二、建模1.一般步骤:分析问题,设出决策变量根据所提问题列出目标函数根据已知条件列出所有约束条件数学模型的一般形式★矩阵形式:假设有n个决策变量,m个约束条件。
目标函数:Max (Min)z = CX约束条件:AX ≤(=, ≥)b.X≥0其中,C=(c1 , c2 , …, cn )(价值向量)X= (x1 , x2 , …, xn )T(决策变量向量)b=(b1 , b2 , …, bm )T (限定向量)a11 a12 (1)a21 a22 …a2n (约束条件系数矩阵) Am×n = ……am1 am2 …amn数学模型的特点(1)由目标函数和约束条件构成;(2)目标函数只有两种情况:求极小或求极大。
管理运筹学ppt11第十一章 图与网络模型

11§.33 最小生成树问题
例4 解法如下
(1)在G中找一个圈(v1,v7,v6,v1),去掉权数最大的边[v1,v6],得图 G1,如图11-13(b)。
表 11-1
年份
1
2
3
4
5
年初价格
11
11
12
12
13
设备维修费如表 11-2 所示。
表 11-2
使用年数
0~1
1~2
2~3
3~4
4~5
每年维修费
5
6
8
11
18
11§.22
最短路问题
例 3 求解如下:将问题转化为最短路问题,如图 11-8 所示。 用 vi 表示“第 i 年年初购进一台新设备”,弧(vi,vj)表示第 i 年年初购进 的设备一直使用到第 j 年年初。
网络:
在赋权的有向图 D 中指定一点,称为发点(记为 vs),指定另一点为 收点(记为 vt),其余点称为中间点,并把 D 中的每一条弧的赋权数 cij 称为弧(vi,vj)的容量,这样的赋权有向图 D 称为网络。
本章内容
1 2 3 4 5
11§.22 最短路问题
最短路问题:对一个赋权的有向图 D 中的指定的两个点 vs 和 vt 找到 一条从 vs 到vt 的路,使这条路上所有弧的权数的总和最小,这条路被 称之为从 vs 到 vt 的最短路。这条路上所有弧的权数的总和被称为从 vs 到 vt 的距离。
终点 v3 标以(22,1)。
11§.22 最短路问题
(4)这时 I={v1, v2, v3},J={v4, v5, v6}。则min (s14, s15, s16, s24, s25, s26, s34, s35, s36) =s14=30。给弧 (v1, v4)的终点 v4 标以(30,1)。 (5)这时 I={v1, v2, v3, v4}, J={v5, v6}。则min(s15,s16,s25,s26,s35,s36,s45,s46)=s15=41。 给弧(v1,v5)的终点 v5 标以(41,1)。 (6)这时 I ={v1, v2, v3, v4, v5}, J={v6}。则min(s16,s26,s36,s46,s56)=s36=s46=53。 给弧(v3 , v6)和(v4,v6)的终点v6标以(53,3)和(53,4),最终得到图 11-10,可知,v1 到 v6 的距离是 53,最短路径有两条:v1→v3→v6 和 v1→v4→v6。
管理运筹学期末复习资料【韩伯棠】

运筹学(Operational Research)复习资料第一章绪论一、名词解释1.运筹学:运筹学是应用分析、试验、量化的方法,对经济管理系统中的人力、物力、财力等资源进行统筹安排,为决策者提供有依据的最优方案,以实现最有效的管理。
二、选择题1.运筹学的主要分支包括(ABDE )A图论B线性规划C非线性规划D整数规划E目标规划2. 最早运用运筹学理论的是( A )A . 二次世界大战期间,英国军事部门将运筹学运用到军事战略部署B . 美国最早将运筹学运用到农业和人口规划问题上C . 二次世界大战期间,英国政府将运筹学运用到政府制定计划D . 50年代,运筹学运用到研究人口,能源,粮食,第三世界经济发展等问题上第二章线性规划的图解法一、选择题/填空题1.线性规划标准式的特点:(1)目标函数最大化(2)约束条件为等式(3 决策变量为非负(4 ) 右端常数项为非负2. 在一定范围内,约束条件右边常数项增加一个单位:(1)如果对偶价格大于0,则其最优目标函数值得到改进,即求最大值时,最优目标函数值变得更大,求最小值时最优目标函数值变得更小。
(2)如果对偶价格小于0,则其最优目标函数值变坏,即求最大值时,最优目标函数值变小了;求最小值时,最优目标函数值变大了。
(3)如果对偶价格等于0,则其最优目标函数值不变。
3.LP模型(线性规划模型)三要素:(1)决策变量(2)约束条件(3)目标函数4. 数学模型中,“s·t”表示约束条件。
5. 将线性规划模型化成标准形式时,“≤”的约束条件要在不等式左端加上松弛变量。
6. 将线性规划模型化成标准形式时,“≥”的约束条件要在不等式左端减去剩余变量。
7.下列图形中阴影部分构成的集合是凸集的是A【解析】:如何判断是凸集?凸集:两点之间连线在图内凹集:两点之间连线在图外8. 线性规划问题有可行解且凸多边形无界,这时CA没有无界解 B 没有可行解 C 有无界解 D 有有限最优解9. 对于线性规划问题,下列说法正确的是( D )A. 线性规划问题可能没有可行解B. 在图解法上,线性规划问题的可行解区域都是“凸”区域C. 线性规划问题如有最优解,则最优解可在可行解区域顶点上到达D. 上述说法都正确第三章线性规划问题的计算机求解一、名词解释1.相差值:相应的决策变量的目标系数需要改进的数量,使得决策变量为正值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§2 最短路问题
v2 A2 2 0 v1 S 4 C 4 ∞ v4 5 2 1 4 7 v3 B 4 4 3 v6
8 D9
1 E7 ∞ v5
5 14 13 T 7
v7
由此而得两条从v 的最短路R 由此而得两条从 1到v7的最短路 7* : {v1, v2, v3, v6, v7}与{v1, v2, v3, v5, v6, v7} 与
§1 图与网络的基本概念
• 有向图:关联边有方向的图。 有向图:关联边有方向的图。 弧:有向图的边 a = ( u , v ),起点 u,终点 v; , , ; 的链,且各方向一致, 路:若有从 u 到 w 的链,且各方向一致,则称 的路; 之为从 u 到 w 的路;
u v
x
回路: 回路:起点与终点相同 的路. 的路
18
§2 最短路问题
v2 A2 2 0 v1 S 4 C 4 ∞ v4 5 2 1 4 7 v3 B5 4 3 v6
∞ D
1 E ∞ v5
5 7
∞ T
v7
Step1:令始点P(v1)=0, 其它点 j) = ∞ :令始点 其它点T(v Step2: 计算:T(vj) = min{T(vj) , P(vi)+wij} 计算: Step3: 令:P(vj) = min{T(vj)},返回 ,返回Step2
24
§2 最短路问题
v2 A2 2 0 v1 S 4 C 4 ∞ v4 5 2 1 4 7 v3 B 4 4 3 v6
8 D9
1 E7 ∞ v5
5 14 13 T 7
v7
Step1:令始点P(v1)=0, 其它点 j) = ∞ :令始点 其它点T(v Step2: 计算:T(vj) = min{T(vj) , P(vi)+wij} 计算: Step3: 令:P(vj) = min{T(vj)},返回 ,返回Step2
发点P标号, 发点P标号, 其余点T 其余点T标号 改为P标号 改为 标号 终点为P 终点为 标号
15
§2 最短路问题
如图是一个单向道路系统。 例 1 : 如图是一个单向道路系统 。 大批物资集中 在出发地S,要求用车尽快运输到目的地T。 A,B,C,D,E是中间站 是中间站。 A,B,C,D,E是中间站。图中数字为相邻两站间的路 程。
运筹学
第十一章 图与网络模型
1
第八章 图与网络模型
• 图与网最短路问络的基本概念 • 最小生成树问题 • 最大流问题 • 最小费用流问题
2
§1 图与网络的基本概念
哥尼斯堡七桥问题 哥尼斯堡(现名加里宁格勒)是欧 哥尼斯堡(现名加里宁格勒) 洲一个城市, 洲一个城市 , Pregei河把该城分成两部 河把该城分成两部 河中有两个小岛,十八世纪时, 分,河中有两个小岛,十八世纪时,河 两边及小岛之间共有七座桥, 两边及小岛之间共有七座桥,当时人们 提出这样的问题: 提出这样的问题 : 有没有办法从某处 ( 如 A)出发,经过各桥一次且仅一次 ) 出发, 最后回到原地呢? 最后回到原地呢?
20
§2 最短路问题
v2 A2 2 0 v1 S 4 C 4 ∞ v4 5 2 1 4 7 v3 B 4 4 3 v6
8 D9
1 E7 ∞ v5
5 7
∞ T
v7
Step1:令始点P(v1)=0, 其它点 j) = ∞ :令始点 其它点T(v Step2: 计算:T(vj) = min{T(vj) , P(vi)+wij} 计算: Step3: 令:P(vj) = min{T(vj)},返回 ,返回Step2
A 2 S 4 C 5 1 2 B 3 4 4 1 E
16
7 D 5 T
7
§2 最短路问题
v2 A ∞ 2 0 v1 S 4 C ∞ v4 5 2 1 4 7 v3 B ∞ 4 3 v6
∞ D
1 E ∞ v5
5 7
∞ T
v7
Step1:令始点P(v1)=0, 其它点 j) = ∞ :令始点 其它点T(v Step2: 计算:T(vj) = min{T(vj) , P(vi)+wij} 计算:
22
§2 最短路问题
v2 A2 2 0 v1 S 4 C 4 ∞ v4 5 2 1 4 7 v3 B 4 4 3 v6
8 D9
1 E7 ∞ v5
5 7
14 ∞ T
v7
Step1:令始点P(v1)=0, 其它点 j) = ∞ :令始点 其它点T(v Step2: 计算:T(vj) = min{T(vj) , P(vi)+wij} 计算: Step3: 令:P(vj) = min{T(vj)},返回 ,返回Step2
8
§1 图与网络的基本概念
v2 e1 v1 e2 e3 v4
10 6 6 10 4 13 12 11 12 14
v5
9
3
v8
5
v3
v6
5 8
v10 v9
10 2
v7
•图 G(V,E): 图 ( , ): •V是顶点集合 是顶点集合,V={vi|i=1,…,n},E是边的集合 是边的集合,E={ej | j=1,…,m} 是顶点集合 , 是边的集合 的端点, 的关联边。 对于边 e3 =[v1, v4 ],v1, v4是e3的端点,e3 是v1, v4的关联边。 ,
6
A D C
B
Euler问题 Euler问题
一笔画 问题
§1 图与网络的基本概念
•图:由若干点以及点间联线构成(P229,230) 图 若干点以及点间联线构成( , ) •点:表示某一具体事物 。 点 •点间联线:表示事物之间某种特殊的关系。 点间联线:表示事物之间某种特殊的关系。 点间联线 不带箭头的点间联线。 边:不带箭头的点间联线。 有向边): 弧(有向边 :带箭头的点间联线。 有向边 带箭头的点间联线。 •无向图 无向图——由点,边构成(P229) 由点, 无向图 由点 边构成( ) •有向图 有向图——由点,弧构成。(P230) 由点, 有向图 由点 弧构成。 ) •网络(赋权图)——图中每一条边(弧)[vi ,vj], 网络( 图中每一条边 网络 赋权图) 图中每一条边( 有一常数w 与之对应, 称为边[ 上的权. 有一常数 ij与之对应,。wij称为边[vi ,vj]上的权. 常表示距离,费用,时间,容量等) (常表示距离,费用,时间,容量等)(P231) )
19
§2 最短路问题
v2 A2 2 0 v1 S 4 C 4 ∞ v4 5 2 1 4 7 v3 B 4 4 3 v6
∞ D9
1 E ∞ v5
5 7
∞ T
v7
Step1:令始点P(v1)=0, 其它点 j) = ∞ :令始点 其它点T(v Step2: 计算:T(vj) = min{T(vj) , P(vi)+wij} 计算: Step3: 令:P(vj) = min{T(vj)},返回 ,返回Step2
14
§2 最短路问题 Dijkstra算法
•求解的过程实际上是一种给点标号的过程。 求解的过程实际上是一种给点标号的过程。 求解的过程实际上是一种给点标号的过程 标号( 是给点记的一个数) 标号(数,是给点记的一个数) •临时标号(T标号)——从发点到本节点的 临时标号( 临时标号 标号) 从发点到本节点的 最短距离的上界; 最短距离的上界; •固定标号(P标号)——从发点到本节点的 固定标号( 固定标号 标号) 从发点到本节点的 最短距离。 最短距离。 某点T标号 某点 标号
3
A C ? D
只经过各桥一 次最后能回到 原地吗? 原地吗?
B
A C
只经过各桥一 次最后能回到 原地吗? 原地吗?
D ? B
§1 图与网络的基本概念
最 后 , 数 学 家 Euler ( 欧 拉 ) 1736年巧妙地给出了这个问题的 在 1736 年巧妙地给出了这个问题的 答案, 并因此奠定了图论的基础, 答案 , 并因此奠定了图论的基础 , Euler把 Euler 把 A 、 B 、 C 、 D 四块陆地分别 收缩成四个顶点, 收缩成四个顶点 , 把桥表示成连接 对应顶点之间的边, 对应顶点之间的边 , 问题转化为从 任意一点出发, 任意一点出发 , 能不能经过各边一 次且仅一次, 最后返回该点。 次且仅一次 , 最后返回该点 。 这就 是著名的Euler问题。 Euler问题 是著名的Euler问题。
9
§1 图与网络的基本概念
设 G1 = [ V1 , E1 ] , G2 = [ V2 , E2 ] 的子图; 子图: 子图:如果 V2 ⊆ V1 , E2 ⊆ E1 称 G2 是 G1 的子图; 真子图: 的真子图; 真子图:如果 V2 ⊂ V1 , E2 ⊂ E1 称 G2 是 G1 的真子图 生成图: 生成图:如果 V2 = V1 , E2 ⊂ E1 称 G2 是 G1 的生成图 部分图) (部分图)。
21
§2 最短路问题
v2 A2 2 0 v1 S 4 C 4 ∞ v4 5 2 1 4 7 v3 B 4 4 3 v6
8 D9
1 E7 ∞ v5
5 7
∞ T
v7
Step1:令始点P(v1)=0, 其它点 j) = ∞ :令始点 其它点T(v Step2: 计算:T(vj) = min{T(vj) , P(vi)+wij} 计算: Step3: 令:P(vj) = min{T(vj)},返回 ,返回Step2
17
§2 最短路问题
v2 A2 ∞ 2 0 v1 S 4 C 4 ∞ v4 5 2 1 4 7 v3 B5 4 ∞ 3 v6
∞ D
1 E ∞ v5
5 7
∞ T
v7
Step1:令始点P(v1)=0, 其它点 j) = ∞ :令始点 其它点T(v Step2: 计算:T(vj) = min{T(vj) , P(vi)+wij} 计算: Step3: 令:P(vj) = min{T(vj)},返回 ,返回Step2
