matlab第七次作业

合集下载

Matlab上机作业部分参考答案.ppt

>> A=[16,2,3,13; 5,11,10,8; 9,7,6,12; 4,14,15,1];B=[1; 3; 4; 7];
[rank(A), rank([A B])]
ans =
34 由得出的结果看，A, [A;B] 两个矩阵的秩不同，故方程是
矛盾方程，没有解。
5. 试求下面齐次方程的基础解系
7. 建立如下一个元胞数组，现在要求计算第一个元胞第4行第 2列加上第二个元胞+第三个元胞里的第二个元素+最后一个元胞的第二个元素。
a={pascal(4),'hello';17.3500,7:2:100}
解： >> a={pascal(4),'hello';17.3500,7:2:100} a=
[ 173/34, 151/34]
6. 求解方程组的通解
x1 2x2 4x3 6x4 3x5 2x6 4 2x1 4x2 4x3 5x4 x5 5x6 3
3x1 6x2 2x3 5x5 9x6 1 2x1 3x2 4x4 x6 8
4x2
5x3
2x4
x5
参考答案：（1） >> limit(sym('(tan(x) - sin(x))/(1cos(2*x))')) ans = 0 （2） >> y = sym('x^3 - 2*x^2 + sin(x)'); >> diff(y) ans = 3*x^2-4*x+cos(x) （3） >> f = x*y*log(x+y); >> fx = diff(f,x) fx = y*log(x+y)+x*y/(x+y)

MATLAB习题及参考答案经典.doc

习题：1，计算⎥⎦⎤⎢⎣⎡=572396a 与⎥⎦⎤⎢⎣⎡=864142b 的数组乘积。

2，对于B AX =，如果⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=753467294A ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=282637B ，求解X 。

3，已知：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321a ，分别计算a 的数组平方和矩阵平方，并观察其结果。

4，角度[]604530=x ，求x 的正弦、余弦、正切和余切。

(应用sin,cos,tan.cot)5，将矩阵⎥⎦⎤⎢⎣⎡=7524a 、⎥⎦⎤⎢⎣⎡=3817b 和⎥⎦⎤⎢⎣⎡=2695c 组合成两个新矩阵：（1）组合成一个4⨯3的矩阵，第一列为按列顺序排列的a 矩阵元素，第二列为按列顺序排列的b 矩阵元素，第三列为按列顺序排列的c 矩阵元素，即 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡237912685574（2）按照a 、b 、c 的列顺序组合成一个行矢量，即 []2965318772546，将(x -6)(x -3)(x -8)展开为系数多项式的形式。

(应用poly,polyvalm)7，求解多项式x 3-7x 2+2x +40的根。

(应用roots)8，求解在x =8时多项式(x -1)(x -2) (x -3)(x -4)的值。

(应用poly,polyvalm)9，计算多项式9514124234++--x x x x 的微分和积分。

(应用polyder,polyint ，poly2sym)10，解方程组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡66136221143092x 。

(应用x=a\b)11，求欠定方程组⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡5865394742x 的最小范数解。

(应用pinv) 12，矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=943457624a ，计算a 的行列式和逆矩阵。

(应用det,inv)13， y =sin(x )，x 从0到2π，∆x =0.02π，求y 的最大值、最小值、均值和标准差。

第七次实验作业1

实验报告（二）院（系）理学院课程名称：数学实验日期班级B1111 学号12 实验室文理楼209 专业数学教育姓名樊美林计算机号实验名称数学实验成绩评定所用软件Matlab 教师签名实验目的或要求1.实验步骤、心得体会1. 求下列函数的极小点：1) ()2123222118294xxxxxXf+-++=；、function f = fun1(x)f=x(1)^2+4*x(2)^2+9*x(3)^2-2*x(1)+18*x(2);x0=[1,1,2]x=fminunc('fun1',x0);y=fun1(x)y=-21.25002)()212122212223xxxxxxXf-+-+=；function f = fun1(x)f=x(1)^2+(3/2)*x(2)^2+2*x(1)*x(2)+x(1)-2*x(2);x0=[1,1]x=fminunc('fun1',x0)y=fun1(x)y =-4.75003)()()42121f X x x=-+.function f = fun2(x)f=(x(1)-1)^4+x(2)^2；x0=[0,1]x=fminunc('fun2',x0);y=fun2(x)y =4.0848e-010第1），2）题的初始点可任意选取，第3）题的初始点取为()TX1,00=.2. 梯子长度问题一楼房的后面是一个很大的花园. 在花园中紧靠着楼房有一个温室,温室伸入花园2m,高3m,温室正上方是楼房的窗台. 清洁工打扫窗台周围,他得用梯子越过温室,一头放在花园中,一头靠在楼房的墙上. 因为温室是不能承受梯子压力的,所以梯子太短是不行的.现清洁工只有一架7m 长的梯子,你认为它能达到要求吗? 能满足要求的梯子的最小长度为多少?问题分析：（对问题作出分析，如果问题过于简单，可以不作分析）模型建立：（建立数学模型）结果：（求解的结果）分析：（对求解结果进行分析）其他：（模型的缺点和优点以及改进方向，如果没有，可以不写）模型的求解：（求解所用的软件，求解该问题的源代码）3. 陈酒出售的最佳时机问题某酒厂有批新酿的好酒,如果现在就出售,可得总收入R 0=50万元(人民币),如果窖藏起来待来日(第n 年)按陈酒价格出售,第n 年末可得总收入60n eR R (万元),而银行利率为r=0.05,试分析这批好酒窖藏多少年后出售可使总收入的现值最大. (假设现有资金X 万元,将其存入银行,到第n 年时增值为R(n)万元,则称X 为R(n)的现值.)并填下表：第一种方案：将酒现在出售，所获50万元本金存入银行；第二种方案：将酒窖藏起来，待第n 年出售。

MATLAB作业7参考答案

MATLAB作业7 参考答案1、试生成满足正态分布2N的30000 个伪随机数，对其均值和方差进行验(0.5,1.4)证，并用直方图的方式观察其分布与理论值是否吻合，若改变直方图区间的宽度会得出什么结论？解:用下面的语句可以生成随机数，并计算均值和方差，可见，其结果接近给定的数值。

>> x=normrnd(0.5,1.4,30000,1);>>m=mean(x), s=std(x)m =0.49974242123102s =1.40033494141044>> xx=-5:0.3:5; yy=hist(x,xx); bar(xx,yy/length(x)/0.3); hold onx0=-5:0.1:5; y0=normpdf(x0,0.5,1.5); plot(x0,y0)>> xx=-5:0.8:5; yy=hist(x,xx); bar(xx,yy/length(x)/0.8);hold on; plot(x0,y0)2、某研究者对随机抽取的一组保险丝进行了实验，测出使保险丝烧断的电流值为10.4, 10.2,12.0, 11.3, 10.7, 10.6, 10.9, 10.8, 10.2, 12.1，假设这些值α≤的条件下求出这些保险丝的溶断电流及其满足正态分布，试在置信水平0.05置信区间。

解:方法①由normfit() 函数可以直接求出置信区间，亦即溶断电流的均值为10.92，其置信区间为(10:43; 11:41)。

>> x=[10.4,10.2,12,11.3,10.7,10.6,10.9,10.8,10.2,12.1];>> [m1,s1,ma,sa]=normfit(x,0.05); m1, mam1 =10.92000000000000ma =10.43271643434768 11.40728356565233方法②采用T 检验函数即可判定是否接受均值为mean(x) 的检验，也能求出同样的均值与置信区间>> x=[10.4,10.2,12,11.3,10.7,10.6,10.9,10.8,10.2,12.1];mean(x)ans =10.92000000000000>> [H,p,ci]=ttest(x,mean(x),0.05)H =p =1ci =10.43271643434768 11.407283565652333、假设测出某随机变量的12 个样本为9.78, 9.17, 10.06, 10.14, 9.43, 10.60, 10.59, 9.98, 10.16,10.09, 9.91, 10.36，试求其方差及方差的置信区间。

数学模型数学建模第七次作业数理统计实验

数学模型第七次作业数理统计实验7.1实验目的与要求●学会对数据的参数进行估计和作相应的假设检验●学会对分布进行检验和数据的秩检验●建立相应的统计模型，并用R软件求解7.2 基本实验1. 区间估计已知某种灯泡寿命服从正态分布，在某星期所生产的该灯泡中随机抽取10只，测得其寿命（单位：小时）为1067 919 1196 785 1126 936 918 1156 920 948(1) 试问这批灯泡中大约95%的灯泡至少使用多少小时；(2) 求这批灯泡能够使用1000小时以上的概率。

解：(1)根据题意，使用R软件求解，编辑程序如下：> X<-c(1067,919,1196,785,1126,936,918,1156,920,948)> t.test(X,al="g")得到如下结果：One Sample t-testdata: Xt = 23.9693, df = 9, p-value = 9.148e-10alternative hypothesis: true mean is greater than 095 percent confidence interval:920.8443 Infsample estimates:mean of x997.1由此知道这批灯泡中大约95%的灯泡至少使用920.8443小时。

(2)> x<-c(1067,919,1196,785,1126,936,918,1156,920,948)> x[1] 1067 919 1196 785 1126 936 918 1156 920 948> pnorm(1000,mean(x),sd(x))[1] 0.5087941由此知道求这批灯泡能够使用1000小时以上的概率为50.87941%2. 假设检验I正常男子血小板计数均值为225×109/L，今测得20名男性油漆作业工人的血小板计数值(单位:109/L)220 188 162 230 145 160 238 188 247 113 126 245 164 231 256 183 190 158 224 175 问油漆工人的血小板计数与正常成年男子有无差异，并说明油漆作业对人体血小板计数是否有影响。

Matlab实验指导书(含答案)汇总

实验Matlab 操作环境熟悉、实验目的1．初步了解Matlab 操作环境。

2．学习使用图形函数计算器命令funtool 及其环境。

二、实验内容熟悉Matlab 操作环境，认识命令窗口、内存工作区窗口、历史命令窗口；学会使用format 命令调整命令窗口的数据显示格式；学会使用变量和矩阵的输入，并进行简单的计算；学会使用who 和whos 命令查看内存变量信息；学会使用图形函数计算器funtool ，并进行下列计算：1．单函数运算操作。

求下列函数的符号导数(1) y=sin(x);(2) y=(1+x)A3*(2-x); 求下列函数的符号积分(1) y=cos(x);(2) y=1/(1+x^2);(3) y=1/sqrt(1-x^2);(4) y=(x-1)/(x+1)/(x+2);求反函数(1) y=(x-1)/(2*x+3);(2) y=exp(x);(3) y=log(x+sqrt(1+x^2));代数式的化简(1) (x+1)*(x-1)*(x-2)/(x-3)/(x-4);(2) sin (x)A2+cos(x)A2;(3) x+sin(x)+2*x-3*cos(x)+4*x*sin(x);2．函数与参数的运算操作。

从y=xA2通过参数的选择去观察下列函数的图形变化(1) y1=(x+1)A2⑵ y2=(x+2)A2(3) y3=2*x^2⑷ y4=x^2+2(5) y5=x^4⑹ y6=x^2/23．两个函数之间的操作求和(1) sin(x)+cos(x)(2) 1+x+x^2+x^3+x^4+x^5乘积(1) exp(-x)*sin(x)(2) sin(x)*x商(1) sin(x)/cos(x);⑵ x/(1+x^2);(3) 1/(x-1)/(x-2);求复合函数(1) y=exp(u) u=sin(x)(2) y=sqrt(u) u=1+exp(xA2)(3) y=sin(u) u=asin(x)(4) y=sinh(u) u=-x三、设计提示1．初次接触Matlab 应该注意函数表达式的文本式描述。

《MATLAB7.x》程序设计语言（第二版）课后题答案

《MATLAB7.x》程序设计语言（第二版）部分课后习题答案（楼顺天，姚若玉，沈俊霞编著）说明：所有答案均是本人在备考过程中亲自整理的，收录了一部分题目的答案。

答案可能存在不足甚至谬误，很多算法也可能不是最优的，仅供参考。

本人尽力整理的一点点心血，希望对大家有所帮助。

第二章8、 a=rand(5,5);[i,j]=find(a>0.5);for u=1:length(i);b(u)=a(i(u),j(u));endb'10、aa=any(a');i=find(aa==0)a(i,:)=[];第四章1、function flag=isprime(m)%m为素数，flag=1%m不为素数，flag=0k=sqrt(m);flag=1;for i=2:k;if rem(m,i)==0;flag=0;breakendendm=input('input an integer\n');flag=isprime(m);if flag==1disp([num2str(m),'是素数'])elsedisp([num2str(m),'不是素数'])end4、function [x1,x2]=jfc(a,b,c)d=b^2-4*a*c;if d>0;x1=(-b-sqrt(d))/(2*a);x2=(-b+sqrt(d))/(2*a);elseif d==0;x1=-b/(2*a);a=input('a=');b=input('b=');c=input('c=');[x1,x2]=jfc(a,b,c);if x1~=x2;disp('原方程存在两个不同的根')disp(['x1=',num2str(x1)])disp(['x2=',num2str(x2)]);elseif x1==x2;disp('原方程存在两个相同的根')disp(['x1=x2=',num2str(x1)])elsedisp('原方程的根不存在')end%MATLAB上机作业，184页习题4，求二次方程的实根function [s1,s2]=solve(a,b,c)d=b^2-4*a*c;if d>0s1=(-b-sqrt(d))/(2*a)s1=(-b-sqrt(d))/(2*a)%disp(['原方程有两个不同的根'num2str(s1)'和'nums2tr(s2)]) elseif d==0s1=(-b-sqrt(d))/(2*a);s1=(-b-sqrt(d))/(2*a);%disp(['原方程有两个相同的根'num2str(s1))elsedisp('原方程无实根')endend5、x=-3:0.01:3;if x>=-3 & x<-1;y=(-x.^2-4*x-3)/2;elseif x>=-1 & x<1;y=-x.^2+1;elsey=(-x.^2+4*x-3)/2;endplot(x,y)6、%MATLAB上机作业，184页习题6，点不同按钮产生不同分布的数s=menu('请选择随机数类型','U[-10,10]','U[-5,5]','U[-1,1]','N(0,1)');switch scase 1,n=(rand(1)-0.5)*20;case 2,n=(rand(1)-0.5)*10;case 3,n=(rand(1)-0.5)*2;endn7、load a.txt[m,n]=size(a);w=zeros(m,1);for i=1:m;w(i)=(2*a(i,1)+3*a(i,2)+2*a(i,3)+4*a(i,4)+2.5*a(i,5)+a(i,6))/14.5;endw8、function k=jj(i)if i<=10k=0.1*i;elseif i<=20k=1+(i-10)*0.05;elseif i<=40k=1.5+(i-20)*0.02;elsek=1.9+(i-40)*0.01;ends=0;a=2;b=1;for i=1:15;s=s+a/b;c=b;b=a;a=a+c;ends9、a=ones(15,1);b=ones(15,1);c=ones(15,1);a(1)=2;c(1)=2;for i=2:15;a(i)=b(i-1)+a(i-1);b(i)=a(i-1);c(i)=a(i)./b(i)endsum(c)第五章3、t=1:1:10;t=t';y=[4.842,4.362,3.754,3.368,3.169,3.083,3.304,3.016,3.012,3.005]';x1=[ones(size(t)),exp(-t)];x2=[ones(size(t)),t.*exp(-t)];p1=x1\y;p2=x2\y;grid on,legend('给定数据','y1拟合','y2拟合')5、（1）function dy=cwf(t,y)dy=[5*y(1)-5*y(2)-6*y(3);3*y(1)-2*y(2)+5*y(3);2*y(1)-y(2)-4*y(3)];x0=[1,-4,5];tspan=[13,16];[t,y]=ode45('cwf',tspan,x0);plot(t,y)（2）function dy=cwf(t,y)dy=[y(1)+2*y(2)-3*y(3)+y(4);3*y(1)+y(3)-2*y(4);y(1)-2*y(2)+5*y(4);2*y(1)+3*y(2)+y(4)];x0=[1,-1,2,1];tspan=[15,16];[t,y]=ode45('cwf',tspan,x0);plot(t,y)7、t=1:10;tt=1:0.01:10;y=[15,39.5,66,85.5,89,67.5,12,-86.4,-236.9,-448.4];p1=polyfit(t,y,2);y1=polyval(p1,tt);p2=polyfit(t,y,3);y2=polyval(p2,tt);plot(t,y,'b*',tt,y1,'r-',tt,y2,'c-');legend('样本点','二次拟合','三次拟合'),grid on10&11、pa=[2 3 -4];pb=[4 -2 5];pc=[3 -2 5 6];d1=conv(pa,pb)[q2,r2]=deconv(pc,pa)[q3,r3]=deconv(pc,pb)dy1=polyder(pa,pb)[q2,r2]=polyder(pc,pa)[q3,r3]=polyder(pc,pb)12、x=-5:1:5;xx=-5:0.01:5;y=10.*exp(-abs(x));y1=interp1(x,y,xx,'nearest');y2=interp1(x,y,xx,'linear');y3=interp1(x,y,xx,'spline');y4=interp1(x,y,xx,'cubic');plot(x,y,'*',xx,y1,'r-',xx,y2,'c-',xx,y3,'k-',xx,y4,'g-')grid on,legend('样本点','最临近内插','线性内插','三次样条内插','三次曲线内插')13、a=rand(1,50);amax=max(a)vara=(std(a))^2b=randn(1,50);bmax=max(a)bmin=min(a)ub=mean(a)varb=(std(a))^214、t=[0,0.2,0.4,0.6,0.8,1,2,5]';tt=0:0.01:5;y=[1,1.51,1.88,2.13,2.29,2.4,2.6,-4]';p1=polyfit(t,y,3);y1=polyval(p1,tt);x=[ones(size(t)),exp(t)];p2=x\y;y2=p2(1)+p2(2)*exp(tt);plot(t,y,'k*',tt,y1,'r-',tt,y2,'b-')legend('样本点','三次多项式拟合','指数拟合'),grid on 17、function y=jifen1(x)y=exp(-2*x);function y=jifen2(x)y=exp(2*x);function y=jifen3(x)y=x.^2-3*x+0.5;z1=quadl('jifen1',0,2)z2=quadl('jifen2',0,2)z3=quadl('jifen3',-1,1)19、function z=jifen(x,y)z=exp(-x*y)-2*x*y;q=dblquad('jifen',0,1,-1,1)20、function dy=cwf(t,y)dy=[0.5-y(1);y(1)-4*y(2)];x0=[1,-0.5];tspan=[0,25];[t,y]=ode45('cwf',tspan,x0);plot(y(1,:),y(2,:));grid on亲爱的朋友，上文已完，为感谢你的阅读，特加送另一篇范文，如果下文你不需要，可以下载后编辑删除，谢谢！道路施工方案1、工程概况2、编制说明及编制依据3、主要施工方法及技术措施3．1施工程序3．2施工准备3．3定位放线3. 4土方开挖3．5卵石路基施工3．6天然砾基层施工3. 7高强聚酯土工格楞3．8水泥稳定砂砾基层施工3．9路缘石施工3. 10玻璃纤维土工格栅施工3．11沥青面层施工3. 12降水施工4、质量控制措施5、雨季施工安排6、安全技术措施1.工程概况本项目建设的厂址位于新疆石河子市。

实验七--离散系统分析的MATLAB实现讲解学习

实验七离散系统分析的MATLAB 实现一、实验目的1、掌握利用MATLAB 绘制系统零极点图的方法；2、掌握离散时间系统的零极点分析方法；3、学习离散系统响应的MATLAB 求解方法；4、掌握用MATALB 实现离散系统频率特性分析的方法；5、深刻理解离散系统的系统函数零极点对系统频响的影响，可以根据零极点知识设计简单的滤波器。

二、基本原理（一）离散系统零极点线性时不变离散系统可用线性常系数差分方程描述，即()()N Miji j a y n i b x n j ==-=-∑∑ （1）其中()y k 为系统的输出序列，()x k 为输入序列。

将式（1）两边进行Z 变换，00()()()()()Mjjj Nii i b zY z B z H z X z A z a z-=-====∑∑ （2）将式（2）因式分解后有：11()()()Mjj Nii z q H z Cz p ==-=-∏∏ （3）其中C 为常数，(1,2,,)j q j M =L 为()H z 的M 个零点，(1,2,,)i p i N =L 为()H z 的N 个极点。

系统函数()H z 的零极点分布完全决定了系统的特性，若某系统函数的零极点已知，则系统函数便可确定下来。

因此，系统函数的零极点分布对离散系统特性的分析具有非常重要意义。

（二）离散系统零极点图及零极点分析 1、零极点图的绘制设离散系统的系统函数为()()()B z H z A z =则系统的零极点可用MATLAB 的多项式求根函数roots()来实现，调用格式为：p=roots(A) 其中A 为待求根多项式的系数构成的行矩阵，返回向量p 则是包含多项式所有根的列向量。

如多项式为231()48B z z z =++，则求该多项式根的MATLAB 命令为为：A=[1 3/4 1/8]; P=roots(A) 运行结果为： P =-0.5000 -0.2500需注意的是，在求系统函数零极点时，系统函数可能有两种形式：一种是分子、分母多项式均按z 的降幂次序排列；另一种是分子、分母多项式均按1z -的升幂次序排列。

matlab第七章课后题答案

matlab第七章课后题答案第⼀题分解因式syms x y z>> A=x^9-1;>> factor(A)ans =(x-1)*(x^2+x+1)*(x^6+x^3+1) 解（1）>> B=x^4+x^3+2*x^2+x+1;>> factor(B)ans =(x^2+1)*(x^2+x+1) 解（2）> C=125*x^6+75*x^4+15*x^2+1;>> factor(C)ans =(5*x^2+1)^3 解（3）> D=x^2+y^2+z^2+z*(x*y+y*z+z*x);>> factor(D)ans =x^2+y^2+z^2+z*x*y+y*z^2+z^2*x 解（4）第⼆题化简表达式syms x y a b>> s=y/x+x/y;>> simplify(s)ans =(x^2+y^2)/x/y 解（1）s=sqrt(a+sqrt(a^2-b))/2+sqrt(a-sqrt(a^2-b))/2; ans =1/2*(a+(a^2-b)^(1/2))^(1/2)+1/2*(a-(a^2-b)^(1/2))^(1/2) 解（2）s=2*cos(x)^2*x-sin(x)^2*x;>> simplify(s)ans =x*(3*cos(x)^2-1) 解（3）s=sqrt(3+2*(sqrt2))第三题求函数的极限> syms x>> f=(x^2-6*x+8)/(x^2-5*x+4);> limit(f,x,4)ans =2/3 解（1）>> f=abs(x)/x;>> limit(f,x,0)ans =NaN 解（2）f=(sqrt(1+x^2)-1)/x;>> limit(f,x,0)ans =0 解（3）f=(x+1/x)^x;>> limit(f,x,inf,'left')ans =Inf 解（4）第四题求函数的符号导数f=3*(x^2)-5*x+1;>> diff(f)ans =6*x-5 解(1)y’>> diff(f,x,2)ans =6 解（1）> y=sqrt(x+sqrt(x+sqrt(x)));>> diff(y)ans =1/2/(x+(x+x^(1/2))^(1/2))^(1/2)*(1+1/2/(x+x^(1/2))^(1/2)*(1+1/2/x^(1/2))) 解（2）diff(y,x,2)ans =-1/4/(x+(x+x^(1/2))^(1/2))^(3/2)*(1+1/2/(x+x^(1/2))^(1/2)*(1+1/2/x^(1/2)))^2+1/2/(x+(x+x^(1/2) )^(1/2))^(1/2)*(-1/4/(x+x^(1/2))^(3/2)*(1+1/2/x^(1/2))^2-1/8/(x+x^(1/2))^(1/2)/x^(3/2)) 解(2)y=sin(x)-x^2/2;> diff(y)ans =cos(x)-x 解（3）>> diff(y,x,2)ans =-sin(x)-1 解（3）syms x y z>> z=x+y-sqrt(x^2+y^2);>> diff(z,x,y)ans =1-1/(x^2+y^2)^(1/2)*y 解（4）>> diff(y,x)ans =0 解（4）第五题求不定积分x=sym('x');>> f=1/(x+a);>> int(f)ans =log(x+a) 解（1）>> f=(1-3*x)^3;>> int(f)ans =-1/12*(1-3*x)^4 解（2）>> f=(1/(sin(x)^2*cos(x)^2));>> int(f)ans =1/sin(x)/cos(x)-2/sin(x)*cos(x) 解（3）>> f=x^2/(sqrt(a^2+x^2));>> int(f)ans =1/2*x*(a^2+x^2)^(1/2)-1/2*a^2*log(x+(a^2+x^2)^(1/2)) 解（4）第六题求定积分> x=sym('x');> int((x*(2-sin(x)^2))^12,0,1)ans =-13072167041243000966100527033032931/1439431206610157332070400000000000*sin(1)^19 *cos(1)-63988617583073709724938474490679159346183608452999323027852007/820274272 498737105178830959457441284892917760000000000*cos(1)*sin(1)+417844027386435896683 78350956709518241555640967463723429593/1230411408748105657768246439186161927339 376640000000000*sin(1)^3*cos(1)-6287598784304532394386769772554886862775718358540 017487607/1794349971090987417578692723813152810703257600000000000*sin(1)^7*cos(1)-117903417317/3522410053632*sin(1)^23*cos(1)+93129118771020938708526771772323524014639/1529945519744217245425650892800000000000*sin(1)^17*cos(1)-2677966496932891906 2789407028617562008014032541099/6567698857381017597043504106365255680000000000* sin(1)^10-90936661567370530014104030508869215332048771345315401/53375584364747317 6140678428961747763200000000*cos(1)^2+2541573211/146767085568*sin(1)^24+940325057 70279736611460220749/16522396770089041920000000000*sin(1)^20+2704734082846637530 0822998906838403821858600396601/4670363631915390291230936253415292928000000000*sin(1)^8+5542192477209543230894137867604219553503/255755814666761099367961067520 00000000*sin(1)^16+6290548805350754451916704658025155325352197570086424587493/20 18643717477360844776029314289796912041164800000000000*sin(1)^9*cos(1)-74888453896 484988301898479573506809/1756135812378578105401344000000000*sin(1)^18-66275838868 9551809679364987359346538465101954279/842854686697230591620583026983541145600000000*sin(1)^14+4741716006420769418428944378170996543275038000761225969993/153801 4260935132072210308048982702409174220800000000000*sin(1)^5*cos(1)-273698005143037 11474211657412466731397670944577/100266509581957021396215456910540800000000000*sin(1)^15*cos(1)+18044178399358284974551495/22109663333532016620601344*sin(1)^21*cos(1)+159018588498544047612814017616772807534595903672788230889/18504234076875807 7437802687143231383603773440000000000*sin(1)^13*cos(1)-42990929319556261053136947 04999192498272936575705473777243/2220508089225096929253632245718776603245281280 000000000*sin(1)^11*cos(1)+72644795857216400572361363249893595045872001672201/160 1267530942419528422035286885243289600000000*sin(1)^4-179168559345113148705406926 00563709435304263998599/3002376620517036615791316162909831168000000000*sin(1)^6-3 228431702614231399553/6979060395685611307008*sin(1)^22+1809464903223467961506769 2014871302547716716561173/8669362491742943228097425420402137497600000000*sin(1)^12+908212034006674534482628671295497731536658010905190650989336891/1066356554248 3582367324802472946736703607930880000000000解（1）int(x/(x^2+x+1),-1,1)ans =1/2*log(3)-1/6*3^(1/2)*pi 解（2）> int((x*sin(x))^2,0,pi)ans =1/6*pi^3-1/4*pi 解（3）第七题求级数之和n=sym('n');>> s1=symsum((-1)*(2*n+1)/2^n,n,0,inf)s1 =-6 解（1）>> s2=symsum(x^(2*n-1)/2^n-1,n,1,inf)s2 =sum(x^(2*n-1)/(2^n)-1,n = 1 .. Inf) 解（2）s3=symsum(1/(2*n+1)^2,n,0,inf)s3 =1/8*pi^2 解（3）s4=symsum(1/n*(n+1)*(n+1),n,1,inf)s4 =Inf 解（4）第⼋题求泰勒展开式>> x=sym('x');f1=x^4-5*x^3+x^2-3*x+4;f2=(exp(x)+exp(-x))/2;f3=tan(x);f4=sin(x)^2;f5=sqrt(x^3+x^2+5*x+3);taylor(f1,4,4)ans =-140+21*x+37*(x-4)^2+11*(x-4)^3 解（1）taylor(f2,5,0)ans =1+1/2*x^2+1/24*x^4 解（2）taylor(f3,3,2)ans =tan(2)+(1+tan(2)^2)*(x-2)+tan(2)*(1+tan(2)^2)*(x-2)^2 解（3）taylor(f4,8,0)ans =x^2-1/3*x^4+2/45*x^6 解（4）taylor(f5,5,0)ans =3^(1/2)+5/6*3^(1/2)*x-13/72*3^(1/2)*x^2+137/432*3^(1/2)*x^3-2909/10368*3^(1/2)* x^4 解（5）第九题求⾮线性⽅程的解x=solve(‘a*x^2+b*x+c=0’,’x’)x =1/2/a*(-b+(b^2-4*a*c)^(1/2))1/2/a*(-b-(b^2-4*a*c)^(1/2)) 解（1）x=solve(‘2*sin(3*x-pi/4)=1’,’x’)x =5/36*pi 解（2）x=solve(‘sin(x)-sqrt(3)*cos(x)=sqrt(2)’,’x’)x =-atan(2*(1/4*2^(1/2)+1/4*3^(1/2)*2^(1/2))*2^(1/2)/(3^(1/2)-1))+pi-atan(2*(1/4*2^(1/2)-1/4*3^(1/2)*2^(1/2))*2^(1/2)/(1+3^(1/2)))-pi 解（3）x=solve(‘x^2+10*(x-1)*sqrt(x)+14*x+1=0’,’x’)x =(2^(1/2)-1)^2(-4+17^(1/2))^2 解（4）第⼗题求⽅程组的解[x,y]=solve(‘ln(x/y)=9’,’exp(x+y)=3’,’x,y’)x =exp(9)*log(3)/(exp(9)+1)y =log(3)/(exp(9)+1) 解（1）[x,y,z]=solve(‘(4*x^2)/(4*x^2+1)=y’,’(4*y^2)/(4*y^2+1)=z’,’(4*z^2)/(4*z^2+ 1)=x’,’x,y,z’) x =y =0 解（2）z =第⼗⼀题求初值y=dsolve('x*(D2y)+(1-n)*(Dy)+y=0','y(0)=Dy(0)=0','x')第⼗⼆题，求特解[x,y]=dsolve(‘Dx=3*x+4*y’,’Dy=5*x-7*y’,’x(0)=0’,’y(0)=0’,’t’)x =y =解（1）。

matlab实验内容答案

m a t l a b实验内容答案(总16页) -本页仅作为预览文档封面，使用时请删除本页-实验报告说明：matlab 课程实验需撰写8个实验报告，每个实验报告内容写每次实验内容中标号呈黑体大号字显示的题目。

第一次实验内容：实验一 MATLAB 运算基础一、实验目的1.熟悉启动和退出MATLAB 的方法。

2.熟悉MATLAB 命令窗口的组成。

3.掌握建立矩阵的方法。

4.掌握MATLAB 各种表达式的书写规则以及常用函数的使用。

二、实验内容1.先求下列表达式的值，然后显示MATLAB 工作空间的使用情况并保存全部变量。

（1）22sin8511z e ︒=+ （2）12ln(2z x =，其中2120.455i +⎡⎤=⎢⎥-⎣⎦（3）0.30.33sin(0.3), 3.0, 2.9, 2.8,,2.8,2.9,3.02a ae e z a a --=+=--- 提示：利用冒号表达式生成a 向量，求各点的函数值时用点乘运算。

（4）2220141122123t t z t t t t t ⎧≤<⎪=-≤<⎨⎪--≤<⎩，其中t ＝0：：提示：用逻辑表达式求分段函数值。

2.已知12344347873657A -⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦，131203327B -⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦求下列表达式的值：（1） A+6=B 和A-B+I(其中I 为单位矩阵)。

（2） A*B 和A.*B 。

（3） A^3和A^.3 。

（4） A/B 和B\A 。

（5）[A ，B]和[A([1,3],;);B^2] 。

3.设有矩阵A 和B12345678910111213141516171819202122232425A ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦， 30161769023497041311B ⎡⎤⎢⎥-⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎣⎦（1）求它们的乘积C 。

（2）将矩阵C 的右下角3×2子矩阵赋给D（3）查看MATLAB 工作空间使用情况。

matlab7[2].0x课后习题答案

第二章1、利用基本矩阵产生3*3和15*8的单位矩阵、全1矩阵、全0矩阵、均匀分布随机阵（[-1,1]之间）、正态分布随机阵（均值为1，方差为4）。

解：A1=eye(3); A2=ones(3); A3=zeros(3); A4=2*rand(3)-1; A5=2*randn(3)+1;B1=eye(15,8); B2=ones(15,8); B3=zeros(15,8); B4=2*rand(15,8)-1; B5=2*randn(15,8)+1; 结果：由于数据是随机产生的，所以在没有给出运行结果。

2、利用diag等函数产生下列矩阵：a=[0 0 8;0 -7 5;2 3 0] b=[2 0 4;0 5 0;7 0 8]然后利用reshape函数将它们变换成行向量。

解：产生a的程序：b=diag([8 -7 2]);c=b+diag([5 3],-1);a=fliplr(c)产生b的程序：s=[2 2 8];t=[4 3 7];v=diag(s);p=diag(t)+fliplr(v);b=fliplr(p)运行结果：a =0 0 80 -7 52 3 0b =2 0 40 5 07 0 8利用reshape函数将它们变换成行向量：reshape(a,1,9)ans =0 0 2 0 -7 3 8 5 03、产生一均匀分布在（-5,5）之间的随机阵（50*2），要求精确到小数点后一位。

解：A=5-round(100*rand(50,2))/10部分数据结果：A =2.4000 4.2000-0.1000 2.7000-4.6000 -3.3000-0.5000 -0.40003.50004.20004、编程实现当t∈[-π,π],间隔为1°时求解正弦和余弦值。

解：t=(-1*pi:1/180:pi);%范围y1=sin(t)y2=cos(t)部分数据结果：Columns 10 through 18（y1）-0.0500 -0.0555 -0.0611 -0.0666 -0.0722 -0.0777 -0.0832-0.0888 -0.09435、利用rand函数产生（0,1）间的均匀分布的10*10随机矩阵A，然后统计A中大于等于0.6的元素的个数。

matlab习题与答案

matlab习题与答案
MATLAB习题与答案
MATLAB是一种强大的数学软件，广泛应用于工程、科学和金融等领域。

通过MATLAB，用户可以进行数据分析、图像处理、模拟建模等多种操作。

为了帮
助大家更好地掌握MATLAB的应用，我们为大家准备了一些习题与答案，希望
能够帮助大家更好地理解和掌握MATLAB的使用。

习题一：编写一个MATLAB程序，实现对给定矩阵的转置操作。

解答：可以使用MATLAB中的transpose函数来实现矩阵的转置操作。

例如，
对于一个3x3的矩阵A，可以使用以下代码实现转置操作：
A = [1 2 3; 4 5 6; 7 8 9];
B = transpose(A);
习题二：编写一个MATLAB程序，实现对给定矩阵的逆矩阵计算。

解答：可以使用MATLAB中的inv函数来实现对矩阵的逆矩阵计算。

例如，对
于一个3x3的矩阵A，可以使用以下代码实现逆矩阵计算：
A = [1 2 3; 4 5 6; 7 8 9];
B = inv(A);
习题三：编写一个MATLAB程序，实现对给定矩阵的特征值和特征向量计算。

解答：可以使用MATLAB中的eig函数来实现对矩阵的特征值和特征向量计算。

例如，对于一个3x3的矩阵A，可以使用以下代码实现特征值和特征向量计算：A = [1 2 3; 4 5 6; 7 8 9];
[V, D] = eig(A);
通过以上习题与答案的学习，相信大家对MATLAB的应用已经有了更深入的了
解。

希望大家能够多加练习，不断提升自己的MATLAB技能，为今后的工作和学习打下坚实的基础。

MATLAB实验七循环结构程序设计

1.根据n3212222211116+⋯+++=π，求π的近似值。

当n 分别取100、1000、10000时，记过是多少？ n=100程序设计： n=100; i=1:n; f=1./i.^2; x=sum(f); y=sqrt(6*x) 运行结果： x =3.1321 n=1000 程序设计： n=1000; i=1:n; f=1./i.^2; x=sum(f); y=sqrt(6*x) 运行结果： x =3.1406 n=10000 程序设计： n=1000; i=1:n; f=1./i.^2; x=sum(f); y=sqrt(6*x) 运行结果： x =3.1415 2.根据y=1+1-n 215131+⋯++,求：（1）y<3时的最大n 值。

（2）与（1）的n 值对应的y 值。

程序设计： y=1;n=1; while(y<3)n=n+2; y=y+1/n; end y=y-1/n n=(n+1)/2 运行结果： y =2.9944 n =57 3.考虑以下迭代公式：x x nn b a+=+1其中a 、b 为正的常数。

（1）编写程序求迭代的结果，迭代的终止条件为1051-+≤-x x n n ，迭代初值x=1.0，迭代次数不超过500次。

程序设计： x=1.0; a=2; b=3;x=a/(b+x); n=1;while(abs(x-(a/x-b))> 10e-5&n<=500) x=a/(b+x); n=n+1; end x n运行结果： x =0.5616 n =6（2）如果迭代过程收敛于r ，那么r 的准确值是242ab b+±-，当（a,b ）的值取（1，1）、（8，3）、（10，0.1）时，分别对迭代结果的准确值进行比较。

（a,b）取（1，1）程序设计：x=1.0;a=1;b=1;x=a/(b+x);n=1;while(abs(x-(a/x-b))>10e-5&n<=500)x=a/(b+x);n=n+1;endxr1=(-b+sqrt(b^2+4*a))/2r2=(-b-sqrt(b^2+4*a))/2运行结果：x =0.6181r1 =0.6180r2 =-1.6180（a,b）取（8，3）程序设计：x=1.0;a=8;b=3;x=a/(b+x);n=1;while(abs(x-(a/x-b))>10e-5&n<=50 0)x=a/(b+x);n=n+1;endxr1=(-b+sqrt(b^2+4*a))/2r2=(-b-sqrt(b^2+4*a))/2运行结果：x =1.7016r1 =1.7016r2 =-4.7016（a,b）取（10，0.1程序设计：x=1.0;a=10;b=0.1;x=a/(b+x);n=1;while(abs(x-(a/x-b))>10e-5&n<=50 0)x=a/(b+x);n=n+1;endxr1=(-b+sqrt(b^2+4*a))/2r2=(-b-sqrt(b^2+4*a))/2运行结果：x =3.1127r1 =3.1127r2 =-3.21274.已知⎪⎪⎩⎪⎪⎨⎧>+-=======---3,23,12,01,1321321nnnnfffffffnnnn求ff1001~中：（1）最大值、最小值、各数之和。

MATLAB作业7.1.1-7.1.2

7.1MATLAB语言平台3)matlab变量精度formata=pia =3.1416b=exp(1)b =2.7183Format shorta=pia =3.1416b=exp(1)b =2.7183Format long>> aa =3.141592653589793>> bb =2.718281828459046 Format short e>> aa =3.1416e+00>> bb =2.7183e+00Format long e>> aa =3.141592653589793e+00>> bb =2.718281828459046e+00Format hex>> aa =400921fb54442d18>> bb =4005bf0a8b14576a4)变量查询>> who您的变量为:a b>> whosName Size Bytes Class Attributes a 1x1 8 doubleb 1x1 8 double5）目录与目录树结构dir. lcdata.xml matlab.exe mex.bat mexutils.pm win64.. lcdata.xsd matlab.lnk mex.pl mw_mpiexec.bat worker.batdeploytool.bat lcdata_utf8.xml mbuild.bat mexext.bat registryexam1.m m3iregistry mcc.bat mexsetup.pm util6）路径函数与搜索路径pathMATLABPATHC:\Users\acer-pc\Documents\MATLABE:\matlab2\toolbox\matlab\datafunE:\matlab2\toolbox\matlab\datatypesE:\matlab2\toolbox\matlab\elfunE:\matlab2\toolbox\matlab\elmatE:\matlab2\toolbox\matlab\funfunE:\matlab2\toolbox\matlab\generalE:\matlab2\toolbox\matlab\iofunE:\matlab2\toolbox\matlab\langE:\matlab2\toolbox\matlab\matfunE:\matlab2\toolbox\matlab\mvm……E:\matlab2\toolbox\rtw\targets\xpc\target\build\xpcblocksE:\matlab2\toolbox\rtw\targets\xpc\target\build\xpcobsoleteE:\matlab2\toolbox\rtw\targets\xpc\xpc\xpcmngrE:\matlab2\toolbox\rtw\targets\xpc\xpcdemos>> which matlab.lnkE:\matlab2\bin\matlab.lnk>> path(path,'c:\newpath')警告: 名称不存在或不是目录: c:\newpath> In path (line 109)7)联机帮助help helphelp Display help text in Command Window.help, by itself, lists all primary help topics. Each primary topiccorresponds to a folder name on the MA TLAB search path.help NAME displays the help for the functionality specified by NAME,such as a function, operator symbol, method, class, or toolbox.NAME can include a partial path.Some classes require that you specify the package name. Events,properties, and some methods require that you specify the classname. Separate the components of the name with periods, using oneof the following forms:help help PACKAGENAME.CLASSNAMEhelp If NAME is the name of both a folder and a function, help displayshelp for both the folder and the function. The help for a folderis usually a list of the program files in that folder.If NAME appears in multiple folders on the MA TLAB path, help displays information about the first instance of NAME found on the path.NOTE:In the help, some function names are capitalized to make themstand out. In practice, type function names in lowercase. Forfunctions that are shown with mixed case (such as javaObject),type the mixed case as shown.EXAMPLES:help close % help for the CLOSE functionhelp database/close % help for CLOSE in the Database Toolboxhelp database % list of functions in the Database Toolbox% and help for the DA TABASE function help containers.Map.isKey % help for isKey methodSee also doc, docsearch, lookfor, matlabpath, which.help 的参考页名为help 的其他函数help whowho List current variables.who lists the variables in the current workspace.In a nested function, variables are grouped into those in the nestedfunction and those in each of the containing functions. who displaysonly the variables names, not the function to which each variablebelongs. For this information, use WHOS.WHOS lists more information about each variable.who GLOBAL and WHOS GLOBAL list the variables in the global workspace.who -FILE FILENAME lists the variables in the specified .MAT file.who ... VAR1 V AR2 restricts the display to the variables specified. Thewildcard character '*' can be used to display variables that match apattern. For instance, who A* finds all variables in the currentworkspace that start with A.who -REGEXP PA T1 PAT2 can be used to display all variables matching the specified patterns using regular expressions. For more information onusing regular expressions, type "doc regexp" at the command prompt.Use the functional form of who, such as who('-file',FILE,V1,V2),when the filename or variable names are stored in strings.S = who(...) returns a cell array containing the names of the variablesin the workspace or file. You must use the functional form of who whenthere is an output argument.Examples for pattern matching:who a* % Show variable names starting with "a"who -regexp ^b\d{3}$ % Show variable names starting with "b"% and followed by 3 digits who -file fname -regexp \d % Show variable names containing any% digits that exist in MAT-file fname See also whos, clear, clearvars, save, load.who 的参考页名为who 的其他函数help pathpath Get/set search path.path, by itself, prettyprints MATLAB's current search path. The initialsearch path list is set by PA THDEF, and is perhaps individualized bySTARTUP.P = path returns a string containing the path in P. path(P) changes thepath to P. path(path) refreshes MA TLAB's view of the directories onthe path, ensuring that any changes to non-toolbox directories arevisible.path(P1,P2) changes the path to the concatenation of the two pathstrings P1 and P2. Thus path(path,P) appends a new directory to thecurrent path and path(P,path) prepends a new directory. If P is alreadyon the path, then path(path,P) moves P to the end of the path,and similarly, path(P,path) moves P to the beginning of the path.For example, the following statements add another directory to MATLAB's search path on various operating systems:Unix: path(path,'/home/myfriend/goodstuff')Windows: path(path,'c:\tools\goodstuff')See also what, cd, dir, addpath, rmpath, genpath, pathtool, savepath, rehash.path 的参考页名为path 的其他函数8）字符串查询help lookforlookfor Search all MA TLAB files for keyword.lookfor XYZ looks for the string XYZ in the first comment line(the H1 line) of the HELP text in all MATLAB files found on MA TLABPATH (including private directories). For all files in which amatch occurs, lookfor displays the H1 line.For example, "lookfor inverse" finds at least a dozen matches,including the H1 lines containing "inverse hyperbolic cosine""two-dimensional inverse FFT", and "pseudoinverse".Contrast this with "which inverse" or "what inverse", which runmore quickly, but which probably fail to find anything becauseMATLAB does not ordinarily have a function "inverse".lookfor XYZ -all searches the entire first comment block ofeach MATLAB file.In summary, WHAT lists the functions in a given directory,WHICH finds the directory containing a given function or file, andlookfor finds all functions in all directories that might havesomething to do with a given key word.See also dir, help, who, what, which.lookfor 的参考页（2）练习MATLAB命令的基本操作1）常数矩阵输入a=[1 2 3]a =1 2 3>> a=[1;2;3]a =123记录结果显示有何不同b=[1 2 5]b =1 2 5>> b=[1 2 5];‘；’有则只执行不显示，无则即执行又显示记录结果显示有何不同> aa =123>> a'ans =1 2 3>> bb =1 2 5>> b'ans =125记录结果，比较变量加“’”>> c=a*bc =1 2 52 4 103 6 15记录结果显示与出错原因>> c=a*b'错误使用*内部矩阵维度必须一致。

数学实验作业七

数学实验作业七题目：P200. 2)；6) 日期：2003-4-9【实验目的】：1、掌握MATLAB 优化工具箱的基本用法，对不同算法进行初步分析、比较。

2、练习实际问题的非线性最小二乘拟合。

【实验内容】：二：求解()12212122min 42421x e x x x x x ++++，初值（－1，1），对不同算法的结果进行分析、比较。

【模型分析】：首先画出函数f=12212122(42421)x e x x x x x ++++的图像和等高线：可以看到：在[0.5,-1]附近为一个“凹地”，最小值应在该凹地中取得。

另外，从（-1,1）到此凹地为一与Rosenbrock 函数类似的狭长通道，不利于沿负梯度方向下降。

可以想象，该函数具有与Rosenbrock 函数类似的性质。

【MATLAB 源程序】比较程序如下：%数学实验作业二.1-dfunction f=ch72fun(x);%第7章第2题的函数f=exp(x(1)).*(4*x(1).^2+2*x(2).^2+4*x(1).*x(2)+2.*x(2)+1);%ch72.m%第7章第2题X0=[-1,1];%赋初值%BFGS,混合二三次插值opt1=optimset('TolX',1e-6,'TolFun',1e-6,'MaxIter',1000);[X1,FV AL,EXITFLAG,OUTPUT]=FMINUNC(@ch72fun,X0,opt1)%BFGS,三次插值opt2=optimset(opt1,'LineSearchType','cubicpoly');[X1,FV AL,EXITFLAG,OUTPUT]=FMINUNC(@ch72fun,X0,opt2)%DFP,混合二三次插值opt3=optimset(opt1,'HessUpdate','dfp');[X1,FV AL,EXITFLAG,OUTPUT]=FMINUNC(@ch72fun,X0,opt3)%DFP,三次插值opt4=optimset(opt3,'LineSearchType','cubicpoly');[X1,FV AL,EXITFLAG,OUTPUT]=FMINUNC(@ch72fun,X0,opt4)%最速下降,混合二三次插值opt5=optimset(opt1,'HessUpdate','steepdesc');[X1,FV AL,EXITFLAG,OUTPUT]=FMINUNC(@ch72fun,X0,opt5)【MATLAB 运行结果】：结果为：所以可以得到本题的解析解：x=(0.5,-1)，f=0。

（完整版）matlab经典习题及解答

（完整版）matlab经典习题及解答第1章 MATLAB 概论1.1 与其他计算机语⾔相⽐较，MATLAB 语⾔突出的特点是什么？MATLAB 具有功能强⼤、使⽤⽅便、输⼊简捷、库函数丰富、开放性强等特点。

1.2 MATLAB 系统由那些部分组成？MATLAB 系统主要由开发环境、MATLAB 数学函数库、MATLAB 语⾔、图形功能和应⽤程序接⼝五个部分组成。

1.4 MATLAB 操作桌⾯有⼏个窗⼝？如何使某个窗⼝脱离桌⾯成为独⽴窗⼝？⼜如何将脱离出去的窗⼝重新放置到桌⾯上？在MATLAB 操作桌⾯上有五个窗⼝，在每个窗⼝的右上⾓有两个⼩按钮，⼀个是关闭窗⼝的Close 按钮，⼀个是可以使窗⼝成为独⽴窗⼝的Undock 按钮，点击Undock 按钮就可以使该窗⼝脱离桌⾯成为独⽴窗⼝，在独⽴窗⼝的view 菜单中选择Dock ……菜单项就可以将独⽴的窗⼝重新防⽌的桌⾯上。

1.5 如何启动M ⽂件编辑/调试器？在操作桌⾯上选择“建⽴新⽂件”或“打开⽂件”操作时，M ⽂件编辑/调试器将被启动。

在命令窗⼝中键⼊edit 命令时也可以启动M ⽂件编辑/调试器。

1.6 存储在⼯作空间中的数组能编辑吗？如何操作？存储在⼯作空间的数组可以通过数组编辑器进⾏编辑：在⼯作空间浏览器中双击要编辑的数组名打开数组编辑器，再选中要修改的数据单元，输⼊修改内容即可。

1.7 命令历史窗⼝除了可以观察前⾯键⼊的命令外，还有什么⽤途？命令历史窗⼝除了⽤于查询以前键⼊的命令外，还可以直接执⾏命令历史窗⼝中选定的内容、将选定的内容拷贝到剪贴板中、将选定内容直接拷贝到M ⽂件中。

1.8 如何设置当前⽬录和搜索路径，在当前⽬录上的⽂件和在搜索路径上的⽂件有什么区别？当前⽬录可以在当前⽬录浏览器窗⼝左上⽅的输⼊栏中设置，搜索路径可以通过选择操作桌⾯的file 菜单中的Set Path 菜单项来完成。

在没有特别说明的情况下，只有当前⽬录和搜索路径上的函数和⽂件能够被MATLAB 运⾏和调⽤，如果在当前⽬录上有与搜索路径上相同⽂件名的⽂件时则优先执⾏当前⽬录上的⽂件，如果没有特别说明，数据⽂件将存储在当前⽬录上。

MATLAB讲义第七章作业及答案

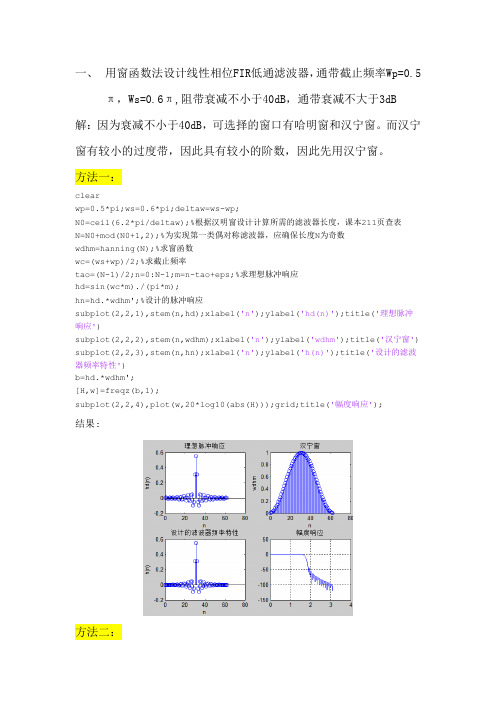
一、用窗函数法设计线性相位FIR低通滤波器，通带截止频率Wp=0.5π，Ws=0.6π,阻带衰减不小于40dB，通带衰减不大于3dB 解：因为衰减不小于40dB，可选择的窗口有哈明窗和汉宁窗。

而汉宁窗有较小的过度带，因此具有较小的阶数，因此先用汉宁窗。

方法一：clearwp=0.5*pi;ws=0.6*pi;deltaw=ws-wp;N0=ceil(6.2*pi/deltaw);%根据汉明窗设计计算所需的滤波器长度，课本211页查表N=N0+mod(N0+1,2);%为实现第一类偶对称滤波器，应确保长度N为奇数wdhm=hanning(N);%求窗函数wc=(ws+wp)/2;%求截止频率tao=(N-1)/2;n=0:N-1;m=n-tao+eps;%求理想脉冲响应hd=sin(wc*m)./(pi*m);hn=hd.*wdhm';%设计的脉冲响应subplot(2,2,1),stem(n,hd);xlabel('n');ylabel('hd(n)');title('理想脉冲响应')subplot(2,2,2),stem(n,wdhm);xlabel('n');ylabel('wdhm');title('汉宁窗') subplot(2,2,3),stem(n,hn);xlabel('n');ylabel('h(n)');title('设计的滤波器频率特性')b=hd.*wdhm';[H,w]=freqz(b,1);subplot(2,2,4),plot(w,20*log10(abs(H)));grid;title('幅度响应');结果:方法二：>> wp=0.5*pi;>> ws=0.6*pi;>> wd=ws-wp;>> N=ceil(8*pi/wd);>> wc=(0.5+0.6)*pi/2;>> window=hanning(N+1); >> b=fir1(N,wc/pi,window); >> freqz(b,1,512)。

MATLAB实用教程(第2版)第七章数学计算

● R=chol(X)，X为对称的正定矩阵，R为上三角矩阵，使得；
● [R,p]=chol(X)，X是正定矩阵时，返回的矩阵R是上三角矩阵，而且满足等式，同时返回参数p=0；X不是正定矩阵时，返回的参数p是正整数，是三角矩阵，且矩阵阶数是p-1，并且满足等式。
例7.8 将对称正定矩阵
23
例7.9 对矩阵
进行LU分解。
（1）新建一个M文件；
（2）在文本编辑器中键入如下内容：
A=[-1 8 -5;9 -1 2;2 -5 7]; [Ll,Ul]=lu(A) Al=Ll*Ul x=inv(A) xl=inv(Ul)*(Ll) d=det(A) dl=det(Ll)*det(Ul)
（3）保存文件，文件名为“exam0709.m”；运行脚本可得到结果下：
• 例7.1 分别求取函数、、、和的极限。在命令窗口输入的具体代码如下：
syms x a t h;
limit(sin(x)/x) limit((x-2)/(x^2-4),2) limit((1+2*t/x)^(3*x),x,inf) limit(1/x,x,0,'right') limit(1/x,x,0,'left')
进行Cholesky分解。
20
（1）新建一个M文件；（2）在文本编辑器中键入如下内容：
X=[1 1 1 1 1;1 2 3 4 5;1 3 6 10 15;1 4 10 12 35;1 5 15 35 70]; R=chol(X) C=transpose(R)*R
（3）保存文件，文件名为“exam0708.m”；运行脚本后可得到如下结果：
18
（3）保存文件，文件名为“exam0707.m”；运行脚本后可得到如下结果：

MATLAB教程2012a习题解答1-7章完整版-张志涌-北航

●MATLAB R2012a●课后习题答案全解●第一章基础准备及入门习题1及解答⏹ 1.数字1.5e2，1.5e3 中的哪个与1500相同吗？〖解答〗1.5e3⏹ 2.请指出如下5个变量名中，哪些是合法的？abcd-2 xyz_3 3chan a变量ABCDefgh〖解答〗2、5是合法的。

⏹ 3.在MATLAB环境中，比1大的最小数是多少？〖解答〗1+eps⏹ 4.设a = -8 , 运行以下三条指令，问运行结果相同吗？为什么？w1=a^(2/3)w2=(a^2)^(1/3)w3=(a^(1/3))^2〖解答〗（1）不同。

具体如下w1=a^(2/3) %仅求出主根w2=(a^2)^(1/3) %求出(-8)^2的主根 w3=(a^(1/3))^2%求出(-8)主根后再平方w1 = -2.0000 + 3.4641iw2 = 4.0000 w3 =-2.0000 + 3.4641i（2）复数的多方根的，下面是求取全部方根的两种方法：（A ）根据复数方根定义a=-8;n=2;m=3;ma=abs(a);aa=angle(a); for k=1:m%m 决定循环次数 sa(k)=(aa+2*pi*(k-1))*n/m;%计算各根的相角 endresult=(ma^(2/3)).*exp(j*sa) %计算各根result =-2.0000 + 3.4641i 4.0000 - 0.0000i -2.0000 - 3.4641i（B ）利用多项式023=-a r 求根p=[1,0,0,-a^2]; r=roots(p) r =-2.0000 + 3.4641i -2.0000 - 3.4641i 4.0000⏹ 5.指令clear, clf, clc 各有什么用处？〖解答〗 clear 清除工作空间中所有的变量。

clf 清除当前图形。

clc 清除命令窗口中所有显示。

⏹ 6.以下两种说法对吗？（1）“MATLAB 进行数值的表达精度与其指令窗中的数据显示精度相同。

matlab参考答案matlab第7次作业至诚2013参考答案

1 t 在[0，10]范围内，)3010sin(02+=-t e y t ，计算y 的最大值，最小值，平均值和积分值。

t=0:10y=exp(-2*t).*sin(10*t+pi/6)max(y)min(y)mean(y)trapz(t,y)2 数据分析（必做）下表为2.1 >> score=[75 81 73;62 85 79;71 68 60;58 92 75;73 90 81]2.2 统计每位学生的平均分和总分>> mean(score,2) %平均分>> sum(score,2) %总分，注意cumsum 用于求累计求和，此处用sum 函数即可 >> max(score,[],2) %最高分%%方法二：mean(score')sum(score')max(score')2.3 统计每门课程的平均分和总分>> mean(score) %平均分>> sum(score) %总分>> max(score) %最高分2.4 统计每门课程的标准差>> std(score,0)2.4 按照数学成绩的升序序列对矩阵进行重新排序>> [x,ind]=sortrows(score,2)2.5 找出语文成绩最高分的学生序号>> [x,ind]=max(score(:,2))2.6 打印语文成绩最高的学生三门课程的成绩信息：显示格式如下：×的数学成绩：××分，语文成绩：××分物理成绩：××分[x,ind]=sortrows(score,2)fprintf('%d 的数学成绩是%d,语文成绩是%d,物理成绩是%d\n',ind,x(4,1),x(4,2),x(4,3))%%方法二:[s,ind]=max(score(:,2))fprintf('%d 的数学成绩是%d,语文成绩是%d,物理成绩是%d\n', ind,score(ind,1),score(ind,2),score(ind,3))。