假设检验 作业
实验7 假设检验(一)

实验7 假设检验(一)一、实验目的:1.掌握重要的参数检验方法(单个总体的均值检验,两个总体的均值检验,成对样本的均值的检验,两个总体方差的检验,二项分布总体的检验);2.掌握若干重要的非参数检验方法(Pearson拟合优度 2检验,Kolmogorov-Smirnov单样本和双样本检验)。
二、实验内容:练习:要求:①完成练习并粘贴运行截图到文档相应位置(截图方法见下),并将所有自己输入文字的字体颜色设为红色(包括后面的思考及小结),②回答思考题,③简要书写实验小结。
④修改本文档名为“本人完整学号姓名1”,其中1表示第1次实验,以后更改为2,3,...。
如文件名为“09张立1”,表示学号为09的张立同学的第1次实,法1Alt,即完法2:图标,工具。
)1.2.H0:H1:alternative hypothesis: true mean is not equal to 22595 percent confidence interval:172.3827 211.9173sample estimates:mean of x192.15P=0.002516<0.05,拒绝原假设,认为油漆工人的血小板计数与正常成年男子有差异3.(习题5.2)已知某种灯泡寿命服从正态分布,在某星期所生产的该灯泡中随机抽取10 只,测得其寿命(单位:小时)为1067 919 1196 785 1126 936 918 1156 920 948求这个星期生产出的灯泡能使用1000小时以上的概率。
解:源代码及运行结果:(复制到此处,不需要截图)> x<-c(1067, 919, 1196, 785, 1126, 936, 918, 1156, 920, 948)> p<-pnorm(1000,mean(x),sd(x))> 1-p[1] 0.4912059结论:这个星期生产出的灯泡能使用1000小时以上的概率为0.49120594.(习题5.3)为研究某铁剂治疗和饮食治疗营养性缺铁性贫血的效果,将16名患者按年龄、体重、病程和病情相近的原则配成8对,分别使用饮食疗法和补充铁剂治疗的方法,3个月后测得两种患者血红资白如下表所示,问两种方法治疗后的患者血红蛋白有无差异?H0:H1:5.,分别测试验组与对照组空腹腔血糖下降值(mmol/L)(1)检验试验组和对照组的的数据是否来自正态分布,采用正态性W检验方法(见第3章)、Kolmogorov-Smirnov检验方法和Pearson拟合优度 2检验;解:提出假设:H0:认为国产四类新药阿卡波糖股嚢与拜唐苹股嚢对空腹血糖的降糖效果不同H1:认为国产四类新药阿卡波糖股嚢与拜唐苹股嚢对空腹血糖的降糖效果相同①正态性W检验方法源代码及运行结果:(复制到此处,不需要截图)>x<-c(-0.70,-5.60,2.00,2.80,0.70,3.50,4.00,5.80,7.10,-0.50,2.50,-1.60,1.70,3.00,0.40,4.50,4.6 0,2.50,6.00,-1.4)> shapiro.test(x)Shapiro-Wilk normality testdata: xW = 0.9699, p-value = 0.7527>y<-c(3.70,6.50,5.00,5.20,0.80,0.20,0.60,3.40,6.60,-1.10,6.00,3.80,2.00,1.60,2.00,2.20,1.20,3②结论:试验组p=0.9771>0.05,对照组p=0.9368>0.05,所以检验试验组和对照组的的数据是来自正态分布③Pearson拟合优度 2检验源代码及运行结果:(复制到此处,不需要截图)>x<-c(-0.70,-5.60,2.00,2.80,0.70,3.50,4.00,5.80,7.10,-0.50,2.50,-1.60,1.70,3.00,0.40,4.50,4.6 0,2.50,6.00,-1.4)> A<-table(cut(x,br=c(-6,-3,0,3,6,9)))> p<-pnorm(c(-3,0,3,6,9),mean(x),sd(x))> p> p<-c(p[1],p[2]-p[1],p[3]-p[2],p[4]-p[3],1-p[4])> p> chisq.test(A,p=p)Chi-squared test for given probabilitiesdata: AX-squared = 0.56387, df = 4, p-value = 0.967Warning message:In chisq.test(A, p = p) : Chi-squared近似算法有可能不准>y<-c(3.70,6.50,5.00,5.20,0.80,0.20,0.60,3.40,6.60,-1.10,6.00,3.80,2.00,1.60,2.00,2.20,1.20,3 .10,1.70,-2.00)> B<-table(cut(y,br=c(-2,1,2,4,7)))> p<-pnorm( c(-2,1,2,4,7),mean(y),sd(y))> p> p(2H0:H1:t = -0.64187, df = 38, p-value = 0.5248alternative hypothesis: true difference in means is not equal to 095 percent confidence interval:-2.326179 1.206179sample estimates:mean of x mean of y2.065 2.625结论:p=0.5248>0.05,不拒绝原假设,两组数据均值没有差异②方差不同模型源代码及运行结果:(复制到此处,不需要截图)>x<-c(-0.70,-5.60,2.00,2.80,0.70,3.50,4.00,5.80,7.10,-0.50,2.50,-1.60,1.70,3.00,0.40,4.50,4.6 0,2.50,6.00,-1.4)>y<-c(3.70,6.50,5.00,5.20,0.80,0.20,0.60,3.40,6.60,-1.10,6.00,3.80,2.00,1.60,2.00,2.20,1.20,3 .10,1.70,-2.00)> t.test(x,y)Welch Two Sample t-testdata: x and yt = -0.64187, df = 36.086, p-value = 0.525alternative hypothesis: true difference in means is not equal to 095 percent confidence interval:(3解:提出假设:H0:试验组与对照组的方差相同H1:试验组与对照组的方差不相同源代码及运行结果:(复制到此处,不需要截图)>x<-c(-0.70,-5.60,2.00,2.80,0.70,3.50,4.00,5.80,7.10,-0.50,2.50,-1.60,1.70,3.00,0.40,4.50,4.6 0,2.50,6.00,-1.4)>y<-c(3.70,6.50,5.00,5.20,0.80,0.20,0.60,3.40,6.60,-1.10,6.00,3.80,2.00,1.60,2.00,2.20,1.20,3 .10,1.70,-2.00)> var.test(x,y)F test to compare two variancesdata: x and yF = 1.5984, num df = 19, denom df = 19, p-value = 0.3153alternative hypothesis: true ratio of variances is not equal to 195 percent confidence interval:0.6326505 4.0381795sample estimates:ratio of variances1.598361结论:p= 0.3153>0.05,不拒绝原假设,试验组与对照组的方差相同6.(习题5.5)为研究某种新药对抗凝血酶活力的影响,随机安排新药组病人12例,对照组病人10例,(1(2(3解:(1H0:H1:H0:H1:> y<-c(162, 172 ,177 ,170 ,175, 152 ,157 ,159, 160 ,162)> ks.test(y,"pnorm",mean(y),sd(y))One-sample Kolmogorov-Smirnov testdata: yD = 0.22216, p-value = 0.707alternative hypothesis: two-sidedWarning message:In ks.test(y, "pnorm", mean(y), sd(y)) :Kolmogorov - Smirnov检验里不应该有连结(2)检验两组样本方差是否相同;提出假设:H0:两组样本方差相同H1:两组样本方差不相同源代码及运行结果:(复制到此处,不需要截图)> x<-c(126,125,136,128,123,138,142,116,110,108,115,140)> y<-c(162, 172 ,177 ,170 ,175, 152 ,157 ,159, 160 ,162)> var.test(x,y)F test to compare two variancesdata: x and yF = 1.9646, num df = 11, denom df = 9, p-value = 0.32alternative hypothesis: true ratio of variances is not equal to 1(3H0:H1:7.靠,随机抽选了400名居民,发现其中有57人是老年人。
应用数理统计作业题及参考答案(第三章)

第三章 假设检验P1313.2 一种元件,要求其使用寿命不得低于1000(小时)。
现在从一批这种元件中随机抽取25件,测得其寿命平均值为950(小时)。
已知该种元件寿命服从标准差100σ=(小时)的正态分布,试在显著水平0.05下确定这批元件是否合格。
解:本题需检验0H :0μμ≥,1H :0μμ<.元件寿命服从正态分布,0σ已知,∴当0H成立时,选取统计量X u μ-=,其拒绝域为{}V u u α=<.其中950X =,01000μ=,25n =,0100σ=.则 2.5u ==-.查表得0.05 1.645u =-,得0.05u u <,落在拒绝域中,拒绝0H ,即认为这批元件不合格。
3.3 某厂生产的某种钢索的断裂强度服从正态分布()2N μσ,,其中40σ=(kg / cm 2)。
现从一批这种钢索的容量为9的一个子样测得断裂强度平均值为X ,与以往正常生产时的μ相比,X 较μ大20(kg / cm 2)。
设总体方差不变,问在0.01α=下能否认为这批钢索质量有显著提高?解:本题需检验0H :0μμ=,1H :0μμ>.钢索的断裂强度服从正态分布,0σ已知,∴当0H成立时,选取统计量u =,其拒绝域为{}1V u u α-=>.其中040σ=,9n =,020X μ-=,0.01α=.则 1.5u ==.查表得10.990.01 2.33u u u u αα-==-=-=,得0.99u u <,未落在拒绝域中,接受0H ,即认为这批钢索质量没有显著提高。
3.5 测定某种溶液中的水分。
它的10个测定值给出0.452%X =,0.035%S =。
设总体为正态分布()2N μσ,,试在水平5%检验假设:(i )0H :0.5%μ>; 1H :0.5%μ<. (ii )0H :0.04%σ≥; 1H :0.04%σ<. 解:(i )总体服从正态分布,0σ未知,当0H成立时,选取统计量t =(){}1V t t n α=<-.查表得()()0.050.9599 1.8331t t =-=-.而()4.114 1.83311t t n α==-<-=-.落在拒绝域中,拒绝0H .(ii )总体服从正态分布,μ未知, 当0H 成立时,选取统计量222nSχσ=,其拒绝域为(){}221V n αχχ=<-.查表得()20.059 3.325χ=.而()()()2222100.035%7.65610.04%n αχχ⨯==>-.未落在拒绝域中,接受0H .3.6 使用A (电学法)与B (混合法)两种方法来研究冰的潜热,样品都是-0.72℃的冰块,下列数据是每克冰从-0.72℃变成0℃水的过程中的吸热量(卡 / 克):方法A :79.98,80.04,80.02,80.04,80.03,80.03,80.04,79.97,80.05,80.03,80.02,80.00,80.02方法B :80.02,79.94,79.97,79.98,79.97,80.03,79.95,79.97假定用每种方法测得的数据都服从正态分布,且它们的方差相等。
作业题07 假设检验

第七章 假设检验 作业习题答案7.1 设总体2(,)N ξμσ~,其中参数μ,2σ为未知,试指出下面统计假设中哪些是简单假设,哪些是复合假设:(1)0:0,1H μσ==; (2)0:0,1H μσ=>; (3)0:3,1H μσ<=; (4)0:03H μ<<; (5)0:0H μ=.7.2 设1225,,,ξξξ 取自正态总体(,9)N μ,其中参数μ未知,x 是子样均值,如对检验问题001:,:H H μμμμ=≠取检验的拒绝域:12250{(,,,):||}c xx x x c μ=-≥ ,试决定常数c,使检验的显著性水平为0.057.3 设子样1225,,,ξξξ 取自正态总体20(,)N μσ,20σ已知,对假设检验0010:,:H H μμμμ=>,取临界域12n 0{(,,,):|}c x x x c ξ=> ,(1)求此检验犯第一类错误概率为α时,犯第二类错误的概率β,并讨论它们之间的关系;(2)设0μ=0.05,20σ=0.004,α=0.05,n=9,求μ=0.65时不犯第二类错误的概率。
7.4 设一个单一观测的ξ子样取自分布密度函数为()f x 的母体,对()f x 考虑统计假设:0011101201:():()00x x x H f x H f x ≤≤≤≤⎧⎧==⎨⎨⎩⎩其他其他试求一个检验函数使犯第一,二类错误的概率满足2min αβ+=,并求其最小值。
7.5 设某产品指标服从正态分布,它的根方差σ已知为150小时。
今由一批产品中随机抽取了26个,测得指标的平均值为1637小时,问在5%的显著性水平下,能否认为该批产品指标为1600小时?7.6 某电器零件的平均电阻一直保持在2.64Ω,根方差保持在0.06Ω,改变加工工艺后,测得100个零件,其平均电阻为2.62Ω,根方差不变,问新工艺对此零件的电阻有无显著差异?去显著性水平α=0.01。
第12章 假设检验典型例题与综合练习

经济数学基础 第12章 假设检验第12章 假设检验典型例题与综合练习一、典型例题1.U 检验例1某切割机在正常工作时,切割的每段金属棒长度服从正态分布,且其平均长度为10.5cm ,标准差为0.15cm.今从一批产品中随机抽取15段进行测量,其结果为(单位:cm )10.5 10.6 10.1 10.4 10.5 10.3 10.3 10.9 10.2 10.6 10.8 10.5 10.7 10.2 10.7假设方差不变,问该切割机工作是否正常?(α=0.05)这是已知方差2σ,对正态总体的均值μ进行检验的问题,用U 检验法解:,5.10:0=μH 5.10:1≠μH选统计量n x U /0σμ-=计算得x =10.48,已知15.0=σ,n =15,计算检验量516.015/15.05.1048.10=-=U查正态分布数值表求临界值λ,因为05.0=αλ,975.021)(=-=Φαλ,得经济数学基础 第12章 假设检验λ=975.0U =1.96,因为975.0U U <,故0H 相容,即在显著水平05.0=α下可以认为该切割机工作正常.2. T 检验例1 随机抽取某班28名学生的英语考试成绩,得平均分数为80=x 分,样本标准差8=s 分,若全年级的英语成绩服从正态分布,且平均成绩为85分,试问在显著水平05.0=α下,能否认为该班的英语成绩与全年级学生的英语平均成绩没有本质的差别这是单个正态总体),(~2σμN X ,方差2σ未知时关于均值μ的假设检验问题,用T 检验法.解85:0=μH ,85:1≠μH选统计量n s x T /0μ-=已知80=x ,8=s ,n =28,850=μ,计算得ns x T /0μ-=31.328/88580=-=查t 分布表,05.0=α,自由度27,临界值λ=052.2)27(975.0=t .经济数学基础 第12章 假设检验由于>T 052.2)27(975.0=t ,故拒绝H ,即在显著水平05.0=α下不能认为该班的英语成绩为85分.3. x 2检验例 1 检验某电子元件可靠性指标15次,计算得指标平均值为95.0=x ,样本标准差为03.0=s ,该元件的订货合同规定其可靠性指标的标准差为0.05,假设元件可靠性指标服从正态分布.问在10.0=α下,该电子元件可靠性指标的方差是否符合合同标准?取10.0=α.这是单个正态总体),(~2σμN X ,关于方差2σ的假设检验问题,用2χ检验法.解22005.0:=σH ,22105.0:≠σH当H 为真时,统计量222)1(σχs n -=~)1(2-χn拒绝域是>2χ)1(205.0-n χ或<2χ)1(295.0-χn n =15,03.0=s ,05.00=σ,检验值22205.003.0)15(-=χ=5.04因为10.0=α,自由度14,查2χ分布表571.6)14(295.0=χ,知571.61=λ ,)14(295.012χλχ=<,所以拒绝H ,即该电子元件可靠性指标的方差不符合合同标准.经济数学基础 第12章 假设检验由于2χ分布的图形是不对称的,所以左右两个临界值是不同的.比较检验值2χ与临界值21,λλ的大小:只要满足2χ>1λ或2χ<2λ之一,就可以H ;否则接受0H .二、综合练习1.填空题1. 对总体);(~θx f X 的未知参数θ的有关命题进行检验,属于 ________问题.2. 小概率原理是指 .3.设),(~2σμN X ,当2σ已知时,检验00:μμ=H ,用 检验法,选用统计量U = ,当H 成立时,统计量服从 分布.2.单选题1.对正态总体方差的假设检验用的是( ).(A) U 检验法 (B) T 检验法 (C) 2χ检验法 (D) F 检验法2.设nx x x ,,,21Λ是来自正态总体),(2σμN (2σ已知)的样本,按给定的显著性水平α检验00:μμ=H (已知);1:μμ≠H 时,判断是否接受H 与( )有关.经济数学基础 第12章 假设检验(A) 样本值,显著水平α (B) 样本值,样本容量n (C) 样本容量n ,显著水平α (D) 样本值,样本容量n ,显著水平α3.在假设检验中,显著水平α表示( ). (A)P {接受00H H 假}=α (B)P {拒绝00H H 真}=α (C)P {接受0H H 真}=α (D)P {拒绝0H H 假}=α1. C 2.D 3.B3.计算题1.某手表厂生产的圆形女表表壳,在正常条件下,直径服从均值为20mm ,方差为1mm 2的正态分布,某天抽查10只表壳,测得直径为(单位:mm ):19 19.5 19.8 20 20.220.5 18.7 19.6 20 20.1问生产情况是否正常?第二天测了5只,测得直径为(单位:mm ):20.2 21.3 22.4 23.5 24.6 结论是什么?取02.0=α.2.洗衣粉包装机包出的洗衣粉重量是一个随机变量),(2σμN ,机器正常工作时,5000=μ克,有一天开机后,随机地抽取9袋洗衣粉,称得重量为(单位:g ):497 506 528 524 498经济数学基础 第12章 假设检验511 520 515 512问以05.0=α显著水平检验这天机器的工作是否正常.3.已知某化纤厂生产的纤度平日服从正态分布)048.0,405.1(2N ,某日抽取5根化纤,测得其纤度为1.32 1.55 1.36 1.40 1.44问该日生产的化纤纤度总体方差2σ是否正常?取05.0=α.三、本章作业1.由经验知某产品重量)05.0,15(~N X ,现抽取6个样品,测得重量为(单位:kg ):14.7 15.1 14.8 15.0 15.2 14.6设方差不变,问平均重量是否仍为15kg ?取05.0=α.2.某机器在正常工作时,生产的产品平均每个应为50克重,从该机器生产的一批产品中抽取9个,分别称得重量为(单位:g ):经济数学基础 第12章 假设检验52.1 50.5 51.2 49.7 49.550.5 58.7 50.5 48.3 设产品重量服从正态分布,问这批产品质量是否正常?取05.0=α3.正常人的脉搏平均72次/分,某医生测得10例慢性中毒者的脉搏为(单位:次/分)54 67 68 70 6667 70 65 69 78 设中毒者的脉搏服从正态分布,问中毒者和正常人的脉搏有无显著性差异?取05.0=α.1.可以认为平均重量仍为15kg ; 2.这批产品的质量正常; 3.没有显著差异.。
假设检验练习题

假设检验练习题在统计学中,假设检验是一种常用的数据分析方法,用于通过样本数据对总体参数的假设进行验证。
通过进行假设检验,我们可以确定样本数据是否足够支持对总体参数的某种特定假设。
一、背景介绍假设检验的基本思想是:假设总体参数服从某种特定的概率分布,然后利用样本数据对这一假设进行检验。
在进行假设检验时,我们通常会提出原假设(H0)和备择假设(H1),其中原假设是我们要进行检验的假设,备择假设则是对原假设的否定或补充。
二、假设检验的步骤1. 提出假设:根据问题的需求和背景,明确原假设和备择假设。
2. 选择显著性水平:显著性水平α代表我们对假设检验结果的接受程度,通常选择0.05或0.01。
3. 计算检验统计量:根据样本数据和所选的假设检验方法,计算出相应的检验统计量。
4. 确定拒绝域:根据显著性水平和假设检验的方法,确定拒绝域的临界值。
5. 判断结论:将计算得到的检验统计量与拒绝域进行比较,根据比较结果作出结论。
三、假设检验的类型1. 单样本检验:当我们只有一个样本数据,想要对总体参数是否符合某个特定值进行判断时,可以使用单样本检验。
2. 独立样本检验:当我们有两个独立的样本数据,并且希望比较两个总体参数是否有差异时,可以使用独立样本检验。
3. 配对样本检验:当我们有两组相关的样本数据,并且希望比较两个总体参数的差异时,可以使用配对样本检验。
四、常见的假设检验方法1. t检验:用于对总体均值进行假设检验,可以进行单样本t检验、独立样本t检验和配对样本t检验。
2. 方差分析(ANOVA):用于比较多个样本均值是否有差异,适用于有两个以上样本的情况。
3. 卡方检验:用于对分类变量的比例进行假设检验,适用于两个或更多分类变量的情况。
4. 相关分析:用于检验两个变量之间是否存在线性相关性。
五、实例分析为了更好地理解假设检验的应用,我们举一个实际例子。
假设一个制药公司研发了一种新药,声称该药物的疗效显著优于市场上已有的药物。
作业三 假设检验

作业三假设检验一、为了研究两种教学方法的效果。
选择了6对智商、年龄、阅读能问:能否认为新教学方法优于原教学方法?问:(1)男性的身高与女性的身高是否相等?(2)学生的体重是否等于45公斤?三、双样本T检验(Independent-Samples T Test过程)分别测得14例老年性慢性支气管炎病人及11例健康人的尿中17酮类固醇实验步骤:1.建立数据文件。
定义变量名:把实际观察值定义为x,再定义一个变量group来区分病人与健康人。
输入原始数据,在变量group中,病人输入1,健康人输入2。
2. 选择菜单“Analyz e→Compare Means→Independent-samples T Test”项,弹出“Independent- samples T Test”对话框。
从对话框左侧的变量列表中选x,进入“Test Variable(s)”框,选择变量“group”,进入“Grouping Variable”框,点击“Define Groups”钮弹出“Define Groups”定义框,在Group 1中输入1,在Group 2中输入2。
3.单击“OK”按钮,得到输出结果。
四.成对样本T检验(Paired-Samples T Test过程)某单位研究饲料中缺乏维生素E与肝中维生素A含量的关系,将大白鼠按性别、体重等配为8对,每对中两只大白鼠分别喂给正常饲料和维生素E缺乏饲料,一段时期后将之宰杀,测定其肝中维生素A含量(μmol/L)如下,问饲料中缺乏维生素E对鼠肝中维生素A含量有无影响?实验步骤:1.建立数据文件。
定义变量名:正常饲料组测定值为x1,维生素E缺乏饲料组测定值为x2,输入原始数据。
2.选择菜单“Analyz e→Compare Means→Paired-samples T Test”项,弹出“Paired - samples T Test”对话框。
从对话框左侧的变量列表中选择变量x1、x2进入Variables框。
概率论与数理统计实验实验3参数估计假设检验

概率论与数理统计实验实验3 参数估计假设检验实验目的实验内容直观了解统计描述的基本内容。
2、假设检验1、参数估计3、实例4、作业一、参数估计参数估计问题的一般提法X1, X2,…, Xn要依据该样本对参数作出估计,或估计的某个已知函数.现从该总体抽样,得样本设有一个统计总体,总体的分布函数向量). 为F(x, ),其中为未知参数( 可以是参数估计点估计区间估计点估计——估计未知参数的值区间估计——根据样本构造出适当的区间,使他以一定的概率包含未知参数或未知参数的已知函数的真?(一)、点估计的求法1、矩估计法基本思想是用样本矩估计总体矩.令设总体分布含有个m未知参数??1 ,…,??m解此方程组得其根为分别估计参数??i ,i=1,...,m,并称其为??i 的矩估计。
2、最大似然估计法(二)、区间估计的求法反复抽取容量为n的样本,都可得到一个区间,这个区间可能包含未知参数的真值,也可能不包含未知参数的真值,包含真值的区间占置信区间的意义1、数学期望的置信区间设样本来自正态母体X(1) 方差?? 2已知, ?? 的置信区间(2) 方差?? 2 未知, ?? 的置信区间2、方差的区间估计未知时, 方差?? 2 的置信区间为(三)参数估计的命令1、正态总体的参数估计设总体服从正态分布,则其点估计和区间估计可同时由以下命令获得:[muhat,sigmahat,muci,sigmaci] = normfit(X,alpha)此命令以alpha 为显著性水平,在数据X下,对参数进行估计。
(alpha缺省时设定为0.05),返回值muhat是X的均值的点估计值,sigmahat是标准差的点估计值, muci是均值的区间估计,sigmaci是标准差的区间估计.例1、给出两列参数?? =10, ??=2正态分布随机数,并以此为样本值,给出?? 和?? 的点估计和区间估计命令:r=normrnd(10,2,100,2);[mu,sigm,muci,sigmci]=normfit(r);[mu1,sigm1,muci1,si gmci1]=normfit(r,0.01);mu=9.8437 9.9803sigm=1.91381.9955muci=9.4639 9.584310.2234 10.3762sigmci=1.68031.75202.2232 2.3181mu1=9.8437 9.9803sigm1=1.91381.9955muci1=9.3410 9.456210.3463 10.5043sigmci1=1.6152 1.68412.3349 2.4346例2、产生正态分布随机数作为样本值,计算区间估计的覆盖率。
计量经济学第3章习题作业

A n ≥ k +1 B n ≤ k +1 C n ≥ 30 D n ≥ 3(k +1)
6. 对于 Yi =βˆ0 + βˆ1Xi +ei ,以σˆ 表示估计标准误差,r 表示相关系数,则有( ) A σˆ=0时,r=1
B σˆ=0时,r=-1
C σˆ=0时,r=0
7. 简述变量显著性检验的步骤。 8. 简述样本相关系数的性质。 9. 试述判定系数的性质。
五、综合题
1. 为了研究深圳市地方预算内财政收入与国内生产总值的关系,得到以下数据:
年份
地方预算内财政收入 Y
国内生产总值(GDP)X
(亿元)
(亿元)
1990
21.7037
171.6665
1991
27.3291
184.7908
1436.0267
2000
225.0212
1665.4652
2001
265.6532
1954.6539
要求:
(1)建立深圳地方预算内财政收入对 GDP 的回归模型;
(2)估计所建立模型的参数,解释斜率系数的经济意义;
(3)对回归结果进行检验;
(4)若是 2005 年的国内生产总值为 3600 亿元,确定 2005 年财政收入的预测值和预
)
A 可靠性
B 合理性
C 线性
D 无偏性
E 有效性
5. 剩余变差是指(
)
A 随机因素影响所引起的被解释变量的变差
B 解释变量变动所引起的被解释变量的变差
C 被解释变量的变差中,回归方程不能做出解释的部分
D 被解释变量的总变差与回归平方和之差
《应用数理统计》第三章假设检验课后作业参考答案

第三章 假设检验课后作业参考答案3.1 某电器元件平均电阻值一直保持2.64Ω,今测得采用新工艺生产36个元件的平均电阻值为2.61Ω。
假设在正常条件下,电阻值服从正态分布,而且新工艺不改变电阻值的标准偏差。
已知改变工艺前的标准差为0.06Ω,问新工艺对产品的电阻值是否有显著影响?(01.0=α)解:(1)提出假设64.2:64.2:10≠=μμH H , (2)构造统计量36/06.064.261.2/u 00-=-=-=nX σμ(3)否定域⎭⎬⎫⎩⎨⎧>=⎭⎬⎫⎩⎨⎧>⋃⎭⎬⎫⎩⎨⎧<=--21212αααu u uu u u V (4)给定显著性水平01.0=α时,临界值575.2575.2212=-=-ααuu ,(5) 2αu u <,落入否定域,故拒绝原假设,认为新工艺对电阻值有显著性影响。
3.2 一种元件,要求其使用寿命不低于1000(小时),现在从一批这种元件中随机抽取25件,测得其寿命平均值为950(小时)。
已知这种元件寿命服从标准差100σ=(小时)的正态分布,试在显著水平0.05下确定这批元件是否合格。
解:{}01001:1000, H :1000X 950 100 n=25 10002.5V=u 0.05H x u αμμσμα-≥<====->=提出假设:构造统计量:此问题情形属于u 检验,故用统计量:此题中:代入上式得:拒绝域:本题中:0.950.950u 1.64u 0.0u H =>∴即,拒绝原假设认为在置信水平5下这批元件不合格。
3.3某厂生产的某种钢索的断裂强度服从正态分布()2,σμN ,其中()2/40cm kg =σ。
现从一批这种钢索的容量为9的一个子样测得断裂强度平均值为X ,与以往正常生产时的μ相比,X 较μ大20(2/cm kg )。
设总体方差不变,问在01.0=α下能否认为这批钢索质量显著提高? 解:(1)提出假设0100::μμμμ>=H H , (2)构造统计量5.13/4020/u 00==-=nX σμ (3)否定域{}α->=1u u V(4)给定显著性水平01.0=α时,临界值33.21=-αu(5) α-<1u u ,在否定域之外,故接受原假设,认为这批钢索质量没有显著提高。
假设检验与方差分析的作业

管理工程学院硕士生《应用统计方法》课程作业I 假设检验与方差分析一、假设检验:(配对均值检验)1、某药厂最近研制出一种新的降压药,为了验证其疗效,选择15个高血压病人进行实验。
数据表是服药前后的血压值。
选用适当的统计方法验证该药是否有效。
patient 1 2 3 4 5 6 7 8 before 115 135 127 130 103 90 101 104 after 109 120 125 130 105 94 90 100patient 9 10 11 12 13 14 15before 109 89 120 113 118 130 120after 90 90 110 103 100 121 108二、方差分析:1、对于硅酸盐水泥的抗折强度,用四种不同的配方方法收集了以下数据:配方法抗折强度1 3129 3000 2865 28902 3200 3300 2975 31503 2800 2900 2985 30504 2600 2700 2600 2765(1)检验配方法影响水泥砂浆强度的假设。
(2)选择一种比较方法对均值进行比较。
2、纺织厂有很多织布机,设每台机器每分钟织出同样的布,为了研究这一假设,随机选取5台织布机并测定它们在不同时间的产量,得出数据:织布机产量1 14.0 14.1 14.2 14.0 14.12 13.9 13.8 13.9 14.0 14.03 14.1 14.2 14.1 14.0 13.94 13.6 13.8 14.0 13.9 13.75 13.8 13.6 13.9 13.8 14.0(1)说明为什么这是一种随机效应实验。
织布机的产量相等吗?(2)估计织布机间的变异。
(3)估计实验的误差方差。
3、电视机厂感兴趣于对彩色显像管四种不同的涂层对显像管的电导率是否有影响。
测得电导率的数据如下:涂层电导率1 143 141 150 1462 152 149 137 1433 134 136 132 1274 129 127 132 129 (1)涂层使电导率有差异吗?(2)估计总均值与处理效应。
作业·假设检验
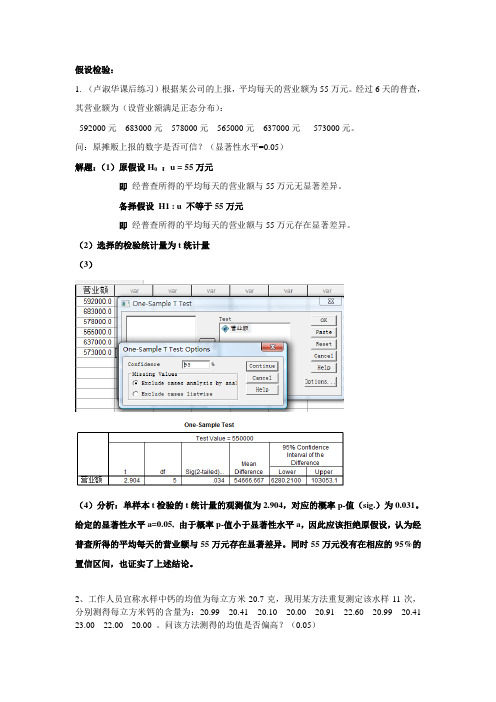
假设检验:1. (卢淑华课后练习)根据某公司的上报,平均每天的营业额为55万元。
经过6天的普查,其营业额为(设营业额满足正态分布):592000元683000元578000元565000元637000元573000元。
问:原摊贩上报的数字是否可信?(显著性水平=0.05)解题:(1)原假设H0:u = 55万元即经普查所得的平均每天的营业额与55万元无显著差异。
备择假设H1 : u 不等于55万元即经普查所得的平均每天的营业额与55万元存在显著差异。
(2)选择的检验统计量为t统计量(3)(4)分析:单样本t检验的t统计量的观测值为2.904,对应的概率p-值(sig.)为0.031。
给定的显著性水平a=0.05, 由于概率p-值小于显著性水平a,因此应该拒绝原假设,认为经普查所得的平均每天的营业额与55万元存在显著差异。
同时55万元没有在相应的95%的置信区间,也证实了上述结论。
2、工作人员宣称水样中钙的均值为每立方米20.7克,现用某方法重复测定该水样11次,分别测得每立方米钙的含量为:20.99 20.41 20.10 20.00 20.91 22.60 20.99 20.41 23.00 22.00 20.00 。
问该方法测得的均值是否偏高?(0.05)解题:(1)(单样本t检验)原假设:用此方法测得的均值与20.7克无显著差异。
备择假设(2)选择的检验统计量为t 统计量分析:t统计量的观测值为1.064,对应的概率p-值为3.312。
给定的显著性水平为a=0.05,由概率p-值大于0.05,因此接受原假设,认为用此方法测得的均值与20.7克无显著差异。
同时20.7克在相应的95%的置信区间内也证实了这点。
3、长春市政府官员宣称,长春市居民的生活水平已经明显提高,平均居民月收入已经达到1200元。
现以抽样调查方法来验证该官员的说法是否正确,随机抽样15名居民,他们的月收入分别为:1350 1300 1100 1200 1250 1000 1100 1350 1200 1150 1050 1100 1150 1200 1250 ,根据这个调查结果,如何评价该官员的说法?解题:(单总体t检验)(1)原假设:居民平均收入与1200无显著差异(2)选择检验统计量为t统计量4. 对两种不同的水稻品种A和B分别统计了8个地区的单位面积产量(公斤),得到下面数据:A品种:86 87 56 93 84 93 75 79B品种:80 79 58 91 77 82 76 66要求检验两个水稻品种的单位面积产量之间是否有显著。
4试验四、 用dps进行假设检验

Ⅶ
Ⅷ Ⅸ
67.2
68.9 62.6
62.4
61.3 56.7
4.8
7.6 5.9
因为要测验新肥料能否比对照增产5kg,故采用一尾测验。
H0:新肥料比对照每亩增收不到5kg,最多5kg,即
H 0:μd 5 ;对HA : 新肥料比对照每亩可增收5kg以上,即
查附表4, v=7-1=6时, t0.01=3.707。实得现|t |>t0.01,故 推断:否定 H 0:μd 0 ,接受 H A:μd 0 ,即A、B两法对
饨化病毒的效应有极显著差异。
[例5] 研究某种新肥料 能否比原肥料每亩增产5kg 以上皮棉,选土壤和其他
表5.5 两种肥料的皮棉产量(kg)
=0.05。 显著水平
测验计算: y (35.6 37.6 34.6) / 8 281 .7 / 8 35.2 g
SS 35.62 37.62 34.62 (281 .7)2 / 8 18.83
1.64 18.83 0.58g s 1.64g s y 8 1 8
18400 3787 .5 1479 .17 78
1 1 s y1 y2 1479 .17 18.688(cm) 8 9 176 .3 233.3 t 3.05 18.688
按 v=7+8=15,查t表得一尾 t0.05 =1.753(一尾测验t0.05等于 两尾测验的t0.10),现实得 t =-3.05<-t0.05=-1.753,P<0.05。 推断:否定 H 0 : 1 2 ,接受 H A : 1 2 ,即认为玉米喷矮
应用统计学——假设检验书面作业和答案

假设检验作业1. 一种罐装饮料采用自动生产线生产,每罐的容量是255ml (总体的均值 ),标准差为5ml (总体的标准差)。
为检验每罐容量是否符合要求,质检人员在某天生产的饮料中随机抽取了40罐进行检验,测得每罐平均容量为255.8ml (样本的均值)。
取显著性水平=0.05 ,检验该天生产的饮料容量是否符合标准要求? 解:正态,总体方差已经,大样本,Z 检验统计量,双侧检验 96.105.040/52558.255)1,0(~n /2552552010==-=-=≠=αασμμμZ N X Z H H :: 若计算的Z 值在(-1.96,1.96)之间,不能拒绝原假设,认为符合标准;反之,拒绝原假设,即产品不符合标准。
2. 某一小麦品种的平均产量为5200kg/hm2 。
一家研究机构对小麦品种进行了改良以期提高产量。
为检验改良后的新品种产量是否有显著提高,随机抽取了36个地块进行试种,得到的样本平均产量为5275kg/hm2,标准差为120/hm2 。
试检验改良后的新品种产量是否有显著提高? (a=0.05)解:不知是否正态总体,总体标准差未知,但因是大样本,可用Z 分布检验统计量,右侧检验(注意临界值或拒绝域的确定,用图形表示更清楚)645.105.036/12052005275)1,0(~n /52005200010==-=-=≤ααμμμZ N s X Z H H ::计算出的Z 值,若Z 值大于1.645则拒绝原假设;反之,不能拒绝原假设。
3. 一种以休闲和娱乐为主题的杂志,声称其读者群中有80%为女性。
为验证这一说法是否属实,某研究部门抽取了由200人组成的一个随机样本,发现有146个女性经常阅读该杂志。
分别取显著性水平 a=0.05和a=0.01 ,检验该杂志读者群中女性的比率是否为80%?注意:(1)有些书,用大写的π表示总体比例。
(2) 不同的显著性水平,可能得出不同的结论。
研究生“应用数理统计”课外作业---初试成绩分布的假设检验

研究生“应用数理统计”课程课外作业学号 XXXXXXX 姓名 XXX 学院 XXXXXX年级专业 XXXXX成绩初试成绩分布的假设检验摘要:数理统计学是一门应用性很强的学科,其方法被广泛应用于现实社会的信息、经济、工程等各个领域,学习和应用数理统计方法已成为当今技术领域里的一种时尚,面对信息时代,为了处理大量的数据以及从中得出有助于决策的量化理论,必须掌握不断更新的数理统计知识,为今后的研究和应用提供新的思路和有效解决方法。
本报告主要应用数理统计的其中一种方法-假设检验,对报考重庆大学2012年机械工程学院工业工程专业的70名学生的初试成绩进行假设检验,首先假设70名学生的初试成绩服从正态分布,然后建立模型,进行模型分析并代入初始数据求解,然后进行检验,通过检验发现报考重庆大学2012年机械工程学院工业工程专业的70名学生的初试成绩服从正态分布。
关键字:假设检验初试成绩正态分布一、问题提出,问题分析。
我是2012年考入重庆大学机械工程学院工业工程专业的一名学生,进入学校几个月来,在选课时,我选了数理统计这门课,刚刚学习了假设检验,其中,书上有一道例题:检验某高校60名学生的英语成绩是否服从正态分布,检验结果是服从正态分布。
这使我想起了我当初参加的研究生考试,我发现我们的考试成绩分布在355-395之间的比较多,小于355或大于395的比较少,那么,我们参加复试的70名考生的初试成绩是否也服从正态分布呢?于是,我根据自己学到的数理统计知识进行了假设检验。
二、数据描述(用表格表达数据信息,指出数据来源或提供原始数据)幸运的是:当初公布复试结果时,我用手机把复试结果照了下来,照片上可以看出我们70名考生的初试成绩,现将其整理如下(原件请见附录):表(2.1.1)重庆大学2012年机械工程学院工业工程专业初试成绩表404 407 415 402 389 387 390 391 388 393 405 378 381 381 369 392 359 362 403 385 381 388 365 358 366 354 368 368 373 349 379 360 360 391 351 367 348 362 372 348 347 340 360 354 349 345 352 353 342 360 351 342 341 340 384 371 324 340 374 340 341 335 335 339 334 317 374 380 359 356三、模型建立:(1)提出假设条件,明确概念,引进参数;设总体X的分布函数为F(x),但未知。
假设检验作业参考答案

(4)计算检测统计量的值
2
n 1 S 2 30 1 2 103.11
02
0.752
(5)作出决策
2 103.11 42.557 ,落入拒绝域,故在 0.05 的显著性水平上拒绝 H 0 。
结论:有证据表明电视的使用寿命的方差显著大于视频录像设备的使用寿命的方差。
2
n=30, S =2, s0 = 0.75 = 0.5625 (1)提出假设
2 2 H0 : 2 0 ; H1 : 2 0
2
2
2
(2)构造检测统计量
n 1 S 2 2 n 1 2
2
0
(3)给定显著性水平 0.05 29 42.557 ,其拒绝域为 42.557, 。
(3)给定显著性水平 0.01 ,确定拒绝域。
0.01 , z0.01 2.33 ,其拒绝域为 2.33, 。
(4)计算检测统计量的值
z
x 0 7.25 6.70 3.11 s / n 2.5 / 200
(5)作出决策
z 3.11 2.33 ,落入拒绝域,故在 0.01 的显著性水平上拒绝 H 0 。
np 356 0.879 313 5 , np 1 p 356 0.879 1 0.879 37.81 5 。
本题为大样本下总体比例的双侧检验问题,应采取 Z 检验法。 (1)已知本题假设为
H 0 : 0.75; H1 : 0.75
n
p 0
0.879 0.75 0.75 1 0.75 356
5.63
(5)作出决策
参数估计和假设检验练习题

参数估计和假设检验练习题作业⼆(⼀)单项选择题1.标准误的英⽂缩写为:A.S B.SE C.S D.SDX2.通常可采⽤以下那种⽅法来减⼩抽样误差:A.减⼩样本标准差B.减⼩样本含量C.扩⼤样本含量D.以上都不对3.配对设计的⽬的:A.提⾼测量精度B.操作⽅便C.为了可以使⽤t检验D.提⾼组间可⽐性4.以下关于参数估计的说法正确的是:A.区间估计优于点估计B.样本含量越⼤,参数估计准确的可能性越⼤C.样本含量越⼤,参数估计越精确D.对于⼀个参数只能有⼀个估计值5.关于假设检验,下列那⼀项说法是正确的A.单侧检验优于双侧检验B.采⽤配对t检验还是成组t检验是由实验设计⽅法决定的C.检验结果若P值⼤于0.05,则接受H0犯错误的可能性很⼩D.⽤u检验进⾏两样本总体均数⽐较时,要求⽅差齐性6.两样本⽐较时,分别取以下检验⽔准,下列何者所取第⼆类错误最⼩A.α=0.05 B.α=0.01 C.α=0.10 D.α=0.207.统计推断的内容是A.⽤样本指标推断总体指标B.检验统计上的“假设”C.A、B均不是D.A、B均是8.当两总体⽅差不齐时,以下哪种⽅法不适⽤于两样本总体均数⽐较A.t检验B.t’检验C.u 检验(假设是⼤样本时)D.F检验A.1X=2X,1S=2SB.作两样本t检验,必然得出⽆差别的结论C.作两⽅差齐性的F检验,必然⽅差齐D.分别由甲、⼄两样本求出的总体均数的95%可信区间,很可能有重叠10.以下关于参数点估计的说法正确的是A.CV越⼩,表⽰⽤该样本估计总体均数越可靠B.σ越⼩,表⽰⽤该样本估计总体均数越准确XC.σ越⼤,表⽰⽤该样本估计总体均数的可靠性越差XD.S越⼩,表⽰⽤该样本估计总体均数越可靠(⼆)名词解释(三)是⾮题1.若两样本均数⽐较的假设检验结果P值远远⼩于0.01,则说明差异⾮常⼤。
P⼩于0.01只能说明两样本均数有差异,但并不能说明差异的⼤⼩。
2.对同⼀参数的估计,99%可信区间⽐90%可信区间好。
《应用数理统计》吴翊李永乐第三章假设检验课后作业

《应⽤数理统计》吴翊李永乐第三章假设检验课后作业第三章假设检验课后作业参考答案3.1 某电器元件平均电阻值⼀直保持2.64Ω,今测得采⽤新⼯艺⽣产36个元件的平均电阻值为2.61Ω。
假设在正常条件下,电阻值服从正态分布,⽽且新⼯艺不改变电阻值的标准偏差。
已知改变⼯艺前的标准差为0.06Ω,问新⼯艺对产品的电阻值是否有显著影响?(01.0=α)解:(1)提出假设64.2:64.2:10≠=µµH H , (2)构造统计量36/06.064.261.2/u 00-=-=-=nX σµ(3)否定域>=><=--21212αααu u uu u u V (4)给定显著性⽔平01.0=α时,临界值575.2575.2212=-=-ααuu ,(5) 2αu u <,落⼊否定域,故拒绝原假设,认为新⼯艺对电阻值有显著性影响。
3.2 ⼀种元件,要求其使⽤寿命不低于1000(⼩时),现在从⼀批这种元件中随机抽取25件,测得其寿命平均值为950(⼩时)。
已知这种元件寿命服从标准差100σ=(⼩时)的正态分布,试在显著⽔平0.05下确定这批元件是否合格。
解:{}01001:1000, H :1000X 950 100 n=25 10002.5V=u 0.05H x u αµµσµα-≥<====->=提出假设:构造统计量:此问题情形属于u 检验,故⽤统计量:此题中:代⼊上式得:拒绝域:本题中:0.950.950u 1.64u 0.0u H =>∴即,拒绝原假设认为在置信⽔平5下这批元件不合格。
3.3某⼚⽣产的某种钢索的断裂强度服从正态分布()2,σµN ,其中()2/40cm kg =σ。
现从⼀批这种钢索的容量为9的⼀个⼦样测得断裂强度平均值为X ,与以往正常⽣产时的µ相⽐,X 较µ⼤20(2/cm kg )。
大作业1: 假设检验在“新旧工艺有无差异”分析中的应用

大作业1:假设检验在“新旧工艺有无差异”分析中的应用姓名:***班级:人力032学号:**********提交日期:2005-12-4假设检验在“新旧工艺有无差异”分析中的应用假设检验原理:假设检验可用于各种场合,其思路是根据实际问题的要求提出一个关于质量特性值的论断(称为原假设),然后,根据样本的有关信息,对原假设的真伪进行判断。
在假设检验里,要提出原假设,同时根据实际问题提出原假设的对立面(称为备择假设),为了叙述方法,原假设用H0表示,备择假设用H1表示,假设检验是对H0的真伪进行判断。
1)编写假设检验实际问题案例:本例中企业为了提高生产效率,让车床更好的加工零件,自动车床采用新旧两种工艺加工同种零件,测得的加工偏差(单位:微米)分别为旧工艺 2.7 2.4 2.5 3.1 2.7 3.5 2.9 2.7 3.5 3.3新工艺 2.6 2.1 2.7 2.8 2.3 3.1 2.4 2.4 2.7 2.3设测量的加工偏差服从正态分布,所得的两个样本相互独立,且总体方差相等。
试问自动车床在新旧两种工艺的加工精度有无显著差异?(α=0.01)2)a.分析案例背景及用假设检验方法解决实际问题的必要性:企业为了提高经济效益,经常要开展QC小组活动或质量改进活动.在这些活动中,会遇到各种各样的问题.如:为了降低成本,改变生产工艺方法或配方,但不知改变工艺后的产品质量特性值和以前相比是否发生了变化;或为了扩大产量,增加了生产设备,但不知新设备生产出的产品质量特性值是否和老设备的一致;进厂原料有一定的质量要求,怎样根据进厂原料的检验结果来决定是接受或退货.b.简述你所运用的假设检验方法的算法步骤:解由题意知要检验的假设为.在H0为真时,检验统计量为:由此可得水平为α的拒绝域为这里m = n,α=0.01,故tα/2(m + n –2)=t0.005(18)=2.8784。
并由样本算得于是:故接受H0,即认为新旧工艺对零件的加工精度无显著差异。
h0h1假设例题

h0h1假设例题
H0和H1是统计学假设检验中的两个基本概念,分别代表零假设(Null Hypothesis, H0)和备择假设(Alternative Hypothesis, H1)。
下面是一个简单的H0与H1的假设检验例题:
例题:
某公司声称其新产品的合格率为95%。
为验证这一说法是否准确,质检部门随机抽取了该新产品200件进行检测,并发现其中190件产品合格。
零假设(H0):
- H0: 新产品的实际合格率为95%,即产品质量符合公司的声明。
-具体数学形式表示为:H0: p = 0.95,其中p代表新产品的实际合格率。
备择假设(H1):
-H1: 新产品的实际合格率不等于95%,即产品质量可能不符合公司的声明。
-双侧备择假设:H1: p ≠0.95,意味着实际合格率可能高于或低于95%。
-单侧备择假设(假设我们只想知道是否合格率偏低):H1: p < 0.95
或者H1: p > 0.95 (取决于问题的具体方向性)
接下来,我们会根据样本数据计算检验统计量,并基于显著性水平α确定拒绝域,通过比较样本结果与拒绝域来决定是否拒绝零假设,从而判断公司声称的产品合格率是否可信。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
假设检验作业
一、单项选择题
1.在假设检验中,第一类错误是指()
A.当原假设正确时拒绝原假设
B.当原假设错误时拒绝原假设
C.当备择假设正确时拒绝备择假设
D.当备择假设不正确时拒绝备择假设
2.对于给定的显著性水平α,根据P 值拒绝原假设的准则是()
A.P=α
B.P<α
C.P>α
D.P=α=0
3.在大样本情况下,当总体方差已知时,检验总体均值所使用的统计量是()A.0/x z n µσ−=B.
x z =C.
x t =D.
x z =
4.检验一个正态总体的方差时所使用的分布是()
A.正态分布
B.t 分布
C.F 分布
D.2
χ分布二、简答题
简述:假设检验依据的基本原理是什么?
三、计算题
1.已知某炼铁厂的产品含碳量服从正态分布N(4.55,0.108),现在测定了9炉铁水,其平均含碳量为4.484。
如果估计方差没有变化,可否认为现在生产的铁水平均含碳量为4.55 (α=0.05)。
2.某地区小麦的一般生产水平为亩产250公斤,其标准差为30公斤。
现用一种化肥进行试验,从35个小区抽样结果,平均产量为270公斤。
问这种化肥是否使小麦明显增产?(α=0.05)
3.某种大量生产的袋装食品,按规定不得少于250克。
今从一批该食品中任意抽取50袋,发现有6袋低于250克。
若规定不符合标准的比例超过5%就不得出厂。
问该批食品能否出厂?(α=0.05)
4.为了控制贷款规模,某商业银行有个内部要求,平均每项贷款数额不能超过60万元。
随着经济的发展,贷款规模有增大的趋势。
银行经理想了解在同样项目条件下,贷款的平均规模是否明显地超过60万元。
一个n=144的随机样本被抽出,测得平均值为68.1万元,标准差为45万元。
在α=0.01的显著性水平下,对贷款平均规模进行检验。
5.某工厂制造螺栓,规定螺栓口径为7.0cm,方差为0.03cm。
今从一批螺栓中抽取80个测量其口径,得平均值为
6.97cm,方差为0.0375cm。
假定螺栓口径为正态分布,问这批螺栓是否达到规定的要求?(α=0.05)。
