磁路和磁路定律
电机学中的基本电磁定理

i2
i3
l
其中 H: 磁场强度,安/米(A/m)
dl
注:若i与l符合右手螺旋关系, 取正号,否则取 负号 。其中大拇指所指为i的方向,四指为l方向。 如图示为: ∑ i = i1 + i2 - i3
当气隙长度δ远远小于两侧 的铁心截面的边长时, 铁心和 气隙中为均匀磁场,则
F Ni H FelFe H
其中 F=Ni:磁路的磁动势 HFelFe:铁心上的磁压降 Hδ δ :气隙上的磁压降
带气隙的铁心磁路
注:i 与 l 符合右手螺旋关系,电机学中习惯大拇指所 指为 l 的方向,四指为多匝线圈中 i 方向。
设有向回路 l 与圆 环的中心圆重合,则沿 着回线 l 磁场强度 H 处 处相等且其方向处处与 回线切线方向相同(称 为均匀磁场),同时闭 合回线所包围的总电流 由通有电流 i 的 N 匝线 圈提供,则:
e blv
运动电势的方向习惯用右手定则确定,如图所示。
2.3. 电磁力定律
载流导体在磁场中要受到电磁力,在导体与磁场 垂直的情况下,若导体中电流为i,导体长度为l,导 体所在处的磁通密度为b,则电磁力为:
f bli
注:电磁力方向由左手定则决定
电机的基本作用原理
三个定律,一个定理 1)安培环路定律(全电流定律):电流在任一导 体中流通,则该导体周围将有磁场产生。 2)电磁感应定律:任一线圈中键链的磁通发生变 化,则在该线圈中将有感应电势产生。
3)电磁力定律:任一载流导体在磁场中将受力的 作用。
4)能量守恒定理:输入能量 = 输出能量 + 损耗能 量
电机的可逆运行原理
机械功率
发电机 电动机
磁性材料和磁路及磁路基本定律

1.饱和——引起电感量减小
2.居里温度——磁导率减小
磁性材料
3
磁化曲线
开关电源技术——
磁性材料
tqzheng@
4
磁滞回线
磁性材料
Fig 1 Typical B vs H Loop
B Magnetic Flux Density(磁通密度[磁感应强度]) Bs Saturation Flux Density(饱和磁密) Br Remanence(剩磁) H magnetic Field Strength(磁场强度) Hc Coercive Force(矫顽力) i Initial Permeability(初始磁导率) a(max) Maximum Amplitude Permeability
开关电源技术——
磁性材料
tqzheng@
8
磁滞损耗Ph
The area enclosed by the hysteresis loop is a measure of hysteresis loss per cycle.
磁性材料
9
涡流损耗Pe
磁性材料
10
剩余损耗Pc
由于磁化弛豫效应或磁性滞后效应引起 的损耗。所谓弛豫是指在磁化或反磁化 的过程中,磁化状态并不是随磁化强度 的变化而立即变化到它的最终状态,而 是需要一个过程,这个‘时间效应’便 是引起剩余损耗的原因。
在退磁曲线中, B 与 H 之积, 在某一点处达到最 大值, 通常记作(BH)m, 叫最大磁能积.
磁性材料
5
磁性材料
6
基本定律
1、安培环路定律
Hdl I IN
2、电磁感应定律 (法拉第+楞次)
磁路基本定律、计算方法

1.7 电机的冷却与防护
气冷(空气、氢气)、液冷(水、油)、混合冷
一、冷却介质
间接—空气冷却(冷却介质只与铁心、绕组、机壳外表面接触) 直接--氢气、水(进入发热体内部)
二、冷却方式
开启式、防护式
三、机壳防护
解 用安培环路定律来求解。
磁场强度
磁动势
Байду номын сангаас
励磁电流
[例2] 若在例l磁路中,开一个长度
的气隙,问铁心中激励1T的磁通密度时,所需的励磁磁动势为多少?已知铁心截面积 。 考虑气隙磁场边缘效应,计算气隙有效面积时通常在长、宽方向增加δ值。
01
解 用磁路的基尔霍夫第二定律来求解。
02
铁心内的磁场强度:
03
气隙磁场强度:
04
铁心磁位降:
05
气隙磁位降:
06
励磁磁动势:
交流磁路的特点 交流磁路中,激磁电流是交流,因此磁路中的磁动势及其所激励的磁通均随时间而交变,但每一瞬时仍和直流磁路一样,遵循磁路的基本定律。就瞬时值而言,通常情况下,可以使用相同的基本磁化曲线。 交变磁通除了会引起铁心损耗之外,还有以下两个效应: 磁通量随时间交变,必然会在激磁线圈内产生感应电动势; 磁饱和现象会导致电流、磁通和电动势波形的畸变。 有关交流磁路和铁心线圈的计算,将在变压器一章内作进一步的说明。
三、磁路计算方法
二、电路分析
一、磁路分析
磁路欧姆定律 =F/Rm=Fm --磁路磁阻;m ---磁路磁导 与电路对应
磁路分析
2、基尔霍夫第一定律
穿入任一封闭面的磁通等于穿出该封闭面的磁通。(穿入任一封闭面的总磁通等于0)。 =0
3、基尔霍夫第二定律
在磁路中沿任何闭合磁路径上,磁动势的代数和等于磁压降的代数和。 F= Hl
磁路与磁路的欧姆定律

例题:铸钢圆环上绕有线圈800匝,通有2A电流,环
平均周长为0.5m,截面积3.25×10-4m2,求线
圈磁动势、磁阻和磁通。(硅钢片的磁导率 为7500H/m)
Fm NI
Rm
l
S
Fm Rm
几点说明:
1. 磁阻Rm 的大小取决于磁路的尺寸和材料的磁导率。
Rm
l
S
2. 很大,但不是常数,因此 Rm 也不是常数。所以磁
#
返回
磁路基础知识
磁路基础知识
磁路基础知识
磁路基础知识
磁路基础知识
磁路基础知识
磁路基础知识
磁路基础知识
磁路欧姆定律
磁通所通过的路径称为磁路。
磁路欧姆定律
磁路欧姆定律
磁路欧姆定律
磁路欧姆定律
磁路欧姆定律
磁路欧姆定律
磁路与电路的比较
电磁铁
电磁铁
电磁铁
电磁铁的实际应用
无
不变
整块铸钢或工业纯铁 组成
交流电磁铁
交流电磁铁
励磁电流随空气间隙的增 大而增大 有 脉动变化
由多层彼此绝缘的硅钢片 叠成
注意:即使是额定电压相同的交、直流电磁铁,也决不能互换使用
电磁铁的特点
1. 励磁电流是由励磁线圈的外加电压U 和线圈电阻R 决定的
I
U R
电流是恒定的,无感应电动势产生。
2. 无磁滞和涡流损耗,铁心可以使用整块的铸钢、软铁。
线圈 衔铁
铁心中的磁通是交变的,空气隙处的磁感应强度为:
B0 Bm sin t
吸力
f 4B02S 105 4Bm2 sin 2 tS0 105
Fm
1 2
(1 cos 2t)
磁路及磁路基本定律

1
10.3
1 磁路
用铁磁性材料制成一个导磁路径,常称为铁心。 将通电线圈绕在铁心上,这样由铁磁性材料所 构成的(包括必须有的气隙在内)通过磁通的 路径即为磁路。
2
永久磁铁
铁心
Φ 气隙
i Φ2
N
S
铁心
(a)磁电式仪表的磁路
Φ 原副 绕绕 组组
(b)心式变压器的磁路
3
边缘 效应
主磁 通
I 漏磁 通
(2) 根据磁路尺寸计算出各段截面积S和平均长度l。
17
Sa (a)(b)ab(ab)
Sb
(r)2
2
r2r
a b
(a)
r
(b)
(a) 矩形截面; (b) 圆形截面
18
(3) 由已知磁通Φ, 算出各段磁路的磁感应强度B=Φ/S。 (4) 根据每一段的磁感应强度求磁场强度, 对于铁磁材 料可查基本磁化曲线。 对于空气隙可用以下公式:
40 180
50
图10-18无分支磁路
20
解:将该无分支磁路按材料和截面不同分为 三段,其各段平均磁路长度为L0、L1、L2。 则: L0=5mm=0.5cm L1=(240-40/2-40/2-5)mm=19.5cm L2=[(240-40/2-40/2)+2(180-40/2-50/2)]
=47cm • 磁路的叠装厚度为:
=(7270×0.5+2.85×19.5+9.96×47)A =4160A • 所以线圈电流I为 I=∑HL/N=4160/200A=20.8A
24
2.已知磁动势求磁通
• (1)先设定一磁通值,然后按照已知磁通求 磁动势的计算步骤求出所需的磁动势。
第一章 磁路基础知识

l1 l2 3l 15 10 2 m 两边磁路长度:
气隙磁位降: B 1.211 2H 2 2 2.5 10 3 A 4818 A 0 4π 10 7
1.211 (2 0.25) 2 B T 1.533T 中间铁心磁位降: 3 4 A 4 10
磁路基础知识
1.2.3涡流与涡流损耗 1、涡流 2、涡流损耗:涡流在铁心中引起的损耗 3、注意:为减小涡流损耗,电机和变压器的铁心都用 含硅量较高的薄硅钢片叠成。 4、铁心损耗:磁滞损耗+涡流损耗
2 pFe f 1.3 BmG
南通大学《电机学》
磁路基础知识
1.3直流磁路的计算
磁路计算正问题——给定磁通量,计算所需的励磁磁动势 磁路计算逆问题——给定励磁磁势,计算磁路内的磁通量 磁路计算正问题的步骤: 1)将磁路按材料性质和不同截面尺寸分段; 2)计算各段磁路的有效截面积Ak和平均长度lk; 3)计算各段磁路的平均磁通密度Ak ,Bk=Φk/Ak; 4)根据Bk求出对应的Hk;
Φ
RmFe
N
F
Rm
i
Φ
串联磁路 南通大学《电机学》 磁路基础知识
模拟电路图
解:铁心内磁通密度为 BFe 0.0009 T 1T
AFe 0.0009
从铸钢磁化曲线查得:与BFe对应的HFe=9×102A/m
H FelFe 9 10 2 0.3A 270 A 铁心段的磁位降:
查磁化曲线:H1 H 2 215 A/m
H1l1 H 2l2 215 15 10 2 A 32.25A
总磁动势和励磁电流为:
Ni 2H H l
3 3
H 1l1
电机学第一章 磁路

H
随着磁场强度H的增大,饱和程度增加,μFe减 小,Rm增大,导磁性能降低.
B
c b
B = f ( H)
d
μFe = f ( H )
a
B = μ0 H
H
设计电机和变压器时,为使主磁路内得到较大的 磁通量而又不过分增大励磁磁动势.通常把铁心 内的工作磁通密度选择在膝点附近
B
c b
膝点 饱和点
B = f ( H)
四、铁心损耗
1.磁滞损耗
定义: 铁磁材料置于交变磁场中时,磁畴相 互间不停地摩擦、消耗能量、造成损耗,这种 损耗称为磁滞损耗。 公式: n h h m
p = C fB V
应用:由于硅钢片磁滞回线的面积较 小,故电机和变压器的铁心常用硅钢片叠成。
2.涡流损耗
¾涡流:铁磁材料在交变磁场将 有围绕磁通呈蜗旋状的感应电动 势和电流产生,简称涡流。 ¾涡流损耗:涡流在其流通路径 上的等效电阻中产生的I2R损耗 称为涡流损耗。 ¾涡流损耗与磁场交变频率f, 厚度d和最大磁感应强度Bm的平 方成正比,与材料的电阻率成反 比。 ¾要减小涡流损耗,首先应减小 厚度,其次是增加涡流回路中的 电阻。电工硅钢片中加入适量的 硅,制成硅钢片,显著提高电阻 率
表1.1 磁路和电路对比表 序 号 1 2 3 4 5 6 7 8 9 电 基本物理量 或基本定律 电 流 电 压 电 阻 电 导 电流密度 电导率 基尔霍夫 第一定律 基尔霍夫 第二定律 欧姆定律 路 符号或 定义 I U R=l/(γA) G=1/R J=I/A 单位 A V Ω S A/m2 S/m 磁 路 单 位 Wb A 1/H H Wb/m2(T) H/m 基本物理量或 符号或 基本定律 定义 磁 通 φ F 磁动势 磁 阻 磁 导 磁通密度 磁导率 磁通连续性 原理 Rm=l/(μA)
磁路定律及磁路、电路的比较

H1l1 H2l2 H0l0 N i
沿任一闭合磁路,各段磁路上的磁压之和恒等于 磁动势的代数和。
8.3.3 磁路的欧姆定律
这段磁路由磁导率为 的
材料构成,长为 l ,横截面积为
S,穿过的磁通为Φ,其磁压为
Um
Hl
B
l
Sl
l
S
Rm
该段磁路 的磁阻
Rm
l
S
Um
Fm
1/亨利(1/H)
应特别注意:铁磁材料的 值不是常数,导致Rm也
不是常数。所以以下公式仅有定性意义,不便实际计算。
Rm
l
S
Fm Rm
B H
计算时需根据基本磁化曲线,对每一个H 值查对应的B。
8.3.4 交流线圈的电抗
交流线圈的电感系数L为
L N N Fm N N i N 2 N 2 S
i
0
1 2 3 0
1 2 3
进入和穿出任一封闭面磁通的代数和等于零。 进入封闭面的磁通量等于穿出该封闭面的磁通量。
8.3.2 磁路的基尔霍夫第二定律
N i ——磁动势 (磁势 ) Hl ——磁压(磁压降)
磁动势是磁路中有磁场存在的根源。
图示无分支磁路,可按磁路材料不同、横截面积 不同分为三段,每段都为匀强磁场。磁路的基尔霍夫 第二定律表达式为:
内容简介
本教材理论推导从简,计算思路交待详细,概念述 明来龙去脉,增加例题数量和难度档次,章节分 “重计 算”及“重概念”两类区别对待,编排讲究逐步引深的 递进关系,联系工程实际,训练动手能力,尽力为后续 课程铺垫。借助类比及对偶手法,语言朴实简练,图文 印刷结合紧密,便于自学与记忆,便于节省理论教学时 数。适用于应用型本科及高职高专电力类、自动化类、 机电类、电器类、仪器仪表类、电子类及测控技术类专 业。
磁路的基本概念和基本定律

磁路的基本概念和基本定律在很多电工设备(象变压器、电机、电磁铁等)中,不仅有电路的问题,同时还有磁路的问题,这一章,我们就学习磁的相关知识。
一、磁铁及其性质:人们把物体能够吸引铁、钴等金属及其合金的性质叫做磁性,把具有磁性的物体叫做磁体(磁铁)。
磁体两端磁性最强的区域叫磁极。
任何磁体都具有两个磁极,而且无论把磁体怎样分割总保持有两个异性磁极,也就是说,N极和S极总是成对出现的。
与电荷间的相互作用力相似,磁极间也存在相互的作用力,且同极性相互排斥,异极性相互吸引。
1.1磁场与磁感应线磁铁周围和电流周围都存在磁场。
磁场具有力和能的特征。
磁感应线能形象地描述磁场。
它们是互不交叉的闭合曲线,在磁体外部有N极指向S极,在磁体内部由S极指向N极,磁感应线上某点的切线方向表示该点的磁场方向,其疏密程度表示磁场的强弱。
1.2描述磁场的物理量:磁感应强度B:在磁场中垂直于磁场方向的通电导线所受电磁力F与电流I和导线有效长度L的乘积IL的比值即为该处的磁感应强度,即B=F/IL,单位:特斯拉。
磁感应强度是表示磁场中某点磁场强弱和方向的物理量,它是一个矢量,它与电流之间的方向关系可用右手螺旋定则来确定。
磁通∮:磁感应强度B和与它垂直方向的某一截面积S的乘积,称为通过该面积的磁通,即∮=BS,由上式可知,磁感应强度在数值上可以看作与磁场方向相垂直的单位面积所通过的磁通,故又称为磁通密度,单位是伏.秒,通常称为“韦”。
磁通∮是描述磁场在空间分布的物理量。
磁导率u是说明媒体介质导磁性能的物理量。
1.3定则电流与其产生磁场的方向可用安培定则(又称右手螺旋法则)来判断。
安培定则既适用于判断电流产生的磁场方向,也可用于在已知磁场方向时判断电流的方向。
1.直线电流产生的磁场,以右手拇指的指向表示电流方向,弯曲四指的指向即为磁场方向。
2.环形电流产生的磁场:以右手弯曲的四指表示电流方向,拇指所指的方向即为磁场方向。
3.通电导体在磁场内的受力方向,用左手定则来判断。
磁路基础知识

基尔霍夫第二定律
NI= Hl ΦRm
电路旳基本物理量及公式
电动势E 电 流I 电 阻R 电 导G 欧姆定律
I E/R
基尔霍夫第一定律
i=0
基尔霍夫第二定律
e=iR
南通大学《电机学》
磁路基础知识
1.2铁磁材料及其特征
1.2.1铁磁材料旳高导磁性 1.铁磁物质旳磁化
将铁、镍、钴等铁磁物质放入磁场后,铁磁物质 呈现很强旳磁性,这种现象,称为铁磁物质旳磁化。
磁畴:在铁磁物质内部存在着许多很小旳天然磁化区。
南通大学《电机学》
磁路基础知识
2.起始磁化曲线
将一块还未磁化旳铁磁材料进行磁化,当磁场 强度H由零逐渐增大时,磁通密度B也将随之增大, 曲线B=f(H)就称为起始磁化曲线
B
c
d
B f (H)
b
a
0
南通大学《电机学》
磁路基础知识
B 0H
H
3.磁滞回线
相应旳模拟电路图
南通大学《电机学》
磁路基础知识
1.1.5磁路旳基尔霍夫定律 1、磁路旳基尔霍夫第一定律
闭合面A显然有:
-Φ1+Φ2+Φ3=0
Φ=0
穿出(或进入)任一闭合面旳总磁通量恒等于零( 或者说,进入任一闭合面旳磁通量恒等于穿出该闭 合面旳磁通量)
南通大学《电机学》
磁路基础知识
2、磁路旳基尔霍夫第二定律
Φ
RmFe
F
Rm
磁路基础知识
模拟电路图
解:铁心内磁通密度为
0.0009
BFe
AFe
T 1T 0.0009
从铸钢磁化曲线查得:与BFe相应旳HFe=9×102A/m
铁心段旳磁位降: H l Fe Fe 9 102 0.3A 270A
磁路及动力学基础知识
矫顽力
磁滞现象是铁磁材料的另一个特性。
第1章
返 回 上 页 下 页
说明1:基本磁化曲线
B
不同的铁磁物 质其磁滞回线 宽窄是不同的, 当铁磁材料的 磁滞回线较窄 时,可用它的 平均磁化曲线, 即基本磁化曲 线进行计算
基 本 磁 化 曲 线
H
基本磁化曲线
定义:对同一铁磁材料,选择 不同的磁场强度进行反复磁 化,可得一系列大小不同的 磁滞回线,再将各磁滞回线的 顶点联接起来,所得的曲线。 第1章
第1章
返 回 上 页 下 页
■磁场强度 磁场强度是计算磁场所用的物理量,其大小等 于磁场中某点的磁感应强度与该点上的磁导率之比。 H的单位:安/米 B 矢量 H B的单位: 特斯拉 的单位:亨/米
讨论 磁场内某一点的磁场强度H与有关吗?
NI Hx lx
磁场内某一点的H只与电流大小、线圈匝数及该点的几何 位臵有关,而与(磁介质的磁性)无关。
问 磁场内某一点的磁感应强度B与有关吗?
第1章
返 回 上 页 下 页
1.1.2 本课程中常用的基本电磁定律
复习电路定律
1.电路欧姆定律 I U ,直流电路
R U I ,交流电路 Z
2.基尔霍夫定律
I 0,直流电路 基尔霍夫第一定律 I 0,交流电路
x Hx
I
Hdl H l I NI
其中
x x
H x 2 x
NI Hx lx
l x=2 x是半径为x的圆周长 Hx是半径 x 处的磁场强度 NI = F即线圈匝数与电流的乘积,称磁动势或磁势 单位为安匝(A)
第1章
返 回 上 页 下 页
磁路的三个基本定律

磁路的三个基本定律一、磁路的欧姆定律1. 内容- 磁路中的磁通Φ(单位为韦伯,Wb)与磁动势F(单位为安匝,At)成正比,与磁阻R_m(单位为H^-1)成反比,即varPhi=(F)/(R_m)。
2. 相关概念- 磁动势F:磁动势是产生磁通的激励,等于线圈的匝数N与通过线圈的电流I 的乘积,即F = NI。
例如,一个线圈匝数为100匝,通过的电流为2A,则磁动势F=100×2 = 200安匝。
- 磁阻R_m:磁阻表示磁路对磁通的阻碍作用,它与磁路的长度l(单位为米,m)成正比,与磁路的横截面积S(单位为平方米,m^2)和磁导率μ(单位为亨/米,H/m)成反比,即R_m=(l)/(μ S)。
例如,对于一段长度l = 0.5m,横截面积S=0.01m^2,磁导率μ = 4π×10^-7H/m的磁路,其磁阻R_m=(0.5)/(4π×10^-7)×0.01≈3.98×10^7H^-1。
二、磁路的基尔霍夫第一定律(磁通连续性定律)1. 内容- 对于磁路中的任一闭合面,进入该闭合面的磁通等于离开该闭合面的磁通,即∑varPhi = 0。
2. 理解与示例- 这一定律类似于电路中的基尔霍夫电流定律。
例如,在一个有分支的磁路中,假设一个节点处有三条磁路分支,磁通分别为varPhi_1、varPhi_2和varPhi_3,如果规定进入节点为正,离开节点为负,则varPhi_1-varPhi_2-varPhi_3 = 0。
也就是说,磁通在磁路的节点处是连续的,不会凭空产生或消失。
三、磁路的基尔霍夫第二定律(安培环路定律的推广)1. 内容- 在磁路的任一闭合回路上,磁动势的代数和等于各段磁路磁压降(Hl,其中H为磁场强度,单位为安/米,A/m)的代数和,即∑ F=∑ Hl。
2. 相关概念与示例- 磁场强度H:磁场强度与磁导率μ和磁感应强度B(单位为特斯拉,T)的关系为B = μ H。
1.1 电机的磁路和磁路定理
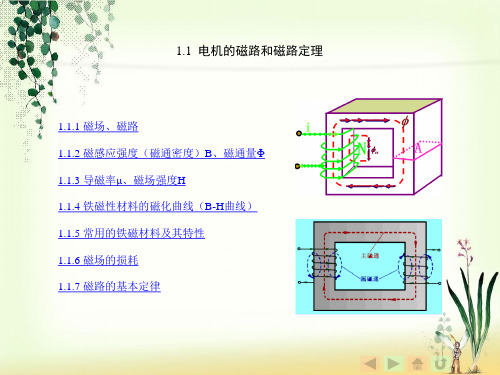
n
Hdl I
l k 1
k
NI F
上式中:N为闭合路径链着的线圈匝数; I为线圈中的电流。 积分回路的绕行方向和产生该磁场电流的方向 符合右手螺旋法则。
I1
B
0.0012 1.2T 4 S 10 10
查硅钢片磁化曲线
H 700A / m
求磁势
F Hl 700A / m 0.6m 420A
问题: 为何不能用 公式H=B/µ 直接求H?
例3.如图所示为一有气隙的电磁铁磁路,S
铁心为 10cm2,l 60cm, 0.2cm,
磁导率μ:表示磁场媒质磁性的物理量,即用来衡量物质的导磁能力。
μ=B/H(单位亨/米)
真空磁导率为
0 4 107 H / m
空气、铜、铝等非磁性物质,磁导率约等于真空磁导率。 磁性材料的磁导率为 μFe=(2000 ~ 6000)μ0 磁性材料的磁导率远远大于空气的磁导率。如:铁、镍、钴及其合金。 单质存在的铁矿,一般具有整体磁性,就是因为被地磁场磁化的原因。磁性材料(铁磁材料)的这一 特性被广泛应用于各种电机电器中。例如,电机、变压器的线圈中都装有铁芯,就是为了以较小的激磁电 流获取较大的磁通。 非磁性材料因为没有磁畴,磁场对单个物质原子不起作用,不具有磁化的特性,磁导率也不会很大。 磁场强度H:表征磁场性质的另一个物理量。它也是一个矢量,其单位为A/m(安/米)。在电机分析 中磁场强度反映了电磁之间的关系,它和磁感应强度间的数量关系是:
B 1.2T
(3)求总的磁动势为:
F
电机学:第一章 磁路2
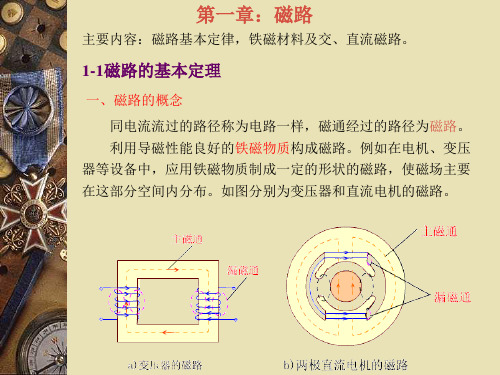
主要内容:磁路基本定律,铁磁材料及交、直流磁路。
1-1磁路的基本定理
一、磁路的概念 同电流流过的路径称为电路一样,磁通经过的路径为磁路。 利用导磁性能良好的铁磁物质构成磁路。例如在电机、变压
器等设备中,应用铁磁物质制成一定的形状的磁路,使磁场主要 在这部分空间内分布。如图分别为变压器和直流电机的磁路。
用直流励磁 用交流励磁
磁路中磁通恒定 磁路中磁通交变
直流磁路 直流电机 交流磁路 变压器、感应电机
二、磁路的基本定律
磁路的基本定律有 安培环路定律,磁路的欧姆定律,磁路的基尔霍 夫第一定律,磁路的基尔霍夫第二定律。 1、安培环路定理(或称全电流定理)
在磁路中沿任一闭合路径L,磁场H的线积分等于该闭合回路所包围 的总电流,即:
基尔霍夫第二定律
Ni Hl Rm
电动势 E=IR 电流 I 电阻 R=L/σA =ρL/A 电导 G=1/R
电导率
欧姆定律 I= E R
基尔霍夫第一定律 i 0
基尔霍夫第二定律
e iR
电路与磁路的不同点:
1、电路中有电流就有功率损耗。磁路中恒定磁通下没有功率损耗。 2、电流全部在导体中流动,而在磁路中没有绝对的磁绝缘体,除
范围内。所以电机和变压器的铁心用导磁率较高的铁磁材料组成。
一、铁磁物质的磁化
1 、铁磁物质
铁磁物质的磁导率都很大,一般是
的几千倍。
0
铁磁物质
金属
铁、钴、镍: B高,居里温度高。缺点是电阻率 低,涡流耗严重。
非金属 铁氧体: 电阻率高,涡流损耗小,抗锈防腐。
2、铁磁物质的磁化
缺点是B低,温度稳定性差。
I
Rm R F E
注:由于铁磁材料的磁导率不是常数,所以Rm一般不是常数。 3、磁路的基尔霍夫第一定律
磁路及其基本定律

磁路及其基本定律
一、磁路的概念
在电机、变压器及各种铁磁元件中常用磁性材料做成一定形状的铁心。
铁心的磁导率比周围空气或其它物质的磁导率高的多,磁通的绝大部分经过铁心形成闭合通路,磁通的闭合路径称为磁路。
二、磁路的欧姆定律
磁路的欧姆定律是分析磁路的基本定律
1.磁路的欧姆定律
若某磁路的磁通为Φ,磁通势为F ,磁阻为R m ,则Φ= F/Rm
2. 磁路与电路的比较
3. 磁路分析的特点
(1) 在处理电路时不涉及电场问题,在处理磁路时离不开磁场的概念;
(2) 在处理电路时一般可以不考虑漏电流,在处理磁路时一般都要考虑漏磁通;
(3) 磁路欧姆定律和电路欧姆定律只是在形式上相似。
由于μ不是常数,其随励磁电流而变,磁路欧姆定律不能直接用来计算,只能用于定性分析;
(4) 在电路中,当E =0 时,I=0 ;但在磁路中,由于有剩磁,当F
=0 时,F 不为零;
9.6.3 磁路的分析计算
主要任务: 预先选定磁性材料中的磁通 F ( 或磁感应强度) ,按照所定的磁通、磁路各段的尺寸和材料, 求产生预定的磁通所需要的磁通势F=NI ,确定线圈匝数和励磁电流。
基本公式: 设磁路由不同材料或不同长度和截面积的n 段组成,则基本公式为:
基本步骤:
(1) 求各段磁感应强度B i
(2) 求各段磁场强度H i 根据各段磁路材料的磁化曲线B i =f ( H i ) , 求B 1 ,B 2 ,……相对应的H 1 ,H 2 ,……。
(3) 计算各段磁路的磁压降(H i l i )
(4) 根据下式求出磁通势(NI )。
电工电子技术-磁路及其基本定律

一个没有铁芯的载流线圈所产生的磁通是分布在整个空 间的,而当此线圈绕在闭合铁芯上时,由于铁芯的磁导率远 比周围空气或其他非磁性材料的磁导率大,因此,绝大多数 磁通将集中于铁芯内部,并构成回路。这部分磁通称为主磁 通。另外一小部分磁通经过铁芯外的非磁性材料而形成回路, 这部分磁通称为漏磁通。
磁路与电路的关系
Hl I
在下图所示磁路中,应用安培环路定律为:
Hl NI
上式中,线圈匝数与电流的乘积NI称为磁通势(磁动势 ),用字母F表示,即
F NI
2.磁路欧姆定律
NI F
l Rm
S 上式与电路的欧姆定律在形式上相似,故称为磁路欧姆 定律。因铁磁性材料的磁导率μ不是常数,因此,磁路的欧 姆定律通常不能用于定量计算,只能用于定性分析。
我们把这种人为造成的主磁通的闭合路径称为磁路。如 下图所示为几种铁芯构成的磁路。
1.安培环路定律
安培环路定律又称为全电流定律,它是计算磁路的基本 公式,其数学表形式, 即在磁场中,任选一磁力线作为闭合回线,若闭合回线上各 点的磁场强度H相等,且其方向与闭合回线的切线方向一致 ,则磁场强度H与闭合回线的长度l的乘积就等于闭合回线内 所包围的电流总和ΣI,其表达式为:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第4章磁路和磁路定律1 磁路与电路的对比电路与磁路对照表磁路与电路的不同1)将磁路与电路对比,这只是定性的,近似的说法。
认真研究磁路和电路有重大不相同。
电路中,导电体的电阻率与绝缘体的电阻率相差1013位以上,所以在空间泄漏的电流是微乎其微的。
磁路中,一般导磁体与空气的磁导体相差不过102-103倍,最优良的磁体的磁导率与空气的磁导率相差不超过106倍。
2)导磁体达到磁饱和以后,磁导率会降到与空气一样所以在空间泄漏的磁通量相当可观。
在低矫顽力永磁材料的磁路中,往往泄漏磁通大于有用磁通。
3)磁性材料的性能参数有达5%的误差,加上计算过程中的估算和假定,磁性计算比电路计算困难大,磁路的计算误差在10%,就被认为较满意。
但是随着计算机在磁路没计算中的应用,计算精度将会提高。
2 磁路的概念观察两种现象:a)在通电螺线管内腔的中部,电流产生的磁力线平行无螺线管的轴线,磁场线渐进螺线管两端时变成的散开的曲线,曲线在螺线管外部空间相接。
如果将一根长铁心插入通电螺线管中,并且让铁心闭合,则泄漏到空间的磁力线很少,由上,我们定义,不管有无铁心,磁力经过的路线,让我们成为磁路。
b)用永磁性作磁源,也产生上述现象。
图1 等效磁路图1 a)给出了永磁体单独存在时的情况。
图b)将永磁体放入软磁体回路的间隙中,磁力线的大部分通过软磁体和永磁体构成的回路。
以上两种也是表示磁回路。
图中磁力线密度表示磁通量的密度。
广义的讲,磁通量所通过的磁介质的路经叫磁路。
磁路是许多以电磁原理作成的机械、器件如电机,电器,磁电式仪表等的主要组成部分之一。
各种磁路传递着磁力线,发挥着应有的机能。
大多数磁路含有磁性材料和工作气隙,完全由磁性材料构成的闭合磁路的情况也有不少。
凡含有空隙的磁路,一部分磁通量作为有用磁场,还有一部分磁通量在空隙的附近泄漏在空间,形成漏磁通。
图2 磁路3磁路欧姆定律软磁圆环,截面积S 平均周长l 磁导率μ线圈匝N 电流为i 则圆环内的磁场H 为 :lNiH =(4-1) H 的方面与环的轴线平行。
无漏磁时,穿过环的截面的磁通Φ为:BS =Φ (4-2)由H B μ=(μ铁环的磁导率,H 磁场)得HS μ=Φ (4-3)将(2-1)代入上式得:S lNiμ=Φ (4-4)由上式得Sl Niμ=Φ (4-5) 磁力势Ni Fm =,SlRm μ=(2-5)可写成 mmR F =Φ (4-6)图3 环形线圈此式与电路的欧姆定律相似。
磁通量Φ对用于电流,磁力势Ni Fm =对用于电势E 。
SlRm μ=为磁阻与电阻相对应。
磁动势与磁化电流i 和线圈总匝数N 成正比。
磁阻与磁路的长度,(铁心的平均周长l )成正比,与磁导率μ及磁路的横截面积A 成反比。
由电路欧姆定律推导出来的电动势叠加原理及电阻的串并联的计算方法,同样适用于磁路中的磁力势叠加和磁阻的串并联。
4 磁路的串联和并联如图,如果磁导率为1μ长为1l 的环式线圈铁心中有一长为0l ,磁导率0μ的空隙,这是串联的例子:图4 有缺口环形线圈磁动势等于各部分磁压降(i i l H )之和:001l H Hl N i += (4-7)因为H B μ=,000H B μ= 则上式可写为:001l B l BN i μμ+=(4-8)将BS =Φ代入(2-8)中,若系统无漏磁通,铁心里的磁通量与空隙的磁通量相同(连续)。
S B Φ=0S B Φ= 代入(2-8)得, )(001S l S l N i μμ+Φ= (4-9) 由i m N F =,S l R mlμ1= ,0000S l R m μ= 得 )(mo ml m R R F +Φ= (4-10)mo ml mR R F +=Φ, 另m o m l m R R R +=, 所以 此时用(2-6)如果组成磁路的几个磁阻是串联的而无分支,根据磁通连续原理,磁路各处的磁通量相等。
Φ=Φ⋅⋅⋅Φ=Φ=Φn 321 (4-11)对磁路各段的每个磁阻均有:1111m R l H =Φ,2222m R l H =Φ,…mn n n n R l H =Φ1 (4-12)将上式代入(2-12)得:nn n m m R I H R l H R l H =⋅⋅⋅===Φ222111 (4-13) 111l H R m =Φ,222l H R m =Φ,…n n m n l H R =Φ (4-14)两边相加得:i ni i n n mn m m l H l H L H l H R R R ∑==+⋅⋅⋅++=⋅⋅⋅++Φ1221121)( (4-15)ini i l H ∑=1为串联磁路的磁位差之和,也即总磁位差,应等于磁动势:m ini i F lH =∑=1(4-16)m ni miR R=∑=1成为串联磁路的总磁阻由此式(2-16)可写成m m F R =Φ 因式(2-6)并联对于并联磁路,其并联磁阻两端的磁位差相等,所以几个磁阻并联有:Hl l H L H l H n n =⋅⋅⋅==2211 (4-17)根据磁通连续原理,即总磁通等于各个并联分磁路磁通之和,即n Φ+⋅⋅⋅+Φ+Φ=Φ21 (4-18)将(2-13)代入上式,并加上(2-18)的条件,则有:)111(21222111mnm m n n n m m R R R Hl R I H R l H R l H +⋅⋅⋅++=+⋅⋅⋅++=Φ (4-19) 与欧姆定律比较可得:mnm m m R R R R 111121+⋅⋅⋅++= (4-20)5 磁路中的基尔霍夫定律基尔霍夫第一定律:0=Φ∑ (4-21)磁通的连续性定律磁路中任意结合点处,进入该处的磁通与离开的磁通的代数和等于零。
磁感应线是封闭曲线,无头无尾。
基尔霍夫第二定律:i N l H R i i i m i i ∑∑==Φ∑ (4-22)上式表明,沿磁路的任一闭合回路中,各部分磁位差的代数和等于通过回路所以磁动势的代数和。
第二定律实质上是磁路的全电流定律,对磁路中某一段而定,它就是欧姆定律。
磁动势又称为磁化力。
6 交流磁路交流电路中,除了有电阻,还有感抗和容抗,合称为电抗。
电抗存在是交流电路的主要特点之一,图5 磁感应强度、磁导率与磁场强度电抗的存在使交流,电路的能耗复杂度。
交流电流和电压按正弦曲线随时间变化,它们常用有效值来表示,其关系可写成:e u u 2max = (4-23) e I I 2max = (4-24)e u ,e I 电压和电流的有效值图6 e u ,e I 电压和电流的有效值当激磁线圈通以交流电时,就是交流磁路的情况,它具有下列特点:1) 线圈的磁势、磁通、磁感应强度,磁场强度都随时间不断变化着,在计算中一般不同瞬时值。
磁通、磁感强度用最大值此m Φ、m B 表示;磁势和磁场强度用有效值来表示,其符号为In 和H 。
2) 线圈中电流的大小决定于电阻和电抗,而且主要决定于线圈的电抗,多数情况下电抗在数值上比电阻大得多,线圈的电抗又和磁阻大小有关。
3) 在交变磁场作用下,磁导体的磁滞回线的形状和大小,随磁场频率的改变而改变。
磁导体中有涡流损耗和磁滞损耗,这种损耗总称为铁损。
铁损的存在不仅使线圈的磁激电流增加,而且使磁路中的磁势和磁通之间有相位差。
沿磁导体各段的磁通相位也不同。
4) 线圈中的磁链(磁通和匝数的乘积)决定于线圈两端的电压值。
外加电压越高,其磁链也越大。
交流磁路,需考虑铁损和分磁损耗的情况,磁路的欧姆定律,磁路的基尔霍夫第一、第二定律均应改为复数形式。
由上式可知交流磁路的情况比直流磁路要复杂得多。
7永磁磁路的分类:1)静态永磁磁路:具有固定工作间隙,使用时保持一定的工作状态。
2)半静态永磁磁路:磁系统本身的空隙不会变化,而在工作时,由于铁磁性工件的位置不同,磁路的工作间隙要发生变化。
右图的例子,当铁磁性工件被放开时,磁路的工作间隙最大,由于磁路的磁阻很大,磁路工作当处在退磁曲线的D上。
当铁磁性工件被吸住时,磁路的工作间隙最小,磁阻最小,磁路工作是移动的变化磁场,所以其工作状态时不断地在DE局部磁滞回线上往返运动。
到回复曲线的E上。
在具有变化工作间隙的半静态磁路中,永磁体所受的退磁场也是变化的。
μ(补充)恢复磁导率seco当永磁材料的磁状态处于退磁曲线上任意点时,受到一个与磁化方向相同的磁场H m的作用,磁状态不是该退磁曲线上升,而是沿mpr曲线回升。
当H m消失时,磁状态由rqm回到m形成mprqmμ,它可用B R处切线的斜回复曲线,用mr代替,称为mr为回复线,它的频率为恢复磁导率seco率近似表示。
则永磁体动态特性好。
在电动条件下工作的永磁路其磁阻,磁通是经常变化的,利用其变化的磁通,可以把机械能转变成电能,也可把电能转换成机械能,如用电动机。
永磁体本身的退磁场在不断变化外,还有一个外加磁通。
8 聚磁技术聚磁技术:运用永磁体和导磁体的各种排列,尽量使更多的磁通量汇聚到工作气隙中去。
因为长温下没有绝缘物质可以帮助汇聚磁力线,而一般物体在正常状态下都是导磁体,磁力线可以进入一般物体内部。
非导磁性物质,磁力线穿入,有相当一部分穿出,此既漏磁。
迄今,只发现超导材料在超导态时表现出绝磁的性质,磁力线不能进入超导体内部。
聚磁技术必须依靠高矫顽力的永磁体。
这种永磁体经得住较活的退磁场,它发出的磁力线不仅可以进入工作气隙,而且还能使其他永磁体的磁力线受到一定约束,更多地进入工作气隙。
聚磁技术的基础正是最普通的同级相斥、异极相吸。
见下图:注意的原则:1)高矫顽力永磁材料的回复磁导率1≈r μ,它自身的磁阻较大,所以当它与高r B ,低C H 的永磁材料联合运用时。
一般须放在后者的根部和侧部。
若放在前部,则气隙磁密反而下降。
2)锶铁氧硅和稀土永磁体的矫顽力都很高,当这两种永磁体联合运用时,前者放在侧部和根部,后者放在中心部位,主要原因是后者的剩磁比前者高,剩磁高的应放在中心和前部。
3)中心磁体要选择合适的材料,这是一个重要问题。
从实验得出下列规律:(1)在小气隙时(15.0/<D Lg ),中心磁体以高s B 的软磁材料为佳,如FeCo ,低碳钢等; (2)在中等气隙时,(5.0/15.0<<D Lg ),中心磁体的高Br 的AlNiCo 或FeCrCo 永磁材料为宜;(3)在大气隙时(5.0/>D Lg ),中心磁体以高Hc 的锶铁氢体和稀土钴永磁体为好。
这里:Lg 是工作气隙的长度,D 是中心磁体的直径,习惯称D Lg /为相对气隙。
若中心体的极面是正方形,D 是正方形边长,若是长方形,D 是它的短边长。
对永磁体,先充磁后但装和先但装后充磁,两者大小一样。
如右图,中心磁体是5AlNiCo , 侧部,根部都是锶铁氧体。
