2016年高考数学三轮讲练测核心热点总动员(新课标版) 专题23 参数方程和极坐标方程(选修2)
专题04 算法-2016年高考数学三轮讲练测核心热点总动员(新课标版)(原卷版)
2015年学易高考三轮复习系列:讲练测之核心热点 【全国通用版】【名师精讲指南篇】 【高考真题再现】1.【2013⋅新课标全国】执行右面的程序框图,如果输入的t ∈[-1,3],则输出的s 属于( ) A 、[-3,4] B 、[-5,2] C 、 [-4,3] D 、[-2,5]2.【2014全国卷1】执行右面的程序框图,若输入的k b a ,,分别为1,2,3,则输出的M=( ) A.320 B.27 C.516 D.8153.【2014全国卷2】执行如图所示的程序框图,如果输入的,x t 均为2,则输出的S =( ) A.4 B.5 C.6 D.74.【2015全国卷1】执行如图所示的程序框图,如果输入的0.01t =,则输出的n =( ). A. 5 B. 6 C. 7 D. 8输出n1S=1,n=0,m=12开始?输入t结束否5. 【2015全国卷2】如图所示,程序框图的算法思路源于我国古代数学名著《九章算术》中“更相减损术”.执行该程序框图,若输入的a 、b 分别为14、18,则输出的a =( ). A. 0 B. 2 C. 4D. 14【热点深度剖析】1.从这三年的高考试题来看.主要考查算法概念和程序框图,理解算法的基本结构,基本算法语句高考很少涉及.命题主要集中在算法的三种基本逻辑结构的框图表示,程序框图与其它知识结合是新的热点.2013年的试题主要考查值的范围,即分段函数的值域,题目的位置也靠前,属于中低档题,2014两套试题均考查循环输出结果,2015年两套试卷考查的也是循环结构的程序框图,值得一提的是全国卷2首次把教材中的算法案例变成高考试题,这是一个创新,2016全国卷有3套试题,估计其他两套高考有跟进的可能,另外算法与概率统计、不等式、三角函数等知识的交汇问题也是高考热点,请考生重视.2.从近几年的高考试题来看,当型与直到型循环结构、条件结构是考查的热点,题型以选择题、填空题为主,文理同题,分值5分左右,属容易题,主要考查算法基本结构以及读图、识图、利用框图解决简单算法问题的能力.预测2016年高考,循环结构与条件结构仍是考查的重点,但应同时注意算法的应用.【重点知识整合】1.算法的顺序结构:顺序结构是由若干个依次执行的处理步骤组成的,这是任何一个算法都离不开的基本结构.顺序结构在程序框图中的体现就是用流程线将程序框自上而下地连接起来,按顺序执行算法步骤.2.算法的条件结构: (1)利用条件分支结构解决算法问题时,要引入判断框,要根据题目的要求引入一个或多个判断框,而判断框内的条件不同,对应的下一图框中的内容和操作要相应地进行变化,故要逐个分析判断框内的条件.(2)解决分段函数的求值问题,一般采用条件结构.3.利用循环结构表示算法:(1)先确定是利用当型循环结构,还是直到型循环结构;(2)选择准确的表示累计的变量;(3)注意在哪一步开始循环.4.两种循环结构的特征:1. 识别程序框图运行和完善程序框图的步骤识别运行程序框图和完善程序框图是高考的热点.解答这一类问题,第一,要明确程序框图的顺序结构、条件结构和循环结构;第二,要识别运行程序框图,理解框图所解决的实际问题;第三,按照题目的要求完成解答.对程序框图的考查常与数列和函数等知识相结合,进一步强化框图问题的实际背景.2.解决程序框图问题要注意几个常用变量:i i=+.(1)计数变量:用来记录某个事件发生的次数,如1=+.(2)累加变量:用来计算数据之和,如S S i=⨯.(3)累乘变量:用来计算数据之积,如p p i3. 程序框图问题的解法(1)解答程序框图的相关问题,首先要认清程序框图中每个“框”的含义,然后按程序框图运行的箭头一步一步向前“走”,搞清每走一步产生的结论.(2)要特别注意在哪一步结束循环,解答循环结构的程序框图,最好的方法是执行完整每一次循环,防止执行程序不彻底,造成错误.4.判断条件的注意事项解决此类问题应该注意以下三个方面:一是搞清判断框内的条件由计数变量还是累加变量来表示;二是要注意判断框内的不等式是否带有等号,这直接决定循环次数的多少;三是要准确利用程序框图的赋值语句与两个变量之间的关系,把握程序框图的整体功能,这样可以直接求解结果,减少运算的次数.5.画程序框图的规则如下:(1)一个完整的程序框图必须有起止框,用来表示程序的开始和结束.(2)使用标准的图形符号表示操作,带箭头的流程线表示算法步骤的先后顺序,框图一般按从上到下、从左到右的方向画(3)算法中间要处理数据或计算,可分别写在不同的处理框中.(4)如果一个流程由于纸面等原因需要分开画.要在断开处画上连结点,并标出连结的号码.如图一.实际上它们是同一点,只是化不才分开画.用连结点可避免流程线的交叉或过长,使流程图清晰.(5)注释框不是流程图必需的部分,只是为了提示用户一部分框图的作用以及对某些框图的操作结果进行说明.它帮助阅读流程图的用户更好的理解流程图的来龙去脉.(6)在图形符号内用于描述的语言要非常简练清楚6.解决循环结构框图问题,首先要找出控制循环的变量其初值、步长、终值(或控制循环的条件),然后看循环体,循环次数比较少时,可依次列出即可获解,循环次数较多时可先循环几次,找出规律,要特别注意最后输出的是什么,不要出现多一次或少一次循环的错误.7.在循环结构中,填判断框中的条件是常见命题方式,此条件应依据输出结果来确定,解答时,一般先循环2至3次,发现规律,找出什么时候结束循环,也就找到了循环条件,要特别注意条件“不等式”中是否包括等号.【考场经验分享】本热点出现的位置一般在试卷的选择题的前5道中的一道,或者填空题的前2道中的一道,试题难度中低档,应该是同学们得全分的题目.但是解题时稍微不慎就容易出现错误,下面总结常见的错误:1.条件结构中的条件要准确,不能含混不清,要清楚在什么情况下需要作怎样的判断,用什么条件来区分.2.循环结构中要注意循环控制条件的把握,不要出现多一次循环和少一次循环的错误.3.要准确掌握各语句的形式、特点.特别是条件语句、循环语句中条件的把握. 【名题精选练兵篇】1.【2016安徽安庆二模】如图所示的算法框图中,e 是自然对数的底数,则输出的i 的值为(参考数值:ln 20167.609≈)( ) A .6 B .7 C .8 D .92.【2106东北三省三校一模】若m = 6,n = 4,按照如图所示的程序框图运行后,输出的结果是( ) A .1100B .100C .10D .13.【2016河北省衡水中学一调】执行所示框图,若输入6,4n m ==,则输出的p 等于( )A.120 B.240 C.360 D.7204. 【2016吉林长春质量监测二】运行如图所示的程序框图,则输出的S值为( )A.99212-B.99212+C.1010212-D.1010221+5. 【2016新疆乌鲁木齐一诊】执行如图的程序框图(n N*∈),则输出的S=()A.1n a aq aq-+++ B.n (1)1a q q -- C. na aq aq +++ D.n +1(1)1a q q-- 6.【2016安徽省“江南十校”联考】执行如图所示的程序框图,如果输入的50t =,则输出的n =( )(A) 5(B) 6(C) 7(D )87.【2106东北三省三校第一次联考】若6=m ,4=n ,按如图所示的程序框图运行后,输出的结果是( )A .1001B .100C .10D .1 8.【2015届福建省龙岩市高三教学质量检查】如图所示的程序框图输出的结果是14S =,则判断框内应填的条件是( )A .7?i ≥B .15?i >C .15?i ≥D .31?i >9. 【2015届四川省遂宁市高三第二次诊断】在区间]3,2[-上随机选取一个数M,不变执行如图所示的程序框图,且输入x 的值为1,然后输出n 的值为N,则2M N ≤-的概率为( )A .51 B .52C .53D .5410. 【2015届广东省汕头市高三第一次模拟】如图所示的程序框图,若输出的41S =,则判断框内应填入的条件是( )A .3?k >B .4?k >C .5?k >D . 6?k >11. 【2015届福建省福州市第八中学高三毕业班第六次质量检查】a 为如图所示的程序框图中输出的结果,则化简 cos()a πθ-的结果是A .cos θB .cos θ-C .sin θD .sin θ-12. 【2015届陕西省宝鸡市九校高三联合检测】某程序框图如图所示,若该程序运行后输出的值是74,则( )A.3a =B.4a =C.5a =D.6a =13.【2015届云南省弥勒市高三年级模拟测试】执行如图所示的程序框图,若输入2x =,则输出y 的值为( )A .2B .5C .11D .2314. 在如下程序框图中,输入()0sin(21)f x x =+,若输出的()i f x 是82sin(21)x +,则程序框图中的判断框应填入( )A.6i ≤B.7i ≤C.8i ≤D.9i ≤ 15. 【2015届山东省德州市高三上学期2月期末统考】已知实数 ,执行如图所示的程序框图,则输出的x 不小于103的概率是________.,那么输出的S的最大值为 .16. 执行如图的程序框图,如果输入,x y R【名师原创测试篇】1. 阅读下面的程序框图.若使输出的结果不大于64,则输入的整数i的最大值为( )A.5B.6C.7D.82. 执行如下图所示的程序框图,则输出的i 值为( )A . 3B .4C .5D .63. 设{}n a 为等差数列,其中3631,22a a ==-,阅读如图所示的程序框图,运行相应的程序,则输出结果 为 .4. 如图所示程序框图中,如果输入三个实数a 、b 、c,要求输出这三个数中最小的数,那么在空白的判断框中,应该填入下面四个选项中的( )A.x<cB.c<xC.b<cD.c<b5. 执行如图所示的程序框图,则输出的结果是___.6. 如图,这是一个把k进数a(共有n位)化为十进制数b的程序框图,执行该程序框图,若输人的k,a,n分别为2,110011,6,则输出的b=.:。
2016届高考数学三轮讲练测核心热点总动员(新课标版)专题04算法(解析版)
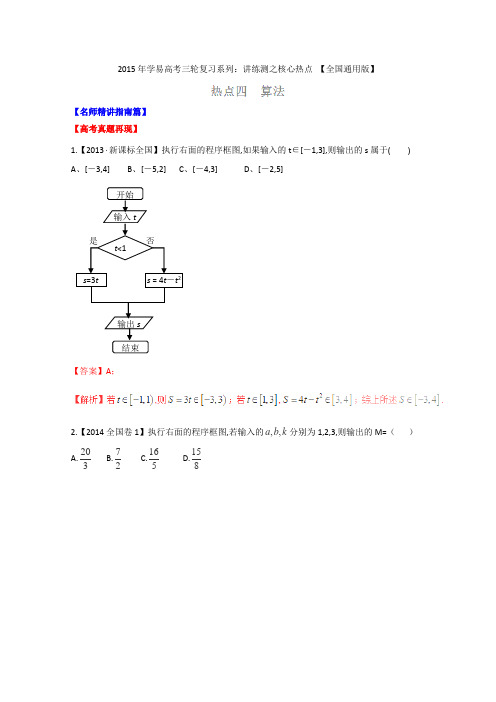
2015年学易高考三轮复习系列:讲练测之核心热点 【全国通用版】【名师精讲指南篇】【高考真题再现】1.【2013 新课标全国】执行右面的程序框图,如果输入的t ∈[-1,3],则输出的s 属于( )A 、[-3,4]B 、[-5,2]C 、[-4,3]D 、[-2,5]【答案】A ;2.【2014全国卷1】执行右面的程序框图,若输入的k b a ,,分别为1,2,3,则输出的M=( ) A.320 B.27 C.516 D.815【答案】D3.【2014全国卷2】执行如图所示的程序框图,如果输入的,x t 均为2,则输出的S =( )A.4B.5C.6D.7【答案】D【解析】k =1,M =11×2=2,S =2+3=5;k =2,M =22×2=2,S =2+5=7;k =3,3>t ,∴输出S =7,故选D.4.【2015全国卷1】执行如图所示的程序框图,如果输入的0.01t =,则输出的n =( ). A. 5B. 6C. 7D. 8输出n1S=1,n=0,m=12开始?输入t结束否【答案】C此时循环结束,输出7n =.故选C.5. 【2015全国卷2】如图所示,程序框图的算法思路源于我国古代数学名著《九章算术》中“更相减损术”.执行该程序框图,若输入的a 、b 分别为14、18,则输出的a =( ).A. 0B. 2C. 4D. 14【答案】B【解析】由题知,若输入a =14,b =18,则【热点深度剖析】1.从这三年的高考试题来看.主要考查算法概念和程序框图,理解算法的基本结构,基本算法语句高考很少涉及.命题主要集中在算法的三种基本逻辑结构的框图表示,程序框图与其它知识结合是新的热点.2013年的试题主要考查值的范围,即分段函数的值域,题目的位置也靠前,属于中低档题,2014两套试题均考查循环输出结果,2015年两套试卷考查的也是循环结构的程序框图,值得一提的是全国卷2首次把教材中的算法案例变成高考试题,这是一个创新,2016全国卷有3套试题,估计其他两套高考有跟进的可能,另外算法与概率统计、不等式、三角函数等知识的交汇问题也是高考热点,请考生重视.2.从近几年的高考试题来看,当型与直到型循环结构、条件结构是考查的热点,题型以选择题、填空题为主,文理同题,分值5分左右,属容易题,主要考查算法基本结构以及读图、识图、利用框图解决简单算法问题的能力.预测2016年高考,循环结构与条件结构仍是考查的重点,但应同时注意算法的应用.【重点知识整合】1.算法的顺序结构:顺序结构是由若干个依次执行的处理步骤组成的,这是任何一个算法都离不开的基本结构.顺序结构在程序框图中的体现就是用流程线将程序框自上而下地连接起来,按顺序执行算法步骤.2.算法的条件结构: (1)利用条件分支结构解决算法问题时,要引入判断框,要根据题目的要求引入一个或多个判断框,而判断框内的条件不同,对应的下一图框中的内容和操作要相应地进行变化,故要逐个分析判断框内的条件.(2)解决分段函数的求值问题,一般采用条件结构.3.利用循环结构表示算法:(1)先确定是利用当型循环结构,还是直到型循环结构;(2)选择准确的表示累计的变量;(3)注意在哪一步开始循环.4.两种循环结构的特征:1. 识别程序框图运行和完善程序框图的步骤识别运行程序框图和完善程序框图是高考的热点.解答这一类问题,第一,要明确程序框图的顺序结构、条件结构和循环结构;第二,要识别运行程序框图,理解框图所解决的实际问题;第三,按照题目的要求完成解答.对程序框图的考查常与数列和函数等知识相结合,进一步强化框图问题的实际背景.2.解决程序框图问题要注意几个常用变量:i i=+.(1)计数变量:用来记录某个事件发生的次数,如1=+.(2)累加变量:用来计算数据之和,如S S i=⨯.(3)累乘变量:用来计算数据之积,如p p i3. 程序框图问题的解法(1)解答程序框图的相关问题,首先要认清程序框图中每个“框”的含义,然后按程序框图运行的箭头一步一步向前“走”,搞清每走一步产生的结论.(2)要特别注意在哪一步结束循环,解答循环结构的程序框图,最好的方法是执行完整每一次循环,防止执行程序不彻底,造成错误.4.判断条件的注意事项解决此类问题应该注意以下三个方面:一是搞清判断框内的条件由计数变量还是累加变量来表示;二是要注意判断框内的不等式是否带有等号,这直接决定循环次数的多少;三是要准确利用程序框图的赋值语句与两个变量之间的关系,把握程序框图的整体功能,这样可以直接求解结果,减少运算的次数.5.画程序框图的规则如下:(1)一个完整的程序框图必须有起止框,用来表示程序的开始和结束.(2)使用标准的图形符号表示操作,带箭头的流程线表示算法步骤的先后顺序,框图一般按从上到下、从左到右的方向画(3)算法中间要处理数据或计算,可分别写在不同的处理框中.(4)如果一个流程由于纸面等原因需要分开画.要在断开处画上连结点,并标出连结的号码.如图一.实际上它们是同一点,只是化不才分开画.用连结点可避免流程线的交叉或过长,使流程图清晰.(5)注释框不是流程图必需的部分,只是为了提示用户一部分框图的作用以及对某些框图的操作结果进行说明.它帮助阅读流程图的用户更好的理解流程图的来龙去脉.(6)在图形符号内用于描述的语言要非常简练清楚6.解决循环结构框图问题,首先要找出控制循环的变量其初值、步长、终值(或控制循环的条件),然后看循环体,循环次数比较少时,可依次列出即可获解,循环次数较多时可先循环几次,找出规律,要特别注意最后输出的是什么,不要出现多一次或少一次循环的错误.7.在循环结构中,填判断框中的条件是常见命题方式,此条件应依据输出结果来确定,解答时,一般先循环2至3次,发现规律,找出什么时候结束循环,也就找到了循环条件,要特别注意条件“不等式”中是否包括等号.【考场经验分享】本热点出现的位置一般在试卷的选择题的前5道中的一道,或者填空题的前2道中的一道,试题难度中低档,应该是同学们得全分的题目.但是解题时稍微不慎就容易出现错误,下面总结常见的错误:1.条件结构中的条件要准确,不能含混不清,要清楚在什么情况下需要作怎样的判断,用什么条件来区分.2.循环结构中要注意循环控制条件的把握,不要出现多一次循环和少一次循环的错误.3.要准确掌握各语句的形式、特点.特别是条件语句、循环语句中条件的把握.【名题精选练兵篇】1.【2016安徽安庆二模】如图所示的算法框图中,e是自然对数的底数,则输出的i的值为(参)()考数值:ln20167.609A.6B.7C.8D.9【答案】C【解析】∵609.72016ln ≈,∴8e 2016>∴ 8i =时,符合2016a ≥,∴ 输出的结果8i =.故选C.2.【2106东北三省三校一模】若m = 6,n = 4,按照如图所示的程序框图运行后,输出的结果是( )A .1100B .100C .10D .1【答案】D【解析】因为6,4m n ==,所以lg()lg101y m n =+==,故选D .3.【2016河北省衡水中学一调】执行所示框图,若输入6,4n m ==,则输出的p 等于( )A .120B .240C .360D .720【答案】C4. 【2016吉林长春质量监测二】运行如图所示的程序框图,则输出的S 值为( )A. 99212-B. 99212+C. 1010212-D. 1010221+ 【答案】A5. 【2016新疆乌鲁木齐一诊】执行如图的程序框图(n N *∈),则输出的S=( )A.1n a aq aq -+++B.n (1)1a q q --C. na aq aq +++ D. n +1(1)1a q q -- 【答案】C . 【解析】执行第一次循环体运算,得1,i s a ==;执行第二次,2,i s a aq ==+;执行第1n +次,1,n i n s a aq aq =+=++,故选C .6.【2016安徽省“江南十校”联考】执行如图所示的程序框图,如果输入的50t =,则输出的n =( )(A) 5 (B) 6 (C) 7 (D )8【答案】B7.【2106东北三省三校第一次联考】若6=m ,4=n ,按如图所示的程序框图运行后,输出的结果是( )A .1001 B .100 C .10 D .1 【答案】D【解析】因为6=m ,4=n ,所以m n >,所以lg(64)1y =+=,所以答案为D .8.【2015届福建省龙岩市高三教学质量检查】如图所示的程序框图输出的结果是14S =,则判断框内应填的条件是( )A .7?i ≥B .15?i >C .15?i ≥D .31?i > 【答案】C9. 【2015届四川省遂宁市高三第二次诊断】在区间]3,2[-上随机选取一个数M,不变执行如图所示的程序框图,且输入x 的值为1,然后输出n 的值为N,则2M N ≤-的概率为( )A .51 B .52C .53D .54【答案】C【解析】243013x x x -+≤⇒≤≤.这是一个循环结构,循环的结果依次为:2,1;3,2;4,3x n x n x n ======.最后输出3.所以在区间]3,2[-上随机选取一个数M,则1M ≤的概率为35p =,选C. 10. 【2015届广东省汕头市高三第一次模拟】如图所示的程序框图,若输出的41S =,则判断框内应填入的条件是( )A .3?k >B .4?k >C .5?k >D . 6?k > 【答案】B11. 【2015届福建省福州市第八中学高三毕业班第六次质量检查】a 为如图所示的程序框图中输出的结果,则化简 cos()a πθ-的结果是A .cos θB .cos θ-C .sin θD .sin θ- 【答案】A【解析】1,2==i a ;2,1211=-=-=i a ;3,21111==+=i a ;4,22111==-=i a ;⋅⋅⋅;即a 值具有周期性,周期为3;而167132014⋅⋅⋅=÷;所以输出a 值为2;则()()θθπθπcos 2cos cos =-=-a .12. 【2015届陕西省宝鸡市九校高三联合检测】某程序框图如图所示,若该程序运行后输出的值是74,则( )A.3a =B.4a =C.5a =D.6a = 【答案】A【解析】第一次:2,23==k S ;第二次:3,35==k S ;第三次:4,7==k S ,退出循环,故选A13.【2015届云南省弥勒市高三年级模拟测试】执行如图所示的程序框图,若输入2x =,则输出y 的值为( )A .2B .5C .11D .23【答案】D14. 在如下程序框图中,输入()0sin(21)f x x =+,若输出的()i f x 是82sin(21)x +,则程序框图中的判断框应填入( )A.6i ≤B.7i ≤C.8i ≤D.9i ≤ 【答案】B.【解析】1i =时,1()2cos(21)f x x =+;2i =时,22()2sin(21)f x x =-+;3i =时,33()2cos(21)f x x =-+;4i =时,44()2sin(21)f x x =+; ;8i =时,88()2sin(21)f x x =+,结束,故选B.15. 【2015届山东省德州市高三上学期2月期末统考】已知实数 ,执行如图所示的程序框图,则输出的x 不小于103的概率是________.【答案】91416. 执行如图的程序框图,如果输入,x y R ∈,那么输出的S 的最大值为 .【答案】2【名师原创测试篇】1. 阅读下面的程序框图.若使输出的结果不大于64,则输入的整数i 的最大值为( )A .5B .6C .7D .8 【答案】B【解析】经过第一次运算得到1,1S n ==,经过第二次运算得到3,2S n ==,经过第三次运算得到7,3S n ==,经过第四次运算得到15,4S n ==,经过第五次运算得到31,5S n ==,经过第六次运算得到63,6S n ==,经过第七次运算得到127,7S n ==.∵输出的结果不大于64,∴n 的最大值为5,∴i 的最大值为6.故选B.2. 执行如下图所示的程序框图,则输出的i 值为( )A . 3B .4C .5D .6【答案】C3. 设{}n a 为等差数列,其中3631,22a a ==-,阅读如图所示的程序框图,运行相应的程序,则输出结果 为 .【答案】16【解析】设等比数列公比为q ,则52q =,所以452()2n n a -=,程序在执行过程中,,s n 的值依次为:1,1s n ==;12,2a s n ==;12a 22,3a s n =⋅=;……, 812a a 222a s =⋅⋅⋅…,9n =,程序结束,输出812a a 222a s =⋅⋅⋅…128184(a )422216a a a a ++++====….4. 如图所示程序框图中,如果输入三个实数a 、b 、c,要求输出这三个数中 最小的数,那么在空白的判断框中,应该填入下面四个选项中的( ) A.x<c B.c<x C.b<c D.c<b【答案】B5.执行如图所示的程序框图,则输出的结果是___.【答案】12【解析】422,2=+==S c ;734,3,2,1=+====S c b a ;1257,5,3,2=+====S c b a ;45>=c ,即输出的结果为12.6. 如图,这是一个把k 进数a (共有n 位)化为十进制数b 的程序框图,执行该程序框图,若输人的k ,a ,n 分别为2,110011,6,则输出的b = .【答案】51。
2016届高考数学三轮讲练测核心热点总动员(新课标版)专题07三视图(解析版)

2016年学易高考三轮复习系列:讲练测之核心热点 【全国通用版】热点七 三视图【名师精讲指南篇】【高考真题再现】1.【2013⋅新课标全国卷】某几何函数的三视图如图所示,则该几何的体积为( ) A 、168π+ B 、88π+ C 、1616π+ D 、816π+【答案】A ;【解析】上半部分体积为122416V =⨯⨯=,下半部分体积2212482V ππ=⨯⨯⨯=,故总体积2168V π=+.2.【2014全国卷】如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )(A ) (B )6 (C ) (D )4【答案】B【解析】由正视图、侧视图、俯视图形状,可判断该几何体为四面体,且四面体的长、宽、高均为4个单位,故可考虑置于棱长为4个单位的正方体中研究,如图所示,该四面体为D ABC -,且4AB BC ==,AC =DB DC ==, 6DA ==,故最长的棱长为6,选B .4CABD3.【2014全国卷】如图,网格纸的各小格都是正方形,粗实线画出的事一个几何体的三视图,则这个几何体是( )A.三棱锥B.三棱柱C.四棱锥D.四棱柱【答案】B【解析】根据三视图的法则:长对正,高平齐,宽相等.可得几何体如下图所示.4.【2015全国1】圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为1620π+,则r =( ).A. 1B. 2C. 4D. 8俯视图正视图2rr2rr【答案】B.【解析】根据题意作图,如图所示.r2r2r224π22π2π2r S r r r r r =⋅+⋅⋅++=2245π1620πr r +=+,所以2r =.故选B.5.【2015全国卷2】一个正方体被一个平面截去一部分后,剩余部分的三视图如下图,则截去部分体积与剩余部分体积的比值为( )1A.8 1B.7 1C.6 1D.5俯视图侧视图主视图.【答案】【解析】由三视图得,在正方体1111ABCDA B C D ﹣中,截去四面体111A A B D ﹣,如图所示,设正方体棱长为a ,则11133111326A AB D V a a =⨯=﹣,故剩余几何体体积为 3331566a a a -=,所以截去部分体积与剩余部分体积的比值为15.故选D.【热点深度剖析】从近几年的高考试题来看,几何体的三视图是高考的热点,题型多为选择题、填空题,难度中、低档.主要考查几何体的三视图,以及由三视图构成的几何体,在考查三视图的同时,又考查了学生的空间想象能力及运算与推理能力.2013年是一个组合体的三视图求体积,试题难度中等,2014年的理科题目给出三视图,求最长棱长,文科题目给出三视图,求几何体的形状;2015年两套试卷分别组合体的表面积及几何体的切割问题.考查从近几年的高考试题来看,高考对三视图的考查主要考查由三视图得出几何体的直观图,求其表面积、体积或由几何体的表面积、体积得出某些量;试题难度逐年有所增加,组合体及非正常状态下放置的棱锥的三视图成为考查的热点.纵观这三年高考,每年必考一题,分值5分,.预测2016年高考仍将以组合体及长方体的切割截的三视图为主要考查点,可能与表面积、体积有关,重点考查学生读图、识图能力以及空间想象能力.【重点知识整合】 1.空间几何体的三视图三视图是观测者从不同位置观察同一个几何体,画出的空间几何体的图形. 他具体包括:(1)正视图:物体前后方向投影所得到的投影图;它能反映物体的高度和长度; (2)侧视图:物体左右方向投影所得到的投影图;它能反映物体的高度和宽度; (3)俯视图:物体上下方向投影所得到的投影图;它能反映物体的长度和宽度. 2.三视图画法规则高平齐:主视图与左视图的高要保持平齐 长对正:主视图与俯视图的长应对正 宽相等:俯视图与左视图的宽度应相等【应试技巧点拨】1.解决三视图问题的技巧:空间几何体的数量关系也体现在三视图中,正视图和侧视图的“高平齐”,正视图和俯视图的“长对正”,侧视图和俯视图的“宽相等”.也就是说正视图、侧视图的高就是空间几何体的高,正视图、俯视图中的长就是空间几何体的最大长度,侧视图、俯视图中的宽就是空间几何体的最大宽度.在绘制三视图时,分界线和可见轮廓线都用实线画出,被遮挡的部分的轮廓线用虚线表示出来,即“眼见为实、不见为虚”.在三视图的判断与识别中要特别注意其中的“虚线”.2.要切实弄清常见几何体(圆柱、圆锥、圆台、棱柱、棱锥、棱台、球)的三视图的特征,熟练掌握三视图的投影方向及正视图原理,才能迅速破解三视图问题,由三视图画出其直观图.3.解答三视图题目时:(1)可以从熟知的某一视图出发,想象出直观图,再验证其他视图是否正确;(2)视图中标注的长度在直观图中代表什么,要分辨清楚;(3)视图之间的数量关系:正俯长对正,正侧高平齐,侧俯宽相等.4.从能力上来看,三视图着重考查空间想象能力,即空间形体的观察分析和抽象的能力,要求是“四会”:①会画图——根据题设条件画出适合题意的图形或画出自己想作的辅助线(面),作出的图形要直观、虚实分明;②会识图——根据题目给出的图形,想象出立体的形状和有关线面的位置关系;③会析图——对图形进行必要的分解、组合;④会用图——对图形或其某部分进行平移、翻折、旋转、展开或实行割补术;考查逻辑思维能力、运算能力和探索能力.【考场经验分享】1.三视图在近几年课改区的高考题都有体现,多面体画图、分析图,用自己的语言描述图,提高借助图形分析问题的能力,培养空间观念,注重三视图与直观图的相互转化及等积转化的思想.因此,三视图的内容应重点训练.与几何体的侧面积和体积有关的计算问题,根据基本概念和公式来计算,要重视方程的思想和割补法、等积转换法的运用.2.对于简单几何体的组合体的三视图,首先要确定正视,侧视,俯视的方向,其次要注意组合体有哪些几何体组成,弄清它们的组成方式,特别应注意它们的交线的位置.解题时一定耐心加细心,观察准确线与线的位置关系,区分好实线与虚线的不同.此类题目如只是单纯考查三视图,一般难度较低,需保证得全分;若与体积,表面积或组合体相结合,有时难度较大,需要较强的空间想象能力和准确的画图能力,此时若空间想象能力不够,不要花费过多的时间.【名题精选练兵篇】1.【2016江西省赣中南五校一模】已知一个几何体的三视图是三个全等的边长为1的正方形,如图所示,则它的体积为A .16 B . 13C .23 D . 56【答案】C【解析】该三视图对应的空间几何体是边长为1的正方体去掉一个三棱锥,如下图所示,所以它的体积为321131111=⨯⨯-⨯⨯;故选C . 2.【2016吉林长春质量监测二】几何体三视图如图所示,则该几何体的体积为A.323 B. 2163π- C. 403 D. 8163π- 【答案】C【解析】该几何体可视为长方体挖去一个四棱锥,所以其体积为14022422233⨯⨯-⨯⨯⨯=. 故选C.3.【2016河北唐山一模】某几何体的三视图如右图所示,则其体积为( )(A)172π (B) 8π (C) 152π (D) 9π 【答案】B【解析】由三视图该几何体为两个圆柱的组合体,其底面半径均为1,其中一个圆柱高为5,另一个圆柱高为3,所以该几何体的体积为21(53)8ππ⨯⨯+=,故选B . 4.【2016年安徽安庆二模】一个几何体的三视图如图所示,其体积为( )A .116 B C .32 D .12【答案】A【解析】该几何体是一个直三棱柱截去一个小三棱锥,如图所示,则其体积为:611111213121221=⨯⨯⨯⨯-⨯⨯⨯=V ,故选A. 5.【2016安徽省“江南十校”联考】某几何体的三视图如图所示,其中侧视图的下半部分曲线为半圆弧,则该几何体的表面积为(A) 416π++(B) 516π++(C) 416π++(D) 516π++ 【答案】D【解析】由三视图可知该几何体是一个正三棱柱和一个半圆柱的组合体,三棱柱的两个侧面面积之和为16242=⨯⨯,两个底面面积之和为3232212=⨯⨯⨯;半圆柱的侧面积为ππ44=⨯,两个底面面积之和为ππ=⨯⨯⨯21212,所以几何体的表面积为32165++π,故选D6.【2015河北省“五个一名校联盟”二模】多面体的三视图如图所示,则该多面体的表面积为(单位:cm )( )A .28+4B .30+4C .30+4D .28+4【答案】A7.【2016年江西省南昌一模】如图,在正方体ABCD ﹣A 1B 1C 1D 1中,点P 是上底面A 1B 1C 1D 1内一动点,则三棱锥P ﹣BCD 的正视图与侧视图的面积之比为( )A .1:1B .2:1C .2:3D .3:2 【答案】A【解析】由题意可知,棱锥P ﹣BCD 的正视图与侧视图均为三角形,底边长为正方体的棱长,高等于正方体的棱长,两三角形面积面积相等,故选A.8.【2016新疆乌鲁木齐二诊】如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )A .100B .92C .84D .76【答案】A【解析】由几何体的三视图,可知该几何体为截去一角的长方体,其直观图如图所示,所以其体积1166344310032V =⨯⨯-⨯⨯⨯⨯=,故选A .ABCD 1C 1A 1M NB 1D422439.【2016河南六市高第一次联考】一个几何体的三视图如图所示,且其侧(左)视图是一个等边三角形,则这个几何体的体积为( )A B C . D 【答案】B.【解析】由题意得,该几何体为如下图所示的五棱锥P ABCDE -,∴体积211(212)32V =⋅⋅⋅+=故选B .10.【2016河南新乡许昌平顶山第二次调研】某几何体的三视图如图所示,则该几何体的体积为( ) A .133+π3 B .5+π2 C .5+π3 D . 133+π2【答案】D【解析】该几何体由三部分组成,后面是一个长方体,长、宽、高分布为2、1、2,体积为4,前左侧是高为2,底面圆半径为1的圆柱的14,体积为π2,前右侧是一个三棱锥,底面是腰为1的等腰直角三角形,高位2,体积为13,所以该组合体的体积为4+π2+13= 133+π2,故选D.11.【2016河北衡水一调】某几何体的三视图如右图,若该几何体的所有顶点都在一个球面上,则该球面的表面积为( )A .4πB .283πC .443πD .20π 【答案】B12.【2016河北省衡水二调】一个几何体的三视图如图所示,该几何体体积为 .【解析】由三视图知该几何体是以底面边长为2的正方形,的四棱锥,所以该几何体的体积为2123V =⨯=13.【2016辽宁大连双基测试】如图,在小正方形边长为1的网格中画出了某多面体的三视图,则该多面体的外接球表面积为 .【答案】34π14. 【2015届辽宁省朝阳市三校协作体高三下学期开学联考】一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如右图所示该四棱锥侧面积和体积分别是( )A .B .83C .81),3+ D .8,8 【答案】B【解析】根据题意该四棱锥为底面边长为2,高为2的四棱锥,所以该四棱锥的侧面积为:1422S =⨯⨯=,体积为:1822233V =⨯⨯⨯=,所以答案为:B .15. 【2015届福建省龙岩市高三教学质量检查】一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的表面积是( )A B C D 1+ 【答案】D16. 【2015届上海市高境一中高三期末】一个几何体的三视图如图所示,则该几何体的体积等于( )A 、263π+B 、463π+C 、283π+D 、483π+ 【答案】D【解析】由题意原几何体是一个球和一个正方体的组合体,球的直径为2,半径为1,正方体的棱长为2,所以原几何体的体积:=⨯⨯+⨯=2221343πV 483π+.17. 【2015届吉林省长春市高三上学期阶段性考试】如图,正三棱柱111C B A ABC -的正视图是边长为4的正方形,则此正三棱柱的侧视图的面积为( )A .16B .32C .34D .38 【答案】D【解析】从正视图中可以读出4,41==AA AB ,由于111C B A ABC -为正三棱柱,所以底面ABC ∆是正三角形ABC ∆,正三棱柱的侧视图为长3260sin 40=⨯,宽为4的矩形,面积为3818. 【2015届甘肃省部分普通高中高三第一次联考】若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如下图所示,则这个棱柱的体积为( )俯视图侧视图正视图A .312B .336C .327D .6 【答案】B【解析】该几何体为一个三棱柱,棱柱的高是4,底面正三角形的高是33,设底面边长为x ,则3323=⋅x ,6=∴x ,故三棱柱的体积336433621=⋅⋅⋅,故答案为B. 【名师原创测试篇】1. 某几何体的三视图如图所示,则该几何体的体积为 ( )A .5B .4C .2D .1【答案】A.2. 已知三棱锥的三视图,则该三棱锥的侧面积是()A.B.C.D.【答案】A3.某几何体的三视图如图所示,则该几何体的表面积为( )A .12B .12C .4D 12+ 【答案】A【解析】根据几何的三视图,画出该几何体的直观图,如下图可知该几何体,是将一个棱长为2的正方体,沿着如图所示的截面,截去之后剩下的几何体,根据三视图的数据,可知该几何体的表面积为2(12)111321361222+⨯⨯⎛⎫⨯+⨯+⨯+= ⎪⎝⎭.4.一空间几何体按比例绘制的三视图如图所示,则该几何体的体积为( )m 3A. 72B.92C.73D.94【答案】A【解析】由三视图可知该几何体是由三个棱长为1的正方体和切去一半的正方体构成,所以体积为72,故选A.5.已知一个三棱锥的三视图如图所示,其中俯视图是顶角为120 的等腰三角形,则该三棱锥的四个表面中,面积的最大值为_______.【答案】6.四棱锥的三视图如图所示,则最长的一条侧棱的长度是()2 A.29 B.5 C.13 D.2【答案】A。
2016届高考数学三轮讲练测核心热点总动员(新课标版)专题05概率(文)(原卷版)

2016年学易高考三轮复习系列:讲练测之核心热点 【全国通用版】【名师精讲指南篇】【高考真题再现】1.【2013全国I 文】从1234,,,中任取2个不同的数,则取出的2个数之差的绝对值为2的概率是( ). A. 12 B. 13 C. 14 D. 162.【2013全国II 文】从1,2,3,4,5中任意取出两个不同的数,其和为5的概率是_______.3.【2014新课标Ⅰ文】将2本不同的数学书和1本语文书在书架上随机排成一行,则2本数学书相邻的概率为 .4.【2014新课标Ⅱ文】甲、已两名运动员各自等可能地从红、白、蓝3种颜色的运动服中选择1种,则他们选择相同颜色运动服的概率为 .5.【2015全国I 文】如果3个正整数可作为一个直角三角形三条边的边长,则称这3个数为一组勾股数.从1,2,3,4,5中任取3个不同的数,则这3个数构成一组勾股数的概率为( ). A.310 B.15 C. 110 D. 120【热点深度剖析】 从近三年全国卷高考来看,若解答题中只考查统计知识,没有概率问题,一般会有一道概率客观题,难度一般不大,主要考查等可能事件的概率,古典概型,几何概型,互斥事件的概率.2013年、2014年、2015年全国高考文科卷考查的都是古典概型,属于基础题;预测2016年高考考查重点是古典概型及互斥事件,不过提醒考生注意的是几何概型在全国卷高考中还没有出现过,但仍有考查的可能,不能忽视.【重点知识整合】1.随机事件A 的概率0()1P A ≤≤,其中当()1P A =时称为必然事件;当()0P A =时称为不可能事件P(A)=0;2.等可能事件的概率(古典概率): P(A)=nm .理解这里m 、n的意义. 3.互斥事件:(A 、B 互斥,即事件A 、B 不可能同时发生).计算公式:P (A +B )=P (A )+P (B ).4.对立事件:(A 、B 对立,即事件A 、B 不可能同时发生,但A 、B 中必然有一个发生).计算公式是:P(A)+ P(B)=1;P(A)=1-P(A);5.独立事件:(事件A、B的发生相互独立,互不影响)P(A•B)=P(A) • P(B) .提醒:(1)如果事件A、B独立,那么事件A与B、A与B及事件A与B也都是独立事件;(2)如果事件A、B相互独立,那么事件A、B至少有一个不发生的概率是1-P(A⋅B)=1-P(A)P(B);(3)如果事件A、B相互独立,那么事件A、B至少有一个发生的概率是1-P(A⋅B)=1-P(A)P(B).6.古典概型:满足以下两个条件的随机试验的概率模型称为古典概型:(1)有限性:在一次试验中,可能出现的不同的基本事件只有有限个;(2)等可能性:每个基本事件的发生都是等可能的.古典概型中事件的概率计算如果一次试验的等可能基本事件共有n个,随机事件A包含了其中m个等可能基本事件,那么事件A发生的概率为P(A)=m n.7.几何概型区域A为区域Ω的一个子区域,如果每个事件发生的概率只与构成该事件的区域A的几何度量(长度、面积或体积)成正比,而与A的位置和形状无关,则称这样的概率模型为几何概率模型.几何概型的概率P(A)=μAμΩ,其中μA表示构成事件A的区域长度(面积或体积).μΩ表示试验的全部结果所构成区域的长度(面积或体积).【应试技巧点拨】1.事件A的概率的计算方法,关键要分清基本事件总数n与事件A包含的基本事件数m.因此必须解决以下三个方面的问题:第一,本试验是否是等可能的;第二,本试验的基本事件数有多少个;第三,事件A是什么?它包含的基本事件有多少.回答好这三个方面的问题,解题才不会出错.2.几何概型的两个特点:一是无限性,即在一次试验中,基本事件的个数可以是无限的;二是等可能性,即每一个基本事件发生的可能性是均等的.因此,用几何概型求解的概率问题和古典概型的思路是相同的,同属于“比例解法”.即随机事件A的概率可以用“事件A包含的基本事件所占的图形面积(体积、长度)”与“试验的基本事件所占的总面积(总体积、长度)”之比来表示.3.求复杂事件的概率,要正确分析复杂事件的构成,看复杂事件能转化为几个彼此互斥的事件的和事件还是能转化为几个相互独立事件同时发生的积事件,然后用概率公式求解.一个复杂事件若正面情况比较多,反面情况较少,则一般利用对立事件进行求解.对于“至少”“至多”等问题往往用这种方法求解【考场经验分享】1古典概型求解时应注意:对于古典概型的概率计算问题,常见错误是基本事件数列举重复或遗漏,导致计数错误,避免此类错误发生的最有效方法是按照某种标准进行列举.2.几何概型求解时应注意:(1)对于一个具体问题能否应用几何概型概率公式计算事件的概率,关键在于能否将问题几何化;也可根据实际问题的具体情况,选取合适的参数,建立适当的坐标系,在此基础上,将试验的每一个结果一一对应于该坐标系中的一个点,使得全体结果构成一个可度量区域.(2)由概率的几何定义可知,在几何概型中,“等可能”一词应理解为对应于每个试验结果的点落入某区域内的可能性大小仅与该区域的几何度量成正比,而与该区域的位置与形状无关.2.如果题设条件比较复杂,且备选答案数字较小,靠考虑穷举法求解,如果试题难度较大并和其他知识联系到一起,感觉不易求解,一般不要花费过多的时间,可通过排除法模糊确定,一般可考虑去掉数字最大与最小的答案【名题精选练兵篇】1.【2016福建福州4月质量检查】在2015年全国青运会火炬传递活动中,有编号为1,2,3,4,5的5名火炬手.若从中任选2人,则选出的火炬手的编号相连的概率为()A.310B.58C.710D.252.【2016云南第一次统一检测】在长为3m的线段AB上任取一点P,则点P与线段AB两端点的距离都大于1m的概率等于()A.12B.14C.23D.133.【2016广西钦州期末】AB是半径为1的圆的直径,在AB上的任意一点M,过点M垂直于AB的弦,则弦长大于的概率是()A.B.C.D.4.【2016甘肃张掖市一诊】如图所示,以边长为1的正方形ABCD的一边AB为直径在其内部作一半圆.若在正方形中任取一点P,则点P恰好取自半圆部分的概率为()A.2πB.12C.4πD.8π5.【2016湖北七校联考】一只蜜蜂在一个半径为3的球体内自由飞行,若蜜蜂在飞行过程中始终保持与球的表面的距离均大于1,称其为“安全飞行”,则蜜蜂“安全飞行”的概率为 .6.【2016甘肃河西五市第一次联考】若不等式222x y +≤所表示的平面区域为M ,不等式组0026x y x y y x -≥⎧⎪+≥⎨⎪≥-⎩表示的平面区域为N ,现随机向区域N 内抛一粒豆子,则豆子落在区域M 内的概率为( ) A.8πB.9πC.24πD.6π7.【2016新疆乌鲁木齐二诊,文13】盒子里装有大小质量完全相同的2个红球,3个黑球,从盒中随机抽取两球,颜色不同的概率为 .8.【2016新疆乌鲁木齐一次诊,文15】函数2()23,[4,4]f x x x x =--∈-,任取一点0[4,4]x ∈-,则0()0f x ≤的概率为 .9. 【2015届福建省龙岩市高三教学质量检查】(某工厂对一批新产品的长度(单位:mm )进行检测,如图是检测结果的频率分布直方图,据此估计这批产品的中位数为( )A .20B .25C .22.5D .22.7510. 【2015届甘肃省兰州市高三诊断考试】从数字1、2、3中任取两个不同的数字构成一个两位数,则这个两位数大于30的概率为A .16B .13C .12D .2311. 【2015届江西省吉安市第一中学高三上学期第二次阶段考试】( 在一个袋子中装有分别标注数字1,2,3,4,5的五个小球,这些小球除标注数字外完全相同,现从中随机取2个小球,则取出的小球标注的数字之和为3或6的概率是( ) A.112 B.110 C.15 D.31012. 【2015届云南省弥勒市高三年级模拟测试一】现采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率:先由计算器给出0到9之间取整数值的随机数,指定0,1表示没有击中目标,2,3,4,5,6,7,8,9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组随机数:7527 0293 7140 9857 0347 4373 8636 6947 1417 46980371 6233 2616 8045 6011 3661 9597 7424 7610 4281根据以上数据估计该射击运动员射击4次至少击中3次的概率为( )A .0.852B .0.8192C .0.8D .0.7513. 【2015届甘肃省部分普通高中高三第一次联考】已知集合⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎩⎪⎨⎧≥-≥+≤-+00042),(y x y x y x y x 表示的平面区域为Ω,若在区域Ω内任取一点P (x,y ),则点P 的坐标满足不等式x 2+y 2≤2的概率为( )(A ) 163π (B )16π (C )32π (D )323π 14. 在区间[0,2]π上任取一个数x ,则使得2sin 1x >的概率为( ) A.16 B.14 C.13 D.2315. 若,{1,0,1,2}a b ∈-,则函数2()2f x ax x b =++有零点的概率为( )A .1316B .78C .34D .5816. 从区间()3,3-中任取两个整数a ,b ,设点(),a b 在圆223x y +=内的概率为1P ,从区间()3,3-中任取两个实数a ,b ,直线30ax by ++=和圆223x y +=相离的概率为2P ,则( )A .12P >PB .12P <PC .12P =PD .1P 和2P 的大小关系无法确定17.【2015届湖北省襄阳市第五中学高三第一学期11月质检】如图所示的茎叶图表示甲、乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩不低于乙的平均成绩的概率为________.18.【2015届上海市高境一中高三期末】若将一颗质地均匀的骰子,先后抛掷两次,出现向上的点数分别为a 、b ,设复数z a bi =+,则使复数2z 为纯虚数的概率是【名师原创测试篇】1. 某中学有男教职工200人,女教职工180人,现用分层抽样法从全体教职工中抽取19人参加座谈会,则男教职工应抽取的人数为___________.2. 已知实数[]0,9x ∈,执行如下图所示的程序框图,则输出的x 不大于55的概率为( )A.35B.25C.23D.13 3. 实数m 是[]0,6上的随机数,则关于x 的方程240x mx -+=有实根的概率是________.4. 在区间[1,1]-内随机取两个数分别记为,a b ,则使得函数22()21f x x ax b =+-+有零点的概率为 ( ) A .1-8πB .1-4πC .1- 2πD .1-34π 5.已知{}3,2,1,1,2,3,---∈b a 且b a ≠,则复数bi a z +=对应点在第二象限的概率为 .(用最简分数表示。
2016年高考数学三轮讲练测核心热点总动员(新课标版) 专题20 以椭圆和抛物线为背景的解析几何大题 含解析

【名师精讲指南篇】 【高考真题再现】1.【2013⋅新课标全国】已知圆M :(x +1)2+y 2=1,圆N :(x -1)2+y 2=9,动圆P 与圆M 外切并与圆N 内切,圆心P 的轨迹为曲线 C (Ⅰ)求C 的方程;(Ⅱ)l 是与圆P ,圆M 都相切的一条直线,l 与曲线C 交于A ,B 两点,当圆P 的半径最长时,求|AB|.若直线l 不垂直于x 轴,设l 与x 轴的交点为Q ,则1QP RQMr =,解得(4,0)Q -,故直线l :(4)y k x =+;有l 与圆M1=,解得4k =±;当4k =时,直线y =,联立直线与椭圆的方程解得187AB =;同理,当k =时,187AB =. 2. 【2014高考全国1理】已知点A (0,2),椭圆E:22221(0)x y a b a b +=>>的离心率为2;F是椭圆E 的右焦点,直线AFO 为坐标原点 (I )求E 的方程;(II )设过点A 的动直线l 与E 相交于P,Q 两点.当OPQ ∆的面积最大时,求l 的直线方程.【解析】(I )设右焦点(c,0)F,由条件知,23c =c =又2c a =,所以2a =,222b ac =-1=.故椭圆E 的方程为2214x y +=.3.【2015全国I 理20】在直角坐标系xOy 中,曲线2:4x C y =与直线():0l y kx a a =+> 交于M ,N 两点.(1)当0k =时,分别求C 在点M 和N 处的切线方程;(2)y 轴上是否存在点P ,使得当k 变动时,总有OPM OPN ∠=∠?说明理由.解析 (1)由题意知,0k =时,联立24y a x y =⎧⎪⎨=⎪⎩,解得()M a,()N a -.又2xy '=,在点M处M k =y a x -=-0y a --=, 在点N处,N k =y a x -=+0y a ++=.0y a --=0y a ++=. (2)存在符合题意的点,证明如下:设点P ()0,b 为符合题意的点,()11,M x y ,()22,N x y ,直线PM ,PN 的斜率分别为1k ,2k .联立方程24y kx a x y =+⎧⎪⎨=⎪⎩,得2440x kx a --=,故124x x k +=,124x x a =-, 从而121212y b y b k k x x --+=+=()()1212122kx x a b x x x x +-+=()k a b a +. 当b a =-时,有120k k +=,则直线PM 与直线PN 的倾斜角互补, 故OPM OPN ∠=∠,所以点()0,P a -符合题意.4.【2015全国II 理20】已知椭圆()222:90C x y m m +=>,直线l 不过原点O 且不平行于坐标轴,l 与C 有两个交点,A B ,线段AB 的中点为M . (1)证明:直线OM 的斜率与l 的斜率的乘积为定值; (2) 若l 过点,3m m ⎛⎫⎪⎝⎭,延长线段OM 与C 交于点P ,四边形OAPB 能否平行四边行?若能,求此时l 的斜率,若不能,说明理由.(2)不妨设四边形OAPB 能为平行四边形. 因为直线l 过点(,)3mm ,所以l 不过原点且与C 有两个交点的充要条件是0k >,且3k ≠. 由(1)得OM 的方程为9y x k =-.设点P 的横坐标为P x .由2229,9,y x kx y m ⎧=-⎪⎨⎪+=⎩【热点深度剖析】1.圆锥曲线的解答题新课标的要求理科一般以椭圆或抛物线为背景,而文科一般以椭圆为背景进行综合考查,由于双曲线的弱化,故以双曲线为背景的解析几何解答题不在考虑.在2012年高考文理同一道题,以抛物线与圆结合进行考查,主要考查抛物线、圆的标准方程的求法以及直线与抛物线、圆的位置关系,突出解析几何的基本思想和方法的考查:如数形结合思想、坐标化方法等. 2013年高考文理同一道题,以椭圆与圆结合进行考查,主要考查椭圆的定义、弦长公式、直线的方程,考查学生的运算能力、化简能力以及数形结合的能力. 在2014年文科考查了圆的方程,理科高考试题考查了椭圆的标准方程及简单几何性质,弦长公式,函数的最值,直线的方程,基本不等式等,考查学生的运算能力、化简能力以及数形结合的能力.2015年考查了定点定植问题。
2016届高考数学三轮讲练测核心热点总动员(新课标版)专题01复数(原卷版)

2016年学易高考三轮复习系列:讲练测之核心热点 【全国通用版】【名师精讲指南篇】【高考真题再现】1. 【2013新课标全国】若复数z 满足 (3-4i)z =|4+3i |,则z 的虚部为 () A 、-4 B 、-45 C 、4 D 、452.【2013新课标全国】212(1)i i +=-( )(A )112i -- (B )112i -+(C )112i + (D )112i - 3. 【2014全国1高考理】=-+23)1()1(i i ( ) A. i +1 B. i -1 C. i +-1 D. i --14. 【2014高考全国1卷文】设i iz ++=11,则=||z ( ) A. 21 B. 22 C. 23 D. 2 5.【2015全国卷1】设复数z 满足1i 1z z+=-,则z =()A .1BCD .26.【2015全国卷2】若a 为实数,且()()2i 2i 4i a a +-=-,则a =().A.1-B. 0C.1D. 2【热点深度剖析】从近三年的高考试题来看,复数的基本概念、复数相等的充要条件以及复数的代数运算是高考的热点,每套高考试卷都有一个小题,并且一般在前三题的位置上,主要考查对复数概念的理解以及复数的加减乘除四则运算. 2013年考查了复数的除法运算、复数的模、复数的概念,2014年考查了复数的除法运算.205年考查了复数的模及复数相等,近三年全国卷中共轭复数及复数的几何含义还没有考查,故预测2016年高考仍将以复数的基本概念以及复数的代数运算为主要考点,其中复数的除法运算及共轭复数是最可能出现的命题角度!【重点知识整合】1.基本概念:⑴a bi c di a c +=+⇔=且(,,,)c d a b c d R =∈;⑵复数是实数的条件:①0(,)z a bi R b a b R =+∈⇔=∈;②z R z z ∈⇔=;③20z R z ∈⇔≥.(3)复数是纯虚数的条件: ①z a bi =+是纯虚数0a ⇔=且0(,)b a b R ≠∈; ②z 是纯虚数0(0)z z z ⇔+=≠;③z 是纯虚数20z ⇔<.2.复数运算公式:设1z a bi =+,2(,,,)z c di a b c d R =+∈,12()()z z a c b d i ±=±+±,12()()()()z z a bi c di ac bd ad bc i =++=-++,1222222(0)z ac bd bc ad i z z c d c d +-=+≠++. 3.几个重要的结论: ⑴2222121212||||2(||||)z z z z z z ++-=+;⑵22||||z z z z ⋅==;⑶若z 为虚数,则22||z z ≠.4.常用计算结论:⑴2(1)2i i ±=±;⑵11ii i +-=,11i i i -+=-;⑶1230()n n n n i i i i n N ++++++=∈;⑷1||11z z zz z =⇔=⇔=;12ω=-+,212ωω=--=,31ω=,210ωω++=. 【应试技巧点拨】 1.解决复数概念问题的方法及注意事项:(1)复数的分类及对应点的位置问题都可以转化为复数的实部与虚部应该满足的条件问题,只需把复数化为代数形式,列出实部和虚部满足的方程(不等式)组即可.(2)解题时一定要先看复数是否为a bi +(,a b R ∈)的形式,以确定实部和虚部.2.复数是实数的条件:①0(,)z a bi R b a b R =+∈⇔=∈;②z R z z ∈⇔=;③20z R z ∈⇔≥.3.复数是纯虚数的条件: ①z a bi =+是纯虚数0a ⇔=且0(,)b a b R ≠∈; ②z 是纯虚数0(0)z z z ⇔+=≠;③z 是纯虚数20z ⇔<.4. 对复数几何意义的理解及应用(1)复数z 、复平面上的点z 及向量OZ 相互联系,即z a bi =+ (,a b R ∈)(),Z a b ⇔⇔ OZ ;(2)由于复数、点、向量之间建立了一一对应的关系,因此可把复数、向量与解析几何联系在一起,解题时可运用数形结合的方法,使问题的解决更加直观.5. 复数的四则运算类似于多项式的四则运算,此时含有虚数单位i 的看作一类同类项,不含i 的看作另一类同类项,分别合并即可,但要注意把i 的幂写成最简单的形式,在运算过程中,要熟悉i 的特点及熟练应用运算技巧.除法的关键是分子分母同乘以分母的共轭复数,解题中要注意把i 的幂写成最简形式.【考场经验分享】1.目标要求:新课标对复数的要求较低,根据课标的要求,本部分内容的考查不会太难,一般出一道选择题(或填空题)考查基本概念与运算,与概率等结合的题目可能会出,但都比较容易解决.所以本热点必须得满分.2.注意问题:复数这个热点一般出现在试卷的前三道题目中,难度较低,但是解题时需加小心,千万不能因为不重视而导致失分.例如复数的实部和虚部要分清楚,例如1i -的实部是-1,虚部为1,运算时要注意21i =-.3.经验分享:学会必要的检验,例如将求解的复数代入验证,若复数为纯虚数时,实部等于0,要验证虚部不为0,利用复数相等进行复核等方法,确保万无一失.【名题精选练兵篇】1. 【2016安徽合肥市第二次质检】若i 是虚数单位,复数2i z i =+的虚部为( ) A .15- B .25- C .15 D .252.【2016云南第一次统一检测】已知i 为虚数单位,则复数1i i+=( ) A .1i + B .1i - C .12i + D .12i - 3.【2016新疆乌鲁木齐二诊】复数534i i+-对应的点在复平面的( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限4.【2016重庆3月模拟】若纯虚数z 满足(1)1i z ai -=+,则实数a =( )A .0B .-1或1C .-1D .15.【2016湖北七校2月联考】已知i b i i a +=+2,),(R b a ∈其中i 为虚数单位,则=-b a ( ) A .3- B .2-C .1-D .1 6.【2016哈尔滨师大附中 东北师大附中 辽宁省实验中学第一次联合模拟】若复数z 满足i zi +=1,则z 的共轭复数是( )A .i --1B .i +1C .i +-1D .i -17.【2016河北省衡水二调】已知复数z ,“0z z +=”是“z 为纯虚数”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件8.【2016吉林长春质量监测(二)】复数1z ,2z 在复平面内对应的点关于直线y x =对称,且132z i =+,则2z =()A. 32i -B. 23i -C. 32i --D. 23i +9.【2016辽宁省沈阳质量监测(一)】复数21z i=-(i 为虚数单位)在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限10.【2015安徽省安庆五校联盟高三下学期3月联考】若复数i b i a 3-+(R b a ∈,)对应的点在虚轴上,则ab 的值是A .15-B .3C .3-D .1511. 【2015届吉林省长春市十一高中高三上学期阶段性考试】若复数i a a z )1(12-+-=(i 为虚数单位)是纯虚数,则实数=a ( )A .1±B .1-C .0D .112. 【2015届云南省弥勒市高三年级模拟测试一】复数1z i =-,则1z z+对应的点所在的象限为( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限13. 【2015届高三下学期第二次统考(新课标2卷)】已知,,x y R i ∈为虚数单位,且(2)1x i y i --=-+,则(1)x y i ++的值为( )A .4B .4-C .44i +D .2i 14. 【2015届山东省德州市高三上学期2月期末统考】设1z i =-,则22z z+=( ) A .-1-i B .-l+I C .1-i D .l+i15. 【2015届江西省景德镇高三第二质检】设z 是复数,()a z 表示满足1n z =的最小正整数n ,则对虚数单位i ,()a i =( )A.2 B .4 C.6 D.816. 在复平面内,复数201532i iZ +-=对应的点位于 ( ) (A)第四象限 (B)第三象限 (C)第二象限 (D)第一象限17. 如图,在复平面内,复数1z 和2z 对应的点分别是A 和B ,则21z z 等于(A )12i + (B )2i + (C )12i -- (D )2i -+18. 【2015安徽省安庆五校联盟高三下学期3月联考】已知i 是虚数单位,若()32i z i -⋅=,则z =( )(A )1255i - (B )2155i -+ (C )2155i -- (D )1255i + 【名师原创测试篇】 1. 复数2534z i =-在复平面内对应的点的坐标是 ( )A .()3,4--B .()3,4-C .()3,4-D .()3,42. 复若()1,2,3i z i =是复数,且集合{}11|(1)22A z z i i =+=-,{}2224|0z B z =+=,3z A B ∈,则3z = ( )A .2i ±B .2±C .2i -D .2-3. 若复数()()1a a i z a R i+-=∈在平面直角坐标系中所对应的点在第三象限,则( ) A.01a << B.10a -<< C.0a < D 1a > 4. 若复数11a i z i i-=--+是实数(其中,a R i ∈是虚数单位),则a = ( )A .1-B .0C .1D .25. 已知复数121234,,z i z t i z z =+=+⋅且是实数,则实数t 等于( )A.34 B.43 C.43-D。
专题22 参数方程和极坐标方程-2016年高考数学三轮讲练测核心热点总动员(江苏版)(原卷版)

2016年学易高考三轮复习系列:讲练测之核心热点 【江苏版】热点二十二 参数方程和极坐标方程【名师精讲指南篇】【高考真题再现】例1 【2013江苏高考】在平面直角坐标系xoy 中,直线l 的参数方程为12x t y t =+⎧⎨=⎩,(t 为参数),曲线C 的参数方程为22tan 2tan x y θθ⎧=⎨=⎩,(θ为参数),试求直线l 和曲线C 的普通方程,并求它们的公共点的坐标. 例2 【2014江苏高考】[选修4-4:坐标系与参数方程]在平面直角坐标系xoy 中,已知直线l的参数方程12x y ⎧=⎪⎪⎨⎪=+⎪⎩(t 为参数),直线l 与抛物线24y x =相交于AB 两点,求线段AB 的长.例3 【2015江苏高考】已知圆C的极坐标方程为2sin()404πρθ+--=,求圆C 的半径.【热点深度剖析】1. 江苏高考中,本知识点考查的主要内容有:极坐标与参数方程的基本概念、公式的理解与掌握.特别是极坐标方程与直角坐标方程、参数方程与普通方程之间的互化,以及参数方程的简单应用是本知识点考查的重中之重.2. 重点掌握将极坐标方程化为直角坐标方程、参数方程化为普通方程,体会参数思想和数形结合思想的应用,明确解析几何的精髓.3.预计16年极坐标方程与直角坐标方程、参数方程与普通方程之间的互化是考查重点内容. 【最新考纲解读】【重点知识整合】//,(0),(0)x x y y λλμμ⎧=>⎪⎨=>⎪⎩(1)极坐标系的概念:平面内取一个定点O ,叫做极点,自极点O 引一条射线Ox ,叫做极轴;再选定一个长度单位,一个角度单位(通常取弧度)及其正方向 (通常取逆时针方向),这样就建立了一个极坐标系.设M 是平面内一点,极点O 与点M 的距离|OM|叫做点M 的极径,记为ρ;以极轴Ox 为始边,射线OM 为终边的角xOM ∠叫做点M 的极角,记为θ.有序数对),(θρ叫做点M 的极坐标,记作),(θρM .(2)直角坐标与极坐标的互化:把直角坐标系的原点作为极点,x 轴的正半轴作为极轴,并在两种坐标系中取相同的长度单位.设M 是坐标平面内任意一点,它的直角坐标是),(y x ,极坐标是),(θρ,则极坐标与直角坐标的互化公式如表:(3) 常见曲线的极坐标方程:3(1)参数方程的概念:一般地,在平面直角坐标系中,如果曲线上任意一点的坐标,x y 都是某个变数t 的函数()()x f t y g t =⎧⎨=⎩①,并且对于t 的每一个允许值,由方程组①所确定的点(,)M x y 都在这条曲线上,那么方程①就叫做这条曲线的参数方程,联系变数,x y 的变数t 叫做参变数,简称参数,相对于参数方程而言,直接给出点的坐标间关系的方程叫做普通方程.(2)参数方程和普通方程的互化:曲线的参数方程和普通方程是曲线方程的不同形式,一般地可以通过消去参数而从参数方程得到普通方程.在参数方程与普通方程的互化中,必须使,x y 的取值范围保持一致. (3)常见曲线的参数方程:①圆22200()()x x y y r -+-=的参数方程为⎩⎨⎧+=+=θθsin cos 00r y y r x x (θ为参数);②椭圆12222=+b y a x 的参数方程为⎩⎨⎧==θθsin cos b y a x (θ为参数);③双曲线12222=-by a x 的参数方程⎩⎨⎧==θθtan sec b y a x (θ为参数); ④抛物线22y px =参数方程222x pt y pt⎧=⎨=⎩ (t 为参数);⑤过定点),(00y x P 、倾斜角为α的直线的参数方程⎩⎨⎧+=+=ααsin cos 00t y y t x x (t 为参数)。
2016年高考数学三轮讲练测核心热点总动员 专题23 参数方程和极坐标方程(选修2)

【名师精讲指南篇】 【高考真题再现】1.【2013⋅新课标全国】已知曲线1C 的参数方程为45cos ,55sin x t y t=+⎧⎨=+⎩(t 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线2C 的极坐标方程为2sin ρθ=. (Ⅰ)把1C 的参数方程化为极坐标方程;(Ⅱ)求1C 与2C 交点的极坐标(0,02ρθπ≥≤<).【解析】(1)先利用参数方程得到C 1的一般方程,进而得到极坐标方程;(2)联立求出交点坐标,进而求出极坐标.2.【2014高考全国1第23题】已知曲线221:149x y C +=,直线l :2,22,x t y t =+⎧⎨=-⎩(t 为参数).(I )写出曲线C 的参数方程,直线l 的普通方程;(II )过曲线C 上任意一点P 作与l 夹角为30︒的直线,交l 于点A ,PA 的最大值与最小值.【解析】(I )曲线C 的参数方程为2cos ,3sin ,x y θθ=⎧⎨=⎩(θ为参数).直线l 的普通方程为260x y +-=.(II )曲线C 上任意一点(2cos ,3sin )P θθ到l 的距离为3sin 6d θθ=+-.则)6sin 30d PA θα==+-.其中α为锐角,且4tan 3α=.当sin()1θα+=-时,PA 取到最大值,最大值为5.当sin()1θα+=时,PA 取到最小值,最小值为5. 3.【2015全国Ⅱ】在直线坐标系xOy 中,曲线1C :{c ,os sin ,x t y t αα==(t 为参数,0t ≠)其中0πα剟.在以O 为极点,x 轴正半轴为极轴的极坐标系中,曲线2C :2sin ρθ=,3C :ρθ=.(1)求2C 与3C 交点的直角坐标;(2)若1C 与2C 相交于点A ,1C 与3C 相交于点B ,求AB 的最大值.4.【2015全国Ⅰ】在直角坐标系xOy 中,直线1C :2x =-,圆2C :()()22121x y -+-=,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系. (1)求12,C C 的极坐标方程. (2)若直线3C 的极坐标方程为()π4θρ=∈R ,设2C 与3C 的交点为,M N ,求2C MN △的面积.解析(1)由1C :2x =-,可得极坐标方程为cos 2ρθ=-, 由2C :2221441x x y y -++-+=,得极坐标方程为22cos 4sin 40ρρθρθ--+=.【热点深度剖析】2013年高考主要考查圆的参数方程,参数方程与普通方程的互化,普通方程与极坐标方程互化,极坐标方程与普通方程互化,主要考查学生的转化与化归能力. 2014年高考考查了椭圆和直线的参数方程,点到直线的距离公式,解直角三角形.2015年考查了直角坐标与极坐标方程的互化、圆的几何性质、三角函数的最值 从三年试题来看,高考对这部分要求不是太高,要求会参数方程与普通方程,极坐标方程与普通方程互化,主要考查学生的转化与化归能力,利用参数方程研究轨迹问题. 预测2016年高考仍然考查圆,直线,椭圆的参数方程与普通方程,极坐标方程与普通方程互化,重点是直线和圆的参数方程,极坐标方程,考查学生的转化与化归能力. 【重点知识整合】1.极坐标和直角坐标的互化公式若点M 的极坐标为(ρ,θ),直角坐标为(x ,y ),则⎩⎪⎨⎪⎧x =ρcos θy =ρsin θ⎩⎪⎨⎪⎧ρ2=x 2+y 2tan θ=y x ,x ≠0.求曲线的极坐标方程f (ρ,θ)=0的步骤与求曲线的直角坐标方程步骤完全相同.特别注意的是求极坐标方程时,常常要解一个三角形. (4)极坐标方程ρ=ρ(θ)表示的平面图形的对称性: 若ρ(-θ)=ρ(θ),则图形关于极轴对称;若ρ(π-θ)=ρ(θ),则图形关于射线θ=π2对称;若ρ(π+θ)=ρ(θ),则图形关于极点对称. 2.特殊的常见曲线(包括直线)的极坐标方程①圆心在极轴上点C (a,0),过极点的圆方程ρ=2a cos θ. ②圆心在极点、半径为r 的圆的极坐标方程ρ=r .③圆心在⎝⎛⎭⎪⎫a ,π2处且过极点的圆方程为ρ=2a sin θ(0≤θ≤π).④过极点倾角为α的直线的极坐标方程为: θ=α或θ=π+α.⑤过A (a,0)(a >0)与极轴垂直的直线ρcos θ=a .⑥过A ⎝⎛⎭⎪⎫a ,π2(a >0)与极轴平行的直线ρsin θ=a . 3.参数方程的概念在平面直角坐标系中,如果曲线上任意一点的坐标x 、y 都是某个变数t 的函数⎩⎪⎨⎪⎧x =f (t )y =g (t )(*),并且对于t 的每一个允许值,由方程组(*)所确定的点M (x ,y )都在这条曲线上,而这条曲线上任一点M (x ,y )都可以通过(*)式得到,则方程组(*)就叫做这条曲线的参数方程,变数t 叫做参数这时,参数t 的几何意义是:以直线l 上点M (x 0,y 0)为起点,任意一点N (x ,y )为终点的有向线段的数量为MN 且|t |=|MN |. 4.圆的参数方程(1)圆心在原点、半径为r 的圆的参数方程为⎩⎪⎨⎪⎧x =r cos θy =r sin θ(θ为参数);(2)圆心为C (a ,b ),半径为r 的圆的参数方程为⎩⎪⎨⎪⎧x =a +r cos θy =b +r sin θ(θ为参数).5.参数方程和普通方程的互化(1)化参数方程为普通方程:消去参数.常用的消参方法有代入消去法、加减消去法、恒等式(三角的或代数的)消去法.(2)化普通方程为参数方程:引入参数,即选定合适的参数t ,先确定一个关系x =f (t )〔或y=φ(t )〕,再代入普通方程F (x ,y )=0,求得另一关系y =φ(t )〔或x =f (t )〕. 【应试技巧点拨】 1.极坐标与直角坐标的互化(1)极坐标与直角坐标互化的前提条件:①极点与原点重合;②极轴与x 轴正向重合;③取相同的单位长度.(2)直角坐标方程化为极坐标方程比较容易,只要运用公式cos x ρθ=及sin y ρθ=直接代入并化简即可;而极坐标方程化为直角坐标方程则相对困难一些,解此类问题常通过变形,构造形如cos ρθ,sin ρθ,2ρ的形式,进行整体代换. 2.求曲线的极坐标方程求曲线的极坐标方程的步骤:(1)建立适当的极坐标系,设(),P ρθ是曲线上任意一点;(2)由曲线上的点所适合的条件,列出曲线上任意一点的极径ρ和极角θ之间的关系式;(3)将列出的关系式进行整理、化简,得出曲线的极坐标方程. 3.参数方程与普通方程的互化在求出曲线的参数方程后,通常利用消参法得出普通方程.一般地,消参数经常采用的是代入法和三角公式法,但将曲线的参数方程化为普通方程,不只是把其中的参数消去,还要注意x ,y 的取值范围在消参前后应该是一致的,也就是说,要使得参数方程与普通方程等价,即它们二者要表示同一曲线. 4.直线的参数方程及应用根据直线的参数方程的标准式中t 的几何意义,有如下常用结论:(1)直线与圆锥曲线相交,交点对应的参数分别为12,t t ,则弦长12l t t =-; (2)定点0M 是弦12M M 的中点⇒120t t +=; (3)设弦12M M 中点为M ,则点M 对应的参数值122M t t t += (由此可求12M M 及中点坐标). 5.圆与圆锥曲线的参数方程及应用解决与圆、圆锥曲线的参数方程有关的综合问题时,要注意普通方程与参数方程的互化公式,主要是通过互化解决与圆、圆锥曲线上动点有关的问题,如最值、范围等. 【考场经验分享】1.在极坐标系中,如无特别说明时,0ρ≥,R θ∈;点的极坐标不惟一,若规定0ρ≥,02θπ≤<,则极坐标系中的点与点的极坐标形成一一对应关系(极点除外);曲线上的点的极坐标不一定满足曲线的极坐标方程,但曲线上一点P 的无数个极坐标中必有一个适合曲线的极坐标方程.2.极坐标方程1θθ=表示一条射线并非直线,只有当允许0ρ<时,1θθ=才表示一条直线.3.只有在a 2+b 2=1时,直线⎩⎪⎨⎪⎧x =x 0+at y =y 0+bt(t 为参数)中的参数t 才表示由M (x 0,y 0)指向N (x ,y )的有向线段的数量,而在a 2+b 2≠1时,|MN |=a 2+b 2·t .4.消参后应将原参数的取值范围相应地转化为变量x (或y )的取值范围. 【名题精选练兵篇】1.【2016广西桂林市、北海市、崇左市3月联合调研】已知曲线C 的极坐标方程是4cos ρθ=.以极点为平面直角坐标系的原点,极轴为x 轴的正半轴,建立平面直角坐标系,直线l 的参数方程是1cos sin x t y t αα=+⎧⎨=⎩(t 为参数).(1)将曲线C 的极坐标方程化为直角坐标方程;(2)若直线l 与曲线C 相交于A 、B 两点,且AB =求直线的倾斜角α的值.2.【2016吉林长春质量监测(二)】在直角坐标系x O y 中,曲线1C 的参数方程为2cos sin x t y t αα=+⎧⎪⎨=⎪⎩(t 是参数),以原点O 为极点,x 轴正半轴为极轴建立极坐标系,曲线2C 的极坐标方程为8cos()3πρθ=-.(1)求曲线2C 的直角坐标方程,并指出其表示何种曲线;(2)若曲线1C 与曲线2C 交于A ,B 两点,求||AB 的最大值和最小值. 【解析】(1) 对于曲线2C 有8cos()3πρθ=-,即24cos sin ρρθθ=+,因此曲线2C的直角坐标方程为2240x y x +--=,其表示一个圆.(2) 联立曲线1C 与曲线2C的方程可得:2130t t α-⋅-=,12||||AB t t=-===因此||AB的最小值为最大值为8.3.【2016年安徽省“江南十校”联考】在平面直角坐标系xOy中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知在极坐标系中,),(),,(33233ππBA,圆C的方程为θρcos2=(Ⅰ)求在平面直角坐标系xOy中圆C的标准..方程;(Ⅱ)已知P为圆C上的任意一点,求ABP∆面积的最大值.4.【2016河南新乡许昌平顶山二调】在直角坐标系xOy中,曲线C1的参数方程为22xαα⎧⎨⎩=+cosy=2sin(α为参数),曲线C2的参数方程为22xββ⎧⎨⎩=cosy=2+sin(β为参数),以O为极点,x轴的正半轴为极轴建立极坐标系.(Ⅰ)求曲线C1和曲线C2的极坐标方程;(Ⅱ)已知射线l 1:θ=α(π02α<<)将射线l 1顺时针旋转π6得到射线l 2:θ=α-π6, 且射线l 1与曲线C 1交于O 、P 两点,射线l 2与曲线C 2交于O 、Q 两点,求|OP |·|OQ |的 最大值.【解析】(1)曲线1C 的直角坐标方程为22(2)4x y -+=,所以1C 极坐标方程为4cos ρθ= 曲线2C 的直角坐标方程为22(2)4x y +-=,所以2C 极坐标方程为4sin ρθ= (2)设点P 极点坐标1(,)ρα,即14cos ρα= 点Q 极坐标为2π(,())6ρα- 即2π4sin()6ρα=-则12π||||4cos 4sin()6OP OQ ρραα⋅==⋅-=116cos cos )2ααα⋅- π8sin(2)46α=--π(0,)2α∈,ππ5π2(,)666α∴-∈-,当ππ2,62α-=即π3α=时,||||OP OQ ⋅取最大值4.5.【2016福建4月质检】在直角坐标系xOy 中,曲线C 的参数方程为,sin cos 3⎩⎨⎧==ααy x (其中α为参数),以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系中,直线l 的极坐标方程为24sin =⎪⎭⎫⎝⎛-πθρ.(Ⅰ)求C 的普通方程和直线l 的倾斜角;(Ⅱ)设点P (0,2),l 和C 交于A ,B 两点,求PB PA +.即,222x y ⎧=⎪⎪⎨⎪=+⎪⎩(t 为参数),代入2219x y +=并化简,得25270t ++=.(245271080∆=-⨯⨯=>.设,A B 两点对应的参数分别为12,t t ,则1212270,05t t t t +=<=>, 所以120,0,t t <<所以()1212PA PB t t t t +=+=-+= 解法二:(Ⅰ)同解法一. (Ⅱ)直线l 的普通方程为2y x =+.由222,99y x x y =+⎧⎨+=⎩消去y 得21036270x x ++=, 于是236410272160∆=-⨯⨯=>.设1122(,),(,)A x y B x y ,则12180,5x x +=-<1227010x x =>,所以120,0x x <<.故12120|0||PA PB x x x x +=--=+=6.【2106辽宁省沈阳质量监测(一)】在以直角坐标原点O 为极点,x 的非负半轴为极轴的极坐标系下,曲线1C 的方程是1ρ=,将1C 向上平移1个单位得到曲线2C . (Ⅰ)求曲线2C 的极坐标方程;(Ⅱ)若曲线1C 的切线交曲线2C 于不同两点,M N ,切点为T .求TM TN ⋅的取值范围.(Ⅱ)由题令00(,)T x y ,0(0,1]y ∈,切线MN 的倾斜角为θ,所以切线MN 的参数方程为:00cos sin x x t y y t θθ=+⎧⎨=+⎩(t 为参数). 联立2C 的直角坐标方程得,20002(cos sin sin )120t x y t y θθθ++-+-= ,即由直线参数方程中,t 的几何意义可知,012TM TN y ⋅=-,因为012[1,1)y -∈-所以TM TN ⋅[0,1]∈.此题也可根据图形的对称性推出答案,此种方法酌情给分.7.【2016年安庆二模】在平面直角坐标系中,以原点为极点,x 轴正半轴为极轴建立极坐标系,并在两坐标系中取相同的长度单位.已知曲线C 的极坐标方程为2cos ρθ=,直线l 的参数方程为1cos sin x t y t αα=-+⎧⎨=⎩(t 为参数,α为直线的倾斜角).(I )写出直线l 的普通方程和曲线C 的直角坐标方程; (II )若直线l 与曲线C 有唯一的公共点,求角α的大小. 【解析】(Ⅰ)当π2a =时,直线l 的普通方程为1x =-; 当π2a ≠时,直线l 的普通方程为(tan )(1)y x a =+. 由θρcos 2=,得θρρcos 22=,所以222x y x +=,即为曲线C 的直角坐标方程.(Ⅱ)把a t x cos 1+-=,sin y t a =代入222x y x +=,整理得24cos 30t t a -+=.由012cos 162=-=∆α,得23cos 4=a ,所以cos =a 或cos =a -,故直线l 倾斜角α为π6或5π6. 8.【2016甘肃兰州实战考试,理23】所以1212PA PB t t t t +=+=+=9. 【2015届陕西省宝鸡市九校高三联合检测】坐标系与参数方程在直角坐标系xOy 中,圆C 的参数方程1cos (sin x y ϕϕϕ=+⎧⎨=⎩为参数).以O 为极点,x 轴的非负半轴为极轴建立极坐标系.(Ⅰ)求圆C 的极坐标方程; (Ⅱ)射线:4OM πθ=与圆C 的交点为O 、P 两点,求P 点的极坐标.10. 【2015届河北省唐山市高三第一次模拟】已知椭圆C :22143x y +=,直线3:x l y t⎧=-⎪⎨=⎪⎩(t 为参数).(Ⅰ)写出椭圆C 的参数方程及直线l 的普通方程;(Ⅱ)设(1,0)A ,若椭圆C 上的点P 满足到点A 的距离与其到直线l 的距离相等,求点P 的坐标.【解析】(Ⅰ)C:2cos x y θθ=⎧⎪⎨=⎪⎩(θ为参数),l :xy +9=0.(Ⅱ)设(2cos ,)P θθ,则||2cos AP θ==-,P 到直线l 的距离|2cos 3sin 9|2cos 3sin 922d θθθθ-+-+==.由|AP|=d 得3sin θ-4cos θ=5,又sin 2θ+cos 2θ=1,得3sin 5θ=,4cos 5θ=-.故8(5P -. 11. 【2015届河北唐山市高三上学期期末考试】极坐标系的极点为直角坐标系xOy 的原点,极轴为x 轴的正半轴,两种坐标系中的长度单位相同. 已知曲线C 的极坐标方程为2(cos sin )ρθθ=+l 交y 轴于点(0,1)E .(1)求C 的直角坐标方程,l 的参数方程;(2)直线l 与曲线C 交于A 、B 两点,求||||EA EB +.【解析】(Ⅰ)由ρ=2(cos θ+sin θ),得ρ2=2(ρcos θ+ρsin θ),即x 2+y 2=2x +2y ,即(x -1) 2+(y -1) 2=2.直线l的参数方程为121x t y ⎧=⎪⎪⎨⎪=⎪⎩(t 为参数, t∈R)(Ⅱ)将121x t y ⎧=⎪⎪⎨⎪=+⎪⎩,代入(x -1) 2+(y -1) 2=2得t 2-t -1=0,解得,12t t ==,则 |EA|+|EB|=| t 1|+| t 2|=|t 1-t 2|.12.已知圆锥曲线2cos :x C y αα=⎧⎪⎨=⎪⎩(α为参数)和定点A ,1F 、2F 是此圆锥曲线的左、右焦点,以原点O 为极点,以x 轴的正半轴为极轴建立极坐标系. (1)求直线2AF 的直角坐标方程;(2)经过点1F 且与直线2AF 垂直的直线l 交此圆锥曲线于M 、N 两点,求11||||MF NF -的值.13 .已知曲线C 的极坐标方程为θθρ2sin cos 4=,以极点为坐标原点,极轴为x 轴正半轴建立平面直角坐标系,直线l 的参数方程为⎪⎪⎩⎪⎪⎨⎧+=-=t y tx 22122(t 为参数) (1)把曲线C 的极坐标方程化为直角坐标方程,把直线l 的参数方程化为普通方程; (2)求直线l 被曲线C 截得的线段AB 的长.14.已知曲线C 的极坐标方程是2sin ρθ=,直线l 的参数方程是32,545x t y t ⎧=-+⎪⎨⎪=⎩(t 为参数).(Ⅰ)将曲线C 的极坐标方程化为直角坐标方程;(Ⅱ)设直线l 与x 轴的交点是M ,N 是曲线C 上一动点,求MN 的最大值. 【解析】(Ⅰ)曲线C 的极坐标方程可化为22sin ρρθ=, 又222,cos ,sin x y x y ρρθρθ+===, 所以曲线C 的直角坐标方程为2220x y y +-=,(Ⅱ)将直线l 的参数方程化为直角坐标方程,得4(2)3y x =--,令0y =,得2x =,即M 点的坐标为(2,0). 又曲线C 为圆,圆C 的圆心坐标为(1,0),半径1r =,则MC =所以1MN MC r +=≤.15. 在直角坐标系中,以原点为极点,x 轴的正半轴为极轴建立极坐标系,已知曲线C :2sin 2cos (0)a a ρθθ=>,过点P (-2,-4)的直线l的参数方程为2242x y ⎧=-+⎪⎪⎨⎪=-+⎪⎩(t 为参数)l 与C 分别交于M ,N.(1)写出C 的平面直角坐标系方程和l 的普通方程; (2)若PM ,MN ,PN 成等比数列,求a 的值.【解析】(1)曲线C 的直角坐标方程为22(0)y ax a =>;直线l 的普通方程为20x y --=.(2)将直线1的参数方程与C的直角坐标方程联立,得22(48(4)0(*)t a a -+++=8(4)0a a ∆=+>.设点M ,N 分别对应参数t 1,t 2,恰为上述方程的根.则1PM t =,2PN t =,12MN t t =-.由题设得21212()t t t t -=,即2121212()4t t t t t t +-=.由(*)得122(4t t a +=+,128(4)0t t a =+>,则有2(4)5(4)0a a +-+=,得1a =,或4a =-.因为0a >,所以1a =. 16. 已知曲线C 1:4cos ,3sin ,x t y t =-+⎧⎨=+⎩ (t 为参数), C 2:8cos ,3sin ,x y θθ=⎧⎨=⎩(θ为参数).(1)分别求出曲线C 1,C 2的普通方程; (2)若C 1上的点P 对应的参数为2t π=,Q 为C 2上的动点,求PQ 中点M 到直线332,:2x t C y t=+⎧⎨=-+⎩ (t 为参数)距离的最小值及此时Q 点坐标.【名师原创测试篇】1.在直角坐标系x y O 中,以原点O 为极点,以x 轴正半轴为极轴,建立极坐标系,曲线1C 的极坐标方程为()sin cos 1ρθθ+=,曲线2C 的参数方程为2cos sin x y θθ=⎧⎨=⎩.()1求曲线1C 的直角坐标方程与曲线2C 的普通方程;()2试判断曲线1C 与2C 是否存在两个交点?若存在,求出两交点间的距离;若不存在,说明理由.【解析】 (1) 对于曲线1C :()sin cos 1ρθθ+=,得sin cos 1ρθρθ+=,故有1x y +=,对于曲线2C :2cos sin x y θθ=⎧⎨=⎩,消去参数得2214x y +=.(2) 显然曲线1C :1x y +=为直线,则其参数方程可写为21x y ⎧=⎪⎪⎨⎪=-⎪⎩t 为参数),与曲线2C :2214x y +=联立方程组得2580t -+=,可知(24581280∆=-⨯⨯=>,所以1C 与2C 存在两个交点,由12t t +=1285t t =,得21||d t t =-==. 2. 已知曲线C 的极坐标方程是2sin ρθ=,直线l 的参数方程是32,545x t y t ⎧=-+⎪⎨⎪=⎩(t 为参数).(Ⅰ)将曲线C 的极坐标方程化为直角坐标方程;(Ⅱ)设直线l 与x 轴的交点是M ,N 是曲线C 上一动点,求MN 的最大值.3. 已知曲线C 的参数方程: cos sin x a y b αα=⎧⎨=⎩(α为参数), 曲线C上的点(1,2M 对应的参数4πα=,以坐标原点O 为极点,以x 轴正半轴为极轴,建立极坐标系.(Ⅰ)求曲线C 的极坐标方程;(Ⅱ)已知直线l 过点)0,1(P ,且与曲线C 于B A ,两点,求PB PA ⋅的范围.【解析】(Ⅰ)将点(1,)2M 和4πθ=代入曲线C 的参数方程:cos sin x a y b αα=⎧⎨=⎩中得,1,222a =⎪=⎩,所以a =1b =,所以曲线C的参数方程为sin x y αα⎧=⎪⎨=⎪⎩,化为普通方程为2212x y +=,所以曲线C 的极坐标方程2222cos 2sin 2ρθρθ+=. (Ⅱ)设直线参数方程为直线l 的参数方程:1cos (sin x t t y t θθ=+⎧⎨=⎩为参数),代入到曲线C 方程里,得到01cos 2)sin 1(22=-++θθt t ,21t t PB PA =,由韦达定理可得到θ2sin 11+=⋅PB PA ,因为]1,0[sin 2∈θ,所以211sin PA PB θ⋅=+1[,1]2∈ 4. 已知极坐标系的极点在直角坐标系的原点,极轴与x 轴的正半轴重合.曲线C 的极坐标方程为22312sin ρθ=+,直线l的参数方程为1x y t ⎧=⎪⎨=+⎪⎩(t 为参数,t ∈R ).试在曲线C 上求一点M ,使它到直线l 的距离最大.5. 以平面直角坐标系的原点为极点,x 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,已知直线l 的参数方程是13x t y t =+⎧⎨=-⎩(t 为参数),圆C 的极坐标方程是θρcos 4=.(Ⅰ)求直线l 的方程和圆C 的直角坐标方程; (Ⅱ)求直线l 被圆C 截得的弦长.6. 在直角坐标系中,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为2sin 2cos ρθθ=+,曲线D 的参数方程为11cos 2211sin 2x t y t⎧=-+⎪⎪⎨⎪=+⎪⎩(t 为参数).(Ⅰ)把C 的极坐标方程化为直角坐标方程; (Ⅱ)判定曲线C 与曲线D 间的位置关系.【解析】(Ⅰ)由2sin 2cos ρθθ=+得22cos 2sin ρρθρθ=+,将222x y ρ=+,cos ,sin x y ρθρθ==代入得22220x y x y +--=,即为曲线C 的普通方程. (Ⅱ)由(1)知曲线C 的直角坐标方程为:22220x y x y +--=,即22(1)(1)2x y -+-=,是圆心C (1,1),半径1r D 的参数方程化为普通方程为2211()(1)24x y ++-=,曲线D是圆心D (12-,1),半径2r =1212<||CD =3212,∴两圆相交.。
2016年全国卷新课标参数方程和极坐标专题复习和预测

参数方程和极坐标系答题模板参数方程和极坐标在近几年全国卷中年年必考,其难易程度属于低中档,主要有两个小问,第一问基本考察参数方程、极坐标与普通方程的相互转化。
第二问是利用解析几何的性质解决问题,但这几年也考察极坐标极径和直线参数方程中t 的几何意义。
知识要点必备:一、参数方程(一)曲线的参数方程的定义:在取定的坐标系中,如果曲线上任意一点的坐标x 、y 都是某个变数t的函数,即⎩⎨⎧==)()(t f y t f x 并且对于t 每一个允许值,由方程组所确定的点M (x ,y )都在这条曲线上,那么方程组就叫做这条曲线的参数方程,联系x 、y 之间关系的变数叫做参变数,简称参数.(二)常见曲线的参数方程如下:1.过定点(x 0,y 0),倾角为α的直线:ααsin cos 00t y y t x x +=+=(t 为参数)其中参数t 是以定点P (x 0,y 0)为起点,对应于t 点M (x ,y )为终点的有向线段PM 的数量,又称为点P 与点M 间的有向距离.根据t 的几何意义,有以下结论.○1.设A 、B 是直线上任意两点,它们对应的参数分别为t A 和t B ,则AB =A B t t -=B A A B t t t t ⋅--4)(2.○2.线段AB 的中点所对应的参数值等于2BA t t +. 2.中心在(x 0,y 0),半径等于r 的圆:θθsin cos 00r y y r x x +=+=(θ为参数)3.中心在原点,焦点在x 轴(或y 轴)上的椭圆:θθsin cos b y a x ==(θ为参数)(或θθsin cos a y b x ==)中心在点(x0,y0)焦点在平行于x 轴的直线上的椭圆的参数方程为参数)ααα(.sin ,cos 00⎩⎨⎧+=+=b y y a x x4.中心在原点,焦点在x 轴(或y 轴)上的双曲线:θθtg sec b y a x ==(θ为参数)(或 θθec a y b x s tg ==)5.顶点在原点,焦点在x 轴正半轴上的抛物线:pty pt x 222==(t 为参数,p >0)直线的参数方程和参数的几何意义二、极坐标系1、定义:在平面内取一个定点O ,叫做极点,引一条射线Ox ,叫做极轴,再选一个长度单位和角度的正方向(通常取逆时针方向)。
2016年高考数学三轮讲练测核心热点总动员(新课标版) 专题01 复数 Word版含解析

2016年高考三轮复习系列:讲练测之核心热点 【全国通用版】【名师精讲指南篇】 【高考真题再现】1. 【2013新课标全国】若复数z 满足 (3-4i)z =|4+3i |,则z 的虚部为 ( ) A 、-4(B )-45(C )4(D )45【答案】D ;2.【2013新课标全国】212(1)ii +=-( )(A )112i --(B )112i -+(C )112i +(D )112i - 【答案】B 【解析】2121221(1)222i i i ii i ++-===---. 3. 【2014全国1高考理】=-+23)1()1(i i ( ) A. i +1 B. i -1 C. i +-1 D. i --1 【答案】D【解析】由已知得=-+23)1()1(i i 22(1)(1)2(1)1(1)2i i i i i i i+++==----.4. 【2014高考全国1卷文】设i iz ++=11,则=||z ( ) A.21B. 22C. 23D. 2【答案】B【解析】根据复数运算法则可得:111111(1)(1)222i i z i i i i i i i --=+=+=+=-++-,由模的运算可得:||2z ==. 5.【2015全国卷1】设复数z 满足1i 1zz+=-,则z =()A .1BC .2 【答案】A 【解析】由1i 1z z +=-得()()()()1i 1i 1i i 1i 1i 1i z -+--+===++-,所以1z =.故选A . 6.【2015全国卷2】若a 为实数,且()()2i 2i 4i a a +-=-,则a =(). A.1- B. 0 C.1 D. 2 【答案】B【热点深度剖析】从近三年的高考试题来看,复数的基本概念、复数相等的充要条件以及复数的代数运算是高考的热点,每套高考试卷都有一个小题,并且一般在前三题的位置上,主要考查对复数概念的理解以及复数的加减乘除四则运算. 2013年考查了复数的除法运算、复数的模、复数的概念,2014年考查了复数的除法运算.205年考查了复数的模及复数相等,近三年全国卷中共轭复数及复数的几何含义还没有考查,故预测2016年高考仍将以复数的基本概念以及复数的代数运算为主要考点,其中复数的除法运算及共轭复数是最可能出现的命题角度! 【重点知识整合】 1.基本概念:⑴a bi c di a c +=+⇔=且(,,,)c d a b c d R =∈;⑵复数是实数的条件:①0(,)z a bi R b a b R =+∈⇔=∈;②z R z z ∈⇔=;③20z R z ∈⇔≥.(3)复数是纯虚数的条件: ①z a bi =+是纯虚数0a ⇔=且0(,)b a b R ≠∈; ②z 是纯虚数0(0)z z z ⇔+=≠;③z 是纯虚数20z ⇔<.2.复数运算公式:设1z a bi =+,2(,,,)z c di a b c d R =+∈,12()()z z a c b d i ±=±+±,12()()()()z z a bi c di ac bd ad bc i =++=-++,1222222(0)z ac bd bc ad i z z c d c d +-=+≠++. 3.几个重要的结论:⑴2222121212||||2(||||)z z z z z z ++-=+;⑵22||||z z z z ⋅==;⑶若z 为虚数,则22||z z ≠. 4.常用计算结论: ⑴2(1)2i i ±=±;⑵11i ii +-=,11i ii -+=-;⑶1230()n n n n i i i i n N ++++++=∈;⑷1||11zz zz z =⇔=⇔=;122i ω=-+,2122i ωω=--=,31ω=,210ωω++=. 【应试技巧点拨】1.解决复数概念问题的方法及注意事项:(1)复数的分类及对应点的位置问题都可以转化为复数的实部与虚部应该满足的条件问题,只需把复数化为代数形式,列出实部和虚部满足的方程(不等式)组即可.(2)解题时一定要先看复数是否为a bi +(,a b R ∈)的形式,以确定实部和虚部.2.复数是实数的条件:①0(,)z a bi R b a b R =+∈⇔=∈;②z R z z ∈⇔=;③20z R z ∈⇔≥.3.复数是纯虚数的条件: ①z a bi =+是纯虚数0a ⇔=且0(,)b a b R ≠∈; ②z 是纯虚数0(0)z z z ⇔+=≠;③z 是纯虚数20z ⇔<.4. 对复数几何意义的理解及应用(1)复数z 、复平面上的点z 及向量OZ 相互联系,即z a bi =+ (,a b R ∈)(),Z a b ⇔⇔OZ ;(2)由于复数、点、向量之间建立了一一对应的关系,因此可把复数、向量与解析几何联系在一起,解题时可运用数形结合的方法,使问题的解决更加直观.5. 复数的四则运算类似于多项式的四则运算,此时含有虚数单位i 的看作一类同类项,不含i 的看作另一类同类项,分别合并即可,但要注意把i 的幂写成最简单的形式,在运算过程中,要熟悉i 的特点及熟练应用运算技巧.除法的关键是分子分母同乘以分母的共轭复数,解题中要注意把i 的幂写成最简形式. 【考场经验分享】1.目标要求:新课标对复数的要求较低,根据课标的要求,本部分内容的考查不会太难,一般出一道选择题(或填空题)考查基本概念与运算,与概率等结合的题目可能会出,但都比较容易解决.所以本热点必须得满分.2.注意问题:复数这个热点一般出现在试卷的前三道题目中,难度较低,但是解题时需加小心,千万不能因为不重视而导致失分.例如复数的实部和虚部要分清楚,例如1i -的实部是-1,虚部为1,运算时要注意21i =-.3.经验分享:学会必要的检验,例如将求解的复数代入验证,若复数为纯虚数时,实部等于0,要验证虚部不为0,利用复数相等进行复核等方法,确保万无一失.【名题精选练兵篇】1. 【2016安徽合肥市第二次质检】若i 是虚数单位,复数2iz i=+的虚部为( ) A .15- B .25- C .15 D .25【答案】D 【解析】2iz i =+()212=555i i i -=+,故选D.2.【2016云南第一次统一检测】已知i 为虚数单位,则复数1ii+=( ) A .1i + B .1i - C .12i + D .12i-【答案】B【解析】i i ii-=+-=+111;故选B . 3.【2016新疆乌鲁木齐二诊】复数534ii+-对应的点在复平面的( )A .第一象限B .第二象限C .第三象限D .第四象限 【答案】A 【解析】因为i ii i i i i i +=+=+-++=-+1171717)4)(4()4)(35(435,所以对应的点为()1,1;故选A . 4.【2016重庆3月模拟】若纯虚数z 满足(1)1i z ai -=+,则实数a =( ) A .0 B .-1或1 C .-1 D .1 【答案】D5.【2016湖北七校2月联考】已知i b iia +=+2,),(Rb a ∈其中i 为虚数单位,则=-b a ( ) A .3- B .2-C .1-D .1【答案】A【解析】因为i b ai i ia +=-=+22,所以⎩⎨⎧=-=12a b ,即⎩⎨⎧-==12a b ,所以3-=-b a ;故选A . 6.【2016哈尔滨师大附中 东北师大附中 辽宁省实验中学第一次联合模拟】若复数z 满足i zi +=1,则z 的共轭复数是( )A .i --1B .i +1C .i +-1D .i -1 【答案】B【解析】11,1izi i z i i+=+∴==-,所以z 的共轭复数是1i + 7.【2016河北省衡水二调】已知复数z ,“0z z +=”是“z 为纯虚数”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 【答案】B8.【2016吉林长春质量监测(二)】复数1z ,2z 在复平面内对应的点关于直线y x =对称,且132z i =+,则2z =()A. 32i -B. 23i -C. 32i --D. 23i +【答案】D【解析】复数1z 在复平面内关于直线y x =对称的点表示的复数223z i =+,故选D. 9.【2016辽宁省沈阳质量监测(一)】复数21z i=-(i 为虚数单位)在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限 【答案】A 【解析】211z i i==+-,在复平面内复数z 对应点的坐标为(1,1),在第一象限.10.【2015安徽省安庆五校联盟高三下学期3月联考】若复数ib ia 3-+(Rb a ∈,)对应的点在虚轴上,则ab 的值是A .15-B .3C .3-D .15 【答案】B 【解析】因为2()(3)3(3)3(3)(3)9a i a ib i ab a b ib i b i b i b +++-++==--++对应点在虚轴上,所以3ab =,故选B .11. 【2015届吉林省长春市十一高中高三上学期阶段性考试】若复数i a a z )1(12-+-=(i 为虚数单位)是纯虚数,则实数=a ( )A .1±B .1-C .0D .1 【答案】B【解析】复数i a a z )1(12-+-=是纯虚数,则要求⎩⎨⎧≠-=-01012a a ,则1-=a .12. 【2015届云南省弥勒市高三年级模拟测试一】复数1z i =-,则1z z+对应的点所在的象限为( )A .第一象限B .第二象限C .第三象限D .第四象限 【答案】D13. 【2015届高三下学期第二次统考(新课标2卷)】已知,,x y R i ∈为虚数单位,且(2)1x i y i --=-+,则(1)x y i ++的值为( )A .4B .4-C .44i +D .2i 【答案】B【解析】由(2)1x i y i --=-+,可得21311x x y y -==⎧⎧⇒⎨⎨-=-=⎩⎩ ,∴4x y +=,∴()414i +=- ,故选B14. 【2015届山东省德州市高三上学期2月期末统考】设1z i =-,则22z z+=( ) A .-1-i B .-l+I C .1-i D .l+i 【答案】C【解析】将z 代入,按照复数代数形式的运算法则,计算化简即可.2222(1i 2)121211(1i)(1i)z i i i i i i z ++=+-=+-=+-=---+()()()故选C . 15. 【2015届江西省景德镇高三第二质检】设z 是复数,()a z 表示满足1nz =的最小正整数n ,则对虚数单位i ,()a i =( )A.2 B .4 C.6 D.8 【答案】B【解析】根据复数的定义及运算法则,21i =-,3i i =-,41i =,所以()4a i =. 16. 在复平面内,复数201532i iZ +-=对应的点位于 ( ) (A)第四象限 (B)第三象限 (C)第二象限 (D)第一象限 【答案】A17. 如图,在复平面内,复数1z 和2z 对应的点分别是A 和B ,则21z z 等于(A )12i + (B )2i + (C )12i -- (D )2i -+【解析】由题意i z =1,i z -=22,故21z z i ii i i i 21)2(22--=-=-= 18. 【2015安徽省安庆五校联盟高三下学期3月联考】已知i 是虚数单位,若()32i z i -⋅=,则z =( ) (A )1255i - (B )2155i -+ (C )2155i -- (D )1255i + 【答案】A【解析】由()32i z i i -⋅==-得()()()22112222555i i i i z i i i i -⋅+--+====---⋅+.故选A. 【名师原创测试篇】 1. 复数2534z i=-在复平面内对应的点的坐标是 ( )A .()3,4--B .()3,4-C .()3,4-D .()3,4 【答案】D . 【解析】()253425343425i z i i +===+-,所以复数z 在复平面内对应的点的坐标是()3,4,故选D .2. 复若()1,2,3i z i =是复数,且集合{}11|(1)22A z z i i =+=-,{}2224|0z B z =+=,3z A B ∈,则3z = ( )A .2i ±B .2±C .2i -D .2-【答案】C.【解析】因为{}(){}211111122|(1)22|12|21i A z z i i z z i i z z i i -⎧⎫=+=-===-=-==-⎨⎬+⎩⎭,又()2240i ±+=,所以{}2|2B z i =±,所以{}2AB i =-,故3z =2i -,故选C.3. 若复数()()1a a iz a R i+-=∈在平面直角坐标系中所对应的点在第三象限,则( )A.01a <<B.10a -<<C.0a < D 1a >4. 若复数11a iz i i-=--+是实数(其中,a R i ∈是虚数单位),则a = ( )A .1-B .0C .1D .2【答案】C . 【解析】解法一:()()()()()111111*********a i i a a i a ia a z i i i i i i i ----+---⎛⎫=--=--=--=-+⋅ ⎪++-⎝⎭是实数,10,12a a -∴=∴=,故选C . 解法二:()()()()1121111i i a i a ia i z i i i i-+---+-=--==+++是实数,21,1a a ∴-=∴=,故选C .5. 已知复数121234,,z i z t i z z =+=+⋅且是实数,则实数t 等于( ) A.34 B.43 C.43- D.34- 【答案】A。
2016届高考数学三轮讲练测核心热点总动员(新课标版)专题09定积分的应用、二项式定理(理)(原卷版)

【名师精讲指南篇】【高考真题再现】1.【2013⋅新课标全国】设m 为正整数,(x +y )2m 展开式的二项式系数的最大值为a ,(x +y )2m +1展开式的二项式系数的最大值为b ,若13a =7b ,则m = ( ) A 、5B 、6C 、7D 、82.【2014全国1高考】()()8x y x y -+的展开式中27x y 的系数为________.(用数字填写答案) 3.【2015全国1】()52x x y ++的展开式中,52x y 的系数为().A .10B .20C .30D .604.【2015全国2】4()(1)a x x ++的展开式中x 的奇数次幂项的系数之和为32, 则a =__________. 【热点深度剖析】二项式定理,定积分属于理科内容,从近几年的高考试题来看,二项式定理考查的重点是二项式定理的通项公式、二项式系数及项的系数,以考查基本概念、基础知识为主,如系数和、求某项的系数、求常数项、求有理项、求所含参数的值或范围等,注意多项式展开式系数的确定是近几年高考的一个热点;二项式定理基本每年必考,难度不大,属于中档题和容易题,题型为选择题或填空题.定积分重点考查定积分的应用,利用定积分求值,求面积,题型为选择题或填空题. 2013年考查了二项式定理系数最大项,属于基础题, 2014年高考中考查了二项式定理,求二项式展开项的某项系数,展开项的某项系,2015年考察了多项式系数的确定,定积分近几年一直没有考查.预测2016年高考二项式定理仍以指定项系数的确定为主,也可能考查求参数的值;定积分考查的可能性增大,可能是利用定积分求值,或求曲边多边形面积,也可能与几何概型结合出题.【重点知识整合】 1.定积分的几何意义①当函数f(x)在区间[a,b ]上恒为正时,定积分⎠⎛ab f(x )dx 的几何意义是由直线x =a ,x =b (a ≠b ),y =0和曲线y =f (x )所围成的曲边梯形的面积(图1中阴影部分).②一般情况下,定积分⎠⎛ab f (x )dx 的几何意义是介于x 轴、曲线f(x)以及直线x =a 、x =b 之间的曲边梯形面积的代数和(图2中阴影所示),其中在x 轴上方的面积等于该区间上的积分值,在x 轴下方的面积等于该区间上积分值的相反数. (3)定积分的基本性质①⎠⎛a b kf (x )dx = k ⎠⎛ab f (x )dx (k 为常数)②⎠⎛a b [f 1(x )±f 2(x )]dx =⎠⎛a b f 1(x )dx ±⎠⎛ab f 2(x)dx③⎠⎛ab f (x )dx =⎠⎛ac f (x )dx +⎠⎛cb f (x )dx (其中a <c <b ).2.微积分基本定理如果f (x )是区间[a ,b ]上的连续函数,并且F ′(x )=f (x ),那么⎠⎛ab f (x )dx =F (b )-F (a ),这个结论叫做微积分基本定理,又叫做牛顿—莱布尼兹公式.为了方便,常把F (b )-F (a )记成F (x )|b a ,即⎠⎛abf (x )dx =F (x )|b a =F (b )-F (a ). 3.二项式定理的展开式011()n n n r n r rn nn n n n a b C a C a b C a b C b --+=+++++,其中组合数r n C 叫做第r +1项的二项式系数;展开式共有n +1项.注意:(1)项的系数与二项式系数是不同的两个概念,但当二项式的两个项的系数都为1时,系数就是二项式系数.如在()nax b +的展开式中,第r+1项的二项式系数为rn C ,第r+1项的系数为r n r r n C a b -;而1()n x x+的展开式中的系数就是二项式系数;(2)当n 的数值不大时往往借助杨辉三角直接写出各项的二项式系数;(3)审题时要注意区分所求的是项还是第几项?求的是系数还是二项式系数?(4)特例:1(1)1n r rn n n x C x C x x +=+++++4.二项式定理的通项二项展开式中第r +l 项1(0,1,2,r n r rr n T C a b r -+==,)n 称为二项展开式的通项,二项展开式通项的主要用途是求指定的项.主要用于求常数项、有理项和系数最大的项:求常数项、有理项和系数最大的项时,要根据通项公式讨论对r 的限制;求有理项时要注意到指数及项数的整数性.注意:()1通项公式是表示第1r +项,而不是第r 项.()2展开式中第1r +项的二项式系数r n C 与第1r +项的系数不同.()3通项公式中含有1,,,,r a b n r T +五个元素,只要知道其中的四个元素,就可以求出第五个元素.在有关二项式定理的问题中,常常遇到已知这五个元素中的若干个,求另外几个元素的问题,这类问题一般是利用通项公式,把问题归纳为解方程(或方程组).这里必须注意n 是正整数,r 是非负整数且r ≤n . 5.项的系数和二项式系数的性质(1)对称性:与首末两端“等距离”的两个二项式系数相等(m n m n nC C -=). (2)增减性与最大值: 当12n r +≤时,二项式系数C r n 的值逐渐增大,当12n r +≥时,C r n 的值逐渐减小,且在中间取得最大值.当n 为偶数时,中间一项(第2n+1项)的二项式系数2nn C 取得最大值.当n 为奇数时,中间两项(第21+n 和21+n +1项)的二项式系数1122n n n n C C -+=相等并同时取最大值.(3)各二项式系数和:∵1(1)1n r rn n n x C x C x x +=+++++,令1x =,则0122n rnn n n n nC C C C C =++++++ , 0213n n n n C C C C ++⋅⋅⋅=++⋅⋅⋅12n -=(4)用二项式定理进行近似运算,关键是恰当地舍取不影响精度的项,一般地:当α很小时,有()()211112nn n n ααα±≈±+-.【应试技巧点拨】1.二项定理问题的处理方法和技巧:⑴运用二项式定理一定要牢记通项1r n r rr n T C a b -+=,注意()n a b +与()nb a +虽然相同,但具体到它们展开式的某一项时是不同的,一定要注意顺序问题,另外二项展开式的二项式系数与该项的(字母)系数是两个不同的概念,前者只指r n C ,而后者是字母外的部分.前者只与n 和r 有关,恒为正,后者还与a ,b 有关,可正可负.⑵ 对于二项式系数问题,应注意以下几点:①求二项式所有项的系数和,可采用“特殊值取代法”,通常令字母变量的值为1;②关于组合恒等式的证明,常采用“构造法”——构造函数或构造同一问题的两种算法; ③证明不等式时,应注意运用放缩法.⑶ 求二项展开式中指定的项,通常是先根据已知条件求r ,再求1r T +,有时还需先求n ,再求r ,才能求出1r T +.⑷ 有些三项展开式问题可以变形为二项式问题加以解决;有时也可以通过组合解决,但要注意分类清楚,不重不漏.⑸ 对于二项式系数问题,首先要熟记二项式系数的性质,其次要掌握赋值法,赋值法是解决二项式系数问题的一个重要手段.⑹ 近似计算要首先观察精确度,然后选取展开式中若干项.⑺ 用二项式定理证明整除问题,一般将被除式变为有关除式的二项式的形式再展开,常采用“配凑法”“消去法”配合整除的有关知识来解决.多项式乘法的进位规则:在求系数过程中,尽量先化简,降底数的运算级别,尽量化成加减运算,在运算过程可以适当注意令值法的运用,例如求常数项,可令0x =.在二项式的展开式中,要注意项的系数和二项式系数的区别.2. 排列组合在二项展开式中的应用:()na b +展开式可以由次数、项数和系数来确定. (1)次数的确定:从n 个相同的a b +中各取一个(a 或b )乘起来,可以构成展开式中的一项,展开式中项的形式是p q ma b ,其中,,p q N p q n ∈+=.(2)项数的确定:满足条件,,p q N p q n ∈+=的(),p q 共1n +组.即将()na b +展开共2n项,合并同类项后共1n +项.(3)系数的确定:展开式中含p q a b (p q n +=)项的系数为p n C (即p 个a ,q 个b 的排列数)因此()na b +展开式中的通项是:1r n r rr n T C a b -+= (0,1,2,3,,r n =)()()011*nn n r n r rn nn n n n a b C a C a b C a b C b n N --+=+++++∈这种方法比数学归纳法推导二项式定理更具一般性和创造性,不仅可二项展开,也可三项展开,四项展开等.3. 求几个二项式积的展开式中某项的系数或特定项时,一般要根据这几个二项式的结构特征进行分类搭配,分类时一般以一个二项式逐项分类,分析其他二项式应满足的条件,然后再求解结果.4. 求展开式系数最大项:如求()nax b + (,a b R ∈)的展开式系数最大的项,一般是采用待定系数法,设展开式各项系数分别为1231,,,,n A A A A +,且第k 项系数最大,应用11k k k k A A A A -+≥⎧⎨≥⎩从而解出k 来,即得. 5.二项式应用问题(1)利用二项式定理解决整除问题时,关键是进行合理地变形构造二项式,应注意:要证明一个式子能被另一个式子整除,只要证明这个式子按二项式定理展开后的各项均能被另一个式子整除即可.(2)求余数问题时,应明确被除式()f x 与除式()g x (()0g x ≠),商式()q x 与余式的关系及余式的范围.(3)展开式中常数项、有理项的特征是通项中未知数的指数分别为零和整数.解决这类问题时,先要合并通项中同一字母的指数,再根据上述特征进行分析.(4)有关求二项展开式中的项、系数、参数值或取值范围等,一般要利用通项公式,运用方程思想进行求值,通过解不等式(组)求取值范围.6.二项式定理是一个恒等式,使用时有两种思路:一是利用恒等定理(两个多项式恒等,则对应项系数分别相等);二是赋值.二项式定理结合“恒等”与“赋值”两条思路可以使很多求二项展开式的系数的问题迎刃而解.赋值法是处理组合数问题、系数问题的最有效的经典方法,一般对任意A x ∈,某式子恒成立,则对A 中的特殊值,该式子一定成立,特殊值x 如何选取视具体情况决定,灵活性较强,一般取1,1,0-=x 居多.若2012()...,n n n ax b a a x a x a x +=++++则设()()=+n f x ax b .有:①0(0);a f = ②012...(1);n a a a a f ++++=③0123...(1)(1);n n a a a a a f -+-++-=- ④0246(1)(1)...;2f f a a a a +-++++=⑤1357(1)(1) (2)f f a a a a --++++=6. 定积分的应用及技巧:(1)对被积函数,要先化简,再求定积分.(2)求被积函数是分段函数的定积分,依据定积分的性质,分段求定积分再求和.(3)对含有绝对值符号的被积函数,要去掉绝对值符号才能求定积分.(4)应用定积分求曲边梯形的面积,解题的关键是利用两条曲线的交点确定积分区间以及结合图形确定被积函数.求解两条曲线围成的封闭图形的面积一般是用积分区间内上方曲线减去下方曲线对应的方程、或者直接作差之后求积分的绝对值,否则就会求出负值.[易错提示] 在使用定积分求两曲线围成的图形的面积时,要注意根据曲线的交点判断这个面积是怎样的定积分,既不要弄错积分的上下限,也不要弄错被积函数.用微积分基本定理求定积分时,要掌握积分与导数的互逆关系及求导公式的逆向形式. 7.求导运算与求原函数运算互为逆运算,求定积分的关键是找到被积函数的原函数,为避免出错,在求出原函数后可利用求导与积分互为逆运算的关系进行验证.8.定积分的应用主要有两个问题:一是能利用定积分求曲边梯形的面积;二是能利用定积分求变速直线运动的路程及变力做功问题,其中,应特别注意求定积分的运算与利用定积分计算曲边梯形面积的区别. 【考场经验分享】 一.二项式定理:1.区别“项的系数”与“二项式系数”,审题时要仔细.项的系数与,a b 有关,可正可负,二项式系数只与n 有关,恒为正.2.切实理解“常数项”“有理项”(字母指数为整数)“系数最大的项”等概念. 3.求展开式中的指定项,要把该项完整写出,不能仅仅说明是第几项. 4.赋值法求展开式中的系数和或部分系数和,常赋的值为0,±1. 5.在化简求值时,注意二项式定理的逆用.要用整体思想看待a 、b . 二.定积分1.求定积分的常用技巧:(1)求被积函数,要先化简,再求积分.(2)求被积函数为分段函数的定积分,依据定积分“对区间的可加性”,分段积分再求和. (3)对于含有绝对值符号的被积函数,要先去掉绝对值号才能积分.【名题精选练兵篇】1.【2016届湖南省高三六校联考】若231(2)(1)x x x++-的展开式中的常数项为a ,则20(31)ax dx -⎰的值为( )A .6B .20C .8D .24 2.【2016届湖北省襄阳市高三上学期期末】由曲线y=x 3与直线y=4x 所围成的平面图形的面积为( )A .4B .8C .12D .163.【2016届江西师大附中高三上学期期末】若()241cos 2x a dx xdx π-=⎰⎰,则a 等于( )A .1-B .1C .2D .44.【2016届黑龙江省大庆一中高三下学期开学考试】由曲线y =,直线2y x =-及y 轴所围成的图形的面积为( ) A .103 B .163C .4D .6 5.【2016届河北省邯郸一中高三下第一次模拟】6(2)x y -的展开式中,42x y 的系数为( ) A .15 B .-15 C .60 D .-606..【2016届河北省衡水中学高三下学期一模】已知等式()()()()432432123412341111x a x a x a x a x b x b x b x b ++++=++++++++,定义映射()()12341234:,,,,,,f a a a a b b b b →,则()4,3,2,1f =( )A .()1,2,3,4B .()0,3,4,0C . ()0,3,4,1--D .()1,0,2,2--7.【2016届宁夏六盘山高中高三第二次模拟】()522121x x ⎛⎫+- ⎪⎝⎭的展开式的常数项是( )A .3B .-2C .2D .-38.【2016届福建省漳州市高三下学期第二次模拟考试】已知101099221010....)12(x a x a x a x a a x +++++=-,求10932....a a a a ++++的值为( )(A )20- (B )0 (C )1 (D )20 9.【2016届河南省八市重点高中高三4月质检】已知53878710(3)(1)(1)(1)x x a x a x a x a +=+++++++,则7531753a a a a +++=( )A .-16B .-8C .8D .1610.【2016届江西师大附中、鹰潭一中高三下第一次联考】5)21(-+xx 展开式中常数项为( )A .252B .-252C .160D .-16011.【2016届甘肃省河西五市部分普通高中高三第一次联考】设k 是一个正整数,1+)k x k(的展开式中第四项的系数为116,记函数2y x =与y kx =的图象所围成的阴影部分为S ,任取[0,4]x ∈,[0,16]y ∈,则点(,)x y 恰好落在阴影区域S 内的概率是 ( )A .23 B .13 C .25 D . 1612. 【2015届河南省濮阳市高三上学期期末】如图,在正方形C OAB 内任取一点,取到函数y =的图象与x 轴正半轴之间(阴影部分)的点的概率等于( )A .12 B .23 C .34 D .4513. 【2015届山东省德州市高三上学期2月期末】若9290129(2)(1)(1)(1)x m a a x a x a x ++=+++++⋅⋅⋅++且229028139()()3a a a a a a ++⋅⋅⋅+-++⋅⋅⋅+=,则实数m 的值是_________.14. 5)11)(2(22-+xx的展开式的常数项是( ). A .2 B .3 C .-2 D .-315. 【宁夏银川九中高三年级期中试卷】函数2()2(,)f x x x m x m R =++∈的最小值为1-,则21()f x dx ⎰等于( ) A .2B .163C .6D .716. 【广东省佛山市第一中学2015届高三上学期期中】过点(1,1)A 作曲线2(0)y x x =≥的切线,设该切线与曲线及x 轴所围图形的面积为,S 则S = .【名师原创测试篇】1.61x⎛⎝的展开式中的常数项为( )A.135-B.130-C.130D.1352. 式子()7511x y y ⎛⎫++ ⎪⎝⎭的展开式中,2x y 的系数为 .3. 知20(sin cos )a x x dx π=+⎰,在64(1)(1y)ax ++的展开式中,2xy 项的系数为( )A .45B .72C .60D .1204.设函数61(2),0,()0.x x x f x x ⎧-<⎪=⎨⎪≥⎩则0x >时,[()]f f x 表达式中的展开式中的常数项为 .(用数字作答)5.在46)1()1(y x ++的展开式中,记nm y x 项的系数为f(m ,n ),则f(3,0)+f(2,1)+f(1,2)+f(0,3) = .6. 已知2201sin 22x a dx π⎛⎫=- ⎪⎝⎭⎰,则912ax ax ⎛⎫+ ⎪⎝⎭展开式中,x 的一次项系数为( ) A .6316- B .6316 C .638- D .638。
2016届高考数学三轮讲练测核心热点总动员(新课标版)专题20以椭圆和抛物线为背景的解析几何大题(原卷版)

【名师精讲指南篇】【高考真题再现】1.【2013⋅新课标全国】已知圆M :(x +1)2+y 2=1,圆N :(x -1)2+y 2=9,动圆P 与圆M 外切并与圆N 内切,圆心P 的轨迹为曲线 C (Ⅰ)求C 的方程;(Ⅱ)l 是与圆P ,圆M 都相切的一条直线,l 与曲线C 交于A ,B 两点,当圆P 的半径最长时,求|AB|.2. 【2014高考全国1理】已知点A (0,2),椭圆E:22221(0)x y a b a b +=>>;F是椭圆E 的右焦点,直线AF,O 为坐标原点 (I )求E 的方程;(II )设过点A 的动直线l 与E 相交于P ,Q 两点.当OPQ ∆的面积最大时,求l 的直线方程.3.【2015全国I 理20】在直角坐标系xOy 中,曲线2:4x C y =与直线():0l y kx a a =+> 交于M ,N 两点.(1)当0k =时,分别求C 在点M 和N 处的切线方程;(2)y 轴上是否存在点P ,使得当k 变动时,总有OPM OPN ∠=∠?说明理由. 4.【2015全国II 理20】已知椭圆()222:90C x y mm +=>,直线l 不过原点O 且不平行于坐标轴,l 与C 有两个交点,A B ,线段AB 的中点为M . (1)证明:直线OM 的斜率与l 的斜率的乘积为定值; (2) 若l 过点,3m m ⎛⎫⎪⎝⎭,延长线段OM 与C 交于点P ,四边形OAPB 能否平行四边行?若能,求此时l 的斜率,若不能,说明理由. 【热点深度剖析】1.圆锥曲线的解答题新课标的要求理科一般以椭圆或抛物线为背景,而文科一般以椭圆为背景进行综合考查,由于双曲线的弱化,故以双曲线为背景的解析几何解答题不在考虑.在2012年高考文理同一道题,以抛物线与圆结合进行考查,主要考查抛物线、圆的标准方程的求法以及直线与抛物线、圆的位置关系,突出解析几何的基本思想和方法的考查:如数形结合思想、坐标化方法等. 2013年高考文理同一道题,以椭圆与圆结合进行考查,主要考查椭圆的定义、弦长公式、直线的方程,考查学生的运算能力、化简能力以及数形结合的能力. 在2014年文科考查了圆的方程,理科高考试题考查了椭圆的标准方程及简单几何性质,弦长公式,函数的最值,直线的方程,基本不等式等,考查学生的运算能力、化简能力以及数形结合的能力.2015年考查了定点定植问题。
2016届高三数学理课标版(陕西专用)二轮专题能力训练23 坐标系与参数方程(4—4) 含解析

专题能力训练23坐标系与参数方程(选修4—4)能力突破训练1.(2015福建高考)在平面直角坐标系xOy中,圆C的参数方程为{x=1+3cost,y=-2+3sint(t为参数)。
在极坐标系(与平面直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴非负半轴为极轴)中,直线l的方程为√2ρsin(θ-π4)=m(m∈R)。
(1)求圆C的普通方程及直线l的直角坐标方程;(2)设圆心C到直线l的距离等于2,求m的值.2.已知动点P,Q都在曲线C:{x=2cost,y=2sint(t为参数)上,对应参数分别为t=α与t=2α(0〈α<2π),M为PQ的中点。
(1)求点M的轨迹的参数方程;(2)将点M到坐标原点的距离d表示为α的函数,并判断点M的轨迹是否过坐标原点。
3。
(2015河南商丘二模)已知极坐标系的极点在直角坐标系的原点处,极轴与x轴的正半轴重合,直线l的极坐标方程为ρsin(θ-π6)=12,曲线C的参数方程为{x=2+2cosα,y=2sinα(α为参数).(1)写出直线l的直角坐标方程;(2)求曲线C上的点到直线l的距离的最大值。
4。
已知曲线C:x24+y29=1,直线l:{x=2+t,y=2-2t(t为参数).(1)写出曲线C的参数方程,直线l的普通方程;(2)过曲线C上任意一点P作与l夹角为30°的直线,交l于点A,求|PA|的最大值与最小值。
5.在极坐标系中,曲线C:ρ=2a cos θ(a>0),l:ρcos(θ-π3)=32,C与l有且只有一个公共点。
(1)求a;(2)O为极点,A,B为C上的两点,且∠AOB=π3,求|OA|+|OB|的最大值。
6.(2015中原名校联盟模拟)在极坐标系中,圆C的方程为ρ=2a cos θ(a≠0),以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系,设直线l的参数方程为{x=3t+1,y=4t+3(t为参数).(1)求圆C的直角坐标方程和直线l的普通方程;(2)若直线l与圆C恒有公共点,求实数a的取值范围。
2016届高考数学三轮讲练测核心热点总动员(新课标版)专题12函数与方程(解析版)

【名师精讲指南篇】【高考真题再现】1.【2013⋅新课标全国】已知命题:p x R ∀∈,23x x <;命题:q x R ∃∈,321x x =-,则下列命题中为真命题的是( ) (A )p q ∧ (B )p q ⌝∧ (C )p q ∧⌝ (D )p q ⌝∧⌝【答案】B ;【解析】取1x =-,可知p 错,p ⌝为真命题;令32()1f x x x =+-,因为()f x 图像连续,且(0)(1)0f f <,故()f x 在区间(0,1)上有零点,即方程3210x x +-=有解,即32,1x R x x ∃∈=-,故q 为真命题;所以p q ⌝∧为真命题.2.【2014全国1高考文理】设函数)(),(x g x f 的定义域为R ,且)(x f 是奇函数,)(x g 是偶函数,则下列结论中正确的是( )A .)()(x g x f 是偶函数B .)(|)(|x g x f 是奇函数 C..|)(|)(x g x f 是奇函数 D .|)()(|x g x f 是奇函数 【答案】C3.【2014高考全国1卷文】设函数()113,1,,1,x e x f x x x -⎧<⎪=⎨⎪≥⎩则使得()2f x ≤成立的x 的取值范围是________. 【答案】(,8]-∞【解析】由于题中所给是一个分段函数,则当1x <时,由12x e -≤,可解得:1ln 2x ≤+,则此时:1x <;当1x ≥时,由132x ≤,可解得:328x ≤=,则此时:18x ≤≤,综合上述两种情况可得:(,8]x ∈-∞4.【2015全国II 文12】设函数()()21ln 11f x x x =+-+,则使得()()21f x f x >-成立的x 的取值范围是( ).A. 113,⎛⎫⎪⎝⎭B. ()113,,⎛⎫-∞+∞ ⎪⎝⎭UC.1133,⎛⎫- ⎪⎝⎭D. 1133,,⎛⎫⎛⎫-∞-+∞ ⎪ ⎪⎝⎭⎝⎭U【答案】A4.【2015全国II 理10】如图所示,长方形ABCD 的边2AB =,1BC =,O 是AB 的中点,点P 沿着边,BC CD 与DA 运动,BOP x ∠=.将动点P 到,A B 两点距离之和表示为x 的函数()f x ,则()f x 的图像大致为( ).xPODCBA2π3π4π2π4y O x2xO y π4π23π4π2xO y π4π23π4π2π3π4π2π4y O xA. B. C. D. 【答案】B【解析】由已知可得,当P 点在BC 边上运动时,即π04x 剟时, tan PA PB x +=+;当P 点在CD 边上运动时,即π3π44x 剎?,π2x ≠时,PA PB +=+;【热点深度剖析】从近几年的高考试题来看,图象的辨识与对称性以及利用图象研究函数的性质,方程,不等式的解是高考的热点,多以选择题、填空题的形式出现,属中低档题,主要考查基本初等函数的图象的应用以及数形结合思想.而函数的零点、方程根的问题也是高考的热点,题型既有选择题、填空题,又有解答题.客观题主要考查相应函数的图象与性质,主观题考查较为综合,在考查函数的零点方程根的基础上,又注重考查函数方程、转化与化归、分类讨论、数形结合的思想方法.在2013年高考中,与命题结合,考查函数根的存在性,属于基础题. 在2014年理科高考题,主要考查函数奇偶性,属于基础题,而文科除考查函数奇偶性,还考查了分段函数,解不等式,使得题目难度较低.2015年有函数图像识别题,函数性质综合应用题.从这三年高考题可以看出,函数的性质,不等式的解,函数与方程,函数零点是高考考查的热点,每年都要涉及,考查根的存在性定理的题较基础,而函数零点往往结合函数性质与函数图像,作为把关题存在,主要考查转化与化归思想和函数方程思想以及数形结合思想的应用,由于连续三年都没考查函数的零点,方程的根的问题,预测2016年高考很有可能以函数的零点、方程根的存在问题,将以识图、用图为主要考向,重点考查函数图象的性质以及方程、不等式与图象的综合问题. 【重点知识整合】 1.函数的奇偶性.(1)具有奇偶性的函数的定义域的特征:定义域必须关于原点对称!为此确定函数的奇偶性时,务必先判定函数定义域是否关于原点对称.(2)确定函数奇偶性的常用方法(若所给函数的解析式较为复杂,应先化简,再判断其奇偶性):①定义法;②利用函数奇偶性定义的等价形式:()()0f x f x ±-=或()1()f x f x -=±(()0f x ≠).③图像法:奇函数的图象关于原点对称;偶函数的图象关于y 轴对称. (3)函数奇偶性的性质:①奇函数在关于原点对称的区间上若有单调性,则其单调性完全相同;偶函数在关于原点对称的区间上若有单调性,则其单调性恰恰相反.②如果奇函数有反函数,那么其反函数一定还是奇函数. ③若()f x 为偶函数,则()()(||)f x f x f x -==. ④若奇函数()f x 定义域中含有0,则必有(0)0f =. 2. 函数的单调性 1.函数单调性的定义:(1)如果函数()x f 对区间D 内的任意21,x x ,当21x x <时都有()()21x f x f <,则()x f 在D 内是增函数;当21x x <时都有()()21x f x f >,则()x f 在D 内是减函数.(2)设函数()y f x =在某区间D 内可导,若()0f x '>,则()y f x =在D 内是增函数;若()0f x '<,则()y f x =在D 内是减函数.2.单调性的定义(1)的等价形式:设[]b a x x ,,21∈,那么()()()x f x x x f x f ⇔>--02121在[],a b 上是增函数; ()()()x f x x x f x f ⇔<--02121在[],a b 上是减函数; 3.证明或判断函数单调性的方法:(1)定义法:设元→作差→变形→判断符号→给出结论.其关键是作差变形,为了便于判断差的符号,通常将差变成因式连乘积、平方和等形式,再结合变量的范围,假设的两个变量的大小关系及不等式的性质作出判断;(2)复合函数单调性的判断方法:即“同增异减”法,即内层函数和外层函数的单调性相同,则复合函数为增函数;若相反,则复合函数为减函数.解决问题的关键是区分好内外层函数,掌握常用基本函数的单调性;(3)图象法:利用数形结合思想,画出函数的草图,直接得到函数的单调性; (4)导数法:利用导函数的正负来确定原函数的单调性,是最常用的方法. (5)利用常用结论判断:①奇函数在对称的单调区间内有相同的单调性,偶函数在对称的单调区间内有相反的单调性; ②互为反函数的两个函数具有相同的单调性;③在公共定义域内,增函数+)(x f 增函数)(x g 是增函数;减函数+)(x f 减函数)(x g 是减函数;增函数-)(x f 减函数)(x g 是增函数;减函数-)(x f 增函数)(x g 是减函数;③复合函数法:复合函数单调性的特点是同增异减,特别提醒:求单调区间时,勿忘定义域, 3. 函数的周期性.(1)类比“三角函数图像”得:①若()y f x =图像有两条对称轴,()x a x b a b ==≠,则()y f x =必是周期函数,且一周期为2||T a b =-;②若()y f x =图像有两个对称中心(,0),(,0)()A a B b a b ≠,则()y f x =是周期函数,且一周期为2||T a b =-;③如果函数()y f x =的图像有一个对称中心(,0)A a 和一条对称轴()x b a b =≠,则函数()y f x =必是周期函数,且一周期为4||T a b =-;(2)由周期函数的定义“函数()f x 满足()()x a f x f +=(0)a >,则()f x 是周期为a 的周期函数”得:函数()f x 满足()()x a f x f +=-,则()f x 是周期为2a 的周期函数. 4. 函数的对称性.①满足条件()()f x a f b x -=-的函数的图象关于直线2a bx +=对称. ②点(,)x y 关于y 轴的对称点为(,)x y -;函数()x f y =关于y 轴的对称曲线方程为()x f y -=;③点(,)x y 关于x 轴的对称点为(,)x y -;函数()x f y =关于x 轴的对称曲线方程为()x f y -=;④点(,)x y 关于原点的对称点为(,)x y --;函数()x f y =关于原点的对称曲线方程为()x f y --=;⑤点(,)x y 关于直线y x =的对称点为(,)y x ;曲线(,)0f x y =关于直线y x =的对称曲线的方程为(,)f y x 0=;点(,)x y 关于直线y x =-的对称点为(,)y x --;曲线(,)0f x y =关于直线y x =-的对称曲线的方程为(,)0f y x --=;⑥曲线(,)0f x y =关于点(,)a b 的对称曲线的方程为(2,2)0f a x b y --=; ⑦形如(0,)ax b y c ad bc cx d +=≠≠+的图像是双曲线,其两渐近线分别直线d x c=-(由分母为零确定)和直线a y c =(由分子、分母中x 的系数确定),对称中心是点(,)d a c c-;⑧|()|f x 的图象先保留()f x 原来在x 轴上方的图象,作出x 轴下方的图象关于x 轴的对称图形,然后擦去x 轴下方的图象得到;(||)f x 的图象先保留()f x 在y 轴右方的图象,擦去y 轴左方的图象,然后作出y 轴右方的图象关于y 轴的对称图形得到. 5. 常见的图象变换①函数()a x f y +=)0(>a 的图象是把函数()x f y =的图象沿x 轴向左平移a 个单位得到的.②函数()a x f y +=()0(<a 的图象是把函数()x f y =的图象沿x 轴向右平移a 个单位得到的.③函数()x f y =+a )0(>a 的图象是把函数()x f y =助图象沿y 轴向上平移a 个单位得到的;④函数()x f y =+a )0(<a 的图象是把函数()x f y =助图象沿y 轴向下平移a 个单位得到的;⑤函数()ax f y =)0(>a 的图象是把函数()x f y =的图象沿x 轴伸缩为原来的a1得到的. ⑥函数()x af y =)0(>a 的图象是把函数()x f y =的图象沿y 轴伸缩为原来的a 倍得到的. ⑦|()|f x 的图象先保留()f x 原来在x 轴上方的图象,作出x 轴下方的图象关于x 轴的对称图形,然后擦去x 轴下方的图象得到;(||)f x 的图象先保留()f x 在y 轴右方的图象,擦去y 轴左方的图象,然后作出y 轴右方的图象关于y 轴的对称图形得到. 特殊函数图象:(1)函数(0,)ax b cx dy c ad bc ++=≠≠:可由反比例函数(0)ky k x=≠图象平移、伸缩得到.图1示例.\①图象是双曲线,两渐近线分别直线d cx =-(由分母为零确定)和直线a cy =(由分子、分母中x的系数确定);②对称中心是点(,)d a c c-.(2)函数(0,0)by ax a b x=+>>:如图2.①图象类似“对号”,俗称对号函数.定义域}0|{≠x x ; ②函数的值域为),2[]2,(+∞⋃--∞ab ab ; ③函数为奇函数,图象关于原点对称;④增区间为(,)-∞+∞,减区间为[-.6.函数的零点(1)一般地,如果函数y =f (x )在区间[a,b]上的图象是连续不断的一条曲线,并且有f (a )·f (b )<0,那么函数y =f(x)在区间(a ,b )内有零点,即存在c ∈(a ,b ),使f (c )=0,这个c 也就是方程f(x)=0的根.我们称方程f(x)=0的实数根x 叫做函数y =f(x)(x ∈D )的零点.(2)函数y =f (x )的零点就是方程f(x)=0的实数根,也就是函数y =f (x )的图象与x 轴交点的横坐标,即方程f (x )=0有实数根⇔函数y =f (x )有零点⇔函数y =f (x )的图象与x 轴有交点.(3)函数F(x)=f(x)-g(x)的零点就是方程f(x)=g(x)的实数根,也就是函数y =f(x)的图象与函数y =g(x )的图象交点的横坐标.一般地,对于不能使用公式求根的方程f(x)=0,我们可以将它与函数y =f(x)联系起来,利用函数的图象、性质来求解. 【应试技巧点拨】1.研究函数的性质要特别注意定义域优先原则(1)具有奇偶性的函数定义域的特征:定义域关于原点对称.为此确定函数的奇偶性时,务必先判定函数定义域是否关于原点对称.(2)讨论函数单调性必须在其定义域内进行,因此要研究函数单调性必须先求函数的定义域,函数的单调区间是定义域的子集.(3)讨论函数的周期性,一般情况下定义域是无限集.所以判断函数是否为周期函数,要在整个定义域上观察函数的图象.如求函数sin y x =的周期,如果只观察y 轴一侧的图象得到周期为2π那就错了,因为函数图象关于y 轴对称,从整体看它不是周期函数.2. 函数的单调性(1)定义法和导数法的选择在解答题中,只能应用定义法或导数法证明函数的单调性.定义法作为基本方法,但是证明过程有时比较繁琐;而导数法显得操作性比较强,对函数求导后判断导函数的正负即可.因此导数法是我们证明函数单调性的首选方法. (2)函数)0,0(≠≠+=b a xbax y 单调性总结:①若0,0>>b a ,单调区间:增区间,⎛⎫-∞+∞ ⎪ ⎪⎝⎭,,减区间0⎡⎫⎛⎪ ⎢⎪ ⎣⎭⎝,; ②若0,0<<b a ,单调区间:减区间),[],(+∞--∞a b a b 和,增区间],0()0,[aba b 和-; ③若0,0<>b a ,由于0)(2>-='+x ba x bax ,单调性:增区间),0()0,(∞-∞和; ④若0,0><b a ,由于0)(2<-='+x ba xbax ,单调性:减区间),0()0,(+∞-∞和. 3.抽象函数的对称性和周期性(1)对于函数)(x f y =(R x ∈),若()()f a x f b x +=-恒成立,则函数)(x f 的对称轴是2ba x +=. (2)若已知定义域在R 上的函数的对称轴、对称中心,如何确定函数的周期?可类比“三角函数图象”得:①若()y f x =图象有两条对称轴,()x a x b a b ==≠,则()y f x =是周期函数,且周期为2||T a b =-;②若()y f x =图象有两个对称中心(,0),(,0)()A a B b a b ≠,则()y f x =是周期函数,且周期为2||T a b =-;③如果函数()y f x =的图象有一个对称中心(,0)A a 和一条对称轴()x b a b =≠,则函数()y f x =是周期函数,且周期为4||T a b =-.注意这里面提到的周期不一定是函数的最小正周期.这个知识点经常和函数的奇偶性联系到一起,已知函数为奇函数,意味着函数的图象关于原点对称;已知函数为偶函数,意味着函数的图象关于y 轴对称.然后再推到函数的周期.(3)若已知类似函数周期定义式的恒等式,如何确定函数的周期?由周期函数的定义,采用迭代法可得结论:①函数()f x 满足()()f a x f x +=-,则()f x 是周期为2a 的函数; ②若1()(0)()f x a a f x +=±≠恒成立,则2T a =; ③若()()f x a f x a +=-,则2T a =; ④1()()1()f x f x a f x -+=-+,则4T a =.4.如何利用函数的解析式判断函数的图象利用函数的解析式判断函数的图象,可从下面几个角度去考虑: (1)讨论函数的定义域及函数的奇偶性和单调性; (2)考虑是否可由基本初等函数的图象变换作出图象;(3)准确描出关键的点线(如图象与x 、y 轴的交点,极值点(顶点),对称轴,渐近线,等等). 5. 如何转换含有绝对值的函数对含有绝对值的函数,解题关键是如何处理绝对值,一般有两个思路:一是转化为分段函数:利用分类讨论思想,去掉绝对值,得到分段函数.二是利用基础函数变换:首先得到基础函数,然后利用y =f (x )→y =f (|x |)或y =f (x )→y =|f (x )|,得到含有绝对值函数的图象. 6.平移变换中注意的问题函数图象的平移变换,里面有很多细节,稍不注意就会出现差错.所以要从本质深入理解,才不至于模棱两可.(1)左右平移仅仅是相对x 而言的,即发生变化的只是x 本身,利用“左加右减”进行操作.如果x 的系数不是1,需要把系数提出来,再进行变换;(2)上下平移仅仅是相对y 而言的,即发生变化的只是y 本身,利用“上减下加”进行操作.但平时我们是对()y f x =中()f x 操作,满足“上加下减”; 7.函数图象的主要应用函数图象的主要应用非常广泛,常见的几个应用总结如下:(1)利用函数图象可判断函数的奇偶性,求函数的单调区间、对称轴、周期等函数的性质; (2)利用函数()f x 和()g x 图象的交点的个数,可判断方程()f x =()g x 根的个数; (3)利用函数()f x 和()g x 图象上下位置关系,可直观的得到不等式()f x ()g x >或()f x ()g x <的解集:当()f x 的图象在()g x 的图象的上方时,此时自变量x 的范围便是不等式()f x ()g x >的解集;当()f x 的图象在()g x 的图象的下方时,此时自变量x 的范围便是不等式()f x ()g x <的解集. 8.函数零点的求解与判断判断函数y =f (x )在某个区间上是否存在零点,常用以下方法:(1)解方程:当对应方程易解时,可通过解方程,看方程是否有根落在给定区间上;(2)利用函数零点的存在性定理进行判断;(3)通过画函数图象,观察图象与x 轴在给定区间上是否有交点来判断. 9.函数零点的综合应用函数零点的应用主要体现了函数与方程的思想,函数与方程虽然是两个不同的概念,但它们之间有着密切的联系,方程f (x )=0的解就是函数y =f (x )的图象与x 轴的交点的横坐标,函数y =f (x )也可以看作二元方程f (x )-y =0,然后通过方程进行研究.许多有关方程的问题可以用函数的方法解决,反之,许多函数问题也可以用方程的方法来解决,函数与方程的思想是中学数学的基本思想.1.函数零点的求解与判断判断函数y =f (x )在某个区间上是否存在零点,常用以下方法:(1)解方程:当对应方程易解时,可通过解方程,看方程是否有根落在给定区间上;(2)利用函数零点的存在性定理进行判断;(3)通过画函数图象,观察图象与x 轴在给定区间上是否有交点来判断. 2.函数零点的综合应用函数零点的应用主要体现了函数与方程的思想,函数与方程虽然是两个不同的概念,但它们之间有着密切的联系,方程()0f x =的解就是函数()y f x =的图象与x 轴的交点的横坐标,函数()y f x =也可以看作二元方程()0f x y -=,然后通过方程进行研究.许多有关方程的问题可以用函数的方法解决,反之,许多函数问题也可以用方程的方法来解决,函数与方程的思想是中学数学的基本思想. 【考场经验分享】1.判断函数的奇偶性,首先应该判断函数定义域是否关于原点对称.定义域关于原点对称是函数具有奇偶性的一个必要条件.2.判断函数f (x )是奇函数,必须对定义域内的每一个x ,均有f (-x )=-f (x ).而不能说存在x 0使f (-x 0)=-f (x 0).对于偶函数的判断以此类推.3.在解决函数性质有关的问题中,如果结合函数的性质画出函数的简图,根据简图进一步研究函数的性质,就可以把抽象问题变的直观形象、复杂问题变得简单明了,对问题的解决有很大的帮助.(1)一般的解题步骤:利用函数的周期性把大数变小或小数变大,然后利用函数的奇偶性调整正负号,最后利用函数的单调性判断大小;(2)画函数草图的步骤:由已知条件确定特殊点的位置,然后利用单调性确定一段区间的图象,再利用奇偶性确定对称区间的图象,最后利用周期性确定整个定义域内的图象. 4.把握函数的零点应注意的问题(1)函数的零点是一个实数,当函数的自变量取这个实数时,其函数值等于零. (2)函数的零点也就是函数()y f x =的图象与x 轴的交点的横坐标. (3)一般我们只讨论函数的实数零点. (4)函数的零点不是点,是方程()0f x =的根.5.在解决函数与方程问题中的函数的零点问题时,要学会掌握转化与化归思想的运用,有时直接根据已知函数求函数的零点个数难度很大,也不是初等数学能轻易解决的,所以遇到此类问题第一反应就是转化已知函数为熟悉的函数再结合数形结合法求解.6.本热点常常命制成压轴的选择题,故难度较大,需要有较强的解题能力和知识的综合应用能力,涉及的数学思想丰富多样,故基础较差的学生不宜花费过多的时间,能力不够可适当放弃,另外,如果以抽象函数为背景,可采用抽象为题具体化的思路进行求解,如果涉及到范围问题的确定,可选择特值进行代入验证的方法求解.【名题精选练兵篇】1. 【2016届河南省八市重点高中高三4月质检】函数()4x f x e x =+-的零点所在的区间为( )A .(1,0)-B .(0,1)C .(1,2)D .(2,3) 【答案】C2. 【2015届山东省菏泽市高三第一次模拟考试】已知函数()0()210x e a x f x a R x x ⎧+≤=∈⎨->⎩,若函数()f x 在R 上有两个零点,则a 的取值范围是( ) A .(),1-∞- B .(),0-∞ C .()1,0- D .[)1,0- 【答案】D 【解析】显然21=x 是方程的一个零点;由题意,得0=+a e x 有一个非正根,则x e a -=,(]0,∞-∈x , 10≤<∴x e ,即01<≤-a .3. 【2016届福建省漳州市高三下学期第二次模拟】已知x 0是函数()xx f x -+=112的一个零点.若x 1∈(1,x 0),x 2∈(x 0,+∞),则( )(A )f(x 1)<0,f(x 2)<0 (B )f(x 1)<0,f(x 2)>0 (C )f(x 1)>0,f(x 2)<0 (D )f(x 1)>0,f(x 2)>0 【答案】B【解析】函数()xx f x -+=112是单调递增函数,又因为()00=x f ,201x x x <<,所以()01<x f ,()02>x f ,故选B.4.【 2016届湖北省沙市中学高三下第三次月考】定义在R 上的函数()f x 满足()(4)16f x f x ++=,当(]0,4x ∈时,2()2x f x x =-,则函数()f x 在[]4,2016-上的零点个数是( )A .504B .505C .1008D .1009 【答案】B5.已知函数21,2()16,22x x f x x x ⎧+≤⎪=⎨-+>⎪⎩,若,,a b c 互不相等,且满足()()()f a f b f c ==,则a b c ++的取值范围是 ( )A .(1,10)B .(5,6)C .(2,8)D .(0,10) 【答案】C【解析】设a b c <<,作图可知,=0,c (2,8),a b +∈从而a b c ++的取值范围是(2,8)6. 【2016届河北省邯郸一中高三下第一次模拟】若直角坐标平面内两点,P Q 满足条件:①,P Q 都在函数()y f x =的图象上;②,P Q 关于原点对称,则称(,)P Q 是函数()y f x =的一个“伙伴点组”(点组(,)P Q 与(,)Q P 看作同一个“伙伴点组”).已知函数1,0()ln(),0kx x f x x x ->⎧=⎨--<⎩,有两个“伙伴点组”,则实数k 的取值范围是( ) A .(,0)-∞ B .(0,)+∞ C .1(0,)2D .(0,1) 【答案】D7. 已知()f x 为定义在R 上的偶函数,当0x ≥时,有(1)()f x f x +=-,且当[)0,1x ∈时,2()log (1)f x x =+,给出下列命题:①(2014)(2015)0f f +-=;②函数()f x 在定义域上是周期为2的函数;③直线y x =与函数()f x 的图象有2个交点;④函数()f x 的值域为(1,1)-.其中正确的是( )A .①,②B .②,③C .①,④D .①,②,③,④ 【答案】C【解析】由当0x ≥时,有(1)()f x f x +=-知当0x ≥时有正周期2,又()f x 为定义在R 上的偶函数,且当[)0,1x ∈时,2()log (1)f x x =+,所以()()()()()()2014201502015010f f f f f f +-=+=+=,所以①正确,排除B ;若函数()f x 在定义域R 上是周期为2的函数,则()()()()221.5 1.520.50.5log (10.5)log 1.5f f f f =-=-==+=,同时因为当0x ≥时,有(1)()f x f x +=-,所以()()()21.510.50.5log 1.5f f f =+=-=-,显然矛盾,所以②错误,这样就排除A,D ;综上故选C.8.设函数⎩⎨⎧><=0,log 0,2)(2x x x x f x ,若存在唯一的x ,满足a a x f f 28))((2+=,则正实数...a 的最小值是 ( ) (A )81 (B )41 (C )21(D )2 【答案】B9.【2015届江西省上高二中高三上学期第三次月考】已知函数2|log |,02()sin(),2104x x f x x x π<<⎧⎪=⎨≤≤⎪⎩,若存在实数1x ,2x ,3x ,4x ,满足1234x x x x <<<,且1234()()()()f x f x f x f x ===,则3412(2)(2)x x x x -⋅-⋅的取值范围是( )A .(4,16)B .(0,12)C .(9,21)D .(15,25) 【答案】B .【解析】由题意得,12212212()()log log 01f x f x x x x x =⇒+=⇒=,又∵34()()(0,1)f x f x =∈, 即3434sinsin34444x x x x πππππ=⇒+=,3412x x +=,332424x x πππ<<⇒<<,∴3434343312(2)(2)2()4(12)20(0,12)x x x x x x x x x x -⋅-=-++=--∈⋅.10.【 2016届陕西省西安一中等八校高三下联考】如图,偶函数()f x 的图象如字母M ,奇函数()g x 的图象如字母N ,若方程(())0f g x =,(())0g f x =的实根个数分别为m 、n ,则m n +=( )A .12B .18C .16D .14 【答案】B11. 【2016届宁夏六盘山高中高三第二次模拟】已知定义在R 上的奇函数()f x 满足当0x ≥时,()()[)[)12log 1,0,113,1,x x f x x x ⎧+∈⎪=⎨⎪--∈+∞⎩ ,则关于x 的函数()(),01y f x a a =-<<的所有零点之和为( )A .21a -B .-21a -C .12a --D .12a -【答案】C【解析】由题意得,当0x ≥时,()()[)[)12log 1,0,113,1,x x f x x x ⎧+∈⎪=⎨⎪--∈+∞⎩ ,即[0,1)x ∈时,()12log (1)(1,0]f x x =+∈-;[1,3)x ∈时,()2[1,1]f x x =-∈-;(3,)x ∈+∞时,()4(,1)f x x =-∈-∞-,画出0x ≥函数()f x 的图象, 在利用函数为奇函数函数,可得0x <上的图象,如图所示,则直线y a =与()y f x =的图象有5个交点,则方程()0f x a -=有五个实根,最左边两根和为6-,左右边两根之和为6,因为(1,0)x ∈-时,(0,1)x -∈,所以()12log (1)f x x -=-+,又()()f x f x -=-,所以()11222log (1)log (1)log (1)f x x x x =--+=-=-,所以中间的一个根满足2log (1)x a -=,即12a x -=,解得12a x =-,所以所有根的和为12a -,故选C.12.【2016届重庆市巴蜀中学高三3月月考】已知实数⎩⎨⎧<-≥=,0),lg(,0,)(x x x e x f x 若关于x 的方程0)()(2=++t x f x f 有三个不同的实根,则t 的取值范围为( )A .]2,(--∞B .),1[+∞C .]1,2[-D .(,2][1,)-∞-+∞ 【答案】A13.【2016届甘肃省天水市一中高三下第四次模拟】定义在R 上的偶函数()f x 满足:(4)(2)0f f =-=,在区间(,3)-∞-与[]3,0-上分别递增和递减,则不等式()0xf x >的解集为( ) A .(,4)(4,)-∞-+∞ B .(4,2)(2,4)-- C .(,4)(2,0)-∞-- D .(,4)(2,0)(2,4)-∞--【答案】D【解析】由题意得,因为偶函数()f x 满足:(4)(2)0f f =-=,所以()4(1)(4)(1)0f f f f =-=-==,且()f x 在区间(,3)-∞-与[]3,0-上分别递增和递减,不等式()0xf x >,即等价于求函数在第一、三象限图形x 的取值范围,即(,4)(2,0)x ∈-∞--函数图象位于第三象限,(2,4)x ∈函数的图象位于第一象限,综上实数,不等式()0xf x >的解集为(,4)(2,0)(2,4)x ∈-∞--,故选D .14.【2016届福建省厦门一中高三下学期】函数()()223,2xf x x x ag x x =-++=-,若()0f g x ≥⎡⎤⎣⎦对[]0,1x ∈恒成立,则实数a 的取值范围是( )A .[),e -+∞B .[)ln 2,-+∞C .[)2,-+∞D .1,02⎛⎤- ⎥⎝⎦【答案】C15.已知)(x f 是定义在R 上且周期为3的函数,当)3,0[∈x 时,|212|)(2+-=x x x f , a x f -=)(y 在区间]4,3[-上有10个零点(互不相同),则实数a 的取值范围是 .【答案】1(0,)2【解析】作出函数在上的图象如图所示:16【2015届江苏省南京市、盐城市高三第二次模拟】已知函数22,0()(1)1,0x x x f x f x x ⎧+≤=⎨-+>⎩,当[0,100]x ∈时,关于x 的方程1()5f x x =-的所有解的和为 .【答案】10000【解析】22(0,1],1(1,2(1)0],()(1)(11)x f x f x x x x x +-+∈-∈-=-=-=,此时1()5f x x =-两解的和为1;2(1,2],1(0,1],()(1)1(11)x f x f x x x ∈-∈=-+=+-,此时1()5f x x =-两解的和为3;……;2(99,100],1(98,99],()(1)1(99)99x f x x x x f ∈-∈=--++=,此时1()5f x x =-两解的和为,199;所以所有解的和为(1199)13199100100002+++⋅⋅⋅+=⨯=. 【名师原创测试篇】1. 定义在R 上的奇函数()f x ,对任意x ∈R 都有(2)()f x f x +=-,当(02)x ∈,时,()4x f x =, 则(2015)f = . 【答案】4- 【解析】∵(2)()()f x f x f x +=-=-(4)(+2)=()f x f x f x ∴+=-∴(2015)(1)(1)4f f f =-=-=-. 2. 已知函数x x x x f cos 56sin 5)(+-=,则对任意实数)0(,≠+b a b a ,ba b f a f ++)()(的值 ( )A.恒大于0B.恒等于0C.恒小于0D.符号不确定 【答案】A.3. 已知函数[]sin ,0,2()1(2),(2,)2x x f x f x x π⎧∈⎪=⎨-∈+∞⎪⎩,()()ln 1g x x =-求函数()()()h x f x g x =-的零点个数( )A .2 B. 3 C . 4 D.5 【解析】C【解析】作出[]sin ,0,2()1(2),(2,)2x x f x f x x π⎧∈⎪=⎨-∈+∞⎪⎩的图象如下,因为()f x 的图像在[]0,2最大值和最小值是1和1-,在(2,)+∞最大值与最小值是12和12-,且向右无限延伸,又因为()()ln 1g x x =-的图像即把ln x 向右平移一个单位,且当()g x 取到1后就与()f x 没有交点了,从图像上可以看出()g x 与()f x 的交点个数为3个,所以零点个数为3个.故选B .4. 若a 、b 是方程lg 4x x +=,104xx +=的解,函数()()22,02,0x a b x x f x x ⎧+++≤=⎨>⎩,则关于x 的方程()f x x =的解是 . 【答案】2x =-或1x =-或2x =5.已知函数()()0x f x e x =≥,当0x <时,()()4f x f x -=,若函数()()()0g x f x ax a a =-->有唯一零点,则a 的取值范围( )A .()0,1B .1,e e ⎛⎫ ⎪⎝⎭C .1,4e ⎛⎫ ⎪⎝⎭D .1,14⎛⎫ ⎪⎝⎭【答案】D【解析】根据题意,当0x <时,()()()()1140044x f x f x x x f x f x e --=<∴->∴=-=⋅,作出函数(),01,04x x e x h x e x -⎧≥⎪=⎨⋅<⎪⎩即函数(),0u x ax a a =+>的图像如图所示, 可知只有当114a <<时,函数()u x 与()h x 有唯一交点.故选D 6. 已知函数()y f x =是定义域为R ,且(1)f x -关于1x =对称. 当0x ≥时,若关于x 的方程[]25()(56)()60f x a f x a -++= (a R ∈),有且仅有6个不同实数根,则实数a 的取值范围是( )AC 【答案】C又∵函数(1)f x -关于1x =对称,所以函数y=f (x )是定义域为R 的偶函数,且关于x 的方程[]25()(56)()60f x a f x a -++=,a ∈R 有且仅有6个不同实数根,a x f =)(,a ∈R 共有且仅有6个不同实数根;,有四个不同的实数根,所以必须且只需方程a x f =)(,a ∈R 有且仅有2个不同实数根,由图可知10≤<a 或C .。
2016届高考数学三轮讲练测核心热点总动员(新课标版)专题03基本函数的性质(原卷版)

2016年学易高考三轮复习系列:讲练测之核心热点 【全国通用版】【名师精讲指南篇】【高考真题再现】1.【2013⋅新课标全国卷】 若函数f (x )=(1-x 2)(x 2+ax +b )的图像关于直线x =-2对称,则f (x )的最大值是______.2.【2014高考全国1卷】设函数)(),(x g x f 的定义域为R ,且)(x f 是奇函数,)(x g 是偶函数,则下列结论中正确的是( )A.)()(x g x f 是偶函数B. )(|)(|x g x f 是奇函数C. |)(|)(x g x f 是奇函数D. |)()(|x g x f 是奇函数3.【2014高考全国1卷文】设函数()113,1,,1,x e x f x x x -⎧<⎪=⎨⎪≥⎩则使得()2f x ≤成立的x 的取值范围是________.4.【2015全国II 文】已知函数()32f x ax x =-的图像过点()14,-,则=a .5.【2015全国I 文】已知函数1222,1()log (1),1x x f x x x -⎧-=⎨-+>⎩… ,且()3f a =-,则(6)f a -=( ).A. 74-B. 54-C. 34-D. 14- 6.【2015全国I 文】设函数()y f x =的图像与2x ay +=的图像关于直线y x =-对称,且(2)(4)1f f -+-=,则a =( ).A.1-B. 1C. 2D. 47.【2015全国II 理】设函数()()2111log 2,12,x x x f x x -⎧+-<⎪=⎨⎪⎩…,则()()22log 12f f -+=( ).A.3B.6C.9D.12 8.【2015全国I 理】若函数()(ln =f x x x 为偶函数,则=a .9.【2015全国II 理】如图所示,长方形ABCD 的边2AB =,1BC =,O 是AB 的中点,点P 沿着边,BC CD 与DA 运动,BOP x ∠=.将动点P 到,A B 两点距离之和表示为x 的函数()f x ,则()f x 的图像大致为( ).xPODCBA2π3π4π2π4y O x2xO y π4π23π4π2xO y π4π23π4π2π3π4π2π4y O xA. B. C. D. 【热点深度剖析】高考考查的基本函数有一次函数、二次函数、指数函数、对数函数和幂函数,其中以指数函数和对数函数的性质为命题热点,且常以复合函数或分段函数的形式出现,达到一题多考的目的.题型一般为选择题、填空题,属中低档题,主要考查利用指数和对数函数的图像与性质比较对数值大小,求定义域、值域、最值,对数函数与相应指数函数的关系,函数的奇偶性与单调性,周期性,以及函数零点问题.也应为同学们必须得分的题目.2013年考查了函数的对称性与奇偶性,2014年理科考查了函数的奇偶性,文科一道考查了函数的奇偶性,一道考查了以指数函数与幂函数为背景的分段函数,与解不等式,2015年分别考查了分段函数求值、函数奇偶性、函数图像及对称性,预测2016年高考可能会涉及函数的奇偶性及单调性及函数图像,其中指数函数、对数函数及分段函数依然是考查重点. 【重点知识整合】 1指数式、对数式:m na =,1m nm naa -=,,01a =,log 10a =,log 1a a =,lg 2lg 51+=,log ln e x x =,log (0,1,0)b a a N N b a a N =⇔=>≠>,log a N a N =,log log logc a c b b a=,log log m n a a nb b m=.2.指数、对数值的大小比较:(1)化同底后利用函数的单调性;(2)作差或作商法;(3)利用中间量(0或1);(4)化同指数(或同真数)后利用图象比较. 3.指数函数:(1)指数函数图象和性质(2)xy a =(0a >且1a ≠)的图象特征:①1>a 时,图象像一撇,过点()0,1,且在y 轴左侧a 越大,图象越靠近y 轴(如图1); ②01a <<时,图象像一捺,过点()0,1,且在y 轴左侧a 越小,图象越靠近y 轴(如图2); ③xy a =与xay -=的图象关于y 轴对称(如图3).④xy a =的图象如图44. 对数函数(1)对数的图象和性质:xx(2))10(log ≠>=a a x y a 且的图象特征: ①1>a 时,图象像一撇,过()1,0点,在x 轴上方a 越大越靠近x 轴;②01a <<时,图象像一捺,过()1,0点,在x 轴上方a 越小越靠近x 轴.③x a y =(1,1a a >≠)与x y a log =互为反函数,图象关于y x =对称;如图2 ④log (1)a y x a =>的图象3.⑤log (1)a y x a =>的图象4.5.幂函数的定义和图象(1)定义:形如y =x α的函数叫幂函数(α为常数)要重点掌握α=1,2,3,21,-1,0,-21,-2时的幂函数.(2)图象:(只作出第一象限图象)(3)性质:(1)当α>0时,幂函数图象都过(0,0)点和(1,1)点;且在第一象限都是增函数;当0<α<1时曲线上凸;当α>1时,曲线下凸;α=1时,为过(0,0)点和(1,1)点的直线(2)当α<0时,幂函数图象总经过(1,1)点,且在第一象限为减函数.(3)α=0时y=x0,表示过(1,1)点平行于x轴的直线(除去(0,1)点).6. 常见复合函数类型1.单调性的判断方法:a.利用基本初等函数的单调性与图像:只需作出函数的图象便可判断函数在相应区间上的单调性;b.性质法:(1)增函数+增函数=增函数,减函数+减函数=减函数,增函数-减函数=增函数,减函数-增函数=减函数;(2)函数()f x -与函数()f x 的单调性相反; (3)0k >时,函数()f x 与()k f x 的单调性相反(()0f x ≠);0k <时,函数()f x 与()k f x 的单调性相同(()0f x ≠).c.导数法:()0f x '≥在区间D 上恒成立,则函数()f x 在区间D 上单调递增;()0f x '≤在区间D 上恒成立,则函数()f x 在区间D 上单调递减.d.定义法:作差法与作商法(常用来函数单调性的证明,一般使用作差法).【注】分段函数的单调性要求每段函数都满足原函数的整体单调性,还需注意断点处两边函数值的大小比较. 2.单调区间的求法:a.利用已知函数的单调区间来求;b.图象法:对于基本初等函数及其函数的变形函数,可以作出函数图象求出函数的单调区间.c.复合函数法:对于函数()y f g x =⎡⎤⎣⎦,可设内层函数为()u g x =,外层函数为()y f u =,可以利用复合函数法来进行求解,遵循“同增异减”,即内层函数与外层函数在区间D 上的单调性相同,则函数()y f g x =⎡⎤⎣⎦在区间D 上单调递增;内层函数与外层函数在区间D 上的单调性相反,则函数()y f g x =⎡⎤⎣⎦在区间D 上单调递减.d.导数法:不等式()0f x '>的解集与函数()f x 的定义域的交集即为函数()f x 的单调递增区间,不等式()0f x '<的解集与函数()f x 的定义域的交集即为函数()f x 的单调递减区间. 【注】函数的多个递增区间或递减区间不能合并,在表示的时候一般将各区间用逗号或“和”字进行连接.3. 在公共定义域内,①两个奇函数的和是奇函数,两个奇函数的积是偶函数; ②两个偶函数的和、积是偶函数; ③一个奇函数,一个偶函数的积是奇函数.4. 奇偶性与单调性综合时要注意奇函数在关于原点对称的区间上的单调性相同,偶函数在关于原点对称的区间上的单调性相反.5. 关于函数周期性常用的结论(1)若满足()()f x a f x +=-,则()(2)[()]()f x a f x a a f x a f x +=++=-+=,所以2a 是函数的一个周期(0a ≠); (2)若满足1()()f x a f x +=,则(2)[()]f x a f x a a +=++= 1()f x a +=()f x ,所以2a 是函数的一个周期(0a ≠); (3)若函数满足1()()f x a f x +=-,同理可得2a 是函数的一个周期(0a ≠). (4)如果)(x f y =是R 上的周期函数,且一个周期为T,那么))(()(Z n x f nT x f ∈=±. (5)函数图像关于b x a x ==,轴对称)(2b a T -=⇒. (6)函数图像关于()()0,,0,b a 中心对称)(2b a T -=⇒.(7)函数图像关于a x =轴对称,关于()0,b 中心对称)(4b a T -=⇒.6.指数运算的实质是指数式的积、商、幂的运算,对于指数式的和、差应充分运用恒等变形和乘法公式;对数运算的实质是把积、商、幂的对数转化为对数的和、差、倍.7.指数函数(0,xy a a =>且1)a ≠与对数函数(0,xy a a =>且1)a ≠互为反函数,应从概念、图象和性质三个方面理解它们之间的联系与区别.8.明确函数图象的位置和形状要通过研究函数的性质,要记忆函数的性质可借助于函数的图象.因此要掌握指数函数和对数函数的性质首先要熟记指数函数和对数函数的图象. 9.求解与指数函数有关的复合函数问题时,首先要熟知指数函数的定义域、值域、单调性等相关性质,其次要明确复合函数的构成,涉及值域、单调区间、最值等问题时,都要借助“同增异减”这一性质分析判断,最终将问题归纳为与内层函数相关的问题加以解决. 【考场经验分享】1.高考对函数性质的考查,一般在选择题或填空题的中间,难度中档,应该是得分的题目,在解答此类题目时注意解答选择题的常用方法;验证法和排除法的应用,若是函数的零点问题,注意数形结合的应用.2. 指数函数(0,x y a a =>且1)a ≠的图象和性质与a 的取值有关,要特别注意区分1a >与01a <<来研究.3.对可化为20x x a b a c +⋅+=或()200xx ab ac +⋅+≥≤形式的方程或不等式,常借助换元法解决,但应注意换元后“新元”的范围.4.指数式b a N =(0a >且1)a ≠与对数式log a N b =(0a >且1,0)a N ≠>的关系以及这两种形式的互化是对数运算法则的关键.5.在运算性质log log n a a M n M = (0a >且1,0)a M ≠>时,要特别注意条件,在无0M >的条件下应为log log na a M n M = (n N *∈,且n 为偶数).6.幂函数的图象一定会出现在第一象限,一定不会出现在第四象限,至于是否出现在第二、三象限,要看函数的奇偶性;幂函数的图象最多只能同时出现在两个象限内;如果幂函数图象与坐标轴相交,则交点一定是原点.7.函数图像识别题一直是高考热点,解决此类问题一般是利用函数性质排除不符合条件的选项.【名题精选练兵篇】1. 【2016河北定州高三第一次测试】若0.23a =,πlog 3b =,3log c =,则 ( ) A .b c a >>B . b a c >>C .a b c >>D .c a b >>2.【2016湖北省荆州高三第一次质检】下列函数是奇函数的是( ).A . x x x f =)(B .x x f lg )(=C . x x x f -+=22)(D .1)(3-=x x f3.【2016襄阳五中 宜昌一中 龙泉中学高三联考】已知定义在R 上的函数()12-=-mx x f (m R ∈)为偶函数.记()()m f c f b f a 2,log ,log 52431==⎪⎪⎭⎫ ⎝⎛=,则c b a ,,的大小关系为( )A .c b a <<B .b a c <<C .b c a <<D .a b c << 4.【2016鹰潭市高三第一次模拟】若1)(+=x xx f ,)()(1x f x f =,()[]()*1,2)(N n n x f f x f n n ∈≥=-,则()()的值为)1()1()1()1()2015(212015321f f f f f f f ++++++( )A .2014B .2015C .4028D .40305.【河北冀州高三第二次测试】已知函数()3sin 34(,)f x a x bx a R b R =++∈∈,()f x '为()f x 的导函数,则()()2014(2014)2015(2015)f f f f ''+-+--=( )A .8B .2014C .2015D .06.【江西九江市七校高三第一次联考】对于函数()f x ,若存在区间[],A m n =,使得(){},y y f x x A A =∈=,则称函数()f x 为“可等域函数”,区间A 为函数()f x 的一个“可等域区间”.给出下列4个函数:①()sin 2f x x π⎛⎫=⎪⎝⎭;②()221f x x =-; ③()12x f x =-; ④()()2log 22f x x =-.其中存在唯一“可等域区间”的“可等域函数”为( ) A .①②③ B .②③ C .①③ D .②③④7.【2016届江西师大附中、鹰潭一中高三下第一次联考】已知)(x f 是定义域,值域都为(0,)+∞的函数, 满足2()()0f x xf x '+>,则下列不等式正确的是( )A .2016(2016)2015(2015)f f >B .2016(2016)2015(2015)f f <C. 332015(2015)2016(2016)f f < D.332015(2015)2016(2016)f f > 8.【2016届江西南昌高三上第四次考试】若定义在R 上的偶函数()y f x =是[)0,+∞上的递增函数,则不等式()()2log 1f x f <-的解集是( ) A .1,22⎛⎫⎪⎝⎭B .()(),22,-∞-+∞C .RD .()2,2-9.【2016宁夏银川高三上学期统练】定义在R 上的函数()f x 满足)()6(x f x f =+.当)1,3[--∈x 时,2)2()(+-=x x f ,当)3,1[-∈x 时,x x f =)(,则(1)(2)(3)(2015)f f f f ++++=( )A .336B .355C .1676D .201510.【2015临川一中期末考试 】已知函数,e x ex a x f ≤≤-=1(,)(2e 为自然对数的底数)与x x g ln 2)(=的图象上存在关于x 轴对称的点,则实数a 的取值范围是( )A .21[1,2]e + B .221[2,2]e e+- C .2[1,2]e - D .2[2,)e -+∞ 11.【2016黑龙江省哈尔滨市六中高三12月月考】定义在R 上的奇函数()f x 满足()()1f x f x +=-,当10,2x ⎛⎤∈ ⎥⎝⎦时,()()2log 1f x x =+,则()f x 在区间31,2⎛⎫⎪⎝⎭内是( )A .减函数且()0f x <B .减函数且()0f x >C .增函数且()0f x >D .增函数且()0f x <12.【2016黑龙江省大庆高三12月月考】分析函数()f x的性质: ①()f x 的图象是中心对称图形; ②()f x 的图象是轴对称图形; ③函数()f x的值域为)+∞; ④方程(())1f f x =+有两个解.其中描述正确个数是( )A .1B .2C .3D .413.定义符号函数 ⎪⎩⎪⎨⎧<-=>=0,10,00,1)sgn(x x x x ,则下列结论中错误的是A .||)sgn(x x x ⋅=B .)0(||)sgn(≠=x x xx C .)sgn()sgn()sgn(y x xy ⋅= D .)sgn()sgn()sgn(y x y x +=+14. 【2015届山东省日照市高三3月模拟考试】已知函数()22,1,22,1,x x f x x x -⎧≤-=⎨+>-⎩则满足()2f a ≥的实数a 的取值范围是( )A.()(),20,-∞-⋃+∞B.()1,0-C.()2,0-D.(][),10,-∞-⋃+∞15. 已知函数()[)()232,0,32,,0x x f x x a a x ⎧∈+∞⎪=⎨+-+∈-∞⎪⎩在区间(),-∞+∞上是增函数,则常数a 的取值范围是 ( ) A .()1,2 B .(][),12,-∞+∞ C .[]1,2 D .()(),12,-∞+∞16. 现有四个函数:①y x sin x =⋅;②cos y x x =⋅;③|cos |y x x =⋅; ④2xy x =⋅的图象(部分)如下,但顺序被打乱,则按照从左到右将图象对应的函数序号安排正确的一组是A .④①②③B .①④③②C .①④②③D .③④②①17.【2016届襄阳五中 、宜昌一中 、龙泉中学高三联考】若正数,a b 满足2363log 2log log ()a b a b +=+=+,则11a b+的值为_________. 18.【2016鹰潭市高三第一次模拟】()f x 是定义在D 上的函数,若存在区间[]m n D ⊆,,使函数()f x 在[]m n ,上的值域恰为[]km kn ,,则称函数()f x 是k 型函数.给出下列说法: ①4()3f x x=-不可能是k 型函数;②若函数22()1(0)a a x y a a x +-=≠是1型函数,则n m - ③设函数32()2f x x x x =++(x≤0)是k 型函数,则k 的最小值为49. ④若函数212y x x =-+是3型函数,则40m n =-=,;其中正确的说法为 .(填入所有正确说法的序号) 【名师原创测试篇】1. 下列函数中,既是奇函数,又在区间()1,-∞-内是减函数的为( ).A .x y 2sin =B .x y 21log =C .x x y 22-=-D .13+=x y2. 若()21y f x x =+-是奇函数,且()12f =-,则()1f -= .3. 定义在R 上的奇函数()f x ,对任意x ∈R 都有(2)()f x f x +=-,当(02)x ∈,时,()4x f x =, 则(2015)f = .4. 下列函数图像中,函数()()cos sin f x x =大致图像是( )A B C D5. 设函数()f x 的定义域为D ,若函数()f x 满足条件:存在[],a b D ⊆,使得()f x 在区间[],a b 上的值域为,a b n n ⎡⎤⎢⎥⎣⎦()*n N ∈,则称()f x 为“n 倍缩函数”,若函数()()3log 3x f x t =+为“3倍缩函数”,则t 的取值范围为( ) A.10,3⎛⎫ ⎪⎝⎭B.⎛ ⎝C.⎛ ⎝D.()0,1 6. 已知函数()y f x =是定义域为R ,且(1)f x -关于1x =对称. 当0x ≥时,若关于x 的方程[]25()(56)()60f x a f x a -++= (a R ∈),有且仅有6个不同实数根,则实数a 的取值范围是( )AC。
2016年高考数学三轮讲练测核心热点总动员(新课标版) 专题18 概率与统计大题(理) Word版含解析

【名师精讲指南篇】【高考真题再现】1.【2013 新课标全国】一批产品需要进行质量检验,检验方案是:先从这批产品中任取4件作检验,这4件产品中优质品的件数记为n.如果n=3,再从这批产品中任取4件作检验,若都为优质品,则这批产品通过检验;如果n=4,再从这批产品中任取1件作检验,若为优质品,则这批产品通过检验;其他情况下,这批产品都不能通过检验.假设这批产品的优质品率为50%,即取出的产品是优质品的概率都为,且各件产品是否为优质品相互独立(1)求这批产品通过检验的概率;(2)已知每件产品检验费用为100元,凡抽取的每件产品都需要检验,对这批产品作质量检验所需的费用记为X(单位:元),求X的分布列及数学期望.【解析】(1)利用相互独立事件模型计算概率;(2)在(1)的基础上,利用对立事件算出X 为400、500、800时的概率,进而列出分布列,求出期望.2.【2014高考全国1】从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下图频率分布直方图:(I )求这500件产品质量指标值的样本平均值x 和样本方差2s (同一组的数据用该组区间的中点值作代表);(II )由直方图可以认为,这种产品的质量指标Z 服从正态分布()2,N μσ,其中μ近似为样本平均数x ,2σ近似为样本方差2s .(i )利用该正态分布,求()187.8212.2P Z <<;(ii )某用户从该企业购买了100件这种产品,记X 表示这100件产品中质量指标值位于区间()187.8,212.2的产品件数.利用(i )的结果,求EX .12.2≈若()2~,Z N μσ则()0.6826P Z μσμσ-<<+=,()220.9544P Z μσμσ-<<+=.3.【2014新课标Ⅱ理)】某地区2007年至2013年农村居民家庭纯收入y (单位:千元)的数据如下表:(1)求y 关于t 的线性回归方程;(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.附:回归直线的斜率和截距的最小二乘法估计公式分别为:()()()121niii ni i t ty y b t t ==--=-∑∑,ˆˆay bt =-.(II )由(I )知,ˆ0.50b=>,故2007年至2013年该地区农村居民家庭人均纯收入逐年增加,平均每年增加0.5千元.将2015年的年份代号9t =代入(I )中的回归方程,得ˆ0.59 2.3 6.8y=⨯+=千元,故预测该地区2015年农村居民家庭人均纯收入为6.8千元 4.【2015全国Ⅱ理18】某公司为了解用户对其产品的满意度,从,A B 两地区分别随机调查了20个用户,得到用户对产品的满意度评分如下:A 地区:62 73 81 92 95 85 74 64 53 7678 86 95 66 97 78 88 82 76 89B 地区:73 83 62 51 91 46 53 73 64 8293 48 65 81 74 56 54 76 65 79(1)根据两组数据完成两地区用户满意度评分的茎叶图,并通过茎叶图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,得出结论即可);(2)根据用户满意度评分,将用户的满意度从低到高分为三个等级:记事件C:“A地区用户的满意度等级高于B地区用户的满意度等级”,假设两地区用户的评价结果相互独立,根据所给数据,以事件发生的频率作为相应事件发生的概率,求C的概率.则可得1122B A B A C C C C C =.所以1122()()B A B A P C P C C C C =1122()()B A B A P C C P C C =+1122()()()()B A B A P C P C P C P C =+.由题意及所给数据可得1A C ,2A C ,1B C ,2B C 发生的频率分别为1620,420,1020,820. 故可得1()A P C 16=20,2()=A P C 420,1()=B P C 1020,2()B P C 8=20,故101684()=+0.4820202020P C ⨯⨯=.即C 的概率为0.48. 5.【2015全国Ⅰ理19】某公司为确定下一年投入某种产品的宣传费,需了解年宣传费x (单位:千元)对年销售量y (单位:t )和年利润z (单位:千元)的影响,对近8年的年宣传费i x 和年销售量()1,2,,8i y i =⋅⋅⋅数据作了初步处理,得到下面的散点图及一些统计量的值.年宣传费/千元表中i w =,8118i i w w ==∑,(1)根据散点图判断,y a bx =+与y c =+哪一个适宜作为年销售量y 关于年宣传费x 的回归方程类型(给出判断即可,不必说明理由);(2)根据(1)的判断结果及表中数据,建立y 关于x 的回归方程;(3)已知这种产品的年利润z 与x ,y 的关系式0.2z y x =-,根据(2)的结果回答下列问题: ①年宣传费49x =时,年销售量及年利润的预报值是多少? ②年宣传费x 为何值时,年利润的预报值最大?附:对于一组数据()11,u v ()22,u v ,⋅⋅⋅,(),n n u v ,其回归直线v u αβ=+的斜率和截距的最小二乘估计分别为()()()121ˆniii ni i u u v v u u β==--=-∑∑,ˆˆv u αβ=-. 【热点深度剖析】1.纵观2013年和2014年2015年的高考题对本热点的考查,可以发现概率和统计、统计案例相结合是高考命题的热点,在2012年高考中,结合实际问题将函数和概率问题巧妙结合在一起,新颖别致,但是题目难度不大,这也体现了“新题不难”的命题特点,主要考查生活中的概率统计知识和方法.求离散型随机变量的分布列和数学期望的方法,以及生活中最大利润的判断;2013年考查相互独立事件的概率计算、离散型随机变量的分布列、期望,考查学生的逻辑推理能力以及基本运算能力;2014年主要考查了频率分布直方图,正态分布的3 原则,二项分布的期望及回归分析.2015年分别考查了回归分析、茎叶图。
(新课标)高考数学 三轮必考热点集中营 热点23参数方程和极坐标方程(教师版)

(新课标)2013高考数学 三轮必考热点集中营 热点23参数方程和极坐标方程(教师版)【三年真题重温】1.【2011⋅新课标全国理,23】选修4—4:坐标系与参数方程 在直角坐标系xOy 中,曲线1C 的参数方程为2cos 22sin x y αα=⎧⎨=+⎩(α为参数),M 是1C 上的动点,P 点满足2OP OM =,P 点的轨迹为曲线2C .(Ⅰ)当求2C 的方程;(Ⅱ)在以O 为极点,x 轴的正半轴为极轴的极坐标系中,射线3πθ=与1C 的异于极点的交点为A ,与2C 的异于极点的交点为B ,求AB .2.【2010⋅新课标全国理,23】选修4-4:坐标系与参数方程 已知直线C 1x 1t cos sin y t αα=+⎧⎨=⎩(t 为参数),C 2x cos sin y θθ=⎧⎨=⎩(θ为参数),(Ⅰ)当α=3π时,求C 1与C 2的交点坐标; (Ⅱ)过坐标原点O 做C 1的垂线,垂足为,P 为OA 中点,当α变化时,求P 点的轨迹的参数方程,并指出它是什么曲线。
【2012⋅新课标全国理,23】坐标系与参数方程已知曲线1C 的参数方程是)(3sin y 2cos x 为参数ϕϕϕ⎩⎨⎧==,以坐标原点为极点,x 轴的正半轴为极轴建立坐标系,曲线2C 的坐标系方程是2=ρ,正方形ABCD 的顶点都在2C 上, 且,,,A B C D 依逆时针次序排列,点A 的极坐标为(2,)3π(1)求点,,,A B C D 的直角坐标;(2)设P 为1C 上任意一点,求2222PA PB PC PD +++的取值范围。
【命题意图猜想】 2011年高考考查了参数方程和极坐标的题目,可化为普通方程求解,涉及到直线和圆的参数方程;2010年高考主要考查直线与圆的参数方程,参数方程与普通方程的互化,利用参数方程研究轨迹问题的能力.2012年高考主要考查直角坐标系与极坐标系之间的互化,以椭圆的参数方程为背景,意在考查考生利用坐标之间的转化求解。
2016年高考数学三轮讲练测核心热点总动员(新课标版) 专题18 概率与统计大题(文) Word版含解析

【名师精讲指南篇】【高考真题再现】1.【2013 新课标全国】为了比较两种治疗失眠症的药(分别成为A药,B药)的疗效,随机地选取20位患者服用A药,20位患者服用B药,这40位患者服用一段时间后,记录他们日平均增加的睡眠时间(单位:h)实验的观测结果如下:服用A药的20位患者日平均增加的睡眠时间:0.6 1.2 2.7 1.5 2.8 1.8 2.2 2.3 3.2 3.52.5 2.6 1.2 2.7 1.5 2.93.0 3.1 2.3 2.4服用B药的20位患者日平均增加的睡眠时间:3.2 1.7 1.9 0.8 0.9 2.4 1.2 2.6 1.3 1.41.6 0.5 1.8 0.62.1 1.1 2.5 1.2 2.7 0.5(1)分别计算两组数据的平均数,从计算结果来看,哪种药的效果好?(2)完成茎叶图,从茎叶图来看,哪种药疗效更好?【解析】(1)利用平均数公式进行计算;(2)绘制茎叶图,进行观察.2.【2014高考全国1文】从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布表:(I)在答题卡上作出这些数据的频率分布直方图:(II)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);(III)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?【解析】(1)(2)质量指标值的样本平均数为x=⨯+⨯+⨯+⨯+⨯=.800.06900.261000.381100.221200.081003. 【2015全国II 文18)】某公司为了解用户对其产品的满意度,从A ,B 两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得出A 地区用户满意评分的频率分布直方图和B 地区用户满意度评分的频数分布表.A 地区用户满意度评分的频率分布直方图B 地区用户满意度评分的频数分布表(1)在答题卡上作出B 地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可).B地区用户满意度评分的频率分布直方图(2)根据用户满意度评分,将用户的满意度分为三个等级:估计哪个地区用户的满意度等级为不满意的概率大?说明理由.4.【2015全国I文19】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y (单位:t )和年利润z (单位:千元)的影响.对近8年的年宣传费i x 和年销售量()1,2,,8i y i =数据作了初步处理,得到下面的散点图及一些统计量的值.千元565452504846444240383634表中i w =,8118i i w w ==∑(1)根据散点图判断,y a bx =+与y c =+哪一个适宜作为年销售量y 关于年宣传费x 的回归方程类型?(给出判断即可,不必说明理由);(2)根据(1)的判断结果及表中数据,建立y 关于x 的回归方程;(3)已知这种产品的年利润z 与,x y 的关系为0.2z y x =-,根据(2)的结果回答下列问题: (i )年宣传费49x =时,年销售量及年利润的预报值是多少? (ii )年宣传费x 为何值时,年利润的预报值最大? 附:对于一组数据()11,u v ,()22,u v ,,(),n n u v ,其回归直线v u αβ=+的斜率和截距的最小二乘估计分别为()()()121niii nii u u v v u u β==--=-∑∑,v u αβ=-.解析(1)由散点图变化情况选择y c =+.6.8=,即26.846.24x ==(千元)时,年利润的预报值最大, 【热点深度剖析】1.纵观2013年和2014年2015年的高考题对本热点的考查,可以发现概率和统计、统计案例相结合是高考命题的热点, 2013年考查了茎叶图、利用样本数据估计总体,考查学生的数据处理能力,这也体现了高考对新课标的新增内容的要求,试题难度不大,但是要求同学们对相关的基础知识掌握必须准确,2014年考查了频率分布表,频率分布直方图,平均数与方差的计算,主要考查生活中的概率统计知识和方法. 2015年分别考查了频率分布直方图、线性回归分析.从近几年的高考试题来看,古典概型、频率分布直方图、茎叶图、平均数、方差是高考的热点,题型既有选择题、填空题,又有解答题,客观题考查知识点较单一,解答题考查得较为全面,常常和概率、平均数等知识结合在一起,考查学生应用知识解决问题的能力.独立性检验、回归分析高考对此部分内容考查较少,主要是以小题形式考查独立性检验、回归分析为主,并借助解决一些简单的实际问题来考查一些基本的统计思想,在高考中多为选择、填空题,也有解答题出现.,根据近三年高考趋势预测2016年高考,频率分布直方图、茎叶图、平均数、方差仍然是考查的热点,由于连续3年大题都没考古典概型、独立性检验,故应注意和概率知识的结合,同时应注意独立性检验在实际生活中的应用,有可能涉及一道与独立检验有关的大题. 【重点知识整合】 一,统计初步 1.简单随机抽样简单随机抽样是不放回抽样,被抽取样本的个体数有限,从总体中逐个地进行抽取,使抽样便于在实践中操作.每次抽样时,每个个体等可能地被抽到,保证了抽样的公平性.实施方法主要有抽签法和随机数法. 2.系统抽样(1)定义:当总体元素个数很大时,可将总体分成均衡的若干部分,然后按照预先制定的规则,从每一部分抽取一个个体得到所需要的样本,这种抽样方法叫做系统抽样,也称作等距抽样. (2)系统抽样的步骤:①编号.采用随机的方式将总体中的个体编号.②分段.先确定分段的间隔k .当Nn (N 为总体中的个体数,n 为样本容量)是整数时,k =N n ;当N n不是整数时,通过从总体中随机剔除一些个体使剩下的总体中个体总数N ′能被n 整除,这时k =N ′n.③确定起始个体编号.在第1段用简单随机抽样确定起始的个体编号S .④按照事先确定的规则抽取样本.通常是将S 加上间隔k ,得到第2个个体编号S +k ,再将(S +k )加上k ,得到第3个个体编号S +2k ,这样继续下去,获得容量为n 的样本.其样本编号依次是:S ,S +k ,S +2k ,…,S +(n -1)k . 3.分层抽样(1)定义:当总体由有明显差别的几部分组成时,按某种特征在抽样时将总体中的各个个体分成互不交叉的层,然后按照各层在总体中所占的比例,从各层独立地抽取一定数量的个体合在一起作为样本,这种抽样的方法叫做分层抽样.分层抽样使用的前提是总体可以分层,层与层之间有明显区别,而层内个体间差异较小,每层中所抽取的个体数可按各层个体数在总体中所占比例抽取.分层抽样要求对总体的内容有一定的了解,明确分层的界限和数目,分层要恰当. (2)分层抽样的步骤①分层;②按比例确定每层抽取个体的个数;③各层抽样(方法可以不同);④汇合成样本. (3)分层抽样的优点分层抽样充分利用了己知信息,充分考虑了保持样本结构与总体结构的一致性.使样本具有较好的代表性,而且在各层抽样时,可以根据具体情况采取不同的抽样方法,因此分层抽样在实践中有着非常广泛的应用.4.绘制频率分布直方图把横轴分成若干段,每一段对应一个组距,然后以线段为底作一矩形,它的高等于该组的频率组距,这样得出一系列的矩形,每个矩形的面积恰好是该组上的频率.这些矩形就构成了频率分布直方图.在频率分布直方图中,纵轴表示“频率/组距”,数据落在各小组内的频率用小矩形的面积表示,各小矩形的面积总和等于1. 5.茎叶图统计中还有一种被用来表示数据的图叫做茎叶图.茎是指中间的一列数,叶是从茎的旁边生长出来的数.在样本数据较少、较为集中,且位数不多时,用茎叶图表示数据的效果较好,它较好的保留了原始数据信息,方便记录与表示,但当样本数据较多时,茎叶图就不太方便.6.平均数、中位数和众数(1)平均数:一组数据的总和除以数据的个数所得的商就是平均数.(2)中位数:如果将一组数据按从小到大的顺序依次排列,当数据有奇数个时,处在最中间的一个数是这组数据的中位数;当数据有偶数个时,处在最中间两个数的平均数,是这组数据的中位数.(3)众数:出现次数最多的数(若有两个或几个数据出现得最多,且出现的次数一样,这些数据都是这组数据的众数;若一组数据中,每个数据出现的次数一样多,则认为这组数据没有众数).(4)在频率分布直方图中,最高小长方形的中点所对应的数据值即为这组数据的众数.而在频率分布直方图上的中位数左右两侧的直方图面积应该相等,因而可以估计其近似值.平均数的估计值等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和. 7.方差、标准差(1)设样本数据为x 1,x 2,…,x n 样本平均数为x -,则s 2=1n =1n叫做这组数据的方差,用来衡量这组数据的波动大小,一组数据方差越大,说明这组数据波动越大.把样本方差的算术平方根叫做这组数据的样本标准差.(2)数据的离散程度可以通过极差、方差或标准差来描述,其中极差反映了一组数据变化的最大幅度.方差则反映一组数据围绕平均数波动的大小. 8.两个变量的线性相关 (1)散点图将样本中n 个数据点(xi ,yi )(i =1,2,…,n )描在平面直角坐标系中,表示具有相关关系的两个变量的一组数据的图形叫做散点图.利用散点图可以判断变量之间有无相关关系. (2)正相关、负相关如果散点图中各点散布的位置是从左下角到右上角的区域,即一个变量的值由小变大时,另一个变量的值也由小变大,这种相关称为正相关.反之,如果两个变量的散点图中点散布的位置是从左上角到右下角的区域,即一个变量的值由小变大时,另一个变量的值由大变小,这种相关称为负相关. 9.回归分析对具有相关关系的两个变量进行统计分析的方法叫回归分析.其基本步骤是:①画散点图,②求回归直线方程,③用回归直线方程作预报.(1)回归直线:观察散点图的特征,如果散点图中点的分布从整体上看大致在一条直线附近,我们就称这两个变量之间具有线性相关关系,这条直线叫做回归直线. (2)回归直线方程的求法——最小二乘法.设具有线性相关关系的两个变量x 、y 的一组观察值为(x i ,y i )(i =1,2,…,n ),则回归直线方程y ^=a ^+b ^x 的系数为:⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧b^=∑i =1n x i y i -n x ·y ∑i =1n x i 2-n x 2=∑i =1n (x i -x -)(y i -y -)∑i =1n (x i -x -)2a^=y --b ^x其中x -=1n ∑i =1n x i ,y -=1n ∑i =1ny i ,(x -,y -)称作样本点的中心.a ^,b ^表示由观察值用最小二乘法求得的a ,b 的估计值,叫回归系数. 10.独立性检验(1)若变量的不同“值”表示个体所属的不同类别,则这些变量称为分类变量. (2)两个分类变量X 与Y 的频数表,称作2×2列联表.二.随机事件的概率1.随机事件和确定事件:在一定的条件下所出现的某种结果叫做事件. (1)在条件S 下,一定会发生的事件叫做相对于条件S 的必然事件. (2)在条件S 下,一定不会发生的事件叫做相对于条件S 的不可能事件. (3)必然事件与不可能事件统称为确定事件.(4)在条件S 下可能发生也可能不发生的事件,叫做随机事件. (5)确定事件和随机事件统称为事件,一般用大写字母,,,A B C 表示.2.频率与概率(1)在相同的条件S 下重复n 次试验,观察某一事件A 是否出现,称n 次试验中事件A 出现的次数A n 为事件A 出现的频数,称事件A 出现的比例()An n f A n=为事件A 出现的频率. (2)对于给定的随机事件A ,如果随着试验次数的增加,事件A 发生的频率()n f A 稳定在某个常数上,把这个常数记作()p A ,称为事件A 的概率,简称为A 的概率. 3.互斥事件与对立事件互斥事件的定义:在一次试验中,不可能同时发生的两个事件叫做互斥事件.即A B 为不可能事件(AB φ=),则称事件A 与事件B 互斥,其含义是:事件A 与事件B 在任何一次试验中不会同时发生. 一般地,如果事件12,,,n A A A 中的任何两个都是互斥的,那么就说事件12,,,n A A A 彼此互斥.对立事件:若不能同时发生,但必有一个发生的两个事件叫做互斥事件;即A B 为不可能事件,而AB 为必然事件,那么事件A 与事件B 互为对立事件,其含义是:事件A 与事件B 在任何一次试验中有且仅有一个发生.互斥事件和对立事件的区别和联系:对立事件是互斥事件,但是互斥事件不一定是对立事件.两个事件互斥是两个事件对立的必要非充分条件.4.事件的关系与运算B或A B +)B (或AB )B 为不可能事件,那么称事件B φ=B 为不可能事件,B 为必然事件,那么称事件与事件B 互为对立事件B φ=且B =Ω5.随机事件的概率事件A 的概率:在大量重复进行同一试验时,事件A 发生的频率nm总接近于某个常数,在它附近摆动,这时就把这个常数叫做事件A 的概率,记作()p A .由定义可知()01p A ≤≤,显然必然事件的概率是1,不可能事件的概率是0. 5.概率的几个基本性质(1)概率的取值范围:()01p A ≤≤. (2)必然事件的概率:()1p A =. (3)不可能事件的概率:()0p A =. (4)互斥事件的概率加法公式: ①()()()p A B p A p B =+(,A B 互斥),且有()()()1p A A p A p A +=+=. ②()()()()1212n n p A A A p A p A p A =+++ (12,,,n A A A 彼此互斥).(5)对立事件的概率:()()1P A P A =-. 三.古典概型1. 一次试验连同其中可能出现的每一个结果称为一个基本事件,通常此试验中的某一事件A 由几个基本事件组成.如果一次试验中可能出现的结果有n 个,即此试验由n 个基本事件组成,而且所有结果出现的可能性都相等,那么每一基本事件的概率都是n1.如果某个事件A 包含的结果有m 个,那么事件A 的概率P (A )=nm . 基本事件的特点(1)任何两个基本事件是互斥的.(2)任何事件都可以表示成基本事件的和(除不可能事件).2.古典概型:具有以下两个特点的概率模型称为古典概率模型,简称古典概型. ①试验中所有可能出现的基本事件只有有限个,即有限性. ②每个基本事件发生的可能性相等,即等可能性. 概率公式:P (A )=A 包含的基本事件的个数基本事件的总数.四.几何概型1.(1)随机数的概念:随机数是在一定范围内随机产生的数,并且得到这个范围内任何一个数的机会是均等的. (2)随机数的产生方法①利用函数计算器可以得到0~1之间的随机数;②在Scilab 语言中,应用不同的函数可产生0~1或a~b 之间的随机数. 2.几何概型(1)定义:如果某个事件发生的概率只与构成该事件区域的长度(面积或体积等)成比例,则称这样的概率模型为为几何概率模型,简称几何概型.(2)特点:①无限性:在一次试验中,可能出现的结果有无限多个; ②等可能性:每个结果的发生具有等可能性. (3)几何概型的解题步骤:首先是判断事件是一维问题还是二维、三维问题(事件的结果与一个变量有关就是一维的问题,与两个变量有关就是二维的问题,与三个变量有关就是三维的问题);接着,如果是一维的问题,先确定试验的全部结果和事件A 构成的区域长度(角度、弧长等),最后代公式()p A =构成事件A 的区域长度面积或体积试验的全部结果所构成的区域长度面积或体积;如果是二维、三维的问题,先设出二维或三维变量,再列出试验的全部结果和事件A 分别满足的约束条件,作出两个区域,最后计算两个区域的面积或体积代公式.(4)求几何概型时,注意首先寻找到一些重要的临界位置,再解答.一般与线性规划知识有联系.3.几种常见的几何概型(1)设线段l 是线段L 的一部分,向线段L 上任投一点.若落在线段l 上的点数与线段L 的长度成正比,而与线段l 在线段l 上的相对位置无关,则点落在线段l 上的概率为: P=l 的长度/L 的长度(2)设平面区域g 是平面区域G 的一部分,向区域G 上任投一点,若落在区域g 上的点数与区域g 的面积成正比,而与区域g 在区域G 上的相对位置无关,则点落在区域g 上概率为: P=g 的面积/G 的面积(3)设空间区域上v 是空间区域V 的一部分,向区域V 上任投一点.若落在区域v 上的点数与区域v 的体积成正比,而与区域v 在区域v 上的相对位置无关,则点落在区域V 上的概率为: P=v 的体积/V 的体积 五.条件概率 1.条件概率及其性质(1)对于任何两个事件A 和B ,在已知事件A 发生的条件下,事件B 发生的概率叫做条件概率,用符号()/p B A 来表示,其公式为()()()/p AB p B A P A =.在古典概型中,若用()n A 表示事件A 中基本事件的个数,则()()()/n AB p B A n A =. (2)条件概率具有的性质: ①()0/1p B A ≤≤;② 如果B 和C 是两互斥事件,则()()()///p B C A p B A p C A =+.2.相互独立事件(1)对于事件A 、B ,若A 的发生与B 的发生互不影响,则称A 、B 是相互独立事件. (2)若A 与B 相互独立,则()()/p B A p B =,()()()()()/p AB p B A P A P A P B =⋅=⋅.(3)若A 与B 相互独立,则A 与B ,A 与B ,A 与B 也都相互独立. (4)若()()()p AB P A P B =⋅,则A 与B 相互独立. 【应试技巧点拨】 1.三种抽样方法的比较2.样本频率直方图与样本的数字特征在频率分布直方图中,平均数的估计值等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和;中位数的估计值,应使中位数左右两边的直方图面积相等;最高小长方形的中点所对应的数据值即为这组数据的众数.3.方差是刻画一组数据离散程度的量,方差越大,这组数据波动越大,越分散.讨论产品质量、售价高低、技术高低、产量高低、成绩高低、寿命长短等等问题,一般都是通过方差来体现.5.判断两变量是否有相关关系很容易将相关关系与函数关系混淆.相关关系是一种非确定性关系,即是非随机变量与随机变量之间的关系,而函数关系是一种因果关系.6.求回归方程,关键在于正确求出系数a,b,由于a,b的计算量大,计算时应仔细谨慎,分层进行,避免因计算而产生错误.(注意回归直线方程中一次项系数为b,常数项为a,这与一次函数的习惯表示不同)7.回归分析是处理变量相关关系的一种数学方法.主要解决:(1)确定特定量之间是否有相关关系,如果有就找出它们之间贴近的数学表达式;(2)根据一组观察值,预测变量的取值及判断变量取值的变化趋势;(3)求出回归直线方程.8.独立性检验是一种假设检验,在对总体的估计中,通过抽取样本,构造合适的随机变量,对假设的正确性进行判断.【考场经验分享】1.进行分层抽样时应注意以下几点:(1)分层抽样中分多少层、如何分层要视具体情况而定,总的原则是:层内样本的差异要小,两层之间的样本差异要大,且互不重叠;(2)为了保证每个个体等可能入样,所有层中每个个体被抽到的可能性应相同;(3)在每层抽样时,应采用简单随机抽样或系统抽样的方法进行抽样.2.在作茎叶图时,容易出现茎两边的数字不是从小到大的顺序排列,从而导致结论分析错误,在使用茎叶图整理数据时,要注意:一是数据不能遗漏,二是数据最好按从小到大顺序排列,对三组以上的数据,也可使用茎叶图,但没有表示两组记录那么直观、清晰.3.回归分析是对具有相关关系的两个变量进行统计分析的方法,只有在散点图大致呈线性时,求出的回归直线方程才有实际意义,否则,求出的回归直线方程毫无意义.4.根据回归方程进行预报,仅是一个预报值,而不是真实发生的值.5.r的大小只说明是否相关并不能说明拟合效果的好坏,R2才是判断拟合效果好坏的依据.6.独立性检验的随机变量K2=2.706是判断是否有关系的临界值,K2<2.076应判断为没有充分证据显示X与Y有关系,而不能作为小于90%的量化值来判断.7. 概率计算题的核心环节就是把一个随机事件进行类似本题的分拆,这中间有三个概念,事件的互斥,事件的对立和事件的相互独立,在概率的计算中只要弄清楚了这三个概念,根据实际情况对事件进行合理的分拆,就能把复杂事件的概率计算转化为一个个简单事件的概率计算,达到解决问题的目的.8.在解含有相互独立事件的概率题时,首先把所求的随机事件分拆成若干个互斥事件的和,其次将分拆后的每个事件分拆为若干个相互独立事件的乘积,这两个事情做好了,问题的思路就清晰了,接下来就是按照相关的概率值进行计算的问题了.9.相当一类概率应用题都是比如掷硬币、掷骰子、摸球等概率模型赋予实际背景后得出来的,我们在解题时就要把实际问题再还原为我们常见的一些概率模型,这就要根据问题的具体情况去分析,对照常见的概率模型,把不影响问题本质的因素去除,抓住问题的本质.【名题精选练兵篇】1.【2016广西钦州上学期期末,文18】某校高一某班的一次数学测试成绩的茎叶图和频率分布直方图因故都受到不同程度的损坏,但可见部分如下,据此解答如下问题:(Ⅰ)求分数在[50,60)的频率及全班人数;(Ⅱ)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;(Ⅲ)若规定:90分(包含90分)以上为优秀,现从分数在80分(包含80分)以上的试卷中任取两份分析学生失分情况,求在抽取的试卷中至少有一份优秀的概率.2.【2016河北唐山二模,文18】二手车经销商小王对其所经营的某一型号二手汽车的使用年数x (0<x ≤10)与销售价格y (单位:万元/辆)进行整理,得到如下的对应数据:(Ⅰ)试求y 关于x 的回归直线方程;(参考公式:b ˆ=ni =1∑x i y i -n ·x -y-ni =1∑x 2i -nx-2,a ˆ=y --b ˆx -.)(Ⅱ)已知每辆该型号汽车的收购价格为w =0.05x 2-1.75x +17.2万元,根据(Ⅰ)中所求的回归方程,预测x 为何值时,小王销售一辆该型号汽车所获得的利润z 最大? 解:(Ⅰ)由已知:x -=6,y -=10,5i =1∑x i y i =242,5i =1∑x 2i =220,^b =ni =1∑x i y i -nx -y-ni =1∑x 2i -nx-2=-1.45,a ˆ=y --^bx-=18.7;所以回归直线的方程为^y =-1.45x +18.7 (Ⅱ)z =-1.45x +18.7-(0.05x 2-1.75x +17.2)=-0.05x 2+0.3x +1.5 =-0.05(x -3)2+1.95,所以预测当x =3时,销售利润z 取得最大值.3.【2016吉林长春质量监测二,文18】近年来我国电子商务行业迎来篷布发展的新机遇,2015年双11期间,某购物平台的销售业绩高达918亿人民币.与此同时,相关管理部门也推出了针对电商的商品和服务的评价体系.现从评价系统中选出200次成功的交易,并对其评价进行统计,对商品的好评率为35,对服务的好评率为34,其中对商品和服务都做出好评的交易为80次. (1)是否可以在犯错误概率不超过0.1%的前提下,认为商品好评与服务好评有关?(2)若针对商品的好评率,采用分层抽样的方式从这200次交易中取出5次交易,并从中选择两次交易进行客户回访,求只有一次好评的概率.2()0.150.100.050.0250.0100.0050.0012.072 2.7063.841 5.024 6.6357.87910.828P K k k≥4.【2016辽宁省沈阳质量监测一,文19】为考查某种疫苗预防疾病的效果,进行动物实验,得到统计数据如下:现从所有试验动物中任取一只,(Ⅰ)求22⨯列联表中的数据x ,y ,A ,B 的值; (Ⅱ)绘制发病率的条形统计图,并判断疫苗是否有效? (Ⅲ)能够有多大把握认为疫苗有效?未注射 注射10000005016.6710.8285020603==≈>⨯⨯.所以至少有99.9%的把握认为疫苗有效.5.【2016新疆乌鲁木齐一诊,文19】某城市居民月生活用水收费标准为1.6,022.7,23.54.0,3.5 4.5t t W t t t t t ≤<⎧⎪≤<⎨⎪≤≤⎩()=(t 为用水量,单位:吨;W 为水费,单位:元),从该市抽取的100户居民的月均用水量的频率分布直方图如图所示.(I)求这100户居民的月均用水量的中位数及平均水费;(II )从每月所交水费在14元-18元的用户中,随机制取户,求2户的水费都超过16元的概率.未注射 注射()()0.50 2.250.28 2.750.12 3.25 2.70.08 3.750.04 4.2540.5⨯+⨯+⨯⨯+⨯+⨯⨯⨯⎤⎦5.05275=(元) …6分6. 【山东省青岛市2015届高三上学期期末】右图为某校语言类专业N 名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的学员数为21人 (I )求该专业毕业总人数N 和90~95分数段内的人数n ;(II )现欲将90~95分数段内的n 名人分配到几所学校,从中安排2人到甲学校去,若n 人中仅有两名男生,求安排结果至少有一名男生的概率.【解析】 (Ⅰ)8090分数段频率为1(0.040.03)50.35p =+⨯=,此分数段的学员总数为21人所以毕业生的总人数N 为21600.35N ==,9095分数段内的人数频率为21(0.010.040.050.040.030.01)50.1p =-+++++⨯=所以9095分数段内的人数600.16n =⨯=;(Ⅱ) 9095分数段内的6人中有两名男生,4名女生,设男生为12,A A ;女生为1234,,,B B B B ,设安排结果中至少有一名男生为事件A ,从中取两名毕业生的所有情况(基本事件空间)为121112131421222324121314232434;;;;;;;;;,,;;;;A A A B A B A B A B A B A B A B A B B B B B B B B B B B B B 共。
2016年高考数学三轮讲练测核心热点总动员(新课标版) 专题02 集合运算、简易逻辑

2016年高考三轮复习系列:讲练测之核心热点 【全国通用版】【名师精讲指南篇】【高考真题再现】1. 【2013⋅新课标全国卷】 已知集合A={1,2,3,4},2{|,}B x x n n A ==∈,则A∩B= ( )(A ){1,4}(B ){2,3} (C ){9,16} (D ){1,2} 【答案】A ;【解析】依题意,{}1,4,9,16B =,故{}1,4A B =.2. 【2013新课标全国卷】已知命题:p x R ∀∈,23x x <;命题:q x R ∃∈,321x x =-,则下列命题中为真命题的是( )(A )p q ∧(B )p q ⌝∧ (C )p q ∧⌝ (D )p q ⌝∧⌝【答案】B ;3. 【2013⋅新课标全国理】已知集合{}220A x x x =->,{B x x =<,则( )A 、A∩B=∅B 、AB=R C 、B ⊆A D 、A ⊆B【答案】B ;【解析】依题意{0A x x =<或}2x >,由数轴可知,选B.4.【2014全国1】已知集合{}{}22|,032|2<≤-=≥--=x x B x x x A ,则=B A ( ) A .]1,2[-- B . )2,1[- C..]1,1[- D .)2,1[【答案】A 【解析】由已知得,{1A x x =≤-或}3x ≥,故{}21A B x x =-≤≤-,选A .5.【2014高考全国1】已知集合{}{}|13,|21M x x N x x =-<<=-<<,则MN =( ) A. )1,2(- B. )1,1(- C. )3,1( D. )3,2(-【答案】B【解析】根据集合的运算法则可得:{}|11MN x x =-<<,即选B . 6.【2015全国I 文】已知集合{32,},{6,8,10,12,14}A xx n n B ==+∈=N ,则集合A B中元素的个数为( ).A. 5B. 4C. 3D. 2【答案】D7.【2015全国II 理】已知集合{}2,1,0,2A =--,()(){}120B x x x =-+<,则AB =(). A.{}1,0- B. {}0,1 C.{}1,0,1- D. {}0,1,2 【答案】A【解析】对于B 集合,由已知得,{}21B x x =-<<,用数轴可得{}1,0AB =-.故选A.8.【2015全国I 理】设命题:p n ∃∈N ,22n n >,则p ⌝为().A .n ∀∈N ,22n n >B .n ∃∈N ,22n n …C .n ∀∈N ,22n n …D .n ∃∈N ,22n n =【答案】C【解析】存在的否定是任意,大于的否定是小于等于,所以:N p n ⌝∀∈,22n n …. 故选C .【热点深度剖析】1.高考对集合问题的考查,主要以考查概念和计算为主,考查两个集合的交集、并集、补集运算;从考查形式上看,主要以小题形式出现,常联系不等式的解集与不等关系,试题难度较低,一般出现在前三道题中,常考查数形结合、分类讨论等数学思想方法, 2013年文科考查集合的运算,理科考查不等式的解集,2014年文科考查集合的运算,理科考查不等式的解集,2015全国卷考查了离散型数集的交集运算及不等式的解法,预测2016年高考仍是考查集合的运算为主,理科可能与指对不等式及分式不等式结合,会涉及到集合的交集、并集、补集, 文科主要考查集合的交集与并集运算.2.命题及其关系,以及逻辑联结词, 全称量词与存在量词,此部分知识在高考命题中多以选择题和填空题的形式出现,主要考查基本概念,四种命题中互为等价的命题, 全称量词与存在量词的否定是考查的重点.常以本节知识作为载体考查函数、立体几何、解析几何等内容;以逻辑推理知识为命题背景的解答题也会出现.2015年全国卷1考查了全称命题的否定,预测2016年全国卷1不会再出现全称命题与特称命题的否定,但全国卷2有可能跟进。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【名师精讲指南篇】 【高考真题再现】1.【2013⋅新课标全国】已知曲线1C 的参数方程为45cos ,55sin x t y t=+⎧⎨=+⎩(t 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线2C 的极坐标方程为2sin ρθ=. (Ⅰ)把1C 的参数方程化为极坐标方程;(Ⅱ)求1C 与2C 交点的极坐标(0,02ρθπ≥≤<).【解析】(1)先利用参数方程得到C 1的一般方程,进而得到极坐标方程;(2)联立求出交点坐标,进而求出极坐标.2.【2014高考全国1第23题】已知曲线221:149x y C +=,直线l :2,22,x t y t =+⎧⎨=-⎩(t 为参数).(I )写出曲线C 的参数方程,直线l 的普通方程;(II )过曲线C 上任意一点P 作与l 夹角为30︒的直线,交l 于点A ,PA 的最大值与最小值.【解析】(I )曲线C 的参数方程为2cos ,3sin ,x y θθ=⎧⎨=⎩(θ为参数).直线l 的普通方程为260x y +-=.(II )曲线C 上任意一点(2cos ,3sin )P θθ到l 的距离为3sin 6d θθ=+-.则)6sin 30d PA θα==+-.其中α为锐角,且4tan 3α=.当sin()1θα+=-时,PA 取到最大值,最大值为5.当sin()1θα+=时,PA 取到最小值,最小值为5. 3.【2015全国Ⅱ】在直线坐标系xOy 中,曲线1C :{c ,os sin ,x t y t αα==(t 为参数,0t ≠)其中0πα剟.在以O 为极点,x 轴正半轴为极轴的极坐标系中,曲线2C :2sin ρθ=,3C :ρθ=.(1)求2C 与3C 交点的直角坐标;(2)若1C 与2C 相交于点A ,1C 与3C 相交于点B ,求AB 的最大值.4.【2015全国Ⅰ】在直角坐标系xOy 中,直线1C :2x =-,圆2C :()()22121x y -+-=,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系. (1)求12,C C 的极坐标方程. (2)若直线3C 的极坐标方程为()π4θρ=∈R ,设2C 与3C 的交点为,M N ,求2C MN △的面积.解析(1)由1C :2x =-,可得极坐标方程为cos 2ρθ=-, 由2C :2221441x x y y -++-+=,得极坐标方程为22cos 4sin 40ρρθρθ--+=.【热点深度剖析】2013年高考主要考查圆的参数方程,参数方程与普通方程的互化,普通方程与极坐标方程互化,极坐标方程与普通方程互化,主要考查学生的转化与化归能力. 2014年高考考查了椭圆和直线的参数方程,点到直线的距离公式,解直角三角形.2015年考查了直角坐标与极坐标方程的互化、圆的几何性质、三角函数的最值 从三年试题来看,高考对这部分要求不是太高,要求会参数方程与普通方程,极坐标方程与普通方程互化,主要考查学生的转化与化归能力,利用参数方程研究轨迹问题. 预测2016年高考仍然考查圆,直线,椭圆的参数方程与普通方程,极坐标方程与普通方程互化,重点是直线和圆的参数方程,极坐标方程,考查学生的转化与化归能力. 【重点知识整合】1.极坐标和直角坐标的互化公式若点M 的极坐标为(ρ,θ),直角坐标为(x ,y ),则⎩⎪⎨⎪⎧x =ρcos θy =ρsin θ⎩⎪⎨⎪⎧ρ2=x 2+y 2tan θ=y x ,x ≠0.求曲线的极坐标方程f (ρ,θ)=0的步骤与求曲线的直角坐标方程步骤完全相同.特别注意的是求极坐标方程时,常常要解一个三角形. (4)极坐标方程ρ=ρ(θ)表示的平面图形的对称性: 若ρ(-θ)=ρ(θ),则图形关于极轴对称;若ρ(π-θ)=ρ(θ),则图形关于射线θ=π2对称;若ρ(π+θ)=ρ(θ),则图形关于极点对称. 2.特殊的常见曲线(包括直线)的极坐标方程①圆心在极轴上点C (a,0),过极点的圆方程ρ=2a cos θ. ②圆心在极点、半径为r 的圆的极坐标方程ρ=r .③圆心在⎝⎛⎭⎪⎫a ,π2处且过极点的圆方程为ρ=2a sin θ(0≤θ≤π).④过极点倾角为α的直线的极坐标方程为: θ=α或θ=π+α.⑤过A (a,0)(a >0)与极轴垂直的直线ρcos θ=a .⑥过A ⎝⎛⎭⎪⎫a ,π2(a >0)与极轴平行的直线ρsin θ=a . 3.参数方程的概念在平面直角坐标系中,如果曲线上任意一点的坐标x 、y 都是某个变数t 的函数⎩⎪⎨⎪⎧x =f (t )y =g (t )(*),并且对于t 的每一个允许值,由方程组(*)所确定的点M (x ,y )都在这条曲线上,而这条曲线上任一点M (x ,y )都可以通过(*)式得到,则方程组(*)就叫做这条曲线的参数方程,变数t 叫做参数这时,参数t 的几何意义是:以直线l 上点M (x 0,y 0)为起点,任意一点N (x ,y )为终点的有向线段的数量为MN 且|t |=|MN |. 4.圆的参数方程(1)圆心在原点、半径为r 的圆的参数方程为⎩⎪⎨⎪⎧x =r cos θy =r sin θ(θ为参数);(2)圆心为C (a ,b ),半径为r 的圆的参数方程为⎩⎪⎨⎪⎧x =a +r cos θy =b +r sin θ(θ为参数).5.参数方程和普通方程的互化(1)化参数方程为普通方程:消去参数.常用的消参方法有代入消去法、加减消去法、恒等式(三角的或代数的)消去法.(2)化普通方程为参数方程:引入参数,即选定合适的参数t ,先确定一个关系x =f (t )〔或y=φ(t )〕,再代入普通方程F (x ,y )=0,求得另一关系y =φ(t )〔或x =f (t )〕. 【应试技巧点拨】 1.极坐标与直角坐标的互化(1)极坐标与直角坐标互化的前提条件:①极点与原点重合;②极轴与x 轴正向重合;③取相同的单位长度.(2)直角坐标方程化为极坐标方程比较容易,只要运用公式cos x ρθ=及sin y ρθ=直接代入并化简即可;而极坐标方程化为直角坐标方程则相对困难一些,解此类问题常通过变形,构造形如cos ρθ,sin ρθ,2ρ的形式,进行整体代换. 2.求曲线的极坐标方程求曲线的极坐标方程的步骤:(1)建立适当的极坐标系,设(),P ρθ是曲线上任意一点;(2)由曲线上的点所适合的条件,列出曲线上任意一点的极径ρ和极角θ之间的关系式;(3)将列出的关系式进行整理、化简,得出曲线的极坐标方程. 3.参数方程与普通方程的互化在求出曲线的参数方程后,通常利用消参法得出普通方程.一般地,消参数经常采用的是代入法和三角公式法,但将曲线的参数方程化为普通方程,不只是把其中的参数消去,还要注意x ,y 的取值范围在消参前后应该是一致的,也就是说,要使得参数方程与普通方程等价,即它们二者要表示同一曲线. 4.直线的参数方程及应用根据直线的参数方程的标准式中t 的几何意义,有如下常用结论:(1)直线与圆锥曲线相交,交点对应的参数分别为12,t t ,则弦长12l t t =-; (2)定点0M 是弦12M M 的中点⇒120t t +=; (3)设弦12M M 中点为M ,则点M 对应的参数值122M t t t += (由此可求12M M 及中点坐标). 5.圆与圆锥曲线的参数方程及应用解决与圆、圆锥曲线的参数方程有关的综合问题时,要注意普通方程与参数方程的互化公式,主要是通过互化解决与圆、圆锥曲线上动点有关的问题,如最值、范围等. 【考场经验分享】1.在极坐标系中,如无特别说明时,0ρ≥,R θ∈;点的极坐标不惟一,若规定0ρ≥,02θπ≤<,则极坐标系中的点与点的极坐标形成一一对应关系(极点除外);曲线上的点的极坐标不一定满足曲线的极坐标方程,但曲线上一点P 的无数个极坐标中必有一个适合曲线的极坐标方程.2.极坐标方程1θθ=表示一条射线并非直线,只有当允许0ρ<时,1θθ=才表示一条直线.3.只有在a 2+b 2=1时,直线⎩⎪⎨⎪⎧x =x 0+at y =y 0+bt(t 为参数)中的参数t 才表示由M (x 0,y 0)指向N (x ,y )的有向线段的数量,而在a 2+b 2≠1时,|MN |=a 2+b 2·t .4.消参后应将原参数的取值范围相应地转化为变量x (或y )的取值范围. 【名题精选练兵篇】1.【2016广西桂林市、北海市、崇左市3月联合调研】已知曲线C 的极坐标方程是4cos ρθ=.以极点为平面直角坐标系的原点,极轴为x 轴的正半轴,建立平面直角坐标系,直线l 的参数方程是1cos sin x t y t αα=+⎧⎨=⎩(t 为参数).(1)将曲线C 的极坐标方程化为直角坐标方程;(2)若直线l 与曲线C 相交于A 、B 两点,且AB =求直线的倾斜角α的值.2.【2016吉林长春质量监测(二)】在直角坐标系x O y 中,曲线1C 的参数方程为2cos sin x t y t αα=+⎧⎪⎨=⎪⎩(t 是参数),以原点O 为极点,x 轴正半轴为极轴建立极坐标系,曲线2C 的极坐标方程为8cos()3πρθ=-.(1)求曲线2C 的直角坐标方程,并指出其表示何种曲线;(2)若曲线1C 与曲线2C 交于A ,B 两点,求||AB 的最大值和最小值. 【解析】(1) 对于曲线2C 有8cos()3πρθ=-,即24cos sin ρρθθ=+,因此曲线2C的直角坐标方程为2240x y x +--=,其表示一个圆.(2) 联立曲线1C 与曲线2C的方程可得:2130t t α-⋅-=,12||||AB t t=-===因此||AB的最小值为最大值为8.3.【2016年安徽省“江南十校”联考】在平面直角坐标系xOy中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知在极坐标系中,),(),,(33233ππBA,圆C的方程为θρcos2=(Ⅰ)求在平面直角坐标系xOy中圆C的标准..方程;(Ⅱ)已知P为圆C上的任意一点,求ABP∆面积的最大值.4.【2016河南新乡许昌平顶山二调】在直角坐标系xOy中,曲线C1的参数方程为22xαα⎧⎨⎩=+cosy=2sin(α为参数),曲线C2的参数方程为22xββ⎧⎨⎩=cosy=2+sin(β为参数),以O为极点,x轴的正半轴为极轴建立极坐标系.(Ⅰ)求曲线C1和曲线C2的极坐标方程;(Ⅱ)已知射线l 1:θ=α(π02α<<)将射线l 1顺时针旋转π6得到射线l 2:θ=α-π6, 且射线l 1与曲线C 1交于O 、P 两点,射线l 2与曲线C 2交于O 、Q 两点,求|OP |·|OQ |的 最大值.【解析】(1)曲线1C 的直角坐标方程为22(2)4x y -+=,所以1C 极坐标方程为4cos ρθ= 曲线2C 的直角坐标方程为22(2)4x y +-=,所以2C 极坐标方程为4sin ρθ= (2)设点P 极点坐标1(,)ρα,即14cos ρα= 点Q 极坐标为2π(,())6ρα- 即2π4sin()6ρα=-则12π||||4cos 4sin()6OP OQ ρραα⋅==⋅-=116cos cos )2ααα⋅- π8sin(2)46α=--π(0,)2α∈,ππ5π2(,)666α∴-∈-,当ππ2,62α-=即π3α=时,||||OP OQ ⋅取最大值4.5.【2016福建4月质检】在直角坐标系xOy 中,曲线C 的参数方程为,sin cos 3⎩⎨⎧==ααy x (其中α为参数),以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系中,直线l 的极坐标方程为24sin =⎪⎭⎫⎝⎛-πθρ.(Ⅰ)求C 的普通方程和直线l 的倾斜角;(Ⅱ)设点P (0,2),l 和C 交于A ,B 两点,求PB PA +.即,222x y ⎧=⎪⎪⎨⎪=+⎪⎩(t 为参数),代入2219x y +=并化简,得25270t ++=.(245271080∆=-⨯⨯=>.设,A B 两点对应的参数分别为12,t t ,则1212270,05t t t t +=<=>, 所以120,0,t t <<所以()1212PA PB t t t t +=+=-+= 解法二:(Ⅰ)同解法一. (Ⅱ)直线l 的普通方程为2y x =+.由222,99y x x y =+⎧⎨+=⎩消去y 得21036270x x ++=, 于是236410272160∆=-⨯⨯=>.设1122(,),(,)A x y B x y ,则12180,5x x +=-<1227010x x =>,所以120,0x x <<.故12120|0||PA PB x x x x +=--=+=6.【2106辽宁省沈阳质量监测(一)】在以直角坐标原点O 为极点,x 的非负半轴为极轴的极坐标系下,曲线1C 的方程是1ρ=,将1C 向上平移1个单位得到曲线2C . (Ⅰ)求曲线2C 的极坐标方程;(Ⅱ)若曲线1C 的切线交曲线2C 于不同两点,M N ,切点为T .求TM TN ⋅的取值范围.(Ⅱ)由题令00(,)T x y ,0(0,1]y ∈,切线MN 的倾斜角为θ,所以切线MN 的参数方程为:00cos sin x x t y y t θθ=+⎧⎨=+⎩(t 为参数). 联立2C 的直角坐标方程得,20002(cos sin sin )120t x y t y θθθ++-+-= ,即由直线参数方程中,t 的几何意义可知,012TM TN y ⋅=-,因为012[1,1)y -∈-所以TM TN ⋅[0,1]∈.此题也可根据图形的对称性推出答案,此种方法酌情给分.7.【2016年安庆二模】在平面直角坐标系中,以原点为极点,x 轴正半轴为极轴建立极坐标系,并在两坐标系中取相同的长度单位.已知曲线C 的极坐标方程为2cos ρθ=,直线l 的参数方程为1cos sin x t y t αα=-+⎧⎨=⎩(t 为参数,α为直线的倾斜角).(I )写出直线l 的普通方程和曲线C 的直角坐标方程; (II )若直线l 与曲线C 有唯一的公共点,求角α的大小. 【解析】(Ⅰ)当π2a =时,直线l 的普通方程为1x =-; 当π2a ≠时,直线l 的普通方程为(tan )(1)y x a =+. 由θρcos 2=,得θρρcos 22=,所以222x y x +=,即为曲线C 的直角坐标方程.(Ⅱ)把a t x cos 1+-=,sin y t a =代入222x y x +=,整理得24cos 30t t a -+=.由012cos 162=-=∆α,得23cos 4=a ,所以cos =a 或cos =a -,故直线l 倾斜角α为π6或5π6. 8.【2016甘肃兰州实战考试,理23】所以1212PA PB t t t t +=+=+=9. 【2015届陕西省宝鸡市九校高三联合检测】坐标系与参数方程在直角坐标系xOy 中,圆C 的参数方程1cos (sin x y ϕϕϕ=+⎧⎨=⎩为参数).以O 为极点,x 轴的非负半轴为极轴建立极坐标系.(Ⅰ)求圆C 的极坐标方程; (Ⅱ)射线:4OM πθ=与圆C 的交点为O 、P 两点,求P 点的极坐标.10. 【2015届河北省唐山市高三第一次模拟】已知椭圆C :22143x y +=,直线3:x l y t⎧=-⎪⎨=⎪⎩(t 为参数).(Ⅰ)写出椭圆C 的参数方程及直线l 的普通方程;(Ⅱ)设(1,0)A ,若椭圆C 上的点P 满足到点A 的距离与其到直线l 的距离相等,求点P 的坐标.【解析】(Ⅰ)C:2cos x y θθ=⎧⎪⎨=⎪⎩(θ为参数),l :xy +9=0.(Ⅱ)设(2cos ,)P θθ,则||2cos AP θ==-,P 到直线l 的距离|2cos 3sin 9|2cos 3sin 922d θθθθ-+-+==.由|AP|=d 得3sin θ-4cos θ=5,又sin 2θ+cos 2θ=1,得3sin 5θ=,4cos 5θ=-.故8(5P -. 11. 【2015届河北唐山市高三上学期期末考试】极坐标系的极点为直角坐标系xOy 的原点,极轴为x 轴的正半轴,两种坐标系中的长度单位相同. 已知曲线C 的极坐标方程为2(cos sin )ρθθ=+l 交y 轴于点(0,1)E .(1)求C 的直角坐标方程,l 的参数方程;(2)直线l 与曲线C 交于A 、B 两点,求||||EA EB +.【解析】(Ⅰ)由ρ=2(cos θ+sin θ),得ρ2=2(ρcos θ+ρsin θ),即x 2+y 2=2x +2y ,即(x -1) 2+(y -1) 2=2.直线l的参数方程为121x t y ⎧=⎪⎪⎨⎪=⎪⎩(t 为参数, t∈R)(Ⅱ)将121x t y ⎧=⎪⎪⎨⎪=+⎪⎩,代入(x -1) 2+(y -1) 2=2得t 2-t -1=0,解得,12t t ==,则 |EA|+|EB|=| t 1|+| t 2|=|t 1-t 2|.12.已知圆锥曲线2cos :x C y αα=⎧⎪⎨=⎪⎩(α为参数)和定点A ,1F 、2F 是此圆锥曲线的左、右焦点,以原点O 为极点,以x 轴的正半轴为极轴建立极坐标系. (1)求直线2AF 的直角坐标方程;(2)经过点1F 且与直线2AF 垂直的直线l 交此圆锥曲线于M 、N 两点,求11||||MF NF -的值.13 .已知曲线C 的极坐标方程为θθρ2sin cos 4=,以极点为坐标原点,极轴为x 轴正半轴建立平面直角坐标系,直线l 的参数方程为⎪⎪⎩⎪⎪⎨⎧+=-=t y tx 22122(t 为参数) (1)把曲线C 的极坐标方程化为直角坐标方程,把直线l 的参数方程化为普通方程; (2)求直线l 被曲线C 截得的线段AB 的长.14.已知曲线C 的极坐标方程是2sin ρθ=,直线l 的参数方程是32,545x t y t ⎧=-+⎪⎨⎪=⎩(t 为参数).(Ⅰ)将曲线C 的极坐标方程化为直角坐标方程;(Ⅱ)设直线l 与x 轴的交点是M ,N 是曲线C 上一动点,求MN 的最大值. 【解析】(Ⅰ)曲线C 的极坐标方程可化为22sin ρρθ=, 又222,cos ,sin x y x y ρρθρθ+===, 所以曲线C 的直角坐标方程为2220x y y +-=,(Ⅱ)将直线l 的参数方程化为直角坐标方程,得4(2)3y x =--,令0y =,得2x =,即M 点的坐标为(2,0). 又曲线C 为圆,圆C 的圆心坐标为(1,0),半径1r =,则MC =所以1MN MC r +=≤.15. 在直角坐标系中,以原点为极点,x 轴的正半轴为极轴建立极坐标系,已知曲线C :2sin 2cos (0)a a ρθθ=>,过点P (-2,-4)的直线l的参数方程为2242x y ⎧=-+⎪⎪⎨⎪=-+⎪⎩(t 为参数)l 与C 分别交于M ,N.(1)写出C 的平面直角坐标系方程和l 的普通方程; (2)若PM ,MN ,PN 成等比数列,求a 的值.【解析】(1)曲线C 的直角坐标方程为22(0)y ax a =>;直线l 的普通方程为20x y --=.(2)将直线1的参数方程与C的直角坐标方程联立,得22(48(4)0(*)t a a -+++=8(4)0a a ∆=+>.设点M ,N 分别对应参数t 1,t 2,恰为上述方程的根.则1PM t =,2PN t =,12MN t t =-.由题设得21212()t t t t -=,即2121212()4t t t t t t +-=.由(*)得122(4t t a +=+,128(4)0t t a =+>,则有2(4)5(4)0a a +-+=,得1a =,或4a =-.因为0a >,所以1a =. 16. 已知曲线C 1:4cos ,3sin ,x t y t =-+⎧⎨=+⎩ (t 为参数), C 2:8cos ,3sin ,x y θθ=⎧⎨=⎩(θ为参数).(1)分别求出曲线C 1,C 2的普通方程; (2)若C 1上的点P 对应的参数为2t π=,Q 为C 2上的动点,求PQ 中点M 到直线332,:2x t C y t=+⎧⎨=-+⎩ (t 为参数)距离的最小值及此时Q 点坐标.【名师原创测试篇】1.在直角坐标系x y O 中,以原点O 为极点,以x 轴正半轴为极轴,建立极坐标系,曲线1C 的极坐标方程为()sin cos 1ρθθ+=,曲线2C 的参数方程为2cos sin x y θθ=⎧⎨=⎩.()1求曲线1C 的直角坐标方程与曲线2C 的普通方程;()2试判断曲线1C 与2C 是否存在两个交点?若存在,求出两交点间的距离;若不存在,说明理由.【解析】 (1) 对于曲线1C :()sin cos 1ρθθ+=,得sin cos 1ρθρθ+=,故有1x y +=,对于曲线2C :2cos sin x y θθ=⎧⎨=⎩,消去参数得2214x y +=.(2) 显然曲线1C :1x y +=为直线,则其参数方程可写为21x y ⎧=⎪⎪⎨⎪=-⎪⎩t 为参数),与曲线2C :2214x y +=联立方程组得2580t -+=,可知(24581280∆=-⨯⨯=>,所以1C 与2C 存在两个交点,由12t t +=1285t t =,得21||d t t =-==. 2. 已知曲线C 的极坐标方程是2sin ρθ=,直线l 的参数方程是32,545x t y t ⎧=-+⎪⎨⎪=⎩(t 为参数).(Ⅰ)将曲线C 的极坐标方程化为直角坐标方程;(Ⅱ)设直线l 与x 轴的交点是M ,N 是曲线C 上一动点,求MN 的最大值.3. 已知曲线C 的参数方程: cos sin x a y b αα=⎧⎨=⎩(α为参数), 曲线C上的点(1,2M 对应的参数4πα=,以坐标原点O 为极点,以x 轴正半轴为极轴,建立极坐标系.(Ⅰ)求曲线C 的极坐标方程;(Ⅱ)已知直线l 过点)0,1(P ,且与曲线C 于B A ,两点,求PB PA ⋅的范围.【解析】(Ⅰ)将点(1,)2M 和4πθ=代入曲线C 的参数方程:cos sin x a y b αα=⎧⎨=⎩中得,1,222a =⎪=⎩,所以a =1b =,所以曲线C的参数方程为sin x y αα⎧=⎪⎨=⎪⎩,化为普通方程为2212x y +=,所以曲线C 的极坐标方程2222cos 2sin 2ρθρθ+=. (Ⅱ)设直线参数方程为直线l 的参数方程:1cos (sin x t t y t θθ=+⎧⎨=⎩为参数),代入到曲线C 方程里,得到01cos 2)sin 1(22=-++θθt t ,21t t PB PA =,由韦达定理可得到θ2sin 11+=⋅PB PA ,因为]1,0[sin 2∈θ,所以211sin PA PB θ⋅=+1[,1]2∈ 4. 已知极坐标系的极点在直角坐标系的原点,极轴与x 轴的正半轴重合.曲线C 的极坐标方程为22312sin ρθ=+,直线l的参数方程为1x y t ⎧=⎪⎨=+⎪⎩(t 为参数,t ∈R ).试在曲线C 上求一点M ,使它到直线l 的距离最大.5. 以平面直角坐标系的原点为极点,x 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,已知直线l 的参数方程是13x t y t =+⎧⎨=-⎩(t 为参数),圆C 的极坐标方程是θρcos 4=.(Ⅰ)求直线l 的方程和圆C 的直角坐标方程; (Ⅱ)求直线l 被圆C 截得的弦长.6. 在直角坐标系中,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为2sin 2cos ρθθ=+,曲线D 的参数方程为11cos 2211sin 2x t y t⎧=-+⎪⎪⎨⎪=+⎪⎩(t 为参数).(Ⅰ)把C 的极坐标方程化为直角坐标方程; (Ⅱ)判定曲线C 与曲线D 间的位置关系.【解析】(Ⅰ)由2sin 2cos ρθθ=+得22cos 2sin ρρθρθ=+,将222x y ρ=+,cos ,sin x y ρθρθ==代入得22220x y x y +--=,即为曲线C 的普通方程. (Ⅱ)由(1)知曲线C 的直角坐标方程为:22220x y x y +--=,即22(1)(1)2x y -+-=,是圆心C (1,1),半径1r D 的参数方程化为普通方程为2211()(1)24x y ++-=,曲线D是圆心D (12-,1),半径2r =1212<||CD =3212,∴两圆相交.。
