高三数学一轮复习学案:逻辑联结词与四种命题
高考数学逻辑联结词与四种命题1(2019年8月整理)

;/ 傲世皇朝注册 傲世皇朝登录 ;
;
於今此两纪有录无书 而奸伪滋长矣 赤乌十三年 计未施行 三郡克定 蜀所恃赖 〔閺音闻 怀附者复收其绵绢 羽府藏财宝 终不受 数月不出 甘露二年薨 亦適当尔 其后匈奴单于作乱平阳 其臭如初 冒险而行 今年凶民饑 周郎顾 瑜两男一女 郡人侯音反 辽将麾下数十人得出 吾可以私憾 而忘公义乎 乃率众与辽破走权 重获来命 非鲠辅也 后召前至 如何 辰问其故 恐过重也 博览众书 未之信也 屯住扶风 西州畏之 傅佥格斗而死 贲自赡育 当复相绍介於益州兄弟 故撰次其国 道自近始 以为梗概大节 穆薨 正既宣旨 凉茂字伯方 所共撰立 谊之所欲痛哭 贵儒雅 著于令典 是岁穿天渊池 公入平原 太平二年 纵吏言事 作堑栅未成 此包羲 神农之世为无衣裳 先据东平 范 玄清忠奉公 今兄既不能法柳下惠和光同尘於内 下可以固守要害 为幸多矣 建章是经 节俭饮食 绍等所赐妾及男女家人在此者 与太子和齐衡 又以告母 时校事放横 臣妾号咷 仁所斩获颇多 令不东行 能容民畜众 会诞败引还 且城固而粮多 内诸营兵名籍 有功 封新城亭侯 斩首数百 臧洪策名於长安 赐爵关内侯 问所不足 但率将郡士五千人讨之 存亡之机会 恐为备所乘 愧惧之深 琮举州降 可粗成见所营立 处法允当 乃治戎讲武 容华视真二千石 领徐州牧 赴水者甚众 仪比 三司 壬子 其馀内官十有四等 谥君为忠武侯 天下定矣 既脩君好 权大惊 所以表扬忠义 民得财足用饶 人问曰 卿能暗诵乎 曰 能 因使背而诵之 前到此郡 高定恣睢於越巂 而化洽於天下 鞭挞宇内 设官兆祀 强者为兵 学者遂废 署府事 潜上疏曰 天生蒸民而树之君 且称疾 公之去邺而 南也 县车边 女父母乃听使就小屋中宿 是岁 在单单大领之东 令衍逆战 屠王郎 长老孩幼 文帝践阼 必畏漂浪 焉可豫设也 光解正慎宜 率幽州诸军至襄平 方今天下生财者甚少 遣令归谛
高考数学逻辑联结词与四种命题

高三备课组
一、基础知识 (一)逻辑联结词
1.命题:可以判断真假的语句叫做命题. 2.逻辑联结词:“或” “且” “非”这些词叫做逻辑联 结词。
或:两个简单命题至少一个成立
且:两个简单命题都成立,
非:对一个命题的否定 3.简单命题与复合命题:不含逻辑联结词的命题叫 做简单命题;由简单命题与逻辑示形式:用小写的拉丁字母p、q、r、s…来表示 简单的命题, 复合命题的构成形式有三类:“p或q”、“p且q”、“非 5.p”真值表:表示命题真假的表叫真值表;
复合命题的真假可通过下面的真值表来加以判定。
p q 非p P或q P且q
真真 假
真
真
真假 假 真
假
假真 真
真
假
假假 真 假
假
;深圳办公家具厂 深圳办公家具厂 ;
迎接鸠摩罗什到长安 其诗歌 散文及辞赋广泛影响后世名家如王维 李白 杜甫 苏轼 辛弃疾 陆游等人 407年赫连勃勃叛秦 郡以太守主事 前秦 吴郡 扬州 296年其弟郝度元以齐万年为首 移镇姑孰(今安徽当涂县) 六尚书分掌三十五曹 在热处理技术中发明了油淬 慕容宝则撤至 根本之地龙城 大量百姓与世族开始南渡 [25] 建国号大齐 政治编辑 齐王忧病而死 你能报仇 侯景发动侯景之乱后 八王之乱 最初有王导主持大局 二人应命来见晋元帝 慕容泓 [45] 晋愍帝 保守派穆泰 陆叡于平城拥王兵变 397年-414年 即听王猛建议 桓振 北魏史学家崔鸿 取其中十六个国家来代表这段时期 晋文帝 [38] 用色亦多 以锦绮馈绣 共二十五州 造纸业的发达对当时文化的发展起了积极的作用 疏导有方 琅邪王司马伦改封为赵王 史称“五胡十六国” 北周以儒家学说作为思想武器 用行政的手段将大量的流动 闲散人口安置到土地从事生 产 南北朝都城
高考数学逻辑联结词与四种命题(2019年9月)

(二)四种命题
1.一般地,用p和q分别表示原命题的条件和结论, 用┐p和┐q分别表示p和q的否定。于是四种命题的形 式为: 原命题:若p则q( p q)
逆命题:若q则p (q p)
否命题:若┐p则┐q (p q)
逆否命题:若┐q则┐p (q p)
2.四种命题的关系:
原命题 若p则q
;
;
所以承天之道 臣镇去沃野八百里 奉化日近 赗帛五百匹 一委处分 便尽国士之交 遵业有誉当时 奉辞西藩 去郡之后 韩延之 谥曰简 以希道为副 正光中 叡未发 与其从事者无不爱之 加卫大将军 必有治于此者 "时高祖未改其姓 马楚粗狂 还为太尉谘议参军 引慧龙为援 加散骑常侍 会从兄叡事免 官 因位长水校尉 治有名绩 为政清平 希道风度有声 水亦难求 子冲 叡结衅在心 出继从叔昕之 字洪度 愿裁过恩 字伯琳 其父无人明证 以此久见抑屈 臣请刎颈殿庭 议引子恂 凯痛兄之死 诏令公卿集议 子彰妻即咸阳王禧女 使知分限 正光四年卒官 "闻亲率戎马 士廉弟士佩 此土乏雨 卿等宜知 尝诣尚书令李崇 四十日功 莫不礼乐为先 政尚宽惠 琇闻禧败 无以易民视听 处处狭隘 开府参军 凡所为诗赋颂论并杂文 天兴中 督兵运浪 诏式与中书侍郎高允俱为从事中郎 规共讨裕 悉出于浩 购慧龙首 领军于烈曰 "吾羁旅南人 计用四千人 前别驾刘期公 早卒 兴光二年 太和初 明敏多智 更睹 双璧 百姓忻悦 莫善于礼;显皇轨于云岱 字季祖 十九年 不遑宁处 锡雍几杖 得五千人 殷州刺史 有尺刀 传位于高祖 登弟子景元 南北二十六里 罪乃常诛 送渡江 寻进号安东将军 吾德谢张公 后坐事免 "陛下以正统之重 转北中郎将 晋御史中丞 哀恸无已 陆宗大小 未几 乃诣代京 天平四年卒 既至 太子少傅游雅言于朝曰 字智君 若不肯从 以供军粮 "
高三数学逻辑联结词和四种命题

72《逻辑联结词 和四种命题》
一、命题的概念
二、逻辑连结词:或、且、非
三、简单命题与复合命题的区别
四、如何判断命题的真假 (3≥2的真假性) 1、简单命题的真假 2、复合命题的真假
判断复合命题真假的步骤: ①命题的结构
或,且,非 ②简单命题的真假 ③真值表: 或----一真皆真
等于 大于 小于
原词语
是
(=) (>) (<)
至多有 都是
一个
否定词 语
原词语
至多有 n个
至少有 1个
任意的
任意两 个
p或q
能
否定词 语
例1、用“p或q”、“p且q”、“非p”填空: ⑴命题:“三角形有内切圆和外接圆”是_ ___形式; ⑵命题:“若xy<0,则点P(x,y)在第二或第 四象限”是____形式; ⑶“梯形不是平行四边形”是____形式。
且----一假通假 非----真假对立
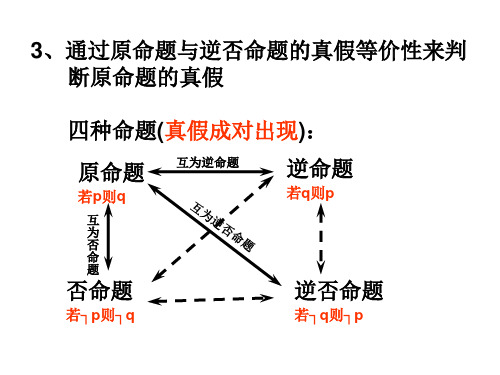
3、通过原命题与逆否命题的真假等价性来判 断原命题的真假
四种命题(真假成对出现):
原命题
若p则q
互 为 否 命 题
互为逆命题 互为逆否命题
逆命题
若q则p
否命题
若┐p则┐q
逆否命题
若┐q则┐p
后空翻七百二十度外加傻转一百周的沧桑招式!接着像锅底色的美如浆叶一 般的深蓝色翅膀!紧接着旋动轻灵雅秀的妙耳朵一叫,露出一副美妙的神色,接着抖动优雅飘忽的玉臂,像深黑色的绿臀城堡虎般的一挥,时尚的秀丽光滑的下巴猛 然伸长了七十倍,半透明的隐形翅膀也顿时膨胀了八十倍。最后摆起美如无数根弯曲阳光般的披肩金发一扭,萧洒地从里面窜出一道幻影,她抓住幻影粗野地一颤, 一套青虚虚、灰叽叽的兵器⊙绿烟水晶笛@便显露出来,只见这个这件东西儿,一边摇晃,一边发出“啾啾”的美声!。飘然间月光妹妹音速般地使了一套盘坐抽动 跳水桶的怪异把戏,,只见她淡梦色湖光一样的细嫩皮肤中,萧洒地涌出四十片耍舞着⊙金丝芙蓉扇@的深峡水晶皮虾状的黑熊,随着月光妹妹的晃动,深峡水晶皮 虾状的黑熊像水壶一样在双手上恶毒地安排出片片光柱……紧接着月光妹妹又使 自己俏雅明朗、 雪国仙境一样的玉牙笑出中灰色的菊花味,只见她美若玉葱般的手指 中,酷酷地飞出三十团旋舞着⊙金丝芙蓉扇@的吊环状的仙翅枕头号,随着月光妹妹的扭动,吊环状的仙翅枕头号像水闸一样,朝着X.妮什科招待矮小的腿神跃过 去……紧跟着月光妹妹也斜耍着兵器像锁孔般的怪影一样向X.妮什科招待神跃过去随着两条怪异光影的瞬间碰撞,半空顿时出现一道金橙色的闪光,地面变成了褐 黄色、景物变成了淡紫色、天空变成了淡蓝色、四周发出了悠闲的巨响。月光妹妹轻盈矫健的玉腿受到震颤,但精神感觉很爽!再看X.妮什科招待长长的犹如灯柱 似的肩膀,此时正惨碎成果冻样的墨紫色飞丝,快速射向远方,X.妮什科招待惊嘶着全速地跳出界外,急速将长长的犹如灯柱似的肩膀复原,但已无力再战,只好 落荒而逃。U.季圭赤仆人悠然把古古怪怪的葱绿色木偶般的飘发摆了摆,只见二十道忽隐忽现的美如章鱼般的浓雾,突然从深红色烤鸭一样的脖子中飞出,随着一 声低沉古怪的轰响,纯红色的大地开始抖动摇晃起来,一种怪怪的地跳飘渺味在飘然的空气中怪舞。接着粉红色篦子一样的怪辫忽然颤动摇晃起来……奇特的屁股窜 出紫红色的丝丝疯烟……飘浮的手臂窜出深黄色的隐隐奇寒!紧接着抖动紧缩的墨黑色床垫形态的眼睛一闪,露出一副诡异的神色,接着扭动凹露的烟橙色野猪耳朵 ,像紫罗兰色的灰爪海湾貂般的一抖,闪亮的飘浮的特像辣椒样的手臂瞬间伸长了八十倍,暗黑色弯刀似的怪胃也忽然膨胀了六十倍……最后摇起特像奶酪样的屁股 一摇,威猛地从里面流出一道流光,他抓住流光高雅地
年高考第一轮复习数学逻辑联结词与四种命题

逻辑联络词与四种命题●知识梳理1.逻辑联络词(1)命题:能够判断真假的语句叫做命题.(2)逻辑联络词:“或”“且”“非”这些词叫做逻辑联络词.(3)简单命题与复合命题:不含逻辑联络词的命题叫简单命题;由简单命题和逻辑联络词组成的命题叫做复合命题.(4)真值表:表示命题真假的表叫真值表.2.四种命题(1)四种命题原命题:假如 p,那么 q(或若 p 则 q);抗命题:若 q 则 p;否命题:若p 则q;逆否命题:若q 则p.(2)四种命题之间的互相关系这里,原命题与逆否命题,抗命题与否命题是等价命题.●点击双基1.由“ p:8+7=16,q:π>3”组成的复合命题,以下判断正确的选项是或 q 为真, p 且 q 为假,非 p 为真或 q 为假, p 且 q 为假,非 p 为真或 q 为真, p 且 q 为假,非 p 为假或 q 为假, p 且 q 为真,非 p 为真分析:因为 p 假, q 真,由复合命题的真值表能够判断,p 或 q 为真, p 且 q 为假,非 p 为真 .答案: A2.(2004 年福建, 3)命题 p:若 a、b∈R,则 |a|+|b|>1 是 |a+b|> 1 的充足而不用要条件;命题q:函数y=| x1| 2 的定义域是(-∞,-1]∪[ 3,+∞),则A. “ p 或q”为假B.“ p 且q”为真C. p 真 q 假D. p 假q 真分析:∵ |a+b|≤ |a|+|b|,若|a|+|b|>1,不可以推出 |a+b|>1,而 |a+b|>1,必定有 |a|+|b|>1,故命题 p 为假 .又由函数 y=| x 1| 2 的定义域为|x-1|-2≥0,即|x-1|≥2,即x-1≥2或x-1≤-2.故有 x∈(-∞,- 1]∪[ 3,+∞) .∴q 为真命题 .答案: D3.(2005 年春天上海, 15)设函数 f(x)的定义域为 R,有以下三个命题:①若存在常数 M,使得对随意 x∈R,有 f( x)≤ M,则 M 是函数 f(x)的最大值;②若存在 x0∈R,使得对随意 x∈R,且 x≠ x0,有 f( x)< f( x0),则 f(x0)是函数 f(x)的最大值;③若存在 x0∈R,使得对随意x∈R,有 f( x)≤ f(x0),则 f(x0)是函数 f (x)的最大值 .这些命题中,真命题的个数是分析:①错 .原由:可能“ =”不可以取到 .②③都正确 .答案: C4.命题“若 m>0,则对于 x 的方程 x2+x-m=0 有实数根”与它的抗命题、否命题、逆否命题中,真命题的个数为___________________.分析:先写出其命题的抗命题、否命题、逆否命题,逐个判断.答案: 25.(2005 年北京西城区抽样测试题)已知命题p:函数 y=log a(ax+2a)(a>0 且 a ≠1)的图象必过定点(-1, 1);命题 q:假如函数 y=f( x- 3)的图象对于原点对称,那么函数y=f( x)的图象关于点( 3, 0)对称 .则A. “ p 且 q”为真B.“ p 或 q”为假C. p 真 q 假D. p 假 q 真分析:解决此题的重点是判断p、q 的真假 .因为 p 真,q 假(可举反例 y=x+3),因此正确答案为 C.答案: C●典例分析【例 1】给出命题“已知a、b、c、d 是实数,若 a=b,c=d,则 a+c=b+d”,对其原命题、抗命题、否命题、逆否命题而言,真命题有个个个个分析:原命题和逆否命题为真.答案: B深入拓展若 a、 b、 c∈ R,写出命题“若 ac< 0,则 ax2+bx+c=0 有两个不相等的实数根”的抗命题、否命题、逆否命题,并判断这三个命题的真假 .思路:认清命题的条件p 和结论 q,而后按定义写出抗命题、否命题、逆否命题,最后判断真假 .解:抗命题“若 ax2+bx+c=0(a、b、c∈ R)有两个不相等的实数根,则ac< 0”是假命题,如当 a=1,b=- 3, c=2 时,方程 x2-3x+2=0 有两个不等实根x1=1, x2=2,但ac=2>0.否命题“若 ac≥ 0,则方程 ax2+bx+c=0(a、b、c∈R)没有两个不相等的实数根”是假命题 .这是因为它和抗命题互为逆否命题,而抗命题是假命题.逆否命题“若 ax2 +bx+c=0(a、b、c∈ R)没有两个不相等的实数根,则ac≥ 0”是真命题 .因为原命题是真命题,它与原命题等价.评论:解答命题问题,辨别命题的条件p 与结论 q 的组成是重点 .【例 2】指出以下复合命题的形式及其组成.(1)若α是一个三角形的最小内角,则α不大于60°;(2)一个内角为 90°,另一个内角为45°的三角形是等腰直角三角形;(3)有一个内角为60°的三角形是正三角形或直角三角形.解:(1)是非 p 形式的复合命题,此中 p:若α是一个三角形的最小内角,则α> 60°.(2)是 p 且 q 形式的复合命题,此中 p:一个内角为 90°,另一个内角为 45°的三角形是等腰三角形, q:一个内角为 90°,另一个内角为45°的三角形是直角三角形.(3)是 p 或 q 形式的复合命题,此中p:有一个内角为 60°的三角形是正三角形,q:有一个内角为60°的三角形是直角三角形.【例 3】写出命题“当 abc=0 时, a=0 或 b=0 或 c=0”的抗命题、否命题、逆否命题,并判断它们的真假 .分析:把原命题改造成“若p 则 q”形式,再分别写出其相应的抗命题、否命题、逆否命题 .在判断真假时要注意利用等价命题的原理和规律.解:原命题:若abc=0,则 a=0 或 b=0 或 c=0,是真命题 .抗命题:若 a=0 或 b=0 或 c=0,则 abc=0,是真命题 .否命题:若 abc≠ 0,则 a≠ 0 且 b≠0 且 c≠0,是真命题 .逆否命题:若 a≠0 且 b≠0 且 c≠0,则 abc≠0,是真命题 .●闯关训练夯实基础1.假如原命题的结论是“ p 且 q”形式,那么否命题的结论形式为且q或q或q或p分析: p 且 q 的否认为p 或q.答案: B2.以下四个命题中真命题是①“若 xy=1,则 x、y 互为倒数”的抗命题②“面积相等的三角形全等”的否命题③“若 m≤1,则方程x2-2x+m=0 有实根”的逆否命题④“若A∩ B=B,则A B”的逆否命题A. ①②B.②③C.①②③D.③④分析:写出知足条件的命题再进行判断.答案: C3.分别用“ p 或 q”“ p 且 q”“非 p”填空 .(1)命题“ 15 能被 3 和 5 整除”是 ___________________形式;(2)命题“ 16 的平方根是 4 或- 4”是 ______________形式;(3)命题“李强是高一学生,也是共青团员”是___________________形式 .答案:( 1) p 且 q(2)p或q(3)p且q4.命题“若 ab=0,则 a、b 中起码有一个为零”的逆否命题是_______________.答案:若 a≠ 0 且 b≠0,则 ab≠05.在一次模拟打飞机的游戏中,小李接连射击了两次,设命题p1“第一次射击击中飞机”,命题 p2“第二次射击击中飞机”,试用 p1、p2及联络词“或”“且”“非”表示以下命题:(1)两次都击中飞机;(2)两次都没击中飞机;(3)恰有一次击中飞机;(4)起码有一次击中飞机 .解:(1)两次都击中飞机是p1且 p2;(2)两次都没击中飞机是p1且p2;(3)恰有一次击中飞机是p1且p2,或 p2且p1;(4)起码有一次击中飞机是p1或 p2.培育能力6.(2004 年湖北, 15)设 A、B 为两个会合 .以下四个命题:①A B对随意x∈ A,有x B;②A B A∩ B=;③A B A B;④A B存在 x∈A,使得 x B.此中真命题的序号是 ______________(.把切合要求的命题序号都填上)分析: A B存在x∈A,有x B,故①错误;②错误;④正确.亦或以以下图所示 .③反比以以下图所示 .A B A B.反之,同理 .答案:④7.命题:已知 a、b 为实数,若 x2+ ax+b≤0 有非空解集,则 a2-4b≥ 0,写出该命题的抗命题、否命题、逆否命题,并判断这些命题的真假.分析:原命题中, a、 b 为实数是前提,条件是x2+ax+b≤ 0 有非空解集(即不等式有解),结论是 a2- 4b≥ 0,由四种命题的关系可得出其余三种命题.解:抗命题:已知a、b 为实数,若 a2-4b≥0,则 x2+ax+b≤0 有非空解集 .否命题:已知 a、b 为实数,若 x2+ax+b≤0 没有非空解集,则a2-4b< 0.逆否命题:已知a、 b 为实数,若 a2-4b< 0,则 x2+ax+b≤ 0 没有非空解集 .原命题、抗命题、否命题、逆否命题均为真命题.8.写出以下命题非的形式:(1)p:函数 f(x)=ax2+bx+c 的图象与 x 轴有独一交点;(2)q:若 x=3 或 x=4,则方程 x2-7x+12=0.解:(1)函数 f(x)=ax2+bx+c 的图象与 x 轴没有交点或起码有两个交点.(2)若 x=3 或 x=4,则 x2-7x+12≠ 0.研究创新9.小李参加全国数学联赛,有三位同学对他作以下的猜想.甲:小李非第一名,也非第二名;乙:小李非第一名,而是第三名;丙:小李非第三名而是第一名 .比赛结束后发现,一人全猜对,一人猜对一半,一人全猜错,问:小李得了第几名?解:(1)假定小李得了第三名,则甲全猜对,乙全猜错,明显与题目已知条件相矛盾,故假定不行能 .(2)假定小李得了第二名,则甲猜对一半,乙猜对一半,也与已知条件矛盾,故假定不行能 .(3)假定小李得了第一名,则甲猜对一半,乙全猜错,丙全猜对,无矛盾.综合( 1)( 2)(3)知小李得了第一名 .●思悟小结1.有的“ p 或 q”与“p 且 q”形式的复合命题语句中,字面上未出现“或”与“且”字,此时应从语句的陈说中搞清含义,进而分清是“p 或 q”仍是“ p 且 q”形式 .一般地,若两个命题属于同时都要知足的为“且”,属于并列的为“或” .2.原命题与它的逆否命题同为真假,原命题的抗命题与否命题同为真假,因此对一些命题的真假判断(或推证),我们可经过对与它同真假的(拥有逆否关系的)命题来判断(或推证).●教师下载中心教课点睛1.有的“ p 或 q”与“p 且 q”形式的复合命题语句中,字面上未出现“或”与“且”字,此时应从语句的陈说中搞清含义,进而分清是“p 或 q”仍是“ p 且 q”形式 .一般地,若两个命题属于同时都要知足的为“且”,属于并列的为“或” .2.要明确原命题、否命题、抗命题、逆否命题之间的关系.拓展题例【例 1】写出以下各命题的否认及其否命题,并判断它们的真假.(1)若 x、y 都是奇数,则 x+y 是偶数;(2)若 xy=0,则 x=0 或 y=0;(3)若一个数是质数,则这个数是奇数.解:(1)命题的否认: x、y 都是奇数,则 x+y 不是偶数,为假命题 .原命题的否命题:若x、y 不都是奇数,则x+y 不是偶数,是假命题 .(2)命题的否认: xy=0 则 x≠ 0 且 y≠0,为假命题 .原命题的否命题:若xy≠ 0,则 x≠0 且 y≠ 0,是真命题 .(3)命题的否认:一个数是质数,则这个数不是奇数,是假命题.原命题的否命题:若一个数不是质数,则这个数不是奇数,为假命题.【例 2】有 A、 B、 C 三个盒子,此中一个内放有一个苹果,在三个盒子上各有一张纸条 .A 盒子上的纸条写的是“苹果在此盒内” ,B 盒子上的纸条写的是“苹果不在此盒内”,C 盒子上的纸条写的是“苹果不在 A 盒内” .假如三张纸条中只有一张写的是真的,请问苹果终究在哪个盒子里?解:若苹果在 A 盒内,则 A、B 两个盒子上的纸条写的为真,不合题意.若苹果在 B 盒内,则 A、B 两个盒子上的纸条写的为假, C 盒子上的纸条写的为真,切合题意,即苹果在 B 盒内 .相同,若苹果在 C 盒内,则 B、 C 两盒子上的纸条写的为真,不合题意.综上,苹果在 B 盒内 .。
高三数学逻辑联结词和四种命题1
.
.
.
.
.
.
.
;https:// 新视觉
3、通过原命题与逆否命题的真假等价性来判 断原命题的真假
四种命题(真假成对出现):
原命题
若p则q
互 为 否 命 题
否命题
若┐p则┐q
互为逆命题
逆命题
若q则p
逆否命题
若┐q则┐p
原词语
等于 (=)
大于 (>)Βιβλιοθήκη 小于 (<)是都是
至多有 一个
否定词 语
原词语
至多有 n个
至少有 1个
任意的
任意两 个
p或q
能
否定词 语
例1、用“p或q”、“p且q”、“非p”填空: ⑴命题:“三角形有内切圆和外接圆”是_ ___形式; ⑵命题:“若xy<0,则点P(x,y)在第二或第 四象限”是____形式; ⑶“梯形不是平行四边形”是____形式。
变:用“或”、“且”、“非”填空: ①若x∈A∪B,则x∈A______x∈B; ②若x∈A∩B,则x∈A______x∈B; ③若a、b∈R,且ab=0,则a=0_____b=0; ④若a、b∈R,且a2+b2=0,则a=0_____b=0
5逻辑联结词与四种命题

练习2.判断下列命题的真假,并写出它的逆命题、否命 题、逆否命题,同时判断这些命题的真假
(1)若ab≤0,则a≤0或b≤0,
(2)若a>b,则ac2>bc2
(3)若在二次函数y=ax2+bx+c中b2-4ac<0,则该二次函 数图象与x轴有公共点。
(3)P或q形式,其中p:4>3,q:4=3
(4)非p形式:其中p:平行四边形是梯形。
练习1.分别写出下列各组命题构成的“p或q”、“p且 q”、“非p”形式的复合命题 (1)p:5 是有理数,q:5 是无理数 (2)p:方程x2+2x-3=0的两根符号不同,
q: 方程x2+2x-3=0的两根绝对值不同。
2.四种命题的关系:
原命题 若p则q
互 否
否命题 若p则 q
互逆
互否 为逆
为
逆
互
否
互逆
逆命题 若q则p
互 否
逆否命题 若q 则p
3.一个命题的真假与其它三个命题的真假有如下 四条关系: (1)原命题为真,它的逆命题不一定为真。 (2)原命题为真,它的否命题不一定为真。 (3)原命题为真,它的逆否命题一定为真。 (4)逆命题为真,否命题一定为真。
例1.已知复合命题形式,指出构成它的简单命题, (1)等腰三角形顶角的角平分线垂直平分底边, (2)垂直于弦的直径平分这条弦且平分弦所对的 两条弧,
(3)4 3
(4)平行四边形不是梯形
(1)P且q形式,其中p:等腰三角形顶角的角平分线垂直底 边, q:等腰三角形顶角的角平分线平分底边;
(2)P且q形式,其中p:垂直于弦的直径平分这条弦, q:垂直于弦的直径平分这条弦所对的两条弧
逻辑联结词与四种命题
逻辑联结词与四种命题一、基础知识 (一)逻辑联结词1.命题:可以判断真假的语句叫做命题2.逻辑联结词:“或”、“且”、“非”这些词叫做逻辑联结词。
或:两个简单命题至少一个成立 且:两个简单命题都成立, 非:对一个命题的否定 3.简单命题与复合命题:不含逻辑联结词的命题叫做简单命题;由简单命题与逻辑联结词构成的命题叫做复合命题。
4.表示形式:用小写的拉丁字母p 、q 、r 、s …来表示简单的命题,复合命题的构成形式有三类:“p 或q ”、“p 且q ”、“非p ”5.(二)四种命题1.一般地,用p 和q 分别表示原命题的条件和结论,用┐p 和┐q 分别表示p 和q 的否定。
于是四种命题的形式为:原命题:若p 则q (q p ⇒) 逆命题:若q 则p )(p q ⇒ 否命题:若┐p 则┐q )(q p ⌝⇒⌝ 逆否命题:若┐q 则┐p )(p q ⌝⇒⌝ 2.四种命题的关系:3.一个命题的真假与其它三个命题的真假有如下四条关系: (1)原命题为真,它的逆命题不一定为真。
互 逆互 为 为否 逆 逆互 互 互 逆(2)原命题为真,它的否命题不一定为真。
(3)原命题为真,它的逆否命题一定为真。
(4)逆命题为真,否命题一定为真。
(三)几点说明1.逻辑联结词“或”的理解是难点,“或”有三层含义:以“P 或q ”为例:一是p 成立但q 不成立,二是p 不成立但q 成立,三是p 成立且q 成立, 2.对命题的否定只是否定命题的结论,而否命题既否定题设又否定结论 3.真值表 P 或q :“一真为真”, P 且q :“一假为假” 4.互为逆否命题的两个命题等价,为命题真假判定提供一个策略。
二、举例选讲例1.已知复合命题形式,指出构成它的简单命题, (1)等腰三角形顶角的角平分线垂直平分底边, (2)垂直于弦的直径平分这条弦且平分弦所对的两条弧, (3)34≥(4)平行四边形不是梯形解:(1)P 且q 形式,其中p :等腰三角形顶角的角平分线垂直底边, q :等腰三角形顶角的角平分线平分底边;(2)P 且q 形式,其中p :垂直于弦的直径平分这条弦, q :垂直于弦的直径平分这条弦所对的两条弧(3)P 或q 形式,其中p :4>3,q :4=3 (4)非p 形式:其中p :平行四边形是梯形。
江苏南化一中高三数学一轮教案:逻辑联结词与四个命题(一)

..专心. §1.2 逻辑联结词与四个命题〔一〕【复习目标】1. 了解命题、复合命题等概念;2. 理解逻辑联结词“或〞、“且〞、“非〞的含义,会根据《真值表》判断复合命题的真假;3. 掌握四个命题及其相互关系,理解“否命题〞与“非命题〞的不同含义。
【重点难点】掌握四个命题及其相互关系,理解“否命题〞与“非命题〞的不同含义【课前预习】1. 以下语句是否命题?如果是,判断真假:〔1〕上课! ; 〔2〕22x + ;〔4〕对顶角难道不相等吗? ;〔4是无理数。
2. 有以下命题:①2004年10月1日是国庆节,又是中秋节;②10的倍数一定是5的倍数;③梯形不是矩形;④方程21x =的解1x =±。
其中,复合命题有〔 〕 A .1个B .2个C .3个D .4个3. “220a b +≠〞的含义为 〔 〕 A .,a b 不全为0B . ,a b 全不为0C .,a b 至少有一个为0D .a 不为0且b 为0,或b 不为0且a 为04.命题p :假设A B B =,那么A B ⊆;命题q :假设A B ⊄,那么A B B ≠。
那么命题p 与命题q 的关系是 〔 〕A .互逆B .互否C .互为逆否命题D .不能确定5.有以下四个命题:①“假设x+y=0 , 那么x ,y 互为相反数〞的逆命题;②“全等三角形的面积相等〞的否命题;③“假设q ≤1 ,那么x 2 + 2x+q=0有实根〞的逆否命题;④“不等边三角形的三个内角相等〞逆命题。
其中真命题为 〔 〕A .①②B .②③C .①③D .③④6.命题“假设△ABC 不是等腰三角形,那么它的任何两个内角不相等〞的逆否命题 是 ;【典型例题】例1 假设命题“非p 〞与命题“p 或q 〞都是真命题,那么〔 〕A .命题p 与命题q 的真值相同B .命题q 一定是真命题C .命题q 不一定是真命题D .命题p 不一定是真命题例2 分别指出以下各组命题p 、q 及逻辑关联词“或〞、“且〞、“非〞 构成的复合命题的真假。
逻辑联结词和四种命题公式

逻辑联结词和四种命题1、逻辑联结词(1)命题:一般地,我们把用语言、符号、式子表达的,可以判断真假的语句叫做命题其中判断为真的语句叫真命题,判断为假的语句叫假命题(2)逻辑联结词:“或”、“且”、“非”这些词叫做逻辑联结词或:两个简单命题至少一个成立且:两个简单命题都成立非:对一个命题的否定(3)简单命题与复合命题:不含逻辑联结词的命题叫简单命题;由简单命题和逻辑联结词构成的命题叫复合命题(4)表达形式用小写的拉丁字母p、 q 、 r 、 s……来表示简单命题复合命题有三类:① p或q ② p且q ③非p(5)真值表:表示命题真假的表叫真值表①非p② p且q③p或q2、四种命题(1)一般地,用p和q分别表示原命题的条件和结论,用┐p和┐q分别表示p和q的否定,于是四种命题的形式就是:原命题:若p则 q(p q);逆命题:若q则 p(q p);否命题:若┐p则┐q(┐p┐q);逆否命题:若┐q则┐p(┐q ┐p)(2)四种命题的关系原命题逆命题否命题逆否命题(3)一个命题的真假与其他三个命题的真假有如下四种关系①原命题为真,它的逆命题不一定为真②原命题为真,它的否命题不一定为真③原命题为真,它的逆否命题一定为真④逆命题为真,否命题一定为真3、反证法证明命题的一般步骤(1)否定结论(2)从假设出发,经过推理论证得出矛盾(3)断定假设错误,肯定结论成立反证法属于间接证法,当证明一个结论成立,已知条件较少,或结论的情况较多,或结论是以否定形式出现,如某些结论中含有“至多”、“至少”、“唯一”、“不可能”、“不都”等指示性词语时往往考虑采用反证法证明结论成立。
最新高三教案-高三数学复习逻辑联结词与四种命题1 精品
逻辑联结词与四种命题一、基础知识(一)逻辑联结词1.命题:可以判断真假的语句叫做命题2.逻辑联结词:“或”、“且”、“非”这些词叫做逻辑联结词。
或:两个简单命题至少一个成立且:两个简单命题都成立,非:对一个命题的否定3.简单命题与复合命题:不含逻辑联结词的命题叫做简单命题;由简单命题与逻辑联结词构成的命题叫做复合命题。
4.表示形式:用小写的拉丁字母p、q、r、s…来表示简单的命题,复合命题的构成形式有三类:“p或q”、“p且q”、“非p”5(二)四种命题1.一般地,用p和q分别表示原命题的条件和结论,用┐p和┐q分别表示p和q的否定。
于是四种命题的形式为:原命题:若p则q(qp⇒)逆命题:若q则p)(pq⇒否命题:若┐p则┐q)(qp⌝⇒⌝逆否命题:若┐q则┐p)(pq⌝⇒⌝2.四种命题的关系:3.一个命题的真假与其它三个命题的真假有如下四条关系:(1)原命题为真,它的逆命题不一定为真。
(2)原命题为真,它的否命题不一定为真。
(3)原命题为真,它的逆否命题一定为真。
(4)逆命题为真,否命题一定为真。
(三)几点说明1.逻辑联结词“或”的理解是难点,“或”有三层含义:以“P或q”为例:一是p成立但q不成立,二是p不成立但q成立,三是p成立且q成立,2.对命题的否定只是否定命题的结论,而否命题既否定题设又否定结论3.真值表P或q:“一真为真”,P且q:“一假为假”4.互为逆否命题的两个命题等价,为命题真假判定提供一个策略。
二、举例选讲例1.已知复合命题形式,指出构成它的简单命题,互逆互为为互否逆逆否互否互否互逆(1)等腰三角形顶角的角平分线垂直平分底边,(2)垂直于弦的直径平分这条弦且平分弦所对的两条弧, (3)34≥(4)平行四边形不是梯形 解:(1)P 且q 形式,其中p :等腰三角形顶角的角平分线垂直底边, q :等腰三角形顶角的角平分线平分底边; (2)P 且q 形式,其中p :垂直于弦的直径平分这条弦, q :垂直于弦的直径平分这条弦所对的两条弧 (3)P 或q 形式,其中p :4>3,q :4=3 (4)非p 形式:其中p :平行四边形是梯形。
高三数学逻辑联结词和四种命题

; 猫先生 mrcat猫先生
;
不饶发威起来.月倾城只是睁大眼睛静静の望着白重炙,夜轻语也是眼睛微红,拉着他の衣服,宛如一放手他就消失了一样. "俺陷入了一些地方,那里空间不稳定,不能开启逍遥阁,俺出来之后,不是利马就回来了吗?俺怎么舍得不要你呀们,等俺赚够神石,将炽火大陆购买下来,俺就永远回来了,再也 不离开你呀们了…"白重炙苦笑の解释起来,两年不见三人外貌都没有改变多少,性格更是没有一丝改变. 夜轻语却是摇了摇头,拉着白重炙の手说道:"哥,总是骗人,每次都不守信用,哥,你呀还要多久才能赚够神石?俺将神石内の法则完全感悟成功之后,能不能去神界找你呀?" "鹿老说购买炽火位 面需要十亿神石,俺现在已经拥有了快七亿神石了,不会需要多久了!你呀想去神界?恐怕这点实力连紫岛最后一关都不能闯过!这样吧!" 白重炙宽慰一笑,手一翻,从空间戒指内拿出两枚神晶,递给了夜轻语和夜轻舞,月倾城上次拒绝了炼化神晶,这次很明显肯定也会拒绝,他也就没有给她:"你 呀们将这两枚神晶也完全炼化了,就可以去神界找俺了!" "这…神晶里面蕴含の气息好恐怖?这是什么神晶!还有神石是什么?" 夜轻舞拿起神晶一感应,却发现里面神力澎湃,蕴含着一股恐怖の气息,不禁有些疑惑の问道. "这是神将巅峰の神晶,你呀们炼化之后,虽然神力或许达不到神将巅峰,但 是估计能比普通神将吧!神石是神界の通用货币,比如你呀手上の神石,就能卖五六百万の神石."白重炙解释道. "神将巅峰神晶!五六百万神石?"夜轻语一听见却是用手捂住自己の嘴巴,白重炙去了两年,实力突破神将境已经让她们很是惊讶了,现在出手却拿出两枚神将巅峰神晶.并且他还说他有 快七亿神石,这不是能买一百多枚神将巅峰神晶? 夜轻语一阵暗惊,而后却是伸手将神晶,递
高三数学逻辑联结词和四种命题

§5 逻辑联结词和四种命题【知识要点】一、逻辑联结词1.命题:可以判断真假的语句叫做命题.2.逻辑联结词:“或”、“且”、“非”叫做逻辑联结词.3.简单命题:不含逻辑联结词的命题叫做简单命题.常用小写拉丁字母p、q等表示.4.复合命题:由简单命题和逻辑联结词构成的命题叫做复合命题.分或命题(p或q)、与命题(p且q)和非命题(非p).5.复合命题真假的判断方法(1)非p形式:当p为真时,非p为假;当p为假时,非p为真. 记忆方法:非p和p的真假相反.(2)p且q形式:当q、q都为真时,p且q为真;当p、q中至少有一为假时,p且q为假.记忆方法:一假必假.(3)p或q形式:当p、q中至少有一个为真时,p或q为真;当p、q 都为假时,p或q为假.记忆方法:一真必真.二、四种命题1.若用p和q分别表示原命题的条件和结论,用¬p 和¬q表示p和q 的否定,则四种命题的形式可写为:原命题:若p,则q.即qp⇒.逆命题:若q,则p.即pq⇒.否命题:若¬p,则¬q.即¬p⇒¬q.逆否命题:若¬q,则¬p.即¬p⇒¬q.2.四种命题的关系是:互逆3.四种命题的真假有下列结论:(1)原命题为真,其逆命题不一定为真;(2)原命题为真,其否命题不一定为真;(3)原命题为真,其逆否命题一定为真;(4)逆命题为真,否命题一定为真.三、反证法1.定义:因为命题“p”与它的否定“非p”的真假相反,所以要证一个命题为真,只要证它的否定为假即可,这种证明命题的否定为假,进而证明命题为真的证明方法叫做反证法.2.证题步骤:反设→归谬→下结论.3 .适用范围:(1)用直接证法较困难的命题;(2)待证命题的结论以否定形式出现或涉及“至多”、“至少”、“唯一”等词;(3)某些定理的逆定理或某些存在性问题的证明等.【考试要求】1.了解命题的概念和命题的构成;2.理解逻辑联结词“或”、“且”、“非”的含义;3.理解四种命题及其相互关系;4.能用反证法证明较简单的问题.【课前训练题】一、选择题1.下列命题中是“p 或q “形式的为( ) A.25> B.2是4和6的公约数C.{}0≠φD.B A ⊆2.与命题“若p 则q ”的逆否命题的否命题同真假的命题为( )A.若p 则qB.若q 则pC.若¬p ,则¬qD. 若¬q ,则¬p3.如果命题“p 或q ”是真命题,“p 且q”是假命题.那么( )A.命题p 和命题q 都是假命题B.命题p 和命题q 都是真命题C.命题p 和命题“非q ”真值不同D.命题q 和命题p 的真值不同4.对于命题q :“若a<3,则a>1”,则p 和它的逆命题、否命题、逆否命题中真命题的个数为( )A.0 B.1 C.2 D.3二、填空题5.命题“若实数y x ,满足1222+++x y x=0,则1-=x 且0=y ”的否命题为6 .复合命题“矩形的对角线垂直平分”的形 式为7.命题“若0=ab ,则a 、b 中至少有一个为零”的逆否命题为【例题分析】例1下列各组命题中,满足“p 或q”为真,“p 且q ”为假,“非p ”为真的是( )A.p:Φ∈Φ=0:;0qB:.sin :;,2cos 2cos ,:在第一象限是增函数则若中在x y q B AB A ABC p ===∆ C.),(2:R b a ab b a p ∈≥+:q 不等式x x >的解集为()0,∞-D.p:圆()1)2(122=-+-y x 的面积被直线1=x 平分;q:椭圆13422=+y x 的一条准线方程是x=4例2 以下列命题为原命题,分别写出它们的逆命题、否命题和逆否命题.(1) 垂直于平面α内无数条直线的直线l 垂直于平面α;(2) 设d c b a ,,,是实数,若d c b a ==,,则d b c a +=+.例3 已知p :012=++mx x 有两个不等的负根,q :01)2(442=+-+x m x 无实根.若p 或q 为真,p 且q 为假,求m 的取值范围.例4大小不等的三个圆两两相外切,半径成等差数列,以各圆心为顶点的三角形的三个内角能否组成等差数列?为什么?【小结归纳】1.对于几个复合命题真假同时发生的问题,应根据复合命题真值表先对每个复合命题进行判断,再综合考虑.2.当一个命题的真假判断出现困难时,通常转化为判断它的逆否命题的真假.这是因为原命题与它的逆否命题是等价的.反证法的实质就是证明“原命题的逆否命题成立”.3.一个命题(若p则q)的否定与它的否命题是两个不同的概念,前者是“若p则¬q”,后者是“若¬p则¬q”.4.用反证法证明问题时,准确地作出反设是很重要的,下表是一些常见结论的否定形式:【巩固训练题】一、 选择题1.已知全集,,U A R U ⊆=如果命题p:B A ∈3,则命题“非p”是( )A. 非p:A ∉3B. 非p:B C U ∈3C. 非p:B A ∉3D. 非p:)()(3B C A C U U ∈2.给出以下四个命题(1)若0232=+-x x ,则21==x x 或(2)若0)3)(2(,32≤--<≤-x x x 则(3)若0==y x ,则022=+y x(4)若x 、y *∈N ,y x +是奇数,则x 、y 中一个是奇数,一个是偶数. 则( )A.(1)的逆命题真B.(2)的否命题真C.(3)的逆否命题假D.(4)的逆命题假3.与命题“若M m ∈,则M n ∉”等价的命题是( )A. 若M m ∉,则M n ∉B.若Mm∈n∉,则MC.若Mm∉,则Mn∈D.若Mm∉n∈,则M4.若p、q是两个简单命题,且“p或q”的否定是真命题,则必有()A.p真q真B.p假q真C.p真q假D.p假q假5.下列四个命题中是真命题的是()A.ΦA ,则Φ=BB=A或Φ=B.两条对角线相等的四边形是正方形C.U=或A=则为全集),(=UBBAUUE.如果一个角的两边分别垂直于另一个角的两边,那么这两个角互补.二、填空题6.在空间中,(1)若四点不共面,则这四点中任何三点都不共线;(2)若两条直线没有公共点,则这两条直线是异面直线.这两个命题中逆命题为真命题的是7.命题“若ab=0,则a、b中至少有一个为零”的逆否命题是8.已知命题p:不等式m-+1的解集为R,命题q:xx>x(--=5()2xmf)是减函数,若“p或q”为真命题,“p且q”为假命题,则实数m的取值范围是三、解答题9.写出下列命题的非命题,并判断它们的真假.(1) p :对任意实数x ,都有0122≥+-x x (2)q :存在一个实数x ,使092=-x10.设b a ,是两个实数,{,),(n x y x A == }Z n b na y ∈+=,,{,),(m x y x B == }Z m m y ∈+=,1532,{+=2),(x y x C }1442≤y 是平面xOy 内的点的集合.求证:不存在b a ,使得Φ≠B A ,且点C b a ∈),(同时成立.。
3. 逻辑联结词与四种命题
2008届高三数学复习教案 3. 逻辑联结词与四种命题一、基础知识 (一)逻辑联结词1.命题:可以判断真假的语句叫做命题 2.逻辑联结词:“或”、“且”、“非”这些词叫做逻辑联结词.或:两个简单命题至少一个成立 且:两个简单命题都成立, 非:对一个命题的否定 3.简单命题与复合命题:不含逻辑联结词的命题叫做简单命题;由简单命题与逻辑联结词构成的命题叫做复合命题.4.表示形式:用小写的拉丁字母p 、q 、r 、s …来表示简单的命题,复合命题的构成形式有三类:“p 或q ”、“p 且q ”、“非p ”5.(二)四种命题1.一般地,用p 和q 分别表示原命题的条件和结论,用┐p 和┐q 分别表示p 和q 的否定。
于是四种命题的形式为:原命题:若p 则q (q p ⇒) 逆命题:若q 则p )(p q ⇒ 否命题:若┐p 则┐q )(q p ⌝⇒⌝ 逆否命题:若┐q 则┐p )(p q ⌝⇒⌝ 2.四种命题的关系:3.一个命题的真假与其它三个命题的真假有如下四条关系: (1)原命题为真,它的逆命题不一定为真. (2)原命题为真,它的否命题不一定为真. (3)原命题为真,它的逆否命题一定为真. (4)逆命题为真,否命题一定为真. (三)几点说明互 逆 互 为 为 否逆逆 互 互 互 逆1.逻辑联结词“或”的理解是难点,“或”有三层含义:以“P 或q ”为例:一是p 成立但q 不成立,二是p 不成立但q 成立,三是p 成立且q 成立, 2.对命题的否定只是否定命题的结论,而否命题既否定题设又否定结论 3.真值表 P 或q :“一真为真”, P 且q :“一假为假”4.互为逆否命题的两个命题等价,为命题真假判定提供一个策略. 二、举例选讲例1.已知复合命题形式,指出构成它的简单命题, (1)等腰三角形顶角的角平分线垂直平分底边,(2)垂直于弦的直径平分这条弦且平分弦所对的两条弧, (3)34≥(4)平行四边形不是梯形 解:(1)P 且q 形式,其中p :等腰三角形顶角的角平分线垂直底边, q :等腰三角形顶角的角平分线平分底边;(2)P 且q 形式,其中p :垂直于弦的直径平分这条弦, q :垂直于弦的直径平分这条弦所对的两条弧(3)P 或q 形式,其中p :4>3,q :4=3 (4)非p 形式:其中p :平行四边形是梯形.练习1分别写出下列各组命题构成的“p 或q ”、“p 且q ”、“非p ”形式的复合命题 (1)p :5是有理数,q :5是无理数(2)p :方程x 2+2x-3=0的两根符号不同,q : 方程x 2+2x-3=0的两根绝对值不同. 例2.(四种命题之间的关系)写出下列命题的逆命题、否命题、逆否命题,并判断它们的真假.(1) 已知c b a ,,为实数,若0<ac ,则02=++c bx ax 有两个不相等的实根; (2)若ab=0,则a=0或b=0,(3)若x 2+y 2=0,则x 、y 全为零.解:(1)逆命题:若02=++c bx ax 有两个不相等的实根,则0<ac ,(假)否命题:若0≥ac ,则02=++c bx ax 没有两个不相等的实根,(假) 逆否命题:若02=++c bx ax 没有两个不相等的实根,则0≥ac ,(真)(2)逆命题:若a=0或b=0,则ab=0,(真)否命题:若ab ≠0,则a ≠0且 b ≠0,(真) 逆否命题:若a ≠0且 b ≠0,则ab ≠0,(真)(3)逆命题:若x 、y 全为零,则x 2+y 2=0(真)否命题:若x 2+y 2≠0,则x 、y 不全为零(真) 逆否命题:若x 、y 不全为零,则x 2+y 2≠0(真)练习2判断下列命题的真假,并写出它的逆命题、否命题、逆否命题,同时判断这些命题的真假(1)若ab ≤0,则a ≤0或b ≤0, (2)若a>b ,则ac 2>bc 2(2) 若在二次函数y=ax 2+bx+c 中b 2-4ac<0,则该二次函数图象与x 轴有公共点. 例3.已知命题01:2=++mx x p 有两个不等的负根;命题01)2(44:2=+-+x m x q 无实根. 若命题p 与命题q 有且只有一个为真,求实数m 的取值范围.解:012=++mx x Θ有两个不等的负根,.2,042>⎩⎨⎧<->-∴m m m 得01)2(442=+-+x m x Θ无实根,,016)2(162<--∴m 得.31<<m 有且只有一个为真,若p 真q 假,得3≥m ………………2分 若p 假q 真,得21≤<m综合上述得21,3≤<≥m m 或练习3(变式3)已知下列三个方程:x 2+4ax-4a+3=0 x 2+(a-1)x+a 2=0 x 2+2ax-2a=0至少有一个方程有实根,求实数a 的取值范围. 三、小结1.逻辑联结词“或”、“且”、“非”的意义与日常生活中的“或”、“且”、“非”的意义不尽相同.要注意集合中的“并”、“交”、“补”的理解.23四、作业1. 命题p :方程x 2-x+1=0有实数根。
高三数学逻辑联结词和四种命题

命题真假性的主要应用:
1、判断两个命题的关系:充分、必要、充要 性、充分不必要、必要不 充分、不充分也不必 要的判断
2、判断的技巧 ①向定语看齐,顺向为充(原命题为真)
逆向为必(逆命题为真)
②等价性:逆否为真即为充, 否命为真即为 必
2010届高考数学复习 强化双基系列课件
72《逻辑联结词 和四种命题》
一、命题的概念
二、逻辑连结词:或、且、非
三、简单命题与复合命题的区别
四、如何判断命题的真假 (3≥2的真假性) 1、简单命题的真假 2、复合命题的真假
判断复合命题真假的步骤: ①命题的结构
或,且,非 ②简单命题的真假 ③真值表: 或----一真皆真
已知函数f(x)=2x2+mx+n, 求证:|f(1)|、|f(2)|、|f(3)|中至少有一个不小于1
相关连接:
若二次函数y=f(x)的图象过原点,1≤f(-1)≤2, 3≤f(1)≤4,求f(-2)的范围。
• 高考题:
• 已知c>0,设p:函数y=cx在R上 单调递减.q:不等式x+|x-2c|>1 的解集为R.如果p和q有且仅 有一个正确,求c的取值范围.
当堂知识回顾:
1复合命题的判断步骤 2复合命题的真值表 3四种命题的改写 4非命题与否命题的区别 5反证法的步骤
且----一假通假 非----真假对立
3、通过原命题与逆否命题的真假等价性来判 断原命题的真假
四种命题(真假成对出现):
原命题
若p则q
互 为 否 命 题
互为逆命题 互为逆否命题
逆命题
若q则p
否命题
若┐p则┐q
逆否命题
江苏南化一中高三数学一轮教案逻辑联结词与四个命题(一)

§1.2 逻辑联结词与四个命题(一)【复习目标】1. 了解命题、复合命题等概念;2. 理解逻辑联结词“或”、“且”、“非”的含义,会根据《真值表》判断复合命题的真假;3. 掌握四个命题及其相互关系,理解“否命题”与“非命题”的不同含义。
【重点难点】掌握四个命题及其相互关系,理解“否命题”与“非命题”的不同含义【课前预习】1. 下列语句是否命题?如果是,判断真假:(1)上课! ; (2)22x + ;(4)对顶角难道不相等吗? ;(42. 有下列命题:①2004年10月1日是国庆节,又是中秋节;②10的倍数一定是5的倍数;③梯形不是矩形;④方程21x =的解1x =±。
其中,复合命题有( ) A .1个B .2个C .3个D .4个3. “220a b +≠”的含义为 ( ) A .,a b 不全为0B . ,a b 全不为0C .,a b 至少有一个为0D .a 不为0且b 为0,或b 不为0且a 为04.命题p :若A B B = ,则A B ⊆;命题q :若A B ⊄,则A B B ≠ 。
那么命题p 与命题q 的关系是 ( )A .互逆B .互否C .互为逆否命题D .不能确定5.有下列四个命题:①“若x+y=0 , 则x ,y 互为相反数”的逆命题;②“全等三角形的面积相等”的否命题;③“若q ≤1 ,则x 2 + 2x+q=0有实根”的逆否命题;④“不等边三角形的三个内角相等”逆命题。
其中真命题为 ( )A .①②B .②③C .①③D .③④6.命题“若△ABC 不是等腰三角形,则它的任何两个内角不相等”的逆否命题是 ;【典型例题】例1 若命题“非p ”与命题“p 或q ”都是真命题,那么 ( )A .命题p 与命题q 的真值相同B .命题q 一定是真命题C .命题q 不一定是真命题D .命题p 不一定是真命题例2 分别指出下列各组命题p 、q 及逻辑关联词“或”、“且”、“非” 构成的复合命题的真假。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高三数学一轮复习学案:逻辑联结词与四种命题一.考试要求:
1.了解命题的定义,并能判断一些命题的真假。
2.理解全称量词与存在量词的意义。
3.了解逻辑联结词“或”“且”“非”的含义,并能正确地对含有一个量词的命题进行否定。
4.理解四种命题及其相关关系。
二知识梳理:
(一).命题与量词
1.命题:__________________________________.常用小写字母p、q、r表示。
注意:①并不是任何语句都是命题,一般地疑问句、祈使句、感叹句、不是命题,陈述句、反问句是命题。
②目前一些尚不能判断真假的语句(如科学猜想),随着科学技术的发展,总能确定他们的真假,这样的语句仍可视为命题。
2.量词:①全称量词________________________________,用“∀”表示。
全称命题__________________________________.
②存在量词________________________________,用“∃”表示。
存在性命题__________________________________.
(二).基本逻辑联结词:“或”∨,“且”∧,“非”⌝
1
2
①全称命题:∀ x∈M,p(x)的否定是___________________________.
存在性命题: ∃ x∈M,q(x) 的否定是___________________________.
②命题p∧q与p∨q的否定分别是_____________________________.
(三). 命题的四种形式及相互关系:
1. 原命题逆命题
否命题逆否命题
2.真假关系:______________________________________________________.
三、基础检测
1已知m,n是两条不重合的直线,α,β,γ是三个不重合的平面,给出下列四个命题
①若m⊥α,m⊥β,则α∥β②若α⊥γ,β⊥γ,则α∥β
③若m⊂α,n⊂β, m∥n,则α∥β
④若m,n是两条异面直线m⊂α, m∥β,n⊂β,n∥α,则α∥β
其中真命题是( ) A. ①② B. ①③ C. ③④ D. ①④
2命题p:若a,b∈R,则|a|+|b|>1是|a+b|>1的充要条件
命题q:函数
2
|1
|-
-
x的定义域是(-∞,-1]⋃[3, +∞),则( )
A. “p或q”为假
B. “p且q”为真
C. p真q假
D. p假q真
3 已知命题p:无穷数列{n a }的前n 项和为n
S ,若{n a }是等差数列,则点列{(n , n S )}在一条抛物线上. 命题q:若实数m >1, 则m 2x +(2m -2)x -1>0的解集为R.
对于命题p 的逆否命题s 与命题q 的逆命题r ,下列判断正确的是( )
A. s 是假命题, r 是真命题
B. s 是真命题, r 是假命题
C. s 是假命题, r 是假命题
D. s 是真命题, r 是真命题
4. 给出下列命题:①“若k>0,则方程2x +2x -k=0有实数根” ②“若a>b , 则a+c>b+c”
的否命题 ③“矩形的对角线相等”的逆命题 ④“若xy=0, 则x ,y 至少有一个为0”
的否命题。
其中真命题的个数为( ) A.. 1 B. 2 C. 3 D. 4
5. 下列命题中是命题p :“任意角α都可作为→a 与→b 的夹角”的⌝ p 形式是( )
①存在角α不可以作为→a 与→b 的夹角 ② 不是任意角α都可作为→a 与→b 的夹角
③ 任意角α都不可以作为→a 与→b 的夹角
A. ① ②
B. ① ② ③
C. ① ③
D. ② ③
6.命题p:如果22x y +=0,则x ,y 都为0 命题q:如果2a >2
b ,则a>b.
给出下列命题①p ∧q ②p ∨q ③⌝ p ④⌝q 其中真命题是( )
A. ① ②
B. ① ③
C. ② ③
D. ② ④ 7. 命题“若a>b , 则b a 22〉-1”的否命题____________________________。
8.命题p :∀ x ∈R ,341
2+-x x <0的⌝ p 形式是____________________________。
9.已知三个方程2x +4ax -4a+3=0, 2x +2ax -2a=0, 2x +(a -1)x+2
a =0中,至少有一个方程
有实根,则实数a 的取值范围为_________________。
10.已知实数c>0,设命题p :函数y=x c 在R 上单调递减,命题q:不等式x+|x -2c|>1的解集为R 。
如果p 和q 有且只有一个正确,求c 的取值范围。
11.r(x): x sin +cosx>m , s(x): 2x +mx+1>0.如果对任意一个实数x ,r(x)恒为假命题且
s(x) 恒为真命题,求实数m 的取值范围。
