2010年第八届小学希望杯全国数学邀请赛六年级第2试及答案
第8届希望杯2试答案

长方形的中间有一个由两个长方形构成的十字形的阴影.如果阴影部分的面积恰 厘米.
【解析】
直线形汁算 首先单独看竖直的阴影正好将长方形分为相等的三份, 要使阴影部分与空白部分面 积相等,那么水平的阴影与竖直阴影不重合的部分应该等于半份, x 3 8 2 (9 3) 2
【例 8】
(2010 年希望杯第八届四年级二试第 8 题) 如图 2,一个边长为 50 米的正方形 围墙,甲、乙两人分别从 A 、C 两点同时出发,沿闹墙按顺时针方向运动,已知甲 每秒走 5 冰,乙每秒走 3 米,则至少经过 条边上。 秒甲、乙走到正方形的同一
【解析】
120 如图,周长 52 厘米- 2 最长边 16 厘米=2 个长.所以长=10 厘米,宽=6 厘米, “ L” 形纸片面积是 2 10 6 120 平方厘米.
【例 12】 (2010 年希望杯第八届四年级二试第 12 题 )48 名学生参加聚会,第一个到会的 男生和全部女生握手,第二个到 A 的男生只差一名女生没握过手,第三个到会的 男生只差 2 名女生没握过手,„„最后一个到会的男生同 9 名女生握过手,这 48 名学生中共有 名女生。 【解析】 和差倍问题 题设中隐含女生比男生多 8 名的条件,那么女生共有 (48 8) 2 8 28 名. 【例 13】 (2010 年希望杯第八届四年级二试第 13 题) 如桌 3 台数控机床 4 小时可以加 工 960 个同样的零件,那么 1 台数控机床加工 400 个相同的零件满要多长时间?.
【解析】
行程问题
50 秒,要在同一条边上,首先路程差应 3 小于一个边长.经过 50 (5 3) 25 秒后,甲、乙路程差为一个边长,此时甲在 CD 边的中
由题设可知,甲走完一条边需要 10 秒,乙需要 点, 而乙在 AD 边的中点. 因此需要再经过 5 秒后, 甲到达 D 点, 甲、 乙才走到同一条边上. 综 上,至少需要 30 秒.
第8届六年级2试试题及详解

第八届“希望杯”二试六年级真题详解作者: | 查看: 338次1、原题:(略)解析:这算是一道送分的题了。
三又四分之三乘零点二,得零点七五;五点四与一点三五约分,得四。
四乘以零点七五,得三。
2、原题:(略)解析:这是一道连分数的问题,在赛假特训班上重点讲过,结课考试时第一题就是这个题的原型。
这道题的结果是1。
3、原题:有一类自然数,从左边第三位开始,每个数位上的数字都是它左边两个数位上的数字之和,如21347,则这类自然数中最大的奇数是。
解析:要想让该自然数尽量大,首先就要努力让它的位数尽量多。
根据该题的特点,左边的数越小,它的位数才可能尽量多。
在最高位上能选的最小数只能是“1”,第二位我们可以选最小的一位数“0”,这两个数确定下来后,就只能是按题目定出的条件,跟着感觉走了。
“1011235”,本来后面可以再加个“8”的,但人家要求是奇数,只能到此为止,最后的结果是:10112354、原题:(略)解析:这个题出的有点太初级了。
我相信所有的同学都能做出来。
27/3=9 63/7=9所以下来就是:8*9=72了。
5、原题:(略)解析:这是六年级“百题培训”资料上的第66题,一字未改。
资料上给的答案有点复杂,在这里我们重点讲一下。
先看图1,因为红色部分、黄色部分和绿部分面积相等,所以:红+黄=绿+黄,甩以点E、F分别在AB、AC上所占位置分点相同,所以:AE:EB=AF:FC再看图2,作辅助线PA,把黄色分成蓝、黄两部分。
根据上面的结论得出:红:蓝=绿;黄,又因为“红=绿”,所以“蓝=黄=4/2=2”所以: BE:AE=2:1。
现知道三角形ACE的面积是:4+4=8,所以,三角形BCE的面积是8*2=16,所以,三角形CPB的面积是:16-4=12。
6、原题:(略)解析:这是一道老题了。
学生能平均分成5组,那学生人数一定是5人倍数,加上老师1人,所以总人数一定是个位数为“1”或“6”的一个数。
每人种树一样多,共种了527棵,把527分解因数,发现527的因数仅有1、17、31、527,在这四个因数中,只有31符合条件,所以师生共有31人,减去老师1人,学生人数就是30人了。
第八届希望杯-六年级-第2试试卷及解析

第八届小学“希望杯”全国数学邀请赛六年级第2试一、填空题(每小题5分,共60分)1.2.已知,其中A、B、C都是大于0但互不相同的自然数,则(A+B)÷C=( )3.有一类自然数,从左边第三位开始,每个数位上的数字都是它左边两个数位上数字之和,如21347,则这类自然数中,最大的奇数是( )4.王老师在黑板上写了这样的乘法算式:12345679×()=□□□□□□□□□,然后说道:只要同学们告诉我你喜欢1,2,3,4,5,6,7,8,9中的哪个数,我在括号里填上适当的乘数,右边的积一定全是你喜欢的数字组成.小明抢着说:我喜欢3.王老师填乘数“27”,结果12345679×(27)=333333333;小宇说:我喜欢7,只见王老师在乘数上填“63”,结果是12345679×(63)=777777777.小丽说:我喜欢8,那么在乘数上应填( )5.如图,三角形ABC中,点E在AB上,点F在AC上,BF与CE交于点P上,如果四边形AEPF与三角形BEP、三角形CFP的面积都是4,则三角形BPC的面积是( )6.张老师带六一班学生去种树,学生恰好可以平均分成5组,已知师生每人种的树一样多,共种树527棵,问六一班学生有( )人.7.两个顽皮的孩子逆着自动扶梯行驶的方向行走,从扶梯的一端到达另一端,男孩走了100秒,女孩走了300秒,已知在电梯静止时,男孩每秒走3米,女孩每秒走2米,则该自动扶梯长( )米8.有7根直径都是5厘米的圆柱形木头,现在用绳子分别在两处把它们捆在一起,则至少需要绳子( )分米(结头处绳子不计,Л取3.14)9. 一个深30厘米的圆柱形容器,外圆直径22厘米,壁厚1厘米,已装深27.5厘米的水.现放入一个底面直径10厘米,高30厘米的圆锥形铁块,则将有( )立方厘米的水溢出?10.新年联欢会共有8个节目,其中有3个非歌唱类节目.排列节目单时规定,非歌唱类节目不相邻,而且第一个和最后一个节目是歌唱类节目,则节目单有( )种不同的排法.11.有一水池,单开进水管3小时可把水池注满,单开出水管4小时把排空满池水.水池建成后,发现水池漏水,这时,若同时打开进水管与出水管14小时才能把水池注满,当水池注满后,并且关闭进水管与出水管,经过( )小时水池会漏完.12.甲乙两人分别从A、B两地同时出发,相向而行,已知甲、乙两人的速度比是6:5,他们相遇时距AB两地的中点5千米,当甲到达B时,乙距A还有( )千米二、解答题(每题15分,共60分)每题都要写出推算过程.13.有一个电子计算器的数字显示屏坏了,有部分区域在该亮时不亮,使原本的一道一位数乘以一位数,积是两位数的乘法算式,出现如图1所示怪样(不妨用火柴棒来表示),小明对此用火柴棒摆出可能算式如图2请问,图中所示的算式有哪几种?14.修一条高速公路,若甲、乙、丙合作,90天可完工;若甲、乙、丁合作,120天可完工;若丙、丁合作,180天完工;若甲、乙合作36天后,剩下的工程由四人合作,还需要多少天完工?15.甲乙两辆车在与铁路并行的道路上相向而行,一列长180米的火车以60千米/小时的速度与甲同向前进,火车从追上甲车到遇上乙车,相隔5分钟,若火车从追上并超过甲车用时30秒,从与乙车相遇到离开用时6秒,求乙车遇到火车后再过多长时间与甲车相遇?16.定义:f(n)=k(其中n是自然数,k是0.987651234658、、、、的小数点后的第n位数字),如f(1)=9,f(2)=8,f(3)=7,求5f (……f ( f ( 5 ) ) )+2f (……f ( f ( 8 ) ) )的值.505个f 2010个f862参考答案。
小学六年级“希望杯”第1-10届试题及详解(第一试和第二试)

第四届小学“希望杯”全国数学邀请赛六年级第1试以下每题5分,共120分。
1.2006×2008×()=________。
2.900000-9=________×99999。
3.=________。
4.如果a=,b=,c=,那么a,b,c中最大的是________,最小的是________。
5.将某商品涨价25%,如果涨价后的销售金额与涨价前的销售金额相同,则销售量减少了________%。
6.小明和小刚各有玻璃弹球若干个。
小明对小刚说:“我若给你2个,我们的玻璃弹球将一样多。
”小刚说:“我若给你2个,我的弹球数量将是你的弹球数量的三分之一。
”小明和小刚共有玻璃弹球________个。
7.一次测验中,小明答错了10道题,小刚答错了8道题,小强答对的题的数量等于小明与小刚答对题的数量之和,且小强答错了3道题。
这次测验共有________道题。
8.一个两位数,加上它的个位数字的9倍,恰好等于100。
这个两位数的各位数字之和的五分之三是________。
9.将一个数A的小数点向右移动两位,得到数B。
那么B+A是B-A的________倍。
(结果写成分数形式)10.用10根火柴棒首尾顺次连接接成一个三角形,能接成不同的三角形有________个。
11.希望小学举行运动会,全体运动员的编号是从1开始的连续整数,他们按图中实线所示,从第1珩第1列开始,按照编号从小到大的顺序排成一个方阵。
小明的编号是30,他排在第3行第6列,则运动员共有________人。
12.将长为5,宽为3,高为1的长方体木块的表面涂上漆,再切成15块棱长为l的小正方体。
则三个面涂漆的小正方体有________块。
13.如图,∠AOB的顶点0在直线l上,已知图中所有小于平角的角之和是400度,则∠AOB=________度。
14.如图,桌面上有A、B、C三个正方形,边长分别为6,8,10。
B的一个顶点在A 的中心处,C的一个顶点在B的中心处,这三个正方形最多能盖住的面积是________。
第八-十二届希望杯全国数学邀请赛六年级试题及答案解析
4. 一个两位数除以一位数,所得的商若是最小的两位数,那么被除数最大是__________.
5. 22012 的个位数字是__________.(其中 2n 表示 n 个 2 相乘)
6. 下图(左)是一个正方体的展开图,图中(右)的四个正方体中只有一个是和这个展开 图对应的,这个正方体是__________.(填序号)
10. 在一个两位数的中间加上小数点,得到一个小数,若这个小数与原来的两位数的和是 86.9 ,则原来的两位数是___________.
11. A、B 两校的男、女生的人数的比分别是 8:7 和 30:31,两校合并后,男、女生人数的比
是 27:26,则 A、B 两校合并前人数的比是___________. 12. 有 2013 名学生参加数学竞赛,共有 20 道竞赛题,每个学生有基础分 25 分,此外,答
b (若a b).
1.1 7 1 0.1
例如: 3.5 2 3.5,1 1.2 1.2, 7 7 1,则
33 4 0.8
___________.
5
7. 有一口无水的井,用一根绳子测井的深度,将绳子对折后垂到井底,绳子的一端高出井 口 9m;将绳子三折后垂到井底,绳子的一端高出井口 2m,则绳子长___________m, 井深___________m.
①
②
③
④
7. 一列快车从甲地开往乙地需要 5 小时,一列慢车从乙地开往甲地所需时间比快车多 1 , 5
两车同时从甲乙两地相对开出 2 小时后,慢车停止前进,快车继续行驶 40 千米后恰与 慢车相遇,则甲乙两地相距__________千米.
8. 对任意两个数 x,y,定义新的运算“*”为: x y x y
1 1
第十届小学“希望杯”全国数学邀请赛六年级第2试

第十届小学 希望杯 全国数学邀请赛六年级㊀㊀第2试一㊁填空题(每小题5分,共60分.)1.计算:12ˑ13ˑ14ˑ15+32ˑ34ˑ3512ˑ23ˑ25=.2.计算:2+3+5+13+299+1163+2535+515=.3.王涛将连续的自然数1,2,3, 逐个相加,一直加到某个自然数为止,由于计算时漏加了一个自然数而得到错误的结果2012,那么,他漏加的自然数是.4.在数0.20120415中的小数点后面的数字上方加上循环点,得到循环小数,这些循环小数中,最大的是,最小的是.5.对任意两个数x ,y ,规定运算 ∗ 的含义是:x ∗y =4ˑx ˑy m ˑx +3ˑy (其中m 是一个确定的数).如果1∗2=1,那么m =,3∗12=.图16.对于一个多边形,定义一种 生长 操作:如图1,将其一边A B 变成向外凸的折线A C D E B ,其中C 和E 是A B 的三等分点,C ㊁D ㊁E 三点可构成等边三角形.那么,一个边长是9的等边三角形,经过两次 生长 操作(如图2),得到的图形的周长是;经过四次 生长 操作,得到的图形的周长是.图2图37.如图3所示的 鱼 形图案中共有个三角形.8.已知自然数N 的个位数字是0,且有8个约数,则N 最小是.9.李华在买某一种商品的时候,将单价中的某一数字 1 错看成了 7 ,准备付款189元,实际应付147元,已知商品的单价及购买的数量都是整数,则这种商品的实际单价是元,李华共买了件.10.如图4,已知A B =40c m ,图中的曲线是由半径不同的三种半圆弧图4平滑连接而成,那么阴影部分的面积是c m 2.(π取3.14)11.快车和慢车同时从甲㊁乙两地相对开出,快车每小时行33千米,相遇时行了全程的47,已知慢车行完全程需要8小时,则甲㊁乙两地相距千米.12.甲㊁乙㊁丙三人去郊游,甲买了9根火腿,乙买了6个面包,丙买了3瓶矿泉水.乙花的钱是甲的1213,丙花的钱是乙的23.丙根据每人所花钱的多少拿出9元钱分给甲和乙,其中,分给甲元,分给乙元.二、解答题(每小题15分,共60分.)㊀每题都要写出推算过程.13.将1到9这9个自然数中的5个数填入图5所示的圆圈内,使任意有线段相连的两个圆圈内的两数之差恰好等于连接这两个圆圈的线段的条数.图6给出了一种填法,请你再给出两种不同的填法.图5图6㊀㊀答:㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀14.甲㊁乙二人分别从A㊁B两地同时出发相向而行,于C地相遇后,甲继续向B地行走,乙则休息14分钟后再继续向A地行走.甲和乙各自到达B地和A地后立即折返,又在C地相遇.已知甲每分钟走60米,乙每分钟走80米.则A㊁B两地相距多少米?15.将100个棱长为1的立方体堆放成一个多面体,将可能堆成的多面体的表面积按从小到大排列,求开始的6个.16.在m行n列的网格中,规定:由上而下的横行依次为第1行,第2行, ,由左向右的竖列依次为第1列,第2列, .点(a,b)表示位于第a行㊁第b列的格点.图7是4行5列的网格,从点A(2,3)出发,按象棋中的马走 日 字格的走法,可到达网格中的格点B(1,1),C(3,1),D(4,2),E(4,4),F(3,5),G(1,5).如果在9行9列的网格中(图8),从点(1,1)出发,按象棋中的马走 日 字格的走法,(1)能否到达网格中的每一个格点?答:.(填 能 或 不能 )(2)如果能,那么沿最短路线到达某个格点,最多的需要几步?这样的格点有几个?写出它们的位置.如果不能,请说明理由.图7图8㊀㊀参考答案及评分标准六年级㊀㊀第2试一㊁填空题(每小题5分㊂其中第4,5,6,9,12题,每空2.5分㊂)题号123456789101112答案5182483340.20120415㊃;0.20㊃120415㊃2;33748;8513353021;76281986;3㊀㊀二㊁解答题㊀13.给出两种答案作为参考:注㊀填对一种答案得8分,填对两种答案得15分㊂14.A ㊁B 两地相距1680米㊂15.前6个依次是:130,160,208,240,250,258㊂16.(1)能㊂(2)最多需要6步,这样的格点有4个,它们是(8,8),(9,9),(7,9),(9,7)㊂。
希望杯六年级近五年真题大全

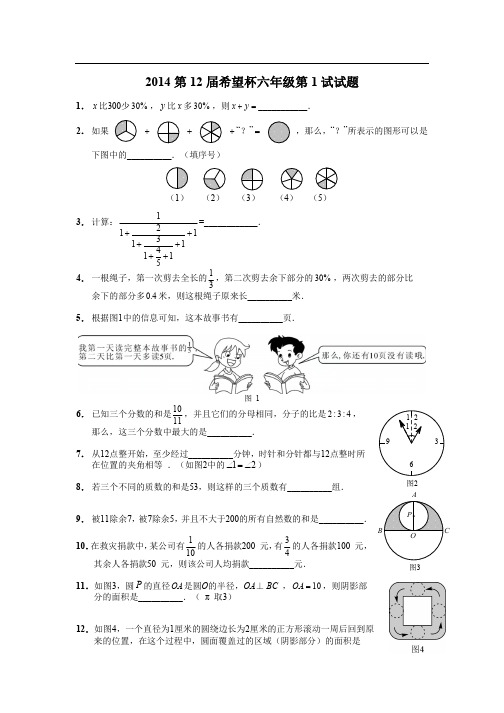
希望杯目录真题希望杯简介 ......................................................................... .. (Ⅰ)近三年真题分析.......................................................................... (Ⅱ)2014第 12 届希望杯六年级第 1 试试题....................................................................... .. (1)2013第 11 届希望杯六年级第 1 试试题....................................................................... .. (3)2012第 10 届希望杯六年级第 1 试试题....................................................................... .. (5)2011 第 9 届希望杯六年级第 1 试试题........................................................................... (7)2010第 8 届希望杯六年级第 1 试试题....................................................................... . (9)2014第 12 届希望杯六年级第 2 试试题...................................................................... . (11)2013第 11 届希望杯六年级第 2 试试题...................................................................... . (13)2012第 10 届希望杯六年级第 2 试试题...................................................................... . (15)2011 第 9 届希望杯六年级第 2 试试题........................................................................... . (17)2010第 8 届希望杯六年级第 2 试试题...................................................................... (19)参考答案2014第 12 届希望杯六年级第 1 试试题分析....................................................................... . (21)2013第 11 届希望杯六年级第 1 试试题分析....................................................................... . (23)2012第 10 届希望杯六年级第 1 试试题分析....................................................................... . (25)2011第 9 届希望杯六年级第 1 试试题分析 (27).........2010第 8 届希望杯六年级第 1 试试题分析....................................................................... (29)2014第 12 届希望杯六年级第 2 试试题分析....................................................................... . (31)2013第 11 届希望杯六年级第 2 试试题分析....................................................................... . (33)2012第 10 届希望杯六年级第 2 试试题分析....................................................................... . (35)2011第 9 届希望杯六年级第 2 试试题分析....................................................................... (37)2010第 8 届希望杯六年级第 2 试试题分析....................................................................... (39)希望杯简介“希望杯”全国数学邀请赛的主办单位“希望杯”是由中国科学技术协会普及部、中国优选法统筹法与经济数学研究会、《数理天地》杂志社、中青在线、华罗庚实验室等主办的全国性数学竞赛.“希望杯”全国数学邀请赛的宗旨鼓励和引导中小学生学好数学课程中最主要的内容,适当地拓宽知识面;启发他们注意数学与其它课程的联系和数学在实际中的应用;激励他们去钻研和探究;培养他们科学的思维能力、创新能力和实践能力;树立他们为振兴中华而努力成才的自信.“希望杯”全国数学邀请赛的命题原则试题内容不超出现行数学教学大纲,不超出教学进度,贴近现行的数学课本,源于课本,高于课本.题目活而不难,巧而不偏;既大众化又富于思考性和启发性.力求体现科学思维之美,寓科学于趣味之中,将知识、能力的考察和思维能力的培养结合起来.“希望杯”全国数学邀请赛的参赛对象初、高中一、二年级学生和小学四、五、六年级学生.每年举行一次,为一届.每次举行两试,三月中旬第 1 试,考小时;四月中旬第 2 试,考 2 小时.“希望杯”全国数学邀请赛的赛前准备杯赛的备考其实非常简单,做到以下两点,希望杯获奖轻松惬意:1.利用寒假做完希望杯 100 题和希望杯历年真题;2.春季再做一遍;3.结合一试的试题,有针对性的准备二试.希望杯全国数学邀请赛的评奖希望杯会设置全国奖项和深圳地区奖项其中含金量最高的是全国一二等奖,整个深圳市也就 20 个左右的名额;而全国三等奖就有好几百个,具体规则如下:根据希望杯的评奖规则,全国一二等奖在赛区内统一标准,按照初赛人数的约千分之三评定.全国三等奖按报名单位初赛人数和规定比例评定,由报名单位按照下述要求评定:1.各单位获奖总指标(一二三等奖):中学每满 30 人初赛给一个指标,不足 30 人不给;小学每满 20 人初赛给一个指标,不足 20 人不给.若评出人数多于计划指标,组委会将按照从后到前的顺序去掉多出指标.2.各单位评奖时应当按照复赛分数由高到低的原则,赛分数相同时按初赛成绩排序.3.各单位指标可在小学内部中学内部调剂使用,得在二者之间调剂.4.凡是列入全国一二等奖推荐名单的,提供该生的一试试卷和二试试卷,奖励等级由全国组委会统一确定.深圳地区奖项设置有特、一、二、三等奖,2014 年 2000 多名进入二试的学生中,有 120 个特等奖,400 个一等奖,所有进入二试的选手至少能获三等奖!!近三年真题分析“希望杯”题型涉及内容广泛,为了更好备战 2015 年“希望杯”,我们需要对历年考试情况有一个详细了解。
2010年第八届小学希望杯六年级初决赛试题及答案

2010年第八届小学“希望杯”全国数学邀请赛六年级第1试以下每题6分,共120分。
1.计算:8-(7.14×13-229÷2.5)+0. 1= . 2.将分子相同的三个最简假分数化成带分数后,分别是:23a ,34b ,35c ,其中a, b, c 是不超过10的自然数,则(2a +b )÷c = 。
3.若用“*”表示一种运算,且满足如下关系:(1)1*1=1; (2)(n +1)*1=3×(n*1)。
则5*12*1= 。
4.一个分数,分子减1后等于23,分子减2后等于12,则这个分数是 。
5.将2,3,4,5,6,7,8,9这八个数分别填入下面的八个方格内(不能重复),可以组成许多不同的减法算式,要使计算结果最小,并且是自然数,则这个计算结果是 。
6.一个箱子里有若干个小球。
王老师第一次从中箱子取出半数的球,再放进去1个球,第二次仍从箱子中取出半数的球,再放进去1个球,…,如此下去,一共操作了2010次,最后箱子里还有两个球。
则未取出球之前,箱子里有小球 个。
7.过年了,同学们要亲手做一些工艺品送给敬老院的老人。
开始时艺术小组的同学们先做一天,随后增加15位同学和他们一起又做了两天,恰好完成。
假设每位同学的工作效率相同,且一位同学单独完成需要60天。
那么艺术小组的同学有 位。
8.某超市平均每小时有60人排队付款,每一个收银台每小时能应付80人,某天某时段内,该超市只有一个收银台工作,付款开始4小时就没有顾客排队了。
如果当时有两个收银台工作,那么付款开始 小时就没有人排队了。
9.下面四个图形都是由六个相同的正方形组成,其中,折叠后不能围成正方体的是 。
(填序号)10.如图1所示的四个正方形的边长都是1,图中的阴影部分的面积依次用S 1,S 2,S 3,S 4表示,则S 1,S 2,S 3,S 4从小到大排列依次是 。
11.如图2,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根铁棒在水面以上的长度是总长的13,另一根铁棒在水面以上的长度是总长的15。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第八届小学“希望杯”全国数学邀请赛六年级 第2试一、填空题(每小题5分,共60分)1.330.245.41.35⨯⨯=。
2.已知111116A 116B 16C C -=+++++,其中A 、B 、C 都是大于0但互不相同的自然数,则(A+B)÷C =。
3.有一类自然数,从左边第三位开始,每个数位上的数字都是它左边两个数位上数字之和,如21347,则这类自然数中,最大的奇数是。
4.王老师在黑板上写了这样的乘法算式:12345679×( )=□□□□□□□□□,然后说道:只要同学们告诉我你喜欢1,2,3,4,5,6,7,8,9中的哪个数,我在括号里填上适当的乘数,右边的积一定全是你喜欢的数字组成。
小明抢着说:我喜欢3。
王老师填乘数“27”,结果12345679×(27)=333333333;小宇说:我喜欢7,只见王老师在乘数上填“63”,结果是12345679×(63)=777777777。
小丽说:我喜欢8,那么在乘数上应填。
5.如图,三角形ABC 中,点E 在AB 上,点F 在AC 上,BF 与CE 交于点P 上,如果四边形AEPF 与三角形BEP 、三角形CFP 的面积都是4,则三角形BPC 的面积是。
6.张老师带六一班学生去种树,学生恰好可以平均分成5组,已知师生每人种的树一样多,共种树527棵,问六一班学生有人。
7.两个顽皮的孩子逆着自动扶梯行驶的方向行走,从扶梯的一端到达另一端,男孩走了100秒,女孩走了300秒,已知在电梯静止时,男孩每秒走3米,女孩每秒走2米,则该自动扶梯长米8.有7根直径都是5厘米的圆柱形木头,现在用绳子分别在两处把它们捆在一起,则至少需要绳子分米(结头处绳子不计,π取3.14)9. 一个深30厘米的圆柱形容器,外圆直径22厘米,壁厚1厘米,已装深27.5厘米的水。
现放入一个底面直径10厘米,高30厘米的圆锥形铁块,则将有立方厘米的水溢出?10.新年联欢会共有8个节目,其中有3个非歌唱类节目.排列节目单时规定,非歌唱类节目不相邻,而且第一个和最后一个节目是歌唱类节目,则节目单有种不同的排法.11.有一水池,单开进水管3小时可把水池注满,单开出水管4小时把排空满池水.水池建成后,发现水池漏水,这时,若同时打开进水管与出水管14小时才能把水池注满,当水池注满后,并且关闭进水管与出水管,经过小时水池会漏完.12.甲乙两人分别从A 、B 两地同时出发,相向而行,已知甲、乙两人的速度比是6:5,他们相遇时距AB 两地的中点5千米,当甲到达B 时,乙距A 还有千米二、解答题(每题15分,共60分)每题都要写出推算过程。
13.有一个电子计算器的数字显示屏坏了,有部分区域在该亮时不亮,使原本的一道一位数乘以一位数,积是两位数的乘法算式,出现如图1所示怪样(不妨用火柴棒来表示),小明对此用火柴棒摆出可能算式如图2。
请问,图中所示的算式有哪几种?14.修一条高速公路,若甲、乙、丙合作,90天可完工;若甲、乙、丁合作,120天可完工;若丙、丁合作,180天完工;若甲、乙合作36天后,剩下的工程由四人合作,还需要多少天完工?15.甲乙两辆车在与铁路并行的道路上相向而行,一列长180米的火车以60千米/小时的速度与甲同向前进,火车从追上甲车到遇上乙车,相隔5分钟,若火车从追上并超过甲车用时30秒,从与乙车相遇到离开用时6秒,求乙车遇到火车后再过多长时间与甲车相遇?16.定义:f (n)=k (其中n 是自然数,k 是0.987651234658……的小数点后的第n 位数字),如f (1)=9,f (2)=8,f (3)=7,求()()()()()()5528f f f f f +…………的值。
第八届小学“希望杯”全国数学邀请赛答案六年级第2试1.原式=0.75/1.35 ×5.4=32.等式左边,经过计算=191/228,再把它转化成等式右边形式可算出A=1,B=5,C=6(A+B)÷C=1(由于博文中不好显示这种形式的分数,故解析较略)3.要想这个奇数最大,那么位数越多越好,要想位数越多,那么该数里面所涉加法的次数越多越好,要想加法的次数越数,那么其中的加数越小越好,依以上考虑,不难找出该数是10112354.由题可知:12345679×27=333333333即12345679×3×9=333333333即12345679×9=111111111可推出12345679×9×8=888888888即12345679×72=8888888885.连接AP、EF因为三角形BPE和三角形CFD的面积相等,都等于4所以三角形BEF和三角形EFC的面积相等,这两个三角形的底边都是EF,所以它们的高肯定相等,可以推出EF∥BC 那么,根据平行线定律,可得CF:FA=BE:EA在三角形CPF和三角形APF中,由于高相同,所以面积之比会等于底边之比,即三角形CPF的面积:三角形APF的面积=CF:FA同理可得:三角形BPE的面积:三角形EPA的面积=BE:EA综合上面三个比,可得三角形CPF的面积:三角形APF的面积=三角形BPE的面积:三角形EPA的面积因为三角形BPE的面积=三角形CPF的面积=4所以,三角形EPA的面积=三角形APF的面积=1/2 四边形EPFA的面积=2那么 BE:EA=2:1即三角形BEC的面积:三角形ECA的面积=BE:EA=2:1三角形ECA的面积=8,所以,三角形BEC的面积=16那么,三角形BPC的面积=16-4=126.527=17×31师生人数可能是17人,或是31人,即学生人数是16人或30人,由于学生人数能平均分成五组,故学生人数应是30人7.牛吃草问题“新草”:扶梯速度:(300×2-100×3)÷(300-100)=1.5米/秒“原草”:扶梯长度:300×2-1.5×300=150米8.每处绳子由6段长度为5分米和6段60°弧形组成,所以,至少需要绳子长度=2×(5×6+6× 60°/360° ×л×5)=91.49.容器的容积=л×[(22-2)÷2]×[(22-2)÷2]×30=3000л容器内水的体积=л×[(22-2)÷2]×[(22-2)÷2]×27.5=2750л圆锥的体积=л×5×5×30×1/3=250л圆锥的体积+水的体积=3000л=容器的容器水刚好满,不会溢出10.先将5个歌唱类节目排列好,有5×4×3×2×1=120种这5个节目中有四个空隔,再将3个非歌唱类节目按插在这四个空隔中,有4×3×2=24种所以共有120×24=2880种11.设x小时排空由题意可列出方程: (1/3 – 1/4 –1/x)×14=1解得 x=8412.第一次相遇时,时间相等,速度与路程成正比,甲乙的速度比是6:5,甲乙所走的路程比也是6:5,即甲比乙多走1份路,由题可知,甲比乙多走5×2=10千米,即1份路就是10千米,总路程即为11×10=110千米,即,第一次相遇时,甲走了60千米,乙走了50千米在接下来行走中,甲乙所用的时间相等,所走路程比仍是6:5,此时,甲到B,走了50千米,那么乙就走了50× 5/6 = 250/6千米,离A地60- 250/6 = 110/6千米13.在数字0---9中,只有4,5,6,8,9,符合题意,所以有以下种情况:5×9=45,9×5=45,6×8=48,8×6=48,6×9=54,9×6=54,8×8=6414. 对应法解工程应用题(此处的甲乙丙丁分别表示其工作效率)甲+乙+丙=1/90甲+乙+丁=1/120丙+丁=1/180以上三个式子相加,得 2甲+2乙+2丙+2丁=9/360甲+乙+丙+丁=1/80可推出甲+乙=1/80 – 1/180 =5/720(1- 5/720 ×36)÷ 1/80 = 60天15.题中”火车追上到超过甲用30秒”,是火车尾追甲,追及路程是火车长可求出甲的速度= 60000/3600 - 180÷30 = 32/3 米/秒题中“火车与乙相遇到离开用6秒”,是火车尾与乙相遇,相遇路程是火车长可求出乙的速度=180÷6 – 60000/3600 = 40/3 米/秒题中“火车追上甲到遇到乙用了5分钟”,此时,火车走了60000× 5/60 =5000米甲走了32/3 × 5×60= 3200米,与乙相隔5000-3200=1800米甲乙相遇时间=1800÷(32/3 + 40/3)=1.25分钟16.由题可知:ƒ(5)=5,505次ƒ(5)结果仍是5,所以,所求的前面部分=5×5=25后一部分:ƒ(8)=3,ƒ(3)=7,ƒ(7)=3,ƒ(3)=7、、、、、2个重复一次,2010÷2没有余数,2010个就应ƒ(3)=7,所以后一部分=2×7=14即,最后结果=25+14=39。
