第五章习题解答
第5章习题答案

第5章5-1传输线长度为1m ,当信号频率分别为975MHz 和6MHz 时,传输线分别是长线还是短线?答:1) 频率为975MHz 时,信号的波长为0.3077m<1m ,传输线是长线;2) 频率为6MHz 时,信号的波长为50m>1m ,传输线是短线;5-2已知同轴电缆的特性阻抗为75Ω,其终端接负载阻抗Z L =25+j50Ω,计算终端反射系数2Γ。
答:217550257550250L 0L 2+-=++-+=+-=Γj j j j Z Z Z Z5-3 一无耗传输线特性阻抗为Z 0=100Ω,负载阻抗Z L =75-j68Ω,试求距离终端为λ/8和λ/4处的输入阻抗。
答:1006850687568257568250L 0L 2+-=++-+=+-=Γj j j j Z Z Z Z100685068)(100685068100685068822'228/++=-+-=+-=Γ=Γ--j j j j j e j j e j z j λλπβλ 100686850)1(100685068100685068422'224/+-=-+-=+-=Γ=Γ--j jj j e j j ej z j λλπβλL 02L 075681002568756810017568Z Z j jZ Z j j-----Γ===+-+-222'8/82256825682568()175681756817568j j z j j j ee j j j j πλβλλ-------Γ=Γ==-=---0256811(8)1756825682000013617568(/8)10010025681(8)175682568150117568in j j j j j Z Z j j j j λλλ-++Γ-+---====--Γ--+-- 222'4/42256825682568(1)175681756817568j j z j j j ee j j jπλβλλ------+Γ=Γ==-=---0256811(4)1756825682000017568(/4)10010025681(4)175682568150136117568in j j j j Z Z j j j j j λλλ+++Γ-++-====+-Γ------5-4设无耗线终端接负载阻抗L L j X Z Z +=0,其实部0Z 为传输线特性阻抗,试证明:负载的归一化电抗L ~X 与驻波系数ρ的关系为ρρ1~L -=X 。
刚体的定轴转动习题解答

- 第五章 刚体的定轴转动一 选择题1. 一绕定轴转动的刚体,某时刻的角速度为,角加速度为,则其转动加快的依据是:( )A. > 0B. > 0,> 0C. < 0,> 0D.> 0,< 0解:答案是B 。
2. 用铅和铁两种金属制成两个均质圆盘,质量相等且具有相同的厚度,则它们对过盘心且垂直盘面的轴的转动惯量。
( )A. 相等;B. 铅盘的大;C. 铁盘的大;D. 无法确定谁大谁小解:答案是C 。
简要提示:铅的密度大,所以其半径小,圆盘的转动惯量为:2/2Mr J =。
3. 一轻绳绕在半径为r 的重滑轮上,轮对轴的转动惯量为J ,一是以力F向下拉绳使轮转动;二是以重量等于F 的重物挂在绳上使之转动,若两种情况使轮边缘获得的切向加速度分别为a 1和a 2,则有: ( )A. a 1 = a 2B. a 1 > a 2C. a 1< a 2D. 无法确定解:答案是B 。
简要提示:(1) 由定轴转动定律,1αJ Fr =和11αr a =,得:J Fr a /21=(2) 受力分析得:⎪⎩⎪⎨⎧===-2222ααr a J Tr ma T mg ,其中m 为重物的质量,T 为绳子的力。
得:)/(222mr J Fr a +=,所以a 1 > a 2。
4. 一半径为R ,质量为m 的圆柱体,在切向力F 作用下由静止开始绕轴线- 作定轴转动,则在2秒F 对柱体所作功为: ( )A. 4 F 2/ mB. 2 F 2 / mC. F 2 / mD. F 2 / 2 m解:答案是A 。
简要提示:由定轴转动定律: α221MR FR =,得:mRF t 4212==∆αθ 所以:m F M W /42=∆=θ5. 一电唱机的转盘正以 0的角速度转动,其转动惯量为J 1,现将一转动惯量为J 2的唱片置于转盘上,则共同转动的角速度应为: ( )A .0211ωJ J J +B .0121ωJ J J +C .021ωJ JD .012ωJ J 解:答案是A 。
第5章 习题参考答案

第五章习题参考答案一、填空题1、MCS-51有5个中断源,2个中断优先级,优先级由软件填写特殊功能寄存器 IP 加以选择。
2、外中断请求标志位是 IE0 和 IE1 。
3、 RETI 指令以及任何访问 IE 和 IP 寄存器的指令执行过后,CPU不能马上响应中断。
4、8051单片机响应中断后,产生长调用指令LCALL,执行该指令的过程包括:首先把 PC的内容压入堆栈,以进行断点保护,然后把长调用指令的16位地址送 PC ,使程序执行转向程序存储器中的中断地址区。
二、选择题:1、在中断服务程序中,至少应有一条( D )。
A、传送指令B、转移指令C、加法指令D、中断返回指令2、要使MCS-51能够响应定时器T1中断,串行接口中断,它的中断允许寄存器IE的内容应是( A )。
A、 98HB、 84HC、 42HD、 22H3、MCS-51响应中断时,下列哪种操作不会发生( A )A、保护现场B、保护PCC、找到中断入口D、保护PC转入中断入口4、MCS-51中断源有( A )A、 5个B、 2个C、 3个D、6个5、计算机在使用中断方式与外界交换信息时,保护现场的工作应该是( C )A、由CPU自动完成B、在中断响应中完成C、应由中断服务程序完成D、在主程序中完成6、MCS-51的中断允许触发器内容为83H,CPU将响应的中断请求是( D )。
A、 INT0,INT1B、 T0,T1C、 T1,串行接口D、 INT0,T07、若MCS-51中断源都编程为同级,当它们同时申请中断时,CPU首先响应( B )。
A、 INT1B、 INT0C、 T1D、T08、当CPU响应串行接口中断时,程序应转到( C )。
A、 0003HB、 0013HC、 0023HD、 0033H9、执行MOV IE,#03H后,MCS-51将响应的中断是( D )。
A、 1个B、 2个C、 3个D、0个10、外部中断1固定对应的中断入口地址为( C )。
第五章练习题参考答案(完整版)
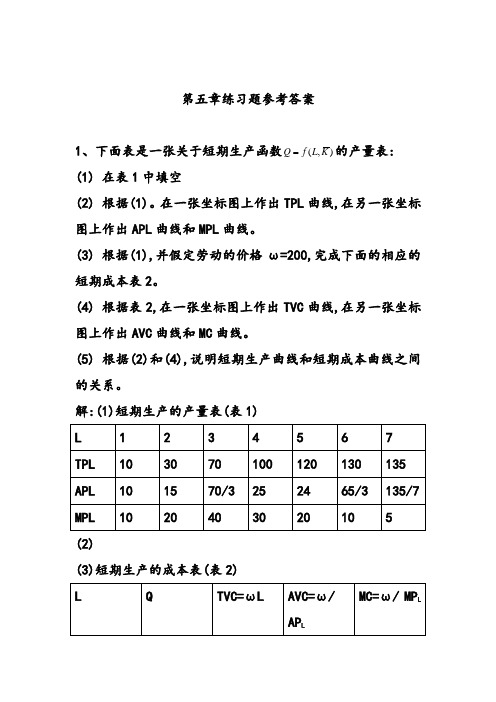
第五章练习题参考答案1、下面表是一张关于短期生产函数),(K L f Q 的产量表:(1) 在表1中填空(2) 根据(1)。
在一张坐标图上作出TPL 曲线,在另一张坐标图上作出APL 曲线和MPL 曲线。
(3) 根据(1),并假定劳动的价格ω=200,完成下面的相应的短期成本表2。
(4) 根据表2,在一张坐标图上作出TVC 曲线,在另一张坐标图上作出AVC 曲线和MC 曲线。
(5) 根据(2)和(4),说明短期生产曲线和短期成本曲线之间的关系。
解:(1)短期生产的产量表(表1)(2)(3)短期生产的成本表(表2)(4)边际产量和边际成本的关系,边际MC和边际产量MPL两者的变动方向是相反的。
总产量和总成本之间也存在着对应关系:当总产量TPL下凸时,总成本TC曲线和总可变成本TVC是下凹的;当总产量曲线存在一个拐点时, 总成本TC曲线和总可变成本TVC也各存在一个拐点。
平均可变成本和平均产量两者的变动方向是相反的。
MC曲线和AVC曲线的交点与MPL曲线和APL曲线的交点是对应的。
2、下图是一张某厂商的LAC曲线和LMC曲线图。
请分别在Q1和Q2的产量上画出代表最优生产规模的SAC曲线和SMC曲线。
解:在产量Q1和Q2上,代表最优生产规模的SAC曲线和SMC曲线是SAC1和SAC2以及SMC1和SMC2。
SAC1和SAC2分别相切于LAC的A和B,SMC1和SMC2则分别相交于LMC的A1和B 1。
3、假定某企业的短期成本函数是TC(Q)=Q 3-5Q 2+15Q+66: (1) 指出该短期成本函数中的可变成本部分和不变成本部分;(2) 写出下列相应的函数:TVC(Q) AC(Q) AVC(Q) AFC(Q)和MC(Q)。
解(1)可变成本部分: Q 3-5Q 2+15Q 不可变成本部分:66 (2)TVC(Q)= Q 3-5Q 2+15Q AC(Q)=Q 2-5Q+15+66/Q AVC(Q)= Q 2-5Q+15 AFC(Q)=66/Q MC(Q)= 3Q 2-10Q+154、已知某企业的短期总成本函数是STC(Q)=0.04 Q 3-0.8Q 2+10Q+5,求最小的平均可变成本值。
第5章 习题答案

第5章 相对论习题5-1 观察者A 测得与他相对静止的XOY 平面上一个圆的面积是12cm 2,另一观察者B 相对A 以0.8C(C 为真空中光速)平行于XOY 平面作匀速直线运动,B 测得这一图形为一椭圆,面积是多少(椭圆面积S=πab ,a 、b 为长短半轴).5-2 一宇宙飞船固有长度,m 900=L 相对地面以v=0.8c 匀速度在一观测站上空飞过,则观测站测得飞船船身通过观测站时间间隔是多少?宇航员测得船身通过观测站的时间隔是多少?解:设地面为S 系,飞船为S ′系,则观测站测飞船长度为2201c L L υ-=.所以,观测站时间间隔是s 1025.28.018.090172220-⨯=-=-==cc L Lt υυυ∆ 宇航员在S ′系测得船身通过的时间是00τυ=='L t ∆,宇航员观察S 系中的钟是以-v 在运动,所以宇航员测得船身通过观测站的时间隔是s 1025.217220-⨯=-==cL t υυγτ∆5-3 半人马星座α星是太阳系最近的恒星,它距地球为 m 。
设有一宇宙飞船,以v =0.999c 的速度飞行,飞船往返一次需多少时间?如以飞船上的时钟计算,往返一次的时间又为多少?解:在地面上观测飞船往返一次的时间为s 1087.2999.0103.42816⨯=⨯⨯=ct ∆;16103.4⨯在飞船上观测距离缩短,测得时间为s 1028.1999.0999.01103.47216⨯=-⨯='ct ∆;或运动的钟测得s 1028.1999.01999.0103.47216⨯=-⨯='ct ∆.5-4 观测者甲和乙分别静止于两个惯性参照系K 和K ′中,甲测得在同一地点发生的两个事件的时间间隔为4S,而乙测得这两个事件的时间间隔为5S,求:(1) K ′相对于K 的运动速度;(2) 乙测得这两个事件发生的地点的距离.解:(1)设两事件的时空坐标见下表事件1 事件2 K 系 ),(11t x ),(21t x K ′系),(11t x '' ),(22t x '' 由洛伦兹变换)/(2c x t t υγ-='得222/1/)/(c t c x t t υυγ-=-='∆∆∆∆解上式得 c c t t c 6.0)54(1)(122=-='-=∆∆υ. (2)由洛伦兹变换)/(2c x t t '+'=υγ得)/(2c x t t '+'=∆∆∆υγ解之得 m 109105)56.014()(882212⨯-=⨯⨯--='-='-'='υγc t tx x x ∆∆∆5-5 惯性系S ′相对另一惯性系S 沿x 轴作匀速直线运动,取两坐标原点重合时刻作为计时起点.在S 系中测得两事件的时空坐标分别为x 1=6×104m,t 1=2×10-4s ,以及x 2=12×104m, t 2=1×10-4s .已知在S ′系中测得该两事件同时发生.试问:(1)S ′系相对S 系的速度是多少? (2)S '系中测得的两事件的空间间隔是多少?解:(1)由洛伦兹变换)/(2c x t t υγ-='得0)/(2=-='c x t t ∆∆∆υγ解之得 m/s 105.110310610)1(10388448⨯-=⨯⨯⨯⨯-⨯⨯==-c x t c ∆∆υ (2)由)(t x x '+'=υγ得x t x x '='+'=∆∆∆∆γυγ)(所以 m 102.55.01106/)(424⨯=-⨯=='+'='γυγx t x x ∆∆∆∆5-6 长度01m =l 的米尺静止于S ′系中,与x '轴的夹角o 30'=θ,S ′系相对S 系沿x 轴运动,在S 系中观测者测得米尺与x 轴夹角为o45=θ. 试求:(1)S ′系和S 系的相对运动速度.(2)S 系中测得的米尺长度.解:(1)由教材p152例题5.3有θγθ'=tan tan 得 c c 816.0)tan tan (12='-=θθυ (2)在x 方向尺会缩短,即m 5.0tan tan cos tan tan 0=''=''='=θθθθθγl x x x ;y 方向没运动,长度不变,即m 5.0sin 0='='=θl y y 。
第5章-习题参考答案

第五章习题参考答案一、填空题1、MCS-51有5个中断源,2个中断优先级,优先级由软件填写特殊功能寄存器 IP 加以选择。
2、外中断请求标志位是 IE0 和 IE1 。
3、 RETI 指令以及任何访问 IE 和 IP 寄存器的指令执行过后,CPU不能马上响应中断。
4、8051单片机响应中断后,产生长调用指令LCALL,执行该指令的过程包括:首先把 PC的内容压入堆栈,以进行断点保护,然后把长调用指令的16位地址送 PC ,使程序执行转向程序存储器中的中断地址区。
二、选择题:1、在中断服务程序中,至少应有一条( D )。
A、传送指令B、转移指令C、加法指令D、中断返回指令2、要使MCS-51能够响应定时器T1中断,串行接口中断,它的中断允许寄存器IE的内容应是( A )。
A、 98HB、 84HC、 42HD、 22H3、MCS-51响应中断时,下列哪种操作不会发生( A )A、保护现场B、保护PCC、找到中断入口D、保护PC转入中断入口4、MCS-51中断源有( A )A、 5个B、 2个C、 3个D、6个5、计算机在使用中断方式与外界交换信息时,保护现场的工作应该是( C )A、由CPU自动完成B、在中断响应中完成C、应由中断服务程序完成D、在主程序中完成6、MCS-51的中断允许触发器内容为83H,CPU将响应的中断请求是( D )。
A、 INT0,INT1B、 T0,T1C、 T1,串行接口D、 INT0,T07、若MCS-51中断源都编程为同级,当它们同时申请中断时,CPU首先响应( B )。
A、 INT1B、 INT0C、 T1D、T08、当CPU响应串行接口中断时,程序应转到( C )。
A、 0003HB、 0013HC、 0023HD、 0033H9、执行MOV IE,#03H后,MCS-51将响应的中断是( D )。
A、 1个B、 2个C、 3个D、0个10、外部中断1固定对应的中断入口地址为( C )。
第五章 习题解答

答:包括以下三个过程:
1热流体以对流传热方式将热量传给管内壁
2热量由内壁面以热传导方式传给外壁面
3热量由外壁面以对流传热的方式传给冷流体
6.简述何谓强化传热?有哪三个主要途径?
答:强化传热是指提高冷热流体间的传热速率。
1增大总传热系数K,这是强化传热的重点。
5.对流传热速率方程的表达式为,其中温度差代表。
流体与壁面(或反之)间温度差的平均值
6.在间壁式换热器中,间壁两边流体都变温时,两流体的流动方向有、、和四种。
并流逆流错流折流
7.对流传热系数的主要影响因素有(1)(2)(3)(4)(5)。
1、流体的种类和相变化的情况2、流体的性质3、流体流动的状态
4、流体流动的原因5、穿热面的形状、分布和大小
已知 ,故
(2)当导热系数小的材料包在里层时,热损失 为:
(3)当导热系数大的材料包在里层时,热损失 为:
(4)可求出: ,说明在圆筒壁当采用两种以上材料保温时,为减少热损失,应将 小的材料包在里层为好。
5.求绝压为140 ,流量为1000 的饱和水蒸汽冷凝后并降温到60℃时所放出的热量。用两种方法计算并比较结果。已知140 水蒸汽的饱和温度为109.2℃,冷凝热为2234.4 ,焓为2692.1 ;60℃的水的焓为251.21 。
解:(1)第一种方法
(2分)
(2)第二种方法
①冷凝水的平均温度为 (1分)
查出84.6℃下的水的比热容为: (1分)
②水蒸气冷凝并降温放出的热量为:
计算表明两种方法结果一样,但是第一种方法较简单。(1分)
6.将0.417 、80℃的有机苯,通过一换热器冷却到40℃;冷却水初温为30℃,出口温度不超过35℃。假设热损失可略,已查出在平均温度下,硝基苯和水的比热容分别为1.6 。求:(1)冷却水用量 ?
第五章 习题解答

Q = ΔU −W = 2090 − (−52.8) = 2143(J)
(c) ΔU , ΔH 同(a)。W = 0 看作向真空膨胀。 Q = ΔU = 2090 (J)
(2)该过程实为部分水蒸气液化的可逆相变过程。
W
=
− p (V2
−V1 )
=
− p( m ρg
− V1 )
=
−101325
×
⎛ ⎜ ⎝
解:先看理想气体:
( ) ΔS = nRT ln
p1 p2
=
8.314
×
300
ln
105 106
= −19.14
J ⋅ K-1
4
ΔA = ΔU − Δ (TS ) = 0 − (−19.14× 300) = 5743(J)
ΔG = ΔH − Δ (TS ) = 0 − (−19.14× 300) = 5743(J)
/
J·mol-1
S
O m
/
J·K-1·mol-1
Cp,m / J·K-1·mol-1
Sn(白锡)
0
52.30
26.15
Sn(灰锡)
-2197
解:计算
10℃时白锡转化为灰锡的
Δ
GΟ
trs m
。
44.76
25.73
( ) ( ) ∫ Δ
trs
H
O m
T
=
Δ trs
H
O m
298.15K +
T
298.15K ΔtrsC p,mdT
2
解:水物质的量: n = pV = 50.663×103 ×100×10−3 = 1.6377 (mol)
第五章习题解答

习 题 五1. 设V 是数域F 上向量空间,假如V 至少含有一个非零向量α,问V 中的向量是有限多还是无限多?有没有n (n ≥ 2)个向量构成的向量空间? 解 无限多;不存在n (n ≥ 2)个向量构成的向量空间(因为如果F 上一个向量空间V 含有至少两个向量, 那么V 至少含有一个非零向量α , 因此V 中含有α , 2α , 3α , 4α , …,这无穷多个向量互不相等,因此V 中必然含有无穷多个向量).2. 设V 是数域F 上的向量空间,V 中的元素称为向量,这里的向量和平面解析几何中的向量α,空间解析几何中的向量β有什么区别?解 这里的向量比平面中的向量意义广泛得多,它可以是多项式,矩阵等,不单纯指平面中的向量.3. 检验以下集合对所指定的运算是否构成数域F 上的向量空间.(1)集合:全体n 阶实对称矩阵;F :实数域;运算:矩阵的加法和数量乘法;(2)集合:实数域F 上全体二维行向量;运算: (a 1, b 1)+ (a 2, b 2)=(a 1+a 2, 0) k • (a 1, b 1)=(ka 1, 0)(3)集合:实数域上全体二维行向量;运算: (a 1, b 1)+ (a 2, b 2)=(a 1+a 2, b 1+b 2)k •( a 1, b 1)=(0, 0)解 (1) 是; (2) 不是(因为零向量不唯一);(3) 不是(不满足向量空间定义中的(8)).4. 在向量空间中,证明,(1) a (-α)=-a α=(-a ) α ,(2) (a -b )α=a α-b α ,a ,b 是数,α是向量.证明 (1) a a a a =+-=+-))(()(αααα 0= 0ααa a -=-∴)(又 ==+-=+-a a a a a 0))(()(ααα 0ααa a -=-∴)(综上, .)()(αααa a a -=-=-(2) ααααααb a b a b a b a -=-+=-+=-)())(()(.5. 如果当k 1=k 2=…=k r =0时,k 1α1+k 2α2+…+k r αr =0, 那么α1, α2, …, αr 线性无关. 这种说法对吗?为什么?解 这种说法不对. 例如设α1=(2,0, -1), α2=(-1,2,3), α3=(0,4,5), 则0α1+0α2+0α3=0. 但α1, α2, α3线性相关, 因为α1+2α2-α3=0.6. 如果α1, α2, …, αr 线性无关,而αr +1不能由α1, α2, …, αr 线性表示,那么α1, α2,…, αr , αr +1线性无关. 这个命题成立吗?为什么? 解 成立. 反设α1, α2,…, αr , αr +1线性相关,由条件α1, α2, …, αr 线性无关知αr +1一定能由α1, α2, …, αr 线性表示,矛盾.7. 如果α1, α2, …, αr 线性无关,那么其中每一个向量都不是其余向量的线性组合. 这种说法对吗?为什么?解 对. 反设 αi = k 1α1+k 2α2+…k i -1αi-1+k i+1αi +1 +…+k r αr ,则 k 1α1+k 2α2+…k i -1αi-1+(-1) αi +k i+1αi +1 +…+k r αr =0. 由于-1≠0, 故α1, α2, …, αr 线性相关.8. 如果向量α1, α2, …, αr 线性相关,那么其中每一个向量都可由其余向量线性表示. 这种说法对吗?为什么?解 不对. 设α1=(1,0) , α2=(2,0) , α3=(0,1) , 则α1, α2, α3线性相关, 但α3不能由α1, α2线性表示.9. 设α1= (1, 0, 0), α2= (1, 2, 0), α3=(1, 2, 3)是F 3中的向量,写出α1, α2, α3的一切线性组合. 并证明F 3中的每个向量都可由{α1, α2, α3}线性表示.解 k 1α1+k 2α2+k 3α3 k 1, k 2 , k 3∈F .设k 1α1+k 2α2+k 3α3=0,则有⎪⎩⎪⎨⎧==+=++030220332321k k k k k k , 解得 k 1= k 2 =k 3=0.故α1, α2, α3线性无关.对任意(a,b,c)∈F 3, (a,b,c)=3213)32())322((αααc c b c ba +-+--,所以F 3中的每个向量都可由{α1, α2, α3}线性表示.10. 下列向量组是否线性相关(1) α1= (1, 0, 0), α2= (1, 1, 0), α3=(1, 1, 1);(2) α1=(3, 1, 4), α2=(2, 5, -1), α3=(4, -3, 7).解 (1) 线性无关; (2) 线性无关.11. 证明,设向量α1, α2, α3线性相关,向量α2, α3, α4线性无关,问:(1) α1能否由α2, α3线性表示?说明理由;(2) α4能否由α1, α2, α3线性表示?说明理由.解 (1)因为α2, α3线性无关而α1, α2, α3线性相关,所以α1能由α2, α3线性表示;(2)反设α4能由α1, α2, α3线性表示,但α1能由α2, α3线性表示,故α4能由α2, α3线性表示,这与α2, α3, α4线性无关矛盾,所以α4不能由α1, α2, α3线性表示.12. 设α1= (0, 1, 2), α2= (3, -1, 0), α3=(2, 1, 0),β1= (1, 0, 0), β2= (1, 2, 0), β3=(1, 2, 3)是F 3中的向量. 证明,向量组{α1, α2, α3}与{β1, β2, β3}等价.证明 (β1, β2, β3)=(321,,εεε)A(α1, α2, α3)= (321,,εεε)B其中A=⎪⎪⎪⎭⎫ ⎝⎛300220111, B=⎪⎪⎪⎭⎫ ⎝⎛-002111230.易验证A , B 均可逆, 这样 (β1, β2, β3) = (α1, α2, α3 )(B -1A )(α1, α2, α3) = (β1, β2, β3)(A -1B ) ,故向量组{α1, α2, α3}与{β1, β2, β3}等价.13. 设数域F 上的向量空间V 的向量组{α1, α2, …, αs }线性相关,并且在这个向量组中任意去掉一个向量后就线性无关. 证明,如果∑=s i i ik 1α=0 (k i ∈F ),那么或者k 1=k 2=…=k s =0, 或k 1,k 2,…,k s 全不为零.证明 由条件∑=s i i ik 1α=0 (k i ∈F )知k i αi = - (k 1α1+k 2α2+…k i -1αi-1+k i+1αi +1 +…+k s αs ) (*)(1) 当k i =0时,(*)式左边等于零,故k 1α1+k 2α2+…k i -1αi-1+k i+1αi +1 +…+k s αs =0. 由于这s -1个向量线性无关,所以k 1=k 2=…=k s =0.(2) 当k i ≠0时, αi = -ik 1(k 1α1+k 2α2+…k i -1αi-1+k i+1αi +1 +…+k s αs ),下证对于任意i j s j ≠∈},,2,1{ 时k j ≠0. 反设k j =0, 则αi 可由s -2个向量线性表示.这与任意s -1个向量线性无关矛盾,所以此时k 1,k 2,…,k s 全不为零.14. 设α1=(1, 1), α2=(2, 2), α3=(0, 1) , α4=(1, 0)都是F 2中的向量. 写出{α1, α2, α3, α4}的所有极大无关组.解 α1, α3 ; α1, α4 ; α2 ,α3 ; α2 ,α4 ; α3 ,α4 .15. 设A 1=⎪⎪⎭⎫ ⎝⎛-2001,A 2=⎪⎪⎭⎫ ⎝⎛-0021, A 3=⎪⎪⎭⎫ ⎝⎛0120,A 4=⎪⎪⎭⎫ ⎝⎛-2142∈M 2×2(F ). 求向量空间M 2×2(F )中向量组{A 1, A 2,A 3, A 4}的秩及其极大无关组. 解 秩{A 1, A 2,A 3, A 4}=3, {A 1, A 2,A 3}是向量组{A 1, A 2, A 3, A 4}的一个极大无关组.16.设由F 4中向量组{α1=(3,1,2,5),α2=(1,1,1,2),α3=(2,0,1,3),α4 =(1,-1,0,1),α5 =(4,2,3,7)}. 求此向量组的一个极大无关组.解 (α1,α2,α3,α4,α5)= (4321,,,εεεε)A , 其中A=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-71325301122101141213, 则秩A =2. 又(α1,α2 )= (4321,,,εεεε)B , 其中B =⎪⎪⎪⎪⎪⎭⎫ ⎝⎛25121113. 秩B =2, 故{α1,α2}线性无关, 它是向量组{α1,α2,α3,α4,α5}的一个极大无关组.17. 证明,如果向量空间V 的每一个向量都可以唯一表成V 中向量α1, α2, …, αn 的线性组合,那么dim V =n .证明 由条件零向量可唯一的表示成α1, α2, …, αn 的线性组合, 这说明α1, α2, …, αn 线性无关, 故可作为V 的基, 从而dim V =n .18. 设β1, β2,…,βn 是F 上n (>0)维向量空间V 的向量,并且V 中每个向量都可以由β1, β2,…,βn 线性表示. 证明, {β1, β2,…,βn }是V 的基.证明 由条件标准正交基{ e 1, e 2, …,e n }可由β1, β2,…,βn 线性表示, 反过来β1, β2,…,βn 又可由{ e 1, e 2, …,e n }线性表示,所以{ e 1, e 2, …,e n }和{β1, β2,…,βn }等价. 由{ e 1, e 2, …,e n }线性无关知{β1, β2,…,βn }线性无关,又因V 中每个向量都可以由β1, β2,…,βn 线性表示, 由基的定义知{β1, β2,…,βn }是V 的基.19. 复数集C 看作实数域R 上的向量空间(运算: 复数的加法,实数与复数的乘法)时,求C 的一个基和维数.解 基为{1, i }; dim C =2.20. 设V 是实数域R 上全体n 阶对角形矩阵构成的向量空间(运算是矩阵的加法和数与矩阵的乘法). 求V 的一个基和维数.解 基为E ii (i =1,2, …,n ); dim V =n .21. 求§5.1中例9给出的向量空间的维数和一个基.解 任意一个不等于1的正实数都可作为V 的基; dim V =1.22. 在R 3中,求向量α=(1, 2, 3)在基ε1=(1, 0, 0),ε2=(1, 1, 0),ε3=(1, 1, 1)下的坐标.解 (-1,-1,3)T .23. 求R 3中由基{α1, α2, αs }到基{β1, β2, β3 }的过渡矩阵,其中α1=(1, 0, -1), α2=(-1, 1, 0), α3=(1, 2, 3),β1=(0, 1, 1), β2=(1, 0, 1), β3=(1, 1, 1).解 所求过渡矩阵为⎪⎪⎪⎭⎫ ⎝⎛-32204230061. 24. 设{α1, α2,…, αn }是向量空间V 的一个基,求由这个基到基{α3, α4, …, αn ,α1, α2}的过渡矩阵.解 所求过渡矩阵为⎪⎪⎭⎫ ⎝⎛-0022n I I . 25. 已知F 3中向量α关于标准基ε1=(1, 0, 0),ε2=(0, 1, 0) ,ε3=(0, 0, 1)的坐标是(1, 2, 3),求α关于基β1=(1, 0, 1), β2=(0, 1, 1), β3=(1, 1, 3)的坐标.解 (1,2,0)T .26. 判断R n 的下列子集哪些是子空间(其中R 是实数域,Z 是整数集).(1) {(a 1, 0, …, 0, a n )| a 1, a n ∈R };(2) {(a 1, a 2, …, a n )|∑==ni i a 10,a 1, a 2, …, a n ∈R };(3) {(a 1, a 2, …, a n )|a i ∈Z , i =1, 2, …, n };解 (1) 是; (2) 是; (3) 不是(数乘不封闭).27. 设V 是一个向量空间,且V ≠{0}. 证明,V 不能表成它的两个真子空间的并集.证明 设W 1与W 2是V 的两个真子空间(1) 若21W W ⊆,则W 1⋃W 2= W 2≠V ;(2) 若21W W ⊇,则W 1⋃W 2= W 1≠V ;(3) 若21W W ⊄且12W W ⊄, 取1W ∈α但2W ∉α,2W ∈β但1W ∉β, 那么1W ∉+βα,否则将有1)(W ∈=-+βαβα,这与1W ∉β矛盾, 同理2W ∉+βα, 所以V 中有向量21W W ∉+βα,即V ≠21W W .28. 设V 是n 维向量空间,证明V 可以表示成n 个一维子空间的直和.证明 设{α1, α2,…, αn }是向量空间V 的一个基, (α1), (α2) ,…, (αn )分别是由α1, α2,…, αn 生成的向量空间, 要证(α1+α2+…+αn )= (α1)⊕ (α2)⊕…⊕ (αn )(1) 因为{α1, α2,…, αn }是V 的一个基, 所以V 中任一向量α都可由α1, α2,…, αn 线性表示, 此即(α1+α2+…+αn )= (α1)+ (α2)+…+ (αn ).(2) 对任意i ≠j ∈{1,2,…, n },下证 (αi )∩ (αj )={0}. 反设存在0 ≠∈x (αi )∩ (αj ),由∈x (αi )知存在k F ∈使得x =k αi ; 由 x ∈ (αj )知存在F l ∈使得x =l αj , 从而αi =kl αj , 即α1与α2线性相关, 矛盾, 所以 (αi )∩ (αj )={0}. 综上, (α1+α2+…+αn )= (α1)⊕ (α2)⊕…⊕ (αn ).29. 在R 3中给定两个向量组α1=(2, -1, 1, -1), α2=(1, 0, -1, 1),β1=(-1, 2, -1, 0), β2=(2, 1, -1, 1).求 (α1, α2)+ (β1, β2) 的维数和一个基.解 取R 4的标准正交基{4321,,,εεεε},于是(α1, α2, β1, β2)= (4321,,,εεεε)A ,其中 A =⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------1011111112012112 , 秩A = 4. 故α1, α2, β1, β2线性无关, 又因为 (α1, α2)∩ (β1, β2)={0},所以dim (α1, α2) + dim (β1, β2)= 4,{ α1, α2, β1, β2}是它的基.30. 设W 1, W 2都是向量空间V 的子空间,证明下列条件是等价的:(1) W 1⊆W 2;(2) W 1∩W 2=W 1;(3) W 1+W 2=W 2.证明 (i) (1)⇒(2) 因为W 1⊆W 2 , 所以W 1∩W 2=W 1. (ii) (2)⇒(3) W 1+W 2 ={α1+α2 | α1∈W 1, α2∈W 2} 由(2)知对任意α∈W 1, 都有α∈W 2 , 所以W 1+W 2 ={α1+α2 | α1, α2∈W 2}=W 2 .(iii) (3)⇒(1) W 1+W 2 ={α1,+α2 | α1∈W 1, α2∈W 2}=W 2 , 说明对任意α∈W 1, 都有α∈W 2 , 此即W 1⊆W 2 .31. 设V 是实数域R 上n 阶对称矩阵所成的α2向量空间;W 是数域R 上n 阶上三角矩阵所成的向量空间,给出V 到W 的一个同构映射.解 对∈∀A V (A =(a ij )且a ij = a ji )和B ∈W (B =(a ij ),当i>j 时, a ij =0) 定义f : V → WA B 易验证f 是V 到W 的一个同构映射.32. 设V 与W 都是数域F 上的向量空间,f 是V 到W 的一个同构映射,证明{α1, α2, …, αn }是V 的基当且仅当{f (α1), f (α2), …, f (αn )}是W 的基.证明 设{α1, α2, …, αn }是V 的基.(1) 由α1, α2, …, αn 线性无关知f (α1), f (α2), …, f (αn ) 线性无关.(2) 任取∈ηW , 由f 是同构映射知存在∈ξV 使得f (ξ)=η.但ξ=∑=n i i ia 1α, a i ∈F , f (ξ)=f (∑=n i i i a 1α)=)(1∑=n i i i f a α=η. 由η的任意性知{f (α1), f (α2), …, f (αn )}是W 的基.反过来, {f (α1), f (α2), …, f (αn )}是W 的基(1) 由f (α1), f (α2), …, f (αn )线性无关知α1, α2, …, αn 线性无关.(2) 任取∈ξV , 由f 是同构映射知存在∈ηW 使得f (ξ)=η.但η=∑=n i i i f k 1)(α= f (∑=n i i i k 1α), k i ∈F , 从而ξ=∑=ni i i k 1α, k i ∈F .由ξ的任意性知{ α1, α2, …, αn }是V 的基.补 充 题1. 设W 1, W 2是数域F 上向量空间V 的两个子空间. α,β是V 的两个向量,其中α∈W 2,但α∉ W 1,β∉W2. 证明:(1)对于任意k ∈F ,αβk +∉W 2;(2)至多有一个k ∈F ,使得αβk +∈W 1.证明 (1)反设存在k 1∈F 使得αβ1k +∈W 2 , 又α∈W 2 , 因此β=β+ k 1α-k 1α∈W 2 , 这与β∉W 2矛盾. 所以对于∀k ∈F ,αβk +∉W 2 .(2)若有k 1, k 2∈F , k 1≠k 2使得αβ1k +, αβ2k +∈W 1, 那么。
第五章习题与解答_高电压技术

第五章绝缘得高压试验一、选择题1)用铜球间隙测量高电压,需满足那些条件才能保证国家标准规定得测量不确定度?A 铜球距离与铜球直径之比不大于0、5B 结构与使用条件必须符合IEC得规定C 需进行气压与温度得校正D 应去除灰尘与纤维得影响2)交流峰值电压表得类型有:A电容电流整流测量电压峰值B整流得充电电压测量电压峰值C 有源数字式峰值电压表D 无源数字式峰值电压表3)关于以下对测量不确定度得要求,说法正确得就是:A 对交流电压得测量,有效值得总不确定度应在±3%范围内B 对直流电压得测量,一般要求测量系统测量试验电压算术平均值得测量总不确定度应不超过±4%C 测量直流电压得纹波幅值时,要求其总不确定度不超过±8%得纹波幅值D 测量直流电压得纹波幅值时,要求其总不确定度不超过±2%得直流电压平均值。
4)构成冲击电压发生器基本回路得元件有冲击电容C1,负荷电容C2,波头电阻R1与波尾电阻R2,为了获得一很快由零上升到峰值然后较慢下降得冲击电压,应使______。
A.C1>>C2、R1>>R2B.C1>>C2、R1<<R2C.C1<<C2、R1>>R2D.C1<<C2、R1<<R25)用球隙测量交直流电压时,关于串接保护电阻得说法,下面哪些就是对得?A 球隙必须串有很大阻值得保护电阻B 串接电阻越大越好C 一般规定串联得电阻不超过500ΩD 冲击放电时间很短,不需要保护球面。
6)电容分压器得低压臂得合理结构就是______。
A低压臂电容得内电感必须很小B 应该用同轴插头,插入低压臂得屏蔽箱C 电缆输入端应尽可能靠近电容C2得两极。
D abc环路线应该比较长7)标准规定得认可得冲击电压测量系统得要求就是:A 测量冲击全波峰值得总不确定度为±5%范围内B 当截断时间时,测量冲击截波得总不确定度在±5%范围内C当截断时间时,测量冲击电压截波得总不确定度在±4%范围内D测量冲击波形时间参数得总不确定度在±15%范围内8)光电测量系统有哪几种调制方式:A 幅度-光强度调制(AM-IM)B 调频-光强度调制(FM-IM)C 数字脉冲调制D 利用光电效应二、填空题9)交流高电压试验设备主要就是指______。
第五章__习题解答

ω φ(ω ) 0 0° 0.1 0.4 0.8 2 8 40 100 -11.3° -34.3° -42.8° -36.5° -22.5° -47.3° -69.1°
对数幅频特性渐进线
对数相频特性曲线
0.032(10s 1) (3) 写成标准形式 G( s) 2 s( s s 1)(0.04s 2 0.16s 1)
起始段的延长线与0dB线的交点频率 a
a K v 400 20(rad / s)
2 c a / 5 80(rad / s)
1800 2 900 arctan( 0.2 c ) arctan( 0.005c ) 650
Ⅱ型系统:ess essp essv
20lg(1 /(2 )) 20dB
要求幅值裕量为20dB。由对数 幅频特性渐进线起始段 20lg( K /(100 g )) 40dB 解得 K 10 开环增益为 10 / 100 0.1
5.14 (a)
20lg( K / 2 ) | 5 24
K 400
400(0.2s 1) G( s) 2 s (0.005s 1)
开环幅相特性曲线如题图5-3(a)所示。
(2) 超前网络的频率特性
jRC G ( j ) jRC 1 RC 幅频特性 A( ) 1 (RC) 2 相频特性 ( ) 900 arctanT
方法一:当ω变化0→∞时,A(ω) 变化0→1,φ(ω) 变化90°→0°,由此可概略绘制开环幅相特性曲线。 方法二:通过列表计算作出开环幅相特性曲线。
第五章 习题解答
4 闭环传递函数 ( s) s 1 s5 4 j ( ) 闭环频率特性 ( j ) M ( )e j 5 4 M ( ) ( ) arctan( / 5) 2 25
第5章课后习题参考答案

第五章习题参考答案3.给定一个单位立方体,一个顶点在(0,0,0),相对的另一个顶点在(1,1,1),过这两个顶点连接一条直线,将单位立方体绕该直线旋转θ角,试导出变换矩阵。
解答:需进行以下复合变换:⑴绕Z轴旋转-45。
角,变换矩阵为:/220 0T1= 2/20 00 1 00 0 1⑵绕Y轴旋转2)角,变换矩阵为:/30 30T2= 0 1 0 030 300 0 0 1⑶绕X轴旋转θ角,变换矩阵为:1 0 0 0T3= 0 cosθs i nθ00 -sinθc o sθ00 0 0 1⑷绕Y轴旋转2)角,变换矩阵为:/30 30T4= 0 1 0 030 300 0 0 1⑸绕Z 轴旋转45。
角,变换矩阵为:/2/20 0 T5= 2/20 0 0 0 1 00 0 0 1 故最后的变换矩阵为: T=T1T2T3T4T5=1/32/3cos θ+ 1/3/3s i n1/3c o s θθ+- 1/3/3s i n 1/3c o s θθ-- 0 1/33sin 1/3cos θθ-- 1/32/3c o s θ+ 1/3/3s i n1/3c o s θθ+- 01/33sin 1/3cos θθ+- 1/3/3s i n1/3c o s θθ-- 1/32/3c o s θ+ 00 0 0 1 6.编程绘制第5题中三棱锥的正等轴测和正二测图。
同上类似,只是变换矩阵改为T 正等=0.70700.40800.70700.4080000.816001-⎡⎤⎢⎥--⎢⎥⎢⎥⎢⎥⎣⎦和T 正二=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---1000943.0000312.00354.00118.00935.07.编程绘制第5题中三棱锥的斜等测和斜二测投影图。
同上类似,变换矩阵改为:T 斜等=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-1001000707.00707.00001T斜二=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-1001000354.00354.000018.编程绘制第5题中三棱锥的立体一点、二点和三点透视图。
第5章-习题解答

第5章-习题解答第5章 习题与答案5-1 机械波的表达式为y = 0.03cos6π(t + 0.01x ) (SI) ,则 [ ](A) 其振幅为3 m (B) 其周期为s 31 (C) 其波速为10 m/s (D) 波沿x 轴正向传播 [答案:B]5-2 一平面简谐波,波速u =5m · s -1. t = 3 s 时波形曲线如题5-2图所示. 则x =0处的振动方程为[ ](A)y =2×10-2cos(πt /2-π/2) ( S I ) . (B) y =2×10-2cos(πt +π ) ( S I ) . (C) y =2×10-2cos(πt /2+π/2) ( S I ) . (D) y =2×10-2cos(πt -3π/2)( SI ) . [答案:A]5-3 如题5-3图所示,两相干波源s 1和s 2相距λ/4(λ为波长), s 1ux y (10· · · · · · · 0 5 1122- PSS题5-2图题5-3图的位相比s 2的位相超前π/2 ,在s 1、s 2的连线上, s 1外侧各点(例如P 点)两波引起的两谐振动的位相差是[ ](A) 0 . (B) π . (C) π /2 . (D) 3π/2 . [答案:B]5-4 一平面简谐波沿ox 正方向传播,波动表达式为]2)42(2cos[10.0π+-π=x t y (SI),该波在t = 0.5 s 时刻的波形如题5-5图中的哪一个? [ ] [答案:B]5-5 横波以波速u 沿x 轴负方向传播.t 时刻波形曲线如题5-5图所示.则该时刻 [ ]题5-4图-(A) A 点振动速度大于零 (B)B 点静止不动(C) C 点向下运动(D) D 点振动速度小于零 [答案:D]5-6 一平面简谐波沿x 轴正方向传播,t = 0 时刻的波形如题5-6图所示,则P 处质点的振动在t = 0时刻的旋转矢量图是[ ][答案:A]5-7 一简谐波沿x 轴正方向传播,t = T /4时的波形曲线如题5-7图所示.若振动以余弦函数表示,且此题各点振动的初相取-π 到π 之间的值,则 [ ] (A) O 点的初相为0=φωS A O ′ωSA ωωSAO ′(A)(B)(C)(D)S题5-5图题5-6图(B) 1点的初相为π-=211φ(C) 2点的初相为π=2φ(D) 3点的初相为π-=213φ[答案:D]5-8 在驻波中,两个相邻波节间各质点的振动[ ](A) 振幅相同,相位相同 (B) 振幅不同,相位相同(C) 振幅相同,相位不同 (D) 振幅不同,相位不同 [答案:B]5-9 一平面简谐波在弹性媒质中传播,在媒质质元从平衡位置运动到最大位移处的过程中:[ ](A) 它的动能转化为势能. (B) 它的势能转化为动能. (C) 它从相邻的一段质元获得能量其能量逐渐增大.(D) 它把自己的能量传给相邻的一段质元,题5-7图其能量逐渐减小. [答案:D]5-10 一横波的波动方程是))(4.0100(2sin 02.0SI x t y -=π,则振幅是__________,波长是__________,频率是__________,波的传播速度是__________。
化工原理习题答案第五章

待求的温度 t,就是 PAo/ PBo=3.5 时的温度,用试差法计算。 假设 t=80℃,PAo=181.1 kPa,PBo=50.93 kPa PAo/ PBo=181.1/50.93=3.556>3.5 温度 t 越小,则 PAo/ PBo 就越大,故所假设的 t 偏小。 假设 t=85℃,PAo=215.9 kPa,PBo=62.78 kPa PAo/ PBo=215.9/62.78=3.44 用比例内插法求 PAo/ PBo=3.5 时的温度 t (t80)/(8580)=(3.53.556)/(3.443.556) 求得 t=82.4℃,在此温度下,PAo=197.2 kPa,PBo=56.35 kPa,则 PAo/ PBo=197.2/56.35=3.5 故 t=82.4℃是待求温度 总压 P= PAox/y=197.2×0.6/0.84=140.9 kPa
解: (1)t=80℃时,PAo=181.1 kPa,PBo=50.93 kPa 总压 P=( PA -PBo)x + PBo=(181.150.93) ×0.5+ 50.93=116 kPa 气相组成 y= PAox/P=181.1×0.5/116=0.781 (2) 已知 P=101.33 kPa,x=0.4,求 t, y P=101.33 kPa 时,甲醇的沸点是 64.7℃,丙醇的沸点是 97.2℃,所求气液相平衡温度必 在 64.7℃与 97.2℃之间。 假设 t=75℃,计算 PAo=151.1 kPa,PBo=41 kPa 液相组成 x=(P PBo)/( PAoPBo)= (101.33 41)/( 151.141)=0.548>0.4 计算 x 值大于已知的 x 值,故所假设的温度 t 偏小,重新假设大一点的 t 进行计算,将三次 假设的 t 与计算的 x 值列于下表,并在习题 5-1 附图 1 上绘成一条曲线,可知 x=0.4 时的平 均温度 t=79.5C 习题 5-1 附表 计算次数 假设 t/℃ x 第一次 75 0.548 第二次 80 0.387 第三次 85 0.252
运筹学习题答案第五章

第五章习题解答
5.11 某城市可划分为11个防火区,已设有4个消 防站,见下图所示。
page 16 2 January 2024
School of Management
运筹学教程
第五章习题解答
上图中,虚线表示该消防站可以在消防允许时间
内到达该地区进行有效的消防灭火。问能否关闭若干 消防站,但仍不影响任何一个防火区的消防救灾工作。 (提示:对每—个消防站建立一个表示是否将关闭的01变量。)
x1, x2 0,且为整数
解:x1 1, x2 3, Z 4
min Z 5x1 x2
3x1 x2 9
(2)
st
x1 x1
x2 5 8x2 8
.
x1, x2 0,且为整数
解:x1 4, x2 1, Z 5
page 8 2 January 2024
School of Management
School of Management
运筹学教程
第五章习题解答
5.12 现有P个约束条件
n
aij xij bi
j 1
i 1,2,, p
需要从中选择q个约束条件,试借助0-1变量列出 表达式。
解:设yi是0 1变量,i 1,2,, p
n
yi ( aij xij bi ) 0 j 1
i 1,2,, p
运筹学教程
第五章习题解答
5.1 某地准备投资D元建民用住宅。可以建住宅
的造分地价别点为建有d几j;n幢处,,:最才A多能1,可使A造建2,a造j幢…的。,住问A宅n应。总当在数在A最i哪处多几每,处幢试建住建住宅立宅的问, 题的数学模型。
解:设xi表示在Ai处所建住宅的数量, i 1,2,, n。
第5章部分习题参考解答

μ 0ε 0
其实,观察题目给定的电场表达式,可知它表征一个沿 + x 方向传播的均匀平面 ω 109 波,其相速为 vp = = = 2 ×108 m/s k 5 1 1 1 1 1 而 vp = = = = × 3 × 108
με
μ 0ε r ε 0
εr
μ 0ε 0
εr
3 故 ε r = ( ) 2 = 2.25 2
G G 5.1 在自由空间中,已知电场 E ( z , t ) = ey 103 sin(ωt − β z ) V/m ,试求磁场强度 G H ( z, t ) 。 解:以余弦为基准,重新写出已知的电场表示式 G π G E ( z , t ) = ey 103 cos(ωt − β z − ) V/m 2 这是一个沿 + z 方向传播的均匀平面波的电场,其初相角为 −90D 。与之相伴的磁 场为 G 1 G G 1 G G π H ( z , t ) = ez × E ( z , t ) = ez × ey 103 cos(ωt − β z − ) η0 η0 2
无损耗媒质中的波阻抗为
9 4
G E E 50 η= G = m = = 500 Ω H H m 0.1
又由于
η=
故
μ r μ0 μr = η0 ε rε 0 εr
(2)
μr η 500 2 ) = ( )2 = ( ε r η0 377
联立式(1)和式(2),得
μr = 1.99 , ε r = 1.13 5.8 在自由空间中,一均匀平面波的相位常数为 β 0 = 0.524 rad/m ,当该波进入到 理想介质后,其相位常数变为 β = 1.81 rad/m 。设该理想介质的 μr = 1 ,试求该理
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章:运输层1、试说明运输层在协议栈中的作用?运输层的通信和网络层的通信有什么重要的区别?为什么运输层是必不可少的?答:(1)首先,从通信和信息处理的角度来看,运输层向它上面的应用层提供通信服务,并为高层用户屏蔽了下层通信通信子网的细节。
其次,运输层的另一个重要功能就是复用和分用功能。
第三,运输层对传输的报文提供了差错检测机制。
第四,根据应用的不同,运输层还采用不同的运输层协议提供不同的服务。
(2)网络层为主机之间提供逻辑通信,而运输层为应用进程之间提供端到端的逻辑通信,如下图所示:(3)虽然无连接的运输服务和无连接的网络服务十分相似,但是运输层依然有它存在的必要性,因为:事实上,网络层是通信子网的一个组成部分,假设网络服务质量不可靠,频繁地丢失分组,网络层系统崩溃或不停的发出网络重置,这将发生什么情况呢?因为用户不能对通信子网加以控制,所以无法采用更好的通信处理机来解决网络层服务质量低劣的问题,更不可能通过改进数据链路层纠错能力来改善低层的条件。
因此,解决这一问题的唯一可行的办法就是在网络层的上面增加一层,即运输层。
运输层的存在使得运输服务比网络服务更可靠,分组的丢失、残缺,甚至网络重置都可以被运输层检测到,并采用相应的补救措施,而且由于运输服务独立于网络服务,故可以采用一个标准的原语集提供运输服务。
2、网络层提供数据报或虚电路服务对上面的运输层有何影响?答:如果下层的网络十分可靠,例如提供虚电路服务,那么用于完成数据传输的运输层协议就不需要做太多的工作。
当网络层仅使用提供不可靠的数据报服务时,运输层就需要使用一些复杂的协议,以便能够提供更优质的服务。
3、当应用程序使用面向连接的TCP和无连接的IP时,这种传输是面向连接的还是面向连接的?答:在网络层IP提供的是无连接的服务,但是在运输层TCP提供的服务是面向连接的。
但是最终,该应用程序使用的还是面向连接的传输服务。
4、试用画图解释运输层的复用。
画图说明许多个运输用户复用到一条运输连接上,而这一条运输连接又复用到IP 数据报上。
答:答案见辅导材料P155页。
5、试举例说明有些应用程序愿意采用不可靠的UDP,而不愿意采用可靠的TCP。
答:6、接收端收到有差错的UDP用户数据报时应如何处理?答:简单的进行丢弃,其他的什么也不做。
7、如果应用程序愿意使用UDP完成可靠的传输,这可能吗?请说明理由?答:不可能。
因为UDP是无连接的,只提供尽最大可能的交付。
并且UDP没有拥塞控制,当很多主机同时向网络发送高速率的数据时,网络就会产生拥塞,结果会致使大家都收不到正确的数据。
8、为什么说UDP是面向报文的,而TCP是面向字节流的?答:在发送方,UDP对应用层送交下来的报文既不合并,也不拆分,按照原样发送,即UDP一次发送一个报文;在接收方,UDP对IP层交上来的UDP数据报,在除去首部后就原封不动的交付给上层的应用进程,即,UDP一次交付一个报文。
TCP是面向字节流的:TCP仅把应用程序交下来的数据看成一连串的无结构的字节流,并不知道所传输的字节流的含义,也不保证接收方应用程序收到的数据块和发送方发送的数据块的大小是否具有对应关系。
即:TCP可能把应用层交下来的数据块分成几个部分发送出去,也可能把几个数据块合并成一个发送出去。
在接收端也同样。
9、端口的作用是什么?为什么端口号要划分为三种?答:端口的作用:发送端:让应用层的各种应用进程都能将其数据通过端口向下交付给运输层,以便组成TPDU;接收端:运输层收到IP层交上来的数据后,要根据目的端口号决定应当通过哪个端口将数据交付给应用层中的相应的进程。
从这个意义上讲,端口是用来标志应用层的进程。
把端口号分成三种不同的类型是为了方便不同的应用程序使用:熟知端口号(系统端口号):其数值标号为0~1023,把它们指派给TCP/IP最重要的一些应用程序使用,让所有的用户都知道。
当一种新型的应用程序出现后,IANA必须要为它指派一个熟知端口号,否者因特网上的其它应用程序就无法和它进行通信。
登记端口号:是为了给没有熟知端口号的应用程序使用的。
客户端使用的端口号:这类端口号仅在客户进程运行时才动态选择的,是留给客户进程选择暂时使用的。
10、试说明运输层中伪首部的作用。
答:伪首部既不向上也不向下传送,仅仅是为了计算检验和。
11、某个应用进程使用运输层的用户数据UDP,然后继续向下交给IP层后组成IP数据报。
既然都是数据报,是否可以跳过UDP直接交给IP层?哪些功能UDP提供了但是IP没有提供?答:虽然都是数据报,但是应用进程不能跳过UDP直接交给IP层,因为IP数据报只能找到目的主机而无法找到目的进程。
UDP提供了IP 所不能提供的复用和分用功能;UDP可以对数据报做包括数据段在内的差错检测,而IP只对其数据报的头部做差错检测。
12、一个应用程序用了UDP,到了IP层之后把数据报再分为4个数据报片发送出去,结果是前两个数据报片丢失,后两个到达了目的站,过了一段时间,应用程序重传UDP,而IP层仍然划分为4个数据报片来传送,结果这次的前两个到达了目的站而后两个丢失了。
试问:在目的站能否将这四个数据报片组装成一个完整的数据报?假设在目的站第一次收到的后两个数据报片仍然保存在目的站的缓存中》答:不行。
重传时,IP数据报的标识字段会有另一个标识符。
仅当标识符相同的数据报片才能组成一个数据报。
前两个数据报片的标识符和后两个数据报片的标识符不同,所以不能组成一个IP数据报。
13、一个UDP用户数据报的数据字段为8192字节,在链路层要使用以太网来传送,试问应当划分为几个IP数据报片?说明每个IP数据报片的长度和片偏移字段的值?答:以太网帧的数据字段的最大长度是1500字节。
UDP数据报的首部是8个字节,所以整个UDP数据报的长度是8200字节。
假定IP数据报的首部没有选项,即首部长度是20字节。
而IP数据报的片偏移量指出了一个片在原IP数据分组中的相对位置,单位是8字节。
通过以上分析,可将UDP数据报分为6个数据报片,前5个的长度是1480字节(IP数据报是1500字节),最后一个的长度是800字节(IP 数据报是820字节),片偏移量分别是:0,185,370,555,740,925.14、一个UDP用户数据报的首部的十六进制表示是:06 32 00 45 00 1C E2 17 。
试求源端口,目的端口,用户数据报的总长度、数据部分长度。
这个用户数据报是从客户发送给服务器的,还是服务器发送给客户的?使用UDP的这个服务器程序是什么?答:把UDP数据报的首部各字段如下(每个字段都是2字节):因此:源端口是1586,目的端口是69,UDP用户数据报总长度是28字节,数据部分是20字节。
此UDP用户数据报是从客户发给服务器的,因为目的端口号69<1023,是熟知端口。
服务程序是TFTP。
(查熟知端口表就会知道)。
15、使用TCP对实时话音数据的传输有没有什么问题?使用UDP在传输数据文件时会有什么问题?答:UDP不保证可靠交付,但是UDP比TCP的开销要小。
因此,只要应用程序接受这样的服务质量就可以使用UDP。
如果话音不是实时数据(边接收边播放)就可以使用TCP,因为TCP传输可靠。
接收端用TCP将话音数据接收完毕后,可以在以后的任何时间进行播放。
但假定是实时传输,则必须使用UDP.16、在停止等待协议中,在什么情况下确认帧可以不使用序号?在停止等待协议中,如果不使用编号是否可行?为什么?答:(1)在停止等待协议中,仅当数据帧和确认帧在传输的过程中既不会丢失也不会有差错的情况下,确认帧才可以不使用序号(其实,如果在传输的过程中既不丢失也无差错时,根本就不用确认了)。
(2)然而在现实的数据传输中,很难保证数据的传输既不丢失也不出现差错,所以在停止等待协议中应当使用序号。
17、在停止等待协议中,如果收到重复的报文段时不予理睬(即悄悄地丢弃它,其他什么也不做)是否可行?试举出具体的例子。
答:不行。
如下图所示:若对收到的重复的报文不进行重传确认,就会让发送方一直认为它所发送的数据没有正确到达接收端,而继续重传下去;当重传达到一定的次数时,就会认为网络出现了故障。
18、假定在运输层使用停止等待协议。
发送方在发送报文段M0后在设定的时间内未收到确认,于是重传M0,但是M0又迟迟不能到达接收方。
不久,发送方收到了迟到的对M0的确认,于是发送下一个报文段M1,不久就收到了对M1的确认。
接着发送方发送新的报文段M0,但是这个新的M0在传送的过程中丢失了。
正巧,一开始就滞留在网络中的M0现在到达了接收方。
接收方无法分辨M0是旧的。
于是收下了M0,并发送确认。
显然,接收方后来收到的M0是重复的,协议失败了。
试画出类似于图5-9所示的双方交换报文段的过程。
答:见教材P38319、试证明:当用n比特进行分组的编号时,若接收窗口等于1(即只能按序接收分组),则仅在发送窗口不超过2n-1时,连续ARQ协议才能正确运行。
窗口的单位是分组。
答:如下图所示:设发送窗口记为W T ,接收窗口记为W R .假定用3个比特进行编号,设接收窗口正好在7号分组处(有阴影的分组)。
发送窗口W T的位置不可能比②更靠前,也不可能比③更靠后,也可能不是这种极端位置,如①。
对于①和②的情况,在W T的范围内无重复序号,即W T≦2n。
对于③的情况,在W T+W R的范围内无重复序号,即W T+W R≦2n。
现在W R =1,故发送窗口的最大值W T≦2n-1。
图见教材P38320、在连续ARQ协议中,若发送窗口等于7,则发送端在开始发送时可以连续发送7个分组,因此,每一个分组发送出去后,都要设置一个超时计时器。
现在计算机中只有一个硬时钟。
设这7个分组发出的时间分别是:t0 ,t1 ,t2 ,t3 ,t4 ,t5 ,t6 ,且t out都一样大,试问如何实现这7个超时计时器(这叫软时钟法)?答:用相对发送时间实现一个链表,见P383图A-5。
21、假定使用连续ARQ协议,发送窗口大小是3,而序号的范围是【0,15】,而传输媒体保证在接收方能够按序收到分组,在某个时刻,在接收方,下一个期望收到的序号是5.试问:(1)在发送方的发送窗口中可能出现的序号组合有哪几种?(2)接收方已经发送出去的、但是在网络中(即还没有到达发送方)的确认分组可能有哪些?说明这些确认分组是用来确认哪些序号的分组?答:(1)接收方期望收到的分组序号是5,说明前5个分组都已经收到了。
若这些确认都已经到达了发送方,则发送窗口的范围是【5,7】。
接收方期望收到序号为5的分组,说明序号为0,1,2,3,4的分组都已经收到,并且发出了确认。
并且对序号为0,1的分组的确认肯定被发送方收到了,否则不可能发送4号分组。
