2015年陕西省分析数据深入
2015年陕西省公务员考试真题答案解析估分:资料分析

2015年陕西省公务员考试真题答案解析估分:资料分析第四部分资料分析一、根据以下资料,回答101-105题。
2013年二季度,我国税收收入同比增速逐步提高,分别为7.9%、8.3%和12.9%。
截止2013年6月,全国税收总收入完成59260.61亿元,同比增长7.9%,较上年同期回落1.9个百分点。
其中,国内增值税、企业所得税同比分别增长6.6%和14.2%,较上年同期增速分别回落1.5和3.1个百分点;房产税同比增长11%,比上年同期增速回落19.1个百分点;进口货物增值税消费税和关税同比分别下降17.1%和16%,比上年同期分别回落24.5和22.9个百分点。
101.2012年1-6月,全国税收总收入比2011年同期增加了( )。
A.4901.94亿B.3108.78亿C.5168.68亿D.4726.35亿102.2013年上半年,房产税、城镇土地使用税及契税三项收入之和约占全国税收总收入的比重( )。
A.1.2%B.6.2%C.16.2%D.19.2%103.2011年1-6月,全国关税收入约为( )。
A.1300亿B.1350亿C.1380亿D.1540亿104.2013年上半年与上年同期相比,下列增长最快的是( )。
A.契税B.国内增值税C.出口货物退增值税消费税D.企业所得税105.根据上述资料,下列说法与资料相符的有几个( )。
①2013年一季度我国税收总收入同比增速低于7.9%②2013年我国税收总收入预计可达到118520亿元③若2013年上半年,进口货物增值税消费税维持上年同期水平,那么2013年上半年税收总收入同比增长将比2012年提高约1.5个百分点。
④2013年我国上半年企业所得税、国内增值税两项之和不到同期税收总收入的50%A.0B.1C.2D.3二、根据以下资料,回答106-110题。
近年由于金融海啸、欧债危机等因素影响,台湾多层次资本市场市场总体成交值从2010年至2012年连续3年下降。
2015年陕西省高考数学试卷(文科)解析

2015年陕西省高考数学试卷(文科)一。
选择题:在每小题给出的四个选项中,只有一项符合题目要求(每小题5分,共60分)1.(5分)(2015•陕西)设集合M={x|x2=x},N={x|lgx≤0},则M∪N=()A.[0,1]B.(0,1]C.[0,1)D.(﹣∞,1]2.(5分)(2015•陕西)某中学初中部共有110名教师,高中部共有150名教师,其性别比例如图所示,则该校女教师的人数为()A.93 B.123 C.137 D.1673.(5分)(2015•陕西)已知抛物线y2=2px(p>0)的准线经过点(﹣1,1),则该抛物线焦点坐标为()A.(﹣1,0) B.(1,0)C.(0,﹣1) D.(0,1)4.(5分)(2015•陕西)设f(x)=,则f(f(﹣2))=()A.﹣1 B.C.D.5.(5分)(2015•陕西)一个几何体的三视图如图所示,则该几何体的表面积为()A.3πB.4πC.2π+4 D.3π+46.(5分)(2015•陕西)“sinα=cosα”是“cos2α=0”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件7.(5分)(2015•陕西)根据如图框图,当输入x为6时,输出的y=()A.1B.2C.5D.10 8.(5分)(2015•陕西)对任意向量、,下列关系式中不恒成立的是()A.||≤|||| B.||≤|||﹣|||C.()2=||2D.()•()=2﹣29.(5分)(2015•陕西)设f(x)=x﹣sinx,则f(x)()A.既是奇函数又是减函数B.既是奇函数又是增函数C.是有零点的减函数D.是没有零点的奇函数10.(5分)(2015•陕西)设f(x)=lnx,0<a<b,若p=f(),q=f(),r=(f(a)+f(b)),则下列关系式中正确的是()A.q=r<p B.p=r<q C.q=r>p D.p=r>q11.(5分)(2015•陕西)某企业生产甲、乙两种产品均需用A、B两种原料.已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产一吨甲、乙产品可获得利润分别为3万元、4万元,则该企业每天可获得最大利润为()甲乙原料限额A(吨) 3 2 12B(吨) 1 2 8A.12万元B.16万元C.17万元D.18万元12.(5分)(2015•陕西)设复数z=(x﹣1)+yi(x,y∈R),若|z|≤1,则y≥x的概率为()A.+B.+C.﹣D.﹣二。
2015年陕西省公务员考试真题答案解析估分:数量关系

2015年陕西省公务员考试真题答案解析估分:数量关系数量关系121.现有若干支铅笔,若只平均分给一年级一班的女生,每名女生可以得到15支,若只平均分给该班的男生,每名男生可以得到10支。
现将这些铅笔平均分给该班的所有同学,则每名同学可以得到( )支铅笔。
A.4B.5C.6D.7E.8F.9G.10H.11122.把一个正方形的四个角分别切除一个等腰三角形,剩下一个长宽不等的矩形。
若被切除部分的总面积为400平方厘米,且切除的三角形的直角边的长度均为整数,则所剩矩形的面积为( )平方厘米。
A.320B.336C.360D.384E.400F.420G.441H.464123.一辆汽车从A地运货到B地,若该车的速度增加20千米/小时,可以提前45分钟到达B地,若该车的速度减少12千米/小时,到达B地的时间将延迟45分钟,则A地与B 地之间的距离为( )千米。
A.164B.176C.180D.196E.200F.212G.244H.256124.若销售团队有5个人,每个人把其他四个人的年龄相加,所得到的和分别为95,102,100,99,104,则这五个人中年龄最大的人为( )岁。
A.25B.26C.27D.28E.29F.30G.31H.32125.设有编号为1,2,3,……,10的10张背面向上的纸牌,现有10名游戏者,第1名游戏者将所有编号是1的倍数的纸牌翻成另一面向上的状态,接着第2名游戏者将所有编号是2的倍数的纸牌翻成另一面向上的状态,……,第n名(n≤10)游戏者,将所有编号是n的倍数的纸牌翻成另一面向上的状态,如此下去,当第10名游戏者翻完纸牌后,那些纸牌正面向上的最大编号与最小编号的差是( )。
A.2B.3C.4D.5E.6F.7G.8H.9126.针对100名旅游爱好者进行调查发现,28人喜欢泰山,30人喜欢华山,42人喜欢黄山,8人既喜欢黄山又喜欢华山,10人既喜欢泰山又喜欢黄山,5人既喜欢华山又喜欢黄山,3人喜欢这三个景点,则不喜欢这三个景点中任何一个的有( )人。
2015年陕西高考0分作文处理结果

2015年陕西高考0分作文处理结果2015年的陕西高考作文题目是《人生的路口》,考生需要就自己人生的选择和未来的规划进行阐述。
然而,有一些考生在作文中没有表达出自己的观点,或者是完全离题,导致了0分的结果。
这些考生的作文被评为“无法理解”、“毫无逻辑”、“内容空洞”等等。
这样的作文不仅无法得分,而且还会影响整个考试的成绩。
因此,陕西省教育考试院采取了一些措施来处理这些0分作文。
首先,教育考试院对这些作文进行了专门的评估。
评估小组由资深的语文教师和专家组成,他们对这些作文进行了详细的阅读和分析。
评估的目的是找出作文中的问题和不足,以便教育考试院在今后的考试中改进评分标准和考试内容。
评估结果显示,这些0分作文中最常见的问题是思路不清、缺乏逻辑性和表达不清。
有些考生只是简单地列举了一些人生的选择,而没有对其进行深入的分析和思考。
还有一些考生没有理解题目的意思,写了与题目完全无关的内容。
针对这些问题,教育考试院采取了多种措施来加以解决。
首先,他们提高了评分标准的严格程度,要求考生必须清晰地表达自己的观点和思路。
其次,他们加强了对考生的指导和培训,帮助考生更好地理解题目和写作技巧。
此外,他们还在考试前提供了更多的样卷和模拟题,让考生更好地适应考试。
这些措施的效果非常显著。
在2016年的陕西高考中,零分作文的数量大大减少,考生的作文质量也有了明显的提高。
这充分证明了教育考试院采取的措施是正确的,也为今后的考试提供了有益的经验。
总的来说,陕西省教育考试院对零分作文的处理是及时、有效的。
他们通过评估、提高评分标准、加强指导和培训等多种措施,成功地解决了这个问题。
我们相信,在教育考试院的不断努力下,未来的高考将会更加公平、公正、科学。
陕西省各地级市人均GDP变化趋势分析

陕西省各地级市人均GDP变化趋势分析作者:刘莹来源:《今日财富》2018年第26期经济高速增长伴随着地区收入差距扩大是世界各国普遍存在的问题,陕西省也不例外。
本文采用线性趋势法,选取了1994年-2015年的数据进行陕西省各市人均GDP分析。
通过分析后得出以下结论:陕西省各市人均GDP总趋势基本都是在不断上升,人均GDP增长速度由大到小的顺序为:榆林市、延安市、西安市、宝鸡市、咸阳市、铜川市、汉中市、渭南市、安康市、商洛市。
改革开放以来,陕西省经济得到快速发展,并且成为全国经济增长较快的省区之一,但是与我国东部有些省份相比,仍有很大差距。
陕西省经济差异的研究很有限,张长宪、单福东等将陕西省划分为关中、陕北、陕南三个地域单元,研究其经济差异问题,张艳芳等使用聚类分析法,对陕西省各地市进行了分类研究。
因此,本文要研究陕西省各市人均GDP变化,测算了1994年以来陕西省各市人均GDP增长的趋势。
一、线性趋势法线性趋势法是一种基本的回归分析方法,其公式为:y=at+b。
式中t为时间,a、b为经验常数,可以用最小二乘法求得,a表示人均GDP速度(万元/10a),当a是正值时,表明是上升趋势,反之亦然。
R 越接近0, y与t之间的线性相关就越小;相反,R 越大, y与t之间的线性相关就越密切。
二、人均GDP变化特征由图1(a)(b)知,1994-2015年,榆林市、延安市人均GDP呈上升趋势,线性拟合的增长速度为4.44万元/10a和3.16万元/10a,相关系数为R=0.82和 R=0.90由图1(c)(d)知,1994-2015年,西安市、宝鸡市人均GDP呈上升趋势,线性拟合的增长速度为2.90万元/10a和2.11万元/10a,相关系数为R=0.87和R=0.87。
由图1(e)(f)可知,1994-2015年,咸阳市、铜川市人均GDP呈上升趋势,线性拟合的增长速度为1.88万元/10a和1.83万元/10a,相关系数R=0.82和R=0.83。
陕西省财政厅关于编制2015年省级部门预算的通知-陕财办预[2014]77号
![陕西省财政厅关于编制2015年省级部门预算的通知-陕财办预[2014]77号](https://img.taocdn.com/s3/m/74034c443a3567ec102de2bd960590c69ec3d833.png)
陕西省财政厅关于编制2015年省级部门预算的通知正文:---------------------------------------------------------------------------------------------------------------------------------------------------- 陕西省财政厅关于编制2015年省级部门预算的通知(陕财办预[2014]77号)根据《中华人民共和国预算法》和《中华人民共和国预算法实施条例》相关规定,现就编制2015年省级单位部门预算有关工作通知如下:一、2015年省级部门预算编制的总体要求2015年省级部门预算编制的总体要求是:全面贯彻落实党的十八届三中全会精神,紧紧围绕建立全面规范、公开透明的预算管理制度目标,健全和完善各项预算管理办法,大力推进预算公开,坚持厉行节约和从紧编制预算,严格控制一般性支出,优化支出结构,创新预算管理方式,完善预算编制体系和分配机制,实施预算绩效管理,切实保证各项支出政策的落实和省级单位重点支出需要。
二、2015年省级部门预算编制的工作重点(一)规范预算编制流程,完善部门预算管理制度。
按照全面规范预算管理的要求,我厅制定了《省级部门预算管理暂行办法》,各部门要按照办法要求,进一步完善单位内部工作流程和管理制度,着力构建规范的省级部门预算制度体系。
要按照办法确定的“两上三下”的预算编制流程,明确部门职责和岗位职责,完善预算编制、执行的内部控制制度体系,切实加强省级预算管理制度建设。
(二)扩大预算公开范围,提高财政预算透明度。
一是进一步扩大部门预算公开范围。
除涉密部门外,所有使用财政拨款的部门都要公开部门预算,纳入预算公开范围的单位要向省人代会报送部门预算草案。
二是细化预算公开内容。
省财政厅批复省级单位的部门预算报表要全部公开,并细化公开到支出功能分类项级科目。
所有财政拨款安排的“三公”经费都要详细公开,并分析增减变化的原因。
2015年陕西省物理中考试题分析

2015年陕西省物理中考试题分析----扶风初中虢军旗 2015年6月29日2015年陕西省中考物理试题,题目难度与题型设计相对稳定,命题依据课标,立足教材,以生活、物理和科学技术发展为平台,注重考查基础知识和基本技能,在物理知识的应用性、探究性和综合性上考查学生的科学素养和探究能力。
整卷重点、难点设置合理,试题所选取素材大部分源于日常生活、生产和科技发展实际,并突出了当今社会注重的能量、环保、节能的意识,符合新课标的“从生活走向物理,从物理走向社会”的课改理念。
首先,注重对三基的考查,促进学生发展。
注重基础,紧扣课标,科学规范,突出考查物理能力。
主要考查知识点包括:光的折射现象,物理量的估测,声现象,物态变化,机械运动,内能,分析电路故障等重点内容。
但是我们要注意基础知识、基本概念的考查是中考的重点,要求能在具体情景中辨认出该知识或规律。
试题对物理知识的应用性、探究性、综合性进行全面考查,给各个不同层次的学生均有一定的答题空间,具有很高的信度和效度。
如第24、29、30题。
第二,联系实际,贴近生活,强调知识应用。
试题着眼于物理科学三维课程目标的考核,较好的联系了生产、生活和社会实践,关心科技与社会的发展,情景设计新颖。
发声、能喝到饮料、走路的时候被石块绊了一下、汽车上流行的感应雨刮器等等”这些生活中最常见事物所包含的物理知识你知道吗?不仅检测了孩子们两年物理学习是否有良好的基础,同时也给物理教学指明了方向。
第三,加强了实验操作能力和探究能力的考查。
试题进一步突出了对实验原理、物理过程和方法、实验结果分析的考查,特别重视实验研究方法。
突出了实验探究的基础性和实践性,多角度、多层次加强了对科学探究过程与方法的考查,以基本实验为载体,实现对基本仪器和基本实验原理的考查;以实验过程中出现的实际问题为载体,较好地体现了新课程标准所倡导的教学方式和学习方式;创新实验为载体,实现对科学探究能力及过程方法目标的考查。
陕西省人口数据的统计分析

陕西省人口数据的统计分析陕西省位于中国西部,是一个人口稠密的省份,下面对陕西省人口数据进行具体的统计分析。
一、人口总量2020年,陕西省总人口为38,107,187人,其中男性为19,563,436人,女性为18,543,751人。
总人口数量在2015年之后出现下降,主要原因是陕西省的出生率逐年下降,而死亡率逐年上升。
二、城乡人口比例陕西省城乡人口比例为43.7:56.3,在全国排名第20位。
城市人口为16,824,905人,占总人口的44.15%,农村人口为21,282,282人,占总人口的55.85%。
随着城镇化的推进,城市人口占比逐渐上升,而农村人口逐年下降。
三、人口密度陕西省的人口密度为225人/平方千米,在全国排名第21位。
其中,城市人口密度为959人/平方千米,而农村人口密度为125人/平方千米。
人口密度显示,陕西省的城市化水平远远高于农村化水平。
四、年龄结构五、性别比例陕西省男女比例为105.4:100,在全国排名第17位。
这个比例表明,在陕西省的人口结构中,男性比女性稍微多一些。
六、民族结构陕西省是一个多民族聚居的省份,其中汉族占总人口的99.09%,其他少数民族占总人口的0.91%。
少数民族主要有回族、满族、蒙古族、朝鲜族等。
七、出生率和死亡率陕西省的出生率呈逐年下降趋势,而死亡率呈逐年上升趋势,表明陕西省的人口总量在逐渐缩小。
2020年,陕西省出生率为9.40‰,死亡率为7.98‰。
综上所述,陕西省的人口总量在逐年下降,城市人口占比逐渐上升,人口年龄结构较为平衡,老年化趋势明显,男性比女性稍微多一些,汉族占绝大多数。
同时,陕西省的出生率呈逐年下降趋势,而死亡率逐年上升趋势,表明陕西省的人口总量在逐渐缩小。
2015年陕西省高考数学试题及答案(理科)及解析
2015年陕西省高考数学试卷(理科)一、选择题,共12小题,每小题5分,共60分1.(5分)(2015•陕西)设集合M={x|x2=x},N={x|lgx≤0},则M∪N=()A .[0,1]B.(0,1]C.[0,1)D.(﹣∞,1]2.(5分)(2015•陕西)某中学初中部共有110名教师,高中部共有150名教师,其性别比例如图所示,则该校女教师的人数为()A .93B.123C.137D.1673.(5分)(2015•陕西)如图,某港口一天6时到18时的水深变化曲线近似满足函数y=3sin (x+φ)+k.据此函数可知,这段时间水深(单位:m)的最大值为()A .5B.6C.8D.104.(5分)(2015•陕西)二项式(x+1)n(n∈N+)的展开式中x2的系数为15,则n=()A .7B.6C.5D.45.(5分)(2015•陕西)一个几何体的三视图如图所示,则该几何体的表面积为()A .3πB.4πC.2π+4D.3π+46.(5分)(2015•陕西)“sinα=cosα”是“cos2α=0”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件7.(5分)(2015•陕西)对任意向量、,下列关系式中不恒成立的是()A.||≤||||B.||≤|||﹣|||C.()2=||2D.()•()=2﹣28.(5分)(2015•陕西)根据如图框图,当输入x为2006时,输出的y=()A .2B.4C.10D.289.(5分)(2015•陕西)设f(x)=lnx,0<a<b,若p=f(),q=f(),r=(f(a)+f(b)),则下列关系式中正确的是()A .q=r<p B.p=r<q C.q=r>p D.p=r>q10.(5分)(2015•陕西)某企业生产甲、乙两种产品均需用A、B两种原料.已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产一吨甲、乙产品可获得利润分别为3万元、4万元,则该企业每天可获得最大利润为()甲乙原料限额A(吨)3212B(吨)128A .12万元B.16万元C.17万元D.18万元11.(5分)(2015•陕西)设复数z=(x﹣1)+yi(x,y∈R),若|z|≤1,则y≥x的概率为()A .+B.+C.﹣D.﹣12.(5分)(2015•陕西)对二次函数f(x)=ax2+bx+c(a为非零整数),四位同学分别给出下列结论,其中有且只有一个结论是错误的,则错误的结论是()A .﹣1是f(x)的零点B.1是f(x)的极值点C .3是f(x)的极值D.点(2,8)在曲线y=f(x)上二、填空题,共4小题,每小题5分,共20分13.(5分)(2015•陕西)中位数为1010的一组数构成等差数列,其末项为2015,则该数列的首项为.14.(5分)(2015•陕西)若抛物线y2=2px(p>0)的准线经过双曲线x2﹣y2=1的一个焦点,则p=.15.(5分)(2015•陕西)设曲线y=e x在点(0,1)处的切线与曲线y=(x>0)上点P 的切线垂直,则P的坐标为.16.(5分)(2015•陕西)如图,一横截面为等腰梯形的水渠,因泥沙沉积,导致水渠截面边界呈抛物线型(图中虚线所示),则原始的最大流量与当前最大流量的比值为.三、解答题,共5小题,共70分17.(12分)(2015•陕西)△ABC的内角A,B,C所对的边分别为a,b,c.向量=(a,b)与=(cosA,sinB)平行.(Ⅰ)求A;(Ⅱ)若a=,b=2,求△ABC的面积.18.(12分)(2015•陕西)如图,在直角梯形ABCD中,AD∥BC,∠BAD=,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点,将ABE沿BE折起到A1BE的位置,如图2.(Ⅰ)证明:CD⊥平面A1OC;(Ⅱ)若平面A1BE⊥平面BCDE,求平面A1BC与平面A1CD夹角的余弦值.19.(12分)(2015•陕西)某校新、老校区之间开车单程所需时间为T,T只与道路通畅状况有关,对其容量为100的样本进行统计,结果如下:T(分钟)2530354020304010频数(次)(Ⅰ)求T的分布列与数学期望ET;(Ⅱ)刘教授驾车从老校区出发,前往新校区做一个50分钟的讲座,结束后立即返回老校区,求刘教授从离开老校区到返回老校区共用时间不超过120分钟的概率.20.(12分)(2015•陕西)已知椭圆E:+=1(a>b>0)的半焦距为c,原点O到经过两点(c,0),(0,b)的直线的距离为c.(Ⅰ)求椭圆E的离心率;(Ⅱ)如图,AB是圆M:(x+2)2+(y﹣1)2=的一条直径,若椭圆E经过A、B两点,求椭圆E的方程.21.(12分)(2015•陕西)设f n(x)是等比数列1,x,x2,…,x n的各项和,其中x>0,n∈N,n≥2.(Ⅰ)证明:函数F n(x)=f n(x)﹣2在(,1)内有且仅有一个零点(记为x n),且x n=+x;(Ⅱ)设有一个与上述等比数列的首项、末项、项数分别相同的等差数列,其各项和为g n(x),比较f n(x)和g n(x)的大小,并加以证明.四、选修题,请在22、23、24中任选一题作答,如果多做则按第一题计分.选修4-1:几何证明选讲22.(10分)(2015•陕西)如图,AB切⊙O于点B,直线AO交⊙O于D,E两点,BC⊥DE,垂足为C.(Ⅰ)证明:∠CBD=∠DBA;(Ⅱ)若AD=3DC,BC=,求⊙O的直径.五、选修4-4:坐标系与参数方程23.(2015•陕西)在直角坐标系xOy中,直线l的参数方程为(t为参数),以原点为极点,x轴正半轴为极轴建立极坐标系,⊙C的极坐标方程为ρ=2sinθ.(Ⅰ)写出⊙C的直角坐标方程;(Ⅱ)P为直线l上一动点,当P到圆心C的距离最小时,求P的直角坐标.六、选修4-5:不等式选讲24.(2015•陕西)已知关于x的不等式|x+a|<b的解集为{x|2<x<4}(Ⅰ)求实数a,b的值;(Ⅱ)求+的最大值.2015年陕西省高考数学试卷(理科)参考答案与试题解析一、选择题,共12小题,每小题5分,共60分1.(5分)考并集及其运算.点:专题:集合.分析:求解一元二次方程化简M,求解对数不等式化简N,然后利用并集运算得答案.解答:解:由M={x|x2=x}={0,1},N={x|lgx≤0}=(0,1],得M∪N={0,1}∪(0,1]=[0,1].故选:A.点评:本题考查了并集及其运算,考查了对数不等式的解法,是基础题.2.(5分)考点:收集数据的方法.专题:计算题;概率与统计.分析:利用百分比,可得该校女教师的人数.解答:解:初中部女教师的人数为110×70%=77;高中部女教师的人数为40×150%=60,∴该校女教师的人数为77+60=137,故选:C.点评:本题考查该校女教师的人数,考查收集数据的方法,考查学生的计算能力,比较基础.3.(5分)考点:由y=Asin(ωx+φ)的部分图象确定其解析式.专题:三角函数的图像与性质.分析:由题意和最小值易得k的值,进而可得最大值.解答:解:由题意可得当sin(x+φ)取最小值﹣1时,函数取最小值y min=﹣3+k=2,解得k=5,∴y=3sin(x+φ)+5,∴当当sin(x+φ)取最大值1时,函数取最大值y max=3+5=8,故选:C.点评:本题考查三角函数的图象和性质,涉及三角函数的最值,属基础题.4.(5分)考点:二项式定理的应用.专题:二项式定理.分析:由题意可得==15,解关于n的方程可得.解答:解:∵二项式(x+1)n(n∈N+)的展开式中x2的系数为15,∴=15,即=15,解得n=6,故选:B.点评:本题考查二项式定理,属基础题.5.(5分)考点:由三视图求面积、体积.专题:计算题;空间位置关系与距离.分析:根据几何体的三视图,得出该几何体是圆柱体的一部分,利用图中数据求出它的表面积.解答:解:根据几何体的三视图,得;该几何体是圆柱体的一半,∴该几何体的表面积为S几何体=π•12+π×1×2+2×2=3π+4.故选:D.点评:本题考查了利用空间几何体的三视图求表面积的应用问题,是基础题目.6.(5分)考点:必要条件、充分条件与充要条件的判断.专题:简易逻辑.分析:由cos2α=cos2α﹣sin2α,即可判断出.解答:解:由cos2α=cos2α﹣sin2α,∴“sinα=cosα”是“cos2α=0”的充分不必要条件.故选:A.点评:本题考查了倍角公式、简易逻辑的判定方法,考查了推理能力,属于基础题.7.(5分)考点:平面向量数量积的运算.专题:平面向量及应用.分析:由向量数量积的运算和性质逐个选项验证可得.解答:解:选项A正确,∵||=|||||cos<,>|,又|cos<,>|≤1,∴||≤||||恒成立;选项B错误,由三角形的三边关系和向量的几何意义可得||≥|||﹣|||;选项C正确,由向量数量积的运算可得()2=||2;选项D正确,由向量数量积的运算可得()•()=2﹣2.故选:B点评:本题考查平面向量的数量积,属基础题.8.(5分)考点:程序框图.专题:图表型;算法和程序框图.分析:模拟执行程序框图,依次写出每次循环得到的x的值,当x=﹣2时不满足条件x≥0,计算并输出y的值为10.解答:解:模拟执行程序框图,可得x=2006,x=2004满足条件x≥0,x=2002满足条件x≥0,x=2000…满足条件x≥0,x=0满足条件x≥0,x=﹣2不满足条件x≥0,y=10输出y的值为10.故选:C.点评:本题主要考查了循环结构的程序框图,属于基础题.9.(5分)考点:不等关系与不等式.专题:不等式的解法及应用.分析:由题意可得p=(lna+lnb),q=ln()≥ln()=p,r=(lna+lnb),可得大小关系.解答:解:由题意可得若p=f()=ln()=lnab=(lna+lnb),q=f()=ln()≥ln()=p,r=(f(a)+f(b))=(lna+lnb),∴p=r<q,故选:B点评:本题考查不等式与不等关系,涉及基本不等式和对数的运算,属基础题.10.(5分)考点:简单线性规划的应用.专题:不等式的解法及应用.分析:设每天生产甲乙两种产品分别为x,y顿,利润为z元,然后根据题目条件建立约束条件,得到目标函数,画出约束条件所表示的区域,然后利用平移法求出z的最大值.解答:解:设每天生产甲乙两种产品分别为x,y顿,利润为z元,则,目标函数为z=3x+4y.作出二元一次不等式组所表示的平面区域(阴影部分)即可行域.由z=3x+4y得y=﹣x+,平移直线y=﹣x+由图象可知当直线y=﹣x+经过点B时,直线y=﹣x+的截距最大,此时z最大,解方程组,解得,即B的坐标为x=2,y=3,∴z max=3x+4y=6+12=18.即每天生产甲乙两种产品分别为2,3顿,能够产生最大的利润,最大的利润是18万元,故选:D.点评:本题主要考查线性规划的应用,建立约束条件和目标函数,利用数形结合是解决本题的关键.11.(5分)考点:几何概型.专题:概率与统计.分析:由题意易得所求概率为弓形的面积与圆的面积之比,分别求面积可得.解答:解:∵复数z=(x﹣1)+yi(x,y∈R)且|z|≤1,∴|z|=≤1,即(x﹣1)2+y2≤1,∴点(x,y)在(1,0)为圆心1为半径的圆及其内部,而y≥x表示直线y=x左上方的部分,(图中阴影弓形)∴所求概率为弓形的面积与圆的面积之比,∴所求概率P==故选:D.点评:本题考查几何概型,涉及复数以及圆的知识,属基础题.12.(5分)考点:二次函数的性质.专题:创新题型;函数的性质及应用;导数的综合应用.分析:可采取排除法.分别考虑A,B,C,D中有一个错误,通过解方程求得a,判断是否为非零整数,即可得到结论.解答:解:可采取排除法.若A错,则B,C,D正确.即有f(x)=ax2+bx+c的导数为f′(x)=2ax+b,即有f′(1)=0,即2a+b=0,①又f(1)=3,即a+b+c=3②,又f(2)=8,即4a+2b+c=8,③由①②③解得,a=5,b=﹣10,c=8.符合a为非零整数.若B错,则A,C,D正确,则有a﹣b+c=0,且4a+2b+c=8,且=3,解得a∈∅,不成立;若C错,则A,B,D正确,则有a﹣b+c=0,且2a+b=0,且4a+2b+c=8,解得a=﹣不为非零整数,不成立;若D错,则A,B,C正确,则有a﹣b+c=0,且2a+b=0,且=3,解得a=﹣不为非零整数,不成立.故选:A.点评:本题考查二次函数的极值、零点等概念,主要考查解方程的能力和判断分析的能力,属于中档题.二、填空题,共4小题,每小题5分,共20分13.(5分)考点:等差数列.专题:等差数列与等比数列.分析:由题意可得首项的方程,解方程可得.解答:解:设该等差数列的首项为a,由题意和等差数列的性质可得2015+a=1010×2解得a=5故答案为:5点评:本题考查等差数列的基本性质,涉及中位数,属基础题.14.(5分)考点:抛物线的简单性质.专题:计算题;圆锥曲线的定义、性质与方程.分析:先求出x2﹣y2=1的左焦点,得到抛物线y2=2px的准线,依据p的意义求出它的值.解答:解:双曲线x2﹣y2=1的左焦点为(﹣,0),故抛物线y2=2px的准线为x=﹣,∴=,∴p=2,故答案为:2.点评:本题考查抛物线和双曲线的简单性质,以及抛物线方程y2=2px中p的意义.15.(5分)考点:利用导数研究曲线上某点切线方程.专题:导数的概念及应用.分析:利用y=e x在某点处的切屑斜率与另一曲线的切线斜率垂直求得另一曲线的斜率,进而求得切点坐标.解答:解:∵f'(x)=e x,∴f'(0)=e0=1.∵y=e x在(0,1)处的切线与y=(x>0)上点P的切线垂直∴点P处的切线斜率为﹣1.又y'=﹣,设点P(x0,y0)∴∴x0=±1,∵x>0,∴x0=1∴y0=1∴点P(1,1)故答案为:(1,1)点评:本题考查导数在曲线切线中的应用,在高考中属基础题型,常出现在选择填空中.16.(5分)考点:直线与圆锥曲线的关系.专题:创新题型;圆锥曲线的定义、性质与方程.分析:建立直角坐标系,求出抛物线方程,然后利用定积分求出泥沙沉积的横截面面积,求出梯形面积,即可推出结果.解答:解:如图:建立平面直角坐标系,设抛物线方程为:y=ax2,因为抛物线经过(5,2),可得a=,所以抛物线方程:y=,横截面为等腰梯形的水渠,泥沙沉积的横截面的面积为:2×=2()=,等腰梯形的面积为:=16,当前最大流量的横截面的面积16﹣,原始的最大流量与当前最大流量的比值为:=1.2.故答案为:1.2.点评:本题考查抛物线的求法,定积分的应用,考查分析问题解决问题的能力,合理建系是解题的关键.三、解答题,共5小题,共70分17.(12分)考点:余弦定理的应用;平面向量共线(平行)的坐标表示.专题:解三角形.分析:(Ⅰ)利用向量的平行,列出方程,通过正弦定理求解A;(Ⅱ)利用A,以及a=,b=2,通过余弦定理求出c,然后求解△ABC的面积.解答:解:(Ⅰ)因为向量=(a,b)与=(cosA,sinB)平行,所以asinB﹣=0,由正弦定理可知:sinAsinB﹣sinBcosA=0,因为sinB≠0,所以tanA=,可得A=;(Ⅱ)a=,b=2,由余弦定理可得:a2=b2+c2﹣2bccosA,可得7=4+c2﹣2c,解得c=3,△ABC的面积为:=.点评:本题考查余弦定理以及宰相肚里的应用,三角形的面积的求法,考查计算能力.18.(12分)考点:二面角的平面角及求法;直线与平面垂直的性质.专题:空间位置关系与距离;空间角.分析:(Ⅰ)根据线面垂直的判定定理即可证明:CD⊥平面A1OC;(Ⅱ)若平面A1BE⊥平面BCDE,建立空间坐标系,利用向量法即可求平面A1BC与平面A1CD夹角的余弦值.解答:证明:(Ⅰ)在图1中,∵AB=BC=1,AD=2,E是AD的中点,∠BAD=,∴BE⊥AC,即在图2中,BE⊥OA1,BE⊥OC,则BE⊥平面A1OC;∵CD∥BE,∴CD⊥平面A1OC;(Ⅱ)若平面A1BE⊥平面BCDE,由(Ⅰ)知BE⊥OA1,BE⊥OC,∴∠A1OC为二面角A1﹣BE﹣C的平面角,∴∠A1OC=,如图,建立空间坐标系,∵A1B=A1E=BC=ED=1.BC∥ED∴B(,0,0),E(﹣,0,0),A1(0,0,),C(0,,0),=(﹣,,0),=(0,,﹣),设平面A1BC的法向量为=(x,y,z),平面A1CD的法向量为=(a,b,c),则得,令x=1,则y=1,z=1,即=(1,1,1),由得,取=(0,1,1),则cos<>===,∵平面A1BC与平面A1CD为钝二面角,∴平面A1BC与平面A1CD夹角的余弦值为﹣.点评:本题主要考查空间直线和平面垂直的判定以及二面角的求解,建立坐标系利用向量法是解决空间角的常用方法.19.(12分)考点:离散型随机变量的期望与方差;离散型随机变量及其分布列.专题:概率与统计.分析:(Ⅰ)求T的分布列即求出相应时间的频率,频率=频数÷样本容量,数学期望ET=25×0.2+30×0.3+35×0.4+40×0.1=32(分钟);(Ⅱ)设T1,T2分别表示往、返所需时间,事件A对应于“刘教授在路途中的时间不超过70分钟”,先求出P()=P(T1=35,T2=40)+P(T1=40,T2=35)+P(T1=40,T2=40)=0.09,即P(A)=1﹣P()=0.91.解答:解(Ⅰ)由统计结果可得T的频率分布为T(分钟)25303540频率0.20.30.40.1以频率估计概率得T的分布列为T25303540P0.20.30.40.1从而数学期望ET=25×0.2+30×0.3+35×0.4+40×0.1=32(分钟)(Ⅱ)设T1,T2分别表示往、返所需时间,T1,T2的取值相互独立,且与T的分布列相同,设事件A表示“刘教授共用时间不超过120分钟”,由于讲座时间为50分钟,所以事件A对应于“刘教授在路途中的时间不超过70分钟”P()=P(T1+T2>70)=P(T1=35,T2=40)+P(T1=40,T2=35)+P(T1=40,T2=40)=0.4×0.1+0.1×0.4+0.1×0.1=0.09故P(A)=1﹣P()=0.91故答案为:(Ⅰ)分布列如上表,数学期望ET=32(分钟)(Ⅱ)0.91点评:本题考查了频率=频数÷样本容量,数学期望,对学生的理解事情的能力有一定的要求,属于中档题.20.(12分)考点:直线与圆锥曲线的综合问题;曲线与方程.专题:创新题型;直线与圆;圆锥曲线的定义、性质与方程.分析:(Ⅰ)求出经过点(0,b)和(c,0)的直线方程,运用点到直线的距离公式,结合离心率公式计算即可得到所求值;(Ⅱ)由(Ⅰ)知,椭圆E的方程为x2+4y2=4b2,①设出直线AB的方程,代入椭圆方程,运用韦达定理和弦长公式,结合圆的直径和中点坐标公式,解方程可得b2=3,即可得到椭圆方程.解答:解:(Ⅰ)经过点(0,b)和(c,0)的直线方程为bx+cy﹣bc=0,则原点到直线的距离为d==c,即为a=2b,e===;(Ⅱ)由(Ⅰ)知,椭圆E的方程为x2+4y2=4b2,①由题意可得圆心M(﹣2,1)是线段AB的中点,则|AB|=,易知AB与x轴不垂直,记其方程为y=k(x+2)+1,代入①可得(1+4k2)x2+8k(1+2k)x+4(1+2k)2﹣4b2=0,设A(x1,y1),B(x2,y2),则x1+x2=.x1x2=,由x1+x2=﹣4,得=﹣4,解得k=,从而x1x2=8﹣2b2,于是|AB|=•|x1﹣x2|=•==,解得b2=3,则有椭圆E的方程为+=1.点评:本题考查椭圆的方程和性质,主要考查椭圆的离心率的求法和椭圆方程的运用,联立直线方程和椭圆方程,运用韦达定理和弦长公式,同时考查直线和圆的位置关系,以及中点坐标公式和点到直线的距离公式的运用,属于中档题.21.(12分)考点:数列的求和;等差数列与等比数列的综合.专题:综合题;创新题型;导数的综合应用;等差数列与等比数列.分析:(Ⅰ)由F n(x)=f n(x)﹣2=1+x+x2+…++x n﹣2,求得F n(1)>0,F n()<0.再由导数判断出函数F n(x)在(,1)内单调递增,得到F n(x)在(,1)内有且仅有一个零点x n,由F n(x n)=0,得到;(Ⅱ)先求出,构造函数h(x)=f n(x)﹣g n(x)=1+x+x2+…++x n﹣,当x=1时,f n(x)=g n(x).当x≠1时,利用导数求得h(x)在(0,1)内递增,在(1,+∞)内递减,得到f n(x)<g n(x).解答:证明:(Ⅰ)由F n(x)=f n(x)﹣2=1+x+x2+…++x n﹣2,则F n(1)=n﹣1>0,F n()=1+.∴F n(x)在(,1)内至少存在一个零点,又,∴F n(x)在(,1)内单调递增,∴F n(x)在(,1)内有且仅有一个零点x n,∵x n是F n(x)的一个零点,∴F n(x n)=0,即,故;(Ⅱ)由题设,,设h(x)=f n(x)﹣g n(x)=1+x+x2+…++x n﹣,x>0.当x=1时,f n(x)=g n(x).当x≠1时,.若0<x<1,h′(x)>=.若x>1,h′(x)<=.∴h(x)在(0,1)内递增,在(1,+∞)内递减,∴h(x)<h(1)=0,即f n(x)<g n(x).综上,当x=1时,f n(x)=g n(x);当x≠1时,f n(x)<g n(x).点评:本题考查了函数零点的判定方法,考查了等比数列的前n项和,训练了利用导数研究函数的单调性,考查了数学转化与化归等思想方法,是中档题.四、选修题,请在22、23、24中任选一题作答,如果多做则按第一题计分.选修4-1:几何证明选讲22.(10分)考点:直线与圆的位置关系.专题:直线与圆.分析:(Ⅰ)根据直径的性质即可证明:∠CBD=∠DBA;(Ⅱ)结合割线定理进行求解即可求⊙O的直径.解答:证明:(Ⅰ)∵DE是⊙O的直径,则∠BED+∠EDB=90°,∵BC⊥DE,∴∠CBD+∠EDB=90°,即∠CBD=∠BED,∵AB切⊙O于点B,∴∠DBA=∠BED,即∠CBD=∠DBA;(Ⅱ)由(Ⅰ)知BD平分∠CBA,则=3,∵BC=,∴AB=3,AC=,则AD=3,由切割线定理得AB2=AD•AE,即AE=,故DE=AE﹣AD=3,即可⊙O的直径为3.点评:本题主要考查直线和圆的位置关系的应用和证明,根据相应的定理是解决本题的关键.五、选修4-4:坐标系与参数方程23.(2015•陕西)考点的极坐标和直角坐标的互化.点:专坐标系和参数方程.题:分析:(I)由⊙C的极坐标方程为ρ=2sinθ.化为ρ2=2,把代入即可得出;.(II)设P,又C.利用两点之间的距离公式可得|PC|=,再利用二次函数的性质即可得出.解答:解:(I)由⊙C的极坐标方程为ρ=2sinθ.∴ρ2=2,化为x2+y2=,配方为=3.(II)设P,又C.∴|PC|==≥2,因此当t=0时,|PC|取得最小值2.此时P(3,0).点评:本题考查了极坐标化为直角坐标方程、参数方程的应用、两点之间的距离公式、二次函数的性质,考查了推理能力与计算能力,属于中档题.六、选修4-5:不等式选讲24.(2015•陕西)考点:不等关系与不等式.专题:不等式的解法及应用.分析:(Ⅰ)由不等式的解集可得ab的方程组,解方程组可得;(Ⅱ)原式=+=+,由柯西不等式可得最大值.解答:解:(Ⅰ)关于x的不等式|x+a|<b可化为﹣b﹣a<x<b﹣a,又∵原不等式的解集为{x|2<x<4},∴,解方程组可得;(Ⅱ)由(Ⅰ)可得+=+=+≤=2=4,当且仅当=即t=1时取等号,∴所求最大值为4点评:本题考查不等关系与不等式,涉及柯西不等式求最值,属基础题.。
2015年陕西省高考数学试卷(理科)答案与解析

62015年陕西省高考数学试卷(理科)参考答案与试题解析一、选择题,共12小题,每小题5分,共60分21. ( 5 分)(2015?陕西)设集合 M={x|x =x} , N={x|lgx O },贝U M U N=( )A . [0, 1]B . (0, 1]C . [0, 1)D . ( - s, 1]考点:并集及其运算. 专题:集合.分析:求解一元二次方程化简 M ,求解对数不等式化简 N ,然后利用并集运算得答案. 解答:解:由 M={x|x 2=x}={0 , 1},N={x|lgx O}= (0, 1], 得 M U N={0 , 1} U (0, 1]=[0 , 1]. 故选:A .点评:本题考查了并集及其运算,考查了对数不等式的解法,是基础题.考点:收集数据的方法. 专题:计算题;概率与统计.分析:利用百分比,可得该校女教师的人数. 解答:解:初中部女教师的人数为110/70%=77 ;高中部女教师的人数为 40XI50%=60,•••该校女教师的人数为 77+60=137, 故选:C .点评:本题考查该校女教师的人数,考查收集数据的方法, 考查学生的计算能力,比较基础. 33 (5分)(2015?陕西)如图,某港口一天6时到18时的水深变化曲线近似满足函数 y=3sinI Kx+ 0) +k .据此函数可知,这段时间水深(单位: m )的最大值为()2. ( 5分)(2015?陕西)某中学初中部共有例如图所示,则该校女教师的人数为(110名教师,高中部共有 150名教师,其性别比 )C . 137D . 167考点:由y=Asin ( w x+ $)的部分图象确定其解析式. 专题:三角函数的图像与性质.分析:由题意和最小值易得 k 的值,进而可得最大值. 解答:解:由题意可得当 sin (-1-X+ 0)取最小值-1时,函数取最小值 y min = - 3+k=2,解得k=5 ,|7T••• y=3sin (—x+ 0) +5,6IT...当当sin ( x+ 0)取最大值1时,6函数取最大值 y max =3+5=8 , 故选:C .点评:本题考查三角函数的图象和性质,涉及三角函数的最值,属基础题.4. ( 5分)(2015?陕西)二项式(x+1 ) n ( n 3 +)的展开式中x 2的系数为15,则n=()A . 7B . 6C . 5D . 4考点:二项式定理的应用. 专题:二项式定理.分析:由题意可得「-=门■ 1=15,解关于n 的方程可得.% 2解答:解:•••二项式(x+1 ) n (n€N + )的展开式中x 2的系数为15,9 n (n _ 1) " + • C ;=15,即 ----- c -------- =15,解得 n=6,故选:B .点评:本题考查二项式定理,属基础题. 44 ( 5分)(2015?陕西)一个几何体的三视图如图所示,则该几何体的表面积为(D . 10#」L考点:由三视图求面积、体积. 专题:计算题;空间位置关系与距离.分析:根据几何体的三视图,得出该几何体是圆柱体的一部分,利用图中数据求出它的表面 积. 解答:解:根据几何体的三视图,得;该几何体是圆柱体的一半, 该几何体的表面积为2V 几何体=n? + n 1>2+2 >2 =3 n +4.故选:D .点评:本题考查了利用空间几何体的三视图求表面积的应用问题,是基础题目6. ( 5 分)(2015?陕西)sin a =cos a 是 cos2a =0”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件考点:必要条件、充分条件与充要条件的判断. 专题:简易逻辑.2 2分析:由cos2 a =cos a- sin a,即可判断出. 解答:解:由 cos2 a =cos 2 a- sin 2 a,• •• sin a =COS a 是“os2 a=0"的充分不必要条件.故选:A .点评:本题考查了倍角公式、简易逻辑的判定方法,考查了推理能力,属于基础题.7. ( 5分)(2015?陕西)对任意向量 &、b ,下列关系式中不恒成立的是()「一 • •冃|叫-M|(日+环? (g-亍)=^2-b 2考点:平面向量数量积的运算.左视團C . 2 n +4D . 3 n +4专题:平面向量及应用.分析:由向量数量积的运算和性质逐个选项验证可得. 解答:i 一一 _.一解:选项 A 正确,•••|mb |=|;a ||b ||cos v 3, b >|,又|c osv & b >鬥,二1/…冃aiHb 恒成立;选项B 错误,由三角形的三边关系和向量的几何意义可得|厂=「|耳|比-|「,||;选项C 正确,由向量数量积的运算可得( 选项D 正确,由向量数量积的运算可得( 故选:B点评:本题考查平面向量的数量积,属基础题.& ( 5分)(2015?陕西)根据如图框图,当输入C . 10考点:程序框图.专题:图表型;算法和程序框图.分析:模拟执行程序框图,依次写出每次循环得到的x 的值,当x= - 2时不满足条件计算并输出y 的值为10.解答:解:模拟执行程序框图,可得x=2006, x=2004满足条件x 为,x=2002满足条件x 为,x=2000满足条件x 为,x=0―* ―e ~* ―■- Q■ ) =i ■ ■-| ;「F ? (;-,■,) = I 2-1〔2.x 为2006时,输出的y (D . 28/输入茫/尸3齐1满足条件x 为,x= - 2 不满足条件x%, y=10 输出y 的值为10.故选:C .点评:本题主要考查了循环结构的程序框图,属于基础题.9. ( 5 分)(2015?陕西)设 f (x ) =lnx , 0v a v b ,若 p=f ( . -h), q=f (关系.解:由题意可得若 p=f (J 十)=ln (.) —Inab=〔 (Ina+lnb ),2 2q=f (r=g (f (a ) +f (b)) 丄(Ina+lnb ), ••• p=r v q ,故选:B点评:本题考查不等式与不等关系,涉及基本不等式和对数的运算,属基础题.10. ( 5分)(2015?陕西)某企业生产甲、乙两种产品均需用A 、B 两种原料.已知生产 1吨每种产品所需原料及每天原料的可用限额如表所示. 如果生产一吨甲、乙产品可获得利润分别为3万元、4万兀,则该企业每天可获得最大利润为()A B ' (吨) (吨)甲3 1乙2 2原料限额12 8 A . 12万元 B . 16万元C . 17力兀D . 18力兀考点 :简单线性规划的应用.专题 :不等式的解法及应用.分析 :设每天生产甲乙两种产品分别为x , y 顿,利润为z 元,然后根据题目条件建立约束条件,得到目标函数,画出约束条件所表示的区域, 然后利用平移法求出 z 的最大值. 解答:解:设每天生产甲乙两种产品分别为 x , y 顿,利润为z 元,f 3x+2y<12则■:1-■:"I &0,卩沁),冷(f ( a )+f ( b )),则下列关系式中正确的是(A . q=r v pB . p=r v q考点:不等关系与不等式. 专题:不等式的解法及应用. 分析:由题意可得(Ina+lnb ), q=D . p=r > q目n (.-]・)=p , ry (Ina+lnb ),可得大小解答: q=r > p )=ln 目n (i :八)=p ,目标函数为z=3x+4y .作出二元一次不等式组所表示的平面区域(阴影部分)即可行域.由z=3x+4y 得y= - - Jx+'-,4 4|平移直线y=-卫x+M由图象可知当直线4 4距最大,此时z最大,解方程组,解得1就1x+2y=8〔尸3即B的坐标为x=2 , y=3,/• z max=3x+4y=6+12=18 .即每天生产甲乙两种产品分别为2, 3顿,能够产生最大的利润,最大的利润是18万元,故选:D.点评:本题主要考查线性规划的应用,建立约束条件和目标函数,利用数形结合是解决本题的关键.11. (5分)(2015?陕西)设复数z= (x- 1)+yi (x, y€R),若|z冃,则y汰的概率为考点:专题:分析:解答:几何概型.概率与统计.由题意易得所求概率为弓形的面积与圆的面积之比,分别求面积可得. 解:•••复数z= (x- 1)+yi (x, y€R)且|z|<1,••• |z|=J (K- 1 )2+异勻,即(x- 1)2+y2勻,点(x, 丫)在(1, 0)为圆心1为半径的圆及其内部,而y孩表示直线y=x左上方的部分,(图中阴影弓形)•••所求概率为弓形的面积与圆的面积之比,y=-卫x+三经过点B时,直线y=-卫x在的截4 4 4 43.114+B. 1,1+2兀丄71A .212. (5分)(2015?陕西)对二次函数f (x ) =ax +bx+c (a 为非零整数),四位同学分别给出 下列结论,其中有且只有一个结论是错误的,则错误的结论是()A . - 1是f (x )的零点B . 1是f (x )的极值点C . 3是f (x )的极值D .点(2, 8)在曲线y=f (x )上 考点:二次函数的性质.专题:创新题型;函数的性质及应用;导数的综合应用.分析:可采取排除法.分别考虑 A , B , C , D 中有一个错误,通过解方程求得a ,判断是否为非零整数,即可得到结论.解答:解:可采取排除法.2若A 错,贝V B , C , D 正确.即有f (x ) =ax +bx+c 的导数为f'(x ) =2ax+b , 即有 f ' (1) =0,即2a+b=0,①又 f (1) =3,即 a+b+c=3②,又f (2) =8,即4a+2b+c=8 ,③ 由①②③ 解得,a=5, b= - 10, c=8.符合a 为非 零整数._ b 2若B 错,则A , C, D 正确,则有a - b+c=0,且4a+2b+c=8,且=3 ,解得a €?,4a不成立;O 若 C 错,贝U A , B , D 正确,则有 a - b+c=0,且 2a+b=0,且 4a+2b+c=8,解得 a=—-3不为非零整数,不成立;isr — b 2若D 错,贝U A , B , C 正确,则有 a - b+c=0 ,且2a+b=0,且=3,解得a=-4a卫不为非零整数,不成立.4故选:A .点评:本题考查二次函数的极值、零点等概念,主要考查解方程的能力和判断分析的能力, 属于中档题.二、填空题,共4小题,每小题5分,共20分•••所求概率卩=厂_ ;n.i 2属基础题.13. (5分)(2015?陕西)中位数为1010的一组数构成等差数列,其末项为2015,则该数列的首项为5 .考点:等差数列.专题:等差数列与等比数列.分析:由题意可得首项的方程,解方程可得.解答:解:设该等差数列的首项为a,由题意和等差数列的性质可得2015+a=1010 X2解得a=5故答案为:5点评:本题考查等差数列的基本性质,涉及中位数,属基础题.14. (5分)(2015?陕西)若抛物线y2=2px (p > 0)的准线经过双曲线x2- y2=1的一个焦点,则p= 2 一'_.考点:抛物线的简单性质.专题:计算题;圆锥曲线的定义、性质与方程.分析:先求出x2-y2=1的左焦点,得到抛物线y2=2px的准线,依据p的意义求出它的值.解答:解:双曲线x2- y2=1的左焦点为(-^/勺,0),故抛物线y2=2px的准线为x= - V2 ,•••"'=-,二p=2:,故答案为:2.':.点评:本题考查抛物线和双曲线的简单性质,以及抛物线方程y2=2px中p的意义.15. (5分)(2015?陕西)设曲线y=e x在点(0, 1 )处的切线与曲线y二•(x> 0)上点P的x切线垂直,则P的坐标为(1, 1).考点:利用导数研究曲线上某点切线方程.专题:导数的概念及应用.分析:利用y=e x在某点处的切屑斜率与另一曲线的切线斜率垂直求得另一曲线的斜率,进而求得切点坐标.解答:解:T f(x)=e x,••• f(0)=e0=1.•/ y=e x在(0, 1)处的切线与『=•• (x>0)上点P的切线垂直•点P处的切线斜率为-1.又y'=-」,设点P (x o, y0)••• X0=±1, •/ x> 0, ••• x0=1y0=1•••点P (1, 1)故答案为:(1, 1)点评:本题考查导数在曲线切线中的应用,在高考中属基础题型,常出现在选择填空中.16. (5分)(2015?陕西)如图,一横截面为等腰梯形的水渠,因泥沙沉积,导致水渠截面边界呈抛物线型(图中虚线所示),则原始的最大流量与当前最大流量的比值为 1.2考点:直线与圆锥曲线的关系.专题:创新题型;圆锥曲线的定义、性质与方程.分析:建立直角坐标系,求出抛物线方程,然后利用定积分求出泥沙沉积的横截面面积,求出梯形面积,即可推出结果.解答:解:如图:建立平面直角坐标系,设抛物线方程为:y=ax2,因为抛物线经过(5, 2), 可得a=-,所以抛物线方程:y= --「,横截面为等腰梯形的水渠,泥沙沉积的横截面的面积为:2畚匸导2 X2)=2(焉』|卜2)冷,等腰梯形的面积为:业§ X2=16,当前最大流量的横截面的面积16-卫,2 316原始的最大流量与当前最大流量的比值为:故答案为:1.2.点评:本题考查抛物线的求法,定积分的应用,考查分析问题解决问题的能力,合理建系是解题的关键.三、解答题,共5小题,共70分17. (12分)(2015?陕西)△ ABC 的内角A , B , C 所对的边分别为 a , b , c.向量i = ( a ,)与 I = (cosA , sinB )平行.(I )求 A ;(n )若a= L, b=2,求厶ABC 的面积.考点:余弦定理的应用;平面向量共线(平行)的坐标表示. 专题:解三角形. 分析:(I )利用向量的平行,列出方程,通过正弦定理求解A ;(n )禾9用A ,以及a=. ; b=2,通过余弦定理求出 c ,然后求解△ ABC 的面积.(I )因为向量 | = (a ,样g b )与 | ,= ( cosA , sinB )平行,所以 asinB - . 一, : =0,由正弦定理可知:sinAsinB - :-;sinBcosA=0 ,因为 sinB 和, 所以 tanA= 一;,可得 A=—L ;■—-1(n ) a=「], b=2,由余弦定理可得:a 2=b 2+c 2- 2bccosA ,可得 7=4+c 2- 2c ,解得c=3,△ABC 的面积为:_ .匸£点评:本题考查余弦定理以及宰相肚里的应用,三角形的面积的求法,考查计算能力.AD=2 , E 是AD 的中点,O 是AC 与BE 的交点,将 ABE 沿BE 折起到 A 1BE 的位置,如 图2.(I )证明:CD 丄平面A 1OC ;(n )若平面A 1BE 丄平面BCDE ,求平面 A 1BC 与平面A 1CD 夹角的余弦值.El 圏2考点:二面角的平面角及求法;直线与平面垂直的性质. 专题:空间位置关系与距离;空间角.分析:(I )根据线面垂直的判定定理即可证明:CD 丄平面A 1OC ;(n )若平面A 1BE 丄平面BCDE ,建立空间坐标系,利用向量法即可求平面 A 1BC与平面A 1CD 夹角的余弦值.解答:II解答 证明:(I )在图1中,•/ AB=BC=1 , AD=2 , E 是AD 的中点,/ BAD=,••• BE 丄 AC ,解答:解:18. (12分)(2015?陕西)如图,在直角梯形ABCD 中,AD // BC , / BAD= ,AB=BC=1 ,A Mi即在图2中,BE 丄0A 1, BE 丄0C , 则BE 丄平面A i OC ;•/ CD // BE , ••• CD 丄平面 A i OC ;(n )若平面A i BE 丄平面BCDE , 由(I)知 BE 丄 OA i , BE 丄 OC , • Z A i OC 为二面角 A i - BE - C 的平面角,Z A i OC 二丄,2如图,建立空间坐标系,CD=BE=(-屈 0, 0)设平面A i BC 的法向量为!T = (X , y , z ),平面A i CD 的法向量为口 = (a , b , c ),取 r= (0, i , i ),•••平面A i BC 与平面 A i CD 为钝二面角,•平面A i BC 与平面A i CD 夹角的余弦值为-点评:本题主要考查空间直线和平面垂直的判定以及二面角的求解, 是解决空间角的常用方法.A i B=A i E=BC=ED=i . BC // ED• B ( ■' 2葩(-夢亨,0),两=,0, 0), E (-羊(0,二::,0),fw&C=0「-玄4■产0\ ----------得[口・止&二y - z=0z=i ,即 I = (i ,i , i ),El •丘[C二。
简析陕西省经济社会转型升级中信息服务业发展

简析陕西省经济社会转型升级中信息服务业发展一、引言信息服务业作为战略性新兴产业的重要组成部分,在推动经济社会转型升级中起着重要的支撑作用。
其发展水平是衡量一个国家和地区现代化程度的重要标志。
加快发展信息服务业,对经济社会转型升级、满足人民群众日益增长的精神文化需求、提高人民生活水平和质量等具有重要意义。
近年来,陕西省信息服务业发展取得显著成效,呈现出整体推进、重点突破、全面提升的良好发展态势。
但当前陕西省信息服务业仍然存在总体发展水平较低,基础设施建设比较薄弱,产业结构不合理等问题,加快发展是新形势下经济社会转型升级中面临的重大任务。
“十二五”期间,陕西经济社会发展取得明显的成就,综合实力得到增强,陕西经济实现了持续和快速的增长。
2014年,全年生产总值17689.94亿元,比上年增长9.7%;人均生产总值46929元,比上年增长9.4%。
2015年,陕西全年生产总值18171.86亿元,比上年增长8.0%。
其中,第一产业增加1597.63亿元,增长5.1%,占生产总值的比重为8.8%;第二产业增加9360.30亿元,增长7.3%,占生产总值的比重为51.5%;第三产业增加7213.93亿元,增长9.6%,占生产总值的比重为39.7%。
人均生产总值48023元,比上年增长7.6%。
2015年陕西人均生产总值达到中等收入国家水平。
财政总收入3300亿元,地方财政收入2055亿元,分别是2010年的1.83倍和2.15倍。
“十二五”期间,陕西地区生产总值年均增长11%、城乡居民收入年均增长11.5%和14.4%。
二、陕西省信息服务业发展现状近年来,伴随着经济的快速发展,陕西省信息服务业也取得了较大的发展。
信息服务业市场规模不断扩大,对经济社会发展和转型升级的支撑作用不断增强,在国民经济和社会发展中起着举足轻重的作用。
(一)软件服务业发展迅速近年来,陕西软件服务业发展势头强劲。
2014年,陕西软件服务业实现业务收入910亿元,同比增长30.8%。
2015年陕西省数据结构试题集(10套题并附带答案)试题及答案

12、一棵左子树为空的二叉树在前序线索化后,其空指针域个数为
A.0 B.1 C.2 D.不确定
13、下述排序方法中,时间性能和待排序记录的初始状态无关的是( )
A 插入排序和快速排序 B 归并排序和快速排序
38、在循环双链表的p所指的结点之前插入s所指结点的操作是 D 。
A.p->prior = s;s->next = p;p->prior->next = s;s->prior = p->prior
B.p->prior = s;p->prior->next = s;s->next = p;s->prior = p->prior
10、衡量查找算法效率的主要标准是( C )。
A)元素个数 B)所需的存储量
C)平均查找长度 D)算法难易程度
11、从一棵二叉搜索树中查找一个元素时,其时间复杂度大致为( )。
A.O(1) B.O(n)
C.O(1Ogzn) D.O(n2)
A.数据元素具有同一特点
B.不仅数据元素所包含的数据项的个数要相同,而且对应的数据项的类型要一致
C.每个数据元素都一样
D.数据元素所包含的数据项的个数要相等
19、数据结构在计算机内存中的表示是指 A 。
A.数据的存储结构 B.数据结构 C.数据的逻辑结构 D.数据元素之间的关系
3、若进栈序列为1,2,3,4,则不可能得到的出栈序列是( C )。
A)3,2,1,4 B)3,2,4,1
C)4,2,3,1 D)2,3,4,1
4、深度为k的完全二叉树所含叶结点的个数最多为( B)。
A)2k B) 2k-1 C)k D) 2k
陕西省教育厅2015年重点科学研究计划

18
研究孙思邈健康文化品牌建 孙思邈健康文 设,研究其生命观、医德思想及医 15JZ018 化品牌建设与 家行为规范,探索孙思邈健康文化 相关产业研究 体验基地建设和健康文化相关产品 开发。 基于微平台的 分析影响中医药健康文化特色 中医药健康文 化设计制作及传播的因素,研究特 15JZ019 化特色化设计 色化设计制作及传播的理念,选择 制作及传播研 部分内容设计制作成样本。 究 梳理中医药高等教育的文化价 中医药高等教 值要素及其内涵与外延,分析中医 育中医药文化 15JZ020 药文化要素缺失的具体表现、主客 要素缺失的影 观原因,提出并论证可资借鉴的策 响与对策研究 略与方法。 调研秦东民俗文化及其现状, 秦东民俗文化 研究秦东民俗文化的文化渊源与传 15JZ021 及其当代价值 承流变,探讨其当代价值和保护策 研究 略。
2.0
第 4 页
陕西省教育厅2015年重点科研计划项目一览表(人文社科)
序号 项目编号 项目名称 研 究 内 容 预期成果 承担单位 依托基地及 主要成员及单 起止时间 项目负责人 位 厅拨经费 (万元) 备 注
23
研究构建《史记》时代文明的 《史记》词汇 百科式词汇系统,考察反映各类文 15JZ023 与汉代文明研 明的词汇在《史记》前后时代的传 究 承与发展的词汇动态规律。
2.0
12
1.0
陕西省教育厅2015年重点科研计划项目一览表(人文社科)
序号 项目编号 项目名称 研 究 内 容 预期成果 承担单位 依托基地及 主要成员及单 起止时间 项目负责人 位 厅拨经费 (万元) 备 注
13
构建基于LPI的丝绸之路经济带 基于LPI的丝绸 物流枢纽城市评价指标体系,研究 研究报告;核心 之路物流枢纽 15JZ013 和评价丝绸之路经济带物流枢纽城 期刊发表研究论 城市评价指标 市物流绩效方面的存在问题与制约 文3篇。 体系研究 因素。 研究工业经济规模、结构、能 陕西省工业碳 源结构等因素对工业碳排放的影响 排放影响因素 15JZ014 规律,构建陕西省工业碳排放总量 分解及减排路 预测模型,探索陕西省工业碳减排 径研究 的路径。 分析王蓬作品与时代背景的关 系及影响,研究其作品对秦岭风光 王蓬文学创作 15JZ015 和民情的描写,探讨王蓬笔下对蜀 研究 道遗迹和丝绸之路沿线风光民俗的 研究。
2015年陕西各县市区GDP及人均GDP
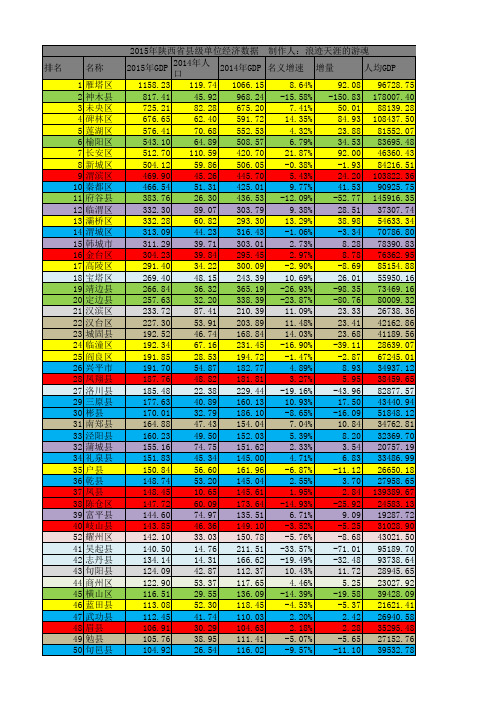
杨陵区 周至县 山阳县 华州区 洋县 洛南县 扶风县 安塞县 华阴市 黄陵县 镇安县 王益区 澄城县 西乡县 丹凤县 汉阴县 合阳县 紫阳县 子长县 延川县 商南县 长武县 平利县 柞水县 印台区 麟游县 宁强县 石泉县 白水县 陇县 绥德县 镇巴县 淳化县 白河县 略阳县 永寿县 子洲县 延长县 米脂县 千阳县 清涧县 富县 岚皋县 潼关县 佳县 宜君县 宜川县 宁陕县 甘泉县 太白县 吴堡县 镇坪县 黄龙县 留坝县
浪迹天涯的游魂2015年gdp2014年人口2014年gdp人均gdp西安1榆林1西安2西安3西安4榆林2西安5西安6宝鸡1咸阳1榆林3渭南1西安7咸阳2渭南2宝鸡2西安8延安1榆林4榆林5安康1汉中1汉中2西安9西安10咸阳3宝鸡3延安2咸阳4咸阳5汉中3咸阳6渭南3咸阳7西安11咸阳8宝鸡4宝鸡5渭南4宝鸡6铜川1延安3延安4安康2商洛1榆林6西安12咸阳9宝鸡7汉中4咸阳10渭南5西安13商洛2渭南6汉中5商洛3宝鸡8延安5渭南7延安6商洛4铜川2渭南8汉中667丹凤县789429647320784574266329368汉阴县7750247268441324906313511369合阳县752044027139534381170831470紫阳县7458285264791511979261500771子长县7222217681121097890331893472延川县704017011001729722977413874273商南县689222286339872553309335774长武县6883170160611356822404644375平利县6790193960591206731350180576柞水县661715436418310199428839977印台区66032194779415281191300957278麟游县644891655751566873703930179宁强县641230886194352218207642580石泉县6298172054761501822366162881白水县615428336630718476217225682陇县597825145716458262237788483绥德县588729645409884478198616784镇巴县583024805642333188235080685淳化县573819575354717384293203986白河县524316424827862416319305788略阳县50462018632020161274250049687永寿县5000186944831153517267522789子洲县4403176552261575823249461890延长县430012644109465191340189991米脂县4153155448661465713267245892千阳县4111125235061726605
2015-2019年陕西省农村订单定向医学生就业履约情况分析

2015-2019年陕西省农村订单定向医学生就业履约情况分析*宋娟(西安医学院卫生管理学院,陕西西安710021)为解决农村基层卫生人力资源紧缺问题,国家发改委等五部门2010年印发了《开展农村订单定向医学生免费培养工作实施意见》,着力为农村基层医疗机构培养输送医学生。
考虑到地区间经济发展不平衡的现实情况,中央财政特别支持中西部地区的五年制本科农村订单定向医学生(以下简称“定向生”)免费培养工作。
本文通过对陕西省承担培养任务的三所医学院校556名本科毕业生的调查,了解其毕业后的履约和工作状况,讨论如何实现定向生“下得去”“留得住”,让此项政策能够实现落到实处,真正充实基层医生队伍。
一、资料和方法(一)资料来源研究对象来源于陕西省承担定向生培养的三所医学院校:西安医学院、延安大学医学院、陕西中医药大学,分别于2018年12月完成对2015、2016、2017、2018届毕业生,2020年1月完成对2019届毕业生的调查,两次调查共回收有效问卷556份。
(二)研究方法采用抽查的方法进行现况调查,问卷内容包括受访者个人信息、履约情况、工作情况和参加规培情况四部分。
其中“履约”被界定为定向生按照定向协议的约定回定向地就业或参加规培。
(三)分析方法利用EXEEL2010软件录入数据,定量资料用SPSS21.0进行数据分析,采用描述性统计、卡方检验进行统计学分析,统计检验水准琢=0.05。
定性资料使用主体框架法进行转录和分析。
二、结果调查对象基本情况:参与调查的总样本量为556人。
其中男性203人,女生353人;2015级93人,2016级91人,2017级98人,2018级145人,2019级129人。
西安医学院毕业生313人,延安大学医学院87人,陕西中医药大学156人。
(一)履约情况摘要:目的:分析陕西省农村订单定向医学生的就业和规培情况,了解毕业定向生就业履约状况及影响因素,为完善相关政策提供依据。
行业收入不平等的区域异质性分析

中图分类号FD61.5
长期以来,收入不平等问题一直受到广泛关注。越来越多的研究表明,结构性因素对中国收人分配产生 着显著的影响。在经济和社会生活中,存在各种对个人社会、经济地位产生重要影响的分割性结构(segmen— tation)(cain,1976)。…在众多分割性结构当中,劳动力市场分割是对劳动就业、经济发展等方面产生重要 影响的分割性结构,收入不平等便是劳动力市场分割产生的显著的分配效应。随着市场转型的不断深化,行 业分割日益成为劳动力市场分割的新结构、新趋势,因此,行业分割以及在此格局下导致的收入不平等十分 引人关注。同时,由于我国实施的显著的异质性的区域政策,我国劳动力市场的区域分割也是明显存在的, 即不同区域的劳动力的收入水平存在较大差异,最为典型的表现在城乡分割和东、中、西部地区的收人不平 等。在行业分割与区域分割的共同作用下,行业收入水平在区域间也存在较大差异。纵观当前研究,专门针 对行业分割的系统研究还比较少见,大多散见于垄断行业与竞争行业的比较研究当中,而对于行业收入不平 等的区域差异分析亦不多见。本研究将从区域异质性的角度考察行业收人不平等问题。 一、区域异质性与收入不平等 区域本是一个地理性概念,然则由于中国特殊的政治经济体制,赋予了它独特的政治经济意涵。我国的 城乡分割、区域分割正是由于这种制度性因素使然。地域、行业、所有制形式和工作单位被认为是社会主义 经济的重要遗产,并且构成了能够直接解释中国城市社会分化的结构和扩展的最重要的制度性根源(王天 夫、王丰,2005)。[21可以说,国家政策是造成区域差异的重要原因。计划经济时期,二元户籍制度造成了对 我国产生影响深远的城乡分割;从改革开放初期,我国实施区域差异化改革,即优先发展南部和东部地区的 经济政策,这样的地区间的不平衡发展得到了延续(王天夫、王丰,2005)。口1在具体的改革实践中,“区域差 异改革”表现为在不同区域引入市场机制的时机、程度和速度不同(郝大海、李路路,2006)。H1显然,我国东
2015年陕西省公务员考试真题答案解析估分:资料分析

2015年陕西省公务员考试真题答案解析估分:资料分析第四部分资料分析一、根据以下资料,回答101-105题。
2013年二季度,我国税收收入同比增速逐步提高,分别为7.9%、8.3%和12.9%。
截止2013年6月,全国税收总收入完成59260.61亿元,同比增长7.9%,较上年同期回落1.9个百分点。
其中,国内增值税、企业所得税同比分别增长6.6%和14.2%,较上年同期增速分别回落1.5和3.1个百分点;房产税同比增长11%,比上年同期增速回落19.1个百分点;进口货物增值税消费税和关税同比分别下降17.1%和16%,比上年同期分别回落24.5和22.9个百分点。
101.2012年1-6月,全国税收总收入比2011年同期增加了( )。
A.4901.94亿B.3108.78亿C.5168.68亿D.4726.35亿102.2013年上半年,房产税、城镇土地使用税及契税三项收入之和约占全国税收总收入的比重( )。
A.1.2%B.6.2%C.16.2%D.19.2%103.2011年1-6月,全国关税收入约为( )。
A.1300亿B.1350亿C.1380亿D.1540亿104.2013年上半年与上年同期相比,下列增长最快的是( )。
A.契税B.国内增值税C.出口货物退增值税消费税D.企业所得税105.根据上述资料,下列说法与资料相符的有几个( )。
①2013年一季度我国税收总收入同比增速低于7.9%②2013年我国税收总收入预计可达到118520亿元③若2013年上半年,进口货物增值税消费税维持上年同期水平,那么2013年上半年税收总收入同比增长将比2012年提高约1.5个百分点。
④2013年我国上半年企业所得税、国内增值税两项之和不到同期税收总收入的50%A.0B.1C.2D.3二、根据以下资料,回答106-110题。
近年由于金融海啸、欧债危机等因素影响,台湾多层次资本市场市场总体成交值从2010年至2012年连续3年下降。
2015年陕西省中考数学总复习教学案:第15讲 数据的收集与整理
第四章统计与概率第15讲数据的收集与整理题,分值为3分,考查形式一般有两种,一种是直接给出一组数据,一种是以表格形式给出一组数据,对于中位数的考查,虽然近三年未考查到,但曾在2011年考查到中位数的计算,因此对中位数的计算考生在复习时不容忽视,2014年中考说明中删除了极差的相关内容,因此以后中考将不会再涉及,预计在2015的中考中,仍会在选择题中可能会考查平均数和众数的计算,也可能会考查中位数的计算.1.数据收集的途径(1)直接手段:__调查、观察、测量、实验__等.(2)间接途径:__查阅文献资料、使用互联网查询__等. 2.数据整理的方法__分类、排序、分组、编码__等.3.平均数、总体、个体、样本及样本容量 (1)总体:把__所要考察对象__的全体叫总体. (2)个体:__每一个考察对象__叫做个体.(3)样本:从总体中所抽取的__一部分个体__叫做总体的一个样本. (4)样本容量:样本中__个体的数目__叫做样本容量.(5)算术平均数:一般地,如果有n 个数x 1,x 2,x 3,…,x n ,那么平均数x =1n(x 1+x 2+x 3+…+x n ).加权平均数:如果在n 个数据中,x 1出现了f 1次,x 2出现了f 2次,…,x k 出现了f k 次,这里f 1+f 2+…+f k =n ,那么这n 个数的算术平均数x =x 1f 1+x 2f 2+…+x k f kn.也叫做x 1,x 2,…,x k 这k 个数的加权平均数,其中f 1,f 2,…f k 分别叫做x 1,x 2,…,x k 的权.4.众数与中位数在一组数据中,出现次数最多的那个数据叫做这组数据的__众数__.将一组数据按大、小依次排列,把排在正中间的一个数据称为__中位数__.但中位数并不一定是数据中的一个数.当数据的个数是偶数个时,最中间有两个数,这两个数的平均数就是这组数据的中位数;如果数据的个数是奇数个时,中位数是正中间的那个数.5.方差设一组数据x 1,x 2,…,x n 中,各数据与它们的平均数x 的差的平方分别是(x 1-x)2,(x 2-x)2,…,(x n -x)2.那么我们用它的平均数即s 2=1n[(x 1-x)2+(x 2-x)2+…+(x n -x)2]来衡量一组数据的波动大小,并把它叫做这组数据的方差.6.由样本特征估计总体特征是统计数据常用的方法“集中”问“三数”平均数、中位数、众数都是数据的代表,它们是“同一家族的三个成员”,都是用来刻画一组数据的平均水平,表示数据的集中趋势.应用平均数时,所有数据都参与运算,它能充分地利用数据所提供的信息,但当一组数据中存在极大值或极小值时,平均数将不能准确地表示数据的集中情况.应用中位数时,计算较简单,不会受极大值或极小值的影响,但不能充分利用所有数据的信息.应用众数时,某些情况下,人们最关心、最重视的是出现次数最多的数据,这时应用众数比较简单且能够直接满足人们的需求,但当各个数据的重复次数大致相等时,众数往往没有意义.“波动”问“方差”方差是刻画数据离散程度的统计量,能反映一组数据的波动情况.1.(2014·陕西)某区10名学生参加市级汉字听写大赛,他们得分情况如下表:那么这10名学生所得分数的平均数和众数分别是( B )A.85和82.5B.85.5和85C.85和85 D.85.5和802.(2013·陕西)我省某市五月份第二周连续七天的空气质量指数分别为:111,96,47,68,70,77,105,则这七天空气质量指数的平均数是( C )A.71.8B.77C.82D.95.73.(2012·陕西)某中学举行歌咏比赛,以班为单位参赛,评委组的各位评委给九(3)班的演唱打分情况(满分100分)如下表,从中去掉一个最高分和一个最低分,则余下的分数的平均分是( C )A.92分B.93选择合适的调查方式【例1】(2014·内江)下列调查中,①调查本班同学的视力;②调查一批节能灯管的使用寿命;③为保证“神舟9号”的成功发射,对其零部件进行检查;④对乘坐某班次客车的乘客进行安检.其中适合采用抽样调查的是( B )A.①B.②C.③D.④【点评】全面调查可以直接获得总体的情况,调查的结果准确,但搜集、整理、计算数据的工作量大;抽样调查的范围小,节省人力、物力,但往往不如全面调查的结果准确.调查范围的大小是相对而言的,类似的问题应联系实际才不会出错.1.(2013·黔西南州)下列调查中,可用普查的是( C )A.了解某市学生的视力情况B.了解某市中学生课外阅读的情况C.了解某市百岁以上老人的健康情况D.了解某市老年人参加晨练的情况平均数、众数、中位数的计算【例2】(2014·孝感)为了解某社区居民的用电情况,随机对该社区10户居民进行了调查,下表是这10户居民2014年4月份用电量的调查结果:那么关于这10户居民月用电量(单位:度),下列说法错误的是( C ) A .中位数是55 B .众数是60 C .方差是29 D .平均数是54 【点评】 平均数、众数、中位数是中考的热点之一,解决这类问题的关键是弄清概念.平均数的大小与一组数据里的每一个数据均有关系,其中任何一个数据的变动都会引起平均数的变动;众数着眼于各数据出现的频率,其大小只与这组数据中的部分数据有关,可以是一个或多个;中位数则与数据的排列位置有关,某些数据的变动对中位数没有影响,计算时要分清数据是奇数个,还是偶数个.2.(1)(2014·襄阳)五箱梨的质量(单位:kg )分别为:18,20,21,18,19,则这五箱梨质量的中位数和众数分别为( D )A .20和18B .20和19C .18和18D .19和18(2)(2013·内江)一组数据3,4,6,8,x 的中位数是x ,且x 是满足不等式组⎩⎪⎨⎪⎧x -3≥0,5-x >0的整数,则这组数据的平均数是__5__.方差的计算【例3】 (1)(2014·呼和浩特)某校五个绿化小组一天的植树棵数如下:10,10,12,x ,8.已知这组数据的平均数是10,那么这组数据的方差是__1.6__.(2)(2014·重庆)2014年8月26日,第二届青奥会将在南京举行,甲、乙、丙、丁四位跨栏运动员在为该运动会积极准备.在某天“110米跨栏”训练中,每人各跑5次,据统计,他们的平均成绩都是13.2秒,甲、乙、丙、丁的成绩的方差分别是0.11,0.03,0.05,0.02.则当天这四位运动员“110米跨栏”的训练成绩最稳定的是( D )A .甲B .乙C .丙D .丁【点评】 理解中位数、方差的概念,灵活运用求平均数、方差的计算公式.3.(2014·湘潭)为测试两种电子表的走时误差,做了如下统计:__B __试题 某校七年级六个班的人数依次为52人,55人,53人,51人,54人,52人,各班的期末数学平均成绩分别为95分,91.5分,`93分,95分,91分,93.5分,求七年级期末数学考试的平均成绩. 错解解:x =16(95+91.5+93+95+91+93.5)≈93.2(分)答:七年级期末数学考试的平均成绩为93.2分.剖析 七年级的平均成绩应该是七年级每个学生成绩的平均数,题目已知六个班各班的平均成绩,求这个年级的平均成绩,只需分别求出每个班的总分数,这些总分数的和就是这个年级所有学生成绩的和,再除以年级总人数,就是所求的这个年级的平均成绩,而上面的错解把六个班的平均成绩的平均数误当成年级的平均成绩,导致了错误.正解x =95×52+91.5×55+93×53+95×51+91×54+93.5×5252+55+53+51+54+52≈93.1(分)答:该校七年级期末数学考试的平均成绩为93.1分.。
陕西省2015年初中毕业学业考试物理试题

物理试卷 第1页(共8页) 物理试卷 第2页(共8页)绝密★启用前陕西省2015年初中毕业学业考试物 理本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
满分70分,考试时间60分钟。
第Ⅰ卷(选择题 共16分)一、选择题(本题共8小题,每小题2分,共16分。
每小题只有一个选项是符合题意的) 1.对图中的自然现象解释正确的是( )A .冰挂的形成是凝华现象 B .云的形成是汽化现象 C .霜的形成是凝固现象 D .雾的形成是液化现象2.关于声现象,下列说法正确的是 ( )A .吹笛子时,手指按压不同的笛孔是为了改变音色B .吉他能发出声音是由于弦在振动C .声呐是利用次声波传递信息的D .市区内禁止鸣笛是在传播过程中减弱噪声3.如图所示为多功能车用安全锤,以下关于安全锤的分析正确的是 ( )A .安全锤上配备的螺丝起子在使用时相当于一个省力杠杆B .要使手电筒中的三个LED 灯工作时互不影响,应将它们串联C .榔头的前端做得很尖锐是通过减小受力面积来减小压强D .利用吸磁杆的磁性可吸引所有金属4.对下列与压强有关的事例,解释不正确的是( )A .用吸管喝饮料利用了大气压强B .高压锅是利用液体的沸点随气压增大而升高的原理制造的C .水坝下部比上部建造得宽是因为液体压强随着深度的增加而减小D .火车进站时旅客不能越过安全黄线,依据的是流体中流速大的地方压强小 5.下列与体育运动有关的描述正确的是 ( )A .初中学生50 m 跑步的测试成绩一般是30 sB .在运动鞋底做有花纹是为了增大摩擦C .掷出的铅球,在下落过程中动能转化为重力势能D .踢足球时,脚对球的作用力和球对脚的作用力是一对平衡力6.如图所示是某老师的自制教具。
他在矿泉水瓶的侧壁上钻一个孔,把电火花发生器紧紧塞进孔中。
实验时从瓶口喷入酒精并盖上锥形纸筒,按动电火花发生器的按钮,点燃瓶内酒精后,纸筒即刻飞出。
关于此实验,分析不正确的是 ( )A .酒精不完全燃烧时热值不变B .能闻到酒精的气味说明分子在永不停息地做无规则运动C .燃气推动纸筒飞出的过程相当于内燃机的压缩冲程D .纸筒飞出后瓶内气体的内能减小,温度降低 7.下列说法正确的是 ( )A .发现有人触电后,应立即用手把触电的人拉离带电体B .家庭电路中,开关必须接在零线上C .目前核电站获得核能的途径是核裂变D .煤、石油、开然气都属于可再生能源8.如图所示电路,闭合开关S 1、S 2,下列对电路的分析正确的是( )A .L 1与L 2串联B .电流表A 1测L 1的电流C .当开关S 2断开时,通过L 1的电流变小D .当开关S 2断开时,电流表A 2的示数变小第Ⅱ卷(非选择题 共54分)二、填空与作图题(本题共6小题,每空1分,每图2分,共19分)毕业学校_____________ 姓名________________ 考生号________________ ________________ ___________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------9.(2分)LED灯是一种特殊的二极管。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、矩阵中元素按行和按列都已排序,要求查找时间复杂度为O(m+n),因此不能采用常规的二层循环的查找。
可以先从右上角(i=a,j=d)元素与x比较,只有三种情况:一是A[i,j]>x,这情况下向j 小的方向继续查找;二是A[i,j]<x,下步应向i大的方向查找;三是A[i,j]=x,查找成功。
否则,若下标已超出范围,则查找失败。
void search(datatype A[ ][ ], int a,b,c,d, datatype x)//n*m矩阵A,行下标从a到b,列下标从c到d,本算法查找x是否在矩阵A中.{i=a; j=d; flag=0; //flag是成功查到x的标志while(i<=b && j>=c)if(A[i][j]==x) {flag=1;break;}else if (A[i][j]>x) j--; else i++;if(flag) printf(“A[%d][%d]=%d”,i,j,x); //假定x为整型.else printf(“矩阵A中无%d 元素”,x);}算法search结束。
[算法讨论]算法中查找x的路线从右上角开始,向下(当x>A[i,j])或向左(当x<A[i,j])。
向下最多是m,向左最多是n。
最佳情况是在右上角比较一次成功,最差是在左下角(A[b,c]),比较m+n次,故算法最差时间复杂度是O(m+n)。
2、矩阵中元素按行和按列都已排序,要求查找时间复杂度为O(m+n),因此不能采用常规的二层循环的查找。
可以先从右上角(i=a,j=d)元素与x比较,只有三种情况:一是A[i,j]>x,这情况下向j 小的方向继续查找;二是A[i,j]<x,下步应向i大的方向查找;三是A[i,j]=x,查找成功。
否则,若下标已超出范围,则查找失败。
void search(datatype A[ ][ ], int a,b,c,d, datatype x)//n*m矩阵A,行下标从a到b,列下标从c到d,本算法查找x是否在矩阵A中.{i=a; j=d; flag=0; //flag是成功查到x的标志while(i<=b && j>=c)if(A[i][j]==x) {flag=1;break;}else if (A[i][j]>x) j--; else i++;if(flag) printf(“A[%d][%d]=%d”,i,j,x); //假定x为整型.else printf(“矩阵A中无%d 元素”,x);}算法search结束。
[算法讨论]算法中查找x的路线从右上角开始,向下(当x>A[i,j])或向左(当x<A[i,j])。
向下最多是m,向左最多是n。
最佳情况是在右上角比较一次成功,最差是在左下角(A[b,c]),比较m+n次,故算法最差时间复杂度是O(m+n)。
3、设有两个集合A和集合B,要求设计生成集合C=A∩B的算法,其中集合A、B和C用链式存储结构表示。
typedef struct node {int data; struct node *next;}lklist;void intersection(lklist *ha,lklist *hb,lklist *&hc){lklist *p,*q,*t;for(p=ha,hc=0;p!=0;p=p->next){ for(q=hb;q!=0;q=q->next) if (q->data==p->data) break;if(q!=0){ t=(lklist *)malloc(sizeof(lklist)); t->data=p->data;t->next=hc; hc=t;} }}4、我们可用“破圈法”求解带权连通无向图的一棵最小代价生成树。
所谓“破圈法”就是“任取一圈,去掉圈上权最大的边”,反复执行这一步骤,直到没有圈为止。
请给出用“破圈法”求解给定的带权连通无向图的一棵最小代价生成树的详细算法,并用程序实现你所给出的算法。
注:圈就是回路。
5、二叉树的层次遍历序列的第一个结点是二叉树的根。
实际上,层次遍历序列中的每个结点都是“局部根”。
确定根后,到二叉树的中序序列中,查到该结点,该结点将二叉树分为“左根右”三部分。
若左、右子树均有,则层次序列根结点的后面应是左右子树的根;若中序序列中只有左子树或只有右子树,则在层次序列的根结点后也只有左子树的根或右子树的根。
这样,定义一个全局变量指针R,指向层次序列待处理元素。
算法中先处理根结点,将根结点和左右子女的信息入队列。
然后,在队列不空的条件下,循环处理二叉树的结点。
队列中元素的数据结构定义如下:typedef struct{ int lvl; //层次序列指针,总是指向当前“根结点”在层次序列中的位置int l,h; //中序序列的下上界int f; //层次序列中当前“根结点”的双亲结点的指针int lr; // 1—双亲的左子树 2—双亲的右子树}qnode;BiTree Creat(datatype in[],level[],int n)//由二叉树的层次序列level[n]和中序序列in[n]生成二叉树。
n是二叉树的结点数{if (n<1) {printf(“参数错误\n”); exit(0);}qnode s,Q[]; //Q是元素为qnode类型的队列,容量足够大init(Q); int R=0; //R是层次序列指针,指向当前待处理的结点BiTree p=(BiTree)malloc(sizeof(BiNode)); //生成根结点p->data=level[0]; p->lchild=null; p->rchild=null; //填写该结点数据for (i=0; i<n; i++) //在中序序列中查找根结点,然后,左右子女信息入队列if (in[i]==level[0]) break;if (i==0) //根结点无左子树,遍历序列的1—n-1是右子树{p->lchild=null;s.lvl=++R; s.l=i+1; s.h=n-1; s.f=p; s.lr=2; enqueue(Q,s);}else if (i==n-1) //根结点无右子树,遍历序列的1—n-1是左子树{p->rchild=null;s.lvl=++R; s.l=1; s.h=i-1; s.f=p; s.lr=1; enqueue(Q,s);}else //根结点有左子树和右子树{s.lvl=++R; s.l=0; s.h=i-1; s.f=p; s.lr=1;enqueue(Q,s);//左子树有关信息入队列s.lvl=++R; s.l=i+1;s.h=n-1;s.f=p; s.lr=2;enqueue(Q,s);//右子树有关信息入队列}while (!empty(Q)) //当队列不空,进行循环,构造二叉树的左右子树{ s=delqueue(Q); father=s.f;for (i=s.l; i<=s.h; i++)if (in[i]==level[s.lvl]) break;p=(bitreptr)malloc(sizeof(binode)); //申请结点空间p->data=level[s.lvl]; p->lchild=null; p->rchild=null; //填写该结点数据if (s.lr==1) father->lchild=p;else father->rchild=p; //让双亲的子女指针指向该结点if (i==s.l){p->lchild=null; //处理无左子女s.lvl=++R; s.l=i+1; s.f=p; s.lr=2; enqueue(Q,s);}else if (i==s.h){p->rchild=null; //处理无右子女s.lvl=++R; s.h=i-1; s.f=p; s.lr=1; enqueue(Q,s);}else{s.lvl=++R; s.h=i-1; s.f=p; s.lr=1; enqueue(Q,s);//左子树有关信息入队列s.lvl=++R; s.l=i+1; s.f=p; s.lr=2; enqueue(Q,s); //右子树有关信息入队列}}//结束while (!empty(Q))return(p);}//算法结束6、若第n件物品能放入背包,则问题变为能否再从n-1件物品中选出若干件放入背包(这时背包可放入物品的重量变为s-w[n])。
若第n件物品不能放入背包,则考虑从n-1件物品选若干件放入背包(这时背包可放入物品仍为s)。
若最终s=0,则有一解;否则,若s<0或虽然s>0但物品数n<1,则无解。
(1)s-w[n],n-1 //Knap(s-w[n],n-1)=true(2)s,n-1 // Knap←Knap(s,n-1)7、设有一个数组中存放了一个无序的关键序列K1、K2、…、Kn。
现要求将Kn放在将元素排序后的正确位置上,试编写实现该功能的算法,要求比较关键字的次数不超过n。
51. 借助于快速排序的算法思想,在一组无序的记录中查找给定关键字值等于key的记录。
设此组记录存放于数组r[l..h]中。
若查找成功,则输出该记录在r数组中的位置及其值,否则显示“not find”信息。
请编写出算法并简要说明算法思想。
