正方体11种展开图课堂

合集下载

正方体11种展开图ppt课件

五棱锥
41
感谢亲观看此幻灯片，此课件部分内容来源于网络，如有侵权请及时联系我们删除，谢谢配合！
可编辑课件
18
(5)
可编辑课件
19
(6)
可编辑课件
20
(7)
可编辑课件
21
(8)
可编辑课件
22
(9)
可编辑课件
23
(10)
可编辑课件
24
(11)
可编辑课件
25
(12)
可编辑课件
26
(13)
可编辑课件
27
(14)
可编辑课件
28
(15)
可编辑课件
29
(16)
可编辑课件
30
(17)
可编辑课件
31
(18)
可编辑课件
32
在展开的过程中注意你剪开了几条棱？
将正方体展开成平面图形需要剪开7条棱
（无论用哪种方案展开）
可编辑课件
33
开始时我们已经在正方体的相对的面上标上相同的数字，现在观察一下这些数字在展开图中有什么规律？
可编辑课件
34
“一四一”型
可编辑课件
35
“二三一”型
“三三”型
“二二二”型
可编辑课件
36
考考你下图是正方体的表面展开图。
1、如果“你”在前面，那么谁在后面？
了！太棒你们
可编辑课件
37
2、“坚”在下，“就”在后，“胜”、 “利”在哪里？
坚
持就是
胜
“胜”在上，
利
“利”在前！
可编辑课件
38
可编辑课件
39
圆柱

正方体展开全图11种情况演示课件

展开5
第一类（6种）：中间四连方，两侧各有一个。
展开6
第一类（6种）：中间四连方，两侧各有一个。
第二类（3种）：中间三连方，两侧各有一、二个。
第二类（3种）：中间三连方，两侧各有一、二个。
第二类（3种）：中间三连方，两侧各有一、二个。
展开10
第三类（1种）：中间二连方，两侧各有二个。
展开11
(√)
在展开的过程中注意你剪开了几条棱？
将正方体展开成平面图形需要剪开 7条棱（无论用哪种方案展开）
(1)
判断下列图形能不能折成正方体？
(3)
(11)
PART 1
(12)
PART 1
(13)
PART 1
(14)
PART 1
(16)
PART 1
(17)
PART 1
你
太
棒
了
！
们
考考你下图是正方体的表面展开图。
1、如果“你”在前面，那么谁在后面？
利
胜
持
是
就
坚
2、“坚”在下，“就”在后，“胜”、“利”在哪里？
Байду номын сангаас
圆柱圆锥
毕业论文答辩
点击此处添加正文，文字是您思想的提炼，请言简意赅的阐述观点。
四棱锥
五棱锥
第四类（1种）：两排各有三个。
练一练
用手势判断下面的平面图形是不是正方体的展开图？
用手势判断下面的平面图形是不是正方体的展开图？
练一练
练一练
用手势判断下面的平面图形是不是正方体的展开图？
想一想：下列的图形都是正方体的展开图吗？
(5)
(2)
(6)
(3)

正方体动态展开图(11种)

练一练
用手势判断下面的平面图形是不是正方体的展开图？
练一练
用手势判断下面的平面图形是不是正方体的展开图？
练一练
用手势判断下面的平面图形是不是正方体的展开图？
你的收获有哪些？
正方体的展开图
动画演示
1
2
3
4
5
6
7
11
8 9 10
归纳总结
第一类，中间四连方，两侧各一个，共六种。
第二类，中间三连方，两侧各有一、二个，共三种。
第三类，中间二连方，两侧各有二个，只有一种。
第四类，两排各三个，只有一种。
பைடு நூலகம் 练一练
用手势判断下面的平面图形是不是正方体的展开图？

正方体11种平面展开图(精心整理)

正方体的11种平面展开图
正方体的平面展开图共有11种（那些经旋转或翻转后方向不同但实质相同的图形不重复计算），具体来讲分以下4类。

口诀：需背诵
正方体：中间四个面，上下各一面（6种摆法-141）
中间三个面，一二隔河见（3种摆法-132/231）
中间二个面，楼梯天天见（1种摆法-222)
中间没有面，三三连一线（1种摆法-33）
“田”“凹”应弃之
第一类：“1—4—1”型，其特点是有4个连成一排的正方形，两侧又各有1个正方形，共有6种。

口诀：中间四个面，上下各一面（上下面随便放）
第二类：“1—3—2”型，其特点是有3个连成一排的正方形，这一排正方形的一侧有1个正方形，另一侧有2个正方形（其中只有1个与中间那一排相连），共有3种。

口诀：中间三个面，一二隔河见（二三位置是固定的）
第三类：“2—2—2”型，其特点是有2个连成一排的正方形，其两侧又各有2个连成一排的正方形，只有1种。

口诀：中间二个面，楼梯天天见
第四类：“3—3”型，其特点是有3个连成一排的正方形，其一侧还有3个连成一排的正方形，只有1种。

中间没有面，三三连一线（1种摆法-33）。

正方体11种平面展开图(精心整理)

正方体的11种平面展开图
正方体的平面展开图共有11种（那些经旋转或翻转后方向不同但实质相同的图形不重复计算），具体来讲分以下4类。

口诀：中间二个面，楼梯天天见
第四类：“3—3”型，其特点是有3个连成一排的正方形，其一侧还有3个连成一排的正方形，只有1种。

中间没有面，三三连一线（1种摆法-33）。

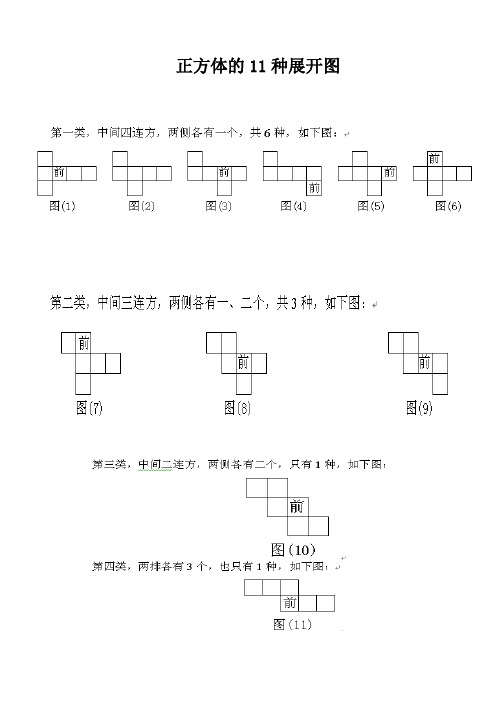
正方体11种展开图

图1
图2
图3
图4
图5
图6
第二类（3种）：中间三连方，两侧各有二、一个。 “二三一”
型
图7
图8
图9
第三类（1种）：中间二连方，两侧各有二个。
图 10 “二二二”型
第四类（1种）：两排各有三个。
“三三”型
图 11
展开1 第一类（6种）：中间四连方，两侧各有一个。
展开第一类（6种）：中间四连方，两侧各有一个。 2
(16)
(17)
(18)
在展开的过程中注意你剪开了几条棱？
将正方体展开成平面图形需要剪开7条棱
（无论用哪种方案展开）
开始时我们已经在正方体的相对的面上标上相同的数字，现在观察一下这些数字在展
开图中有什么规律？
“一四一” 型
“二三一”型
“三三”型
“二二二”型
考考你下图是正方体的表面展开图。
1、如果“你”在前面，那么谁在后面？
了！
太棒
你们
2、“坚”在下，“就”在后， “胜”、“利”在哪里？
坚
持就是
胜
利
圆柱圆锥
三棱锥
四棱锥
五棱锥
展开第3 一类（6种）：中间四连方，两侧各有一个。
展开4 第一类（6种）：中间四连方，两侧各有一个。
展开5 第一类（6种）：中间四连方，两侧各有一个。
展开6 第一类（6种）：中间四连方，两侧各有一个。
展开7
第二类（3种）：中间三连方，两侧各有一、二个。
展开8
第二类（3种）：中间三连方，两侧各有一、二个。
展开9
第二类（3种）：中间三连方，两侧各有一、二个
展开10
第三类（1种）：中间二连方，两侧各有二个。

正方体的11种展开图课件

正方体展开图
.
1
将正方体剪开展成一个平面图形。
.
2
• 1、在正方体的相对的面上标上相同的数字
• 2、在展开的过程中注意你剪开了几条棱？
.
3
“一四一”
型
.
4
“二三一” 型
“三三” 型
“二二二”
.型
5
判断下列图形能不能折成正方体？
(1)
(2)
.
7
(3)
.
8
(4)
.
9
(5)
.
10
(6 )
开始时我们已经在正方体的相对的面上标上相同的数字，现在观察一下这些数字在展开图中有什么规律？
.
25
“一四一”
型
.
26
“二三一” 型
“三三” 型
“二二二”
型 .
27
考考你下图是正方体的表面展开图。
1、如果“你”在前面，那么谁在后面？
了！太棒你们
.
28
2、“坚”在下，“就”在后，“胜”、 “利”在哪里？
坚
持就是
胜
利
.
29
.
30
圆柱
圆锥
.
31
三棱锥
四棱锥 .
五棱锥
32
感谢亲观看此幻灯片，此课件部分内容来源于网络，如有侵权请及时联系我们删除，谢谢配合！
.
11
(7 )
.
12
(8)
.
13
(9)
.
14
பைடு நூலகம்10 )
.
15
(11)
.
16
(12 )
.
17

正方体的11种展开图(课堂PPT)

A
B
23
变形：如图有一长方体房间，在房间内一角A 处有一只小虫，它想到房间的另一角B处去吃食物，它采取怎样的行走路线最近？
A
B
24
课堂小结:
这节课我们探索了．．．．．．这节课我体验到了．．．．．．这节课我还想．．．．．．
25
Bye Bye !
26
在正方体涂相同的颜色或者画上相同的符号14101511161217131814191520162117221824我们已经在正方体的上涂上相同的颜色现在观察一下相对的两个面在展开图中有什么规律
正方体展开图
1
自主探索尝试发现将正方体剪开展成一个平面图形。
2
展示成果归纳总结
“一四一”型
3“二三一”型“三三”型“二二二”型4
判断下列图形能不能折成正方体？
(1)
(2)
6
(3)
7
(4)
8
(5)
9
(6)
10
(7)
11
(8)
12
(9)
13
(10)
14
(11)
15
(12)
16
(13)
17
(14)
18
(15)
19
(16)
20
(17)
21
(18)
22
2.如图有一正方体房间，在房间内的一角A 处有一只小虫，它想到房间的另一角B处去吃食物，它采取怎样的行走路线最近？

(完整版)正方体的11种展开图

正方体的11种展开图
判断技巧
我们知道，同一个立方体图形，按不同的方式展开得到的平面展开图形一般是不一样的。

常见的正方体平面展开图究竟有几种不同的形状呢？
同学们一定熟悉这样一种操作：把一个正方形纸片平均分成9个小正方形，剪去角上四个小正方形，可以拼成一个无盖的正方体纸盒，其中五个面按习惯不妨记为下、左、右、前、后，如图一。

好啦！现在只要把刚才剪去的一个小正方形作为“上”面，就可拼成一个正方体。

作为正方体平面展开图，这个“上”应该和图1（1）中哪个面拼接在一起呢？观察图1（2），知“上”和前、后、左、右任一个面拼接都行（这四种拼接看作同一种情形），不妨和“后”拼接在一起，如图2。

根据上和下、左和右、前和后相间隔这一规律，现在我们把图2中的“左”或“右”平移，可得图3～图7五种情形。

平移图2中的“前”，可得图8；再平移图8中的“左”，可得图9、图10；把图10中的“上”向左平移，得图11；若移动图8（或图9、图10）中的“左”，又可得图12。

同学们，当你和我一样，把图2～图12这11个图剪下来，动手折一折，得到11个漂亮的小正方体时，你一定为我们的收获感到欢欣鼓舞吧！
对正方体表面展开图的11种情况，为加深记忆，可编成如下口诀：一四一呈6种，一三二有3种，二二二与三三各1种，展开图共有11种。

“动手实践，自主探索和合作交流”是新课程标准倡导学习数学的三种重要方法，而实践活动是培养我们进行主动探索与合作交流的重要途径。

只要通过自己主动观察、实验、猜想、验证等数学活动，就能使我们“建立空间观念，发展几何直觉”，提高思维能力。

正方体11种展开图

类型六：十字型
总结词
由两个相同的等腰直角三角形和两个相同的矩形组成的展开图，呈十字形状。
详细描述
这种类型的展开图在正方体的两个相对的面上保留了一个矩形，而其他面则由两个等腰直角三角形组成，整体呈十字形状。
类型七：二字型
总结词
由两个相同的矩形和两个相同的等腰直角三角形组成的展开图，呈二字形状。
详细描述
正方体11种展开图
• 正方体的基本特性 • 正方体的11种展开图 • 正方体展开图的制作方法 • 正方体展开图的应用场景 • 正方体展开图的挑战与未来发展
01
正方体的基本特性
定义与特性
01
正方体是一种三维几何体，由六个正方形面组成，每个面都是等大的正方形。
02
正方体的体对角线、棱和面都是对称的，具有高度的空间对称性。
05
正方体展开图的挑战与未来发展
当前面临的挑战
寻找新的展开方式
目前已知的正方体展开图种类有限，需要探索新的展开方式以丰
富其多样性。
证明无解的存在
对于某些特定条件下的正方体展开问题，需要证明无解的存在，这需要深入的数学理论支持。
实际应用中的限制
正方体展开图在实际应用中可能受到材料、工艺等因素的限制，需要解决这些实际问题。
正方体的几何属性
正方体的体积是边长的三次方，记作 V=a^3，其中a是正方体的边长。
正方体的表面积是6倍的边长的平方，记作A=6a^2。
正方体的展开与折叠
正方体的展开是将正方体的表面沿某些边展开成平面的过程，通常用于制作纸盒等包装材料。
正方体的折叠则是将展开的平面重新折回成立体的过程，常用于制作纸艺模型和玩具。
详细描述

正方体11种平面展开图(精心整理)

正方体的11种平面展开图
正方体的平面展开图共有11种（经旋转或翻转后方向不同但实质相同的图形不重复计算），具体来讲分以下4类:
口诀：需背诵
正方体：中间四个面，上下各一面（6种摆法-141）
中间三个面，一二隔河见（3种摆法-132/231）
中间二个面，楼梯天天见（1种摆法-222)
中间没有面，三三连一线（1种摆法-33）
“田”“凹”应弃之
第一类：“1—4—1”型，其特点是有4个连成一排的正方形，两侧又各有1个正方形，共有6种。

口诀：中间二个面，楼梯天天见
第四类：“3—3”型，其特点是有3个连成一排的正方形，其一侧还有3个连成一排的正方形，只有1种。

中间没有面，三三连一线（1种摆法-33）。

正方体11种平面展开图

正方体的11种平面展开图正方体的平面展开图共有11种（那些经旋转或翻转后方向不同但实质相同的图形不重复计算），具体来讲分以下4类。

第一类：“1—4—1”型，其特点是有4个连成一排的正方形，两侧又各有1个正方形，共有6种。

第二类：“1—3—2”型，其特点是有3个连成一排的正方形，这一排正方形的一侧有1个正方形，另一侧有2个正方形（其中只有1个与中间那一排相连），共有3种。

第三类：“2—2—2”型，其特点是有2个连成一排的正方形，其两侧又各有2个连成一排的正方形，只有1种。

第四类：“3—3”型，其特点是有3个连成一排的正方形，其一侧还有3个连成一排的正方形，只有1种。

注：①将长方体、正方体展开：无论怎么剪，都要剪7条棱。

②“隔”的原理：相对的面如果在同一行或同一排，中间一定只隔一个面；相对的面如果不在同一行或同一排，中间可以隔着一些面。

③长方体、正方体中各面的关系：相对、相邻。

每个面都有1个相对的面，4个相邻的面。

注：立体图中相对的面在展开图中符合“隔”的原理，而相邻的面在展开图中不符合“隔”的原理。

④长方体、正方体中最多可以同时看到三个面，且这三个面都是相邻的面。

⑤要区分好是从“立体图”到“展开图”，还是从“展开图”到“立体图”：正方体、长方体展开图⑥长方体（不包含正方体）最多有1组相对的面是正方形；当有2组相对的面是正方形时，长方体就变成了正方体（特殊的长方体）。

长方体（不包含正方体）的6个面中，最多有4个面的面积相等；12条棱中，最多有8条棱长度相等。

（即2个相对的面是正方形，其余四个面变为完全相同的长方形。

）⑦正方体的棱长扩大a倍：棱长和扩大a倍，表面积扩大a2倍，体积扩大a3倍。

（给出其中一个，要能将其余的都求出来）⑧常见的平方、立方（需熟记在心）12=1 22=4 32=9 42=16 52= 25 62=36 72=49 82=64 92=81 ……13=1 23=8 33=27 43=64 53= 125 63=216 ……互逆。