第六章单元作业

合集下载

人教版七年级数学下册第六章实数。单元测试题精选(Word版附答案)

人教版七年级数学下册第六章实数。

单元测试题精选(Word版附答案)人教版七年级数学第6章《实数》单元测试题精选完成时间：120分钟满分：150分得分评卷人：______________ 姓名：______________ 成绩：______________一、选择题（本大题10小题，每小题4分，共40分。

每小题给出的四个选项中，只有一个选项是符合题意的，请将该选项的标号填入表格内）题号 1 2 3 4 5 6 7 8 9 10答案 B A D A A C D C B B二、填空题（每题5分，共20分）11.m = 3.n = 1.(m+n)^5 = 243.12.(1) 0.000 521 7 (2) 0.002 284.13.3.14.x = 8.三、解答题（共90分）15.1) x = ±5/3;2) x = 3/5.16.1.17.a = 9.b = -8.3a+b的算术平方根为 5.18.已知 $m=\lfloor 313\rfloor$。

$n=0.13$，求 $m-n$ 的值。

19.如图，计划围一个面积为 $50\text{ m}^2$ 的长方形场地，一边靠旧墙（墙长为 $10$ m），另外三边用篱笆围成，并且它的长与宽之比为 $5:2$。

讨论方案时，XXX说：“我们不可能围成满足要求的长方形场地。

”小军说：“面积和长宽比例是确定的，肯定可以围得出来。

”请你判断谁的说法正确，为什么？解：设长为 $5x$，宽为 $2x$，则面积为 $10x^2$，另一条边长为 $10-5x$，由题意得 $10x^2=(10-5x)\times2x$，解得$x=1$，长为 $5$，宽为 $2$，可以围成满足要求的长方形场地，小军的说法正确。

20.若 $x+3+(y-3)^2=3$，则 $(xy)^{\frac{2015}{3}}$ 等于多少？解：移项得 $(y-3)^2=3-x-3=-x$，所以 $xy=\frac{3-x}{y-3}$，将其代入 $(xy)^{\frac{2015}{3}}$ 得 $\left(\frac{3-x}{y-3}\right)^{\frac{2015}{3}}$，根据乘方的运算法则，得$\left(\frac{3-x}{y-3}\right)^{671}$。

人教版七年级数学下册第六章实数单元练习

第六章实数一、单选题1．1.44的算术平方根是（）A ．1.2B ．﹣1.2C ．±1.2D ．以上都是 2．9的平方根是（）A ．±3B ．3C ．±4.5D ．4.533m -的立方根，则（）A ．3m =B ．m 是小于3的实数C ．m 是大于3的实数D ．m 可以是任意实数 4．下列各式正确的是（）A 4=±B ．2=C ．3=D 2=- 5．下列各数中，无理数是（）A B C D ．236 ）A ．0和1之间B ．1和2之间C ．2和3之间D ．3和4之间7．在下列实数中：120192019，0，最大的数是（）A ．12019B C ．2019 D ．0 8．已知实数a 、b 在数轴上的位置如图所示，下列结论错误的是（）A ．a ＜0＜bB ．1＜b ＜|a|C ．1＜﹣a ＜bD ．﹣b ＜a ＜19．填在下面各正方形中四个数之间都有相同的规律，根据这种规律m 的值为( )A ．180B ．182C ．184D ．186 10．现规定一种新的运算“*”；m*n=(m +n)m−n ，那么51*22=（） A ．B ．5C ．3D ．9二、填空题 11．若一个数的平方根就是它本身，则这个数是______．12．已知a 是64的立方根，2b -3是a 的平方根，则11a - 4b 的算术平方根为______．13_________12（填“＞”或“＜”） 14．规定一种新运算:2,b a b a ⊗=÷如4343240.5 ,⊗=÷=则23-⊗=_____．三、解答题15．已知m 、n ＝0，求2m ﹣n 的值．16．求下列各式中的x（1）x 3﹣0.027＝0（2）（x ﹣2）2＝9．17．设2x =+x 的整数部分为a ，小数部分为b ，求a 、b 的值．18．观察下列等式：11283274641,2,3,4,225510101717-=-=-=-=⋅⋅⋅根据你发现的规律，解答下列问题：（1）写出第6个等式．（2）用关于n （n 是正整数）的等式表示这个规律．19．定义：如果2b n =，那么称b 为n 的布谷数，记为()b g n =. 例如：因为328=，所以()3(8)23g g ==，因为1021024=，所以()10(1024)210g g ==. （1）根据布谷数的定义填空：g （2）=________________,g （32）=___________________. （2）布谷数有如下运算性质：若m ，n 为正整数，则()()()=+g mn g m g n ，()()m g g m g n n ⎛⎫=- ⎪⎝⎭. 根据运算性质解答下列各题：①已知(7) 2.807g =，求 (14)g 和74g ⎛⎫ ⎪⎝⎭的值； ①已知(3)g p =.求(18)g 和316g ⎛⎫ ⎪⎝⎭的值.答案1．A 2．A 3．D 4．D 5．A 6．C 7．C 8．B 9．C 10．D 11．01213．＞14．4-15．816．（1）x ＝0.3；（2）x ＝5或x ＝﹣117．a ，b 的值分别为3．18．（1）21637；（2）32211n n n n n -=++. 19．（1）1；5；（2）①3.807，0.807；①12p +；4p -。

人教版七年级下册第六章《实数》单元测试题及答案

第六章《实数》单元测试题一、用心填一填，一定能填对：（每空1分，共53分）1. 正数a 的平方根记作 ,正数a 的正的平方根记作，正数a 的负的平方根记作 .2. 如果x 2=4，则x 叫作4的，记作 .3。

81的平方根是，0。

64的算术平方根是 . 5的平方根是 ,0的平方根是 .４. 491的算术平方根的相反数是，平方根的倒数是，平方根的绝对值是 . ５。

24-的相反数的倒数是，这个结果的算术平方根是。

６. 当a 时，1-a 有意义，当a 时，1-a =0。

７. 如果2x =5，则x = 。

８。

如果一个正数的一个平方根是m,那么这个数的另一个平方根是，这个数的算术平方根是 ,两个平方根的和是。

９。

当x >0时，x -表示x 的，当x <0时,3x -表示x的。

10。

16 的负的平方根是，2)5(-的平方根是 .11. 962+-x x 的平方根是 .12. 如果a x =3那么x 是a 的，a 是x 的。

13。

0.064的立方根是，1-的立方根是，3的立方根是，0的立方根是，9-的立方根是 .14．35是5的，一个数的立方根是2-，则这个数是。

15．=-364 ，=-327 ，=--3125 。

16．=--33)0001.0( . 17．当x 时，32-x 有意义。

18、若22)3(-=a ，则a = ,若23)3(-=a ，则a = .19．=--32)125.0( 。

20．若12-x 是225的算术平方根，则x 的立方根是。

21。

3343的平方根是。

22. 若x 是64125的立方根，则x 的平方根是 . 23.25-的相反数是。

2４.若1.1001.102=，则=±0201.1 。

25. 若x x -+有意义，则=+1x26. 1- ，-22 ， 33 27. 数轴上离原点距离是5的点表示的数是。

28. 无理数a 满足14-<<-a , 请写出两个你熟悉的无理数a .二、你很聪明,一定能选对：（每小题1分，共10分）1. 0.0196的算术平方根是（）A 0。

第六章实数单元测试卷

第六章实数单元测试卷一、选择题1. 25 的平方根是 ( )A ． 5B ． −5C ． ±√5D ． ±5 2. 下列等式正确的是 ( )A ． ±√(−2)2=2B ． √(−2)2=−2C ． √−83=−2D ． √0.013=0.1 3. 下列各数中，无理数的个数是 ( )3.141，−227，√−273，π，0，0.1010010001⋯A ． 2B ． 3C ． 4D ． 5 4. 设 7−√10 的整数部分为 a ，小数部分为 b ，则 (a +√10)(b −1) 的值是 ( ) A ． 6 B ． 2−√10 C ． 1 D ． −1 5. 若 a ，b 为实数，且满足 ∣a −2∣+√3−b =0，则 b −a 的值为 ( ) A ． 1 B ． 0 C ． −1 D ．以上都不对 6. 计算 ∣∣√6−3∣∣+∣∣2−√6∣∣ 的值为 ( )A ． 5B ． 5−2√6C ． 1D ． 2√6−1 7. 下列说法不正确的有 ( )①任何数都有算术平方根；②一个数的算术平方根一定是正数；③ a 2 的算术平方根是 a ；④ (π−4)2 的算术平方根是 π−4；⑤算术平方根不可能是负数．A ． 5 个B ． 4 个C ． 3 个D ． 2 个 8. 若 √a 2=−a ，则实数 a 在数轴上的对应点一定在 ( )A ．原点左侧B ．原点右侧C ．原点或原点左侧D ．原点或原点右侧二、填空题9. 比较大小：√5−3 √5−22（填“>”“<”或“=”）．10. 下列关于 √13 的说法中，正确的有（填序号）．① 13 的平方根是 √13；② √13 是 13 的算术平方根；③ √13 是无理数；④ 3<√13<4．11. 若 √2+a 的值为有理数，请你写出一个符合条件的实数 a 的值． 12. 若 y =√x −12+√12−x −6，则 xy 的值为． 13. 若 a <√6<b ，且 a ，b 是两个连续的整数，则 a b = ．14. 大家知道 √2 是无理数，而无理数是无限不循环小数，因此 √2 的小数部分我们不可能全部写出来，于是小林用 √2−1 来表示 √2 的小数部分．事实上，小林的表示方法是有道理的，因为 1<√2<2，即 √2 的整数部分是 1，所以将这个数减去其整数部分就是小数部分．如果 √5 的小数部分为 a ，√13 的整数部分为 b ，那么 a +b −√5= ．15. 规定用符号 [m ] 表示一个实数 m 的整数部分，例如：[23]=0，[3.14]=3．按此规定，[√10+1] 的值为．三、解答题16. 把下列各数填入相应的大括号内．√3，−2，√93，0，√−83，16113，3.1415，3−π，√144，3−√29，3√2，0.2121121112⋯ 整数集合：{ ⋯}；非负数集合：{ ⋯}；无理数集合：{ ⋯}．17. 计算：(1) √144−√169+√83；(2) ∣∣√3−2∣∣+√3；(3) √−13−√16−√(−6)2+∣∣√2−1∣∣．18. 求 x 的值：(1) x 2−24=25； (2) 8x 3=125； (3) (x −2)2=25．19. 计算并回答问题：(1) √169= ，√1.69= ，√0.0169= ．(2) √21973= ，√2.1973= ，√0.0021973= ．(3) 根据上述结果你发现了什么规律？请用语言概括出来；(4) 根据你发现的规律填空：如果 √15≈3.873，√150≈12.25，√613≈3.936，√6103≈8.481，则 √1.5≈ ，√0.0613≈ ．20. 已知一个正方体的棱长是 7 cm ，要再做一个正方体，使它的体积是原正方体体积的 8倍，求新做的正方体的棱长．（提示：设未知数列方程）21. 若 √2a +b 与 √c −b 的值互为相反数，√1−3b 3 与 √b +13 互为相反数，求 a ，b ，c 的值．22. 已知 a 是 √10 的整数部分，b 是它的小数部分，求 (−a )3+(b +3)2 的值．23. 王老师给同学们布置了这样一道习题：一个数的算术平方根为 2m −6，它的平方根为±(m −2)，求这个数．小张的解法如下：依题意可知，2m −6 是 m −2，−(m −2) 两数中的一个． ⋯⋯（1）当 2m −6=m −2 时，解得 m =4． ⋯⋯（2）所以这个数为 2m −6=2×4−6=2． ⋯⋯（3）当 2m −6=−(m −2) 时，解得 m =83． ⋯⋯（4）所以这个数为 2m −6=2×83−6=−23． ⋯⋯（5）综上可得，这个数为 2 或 −23． ⋯⋯（6）王老师看后说，小张的解法是错误的．你知道小张错在哪里吗？为什么？请改正．24.先阅读，然后解答提出的问题．设a，b是有理数，且满足a+√2b=3−2√2，求b a的值．解：由题意得(a−3)+(b+2)√2=0，因为a，b都是有理数，所以a−3，b+2也是有理数，又因为√2是无理数，所以a−3=0，b+2=0，所以a=3，b=−2，所以b a=(−2)3=−8．问题：设x，y都是有理数，且满足x2−2y+√5y=10+3√5，求x+y的值．。

第六章单元测试题

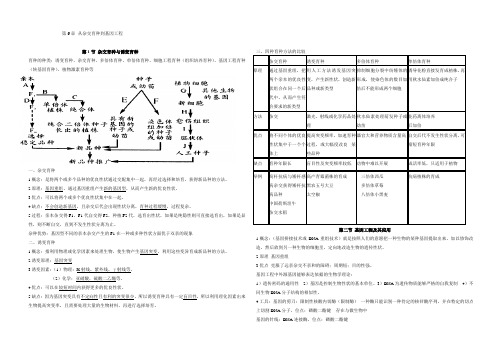
第6章从杂交育种到基因工程第1节杂交育种与诱变育种育种的种类：诱变育种、杂交育种、多倍体育种、单倍体育种、细胞工程育种（组织培养育种）、基因工程育种（转基因育种）、植物激素育种等一、杂交育种1.概念：是将两个或多个品种的优良性状通过交配集中一起，再经过选择和培育，获得新品种的方法。

2.原理：基因重组。

通过基因重组产生新的基因型，从而产生新的优良性状。

3.优点：可以将两个或多个优良性状集中在一起。

4.缺点：不会创造新基因，且杂交后代会出现性状分离，育种过程缓慢，过程复杂。

5过程：亲本杂交得F1，F1代自交得F2，种植F2代，选育出性状，如果是纯隐性则可直接选育出，如果是显性，则不断自交，直到不发生性状分离为止。

杂种优势：基因型不同的亲本杂交产生的F1在一种或多种性状方面优于双亲的现象二、诱变育种1.概念：指利用物理或化学因素来处理生物，使生物产生基因突变，利用这些变异育成新品种的方法。

2.诱变原理：基因突变3.诱变因素：（1）物理：X 射线，紫外线，γ射线等。

（2）化学：亚硝酸，硫酸二乙酯等。

4.优点：可以在较短时间内获得更多的优良性状。

5.缺点：因为基因突变具有不定向性且有利的突变很少，所以诱变育种具有一定盲目性，所以利用理化因素出来生物提高突变率，且需要处理大量的生物材料，再进行选择培育。

三、四种育种方法的比较杂交育种诱变育种多倍体育种单倍体育种原理通过基因重组，把两个亲本的优良性状组合在同一个后代中，从而产生符合要求的新类型用人工方法诱发基因突变，产生新性状，创造新品种或新类型抑制细胞分裂中纺锤体的形成，使染色体的数目加倍后不能形成两个细胞诱导花粉直接发育成植株，再用秋水仙素加倍成纯合子方法杂交激光、射线或化学药品处理秋水仙素处理萌发种子或幼苗花药离体培养后加倍优点将不同个体的优良性状集中于一个个体上提高突变频率，加速育种过程，或大幅度改良某些品种器官大和营养物质含量高自交后代不发生性状分离，可缩短育种年限缺点育种年限长盲目性及突变频率较低动物中难以开展成活率低，只适用于植物举例高杆抗病与矮杆感病杂交获得矮杆抗病品种中国荷斯坦牛杂交水稻高产青霉菌株的育成黑农五号大豆太空椒三倍体西瓜多倍体草莓八倍体小黑麦抗病植株的育成第二节基因工程及其应用1.概念：（基因拼接技术或DNA 重组技术）就是按照人们的意愿把一种生物的某种基因提取出来，加以修饰改造，然后放到另一种生物的细胞里，定向地改造生物的遗传性状。

人教版七年级数学下册《第六章实数》单元练习题(含答案)

第六章实数一、选择题1.若81x2＝49，则x的值是()A．B．C．D． ±72.的算术平方根是()A． ±3B． 3C．D．3.若a＜－2＜b，且a、b是两个连续整数，则a＋b的值是() A． 1B． 2C． 3D． 44.下列说法正确的是()A．－4没有立方根B． 1的立方根为±1C．的立方根是D． 5的立方根为5.下列说法错误的是()A． 5是25的算术平方根B． ±4是64的立方根C． (－4)3的立方根是－4D． (－4)2的平方根是±46.的平方根是()A．B．C．D．7.下列判断中，正确的是()A．有理数是有限小数B．无理数都是无限小数C．无限小数是无理数D．无理数没有算术平方根8.实数，－3.14,0，中，无理数共有()A． 1个B． 2个C． 3个D． 4个二、填空题9.x是16的算术平方根，那么x的算术平方根是______．10.按规律填空：，，，，，，…，________.(第n个数)11.2－的绝对值是________．12.用代数式表示实数a(a＞0)的平方根________．13.若a＜＜b，且a、b是两个连续的整数，则a5＝________.14.数轴上有A、B、C三个点，B点表示的数是1，C点表示的数是，且AB＝BC，则A点表示的数是________．15.如图，M、N、P、Q是数轴上的四个点，这四个点中最适合表示的点是________．16.已知某数的两个平方根分别是a＋3与2a－15，则a＝________，这个数是________．三、解答题17.已知某正数的两个平方根分别是m＋4和2m－16，n的立方根是－2，求－n－m的算术平方根．18.已知2a－3的平方根是±5,2a＋b＋4的立方根是3，求a＋b的平方根．19.实数a，b，c在数轴上的对应关系如图，化简下面的式子：|a－b|－|c－a|＋|b－c|＋|a|.20.如图所示，数轴上表示1和对应点分别为A、B，点B到点A的距离等于点C到点O的距离相等，设点C表示的数为x.(1)请你写出数x的值；(2)求(x－)2的立方根．21.计算：－＋.答案解析1.【答案】A【解析】由81x2＝49得：x2＝，得：x＝.2.【答案】D【解析】因为＝3，所以的算术平方根是.3.【答案】A【解析】因为的整数部分是2，所以0＜－2＜1，因为a、b是两个连续整数，所以a＝0，b＝1，所以a＋b＝1.4.【答案】D【解析】A.－4的立方根是，故此选项错误；B．1的立方根是1，故此选项错误；C.的立方根是，故此选项错误；D．5的立方根是，故此选项正确．5.【答案】B【解析】因为＝5，＝4，＝－4，＝±4，所以选项B错误．6.【答案】B【解析】因为＝，所以的平方根是.7.【答案】B【解析】A.有理数是有限小数和无限循环小数，所以A选项错误；B．无理数是无限不循环小数，都是无限小数，所以B选项正确；C．无限小数分为无限循环小数和无限不循环小数，而无限不循环小数是无理数，所以C选项错误；D．负数没有算术平方根，而无理数可分为正无理数和负无理数，其中正无理数有算术平方根，所以D选项错误．8.【答案】A【解析】是无理数，－3.14,0，是有理数．9.【答案】2【解析】因为42＝16，所以16的算术平方根是4，即x＝4，因为22＝4，所以x的算术平方根是2.10.【答案】【解析】因为＝，＝，＝，＝，＝，……所以第n个数为＝.11.【答案】－2【解析】2－的绝对值是－2.12.【答案】【解析】用代数式表示实数a(a＞0)的平方根为：.13.【答案】32【解析】因为4＜6＜9，所以2＜＜3，由a＜＜b，且a、b是两个连续的整数，得到a＝2，b＝3，则a5＝25＝32.14.【答案】2－【解析】设A点表示x，因为B点表示的数是1，C点表示的数是，且AB＝BC，所以1－x＝－1.解得：x＝2－.15.【答案】P【解析】因为4＜7＜9，所以2＜＜3，所以在2与3之间，且更靠近3.16.【答案】449【解析】由题意得：a＋3＋(2a－15)＝0，解得：a＝4，所以(a＋3)2＝72＝49.17.【答案】解：因为某正数的两个平方根分别是m＋4和2m－16，可得：m＋4＋2m－16＝0，解得：m＝4，因为n的立方根是－2，所以n＝－8，把m＝4，n＝－8代入－n－m＝8－4＝4，所以－n－m的算术平方根是2.【解析】首先根据平方根的性质，求出m值，再根据立方根的性质求出n，代入－n－m，求出这个值的算术平方根即可．18.【答案】解：因为2a－3的平方根是±5，所以2a－3＝52＝25，解得a＝14；因为2a＋b＋4的立方根是3，所以2a＋b＋4＝33＝27，所以2×14＋b＋4＝27，解得b＝－5；所以a＋b＝14－5＝9，所以a＋b的平方根是±3.【解析】首先根据2a－3的平方根是±5，可得2a－3＝52＝25，据此求出a的值；然后根据2a＋b ＋4的立方根是3，可得2a＋b＋4＝33＝27，据此求出b的值；最后求出a＋b的值，进而求出a ＋b的平方根．19.【答案】解：因为由图可知，a＜b＜0＜c，|a|＞c＞|b|，所以a－b＜0，c－a＞0，b－c＜0，所以原式＝b－a－(c－a)＋(c－b)－a＝b－a－c＋a＋c－b－a＝－a.【解析】根据各点在数轴上的位置判断出a、b、c的符号及绝对值的大小，再去绝对值符号，合并同类项即可．20.【答案】解：(1)因为点A、B分别表示1，，所以AB＝－1，即x＝－1；(2)因为x＝－1，所以(x－)2＝(－1－)2＝(－1)2＝1，故(x－)2的立方根为1.【解析】(1)根据数轴上两点间的距离求出AB之间的距离即为x的值；(2)把x的值代入所求代数式进行计算即可．21.【答案】解：原式＝0.5－＋＝0.5－1.5＝－1.【解析】原式利用平方根及立方根定义计算即可得到结果．。

2023年春学期人教版七年级数学下册第六章《实数》单元综合练附答案解析

2023年春学期七年级数学下册第六章《实数》单元综合练一．选择题1．下列各数中的无理数是（）A．6.2B．C．D．π﹣3.142．下列说法中，正确的是（）A．无理数包括正无理数、零和负无理数B．无限小数都是无理数C．正实数包括正有理数和正无理数D．实数可以分为正实数和负实数两类3．|﹣|的平方是（）A．﹣B．C．﹣2D．24．在实数﹣1，﹣，0，中，最小的实数是（）A．﹣1B．C．0D．﹣5．下列各组数中，互为相反数的一组是（）A．﹣2与﹣B．﹣2与C．﹣2与D．|﹣2|与6．若实数a、b、c在数轴上对应点的位置如图所示，则|c﹣a|﹣|b+a|+|b﹣c|等于（）A．﹣2c B．﹣a+2b C．﹣a﹣b D．a﹣2b7．计算：|1﹣|+|3﹣|﹣|3.14﹣π|＝（）A．0.86﹣2+πB．5.14﹣πC．2﹣7.14+πD．﹣1.14+π8．已知：，比较m、n的大小（）A．m＞n B．m＜n C．m＝n D．无法确定9．如图，在数轴上，AB＝AC，A，B两点对应的实数分别是和﹣1，则点C对应的实数是（）A．2B．2﹣2C．+1D．2+110．已知2a﹣1和﹣a+4是一个正数的平方根，则这个正数的值是（）A．9B．1C．7D．49或二．填空题11．写出一个比4大且比5小的无理数：．12．的算术平方根为．13．的倒数是，3﹣的绝对值是．14．已知，a、b互为倒数，c、d互为相反数，求＝．15．已知：≈1.421267…，≈4.494441…，则（精确到0.1）≈．16．用“*”表示一种新运算：对于任意正实数a、b，都有a*b＝．例如8*9＝，那么15*196＝，当m*（m*16）＝．三．解答题17．计算：．18．计算：+++．19．计算：（1）；（2）|﹣2|+．20．计算：（1）；（2）；（3）3（x﹣2）2＝27；（4）2（x﹣1）3+16＝0．21．实数a、b互为相反数，c、d互为倒数，x的绝对值为，y2＝9，求x2+（a+b）x﹣y的值．22．已知2a+3的立方根是3，a+b﹣1的算术平方根是4，c是的整数部分．（1）求a，b，c的值．（2）求a﹣4b+3c的平方根．23．已知a的立方根是3，b的算术平方根是4，一个正数c的两个平方根分别是d+1和2d﹣7，求a+b﹣2c的平方根．24．阅读下面的文字，解答问题：大家知道是无理数，而无理数是无限不循环小数，因此的小数部分我们不可能全部地写出来，于是小明用﹣1来表示的小数部分，因为的整数部分是1，将这个数减去其整数部分，差就是小数部分又例如：因为＜＜，即2＜＜3，所以的整数部分为2，小数部分为（﹣2）请解答：（1）的整数部分是，小数部分是；（2）如果的小数部分为a，的整数部分为b，求a+b﹣的值．参考答案一．选择题1．解：A、6.2是有限小数，是有理数，选项错误；B、是分数，是有理数，选项错误；C、＝3是整数，是有理数，选项错误；D、π﹣3.14是无限不循环小数，是无理数，选项正确．故选：D．2．解：（A）无理数包括正无理数和负无理数，故A错误；（B）无限循环小数是有理数，无限不循环小数是无理数，故B错误；（D）实数可分为正实数，零，负实数，故D错误；故选：C．3．解：|﹣|的平方是2，故选：D．4．解：∵|﹣|＞|﹣1|，∴﹣1＞﹣，∴实数﹣1，﹣，0，中，﹣＜﹣1＜0＜．故4个实数中最小的实数是：﹣．故选：D．5．解：A、绝对值不同不是相反数，故A错误；B、都是﹣2，故B错误；C、只有符号不同的两个数互为相反数，故C正确；D、都是2，故D错误；故选：C．6．解：由图知，c＜b＜0＜a，|b|＜|a|，∴|c﹣a|﹣|b+a|+|b﹣c|＝a﹣c﹣（a+b）+b﹣c＝a﹣c﹣a﹣b+b﹣c＝﹣2c．故选：A．7．解：原式＝﹣1+3﹣﹣π+3.14＝5.14﹣π，故选：B．8．解：∵，∴m﹣n＝﹣（﹣1）＝+﹣+1＝﹣＝，∵9＜10，∴3＜，∴3﹣＜0，∴＜0，∴m＜n，故选：B．9．解：AB＝﹣（﹣1）＝+1，∵AB＝AC，A所表示的实数为，点C在点A的右侧，∴点C所表示的数为：+（+1）＝2+1，故选：D．10．解：∵2a﹣1和﹣a+4是一个正数的平方根，∴①2a﹣1+4﹣a＝0，解得a＝﹣3，把a＝﹣3代入4﹣a得7，∴这个正数的值是49；②2a﹣1＝4﹣a，解得a＝，把a＝代入4﹣a得＝，∴这个正数的值是；故选：D．二．填空题11．解：比4大且比5小的无理数可以是．故答案为．12．解：∵，∴，∵，∴的算术平方根是，故答案为：．13．解：∵＝﹣4，∴的倒数是﹣，∵3＜＜4，∴3﹣＜0，∴3﹣的绝对值是﹣3．故答案为：﹣，﹣3．14．解：∵a、b互为倒数，∴ab＝1，∵c、d互为相反数，∴c+d＝0，∴＝﹣++1＝0．故答案为0．15．解：∵≈4.494，∴≈44.9（精确到0.1），故答案为：44.9．16．解：15*196＝+1＝14+1＝15；m*（m*16）＝m*（+1）＝m*5＝+1．故答案为：15，+1．三．解答题17．解：原式＝﹣1+﹣2﹣＝．18．解：+++＝﹣2+5+2﹣3＝+2．19．解：（1）＝﹣+3+1＝4．（2）|﹣2|+＝2﹣3﹣2+1＝﹣2．20．解：（1）＝2÷+1＝2×+1＝；（2）＝﹣+﹣1＝﹣1；（3）3（x﹣2）2＝27，（x﹣2）2＝9，x﹣2＝±3，x﹣2＝3或x﹣2＝﹣3，x＝5或x＝﹣1；（4）2（x﹣1）3+16＝0，2（x﹣1）3＝﹣16，（x﹣1）3＝﹣8，x﹣1＝﹣2，x＝﹣1．21．解：由题意得，a+b＝0，cd＝1，|x|＝，y2＝9，则x2＝6，y＝±3，当y＝3时，原式＝6+0﹣1×3＝6﹣3＝3，当y＝﹣3时，原式＝6+0﹣1×（﹣3）＝6+3＝9，∴式子的值为3或9．22．解：（1）∵2a+3的立方根是3，∴2a+3＝27，解得a＝12，∵a+b﹣1的算术平方根是4，∴a+b﹣1＝16，解得b＝5，∵3＜＜4，∴的整数部分是3，∴c＝3，综上所述：a＝12，b＝5，c＝3；（2）∵a＝12，b＝5，c＝3．∴a﹣4b+3c＝12﹣20+9＝1，∵1的平方根是±1∴a﹣4b+3c的平方根是±1．23．解：∵a的立方根是3，b的算术平方根是4，∴a＝27，b＝16，∵个正数c的两个平方根分别是d+1和2d﹣7，∴d+1+2d﹣7＝0，解得d＝2，∴c＝（2+1）2＝9，把a＝27，b＝16，c＝9，代入a+b﹣2c＝27+16﹣2×9＝25，∴a+b﹣2c的平方根是±5．24．解：（1）∵，∴的整数部分是3，小数部分是﹣3，故答案为：3，﹣3；（2）∵2＜＜3，a＝﹣2，3＜＜4，∴b＝3，a+b﹣＝﹣2+3﹣＝1．。

人教版八年级上册物理第六章质量和密度单元测试题含答案

八年级上册物理《第六章质量和密度》同步训练一、填空题1．小东买了一瓶矿泉水，喝去了一半后，剩余的矿泉水的密度________（选填“变大”、“变小“或“不变”）。

水的密度是1.0×103kg/m3，表示的物理意义是________。

2．某合金块的体积是20cm3，用天平测量合金块的质量时，砝码质量和游码的如图所示，则该合金块的质量是________g，密度是________kg/m3．3．某物理课外兴趣小组的同学利用天平和一个小塑料杯测量酸奶的密度。

实验过程如下：用调节好的天平测出空塑料杯的质量为5g，将塑料杯中装满水，测出塑料杯和水的总质量为77g；再将塑料杯中的水倒净擦干后装满酸奶，测出塑料杯和酸奶的总质量为95g，则塑料杯中酸奶的质量为_____g，酸奶的密度为_____g/cm34．小明用天平测量苹果质量，在调节天平平衡的过程中，发现指针如图甲所示，他应将平衡螺母向_____（填“左”或“右”）移动，直到指针指在分度盘中央，然后将苹果放到天平的左盘，向右盘加减砝码并移动游码，使天平再次平衡时，砝码质量和游码对应的刻度值如图乙所示，则苹果质量为_____g。

5．有一辆汽车，油箱的容积为250L，每千米消耗汽油0.4kg。

如果一箱油加满后在相距15km 的甲、乙两地往返运输，汽车开始从甲地出发，往返______次后需在甲地重新加油。

(汽油密度是0.71×103kg/m3)6．现在树脂镜片广泛取代了玻璃镜片，已知某种树脂镜片的密度为1.3g/cm3，玻璃的密度为2.5×103kg/m3，每一只眼镜片的体积约为4×10－6m3，则用树脂镜片代替玻璃镜片后，一副眼镜质量约可以减少__________g。

7．某小组测量酱油的密度，在烧杯中倒入适量的酱油，测出烧杯和酱油的总质量是824g,将烧杯中一部分酱油倒入量筒中，如甲图所示，测量烧杯和剩余酱油的质量时，所加砝码和游码位置如乙图所示，那么量筒中酱油的质量为_________g,由此可计算出酱油的密度为________kg/m38．用天平正确测量盛水烧杯质量的场景如图所示，已知干燥的空烧杯质量为33.4g，则烧杯中水的质量为________g，大约含有_____________个水分子（不考虑分子间空隙，水分子的体积约为10－29m3）。

八年级物理上册《第六章质量和密度》单元检测卷及答案-人教版

八年级物理上册《第六章质量和密度》单元检测卷及答案-人教版学校:___________班级：___________姓名：___________考号：___________一、单选题1．甲、乙两个物体质量之比3:2，体积之比1:3，那么它们的密度之比为（）A．9:2 B．2:9 C．1:2 D．2:12．运动会发奖用的金、银、铜制成的体积、图案及形状完全相同的奖牌，其中奖牌质量最大的是（ρ金＞ρ银＞ρ铜）（）A．金牌B．银牌C．铜牌D．无法确定3．甲物质的密度为2.5t/m3，乙物质的密度为2.5kg/dm3，丙物质的密度为250kg/m3，丁物质的密度为2.5g/cm3，其中密度最小的物质是（）A．甲B．乙C．丙D．丁4．一钢瓶中贮有质量m，密度为ρ的氧气，当用去质量为m/4的氧气后，钢瓶内所剩氧气的密度为（）A．ρB．3ρ/4 C．ρ/4 D．4ρ5．如图所示是甲和乙两种物质的质量和体积关系图象，下列说法正确的是（）A．乙物质的密度比水大B．体积为50cm3的乙物质的质量为35gC．质量为25g的甲物质的体积为20cm3D．当甲和乙两物质的质量相同时，甲物质的体积较大6．我国研制的“全碳气凝胶”是目前世界上密度最小的固体材料，其密度仅为0.16kg/m3，则（）A．该材料体积越大，密度越大B．1m3的该材料质量为0.16kgC．该材料制的物品带到太空，质量减小D．该材料适合做打桩用的重锤7．密度公式ρ=m因能被写成如图所示的样式而被称为“物理最美公式”。

关于该公式的说法正确的是（）VA．由不同种类的物质组成的物体的质量和体积的比值一定不同B．同种物质的密度和由该物质组成的物体的体积成反比C．同种物质的密度和由该物质组成的物体的质量成正比是密度的定义式，实质上是密度与物体质量体积无关D．ρ=mV8．下表给出了常温常压下一些物质的密度，阅读后请判断下面一些结论，其中正确的是（）一些物质的密度（kg/m3）水 1.0×103水银13.6×103冰0.9×103干松木0.5×103煤油0.8×103铜8.9×103酒精0.8×103铅11.3×103A．1kg水凝固成冰后体积不变B．酒精用掉一半后密度将变为0.4×103kg/m3C．一个最多能装1kg的酒精的瓶子，它一定不能装1kg水D．一个体积为2cm3纯铜球的质量是16g，此铜球一定不是实心二、多选题9．体积和质量都相等的铁球、铜球和铅球，已知ρ铅＞ρ铜＞ρ铁，则下列说法中正确的是（）A．如果铁球是实心的，则铜球和铅球一定是空心的B．如果铅球是实心的，则铜球和铁球一定是空心的C．铅球、铜球和铁球可能都是空心的D．铅球、铜球和铁球不可能都是实心的10．为测量某种液体的密度，小明利用天平和量杯测量了液体和量杯的总质量m及液体的体积V，得到了几组数据并绘出了m -V图像，如图所示，下列说法正确的是（）A．量杯质量为20g B．该液体密度为1.25g/cm³C．该液体密度为1g/cm³D．40cm³的该液体质量为40g三、填空题11．水在4℃时候密度最，低于4℃或者高于4℃时密度变．12．在国际单位制中，长度的主单位是，质量的主单位是，时间的主单位是。

第六章实数单元测试及答案

第六章实数单元测试及答案一、选择题1．一列数1a ， 2a ， 3a ，…… n a ，其中1a =﹣1， 2a =111a -， 3a =211a -，……， n a =111n a --，则1a ×2a ×3a ×…×2017a =（）A ．1B ．-1C ．2017D ．-20172．圆的面积增加为原来的m 倍，则它的半径是原来的（）A ．m 倍B ．2m 倍 C倍 D ．2m 倍3．下列命题中，真命题是（）A ．实数包括正有理数、0和无理数B ．有理数就是有限小数C ．无限小数就是无理数D ．无论是无理数还是有理数都是实数4．下列说法中正确的个数有（）①0是绝对值最小的有理数；②无限小数是无理数；③数轴上原点两侧的数互为相反数；④相反数等于本身的数是0；⑤绝对值等于本身的数是正数；A ．2个B ．3个C ．4个D ．5个5．若a ，b均为正整数，且a >b <+a b 的最小值是（） A ．3 B ．4 C ．5 D ．66．有下列四种说法：①数轴上有无数多个表示无理数的点；②带根号的数不一定是无理数；③平方根等于它本身的数为0和1；④没有最大的正整数，但有最小的正整数；其中正确的个数是( )A ．1B ．2C ．3D ．47．已知|x |＝2，y 2＝9，且xy ＜0，则x +y 的值为（）A ．1或﹣1B ．-5或5C ．11或7D ．-11或﹣7830b -=）A ．0B ．±2C ．2D ．49．下列各数中3.14，0.1010010001…，﹣17，2π有理数的个数有（）A ．1个B ．2个C ．3个D ．4个10．已知m 是整数，当|m ﹣40|取最小值时，m 的值为（） A ．5 B ．6 C ．7 D ．8二、填空题11．若x +1是125的立方根，则x 的平方根是_________．12．若()2320m n ++-=，则m n 的值为 ____.13．估计51-与0.5的大小关系是：51-_____0.5．（填“＞”、“=”、“＜”） 14．观察下列各式：(1)123415⨯⨯⨯+=；(2)2345111⨯⨯⨯+=；(3)3456119⨯⨯⨯+=；根据上述规律，若121314151a ⨯⨯⨯+=，则a =_____．15．比较大小：512-__________0.5．（填“>”“<”或“=”） 16．已知31.35 1.105≈，3135 5.130≈，则30.000135-≈________．17．已知a 、b 为两个连续的整数，且a ＜19＜b ，则a +b ＝_____．18．如图，直径为1个单位长度的半圆，从原点沿数轴向右滚动一周，圆上的一点由原点O 到达点'O ，则点'O 对应的数是_______．19．若一个正数的平方根是21a +和2a +，则这个正数是____________．20．若x ，y 为实数，且|2|30x y ++-=，则(x+y) 2012的值为____________．三、解答题21．先阅读然后解答提出的问题：设a 、b 是有理数，且满足2322+=-a b b a 的值．解：由题意得(3)(20-++=a b ，因为a 、b 都是有理数，所以a ﹣3，b+2也是有理数，2是无理数，所以a-3=0，b+2=0，所以a=3，b=﹣2，所以3(2)8=-=-a b ．问题：设x 、y 都是有理数，且满足225y 1035x y -+=+x+y 的值．22．阅读下面文字：对于5231591736342⎛⎫⎛⎫⎛⎫-+-++- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭可以如下计算：原式()()()5231591736342⎡⎤⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-+-+++-+- ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦⎣⎦ ()()()5231591736342⎡⎤⎛⎫⎛⎫⎛⎫=-+-++-+-+-++-⎡⎤ ⎪ ⎪ ⎪⎢⎥⎣⎦⎝⎭⎝⎭⎝⎭⎣⎦ 1014⎛⎫=+- ⎪⎝⎭ 114=- 上面这种方法叫拆项法，你看懂了吗？仿照上面的方法，计算：（1）115112744362⎛⎫⎛⎫-+-++- ⎪ ⎪⎝⎭⎝⎭ （2）235120192018201720163462⎛⎫⎛⎫-++-+ ⎪ ⎪⎝⎭⎝⎭ 23．阅读理解：计算1111234⎛⎫+++ ⎪⎝⎭×11112345⎛⎫+++ ⎪⎝⎭﹣111112345⎛⎫++++ ⎪⎝⎭×111234⎛⎫++ ⎪⎝⎭时，若把11112345⎛⎫+++ ⎪⎝⎭与111234⎛⎫++ ⎪⎝⎭分别各看着一个整体，再利用分配律进行运算，可以大大简化难度．过程如下：解：设111234⎛⎫++ ⎪⎝⎭为A ，11112345⎛⎫+++ ⎪⎝⎭为B ，则原式=B （1+A ）﹣A （1+B ）=B+AB ﹣A ﹣AB=B ﹣A=15．请用上面方法计算： ①11111123456⎛⎫+++++ ⎪⎝⎭×111111234567⎛⎫+++++ ⎪⎝⎭-1111111234567⎛⎫++++++ ⎪⎝⎭×1111123456⎛⎫++++ ⎪⎝⎭②111123n ⎛⎫++++ ⎪⎝⎭111231n ⎛⎫+++ ⎪+⎝⎭-1111231n ⎛⎫++++ ⎪+⎝⎭11123n ⎛⎫+++ ⎪⎝⎭． 24．你能找出规律吗？（1＝，＝；＝，＝．“＜”）．（2）请按找到的规律计算：；（3）已知：a，b＝（可以用含a ，b 的式子表示）．25．阅读理解．23．∴11＜21的整数部分为1，12．解决问题：已知a﹣3的整数部分，b﹣3的小数部分．（1）求a ，b 的值；（2）求（﹣a ）3+（b +4）22＝17．26．阅读下列解题过程：为了求23501222...2+++++的值，可设23501222...2S =+++++，则2345122222...2S =+++++，所以得51221S S -=-，所以5123505121:1222...221S =-+++++=-，即；仿照以上方法计算：（1）2320191222...2+++++= .（2）计算：2320191333...3+++++（3）计算：101102103200555...5++++【参考答案】***试卷处理标记，请不要删除一、选择题1．B解析：B【解析】因为1a =﹣1,所以2a =11111112a ==---（）,3 a =21121112a ==--,4 a =3111112a ==---,通过观察可得:1 a ,2a ,3a ,4 a ……的值按照﹣1,1 2, 2三个数值为一周期循环,将2017除以3可得372余1,所以2017a 的值是第273个周期中第一个数值﹣1,因为每个周期三个数值的乘积为: 11212-⨯⨯=-,所以1a ×2a ×3a ×…×2017a =()()372111,-⨯-=-故选B. 2．C解析：C【分析】设面积增加后的半径为R ，增加前的半径为r ，根据题意列出关系式计算即可．【详解】设面积增加后的半径为R ，增加前的半径为r ，根据题意得：πR 2=mπr 2，∴，故选：C ．【点睛】此题主要考查了实数的运算，要注意，圆的面积和半径之间是平方关系而非正比例关系．3．D解析：D【分析】直接利用实数以及有理数、无理数的定义分析得出答案．【详解】A 、实数包括有理数和无理数，故此命题是假命题；B 、有理数就是有限小数或无限循环小数，故此命题是假命题；C 、无限不循环小数就是无理数，故此命题是假命题；D 、无论是无理数还是有理数都是实数，是真命题．故选：D ．【点睛】此题主要考查了命题与定理，正确掌握相关定义是解题关键．4．A解析：A【分析】分别利用绝对值的定义、无理数、有理数的定义、相反数的定义分别进行判断即可得出答案．【详解】①0是绝对值最小的有理数；根据绝对值的性质得出，故此选项正确；②无限小数是无理数；根据无限循环小数是有理数判断，故此选项错误；③数轴上原点两侧的数互为相反数；根据到原点距离相等的点是互为相反数，故此选项错误；④相反数等于本身的数是0；根据相反数的定义判断，故此选项正确；⑤绝对值等于本身的数是正数；还有0的绝对值也等于本身，故此选项错误.∴正确的个数有2个故选：A.【点睛】本题主要考查了绝对值的定义、无理数、有理数的定义、相反数的定义等知识，熟练掌握其性质是解题关键.5．B解析：B【分析】的范围，然后确定a、b的最小值，即可计算a+b的最小值．【详解】23．∵a a为正整数，∴a的最小值为3．12．∵b b为正整数，∴b的最小值为1，∴a+b的最小值为3+1=4．故选B．【点睛】本题考查了估算无理数的大小，解题的关键是：确定a、b的最小值．6．C解析：C【分析】根据实数的定义，实数与数轴上的点一一对应，平方根的定义可得答案．【详解】①数轴上有无数多个表示无理数的点是正确的；；2③平方根等于它本身的数只有0，故本小题是错误的；④没有最大的正整数，但有最小的正整数，是正确的．综上，正确的个数有3个，故选：C．【点睛】本题主要考查了实数的有关概念，正确把握相关定义是解题关键．7．A解析：A【分析】根据题意，利用平方根定义，绝对值的代数意义，以及有理数的乘法法则判断确定出x与y 的值即可．【详解】解：∵|x |＝2，y 2＝9，且xy ＜0，∴x=2或-2，y=3或-3，当x=2，y=-3时，x+y=2-3=-1；当x=-2，y=3时，原式=-2+3=1，故选：A ．【点睛】此题考查了有理数的乘方，绝对值，以及有理数的加法，熟练掌握运算法则是解本题的关键．8．C解析：C【分析】由算术平方根和绝对值的非负性，求出a 、b 的值，然后进行计算即可．【详解】解：根据题意，得a ﹣1＝0，b ﹣3＝0，解得：a ＝1，b ＝3，∴a +b ＝1+3＝4，∴2．故选：C ．【点睛】本题考查了算术平方根和绝对值的非负性，解题的关键是正确求出a 、b 的值．9．C解析：C【分析】直接利用有理数的定义进而判断得出答案．【详解】解：3.14，0.1010010001…，-17 ，2π 3.14，-17＝-2共3个.故选C ．【点睛】此题主要考查了有理数，正确把握有理数的定义是解题关键． 10．B解析：B【分析】根据绝对值是非负数，所以不考虑m 为整数,则m 取最小值是0，又0的绝对值为0，令0m=，得出m=m的整数可得：m ＝6．【详解】解：因为m取最小值，m∴=，∴=，m解得：m=240m=，∴<<，且m更接近6，67m∴当6m=时，m有最小值.故选：B．【点睛】本题考查绝对值的非负性，以及估算二次根式的大小，理解并熟练掌握绝对值的非负性是本题解题关键；在估算二次根式大小的时候，先算出二次根式的平方，再看这个平方在哪两个平方数之间，就相应的得出二次根式在哪两个整数之间，即可估算出二次根式的大小.二、填空题11．±2【分析】先根据立方根得出x的值，然后求平方根．【详解】∵x+1是125的立方根∴x+1=，解得：x=4∴x的平方根是±2故答案为：±2【点睛】本题考查立方根和平方根，注意一个正解析：±2【分析】先根据立方根得出x的值，然后求平方根．【详解】∵x+1是125的立方根∴x=4∴x的平方根是±2故答案为：±2本题考查立方根和平方根，注意一个正数的平方根有2个，算术平方根只有1个．12．【分析】根据非负数的性质列式求出m 、n 的值，然后代入代数式进行计算即可得解．【详解】由题意得，m+3=0，n-2=0，解得m=-3，n=2，所以，mn=（-3）2=9．故答案为9．【解析：【分析】根据非负数的性质列式求出m 、n 的值，然后代入代数式进行计算即可得解．【详解】由题意得，m+3=0，n-2=0，解得m=-3，n=2，所以，m n =（-3）2=9．故答案为9．【点睛】此题考查绝对值和算术平方根非负数的性质，解题关键在于掌握几个非负数的和为0时，这几个非负数都为0．13．>【解析】∵ . , ∴ , ∴ ,故答案为>.解析：>【解析】∵10.52-=-=20-> , ∴0> , ∴0.5> ,故答案为>.14．181【分析】观察各式得出其中的规律，再代入求解即可．【详解】由题意得将代入原式中故答案为：181．本题考查了实数运算类的规律题，掌握各式中的规律是解题的关键．解析：181【分析】观察各式得出其中的规律，再代入12n=求解即可．【详解】由题意得()31n n=⨯++将12n=代入原式中12151181a==⨯+=故答案为：181．【点睛】本题考查了实数运算类的规律题，掌握各式中的规律是解题的关键．15．＞【分析】首先把两个数采用作差法相减，根据差的正负情况即可比较两个实数的大小．【详解】∵，∵-2＞0，∴＞0．故＞0.5．故答案为：＞.【点睛】此题考查实数大小比较，解题关键在于解析：＞【分析】首先把两个数采用作差法相减，根据差的正负情况即可比较两个实数的大小．【详解】12＞0，∴22＞0．＞0.5．故答案为：＞.【点睛】此题考查实数大小比较，解题关键在于掌握比较两个实数的大小，可以采用作差法、取近似值法等．16．-0.0513【分析】根据立方根的意义，中，m的小数点每移动3位，n的小数点相应地移动1位．【详解】因为所以-0.0513故答案为：-0.0513【点睛】考核知识点：立方根．理解立方解析：-0.0513【分析】=中，m的小数点每移动3位，n的小数点相应地移动1位．n【详解】≈5.130≈-0.0513故答案为：-0.0513【点睛】考核知识点：立方根．理解立方根的定义是关键．17．9【分析】首先根据的值确定a、b的值，然后可得a+b的值．【详解】∵＜，∴4＜＜5，∵a＜＜b，∴a＝4，b＝5，∴a+b＝9，故答案为：9．【点睛】本题主要考查了估算无理数的解析：9【分析】a 、b 的值，然后可得a +b 的值．【详解】<∴45，∵a b ，∴a ＝4，b ＝5，∴a +b ＝9，故答案为：9．【点睛】本题主要考查了估算无理数的大小，关键是正确确定a 、b 的值． 18．【分析】点对应的数为该半圆的周长．【详解】解：半圆周长为直径半圆弧周长即故答案为：．【点睛】本题考查数轴上的点与实数的关系．明确的长即为半圆周长是解答的关键．解析：12π+【分析】点O '对应的数为该半圆的周长．【详解】解：半圆周长为直径+半圆弧周长即12π+ 故答案为：12π+．【点睛】本题考查数轴上的点与实数的关系．明确OO '的长即为半圆周长是解答的关键． 19．1【分析】一个正数有两个平方根，它们互为相反数，由此即可列式2a+1+a+2=0，求出a 再代回一个根再平方即可得到该正数.【详解】由题意得2a+1+a+2=0，解得a=-1,∴a+2=1解析：1【分析】一个正数有两个平方根，它们互为相反数，由此即可列式2a+1+a+2=0，求出a 再代回一个根再平方即可得到该正数.【详解】由题意得2a+1+a+2=0，解得a=-1,∴a+2=1,∴这个正数是22(2)11a +==，故答案为：1.【点睛】此题考查平方根的性质：一个正数有两个平方根，它们互为相反数，0的平方根是0，负数没有平方根.20．1【分析】先根据绝对值的非负性、算术平方根的非负性求出x 、y 的值，再代入计算有理数的乘方即可．【详解】由绝对值的非负性、算术平方根的非负性得：解得则故答案为：1．【点睛】本题考查了解析：1【分析】先根据绝对值的非负性、算术平方根的非负性求出x 、y 的值，再代入计算有理数的乘方即可．【详解】由绝对值的非负性、算术平方根的非负性得：2030x y +=⎧⎨-=⎩解得23x y =-⎧⎨=⎩则201220122012()(23)11x y +=-+==故答案为：1．【点睛】本题考查了绝对值的非负性、算术平方根的非负性、有理数的乘方运算，利用绝对值的非负性、算术平方根的非负性求解是常考知识点，需重点掌握．三、解答题21．7或-1.【分析】根据题目中给出的方法，对所求式子进行变形，求出x 、y 的值，进而可求x+y 的值.【详解】解：∵2210x y -=+∴()22100x y --+-=，∴2210x y --=0-=0∴x=±4，y=3当x=4时，x+y=4+3=7当x=-4时，x+y=-4+3=-1∴x+y 的值是7或-1.【点睛】本题考查实数的运算，解题的关键是弄清题中给出的解答方法，然后运用类比的思想进行解答.22．（1）14-（2）124- 【分析】（1）根据例子将每项的整数部分相加，分数部分相加即可解答；（2）根据例子将每项的整数部分相加，分数部分相加即可解答.【详解】（1）115112744362⎛⎫⎛⎫-+-++- ⎪ ⎪⎝⎭⎝⎭()115112744362⎛⎫=--+-+--+- ⎪⎝⎭ 104⎛⎫=+- ⎪⎝⎭ 14=- （2）原式()235120192018201720163462⎛⎫=-+-++-+-+ ⎪⎝⎭ 124⎛⎫=-+- ⎪⎝⎭124=- 【点睛】此题考察新计算方法，正确理解题意是解题的关键，根据例子即可仿照计算.23．（1）17；（2）11n +. 【解析】【分析】①根据发现的规律得出结果即可；②根据发现的规律将所求式子变形，约分即可得到结果．【详解】（1）设1111123456⎛⎫++++ ⎪⎝⎭为A ，111111234567⎛⎫+++++ ⎪⎝⎭为B ，原式=（1+A ）B ﹣（1+B ）A=B+AB ﹣A ﹣AB=B ﹣A=17；（2）设11123n ⎛⎫+++ ⎪⎝⎭为A ，111231n ⎛⎫+++ ⎪+⎝⎭为B ，原式=（1+A ）B ﹣（1+B ）A=B+AB ﹣A ﹣AB=B ﹣A=11n +．【点睛】考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．24．（1）6，6，20，20，＝，＝；（2）①10，②4；（3）2a b【分析】（1)0,0a b =≥≥，据此判断即可．（2=10===，4===，据此解答即可．（3）根据a =b =2a b ==，据此解答即可．【详解】解：（1236=⨯=6==；4520=⨯=20==．==故答案为：6，6，20，20，＝，＝；（210===；4===；（3）∵a =b =2a b ==，故答案为：2a b ．【点睛】本题考查算数平方根，掌握求一个数算术平方根的方法为解题关键．25．（1）a ＝1，b ﹣4；（2）±4．【分析】（1）根据被开饭数越大算术平方根越大，可得a ，b 的值，（2）根据开平方运算，可得平方根．【详解】解：（1<，∴4<＜5，∴1﹣3＜2，∴a ＝1，b 4；（2）（﹣a ）3+（b+4）2＝（﹣1）3+﹣4+4）2＝﹣1+17＝16，∴（﹣a ）3+（b+4）2的平方根是：±4．【点睛】本题考查了估算无理数的大小，利用被开方数越大算术平方根越大得出4＜5是解题关键．26．（1）202021-；（2）2020312-；（3）201101554-. 【分析】仿照阅读材料中的方法求出所求即可．【详解】解：（1）根据2350511222...221+++++=-得：2320191222...2+++++=202021-（2）设2320191333...3S =+++++，则234202033333...3S =+++++，∴2020331S S -=-， ∴2020312S -= 即：2020232019311333 (32)-+++++= （3）设232001555...5S =+++++，则23420155555...5S =+++++，∴201551S S -=-，∴201514S -= 即：20123200511555 (5)4-+++++= 同理可求⸫10123100511555 (5)4-+++++= ∵1011021032002320023100555...51555...5)(1555...5)++++=+++++-+++++（ 201101201101101102103200515155555 (5444)---∴++++=-= 【点睛】此题考查了规律型：数字的变化类，弄清题中的规律是解本题的关键．。

第六章单元测试

第六章《质量和密度》单元测试题一、选择题（每空？分，共？分）1、一瓶矿泉水放入冰箱结冰后，下列物理量不发生改变的是（）A．质量 B．温度 C．体积 D．密度2、一块金属的密度为ρ，质量为m，把它分割成三等份，那么每一块的密度和质量分别是（）A. ρ/3, mB. ρ/3, m/3C. ρ, mD. ρ, m/33、1 m3的冰和1 m3的水相比较（）A.冰和水的体积相同，水比冰的质量大B.冰的体积跟它全部溶化成水后的体积相同C.水全部结成冰后，与1 m3冰的质量相同D.冰的密度比水小，冰的质量比水大4、一把汤匙的质量是18.4 g，体积是8 cm3，则根据如下密度表，可知做成汤匙的材料可能是( )5、一个实心金属球放在盛满水的杯子里，从杯中溢出10g的水，若把这个金属球放入满煤油（ρ水=1.0×103kg/m3，ρ煤油=0.8×103kg/m3）的杯子里，溢出煤油的质量为A．12.5g B．10g C．8g D．6.4g6、把一蜡块放入盛满酒精的容器中，溢出酒精的质量是4克；若把该蜡块放入盛满水的容器中，已知ρ蜡＝0.9×103kg／m3，ρ酒精＝0.8×103kg／m3，则溢出水的的质量是（容器足够大）（）A．4g B．4.5g C．5g D．3.6g7、有一不吸水木球，其质量为10g，体积为20cm3，先把它轻轻放人盛满水的溢水杯中.当木球球静止时，溢出水的质量为10g;把它取出擦干，再轻轻放人盛满煤油的溢水杯中，当木球静止时，溢出煤油的质量是(煤油的密度是0.8×103 g／cm3) ( ) A. 5g B. 8g C. 10g D. 16g8、分别用铅、铁、铝制成三个体积、质量都相等的空心球（密度大小：铅>铁>铝），比较它们中间空心部分的体积，则（）A、铅球最大B、铁球最大C、铝球最大D、三球一样大9、一枝蜡烛燃烧一半后，剩下部分的（）A.质量、密度都减半B.质量减半，密度不变C.质量不变，密度减半D.质量和密度都不变10、关于物体的质量和物质的密度，下列说法中正确的是（）A．一块冰全部溶化成水后，质量变小，密度不变B．把铜块碾成铜片，质量和密度均不变C．宇航员在太空处于失重状态，故质量和密度均为零D．把铁球加热，质量变大，密度变小11、关于物体的质量和物质的密度，下列说法中正确的是（）A．一块冰全部溶化成水后，质量变小，密度不变B．把铜块碾成铜片，质量和密度均不变C．宇航员在太空处于失重状态，故质量和密度均为零D．把铁球加热，质量变大，密度变小12、一个小药瓶质量为5g，装满药液时总质量为21g，装满水的总质量为25g，则药液的密度为 ( )A. 1.2×lo3kg／m3 B .0. 92×103kg／m3 C. 0.84×l03kg／m3 D．0.8×103kg／m313、—瓶子装满水时总质量是400g，装满酒精时总质量是350g。

八年级物理下册第六章《常见光学仪器》单元测试题

八年级物理下册第六章《常见的光学仪器》单元测试姓名：班级：分数：（满分：100分时间：90分钟）一、选择题（36分）（每小题只有一个选项最符合题意）1.如图方框中透镜放置正确的有（）①②图1③④A．①②③B．②③④C．①③D．①②③④2．如图2所示，让一束平行于主光轴的光线经过一透镜，在光屏上得到一个最小、最亮的光斑。

下列说法不正确的是（）图2A.凸透镜的特点是中间厚、边缘薄B.凸透镜是虚焦点C.凸透镜对光有会聚作用D.该凸透镜的焦距10cm3．如图所示，图中成实像的是（）①放大镜看字②照相机照相③用幻灯机放幻灯片④平面镜中的像A．①②B．②③C．①③D．③④4．如图，同学们正在用“自拍神器”摄影留念。

与用手直接拿手机自拍相比，利用自拍杆可以（）A．增大物距，减小像的大小，从而增大取景范围B．减小物距，减小像的大小，从而减小取景范围C．增大物距，增大像的大小，从而减小取景范围D．减小物距，增大像的大小，从而增大取景范围5．小乐用放大镜看指纹时，觉得指纹的像太小，为使指纹的像大一些，正确的做法是（）A．眼睛和手指不动，让放大镜离手指稍近些B．眼睛和手指不动，让放大镜离手指稍远些C．放大镜和手指不动，让眼睛离放大镜稍近些D．放大镜和手指不动，让眼睛离放大镜稍远些6．在探究凸透镜成像规律实验中，当烛焰位于距离凸透镜一倍焦距以内时，人眼观察到烛焰成像的情形是图中的（）7．如图所示，a、b、c、d在凸透镜主光轴上，F为焦点。

若保持凸透镜和光屏的位置不变，则物体放在哪个位置时，可能在光屏上观察到物体的像（）A．a点B．b点C．c点D．d点8．物体放在凸透镜前12cm时，在透镜另一侧的光屏上成一个倒立放大的像；则当物体距该透镜8cm时，所成的像可能是（）A倒立缩小的像B倒立等大的像C倒立放大的像D正立等大的虚像9．在“探究凸透镜成像的规律”实验中，下列说法正确的是（）A．将蜡烛移至a处时，移动光屏，可看见放大、正立的实像B．将蜡烛移至b处时，移动光屏，可看见缩小、倒立的实像C．将蜡烛移至c处时，移动光屏，可看见放大、倒立的实像D．将蜡烛移至d处时，移动光屏，可看见放大、正立的虚像10.小红同学学习了“小孔成像”、“平面镜成像”和“凸透镜成像”的知识后，总结出关于“实像”和“虚像”的一些特点，错误的是（）A．虚像不可以用光屏承接B．实像可以是放大的，也可以是缩小的C．既有等大实像，也有等大虚像D．观察实像时有光进入人眼，观察虚像时没有光进入人眼11．关于显微镜和天文望远镜所成的像和所观察到的像，下列说法中正确的是（）A.用显微镜观察到的是虚像，用望远镜看到的是实像B.用显微镜观察到的是实像，用望远镜看到的是虚像C.目镜成的是实像，物镜成的是虚像D.目镜成的是虚像，物镜成的是实像12．如图4所示，关于近视眼和远视眼，下列说法正确的是（）A．甲为近视眼，应佩戴凸透镜矫正B．乙为近视眼，应佩戴凹透镜矫正C．甲为远视眼，应佩戴凹透镜矫正D．乙为远视眼，应佩戴凸透镜矫正图4图513．在探究凸透镜成像规律的实验中，将蜡烛放在凸透镜前适当位置，调节光屏位置得到清晰的像。

第六章圆周运动单元练习 -2023年高一下学期物理人教版(2019)必修第二册

第六章圆周运动同步练习题一、选择题。

1、如图所示，一偏心轮绕垂直纸面的轴O匀速转动，a和b是轮边缘上的两个点，则偏心轮转动过程中，a、b两点()A．角速度大小相同B．线速度大小相同C．周期大小不同D．转速大小不同2、关于向心力的说法正确的是()A．物体由于做圆周运动还受到一个向心力B．向心力可以是任何性质的力C．做匀速圆周运动的物体其向心力是恒力D．做圆周运动的物体所受各力的合力一定指向圆心3、如图所示，M能在水平光滑杆上自由滑动，滑杆连架装在转盘上。

M用绳跨过在圆心处的光滑滑轮与另一质量为m的物体相连。

当转盘以角速度ω转动时，M离轴距离为r，且恰能保持稳定转动。

当转盘转速增至原来的2倍，调整r使之达到新的稳定转动状态，则滑块M()A.所需要的向心力变为原来的4倍B.线速度变为原来的1 2C.半径r变为原来的12 D.M的角速度变为原来的124、（多选）一小球被细绳拴着，在水平面内做半径为R的匀速圆周运动，向心加速度为a，那么()A．角速度ω＝aR B．时间t内通过的路程s＝t aRC．周期T＝Ra D．时间t内可能发生的最大位移为2R5、如图所示，质量为m的小球固定在杆的一端，在竖直面内绕杆的另一端O做圆周运动。

当小球运动到最高点时，瞬时速度为v ＝12Lg ，L 是球心到O 点的距离，则球对杆的作用力是( )A.12mg 的拉力B.12mg 的压力C.零D.32mg 的压力6、(双选)下列说法正确的是( )A.匀速圆周运动是线速度不变的运动B.匀速圆周运动是角速度不变的运动C.匀速圆周运动是周期不变的运动D.做匀速圆周运动的物体经过相等时间的速度变化量相等7、（双选）变速自行车靠变换齿轮组合来改变行驶速度，如图是某一变速车齿轮转动结构示意图，图中A 轮有48齿，B 轮有42齿，C 轮有18齿，D 轮有12齿，则( )A ．该车可变换两种不同挡位B ．该车可变换四种不同挡位C ．当A 轮与D 轮组合时，两轮的角速度之比ωA ∶ωD ＝1∶4D ．当A 轮与D 轮组合时，两轮角速度之比ωA ∶ωD ＝4∶18、（双选）在光滑的水平面上，用长为l 的细线拴一质量为m 的小球，以角速度ω做匀速圆周运动，下列说法中正确的是( )A ．l 、ω不变，m 越大线越易被拉断B ．m 、ω不变，l 越小线越易被拉断C ．m 、l 不变，ω越大线越易被拉断D ．m 不变，l 减半且角速度加倍时，线的拉力不变9、（双选）如图所示：是甲、乙两球做圆周运动的向心加速度随半径变化的关系图像，下列说法中正确的是()A．甲球线速度大小保持不变B．乙球线速度大小保持不变C．甲球角速度大小保持不变D．乙球角速度大小保持不变10、(多选)如图所示，电风扇在闪光灯下运转，闪光灯每秒闪30次，风扇转轴O 上装有3个扇叶，它们互成120°角，当风扇转动时，观察者感觉扇叶不动，则风扇转速可能是()A.600 r/minB.900 r/minC.1 200 r/minD.3 000 r/min11、（双选）一辆卡车在水平路面上行驶，已知该车轮胎半径为R，轮胎转动的角速度为ω，关于各点的线速度大小，下列说法正确的是()A．相对于地面，轮胎与地面的接触点的速度为ωRB．相对于地面，车轴的速度大小为ωRC．相对于地面，轮胎上缘的速度大小为ωRD．相对于地面，轮胎上缘的速度大小为2ωR*12、两个小球固定在一根长为L的杆的两端，且绕杆上的O点做匀速圆周运动，如图所示．当小球1的速度为v1，小球2的速度为v2时，则转轴O到小球2的距离为()A.v1v1＋v2L B.v2v1＋v2L C.v1＋v2v1L D.v1＋v2v2L13、如图所示，某物体沿14光滑圆弧轨道由最高点滑到最低点的过程中，物体的速率逐渐增大，则()A．物体的合力为零B．物体的合力大小不变，方向始终指向圆心OC．物体的合力就是向心力D．物体的合力方向始终与其运动方向不垂直(最低点除外) 14、关于向心加速度，下列说法正确的是()A．向心加速度是描述线速度大小变化快慢的物理量B．向心加速度只改变线速度的方向，不改变线速度的大小C．向心加速度的大小恒定，方向时刻改变D．向心加速度是平均加速度，大小可用a＝v－v0t来计算15、为了测定子弹的飞行速度，在一根水平放置的轴杆上固定两个薄圆盘A、B，盘A、B平行且相距l＝2 m，轴杆的转速为n＝3 600 r/min。

七年级数学下册《第六章实数》单元检测卷(附带答案)

七年级数学下册《第六章实数》单元检测卷(附带答案)一、选择题(每题3分,共30分)1.9的平方根是（） A.3 B.-3C.±3D.不存在 2.38=（）A.2B.-2C.±2D.不存在3.下列说法正确的是（） A.-0.064的立方根是0.4 B.-9的平方根是±3 C.16316D.0.01的立方根是0.0000014．若a 3＝－27，则a 的倒数是( )A ．3B ．－3C.13D ．－135．面积为8的正方形的边长在( )5. ，且，则的值为（）A ．B ．C ．1D ．1或6. 已知x ，y ，则y x 的立方根是( )AB ．－2C ．－8D ．±27．下列命题中正确的是（）①0.027的立方根是0.3 不可能是负数 ③如果a 是b 的立方根，那么ab≥0 ④一个数的平方根与其立方根相同，则这个数是1． A ．①③ B ．②④ C ．①④ D ．③④8.一个数的算术平方根等于这个数的立方根，那么这个数是（）A.1B.0或1C.0D. ±19.下列实数317 -π 3.14159 8 327 12中无理数有（）A.2个B.3个C.4个D.5个10.如图，数轴上A ，B 两点对应的实数分别是1和3，若AB=BC ，则点C 所对应的实数是（）A.231B.13+C.23D.231二、填空题(每题3分,共24分) 11．4是_____的算术平方根．2316,27a b ==-||a b a b -=-+a b 1-7-7-()2320x y -+=363a12．25的算术平方根是_______.13．若一个正数的两个不同的平方根分别是2a﹣1和﹣a+2，则这个正数是．14．若a＜0，化简＝．15．已知10+的整数部分是x，小数部分是y，求x﹣y的相反数．16．已知x，y都是实数，且y＝x－3＋3－x＋4，则y x＝________.17．点A在数轴上和表示1的点相距6个单位长度，则点A表示的数为________．18．若两个连续整数x，y满足x＜5＋1＜y，则x＋y的值是________．三、解答题(满分46分,19题6分，20、21、22、23、24题每题8分)19．(6分)计算：(1)|－2|＋3－8－(－1)2017(2)9－（－6）2－3－27.20．(8分)求下列各式中x的值．(1)(x－3)2－4＝21 (2)27(x＋1)3＋8＝0.21．(本题8分)已知与互为相反数，求的平方根．22．你能找出规律吗？(1)计算：9×16＝________，9×16＝________ 25×36＝________，25×36＝________．(2)请按找到的规律计算：5×125 ②123×935.(3)已知a＝2，b＝10，用含a，b的式子表示40.23.如图，用两个面积为28cm的小正方形纸片剪拼成一个大的正方形．（1）大正方形的边长是________cm（2）请你探究是否能将此大正方形纸片沿着边的方向裁出一个面积为214cm的长方形纸片，使它的长宽之比为2:1，若能，求出这个长方形纸片的长和宽，若不能，请说明理由．24.已知：31a+的立方根是2-，21b-的算术平方根3，c43（1）求,,a b c的值（2）求922a b c-+的平方根．参考答案一.填空题题号12345678910答案C B C D B C A B A A二.选择题11．【答案】16【解析】试题解析：∵42=16∴4是16的算术平方根12．【答案】513．【解答】解：∵一个正数的两个平方根分别是2a﹣1与﹣a+2∴2a﹣1﹣a+2＝0解得：a＝﹣1故2a﹣1＝﹣3则这个正数是：（﹣3）2＝9故答案为：914．【答案】1﹣a15．【答案】16．【答案】6417．【答案】1－6或1＋6点拨：数轴上到某个点距离为a(a＞0)个单位长度的点有两个．注意运用数形结合思想，利用数轴帮助分析．18．【答案】7点拨：∵2＜5＜3，∴3＜5＋1＜4.∵x＜5＋1＜y，且x，y为两个连续整数，∴x＝3，y＝4.∴x＋y＝3＋4＝7.三.解答题19．【答案】解：(1)原式＝2－2＋1＝1.(4分)(2)原式＝3－6＋3＝0.(8分)20．【答案】解：(1)移项得(x－3)2＝25，∴x－3＝5或x－3＝－5，∴x＝8或－2.(5分)(2)移项整理得(x＋1)3＝－827，∴x＋1＝－23，∴x＝－53.(10分)21．【答案】解：根据相反数的定义可知：解得：a=-8,b=364的平方根是：22．【答案】解：(1)12 12 30 30(2)①原式＝5×125＝625＝25②原式＝53×485＝16＝4(3)40＝2×2×10＝2×2×10＝a2b.23．【答案】（1）4 （2）不能，理由见解析．【解析】（1）根据已知正方形的面积求出大正方形的边长即可（2）先设未知数根据面积=14（cm2）列方程，求出长方形的边长，将长方形的长与正方形边长比较大小再判断即可．解：（1）两个正方形面积之和为：2×8=16（cm2）∴拼成的大正方形的面积=16（cm 2） ∴大正方形的边长是4cm 故答案为：4（2）设长方形纸片的长为2xcm ，宽为xcm 则2x •x =14 解得：7x =2x 7>4∴不存在长宽之比为2:1且面积为214cm 的长方形纸片． 24．【答案】（1）3,5,6a b c =-== （2）其平方根为4± 【解析】（1）根据立方根，算术平方根，无理数的估算即可求出,,a b c 的值（2）将（1）题求出的值代入922a b c -+，求出值之后再求出平方根．解：（1）由题得318,219a b +=--= 3,5a b ∴=-= 364349<6437∴<6c ∴=3,5,6a b c ∴=-==（2）当3,5,6a b c =-==时()99223561622a b c -+=⨯--+⨯=∴其平方根为164±±。

人教版数学七年级下册-第六章《实数》单元测试(含答案)

第六章《实数》单元测试姓名：班级：座号：一、单选题（共8题；共32分）1. 9的算术平方根是（）A. 81B. ±81C. 3D. ±32. -8的立方根是（）A. B. C.D.3.在，1.01001000100001，2 ，3.1415，- ，，0，，这些数中，无理数共有（）A. 2个B. 3个C. 4个D. 5个4.下列说法中错误的是( )A. 0的算术平方根是0B. 36的平方根为±6C.D. -4的算术平方根是-25.已知a2=25， =7，且|a+b|=a+b，则a﹣b的值为（）A. 2或12B. 2或﹣12C. ﹣2或12D. ﹣2或﹣126.，则a与b的关系是（）A. B. a与b相等 C. a与b互为相反数 D. 无法判定7.下列计算或说法：①±3都是27的立方根；②=a；③的立方根是2；④=±4，其中正确的个数是（）A. 1个B. 2个C. 3个 D. 4个8.下列六种说法正确的个数是（）①无限小数都是无理数；②正数、负数统称实数；③无理数的相反数还是无理数；④无理数与无理数的和一定还是无理数；⑤无理数与有理数的和一定是无理数；⑥无理数与有理数的积一定仍是无理数．A. 1B. 2C. 3 D . 4二、填空题（共24分）1.算术平方根等于本身的实数是________.2.﹣125的立方根是________．3.比较大小：﹣π________﹣3.14（选填“＞”、“=”、“＜”）．4.某正数的平方根是n+l和n﹣5，则这个数为________．5.已知一个正数的两个平方根是x﹣7和3x﹣1，则x的值是________．6.方程（x﹣1）3﹣8=0的根是 ________7.若=2﹣x，则x的取值范围是________；若3+ 的小数部分是m，3﹣的小数部分是n，则m+n=________．三、求下列各式中x的值（共10分）（1）（2x﹣1）2=9 （2）2x3﹣6=四、解答题（共10分）1.已知某数的平方根是a+3和2a﹣15，求1﹣7a的立方根。

第六章实数单元精练

人教版七年级下册实数单元精练一.选择题1．下列实数 210.3,,,,4247π中，无理数共有（） A ．1个 B ．2个 C ．3个 D ．4个2. 下面说法正确的是（）A. 4是2的平方根B. 2是4的算术平方根C. 0的算术平方根不存在D. -1的平方的算术平方根是-13. ()25- 的平方根是（）A. -5B. ±5C. 5D. 25 4.若一个数的算术平方根等于它本身，则这个数是 (??)A ．1B ．−1C ．0D ．0 或 15．下列各式中，正确的是（）A ．2(3)3-=-B ． 6.40.8-=-C ．164=±D ．382-=-6．已知|a －3|＋2b +＝0，则3ab -的值为( )A ．23B ．－23C ．32D ．－327.若 a 2=4，b 2=9，且 ab <0，则 a −b 的值为 (??)A ． −2B ．C ． 5D ． −58．一个正数b 的平方根为a +1和2a ﹣7，则9a +b 的立方根是（）A ．2B ．3C ．9D ．±39.一个正方体的水晶砖，体积为 100?cm 3，它的棱长大约在 (??)A ． 3?cm 与 4?cm 之间B ． 4?cm 与 5?cm 之间C ． 5?cm 与 6?cm 之间D ． 6?cm 与 7?cm 之间10．在一个正方形的内部按照如图方式放置大小不同的两个小正方形，其中较大的正方形面积为12，重叠部分的面积为3，空白部分的面积为306，则较小的正方形面积为（）A ．11B ．10C ．9D ．8 二.填空题 11.149 的算术平方根是______，即 √149=______．12.已知 a ，b 为两个连续的整数，且 a <√33<b ，则 a +b =______．13.已知a ，b 分别是13的整数部分和小数部分，则2a ﹣b 的值为______．14. 一个正方形的面积是6平方厘米，则这个正方形的边长等于_____________厘米．15.有一个数值转换器，流程如图．当输入x 的值为27时，输出y 的值是__________．16.如图，四边形ABCD CEFG 、均为正方形，其中正方形ABCD 面积为28cm ．图中阴影部分面积为25cm ，正方形CEFG 面积为_________．三.解答题17.请把下列各数填在相应的集合里：①0，②，③0.，④﹣|﹣2|，⑤﹣（﹣3），⑥π，⑦3.14，⑧1.010010001…（每两个1之间依次增加一个0）（将序号写在横线上即可）负数集合：{ …}；分数集合：{ …}；有理数集合：{ …}；无理数集合：{ …}．18.计算（1）；（2）﹣22×（）2|﹣2|．19.计算下列各式的值：(1) 9x2-25=0； (2) 4(2x-1)2=36.20.已知：3a+21的立方根是3，4a﹣b﹣1的算术平方根是2，c的平方根是它本身．（1）求a，b，c的值；（2）求3a+10b+c的平方根．21.我家客厅的面积为21.6m2，要想用240块相同的正方形地砖铺设，问每块地砖的边长应为多少？。

第六章实数单元练习2022-2023学年人教版七年级数学下册

第六章实数姓名：得分：日期：一、选择题（本大题共 10 小题）1、若a和b是连续整数，且a＜2√7＜b，则a和b的值分别是（）A.3和4B.4和5C.5和6D.6和72、在实数-3、2、0、-π中，最小的数是（）A.-3B.2C.0D.-π3、下列计算正确的是()A. √9=±3B. √5−√4=1C. √(3−π)2=3−πD. √233=24、下列说法正确的是A.-3是-9的平方根B.3是(−3)2的算术平方根C.(−2)2的平方根是2D.8的立方根是±25、有下列说法：(1)无理数就是开方开不尽的数；(2)无理数是无限不循环小数；(3)无理数包括正无理数、零、负无理数；(4)无理数都可以用数轴上的点来表示.其中正确的说法的个数是() A. 1 B. 2 C. 3 D. 46、下列各数中，是无理数的是（）A.0B.1.010010001C.πD.22 77、关于√2下列说法中不正确的是（）A.√2是无理数B.√2的平方是2C.2的平方根是√2D.面积为2的正方形的边长可表示为√28、下列语句正确的是()A. √64的立方根是±2B. ±87是11549的平方根C. -3是27的负立方根D. (−2)2的平方根是-29、下列各式计算正确的是()A. √(−2)2=−2B. −√22=−2C. −√(±2)2=±2D. √22=±210、√16的平方根是()A. 2B. ±2C. 4D. ±4二、填空题（本大题共 11 小题）11、-27的立方根为______，√16的平方根为______．12、比较大小：√10______3．（填“＞”、“=”或“＜”）13、比较大小：√2018______20.18（用“＞”，“＜”，“=”填空）．14、写出一个大于-3的负无理数______．15、请写出一个比3大比4小的无理数：______．16、计算：√−83-|-2|=______．17、算术平方根和立方根等于本身的数是______．18、若a、b互为相反数，m、n互为倒数，k的立方根等于-2，则2014a+2013b+mnb+k的值为______ ．19、√3-2的绝对值是______．20、下列数中：√4，-π，-227，3.131131113…（相邻两个3之间依次多一个1），无理数有______个．21、-8的立方根是 ______ ，√81的算术平方根是 ______ ．三、计算题（本大题共 2 小题）22、计算√0.04-√−273+√(−1)223、求下列各式中x的值（1）2x2=10（2）（x+3）3=-8四、解答题（本大题共 2 小题）24、若√2−π+(1−π)2=0．(1)求x，y的值；(2)求1ππ+1(π+1)(π+1)+1(π+2)(π+2)+⋯+1(π+2016)(π+2016)的值．25、小明想用一块面积为36ππ2的正方形纸片，沿边的方向裁出一块面积为18ππ2的长方形纸片，使它的长度之比为3:2，他能裁出吗？请说明理由．。