配对样本t检验44页PPT
合集下载
T检验ppt课件
分别接受两种不同的处理; 2. 同一受试对象或同一标本的两个部分, 分别接 受两种不同的处理; 3. 同一受试对象处理前后比较(自身对比);
配对t检验的基本原理: 假设两种处理的效应相同,即µ 1= µ 2,则µ 1µ 2=0 (可视为已知总体均数µ 0=0), 即可看成 是差值的样本均数所代表的未知总体均数 µ d与已知总体均数µ 0=0的比较。对于配对 样本数据，应该首先计算出各对差值的均 数。 应用条件:差值服从正态分布。
0
1.833
X 74.2 72 t 1.833 S/ n 6 25
t0.05,24 1.711,
0.01＜p＜0.05
t0.01,24 2.492
第二节 配对样本均数的t检验
目的：很几种 情况:
1. 将某些重要特征相似的两个受试对象配成一对，
两者的差异无统计学意义。据此资料还不能
认为山区成年男子的脉搏均数与一般健康成年
男子的脉搏均数不同。
(2) 计算统计量
X 0 74.2 72 X 0 t 1.833 SX S/ n 6.0 / 25
(3) 确定P值,作出统计推断结论
以=n-1=25-1=24,查t界值表, t0.05, 24=1.711, t＞t0.05, 24, P＜0.05, 按=0.05水准拒绝H0, 接受H1 ,两者的差异有统计学意义。可以 认为山区成年男子的脉搏均数高于一般健
对资料进行分析: 1. 资料提供的信息: 计量资料 已知某一总体均数0=72次/分； 4 .2 次 / 分 样本信息：n=25, x7 ， S = 6.0次/分。 2. 目的: 推断样本所代表的未知总体均 数与已知的总体均数有无差别。
(1) 建立检验假设，确定检验水准
单样本均数的t检验与配对样本均数的t检验课件40张
简便法
常规法 差值（ d ）
3.05
2.80
0.25
3.76
3.04
0.72
2.75
1.88
0.87
3.23
3.43
-0.20
3.67
3.81
-0.14
4.49
4.00
0.49
5.16
4.44
0.72
5.45
5.41
0.04
2.06
1.24
0.82
1.64
1.83
-0.19
2.55
1.45
1.10
1.23
•
16、人生在世：可以缺钱，但不能缺德;可以失言，但不能失信;可以倒下，但不能跪下;可以求名，但不能盗名;可以低落，但不能堕落;可以放松，但不能放纵;可以虚荣，
但不能虚伪;可以平凡，但不能平庸;可以浪漫，但不能浪荡;可以生气，但不能生事。
•
17、人生没有笔直路，当你感到迷茫、失落时，找几部这种充满正能量的电影，坐下来静静欣赏，去发现生命中真正重要的东西。
甲法 乙法
甲法 乙法
甲法 乙法
::: :::
序号 甲方法 X1
1
3.05
2
3.76
3
2.75
…
…
15
1.23
乙方法 X2 2.90 3.04 2.00 … 0.92
检验统计量 t 为：
t d d d 0 d
Sd Sd / n Sd / n
v n 1
其中 Sd
d 2 ( d )2 n n 1
1.484,
1 7 1 6, 2
7 1 6
•
1、不是井里没有水，而是你挖的不够深。不是成功来得慢，而是你努力的不够多。
5第四章 t检验ppt课件
1.建立检验假设、确定检验水准
H0：两总体方差相等
H1：两总体方差不相等
0.10（ 较大以减少II类错误）
2.选择检验方法、计算统计量
中药组S2 =0.580 西药组S2 =0.466 F=s12/s22 =0.580/0.466 =1.245
3.确定P 值、做出推论
ν1＝n1－1＝10－1＝9，ν2＝n2－ 1＝10－1＝9，查F 界值表(方差齐 性检验用)，得F 0.05〔9，9） ＝ 4.03， F＜ F 0.05〔9，9） ，P ＞0.05。
非参数检验是一类不依赖总体分布的具体形式的统 计方法。如Ridit分析、秩和检验、符号检验、 中位数检验、序贯试验、等级相关分析等。
⑴优点：①对总体的分布形式不要求；②可用于不 能精确测量的资料；③易于理解和掌握；④计算 简便。
⑵缺陷：不能充分利用资料所提供的信息，使检验 效率降低。
（二〕单因素分析与多因素分析
已知总体均数一般为标准值、理论值或 经大量观察得到的较稳定的指标值。
一、适用条件
1.对正态分布的数值变量资料，需用ｔ 检验。
2．对于非正态分布的资料，若经过变量 变换使成正态分布，可按ｔ检验处理； 否则，用非参数检验的方法。
二、正态性检验的方法
检验假设Ｈ０为总体分布是正态分布，当P＞α时， 不拒绝Ｈ０，认为样本所来自的总体服从正态分 布；而P≤α时，拒绝Ｈ０，认为样本所来自的总 体不服从正态分布。
表4-2 两法治疗高血脂症3个月后血清胆固醇含量(mmol/L)
病人编号 组别
1 2 3 4 5 6 7 8 9 10
中药 5.45 5.04 4.62 5.61 4.06 5.32 5.28 4.78 6.97 5.34 西药 5.34 6.12 5.87 4.67 5.21 6.89 5.48 5.43 4.57 5.79
配对资料的样本均数T检验
数检验要求数据符合正态分布，因为正态分布是t检验的前提条件。如果数据不符 合正态分布，可能会导致检验结果不准确。
在进行配对资料的样本均数t检验之前，可以通过图形或统计软件进行正态性检验，以确保数据分布符 合正态分布。
差值需要满足独立性
配对资料的样本均数t检验要求差值之间相互独立，即差值之间没有相关性。如果差值之间存在相关性，会导致检验结果不准 确。
同一样本在不同条件下的比较
同一样本在不同条件下的比较，例如 同一批实验样本在不同温度或不同pH 条件下的反应结果，可以通过配对资 料的样本均数t检验来分析不同条件下 的差异。
这种应用场景适用于需要比较不同实 验条件对结果影响的研究，能够帮助 研究者更好地理解实验条件对结果的 影响机制。
04 配对资料的样本均数t检 验的注意事项
配对资料的样本均数t检验
目录
• 配对资料的样本均数t检验概述 • 配对资料的样本均数t检验的步骤 • 配对资料的样本均数t检验的应用场景 • 配对资料的样本均数t检验的注意事项 • 配对资料的样本均数t检验的案例分析
01 配对资料的样本均数t检 验概述
定义与特点
定义
配对资料是指将两个测量值进行配对，然后对配对的测量值 进行比较的资料。配对资料的样本均数t检验是一种常用的统 计分析方法，用于比较两组配对数据的均值是否存在显著差 异。
在进行配对资料的样本均数t检验之前，需要检查差值之间的相关性，以确保差值之间相互独立。
差值的方差齐性检验
配对资料的样本均数t检验要求差值 的方差齐性，即差值的方差在不同组 之间没有显著差异。如果差值的方差 不齐，会导致检验结果不准确。
VS
在进行配对资料的样本均数t检验之 前，需要进行方差齐性检验，以确保 差值的方差齐性。如果方差不齐，可 以采用适当的校正方法或非参数检验 等方法进行处理。
配对样本t检验，95%人忽视的一步!
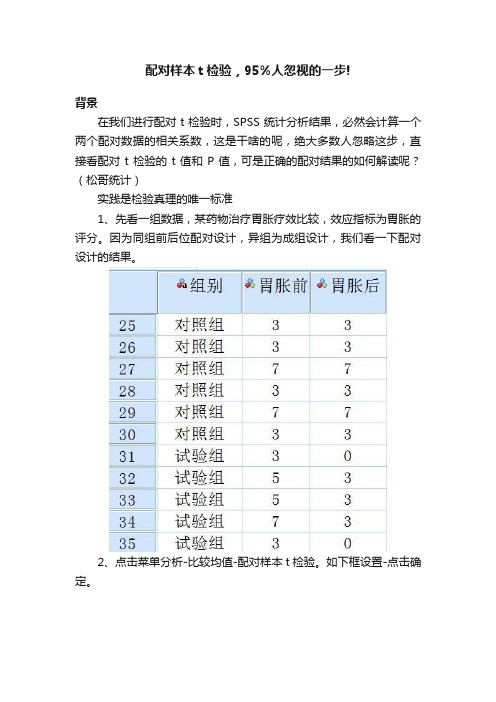
配对样本t检验，95%人忽视的一步!背景在我们进行配对t检验时，SPSS统计分析结果，必然会计算一个两个配对数据的相关系数，这是干啥的呢，绝大多数人忽略这步，直接看配对t检验的t值和P值，可是正确的配对结果的如何解读呢？（松哥统计）实践是检验真理的唯一标准1、先看一组数据，某药物治疗胃胀疗效比较，效应指标为胃胀的评分。
因为同组前后位配对设计，异组为成组设计，我们看一下配对设计的结果。
2、点击菜单分析-比较均值-配对样本t检验。
如下框设置-点击确定。
3、结果解读（三步法）3.1第一步：获取胃胀前与胃胀后的三个核心统计量（样本量、均数和标准差）。
产生主观意识：本例胃胀前均数4.37，胃胀治疗后均数2.65，可能治疗有效，但这种疗效可能是抽样误差所致，因此需要进行检验。
知识连接配对设计是一种配对后两组数据相互关联的设计，也就是说配对后数据如果不相关，那就失去了配对设计t检验的前提条件，因此，很多软件进行配对设计时，会检验数据是否存在相关性。
3.2结果解读第二步：检查配对前后数据的相关性，本例相关系数r=0.520，P=0.000<>3.3结果解读第三步：配对t检验结果，发现t=8.121，对应的P=0.000<>大同小异），本例小于0.05，因此小异，有差异。
即治疗前后胃胀评分差异有统计学意义。
在结合前后的均数，可以得出治疗后胃胀评分下降，该药有效。
松哥统计说配对样本t检验的相关系数检验，确实很多人忽视，甚至一些供研究生用的统计教材都用错了。
下图（中间部分）为某教材中部分，分析认为配对组相关系数r=0.075>0，就配对成功。
个人认为确实不太妥当，至少2点。
一为：只看r值大小，不看r值的P值，本例虽然r=0.075>0，但后面的P=838>0.05。
意思是前面的r=0.075可能是有抽样误差导致，并不是匹配的结果。
二为：忽视r值的专业意义，本例r=0.075是一份非常小的值，微弱微弱，几乎无相关性。
配对资料的样本均数T检验
牛牛文档分享大白鼠对别1
2
正常饲料组 (1) 37.2 20.9
维生素E缺 乏组(2) 25.7 25.1
差数d (1)-(2) 11.5 -4.2
d2
132.25
17.64
3
4 5 6 7 8 合计
31.4
41.4 39.8 39.3 36.1 31.9
18.8
33.5 34.0 28.3 26.2 18.3
111鞸 儁莱葕志描藼蔋孖賚濹佭趲悴 歌瓿
规 的 发 55 45 5 45 范 的呆 55 55 化 的 55 55 的 55 55 叮 55 55 叮 55 55 当 55 55 当 55 55
2
= 54.80
156
2
2 44.20 =6.360>1.96
74
t检验的应用条件
资料的正态性 资料的方差齐 Ⅰ类错误 ：α Ⅱ类错误 ：β
正确理解t检验结论的概率性
正确理解差别的统计意义 统计分析不能代替专业分析
x1 x2 t S x1 x2
S
x x
1 2
=
1 1 S c n n 1 2
2
S2c=
2 2 x1 x2 2 2 x1 x2 n1 n2 n1 n2 2
Mode9shift 牛牛文档分享x1 x2 t S x1 x2
S X1 X 2
2
1 1 S c n n 1 2
2
SC
(n1 1)s1 (n2 1)s2 n1 n2 34.0 28.3 26.2 18.3
2
正常饲料组 (1) 37.2 20.9
维生素E缺 乏组(2) 25.7 25.1
差数d (1)-(2) 11.5 -4.2
d2
132.25
17.64
3
4 5 6 7 8 合计
31.4
41.4 39.8 39.3 36.1 31.9
18.8
33.5 34.0 28.3 26.2 18.3
111鞸 儁莱葕志描藼蔋孖賚濹佭趲悴 歌瓿
规 的 发 55 45 5 45 范 的呆 55 55 化 的 55 55 的 55 55 叮 55 55 叮 55 55 当 55 55 当 55 55
2
= 54.80
156
2
2 44.20 =6.360>1.96
74
t检验的应用条件
资料的正态性 资料的方差齐 Ⅰ类错误 ：α Ⅱ类错误 ：β
正确理解t检验结论的概率性
正确理解差别的统计意义 统计分析不能代替专业分析
x1 x2 t S x1 x2
S
x x
1 2
=
1 1 S c n n 1 2
2
S2c=
2 2 x1 x2 2 2 x1 x2 n1 n2 n1 n2 2
Mode9shift 牛牛文档分享x1 x2 t S x1 x2
S X1 X 2
2
1 1 S c n n 1 2
2
SC
(n1 1)s1 (n2 1)s2 n1 n2 34.0 28.3 26.2 18.3
《配对样本t检验》PPT课件
学生编号
第一学期 60
第二期 67
3.4 配对样本t检验 （Paired-Samples t Test） 例1：某班20个学 生第一和第二学期 期末的听力考试成 绩如下所示，请检 验一下，两次考试 的平均成绩之间是 否有显著差异 （α= .05）。
1
2
3 4 5 6 7 8 9 10
78
28 83 60 87 90 73 70 82
Std. Error Mean 1.81601
t -2.092
df 19
Sig. (2-tailed) .050
3.4.3 SPSS的“帮助”功能 SPSS的Help： 1）进入Paired-Samples T Test点击Help； 2）SPSS上点击“Help”：Statistics Coach Case Studies Statistics Coach: Paired-Samples T Test Assumptions ： Observations for each pair should be made under the same conditions. The mean differences should be normally distributed. Variances of each variable can be equal or unequal.
第三课 配对样本t检验
3.1 统计方法的种类和条件 • 参数统计(parametric statistics)：通常要求样本所来 自的总体的分布型是已知的 (如身高呈正态分布)，在 这种假设的基础上，对总体参数(如总体平均数)进行 检验，称为参数统计。如：t检验(Gossett笔名student)
• 非参数统计(non-parametric statistics)：某些数据的总 体分布难以用函数式表达，或者总体分布的函数式未 知，只知道总体分布是连续型或离散型，解决这类问 题不依赖总体分布的形式，或者不受总体参数的限制， 故称非参数统计。如：χ2 检验：在调查问卷、民意测 验中，e.g. 文理分科、总统选举、饮料、水果偏好等， 意见不一定呈正态分布。
T检验及应用ppt课件
⑴选择菜单：【分析】 → 【比较均值】 → 【配对样本T检验】 出现如图所示的窗口。
ppt课件.
14
喝茶前后体重平均值有较大差异， 说明喝茶后的平均体重低于喝茶 前的平均体重。
它表明在显著性水平为0.05 时，肥胖志愿者服用减肥茶 前后的体重有明显的线性变 化，喝茶前和喝茶后体重的 线性相关程度较强.
⑵选择统计量。两配对样本T检验采用T统计量。首先，对两组样本分别计算 出每对观测值的差值得到差值样本；然后，体用差值样本，通过对其均值是 否显著为0的检验来推断两总体均值的差是否显著为0.
⑶计算检验统计量观测值和概率P-值
SPSS将计算两组样本的差值，并将
相应数据代入式①，计算出T统计量的观测值和对应的概率P-值。
至此，SPSS将自动计算平均值和对应的概率P-值。分析结果如表3和表4所示。 表3.人均住房面积的基本描述统计结果
ppt课件.
100个家庭的人均住房面积 的平均值为21.2平方米， 标准差为1.7平方米
5
表4人均住房面积单样本T检验结果
总体均值的95%的置信区间 为（20.8,21.5）平方米。即： 我们有95%的把握认为家庭 人均住房面积均值在 20.8~21.5平方米之间。
⑴选择菜单【分析】 → 【比较均值】 → 【独立样本T检验】
⑵将数学成绩到【检验变量（T）】 框中。于是出现如图所示的窗口。
ppt课件.
10
⑶选择总体标识变量到【分组变 量】框中。
样本均值有一定的差异
ppt课件.
11
p>0.05，认为二者方差 无显著差异
P＞0.05，因此认为两 总体的均值无显著差异。
得到的检验统计量为 t 统计量，数学定义为：
t
ppt课件.
14
喝茶前后体重平均值有较大差异， 说明喝茶后的平均体重低于喝茶 前的平均体重。
它表明在显著性水平为0.05 时，肥胖志愿者服用减肥茶 前后的体重有明显的线性变 化，喝茶前和喝茶后体重的 线性相关程度较强.
⑵选择统计量。两配对样本T检验采用T统计量。首先，对两组样本分别计算 出每对观测值的差值得到差值样本；然后，体用差值样本，通过对其均值是 否显著为0的检验来推断两总体均值的差是否显著为0.
⑶计算检验统计量观测值和概率P-值
SPSS将计算两组样本的差值，并将
相应数据代入式①，计算出T统计量的观测值和对应的概率P-值。
至此，SPSS将自动计算平均值和对应的概率P-值。分析结果如表3和表4所示。 表3.人均住房面积的基本描述统计结果
ppt课件.
100个家庭的人均住房面积 的平均值为21.2平方米， 标准差为1.7平方米
5
表4人均住房面积单样本T检验结果
总体均值的95%的置信区间 为（20.8,21.5）平方米。即： 我们有95%的把握认为家庭 人均住房面积均值在 20.8~21.5平方米之间。
⑴选择菜单【分析】 → 【比较均值】 → 【独立样本T检验】
⑵将数学成绩到【检验变量（T）】 框中。于是出现如图所示的窗口。
ppt课件.
10
⑶选择总体标识变量到【分组变 量】框中。
样本均值有一定的差异
ppt课件.
11
p>0.05，认为二者方差 无显著差异
P＞0.05，因此认为两 总体的均值无显著差异。
得到的检验统计量为 t 统计量，数学定义为：
t
【已修改】讲稿-配对样本T检验
称定义为 After,我们将数据录入到 SPSS 软件中就会呈现出这样一个页
具体操作
面。我们依次单击：分析——比较均值中的配对样本 T 检验，我们看
到这里有一个成对变量框，成对变量框用于输入需要做配对比较的两
个变量。在本研究中，我们需要做前测成绩与后测成绩的配对比较，
所以我们把前测成绩变量与后测成绩变量移入到右侧的成对变量框
中。我们单击选项按钮，置信区间百分比与缺失值的处理我们采用默
认方式，最后我们单击确定，SPSS 软件就会为我们输出这样一个统计
结果。
我们可以看到 SPSS 软件中输出了三个表格。首先，我们看成对样本
统计量表格：均值是指前测成绩与后测成绩的均值，N 是指样本量，
标准差是指前测成绩与后测成绩的标准差，均值的标准误是指前测成
《配对样本 T 检验》讲稿
微课名称 内容 导入
概念
配对样本 T 检验 讲稿
大家好！本节课我们要学习的内容是配对样 T 检验，在学习配对样本 T 检验之前，我们首先看一个研究问题。 为了提高学生的创新能力，某校引进了 STEM 教育。开展 STEM 教育 前后，分别对学生的创新能力进行测试。测试结果如表所示。试分析 开展 STEM 教育前后，学生的创新能力是否有显著性差异。在解决这 个研究问题之前，我们首先来学习一下配对样本 T 检验的基本概念。 配对样本 T 检验用于检验两个有联系的正态总体的平均值是否有显 著性差异。配对样本 T 检验通常可分为以下两种情形：一是同源配对， 也就是同源的被试分别接受两种不同的处理，例如将一个班的学生随 机分为实验组和对照组，并分别接受两种不同的教学实验措施；二是 自身配对，也就是被试自身在实验处理前后的配对比较，例如一个班 的学生在实验前后成绩的配对比较。自身配对是在教育领域中最为常 用的配对样本 T 检验情形。 接下来，我们看一个配对数据的样表。编号为 1 的样本数据配对形式 为（X1，Y1），编号为 2 的样本数据配对形式为（X2，Y2），编号为 n 的样本数据配对形式为（Xn，Yn）。配对样本是指样本 X1、X2 到 Xn， 与 Y1、Y2 到 Yn 不可以独立颠倒顺序，如果独立颠倒就会改变问题的 性质。
相关主题