2009年中考试题专题之-正多边形与圆试题及答案

合集下载

人教版九年级上册数学《正多边形和圆》同步习题(含答案)

24.3正多边形和圆同步习题一、选择题1．如图，四边形ABCD是⊙O的内接四边形，若∠D＝3∠B，则∠B的度数为（）A．30°B．36°C．45°D．60°2．如图，四边形ABCD是⊙O的内接四边形，BE平分∠ABC，若∠D＝110°，则∠ABE 的度数是（）A．30°B．35°C．50°D．55°3．对于以下说法：①各角相等的多边形是正多边形；②各边相等的三角形是正三角形；③各角相等的圆内接多边形是正多边形；④各顶点等分外接圆的多边形是正多边形．正确的有（）A．1个B．2个C．3个D．4个4．一个三角形的外接圆的圆心在这个三角形的外部，则该三角形一定是（）A、锐角三角形B、直角三角形C、钝角三角形D、等腰三角形5．如图，△ABC是半径为1的⊙O的内接正三角形，则圆的内接矩形BCDE的面积为（）A．3 B．32C．3D．326．如图，正五边形ABCDE内接于O，点P是劣弧BC上一点（点P不与点C重合），则CPD∠=（）A．45︒B．36︒C．35︒D．307．如图，四边形ABCD内接于⊙O ，110BOD︒∠=，那么BCD∠等于（）A．110°B．135°C．55°D．125°8．如图，△ABC为⊙O的内接三角形，若∠AOC=160°，则∠ADC的度数是（）A．80°B．160°C．100°D．40°9．如图，将正五边形绕中心O顺时针旋转a角度，与原正五边形构成新的图形，若要使该图形既是轴对称又是中心对称图形，则a的最小角度为（）A ．30B ．36C ．72D ．90 10．如图，正五边形ABCDE 和等边AFG 内接于O ，则GFD ∠的度数是（）A ．10︒B ．12︒C ．15︒D ．20︒二、填空题 11．如图，四边形ABCD 为O 的内接四边形，已知BOD 110∠=，则BCD ∠的度数为____________________．12．一个正多边形的一个外角为30°，则它的内角和为_____．13．如图，四边形ABCD 内接于⊙O ，点E 在BC 的延长线上，若∠BOD ＝100°，则∠DCE ＝_____°．14．如图，四边形ABCD 是⊙O 的内接四边形，∠B＝135°，则∠AOC 的度数为_____．15．如图，点A ，B ，C ，D 在O 上，CD CB =，30CAD ∠=︒，50ACD ∠=︒，则ADB =∠_______．三、解答题16．如图，四边形ABCD 内接于O ，AC 与BD 为对角线，BCA BAD ∠=∠，过点A 作//AE BC 交CD 的延长线于点E ．求证：EC AC =．17．如图，ABC 的外角BAM ∠的平分线与它的外接圆相交于点E ，连接BE ，CE ，过点E 作//EF BC ，交CM 于点D求证：（1）BE CE =；（2）EF 为⊙O 的切线．18．如图，⊙O 外接于正方形,ABCD P 为弧AD 上一点，且1,3AP PC ==，求正方形ABCD 的边长和PB 的长．参考答案1-5 CBBCC6-10 BDCBB11．125°12．1800°13．5014．9015．70°16．证明：∵//AE BC ，∴ACB EAC ∠=∠．∵ACB BAD ∠=∠，∴EAC BAD ∠=∠，∴EAD CAB ∠=∠，∵180ADE ADC ∠+∠=︒，180ADC ABC ∠+∠=︒，∴ADE ABC =∠∠，∵180EAD ADE E ∠+∠+∠=︒，180BAC ABC ACB ∠+∠+∠=︒， ∴E ACB EAC ∠=∠=∠，∴CE CA =．17．证明：（1）∵四边形ACBE 是圆内接四边形，∴∠EAM ＝∠EBC ，∵AE 平分∠BAM ，∴∠BAE ＝∠EAM ，∵∠BAE ＝∠BCE ，∴∠BCE ＝∠EAM ，∴∠BCE ＝∠EBC ，∴BE ＝CE ；（2）如图，连接EO 并延长交BC 于H ，连接OB ，OC ，∵OB ＝OC ，EB ＝EC ，∴直线EO 垂直平分BC ，∴EO ⊥BC ，∵EF//BC ，∴EO ⊥EF ，∵OE 是⊙O 的半径，∴EF 为⊙O 的切线．18．解：连接AC ，作AE PB ⊥于点E ，如图所示．∵四边形ABCD 是正方形，,AB BC CD AD ∴===90,45ABC D BCD ACB ︒︒∠=∠=∠=∠=， AC ∴是O 的直径，ABC 是等腰直角三角形， 90,2,APC AC ︒∴∠==22221310,AC AP PC ∴=+=+= 52AB ∴== 45,,APB ACB AE PB ︒∠=∠=⊥APE ∴是等腰直角三角形，22PE AE AP ∴=== 2222232(5)22BE AB AE ⎛⎫∴=-=-= ⎪ ⎪⎝⎭，232∴=+=+=．PB PE BE22正方形ABCD的边长为5,PB的长为22．。

正多边形与圆-练习题含答案

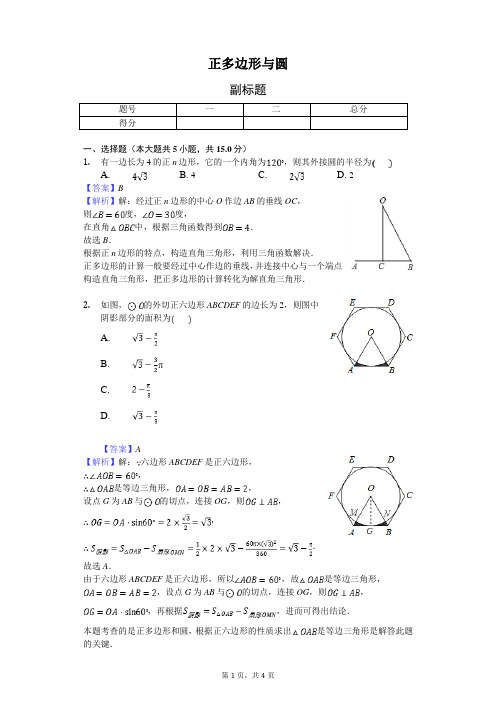
正多边形与圆副标题一、选择题（本大题共5小题，共15.0分）1.有一边长为4的正n边形，它的一个内角为，则其外接圆的半径为B. 4C.D. 2A.【答案】B【解析】解：经过正n边形的中心O作边AB的垂线OC，则度，度，在直角中，根据三角函数得到．故选B．根据正n边形的特点，构造直角三角形，利用三角函数解决．正多边形的计算一般要经过中心作边的垂线，并连接中心与一个端点构造直角三角形，把正多边形的计算转化为解直角三角形．2.如图，的外切正六边形ABCDEF的边长为2，则图中阴影部分的面积为A.B.C.D.【答案】A【解析】解：六边形ABCDEF是正六边形，，是等边三角形，，设点G为AB与的切点，连接OG，则，，．故选A．由于六边形ABCDEF是正六边形，所以，故是等边三角形，，设点G为AB与的切点，连接OG，则，，再根据，进而可得出结论．本题考查的是正多边形和圆，根据正六边形的性质求出是等边三角形是解答此题的关键．3.如图，是等边三角形ABC的外接圆，的半径为2，则等边的边长为A.1 B. C. D.【答案】D【解析】解：作于D，连接OB，如图所示：则，是等边三角形ABC的外接圆，，，，，即等边的边长为；故选：D．作于D，连接OB，由垂径定理得出，由等边三角形的性质和已知条件得出，求出OD，再由三角函数求出BD，即可得出BC的长．本题考查了等边三角形的性质、垂径定理、含角的直角三角形的性质、三角函数；熟练掌握等边三角形的性质，并能进行推理计算是解决问题的关键．4.如图，正六边形ABCDEF内接于，半径为4，则这个正六边形的边心距OM和的长分别为A. 2，B.，C.，D.，【答案】D【解析】解：连接OB，，，，，故选：D．正六边形的边长与外接圆的半径相等，构建直角三角形，利用直角三角形的边角关系即可求出OM，再利用弧长公式求解即可．本题考查了正多边形和圆以及弧长的计算，将扇形的弧长公式与多边形的性质相结合，构思巧妙，利用了正六边形的性质，是一道好题．5.以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形，则该三角形的面积是B. C. D.A.【答案】A【解析】解：如图1，，；如图2，，；如图3，，，则该三角形的三边分别为：1，，，，该三角形是直角三角形，该三角形的面积是：．故选：A．由于内接正三角形、正方形、正六边形是特殊内角的多边形，可构造直角三角形分别求出边心距的长，由勾股定理逆定理可得该三角形是直角三角形，进而可得其面积．本题主要考查多边形与圆，解答此题要明确：多边形的半径、边心距、中心角等概念，根据解直角三角形的知识解答是解题的关键．二、填空题（本大题共1小题，共3.0分）6.已知一个正六边形的边心距为，则它的半径为______ ．【答案】2【解析】解：如图，在中，，，；故答案为：2．设正六边形的中心是O，一边是AB，过O作与G，在直角中，根据三角函数即可求得OA．本题主要考查正多边形的计算问题，常用的思路是转化为直角三角形中边和角的计算，属于常规题．。

2009年145套中考试卷精品分类24.正多边形与圆、弧长、扇形面积(解答题)

24．正多边形与圆. 弧长.扇形面积（解答题）一．解答56.（2009年杭州市）如图，有一个圆O 和两个正六边形1T ，2T ．1T 的6个顶点都在圆周上，2T 的6条边都和圆O 相切（我们称1T ，2T 分别为圆O 的内接正六边形和外切正六边形）．（1）设1T ，2T 的边长分别为a ，b ，圆O 的半径为r ，求a r :及b r :的值；（2）求正六边形1T ，2T 的面积比21:S S 的值．【关键词】弧长.弓形面积及简单组合图形的面积【答案】（1）连接圆心O 和T 的6个顶点可得6个全等的正三角形.所以r ∶a=1∶1;连接圆心O 和T 相邻的两个顶点，得以圆O 半径为高的正三角形，所以r ∶b=3∶2;（2） T ∶T 的连长比是3∶2，所以S ∶S =4:3):(2b a .57.（2009年宁波市）（1）如图1，把等边三角形的各边三等分，分别以居中那条线段为一边向外作等边三角形，并去掉居中的那条线段，得到一个六角星，则这个六角星的边数是．（2）如图2，在5×5的网格中有一个正方形，把正方形的各边三等分，分别以居中那条线段为一边向外作正方形，并去掉居中的那条线段．请你把得到的图形画在图3中，并写出这个图形的边数．（3）现有一个正五边形，把正五边形的各边三等分，分别以居中那条线段为一边向外作正五边形，并去掉居中的那条线段，得到的图形的边数是多少？【关键词】正多边形【答案】（1）12．（2）这个图形的边数是20．（3）得到的图形的边数是30358．（2009年内蒙古包头）如图，在ABC△中，120AB AC A BC=∠==，°，，A⊙与BC相切于点D，且交AB AC、于M N、两点，则图中阴影部分的面积是（保留π）．3π【解析】本题考查三角形和扇形面积的求法及三角函数有内容。

图中阴影部分的面积等于AMNABCS S∆-扇形，连结AD，在ΔABC中，AB=AC，A=120∠︒，⊙A与BC相交于点D，则AD⊥BC，1122BD BC==⨯=11BAD=BAC=120=6022∠∠⨯︒︒，∴∠B=30°，AD=BD tan tan3013⨯∠︒=，D（图1）（图2）（图3）∴2AMN 112011.23603ABC S S ππ∆⨯-=⨯⨯=扇形59．图中的粗线CD 表示某条公路的一段，其中AmB 是一段圆弧，AC .BD 是线段，且AC .BD 分别与圆弧AmB 相切于点A .B ，线段AB =180m ，∠ABD =150°．（1）画出圆弧AmB 的圆心O ；（2）求A 到B 这段弧形公路的长．【关键词】切线性质.等边三角形判定和性质.弧长计算. 【答案】解：（1）如图，过A 作AO ⊥AC ，过B 作BO ⊥BD ，AO 与BO 相交于O ，O 即圆心．说明：若不写作法，必须保留作图痕迹．其它作法略．（2）∵ AO .BO 都是圆弧AmB 的半径，O 是其圆心，∴ ∠OBA =∠OAB =150°-90°=60°．∴ △AOB 为等边三角形．∴ AO =BO =AB =180． ∴ π6018060π180AB ⨯⨯== (m)．∴ A 到B 这段弧形公路的长为60πm ．60.（2009年衡阳市）如图，圆心角都是90º的扇形OAB 与扇形OCD 叠放在一起，连结AC ，BD ．（1）求证：AC=BD ；O（2）若图中阴影部分的面积是243cm π，OA=2cm ，求OC 的长．【关键词】扇形.阴影面积【答案】（1）证明：BDAC BOD AOC DO CO BO AB BOD AOC AODBOD AOD AOC COD AOB =⇒∆≅∆⇒⎪⎭⎪⎬⎫==∠=∠⇒∠+∠=∠+∠⇒∠∠ 900＝＝（2）根据题意得：360)(9036090360902222OC OA OC OA S -=-=πππ阴影；∴360)2(904322OC -=ππ解得：OC ＝1cm ．61．（2009年广东省）（1）如图1，圆内接ABC △中，AB BC CA OD ==，.OE 为O ⊙的半径，OD BC ⊥于点F ，OE AC ⊥于点G ，求证：阴影部分四边形OFCG 的面积是ABC △的面积的13．（2）如图2，若DOE ∠保持120°角度不变，求证：当DOE ∠绕着O 点旋转时，由两条半径和ABC △的两条边围成的图形（图中阴影部分）面积始终是ABC △的面积的13．【关键词】等边三角形；全等三角形的性质与判定；旋转【答案】证明：（1）如图1，连结OA .OC ，因为点O 是等边三角形ABC 的外心，图1D 图2所以Rt Rt Rt OFC OGC OGA △≌△≌△．2OFCG OFC OAC S S S ==△△，因为13OAC ABC S S =△△，所以13OFCGABC S S =△．（2）解法一：连结OA .OB 和OC ，则12AOC COB BOA ∠=∠△≌△≌△，，不妨设OD 交BC 于点F OE ，交AC 于点G ，3412054120AOC DOE ∠=∠+∠=∠=∠+∠=°，°， 35∴∠=∠，在OAG △和OCF △中1235OA OC ∠=∠⎧⎪=⎨⎪∠=∠⎩OAG OCF ∴△≌△，13OFCG AOC ABC S S S ∴==△△解法二：不妨设OD 交BC 于点F ，OE 交AC 于点G ，作OH BC OK AC ⊥，⊥，垂足分别为点H .K ，在四边形HOKC 中，9060OHC OKC C ∠=∠=∠=°，°，360909060120HOK ∴∠=︒-︒-︒-︒=︒答案20题图（3）A E O G FBCD13 2 H K（2）AEO G FB CD1 2 3 45即12120∠+∠=°, 又23120GOF ∠=∠+∠=°， 13∴∠=∠ AC BC =，OH OK ∴=，OGK OFH ∴△≌△，13OFCG OHCK ABC S S S ∴==△．62．（2009年甘肃庆阳），在平面直角坐标系中，等腰Rt △OAB 斜边OB 在y 轴上，且OB =4．（1）画出△OAB 绕原点O 顺时针旋转90°后得到的三角形；（2）求线段OB 在上述旋转过程中所扫过部分图形的面积（即旋转前后OB 与点B 轨迹所围成的封闭图形的面积）．【关键词】平面直角坐标系；旋转【答案】本小题满分8分解：（1）画图正确（如图）；（2）所扫过部分图形是扇形，它的面积是：290π44π360⨯=．63．（2009年广西南宁）如图，PA .PB 是半径为1的O ⊙的两条切线，点A .B 分别为切点，60APB OP AB C O D ∠=°，与弦交于点，与⊙交于点．（1）在不添加任何辅助线的情况下，写出图中所有的全等三角形；（2）求阴影部分的面积（结果保留π）．【关键词】直线与圆的位置关系；弧长.弓形面积及简单组合图形的面积【答案】解：（1）ACO BCO APC BPC PAO PBO △≌△，△≌△，△≌△（2）PA .PB 为O ⊙的切线PO ∴平分90APB PA PB PAO ∠=∠=，，°PO AB∴⊥∴由圆的对称性可知：AOD S S =阴影扇形在Rt PAO △中，11603022APO APB ∠=∠=⨯=︒° 90903060AOP APO ∴∠=-∠=-︒=︒°°260π1360AOD S S ⨯⨯∴==阴影扇形π6=64.（2009青海）如图，一个圆锥的高为，侧面展开图是半圆．求：（1）圆锥的母线长与底面半径之比；（2）求BAC ∠的度数；（3）圆锥的侧面积（结果保留π）．【关键词】弧长、弓形面积及简单组合图形的面积【答案】（1）设此圆锥的高为h ，底面半径为r ，母线长AC l =．∵2ππr l =，∴2lr=．（2）∵2lr=，∴圆锥高与母线的夹角为30°，则60BAC ∠=° （3）由图可知222l h r h =+=，， ∴222(2)r r =+，即22427r r =+．解得 3cm r =． ∴26cm l r ==．∴圆锥的侧面积为22π18π(cm )2l =．。

人教版九年级数学上册《24.3 正多边形和圆》同步练习题-附答案

人教版九年级数学上册《24.3 正多边形和圆》同步练习题-附答案学校:___________班级：___________姓名：___________考号：___________考点正多边形与圆1.定义：正多边形的圆的圆心叫做这个正多边形的中心圆的半径叫做正多边形的半径正多边形每一边所对的角叫做正多边形的中心角到正多边形的一边的距离叫做正多边形的边心距。

2.公式：正多边形的有关概念：边长（a ）中心（O ）中心角（∠AOB ）半径（R ））边心距（r ）如图所示①．边心距222a r R ⎛⎫=- ⎪⎝⎭中心角360n ︒=关键点:三角形的内切圆与外接圆关系定义圆心实质半径图示外接圆经过三角形各顶点的圆外心三角形各边垂直平分线的交点交点到三角形三个顶点的距离相等内切圆与三角形各边都相切的圆内心三角形各内角平分线的交点交点到三角形各边的距离相等名校提高练习:一选择题：本题共10小题每小题3分共30分。

在每小题给出的选项中只有一项是符合题目要求的。

1.(2024·四川省泸州市·月考试卷)已知圆内接正三角形的面积为√ 3则该圆的内接正六边形的边心距是( )A. 2B. 1C. √ 3D. √ 322.同一个圆的内接正三角形正方形正六边形的边心距分别为r3r4r6则r3：r4：r6等于( )A. 1:√2:√3B. √3:√2:1C. 1：2：3D. 3：2：13.如图若干个全等的正五边形排成环状图中所示的是前3个正五边形要完成这一圆环还需正五边形的个数为( )A. 10B. 9C. 8D. 74.(2024·贵州省黔东南苗族侗族自治州·月考试卷)正六边形ABCDEF内接于⊙O正六边形的周长是12则⊙O的半径是( )A. √ 3B. 2C. 2√ 2D. 2√ 35.(2024·山东省·单元测试)《几何原本》中记载了用尺规作某种六边形的方法其步骤是：①在⊙O上任取一点A连接AO并延长交⊙O于点B②以点B为圆心BO为半径作圆弧分别交⊙O于C D两点③连接CO DO并延长分别交⊙O于点E F④顺次连接BC CF FA AE ED DB得到六边形AFCBDE.再连接AD EF AD EF交于点G.则下列结论不正确的是( )A. GF=GDB. ∠FGA=60°C. EFAE=√ 2 D. AF⊥AD6.(2024·江苏省·同步练习)以半径为2的圆的内接正三角形正方形正六边形的边心距为三边作三角形则该三角形的面积是( )A. √ 22B. √ 32C. √ 2D. √ 37.(2024·江苏省·同步练习)如图正十二边形A1A2…A12连接A3A7A7A10则∠A3A7A10的度数为( )A. 60°B. 65°C. 70°D. 75°8.(2024·江苏省·同步练习)如图若干个全等的正五边形排成环状．图中所示的是前3个正五边形要完成这一圆环还需正五边形的个数为( )A. 6B. 7C. 8D. 99.(2024·北京市市辖区·期末考试)如图正方形ABCD的边长为6且顶点A B C D都在⊙O上则⊙O 的半径为()．A. 3B. 6C. 3√ 2D. 6√ 210.(2024·广东省广州市·月考试卷)如图已知⊙O的周长等于4πcm则圆内接正六边形的边长为()cm．A. √ 3B. 2C. 2√ 3D. 4二填空题：本题共6小题每小题3分共18分。

专题37 正多边形和圆-中考数学二轮复习之难点突破+热点解题方法

专题37 正多边形和圆一、单选题1．如图所示，ABC 为O 的内接三角形，2,30AB C =∠=︒，则O 的内接正方形的面积（）A ．2B ．4C ．8D ．16【答案】C【分析】先连接BO ，并延长交⊙O 于点D ，再连接AD ，根据同圆中同弧所对的圆周角相等，可得⊙ADB=30°，而BD 是直径，那么易知⊙ADB 是直角三角形，再利用直角三角形中30°的角所对的边等于斜边的一半，那么可求BD ，进而可知半径的长，任意圆内接正方形都是以两条混响垂直的直径作为对角线的四边形，故利用勾股定理可求正方形的边长，从而可求正方形的面积．【详解】解：连接BO ，并延长交⊙O 于点D ，再连接AD ，如图，⊙⊙ACB=30°，⊙⊙BDA=30°，⊙BD 是直径，⊙⊙BAD=90°，在Rt⊙ADB 中，BD=2AB=4，⊙⊙O 的半径是2，⊙⊙O 的内接正方形是以两条互相垂直的直径为对角线的，⊙正方形的边长=⊙S 正方形=8=．【点睛】本题考查了圆周角定理、含有30角的直角三角形的性质，解题的关键是作辅助线，构造直角三角形． 2．如图，在一张正六边形纸片中剪下两个全等的直角三角形（阴影部分），拼成一个四边形，若拼成的四边形的周长为12，则纸片的剩余部分拼成的五边形的面积为（）A ．B ．C ．8D ．16【答案】B【分析】由题可知，求解剩余部分拼成的五边形的面积，需要利用Rt⊙OBC ，求解正六边形面积和两个直角三角形面积；最后正六边形面积减去两倍Rt⊙OBC 的面积即可．【详解】依题意，如图，根据题意得：⊙BOC ＝30°，设BC ＝x ，则OB ＝2x ，OC =， ⊙2（x +2x ）＝12，解得x ＝2，⊙OC ＝⊙ 11222OBC S BC OC ∆=⨯⨯=⨯⨯=⊙ 正六边形的面积＝1212OBC S ∆⨯=⨯=⊙ 拼成一个四边形的面积为：2OBC S ∆⨯=⊙纸片的剩余部分拼成的五边形的面积为：=故选：B ．本题考查正六边形的性质及面积求法，重点在于利用正六边形分解成12个全等直角三角形的方法． 3．如图，两个正六边形ABCDEF 、EDGHIJ 的顶点A 、B 、H 、I 在同一个圆上，点P 在ABI 上，则tan⊙API 的值是（）A ．B ．C ．2D ．1【答案】A【分析】连接AE ，EI ，AH ，过点J 作JM ⊙EI 于M ，证明90AIH ∠=︒，设HI JI JE a ===，求出AI 即可．【详解】解：如图，连接AE ，EI ，AH ，过点J 作JM ⊙EI 于M ．⊙ABCDEF 是正六边形，⊙⊙DEF ＝⊙F ＝120°，⊙F A ＝FE ，⊙⊙FEA ＝⊙F AE ＝30°，⊙⊙AED ＝90°，同法可证，⊙DEI ＝⊙EIH ＝90°，⊙⊙AED +⊙DEI ＝180°，⊙A ，E ，I 共线，设HI JI JE a ===，⊙JM ⊙EI ，⊙EM ＝MI， ⊙AI ＝2EI ＝a ，⊙⊙API ＝⊙AHI ，⊙tan⊙API ＝tan⊙AHI ＝AI HI＝a= 故选：A ．【点睛】本题考查了正多边形和圆，解直角三角形，圆周角定理等知识，解题关键是正确添加辅助线，构造直角三角形解决问题．4，这个正六边形的面积为（）A ．12B．C．D．【答案】B【分析】根据正六边形的特点，通过中心作边的垂线，连接半径，结合解直角三角形的有关知识解决．【详解】解：如图，连接OA 、OB ；过点O 作OG ⊙AB 于点G ．在Rt⊙AOG 中，OG =⊙AOG ＝30°，⊙OG ＝OA •cos 30°， ⊙OA 30OG cos ===︒2，⊙这个正六边形的面积＝6S ⊙OAB ＝612⨯⨯2=．故选：B【点睛】此题主要考查正多边形和圆，根据题意画出图形，再根据正多边形的性质及锐角三角函数的定义解答即可．5．已知⊙O的半径是2，一个正方形内接于⊙O，则这个正方形的边长是（）A．B．2C D．4【答案】A【分析】利用正方形的性质结合勾股定理可得出正方形的边长．【详解】解：如图所示：⊙⊙O的半径为2，四边形ABCD是正方形，⊙OA＝OB＝2，⊙AOB＝90°，⊙AB＝=故选：A．【点睛】此题主要考查了正多边形和圆，熟练掌握正方形的性质是解题的关键．6．将一枚飞镖投掷到如图所示的正六边形镖盘上，飞镖落在白色区域的概率为（）A ．12B ．25C ．35D ．23【答案】A【分析】算出白色区域的面积与整个图形的面积之比即为所求概率．【详解】解：如图，过点A 作AG BF ⊥于点G⊙ 六边形ABCDEF 为正六边形，⊙BAF=120∠︒，=60FAG ∠︒设正六边形的边长为a，则22aAG FG ==⨯=，BF=2⊙空白部分的面积为：13322ABF a S S ==⨯⨯=△空白正六边形的面积为：226S ==六⊙飞镖落在白色区域的概率为：12S P S ==空白六故选：A【点睛】本题考查概率的求解，确定白色区域面积占整个图形面积的占比是解题的关键．7．已知正六边形ABCDEF内接于O，若O的直径为2，则该正六边形的周长是（）A．12B．C．6D．【答案】C【分析】如图，连接OA、OB，由正六边形ABCDEF内接于O可得⊙AOB=60°，即可证明⊙AOB是等边三角形，根据O直径可得OA的长，进而可得正六边形的周长．【详解】如图，连接OA、OB，⊙O的直径为2，⊙OA=1，⊙正六边形ABCDEF内接于O，⊙⊙AOB=60°，⊙OA=OB，⊙⊙AOB是等边三角形，⊙AB=OA=1，⊙该正六边形的周长是1×6=6，故选：C．【点睛】本题考查正多边形和圆，正确得出⊙AOB=60°是解题关键．8．若正六边形的半径长为6，则它的边长等于（）A．6B．3C．D．【答案】A【分析】根据正六边形的外接圆半径和正六边形的边长将组成一个等边三角形，即可求解．【详解】正六边形的中心角为360660，那么外接圆的半径和正六边形的边长将组成一个等边三角形，故正六边形的外接圆半径等于6，则正六边形的边长是6．故选：A．【点睛】此题主要考查了正多边形和圆，利用正六边形的外接圆半径和正六边形的边长将组成一个等边三角形得出是解题关键．9．如图，AB，AC分别为O的内接正三角形和内接正四边形的一边，若BC恰好是同圆的一个内接正n边形的一边，则n的值为（）A ．8B ．10C ．12D ．14【答案】C【分析】连接OB ，OC ，OA ，根据圆内接正三角形，正方形可求出AOB ∠，AOC ∠的度数，进而可求BOC ∠的度数，利用360BOC n︒∠=，即可求得答案．【详解】如图：连接OB ，OC ，OA ，ABE △为圆内接正三角形3601203AOB ︒∴∠==︒ 四边形ACDF 为圆内接正方形 360904AOC ︒∴∠==︒ 1209030BOC AOB AOC ∴∠=∠-∠=︒-︒=︒ 若以BC 为边的圆内接正n 边形，则有36030BOC n ︒∠==︒ 12n ∴=故选：C ．【点睛】本题考查了圆内接正多边形中心角的求法，熟练掌握圆内接正多边形的中心角等于360n︒（n 为正多边形的边数）是解题关键．10．如图，圆内接正方形的边长为2，以其各边为直径作半圆，则图中阴影部分的面积为（）A．4B．24π-C．2πD．2π+【答案】A【分析】设正方形的中心为O，连接OA，OB首先求出其长度，再根据阴影部分面积等于四个直径为2的半圆面积之和加上一个边长为2的圆的面积求解即可．【详解】解：设正方形的中心为O，连接OA，OB，由题意可得OA=OB，⊙AOB=90°，AB=2⊙在Rt⊙AOB中，⊙2221=42424 22ABS AB OAππππ⎛⎫⨯⨯+-⨯=+-=⎪⎝⎭阴影故选：A【点睛】本题考查正多边形和圆，勾股定理，正方形的性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题．11．如图，螺母的外围可以看作是正六边形ABCDEF，己知这个正六边形的半径是2，则它的周长是（）A．B．C．12D．24【答案】C【分析】如图，先求解正六边形的中心角AOB ∠，再证明AOB 是等边三角形，从而可得答案．【详解】解：如图，O 为正六边形的中心，,OA OB 为正六边形的半径，1360606AOB ∴∠=⨯︒=︒，2OA OB ==，AOB ∴为等边三角形，2AB ∴=，∴ 正六边形ABCDEF 的周长为62=12.⨯故选：.C【点睛】本题考查的是正多边形与圆，正多边形的半径，中心角，周长，掌握以上知识是解题的关键．12．如图，有一个半径为4cm 的圆形纸片，若在该纸片上沿虚线剪一个最大正六边形纸片，则这个正六边形纸片的边心距是（）．AB ．2cmC ．D ．4cm【答案】C【分析】连接OA 、OB ，根据圆内接正六边形的性质得到⊙AOB 是等边三角形，作OC⊙AB 于C ，求得⊙AOC=30，由OA=4cm ，得到AC=2cm ，根据勾股定理求出=．【详解】如图，连接OA、OB，则⊙AOB是等边三角形，作OC⊙AB于C，⊙⊙AOB是等边三角形，⊙⊙OAB=60︒，⊙⊙AOC=30，⊙OA=4cm，⊙AC=2cm，=，故选：C．．【点睛】此题考查圆内接正六边形的性质，等边三角形的性质，勾股定理，直角三角形30度角所对的直角边等于斜边的一半的性质，熟记圆内接正六边形的性质是解题的关键．13．如图，正六边形ABCDEF内接于O，连接AC，则BAC∠的度数是（）A．60︒B．50︒C．40︒D．30【答案】D【分析】连接BO、CO，根据正六边形的性质可求⊙BOC，再根据圆周角的性质可求BAC∠．【详解】解：连接BO、CO，在正六边形ABCDEF中，⊙BOC=3606︒=60°，⊙⊙BAC=12⊙BOC=30°，故选：D ．【点睛】本题考查了正六边形的性质和圆周角的性质，连接半径，求圆心角是解题关键．14．如图，正ABC 内接于半径是1的圆，则阴影部分的面积是（）A ．4π-B ．4π-C ．2π-D ．2π- 【答案】A【分析】设该圆的圆心为O ，连接OA 、OB ，延长AO 交BC 于点D ，根据题意可知：O 为ABC 的中心，OA=OB=1，⊙ABC=60°从而求出⊙1，然后根据30°所对的直角边是斜边的一半和勾股定理即可求出OD 和BD ，然后根据垂径定理求出BC ，最后根据S 阴影=S 圆－S ⊙ABC 即可求出结论．【详解】解：设该圆的圆心为O ，连接OA 、OB ，延长AO 交BC 于点D ，⊙正ABC内接于半径是1的圆，⊙O为ABC的中心，OA=OB=1，⊙ABC=60°⊙⊙1=12⊙ABC=30°，AD⊙BC在Rt⊙ODB中，OD=12OB=12，=⊙AD=OA＋OD=32，⊙S阴影=S圆－S⊙ABC=21π－12 BC·AD=π－4故选A．【点睛】此题考查的是正多边形与圆、垂径定理、等边三角形的性质和直角三角形的性质，掌握正多边形中心的性质、垂径定理、等边三角形的性质和直角三角形的性质是解题关键．15．公元3世纪，刘徽发现可以用圆内接正多边形的周长近似地表示圆的周长．如图所示，他首先在圆内画一个内接正六边形，再不断地增加正多边形的边数；当边数越多时，正多边形的周长就越接近于圆的周长．刘徽在《九章算术》中写道：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣．”我们称这种方法为刘徽割圆术，它开启了研究圆周率的新纪元．小牧通过圆内接正n边形，使用刘徽割圆术，得到π的近似值为（）A ．360sin 2n n ︒⋅B ．3602sin n n ︒⋅C ．3602sin 2n n ︒⋅D ．360sin n n︒⋅ 【答案】A【分析】如详解图，先利用三角函数的知识把正n 边形的边长用含有n 的式子表达出来，求解出正n 边形的周长，再利用正n 边形的周长无限接近圆的周长即可求解．【详解】如图：36012n︒∠= ， 360sin 2a b n︒= 360sin 2a b n︒=，则正n 边形的周长为：36022sin 2L an bn n︒== ，圆的周长为：2L b π=，由圆的内接正n 边形的周长无限接近圆的周长可得：3602sin22bn b n π︒≈ 整理得：360sin2n nπ︒≈ 故选：A ．【点睛】本题考查了极限的思想，抓住圆内接正n 边形的周长无限接近圆的周长是解题关键．16．如图，O 的内接正六边形ABCDEF 的边长为1，则BC 的长为（）A ．14πB ．13π C ．23π D ．π【答案】B【分析】如图（见解析），先根据圆内接正六边形的性质求出中心角60BOC ∠=︒，再根据等边三角形的判定与性质可得1OB OC BC ===，然后利用弧长公式即可得．【详解】如图，连接OB 、OC ，由题意得：1BC =，正六边形ABCDEF 是O 的内接正六边形，∴中心角360606BOC ︒∠==︒，又OB OC =， BOC ∴是等边三角形，1OB OC BC ∴===，则BC 的长为60111803ππ⨯=，故选：B ．【点睛】本题考查了圆内接正六边形的性质、弧长公式等知识点，熟练掌握圆内接正六边形的性质是解题关键．17．如图，⊙O与正六边形OABCDE的边OA、OE分别交于点F、G，点M为劣弧FG的中点．若FM＝，则⊙O的半径为（）A．2B C．D．【答案】C【分析】连接OM，根据正六边形OABCDE和点M为劣弧FG的中点，可得⊙OFM是等边三角形，进而可得⊙O的半径．【详解】解：如图，连接OM，⊙正六边形OABCDE，⊙⊙FOG＝120°，⊙点M为劣弧FG的中点，⊙⊙FOM＝60°，OM＝OF，⊙⊙OFM是等边三角形，⊙OM＝OF＝FM＝则⊙O的半径为．故选：C．【点睛】本题考查正多边形与圆，解题的关键是学会添加常用辅助线．18．如图，正方形ABCD 和正三角形AEF 内接于O ，DC 、BC 交EF 于G 、H ，若正方形ABCD 的边长是4，则GH 的长度为( )A ．B ．CD 【答案】A【分析】连接AC 交EF 于M ，连接OF ，根据正方形的性质、等边三角形的性质及等腰三角形的性质即可求解．【详解】解：连接AC 交EF 于M ，连接OF ，四边形ABCD 是正方形，90B ∴∠=︒，AC ∴是O 的直径，ACD ∴∆是等腰直角三角形，AC ∴==OA OC ∴==AEF ∆是等边三角形，AM EF ∴⊥，30OFM ∠=︒，12OM OF ∴==CM ∴=45ACD ∴∠=︒，90CMG ∠=︒，45CGM ∴∠=︒，CGH ∴∆是等腰直角三角形，2GH CM ∴==故选：A ．【点睛】本题考查正多边形与圆的关系，涉及到特殊锐角三角函数值、正方形的性质、等边三角形的性质及等腰三角形的性质，解题的关键是综合运用所学知识．19．如图，圆内接正八边形的边长为1，以正八边形的一边AB 作正方形ABCD ，将正方形ABCD 绕点B 顺时针旋转，使AB 与正八边形的另一边BC '重合，则正方形ABCD 与正方形A BC D '''重叠部分的面积为（）A 1B ．12CD 【答案】A【分析】先计算出正八边形的内角⊙ABC′=135°，再利用旋转的性质得⊙ABC=⊙A′BC′=90°，⊙BA′D′=⊙BAD=90°，所以⊙ABA′=135°-90°=45°，则延长BA′过点D ，如图，然后利用正方形ABCD 与正方形A′BC′D′重叠部分的面积=S ⊙BDC -S ⊙DA′E 进行计算．【详解】正八边形的内角(82)1801358ABC ︒'︒-⨯∠==，正方形ABCD 绕点B 顺时针旋转，使BC 与正八边形的另一边BC '重合，90,90ABC A BC BA D BAD ∴∠=∠''=︒∠''=∠=︒．1359045ABA ∴∠'=︒-︒=︒．如解图，延长BA '至点D ，DC 与A D ''相交于点E ，,,11AB A B AB BD =∴'==='1A D ∴=．⊙正方形ABCD 与正方形A BC D '''重叠部分的面积11111)1)122BDC DA E S S '=-=⨯⨯-⨯⨯= 故选：A ．【点睛】本题考查正多边形与圆，把一个圆分成n 等分，依次连接各点所得的多边形是这个圆的内接正多边形，也考查了正方形和正八边形的性质．20．如图，正六边形ABCDEF 内接于O ，过点O 作OM ⊥弦BC 于点M ，若O 的半径为4，则弦心距OM 的长为（）A ．BC ．2D ．【答案】A【分析】如图，连接OB 、OC ．首先证明⊙OBC 是等边三角形，求出BC 、BM ，根据勾股定理即可求出OM ．【详解】解：如图，连接OB 、OC ．⊙ABCDEF是正六边形，⊙⊙BOC=60°，OB=OC=4，⊙⊙OBC是等边三角形，⊙BC=OB=OC=4，⊙OM⊙BC，⊙BM=CM=2，在Rt⊙OBM中，2222OM OB BM=-=-=，4223故选：A．【点睛】本题考查正多边形与圆、等边三角形的性质、勾股定理、弧长公式等知识，解题的关键是记住等边三角形的性质，弧长公式，属于基础题，中考常考题型．21．如图，⊙O是正方形ABCD与正六边形AEFCGH的外接圆．则正方形ABCD与正六边形AEFCGH的周长之比为（）A．⊙ 3B C D．【答案】A【分析】计算出在半径为R的圆中，内接正方形和内接正六边形的边长即可求出．【详解】解：设此圆的半径为R，R ，它的内接正六边形的边长为R ，内接正方形和内接正六边形的周长比为：R ：6R ＝．故选：A ．【点睛】本题考查了正多边形和圆，找出内接正方形与内接正六边形的边长关系，是解决问题的关键．22．如图，正五边形ABCDE 和等边AFG 内接于O ，则GFD ∠的度数是（）A ．10︒B ．12︒C ．15︒D ．20︒【答案】B【分析】如图（见解析），先根据正五边形的内角和定理与性质可得108ABC BCD ∠=∠=︒，BC CD =，再根据三角形的内角和定理、等腰三角形的性质可得36CBD ∠=︒，从而可得72ABD ∠=︒，然后根据圆周角定理可得72AFD ABD ∠=∠=︒，最后根据等边三角形的性质可得60AFG =︒∠，据此即可得出答案．【详解】如图，连接BD ，五边形ABCDE 是正五边形，()521801085ABC BCD -⨯︒∴∠=∠==︒，BC CD =， 1(180)362CBD CDB BCD ∴∠=∠=︒-∠=︒， 72ABD ABC CBD ∴∠=∠-∠=︒，由圆周角定理得：72AFD ABD ∠=∠=︒，又AFG 是等边三角形，60AFG ∴∠=︒，726012GFD AFD AFG ∴∠=∠-∠=︒-︒=︒，故选：B ．【点睛】本题考查了正五边形的内角和与性质、等腰三角形和等边三角形的性质、圆周角定理等知识点，通过作辅助线，利用到圆周角定理是解题关键．23．如图，在平面直角坐标系中，将边长为1的正六边形OABCDE 绕点O 顺时针旋转i 个45°，得到正六边形i i i i i OA B C D E ，则正六边形(2020)i i i i i OA B C D E i =的顶点i C 的坐标是（）A ．(1,B ．C ．(1,2)-D ．(2,1)【答案】A【分析】如图，以O 为圆心，OC 为半径作,O 得到将边长为1的正六边形OABCDE 绕点O 顺时针旋转i 个45°，即把OC 绕点O 顺时针旋转i 个45°，2020C 与4C 重合，利用正六边形的性质与锐角三角函数求解C 的坐标，利用4,C C 关于原点成中心对称，从而可得答案．【详解】解：如图，以O 为圆心，OC 为半径作,O将边长为1的正六边形OABCDE 绕点O 顺时针旋转i 个45°，即把OC 绕点O 顺时针旋转i 个45°，C 旋转后的对应点依次记为12,...C C ， 1周角＝360,︒OC ∴绕点O 顺时针旋转顺时针旋转8次回到原位置，20208252...4,÷=2020C ∴与4C 重合，4,C C 关于原点成中心对称，连接,CE正六边形OABCDE ，,120.DC DE CDE DEO EOA ∴=∠=∠=∠=︒30,90,60,DEC CEO COE ∴∠=︒∠=︒∠=︒1,OE =tan tan 60CE COE OE∴∠=︒==CE ∴= (,C ∴- 4,C C 关于原点成中心对称，((420201,,1,.C C ∴故选A ．【点睛】本题考查的是旋转的旋转，正六边形的性质，圆的对称性，锐角三角函数，掌握以上知识是解题的关键． 24．设边长为a 的等边三角形的高、内切圆的半径、外接圆的半径分别为h 、r 、R ，则下列结论不正确．．．的是（）A ．h R r =+B ．2R r =C ．4r a =D ．3R a = 【答案】C【分析】将图形标记各点,即可从图中看出长度关系证明A 正确,再由构造的直角三角形和30°特殊角证明B 正确,利用勾股定理求出r 和R,即可判断C 、D ．【详解】如图所示,标上各点⊙AO 为R⊙OB 为r ⊙AB 为h，从图象可以得出AB=AO+OB⊙即h R r =+⊙A 正确⊙⊙三角形为等边三角形⊙⊙⊙CAO=30°⊙根据垂径定理可知⊙ACO=90°⊙⊙AO=2OC⊙即R=2r ⊙B 正确⊙在Rt⊙ACO 中，利用勾股定理可得⊙AO 2=AC 2+OC 2⊙即22212R a r ⎛⎫=+ ⎪⎝⎭⊙由B 中关系可得⊙()222122r a r ⎛⎫=+ ⎪⎝⎭，解得6=r a ⊙则3R a =⊙所以C 错误，D 正确；故选：C ．【点睛】本题考查圆与正三角形的性质结合,关键在于巧妙利用半径和构建直角三角形．25．如图，在边长为1的正六边形ABCDEF 中，M 是边DE 上一点，则线段AM 的长可以是（）A ．1.4B ．1.6C ．1.8D ．2.2【答案】C【分析】连接AE，AD，过点F作FH⊙AE于点H，则AM的长介于AE和AD之间，分别求出AE，AD的长，再结合选项即可得到问题答案．【详解】解：连接AE，AD，，过点F作FH⊙AE于点H，⊙多边形ABCDEF是正六边形，⊙⊙AFE=⊙DEF=(6-2) ×180°÷6=120°，⊙⊙FEH=30°，⊙AEM=90°，⊙HF=12AF=12，=，＜AM＜2，故选：C．【点睛】本题考查了正多边形，以及勾股定理等知识，熟记和正多边形有关的各种性质以及正确的添加出图形的辅助线是解题的关键．26．如图，圆内接正六边形的边长为4，以其各边为直径作半圆，则图中阴影部分的面积为（）A ．4πB ．4πC ．8πD ．4π 【答案】A【分析】正六边形的面积加上六个小半圆的面积，再减去中间大圆的面积即可得到结果．【详解】解：正六边形的面积为：1462⨯⨯=，六个小半圆的面积为：22312ππ⋅⨯=，中间大圆的面积为：2416ππ⋅=，所以阴影部分的面积为：12164πππ+-=-，故选：A ．【点睛】本题考查了正多边形与圆，圆的面积的计算，正六边形的面积的计算，正确的识别图形是解题的关键． 27．如图，AB 是O 的直径，O 的半径为2，AD 为正十边形的一边，且//AD OC ，则劣弧BC 的长为（）A ．πB ．32πC ．43πD ．65π 【答案】D【分析】利用正十边形的中心角求法得⊙AOD=36º，再根据等腰三角形的性质及由平行线的性质求得⊙AOC 的度数，进而求得⊙BOC ，然后用弧长公式求解即可．【详解】⊙AD 为正十边形的一边， ⊙⊙AOD=36010=36º， ⊙OA=OD ， ⊙⊙OAD=⊙ODA=180362-=72º， ⊙AD⊙OC ，⊙⊙AOC=⊙OAD=72º，⊙⊙BOC=180º-⊙AOC=180º-72º=108º，⊙劣弧BC 的长为108261805ππ⨯=，故选D ．【点睛】本题考查了正多边形的中心角、圆的定义、等腰三角形的性质、平行线的性质、弧长公式，熟练掌握基本图形的性质，会利用弧长公式求解弧长是解答的关键．二、填空题28．公元263年左右，我国数学家刘徽发现当正多边形的边数无限增加时，这个正多边形面积可无限接近它的外接圆的面积，因此可以用正多边形的面积来近似估计圆的面积，如图，O 是正十二边形的外接圆，设正十二边形的半径OA 的长为1，如果用它的面积来近似估计O 的面积，那么O 的面积约是___．【答案】3【分析】设AB 为正十二边形的边，连接OB ，过A 作AD OB ⊥于D ，由正十二边形的性质得出30AOB ∠=，由直角三角形的性质得出1122AD OA ==，求出AOB 的面积1124OB AD ⨯==，即可得出答案．【详解】解：设AB 为正十二边形的边，连接OB ，过A 作AD OB ⊥于D ，如图所示：3601130,,1222AOB AD OB AD OA ∠∴==⊥∴==， AOB ∴的面积111112224OB AD =⨯=⨯⨯= ∴正十二边形的面积11234=⨯=， O ∴的面积≈正十二边形的面积3=，故答案为：3．【点睛】本题考查了正多边形和圆、正十二边形的性质、直角三角形的性质以及三角形面积等知识；熟练掌握正十二边形的性质是解题的关键．29．如图，在正五边形ABCDE 中，AC 为对角线，以点A 为圆心，AE 为半径画圆弧交AC 于点F ，连结EF ，则⊙1的度数为__．【答案】54°【分析】根据五边形的内角和公式求出⊙ABC ，根据等腰三角形的性质，三角形内角和的定理计算⊙BAC ，再求⊙EAF ，利用圆的性质得AE=AF ，最后求出⊙1即可．【详解】解：⊙五边形ABCDE 是正五边形，⊙⊙EAB ＝⊙ABC ＝()5-21805⨯︒＝108°， ⊙BA ＝BC ，⊙⊙BAC＝⊙BCA＝180-1082︒︒＝36°，⊙⊙EAF＝108°﹣36°＝72°，⊙以点A为圆心，AE为半径画圆弧交AC于点F，⊙AE＝AF，⊙⊙1＝180-722︒︒＝54°．故答案为：54°．【点睛】本题考查了正多边形的内角与圆，熟练掌握正多边形的内角的计算公式、和圆的性质，等腰三角形的性质是解题的关键．30．如图，有一个圆O和两个正六边形T1，T2．T1的6个顶点都在圆周上，T2的6条边都和圆O相切(我们称T1，T2分别为圆O的内接正六边形和外切正六边形)．若设T1，T2的边长分别为a，b，圆O的半径为r，则r：a=____；r：b=____；正六边形T1，T2的面积比S1：S2的值是____．【答案】1：1 2 3：4【分析】根据圆内接正六边形的边长等于它的半径可得r与a比值，在由圆的半径和正六边形的半边及正六边形对角线的一半组成的直角三角形中，根据锐角三角函数即可求得r与b的比值；根据相似多边形的面积比是相似比的平方，由r：a与r：b 可求a：b，继而即可求解．【详解】连接OE，OG，OF，⊙EF=a，T1为正六边形，⊙⊙OEF为等边三角形，OE为圆O的半径r，⊙a：r=1：1，即r：a=1：1⊙，由题意可知：OG为⊙FOE的平分线，即⊙EOG=12⊙EOF=30°，在Rt⊙OEG中，OE=r，OG=b，⊙OE OG =r b=cos⊙EOG=cos30°，即r b⊙r ：2⊙，⊙由⊙⊙得，a ：2，且两个正六边形T 1，T 2相似，⊙S 1：S 2=a 2：b 2=3：4，故答案为：1：12；3：4．【点睛】本题考查正多边形与圆的有关知识，解题的关键是学会构造由正多边形半径，边心距、半边组成的直角三角形，掌握锐角三角函数，注意相似多边形的面积比即是相似比的平方．31．如图，正六边形ABCDEF 的边长为2，以点A 为圆心，AB 的长为半径，作扇形ABF ，则图中阴影部分的面积为_____（结果保留根号和π）．【答案】43π 【分析】设正六边形的中心为点O ，连接OD 、OE ，作OH⊙DE 于H ，根据正多边形的中心角公式求出⊙DOE ，求出OH 和正六边形ABCDEF 的面积，再求出⊙A ，利用扇形面积公式求出扇形ABF 的面积，即可得出结果．【详解】解：设正六边形的中心为点O ，连接OD 、OE ，作OH⊙DE 于H ，如图所示：⊙DOE ＝3606︒＝60°， ⊙OD ＝OE ＝DE ＝2，⊙OH⊙正六边形ABCDEF 的面积＝12＝ ⊙A ＝()621801206-⨯︒=︒， ⊙扇形ABF 的面积2120243603ππ⨯==，⊙图中阴影部分的面积43π=，故答案为：43π．【点睛】本题考查的是正多边形和圆、扇形面积计算，掌握正多边形的中心角、内角的计算公式、扇形面积公式是解题的关键．32．如图，等边⊙ABC 内接于⊙O ，BD 为⊙O 内接正十二边形的一边，CD=等于_________．【答案】252542π- 【分析】首先连接OB，OC，OD，由等边⊙ABC内接于⊙O，BD为内接正十二边形的一边，可求得⊙BOC，⊙BOD 的度数，则证得⊙COD是等腰直角三角形，并利用勾股定理求得圆的半径，最后利用S阴影=S扇形OCD-S⊙OCD 进行计算后即可得出答案．【详解】解：连接OB，OC，OD，⊙等边⊙ABC内接于⊙O，BD为内接正十二边形的一边，⊙⊙BOC＝13×360°＝120°，⊙BOD＝112×360°＝30°，⊙⊙COD＝⊙BOC−⊙BOD＝90°，⊙OC＝OD，⊙⊙OCD＝45°，⊙OC2+ OD2＝CD2．即2OC2=50，⊙OC=5，⊙S阴影=S扇形OCD-S⊙OCD=90251252555360242ππ-⨯⨯=-．故答案为：2525 42π-．【点睛】此题考查了正多边形与圆、扇形面积的计算等知识，掌握辅助线的作法以及数形结合思想的应用是解题的关键．三、解答题33．已知：如图，A为⊙O上一点；求作：⊙O的内接正方形ABCD．【答案】见解析【分析】先作直径AC，再过O点作AC的垂线交⊙O于D、B，然后连接AB、AD、CD、CB即可．【详解】解：如图，四边形ABCD为所作．【点睛】本题考查了作图——复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．的余角34．如图，正五边形ABCDE内接于O，P为DE上的一点（点P不与点,D E重合），求CPD的度数．【答案】54°【分析】连接OC，OD．求出⊙COD的度数，再根据圆周角定理即可解决问题．【详解】如图，连接,OC OD．⊙五边形ABCDE是正五边形，⊙360725COD︒∠==︒，⊙1362CPD COD∠=∠=︒，⊙90°-36°=54°，⊙CPD∠的余角的度数为54°．【点睛】本题考查了正多边形和圆、圆周角定理等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．35．如图1，等边ABC内接于⊙O，连接CO并延长交⊙O于点D．（1）可以证明CD垂直平分AB，写出AD与DB的数量关系：___．（2）请你仅使用无刻度的直尺按要求作图：⊙在图1中作出一个正六边形，保留作图痕迹（作图过程用虚线表示，作图结果用实线表示）．⊙请在图2中作出⊙O的内接正六边形ADBECF的一条不经过顶点的对称轴，保留作图痕迹(作图过程用虚线表示，作图结果用实线表示）．【答案】（1）AD DB=；（2）⊙见解析，⊙见解析【分析】（1）结合外心的定义和等边三角形的性质推断出CD垂直平分AB，从而利用垂径定理得出结论即可；（2）⊙结合（1）的结论，可直接连接AO，BO，分别延长与圆相交，再顺次连接各交点即可；⊙如图，延长AF，EC，交于一点，此时可构成等边三角形，从而连接交点与圆心的直线即为所求的对称轴．【详解】（1）AD DB=，⊙O为三角形的外心，⊙O为三角形三边中垂线的交点，又⊙三角形为等边三角形，⊙可得CD垂直平分AB，根据垂径定理可得：AD DB=；（2）⊙如图所示，在（1）的基础之上，连接AO，并延长至E，连接BO，并延长至F，顺次连接圆周上各点即可；⊙如图所示：（方法不唯一）【点睛】本题主要考查复杂作图，以及正多边形与圆之间的关系，熟练掌握正多边形的性质是解题关键．36．如图M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDEFG…的边AB、BC上的点，且BM＝CN，连接OM、ON（1）求图1中⊙MON 的度数（2）图2中⊙MON 的度数是，图3中⊙MON 的度数是（3）试探究⊙MON 的度数与正n 边形边数n 的关系是____【答案】（1）120︒；（2）90︒，72︒；（3）360MON n︒∠=．【分析】（1）如图（见解析），先根据圆内接正三角形的性质可得3603120BOC ，再根据圆内接正三角形的性质可得30OBM OCN ∠=∠=︒，然后根据三角形全等的判定定理与性质可得BOM CON ∠=∠，最后根据角的和差、等量代换即可得；（2）如图（见解析），先根据圆内接正方形的性质可得360904BOC ︒∠==︒，再根据（1）同样的方法可得90MON BOC ∠=∠=︒；先根据圆内接正五边形的性质可得中心角360725BOC ︒∠==︒，再根据（1）同样的方法可得72MON BOC ∠=∠=︒；（3）根据（1）、（2）归纳类推出一般规律即可得．【详解】（1）如图，连接OB 、OC ，则OC OB =，ABC 是O 内接正三角形，∴中心角3603120BOC， ⊙点O 是O 内接正三角形ABC 的内心，⊙1130,3022OBM ABC OCN ACB ∠=∠=︒∠=∠=︒， ⊙OBM OCN ∠=∠，在OMB △和ONC 中，BM CN OBM OCN OB OC =⎧⎪∠=∠⎨⎪=⎩，。

人教版九年级数学上册24.3 正多边形和圆同步练习含答案

第24章 24.3《正多边形和圆》同步练习及答案 (1) 1．边长为a的正六边形的边心距是__________，周长是____________，面积是___________。

2．如图1，正方形的边长为a，以顶点B、D为圆心，以边长a为半径分别画弧，在正方形内两弧所围成图形的面积是___________。

(1) (2) (3)3．圆内接正方形ABCD的边长为2，弦AE平分BC边，与BC交于F，则弦AE的长为__________。

4．正六边形的面积是183，则它的外接圆与内切圆所围成的圆环面积为_________。

5．圆内接正方形的一边截成的小弓形面积是2π-4，则正方形的边长等于__________。

6．正三角形的内切圆半径、外接圆半径和高的比为___________。

7．在半径为R的圆中，内接正方形与内接正六边形的边长之比为___________。

8．同圆的内接正n边形与外切正n边形边长之比是______________。

9．正三角形与它的内切圆及外接圆的三者面积之比为_____________。

10．正三角形的外接圆半径为4cm，以正三角形的一边为边作正方形，则此正方形的外接圆半径长为___________。

B卷1．正方形的内切圆半径为r，这个正方形将它的外接圆分割出四个弓形，其中一个弓形的面积为_________。

2．如果正三角形的边长为a，那么它的外接圆的周长是内切圆周长的_______倍。

3．如图2，正方形边长为2a，那么图中阴影部分的面积是__________。

4．正多边形的一个内角等于它的一个外角的8倍，那么这个正多边形的边数是________。

5．半径为R的圆的内接正n边形的面积等于__________。

6．如果圆的半径为a，它的内接正方形边长为b，该正方形的内切圆的内接正方形的边长为c，则a,b,c间满足的关系式为___________。

7．如图3，正△ABC内接于半径为1cm的圆，则阴影部分的面积为___________。

人教版九年级数学上《正多边形和圆》练习题含答案

24.3正多边形和圆知识点1正多边形与圆的关系1．如果一个四边形的外接圆与内切圆是同心圆，那么这个四边形一定是()A．矩形B．菱形C．正方形D．不能确定2．如图24－3－1所示，已知△ABC是⊙O的内接等腰三角形，顶角∠BAC＝36°，弦BD，CE分别平分∠ABC，∠ACB.求证：五边形AEBCD是正五边形．图24－3－1知识点2与正多边形有关的计算3．如果一个正多边形的中心角为72°，那么这个正多边形的边数是()A．4 B．5 C．6 D．74．若正方形的边长为6，则其内切圆半径的大小为()A．3 2 B．3 C．6 D．6 25．2016·南平若正六边形的半径为4，则它的边长等于()A．4 B．2 C．2 3 D．4 36．如图24－3－2所示，正六边形ABCDEF内接于⊙O，则∠ADB的度数是()图24－3－2A．60°B．45°C．30°D．22.5°7．正八边形的中心角等于________度．8．将一个边长为1的正八边形补成如图24－3－3所示的正方形，这个正方形的边长等于________．(结果保留根号)图24－3－39．2017·资阳边长相等的正五边形和正六边形如图24－3－4所示拼接在一起，则∠ABC ＝________°.图24－3－410．如图24－3－5，已知正五边形ABCDE，M是CD的中点，连接AC，BE，AM.求证：(1)AC＝BE；(2)AM⊥CD.图24－3－5知识点3与正多边形有关的作图11．已知⊙O和⊙O上的一点A，作⊙O的内接正方形和内接正六边形(点A为正方形和正六边形的顶点)．12．如图24－3－6所示，⊙O的内接多边形的周长为3，⊙O的外切多边形的周长为3.4，则下列各数中与此圆的周长最接近的是()图24－3－6A. 6B.8C.10D.1713．若AB是⊙O内接正五边形的一边，AC是⊙O内接正六边形的一边，则∠BAC等于()A．120°B．6°C．114°D．114°或6°14．若等腰直角三角形的外接圆半径的长为2，则其内切圆半径的长为()A. 2 B．2 2－2C．2－ 2 D.2－115．2017·达州以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形，则该三角形的面积是()A.22 B.32 C. 2 D.316．2017·云南如图24－3－7，边长为4的正方形ABCD外切于⊙O，切点分别为E，F，G，H.则图中阴影部分的面积为________．图24－3－717．如图24－3－8，正六边形ABCDEF内接于⊙O，若⊙O的内接正三角形ACE的面积为48 3，试求正六边形的周长．图24－3－818．如图24－3－9①②③④，M，N分别是⊙O的内接正三角形ABC，正方形ABCD，正五边形ABCDE，…，正n边形ABCDEFG…的边AB，BC上的点，且BM＝CN，连接OM，ON.图24－3－9(1)求图①中∠MON的度数；(2)图②中，∠MON的度数是________，图③中∠MON的度数是________；(3)试探究∠MON的度数与正n边形的边数n的关系(直接写出答案)．教师详解详析1．C [解析] 只有正多边形的外接圆与内切圆才是同心圆，故这个四边形是正方形．故选C .2．证明：∵△ABC 是等腰三角形，且∠BAC ＝36°， ∴∠ABC ＝∠ACB ＝72°.又∵BD 平分∠ABC ，CE 平分∠ACB ， ∴∠ABD ＝∠CBD ＝∠BCE ＝∠ACE ＝36°，即∠BAC ＝∠ABD ＝∠CBD ＝∠BCE ＝∠ACE ， ∴BC ︵＝AD ︵＝CD ︵＝BE ︵＝AE ︵，∴A ，E ，B ，C ，D 是⊙O 的五等分点， ∴五边形AEBCD 是正五边形．3．B [解析] 设这个正多边形为正n 边形，由题意可知72n ＝360，解得n ＝5.故选B . 4．B5．A [解析] 正六边形的中心角为360°÷6＝60°，那么外接圆的半径和正六边形的边组成一个等边三角形．因为正六边形的外接圆半径等于4，所以正六边形的边长等于4.6．C [解析] 连接OB ，则∠AOB ＝60°， ∴∠ADB ＝12∠AOB ＝30°.7．45 8．1＋2[解析] 如图，∵△BDE 是等腰直角三角形，BE ＝1，∴BD ＝22， ∴正方形的边长等于AB ＋2BD ＝1＋ 2.9．24 [解析] 正六边形的一个内角＝16×(6－2)×180°＝120°，正五边形的一个内角＝15×(5－2)×180°＝108°，∴∠BAC ＝360°－(120°＋108°)＝132°.∵两个正多边形的边长相等，即AB ＝AC ，∴∠ABC ＝12×(180°－132°)＝24°.10．证明：(1)由五边形ABCDE 是正五边形，得AB ＝AE ，∠ABC ＝∠BAE ，AB ＝BC ， ∴△ABC ≌△EAB ，∴AC ＝BE.(2)连接AD ，由五边形ABCDE 是正五边形，得AB ＝AE ，∠ABC ＝∠AED ，BC ＝ED ， ∴△ABC ≌△AED ， ∴AC ＝AD.又∵M 是CD 的中点， ∴AM ⊥CD. 11．解：如图所示．作法：①作直径AC ；②作直径BD ⊥AC ，依次连接AB ，BC ，CD ，DA ，则四边形ABCD 是⊙O 的内接正方形；③分别以点A ，C 为圆心，OA 的长为半径画弧，交⊙O 于点E ，H 和F ，G ，顺次连接AE ，EF ，FC ，CG ，GH ，HA ，则六边形AEFCGH 为⊙O 的内接正六边形．12．C [解析] 根据两点之间，线段最短可得圆的周长大于3而小于3.4，选项中只有C 满足要求．13．D [解析] 分两种情况考虑：(1)如图①所示，∵AB 是⊙O 内接正五边形的一边，∴∠AOB ＝360°5＝72°.∵AC 是⊙O 内接正六边形的一边，∴∠AOC ＝360°6＝60°，∴∠BOC ＝72°－60°＝12°，∴∠BAC ＝12∠BOC ＝6°.(2)如图②所示，∠AOB ＝72°，∠AOC ＝60°，∴∠OAB ＝54°，∠OAC ＝60°，∴∠BAC ＝60°＋54°＝114°.综上所述，可知选D .14．B [解析] ∵等腰直角三角形的外接圆半径为2，∴此直角三角形的斜边长为4，两条直角边的长均为2 2.如图，根据三角形内切圆的性质可得CD ＝CE ＝r ，AD ＝BE ＝AO ＝BO ＝2 2－r ，∴AB ＝AO ＋BO ＝4 2－2r ＝4，解得r ＝2 2－2.故选B .15．A [解析] 如图①，∵OC ＝2，∴OD ＝1；如图②，∵OB ＝2，∴OE ＝2；如图③，∵OA ＝2，∴OD ＝3，则该三角形的三边长分别为1，2， 3. ∵12＋(2)2＝(3)2， ∴该三角形是直角三角形，∴该三角形的面积是12×1×2＝22.故选A .16．2π＋4 [解析] 如图，连接HO ，并延长交BC 于点P ，连接EO ，并延长交CD 于点M.∵正方形ABCD 外切于⊙O ， ∴∠A ＝∠B ＝∠AHP ＝90°，∴四边形AHPB 为矩形，∴∠OPB ＝90°. 又∵∠OFB ＝90°，∴点P 与点F 重合， ∴HF 为⊙O 的直径，同理：EG 为⊙O 的直径．由∠D ＝∠OGD ＝∠OHD ＝90°且OH ＝OG 知，四边形DGOH 为正方形．同理：四边形OGCF 、四边形OFBE 、四边形OEAH 均为正方形， ∴DH ＝DG ＝GC ＝CF ＝2，∠HGO ＝∠FGO ＝45°， ∴∠HGF ＝90°，GH ＝GF ＝GC 2＋CF 2＝2 2，则阴影部分面积＝12S ⊙O ＋S △HGF＝12·π·22＋12×2 2×2 2 ＝2π＋4. 故答案为2π＋4.17．解：如图，连接OA ，作OH ⊥AC 于点H ，则∠OAH ＝30°.在Rt △OAH 中，设OA ＝R ，则OH ＝12R ，由勾股定理可得AH ＝OA 2－OH 2＝R 2－（12R ）2＝123R. 而△ACE 的面积是△OAH 面积的6倍，即6×12×12 3R ×12R ＝48 3，解得R ＝8，即正六边形的边长为8，所以正六边形的周长为48.18．解：(1)方法一：如图①，连接OB ，OC.图①∵正三角形ABC 内接于⊙O ，∴∠OBM ＝∠OCN ＝30°，∠BOC ＝120°.又∵BM ＝CN ，OB ＝OC ，∴△OBM ≌△OCN ，∴∠BOM ＝∠CON ，∴∠MON ＝∠BOC ＝120°.方法二：如图②，连接OA ，OB.图②∵正三角形ABC内接于⊙O，∴AB＝BC，∠OAM＝∠OBN＝30°，∠AOB＝120°.∵BM＝CN，∴AM＝BN.又∵OA＝OB，∴△AOM≌△BON，∴∠AOM＝∠BON，∴∠MON＝∠AOB＝120°.(2)90°72°(3)∠MON＝360°n.。

中考数学一轮复习几何部分专题3：正多边形和圆(教师用,附答案)

中考数学一轮复习几何部分专题3：正多边形和圆必考知识点：1、掌握正多边形的边长、半径、中心角、边心距、周长、面积等的计算；2、掌握圆周长、弧长的计算公式，能灵活运用它们来计算组合图形的周长；3、掌握圆、扇形、弓形的面积计算方法，会通过割补、等积变换求组合图形的面积；4、掌握圆柱、圆锥的侧面展开图的有关计算。

必考例题：【例1】如图，两相交圆的公共弦AB 为32，在⊙O 1中为内接正三角形的一边，在⊙O 2中为内接正六边形的一边，求这两圆的面积之比。

分析：欲求两圆的面积之比，根据圆的面积计算公式，只须求出两圆的半径3R 与6R 的平方比即可。

解：设正三角形外接圆⊙O 1的半径为3R ，正六边形外接圆⊙O 2的半径为6R ，由题意得：AB R 333=，AB R =6，∴3R ∶6R ＝3∶3；∴⊙O 1的面积∶⊙O 2的面积＝1∶3。

【例2】已知扇形的圆心角为1500，弧长为π20，求扇形的面积。

分析：此题欲求扇形的面积，想到利用扇形的面积公式，lR R n S 213602=π＝扇形，由条件n ＝1500，π20=l 看到，不管是用前者还是用后者都必须求出扇形的半径，怎么求？由条件想到利用弧长公式不难求出扇形半径。

解：设扇形的半径为R ，则180Rn l π＝，n ＝1500，π20=l ∴18015020Rππ＝，24=R ∴ππ24024202121=⨯⨯=lR S ＝扇形。

【例3】如图，已知PA 、PB 切⊙O 于A 、B 两点，PO ＝4cm ，∠APB ＝600，求阴影部分的周长。

分析：此题欲求阴影部分的周长，须求PA 、PB 和⋂AB 的长，连结OA 、OB ，根据切线长定理得PA ＝PB ，∠PAO ＝∠PBO ＝Rt ∠，∠APO ＝∠BPO ＝300，在Rt △PAO 中可求出PA 的长，根据四边形内角和定理可得∠AOB ＝1200，因此可求出⋂AB 的长，从而能求出阴影部分的周长。

初中数学人教版(五四制)九年级上册第三十一章圆31.3 正多边形和圆-章节测试习题(3)

章节测试题1.【答题】半径相等的圆的内接正三角形、正方形、正六边形的边长之比为（）A. 1∶∶B. ∶∶1C. 3∶2∶1D. 1∶2∶3【答案】B【分析】本题考查了正多边形和圆,根据正多边形的性质解答即可.【解答】设圆的半径为R，如图(一)，连接OB，过O作OD⊥BC于D，则∠OBC=30∘,BD=OB⋅cos30∘=R，故BC=2BD=R；如图(二)，连接OB、OC，过O作OE⊥BC于E，则△OBE是等腰直角三角形，2BE2=OB2,即BE=R，故BC=R；如图(三)，连接OA、OB，过O作OG⊥AB，则△OAB是等边三角形，故AG=OA⋅cos60∘=R，AB=2AG=R，故圆内接正三角形、正方形、正六边形的边长之比为R: R:R=::1.2.【答题】使用同一种规格的下列地砖，不能进行平面镶嵌的是（）A. 正三角形地砖B. 正四边形地砖C. 正五边形地砖D. 正六边形地砖【答案】C【分析】本题考查了正多边形和圆,根据正多边形的性质解答即可.【解答】解：A、正三角形的每个内角是60°，能整除360°，能密铺，故A不符合题意；B、正四边形每个内角是90°，能整除360°，能密铺，故B不符合题意；C、正五边形每个内角是180°-360°÷5=108°，不能整除360°，不能密铺，故C符合题意；D、正六边形每个内角是120°，能整除360°，能密铺，故D不符合题意．选C.3.【答题】正六边形的两条平行边之间的距离为1，则它的边长为（）A.B.C.D.【答案】D【分析】本题考查了正多边形和圆,根据正多边形的性质解答即可.【解答】根据题意画出图形,再根据正六边形的性质求出正六边形的一个内角度数,利用垂径定理求出这个内角度数的一半,再利用锐角三角函数的定义求出答案.4.【答题】同圆的内接正三角形与内接正方形的边长的比是（）A.B.C.D.【答案】A【分析】本题考查了正多边形和圆,根据正多边形的性质解答即可.【解答】根据题意画出图形,设出圆的半径,再根据垂径定理,由正多边形及直角三角形的性质求解即可.5.【答题】用若干个全等的正五边形可以拼成一个环状，图中所示的是前3个正五边形的拼接情况，要完全拼成一个圆环还需要的正五边形个数是（）A. 5B. 6D. 8【答案】C【分析】本题考查了正多边形和圆,根据正多边形的性质解答即可.【解答】解：如图，圆心角为∠1，∵五边形的内角和为：（5-2）×180°=3×180°=540°，∴五边形的每一个内角为：540°÷5=108°，∴∠1=108°×2-180°=216°-180°=36°，∵360°÷36°=10，∵360°÷36°=10，∴他要完成这一圆环共需10个全等的五边形．∴要完全拼成一个圆环还需要的正五边形个数是：10-3=7选C.6.【答题】一个边长为2的正多边形的内角和是其外角和的2倍，则这个正多边形的半径是（）B.C. 1D.【答案】A【分析】本题考查了正多边形和圆,根据正多边形的性质解答即可.【解答】解：设多边形的边数为n．因为正多边形内角和为（n-2）•180°，正多边形外角和为360°，根据题意得：（n-2）•180°=360°×2，解得：n=6故正多边形为6边形．边长为2的正六边形可以分成六个边长为2的正三角形，所以正多边形的半径等于2.选A.7.【答题】如图，正十二边形A1A2…A12，连接A3A7，A7A10，则∠A3A7A10的度数为（）A. 60°B. 65°C. 70°D. 75°【答案】D【分析】本题考查了正多边形和圆,根据正多边形的性质解答即可. 【解答】设该正十二边形的中心为O，如图，连接A10O和A3O，由题意知，=⊙O的周长，∴∠A3OA10==150°，∴∠A3A7A10=75°.选D.8.【答题】如图，正六边形ABCDEF内接于⊙O，若直线PA与⊙O相切于点A，则∠PAB=（）A. 30°B. 35°C. 45°D. 60°【答案】A【分析】本题考查了正多边形和圆,根据正多边形的性质和切线的性质解答即可.【解答】解：连接OA，根据直线PA为切线可得∠OAP=90°，根据正六边形的性质可得∠OAB=60°，则∠PAB=∠OAP－∠OAB=90°－60°=30°．9.【答题】正多边形的中心角与该正多边形一个内角的关系是（）A. 互余B. 互补C. 互余或互补D. 不能确定【答案】B【分析】本题考查了正多边形和圆,根据正多边形的性质解答即可.【解答】设正多边形的边数为n，则正多边形的中心角为，正多边形的一个外角等于，所以正多边形的中心角等于正多边形的一个外角，而正多边形的一个外角与该正多边形相邻的一个内角的互补，所以正多边形的中心角与该正多边形一个内角互补．选B.10.【答题】顺次连接正六边形的的三个不相邻的顶点，得到如图所示的图形，该图形（）A. 既是轴对称图形也是中心对称图形B. 是轴对称图形但不是中心对称图形C. 是中心对称图形但不是轴对称图形D. 既不是轴对称图形也不是中心对称图形【答案】B【分析】本题考查了正多边形和圆,根据正多边形的性质解答即可.【解答】解：此图形是等边三角形，等边三角形是轴对称图形但并不是中心对称图形，选B.11.【答题】圆的半径扩大一倍，则它的相应的圆内接正n边形的边长与半径之比（）A. 扩大了一倍B. 扩大了两倍C. 扩大了四倍D. 没有变化【答案】D【分析】本题考查了正多边形和圆,根据正多边形的性质解答即可.【解答】解：圆的半径扩大一倍，则它的相应的圆内接正n边形的边长与半径之比没有发生变化.选D.12.【答题】如图，半径为1的⊙O与正六边形ABCDEF相切于点A、D，则弧AD的长为（）A.B.C.D.【答案】C【分析】本题考查了正多边形和圆,根据正多边形的性质解答即可.【解答】解：如图，可由正六边形的性质可知：∠F=∠E=120°，∠DAF=∠EDA=60°，然后根据切线的性质，可知∠OAF=∠ODE=90°，因此可得∠ODA=∠OAD=30°，再由三角形的内角和求得∠O=120°，因此可知的度数为120°，根据弧长公式可知的长为：.选C.13.【答题】一元钱硬币的直径约为24 mm，则用它能完全覆盖住的正六边形的边长最大不能超过（）A. 12 mmB. 12mmC. 6 mmD. 6mm【答案】A【分析】本题考查了正多边形和圆,根据正多边形的性质解答即可.【解答】解：已知圆内接半径r为12mm，则OB=12，∴BD=OB•sin30°=12×=6，则BC=2×6=12，可知边长为12mm，就是完全覆盖住的正六边形的边长最大．选A.14.【答题】以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形，则该三角形的面积是（）A.B.C.D.【答案】D【分析】本题考查了正多边形和圆,根据正多边形的性质解答即可.【解答】解：如图1，∵OC=2，∴OD=2×sin30°=1；如图2，∵OB=2，∴OE=2×sin45°=；如图3，∵OA=2，∴OD=2×cos30°=，则该三角形的三边分别为：1，，，∵（1）2+（）2=（）2，∴该三角形是直角边，∴该三角形的面积是×1××=，选D.15.【答题】若正六边形的半径长为4，则它的边长等于（）A.4B.2C.D.【答案】A【分析】本题考查了正多边形和圆,根据正多边形的性质解答即可.【解答】解：正六边形的中心角为360°÷6=60°，那么外接圆的半径和正六边形的边长将组成一个等边三角形，故正六边形的半径等于4，则正六边形的边长是4选A.16.【答题】如图，一张半径为1的圆形纸片在边长为a(a≥3)的正方形内任意移动，则在该正方形内，这张圆形纸片“不能接触到的部分”的面积是（）A. a2－πB. (4－π)a2C. πD. 4－π【答案】D【分析】本题考查了正多边形和圆,根据正多边形的性质解答即可.【解答】解：小正方形的面积是：1；当圆运动到正方形的一个角上时，形成扇形BAO，它的面积是：．则这张圆形纸片“不能接触到的部分”的面积是4（1﹣）=4﹣π．选D.17.【答题】若正三角形、正方形、正六边形的周长相等，它们的面积分别是S1，S2，S3，则下列关系成立的是（）A.B.S1＜S2＜S3C.S1＞S2＞S3D.S2＞S3＞S1【答案】B【分析】本题考查了正多边形和圆,根据正多边形的性质解答即可.【解答】解：首先假设周长都是12，则正三角形的边长为4，面积为；正方形的边长为3，面积为9,；正六边形的边长为2，面积为：，则.18.【答题】如果一个正多边形的中心角为72°，那么这个正多边形的边数是( )A. 4B. 5C. 6D. 7【答案】B【分析】本题考查了正多边形和圆,根据正多边形的性质解答即可.【解答】解：这个多边形的边数是360÷72=5，选B.19.【答题】如图，圆内接正五边形ABCDE中，对角线AC和BD相交于点P，则∠APB的度数是（）A. 36°B. 60°C. 72°D. 108°【答案】C【分析】本题考查了正多边形和圆,根据正多边形的性质解答即可.【解答】解：∵五边形ABCDE为正五边形，∴AB=BC=CD，∠ABC=∠BCD=108度，∴∠BAC=∠BCA=∠CBD=∠BDC==36°，∴∠APB=∠DBC+∠ACB=72°，选C.20.【答题】正多边形的中心角是36°，那么这个正多边形的边数是（）A. 10B. 8C. 6D. 5【答案】A【分析】本题考查了正多边形和圆,根据正多边形的性质解答即可.【解答】解：一个正多边形的中心角都相等，且所有中心角的和是360度，用360度除以中心角的度数，就得到中心角的个数，即多边形的边数．解：由题意可得：边数为360°÷36°=10，则它的边数是10故答案为10.。

初三数学正多边形和圆同步测试题含答案新人教版

适用精选文件资料分享初三数学正多边形和圆同步测试题（含答案新人教版）初三数学正多边形和圆同步测试题（含答案新人教版）知识点相等，______________也相等的多边形叫做正多边形 . 2 ．把一个圆分成几等份，连接各点所获得的多边形是________________，它的中心角等于______________________________________________. 3.一个正多边形的外接圆的 ____________叫做这个正多边形的中心，外接圆的__________叫做正多边形的半径，正多边形每一边所对的 __________叫做正多边形的中心角，中心到正多边形的一边的____________叫做正多边形的边心距 . 4. 正 n 边形的半径为 R，边心距为 r ，边长为 a，（1）中心角的度数为： ______________. （2）每个内角的度数为：_______________________. （3）每个外角的度数为： ____________.（4）周长为： _________，面积为： _________. 5. 正 n 边形都是轴对称图形，当边数为偶数时，它的对称轴有 _______条，而且还是中心对称图形；当边数为奇数时，它不过 _______________.（填“轴对称图形”或“中心对称图形”）一、选择题 1. 以下说法正确的选项是（）A. 各边相等的多边形是正多边形B. 各角相等的多边形是正多边形C.各边相等的圆内接多边形是正多边形 D. 各角相等的圆内接多边形是正多边形 2.（2013?天津）正六边形的边心距与边长之比为（）A．：3 B．：2 C． 1 ：2 D．：2 3.(2013山东滨州)若正方形的边长为 6，则其外接圆半径与内切圆半径的大小分别为 ( ) A．6，B ．，3 C．6，3 D．， 4. 以以下图，正六边形 ABCDEF内接于⊙ O，则∠ADB的度数是（）． A ．60° B ．45° C．30° D． 22．5°5.半径相等的圆的内接正三角形，正方形，正六边形的边长的比为（）A. B. C.3:2:1 D.1:2:36.圆内接正五边形 ABCDE中，对角线 AC和 BD订交于点 P，则∠ APB 的度数是（）． A ．36° B ．60° C．72° D．108°7. （2013?自贡）如图，点 O是正六边形的对称中心，假如用一副三角板的角，借助点O（使该角的极点落在点O处），把这个正六边形的面积n 均分，那么 n 的全部可能取值的个数是（）A.4B.5C.6D. 78.如图，△PQR是⊙O的内接正三角形，四边形ABCD是⊙O 的内接正方形，BC∥QR，则∠ AOQ的度数是（）°°°°二、填空题 9. 一个正 n 边形的边长为 a，面积为 S，则它的边心距为__________. 10. 正多边形的一此中心角为36度,那么这个正多边形的一个内角等于 __________度. 11. 若正六边形的面积是cm 2，则这个正六边形的边长是__________. 12.已知正六边形的边心距为，则它的周长是 _______. 13. 点 M、N分别是正八边形相邻的边AB、BC 上的点，且 AM=BN，点 O是正八边形的中心，则∠ MON=_____________.14.边长为 a 的正三角形的边心距、半径（外接圆的半径）和高之比为_________________. 15. 要用圆形铁片截出边长为 4cm的正方形铁片，则采纳的圆形铁片的直径最小要__________cm. 16. 若正多边形的边心距与边长的比为 1:2 ，则这个正多边形的边数是 __________. 17.一个正三角形和一个正六边形的周长相等，则它们的面积比为__________.18.(2 013? 徐州 ) 如图，在正八边形 ABCDEFGH中，四边形 BCFG的面积为 20cm2，则正八边形的面积为 ________cm2.三、解答题 19. 比较正五边形与正六边形，可以发现它们的同样点与不一样点 .正五边形正六边形比方它们的一个同样点：正五边形的各边相等，正六边形的各边也相等 . 它们的一个不一样点：正五边形不是中心对称图形，正六边形是中心对称图形 . 请你再写出它们的两个同样点和不一样点 . 同样点：（1）___________________________________________________________ _________; （2）___________________________________________________________ ________. 不一样点：（1）___________________________________________________________ _________; （2）__________________________________________________________________. 20. 已知，如，正六形ABCDEF的 6cm，求个正六形的外接半径R、心距 r6 、面 S6.21.如，⊙O的半径，⊙O的内接一个正多形，心距 1，求它的中心角、、面 .22.已知⊙O和⊙O上的一点A. （1）作⊙O的内接正方形ABCD和内接正六形 AEFCGH；（2）在（ 1）的作中，假如点 E 在弧 AD上，求： DE是⊙O内接正十二形的一 .23.如 1、 2、 3、⋯、 n，M、N分是⊙O 的内接正三角形ABC、正方形 ABCD、正五形 ABCDE、⋯、正 n 形 ABCDE⋯的 AB、BC 上的点，且 BM=CN， OM、ON.(1)求 1 中∠ MON的度数； (2) 2 中∠ MON的度数是 _________， 3 中∠ MON的度数是 _________；(3) 研究∠ MON的度数与正 n形数 n 的关系 ( 直接写出答案 ).24.3 正多形和知点 1. 各各角 2.正多形正多形每一所的心角 3. 心半径心角距离称形一、解：依据内接正多形的性可知，只要把此正六形再化正多形即可，即周角除以 30 的倍数就可以解决． 360÷30=12； 360÷60=6； 360÷90=4；360÷120=3； 360÷180=2．所以 n 的全部可能的共五种状况，故B． 8.D 二、填空 9. 10.144 11.4cm 12.12 13.45 ° 14.1:2:315.16. 四 17.2:3 18.40 三、解答题 19. 同样点：（1）每个内角都相等（或每个外角都相等或对角线都相等）；（2）都是轴对称图形（或都有外接圆和内切圆） . 不一样点：（1）正五边形的每个内角是108°，正六边形的每个内角是120°；（2）正五边形的对称轴是5 条，正六边形的对称轴是 6 条. 20. 21. 解：连接 OB ∵在 Rt△AOC 中，AC==1 ∴AC=OC∴∠ AOC=∠OAC=45° ∵OA=OBOC⊥AB∴AB=2AC=2 ∠AOB=2∠OAC=2×45°=90° ∴这个内接正多边形是正方形 . ∴面积为 22=4 ∴中心角为 90°，边长为 2，面积为 4. 22. (1) 作法：①作直径 AC; ②作直径 BD⊥AC; ③挨次连接 A、B、C、D 四点 ,四边形ABCD即为⊙O的内接正方形 ; ④分别以 A、C为圆心，以 OA长为半径作弧，交⊙O于 E、H、F、G; ⑤按序连接 A、E、F、C、G、H 各点 . 六边形 AEFCGH即为⊙O的内接正六边形 . (2) 证明：连接 OE、DE.∵∠ AOD＝＝90°，∠ AOE＝＝60°，∴∠ DOE＝∠ AOD－∠ AOE＝90°- 60°=30°. ∴DE为⊙O的内接正十二边形的一边 . 23.(1) 方法一：连接 OB、OC. ∵正△ ABC内接于⊙ O，∴∠ OBM=∠OCN＝30°，∠ BOC=120°. 又∵ BM=CN， OB=OC，∴△ OBM≌△ OCN（SAS）. ∴∠ BOM ＝∠ CON.∴∠ MON=∠BOC=120°. 方法二：连接 OA、OB. ∵正△ ABC 内接于⊙ O，∴AB=AC，∠ OAM=∠OBN=30°, ∠AOB=120°. 又∵ BM＝CN，∴AM=BN.又∵ OA=OB,∴△ AOM≌△ BON（SAS）. ∴∠ AOM=∠BON.∴∠ MON=∠AOB=120°. (2)90° 72° (3)∠MON= .。

人教版九年级上册数学《正多边形和圆》同步辅导与测试(含解析)

九年级数学同步指导与测试正多边形和圆要点、难点：1.正多边形的定义：各边相等、各内角也相等的多边形叫正多边形。

2. 正多边形与圆的关系（ 1）把圆分红 n （ n ≥ 3）等份，有以下结论：其一：挨次连接各分点所得的多边形是这个圆的内接正n 边形，这圆是正n 边形的外接圆。

其二：经过各分点作圆的切线以相邻切线的交点为极点的多边形是这个圆的外切正边形，这圆是正 n 边形的内切圆。

n（ 2）任何正多边形都有一个外接圆和一个内切圆，这两个圆是齐心圆。

3.相关的观点（ 1）正多边形的中心（ 2）正多边形的半径（ 3）正多边形的边心距（ 4）正多边形的中心角4.正 n 边形的半径和边心距把正 n 边形分红 2n 个全等的直角三角形。

这里我们设：正 n 边形的中心角为 α，半径为 R ，边心距为 r ，边长为 a n ，周长为 P n ，面积为 S n ，则有（）360 ；（ 2 ） a n2 R180 ；（）180 ；1nsin3 rR cosnn22 1 211（ 4）Rr4an ；（ 5）P n n a n ；（ 6） S n2n r an2r Pn ；（ 7 ）正多边形的每一个内角( n2) 180，内角和(n 2) 180 .n5. 每一个正多边形都是轴对称图形，当边数为偶数时，它仍是中心对称图形。

6.要点和难点：（ 1）要点是正多边形的计算问题，计算往常是经过解直角三角形来解决的，所以在解这种题时，要尽量创建直角三角形，把所求的问题放到直角三角形中去，特别是含30°、 60°角的直角三角形和等腰直角三角形更重要。

（ 2）难点是灵巧运用正多边形的知识和观点解题。

〖知识总结〗正多边形的定义要理解后记牢，这里各边都相等，各角都相等，缺一不行，边数同样多的正多边形是相像多边形。

关于随意三角形来讲都有外接圆和内切圆，但注意只有正三角形的外接圆和内切圆是齐心圆。

相关正多边形的计算本质是把问题转变为解直角三角形的计算，所以这里要用到三角函数及勾股定理等相关知识。

初中数学中考正多边形与圆的关系(含答案解析)

正多边形与圆的关系一、选择题（本大题共10小题，共30.0分）1.半径为R的圆内接正三角形、正方形、正六边形的边心距分别为a，b，c，则a，b，c的大小关系是()A. a<b<cB. b<a<cC. a<c<bD. c<b<a2.若正方形的外接圆半径为2，则其内切圆半径为()A. √2B. 2√2C. √22D. 13.一个正方形的边长为a，则它的内切圆的面积为()A. 34a2π B. 14a2π C. 32a2π D. a2π4.若一个正多边形的边长与半径相等，则这个正多边形的中心角是()A. 45°B. 60°C. 72°D. 90°5.有下列四个命题：①各边相等的圆内接多边形是正多边形；②各边相等的圆外切多边形是正多边形；③各角相等的圆内接多边形是正多边形；④各角相等的圆外切多边形是正多边形．其中正确的个数为()A. 1B. 2C. 3D. 46.下列正多边形，通过直尺和圆规不能作出的是()A. 正三角形B. 正四边形C. 正五边形D. 正六边形7.正六边形的半径与边心距之比为()A. 1：√3B. √3：1C. √3：2D. 2：√38.若正六边形的边长为4，则它的外接圆的半径为()．A. 4√3B. 4C. 2√3D. 29.正四边形的边心距为1，则它的半径是A. 2√2B. √2C. 2D. 110.如图，五边形ABCDE是⊙O的内接正五边形，则∠OCD的度数是()A. 60°B. 54∘C. 76°D. 72°二、填空题（本大题共10小题，共30.0分）11.若点O是正六边形ABCDEF的中心，∠MON=120°且角的两边分别交六边形的边AB、EF于M、N两点。

若多边形AMONF的面积为2√3，则正六边形ABCDEF的边长是____.12.半径为2的圆内接正六边形的边心距等于_____．13.圆内接正六边形的边长为10cm，它的边心距等于__________cm．14.正六边形的半径为1，则正六边形的面积为____________________；15.如图，点O为正六边形ABCDEF的中心，连接EA，则∠AED=____度；若OA=4，则该正六边形的面积为__________.16.半径为4的正n边形边心距为2√3，则此正n边形的边数为_____．17.已知一个正六边形的外接圆半径为2，则这个正六边形的周长为________．18.如图，⊙O是正五边形ABCDE的外接圆，则∠ADC的度数是________．19.如图，五边形ABCDE是⊙O的内接正五边形，AF是⊙O的直径，则∠BDF的度数是______°.20.半径为3的圆的内接正方形的边长是________．答案和解析1.【答案】A【解析】【分析】此题主要考查了正多边形和圆的性质，解决本题的关键是构造直角三角形，得到用半径表示的边心距；注意：正多边形的计算一般要转化为解直角三角形的问题来解决．根据三角函数即可求解．【解答】解：设圆的半径为R，则正三角形的边心距为a=R×cos60°=12R.四边形的边心距为b=R×cos45°=√22R，正六边形的边心距为c=R×cos30°=√32R.∵12R<√22R<√32R，∴a<b<c，故选：A．2.【答案】A【解析】【分析】本题考查的是正方形和圆、等腰直角三角形的性质等知识，解题的关键是根据题意画出图形，属于中考常考题型．根据题意画出图形，再由正方形及等腰直角三角形的性质求解即可．【解答】解：如图所示，连接OA、OE，∵AB是小圆的切线，∴OE⊥AB，∵四边形ABCD是正方形，∴AE=OE，∴△AOE是等腰直角三角形，AE2+OE2=AO2，∴OE=√22OA=√2．故选：A．3.【答案】B【解析】【分析】本题考查了正多边形与圆的关系，知道正方形的内切圆的直径等于正方形的边长是解题的关键.根据正方形的内切圆的直径等于正方形的边长求得圆的半径，最后再求出圆的面积即可．【解答】解：因为正方形的内切圆的直径等于正方形的边长，所以r=a2，所以正方形的内切圆的面积为πr2=π(a2)2=14a2π，故选B．4.【答案】B【解析】【分析】本题考查正多边形与圆的关系、等边三角形的判定与性质；解题的关键是作辅助线，灵活运用等边三角形的判定与性质来分析、解答．如图，作辅助线，由题意可得OA=OB= AB，从而得出△OAB是等边三角形，进而求出∠AOB的度数，问题即可解决．【解答】解：如图，连接OA、OB；AB为⊙O的内接正多边形的一边，∵正多边形的边长与半径相等，∴OA=OB=AB，∴△OAB是等边三角形，∴∠AOB=60°，即这个正多边形的中心角为60°．故选B．5.【答案】B【解析】【分析】本题考查了命题与定理：判断事物的语句叫命题；正确的命题称为真命题，错误的命题称为假命题，经过推理论证的真命题称为定理.根据命题的“真”“假”进行判断即可．【解答】解：①各边相等的圆内接多边形是正多边形，正确；②各边相等的圆外切多边形不一定正多边形，比如菱形，所以错误；③各角相等的圆内接多边形不一定是正多边形，比如长方形，所以错误；④各角相等的圆外切多边形是正多边形，正确．故选B．6.【答案】C【解析】【分析】本题主要考查作图−复杂作图，解题的关键是熟练掌握圆上等分点的尺规作图．根据尺规作图取圆的等分点的作法即可得出答案．【解答】解：取圆上一点为圆心，相同的长度为半径画弧，重复此种作法可得到圆的六等分点，据此可得圆的内接正六边形；在以上所得六等分点中，间隔取点，首尾连接可得圆的内接正三角形；由于圆的直径可以将圆二等分、两条互相垂直的直径可以将圆四等分，据此可作出圆的内接正四边形；综上可知，不可以用尺规作图作出的是圆的内接正五边形，故选C．7.【答案】D【解析】【试题解析】【分析】此题主要考查正多边形与圆的知识，等边三角形高的计算，要求学生熟练掌握应用.可设正六边形的半径为R，欲求半径与边心距之比，我们画出图形，通过构造直角三角形，解直角三角形即可得出．解：如图所示，设正六边形的半径为R，又该多边形为正六边形，故∠OBA=60°，R，在Rt△BOG中，OG=√32∴边心距r=√3R2即半径与边心距之比2：√3，故选D．8.【答案】B【解析】【分析】本题考查正多边形与圆，用到的知识点为：n边形的中心角为360÷n，有一个角是60°的等腰三角形是等边三角形．根据正六边形的边长等于正六边形的半径，即可求解．【解答】解：正六边形的中心角为360°÷6=60°．那么外接圆的半径和正六边形的边长将组成一个等边三角形．∴它的外接圆半径是4．故选B．9.【答案】B【解析】【分析】本题考查了正多边形和圆的知识，解题的关键是正确的构造如图所示的直角三角形并求解．利用正四边形的外接圆的半径是边心距的√2倍计算．【解答】解：如图，∵正四边形的边心距为1，∴OB=1，∵∠OAB=45°，∴OA=√2OB=√2，故选：B．10.【答案】B【解析】【分析】是解题的关键．本题考查的是正多边形和圆，掌握正多边形的中心角的计算公式：360°n根据正多边形的中心角的计算公式：360°计算出∠COD，再由等腰三角形的性质可得．n【解答】解：∵五边形ABCDE是⊙O的内接正五边形，=72°，∴五边形ABCDE的中心角∠COD的度数为360°5∵OC=OD，∴∠OCD=∠ODC，∴∠OCD=(180°−72°)÷2=54°．故选B．11.【答案】2【解析】略12.【答案】√3【解析】【分析】此题主要考查了正多边形和圆、解直角三角形，正确掌握正六边形的性质是解题关键．构建直角三角形，利用直角三角形的边角关系即可求出．【解答】解：连接OA，作OM⊥AB，得到∠AOM=30°，AB=2，则AM=1，∴OM=OA⋅cos30°=√3∴正六边形的边心距是√3．故答案为√3．13.【答案】5√3【解析】【分析】本题考查的是正多边形与圆，熟知正六边形的性质是解答此题的关键．根据题意画出图形，利用等边三角形的性质及勾股定理直接计算即可．【解答】解：如图所示，连接OB、OC，过O作OG⊥BC于G，∵此多边形是正六边形，∴△OBC是等边三角形，∴∠OBG=60°，∴BG=5cm，OB=10cm，根据勾股定理可得：边心距OG=5√3cm；故答案为：5√3．14.【答案】3√32【解析】略15.【答案】90°；24√3【解析】【试题解析】【分析】本题考查了正多边形的性质，勾股定理的应用，等腰三角形的性质，属于中档题．六边形ABCDEF为正六边形，可得出∠AFE和∠FED的度数，进而得出∠AEF的度数，从而得出∠AED；连接OA，OF，过O作OG⊥AF于点G，先得出△AOF的面积，再乘以6，即可得出该正六边形的面积．【解答】解：∵六边形ABCDEF为正六边形，∴AF=FE，且∠AFE=∠FED=(6−2)×180°=120°，6=30°，则∠AEF=180°−120°2∴∠AED=∠FED−∠AEF=120°−30°=90°，连接OA，OF，过O作OG⊥AF于点G，∵点O为正六边形ABCDEF的中心，∴∠OAF=60°，则△AOF为等边三角形，∠AOG=30°，(三线合一)在Rt△OGA中，GA=12OA=12×4=2，则OG=√OA2−AG2=√42−22=2√3，故该正六边形的面积为：6S△AOF=6×12×4×2√3=24√3．故答案为90°；24√3．16.【答案】6【解析】【分析】此题主要考查了正多边形和圆的有关计算，根据已知得出中心角∠AOB=60°是解题关键．由三角函数求出∠DAO=60°，得出∠AOD=30°，求出中心角∠AOB=60°，即可得出答案．【解答】解：如图所示AB为正n边形的边长，OA为半径，OD为边心距，∵半径为4的正n边形边心距为2√3，∴sin∠DAO=DO AO =2√34=√32，∴∠DAO=60°，∴∠AOD=30°，∴∠AOB=60°，∴n=360°60°=6故答案为6．17.【答案】12【解析】解：∵l正六边形的半径等于边长，∴正六边形的边长a=2，正六边形的周长=6a=12，故答案为12．根据正六边形的半径等于边长进行解答即可．本题考查的是正六边形的性质，解答此题的关键是熟知正六边形的边长等于半径．18.【答案】72°【解析】【分析】本题主要考查了正多边形和圆的关系，以及圆周角定理的应用由正五边形的性质得出∠CDE=(5−2)×180°÷5=108°，AE=AB=BC，得出AE⏜= AB⏜=BC⏜，由圆周角定理即可得出答案．【解答】解：∵⊙O是正五边形ABCDE的外接圆，∴∠CDE=(5−2)×180°÷5=108°，AE=AB=BC，∴AE⏜=AB⏜=BC⏜，×108°=72°；∴∠ADC=23故答案为72°．19.【答案】54【解析】【分析】本题考查正多边形与圆，圆周角定理等知识，解题的关键灵活运用所学知识解决问题，属于中考常考题型．连接AD，根据圆周角定理得到∠ADF=90°，根据五边形的内角和得到∠ABC=∠C= 108°，求得∠ABD=72°，由圆周角定理得到∠F=∠ABD=72°，求得∠FAD=18°，于是得到结论．【解答】解：连接AD，∵AF 是⊙O 的直径，∴∠ADF =90°，∵五边形ABCDE 是⊙O 的内接正五边形，∴∠ABC =∠C =108°，∵BC =CD ，，∴∠ABD =72°，∴∠F =∠ABD =72°，∴∠FAD =18°，∴∠CDF =∠DAF =18°，∴∠BDF =36°+18°=54°，故答案为54．20.【答案】3√2 【解析】【分析】该题主要考查了正多边形和圆，解直角三角形，正方形的性质，正确的理解题意是解题的关键．画出图形，先根据题意首先求出BE 的长，即可解决问题．【解答】解：如图，∵四边形ABCD 是⊙O 的内接正方形，∴∠OBE =45°；∵OE ⊥BC ，∴BE =CE ；又OB =3，∴sin45°=OE OB ，cos45°=BE OB ，∴OE =3√22，即BE =3√22，∴BC=3√2，故答案为3√2．。

人教版九年级数学上册24.3正多边形和圆同步测试及答案【精】

正多边形和圆1．正六边形的边心距与边长之比为( B ) A.3∶3 B.3∶2 C ．1∶2 D.2∶2【解析】如图：设正六边形的边长是a ，则半径长也是a ；经过正六边形的中心O 作边AB 的垂线OC ，则AC ＝12AB ＝12a ， ∴OC ＝OA 2－AC 2＝32a ， ∴正六边形的边心距与边长之比为：32a ∶a ＝3∶2. 3－1，在⊙O 中，OA ＝AB ，OC ⊥AB ，则下列结论错误的是( D ) 图24－3－1A ．弦AB 的长等于圆内接正六边形的边长B ．弦AC 的长等于圆内接正十二边形的边长C.AC ︵＝BC ︵D ．∠BAC ＝30°【解析】因为OA ＝AB ＝OB ，所以△OAB 是等边三角形，又OC ⊥AB ，所以∠AOC ＝∠BOC ＝30°，所以∠BAC ＝15°，D 不正确．3．如图24－3－2，点O 是正六边形的对称中心，如果用一副三角板的角，借助点O (使该角的顶点落在点O 处)，把这个正六边形的面积n 等分，那么n 的所有可能取值的个数是( B )图24－3－2A ．4B ．5C ．6D ．7【解析】 360÷30＝12；360÷60＝6；360÷90＝4；360÷120＝3；360÷180＝2.因此n 的所有可能的值共五种情况．4．如图24－3－3，要拧开一个边长为a ＝6 mm 的正六边形螺帽，扳手张开的开口b 至少为( C )图24－3－3 A ．6 2 mm B ．12 mmC ．6 3 mmD ．4 3 mm5．已知正六边形的边心距为3，则它的周长是( B )A ．6B ．12C ．6 3D ．12 3【解析】正六边形的边长等于半径，设半径为R ，则⎝⎛⎭⎫12R 2＋(3)2＝R 2，∴R ＝2，它的周长是6R＝6×2＝12，故选B.6．若正六边形的边长为4 cm ，那么正六边形的中心角是__60__度，半径是__4__cm ，边心距是__23__cm ，它的每一个内角是__120°__．7．[2012·巴中]已知一个圆的半径为5 cm ，则它的内接正六边形的边长为__5__cm.8．已知一个正n 边形的中心角是它的一个内角的三分之一，则n ＝__8__．【解析】由360n ＝180（n －2）n ×13，得n ＝8. 9．已知⊙O 和⊙O 上的一点A ，如图24－3－4所示．图24－3－4(1)作⊙O 的内接正方形ABCD 和内接正六边形AEFCGH ；(2)在(1)题所作的图中，如果点E 在AB ︵上，试证明EB 是⊙O 的内接正十二边形的一边．【解析】 (1)根据正四边形和正六边形的作图方法分别作出⊙O 的内接正方形ABCD 和内接正六边形AEFCGH ；(2)计算EB 所对的圆心角的度数．解：(1)如图所示，在⊙O 中，用直尺和圆规作两条互相垂直的直径AC 和BD ，连接AB ，BC ，CD ，DA ，得⊙O 的内接正方形ABCD ；按正六边形的作法用直尺和圆规在⊙O 中作出正六边形AEFCGH . (2)如图，连接OE .∵AE 是正六边形的一边，∴∠AOE ＝360°6＝60°.∵AB 是正方形的一边，∴∠AOB ＝360°4＝90°，∴∠BOE ＝∠AOB －∠AOE ＝90°－60°＝30°.设EB 是⊙O 的内接正n 边形的一边，则360°n＝30°，∴n ＝12， ∴EB 是⊙O 的内接正十二边形的一边．10．小敏在作⊙O 的内接正五边形时，先做了如下几个步骤：(1)作⊙O 的两条互相垂直的直径，再作OA 的垂直平分线交OA 于点M ，如图1；(2)以M 为圆心，BM 长为半径作圆弧，交CA 于点D ，连接BD ，如图2.若⊙O 的半径为1，则由以上作图得到的关于正五边形边长BD 的等式是( C )图24－3－5 A ．BD 2＝5－12OD B ．BD 2＝5＋12OD C ．BD 2＝5ODD ．BD 2＝52OD 11．[2013·徐州]如图24－3－6，在正八边形ABCDEFGH 中，四边形BCFG 的面积为20 cm 2，则正八边形的面积为____________cm 2.图24－3－6【解析】连接HE ，AD ，在正八边形ABCDEFGH 中，可得：HE ⊥BG 于点M ，AD ⊥BG 于点N ，∵正八边形每个内角为：（8－2）×180°8＝135°， ∴∠HGM ＝45°，∴MN ＝MG ，设MH ＝MG ＝x ，则HG ＝AH ＝AB ＝GF ＝2x ，∴BG ×GF ＝2(2＋1)x 2＝20，四边形ABGH 面积＝12(AH ＋BG )×HM ＝(2＋1)x 2＝10， ∴正八边形的面积为：10×2＋20＝40(cm 2)．12．将固定宽度的纸条打个简单的结，然后系紧，使它成为平面的结(如图24－3－7)，求证：五边形ABCDE 是正五边形．图24－3－7第13题答图证明：如图所示，连接BE ，AD ，设纸条的宽度为h ，则S △ABE ＝12AB ·h ＝12AE ·h ， ∴AB ＝AE ，同理得AB ＝BC ，BC ＝CD ，∴AE ＝AB ＝BC ＝CD .∵纸条的宽度固定，∴AE ∥BD ，CD ∥BE ，∴∠1＝∠2＝∠3＝∠4＝∠5.由折叠性质得∠ABD ＋∠ABC ＝180°，从而得∠1＝∠2＝∠3＝∠4＝∠5＝36°，由此易得∠ABC ＝∠BCD ＝∠CDE ＝∠DEA ＝∠EAB ，AE ＝AB ＝BC ＝CD ＝DE ，∴五边形ABCDE 是正五边形．13．如图24－3－8所示，已知△ABC 是⊙O 的内接等腰三角形，顶角∠BAC ＝36°，弦BD ，CE 分别平分∠ABC ，∠ACB ，求证：五边形AEBCD 是正五边形．图24－3－8 【解析】要证明五边形AEBCD 是正五边形，只需证AE ︵＝EB ︵＝BC ︵＝CD ︵＝DA ︵即可．证明：∵△ABC 是等腰三角形，且∠BAC ＝36°，∴∠ABC ＝∠ACB ＝72°.又∵BD 平分∠ABC ，CE 平分∠ACB ，∴∠ABD ＝∠CBD ＝∠BCE ＝∠ACE ＝36°，即∠BAC ＝∠ABD ＝∠CBD ＝∠BCE ＝∠ACE ，∴BC ︵＝AD ︵＝CD ︵＝BE ︵＝AE ︵，∴A ，E ，B ，C ，D 是⊙O 的五等分点，∴五边形AEBCD 是正五边形．14．如图24－3－9，正五边形ABCDE ，连接对角线AC ，BD ，设AC 与BD 相交于O .(1)写出图中所有的等腰三角形；(2)判断四边形AODE 的形状，并说明理由．:学科图24－3－9解：(1)△ABO ，△ABC ，△BOC ，△DOC ，△BCD .(2)四边形AODE 是菱形，理由如下：∵AB ＝BC ，∠ABC ＝（5－2）×180°5＝108°， ∴∠BAC ＝∠BCA ＝12×(180°－108°)＝36°，同理得∠CBD ＝∠CDB ＝36°，∴∠ABO ＝∠ABC －∠CBD ＝72°，∠AOB ＝180°－∠ABO －∠BAC ＝72°，∴AB ＝AO ，同理得DO ＝DC ，∴OA ＝AE ＝ED ＝DO ，∴四边形AODE 是菱形．15．小刚现有一边长为a m 的正方形花布，准备做一个形状为正八边形的风筝，参加全校组织的风筝比赛，问：在这样的花布上怎样裁剪，才能得到一个面积最大的风筝？解：如图所示，在正方形ABCD 中，△DEF ，△CGH ，△BOP ，△AMN 为全等的等腰直角三角形，八边形EMNOPHGF 为正八边形．设直角边DE ＝DF ＝CG ＝CH ＝x .在Rt △DEF 中，EF ＝2x . ∵EF ＝FG ，且DC ＝DF ＋FG ＋CG ，∴x ＋x ＋2x ＝a ，解得x ＝2－22a ≈0.3a ，因此，从四个角上各剪去一个直角边长约为0.3a m 的等腰直角三角形，即可得到一个面积最大的正八边形风筝．16．小赵对芜湖科技馆富有创意的科学方舟形象设计很有兴趣，他回家后将一正五边形纸片沿其对称轴对折，旋转放置，做成科学方舟模型，如图24－3－10所示，该正五边形的边心距OB 长为2，AC 为科学方舟船头A 到船底的距离，请你计算AC ＋12AB ＝__522__．图24－3－10【解析】设正五边形的边长为a ，根据正五边形的面积等于科学方舟面积的2倍列方程求解，依题意，有12×2×a ×5＝⎝⎛⎭⎫12×AB ×a 2＋12×a ×AC ×2，即522a ＝⎝⎛⎭⎫12AB ＋AC ×a ，∴12AB ＋AC ＝522.。

初中数学正多边形和圆考试卷及答案.docx

xx学校xx学年xx 学期xx试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx 题xx题xx题总分得分一、xx题（每空xx 分，共xx分）试题1:下列命题中，是假命题的是( )A．各边相等的圆内接多边形是正多边形B．正多边形的任意两个角的平分线如果相交，则交点为正多边形的中心C．正多边形的任意两条边的中垂线如果相交，则交点是正多边形的中心D．一个外角小于一个内角的正多边形一定是正五边形试题2:如图2433，正六边形螺帽的边长是2 cm，这个扳手的开口a的值应是( )A．2 cm B. cmC. cm D．1 cm试题3:已知正六边形的边长为10 cm，则它的边心距为( )评卷人得分A. cm B．5 cm C．5 cm D．10 cm试题4:正六边形的两条平行边之间的距离为1，则它的边长为( )A. B. C. D.试题5:正多边形的一个中心角为36°，那么这个正多边形的一个内角等于________．试题6:某工人师傅需要把一个半径为6 cm的圆形铁片加工成边长最大的正六边形铁片，求此正六边形的边长．试题7:如图2434，在圆内接正五边形ABCDE中，对角线AC，BD相交于点P，求∠APB的度数．试题8:圆的半径为8，那么它的外切正方形的周长为____，内接正方形的周长为________．试题9:将一块正五边形纸片[图2435(1)]做成一个底面仍为正五边形且高相等的无盖纸盒[侧面均垂直于底面，见图2435(2)]，需在每一个顶点处剪去一个四边形，例如图中的四边形ABCD，则∠BAD的大小是________．试题10:如图2436，施工工地的水平地面上，有三根外径都是1 m的水泥管，两两相切地堆放在一起，求其最高点到地面的距离？试题11:(1)如图2437(1)，在圆内接△ABC中，AB＝BC＝CA，OD，OE为⊙O的半径，OD⊥BC于点F，OE⊥AC于点G，求证：阴影部分四边形OFCG的面积是△ABC面积的；(2)如图2437(2)，若∠DOE保持120°不变，求证：当∠DOE绕着点O旋转时，由两条半径和△ABC的两条边围成的图形(图中阴影部分)面积始终是△ABC面积的.(1) (2)试题1答案:D试题2答案:A试题3答案:C试题4答案:D试题5答案:144°试题6答案:解：如图D35，只有当正六边形是圆的内接正六边形时，此正六边形的边长最大，最大边长为6 cm.试题7答案:解：如图D36，连接OA，OB.∵五边形ABCDE是正五边形，∴∠AOB＝＝72°.∵AB＝CD，∴＝.∴∠2＝∠1＝∠AOB＝36°.∴∠APB＝∠1＋∠2＝72°.试题8答案:64 32试题9答案:72°试题10答案:解：由于三个圆两两外切，所以圆心距等于半径之和．所以以三个圆心为顶点的三角形是边长为1 m的等边三角形，最高点到地面距离是等边三角形的高加上一个直径．因为等边三角形的高是，故最高点到地面的距离是m. 试题11答案:证明：(1)连接OA，OC.∵点O是等边三角形ABC的外心，∴Rt△OFC≌Rt△OGC≌Rt△OGA.∴S四边形OFCG＝2S△OFC＝S△OAC.∵S△OAC＝S△ABC，∴S四边形OFCG＝S△ABC.(2)如图D37，连接OA，OB和OC.图D37则△AOC≌△COB≌△BOA，∠1＝∠2.不妨设OD交BC于点F，OE交AC于点G.∵∠AOC＝∠3＋∠4＝120°，∠DOE＝∠5＋∠4＝120°，∴∠3＝∠5.在△OAG和△OCF中，∴△OAG≌△OCF.∴S四边形OFCG＝S△AOC＝S△ABC.。

人教版九年级《24.3正多边形和圆》精讲精练(含答案)

一、基础知识1.使学生认识正多边形的定义及正多边形的相关观点。

各边相等，各角也相等的多边形叫做正多边形。

一个正多边形的外接圆的圆心叫做这个正多边形的中心，外接圆的半径叫做正多边形的半径，正多边形每一边所对的圆心角叫做正多边形的中心角，中心到正多边形的一边的距离叫做正多边形的边心距。

注：正多边形都是轴对称图形，正 n 边形有 n 条对称轴，当 n 是偶数时，该正多边形又是中心对称图形，对称中心为正多边形的中心，当n 为奇数时，该正多边形不是中心对称图形。

2.能娴熟的进行正多边形的相关计算注: ①正n 边形的中心角为（360 ）°，正n 边形的每个外角也是（360）°，所以正n n n边形的中心角和正n 边形的外角相等，正n 边形的中心角和每个内角是互补的关系②正 n 边形的半径和边心距，把正n 边形分红2n 个全等的直角三角形3.能利用正多边形和圆解决问题。

二、重难点剖析本课教课要点：会进行正多边形的相关计算并利用正多边形和圆解决问题。

本课教课难点：利用正多边形和圆解决问题。

三、典例精析：例 1：（ 2014?天津）正六边形的边心距为 3 ，则该正六边形的边长是（）A．3 B ． 2C． 3D． 23应选 B．【评论】本题主要观察了正六边形和圆，注意：外接圆的半径等于正六边形的边长．例 2（2014 ?南京）如图，AD是正五边形 ABCDE的一条对角线，则∠BAD=。

四、感悟中考1 、（ 2014 ?河北）如图，边长为 a 的正六边形内有两个三角形（数据如图），则S暗影=（）S空白A．3B．4C．5D．62、（ 2014 ?莱芜）如图，在正五边形 ABCDE中，连接 AC、AD、 CE，CE交 AD于点F，连结 BF，以下说法不正确的选项是（）A．△ CDF的周长等于 AD+CD2222B ． FC均分∠ BFDC ．AC+BF =4CD D． DE=EF?CE应选：B．【评论】本题观察了正五边形的性质，全等三角形的判断，综合观察的知识点许多，熟记定理内容和娴熟运用是解题要点。