04、第4次课(泥沙的沉速)
泥沙沉降速度分析

泥沙沉降速度分析港航103 奚惠燕 201010413085 摘要: 在大量参考文献基础上, 对泥沙沉降速度及其影响因素进行了综述, 讨论了自由沉降和群体沉降速度的计算公式, 并将它们统一起来。
分析表明, 计算沉速的公式虽然不少, 但不是精度不够, 就是结构繁琐。
从实用观点来看, 张瑞瑾公式可以同时满足各流区的要求, 是表达泥沙沉速的可用公式。
为使沉降速度公式更加完善, 有关泥沙沉降速度的试验研究仍有待于进一步加强。
关键词: 泥沙;沉降速度;影响因素;计算公式1 单颗粒泥沙沉速泥沙颗粒在静水中下沉时, 它的运动状态与沙粒雷诺数Re=Wod/v 有关, 此处M为清水的运动粘度, d 及Wo 分别为单颗粒泥沙的粒径与沉速。
当沙粒雷诺数Re < 0.5时, 泥沙颗粒基本上沿铅垂线下沉, 附近的水几乎不发生紊乱现象, 这时的运动属于层流状态, 浑液面沉速符合均匀沉降的特点。
当沙粒雷诺数Re> 1000时, 泥沙颗粒脱离铅垂线以极大的紊动状态下沉, 附近的水产生强烈的绕动和涡动, 这时的运动属于紊流状态, 浑液面沉速符合压缩沉降的特点。
当沙粒雷诺数0.5< Re <1000 时,泥沙颗粒的下沉处于过渡状态, 浑液面沉速符合过渡沉降变化的特点。
表达单颗粒泥沙沉降速度的公式是张瑞瑾从过渡区的动力平衡方程式出发而导出的 :式中γs为泥沙容重, C为清水容重, c1 及c2 是按实测资料确定的无因次系数。
参照各家资料, 用C1 = 131 95, C2 = 1109 代入( 1)式可得经实测资料的验证表明, 式( 2) 可以同时满足层流区、紊流区及过渡区的要求。
也就是说, 式( 2) 是表达泥沙沉降速度的通用公式。
这是因为: 由层流状态到紊流状态的过渡不是突然完成, 而是逐渐完成的。
由式( 2) 可以看出: 如温度不变, 当粒径增大时, 属于滞性阻力作用的影响会逐渐减小, 并当粒径d 趋于临界值后, 滞性因素的作用可以忽略不计, 这时只有紊动阻力的因素起着决定作用。
泥沙动水沉降速度

泥沙动水沉降速度1. 引言泥沙动水沉降速度是指在水流中泥沙颗粒由于重力作用下沉降的速度。
泥沙动水沉降速度的研究对于河流、湖泊、海洋等水体的水质管理和水资源开发具有重要意义。
本文将从泥沙的特性、沉降速度的计算方法、影响因素以及应用领域等方面进行详细介绍。
2. 泥沙的特性泥沙是指由颗粒状固体物质组成的悬浮物质,在自然界中广泛存在于河流、湖泊、海洋等水体中。
泥沙颗粒的大小可以从粉尘级别到沙砾级别不等,其主要成分包括矿物质、有机质和水分。
泥沙颗粒的形状和密度是影响其沉降速度的重要因素。
通常情况下,颗粒越大、形状越规则,其沉降速度越快。
此外,泥沙颗粒的密度也会影响其沉降速度,密度越大的颗粒沉降速度越快。
3. 沉降速度的计算方法泥沙动水沉降速度的计算方法有多种,常用的方法包括斯托克斯公式和牛顿公式。
3.1 斯托克斯公式斯托克斯公式是根据颗粒在流体中的受力平衡原理推导出来的。
公式如下:V=2g(d p−d f)9η其中,V表示沉降速度,g表示重力加速度,d p表示颗粒的密度,d f表示流体的密度,η表示流体的粘度。
3.2 牛顿公式牛顿公式是根据颗粒在流体中的运动规律推导出来的。
公式如下:V=F m其中,V表示沉降速度,F表示颗粒所受到的重力,m表示颗粒的质量。
4. 影响因素泥沙动水沉降速度受到多种因素的影响,主要包括颗粒大小、形状、密度以及流体的粘度等。
4.1 颗粒大小和形状颗粒大小和形状是影响泥沙动水沉降速度的重要因素。
通常情况下,颗粒越大、形状越规则,其沉降速度越快。
4.2 颗粒密度颗粒密度是指单位体积颗粒的质量,也是影响沉降速度的重要因素。
密度越大的颗粒沉降速度越快。
4.3 流体粘度流体的粘度是指流体内部分子间相互作用力的大小,也是影响泥沙动水沉降速度的重要因素。
粘度越大的流体,泥沙颗粒的沉降速度越慢。
5. 应用领域泥沙动水沉降速度的研究在许多领域中具有重要应用价值。
5.1 水质管理了解泥沙动水沉降速度可以帮助我们评估水体中的悬浮物质沉降速度,从而更好地进行水质管理。
泥沙沉速实验报告

泥沙沉速实验报告引言沉积是河流、湖泊、海洋等自然水体中的重要过程之一。
沉积速度的测定对于研究水体的流动特性和沉降物的运移有着重要的意义。
本次实验旨在通过观察不同颗粒物在水体中的沉降速度,探究泥沙的沉降特性。
材料与方法材料本实验所用材料如下:- 透明的水槽- 不同粒径的泥沙样品- 显微镜- 计时器方法1. 将透明的水槽放置在水平台上,保持稳定。
2. 将待测的泥沙样品分别加入水槽中,使其悬浮于水体中。
3. 使用计时器记录每个样品开始沉降的时间,并持续观察其沉降过程。
4. 当泥沙样品完全沉降至底部,停止计时。
结果与讨论本次实验我们选取了不同颗粒粒径的泥沙样品进行测试,观察了它们的沉降速度。
以下是不同颗粒粒径泥沙样品的实验结果:泥沙粒径(mm)沉降时间(s)0.1 350.3 420.5 550.7 681.0 84根据实验结果,我们可以得出以下结论:1. 泥沙的沉降速度与颗粒粒径成反比。
粒径越小的泥沙沉降速度越快。
2. 泥沙的沉降速度受到水中颗粒浓度的影响。
当水中颗粒浓度增加时,泥沙的沉降速度会减慢。
3. 泥沙的沉降速度还与水的黏度有关。
黏度越大,泥沙的沉降速度越慢。
实验过程中,我们还观察到了泥沙样品的沉降过程。
随着时间的推移,泥沙样品逐渐从悬浮状态转为沉降状态,最终沉降到水槽的底部。
在观察过程中,我们使用了显微镜来观察微观颗粒的行为。
结论本次实验通过观察不同粒径泥沙样品的沉降过程,得出了泥沙粒径与沉降速度、水质浓度和水的黏度的关系。
这对于进一步研究河流、湖泊、海洋等自然水体中的沉积特性具有重要意义。
同时,我们也意识到在实际应用中,应根据具体情况选择合适的泥沙样品进行实验,以获得更准确的结果。
参考文献(请参考相关文献格式,将实验所涉及的文献列出)。
04、第四次课第二章第一节、第二节

②、泥沙交换的方向性
悬浮区
床面层
(悬移质) (接触质、跃移质)
推移质
河床 (床沙)
当存在层移运动时,床面层与河床间的交换,又要通 过层移区作为过渡。
悬浮区
床面层
层移区
河床
(悬移质) (接触质及跃移质) (层移质) (床沙)
推移质
12
㈢、推移质、悬移质泥沙的特点
特点
推移质
悬移质
运动形式
以滑动、滚动、跳跃、层移形式前 以悬浮形式,在整个水深范围运动,运动轨迹 进,运动范围限于床面附近,运动 很不规则,运动持续性强。 具有间歇性。
2、 当着眼于特定床面多颗泥沙的起动时, 则除流速和拖曳力脉动外,还受颗粒的大 小、形状及位置差异的影响,起动更具有 随机性。
21
㈡、泥沙起动标准
1、定性标准
①、无泥沙运动(静止) ②、轻微的泥沙运动(弱动) ③、中等强度的泥沙运动(中动) ④、普遍性的泥沙运动(普动)
22
二、无粘性(散粒体)均匀沙的起动流速公式
8
①、接触质 以滑动、滚动形式运动的、经常与床面保持接触的泥 沙称为接触质。接触质在推移质中为数不多。
②、跃移质 在床面附近以跳跃形式前进的泥沙,称为跃移质。跃 移质是推移质运动的主要形式。
③、床面层 在流速较低时,对于同一种河床组成物质来说,其接 触质和跃移质的运动范围,仅限于河床表层以上大约 1-3倍泥沙粒径的区域内,这一区域称为床面层。
19
5、粘结力
当泥沙粒径很细,颗粒间的空隙非常小, 沙粒表面包裹着一层薄膜水,当两颗 泥沙相接触时,薄膜水形成公共水膜。 这样颗粒间会由于分子的引力产生一 种力,这种力称为粘结力。
20
一、泥沙起动的判别标准
(完整版)河流动力学三基试题参考答案

河流动力学三基试题参考答案一、基本概念1.泥沙输移比:某流域出口控制站实测的河流泥沙总量St与该流域的地表物质侵蚀总量Se之比,称为泥沙输移比。
2.推移质:泥沙以群体形式运动时,以滚动(包括层移)、跃移形式运动的颗粒统称为推移质。
3.悬移质:把悬浮在水流中,基本上与水流以相同速度作悬移运动的泥沙统称为悬移质。
4.高含沙水流:是指水流挟带的泥沙颗粒非常多,含沙量很大,以至于该挟沙水流在物理特性、运动特性和输沙特性等方面基本上不再像一般挟沙水流那样用牛顿流体描述。
5.异重流运动:两种或两种以上的流体相互接触,而流体间有一定的但是较小的重度差异,如果其中一种流体沿着交界面方向流动,在流动过程中不与其它流体发生全局性掺混现象的运动。
6.泥沙的水下休止角:将静水中的泥沙颗粒堆积起来,其堆积体边坡形成的稳定倾斜面与水平面的夹角称为泥沙的水下休止角。
7.含沙量:单位体积浑水中固体泥沙颗粒所占的比例,一般有重量含沙量和体积比含沙量。
8.等容粒径:与泥沙颗粒体积相同的球体直径。
9.中值粒径D50:累计频率曲线上纵坐标取值为50%时所对应的粒径值。
10.算术平均粒径D m:各粒径组平均粒径的重量百分比的加权平均值。
11.风化作用:岩石和矿物在地表环境中,受物力、化学和生物作用,发生体积破坏和化学成分变化的过程,称为风化作用。
12.泥沙的沉速:泥沙在静止清水中沉降速度达到恒定极限速度时,对应的沉速叫做泥沙的沉速。
13.泥沙的干容重:一般把单位体积沙样干燥后的重量称为干容重。
14.泥沙的容重:泥沙颗粒的实有重量于实有体积的比值(即排出空隙率在外)。
15.推移质输沙率:在一定水力、泥沙条件下,单位时间内通过过水断面的推移质数量称为推移质输沙率,用G b表示,单位一般用kg/s或者t/s。
16.泥沙的起动:设想在具有一定泥沙组成的床面上,使水流的速度由小到大逐渐增加,直到使床面泥沙(简称床沙)由静止转入运动,这种现象称为泥沙的起动。
泥沙的沉速讲解

1/
3
s
1
/
3
1/
3
4 3
ReD CD
1/ 3
ReD
Sa
d
g1/
3
s
1/
3
1
/
3
g1/
3
s
2/3
1/ 3 d
上述公式中单位用国际单位:ω:m/s,g:m/s2,d:m
公式单位若为:ω: cm/s,g:cm/s2,d:mm
g1
/
3
s
1/ 3 d
10 2/ 3
F 3 d 3 d
(2-4)
圆球绕流阻力的一般表达式 (2-2)
F
Cd
d2
4
2
2
得
Cd
24
d
24 Red
(2-5)
8
5、层流区、紊流区和过渡区圆球沉速公式 ①、层流区圆球沉速公式( Red<0.5)源自将CD24
d
代入球体在静水中沉速的一般表达式
(2-5)
4 s gd 3Cd
得
第2章 泥沙的沉速 2.1 泥沙沉降的不同形式 1、沉速的定义
单颗粒泥沙在足够大的静止清水中等速下沉时的速度, 称为泥沙的沉速。用符号ω表示。
定义的理解,应注意的几点 ⒉ 泥沙在水中沉降时所受作用力 ⒊ 泥沙在水中沉降特点 ⒋ 研究泥沙沉降的意义
5. 泥沙在静水中下沉时的运动状态
沙粒雷诺数
Red
D
泥沙在层流区的岗恰洛夫沉速公式为
0.75 1 s gd 2 1 s gd 2 18 24
(2-21)
13
3、岗恰洛夫公式 ②紊流区沉速公式(d>1.5mm)
泥沙沉速公式讲解学习

泥沙沉速公式泥沙沉速公式研究泥沙沉速时很多方法都是从球体出发,但天然泥沙并非球体,它在下沉时受到的阻力比球体大,其阻力系数通常根据实验确定,关于泥沙的沉速,中外学者提出不少计算公式。
岗恰洛夫公式(1)层流区 ( D < 0.15㎜ ):):(2)紊流区 ( D > 1.5㎜(3)过渡区 ( 0.15 < D < 1.5㎜ ):考虑层流区和紊流区沉速公式的结构形式,认为在过渡区来说,几个主要变量的次方,应该介于层流区与紊流区之间。
考虑量纲法则得到过渡区沉速公式β反映粒径和温度变化改变粘滞性影响的一个附加因素。
D0=0.15cm,计算时D 应与D0的单位一致。
沙玉清公式(1)层流区 ( D < 0.1㎜ ):(2)紊流区 ( D > 2㎜ ):(3)过渡区 ( 0.1 < D < 2㎜ ) :引进两个无因次判数,一个名为沉速判数Sa ,是沙粒雷诺数ωD/ν及阻力系数CD 的函数。
另一个名为粒径判数Φ,是沙粒雷诺数与沉速判数的函数 。
aS S D Dgνωνγγγφ=⎪⎪⎭⎫ ⎝⎛-=3/23/13/1适用条件:当粒径为0.062到2.0mm 时张瑞瑾公式泥沙下沉时的有效重力31)(DK W S γγ-=K1为泥沙体积系数 泥沙下沉时颗粒所受阻力2232ωρωρυD K D K F +=K2和K3都是无因次系数 由W=F 得到gD K K D K K D K K S γγγυυω-+⎪⎪⎭⎫ ⎝⎛+-=31232322121D C gD C D C S υγγγυ1221--+⎪⎭⎫⎝⎛= 并通过大量的泥沙实测资料得出: C1= 13.95 , C2= 1.09则此公式可满足层流区、紊流区和过渡区的要求。
(1)层流区:(2)紊流区:窦国仁公式①既然在过渡区,绕流阻力有表面阻力和形状阻力两部分组成,所以过渡区总阻力F 总=F 表+F 形 。
②绕流属层流状态时,因为泥沙颗粒背后不发生分离现象,在泥沙的表面全部处于滞性状态,泥沙所受的阻力是F 表 。
泥沙的起动与沉降

阻力系数 CD、CL 与沙粒形状和 沙粒雷诺数有关,最后得出起动拖 曳力公式:
(s c)Df(u D)
(4-32)
上式的关系见图 4-10,即著名的 希尔兹关系曲线。
c s - D
10 20 30 40 60 80
1
0.8 0.6
层流曲线
0.4
0.2 0.1 0.08 0.06 0.04
0.02
• 这就给确定泥沙的临界水流条件带来了困 难,究竟怎样判别泥沙是否起动,目前还 没有一致的看法。
克雷默(1935) 根据试验观察的现象,把 推移质的运动分为四个阶段:
1). 无泥沙运动 2). 轻微的泥沙运动 3). 中等强度泥沙运动 4). 普遍的泥沙运动
窦国仁的理论分析
瞬时底流速表示的起动条件:
粉沙在油中 (层流)
D 0.1
s -
gD
102
103
希尔兹紊流曲线
0.01 0.01 0.02 0.04 0.1 0.2 0.4
12 4
10 20 40 100 200 400 1000
Re *
uD
图 4-10 希尔兹起动拖曳力曲线
希尔兹起动拖曳力曲线具有以下特点:
Re * = 10 ,最易于起动; Re * < 10 ,不易于起动,起动拖曳力随粒 径的减小而加大;
Re* > 10 ,起动拖曳力随粒径的增大而加 大;
Re* > 1000 ,接近一常数0.06。
2 起动流速
由于流速场和剪力场之间存在着一定的 关系,所以可以从起动拖曳力的表达式 推导出泥沙的起动流速公式。如采用对
数流速公式, 可得用UC 代表在临界起动
时的垂线平均流速: 即为Shields数
04、第4次课(泥沙的沉速)

-
ω = 1 . 044
γ
s
− γ
γ
− γ
gD
(D>4mm)
ν ρ −ρ ν ω = 1395 +1.09 s gD−13.95 . ρ D D
2
冈恰洛夫
2/ 3 1 γ s − γ gD 2 g2 / 3 γ s − γ ω= D 24 γ ν ω = β 1/ 3 ν γ 0.15mm) (D<0.15mm)
令
ReD 3 3 = Sa CD 4
Sa =
ω
γ s −γ g ν 1/ 3 γ
1/ 3 1/ 3
4 ReD = 3 C D
1/ 3
6
令
ReD φ= = Sa
ω
ωD ν
1/ 3 γ − γ 1/ 3 s g γ ν
8
⒉ 张瑞瑾层流区与紊流区沉速公式 泥沙在紊流区的阻力为 泥沙在层流区的阻力为 F = k2ρ Dω W = k1 (γ s − γ )D3 泥沙的有效重力为
F = k3 ρ D2ω2
分别解泥沙沉降时力的平衡方程, 分别解泥沙沉降时力的平衡方程,同时利用 实测资料确定系数 紊流区 ω = 1.044 γ s −γ gD (D > 4mm )
ω = 1 . 068
γ
s
γ γ
− γ
gD
-
(D> (D>1.5mm)
沙玉清
2 1 γ s − γ gD 2 [lg S a + 3 .790 ] + ω ω= 24 γ ν [lg Φ − 5 .777 ]2 = 39
河流动力学复习

河流动力学复习第一章绪论考核内容为学科的发展概况、课程的内容及学习任务。
1、了解河流动力学发展的历史;认识水流~泥沙~水电工程可持续发展间的相互关系。
2、了解水流运动与泥沙运动的重要性;3、理解课程的任务与特点;4、了解课程的主要内容。
考核知识点:1、河流动力学的任务2、水流~泥沙~水电工程可持续发展间的相互关系3、河流动力学的研究方法及特点第二章河流动力学基本概念考核内容为河流动力学基本概念1. 河道水流的基本特性:二相性、非恒定性、三维性、非均匀性2. 水沙运动的不平衡性3. 河道水流的水流结构及阻力损失考核知识点:1、河道水流的基本特性2、河道水流的水流结构及阻力损失第三章泥沙特性考核内容为泥沙的分类、泥沙的来源、泥沙的几何特性及泥沙的重力特性。
1. 泥沙的分类2. 泥沙几何特性:粒径,级配曲线,特征值3. 泥沙的重力特性:含沙量、浑水容重考核知识点: 1、泥沙的分类2、泥沙的几何特性及重力特性。
第四章泥沙的沉速考核内容为泥沙沉速的定义、沉降过程中的三种状态、沉速公式、影响沉速的主要因素、泥沙沉速的测定。
考核知识点:1、泥沙沉速的定义、沉速公式2、影响沉速的主要因素、泥沙沉速的测定。
第五章泥沙的起动考核内容为泥沙起动的物理机理,泥沙起动的物理现象及受力分析。
考核知识点:1、均匀沙起动条件:力的表达式,散体及粘性泥沙的统一起动流速公式,2、散体泥沙的起动拖曳力公式,止动与扬动流速。
第六章沙波运动与动床阻力考核内容为沙波运动规律与动床阻力计算。
1. 沙波形态与运动状态,沙坡的发展过程及形成机理,床面形态判别标准,沙波尺度及其运行速度,推求推移质输沙率,沙波运动对河流的影响。
2. 动床阻力:河床与河岸阻力划分,沙粒与沙波阻力的划分,动床阻力的计算。
考核知识点:1. 沙坡的发展过程及形成机理,床面形态判别标准,沙波运动对河流的影响。
2. 动床阻力的计算。
第七章推移质输沙率考核内容为推移质输沙率计算方法。
最新泥沙沉速公式

泥沙沉速公式研究泥沙沉速时很多方法都是从球体出发,但天然泥沙并非球体,它在下沉时受到的阻力比球体大,其阻力系数通常根据实验确定,关于泥沙的沉速,中外学者提出不少计算公式。
岗恰洛夫公式(1)层流区( D < 0.15㎜):):(2)紊流区( D > 1.5㎜(3)过渡区( 0.15 < D < 1.5㎜):考虑层流区和紊流区沉速公式的结构形式,认为在过渡区来说,几个主要变量的次方,应该介于层流区与紊流区之间。
考虑量纲法则得到过渡区沉速公式β反映粒径和温度变化改变粘滞性影响的一个附加因素。
D0=0.15cm,计算时D应与D0的单位一致。
沙玉清公式(1)层流区 ( D < 0.1㎜ ):(2)紊流区 ( D > 2㎜ ):(3)过渡区 ( 0.1 < D < 2㎜ ) :引进两个无因次判数,一个名为沉速判数Sa ,是沙粒雷诺数ωD/ν及阻力系数CD 的函数。
另一个名为粒径判数Φ,是沙粒雷诺数与沉速判数的函数 。
aS S D Dgνωνγγγφ=⎪⎪⎭⎫ ⎝⎛-=3/23/13/1适用条件:当粒径为0.062到2.0mm 时张瑞瑾公式泥沙下沉时的有效重力31)(D K W S γγ-=K1为泥沙体积系数 泥沙下沉时颗粒所受阻力2232ωρωρυD K D K F +=K2和K3都是无因次系数 由W=F 得到gD K K D K K DK K S γγγυυω-+⎪⎪⎭⎫ ⎝⎛+-=31232322121D C gD C D C S υγγγυ1221--+⎪⎭⎫⎝⎛= 并通过大量的泥沙实测资料得出: C1= 13.95 , C2= 1.09此公式可满足层流区、紊流区和过渡区的要求。
(1)层流区:(2)紊流区:窦国仁公式①既然在过渡区,绕流阻力有表面阻力和形状阻力两部分组成,所以过渡区总阻力F总=F 表+F形。
②绕流属层流状态时,因为泥沙颗粒背后不发生分离现象,在泥沙的表面全部处于滞性状态,泥沙所受的阻力是F表。
第四节 河流泥沙的运动

第四节河流泥沙的运动一、推移质运动推移质的运动来源于床面泥沙的起动。
当床面泥沙起动达到一定程度后,床面会出现起伏不平的沙波,而沙波运动又往往是推移质运动的主要形式。
因此,在介绍推移质运动时,往往需要涉及到河床泥沙的起动、起动流速及沙波运动的相关概念。
1.泥沙的起动流速设想床面为泥沙组成且具有一定厚度,在这种水槽中施放水流,使水流的速度由小到大逐渐增加,直到使床面泥沙(床沙)由静止转入运动,这种现象称为泥沙的起动。
泥沙颗粒由静止状态变为运动状态的临界水流条件,称为泥沙的起动条件。
泥沙的起动条件常用起动流速Uc表示,它相当于床面泥沙开始起动时的水流平均流速U。
对于天然沙,其起动流速常由下式计算:U c = 4.66131hd(3-3)式中,d为泥沙粒径;h为水深。
适用范围:d>0.15~0.2mm。
泥沙的起动流速是关系到河床冲刷状态的重要判据,因此,对它的研究具有重要的理论与实践意义。
例如,在研究坝下游河床冲刷时,首先需计算河床泥沙的起动流速。
当河道实际水流流速U超过床沙的起动流速Uc时,就可判定,河床就会被冲刷;反之,河床就不会发生冲刷。
河床在冲刷过程中,水深随之增加,流速降低,当发展到水流条件不足以使床面泥沙继续起动时,冲刷便会自动停止。
再如,组成河床的泥沙粗细不均时,则细的颗粒被水流优先冲走,粗的颗粒留下来逐渐形成一层抗冲覆盖层,冲刷逐渐停止下来。
河床冲刷前的高程与冲刷终止后的高程之差,即为河床的冲刷深度。
下面举例说明泥沙起动流速公式的具体实际应用方法及其意义。
算例:已知某水库下游河段河床沙质组成,河宽B=200m, 过水面积A=500m2,床沙平均粒径d=5.5mm, 问当水库下泄流量Q=500m3/s时,河床会否发生冲刷?可能冲深多少?解:(1)判断河床会否发生冲刷?V = Q/A = 500/500 = 1.0 m/sH = 500/200 = 2.5 m由沙莫夫公式Vc= 4.6d1/3H1/6 = 4.6×(5.5×10-3)1/3×2.51/6= 0.946 m/s∵ V > Vc,∴河床会发生冲刷。
泥沙课后习题讲解

1.泥沙主要有哪些特性?(1)矿物的物理特性①比重——矿物容重与水容重之比:泥沙的比重一般都在2.60~2.70之间,通常取用2.65。
②硬度——硬度是表示矿物抵抗外界机械作用的能力。
(2)几何特性泥沙的几何特征指泥沙的形状和粒径。
①泥沙的粒径:泥沙颗粒的大小,以颗粒直径来表示,简称粒径,其符号为D(或d),单位mm。
1)等容粒径:等容粒径是指体积与泥沙颗粒相等的球体直径。
D=abc/3,或者D=3√abc。
2)筛分粒径(筛径):沙粒的中轴长度是比较接近等容粒径的,因此筛析法所测的粒径可近似地看成等容粒径。
3)沉降粒径(沉径)②圆度——指颗粒棱和角的尖锐程度。
定义:颗粒最尖锐棱角的曲率半径除以颗粒最大内切圆的半径。
③球度—反映沙粒形状的特征系数,沃德尔(wadell)定义:与颗粒体积的球体直径(等容粒径)和颗粒外接球直径之比。
用Ψ表示。
④比表面积,定义——泥沙颗粒的表面积与其体积之比。
⑤泥沙的群体特性(级配曲线)。
粒配曲线:表示天然沙颗粒组成的曲线。
⑥孔隙率与孔隙比。
孔隙率n:沙样中孔隙的体积与沙样总体积之比:n=V孔隙/V总。
孔隙比e:沙样中孔隙的体积与沙样颗粒体积之比:e=V孔隙/(V总-V孔隙)(3)泥沙的重力特性①密度:密度——颗粒单位体积内所含的质量。
②容重(重度):容重(重度)——泥沙颗粒实有重量与实有体积的比值。
③比重:比重——固体泥沙颗粒重量与同体积4℃水的重量之比。
无量纲,一般泥沙比重:=2.65。
④有效容重系数(有效密度系数)泥沙在水中运动状态,既与泥沙容重有关,又与水的容重有关,在分析计算时,常出现相对数值,为简便起见,令:γγγ-=saρρρ-=sa常取a=1.65。
⑤干容重单位体积沙样经过100~105℃温度烘干后,其重量与原状沙样整个体积的比值,称为泥沙的干容重。
符号:sγ'单位:N/m3,tf/m3,kgf/m3;⑥浑水容重:单位体积浑水的重量,单位:N/m3,tf/m3,kgf/m3;⑦含沙量:单位体积浑水中固体泥沙颗粒所占比例,⑧水下休止角(φ)在静水中的泥沙,由于摩擦力的作用,可以形成一定的稳定的倾斜面,此面与水平面的交角称为泥沙的水下休止角。
《泥沙的沉速》课件

05 泥沙的沉速研究展望
研究方向
1 2
泥沙沉速与环境因素的关系
研究泥沙沉速与水流速度、水深、水质等因素的 关系,揭示泥沙运动规律。
泥沙沉速与河床演变
探讨泥沙沉速与河床演变的关系,预测河床形态 变化趋势。
3
泥沙沉速与人类活动影响
分析人类活动对泥沙沉速的影响,提出相应的治 理措施。
03
探讨影响泥沙颗粒沉速的主要因 素,如颗粒形状、大小、密度、
水的温度和流速等。
04
04 泥沙的沉速应用
水库淤积预测
泥沙淤积对水库寿命的影响
水库淤积速度过快会导致水库寿命缩短,影响水库的正常运行。通过泥沙的沉 速研究,可以预测水库淤积情况,为水库的维护和管理提供科学依据。
沉速与水库淤积量的关系
水库淤积量与泥沙的沉速密切相关。通过研究泥沙的沉速,可以推算水库淤积 量,进而制定合理的清淤计划,保持水库的库容和功能。
牛顿公式是描述泥沙颗粒在流动水体中受 到的阻力与流速、颗粒粒径、水的粘滞系 数之间的关系的公式。它基于牛顿第二定 律和斯托克斯阻力理论推导得出。公式表 达为:F=Cdv/2,其中F为阻力,C为阻 力系数,d为颗粒粒径,v为水的粘滞系 数。
修正公式
总结词
对斯托克斯公式和牛顿公式进行修正,以考虑实际水体中的复杂因素对泥沙沉速和阻力的影响。
环境保护
揭示人类活动对河床演变的影响,保护生态 环境。
泥沙资源利用
泥沙资源化利用
随着城市化进程的加速,建筑、道路等工程 需要大量的砂石材料。通过研究泥沙的沉速 ,可以从河床中提取符合工程要求的砂石材 料,实现泥沙资源化利用。
沉速与泥沙资源利用的关 系
泥沙的沉速与砂石材料的粒径、级配等密切 相关。通过对泥沙沉速的研究,可以优化砂 石材料的提取和加工工艺,提高泥沙资源的
泥沙的特性
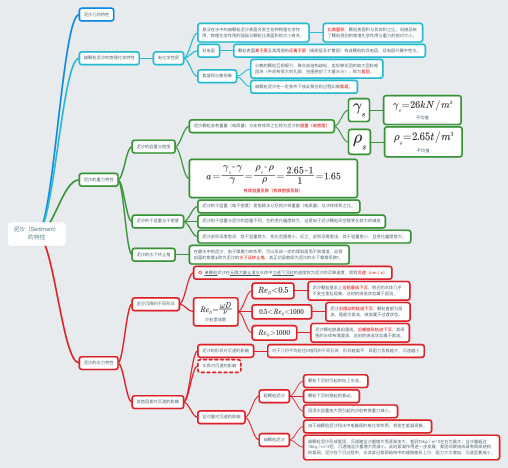
泥沙(Sediment)的特性泥沙几何特性细颗粒泥沙的物理化学特性电化学性质悬浮在水中的细颗粒泥沙表面会发生各种物理化学作用,物理化学作用的强弱与颗粒比表面积的大小有关。
比表面积:颗粒表面积与其体积之比。
间接反映了颗粒受到的物理化学作用与重力的相对大小。
双电层颗粒表面离子层及其周围的反离子层(吸附层及扩散层)构成颗粒的双电层,双电层外属中性水。
絮凝和分散现象分散的颗粒互相吸引,聚合成结构疏松、类似棉花团的较大团粒或团块(中间有很大的孔隙,包围密封了大量水分),称为絮团。
细颗粒泥沙在一定条件下彼此聚合的过程叫做絮凝。
泥沙的重力特性泥沙的容重与密度泥沙颗粒实有重量(或质量)与实有体积之比称为泥沙的容重(或密度)平均值平均值有效容重系数(有效密度系数)泥沙的干容重与干密度泥沙的干容重(或干密度)是指除水分后的沙样重量(或质量)与沙样体积之比。
泥沙的干容重与泥沙的容重不同,它的变化幅度较大,这是由于泥沙颗粒间空隙变化较大的缘故泥沙淤积深度愈深,其干容重愈大,变化范围愈小;反之,淤积深度愈浅,其干容重愈小,且变化幅度愈大。
泥沙的水下休止角在静水中的泥沙,由于摩擦力的作用,可以形成一定的倾斜面而不致塌落,此倾斜面的角度φ称为泥沙的水下远休止角,其正切函数即为泥沙的水下摩擦系数f。
泥沙的水力特性泥沙沉降的不同形式单颗粒泥沙在无限大静止清水水体中匀速下沉时的速度称为泥沙的沉降速度,简称沉速(cm/s)沙粒雷诺数泥沙颗粒基本上沿铅垂线下沉,附近的水体几乎不发生紊乱现象,这时的绕流状态属于层流。
泥沙沿摆动的轨迹下沉;颗粒首部为层流,尾部为紊流,绕流属于过渡状态。
泥沙颗粒脱离铅垂线,沿螺旋形轨迹下沉,其周围的水体布满漩涡,这时的绕流状态属于紊流。
其他因素对沉速的影响泥沙的形状对沉速的影响对于几何平均粒径D相同的不同石块,形状越扁平,其阻力系数越大,沉速越小水质对沉速的影响含沙量对沉速的影响粗颗粒泥沙颗粒下沉时引起的向上水流。
泥沙沉速公式

泥沙沉速公式研究泥沙沉速时很多方法都是从球体出发,但天然泥沙并非球体,它在下沉时受到的阻力比球体大,其阻力系数通常根据实验确定,关于泥沙的沉速,中外学者提出不少计算公式。
岗恰洛夫公式(1)层流区 ( D < 0.15㎜ ):(2)紊流区 ( D > 1.5㎜ ):(3)过渡区 ( 0.15 < D < 1.5㎜ ):考虑层流区和紊流区沉速公式的结构形式,认为在过渡区来说,几个主要变量的次方,应该介于层流区与紊流区之间。
考虑量纲法则得到过渡区沉速公式β反映粒径和温度变化改变粘滞性影响的一个附加因素。
D0=0.15cm,计算时D应与D0的单位一致。
沙玉清公式(1)层流区 ( D < 0.1㎜ ):(2)紊流区 ( D > 2㎜ ):(3)过渡区 ( 0.1 < D < 2㎜ ) :引进两个无因次判数,一个名为沉速判数Sa ,是沙粒雷诺数ωD/ν及阻力系数CD 的函数。
另一个名为粒径判数Φ,是沙粒雷诺数与沉速判数的函数 。
aS S D Dgνωνγγγφ=⎪⎪⎭⎫ ⎝⎛-=3/23/13/1适用条件:当粒径为0.062到2.0mm 时张瑞瑾公式泥沙下沉时的有效重力31)(DK W S γγ-=K1为泥沙体积系数 泥沙下沉时颗粒所受阻力2232ωρωρυD K D K F +=K2和K3都是无因次系数 由W=F 得到gD K K D K K DK K S γγγυυω-+⎪⎪⎭⎫ ⎝⎛+-=31232322121D C gD C D C S υγγγυ1221--+⎪⎭⎫⎝⎛= 并通过大量的泥沙实测资料得出:C1= 13.95 , C2= 1.09则此公式可满足层流区、紊流区和过渡区的要求。
(1)层流区:(2)紊流区:窦国仁公式①既然在过渡区,绕流阻力有表面阻力和形状阻力两部分组成,所以过渡区总阻力F总=F 表+F形。
②绕流属层流状态时,因为泥沙颗粒背后不发生分离现象,在泥沙的表面全部处于滞性状态,泥沙所受的阻力是F表。
泥沙颗粒团沉速

泥沙颗粒团沉速
匡翠萍;郑宇华;顾杰;马丹青
【期刊名称】《同济大学学报(自然科学版)》
【年(卷),期】2016(044)012
【摘要】针对现有的泥沙沉速公式大多适用于单颗粒泥沙沉降的情形,基于前人对单颗粒泥沙沉速规律的研究成果,利用试验测得不同泥沙颗粒团在水中沉降时的沉速数据,引入泥沙颗粒团特征粒径及附加粒径2个因子,对多个广泛运用的单颗粒泥沙沉速公式进行了修正.用修正后的公式计算得到的泥沙颗粒团沉速与用试验测得的泥沙颗粒团沉速较接近,可推广运用到计算泥沙颗粒团在水中的沉降速率.
【总页数】7页(P1845-1850,1866)
【作者】匡翠萍;郑宇华;顾杰;马丹青
【作者单位】同济大学土木工程学院,上海200092;上海海洋大学海洋科学学院,上海201306;上海海洋大学海洋科学学院,上海201306;上海海洋大学海洋科学学院,上海201306
【正文语种】中文
【中图分类】TV142+.1
【相关文献】
1.单颗粒泥沙沉速公式的对比研究 [J], 赵德招;陈立;周银军;桂波
2.基于光谱特征的长江口细颗粒泥沙絮凝体投影表面积和沉速分析 [J], 程江;蒋雪中
3.刚性植物条件下静水中粗颗粒泥沙沉速研究 [J], 唐洪武;吕升奇;龙涧川
4.潮汐环境下细颗粒泥沙沉降速度研究述评Ⅲ——沉速的影响因子 [J], 万远扬;吴华林;沈淇;顾峰峰
5.基于高速摄像的单颗粒泥沙沉速试验 [J], 宋佳苑;孙志林
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
㈠、岗恰洛夫公式 层流区沉速公式( ⒈ 层流区沉速公式( D < 0.15mm ) 球体层流区沉速公式(Stokes公式 公式) 球体层流区沉速公式(Stokes公式)
1 γ s − γ gD2 ω= 18 γ ν
泥沙沉降阻力大于球体沉降阻力,天然泥沙 泥沙沉降阻力大于球体沉降阻力, 沉速应较球体沉速小, 沉速应较球体沉速小,所以应该乘以一个小 的系数。 于1的系数。 泥沙在层流区的岗恰洛夫沉速公式为
14
−4 / 3
考虑形状影响的沉速公式为
c ω = 1.72 ab
2/ 3
γ s −γ gD γ
11
㈡、水质对沉速的影响 泥沙絮凝及絮团的沉速主要受以下因素影响: 泥沙絮凝及絮团的沉速主要受以下因素影响: 1、泥沙粒径 2、水中电解质的离子浓度与价位 3、含盐度 4、含沙量
12
㈢、含沙量对沉速的影响 1、对于水体中含较多粗颗粒泥沙 、 下沉的泥沙引起的向上水流和激起的紊动; 下沉的泥沙引起的向上水流和激起的紊动;浑水容重 增加; 增加; 沉速减小 2、对于水体中含较多细颗粒泥沙时 、 下沉的泥沙引起的向上水流和激起的紊动; 下沉的泥沙引起的向上水流和激起的紊动;浑水容重 增加;浑水粘滞性增加; 增加;浑水粘滞性增加; 沉速减小 细颗粒泥沙和水中的电解质作用, 细颗粒泥沙和水中的电解质作用,将发生絮凝现象 含沙量较低(小于15kg/m ),形成互不相连的絮团 形成互不相连的絮团, 含沙量较低(小于15kg/m3),形成互不相连的絮团, 沉速增加; 增大了颗粒粒径 沉速增加; 含沙量进一步增大(大于15kg/m ),絮团联成絮网结 含沙量进一步增大(大于15kg/m3),絮团联成絮网结 13 构 沉速将大幅降低。 沉速将大幅降低。
层流区,采用Stokes公式; 层流区,采用Stokes公式; Stokes公式 过渡区,采用沙玉清的过渡区公式; 过渡区,采用沙玉清的过渡区公式; 紊流区,采用岗恰洛夫紊流区公式; 紊流区,采用岗恰洛夫紊流区公式; 在实际工作中,常采用张瑞瑾各区统一公式计算沉速。 在实际工作中,常采用张瑞瑾各区统一公式计算沉速。
备注
3.7D 1− 0.037T β = 0.081lg 83 D 0
4
T为水温,D0=1.5mm,计算时D与D0的单位应该一致。 为水温,D0=1.5mm,计算时D D0的单位应该一致。 的单位应该一致
㈡、沙玉清沉速公式 层流区沉速公式( ⒈ 层流区沉速公式( D < 0.1mm ) 与岗恰洛夫的考虑相同, 与岗恰洛夫的考虑相同,得出与岗恰洛夫完 全一致的公式 γ − γ gD2 1
8
⒉ 张瑞瑾层流区与紊流区沉速公式 泥沙在紊流区的阻力为 泥沙在层流区的阻力为 F = k2ρ Dω W = k1 (γ s − γ )D3 泥沙的有效重力为
F = k3 ρ D2ω2
分别解泥沙沉降时力的平衡方程, 分别解泥沙沉降时力的平衡方程,同时利用 实测资料确定系数 紊流区 ω = 1.044 γ s −γ gD (D > 4mm )
1 γ s − γ gD2 1 γ s − γ gD2 ω = 0.75× = 18 γ ν 24 γ ν
2
紊流区沉速公式( ⒉ 紊流区沉速公式( D > 1.5mm ) 紊流区泥沙沉降阻力值大致在0.9 1.4之间 0.9紊流区泥沙沉降阻力值大致在0.9-1.4之间 岗恰洛夫取 CD = 1.17 泥沙沉降阻力为 2 2
2 2
7
㈢、张瑞瑾公式
过渡区沉速公式( ⒈ 过渡区沉速公式( 0.1 < D < 4mm ) F = k2ρν Dω + k3ρ D2ω2 过渡区的阻力 W = k1 (γ s − γ )D3 泥沙的有效重力 F =W 取 1 k2 k1 C1 = ,C2 = 经简单换算, 并令 ,经简单换算,得 2k k
3 3
γ s −γ ν ν gD − C1 ω = C1 + C2 d γ d
2
利用实测资料, 利用实测资料,确定
2
C1 = 13.95,C2 = 1.09
ν γ −γ ν gD −13.95 ω = 13.95 +1.09 s 得, D D γ
——张瑞瑾各区统一沉速公式
令
ReD 3 3 = Sa CD 4
Sa =
ω
γ s −γ g ν 1/ 3 γ
1/ 3 1/ 3
4 ReD = 3 C D
1/ 3
6
令
ReD φ= = Sa
ω
ωD ν
1/ 3 γ − γ 1/ 3 s g γ ν
1/ 3
γ s −γ g γ D = 2/ 3
1/ 3 1/ 3
ν
Sa = f (ω) , =f ( D) φ
(lg Sa + 3.790)2 + (lgφ − 5.777)2 = 39
沙玉清过渡区泥沙沉速的实用算式
D ω lg 1/ 3 + 3.386 + lg 2/ 3 − 5.374 = 39 ν ν
F = CD
πD γ ω
4
2g
泥沙在水流中的有效重力为
6 将阻力系数带入 F ,并令 F = W W = (γ s − γ )
πD3
便得泥沙在紊流区的沉速公式
γ s −γ gD ω = 1.068 γ
3
⒊ 过渡区沉速公式( 0.15 < D < 1.5mm )
沉速公式 沉速与各变量的关系
层流区
1 γ s − γ gD 2 ω= 24 γ ν g2 / 3 γ s − γ ω = β 1/3 ν γ
γ
层流区
1 γ s −γ gD2 ω= 25.6 γ ν
( D < 0.1mm )
9
四、天然沙的沉速公式的选用
作者 Stokes 层流区 层流区 过渡区 - 紊流区 - 各区统一式 -
ω =
1 γ s − γ gD 2 18 γ ν 0.1mm) (D<0.1mm)
张瑞瑾
1 γ s − γ gD2 ω= 25.6 γ ν
ω 与 D 2 , g、
γs −γ −1 有效容重系数) (有效容重系数)的一次方及ν 成正比 γ γs −γ 1/3 次方、 的 2/3 次方、及ν − 成正比 γ
过渡区
2 /3
D
ω 与 D 、与 g 和
紊流区
ω = 1.068
γs −γ gD γ
ω 与 D 、g 和
γs −γ 有效容重系数) 次方及 0 (有效容重系数)的 1/2 次方及ν 成正比 γ
(D<0.1mm) 0.1mm)
-
ω = 1 . 044
γ
s
− γ
γ
− γ
gD
(D>4mm)
ν ρ −ρ ν ω = 1395 +1.09 s gD−13.95 . ρ D D
2
冈恰洛夫
2/ 3 1 γ s − γ gD 2 g2 / 3 γ s − γ ω= D 24 γ ν ω = β 1/ 3 ν γ 0.15mm) (D<0.15mm)
ω = 1 . 068
γ
s
γ γ
− γ
gD
-
(D> (D>1.5mm)
沙玉清
2 1 γ s − γ gD 2 [lg S a + 3 .790 ] + ω ω= 24 γ ν [lg Φ − 5 .777 ]2 = 39
= 1 . 14
s
γ
gD
-
(D<0.1mm) 0.1mm)
(D> (D>2.0mm)
24 γ mm )
ω=
s
沙玉清取紊流区泥沙沉降的阻力系数 CD = 1.02 得,
γ s −γ ω = 1.14 gD γ
5
过渡区沉速公式( ⒊ 过渡区沉速公式( 0.1 < D < 2mm ) ①、沉降判数 Sa 与粒径判数 φ
ωD ReD 3 ω3 ν = = 4 γ s − γ gD 4 γ s CD g −1ν 2 γ 3 γ ω
含沙量对沉速的影响, 含沙量对沉速的影响,取决于以上各因素的对比关 系。 巴切勒用统计理论考虑均匀球体在水中沉降时的相 互影响, 互影响,对非粘性均匀沙得出如下含沙量对沉速影 ω s = ω (1 − 6.55 SV ) 响的公式 体积比含沙量, 含沙量为S 时的均匀沙沉速, SV体积比含沙量,ωs含沙量为SV时的均匀沙沉速, 清水单颗粒泥沙沉速。 ω清水单颗粒泥沙沉速。 该式适用于S <0.05( 该式适用于SV<0.05(即S<130kg/m3)的非粘性粗颗 粒泥沙在本身悬浮液中的沉降情况。 粒泥沙在本身悬浮液中的沉降情况。
10
四、其他因素对沉速的影响 ㈠、泥沙的形状对沉速的影响 形状不同,颗粒在水中下沉所受的阻力不同, 形状不同,颗粒在水中下沉所受的阻力不同, 同粒径的泥沙形状愈扁平,阻力愈大, 同粒径的泥沙形状愈扁平,阻力愈大,沉速 愈小。 愈小。 阻力系数与形状系数的经验关系为
c CD = 0.45 ab
三、泥沙的沉速
泥沙与圆球具有同样的沉降机理, 泥沙与圆球具有同样的沉降机理,球体沉降的阻 力规律同样适用于泥沙,只是泥沙的形状复杂, 力规律同样适用于泥沙,只是泥沙的形状复杂, 沉降中所受到的阻力较球体沉降阻力大, 沉降中所受到的阻力较球体沉降阻力大,同粒径 的沉速有所减小。 的沉速有所减小。 由于泥沙的形状各不相同, 由于泥沙的形状各不相同,无法得类似于球体那 关系曲线, 样的简单的泥沙的 CD ~ ReD 关系曲线,在过渡 区球体沉速可通过试算求解的办法, 区球体沉速可通过试算求解的办法,对求解泥沙 沉速来讲行不通。 沉速来讲行不通。
