流体力学课后答案包括过程
流体力学课后答案
1-2 一盛水封闭容器从空中自由下落,则器内水体质点所受单位质量力等于多少 解:受到的质量力有两个,一个是重力,一个是惯性力。
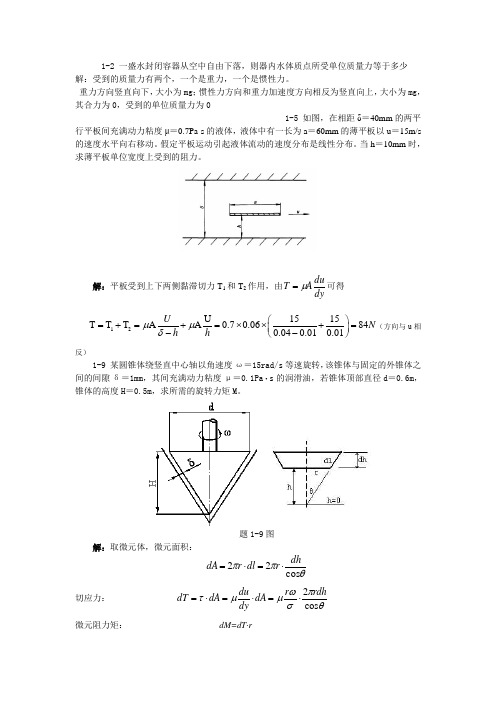
重力方向竖直向下,大小为mg ;惯性力方向和重力加速度方向相反为竖直向上,大小为mg ,其合力为0,受到的单位质量力为01-5 如图,在相距δ=40mm 的两平行平板间充满动力粘度μ=0.7Pa·s 的液体,液体中有一长为a =60mm 的薄平板以u =15m/s 的速度水平向右移动。
假定平板运动引起液体流动的速度分布是线性分布。
当h =10mm 时,求薄平板单位宽度上受到的阻力。
解:平板受到上下两侧黏滞切力T 1和T 2作用,由dyduAT μ=可得 12U 1515T T T AA 0.70.06840.040.010.01U N h h μμδ⎛⎫=+=+=⨯⨯+= ⎪--⎝⎭(方向与u 相反)1-9 某圆锥体绕竖直中心轴以角速度ω=15rad/s 等速旋转,该锥体与固定的外锥体之间的间隙δ=1mm ,其间充满动力粘度μ=0.1Pa ·s 的润滑油,若锥体顶部直径d =0.6m ,锥体的高度H =0.5m ,求所需的旋转力矩M 。
题1-9图解:取微元体,微元面积:θππcos 22dhr dl r dA ⋅=⋅= 切应力: θπσωμμτcos 2rdh r dA dy du dA dT ⋅=⋅=⋅= 微元阻力矩: dM=dT·r阻力矩:2-12 圆柱形容器的半径cm R 15=,高cm H 50=,盛水深cm h 30=,若容器以等角速度ω绕z 轴旋转,试求ω最大为多少时不致使水从容器中溢出。
解:因旋转抛物体的体积等于同底同高圆柱体体积的一半,因此,当容器旋转使水上升到最高时,旋转抛物体自由液面的顶点距容器顶部h’= 2(H-h)= 40cm等角速度旋转直立容器中液体压强的分布规律为0222p gz r p +⎪⎪⎭⎫⎝⎛-=ωρ对于液面,p=p 0 , 则gr z 222ω=,可得出22r gz =ω 将z=h ’,r=R 代入上式得s R gh /671.1815.04.08.92'222=⨯⨯==ω2-13装满油的圆柱形容器,直径cm D 80=,油的密度3/801m kg =ρ,顶盖中心点装有真空表,表的读数为Pa 4900,试求:(1)容器静止时,作用于顶盖上总压力的大小和方向;(2)容器以等角速度120-=s ω旋转时,真空表的读数值不变,作用于顶盖上总压力的大小和方向。
流体力学课后习题答案(第一章)

F 13.1N
M F d 1 13.1 2 2 M 6.55 N m
P F P 13.11 13.1W
答:所需扭矩 M 6.55 N m ,轴功率 P 13.1W 。 1-6 如题图 1-6 所示,两无限大的平板、间隙为 d,假定液体速度 分布呈线性分布。液体动力粘度 m=0.6510-3Pa,密度 r=879.12kg/m3 。 计算:
E 1 2 1 2 m 1 30.48 2 2 E 464.5W 464.5 N m2
的速度移动。
E 464.5W kg 464.5 N m2
(2)求空气的单位体积动能
p RT , R 287 J kg K
p 2.756 105 3.265 kg m3 RT 287 273 21.1
-7-
滑表面匀速下滑,已知:u=1m/s,油膜厚度 d=1mm。求润滑油的动力粘 度系数?
δ=1mm F N u=1m/s mg
5
13
12
题图 1-8 解:因油膜很薄,可以认为速度梯度成直线,符合牛顿内摩擦定律。
F A A
1 180 1 103
F 0.4 0.45
又因为物体做匀速运动,所以有
180 mg 12 13 5 13
180 5 9.81
0.105 Pa s
答:润滑油的动力粘度系数为 0.105 Pa s 。 1-9 如题图 1-9 所示,旋转圆锥体,底 边直径 D=15.2mm,高 h=20cm,油膜充 满锥体和容器的隙缝, 缝隙=0.127mm, 油的动力粘度系数=1.8410-3Pa。 求圆 锥相对容器以等 角速度 120r/min 旋转时所需要的力矩。
流体力学课后答案包括过程
第1章 绪论1.1 解:339005.08.94410m kg m kg gV G V m =⨯===ρ 1.2 解:3132-⎪⎭⎫ ⎝⎛=h y h u dy du m 当25.0=h y 时,此处的流速梯度为h uhu dy du m m0583.1413231=⎪⎭⎫⎝⎛=-当50.0=h y 时,此处的流速梯度为huh u dy du m m 8399.0213231=⎪⎭⎫ ⎝⎛=-1.3 解:N N A dy du A T 1842.08.0001.0115.1=⨯⨯⨯===μτ 1.4 解:充入内外筒间隙中的实验液体,在外筒的带动下做圆周运动。
因间隙很小,速度可视为近似直线分布,不计内筒端面的影响,内桶剪切应力由牛顿内摩擦定律推得:δδωμδμμτ)(0+===r u dy du 作用于内筒的扭矩:h r r Ar M 22)(πδδωμτ+==()()s Pa s Pa hr r M ⋅=⋅+⨯⨯⨯⨯⨯=+=3219.4003.02.04.02.060102003.09.4222πδπωδμ1.5 解:体积压缩系数:dpV dV -=κmlPa ml N m VdpdV 8905.1)1011020(2001075.456210-=⨯-⨯⨯⨯⨯-=-=-κ(负号表示体积减少)手轮转数:122.0418905.1422≈⨯⋅==πδπd dV n1.6 解:νρμ=1()()νρρνμ035.1%101%1512=-+= 035.112=μμ,即2μ比1μ增加了3.5%。
1.7 解:测压管内液面超高:mm d h O H 98.28.292==mm dh Hg05.15.10-=-=当测压管内液面标高为5.437m 时,若箱内盛水,水箱液面高程为:m m m 34402.5100098.2347.5=-若箱内盛水银,水箱液面高程为:m m m 34805.5)100005.1(347.5=-- 1.8 解:当液体静止时,它所受到的单位质量力:{}}{g f f f f z y x -==,0,0,,。
华中科技大学流体力学课后习题答案完整版

解: v |(1,2) =
v
2 x
+
v
2 y
|(1,2) = 30.41m / s ;
a=
a
2 x
+
a
2 y
|(1,2) =
(∂vx / ∂x ⋅ vx )2 + (∂vy / ∂x ⋅ vx + ∂vy / ∂y ⋅ vy )2 = 167.71m / s2 。
2.4 (1) ax = 35, a y = 15 ;(2)260。
直立部分: P2
=
ρg⎜⎛ h ⎝
+
h ⎟⎞ ⋅ hB 2⎠
=
3 2
ρgh 2 B
方向向左;作用点距离水平面为
yD
=
3 2
h+
Bh3 12 3h 2 ⋅ Bh
=
14 h 9
⇒ L2 = 2h −14h 9 = 4h 9 M 2 = P2 ⋅ L2 = 2ρgh3 B 3
于是关闭闸门所需的力 P 由力矩平衡方程
H2
− h2
设此合力的作用点距底部 x 处,则
( ) R ⋅ x = P1 ⋅ H 3 − P2 ⋅ h 3 = ρgB H 3 − h3 6
将 H = 7.5m
⇒
x
=
H
2 + Hh + h2
3(H + h)
h = 3m B = 5m 代入得 R = 1160KN
x = 2.79m
1.29 解:闸门自动开启,此时压力中心 D 应与 O 点重合;水位超过 H,则压力中心 D 高
解:(1) ax |(2,1) = (∂vx / ∂x ⋅ vx + ∂vx / ∂y ⋅ v y ) |(2,1) = 35 ,
流体力学课后答案

流体力学课后答案第1章绪论1.1 若某种牌号的汽油的重度γ为7000N/m 3,求它的密度ρ。
解:由g γρ=得,3327000N/m 714.29kg/m 9.8m /m γρ===g1.2 已知水的密度ρ=997.0kg/m 3,运动黏度ν=0.893×10-6m 2/s ,求它的动力黏度μ。
解:ρμ=v 得,3624997.0kg/m 0.89310m /s 8.910Pa s μρν--==??=?? 1.3 一块可动平板与另一块不动平板同时浸在某种液体中,它们之间的距离为0.5mm ,可动板若以0.25m/s 的速度移动,为了维持这个速度需要单位面积上的作用力为2N/m 2,求这两块平板间流体的动力黏度μ。
解:假设板间流体中的速度分布是线性的,则板间流体的速度梯度可计算为13du u 0.25500s dy y 0.510--===? 由牛顿切应力定律d d uyτμ=,可得两块平板间流体的动力黏度为 3d 410Pa s d yuτμ-==??1.4上下两个平行的圆盘,直径均为d ,间隙厚度为δ,间隙中的液体动力黏度系数为μ,若下盘固定不动,上盘以角速度ω旋转,求所需力矩T 的表达式。
题1.4图解:圆盘不同半径处线速度不同,速度梯度不同,摩擦力也不同,但在微小面积上可视为常量。
在半径r 处,取增量dr ,微面积,则微面积dA 上的摩擦力dF 为du r dF dA2r dr dz ωμπμδ== 由dF 可求dA 上的摩擦矩dT32dT rdF r dr πμωδ==积分上式则有d 43202d T dT r dr 32πμωπμωδδ===??1.5 如下图所示,水流在平板上运动,靠近板壁附近的流速呈抛物线形分布,E 点为抛物线端点,E 点处0d d =y u ,水的运动黏度ν=1.0×10-6m 2/s ,试求y =0,2,4cm 处的切应力。
(提示:先设流速分布C By Ay u ++=2,利用给定的条件确定待定常数A 、B 、C )题1.5图解:以D 点为原点建立坐标系,设流速分布C By Ay u ++=2,由已知条件得C=0,A=-625,B=50则2u 625y 50y =-+ 由切应力公式du dyτμ=得du(1250y 50)dy τμρν==-+ y=0cm 时,221510N /m τ-=?;y=2cm 时,222 2.510N /m τ-=?;y=4cm 时,30τ= 1.6 某流体在圆筒形容器中。
《流体力学》课后习题答案.pdf

得:T1 = t1 + 273 = 50 + 273 = 323K ,T2 = t2 + 273 = 78 + 273 = 351K
根据
p
=
mRT V
,有:
p1
=
mRT1 V1
,
p2
=
mRT2 V2
得: V2 V1
=
p1 p2
T2 T1
=
9.8067 104 5.8840 105
351 323
=
0.18
设管段长度 l,管段表面积: A = dl
单位长度管壁上粘滞力: = A u = dl u − 0 = 3.14 0.025 0.03
l y l
0.001
1-8 解: A = 0.8 0.2 = 0.16m2 ,u=1m/s, = 10mm , = 1.15Pa s
T = A u = A u − 0 = 1.15 0.16 1 = 18.4N
1
=
T1 b
=
A b
u
−0 −h
=
0.7 0.06b b
15 − 0 0.04 − 0.01
=
21N
/m,方向水平向左
下表面单位宽度受到的内摩擦力:
2
=
T2 b
=
Au−0 b h−0
=
0.7 0.06b 15 − 0
b
0.01− 0
= 63N
/m,方向水平向左
平板单位宽度上受到的阻力:
= 1 + 2 = 21+ 63 = 84N ,方向水平向左。
h1 = 5.6m
2.4 解:如图 1-2 是等压面,3-4 是等压面,5-6 段充的是空气,因此 p6 = p5 ,6-7 是等压面,
(完整版)工程流体力学课后习题(第二版)答案

第一章绪论31-1. 20C的水2.5m,当温度升至80C时,其体积增加多少?[解]温度变化前后质量守恒,即V 2V3又20C时,水的密度i 998.23kg /m380C 时,水的密度 2 971.83kg/m3V2— 2.5679m323则增加的体积为V V V i 0.0679m1-2.当空气温度从0C增加至20C时,运动粘度增加15%,重度减少10%,问此时动力粘度增加多少(百分数)?[解](1 0.15)原(1 0.1)原1.035原原1.035原原 1.035原原0.035原原此时动力粘度增加了 3.5%1-3•有一矩形断面的宽渠道,其水流速度分布为u 0.002 g(hy 0.5y2)/ ,式中、分别为水的密度和动力粘度,h为水深。
试求h 0.5m时渠底(y=0)处的切应力。
[解]——0.002 g(h y)/dy0.002 g(h y) dy当h =0.5m , y=0 时0.002 1000 9.807(0.5 0)9.807Pa1-4.一底面积为45 x 50cm2,高为1cm的木块,质量为5kg,沿涂有润滑油的斜面向下作等速运动,木块运动速度u=1m/s,油层厚1cm,斜坡角22.620(见图示),求油的粘度。
[解]木块重量沿斜坡分力F与切力T平衡时,等速下滑mg sindu T Adymg sin A U 5 9.8 sin 22.621 0.4 0.45 -0.0010.1047 Pa s1-5.已知液体中流速沿y方向分布如图示三种情况,试根据牛顿内摩擦定律沿y方向的分布图。
3 3 5 2 [解] A dl 3.14 0.8 10 20 10 5.024 10 m 石,定性绘出切应力1-6 •为导线表面红绝缘,将导线从充满绝缘涂料的模具中拉过。
已知导线直径的粘度=0.02Pa. s。
若导线以速率50m/s拉过模具,试求所需牵拉力。
0.9mm,长度20mm,涂料(1.O1N)yU 50 5F R A 0.02 3 5.024 10 1.01Nh 0.05 10 31-7.两平行平板相距0.5mm,其间充满流体,下板固定,上板在2Pa的压强作用下以0.25m/s匀速移动,求该流体的动力粘度。
《流体力学》课后习题答案详解

习题【1】1-1 解:已知:120t =℃,1395p kPa '=,250t =℃ 120273293T K =+=,250273323T K =+= 据p RT ρ=,有:11p RT ρ'=,22p RT ρ'= 得:2211p T p T '=',则2211323395435293T p p kPa T ''=⋅=⨯=1-2 解:受到的质量力有两个,一个是重力,一个是惯性力。
重力方向竖直向下,大小为mg ;惯性力方向和重力加速度方向相反为竖直向上,大小为mg ,其合力为0,受到的单位质量力为01-3 解:已知:V=10m 3,50T ∆=℃,0.0005V α=℃-1根据1V V V Tα∆=⋅∆,得:30.000510VVV Tα∆=⋅⋅∆=⨯⨯1-4 解:已知:419.806710Pa p '=⨯,52 5.884010Pa p '=⨯,150t =℃,278t =℃得:1127350273323T t K=+=+=,G =mg自由落体: 加速度a =g2227378273351T t K =+=+=根据mRTp V=,有:111mRT p V '=,222mRT p V '=得:421251219.8067103510.185.884010323V p T V p T '⨯=⋅=⨯='⨯,即210.18V V = 体积减小了()10.18100%82%-⨯=1-5 解:已知:40mm δ=,0.7Pa s μ=⋅,a =60mm ,u =15m/s ,h =10mm根据牛顿内摩擦力定律:uT Ayμ∆=∆ 设平板宽度为b ,则平板面积0.06A a b b =⋅=上表面单位宽度受到的内摩擦力:1100.70.06150210.040.01T A u b N b b h b μτδ-⨯-==⋅=⨯=--/m ,方向水平向左下表面单位宽度受到的内摩擦力: 2200.70.061506300.010T A u b N b b h b μτ-⨯-==⋅=⨯=--/m ,方向水平向左平板单位宽度上受到的阻力:12216384N τττ=+=+=,方向水平向左。
流体力学三课后答案

流体力学三课后答案———————————————————————————————————————————————————————————————— 作者:作者: ———————————————————————————————————————————————————————————————— 日期:日期:第一章 流体的基本概念1-1 单位换算:1. 1.海水的密度海水的密度ρ=1028公斤公斤//米3,以达因以达因//厘米3,牛/米3为单位,表示此海水的重度γ值。
值。
解:解:2.2.酒精在酒精在0℃时的比重为0.8070.807,,其密度ρ为若干公斤为若干公斤//米3? ? 若若干克干克//厘米3? ? 其重度其重度γ为若干达因为若干达因//厘米3? ? 若干牛若干牛若干牛//米3?解:l-2 粘度的换算:1. 1.石油在石油在5050℃时的重度℃时的重度γ=900达因达因//厘米3,动力粘度μ=58.86×10-4牛.秒/米2。
求此石油的运动粘性系数ν。
解:解:2.2.某种液体的比重为某种液体的比重为1.0461.046,动力粘性系数,动力粘性系数μ=1.85厘泊,其运动粘性系数为若干斯动粘性系数为若干斯? ?3323333w w/8.790/7908/8.9/807 0.807g/cm 807kg/m 1000kg/m 0.807; cmdy m N s m m kg g ==⨯===⨯=⨯=∴==γρρργρρ比重比重酒精酒精√sm s cm cm dy s cm cm s dy g g /104.6/1064 /900/)/980101086.58( ; 26233224--⨯=⨯=⨯⋅⨯==∴==γμνργρμν33235/44.1007/4.10074/8.9/1028 101; cm dy m N s m m kg dy N g ==⨯=∴==γργ解:3.3.求在求在1大气压下,3535℃时空气的动力粘性系数℃时空气的动力粘性系数μ及运动粘性系数ν之值。
流体力学课后习题与答案

第三、四章 流体动力学基础习题及答案3-8已知流速场u x =xy 2, 313y u y =-, u z =xy, 试求:(1)点(1,2,3)的加速度;(2)是几维流动;(3)是恒定流还是非恒定流;(4)是均匀流还是非均匀流?解:(1)411633x x x x x x y z u u u u a u u u xy t x y z ∂∂∂∂=+++==∂∂∂∂25333213313233312163. 06m/s y y z x y a y u y a yu xu xy xy xy a =-===+=-====(2)二元流动 (3)恒定流(4)非均匀流41xy 33-11已知平面流动速度分布为x y 2222cxu u x ycy x y =-=++,, 其中c 为常数。
求流线方程并画出若干条流线。
解:2222-xdx=ydyx ydx dydx dy cy cx u u x y x y =⇒-=⇒++积分得流线方程:x 2+y 2=c方向由流场中的u x 、u y 确定——逆时针3-17下列两个流动,哪个有旋?哪个无旋?哪个有角变形?哪个无角变形?(1)u x =-ay,u y =ax,u z =0 (2)z 2222,,0,a c x ycy cxu u u x y x y =-==++式中的、为常数。
z 2222,,0,a c x y cy cxu u u x y x y =-==++式中的、为常数。
解:(1)110 ()()22yx x y z u u a a a xy ωωω∂∂===-=+=∂∂有旋流动 xy 11()()0 22y x xy zx u u a a x y εεε∂∂=+=-==∂∂ 无角变形 (2)222222222222222222211()2()2()22()()12()2()0 0 2()y x z x y u u x y c cx x y c cy x y x y x y c x y c x y x y ωωω∂⎡⎤∂+-+-=-=+⎢⎥∂∂++⎣⎦⎡⎤+-+====⎢⎥+⎣⎦无旋流动2222xy 22222112()()()022()()y x u u c x y c x y x y x y x y ε∂⎡⎤∂---=+==-≠⎢⎥∂∂++⎣⎦ 有角变形4—7变直径管段AB ,d A =0.2m,d B =0.4m ,高差△h=1.5m ,测得p A =30kPa ,p B =40kPa ,B 点处断面平均流速v B =1.5m/s ,试判断水在管中的流动方向。
流体力学部分课后题答案详解中国建筑工业出版社

2-15解:(1)当1γ为空气 21p p = ()A B p h z p =++γ ()h z p p p B A +=-=∆γ 3.010008.9⨯⨯= kpa pa 94.22940== (2)当1γ为油 31p p =()z H h p p A +++=γ1 ()H h p p B γγ++=13H h z H h p p p p p B A γγγγγ--+++-=-=∆131h z h 1γγγ-+=1.090002.010008.91.010008.9⨯-⨯⨯+⨯⨯= k p a pa 04.22040== 2-16 解:21p p =()211h h H p p M +++=水γ 212h h p p a 汞油γγ++=()2121h h p h h H p a M 汞油水γγγ++=+++()2.010008.96.1378502.05.110008.998011⨯⨯⨯+⨯=++⨯⨯+-h h 26656785098002.098005.1980098011+=+⨯+⨯+-h h 1960147009802665619501--+=hm h 63.51= 2-28解:()21h h p -=γ()()()b h h h b h h h h P 02210212145sin 45sin 21-+--=γγ ()()145sin 22310008.9145sin 232310008.92100⨯-⨯⨯+⨯-⨯-⨯⨯⨯= kN N 65.343465022510008.9==⨯⨯=()()()Pbl h h h bl h h h h l D D D 2022110212145sin 45sin 21-+--=γγ m 45.222510008.9222210008.92322210008.9=⨯⨯⨯⨯⨯+⨯⨯⨯=2-32 解:b h h b h h P 02202145sin 2145sin γγ+= 2222210008.9212222110008.9⨯⨯⨯⨯⨯+⨯⨯⨯⨯=kN N 8576.1106.1108572810008.9==⨯⨯=Ph h b h h h h b h h l D 02102202102145sin 3245sin 2145sin 245sin ⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=γγ2810008.92372410008.9222410008.9⨯⨯⨯⨯⨯+⨯⨯⨯=2613= 26722613=-=p lT P G l T l P l G ⨯=⨯+⨯22672810008.9162.19⨯=⨯⨯⨯+⨯T kN T 31.10134.27481.9=+= 2-41解:245sin 0=⨯=r hb h h P x ⨯⨯⋅⋅=21γ 4212210008.9⨯⨯⨯⨯⨯=kN N 2.3939200==V P z γ=b r r r⎪⎭⎫⎝⎛⨯⨯⨯-=00245cos 45sin 2136045πγ 4212281214.310008.92⨯⎪⎭⎫ ⎝⎛⨯⨯-⨯⨯⨯⨯= kN N 344.2222344==kN P 1.45344.222.3922=+=03057.0arctan 2.39344.22arctan arctan≈===x z P P α3-3解:(1)s m v d Q /0049.010025.04432323=⋅⋅=⋅=ππs kg Q /9.4=ρ(2)s m v d d v /625.032131=⎪⎪⎭⎫⎝⎛= s m v d d v /5.232232=⎪⎪⎭⎫ ⎝⎛=3-5解:s m h m Q /778.2/1000033==s m d Qv /2042≤=π所以,177.04=≥πv Qd 所以,mm m d 45045.0== 此时,s m d Q d Qv /4.1763585.0112.114422====ππ3-6解:22543212054d d A A A A A ππ======22114012021d d A A ππ=⋅="=' 22224012021d d A A ππ=⋅="='22334012021d d A A ππ=⋅="='22444012021d d A A ππ=⋅="='22554012021d d A A ππ=⋅="='2214014d d ππ=d d 1011=d r 10211= 2224034d d ππ=d d 1032= d r 10232= 2234054d d ππ=d d 1053= d r 10253= 2244074d d ππ=d d 1074= d r 10274=2254094d d ππ=d d 1035=d r 10235= ()()54321254321220240u u u u u d u u u u u d Q G ++++=++++==πρπρρ3-7解:干管前端的质量流量为:42562.2211111d A v Q πρρ⨯⨯==()s kg /128544.005.042562.22=⨯⨯⨯=πs kg Q Q Q /064272.02132===ρρρ ()s m A Q v /247.2204.043.2064272.022222=⋅⋅==πρρ()s m A Q v /05.18045.0424.2064272.023333=⋅⋅==πρρ 3-10解:将基准面建立在B 点经过的水平面上,列能量方程:gv p z gv p z 222222221111αγαγ++=++其中,m z 2.11= m p 5.11=γ s m v /21= s m v d d v /5.4122212== 121==αα gp g 25.40225.12.1222++=++γ871.125.4225.12.1222=-++=gg p γ 3-11解:将2点所在的水平面作为基准面,列能量方程: gv p z gv p z 222222221111αγαγ++=++31=z 02=zγγ21p p =s m v /31=gv p g p 2023322221++=++γγ s m gh v /2.83222=+=32.822112=⎪⎪⎭⎫ ⎝⎛=d d v v 所以,m d 12.02= 3-14解:以水面为基准面,列0-0和D-D 的能量方程:gv p z gv p z DD DD 22220000αγαγ++=++00=z00=γp02200=gv α 4-=D z0=γDpgv DD 2040002α++-=++ 所以,422=gv DD α,即,s m v D /85.88.924=⋅⋅=所以,s m v d Q D /017368.085.805.044322=⋅⋅==ππ81:1:2:24422==A D DD A A d d gv gv αα列0-0和A-A 断面的能量方程:gv p z gv p z AA AA 22220000αγαγ++=++8147000++-=++γAp 所以,8147-=γAp 所以,kpa p A 1.68= 列0-0和B-B 断面的能量方程:gv p z gv p z BB BB 22220000αγαγ++=++kpa p B 484.08.9814-=⋅-= 列0-0和C-C 断面的能量方程:gv p z gv p z CC CC 22220000αγαγ++=++kpa p C 1.208.98142-=⨯⎪⎭⎫ ⎝⎛+-=0=D p3-18解:将基准面建在管道所在的水平面上,列能量方程:21222222111122-+++=++l h gv p z gv p z αγαγ128.998.0008.9490222+++=++g v α9.3222=gv s m v /74.82= 3-19 解:(1)(a )将基准面建在A 所在的水平面上,列0-0和C-C 断面的能量方程:gv p z gv p z CC CC 2222000αγαγ++=++gv CC 2000042α++=++422=gv CC α s m v C /85.88.98=⨯=1:4:2:22222==B C CC B B s s gv gv αα122=gv BB α s m v /43.48.921=⨯= 且 B A v v =(b )(c )gv p z gv p z AA AA 22220000αγαγ++=++10004++=++γAp3=γAp k p a p A 4.29=(2)(a )212200022-+++=++l CC CC h gv p z gv p z αγαγ其中,gv g v h l 2324222121+=-g v g v g v 223200004222222++++=++54222=g v 所以,s m v /96.32= s m v v /96.12121==(b )(c )gv g v p z g v p z 2222212111120000+++=++αγαγ 5300041++=++γp5341-=γp k p a p 32.331= gv g v g v p z g v p z 223242222222222220000++++=++αγαγ5423545400042⋅++++=++γp kpa p 76.112=3-20 解:()()212221221122-++=--++l a p v p z z v p ργγρs m d Qv /38.2005.014.34202.042221=⨯⨯⨯==πs m d Qv /19.1005.014.3402.04222=⨯⨯==π2423222121v v p l ρρ+=-()()242322222122212211v v v p z z v p a ρρργγρ+++=--++22214v v =()()8.930306.02.1224232300212221221⨯+---+++=v v v v p ρρρρ()()8.930306.02.12424212230022222222⨯+---+++=v v v v ρρρρ8.9606.019.1026.0133002⨯⨯-⨯⨯+= pa 16.352= mm p h 6.449.716.3521===γ3-22解:s kN h kN G /048944.0/2.176==s m GQ /1347.77.08.910048944.033=⨯⨯==γs m d Q d Qv /09.914.31347.7444222=⨯===ππ()2122221122-++=-++l a p v p H v p ργγρ其中,01≈v ,pa h p 988.9101010331=⨯⨯⨯==-γ()γgv d H H 2035.0209.97.008.97.02.1098222+⨯+=⨯⨯-++-()8.97.08.9209.9035.0209.97.008.97.02.109822⨯⨯⨯+⨯+=⨯⨯-++-H HH H 0122.19.289.498+=+-所以,m H 64.32=()212211212212-++=-++l M M a p v p H v p ργγρ()8.97.08.9209.9164.322035.0209.97.064.328.97.02.12109822⨯⨯⨯+⨯+=⨯⨯-++-M p 52.169.28968.7998++=+-M p所以,pa p M 45.63-=3-263-28解:列连续性方程:s m D Qv /18.34.014.344.04221=⨯⨯==π s m d Q v /96.501.014.344.04222=⨯⨯==π列能量方程: g v p z g v p z 222222221111αγαγ++=++ g v g v p 222112221ααγ-=m 98.1318.9218.396.5022=⨯-= kpa p 404.12938.998.1311=⨯=列动量方程:()12v vQ F -=∑ρ ()12222144v v Q R d p D p -=-⨯-⨯ρππ()18.396.504.04.04404.12932-⨯=-⨯⨯R πkN R 339.14378.474.04.04404.12932=⨯-⨯⨯=π kN R 94.1112=3-33解:列能量方程:g v p z g v p z 222222221111αγαγ++=++ 其中,5321=v v 2221259v v = g v g v 209.0205.1222211αα++=++gv g v 225926.02222-= s m v /3.42= s m v /58.21=()12v v Q F -=∑ρ()1222212121v v Q R b h b h -=--ργγ 其中,s m Q /644.45.12.158.23=⨯⨯= 72.1644.410009.0108.9215.1108.9212323⨯⨯=-⨯⨯⨯-⨯⨯⨯R N R 2.480=4-2 (1) m mm d 1.0100== s kg Q /10=ρ s m Q Q /01.03==ρρs m d Q v /274.11.014.301.04422=⨯⨯==π s m /10519.126-⨯=ν 8387110519.11.0274.1Re 6=⨯⨯==-νvd (紊流) (2) s kg Q /10=ρ s m Q Q /011765.0850103===ρρ s m d Q v /4987.11.014.3011765.04422=⨯⨯==π s m /1014.124-⨯=ν 13151014.11.04987.1Re 4=⨯⨯==-νvd 4-3 解:m d 3.0= C T 020= s m /107.1526-⨯=νs m d v /1067.1043.0107.152000Re 36max --⨯=⨯⋅=⋅=ν s m A v Q /103947.743.014.31067.1043323max max --⨯=⨯⨯⨯=⋅= h kg Q /9.3136002.1103947.73=⨯⨯⨯=-ρ4-4 解:212=d d 4212221==d d v v 222111Re 2214Re ===ννd v d v 所以,2Re Re 21= 4-12 紊流粗糙区,5106Re ⨯> νvd=Re ,所以,s m d v /14.325.010308.1106Re 65=⨯⨯⨯==-ν s m d v Q /154.0425.014.314.34322=⨯==π 4-13 s m s L Q /2.0/20031==s m d Q v /076433.44211==π 661107791.010308.125.0076433.4Re ⨯=⨯⨯==-νvd s L Q /202= s m v /4076433.02=4210791.7Re ⨯=s L Q /53= s m v /1019.03= 43109478.1Re ⨯=查尼氏图,得到, 5106Re ⨯=u 4104Re ⨯=l123Re Re Re Re Re <<<<u l ,所以,1Q 属于紊流粗糙区,2Q 属于紊流过渡区,3Q 属于紊流光滑区,(1) 对于1Q ,采用希弗林松公式,02326.025.0105.011.011.025.0325.01=⎪⎪⎭⎫ ⎝⎛⨯=⎪⎭⎫ ⎝⎛=-d K λm g v d l h f 888.78.92076433.425.010002326.0222111=⨯⨯⨯==λ (2) 对于2Q ,采用阿公式,02547.010791.76825.0105.011.0Re 6811.025.04325.02=⎪⎪⎭⎫ ⎝⎛⨯+⨯=⎪⎭⎫ ⎝⎛+=-d K λ m g v d l h f 086.08.924076433.025.010002547.0222222=⨯⨯⨯==λ(3) 对于3Q ,采用布公式02678.05.194773164.0Re 3164.025.025.03===λ m g v d l h f 005676.08.9244076433.025.010002678.0222333=⨯⎪⎭⎫ ⎝⎛⨯⨯==λ 4-15 5102Re ⨯=u 4000Re =lm d 05.0= m K 31025.0-⨯= s m d v u /028.405.010007.1102Re 65max =⨯⨯⨯==-νs L d v Q /905.7405.014.3028.4422max max =⨯==π 26m i n 10056.805.010007.14000Re --⨯=⨯⨯==d v l ν s L s m d v Q /1581.0/1001581.0405.014.310056.8432222min min =⨯=⨯⨯==--π 4-21 (1) a d d =21 2211av v = gv d l d v g v d l g v d l h f 2642Re 64221111211121111νλ=== 4212221211ad d v v h h f f == 19.1=a (2)75.425.12275.12122225.0225.0225.021125.0125.0125.021123164.023164.0a d d v v gv d l d v g v d l d v h h f f =⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛==νν 16.1=a (3)25.525.11222122225.0221125.01211211.0211.0a d d v v g v d l d K g v d l d K h h f f =⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛= 14.1=a 4-24 解:s m Q /002742.0602329.03=⨯=s m d Q v /3972.105.014.3002742.04422=⨯⨯==π 629.022=⎪⎭⎫ ⎝⎛+g v d l ζλ ()629.08.923972.162=⨯+ζ 3151.0=ζ 4-26 解:(1) 突然缩小375.03145.7815.015.0121=⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-=A A ζmm m g v h j 5.760765.08.922375.022211==⨯==ζ (2)5.02=ζmm m g v h j 102102.08.9225.022222==⨯==ζ (3)1693145.781122213=⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-=A A ζ mm m h j 115115.08.92216923==⨯= (4)14=ζ mm m h j 204204.08.922124==⨯= 4-27 解:()()gv v g v v h h m m j j 222121-+-=''+' ()()()()02212221=-+--=''+'gv v g v v h h m m vm j j 所以,221v v v m += 此时,()j j j h gv v g v v v g v v v h h 2221222222121212211=-=⎪⎭⎫ ⎝⎛-++⎪⎭⎫ ⎝⎛+-=''+' 4-29 解:s m h m Q /1044.4/16333-⨯== s m d Q v /2624.205.014.31044.44423211=⨯⨯⨯==-π s m d Q v /5656.01.014.31044.44423222=⨯⨯⨯==-π m g v v p p h j 140674.08.925656.02624.28.910001739.522222121=⨯-+⨯⨯-=-+-=γ g v h j 2211ζ= 5387.01=ζ gv h j 2222ζ= 619.82=ζ5-17 解:5.6082.014.32.12.01002.08842412111=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=d d l S p πρλ 7.30422.014.32.12.05002.08842422222=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=d d l S p πρλ 973671.014.32.11.05002.08842432333=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=d d l S p πρλ 3.101018973677.30425.608321=++=++=p p p p S S S S 22211/91.227215.03.101018m N Q S p p =⨯==22222/1.258616.03.101018m N Q S p p =⨯==5-25 解:()()⎪⎩⎪⎨⎧=++=++=1021520232322223221SQ Q Q S SQ Q Q S SQ 610=S解得,s m Q /10472.4331-⨯= s m Q /1041.2332-⨯= s m Q /1063.0333-⨯=5-27 解:94.10348.92.014.32.020002.08842412111=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=g d d l S πλ 8.206988.91.014.31.0100025.08842422222=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=g d d l S πλ 78.37258.92.014.32.072002.08842432333=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=g d d l S πλ 038035.087.14311705.321111211=+=+='S S S 所以,25.6911='S 1)()H Q S S =+'231s m S S H Q /10186.604417163331-⨯==+'=2)H SQ =2 H Q S =⎪⎭⎫ ⎝⎛'221 1325133831432=+'=-'=S S S S gd πζ ()1.25688.92.014.31325142=⨯⨯⨯=ζ 5-28 解:286.1368.93.014.383.020002.084242=⨯⨯⨯⨯==g d d l S AB AB AB AB πλ 029.1098.93.014.383.016002.084242=⨯⨯⨯⨯==g d d l S AC AC AC AC πλ 34.328.94.014.384.020002.084242=⨯⨯⨯⨯==g d d l S AD AD AD AD πλ 772.818.93.014.383.012002.084242=⨯⨯⨯⨯===g d d l S S BC BC BC CD BC πλ 5108.2⨯=A p2AB AB A Q S p γ= s m S p Q AB A AB /457868.08.91000286.136108.235=⨯⨯⨯==γ 2AD AD A Q S p γ= s m S p Q AD AAD /93993.08.9100034.32108.235=⨯⨯⨯==γ ()()222BC BC BC AC A Q S Q S p += ()s m S S p Q Q BC AC A CD BC /23488.043=+==γs m Q Q Q BC AB /69275.022=+= s m Q Q Q CD AD /17481.123=+=s m Q Q Q /86756.13321=+= 22/2.44m kN Q S p BC BC C ==γ。
流体力学课后作业答案

49
2.37 圆柱体直径d=2m,长l=5m,放置于60°的斜
面上,求水作用于圆柱体上的静水总压力大小及其
流
作用方向。
体
力
解: Px ghxC Ax
学
9800 d cos 60 d cos 60 5
2
60°
24.5kN
V
1 2
V圆
V三角
[1 (d )2
22
1 d sin 60 2
0
R3 H3
h3dh
=39.6N m
33
1-13 水暖系统为防止水温升高时体积膨胀将水管胀裂, 在系统顶部设膨胀水箱,若系统内水的总体积V=8m3,
流 体 力
加温前后温差为50ºC,水的体膨胀系数为0.0005 1/ºC, 学
求膨胀水箱的最小容积。
dV
解:由
V
V dt
dV V dt V 0.0005508 0.2m3
若反向流动,Q不变,Re不变,λ不变,hf不变,
所以h不变,只是反向高差为9cm。
26
4-20 环形断面管道中水温10℃,流量Q=400L/min,
当量粗糙高度K=0.15mm,d=75mm,D=100mm。求 流
在管长l=300m管段上的沿程水头损失。
体
解: v Q 4Q 1.94m/s
34
第二章习题解答
2-29 有一容器上部盛油h1=1m,ρ1=800kg/m3,下部盛水 h2=2m,侧壁倾角θ=60º。求容器壁上单宽静水压力及作用 位置。
解:F1 1gh1C A1
油 h1
8009.8 0.5 (1/ sin 60) 1 4.52kN
流体力学课后答案

第一章 流体及其物理性质1-1 已知油的重度为7800N/m 3,求它的密度和比重。
又,0.2m 3此种油的质量和重量各为多少?已已知知::γ=7800N/m 3;V =0.2m 3。
解解析析::(1) 油的密度为 3kg/m 79581.97800===gγρ; 油的比重为 795.01000795OH 2===ρρS (2) 0.2m 3的油的质量和重量分别为 kg 1592.0795=⨯==V M ρ N 15602.07800=⨯==V G γ1-2 已知300L(升)水银的质量为4080kg ,求其密度、重度和比容。
已已知知::V =300L ,m =4080kg 。
解解析析::水银的密度为 33kg/m 13600103004080=⨯==-V m ρ 水银的重度为 3N/m 13341681.913600=⨯==g ργ 水银的比容为 kg /m 10353.7136001135-⨯===ρv1-3 某封闭容器内空气的压力从101325Pa 提高到607950Pa ,温度由20℃升高到78℃,空气的气体常数为287.06J/k g ·K 。
问每kg 空气的体积将比原有体积减少多少?减少的百分比又为多少?已已知知::p 1=101325Pa ,p 2=607950Pa ,t 1=20℃,t 2=78℃,R =287.06J/k g ·K 。
解解析析::由理想气体状态方程(1-12)式,得 kg /m 83.0101325)27320(06.2873111=+⨯==p RT v kg /m 166.0607950)27378(06.2873222=+⨯==p RT v kg /m 664.0166.083.0321=-=-v v%80%10083.0166.083.0%100121=⨯-=⨯-v v v每kg 空气的体积比原有体积减少了0.664m 3;减少的百分比为80%。
《流体力学》课后习题详细解答

1-8解:
或,由 积分得
1-9解:法一:5atm
10atm
=0.537 x 10-9x (10-5) x98.07 x 103= 0.026%
法二: ,积分得
1-10解:水在玻璃管中上升高度
h =
水银在玻璃管中下降的高度
H= mm
第二章流体静力学
2-1解:已知液体所受质量力的x向分量为–a ,z向分量为-g。液体平衡方程为
重心C位于浮心之上,偏心距
沉箱绕长度方向的对称轴y轴倾斜时稳定性最差。浮面面积A=15m2。浮面关于y
轴的惯性矩和体积排量为
定倾半径
可见, >e,定倾中心高于重心,沉箱是稳定的。
第三章流体运动学
3-1解:质点的运动速度
质点的轨迹方程
3-Байду номын сангаас解:
由 和 ,得
故
3-3解:当t=1s时,点A(1,2)处的流速
线速度u = 0r,速度环量
(2)半径r+dr的圆周封闭流线的速度环量为
得
忽略高阶项2 0dr2,得d
(3)设涡量为 ,它在半径r和r+dr两条圆周封闭流线之间的圆环域上的积分为d 。因为 在圆环域上可看作均匀分布,得
将圆环域的面积dA=2 rdr代入该式,得
可解出 =2 + dr/r。忽略无穷小量 dr/r,最后的涡量
沉箱绕长度方向的对称轴y倾斜时稳定性最差。浮面面积A=15m2.浮面关于y轴的惯性矩和体积排量为
定倾半径
可见, ,定倾中心低于重心,沉箱是不稳定的。
(2)沉箱的混凝土体积
沉箱的重量
沉箱水平截面面积
设吃水深度为h,取水的密度 =1000kg/m3.浮力F等于重量G。有
流体力学课后答案

流体力学课后答案(共112页) -本页仅作为预览文档封面,使用时请删除本页-第一章 流体及其物理性质1-1 已知油的重度为7800N/m 3,求它的密度和比重。
又,此种油的质量和重量各为多少已已知知::γ=7800N/m 3;V =。
解解析析::(1) 油的密度为 3kg/m 79581.97800===g γρ;油的比重为 795.01000795OH 2===ρρS (2) 的油的质量和重量分别为 kg 1592.0795=⨯==V M ρ N 15602.07800=⨯==V G γ1-2 已知300L(升)水银的质量为4080kg ,求其密度、重度和比容。
已已知知::V =300L ,m =4080kg 。
解解析析::水银的密度为 33kg/m 13600103004080=⨯==-V m ρ水银的重度为 3N/m 13341681.913600=⨯==g ργ 水银的比容为 kg /m 10353.7136001135-⨯===ρv 1-3 某封闭容器内空气的压力从101325Pa 提高到607950Pa ,温度由20℃升高到78℃,空气的气体常数为kg ·K 。
问每kg 空气的体积将比原有体积减少多少减少的百分比又为多少已已知知::p 1=101325Pa ,p 2=607950Pa ,t 1=20℃,t 2=78℃,R =kg ·K 。
解解析析::由理想气体状态方程(1-12)式,得kg /m 83.0101325)27320(06.2873111=+⨯==p RT v kg /m 166.0607950)27378(06.2873222=+⨯==p RT v kg /m 664.0166.083.0321=-=-v v%80%10083.0166.083.0%100121=⨯-=⨯-v v v每kg 空气的体积比原有体积减少了;减少的百分比为80%。
1-4 图示为一水暖系统,为了防止水温升高时体积膨胀将水管胀裂,在系统顶部设一膨胀水箱,使水有膨胀的余地。
流体力学课后答案.
第1章 绪论1.1 若某种牌号的汽油的重度γ为7000N/m 3,求它的密度ρ。
解:由g γρ=得,3327000N/m 714.29kg/m9.8m /m γρ===g1.2 已知水的密度ρ=997.0kg/m 3,运动黏度ν=0.893×10-6m 2/s ,求它的动力黏度μ。
解:ρμ=v 得,3624997.0kg/m 0.89310m /s 8.910Pa s μρν--==⨯⨯=⨯⋅ 1.3 一块可动平板与另一块不动平板同时浸在某种液体中,它们之间的距离为0.5mm ,可动板若以 0.25m/s 的速度移动,为了维持这个速度需要单位面积上的作用力为2N/m 2,求这两块平板间流体的动力黏度μ。
解:假设板间流体中的速度分布是线性的,则板间流体的速度梯度可计算为13du u 0.25500s dy y 0.510--===⨯ 由牛顿切应力定律d d uyτμ=,可得两块平板间流体的动力黏度为 3d 410Pa s d yuτμ-==⨯⋅1.4上下两个平行的圆盘,直径均为d ,间隙厚度为δ,间隙中的液体动力黏度系数为μ,若下盘固定不动,上盘以角速度ω旋转,求所需力矩T 的表达式。
题1.4图解:圆盘不同半径处线速度 不同,速度梯度不同,摩擦力也不同,但在微小面积上可视为常量。
在半径r 处,取增量dr ,微面积 ,则微面积dA 上的摩擦力dF 为du r dF dA2r dr dz ωμπμδ== 由dF 可求dA 上的摩擦矩dT32dT rdF r dr πμωδ==积分上式则有d 43202d T dT r dr 32πμωπμωδδ===⎰⎰1.5 如下图所示,水流在平板上运动,靠近板壁附近的流速呈抛物线形分布,E 点为抛物线端点,E 点处0d d =y u ,水的运动黏度ν=1.0×10-6m 2/s ,试求y =0,2,4cm 处的切应力。
(提示:先设流速分布C By Ay u ++=2,利用给定的条件确定待定常数A 、B 、C )题1.5图解:以D 点为原点建立坐标系,设流速分布C By Ay u ++=2,由已知条件得C=0,A=-625,B=50则2u 625y 50y =-+ 由切应力公式du dyτμ=得du(1250y 50)dy τμρν==-+ y=0cm 时,221510N/m τ-=⨯;y=2cm 时,222 2.510N/m τ-=⨯;y=4cm 时,30τ= 1.6 某流体在圆筒形容器中。
流体力学课后答案(莫乃榕)

1.gh p p a ρ=- ,(G A p p a =-),所以G ghA =ρ,h=gd Gdg G gAGρππρρ2244==2.)(``12h h g p gh h g p ∆-+=+∆+ρρρ, )2(`21h h g gh p p -∆+=-ρρ,因为42422d h D h ππ=∆、所以22)(D d h h =∆ 。
Pa Dd gh h Dd g gh p p 69.10)]1(`1[]1)[(`2221=-+=-+=-ρρρρρ3.初始时p=p a , )(32y x g p gx p a a -+=+ρρ,当a p p >时,)()(),()(3232232322h h g h h g p p h h y x g p h h x g p a a ∆+∆+∆-=-∆+∆+-+=∆+-+ρρρρ)44(442223322221d d h d h d hππππ-∆=∆= ,所以有:)]()(1[)]()1([22232122212322122223212221322212d d d d d d d gh d d d d d g d d g h p p a -++-=-++-=-ρρρρρ=268.3Pa4.Z=8848m,=β0.0065K/m,T=T 8003055.0/,488.23028800==-=-T T K z z ββ310076.0)443081(2565.50=-=z p p ,0003874.08.0310076.0ρρ=⨯==T R p RTp5,G=20KN ,h=2.5m, μ=0.3 ,F=KN ghG F G T h h g19.2921,122=+=+=⨯⨯μρμρ7.l AA g p p )(sin `021+=-θρ,或者δρδρgl K p gl K p `,`== ,Pa p p )4~2(==ηδ3105.05.0-⨯==mm l δ ,5.0,1~5.0`===∴K lg p K 取δρδ8.2[Pa dp pd 51030][2,]⨯===δσδσ9.80=θ°,3/1900m kg =ρ ,G=1*21,)cos (`1*2cos 2`ghL F h L l g h lL l gρθρθρ=-=+-)c o s `2),cos 3(2),cos 3(2θρρθθ-=->->LlF GlL FG l L F l G(即即θθρρθθρρc o s 31)c o s `,/),cos 3(2)cos (`2->-=->-∴x x x L l l LLl (则令负根舍去)有(4620.0,07.5108215.0,9.1`,cos 31)cos (`22=>--∴=->-x x x x x x ρρθθρρ, 4091.0s i n 4620.0s i n ===θθL l hl 9.Pa pR T m R Pa p T R p 4410735.0,5.0,1047.1,22⨯===⨯== 10.L=0.3m,,h=0.2m,2/5373.6,,s m g lh a lh ga x ga z ===∴-=11.如图坐标轴的原点取在液面的中心,0,cos ,sin =-=--=z y x f g f g a f αα 等压面上ααρcos sin ,0,0)(g g a f f dxdy dy f dx f dz f dy f dx f dp yx y x z y x +-=-==+=++=斜率69,3834.0cos sin ,2,2,cos sin ==+==-=-=-=+-θααβθθπββπθβααg g a tg ctg tg g g a °12.根据旋转抛物面所围体积等于同高同底圆柱体体积的原理,可知自由面恰好经过容器口周边及底面中心,自由面:gR h R r h z r gz 22,2,22222ωω=∴===时,压强分布:2222210),2(r p p z z gr g p p a a ρωωρ=-=-=-时,总压力:F=h R g F Rgh Rhg R rdr p p Ra 222240,2,4,412)(πρωωρωππ=∴==∴=-⎰13.压强分布:C gr gp p p r r z C z grg p a a +====+-=2,,0,)2(22022ωρωρ时,当所以].)(2[2022z r r gg p p a --=-ωρrdr r r ggrdr p p RRa πωρπσ2)(22)(20202-=-=⎰⎰即22/22/,2/,024)(0220224202=====-=-⎰R r R r Rr Rrdr r r R14.初始时,支管液面在0-0上,则活塞盖自重G 等于G=gx d ρπ421,旋转时,以盖心为原点C z gr g p +-=)2(22ωρ,r=R,z=x+h+H 时,p=p )](2[,22H h x gR g p a a ++-=ωρ所以2/)],()(2[11222d R H h x z R r gg p p a =+++--=-令ωρG=2121221412,2]2)()24(2[2)(1R gx G R H h x R R R gg rdr p p R a πρπωρπ=+++-=-⎰所以02)()24(221221412=++-R H h R R R gω2221212222121222212122)(211822/)/(12/2,)(21,44d d d R gd d R R g h d d h H h d d H+-=+-===⨯ωωππ代入上式得2-14有三种思路:一积分;二把力分成两部分;三根据压力中心的公式来求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1章 绪论1.1 解:339005.08.94410m kg m kg gV G V m =⨯===ρ 1.2 解:3132-⎪⎭⎫ ⎝⎛=h y h u dy du m 当25.0=h y 时,此处的流速梯度为h u h u dy du mm 0583.1413231=⎪⎭⎫⎝⎛=-当50.0=h y 时,此处的流速梯度为hu h u dy du mm 8399.0213231=⎪⎭⎫ ⎝⎛=-1.3 解:N N A dy du A T 1842.08.0001.0115.1=⨯⨯⨯===μτ 1.4 解:充入内外筒间隙中的实验液体,在外筒的带动下做圆周运动。
因间隙很小,速度可视为近似直线分布,不计内筒端面的影响,内桶剪切应力由牛顿内摩擦定律推得:δδωμδμμτ)(0+===r u dy du 作用于内筒的扭矩:h r r Ar M 22)(πδδωμτ+==()()s Pa s Pa hr r M ⋅=⋅+⨯⨯⨯⨯⨯=+=3219.4003.02.04.02.060102003.09.4222πδπωδμ1.5 解:体积压缩系数:dp V dV-=κmlPa ml N m VdpdV 8905.1)1011020(2001075.456210-=⨯-⨯⨯⨯⨯-=-=-κ(负号表示体积减少)手轮转数:122.0418905.1422≈⨯⋅==πδπd dV n1.6 解:νρμ=1()()νρρνμ035.1%101%1512=-+= 035.112=μμ,即2μ比1μ增加了3.5%。
1.7 解:测压管内液面超高:mm d h O H 98.28.292==mm dh Hg05.15.10-=-=当测压管内液面标高为5.437m 时,若箱内盛水,水箱液面高程为:m m m 34402.5100098.2347.5=-若箱内盛水银,水箱液面高程为:m m m 34805.5)100005.1(347.5=-- 1.8 解:当液体静止时,它所受到的单位质量力:{}}{g f f f f z y x -==,0,0,,。
当封闭容器自由下落时,它所受到质量力除向下的重力G =mg 外,还有与重力加速度方向相反(即向上)的惯性力F =-mg ,所以0=-=+=mmgmg m F G f z 其单位质量力为{}}{0,0,0,,==z y x f f f f1.9 解:2222y x m r m F +∆=∆=ωω离心水平方向(法向)的单位质量力为:2222y x r mF f +⋅=⋅=∆=ωω离心水平x m y x x y x m F x 222222ωω∆=+⋅+∆=x mxm f x 22ωω=∆∆=同理可求:y f y 2ω=2/8.9s m g mmgf z ---==∆∆=则A 点处单位质量力为:()22242y x g f ++=ω与水平方向夹角为:()22242arcsin arcsin y x g g f g ++==ωθ1.10 解:体积膨胀系数:dtV dVV =α33408.0801000051.0m m Vdt dV V =⨯⨯==α 解法二:dt V dVV α= 积分: ⎰⎰=TT V V V dt V dV 00α()0408.08000051.0ln00=⨯=-=T T V VV α ()30408.004164.100416.110100m e e V V T T V =⨯===-α所以,膨胀水箱的最小容积为:34164.0m V =∆1.11 答:运动粘度ν——[]T L 2切应力τ——[]2LT M 体积模量κ——[]M LT2表面张力系数σ——[]2TM 动量p ——[]T ML 功E ——[]22ML1.12 答:① u E v p =2ρ(欧拉数) ② ③ QA ω23 ④ We lv =σρ2(韦伯数) 1.13 解:由已知条件可将溢流堰过流时单宽流量q 与堰顶水头H 、水的密度ρ和重力加速度g 的关系写成下面的一般表达式:γβαρH g K q =其量纲公式: [][][][][][][]βγβααγβα232312--+----==T L M L LT ML TL根据量纲一致性原则:[]M :0=α []L :23=++-γβα[]T :12-=-β解得: 23210===γβα锅炉散热器令2K m =(即堰流流量系数),得堰流单宽流量计算公式: 2302H g m q =1.14 解:根据题意已知列出水泵输出功率N 与有关的物理量的关系式:()0,,,,=H Q g N f ρ由于用瑞利法求力学方程,有关物理量不能超过4个,当有关物理量超过4个时,则需要归并有关物理量,令g ργ=写出指数乘积关系式:cb a H Q K N γ=写出量纲式:[][][][]cbaH Q N γ=以基本量纲(M 、L 、T )表示各物理量量纲: ()()()cbaL T L T ML TML 132232----=根据量纲和谐原理求量纲指数: M :a =1L :c b a ++-=322 T :b a --=-23 得:1=a ,1=b ,1=c整理方程:令K 为试验确定的系数: gQH K QH K N ργ== 1.15 解:列出有关物理量的关系式:()0,,,,,21=∆νρd d p v f取v ,2d ,ρ为基本量11121c b a d v p ρπ∆=,222212c b a d v d ρπ=,33323c b a d v ρνπ= 1π:[][][][]1112cbad v p ρ=∆ ()()()111321c baML L LT TML ---=M :11c =L :11131c b a -+=- T :12a -=-得:1,0,2111===c b a , ρπ21v p∆=同理可得:212d d =π 3π:[][][][]3332cbad v ρν= 解得:13=a ,13=b ,03=c ,23vd υπ=即:0,,2212=⎪⎪⎭⎫⎝⎛∆vd d d v p f υρ ⎪⎪⎭⎫ ⎝⎛Φ∆=⎪⎪⎭⎫⎝⎛Φ=∆⎪⎪⎭⎫ ⎝⎛=∆1212221212Re,Re,,d d p v d d v vd d d f v pρρρυρ 第2章 流体静力学2.1 解:相对压强:gh p ρ=333/0204.1051/100510.13008.93090m kg m kg gh p =⨯=⨯==ρ 2.2 解:设小活塞顶部所受的来自杠杆的压力为F ,则小活塞给杠杆的反力亦为F ,对杠杆列力矩平衡方程:Fa b a T =+)(a b a T F )(+=小活塞底部的压强为:22)(44adb a T d F p ππ+==根据帕斯卡原理,p 将等值的传递到液体当中各点,大活塞底部亦如此。
222)(4adD b a T D p G +==∴πcm cm b a T Gad D 28.28)7525(201000825)(22=+⨯⨯⨯=+=2.3 解:(1)at at kPa p p p a 3469.19813213295227'===-=-= (2)kPa p p p a v 257095'=-=-=m g p h v v 55.28.925===ρ水柱高 2.4 解:2.5 解:1-1为等压面:gh p gH p a ρρ+=+0kPa m N m N m N H h g p p a 94.100/100940/)2.15.1(8.91000/108.9)('22240==-⨯⨯+⨯=-+=ρ kPa p 94.20=2.6 解: kPa gL p c 45.230sin 5.08.9sin =⨯⨯==αρ 2.7 解:如图所示,过1、2、3点的水平面是等压面。
)()()(322341121z z g z z g gh p z z g gh p B B A A ---++=--+ρρρρρ[])()()()(32212341z z g z z z z g h h g p p A B B A ---+-+-=-ρρρ[])()()()(3221234141z z g z z z z g z z g ---+-+-=ρρρ[]{}310)3262(8.0)1862()3253(6.13)5318(8.9-⨯---+-+-⨯=Pa 8085=2.8 解:1(a)ρ(d)hgh gh p gh p p B B A A ρρρ+-=- ()gh h h g p p p B A B A ρρ+-=-=()[]gh h g p ρρ++-1=()[]31036.08.96.13136.08.9-⨯⨯⨯++-=34.6528kPa2.9 解:如图所示,A 、B 、C 点水平面是等压面。
)9.05.2()9.00.2()7.00.2()7.08.1(---+---=g g g g p p p A ρρρρ g g p ρρ)6.13.1()1.11.1(+-+=g p )9.22.2(ρρ-=8.9)19.26.132.2(⨯⨯-⨯=kPa 796.264=2.10 解:对上支U 形管:()11gh g h h H p ρρ=+- 所以 1)()(h h H p ρρρ-=- (1) 对下支U 形管:221)(gh g h h h H p ρρ=-++ 221)(gh g h h h H p ρρ=-++ (2)将(2)代入(1)得: 212)(h h h p ρρ=- ()()32124950405.264013600m kg h h h p =-⨯=-=ρρ代入(2)得:212h h h h H p--+=ρρ mm39.1435.2610040)1495013600(=-+⨯-=2.11 解:O mH gp A25.1405.0140=+=ρO mH gp C28.1423.25.140=+=ρ O mH gp B25.45.04=+=ρ O mH gpg p B D 25.4==ρρ 2.12 解:静水总压力:()BL L L g P ⨯⨯+=60sin 2211ρ ()kN4329.1035.15.260sin 5.2228.9121=⨯⨯⨯+⨯⨯⨯⨯=或:m L L h C 8146.260sin 21=⎪⎭⎫ ⎝⎛+=kN A gh P C 4359.1035.25.18146.28.91=⨯⨯⨯⨯==ρ 合力作用点D 距A 点的距离: ()[]()[]60sin 60sin 360sin 260sin 1111g L L g L g L L g L L L L DAρρρρ+++⨯+-=()()()m 4103.10.25.20.25.20.220.235.25.2=++++⨯-= 或:压力中心至闸门底边的距离:m m h h h h L e 09.1)60sin 5.460sin 2(3)60sin 5.460sin 22(5.2)(3)2(2121=︒⨯+︒⨯⨯︒⨯+︒⨯⨯⨯=++=或:压力中心的位置:Ay I y y C CxC D += ()m 4103.35.25.125.20.25.25.112125.20.23=⨯⨯⎪⎭⎫ ⎝⎛+⨯⨯+⎪⎭⎫ ⎝⎛+= 0=∑A M : 60cos TL PL DA =()kN L PL T DA 6969.11660cos 5.24103.14359.10360cos =⨯⨯==ρ2.13 解:(1)求闸门所受的静水总压力P 及力矩M对角式转动闸门铅垂边:静水总压力:[])2(2)(2111111R H g BR B R H R H g P P x -=+-==ρρkN 6.19)15.22(8.921=-⨯⨯⨯=作用点距O 点的距离:[][]B R H R H R B H R H H R H R e )2(3)23()(3)(21111111--=+-+-=m 4583.0)15.22(3125.23=-⨯⨯-⨯=力矩:)23(6121111R H g BR e P M -==ρ m kN ⋅=-⨯⨯⨯=9833.8)25.23(8.961对角式转动闸门水平边:静水总压力:kN B gHR P P z 5.2415.28.922=⨯⨯===ρ 作用点距O 点的距离:m R e 5.05.022== 力矩:m kN B gHR e P M ⋅=⨯⨯===25.125.28.9212122222ρ 对整个角式转动闸门:静水总压力:kN P P P z x 3753.315.246.1922=+=+=力矩:m kN M M M ⋅=-=2667.312(2)求当?2=R 时闸门所受的力矩M =0当21M M =时,即22121)23(3HR R H R =-时,M =0 m R H HR R 8563.0)125.23(5.231)23(31212=⨯-⨯⨯=-=2.14 解:设阀门形心点的水深为h c 阀门上受的静水总压力:24d gh P cπρ=P 的作用点距水面的斜长:Ay I y y C CxC D += 2460sin 460sin r h r h c cππ+= c c h r h 460sin 60sin 2+=阀门上受的静水总力矩:)(C D y y P M -=)460sin 4(422CC h d d gh⨯=πρ)1660sin 5.0(5.048.922CC h h⨯⨯⨯⨯=πm kN m kN ⋅=⋅=04.260260.02.15 解:受力示意图:(1)水压力 kN gh P x 490108.921212211=⨯⨯==ρ 01=z P()()2221222121540401028.921221+⨯+⨯⨯⨯=+⨯+=b h h h g P ρ kN 6855.12559=kN h b P P x 117604015arctan cos 6855.12559arctan cos 2122=⎪⎭⎫ ⎝⎛⨯=⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛= kN h b P P z 44104015arctan sin 6855.12559arctan sin 2122=⎪⎭⎫ ⎝⎛⨯=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫⎝⎛=ρkN P P P x x x 122501176049021=+=+= kN P P P z z z 441021=+= kN P P P z x 5237.1301922=+=(2)对O 点的矩 P 1的矩:)(33.21233401031490312111顺时针m kN h h P M x P ⋅=⎪⎭⎫⎝⎛+⨯⨯=⎪⎭⎫ ⎝⎛+⨯=或:m A y I y y C C C D 6667.611111=+=P 2至坝踵的距离(沿坝面方向): ()()()()m h h h h b h L DB 0880.1740104010231540232221212122=++⨯+=+++=()()m b b L AB 3118.194015arctan sin 40154015arctan sin 21=⎪⎭⎫ ⎝⎛⨯+=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+=或:m arctg h arctg h y C 0400.32)4015cos(2)4015cos(212=+=m A y I y y C C C D 7866.3622222=+=P 2的矩:(逆时针)m kN L L P M DB AB P ⋅=-⨯=-⨯=00.27930)0880.173118.19(6855.12559)(22 (逆时针)--m kN M M M P P ⋅==∑67.6696212.16 解:闸门左侧流体静压力:kN b gh b h gh b A P P 632.22sin 2sin 21211111====αραρ左侧压力中心距B 点的距离:m h e 7698.0sin 311==α或:左侧压力中心D 1的位置(距水面的距离):m Ay I y y C xC CD 5396.11111=+= 闸门右侧流体静压力:kN bgh b A P P 905.0sin 22222===αρ右侧压力中心距B 点的距离:m h e 1534.0sin 322==α或:右侧压力中心D 2的位置(距水面的距离):m Ay I y y C xC CD 3079.02222=+= 对铰链O 列力矩平衡方程(此时x>e 1):()()2211e x P e x P -=-mm h h h h h h h h h h P P e P e P x 7955.0)4.02(60sin 34.04.022)(sin 3)(sin 3222122212122213231212211=+︒+⨯+=+++=--=--=αα另一种情况(此时e 1> x ,e 2> x ):对铰链O 列力矩平衡方程:()()x e P x e P -=-2211m P P e P e P x 7955.0212211=--=2.17 解:2.18 解:(1)求铅直分力P z三角形半圆+V V V =30cos 30sin 21422⨯⨯⨯⨯+⨯=d d d π 3227473.930cos 30sin 421442m =⨯⨯⨯+⨯=πkN gV P z 5234.957473.98.9=⨯==ρ(2)求水平分力P xm d L x 4641.330cos ==kN A gh P x xC x 8.584641.3218.92=⨯⨯==ρ2.19 解:解法一: 水平分力: ()()kN b r g P x 2.39445sin 28.92145sin 2122=⨯⨯⨯⨯=⨯=ρ铅直分力: ()()2222225708.045sin 22123604545sin 2136045m r r A P =⨯-⨯⨯=⋅-=ππkN g b A P P z 3752.228.945708.02=⨯⨯=⨯⨯=ρ kN P P P z x 1364.4522=+=''3'43297175.292.393752.22arctan arctan 2 ====x P P β 解法二:水平分力:7071.045sin 221sin 21=⨯⨯==αr h c 26568.545sin 24sin m br A x =⨯⨯== αkN A gh P x c x 2.396568.57071.08.9=⨯⨯==ρ铅直分力:b r r r gV P z ⎥⎦⎤⎢⎣⎡⋅-⨯==ααπρsin cos 21818.92kN 3752.224212212818.922=⨯⎥⎦⎤⎢⎣⎡⨯⨯-⨯⨯⨯=π 其余同解法一。
