2019台湾省中考数学试题(word版,含解析)

合集下载

2020年春人教版九年级数学下册 2019台湾省中考数学试题(word版,含解析)

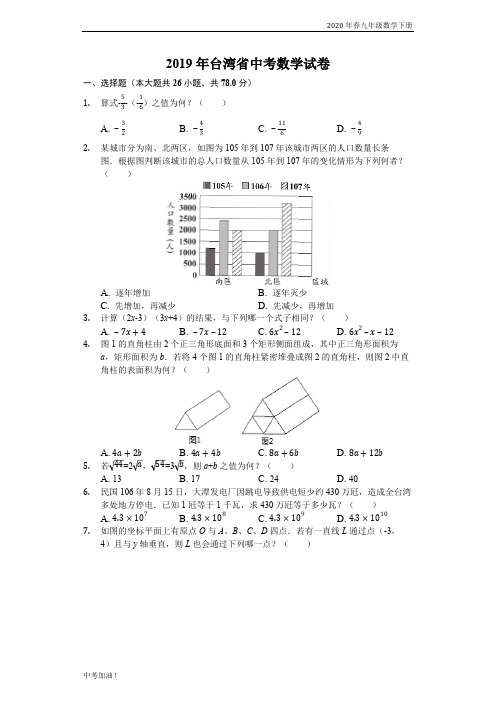
2020年春九年级数学下册中考加油！2019年台湾省中考数学试卷一、选择题（本大题共26小题，共78.0分）1.算式--（-）之值为何？（）5316A. B. C. D. ‒32‒43‒116‒492.某城市分为南、北两区，如图为105年到107年该城市两区的人口数量长条图．根据图判断该城市的总人口数量从105年到107年的变化情形为下列何者？（）A. 逐年增加B. 逐年灭少C. 先增加，再减少D. 先减少，再增加3.计算（2x -3）（3x +4）的结果，与下列哪一个式子相同？（）A. B. C. D. ‒7x +4‒7x ‒126x 2‒126x 2‒x ‒124.图1的直角柱由2个正三角形底面和3个矩形侧面组成，其中正三角形面积为a ，矩形面积为b ．若将4个图1的直角柱紧密堆叠成图2的直角柱，则图2中直角柱的表面积为何？（）A. B. C. D. 4a +2b4a +4b 8a +6b 8a +12b 5.若=2，=3，则a +b 之值为何？（）44a 54b A. 13B. 17C. 24D. 406.民国106年8月15日，大潭发电厂因跳电导致供电短少约430万瓩，造成全台湾多处地方停电．已知1瓩等于1千瓦，求430万瓩等于多少瓦？（）A. B. C. D. 4.3×1074.3×1084.3×1094.3×10107.如图的坐标平面上有原点O 与A 、B 、C 、D 四点．若有一直线L 通过点（-3，4）且与y 轴垂直，则L 也会通过下列哪一点？（）第2页，共19页A. AB. BC. CD. D8.若多项式5x 2+17x -12可因式分解成（x +a ）（bx +c ），其中a 、b 、c 均为整数，则a +c 之值为何？（）A. 1B. 7C. 11D. 139.公园内有一矩形步道，其地面使用相同的灰色正方形地砖与相同的白色等腰直角三角形地砖排列而成．如图表示此步道的地砖排列方式，其中正方形地砖为连续排列且总共有40个．求步道上总共使用多少个三角形地砖？（）A. 84B. 86C. 160D. 16210.数线上有O 、A 、B 、C 四点，各点位置与各点所表示的数如图所示．若数线上有一点D ，D 点所表示的数为d ，且|d -5|=|d -c |，则关于D 点的位置，下列叙述何者正确？（）A. 在A 的左边B. 介于A 、C 之间C. 介于C 、O 之间D. 介于O 、B 之间11.如图，将一长方形纸片沿着虚线剪成两个全等的梯形纸片．根据图中标示长度与角度，求梯形纸片中较短的底边长度为何？（）A. 4B. 5C. 6D. 712.阿慧在店内购买两种蛋糕当伴手礼，如图为蛋糕的价目表．已知阿慧购买10盒蛋糕，花费的金额不超过2500元．若他将蛋糕分给75位同事，每人至少能拿到一个蛋糕，则阿慧花多少元购买蛋糕？（）A. 2150B. 2250C. 2300D. 245013.如图，△ABC 中，D 点在BC 上，将D 点分别以AB 、AC 为对称轴，画出对称点E 、F ，并连接AE 、AF ．根据图中标示的角度，求∠EAF 的度数为何？（）A. 113B. 124C. 129D.1342020年春九年级数学下册中考加油！14.箱子内装有53颗白球及2颗红球，小芬打算从箱子内抽球，以毎次抽出一球后将球再放回的方式抽53次球．若箱子内每颗球被抽到的机会相等，且前52次中抽到白球51次及红球1次，则第53次抽球时，小芬抽到红球的机率为何？（）A. B. C. D. 121325325515.如图，△ABC 中，AC =BC ＜AB ．若∠1、∠2分别为∠ABC 、∠ACB 的外角，则下列角度关系何者正确（）A. ∠1<∠2B. ∠1=∠2C. ∠A +∠2<180∘D. ∠A +∠1>180∘16.小涵与阿嘉一起去咖啡店购买同款咖啡豆，咖啡豆每公克的价钱固定，购买时自备容器则结帐金额再减5元．若小涵购买咖啡豆250公克且自备容器，需支付295元；阿嘉购买咖啡豆x 公克但没有自备容器，需支付y 元，则y 与x 的关系式为下列何者？（）A. B. C. D. y =295250xy =300250xy =295250x +5y =300250x +517.如图，将一张面积为14的大三角形纸片沿着虚线剪成三张小三角形纸片与一张平行四边形纸片．根据图中标示的长度，求平行四边形纸片的面积为何？（）A. B. C. D. 21542524748718.图1的摩天轮上以等间隔的方式设置36个车厢，车厢依顺时针方向分别编号为1号到36号，且摩天轮运行时以逆时针方向等速旋转，旋转一圈花费30分钟．若图2表示21号车厢运行到最高点的情形，则此时经过多少分钟後，9号车厢才会运行到最高点？（）A. 10B. 20C. D. 15245219.如图，直角三角形ABC 的内切圆分别与AB 、BC 相切于D 点、E 点，根据图中标示的长度与角度，求AD 的长度为何？（）第4页，共19页A. 32B. 52C. 43D. 5320.某旅行团到森林游乐区参观，如表为两种参观方式与所需的缆车费用．已知旅行团的每个人皆从这两种方式中选择一种，且去程有15人搭乘缆车，回程有10人搭乘缆车．若他们缆车费用的总花费为4100元，则此旅行团共有多少人？（）参观方式缆车费用去程及回程均搭乘缆车300元单程搭乘缆车，单程步行200元A. 16B. 19C. 22D. 2521.小宜跟同学在某餐厅吃饭，如图为此餐厅的菜单．若他们所点的餐点总共为10份意大利面，x 杯饮料，y 份沙拉，则他们点了几份A 餐？（）A. B. C. D. 10‒x 10‒y 10‒x +y 10‒x ‒y22.若正整数a 和420的最大公因数为35，则下列叙何者正确？（）A. 20可能是a 的因数，25可能是a 的因数B. 20可能是a 的因数，25不可能是a 的因数C. 20不可能是a 的因数，25可能是a 的因数D. 20不可能是a 的因数，25不可能是a 的因数23.如图，有一三角形ABC 的顶点B 、C 皆在直线L 上，且其内心为I ．今固定C点，将此三角形依顺时针方向旋转，使得新三角形A 'B 'C 的顶点A ′落在L 上，且其内心为I ′．若∠A ＜∠B ＜∠C ，则下列叙述何者正确？（）#JYA. IC 和平行，和L 平行B. IC 和平行，和L 不平行I 'A 'II 'I 'A 'II 'C. IC 和不平行，和L 平行D. IC 和不平行，和L 不平行I 'A 'II 'I 'A 'II '24.如图表示A 、B 、C 、D 四点在O 上的位置，其中⏜AD=180°，且=，=．若阿超在上取一点P ，在⏜AB⏜BD⏜BC ⏜CD⏜AB⏜BD上取一点Q ，使得∠APQ =130°，则下列叙述何者正确？（）2020年春九年级数学下册中考加油！A. Q 点在上，且⏜BC⏜BQ>⏜QCB. Q 点在上，且⏜BC⏜BQ<⏜QCC. Q 点在上，且⏜CD⏜CQ>⏜QDD. Q 点在上，且⏜CD⏜CQ<⏜QD25.如图的△ABC 中，AB ＞AC ＞BC ，且D 为BC 上一点．今打算在AB 上找一点P ，在AC 上找一点Q ，使得△APQ 与△PDQ 全等，以下是甲、乙两人的作法：（甲）连接AD ，作AD 的中垂线分别交AB 、AC 于P 点、Q 点，则P 、Q 两点即为所求（乙）过D 作与AC 平行的直线交AB 于P 点，过D 作与AB 平行的直线交AC 于Q 点，则P 、Q 两点即为所求对于甲、乙两人的作法，下列判断何者正确？（）A. 两人皆正确B. 两人皆错误C. 甲正确，乙错误D. 甲错误，乙正确26.如图，坐标平面上有一顶点为A 的抛物线，此抛物线与方程式y =2的图形交于B 、C 两点，△ABC 为正三角形．若A 点坐标为（-3，0），则此抛物线与y 轴的交点坐标为何？（）A. (0,92)B. (0,272)C. (0,9)D. (0,19)二、解答题（本大题共2小题，共16.0分）27.市面上贩售的防晒产品标有防晒指数SPF ，而其对抗紫外线的防护率算法为：防护率=×100%，其中SPF ≥1．SPF ‒1SPF 请回答下列问题：（1）厂商宣称开发出防护率90%的产品，请问该产品的SPF 应标示为多少？（2）某防晒产品文宣内容如图所示．请根据SPF与防护率的转换公式，判断此文宣内容是否合理，并详细解释或完整写出你的理由．28.在公园有两座垂直于水平地面且高度不一的图柱，两座圆柱后面有一堵与地面互相垂直的墙，且圆柱与墙的距离皆为120公分．敏敏观察到高度90公分矮圆柱的影子落在地面上，其影长为60公分；而高圆柱的部分影子落在墙上，如图所示．已知落在地面上的影子皆与墙面互相重直，并视太阳光为平行光，在不计圆柱厚度与影子宽度的情况下，请回答下列问题：（1）若敏敏的身高为150公分，且此刻她的影子完全落在地面上，则影长为多少公分？（2）若同一时间量得高圆柱落在墙上的影长为150公分，则高图柱的高度为多少公分？请详细解释或完整写出你的解题过程，并求出答案．第6页，共19页2020年春九年级数学下册中考加油！答案和解析1.【答案】A 【解析】解：原式=-+=-+==-=-，故选：A．根据有理数的加减法法则计算即可．本题主要考查了有理数的加减法．有理数的减法法则：减去一个数，等于加上这个数的相反数．2.【答案】A【解析】解：由图中数据可知：105年该城市的总人口数量＜106年该城市的总人口数量＜107年该城市的总人口数量，∴该城市的总人口数量从105年到107年逐年增加，故选：A．根据图中数据计算可直接得105年该城市的总人口数量＜106年该城市的总人口数量＜107年该城市的总人口数量，据此作答．本题考查条形统计图，解答本题的关键是明确题意，利用数形结合的思想解答．3.【答案】D【解析】解：由多项式乘法运算法则得（2x-3）（3x+4）=6x2+8x-9x-12=6x2-x-12．故选：D．由多项式乘法运算法则：两多项式相乘时，用一个多项式的各项去乘另一个多项式的每一项，再把所得的积相加，合并同类项后所得的式子就是它们的积．本题考查多项式乘法运算法则，牢记法则，不要漏项是解答本题的关键．4.【答案】C【解析】解：∵正三角形面积为a，矩形面积为b，∴图2中直角柱的表面积=2×4a+6b=8a+6b，故选：C．根据已知条件即可得到结论．本题考查了等边三角形的性质，矩形的性质，列代数式，正确的识别图形是解题的关键．5.【答案】B【解析】解：∵==2，∴a=11，∵==3，∴b=6，∴a+b=11+6=17．故选：B．根据二次根式的定义求出a、b的值，代入求解即可．本题主要考查了二次根式的定义，熟练掌握定义是解答本题的关键．6.【答案】C【解析】解：430万瓩=4300000瓩，∵1瓩等于1千瓦，∴4300000瓩=4300000千瓦=4.3×106千瓦=4.3×109瓦；故选：C．根据题意将430万瓩化为4.3×109瓦即可解题；本题考查科学记数法；能够将单位进行准确的换算，将大数用科学记数法表示出来是解题的关键．7.【答案】D【解析】第8页，共19页2020年春九年级数学下册中考加油！解：如图所示：有一直线L 通过点（-3，4）且与y 轴垂直，故L 也会通过D 点．故选：D ．直接利用点的坐标，正确结合坐标系分析即可．此题主要考查了点的坐标，正确结合平面直角坐标系分析是解题关键．8.【答案】A【解析】解：利用十字交乘法将5x 2+17x-12因式分解，可得：5x 2+17x-12=（x+4）（5x-3）． ∴a=4，c=-3， ∴a+c=4-3=1．故选：A ．首先利用十字交乘法将5x 2+17x-12因式分解，继而求得a ，c 的值．此题考查了十字相乘法分解因式的知识．注意ax 2+bx+c （a≠0）型的式子的因式分解：这种方法的关键是把二次项系数a 分解成两个因数a 1，a 2的积a 1•a 2，把常数项c 分解成两个因数c 1，c 2的积c 1•c 2，并使a 1c 2+a 2c 1正好是一次项b ，那么可以直接写成结果：ax 2+bx+c=（a 1x+c 1）（a 2x+c 2）．9.【答案】A【解析】解：3+40×2+1=84．答：步道上总共使用84个三角形地砖．故选：A ．中间一个正方形对应两个等腰直角三角形，从而得到三角形的个数为3+40×2+1．本题考查了等腰直角三角形：两条直角边相等的直角三角形叫做等腰直角三角形．也考查了规律型问题的解决方法，探寻规律要认真观察、仔细思考，善用联想来解决这类问题．10.【答案】D【解析】解：∵c＜0，b=5，|c|＜5，|d-5|=|d-c|，∴BD=CD，∴D点介于O、B之间，故选：D．根据O、A、B、C四点在数轴上的位置和绝对值的定义即可得到结论．本题考查的是实数与数轴，熟知实数与数轴上各点是一一对应关系是解答此题的关键．11.【答案】C【解析】解：过F作FQ⊥AD于Q，则∠FQE=90°，∵四边形ABCD是长方形，∴∠A=∠B=90°，AB=DC=8，AD∥BC，∴四边形ABFQ是矩形，∴AB=FQ=DC=8，∵AD∥BC，∴∠QEF=∠BFE=45°，∴EQ=FQ=8，∴AE=CF=×（20-8）=6，故选：C．根据矩形的性质得出∠A=∠B=90°，AB=DC=8，AD∥BC，根据矩形的判定得出四边形ABFQ是矩形，求出AB=FQ=DC=8，求出EQ=FQ=8，即可得出答案．本题考查了矩形的性质和判定，能灵活运用定理进行推理是解此题的关键．12.【答案】D【解析】解：设阿慧购买x盒桂圆蛋糕，则购买（10-x）盒金爽蛋糕，依题意有，解得2≤x≤3，第10页，共19页2020年春九年级数学下册∵x是整数，∴x=3，350×3+200×（10-3）=1050+1400=2450（元）．答：阿慧花2450元购买蛋糕．故选：D．可设阿慧购买x盒桂圆蛋糕，则购买（10-x）盒金爽蛋糕，根据不等关系：①购买10盒蛋糕，花费的金额不超过2500元；②蛋糕的个数大于等于75个，列出不等式组求解即可．本题考查一元一次不等式组的应用，解答此类问题的关键是明确题意，列出相应的一元一次不等式组，注意要与实际相联系．13.【答案】D【解析】解：连接AD，∵D点分别以AB、AC为对称轴，画出对称点E、F，∴∠EAB=∠BAD，∠FAC=∠CAD，∵∠B=62°，∠C=51°，∴∠BAC=∠BAD+∠DAC=180°-62°-51°=67°，∴∠EAF=2∠BAC=134°，故选：D．连接AD，利用轴对称的性质解答即可．此题考查轴对称的性质，关键是利用轴对称的性质解答．14.【答案】D【解析】解：∵一个盒子内装有大小、形状相同的53+2=55个球，其中红球2个，白球53个，∴小芬抽到红球的概率是：=．故选：D．让红球的个数除以球的总数即为所求的概率．本题考查了概率公式，熟练掌握概率的概念是解题的关键．15.【答案】C【解析】解：∵AC=BC＜AB，∴∠A=∠ABC＜∠ACB，∵∠1、∠2分别为∠ABC、∠ACB的外角，∴∠2=∠A+∠ABC，∴∠A+∠2=∠A+∠A+∠ABC＜∠ACB+∠A+∠ABC=180°，故选：C．由AC=BC＜AB，得∠A=∠ABC＜∠ACB，再由三角形的外角性质定理和三角形的内角和可得正确答案．本题考查了等腰三角形的性质定理，三角形的外角性质定理及三角形的内角和，这些都是一些基础知识点，难度不大．16.【答案】B【解析】解：根据题意可得咖啡豆每公克的价钱为：（295+5）÷250=（元），∴y与x的关系式为：．故选：B．根据若小涵购买咖啡豆250公克且自备容器，需支付295元，可得咖啡豆每公克的价钱为（295+5）÷250=（元），据此即可y与x的关系式．本题主要考查了一次函数的应用，根据题意得出咖啡豆每公克的单价是解答本题的关键．17.【答案】D【解析】解：如图，设△ADE，△BDF，△CEG，平行四边形DEGF的面积分别为S1，S2，S3和S，过点D作DH∥EC，则由DFGE为平行四边形，易得四边形DHCE也为平行2020年春九年级数学下册四边形，从而△DFH≌△EGC，∴S△DFH=S3，∵DE∥BC，∴△ADE∽△ABC，DE=3，BC=7，∴=，∵S△ABC=14，∴S1=×14，∴S△BDH：S=（×4）：3=2：3，∴S△BDH=S，∴+S=14-×14，∴S=．故选：D．如图，设△ADE，△BDF，△CEG，平行四边形DEGF的面积分别为S1，S2，S3和S，过点D作DH∥EC，则由DFGE为平行四边形，易得四边形DHCE也为平行四边形，从而△DFH≌△EGC，利用面积比等于相似比的平方可求．本题是巧求面积的选择题，综合考查了平行四边形，相似三角形的性质等，难度较大．18.【答案】B【解析】解：=20（分钟）．所以经过20分钟後，9号车厢才会运行到最高点．故选：B．先求出从21号旋转到9号旋转的角度占圆大小比例，再根据旋转一圈花费30分钟解答即可．本题主要考查了生活中的旋转现象，理清题意，得出从21号旋转到9号旋转的角度占圆大小比例是解答本题的关键．19.【答案】D【解析】解：设AD=x，∵直角三角形ABC的内切圆分别与AB、BC相切于D点、E点，∴BD=BE=1，∴AB=x+1，AC=AD+CE=x+4，在Rt△ABC中，（x+1）2+52=（x+4）2，解得x=，即AD的长度为．故选：D．设AD=x，利用切线长定理得到BD=BE=1，AB=x+1，AC=AD+CE=x+4，然后根据勾股定理得到（x+1）2+52=（x+4）2，最后解方程即可．本题考查了三角形的内切圆与内心：三角形的内心到三角形三边的距离相等；三角形的内心与三角形顶点的连线平分这个内角．也考查了切线长定理．20.【答案】A【解析】解：设此旅行团有x人单程搭乘缆车，单程步行，其中去程及回程均搭乘缆车的有y人，根据题意得，，解得，，则总人数为7+9=16（人）故选：A．设此旅行团有x人单程搭乘缆车，单程步行，其中去程及回程均搭乘缆车的有y人，根据题意列出二元一次方程，求出其解．2020年春九年级数学下册本题是二元一次方程组的应用，主要考查了列二元一次方程组解应用题，关键是读懂题意，找出等量关系，列出方程组．21.【答案】D【解析】解：x杯饮料则在B餐中点了x份意大利面，y份沙拉则在C餐中点了y份意大利面，∴点A餐为10-x-y；故选：D．根据点的饮料和沙拉能确定点了x+y份意大利面，根据题意可得点A餐10-x-y；本题考查列代数式；能够根据题意，以意大利面为依据，准确列出代数式是解题的关键．22.【答案】C【解析】解：正整数a和420的最大公因数为35，则a必须是35的倍数，∵420÷35=12，12=3×4，20=4×5，25=5×5，∴20不可能是a的因数，25可能是a的因数；故选：C．由420÷35=12，12=3×4，20=4×5，25=5×5，即可求解；本题考查有理数的乘法；理解因数的概念，熟练掌握有理数的乘法是解题的关键．23.【答案】C【解析】解：作ID⊥BA'于D，IE⊥AC于E，I'F⊥BA'于F，如图所示：则ID∥I'F，∵△ABC的内心为I，△A'B'C的内心为I′，∴ID=IE=IF，∠ICD-∠ACB，∠I'A'C=∠B'A'C，∴四边形IDFI'是矩形，∴II'∥L，∵∠A＜∠B＜∠C，∴∠A'＜∠B'＜∠C，∴∠ICD＞∠I'A'C，∴IC和I'A'不平行，故选：C．作ID⊥BA'于D，IE⊥AC于E，I'F⊥BA'于F，由内心的性质得出ID=IE=IF，∠ICD=∠ACB，∠I'A'C=∠B'A'C，证出四边形IDFI'是矩形，得出II'∥L，证出∠ICD＞∠I'A'C，得出IC和I'A'不平行，即可得出结论．本题考查了三角形的内心、平行线的判定、旋转的性质；熟练掌握三角形的内心性质和平行线的判定是解题的关键．24.【答案】B【解析】解：连接AD，OB，OC，∵=180°，且=，=，∴∠BOC=∠DOC=45°，在圆周上取一点E连接AE，CE，∴∠E=AOC=67.5°，∴∠ABC=122.5°＜130°，取的中点F，连接OF，则∠AOF=67.5°，∴∠ABF=123.25°＜130°，∴Q点在上，且＜，故选：B．连接AD，OB，OC，根据题意得到∠BOC=∠DOC=45°，在圆周上取一点E连接AE，CE，由圆周角定理得到∠E=AOC=67.5°，求得∠ABC=122.5°＜130°，取的中点F，连接OF，得到∠ABF=123.25°＜130°，于是得到结论．2020年春九年级数学下册本题考查了圆心角，弧，弦的关系，圆内接四边形的性质，圆周角定理，正确的理解题意是解题的关键．25.【答案】A【解析】解：如图1，∵PQ垂直平分AD，∴PA=PD，QA=QD，而PQ=PQ，∴△APQ≌△DPQ（SSS），所以甲正确；如图2，∵PD∥AQ，DQ∥AP，∴四边形APDQ为平行四边形，∴PA=DQ，PD=AQ，而PQ=QP，∴△APQ≌△DQP（SSS），所以乙正确．故选：A．如图1，根据线段垂直平分线的性质得到PA=PD，QA=QD，则根据“SSS”可判断△APQ≌△DPQ，则可对甲进行判断；如图2，根据平行四边形的判定方法先证明四边形APDQ为平行四边形，则根据平行四边形的性质得到PA=DQ，PD=AQ，则根据“SSS”可判断△APQ≌△DQP，则可对乙进行判断．本题考查了作图-复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了线段垂直平分线的性质、平行四边形的判定与性质和三角形全等的判定．26.【答案】B【解析】解：设B（-3-m，2），C（-3+m，2），（m＞0）∵A点坐标为（-3，0），∴BC=2m，∵△ABC 为正三角形，∴AC=2m ，∠DAO=60°，∴m=∴C （-3+，2）设抛物线解析式y=a （x+3）2，a （-3++3）2=2，∴a=，∴y=（x+3）2，当x=0时，y=；故选：B ．设B （-3-m ，2），C （-3+m ，2），（m ＞0），可知BC=2m ，再由等边三角形的性质可知C （-3+，2），设抛物线解析式y=a （x+3）2，将点C 代入解析式即可求a ，进而求解；本题考查二次函数的图象及性质，等边三角形的性质；结合函数图象将等边三角形的边长转化为点的坐标是解题的关键．27.【答案】解：（1）根据题意得，，SPF ‒1SPF ×100%=90%解得，SPF =10，答：该产品的SPF 应标示为10；（2）文宣内容不合理．理由如下：当SPF =25时，其防护率为：；25‒125×100%=96%当SPF =50时，其防护率为：；50‒150×100%=98%98%-96%=2%，∴第二代防晒乳液比第一代防晒乳液的防护率提高了2%，不是提高了一倍．∴文宣内容不合理．【解析】（1）根据公式列出方程进行计算便可；（2）根据公式计算两个的防护率，再比较可知结果．2020年春九年级数学下册本题是分式方程的应用，根据公式列出方程是解第一题的关键，第二题的关键是根据公式正确算出各自的防护率．28.【答案】解：（1）设敏敏的影长为x 公分．由题意：=，150x 9060解得x =100（公分），经检验：x =100是分式方程的解．∴敏敏的影长为100公分．（2）如图，连接AE ，作FB ∥EA ．∵AB ∥EF ，∴四边形ABFE 是平行四边形，∴AB =EF =150公分，设BC =y 公分，由题意BC 落在地面上的影从为120公分．∴=，y 1209060∴y =180（公分），∴AC =AB +BC =150+180=330（公分），答：高图柱的高度为330公分．【解析】（1）根据同一时刻，物长与影从成正比，构建方程即可解决问题．（2）如图，连接AE ，作FB ∥EA ．分别求出AB ，BC 的长即可解决问题．本题考查相似三角形的应用，平行投影，平行四边形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．。

2019年台湾省中考数学试卷-含详细解析

2019年台湾省中考数学试卷含详细解析一、选择题（本大题共26小题，共78.0分）1.算式−53−(−16)之值为何？()A. −32B. −43C. −116D. −492.某城市分为南、北两区，如图为105年到107年该城市两区的人口数量长条图．根据图判断该城市的总人口数量从105年到107年的变化情形为下列何者？()A. 逐年增加B. 逐年减少C. 先增加，再减少D. 先减少，再增加3.计算(2x−3)(3x+4)的结果，与下列哪一个式子相同？()A. −7x+4B. −7x−12C. 6x2−12D. 6x2−x−124.图1的直角柱由2个正三角形底面和3个矩形侧面组成，其中正三角形面积为a，矩形面积为b.若将4个图1的直角柱紧密堆叠成图2的直角柱，则图2中直角柱的表面积为何？()A. 4a+2bB. 4a+4bC. 8a+6bD. 8a+12b5.若√44=2√a，√54=3√b，则a+b之值为何？()A. 13B. 17C. 24D. 406.民国106年8月15日，大潭发电厂因跳电导致供电短少约430万瓩，造成全台湾多处地方停电．已知1瓩等于1千瓦，求430万瓩等于多少瓦？()A. 4.3×107B. 4.3×108C. 4.3×109D. 4.3×10107.如图的坐标平面上有原点O与A、B、C、D四点．若有一直线L通过点(−3,4)且与y轴垂直，则L也会通过下列哪一点？()A. AB. BC. CD. D8.若多项式5x2+17x−12可因式分解成(x+a)(bx+c)，其中a、b、c均为整数，则a+c之值为何？()A. 1B. 7C. 11D. 139.公园内有一矩形步道，其地面使用相同的灰色正方形地砖与相同的白色等腰直角三角形地砖排列而成．如图表示此步道的地砖排列方式，其中正方形地砖为连续排列且总共有40个．求步道上总共使用多少个三角形地砖？()A. 84B. 86C. 160D. 16210.数线上有O、A、B、C四点，各点位置与各点所表示的数如图所示．若数线上有一点D，D点所表示的数为d，且|d−5|=|d−c|，则关于D点的位置，下列叙述何者正确？()A. 在A的左边B. 介于A、C之间C. 介于C、O之间D. 介于O、B之间11.如图，将一长方形纸片沿着虚线剪成两个全等的梯形纸片．根据图中标示长度与角度，求梯形纸片中较短的底边长度为何？()A. 4B. 5C. 6D. 712.阿慧在店内购买两种蛋糕当伴手礼，如图为蛋糕的价目表．已知阿慧购买10盒蛋糕，花费的金额不超过2500元．若他将蛋糕分给75位同事，每人至少能拿到一个蛋糕，则阿慧花多少元购买蛋糕？()A. 2150B. 2250C. 2300D. 245013.如图，△ABC中，D点在BC上，将D点分别以AB、AC为对称轴，画出对称点E、F，并连接AE、AF.根据图中标示的角度，求∠EAF的度数为何？()A. 113B. 124C. 129D. 13414.箱子内装有53颗白球及2颗红球，小芬打算从箱子内抽球，以毎次抽出一球后将球再放回的方式抽53次球．若箱子内每个球被抽到的机会相等，且前52次中抽到白球51次及红球1次，则第53次抽球时，小芬抽到红球的机率为何？()A. 12B. 13C. 253D. 25515.如图，△ABC中，AC=BC<AB.若∠1、∠2分别为∠ABC、∠ACB的外角，则下列角度关系何者正确()A. ∠1<∠2B. ∠1=∠2C. ∠A+∠2<180°D. ∠A+∠1>180°16.小涵与阿嘉一起去咖啡店购买同款咖啡豆，咖啡豆每公克的价钱固定，购买时自备容器则结帐金额再减5元．若小涵购买咖啡豆250公克且自备容器，需支付295元；阿嘉购买咖啡豆x公克但没有自备容器，需支付y元，则y与x的关系式为下列何者？()A. y=295250x B. y=300250x C. y=295250x+5 D. y=300250x+517.如图，将一张面积为14的大三角形纸片沿着虚线剪成三张小三角形纸片与一张平行四边形纸片．根据图中标示的长度，求平行四边形纸片的面积为何？()A. 215B. 425C. 247D. 48718.图1的摩天轮上以等间隔的方式设置36个车厢，车厢依顺时针方向分别编号为1号到36号，且摩天轮运行时以逆时针方向等速旋转，旋转一圈花费30分钟．若图2表示21号车厢运行到最高点的情形，则此时经过多少分钟後，9号车厢才会运行到最高点？()A. 10B. 20C. 152D. 45219.如图，直角三角形ABC的内切圆分别与AB、BC相切于D点、E点，根据图中标示的长度与角度，求AD的长度为何？()A. 32B. 52C. 43D. 5320.某旅行团到森林游乐区参观，如表为两种参观方式与所需的缆车费用．已知旅行团的每个人皆从这两种方式中选择一种，且去程有15人搭乘缆车，回程有10人搭乘缆车．若他们缆车费用的总花费为4100元，则此旅行团共有多少人？()参观方式缆车费用去程及回程均搭乘缆车300元单程搭乘缆车，单程步行200元1619222521.小宜跟同学在某餐厅吃饭，如图为此餐厅的菜单．若他们所点的餐点总共为10份意大利面，x杯饮料，y份沙拉，则他们点了几份A餐？()A. 10−xB. 10−yC. 10−x+yD. 10−x−y22.若正整数a和420的最大公因数为35，则下列叙何者正确？()A. 20可能是a的因数，25可能是a的因数B. 20可能是a的因数，25不可能是a的因数C. 20不可能是a的因数，25可能是a的因数D. 20不可能是a的因数，25不可能是a的因数23.如图，有一三角形ABC的顶点B、C皆在直线L上，且其内心为I.今固定C点，将此三角形依顺时针方向旋转，使得新三角形A′B′C的顶点A′落在L上，且其内心为I′.若∠A<∠B<∠C，则下列叙述何者正确？()#JYA. IC和I′A′平行，II′和L平行B. IC和I′A′平行，II′和L不平行C. IC和I′A′不平行，II′和L平行D. IC和I′A′不平行，II′和L不平行24.如图表示A、B、C、D四点在O上的位置，其中AD⏜=180°，且AB⏜=BD⏜，BC⏜=CD⏜.若阿超在AB⏜上取一点P，在BD⏜上取一点Q，使得∠APQ=130°，则下列叙述何者正确？()A. Q点在BC⏜上，且BQ⏜>QC⏜B. Q点在BC⏜上，且BQ⏜<QC⏜C. Q点在CD⏜上，且CQ⏜>QD⏜D. Q点在CD⏜上，且CQ⏜<QD⏜25.如图的△ABC中，AB>AC>BC，且D为BC上一点．今打算在AB上找一点P，在AC上找一点Q，使得△APQ与△PDQ全等，以下是甲、乙两人的作法：(甲)连接AD，作AD的中垂线分别交AB、AC于P点、Q点，则P、Q两点即为所求(乙)过D作与AC平行的直线交AB于P点，过D作与AB平行的直线交AC于Q点，则P、Q两点即为所求对于甲、乙两人的作法，下列判断何者正确？()A. 两人皆正确B. 两人皆错误C. 甲正确，乙错误D. 甲错误，乙正确26.如图，坐标平面上有一顶点为A的抛物线，此抛物线与方程式y=2的图形交于B、C两点，△ABC为正三角形．若A点坐标为(−3,0)，则此抛物线与y轴的交点坐标为何？())A. (0,92)B. (0,272C. (0,9)D. (0,19)二、解答题（本大题共2小题，共16.0分）27.市面上贩售的防晒产品标有防晒指数SPF，而其对抗紫外线的防护率算法为：防护×100%，其中SPF≥1．率=SPF−1SPF请回答下列问题：(1)厂商宣称开发出防护率90%的产品，请问该产品的SPF应标示为多少？(2)某防晒产品文宣内容如图所示．请根据SPF与防护率的转换公式，判断此文宣内容是否合理，并详细解释或完整写出你的理由．28.在公园有两座垂直于水平地面且高度不一的图柱，两座圆柱后面有一堵与地面互相垂直的墙，且圆柱与墙的距离皆为120公分．敏敏观察到高度90公分矮圆柱的影子落在地面上，其影长为60公分；而高圆柱的部分影子落在墙上，如图所示．已知落在地面上的影子皆与墙面互相重直，并视太阳光为平行光，在不计圆柱厚度与影子宽度的情况下，请回答下列问题：(1)若敏敏的身高为150公分，且此刻她的影子完全落在地面上，则影长为多少公分？(2)若同一时间量得高圆柱落在墙上的影长为150公分，则高图柱的高度为多少公分？请详细解释或完整写出你的解题过程，并求出答案．答案和解析1.【答案】A【解析】解：原式=−53+16=−106+16=−10+16=−96=−32，故选：A．根据有理数的加减法法则计算即可．本题主要考查了有理数的加减法．有理数的减法法则：减去一个数，等于加上这个数的相反数．2.【答案】A【解析】【分析】本题考查条形统计图，解答本题的关键是明确题意，属于基础题．根据图中数据计算可直接得105年该城市的总人口数量<106年该城市的总人口数量< 107年该城市的总人口数量，据此作答．【解答】解：由图中数据可知：105年该城市的总人口数量<106年该城市的总人口数量<107年该城市的总人口数量，∴该城市的总人口数量从105年到107年逐年增加，故选：A．3.【答案】D【解析】解：由多项式乘法运算法则得(2x−3)(3x+4)=6x2+8x−9x−12=6x2−x−12．故选：D．由多项式乘法运算法则：两多项式相乘时，用一个多项式的各项去乘另一个多项式的每一项，再把所得的积相加，合并同类项后所得的式子就是它们的积．本题考查多项式乘法运算法则，牢记法则，不要漏项是解答本题的关键．4.【答案】C【解析】解：∵正三角形面积为a，矩形面积为b，∴图2中直角柱的表面积=2×4a+6b=8a+6b，故选：C．根据已知条件即可得到结论．本题考查了等边三角形的性质，矩形的性质，列代数式，正确的识别图形是解题的关键．5.【答案】B【解析】解：∵√44=2√11=2√a，∴a=11，∵√54=3√6=3√b，∴b=6，∴a+b=11+6=17．故选：B．根据二次根式的定义求出a、b的值，代入求解即可．本题主要考查了二次根式的定义，熟练掌握定义是解答本题的关键．6.【答案】C【解析】解：430万瓩=4300000瓩，∵1瓩等于1千瓦，∴4300000瓩=4300000千瓦=4.3×106千瓦=4.3×109瓦；故选：C．根据题意将430万瓩化为4.3×109瓦即可解题；本题考查科学记数法；能够将单位进行准确的换算，将大数用科学记数法表示出来是解题的关键．7.【答案】D【解析】解：如图所示：有一直线L通过点(−3,4)且与y轴垂直，故L也会通过D点．故选：D．直接利用点的坐标，正确结合坐标系分析即可．此题主要考查了点的坐标，正确结合平面直角坐标系分析是解题关键．8.【答案】A【解析】解：利用十字交乘法将5x2+17x−12因式分解，可得：5x2+17x−12=(x+4)(5x−3)．∴a=4，c=−3，∴a+c=4−3=1．故选：A．首先利用十字交乘法将5x2+17x−12因式分解，继而求得a，c的值．此题考查了十字相乘法分解因式的知识．注意ax2+bx+c(a≠0)型的式子的因式分解：这种方法的关键是把二次项系数a分解成两个因数a1，a2的积a1⋅a2，把常数项c分解成两个因数c1，c2的积c1⋅c2，并使a1c2+a2c1正好是一次项系数b，那么可以直接写成结果：ax2+bx+c=(a1x+c1)(a2x+c2).9.【答案】A【解析】解：3+40×2+1=84．答：步道上总共使用84个三角形地砖．故选：A．中间一个正方形对应两个等腰直角三角形，从而得到三角形的个数为3+40×2+1．本题考查了等腰直角三角形：两条直角边相等的直角三角形叫做等腰直角三角形．也考查了规律型问题的解决方法，探寻规律要认真观察、仔细思考，善用联想来解决这类问题．10.【答案】D【解析】【分析】本题考查的是实数与数轴，熟知实数与数轴上各点是一一对应关系是解答此题的关键．根据O、A、B、C四点在数轴上的位置和绝对值的定义即可得到结论．【解答】解：∵c<0，b=5，|c|<5，|d−5|=|d−c|，∴BD=CD，∴D点介于O、B之间，故选：D．11.【答案】C【解析】解：过F 作FQ ⊥AD 于Q ，则∠FQE =90°， ∵四边形ABCD 是长方形，∴∠A =∠B =90°，AB =DC =8，AD//BC ， ∴四边形ABFQ 是矩形， ∴AB =FQ =DC =8， ∵AD//BC ，∴∠QEF =∠BFE =45°， ∴EQ =FQ =8，∴AE =CF =12×(20−8)=6，故选：C ．根据矩形的性质得出∠A =∠B =90°，AB =DC =8，AD//BC ，根据矩形的判定得出四边形ABFQ 是矩形，求出AB =FQ =DC =8，求出EQ =FQ =8，即可得出答案．本题考查了矩形的性质和判定，能灵活运用定理进行推理是解此题的关键． 12.【答案】D【解析】解：设阿慧购买x 盒桂圆蛋糕，则购买(10−x)盒金爽蛋糕，依题意有 {350x +200(10−x)≤250012x +6(10−x)≥75，解得212≤x ≤313， ∵x 是整数， ∴x =3，350×3+200×(10−3) =1050+1400=2450(元)．答：阿慧花2450元购买蛋糕．故选：D ．可设阿慧购买x 盒桂圆蛋糕，则购买(10−x)盒金爽蛋糕，根据不等关系：①购买10盒蛋糕，花费的金额不超过2500元；②蛋糕的个数大于等于75个，列出不等式组求解即可．本题考查一元一次不等式组的应用，解答此类问题的关键是明确题意，列出相应的一元一次不等式组，注意要与实际相联系． 13.【答案】D【解析】解：连接AD ，∵D 点分别以AB 、AC 为对称轴，画出对称点E 、F ，∴∠EAB=∠BAD，∠FAC=∠CAD，∵∠B=62°，∠C=51°，∴∠BAC=∠BAD+∠DAC=180°−62°−51°=67°，∴∠EAF=2∠BAC=134°，故选：D．连接AD，利用轴对称的性质解答即可．此题考查轴对称的性质，关键是利用轴对称的性质解答．14.【答案】D【解析】解：∵一个盒子内装有大小、形状相同的53+2=55个球，其中红球2个，白球53个，∴小芬抽到红球的概率是：253+2=255．故选：D．让红球的个数除以球的总数即为所求的概率．本题考查了概率公式，熟练掌握概率的概念是解题的关键．15.【答案】C【解析】解：∵AC=BC<AB，∴∠A=∠ABC<∠ACB，∵∠1、∠2分别为∠ABC、∠ACB的外角，∴∠2=∠A+∠ABC，∴∠A+∠2=∠A+∠A+∠ABC<∠ACB+∠A+∠ABC=180°，故选：C．由AC=BC<AB，得∠A=∠ABC<∠ACB，再由三角形的外角性质定理和三角形的内角和可得正确答案．本题考查了等腰三角形的性质定理，三角形的外角性质定理及三角形的内角和，这些都是一些基础知识点，难度不大．16.【答案】B【解析】解：根据题意可得咖啡豆每公克的价钱为：(295+5)÷250=300250(元)，∴y与x的关系式为：y=300250x．故选：B．根据若小涵购买咖啡豆250公克且自备容器，需支付295元，可得咖啡豆每公克的价钱为(295+5)÷250=300250(元)，据此即可得到y与x的关系式．本题主要考查了一次函数的应用，根据题意得出咖啡豆每公克的单价是解答本题的关键．17.【答案】D【解析】解：如图，设△ADE，△BDF，△CEG，平行四边形DEGF的面积分别为S1，S2，S3和S，过点D作DH//EC，则由DFGE为平行四边形，易得四边形DHCE也为平行四边形，从而△DFH≌△EGC，∴S△DFH=S3，∵DE//BC，∴△ADE∽△ABC，DE=3，BC=7，∴S1S△ABC =949，∵S△ABC=14，∴S1=949×14，∴S△BDH：S=(12×4)：3=2：3，∴S△BDH=23S，∴23S+S=14−949×14，∴S=487．故选：D．如图，设△ADE，△BDF，△CEG，平行四边形DEGF的面积分别为S1，S2，S3和S，过点D作DH//EC，则由DFGE为平行四边形，易得四边形DHCE也为平行四边形，从而△DFH≌△EGC，利用面积比等于相似比的平方可求．本题是巧求面积的选择题，综合考查了平行四边形，相似三角形的性质等，难度较大．18.【答案】B【解析】解：36−21+936×30=20(分钟)．所以经过20分钟後，9号车厢才会运行到最高点．故选：B．先求出从21号旋转到9号旋转的角度占圆大小比例，再根据旋转一圈花费30分钟解答即可．本题主要考查了生活中的旋转现象，理清题意，得出从21号旋转到9号旋转的角度占圆大小比例是解答本题的关键．19.【答案】D【解析】解：设AD=x，∵直角三角形ABC的内切圆分别与AB、BC相切于D点、E点，∴BD=BE=1，∴AB=x+1，AC=AD+CE=x+4，在Rt△ABC中，(x+1)2+52=(x+4)2，解得x=53，即AD的长度为53．故选：D．设AD=x，利用切线长定理得到BD=BE=1，AB=x+1，AC=AD+CE=x+4，然后根据勾股定理得到(x+1)2+52=(x+4)2，最后解方程即可．本题考查了三角形的内切圆与内心：三角形的内心到三角形三边的距离相等；三角形的内心与三角形顶点的连线平分这个内角．也考查了切线长定理．20.【答案】A【解析】解：设此旅行团有x 人单程搭乘缆车，单程步行，其中去程及回程均搭乘缆车的有y 人，根据题意得，{200x +300y =4100(15−y)+(10−y)=x，解得，{x =7y =9，则总人数为7+9=16(人)故选：A ．设此旅行团有x 人单程搭乘缆车，单程步行，其中去程及回程均搭乘缆车的有y 人，根据题意列出二元一次方程，求出其解．本题是二元一次方程组的应用，主要考查了列二元一次方程组解应用题，关键是读懂题意，找出等量关系，列出方程组．21.【答案】D【解析】解：x 杯饮料则在B 餐中点了x 份意大利面，y 份沙拉则在C 餐中点了y 份意大利面，∴点A 餐为10−x −y ；故选：D ．根据点的饮料和沙拉能确定点了x +y 份意大利面，根据题意可得点A 餐10−x −y ；本题考查列代数式；能够根据题意，以意大利面为依据，准确列出代数式是解题的关键． 22.【答案】C【解析】解：正整数a 和420的最大公因数为35，则a 必须是35的倍数，∵420÷35=12，12=3×4，20=4×5，25=5×5，∴20不可能是a 的因数，25可能是a 的因数；故选：C ．由420÷35=12，12=3×4，20=4×5，25=5×5，即可求解；本题考查有理数的乘法；理解因数的概念，熟练掌握有理数的乘法是解题的关键． 23.【答案】C【解析】解：作ID ⊥BA′于D ，IE ⊥AC 于E ，I′F ⊥BA′于F ，如图所示：则ID//I′F ，∵△ABC 的内心为I ，△A′B′C 的内心为I′，∴ID =IE =IF ，∠ICD −12∠ACB ，∠I′A′C =12∠B′A′C ， ∴四边形IDFI′是矩形，∴II′//L ，∵∠A <∠B <∠C ，∴∠A′<∠B′<∠C ，∴∠ICD >∠I′A′C ，∴IC 和I′A′不平行，作ID⊥BA′于D，IE⊥AC于E，I′F⊥BA′于F，由内心的性质得出ID=IE=IF，∠ICD=1 2∠ACB，∠I′A′C=12∠B′A′C，证出四边形IDFI′是矩形，得出II′//L，证出∠ICD>∠I′A′C，得出IC和I′A′不平行，即可得出结论．本题考查了三角形的内心、平行线的判定、旋转的性质；熟练掌握三角形的内心性质和平行线的判定是解题的关键．24.【答案】B【解析】解：连接AD，OB，OC，∵AD⏜=180°，且AB⏜=BD⏜，BC⏜=CD⏜，∴∠BOC=∠DOC=45°，在圆周上取一点E连接AE，CE，∴∠E=12∠AOC=67.5°，∴∠ABC=122.5°<130°，取BC⏜的中点F，连接OF，则∠AOF=67.5°，∴∠ABF=123.25°<130°，∴Q点在BC⏜上，且BQ⏜<QC⏜，故选：B．连接AD，OB，OC，根据题意得到∠BOC=∠DOC=45°，在圆周上取一点E连接AE，CE，由圆周角定理得到∠E=12∠AOC=67.5°，求得∠ABC=122.5°<130°，取BC⏜的中点F，连接OF，得到∠ABF=123.25°<130°，于是得到结论．本题考查了圆心角，弧，弦的关系，圆内接四边形的性质，圆周角定理，正确的理解题意是解题的关键．25.【答案】A【解析】解：如图1，∵PQ垂直平分AD，∴PA=PD，QA=QD，而PQ=PQ，∴△APQ≌△DPQ(SSS)，所以甲正确；如图2，∵PD//AQ，DQ//AP，∴四边形APDQ为平行四边形，∴PA=DQ，PD=AQ，而PQ=QP，∴△APQ≌△DQP(SSS)，所以乙正确．故选：A．如图1，根据线段垂直平分线的性质得到PA=PD，QA=QD，则根据“SSS”可判断△APQ≌△DPQ，则可对甲进行判断；如图2，根据平行四边形的判定方法先证明四边形APDQ为平行四边形，则根据平行四边形的性质得到PA=DQ，PD=AQ，则根据“SSS”可判断△APQ≌△DQP，则可对乙进行判断．本题考查了作图−复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了线段垂直平分线的性质、平行四边形的判定与性质和三角形全等的判定．【解析】解：设B(−3−m,2)，C(−3+m,2)，(m>0)∵A点坐标为(−3,0)，∴BC=2m，∵△ABC为正三角形，∴AC=2m，∠DAO=60°，∴m=2√3 3∴C(−3+23√3,2)设抛物线解析式y=a(x+3)2，a(−3+2√33+3)2=2，∴a=32，∴y=32(x+3)2，当x=0时，y=272；故选：B．设B(−3−m,2)，C(−3+m,2)，(m>0)，可知BC=2m，再由等边三角形的性质可知C(−3+23√3,2)，设抛物线解析式y=a(x+3)2，将点C代入解析式即可求a，进而求解；本题考查二次函数的图象及性质，等边三角形的性质；结合函数图象将等边三角形的边长转化为点的坐标是解题的关键．27.【答案】解：(1)根据题意得，SPF−1SPF×100%=90%，解得，SPF=10，答：该产品的SPF应标示为10；(2)文宣内容不合理．理由如下：当SPF=25时，其防护率为：25−125×100%=96%；当SPF=50时，其防护率为：50−150×100%=98%；98%−96%=2%，∴第二代防晒乳液比第一代防晒乳液的防护率提高了2%，不是提高了一倍．∴文宣内容不合理．【解析】(1)根据公式列出方程进行计算便可；(2)根据公式计算两个的防护率，再比较可知结果．本题是分式方程的应用，根据公式列出方程是解第一题的关键，第二题的关键是根据公式正确算出各自的防护率．28.【答案】解：(1)设敏敏的影长为x公分．由题意：150x =9060，解得x=100(公分)，经检验：x=100是分式方程的解．∴敏敏的影长为100公分．(2)如图，连接AE，作FB//EA．∵AB//EF，∴四边形ABFE是平行四边形，∴AB=EF=150公分，设BC=y公分，由题意BC落在地面上的影从为120公分．∴y120=9060，∴y=180(公分)，∴AC=AB+BC=150+180=330(公分)，答：高图柱的高度为330公分．【解析】(1)根据同一时刻，物长与影从成正比，构建方程即可解决问题．(2)如图，连接AE，作FB//EA.分别求出AB，BC的长即可解决问题．本题考查相似三角形的应用，平行投影，平行四边形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．。

2019台湾第一次中考(台北卷) 与简答

经典精品试卷2019台湾第一次中考(台北) 数学真题与简答（A） 1. 图(一)数在线的O是原点，A、B、C三点所表示的数分别为a、b、c。

根据图中各点的位置，下列各数的絶对值的比较何者正确？(A) |b |＜|c | (B) |b |＞|c | (C) |a |＜|b | (D) |a |＞|c |（D ） 2. 计算(－3)3＋52－(－2)2之值为何？ (A) 2 (B) 5 (C)－3 (D)－6（D ） 3. 表(一)表示某签筒中各种签的数量。

已知每支签被抽中的机会均相等，若自此筒中抽出一支签，则抽中红签的机率为何？31 (B)21 (C)53 (D)32 （A ） 4. 计算75147-＋27之值为何？(A) 53 (B) 333 (C) 311 (D) 911（A ） 5. 计算x 2(3x ＋8)除以x 3后，得商式和余式分别为何？(A)商式为3，余式为8x 2 (B)商式为3，余式为8(C)商式为3x ＋8，余式为8x 2 (D)商式为3x ＋8，余式为0（A ） 6. 若下列有一图形为二次函数y ＝2x 2－8x ＋6的图形，则此图为何？（D ） 7. 化简41(－4x ＋8)－3(4－5x )，可得下列哪一个结果？ (A)－16x －10 (B)－16x －4 (C) 56x －40 (D) 14x －10（C ） 8. 图(二)中有四条互相不平行的直线L 1、L 2、L 3、L 4所截出的七个角。

关于这七个角的度数关系，下列何者正确？(A)742∠∠∠＋＝(B)613∠∠∠＋＝(C)︒∠∠∠180641＝＋＋(D)︒∠∠∠360532＝＋＋（C ） 9. 图(三)的坐标平面上，有一条通过点(－3,－2)的直线L 。

若四点(－2 ,a )、(0 ,b )、(c , 0)、(d ,－1)在L 上，则下列数值的判断，何者正确？(A) a ＝3 (B) b ＞－2(C) c ＜－3 (D) d ＝2（B ）10. 在1～45的45个正整数中，先将45的因子全部删除，再将剩下的整数由小到大排列，求第10个数为何？(A) 13 (B) 14 (C) 16 (D) 17（C ）11. 计算45.247)6.1(÷÷－－之值为何？ (A)－1.1 (B)－1.8 (C)－3.2 (D)－3.9 （B ）12. 已知世运会、亚运会、奥运会分别于公元2009年、2010年、2012年举办。

【真题】2019年台湾地区中考数学试题含答案解析(Word版)

台湾省2019年中考数学试题(解析版)一、选择题（本大题共26小题）1．（2019•台湾）算式（﹣2）×|﹣5|﹣|﹣3|之值为何（）A．13 B．7 C．﹣13 D．﹣7【分析】原式先计算绝对值运算，再计算乘法运算，最后算加减运算即可得到结果．【解答】解：原式=﹣2×5﹣3=﹣10﹣3=﹣13，故选C【点评】此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．2．（2019•台湾）下列哪一个选项中的等式成立（）A．=2 B．=3 C．=4 D．=5【分析】根据二次根式的性质和化简方法，逐项判断即可．【解答】解：∵=2，∴选项A符合题意；∵=3，∴选项B不符合题意；∵=16，∴选项C不符合题意；∵=25，∴选项D不符合题意．故选：A．【点评】此题主要考查了二次根式的性质和化简，要熟练掌握，化简二次根式的步骤：①把被开方数分解因式；②利用积的算术平方根的性质，把被开方数中能开得尽方的因数（或因式）都开出来；③化简后的二次根式中的被开方数中每一个因数（或因式）的指数都小于根指数2．3．（2019•台湾）计算6x•（3﹣2x）的结果，与下列哪一个式子相同（）A．﹣12x2+18x B．﹣12x2+3 C．16x D．6x【分析】根据单项式乘以多项式法则可得．【解答】解：6x•（3﹣2x）=18x﹣12x2，故选：A．【点评】本题主要考查整式的乘法，熟练掌握单项式乘以多项式的法则是解题的关键．4．（2019•台湾）若阿光以四种不同的方式连接正六边形ABCDEF的两条对角线，连接后的情形如下列选项中的图形所示，则下列哪一个图形不是轴对称图形（）A．B．C．D．【分析】根据轴对称图形的概念：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．【解答】解：A、是轴对称图形，故此选项错误；B、是轴对称图形，故此选项错误；C、不是轴对称图形，故此选项错误；D、不是轴对称图形，故此选项正确；故选：D．【点评】此题主要考查了轴对称图形，关键是掌握轴对称图形的概念．5．（2019•台湾）已知坐标平面上有两直线相交于一点（2，a），且两直线的方程式分别为2x+3y=7，3x﹣2y=b，其中a，b为两数，求a+b之值为何（）A．1 B．﹣1 C．5 D．﹣5【分析】把问题转化为关于a、b的方程组即可解决问题．【解答】解：由题意，解得，∴a+b=5，故选C．【点评】本题考查两条直线相交或平行的性质，二元一次方程组等知识，解题的关键是灵活运用所学知识解决问题，学会用转化的思想思考问题．6．（2019•台湾）阿信、小怡两人打算搭乘同一班次电车上学，若此班次电车共有5节车厢，且阿信从任意一节车厢上车的机会相等，小怡从任意一节车厢上车的机会相等，则两人从同一节车厢上车的概率为何（）A．B．C．D．【分析】根据阿信、小怡各有5节车厢可选择，共有25种，两人在不同车厢的情况数是20种，得出在同一节车厢上车的情况数是5种，根据概率公式即可得出答案．【解答】解：二人上5节车厢的情况数是：5×5=25，两人在不同车厢的情况数是5×4=20，则两人从同一节车厢上车的概率是=；故选B．【点评】此题主要考查了概率的求法．用到的知识点为：概率=所求情况数与总情况数之比．7．（2019•台湾）平面上有A、B、C三点，其中AB=3，BC=4，AC=5，若分别以A、B、C为圆心，半径长为2画圆，画出圆A，圆B，圆C，则下列叙述何者正确（）A．圆A与圆C外切，圆B与圆C外切B．圆A与圆C外切，圆B与圆C外离C．圆A与圆C外离，圆B与圆C外切D．圆A与圆C外离，圆B与圆C外离【分析】根据圆和圆的位置与两圆的圆心距、半径的数量之间的关系，即可判定．【解答】解：∵AC=5＞2+2，即AC＞R A+R B，∴⊙A与⊙C外离，∵BC=4=2+2，即BC=R B+R C，∴⊙B与⊙C相切．故选C．【点评】本题考查圆与圆的位置关系，记住：①两圆外离⇔d＞R+r；②两圆外切⇔d=R+r；③两圆相交⇔R﹣r＜d＜R+r（R≥r）；④两圆内切⇔d=R﹣r（R＞r）；⑤两圆内含⇔d＜R﹣r（R＞r）是解题的关键．8．（2019•台湾）下列选项中所表示的数，哪一个与252的最大公因数为42（）A．2×3×52×72B．2×32×5×72C．22×3×52×7 D．22×32×5×7【分析】先将42与252分别分解质因数，再找到与252的最大公因数为42的数即可．【解答】解：∵42=2×3×7，252=22×32×7，∴2×3×52×72与252的最大公因数为42．故选：A．【点评】考查了有理数的乘方，有理数的乘法，关键是将42与252分解质因数．9．（2019•台湾）某高中的篮球队球员中，一、二年级的成员共有8人，三年级的成员有3人，一、二年级的成员身高（单位：公分）如下：172，172，174，174，176，176，178，178若队中所有成员的平均身高为178公分，则队中三年级成员的平均身高为几公分（）A．178 B．181 C．183 D．186【分析】先求出一、二年级的成员的总共身高，再根据总数=平均数×数量可求一、二、三年级的成员的总共身高，依此可求三年级成员的总共身高，再除以3即可求解．【解答】解：172+172+174+174+176+176+178+178=1400（公分），（178×11﹣1400）÷3=（1958﹣1400）÷3=186（公分）．答：队中三年级成员的平均身高为186公分．故选：D．【点评】考查了平均数问题，关键是熟练掌握平均数的计算公式．10．（2019•台湾）已知在卡乐芙超市内购物总金额超过190元时，购物总金额有打八折的优惠，安妮带200元到卡乐芙超市买棒棒糖．若棒棒糖每根9元，则她最多可买多少根棒棒糖（）A．22 B．23 C．27 D．28【分析】设买x根棒棒糖，根据题意列出不等式，解不等式即可．【解答】解：设买x根棒棒糖，由题意得，9x×0.8≤200，解得，x≤，∴她最多可买27根棒棒糖，故选：C．【点评】本题考查的是一元一次不等式的应用，根据题意正确列出不等式、并正确解出不等式是解题的关键．11．（2019•台湾）如图，△ABC中，D，E两点分别在AB，BC上，若AD：DB=CE：EB=2：3，则△DBE与△ADC的面积比为（）A．3：5 B．4：5 C．9：10 D．15：16【分析】根据三角形面积求法进而得出S△BDC ：S△ADC=3：2，S△BDE：S△DCE=3：2，即可得出答案．【解答】解：∵AD：DB=CE：EB=2：3，∴S△BDC ：S△ADC=3：2，S△BDE：S△DCE=3：2，∴设S△BDC =3x，则S△ADC=2x，S△BED=1.8x，S△DCE=1.2x，故△DBE与△ADC的面积比为：1.8x：2x=9：10．故选：C．【点评】此题主要考查了三角形面积求法，正确利用三角形边长关系得出面积比是解题关键．12．（2019•台湾）一元二次方程式x2﹣8x=48可表示成（x﹣a）2=48+b的形式，其中a、b为整数，求a+b之值为何（）A．20 B．12 C．﹣12 D．﹣20【分析】将一元二次方程式x2﹣8x=48配方，可求a、b，再代入代数式即可求解．【解答】解：x2﹣8x=48，x2﹣8x+16=48+16，（x﹣4）2=48+16，a=4，b=16，a+b=20．故选：A．【点评】此题考查了配方法解一元二次方程，解题时要注意解题步骤的准确应用．选择用配方法解一元二次方程时，最好使方程的二次项的系数为1，一次项的系数是2的倍数．13．（2019•台湾）已知坐标平面上有一长方形ABCD，其坐标分别为A（0，0），B（2，0），C（2，1），D（0，1），今固定B点并将此长方形依顺时针方向旋转，如图所示．若旋转后C点的坐标为（3，0），则旋转后D点的坐标为何（）A．（2，2） B．（2，3） C．（3，3） D．（3，2）【分析】先根据旋转后C点的坐标为（3，0），得出点C落在x轴上，再根据AC=3，DC=2，即可得到点D的坐标为（3，2）．【解答】解：∵旋转后C点的坐标为（3，0），∴点C落在x轴上，∴此时AC=3，DC=2，∴点D的坐标为（3，2），故选：D．【点评】本题主要考查了旋转的性质以及矩形的性质的运用，解题时注意：矩形的四个角都是直角，对边相等．14．（2019•台湾）如图为平面上五条直线L1，L2，L3，L4，L5相交的情形，根据图中标示的角度，判断下列叙述何者正确（）A．L1和L3平行，L2和L3平行B．L1和L3平行，L2和L3不平行C．L1和L3不平行，L2和L3平行D．L1和L3不平行，L2和L3不平行【分析】根据同旁内角不互补，可得两直线不平行；根据内错角相等，可得两直线平行．【解答】解：∵92°+92°≠180°，∴L1和L3不平行，∵88°=88°，∴L2和L3平行，故选：C．【点评】本题主要考查了平行线的判定，解题时注意：同旁内角互补，两直线平行；内错角相等，两直线平行．15．（2019•台湾）威立到小吃店买水饺，他身上带的钱恰好等于15粒虾仁水饺或20粒韭菜水饺的价钱，若威立先买了9粒虾仁水饺，则他身上剩下的钱恰好可买多少粒韭菜水饺（）A．6 B．8 C．9 D．12【分析】可设1粒虾仁水饺为x元，1粒韭菜水饺为y元，由题意可得到y与x 之间的关系式，再利用整体思想可求得答案．【解答】解：设1粒虾仁水饺为x元，1粒韭菜水饺为y元，则由题意可得15x=20y，∴3x=4y，∴15x﹣9x=6x=2×3x=2×4y=8y，∴他身上剩下的钱恰好可买8粒韭菜水饺，故选B．【点评】本题主要考查方程的应用，利用条件找到1粒虾仁水饺和1粒韭菜水饺的价钱之间的关系是解题的关键，注意整体思想的应用．16．（2019•台湾）将图1中五边形纸片ABCDE的A点以BE为折线往下折，A点恰好落在CD上，如图2所示，再分别以图2的AB，AE为折线，将C，D两点往上折，使得A、B、C、D、E五点均在同一平面上，如图3所示，若图1中∠A=124°，则图3中∠CAD的度数为何（）A．56 B．60 C．62 D．68【分析】根据三角形内角和定理和折叠的性质来解答即可．【解答】解：由图（2）知，∠BAC+∠EAD=180°﹣124°=56°，所以图（3）中∠CAD=180°﹣56°×2=68°．故选：D．【点评】本题考查了多边形内角与外角，结合图形解答，需要学生具备一定的读图能力和空间想象能力．17．（2019•台湾）若a，b为两质数且相差2，则ab+1之值可能为下列何者（）A．392B．402C．412D．422【分析】根据选项的数值，得到ab+1的值，进一步根据平方差公式得到ab的乘积形式，再根据质数的定义即可求解．【解答】解：A、当ab+1=392时，ab=392﹣1=40×38，与a，b为两质数且相差2不符合，故本选项错误；B、当ab+1=402时，ab=402﹣1=41×39，与a，b为两质数且相差2不符合，故本选项错误；C、当ab+1=412时，ab=412﹣1=42×40，与a，b为两质数且相差2不符合，故本选项错误；D、当ab+1=422时，ab=422﹣1=43×41，正好与a，b为两质数且相差2符合，故本选项正确，故选：D．【点评】本题考查的是因式分解的应用，质数的定义，解答此类题目的关键是得到ab是哪两个相差为2的数的积．18．（2019•台湾）如图，O为锐角三角形ABC的外心，四边形OCDE为正方形，其中E点在△ABC的外部，判断下列叙述何者正确（）A．O是△AEB的外心，O是△AED的外心B．O是△AEB的外心，O不是△AED的外心C．O不是△AEB的外心，O是△AED的外心D．O不是△AEB的外心，O不是△AED的外心【分析】根据三角形的外心的性质，可以证明O是△ABE的外心，不是△AED的外心．【解答】解：如图，连接OA、OB、OD．∵O是△ABC的外心，∴OA=OB=OC，∵四边形OCDE是正方形，∴OA=OB=OE，∴O是△ABE的外心，∵OA=OE≠OD，∴O表示△AED的外心，故选B．【点评】本题考查三角形的外心的性质．正方形的性质等知识，解本题的关键是灵活运用所学知识解决问题，属于中考常考题型．19．（2019•台湾）如图为互相垂直的两直线将四边形ABCD分成四个区域的情形，若∠A=100°，∠B=∠D=85°，∠C=90°，则根据图中标示的角，判断下列∠1，∠2，∠3的大小关系，何者正确（）A．∠1=∠2＞∠3 B．∠1=∠3＞∠2 C．∠2＞∠1=∠3 D．∠3＞∠1=∠2【分析】根据多边形的内角和与外角和即可判断．【解答】解：∵（180°﹣∠1）+∠2=360°﹣90°﹣90°=180°∴∠1=∠2∵（180°﹣∠2）+∠3=360°﹣85°﹣90°=185°∴∠3﹣∠2=5°，∴∠3＞∠2∴∠3＞∠1=∠2故选（D）【点评】本题考查多边形的内角与外角，解题的关键是熟练运用多边形的内角和与外角和，本题属于基础题型．20．（2019•台湾）如图的数轴上有O、A、B三点，其中O为原点，A点所表示的数为106，根据图中数轴上这三点之间的实际距离进行估计，下列何者最接近B点所表示的数（）A．2×106B．4×106C．2×107D．4×108【分析】根据数轴上的数据求出OA的长度，从而估算出OB的长度，即可估算出点B表示的数，从而得解．【解答】解：由数轴的信息知：OA=106；∴B点表示的实数为：20=2×107；故选C．【点评】本题考查了数轴与有理数的加法运算，求出点D表示的数是解题的关键．21．（2019•台湾）如图，△ABC、△ADE中，C、E两点分别在AD、AB上，且BC 与DE相交于F点，若∠A=90°，∠B=∠D=30°，AC=AE=1，则四边形AEFC的周长为何（）A．2 B．2 C．2+D．2+【分析】根据三角形的内角和得到∠AED=∠ACB=60°，根据三角形的外角的性质得到∠B=∠EFB=∠CFD=∠D，根据等腰三角形的判定得到BE=EF=CF=CD，于是得到四边形AEFC的周长=AB+AC．【解答】解：∵∠A=90°，∠B=∠D=30°，∴∠AED=∠ACB=60°，∵∠AED=∠B+∠EFB=∠ACB=∠CFD+∠D=60°，∴∠EFB=∠CFD=30°，∴∠B=∠EFB=∠CFD=∠D，∴BE=EF=CF=CD，∴四边形AEFC的周长=AB+AC，∵∠A=90°，AE=AC=1，∴AB=AD=，∴四边形AEFC的周长=2．故选B．【点评】本题考查了等腰三角形的性质，解直角三角形，三角形的外角的性质，熟练掌握等腰三角形的判定与性质是解题的关键．22．（2019•台湾）已知坐标平面上有两个二次函数y=a（x+1）（x﹣7），y=b（x+1）（x﹣15）的图形，其中a、b为整数．判断将二次函数y=b（x+1）（x﹣15）的图形依下列哪一种方式平移后，会使得此两图形的对称轴重叠（）A．向左平移4单位 B．向右平移4单位C．向左平移8单位 D．向右平移8单位【分析】将二次函数解析式展开，结合二次函数的性质找出两二次函数的对称轴，二者做差后即可得出平移方向及距离．【解答】解：∵y=a（x+1）（x﹣7）=ax2﹣6ax﹣7a，y=b（x+1）（x﹣15）=bx2﹣14bx ﹣15b，∴二次函数y=a（x+1）（x﹣7）的对称轴为直线x=3，二次函数y=b（x+1）（x﹣15）的对称轴为直线x=7，∵3﹣7=﹣4，∴将二次函数y=b（x+1）（x﹣15）的图形向左平移4个单位，两图形的对称轴重叠．故选A．【点评】本题考查了二次函数图象与几何变换以及二次函数的性质，根据二次函数的性质找出两个二次函数的对称轴是解题的关键．23．（2019•台湾）如图为阿辉，小燕一起到商店分别买了数杯饮料与在家分饮料的经过．若每杯饮料的价格均相同，则根据图中的对话，判断阿辉买了多少杯饮料（）A．22 B．25 C．47 D．50【分析】根据题意列出算式，计算即可得到结果．【解答】解：根据题意得：[（1000+120）﹣（2000﹣1120）]÷6=40，880÷40=22（杯），则阿辉买了22杯饮料，故选A【点评】此题考查了有理数的混合运算，列出正确的算式是解本题的关键．24．（2019•台湾）如图，水平桌面上有个内部装水的长方体箱子，箱内有一个与底面垂直的隔板，且隔板左右两侧的水面高度为别为40公分，50公分，今将隔板抽出，若过程中箱内的水量未改变，且不计箱子及隔板厚度，则根据图中的数据，求隔板抽出后水面静止时，箱内的水面高度为多少公分（）A．43 B．44 C．45 D．46【分析】设长方形的宽为x公分，抽出隔板后之水面高度为h公分，根据题意列出方程，求出方程的解即可．【解答】解：设长方形的宽为x公分，抽出隔板后之水面高度为h公分，长方形的长为130+70=200（公分）×40+×50=200•x•h，解得：h=44，故选B．【点评】本题考查了一元一次方程的应用，能根据题意列出方程是解此题的关键．25．（2019•台湾）如图，某计算机中有、、三个按键，以下是这三个按键的功能．1．：将荧幕显示的数变成它的正平方根，例如：荧幕显示的数为49时，按下后会变成7．2．：将荧幕显示的数变成它的倒数，例如：荧幕显示的数为25时，按下后会变成0.04．3．：将荧幕显示的数变成它的平方，例如：荧幕显示的数为6时，按下后会变成36．若荧幕显示的数为100时，小刘第一下按，第二下按，第三下按，之后以、、的顺序轮流按，则当他按了第100下后荧幕显示的数是多少（）A．0.01 B．0.1 C．10 D．100【分析】根据题中的按键顺序确定出显示的数即可．【解答】解：根据题意得：=10，=0.1，0.12=0.01，=0.1，=10，102=100，100÷6=16…4，则第100次为0.1．故选B【点评】此题考查了计算器﹣数的平方，弄清按键顺序是解本题的关键．26．（2019•台湾）如图为两正方形ABCD，BPQR重叠的情形，其中R点在AD上，CD与QR相交于S点．若两正方形ABCD、BPQR的面积分别为16、25，则四边形RBCS的面积为何（）A．8 B．C．D．【分析】根据正方形的边长，根据勾股定理求出AR ，求出△ABR ∽△DRS ，求出DS ，根据面积公式求出即可．【解答】解：∵正方形ABCD 的面积为16，正方形BPQR 面积为25， ∴正方形ABCD 的边长为4，正方形BPQR 的边长为5，在Rt △ABR 中，AB=4，BR=5，由勾股定理得：AR=3， ∵四边形ABCD 是正方形， ∴∠A=∠D=∠BRQ=90°，∴∠ABR +∠ARB=90°，∠ARB +∠DRS=90°， ∴∠ABR=∠DRS ， ∵∠A=∠D ， ∴△ABR ∽△DRS ， ∴=， ∴=，∴DS=，∴阴影部分的面积S=S 正方形ABCD ﹣S △ABR ﹣S △RDS =4×4﹣﹣1××=，故选D ．【点评】本题考查了正方形的性质，相似三角形的性质和判定，能求出△ABR 和△RDS 的面积是解此题的关键．二、解答题（本大题共2小题）27．（2019•台湾）今有甲、乙、丙三名候选人参与某村村长选举，共发出1800张选票，得票数最高者为当选人，且废票不计入任何一位候选人之得票数内，全村设有四个投开票所，目前第一、第二、第三投开票所已开完所有选票，剩下第四投开票所尚未开票，结果如表所示：投开票所候选人废票合计甲乙丙一20021114712570二2868524415630三97412057350四250（单位：票）请回答下列问题：（1）请分别写出目前甲、乙、丙三名候选人的得票数；（2）承（1），请分别判断甲、乙两名候选人是否还有机会当选村长，并详细解释或完整写出你的解题过程．【分析】（1）直接根据题意将三个投票所得所有票数相加得出答案；（2）利用（1）中所求，进而分别分析得票的张数得出答案．【解答】解：（1）由图表可得：甲得票数为：200+286+97=583；乙得票数为：211+85+41=337；丙得票数为：147+244+205=596；（2）由（1）得：596﹣583=13，即丙目前领先甲13票，所以第四投票所甲赢丙14票以上，则甲当选，故甲可能当选；596﹣337=259＞250，若第四投票所250票皆给乙，乙的总票数仍然比丙低，故乙不可能当选．【点评】此题主要考查了推理与论证，正确利用表格中数据分析得票情况是解题关键．28．（2019•台湾）如图，在坐标平面上，O为原点，另有A（0，3），B（﹣5，0），C（6，0）三点，直线L通过C点且与y轴相交于D点，请回答下列问题：（1）已知直线L的方程为5x﹣3y=k，求k的值．（2）承（1），请完整说明△AOB与△COD相似的理由．【分析】（1）利用函数图象上的点的特点，即可求出k的值；（2）先求出OA，OB，OC，OD，即可得出，即可得出结论．【解答】解：（1）∵直线L：5x﹣3y=k过点C（6，0），∴5×6﹣3×0=k，∴k=30，（2）由（1）知，直线L：5x﹣3y=30，∵直线L与y轴的交点为D，令x=0，∴﹣3y=30，∴y=﹣10，∴D（0，﹣10），∴OD=10，∵A（0，3），B（﹣5，0），C（6，0），∴OA=3，OB=5，OC=6，∴=，=，∴，∵∠AOB=∠COD=90°，∴△AOB∽△COD．【点评】此题是一次函数综合题，主要考查了函数图象上点的特点，相似三角形的判定，解本题的根据是求出点D的坐标．。

2019年台湾省中考数学试卷

免费更新全国各地各科真题及解析。

不费力气找真题，我们不做“大多数”！先驱助考，守护我们的中学时代！➕微信：2020258934 考后第一时间领真题包。

2019年中考数学试题含答案及名家点评：台湾省

∴空竹篮的重量为：15﹣12.5＝2.5kg．故选C．名家点评：本题考查了总价÷数量＝单价的运用，总价÷单价＝数量的运用，解答时求出西红柿的单价是解答本题的关键． 8．(3分)(2020•台湾)下列选项中有一张纸片会与如图紧密拼凑成正方形纸片，且正方形上的黑色区域会形成一个轴对称图形，则此纸片为何？( )
名家点评：本题考查了坐标与图象的性质的运用，垂直的性质的运用，全等三角形的判定及性质的运用，等腰三角形的性质的运用，解答时证明三角形全等是关键． 10．(3分)(2020•台湾)如图，有一圆通过△ABC的三个顶点，且的中垂线与相交于D点．若∠B＝74°，∠C ＝46°，则的度数为何？( )
解：原式＝743×(370﹣1)﹣741×370
＝370×(743﹣741)﹣743
＝370×2﹣743＝﹣3，
故选：A．
名家点评：本题考查了有理数的乘法，乘法分配律是解题关键．
6．(3分)(2020•台湾)若二元一次联立方程式的解为x＝a，y＝b，则a＋b之值为何？( )
A． B．
C．
D．
思路分析：首先解方程组求得x、y的值，即可得到a、b的值，进而求得a＋b的值．
D．6

思路分析：利用勾股定理列式求出AE，再根据两直线平行，内错角相等可得∠DAE＝90°，然后利用勾股
定理列式计算即可得解．
解：∵AE⊥BC，
∴∠AEB＝90°，
∵AB＝10，BE＝8，
∴AE＝＝＝6，
∵AD∥BC，
∴∠DAE＝∠AEB＝90°，
∴AD＝＝＝6．
故选C．
名家点评：本题考查了梯形，勾股定理，是基础题，熟记定理并确定出所求的边所在的直角三角形是解
所有可能的结果，列表法适合于两步完成的事件，树状图法适合两步或两步以上完成的事件．用到的知

2019年台湾省中考数学试题(word版,含解析)

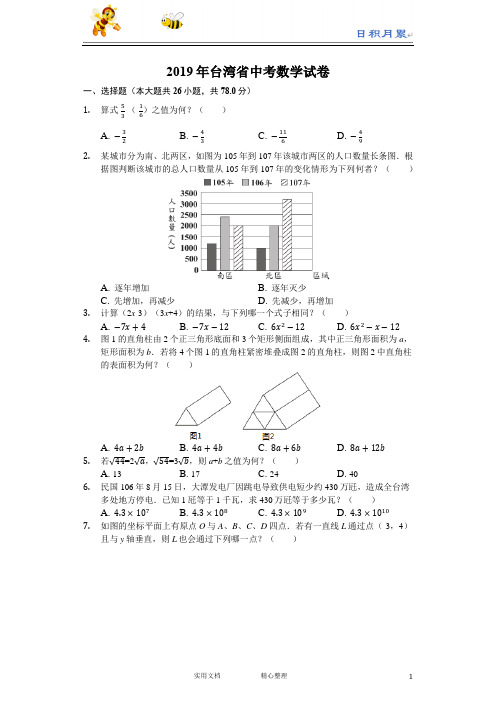
2019年台湾省中考数学试卷一、选择题（本大题共26小题，共78.0分） 1. 算式-53-（-16）之值为何？（）A. −32B. −43C. −116D. −492. 某城市分为南、北两区，如图为105年到107年该城市两区的人口数量长条图．根据图判断该城市的总人口数量从105年到107年的变化情形为下列何者？（）A. 逐年增加B. 逐年灭少C. 先增加，再减少D. 先减少，再增加3. 计算（2x -3）（3x +4）的结果，与下列哪一个式子相同？（）A. −7x +4B. −7x −12C. 6x 2−12D. 6x 2−x −12 4. 图1的直角柱由2个正三角形底面和3个矩形侧面组成，其中正三角形面积为a ，矩形面积为b ．若将4个图1的直角柱紧密堆叠成图2的直角柱，则图2中直角柱的表面积为何？（）A. 4a +2bB. 4a +4bC. 8a +6bD. 8a +12b5. 若√44=2√a ，√54=3√b ，则a +b 之值为何？（）A. 13B. 17C. 24D. 406. 民国106年8月15日，大潭发电厂因跳电导致供电短少约430万瓩，造成全台湾多处地方停电．已知1瓩等于1千瓦，求430万瓩等于多少瓦？（）A. 4.3×107B. 4.3×108C. 4.3×109D. 4.3×10107. 如图的坐标平面上有原点O 与A 、B 、C 、D 四点．若有一直线L 通过点（-3，4）且与y 轴垂直，则L 也会通过下列哪一点？（）A. AB. BC. CD. D8.若多项式5x2+17x-12可因式分解成（x+a）（bx+c），其中a、b、c均为整数，则a+c之值为何？（）A. 1B. 7C. 11D. 139.公园内有一矩形步道，其地面使用相同的灰色正方形地砖与相同的白色等腰直角三角形地砖排列而成．如图表示此步道的地砖排列方式，其中正方形地砖为连续排列且总共有40个．求步道上总共使用多少个三角形地砖？（）A. 84B. 86C. 160D. 16210.数线上有O、A、B、C四点，各点位置与各点所表示的数如图所示．若数线上有一点D，D点所表示的数为d，且|d-5|=|d-c|，则关于D点的位置，下列叙述何者正确？（）A. 在A的左边B. 介于A、C之间C. 介于C、O之间D. 介于O、B之间11.如图，将一长方形纸片沿着虚线剪成两个全等的梯形纸片．根据图中标示长度与角度，求梯形纸片中较短的底边长度为何？（）A. 4B. 5C. 6D. 712.阿慧在店内购买两种蛋糕当伴手礼，如图为蛋糕的价目表．已知阿慧购买10盒蛋糕，花费的金额不超过2500元．若他将蛋糕分给75位同事，每人至少能拿到一个蛋糕，则阿慧花多少元购买蛋糕？（）A. 2150B. 2250C. 2300D. 245013.如图，△ABC中，D点在BC上，将D点分别以AB、AC为对称轴，画出对称点E、F，并连接AE、AF．根据图中标示的角度，求∠EAF的度数为何？（）A. 113B. 124C. 129D. 13414.箱子内装有53颗白球及2颗红球，小芬打算从箱子内抽球，以毎次抽出一球后将球再放回的方式抽53次球．若箱子内每颗球被抽到的机会相等，且前52次中抽到白球51次及红球1次，则第53次抽球时，小芬抽到红球的机率为何？（）A. 12B. 13C. 253D. 25515.如图，△ABC中，AC=BC＜AB．若∠1、∠2分别为∠ABC、∠ACB的外角，则下列角度关系何者正确（）A. ∠1<∠2B. ∠1=∠2C. ∠A+∠2<180∘D. ∠A+∠1>180∘16.小涵与阿嘉一起去咖啡店购买同款咖啡豆，咖啡豆每公克的价钱固定，购买时自备容器则结帐金额再减5元．若小涵购买咖啡豆250公克且自备容器，需支付295元；阿嘉购买咖啡豆x公克但没有自备容器，需支付y元，则y与x的关系式为下列何者？（）A. y=295250x B. y=300250x C. y=295250x+5 D. y=300250x+517.如图，将一张面积为14的大三角形纸片沿着虚线剪成三张小三角形纸片与一张平行四边形纸片．根据图中标示的长度，求平行四边形纸片的面积为何？（）A. 215B. 425C. 247D. 48718.图1的摩天轮上以等间隔的方式设置36个车厢，车厢依顺时针方向分别编号为1号到36号，且摩天轮运行时以逆时针方向等速旋转，旋转一圈花费30分钟．若图2表示21号车厢运行到最高点的情形，则此时经过多少分钟後，9号车厢才会运行到最高点？（）A. 10B. 20C. 152D. 45219.如图，直角三角形ABC的内切圆分别与AB、BC相切于D点、E点，根据图中标示的长度与角度，求AD的长度为何？（）A. 32B. 52C. 43D. 5320.某旅行团到森林游乐区参观，如表为两种参观方式与所需的缆车费用．已知旅行团的每个人皆从这两种方式中选择一种，且去程有15人搭乘缆车，回程有10人搭乘缆车．若他们缆车费用的总花费为4100元，则此旅行团共有多少人？（）参观方式缆车费用去程及回程均搭乘缆车300元单程搭乘缆车，单程步行200元1619222521.小宜跟同学在某餐厅吃饭，如图为此餐厅的菜单．若他们所点的餐点总共为10份意大利面，x杯饮料，y份沙拉，则他们点了几份A餐？（）A. 10−xB. 10−yC. 10−x+yD. 10−x−y22.若正整数a和420的最大公因数为35，则下列叙何者正确？（）A. 20可能是a的因数，25可能是a的因数B. 20可能是a的因数，25不可能是a的因数C. 20不可能是a的因数，25可能是a的因数D. 20不可能是a的因数，25不可能是a的因数23.如图，有一三角形ABC的顶点B、C皆在直线L上，且其内心为I．今固定C点，将此三角形依顺时针方向旋转，使得新三角形A'B'C的顶点A′落在L上，且其内心为I′．若∠A＜∠B＜∠C，则下列叙述何者正确？（）#JYA. IC和I′A′平行，II′和L平行B. IC和I′A′平行，II′和L不平行C. IC和I′A′不平行，II′和L平行D. IC和I′A′不平行，II′和L不平行24.如图表示A、B、C、D四点在O上的位置，其中AD⏜=180°，且AB⏜=BD⏜，BC⏜=CD⏜．若阿超在AB⏜上取一点P，在BD⏜上取一点Q，使得∠APQ=130°，则下列叙述何者正确？（）A. Q点在BC⏜上，且BQ⏜>QC⏜B. Q点在BC⏜上，且BQ⏜<QC⏜C. Q点在CD⏜上，且CQ⏜>QD⏜D. Q点在CD⏜上，且CQ⏜<QD⏜25.如图的△ABC中，AB＞AC＞BC，且D为BC上一点．今打算在AB上找一点P，在AC上找一点Q，使得△APQ与△PDQ全等，以下是甲、乙两人的作法：（甲）连接AD，作AD的中垂线分别交AB、AC于P点、Q点，则P、Q两点即为所求（乙）过D作与AC平行的直线交AB于P点，过D作与AB平行的直线交AC于Q 点，则P、Q两点即为所求对于甲、乙两人的作法，下列判断何者正确？（）A. 两人皆正确B. 两人皆错误C. 甲正确，乙错误D. 甲错误，乙正确26.如图，坐标平面上有一顶点为A的抛物线，此抛物线与方程式y=2的图形交于B、C两点，△ABC为正三角形．若A点坐标为（-3，0），则此抛物线与y轴的交点坐标为何？（）)A. (0,92)B. (0,272C. (0,9)D. (0,19)二、解答题（本大题共2小题，共16.0分）27.市面上贩售的防晒产品标有防晒指数SPF，而其对抗紫外线的防护率算法为：防护×100%，其中SPF≥1．率=SPF−1SPF请回答下列问题：（1）厂商宣称开发出防护率90%的产品，请问该产品的SPF应标示为多少？（2）某防晒产品文宣内容如图所示．请根据SPF与防护率的转换公式，判断此文宣内容是否合理，并详细解释或完整写出你的理由．28.在公园有两座垂直于水平地面且高度不一的图柱，两座圆柱后面有一堵与地面互相垂直的墙，且圆柱与墙的距离皆为120公分．敏敏观察到高度90公分矮圆柱的影子落在地面上，其影长为60公分；而高圆柱的部分影子落在墙上，如图所示．已知落在地面上的影子皆与墙面互相重直，并视太阳光为平行光，在不计圆柱厚度与影子宽度的情况下，请回答下列问题：（1）若敏敏的身高为150公分，且此刻她的影子完全落在地面上，则影长为多少公分？（2）若同一时间量得高圆柱落在墙上的影长为150公分，则高图柱的高度为多少公分？请详细解释或完整写出你的解题过程，并求出答案．答案和解析1.【答案】A【解析】解：原式=-+=-+==-=-，故选：A．根据有理数的加减法法则计算即可．本题主要考查了有理数的加减法．有理数的减法法则：减去一个数，等于加上这个数的相反数．2.【答案】A【解析】解：由图中数据可知：105年该城市的总人口数量＜106年该城市的总人口数量＜107年该城市的总人口数量，∴该城市的总人口数量从105年到107年逐年增加，故选：A．根据图中数据计算可直接得105年该城市的总人口数量＜106年该城市的总人口数量＜107年该城市的总人口数量，据此作答．本题考查条形统计图，解答本题的关键是明确题意，利用数形结合的思想解答．3.【答案】D【解析】解：由多项式乘法运算法则得（2x-3）（3x+4）=6x2+8x-9x-12=6x2-x-12．故选：D．由多项式乘法运算法则：两多项式相乘时，用一个多项式的各项去乘另一个多项式的每一项，再把所得的积相加，合并同类项后所得的式子就是它们的积．本题考查多项式乘法运算法则，牢记法则，不要漏项是解答本题的关键．4.【答案】C【解析】解：∵正三角形面积为a，矩形面积为b，∴图2中直角柱的表面积=2×4a+6b=8a+6b，故选：C．根据已知条件即可得到结论．本题考查了等边三角形的性质，矩形的性质，列代数式，正确的识别图形是解题的关键．5.【答案】B【解析】解：∵==2，∴a=11，∵==3，∴b=6，∴a+b=11+6=17．故选：B．根据二次根式的定义求出a、b的值，代入求解即可．本题主要考查了二次根式的定义，熟练掌握定义是解答本题的关键．6.【答案】C【解析】解：430万瓩=4300000瓩，∵1瓩等于1千瓦，∴4300000瓩=4300000千瓦=4.3×106千瓦=4.3×109瓦；故选：C．根据题意将430万瓩化为4.3×109瓦即可解题；本题考查科学记数法；能够将单位进行准确的换算，将大数用科学记数法表示出来是解题的关键．7.【答案】D【解析】解：如图所示：有一直线L通过点（-3，4）且与y轴垂直，故L也会通过D点．故选：D．直接利用点的坐标，正确结合坐标系分析即可．此题主要考查了点的坐标，正确结合平面直角坐标系分析是解题关键．8.【答案】A【解析】解：利用十字交乘法将5x2+17x-12因式分解，可得：5x2+17x-12=（x+4）（5x-3）．∴a=4，c=-3，∴a+c=4-3=1．故选：A．首先利用十字交乘法将5x2+17x-12因式分解，继而求得a，c的值．此题考查了十字相乘法分解因式的知识．注意ax2+bx+c（a≠0）型的式子的因式分解：这种方法的关键是把二次项系数a分解成两个因数a1，a2的积a1•a2，把常数项c分解成两个因数c1，c2的积c1•c2，并使a1c2+a2c1正好是一次项b，那么可以直接写成结果：ax2+bx+c=（a1x+c1）（a2x+c2）．9.【答案】A【解析】解：3+40×2+1=84．答：步道上总共使用84个三角形地砖．故选：A．中间一个正方形对应两个等腰直角三角形，从而得到三角形的个数为3+40×2+1．本题考查了等腰直角三角形：两条直角边相等的直角三角形叫做等腰直角三角形．也考查了规律型问题的解决方法，探寻规律要认真观察、仔细思考，善用联想来解决这类问题．10.【答案】D【解析】解：∵c＜0，b=5，|c|＜5，|d-5|=|d-c|，∴BD=CD，∴D点介于O、B之间，故选：D．根据O、A、B、C四点在数轴上的位置和绝对值的定义即可得到结论．本题考查的是实数与数轴，熟知实数与数轴上各点是一一对应关系是解答此题的关键．11.【答案】C【解析】解：过F作FQ⊥AD于Q，则∠FQE=90°，∵四边形ABCD是长方形，∴∠A=∠B=90°，AB=DC=8，AD∥BC，∴四边形ABFQ是矩形，∴AB=FQ=DC=8，∵AD∥BC，∴∠QEF=∠BFE=45°，∴EQ=FQ=8，∴AE=CF=×（20-8）=6，故选：C．根据矩形的性质得出∠A=∠B=90°，AB=DC=8，AD∥BC，根据矩形的判定得出四边形ABFQ是矩形，求出AB=FQ=DC=8，求出EQ=FQ=8，即可得出答案．本题考查了矩形的性质和判定，能灵活运用定理进行推理是解此题的关键．12.【答案】D【解析】解：设阿慧购买x盒桂圆蛋糕，则购买（10-x）盒金爽蛋糕，依题意有，解得2≤x≤3，∵x是整数，∴x=3，350×3+200×（10-3）=1050+1400=2450（元）．答：阿慧花2450元购买蛋糕．故选：D．可设阿慧购买x盒桂圆蛋糕，则购买（10-x）盒金爽蛋糕，根据不等关系：①购买10盒蛋糕，花费的金额不超过2500元；②蛋糕的个数大于等于75个，列出不等式组求解即可．本题考查一元一次不等式组的应用，解答此类问题的关键是明确题意，列出相应的一元一次不等式组，注意要与实际相联系．13.【答案】D【解析】解：连接AD，∵D点分别以AB、AC为对称轴，画出对称点E、F，∴∠EAB=∠BAD，∠FAC=∠CAD，∵∠B=62°，∠C=51°，∴∠BAC=∠BAD+∠DAC=180°-62°-51°=67°，∴∠EAF=2∠BAC=134°，故选：D．连接AD，利用轴对称的性质解答即可．此题考查轴对称的性质，关键是利用轴对称的性质解答．14.【答案】D【解析】解：∵一个盒子内装有大小、形状相同的53+2=55个球，其中红球2个，白球53个，∴小芬抽到红球的概率是：=．故选：D．让红球的个数除以球的总数即为所求的概率．本题考查了概率公式，熟练掌握概率的概念是解题的关键．15.【答案】C【解析】解：∵AC=BC＜AB，∴∠A=∠ABC＜∠ACB，∵∠1、∠2分别为∠ABC、∠ACB的外角，∴∠2=∠A+∠ABC，∴∠A+∠2=∠A+∠A+∠ABC＜∠ACB+∠A+∠ABC=180°，故选：C．由AC=BC＜AB，得∠A=∠ABC＜∠ACB，再由三角形的外角性质定理和三角形的内角和可得正确答案．本题考查了等腰三角形的性质定理，三角形的外角性质定理及三角形的内角和，这些都是一些基础知识点，难度不大．16.【答案】B【解析】解：根据题意可得咖啡豆每公克的价钱为：（295+5）÷250=（元），∴y与x的关系式为：．故选：B．根据若小涵购买咖啡豆250公克且自备容器，需支付295元，可得咖啡豆每公克的价钱为（295+5）÷250=（元），据此即可y与x的关系式．本题主要考查了一次函数的应用，根据题意得出咖啡豆每公克的单价是解答本题的关键．17.【答案】D【解析】解：如图，设△ADE，△BDF，△CEG，平行四边形DEGF的面积分别为S1，S2，S3和S，过点D作DH∥EC，则由DFGE为平行四边形，易得四边形DHCE也为平行四边形，从而△DFH≌△EGC，∴S△DFH=S3，∵DE∥BC，∴△ADE∽△ABC，DE=3，BC=7，∴=，∵S△ABC=14，∴S1=×14，∴S△BDH：S=（×4）：3=2：3，∴S△BDH=S，∴+S=14-×14，∴S=．故选：D．如图，设△ADE，△BDF，△CEG，平行四边形DEGF的面积分别为S1，S2，S3和S，过点D作DH∥EC，则由DFGE为平行四边形，易得四边形DHCE也为平行四边形，从而△DFH≌△EGC，利用面积比等于相似比的平方可求．本题是巧求面积的选择题，综合考查了平行四边形，相似三角形的性质等，难度较大．18.【答案】B【解析】解：=20（分钟）．所以经过20分钟後，9号车厢才会运行到最高点．故选：B．先求出从21号旋转到9号旋转的角度占圆大小比例，再根据旋转一圈花费30分钟解答即可．本题主要考查了生活中的旋转现象，理清题意，得出从21号旋转到9号旋转的角度占圆大小比例是解答本题的关键．19.【答案】D【解析】解：设AD=x，∵直角三角形ABC的内切圆分别与AB、BC相切于D点、E点，∴BD=BE=1，∴AB=x+1，AC=AD+CE=x+4，在Rt△ABC中，（x+1）2+52=（x+4）2，解得x=，即AD的长度为．故选：D．设AD=x，利用切线长定理得到BD=BE=1，AB=x+1，AC=AD+CE=x+4，然后根据勾股定理得到（x+1）2+52=（x+4）2，最后解方程即可．本题考查了三角形的内切圆与内心：三角形的内心到三角形三边的距离相等；三角形的内心与三角形顶点的连线平分这个内角．也考查了切线长定理．20.【答案】A【解析】解：设此旅行团有x人单程搭乘缆车，单程步行，其中去程及回程均搭乘缆车的有y人，根据题意得，，解得，，则总人数为7+9=16（人）故选：A．设此旅行团有x人单程搭乘缆车，单程步行，其中去程及回程均搭乘缆车的有y人，根据题意列出二元一次方程，求出其解．本题是二元一次方程组的应用，主要考查了列二元一次方程组解应用题，关键是读懂题意，找出等量关系，列出方程组．21.【答案】D【解析】解：x杯饮料则在B餐中点了x份意大利面，y份沙拉则在C餐中点了y份意大利面，∴点A餐为10-x-y；故选：D．根据点的饮料和沙拉能确定点了x+y份意大利面，根据题意可得点A餐10-x-y；本题考查列代数式；能够根据题意，以意大利面为依据，准确列出代数式是解题的关键．22.【答案】C【解析】解：正整数a和420的最大公因数为35，则a必须是35的倍数，∵420÷35=12，12=3×4，20=4×5，25=5×5，∴20不可能是a的因数，25可能是a的因数；故选：C．由420÷35=12，12=3×4，20=4×5，25=5×5，即可求解；本题考查有理数的乘法；理解因数的概念，熟练掌握有理数的乘法是解题的关键．23.【答案】C【解析】解：作ID⊥BA'于D，IE⊥AC于E，I'F⊥BA'于F，如图所示：则ID∥I'F，∵△ABC的内心为I，△A'B'C的内心为I′，∴ID=IE=IF，∠ICD-∠ACB，∠I'A'C=∠B'A'C，∴四边形IDFI'是矩形，∴II'∥L，∵∠A＜∠B＜∠C，∴∠A'＜∠B'＜∠C，∴∠ICD＞∠I'A'C，∴IC和I'A'不平行，故选：C．作ID⊥BA'于D，IE⊥AC于E，I'F⊥BA'于F，由内心的性质得出ID=IE=IF，∠ICD=∠ACB，∠I'A'C=∠B'A'C，证出四边形IDFI'是矩形，得出II'∥L，证出∠ICD＞∠I'A'C，得出IC和I'A'不平行，即可得出结论．本题考查了三角形的内心、平行线的判定、旋转的性质；熟练掌握三角形的内心性质和平行线的判定是解题的关键．24.【答案】B【解析】解：连接AD，OB，OC，∵=180°，且=，=，∴∠BOC=∠DOC=45°，在圆周上取一点E连接AE，CE，∴∠E=AOC=67.5°，∴∠ABC=122.5°＜130°，取的中点F，连接OF，则∠AOF=67.5°，∴∠ABF=123.25°＜130°，∴Q点在上，且＜，故选：B．连接AD，OB，OC，根据题意得到∠BOC=∠DOC=45°，在圆周上取一点E连接AE，CE，由圆周角定理得到∠E=AOC=67.5°，求得∠ABC=122.5°＜130°，取的中点F，连接OF，得到∠ABF=123.25°＜130°，于是得到结论．本题考查了圆心角，弧，弦的关系，圆内接四边形的性质，圆周角定理，正确的理解题意是解题的关键．25.【答案】A【解析】解：如图1，∵PQ垂直平分AD，∴PA=PD，QA=QD，而PQ=PQ，∴△APQ≌△DPQ（SSS），所以甲正确；如图2，∵PD∥AQ，DQ∥AP，∴四边形APDQ为平行四边形，∴PA=DQ，PD=AQ，而PQ=QP，∴△APQ≌△DQP （SSS），所以乙正确．故选：A．如图1，根据线段垂直平分线的性质得到PA=PD，QA=QD，则根据“SSS”可判断△APQ≌△DPQ，则可对甲进行判断；如图2，根据平行四边形的判定方法先证明四边形APDQ为平行四边形，则根据平行四边形的性质得到PA=DQ，PD=AQ，则根据“SSS”可判断△APQ≌△DQP，则可对乙进行判断．本题考查了作图-复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了线段垂直平分线的性质、平行四边形的判定与性质和三角形全等的判定．26.【答案】B【解析】解：设B（-3-m，2），C（-3+m，2），（m＞0）∵A点坐标为（-3，0），∴BC=2m，∵△ABC为正三角形，∴AC=2m，∠DAO=60°，∴m=∴C（-3+，2）设抛物线解析式y=a（x+3）2，a（-3++3）2=2，∴a=，∴y=（x+3）2，当x=0时，y=；故选：B．设B（-3-m，2），C（-3+m，2），（m＞0），可知BC=2m，再由等边三角形的性质可知C（-3+，2），设抛物线解析式y=a（x+3）2，将点C代入解析式即可求a，进而求解；本题考查二次函数的图象及性质，等边三角形的性质；结合函数图象将等边三角形的边长转化为点的坐标是解题的关键．×100%=90%，27.【答案】解：（1）根据题意得，SPF−1SPF解得，SPF=10，答：该产品的SPF应标示为10；（2）文宣内容不合理．理由如下：×100%=96%；当SPF=25时，其防护率为：25−125×100%=98%；当SPF=50时，其防护率为：50−15098%-96%=2%，∴第二代防晒乳液比第一代防晒乳液的防护率提高了2%，不是提高了一倍．∴文宣内容不合理．【解析】（1）根据公式列出方程进行计算便可；（2）根据公式计算两个的防护率，再比较可知结果．本题是分式方程的应用，根据公式列出方程是解第一题的关键，第二题的关键是根据公式正确算出各自的防护率．28.【答案】解：（1）设敏敏的影长为x 公分．由题意：150x=9060，解得x =100（公分），经检验：x =100是分式方程的解． ∴敏敏的影长为100公分．（2）如图，连接AE ，作FB ∥EA ． ∵AB ∥EF ，∴四边形ABFE 是平行四边形， ∴AB =EF =150公分，设BC =y 公分，由题意BC 落在地面上的影从为120公分． ∴y120=9060，∴y =180（公分），∴AC =AB +BC =150+180=330（公分），答：高图柱的高度为330公分．【解析】（1）根据同一时刻，物长与影从成正比，构建方程即可解决问题．（2）如图，连接AE ，作FB ∥EA ．分别求出AB ，BC 的长即可解决问题．本题考查相似三角形的应用，平行投影，平行四边形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．。

2019年台湾省中考数学试卷及解析

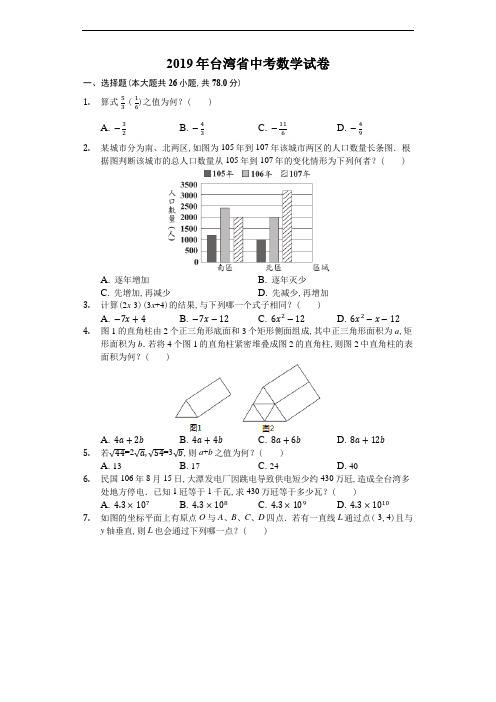
2019年台湾省中考数学试卷一、选择题(本大题共26小题,共78.0分)1. 算式-53-(-16)之值为何？( ) A. −32 B. −43 C. −116 D. −49 2. 某城市分为南、北两区,如图为105年到107年该城市两区的人口数量长条图．根据图判断该城市的总人口数量从105年到107年的变化情形为下列何者？( )A. 逐年增加B. 逐年灭少C. 先增加,再减少D. 先减少,再增加 3. 计算(2x -3)(3x +4)的结果,与下列哪一个式子相同？( )A. −7x +4B. −7x −12C. 6x 2−12D. 6x 2−x −12 4. 图1的直角柱由2个正三角形底面和3个矩形侧面组成,其中正三角形面积为a ,矩形面积为b ．若将4个图1的直角柱紧密堆叠成图2的直角柱,则图2中直角柱的表面积为何？( )A. 4a +2bB. 4a +4bC. 8a +6bD. 8a +12b5. 若√44=2√a,√54=3√b ,则a +b 之值为何？( )A. 13B. 17C. 24D. 406. 民国106年8月15日,大潭发电厂因跳电导致供电短少约430万瓩,造成全台湾多处地方停电．已知1瓩等于1千瓦,求430万瓩等于多少瓦？( )A. 4.3×107B. 4.3×108C. 4.3×109D. 4.3×10107. 如图的坐标平面上有原点O 与A 、B 、C 、D 四点．若有一直线L 通过点(-3,4)且与y 轴垂直,则L 也会通过下列哪一点？( )A. AB. BC. CD. D8.若多项式5x2+17x-12可因式分解成(x+a)(bx+c),其中a、b、c均为整数,则a+c之值为何？( )A. 1B. 7C. 11D. 139.公园内有一矩形步道,其地面使用相同的灰色正方形地砖与相同的白色等腰直角三角形地砖排列而成．如图表示此步道的地砖排列方式,其中正方形地砖为连续排列且总共有40个．求步道上总共使用多少个三角形地砖？( )A. 84B. 86C. 160D. 16210.数线上有O、A、B、C四点,各点位置与各点所表示的数如图所示．若数线上有一点D,D点所表示的数为d,且|d-5|=|d-c|,则关于D点的位置,下列叙述何者正确？( )A. 在A的左边B. 介于A、C之间C. 介于C、O之间D. 介于O、B之间11.如图,将一长方形纸片沿着虚线剪成两个全等的梯形纸片．根据图中标示长度与角度,求梯形纸片中较短的底边长度为何？( )A. 4B. 5C. 6D. 712.阿慧在店内购买两种蛋糕当伴手礼,如图为蛋糕的价目表．已知阿慧购买10盒蛋糕,花费的金额不超过2500元．若他将蛋糕分给75位同事,每人至少能拿到一个蛋糕,则阿慧花多少元购买蛋糕？( )A. 2150B. 2250C. 2300D. 245013.如图,△ABC中,D点在BC上,将D点分别以AB、AC为对称轴,画出对称点E、F,并连接AE、AF．根据图中标示的角度,求∠EAF的度数为何？( )A. 113B. 124C. 129D. 13414.箱子内装有53颗白球及2颗红球,小芬打算从箱子内抽球,以毎次抽出一球后将球再放回的方式抽53次球．若箱子内每颗球被抽到的机会相等,且前52次中抽到白球51次及红球1次,则第53次抽球时,小芬抽到红球的机率为何？( )A. 12B. 13C. 253D. 25515.如图,△ABC中,AC=BC＜AB．若∠1、∠2分别为∠ABC、∠ACB的外角,则下列角度关系何者正确( )A. ∠1<∠2B. ∠1=∠2C. ∠A+∠2<180∘D. ∠A+∠1>180∘16.小涵与阿嘉一起去咖啡店购买同款咖啡豆,咖啡豆每公克的价钱固定,购买时自备容器则结帐金额再减5元．若小涵购买咖啡豆250公克且自备容器,需支付295元；阿嘉购买咖啡豆x公克但没有自备容器,需支付y元,则y与x的关系式为下列何者？( )A. y=295250x B. y=300250x C. y=295250x+5 D. y=300250x+517.如图,将一张面积为14的大三角形纸片沿着虚线剪成三张小三角形纸片与一张平行四边形纸片．根据图中标示的长度,求平行四边形纸片的面积为何？( )A. 215B. 425C. 247D. 48718.图1的摩天轮上以等间隔的方式设置36个车厢,车厢依顺时针方向分别编号为1号到36号,且摩天轮运行时以逆时针方向等速旋转,旋转一圈花费30分钟．若图2表示21号车厢运行到最高点的情形,则此时经过多少分钟後,9号车厢才会运行到最高点？( )A. 10B. 20C. 152D. 45219.如图,直角三角形ABC的内切圆分别与AB、BC相切于D点、E点,根据图中标示的长度与角度,求AD的长度为何？( )A. 32B. 52C. 43D. 5320.某旅行团到森林游乐区参观,如表为两种参观方式与所需的缆车费用．已知旅行团的每个人皆从这两种方式中选择一种,且去程有15人搭乘缆车,回程有10人搭乘缆4100参观方式缆车费用去程及回程均搭乘缆车300元单程搭乘缆车,单程步行200元1619222521.小宜跟同学在某餐厅吃饭,如图为此餐厅的菜单．若他们所点的餐点总共为10份意大利面,x杯饮料,y份沙拉,则他们点了几份A餐？( )A. 10−xB. 10−yC. 10−x+yD. 10−x−y22.若正整数a和420的最大公因数为35,则下列叙何者正确？( )A. 20可能是a的因数,25可能是a的因数B. 20可能是a的因数,25不可能是a的因数C. 20不可能是a的因数,25可能是a的因数D. 20不可能是a的因数,25不可能是a的因数23.如图,有一三角形ABC的顶点B、C皆在直线L上,且其内心为I．今固定C点,将此三角形依顺时针方向旋转,使得新三角形A'B'C的顶点A′落在L上,且其内心为I′．若∠A＜∠B＜∠C,则下列叙述何者正确？( )#JYA. IC和I′A′平行,II′和L平行B. IC和I′A′平行,II′和L不平行C. IC和I′A′不平行,II′和L平行D. IC和I′A′不平行,II′和L不平行24.如图表示A、B、C、D四点在O上的位置,其中AD⏜=180°,且AB⏜=BD⏜,BC⏜=CD⏜．若阿超在AB⏜上取一点P,在BD⏜上取一点Q,使得∠APQ=130°,则下列叙述何者正确？( )A. Q点在BC⏜上,且BQ⏜>QC⏜B. Q点在BC⏜上,且BQ⏜<QC⏜C. Q点在CD⏜上,且CQ⏜>QD⏜D. Q点在CD⏜上,且CQ⏜<QD⏜25.如图的△ABC中,AB＞AC＞BC,且D为BC上一点．今打算在AB上找一点P,在AC上找一点Q,使得△APQ与△PDQ全等,以下是甲、乙两人的作法:(甲)连接AD,作AD的中垂线分别交AB、AC于P点、Q点,则P、Q两点即为所求(乙)过D作与AC平行的直线交AB于P点,过D作与AB平行的直线交AC于Q点,则P、Q两点即为所求对于甲、乙两人的作法,下列判断何者正确？( )A. 两人皆正确B. 两人皆错误C. 甲正确,乙错误D. 甲错误,乙正确26.如图,坐标平面上有一顶点为A的抛物线,此抛物线与方程式y=2的图形交于B、C两点,△ABC为正三角形．若A点坐标为(-3,0),则此抛物线与y轴的交点坐标为何？( ))A. (0,92)B. (0,272C. (0,9)D. (0,19)二、解答题(本大题共2小题,共16.0分)27.市面上贩售的防晒产品标有防晒指数SPF,而其对抗紫外线的防护率算法为:防护×100%,其中SPF≥1．率=SPF−1SPF请回答下列问题:(1)厂商宣称开发出防护率90%的产品,请问该产品的SPF应标示为多少？(2)某防晒产品文宣内容如图所示．请根据SPF与防护率的转换公式,判断此文宣内容是否合理,并详细解释或完整写出你的理由．28.在公园有两座垂直于水平地面且高度不一的图柱,两座圆柱后面有一堵与地面互相垂直的墙,且圆柱与墙的距离皆为120公分．敏敏观察到高度90公分矮圆柱的影子落在地面上,其影长为60公分；而高圆柱的部分影子落在墙上,如图所示．已知落在地面上的影子皆与墙面互相重直,并视太阳光为平行光,在不计圆柱厚度与影子宽度的情况下,请回答下列问题:(1)若敏敏的身高为150公分,且此刻她的影子完全落在地面上,则影长为多少公分？(2)若同一时间量得高圆柱落在墙上的影长为150公分,则高图柱的高度为多少公分？请详细解释或完整写出你的解题过程,并求出答案．。

DA2019年台湾省中考数学

答案和解析1.【答案】A【解析】解：原式=-+=-+==-=-，故选：A．根据有理数的加减法法则计算即可．本题主要考查了有理数的加减法．有理数的减法法则：减去一个数，等于加上这个数的相反数．2.【答案】A【解析】解：由图中数据可知：105年该城市的总人口数量＜106年该城市的总人口数量＜107年该城市的总人口数量，∴该城市的总人口数量从105年到107年逐年增加，故选：A．根据图中数据计算可直接得105年该城市的总人口数量＜106年该城市的总人口数量＜107年该城市的总人口数量，据此作答．本题考查条形统计图，解答本题的关键是明确题意，利用数形结合的思想解答．3.【答案】D【解析】解：由多项式乘法运算法则得（2x-3）（3x+4）=6x2+8x-9x-12=6x2-x-12．故选：D．由多项式乘法运算法则：两多项式相乘时，用一个多项式的各项去乘另一个多项式的每一项，再把所得的积相加，合并同类项后所得的式子就是它们的积．本题考查多项式乘法运算法则，牢记法则，不要漏项是解答本题的关键．4.【答案】C【解析】解：∵正三角形面积为a，矩形面积为b，∴图2中直角柱的表面积=2×4a+6b=8a+6b，故选：C．根据已知条件即可得到结论．本题考查了等边三角形的性质，矩形的性质，列代数式，正确的识别图形是解题的关键．5.【答案】B【解析】解：∵==2，∴a=11，∵==3，∴b=6，∴a+b=11+6=17．故选：B．根据二次根式的定义求出a、b的值，代入求解即可．本题主要考查了二次根式的定义，熟练掌握定义是解答本题的关键．6.【答案】C【解析】解：430万瓩=4300000瓩，∵1瓩等于1千瓦，∴4300000瓩=4300000千瓦=4.3×106千瓦=4.3×109瓦；故选：C．根据题意将430万瓩化为4.3×109瓦即可解题；本题考查科学记数法；能够将单位进行准确的换算，将大数用科学记数法表示出来是解题的关键．7.【答案】D【解析】解：如图所示：有一直线L通过点（-3，4）且与y轴垂直，故L也会通过D点．故选：D．直接利用点的坐标，正确结合坐标系分析即可．此题主要考查了点的坐标，正确结合平面直角坐标系分析是解题关键．8.【答案】A【解析】解：利用十字交乘法将5x2+17x-12因式分解，可得：5x2+17x-12=（x+4）（5x-3）．∴a=4，c=-3，∴a+c=4-3=1．故选：A．首先利用十字交乘法将5x2+17x-12因式分解，继而求得a，c的值．此题考查了十字相乘法分解因式的知识．注意ax2+bx+c（a≠0）型的式子的因式分解：这种方法的关键是把二次项系数a分解成两个因数a1，a2的积a1•a2，把常数项c分解成两个因数c1，c2的积c1•c2，并使a1c2+a2c1正好是一次项b，那么可以直接写成结果：ax2+bx+c=（a1x+c1）（a2x+c2）．9.【答案】A【解析】解：3+40×2+1=84．答：步道上总共使用84个三角形地砖．故选：A．中间一个正方形对应两个等腰直角三角形，从而得到三角形的个数为3+40×2+1．本题考查了等腰直角三角形：两条直角边相等的直角三角形叫做等腰直角三角形．也考查了规律型问题的解决方法，探寻规律要认真观察、仔细思考，善用联想来解决这类问题．10.【答案】D【解析】解：∵c＜0，b=5，|c|＜5，|d-5|=|d-c|，∴BD=CD，∴D点介于O、B之间，故选：D．根据O、A、B、C四点在数轴上的位置和绝对值的定义即可得到结论．本题考查的是实数与数轴，熟知实数与数轴上各点是一一对应关系是解答此题的关键．11.【答案】C【解析】解：过F作FQ⊥AD于Q，则∠FQE=90°，∵四边形ABCD是长方形，∴∠A=∠B=90°，AB=DC=8，AD∥BC，∴四边形ABFQ是矩形，∴AB=FQ=DC=8，∵AD∥BC，∴∠QEF=∠BFE=45°，∴EQ=FQ=8，∴AE=CF=×（20-8）=6，故选：C．根据矩形的性质得出∠A=∠B=90°，AB=DC=8，AD∥BC，根据矩形的判定得出四边形ABFQ是矩形，求出AB=FQ=DC=8，求出EQ=FQ=8，即可得出答案．本题考查了矩形的性质和判定，能灵活运用定理进行推理是解此题的关键．12.【答案】D【解析】解：设阿慧购买x盒桂圆蛋糕，则购买（10-x）盒金爽蛋糕，依题意有，解得2≤x≤3，∵x是整数，∴x=3，350×3+200×（10-3）=1050+1400=2450（元）．答：阿慧花2450元购买蛋糕．故选：D．可设阿慧购买x盒桂圆蛋糕，则购买（10-x）盒金爽蛋糕，根据不等关系：①购买10盒蛋糕，花费的金额不超过2500元；②蛋糕的个数大于等于75个，列出不等式组求解即可．本题考查一元一次不等式组的应用，解答此类问题的关键是明确题意，列出相应的一元一次不等式组，注意要与实际相联系．13.【答案】D【解析】解：连接AD，∵D点分别以AB、AC为对称轴，画出对称点E、F，∴∠EAB=∠BAD，∠FAC=∠CAD，∵∠B=62°，∠C=51°，∴∠BAC=∠BAD+∠DAC=180°-62°-51°=67°，∴∠EAF=2∠BAC=134°，故选：D．连接AD，利用轴对称的性质解答即可．此题考查轴对称的性质，关键是利用轴对称的性质解答．14.【答案】D【解析】解：∵一个盒子内装有大小、形状相同的53+2=55个球，其中红球2个，白球53个，∴小芬抽到红球的概率是：=．故选：D．让红球的个数除以球的总数即为所求的概率．本题考查了概率公式，熟练掌握概率的概念是解题的关键．15.【答案】C【解析】解：∵AC=BC＜AB，∴∠A=∠ABC＜∠ACB，∵∠1、∠2分别为∠ABC、∠ACB的外角，∴∠2=∠A+∠ABC，∴∠A+∠2=∠A+∠A+∠ABC＜∠ACB+∠A+∠ABC=180°，故选：C．由AC=BC＜AB，得∠A=∠ABC＜∠ACB，再由三角形的外角性质定理和三角形的内角和可得正确答案．本题考查了等腰三角形的性质定理，三角形的外角性质定理及三角形的内角和，这些都是一些基础知识点，难度不大．16.【答案】B【解析】解：根据题意可得咖啡豆每公克的价钱为：（295+5）÷250=（元），∴y与x的关系式为：．故选：B．根据若小涵购买咖啡豆250公克且自备容器，需支付295元，可得咖啡豆每公克的价钱为（295+5）÷250=（元），据此即可y与x的关系式．本题主要考查了一次函数的应用，根据题意得出咖啡豆每公克的单价是解答本题的关键．17.【答案】D【解析】解：如图，设△ADE，△BDF，△CEG，平行四边形DEGF的面积分别为S1，S2，S3和S，过点D作DH∥EC，则由DFGE为平行四边形，易得四边形DHCE也为平行四边形，从而△DFH≌△EGC，∴S△DFH=S3，∵DE∥BC，∴△ADE∽△ABC，DE=3，BC=7，∴=，∵S△ABC=14，∴S1=×14，∴S△BDH：S=（×4）：3=2：3，∴S△BDH=S，∴+S=14-×14，∴S=．故选：D．如图，设△ADE，△BDF，△CEG，平行四边形DEGF的面积分别为S1，S2，S3和S，过点D作DH∥EC，则由DFGE为平行四边形，易得四边形DHCE也为平行四边形，从而△DFH≌△EGC，利用面积比等于相似比的平方可求．本题是巧求面积的选择题，综合考查了平行四边形，相似三角形的性质等，难度较大．18.【答案】B【解析】解：=20（分钟）．所以经过20分钟後，9号车厢才会运行到最高点．故选：B．先求出从21号旋转到9号旋转的角度占圆大小比例，再根据旋转一圈花费30分钟解答即可．本题主要考查了生活中的旋转现象，理清题意，得出从21号旋转到9号旋转的角度占圆大小比例是解答本题的关键．19.【答案】D【解析】解：设AD=x，∵直角三角形ABC的内切圆分别与AB、BC相切于D点、E点，∴BD=BE=1，∴AB=x+1，AC=AD+CE=x+4，在Rt△ABC中，（x+1）2+52=（x+4）2，解得x=，即AD的长度为．故选：D．设AD=x，利用切线长定理得到BD=BE=1，AB=x+1，AC=AD+CE=x+4，然后根据勾股定理得到（x+1）2+52=（x+4）2，最后解方程即可．本题考查了三角形的内切圆与内心：三角形的内心到三角形三边的距离相等；三角形的内心与三角形顶点的连线平分这个内角．也考查了切线长定理．20.【答案】A【解析】解：设此旅行团有x人单程搭乘缆车，单程步行，其中去程及回程均搭乘缆车的有y人，根据题意得，，解得，，则总人数为7+9=16（人）故选：A．设此旅行团有x人单程搭乘缆车，单程步行，其中去程及回程均搭乘缆车的有y人，根据题意列出二元一次方程，求出其解．本题是二元一次方程组的应用，主要考查了列二元一次方程组解应用题，关键是读懂题意，找出等量关系，列出方程组．21.【答案】D【解析】解：x杯饮料则在B餐中点了x份意大利面，y份沙拉则在C餐中点了y份意大利面，∴点A餐为10-x-y；故选：D．根据点的饮料和沙拉能确定点了x+y份意大利面，根据题意可得点A餐10-x-y；本题考查列代数式；能够根据题意，以意大利面为依据，准确列出代数式是解题的关键．22.【答案】C【解析】解：正整数a和420的最大公因数为35，则a必须是35的倍数，∵420÷35=12，12=3×4，20=4×5，25=5×5，∴20不可能是a的因数，25可能是a的因数；故选：C．由420÷35=12，12=3×4，20=4×5，25=5×5，即可求解；本题考查有理数的乘法；理解因数的概念，熟练掌握有理数的乘法是解题的关键．23.【答案】C【解析】解：作ID⊥BA'于D，IE⊥AC于E，I'F⊥BA'于F，如图所示：则ID∥I'F，∵△ABC的内心为I，△A'B'C的内心为I′，∴ID=IE=IF，∠ICD-∠ACB，∠I'A'C=∠B'A'C，∴四边形IDFI'是矩形，∴II'∥L，∵∠A＜∠B＜∠C，∴∠A'＜∠B'＜∠C，∴∠ICD＞∠I'A'C，∴IC和I'A'不平行，故选：C．作ID⊥BA'于D，IE⊥AC于E，I'F⊥BA'于F，由内心的性质得出ID=IE=IF，∠ICD=∠ACB，∠I'A'C=∠B'A'C，证出四边形IDFI'是矩形，得出II'∥L，证出∠ICD＞∠I'A'C，得出IC和I'A'不平行，即可得出结论．本题考查了三角形的内心、平行线的判定、旋转的性质；熟练掌握三角形的内心性质和平行线的判定是解题的关键．24.【答案】B【解析】解：连接AD，OB，OC，∵=180°，且=，=，∴∠BOC=∠DOC=45°，在圆周上取一点E连接AE，CE，∴∠E=AOC=67.5°，∴∠ABC=122.5°＜130°，取的中点F，连接OF，则∠AOF=67.5°，∴∠ABF=123.25°＜130°，∴Q点在上，且＜，故选：B．连接AD，OB，OC，根据题意得到∠BOC=∠DOC=45°，在圆周上取一点E连接AE，CE，由圆周角定理得到∠E=AOC=67.5°，求得∠ABC=122.5°＜130°，取的中点F，连接OF，得到∠ABF=123.25°＜130°，于是得到结论．本题考查了圆心角，弧，弦的关系，圆内接四边形的性质，圆周角定理，正确的理解题意是解题的关键．25.【答案】A【解析】解：如图1，∵PQ垂直平分AD，∴PA=PD，QA=QD，而PQ=PQ，∴△APQ≌△DPQ（SSS），所以甲正确；如图2，∵PD∥AQ，DQ∥AP，∴四边形APDQ为平行四边形，∴PA=DQ，PD=AQ，而PQ=QP，∴△APQ≌△DQP （SSS），所以乙正确．故选：A．如图1，根据线段垂直平分线的性质得到PA=PD，QA=QD，则根据“SSS”可判断△APQ≌△DPQ，则可对甲进行判断；如图2，根据平行四边形的判定方法先证明四边形APDQ为平行四边形，则根据平行四边形的性质得到PA=DQ，PD=AQ，则根据“SSS”可判断△APQ≌△DQP，则可对乙进行判断．本题考查了作图-复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了线段垂直平分线的性质、平行四边形的判定与性质和三角形全等的判定．26.【答案】B【解析】解：设B（-3-m，2），C（-3+m，2），（m＞0）∵A点坐标为（-3，0），∴BC=2m，∵△ABC为正三角形，∴AC=2m，∠DAO=60°，∴m=∴C（-3+，2）设抛物线解析式y=a（x+3）2，a（-3++3）2=2，∴a=，∴y=（x+3）2，当x=0时，y=；故选：B．设B（-3-m，2），C（-3+m，2），（m＞0），可知BC=2m，再由等边三角形的性质可知C（-3+，2），设抛物线解析式y=a（x+3）2，将点C代入解析式即可求a，进而求解；本题考查二次函数的图象及性质，等边三角形的性质；结合函数图象将等边三角形的边长转化为点的坐标是解题的关键．27.【答案】解：（1）根据题意得，，解得，SPF=10，答：该产品的SPF应标示为10；（2）文宣内容不合理．理由如下：当SPF=25时，其防护率为：；当SPF=50时，其防护率为：；98%-96%=2%，∴第二代防晒乳液比第一代防晒乳液的防护率提高了2%，不是提高了一倍．∴文宣内容不合理．【解析】（1）根据公式列出方程进行计算便可；（2）根据公式计算两个的防护率，再比较可知结果．本题是分式方程的应用，根据公式列出方程是解第一题的关键，第二题的关键是根据公式正确算出各自的防护率．28.【答案】解：（1）设敏敏的影长为x公分．由题意：=，解得x=100（公分），经检验：x=100是分式方程的解．∴敏敏的影长为100公分．（2）如图，连接AE，作FB∥EA．∵AB∥EF，∴四边形ABFE是平行四边形，∴AB=EF=150公分，设BC=y公分，由题意BC落在地面上的影从为120公分．∴=，∴y=180（公分），∴AC=AB+BC=150+180=330（公分），答：高图柱的高度为330公分．【解析】（1）根据同一时刻，物长与影从成正比，构建方程即可解决问题．（2）如图，连接AE，作FB∥EA．分别求出AB，BC的长即可解决问题．本题考查相似三角形的应用，平行投影，平行四边形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．。

2019年台湾地区初中教育会考(中考)数学科题本与详解

台湾2019年初中教育会考(中考)数学科题本与详解(5月14日 10:30 ~ 11:50)第一部分：选择题 (1~25题)1. x = -3，y = 1为下列哪一个二元一次方程式的解？(A) x +2y = -1 (B) x -2y = 1 (C) 2x +3y = 6 (D) 2x -3y = -6 [解] 将x ＝－3，y ＝1代入各式，(A) (－3)＋2‧1＝－1； (B) (－3)－2‧1＝－5≠1； (C) 2‧(－3)＋3‧1＝－3≠6 (D) 2‧(－3)－3‧1＝－9≠－6；故选(A)。

2. 算式 [ -5 -(-11) ]÷(3 2 ⨯4 ) 之值为何？ (A) 1 (B) 16 (C) - 8 3 (D) - 1283[解] [－5－(－11)]÷( 32 ×4)＝[－5＋11]÷(3×2)＝6÷6＝1，故选(A)。

3. 计算 (2x +1)(x -1)-(x 2+x -2)的结果，与下列哪一个式子相同？(A) x 2-2x +1 (B) x 2-2x -3 (C) x 2+x -3 (D) x 2-3[解] (2x ＋1)(x －1)－(x 2＋x －2)＝(2x 2－2x ＋x －1)－(x 2＋x －2)＝2x 2－x －1－x 2－x ＋2 ＝x 2－2x ＋1，故选(A)。

4. 如图(一)，已知扇形AOB 的半径为10公分，圆心角为54°，则此扇形面积为多少平方公分？ (A) 100π (B) 20π (C) 15π (D) 5π[解] 扇形AOB 面积＝10×10×π×54360 ＝15π(平方公分)，故选(C)。

5. 图(二)数在线的A 、B 、C 三点所表示的数分别为a 、b 、c 。

若| a -b | = 3，| b -c | = 5，且原点O 与A 、B 的距离分别为4、 1，则关于O 的位置，下列叙述何者正确？(A) 在A 的左边 (B) 介于A 、B 之间 (C) 介于B 、C 之间 (D) 在C 的右边[解] ∵OB ＝1，∴O 点在B 点左侧1单位处或右侧1单位处，已知OA ＝4： ○1 若O 点在B 点左侧1单位处，∵∣a －b ∣＝3，∴OA ＝3－1＝2(不合)； ○2 若O 点在B 点右侧1单位处，∵∣a －b ∣＝3，∴OA ＝3＋1＝4(合)；因此O 点在B 、C 之间，故选(C)。

2019年台湾第二次中考数学试题及答案

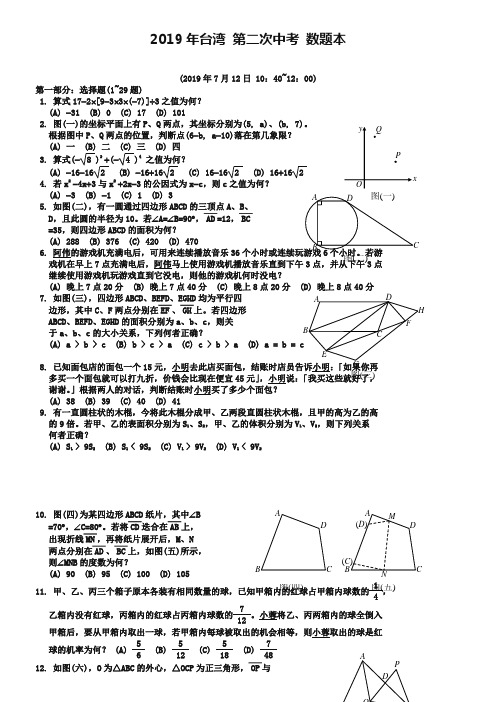
2019年台湾第二次中考数题本(2019年7月12日 10：40~12：00)第一部分：选择题(1~29题)1. 算式17-2⨯[9-3⨯3⨯(-7)]÷3之值为何？ (A) -31 (B) 0 (C) 17 (D) 1012. 图(一)的坐标平面上有P 、Q 两点，其坐标分别为(5, a)、(b, 7)。

根据图中P 、Q 两点的位置，判断点(6-b, a -10)落在第几象限？ (A) 一 (B) 二 (C) 三 (D) 四3. 算式(-8 )3 +(- 4 )4 之值为何？(A) -16-16 2 (B) -16+16 2 (C) 16-16 2 (D) 16+16 24. 若x 2 -4x +3与x 2+2x -3的公因式为x -c ，则c 之值为何？ (A) -3 (B) -1 (C) 1 (D) 3 5. 如图(二)，有一圆通过四边形ABCD 的三顶点A 、B 、 D ，且此圆的半径为10。

若∠A=∠B=90︒，AD ￣=12，BC ￣ =35，则四边形ABCD 的面积为何？(A) 288 (B) 376 (C) 420 (D) 470 6. 阿伟的游戏机充满电后，可用来连续播放音乐36个小时或连续玩游戏6个小时。

若游戏机在早上7点充满电后，阿伟马上使用游戏机播放音乐直到下午3点，并从下午3点继续使用游戏机玩游戏直到它没电，则他的游戏机何时没电？(A) 晚上7点20分 (B) 晚上7点40分 (C) 晚上8点20分 (D) 晚上8点40分7. 如图(三)，四边形ABCD 、BEFD 、EGHD 均为平行四边形，其中C 、F 两点分别在EF ￣、GH ￣上。

若四边形 ABCD 、BEFD 、EGHD 的面积分别为a 、b 、c ，则关于a 、b 、c 的大小关系，下列何者正确？ (A) a > b > c (B) b > c > a (C) c > b > a (D) a = b = c8. 已知面包店的面包一个15元，小明去此店买面包，结账时店员告诉小明：「如果你再多买一个面包就可以打九折，价钱会比现在便宜45元」，小明说：「我买这些就好了，谢谢。

2019台湾第一次中考(全区卷) 与简答

经典精品试卷2019台湾第一次中考(全区) 数学真题与简答（A） 1. 坐标平面上，若点(3, b)在方程式9y的图形上，则b值为何？=x3-2(A)－1 (B) 2 (C) 3 (D) 9（C ） 2. 计算33)4(7-+之值为何？(A) 9 (B) 27 (C) 279 (D) 407（D ） 3. 化简)23(4)32(5x x ---之后，可得下列哪一个结果？(A) 2x －27 (B) 8x －15 (C) 12x －15 (D) 18x －27（D ） 4. 下列有一面国旗是线对称图形，根据选项中的图形，判断此国旗为何？ (A)(B) (C) (D)（A ） 5. 下列四个多项式，哪一个是3522-+x x 的因式？(A) 2x －1 (B) 2x －3 (C) x －1 (D) x －3（A ） 6. 图(一)为某校782名学生小考成绩的次数分配直方图，若下列有一选项为图(一)成绩的累积次数分配直方图，则此图为何？ (A) (B) (C) (D)（C ） 7. 若△ABC 中，2（∠A ＋∠C ）＝3∠B ，则∠B 的外角度数为何？ (A) 36 (B) 72 (C) 108 (D) 144 （D ） 8. 若949)7(22+-=-bx x a x ，则b a +之值为何？(A) 18 (B) 24 (C) 39 (D) 45（B ） 9. 在早餐店里，王伯伯买5颗馒头，3颗包子，老板少拿2元，只要50元。

李太太买了11颗馒头，5颗包子，老板以售价的九折优待，只要90元。

若馒头每颗x 元，包子每颗y 元，则下列哪一个二元一次联立方程式可表示题目中的数量关系？(A)⎩⎨⎧⨯=++=+9.09051125035y x y x (B)⎩⎨⎧÷=++=+9.09051125035y x y x (C)⎩⎨⎧⨯=+-=+9.09051125035y x y x (D)⎩⎨⎧÷=+-=+9.09051125035y x y x （C ）10. 若(a －1)：7＝4：5，则10a ＋8之值为何？(A) 54 (B) 66 (C) 74 (D) 80（C ）11. 图(二)数在线有O 、A 、B 、C 、D 五点，根据图中各点所表示的数，判断18在数在线的位置会落在下列哪一线段上？(A)OA (B)AB (C)BC (D)CD（A ）12. 判断312是96的几倍？(A) 1 (B) (31)2 (C) (31)6 (D) (－6)2 （A ）13. 解不等式－51x －3＞2，得其解的范围为何？(A) x ＜－25 (B) x ＞－25 (C) x ＜5 (D) x ＞5（B ）14. 计算)4(433221-⨯++之值为何？ (A)－1 (B)－611 (C)－512 (D)－323 （B ）15. 图(三)的坐标平面上有一正五边形ABCDE ，其中C 、D 两点坐标分别为(1,0)、(2,0) 。