二倍角及正余弦定理【教师版本】

合集下载

二倍角的正弦、余弦、正切公式2 人教课标版精品课件

时光就是这么不经用，很快自己做了母亲，我才深深的知道，这样的爱，不带任何附加条件，不因万物毁灭而更改。只想守护血浓于水的旧时光，即便峥嵘岁月将容颜划伤，相信一切都是最好的安排。那时的时光无限温柔，当清水载着陈旧的往事，站在时光这头，看时光那头，一切变得分明。执笔书写，旧时光的春去秋来，欢喜也好，忧伤也好，时间窖藏，流光曼卷里所有的宠爱，疼惜，活色生香的脑海存在。
唯用一枝瘦笔，剪一段旧时光，剪掉喧嚣尘世的纷纷扰扰，剪掉终日的忙忙碌碌。情也好，事也罢，细品红尘，文字相随，把寻常的日子，过得如春光般明媚。光阴珍贵，指尖徘徊的时光唯有珍惜，朝圣的路上做一个谦卑的信徒，听雨落，嗅花香，心上植花田，蝴蝶自会来，心深处自有广阔的天地。旧时光难忘，好的坏的一一纳藏，不辜负每一寸光阴，自会花香满径，盈暗香满袖。每个人都有自己的精神家园，而对于记忆中的几户人家，我更有着刻骨铭心的情感。上个世纪六七十年代，在陕西的某城市的郊区一个大院子里住了四家人。一家人姓赵四十岁左右，是一个食堂的采购员；姓李的一家人是个老离休干部，也是一个军人。曾经在解放战争时期受过伤，当时他的腿上留有敌人手榴弹炸的弹片在里头呢；东面的一家姓石，是一个搞电子的工程师；西面一家姓吴，老吴是一个中学教师。
老吴走后每一天孩子起床都是老李叫他们起床，洗脸，吃饭上学，都是老李管的。孩子们放学就在老李家里学习，写作业，吃饭。每到星期天老石钓来鱼做熟以后，就端到老李家让老吴的孩子打牙祭。老赵的孩子学习好，只要有时间就去老吴家帮助他的孩子辅导功课。就这样两个多月很快过去了，老吴两口子回来了，他们看到家里面收拾的整整齐齐的。孩子们也长胖了，也爱学习了。他当面给老李鞠了一躬表示十分的感激，还给老石的孩子带了一些当地的土特产，给老赵的孩子买了几件衣服。老干部老李当时家里有一部电话机，这个电话机就成了几家人共同使用的了。那个时候打个电话一般不太容易，当时电话机是个除了单位有一部以外，根本很少有个人电话的。老石在休息的时候喜欢出去钓鱼，他这个人喜欢钓鱼，就是不太喜欢吃鱼。钓的鱼一部分留下给自家孩子吃一些，大部分的鱼都分给邻居吃了。老李特别喜欢吃鱼，老石就经常把钓的鱼给他吃。老赵是个食堂的采购员，经常可以买到别人还没有吃到的反季节蔬菜，大家经常让他给代买一点便宜的蔬菜，或者便宜的鸡蛋，或者便宜的肉和其他调味品。当时一般的人家里都没有电视机，最多有个半导体收音机就是很好的了。大多数人下班吃完饭没有事就是喜欢串串门，一起都聊的是过去的事情，以及现在的工作和家常事。串门是特别普遍的现象。现在这个年代在一起住了好久也不知道邻居是干啥的，或者姓啥叫啥，哪里的人都不知道。就是住在隔壁的也就是看见了打个招呼点个头，各自开门关门就走开了，与那个时候的邻里关系没法相比。老吴是个老师，也是一个戏迷，爱听京剧，也是一个爱下象棋的。老吴一有空就和老李下棋玩，于是他们有了深厚的情谊。他们几家人的孩子相处得也是特别的好，一般放了学就在一起学习玩耍。在那个时候，人们心里都是充满着英雄主义和共产主义的理想，就是跟着毛主席共产党好好的为人民服务。小孩玩的游戏，多是是刀枪、打仗的游戏，还有电影里看见的剧情。他们拿着玩具枪，还有木头做的宝剑，或者花五角钱可以买一根长杆木头大刀。他们拿着这些玩具就分出两个队伍。你这个队伍藏起来，他们埋伏起来之前还要伪装好，他们一般都是藏在山坡底下或者是草多的地方。有的头上还要带上细树枝编的帽子或者是柳树条编的头箍，他们就趴在草丛里一般很难被另外一群小伙伴发现的。那个队伍就到处找他们，这个游戏叫做抓特务，或者叫做打伏击抓俘虏。他们一有时间，或者一放寒暑假，一群孩子就喜欢玩这个游戏，特别好玩。那一两个月就是孩子们的天下了，非常热闹。除此之外就是滚铁环、碰膝盖游戏。女孩子喜欢跳皮筋、跳格子、跳绳、打沙包、唱歌，也喜欢玩抓

二倍角的正弦、余弦、正切公式(同步讲义)(教师版)

人教A 版必修1第5章三角函数：5.1第3课时二倍角的正弦、余弦、正切公式（同步讲义）(教师独具内容)课程标准：1.会从两角和的正弦、余弦、正切公式推导出二倍角的正弦、余弦、正切公式.2.能熟练运用二倍角的公式进行简单的恒等变换，并能灵活地将公式变形运用．教学重点：二倍角的正弦、余弦、正切公式以及公式的变形，二倍角公式的简单应用．教学难点：倍角公式与以前学过的同角三角函数的基本关系式、诱导公式、和(差)角公式的综合应用.【知识导学】知识点一二倍角的正弦、余弦、正切公式公式的适用条件：在S 2α，C 2α中，α∈□07R ，在T 2α中，α≠□08k π2＋π4(k ∈Z )，且α≠□09k π＋π2(k ∈Z )．知识点二二倍角公式的变形形式(1)(sin α±cos α)2＝□011±sin2α；(2)cos 2α＝□021＋cos2α2； (3)sin 2α＝□031－cos2α2. 【新知拓展】1．“二倍”的含义倍角公式中的“倍角”是相对的，对于两个角的比值等于2的情况都成立，如6α是3α的2倍，3α是3α2的2倍．这就是说，“倍”是相对而言的，是描述两个数量之间的关系的．2．用正切来表示正弦、余弦的倍角公式，也叫“万能公式”，公式如下：(1)sin2α＝2sin αcos α＝2sin αcos αsin 2α＋cos 2α＝2tan α1＋tan 2α，即sin2α＝2tan α1＋tan 2α. (2)cos2α＝cos 2α－sin 2α＝cos 2α－sin 2αsin 2α＋cos 2α＝1－tan 2α1＋tan 2α，即cos2α＝1－tan 2α1＋tan 2α.1．判一判(正确的打“√”，错误的打“×”)(1)二倍角的正弦、余弦、正切公式的适用范围是任意角．( )(2)存在角α，使得sin2α＝2sin α成立．( ) (3)对任意角α，总有tan2α＝2tan α1－tan 2α.( )答案 (1)× (2)√ (3)×2．做一做(1)计算cos 215°－sin 215°结果等于( )A.12B.22 C.33 D.32 (2)12sin15°cos15°的值等于( )A.14B.18C.116D.12 (3)已知cos α＝13，则cos2α等于( )A.13B.23 C ．－79 D.79(4)若tan α＝12，则tan2α＝( )A.43 B.34 C.15 D ．－43答案 (1)D (2)B (3)C (4)A题型一给角求值问题【例1】求下列各式的值：(1)sin π12cos π12；(2)1－2sin 2750°；(3)2tan150°1－tan 2150°；(4)cos20°cos40°cos80°.[解] (1)原式＝2sin π12cos π122＝sin π62＝14. (2)原式＝cos(2×750°)＝cos1500°＝cos(4×360°＋60°)＝cos60°＝12. (3)原式＝tan(2×150°)＝tan300°＝tan(360°－60°)＝－tan60°＝－ 3.(4)原式＝2sin20°cos20°cos40°cos80°2sin20°＝2sin40°cos40°cos80°4sin20°＝2sin80°cos80°8sin20°＝sin160°8sin20° ＝18. 金版点睛正用、逆用二倍角公式求值对于给角求值问题，需观察题中角度间的关系，发现其特征，并能根据式子的特点构造出二倍角的形式，正用、逆用二倍角公式求值．注意利用诱导公式和同角三角函数基本关系对已知式进行转化．【跟踪训练1】求下列各式的值：(1)cos π5cos 2π5；(2)12－cos 2π8； (3)tan π12－1tan π12. 解 (1)原式＝2sin π5cos π5cos 2π52sin π5＝sin 2π5cos 2π52sin π5＝sin 4π54sin π5＝sin π54sin π5＝14. (2)原式＝1－2cos 2π82＝－2cos 2π8－12＝－12cos π4＝－24.(3)原式＝tan 2π12－1tan π12＝－2×1－tan 2π122tan π12＝－2×1tan π6＝－233＝－2 3. 题型二给值求值问题【例2】已知cos ⎝⎛⎭⎫α＋π4＝35，π2≤α<3π2，求cos ⎝⎛⎭⎫2α＋π4的值． [解] ∵π2≤α<3π2，∴3π4≤α＋π4<7π4. ∵cos ⎝⎛⎭⎫α＋π4>0，∴3π2<α＋π4<7π4. ∴sin ⎝⎛⎭⎫α＋π4＝－1－cos 2⎝⎛⎭⎫α＋π4 ＝－1－⎝⎛⎭⎫352＝－45. ∴cos2α＝sin ⎝⎛⎭⎫2α＋π2＝2sin ⎝⎛⎭⎫α＋π4cos ⎝⎛⎭⎫α＋π4 ＝2×⎝⎛⎭⎫－45×35＝－2425， sin2α＝－cos ⎝⎛⎭⎫2α＋π2＝1－2cos 2⎝⎛⎭⎫α＋π4 ＝1－2×⎝⎛⎭⎫352＝725.∴cos ⎝⎛⎭⎫2α＋π4＝22cos2α－22sin2α＝22×⎝⎛⎭⎫－2425－725＝－31250. [结论探究] 若本例条件不变，求cos2αsin ⎝⎛⎭⎫π4＋α的值．解 ∵π2≤α<3π2，∴3π4≤π4＋α<7π4. 又cos ⎝⎛⎭⎫α＋π4＝35>0，∴3π2<π4＋α<7π4， ∴sin ⎝⎛⎭⎫π4＋α＝－45， ∴cos2α＝sin ⎝⎛⎭⎫2α＋π2＝2sin ⎝⎛⎭⎫α＋π4cos ⎝⎛⎭⎫α＋π4 ＝2×⎝⎛⎭⎫－45×35＝－2425，∴cos2αsin ⎝⎛⎭⎫π4＋α＝－2425－45＝65. 金版点睛解决条件求值问题的方法给值求值问题，注意寻找已知式与未知式之间的联系，有两个观察方向：(1)有方向地将已知式或未知式化简，使关系明朗化；(2)寻找角之间的关系，看是否适合相关公式的使用，注意常见角的变换和角之间的二倍关系．【跟踪训练2】已知x ∈⎝⎛⎭⎫π4，π2，sin ⎝⎛⎭⎫π4－x ＝－35，求cos2x 的值．解解法一：由已知条件得cos x －sin x ＝－325，将此式两边平方得2sin x cos x ＝725. 由此可得(cos x ＋sin x )2＝3225. 因为x ∈⎝⎛⎭⎫π4，π2，所以sin x >0，cos x >0.所以cos x ＋sin x ＝425. 故cos2x ＝cos 2x －sin 2x ＝(cos x ＋sin x )(cos x －sin x ) ＝425×⎝⎛⎭⎫－325＝－2425. 解法二：∵sin ⎝⎛⎭⎫π4－x ＝－35，x ∈⎝⎛⎭⎫π4，π2， ∴π4－x ∈⎝⎛⎭⎫－π4，0，cos ⎝⎛⎭⎫π4－x ＝45. cos2x ＝sin ⎝⎛⎭⎫π2－2x ＝2sin ⎝⎛⎭⎫π4－x cos ⎝⎛⎭⎫π4－x ＝2×⎝⎛⎭⎫－35×45＝－2425. 题型三给值求角问题【例3】已知tan α＝13，tan β＝－17，且α，β∈(0，π)，求2α－β的值． [解] ∵tan α＝13>0，α∈(0，π)，∴α∈⎝⎛⎭⎫0，π2，2α∈(0，π)， ∴tan2α＝2tan α1－tan 2α＝2×131－⎝⎛⎭⎫132＝34>0，∴2α∈⎝⎛⎭⎫0，π2. 又∵tan β＝－17<0，β∈(0，π)，∴β∈⎝⎛⎭⎫π2，π， ∴tan(2α－β)＝tan2α－tan β1＋tan2αtan β＝34－⎝⎛⎭⎫－171＋34×⎝⎛⎭⎫－17＝1，又∵2α∈⎝⎛⎭⎫0，π2，β∈⎝⎛⎭⎫π2，π， ∴2α－β∈(－π，0)，∴2α－β＝－3π4. 金版点睛在给值求角时，一般选择一个适当的三角函数，根据题设确定所求角的范围，然后再求出角.其中确定角的范围是关键的一步.【跟踪训练3】已知tan α＝17，sin β＝1010，且α，β为锐角，求α＋2β的值．解 ∵tan α＝17<1，且α为锐角，∴0<α<π4，又∵sin β＝1010<22，且β为锐角，∴0<β<π4， ∴0<α＋2β<3π4. 由sin β＝1010，β为锐角，得cos β＝31010，∴tan β＝13， ∴tan(α＋β)＝tan α＋tan β1－tan αtan β＝12， ∴tan(α＋2β)＝tan (α＋β)＋tan β1－tan (α＋β)tan β＝12＋131－12×13＝1，故α＋2β＝π4. 题型四有关化简与证明问题【例4】(1)化简：11－tan θ－11＋tan θ； (2)证明：1＋sin4α＋cos4α1＋sin4α－cos4α＝1tan2α. [解] (1)原式＝(1＋tan θ)－(1－tan θ)(1－tan θ)(1＋tan θ)＝2tan θ1－tan 2θ＝tan2θ. (2)证明：左边分子为2cos 22α＋2sin2αcos2α＝2cos2α·(cos2α＋sin2α)．左边分母为2sin 22α＋2sin2αcos2α＝2sin2α(sin2α＋cos2α)．故两式相除，即cos2αsin2α＝1tan2α. 金版点睛证明的本质问题实际上就是化简三角函数的化简与证明有四个方向，即分别从“角”“函数名”“幂”“形”着手分析，消除差异，化繁为简，或用“两头凑”的方法．【跟踪训练4】(1)化简cos10°＋3sin10°1－cos80°＝________； (2)求证：(sin2x ＋cos2x －1)(sin2x －cos2x ＋1)sin4x＝tan x . 答案 (1)2 (2)见解析解析 (1)cos10°＋3sin10°1－cos80°＝2(sin30°cos10°＋cos30°sin10°)2sin 240°＝2sin40°2sin40°＝ 2. (2)证法一：左边＝(2sin x cos x －2sin 2x )(2sin x cos x ＋2sin 2x )sin4x＝4sin 2x (cos 2x －sin 2x )sin4x ＝4sin 2x cos2x 2sin2x cos2x＝4sin 2x 2×2sin x cos x＝tan x ＝右边．故原等式成立．证法二：左边＝(sin2x ＋cos2x －1)(sin2x －cos2x ＋1)(sin2x ＋cos2x )2－1＝(sin2x ＋cos2x －1)(sin2x －cos2x ＋1)(sin2x ＋cos2x －1)(sin2x ＋cos2x ＋1)＝sin2x ＋1－cos2x sin2x ＋1＋cos2x ＝2sin x cos x ＋2sin 2x 2sin x cos x ＋2cos 2x＝2sin x (cos x ＋sin x )2cos x (sin x ＋cos x )＝tan x ＝右边．故原等式成立．随堂水平达标1．若tan α＝3，则sin2αcos 2α的值等于( ) A ．2 B ．3 C ．4 D ．6答案 D解析 sin2αcos 2α＝2sin αcos αcos 2α＝2tan α＝2×3＝6. 2．下列各式中，值为32的是( ) A ．2sin15°cos15° B ．cos 215°－sin 215°C ．2sin 215°D ．sin 215°＋cos 215° 答案 B解析 A 项，2sin15°cos15°＝sin30°＝12；B 项，cos 215°－sin 215°＝cos30°＝32；C 项，2sin 215°＝1－cos30°＝1－32；D 项，sin 215°＋cos 215°＝1.故选B. 3．cos 4π8－sin 4π8的值为( ) A ．0 B.22 C ．1 D ．－22答案 B解析 cos 4π8－sin 4π8＝⎝⎛⎭⎫cos 2π8＋sin 2π8⎝⎛⎭⎫cos 2π8－sin 2π8＝cos π4＝22. 4．设sin2α＝－sin α，α∈⎝⎛⎭⎫π2，π，则tan2α的值是________．答案 3 解析 ∵α∈⎝⎛⎭⎫π2，π，∴sin α>0，又∵sin2α＝2sin αcos α＝－sin α，∴cos α＝－12，∴sin α＝32，tan α＝－3， ∴tan2α＝2tan α1－tan 2α＝－231－(－3)2＝ 3. 5．已知cos α＝－1213，α∈⎝⎛⎭⎫π，3π2，求sin2α，cos2α，tan2α的值．解 ∵cos α＝－1213，α∈⎝⎛⎭⎫π，3π2， ∴sin α＝－1－cos 2α＝－513， ∴sin2α＝2sin αcos α＝2×⎝⎛⎭⎫－513×⎝⎛⎭⎫－1213＝120169， cos2α＝1－2sin 2α＝1－2×⎝⎛⎭⎫－5132＝119169， tan2α＝sin2αcos2α＝120119.。

二倍角及正余弦定理【教师版本】

3如图一船在海上自西向东航行在a处测得某岛m的方位角为北偏东角前进m海里后在处测得该岛的方位角为北偏东角已知该岛周围n海里范围内包括边界有暗礁现该船继续东行当解析由题可知在abm根据正弦定理得bmsin90解得bmmcos要使该船没有触礁危险需满足bmsin90时该船没有触礁危险
东方教育学科教师辅导讲义
讲义编号SH12sx00021
学员编号：年级：高一课时数：2
学员姓名：辅导科目：数学学科教师：李生
学科组长签名及日期
剩余课时数
课题
二倍角及正余弦定理
授课时间
备课时间：
教学目标
1.掌握二倍角及半角公式
2.利用正余弦定理解斜三角形
重点、难点
1、二倍角及半角公式
2、正余弦定理
考点及考试要求
1.二倍角及半角公式的应用
（2）已知三角形的两边及夹角，可求出第三边．
例题一：在△ABC中已知acosB=bcosA,试判断△ABC的形状.
【答案】解法1：由扩充的正弦定理：代入已知式
2RsinAcosB=2RsinBcosA
sinAcosB-cosAsinB=0，sin(A-B)=0
A-B=0∴A=B即△ABC为等腰三角形
解析AB＝1 000×1 000×＝(m)，
∴BC＝·sin 30°＝(m)．
∴航线离山顶h＝×sin 75°≈11.4 (km)．
∴山高为18－11.4＝6.6 (km)．
3、如图，一船在海上自西向东航行，在A处测得某岛M的方位角为北偏东α角，前进m海里后在B处测得该岛的方位角为北偏东β角，已知该岛周围n海里范围内(包括边界)有暗礁，现该船继续东行，当α与β满足条件__________________时，该船没有触礁危险．

【课件】二倍角的正弦、余弦、正切公式(人教A版2019必修第一册)

T2
tan
2
2
1
tan tan2
公式说明
1.角的倍半关系是相对而言的, 2 是的二倍, 4 是
2 的二倍,
2
是
4
的二倍等;
2.当 =k (k Z ) 时， tan 的值不存在，
2
求 tan 2 的值可利用诱导公式.
练一练
若为锐角，且 sin : sin 8 : 5,则cos 的值为（） 2
答案： C
3 典型例题
例4.求8sin cos cos cos 的值.
48 48 24 12
解：8sin cos cos cos
48 48 24 12
=4 （2 sin cos ）cos cos
48 48
24 12
=4sin cos cos
24 24 12
2 (2sin cos ) cos
所以
tan
2B
1
2
tan tan
B 2B
22 1 22
4. 3
所以tan(2A 2B) tan 2A tan 2B 1 tan 2A tan 2B
1
24 4 73 24 (
4)
44 . 117
73
解法2 在ABC中，由cos A 4 , 0 A , 得 5
sin A 1 cos2 A 1 ( 4 )2 3 . 55
简记为S2α
2 二倍角公式
cos 2 co（ s )
cos2 sin2 2cos2 1 1 2sin2 .
简记为 C2 .
2 二倍角公式
tan
2
tan（
)
2 tan 1 tan2
简记为 T2 .

高中数学人教版必修二倍角的正弦、余弦、正切公式教案(系列五)

3.1.3 二倍角的正弦、余弦、正切公式整体设计教学分析“二倍角的正弦、余弦、正切公式”是在研究了两角和与差的三角函数的基础上，进一步研究具有“二倍角”关系的正弦、余弦、正切公式的，它既是两角和与差的正弦、余弦、正切公式的特殊化，又为以后求三角函数值、化简、证明提供了非常有用的理论工具、通过对二倍角的推导知道，二倍角的内涵是：揭示具有倍数关系的两个三角函数的运算规律、通过推导还让学生加深理解了高中数学由一般到特殊的化归思想、因此本节内容也是培养学生运算和逻辑推理能力的重要内容，对培养学生的探索精神和创新能力、发现问题和解决问题的能力都有着十分重要的意义.本节课通过教师提出问题、设置情境及对和角公式中α、β关系的特殊情形α=β时的简化，让学生在探究中既感到自然、易于接受，还可清晰知道和角的三角函数与倍角公式的联系，同时也让学生学会怎样发现规律及体会由一般到特殊的化归思想.这一切教师要引导学生自己去做,因为，《数学课程标准》提出：“要让学生在参与特定的数学活动，在具体情境中初步认识对象的特征，获得一些体验”.在实际教学过程中不要过多地补充一些高技巧、高难度的练习，更不要再补充一些较为复杂的积化和差或和差化积的恒等变换，否则就违背了新课标在这一章的编写意图和新课改精神.三维目标1.通过让学生探索、发现并推导二倍角公式,了解它们之间、以及它们与和角公式之间的内在联系,并通过强化题目的训练,加深对二倍角公式的理解，培养运算能力及逻辑推理能力,从而提高解决问题的能力.2.通过二倍角的正弦、余弦、正切公式的运用，会进行简单的求值、化简、恒等证明.体会化归这一基本数学思想在发现中和求值、化简、恒等证明中所起的作用.使学生进一步掌握联系变化的观点，自觉地利用联系变化的观点来分析问题，提高学生分析问题、解决问题的能力.3.通过本节学习，引导学生领悟寻找数学规律的方法，培养学生的创新意识，以及善于发现和勇于探索的科学精神.重点难点教学重点：二倍角公式推导及其应用.教学难点：如何灵活应用和、差、倍角公式进行三角式化简、求值、证明恒等式.安排1教学过程导入新课思路1.(复习导入)请学生回忆上两节共同探讨的和角公式、差角公式，并回忆这组公式的来龙去脉，然后让学生默写这六个公式.教师引导学生：和角公式与差角公式是可以互相化归的.当两角相等时,两角之和便为此角的二倍,那么是否可把和角公式化归为二倍角公式呢?今天,我们进一步探讨一下二倍角的问题，请同学们思考一下，应解决哪些问题呢？由此展开新课.思路2.(问题导入)出示问题，让学生计算，若sinα=53,α∈(2,π),求sin2α，cos2α的值.学生会很容易看出：sin2α=sin(αα)=sinαcosαcosαsinα=2sinαcosα的，以此展开新课，并由此展开联想推出其他公式.推进新课新知探究提出问题①还记得和角的正弦、余弦、正切公式吗？(请学生默写出来，并由一名学生到黑板默写) ②你写的这三个公式中角α、β会有特殊关系α=β吗？此时公式变成什么形式？③在得到的C 2α公式中，还有其他表示形式吗？④细心观察二倍角公式结构，有什么特征呢？⑤能看出公式中角的含义吗？思考过公式成立的条件吗？⑥让学生填空：老师随机给出等号一边括号内的角，学生回答等号另一边括号内的角，稍后两人为一组，做填数游戏：sin( )=2sin( )cos( )，cos( )=cos 2( )sin 2( ). ⑦思考过公式的逆用吗？想一想C 2α还有哪些变形？⑧请思考以下问题：sin2α=2sinα吗？cos2α=2cosα吗？tan2α=2tanα？活动：问题①,学生默写完后，教师打出课件，然后引导学生观察正弦、余弦的和角公式，提醒学生注意公式中的α,β，既然可以是任意角，怎么任意的？你会有些什么样的奇妙想法呢？并鼓励学生大胆试一试.如果学生想到α,β会有相等这个特殊情况，教师就此进入下一个问题，如果学生没想到这种特殊情况，教师适当点拨进入问题②，然后找一名学生到黑板进行简化，其他学生在自己的座位上简化、教师再与学生一起集体订正黑板的书写，最后学生都不难得出以下式子，鼓励学生尝试一下，对得出的结论给出解释.这个过程教师要舍得花时间，充分地让学生去思考、去探究，并初步地感受二倍角的意义.同时开拓学生的思维空间，为学生将来遇到的3α或3β等角的探究附设类比联想的源泉.sin(αβ)=sinαcosβcosαsinβsin2α=2sinαcosα（S 2α）cos(αβ)=cosαcosβsinαsinβcos2α=cos 2αsin 2α(C 2α)tan(αβ)=)(tan 1tan 22tan tan tan 1tan tan 22ααααβαβαT -=⇒-+ 这时教师适时地向学生指出，我们把这三个公式分别叫做二倍角的正弦，余弦，正切公式，并指导学生阅读教科书，确切明了二倍角的含义，以后的“倍角”专指“二倍角”、教师适时提出问题③，点拨学生结合sin 2αcos 2α=1思考,因此二倍角的余弦公式又可表示为以下右表中的公式.这时教师点出，这些公式都叫做倍角公式（用多媒体演示）.倍角公式给出了α的三角函数与2α的三角函数之间的关系.问题④,教师指导学生，这组公式用途很广，并与学生一起观察公式的特征与记忆，首先公式左边角是右边角的2倍；左边是2α的三角函数的一次式，右边是α的三角函数的二次式，即左到右→升幂缩角，右到左→降幂扩角、二倍角的正弦是单项式，余弦是多项式，正切是分式.问题⑤,因为还没有应用，对公式中的含义学生可能还理解不到位，教师要引导学生观察思考并初步感性认识到：(Ⅰ)这里的“倍角”专指“二倍角”,遇到“三倍角”等名词时,“三”字等不可省去；(Ⅱ)通过二倍角公式,可以用单角的三角函数表示二倍角的三角函数；(Ⅲ)二倍角公式是两角和的三角函数公式的特殊情况；(Ⅳ)公式(S 2α),(C 2α)中的角α没有限制，都是α∈R .但公式(T 2α)需在α≠21kπ4π和α≠kπ2π(k ∈Z )时才成立，这一条件限制要引起学生的注意.但是当α=kπ2π,k ∈Z 时,虽然tanα不存在,此时不能用此公式，但tan2α是存在的,故可改用诱导公式.问题⑥,填空是为了让学生明了二倍角的相对性，即二倍角公式不仅限于2α是α的二倍的形式,其他如4α是2α的二倍,2a 是4a 的二倍,3α是23a 的二倍,3a 是6a 的二倍，2πα是4π2a 的二倍等,所有这些都可以应用二倍角公式.例如:sin 2a =2sin 4a cos 4a ,cos 3a =cos 26a sin 26a 等等. 问题⑦,本组公式的灵活运用还在于它的逆用以及它的变形用，这点教师更要提醒学生引起足够的注意.如:sin3αcos3α=21sin6α，4sin 4a cos 4a =2(2sin 4a cos 4a )=2sin 2a ,40tan 140tan 22-=tan80°，cosαsinα=cos4α，tan2α=2tanα(1tan 2α)等等. 问题⑧,一般情况下:sin2α≠2sinα,cos2α≠2cosα,tan2α≠2tanα.若sin2α=2sinα,则2sinαcosα=2sinα,即sinα=0或cosα=1,此时α=kπ(k ∈Z ).若cos2α=2cosα,则2cos 2α2cosα1=0,即cosα=231-(cosα=231+舍去). 若tan2α=2tanα,则aa 2tan 1tan 2-=2tanα,∴tanα=0,即α=kπ(k ∈Z ). 解答：①—⑧（略）应用示例思路1例1 已知sin2α=135,4π<α<2π,求si n4α,cos4α,tan4α的值. 活动：教师引导学生分析题目中角的关系，观察所给条件与结论的结构，注意二倍角公式的选用，领悟“倍角”是相对的这一换元思想.让学生体会“倍”的深刻含义，它是描述两个数量之间关系的.本题中的已知条件给出了2α的正弦值.由于4α是2α的二倍角,因此可以考虑用倍角公式.本例是直接应用二倍角公式解题，目的是为了让学生初步熟悉二倍角的应用，理解二倍角的相对性，教师大胆放手，可让学生自己独立探究完成.解:由4π<α<2π,得2π<2α<π.又∵sin2α=135, ∴cos2α=a 2sin 12--=1312)135(12-=--.于是sin4α=sin[2×(2α)]=2sin2αcos2α=2×135×(1312-)=169120- cos4α=cos[2×(2α)]=12sinα=12×(135)2=129119 tan4α=a a 4cos 4sin =(169120)×119169=119120-. 点评：学生由问题中条件与结论的结构不难想象出解法，但要提醒学生注意,在解题时注意优化问题的解答过程，使问题的解答简捷、巧妙、规范，并达到熟练掌握的程度.本节公式的基本应用是高考的热点.变式训练1.不查表,求值:sin15°cos15°.解:原式=2615cos 15sin 215sin )15cos 15(sin 222=++=+ 点评：本题在两角和与差的学习中已经解决过，现用二倍角公式给出另外的解法，让学生体会它们之间的联系，体会数学变化的魅力.2.(2007年高考海南卷,9) 若22)4sin(2cos -=-πa a,则cosαsinα的值为……( ) A.27- B.21- C.21 D.27 答案:C3.(2007年高考重庆卷,6) 下列各式中,值为23的是( ) A.2sin15°cos15° B.cos 215°sin 215°C.2sin 215°1D.sin 215°cos 215°答案:B例2 证明θθθθ2cos 2sin 12cos 2sin 1++-+=tanθ. 活动：先让学生思考一会，鼓励学生充分发挥聪明才智，战胜它，并力争一题多解.教师可点拨学生想一想，到现在为止，所学的证明三角恒等式的方法大致有几种：从复杂一端化向简单一端；两边化简，中间碰头；化切为弦；还可以利用分析综合法解决，有时几种方法会同时使用等.对找不到思考方向的学生，教师点出：可否再添加一种，化倍角为单角？这可否成为证明三角恒等式的一种方法？再适时引导，前面学习同角三角函数的基本关系时曾用到“1”的代换，对“1”的妙用大家深有体会，这里可否在“1”上做做文章？待学生探究解决方法后，可找几个学生到黑板书写解答过程，以便对照点评及给学生以启发.点评时对能够善于运用所学的新知识解决问题的学生给予赞扬；对暂时找不到思路的学生给予点拨、鼓励.强调“1”的妙用很妙，妙在它在三角恒等式中一旦出现，在证明过程中就会起到至关重要的作用，在今后的证题中，万万不要忽视它.证明:方法一:左=)1cos 21(cos sin 2)cos 211(cos sin 2)2cos 1(2sin )2cos 1(2sin 22-++-++=+-+θθθθθθθθθθ =θθθθθθ22cos cos sin cos 1cos sin +-+ =θθθθθθ22cos cos sin sin cos sin ++ )cos (sin cos )sin (cos sin θθθθθθ++=tanθ=右. 所以,原式成立.方法二:左= =)cos (sin cos 2)cos (sin sin 2θθθθθθ++=tanθ=右. 方法三:左=)sin (cos )cos sin 2cos (sin )sin (cos )cos sin 2cos (sin 2cos )2sin 1(2cos )2sin 1(22222222θθθθθθθθθθθθθθθθ-+•++--•++=++-+ =)sin )(cos sin (cos )cos (sin )sin )(cos sin (cos )cos (sin 22θθθθθθθθθθθθ-+++-+-+ =)sin cos cos )(sin cos (sin )cos sin cos )(sin cos (sin θθθθθθθθθθθθ-+++-+++ =θθθθθθcos 2)cos (sin sin 2)cos (sin •+•+=tanθ=右.点评：以上几种方法大致遵循以下规律：首先从复杂端化向简单端；第二，化倍角为单角，这是我们今天刚刚学习的；第三，证题中注意对数字的处理，尤其“1”的代换的妙用，请同学们在探究中仔细体会这点.在这道题中通常用的几种方法都用到了，不论用哪一种方法，都要思路清晰，书写规范才是.思路2例1 求sin10°sin30°sin50°sin70°的值.活动：本例是一道灵活应用二倍角公式的经典例题，有一定难度，但也是训练学生思维能力的一道好题.本题需要公式的逆用，逆用公式的先决条件是认识公式的本质，要善于把表象的东西拿开，正确捕捉公式的本质属性，以便合理运用公式.教学中教师可让学生充分进行讨论探究，不要轻易告诉学生解法，可适时点拨学生需要做怎样的变化，又需怎样应用二倍角公式.并点拨学生结合诱导公式思考.学生经过探索发现，如果用诱导公式把10°，30°，50°，70°正弦的积化为20°,40°,60°,80°余弦的积,其中60°是特殊角,很容易发现40°是20°的2倍,80°是40°的2倍,故可考虑逆用二倍角公式.解:原式=cos80°cos60°cos40°cos20° =20sin 2280cos 40cos 20cos 20sin 233•• =.16120sin 1620sin 20sin 16160sin == 点评：二倍角公式是中学数学中的重要知识点之一，又是解答许多数学问题的重要模型和工具，具有灵活多变，技巧性强的特点，要注意在训练中细心体会其变化规律.例2 在△ABC 中,cosA=54,tanB=2,求tan(2A2B)的值. 活动：这是本节课本上最后一个例题，结合三角形，具有一定的综合性,同时也是和与差公式的应用问题.教师可引导学生注意在三角形的背景下研究问题,会带来一些隐含的条件,如ABC=π,0<A<π,0<B<π,0<C<π,就是其中的一个隐含条件.可先让学生讨论探究，教师适时点拨.学生探究解法时教师进一步启发学生思考由条件到结果的函数及角的联系.由于对2A2B 与A,B 之间关系的看法不同会产生不同的解题思路,所以学生会产生不同的解法，不过它们都是对倍角公式、和角公式的联合运用，本质上没有区别.不论学生的解答正确与否，教师都不要直接干预.在学生自己尝试解决问题后,教师可与学生一起比较各种不同的解法，并引导学生进行解题方法的归纳总结.基础较好的班级还可以把求tan(2A2B)的值改为求tan2C 的值.解：方法一:在△ABC 中,由cosA=54,0<A<π,得 sinA=.53)54(1cos 122=-=-A 所以tanA=A A cos sin =53×45=43, tan2A=724)43(1432tan 1tan 222=-⨯=-A A 又tanB=2,所以tan2B=.342122tan 1tan 222-=-⨯=-B B 于是tan(2A2B)=.17744)34(7241347242tan 2tan 12tan 2tan =-⨯--=-+B A B A 方法二:在△ABC 中,由cosA=54,0<A<π,得 sinA=.53)54(1cos 122=-=-A 所以tanA==A A cos sin 53×45=43.又tanB=2, 所以tan(AB)=2112431243tan tan 1tan tan -=⨯-+=-+B A B A 于是tan(2A2B)=tan[2(AB)]=.11744)211(1)211(2)(tan 1)tan(222=---⨯=+-+B A B A 点评：以上两种方法都是对倍角公式、和角公式的联合运用,本质上没有区别,其目的是为了鼓励学生用不同的思路去思考,以拓展学生的视野.变式训练化简：.4sin 4cos 14sin 4cos 1aa a a +-++解：原式＝aa a a a a 2cos 2sin 22sin 22cos 2sin 22cos 222++ =)2cos 2(sin 2sin 2)2sin 2(cos 2cos 2a a a a a a ++ =cot2α.知能训练(2007年高考四川卷,17) 已知cosα=71,cos(αβ)=1413,且0<β<α<2π, (1)求tan2α的值(2)求β.解:(1)由cosα=71,0<α<2π,得sinα=a 2cos 1-=.734)71(12=- ∴tanα=a a cos sin =17734⨯=43.于是tan2α=.4738tan 1342tan 1tan 222-=-⨯--aa a (2)由0<α<β<2π,得0<αβ<2π.又∵cos(αβ)=1413,∴sin(αβ)=.1433)1413(1)(cos 122=-=--βa 由β=α(αβ),得 cosβ=cos ［α(αβ)］=cosαcos(αβ)sinαsin(αβ)=71×14131433734⨯=21. ∴β=3π.点评:本题主要考查三角恒等变形的主要基本公式、三角函数值的符号,已知三角函数值求角以及计算能力.作业课本习题3.1 A 组15、16、17.课题小结1.先由学生回顾本节课都学到了什么？有哪些收获？对前面学过的两角和公式有什么新的认识？对三角函数式子的变化有什么新的认识？怎样用二倍角公式进行简单三角函数式的化简、求值与恒等式证明.2.教师画龙点睛：本节课要理解并掌握二倍角公式及其推导，明白从一般到特殊的思想，并要正确熟练地运用二倍角公式解题.在解题时要注意分析三角函数名称、角的关系，一个题目能给出多种解法，从中比较最佳解决问题的途径，以达到优化解题过程，规范解题步骤，领悟变换思路，强化数学思想方法之目的.。

江苏高考数学复习三角函数解三角形第24课二倍角的三角函数教师用书

第24课二倍角的三角函数[最新考纲]1．二倍角的正弦、余弦、正切公式 (1)sin 2α＝2sin αcos α；(2)cos 2α＝cos 2α－sin 2α＝2cos 2α－1＝1－2sin 2α； (3)tan 2α＝2tan α1－tan 2α. 2．二倍角公式的变形及逆用 (1)公式C 2α的变形： ①sin 2α＝12(1－cos 2α)；②cos 2α＝12(1＋cos 2α)．(2)公式的逆用：①1±sin 2α＝(sin α±cos α)2； ②sin α±cos α＝2sin ⎝⎛⎭⎪⎫α±π4.1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”) (1)对∀α∈R ，sin 2α＝2sin α均不成立．( ) (2)sin2π8－cos 2π8＝cos π4＝22.( ) (3)sin α＋cos α＝1＋sin 2α.( ) (4)等式1＋cos α＝2sin 2α2对∀α∈R 均成立．( )[答案] (1)× (2)× (3)× (4)×2．下列各式中值为32的是________．(填序号) ①2sin 15°cos 15°；②cos 215°－sin 215°；③2sin 215°－1；④sin 215°＋cos 215°. ② [2sin 15°cos 15°＝sin 30°＝12，cos 215°－sin 215°＝cos 30°＝32，2sin 215°－1＝－cos 30°＝－32， sin 215°＋cos 215°＝1.]3．若sin α＝255，α∈⎝ ⎛⎭⎪⎫0，π2，则tan 2α＝________.－43 [∵α∈⎝ ⎛⎭⎪⎫0，π2，sin α＝255，∴cos α＝1－sin 2α＝55， ∴tan α＝2，∴tan 2α＝2tan α1－tan 2α＝41－4＝－43.] 4．(2017·南京模拟)若tan α＝3，则sin 2α1＋cos 2α＝________.3 [sin 2α1＋cos 2α＝2sin αcos α2cos 2α＝tan α＝ 3.] 5．(教材改编)函数 f (x )＝3sin x ＋cos x 的最小值为________．－2 [函数f (x )＝2sin ⎝⎛⎭⎪⎫x ＋π6的最小值是－2.](2017·无锡模拟)已知cos ⎝ ⎛⎭⎪⎫6＋αcos ⎝ ⎛⎭⎪⎫3－α＝－4，α∈⎝ ⎛⎭⎪⎫π3，π2.(1)求sin 2α的值； (2)求tan α－1tan α的值． [解] (1)cos ⎝ ⎛⎭⎪⎫π6＋α·cos ⎝ ⎛⎭⎪⎫π3－α ＝cos ⎝ ⎛⎭⎪⎫π6＋α·sin ⎝ ⎛⎭⎪⎫π6＋α＝12sin ⎝ ⎛⎭⎪⎫2α＋π3＝－14，即sin ⎝ ⎛⎭⎪⎫2α＋π3＝－12. ∵α∈⎝⎛⎭⎪⎫π3，π2， ∴2α＋π3∈⎝ ⎛⎭⎪⎫π，4π3，∴cos ⎝ ⎛⎭⎪⎫2α＋π3＝－32， ∴sin 2α＝sin ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫2α＋π3－π3＝sin ⎝ ⎛⎭⎪⎫2α＋π3cos π3－cos ⎝⎛⎭⎪⎫2α＋π3·sin π3＝12.(2)∵α∈⎝ ⎛⎭⎪⎫π3，π2，∴2α∈⎝ ⎛⎭⎪⎫2π3，π. 又由(1)知sin 2α＝12，∴cos 2α＝－32.∴tan α－1tan α＝sin αcos α－cos αsin α＝sin 2α－cos 2αsin αcos α＝－2cos 2αsin 2α＝－2×－3212＝2 3.[规律方法] 给出某些角的三角函数式的值，求另外一些角的三角函数值，解题关键在于“变角”，使其角相同或具有某种关系．如本题中⎝ ⎛⎭⎪⎫π6＋α＋⎝ ⎛⎭⎪⎫π3－α＝π2，从而先利用诱导公式变换函数名，进而逆用二倍角公式求值．[变式训练1] (2017·南京、盐城二模)已知α为锐角，cos ⎝ ⎛⎭⎪⎫α＋π4＝55.(1)求tan ⎝⎛⎭⎪⎫α＋π4的值；(2)求sin ⎝ ⎛⎭⎪⎫2α＋π3的值. 【导学号：62172133】 [解] (1)因为α∈⎝ ⎛⎭⎪⎫0，π2，所以α＋π4∈⎝ ⎛⎭⎪⎫π4，3π4，所以sin ⎝⎛⎭⎪⎫α＋π4＝1－cos 2⎝⎛⎭⎪⎫α＋π4＝255，所以tan ⎝ ⎛⎭⎪⎫α＋π4＝sin ⎝ ⎛⎭⎪⎫α＋π4cos ⎝⎛⎭⎪⎫α＋π4＝2.(2)因为sin ⎝ ⎛⎭⎪⎫2α＋π2＝sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫α＋π4＝2sin ⎝ ⎛⎭⎪⎫α＋π4cos ⎝ ⎛⎭⎪⎫α＋π4＝45，cos ⎝ ⎛⎭⎪⎫2α＋π2＝cos ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫α＋π4＝2cos 2⎝⎛⎭⎪⎫α＋π4－1＝－35，所以sin ⎝ ⎛⎭⎪⎫2α＋π3＝sin ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫2α＋π2－π6＝sin ⎝ ⎛⎭⎪⎫2α＋π2cos π6－cos ⎝ ⎛⎭⎪⎫2α＋π2sinπ6＝43＋310.(1)化简：sin 2α－2cos 2αsin ⎝ ⎛⎭⎪⎫α－π4＝________.(2)化简：2cos 4x －2cos 2x ＋122tan ⎝ ⎛⎭⎪⎫π4－x sin 2⎝ ⎛⎭⎪⎫π4＋x .(1)22cos α [原式＝2sin αcos α－2cos 2α22α－cos α＝22cos α.](2)原式＝－2sin 2x cos 2x ＋122sin ⎝ ⎛⎭⎪⎫π4－x cos 2⎝ ⎛⎭⎪⎫π4－x cos ⎝ ⎛⎭⎪⎫π4－x＝12－sin 22x2sin ⎝ ⎛⎭⎪⎫π4－x cos ⎝ ⎛⎭⎪⎫π4－x ＝12cos 22x sin ⎝ ⎛⎭⎪⎫π2－2x ＝12cos 2x .[规律方法] 1.三角函数式的化简要遵循“三看”原则(1)一看“角”，通过看角之间的差别与联系，把角进行合理的拆分，从而正确使用公式．(2)二看“函数名称”，看函数名称之间的差异，从而确定使用的公式，最常见的是“切化弦”．(3)三看“结构特征”，分析结构特征，找到变形的方向．2．三角函数式化简的方法弦切互化，异名化同名，异角化同角，降幂或升幂．[变式训练2] 化简sin 2⎝ ⎛⎭⎪⎫α－π6＋sin 2⎝ ⎛⎭⎪⎫α＋π6－sin 2α＝________.12 [法一：原式＝1－cos ⎝ ⎛⎭⎪⎫2α－π32＋1－cos ⎝ ⎛⎭⎪⎫2α＋π32－sin 2α ＝1－12⎣⎢⎡⎦⎥⎤cos ⎝ ⎛⎭⎪⎫2α－π3＋cos ⎝ ⎛⎭⎪⎫2α＋π3－sin 2α＝1－cos 2α·cos π3－sin 2α＝1－cos 2α2－1－cos 2α2＝12. 法二：令α＝0，则原式＝14＋14＝12.]已知函数f (x )＝sin 2x －sin 2⎝ ⎛⎭⎪⎫x －6，x ∈R . (1)求f (x )的最小正周期；(2)求f (x )在区间⎣⎢⎡⎦⎥⎤－π3，π4上的最大值和最小值. 【导学号：62172134】[解] (1)由已知，有f (x )＝1－cos 2x 2－1－cos ⎝⎛⎭⎪⎫2x －π32＝12⎝ ⎛⎭⎪⎫12cos 2x ＋32sin 2x －12cos 2x ＝34sin 2x －14cos 2x ＝12sin ⎝⎛⎭⎪⎫2x －π6.所以f (x )的最小正周期T ＝2π2＝π. (2)因为f (x )在区间⎣⎢⎡⎦⎥⎤－π3，－π6上是减函数，在区间⎣⎢⎡⎦⎥⎤－π6，π4上是增函数，且f ⎝ ⎛⎭⎪⎫－π3＝－14，f ⎝ ⎛⎭⎪⎫－π6＝－12，f ⎝ ⎛⎭⎪⎫π4＝34，所以f (x )在区间⎣⎢⎡⎦⎥⎤－π3，π4上的最大值为34，最小值为－12.[规律方法] 1.进行三角恒等变换要抓住：变角、变函数名称、变结构，尤其是角之间的关系；注意公式的逆用和变形使用．2．把形如y ＝a sin x ＋b cos x 化为y ＝a 2＋b 2sin(x ＋φ)，可进一步研究函数的周期、单调性、最值与对称性．[变式训练3] 已知函数f (x )＝sin ⎝ ⎛⎭⎪⎫π2－x sin x －3cos 2x .(1)求f (x )的最小正周期和最大值； (2)讨论f (x )在⎣⎢⎡⎦⎥⎤π6，2π3上的单调性．[解] (1)f (x )＝sin ⎝ ⎛⎭⎪⎫π2－x sin x －3cos 2x ＝cos x sin x －32(1＋cos 2x )＝12sin 2x －32cos 2x －32＝sin ⎝⎛⎭⎪⎫2x －π3－32.因此f (x )的最小正周期为π，最大值为2－32.(2)当x ∈⎣⎢⎡⎦⎥⎤π6，2π3时，0≤2x －π3≤π，从而当0≤2x －π3≤π2，即π6≤x ≤5π12时，f (x )单调递增，当π2≤2x －π3≤π，即5π12≤x ≤2π3时，f (x )单调递减．综上可知，f (x )在⎣⎢⎡⎦⎥⎤π6，5π12上单调递增；在⎣⎢⎡⎦⎥⎤5π12，2π3上单调递减．[思想与方法]1．三角函数的求值与化简要注意观察角、函数名称、式子结构之间的联系，然后进行变换．2．利用三角函数值求角要考虑角的范围．3．与三角函数的图象与性质相结合的综合问题．借助三角恒等变换将已知条件中的函数解析式整理为f (x )＝A sin(ωx ＋φ)的形式，然后借助三角函数图象解决．[易错与防范]1．利用辅助角公式a sin x ＋b cos x 转化时，一定要严格对照和差公式，防止弄错辅助角．2．计算形如y ＝sin(ωx ＋φ)，x ∈[a ，b ]形式的函数最值时，不要将ωx ＋φ的范围和x 的范围混淆．课时分层训练(二十四)A 组基础达标 (建议用时：30分钟)一、填空题1．已知sin 2α＝23，则cos 2⎝ ⎛⎭⎪⎫α＋π4等于________．16 [因为cos 2⎝ ⎛⎭⎪⎫α＋π4＝1＋cos 2⎝ ⎛⎭⎪⎫α＋π42＝1＋cos ⎝⎛⎭⎪⎫2α＋π22＝1－sin 2α2＝1－232＝16.]2．设sin 2α＝－sin α，α∈⎝ ⎛⎭⎪⎫π2，π，则tan 2α的值是________.【导学号：62172135】3 [∵sin 2α＝2sin αcos α＝－sin α， ∴cos α＝－12，又α∈⎝ ⎛⎭⎪⎫π2，π， ∴sin α＝32，tan α＝－3， ∴tan 2α＝2tan α1－tan 2α＝－231－－32＝ 3.]3．(2016·全国卷Ⅲ改编)若tan θ＝－13，则cos 2θ＝________.45 [∵cos 2θ＝cos 2θ－sin 2θcos 2θ＋sin 2θ＝1－tan 2θ1＋tan 2θ. 又∵tan θ＝－13，∴cos 2θ＝1－191＋19＝45.]4．已知sin α＝35，α∈⎝ ⎛⎭⎪⎫π2，π，则cos 2α2sin ⎝⎛⎭⎪⎫α＋π4＝________.－75[cos 2α2sin ⎝⎛⎭⎪⎫α＋π4＝cos 2α－sin 2α2⎝ ⎛⎭⎪⎫22sin α＋22cos α＝cos α－sin α.∵sin α＝35，α∈⎝ ⎛⎭⎪⎫π2，π，∴cos α＝－45.∴原式＝－75.]5．(2017·苏州模拟)已知sin(α－45°)＝－210且0°<α<90°，则cos 2α的值为________. 【导学号：62172136】725 [∵sin(α－45°)＝－210， ∴sin α－cos α＝－15，∴2sin αcos α＝2425，∴sin α＋cos α＝1＋sin 2α＝75，∴sin α＝35，cos α＝45.∴cos 2α＝cos 2α－sin 2α＝725.]6．(2016·山东高考改编)函数f (x )＝(3sin x ＋cos x )(3cos x －sin x )的最小正周期是________．π [法一：∵f (x )＝(3sin x ＋cos x )(3cos x －sin x ) ＝4⎝⎛⎭⎪⎫32sin x ＋12cos x ⎝ ⎛⎭⎪⎫32cos x －12sin x＝4sin ⎝ ⎛⎭⎪⎫x ＋π6cos ⎝ ⎛⎭⎪⎫x ＋π6＝2sin ⎝ ⎛⎭⎪⎫2x ＋π3， ∴T ＝2π2＝π.法二：∵f (x )＝(3sin x ＋cos x )(3cos x －sin x ) ＝3sin x cos x ＋3cos 2x －3sin 2x －sin x cos x ＝sin 2x ＋3cos 2x ＝2sin ⎝ ⎛⎭⎪⎫2x ＋π3， ∴T ＝2π2＝π.]7．(2017·苏州模拟)若sin ⎝ ⎛⎭⎪⎫π3－α＝14，则cos ⎝ ⎛⎭⎪⎫π3＋2α＝________.【导学号：62172137】－78 [cos ⎝ ⎛⎭⎪⎫π3＋2α＝cos ⎣⎢⎡⎦⎥⎤π－⎝ ⎛⎭⎪⎫23π－2α ＝－cos ⎝ ⎛⎭⎪⎫23π－2α＝－⎣⎢⎡⎦⎥⎤1－2sin 2⎝ ⎛⎭⎪⎫π3－α＝－⎣⎢⎡⎦⎥⎤1－2×⎝ ⎛⎭⎪⎫142＝－78.]8．化简2＋2cos 8＋21－sin 8＝________. －2sin 4 [2＋2cos 8＋21－sin 8 ＝＋＋21－2sin 4cos 4＝2×2cos 24＋2－2＝－2cos 4＋2(cos 4－sin 4)＝－2sin 4.] 9．(2017·南通模拟)若α∈⎝ ⎛⎭⎪⎫π2，π，且3cos 2α＝sin ⎝ ⎛⎭⎪⎫π4－α，则sin 2α的值为________．－1718 [∵3cos 2α＝sin ⎝ ⎛⎭⎪⎫π4－α，∴3sin ⎝⎛⎭⎪⎫π2－2α＝sin ⎝⎛⎭⎪⎫π4－α，∴3×2sin ⎝ ⎛⎭⎪⎫π4－αcos ⎝ ⎛⎭⎪⎫π4－α＝sin ⎝ ⎛⎭⎪⎫π4－α.∴sin ⎝ ⎛⎭⎪⎫π4－α≠0，∴cos ⎝ ⎛⎭⎪⎫π4－α＝16，即sin α＋cos α＝26， ∴sin 2α＝－3436＝－1718.]10．已知cos 4α－sin 4α＝23，且α∈⎝ ⎛⎭⎪⎫0，π2，则cos ⎝⎛⎭⎪⎫2α＋π3＝______________.2－156 [∵cos 4α－sin 4α＝cos 2α－sin 2α＝cos 2α＝23，又α∈⎝⎛⎭⎪⎫0，π2，∴2α∈(0，π)．∴sin 2α＝53. ∴cos ⎝ ⎛⎭⎪⎫2α＋π3＝cos 2αcos π3－sin 2αsin π3 ＝12cos 2α－32sin 2α ＝12×23－32×53 ＝2－156.] 二、解答题11．(2017·盐城期中)已知函数f (x )＝3sin x cos x －cos 2x . (1)求f (x )的最小正周期； (2)若f (x )＝－1，求cos ⎝ ⎛⎭⎪⎫2π3－2x 的值． [解] (1)因为f (x )＝32sin 2x －1＋cos 2x 2＝32sin 2x －cos 2x 2－12＝sin ⎝⎛⎭⎪⎫2x －π6－12，所以f (x )的最小正周期为T ＝2π2＝π.(2)因为f (x )＝－1，所以sin ⎝ ⎛⎭⎪⎫2x －π6－12＝－1，即sin ⎝⎛⎭⎪⎫2x －π6＝－12，所以cos ⎝ ⎛⎭⎪⎫2π3－2x ＝cos ⎝ ⎛⎭⎪⎫π2－⎝⎛⎭⎪⎫2x －π6＝sin ⎝ ⎛⎭⎪⎫2x －π6＝－12. 12．已知函数f (x )＝cos 2x ＋sin x cos x ，x ∈R . (1)求f ⎝ ⎛⎭⎪⎫π6的值； (2)若sin α＝35，且α∈⎝ ⎛⎭⎪⎫π2，π，求f ⎝ ⎛⎭⎪⎫α2＋π24. [解] (1)f ⎝ ⎛⎭⎪⎫π6＝cos 2π6＋sin π6cos π6 ＝⎝ ⎛⎭⎪⎫322＋12×32＝3＋34. (2)因为f (x )＝cos 2x ＋sin x cos x ＝1＋cos 2x 2＋12sin 2x ＝12＋12(sin 2x ＋cos 2x )＝12＋22sin ⎝ ⎛⎭⎪⎫2x ＋π4. 所以f ⎝ ⎛⎭⎪⎫α2＋π24＝12＋22sin ⎝ ⎛⎭⎪⎫α＋π12＋π4 ＝12＋22sin ⎝ ⎛⎭⎪⎫α＋π3＝12＋22⎝ ⎛⎭⎪⎫12sin α＋32cos α. 又因为sin α＝35，且α∈⎝ ⎛⎭⎪⎫π2，π，所以cos α＝－45，所以f ⎝ ⎛⎭⎪⎫α2＋π24＝12＋22⎝ ⎛⎭⎪⎫12×35－32×45 ＝10＋32－4620. B 组能力提升(建议用时：15分钟)1．函数f (x )＝3sin x 2cos x 2＋4cos 2x 2(x ∈R )的最大值等于________． 92 [由题意知f (x )＝32sin x ＋4×1＋cos x 2＝32sin x ＋2cos x ＋2≤94＋4＋2＝92.] 2．如图241，圆O 与x 轴的正半轴的交点为A ，点C ，B 在圆O 上，且点C 位于第一象限，点B 的坐标为⎝ ⎛⎭⎪⎫1213，－513，∠AOC ＝α.若|BC |＝1，则3cos 2α2－sin α2cos α2－32的值为________．图241513[由题意得|OB |＝|OC |＝|BC |＝1，从而△OBC 为等边三角形，∴sin ∠AOB ＝sin ⎝ ⎛⎭⎪⎫π3－α＝513， ∴3cos 2α2－sin α2·cos α2－32＝3·1＋cos α2－sin α2－32＝－12sin α＋32cos α＝sin ⎝ ⎛⎭⎪⎫α＋2π3＝sin ⎣⎢⎡⎦⎥⎤π－⎝ ⎛⎭⎪⎫α＋2π3＝sin ⎝ ⎛⎭⎪⎫π3－α＝513.] 3．已知α，β∈(0，π)，且tan(α－β)＝12，tan β＝－17，求2α－β的值． [解] ∵tan α＝tan[(α－β)＋β]＝α－β＋tan β1－α－ββ＝12－171＋12×17＝13＞0， ∴0＜α＜π2. 又∵tan 2α＝2tan α1－tan 2α＝2×131－⎝ ⎛⎭⎪⎫132＝34＞0， ∴0＜2α＜π2， ∴tan(2α－β)＝tan 2α－tan β1＋tan 2αtan β＝34＋171－34×17＝1. ∵tan β＝－17＜0，∴π2＜β＜π，－π＜2α－β＜0，∴2α－β＝－3π4. 4．已知函数f (x )＝2sin x sin ⎝⎛⎭⎪⎫x ＋π6. (1)求函数f (x )的最小正周期和单调递增区间；(2)当x ∈⎣⎢⎡⎦⎥⎤0，π2时，求函数f (x )的值域． [解] (1)f (x )＝2sin x ⎝⎛⎭⎪⎫32sin x ＋12cos x ＝3×1－cos 2x 2＋12sin 2x ＝sin ⎝ ⎛⎭⎪⎫2x －π3＋32. 所以函数f (x )的最小正周期为T ＝π.由－π2＋2k π≤2x －π3≤π2＋2k π，k ∈Z ，解得－π12＋k π≤x ≤5π12＋k π，k ∈Z ，所以函数f (x )的单调递增区间是⎣⎢⎡⎦⎥⎤－π12＋k π，5π12＋k π，k ∈Z . (2)当x ∈⎣⎢⎡⎦⎥⎤0，π2时，2x －π3∈⎣⎢⎡⎦⎥⎤－π3，2π3， sin ⎝ ⎛⎭⎪⎫2x －π3∈⎣⎢⎡⎦⎥⎤－32，1， f (x )∈⎣⎢⎡⎦⎥⎤0，1＋32. 故f (x )的值域为⎣⎢⎡⎦⎥⎤0，1＋32.。

5.5.1 第3课时二倍角的正弦、余弦、正切公式(课件)

经典例题
题型二条件求值
例 2(1)已知 tan α＝2，则 tan 2α＝________；
(2)已知 0<α<π2，cosπ6＋α＝13，则 sin3π＋2α＝________.
解：(1)∵tan α＝2， ∴tan 2α＝1－2tatnanα2α ＝12－×222＝－43.
(2)∵0<α<π2，∴π6<α＋π6<23π.
＝cos2( ＋α)＝2cos2( ＋α)－1＝2×( )2－1＝－ .
经典例题
题型二条件求值
跟踪训练2 (2)设 α 为锐角，若 cosα＋π6＝45，则 sin2α＋1π2的值为________．
(2)∵α 为锐角，∴α＋π6∈π6，23π. 又∵cosα＋π6＝45，∴sinα＋π6＝35，
公式
简记
正弦 sin2α＝ 2sinαcosα
S2α
余弦 cos2α＝ cos2α－sin2α
C2α
正切 tan2α＝
2tan α 1－tan2α
T2α
解读：倍角公式中的“倍角”是相对的，对于两个角的比值等于 2 的情况都成立，如 4α 是 2α 的二倍，α 是α2的二倍等.
自主学习
二．正弦的二倍角公式的变形 1.sin αcos α＝12sin 2α； 2.1±sin 2α＝(sin α±cos α)2.
－解析：因为 tanα＝－，所以 tan2α＝
＝
＝－ .
经典例题
题型一给角求值
例 1 求下列各式的值：
(1)sin2 π－cos2 π；
(2)sin1π2cos1π2；
(3)
；
(4)cos20°·cos40°·cos80°.

3.3.1二倍角的正弦、余弦和正切公式课件(北师大版必修4)

倍角公式Βιβλιοθήκη 1．sin15°cos15° · 的值为( 1 A. 2 1 C. 4
答案： C
) 1 B. 3 D．1
π 4π 2．sin －cos 等于( 12 12 1 A．－ 2 1 C. 2
4
) 3 B．－ 2 3 D. 2
答案：
B
3．若tanα＝2，则tan2α＝________.
答案：
1 2.cos α－sin α－cos 2α＝－ sin 2αsin 4α. 4
8 8
解析：左边＝(cos4α＋sin4α)(cos4α－sin4α)－cos 2α ＝[(cos2α＋sin2α)2－2cos2αsin2α]· 2α－cos 2α cos 1 2 1 ＝－ sin 2α· 2α＝－ sin 2αsin 4α. cos 2 4 ∴原式得证．
1．对于“二倍角”应该有广义上的理解，如： 8α 是 4α 的二倍；6α 是 3α 的二倍；4α 是 2α 的二 3 α α α α 倍；是 α 的二倍；是的二倍；是的二倍； 3α 2 2 4 3 6 α α n＝2·n＋1(n∈N＋)． 2 2
2．二倍角余弦公式的运用在二倍角公式中，二倍角的余弦公式最为灵活多样，应用广泛．二倍角的常用形式：①1＋cos 2α 1＋cos 2α 2 2 ＝2cos α，②cos α＝，③1－cos 2α＝ 2 1－cos 2α 2 2 2sin α，④sin α＝ . 2
4 － 3
1 4．已知 cos 2α＝－，则 sin2α＝________. 9 5 答案： 9
化简求值求下列各式的值： π π π π (1)(cos －sin )(cos ＋sin )； 12 12 12 12 1 2π (2) －cos ； 2 8 π 2π (3)cos cos . 5 5

二倍角的正弦、余弦和正切教案北师大版必修四

二倍角的正弦、余弦和正切一.教学目标：1.知识与技能（1）能够由和角公式而导出倍角公式；（2）能较熟练地运用公式进行化简、求值、证明，增强学生灵活运用数学知识和逻辑推理能力；（3）能推导和理解半角公式；（4）揭示知识背景，引发学生学习兴趣，激发学生分析、探求的学习态度，强化学生的参与意识. 并培养学生综合分析能力.2.过程与方法让学生自己由和角公式而导出倍角公式和半角公式，领会从一般化归为特殊的数学思想，体会公式所蕴涵的和谐美，激发学生学数学的兴趣；通过例题讲解，总结方法.通过做练习,巩固所学知识.3.情感态度价值观通过本节的学习，使同学们对三角函数各个公式之间有一个全新的认识；理解掌握三角函数各个公式的各种变形，增强学生灵活运用数学知识、逻辑推理能力和综合分析能力.提高逆用思维的能力.二.教学重、难点重点:倍角公式的应用.难点:公式的推导.三.学法与教学用具学法：(1)自主+探究性学习：让学生自己由和角公式导出倍角公式，领会从一般化归为特殊的数学思想，体会公式所蕴涵的和谐美，激发学生学数学的兴趣。

(2)反馈练习法：以练习来检验知识的应用情况，找出未掌握的内容及其存在的差距.教学用具:电脑、投影机.四.教学设想【探究新知】1、复习两角和与差的正弦、余弦、正切公式：2、提出问题：公式中如果β=α，公式会变得如何？3、让学生板演得下述二倍角公式：α-=-α=α-α=ααα=α2222sin 211cos 2sin cos 2cos cos sin 22sin ααα2tan 1tan 22tan -=[展示投影]这组公式有何特点？应注意些什么？注意：1．每个公式的特点，嘱记：尤其是“倍角”的意义是相对的，如：4α是8α的倍角.2．熟悉“倍角”与“二次”的关系（升角——降次，降角——升次）3．特别注意公式的三角表达形式，且要善于变形： 22cos 1sin ,22cos 1cos 22α-=αα+=α 这两个形式今后常用. [展示投影]例题讲评（学生先做，学生讲，教师提示或适当补充）例1.（公式巩固性练习）求值：①．sin22︒30’cos22︒30’=4245sin 21= ②．=-π18cos 22224cos =π ③．=π-π8cos 8sin 22224cos -=π- ④．=ππππ12cos 24cos 48cos 48sin 8216sin 12cos 12sin 212cos 24cos 24sin 4=π=ππ=πππ例2.化简 ①．=π-ππ+π)125cos 125)(sin 125cos 125(sin 2365cos 125cos 125sin 22=π-=π-π ②．=α-α2sin 2cos 44α=α-αα+αcos )2sin 2)(cos 2sin 2(cos 2222 ③．=α+-α-tan 11tan 11α=α-α2tan tan 1tan 22 ④．=θ-θ+2cos cos 21221cos 2cos 2122=+θ-θ+例3、已知),2(,135sin ππ∈α=α，求sin2α，cos2α，tan2α的值。

二倍角的正弦、余弦、正切公式 PPT教学课件(高一数学人教A版必修一册)

B
2
，
高中数学
例2
在△
ABC
中，
cos A 4 5
，
tan B 2
，求
tan2A 2B 的值.
tan
A
B
tan A tan B 1 tan A tan B
3 4 1
2 32
11 2
，
4
. tan 2A
2B
tan
2
A
B
2 tan
1 tan2
A B A B
2
11 2
1
11 2
2
44 117
刚刚我们的推导过程是借助 S 来完成的，如果用 S 来完成推导方法也基本相同，把公式中的替换为即可.
二倍角的正弦公式： sin 2 2sin cos
一【问题1.3】
你能仿照刚刚的推导过程，利用 C,T 得到 cos 2, tan 2 的公式吗？
高中数学
高中数学
一【问题1.3】
和刚才一样，我们将 cos ，tan 公式中的换为后，得到：
即 sin2
1
cos 2
2
.
这两个公式的变形从左向右看，角之间是倍角关系，
从结构上是和、差转化到乘积，从次数上是从一次
变成了二次.
这样无论从右向左，还是从左向右，它能实现角的
改变，和式子结构、次数的改变.
1 cos 2 cos2
2
sin2 15 1 cos 30 1 3
2
24
公式的正向使用与反向使用需要依据求解内容和所给条件灵活判断.
解：在△
ABC
中，由
cos
A
4 5
，0

二倍角的正弦、余弦、正切说课稿北师大版

1.二倍角的正弦公式：\[ \sin 2\alpha = 2\sin\alpha\cos\alpha \]
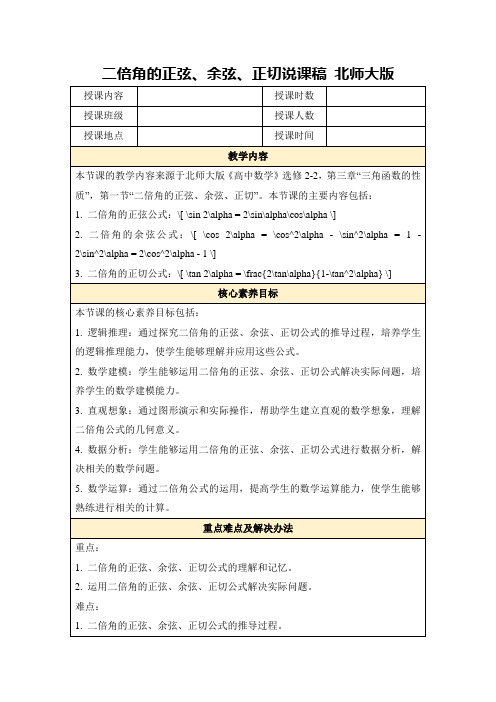
2.二倍角的余弦公式：\[ \cos 2\alpha = \cos^2\alpha - \sin^2\alpha = 1 - 2\sin^2\alpha = 2\cos^2\alpha - 1 \]
学生活动：
-自主阅读预习资料：按照预习要求，自主阅读预习资料，理解二倍角的正弦、余弦、正切知识点。
-思考预习问题：针对预习问题，进行独立思考，记录自己的理解和疑问。
-提交预习成果：将预习成果（如笔记、思维导图、问题等）提交至平台或老师处。
教学方法/手段/资源：
-自主学习法：引导学生自主思考，培养自主学习能力。
2.二倍角的余弦公式：\[ \cos 2\alpha = \cos^2\alpha - \sin^2\alpha = 1 - 2\sin^2\alpha = 2\cos^2\alpha - 1 \]
3.二倍角的正切公式：\[ \tan 2\alpha = \frac{2\tan\alpha}{1-\tan^2\alpha} \]
-反思总结法：引导学生对自己的学习过程和成果进行反思和总结。
作用与目的：
-巩固学生在课堂上学到的二倍角的正弦、余弦、正切知识点和技能。
-通过拓展学习，拓宽学生的知识视野和思维方式。
-通过反思总结，帮助学生发现自己的不足并提出改进建议，促进自我提升。
学生学习效果
1.知识与技能：
-学生能够准确地记忆和理解二倍角的正弦、余弦、正切公式。
4.数据分析：学生能够运用二倍角的正弦、余弦、正切公式进行数据分析，解决相关的数学问题。
5.数学运算：通过二倍角公式的运用，提高学生的数学运算能力，使学生能够熟练进行相关的计算。

二倍角的正弦余弦公式省名师优质课赛课获奖课件市赛课一等奖课件

1
2
tan tan
22.5 2 22.5
1 tan 45 2
1 2
例题讲解
例1. 已知sin 2 3 ,且 ,求sin 4, cos 4, tan 4的值
54
2
解：由 ,得 2 ,
4
22
cos 2 1 sin2 4
5
sin 4 sin(2 2 ) 2sin 2 cos 2 2 3 ( 4) 24
3.1.３二倍角旳正弦、余弦、正切公式
复习回忆
正弦、余弦、正切旳和角公式：
sin( ) sin cos cos sin
cos( ) cos cos sin sin
tan( ) tan tan 1 tan tan
思索探索
你能否利用三角函数旳和角公式推导出下列公式？
5 5 25
cos 4 cos2 2 sin2 2 16 9 7
tan 4sin 424 2525 24
25
25
cos 4 7
7
25
24
(1)已知是第三象限角，sin 3 ,则sin 2 __2_5__
(2)已知cos 2
1 ，则 cos 4 3
5 sin 4
1 ___3__
4
sin 2
sin( ) sin cos cos sin 2sin cos
cos 2
cos( ) cos cos sin sin cos2 sin2
tan 2
tan( ) tan tan 1 tan tan
1
2
tan tan2
思索探究
仔细观察余弦旳二倍角公式，结合我们前面所学旳知识，你还能得出哪些不同旳体现式？

3.1.3二倍角的正弦、余弦、正切公式课件人教新课标

2、cos cos2 sin2
2
4
4
3、tan 3
2
2 tan 3
4
1 tan 2 3
4
4、cos 2cos2 1
2
4
3、已知
tan2α = 1 , 3
求 tanα的值
解：
tan2α
=
2tanα 1- tan2α
=
1 3
由此得 tan2α + 6tanα -1 = 0
新课导入
已知：α的三角函数值，求sin2α、 cos2α、tab2α ?
利用已知的和（差）角公式，能否找到解决问题的线索呢？
复习:两角和的正弦、余弦、正切公式:
sin( ) sin cos cos sin cos( ) coscossinsin
tan( ) tan tan 1 tan tan
例 6:化简
1、
5
(sin
cos
5
5
)(sin
cos 5 )
12 12 12 12
= sin2 5π - cos2 5π = -cos 5π = 3
12
12
62
2、 cos4 sin4
2
2
= cos2 α + sin2 α cos2 α - sin2 α = cosα
2
2
2
2
3、 1 2cos2 cos 2
原式 sin cos2 ,
2sin cos cos2
因为 tan 1 时,sin 0, cos2 0,
2
所以原式 1
因为
2cos
为锐角，由所以原式
tan 1 得 cos 2 ,

2017北师大版必修四二倍角的正弦余弦和正切公式word教

§3.1.3 二倍角的正弦、余弦和正切公式一、教学目标以两角和正弦、余弦和正切公式为基础，推导二倍角正弦、余弦和正切公式，理解推导进程，掌握其应用.二、教学重、难点教学重点：以两角和的正弦、余弦和正切公式为基础，推导二倍角正弦、余弦和正切公式；教学难点：二倍角的理解及其灵活运用.三、学法与教学用具学法：研讨式教学四、教学假想：（一）温习式导入：大家首先回顾一下两角和的正弦、余弦和正切公式，()sin sin cos cos sin αβαβαβ+=+；()cos cos cos sin sin αβαβαβ+=-；()tan tan tan 1tan tan αβαβαβ++=-．咱们由此可否取得sin 2,cos 2,tan 2ααα的公式呢？（学生自己动手，把上述公式中β看成α即可），（二）公式推导：()sin 2sin sin cos cos sin 2sin cos ααααααααα=+=+=；()22cos2cos cos cos sin sin cos sin ααααααααα=+=-=-；试探：把上述关于cos2α的式子可否变成只含有sin α或cos α形式的式子呢？22222cos 2cos sin 1sin sin 12sin αααααα=-=--=-；22222cos 2cos sin cos (1cos )2cos 1αααααα=-=--=-．()2tan tan 2tan tan 2tan 1tan tan 1tan ααααααααα+=+==--．注意：2,22k k ππαπαπ≠+≠+ ()k z ∈（三）例题讲解例一、已知5sin 2,,1342ππαα=<<求sin 4,cos 4,tan 4ααα的值．解：由,42ππα<<得22παπ<<．又因为5sin 2,13α=22512cos 21sin 211313αα⎛⎫=-=-=- ⎪⎝⎭．于是512120sin 42sin 2cos 221313169ααα⎛⎫==⨯⨯-=- ⎪⎝⎭； 225119cos 412sin 21213169αα⎛⎫=-=-⨯= ⎪⎝⎭；120sin 4120169tan 4119cos 4119169ααα-===-．例２、已知1tan 2,3α=求tan α的值．解：22tan 1tan 21tan 3ααα==-，由此得2tan 6tan 10αα+-= 解得tan 25α=-+tan 25α=--（四）小结：本节咱们学习了二倍角的正弦、余弦和正切公式，咱们要熟记公式，在解题进程中要擅长发觉规律，学会灵活运用.（五）作业：15034.P T T -。

《二倍角的正弦、余弦、正切公式》教案(优选.)

最新文件---------------- 仅供参考--------------------已改成-----------word文本 --------------------- 方便更改赠人玫瑰，手留余香。

《二倍角的正弦、余弦、正切公式》教学设计高一A组韩慧芳年级：高一科目：数学内容：二倍角的正弦、余弦、正切公式课型：新课一、教学目标1、知识目标：（1）在理解两角和的正弦、余弦和正切公式的基础上，能够推导二倍角的正弦、余弦和正切公式，并能运用这些公式解决简单的三角函数问题。

（2）通过公式的应用（正用、逆用、变形用），使学生掌握有关化简技巧，提高分析、解决问题的能力。

2、能力目标：通过二倍角公式的推导，了解知识之间的内在联系，完善知识结构，培养逻辑推理能力。

3、情感目标：通过二倍角公式的推导，感受二倍角公式是和角公式的特例，进一步体会从一般化归为特殊的基本数学思想。

在运用二倍角公式的过程中体会换元的数学思想。

二、教学重难点、关键1、教学重点：以两角和的正弦、余弦和正切公式为基础，推导二倍角的正弦、余弦和正切公式2、教学难点：二倍角的理解及其正用、逆用、变形用。

3、关键：二倍角的理解三、学法指导学法：研讨式教学四、教学设想：1、问题情境复习回顾两角和的正弦、余弦、正切公式()sin sin cos cos sin αβαβαβ+=+；()cos cos cos sin sin αβαβαβ+=-；()tan tan tan 1tan tan αβαβαβ++=-。

思考：在这些和角公式中，如果令βα=，会有怎样的结果呢？2、建构数学公式推导：()sin 2sin sin cos cos sin 2sin cos ααααααααα=+=+=；()22cos2cos cos cos sin sin cos sin ααααααααα=+=-=-；思考：把上述关于cos2α的式子能否变成只含有sin α或cos α的式子呢？22222cos 2cos sin 1sin sin 12sin αααααα=-=--=-；22222cos 2cos sin cos (1cos )2cos 1αααααα=-=--=-．以上这些公式都叫做倍角公式，从形式上看，倍角公式给出了αα与2的三角函数之间的关系。

第9课二倍角的正弦、余弦和正切

合作探究的
= −
=
1 例题分析
例1
能力

.
−
学生积极思考，认真
求值.
听讲，积极回答问题
(1)15° 15° ；(2) 2
(3)

− 2 ；
8
8
215°
1 − 2 15°
例 1 当发现三
角式的形式
与二倍角公
的值.
解
1
已知2 = 2 2 − 1 = − 2
1
求得 2 = 4

1
又因为 ∈ ( 2 ，) ，所以 = − 2.
练习 3
1

已知 − = 2 , 且 ∈ ( 2 ，)，
求2.
解已知
1
− = 2
1
两边平方，得2 − 2 + 2 = 4
1
即1 − 2=4
3
所以2 = 4
通过学生小
通过学生小结，梳理结，梳理所学
所学内容提升对本节内容提升对
四、归纳小结
知识的学习理解。
本节知识的
本节课学习了正弦、余弦、正切的二倍角
学习理解，回
公式，并运用此公式求解某些具体问题，对于
顾本节课重
二倍角变形公式，根据具体情况需要灵活使用。
30°
√3
= .
3
4

已知 = 5, 且 ∈ ( 2 ，)，求
例2
4
角的三个公
式，正切的值
直接由同角
三角函数的
2,2,2的值.
解
例 2 熟练二倍

因为 = 5,且 ∈ (2 ，)，
3
所以 = − .

二倍角及正余弦定理【教师版本】

二倍角的正弦、余弦、正切公式2 人教课标版精品课件

二倍角的正弦、余弦、正切公式(同步讲义)(教师版)

二倍角及正余弦定理【教师版本】

【课件】二倍角的正弦、余弦、正切公式(人教A版2019必修第一册)

高中数学人教版必修二倍角的正弦、余弦、正切公式教案(系列五)

江苏高考数学复习三角函数解三角形第24课二倍角的三角函数教师用书

5.5.1 第3课时 二倍角的正弦、余弦、正切公式(课件)

3.3.1二倍角的正弦、余弦和正切公式 课件(北师大版必修4)

二倍角的正弦、余弦和正切教案北师大版必修四

二倍角的正弦、余弦、正切公式 PPT教学课件(高一数学人教A版 必修一册)

二倍角的正弦、余弦、正切说课稿北师大版

二倍角的正弦余弦公式省名师优质课赛课获奖课件市赛课一等奖课件

3.1.3二倍角的正弦、余弦、正切公式课件人教新课标

2017北师大版必修四二倍角的正弦余弦和正切公式word教

《二倍角的正弦、余弦、正切公式》教案(优选.)

第9课 二倍角的正弦、余弦和正切

5.5.1 第3课时二倍角的正弦、余弦、正切公式(课件)

3.3.1二倍角的正弦、余弦和正切公式课件(北师大版必修4)

二倍角的正弦、余弦、正切公式 PPT教学课件(高一数学人教A版必修一册)

第9课二倍角的正弦、余弦和正切