知识讲解_相遇和追及问题(基础).pdf
相遇追及问题详解

必背知识点:速度×时间=路程路程÷速度和=相遇时间追及路程÷速度差=追及时间一、相遇问题例1. 甲、乙二人同时从学校出发到少年宫去,已知学校到少年宫的距离是2400米,甲到少年宫后立即返回学校,在距离少年宫300米处遇到乙,此时他们离开学校已30分钟。
甲每分钟走多少米?乙每分钟走多少米?例2. 甲、乙两车分别从相距240千米的A、B两城同时出发,相向而行,已知甲车到达B城需4小时,乙车到达A城需6小时,问:两车出发后多长时间相遇?例3. 东西两地间有一条公路长217.5千米,甲车以每小时25千米的速度从东到西地,1.5小时后,乙车从西地出发,再经过3小时两车还相距15千米。
乙车每小时行多少千米?例4. 两城市相距328千米,甲、乙两人骑自行车同时从两城出发,相向而行。
甲每小时行28千米,乙每小时行22千米,乙在中途修车耽误1小时,然后继续行驶,与甲相遇,求出发到相遇经过多少时间?例5. AB两城间有一条公路长240千米,甲乙两车同时从A、B两城出发,甲以每小时45千米的速度从A城到B城,乙以每小时35千米的速度从B城到A城,各自到达对方城市后立即以原速沿原路返回,几小时后,两车在途中第二次相遇?相遇地点离A 城多少千米?例6. 甲、乙两车同时从A、B两地出发相向而行,两车在离B地64千米处第一次相遇.相遇后两车仍以原速继续行驶,并且在到达对方出发点后,立即沿原路返回,途中两车在距A地48千米处第二次相遇,问两次相遇点相距多少千米?随堂小试1. 甲、乙两辆汽车从A、B两地同时相向开出,出发后2小时,两车相距141千米:出发后5小时,两车相遇.A、B两地相距多少千米.2. 快车和慢车同时从甲乙两地相对开出,已知快车每小时行40千米,经过3小时快车已过中点12千米与慢车相遇,慢车每小时行多少千米?3. 兄妹二人同时从家里出发到学校去,家与学校相距1400米。
哥哥骑自行车每分钟行200米,妹妹每分钟走80米。
(完整版)高中物理相遇和追及问题(完整版)

、考点、热点回顾一、追及问题1. 类型图象 说明匀加速追匀速①t=t 0 以前,后面物体与 前面物体间距离增大②t=t 0 时,两物体相距最 远为 x 0+Δx③t=t 0 以后,后面物体与前面物体间距离减小④能追及且只能相遇一 次匀速追匀减速匀加速追匀减速2. 速度大者追速度小者度大者追速度小者 开始追及时, 后面物体与 前面物体间的距离在减小, 当 两物体速度相等时,即 t=t0 时刻:① 若Δ x=x0, 则恰能追 及,两物体只能相遇一次, 这相遇追及问题匀减速追匀速也是避免相撞的临界条件② 若Δ x<x0, 则不能追 及,此时两物体最小距离为x0- Δ x③ 若Δ x>x0, 则相遇两次,设t1 时刻Δ x1=x0, 两物体第一次相遇 ,则 t2 时刻两物体第 二次相遇① 表中的Δ x 是开始追及以后,后面物体因速度大而比前面物体多运动的位移; ② x 0是开始追及以前两物体之间的距离; ③ t 2-t 0=t 0-t 1;④ v 1 是前面物 体的速度, v 2是后面物体的速度 . 二、相遇问题这一类 : 同向运动的两物体的相遇问题 , 即追及问题 .第二类 : 相向运动的物体 , 当各自移动的位移大小之和等于开始时两物体的距离时相遇 . 解此类问题首先应注意先画示意图 , 标明数值及物理量 ; 然后注意当被追赶的物体做匀 减速运动时 , 还要注意该物体是否停止运动了 .求解追及问题的分析思路(1) 根据追赶和被追赶的两个物体的运动性质,列出两个物体的位移方程,并注意两物 体运动时间之间的关系.(2) 通过对运动过程的分析,画出简单的图示,找出两物体的运动位移间的关系式.追 及的主要条件是两个物体在追上时位置坐标相同.(3)寻找问题中隐含的临界条件.例如速度小者加速追赶速度大者,在两物体速度相等 时有最大距离; 速度大者减速追赶速度小者, 在两物体速度相等时有最小距离,等等. 利用 这些临界条件常能简化解题 过程.(4)求解此类问题的方法, 除了以上所述根据追及的主要条件和临界条件解联立方程外, 还有利用二次函数求极值,及应用图象法和相对运动知识求解.相遇问题相遇问题的分析思路:匀速追匀加速匀减速追匀加速相遇问题分为追及相遇和相向运动相遇两种情形, 其主要条件是两物体在相遇处的位置 坐标相同.(1) 列出两物体运动的位移方程、注意两个物体运动时间之间的关系. (2) 利用两物体相遇时必处在同一位置,寻找两物体位移间的关系. (3)寻找问题中隐含的临界条件.(4) 与追及中的解题方法相同.【例 1】物体 A 、B 同时从同一地点, 沿同一方向运动, A 以 10m/s 的速度匀速前进, B 以2m/s 2 的加速度从静止开始做匀加速直线运动,求 A 、 B 再次相遇前两物体间的最大距离.【 解析一 】 物理分析法A 做 υA =10 m/s 的匀速直线运动,B 做初速度为零、加速度 a =2 m/s 2的匀加速直线运动.根据题意,开始一小段时间内, A 的速度大于 B 的速度,它们间的距离逐渐变大,当 B 的速度加速到大于 A 的速度后,它们间的距离又逐渐变小; A 、B 间距离有最大值的临界条 件是 υA = υB .①设两物体经历时间 t 相距最远,则 υA = at ② 把已知数据代入①②两式联立得 t =5 s 在时间 t 内, A 、B 两物体前进的距离分别为 s A = υA t =10×5 m = 50 m1 2 1 2s B = at 2= ×2×52 m = 25 m22A 、B 再次相遇前两物体间的最大距离为Δ s m = s A - s B = 50 m -25 m = 25 m解析二 】 相对运动法因为本题求解的是 A 、B 间的最大距离,所以可利用相对运动求解.选 B 为参考系,则 A2 相对 B 的初速度、末速度、加速度分别是 υ0=10 m/s 、υt =υA -υB =0、a =- 2 m/s .22 根据 υt 2-υ0=2as .有 0- 102=2× (-2) ×s AB 解得A、 B 间的最大距离为 s AB =25 m . 解析三 】 极值法11物体 A 、 B 的位移随时间变化规律分别是 s A =10t ,s B =2at 2=2×2×t 2 =t 5.B 间 的 距 离 Δs =10t -t 2, 可 见 ,4×( -1)×0- 102 4×(-1) m =25 m【解析四 】 图象法根据题意作出 A 、B 两物体的 υ-t 图象,如图 1-5-1 所示.由图可知,B 再次相遇前它们之间距离有最大值的临界条件是υA =υB ,得 t 1=5 s A 、 B 间 距 离 的 最 大 值 数 值 上 等 于 ΔO υA P 的 面 积 , 1 Δs m = 2×5×10 m = 25 m .【答案 】25 m【点拨 】相遇问题的常用方法(1) 物理分析法:抓好“两物体能否同时到达空间某位置”这一关键,典型例题且最大值为按(解法一)中的思Δ s m = A 、即设甲、乙两车行驶的总路程分别为 s 、 s ′,则有路分析.(2)相对运动法:巧妙地选取参考系,然后找两物体的运动关系.(3) 极值法:设相遇时间为 t ,根据条件列方程,得到关于 t 的一元二次方程,用判别 式进行讨论,若△> 0,即有两个解,说明可以相遇两次;若△= 0,说明刚好追上或相碰;若△< 0,说明追不上或不能相碰.(4) 图象法:将两者的速度时间图象在同一个坐标系中画出,然后利用图象求解.拓展如图 1-5-2 所示是甲、乙两物体从同一地点,沿同一方向做直线运动的 υ- t 图象,由图象可以看出 ( 〕A .这两个物体两次相遇的时刻分别是 1s 末和 4s 末B .这两个物体两次相遇的时刻分别是 2s 末和 6s 末C .两物体相距最远的时刻是 2s 末D . 4s 末以后甲在乙的前面【解析 】从图象可知两图线相交点 1s 末和 4s 末是两物速度相等时刻,从 4s 末两物相距最远,到 6s 末追上乙.故选 B . 答案 】 B的加速度大小减小为原来的一半。
六年级下册数学讲义-竞赛思维训练专题:第12讲.多次相遇与追及(PDF 解析版)人教版

漫画释义五年级寒假时钟问题五年级春季比例法解行程问题六年级暑期多次相遇与追及六年级秋季变速问题六年级寒假行程模块综合选讲总结多次相遇与追及的规律,利用比例、线段图、柳卡图解决多次相遇与追及问题知识站牌人与人的相遇是一种缘不管是擦肩而过,还是一次美丽的邂逅,都是一种缘缘会让来自不同世界的人走到一起例如今天我们是来自不同学校的同学,汇集到一起来学而思学习,这就是缘分,而且我们已是多次相遇,恰巧今天又要学习多次相遇与追及问题,那该是多大的缘分呀!缘是一个经历了心灵的过程,在这个过程里有些东西不仅仅是灵魂的一种体验,而且还是精神上的一种拥有为了这来之不易的缘分,让我们一起进入今天的课程,体会那精神上的享受!1.理解多次相遇与追及的规律,并能运用相应规律解决行程相关的问题2.掌握用柳卡图解决多次相遇与追及问题的技巧,体会柳卡图与线段图在解决行程问题中的联系与区别一、往返相遇问题的重要结论:设一个全程中甲走的路程为M ,乙走的路程为N ⑴甲乙二人从两端出发的直线型多次相遇问题:⑵同一出发点的直线型多次相遇问题二、柳卡图柳卡图实质上是中学学习的S -T 图的变形,即出现两条横轴(时间),纵轴(路程)忽略在画柳卡图时,最好是先画一个人往返于两地间的路线,并标注到达两地的时刻,接着再画另一人所走路线并标注到达两地的时刻,相交点即相遇地点,最后再利用几何中沙漏模型解决相关问题相遇次数甲乙共走的路程和甲共走的路程乙共走的路程11M N 233M 3N 355M 5N …………n21n -(21)n M-(21)n N-相遇次数甲乙共走的路程和甲共走的路程乙共走的路程122M 2N 244M 4N 366M 6N …………n2n2nM2nN经典精讲教学目标课堂引入1小白从家骑车去学校,每小时15千米,用时2小时,回来以每小时10千米的速度行驶,需要多少时间?【分析】从家到学校的路程:15230⨯=(千米),回来的时间30103÷=(小时).2两地间的路程有255千米,两辆汽车同时从两地相对开出,甲车每小时行45千米,乙车每小时行40千米甲、乙两车相遇时,用了___小时【分析】根据相遇公式知道相遇时间是:255÷(45+40)=255÷85=3(小时),3两列火车从相距480千米的两城相向而行,甲列车每小时行40千米,乙列车每小时行42千米,5小时后,甲、乙两车还相距多少千米?【分析】两车的相距路程减去5小时两车共行的路程,就得到了两车还相距的路程:480(4042)548041070-+⨯=-=(千米).4甲、乙二人同时从相距10千米的两地出发,同向而行,甲每小时行6千米,乙每小时行4千米,经过几小时甲追上乙?【分析】10÷(6—4)=5(小时)5A 、B 两地相距28千米,甲乙两车同时分别从A 、B 两地同一方向开出,甲车每小时行32千米,乙车每小时行25千米,乙车在前,甲车在后,几小时后甲车能追上乙车?【分析】28÷(32-25)=28÷7=4(小时)6①同样的路程,甲乙的速度比为3:2,则甲乙的时间之比为____;②同样的时间,甲乙的速度比为3:2,则甲乙走的路程之比为____;③同样的速度,甲乙用的时间比为3:2,则甲乙走的路程之比为_____.【分析】①2:3②3:2③3:2模块一:多次相遇的认识例1:求全程个数例2:柳卡图的认识模块二:多次相遇与追及规律的应用例3、例4:两次相遇与追及的应用例5:多次相遇与追及的规律运用例题思路知识回顾甲、乙两人在一条长100米的直路上来回跑步,甲的速度3米/秒,乙的速度2米/秒.如果他们同时分别从直路的两端出发,当他们跑了10分钟后,共相遇多少次?(学案对应:学案1)【分析】方法一:10分钟两人共跑了(3+2)⨯60⨯10=3000米3000÷100=30个全程.我们知道两人同时从两地相向而行,他们总是在奇数个全程时相遇(不包括追上)1,3,5,7,…,29共15次.方法二:第一次两个人相遇需要100÷(3+2)=20(秒),从第一次开始到第二次相遇要走两个全程需要:200÷(3+2)=40(秒)所以一共相遇:(10⨯60-20)÷40+1=15.5(次),即为15次.【想想练练】小明和小红两人在长100米的直线跑道上来回跑步,做体能训练,小明的速度为6米/秒,小红的速度为4米/秒.他们同时从跑道两端出发,连续跑了12分钟.在这段时间内,他们迎面相遇了多少次?【分析】第一次相遇时,两人共跑完了一个全程,所用时间为:1006410÷+=()(秒).此后,两人每相遇一次,就要合跑2倍的跑道长,也就是每20秒相遇一次,除去第一次的10秒,两人共跑了126010710⨯-=(秒).求出710秒内两人相遇的次数再加上第一次相遇,就是相遇的总次数.列式计算为:1006410÷+=()(秒),(126010)(102)3510⨯-÷⨯= ,共相遇35136+=(次).注:解决问题的关键是弄清他们首次相遇以及以后每次相遇两人合跑的路程长.如图,甲、乙两人在相距70米的甲乙两端同时出发来回步行,甲的速度和乙的速度之比为3:4,他们相遇的地点分别用A 、B 、…、G 表示,问:(1)A 点到甲地的距离为米;(2)B 点到甲地的距离:B 点到乙地的距离=:;(3)C 点到乙地的距离为米;(4)F 点到G 点的距离为米(提示:F 点到甲地的距离减去G 点到甲地的距离)【分析】(1)30米;(2)5:2;(3)60米;(4)20米D甲2420164242118151296甲、乙两车分别从,A B 两地同时出发相向而行,甲的速度是每小时30千米,乙的速度是每小时20千米,两车相遇后继续行进,各自达到B 、A 两地后,立即沿原路返回.已知两车第二次相遇的地点距第一次相遇的地点是50千米(两人相遇指迎面相遇),那么,A 、B 两地相距___千米.(学案对应:学案2)【分析】方法一:线段图,根据题意甲乙速度比是3:2,因此可以设全程为5份,画图如下:(甲走的用实线表示,乙走的用虚线表示)因此甲、乙两地间的距离是5025125÷⨯=(千米)方法二:柳卡图,由于甲乙速度比是3:2,因此甲乙各走一个全程所用的时间比是2:3,画图如下(甲走的用实线表示,乙走的用虚线表示)因此甲、乙两地间的距离是3150()12555÷-=(千米)【想想练练】甲、乙两人同时从A 、B 两地同时出发,甲的速度是乙的速度的1.5倍,到达对方出发点后立即返回,如果第一次相遇点和第二次相遇点相距300米,那么,A 、B 两地的距离为__米.【分析】方法一:将,A B 间等分为5份,甲每走3份乙走2份,甲、乙相遇情况如下图:,A B 两地的距离为30025750=÷⨯(米).方法二:利用柳卡图,甲乙两人的速度比是3:2,因此走完一个全程所用时间的比是2:3,利用相似知识得CD 间对应的分率是312555-=,,A B 两地的距离为23007505÷=(米).FED CA 062AB乙BA(A 版(1)~(2))⑴甲、乙两车同时从A 、B 两地相对驶,各自达到B 、A 两地后,立即沿距离是千米⑵甲、乙两车同时从A 、B 两地相对驶,各自达到B 、A 两地后,立即沿距离是千米⑶甲、乙两车同时从A 、B 两地相对驶,各自达到B 、A 两地后,立即沿时,距A 地千米⑷如图,A 、B 是圆的直径的两端次相遇,C 离A 点80米;在例4法国数学家柳卡·斯图射影几何与微分几何都作出了世界各国的许多著名数学家“最困难”的题目:“某轮船也有一艘轮船从纽约开往哈佛条航线上问今天中午从哈佛开船从对面开来?”问题提出后讨与激烈的争论,但直到会议称为“柳卡趣题”下面介绍的是柳卡·斯图姆给如下图:地相对开出,两车第一次在距A 地30千米处相遇立即沿原路返回,第二次在距B 地20千米处相遇地相对开出,两车第一次在距A 地30千米处相遇立即沿原路返回,第二次在距A 地60千米处相遇地相对开出,两车第一次在距A 地80千米处相遇立即沿原路返回,第二次在距B 地60千米处相遇的两端,小张在A 点,小王在B 点同时出发反向行走D 点第二次相遇,D 点离B 点60米.求这个圆的周姆生于瑞士,因数学上的成就,于1836年当选为法作出了重要贡献在十九世纪的一次国际数学会议期间学家的晨宴快要结束的时候,柳卡向在场的数学家提出某轮船公司每天中午都有一艘轮船从哈佛开往纽约,往哈佛轮船在途中所花的时间来去都是七昼夜,而且都哈佛开出的轮船,在开往纽约的航行过程中,将会遇到出后,果然一时难住了与会的数学家们尽管为此问题大到会议结束竟还没有人真正解决这个问题这个有趣的数图姆给出的一个非常直观巧妙的解法.遇,相遇后两车继续行相遇,则A 、B 两地间的遇,相遇后两车继续行相遇,则A 、B 两地间的遇,相遇后两车继续行相遇,当甲乙第三次相遇行走,他们在C 点第一圆的周长.选为法国科学院院士他对期间,有一天,正当来自家提出困扰他很久、自认,并且每天的同一时刻而且都是匀速航行在同一会遇到几艘同一公司的轮问题大家进行了广泛的探趣的数学问题,被数学界⑸小王、小李二人往返于甲、乙两地,小王从甲地、小李从乙地同时出发,相向而行,两人第一次在距甲地3千米处相遇,第二次在距甲地6千米处相遇(追上也算作相遇),则甲、乙两地的距离为千米(学案对应:学案3)【分析】⑴3032070⨯-=(千米)⑵(30360)275⨯+÷=(千米)⑶,A B 两地间相距80360180⨯-=千米当第三次相遇时,两车所走路程和是5个全程,那么其中甲车走了805400⨯=千米,400180240÷= ,所以距A 地40千米⑷第一次相遇,两人合起来走了半个周长;第二次相遇,两个人合起来又走了一个周长.从出发开始算,两个人合起来走了一周半.因此,第二次相遇时两人合起来所走的路程是第一次相遇时合起来所走的路程的3倍,那么从A 经过C 到D 的距离,应该是从A 到C 距离的3倍,即A 到D 是803240⨯=(米).那么圆周上A 到B 的距离是24060180-=(米).圆的周长为1802360⨯=(米).⑸由于两人同时出发相向而行,所以第一次相遇一定是迎面相遇;由于本题中追上也算相遇,所以两人第二次相遇可能为迎面相遇,也可能为同向追及.①如果第二次相遇为迎面相遇,如下图所示,两人第一次在A 处相遇,第二次在B 处相遇.则甲、乙两地的距离为(336)27.5⨯+÷=千米;②如果第二次相遇为同向追及,如上图,两人第一次在A 处相遇,相遇后小王继续向前走,小李走到甲地后返回,在B 处追上小王.在这个过程中,小王走了633-=千米,小李走了639+=千米,两人的速度比为3:91:3=.所以第一次相遇时小李也走了9千米,甲、乙两地的距离为9312+=千米.所以甲、乙两地的距离为7.5千米或12千米【想想练练】如图,有一个圆,两只小虫分别从直径的两端A 与C 同时出发,绕圆周相向而行.它们第一次相遇在离A 点8厘米处的B 点,第二次相遇在离C 点6厘米处的D 点,问,这个圆周的长是多少?【分析】如图所示,第一次相遇,两只小虫共爬行了半个圆周,其中从A 点出发的小虫爬了8厘米,第二次相遇,两只小虫又爬了一个圆周,所以两只小虫从出发共爬行了1个半圆周,其中从A 点出发的应爬行8324⨯=(厘米),比半个圆周多6厘米,半个圆周长为83618⨯-=(厘米),一个圆周长就是:(836)236⨯-⨯=(厘米)李王乙甲甲王乙C A甲、乙两车分别从A 、B 两地同时出发相向而行,在A 、B 两地之间不断往返行驶.甲车速度是乙车速度的37,并且甲、乙两车第2012次相遇的地点和第2013次相遇的地点恰好相距120千米(注:当甲、乙两车同向时,乙车追上甲车不算作相遇),那么,A 、B 两地之间的距离是多少千米?(学案对应:学案4)【分析】因为甲乙同时出发,同时相遇,所以甲、乙相遇时间相同,因此3:7S V V ==乙乙甲甲:S :,设全程为10份,则一个全程中,甲走了3份,乙走了7份,通过总结的规律分析第2012次相遇时,甲走:(2012⨯2-1)⨯3=12069(份),120691012069÷= ,所以第2012次相遇地点是在从A 地向右数9份的C 点,第2013次相遇时,甲继续向右数6份即可,到达D 由图看出CD 间距离为4份,A 、B 两地之间的距离是120410300÷⨯=(千米).D C BA四龟问题四只乌龟在边长为3米的正方形四个角上,以每秒1厘米的速度同时匀速爬行,每只乌龟的爬行方向时刻指向另一只.问:经过多少时间它们才能在正方形的中心碰头?答案:对于任意一只乌龟A ,它始终朝着它面对的那只乌龟B 爬行,因此无论如何,A 与B 的距离都是以1cm /s 的速度在减小的,一开始两者距离是3m ,所以就是300s 之后,两只乌龟的距离变成0,即碰头.A 、B 两地相距2400米,甲从A 地、乙从B 地同时出发,在A 、B 间往返长跑甲每分钟跑300米,乙每分钟跑240米,在30分钟后停止运动甲、乙两人在第几次相遇时距A 地最近?最近距离是多少米?【分析】方法一:()300240302400 6.75+⨯÷=(个),即甲乙共行了6.75个全程,共相遇了3次,甲乙两人的速度比是300:2405:4=,设全程为9份①如图所示,甲走路线用实线表示,乙走路线用虚线表示第一次相遇甲行5份,乙行4份,所以第一次相遇地点距A 地是全程的59②第二次相遇时两人共行了3个全程,甲行的距A 地()93593-⨯-=份,所以第二次相遇地点距A 地是全程的13③第三次相遇时两人共行了5个全程,55927⨯÷= 甲行的距A 地7份,所以第三次相遇地点距A 地是全程的79,所以第二次相遇距A 地最近,最近距离是124008003⨯=(米)方法二:柳卡图法,其中实线表示甲所走的路程,虚线表示乙走的路程,实线与虚线的交点就是相遇点由图可以看出两人共相遇了3次,其中第2次距A 地最近,最近距离为D 到A 地的距离,由图看出:6:121:2MN PQ ==,根据沙漏模型:1:2DA DB ''=,所以最近距离为124008003⨯=(米)杯赛提高1.A 、B 两地相距950米甲、乙两人同时由A 地出发往返锻炼半小时甲步行,每分钟走40米;乙跑步,每分钟行150米则甲、乙两车第次迎面相遇时距B 地最近【分析】半小时,两人一共行走(40+150)×30=5700(米),相当于5700÷950=6(个)全程,由于两人同时同地出发,两人行程每2个全程就会有一次相遇,而两人的速度比15:4,所以相同时间内两人的行程比为15:4,那么第一次相遇甲走了全程的48215419⨯=+,距离B 地1119个全程;第二次相遇甲走了全程的1619,距离B 地319个全程;第三次相遇甲走了全程的2419,距离B地519个全程,比较可知甲、乙两人第二次迎面相遇时距离B 地最近2.两名游泳运动员在长30米的游泳池里来回游泳,甲的速度是每秒1米,乙的速度是每秒0.6米,他们同时从游泳池的一端出发,来回一共游了21分钟,他们一共遇上(迎面或同向)几次?【分析】甲游全程用30130÷=秒,乙游全程用300.650÷=秒,画出柳卡图:21分钟一共1260秒,一共相遇84133⨯+=次3.男、女两名田径运动员在长110米的斜坡上练习跑步(坡顶为A ,坡底为B ).两人同时从A点出发,在A ,B 之间不停地往返奔跑.已知男运动员上坡速度是每秒3米,下坡速度是每秒5米,女运动员上坡速度是每秒2米,下坡速度是每秒3米.那么两人第二次迎面相遇的地点离A 点多少米?【分析】方法一:柳卡图法如上图所示,A 为坡顶,B 为坡底,从A 到B 的方向表示下坡,从B 到A 的方向表示上坡,折线图向右的方向的距离表示上(下)坡的时间.根据题意,男、女运动员下坡、上坡的时间比为1111:::6:10:10:155332=,男运动员跑的路线为实线,女运动员跑的路线为虚线,从图中可以看出,两人第一次迎面相遇在C ,第二乙甲03060901201501802102402703003002702402101501209060300B A 35102260附加题次迎面相遇在D ,所以需要求D 到A 的距离.根据几何中的相似三角形性质,可得D 到A 的距离与到B 的距离之比等于(2516):(2210)9:123:4--==,而A 、B 之间的距离为110米,所以D 到A 的距离为3111047347⨯=+(米),故第二次相遇的地点距A 点1477米.方法二:方程法.设第二次迎面相遇的地点离A 点x 米.由于第二次相遇时男运动员走了一个下坡、一个上坡和x 米下坡,女运动员走了一个下坡和()110x -米上坡,可得方程:1101101101105332x x +-+=+解得1477x =,即第二次迎面相遇的地点离A 点1477米.4.甲乙两人都从A 地去往B 地,甲先出发1小时后乙再出发.结果乙比甲提前1小时到达B地,问:乙在什么地方追上甲?【分析】由图可看出,乙在A,B 中点处追上甲.多次迎面相遇规律1.相向而行:第一次相遇两人合走一个全程,以后每相遇一次都要合走两个全程,因此第n 次相遇,两人合走21n -个全程(n 为正整数)2.同向而行:每相遇一次都要合走两个全程,因此第n 次相遇,两人合走2n 个全程(n 为正整数)1.甲、乙二人在相距180米的直路两端同时出发来回散步,甲每秒走2米,乙每秒走2.5米.每人都走了6.5分钟,那么在这段时间内他们共相遇了多少次.【分析】方法一:甲乙6.5分钟共走了(2 2.5) 6.5601755+⨯⨯=米,共走了17551809.75÷=个全程.两人第一次相遇合走了一个全程,以后每2个全程相遇一次.那么,9.75个全程共相遇了5次.方法二:甲行全程用180290÷=秒,乙行全程用180 2.572÷=秒画出柳卡图:乙甲AB 家庭作业知识点总结由图得,一共相遇5次2.如图,A,B 两地相距70米,甲、乙两人同时从A 地同向出发来回步行,甲的速度和乙的速度之比为3:4,则第二次相遇地点与第一次相遇地点间相距多少米?【分析】6270()406125⨯-=++(米)3.甲、乙两车同时从A 地出发同向而行去往B 地,甲车的速度是乙车速度的1.5倍,在,A B 两地间做往返运动.已知两车第二次相遇的地点距第一次相遇的地点是50千米(两人相遇指迎面相遇),那么,A 、B 两地相距___千米.【分析】方法一:线段图,根据题意甲乙速度比是3:2,因此可以设全程为5份,画图如下:(甲走的用实线表示,乙走的用虚线表示)因此甲、乙两地间的距离是5025125÷⨯=(千米)方法二:柳卡图,由于甲乙速度比是3:2,因此甲乙各走一个全程所用的时间比是2:3,画图如下(甲走的用实线表示,乙走的用虚线表示)因此甲、乙两地间的距离是3150()12555÷-=(千米)010836乙912034A B A BC D E F 6B A 26304.甲、乙二人同时从A 地出发去B 地,在A 、B 两地间往返而行,甲的速度是每小时30千米,乙的速度是每小时20千米.已知二人第二次相遇的地点距第一次相遇的地点是40千米,那么,A 、B 两地相距多少千米.【分析】因为甲乙同时出发,同时相遇,所以甲、乙相遇时间相同,因此:30:203:2S V V ===乙乙甲甲:S ,设全程为5份,第一次相遇甲、乙共同行了两个全程,则两个全程中,甲走了6份,乙走了4份,所以F 是第一次相遇地点,第一次相遇到第二次相遇,甲、乙共走2个AB ,因此从开始到第二次相遇,甲、乙共走了4个全程,一个全程甲走3份,8个全程甲共走3412⨯=份,所以D 是第二次相遇地点,由图看出DF 是2份.但已知DF 是40千米,所以AB 的长度是40÷2⨯(2+3)=100(千米).(也可以用乙进行计算)5.甲、乙两车同时从A B 、两地相向出发,第一次在距A 地3000米处相遇相遇后两车继续前行,各自到达目的地后立即返回,在距A 地500米处第二次相遇A B 、两地相距()米【分析】两人第一次相遇共同走了一个全程,第二次相遇共同走了三个全程,第二次相遇所用时间是第一次相遇时间的三倍甲第一次相遇时走了3000米,第二次相遇时走了3个3000米即9000米甲一去一回走了9000米后离出发点还有500米,即两个全程的长度是9000+500=9500米,一个全程的长度是4750米6.甲、乙二人分别从A 、B 两地同时出发,往返跑步.甲每分跑180米,乙每分跑240米.如果他们的第100次相遇点与第101次相遇点的距离是160米,求A 、B 两点间的距离为多少米?【分析】因为甲乙同时出发,同时相遇,所以甲、乙相遇时间相同,因此180:2403:4S V V ===乙乙甲甲:S :,设全程为7份,则一个全程中,甲走了3份,乙走了4份,通过总结的规律分析第100次相遇时,甲走:(100⨯2-1)⨯3=597(份),5977852÷= ,所以第100次相遇地点是在从B 地向左数2份的C 点,第101次相遇时甲走:(101⨯2-1)3⨯=603(份),6037861÷= ,所以第101次相遇地点在从A 点向右数1份的D 点,由图看出CD 间距离为4份,A 、B 两地之间的距离是16047280÷⨯=(米).【学案1】甲、乙两人在一条长100米的直路上来回跑步,甲的速度3米/秒,乙的速度2米/秒.如果他们同时从直路的同一端出发,当他们跑了10分钟后,共相遇多少次?【分析】方法一:10分钟两人共跑了(3+2)⨯60⨯10=3000米3000÷100=30个全程.我们知道两人同时从一端同向而行,每两个全程相遇一次,共15次.方法二:第一次两个人相遇需要200÷(3+2)=40(秒),从第一次开始到第二次相遇要走两个全程需要:200÷(3+2)=40(秒)所以一共相遇:10⨯60÷40=15(次)BBA版学案【学案2】甲、乙二人分别从A 、B 两地同时相向而行,甲的速度是每小时30千米,乙的速度是每小时20千米,二人相遇后继续行进,甲到B 地、乙到A 地后立即返回.已知二人第二次相遇的地点距第一次相遇的地点是20千米,那么,A 、B 两地相距多少千米.【分析】因为甲乙同时出发,同时相遇,所以甲、乙相遇时间相同,因此:30:203:2S V V ===乙乙甲甲:S ,设全程为5份,则一个全程中,甲走了3份,乙走了2份,所以C 是第一次相遇地点,第一次相遇到第二次相遇,甲、乙共走2个AB ,因此从开始到第二次相遇,甲、乙共走了3个全程,一个全程甲走3份,3个全程甲共走339⨯=份,所以D 是第二次相遇地点,由图看出DC 是2份.但已知DC 是20千米,所以AB 的长度是20÷2⨯(2+3)=50(千米).(也可以用乙进行计算)【学案3】甲、乙两车的速度分别为52千米/时和40千米/时.他们同时从A 地出发去B 地,在A 、B 两地间往返而行,从开始走到第三次相遇,共用了6小时.A 、B 两地相距多少千米?【分析】从开始走到第一次相遇,两车走的路程是两个AB 之长;而到第三次相遇,两车走的路程总共就是6个AB 之长,是(52+40)⨯6=552(千米),所以A 、B 两地相距552÷6=92(千米).【学案4】甲、乙两车同时从A 地出发同向而行,在A 、B 两地之间不断往返行驶.甲车速度是乙车速度的37,并且甲、乙两车第2012次相遇的地点和第2013次相遇的地点恰好相距120千米(注:当甲、乙两车同向时,乙车追上甲车不算作相遇),那么,A 、B 两地之间的距离是多少千米?【分析】因为甲乙同时出发,同时相遇,所以甲、乙相遇时间相同,因此3:7S V V ==乙乙甲甲:S :,设全程为10份,则一个全程中,甲走了3份,乙走了7份,通过总结的规律分析第2012次相遇时,甲走:(2012⨯2)⨯3=12072(份),120721012072÷= ,所以第2012次相遇地点是在从B 地向左数2份的C 点,第2013次相遇时,甲继续向左数6份即可,到达D 由图看出CD 间距离为6份,A 、B 两地之间的距离是120610200÷⨯=(千米).BC D BA。
四年级相遇与追击综合问题知识点总结

相遇和追及综合知识点总结一、基础知识点(相遇和追及):其实相遇和追及最核心的问题就是路程S、速度V和时间T的问题,基本公式就是S÷V=T以及这个公式的变形S÷T=V,V×T=S。
相遇问题:路程和S和------相遇时间T------ 速度和V和⏹S和:一定是甲乙两者共同时间内走过的路程。
如果其中一方提前走了一段路程,这个不算,需要去掉。
⏹T相遇时间:一定是在相遇过程中共同经历过的时间。
需要小心题目陷阱,如其中一方休息了一段时间,其中一方提前出发了一段时间都应该剔除。
⏹V和=V甲+ V乙⏹路程和÷速度和=相遇时间路程和÷相遇时间=速度和速度和×相遇时间=路程和追击问题:路程差S差-------追及时间T -------速度差V差⏹S差:有些题没有明确给出路程差,而是隐含在一些条件中,如甲先出发一段时间。
⏹T追及时间:一定是在追及过程中共同经历过的时间。
需要小心题目陷阱,如其中一方休息了一段时间,其中一方提前出发了一段时间都应该剔除。
⏹V和=V甲- V乙路程差÷速度差=追及时间路程差÷追及时间=速度差速速度差×追及时问=路程差二、直线的相遇与追击略三、环形跑道的相遇与追击1、同时同地每次相遇都是合走一圈S和=S甲+S乙=1圈2、同时不同地首次相遇等于初始距离,初始距离需要依据双方的运动方向确定。
每次相遇都是合走一圈S和=S甲+S乙=1圈四、火车过桥火车过杆:S火=车长火车完全过桥:S火=车长+桥长火车完全在桥上:S火= 桥长-车长超人(同向):S差=车长---等效为:人追行人错人(相向):S和=车长---等效为:车尾人与行人相遇超车(同向):S差=车长1+车长2 ---等效为:快车车尾人追慢车车头人错车(相向):S和==车长1+车长2 ---等效为:两个车尾的人相遇五、流水行船静水速度(船速),水速,顺水速度,逆水速度顺水速度=船速+ 水速逆水速度=船速- 水速船速=(顺水速度+逆水速度)÷2水速=(顺水速度-逆水速度)÷2。
高中物理追击和相遇问题专题(含详解)

第3页 共8页
13.汽车以 3 m/s2 的加速度开始启动的瞬间,一辆以 6 m/s 的速度沿同方向做匀速直线运动的自行车
12
x v(t0 t1) at1 60m
此时
2
(2)警车发动到达到最大速度需要 t2= vm/a=8s
(1) 小汽车从开动到追上自行车之前经过多长时间两者相距最远?此时距离是多少?
(2) 小汽车什么
时候追上自行车,此时小汽车的速度是多少?
( 二 ) .匀速运动追匀加速运动的情况 (开始时 v1> v 2):
1.当 v1> v 2 时,两者距离变小;
2.当 v1= v 2 时,①若满足 x1< x 2+Δ x,则永远追不上,此时两者距离最近;
———— -( 3)
由上面 3 式可解得 sAB 60km sAB 表示 AB 间的距离
4.设轿车行驶的速度为 v1,卡车行驶的速度为 v2,
则 v1= 108 km/h=30 m/s ,
v2=72 km/h=20 m/s , 在反应时间Δ t 内两车行驶的距离分别为 s1、 s2,则
s1= v1Δt ① s2= v2Δt ② 轿车、卡车刹车所通过的距离分别为
直线运动中的追及和相遇问题
一、相遇和追及问题的实质
研究的两物体能否在相同的时刻到达相同的空间位置的问题。
二、 解相遇和追及问题的关键 1. 画出物体运动的情景图 2. 理清三大关系
( 1)时间关系 : tA tB t0
( 2)位移关系: xA xB x0
(完整版)相遇问题与追及问题

相遇与追及问题一、学习目标1. 理解相遇与追及的运动模型,掌握相遇与追及这两种情况下路程、时间、速度这三个基本量之间的关系.会利用这个关系来解决一些简单的行程问题.2. 体会数形结合的数学思想方法.二、主要内容1. 行程问题的基本数量关系式:路程=时间×速度;速度=路程÷时间;时间=路程÷速度.2.相遇问题的数量关系式:相遇路程=相遇时间×速度和;速度和=相遇路程÷相遇时间;相遇时间=相遇路程÷速度和.3.追及问题的数量关系式:追及距离=追及时间×速度差;速度差=追及距离÷追及时间;追及时间=追及距离÷速度差.4. 能熟练运用路程、时间、速度这三个基本量的关系,结合图形分析,解决一些简单的行程问题.三、例题选讲例1两辆汽车同时分别从相距500千米的A,B两地出发,相向而行,速度分别为每小时40千米和每小时60千米.求几小时后两车相遇.例2甲车在乙车前200千米,同时出发,速度分别为每小时40千米与60千米.问多少小时后,乙车追上甲车.例3一辆公共汽车和一辆小轿车同时从相距598千米的两地相向而行.公共汽车每小时行40千米,小轿车每小时行52千米,问几小时后两车相距138千米?例4甲、乙两辆汽车同时从东、西两地相向开出,甲车每小时行56千米,乙车每小时行48千米,两车在离中点32千米处相遇.求东、西两地相距多少千米?例6一辆卡车和一辆摩托车同时从A、B两地相对开出,两车在途中距A地60千米处第一次相遇.然后,两车继续前进,卡车到达B地,摩托车到达A地后都立即返回,两车又在途中距B地30千米处第二次相遇.求A、B两地相距多少千米?例7甲、乙、丙三人进行100米赛跑.当甲到达终点时,乙离终点还有20米,丙离终点还有40米.如果甲、乙、丙赛跑的速度都不变,那么当乙到达终点时,丙离终点还有多远?例8小明步行上学,每分行75米,小明离家12分后,爸爸骑单车去追,每分行375米.问爸爸出发多少分后能追上小明?例9解放军某部快艇追击敌舰,追到A岛时,敌舰已逃离该岛15分钟,已测出敌舰每分钟行驶1000米,解放军快艇每分钟行驶1360米,在距离敌舰600米处可开炮射击.问解放军快艇从A岛出发经过多少分钟就可以开炮射击敌舰?例10甲、乙两人在环形跑道上以各自的不变速度跑步,如果两人同时从同地相背而行,乙跑4分钟后两人第一次相遇,已知甲跑一周需6分钟,那么乙跑一周需要多少分钟?例11两名运动员在湖周围环形道上练习长跑,甲每分跑250米,乙每分跑200米,两人同时从两地同向出发,经过45分甲追上乙,如果两人同时同地反向出发,经过多少分两人相遇?例12甲、乙两人在相距90米的直路上来回跑步,甲的速度是每秒3米,乙的速度是每秒2米,如果她们同时分别从直路两端点出发,跑了6分,那么,这段时间内,两人共迎面相遇了多少次?巩固练习:1、甲、乙两站相距980千米,两列火车由两站相对开出,快车每小时行50千米,慢车每小时行多少千米,两车经10小时能相遇?2、甲车每小时行60千米,1小时后,乙车紧紧追赶,速度为每小时80千米,几小时后乙车可追上甲车?3、早晨6时,有一列货车和一列客车同时从相距360千米的甲、乙两城相对开出,中途相遇,这期间,货车停车一次60分钟,客车停车两次各30分钟,已知货车每小时行42千米,客车每小时行78千米,问两车在几点钟相遇?4、东、西两镇相距240千米,一辆客车从上午8时从东镇开往西镇,一辆货车在上午9时从西镇开往东镇,到正午12点,两车恰好在两镇间的中点相遇,如果两车都从上午8时由两地相向开出,速度不变,到上午10时,两车还相距多少千米?5、骑单车从甲地到乙地,以每小时10千米的速度行进,下午1点到,以每小时15千米的速度行进,上午11点到.如果希望中午12点到,那么应以怎样的速度行进呢?6、某人由甲地去乙地,如果他从甲地先骑摩托车行了12小时,再换骑自行车行9小时,恰好到达乙地.如果他从甲地先骑自行车行了21小时,再换骑摩托车行8小时,也恰好到达乙地.问:全程骑摩托车需要多少小时才能到达乙地?7、兄妹两人同时由家上学,哥哥每分钟走90米,妹妹每分钟走60米,哥哥到校门口时,发现忘了带课本,立即沿原路返回去取,行至离校门口180米处与妹妹相遇,他们家离学校多少米?8、兄妹两人在周长300米的圆形水池边玩.从同一地点同时背向饶水池而行.哥哥每分钟走13米,妹妹每分钟走12米.他们第5次相遇时,哥哥共走了多长的路?课后作业:1.甲以每小时4千米的速度步行去学校,乙比甲晚4小时骑自行车从同一地点出发去追甲,乙每小时行12千米,乙多少小时可追上甲?2.小张从家到公园,原打算每分钟走50米,为了提早10分钟到,他把速度加快,每分钟走75米.小张家到公园有多少米?3.父亲和儿子都在某厂工作,他们从家里出发步行到工厂,父亲用40分钟,儿子用30分钟.如果父亲比儿子早5分钟离家,问儿子用多少分钟可赶上父亲?4.解放军某部小分队,以每小时6千米的速度到某地执行任务,途中休息30分后继续前进,在出发5.5小时后,通讯员骑摩托车以56千米的速度追赶他们。
追及与相遇问题公式

追及与相遇问题公式摘要:一、问题背景二、追及与相遇问题的基本公式1.追及问题的基本公式2.相遇问题的基本公式三、公式推导与解释1.追及问题的公式推导与解释2.相遇问题的公式推导与解释四、例题解析1.追及问题例题解析2.相遇问题例题解析五、结论正文:一、问题背景在日常生活中,我们经常会遇到这样的场景:两个人在同一直线上相向而行,其中一个人速度较快,另一个人速度较慢。
当他们相遇之后,速度较快的人继续向前走,速度较慢的人则停下来。
这时,速度较快的人与停留在原地的速度较慢的人之间的距离会逐渐增大。
这就是追及与相遇问题。
二、追及与相遇问题的基本公式1.追及问题的基本公式假设甲乙两人分别在某一直线上相向而行,甲的速度为v1,乙的速度为v2,甲从起点出发,乙从终点出发。
设他们相遇的时间为t,此时甲所走的路程为s1,乙所走的路程为s2。
根据题意,我们可以得到以下关系式:s1 = v1 * ts2 = v2 * ts1 + s2 = 总路程2.相遇问题的基本公式同样假设甲乙两人分别在某一直线上相向而行,甲的速度为v1,乙的速度为v2,甲从起点出发,乙从终点出发。
设他们相遇的时间为t,此时甲所走的路程为s1,乙所走的路程为s2。
根据题意,我们可以得到以下关系式:s1 = v1 * ts2 = v2 * ts1 + s2 = 总路程三、公式推导与解释1.追及问题的公式推导与解释假设甲乙两人分别在某一直线上相向而行,甲的速度为v1,乙的速度为v2,甲从起点出发,乙从终点出发。
设他们相遇的时间为t,此时甲所走的路程为s1,乙所走的路程为s2。
根据题意,我们可以得到以下关系式:s1 = v1 * ts2 = v2 * ts1 + s2 = 总路程当甲乙两人相遇后,甲继续向前走,乙停留在原地。
设他们再次相遇的时间为t",此时甲所走的路程为s1",乙所走的路程为s2"。
根据题意,我们可以得到以下关系式:s1" = v1 * (t + t")s2" = v2 * t"s1" - s2" = 甲乙两人之间的距离2.相遇问题的公式推导与解释同样假设甲乙两人分别在某一直线上相向而行,甲的速度为v1,乙的速度为v2,甲从起点出发,乙从终点出发。
相遇与追及问题

相遇与追及一、必备基础知识:1、行程问题的三个基本量是距离、速度和时间。
2、按所行方向的不同可分为三种:(1)相遇问题;(2)相离问题;(3)追及问题。
其中,相遇与追及问题是最常见考试题型。
3、我们熟悉的:多远——路程多久——时间多快——速度路程=速度×时间4、区别运动形式(1)相向而行:也就是相对而行,面对面(2)相背而行:背对背(3)同向而行:相同的方向5、行程问题的主要数量关系是:距离=速度×时间。
它大致分为以下三种情况:(1)相向而行:相遇时间=距离÷速度和(2)相背而行:相背距离=速度和×时间。
(3)同向而行:速度慢的在前,快的在后。
(4)追及时间=追及距离÷速度差(5)追及距离=速度差×时间。
(6)水船顺V V V +=(7)水船逆V V V -=6、解决行程问题时,要注意充分利用图示把题中的情节形象地表示出来,有助于分析数量关系,有助于迅速地找到解题思路。
二、例题精讲例1两辆汽车同时从某地出发,运送一批货物到距离165千米的工地。
甲车比乙车早到48分钟,当甲车到达时,乙车还距工地24千米。
甲车行完全程用了多少小时?练:甲、乙两地之间的距离是420千米。
两辆汽车同时从甲地开往乙地。
第一辆每小时行42千米,第二辆汽车每小时行28千米。
第一辆汽车到乙地立即返回。
两辆汽车从开出到相遇共用多少小时?例2客车和货车同时从A、B两地相对开出。
客车每小时行驶50千米,货车的速度是客车的80%,相遇后客车继续行3.2小时到达B地。
A、B两地相距多少千米?练:甲、乙两车分别从A、B两地同时出发相向而行,相遇点距中点320米。
已知甲的速度是乙的速度的56,甲每分钟行800米。
求A、B两地的路程。
例3从甲地到乙地的路程分为上坡、平路、下坡三段,各段路程之比是1:2:3,某人走这三段路所用的时间之比是4:5:6。
已知他上坡时的速度为每小时2.5千米,路程全长为20千米。
第2讲 相遇和追及问题

相遇和追及问题知识要点:追及问题与相遇问题的区别在于运动的方向,及由此而引出的速度和与速度差;共同点是双方所用的时间是相等的。
在解答追及问题时,关键是抓住速度差去分析和思考,同时画线段图辅助解题是一种行之有效的方法。
一、三种运动方式:1、相向而行:面对面而行2、同向而行:面朝的方向相同而行3、背向而行:背靠背方向,方向相反而行一、相遇甲从A地到B地,乙从B地到A地,然后两人在途中相遇,实质上是甲和乙一起走了A,B之间这段路程,如果两人同时出发,那么相遇路程=甲走的路程+乙走的路程=甲的速度×相遇时间+乙的速度×相遇时间=(甲的速度+乙的速度)×相遇时间=速度和×相遇时间.一般地,相遇问题的关系式为:速度和×相遇时间=路程和,即=tS V和和二、追及有两个人同时行走,一个走得快,一个走得慢,当走得慢的在前,走得快的过了一些时间就能追上他.这就产生了“追及问题”.实质上,要算走得快的人在某一段时间内,比走得慢的人多走的路程,也就是要计算两人走的路程之差(追及路程).如果设甲走得快,乙走得慢,在相同的时间(追及时间)内:追及路程=甲走的路程-乙走的路程=甲的速度×追及时间-乙的速度×追及时间=(甲的速度-乙的速度)×追及时间=速度差×追及时间.一般地,追击问题有这样的数量关系:追及路程=速度差×追及时间,即=tS V差差例如:假设甲乙两人站在100米的跑道上,甲位于起点(0米)处,乙位于中间5米处,经过时间t后甲乙同时到达终点,甲乙的速度分别为v甲和v乙,那么我们可以看到经过时间t后,甲比乙多跑了5米,或者可以说,在时间t内甲的路程比乙的路程多5米,甲用了时间t追了乙5米三、在研究追及和相遇问题时,一般都隐含以下两种条件:(1)在整个被研究的运动过程中,2个物体所运行的时间相同(2)在整个运行过程中,2个物体所走的是同一路径。
基础相遇追及问题

行程问题(基础)
相遇问题:
相背问题:
追及问题:
【相遇问题】例1:甲乙两人分别从相距20千米的两地同时出发相向而行,甲每小时走6千米,乙每小时走4千米。
两人几小时后相遇?
练习1:一辆汽车和一辆摩托车同时分别从相距900千米的甲、乙两地出发,汽车每小时行40千米,摩托车每小时行50千米。
8小时后两车相距多少千米?
2、甲乙两车分别从相距480千米的A、B两城同时出发,相向而行,已知甲车从A城到B城需6小时,乙车从B 城到A城需12小时。
两车出发后多少小时相遇?
【相背问题】甲每小时行7千米,乙每小时行5千米,两人于相隔18千米的两地同时相背而行,几小时后两人相隔54千米?
1、甲车每小时行6千米,乙车每小时行5千米,两车于相隔10千米的两地同时相背而行,几小时后两人相隔65千米?
2、甲每小时行9千米,乙每小时行7千米,甲从南庄向南行,同时乙从北庄向北行。
经过3小时后,两人相隔60千米。
南北两庄相距多少千米?
【追及问题】例1:甲乙两人分别从相距24千米的两地同时向东而行,甲骑自行车每小时行13千米,乙步行每小时走5千米。
几小时后甲可以追上乙?
2、东西两镇相距20千米,甲、乙两人分别从两镇同时出发相背而行,甲每小时的路程是乙的2倍,3小时后两人相距56千米。
两人的速度各是多少?
3、甲、乙两个车队同时从相隔330千米的两地相向而行,甲队每小时行60千米,乙队每小时行50千米。
问两车队几小时后相遇相遇?
4、甲、乙两人相距40千米的两地同时相向出发,5小时后相遇;如果他们从同一地点出发,则3小时后甲在乙前6千米,求甲、乙两人的速度?(相遇追及结合题)。
(完整版)高中物理相遇和追及问题(完整版)

相遇追及问题一、考点、热点回顾一、追及问题1.速度小者追速度大者类型图象说明匀加速追匀速①t=t0以前,后面物体与前面物体间距离增大②t=t0时,两物体相距最远为x0+Δx③t=t0以后,后面物体与前面物体间距离减小匀速追匀减速④能追及且只能相遇一次匀加速追匀减速2.速度大者追速度小者度大者追速度小者匀减速追匀速开始追及时,后面物体与前面物体间的距离在减小,当两物体速度相等时,即t=t0时刻:①若Δx=x0,则恰能追及,两物体只能相遇一次,这也是避免相撞的临界条件匀速追匀加速②若Δx<x0,则不能追及,此时两物体最小距离为x0-Δx③若Δx>x0,则相遇两次,设t1时刻Δx1=x0,两物体第一次相遇,则t2时刻两物体第二次相遇匀减速追匀加速①表中的Δx是开始追及以后,后面物体因速度大而比前面物体多运动的位移;②x0是开始追及以前两物体之间的距离;③t2-t0=t0-t1;④v1是前面物体的速度,v2是后面物体的速度.二、相遇问题这一类:同向运动的两物体的相遇问题,即追及问题.第二类:相向运动的物体,当各自移动的位移大小之和等于开始时两物体的距离时相遇.解此类问题首先应注意先画示意图,标明数值及物理量;然后注意当被追赶的物体做匀减速运动时,还要注意该物体是否停止运动了.求解追及问题的分析思路(1)根据追赶和被追赶的两个物体的运动性质,列出两个物体的位移方程,并注意两物体运动时间之间的关系.(2)通过对运动过程的分析,画出简单的图示,找出两物体的运动位移间的关系式.追及的主要条件是两个物体在追上时位置坐标相同.(3)寻找问题中隐含的临界条件.例如速度小者加速追赶速度大者,在两物体速度相等时有最大距离;速度大者减速追赶速度小者,在两物体速度相等时有最小距离,等等.利用这些临界条件常能简化解题过程.(4)求解此类问题的方法,除了以上所述根据追及的主要条件和临界条件解联立方程外,还有利用二次函数求极值,及应用图象法和相对运动知识求解.相遇问题相遇问题的分析思路:相遇问题分为追及相遇和相向运动相遇两种情形,其主要条件是两物体在相遇处的位置坐标相同.(1)列出两物体运动的位移方程、注意两个物体运动时间之间的关系. (2)利用两物体相遇时必处在同一位置,寻找两物体位移间的关系. (3)寻找问题中隐含的临界条件.(4)与追及中的解题方法相同.二、典型例题【例1】物体A 、B 同时从同一地点,沿同一方向运动,A 以10m/s 的速度匀速前进,B 以2m/s 2的加速度从静止开始做匀加速直线运动,求A 、B 再次相遇前两物体间的最大距离. 【解析一】 物理分析法A 做 υA =10 m/s 的匀速直线运动,B 做初速度为零、加速度a =2 m/s 2的匀加速直线运动.根据题意,开始一小段时间内,A 的速度大于B 的速度,它们间的距离逐渐变大,当B 的速度加速到大于A 的速度后,它们间的距离又逐渐变小;A 、B 间距离有最大值的临界条件是υA =υB . ① 设两物体经历时间t 相距最远,则υA =at ② 把已知数据代入①②两式联立得t =5 s 在时间t 内,A 、B 两物体前进的距离分别为 s A =υA t =10×5 m=50 ms B =12at 2=12×2×52m =25 mA 、B 再次相遇前两物体间的最大距离为 Δs m =s A -s B =50 m -25 m =25 m 【解析二】 相对运动法因为本题求解的是A 、B 间的最大距离,所以可利用相对运动求解.选B 为参考系,则A 相对B 的初速度、末速度、加速度分别是υ0=10 m/s 、υt =υA -υB =0、a =-2 m/s 2. 根据υt 2-υ0=2as .有0-102=2×(-2)×s AB 解得A、B 间的最大距离为s AB =25 m . 【解析三】 极值法物体A 、B 的位移随时间变化规律分别是s A =10t ,s B =12at 2=12×2×t 2 =t 5.则A 、B 间的距离Δs =10t -t 2,可见,Δs 有最大值,且最大值为Δs m =4×(-1)×0-1024×(-1) m =25 m【解析四】 图象法根据题意作出A 、B 两物体的υ-t 图象,如图1-5-1所示.由图可知,A 、B 再次相遇前它们之间距离有最大值的临界条件是υA =υB ,得t 1=5 s . A 、B 间距离的最大值数值上等于ΔOυA P 的面积,即Δs m =12×5×10 m=25 m .【答案】25 m【点拨】相遇问题的常用方法(1)物理分析法:抓好“两物体能否同时到达空间某位置”这一关键,按(解法一)中的思路分析.(2)相对运动法:巧妙地选取参考系,然后找两物体的运动关系.(3)极值法:设相遇时间为t ,根据条件列方程,得到关于t 的一元二次方程,用判别式进行讨论,若△>0,即有两个解,说明可以相遇两次;若△=0,说明刚好追上或相碰;若△<0,说明追不上或不能相碰.(4)图象法:将两者的速度时间图象在同一个坐标系中画出,然后利用图象求解. 拓展如图1-5-2所示是甲、乙两物体从同一地点,沿同一方向做直线运动的υ-t 图象,由图象可以看出 ( 〕A .这两个物体两次相遇的时刻分别是1s 末和4s 末B .这两个物体两次相遇的时刻分别是2s 末和6s 末C .两物体相距最远的时刻是2s 末D .4s 末以后甲在乙的前面【解析】从图象可知两图线相交点1s 末和4s 末是两物速度相等时刻,从0→2s,乙追赶甲到2s 末追上,从2s 开始是甲去追乙,在4s 末两物相距最远,到6s 末追上乙.故选B . 【答案】B【实战演练1】(2011·新课标全国卷)甲乙两辆汽车都从静止出发做加速直线运动,加速度方向一直不变。
相遇与追击知识点总结

相遇与追击知识点总结1. 基本概念相遇与追击中的基本概念主要包括相遇的条件和追击的方式。
相遇的条件通常有两种,一种是两个物体在相同的时间和地点相遇;另一种是两个物体在不同的时间但在同一条路径上相遇。
而追击包括追击角度、速度和距离等概念。
追击角度指的是两个物体在追击的过程中夹角的大小,速度指的是两个物体在运动中的速度,距离指的是两个物体之间的距离。
2. 运动规律在相遇与追击中,我们需要掌握一些运动规律,包括运动的基本公式、匀速直线运动、加速直线运动、圆周运动等等。
这些基本的运动规律能够帮助我们更好地理解相遇与追击的过程,能够用来计算和预测物体的运动轨迹,找出物体相遇的条件和方式。
3. 实际应用相遇与追击并不是一种抽象的物理现象,它在现实生活中有着许多应用。
比如在航空领域中,飞机的追击和相遇问题经常会出现,这需要考虑到飞机的速度、风速、飞行轨迹等因素。
在车辆追击和相遇中,汽车的速度、路程、时间等因素也需要被考虑。
另外,在天文学领域中,行星、卫星、彗星等天体相互追击的情况也是需要被研究和分析的。
4. 经典问题解答在相遇与追击中,有一些经典问题是非常值得我们去思考和解答的。
比如在地理学中的两船追逐问题、在足球比赛中球员的追击问题、在天文学中行星的相遇问题等等。
这些经典问题涉及到了相遇与追击的各种因素,通过解答这些问题,可以更好地理解相遇与追击的知识点,并且能够培养我们的分析和解决问题的能力。
总结来说,相遇与追击是一个涉及到物理学、数学、天文学等多个领域的现象,它包含了丰富的知识点和应用场景。
通过学习和掌握这些知识,我们不仅可以更好地理解自然界中的各种现象,还可以将其应用到实际生活中,解决一些实际问题。
希望通过本文的介绍,读者能够更加深入地了解相遇与追击的知识,能够从中受益,并且应用到实际生活中。
第五课时追及与相遇问题
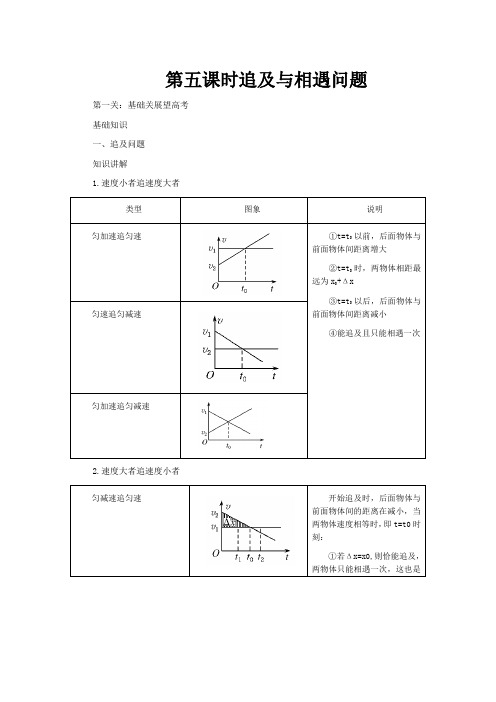
第五课时追及与相遇问题第一关:基础关展望高考基础知识一、追及问题知识讲解1.速度小者追速度大者前面物体间距离增大远为前面物体间距离减小2.速度大者追速度小者前面物体间的距离在减小,当两物体速度相等时,刻:两物体只能相遇一次,这也是避免相撞的临界条件此时两物体最小距离为设一次相遇,二次相遇说明:①表中的Δx是开始追及以后,后面物体因速度大而比前面物体多运动的位移;②x0是开始追及以前两物体之间的距离;③t2-t0=t0-t1;④v1是前面物体的速度,v2是后面物体的速度.三、追及,相遇问题的处理方法技法讲解方法1:临界条件法(物理法):当追者与被追者到达同一位置,两者速度相同,则恰能追上或恰追不上(也是二者避免碰撞的临界条件)方法2:判断法(数学方法):若追者甲和被追者乙最初相距d0令两者在t时相遇,则有x甲-x乙=d0,得到关于时间t的一元二次方程:当Δ=b2-4ac>0时,两者相撞或相遇两次;当Δ=b2-4ac=0时,两者恰好相遇或相撞;Δ=b2-4ac<0时,两者不会相撞或相遇.方法3:图象法.典例剖析典例一辆汽车在十字路口等待绿灯,当绿灯亮时汽车以3m/s2的加速度开始行驶,恰在这时一辆自行车以6m/s的速度匀速驶来,从后边超过汽车.试问:汽车从路口开动后,在赶上自行车之前经过多长时间两车相距最远?此时距离是多少?解析:方法一:函数法当运行时间为t 时,两车相距的距离 当,有极值Δx=6m.(其中字母A 、B 分别是二次函数中二次项、一次项的系数)方法二:方程法当运行时间为t 时,两车相距的距离当判别式Δ≥0时方程有实数解,即Δx ≤6m,当且仅当等式成立时有极值.取Δx=6m 时相距最远,有6t+6=0,得t=2s. 方法三:物理分析法当两车的速度相等时,两车间的距离最大,则at=6m/s,t=2s. Δx=6t-=6m 方法四:图象法画出v —t 图象,如图所示.经分析得两车的速度相等时,两车间的距离最大,则,解得t=2s,Δx=6m. 答案:2s6m第三关:训练关笑对高考 随堂训练1.汽车甲沿着平直的公路以速度v 0匀速行驶.当它路过某处的同时,该处有一辆汽车乙从静止开始匀加速去追赶甲车.根据上述已知条件()A.可求出乙车追上甲车时乙车的速度B.可求出乙车追上甲车时乙车的路程C.可求出乙车从开始起到追上甲车所用的时间D.不能求出上述三者中的任何一个2.如图所示,公路上一辆汽车以v 1=10m/s 的速度匀速行驶,汽车行至A 点时,一人为搭车,从距公路30m 的C 处开始以v 2=3m/s 的速度正对公路匀速跑去,司机见状途中刹车,汽车做匀22013x v t at 6t t .22∆=-=-Bt 2s 2A=-=时2220133x v t at 6t t ,t 6t x 0.222∆=-=--+∆=则23t 2-23t 22236m /s 3m /s t,x 6t t 2=∆=-减速运动,结果人到达B 点时,车也恰好在B 点.已知AB=80m,求:(1)汽车在距A 多远处开始刹车? (2)刹车后汽车的加速度有多大?3.一辆客车以v 1的速度前进,司机发现前面在同一轨道上有辆货车正在以v 2匀速前进,且v 2<v 1,货车车尾与客车车头距离为s ,客车立即刹车,做匀减速运动,而货车仍保持原速度前进.求客车的加速度符合什么条件时,客车与货车不会相撞?5.一辆值勤的警车停在公路边,当警员发现从他旁边以10m/s 的速度匀速行驶的货车严重超载时,决定前去追赶,经过5.5s 后警车发动起来,并以2.5m/s 2的加速度做匀加速运动,但警车的行驶速度必须控制在90km/h 以内.(1)警车在追赶货车的过程中,两车间的最大距离是多少? (2)判定警车在加速阶段能否追上货车.(要求通过计算说明) (3)警车发动后要多长时间才能追上货车? 课时作业十追及与相遇问题 1.甲乙两车在公路上沿同一方向做直线运动,它们的v-t 图象如图所示.两图象在t=t1时相交于P 点,P 在横轴上的投影为Q ,△OPQ 的面积为S.在t=0时刻,乙车在甲车前面,相距为d.已知此后两车相遇两次,且第一次相遇的时刻为t ′,则下面四组t ′和d 的组合可能的是()A.t ′=t 1,d=SB.t ′=t 1,d=S C.t ′=t 1,d=S D.t ′=t 1,d=S 2.两辆游戏赛车a 、b 在两条平行的直车道上行驶.t=0时两车都在同一计时线处,此时比赛开始.它们在四次比赛中的v-t 图象如图所示.哪些图对应的比赛中,有一辆赛车追上了另一辆()1214121212343.甲、乙两辆汽车在平直的公路上沿同一方向做直线运动,t=0时刻同时经过公路旁的同一个路标.在描述两车运动的v-t图中(如图),直线a、b分别描述了甲、乙两车在0~20s的运动情况.关于两车之间的位置关系,下列说法正确的是()A.在0~10s内两车逐渐靠近B.在10~20s内两车逐渐远离C.在5~15s内两车的位移相等D.在t=10s时两车在公路上相遇4.两辆完全相同的汽车,沿水平直线一前一后匀速行驶,速度均为v0,若前车突然以恒定的加速度刹车,在它刚停住后,后车以前车刹车的加速度开始刹车,已知前车在刹车过程中所行的距离为s,若要保证两辆车在上述情况中不相撞,则两车在匀速行驶时保持的距离至少应为()A.1sB.2sC.3sD.4s5.汽车甲沿着平直的公路以速度v0做匀速直线运动,当它路过某处的同时,汽车乙从此处开始以加速度a做初速度为零的匀加速直线运动去追赶汽车甲,根据上述已知条件()A.可求出乙车追上甲车时,乙车的速度B.可求出乙车追上甲车时,乙车走的路程C.可求出乙车从开始运动到追上甲车时,乙车运动的时间D.不能求出上述三者中任何一个6.A、B两辆汽车在平直公路上朝同一方向运动,如图所示为两车运动的v-t图象.下面对阴影部分的说法正确的是()A.若两车从同一点出发,它表示两车再次相遇前的最大距离B.若两车从同一点出发,它表示两车再次相遇前的最小距离C.若两车从同一点出发,它表示两车再次相遇时离出发点的距离D.表示两车出发时相隔的距离7.甲、乙两物体同时开始运动,它们的x-t图象如图所示,下面说法正确的是()A.乙物体做曲线运动B.甲、乙两物体从同一地点出发C.当甲、乙两物体两次相遇时,二者的速度大小不相等D.当甲、乙两物体速度相同时,二者之间的距离最大8.如图所示是两个由同一地点出发,沿同一直线向同一方向运动的物体A和B的速度图象.运动过程中A、B的情况是()A.A的速度一直比B大,B没有追上AB.B的速度一直比A大,B追上AC.A在t1s后改做匀速直线运动,在t2s时追上AD.在t2s时,A、B的瞬时速度相等,A在B的前面,尚未被B追上,但此后总是要被追上的9.在十字路口,汽车以0.5m/s2的加速度从停车线起动做匀加速直线运动时,恰有一辆自行车以5m/s的速度匀速驶过停车线与汽车同方向行驶,求:(1)什么时候它们相距最远;最大距离是多少;(2)在什么地方汽车追上自行车;追到时汽车速度是多少.10.汽车以25m/s的速度匀速直线行驶,在它后面有一辆摩托车,当两车相距1000m时,摩托车从静止开始起动追赶汽车,摩托车的最大速度达30m/s ,若使摩托车在4min 时刚好追上汽车,求摩托车的加速度应该是多少.答案:A解析:甲做匀速运动,乙做匀加速运动,速度越来越大,甲、乙同时异地运动,当t=t 1时,乙的位移为s ,甲的位移为2s 且v 甲=v 乙,若两者第一次相遇在t ′=t 1时,则d+s=2s 可得d=s.不过不会出现第二次相遇,所以A 错误.若两者第一次相遇在t ′=t 1时,则乙的位移为s ,甲的位移为s ,由d+s=s 可得d=s ,所以D 正确,B 、C 错误. 答案:D解析:(1)人,车到达B 点所用时间,设汽车匀速运动时间为t 1,解得t 1=6s汽车刹车处离A 点距离L=v 1t 1=60m. (2)刹车加速度方向与v 1反向. 答案:(1)60m(2)2.5m/s 2解析:解法一:设客车的加速度大小为a 时,刚好能撞上货车,所用时间为t,则 s 货车=v 2ts 客车=v 1t-at 2① 当客车刚与货车相撞时,客车速度:v 2=v 1-at 则而s=s 客车-s 货车=(v 1-v 2)t-at 2③ ②式代入③式中得 121414342CB 30t s 10s v 3===()1111v x v t t t 2=+-22120v 10a m /s 2.5m /s ,t 4-==-=-121212v v v v att a-=+=②12()()()222121212min v v v v 1s v v a a a 22s--=--=故得可见只要客车刹车后的加速度就可避免两车相撞.解法二:以货车为参照物,以客车为研究对象,客车的初速度为v1-v2,加速度为a,方向与初速度的方向反向,做类似于竖直上抛方式的匀减速运动.那么客车不与货车相撞的条件是,客车对货车的最大相对位移应小于s.解析:(1)警车在追赶货车的过程中,当两车速度相等时,它们的距离最大,设警车发动后经过t1时间两车的速度相等,则t 1=v 货a=4s4s 内两车的位移分别为x 货=(t 0+t 1)×v 货=(5.5+4)×10m=95m x 警=×2.5×42m=20m 所以两车间的最大距离Δx=x 货-x 警=75m.(2)v m =90km/h=25m/s,当警车刚达到最大速度时,运动时间 x 货1=(t 0+t 2)×v 货=(5.5+10)×10m=155m x 警1=×2.5×102m=125m 因为x 货1>x 警1,故此时警车尚未追上货车. (3)警车刚达到最大速度时两车距离 Δx 1=x 货1-x 警1=30m警车达到最大速度后做匀速运动,设再经过Δt 时间追赶上货车,以货车为参考系,则所以警车发动后要经过t=t 2+Δt=12s 才能追上货车. 答案:(1)75m(2)不能(3)12s解析:由v-t 图象的特点可知,图线与t 轴所围面积的大小,即为物体位移的大小.观察4个图象,只有A 、C 选项中,a 、b 所围面积的大小有相等的时刻,故选项A 、C 正确.答案:AC解析:由题图知乙做匀减速运动,初速度v 乙=10m/s ,加速度大小a 乙=0.5m/s 2;甲做匀速()212v v a 2s->()()221212v v v v s a 2a2s--<>故得2111at 22=m 2v 25t s 10s a 2.5===2211at 22=1m x t 2s v v ∆∆==-货直线运动,速度v 甲=5m/s.当t=10s 时v 甲=v 乙,甲、乙两车距离最大,所以0~10s 内两车越来越远,10~15s 内两车距离越来越小,t=20s 时,两车距离为零,再次相遇.故A 、B 、D 错误.因5~15s 时间内v 甲=乙,所以两车位移相等,故C 正确.答案:C解析:前车刹车的位移,后车在前车刹车过程中匀速行驶的位移s 1=v 0t , ,后车刹车的位移,后车的总位移s ′=s 1+s 2==3s,所以两车在匀速行驶时保持的距离至少为Δs=s ′-s=2s.答案:B解析:当两车相遇时,对甲车有:s=v 0t ,对乙车有:s=12at2,所以可以求出乙车追上甲车的时间,并求出乙车追上甲车时乙车的路程,B 、C 正确;对乙车:v=at,所以可以求出乙车此时的速度,A 正确.答案:ABC解析:在v-t 图象中,图象与时间轴所包围的图形的面积表示位移,两条线的交点为二者速度相等的时刻,若两车从同一点出发,则题图中阴影部分的面积就表示两车再次相遇前的最大距离,故A 正确.答案:A解析:乙物体的位移图是曲线,并不代表做曲线运动,A 错.甲从参考原点出发,乙从x 0出发,B 错.甲、乙两图线相交代表相遇,此时斜率不同,即速度大小不等,C 对.乙超甲后,两物体距离越来越大,D 错.答案:C 8. 答案:D9. 解析:(1)初始阶段,自行车速度大于汽车速度,只要汽车速度小于自行车速度,两车距离总是在不断增大.当汽车速度增大到大于自行车速度时,两车距离逐渐减小,所以两车速度相等时,距离最大.(1)设自行车速度为v ,汽车加速度为a ,经时间t 两车相距最远.则v=at ,所以t=最大距离(2)若经过时间t ′,汽车追上自行车,则vt ′=at ′2v 20s v 2a =2001v v t s a a==且,202v s 2a =23v 2av a 221515s vt at 50.525m 20.520.5⎛⎫∆=-=⨯-⨯⨯= ⎪⎝⎭12解得 追上自行车时汽车的速度v ′=at ′=0.5×20=10m/s.10.解析:汽车在4min 内的位移s 汽=v 汽t=25×240=6000m摩托车要追上汽车,应有的位移s 摩=s 汽+s 0=6000+1000=7000m若摩托车在4min 内一直加速行驶,由 在4min 末速度可达v t =at=0.243×240=58.3m/s >30m/s所以摩托车应是先加速,待达到最大速度时,再做匀速运动.设摩托车加速运动的时间为t ′,匀速运动的时间为t-t ′,s 摩=at ′2+v m (t-t ′)①v m =at ′② 由②得t ′=③ ③代入①,整理得 2v 25t 20s a 0.5⨯'===22222s 127000s at a 0.243m /s 2t 240⨯====摩摩,得12vm a 222m m v 30a 2.25m /s .2(v t s )2(302407000)===-⨯⨯-摩。
《追及与相遇问题》 知识清单

《追及与相遇问题》知识清单一、追及与相遇问题的概念追及问题,简单来说,就是两个物体在同一直线上运动时,速度快的物体追赶速度慢的物体的过程。
而相遇问题,则是两个物体相向运动,最终在某一时刻在同一位置相遇的情况。
在实际生活中,追及与相遇问题的例子随处可见。
比如警察追捕罪犯、汽车超车、两艘船在海上相向行驶最终相遇等等。
二、追及与相遇问题的基本公式1、速度差×追及时间=路程差这是追及问题中最基本的公式。
速度差指的是两个物体速度的差值,追及时间是从开始追及到追上所用的时间,路程差则是开始追及时两个物体之间的距离。
2、速度和×相遇时间=总路程在相遇问题中,速度和是两个物体速度相加的结果,相遇时间是从出发到相遇所用的时间,总路程就是两个物体一开始相距的距离。
三、追及问题的常见类型1、同地不同时出发比如A 物体先出发一段时间t1,B 物体后出发去追A 物体。
这时,A 物体先走的路程就是 vA×t1,然后两者的路程差就是这个值,再根据速度差来计算追及时间。
2、同时不同地出发A、B 两物体同时出发,但出发地点不同,两者之间存在初始距离 s。
这时,路程差就是这个初始距离 s,同样根据速度差来计算追及时间。
四、相遇问题的常见类型1、相向而行两个物体从两地同时出发,面对面地相向而行,最终相遇。
2、同向而行且中途相遇这种情况比较特殊,比如 A、B 两物体同向而行,A 物体速度较慢在前,B 物体速度较快在后,在一段时间后 B 追上 A 并超过,然后又在前方的某一点相遇。
五、解决追及与相遇问题的关键步骤1、认真审题仔细分析题目中给出的条件,确定是追及问题还是相遇问题,以及物体的运动状态、初始条件等。
2、选择合适的公式根据题目类型和已知条件,选择相应的追及或相遇公式。
3、画出示意图有时候,通过画出物体运动的示意图,可以更直观地理解问题,找出各个量之间的关系。
4、列方程求解将已知量和未知量代入公式,列出方程,然后求解方程得到答案。
追及与相遇问题公式

追及与相遇问题公式摘要:1.追及问题的基本概念2.相遇问题的基本概念3.追及与相遇问题的公式4.实例解析5.结论与启示正文:在我们日常生活中,追及与相遇问题常常出现在交通、竞赛等领域。
为了更好地理解和解决这类问题,我们可以通过数学公式来描述和分析。
一、追及问题的基本概念追及问题是指在一定时间内,一个物体在另一个物体前不断追赶的过程。
我们可以用以下公式来表示:设物体A的速度为v1,物体B的速度为v2,两物体之间的距离为d,追及所需时间为t。
则有:d = v1 * t 和d = v2 * t二、相遇问题的基本概念相遇问题是指在一定时间内,两个物体在运动过程中相遇的次数。
我们可以用以下公式来表示:设物体A的速度为v1,物体B的速度为v2,两物体之间的距离为d,相遇所需时间为t。
则有:d = v1 * t + v2 * t三、追及与相遇问题的公式通过以上两个基本概念,我们可以得到追及与相遇问题的通用公式:设物体A的速度为v1,物体B的速度为v2,两物体之间的距离为d,追及或相遇所需时间为t。
则有:d = (v1 + v2) * t四、实例解析以两个人跑步比赛为例,设甲、乙两人的速度分别为v1和v2,比赛时间为t。
假设他们在比赛开始时相距d0,我们需要求出比赛结束时他们的距离。
根据公式,我们有:d = (v1 + v2) * t五、结论与启示通过以上分析,我们可以发现追及与相遇问题实际上是一个线性方程求解的问题。
在解决这类问题时,我们需要关注物体的速度、时间和距离三个要素,利用公式进行计算。
同时,我们还可以将这类问题应用到日常生活和工作中,提高解决实际问题的能力。
总之,掌握追及与相遇问题的基本概念和公式,能够帮助我们更好地理解这类问题,并运用到实际生活中。
相遇和追及问题

www. 小学奥数知识讲座(一)相遇和追及问题知识要点:行程问题是研究物体运动的,它研究的是物体速度·时间·路程三者之间的关系。
相遇和追及是行程问题中常见的类型。
解决行程问题的关键是要确定运动过程中的位置和方向。
基本公式是:1.行程问题:速度和×相遇时间=相遇路程。
2.追击问题:追及时间=路程差÷速度差典型例题:例1. 小张和小明同时从各自的家中出发,小明每分钟走100米,小张每分钟走80米,15分钟两人相遇,小明的家距小张的家多少米?分析与解:解法一:可以根据公式“速度和×相遇时间=相遇路程”直接求出小明家与小张家的距离。
(100+80)×15=180×15=2700(米)解法二:小明家与小张家的距离由小明和小张走的路程组成,所以可以求出他们两人所走路程的和就是两家的距离。
100×15+80×15=1500+1200=2700(米)练一练1.甲乙两站间的铁路长840千米,两列火车同时从两站相对开出,甲车每小时行50千米,乙车每小时行70千米,两车开出几小时还相距240千米?例2. 甲·乙两人同时从两地出发,相向而行,距离是100千米。
甲每小时行6千米,乙每小时行4千米。
甲带着一只狗,狗每小时行9千米。
这只狗同甲一道出发,碰到乙的时候,它就掉头朝甲这边走,碰到乙是又往乙那边走,直到两人相遇时,这只狗一共走了多少千米?分析与解:从条件看,狗多次与甲·乙相遇,每次走的路程不相同,要求狗一共走了多少千米,如果把每次走的路程加起来,比较复杂。
但我们可以反过来想,从甲·乙同时出发到相遇的过程中,狗在不停地跑,只要算出狗跑了多长时间,就可以求出狗跑了多少千米,而狗跑的时间与甲·乙的相遇时间是相同的。
甲·乙的相遇时间:100÷(6+4)=100÷10=10(时)狗一共走的路程:9×10=90(千米)练一练2.甲·乙两队学生从相距18千米的两地同时出发,相向而行。
知识讲解_相遇和追及问题(基础)(2)

相遇和追及问题编稿:周军审稿:吴楠楠【学习目标】1、掌握追及及相遇问题的特点;2、能熟练解决追及及相遇问题。
【要点梳理】要点一、机动车的行驶安全问题:要点诠释:1、反应时间:人从发现情况到采取相应措施经过的时间为反应时间。
2、反应距离:在反应时间内机动车仍然以原来的速度v匀速行驶的距离。
3、刹车距离:从刹车开始,到机动车完全停下来,做匀减速运动所通过的距离。
4、停车距离与安全距离:反应距离和刹车距离之和为停车距离。
停车距离的长短由反应距离和刹车距离共同决定。
安全距离大于一定情况下的停车距离。
要点二、追及与相遇问题的概述要点诠释:1、追及与相遇问题的成因:当两个物体在同一直线上运动时,由于两物体的运动情况不同,所以两物体之间的距离会不断发生变化,两物体间距越来越大或越来越小,这时就会涉及追及、相遇或避免碰撞等问题.2、追及问题的两类情况(1)速度小者追速度大者(2)速度大者追速度小者说明:①表中的Δx 是开始追及以后,后面物体因速度大而比前面物体多运动的位移; ②x 0是开始追及以前两物体之间的距离; ③t 2-t 0=t 0-t 1;④v 1是前面物体的速度,v 2是后面物体的速度. 特点归类:(1)若后者能追上前者,则追上时,两者处于同一位置,后者的速度一定不小于前者的速度. (2)若后者追不上前者,则当后者的速度与前者相等时,两者相距最近. 3、 相遇问题的常见情况(1) 同向运动的两物体的相遇问题,即追及问题.(2) 相向运动的物体,当各自移动的位移大小之和等于开始时两物体的距离时相遇.解此类问题首先应注意先画示意图,标明数值及物理量;然后注意当被追赶的物体做匀减速运动时,还要注意该物体是否停止运动了.要点三、追及、相遇问题的解题思路 要点诠释:追及、相遇问题最基本的特征相同,都是在运动过程中两物体处在同一位置. ①根据对两物体运动过程的分析,画出物体运动情况的示意草图.②根据两物体的运动性质,分别列出两个物体的位移方程,注意要将两个物体运动时间的关系反映在方程中;③根据运动草图,结合实际运动情况,找出两个物体的位移关系; ④将以上方程联立为方程组求解,必要时,要对结果进行分析讨论. 要点四、分析追及相遇问题应注意的两个问题 要点诠释:分析这类问题应注意的两个问题:(1)一个条件:即两个物体的速度所满足的临界条件,例如两个物体距离最大或距离最小、后面的物体恰好追上前面的物体或恰好追不上前面的物体等情况下,速度所满足的条件.常见的情形有三种:一是做初速度为零的匀加速直线运动的物体甲,追赶同方向的做匀速直线运动的物体乙,这种情况一定能追上,在追上之前,两物体的速度相等(即v v =甲乙)时,两者之间的距离最大;二是做匀速直线运动的物体甲,追赶同方向的做匀加速直线运动的物体乙,这种情况不一定能追上,若能追上,则在相遇位置满足v v ≥甲乙;若追不上,则两者之间有个最小距离,当两物体的速度相等时,距离最小;三是做匀减速直线运动的物体追赶做匀速直线运动的物体,情况和第二种情况相似.(2)两个关系:即两个运动物体的时间关系和位移关系.其中通过画草图找到两个物体位移之间的数值关系是解决问题的突破口.要点五、追及、相遇问题的处理方法方法一:临界条件法(物理法):当追者与被追者到达同一位置,两者速度相同,则恰能追上或恰追不上(也是二者避免碰撞的临界条件)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
速直线运动的物体甲,追赶同方向的做匀加速直线运动的物体乙,这种情况不一定能追上,若能追上,则在
相遇位置满足 v甲 v乙;若追不上,则两者之间有个最小距离,当两物体的速度相等时,距离最小;三是做匀
所以饮酒的驾驶员从发现情况到汽车停止所需时间
t=t2+t3 解得 t=5.25 s
类型二、追及问题一:速度小者追赶同向速度大者 例 2、一辆汽车在十字路口等候绿灯,当绿灯亮时汽车以 3m/s2 的加速度开始加速行驶,恰在这时一辆自 行车以 6m/s 的速度匀速驶来,从后边超过汽车。试求:(1)汽车从路口开动后,在追上自行车之前经过 多长时间两车相距最远?此时距离是多少?
所以两车至少相距 s = s1 + s2 = 156m 。
【点评】刹车问题实际上是匀变速直线运动的有关规律在减速情况下的具体应用,要解决此类问题,首先 要搞清楚在反应时间里汽车仍然做匀速直线;其次也要清楚汽车做减速运动,加速度为负值;最后要注意 单位统一。 举一反三
【变式】酒后驾车严重威胁交通安全.其主要原因是饮酒会使人的反应时间(从发现情况到实施操作制动
方法二:判断法(数学方法):若追者甲和被追者乙最初相距 d0 令两者在 t 时相遇,则有 x甲 − x乙 = d0 ,得到关
于时间 t 的一元二次方程:当 = b2 − 4ac 0 时,两者相撞或相遇两次;当 = b2 − 4ac = 0 时,两者恰好
相遇或相撞; = b2 − 4ac 0 时,两者不会相撞或相遇。
【解析】(1)乙车追上甲车时,二者位移相同,设甲车位移为 x1,乙车位移为 x2,则 x1=x2,即 v1t1=12 at12 , 解得 t1=10 s,v2=at1=20 m / s ,因此 v2=2v1 .
(2)设追上前二者之间的距离为 x ,则 Δx=x1-x2=v1t2-12 at22 =10t2-t 由数学知识知:当 t2=2101s = 5s 时,两者相距最远,此时 v2=v1 .
于图线Ⅱ与时间轴围成的三角形的面积。两车之间的距离则等于图中矩形的面积与三角形面积的差,不难
学海无涯
看出,当 t=t0 时矩形与三角形的面积之差最大。 v/m/s Ⅱ
6Ⅰ
0
t0
t/s
此时 v汽 = at0 = v自
t0
=
v自 a
=
6 3
s
=
2s
Sm
=
1 2
t0
v自
=
1 2
2 6m
=
6m
方法三:二次函数极值法
的时间)变长,造成制动距离(从发现情况到汽车停止的距离)变长,假定汽车以 108 km/h 的速度匀速行驶, 刹车时汽车的加速度大小为 8 m/s2,正常人的反应时间为 0.5 s,饮酒人的反应时间为 1.5 s,试问:
(1)驾驶员饮酒后的反制距离比正常时多几米? (2)饮酒的驾驶员从发现情况到汽车停止需多少时间? 【答案】 (1)30 m (2)5.25 s 【解析】 (1)汽车匀速行驶 v=108 km/h=30 m/s
【答案】98m 24.5m
学海无涯
【变式 2】甲、乙两车同时从同一地点出发,向同一方向运动,其中甲以 10 m/s 的速度匀速行驶,乙以 2 m/s2 的加速度由静止启动,求:
(1)经多长时间乙车追上甲车?此时甲、乙两车速度有何关系? (2)追上前经多长时间两者相距最远?此时二者的速度有何关系? 【答案】(1)10 s 2 倍 (2)5 s 相等
v汽 = at = v自
∴ t = v自 = 6 s = 2s a3
x m
=
x自 −
x汽 =
v自t
− 1 at2 2
= 6 2m
− 1 3 22m 2
= 6m
方法二:图象法
在同一个 v-t 图象中画出自行车和汽车的速度-时间图线,如图所示。其中Ⅰ表示自行车的速度图线,
Ⅱ表示汽车的速度图线,自行车的位移 x自等于图线Ⅰ与时间轴围成的矩形的面积,而汽车的位移 x汽 则等
设经过时间 t 汽车和自行车之间的距离 x ,则
x
=
x自 −
x汽
=
v自t
−
1 2
at 2
=
6t
−
3 2
t2
=
−
3 2
(t
−
2)2
+
6
当 t = 2s 时两车之间的距离有最大值 xm ,且 xm = 6m.
【点评】(1)在解决追及相遇类问题时,要紧抓“一图三式”,即:过程示意图,时间关系式、速度关系式
【解析】方法一:设两车恰好相撞(或不相撞),所用时间为 t,此时两车速度相等
v1 t
+
1 2
at 2
=
v2t
+
s
v1 + at = v2
解之可得: a = (v2 − v1)2 2s
即,当 a (v2 − v1)2 时,两车不会相撞。 2s
方法二:要使两车不相撞,其位移关系应为:
v1 t
+
1 2
at 2
学海无涯
举一反三 【高清课程:相遇和追及问题例 3】 【变式】汽车正以 10m/s 的速度在平直公路上前进,突然发现正前方 s 处有一辆自行车以 4m/s 的速度做 同方向的匀速直线运动,汽车立即关闭油门做匀减速运动,加速度大小为 6m/s2,若汽车恰好不碰上自行 车,则 s 大小为多少? 【答案】3m 类型四、相遇问题
【思路点拨】画好汽车和自行车的运动示意图是关键。 【答案】2s 6m 【解析】: 方法一:临界状态法
运动示意图如图:
x汽
△x
x自
汽车在追击自行车的过程中,由于汽车的速度小于自行车的速度,汽车与自行车之间的距离越来越大; 当汽车的速度大于自行车的速度以后,汽车与自行车之间的距离便开始缩小。很显然,当汽车的速度与自 行车的速度相等时,两车之间的距离最大。设经时间 t 两车之间的距离最大。则
例 4、在某市区内,一辆小汽车在公路上以速度 vA 向东行驶,一位观光游客正由南向北从斑马线上横过马 路。汽车司机发现游客途经 D 处时,经过 0.7s 作出反应紧急刹车,但仍将正步行至 B 处的游客撞伤,该 汽车最终在 C 处停下,如图所示。为了判断汽车司机是否超速行驶以及游客横穿马路的速度是否过快,警 方派一车胎磨损情况与肇事汽车相当的警车以法定最高速度 vm=14.0m / s 行驶在同一马路的同一地段,在
v2t
+
s
对任一时间 t,不等式都成立的条件为 =(v2 − v1)2 − 2as 0
由此得 a (v2 − v1)2 2s
【点评】分析解决两物体的追及、相遇类问题,应首先在理解题意的基础上,认清两物体在位移、速度、 时间等方面的关联,必要时须画出运动关联的示意图。这类问题的特殊之处是常与极值条件或临界条件相 联系。分析解决这类问题的方法有多种,无论哪一种方法,分析临界条件、解决相关的临界条件方程或用 数学方法找出相关的临界值,是解决这类问题的关键和突破口。
学海无涯 相遇和追及问题 【学习目标】 1、掌握追及及相遇问题的特点; 2、能熟练解决追及及相遇问题。 【要点梳理】 要点一、机动车的行驶安全问题: 要点诠释: 1、 反应时间:人从发现情况到采取相应措施经过的时间为反应时间。 2、 反应距离:在反应时间内机动车仍然以原来的速度 v 匀速行驶的距离。 3、 刹车距离:从刹车开始,到机动车完全停下来,做匀减速运动所通过的距离。 4、 停车距离与安全距离:反应距离和刹车距离之和为停车距离。停车距离的长短由反应距离和刹车距离 共同决定。安全距离大于一定情况下的停车距离。 要点二、追及与相遇问题的概述 要点诠释: 1、 追及与相遇问题的成因: 当两个物体在同一直线上运动时,由于两物体的运动情况不同,所以两物体之间的距离会不断发生变 化,两物体间距越来越大或越来越小,这时就会涉及追及、相遇或避免碰撞等问题. 2、 追及问题的两类情况 (1)速度小者追速度大者
方法三:图象法.利用速度时间图像可以直观形象的描述两物体的运动情况,通过分析图像,可以较方便的 解决这类问题。 【典型例题】 类型一、机动车的行驶安全问题 例 1、为了安全,在高速公路上行驶的汽车之间应保持必要的距离。已知某高速公路的最高限速为 v=120km/h。假设前方车辆突然停止运动,后面汽车的司机从眼睛发现这一情况,经过大脑反应,指挥手、 脚操纵汽车刹车,到汽车真正开始减速,所经历的时间需要 0.50s(即反应时间),刹车时汽车所受阻力是 车重的 0.40 倍,为了避免发生追尾事故,在该高速公路上行驶的汽车之间至少应保留多大的距离?
【思路点拨】理解各个时间段汽车的运动情况是关键。 【答案】156m
【解析】 v =120km / h = 33.3m / s 匀减速过程的加速度大小为 a = kmg / m = 4m / s2 。
匀速阶段的位移 s1 = vt1 = 16.7m ,
减速阶段的位移 s2 = v2 / 2a = 139m ,
类型三、追及问题二:速度大者减速追赶同向速度小者
例 3、火车以速度 v1 匀速行驶,司机发现前方同轨道上相距 S 处有另一列火车沿同方向以速度 v2 (对地、
且 v1 v2 )做匀速运动,司机立即以加速度 a 紧急刹车,要使两车不相撞, a 应满足什么条件?
【思路点拨】理解两车不相撞的临界条件。
【答案】 a (v2 − v1)2 2s
(2)速度大者追速度小者
学海无涯
说明:①表中的 Δx 是开始追及以后,后面物体因速度大而比前面物体多运动的位移; ②x0 是开始追及以前两物体之间的距离; ③t2-t0=t0-t1; ④v1 是前面物体的速度,v2 是后面物体的速度. 特点归类: (1)若后者能追上前者,则追上时,两者处于同一位置,后者的速度一定不小于前者的速度. (2)若后者追不上前者,则当后者的速度与前者相等时,两者相距最近. 3、 相遇问题的常见情况 (1) 同向运动的两物体的相遇问题,即追及问题. (2) 相向运动的物体,当各自移动的位移大小之和等于开始时两物体的距离时相遇. 解此类问题首先应注意先画示意图,标明数值及物理量;然后注意当被追赶的物体做匀减速运动时,还要注 意该物体是否停止运动了. 要点三、追及、相遇问题的解题思路 要点诠释: 追及、相遇问题最基本的特征相同,都是在运动过程中两物体处在同一位置. ①根据对两物体运动过程的分析,画出物体运动情况的示意草图. ②根据两物体的运动性质,分别列出两个物体的位移方程,注意要将两个物体运动时间的关系反映在方程 中; ③根据运动草图,结合实际运动情况,找出两个物体的位移关系; ④将以上方程联立为方程组求解,必要时,要对结果进行分析讨论. 要点四、分析追及相遇问题应注意的两个问题 要点诠释: 分析这类问题应注意的两个问题: (1)一个条件:即两个物体的速度所满足的临界条件,例如两个物体距离最大或距离最小、后面的物体恰好 追上前面的物体或恰好追不上前面的物体等情况下,速度所满足的条件. 常见的情形有三种:一是做初速度为零的匀加速直线运动的物体甲,追赶同方向的做匀速直线运动的物体
