2014年苏教版选修1-2 3

合集下载

2014年江苏省普通高中学业水平测试(选修科目)说明

2014年江苏省普通高中学业水平测试（选修科目）物理科说明表2 考试内容范围及要求物理1内容要求说明1.质点参考系和坐标系I2.路程和位移速度和速率加速度Ⅱ3.匀变速直线运动自由落体运动Ⅱ4.速度随时间的变化规律（实验、探究）Ⅱ5.形变和弹力胡克定律I6.静摩擦滑动摩擦摩擦力动摩擦因数I7.力的合成和分解Ⅱ力的合成和分解计算，只限于用作图法或直角三角形知识解决8.共点力作用下物体的平衡I 只要求解决在一个平面内的共点力平衡问题9.力的平行四边形定则（实验、探究）Ⅱ10.牛顿运动定律及其应用Ⅱ加速度大小不同的连接体问题的计算仅限于两个物体的情况；11.加速度与物体质量、物体受力的关系（实验、探究）Ⅱ物理2内容要求说明12.功和功率Ⅱ13.动能动能定理Ⅱ选修3-1内容要求说明 26. 电荷电荷守恒定律 I 27. 点电荷库仑定律I 28. 静电场电场线电势能电势等势面 I29. 电场强度点电荷的场强电势差 Ⅱ电场强度的计算最多考虑两个电场的叠加 30. 匀强电场中电势差与电场强度的关系 I31. 带电粒子在匀强电场中的运动Ⅱ 只限于带电粒子进入电场时速度平行或垂直于场强的情况 32. 电容电容器 I 33. 电阻定律I 34.决定导体电阻的因素（实验、探究） Ⅱ 35. 电阻的串联与并联I 36. 电流电源的电动势和内阻 I 37. 欧姆定律闭合电路的欧姆定律Ⅱ 38.描绘小灯泡的伏安特性曲线（实验、探究） Ⅱ 39. 测量电源的电动势和内阻（实验、探究） Ⅱ 40. 电功电功率焦耳定律I14.重力势能 Ⅱ15.弹性势能I 弹性势能的表达式不作要求 16.机械能守恒定律及其应用Ⅱ 17.验证机械能守恒定律（实验、探究） Ⅱ 18.能量守恒 I 19.运动的合成与分解 Ⅱ20.抛体运动 Ⅱ 斜抛运动的计算不作要求 21.圆周运动的描述 I22.匀速圆周运动的向心力 Ⅱ 向心力的计算只限于向心力是由一条直线上的力合成的情况 23.开普勒行星运动定律 I 计算不作要求24.万有引力定律及其应用Ⅱ 地球表面附近，重力近似等于万有引力25.第一宇宙速度第二宇宙速度第三宇宙速度I定量计算只限第一宇宙速度41. 磁场磁感应强度磁感线磁通量I42. 通电直导线和通电线圈周围磁场的方向I43. 安培力Ⅱ计算限于直导线跟磁感应强度平行或垂直两种情况44. 洛仑兹力Ⅱ45. 带电粒子在匀强磁场中的运动Ⅱ计算限于速度与磁感应强度平行或垂直两种情况46. 质谱仪和回旋加速器的基本原理I选修3-2内容要求说明47. 电磁感应现象I48.感应电流的产生条件Ⅱ49. 法拉第电磁感应定律楞次定律Ⅱ限于导线方向与磁场方向、运动方向垂直的情况；有关反电动势的计算不作要求50. 互感涡流I51. 交变电流描述交变电流的物理量和图像I52. 正弦交变电流的函数表达式I53.电感和电容对交变电流的影响I54. 理想变压器Ⅱ限于单个副线圈的理想变压器55.远距离输电I56.传感器的工作原理及其应用I选修3-3内容要求说明57.分子动理论的基本观点阿伏加德罗常数I58.用油膜法估测分子的大小（实验、探究）I59.布朗运动I60.分子热运动速率的统计分布规律I61.温度和内能I62.气体压强的微观解释I63.晶体和非晶体晶体的微观结构I64.液晶I65.液体的表面张力I 对浸润和不浸润现象、毛细现象的解释不作要求66.气体实验定律I67.理想气体I68.热力学第一定律I69.能源与可持续发展I选修3-4内容要求说明70. 简谐运动简谐运动的表达式和图像I71. 单摆的周期与摆长的关系（实验、探究）I72. 受迫振动和共振I73. 机械波横波和纵波横波的图像I74. 波长、波速和频率(周期)的关系I 仅限于单一方向传播75. 波的干射和衍射I76.多普勒效应I77. 电磁波谱电磁波及其应用I78. 光的折射定律折射率I79.测定玻璃的折射率（实验、探究）I80.光的全反射光导纤维I81. 光的干涉、衍射和偏振I82.激光的特性和应用I83. 狭义相对论的基本假设狭义相对论时空观与经典时空观的区别I84.同时的相对性长度的相对性质能关系I 定量计算不作要求选修3-5内容要求说明85. 动量动量守恒定律I86.验证动量守恒定律（实验、探究）I87. 弹性碰撞和非弹性碰撞I 只限于一维碰撞的问题88.原子核式结构模型I89. 氢原子光谱原子的能级I90. 原子核的组成I91. 原子核的衰变半衰期I92.放射性同位素放射性的应用与防护I93. 核力与结合能质量亏损I94. 核反应方程I95. 裂变反应聚变反应链式反应I96.普朗克能量子假说黑体和黑体辐射97.光电效应I98.光的波粒二象性物质波I。

苏教版高三数学选修1-2电子课本课件【全册】

苏教版高三数学选修1-2电子课本课件【全册】目录
0002页 0056页 0108页 0161页 0201页 0251页 0298页
第一章统计案例 1.2回归分析 2.1合情推理与演绎推理第三章数系的扩充与复数的引入 3.2复数的四则运算第四章框图 4.2结构图
第一章统计案例
苏教版高三数学选修1-2电子课本源自件【全册】2.1合情推理与演绎推理
苏教版高三数学选修1-2电子课本课件【全册】
2.2直接证明与间接证明
苏教版高三数学选修1-2电子课本课件【全册】
第三章数系的扩充与复数的引入
苏教版高三数学选修1-2电子课本课件【全册】
3.1数系的扩充
苏教版高三数学选修1-2电子课本课件【全册】
3.2复数的四则运算
苏教版高三数学选修1-2电子课本课件【全册】
3.3复数的几何意义
苏教版高三数学选修1-2电子课本课件【全册】
第四章框图
苏教版高三数学选修1-2电子课本课件【全册】
4.1流程图
苏教版高三数学选修1-2电子课本课件【全册】
1.1独立性检验
苏教版高三数学选修1-2电子课本课件【全册】
1.2回归分析
苏教版高三数学选修1-2电子课本课件【全册】
第二章推理与证明
苏教版高三数学选修1-2电子课本课件【全册】

苏教版高中数学选修1-2 第3章 3.2 复数的四则运算学案

3.2复数的四则运算第1课时复数的加法、减法、乘法运算学习目标 1.掌握复数代数形式的加减运算.2.理解复数乘法运算法则，能进行复数的乘法运算.3.掌握共轭复数的概念及应用．知识点一复数的加减运算思考1类比多项式的加减法运算，想一想复数如何进行加减法运算？答案两个复数相加(减)就是把实部与实部、虚部与虚部分别相加(减)，即(a＋b i)±(c＋d i)＝(a±c)＋(b±d)i(a，b，c，d∈R)．思考2复数的加法满足交换律和结合律吗？答案满足．梳理(1)运算法则设z1＝a＋b i，z2＝c＋d i(a，b，c，d∈R)是任意两个复数，那么(a＋b i)＋(c＋d i)＝(a＋c)＋(b ＋d)i，(a＋b i)－(c＋d i)＝(a－c)＋(b－d)i.(2)加法运算律对任意z1，z2，z3∈C，有z1＋z2＝z2＋z1，(z1＋z2)＋z3＝z1＋(z2＋z3)．知识点二复数的乘法运算思考复数的乘法与实数的乘法有何联系与区别？答案复数的乘法类似于多项式的乘法，相当于把复数的代数形式看成关于“i”的多项式，运算过程中要把i2换成－1，然后把实部与虚部分别合并．梳理(1)复数的乘法法则设z1＝a＋b i，z2＝c＋d i(a，b，c，d∈R)，z1z2＝(a＋b i)(c＋d i)＝(ac－bd)＋(ad＋bc)i.(2)乘法运算律对于任意z1，z2，z3∈C，有知识点三共轭复数思考复数3＋4i与3－4i，a＋b i与a－b i(a，b∈R)有什么特点？答案这两组复数的特点：①实部相等，②虚部互为相反数．梳理(1)把实部相等、虚部互为相反数的两个复数叫做互为共轭复数．(2)复数z＝a＋b i(a，b∈R)的共轭复数记作z，即z＝a－b i.(3)当复数z＝a＋b i(a，b∈R)的虚部b＝0时，z＝z，也就是说，实数的共轭复数仍是它本身．1．两个实数的和、差、积仍是实数，两个虚数的和、差、积仍是虚数．(×)2．任意有限个复数的含加、减、乘法的混合运算中，应先进行乘法，再进行加、减法，有括号时先算括号内的．(√)3．两个互为共轭复数的和是实数，差是纯虚数．(×)类型一复数的加减运算例1计算：(1)(3＋5i)＋(3－4i)；(2)(－3＋2i)－(4－5i)；(3)(5－5i)＋(－2－2i)－(3＋3i)．解(1)(3＋5i)＋(3－4i)＝(3＋3)＋(5－4)i＝6＋i.(2)(－3＋2i)－(4－5i)＝(－3－4)＋[2－(－5)]i＝－7＋7i.(3)(5－5i)＋(－2－2i)－(3＋3i)＝(5－2－3)＋[－5＋(－2)－3]i＝－10i.反思与感悟复数加减运算法则的记忆方法(1)复数的实部与实部相加减，虚部与虚部相加减．(2)把i看作一个字母，类比多项式加减中的合并同类项．跟踪训练1(1)计算：(5－6i)＋(－2－i)－(3＋4i)；(2)已知复数z满足z＋1－3i＝5－2i，求z.解(1)(5－6i)＋(－2－i)－(3＋4i)＝[(5－2)＋(－6－1)i]－(3＋4i)＝(3－7i)－(3＋4i)＝(3－3)＋(－7－4)i ＝－11i. (2)由z ＋1－3i ＝5－2i ，得z ＝(5－2i)－(1－3i)＝(5－1)＋(－2＋3)i ＝4＋i. 类型二复数的乘法例2 计算：(1)(1－i)(1＋i)＋(－1＋i)； (2)(2－i)(－1＋5i)(3－4i)＋2i.解 (1)(1－i)(1＋i)＋(－1＋i)＝1－i 2－1＋i ＝1＋i. (2)(2－i)(－1＋5i)(3－4i)＋2i ＝(－2＋10i ＋i －5i 2)(3－4i)＋2i ＝(－2＋11i ＋5)(3－4i)＋2i ＝(3＋11i)(3－4i)＋2i ＝(9－12i ＋33i －44i 2)＋2i ＝53＋21i ＋2i ＝53＋23i.反思与感悟 (1)三个或三个以上的复数相乘，可按从左向右的顺序运算，或利用结合律运算．混合运算的顺序与实数的运算顺序一样．(2)平方差公式、完全平方公式等在复数范围内仍然成立．一些常见的结论要熟悉：i 2＝－1，(1±i)2＝±2i.跟踪训练2 若复数(m 2＋i)(1＋m i)是实数，则实数m ＝________. 答案－1解析 ∵(m 2＋i)(1＋m i)＝m 2－m ＋(m 3＋1)i 是实数，∴m 3＋1＝0，则m ＝－1. 类型三共轭复数的概念例3 复数z 满足z ·z ＋2i z ＝4＋2i ，求复数z 的共轭复数．解设z ＝x ＋y i(x ，y ∈R )，则z ＝x －y i. ∵z ·z ＋2i z ＝4＋2i ， ∴x 2＋y 2＋2i(x ＋y i)＝4＋2i ，因此(x 2＋y 2－2y )＋2x i ＝4＋2i ，得⎩⎪⎨⎪⎧ x 2＋y 2－2y ＝4，2x ＝2，解得⎩⎪⎨⎪⎧ x ＝1，y ＝3，或⎩⎪⎨⎪⎧x ＝1，y ＝－1， ∴z ＝1＋3i 或z ＝1－i.因此z 的共轭复数z ＝1－3i 或z ＝1＋i.反思与感悟 (1)有关复数z 及其共轭复数的题目，注意共轭复数的性质：①设z ＝a ＋b i(a ，b ∈R )，则z ·z ＝a 2＋b 2.②z ∈R ⇔z ＝z .(2)紧紧抓住复数相等的充要条件，把复数问题转化成实数问题是解决本题的关键，正确熟练地进行复数运算是解题的基础．跟踪训练3 已知z ∈C ，z 为z 的共轭复数，若z ·z －3i z ＝1＋3i ，求z . 解设z ＝a ＋b i(a ，b ∈R )，则z ＝a －b i(a ，b ∈R )．由题意得(a ＋b i)(a －b i)－3i(a －b i)＝1＋3i ，即a 2＋b 2－3b －3a i ＝1＋3i ，则有⎩⎪⎨⎪⎧ a 2＋b 2－3b ＝1，－3a ＝3，解得⎩⎪⎨⎪⎧ a ＝－1，b ＝0或⎩⎪⎨⎪⎧a ＝－1，b ＝3，所以z ＝－1或z ＝－1＋3i.1．已知复数z 1＝12－32i 和复数z 2＝cos 60°＋isin 60°，则z 1＋z 2＝________.答案 1解析 ∵z 2＝12＋32i ，∴z 1＋z 2＝1.2．已知i 是虚数单位，则(－1＋i)(2－i)＝________. 答案－1＋3i解析 (－1＋i)(2－i)＝－2＋3i －i 2＝－1＋3i.3．若复数z 满足z ＋(2－3i)＝－1＋2i ，则z ＋2－5i ＝________. 答案－1解析 ∵z ＝－1＋2i －2＋3i ＝－3＋5i ， ∴z ＋2－5i ＝－3＋5i ＋2－5i ＝－1.4．设复数z 1＝x ＋2i ，z 2＝3－y i(x ，y ∈R )，若z 1＋z 2＝5－6i ，则z 1－z 2＝________. 答案－1＋10i解析 ∵z 1＋z 2＝x ＋2i ＋(3－y i)＝(x ＋3)＋(2－y )i ， ∴(x ＋3)＋(2－y )i ＝5－6i(x ，y ∈R )，由复数相等的定义，得x ＝2且y ＝8， ∴z 1－z 2＝2＋2i －(3－8i)＝－1＋10i.5．复数z 1＝a ＋4i ，z 2＝－3＋b i ，若它们的和z 1＋z 2为实数，差z 1－z 2为纯虚数，则a ，b 的值分别为________．答案－3，－4解析 ∵z 1＋z 2＝a －3＋(4＋b )i 为实数， ∴4＋b ＝0，即b ＝－4.又z 1－z 2＝(a ＋3)＋(4－b )i 为纯虚数， ∴a ＋3＝0且4－b ≠0，∴a ＝－3.1．复数的加减运算把复数的代数形式z ＝a ＋b i(a ，b ∈R )看作关于“i ”的多项式，则复数的加法、减法运算，类似于多项式的加法、减法运算，只需要“合并同类项”就行，不需要记加法、减法法则． 2．两个复数的和(差)是复数，但两个虚数的和(差)不一定是虚数，例如(3－2i)＋2i ＝3. 3．复数的乘法与多项式乘法是类似的，有一点不同即必须在所得结果中把i 2换成－1，再把实部、虚部分别合并，两个复数的积仍然是一个复数． 4．理解共轭复数的性质 (1)z ∈R ⇔z ＝z .(2)当a ，b ∈R 时，有a 2＋b 2＝(a ＋b i)(a －b i)，这是虚数问题实数化的一个重要依据.一、填空题1．复数z 满足z －(1－i)＝2i ，则z ＝________. 答案 1＋i解析 ∵z －(1－i)＝2i ， ∴z ＝1－i ＋2i ＝1＋i.2．若复数(1＋b i)(2＋i)是纯虚数(i 是虚数单位，b 是实数)，则b ＝________. 答案 2解析 (1＋b i)(2＋i)＝(2－b )＋(2b ＋1)i ，令2－b ＝0，且2b ＋1≠0， ∴b ＝2.3．已知复数z 1＝(a 2－2)＋(a －4)i ，z 2＝a －(a 2－2)i(a ∈R )，且z 1－z 2为纯虚数，则a ＝________. 答案－1解析 ∵z 1－z 2＝(a 2－a －2)＋(a －4＋a 2－2)i(a ∈R )为纯虚数，∴⎩⎪⎨⎪⎧a 2－a －2＝0，a 2＋a －6≠0，解得a ＝－1.4．复数z ＝i(i ＋1)(i 为虚数单位)的共轭复数是________．答案－1－i解析 ∵z ＝i(i ＋1)＝i 2＋i ＝－1＋i ， ∴z 的共轭复数是z ＝－1－i.5．若复数z ＝1－2i(i 为虚数单位)，则z ·z ＋z 的实部是________．答案 6解析 ∵z ＝1－2i ， ∴z ＝1＋2i ，∴z ·z ＝(1－2i)(1＋2i)＝5， ∴z ·z ＋z ＝5＋1－2i ＝6－2i. ∴z ·z ＋z 的实部是6. 6．复数z ＝32－a i ，a ∈R ，且z 2＝12－32i ，则a ＝________. 答案 12解析 ∵z 2＝⎝⎛⎭⎫32－a i 2＝⎝⎛⎭⎫34－a 2－3a i ， ∴⎝⎛⎭⎫34－a 2－3a i ＝12－32i(a ∈R )，则⎩⎨⎧34－a 2＝12，3a ＝32，∴a ＝12.7．把复数z 的共轭复数记作z ，已知(1＋2i)z ＝4＋3i ，则z ＝________. 答案 2＋i解析设z ＝a ＋b i ，则z ＝a －b i(a ，b ∈R )， (1＋2i)z ]＝(1＋2i)(a －b i)＝(a ＋2b )＋(2a －b )i ＝4＋3i ，由复数相等的充要条件可得⎩⎪⎨⎪⎧ a ＋2b ＝4，2a －b ＝3，解得⎩⎪⎨⎪⎧a ＝2，b ＝1.∴z ＝2＋i.8．已知z 1＝(3x ＋y )＋(y －4x )i(x ，y ∈R )，z 2＝(4y －2x )－(5x ＋3y )i(x ，y ∈R )．设z ＝z 1－z 2，且z ＝13－2i ，则z 1＝________，z 2＝________. 考点复数的加减法运算法则题点复数加减法的综合应用答案 5－9i －8－7i解析 ∵z ＝z 1－z 2＝(3x ＋y －4y ＋2x )＋(y －4x ＋5x ＋3y )i ＝(5x －3y )＋(x ＋4y )i ＝13－2i ，∴⎩⎪⎨⎪⎧ 5x －3y ＝13，x ＋4y ＝－2，解得⎩⎪⎨⎪⎧x ＝2，y ＝－1.∴z 1＝5－9i ，z 2＝－8－7i. 9．已知z 1＝32a ＋(a ＋1)i ，z 2＝－33b ＋(b ＋2)i(a ，b ∈R )，若z 1－z 2＝43，则z 1·z 2＝________. 答案－18－63i 解析 z 1－z 2＝32a ＋(a ＋1)i －[－33b ＋(b ＋2)i] ＝⎝⎛⎭⎫32a ＋33b ＋(a －b －1)i ＝4 3. ∴⎩⎪⎨⎪⎧32a ＋33b ＝43，a －b －1＝0，解得⎩⎪⎨⎪⎧a ＝2，b ＝1，∴z 1＝3＋3i ，z 2＝－33＋3i.z 1·z 2＝(3＋3i)(－33＋3i)＝－18－63i.10．已知3＋i －(4＋3i)＝z －(6＋7i)，则z ＝________. 答案 5＋5i解析 ∵3＋i －(4＋3i)＝z －(6＋7i)， ∴z ＝3＋i －(4＋3i)＋(6＋7i) ＝(3－4＋6)＋(1－3＋7)i ＝5＋5i.11．若(x ＋i)i ＝－1＋2i(x ∈R )，则x ＝________. 答案 2解析由题意知x i －1＝－1＋2i ，又x ∈R ，由复数相等，得x ＝2. 二、解答题12．已知z －1＋2z i ＝－4＋4i ，求复数z .解设z ＝x ＋y i(x ，y ∈R )，代入z －1＋2z i ＝－4＋4i ，整理，得(x －2y －1)＋(2x ＋y )i ＝－4＋4i ，故有⎩⎪⎨⎪⎧ x －2y －1＝－4，2x ＋y ＝4.解得⎩⎪⎨⎪⎧x ＝1，y ＝2，所以复数z ＝1＋2i.13．已知复数z ＝(1－i)2＋1＋3i ，若z 2＋az ＋b ＝1－i(a ，b ∈R )，求b ＋a i 的共轭复数．解 z ＝(1－i)2＋1＋3i ＝－2i ＋1＋3i ＝1＋i ，由z 2＋az ＋b ＝1－i ，得(1＋i)2＋a (1＋i)＋b ＝1－i ，∴a ＋b ＋i(a ＋2)＝1－i(a ，b ∈R )，∴⎩⎪⎨⎪⎧a ＋b ＝1，a ＋2＝－1，解得⎩⎪⎨⎪⎧a ＝－3，b ＝4.所以b ＋a i ＝4－3i ，则b ＋a i 的共轭复数是4＋3i. 三、探究与拓展14．已知z 1＝3＋4i ，z 2＝t ＋i ，且z 1·z 2是实数，则实数t ＝________. 答案 34解析 ∵z 2＝t ＋i ，∴z 2＝t －i ， ∴z 1·z 2＝(3＋4i)(t －i) ＝3t －3i ＋4t i －4i 2 ＝(3t ＋4)＋(4t －3)i. 又∵z 1·z 2是实数， ∴4t －3＝0，即t ＝34.15．已知复数z ＝1＋i ，实数a ，b 满足az ＋2bz ＝(a ＋2z )2成立，求a ，b 的值．解 az ＋2bz ＝(a ＋2b )＋(a ＋2b )i ， (a ＋2z )2＝(a ＋2)2－4＋4(a ＋2)i ＝(a 2＋4a )＋4(a ＋2)i ，∴(a ＋2b )＋(a ＋2b )i ＝(a 2＋4a )＋4(a ＋2)i.∴⎩⎪⎨⎪⎧a ＋2b ＝a 2＋4a ，a ＋2b ＝4(a ＋2)，解得⎩⎨⎧ a ＝－22，b ＝4－32，或⎩⎨⎧a ＝22，b ＝4＋3 2.∴所求实数a ＝－22，b ＝4－32或a ＝22，b ＝4＋3 2.。

苏教版高中数学(选修1-2)(基础版)(全册知识点考点梳理、重点题型分类巩固练习)(家教、补习、复习用)

苏教版高中数学（选修1-2）重难点突破全册知识点梳理及重点题型举一反三巩固练习独立性检验的基本思想及其初步应用【学习目标】1. 了解独立性检验（只要求2×2列联表）的基本思想、方法及初步应用2. 通过典型案例的探究，了解实际推断原理和假设检验的基本思想、方法及初步应用.【要点梳理】要点一、分类变量有一种变量，这种变量所取不同的“值”表示的是个体所属不同类别，称这种变量为分类变量。

要点诠释：（1）对分类变量的理解。

这里的“变量”和“值”都应作为广义的“变量”和“值”进行理解。

例如：“性别变量”有“男”和“女”两种类别，这里的变量指的是性别，同样这里的“值”指的是“男”和“女”。

因此，这里所说的“变量”和“值”取的不一定是具体的数值。

（2）分类变量可以有多种类别。

例如：吸烟变量有“吸烟”与“不吸烟”两种类别，而国籍变量则有多种类别。

要点二、2×2列联表1. 列联表用表格列出的分类变量的频数表，叫做列联表。

2. 2×2列联表对于两个事件A，B，列出两个事件在两种状态下的数据，如下表所示：这样的表格称为2×2列联表。

要点三：卡方统计量公式为了研究分类变量X与Y的关系，经调查得到一张2×2列联表，如下表所示统计中有一个有用的（读做“卡方”）统计量，它的表达式是：22()()()()()n ad bc K a b c d a c b d -=++++（n a b c d =+++为样本容量）。

要点四、独立性检验1. 独立性检验通过2×2列联表，再通过卡方统计量公式计算2K 的值，利用随机变量2K 来确定在多大程度上可以认为“两个分类变量有关系”的方法称为两个分类变量的独立性检验。

2. 变量独立性的判断通过对2K 统计量分布的研究，已经得到两个临界值：3.841和6.635。

当数据量较大时，在统计中，用以下结果对变量的独立性进行判断：①如果2K ≤3.841时，认为事件A 与B 是无关的。

苏教版数学高二-2014版选修1-2检测模块学习评价

模块学习评价(时间：120分钟，满分：160分)一、填空题(本大题共14小题，每小题5分，共70分，请把答案填写在题中的横线上．)1．(2013·重庆高考)设复数z ＝1＋2i(i 是虚数单位)，则|z |＝________. 【解析】 ∵z ＝1＋2i ，∴|z |＝12＋22＝ 5.【答案】52．①正方形的对角线互相平分；②平行四边形的对角线互相平分；③正方形是平行四边形．根据“三段论”推理推出一个结论，则这个结论是________(填序号)．【解析】根据三段论的一般形式，可以得到大前提是②，小前提为③，故得到结论为①.【答案】 ①3．设复数z 满足1＋2iz ＝i ，i 为虚数单位，则z 等于______．【解析】 ∵1＋2i z ＝i ，∴z ＝1＋2i i ＝(1＋2i )(－i )i (－i )＝2－i.【答案】 2－i4．用反证法证明某命题时，对结论“自然数a ，b ，c 中恰有一个偶数“正确的反设为________．【答案】 a ，b ，c 中至少有两个偶数或都是奇数． 5．已知a ∈R ，复数z ＝1＋a i1－a i在复平面内对应的点位于y 轴的负半轴上，那么实数a 的值是________．【解析】 z ＝1＋a i 1－a i＝(1＋a i )2(1－a i )(1＋a i )＝1－a 21＋a 2＋2a 1＋a2i ， ∵z 对应的点位于y 轴的负半轴上， ∴1－a 21＋a 2＝0且2a 1＋a 2＜0，解得a ＝－1. ∴a ＝－1. 【答案】－16．如图1(1)中，小正方体的个数为1，图(2)中，小正方体的个数为5，图(3)中，小正方体的个数为14，依此规律堆积，则第6个图形中小正方体的个数为________．图1【解析】 a n ＝12＋22＋…＋n 2，∴a 6＝12＋22＋…＋62＝91. 【答案】 917．(2013·广东高考改编)若i(x ＋y i)＝3＋4i ，x ，y ∈R ，则复数x ＋y i 的模是________．【解析】法一因为i(x ＋y i)＝3＋4i ，所以x ＋y i ＝3＋4i i ＝(3＋4i )(－i )i (－i )＝4－3i ，故|x ＋y i|＝|4－3i|＝42＋(－3)2＝5.法二因为i(x ＋y i)＝3＋4i ，所以－y ＋x i ＝3＋4i ，所以x ＝4，y ＝－3，故|x ＋y i|＝|4－3i|＝42＋(－3)2＝5.法三因为i(x ＋y i)＝3＋4i ，所以(－i)i(x ＋y i)＝(－i)·(3＋4i)＝4－3i ，即x ＋y i ＝4－3i ，故|x ＋y i|＝|4－3i|＝42＋(－3)2＝5.【答案】 58．下列推理：①留长头发的都是艺术家，小孙留了长头发，所以小孙也是艺术家；②因为a＞1时，指数函数y＝a x是增函数，而a＝tan 196π＞1，所以y＝(tan 196π)x是增函数；③平行四边形的对角线互相平分，因为菱形是平行四边形，所以菱形的对角线互相平分；④无理数都是实数，3是实数，所以3是无理数．其中错误的命题序号是________．【解析】①中“留长头发的都是艺术家”不正确，大前提错误；②中0＜a＝tan 196π＝33＜1，小前提错误；④中小前提中的特殊对象必须是大前提中一般对象的子集，正确的小前提应为“3”是无理数；只有③的推理是正确的．∴①②④错误．【答案】①②④9．(2013·湖北高考改编)在复平面内，复数z＝2i1＋i(i为虚数单位)的共轭复数对应的点位于第________象限．【解析】z＝2i1＋i＝2i(1－i)(1＋i)(1－i)＝1＋i，所以z＝1－i，故复数z的共轭复数对应的点位于第四象限．【答案】四10．若三角形内切圆半径为r，三边长为a、b、c，则三角形的面积S＝12r(a＋b＋c)，运用类比思想，对于空间中的四面体的内切球，存在一个类似的结论为________．【解析】“面积”类比为“体积”，“长度”类比为“面积”．【答案】若四面体内切球半径为R，四个面的面积分别为S1、S2、S3、S4，则四面体的体积为V＝13R(S1＋S2＋S3＋S4)11．在古希腊毕达哥拉斯学派把1,3,6,10,15,21,28，…这些数叫做三角形数，因为这些数对应的点可以排成一个正三角形．图2则第n 个三角形数为________．【解析】转化为⎩⎪⎨⎪⎧a 1＝1，a n ＝a n －1＋n ，∴a n ＝a n －1＋n ＝a n －2＋(n －1)＋n ＝a n －3＋(n －2)＋(n －1)＋n ＝… ＝1＋2＋3＋…＋n ＝n (n ＋1)2. 【答案】 12n (n ＋1)12．设a ＝2，b ＝7－3，c ＝6－2，则a ，b ，c 的大小关系为________．【解析】 ∵b ＝47＋3，c ＝46＋2，显然b <c ，又∵c 2＝(6－2)2＝8－43＜2＝a 2， ∴a >c ，∴a >c >b . 【答案】 a >c >b13．(2013·无锡高二检测)对于两个复数：α＝12＋32i ，β＝12－32i ，有如下几个结论：①在复平面内，α，β表示的点关于实轴对称；②α＝β2；③α2 010＋β2 010＝2；④α＞β.其中正确结论的序号为________．【解析】 ①正确．因为α，β对应的点分别为(12，32)，(12，－32)，关于实轴对称．②错误，α＝12－32i ，β2＝(12－32i)2＝－12－32i ， ∴α≠β2.③正确，α3＝(12＋32i)3＝－1，β3＝(12－32i)3＝－1，∴α2 010＝(α3)670＝(－1)2＝1，β2 010＝(β3)670＝(－1)2＝1.④错误，因为复数不能比较大小．【答案】 ①③14．(2013·徐州高二检测)在平面几何中，△ABC 的内角平分线CE 分AB 所成线段的比AE EB ＝AC BC ，把这个结论类比到空间：在三棱锥A —BCD 中(如图3所示)，面DEC 平分二面角A —CD —B 且与AB 相交于E ，则得到的类比的结论是________．图3【解析】 CE 平分角ACB ，而面CDE 平分二面角A —CD —B ， ∴AC BC 可类比成S △ACD S △BCD ，故结论为AE EB ＝S △ACDS △BCD .【答案】 AE EB ＝S △ACDS △BCD二、解答题(本大题共6小题，共90分．解答应写出文字说明、证明过程或演算步骤)15．(本小题满分14分)已知：x ∈R ，a ＝x 2－1，b ＝2x ＋2. 求证：a ，b 中至少有一个不小于0.【证明】假设a ，b 中没有一个不小于0，即a <0，b <0，则a ＋b <0，又∵a ＋b ＝x 2－1＋2x ＋2 ＝x 2＋2x ＋1＝(x ＋1)2≥0.这与假设所得结论矛盾，故假设不成立， ∴a ，b 中至少有一个不小于0.16．(本小题满分14分)(2013·湛江高二检测)已知关于x 的方程x 2－(6＋i)x ＋9＋a i ＝0(a ∈R )有实根b .(1)求实数a ，b 的值；(2)若复数z 满足|z －a －b i|－2|z |＝0，则z 为何值时，|z |有最小值，并求出|z |的最小值．【解】 (1)因为b 是方程的根，所以(b 2－6b ＋9)＋(a －b )i ＝0，故⎩⎪⎨⎪⎧b 2－6b ＋9＝0，a ＝b ，解得a ＝b ＝3.(2)设z ＝x ＋y i(x ，y 是实数)，由|z －3－3i|＝2|z |，得：(x －3)2＋(y ＋3)2＝4(x 2＋y 2)，即(x ＋1)2＋(y －1)2＝8.∴z 的对应点Z 的轨迹是以(－1,1)为圆心，22为半径的圆．所以z ＝1－i 时，|z |最小值为 2.17．(本小题满分14分)已知：sin 2 30°＋sin 290°＋sin 2150°＝32，sin 25°＋sin 265°＋sin 2125°＝32，通过观察上述两等式的规律，请你写出一个一般性的结论，并给出证明．【解】一般性的结论为： sin 2(α－60°)＋sin 2α＋sin 2(α＋60°)＝32.证明：左边＝1－cos (2α－120°)2＋1－cos 2α2＋1－cos (2α＋120°)2＝32－12[cos(2α－120°)＋cos 2α＋cos(2α＋120°)] ＝32－12(cos 2αcos 120°＋cos 2α＋cos 2αcos 120°) ＝32－12[2cos 2α·(－12)＋cos 2α] ＝32.∴左边＝右边，故一般性结论成立．18．(本小题满分16分)(2013·连云港高二检测)设实部为正数的复数z 满足|z |＝10，且(1＋2i)z 在复平面上对应的点在第一、三象限的角平分线上．(1)求复数z ； (2)若z ＋m －i1＋i(m ∈R )为纯虚数，求m 的值．【解】 (1)设z ＝a ＋b i(a ＞0，b ∈R )． ∴(1＋2i)z ＝(1＋2i)(a ＋b i)＝(a －2b )＋(2a ＋b )i ，由题意可知⎩⎪⎨⎪⎧a －2b ＝2a ＋b ，①a 2＋b 2＝10.②由①得a ＝－3b . ∵a ＞0，∴b ＜0. 解得a ＝3，b ＝－1， ∴z ＝3－i.(2)由(1)知z ＝3－i ，∴z ＝3＋i ，∴z＋m－i1＋i＝3＋i＋(m－i)(1－i)(1＋i)(1－i)＝m＋52－m－12i.∵z＋m－i1＋i为纯虚数，∴m＋5＝0且m－1≠0，即m＝－5.故实数m的值是－5.19．(本小题满分16分)图4(2013·山东高考)如图4，四棱锥P—ABCD中，AB⊥AC，AB⊥PA，AB∥CD，AB＝2CD，E，F，G，M，N分别为PB，AB，BC，PD，PC的中点．(1)求证：CE∥平面PAD；(2)求证：平面EFG⊥平面EMN.(1)【证明】法一如图(1)，取PA的中点H，连接EH，DH.因为E为PB的中点，所以EH∥AB，EH＝12AB.又因为AB∥CD，CD＝12AB，所以EH∥CD，EH＝CD.所以四边形DCEH是平行四边形．所以CE∥DH.又DH⊂平面PAD，CE⊄平面PAD，所以CE∥平面PAD.(2)法二如图(2)，连接CF.因为F为AB的中点，所以AF＝12AB.又因为CD＝12AB，所以AF＝CD.又因为AF∥CD，所以四边形AFCD为平行四边形．所以CF∥AD. 又因为CF⊄平面PAD，所以CF∥平面PAD.因为E，F分别为PB，AB的中点，所以EF∥PA. 又因为EF⊄平面PAD，所以EF∥平面PAD.因为CF∩EF＝F，故平面CEF∥平面PAD.又因为CE⊂平面CEF，所以CE∥平面PAD. (2)因为E，F分别为PB，AB的中点，所以EF∥PA.又因为AB⊥PA，所以AB⊥EF.同理可证AB⊥FG.又因为EF ∩FG ＝F ，EF ⊂平面EFG ，FG ⊂平面EFG ，因此AB ⊥平面EFG . 又因为M ，N 分别为PD ，PC 的中点，所以MN ∥DC . 又因为AB ∥DC ，所以MN ∥AB ，所以MN ⊥平面EFG . 又因为MN ⊂平面EMN ，所以平面EFG ⊥平面EMN .20．(本小题满分16分)已知△ABC 的三边长为a 、b 、c ，且其中任意两边长均不相等，若1a ，1b ，1c 成等差数列．(1)比较b a 与cb 的大小，并证明你的结论．(2)求证B 不可能是钝角．【解】 (1)大小关系为b a ＜cb ，证明如下：要证明b a ＜c b ，只需证明b a ＜cb ，又a ，b ，c 大于0，只需证明b 2＜ac ，(*) ∵1a ，1b ，1c 成等差数列， ∴2b ＝1a ＋1c ≥21ac ，因此b 2≤ac ，(**) ∵a ，b ，c 均不相等，∴(**)式等号不成立，则b 2＜ac 成立，故b a ＜cb 成立．(2)假设B 为钝角，则cos B ＜0，打印版高中数学又cos B ＝a 2＋c 2－b 22ac ＞2ac －b 22ac ＞ac －b 22ac ＞0，这与cos B ＜0矛盾，故假设不成立，所以角B 不可能是钝角．。

苏教版高中数学选修1-2典型例题：综合法的应用

例谈综和法在解题中的应用综合法是一种常用的解题思考方法，它是一种从已知到未知的逻辑推理方法。

具体说，就是从题设中的已知条件或已证的命题出发，经过一系列的逻辑推理，最后推出所要求证的结论成立。

在中学数学中，综合法在不等式、几何、三角、解析等证明中有着广泛的应用。

举例说明。

例1.已知R n m b a ∈,,,，求证：m n n m n m n m b a b a b a +≥+++。

.证明：=+-+++)()(m n n m n m n m b a b a b a m n n m n m n m b a b b a a -+-++))((n n m m b a b a --=因为n n m m b a b a --与同号，且b a =时二式都为0，m n n m n m n m b a b a b a +≥+∴++。

例2已知],0(πα∈，求证：αααcos 1sin 2sin 2-≤。

证明：αααααααcos 1sin cos sin 4cos 1sin 2sin 2--=-- ααααcos 1)1cos 4cos 4(sin 2---= αααcos 1)1cos 2(sin 2---=，因为],0(πα∈，0)1cos 2(,0cos 1,0sin 2≥->-≥∴ααα，0cos 1sin 2sin 2≤--∴ααα， ∴αααcos 1sin 2sin 2-≤。

例3设ABCD 是空间四边形，CD CB AD AB ==,，求证：BD AC ⊥。

证明：设BD 的中点为E ，连结CE AE ,。

因为AD AB =，A B CD EBD AE ⊥∴，同理BD CE ⊥，又E CE AE = ，AEC BD 平面⊥∴，又AEC AC 平面⊂AC BD ⊥∴。

例4过抛物线)0(22>=p px y 的焦点F 作倾斜角为π43的直线，交抛物线于B A ,两点。

求证：p AB 4||=。

苏教版数学高二-2014版苏教数学选修1-2练习第3章《数系的扩充与复数的引入》高考

命题趋势复数的乘除运算是本章考查的重点，其中往往结合复数的实、虚部、几何意义、模的求法、共轭复数等一起考查．很少以解答题形式出现题目较易，主要考查学生的基本运算能力．高考真题1．(2011·江苏)设复数i 满足i(z ＋1)＝－3＋2i(i 是虚数单位)，则z 的实部是__________．解析因为z ＋1＝－3＋2i i＝(－3＋2i)(－i)＝2＋3i ，所以z ＝1＋3i ，故z 的实部是1.答案 12．(2011·山东卷改编)复数z ＝2－i 2＋i(i 为虚数单位)在复平面内对应的点所在第________象限．解析因为z ＝2－i2＋i ＝(2－i )25＝3－4i 5，故复数z 对应点⎝ ⎛⎭⎪⎫35，－45在第四象限．答案四3．(2011·海南卷改编)复数5i 1－2i＝________. 解析因为5i 1－2i＝5i (1＋2i )5＝－2＋i. 答案－2＋i4．(2011·安徽卷改编)设i 是虚数单位，复数1＋a i 2－i为纯虚数，则实数a 为________．解析设1＋a i 2－i ＝b i(b ∈R )，则1＋a i ＝b i(2－i)＝b ＋2b i ，所以b ＝1，a ＝2.答案 25．(2011·江西)若(x －i)i ＝y ＋2i ，x ，y ∈R ，则复数x ＋y i ＝________.解析 ∵(x －i)i ＝y ＋2i ，x i ＋1＝y ＋2i∴y ＝1，x ＝2∴x ＋y i ＝2＋i.答案 2＋i6．(2011·重庆卷改编)复数i 2＋i 3＋i 41－i＝________. 解析 i 2＋i 3＋i 41－i ＝－1－i ＋11－i ＝－i (1＋i )(1－i )(1＋i )＝1－i 2＝12－12i 答案 12－12i7．(2011·辽宁)a 为正实数，i 为虚数单位，⎪⎪⎪⎪⎪⎪a ＋i i ＝2，则a ＝________.A ．2 B. 3 C. 2 D ．1解析 ⎪⎪⎪⎪⎪⎪a ＋i i ＝|1－a i|＝ 1＋a 2＝2，a >0，故a ＝ 3.答案 3 8．(2011·浙江卷改编)把复数z 的共轭复数记作z ，若z ＝1＋i ，i 为虚数单位，则(1＋z )z ＝________.解析 (1＋z )z ＝z ＋z z ＝1－i ＋(1＋i)(1－i)＝1－i ＋2＝3－i.答案 3－i9．(2011·上海)已知复数z 1满足(z 1－2)(1＋i)＝1－i(i 为虚数单位)，复数z 2的虚部为2，z 1·z 2是实数，求z 2.解 (z 1－2)(1＋i)＝1－i ⇒z 1＝2－i设z 2＝a ＋2i ，a ∈R ，则z 1z 2＝(2－i)(a ＋2i)＝(2a ＋2)＋(4－a )i ，∵z1z2∈R，∴a＝4. ∴z2＝4＋2i.。

苏教版数学高二-2014版苏教数学选修1-2练习第1章《统计案例》解读高考

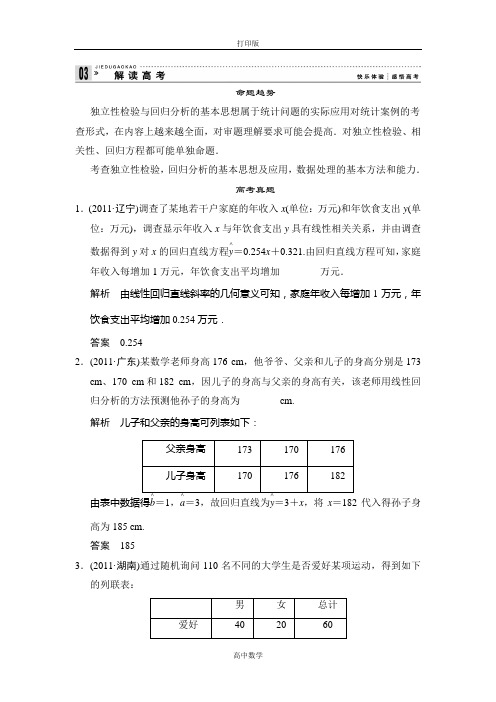
命题趋势独立性检验与回归分析的基本思想属于统计问题的实际应用对统计案例的考查形式，在内容上越来越全面，对审题理解要求可能会提高．对独立性检验、相关性、回归方程都可能单独命题．考查独立性检验，回归分析的基本思想及应用，数据处理的基本方法和能力．高考真题1．(2011·辽宁)调查了某地若干户家庭的年收入x (单位：万元)和年饮食支出y (单位：万元)，调查显示年收入x 与年饮食支出y 具有线性相关关系，并由调查数据得到y 对x 的回归直线方程y ^＝0.254x ＋0.321.由回归直线方程可知，家庭年收入每增加1万元，年饮食支出平均增加________万元．解析由线性回归直线斜率的几何意义可知，家庭年收入每增加1万元，年饮食支出平均增加0.254万元．答案 0.2542．(2011·广东)某数学老师身高176 cm ，他爷爷、父亲和儿子的身高分别是173 cm 、170 cm 和182 cm ，因儿子的身高与父亲的身高有关，该老师用线性回归分析的方法预测他孙子的身高为________cm. 解析儿子和父亲的身高可列表如下：父亲身高 173 170 176 儿子身高170176182由表中数据得b ＝1，a ＝3，故回归直线为y ＝3＋x ，将x ＝182代入得孙子身高为185 cm. 答案 1853．(2011·湖南)通过随机询问110名不同的大学生是否爱好某项运动，得到如下的列联表：男女总计爱好402060由χ2＝n (ad －bc )(a ＋b )(c ＋d )(a ＋c )(b ＋d )算得，χ2＝110×(40×30－20×30)260×50×60×50≈7.8附表：①有99%以上的把握认为“爱好该项运动与性别有关”； ②有99%以上的把握认为“爱好该项运动与性别无关”；③在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别有关”；④在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别无关”。

高中数学苏教版选修1-2【备课资源】3.1

栏
目
开
关
探究点一复数的概念
问题 1 为解决方程 x2＝2，数系从有理数扩充到实数；那么
本
课怎样解决方程 x2＋1＝0 在实数系中无根的问题呢？
时
栏目
答设想引入新数 i，使 i 是方程 x2＋1＝0 的根，即 i·i＝
开关
－1，方程 x2＋1＝0 有解，同时得到一些新数.
问题 2 如何理解虚数单位 i?
②两个复数不相等的一个充分条件是它们的虚部不相等；
本
③1－ai(a∈R)是一个复数；
课时
④虚数的平方不小于 0；
栏目
⑤－1 的平方根只有一个，即为－i；
开 ⑥i 是方程 x4－1＝0 的一个根；
关
⑦ 2i 是一个无理数.
其中正确命题的个数为___4_____.
解析命题①②③⑥正确，④⑤⑦错误.
本 1.对于复数 z＝a＋bi(a，b∈R)，可以限制 a，b 的值得到复数
课
时 z 的不同情况；
栏
目 2.两个复数相等，要先确定两个复数的实、虚部，再利用两个
开关
复数相等的条件进行判断；
编后语
老师上课都有一定的思路，抓住老师的思路就能取得良好的学习效果。在上一小节中已经提及听课中要跟随老师的思路，这里再进一步论述听课时如何抓住老师的思路。
本课
答如果两个复数不全是实数，那么它们不能比较大小.
时
栏目
问题 2 两个复数相等的充要条件是什么？
开
关
答复数 a＋bi 与 c＋di 相等的充要条件是 a＝c 且 b＝d(a，
b，c，d∈R).
例 3 已知 x，y 均是实数，且满足(2x－1)＋i＝－y－(3－y)i，求 x 与 y.