2014-2015海淀区九年级第一学期期中练习(附答案)
北京市海淀区2014届九年级上学期期中考试英语试题

海淀区九年级第一学期期中练习英语2013.11一、听对话,从下面各题所给的A、B、C三幅图片选项与对话内容相符的图片。
每段对话你将听两遍。
(共4分,每小题1分)二、听对话或独白,根据对话或独白的内容,从下面各题所给的A、B、C三个选项中选择最佳选项。
每段对话或独白你将听两遍。
(共12分,每小题1分)5. What’s in the backpack?A. A notebook.B. A pencil box.C. A hair hand6. Whose backpack could it be?A. Jack’sB. Lily’sC. Maria’s请听一段对话,完成第7至8小题。
7. What is John doing now?A. Watching TV.B. Doing homework.C. Playing baseball.8. What does John hate?A. The shows.B. The rulesC. The games.请听一段对话,完成第9至10小题。
9.How long will the holiday be?A. Two days.B. Three days.C. Four days.10. What is Tina going to do during the holiday?A. Go hiking and camping.B. Go to the beach.C. Visit the museum.请听一段对话,完成第11至13小题。
11. When is the party?A. Next Sunday evening.B. Next Saturday evening.C. Next Friday evening.12. What will the boy probably wear for the party?A. A shirt and tie.B. A suit and shirt.C. A suit and tie.13. What can we know about the boy?A. He has no friends.B. He needs more time.C. He wants some advice.请听一段对话,完成第14至16小题。
2014年海淀区初三物理期中考试试卷及答案
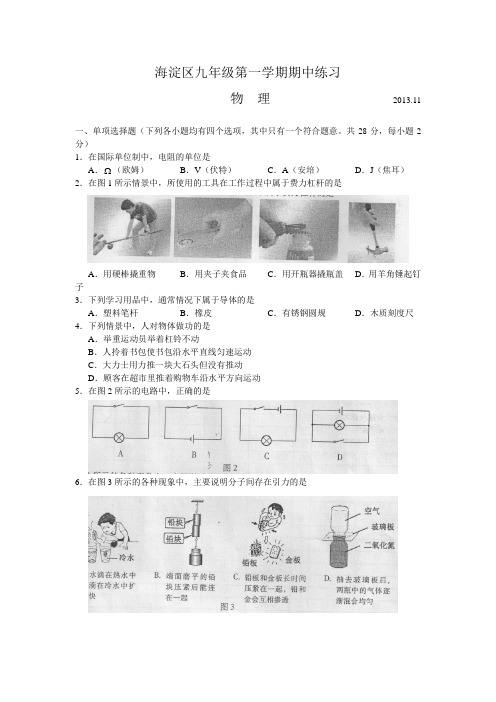
海淀区九年级第一学期期中练习物理2013.11一、单项选择题(下列各小题均有四个选项,其中只有一个符合题意。
共28分,每小题2分)1.在国际单位制中,电阻的单位是A. (欧姆)B.V(伏特)C.A(安培)D.J(焦耳)2.在图1所示情景中,所使用的工具在工作过程中属于费力杠杆的是A.用硬棒撬重物B.用夹子夹食品C.用开瓶器撬瓶盖D.用羊角锤起钉子3.下列学习用品中,通常情况下属于导体的是A.塑料笔杆B.橡皮C.有锈钢圆规D.木质刻度尺4.下列情景中,人对物体做功的是A.举重运动员举着杠铃不动B.人拎着书包使书包沿水平直线匀速运动C.大力士用力推一块大石头但没有推动D.顾客在超市里推着购物车沿水平方向运动5.在图2所示的电路中,正确的是6.在图3所示的各种现象中,主要说明分子间存在引力的是7.关于电路,下列说法中错误的是A.电源是提供电能的装置B.可以通过开关控制电路的通、断C.将电源的正、负极直接用导线连接在一起的电路称为短路D.用电器是将其他形式的能转化为电能的装置8.下列现象中,属于用热传递的方式改变物体内能的是A.在火炉上将一壶凉水烧开B.菜刀在砂轮上磨得发烫C.两手互相摩擦使手发热D.用锯锯木头锯条会发热9.图4中能够说明动能和重力势能相互转化的过程是10.下列说法中正确的是A.水蒸气、水和冰的分子间的距离都是相同的B.打扫卫生时房间内尖土飞扬,说明分子在不停地运动C.扩散只能在气体或液体中进行D.同一物体温度越高,其内部大量分子的热运动越剧烈11.对于功率和机械效率的理解,下列说法中正确的是A.机械工作时的功率越大,其工作时机械效率一定越高B.机械工作时的功率越大,其工作时一定越省力C.机械做的有用功相同,总功越少,其机械效率一定越高D.机械工作时越省力,其机械效率一定越高12.击剑比赛中,当甲方运动员的剑击中乙方的导电服时(相当于图5中“S甲”闭合),乙方指示灯L乙亮;当乙方运动员的剑击中甲方的导电服时,(相当于图5中“S乙”闭合),甲方指示灯L甲亮。
北京海淀2015初三期中试题答案

海淀区九年级第一学期期中测评数学试卷参考答案一、选择题(本题共30分,每小题3分)题 号1 2 3 45 6 7 8 9 10 答 案D A A ABBCDBC二、填空题(本题共18分,每小题3分)题 号11 12 13 14 15 16 答 案,21=x 22-=x21y x =+(答案不唯一)<1300.6120,150三、解答题(本题共72分,第17~26题,每小题5分,第27题7分,第28题7分,第29题8分) 17.解:2320.x x -+=……………………………………………1分0)2)(1(=--x x . ……………………………………………3分∴01=-x 或02=-x .∴2,121==x x . ………………………………………………………5分18.解:∵抛物线a x x y ++=32与x 轴只有一个交点,∴0∆=,………………………………………2分即940a -=.……………………………………………4分∴49=a .……………………………………………5分19.解:∵点(3, 0)在抛物线k x k x y -++-=)3(32上,∴k k -++⨯-=)3(33302.………………………………………2分 ∴9=k .……………………………………………3分∴抛物线的解析式为91232-+-=x x y .∴对称轴为2=x .……………………………………………5分20.解:∵PA ,PB 是⊙O 的切线,∴PA =PB .………………………………………1分∴PBA PAB ∠=∠.………………………………………2分 ∵AC 为⊙O 的直径, ∴CA ⊥PA .∴90=∠PAC º.………………………………………3分 ∵25=∠BAC º,∴65=∠PAB º.………………………………………4分∴502180=∠-=∠PAB Pº.………………………………………5分21.解:∵1=x 是方程0522=+-a ax x 的一个根,∴0512=+-a a .………………………………………2分 ∴152-=-a a .…………………………………………3分 ∴原式7)5(32--=a a ………………………………………4分10-=.………………………………………5分22.解:如图,下降后的水面宽CD 为1.2m ,连接OA , OC ,过点O 作ON ⊥CD 于N ,交AB 于M .………………………… 1分∴90ONC ∠=º.∵AB ∥CD ,∴90OMA ONC ∠=∠=º. ∵ 1.6AB =, 1.2CD =, ∴10.82AM AB ==,10.62CN CD ==.…………………………2分 在Rt △OAM 中,∵1OA =,∴220.6OM OA AM =-=. ………………………………3分 同理可得0.8ON =.………………………………4分 ∴0.2.MN ON OM =-=答:水面下降了0.2米.…………………………5分23.(1)证明:22)3()(34)3(+=-⨯⨯--=∆a a a .……………………………1分∵0>a ,∴2(3)0a +>.即0>∆.∴方程总有两个不相等的实数根.……………………………………………2分(2)解方程,得3,121ax x =-=.……………………………………………4分 ∵方程有一个根大于2,∴23>a. ∴6>a .……………………………………………5分24.解:如图,雕像上部高度AC 与下部高度BC 应有2::BC BC AC =,即AC BC 22=.设BC 为x m.…………………………………1分依题意,得)2(22x x -=..………………………………………3分解得,511+-=x 512--=x (不符合题意,舍去).……4分51 1.2-≈.答:雕像的下部应设计为1.2m .…………………………5分25.解:如图1,当点D 、C 在AB 的异侧时,连接OD 、BC . ………1分∵AB 是⊙O 的直径,∴90ACB ∠=º. 在Rt △ACB 中,∵2=AB ,2AC =,∴2BC =.∴45BAC ∠=º.………………2分 ∵1OA OD AD ===,∴60BAD ∠=º.………………3分∴105CAD BAD BAC ∠=∠+∠=º.………………4分当点D 、C 在AB 的同侧时,如图2,同理可得45BAC ∠=︒,60BAD ∠=︒.∴15CAD BAD BAC ∠=∠-∠=º. ∴CAD ∠为15º或105º.…………………5分26.解:(1)∵直线m x y +-=22经过点B (2,-3),∴m +⨯-=-223.∴1=m .……………………………………………1分 ∵直线22y x m =-+经过点A (-2,n ), ∴5n =.……………………………………………2分 ∵抛物线21y xbx c =++过点A 和点B ,∴⎩⎨⎧++=-+-=.243,245c b c b∴⎩⎨⎧-=-=.3,2c b ∴3221--=x x y .……………………………………………4分 (2)12-.……………………………………………5分27.(1)证明:连接OC . ……………………………1分∵∠PCD =2∠BAC ,∠POC =2∠BAC ,∴∠POC =∠PCD .……………………………2分 ∵CD ⊥AB 于点D , ∴∠ODC =90︒.∴∠POC+∠OCD =90º. ∴∠PCD+∠OCD =90º. ∴∠OCP =90º. ∴半径OC ⊥CP .∴CP 为⊙O 的切线. ……………………………………………3分 (2)解:①设⊙O 的半径为r.在Rt △OCP 中,222OC CP OP +=.∵1,5,BP CP ==∴222(5)(1)r r +=+. ………………………4分解得2r =.∴⊙O 的半径为2. ……………………………………………5分 ②2143. ……………………………………………7分28.解:(1)1x ≤或2x ≥;……………………………………………2分(2)如图所示:……………………………………5分1342x x x x <<<. .……………………………………………7分29.解:(1)60. ……………………………………………2分(2).……………………………………………3分连接,MQ MP .记,MQ PQ 分别交x 轴于,E F .∵将点M 绕点A 顺时针旋转60︒得到点Q ,将点M 绕点N 顺时针旋转60︒得到点P , ∴△MAQ 和△MNP 均为等边三角形. ………………4分 ∴MA MQ =,MN MP =,60AMQ NMP ∠=∠=︒. ∴AMN QMP ∠=∠.∴△MAN ≌△MQP . .………………………………5分 ∴MAN MQP ∠=∠. ∵AEM QEF ∠=∠, ∴60QFE AMQ ∠=∠=︒.∴60α=︒. .…………………………………………….6分 (3)(32,12)或(32-,12-). ………………………8分xyF EPQAO MN。
2014-2015海淀区九年级第一学期期中考试及答案

ODCB A 海淀区九年级第一学期期中测评数学试卷(分数:120分时间:120分钟)班级 姓名 学号 成绩 一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个..是符合题意的. 1.下列图形是中心对称图形的是( )A B C D2.将抛物线2y x =向上平移1个单位,得到的抛物线的解析式为( )A.21y x =+ B.21y x =- C.()21y x =+D.()21y x =-3.袋子中装有4个黑球、2个白球,这些球的形状、大小、质地等完全相同,即除颜色外无其他差别.在看不到球的情况下,随机从袋子中摸出1( )A.这个球一定是黑球B.这个球一定是白球C.“摸出黑球”的可能性大D.“摸出黑球”和“摸出白球”的可能性一样大4.用配方法解方程2230x x --=时,配方后得到的方程为( )A.2(1)=4x - B.2(1)4x -=- C.2(1)=4x + D.2(1)=4x +- 5.如图,O 为正五边形ABCDE 的外接圆,O 的半径为2,则AB 的长为( )A.5πB.25πC.35πD.45π6.如图,AB 是O 的直径,CD 是O 的弦,59ABD ∠=︒,则C ∠等于( )A.29︒B.31︒C.59︒D.62︒7.已知二次函数24y x x m =-+(m 为常数)的图象与x 点为(1,0),则关于B AO CDAx 的一元二次方程240x x m -+=的两个实数根是( )A.121,1x x ==-B.121,2x x =-=C.121,0x x =-=D.121,3x x ==8.如图,C 是半圆O 的直径AB 上的一个动点(不与A ,B 重合),过C 作AB 的垂线交半圆于点D ,以点D ,C ,O 为顶点作矩形DCOE . 若AB =10,设AC =x ,矩形DCOE 的面积为y ,则下列图象中能表示y 与x 的函数关系的图象大致是( )A B C D二、填空题(本题共16分,每小题4分)9.如图,PA ,PB 分别与O 相切于点A ,B ,连接AB .60APB ∠=︒,5AB =,则PA 的长是 .10.若关于x 的一元二次方程240x x k -+=有两个相等的实数根,则k 的值为_________.11.在平面直角坐标系xOy 中,函数2y x =的图象经过点11(,)M x y ,22(,)N x y 两点,若1 42x -<<-,202x <<,则1y 2y .(用“<”,“=”或“>”号连接)12.如图,正方形ABCD 中,点G 为对角线AC 上一点,AG=AB . ∠CAE =15°且AE=AC ,连接GE .将线段AE 绕点A 逆时针旋转得到 线段AF ,使DF=GE ,则∠CAF 的度数为____________.三、解答题(本题共30分,每小题5分) 13.解方程:2310x x +-=.14.如图,∠DAB =∠EAC ,AB =AD ,AC =AE .求证:BC =DE .GDCEDCBOA OBA P15.已知二次函数的图象经过点(0,1),且顶点坐标为(2,5),求此二次函数的解析式.16.如图,四边形ABCD 内接于⊙O ,∠ABC =130°,求∠OAC 的度数.17.若1x =是关于x 的一元二次方程22420x mx m -+=的根,求代数式()2213+m -的值.18.列方程解应用题:某工厂废气年排放量为450万立方米,为改善空气质量,决定分两期治理,使废气的排放量减少到288万立方米.如果每期治理中废气减少的百分率相同,求每期减少的百分率.四、解答题(本题共20分,每小题5分)19.下图是某市某月1日至15日的空气质量指数趋势图,空气质量指数不大于100表示空气质量优良,空气质量指数大于200表示空气重度污染.(1)由图可知,该月1日至15日中空气重度污染的有 天;(2)小丁随机选择该月1日至15日中的某一天到达该市,求小丁到达该市当天空气质量优良的概率.20.已知关于x 的方程2(3)30ax a x +--=(0)a ≠. (1)求证:方程总有两个实数根;(2)若方程有两个不相等的负整数根,求整数a 的值.21.如图,AB 是⊙O 的直径,CD 是弦,CD ⊥AB 于点E ,点G 在直径DF 的延长线上,∠D =∠G =30.(1)求证:CG 是⊙O 的切线; (2)若CD =6,求GF 的长.空气质量指数FD CE O A B22.阅读下面材料:小丁在研究数学问题时遇到一个定义:对于排好顺序的三个数:123,,x x x ,称为数列123,,x x x .计算1x ,122x x +,1233x x x ++,将这三个数的最小值称为数列123,,x x x 的价值.例如,对于数列2,1-,3,因为22=,2(1)122=+-,2(1)3433+-+=,所以数列2,1-,3的价值为12. 小丁进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的价值.如数列1-,2,3的价值为12;数列3,1-,2的价值为1;….经过研究,小丁发现,对于“2,1-,3”这三个数,按照不同的排列顺序得到的不同数列中,价值的最小值为12.根据以上材料,回答下列问题:(1)数列4-,3-,2的价值为______;(2)将“4-,3-,2”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的价值的最小值为______ ,取得价值最小值的数列为___________(写出一个即可); (3)将2,9-,a (1)a >这三个数按照不同的顺序排列,可得到若干个数列.若这些数列的价值的最小值为1,则a 的值为__________.五、解答题(本题共22分,第23题7分,第24题7分,第25题8分)23.在平面直角坐标系xOy 中,抛物线2(1)y x m x m =---(0)m >与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C . (1)求点A 的坐标;(2)当15ABC S △=时,求该抛物线的表达式;(3)在(2)的条件下,经过点C 的直线l :y kx b =+(0)k <与抛物线的另一个交点为D . 该抛物线在直线l 上方的部分与线段CD 组成一个新函数的图象. 请结合图象回答:若新函数的最小值大于8-,求k 的取值范围.24.将线段AB 绕点A 逆时针旋转60°得到线段AC ,继续旋转α(0120)α<<得到线段AD ,连接CD .(1)连接BD ,①如图1,若α=80°,则∠BDC 的度数为 ;②在第二次旋转过程中,请探究∠BDC 的大小是否改变.若不变,求出∠BDC 的度数;若改变,请说明理由.(2)如图2,以AB 为斜边作直角三角形ABE ,使得∠B =∠ACD ,连接CE ,DE . 若∠CED =90°,求α的值.DCB A25.如图,在平面直角坐标系xOy 中,点(,)P a b 在第一象限.以P 为圆心的圆经过原点,与y 轴的另一个交点为A .点Q 是线段OA 上的点(不与O ,A 重合),过点Q 作PQ 的垂线交⊙P 于点(,)B m n ,其中0≥m .图1图2(1)若5b =,则点A 坐标是________________; (2)在(1)的条件下,若OQ =8,求线段BQ 的长;(3)若点P 在函数2y x =(0)x >的图象上,且△BQP 是等腰三角形.①直接写出实数a 的取值范围:__________________;②在12,4PQ 的长度可以为 ,并求出此时点B 的坐标.海淀区九年级第一学期期中练习数学试卷答案及评分参考阅卷须知:1. 为便于阅卷,本试卷答案中有关解答题的推导步骤写的较为详细,阅卷时,只要考生将主要过程正确写出即可.2. 若考生的解法与给出的解法不同,正确者可参照评分参考相应给分.备用图3. 评分参考中所注分数,表示考生正确做到此步应得的累加分数.二、填空题(本题共16分,每小题4分) 9. 5 ;10. 4 ; 11. > ;12. 30°或60°.(注:每个答案2分)三、解答题(本题共30分,每小题5分) 13.(本小题满分5分)解:∵131a ,b ,c ===-, …………………………………………………………………1分∴2341(1)=13>0∆=-⨯⨯-. … ……………………………………………………2分∴x =. ∴12x =. ……………………………………………………5分 14.(本小题满分5分)证明:∵∠DAB =∠EAC ,∴∠DAB +∠BAE =∠EAC+∠BAE .∴∠DAE =∠BAC . ………………………………………………………………1分 在△BAC 和△DAE 中,AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩,,, ∴△BAC ≌△DAE . ………………………………………………………………4分 ∴BC =DE . ………………………………………………………………………5分 15.(本小题满分5分)解:设二次函数的解析式为()225y a x =-+ (0)a ≠.……………………………1分∵二次函数的图象经过点(0,1).∴()21025a =-+.………………………………………………………………2分 ∴1a =-. …………………………………………………………………………4分 ∴二次函数的解析式为241y x x =-++.………………………………………5分16. (本小题满分5分)解:∵四边形ABCD 内接于⊙O ,∴∠ADC +∠ABC =180°. …………………………………………………………1分 ∵∠ABC =130°,∴∠ADC =180°-∠ABC =50°. …………………………………………………2分∴∠AOC =2∠ADC =100°. ………………………………………………………3分 ∵OA=OC ,∴∠OAC =∠OCA . ……………………………………………………………4分∴∠OAC =1(180)402AOC -∠=. ……………………………………………… 5分17. (本小题满分5分)解:依题意,得 21420m m -+=. ……………………………………………………2分∴2241m m -=-. ………………………………………………………………3分 ∴()()2222132213245154+=m m m m m --++=-+=-+=. …………5分18. (本小题满分5分)解:设每期减少的百分率为x .…………………………………………………… ……1分 由题意,得()24501288x -=. ……………………………………………… ………2分解方程得 115x =,295x =. ………………………………………………… ……3分 经检验,915x =>不合题意,舍去;15x = 符合题意. ……………… …………4分答:每期减少的百分率为20%. ……………………………………………… ………5分四、解答题(本题共20分,每小题5分) 19. (本小题满分5分)解:(1)3. …………………………………………………………………………… 2分 (2)小丁随机选择该月1日至15日中的某一天到达该市,则到达该市的 日期有15种不同的选择,在其中任意一天到达的可能性相等. ……………3分 由图可知,其中有9天空气质量优良. ………………………………… ……4分 所以,P (到达当天空气质量优良)93155==. …………………… ………5分20. (本小题满分5分)解:(1)∵0a ≠,∴原方程为一元二次方程.∴()234(3)a a ∆=--⨯⨯- ………………………………………………1分()23a =+.∵()230≥a +.∴此方程总有两个实数根. …………………………………………………2分(2)解原方程,得 11x =-,23x a=. ……………………………………………3分 ∵此方程有两个负整数根,且a 为整数,∴1a =-或3-. …………………………………………………………………4分 ∵12x x ≠,∴3a ≠-.∴1a =-. ………………………………………………………………………5分 21. (本小题满分5分) (1)证明:连接OC .∵OC=OD ,∠D =30°, ∴∠OCD =∠D = 30°.…………………………………1分 ∵∠G =30°,∴∠DCG =180°-∠D -∠G =120°. ∴∠GCO =∠DCG -∠OCD =90°. ∴OC ⊥CG .又∵OC 是⊙O 的半径.∴CG 是⊙O 的切线.……………………………………2分(2)解:∵AB 是⊙O 的直径,CD ⊥AB ,∴132CE CD ==. ………………………………………………………3分∵在Rt △OCE 中,∠CEO =90°,∠OC E =30°, ∴12OE OC =,222OC OE CE =+.设OE x =,则2OC x =.∴()22223x x =+.解得3x =(舍负值).∴23OC =. ………………………………………………………………4分 ∴23OF =.在△OCG 中,∵∠OCG =90°,∠G =30°, ∴243OG OC ==.∴23GF GO OF =-=. ……………………………………………………5分22. (本小题满分5分) 答:(1)53. …………………………………………………………………………………1分 (2)12, ………………………………………………………………………………2分3,2,4--或2,3,4--.(写出一个即可)…………………………………………3分(3)11或4.(每个答案各1分) ……………………………………………………5分五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23. (本小题满分7分)解:(1)∵ 抛物线2(1)y x m x m =---(0)m >与x 轴交于A 、B 两点,∴ 令0y =,即 2(1)0x m x m ---=.解得 11x =-,2x m =. …………………………………………………1分 又∵ 点A 在点B 左侧,且0m >,∴ 点A 的坐标为(1,0)-. …………………………………………………2分(2)由(1)可知点B 的坐标为(0)m ,.∵抛物线与y 轴交于点C ,∴点C 的坐标为(0,)m -. ……………………………………………………3分 ∵0m >,∴1AB m =+,OC m =. ∵15△ABC S =, ∴1(1)152m m +=. ∴6m =-或5m =. ∵0m >,∴5m =.∴抛物线的表达式为245y x x =--. ………………………4分(3)由(2)可知点C 的坐标为(0,5)-.∵直线l :y kx b =+(0)k <经过点C ,∴5b =-. ………………………………………5分 ∴直线l 的解析式为5y kx =-(0)k <. ∵2245(2)9y x x x =--=--,∴当点D 在抛物线顶点处或对称轴左侧时,新函数的最小值为9-,不符合题意. 当点D 在抛物线对称轴右侧时,新函数的最小值有可能大于8-. 令8y =-,即2458x x --=-.解得 11x =(不合题意,舍去),23x =. ∴抛物线经过点(3,8)-.当直线5y kx =-(0)k <经过点(3,8)-时,可求得1k =-.…………………6分由图象可知,当10k -<<时新函数的最小值大于8-. ………………………7分 24.(本小题满分7分) 解:(1)①30°. …………………………………………………………………………1分②不改变,∠BDC 的度数为30.方法一:由题意知,AB=AC=AD .∴点B 、C 、D 在以A 为圆心,AB 为半径的圆上.…………………………2分 ∴∠BDC=12∠BAC =30.……………………………………………………3分 方法二:由题意知,AB=AC=AD . ∵AC =AD ,∠CAD =α, ∴1801=9022ADC C αα-==-∠∠.…………………………………2分 ∵AB=AD ,∠BAD =60α+,∴()18060120160222ADB B ααα-+-====-∠∠. ∴11(90)(60)3022BDC ADC ADB αα=-=---=∠∠∠.…………3分 (2)过点A 作AM ⊥CD 于点M ,连接EM .∴90AMC ∠=. 在△AEB 与△AMC 中,AEB AMC B ACD AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩,,, ∴△AEB ≌△AMC . ………………………………………………………4分∴AE AM =,BAE CAM ∠=∠.∴60EAM EAC CAM EAC BAE BAC ∠=∠+∠=∠+∠=∠=.∴△AEM 是等边三角形.∴EM AM AE ==. …………………………………………………………5分 ∵AC AD =,AM CD ⊥ , ∴CM DM =. 又90DEC ∠=,∴EM CM DM ==.∴AM CM DM ==. …………………………………………………………6分 ∴点A 、C 、D 在以M 为圆心,MC 为半径的圆上.∴90CAD α=∠=. …………………………………………………………7分 25. (本小题满分8分) 解: (1)(0,10). …………………………………………………………………1分(2)连接BP 、OP ,作PH ⊥OA 于点H .∵5,b =PH ⊥OA , ∴152OH AH OA ===.∵OQ =8,∴3QH OQ OH =-=.在Rt △QHP 中,22229PQ QH PH PH =+=+.在Rt PHO △中,2222225PO OH PH PH BP =+=+=.在Rt △BQP 中,22222(25)(9)16BQ BP PQ PH PH =-=+-+=. ∴4BQ =.……………………………………………………………………3分(3)①1≥a .……………………………………………………………………………4分……………………………………………………………………………5分 解:∵△BQP是等腰直角三角形,PQ =∴半径BP = 又∵2(,)P a a ,∴2242OP a a =+=.即42200a a +-=.解得2a =±.∵0a >,∴2a =. ……………………………………………………………………………6分 ∴(2,4)P .如图,作BM y ⊥轴于点M ,则△QBM ≌△PQH . ∴2MQ PH ==,MB QH ===B.…………………………………7分∴1若点Q在OH上,由对称性可得2B.……………………………8分综上,当PQ=B点坐标为+或2-.。
北京市海淀区2014届九年级数学上学期期中试题(含答案)

海淀区九年级第一学期期中测评数学试卷(分数:120分时间:120分钟)班级姓名学号 成绩试题答案一律填涂或书写在答题卡上,在试卷上做答无效. 一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个..是符合题意的. 1.一元二次方程2230x x --=的二次项系数、一次项系数、常数项分别是A. 1,2,3--B. 1,-2,3C. 1,2,3D. 1,2,3- 2.在角、等边三角形、平行四边形、圆中,既是中心对称图形又是轴对称图形的是 A .角B .等边三角形 C .平行四边形 D .圆 3.函数y =x 的取值范围是A .2≠xB .2≤xC .2>xD .2≥x4.如图,点A 、B 、C 在O ⊙上,若110AOB ∠=,则ACB ∠的大小是 A .35B .45 C .55D .1105.用配方法解方程09102=++x x ,配方正确的是 A .16)5(2=+x B .34)5(2=+x C .16)5(2=-x D .25)5(2=+x6.如图所示的图案绕旋转中心旋转一定角度后能够与自身重合,那么这个旋转角可能是 A .60B .72 C .90D .120 7.若0a +=,则a b +的值为A .-1B .1C .5D .68.如图,⊙O 的半径为5,点P 到圆心O 的距离为10,如果过点P 作弦,那么长度为整数值的弦的条数为 A .3 B .4C .5D .6二、填空题(本题共16分,每小题4分)9.如图,将ABC △绕点C 顺时针旋转至''A B C △的位置,若 15ACB ∠=,120B ∠=,则'A ∠的大小为________.10.已知一元二次方程有一个根是0,那么这个方程可以是(填上你认为正确的一个方程即可).11.如图,AB 是⊙O 的直径,点C 、D 为⊙O 上的两点,若40=∠ABD ,则BCD ∠的大小为.12.下面是一个按某种规律排列的数阵:1 第1行2 第2行3第3行4第4行根据数阵排列的规律,则第5行从左向右数第5个数为,第n (3≥n ,且n 是整数)行从左向右数第5个数是(用含n 的代数式表示). 三、解答题(本题共30分,每小题5分) 13.计算:36324⨯+÷.14.用公式法解一元二次方程:241x x +=.15.如图,ABC △与AED △均是等边三角形,连接BE 、CD .请在图中找出一条与CD 长度相等的线段,并证明你的结论. 结论:CD =.证明:A POD C B A16.当15-=x 时,求代数式522-+x x 的值.17.如图,两个圆都以点O 为圆心,大圆的弦AB 交小圆于C 、D 两点.求证:AC =BD . 证明:18.列方程(组)解应用题:如图,有一块长20米,宽12米的矩形草坪,计划沿水平和竖直方向各修一条宽度相同的小路,剩余的草坪面积是原来的34,求小路的宽度.解:四、解答题(每小题5分,共20分)19.已知关于x 的一元二次方程210x mx m -++=的一个根为2. (1) 求m 的值及另一根;(2)若该方程的两个根分别是等腰三角形的两条边的长,求此等腰三角形的周长.20.如图,DE 为半圆的直径,O 为圆心,DE =10,延长DE 到A ,使得EA =1,直线AC 与半圆交于B 、C 两点,且 30=∠DAC .(1)求弦BC 的长; (2)求AOC △的面积.21.已知关于x 的方程0)1(222=++-k x k x 有两个不相等的实数根. (1)求k 的取值范围;(2)求证:1-=x 不可能是此方程的实数根.DCBA O22.阅读下面的材料:小明在研究中心对称问题时发现:如图1,当点1A 为旋转中心时,点P 绕着点1A 旋转180°得到1P 点,点1P 再绕着点1A 旋转180°得到2P 点,这时点P 与点2P 重合.如图2,当点1A 、2A 为旋转中心时,点P 绕着点1A 旋转180°得到1P 点,点1P 绕着点2A 旋转180°得到2P 点,点2P 绕着点1A 旋转180°得到3P 点,点3P 绕着点2A 旋转180°得到4P 点,小明发现P 、4P 两点关于点2P 中心对称.(1)请在图2中画出点3P 、4P , 小明在证明P 、4P 两点关于点2P 中心对称时,除了说明P 、2P 、4P 三点共线之外,还需证明;(2)如图3,在平面直角坐标系xOy 中,当)3,0(1A 、)0,2(2 A 、)0,2(3A 为旋转中心时,点)4,0(P 绕着点1A 旋转180°得到1P 点;点1P 绕着点2A 旋转180°得到2P 点;点2P 绕着点3A 旋转180°得到3P 点;点3P 绕着点1A 旋转180°得到点4P 点. 继续如此操作若干次得到点56P P 、、,则点2P 的坐标为,点2017P 的坐为.五、解答题(本题共22分,第23题7分,第24题8分,第25题7分) 23.已知关于x 的一元二次方程02)12(2=++-x m mx . (1)求证:此方程总有两个实数根;(2)若此方程的两个实数根都是整数,求m 的整数值; (3)若此方程的两个实数根分别为1x 、2x ,求代数式5)(2))(12()(2122213231+++++-+x x x x m x x m 的值.24.已知在ABC △中,90=∠ACB ,26==CB CA ,AB CD ⊥于D ,点E 在直线CD 上,CD DE 21=,点F 在线段AB 上,M 是DB 的中点,直线AE 与直线CF 交于N 点. (1)如图1,若点E 在线段CD 上,请分别写出线段AE 和CM 之间的位置关系和数量关系:___________,___________;(2)在(1)的条件下,当点F 在线段AD 上,且2AF FD =时,求证:45=∠CNE ; (3)当点E 在线段CD 的延长线上时,在线段AB 上是否存在点F ,使得 45=∠CNE .若存在,请直接写出AF 的长度;若不存在,请说明理由.DCBANM FED CBA25.在平面直角坐标系xOy 中,点A 、B 分别在x 轴、y 轴的正半轴上,且10=AB ,点M 为线段AB 的中点.(1)如图1,线段OM 的长度为________________;(2)如图2,以AB 为斜边作等腰直角三角形ACB ,当点C 在第一象限时,求直线OC 所对应的函数的解析式; (3)如图3,设点D 、E 分别在x 轴、y 轴的负半轴上,且10=DE ,以DE 为边在第三象限内作正方形DGFE ,请求出线段MG 长度的最大值,并直接写出此时直线MG 所对应的函数的解析式.GFEDxy O ABM海淀区九年级第一学期期中练习2013.11数学试卷答案及评分参考阅卷须知:1.为便于阅卷,本试卷答案中有关解答题的推导步骤写的较为详细,阅卷时,只要考生将主要过程正确写出即可.2.若考生的解法与给出的解法不同,正确者可参照评分参考相应给分.3.评分参考中所注分数,表示考生正确做到此步应得的累加分数. 二、填空题(本题共16分,每小题4分)9.45°;10.20x x -=(二次项系数不为0,且常数项为0均正确);11.50°;12.21,622+-n n (每空2分).三、解答题(本题共30分,每小题5分) 13.(本小题满分5分)解:36324⨯+÷=………………………………………………………………………2分图1图2CxyOABM BAOyx图32322+=…………………………………………………………………4分 25=.……………………………………………………………………………5分14.(本小题满分5分)解:原方程可化为2+410x x -=,……………………………………………………1分141a ,b ,c ===-,2441(1)=20>0,∆=-⨯⨯-…………………………………………………………2分方程有两个不相等的实数根,2x ===-4分即1222x =-=-.……………………………………………………5分15.(本小题满分5分)结论:CD BE =.……………………………………………………………………1分 证明: △ABC 与△AED 是等边三角形,∴AE AD =,AB AC =,60CAB DAE ∠=∠=.…2分 ∴CAB DAB DAE DAB ∠-∠=∠-∠,即CAD BAE ∠=∠.………………………………3分在△CAD 和△BAE 中,AC AB,CAD BAE,AD AE,=⎧⎪∠=∠⎨⎪=⎩∴△CAD ≌△BAE .…………………………………………………………4分 ∴CD =BE .…………………………………………………………………5分16.(本小题满分5分)解: 15-=x ,∴1x +=.∴5)1(2=+x .………………………………………………………………1分∴2215x x ++=.………………………………………………………………2分∴224x x +=.…………………………………………………………………3分 ∴225451x x +-=-=-.……………………………………………………5分17.(本小题满分5分)证明:过点O 作AB OM ⊥于M ,…………………………1分由垂径定理可得DM CM BM AM ==,.……………3分∴DM BM CM AM -=-.…………………………4分 即BD AC =.…………………………………………5分ED CBA18.(本小题满分5分)解:设小路的宽度是x 米.………………………………………………………1分由题意可列方程,3(20)(12)20124x x --=⨯⨯.……………………………2分化简得, 232600x x -+=.解得, 12302x ,x ==.………………………………………………………3分由题意可知3020x =>不合题意舍去,2x =符合题意.…………………4分 答:小路的宽度是2米.……………………………………………………5分四、解答题(本题共20分,每小题5分) 19.(本小题满分5分)解:(1)∵关于x 的一元二次方程210x mx m -++=的一个根为2,∴22210m m -++=.……………………………………………………1分 ∴5m =.……………………………………………………………………2分∴一元二次方程为2560x x -+=.解得1223x ,x ==.…………………………………………………………3分∴5m =,方程另一根为3.(2)当长度为2的线段为等腰三角形底边时,则腰长为3,此时三角形的周长为2+3+3=8;………………………………………………………………4分 当长度为3的线段为等腰三角形底边时,则腰长为2,此时三角形的周长为2+2+3=7. ………………………………………………………………5分20.(本小题满分5分)解:(1)过点O 作OM ⊥BC 于M .由垂径定理可得:BM=CM .…1分∵30DAC ∠=, ∴12OM OA =.∵直径DE =10, EA =1,∴=5OD OC OE ==.∴516OA OE EA =+=+=. ∴3OM =.…………………2分在R t △COM 中,222225316CM OC OM =-=-=. ∴4CM =. ∴4BM =.∴+8BC BM CM ==.……………………………………………………3分 (2)在R t △AOM 中,222226327AM OA OM =-=-=.∴AM =.……………………………………………………………………4分∴+4AC AM CM ==. ∵OM ⊥AC ,∴114)3622AOCSAC OM =⋅=⨯⨯=.……………………………5分21.(本小题满分5分)解:(1)∵关于x 的方程0)1(222=++-k x k x 有两个不相等的实数根,MECA DB O∴224(1)4=8+4>0k k k ∆=+-.………………………………………………2分 ∴1>2k -.…………………………………………………………………3分 (2)∵当1-=x 时,左边=222(1)x k x k -++22(1)2(1)(1)k k =--+⨯-+223k k =++…………………………………………4分2(+1)20k =+>.而右边=0,∴左边≠右边.∴1-=x 不可能是此方程的实数根.……………………………………5分22.(本小题满分5分)(1)正确画出34P P 、点(图略).………………………………………………1分224=P P P P .……………………………………………………………………2分(2)(-4,-2).…………………………………………………………………3分(0,2).……………………………………………………………………5分五、解答题(本题共22分,第23题7分,第24题8分,第25题7分) 23.(本小题满分7分)解:(1)由题意可知0m ≠.2(21)42m m ∆=+-⨯⨯22=441(21)0m m m -+=-≥.……………………………………………2分∴此方程总有两个实数根.(2)方程的两个实数根为x =,∴1212x ,x m==.…………………………………………………………4分 ∵方程的两个实数根都是整数,且m 为整数,∴1m =±.…………………………………………………………………5分(3)∵原方程的两个实数根分别为1x 、2x ,∴211(21)20mx m x -++=222(21)20mx m x -++=.……………………………………………………6分∴5)(2))(12()(2122213231+++++-+x x x x m x x m=1323211222[(21)2]+[(21)2]+5mx m x x mx m x x -++-++=12211222[(21)2]+[(21)2]+5x mx m x x mx m x -++-++=12005x x ⨯+⨯+=5.…………………………………………………………………………7分24.(本小题满分8分)(1)AE ⊥CM ,AE =CM .……………………………………………………2分(2)如图,过点A 作AG ⊥AB ,且AG =BM,,连接CG 、FG ,延长AE 交CM 于H .∵90=∠ACB ,26==CB CA ,∴∠CAB =∠CBA =45°,12=. ∴∠GAC =∠MBC =45°. ∵AB CD ⊥,∴CD=AD=BD =162AB =. ∵M 是DB 的中点, ∴3BM DM ==. ∴3AG =. ∵2AF FD =,∴4 2.AF DF ==,∴+2+3=5.FM FD DM == ∵AG ⊥AF , ∴FG ==∴.FG FM =……………………………………………………………………3分 在△CAG 和△CBM 中, CA CB CAG CBM AG BM =⎧⎪∠=∠⎨⎪=⎩,,, ∴△CAG ≌△CBM .∴CG =CM ,ACG BCM ∠=∠.∴++90MCG ACM ACG ACM BCM ∠=∠∠=∠∠=.………………………4分 在△FCG 和△FCM 中, CG CM FG FM CF CF =⎧⎪=⎨⎪=⎩,,, ∴△FCG ≌△FCM .∴FCG FCM ∠=∠.………………………………………………………5分 ∴45FCH ∠=.由(1)知AE ⊥CM , ∴90CHN ∠=∴ 45=∠CNE .………………………………………………………………6分 (3)存在.FHNGM EDCBAAF =8.…………………………………………………………………………8分25.(本小题满分7分)(1)5;…………………………………………………………………………………1分 (2)如图1, 过点C 分别作CP ⊥x 轴于P ,CQ ⊥y 轴于Q .∴∠CQB =∠CPA =90°,∵∠QOP =90°,∴∠QCP =90°.∵∠BCA =90°, ∴∠BCQ =∠ACP . ∵BC=AC ,∴△BCQ ≌△ACP .∴CQ=CP .………………………………3分 ∵点C 在第一象限,∴不妨设C 点的坐标为(a ,a )(其中0a ≠).设直线OC 所对应的函数解析式为kx y =,∴a ka =,解得k =1,∴直线OC 所对应的函数解析式为x y =.…………………………………4分 (3)取DE 的中点N ,连结ON 、NG 、OM .∵∠AOB=90°,∴OM =152AB =.同理ON =5.∵正方形DGFE ,N 为DE 中点,DE=10, ∴NG===.在点M 与G 之间总有MG ≤MO +ON +NG (如图2),由于∠DNG 的大小为定值,只要12DON DNG ∠=∠,且M 、N 关于点O 中心对称时,M 、O 、N 、G 四点共线,此时等号成立(如图3).………………………5分∴线段MG 取最大值10+55.………………6分此时直线MG 的解析式x y 251+-=.……………………………………7分。
2015届海淀区九年级第一学期期中练习 答案

2015届海淀区九年级第一学期期中练习答案2015届海淀区九年级第一学期期中练习语文参考答案及评分标准2014.11一、基础.运用(共25分)(一)选择(共12分。
每小题2分)题号123456答案BDBCAB(二)填空(共13分)7.答案:(1)长河落日圆(2)人不知而不愠(3)醉里挑灯看剑(4)道阻且跻(5)黄发垂髫并怡然自乐(6)但愿人长久千里共婵娟(共8分。
每空1分,有错字该空不得分)8.答案:章回《西游记》花果山(或水帘洞)大人国(或飞岛国、智马国、慧骃国,若填其他译名如布罗卜丁奈格等也可)比赛绳技(或绳上跳舞、表演绳技)(共5分。
每空1分,该空有错不得分)二、文言文阅读(共10分)9.答案:B(共2分)10. 答案:(1) (湖面上的)大片烟雾完全消散。
(2)宴会喝酒的乐趣,不在于音乐。
(或宴饮酣畅的乐趣,不在于音乐。
)(共4分。
共2小题,每小题2分)11.答案要点:选文(一)寄寓了作者不以个人沉浮为意,以天下为己任的情怀。
(或寄寓了作者“不以物喜,不以己悲”的阔大情怀和“先天下之忧而忧,后天下之乐而乐”的壮志豪情);选文(二)寄寓了作者与民同乐的情怀。
(共2分。
两个答案要点各1分,选文(一)若用原文回答,则“不以物喜,不以己悲”“先天下之忧而忧,后天下之乐而乐”任意一句得1分)(共2分。
能紧扣所选文段情怀谈启示,言之成理即可)三、现代文阅读(共35分)(一)(共14分)12. 答案示例:刚中带柔(或“刚硬中透着柔情”)顽强美丽(或“顽强”)惊叹(或“惊奇赞叹”)敬畏(共4分。
共4空,每空1分)13.答案示例一:【甲】采用“冲入”“喊着”“叫着”这样的动词,生动形象地写出了绿水碧波快速流入石林时的力与美;又采用“欢快”“朵朵”“蒙蒙”这样的形容词和叠词,写出了流水撞击在石林中水花四溅、水雾弥漫的情景,表达了作者的喜爱之情。
答案示例二:【乙】采用比喻的修辞手法,把水波划过整石为底的沟坡形成的水珠比喻成一颗颗珍珠,生动形象地写出了水珠的圆润、晶莹剔透。
北京市海淀区2014-2015学年九年级上期期中考试物理试卷及答案
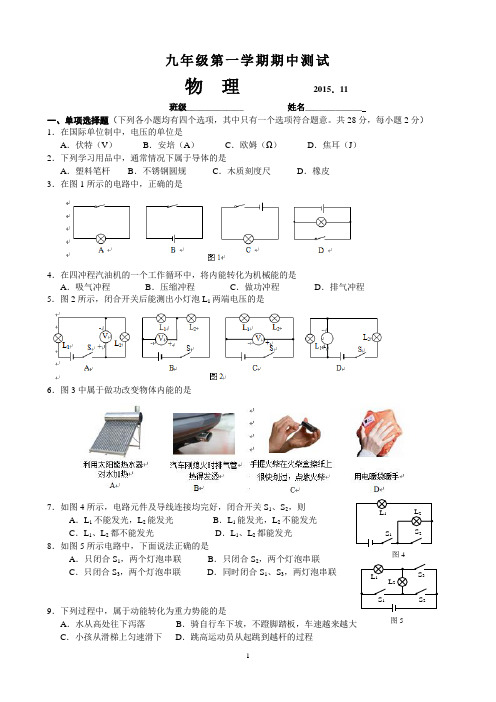
九年级第一学期期中测试物理2015.11班级_____________ 姓名_____________一、单项选择题(下列各小题均有四个选项,其中只有一个选项符合题意。
共28分,每小题2分)1.在国际单位制中,电压的单位是A.伏特(V)B.安培(A)C.欧姆(Ω)D.焦耳(J)2.下列学习用品中,通常情况下属于导体的是A.塑料笔杆B.不锈钢圆规C.木质刻度尺D.橡皮3.在图1所示的电路中,正确的是4.在四冲程汽油机的一个工作循环中,将内能转化为机械能的是A.吸气冲程B.压缩冲程C.做功冲程D.排气冲程5.图2所示,闭合开关后能测出小灯泡L1两端电压的是6.图3中属于做功改变物体内能的是7.如图4所示,电路元件及导线连接均完好,闭合开关S1、S2,则A.L1不能发光,L2能发光B.L1能发光,L2不能发光C.L1、L2都不能发光D.L1、L2都能发光8.如图5所示电路中,下面说法正确的是A.只闭合S1,两个灯泡串联B.只闭合S2,两个灯泡串联C.只闭合S3,两个灯泡串联D.同时闭合S1、S3,两灯泡串联9.下列过程中,属于动能转化为重力势能的是A.水从高处往下泻落B.骑自行车下坡,不蹬脚踏板,车速越来越大C.小孩从滑梯上匀速滑下D.跳高运动员从起跳到越杆的过程图5L1L2S1 S2S3图4L1 L2S2S110.图6所示为滑动变阻器的结构示意图,将滑动变阻器的两个接线柱接到电路中,要求滑片向左移动时,电路中的电流逐渐变小,连入电路中的接线柱可能是 A .A 和BB .A 和CC .C 和DD .D 和B11.“回力”玩具车,玩耍时要先用手压住,往后退一点,松手后才能往前跑。
“用手压住,往后退”是存贮了A .弹性势能B .重力势能C .动能D .惯性12.如图7所示,灯L 1和L 2是两只相同的灯泡,a 、b 是电流表或电压表。
闭合开关S 后,两灯都能发光,则下列判断正确的是A .a 、b 均为电流表B .a 、b 均为电压表C .a 为电流表,b 为电压表D .a 为电压表,b 为电流表13.如图8的滑片P 向左移动,在此过程中下列判断正确的是 A .电压表V 1示数变小,电压表V 2示数变小B .电流表A 示数变小,电压表V 1示数不变C .电压表V 1示数不变,灯泡L 亮度变亮D .电压表V 1示数变小,电压表V 2示数变大14.如图9所示电路,电源两端电压保持不变。
北京市海淀区2014届九年级上学期期中考试英语试题(WORD精校版)

海淀区九年级第一学期期中练习英语2013.11一、听对话,从下面各题所给的A、B、C三幅图片选项与对话内容相符的图片。
每段对话你将听两遍。
(共4分,每小题1分)二、听对话或独白,根据对话或独白的内容,从下面各题所给的A、B、C三个选项中选择最佳选项。
每段对话或独白你将听两遍。
(共12分,每小题1分)5. What’s in the backpack?A. A notebook.B. A pencil box.C. A hair hand6. Whose backpack could it be?A. Jack’sB. Lily’sC. Maria’s请听一段对话,完成第7至8小题。
7. What is John doing now?A. Watching TV.B. Doing homework.C. Playing baseball.8. What does John hate?A. The shows.B. The rulesC. The games.请听一段对话,完成第9至10小题。
9.How long will the holiday be?A. Two days.B. Three days.C. Four days.10. What is Tina going to do during the holiday?A. Go hiking and camping.B. Go to the beach.C. Visit the museum.请听一段对话,完成第11至13小题。
11. When is the party?A. Next Sunday evening.B. Next Saturday evening.C. Next Friday evening.12. What will the boy probably wear for the party?A. A shirt and tie.B. A suit and shirt.C. A suit and tie.13. What can we know about the boy?A. He has no friends.B. He needs more time.C. He wants some advice.请听一段对话,完成第14至16小题。
2014-2015海淀区九年年级第一学期期中练习

(5)《桃花源记》中,表现老人孩子皆有所养,生活幸福的语句是“__________,__________”。
(6)中秋佳节,遥望明月,请你把苏轼《水调歌头
明月几时有》中的名句“__________,
__________”写下来寄给远方的亲人,希望家人都能平平安安,虽然相隔千里,仍能共享这一轮
2! / 1! 3
理解:采用设问的修辞方法。先提出问题,再通过回答给出新闻事实,引起读者的关注和思考,也
点明一些中国留学生误以为国外大学教育更轻松自由,导致刚去国外读大学时的不适应。
B.“蛟龙”携手“龙珠”探大洋
理解:采用比喻的修辞方法。把我国微型遥控潜水器“龙珠号”和另一艘载人潜水器“蛟龙号”联合进行
海洋科考的事实,比喻成“蛟龙号”牵着“龙珠号”在海底游弋,生动有趣。
薄暮冥冥,虎啸猿啼。登斯楼也,则有去国怀乡,忧谗畏讥,满目萧然,感极而悲者矣。 至若春和景明,波澜不惊,上下天光,一碧万顷;沙鸥翔集,锦鳞游泳;岸芷汀兰,郁郁青青。
而或长烟一空,皓月千里,浮光跃金,静影沉璧,渔歌互答,此乐何极!登斯楼也,则有心旷神, 宠辱偕忘,把酒临风,其喜洋洋者矣。
嗟夫!予尝求古仁人之心,或异二者之为。何哉?不以物喜,不以己悲;居庙堂之高则忧其民; 处江湖之远则忧其君。是进亦忧,退亦忧。然则何时而乐耶?其必曰:“先天下之忧而忧,后天下之
时节,冬觅黄精度岁华”一诗描写了他带领众猴在__________③__________(地名)的欢乐生活。孙 悟空后来保护唐僧赴西天取经,历经千难万险方修成正果。《格列佛游记》主要描写格列佛在小人
国、__________④__________等虚构国度的冒险经历,情节离奇。但两部作品都有着深厚的现实根 基,前者以唐代高僧玄奘到天竺(古印度)取经的历史事实为依托,后者原本就是一部借幻想批评
2015届海淀初三期中试卷(精校版)

海淀区九年级第一学期期中练习语文2014. 11一、基础•运用(共25分)(一)选择。
下面各题均有四个选项,其中只有一个符合题意,选出答案后在答题纸上用铅笔把对应题目的选项字母涂黑涂满。
(共12分。
每小题2分)1.下列词语中加点字的读音完争正确的一项是A.和煦(x u)机械(ji e)记载(z①不屈不挠(n do)B.拮据(j ®解剖(p cu)倔强(ju ®刚正不阿.(eC.逮捕(d①氛围(f en)教诲(hu i)一筹莫展(ch du)D.庇护(b i)薄弱(b ©胆怯(qi e)称心如意(ch e ng)2.班上玩“词语接龙”游戏,下列四个选项中的两组接龙词语书写完全正确..的一项是A.缓慢- ——慢不经心不折不扣一扣人心弦B风气-一气冲霄汉班门弄斧一-一斧底抽薪C..淡漠- 漠不关心变本加厉厉厉在目D.•惦记- -—记忆犹新名列前矛矛塞顿开3. 下列句子中加点成语或俗语使用有误..的一项是A. 经过外墙粉刷、护栏改装、地面平整等系列改造,老旧小区的面貌终于焕然一新。
B. 星期天,亮亮一边戴着耳机听音乐,一边欣赏湖边的美景,耳濡目染,十分惬意!C. 只有品行优良的人才能在与他人的长期交往小最终赢得别人的信赖和尊敬,正所谓“路遥知马力,日久见人心”。
D. 网络技术日新月异,几大互联网综合服务商八仙过海,各显其能..,推出了诸如博客、飞信、傲信等社交软件。
4. 结合语境,将下列句子填人横线处,顺序最恰当..的一项是汉字是先民生活与智慧的结晶,有着深厚的文化内蕴。
有的汉字最初就是一幅美丽的图画,记录了某些生活场景。
①现代汉语中“客”字的本义正是“外来者”,它与“主”相对,表示宾从的一方。
客人、客座、客卿中的“客”都包含此意。
②在水利行业,人们就把来自本地以外的水称为“客水”。
③例如,“客”字的甲骨文,俨然一幅简笔画:穹窿似的屋宇下,左方是背着行囊的旅人,右方是拱手相迎的主人。
2013-2014学年北京市海淀区2014届九年级上学期期中考试英语试题(含答..

海淀区九年级第一学期期中练习英语2013.11一、听对话,从下面各题所给的A、B、C三幅图片选项与对话内容相符的图片。
每段对话你将听两遍。
(共4分,每小题1分)二、听对话或独白,根据对话或独白的内容,从下面各题所给的A、B、C三个选项中选择最佳选项。
每段对话或独白你将听两遍。
(共12分,每小题1分)5. What’s in the backpack?A. A notebook.B. A pencil box.C. A hair hand6. Whose backpack could it be?A. Jack’sB. Lily’sC. Maria’s请听一段对话,完成第7至8小题。
7. What is John doing now?A. Watching TV.B. Doing homework.C. Playing baseball.8. What does John hate?A. The shows.B. The rulesC. The games.请听一段对话,完成第9至10小题。
9.How long will the holiday be?A. Two days.B. Three days.C. Four days.10. What is Tina going to do during the holiday?A. Go hiking and camping.B. Go to the beach.C. Visit the museum.请听一段对话,完成第11至13小题。
11. When is the party?A. Next Sunday evening.B. Next Saturday evening.C. Next Friday evening.12. What will the boy probably wear for the party?A. A shirt and tie.B. A suit and shirt.C. A suit and tie.13. What can we know about the boy?A. He has no friends.B. He needs more time.C. He wants some advice.请听一段对话,完成第14至16小题。
2014-2015北京市海淀初三第一学期化学期中试卷(带答案)

2014-2015 北京市海淀区九年级第一学期期中试卷化 学 2014年11月13日考生须知 1. 本试卷共8页,共四道大题,33个小题,满分80分。
考试时间100分钟。
2. 在答题纸指定位置上准确填写学校名称、班级名称、姓名。
3. 试题答案填涂或书写在答题纸上,在试卷上作答无效。
考试结束,将答题纸交回。
4. 请使用黑色字迹笔答题。
可能用到的相对原子质量:H 1 O 16 S 32 Fe 56一、选择题(每小题只有1个选项符合题意,共25个小题,每小题1分,共25分) 1.空气中体积分数约占78%的是A .氮气B .氧气C .稀有气体D .二氧化碳2.下列变化中,属于化学变化的是A .石蜡熔化B .河水结冰C .岩石粉碎D .木炭燃烧 3.下列物质中,属于纯净物的是A .清新空气B .液态氧气C .蔚蓝海水D .澄清石灰水 4.水是宝贵的资源。
下列有关水的说法中,不正确...的是 A .工业用水应该循环利用 B .生活污水直接排放不会造成水污染 C .喷灌、滴灌可以减少大量用水 D .水被严重污染后会给人类带来灾难 5.下列物质在空气中燃烧,生成大量白烟的是A .木炭B .硫粉C .红磷D .铁丝6.我国在大气污染物监测方面取得了一定的进展,下列项目不属于...其基本监测项目的是 A .二氧化碳 B .二氧化氮 C .二氧化硫 D .PM 2.5 7.下列图标中,表示爆炸品的标志是A B C D 8.能保持氧气化学性质的微观粒子是 A .O B .2O C .O 2 D .CO 29.下列符号中,表示2个氢原子的是A .2HB .H 2C .H 2OD .H 2O 2 10.下列关于原子的说法中,不正确...的是 A .物质都是由原子直接构成的 B .原子由原子核和核外电子构成 C .原子核显正电性 D .原子核一般由质子和中子构成 11.可以降低水的硬度的方法是A .沉降B .吸附C .过滤D .蒸馏 12.氧化锆(ZrO 2)纤维是一种耐火纤维材料,其中锆元素的化合价是A .-4B . -2C .+2D .+4 13.下列做法中,符合实验室中化学药品取用规则的是A .鼻孔凑到容器口闻药品的气味B .用药匙取少量氯化钠,尝一尝味道C .若没有说明用量,固体只需盖满试管底部D .为了节约药品,实验剩余的药品应放回原瓶 14.下列物质的用途主要利用了其物理性质的是A .氢气是清洁燃料B .液氮用做制冷剂C .氧气用于气割气焊D .氮气充于食品袋中防腐 15.下列图示的实验操作中,正确的是A .倾倒液体B .过滤液体C .给液体药品加热D .读出液体的体积 16.下列关于催化剂的说法中,正确的是A .只有二氧化锰能做催化剂B .催化剂在反应前后质量不改变C .催化剂只能加快化学反应速率D .所有的化学反应都需要催化剂 17.下列物质中,化学式书写正确的是A .氧化钠 NaOB .氯化钠 KClC .碳酸钙 CaCO 3D .氯化铝 ALCl 3 18.下列化学反应中,既不是化合反应也不是分解反应的是 A . 镁 + 氧气 氧化镁 B .乙烯 + 氧气 二氧化碳 + 水C . 氧化汞 汞 + 氧气D .二氧化碳 + 碳 一氧化碳点燃点燃加热高温19.鉴别空气、氮气和氧气三种气体,最简单的方法是A.分别观察气体的颜色B.分别测量气体的密度C.分别伸入燃着的木条D.分别通入澄清石灰水20.下列加热高锰酸钾并用排水法收集氧气的操作中,正确的是A.组装好仪器后,先装药品再检查装置气密性B.先使试管均匀受热,然后对药品所在部位固定加热C.导管口开始有气泡冒出时,立即收集气体D.收集满气体后,将集气瓶移出水面迅速盖上玻璃片21.某些水果散发的香味来自乙酸乙酯。
北京市海淀区2014-2015年初三语文第一学期期中检测(含答案)

1、基础-运用(共23分)(一)选择。
下面各题均有四个选项,其中只有一个符合题意,选出答案后在答题卡上用铅笔把对应的选项字母涂黑涂满。
(共14分)1、下列加点字注音完全正确的一项是()A.卑鄙(bǐ)颠簸(bǒ)负载(zǎi)毛遂自荐(suì)B.庇护( bì )怪癖(pì)处理(chǔ)高屋建瓴( líng)C.蓓蕾(lěi)订正(dīng)巢穴(xuè )既往不咎 ( jiù )D.笨拙(zhuō)刹那( chà )逮捕(dài )得陇望蜀(lǒng)2、下列词语的书写完全正确的一项是()A.安详濒临对诀承前启后B.爆怒脊梁筹备不屑置辩C.陡峭开辟恻隐焕然一新D.荒费崇拜教诲各行其是3.下列句子中加点成语或俗语使用有误的一项是()A.他们一位是画家,一位是摄影家,却不谋而合地选择了同一题材进行创作。
B.有关岳阳楼的诗赋很多,范仲淹受滕子京之托班门弄斧,写出了《岳阳楼记》。
C. 他山之石,可以攻玉,外聘老师可以学校带来解决问题的新思维、新方法。
D. 在“金牌明星教师”评选中,选手们八仙过海,各显其能,精彩说课掀起微博热议。
4.初三(1)班的准备出一期黑板报参加学校优秀板报的评选。
宣传委员征集同学们的意见,同学们积极响应。
有的同学在内容设计方面提出了十分巧妙的想法,有的同学在版式编排方面提出了极富创见的构思。
根据这些建议,班委会出了黑板报,效果出色。
同学们请你为这期黑板报的参评说出一句推荐的话。
最恰当的一句是()A.由于同学们的精雕细刻,没有人不夸这期黑板报是优秀的。
B.同学们别具匠心的设计,使黑板报的效果十分出色,你说呢?C.在同学们的精雕细刻下,这期黑板报的效果太棒了!D.同学们的设计别具匠心,黑板报的效果十分出色。
5、下列文学常识搭配有误的一项是()A.《使至塞上》》——王维——唐代B.《小石潭记》《捕蛇者说》——柳宗元——南宋C.《绿》《背影》——朱自清——现代D.《我的叔叔于勒》——莫泊桑——法国6.结合语境,将下列句子填入横线处,顺序最恰当的一项是()说起京剧,有些人误以为它是北京的地方戏,其实不然。
海淀区2015届九年级数学上学期期中试题有答案

海淀区九年级第一学期期中练习2014.11数学试卷答案及评分参考阅卷须知:1. 为便于阅卷,本试卷答案中有关解答题的推导步骤写的较为详细,阅卷时,只要考生将主要过程正确写出即可.2. 若考生的解法与给出的解法不同,正确者可参照评分参考相应给分.3. 评分参考中所注分数,表示考生正确做到此步应得的累加分数.二、填空题(本题共16分,每小题4分)9. 5 ;10. 4 ;11. >;12. 30°或60°.(注:每个答案2分)三、解答题(本题共30分,每小题5分)13.(本小题满分5分)解:∵131a ,b ,c ===-, …………………………………………………………………1分∴2341(1)=13>0∆=-⨯⨯-. … ……………………………………………………2分∴x = ∴12x =. ……………………………………………………5分 14.(本小题满分5分)证明:∵∠DAB =∠EAC ,∴∠DAB +∠BAE =∠EAC+∠BAE .∴∠DAE =∠BAC . ………………………………………………………………1分在△BAC 和△DAE 中,AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩,,, ∴△BAC ≌△DAE . ………………………………………………………………4分∴BC =DE . ………………………………………………………………………5分15.(本小题满分5分)解:设二次函数的解析式为()225y a x =-+ (0)a ≠.……………………………1分∵二次函数的图象经过点(0,1).∴()21025a =-+.………………………………………………………………2分 ∴1a =-. …………………………………………………………………………4分 ∴二次函数的解析式为241y x x =-++.………………………………………5分16. (本小题满分5分)解:∵四边形ABCD 内接于⊙O ,∴∠ADC +∠ABC =180°. …………………………………………………………1分 ∵∠ABC =130°,∴∠ADC =180°-∠ABC =50°. …………………………………………………2分∴∠AOC =2∠ADC =100°. ………………………………………………………3分 ∵OA=OC ,∴∠OAC =∠OCA . ……………………………………………………………4分∴∠OAC =1(180)402AOC -∠=. ……………………………………………… 5分 17. (本小题满分5分)解:依题意,得 21420m m -+=. ……………………………………………………2分∴2241m m -=-. ………………………………………………………………3分 ∴()()2222132213245154+=m m m m m --++=-+=-+=. …………5分18. (本小题满分5分)解:设每期减少的百分率为x .…………………………………………………… ……1分 由题意,得()24501288x -=. ……………………………………………… ………2分 解方程得 115x =,295x =. ………………………………………………… ……3分 经检验,915x =>不合题意,舍去;15x = 符合题意. ……………… …………4分 答:每期减少的百分率为20%. ……………………………………………… ………5分四、解答题(本题共20分,每小题5分)19. (本小题满分5分)解:(1)3. …………………………………………………………………………… 2分(2)小丁随机选择该月1日至15日中的某一天到达该市,则到达该市的日期有15种不同的选择,在其中任意一天到达的可能性相等. ……………3分 由图可知,其中有9天空气质量优良. ………………………………… ……4分所以,P (到达当天空气质量优良)93155==. …………………… ………5分20. (本小题满分5分)解:(1)∵0a ≠,∴原方程为一元二次方程. ∴()234(3)a a ∆=--⨯⨯- ………………………………………………1分 ()23a =+.∵()230≥a +.∴此方程总有两个实数根. …………………………………………………2分(2)解原方程,得 11x =-,23x a=. ……………………………………………3分 ∵此方程有两个负整数根,且a 为整数,∴1a =-或3-. …………………………………………………………………4分 ∵12x x ≠,∴3a ≠-.∴1a =-. ………………………………………………………………………5分21. (本小题满分5分)(1)证明:连接OC .∵OC=OD ,∠D =30°,∴∠OCD =∠D = 30°.…………………………………1分∵∠G =30°,∴∠DCG =180°-∠D -∠G =120°.∴∠GCO =∠DCG -∠OCD =90°.∴OC ⊥CG .又∵OC 是⊙O 的半径.∴CG 是⊙O 的切线.……………………………………2分(2)解:∵AB 是⊙O 的直径,CD ⊥AB ,∴132CE CD ==. ………………………………………………………3分 ∵在Rt △OCE 中,∠CEO =90°,∠OC E =30°,∴12OE OC =,222OC OE CE =+. 设OE x =,则2OC x =.∴()22223x x =+. 解得3x =(舍负值).∴23OC =. ………………………………………………………………4分∴OF =在△OCG 中,∵∠OCG =90°,∠G =30°,∴2OG OC ==∴GF GO OF =-= ……………………………………………………5分22. (本小题满分5分)答:(1)53. …………………………………………………………………………………1分(2)12, ………………………………………………………………………………2分3,2,4--或2,3,4--.(写出一个即可)…………………………………………3分(3)11或4.(每个答案各1分) ……………………………………………………5分五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23. (本小题满分7分)解:(1)∵ 抛物线2(1)y x m x m =---(0)m >与x 轴交于A 、B 两点,∴ 令0y =,即 2(1)0x m x m ---=.解得 11x =-,2x m =. …………………………………………………1分 又∵ 点A 在点B 左侧,且0m >,∴ 点A 的坐标为(1,0)-. …………………………………………………2分(2)由(1)可知点B 的坐标为(0)m ,.∵抛物线与y 轴交于点C ,∴点C 的坐标为(0,)m -. ……………………………………………………3分 ∵0m >,∴1AB m =+,OC m =. ∵15△ABC S =, ∴1(1)152m m +=. ∴6m =-或5m =. ∵0m >, ∴5m =.∴抛物线的表达式为245y x x =--. ………………………4分(3)由(2)可知点C 的坐标为(0,5)-.∵直线l :y kx b =+(0)k <经过点C ,∴5b =-. ………………………………………5分 ∴直线l 的解析式为5y kx =-(0)k <. ∵2245(2)9y x x x =--=--,∴当点D 在抛物线顶点处或对称轴左侧时,新函数的最小值为9-,不符合题意. 当点D 在抛物线对称轴右侧时,新函数的最小值有可能大于8-. 令8y =-,即2458x x --=-.解得 11x =(不合题意,舍去),23x =. ∴抛物线经过点(3,8)-.当直线5y kx =-(0)k <经过点(3,8)-时,可求得1k =-.…………………6分 由图象可知,当10k -<<时新函数的最小值大于8-. ………………………7分24.(本小题满分7分)解:(1)①30°. …………………………………………………………………………1分②不改变,∠BDC 的度数为30.方法一:由题意知,AB=AC=AD .∴点B 、C 、D 在以A 为圆心,AB 为半径的圆上.…………………………2分 ∴∠BDC=12∠BAC =30.……………………………………………………3分 方法二:由题意知,AB=AC=AD . ∵AC =AD ,∠CAD =α, ∴1801=9022ADC C αα-==-∠∠.…………………………………2分 ∵AB=AD ,∠BAD =60α+,∴()18060120160222ADB B ααα-+-====-∠∠. ∴11(90)(60)3022BDC ADC ADB αα=-=---=∠∠∠.…………3分(2)过点A 作AM ⊥CD 于点M ,连接EM .∴90AMC ∠=. 在△AEB 与△AMC 中,AEB AMC B ACD AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩,,, ∴△AEB ≌△AMC . ………………………………………………………4分∴AE AM =,BAE CAM ∠=∠.∴60EAM EAC CAM EAC BAE BAC ∠=∠+∠=∠+∠=∠=.∴△AEM 是等边三角形.∴EM AM AE ==. …………………………………………………………5分 ∵AC AD =,AM CD ⊥ , ∴CM DM =. 又90DEC ∠=,∴EM CM DM ==.∴AM CM DM ==. …………………………………………………………6分 ∴点A 、C 、D 在以M 为圆心,MC 为半径的圆上.∴90CAD α=∠=. …………………………………………………………7分 25. (本小题满分8分)解: (1)(0,10). …………………………………………………………………1分(2)连接BP 、OP ,作PH ⊥OA 于点H .∵5,b =PH ⊥OA , ∴152OH AH OA ===.∵OQ =8,∴3QH OQ OH =-=.在Rt △QHP 中,22229PQ QH PH PH =+=+.在Rt PHO △中,2222225PO OH PH PH BP =+=+=.在Rt △BQP 中,22222(25)(9)16BQ BP PQ PH PH =-=+-+=. ∴4BQ =.……………………………………………………………………3分(3)①1≥a .……………………………………………………………………………4分……………………………………………………………………………5分 解:∵△BQP是等腰直角三角形,PQ =∴半径BP = 又∵2(,)P a a ,∴2242OP a a =+=.即42200a a +-=.解得2a =±.∵0a >,∴2a =. ……………………………………………………………………………6分 ∴(2,4)P .如图,作BM y ⊥轴于点M ,则△QBM ≌△PQH . ∴2MQ PH ==,MB QH ===∴1B +. …………………………………7分若点Q 在OH上,由对称性可得2B . ……………………………8分综上,当PQ =B点坐标为+或2.。
北京市海淀区2014届九年级上学期期中考试物理试题(word版).
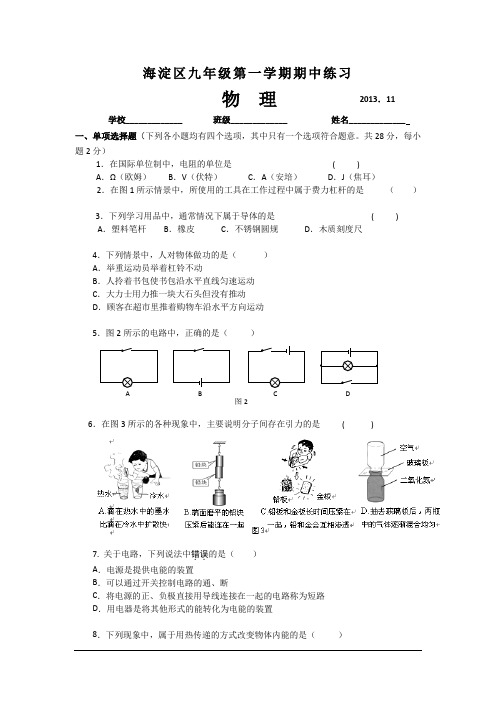
海淀区九年级第一学期期中练习物 理 2013.11学校_____________ 班级_____________ 姓名_____________一、单项选择题(下列各小题均有四个选项,其中只有一个选项符合题意。
共28分,每小 题2分)1.在国际单位制中,电阻的单位是 ( )A .Ω(欧姆)B .V (伏特)C .A (安培)D .J (焦耳)2.在图1所示情景中,所使用的工具在工作过程中属于费力杠杆的是 ( )3.下列学习用品中,通常情况下属于导体的是 ( ) A .塑料笔杆 B .橡皮 C .不锈钢圆规 D .木质刻度尺4.下列情景中,人对物体做功的是( ) A .举重运动员举着杠铃不动B .人拎着书包使书包沿水平直线匀速运动C .大力士用力推一块大石头但没有推动D .顾客在超市里推着购物车沿水平方向运动5.图2所示的电路中,正确的是( )6.在图3所示的各种现象中,主要说明分子间存在引力的是 ( )7. 关于电路,下列说法中错误..的是( ) A .电源是提供电能的装置B .可以通过开关控制电路的通、断C .将电源的正、负极直接用导线连接在一起的电路称为短路D .用电器是将其他形式的能转化为电能的装置8.下列现象中,属于用热传递的方式改变物体内能的是( )图2 A B C DA .在火炉上将一壶凉水烧开B .菜刀在砂轮上磨得发烫C .两手互相摩擦使手发热D .用锯锯木头锯条会发热 9.图4中能够说明动能和重力势能相互转化的过程是( )10.下列说法中正确的是( )A .水蒸气、水和冰的分子间的距离都是相同的B .打扫卫生时房间内尘土飞扬,说明分子在不停地运动C .扩散只能在气体或液体中进行D .同一物体温度越高,其内部大量分子运动越剧烈11.对于功率和机械效率的理解,下列说法中正确的是( ) A .机械工作时的功率越大,其工作时机械效率一定越高 B .机械工作时的功率越大,其工作时一定越省力C .机械做的有用功相同,总功越少,其机械效率一定越高D .机械工作时越省力,其机械效率一定越高12.击剑比赛中,当甲方运动员的剑击中乙方的导电服时(相当于图5中 “S 甲”闭合),乙方指示灯L 乙亮;当乙方运动员的剑击中甲方的导电服时(相当于图5中 “S 乙”闭合),甲方指示灯L 甲亮。
北京市海淀区九年级上学期期中考试数学试题

海淀区九年级第一学期期中测评数学试卷(分数:120分时间:120分钟)2015.11学校姓名准考证号一、选择题(本题共30分,每小题3分)下面各题均有四个选项,其中只有一个..是符合题意的.请将正确选项前的字母填在表格中相应的位置.1.一元二次方程的二次项系数、一次项系数、常数项分别是A.B.C.D.2.下列图形是中心对称图形的是A .B.C.D.3.二次函数的最大值是A.B.C.1 D.24.已知⊙O的半径是4,OP的长为3,则点P与⊙O的位置关系是A.点P在圆内B.点P在圆上C.点P在圆外D.不能确定5.将抛物线沿y轴向下平移2个单位,得到的抛物线的解析式为A.B.C.D.6.已知扇形的半径为,圆心角为,则这个扇形的面积为A.B.C.D.7.用配方法解方程,下列配方正确的是A.B.C.D.8.已知二次函数的图象如图所示,则下列选的是项中不正确...A.B.C.0 < D.9.如图,△ABC内接于⊙O,BD是⊙O的直径.若,则等于A.B.C.D.10.小明乘坐摩天轮转一圈,他离地面的高度y(米)与旋转时间x(分)之间的关系可以近似地用二次函数来刻画.经测试得出部分数据如下表:下列选项中,最接近摩天轮转一圈的时间的是A.7分B.6.5分C.6分D.5.5分二、填空题(本题共18分,每小题3分)11.方程的解为_______________.12. 请写出一个开口向上且经过(0, 1)的抛物线的解析式_________.13.若二次函数的图象上有两个点、,则a____(填“<”或“=”或“>”).14.如图,A、B、C三点在⊙O上,∠AOC=100°,则∠ABC=______°.15.用一块直径为4米的圆桌布平铺在对角线长为4米的正方形桌面上(如示意图),若四周下垂的最大长度相等,则这个最大长度x为_______米(取1.4).16.如图,O是边长为1的等边△ABC的中心,将AB、BC、CA分别绕点A、点B、点C顺时针旋转(),得到、、,连接、、、、.(1)_______〬;(2)当〬时,△的周长最大.三、解答题(本题共72分,第17~26题,每小题5分,第27题7分,第28题7分,第29题8分)17.解方程:.18.若抛物线与轴只有一个交点,求实数的值.k x k x y -++-=)3(32上,求此19.已知点(3, 0)在抛物线抛物线的对称轴.20.如图,AC 是⊙O 的直径,P A , PB 是⊙O 的切线,A , B 为切点,.求∠P 的度数.21.已知x =1是方程的一个根,求代数式的值.22.一圆柱形排水管的截面如图所示,已知排水管的半径为1m ,水面宽AB 为1.6m .由于天气干燥,水管水面下降,此时排水管水面宽变为1.2m ,求水面下降的高度.23.已知关于x 的方程)0(0)3(32>=---a a x a x . (1)求证:方程总有两个不相等的实数根; (2)若方程有一个根大于2,求a 的取值范围.24.在设计人体雕像时,若使雕像的上部(腰以上)与下部(腰以下)的高度的比等于下部与全部(全身)的高度比,则可以增加视觉美感.按此比例,如果雕像的高为2m ,那么它的下部应设计为多高(取2.2 ).25.已知AB 是⊙O 的直径,AC 、AD 是⊙O 的弦,AB =2,AC =,AD =1,求∠CAD 的度数.26.抛物线与直线相交于A、B两点.(1)求这条抛物线的解析式;(2)若,则的最小值为________.27.如图,AB为⊙O的直径,C为⊙O上一点,CD⊥AB于点D. P为AB延长线上一点,. (1)求证:CP为⊙O的切线;(2)BP=1,.①求⊙O的半径;②若M为AC上一动点,则OM+DM的最小值为.28.探究活动:利用函数的图象(如图1)和性质,探究函数的图象与性质.下面是小东的探究过程,请补充完整:(1)函数的自变量x的取值范围是___________;(2)如图2,他列表描点画出了函数图象的一部分,请补全函数图象;图1 图2解决问题:14x b-=的两根为、,且,方程的两根为、,且.若,则、、、的大小关系为(用“<”连接).29.在平面直角坐标系xOy中,半径为1的⊙O与x轴负半轴交于点A,点M在⊙O上,将点M绕点A顺时针旋转60︒得到点Q. 点N为x轴上一动点(N不与A重合),将点M绕点N顺时针旋转60︒得到点P. PQ与x轴所夹锐角为.(1)如图1,若点M的横坐标为,点N与点O重合,则=________︒;(2)若点M、点Q的位置如图2所示,请在x轴上任取一点N,画出直线PQ,并求的度数;(3)当直线PQ与⊙O相切时,点的坐标为_________.图1 图2 备用图海淀区九年级第一学期期中测评数学试卷参考答案一、选择题(本题共30分,每小题3分)三、解答题(本题共72分,第17~26题,每小题5分,第27题7分,第28题7分,第29题8分) 17.解: ……………………………………………1分. ……………………………………………3分 ∴或.∴. ………………………………………………………5分18.解:∵抛物线与轴只有一个交点,∴,………………………………………2分 即.……………………………………………4分 ∴.……………………………………………5分19.解:∵点(3, 0)在抛物线k x k x y -++-=)3(32上,∴k k -++⨯-=)3(33302.………………………………………2分 ∴.……………………………………………3分 ∴抛物线的解析式为.∴对称轴为.……………………………………………5分20.解:∵P A ,PB 是⊙O 的切线,∴P A =PB .………………………………………1分 ∴.………………………………………2分 ∵AC 为⊙O 的直径, ∴CA ⊥P A .∴º.………………………………………3分 ∵º,∴º.………………………………………4分∴502180=∠-=∠PAB Pº.………………………………………5分21.解:∵是方程的一个根,∴.………………………………………2分 ∴.…………………………………………3分∴原式………………………………………4分.………………………………………5分22.解:如图,下降后的水面宽CD 为1.2m ,连接OA , OC ,过点O 作ON ⊥CD 于N ,交AB 于M .………………………… 1分∴º.∵AB ∥CD ,∴90OMA ONC ∠=∠=º. ∵,, ∴,. …………………………2分 在Rt △OAM 中, ∵,∴0.6OM =. ………………………………3分 同理可得.………………………………4分 ∴0.2.MN ON OM =-=答:水面下降了0.2米.…………………………5分23.(1)证明: 22)3()(34)3(+=-⨯⨯--=∆a a a .……………………………1分∵,∴. 即.∴方程总有两个不相等的实数根.……………………………………………2分(2)解方程,得.……………………………………………4分 ∵方程有一个根大于2, ∴. ∴.……………………………………………5分24.解:如图,雕像上部高度AC 与下部高度BC 应有,即.设BC 为x m. …………………………………1分 依题意,得..………………………………………3分解得(不符合题意,舍去).……4分 .答:雕像的下部应设计为1.2m .…………………………5分25. 解:如图1,当点D 、C 在AB 的异侧时,连接OD 、BC . ………1分∵AB 是⊙O 的直径,∴º.在Rt △ACB 中, ∵,, ∴. ∴º.………………2分 ∵,∴º.………………3分 ∴105CAD BAD BAC ∠=∠+∠=º.………………4分当点D 、C 在AB 的同侧时,如图2,同理可得,. ∴15CAD BAD BAC ∠=∠-∠=º. ∴为15º或º. …………………5分26.解:(1)∵直线经过点B (2,-3),∴.∴.……………………………………………1分 ∵直线经过点A (-2,n ),∴.……………………………………………2分∵抛物线过点A 和点B , ∴ ∴∴.……………………………………………4分 (2). ……………………………………………5分27.(1)证明:连接OC . ……………………………1分∵∠PCD =2∠BAC ,∠POC =2∠BAC , ∴∠POC =∠PCD .……………………………2分∵CD ⊥AB 于点D ,∴∠ODC =90︒.∴∠POC+∠OCD =90º. ∴∠PCD+∠OCD =90º. ∴∠OCP =90º. ∴半径OC ⊥CP .∴CP 为⊙O 的切线. ……………………………………………3分 (2)解:①设⊙O 的半径为r . 在Rt △OCP 中,. ∵∴. ………………………4分 解得.∴⊙O 的半径为2. ……………………………………………5分②. ……………………………………………7分或;……………………………………………2分28.解:(1)(2)如图所示:……………………………………5分. .……………………………………………7分29. 解:(1). ……………………………………………2分(2).……………………………………………3分连接.记分别交轴于.∵将点M 绕点A 顺时针旋转60︒得到点Q ,将点M 绕点N 顺时针旋转60︒得到点P , ∴△和△均为等边三角形. ………………4分∴,,60AMQ NMP ∠=∠=︒.∴.∴△≌△. .………………………………5分∴.∵,∴60QFE AMQ ∠=∠=︒.∴. .…………………………………………….6分(3)(,)或(,). ………………………8分。
北京海淀初三期中数学(含解析)

2015北京海淀初三上期中数学试卷一、选择题(本题共30分,每小题3分)下面各题均有四个选项,其中只有一个..是符合题意的.请将正确选项前的字母填在表格中相应的位置. 1.一元二次方程2230x x --=的二次项系数、一次项系数、常数项分别是( ).A .2,1,3B .2,1,3-C .2,1-,3D .2,1-,3-2.下列图形是中心对称图形的是( ).A .B .C .D .3.二次函数2(+1)2y x =--的最大值是( ).A .2-B .1-C .1D .24.已知⊙O 的半径是4,OP 的长为3,则点P 与⊙O 的位置关系是( ).A .点P 在圆内B .点P 在圆上C .点P 在圆外D .不能确定5.将抛物线2y x =沿y 轴向下平移2个单位,得到的抛物线的解析式为( ).A .22y x =+B .22y x =-C .()22y x =+D .()22y x =-6.已知扇形的半径为6,圆心角为60︒,则这个扇形的面积为( ).A .9πB .6πC .3πD .π7.用配方法解方程243x x +=,下列配方正确的是( ).A .2(2)1x -=B .2(2)7x -=C .2(2)7x +=D .2(2)1x +=8.已知二次函数2y ax bx c =++的图象如图所示,则下列选项中不正确...的是( ). A .0a < B .0c > C .012ba<-< D .0a b c ++<9.如图,ABC △内接于⊙O ,BD 是⊙O 的直径.若33DBC ∠=︒,则A ∠等于( ).A .33︒B .57︒C .67︒D .66︒10.小明乘坐摩天轮转一圈,他离地面的高度y (米)与旋转时间x (分)之间的关系可以近似地用二次函数来刻画.经测试得出部分数据如下表:/x 分L 2.66 3.23 3.46 L /y 米L69.1669.6268.46L下列选项中,最接近摩天轮转一圈的时间的是( ). A .7分B .6.5分C .6分D .5.5分二、填空题(本题共18分,每小题3分) 11.方程(1)(2)0x x --=的解为__________.12.请写出一个开口向上且经过(0,1)的抛物线的解析式__________.13.若二次函数225y x =-的图象上有两个点(2,)A a 、,则a __________b (填“<”或“=”或“>”).14.如图,A 、B 、C 三点在⊙O 上,100AOC ∠=︒,则ABC ∠=__________︒.15.用一块直径为4米的圆桌布平铺在对角线长为4米的正方形桌面上(如示意图),若四周下垂的最大长度相等,则这个最大长度x 为_______米(2取1.4).16.如图,O 是边长为1的等边ABC △的中心,将AB 、BC 、CA 分别绕点A 、点B 、点C 顺时针旋转α(0180α︒<<︒),得到AB '、BC '、CA ',连接A B ''、B C ''、A C ''、OA '、OB '. (1)A OB ''∠=__________︒.(2)当α=__________︒时,A B C '''△的周长最大.三、解答题(本题共72分,第17~26题,每小题5分,第27题7分,第28题7分,第29题8分)17.解方程:232x x =-.(3,)B b18.若抛物线23y x x a =++与x 轴只有一个交点,求实数a 的值.19.已知点(3,0)在抛物线23(3)y x k x k =-++-上,求此抛物线的对称轴.20.如图,AC 是⊙O 的直径,PA ,PB 是⊙O 的切线,A ,B 为切点,25BAC ∠=︒.求P ∠的度数.21.已知1x =是方程2250x ax a -+=的一个根,求代数式23157a a --的值.22.一圆柱形排水管的截面如图所示,已知排水管的半径为1m ,水面宽AB 为1.6m .由于天气干燥,水管水面下降,此时排水管水面宽变为1.2m ,求水面下降的高度.23.已知关于x 的方程23(3)0(0)x a x a a ---=>. (1)求证:方程总有两个不相等的实数根. (2)若方程有一个根大于2,求a 的取值范围.24.在设计人体雕像时,若使雕像的上部(腰以上)与下部(腰以下)的高度的比等于下部与全部(全身)的高度比,则可以增加视觉美感.按此比例,如果雕像的高为2m ,那么它的下部应设计为多高(5取2.2).25.已知AB 是⊙O 的直径,AC 、AD 是⊙O 的弦,2AB =,2AC =,1AD =,求CAD ∠的度数.26.抛物线21y x bx c =++与直线22y x m =-+相交于(2,)A n -、(2,3)B -两点.(1)求这条抛物线的解析式.(2)若41≤≤x -,则21y y -的最小值为________.27.如图,AB 为⊙O 的直径,C 为⊙O 上一点,CD AB ⊥于点D .P 为AB 延长线上一点,2PCD BAC ∠=∠.(1)求证:CP 为⊙O 的切线. (2)1BP =,5CP =. ①求⊙O 的半径;②若M 为AC 上一动点,则OM DM +的最小值为__________.28.探究活动:利用函数(1)(2)y x x =--的图象(如图1)和性质,探究函数(1)(2)y x x =--的图象与性质. 下面是小东的探究过程,请补充完整:(1)函数(1)(2)y x x =--的自变量x 的取值范围是___________;(2)如图2,他列表描点画出了函数(1)(2)y x x =--图象的一部分,请补全函数图象;图1 图2解决问题:设方程1(1)(2)04x x x b ----=的两根为1x 、2x ,且12x x <,方程21324x x x b -+=+的两根为3x 、4x ,且34x x <.若12b <<,则1x 、2x 、3x 、4x 的大小关系为__________(用“<”连接).29.在平面直角坐标系xOy中,半径为1的⊙O与x轴负半轴交于点A,点M在⊙O上,将点M绕点A顺时针旋转60︒得到点Q.点N为x轴上一动点(N不与A重合),将点M绕点N顺时针旋转60︒得到点P.PQ与x轴所夹锐角为α.(1)点M的横坐标为12,点N与点O重合,则α=________︒.(2)若点M、点Q的位置如图2所示,请在x轴上任取一点N,画出直线PQ,并求α的度数;(3)当直线PQ与⊙O相切时,点M的坐标为_________.图1 图2 备用图2015北京海淀初三上期中数学试卷答案一、选择题(本题共30分,每小题3分) 题号 1 2 3 4 5 6 7 8 9 10 答案DAAABBCDBC二、填空题(本题共18分,每小题3分)题号 11 12 1314 15 16 答案11x =,22x =21y x =+ (答案不唯一)<1300.6120,150三、解答题(本题共72分,第17~26题,每小题5分,第27题7分,第28题7分,第29题8分) 17.解:2320x x -+=,(1)(2)0x x --=.∴10x -=或20x -=. ∴11x =,22x =.18.解:∵抛物线23y x x a =++与x 轴只有一个交点,∴0∆=, 即940a -=. ∴94a =.19.解:∵点(3,0)在抛物线23(3)y x k x k =-++-上,∴20333(3)k k =-⨯++-, ∴9k =.∴抛物线的解析式为23129y x x =-+-. ∴对称轴为2x =.20.解:∵PA ,PB 是⊙O 的切线,∴PA PB =. ∴PAB PBA ∠=∠. ∵AC 为⊙O 的直径, ∴CA PA ⊥. ∴90PAC ∠=︒. ∵25BAC ∠=︒, ∴65PAB ∠=︒.∴180250P PAB ∠=︒-∠=︒.21.解:∵1x =是方程2250x ax a -+=的一个根,∴2150a a -+=,∴原式23(5)7a a =--10=-.22.解:如图,下降后的水面宽CD 为1.2m ,连接OA ,OC ,过点O 作ON CD ⊥于N ,交AB 于M .∴90ONC ∠=︒. ∵∥AB CD ,∴90OMA ONC ∠=∠=︒. ∵ 1.6AB =, 1.2CD =,∴10.82AM AB ==,10.62CN CD ==. 在Rt OAM △中,∵1OA =,∴220.6OM OA AM =-=. 同理可得0.8ON =. ∴0.2MN ON OM =-=. 答:水面下降了0.2米.23.(1)证明:22(3)43()(3)a a a ∆=--⨯⨯-=+.∵0a >, ∴2(3)0a +>. 即0∆>.∴方程总有两个不相等的实数根. (2)解方程,得11x =-,23a x = ∵方程有一个根大于2, ∴23a>. ∴6a >.24.解:如图,雕像上部高度AC 与下部高度BC 应有::2AC BC BC =,即22BC AC =. 设BC 为m x .依题意,得22(2)x x =-.解得115x =-+,215x =--(不符合题意,舍去). 51 1.2-≈.答:雕像的下部应设计为1.2m .25.解:如图1,当点D 、C 在AB 的异侧时,连接OD 、BC .∵AB 是⊙O 的直径, ∴90ACB ∠=︒. 在Rt ACB △中, ∵2AB =,2AC =, ∴2BC =.∵1OA OD AD ===, ∴60BAD ∠=︒.∴105CAD BAD BAC ∠=∠+∠=︒.当点D 、C 在AB 的同侧时,如图2,同理可得45BAC ∠=︒,60BAD ∠=︒. ∴15CAD BAD BAC ∠=∠-∠=︒. ∴CAD ∠为15︒或105︒.26.解:(1)∵直线22y x m =-+经过点(2,3)B -,∴322m -=-⨯+. ∴1m =.∵直线22y x m =-+经过点(2,)A n -, ∴5n =.∵抛物线21y x bx c =++过点A 和点B , ∴542342b cb c =-+⎧⎨-=++⎩,∴解得23b c =-⎧⎨=-⎩.∴2123y x x =--. (2)12-.27.(1)证明:连接OC .∵2PCD BAC ∠=∠,2POC BAC ∠=∠, ∴POC PCD ∠=∠. ∵CD AB ⊥于点D , ∴90ODC ∠=︒. ∴90POC OCD ∠+∠=︒. ∴90PCD OCD ∠+∠=︒. ∴90OCP ∠=︒. ∴半径OC CP ⊥. ∴CP 为⊙O 的切线. (2)①设⊙O 的半径为r . 在Rt OCP △中,222OC CP OP +=. ∵1BP =,5CP =, ∴222(5)(1)r r +=+. 解得2r =. ∴⊙O 的半径为2.②2143. 过点O 作AC 的对称点E ,连结CE 、CO 、CD ,线段ED 与线段AC 交于M 点,由轴对称可知,CO CE =,OCA ECA ∠=∠,在Rt OCP △中,2OC =,3OP =,5CP =, 253OC PC CD OP ⋅==. 在Rt ECD △中,由勾股定理可得, 222225214()233DE CD CE =+=+=. 即OM DM +的最小值为2143.28.解:(1)1x ≤或2x ≥.(2)如图所示:1342x x x x <<<.29.解:(1)60.(2).连接MQ ,MP .记MQ ,PQ 分别交x 轴于E ,F .∵将点M 绕点A 顺时针旋转60︒得到点Q ,将点M 绕点N 顺时针旋转60︒得到点P , ∴MAQ △和MNP △均为等边三角形.∴MA MQ =,MN MP =,60AMQ NM ∠=∠=︒. ∴AMN QMP ∠=∠. ∴MAN △≌MQP △. ∴MAN MQP ∠=∠. ∵AEM QEF ∠=∠, ∴60QFE AMQ ∠=∠=︒. ∴60α=︒. (3)31(,)22或31(,)22--. 连结OK ,过M 作ME x ⊥轴于E ,由(2)可知,α始终等于60︒,直线PQ 与x 轴交于H ,以AH 为边向下构建等边AHG △, xyF EPQAO MN在MAH △和QAG △中,AM AQ MAH QAG AH AG =⎧⎪∠=∠⎨⎪=⎩, ∴MAH △≌QAG △(SAS ),∴60AHM AGQ ∠=∠=︒.∵PQ 与⊙O 相切,∴OK PQ ⊥,1OK =.在Rt OKH △中,60OHK ∠=︒, ∴233OH =. 设EH x =,则3ME x =,233OE x =-, 在Rt OME △中,由勾股定理可知,22223()(3)13x x -+=, 解得36x =. ∴32OE =,12ME =, 即31(,)22M . 同理31(,)22M --. ∴当直线PQ 与⊙O 相切时,点M 的坐标为31(,)22或31(,)22--.2015北京海淀初三上期中数学试卷部分答案解析一、选择题(本题共30分,每小题3分)1.【答案】D【解析】一元二次方程2230x x --=的二次项系数是2、一次项系数1-、常数项分别是3-.2.【答案】A【解析】依据中心对称图形的定义可知,只有图形A 是中心对称图形.3.【答案】A【解析】二次函数2(+1)2y x =--的最大值是为2-.4.【答案】A【解析】已知⊙O 的半径是4,OP 的长为3,OP R <,则点P 在⊙O 内.5.【答案】B【解析】将抛物线2y x =沿y 轴向下平移2个单位,得到的抛物线的解析式为22y x =-.6.【答案】B【解析】已知扇形的半径为6,圆心角为60︒,则这个扇形的面积为260π66π360S ⨯==.7.【答案】C【解析】用配方法解方程243x x +=,24434x x ++=+,2(2)7x +=.8.【答案】D【解析】依题可知,0a <,0b >,0c >,012b a<-<,0a b c ++>.9.【答案】B【解析】连结DC ,∵BD 是⊙O 的直径,∴90BCD ∠=︒.∵33DBC ∠=︒,∴9057A BDC DBC ∠=∠=︒-∠=︒.10.【答案】C【解析】依表格可知,二次函数的对称轴接近3,所以摩天轮转一圈最接近的时间为6分钟.二、填空题(本题共18分,每小题3分)11.【答案】11x =,22x =【解析】方程(1)(2)0x x --=的解为11x =,22x =.12.【答案】21y x =+(答案不唯一)【解析】开口向上且经过(0,1)的抛物线的解析式21y x =+(答案不唯一),0a >,1c =即可.13.【答案】<【解析】若二次函数225y x =-的图象上有两个点(2,)A a 、,开口向上,对称轴为y 轴,点B 离对称轴更远,则a b <.14.【答案】130(3,)B b【解析】∵100AOC ∠=︒,∴»AC 所对的圆周角为50︒, ∴130ABC ∠=︒.15.【答案】0.6【解析】依题可知,正方形的对角线即为圆桌的直径4, ∴正方形的边长为22,圆心到正方形的边心距为2, 即220.6x =-≈.16.【答案】120,150【解析】(1)连接OA 、OB 、OC 、OC '. 依题可知,AB AB '=BC BC '==CA CA '==, BAB CBC ACA α'''∠===.∵O 是等边ABC △的中心,∴OA OB OC ==,30OAB OBC OCA ∠=∠=∠=︒, 120AOB BOC AOC ∠=∠=∠=︒,OAB '△≌OBC '△≌OCA '△,∴AOB COA ''∠=∠,∴120A OB AOC ''∠=∠=︒.(2)OAB '△≌OBC '△≌OCA '△,∴OA OB OC '''==,120A OB A OC B OC ''''''∠=∠=∠=︒, ∴A B C '''△为等边三角形.A B C '''△周长最大,OB '要最大,当且仅当O 、A 、B '三点共线时,OB '最大, 180OAB BAB '∠+∠=︒,即150α=︒.OB '最大值为313OA AB OA AB '+=+=+,A B C '''△的周长最大值为33+.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
D海淀区九年级第一学期期中测评数学试卷(分数:120分时间:120分钟) 2014.11班级 姓名 学号 成绩 一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个..是符合题意的. 1.下列图形是中心对称图形的是( )A B C D2.将抛物线2y x =向上平移1个单位,得到的抛物线的解析式为( ) A.21y x =+ B.21y x =- C.()21y x =+D.()21y x =-3.袋子中装有4个黑球、2个白球,这些球的形状、大小、质地等完全相同,即除颜色外无其他差别.在看不到球的情况下,随机从袋子中摸出1个球.下面说法正确的是( ) A.这个球一定是黑球 B.这个球一定是白球C.“摸出黑球”的可能性大D.“摸出黑球”和“摸出白球”的可能性一样大4.用配方法解方程2230x x --=时,配方后得到的方程为( )A.2(1)=4x - B.2(1)4x -=- C.2(1)=4x + D.2(1)=4x +- 5.如图,O 为正五边形ABCDE 的外接圆,O 的半径为2,则AB 的长为( )A.5π B.25π C.35π D.45π6.如图,AB 是O 的直径,CD 是O 的弦,59ABD ∠=︒,则C ∠等于( )A.29︒B.31︒C.59︒D.62︒7.已知二次函数24y x x m =-+(m 为常数)的图象与x 轴的一个交点为(1,0),则关于x 的一元二次方程240x x m -+=的两个实数根是( ) A.121,1x x ==- B.121,2x x =-= C.121,0x x =-=D.121,3x x ==8.如图,C 是半圆O 的直径AB 上的一个动点(不与A ,B 重合),过C 作AB 的垂线交半圆于点D ,以点D ,C ,O 为顶点作矩形DCOE . 若AB =10,设AC =x ,矩形DCOE 的面积为y ,则下列图象中能表示y 与x 的函数关系的图象大致是( )A B C D二、填空题(本题共16分,每小题4分)9.如图,PA ,PB 分别与O 相切于点A ,B ,连接AB .60APB ∠=︒,5AB =,则PA 的长是 .10.若关于x 的一元二次方程240x x k -+=有两个相等的实数根,则k 的值为_________.11.在平面直角坐标系xOy 中,函数2y x =的图象经过点11(,)M x y ,22(,)N x y 两点,若1 42x -<<-,202x <<,则1y 2y .(用“<”,“=”或“>”号连接)12.如图,正方形ABCD 中,点G 为对角线AC 上一点,AG=AB . ∠CAE =15°且AE=AC ,连接GE .将线段AE 绕点A 逆时针旋转得到 线段AF ,使DF=GE ,则∠CAF 的度数为____________.三、解答题(本题共30分,每小题5分) 13.解方程:2310x x +-=.ED BO PEDCBA14.如图,∠DAB =∠EAC ,AB =AD ,AC =AE .求证:BC =DE .15.已知二次函数的图象经过点(0,1),且顶点坐标为(2,5),求此二次函数的解析式.16.如图,四边形ABCD 内接于⊙O ,∠ABC =130°,求∠OAC 的度数.17.若1x =是关于x 的一元二次方程22420x mx m -+=的根,求代数式()2213+m -的值.18.列方程解应用题:某工厂废气年排放量为450万立方米,为改善空气质量,决定分两期治理,使废气的排放量减少到288万立方米.如果每期治理中废气减少的百分率相同,求每期减少的百分率.四、解答题(本题共20分,每小题5分)19.下图是某市某月1日至15日的空气质量指数趋势图,空气质量指数不大于100表示空气质量优良,空气质量指数大于200表示空气重度污染.(1)由图可知,该月1日至15日中空气重度污染的有 天; (2)小丁随机选择该月1日至15日中的某一天到达该市,求小丁到达该市当天空气质量优良的概率.20.已知关于x 的方程2(3)30ax a x +--=(0)a ≠. (1)求证:方程总有两个实数根;(2)若方程有两个不相等的负整数根,求整数a 的值.空气质量指数21.如图,AB 是⊙O 的直径,CD 是弦,CD ⊥AB 于点E ,点G 在直径DF 的延长线上,∠D =∠G =30.(1)求证:CG 是⊙O 的切线; (2)若CD =6,求GF 的长.22.阅读下面材料:小丁在研究数学问题时遇到一个定义:对于排好顺序的三个数:123,,x x x ,称为数列123,,x x x .计算1x ,122x x +,1233x x x ++,将这三个数的最小值称为数列123,,x x x 的价值.例如,对于数列2,1-,3,因为22=,2(1)122=+-,2(1)3433+-+=,所以数列2,1-,3的价值为12. 小丁进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的价值.如数列1-,2,3的价值为12;数列3,1-,2的价值为1;….经过研究,小丁发现,对于“2,1-,3”这三个数,按照不同的排列顺序得到的不同数列中,价值的最小值为12. 根据以上材料,回答下列问题:(1)数列4-,3-,2的价值为______;(2)将“4-,3-,2”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的价值的最小值为______ ,取得价值最小值的数列为___________(写出一个即可); (3)将2,9-,a (1)a >这三个数按照不同的顺序排列,可得到若干个数列.若这些数列的价值的最小值为1,则a 的值为__________.五、解答题(本题共22分,第23题7分,第24题7分,第25题8分)23.在平面直角坐标系xOy 中,抛物线2(1)y x m x m =---(0)m >与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C . (1)求点A 的坐标;(2)当15ABC S △=时,求该抛物线的表达式;(3)在(2)的条件下,经过点C 的直线l :y kx b =+(0)k <与抛物线的另一个交点为D . 该抛物线在直线l 上方的部分与线段CD 组成一个新函数的图象. 请结合图象回答:若新函数的最小值大于8-,求k 的取值范围.D C BA24.将线段AB 绕点A 逆时针旋转60°得到线段AC ,继续旋转α(0120)α<<得到线段AD ,连接CD .(1)连接BD ,①如图1,若α=80°,则∠BDC 的度数为 ;②在第二次旋转过程中,请探究∠BDC 的大小是否改变.若不变,求出∠BDC 的度数;若改变,请说明理由.(2)如图2,以AB 为斜边作直角三角形ABE ,使得∠B =∠ACD ,连接CE ,DE . 若∠CED =90°,求α的值.图1 图225.如图,在平面直角坐标系xOy 中,点(,)P a b 在第一象限.以P 为圆心的圆经过原点,与y 轴的另一个交点为A .点Q 是线段OA 上的点(不与O ,A 重合),过点Q 作PQ 的垂线交⊙P 于点(,)B m n ,其中0≥m .(1)若5b =,则点A 坐标是________________; (2)在(1)的条件下,若OQ =8,求线段BQ 的长;(3)若点P 在函数2y x =(0)x >的图象上,且△BQP 是等腰三角形. ①直接写出实数a 的取值范围:__________________; ②在12PQ 的长度可以为 ,并求出此时点B 的坐标.海淀区九年级第一学期期中练习2014.11数学试卷答案及评分参考阅卷须知:1. 为便于阅卷,本试卷答案中有关解答题的推导步骤写的较为详细,阅卷时,只要考生将主要过程正确写出即可.2. 若考生的解法与给出的解法不同,正确者可参照评分参考相应给分.3. 评分参考中所注分数,表示考生正确做到此步应得的累加分数.二、填空题(本题共16分,每小题4分) 9. 5 ; 10. 4 ;11. > ; 12. 30°或60°.(注:每个答案2分)三、解答题(本题共30分,每小题5分) 13.(本小题满分5分)解:∵131a ,b ,c ===-, …………………………………………………………………1分∴2341(1)=13>0∆=-⨯⨯-. … ……………………………………………………2分∴x ==∴12x . ……………………………………………………5分 14.(本小题满分5分)证明:∵∠DAB =∠EAC ,∴∠DAB +∠BAE =∠EAC+∠BAE .∴∠DAE =∠BAC . ………………………………………………………………1分 在△BAC 和△DAE 中,AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩,,, ∴△BAC ≌△DAE . ………………………………………………………………4分 ∴BC =DE . ………………………………………………………………………5分 15.(本小题满分5分)解:设二次函数的解析式为()225y a x =-+ (0)a ≠.……………………………1分∵二次函数的图象经过点(0,1).∴()21025a =-+.………………………………………………………………2分 ∴1a =-. …………………………………………………………………………4分 ∴二次函数的解析式为241y x x =-++.………………………………………5分16. (本小题满分5分)解:∵四边形ABCD 内接于⊙O ,∴∠ADC +∠ABC =180°. …………………………………………………………1分 ∵∠ABC =130°,∴∠ADC =180°-∠ABC =50°. …………………………………………………2分∴∠AOC =2∠ADC =100°. ………………………………………………………3分 ∵OA=OC ,∴∠OAC =∠OCA . ……………………………………………………………4分∴∠OAC =1(180)402AOC -∠=. ……………………………………………… 5分17. (本小题满分5分)解:依题意,得 21420m m -+=. ……………………………………………………2分∴2241m m -=-. ………………………………………………………………3分 ∴()()2222132213245154+=m m m m m --++=-+=-+=. …………5分18. (本小题满分5分)解:设每期减少的百分率为x .…………………………………………………… ……1分 由题意,得()24501288x -=. ……………………………………………… ………2分解方程得 115x =,295x =. ………………………………………………… ……3分经检验,915x =>不合题意,舍去;15x = 符合题意. ……………… …………4分答:每期减少的百分率为20%. ……………………………………………… ………5分四、解答题(本题共20分,每小题5分) 19. (本小题满分5分)解:(1)3. …………………………………………………………………………… 2分(2)小丁随机选择该月1日至15日中的某一天到达该市,则到达该市的 日期有15种不同的选择,在其中任意一天到达的可能性相等. ……………3分 由图可知,其中有9天空气质量优良. ………………………………… ……4分 所以,P (到达当天空气质量优良)93155==. …………………… ………5分20. (本小题满分5分)解:(1)∵0a ≠,∴原方程为一元二次方程.∴()234(3)a a ∆=--⨯⨯- ………………………………………………1分()23a =+.∵()230≥a +.∴此方程总有两个实数根. …………………………………………………2分 (2)解原方程,得 11x =-,23x a=. ……………………………………………3分 ∵此方程有两个负整数根,且a 为整数,∴1a =-或3-. …………………………………………………………………4分 ∵12x x ≠,∴3a ≠-.∴1a =-. ………………………………………………………………………5分 21. (本小题满分5分) (1)证明:连接OC .∵OC=OD ,∠D =30°, ∴∠OCD =∠D = 30°.…………………………………1分 ∵∠G =30°,∴∠DCG =180°-∠D -∠G =120°. ∴∠GCO =∠DCG -∠OCD =90°. ∴OC ⊥CG .又∵OC 是⊙O 的半径.∴CG 是⊙O 的切线.……………………………………2分(2)解:∵AB 是⊙O 的直径,CD ⊥AB ,∴132CE CD ==. ………………………………………………………3分∵在Rt △OCE 中,∠CEO =90°,∠OC E =30°, ∴12OE OC =,222OC OE CE =+.设OE x =,则2OC x =. ∴()22223x x =+.解得x =.∴OC = ………………………………………………………………4分∴OF =在△OCG 中,∵∠OCG =90°,∠G =30°,∴2OG OC ==∴GF GO OF =-= ……………………………………………………5分22. (本小题满分5分) 答:(1)53. …………………………………………………………………………………1分 (2)12, ………………………………………………………………………………2分3,2,4--或2,3,4--.(写出一个即可)…………………………………………3分 (3)11或4.(每个答案各1分) ……………………………………………………5分五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23. (本小题满分7分)解:(1)∵ 抛物线2(1)y x m x m =---(0)m >与x 轴交于A 、B 两点,∴ 令0y =,即 2(1)0x m x m ---=.解得 11x =-,2x m =. …………………………………………………1分 又∵ 点A 在点B 左侧,且0m >,∴ 点A 的坐标为(1,0)-. …………………………………………………2分(2)由(1)可知点B 的坐标为(0)m ,.∵抛物线与y 轴交于点C ,∴点C 的坐标为(0,)m -. ……………………………………………………3分 ∵0m >,∴1AB m =+,OC m =. ∵15△ABC S =,∴1(1)152m m +=. ∴6m =-或5m =.∵0m >,∴5m =.∴抛物线的表达式为245y x x =--. ………………………4分(3)由(2)可知点C 的坐标为(0,5)-.∵直线l :y kx b =+(0)k <经过点C ,∴5b =-. ………………………………………5分 ∴直线l 的解析式为5y kx =-(0)k <. ∵2245(2)9y x x x =--=--,∴当点D 在抛物线顶点处或对称轴左侧时,新函数的最小值为9-,不符合题意. 当点D 在抛物线对称轴右侧时,新函数的最小值有可能大于8-. 令8y =-,即2458x x --=-.解得 11x =(不合题意,舍去),23x =. ∴抛物线经过点(3,8)-.当直线5y kx =-(0)k <经过点(3,8)-时,可求得1k =-.…………………6分由图象可知,当10k -<<时新函数的最小值大于8-. ………………………7分 24.(本小题满分7分) 解:(1)①30°. …………………………………………………………………………1分②不改变,∠BDC 的度数为30.方法一:由题意知,AB=AC=AD .∴点B 、C 、D 在以A 为圆心,AB 为半径的圆上.…………………………2分 ∴∠BDC=12∠BAC =30.……………………………………………………3分 方法二:由题意知,AB=AC=AD . ∵AC =AD ,∠CAD =α, ∴1801=9022ADC C αα-==-∠∠.…………………………………2分 ∵AB=AD ,∠BAD =60α+,∴()18060120160222ADB B ααα-+-====-∠∠. ∴11(90)(60)3022BDC ADC ADB αα=-=---=∠∠∠.…………3分 (2)过点A 作AM ⊥CD 于点M ,连接EM .∴90AMC ∠=. 在△AEB 与△AMC 中,AEB AMC B ACD AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩,,, ∴△AEB ≌△AMC . ………………………………………………………4分∴AE AM =,BAE CAM ∠=∠.∴60EAM EAC CAM EAC BAE BAC ∠=∠+∠=∠+∠=∠=.∴△AEM 是等边三角形.∴EM AM AE ==. …………………………………………………………5分 ∵AC AD =,AM CD ⊥ , ∴CM DM =. 又90DEC ∠=,B∴EM CM DM ==.∴AM CM DM ==. …………………………………………………………6分 ∴点A 、C 、D 在以M 为圆心,MC 为半径的圆上.∴90CAD α=∠=. …………………………………………………………7分 25. (本小题满分8分) 解: (1)(0,10). …………………………………………………………………1分(2)连接BP 、OP ,作PH ⊥OA 于点H .∵5,b =PH ⊥OA , ∴152OH AH OA ===.∵OQ =8,∴3QH OQ OH =-=.在Rt △QHP 中,22229PQ QH PH PH =+=+.在Rt PHO △中,2222225PO OH PH PH BP =+=+=.在Rt △BQP 中,22222(25)(9)16BQ BP PQ PH PH =-=+-+=. ∴4BQ =.……………………………………………………………………3分(3)①1≥a .……………………………………………………………………………4分……………………………………………………………………………5分解:∵△BQP是等腰直角三角形,PQ =∴半径BP = 又∵2(,)P a a ,∴2242OP a a =+=. 即42200a a +-=.解得2a =±.∵0a >,∴2a =. ……………………………………………………………………………6分 ∴(2,4)P .如图,作BM y ⊥轴于点M ,则△QBM ≌△PQH . ∴2MQ PH ==,MB QH ===B.…………………………………7分∴1若点Q在OH上,由对称性可得2B.……………………………8分综上,当PQ=B点坐标为或.。
