统计概率练习题五

合集下载

概率论与数理统计习题5答案

2 / 5
AJ Lin
2013.12
5. 一本书共有 100 万个印刷符号，排版时每个符号被排错的概率为 0.0001，校对时每个排版错误
被改正的概率为 0.9，求校对后错误不多于 15 个的概率。 1, 第n个印刷符号校对后仍印错解：设随机变量 X n , 0, 其它. 则 X n , n 1 是独立同分布随机变量序列，有 p P{xn 1} 0.0001 0.1 10 5 。作 Yn X k ， (n 106 ) ， Yn 为校对后错误总数。按中心极限定理，有 Y np 15 np 3 5 5 P{Yn 15} P n (5 / [10 10 (1 10 )]) (1.58) 0.9495 . npq npq
AJ Lin
2013.12
习题 5 答案
1. 一部件包括 10 部分，每部分的长度是一个随机变量，它们相互独立，服从同一分布，其数学期望为 2mm，均方差为 0.05mm，规定总长度为（ 20 0.1 ）mm 时产品合格，试求产品合格的概率。（其中 (0.63) 0.7357 ， (1.63) 0.9484 ）解：令 X i 表示第 i 部分的长度， i 1, 2, ,10 ，据题意知， X 1 , X 2 , , X 10 相互独立同分布，且 E ( X i ) 2 ， D ( X i ) 0.052 ，故产品合格的概率为
300 X k 300 1.29 400 300 1.29 1 P k 1 300 0.0489 300 0.0489
300 X k 300 1.29 1 P k 1 3.39 1 3.39 1 0.9997 0.0003 . 300 0.0489 (2)设 Y 表示这天售出价格为 1.2 元的蛋糕个数，则 Y ~ B 300, 0.2 ，又 np 300 0.2 60, np (1 p ) 60 0.8 48 ， Y ~ N 60, 48 ，所求概率为 Y 60 60 60 P Y 60 1 P Y 60 1 P 1 (0) 0.5 . 48 48 8. (1)一个复杂系统由 100 个相互独立的元件组成，在系统运行期间每个元件损坏的概率为 0.1，

概率统计试题5

《概率论与数理统计》试卷（A ）注：可能用到的数据()()()()()()()()()()()0.050.0250.050.050.0250.02522220.9750.9750.0250.0251.645,1.96,4 2.3138,5 2.0150,004 2.7764,5 2.5706, 1.6450.95, 1.960.9756 1.237,7 1.1.690,614.449,716.013z z t t t t χχχχ====Φ===Φ=Φ=====一、填空题（每小题4分，共40分）1．设3/1)()(==B P A P ，()1/2P A B = ，则()|P A B = 3/4 2．设随机变量X 的概率密度为()⎩⎨⎧<<=其他,010,2x x x fY 表示对X 的三次独立重复观察试验中事件{}2/1≤X 出现的次数，则{}==2Y P 9/643．设随机变量()()0,~2>σσμN X ，且二次方程042=++X y y 无实根的概率为12，则=μ 44．设随机变量1X 与2X 有相同的分布，其分布律为{}114i P X =-=， {}102i P X ==， {}114i P X ==， 1,2i =且满足1}0{21==X X P ，则==}{21X X P 05．已知随机变量X 服从参数为λ的泊松分布，令1232-+=X X Y ，则Y的数学期望()E Y = 1532-+λλ6．设随机变量X 的数学期望()μ=X E ，方差()2σ=X D ，则由切比雪夫不等式，有{}≤≥-σμ3X P 1/97．设121,,,,+n n X X X X 是来自正态总体()2,σμN 的样本，记∑==ni i X nX 11， ()∑=--=ni iXX n S 12211，则统计量1n X Sμ+-服从___t____分布，自由度为 n-18．已知总体X 的概率密度为()1,01()0,x x f x θθ⎧+<<=⎨⎩其他1θ>-设n X X X ,,,21 为X 的样本，则参数θ的矩估计量为ˆθ= ˆθ=211X X--9．设随机变量X 的分布函数为⎪⎩⎪⎨⎧≥<≤-+-<=1,111,16751,0)(x x x x x F则==}1{2XP ____ 3/8_10．随机变量X 在区间[]1,2-上服从均匀分布，随机变量1,00,01,0X Y X X >⎧⎪==⎨⎪-<⎩则Y 的方差()D Y = 8/9二、（10分）设有来自A 、B 、C 三个地区考生报名表各10份、15份和25份，其中女生的报名表分别为3份、7份和5份，今随机地抽取一份报名表。

概率论与数理统计练习册(理工类) - 第5,6章答案

答；收入至少400元的概率几乎为0.
(2)设出售1.2元的蛋糕数量为Y，则Y ~ B(300, 0.2), E(Y ) = 60, D(Y ) = 48.
P{Y

60}
=
Y P{
− 60

0}
=
(0)
=
0.5
48
答：售出价格为1.2元的蛋糕多于60只的概率0.5.
28
一、选择题：
概率论与数理统计练习题
x} = (x)
n→
n
n
Xi −n
(C) lim P{ i=1
x} = (x)
n→
n
n
Xi −
(D) lim P{ i=1
x} = (x)
n→
n
二、填空题：
224
1．对于随机变量 X，仅知其 E( X ) = 3，D( X ) = 1 ，则可知 P{| X − 3 | 3} 225
一、选择题：
概率论与数理统计练习题
系
专业
班姓名
学号
第五章大数定律与中心极限定理
1．设 n 是 n 次重复试验中事件 A 出现的次数，p 是事件 A 在每次试验中出现的概率，则对任意
的

0
均有
lim
P

n
−
p

n→ n

[A ]
(A) = 0
(B) = 1
(C) 0
(D) 不存在
系
专业
班姓名
学号
第六章数理统计的基本知识
§6.1 总体、样本与统计量、§6.2 抽样分布
1．设 X1, X 2 , X 3 是取自总 X 体的样本，a 是一个未知参数，下述哪个样本函数是统计量[ B ]

高一数学复习专题练习5 概率与统计

高一数学复习专题练习专题5 概率与统计一、选择题1．某校有40个班，每班50人，要求每班随机选派3人参加“学生代表大会”．在这个问题中样本容量是( )A ．40B ．50C ．120D ．150【答案】 C【解析】由于样本容量即样本的个数，故抽取的样本的个数为40×3＝120. 2.从6个篮球、2个排球中任选3个球，则下列事件中，是必然事件的是( ) A.3个都是篮球 B.至少有1个是排球 C.3个都是排球D.至少有1个是篮球【答案】 D【解析】从6个篮球、2个排球中任选3个球，A ，B 是随机事件，C 是不可能事件，D 是必然事件，故选D.3．一个射手进行射击，记事件E 1：“脱靶”，E 2：“中靶”，E 3：“中靶环数大于4”，E 4：“中靶环数不小于5”，则在上述事件中，互斥而不对立的事件共有( ) A ．1对 B ．2对 C ．3对D ．4对【答案】 B【解析】 E 1与E 3，E 1与E 4均为互斥而不对立的事件．4．袋中装有白球和黑球各3个，从中任取2个，则至多有一个黑球的概率是( ) A.15 B.45 C.13 D.12【答案】 B【解析】把白球编号为1,3,5，黑球编号为2,4,6.从中任取2个，基本事件为12,13,14,15,16,23,24,25,26,34,35,36,45,46,56，共15个．其中至多一个黑球的事件有12个．由古典概型公式得P ＝1215＝45.学-科网5.某中学举办电脑知识竞赛，满分为100分，80分以上为优秀(含80分)，现将高一两个班参赛学生的成绩进行整理后分成五组：第一组[50,60)，第二组[60,70)，第三组[70,80)，第四组[80,90)，第五组[90,100]，其中第一、三、四、五小组的频率分别为0.30,0.15,0.10,0.05，而第二小组的频数是40，则参赛的人数以及成绩优秀的概率分别是( ) A.50,0.15 B.50,0.75 C.100,0.15D.100,0.75【答案】 C【解析】由已知得第二小组的频率是1－0.30－0.15－0.10－0.05＝0.40，频数为40，设共有参赛学生x 人，则x ×0.4＝40，∴x ＝100. 成绩优秀的概率为0.15，故选C.6.如图所示，现有一迷失方向的小青蛙在3处，它每跳动一次可以等可能地进入相邻的任意一格(若它在5处，跳动一次，只能进入3处，若在3处，则跳动一次可以等机会地进入1,2,4,5处)，则它在第三次跳动后，首次进入5处的概率是( )A.12B.14C.316D.16【答案】 C7.样本中共有五个个体，其值分别为a,0,1,2,3.若该样本的平均数为1，则样本方差为( ) A.65 B.65C. 2D.2 【答案】 D【解析】 ∵样本的平均数为1，即15×(a ＋0＋1＋2＋3)＝1，∴a ＝－1. ∴样本方差s 2＝15×[(－1－1)2＋(0－1)2＋(1－1)2＋(2－1)2＋(3－1)2]＝2.8．已知集合A ＝{－5，－3，－1,0,2,4}，在平面直角坐标系中，点(x ，y )的坐标满足x ∈A ，y ∈A ，且x ≠y ，则点(x ，y )不在x 轴上的概率( ) A.13B.12C.56D.14【答案】 C【解析】因为x ∈A ，y ∈A ，且x ≠y ，所以x 有6种可能，y 有5种可能，所以试验的所有结果有6×5＝30(种)，且每种结果的出现是等可能的．设事件A 为“点(x ，y )不在x 轴上”，那么y ≠0，有5种可能，x 有5种可能，事件A 包含基本事件个数为5×5＝25种．因此所求事件的概率为P (A )＝2530＝56.9.为了调查某厂2 000名工人生产某种产品的能力，随机抽查了20位工人某天生产该产品的数量，产品数量的分组区间为[10,15)，[15,20)，[20,25)，[25,30)，[30,35]，频率分布直方图如图所示.工厂规定从生产低于20件产品的工人中随机地选取2位工人进行培训，则这2位工人不在同一组的概率是( )A.110B.715C.815D.1315【答案】 C【解析】根据频率分布直方图，可知产品件数在[10,15)，[15,20)内的人数分别为5×0.02×20＝2,5×0.04×20＝4.设生产产品件数在[10,15)内的2人分别是A ，B ，生产产品件数在[15,20)内的4人分别为C ，D ，E ，F ，则从生产低于20件产品的工人中随机地选取2位工人的结果有(A ，B )，(A ，C )，(A ，D )，(A ，E )，(A ，F )，(B ，C )，(B ，D )，(B ，E )，(B ，F )，(C ，D )，(C ，E )，(C ，F )，(D ，E )，(D ，F )，(E ，F )，共15种.2位工人不在同一组的结果有(A ，C )，(A ，D )，(A ，E )，(A ，F )，(B ，C )，(B ，D )，(B ，E )，(B ，F )，共8种.故选取的2位工人不在同一组的概率为815.二、填空题(本大题共4小题，每小题5分，共20分)10．某企业共有职工150人，其中高级职称15人，中级职称45人，低级职称90人，现采用分层抽样来抽取30人，则抽取的高级职称的人数为________．【答案】 3【解析】由题意得抽样比为30150＝15，所以抽取的高级职称的人数为15×15＝3.11．一批产品共有100件，其中5件是次品，95件是合格品，从这批产品中任意抽5件，记A 为“恰有1件次品”，B 为“至少有2件次品”，C 为“至少有1件次品”，D 为“至多有1件次品”．现给出下列结论：①A ＋B ＝C ；②B ＋D 是必然事件；③A ＋C ＝B ；④A ＋D ＝C .其中正确的结论为________．(写出序号即可) 【答案】 ①②【解析】由互斥、对立事件的概念得A ＋B ＝C ，故③错；A ＋D 表示“至多有1件次品”，所以④错． 12.为了了解《中华人民共和国道路交通安全法》在学生中的普及情况，调查部门对某校6名学生进行问卷调查，6人得分情况如下：5,6,7,8,9,10.把这6名学生的得分看成一个总体.如果用简单随机抽样方法从这6名学生中抽取2名，他们的得分组成一个样本，则该样本平均数与总体平均数之差的绝对值不超过0.5的概率为________. 【答案】715三、解答题13.(12分)一个包装箱内有6件产品，其中4件正品，2件次品.现随机抽出两件产品. (1)求恰好有一件次品的概率； (2)求都是正品的概率； (3)求抽到次品的概率.解将6件产品编号，abcd (正品)，ef (次品)，从6件产品中选2件，其包含的基本事件为ab ，ac ，ad ，ae ，af ，bc ，bd ，be ，bf ，cd ，ce ，cf ，de ，df ，ef ，共15种.(1)设恰好有一件次品为事件A ，事件A 包含的基本事件为ae ，af ，be ，bf ，ce ，cf ，de ，df ，共有8种，则P (A )＝815.(2)设都是正品为事件B ，事件B 包含的基本事件数为6，则P (B )＝615＝25.(3)设抽到次品为事件C ，事件C 与事件B 是对立事件，则P (C )＝1－P (B )＝1－25＝35.14.已知关于x 的一元二次方程x 2－2(a －2)x －b 2＋16＝0.若a ，b 是一枚骰子掷两次所得到的点数，求方程有两正根的概率；解 a ，b 是一枚骰子掷两次所得到的点数，总的基本事件(a ，b )共有36个. 设事件A 表示“方程有两正根”，则∆≥0，a －2>0，16－b 2>0，即a －2 2＋b 2≥16，a >2，－4<b <4，则事件A 包含的基本事件有(6,1)，(6,2)，(6,3)，(5,3)，共4个，故方程有两正根的概率为P (A )＝436＝19.15．(12分)先后2次抛掷一枚骰子，将得到的点数分别记为a ，b . (1)求直线ax ＋by ＋5＝0与圆x 2＋y 2＝1相切的概率；(2)将a ，b,5的值分别作为三条线段的长，求这三条线段能围成等腰三角形的概率．解先后2次抛掷一枚骰子，将得到的点数分别记为a ，b 包含的基本事件：(1,1)，(1,2)，(1,3)，(1,4)，(1,5)，(1,6)，(2,1)，…，(6,5)，(6,6)，共36个． (1)∵直线ax ＋by ＋5＝0与圆x 2＋y 2＝1相切，∴5a 2＋b2＝1，整理得a 2＋b 2＝25. 由于a ，b ∈{1,2,3,4,5,6}，∴满足条件的情况只有a ＝3，b ＝4或a ＝4，b ＝3两种情况． ∴直线ax ＋by ＋5＝0与圆x 2＋y 2＝1相切的概率是236＝118.(2)∵三角形的一条边长为5，三条线段围成等腰三角形，∴当a ＝1时，b ＝5，共1个基本事件；当a ＝2时，b ＝5，共1个基本事件；当a ＝3时，b ＝3,5，共2个基本事件；当a ＝4时，b ＝4,5，共2个基本事件；当a ＝5时，b ＝1,2,3,4,5,6，共6个基本事件；当a ＝6时，b ＝5,6，共2个基本事件；∴满足条件的基本事件共有1＋1＋2＋2＋6＋2＝14(个)． ∴三条线段能围成等腰三角形的概率为1436＝718.学-科网16．(12分)有7位歌手(1至7号)参加一场歌唱比赛，由500名大众评委现场投票决定歌手名次，根据年龄将大众评委分为五组，各组的人数如下：组别 A B C D E人数5010015015050(1)为了调查大众评委对7位歌手的支持情况，现用分层抽样方法从各组中抽取若干评委，其中从B组中抽取了6人．请将其余各组抽取的人数填入下表．组别 A B C D E人数5010015015050抽取人数 6(2)在(1)中，若A，B两组被抽到的评委中各有2人支持1号歌手，现从这两组被抽到的评委中分别任选1人，求这2人都支持1号歌手的概率．解 (1)由题设知，分层抽样的抽取比例为6%，所以各组抽取的人数如下表：组别 A B C D E50[来人数50100150150源:Z*xx*]抽取人数3699 3(2)记从A组抽到的3个评委为a1，a2，a3，其中a1，a2支持1号歌手；从B组抽到的6个评委为b1，b2，b3，b4，b5，b6，其中b1，b2支持1号歌手．从{a1，a2，a3}和{b1，b2，b3，b4，b5，b6}中各抽取1人的所有结果为：由以上树状图知所有结果共18种，其中2人都支持1号歌手的有a1b1，a1b2，a2b1，a2b2，共4种，故所求概率P＝418＝29.。

小学三年级概率与统计练习题

小学三年级概率与统计练习题一、选择题1. 以下哪一项不是概率的表示方法？A. 小数B. 百分数C. 分数D. 字母符号2. 甲班有24个学生，其中有8个女生，男生占总人数的几分之几？A. 1/3B. 1/2C. 2/3D. 3/43. 某班级学生中，29名同学会游泳，其中有15名男生，占全班学生总数的几分之几？A. 1/2B. 1/3C. 2/3D. 3/44. 在一副扑克牌中，黑色牌的数量是红色牌数量的2倍，若从中随机抽取一张牌，则抽到黑色牌的概率是多少？A. 1/4B. 1/3C. 2/5D. 1/25. 某班级有30个学生，其中15个是男生，抽到一个男生学生的概率是多少？A. 1/2B. 1/3C. 2/3D. 3/4二、填空题1. 用“A”、“B”、“C”、“D”四个字母组成三位数，一个字母只能使用一次，则可以组成多少个不同的三位数？答：_______个2. 同学们投掷了一枚骰子20次，投掷结果中出现6的次数为8次，出现6的概率是多少？答：_______3. 一架鸟在一根电线上停留，有50%的概率选择向左边飞去，有50%的概率选择向右边飞去。

如果一只鸟飞行5次，那么它全部向左边飞的可能性是多少？答：_______%三、解答题1. 黎明在箱子中装有30个红色球和20个蓝色球，她先从箱子中随机取出一个球，记录颜色后将球放回，然后再次随机取出一个球。

求以下概率：（1）两次取出的球都是红色球的概率；（2）第一次取出的是蓝色球，第二次取出的是红色球的概率。

2. 小明在一堆卡片中找出数字3的概率是1/5，若他连续随机取出3张卡片，则取出至少1张数字3的概率是多少？3. 某班级有40名学生，其中20名学生会游泳，15名学生会跳绳，有8名学生既会游泳又会跳绳。

如果从班级中随机选取一个学生，请你求这个学生会游泳或会跳绳的概率。

答案：一、选择题1. D2. B3. C4. A5. A二、填空题1. 24个2. 8/20=2/53. 1/2×1/2×1/2×1/2×1/2=1/32三、解答题1. （1）30/50×29/49=174/245（2）20/50×30/49=12/492. 不取到数字3的概率是4/5，连续取3次不取到数字3的概率是(4/5)×(4/5)×(4/5)=64/125，取出至少1张数字3的概率是1-64/125=61/125。

概率统计习题集（含答案）

第一章随机事件及其概率一、选择题：1．设A 、B 、C 是三个事件，与事件A 互斥的事件是：（）A ．AB AC + B ．()A B C + C ．ABCD ．A B C ++2．设B A ⊂ 则（）A ．()P AB =1-P （A ） B ．()()()P B A P B A -=-C ． P(B|A) = P(B)D ．(|)()P AB P A =3．设A 、B 是两个事件，P （A ）> 0，P （B ）> 0,当下面的条件（）成立时，A 与B 一定独立A ．()()()P AB P A P B = B ．P （A|B ）=0C ．P （A|B ）= P （B ）D ．P （A|B ）= ()P A4．设P （A ）= a ，P （B ）= b, P （A+B ）= c, 则 ()P AB 为：（）A ．a-bB ．c-bC ．a(1-b)D ．b-a5．设事件A 与B 的概率大于零，且A 与B 为对立事件，则不成立的是（）A ．A 与B 互不相容 B ．A 与B 相互独立C ．A 与B 互不独立D ．A 与B 互不相容6．设A 与B 为两个事件，P （A ）≠P （B ）> 0，且A B ⊃，则一定成立的关系式是（）A ．P （A|B ）=1 B ．P(B|A)=1C ．(|A)1p B =D ．(A|)1p B =7．设A 、B 为任意两个事件，则下列关系式成立的是（）A ．()AB B A -= B ．()A B B A -⊃C ．()A B B A -⊂D ．()A B B A -=8．设事件A 与B 互不相容，则有（）A ．P （AB ）=p （A ）P （B ） B ．P （AB ）=0C ．A 与B 互不相容D ．A+B 是必然事件9．设事件A 与B 独立，则有（）A ．P （AB ）=p （A ）P （B ） B ．P （A+B ）=P （A ）+P （B ）C ．P （AB ）=0D ．P （A+B ）=110．对任意两事件A 与B ，一定成立的等式是（）A ．P （AB ）=p （A ）P （B ） B ．P （A+B ）=P （A ）+P （B ）C ．P （A|B ）=P （A ）D ．P （AB ）=P （A ）P （B|A ）11．若A 、B 是两个任意事件，且P （AB ）=0，则（）A ．A 与B 互斥 B ．AB 是不可能事件C ．P （A ）=0或P （B ）=0D ．AB 未必是不可能事件12．若事件A 、B 满足A B ⊂，则（）A ．A 与B 同时发生 B ．A 发生时则B 必发生C ．B 发生时则A 必发生D ．A 不发生则B 总不发生13．设A 、B 为任意两个事件，则P （A-B ）等于（）A ． ()()PB P AB - B ．()()()P A P B P AB -+C ．()()P A P AB -D ．()()()P A P B P AB --14．设A 、B 、C 为三事件，则AB BC AC 表示（）A ．A 、B 、C 至少发生一个 B ．A 、B 、C 至少发生两个C ．A 、B 、C 至多发生两个D ．A 、B 、C 至多发生一个15．设0 < P (A) < 1. 0 < P (B) < 1. P(|B)+P(A B A )=1. 则下列各式正确的是（）A ．A 与B 互不相容 B ．A 与B 相互独立C ．A 与B 相互对立D ．A 与B 互不独立16．设随机实际A 、B 、C 两两互斥，且P （A ）=0.2，P （B ）=0.3，P （C ）=0.4，则PA B C -= （）（）. A ．0.5 B ．0.1 C ．0.44 D ．0.317掷两枚均匀硬币，出现一正一反的概率为（）A ．1/2B ．1/3C ．1/4D ．3/418．一种零件的加工由两道工序组成，第一道工序的废品率为 1p ，第二道工序的废品率为2p ，则该零件加工的成品率为（）A ．121p p --B ．121p p -C ．12121p p p p --+D ．122p p --19．每次试验的成功率为)10(<<p p ，则在3次重复试验中至少失败一次概率为（）。

概率统计练习题

第一章随机事件及其概率习题一、填空题：1.设A ，B ，C 为三个事件，用A 、B 、C 的运算关系表示（1）A 和B 都发生，而C 不发生为，（2）A 、B 、C 至少有两个发生的事件为。

2.设A ，B 为两个互不相容的事件，P(A)=0.2, P(B)=0.4, P(A+B)= 。

3.设A ，B ，C 为三个相互独立的事件，已知P(A)=a, P(B)=b, P(C)=c,则A ，B ，C 至少有一个发生的概率为。

4.把一枚硬币抛四次，则无反面的概率为，有反面的概率为。

5.电话号码由0，1，……9中的8数字排列而成，则电话号码后四位数字全都不相同的概率表示为。

6.设公寓中的每一个房间都有4名学生，任意挑选一个房间，则这4人生日无重复的概率表示为（一年以365天计算）。

7. 设A ，B 为两个事件，P(A)=0.4, ,P(B)=0.8,P(B A )=0.5,则P(B|A)= 。

8.设A ，B ，C 构成一个随机试验的样本空间的一个划分，且7.0)(,5.0)(==B P A P ,则P(C)= ,P(AB)= 。

9.设A ，B 为两个相互独立的事件，P(A)=0.4，P(A+B)=0.7，则P(B)= 。

10.3个人独立地猜一谜语，他们能够猜出的概率都是31，则此谜语被猜出的概率为。

二、选择题：1. 设A 与B 是两随机事件，则AB 表示（）（A ）A 与B 都不发生（B ）A 与B 同时发生（C ）A 与B 中至少有一个发生（D ）A 与B 中至少有一个不发生 2.设c B A P b B P a A P =⋃==)(,)(,)(，则)(B A P 为（A ）b a -（B ）b c -（C ）)1(b a -（D ）)1(c a -3.若A ，B 是两个互不相容的事件，P （A ）>0，P （B ）>0，则一定有（）（A ）P （A ）=1—P （B ）（B ） P （A|B ）=0 （C ） P （A|B ）=1 （D ）P （A |B ）=04. 每次试验失败的概率为p (0<p<1),则在3次重复试验中至少成功一次的概率为（）（A ）)1(3p - (B)3)1(p -(C) 31p - (D)13C 3)1(p p -三、计算：1.掷两颗质地均匀的骰子，求出现的两个点数之和等于5的概率。

小学一年级概率与统计练习题

小学一年级概率与统计练习题请按照以下格式进行练习题的编写：
一、选择题
1. 在下列数字中，属于偶数的是：
A. 1
B. 2
C. 3
D. 4
2. 从一副扑克牌中随机抽取一张牌，红心牌的概率是：
A. 1/4
B. 1/3
C. 1/2
D. 1/5
3. 小明有3个红色的糖果和2个蓝色的糖果，他从中随机抽取一个
糖果，红色糖果的概率是：
A. 2/3
B. 3/5
C. 1/2
D. 5/7
二、填空题
1. 抛掷一枚骰子，出现偶数的概率是______。

2. 从26个字母中随机抽取一个字母，抽到元音字母的概率是
______。

三、解答题
1. 小明有4张扑克牌，分别是红心A、黑桃A、方块2、梅花2，
请问抽到红心A的概率是多少？
2. 从一副扑克牌中同时抽取两张牌，抽到两张红心牌的概率是多少？
写作时要注意题目的难度和递进关系，按照从易到难的顺序编排题目。

每个题目后都要有四个选项，其中一个是正确答案。

填空题需要在空格中填写正确的数字。

解答题需要学生自己写出答案，并给出解题思路。

以上只是一部分题目的示例，您可以根据需要进一步扩充或修改题目。

希望对您有所帮助！。

统计与概率练习题六年级

统计与概率练习题六年级一、选择题（每题5分，共15分）1. 某班级有40名学生，其中有15名男生，则女生人数是多少？A. 15B. 20C. 25D. 302. 在一次抽奖活动中，参与者购买了200张彩票，其中5张中奖，中奖率是多少？A. 2.5%B. 5%C. 7.5%D. 10%3. 如果一个骰子掷出6个面中的1、2、3、4、5，每个面的概率相等，则掷到1的概率是多少？A. 1/6B. 1/5C. 1/4D. 1/3二、计算题（每题10分，共30分）1. 篮球队在一个赛季中进行了40场比赛，其中赢了30场，输了8场，平局2场。

请计算篮球队的胜率和输率各是多少？2. 一共有5个苹果，其中有2个是绿色的，其余是红色的。

现从这些苹果中随机选择一个，问选择的是红色苹果的概率是多少？3. 一副扑克牌有52张牌，其中有4张A（Ace），如果从中随机抽取一张牌，请计算抽取到A的概率是多少？三、应用题（每题20分，共40分）1. 甲、乙两个班级的学生人数之比是3:5，其中甲班人数比乙班少10人。

请计算甲班和乙班的学生人数各是多少？2. 某球队共有30个人，其中有10个队员会射门，20个队员不会射门。

现从这些队员中随机抽取一人，请计算抽取到会射门的概率是多少？3. 根据一份问卷调查结果，某商店的顾客购买商品的原因分为三类：价格因素、品质因素、服务因素。

问卷中显示，价格因素对购买的影响比例为55%，品质因素为30%，服务因素为15%。

如果有一位顾客购买了该商店的商品，那么他选择购买的主要因素是什么？四、拓展题（每题15分，共30分）1. 小明家有4个孩子，其中一个是小花。

请问有几种可能的情况？2. 某市一天的天气预报可以分为晴天、多云、阴天和雨天四种情况。

根据气象数据，该市的晴天概率为40%，多云为30%，阴天为20%，则该市下雨的概率是多少？3. 某次抽奖活动有100个奖品，共有2000人参与。

每个人只能中1次奖，请计算一个人中奖的概率是多少？总分：115分以上是统计与概率练习题六年级的内容，希望对于你的练习有所帮助。

高三数学练习题：概率与统计

高三数学练习题：概率与统计
问题1：
某班有40名学生，其中有30名学生参加了一个数学竞赛。

现在我们从这些学生中随机抽取一名学生，请计算以下概率：
a) 抽中一位参加了数学竞赛的学生；
b) 抽中一位未参加数学竞赛的学生。

问题2：
某班有50名学生，其中30人喜欢数学，20人喜欢英语，15人同时喜欢数学和英语。

现在我们从这些学生中随机选择一位学生，请计算以下概率：
a) 抽中一位喜欢数学的学生；
b) 抽中一位喜欢英语的学生；
c) 抽中一位同时喜欢数学和英语的学生。

问题3：
某地区的天气预报表明，星期一下雨的概率是0.3，星期二下雨的概率是0.4。

而星期一和星期二都下雨的概率是0.15。

现在，我们从这两个星期中随机选择一个天气预报，请计算以下概率：
a) 抽中星期一下雨；
b) 抽中星期二下雨；
c) 抽中星期一和星期二都下雨。

问题4：
某班有90名学生，其中40人喜欢数学，60人喜欢英语，20人同时喜欢数学和英语。

现在我们从这些学生中选择两个学生，请计算以下概率：
a) 抽中两位喜欢数学的学生；
b) 抽中两位喜欢英语的学生；
c) 抽中一位喜欢数学的学生和一位喜欢英语的学生。

问题5：
某打印店收到100份订单，其中有20份订单有错误。

现在，我们从这些订单中随机抽取一份，请计算以下概率：
a) 抽中一份有错误的订单；
b) 抽中一份没有错误的订单。

小学四年级概率与统计练习题

小学四年级概率与统计练习题题目：小学四年级概率与统计练习题第一部分：概率计算1. 某班级有30个学生，其中20个是男生，10个是女生。

请问从班级中随机选择一个学生，他是女生的概率是多少？2. 一副标准扑克牌共有52张牌，其中红心和黑桃各有13张，梅花和方块各有13张。

请问从一副扑克牌中随机抽取一张牌，它是红心的概率是多少？3. 一枚公平的硬币抛掷一次，正面朝上的概率是多少？4. 甲、乙、丙三个学生参加一场考试，其考试成绩如下：甲：60分乙：80分丙：90分请问从他们中随机选择一个人，他的考试成绩大于70分的概率是多少？第二部分：数据统计与图表1. 下图是小明家的月度用水量统计表，请根据图表回答问题。

![image](image_link)a. 小明家一月份的用水量是多少？b. 二月份的用水量比一月份多还是少？c. 三月份的用水量是多少？d. 四月份的用水量比三月份多还是少？2. 下表是某小学四年级学生的身高统计表，请根据表格回答问题。

| 班级 | 身高范围（cm） | 学生数量 ||------|---------------|----------|| 1班 | 120 - 130 | 5 || 1班 | 131 - 140 | 8 || 1班 | 141 - 150 | 6 || 2班 | 120 - 130 | 4 || 2班 | 131 - 140 | 6 || 2班 | 141 - 150 | 7 |a. 1班的学生数量是多少？b. 2班身高在131cm以上的学生数量是多少？c. 班级1和班级2的学生数量总共是多少？d. 身高在141cm以上的学生数量是多少？第三部分：数据分析1. 某班级12个学生参加一场语文测试，他们的得分如下： 78, 86, 92, 73, 64, 80, 89, 77, 85, 91, 68, 79a. 这组数据的平均分是多少？b. 这组数据的中位数是多少？c. 这组数据的众数是多少？d. 这组数据的范围是多少？2. 某小区住户的家庭成员数统计如下：| 家庭成员数 | 家庭数量 ||------------|----------|| 1人 | 10 || 2人 | 15 || 3人 | 20 || 4人 | 25 || 5人以上 | 30 |a. 该小区共有多少个家庭？b. 平均每个家庭有几人？c. 家庭成员数最多的家庭有多少人？请按照题号完成相应的题目。

统计与概率初三练习题

统计与概率初三练习题在初三学习统计与概率时，练习题是非常重要的一部分。

通过做题，我们可以巩固所学知识，提高解决问题的能力。

本文将提供一些统计与概率的初三练习题，并给出详细解析，希望对同学们的学习有所帮助。

一、统计题1. 某班有60名学生，他们的身高数据如下（单位：cm）：155, 165, 160, 165, 155, 170, 160, 155, 170, 165, 160, 155, 155, 165, 160, 160, 155, 165, 160, 165, 170, 155, 165, 170, 165, 160, 155, 160, 170, 160, 155, 155, 165, 160, 160, 165, 155, 160, 170, 165, 160, 155, 155, 165, 160, 165, 160, 170, 155, 165, 160, 155, 160, 155, 170, 165, 155, 165, 160, 165请计算这60名学生的平均身高和中位数。

解析：要计算平均身高，只需要将所有学生的身高加起来，然后除以学生人数。

平均身高 = (155 + 165 + 160 + 165 + 155 + 170 + 160 + 155 + 170 + 165 + 160 + 155 + 155 + 165 + 160 + 160 + 155 + 165 + 160 + 165 + 170 + 155 + 165 + 170 + 165 + 160 + 155 + 160 + 170 + 160 + 155 + 155 + 165 + 160 + 160 + 165 + 155 + 160 + 170 + 165 + 160 + 155 + 155 + 165 + 160 + 165 + 160 + 170 + 155 + 165 + 160 + 155 + 160 + 155 + 170 + 165 + 155 + 165 + 160 + 165) / 60中位数是指将所有数据按照大小顺序排列，取中间的数。

统计与概率练习题

统计与概率练习题一、选择题1. 假设我们有一个随机变量X，它服从正态分布N(μ, σ²)。

如果μ=50，σ=10，那么P(X>60)的值是多少？A. 0.9772B. 0.8413C. 0.1587D. 0.02282. 在一次掷骰子的实验中，掷出偶数点的概率是多少？A. 0.5B. 0.33C. 0.66D. 0.253. 某工厂生产的产品中有5%是次品。

如果随机抽取100个产品，那么至少有5个次品的概率是多少？A. 0.95B. 0.90C. 0.70D. 0.50二、填空题4. 如果一个随机变量X服从二项分布B(n, p)，其中n=10，p=0.3，那么P(X=3)等于______。

5. 假设随机变量Y服从泊松分布，参数λ=4。

那么P(Y=2)等于______。

6. 某公司有100名员工，其中10名员工有心脏病。

如果随机选择一名员工进行体检，那么这名员工有心脏病的概率是______。

三、简答题7. 解释什么是标准正态分布，并给出其均值和标准差。

8. 描述什么是中心极限定理，并简述其在实际应用中的意义。

9. 什么是条件概率？请给出一个条件概率的例子，并解释其含义。

四、计算题10. 某公司进行一项调查，发现60%的员工支持公司的新政策。

如果随机抽取5名员工进行访谈，计算至少有3名员工支持新政策的概率。

11. 假设有一批零件，其中有10%的零件是次品。

如果从这批零件中随机抽取20个进行检查，求恰好有2个次品的概率。

12. 一个袋子里有10个红球和5个蓝球。

如果随机抽取3个球，求抽到至少2个红球的概率。

五、应用题13. 某学校进行一次数学竞赛，共有100名学生参加。

竞赛结果显示，平均分为70分，标准差为10分。

如果一个学生的成绩超过平均分两个标准差，那么这个学生的成绩至少是多少？14. 某医院对100名患者进行某种疾病的检测，结果发现有5名患者被误诊为健康。

如果随机选择一名患者进行检查，求这名患者被误诊的概率。

小学五年级概率与统计练习题

小学五年级概率与统计练习题
一、选择题
1. 小明有4个红球和6个蓝球，他从中随机抽取一球，那么得到红球的概率是多少？
A. 1/5
B. 2/5
C. 3/5
D. 4/5
2. 一副标准扑克牌共有52张牌，其中有4个A，小明从中随机抽取一张牌，那么不是A的概率是多少？
A. 1/13
B. 3/4
C. 3/13
D. 12/13
3. 小红有10只袜子，其中4只是黑色的，她闭着眼睛随机拿出一只袜子，那么拿到黑色袜子的概率是多少？
A. 2/5
B. 1/2
C. 3/5
D. 2/3
二、填空题
1. 抛一个均匀的六面骰子，出现奇数的概率是____。

2. 从26个大写字母中随机选取一个字母，是辅音字母的概率是
____。

3. 一共有12张牌，其中有4张红心牌和8张黑桃牌，从中随机抽
取一张牌，不是红心牌的概率是____。

三、应用题
小明家里有12只袜子，其中6只是黑色的，4只是蓝色的，2只是
白色的。

小明闭着眼睛随机拿了两只袜子，问他拿到两只黑袜子的概
率是多少？
将问题转化为概率计算，我们可以先计算拿到第一只黑袜子的概率，即 6/12，然后再计算拿到第二只黑袜子的概率，由于已经拿出了一只
黑袜子，所以剩下的黑袜子只有5只，剩下的袜子有11只，所以拿到
第二只黑袜子的概率是 5/11。

根据概率的乘法原理，拿到两只黑袜子的概率等于拿到第一只黑袜
子的概率乘以拿到第二只黑袜子的概率，即 (6/12) * (5/11) = 30/132。

所以小明拿到两只黑袜子的概率是 30/132。

挑战统计问题的数学练习题

挑战统计问题的数学练习题统计学是应用数学的一个分支，致力于收集、分析和解释数据。

在日常生活中，我们常常会遇到各种各样的统计问题，比如调查结果的解读、概率计算等等。

本文将为大家提供一些挑战性的统计问题数学练习题，帮助大家提升解决统计问题的能力。

一、概率计算题1. 在一副标准的扑克牌中，红心牌和黑桃牌各有13张，方块牌和梅花牌各有13张。

从扑克牌中随机抽取一张牌，求抽到红心牌和红色牌的概率。

2. 有一口袋中有3个红球和2个蓝球，在不放回的情况下，依次从袋中抽取两个球，求抽到两个红球的概率。

3. 某市交通事故发生率为0.03，如果发生事故，驾驶员酒驾的概率为0.1。

某天，该市发生了交通事故，求该事故中驾驶员酒驾的概率。

二、数据分析题1. 某班级学生的身高数据如下：165 cm、167 cm、170 cm、172 cm、175 cm、180 cm、182 cm。

计算这组数据的平均身高。

2. 某城市一周七天的降雨量数据如下：10 mm、15 mm、8 mm、0 mm、6 mm、20 mm、5 mm。

计算这组数据的总降雨量。

3. 某公司某年度每个季度的销售额分别为150万元、180万元、120万元、200万元。

计算该年度的总销售额和平均季度销售额。

三、统计推断题1. 一项调查显示，某市民10%的人喜欢做户外运动。

现从该市随机抽取200人进行调查，结果有25人表示喜欢户外运动。

根据这个样本调查结果，估计整个市民中喜欢户外运动的比例。

2. 某电商平台进行了一次广告宣传活动，判断这次活动对销售额的提升是否有效。

在活动前后各随机选择了100名用户进行调查，结果在活动前有50人购买了商品，在活动后有70人购买了商品。

根据这个样本调查结果，判断这次广告宣传活动对销售额的提升是否有效。

3. 某厂家生产的产品合格率为99%，质检员从中随机抽取20个产品进行检验，结果有1个产品不合格。

根据这个样本调查结果，估计该厂家生产的产品的整体合格率。

六年级数学统计与概率练习题

六年级数学统计与概率练习题
1. 从一个玩具袋中随机取一个玩具，这个玩具是车的概率是1/3，是娃娃的概率是2/3。

如果从袋子里取出的是车，那么取出的是娃娃的概率是多少？
2. 一箱中有4个红球，2个蓝球，3个绿球。

如果从箱子中随机取出一个球，那么取出一个红球或者蓝球的概率是多少？
3. 在一个班级里，有25个男生和20个女生。

如果从班级中随机选择一个学生，那么选择一个男生的概率是多少？
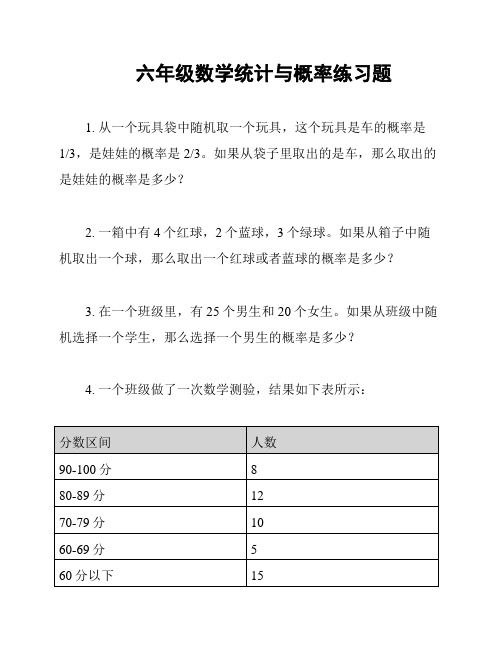
4. 一个班级做了一次数学测验，结果如下表所示：
如果从班级中随机选择一个学生，那么该学生得到60分以下的概率是多少？
5. 请列举三个例子，说明概率为0的情况。

6. 如果一个筛子投掷10次，每次投掷的结果相互独立，那么在这十次投掷中至少出现一次1点的概率是多少？
7. 在一个扑克牌的52张牌中，红桃的数量是13张。

如果从扑克牌中随机选择一张牌，那么选择一张红桃的概率是多少？
8. 一个袋子里有3个红球，4个蓝球，2个绿球。

从袋子中连续取出两个球，不放回。

那么第一次取出红球，第二次取出蓝球的概率是多少？
9. 一个骰子被投掷6次，每次投掷的结果相互独立。

如果每次投掷结果都不是6点，那么总共投掷了多少次？
10. 在一次抽奖活动中，总共有100个参与者，其中40人是男性，60人是女性。

如果从参与者中随机抽取一个人，那么该人是男性并且中奖的概率是多少？
以上是六年级数学统计与概率的练题。

数的概率与统计练习题

数的概率与统计练习题
以下是一份关于数的概率与统计的练习题：
题目一：选择题
1. 下面哪个不是随机事件？
A. 抛硬币结果是正面朝上
B. 从扑克牌中抽取一张A
C. 掷骰子结果为偶数
D. 爬山时碰到下雨
2. 一副标准扑克牌共有52张，其中红心牌有13张，那么从中随机抽取一张牌是红心牌的概率是多少？
A. 1/13
B. 1/26
C. 1/52
D. 13/52
3. 从一个装有8个红球和4个蓝球的袋子中随机取出一球，取出红球的概率是多少？
A. 1/12
B. 2/3
C. 2/12
D. 1/4
题目二：计算题
1. 小明家有三个抽屉，每个抽屉里有红球3个和蓝球2个。

小明先随机选择一个抽屉，然后从该抽屉中随机取球。

若小球为红色，求其来自第一个抽屉的概率。

2. 有一个含有8只白球和5只黑球的袋子，从袋子中依次取球不放回，取出3只，求：
a) 相同颜色的球至少有2只的概率；
b) 取出的3只球均为黑球的概率。

题目三：应用题
甲、乙、丙三位同学分别参加英语和数学两门科目的考试。

已知甲的英语成绩优秀，乙的数学成绩优秀，那么丙同学同时在英语和数学两门科目上优秀的概率是多少？
请将答案写在纸上，答案不唯一。

注意：本试卷是一份练习题，可以根据自己的实际情况适当调整题目。

以上题目仅供参考，不保证完全无误。

祝您学习进步！。

《概率论与数理统计》习题五答案

《概率论与数理统计》习题及答案习题五1.一颗骰子连续掷4次，点数总和记为X .估计P {10<X <18}.【解】设i X 表每次掷的点数，则41i i X X==∑22222221111117()123456,666666211111191()123456,6666666i i E X E X =⨯+⨯+⨯+⨯+⨯+⨯==⨯+⨯+⨯+⨯+⨯+⨯= 从而 22291735()()[()].6212i i i D X E X E X ⎛⎫=-=-= ⎪⎝⎭ 又X 1,X 2,X 3,X 4独立同分布.从而44117()()()414,2i i i i E X E X E X =====⨯=∑∑ 44113535()()()4.123i i i i D X D X D X =====⨯=∑∑ 所以 235/3{1018}{|14|4}10.271,4P X P X <<=-<≥-≈ 2. 假设一条生产线生产的产品合格率是0.8.要使一批产品的合格率达到在76%与84%之间的概率不小于90%，问这批产品至少要生产多少件？【解】令1,,0,i i X ⎧⎨⎩若第个产品是合格品其他情形.而至少要生产n 件，则i =1,2,…,n ,且X 1，X 2，…，X n 独立同分布，p =P {X i =1}=0.8.现要求n ,使得1{0.760.84}0.9.n i i X P n =≤≤≥∑即0.80.9ni X n P -≤≤≥∑ 由中心极限定理得0.840.80.760.80.9,0.160.16n n n n n n --⎛⎫⎛⎫Φ-Φ≥ ⎪ ⎪⎝⎭⎝⎭ 整理得0.95,10n ⎛⎫Φ≥ ⎪ ⎪⎝⎭查表 1.64,10n ≥ n ≥268.96, 故取n =269.3. 某车间有同型号机床200部，每部机床开动的概率为0.7，假定各机床开动与否互不影响，开动时每部机床消耗电能15个单位.问至少供应多少单位电能才可以95%的概率保证不致因供电不足而影响生产.【解】要确定最低的供应的电能量，应先确定此车间同时开动的机床数目最大值m ，而m要满足200部机床中同时开动的机床数目不超过m 的概率为95%,于是我们只要供应15m 单位电能就可满足要求.令X 表同时开动机床数目，则X ~B （200，0.7）,()140,()42,E X D X ==1400.95{0}().42m P X m P X m -⎛⎫=≤≤=≤=Φ ⎪⎝⎭查表知 140 1.64,42m -= ,m =151. 所以供电能151×15=2265（单位）.4. 一加法器同时收到20个噪声电压V k （k =1，2，…，20），设它们是相互独立的随机变量，且都在区间（0，10）上服从均匀分布.记V =∑=201k k V，求P {V ＞105}的近似值.【解】易知:E (V k )=5,D (V k )=10012,k =1,2,…,20 由中心极限定理知，随机变量201205~(0,1).10010020201212k k V Z N =-⨯==⨯⨯∑近似的于是105205{105}1010020201212P V P ⎧⎫⎪⎪-⨯⎪>=>⎨⎬⎪⎪⨯⎪⎪⎩⎭1000.3871(0.387)0.348,102012V P ⎧⎫⎪⎪-⎪⎪=>≈-Φ=⎨⎬⎪⎪⎭即有 P {V >105}≈0.3485. 有一批建筑房屋用的木柱，其中80%的长度不小于3m.现从这批木柱中随机地取出100根，问其中至少有30根短于3m 的概率是多少？【解】设100根中有X 根短于3m ，则X ~B （100，0.2）从而{30}1{30}11000.20.8P X P X ≥=-<≈-Φ⨯⨯ 1(2.5)10.99380.0062.=-Φ=-=6. 某药厂断言，该厂生产的某种药品对于医治一种疑难的血液病的治愈率为0.8.医院检验员任意抽查100个服用此药品的病人，如果其中多于75人治愈，就接受这一断言，否则就拒绝这一断言.（1）若实际上此药品对这种疾病的治愈率是0.8，问接受这一断言的概率是多少？（2）若实际上此药品对这种疾病的治愈率是0.7，问接受这一断言的概率是多少？【解】1,,1,2,,100.0,.i i X i ⎧==⎨⎩第人治愈其他令1001.ii X X ==∑ (1) X ~B (100,0.8)，1001{75}1{75}11000.80.2i i P X P X =>=-≤≈-Φ⨯⨯∑1( 1.25)(1.25)0.8944.=-Φ-=Φ=(2) X ~B (100,0.7)， 1001{75}1{75}11000.70.3i i P X P X =>=-≤≈-Φ⨯⨯∑1(1(1.09)0.1379.21=-Φ=-Φ= 7. 用Laplace 中心极限定理近似计算从一批废品率为0.05的产品中，任取1000件，其中有20件废品的概率.【解】令1000件中废品数X ，则 p =0.05,n =1000,X ~B (1000,0.05)，E (X )=50，D (X )=47.5.故130{20} 6.895 6.89547.547.5P X ϕ⎛⎫===- ⎪⎝⎭6130 4.510.6.895 6.895ϕ-⎛⎫==⨯ ⎪⎝⎭8. 设有30个电子器件.它们的使用寿命T 1，…，T 30服从参数λ=0.1[单位：（小时）-1]的指数分布，其使用情况是第一个损坏第二个立即使用，以此类推.令T 为30个器件使用的总计时间，求T 超过350小时的概率. 【解】11()10,0.1i E T λ=== 21()100,i D T λ== ()1030300,E T =⨯= ()3000.D T =故{350}111(0.913)0.1814.P T >≈-Φ=-Φ=-Φ= 9. 上题中的电子器件若每件为a 元，那么在年计划中一年至少需多少元才能以95%的概率保证够用（假定一年有306个工作日，每个工作日为8小时）.【解】设至少需n 件才够用.则E (T i )=10，D (T i )=100，E (T )=10n ，D (T )=100n .从而1{3068}0.95,n i i P T =≥⨯=∑即0.05.≈Φ 故0.95, 1.64272.n =Φ=≈所以需272a 元.10. 对于一个学生而言，来参加家长会的家长人数是一个随机变量，设一个学生无家长、1名家长、2名家长来参加会议的概率分别为0.05,0.8,0.15.若学校共有400名学生，设各学生参加会议的家长数相与独立，且服从同一分布.（1）求参加会议的家长数X 超过450的概率？（2）求有1名家长来参加会议的学生数不多于340的概率.易知E （X i =1.1）,D (X i )=0.19,i =1,2, (400)而400i i X X=∑,由中心极限定理得400400 1.1~(0,1).i X N -⨯=∑近似地于是{450}1{450}1P X P X >=-≤≈-Φ1(1.147)0.1357.=-Φ=(2) 以Y 记有一名家长来参加会议的学生数.则Y ~B (400,0.8)由拉普拉斯中心极限定理得3404000.8{340(2.5)0.9938.4000.80.2P Y -⨯⎛⎫≤≈Φ=Φ= ⎪⨯⨯⎝⎭11. 设男孩出生率为0.515，求在10000个新生婴儿中女孩不少于男孩的概率？【解】用X 表10000个婴儿中男孩的个数，则X ~B （10000，0.515）要求女孩个数不少于男孩个数的概率，即求P {X ≤5000}. 由中心极限定理有5000100000.515{5000}(3)1(3)0.00135.100000.5150.485P X -⨯⎛⎫≤≈Φ=Φ-=-Φ= ⎪⨯⨯⎝⎭12. 设有1000个人独立行动，每个人能够按时进入掩蔽体的概率为0.9.以95%概率估计，在一次行动中：（1）至少有多少个人能够进入？（2）至多有多少人能够进入？【解】用X i 表第i 个人能够按时进入掩蔽体（i =1,2,…,1000）.令 S n =X 1+X 2+…+X 1000.(1) 设至少有m 人能够进入掩蔽体，要求P {m ≤S n ≤1000}≥0.95，事件90010000.9{}.10000.90.190n n S m m S --⨯⎛⎫≤=≤ ⎪⨯⨯⎝⎭ 由中心极限定理知：10000.9{}1{}10.95.10000.90.1n n m P m S P S m -⨯⎛⎫≤=-<≈-Φ≥ ⎪⨯⨯⎝⎭从而 9000.05,90m -⎛⎫Φ≤ ⎪⎝⎭ 故900 1.65,90m -=- 所以 m =900-15.65=884.35≈884人(2) 设至多有M 人能进入掩蔽体，要求P {0≤S n ≤M }≥0.95.{}0.95.90n P S M ≤≈Φ= 90M =900+15.65=915.65≈916人. 13. 在一定保险公司里有10000人参加保险，每人每年付12元保险费，在一年内一个人死亡的概率为0.006,死亡者其家属可向保险公司领得1000元赔偿费.求：（1）保险公司没有利润的概率为多大；（2）保险公司一年的利润不少于60000元的概率为多大？【解】设X 为在一年中参加保险者的死亡人数，则X ~B （10000，0.006）.(1) 公司没有利润当且仅当“1000X =10000×12”即“X =120”.于是所求概率为1120100000.006{120}100000.0060.994100000.0060.994P X ϕ-⨯⎛⎫=≈ ⎪⨯⨯⨯⨯⎝⎭21(60/59.64)230.181116011e 59.6459.64259.640.0517e 0ϕπ--⎛⎫== ⎪⎝⎭=⨯≈(2) 因为“公司利润≥60000”当且仅当“0≤X ≤60”于是所求概率为{060}100000.0060.994100000.0060.994P X ≤≤≈Φ-Φ⨯⨯⨯⨯ (0)0.5.59.64⎛=Φ-Φ≈ ⎝ 14. 设随机变量X 和Y 的数学期望都是2，方差分别为1和4，而相关系数为0.5试根据契比雪夫不等式给出P {|X -Y |≥6}的估计. （2001研考）【解】令Z =X -Y ，有()0,()()()()2()() 3.E Z D Z D X Y D X D Y D X D Y ρ==-=+-=所以 2()31{|()|6}{||6}.63612D X Y P ZE Z P X Y --≥=-≥≤== 15. 某保险公司多年统计资料表明，在索赔户中，被盗索赔户占20%，以X 表示在随机抽查的100个索赔户中，因被盗向保险公司索赔的户数.（1）写出X 的概率分布；（2）利用中心极限定理，求被盗索赔户不少于14户且不多于30户的概率近似值.（1988研考）【解】（1） X 可看作100次重复独立试验中，被盗户数出现的次数，而在每次试验中被盗户出现的概率是0.2，因此，X ~B (100,0.2)，故X 的概率分布是100100{}C 0.20.8,1,2,,100.k k k P X k k -===(2) 被盗索赔户不少于14户且不多于30户的概率即为事件{14≤X≤30}的概率.由中心极限定理，得{1430}1000.20.81000.20.8P X ≤≤≈Φ-Φ⨯⨯⨯⨯ (2.5)( 1.5)0.994[9.33]0.927.=Φ-Φ-=--=16. 一生产线生产的产品成箱包装，每箱的重量是随机的.假设每箱平均重50千克，标准差为5千克，若用最大载重量为5吨的汽车承运，试利用中心极限定理说明每辆车最多可以装多少箱，才能保障不超载的概率大于0.977.【解】设X i （i =1,2,…,n ）是装运i 箱的重量（单位：千克），n 为所求的箱数，由条件知，可把X 1，X 2，…，X n 视为独立同分布的随机变量，而n 箱的总重量T n =X 1+X 2+…+X n 是独立同分布随机变量之和，由条件知：()50,i E X = 5,=()50,n E T n = =依中心极限定理，当n ~(0,1)N 近似地,故箱数n 取决于条件{5000}n P T P ≤=≤0.977(2).≈Φ>=Φ 2>解出n <98.0199,即最多可装98箱.。