第8章 时间序列分析(2)
第八章时间序列分析

第⼋章时间序列分析第⼋章时间序列分析与预测【课时】6学时【本章内容】§ 时间序列的描述性分析时间序列的含义、时间序列的图形描述、时间序列的速度分析§ 时间序列及其构成分析时间序列的构成因素、时间序列构成因素的组合模型§ 时间序列趋势变动分析移动平均法、指数平滑法、模型法§ 时间序列季节变动分析[原始资料平均法、趋势-循环剔除法、季节变动的调整§ 时间序列循环变动分析循环变动及其测定⽬的、测定⽅法本章⼩结【教学⽬标与要求】1.掌握时间序列的四种速度分析2.掌握时间序列的四种构成因素3.掌握时间序列构成因素的两种常⽤模型4.掌握测定长期趋势的移动平均法5.了解测定长期趋势的指数平滑法6.;7.掌握测定长期趋势的线性趋势模型法8.了解测定长期趋势的⾮线性趋势模型法9.掌握分析季节变动的原始资料平均法10.掌握分析季节变动的循环剔出法11.掌握测定循环变动的直接法和剩余法【教学重点与难点】1.对统计数据进⾏趋势变动分析,利⽤移动平均法、指数平滑法、线性模型法求得数据的长期趋势;2.对统计数据进⾏季节变动分析,利⽤原始资料平均法、趋势-循环剔除法求得数据的季节变动;3.对统计数据进⾏循环变动分析,利⽤直接法、剩余法求得循环变动。
【导⼊】;很多社会经济现象总是随着时间的推移不断发展变化,为了探索现象随时间⽽发展变化的规律,不仅要从静态上分析现象的特征、内部结构以及相互关联的数量关系,⽽且应着眼于现象随时间演变的过程,从动态上去研究其发展变动的过程和规律。
这时需要⼀些专门研究按照时间顺序观测的序列数据的统计分析⽅法,这就是统计学中的时间序列分析。
通过介绍⼀些时间序列分析的例⼦,让同学们了解时间序列的应⽤,并激发学⽣学习本章知识的兴趣。
1.为了表现中国经济的发展状况,把中国经济发展的数据按年度顺序排列起来,据此来研究。
2.公司对未来的销售量作出预测。
这种预测对公司的⽣产进度安排、原材料采购、存货策略、资⾦计划等都⾄关重要。
时间序列分析

时期序列
计算公式:
n
YY1Y2Yn
Yi i1
n
n
【例8.1】 根据表8.1中的国内生产总值序 列,计算各年度的平均国内生产总值
n
Yi
Yi1
4288.585 476.95( 43 亿元)
n
9
绝对数序列的序时平均数
(计算方法)
时点序列— 间隔不相等
Y1 Y2
Y3 Y4
T1
T2
T3
Yn-1
发展速度与增长速度的计算(实例)
【例8.5】 根据表8-3中第三产业国内生产总值序列, 计算各年的环比发展速度和增长速度,及以1994年 为基期的定基发展速度和增长速度
表8- 4 第三产业国内生产总值速度计算表
年份
1994 1995 1996 1997 1998
国内生产总值(亿元)
发展速度 (%)
第8章 时间序列分析
第一节 时间序列的对比分析 第二节 时间序列及其构成因素 第三节 长期趋势分析 第四节 季节变动分析 第五节 循环波动分析
第一节 时间序列的对比分析
一. 时间序列及其分类 二. 时间序列的水平分析 三. 时间序列的速度分析
时间序列及其分类
1. 同一现象在不同时间上的相继观察值排 列而成的数列
803 896 1070 1331 1781 2311 2726 2944 3094
时间序列的分类
时间序列
绝对数序列 相对数序列 平均数序列
时期序列 时点序列
时间序列的分类
1. 绝对数时间序列 一系列绝对数按时间顺序排列而成 时间序列中最基本的表现形式 反映现象在不同时间上所达到的绝对水平 分为时期序列和时点序列
统计学罗文宝主编 第八章时间序列分析单选题多选题参考答案

第八章 时间序列分析二、单项选择题1.根据时期数列计算序时平均数应采用( C )。
A 、几何平均法 B.加权算术平均法 C.简单算术平均法 D.首末折半法2.间隔相等的时点数列计算序时平均数应采用(D )。
A.几何平均法B.加权算术平均法C.简单算术平均法D.首末折半法3.数列中各项数值可以直接相加的时间数列是(B )。
A.时点数列B.时期数列C.平均指标动态数列D.相对指标动态数列4.时间数列中绝对数列是基本数列,其派生数列是(D )。
A. 时期数列和时点数列B. 绝对数时间数列和相对数时间数列C. 绝对数时间数列和平均数时间数列D.相对数时间数列和平均数时间数列5.下列数列中哪一个属于动态数列( D )。
A.学生按学习成绩分组形成的数列B.工业企业按地区分组形成的数列C.职工按工资水平高低排列形成的数列D.出口额按时间先后顺序排列形成的数列6.已知某企业1月、2月、3月、4月的平均职工人数分别为190人、195人、193人和201人。
则该企业一季度的平均职工人数的计算方法为(B )。
7.说明现象在较长时期内发展的总速度的指标是(C )。
A 、环比发展速度 B.平均发展速度 C.定基发展速度 D.环比增长速度8.已知各期环比增长速度为2%、5%、8%和7%,则相应的定基增长速度的计算方法为(A )。
A.(102%×105%×108%×107%)-100%B. 102%×105%×108%×107%C. 2%×5%×8%×7%D. (2%×5%×8%×7%)-100%4201193195190+++、A 3193195190++、B 1422011931952190-+++、C 422011931952190+++、D9.平均发展速度是( C )。
A.定基发展速度的算术平均数B.环比发展速度的算术平均数C.环比发展速度的几何平均数D.增长速度加上100%10.若要观察现象在某一段时期内变动的基本趋势,需测定现象的( C )。
计量经济学中的时间序列分析

计量经济学中的时间序列分析时间序列分析是计量经济学中的重要内容之一,它主要研究特定变量随时间变化的规律性和趋势。
通过时间序列分析,我们可以更好地理解经济现象,预测未来变化趋势,制定合适的政策和策略。
本文将从时间序列的概念入手,介绍时间序列分析的基本原理、方法和应用。
一、时间序列的概念时间序列是按照时间顺序排列的一系列数据观测值的集合。
在计量经济学中,时间序列通常用来观察和研究某一经济变量在不同时间点上的变化情况。
时间序列数据可以是连续的,也可以是间断的,常见的时间单位包括年、季、月、周等。
通过对时间序列数据的分析,我们可以揭示出其中的规律性和特征。
二、时间序列分析的基本原理时间序列分析的基本原理是利用过去的数据来预测未来的发展趋势。
在时间序列分析中,常用的方法包括趋势分析、周期性分析、季节性分析和不规则波动分析。
趋势分析主要用来观察时间序列数据的长期变化趋势,周期性分析则是研究数据是否存在固定长度的周期性波动,季节性分析则是研究数据是否呈现出固定的季节性变化规律,而不规则波动分析则是研究一些随机因素对数据的影响。
三、时间序列分析的方法时间序列分析的方法有很多种,其中常用的包括移动平均法、指数平滑法、回归分析法、ARIMA模型等。
移动平均法通过计算连续几个期间的平均值来平滑数据,达到去除数据波动的目的;指数平滑法则是通过计算加权平均来对数据进行平滑处理,使得预测值更加准确;回归分析法则是通过建立经济模型来研究时间序列数据之间的关系,进行预测和分析;ARIMA模型则是一种时间序列的自回归与移动平均模型,可以对时间序列数据进行拟合和预测。
四、时间序列分析的应用时间序列分析在经济学、金融学、管理学等领域有着广泛的应用。
在经济学中,时间序列分析可以用来研究经济增长、通货膨胀、失业等经济现象的发展趋势;在金融学中,时间序列分析可以用来预测股票价格、汇率、利率等金融变量的变化情况;在管理学中,时间序列分析可以用来制定企业的生产计划和销售策略,提高企业的运营效率。
第8章 时间序列趋势分析

我国年末人口数(万人) 我国人口自然增长率(‰)
某厂职工年平均工资(元/人)
12000
13000
15000……
.
时间序列的构成要素
现象在各时间上的指标数值 时间序列分析的目的
描述现象在过去时间的状态。 分析现象发展变化的规律性。 根据现象的过去行为预测其未来行为。 将相互联系的时间序列进行对比,研究有关现象之 间的联系程度。
4.
不规则变动 (Irregular Variations )
包括随机变动和突然变动。 随机变动—现象受到各种偶然因素影响而呈现出方 向不定、时起时伏、时大时小的变动。 突然变动—战争、自然灾害或其它社会因素等意外 事件引起的变动。影响作用无法相互抵消,影响幅 度很大。 一般只讨论有随机波动而不含突然异常变动的情况。 随机变动与时间无关,是一种无规律的变动,难以 测定,一般作为误差项处理。
8.2.2 长期趋势的测定
长期趋势分析主要是指长期趋势的测定,采用一定的方法
对时间序列进行修匀,使修匀后的数列排除季节变动、循环
.
变动和无规则变动因素的影响,显示出现象变动的基本趋势, 作为预测的依据。
测定长期趋 势的方法
移动平均法 趋势方程拟和法(数学模型法)
.
研究长期趋势的目的和意义
1. 认识和掌握现象随时间演变的趋势和规律,为 制定相关政策和进行管理提供依据;
表8- 2 1981-1998年我国汽车产量数据
年 份
1981 1982 1983 1984 1985 1986 1987 1988 1989
产量(万辆)
17.56 19.63 23.98 31.64 43.72 36.98 47.18 64.47 58.35
第八章时间序列分析

第八章时间序列分析一、填空题:1. 由于决定时间数列变化的因数是多方面的,因此通常把时间数列上各期发展水平按其影响因素的不同分解成几个不同的组成部分,即长期趋势、、循环波动和不规则变动。
2.时间序列按照数列中排列指标的性质不同,可分为、和。
3. “增长1%绝对值”指标其实质是水平的1%。
4. 是把原动态数列的时距扩大,再采用逐项移动的方法计算扩大了时距的序时平均数。
5.就是研究某种现象在一个相当长的时期内持续向上或向下发展变动的趋势。
6. 就是指某些社会现象由于受生产条件或自然条件因素的影响,在一年内随着季节的更换而呈现出比较有规律的变动。
二、单项选择题:1. 时间序列在一年内重复出现的周期性波动称为()A、趋势B、季节性C、周期性D、随机性2. 增长一个百分点而增加的绝对数量称为()A、环比增长率B、平均增长率C、年度化增长率D、增长1%绝对值3. 某银行投资额2004年比2003年增长了10%,2005年比2003年增长了15%,2005年比2004年增长了()A、15%÷10%B、115%÷110%C、(110%×115%)+1D、(115%÷110%)-14.某种股票的价格周二上涨了10%,周三上涨了5%,两天累计张幅达()A、15%B、15.5%C、4.8%D、5%5.如果某月份的商品销售额为84万元,该月的季节指数为1.2,在消除季节因素后该月的销售额为()A、60万元B、70万元C、90.8万元D、100.8万元6. 时间数列的构成要素是()。
A、变量和次数B、时间和指标数值C、时间和次数D、主词和宾词7. 定基增长速度与环比增长速度的关系为()。
A、定基增长速度等于相应的环比增长速度各个的算术和B、定基增长速度等于相应的环比增长速度各个的连乘积C、定基增长速度等于相应的环比增长速度加1后的连乘积再减1D、定基增长速度等于相应的环比增长速度各个的连乘积加18. 以1950年a0为最初水平,1997年a n为最末水平,计算钢产量的年平均发展速度时,须开()。
时间序列分析课后习题解答

第八章 时间序列分析一、选择题1.设(甲)代表时期数列;(乙)代表时点数列;(丙)代表几何序时平均数;(丁)代表“首末折半法”序时平均数。
现已知1996~2000年某银行的年末存款余额,要求计算各年平均存款余额,需计算的是( D )。
A.甲、丙B.乙、丙C.甲、乙D.乙、丁2.某商业集团2000~2001年各季度销售资料如表8—1所示。
表8—1资料中,是总量时期数列的有( D )。
A.1、2、3B.1、3、4C.2、4D.1、33.某地区粮食增长量1990~1995年为12万吨,1996~2000年也为12万吨。
那么,1990~2000年期间,该地区粮食环比增长速度( D )。
A.逐年上升B.逐年下降C.保持不变D.不能做结论4.利用第2题数据计算零售额移动平均数(简单,4项移动平均),2001年第二季度移动平均数为( A )。
A.47.5B.46.5C.49.5D.48.45.利用第3题数据计算2000年商品季平均流转次数(=零售额/库存额)( C )。
A.1.885B.1.838C.1.832D.1.829二、判断题1.连续12个月逐期增长量之和等于年距增长量。
(×)2.计算固定资产投资额的年平均发展速度应采用几何平均法。
(×)3.用移动平均法分析企业季度销售额时间序列的长期趋势时,一般应取4项进行移动平均。
(√)4.计算平均发展速度的水平法只适合时点指标时问序列。
(×)5.某公司连续四个季度销售收入增长率分别为9%、12%、20%和18%,其环比增长速度为0.14%。
(×)三、计算题1.某地区“九五”时期国内生产总值资料如表8—2所示。
试计算该地区“九五”时期国内生产总值和各产业产值的平均发展水平。
表8—2 单位:百万元解:国内生产总值和各产业产值均为时期指标,应采用时期指标序时平均数计算公式计算。
计算公式:国内生产总值平均发展水平:第一产业平均发展水平:第二产业平均发展水平:第三产业平均发展水平:2.某企业2000年8月几次员工数变动登记如表8—3所示。
第八章 时间序列分析 思考题及练习题

第八章思考题及练习题(一) 填空题1、时间数列又称数列,一般由和两个基本要素构成。
2、动态数列按统计指标的表现形式可分为、和三大类,其中最基本的时间数列是。
3、编制动态数列最基本的原则是。
4、时间数列中的四种变动(构成因素)分别是:、、、和5、时间数列中的各项指标数值,就叫,通常用a表示。
6、平均发展水平是对时间数列的各指标求平均,反映经济现象在不同时间的平均水平或代表性水平,又称:平均数,或平均数。
7、增长量由于采用的基期不同,分为增长量和增长量,各增长量之和等于相应的增长量。
8、把报告期的发展水平除以基期的发展水平得到的相对数叫,亦称动态系数。
根据采用的基期不同,它又可分为发展速度和发展速度两种。
9、平均发展速度的计算方法有法和法两种。
10、某企业2000年的粮食产量比90年增长了2倍,比95年增长了0.8倍,则95年粮食产量比90年增长了倍。
11、把增长速度和增长量结合起来而计算出来的相对指标是:。
12、由一个时期数列各逐期增长量构成的动态数列,仍属时期数列;由一个时点数列各逐期增长量构成的动态数列,属数列。
13、在时间数列的变动影响因素中,最基本、最常见的因素是,举出三种常用的测定方法、、。
14、若原动态数列为月份资料,而且现象有季节变动,使用移动平均法对之修匀时,时距宜确定为项,但所得各项移动平均数,尚需,以扶正其位置。
15、使用最小平方法配合趋势直线时,求解 a、b参数值的那两个标准方程式为。
16、通常情况下,当时间数列的一级增长量大致相等时,可拟合趋势方程,而当时间数列中各二级增长量大致相等时,宜配合趋势方程。
17、用半数平均法求解直线趋势方程的参数时,先将时间数列分成的两部分,再分别计算出各部分指标平均数和的平均数,代入相应的联立方程求解即得。
18、分析和测定季节变动最常用、最简便的方法是。
这种方法是通过对若干年资料的数据,求出与全数列总平均水平,然后对比得出各月份的。
19、如果时间数列中既有长期趋势又有季节变动,则应用法来计算季节比率。
关于时间序列分析

1.全然概念(1)一般概念:系统中某一变量的瞧测值按时刻顺序〔时刻间隔相同〕排列成一个数值序列,展示研究对象在一定时期内的变动过程,从中寻寻和分析事物的变化特征、开展趋势和规律。
它是系统中某一变量受其它各种因素碍事的总结果。
(2)研究实质:通过处理推测目标本身的时刻序列数据,获得事物随时刻过程的演变特性与规律,进而推测事物的今后开展。
它不研究事物之间相互依存的因果关系。
(3)假设根底:惯性原那么。
即在一定条件下,被推测事物的过往变化趋势会连续到今后。
暗示着历史数据存在着某些信息,利用它们能够解释与推测时刻序列的现在和今后。
近大远小原理〔时刻越近的数据碍事力越大〕和无季节性、无趋势性、线性、常数方差等。
(4)研究意义:许多经济、金融、商业等方面的数据根基上时刻序列数据。
时刻序列的推测和评估技术相对完善,其推测情景相对明确。
尤其关注推测目标可用数据的数量和质量,即时刻序列的长度和推测的频率。
2.变动特点(1)趋势性:某个变量随着时刻进展或自变量变化,呈现一种比立缓慢而长期的持续上升、下落、停留的同性质变动趋向,但变动幅度可能不等。
(2)周期性:某因素由于外部碍事随着自然季节的交替出现顶峰与低谷的规律。
(3)随机性:个不为随机变动,整体呈统计规律。
(4)综合性:实际变化情况一般是几种变动的叠加或组合。
推测时一般设法过滤除往不规那么变动,突出反映趋势性和周期性变动。
3.特征识不熟悉时刻序列所具有的变动特征,以便在系统推测时选择采纳不同的方法。
(1)随机性:均匀分布、无规那么分布,可能符合某统计分布。
(用因变量的散点图和直方图及其包含的正态分布检验随机性,大多数服从正态分布。
)(2)平稳性:样本序列的自相关函数在某一固定水平线四面摆动,即方差和数学期瞧稳定为常数。
样本序列的自相关函数只是时刻间隔的函数,与时刻起点无关。
其具有对称性,能反映平稳序列的周期性变化。
特征识不利用自相关函数ACF:ρk =γk/γ其中γk是y t的k阶自协方差,且ρ0=1、-1<ρk<1。
第八章 季节性时间序列分析方法

81❝§8.1 季节性时间序列的重要特征82❝§8.2 季节性时间序列模型❝§8.3 季节性检验❝§8.4 季节性时间序列模型的建立所谓是指具有某种周期性变化季节性时间序列,是指具有某种周期性变化规律的随机序列,并且这种周期性的变化规律往往是由于季节变化引起由于季节变化引起。
如果一个随机序列经过个时间间隔后观测数据呈现相似性比如同处于波峰或波谷则我们称该序S 呈现相似性,比如同处于波峰或波谷,则我们称该序列具有以为周期的周期特征,并称其为季节性时S 间序列,为季节长度。
S季节性时间序列存在着规则的周期如果我们把季节性时间序列存在着规则的周期,如果我们把原序列按周期重新排列,即可得到一个所谓的二维表。
对于季节性时间序列按周期进行重新排列是极其有益的不仅有助于考察同周期点的变化情况加有益的,不仅有助于考察同一周期点的变化情况、加深对序列周期性的理解,而且对于形成建模思想和理解季节模型的结构也都是很有帮助的。
影响一个季节性时间序列的因素除了季节因素外❝影响一个季节性时间序列的因素除了季节因素外,往往还存在趋势变动和随机变动等。
t t t tX S T I =++❝研究季节性时间序列的目的,就是分解影响经济指标变动的季节因素、趋势因素和随机因素,从而了解它们对经济的影响。
❝1. 简单季节模型❝2. 乘积季节模型季节性时间序列表现出也就是说时间 同期相关性,也就是说时间相隔为的两个时间点上的随机变量有较强的相关性。
比如对于月度数据S 12比如,对于月度数据则与相关性较强。
我们可以利用这种同期相关性在与之12,S =t X 12t X -t X 12t X -间进行拟合。
简单季节模型通过简单的趋势差分季节差分之通过简单的趋势差分、季节差分之后序列即可转化为平稳,它的模型结构通常表示如下:()(1)(),(*)S S D St tB B X B aΦ-=ΘSAR算子其中为白噪声序列,{}ta2()1,S S S pSB B B BΦ=-Φ-Φ--Φ12212()1.pS S S qSqB B B BΘ=-Θ-Θ--ΘSMA算子称(*)为简单季节模型,或季节性自回归求和移动SARIMA p D q平均模型,简记为模型。
统计学第八章 时间序列分析

季节指数
乘法模型中的季节成分通过季节指数来反映。 季节指数(季节比率):反映季节变动的相
对数。 1、月(或季)的指数之和等于1200%(或
400%) 。 2、季节指数离100%越远,季节变动程度
越大,数据越远离其趋势值。
用移动平均趋势剔除法计算季节指数
1、计算移动平均值(TC),移动期数为4或 12,注意需要进行移正操作。
移动平均的结果 4000 3500 3000 2500 2000 1500 1000 500 0
Example 2
移动平均法可以作为测定长期趋势的一种 较为简单的方法,在股市技术分析中有广 泛的应用。比如对某只股票的日收盘价格 序列分别求一次5日、10日、一个月的移动 平均就可以得到其5日、10日、一个月的移 动平均股价序列,进而得到5日线、10日线、 月线,用以反映股价变动的长期趋势。
1987 1800 1992 1980 1997 2880
1988 1620 1993 2520 1998 3060
1989 1440 1994 2559 1999 2700
4000
3500
销售收入
3000
2500
2000
1500
1000
500
0
年份
2000 2001 2002 2003 2004
销售 收入 3240 3420 3240 3060 3600
部分数据
销售 收入
t
1985 1080
1
1986 1260
2
1987 1800
3
1988 1620
4
1989 1440
5
……
…
2003 3060
19
第8章时间序列趋势分析

第8章时间序列趋势分析时间序列趋势分析是一种用于分析时间序列数据中趋势变化的方法。
它可以帮助我们理解时间序列数据中的长期趋势,并预测未来的发展趋势。
本章将介绍时间序列趋势分析的基本概念和常用方法。
1.时间序列的趋势:时间序列是按照时间先后顺序排列的一系列数据观测值的集合。
时间序列的趋势是指其长期平均水平的变化趋势,包括上升、下降或平稳变化。
趋势可以是线性的,也可以是非线性的。
2.趋势分析的目的:趋势分析的目的是识别和描述时间序列数据中的趋势变化,以便预测未来的发展趋势。
趋势分析可以帮助我们了解时间序列数据的长期变化趋势,从而做出有效的决策。
3.常用的趋势分析方法:(1)平均移动方法:平均移动方法是一种简单的趋势分析方法,它利用移动平均值来平滑原始数据,从而识别出数据的长期趋势。
平均移动方法有简单移动平均法、加权移动平均法和指数移动平均法等。
(2)线性趋势分析:线性趋势分析是一种通过拟合线性模型来描述时间序列数据的趋势变化的方法。
它可以用来估计趋势的斜率和截距,从而判断趋势的上升或下降趋势。
(3)非线性趋势分析:非线性趋势分析是一种通过拟合非线性模型来描述时间序列数据的趋势变化的方法。
它可以用来捕捉数据中的曲线、周期性和季节性等非线性特征。
(4)季节性调整:季节性调整是一种用来消除时间序列数据季节性变化影响的方法。
它可以使得数据更加稳定,更容易分析长期趋势。
4.趋势分析的应用领域:时间序列趋势分析在许多领域都有广泛的应用,包括经济学、金融学、市场研究、气象学、环境科学、交通规划等。
它可以用来预测市场走势、分析经济周期、预测天气变化等。
5.趋势分析的局限性:趋势分析的结果受到许多因素的影响,如数据质量、样本大小和选择的分析方法等。
此外,趋势分析只能应用于具有明显趋势的时间序列数据,对于无趋势或具有周期性的数据效果不佳。
总结起来,时间序列趋势分析是一种用于分析时间序列数据中趋势变化的方法。
它可以帮助我们理解时间序列数据的长期趋势,并预测未来的发展趋势。
时间序列分析

Yangshucheng
第八章 时间序列分析与预测
第一节 时间序列概述
2 July 2016
Statistics
二、时间序列的种类
2、时点指标的特点 第一,不可加性。不同时点的总量指标不可相加,这是 因为把不同时点的总量指标相加后,无法解释所得数值的时 间状态。 第二,指标数值的大小与时点间隔的长短一般没有直接 关系。在时点数列中,相邻两个指标所属时间的差距为时点 间隔。 第三,指标值采用间断统计的方式获得。
以时期指标时间数列计算序时平均数的方法比较简单, 通常采用简单算术平均数方法计算。用公式表示为:
1 n a ai n i1
Yangshucheng
(8.1)
第八章 时间序列分析与预测
第二节 时间序列的分析指标
2 July 2016
Statistics
一、发展水平与平均发展水平
(2)以时点指标时间序列计算序时平均数 ①间隔相等的时点数列序时平均数的计算,间隔相等的 时点数列序时平均数的计算采用“首末折半法”,具体公式 如下: an 1 a1 a ( a2 an1 ) (8.2) n 1 2 2 时点数据具有不可加的特点,式(8.2)是将先转化为时期数 据得到的。我们通过【例8-1】说明这一点。 【例 8-1】根据表 8-1 的数据计算“十五”期间( 2001— 2005年)我国年平均人口数。
非平稳时间序列又可以分为有长期趋势的时间序列,或 有长期趋势、季节波动、周期性等因素共同影响的时间序列。
Yangshucheng
第八章 时间序列分析与预测
第一节 时间序列概述
2 July 2016
Statistics
三、时间序列的编制原则
(一)时间一致 对于总量指标时间序列,各指标值所属时期长短应一致。 对于时点指标时间序列,各指标的时点间隔应一致。 (二)口径一致 一是现象总体范围应一致。 二是计算价格应一致。 三是计量单位一致。 四是经济内容要一致。 (三)计算方法一致 在编制时间序列时,应注意各指标的计算方法是否统一, 以确保指标可比。
时间序列分析(二)--指数平滑

时间序列分析(⼆)--指数平滑本系列⽂章翻译⾃NIST(美国国家标准与技术研究院)的(⼯程统计⼿册) 的第6章第4节关于时间序列分析的内容。
本⽂的翻译会先使⽤翻译软件进⾏初步翻译,笔者在对不恰当之处进⾏修正。
由于笔者⽔平有限,翻译过程难免有疏漏之处,欢迎⼤家评论区指出。
本站所有⽂章均为原创,转载请注明出处。
3. 什么是指数平滑这是⼀种⾮常流⾏的产⽣平滑时间序列的⽅案。
在单⼀移动平均(Single Moving Averages)中,过去的观测值的权重是相等的,⽽指数平滑则随着观测值的变久赋予指数递减的权重。
换句话说,最近的观测结果在预测⽅⾯⽐过去的观测结果具有相对更⼤的权重。
在移动平均的情况下,分配给观察值的权重是相同的,等于1/N。
然⽽,在指数平滑中,有⼀个或多个平滑参数需要确定(或估计),这些选择决定了分配给观察的权重。
本节将介绍单指数平滑、双指数平滑和三指数平滑。
3.1 单指数平滑(Single Exponential Smoothing)该平滑⽅案⾸先设置\(S_2\)为\(y_1\),其中\(S_i\)为平滑观测值或EWMA, \(y\)为原始观测值,下标表⽰时间段,1,2,...n。
第3期\(S_3 = αy_2 + (1-α)S_2\),等等。
没有\(S_1\),平滑序列从第2个观察值的平滑版本开始。
对于任意时刻\(t\),通过计算得到平滑后的值\(S_t\)\[S_t = αy_{t-1} + (1-α)S_{t-1} \qquad 0< α \leq 1 \quad t \geq 3 \]这是指数平滑的基本⽅程,常数或参数\(α\)称为平滑常数。
注意:有⼀种指数平滑的替代⽅法,⽤当前观察值\(y_t\)替换基本⽅程中的\(y_{t-1}\)。
这个公式,由Roberts(1959)提出,在EWMA控制图⼀节中有描述。
这⾥的公式遵循了Hunter(1986)。
设置第⼀个EWMA初始EWMA在后续所有EWMA的计算中起着重要的作⽤。
第八章 时间序列

环比 定基 环比 定基
120.2 120.2 20.2 20.2
113.8 136.8 13.8 36.8
117.7 161.0 17.7 61.0
108.6 174.8 8.6 74.8
33
三、平均发展速度和平均增长速度
1. 观察期内各环比发展速度 的平均数 2. 说明现象在整个观察期内平均发展变化的 程度
动态速度指标
10
第二节
时间序列的水平分析
一、发展水平
• 是时间序列中每一项具体的指标数值。说明
现象在某一时间上所达到的水平。可是绝对数、 相对数、平均数。
• 假如时间序列为: a 0
a1
a 2 an 1 an
• a 0 叫最初水平, an 叫最末水平。 • 还有中间各项水平、基期水平和报告期水平
ai a0 ai Gi 1 a0 a0
(i 1,2,, n)
32
发展速度与增长速度的计算
第三产业国内生产总值速度计算表
年 份
国内生产总值(亿元)
2004
14930.0 — — — —
2005
17947.2
2006
20427.5
2007
24033.3
2008
26104. 3
发展速度 (%) 增长速度 (%)
18
日期 人数
•
12.31 1000
1.31 1050
3.31 1070
6.30 1100
• 求前半年的平均人数 。 1月份平均人数= (1000 1050) 2、3月份平均人数= (1050 1070)
2
2
1025
1060
4、5、6月份平均人数= (1070 1100)
统计学_第八章__时间序列分析
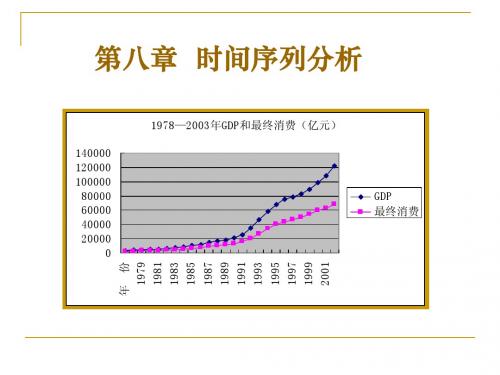
1978—2003年GDP和最终消费(亿元) 140000 120000 100000 80000 60000 40000 20000 0
年 份 1979 1981 1983 1985 1987 1989 1991 1993 1995 1997 1999 2001
GDP 最终消费
4、二者关系 (1)各逐期增长量之和等于相应的累计增长量
an a0 (a1 a0 ) (a2 a1 ) (a3 a2 ) (an an1 )
(2)相邻两期的逐期增长量之和等于相应的 累计增长量;相邻两期的累计增长量之差等于 相应的逐期增长量
(二)平均增长量 1、概念 一段时期内平均每期增加或者减少的绝 对数量。或者说是逐期增长量的序时平均数。 2、计算公式
a0 a1 a 2 a n 或 a n 1
af a f
B、如果是间断时点数列,计算方法为: 『两个假设条件: 一是假设上期期末水平等于本期期初水平; 二是假设现象在间隔期内数量变化是均匀的。』 Ⅰ、间隔期相等的时点数列,采用“首尾(首末)折半 法”计算。 先计算各间隔期的平均数;然后再将这些平均数进行 简单算术平均。例如:
第一节
时间序列分析概述
一、时间序列的概念和作用
(一)、概念: 1、时间序列:将不同时间的某一统计指标数据按照 时间的先后顺序排列起来而形成的统计序列,也称时间 数列或动态数列。 2、基本构成要素(从形式上看): 一是时间顺序(现象所属的时间)。可以是年份、季 度、月份或其他任何时间,称时间要素(常用t表示); 二是不同时间的统计数据(现象在不同时间上的观察 值)。可以是绝对数、相对数、平均数,称数据要素 (常用小写的英文字母a、b、c表示)。
时间序列分析(统计分析学概念)

统计分析学概念
01 基础知识
03 分类 05 主要用途
目录
02 性质特点 04 具体方法
时间序列分析(Time-Series Analysis)是指将原来的销售分解为四部分来看——趋势、周期、时期和不 稳定因素,然后综合这些因素,提出销售预测。强调的是通过对一个区域进行一定时间段内的连续遥感观测,提 取图像有关特征,并分析其变化过程与发展规模。当然,首先需要根据检测对象的时相变化特点来确定遥感监测 的周期,从而选择合适的遥感数据。
主要用途
时间序列分析常用在国民经济宏观控制、区域综合发展规划、企业经营管理、市场潜量预测、气象预报、水 文预报、地震前兆预报、农作物病虫灾害预报、环境污染控制、生态平衡、天文学和海洋学等方面。主要包括从 以下几个方面入手进行研究分析。
系统描述 根据对系统进行观测得到的时间序列数据,用曲线拟合方法对系统进行客观的描述。 系统分析 当观测值取自两个以上变量时,可用一个时间序列中的变化去说明另一个时间序列中的变化,从而深入了解 给定时间序列产生的机理。 预测未来 一般用ARMA模型拟合时间序列,预测该时间序列未来值。 决策和控制 根据时间序列模型可调整输入变量使系统发展过程保持在目标值上,即预测到过程要偏离目标时便可进行必 要
特点:简单易行,便于掌握,但准确性差,一般只适用于短期预测。
分类
时间序列依据其特征,有以下几种表现形式,并产生与之相适应的分析方法: 1.长期趋势变化:受某种基本因素的影响,数据依时间变化时表现为一种确定倾向,它按某种规则稳步地增 长或下降。使用的分析方法有:移动平均法、指数平滑法、模型拟和法等。 2.季节性周期变化:受季节更替等因素影响,序列依一固定周期规则性的变化,又称商业循环。采用的方法: 季节指数。 3.循环变化:周期不固定的波动变化。 4.随机性变化:由许多不确定因素引起的序列变化。 时间序列分析主要有确定性变化分析和随机性变化分析。其中,确定性变化分析包括趋势变化分析、周期变 化分析、循环变化分析。随机性变化分析:有AR、MA、ARMA模型等。
第八章 时间序列分析

y ab
t
某企业某种产品销售量及有关数据(二次曲线)
时间(季) 1997.1 1997.2 1997.3 1997.4 1998.1 1998.2 1998.3 1998.4 1999.1 1999.2 1999.3 合计 销售量 1000 1200 1440 1721 2040 2402 2803 3243 3725 4246 4808 28028 逐期增长 —— 200 240 281 320 361 401 440 482 521 562 二级增长 —— —— 40 41 39 41 40 39 42 39 41
长期趋势的测定方法
时间序列的长期趋势可分为线性趋势和非线性趋 势。 线性趋势:当时间序列的长期趋势近似的呈现为 直线发展,每期的增减数量大致相同。 测定方法:
时距扩大法 移动平均法 趋势方程拟合法。
移动平均法
基本思想:扩大原时间序列的时间间隔, 并按一定的间隔长度逐期移动,分别计 算出一系列移动平均数,由这些移动平 均数形成的新的时间序列对原序列的波 动起到一定的修匀作用,削弱了原序列 中短期偶然因素的影响,从而呈现出现 象在较长时期的发展趋势。 计算方法:见下页
合计 274978.1 162562.6
——
——
——
编制原则
保持数列中各项指标数值的可比性。
时间长短和时点间隔应该前后一致。 总体范围统一。 经济内容统一。 计算方法和计量单位统一。
时间序列的速度分析
发展速度 增长速度 平均发展速度和平均增长速度 速度的分析与应用
发展速度
用于描述现象在观察期内相对的发展变化 速度。 报告期发展水平与基期发展水平之比。 由于采用的基期不同,发展速度分为:
时间序列分析

时间序列分析时间序列分析是一种统计学方法,用于分析时间序列数据的模式、趋势和周期性。
它可以帮助我们了解随着时间推移,数据如何变化,并预测未来的发展趋势。
本文将介绍时间序列分析的基本概念、常用方法和实际应用。
一、时间序列分析的基本概念时间序列是按照时间顺序排列的一系列数据点。
它可以是连续的,例如每天的股票价格,也可以是离散的,例如每个月的销售量。
时间序列分析旨在通过观察数据中的模式和趋势,揭示数据背后的规律和关系。
二、时间序列分析的常用方法1. 描述统计法描述统计法用于计算数据的统计指标,如平均值、标准差和相关系数。
这些指标可以帮助我们了解数据的分布情况和相关性。
2. 组件分析法组件分析法将时间序列分解为趋势、季节和随机成分。
趋势表示长期的变化趋势,季节表示重复出现的周期性变化,随机成分表示无法通过趋势和季节解释的随机波动。
通过对组成部分的分析,可以更好地理解时间序列的内在规律。
3. 平稳性检验法平稳性是时间序列分析的基本假设之一。
平稳时间序列的统计特性不随时间变化而改变。
平稳性检验可以通过观察时间序列的趋势、自相关图和单位根检验等方法进行。
4. 预测方法时间序列分析的一个重要应用是预测未来的数值。
常用的预测方法包括移动平均法、指数平滑法和ARIMA模型等。
这些方法基于过去的数据,通过建立模型来预测未来的趋势和周期性。
三、时间序列分析的实际应用时间序列分析在各个领域都有广泛的应用。
在金融领域,它可以用于股票价格的预测和风险管理;在经济学领域,它可以用于 GDP 的预测和经济政策制定;在气象学领域,它可以用于天气预报和气候变化研究。
除了上述领域外,时间序列分析还用于交通流量预测、销售预测、生态学研究等。
通过对历史数据的分析,我们可以更好地理解和预测未来的发展趋势,为决策提供依据。
结论时间序列分析是一种强大的工具,可以帮助我们理解时间序列数据中的模式和趋势。
通过对数据的描述统计、组件分析和预测,我们可以揭示数据背后的规律,并用于实际问题的解决。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8.1 时间序列的分解 8.2 指数平滑 8.3 ARIMA模型
8.2 指数平滑 Exponential smoothing
8.2.1 单参数(一次)指数平滑 8.2.2 双参数指数平滑 8.2.3 三参数指数平滑
指数平滑方法的基本原理
模型(序列) AR(p) 自相关函数 拖尾 偏自相关函数 第p个后截尾 MA(q) 第q个后截尾 拖尾 ARMA(p,q) 拖尾 拖尾
拖尾是指以指数率单调或振荡衰减, 截尾是指从某个开始非常小(不显著非 零)。
Example:一个零均值时间序列
一个零均值时间序列的ACF和PACF
下图图中横线为0±两倍标准差,可以判断ACF和 PACF是否显著非零)。可以看出ACF呈拖尾状,PACF 第2个后截尾,可初步断定序列适合AR(2)模型。
Yt
ˆ Yt
适用场合
单参数(一次)指数平滑适用于不包含长 期趋势和季节成分的时间序列预测 如果原序列有增长趋势,平滑序列将系统 的低于实际值 如果原序列有下降趋势,平滑序列将系统 的高于实际值
平滑系数的确定
选择合适的平滑系数是提高预测精度的关键。 如果序列波动较小,则平滑系数应取小一些,不 同时期数据的权数差别小一些,使预测模型能包 含更多历史数据的信息; 如果序列趋势波动较大,则平滑系数应取得大一 些。这样,可以给近期数据较大的权数,以使预 测模型更好地适序列趋势的变化。 统计软件中可以根据拟合误差的大小自动筛选最 优的平滑系数值。
Example : 销售额时间序列的温 特指数平滑预测
8.3 ARIMA模型
8.2.1 平稳时间序列模型 (ARMA模型) 8.2.2 ARIMA模型
ARIMA: Autoregressive Integrated Moving Average
时间序列的平稳性
ቤተ መጻሕፍቲ ባይዱ
随机时间序列分析的一个重要概念是平稳性。 时间序列平稳性的直观含义是指时间序列没有明 显的长期趋势、循环变动和季节变动。 从统计意义上讲,如果序列的一、二阶矩存在, 而且对任意时刻满足:(1)均值为常数;(2)协方差 仅与时间间隔有关,则称该序列为宽平稳时间序 列,也叫广义平稳时间序列。
MA模型 ( X t ) at 1at 1 q at q
ARMA模型 ( X t ) 1 ( X t 1 ) p ( X t p ) at
1at 1 q at q
(2) ARMA模型的识别与估计
• Box-Jenkins 的模型识别方法: • 根据ACF和PACF确定模型的形式。 • 自相关函数(ACF)描述时间序列观测值与其 过去的观测值之间的线性相关性。 • 偏自相关函数(PACF)描述在给定中间观测 值的条件下时间序列观测值与其过去的观 测值之间的线性相关性。
Box-Jenkins 的模型识别方法
例子:销售额时间序列
某企业1990-2002年各月销售额数据。
Example : 销售额时间序列的温 特指数平滑预测
软件操作:分析预测创建模型方法选择 “指数平滑”; 设置“条件”,选择季节性模型中 的“Winter(冬季)加法或乘法模型),这里选的 是乘法模型。 从图形看拟合效果很好。
初始预测值的确定
初始预测值的确定 等于第一个观测值 等于前k个值的算术平均 适用场合:单参数(一次)指数平滑适用 于不包含长期趋势和季节成分的平稳时间 序列预测
案例分析
新卫机械厂销售额的单参数指数平滑预测 分析预测创建模型方法选择“指数平 滑”;根据需要设置“条件”。 拟合情况与2年的预测值(下页图)。 SPSS Statistics 估计的=0.689. 拟合数据的MAPE=12.847%.
态分布。
平稳时间序列模型
• 滑动平均(Moving Average)模型-MA(q)
X t at 1at 1 q at q
• 自回归滑动平均(Autoregressive and Moving Average)模型 ARMA(p,q)
X t 1 X t 1 p X t p at 1at 1 q at q
模型的正态化的BIC=4.91;R2=0.166 根据BIC分析 AR(1)要好一点。
AR(1)的拟合效果图
残差自相关图(AR(1)模型)
根据残差自相关图判断AR(1)模型是适合的。
8.2.2 ARIMA模型
在实际问题中我们常遇到的序列,特别是 反映社会、经济现象的序列,大多数并不 平稳,而是呈现出明显的趋势性或季节性。 对于有趋势性时间序列通常采用ARIMA模 型进行分析。 对于有季节性的时间序列可以采用乘积季 节ARIMA模型进行预测。由于这类模型比 较复杂,本课程不做介绍。
ˆ ˆ Yt 1 Yt (1 )Yt ˆ Yt (1 )Yt 1 (1 ) Yt 2 (1 ) Y1 (1 ) Y1
2 t 1 t
式中:
ˆ Yt 1
表示时间序列第t+1期的预测值; 表示时间序列第t期的实际观测值; 表示时间序列第t期的预测值; 表示平滑系数,0< <1。
时间序列的平稳性(图形)
Yt t X
非平稳序列
平稳序列
1 平稳时间序列模型
• (1)ARMA模型的基本形式 P阶自回归(Autoregressive)模型-AR(p)
X t 1 X t 1 p X t p at
X t 为零均值平稳时间序列
a t 是互不相关的序列,且均值为零,方差 2 a 为 (即为白噪声序列),一般假定其服从正
差分(Difference)运算
ARIMA模型需要用到差分工具。用原序列的每 一个观测值减去其前面的一个观测值,就形 成原序列的一阶差分序列:
1 X t X t X t 1
对一阶差分后的序列再进行一次差分运算, 称为二阶差分。
差分(Difference)运算
一阶差分可以消除原序列存在的线性趋势。 有时候需要进行高阶差分才能够使得变换后 的时间序列平稳。 大部分经济时间序列进行一阶或二阶差分后 都可以变为平稳序列。 对有季节性的时间序列,进行季节差分(当 年的可以消除季节成分:
应用实例
利用指数平滑法对我国人均原油产量(单位: 公斤/人)进行预测。 。 从图形看具有增长 趋势,可以用双参数 指数平滑法进行 预测。
应用实例
软件操作:分析预测创建模型方法选 择“指数平滑”;根据需要设置“条件”(选 择Holt线性趋势模型)
由SPSS软件搜索出的最终平滑系数 、 , 分别为1.00和0.001,预测2007-2010年我国 人均原油产量的预测值分别为: 141.74 142.56 143.37 144.18
ARMA模型的参数估计
• 对时间序列所适合的ARMA模型进行初步识 别后,接下来就需要估计出其中的参数, 以便进一步识别和应用模型。 • 主要的参数估计方法有矩估计法、最小二 乘估计法和极大似然估计法等,一般都由 计算机软件实现,这里不作介绍。
(3)ARMA模型的适应性检验
• 模型的适应性检验主要是残差序列的独立 性检验。残差序列可由估计出来的模型计 算得到。如果残差序列的自相关函数不显 著非零,可以认为是独立的。
2 ˆ a ( p, q)] 2 ( p q) N AIC ( p, q) ln[
2 ˆ a ( p, q)] ( p q) ln( N ) N BIC ( p, q) ln[
ˆ2 a ( p, q) 是对序列拟合ARMA(p,q)模型的残差 方差,N为观测值的个数。相对于AIC信息准则, BIC信息准则更多的考虑了模型的参数个数。
例1:AR模型
对前面例子,由SPSS可以得到参数估计,模型 表达式为:
X t 0.42 X t 1 0.39 X t 2 at (4.54)
(4.17)
括号中为参数的t检验值,各参数都是显著的。
例1:AR模型
由下图可以看出残差不存在显著的自相关性,可以认为是 独立的,因而模型是适应的。
单参数指数平滑的图形结果
8.2.2 双参数指数平滑
双参数指数平滑包含两个平滑参数 适用于包含长期趋势、不包含季节成分的 时间序列预测。 其基本思想是:首先对序列选定其随时间 变化的线性模型,再通过对序列水平和增 长量分别进行平滑来估计模型中的参数。
双参数指数平滑模型
ˆ YT l Ft bt l
一个模拟的AR(1)序列
X t 0.6 X t 1 at
~ at NID(0,1)
一个模拟的MA(1)序列
X t at 0.6at 1
at ~ NID(0,1)
有均值项的ARMA模型
对于均值是否为零未知的情况下,建模时 需要给ARMA模型加上一个均值项。 AR模型: ( X t ) 1 ( X t 1 ) p ( X t p ) at
l 1,2,
Ft Yt (1 )(Ft 1 bt 1 ) bt ( Ft Ft 1 ) (1 )bt 1
第一个平滑方程得到原序列经趋势调整的平滑值, 第二个平滑方程是对增量进行指数平滑。初始值 取为:
F1 Y1
Ym Y1 b1 m 1
三参数指数平滑模型
预测公式 (L为季节长度)
