第八章时间序列分析下09统计学共30页文档
统计学 第8章 时间序列分析

统计学文档时间序列分析

第5章时间序列分析5.1时间序列的基本问题5.1.1时间序列的概念时间序列是指反映客观现象的同一指标在不同时间上的数值,按时间先后顺序排列而形成的序列,它由两个基本要素组成:一个是现象的所属时间;另一个是反映该现象的同一指标在不同时间条件下的具体数值。
也称为时间数列,或动态数列。
时间序列的一般形式是:例如,表5.1是一个国内生产总值及其部分构成统计表。
表时间序列可以描述客观现象发展变化的状况、过程和规律,利用时间序列资料可以计算一系列动态分析指标,通过时间序列分析,可以揭示客观现象发展变化的趋势,为预测、决策提供依据。
5.1.2时间序列的分类时间序列可以分为绝对数时间序列、相对数时间序列和平均数时间序列三种。
其中绝对数时间序列是最基本的时间序列,其余两种是在其基础上派生的。
1、绝对数时间序列,简称绝对序列:它是把同一总量指标在不同时间上的数值按时间先后顺序排列而形成的时间序列。
绝对序列反映现象在不同时间上所达到的总量及其增减变化的过程。
绝对序列有时期序列和时点序列两种。
时期序列是由时期绝对数数据所构成的时间序列,其中的每个数值反映现象在一段时间内发展过程的总量。
时点序列是由时点绝对数数据所构成的时间序列,其中的每个数值反映现象在某一时点上所达到的水平。
时期序列中的各个数数值可以相加,各个数数值的和表示了在所对应的时期之内事物及其现象的发展总量。
而时点序列中各个数数值相加通常没有明确的意义;时期序列中各项数值的大小与所包括的时期长短有直接关系,时点序列中各数数值与其时点间隔长短没有直接关系。
2、相对数时间序列:它是把一系列同类的统计相对数按照时间先后顺序排列起来而形成的时间序列,反映事物之间对比关系的变化情况。
3、平均数时间序列:它是把一系列同类的统计平均数按照时间先后顺序排列起来而形成的时间序列,表现事物一般水平的变化过程的发展趋势。
参看上表格。
5.1.3编制时间序列的原则编制时间序列的目的是要通过对序列中各个时期指标值进行比较,以达到研究客观现象的发展变化状况、过程及其规律。
统计学 时间序列分析

三 11.0
四 12.6
五 14.6
六 16.3
七 18.0
月末全员人数(人) a 2000 2000 2200 2200 2300
b
要求计算:①该企业第二季度各月的劳动生产率 ; ②该企业第二季度的月平均劳动生产率; ③该企业第二季度的劳动生产率。
6.2 时间序列分析的水平指标
6.2.1 发展水平与平均发展水平 --相对数(平均数)时间序列
时间 1月1日 5月31日 8月31日 12月31日
社会劳动者 人数
362
390
416
420
解:则该地区该年的月平均人数为:
362390539041634164204
y 2
2
2
534
39.765万人
6.2 时间序列分析的水平指标
6.2.1 发展水平与平均发展水平 --相对数(平均数)时间序列
月份 工业增加值(万元)
6.1 时间序列概述
6.1.2 时间序列的种类
绝对数序列
时期序列
时
派生
时点序列
间
序 列
相对数序列
平均数序列
6.1 时间序列概述
6.1.2 时间序列的种类
年 份 1992 1993 1994 1995 1996 1997
职工工资总额 3939.2 4916.2 6656.4 8100.0时90期80数.0数94列05.3 (亿元)
解:①第二季度各月的劳动生产率:
四月份: y12 10 .6 2 0 1 20 0 00 0 2 0 0 603元 0人 0
五月份: y22 10 .6 4 0 1 20 0 20 0 2 0 0 60 9.4 5 元 2 人
统计学基础(第六版)教学课件第8章

2009
呈现出一定的抛物
2008
趋势;管理成本则
2007
现一定的指数变化
2005
净利润呈现一定的
2006
2005
线性趋势;产量呈
净利润
《统计学基础》(第六版)
管理成本
第8章
8.3 时间序列预测的程序和方法
确定时间序列的成分
4000
年份
8 - 13
第8章
《统计学基础》(第六版)
8.3 时间序列预测的程序和方法
84
60
233
2007
2938
124
73
213
➢
第2步,找出适合该时间序列的预测方法。
2008
3125
214
121
230
2009
3250
216
126
223
第3步,对可能的预测方法进行评估,以确定最
2010
3813
354
172
240
➢
2011
4616
420
218
208
佳预测方案。
2012
4125
514
110.94
110.61
109.60
110.29
110.50
110.00
108.61
—
119.87
133.41
148.01
163.71
179.42
197.89
218.63)根据式(8.5)得:
ҧ =
− 1 × 100 =
0
9
27563
− 1 × 100 = 11.26%
2021/11/5
经济应用统计学-第八章时间数列分析.ppt

时间数列分析
STAT
简单算术平均 间隔相等 简单算术平均
间隔不等 加权算术平均
间隔相等 两次简单平均 间隔不等 先简单后加权
分子分母先分别平均再相除
静态平均指标:同相对指标
平均指标 序时平均指标:视情况选用简单平均和 加权算术平均
n项环比发展速度的连乘积等于第n期的定基发展速度相邻两个时期的定基发展速度之商等于相应时期的环比发展速度stat时间数列分析年份199519961997199819992000200120021995gdp58478678447446378345820688946897315105172117252环比发展速度定基发展速度11602109761052110475109021087710807111491160212734133971403415299166411798520051我国19952003年国内生产总值资料stat时间数列分析增长速度上年同期本期上年同期上年同期本期stat时间数列分析逐期增长水平与前一期水平之比stat时间数列分析累积增长水平与前一期水平之比stat时间数列分析stat时间数列分析stat时间数列分析1时间数列速度分析stat时间数列分析平均发展速度stat时间数列分析平均发展速度stat时间数列分析平均发展速度stat时间数列分析平均发展速度stat时间数列分析年份国内生产总值指数上年100年份国内生产总值指数上年10019781979198019811982198319841985198619871988100107610781052109111091152113510881116111319891990199119921993199419951996199719981041103810921142113511261105109610881078求
统计学第八章 时间序列分析

季节指数
乘法模型中的季节成分通过季节指数来反映。 季节指数(季节比率):反映季节变动的相
对数。 1、月(或季)的指数之和等于1200%(或
400%) 。 2、季节指数离100%越远,季节变动程度
越大,数据越远离其趋势值。
用移动平均趋势剔除法计算季节指数
1、计算移动平均值(TC),移动期数为4或 12,注意需要进行移正操作。
移动平均的结果 4000 3500 3000 2500 2000 1500 1000 500 0
Example 2
移动平均法可以作为测定长期趋势的一种 较为简单的方法,在股市技术分析中有广 泛的应用。比如对某只股票的日收盘价格 序列分别求一次5日、10日、一个月的移动 平均就可以得到其5日、10日、一个月的移 动平均股价序列,进而得到5日线、10日线、 月线,用以反映股价变动的长期趋势。
1987 1800 1992 1980 1997 2880
1988 1620 1993 2520 1998 3060
1989 1440 1994 2559 1999 2700
4000
3500
销售收入
3000
2500
2000
1500
1000
500
0
年份
2000 2001 2002 2003 2004
销售 收入 3240 3420 3240 3060 3600
部分数据
销售 收入
t
1985 1080
1
1986 1260
2
1987 1800
3
1988 1620
4
1989 1440
5
……
…
2003 3060
19
统计学第八章时间序列分析..

a 118729 129034 132616 132410 124000 a n 5 127357.8 万吨标准煤
Statistics
⑵由时点数列计算 ①由连续时点数列计算 ※间隔相等时,采用简单算术平均法
a1 a2 a n
an
a
i 1
n
i
序 时 总量指标 平 均 方 法 相对指标、 平均指标
时点 数列
视情况选用:先平均再相除、先加总再 相除、加权算术平均、加权调和平均等
Statistics
• 平均发展水平指标的计算
一、时期数列序时平均数的计算 二、时点数列序时平均数的计算 (一)连续登记间隔相同的时点数列 (二)连续登记间隔不同的时点数列 (三)不连续登记间隔相等的时点数列 (四)不连续登记间隔不等的时点数列 三、相对数和平均数序时平均数的计算
• 构成时间数列有两个基本要素: 一、现象所属的时间,实践中,构成时 间数列的时间单位长短视研究目的与现 象性质而定。 二、现象在相应时间所达到的水平(即 指标数值)。
Statistics
要素一:时间t
年份 1986 1987 1988 1989 国内生产总值
要素二:指标数值a
年份 1996 1997 1998 1999 国内生产总值
Statistics
序时平均数的计算方法
⒈计算绝对数时间数列的序时平均数 ⑴由时期数列计算,采用简单算术平均法
a1 a2 a n
an
a
i 1
n
i
n
Statistics
例
2006-2010年某地原煤产量 时期 原煤产量(万吨)
2006 2007 2008 2009 2010
统计学_第八章__时间序列分析
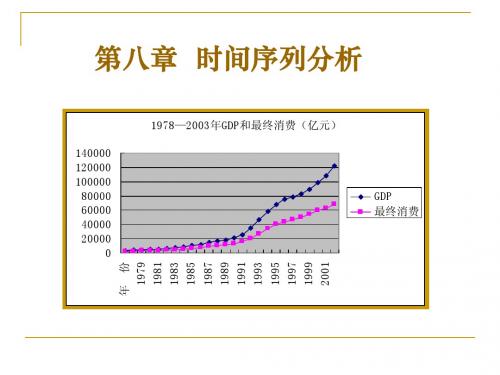
1978—2003年GDP和最终消费(亿元) 140000 120000 100000 80000 60000 40000 20000 0
年 份 1979 1981 1983 1985 1987 1989 1991 1993 1995 1997 1999 2001
GDP 最终消费
4、二者关系 (1)各逐期增长量之和等于相应的累计增长量
an a0 (a1 a0 ) (a2 a1 ) (a3 a2 ) (an an1 )
(2)相邻两期的逐期增长量之和等于相应的 累计增长量;相邻两期的累计增长量之差等于 相应的逐期增长量
(二)平均增长量 1、概念 一段时期内平均每期增加或者减少的绝 对数量。或者说是逐期增长量的序时平均数。 2、计算公式
a0 a1 a 2 a n 或 a n 1
af a f
B、如果是间断时点数列,计算方法为: 『两个假设条件: 一是假设上期期末水平等于本期期初水平; 二是假设现象在间隔期内数量变化是均匀的。』 Ⅰ、间隔期相等的时点数列,采用“首尾(首末)折半 法”计算。 先计算各间隔期的平均数;然后再将这些平均数进行 简单算术平均。例如:
第一节
时间序列分析概述
一、时间序列的概念和作用
(一)、概念: 1、时间序列:将不同时间的某一统计指标数据按照 时间的先后顺序排列起来而形成的统计序列,也称时间 数列或动态数列。 2、基本构成要素(从形式上看): 一是时间顺序(现象所属的时间)。可以是年份、季 度、月份或其他任何时间,称时间要素(常用t表示); 二是不同时间的统计数据(现象在不同时间上的观察 值)。可以是绝对数、相对数、平均数,称数据要素 (常用小写的英文字母a、b、c表示)。
统计学 时间序列分析

7
商品流转次数(c)
1.9 65 75 2.41 2.22 2.4 80.7
2 2.0 2.4
4 2.27
72
120 145+185+190+200+250
c
a(平均销售额) b(平均库存额)
60
6 65 75 78 80 100 105
2.27次
2
2
6
3. 增长量和平均增长量
增长量说明社会经济现象在一定时期内所增长的绝对数量, 它是报告期水平与基期水平之差。 由于采用的基期不同,增长量分为逐期增长量和累积增长量
某企业1996-2000年产量增长速度
年份
1996 1997 1998 1999 2000
环比增长速度(%) 20 (2) 25 15 (5)
定基增长速度(%) (1) 50 (3) (4) 132.5
解: 1996年定基增长速度=20%
1997年环比增长速度=
1+50% 1+20%
1
25%
1998年定基增长速度
535 552 562 676
a 2
2 573人
4 1
例.某地区2008年城乡居民储蓄余款额资料如下
日期
1月1日 3月1日 7月1日 8月1日 12月31日
储蓄余款额
38
42
54
56
60
(亿元)
38 42 2 42 54 4 54 56 1 56 60 5
a 2
2
2
2
53.29万元
定基发展速度: 环比发展ቤተ መጻሕፍቲ ባይዱ度:
x1 , x2 , , xn
x0 x0
x0
统计学第8章 时间序列分析

a n 1
a0
(二)增长速度(增减速度)
增长速度=
增减量 基期水平
报告期水平 基期水平 基期水平
报告期水平 基期水平 1
发展速度1
环比增长速度= an an1 an 1
an1
an1
=环比发展速度 - 100%
定基增长速度= an a0 an 1
a0
a0
=定基发展速度 - 100%
例题:
时间序列的构成要素与模型
(构成要素与测定方法)
时间序列的构成要素
长期趋势
季节变动
循环波动 不规则波动
线性趋势 非线性趋势
按月(季)平均法
移动平均法
二次曲线 指数曲线
趋势剔出法
半数平均法
修正指数曲线
最小平方法
Gompertz曲线 Logistic曲线
剩余法
线性趋势
一、移动平均法
(Moving Average Method)
移动平均法(趋势图)
200
汽 150
车
产 100
量
(万辆)50
产量 五项移动平均趋势值 五项移动中位数
0
1981
1985
1989
1993
1997
(年份)
图11-1 汽车产量移动平均趋势图
移动平均法特点
1、对原数列有修匀作用,移动项数越大,修匀 作用越强。
2、移动平均时,项数为奇数时,只需一次移动 平均,其平均值作为移动平均项中间一期; 当为偶数时,需再进行一次相邻两平均值的 移动平均。
年份
销售额 逐 期 增 减 量 环比发展速度 定基增长速
(万元) (万元)
(%)
度(%)
统计学第八章时间数列

=(报告期水平-前一期水平)/前一期水平 =环比发展速度-1(或100%)
发展速度与增长速度
2、定基增长速度。 定基增长速度是报告期的累计增长量与 某一固定基期水平之比,说明现象在较 长时间内总的增长速度。公式如下:
定基增长速度=累计增长量/某一固定期水平 =报告期水平-某一固定期水平)/某一固定期 水平 =定基发展速度-1(或100%)
1、移动平均法。 移动平均法是对原时间数列逐项求 序时平均数,平均项数固定,并逐 项移动得出由这些平均数构成的新 数列,它可以消除某些因素及随机 因素的影响,显示出现象的长期趋 势。
测定长期趋势的方法
设时间数列的水平顺次为: a1,a2,a3, an 若取三项平均移动平均形成的新数 列为:
a1 a 2 a 3 a 2 a3 a 4 a2 , a3 , 3 3
第八章 时间数列
第一节 第二节 第三节 第四节 时间数列概述 时间数列的水平指标 时间数列的速度指标 动态数列的因素分析
第八章 时间数列
第一节 时间数列概述 一、时间数列的概念及作用 二、时间数列的种类 三、编制时间数列的原则
时间数列的概念及作用
一)时间数列的概念
时间数列亦称动态数列,是将反映某现象的 统计指标在不同时间上的数值,按时间先后 顺序排列而形成的一种数列;如:
动态数列影响因素及其分解 模型
3、循环变动(以C表示) 循环变动是指现象以若干年为一周 期,近乎规律性的盛衰交替变动。 如经济危机就是循环变动,每一循 环周期都要经历危机、萧条、复苏 和高涨四个阶段。
动态数列影响因素及其分解 模型
4、随机变动(以I表示) 随机变动亦称不规则变动或剩余变 动,是动态数列除了上述三种变动 之外剩余的一种变动,是偶然因素 引起的一种随机波动。如自然灾害、 战争等无法预见的因素引起的波动。
统计学第八章时间序列分析与预测

分析目的
分析过去
描述动态变化
9
认识规律
揭示变化规律
统计学第八章时间序列分析与预测
预测未来
未来的数量趋势
统计学
STATISTICS
编制时间序列的基本原则
编制时间序列的目的是通过对各时间的变量数值 进行比较,分析其随时间变化的过程和规律。
各指标数值应当可比
▲所属时间可比
▲总体范围可比
▲经济内容可比
▲计算口径可比
统计学
STATISTICS
8.3 时间序列趋势变动分析
一、测定长期趋势的移动平均法 二、测定长期趋势的指数平滑法 三、测定长期趋势的模型法
统计学第八章时间序列分析与预测
统计学
STATISTICS
趋势变动分析
9
统计学第八章时间序列分析与预测
统计学 STATISTICS 一、测定长期趋势的移动平均法
9
统计学第八章时间序列分析与预测
增长速度 统计学
STATISTICS
增 长 速 度 = 基 增 期 长 水 量 平 = 报 告 水 基 平 期 - 水 基 平 期 水 平 = 发 展 速 度 - 1
环比增长速度=环比发展速度—1 定基增长速度=定基发展速度—1
平均发展速度和平均增长速度 平均增长速度 = 平均发展速度 — 1
9
统计学第八章时间序列分析与预测
平S统TAT计均IST学I发CS 展速度和平均增长速度
几何平均法(水平法)
特点:着眼于期末水平
GnG1G2
n
Gn n Gi i1
Gn x1x2
xn n xn
G = G x0-1 x= 1 ni xn = n 1 1G xi 0 -1
8统计学 第八章 时间序列

库存量
66
72
64
68
66 72 10月份份平均库存 : 69 (百件) 2 72 64 11月份份平均库存 : 68 (百件) 2 64 68 12月份份平均库存 : 66 (百件) 2
2005
2006 2007
182321
210871 246619
45806
28550 35748
2008
2009 2010
300670
335353 397983
54051
34683 62630
第八章 时间序列分析
第二节 时间序列的指标分析
时间序列的水平分析 (一)增长量与平均增长量
年份 国内生产总值(亿元) 2001 95933 2002 102398 2003 2004 116694 136515
基本构成要素
时间数列由互相对应的两个数列构成: (一)时间顺序变化数列 (二)统计指标变化数列
第八章 时间序列分析
第一节 时间序列分析概述
时间序列的类型
时期数列 总量指标时间数列 时点数列
相对指标时间数列
平均指标时间数列
第八章 时间序列分析
第一节 时间序列分析概述
时间序列的类型
月份 1 2 3 4 5 6 7 8 9 10 11 12 超市营业额 (万元) 295 283 322 355 286 379 381 431 424 473 470 481
逐期增长量
增长量(亿元) —— 6465 14296 19821
累积增长量
增长量(亿元)
2005
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
步骤2. 若两变量是同阶单整的,如I(1),则用OLS法估
计长期均衡方程(称为协整回归): Yt=β0+β1Xt+εt
并保存残差et,作为均衡误差εt的估计值。
9
步骤3. 对于两个协整变量来说,均衡误差必须是平稳的。
为检验其平稳性,对上一步保存的均衡误差估计值 (即协整回归的残差et)应用单位根方法。具体作法 是 将 Dickey—Fuller 检 验 法 用 于 时 间 序 列 et , 也 就 是 用OLS法估计形如下式的方程:
2
协整的定义
如果两时间序列Yt~I(d),Xt~I(d),并且这两个时 间序列的线性组合a1Yt+a2Xt 是(d-b)阶单整的,即 a1Yt+a2Xt~I(d-b)(d≥b≥0),则Yt 和Xt被称为是(d, b)阶协整的。记为
Yt, Xt~CI(d , b) 这里CI是协整的符号。构成两变量线性组合的系数向 量(a1,a2)称为“协整向量”。
△et =δet-1 + νt
(3)
有两点须提请注意:
(1)(3)式不包含常数项,这是因为OLS残差et应以0为中 心波动。 (2)Dickey—Fullerτ统计量不适于此检验,表1提供了用于协 整检验的临界值表。
10
表 1 协整检验 EG 或 AEG 的临界值
变量个数
m=2
m=3 显著性水平
样本容量 0.01 0.05 0.10 0.01
CP t 4 C.7 9640 1 .4056 G 83 D1 tPP R2=C 0.9981
通过对该式计算的残差序列作ADF检验,得适当检验模型
e ˆ t 1 .5 e ˆ t 1 5 1 .4 e ˆ t 9 1 2 .2 e ˆ t 7 3
(-4.47) (3.93) (3.05)
经济理论指出,某些经济变量间确实存在着长期均衡关 系,这种均衡关系意味着经济系统不存在破坏均衡的内在 机制,如果变量在某时期受到干扰后偏离其长期均衡点, 则均衡机制将会在下一期进行调整以使其重新回到均衡状 态。
7
(三)协整的检验 Engle-Granger法
步骤1. 用上一节介绍的单位根方法求出两变量的单整的阶, 然后分情况处理, 共有三种情况: (1)若两变量的单整的阶相同,进入下一步; (2)若两变量的单整的阶不同,则两变量不是协整 的; (3)若两变量是平稳的,则整个检验过程停止,因 为可以采用标准回归技术处理。
t=-4.47<-3.75=ADF0.05,拒绝存在单位根的假设,残差项是平 稳的,因此中国居民人均消费水平与人均GDP是(2,2)阶协整的, 说明了该两变量间存在长期稳定的“均衡”关系。
12
二、 误差修正模型(ECM)
协整分析中最重要的结果可能是所谓的“格兰杰代表定 理”(Granger representation theorem)。按照此定理,如果 两变量Yt和Xt是协整的,则它们之间存在长期均衡关系。
εt~I(0),E(εt)= 0。 按照协整的定义,由于
Yt~I(1),Xt~I(1),且线性组合
εt=Yt-β0-β1Xt~I(0)
因此,Yt 和Xt是(1,1)阶协整的,即
Yt,Xt~CI(1, 1)
协整向量是(1, -β0, -β1)
5
综合以上结果,可以说,两时间序列之间的协整是
表示它们之间存在长期均衡关系的另一种方式。因此, 若Yt 和Xt是协整的, 并且均衡误差是平稳的且具有零 均值,则可以确信,方程
m=4
0.01 -5.43 -5.02 -4.83 -4.65
0.05 -4.56 -4.32 -4.21 -4.10
0.10 -4.15 -3.98 -3.89 -3.81
11
例1
检验中国居民人均消费水平CPC与人均国内生产总值GDPPC的 协整关系。
假设已知CPC与GDPPC都是I(2)序列,它们的回归式为
第二节 协整分析与ECM
1
一、协整(cointegrated)分析
(一)协整的提出及定义
大多数序列都是非平稳的,为防止伪回归,这时的处理办法 有两个: 差分:使用变量为差分形式的关系式更适合描述所研究的 经济现象的短期状态或非均衡状态,而不是其长期或均衡 状态,描述所研究经济现象的长期或均衡状态应采用变量 本身。 协整:是指多个非平稳经济变量的某种线性组合是平稳的。 (若平稳就是协整的)
一般:同阶单整序列,如果线性组合后单整阶数降低,则变量之 间存在协整关系。
3
考虑下面的关系
Yt = β0+β1Xt
(1)
其中,Yt~I(1),Xt~I(1)。
当0= Yt-β0-β1Xt时,该关系处于长期均衡状态。
对长期均衡的偏离,称为“均衡误差”,记为εt:
εt = Yt-β0-β1Xt
4
若长期均衡存在,则均衡误差应当围绕均衡值0波动。 也就是说,均衡误差εt应当是一个平稳时间序列,即 应有
0.05
25 -4.37 -3.59 -3.22 -4.92
-4.10
50 -4.12 -3.46 -3.13 -4.59Fra bibliotek-3.92
100 -4.01 -3.39 -3.09 -4.44 ∞ -3.90 -3.33 -3.05 -4.30
-3.83 -3.74
0.10 -3.71 -3.58 -3.51 -3.45
Yt =β0+β1Xt+εt
(2)
将不会产生伪回归结果。 由上可知,如果我们想避免伪回归问题,就应该在
进行回归之前检验一下所涉及的变量是否协整。
“可以把协整检验看成是避免出现伪回归”情况的 一个预检验----格兰杰。
6
(二)协整检验的意义
经济意义:两个变量,虽然它们具有各自的长期波动规律,但是
如果它们是(d,d)阶协整的,则它们之间存在着一个长期稳定的 比例关系。这也解释了尽管这两时间序列是非稳定的,但却可以用 经典的回归分析方法建立回归模型的原因。
当然,在短期内,这些变量可以是不均衡的,扰动项是均衡 误差εt。两变量间这种短期不均衡关系的动态结构可以由误差 修正模型(error correction model)来描述。(变量间这种长 期的稳定关系是在短期动态过程的不断调整下得以维持,这种 短期动态的调整过程就是误差修正机制,它防止了变量间长期 关系的偏差在规模上或数量上的扩大)。
