苏州大学333教育综合真题2010-2019
考研教育学专业基础综合教育学原理历年真题试卷汇编8_真题无答案

考研教育学专业基础综合(教育学原理)历年真题试卷汇编8(总分300, 做题时间180分钟)单项选择题1.【2010-1】根据经验科学的标准,科学教育学的研究任务是( )。
SSS_SINGLE_SELA描述教育现象,揭示教育规律B揭示教育规律,确立教育理想C揭示教育规律,规范教育行为D研究教育实践,解决实际问题2.【2018-1】主张用“理解”和“解释”的立场与方法研究教育问题的教育学流派是( )。
SSS_SINGLE_SELA实验教育学B文化教育学C批判教育学D元教育学3.【2011-2】世界近代教育发展的重要成就之一是实施了( )。
SSS_SINGLE_SELA补偿教育B义务教育C终身教育D回归教育4.【2019-l】苏格拉底说,我不是教给你们知识,我只是知识的产婆。
从教育陈述的角度看,这属于( )。
SSS_SINGLE_SELA描述性定义B口号性定义C术语性定义D隐喻性定义5.【2007-6】在一个人的发展过程中.有的方面在较低的年龄阶段就达到了较高的水平,有的方面则要到较高的阶段才能达到成熟的水平。
这反映人的身心发展具有( )。
SSS_SINGLE_SELA顺序性B阶段性C差异性D不均衡性6.【2013-4】教育之所以能促进儿童发展,根本在于儿童发展上具有( )。
SSS_SINGLE_SELA阶段性B顺序性C不平衡性D可塑性7.【2019-6】人的感知、思维、记忆、想象等方面发展存在不同的关键期,这表明个体的身心发展:具有( )。
SSS_SINGLE_SELA顺序性B阶段性C不平衡性D差异性8.【2018-3】对人力资本理论提出质疑,认为教育并不提高人的能力,只是用来区别不同人的能力的手段,这种观点属于( )。
SSS_SINGLE_SELA冲突论B文凭理论C结构功能论D劳动力市场理论9.【2011-4】把教育方针规定为“教育必须为社会主义现代化建设服务,必须与生产劳动相结合,培养德、智、体等方面全面发展的社会主义事业的建设者和接班人”的文献是( )。
历年苏州大学考研真题试卷与答案汇总-苏州大学考研真题试卷-苏大考研真题答案-苏大考研真题哪里找?

历年苏州大学考研真题试卷与答案汇总-苏大考研真题哪里找?东吴苏大考研网(苏州大学考研在线咨询入口)汇集了苏州大学各专业历年考研真题试卷(原版),同时与苏州大学专业课成绩前三名的各专业硕士研究生合作编写了配套的真题答案解析,答案部分包括了(解题思路、答案详解)两方面内容。
首先对每一道真题的解答思路进行引导,分析真题的结构、考察方向、考察目的,向考生传授解答过程中宏观的思维方式;其次对真题的答案进行详细解答,方便考生检查自身的掌握情况及不足之处,并借此巩固记忆加深理解,培养应试技巧与解题能力。
具体请点击进入【历年苏州大学考研真题答案下载】[东吴苏大考研网] 2019苏大考研817国际法学考试解读与真题答案详解[东吴苏大考研网] 苏州大学347心理学专业综合考研真题试卷(2011-2018)[东吴苏大考研网] 苏州大学333教育综合历年考研真题试卷(2007-2018年)[东吴苏大考研网] 2015年苏州大学335出版综合素质与能力考研真题与答案[东吴苏大考研网] 苏州大学889英语教学论考研真题(2017-2018年,回忆版)[东吴苏大考研网] 苏州大学808管理学考研真题试卷(2000-2015)[东吴苏大考研网] 苏州大学884高分子材料化学考研真题与答案(2015-2018年)[东吴苏大考研网] 苏州大学823艺术史考研真题试卷(2004-2015年)[东吴苏大考研网] 苏州大学822新闻传播专业基础考研真题试卷(2000-2018)[东吴苏大考研网] 苏州大学633教育学专业基础综合真题答案(2007-2018)[东吴苏大考研网] 苏州大学832普通物理考研真题与答案(2003-2015年)[东吴苏大考研网] 苏州大学807微观与宏观经济学考研真题试卷(1999-2017,不含06)[东吴苏大考研网] 苏大637药学基础综合(1)考研真题试卷(09-17)[东吴苏大考研网] 苏大872数据结构与操作系统考研真题答案(真题99-17,答案05-17)[东吴苏大考研网] 2019苏州大学考研889英语教学论复习全析(含真题,共三册)[东吴苏大考研网] 2013-2015年苏州大学612绘画基础(素描命题画)考研真题试卷[东吴苏大考研网] 2019苏大考研398法硕联考专业基础课(非法学)强化冲刺题库(共两册)[东吴苏大考研网] 2019苏大考研498法硕联考综合课(非法学)强化冲刺题库(共三册)[东吴苏大考研网] 2019苏大878电磁学考研强化冲刺题库[东吴苏大考研网] 2019苏大842自动控制原理考研强化冲刺题库(共两册)[东吴苏大考研网] 2019苏大电子技术基础考研强化冲刺题库(共两册)【历年苏州大学考研真题答案下载】[东吴苏大考研网] 2019苏大理论力学考研强化冲刺题库[东吴苏大考研网] 2019苏大837信号系统与数字逻辑考研强化冲刺题库(共三册)[东吴苏大考研网] 2019苏大考研856物理化学(F)冲刺题库(共两册)[东吴苏大考研网] 2019苏大考研629无机化学(F)强化冲刺题库(共两册)[东吴苏大考研网] 2019苏大考研628有机化学(F)强化冲刺题库(共两册)[东吴苏大考研网] 2019苏大602高等数学(F)考研强化冲刺题库【共两册】[东吴苏大考研网] 2019苏大考研861高分子化学强化冲刺题库[东吴苏大考研网] 2019苏大考研853物理化学强化冲刺题库(共两册)[东吴苏大考研网] 2019苏大考研884高分子材料化学强化冲刺题库[东吴苏大考研网] 2019苏大考研835有机化学B强化冲刺题库[东吴苏大考研网] 2019苏大考研834分析化学强化冲刺题库[东吴苏大考研网] 2019苏大考研620无机化学强化冲刺题库(共两册)[东吴苏大考研网] 2019苏大考研635有机化学A强化冲刺题库[东吴苏大考研网] 2019苏大考研862材料科学基础强化冲刺题库[东吴苏大考研网] 2019苏大838信号与线性系统考研强化冲刺题库[东吴苏大考研网] 2019苏大832普通物理考研强化冲刺题库【共两册】[东吴苏大考研网] 2019苏大601高等数学考研强化冲刺题库【共两册】[东吴苏大考研网] 2019苏大831高等代数考研强化冲刺题库(共两册)[东吴苏大考研网] 2019苏大618数学分析考研强化冲刺题库(共两册)[东吴苏大考研网] 2019苏大432统计学考研强化冲刺题库[东吴苏大考研网] 2019苏州大学基础日语考研强化冲刺题库[东吴苏大考研网] 2019苏大448汉语写作与百科知识考研强化冲刺题库[东吴苏大考研网] 2019苏大357英语翻译基础考研强化冲刺题库[东吴苏大考研网] 2019苏大211翻译硕士英语考研强化冲刺题库[东吴苏大考研网] 2019苏大历史学基础考研强化冲刺题库[东吴苏大考研网] 2019苏大826社会保障学考研强化冲刺题库(共两册)[东吴苏大考研网] 2019苏大658公共管理学考研强化冲刺题库(共两册)[东吴苏大考研网] 2019苏大考研660世界史专业基础综合强化冲刺题库(共六册)[东吴苏大考研网] 2019苏大考研659中国史专业基础综合强化冲刺题库(共五册)[东吴苏大考研网] 2019苏大考研824社会研究方法强化冲刺题库[东吴苏大考研网] 2019苏大考研613社会学原理强化冲刺题库[东吴苏大考研网] 2019苏大戏剧与影视学考研核心考点与名校真题详解(共两册)[东吴苏大考研网] 2019苏州大学出版专硕考研强化冲刺题库【共4册】[东吴苏大考研网] 2019苏大822新闻传播专业基础考研强化冲刺题库(共两册)[东吴苏大考研网] 2019苏大334新闻与传播专业综合能力考研强化冲刺题库[东吴苏大考研网] 2019苏大440新闻与传播专业基础考研强化冲刺题库(共两册)[东吴苏大考研网] 2019苏大820评论写作(1)考研强化冲刺题库[东吴苏大考研网] 2019苏大625汉语言文字基础考研冲刺题库【共5册】[东吴苏大考研网] 2019苏大445汉语国际教育基础考研强化冲刺题库[东吴苏大考研网] 2019苏大354汉语基础考研强化冲刺题库[东吴苏大考研网] 2019苏州大学心理学考研强化冲刺题库(共七册)【历年苏州大学考研真题答案下载】[东吴苏大考研网] 2019苏大802中西政治思想史考研强化冲刺题库[东吴苏大考研网] 2019苏大801中西哲学史考研强化冲刺题库(共两册)[东吴苏大考研网] 2019苏大654公共管理基础理论考研强化冲刺题库(共两册)[东吴苏大考研网] 2019苏大652政治学原理考研强化冲刺题库(共两册)[东吴苏大考研网] 2019苏大651哲学概论考研强化冲刺题库[东吴苏大考研网] 2019苏大633教育学专业基础综合考研冲刺题库【共六册】[东吴苏大考研网] 2019苏大665中外音乐史考研复习全析(含历年真题)[东吴苏大考研网] 2019苏州大学666生物化学(农)考研复习全析(含历年真题,共两册)[东吴苏大考研网] 2019苏大842自动控制原理考研复习全析(含历年真题)[东吴苏大考研网] 2019苏大841电子技术基础(机电)考研复习全析(含历年真题)【共两册】[东吴苏大考研网] 2019苏大839管理信息系统与数据结构考研复习全析(含历年真题,共两册)[东吴苏大考研网] 2019苏大850高等数学基础考研复习全析(含历年真题,共两册)[东吴苏大考研网] 2019苏大627生物化学考研复习全析(含历年真题,共两册)[东吴苏大考研网] 2019苏大862材料科学基础考研复习全析(含历年真题)[东吴苏大考研网] 2019苏大858材料学(F)考研复习全析(共两册,含历年真题)[东吴苏大考研网] 2019苏大857细胞生物学(F)考研复习全析(含历年真题)[东吴苏大考研网] 2019苏大631生物化学(F)考研复习全析(含历年真题,共两册)[东吴苏大考研网] 2019苏大856物理化学(F)考研复习全析(含历年真题)[东吴苏大考研网] 2019苏大629无机化学(F)考研复习全析(含历年真题,共三册)[东吴苏大考研网] 2019苏大628有机化学(F)考研复习全析(含历年真题,共两册)[东吴苏大考研网] 2019苏大602高等数学(F)考研复习全析(含历年真题,共两册)[东吴苏大考研网] 2019苏大838信号与线性系统考研复习全析(含历年真题)[东吴苏大考研网] 2019苏大601高等数学考研复习全析(含历年真题,共两册)[东吴苏大考研网] 2019苏大625汉语言文字基础考研复习全析(含历年真题,共六册)[东吴苏大考研网] 2019苏大847金融学概论考研复习全析(含历年真题,共两册)[东吴苏大考研网] 2019苏州大学432统计学考研复习全析(含历年真题)[东吴苏大考研网] 2019苏大831高等代数考研复习全析(含真题答案,共三册)[东吴苏大考研网] 2019苏大618数学分析考研复习全析(含真题答案,共四册)[东吴苏大考研网] 2019苏大616基础俄语考研复习全析(含真题答案,共五册)[东吴苏大考研网] 2019苏大考研243日语强化冲刺题库[东吴苏大考研网] 2019苏大考研241英语强化冲刺题库[东吴苏大考研网] 2019苏大考研245德语强化冲刺题库[东吴苏大考研网] 2019苏大241英语考研复习全析(含历年真题,共五册)[东吴苏大考研网] 2019苏大826社会保障学考研复习全析(含历年真题)[东吴苏大考研网] 2019苏大658公共管理学考研复习全析(含历年真题,共三册)[东吴苏大考研网] 2019苏大660世界史专业基础综合考研复习全析(含历年真题,共六册)【历年苏州大学考研真题答案下载】[东吴苏大考研网] 2019苏大824社会研究方法考研复习全析(含历年真题,共三册)[东吴苏大考研网] 2019苏大613社会学原理考研复习全析(含历年真题,共三册)[东吴苏大考研网] 2019苏大437社会工作实务考研复习全析(含历年真题,共四册)[东吴苏大考研网] 2019苏大331社会工作原理考研复习全析(含历年真题,共三册)[东吴苏大考研网] 2019苏大337设计基础考研复习全析(含历年真题)[东吴苏大考研网] 2019苏大875设计艺术史考研复习全析(含历年真题)[东吴苏大考研网] 2019苏大346体育综合考研强化冲刺题库(共三册)[东吴苏大考研网] 2019苏大考研《经济法》强化冲刺题库[东吴苏大考研网] 2019苏大817国际法学考研复习全析(含真题答案,共四册)[东吴苏大考研网] 2019苏大816环境与资源保护法学考研复习全析(含历年真题)[东吴苏大考研网] 2019苏大815经济法学考研复习全析(含历年真题,共三册)[东吴苏大考研网] 2019苏大813民商法学考研复习全析(含历年真题,共三册)[东吴苏大考研网] 苏大《行政法与行政诉讼法》考试重难点与历年考研真题[东吴苏大考研网] 2019苏大809法学理论考研复习全析(含历年真题)[东吴苏大考研网] 2019苏大852土地资源管理考研复习全析(含历年真题)[东吴苏大考研网] 2019苏大805行政管理学考研复习全析(含真题答案,共三册)[东吴苏大考研网] 2019苏大804管理学基础考研复习全析(含历年真题,共两册)[东吴苏大考研网] 2019苏大802中西政治思想史考研复习全析(含历年真题)[东吴苏大考研网] 2019苏大654公共管理基础理论考研复习全析(共两册,含真题答案)[东吴苏大考研网] 2019苏州大学652政治学原理考研复习全析(含真题,共两册)[东吴苏大考研网] 2019苏州大学333教育综合考研强化冲刺题库[东吴苏大考研网] 2019苏州大学333教育综合考研复习全析(含真题答案,共八册)[东吴苏大考研网] 2019苏大637药学基础综合(1)考研复习全析[东吴苏大考研网] 2019苏大623生物综合考研复习全析(含历年真题)[东吴苏大考研网] 2019苏大854电子技术基础(城市轨道)考研复习全析(含历年真题)[东吴苏大考研网] 2019苏大818理论力学(城市轨道)考研复习全析(含历年真题)[东吴苏大考研网] 2019苏大832普通物理考研复习全析(含历年真题答案,共三册)[东吴苏大考研网] 2019苏大659中国史专业基础综合考研复习全析(含历年真题答案)[东吴苏大考研网] 2019苏大872数据结构与操作系统考研复习全析(含历年真题答案,共三册)[东吴苏大考研网] 2019苏大837信号系统与数字逻辑考研复习全析(含历年真题,共三册)[东吴苏大考研网] 2019苏大848植物生理与生物化学考研复习全析(含历年真题)[东吴苏大考研网] 2019苏大840理论力学(机电)考研复习全析(含历年真题)[东吴苏大考研网] 2019苏大346体育综合考研复习全析(含历年真题答案,共五册)[东吴苏大考研网] 2019苏大656体育学专业基础综合考研复习全析(含历年真题,共三册)[东吴苏大考研网] 2019苏州大学867化工原理考研复习全析(含历年真题)【历年苏州大学考研真题答案下载】[东吴苏大考研网] 2019苏大835有机化学B考研复习全析(含历年真题)[东吴苏大考研网] 2019苏大884高分子材料化学考研复习全析(含真题答案,共三册)[东吴苏大考研网] 2019苏大843材料科学基础考研复习全析(含历年真题)[东吴苏大考研网] 2019苏大861高分子化学考研复习全析(含历年真题答案,共两册)[东吴苏大考研网] 2019苏大853物理化学考研复习全析(含历年真题)[东吴苏大考研网] 2019苏大834分析化学考研复习全析(含历年真题)[东吴苏大考研网] 2019苏大635有机化学A考研复习全析(含历年真题)[东吴苏大考研网] 2019苏大620无机化学考研复习全析(含历年真题,共三册)[东吴苏大考研网] 2019苏大307中医综合考研复习全析(共五册)[东吴苏大考研网] 2019苏大645西医医学综合考研复习全析(共五册)[东吴苏大考研网] 2019苏大653马克思主义基本原理概论考研复习全析(含历年真题)[东吴苏大考研网] 2019苏大803思想政治教育学考研复习全析(含历年真题,共三册)[东吴苏大考研网] 2019苏大634心理学专业基础综合考研复习全析(含真题,共10册)[东吴苏大考研网] 2019苏大347心理学专业综合考研复习全析(含真题答案)(共12册)[东吴苏大考研网] 2019苏大考研397法硕联考专业基础(法学)强化冲刺题库(共两册)[东吴苏大考研网] 2019苏大考研497法硕联考综合课(法学)强化冲刺题库(共三册)[东吴苏大考研网] 2019苏大中国法制史考研强化冲刺题库(张晋藩版)[东吴苏大考研网] 2019苏大考研《刑法》强化冲刺题库[东吴苏大考研网] 2019苏大考研《民法》强化冲刺题库[东吴苏大考研网] 2019苏大考研《行政法与行政诉讼法》强化冲刺题库[东吴苏大考研网] 2019苏大考研《宪法》强化冲刺题库[东吴苏大考研网] 2019苏大考研《法理学》强化冲刺题库[东吴苏大考研网] 2019苏大考研808管理学强化冲刺题库[东吴苏大考研网] 2019苏州大学微观经济学考研强化冲刺题库[东吴苏大考研网] 2019苏州大学宏观经济学考研强化冲刺题库[东吴苏大考研网] 2019苏大801中西哲学史考研复习全析(含历年真题,共三册)[东吴苏大考研网] 2019苏州大学651哲学概论考研复习全析(含历年真题,共三册)[东吴苏大考研网] 2019苏大433税务专业基础考研复习全析(含真题与答案)[东吴苏大考研网] 2019苏州大学431金融学综合考研复习全析(含历年真题答案,共六册)[东吴苏大考研网] 2019苏大398法硕联考基础课(非法学)考研复习全析(含真题答案,共三册)[东吴苏大考研网] 2019苏大397法硕联考专业基础课(法学)考研复习全析【含真题答案,共三册】东吴苏大考研网(苏州大学考研在线咨询入口)【历年苏州大学考研真题答案下载】[东吴苏大考研网] 2019苏大497法硕联考综合课(法学)考研复习全析(含真题答案,共四册)[东吴苏大考研网] 2019苏大498法硕联考综合课(非法学)考研复习全析(含真题答案,共四册)[东吴苏大考研网] 2019苏大考研《文体与翻译》复习全析(刘宓庆,含历年真题答案)[东吴苏大考研网] 2019苏大考研661教育经济学强化冲刺题库[东吴苏大考研网] 2019苏大考研819教育管理学强化冲刺题库(共两册)[东吴苏大考研网] 2019苏大考研819教育管理学复习全析(含历年真题)[东吴苏大考研网] 2019苏大考研661教育经济学复习全析(含历年真题)[东吴苏大考研网] 2019苏大考研845细胞生物学强化冲刺题库[东吴苏大考研网] 2019苏大考研845细胞生物学复习全析(含历年真题)[东吴苏大考研网] 2019苏大考研621生物化学复习全析(含历年真题,共三册)[东吴苏大考研网] 2019苏大857细胞生物学(F)考研冲刺题库[东吴苏大考研网] 2019苏大生物化学考研强化冲刺题库【共两册】[东吴苏大考研网] 2012-2015年苏州大学880和声写作与分析考研真题[东吴苏大考研网] 2012-2015年苏州大学665中外音乐史考研真题[东吴苏大考研网] 2019苏州大学考研308护理综合考试解读与真题答案[东吴苏大考研网] 2011-2013年苏州大学850普通物理(生物医学工程)考研真题[东吴苏大考研网] 2011-2015年苏州大学859普通动物学考研真题[东吴苏大考研网] 2005、2013-2015年苏州大学882遗传学考研真题[东吴苏大考研网] 2011-2015年苏州大学879普通动物学与普通生态学考研真题[东吴苏大考研网] 2009-2010、2014-2015年苏州大学878电磁学考研真题[东吴苏大考研网] 2011-2015年苏州大学874药剂学考研真题[东吴苏大考研网] 2011-2015年苏州大学868生物教学论考研真题[东吴苏大考研网] 2013-2015年苏州大学860水产养殖学考研真题[东吴苏大考研网] 2009-2015年苏州大学851社会医学考研真题[东吴苏大考研网] 2004-2015年苏州大学845细胞生物学考研真题[东吴苏大考研网] 2013-2015年苏州大学666生物化学(农)考研真题[东吴苏大考研网] 2013-2015年苏州大学664动物生物化学与鱼类生理考研真题[东吴苏大考研网] 2006/2009-2016年苏州大学632卫生事业管理学考研真题[东吴苏大考研网] 2005-2015年苏州大学626预防综合考研真题[东吴苏大考研网] 2001-2015年苏州大学621生物化学考研真题[东吴苏大考研网] 2010-2015年苏州大学353卫生综合考研真题[东吴苏大考研网] 2011-2015年苏州大学349药学综合考研真题[东吴苏大考研网] 2011-2015年苏州大学340农业知识综合二考研真题[东吴苏大考研网] 2011-2013年苏州大学627园林设计基础考研真题[东吴苏大考研网] 2011-2013年苏州大学846中外建筑史考研真题[东吴苏大考研网] 2011、2013年苏州大学622建筑设计基础考研真题[东吴苏大考研网] 2014-2015年苏州大学846设计理论考研真题【历年苏州大学考研真题答案下载】[东吴苏大考研网] 2014-2015年苏州大学622快题设计与表现考研真题[东吴苏大考研网] 2009-2015年苏州大学848植物生理与生物化学考研真题[东吴苏大考研网] 2009-2015年苏州大学662植物学考研真题[东吴苏大考研网] 2013年苏州大学663普通昆虫学考研真题[东吴苏大考研网] 2014-2015年苏州大学877土力学考研真题[东吴苏大考研网] 2012-2015年苏州大学873交通工程学考研真题[东吴苏大考研网] 2009-2015年854苏州大学电子技术基础(城市轨道)考研真题[东吴苏大考研网] 2011-2014年苏州大学818理论力学(城市轨道)考研真题[东吴苏大考研网] 2014-2015年苏州大学870生产计划与控制考研真题[东吴苏大考研网] 2004-2015年苏州大学842自动控制原理考研真题[东吴苏大考研网] 2008-2015年苏州大学841电子技术基础考研真题[东吴苏大考研网] 2000-2015年苏州大学840理论力学(机电)考研真题[东吴苏大考研网] 2014-2015年苏州大学833钢铁冶金学考研真题[东吴苏大考研网] 1999-2017年苏州大学872数据结构与操作系统考研真题[东吴苏大考研网] 2009-2015年苏州大学839管理信息系统与数据结构考研真题[东吴苏大考研网] 2010-2013年苏州大学871数字电路考研真题[东吴苏大考研网] 2014-2015年苏州大学850专业综合(2)考研真题【高等数学基础+生物信息学基础】[东吴苏大考研网] 2004-2015年苏州大学836半导体物理考研真题(换05、08)[东吴苏大考研网] 2014-2015年苏州大学627专业综合(1)考研真题(线性代数+生物化学)[东吴苏大考研网] 2010-2015年苏州大学858材料学(F)考研真题(不含11年)[东吴苏大考研网] 2011-2015年苏州大学857细胞生物学(F)考研真题[东吴苏大考研网] 苏州大学856物理化学(F)考研真题(2001-2006、2010-2015年)[东吴苏大考研网] 2010-2015年苏州大学855普通物理(F)考研真题[东吴苏大考研网] 2010-2015年苏州大学631生物化学(F)考研真题[东吴苏大考研网] 2010-2015年苏州大学629无机化学(F)考研真题[东吴苏大考研网] 2012-2015年苏州大学628有机化学(F)考研真题[东吴苏大考研网] 2010-2015年苏州大学602高等数学(F)考研真题[东吴苏大考研网] 2010-2011年苏州大学867化学教学论考研真题[东吴苏大考研网] 2009-2011年苏州大学834化学原理考研真题[东吴苏大考研网] 2001-2006、2010-2015年苏州大学853物理化学考研真题[东吴苏大考研网] 2013-2015年苏州大学867化工原理考研真题[东吴苏大考研网] 2001-2015年苏州大学835有机化学B考研真题[东吴苏大考研网] 2004-2006、2013-2015年苏州大学834分析化学考研真题[东吴苏大考研网] 2001-2015年苏州大学635有机化学A考研真题[东吴苏大考研网] 1999-2018年苏州大学861高分子化学考研真题[东吴苏大考研网] 2005-2015年苏州大学843材料结构基础考研真题[东吴苏大考研网] 2011-2015年苏州大学838普通物理(光学工程)考研真题[东吴苏大考研网] 2003-2015年苏州大学832普通物理考研真题[东吴苏大考研网] 2009-2015年苏州大学838信号与线性系统考研真题【历年苏州大学考研真题答案下载】[东吴苏大考研网] 2014-2015年苏州大学821材料物理化学考研真题[东吴苏大考研网] 2010-2015年苏州大学866中学物理教学法考研真题[东吴苏大考研网] 2014-2015年苏州大学化学综合考研真题[东吴苏大考研网] 2003-2015年苏州大学601高等数学考研真题[东吴苏大考研网] 2012年苏州大学632艺术理论考研真题[东吴苏大考研网] 2012-2013年苏州大学619戏剧戏曲艺术学考研真题[东吴苏大考研网] 2009-2015年苏州大学245德语考研真题(不含13)[东吴苏大考研网] 2001-2015年苏州大学244法语考研真题(不含03、13)[东吴苏大考研网] 2003-2015年苏州大学243日语考研真题(不含13)[东吴苏大考研网] 2005-2015年苏州大学242俄语考研真题与答案【不含07、08、13】[东吴苏大考研网] 2005-2015年苏州大学241英语考研真题(不含08、13)[东吴苏大考研网] 2010-2015年苏州大学211翻译硕士英语考研真题答案[东吴苏大考研网] 2002-2004、2011年苏州大学会计学考研真题[东吴苏大考研网] 2013-2015年苏州大学661教育学原理考研真题[东吴苏大考研网] 2002-2015年苏州大学634心理学专业基础综合(自命题)考研真题[东吴苏大考研网] 2012-2015年苏州大学881知识产权法学考研真题(无13)[东吴苏大考研网] 2011-2015年苏州大学434国际商务专业基础考研真题与答案[东吴苏大考研网] 1999、2007、2009-2015年苏州大学844纺织材料学考研真题[东吴苏大考研网] 2002-2017年苏州大学431金融学综合考研真题与答案解析[东吴苏大考研网] 2019苏州大学考研新闻与传播专业硕士复习全析(含真题与答案,共六册)[东吴苏大考研网] 2003-2015年苏州大学612绘画基础(色彩命题画)考研真题试卷[东吴苏大考研网] 2019苏大考研633教育学专业基础综合复习全析【含真题答案,共八册】[东吴苏大考研网] 2019苏大考研汉语国际教育硕士复习全析(共四册,含真题答案)[东吴苏大考研网] 2013-2015年苏州大学847金融学概论考研真题[东吴苏大考研网] 2007-2015年苏州大学617综合日语考研真题[东吴苏大考研网] 1998-2015年苏州大学658公共管理学考研真题(不含1999)[东吴苏大考研网] 2000、2004、2013-2016年苏州大学660世界史专业基础综合(自命题)考研真题[东吴苏大考研网] 2000-2017年苏州大学659中国史专业基础综合(自命题)考研真题与答案[东吴苏大考研网] 2002、2006-2015年苏州大学624药学基础综合(2)考研真题[东吴苏大考研网] 2006、2009-2017年苏州大学623生物综合考研真题[东吴苏大考研网] 2012-2015年苏州大学865影视评论写作考研真题[东吴苏大考研网] 2011-2015年苏州大学611影视艺术学考研真题[东吴苏大考研网] 2000-2015年苏州大学819教育管理学考研真题(不含03、04、07、08、09、11年)[东吴苏大考研网] 苏州大学311教育学专业基础综合真题与答案(2007-2017年)[东吴苏大考研网] 2000-2006,2010-2015年苏州大学856物理化学(F)考研真题。
考研教育学专业基础综合(教育研究方法)历年真题试卷汇编3

考研教育学专业基础综合(教育研究方法)历年真题试卷汇编3(总分:300.00,做题时间:180分钟)单项选择题(总题数:18,分数:208.00)1.【2010-39】近年来,一些教育研究者开始关注教育活动过程的动态生成、非线性特征及其中潜在的、无序的和偶然的因素。
这种发展方向体现了教育研究的( )。
(分数:11.60)A.经验一分析范式B.社会批判范式C.诠释一理解范式D.复杂思想范式2.【2014-39】教育测验运动和实验教育学在研究方法上主要体现了( )。
(分数:11.60)A.人本主义取向B.科学主义取C.解释主义取向D.历史主义取向3.【2019-40】张老师对小学生作业上的错字进行统计,分析错字类型,为探讨成因及教育对策提供依据,他采用的研究方法为( )。
(分数:11.60)A.测量法B.观察法C.文献研究法D.内容分析法4.【2013-40】某本科生将自己的毕业论文选题定为“中国大学生就业观调查研究”。
这一选题最容易受到质疑的地方是其( )。
(分数:11.60)A.创新性B.价值性C.规范性D.可行性5.【2016-41】如果抽样总体中存在周期性的波动和变化,为了保证样本的代表性,研究者应该避免采用的取样方法是( )。
(分数:11.60)A.简单随机抽样B.系统随机抽样C.分层随机抽样D.整群随机抽样6.【2013-41】在文献检索时,研究者不仅要搜集那些与自己观点一致的材料,也要搜集与自己观点不一致甚至对立的资料。
这体现了文献检索的( )。
(分数:11.60)A.矛盾性原则B.逆时性原则C.选择性原则D.全面性原则7.【2018-41】某研究者欲全面了解并研读近五年来国内核心期刊上发表的有关“教师教学自主权”的研究成果,应检索( )。
(分数:11.60)A.人大报刊复印资料B.中文核心期刊要目总览KI中国期刊全文数据库KI中国年鉴全文数据库8.【2011-41】某研究者欲考察教师对学生期望值的高低与师生关系之间的相关性,他每天用一小时的时间去教室随机观察师生互动行为,并根据实际情况灵活记录观察结果。
2019年苏州大学教育综合333真题

2019年苏州大学教育综合333真题(凯程首发)
凯程教育学/教育硕士教研组整理
一、填空
二、名词解释
1.道尔顿制
2.三舍法
3.先行组织者
4.五育并举
三、简答
1.简述人身心发展的特点
2.简述科尔伯格道德阶段发展论
3.简述教育生物起源说
4.简述孔子的教师观
5.简述夸美纽斯的教育原则
四、论述
1.赫尔巴特四形式教学
2.教育对人的功能和社会的功能的关系
五、材料分析题
材料学生给老师打评价,一个年轻语文老师得了D很生气,不上课了,学生只能自习,耽误了一周影响了班级学习成绩和师生关系。
联系材料运用教育学原理解读,并提出建立良好师生关系的建议。
苏州大学333教育综合考研真题试卷.docx

苏州大学2010年全日制教育硕士教育综合333 真题一、名词解释(每小题 5 分,共 30 分)1、人的发展2、教育的社会流动功能3、终身教育4、元认知5、骑士教育6、有教无类二、简答题(每小题10 分,共 40 分)1、教师角色的冲突有哪些?如何解决?2、比较孟子与荀子人性观及他们对教育的作用的认识。
3、学生认知的差异有哪些表现?为此,教学应注意哪些方面?4、简述卢梭的自然教育思想。
三、分析论述题(每题20 分,共 80 分)1、教育的相对独立性表现在哪些方面?并就此谈谈你对教育与社会发展的关系的认识。
2、试论隋唐科举制与学校教育的关系,并分析其在历史上的影响。
3、论述皮亚杰的道德认知发展理论,并联系实际加以评价。
4、论述文艺复兴时期人文主义教育的主要特征、影响及其贡献。
苏州大学 2011 年全日制教育硕士教育综合333 真题一、名词解释(每小题 5 分,共 30分)1、狭义的课程2、终身教育3、鸿都门学4、元认知 5 、白板说 6 、教育的社会流动功能二、简答题(每小题10 分,共 40 分)1、教师个体专业性发展的内涵包括哪些方面2、简述梁启超“新民”的教育目的观3、简述杜威的道德教育思想4、简述建构主义的学习观三、分析论述题(每题20 分,共 80 分)1、结合现实分析全面发展教育各组成部分的相互关系2、论陶行知“生活即教育”的思想内涵,并联系实际分析其现实意义3、在外国近现代教育史上,你喜欢哪一位教育家,并就此阐释喜欢的原因。
4、联系当前实际,阐述学生品德不良的成因及其教育策略苏州大学 2012 年教育综合考研试题(回忆版)一、名词解释:1. 学习策略2.学制3. 太学4.恩物5. 教育6. 教学二、简答题:1.教育目的与教育方针的不同之处? 2.学校管理校本化基本含义和意义3.科尔伯格道德发展阶段理论 4.三、论述题:1.试述有教无类2.学习动机的激发措施 3 .永恒主义教育4 .教师专业发展苏州大学 2013 年 333 教育综合真题回忆版一、名词解释题1. 教育家2.双轨制3.稷下学宫4.爱弥儿5.恩物6.倒摄抑制7.心智技能8. 皮格马利翁效应二、简答题1、简述欧洲文艺复兴时期人文主义教育思想的基本特征有哪些?(有点模糊)2、简述德育过程的基本特征有哪些?3、简述夸美纽斯的教育思想的基本主张有?4、简述建构主义学习理论的基本特征?5、简述一下创造(还是创新)型心理结构的特征?三、论述题1、根据教育过程的性质,阐述一下你在教育过程中应该注意处理好的几种关系?2、根据教育对社会的发展作用,论述下孔子“庶,富,教。
2018 年苏州大学 333 教育综合考研真题

2018 年苏州大学 333 教育综合真题
一、名词解释(每小题 5 分,共 30 分)
1、发现学习
2、义务教育
3、教学模式
4、进步主义教育运动
5、朱子读书法
6、学习动机
二、简答题(每小题 10 分,共 50 分)
1、布鲁纳的认知结构教学原则
2、教育起源学说的主要观点
3、影响人的身心发展的主要因素
4、经验主义课程论代表人物及观点
5、社会本位论主要观点
三、论述题(每小题 20 分,共 40 分)
1、教学中有哪些教学原则,任选一个举例展开论述
2、结合人的全面发展理论,说明中国学生核心素养的构成四、案例分析(30 分)1、大意是学生英语成绩差,老师说他蠢猪,好好学习后英语考试第二名,老师说他的成绩是抄的,然后任选角度,进行论述
2、谈谈你对教学回归学生生活的理解。
十年真题(2010_2019)高考数学真题分类汇编专题17不等式选讲(理)(含解析)
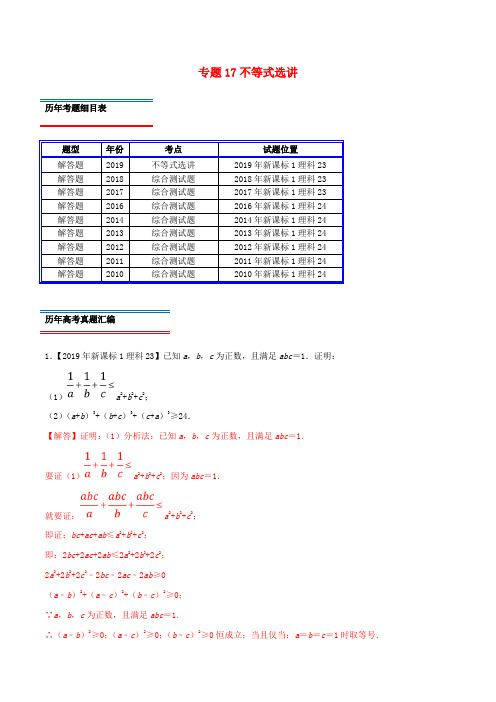
专题17不等式选讲历年考题细目表题型年份考点试题位置解答题2019 不等式选讲2019年新课标1理科23解答题2018 综合测试题2018年新课标1理科23解答题2017 综合测试题2017年新课标1理科23解答题2016 综合测试题2016年新课标1理科24解答题2014 综合测试题2014年新课标1理科24解答题2013 综合测试题2013年新课标1理科24解答题2012 综合测试题2012年新课标1理科24解答题2011 综合测试题2011年新课标1理科24解答题2010 综合测试题2010年新课标1理科24历年高考真题汇编1.【2019年新课标1理科23】已知a,b,c为正数,且满足abc=1.证明:(1)a2+b2+c2;(2)(a+b)3+(b+c)3+(c+a)3≥24.【解答】证明:(1)分析法:已知a,b,c为正数,且满足abc=1.要证(1)a2+b2+c2;因为abc=1.就要证:a2+b2+c2;即证:bc+ac+ab≤a2+b2+c2;即:2bc+2ac+2ab≤2a2+2b2+2c2;2a2+2b2+2c2﹣2bc﹣2ac﹣2ab≥0(a﹣b)2+(a﹣c)2+(b﹣c)2≥0;∵a,b,c为正数,且满足abc=1.∴(a﹣b)2≥0;(a﹣c)2≥0;(b﹣c)2≥0恒成立;当且仅当:a=b=c=1时取等号.即(a﹣b)2+(a﹣c)2+(b﹣c)2≥0得证.故a2+b2+c2得证.(2)证(a+b)3+(b+c)3+(c+a)3≥24成立;即:已知a,b,c为正数,且满足abc=1.(a+b)为正数;(b+c)为正数;(c+a)为正数;(a+b)3+(b+c)3+(c+a)3≥3(a+b)•(b+c)•(c+a);当且仅当(a+b)=(b+c)=(c+a)时取等号;即:a=b=c=1时取等号;∵a,b,c为正数,且满足abc=1.(a+b)≥2;(b+c)≥2;(c+a)≥2;当且仅当a=b,b=c;c=a时取等号;即:a=b=c=1时取等号;∴(a+b)3+(b+c)3+(c+a)3≥3(a+b)•(b+c)•(c+a)≥3×8••24abc=24;当且仅当a=b=c=1时取等号;故(a+b)3+(b+c)3+(c+a)3≥24.得证.故得证.2.【2018年新课标1理科23】已知f(x)=|x+1|﹣|ax﹣1|.(1)当a=1时,求不等式f(x)>1的解集;(2)若x∈(0,1)时不等式f(x)>x成立,求a的取值范围.【解答】解:(1)当a=1时,f(x)=|x+1|﹣|x﹣1|,由f(x)>1,∴或,解得x,故不等式f(x)>1的解集为(,+∞),(2)当x∈(0,1)时不等式f(x)>x成立,∴|x+1|﹣|ax﹣1|﹣x>0,即x+1﹣|ax﹣1|﹣x>0,即|ax﹣1|<1,∴﹣1<ax﹣1<1,∴0<ax<2,∵x∈(0,1),∴a>0,∴0<x,∴a∵2,∴0<a≤2,故a的取值范围为(0,2].3.【2017年新课标1理科23】已知函数f(x)=﹣x2+ax+4,g(x)=|x+1|+|x﹣1|.(1)当a=1时,求不等式f(x)≥g(x)的解集;(2)若不等式f(x)≥g(x)的解集包含[﹣1,1],求a的取值范围.【解答】解:(1)当a=1时,f(x)=﹣x2+x+4,是开口向下,对称轴为x的二次函数,g(x)=|x+1|+|x﹣1|,当x∈(1,+∞)时,令﹣x2+x+4=2x,解得x,g(x)在(1,+∞)上单调递增,f(x)在(1,+∞)上单调递减,∴此时f(x)≥g(x)的解集为(1,];当x∈[﹣1,1]时,g(x)=2,f(x)≥f(﹣1)=2.当x∈(﹣∞,﹣1)时,g(x)单调递减,f(x)单调递增,且g(﹣1)=f(﹣1)=2.综上所述,f(x)≥g(x)的解集为[﹣1,];(2)依题意得:﹣x2+ax+4≥2在[﹣1,1]恒成立,即x2﹣ax﹣2≤0在[﹣1,1]恒成立,则只需,解得﹣1≤a≤1,故a的取值范围是[﹣1,1].4.【2016年新课标1理科24】已知函数f(x)=|x+1|﹣|2x﹣3|.(Ⅰ)在图中画出y=f(x)的图象;(Ⅱ)求不等式|f(x)|>1的解集.【解答】解:(Ⅰ)f(x),由分段函数的图象画法,可得f(x)的图象,如右:(Ⅱ)由|f(x)|>1,可得当x≤﹣1时,|x﹣4|>1,解得x>5或x<3,即有x≤﹣1;当﹣1<x时,|3x﹣2|>1,解得x>1或x,即有﹣1<x或1<x;当x时,|4﹣x|>1,解得x>5或x<3,即有x>5或x<3.综上可得,x或1<x<3或x>5.则|f(x)|>1的解集为(﹣∞,)∪(1,3)∪(5,+∞).5.【2014年新课标1理科24】若a>0,b>0,且.(Ⅰ)求a3+b3的最小值;(Ⅱ)是否存在a,b,使得2a+3b=6?并说明理由.【解答】解:(Ⅰ)∵a>0,b>0,且,∴2,∴ab≥2,当且仅当a=b时取等号.∵a3+b3 ≥224,当且仅当a=b时取等号,∴a3+b3的最小值为4.(Ⅱ)∵2a+3b≥22,当且仅当2a=3b时,取等号.而由(1)可知,2246,故不存在a,b,使得2a+3b=6成立.6.【2013年新课标1理科24】已知函数f(x)=|2x﹣1|+|2x+a|,g(x)=x+3.(Ⅰ)当a=﹣2时,求不等式f(x)<g(x)的解集;(Ⅱ)设a>﹣1,且当x∈[,]时,f(x)≤g(x),求a的取值范围.【解答】解:(Ⅰ)当a=﹣2时,求不等式f(x)<g(x)化为|2x﹣1|+|2x﹣2|﹣x﹣3<0.设y=|2x﹣1|+|2x﹣2|﹣x﹣3,则y,它的图象如图所示:结合图象可得,y<0的解集为(0,2),故原不等式的解集为(0,2).(Ⅱ)设a>﹣1,且当x∈[,]时,f(x)=1+a,不等式化为1+a≤x+3,故x≥a﹣2对x∈[,]都成立.故a﹣2,解得a,故a的取值范围为(﹣1,].7.【2012年新课标1理科24】已知函数f(x)=|x+a|+|x﹣2|①当a=﹣3时,求不等式f(x)≥3的解集;②f(x)≤|x﹣4|若的解集包含[1,2],求a的取值范围.【解答】解:(1)当a=﹣3时,f(x)≥3 即|x﹣3|+|x﹣2|≥3,即,可得x≤1;,可得x∈∅;,可得x≥4.取并集可得不等式的解集为 {x|x≤1或x≥4}.(2)原命题即f(x)≤|x﹣4|在[1,2]上恒成立,等价于|x+a|+2﹣x≤4﹣x在[1,2]上恒成立,等价于|x+a|≤2,等价于﹣2≤x+a≤2,﹣2﹣x≤a≤2﹣x在[1,2]上恒成立.故当 1≤x≤2时,﹣2﹣x的最大值为﹣2﹣1=﹣3,2﹣x的最小值为0,故a的取值范围为[﹣3,0].8.【2011年新课标1理科24】设函数f(x)=|x﹣a|+3x,其中a>0.(Ⅰ)当a=1时,求不等式f(x)≥3x+2的解集(Ⅱ)若不等式f(x)≤0的解集为{x|x≤﹣1},求a的值.【解答】解:(Ⅰ)当a=1时,f(x)≥3x+2可化为|x﹣1|≥2.由此可得x≥3或x≤﹣1.故不等式f(x)≥3x+2的解集为{x|x≥3或x≤﹣1}.(Ⅱ)由f(x)≤0得|x﹣a|+3x≤0此不等式化为不等式组或即或因为a>0,所以不等式组的解集为{x|x}由题设可得1,故a=29.【2010年新课标1理科24】设函数f(x)=|2x﹣4|+1.(Ⅰ)画出函数y=f(x)的图象:(Ⅱ)若不等式f (x )≤ax 的解集非空,求a 的取值范围. 【解答】解:(Ⅰ)由于f (x ),函数y =f (x )的图象如图所示.(Ⅱ)由函数y =f (x )与函数y =ax 的图象可知,极小值在点(2,1)当且仅当a <﹣2或a 时,函数y =f (x )与函数y =ax 的图象有交点.故不等式f (x )≤ax 的解集非空时,a 的取值范围为(﹣∞,﹣2)∪[,+∞).考题分析与复习建议本专题考查的知识点为:解绝对值不等式、证明不等式、利用不等式恒成立求参数的值或范围,求含有绝对值的函数最值也是考查的热点.求解的一般方法是去掉绝对值,也可以借助数形结合求解.历年考题主要以解答题题型出现,重点考查的知识点为解绝对值不等式、证明不等式、利用不等式恒成立求参数的值或范围,求含有绝对值的函数最值也是考查的热点.预测明年本考点题目会比较稳定,备考方向以知识点解绝对值不等式、利用不等式恒成立求参数的值或范围,证明不等式为重点较佳.最新高考模拟试题1.已知函数()22()f x x a x a R =-+-∈. (1)当2a =时,求不等式()2f x >的解集;(2)若[2,1]x ∈-时不等式()32f x x ≤-成立,求实数a 的取值范围. 【答案】(1)2{|3x x <或()4cos(2)6f x x π=-;(2)空集. 【解析】解:(1)不等式()2f x >,即2222x x -+->.可得22222x x x ≥⎧⎨-+->⎩,或122222x x x <<⎧⎨-+->⎩或12222x x x ≤⎧⎨--+>⎩,解得23x <或2x >,所以不等式的解集为2{|2}3x x x <>或.(2)当[2,1]x ∈-时,220x -<,所以()22f x x a x =-+-, 由()32f x x ≤-得1x a -≤,即11a x a -≤≤+,则1211a a -≤-⎧⎨+≥⎩,该不等式无解,所以实数a 的取值范围是空集(或者∅). 2.已知()221f x x x =-++. (1)求不等式()6f x <的解集;(2)设m 、n 、p 为正实数,且()3m n p f ++=,求证:12mn np pm ++≤. 【答案】(1) ()1,3- (2)见证明 【解析】(1)①2x ≥时,()24133f x x x x =-++=-, 由()6f x <,∴336x -<,∴3x <,即23x ≤<,②12x -<<时,()4215f x x x x =-++=-,由()6f x <,∴56x -<,∴1x >-,即12x -<<, ③1x ≤-时,()42133f x x x x =---=-,由()6f x <,∴336x -<,∴1x >-,可知无解, 综上,不等式()6f x <的解集为()1,3-; (2)∵()221f x x x =-++,∴()36f =,∴()36m n p f ++==,且,,m n p 为正实数∴()222222236m n p m n p mn mp np ++=+++++=, ∵222m n mn +≥,222m p mp +≥,222n p np +≥, ∴222m n p mn mp np ++≥++,∴()()2222222363m n p m n p mn mp np mn mp np ++=+++++=≥++ 又,,m n p 为正实数,∴可以解得12mn np pm ++≤. 3.[选修4—5:不等式选讲]已知函数()|||2|(0)f x x m x m m =--+>. (1)当1m =,求不等式()1f x ≥的解集;(2)对于任意实数,x t ,不等式()21f x t t <++-恒成立,求实数m 的取值范围. 【答案】(1)113x x ⎧⎫-≤≤-⎨⎬⎩⎭;(2)()0,2 【解析】(1)当1m =时,()1f x ≥为:1211x x --+≥当1x ≥时,不等式为:1211x x ---≥,解得:3x ≤-,无解当112x -≤<时,不等式为:1211x x -+--≥,解得:13x ≤-,此时1123x -≤≤- 当12x <-时,不等式为:1211x x -+++≥,解得:1x -≥,此时112x -≤<-综上所述,不等式的解集为113x x ⎧⎫-≤≤-⎨⎬⎩⎭(2)对于任意实数x ,t ,不等式()21f x t t <++-恒成立等价于()()max min |2||1|f x t t <++- 因为|2||1||(2)(1)|3t t t t ++-≥+--=,当且仅当(2)(1)0t t +-≤时等号成立 所以()min |2||1|3t t ++-=因为0m >时,()2f x x m x m =--+=2,23,22,m x m x m x x m x m x m ⎧+<-⎪⎪⎪--≤≤⎨⎪-->⎪⎪⎩,函数()f x 单调递增区间为(,)2m -∞-,单调递减区间为(,)2m-+∞ ∴当2m x =-时,()max 322m mf x f ⎛⎫=-= ⎪⎝⎭332m∴<,又0m >,解得:02m << ∴实数m 的取值范围()0,24.选修4-5不等式选讲已知关于x 的不等式20x m x -+≤的解集为{|2}x x ≤-,其中0m >. (1)求m 的值;(2)若正数a ,b ,c 满足a b c m ++=,求证:2222b c aa b c++≥.【答案】(1)2m =(2)见证明 【解析】(1)由题意知:20x m x -+≤即20x m x m x ≥⎧⎨-+≤⎩或20x mm x x ≤⎧⎨-+≤⎩化简得:3x mm x ≥⎧⎪⎨≤⎪⎩或x m x m ≤⎧⎨≤-⎩ 0m >Q ∴不等式组的解集为{}x x m ≤- 2m ∴-=-,解得:2m =(2)由(1)可知,2a b c ++=由基本不等式有:22b a b a +≥,22c b c b+≥,22a c a c +≥三式相加可得:222222b c a a b c b c a a b c +++++≥++222b c a a b c a b c ∴++≥++,即:2222b c a a b c++≥ 5.选修4-5:不等式选讲 已知函数()13f x x x a =+++ (1)当1a =-时,解不等式()2f x ≥;(2)若存在0x 满足00()211f x x ++<,求实数a 的取值范围. 【答案】(1) 1|02x x x ⎧⎫≤≥⎨⎬⎩⎭或 (2) 24a << 【解析】(1)当1a =-时,()|1||31|f x x x =++-,当13x ≥时,不等式等价于1312x x ++-≥,解得12x ≥,12x ∴≥; 当113x -<<时,不等式等价于1312x x +-+≥,解得0x ≤,10x ∴-<≤;当1x ≤-时,不等式等价于1312x x ---+≥,解得12x ≤-,1x -∴≤.综上所述,原不等式的解集为1|02x x x ⎧⎫≤≥⎨⎬⎩⎭或. (2)由()00211f x x ++<,得003131x x a +++<,而()()000000313333333|3|x x a x x a x x a a +++=+++≥+-+=-, (当且仅当()()003330x x a ++≤时等号成立) 由题可知min (()2|1|)1f x x ++<,即31a -<, 解得实数a 的取值范围是24a <<. 6.已知函数()|2|f x ax =-.(Ⅰ)当4a =时,求不等式()|42|8f x x ++≥的解集;(Ⅱ)若[2,4]x ∈时,不等式()|3|3f x x x +-≤+成立,求a 的取值范围.【答案】(I )(,1][1,)-∞-+∞U ;(II )[1,2]- 【解析】(I )当4a =时,原不等式即|42||42|8x x -++≥,即|21||21|4x x -++≥.当12x ≥时,21214x x -++≥,解得1x ≥,∴1x ≥; 当1122x -≤≤时,12214x x -++≥,无解;当12x ≤-时,12214x x ---≥,解得1x ≤-,∴1x ≤-;综上,原不等式的解集为(,1][1,)-∞-+∞U(II )由()|3|3f x x x +-≤+得|2||3|3ax x x -+-≤+(*) 当[2,3]x ∈时,(*)等价于|2|33|2|2ax x x ax x -+-≤+⇔-≤即22a x -≤,所以2222a x x -+≤≤+恒成立,所以813a -≤≤ 当(3,4]x ∈时,(*)等价于|2|33|2|6ax x x ax -+-≤+⇔-≤ 即48ax -≤≤,所以48a x x-≤≤恒成立,所以12a -≤≤ 综上,a 的取值范围是[1,2]-7.已知函数()21f x x x a =-++,()2g x x =+. (1)当1a =-时,求不等式()()f x g x <的解集;(2)设12a >-,且当1,2x a ⎡⎫∈-⎪⎢⎣⎭,()()f x g x ≤,求a 的取值范围.【答案】(1)()0,2;(2)11,23⎛⎤- ⎥⎝⎦ 【解析】(1)当1a =-时,不等式()()f x g x <化为:21120x x x -+---<当12x ≤时,不等式化为12120x x x -+---<,解得:102x <≤当112x <≤时,不等式化为21120x x x -+---<,解得:112x <≤当1x >时,不等式化为21120x x x -+---<,解得:12x << 综上,原不等式的解集为()0,2 (2)由12a x -≤<,得221a x -≤<,21210a x --≤-< 又102x a a ≤+<+ 则()()211f x x x a x a =--++=-++∴不等式()()f x g x ≤化为:12x a x -++≤+得21a x ≤+对1,2x a ⎡⎫∈-⎪⎢⎣⎭都成立 21a a ∴≤-+,解得:13a ≤又12a >-,故a 的取值范围是11,23⎛⎤- ⎥⎝⎦8.已知函数()|2|f x x =-.(Ⅰ)求不等式()|1|f x x x <++的解集;(Ⅱ)若函数5log [(3)()3]y f x f x a =++-的定义域为R ,求实数a 的取值范围.【答案】(I )1,3⎛⎫+∞ ⎪⎝⎭(II )(,1)-∞【解析】解:(I )由已知不等式()|1|f x x x <++,得|2||1|x x x -<++, 当2x ≥时,不等式为21x x x -<++,解得3x >-,所以2x ≥; 当12x -<<时,不等式为21x x x -<++,解得13x >,所以123x <<; 当1x ≤-时,不等式为21x x x -<--,解得3x >,此时无解. 综上:不等式的解集为1,3⎛⎫+∞ ⎪⎝⎭.(II )若5log [(3)()3]y f x f x a =++-的定义域为R ,则(3)()30f x f x a ++->恒成立. ∵|1||2|3|12|333x x a x x a a ++--≥+-+-=-,当且仅当[1,2]x ∈-时取等号. ∴330a ->,即1a <.所以实数a 的取值范围是(,1)-∞. 9.已知函数()123f x x x =-+-. (Ⅰ)解关于x 的不等式()4f x ≤;(Ⅱ)若()20f x m m -->恒成立,求实数m 的取值范围.【答案】(Ⅰ)111,3⎡⎤⎢⎥⎣⎦;(Ⅱ)()2,1-.【解析】解:(I )当1x ≤时,不等式为:()1234x x -+-≤,解得1x ≥,故1x =. 当13x <<时,不等式为:()1234x x -+-≤,解得1x ≥,故13x <<1<x <3, 当3x ≥时,不等式为:()1234x x -+-≤,解得113x ≤,故1133x ≤≤. 综上,不等式()4f x ≤的解集为111,3⎡⎤⎢⎥⎣⎦.(II )由()20f x m m -->恒成立可得()2m m f x +<恒成立.又()37,35,1337,1x x f x x x x x -≥⎧⎪=-+<<⎨⎪-+≤⎩,故()f x 在(],1-∞上单调递减,在()1,3上单调递减,在[)3,+∞上单调递增,∴()f x 的最小值为()32f =. ∴22m m +<,解得21m -<<. 即m 的最值范围是()2,1-.10.已知函数()211f x x x =-++. (Ⅰ)解不等式()3f x ≥;(Ⅱ)记函数()f x 的最小值为m ,若,,a b c 均为正实数,且232a b c m ++=,求222a b c ++的最小值. 【答案】(Ⅰ){}11x x x ≤-≥或;(Ⅱ)914. 【解析】(Ⅰ)由题意, 3,11()2,1213,2x x f x x x x x ⎧⎪-≤-⎪⎪=--<<⎨⎪⎪≥⎪⎩,所以()3f x ≥等价于133x x ≤-⎧⎨-≥⎩或11223x x ⎧-<<⎪⎨⎪-≥⎩或1233x x ⎧≥⎪⎨⎪≥⎩.解得:1x ≤-或1x ≥,所以不等式的解集为{}11x x x ≤-≥或; (Ⅱ)由(1)可知,当12x =时, ()f x 取得最小值32,所以32m =,即233a b c ++=, 由柯西不等式得2222222()(123)(23)9a b c a b c ++++≥++=, 整理得222914a b c ++≥, 当且仅当123a b c ==时, 即369,,141414a b c ===时等号成立.所以222a b c ++的最小值为914.11.已知函数()12f x x a x =+++. (Ⅰ)求1a =时,()3f x ≤的解集;(Ⅱ)若()f x 有最小值,求a 的取值范围,并写出相应的最小值. 【答案】(Ⅰ)[3,0]-; (Ⅱ)见解析. 【解析】(Ⅰ)当1a =时,232()12121231x x f x x x x x x --≤-⎧⎪=+++=-<<-⎨⎪+≥-⎩∵()3f x ≤当2x -≤时()233f x x =--≤解得32x -≤≤-当21x -<<-时()13f x =≤恒成立当1x -≥时()233f x x =+≤解得10x -≤≤ 综上可得解集[3,0]-.(Ⅱ)(1)212()12(1)2121(1)211a x a x f x x a x a x a x a x a x -+--≤-⎧⎪=+++=-+--<<-⎨⎪+++≥-⎩当(1)0a -+>,即1a <-时,()f x 无最小值; 当(1)0a -+=,即1a =-时,()f x 有最小值1-;当(1)0a -+<且10a -≤,即11a -<≤时, min ()(1)f x f a =-= 当(1)0a -+<且10a ->,即1a >时, min ()(2)1f x f =-= 综上:当1a <-时,()f x 无最小值; 当1a =-时,()f x 有最小值1-;当11a -<≤时, min ()(1)f x f a =-= ; 当1a >时, min ()(2)1f x f =-=; 12.选修4-5:不等式选讲 已知函数()|23||1|f x x x =--+. (1)求不等式()6f x ≤的解集;(2)设集合M 满足:当且仅当x M ∈时,()|32|f x x =-,若,a b M ∈,求证:228223a b a b -++≤. 【答案】(1) {}210x x -≤≤;(2)见解析. 【解析】(1)()4,1323132,1234,2x x f x x x x x x x ⎧⎪-+<-⎪⎪=--+=-+-≤≤⎨⎪⎪->⎪⎩当1x <- 时,46x -+≤ ,得2x -≥ ,故21x -≤<-; 当312x -≤≤时,326x -+≤ ,得43x ≥- ,故312x -≤<;当32x >时,46x -≤ ,得10x ≤ ,故3102x <≤; 综上,不等式()6f x ≤的解集为{}210x x -≤≤(2)由绝对值不等式的性质可知()231(23)(1)32f x x x x x x =--+≤-++=- 等价于23(1)32x x x -≤-++-,当且仅当(23)(1)0x x -+≤,即213x -≤≤时等号成立,故21,3M ⎡⎤=-⎢⎥⎣⎦所以221,133a b -≤≤-≤≤, 所以222510(1),4(1)99a b ≤-≤-≤--≤-, 即228(1)(1)3a b ---≤.13.[选修4—5:不等式选讲] 已知函数()31f x x m x m =---- (1)若1m =,求不等式()1f x <的解集.(2)对任意的x R ∈,有()(2)f x f ≤,求实数m 的取值范围. 【答案】(1)(,3)-∞;(2)1123m -≤≤ 【解析】(1)()141f x x x =---<,所以11441(4)11(4)1141x x x x x x x x x <≤≤>⎧⎧⎧⎨⎨⎨---<---<--+<⎩⎩⎩或或解之得不等式()1f x <的解集为(,3)-∞. (2)当131,2m m m +>>-时,由题得2必须在3m+1的右边或者与3m+1重合, 所以1231,3m m ≥+∴≤,所以1123m -<≤,当131,2m m m +==-时,不等式恒成立,当131,2m m m +<<-时,由题得2必须在3m+1的左边或者与3m+1重合,由题得1231,3m m ≤+≥,所以m 没有解.综上,1123m -≤≤. 14.已知()21f x x x =+-. (1)证明()1f x x +≥; (2)若,,a b c +∈R ,记33311134abc a b c +++的最小值为m ,解关于x 的不等式()f x m <. 【答案】(1)见证明;(2) 2433x x ⎧⎫-<<⎨⎬⎩⎭【解析】(1)()2212211f x x x x x x +=+-≥-+=.当且仅当()2x 2x 10-≤,等号成立(2)∵333333311131333333234444abc abc abc abc m a b c a b c abc abc +++≥+=+≥⋅==,当且仅当a=b=c 等号成立由不等式()3f x <即()213f x x x =+-<.由()31,01211,02131,2x x f x x x x x x x ⎧⎪-+≤⎪⎪=+-=-<<⎨⎪⎪-≥⎪⎩得:不等式()3f x <的解集为2433x x ⎧⎫-<<⎨⎬⎩⎭.15.选修4—5:不等式选讲已知函数()11f x x mx =++-,m R ∈。
2010年苏州大学教育综合真题)

2010年苏州大学教育综合真题一、名词解释(每小题5分,共30分)1.人的发展2.教育的社会流动功能3.终身教育4.元认知5.骑士教育6.有教无类二、简答题(每小题10分,共40分)1.教师角色的冲突有哪些?如何解决?2.比较孟子与苟子人性观及他们对教育的作用的认识。
3.学生认知的差异有哪些表现?为此,教学应注意哪些方面?4.简述卢梭的自然教育思想。
三、分析论述题(每题20分,共80分)1.教育的相对独立性表现在哪些方面?并就此谈谈你对教育与社会发展的关系的认识。
2.试论隋唐科举制与学校教育的关系,并分析其在历史上的影响。
3.论述皮亚杰的道德认知发展理论,并联系实际加以评价。
4.论述文艺复兴时期人文主义教育的主要特征、影响及其贡献。
2010年苏州大学教育综合真题详解一、名词解释1.人的发展:“人的发展”一般有两种释义。
一种是把它与物种发展史联系起来,将它看成是人类在地球上出现及其进化的过程,即人类的发展或进化;另一种更为通常的解释是把它与个体发展联系起来,将它看成是人类个体的成长变化过程。
从这个层面上说,人的发展主要是指随着年龄的增长,个体蕴涵的潜能在社会实践活动中不断解放并转化为现实个性的过程,这是一种包含着量和质、内容和结构的不断变化的过程,是从简单到复杂的演化过程。
22.教育的社会流动功能:教育的社会流动功能是指社会成员通过教育的培养、筛选与提高,能够在不同的社会区域、社会层次、职业岗位、科层组织之间转换、调整与变动,以充分发挥其个性特长,展现其智慧才能,实现其人生抱负。
教育的社会流动功能,按其流向可分为横向流动功能与纵向流动功能。
3.【解析】参考答案参见2010年东北师大教育综合真题外教史部分名词解释第1题。
元认知:元认知是对个人自己认知过程的知识以及调节认知过程的能力,它是对思维和学习活动的知识和控制。
简单地说,元认知就是“对认知的认知”,其实质是对认知活动的自我意识和自我调节,其结构包括三个方面:元认知知识、元认知体验和元认知监控。
2011年苏州大学333教育综合[专业硕士]考研真题及部分详解(附赠)【圣才出品】
![2011年苏州大学333教育综合[专业硕士]考研真题及部分详解(附赠)【圣才出品】](https://img.taocdn.com/s3/m/60db835a4b73f242326c5f1d.png)
2011年苏州大学333教育综合[专业硕士]考研真题(附赠)一、名词解释(每小题5分,共30分)1.狭义的课程2.终身教育3.鸿都门学4.元认知5.白板说6.教育的社会流动功能二、简答题(每小题10分,共40分)1.教师个体专业性发展的内涵包括哪些方面?2.简述梁启超“新民”的教育目的观。
3.简述杜威的道德教育思想。
4.简述建构主义的学习观。
三、分析论述题(每题20分,共80分)1.结合现实分析全面发展教育各组成部分的相互关系。
2.论陶行知“生活即教育”的思想内涵,并联系实际分析其现实意义。
3.在外国近现代教育史上,你喜欢哪一位教育家,并就此阐释喜欢的原因。
4.联系当前实际,阐述学生品德不良的成因及其教育策略。
2011年苏州大学333教育综合[专业硕士]考研真题及部分详解(附赠)一、名词解释(每小题5分,共30分)1.狭义的课程答:“课程”狭义指某一门学科。
如数学课程,历史课程等。
课程,简单是指课业及其进程而言。
我国宋代教育家朱熹说过:“宽著期限,紧著课程。
”其中“课程”一词就包含有学习的范围和进程的意思。
在西方,“课程”一词的英语是Curriculum,来源于拉丁文,意为“跑马道”,指赛马场上的跑道而言。
用在教育上,指学校的课程。
意思是学校学生所应学习的学科总和及其进程和安排。
近代学校兴起以来,课程有广义、狭义之分,广义指为了实现学校培养目标而规定的所有学科(即教学科目)的总和,或指学生在教师指导下各种活动的总和。
如中学课程,小学课程。
2.终身教育答:终身教育是指人们在一生各阶段当中所受各种教育的总和,是人所受不同类型教育的统一综合。
包括教育体系的各个阶段和各种方式,既有学校教育,又有社会教育;既有正规教育,也有非正规教育。
主张在每一个人需要的时刻以最好的方式提供必要的知识和技能。
终身教育思想成为很多国家教育改革的指导方针。
终身教育首先重视作为教育基础的个人和小组,学习的主体是个人、小组,而不是课程和教师。
333教育综合试题及答案

333教育综合试题及答案本文旨在提供关于333教育综合试题及答案的详细信息,帮助读者了解该套试题,并给予解析和答案,以便读者进行学习和复习。
一、选择题1. 下列哪个城市被称为“东方的威尼斯”?A. 东京B. 上海C. 巴黎D. 纽约答案:B解析:上海因其众多的河道和水网而被称为“东方的威尼斯”,是历史和现代文化交融的城市。
2. 以下哪个是地球上面积最大的洲?A. 亚洲B. 欧洲C. 非洲D. 北美洲答案:A解析:亚洲是地球上面积最大的洲,占地球陆地面积的三分之二以上。
3. 以下哪个科学家发现了万有引力定律?A. 爱因斯坦B. 牛顿C. 达尔文D. 狄拉克答案:B解析:牛顿发现了万有引力定律,是经典物理学的基石之一。
二、填空题1. 中国的首都是________。
答案:北京2. 2022年冬奥会将在中国的哪个城市举办?答案:北京3. 世界上最长的河流是________。
答案:尼罗河三、简答题1. 请简要描述人体呼吸系统的主要功能。
答案:人体呼吸系统的主要功能包括供氧和排出二氧化碳。
通过呼吸系统,人体吸入氧气,经过肺部的呼吸作用,将氧气输送到全身各个组织和器官,以满足身体的需氧代谢。
同时,呼吸系统也负责排出体内产生的二氧化碳,维持酸碱平衡。
2. 什么是气候变化?列举至少两个导致气候变化的原因。
答案:气候变化是指长期时间尺度上大气环境的变化,包括气温、降水量、风向和风速等方面的变化。
导致气候变化的原因主要包括自然因素和人为因素。
自然因素包括太阳辐射、地球自转和地球轨道变化等;人为因素包括森林砍伐、化石燃料的燃烧和工业化排放等。
四、解答题1. 请简要介绍一种环保措施,以减少塑料污染。
答案:减少塑料污染的一种环保措施是推广使用可降解塑料。
可降解塑料是指在特定条件下可以被微生物分解成水和二氧化碳,对环境影响较小。
相比于传统塑料,可降解塑料可以快速降解,减少对海洋和土壤的污染。
政府和企业可以加大对可降解塑料的研发和推广力度,同时鼓励消费者使用可降解塑料制品。
精选-苏州大学333历年真题

2013苏州大学333教育综合真题回忆版一、名词解释题1.教育家2.双轨制3.稷下学宫4.爱弥儿5.恩物6.倒摄抑制7.心智技能8.皮格马利翁效应二、简单题1.简述欧洲文艺复兴时期人文主义教育思想的基本特征有哪些?(有点模糊)2.简述德育过程的基本特征有哪些?3.简述夸美纽斯的教育思想的基本主张有?4.简述建构主义学习理论的基本特征?(有点模糊)5.简述一下创造(还是创新)型心理结构的特征?(有点模糊)三、论述题1.根据教育过程的性质,阐述一下你在教育过程中应该注意处理好的几种关系?2.根据教育对社会的发展作用,论述下孔子“庶,富,教。
”的思想。
2014苏州大学333一:名词解释1.颜氏家训2.七艺3.莫雷尔法案4.教育目的5.6.校长负责制二:简答题1.马克思关于人的全面发展的学说2.永恒主义教育思想3.建构主义学习观4.简述道德过程的性质三:论述题1.朱熹的道德教育方法2.蔡元培关于北京大学的改革措施及影响3.我国新一轮课程标准的变革4.结合实际谈谈如何提高教师的心理健康2015 苏州大学333教育综合所有真题一,名词解释(5 分*6)1.班级授课制2.学制3.课程4.中世纪大学5.教学模式6.癸卯学制二,简单(10 分*4)1 教育对人的发展的作用?2 罗杰斯的人本主义教学观。
34三,论述题 20*41 洋务学堂有哪些特点?结合洋务教育的背景谈谈洋务教育对我国教育史的意义2 卢梭自然主义教育及影响3 从教育的社会流动功能分析教育不公平的现象4 结合实例谈谈如何培养学生的创造力苏州大学 2016年333教育综合真题一、名词解释 6*5=301、义务教育2、发现学习3、要素主义教育4、庚款兴学5、最近发展区6、总结性评价二、简答题1、教师劳动的特点2、精细加工策略3、黄炎培职业教育思想4、欧洲文艺复兴时期,人文主义教育的特征及意义三、论述题1、学校管理的发展趋势2、柏拉图的教育思想3、学科结构课程理论的主要观点4、董仲舒的教育思想苏州大学2017年333教育综合真题回忆一、名词解释1、稷下学宫2、学习动机3、学制4、绅士教育5、进步主义教育6、《国防教育法》二、简答题1、请列举 19 世纪末 20 世纪前期主要教育思潮和教育实验。
2019苏州大学学科教学(英语)333教育综合与889英语教学论考研复习全析【含真题答案】

2019苏州大学学科教学(英语)333教育综合与889英语教学论考研复习全析【含真题答案】《2019苏州大学333教育综合考研复习全析(含真题答案)》分为八册,由东吴苏大考研网依托多年丰富的教学与辅导经验,组织官方教学研发团队与苏州大学教育学院的优秀研究生共同合作编写而成。
全书内容紧凑权威细致,编排结构科学合理,为参加2019苏州大学考研的考生量身定做的必备专业课资料。
2019苏州大学333教育综合考研复习全析(含真题答案)全书编排根据参考书目:《教育学(王道俊)》《当代教育心理学(修订版)(陈琦、刘儒德)》《中国教育史(孙培青)》《简明中国教育史(王炳照)》《外国教育史(张斌贤)》《外国教育史教程(吴式颖)》《教育心理学(张大均)》结合往年苏州大学考研真题内容,帮助报考苏州大学考研的同学通过苏大教材章节框架分解、配套的课后习题讲解及相关985、211名校考研真题与解答,帮助考生梳理指定教材的各章节内容,深入理解核心重难点知识,把握考试要求与考题命题特征。
通过研读演练本书,达到把握教材重点知识点、适应多样化的专业课考研命题方式、提高备考针对性、提升复习效率与答题技巧的目的。
同时,透过测试演练,以便查缺补漏,为初试高分奠定坚实基础。
适用院系:马克思主义学院:学科教学(思政)(专业学位)教育学院、教育科学研究院:教育管理硕士(专业学位)、职业技术教育硕士(专业学位)文学院:学科教学(语文)(专业学位)社会学院:学科教学(历史)(专业学位)数学科学学院:学科教学(数学)(专业学位)物理与光电·能源学部:学科教学(物理)(专业学位)医学部:学科教学(生物)(专业学位)外国语学院:学科教学(英语)(专业学位)材化部:学科教学(化学)(专业学位)适用科目:333教育综合内容详情本书包括了以下几个部分内容:一、考试重难点(复习笔记):通过总结和梳理《教育学》、《当代教育心理学》、《中国教育史》、《简明中国教育史》、《外国教育史》、《外国教育史教程》、《教育心理学》七本教材各章节复习和考试的重难点,浓缩精华内容,令考生对各章节内容考察情况一目了然,从而明确复习方向,提高复习效率。
苏州大学333教育综合真题2010-2019

2010苏州大学333教育综合真题一、名词解释(每小题5分,共30分)1、人的发展2、教育的社会流动功能3、终身教育4、元认知5、骑士教育6、有教无类二、简答题(每小题10分,共40分)1、教师角色的冲突有哪些?如何解决?2、比较孟子与荀子人性观及他们对教育的作用的认识。
3、学生认知的差异有哪些表现?为此,教学应注意哪些方面?4、简述卢梭的自然教育思想。
三、分析论述题(每小题20分,共80分)1、教育的相对独立性表现在哪些方面?并就此谈谈你对教育与社会发展的关系的认识。
2、试论隋唐科举制与学校教育的关系,并分析其在历史上的影响。
3、论述皮亚杰的道德认知发展理论,并联系实际加以评价。
2011苏州大学333教育综合真题一、名词解释(每小题5分,共30分)1、狭义的课程2、终身教育3、鸿都门学4、元认知5、白板说6、教育的社会流动功能二、简答题(每小题10分,共40分)1、教师个体专业性发展的内涵包括哪些方面?2、简述梁启超“新民”的教育目的观。
3、简述杜威的道德教育思想。
4、简述建构主义的学习观。
三、分析论述题(每小题20分,共80分)1、结合现实分析全面发展教育各组成部分的相互关系。
2、论陶行知“生活即教育”的思想内涵,并联系实际分析其现实意义。
3、在外国近现代教育史上,你喜欢哪一位教育家,并就此阐释喜欢的原因。
4、联系当前实际,阐述学生品德不良的成因及其教育策略。
2012苏州大学333教育综合真题一、名词解释(每小题5分,共30分)1、教育2、教学3、学制4、太学5、恩物6、学习策略二、简答题(每小题10分,共40分)1、教育目的与教育方针的主要区别?2、学校管理校本化的基本含义和意义。
3、《学记》“导而弗牵,强而弗抑,开而弗达”的基本含义。
三、论述题(每小题20分,共80分)1、孔子“有教无类”思想评述。
2、试述永恒主义教育思想的基本内容及其对现代教育的启示。
3、试述教师专业发展的内涵、意义以及主要途径。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
苏州大学
2010年苏州大学333教育综合真题
一、名词解释
1、人的发展
2、教育的社会流动功能
3、终身教育
4、元认知
5、骑士教育
6、有教无类
二、简答题
1、教师角色的冲突有哪些?如何解决?
2、比较孟子与荀子人性观及他们对教育的作用的认识。
3、学生认知的差异有哪些表现?为此,教学应注意哪些方面?
4、简述卢梭的自然教育思想。
三、分析论述题
1、教育的相对独立性表现在哪些方面?并就此谈谈你对教育与社会发展的关系的认识。
2、试论隋唐科举制与学校教育的关系,并分析其在历史上的影响。
3、论述皮亚杰的道德认知发展理论,并联系实际加以评价。
4、论述文艺复兴时期人文主义教育的主要特征、影响及其贡献。
一、名词解释
1、狭义的课程
2、终身教育
3、鸿都门学
4、元认知
5、白板说
6、教育的社会流动功能
二、简答题
1、教师个体专业性发展的内涵包括哪些方面?
2、简述梁启超“新民"的教育目的观。
3、简述杜威的道德教育思想。
4、简述建构主义的学习观。
三、分析论述题
1、结合现实分析全面发展教育各组成部分的相互关系。
2、论陶行知“生活即教育”的思想内涵,并联系实际分析其现实意义。
3、在外国近现代教育史上,你喜欢哪一位教育家,并就此阐释喜欢的原因。
4、联系当前实际,阐述学生品德不良的成因及其教育策略。
一、名词解释
1、教育
2、教学
3、学制
4、太学
5、恩物
6、学习策略
二、简答题
1、教育目的与教育方针的主要区别?
2、学校管理校本化的基本含义和意义。
3、《学记》“导而弗牵,强而弗抑,开而弗达”的基本含义。
三、论述题
1、孔子“有教无类”思想评述。
2、试述永恒主义教育思想的基本内容及其对现代教育的启示。
3、试述教师专业发展的内涵、意义以及主要途径。
4、举例说明你是如何激发学生的学习动机的。
一、名词解释题
1、教育家
2、双轨制
3、稷下学宫
4、爱弥儿
5、恩物
6、倒摄抑制
7、心智技能
8、皮格马利翁效应
二、简答题
1、简述欧洲文艺复兴时期人文主义教育的基本特征是什么?
2、简述德育过程的基本特征是什么?
3、简述夸美纽斯的教育思想的基本主张有哪些?
4、简述建构主义学习理论的基本观点。
5、简述创造性的心理结构及其培养措施。
三、论述题
1、论述教学过程的性质,并结合实际,论述进行教学所应处理的一些关系?
2、根据教育对社会的发展作用,论述下孔子“庶,富,教”的思想。
一、名词解释
1、颜氏家训
2、七艺
3、莫雷尔法案
4、教育目的
5、学习策略
6、校长负责制
二、简答题
1、简述朱熹的道德教育方法。
2、简述永恒主义教育思想。
3、简述建构主义学习观理论的基本观点。
4、简述德育过程的性质。
三、论述题
1、试述蔡元培在北京大学的改革措施及其影响。
2、论述马克思关于人的全面发展的教育思想。
3、评述我国新课程改革的基本理念。
4、结合实际谈谈如何维护教师的心理健康。
一、名词解释
1、班级授课制
2、学制
3、课程
4、中世纪大学
5、教学模式
6、癸卯学制
二、简答
1、简述教育对人的发展的作用。
2、罗杰斯的人本主义教学观
3、简述英国《1944年。
教育法》
4、简述教学过程的性质
三、论述题
1、论述洋务运动的特点,洋务教育兴起背景及在近代教育中的作用。
2、论述卢梭自然主义教育思想内容及影响。
3、结合教育的社会流动功能,试分析现阶段我国教育的公平问题。
4、结合自身实际,谈谈如何培养和发展学生的创造性思维能力。
一、名词解释
1、义务教育
2、庚款兴学
3、最近发展区
4、终结性评价
5、发现学习
6、要素主义教育
二、简答题
1、简述教师劳动的特点。
2、简述欧洲人文主义教育的特征和贡献。
3、简述黄炎培的职业教育思想。
4、简述精细加工策略的主要内容。
三、论述题
1、论述柏拉图的教育思想。
2、论述董仲舒的教育思想。
3、论述学科结构课程的主要观点。
4、论述学校管理的发展趋势。
一、名词解释
1、稷下学宫
2、学习动机
3、学制
4、绅士教育
5、进步主义教育
6、国防教育法
二、简答题
1、19世纪末20世纪初期的教育思潮和教育实验
2、简述埃里克森的心理社会发展理论
3、简述《大学》的三纲领八条目
4、简述科尔伯格的道德发展阶段理论
三、论述题
1、请结合实际论述教育对社会的功能
2、为什么教育对于人的发展起主导作用?试分析教育起主导作用的条件
3、试述《学记》的教育思想
4、试述并评价主要的学习理论
一、名词解释6道(每题5分)
1、学习动机
2、教学模式
3、朱子读书法
4、发现学习
5、义务教育
6、进步主义教育
二、简答5道(每题10分)
1、简述教育起源的主要观点
2、简述经验主义课程论的代表人物和主要观点
3、简述社会本位论的主要观点
4、简述影响人身心发展的主要因素
5、简述布鲁纳认知结构教学论的基本原则
三、论述2道(每题20分)
1、教学中应该遵循哪些原则,选择一个你喜欢的进行举例论证
2、结合人的全面发展的思想,论述中国学生核心素质的构成要素
四、案例分析2道(每题15分)
1、教师不管后进生轻视后进生,而后某后进生努力到班级第一,英语老师怀疑他。
在全班
同学面前去质疑他,自选角度结合教育原理进行分析
2、问儿童:
(1)雪融化了变成什么呢?孩子说春天,教师说正确答案是水
(2)树梢5只鸟,开一枪还有几只,儿童说3只,儿童的理由是鸟爸爸死了,鸟妈妈难受的飞走了,就剩3个鸟宝宝了
案例分析:根据案例,谈谈你对教学回归儿童生活世界的理解
2019年苏州大学333教育综合真题
一、填空(15分)
二、名词解释(4个,一个5分)
1、道尔顿制
2、三舍法
3、先行组织者
4、五育并举
三、简答(5个,一个10分)
1、夸美纽斯的教学原则
2、孔子的教师观
3、科尔伯格道德发展阶段论
4、人身心发展的特点
5、教育生物源说观点
四、论述(2个,一个20分)
1、赫尔巴特四形式教学
2、教育对人的功能和社会的功能的关系
五、案例分析(25分)材料;大意是学生给老师评等级,但是平时上完课就走的老师得了较好的评分而认真负责, 要求严格的老师却得了低等级,语文老师很失望伤心,停课一段时间后还是继续教学了。
用教育理论评述材料,并对良好师生关系提出建议。
