内蒙古第一机械制造(集团)有限公司第一中学2018-2019学年高二下学期期中考试语文试卷附答案
2022-2023学年内蒙古阿拉善盟第一中学高二下学期期末地理试题
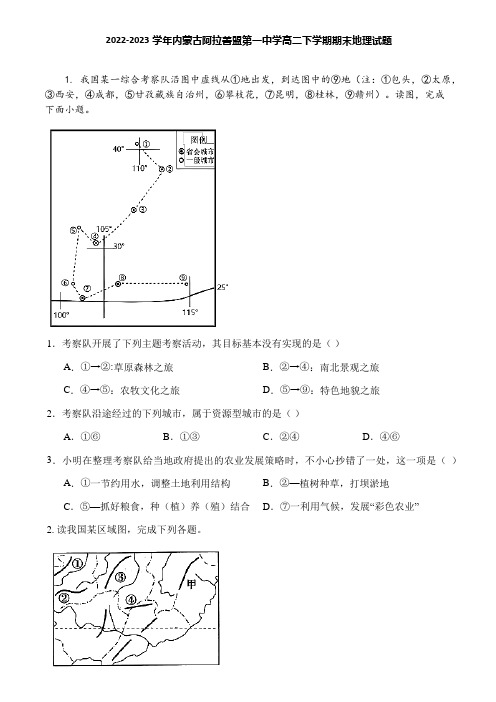
2022-2023学年内蒙古阿拉善盟第一中学高二下学期期末地理试题1. 我国某一综合考察队沿图中虚线从①地出发,到达图中的⑨地(注:①包头,②太原,③西安,④成都,⑤甘孜藏族自治州,⑥攀枝花,⑦昆明,⑧桂林,⑨赣州)。
读图,完成下面小题。
1.考察队开展了下列主题考察活动,其目标基本没有实现的是()A.①→②:草原森林之旅B.②→④:南北景观之旅C.④→⑤:农牧文化之旅D.⑤→⑨:特色地貌之旅2.考察队沿途经过的下列城市,属于资源型城市的是()A.①⑥B.①③C.②④D.④⑥3.小明在整理考察队给当地政府提出的农业发展策略时,不小心抄错了一处,这一项是()A.①一节约用水,调整土地利用结构B.②—植树种草,打坝淤地C.⑤—抓好粮食,种(植)养(殖)结合D.⑦一利用气候,发展“彩色农业”2. 读我国某区域图,完成下列各题。
1.图中①②③④四条山脉中,同为长江、珠江两大河流分水岭的是( )A.①②B.②③C.②④D.③④2.下列关于甲山脉的叙述,正确的是( )A.东南坡的降水少于西北坡B.为我国赣、闽两省的分界线C.我国季风区与非季风区的分界线D.是我国地势第二、三级阶梯的分界线3. 济州岛位于朝鲜半岛南部,广泛分布玄武熔岩,土壤渗透性强,以旱田为主,当地农民在旱田多种植柑橘。
近年来,济州岛柑橘种植园范围不断扩大,且呈现“由北向南、由下向上”的发展趋势。
如图示意济州岛柑橘园分布。
据此完成下面小题。
1.与济州岛南部柑橘林相比,岛屿北部柑橘林面临的主要自然灾害是()A.洪涝B.冻害C.台风D.高温2.近年来,济州岛南部柑橘种植区能从海拔100米以下地区逐渐扩展到海拔200米左右地区,主要得益于改善其()A.热量B.土壤C.水源D.光照4. 下图是中国雨季类型图,读图,完成下面小题。
1.图中①地区雨季类型为()A.全年干旱多晴区B.夏半年多雨区C.夏雨集中区D.夏雨区2.图中M地区夏秋季节多雨的主要原因是()A.受西南季风影响B.受高压脊的影响C.受台风影响D.多对流雨5. 西藏阿里地区是典型的高寒山地荒漠,多大风。
【广宁第一中学2018-2019学年第二学期高二政治期中考试(理科)新】全年级考生成绩统计表

3
82
3314541223200104184高11二0 7班 陈健昌 66.00
5
82
3424341223200108192高33二7 9班 龚朝政 66.00
6
82
344841223200110303高52二6 9班 梁沛君 66.00
6
82
346441223200112150高41二2 9班 高祖宏 66.00
28
98
3014941223200112133高51二6 1班 陈振辉 65.00
28
98
302441223200110125高32二8 1班 曾乐乐 65.00
28
98
304041223200106020高41二9 1班 陈显立 65.00
28
98
304541223200208021高11二3 1班 冯嘉远 65.00
27
82
3124841223200010294高71二4 3班 林延明 66.00
6
82
3174941223200106284高42二2 4班 周凤仪 66.00
9
82
3214141223200109241高11二0 5班 冯国远 66.00
6
82
3274341223200107111高71二8 6班 江浩生 66.00
67.00
1
71
393441223200104214高71二119班 冯达滨 67.00
1
71
394141223200108135高61二519班 叶伟民 67.00
1
71
394941223200207044高71二919班 欧乐谋 67.00
2018-2019学年重庆市第一中学高二下学期期中考试数学试题(文)

重庆市第一中学2018-2019学年高二下学期期中考试(文) 注意事项:1. 答卷前,考生务必将自己的姓名、准考证号码填写在答卷上。
2. 作答时,务必将答案写在答题卡上,写在本试卷及草稿纸上无效。
3. 考试结束后,将答题卡交回。
第Ⅰ卷(选择题,共60分)一、选择题(本题共12小题,每小题5分,共60分. 在下列各题的四个选项中,只有一个选项是符合题意的)1.已知集合{}=1,0,1,2M -,{}230N x x x =-<,则MN =( ) A .{}0,1 B .{}1,0- C .{}1,2 D .{}1,2-2.当1m <时,复数2(1))m i i +-(为虚数单位在复平面内对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限3.已知命题p q ∨为真,p ⌝为真,则下列说法正确的是( )A .p 真q 真B .p 假q 真C .p 真q 假D .p 假q 假4.设函数()241,0,log ,0x x f x x x ⎧-≤=⎨>⎩则12f ⎛⎫= ⎪⎝⎭( ) A .1- B .1 C .12-D .22 5.设,x R ∈则2x ≤“”是11x +≤“”的( ) A .充分而不必要条件 B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件6.根据如下样本数据: x1 2 3 4 5 y 1a - 1- 0.5 1b + 2.5得到的回归方程为,y bx a =+若样本点的中心为(3,0.1),则b 的值为( )A .0.8B .0.8-C .2.3D . 2.3-7.已知双曲线()222210,0x y a b a b -=>>的渐近线与圆()2224a x a y ++=相切,则双曲线的离心率等于( )A .2B .3C .2D .233 8.下列函数中,既是奇函数,又在0+∞(,)上是增函数的是( ) A .()sin f x x = B .()x x f x e e -=+ C .3()f x x x =+ D. ()ln f x x x = 9.如右图所示是某几何体的三视图,则该几何体的体积为( )A .6432π+B .6464π+C .25664π+D .256128π+ 10.已知函数1,0(=2,0x x x f x x +<⎧⎨≥⎩())(),则不等式2(2)(34)f x x f x -<-的解集为( ) A .(1,2) B .(1,4) C .(0,2) D .4(1,]311.函数()f x 对于任意实数,都有()()f x f x -=与(1)(1)f x f x +=-成立,并且当01x ≤≤时,2()f x x =.则方程()02019x f x -=的根的个数是( ) A .2020 B .2019 C .1010 D .1009 12.已知函数()g x 满足121()(1)(0),2x g x g e g x x -'=-+且存在实数0x 使得不等式021()m g x -≥成立,则m 的取值范围为( )A .[0,)+∞B .[1,)+∞C .2∞(-,] D . 3∞(-,] 第Ⅱ卷(非选择题,共90分)二、填空题(本题共4小题,每小题5分,共20分)13.若函数()f x 的定义域为[2,3],-则函数(2)f x 的定义域是__________.14.若函数3()(1)2f x a x x a =+-+为奇函数,则曲线()y f x =在点(1,(1))f 处的切线方程为__________.15. 直线(1)y k x =-与抛物线24y x =交于,A B 两点,若4,AB =则弦AB 的中点到抛物线的准线的距离为__________.16.在正三棱锥P ABC -中,,,PA PB PC 两两垂直,且2,PA PB PC ===则正三棱锥P ABC -的内切球的半径为__________.解答题;共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.17.(本小题满分12分)已知函数21lg(43)x y x x x-=+-+的定义域为M . (1)求M ;(2)当[0,1]x ∈时,求()42x x f x =+的最小值.18.(本小题满分12分)某校开展了知识竞赛活动.现从参加知识竞赛活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为6组:[)40,50,[)50,60,[)60,70,[)70,80,[)80,90,[]90,100,得到如右图所示的频率分布直方图.(1)求a 的值;(2)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”.请将下面的22⨯列联表补充完整,并判断是否有99.9%的把握认为“比赛成绩是否优秀与性别有关”?(结果精确到0.001) 优秀 非优秀 合计 男生40 女生 50合计100 参考公式及数据:22(),()()()()n ad bc K n a b c d a b c d a c b d -==+++++++19.(本小题满分12分)如右图所示,直三棱柱111ABC A B C -中,D 是BC 的中点,四边形11A B BA 为正方形.(1)求证:1A C //平面1AB D ;(2)若ABC ∆为等边三角形, 4BC =,求点B 到平面1AB D 的距离.20.(本小题满分12分)已知椭圆C 的中心在坐标原点,焦点在x 轴上,离心率为12,椭圆C 上的点到焦点距离的最大值为3.(1)求椭圆C 的标准方程;(2)斜率为12的直线l 与椭圆C 交于不同的两点,A B ,且线段AB 的中垂线交x 轴于点P ,求点P 横坐标的取值范围.21.(本小题满分12分)已知215(),(=122x f x e g x x x =--)(为自然对数的底数). (1)记()ln (),F x x g x =+求函数()F x 在区间[]1,3上的最大值与最小值;(2)若,k Z ∈且()()0f x g x k +-≥对任意x R ∈恒成立,求k 的最大值.选考题:共10分.请考生在第22、23题中任选一题作答,如果多做,则按第一题计分.22.(本小题满分10分)选修4—4:坐标系与参数方程已知在平面直角坐标系xOy 中,直线14:23x t l y t=--⎧⎨=+⎩(t 为参数),以原点为极点,轴的非负半轴为极轴,且取相同的单位长度建立极坐标系,曲线C 的极坐标方程为22sin().4πρθ=+ (1)求直线l 的普通方程及曲线C 的直角坐标方程;(2)设点P 的直角坐标为(1,2),-直线l 与曲线C 交于,A B 两点,求PA PB ⋅的值.23.(本小题满分10分)选修4—5:不等式选讲已知函数()21f x x a x =+--(1)当1a =时,求不等式()0f x >的解集;(2)若0a >,不等式()1f x <对x R ∈都成立,求a 的取值范围.。
岭东区第一中学2018-2019学年下学期高二期中数学模拟题

岭东区第一中学2018-2019学年下学期高二期中数学模拟题一、选择题1. 已知集合A={x|a ﹣1≤x ≤a+2},B={x|3<x <5},则A ∩B=B 成立的实数a 的取值范围是( ) A .{a|3≤a ≤4} B .{a|3<a ≤4} C .{a|3<a <4} D .∅2. 3名医生和6名护士被分配到3所学校为学生体检,每校分配1名医生和2名护士.不同的分配方法共有( ) A .90种 B .180种 C .270种D .540种3. 若函数()()()()()1cos sin cos sin 3sin cos 412f x x x x x a x x a x =-++-+-在02π⎡⎤-⎢⎥⎣⎦,上单调递增,则实数的取值范围为( ) A .117⎡⎤⎢⎥⎣⎦, B .117⎡⎤-⎢⎥⎣⎦,C.1(][1)7-∞-+∞,,D .[1)+∞,4. 62)21(x x -的展开式中,常数项是( ) A .45- B .45 C .1615- D .16155. 已知函数1()1x f x ae x a -=+--有两个零点,则实数a 的取值范围是( )A .[1,1]-B .[0,1]C .{1}(0,1]-D .{1}[0,1)- 6. 已知抛物线24y x =的焦点为F ,(1,0)A -,点P 是抛物线上的动点,则当||||PF PA 的值最小时,PAF ∆的 面积为( )A.2B.2C. D. 4【命题意图】本题考查抛物线的概念与几何性质,考查学生逻辑推理能力和基本运算能力.7. 已知f (x )是定义在R 上周期为2的奇函数,当x ∈(0,1)时,f (x )=3x ﹣1,则f (log 35)=( ) A.B.﹣ C .4D.8. 下列结论正确的是( )A .若直线l ∥平面α,直线l ∥平面β,则α∥β.B .若直线l ⊥平面α,直线l ⊥平面β,则α∥β.C .若直线l 1,l 2与平面α所成的角相等,则l 1∥l 2D .若直线l 上两个不同的点A ,B 到平面α的距离相等,则l ∥α9. 已知集合M={1,4,7},M ∪N=M ,则集合N 不可能是( ) A .∅ B .{1,4}C .MD .{2,7}班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________10.一个几何体的三视图如图所示,如果该几何体的侧面面积为12π,则该几何体的体积是()A.4πB.12πC.16πD.48π11.已知函数f(x)的定义域为R,其导函数f′(x)的图象如图所示,则对于任意x1,x2∈R(x1≠x2),下列结论正确的是()①f(x)<0恒成立;②(x1﹣x2)[f(x1)﹣f(x2)]<0;③(x1﹣x2)[f(x1)﹣f(x2)]>0;④;⑤.A.①③B.①③④ C.②④D.②⑤12.下列函数中哪个与函数y=x相等()A.y=()2B.y=C.y=D.y=二、填空题13.阅读如图所示的程序框图,则输出结果S的值为.【命题意图】本题考查程序框图功能的识别,并且与数列的前n项和相互联系,突出对逻辑判断及基本运算能力的综合考查,难度中等.14.在复平面内,记复数+i对应的向量为,若向量饶坐标原点逆时针旋转60°得到向量所对应的复数为.15.在(x2﹣)9的二项展开式中,常数项的值为.16.如图,是一回形图,其回形通道的宽和OB1的长均为1,回形线与射线OA交于A1,A2,A3,…,若从点O到点A3的回形线为第1圈(长为7),从点A3到点A2的回形线为第2圈,从点A2到点A3的回形线为第3圈…依此类推,第8圈的长为.17.如图为长方体积木块堆成的几何体的三视图,此几何体共由块木块堆成.18.若在圆C:x2+(y﹣a)2=4上有且仅有两个点到原点O距离为1,则实数a的取值范围是.三、解答题19.(本题满分12分)如图1在直角三角形ABC中,∠A=90°,AB=2,AC=4,D,E分别是AC,BC边上的中点,M为CD的中点,现将△CDE沿DE折起,使点A在平面CDE内的射影恰好为M.(I)求AM的长;(Ⅱ)求面DCE与面BCE夹角的余弦值.20.在△ABC中,内角A,B,C所对的边分别是a,b,c,已知tanA=,c=.(Ⅰ)求;(Ⅱ)若三角形△ABC的面积为,求角C.215(Ⅱ)若同一次考试成绩之差的绝对值不超过5分,则称该次考试两人“水平相当”.由上述5次摸底考试成绩统计,任意抽查两次摸底考试,求恰有一次摸底考试两人“水平相当”的概率.22.(本题满分12分)在ABC ∆中,已知角,,A B C 所对的边分别是,,a b c ,边72c =,且tan tan tan 3A B A B +=-ABC ∆的面积为ABC S ∆=a b +的值.23.【南京市2018届高三数学上学期期初学情调研】已知函数f (x )=2x 3-3(a +1)x 2+6ax ,a ∈R . (Ⅰ)曲线y =f (x )在x =0处的切线的斜率为3,求a 的值;(Ⅱ)若对于任意x ∈(0,+∞),f (x )+f (-x )≥12ln x 恒成立,求a 的取值范围; (Ⅲ)若a >1,设函数f (x )在区间[1,2]上的最大值、最小值分别为M (a )、m (a ), 记h (a )=M (a )-m (a ),求h (a )的最小值.24.已知p :x ∈A={x|x 2﹣2x ﹣3≤0,x ∈R},q :x ∈B={x|x 2﹣2mx+m 2﹣4≤0,x ∈R ,m ∈R} (1)若A ∩B=[0,3],求实数m 的值;(2)若p 是¬q 的充分条件,求实数m 的取值范围.岭东区第一中学2018-2019学年下学期高二期中数学模拟题(参考答案)一、选择题1. 【答案】A【解析】解:∵A={x|a ﹣1≤x ≤a+2}B={x|3<x <5} ∵A ∩B=B ∴A ⊇B∴解得:3≤a ≤4 故选A【点评】本题考查集合的包含关系判断及应用,通过对集合间的关系转化为元素的关系,属于基础题.2. 【答案】D【解析】解:三所学校依次选医生、护士,不同的分配方法共有:C 31C 62C 21C 42=540种. 故选D .3. 【答案】D 【解析】考点:1、导数;2、单调性;3、函数与不等式.4. 【答案】D【解析】2612316611()()()22rr r r r rr T C x C xx --+=-=-, 令1230r -=,解得4r =.∴常数项为446115()216C -=.5. 【答案】D【解析】当1a =时,1()11x f x e x -=+--. 当1x ≥时,1()2x f x e x -=+-为增函数, ∴()(1)0f x f ≥=,有唯一零点1.当1x <时,1()x f x e x -=-,1()1x f x e -'=-. ∵1x <,∴()0f x '<,()f x 单调减, ∴()(1)0f x f <=,没有零点, 综上: 1a =时,原函数只有一个零点, 故不成立,从而排除,,A B C . 6. 【答案】B【解析】设2(,)4y P y,则21||||y PF PA +=.又设214y t +=,则244y t =-,1t …,所以||||PF PA ==,当且仅当2t =,即2y =±时,等号成立,此时点(1,2)P ±,PAF ∆的面积为1||||22222AF y ⋅=⨯⨯=,故选B.7. 【答案】B【解析】解:∵f (x )是定义在R 上周期为2的奇函数, ∴f (log 35)=f (log 35﹣2)=f (log3), ∵x ∈(0,1)时,f (x )=3x﹣1∴f (log 3)═﹣ 故选:B8. 【答案】B【解析】解:A 选项中,两个平面可以相交,l 与交线平行即可,故不正确; B 选项中,垂直于同一平面的两个平面平行,正确;C 选项中,直线与直线相交、平行、异面都有可能,故不正确;D 中选项也可能相交. 故选:B .【点评】本题考查平面与平面,直线与直线,直线与平面的位置关系,考查学生分析解决问题的能力,比较基础.9. 【答案】D【解析】解:∵M ∪N=M ,∴N ⊆M ,∴集合N不可能是{2,7},故选:D【点评】本题主要考查集合的关系的判断,比较基础.10.【答案】B【解析】解:由三视图可知几何体是底面半径为2的圆柱,∴几何体的侧面积为2π×2×h=12π,解得h=3,∴几何体的体积V=π×22×3=12π.故选B.【点评】本题考查了圆柱的三视图,结构特征,体积,表面积计算,属于基础题.11.【答案】D【解析】解:由导函数的图象可知,导函数f′(x)的图象在x轴下方,即f′(x)<0,故原函数为减函数,并且是,递减的速度是先快后慢.所以f(x)的图象如图所示.f(x)<0恒成立,没有依据,故①不正确;②表示(x1﹣x2)与[f(x1)﹣f(x2)]异号,即f(x)为减函数.故②正确;③表示(x1﹣x2)与[f(x1)﹣f(x2)]同号,即f(x)为增函数.故③不正确,④⑤左边边的式子意义为x1,x2中点对应的函数值,即图中点B的纵坐标值,右边式子代表的是函数值得平均值,即图中点A的纵坐标值,显然有左边小于右边,故④不正确,⑤正确,综上,正确的结论为②⑤.故选D.12.【答案】B【解析】解:A.函数的定义域为{x|x≥0},两个函数的定义域不同.B.函数的定义域为R,两个函数的定义域和对应关系相同,是同一函数.C.函数的定义域为R,y=|x|,对应关系不一致.D.函数的定义域为{x|x≠0},两个函数的定义域不同.故选B . 【点评】本题主要考查判断两个函数是否为同一函数,判断的标准是判断函数的定义域和对应关系是否一致,否则不是同一函数.二、填空题13.【答案】20172016 【解析】根据程序框图可知,其功能是求数列})12)(12(2{+-n n 的前1008项的和,即 +⨯+⨯=532312S =-++-+-=⨯+)2017120151()5131()311(201720152 20172016. 14.【答案】 2i .【解析】解:向量饶坐标原点逆时针旋转60°得到向量所对应的复数为(+i )(cos60°+isin60°)=(+i )()=2i,故答案为 2i .【点评】本题考查两个复数代数形式的乘法及其集合意义,判断旋转60°得到向量对应的复数为(+i )(cos60°+isin60°),是解题的关键.15.【答案】 84 .【解析】解:(x 2﹣)9的二项展开式的通项公式为 T r+1=•(﹣1)r •x 18﹣3r ,令18﹣3r=0,求得r=6,可得常数项的值为T 7===84,故答案为:84.【点评】本题主要考查二项式定理的应用,二项展开式的通项公式,属于基础题.16.【答案】 63 .【解析】解:∵第一圈长为:1+1+2+2+1=7 第二圈长为:2+3+4+4+2=15第三圈长为:3+5+6+6+3=23 …第n 圈长为:n+(2n ﹣1)+2n+2n+n=8n ﹣1 故n=8时,第8圈的长为63, 故答案为:63.【点评】本题主要考查了归纳推理,解答的一般步骤是:先通过观察第1,2,3,…圈的长的情况发现某些相同性质,再从相同性质中推出一个明确表达的一般性结论,最后将一般性结论再用于特殊情形.17.【答案】4【解析】解:由三视图可以看出此几何体由两排两列,前排有一个方块,后排左面一列有两个木块右面一列有一个,故后排有三个,故此几何体共有4个木块组成.故答案为:4.18.【答案】﹣3<a<﹣1或1<a<3.【解析】解:根据题意知:圆x2+(y﹣a)2=4和以原点为圆心,1为半径的圆x2+y2=1相交,两圆圆心距d=|a|,∴2﹣1<|a|<2+1,∴﹣3<a<﹣1或1<a<3.故答案为:﹣3<a<﹣1或1<a<3.【点评】本题体现了转化的数学思想,解题的关键在于将问题转化为:圆x2+(y﹣a)2=4和以原点为圆心,1为半径的圆x2+y2=1相交,属中档题.三、解答题19.【答案】解:(I)由已知可得AM⊥CD,又M为CD的中点,∴;3分(II)在平面ABED内,过AD的中点O作AD的垂线OF,交BE于F点,以OA为x轴,OF为y轴,OC为z轴建立坐标系,可得,∴,,5分设为面BCE的法向量,由可得=(1,2,﹣),∴cos<,>==,∴面DCE与面BCE夹角的余弦值为4分20.【答案】【解析】解:(Ⅰ)由题意知,tanA=,则=,即有sinA﹣sinAcosC=cosAsinC,所以sinA=sinAcosC+cosAsinC=sin(A+C)=sinB,由正弦定理,a=b,则=1;…(Ⅱ)因为三角形△ABC的面积为,a=b、c=,所以S=absinC=a2sinC=,则,①由余弦定理得,=,②由①②得,cosC+sinC=1,则2sin(C+)=1,sin(C+)=,又0<C<π,则C+<,即C+=,解得C=….【点评】本题考查正弦定理,三角形的面积公式,以及商的关系、两角和的正弦公式等,注意内角的范围,属于中档题.21.【答案】【解析】解:(Ⅰ)解法一:依题意有,答案一:∵∴从稳定性角度选甲合适.(注:按(Ⅱ)看分数的标准,5次考试,甲三次与乙相当,两次优于乙,所以选甲合适.答案二:∵乙的成绩波动大,有爆发力,选乙合适.解法二:因为甲5次摸底考试成绩中只有1次90,甲摸底考试成绩不低于90的概率为;乙5次摸底考试成绩中有3次不低于90,乙摸底考试成绩不低于90的概率为.所以选乙合适.(Ⅱ)依题意知5次摸底考试,“水平相当”考试是第二次,第三次,第五次,记为A,B,C.“水平不相当”考试是第一次,第四次,记为a,b.从这5次摸底考试中任意选取2次有ab,aA,aB,aC,bA,bB,bC,AB,AC,BC共10种情况.恰有一次摸底考试两人“水平相当”包括共aA,aB,aC,bA,bB,bC共6种情况.∴5次摸底考试成绩统计,任意抽查两次摸底考试,恰有一次摸底考试两人“水平相当”概率.【点评】本题主要考查平均数,方差,概率等基础知识,运算数据处理能力、运算求解能力、应用意识,考查化归转化思想、或然与必然思想.22.【答案】112. 【解析】试题解析:由tan tan tan 3A B A B +=-可得tan tan 1tan tan A BA B+=-,即tan()A B +=∴tan()C π-=tan C -=tan C =∵(0,)C π∈,∴3C π=.又ABC ∆的面积为2ABC S ∆=,∴1sin 22ab C =,即1222ab ⨯=,∴6ab =. 又由余弦定理可得2222cos c a b ab C =+-,∴2227()2cos 23a b ab π=+-,∴22227()()32a b ab a b ab =+-=+-,∴2121()4a b +=,∵0a b +>,∴112a b +=.1 考点:解三角形问题.【方法点晴】本题主要考查了解三角形问题,其中解答中涉及到两角和与两角差的正切函数公式、三角形的面积、正弦定理和余弦定理,以及特殊角的三角函数值等知识点的综合考查,着重考查了学生分析问题和解答问题的能力,以及推理与运算能力,其中熟练掌握基本公式和灵活运用公式是解答本题的关键,属于中档试题. 23.【答案】(1)a =12(2)(-∞,-1-1e ].(3)827【解析】(2)f (x )+f (-x )=-6(a +1)x 2≥12ln x 对任意x ∈(0,+∞)恒成立, 所以-(a +1)≥22ln xx. 令g (x )=22ln xx ,x >0,则g '(x )=()3212ln x x -.令g '(x )=0,解得x当x ∈(0g '(x )>0,所以g (x )在(0当x ∞)时,g '(x )<0,所以g (x ∞)上单调递减.所以g (x )max =g 1e, 所以-(a +1)≥1e ,即a ≤-1-1e,所以a 的取值范围为(-∞,-1-1e].(3)因为f (x )=2x 3-3(a +1)x 2+6ax ,所以f ′(x )=6x 2-6(a +1)x +6a =6(x -1)(x -a ),f (1)=3a -1,f (2)=4. 令f ′(x )=0,则x =1或a . f (1)=3a -1,f (2)=4.②当53<a <2时, 当x ∈(1,a )时,f '(x )<0,所以f (x )在(1,a )上单调递减; 当x ∈(a ,2)时,f '(x )>0,所以f (x )在(a ,2)上单调递增.又因为f (1)>f (2),所以M (a )=f (1)=3a -1,m (a )=f (a )=-a 3+3a 2,所以h(a)=M(a)-m(a)=3a-1-(-a3+3a2)=a3-3a2+3a-1.因为h'(a)=3a2-6a+3=3(a-1)2≥0.所以h(a)在(53,2)上单调递增,所以当a∈(53,2)时,h(a)>h(53)=827.③当a≥2时,当x∈(1,2)时,f '(x)<0,所以f(x)在(1,2)上单调递减,所以M(a)=f(1)=3a-1,m(a)=f(2)=4,所以h(a)=M(a)-m(a)=3a-1-4=3a-5,所以h(a)在[2,+∞)上的最小值为h(2)=1.综上,h(a)的最小值为827.点睛:已知函数最值求参数值或取值范围的一般方法:(1)利用导数结合参数讨论函数最值取法,根据最值列等量关系,确定参数值或取值范围;(2)利用最值转化为不等式恒成立问题,结合变量分离转化为不含参数的函数,利用导数求新函数最值得参数值或取值范围.24.【答案】【解析】解:由已知得:A={x|﹣1≤x≤3},B={x|m﹣2≤x≤m+2}.(1)∵A∩B=[0,3]∴∴,∴m=2;(2)∵p是¬q的充分条件,∴A⊆∁R B,而C R B={x|x<m﹣2,或x>m+2}∴m﹣2>3,或m+2<﹣1,∴m>5,或m<﹣3.。
陵城区第一中学2018-2019学年下学期高二期中数学模拟题

陵城区第一中学2018-2019学年下学期高二期中数学模拟题一、选择题1. 函数f (x ﹣)=x 2+,则f (3)=( )A .8B .9C .11D .102. 某几何体的三视图如图所示,则该几何体为()A .四棱柱B .四棱锥C .三棱台D .三棱柱3. 高三年上学期期末考试中,某班级数学成绩的频率分布直方图如图所示,数据分组依次如下:[70,90),[90,110),[100,130),[130,150),估计该班级数学成绩的平均分等于()A .112B .114C .116D .1204. 设x ∈R ,则x >2的一个必要不充分条件是()A .x >1B .x <1C .x >3D .x <35. 如图所示为某几何体的正视图和侧视图,则该几何体体积的所有可能取值的集合是()A .{, }B .{,, }C .{V|≤V≤}D .{V|0<V ≤}6. 现准备将7台型号相同的健身设备全部分配给5个不同的社区,其中甲、乙两个社区每个社区至少2台,其它社区允许1台也没有,则不同的分配方案共有( )A .27种B .35种C .29种D .125种7. 若复数a 2﹣1+(a ﹣1)i (i 为虚数单位)是纯虚数,则实数a=()A .±1B .﹣1C .0D .1班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________8. 已知i 是虚数单位,则复数等于( )A .﹣ +iB .﹣ +iC .﹣iD .﹣i9. 某单位综合治理领导小组成员之问的领导关系可以用框图表示,这种框图通常称为( )A .程序流程图B .工序流程图C .知识结构图D .组织结构图10.设f (x )=(e -x -e x )(-),则不等式f (x )<f (1+x )的解集为( )12x +112A .(0,+∞)B .(-∞,-)12C .(-,+∞)D .(-,0)121211.设偶函数f (x )在[0,+∞)单调递增,则使得f (x )>f (2x ﹣1)成立的x 的取值范围是( )A .(,1)B .(﹣∞,)∪(1,+∞)C .(﹣,)D .(﹣∞,﹣)∪(,+∞)12.设1m >,在约束条件,,1.y x y mx x y ≥⎧⎪≤⎨⎪+≤⎩下,目标函数z x my =+的最大值小于2,则m 的取值范围为()A.(1,1+B.(1)+∞C. (1,3)D .(3,)+∞二、填空题13.函数的定义域是,则函数的定义域是__________.111]()y f x =[]0,2()1y f x =+14.求函数在区间[]上的最大值 .15.设全集______.16.抛物线y=x 2的焦点坐标为( )A .(0,)B .(,0)C .(0,4)D .(0,2)17. 设函数,.有下列四个命题:()xf x e =()lng x x m =+①若对任意,关于的不等式恒成立,则;[1,2]x ∈x ()()f x g x >m e <②若存在,使得不等式成立,则;0[1,2]x ∈00()()f x g x >2ln 2m e <-③若对任意及任意,不等式恒成立,则;1[1,2]x ∈2[1,2]x ∈12()()f x g x >ln 22em <-④若对任意,存在,使得不等式成立,则.1[1,2]x ∈2[1,2]x ∈12()()f x g x >m e <其中所有正确结论的序号为 .【命题意图】本题考查对数函数的性质,函数的单调性与导数的关系等基础知识,考查运算求解,推理论证能力,考查分类整合思想.18.若函数f (x ),g (x )满足:∀x ∈(0,+∞),均有f (x )>x ,g (x )<x 成立,则称“f (x )与g (x )关于y=x 分离”.已知函数f (x )=a x 与g (x )=log a x (a >0,且a ≠1)关于y=x 分离,则a 的取值范围是 . 三、解答题19.(本小题满分10分)选修:几何证明选讲41- 如图所示,已知与⊙相切,为切点,过点的割线交圆于两点,弦,相PA O A P C B ,AP CD //BC AD , 交于点,为上一点,且.E F CE EC EF DE ⋅=2(Ⅰ)求证:;P EDF ∠=∠(Ⅱ)若,求的长.2,3,2:3:===EF DE BE CE PA20.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:零件的个数x (个)2345加工的时间y (小时)2.5344.5(1)在给定的坐标系中画出表中数据的散点图;(2)求出y 关于x 的线性回归方程=x+,并在坐标系中画出回归直线;(3)试预测加工10个零件需要多少时间?参考公式:回归直线=bx+a ,其中b==,a=﹣b .21.已知平面直角坐标系xoy中的一个椭圆,它的中心在原点,左焦点为,右顶点为D(2,0),设点A(1,).(1)求该椭圆的标准方程;(2)若P是椭圆上的动点,求线段PA的中点M的轨迹方程;(3)过原点O的直线交椭圆于B,C两点,求△ABC面积的最大值,并求此时直线BC的方程.22.如图,AB是⊙O的直径,C,F为⊙O上的点,CA是∠BAF的角平分线,过点C作CD⊥AF交AF的延长线于D点,CM⊥AB,垂足为点M.(1)求证:DC是⊙O的切线;(2)求证:AM•MB=DF•DA.23.已知函数f (x )=e x ﹣ax ﹣1(a >0,e 为自然对数的底数).(1)求函数f (x )的最小值;(2)若f (x )≥0对任意的x ∈R 恒成立,求实数a 的值.24.(本题12分)已知数列{}n x 的首项13x =,通项2n n x p nq =+(*n N ∈,p ,为常数),且145x x x ,,成等差数列,求:(1)p q ,的值;(2)数列{}n x 前项和n S 的公式.陵城区第一中学2018-2019学年下学期高二期中数学模拟题(参考答案)一、选择题1.【答案】C【解析】解:∵函数=,∴f(3)=32+2=11.故选C.2.【答案】A【解析】试题分析:由三视图可知,该几何体是底面为直角梯形的直四棱柱,直角梯形的上下底分别为3和4,直角腰为1,棱柱的侧棱长为1,故选A.考点:三视图【方法点睛】本题考查了三视图的问题,属于基础题型,三视图主要还是来自简单几何体,所以需掌握三棱锥,四棱锥的三视图,尤其是四棱锥的放置方法,比如正常放置,底面就是底面,或是以其中一个侧面当底面的放置方法,还有棱柱,包含三棱柱,四棱柱,比如各种角度,以及以底面当底面,或是以侧面当底面的放置方法,还包含旋转体的三视图,以及一些组合体的三视图,只有先掌握这些,再做题时才能做到胸有成竹.3.【答案】B【解析】解:根据频率分布直方图,得;该班级数学成绩的平均分是=80×0.005×20+100×0.015×20+120×0.02×20+140×0.01×20=114.故选:B.【点评】本题考查了根据频率分布直方图,求数据的平均数的应用问题,是基础题目.4.【答案】A【解析】解:当x>2时,x>1成立,即x>1是x>2的必要不充分条件是,x<1是x>2的既不充分也不必要条件,x>3是x>2的充分条件,x<3是x>2的既不充分也不必要条件,故选:A【点评】本题主要考查充分条件和必要条件的判断,比较基础.5.【答案】D【解析】解:根据几何体的正视图和侧视图,得;当该几何体的俯视图是边长为1的正方形时,它是高为2的四棱锥,其体积最大,为×12×2=;当该几何体的俯视图为一线段时,它的底面积为0,此时不表示几何体;所以,该几何体体积的所有可能取值集合是{V|0<V≤}.故选:D.【点评】本题考查了空间几何体的三视图的应用问题,解题的关键是根据三视图得出几何体的结构特征是什么,是基础题目.6.【答案】B【解析】排列、组合及简单计数问题.【专题】计算题.【分析】根据题意,可将7台型号相同的健身设备看成是相同的元素,首先分给甲、乙两个社区各台设备,再将余下的三台设备任意分给五个社区,分三种情况讨论分配方案,①当三台设备都给一个社区,②当三台设备分为1和2两份分给2个社区,③当三台设备按1、1、1分成三份时分给三个社区,分别求出其分配方案数目,将其相加即可得答案.【解答】解:根据题意,7台型号相同的健身设备是相同的元素,首先要满足甲、乙两个社区至少2台,可以先分给甲、乙两个社区各2台设备,余下的三台设备任意分给五个社区,分三种情况讨论:①当三台设备都给一个社区时,有5种结果,②当三台设备分为1和2两份分给2个社区时,有2×C52=20种结果,③当三台设备按1、1、1分成三份时分给三个社区时,有C53=10种结果,∴不同的分配方案有5+20+10=35种结果;故选B.【点评】本题考查分类计数原理,注意分类时做到不重不漏,其次注意型号相同的健身设备是相同的元素.7.【答案】B【解析】解:因为复数a2﹣1+(a﹣1)i(i为虚数单位)是纯虚数,所以a2﹣1=0且a﹣1≠0,解得a=﹣1.故选B.【点评】本题考查复数的基本概念的应用,实部为0并且虚部不为0,是解题的关键.8.【答案】A【解析】解:复数===,故选:A.【点评】本题考查了复数的运算法则,属于基础题.9.【答案】D【解析】解:用来描述系统结构的图示是结构图,某单位综合治理领导小组成员之问的领导关系可以用组织结构图表示.故选D .【点评】本题考查结构图和流程图的概念,是基础题.解题时要认真审题,仔细解答. 10.【答案】【解析】选C.f (x )的定义域为x ∈R ,由f (x )=(e -x -e x )(-)得12x +112f (-x )=(e x -e -x )(-)12-x+112=(e x -e -x )(+)-12x +112=(e -x -e x )(-)=f (x ),12x +112∴f (x )在R 上为偶函数,∴不等式f (x )<f (1+x )等价于|x |<|1+x |,即x 2<1+2x +x 2,∴x >-,12即不等式f (x )<f (1+x )的解集为{x |x >-},故选C.1211.【答案】A【解析】解:因为f (x )为偶函数,所以f (x )>f (2x ﹣1)可化为f (|x|)>f (|2x ﹣1|)又f (x )在区间[0,+∞)上单调递增,所以|x|>|2x ﹣1|,即(2x ﹣1)2<x 2,解得<x <1,所以x 的取值范围是(,1),故选:A . 12.【答案】A【解析】考点:线性规划.【方法点晴】本题是一道关于线性规划求最值的题目,采用线性规划的知识进行求解;关键是弄清楚的几何意义直线z x my =+截距为zm,作0my x :L =+,向可行域内平移,越向上,则的值越大,从而可得当直线直线z x my =+过点A 时取最大值,⎩⎨⎧==+00001mx y y x 可求得点A 的坐标可求的最大值,然后由z 2,>解不等式可求m 的范围. 二、填空题13.【答案】[]1,1-【解析】考点:函数的定义域.14.【答案】 .【解析】解:∵f(x)=sin2x+sinxcosx=+sin2x=sin(2x﹣)+.又x∈[,],∴2x﹣∈[,],∴sin(2x﹣)∈[,1],∴sin(2x﹣)+∈[1,].即f(x)∈[1,].故f(x)在区间[,]上的最大值为.故答案为:.【点评】本题考查二倍角的正弦与余弦,考查辅助角公式,着重考查正弦函数的单调性与最值,属于中档题. 15.【答案】{7,9}【解析】∵全集U={n∈N|1≤n≤10},A={1,2,3,5,8},B={1,3,5,7,9},∴(∁U A)={4,6,7,9 },∴(∁U A)∩B={7,9},故答案为:{7,9}。
天津市第一中学2018-2019学年高一下学期期中考试数学试题(附答案)

天津一中2018-2019-2 高一年级数学学科模块质量调查试卷本试卷分为第I 卷(选择题)、第II 卷(非选择题)两部分,共100 分,考试用时90 分钟。
第I 卷1 页,第II 卷至2 页。
考生务必将答案涂写在规定的位置上,答在试卷上的无效。
一.选择题1.以下说法正确的有几个()①四边形确定一个平面;②如果一条直线在平面外,那么这条直线与该平面没有公共点;③过直线外一点有且只有一条直线与已知直线平行;④如果两条直线垂直于同一条直线,那么这两条直线平行;A.0 个B.1 个C.2 个D.3 个2.在△ABC 中,角A, B, C的对边分别是a, b, c ,且a cos B = ( 2c - A ,则角A 的大小为()ππππA.B.C.D.6 4 3 23.在∆ABC 中,若AB ⋅AC = 2 且∠BAC = 30 ,则∆ABC 的面积为()A B.C D4.设α、β、γ为平面,为m、n、l 直线,则下列判断正确的是()A.若α⊥β,α⋂β=l, m ⊥l ,则m ⊥β B.若α⋂γ=m,α⊥γ, β⊥γ,则m ⊥βC.若α⊥γ, β⊥γ, m ⊥α,则m ⊥β D.若n ⊥α,n ⊥β, m ⊥α,则m ⊥βB.C.D.2 3 4 151 1 1 1 1 1A.13B.23C.43D.26.点G 为∆ABC 的重心,AB = 2, BC =1, ∠ABC = 60 ,则AG ⋅CG =()A.-59B.-98C.59D.197.在正方体ABCD -A1B1C1D1中,点O 是正方形ABCD 的中心,关于直线A1O 下列说法正确的()A.A1O / / D1C B.A1O / / 平面B1CD1C.A1O ⊥BC D.A1O ⊥平面AB1D18.一个圆锥SC 的高和底面直径相等,且这个圆锥SC 和圆柱OM 的底面半径及体积也都相等, 则圆锥SC 和圆柱OM 的侧面积的比值为()A.39.平行六面体ABCD -A B C D 的底面ABCD 是菱形,且∠C CB =∠C CD =∠BCD = 60 ,CD = 2, C C =3 ,则二面角C-BD -C 的平面角的余弦值为()1 2 1A.12B.13C3D310.如图,在 ∆ABC 的边 AB 、AC 上分别取点 M 、N ,使AM = 1 AB , AN = 1 AC , BN 与 CM 交于点 P ,若 BP = λ PN , PM = μCP ,3 2则 λ的值为( ) μA . 83B . 38C . 16D . 6二.填空题11.已知向量 a , b 满足 | a |= 1 ,| b |= 2 , | a + b |=,则 | 2a - b |=.12 如图, PA ⊥ 平面ABC , ∠ACB = 90 且PA = AC ,AC = 2BC ,则异面直线 PB 与 AC 所成的角的正切值等于.13.如图,在直棱柱 ABC - A 1 B 1C 1 中, AB ⊥ AC , AB = AC = AA 1 = 2 , 则二面角 A 1 - BC 1 - C 的平面角的正弦值为.14.在 △ABC 中,角 A 、B 、C 的对边分别为a 、b 、c , 2b (2b - c ) cos A = a 2 + b 2 - c 2 ,则内角 A 的值为 .15.已知正方体 ABCD - A 1 B 1C 1 D 1 的棱长为1 ,点 E 是棱 BB 1 的中点,则点 B 1 到平面 ADE 的距离为.16.如图,在直角梯形 ABCD 中, ∠BAD = π, AB = AD = 2 ,若 M 、N3分别是边 AD 、BC 上的动点,满足 AM = λ AD , BN = (1 - λ )BC ,其中λ ∈ (0,1) ,若 AN ⋅ BM = -2 ,则 λ 的值为 .Nα 1 αα17. 设f (α) =m ⋅n ,其中向量m = ( n = (2 in , cos-1) .2 4 2(1)若f (α) =-1 ,求cos( π-α) 的值;3 2(2)在△ABC 中,角A, B, C的对边分别是a, b, c ,若a cos B +b cos A + 2c ⋅ cos C = 0 ,求函数f ( A) 的取值范围.18. 如图,在几何体中,四边形ABCD 是菱形,ADNM 是矩形,平面ADNM ⊥平面ABCD , E 为AB 中点.(1)求证:AN / / 平面MEC ;(2)求证:AC ⊥BN .19.如图1 所示,在矩形ABCD 中,AB = 2 A D = 4 ,E 为CD 的中点,沿AE 将∆AED 折起,如图2 所示,O、H、M 分别为AE、BD、AB 的中点,且DM = 2 .(1)求证:OH / / 平面DEC ;(2)求证:平面ADE ⊥平面ABCE .20.如图,四棱锥P -ABCD 的底面是菱形,PO ⊥底面ABCD ,O、E 分别是AD、AB 的中点,AB = 6, AP =5,∠BAD = 60 . (1)求证:平面PAC ⊥平面POE ;(2)求直线PB 与平面POE 所成角的正弦值;(3)若F 是边DC 的中点,求异面直线BF 与PA 所成角的正切值。
2018-2019学年第一学期高二语文考试试卷(二)

大连市烹饪职业中专期末考试试卷2018~2019学年第一学期高二年级(语文)一、基础知识应用(每题3分,共33分)1.下列词语中,加点字注音完全正确的一组是()A.恪(kè)守广袤(mào)倏(shū)忽嘈(cáo)杂B.梦寐(mèi)藐(miǎo)视寥(liáo)廓端倪(nì)C.颠簸(bǒ)半响(xiǎng)摇曳(yì)精湛(shěn)D.怦(pīng)然神侃(kǎn)熨(yùn)帖糟蹋(tà)2.下列词语中,书写完全正确的一项是()A.停止不前刻勤刻俭目瞪口呆B.价值连城振振有词眼花缭乱C.竭斯底里人声鼎沸心无旁骛D.浅谈辄止碌碌无为花团锦簇3.下列词语中,加点字解释全部正确的一项是()A.意蕴(包含)不求甚解(过多)迫在眉睫B.倏忽(很快地)美不胜收(能够承受)亘古不变(延绵不断)C.漫江(蔓延)鞭长莫及(达到)怨天尤人(钟爱)D.方遒(强劲有力)肆无忌惮(担心)无动于衷(钟爱)4.结合语境,下列句子中加点语解释有误的一项是()A.为满足人们的健康需求,厂家纷纷推出了绿色食品。
(指绿颜色蔬菜)B.针对城乡接合部急诊的压力,医院持续全方位建设急救绿色通道。
(之方便快捷的途径)C.“绿之翼”环保社团,吸引了不少“阳光少年”。
(指活泼、富有生气的少年)D.教育局要求各职业学校实行“阳光招生”。
(指公开、公平、公正的招生)5.下列句中加横线的成语,使用不当的一项是()A.我们一起谈天说地,打牌下棋,还扯着喉咙参差不齐地唱着流行歌曲。
B.考古工作者在这里发现大量木俑,斑驳陆离,为其他古墓出土的文物所罕见。
C.山上有了小屋,好比一望无际的水面飘过一片风帆。
D.它不再是清晰的小屋,而是烟雾之中、星点之下、月影之侧的海市蜃楼。
7.下列各句中,没有使用修辞手法的一句()A.林巧雅一生的业绩,是一颗伟岸高大的常青树;给我们的诊断书,是长青树上的一片绿叶。
河南省郑州市第一中学2018-2019学年高二下学期期中考试数学(理)试题(解析版)

2018-2019学年河南省郑州市第一中学高二下学期期中考试数学(理)试题一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.用反证法证明命题55整除”时,其反设正确的是()A. 5整除B. 5整除C. 5整除5整除【答案】C【解析】【分析】5整除的否定即可.55整除,选C.【点睛】本题考查反证法,考查基本分析判断能力,属基础题.2.)A. B. D.【答案】B【解析】【分析】,,对应点为 B.【点睛】本题考查复数代数形式以及复数几何意义,考查基本分析求解能力,属基础题.3.)A. B. D.【答案】D【解析】【分析】先求导数,再根据导数几何意义得结果.D.【点睛】本题考查导数几何意义,考查基本分析求解能力,属基础题.4.a、b、c S,内切圆半径为r可知,四面体S−ABC的四个面的面积分别为S1、S2、S3、S4,内切球半径为R,四面体S−ABC的体积为V,则R等于C.【答案】C【解析】解:设四面体的内切球的球心为O,则球心O到四个面的距离都是R,所以四面体的体积等于以O为顶点,分别以四个面为底面的4个三棱锥体积的和.则四面体的体积为R=B5.)A. 60B. 64C. 160D.【答案】A【解析】【分析】根据二项展开式通项公式求特定项系数.,因此含项的系数为 A.【点睛】本题考查二项展开式通项公式,考查基本分析求解能力,属基础题.6.高二年级的三个班去甲、乙、丙、丁四个工厂参加社会实践,但去哪个工厂可以自由选择,甲工厂必须有班级要去,则不同的分配方案有()A. B. 37种 C. 18种 D. 16种【答案】B【解析】【分析】根据间接法求解甲工厂没有班级去的方法数即可.【详解】高二年级的B.【点睛】本题考查排列组合,考查基本分析求解能力,属基础题. 7.的模等于()A. B. D. 2【答案】D【解析】【分析】.,所以 D.【点睛】本题考查纯虚数以及复数的模,考查基本分析求解能力,属基础题.8.停车场划出一排9个停车位置,今有5辆不同的车需要停放,若要求剩余的4个空车位连在一起,则不同的停车方法有()A. B. D.【答案】D【解析】【分析】剩余的4个空车位看作一个元素,由相邻问题用捆绑法求排列数.【详解】剩余的4个空车位看作一个元素,则不同的停车方法有 D. 【点睛】本题考查排列组合,考查基本分析求解能力,属基础题.9.()A. B. D. 【答案】A【解析】【分析】.得,所以A,【点睛】本题考查利用定积分求面积,考查基本分析求解能力,属基础题.10.)A. B. C. D. 【答案】B【解析】【分析】.,选B.【点睛】本题考查函数极值,考查等价转化思想方法与基本求解能力,属中档题.11.在二项式则有理项不相邻的概率为()A. B. D.【答案】A【解析】【分析】.有理项不相邻有种方法,因此所求概率为选A.【点睛】本题考查二项式定理以及古典概型概率,考查综合分析求解能力,属中档题.12.,则称函数.已知函数是区间上的双中值函数,则实数)A. B. D.【答案】C【解析】【分析】转化为函数有两个零点问题,再根据二次函数图象可得不等式,即得结果.或C.【点睛】本题考查函数零点,考查综合分析求解能力,属中档题二、填空题: 本大题共4小题,每小题5分,共20分.13.袋中有3个白球2个黑球共5个小球,现从袋中每次取一个小球,每个小球被抽到的可能性均相同,不放回地抽取两次,则在第一次取到黑球的条件下,第二次仍取到黑球的概率是________.【解析】 试题分析:记事件A 为“第一次取到白球”,事件B 为“第二次取到白球”,则事件AB 为“两次都取到白球”,考点:条件概率与独立事件. 点评:本题考查条件概率,是高中阶段见到的比较少的一种题目,针对于这道题同学们要好好分析,再用事件数表示的概率公式做一遍,有助于理解本题.14.【解析】 【分析】根据正态分布对称性求解. 【点睛】本题考查正态分布,考查综合分析求解能力,属中档题15.________.【解析】【分析】.,增,时,【点睛】本题考查利用导数研究函数单调性以及利用导数解决不等式恒成立问题,考查综合分析求解能力,属中档题16.________.【答案】【解析】【分析】利用导数求函数最值.【详解】因,对应值为时,,对应值为,【点睛】本题考查利用导数求函数最值,考查综合分析求解能力,属中档题三、解答题:本大题共6小题,共70分. 解答应写出文字说明,证明过程或演算步骤.17.【答案】(Ⅰ)【解析】【分析】(Ⅰ)根据复数相等列方程组,(Ⅱ)先化复数为代数形式,再根据复数为实数列式,解得实数值.【详解】解:,即为所求.【点睛】本题考查复数相等以及复数概念,考查基本分析求解能力,属中档题18.的通项公式;【答案】【解析】【分析】(Ⅰ)根据递推关系逐一代入求解,再根据规律归纳,(Ⅱ)根据和项与通项关系得递推关系式,再利用求根公式解得相邻项关系,最后根据数学归纳法证明.【详解】解:,解得.时,由(Ⅰ)可知成立,所以当时猜想也成立.【点睛】本题考查数学归纳法求与证数列通项公式,考查基本分析求解能力,属中档题19.(2013•重庆)设f(x)=a(x﹣5)2+6lnx,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线与y轴相交于点(0,6).(1)确定a的值;(2)求函数f(x)的单调区间与极值.【答案】(1)(2)见解析【解析】试题分析:(1(2的单调性可知是极大值点还是极小值点.试题解析:(1,得(2)由(1),.令,解得,.考点:导数的几何意义,用导数研究函数的单调性与极值.【名师点睛】导数的几何意义是切点处切线的斜率,应用时主要体现在以下几个方面(1)已知切点A(x0,f(x0))求斜率k,即求该点处的导数值:k=f′(x0);(2)已知斜率k,求切点A(x1,f(x1)),即解方程f′(x1)=k;(3)已知过某点M(x1,f(x1))(不是切点)的切线斜率为k时,常需设出切点A(x0,f(x0)),利用k20..(Ⅰ)假设这名射手射击3次,求至少1次击中目标的概率;(Ⅱ)假设这名射手射击3次,每次击中目标得10分,未击中目标得0分.在3次射击中,若有2次连续3次全部击中,则额外加10分.手射击3次后的总得分,求.【答案】(I(II 的分布列是【解析】试题分析:解:⑴3,所以所求概率为.⑵的所有可能取值为“”,,,.考点:n次独立重复试验中恰好发生k次的概率;离散型随机变量的期望与方差.点评:本题主要考查n次独立重复实验中恰好发生k次的概率,离散型随机变量的数学期望的求法,属于中档题.21.某分公司经销某种品牌产品,每件产品的成本为30然对数的底数)万件.已知每件产品的售价为40元时,该产品一年的销售量为500万件.经物价部门核定每35元,最高不超过41元.【答案】(1) L(x)= 500(x-30-a)e40-x(35≤x≤41);(2) 当2≤a≤4时,每件产品的售价为35元,该产品一年的利润L(x)最大,最大为500(5-a)e5万元;当4<a≤5时,每件产品的售价为(31+a)元时,该产品一年的利润L(x)最大,最大为500e9-a万元.【解析】试题分析:(1)先根据条件求出k,再根据利润等于销售量乘以单个利润得函数解析式,最后交代定义域(2)先求导数,再求导函数零点,根据零点与定义区间关系分类讨论,确定导函数符号,进而确定最大值试题解析:(1)由题意,该产品一年的销售量为y=.将x=40,y=500代入,得k=500e40.故该产品一年的销售量y(万件)关于x(元)的函数关系式为y=500e40-x.所以L(x)=(x-30-a)y=500(x-30-a)e40-x(35≤x≤41).(2)由(1)得,L′(x)=500[e40-x-(x-30-a)e40-x]=500e40-x(31+a-x).①当2≤a≤4时,L′(x)≤500e40-x(31+4-35)=0,当且仅当a=4,x=35时取等号.所以L(x)在[35,41]上单调递减.因此,L(x)max=L(35)=500(5-a)e5.②当4<a≤5时,L′(x)>0⇔35≤x<31+a,L′(x)<0⇔31+a<x≤41.所以L(x)在[35,31+a)上单调递增,在[31+a,41]上单调递减.因此,L(x)max=L(31+a)=500e9-a.综上所述当2≤a≤4时,每件产品的售价为35元,该产品一年的利润L(x)最大,最大为500(5-a)e5万元;当4<a≤5时,每件产品的售价为(31+a)元时,该产品一年的利润L(x)最大,最大为500e9-a万元.22.【答案】(1)函数的递增区间为,函数的递减区间为23)见解析.【解析】试题分析:(1(2)由(1上是增函数,由(1)可;(3)由(2)知,,,进而换元可得即可得证.试题解析:(1在上单调递增时,在上单调递增;(2)由(1)知,时,不可能成立;(3)由(2.点睛:(1)导数综合题中对于含有字母参数的问题,一般用到分类讨论的方法,解题时要注意分类要不重不漏;(2)对于恒成立的问题,直接转化为求函数的最值即可;(3)对于导数中,数列不等式的证明,解题时常常用到前面的结论,需要根据题目的特点构造合适的不等式,然后转化成数列的问题解决,解题时往往用到数列的求和.。
2018-2019学年新高一开学第一周 语文 第2课诗两首《雨巷》(第二课时)课件

他这时候所写的《雨巷》等诗中便自然贮满了彷徨失望和感伤痛苦的情绪。
2.失恋的痛苦
在爱情上,戴望舒第一次的恋爱在1927年,他 爱恋着好友施蜇存的妹妹施绛年,后来两人订婚, 终因她的变心而解除婚约,戴望舒十分痛苦。
诗中“雨巷”“我”“丁香一样的姑娘”各象征着什么?
象征:象征手法是根据事物之间的某种联系,借助某 人某物的具体形象(象征体),以表现某种抽象的概念、 思想和情感。
主题探讨 联系诗人的经历和写作背景,展开联想,诗中的“雨巷……丁 香般的姑娘”和“我”让你联想到了什么?作者想要表达的主题 到底是什么?
诗人借“丁香一样的姑娘”表达一种追求美好理想的愿望, 以及理想幻灭后的空虚和伤感,从而反映了诗人对现实的不满和 失望,也是当时不满现实又找不到出路的知识分子共同的复杂内 心世界的表露。
1.前途的迷惘
背景 简 黑暗的时代。反动派对革命者的血腥
屠杀,造成了笼罩全国的白色恐怖。原来热烈响应了革命的青年,一下子从火热的高潮
坠入了黑暗的深渊。他们中的一部分人,找不到革命的前途。他们在痛苦中陷于彷徨迷
惘,他们在失望中渴求着新的希望的出现,在阴霾中盼望飘起绚丽的彩虹。《雨巷》就
文学常识: (1)现代派诗歌:现代派诗歌产生于20世纪30年代,受到法国象征主义诗歌的启发
和影响,又承接了20年代中国象征诗派的某些艺术追求。追求诗歌创作的朦胧美,以奇 特观念和繁复的意象来结构诗的内涵。现代派诗人往往以其特有的青春病态的心灵,咏 叹着浊世的哀音,表达着对社会的不满和抗争,也流露出对人生深深的寂寞和惆怅。
戴望舒(1905-1950),笔名戴梦鸥、江恩、艾昂甫, 浙江杭州人。现代派象征主义诗人。1924年考入上海大学 文学系,1925年转入震旦大学法文班,1928年发表成名作 《雨巷》,1932年参加施蛰存主编《现代》杂志的创作, 并成为30年代“现代派”诗人群体的领袖。
公安县第一中学2018-2019学年下学期高二期中数学模拟题

公安县第一中学2018-2019学年下学期高二期中数学模拟题一、选择题1. 若A (3,﹣6),B (﹣5,2),C (6,y )三点共线,则y=( )A .13B .﹣13C .9D .﹣92. 已知,,x y z 均为正实数,且22log x x =-,22log y y -=-,22log zz -=,则( )A .x y z <<B .z x y <<C .z y z <<D .y x z << 3. 函数f (x )=x 2﹣2ax ,x ∈[1,+∞)是增函数,则实数a 的取值范围是( ) A .RB .[1,+∞)C .(﹣∞,1]D .[2,+∞)4. A 是圆上固定的一定点,在圆上其他位置任取一点B ,连接A 、B 两点,它是一条弦,它的长度大于等于半径长度的概率为( )A .B .C .D . 5. sin45°sin105°+sin45°sin15°=( )A .0B .C .D .16. 两个圆锥有公共底面,且两圆锥的顶点和底面圆周都在同一个球面上.若圆锥底面面积是球面面积的,则这两个圆锥的体积之比为( ) A .2:1 B .5:2 C .1:4 D .3:17. 设b ,c 表示两条直线,α,β表示两个平面,则下列命题是真命题的是( ) A .若b ⊂α,c ∥α,则b ∥cB .若c ∥α,α⊥β,则c ⊥β C .若b ⊂α,b ∥c ,则c ∥α D .若c ∥α,c ⊥β,则α⊥β8. 下列说法正确的是( ) A .类比推理是由特殊到一般的推理 B .演绎推理是特殊到一般的推理 C .归纳推理是个别到一般的推理 D .合情推理可以作为证明的步骤9. 设函数)(x f 是定义在)0,(-∞上的可导函数,其导函数为)('x f ,且有2')()(2x x xf x f >+,则不等式0)2(4)2014()2014(2>--++f x f x 的解集为A 、)2012,(--∞B 、)0,2012(-C 、)2016,(--∞D 、)0,2016(- 10.等差数列{a n }中,a 2=3,a 3+a 4=9 则a 1a 6的值为( ) A .14 B .18C .21D .2711.在△ABC 中,sinB+sin (A ﹣B )=sinC 是sinA=的( )A .充分非必要条件B .必要非充分条件班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________C .充要条件D .既不充分也非必要条件12.集合U=R ,A={x|x 2﹣x ﹣2<0},B={x|y=ln (1﹣x )},则图中阴影部分表示的集合是( )A .{x|x ≥1}B .{x|1≤x <2}C .{x|0<x ≤1}D .{x|x ≤1}二、填空题13.某工厂的某种型号的机器的使用年限x 和所支出的维修费用y (万元)的统计资料如表: x 6 8 10 12 y 2 3 5 6 根据上表数据可得y 与x 之间的线性回归方程=0.7x+,据此模型估计,该机器使用年限为14年时的维修费用约为 万元.14.【徐州市第三中学2017~2018学年度高三第一学期月考】函数()3f x x x =-+的单调增区间是__________. 15.抛物线y 2=4x 的焦点为F ,过F 且倾斜角等于的直线与抛物线在x 轴上方的曲线交于点A ,则AF 的长为 .16.【南通中学2018届高三10月月考】定义在上的函数满足,为的导函数,且对恒成立,则的取值范围是__________________.17.已知函数y=f (x ),x ∈I ,若存在x 0∈I ,使得f (x 0)=x 0,则称x 0为函数y=f (x )的不动点;若存在x 0∈I ,使得f (f (x 0))=x 0,则称x 0为函数y=f (x )的稳定点.则下列结论中正确的是 .(填上所有正确结论的序号)①﹣,1是函数g (x )=2x 2﹣1有两个不动点;②若x 0为函数y=f (x )的不动点,则x 0必为函数y=f (x )的稳定点; ③若x 0为函数y=f (x )的稳定点,则x 0必为函数y=f (x )的不动点; ④函数g (x )=2x 2﹣1共有三个稳定点;⑤若函数y=f (x )在定义域I 上单调递增,则它的不动点与稳定点是完全相同.18.函数f (x )=a x +4的图象恒过定点P ,则P 点坐标是 .三、解答题19.【盐城中学2018届高三上第一次阶段性考试】已知函数f (x )=ax 2+lnx (a ∈R ). (1)当a=12时,求f (x )在区间[1,e]上的最大值和最小值; (2)如果函数g (x ),f 1(x ),f 2(x ),在公共定义域D 上,满足f 1(x )<g (x )<f 2(x ),那么就称g (x )为f 1(x ),f 2(x )的“活动函数”.已知函数()()221121-a ln ,2f x a x ax x ⎛⎫=-++ ⎪⎝⎭.()22122f x x ax =+。
河南省郑州市第一中学高二下学期期中考试化学试题(含答案)

郑州市第一中学2023-2024学年高二下学期期中考试化学试题说明:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题),满分100分. 2.考试时间:75分钟.3.将第Ⅰ卷的答案代表字母填(涂)在答题卡上.可能用到的原子:H1C12N14S32Na23Al27P31Zn65As75第Ⅰ卷(选择题,共42分)一、选择题:本题共14小题,每小题3分,共42分.1.下列有关氧原子结构的化学用语中,对电子运动状态描述最详尽的是( )A .168O B .C .2241s 2s 2p D .2.下列分离混合物的实验方法中不正确的是( )A .分离乙酸(沸点77.1℃)与某种液态有机物(沸点120℃)的混合物-蒸馏B .从含有少量NaCl 的3KNO 溶液中提取3KNO 的操作为热水溶解、蒸发浓缩、降温结晶、过滤C .用CCl4萃取碘水中的碘,液体分层后,下层液体从下口放出,上层液体从上口倒出D .将溴水中的溴转移到有机溶剂中-加入乙醇萃取3.某烯烃分子的结构简式为用系统命名法命名其名称为( )A .2,2,4-三甲基-3-乙基-3-戊烯B .2,4,4-三甲基-3-乙基-2-戊烯C .2,2,4-三甲基3-乙基-2-戊烯D .2-甲基-3-叔丁基-2-戊烯 4.下列有关性质的比较不正确的是( )A .沸点:23H O>HF>NHB .熔点:二氧化硅2>NaCl>IC .硬度:碳化硅<金刚石D .沸点:5.日光灯中用到的某种荧光粉的主要成分为()34223W ZX WY ⋅.已知:X 、Y 、Z 和W 为原子序数依次增大的前20号元素,W 为金属元素.基态X 原子s 轨道上的电子数和p 轨道上的电子数相等,基态X 、Y 、Z 原子的未成对电子数之比为2:1:3,下列说法正确的是( ) A .电负性:X Y Z W >>> B .原子半径:X<Y<Z<WC .Y 和W 的单质都能与水反应生成气体D .Z 元素最高价氧化物对应的水化物具有强氧化性 6.下列说法中正确的有( )①金属晶体的导电性、导热性均与自由电子有关 ②若晶体中有阳离子,必然有阴离子 ③分子晶体的熔点一定比金属晶体低 ④共价键的强弱决定分子晶体熔、沸点的高低 ⑤共价晶体中一定含有共价键 ⑥含有离子的晶体一定是离子晶体 ⑦硬度由大到小:金刚石>碳化硅>晶体硅⑧NaCl 和CsCl 晶体中,阴离子周围紧邻的阳离子数均为8 A .2个 B .3个 C .4个 D .5个7.一种锌的配合物结构如图所示,下列有关说法正确的是( )A .中心离子提供空轨道的能级是3d 和4sB .该配合物中H N H --的键角比3NH 中H N H --的键角小C .溴原子不同形状的轨道上的电子数之比是8:17:10D .该化合物中C 、N 的杂化类型相同8.科学家合成了一种高温超导材料,其晶胞结构如图所示,该立方晶胞参数为apm .阿伏加德罗常数的值为A N .下列说法错误的是( )A .晶体最简化学式为66KCaBC B .晶体中与K +最近且距离相等的2Ca+有8个C .晶胞中B 和C 原子构成的多面体有12个面D .晶体的密度为3233A2.1710g cm a N -⨯⋅⋅ 9.某有机物分子的结构简式如图所示,下列相关叙述正确的是( )A .该有机化合物含有3种官能团B .该有机物分子中最多有12个碳原子在同一平面内C .该有机物分子中最多有6个碳原子共线D .该有机物分子中最多有14个碳原子在同一平面内10.抗癌药物CADD522的结构如图.关于该药物的说法错误..的是( )A .能发生水解反应B .含有2个手性碳原子C .能使2Br 的4CCl 溶液褪色D .碳原子杂化方式有2sp 和3sp11.中国工程院李兰娟院士团队公布研究成果,药物阿比朵尔对新冠病毒有明显抑制作用,其分子结构如图所示,下列说法正确的是( )A .其分子式为222523C H BrN O SB .分子中碳原子均采取2sp 杂化 C .阿比朵尔为芳香烃D .分子结构中含有多个官能团,如羟基,酯基,碳溴键,苯环12.下列关于烃的说法正确的是( )A .共面的C 原子最多为14个B .共直线的C 原子只能为4个C .1mol 该烃最多可以和26molH 发生加成反应D .1mol 该烃最多可以消耗26molBr13.某烃的分子式为1014C H ,它不能使溴水褪色,可使酸性4KMnO 溶液褪色,分子结构中只含有一个烷基,符合上述条件的烃有( )A .2种B .3种C .4种D .5种14.下列关于物质的结构或性质及解释都正确的是( )A .AB .BC .CD .D第Ⅱ卷(非选择题,共58分)二、非选择题:本题共4小题,共58分.15.(10分)用系统命名法给有机物命名①_____________;②_____________;③22CH CHCH Cl _____________;④2223|CH CH CCH CH CH 命名为____________________;⑤49C H Cl 的核磁共振氢谱表明其只有一种化学环境的氢,则其化学名称为______________________;⑥2CH CHCOONa 发生聚合反应可得到一种高吸水性树脂,该树脂名称为_____________.16.(22分)东晋《华阳国志·南中志》卷四中已有关于白铜的记载,云南镍白铜(铜镍合金)闻名中外,曾主要用于造币,亦可用于制作仿银饰品.回答下列问题: (1)硫酸镍溶于氨水形成()346Ni NH SO ⎡⎤⎣⎦蓝色溶液. ①()346Ni NH SO ⎡⎤⎣⎦中阴离子的立体构型是_____________.②在()346Ni NH SO ⎡⎤⎣⎦所含非金属元素的电负性由大到小为_______________.③333NH PH AsH 、、的沸点由高到低的顺序为_____________(填化学式,下同),键角由小到大的顺序为_____________.④基态Zn 原子的价电子排布式为_____________,在周期表中位置为_____________.(2)丁二酮肟是检验N2+的灵敏试剂.丁二酮肟分子(||CH3CH3HON C CNOH—)中C 原子轨道杂化类型为_____________,1mol 丁二酮肟分子所含σ键的数目为_____________.(3)配合物[]4Ni(CO)常温下为液体,易溶于4CCl 、苯等有机溶剂.[]4Ni(CO)中Ni 与CO 的C 原子形成配位键.不考虑空间构型,[]4Ni(CO)的结构可用示意图表示为_____________(用“→”表示出配位键). (4)33NH BH 分子中,N B —化学键称为_____________键,其电子对由_____________提供.氨硼烷在催化剂作用下水解释放氢气:333243623NH BH 6H O 3NH B O 9H +-+=++↑.336B O -的结构为.在该反应中,B 原子的杂化轨道类型由_____________变为_____________.17.(14分)晶体世界丰富多彩,复杂多样,各类晶体具有不同的结构特点,决定着它具有不同的性质和用途,回答下列问题:(I )氢化铝钠()4NaAlH 是一种新型轻质储氢材料,其晶胞结构如图所示,为长方体.4NaAlH 晶体中,与4AlH -紧邻且等距的Na +有_____________个;4NaAlH 晶体的密度为_____________3g cm -⋅(用含a 、A N 的代数式表示).(2)氮化钼作为锂离子电池负极材料具有很好的发展前景.它属于填隙式氮化物,N 原子部分填充在Mo 原子立方晶格的八面体空隙中,晶胞结构如图所示.氮化钼的化学式为_____________,Mo 原子周围与之等距离的Mo 原子个数为_____________. (3)ZnS 的晶胞结构如图所示:晶体中2S -填充在2Zn +围成的四面体空隙中,则四面体空隙的填充率为_____________;已知ZnS 的晶胞密度是3ag /cm ,则2Zn +与2S -的最短距离为_____________pm (用含a 、A N 的代数式表示).(4)已知Co 可形成晶胞结构如图所示,以晶胞参数为单位长度建立的坐标系可表示晶胞中各原子的位置,称作原子的分数坐标,已知晶胞含对称中心,其中1号O 原子的分数坐标为(0.6667,0.3333,0.1077),2号O 原子的分数坐标为_____________.18.(12分)异戊二烯()232CH =C CH CH=CH ⎡⎤⎣⎦是一种重要的化工原料,能发生以下反应:已知:①烯烃与酸性4KMnO 溶液反应的氧化产物对应关系:②请回答下列问题:(1)异戊二烯的一氯代物有_____________种;写出一种反应①发生1,2—加成所得有机产物的结构简式为_____________.(2)X 存在顺反异构,写出它的反式异构体的结构简式:_____________;可能发生的反应有_____________(填字母).A .加成反应B .氧化反应C .酯化反应(3)Y 的结构简式为_____________;B 为含有六元环的有机物,其结构简式为_____________.郑州市第一中学2023-2024学年高二下学期期中考试化学参考答案一、选择题:本题共14小题,每小题3分,共42分.二、非选择题:本题共4小题,共58分.15.(10分)【除标注分值外,每空2分】(1)3,3,4-三甲基己烷(1分) (2)乙苯(1分) (3)3-氯-1-丙烯 (4)2-乙基-1,3-丁二烯 (5)2-甲基-2-氯丙烷 (6)聚丙烯酸钠 16.(22分)【除标注分值外,每空2分】(1)①.正四面体形(1分) ②.O 、N 、S 、H (1分) ③.333NH AsH PH 、、 333AsH PH NH 、、 ④1023d 4s 第四周期B Ⅱ族 (2)3sp 和2sp A 15N(3)(4)配位(1分) N (或氮原子)(1分) 3sp 2sp 17.(14分)【每空2分】(1)8 233A1.0810a N ⨯ (2)2Mo N 12 (3)50% 10104 (4)(0.3333,0.6667,0.6077) 18.(12分)【每空2分】(1)6 ()232BrCH CBr CH CH CH =或()232CH C CH CHBrCH Br =(2) AB(3)3||O C CH COOH ——。
红安县第一中学2018-2019学年下学期高二期中数学模拟题

红安县第一中学2018-2019学年下学期高二期中数学模拟题一、选择题1. 已知函数f (x )=3cos (2x ﹣),则下列结论正确的是( )A .导函数为B .函数f (x )的图象关于直线对称C .函数f (x )在区间(﹣,)上是增函数D .函数f (x )的图象可由函数y=3co s2x 的图象向右平移个单位长度得到2.平面向量与的夹角为60°,=(2,0),||=1,则|+2|=( )A. B. C .4 D .123. 已知集合A={0,m ,m 2﹣3m+2},且2∈A ,则实数m 为( )A .2B .3C .0或3D .0,2,3均可4. 已知复数11i z a =+,232i z =+,a ∈R ,i 是虚数单位,若12z z 是实数,则a =( )A . 23-B .13-C .13D .235. 12,e e 是平面内不共线的两向量,已知12AB e ke =-,123CD e e =-,若,,A B D 三点共线,则的值是( )A .1B .2C .-1D .-26. 若函数)1(+=x f y 是偶函数,则函数)(x f y =的图象的对称轴方程是( )] A .1=x B .1-=x C .2=x D .2-=x 7. 某程序框图如图所示,该程序运行后输出的S 的值是( )A .﹣3 B.﹣ C. D .28. 已知命题p :“∀x ∈R ,e x >0”,命题q :“∃x 0∈R ,x 0﹣2>x 02”,则( )A .命题p ∨q 是假命题B .命题p ∧q 是真命题C .命题p ∧(¬q )是真命题D .命题p ∨(¬q )是假命题班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________9. 已知 m 、n 是两条不重合的直线,α、β、γ是三个互不重合的平面,则下列命题中 正确的是( ) A .若 m ∥α,n ∥α,则 m ∥n B .若α⊥γ,β⊥γ,则 α∥βC .若m ⊥α,n ⊥α,则 m ∥nD .若 m ∥α,m ∥β,则 α∥β10.若多项式 x 2+x 10=a 0+a 1(x+1)+…+a 8(x+1)8+a 9(x+1)9+a 10(x+1)10,则 a 8=( ) A .45 B .9 C .﹣45 D .﹣911.下面的结构图,总经理的直接下属是( )A .总工程师和专家办公室B .开发部C .总工程师、专家办公室和开发部D .总工程师、专家办公室和所有七个部 12.若命题p :∀x ∈R ,2x 2﹣1>0,则该命题的否定是( )A .∀x ∈R ,2x 2﹣1<0B .∀x ∈R ,2x 2﹣1≤0C .∃x ∈R ,2x 2﹣1≤0D .∃x ∈R ,2x 2﹣1>0二、填空题13.正六棱台的两底面边长分别为1cm ,2cm ,高是1cm ,它的侧面积为 .14.(﹣2)7的展开式中,x 2的系数是 .15.已知过双曲线22221(0,0)x y a b a b-=>>的右焦点2F 的直线交双曲线于,A B 两点,连结11,AF BF ,若1||||AB BF =,且190ABF ∠=︒,则双曲线的离心率为( )A .5-BC .6- D【命题意图】本题考查双曲线定义与几何性质,意要考查逻辑思维能力、运算求解能力,以及考查数形结合思想、方程思想、转化思想.16.已知一组数据1x ,2x ,3x ,4x ,5x 的方差是2,另一组数据1ax ,2ax ,3ax ,4ax ,5ax (0a >)的标准差是a = .17.设幂函数()f x kx α=的图象经过点()4,2,则k α+= ▲ . 18.已知函数f (x )=,则关于函数F (x )=f (f (x ))的零点个数,正确的结论是 .(写出你认为正确的所有结论的序号)①k=0时,F (x )恰有一个零点.②k <0时,F (x )恰有2个零点. ③k >0时,F (x )恰有3个零点.④k >0时,F (x )恰有4个零点.三、解答题19.(本题满分12分)已知向量(sin cos ))a x x x =+,)cos sin ,(cos x x x b -=,R x ∈,记函数 x f ⋅=)(.(1)求函数)(x f 的单调递增区间;(2)在ABC ∆中,角C B A ,,的对边分别为c b a ,,且满足C a c b cos 22=-,求)(B f 的取值范围.【命题意图】本题考查了向量的内积运算,三角函数的化简及性质的探讨,并与解三角形知识相互交汇,对基本运算能力、逻辑推理能力有一定要求,但突出了基础知识的考查,仍属于容易题.20.已知直线l 的方程为y=x+4,圆C 的参数方程为(θ为参数),以原点为极点,x 轴正半轴为极轴.建立极坐标系.(Ⅰ)求直线l 与圆C 的交点的极坐标;(Ⅱ)若P 为圆C 上的动点.求P 到直线l 的距离d 的最大值.21.已知函数f (x )=sin2x •sin φ+cos 2x •cos φ+sin (π﹣φ)(0<φ<π),其图象过点(,.)(Ⅰ)求函数f (x )在[0,π]上的单调递减区间;(Ⅱ)若x0∈(,π),sinx0=,求f(x0)的值.22.如图,四边形ABCD是圆内接四边形,BA、CD的延长线交于点P,且AB=AD,BP=2BC(Ⅰ)求证:PD=2AB;(Ⅱ)当BC=2,PC=5时.求AB的长.23.在平面直角坐标系XOY中,圆C:(x﹣a)2+y2=a2,圆心为C,圆C与直线l1:y=﹣x的一个交点的横坐标为2.(1)求圆C的标准方程;(2)直线l2与l1垂直,且与圆C交于不同两点A、B,若S△ABC=2,求直线l2的方程.24.某小区在一次对20岁以上居民节能意识的问卷调查中,随机抽取了100份问卷进行统计,得到相关的数(2)据了解到,全小区节能意识强的人共有350人,估计这350人中,年龄大于50岁的有多少人?(3)按年龄分层抽样,从节能意识强的居民中抽5人,再从这5人中任取2人,求恰有1人年龄在20至50岁的概率.红安县第一中学2018-2019学年下学期高二期中数学模拟题(参考答案)一、选择题1.【答案】B【解析】解:对于A,函数f′(x)=﹣3sin(2x﹣)•2=﹣6sin(2x﹣),A错误;对于B,当x=时,f()=3cos(2×﹣)=﹣3取得最小值,所以函数f(x)的图象关于直线对称,B正确;对于C,当x∈(﹣,)时,2x﹣∈(﹣,),函数f(x)=3cos(2x﹣)不是单调函数,C错误;对于D,函数y=3co s2x的图象向右平移个单位长度,得到函数y=3co s2(x﹣)=3co s(2x﹣)的图象,这不是函数f(x)的图象,D错误.故选:B.【点评】本题考查了余弦函数的图象与性质的应用问题,是基础题目.2.【答案】B【解析】解:由已知|a|=2,|a+2b|2=a2+4ab+4b2=4+4×2×1×cos60°+4=12,∴|a+2b|=.故选:B.【点评】本题是对向量数量积的考查,根据两个向量的夹角和模之间的关系,根据和的模两边平方,注意要求的结果非负,舍去不合题意的即可.两个向量的数量积是一个数量,它的值是两个向量的模与两向量夹角余弦的乘积,结果可正、可负、可以为零,其符号由夹角的余弦值确定.3.【答案】B【解析】解:∵A={0,m,m2﹣3m+2},且2∈A,∴m=2或m2﹣3m+2=2,解得m=2或m=0或m=3.当m=0时,集合A={0,0,2}不成立.当m=2时,集合A={0,0,2}不成立.当m=3时,集合A={0,3,2}成立.故m=3.故选:B.【点评】本题主要考查集合元素和集合之间的关系的应用,注意求解之后要进行验证.4. 【答案】A【解析】1232(32)i z z a a =-++, ∵12z z 是实数,∴320a +=,∴23a =-. 5. 【答案】B 【解析】考点:向量共线定理. 6. 【答案】A 【解析】试题分析:∵函数)1(+=x f y 向右平移个单位得出)(x f y =的图象,又)1(+=x f y 是偶函数,对称轴方程为0=x ,∴)(x f y =的对称轴方程为1=x .故选A . 考点:函数的对称性. 7. 【答案】 B【解析】解:由程序框图得:第一次运行S==﹣3,i=2;第二次运行S==﹣,i=3;第三次运行S==,i=4;第四次运行S==2,i=5;第五次运行S==﹣3,i=6,…S 的值是成周期变化的,且周期为4,当i=2015时,程序运行了2014次,2014=4×503+2,∴输出S=﹣. 故选:B .【点评】本题考查了循环结构的程序框图,根据程序的运行功能判断输出S 值的周期性变化规律是关键.8.【答案】C【解析】解:命题p:“∀x∈R,e x>0”,是真命题,命题q:“∃x0∈R,x0﹣2>x02”,即﹣x0+2<0,即:+<0,显然是假命题,∴p∨q真,p∧q假,p∧(¬q)真,p∨(¬q)假,故选:C.【点评】本题考查了指数函数的性质,解不等式问题,考查复合命题的判断,是一道基础题.9.【答案】C【解析】解:对于A,若m∥α,n∥α,则m与n相交、平行或者异面;故A错误;对于B,若α⊥γ,β⊥γ,则α与β可能相交,如墙角;故B错误;对于C,若m⊥α,n⊥α,根据线面垂直的性质定理得到m∥n;故C正确;对于D,若m∥α,m∥β,则α与β可能相交;故D错误;故选C.【点评】本题考查了空间线线关系.面面关系的判断;熟练的运用相关的定理是关键.10.【答案】A【解析】解:a8 是x10=[﹣1+(x+1)]10的展开式中第九项(x+1)8的系数,∴a8==45,故选:A.【点评】本题主要考查二项展开式的通项公式,二项展开式系数的性质以及多项恒等式系数相等的性质,属于基础题.11.【答案】C【解析】解:按照结构图的表示一目了然,就是总工程师、专家办公室和开发部.读结构图的顺序是按照从上到下,从左到右的顺序.故选C.【点评】本题是一个已知结构图,通过解读各部分从而得到系统具有的功能,在解读时,要从大的部分读起,一般而言,是从左到右,从上到下的过程解读.12.【答案】C【解析】解:命题p:∀x∈R,2x2﹣1>0,则其否命题为:∃x∈R,2x2﹣1≤0,故选C;【点评】此题主要考查命题否定的定义,是一道基础题;二、填空题13.【答案】cm2.【解析】解:如图所示,是正六棱台的一部分,侧面ABB1A1为等腰梯形,OO1为高且OO1=1cm,AB=1cm,A1B1=2cm.取AB和A1B1的中点C,C1,连接OC,CC1,O1C1,则C1C为正六棱台的斜高,且四边形OO1C1C为直角梯形.根据正六棱台的性质得OC=,OC1==,1∴CC1==.又知上、下底面周长分别为c=6AB=6cm,c′=6A1B1=12cm.∴正六棱台的侧面积:S=.==(cm2).故答案为:cm2.【点评】本题考查正六棱台的侧面积的求法,是中档,解题时要认真审题,注意空间思维能力的培养.14.【答案】﹣280解:∵(﹣2)7的展开式的通项为=.由,得r=3.∴x 2的系数是.故答案为:﹣280. 15.【答案】B 【解析】16.【答案】2 【解析】试题分析:第一组数据平均数为2)()()()()(,2524232221=-+-+-+-+-∴x x x x x x x x x x x ,22222212345()()()()()8,4,2ax ax ax ax ax ax ax ax ax ax a a -+-+-+-+-=∴=∴=.考点:方差;标准差.17.【答案】32【解析】试题分析:由题意得11,422k αα==⇒=∴32k α+=考点:幂函数定义18.【答案】 ②④【解析】解: ①当k=0时,,当x ≤0时,f (x )=1,则f (f (x ))=f (1)==0,此时有无穷多个零点,故①错误;②当k <0时,(Ⅰ)当x ≤0时,f (x )=kx+1≥1, 此时f (f (x ))=f (kx+1)=,令f (f (x ))=0,可得:x=0; (Ⅱ)当0<x ≤1时,,此时f (f (x ))=f ()=,令f (f (x ))=0,可得:x=,满足;(Ⅲ)当x >1时,,此时f (f (x ))=f ()=k +1>0,此时无零点. 综上可得,当k <0时,函数有两零点,故②正确;③当k >0时,(Ⅰ)当x ≤时,kx+1≤0,此时f (f (x ))=f (kx+1)=k (kx+1)+1, 令f (f (x ))=0,可得:,满足; (Ⅱ)当时,kx+1>0,此时f (f (x ))=f (kx+1)=,令f (f (x ))=0,可得:x=0,满足;(Ⅲ)当0<x ≤1时,,此时f (f (x ))=f ()=,令f (f (x ))=0,可得:x=,满足;(Ⅳ)当x >1时,,此时f (f (x ))=f ()=k +1,令f (f (x ))=0得:x=>1,满足;综上可得:当k >0时,函数有4个零点.故③错误,④正确.故答案为:②④.【点评】本题考查复合函数的零点问题.考查了分类讨论和转化的思想方法,要求比较高,属于难题. 三、解答题19.【答案】【解析】(1)由题意知,)cos )(sin cos (sin 23cos sin )(x x x x x x x f +-+=⋅= )32sin(2cos 232sin 21π-=-=x x x ……………………………………3分 令223222πππππ+≤-≤-k x k ,Z k ∈,则可得12512ππππ+≤≤-k x k ,Z k ∈. ∴)(x f 的单调递增区间为]125,12[ππππ+-k k (Z k ∈).…………………………5分20.【答案】【解析】解:(I)由圆C的参数方程为(θ为参数),利用cos2θ+sin2θ=1化为:x2+(y﹣2)2=4,联立,解得或.可得极坐标分别为:,.(II)圆心(0,2)到直线l的距离=,∴P到直线l的距离d的最大值为+r=+2.【点评】本题考查了参数方程化为普通方程、极坐标方程化为直角坐标方程、直线与圆的位置关系,考查了推理能力与计算能力,属于中档题.21.【答案】【解析】(本小题满分12分)φ解:(Ⅰ)f(x)=+﹣=+=)由f(x)图象过点()知:所以:φ=所以f(x)=令(k∈Z)即:所以:函数f(x)在[0,π]上的单调区间为:(Ⅱ)因为x0∈(π,2π),则:2x0∈(π,2π)则:=sin所以=)=【点评】本题考查的知识要点:三角函数关系式的恒等变换,正弦型函数单调区间的确定,三角函数的求值问题,属于基础题型.22.【答案】【解析】(Ⅰ)证明:∵四边形ABCD是圆内接四边形,∴∠PAD=∠PCB,∴∠APD=∠CPB,∴△APD∽△CPB,∴=,∵BP=2BC∴PD=2AD,∴AB=AD,∴PD=2AB;(Ⅱ)解:由题意,BP=2BC=4,设AB=t,由割线定理得PD•PC=PA•PB,∴2t×5=(4﹣t)×4∴t=,即AB=.【点评】本题考查三角形相似的判断,考查割线定理,考查学生分析解决问题的能力,属于中档题.23.【答案】【解析】解:(1)由圆C与直线l1:y=﹣x的一个交点的横坐标为2,可知交点坐标为(2,﹣2),∴(2﹣a)2+(﹣2)2=a2,解得:a=2,所以圆的标准方程为:(x﹣2)2+y2=4,(2)由(1)可知圆C的圆心C的坐标为(2,0)由直线l2与直线l1垂直,直线l1:y=﹣x可设直线l2:y=x+m,则圆心C到AB的距离d=,|AB|=2=2所以S△ABC=|AB|•d=•2•=2令t=(m+2)2,化简可得﹣2t2+16t﹣32=﹣2(t﹣4)2=0,解得t=(m+2)2=4,所以m=0,或m=﹣4∴直线l2的方程为y=x或y=x﹣4.24.【答案】【解析】解(1)因为20至50岁的54人有9人节能意识强,大于50岁的46人有36人节能意识强,与相差较大,所以节能意识强弱与年龄有关(2)由数据可估计在节能意识强的人中,年龄大于50岁的概率约为∴年龄大于50岁的约有(人)(3)抽取节能意识强的5人中,年龄在20至50岁的(人),年龄大于50岁的5﹣1=4人,记这5人分别为a,B1,B2,B3,B4.从这5人中任取2人,共有10种不同取法:(a,B1),(a,B2),(a,B3),(a,B4),(B1,B2),(B1,B3),(B1,B4),(B2,B3),(B2,B4),(B3,B4),设A表示随机事件“这5人中任取2人,恰有1人年龄在20至50岁”,则A中的基本事件有4种:(a,B1),(a,B2),(a,B3),(a,B4)故所求概率为。
内蒙古巴彦淖尔市临河区第一中学2023-2024学年高二下学期升级考试数学试题

内蒙古巴彦淖尔市临河区第一中学2023-2024学年高二下学期升级考试数学试题一、单选题1.若集合{}1,1A =-,{}2B x mx ==,且B A ⊆,则实数m 的值是( ) A .2-B .2C .2或2-D .2或2-或02.已知命题:0,e 1x p x ∀≥≥或sin 1x <,则p ⌝为( ) A .0,e 1x x ∃<<且sin 1x ≥ B .0,e 1x x ∃≥<且sin 1x ≥ C .0,e 1x x ∃≥≥或sin 1x ≥ D .0,e 1x x ∃<≥或sin 1x ≤3.“02x <<”是“13x -<<”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充要条件 D .既不充分也不必要条件4.当0x >时,92x x+的最小值为( )A .3B .32C .D .5.函数()()01f x x -的定义域为( ) A .()2,11,3∞⎡⎫⋃+⎪⎢⎣⎭ B .()2,11,3∞⎛⎫⋃+ ⎪⎝⎭C .2,3⎡⎫-+∞⎪⎢⎣⎭D .2,3⎛⎫+∞ ⎪⎝⎭6.已知多项式()()562560125621x x a a x a x a x a x -+-=+++⋅⋅⋅++,则1a =( ) A .11B .74C .86D .1-7.已知随机变量X 服从二项分布()4,B p ,其期望()3E X =,随机变量Y 服从正态分布()1,2N ,若()0P Y p >=,则()02P Y <<=( ) A .23B .34C .14D .128.已知函数()f x 是定义域为R 的偶函数,且()1f x +为奇函数,当[]0,1x ∈时,()3x f x k a =⋅+.若()()034f f +=,则()3log 2f =( ) A .2B .0C .3-D .6-二、多选题9.若0a b >>,则下列结论正确的是( ) A .22a b > B .22ac bc > CD .1122ab⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭10.设函数()ln 21ln 21f x x x =+--,则()f x ( )A .是偶函数B .是奇函数C .在11,22⎛⎫- ⎪⎝⎭上单调递增D .在1,2⎛⎫-∞- ⎪⎝⎭上单调递减11.已知函数()ln ex xf x =,则( )A .曲线()y f x =在点()1,0处的切线方程是e 10x y +-=B .函数()f x 有极大值,且极大值点x 0∈ 1,2C .()()23f f <D .函数()f x 只有1个零点三、填空题12.已知函数2()2,[0,]f x x x x b =-∈,且该函数的值域为[1,3]-,则b 的值为. 13.若()f x 是一次函数,()41f f x x =-⎡⎤⎣⎦且,则()f x =.14.已知函数()22ln f x x a x =-.若()0f x ≥在()1,+∞恒成立,则a 的范围为.四、解答题15.在ABC V 中,角A ,B ,C 所对的边分别为a ,b ,c .若c =1b =,120C =o ,求: (1)角B ; (2)ABC V 的面积S .16.记n S 为数列{}n a 的前n 项和.已知221nn S n a n+=+.(1)证明:{}n a 是等差数列;(2)若479,,a a a 成等比数列,求n S 的最小值.17.“五一”假期期间,某餐厅对选择A 、B 、C 三种套餐的顾客进行优惠.对选择A 、B 套餐的顾客都优惠10元,对选择C 套餐的顾客优惠20元.根据以往“五一”假期期间100名顾客对选择A 、B 、C 三种套餐的情况得到下表:将频率视为概率.(I )若有甲、乙、丙三位顾客选择某种套餐,求三位顾客选择的套餐至少有两样不同的概率;(II )若用随机变量X 表示两位顾客所得优惠金额的综合,求X 的分布列和期望. 18.函数2()1ax bf x x +=+是定义在(1,1)-上的单调递增的奇函数,且1225f ⎛⎫= ⎪⎝⎭. (1)求函数()f x 的解析式;(2)求满足(1)()0f t f t -+<的t 的范围; 19.已知函数()()e 1=--∈x f x ax a R (1)讨论函数()f x 的单调性与极值;(2)若[)0,x ∈+∞时,函数()f x 有两个零点,求实数a 的取值范围。
海伦市第一中学2018-2019学年下学期高二期中数学模拟题

海伦市第一中学2018-2019学年下学期高二期中数学模拟题一、选择题1. 如图甲所示, 三棱锥P ABC - 的高8,3,30PO AC BC ACB ===∠=o,,M N 分别在BC 和PO 上,且(),203CM x PN x x ==∈(,,图乙的四个图象大致描绘了三棱锥N AMC -的体积y 与 的变化关系,其中正确的是( )A .B . C. D .1111]2. 下列函数中,与函数()3x xe ef x --=的奇偶性、单调性相同的是( )A .()2ln 1y x x =++ B .2y x = C .tan y x = D .xy e =3. 若x ,y 满足且z=y ﹣x 的最小值为﹣2,则k 的值为( ) A .1B .﹣1C .2D .﹣24. 已知命题p ;对任意x ∈R ,2x 2﹣2x+1≤0;命题q :存在x ∈R ,sinx+cosx=,则下列判断:①p 且q是真命题;②p 或q 是真命题;③q 是假命题;④¬p 是真命题,其中正确的是( ) A .①④ B .②③C .③④D .②④5. 关于x 的方程ax 2+2x ﹣1=0至少有一个正的实根,则a 的取值范围是( )A .a ≥0B .﹣1≤a <0C .a >0或﹣1<a <0D .a ≥﹣16. 在ABC ∆中,3b =,3c =,30B =o ,则等于( )A .3B .123C .3或23D .2 7. 下列命题中的假命题是( )A .∀x ∈R ,2x ﹣1>0B .∃x ∈R ,lgx <1C .∀x ∈N +,(x ﹣1)2>0D .∃x ∈R ,tanx=28. 在△ABC 中,已知a=2,b=6,A=30°,则B=( )A .60°B .120°C .120°或60°D .45°9. 已知两条直线ax+y ﹣2=0和3x+(a+2)y+1=0互相平行,则实数a 等于( ) A .1或﹣3 B .﹣1或3 C .1或3D .﹣1或﹣310.已知点F 是抛物线y 2=4x 的焦点,点P 在该抛物线上,且点P 的横坐标是2,则|PF|=( ) A .2 B .3 C .4 D .511.已知抛物线C :y x 82=的焦点为F ,准线为l ,P 是l 上一点,Q 是直线PF 与C 的一个交点,若2=,则=QF ( )班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________A .6B .3C .38 D .34 第Ⅱ卷(非选择题,共100分)12.若关于x 的方程x 3﹣x 2﹣x+a=0(a ∈R )有三个实根x 1,x 2,x 3,且满足x 1<x 2<x 3,则a 的取值范围为( ) A .a >B .﹣<a <1 C .a <﹣1D .a >﹣1二、填空题13.某慢性疾病患者,因病到医院就医,医生给他开了处方药(片剂),要求此患者每天早、晚间隔小时各服一次药,每次一片,每片毫克.假设该患者的肾脏每小时从体内大约排出这种药在其体内残留量的,并且医生认为这种药在体内的残留量不超过毫克时无明显副作用.若该患者第一天上午点第一次服药,则第二天上午点服完药时,药在其体内的残留量是 毫克,若该患者坚持长期服用此药 明显副作用(此空填“有”或“无”) 14.已知z ,ω为复数,i 为虚数单位,(1+3i )z 为纯虚数,ω=,且|ω|=5,则复数ω= .15.在ABC ∆中,已知角C B A ,,的对边分别为c b a ,,,且B c C b a sin cos +=,则角B 为 .16.(﹣)0+[(﹣2)3]= .17.已知条件p :{x||x ﹣a|<3},条件q :{x|x 2﹣2x ﹣3<0},且q 是p 的充分不必要条件,则a 的取值范围是 .18.若关于x ,y 的不等式组(k 是常数)所表示的平面区域的边界是一个直角三角形,则k= .三、解答题19.如图,在几何体SABCD 中,AD ⊥平面SCD ,BC ⊥平面SCD ,AD=DC=2,BC=1,又SD=2,∠SDC=120°. (1)求SC 与平面SAB 所成角的正弦值;(2)求平面SAD 与平面SAB 所成的锐二面角的余弦值.20.已知函数.(Ⅰ)若函数f(x)在区间[1,+∞)内单调递增,求实数a的取值范围;(Ⅱ)求函数f(x)在区间[1,e]上的最小值.21.已知p:,q:x2﹣(a2+1)x+a2<0,若p是q的必要不充分条件,求实数a的取值范围.22.已知等差数列{a n}的前n项和为S n,公差d≠0,S2=4,且a2,a5,a14成等比数列.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)从数列{a n }中依次取出第2项,第4项,第8项,…,第2n 项,…,按原来顺序组成一个新数列{b n },记该数列的前n 项和为T n ,求T n 的表达式.23.已知函数f (x )=alnx+,曲线y=f (x )在点(1,f (1))处的切线方程为y=2.(I )求a 、b 的值;(Ⅱ)当x >1时,不等式f (x )>恒成立,求实数k 的取值范围.24.(本题满分12分)已知数列}{n a 的前n 项和为n S ,且332-=n n a S ,(+∈N n ). (1)求数列}{n a 的通项公式; (2)记nn a n b 14+=,n T 是数列}{n b 的前n 项和,求n T . 【命题意图】本题考查利用递推关系求通项公式、用错位相减法求数列的前n 项和.重点突出对运算及化归能力的考查,属于中档难度.海伦市第一中学2018-2019学年下学期高二期中数学模拟题(参考答案)一、选择题1. 【答案】A 【解析】考点:几何体的体积与函数的图象.【方法点晴】本题主要考查了空间几何体的体积与函数的图象之间的关系,其中解答中涉及到三棱锥的体积公式、一元二次函数的图象与性质等知识点的考查,本题解答的关键是通过三棱锥的体积公式得出二次函数的解析式,利用二次函数的图象与性质得到函数的图象,着重考查了学生分析问题和解答问题的能力,是一道好题,题目新颖,属于中档试题.2. 【答案】A 【解析】试题分析:()()f x f x -=-所以函数为奇函数,且为增函数.B 为偶函数,C 定义域与()f x 不相同,D 为非奇非偶函数,故选A.考点:函数的单调性与奇偶性. 3. 【答案】B【解析】解:由z=y ﹣x 得y=x+z , 作出不等式组对应的平面区域如图:平移直线y=x+z 由图象可知当直线y=x+z 经过点A 时,直线y=x+z 的截距最小, 此时最小值为﹣2,即y ﹣x=﹣2,则x ﹣y ﹣2=0, 当y=0时,x=2,即A (2,0),同时A 也在直线kx ﹣y+2=0上,代入解得k=﹣1, 故选:B【点评】本题主要考查线性规划的应用,利用数形结合是解决线性规划问题中的基本方法.本题主要考查的难点在于对应的区域为线段.4.【答案】D【解析】解:∵命题p;对任意x∈R,2x2﹣2x+1≤0是假命题,命题q:存在x∈R,sinx+cosx=是真命题,∴①不正确,②正确,③不正确,④正确.故选D.5.【答案】D【解析】解:(1)当a=0时,方程是2x﹣1=0,可知有一个正实根.(2)当a≠0,当关于x的方程ax2+2x﹣1=0有实根,△≥0,解可得a≥﹣1;①当关于x的方程ax2+2x﹣1=0有一个正实根,有﹣<0,解可得a>0;②当关于x的方程ax2+2x﹣1=0有二个正实根,有,解可得a<0;,综上可得,a≥﹣1;故选D.【点评】本题主要考查一个一元二次根的分布问题,属于中档题.在二次项系数不确定的情况下,注意一定要分二次项系数分为0和不为0两种情况讨论.6.【答案】C【解析】考点:余弦定理. 7. 【答案】C【解析】解:A .∀x ∈R ,2x ﹣1=0正确;B .当0<x <10时,lgx <1正确;C .当x=1,(x ﹣1)2=0,因此不正确;D .存在x ∈R ,tanx=2成立,正确. 综上可知:只有C 错误.故选:C .【点评】本题考查了指数函数与对数函数、正切函数的单调性,属于基础题.8. 【答案】C 【解析】解:∵a=2,b=6,A=30°,∴由正弦定理可得:sinB===,∵B ∈(0°,180°), ∴B=120°或60°. 故选:C .9. 【答案】A【解析】解:两条直线ax+y ﹣2=0和3x+(a+2)y+1=0互相平行, 所以=≠,解得 a=﹣3,或a=1.故选:A .10.【答案】B【解析】解:抛物线y 2=4x 的准线方程为:x=﹣1, ∵P 到焦点F 的距离等于P 到准线的距离,P 的横坐标是2,∴|PF|=2+1=3. 故选:B .【点评】本题考查抛物线的性质,利用抛物线定义是解题的关键,属于基础题.11.【答案】A解析:抛物线C :y x 82的焦点为F (0,2),准线为l :y=﹣2,设P (a ,﹣2),B (m ,),则=(﹣a ,4),=(m ,﹣2),∵,∴2m=﹣a,4=﹣4,∴m2=32,由抛物线的定义可得|QF|=+2=4+2=6.故选A.12.【答案】B【解析】解:由x3﹣x2﹣x+a=0得﹣a=x3﹣x2﹣x,设f(x)=x3﹣x2﹣x,则函数的导数f′(x)=3x2﹣2x﹣1,由f′(x)>0得x>1或x<﹣,此时函数单调递增,由f′(x)<0得﹣<x<1,此时函数单调递减,即函数在x=1时,取得极小值f(1)=1﹣1﹣1=﹣1,在x=﹣时,函数取得极大值f(﹣)=(﹣)3﹣(﹣)2﹣(﹣)=,要使方程x3﹣x2﹣x+a=0(a∈R)有三个实根x1,x2,x3,则﹣1<﹣a<,即﹣<a<1,故选:B.【点评】本题主要考查导数的应用,构造函数,求函数的导数,利用导数求出函数的极值是解决本题的关键.二、填空题13.【答案】, 无.【解析】【知识点】等比数列【试题解析】设该病人第n次服药后,药在体内的残留量为毫克,所以)=300,=350.由,所以是一个等比数列,所以所以若该患者坚持长期服用此药无明显副作用。
岭东区第一中学2018-2019学年下学期高二期中数学模拟题

岭东区第一中学2018-2019学年下学期高二期中数学模拟题一、选择题1. 已知集合A={x|a ﹣1≤x ≤a+2},B={x|3<x <5},则A ∩B=B 成立的实数a 的取值范围是( )A .{a|3≤a ≤4}B .{a|3<a ≤4}C .{a|3<a <4}D .∅2. 3名医生和6名护士被分配到3所学校为学生体检,每校分配1名医生和2名护士.不同的分配方法共有()A .90种B .180种C .270种D .540种3. 若函数()()()()()1cos sin cos sin 3sin cos 412f x x x x x a x x a x =-++-+-在02π⎡⎤-⎢⎥⎣⎦,上单调递增,则实数的取值范围为()A .117⎡⎤⎢⎥⎣⎦, B .117⎡⎤-⎢⎥⎣⎦,C.1([1)7-∞-+∞U ,,D .[1)+∞,4. 的展开式中,常数项是( )62)21(x x -A .B .C .D .45-451615-16155. 已知函数有两个零点,则实数的取值范围是( )1()1x f x ae x a -=+--a A .B .C .D .[1,1]-[0,1]{1}(0,1]-U {1}[0,1)-U 6. 已知抛物线的焦点为,,点是抛物线上的动点,则当的值最小时,24y x =F (1,0)A -P ||||PF PA PAF ∆的面积为( )B. C.D. 24【命题意图】本题考查抛物线的概念与几何性质,考查学生逻辑推理能力和基本运算能力.7. 已知f (x )是定义在R 上周期为2的奇函数,当x ∈(0,1)时,f (x )=3x ﹣1,则f (log 35)=( )A .B .﹣C .4D .8. 下列结论正确的是()A .若直线l ∥平面α,直线l ∥平面β,则α∥β.B .若直线l ⊥平面α,直线l ⊥平面β,则α∥β.C .若直线l 1,l 2与平面α所成的角相等,则l 1∥l 2D .若直线l 上两个不同的点A ,B 到平面α的距离相等,则l ∥α 9. 已知集合M={1,4,7},M ∪N=M ,则集合N 不可能是( )A .∅B .{1,4}C .MD .{2,7}班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________10.一个几何体的三视图如图所示,如果该几何体的侧面面积为12π,则该几何体的体积是()A.4πB.12πC.16πD.48π11.已知函数f(x)的定义域为R,其导函数f′(x)的图象如图所示,则对于任意x1,x2∈R(x1≠x2),下列结论正确的是()①f(x)<0恒成立;②(x1﹣x2)[f(x1)﹣f(x2)]<0;③(x1﹣x2)[f(x1)﹣f(x2)]>0;④;⑤.A.①③B.①③④C.②④D.②⑤12.下列函数中哪个与函数y=x相等()A.y=()2B.y=C.y=D.y=二、填空题S13.阅读如图所示的程序框图,则输出结果的值为.n【命题意图】本题考查程序框图功能的识别,并且与数列的前项和相互联系,突出对逻辑判断及基本运算能力的综合考查,难度中等.14.在复平面内,记复数+i对应的向量为,若向量饶坐标原点逆时针旋转60°得到向量所对应的复数为 .15.在(x2﹣)9的二项展开式中,常数项的值为 .16.如图,是一回形图,其回形通道的宽和OB1的长均为1,回形线与射线OA交于A1,A2,A3,…,若从点O到点A3的回形线为第1圈(长为7),从点A3到点A2的回形线为第2圈,从点A2到点A3的回形线为第3圈…依此类推,第8圈的长为 .17.如图为长方体积木块堆成的几何体的三视图,此几何体共由 块木块堆成.18.若在圆C:x2+(y﹣a)2=4上有且仅有两个点到原点O距离为1,则实数a的取值范围是 .三、解答题19.(本题满分12分)如图1在直角三角形ABC中,∠A=90°,AB=2,AC=4,D,E分别是AC,BC边上的中点,M为CD的中点,现将△CDE沿DE折起,使点A在平面CDE内的射影恰好为M.(I)求AM的长;(Ⅱ)求面DCE与面BCE夹角的余弦值.20.在△ABC中,内角A,B,C所对的边分别是a,b,c,已知tanA=,c=.(Ⅰ)求;(Ⅱ)若三角形△ABC的面积为,求角C.21.某校高一数学兴趣小组开展竞赛前摸底考试.甲、乙两人参加了5次考试,成绩如下:第一次第二次第三次第四次第五次甲的成绩8287868090乙的成绩7590917495(Ⅰ)若从甲、乙两人中选出1人参加比赛,你认为选谁合适?写出你认为合适的人选并说明理由;(Ⅱ)若同一次考试成绩之差的绝对值不超过5分,则称该次考试两人“水平相当”.由上述5次摸底考试成绩统计,任意抽查两次摸底考试,求恰有一次摸底考试两人“水平相当”的概率. 22.(本题满分12分)在中,已知角所对的边分别是,边,且ABC ∆,,A B C ,,a b c 72c =,又的面积为,求的值.tan tan tan A B A B +=-g ABC ∆ABC S ∆=a b +23.【南京市2018届高三数学上学期期初学情调研】已知函数f (x )=2x 3-3(a +1)x 2+6ax ,a ∈R .(Ⅰ)曲线y =f (x )在x =0处的切线的斜率为3,求a 的值;(Ⅱ)若对于任意x ∈(0,+∞),f (x )+f (-x )≥12ln x 恒成立,求a 的取值范围;(Ⅲ)若a >1,设函数f (x )在区间[1,2]上的最大值、最小值分别为M (a )、m (a ),记h (a )=M (a )-m (a ),求h (a )的最小值.24.已知p :x ∈A={x|x 2﹣2x ﹣3≤0,x ∈R},q :x ∈B={x|x 2﹣2mx+m 2﹣4≤0,x ∈R ,m ∈R}(1)若A ∩B=[0,3],求实数m 的值;(2)若p 是¬q 的充分条件,求实数m 的取值范围.岭东区第一中学2018-2019学年下学期高二期中数学模拟题(参考答案)一、选择题1. 【答案】A【解析】解:∵A={x|a ﹣1≤x ≤a+2}B={x|3<x <5}∵A ∩B=B ∴A ⊇B∴解得:3≤a ≤4故选A【点评】本题考查集合的包含关系判断及应用,通过对集合间的关系转化为元素的关系,属于基础题. 2. 【答案】D【解析】解:三所学校依次选医生、护士,不同的分配方法共有:C 31C 62C 21C 42=540种.故选D . 3. 【答案】D 【解析】考点:1、导数;2、单调性;3、函数与不等式.4. 【答案】D【解析】,2612316611()()()22r r r r r r r T C x C x x --+=-=-令,解得.1230r -=4r =∴常数项为.446115()216C -=5. 【答案】D【解析】当时,.1a =1()11x f x e x -=+--当时,为增函数,1x ≥1()2x f x e x -=+-∴,有唯一零点.()(1)0f x f ≥=1当时,,.1x <1()x f x ex -=-1()1x f x e -'=-∵,∴,单调减,1x <()0f x '<()f x ∴,没有零点,()(1)0f x f <=综上: 时,原函数只有一个零点,1a =故不成立,从而排除.,,A B C 6. 【答案】B【解析】设,则.又设,则,,所以2(,)4y P y 2||||PF PA=214y t +=244y t =-1t …,当且仅当,即时,等号成立,此时点,||||PF PA ==2t =2y =±(1,2)P ±的面积为,故选B.PAF ∆11||||22222AF y ⋅=⨯⨯=7. 【答案】B【解析】解:∵f (x )是定义在R 上周期为2的奇函数,∴f (log 35)=f (log 35﹣2)=f (log 3),∵x ∈(0,1)时,f (x )=3x ﹣1∴f (log 3)═﹣故选:B8. 【答案】B【解析】解:A 选项中,两个平面可以相交,l 与交线平行即可,故不正确;B 选项中,垂直于同一平面的两个平面平行,正确;C 选项中,直线与直线相交、平行、异面都有可能,故不正确;D 中选项也可能相交.故选:B .【点评】本题考查平面与平面,直线与直线,直线与平面的位置关系,考查学生分析解决问题的能力,比较基础. 9. 【答案】D【解析】解:∵M ∪N=M ,∴N ⊆M ,∴集合N不可能是{2,7},故选:D【点评】本题主要考查集合的关系的判断,比较基础.10.【答案】B【解析】解:由三视图可知几何体是底面半径为2的圆柱,∴几何体的侧面积为2π×2×h=12π,解得h=3,∴几何体的体积V=π×22×3=12π.故选B.【点评】本题考查了圆柱的三视图,结构特征,体积,表面积计算,属于基础题.11.【答案】D【解析】解:由导函数的图象可知,导函数f′(x)的图象在x轴下方,即f′(x)<0,故原函数为减函数,并且是,递减的速度是先快后慢.所以f(x)的图象如图所示.f(x)<0恒成立,没有依据,故①不正确;②表示(x1﹣x2)与[f(x1)﹣f(x2)]异号,即f(x)为减函数.故②正确;③表示(x1﹣x2)与[f(x1)﹣f(x2)]同号,即f(x)为增函数.故③不正确,④⑤左边边的式子意义为x1,x2中点对应的函数值,即图中点B的纵坐标值,右边式子代表的是函数值得平均值,即图中点A的纵坐标值,显然有左边小于右边,故④不正确,⑤正确,综上,正确的结论为②⑤.故选D.12.【答案】B【解析】解:A.函数的定义域为{x|x≥0},两个函数的定义域不同.B.函数的定义域为R,两个函数的定义域和对应关系相同,是同一函数.C.函数的定义域为R,y=|x|,对应关系不一致.D.函数的定义域为{x|x≠0},两个函数的定义域不同.故选B .【点评】本题主要考查判断两个函数是否为同一函数,判断的标准是判断函数的定义域和对应关系是否一致,否则不是同一函数. 二、填空题13.【答案】20172016【解析】根据程序框图可知,其功能是求数列的前1008项的和,即})12)(12(2{+-n n+⨯+⨯=532312S .=-++-+-=⨯+2017120151()5131(311(201720152 2017201614.【答案】 2i .【解析】解:向量饶坐标原点逆时针旋转60°得到向量所对应的复数为(+i )(cos60°+isin60°)=(+i )()=2i,故答案为 2i .【点评】本题考查两个复数代数形式的乘法及其集合意义,判断旋转60°得到向量对应的复数为(+i )(cos60°+isin60°),是解题的关键. 15.【答案】 84 .【解析】解:(x 2﹣)9的二项展开式的通项公式为 T r+1=•(﹣1)r •x 18﹣3r ,令18﹣3r=0,求得r=6,可得常数项的值为T 7===84,故答案为:84.【点评】本题主要考查二项式定理的应用,二项展开式的通项公式,属于基础题. 16.【答案】 63 .【解析】解:∵第一圈长为:1+1+2+2+1=7第二圈长为:2+3+4+4+2=15第三圈长为:3+5+6+6+3=23…第n 圈长为:n+(2n ﹣1)+2n+2n+n=8n ﹣1故n=8时,第8圈的长为63,故答案为:63.【点评】本题主要考查了归纳推理,解答的一般步骤是:先通过观察第1,2,3,…圈的长的情况发现某些相同性质,再从相同性质中推出一个明确表达的一般性结论,最后将一般性结论再用于特殊情形. 17.【答案】 4 【解析】解:由三视图可以看出此几何体由两排两列,前排有一个方块,后排左面一列有两个木块右面一列有一个,故后排有三个,故此几何体共有4个木块组成.故答案为:4.18.【答案】 ﹣3<a<﹣1或1<a<3 .【解析】解:根据题意知:圆x2+(y﹣a)2=4和以原点为圆心,1为半径的圆x2+y2=1相交,两圆圆心距d=|a|,∴2﹣1<|a|<2+1,∴﹣3<a<﹣1或1<a<3.故答案为:﹣3<a<﹣1或1<a<3.【点评】本题体现了转化的数学思想,解题的关键在于将问题转化为:圆x2+(y﹣a)2=4和以原点为圆心,1为半径的圆x2+y2=1相交,属中档题.三、解答题19.【答案】解:(I)由已知可得AM⊥CD,又M为CD的中点,∴;3分(II)在平面ABED内,过AD的中点O作AD的垂线OF,交BE于F点,以OA为x轴,OF为y轴,OC为z轴建立坐标系,可得,∴,,5分设为面BCE的法向量,由可得=(1,2,﹣),∴cos<,>==,∴面DCE与面BCE夹角的余弦值为4分20.【答案】【解析】解:(Ⅰ)由题意知,tanA=,则=,即有sinA﹣sinAcosC=cosAsinC,所以sinA=sinAcosC+cosAsinC=sin(A+C)=sinB,由正弦定理,a=b,则=1;…(Ⅱ)因为三角形△ABC的面积为,a=b、c=,所以S=absinC=a2sinC=,则,①由余弦定理得,=,②由①②得,cosC+sinC=1,则2sin(C+)=1,sin(C+)=,又0<C<π,则C+<,即C+=,解得C=….【点评】本题考查正弦定理,三角形的面积公式,以及商的关系、两角和的正弦公式等,注意内角的范围,属于中档题.21.【答案】【解析】解:(Ⅰ)解法一:依题意有,答案一:∵∴从稳定性角度选甲合适.(注:按(Ⅱ)看分数的标准,5次考试,甲三次与乙相当,两次优于乙,所以选甲合适.答案二:∵乙的成绩波动大,有爆发力,选乙合适.解法二:因为甲5次摸底考试成绩中只有1次90,甲摸底考试成绩不低于90的概率为;乙5次摸底考试成绩中有3次不低于90,乙摸底考试成绩不低于90的概率为.所以选乙合适.(Ⅱ)依题意知5次摸底考试,“水平相当”考试是第二次,第三次,第五次,记为A,B,C.“水平不相当”考试是第一次,第四次,记为a,b.从这5次摸底考试中任意选取2次有ab,aA,aB,aC,bA,bB,bC,AB,AC,BC共10种情况.恰有一次摸底考试两人“水平相当”包括共aA,aB,aC,bA,bB,bC共6种情况.∴5次摸底考试成绩统计,任意抽查两次摸底考试,恰有一次摸底考试两人“水平相当”概率.【点评】本题主要考查平均数,方差,概率等基础知识,运算数据处理能力、运算求解能力、应用意识,考查化归转化思想、或然与必然思想.22.【答案】.112【解析】试题解析:由tan tan tan A B A B +=g可得,即.tan tan 1tan tan A B A B+=-g tan()A B +=∴,∴,∴tan()C π-=tan C -=tan C =∵,∴.(0,)C π∈3C π=又的面积为,∴,即.ABC ∆ABC S ∆=1sin 2ab C =12ab =6ab =又由余弦定理可得,∴,2222cos c a b ab C =+-2227(2cos 23a b ab π=+-∴,∴,∵,∴.122227()()32a b ab a b ab =+-=+-2121()4a b +=0a b +>112a b +=考点:解三角形问题.【方法点晴】本题主要考查了解三角形问题,其中解答中涉及到两角和与两角差的正切函数公式、三角形的面积、正弦定理和余弦定理,以及特殊角的三角函数值等知识点的综合考查,着重考查了学生分析问题和解答问题的能力,以及推理与运算能力,其中熟练掌握基本公式和灵活运用公式是解答本题的关键,属于中档试题.23.【答案】(1)a =(2)(-∞,-1-].(3)121e 827【解析】(2)f (x )+f (-x )=-6(a +1)x 2≥12ln x 对任意x ∈(0,+∞)恒成立,所以-(a +1)≥.22ln x x 令g (x )=,x >0,则g '(x )=.22ln x x()3212ln x x -令g '(x )=0,解得x 当x ∈(0g '(x)>0,所以g (x )在(0当x,+∞)时,g '(x )<0,所以g (x ,+∞)上单调递减.所以g (x )max =g )=,1e 所以-(a +1)≥,即a ≤-1-,1e 1e所以a 的取值范围为(-∞,-1-].1e(3)因为f (x )=2x 3-3(a +1)x 2+6ax ,所以f ′(x )=6x 2-6(a +1)x +6a =6(x -1)(x -a ),f (1)=3a -1,f (2)=4.令f ′(x )=0,则x =1或a .f (1)=3a -1,f (2)=4.②当<a <2时,53当x ∈(1,a )时,f '(x )<0,所以f (x )在(1,a )上单调递减;当x ∈(a ,2)时,f '(x )>0,所以f (x )在(a ,2)上单调递增.又因为f (1)>f (2),所以M (a )=f (1)=3a -1,m (a )=f (a )=-a 3+3a 2,所以h (a )=M (a )-m (a )=3a -1-(-a 3+3a 2)=a 3-3a 2+3a -1.因为h ' (a )=3a 2-6a +3=3(a -1)2≥0.所以h (a )在(,2)上单调递增,53所以当a ∈(,2)时,h (a )>h ()=.5353827③当a ≥2时,当x ∈(1,2)时,f '(x )<0,所以f (x )在(1,2)上单调递减,所以M (a )=f (1)=3a -1,m (a )=f (2)=4,所以h (a )=M (a )-m (a )=3a -1-4=3a -5,所以h (a )在[2,+∞)上的最小值为h (2)=1.综上,h (a )的最小值为.827点睛:已知函数最值求参数值或取值范围的一般方法:(1)利用导数结合参数讨论函数最值取法,根据最值列等量关系,确定参数值或取值范围;(2)利用最值转化为不等式恒成立问题,结合变量分离转化为不含参数的函数,利用导数求新函数最值得参数值或取值范围.24.【答案】【解析】解:由已知得:A={x|﹣1≤x ≤3},B={x|m ﹣2≤x ≤m+2}.(1)∵A ∩B=[0,3]∴∴,∴m=2;(2)∵p 是¬q 的充分条件,∴A ⊆∁R B ,而C R B={x|x <m ﹣2,或x >m+2}∴m ﹣2>3,或m+2<﹣1,∴m >5,或m <﹣3.。
安徽省合肥市第一中学等学校2023-2024学年高二下学期期中联考地理试题3

①位于珠三角,邻近香港和澳门②科技力量雄厚,高端人才集聚
③拥有与总部经济相适应的服务支撑体系④交通、通讯网络完善通畅
A.①②③B.①②④C.①③④D.②③④
24.广州市总部经济的分布特点是()
A.区域性、特色化B.分散性、规模化C.均衡性、个性化D.集中性、多元化
(1)与皖江城市带其他城市相比,说明合肥市承接长三角地区产业转移的有利条件。
(2)从城市化的角度说明承接产业转移对合肥市发展的促进作用。
(3)从产业发展的角度提出构建合肥都市圈的合理措施。
27.阅读图文材料,完成下列要求。
20世纪60年代以来,由于注入水量显著减少,咸海急剧萎缩,至1987年咸海分裂成南、北两部分。锡尔河发源于西天山,流经中亚地区重要的灌溉农业区后,在咸海入湖口形成三角洲湿地,湿地主要沿锡尔河南、北入湖口主河道、河汊、支流及湖泊周边分布,包括湿地植被和湿地水体两个主要部分。1975—1991年,锡尔河入湖口附近耕地大幅扩张,灌渠等水利设施增多,湿地植被也随之扩张,20世纪90年代以后,锡尔河入湖口附近耕地停止扩张。下图分别表示锡尔河三角洲湿地分布及1960—2019年南北咸海及南北入湖口湿地面积变化。
3.图示区域最适合建设移土培肥工程 覆土耕地是( )
A.①B.②C.③D.④
4.除“坡改梯”工程外,该地耕地建设需要的其他配套工程不包括( )
A.农田水利建设工程B.道路工程
C.农田防护林工程D.温室大棚和遮阳设施
5.库区实施移土培肥工程的生态意义主要是( )
①减轻库区的土壤盐碱化②增加库区周边的耕地数量
20.关于上海及全国IC产业的销售情况,下列说法正确的是( )
A.全国的IC产业销售额在20162017年增加最多
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一机械制造(集团)有限公司第一中学2018-2019学年高二下学期期中考试语文试题注意事项:1、答卷前,考生务必将自己的姓名、准考证号填写在答题卡上,本试卷满分150分,考试时间150分钟。
2、回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时将答案写在答题卡上相应题号的位置上,写在非对应题号处或本试卷上无效。
3、考试结束后将答题卡交回。
一、现代文阅读(36分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成1—3题。
君子人格,是中华传统文化在数千年发展进程中不断塑造和培育的正面人格,被历代中国人广泛接受并尊崇。
“君子”一词在西周时早已流行,主要指称贵族和执政者。
春秋末期,孔子赋予“君子”概念许多优秀道德的意蕴。
冯友兰说,孔子一生思考的问题很广泛,其中最根本的就是对如何做人的反思。
如果说,孔子思想的核心是探求如何做人的道理,那么他求索的结果,就是做人要做君子。
君子作为孔子心目中崇德向善的人格,既理想又现实,既高尚又平凡,是可见可感、可学可做、应学应做的人格范式。
孔子一生最大的成就,是创立了儒家学派。
什么是儒学?有一种观点回答得很干脆:儒学就是君子之学。
具体来说,在修己和治人两方面,儒学都以“君子的理想”为枢纽观念:修己即所以成为“君子”,治人则必须先成为“君子”。
从这一角度说,儒学事实上便是“君子之学”。
这种观点从儒学的目标追求和功能作用上说明儒学的特点,无疑抓住了本质,对于我们理解儒学乃至整个中华传统文化的特质,在今天继承和弘扬以儒学为主干的中华优秀传统文化,都具有不可忽视的积极意义。
儒学乃至整个中华传统文化,更多的时候是一种面向现实人生的伦理学说,与西方文化大相径庭。
西方文化热衷于构造能够解释思维与存在、精神与物质关系的严密理论系统,热衷于探寻认识论、方法论、辩证法等。
中华传统文化虽然也包括对认识论、方法论和辩证法的思考,却并不层层追问“是什么、为什么”,而是直截了当地告诉你“做什么、怎么做”。
这种不仅讲究“知”,更看重“行”的“知行合一”的理念,在有关君子及君子文化的论述中尤为突出。
“君子欲讷于言而敏于行”,“君子耻其言而过其行”,《论语》中的这些论述,鲜明体现出儒家乃至整个中华传统文化洋溢的“实用理性”精神。
这种重行动、轻言辞,重实践、轻思辨的精神,使历代士大夫、知识分子都不是只把仁、义、忠、孝、廉、悌等当作理论,而是当作值得遵循也应该遵循的伦理规范。
其目的就是在全社会尽可能多地培育和塑造君子人格,并以其引导、带动各阶层大倡君子之风、大行君子之道。
当前,培育和践行社会主义核心价值观,离不开激活传统文化中优秀的价值理念,有必要通过挖掘、整理、阐发和弘扬,让君子文化这颗最能体现中华优秀传统文化“精气神”的种子在新时代春风吹拂下生根发芽、开花结果。
(摘编自钱念孙《君子文化的传统魅力与当代张力》)1.下列关于原文内容的理解和分析,不正确的一项是(3分)A.“君子”一词在中华文化中出现甚早,孔子将许多优秀道德融入其中,使其成为崇德向善的人格范式。
B.冯友兰认为,如何做人是孔子一生都在思考的问题,而做人要做君子也正是冯先生思考的结果。
C.修己是成为君子的途径,而成为君子又是治人的前提,这说明儒学“修己”与“治人”的核心观念是一致的。
D.《论语》作为儒学的经典著作,很能体现儒学不追求系统的理论构建,而是直接告诉人们“做什么、怎么做”这一特点。
2.下列对原文论证的相关分析,不正确的一项是(3分)A.文章肯定了“儒学就是君子之学”这一观点,并指出其对于当今继承和弘扬中华优秀传统文化等方面的积极意义。
B.文章第四段通过对比分析,呈现了中华传统文化与西方文化的不同之处,指出了各自的优缺点。
C.文章引用《论语》中有关君子“言”与“行”的论述,体现了传统文化“知行合一”的观念和“实用理性”精神。
D.文章从“君子之学”和“实用理性”精神两方面展开论述,彰显了君子文化的传统魅力和当代意义。
3.根据原文内容,下列说法不正确的一项是(3分)A.君子人格具有现实和平凡的特点,这是它能被历代中国人广泛接受并践行的重要原因之一。
B.是不是热衷于构建一套严密的理论系统,可作为观察中西方文化基本差异的一个视角。
C.中国传统文化重行动、轻言辞,重实践、轻思辨,所以不会层层追问“是什么、为什么”。
D.若想让君子文化在当代社会蔚然成风,也离不开广大官员和知识分子的身体力行与引导带动。
(二)实用类文本阅读(本题共3小题,12分)阅读下面的文字,完成4—6题。
材料一:黄河之滨,白塔山下,伫立着一座非物质文化遗产陈列馆,阮熙越就在这里坚守着。
阮熙越是兰州阮氏刻葫芦第四代传人,其作品被英国等国家博物馆收藏,她的家族传承刻葫芦技艺已有百年历史。
谈及刻葫芦民间艺术现状,阮熙越表示,这些年来当地政府在民间艺术上投入很大,很多民间传统工艺的生存环境有了改观。
据兰州市文化和旅游局社会文化处介绍,近两年,政府加大对当地民间艺术的保护力度,现在已建成4个“非物质文化遗产”保护基地,建立了44个“非遗”传习所,给予市级以上“非遗”传习所每年5000元到8000元的资金扶持,提供免费的传习场地,还给予资金支持或提供交流机会去国外展示展演。
(选自《甘肃兰州:政府多措施保护民间工艺实现文化传承》)材料二:对待传统手工技艺程式化和已成为法度套路的东西,如法式、规矩、惯例、艺诀等,我们应该加以尊重,不要以“创新”的名义或为经济效益而轻率地改变。
创新不是告别传统的使用功能,而是以适应当代生活需要为突破点,在不违背手工业生产规律,不扭曲其自然衍变趋势的前提下,生产符合现代人审美观念的产品。
成功的设计能够创立新的“典范”,引领新的手工艺潮流与时尚。
而设计的主要任务是培育民族工艺品牌,重塑民族的工艺意象。
但是,这么多年,中国一直都缺乏叫得响的国际一流“手工品牌”,原因在于掌握技艺的民间手工艺人,大都年龄偏大,文化水平有限,视野思维也不够开阔,而年轻一代则在技艺上不够成熟,这些阻碍了现代设计与传统民间手工艺的融合。
科技代替不了双手,后工业时代更需要“工匠精神”,这样产品才有温度。
手艺人是民间手工艺的传承者,也是“工匠精神”的践行者,因此振兴传统民间手工艺,传承“工匠精神”,首先要给予职业手艺人以职业尊重。
为此,有学者指出,完善制度建设势在必行,还有学者建议学习日本的手工艺人才培养方式——先培养其基本心性、品德,再进行技艺传承,同时将“工匠精种”融入现代教育体系中,培养现代学徒。
(摘编自《光明日报》《传统民间手工艺如何走出“深闺”》)材料三:凤翔城关镇六营村是凤翔泥塑发源地,经过不断地完善加工,逐步形成了今天的彩绘泥塑。
当我们打开“中国泥塑网”时,便可以看到绚丽多姿的泥塑产品正在进行当今最迅捷最远程的网上交易。
据统计资料显示,近些年来仅泥塑产业一项就带动了宝鸡地区旅游等相关产业收入近千万元,当地村民把这项传统的民间工艺发展成为了六营村的主要致富手段。
可喜消息的背后伴随着新的忧虑。
市场经济挽救了民间艺术,同时也激励它发生新旧交替的巨变,这巨变会不会正是原始艺术特征的可悲的消逝过程的开始呢?我们如何才能尽可能长久地保持民间艺术的原汁原味呢?(摘编自《产业化经营让凤翔彩绘泥塑走向世界》)材料四:由于手工工艺品主要以手工制作为主,既费时又耗力,所以手工工艺品大多都是以个人生产经营为主,生产规模相对较小。
虽然有一部分的手工工艺品进入国际市场,但是我国手工艺品的整体发展水平还不是很成熟,其生产规模和经营手段的规模化、市场化以及产业化程度相对较低,所以市场的核心竞争力也较低下。
目前,传统手工艺的生产和形式严重的脱离了人们的生活实际,使得传统手工艺品逐渐萎缩。
现代人的生活方式和审美观念发生了很大的改变,尤其是互联网+时代的到来,消费者的审美越来越国际化、个性化、生活化,对那些造型老套、形象土气、材质普通、品相不佳的非遗手工产品提不起兴趣,这就倒逼手工艺术家们要从传统思维定式中走出来,要融入现代审美情趣、融合当代流行工艺、融汇当下时尚元素,打造出令消费者眼前一亮,而又爱不释手的好作品、好产品。
(摘编自《传统手工艺活态传承的困境与出路》)4.下列对材料相关内容的理解,不正确的一项是(3分)A.手工艺术品主要以手工制作为主,手艺人在振兴传统民间手工艺方面起着至关重要的作用。
因此,重视民间手工艺,首先要重视手艺人。
B.对待传统手工技艺程式化和已成法度套路的东西,如法式、规矩、惯例、艺诀等,我们应该加以尊重,不要以“创新”的名义或为经济效益而做出任何改变。
C.材料三表明,市场经济不但可以挽救民间艺术,使其获得新的发展,还可以带动相关产业的发展,成为致富的新途径。
D.手工工艺品要想获得新的生命力,需要手工艺术家们从传统思维定式中走出来,满足现代人的生活方式和审美情趣。
5.下列对材料相关内容的概括和分析,正确的一顶是(3分)A.中国的民间手工艺人,无论年龄大小,其自身都存在着一定的不足,导致了中国缺乏国际一流的民族工艺品牌。
B.在不违背手工业生产规律的前提下,融入现代审美情趣后,创新的改变手工艺产品的使用功能,就能打造出令消费者眼前一亮的好产品。
C.在市场经济的帮助下,民间艺术不但焕发出了新的活力,还带动了一些地区的经济发展,所以市场经济对民间艺术来说,是百利而无一害的。
D.由于手工艺品主要以手工制作为主,既费时又耗力,生产规模相对较小,所以必须走机械化生产道路,以提高生产效率。
6.怎样才能让民间手工艺走出困境,传承并发扬光大?请结合材料简要概括。
(6分)(三)文学类文本阅读(本题共3小题,15分)阅读下面的文字,完成7—9题。
抬头见喜①老舍对于时节,我向来不特别的注意。
拿清明说吧,上坟烧纸不必非我去不可,又搭着不常住在家乡,所以每逢看见柳枝发青便晓得快到了清明,或者是已经过去。
对重阳也是这样,生平没在九月九登过高,于是重阳和清明一样的没有多大作用。
端阳,中秋,新年,三个大节可不能这么马虎过去。
即使我故意躲着它们,账条是不会忘记了我的。
也奇怪,一个无名之辈,到了三节会有许多人惦记着,不但来信,送账条,而且要找上门来!设若专讲三节的热闹有趣那一面儿,我似乎是最喜爱中秋。
我至少有三次喝醉是在中秋;酒入愁肠呀!这三次“非杨贵妃式”的醉酒我还都记得很清楚。
第一次是在北平,好友卢嵩庵从柳泉居运来一坛子“竹叶青”。
又约来两位朋友——内中有一位是不会喝的。
大家就抄起茶碗来。
坛子虽大,架不住茶碗一个劲进攻;月亮还没上来,坛子已空。
干什么去呢?打牌玩吧。
各拿出铜元百枚,第一把牌将立起来,不晓得——至今还不晓得——我怎么上了床。
牌必是没打成,因为我一睁眼已经红日东升了。
第二次是在天津,和朱荫棠在同福楼吃饭,各饮绿茵陈二两。
