选修2-2课件211合情推理与演绎推理
合集下载
(选修2-2)2.1.1合情推理课件2.24
偶数=奇质数+奇质数
通过更多特例的检验, 从6开始,没有出现反例.
任何一个不小于6 的偶数都等于两个 奇质数的和.
2n p1 p2 (n N , n 3)
大胆猜想:
成语“一叶知秋” 意思是从一片树叶的凋落,知道秋
天将要来到.比喻由细微的迹象看出整体 形势的变化,由个别推知一般.
谚语“瑞雪兆丰年” 物理学中牛顿发现万有引力
由某类事物的部分对象具有某些特征,推出 该类事物的全部对象都具有这些特征的推理,或 者由个别事实概括出一般结论的推理,称为归纳 推理(简称归纳).
即是由部分到整体,由个别到一般的推理.
你能举出归纳推理 的例子吗?
观察下列等式
6=3+3, 12=5+7,
8=3+5, 14=3+11,
10=3+7, 16=5+11 归纳出一个规律:
蛇类是用肺呼吸的
鳄鱼是用肺呼吸的 海龟是用肺呼吸的
爬行动 物都是 用肺呼
整 体 蜥蜴是用肺呼吸的
吸的
一般
共 第一个数为2
第二个数为4 第三个数为6
性
第n个 数为2n.
第四个数为8
由某类事物的部分对象具有某些特征,推出 该类事物的全部对象都具有这些特征的推理,或 者由个别事实概括出一般结论的推理,称为归纳 推理(简称归纳).
化学中的门捷列夫元素周期表Fra bibliotek天文学中开普勒行星运动定律
歌德巴赫猜想 四色定理 牛顿发现万有引力 门捷列夫发现元素周期律等等
应用归纳推理可以 发现新事实,获得新结论!
归纳推理的过程: 归纳推理的特点:
实验观察
在同一类事物中 (1)从特殊到一般;
通过更多特例的检验, 从6开始,没有出现反例.
任何一个不小于6 的偶数都等于两个 奇质数的和.
2n p1 p2 (n N , n 3)
大胆猜想:
成语“一叶知秋” 意思是从一片树叶的凋落,知道秋
天将要来到.比喻由细微的迹象看出整体 形势的变化,由个别推知一般.
谚语“瑞雪兆丰年” 物理学中牛顿发现万有引力
由某类事物的部分对象具有某些特征,推出 该类事物的全部对象都具有这些特征的推理,或 者由个别事实概括出一般结论的推理,称为归纳 推理(简称归纳).
即是由部分到整体,由个别到一般的推理.
你能举出归纳推理 的例子吗?
观察下列等式
6=3+3, 12=5+7,
8=3+5, 14=3+11,
10=3+7, 16=5+11 归纳出一个规律:
蛇类是用肺呼吸的
鳄鱼是用肺呼吸的 海龟是用肺呼吸的
爬行动 物都是 用肺呼
整 体 蜥蜴是用肺呼吸的
吸的
一般
共 第一个数为2
第二个数为4 第三个数为6
性
第n个 数为2n.
第四个数为8
由某类事物的部分对象具有某些特征,推出 该类事物的全部对象都具有这些特征的推理,或 者由个别事实概括出一般结论的推理,称为归纳 推理(简称归纳).
化学中的门捷列夫元素周期表Fra bibliotek天文学中开普勒行星运动定律
歌德巴赫猜想 四色定理 牛顿发现万有引力 门捷列夫发现元素周期律等等
应用归纳推理可以 发现新事实,获得新结论!
归纳推理的过程: 归纳推理的特点:
实验观察
在同一类事物中 (1)从特殊到一般;
人教版选修2-2《2.1.1合情推理》课件(共23张PPT)
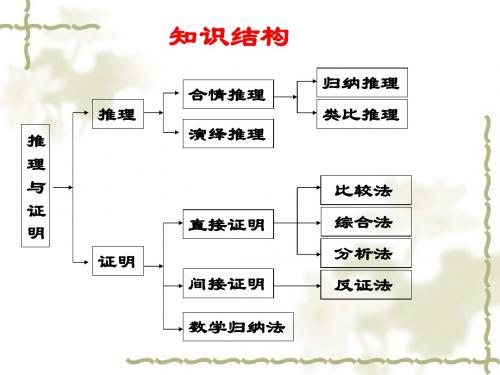
三棱锥
4
4
6
四棱锥
5
5
8
三棱柱
5
6
9
五棱锥
6
6
10
立方体
6
8
12
正八面体
8
6
12
五棱柱
截角正方体
尖顶塔
猜想 F+V-E=2 欧拉公式
多面体 面数(F) 顶点数(V) 棱数(E)
三棱锥
4
4
6
四棱锥
5
5
8
三棱柱
5
6
9
五棱锥
6
6
10
立方体
6
8
12
正八面体86Fra bibliotek12五棱柱
7
10
15
截角正方体 7
10
15
尖顶塔
7.利用等差数列性质类比等比数列性质
歌德巴赫猜想的提出过程:
3+7=10,3+17=20,13+17=30,
改写为:10=3+7,20=3+17,30=13+17.
6=3+3, 8=3+5,
10=5+5, 12=5+7, 14=7+7, 16=5+11,
18 =7+11, …,
1000=29+971, 1002=139+863,
…
这种由某类事物的部分对象具有某些特征, 推出该类事物的全部对象都具有这些特征 的推理,或者由个别事实概栝出一般结论 的推理,称为归纳推理.(简称;归纳)
解;设an表示移动n块金属片时的移动次数. 当n=1时,a1=1 当n=2时,a2= 3
2
1
3
解;设an表示移动n块金属片时的移动次数. 当n=1时,a1=1
人教a版数学【选修2-2】2.1.2《演绎推理》ppt课件

重点:演绎推理的含义及演绎推理规则. 难点:演绎推理的应用.
演绎推理 思维导航 日常生活中我们经常接触这样的推理形式:“所有金属都导 电,因为铁是金属,所以铁导电”,它是合情推理吗?这种 推理形式正确吗?
新知导学 1.演绎推理 从________________出发,推出__________情况下的结论, 一般性的原理 某个特殊 我们把这种推理称为演绎推理,简言之,演绎推理是由 _____________的推理. 一般到特殊
6.判断下列推理是否正确?为什么? “因为过不共线的三点有且仅有一个平面(大前提),而A、B 、C为空间三点(小前提),所以过A、B、C三点只能确定一个 平面(结论).” [解析] 不正确,因为大前提中的“三点”不共线,而小前 提中的“三点”的基本形式——三段论
3.三段论 (1)“三段论”是演绎推理的一般模式,包括: ①大前提——已知的__________; 一般原理 ②小前提——所研究的__________; 特殊情况 ③结论——根据一般原理,对特殊情况做出的________. 判断 其一般推理形式为 大前提:M是P. 小前提:S是M. 结 论:__________.
成才之路 · 数学
人教A版 · 选修2-2
路漫漫其修远兮 吾将上下而求索
第二章
推理与证明
第二章 2.1 合情推理与演绎推理
2.1.2 演绎推理
1
自主预习学案
2
典例探究学案
3
巩固提高学案
4
备 选 练 习
自主预习学案
理解演绎推理的概念,掌握演绎推理的形式,并能用它们进 行一些简单的推理,了解合情推理与演绎推理的联系与区别 .
牛刀小试 1 . (2014· 微山一中高二期中 )关于下面推理结论的错误: “因为对数函数 y=logax 是增函数(大前提),又 y=log1 x 是对
高中数学选修2-2课件:2.1 2.1.2 演绎推理

(4)演绎推理得到结论的正确与否与大前提、小前提和推理形式有 关.( )
课 时 分 层 作 业
[ 答案]
(1)×(2)×(3)× (4)√
返 首 页
自 主 预 习 • 探 新 知
2.“四边形ABCD是矩形,所以四边形ABCD的对角线相等”,补充该 推理的大前提是( )
A.正方形的对角线相等 B.矩形的对角线相等 C.等腰梯形的对角线相等 D.矩形的对边平行且相等
当 堂 达 标 • 固 双 基
合 作 探 究 • 攻 重 难
课 时 分 层 作 业
返 首 页
自 主 预 习 • 探 新 知
[规律方法]
把演绎推理写成“三段论”的一般方法:
1用“三段论”写推理过程时,关键是明确大、小前提,三段论中大前 提提供了一个一般性原理,小前提提供了一种特殊情况,两个命题结合起 来,揭示一般性原理与特殊情况的内在联系
当 堂 达 标 • 固 双 基
A [ 要分析一个演绎推理是否正确,主要观察所给的大前提、小前提和
合 作 探 究 • 攻 重 难
结论及推理形式是否都正确,若这几个方面都正确,才能得到这个演绎推理 正确.因为任何实数的平方都大于0,又因为a是实数,所以a2>0,其中大前 提是:任何实数的平方都大于0,它是不正确的.]
当 堂 达 标 • 固 双 基
合 作 探 究 • 攻 重 难
制造潜艇.
[ 解析] [ 答案] ①是演绎推理;②是归纳推理;③④是类比推理. ①
课 时 分 层 作 业
返 首 页
自 主 预 习 • 探 新 知
[合 作 探 究· 攻 重 难]
演绎推理与三段论
例
(1)下面四个推导过程符合演绎推理三段论形式且推理正确的是(
人教a版数学【选修2-2】2.1.1《合情推理》ppt课件

牛刀小试 1.已知a1=3,a2=6,且an+2=an+1-an,则a33为( A.3 B.-3 C.6 D.-6 [答案] A
)
[解析] a3=a2-a1=6-3=3, a4=a3-a2=3-6=-3, a5=a4-a3=-3-3=-6, a6=a5-a4=-6-(-3)=-3, a7=a6-a5=-3-(-6)=3, a8=a7-a6=6. 归纳猜想该数列为周期数列,且周期为6,所以a33=a6×5+3 =a3=3,故应选A.
(3)∵2 Sn=an+1, ∴2 S1=a1+1,即 2 a1=a1+1,∴a1=1. 又 2 S2=a2+1,∴2 a1+a2=a2+1, ∴a2 2-2a2-3=0. ∵对一切的 n∈N*,an>0,∴a2=3. 同理可求得 a3=5,a4=7,猜测出 an=2n-1.
[解析] (1)由已知有a1=3=22-1, a2=2a1+1=2×3+1=7=23-1, a3=2a2+1=2×7+1=15=24-1, a4=2a3+1=2×15+1=31=25-1. 猜测出an=2n+1-1,n∈N* (n≥2).
(2)由已知有 a1=a, 2-a 1 1 1 a2 = = ,a3= = , 2-a1 2-a 2-a2 3-2a 3-2a 1 a4 = = . 2-a3 4-3a n-1-n-2a 猜测出 an= .(n≥2) n-n-1a
-1
) B.nn D.(2n)2
[答案] B
1 4 x x 4 [解析] 由 x+x ≥2,x+x2=2+2+x2≥3, b x x x b 可推广 x+x3=3+3+3+x3≥4,知 b=33, a x x x a 所以对于结论 x+xn=n+n+…+n+xn≥n+1 知 a=nn, 故 应选 B.
(人教)2015高中数学选修2-2课件 2.1.2合情推理与演绎推理

������2 2 小前提:曲线 C: 2 +y =1
是椭圆.
结论:曲线 C 的离心率 e 的取值范围为(0,1). ②大前提:等比数列的公比都不为零. 小前提:数列{2n}(n∈N*)是等比数列. 结论:数列{2n}的公比不为零.
2.1.2
问题导学
演绎推理
当堂检测
课前预习导学
KEQIAN YUXI DAOXUE
问题导学演绎Biblioteka 理当堂检测课前预习导学
KEQIAN YUXI DAOXUE
课堂合作探究
KETANG HEZUO TANJIU
思路分析:(1)根据三段论推理的模式逐一进行分析对比判断. (2)先确定各题中的大前提、小前提和结论,按三段论形式写出. 答案:① (1)解析:根据三段论推理的模式要求,只有①这种推理形式符合三 段论推理模式,其余均不符合. (2)解:①大前提:所有椭圆的离心率 e 的取值范围为(0,1).
2.1.2
问题导学
演绎推理
当堂检测
课前预习导学
KEQIAN YUXI DAOXUE
课堂合作探究
KETANG HEZUO TANJIU
例 1(1)给出以下推理形式:①所有的 S 都是 M,P 是 S,所以 P 是 M;②所有的 S 都是 M,P 是 M,所以 P 是 S;③所有的 S 都是 M,P 是 Q, 所以 S 是 Q;④所有的 S 都是 M,P 不是 S,所以 P 不是 M.则符合三段论 推理模式的是 .
2.1.2
演绎推理
2.1.2
目标导航
演绎推理
预习导引
课前预习导学
KEQIAN YUXI DAOXUE
课堂合作探究
KETANG HEZUO TANJIU
是椭圆.
结论:曲线 C 的离心率 e 的取值范围为(0,1). ②大前提:等比数列的公比都不为零. 小前提:数列{2n}(n∈N*)是等比数列. 结论:数列{2n}的公比不为零.
2.1.2
问题导学
演绎推理
当堂检测
课前预习导学
KEQIAN YUXI DAOXUE
问题导学演绎Biblioteka 理当堂检测课前预习导学
KEQIAN YUXI DAOXUE
课堂合作探究
KETANG HEZUO TANJIU
思路分析:(1)根据三段论推理的模式逐一进行分析对比判断. (2)先确定各题中的大前提、小前提和结论,按三段论形式写出. 答案:① (1)解析:根据三段论推理的模式要求,只有①这种推理形式符合三 段论推理模式,其余均不符合. (2)解:①大前提:所有椭圆的离心率 e 的取值范围为(0,1).
2.1.2
问题导学
演绎推理
当堂检测
课前预习导学
KEQIAN YUXI DAOXUE
课堂合作探究
KETANG HEZUO TANJIU
例 1(1)给出以下推理形式:①所有的 S 都是 M,P 是 S,所以 P 是 M;②所有的 S 都是 M,P 是 M,所以 P 是 S;③所有的 S 都是 M,P 是 Q, 所以 S 是 Q;④所有的 S 都是 M,P 不是 S,所以 P 不是 M.则符合三段论 推理模式的是 .
2.1.2
演绎推理
2.1.2
目标导航
演绎推理
预习导引
课前预习导学
KEQIAN YUXI DAOXUE
课堂合作探究
KETANG HEZUO TANJIU
高中数学选修2-2第2章第1节合情推理与演绎推理课件

答案: 66 2n2-n
数学 选修2-2
图形中归纳推理的特点及思路 1.此类题目的特点: 由一组平面或空间图形,归纳猜想其数量的变化规律,这 类题颇有智力趣题的味道,解答时常用归纳推理的方法解决, 分析时要注意规律的寻找. 2.解决这类问题从哪入手: (1)从图形的数量规律入手,找到数值变化与数量的关系. (2)从图形的结构变化规律入手,找到图形的结构每发生一 次变化后,与上一次比较,数值发生了怎样变化.
=13(S1+S2+S3+S4)r.∴r=S1+S23+VS3+S4.
答案:
3V S1+S2+S3+S4
数学 选修2-2
4.已知数列{an}满足a1=1,an+1=2an+1(n=1,2,3…) (1)求a2,a3,a4,a5; (2)归纳猜想通项公式an. 解析: (1)a1=1, a2=3=22-1, a3=7=23-1, a4=15=24-1, a5=31=25-1. (2)可归纳猜想出an=2n-1(n∈N*).
数学 选修2-2
类比推理
定义
由两类对象具有某些__类__似____特征和其 中一类对象的某些_已__知__特__征___,推出另 一类对象也具有这些特征的推理,称为 类比推理
特征
类比推理是由 __特__殊__到__特__殊____ 的推理
数学 选修2-2
2.类比推理的特点及适用前提 (1)类比推理的特点 ①类比是由已经解决的问题和已经获得的知识出发,推测 正在研究的事物的属性,提出新问题,作出新发现. ②类比的结果是猜测性的,不一定可靠,但它有发现功 能.
所成二面角的大小.
8分
我们猜想射影定理类比推理到三维空间,其表现形式应为
S=S1·cos α+S2·cos β+S3·cos γ.
数学 选修2-2
图形中归纳推理的特点及思路 1.此类题目的特点: 由一组平面或空间图形,归纳猜想其数量的变化规律,这 类题颇有智力趣题的味道,解答时常用归纳推理的方法解决, 分析时要注意规律的寻找. 2.解决这类问题从哪入手: (1)从图形的数量规律入手,找到数值变化与数量的关系. (2)从图形的结构变化规律入手,找到图形的结构每发生一 次变化后,与上一次比较,数值发生了怎样变化.
=13(S1+S2+S3+S4)r.∴r=S1+S23+VS3+S4.
答案:
3V S1+S2+S3+S4
数学 选修2-2
4.已知数列{an}满足a1=1,an+1=2an+1(n=1,2,3…) (1)求a2,a3,a4,a5; (2)归纳猜想通项公式an. 解析: (1)a1=1, a2=3=22-1, a3=7=23-1, a4=15=24-1, a5=31=25-1. (2)可归纳猜想出an=2n-1(n∈N*).
数学 选修2-2
类比推理
定义
由两类对象具有某些__类__似____特征和其 中一类对象的某些_已__知__特__征___,推出另 一类对象也具有这些特征的推理,称为 类比推理
特征
类比推理是由 __特__殊__到__特__殊____ 的推理
数学 选修2-2
2.类比推理的特点及适用前提 (1)类比推理的特点 ①类比是由已经解决的问题和已经获得的知识出发,推测 正在研究的事物的属性,提出新问题,作出新发现. ②类比的结果是猜测性的,不一定可靠,但它有发现功 能.
所成二面角的大小.
8分
我们猜想射影定理类比推理到三维空间,其表现形式应为
S=S1·cos α+S2·cos β+S3·cos γ.
2015高中数学选修2-2课件 2.1.1合情推理与演绎推理

KETANG HEZUO TANJIU
预习导引
2.类比推理
(1)类比推理的含义
由两类对象具有某些类似特征和其中一类对象的某些已知特征,
推出另一类对象也具有这些特征的推理称为类比推理.
(2)类比推理的特征
类比推理是由特殊到特殊的推理.
预习交流 2
思考:类比推理适合在什么情况下使用?它得出的结论一定正确吗?
提示:当给出的是两类不同的对象,且它们具有一些类似的特征时,
可以使用类比推理.它得出的结论也是猜测性的,不一定正确.
第七页,编辑于星期五:十二点 十四分。
2.1.1
目标导航
合情推理
课前预习导学
课堂合作探究
KEQIAN YUXI DAOXUE
KETANG HEZUO TANJIU
预习导引
3.合情推理及其推理过程
当堂检测
问题导学
例 1(1)已知数列{an}的第 1 项 a1=1,且
an+1=1+
(n=1,2,3,…),试归纳出这个数列的一个通项公式.
(2)观察下列各式:
1=1,
1
4
1+1+2 = 3,
1
1
6
1+1+2 + 1+2+3 = 4,
1
1+
1+2
1
+
1+2+3
1
+
1+2+3+4
=
8
.
5
由上述等式能得出怎样的结论?请写出结论,并证明.
(2)解决数列中的归纳推理问题时,通常是将所给等式中的 n 取具体
【高中数学选修2-2】2.1.1合情推理 PPT 课件

圆的概念和性质
圆的周长 S = 2πR
圆的面积 S =πR2
圆心与弦(非直径)中点的连线 垂直于弦
球的概念和性质
球的表面积 S = 4πR2
球的体积 V = 4 π R 3
3
球心与不过球心的截面(圆面) 的圆心的连线垂直于截面
与圆心距离相等的两弦相等 与球心距离相等的两截面面积相等
与圆心距离不相等的两弦不相 与球心距离不相等的两截面面积
10=3+7,20=3+17,30=13+17.
6=3+3,
1000=29+971,
8=3+5,
1002=139+863,
10=5+5,
…
12=5+7, 14=7+7,
综上述他得出一个规律:
16=5+11, 18 =7+11,
偶数=奇质数+奇质数
…,
歌德巴赫猜想:“任何一个不小于6的偶数都等 于两个奇质数之和”
(3) a=ba2=b2;等等。 (3) a>ba2>b2;等等。
问:这样猜想出的结论是否一定正确? 不一定正确,需要证明。
观察下面推理问题
火星上是否有生命?
火星
地球
相似点:绕太阳运转、绕轴自转、有大气层、有季节变换、大部 分时间的温度适合地球上的某些已知生物的生存等。
地球上有生命 猜想 火星上可能有生命
属未知的现象,因而结论具有猜测性.
3.归纳的前提是特殊的情况,因而归纳是立足于观
察、经验和实验的基础之上,提出带有规律性的结
论。
需证明
我们见过的归纳推理,你想起来了吗?
1,3,5,7,…,由此你猜想出第n 个数是__2_n__1__.
