专题复习最短路径
专题—最短路径问题(含解答)

专题—最短路径问题一.选择题(共7小题)1.如图所示,四边形OABC为正方形,边长为3,点A,C分别在x轴,y轴的正半轴上,点D在OA上,且D的坐标为(1,0),P是OB上的一动点,则“求PD+PA和的最小值”要用到的数理依据是()A.“两点之间,线段最短”B.“轴对称的性质”C.“两点之间,线段最短”以及“轴对称的性质”D.以上答案都不正确解:∵四边形OABC为正方形,∴A、C两点关于直线OB对称(轴对称的性质),∴连接CD,则CD即为PD+PA和的最小值(两点之间,线段最短),∴用到的数理依据是“两点之间,线段最短”以及“轴对称的性质”.故选:C.2.点A、B均在由面积为1的相同小矩形组成的网格的格点上,建立平面直角坐标系如图所示.若P是x轴上使得|PA﹣PB|的值最大的点,Q是y轴上使得QA+QB的值最小的点,则OP•OQ=()A.5B.4C.3D.2解:连接AB并延长交x轴于点P,由三角形的三边关系可知,点P即为x轴上使得|PA﹣PB|的值最大的点,∵点B是矩形ACPD的中心,∴点P即为AB延长线上的点,此时P(3,0)即OP=3;作A点关于y轴的对称点A′连接A′B交y轴于点Q,则A′B即为QA+QB的最小值,∵A′(﹣1,2),B(2,1),设过A′B的直线为:y=kx+b,则,解得,∴Q(0,),即OQ=,∴OP•OQ=3×=5.故选:A.3.已知∠MON=40°,P为∠MON内一定点,OM上有一点A,ON上有一点B,当△PAB的周长取最小值时,∠APB的度数是()A.40°B.100°C.140°D.50°解:分别作点P关于OM、ON的对称点P′、P″,连接OP′、OP″、P′P″,P′P″交OM、ON于点A、B,连接PA、PB,此时△PAB周长的最小值等于P′P″.由轴对称性质可得,OP′=OP″=OP,∠P′OA=∠POA,∠P″OB=∠POB,∴∠P′OP″=2∠MON=2×40°=80°,∴∠OP′P″=∠OP″P′=(180°﹣80°)÷2=50°,又∵∠BPO=∠OP″B=50°,∠APO=∠AP′O=50°,∴∠APB=∠APO+∠BPO=100°.故选:B.4.如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF 分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为()A.6B.8C.10D.12解:连接AD,∵△ABC是等腰三角形,点D是BC边的中点,∴AD⊥BC,=BC•AD=×4×AD=16,解得AD=8,∴S△ABC∵EF是线段AC的垂直平分线,∴点C关于直线EF的对称点为点A,∴AD的长为CM+MD的最小值,∴△CDM的周长最短=(CM+MD)+CD=AD+BC=8+×4=8+2=10.故选:C.5.如图,点P是∠AOB内的一点,且OP=5,且∠AOB=30°,点M、N分别是射线OA、OB上的动点,则△PMN周长的最小值为()A.5B.6C.8D.10解:分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OP、OC、OD、PM、PN.∵点P关于OA的对称点为C,关于OB的对称点为D,∴PM=CM,OP=OC,∠COA=∠POA;∵点P关于OB的对称点为D,∴PN=DN,OP=OD,∠DOB=∠POB,∴OC=OD=OP=5,∠COD=∠COA+∠POA+∠POB+∠DOB=2∠POA+2∠POB=2∠AOB=60°,∴△COD是等边三角形,∴CD=OC=OD=5.∴△PMN的周长的最小值=PM+MN+PN=CM+MN+DN≥CD=5,故选:A.6.如图,A和B两地在一条河的两岸,现要在河上造一座桥MN,使从A到B 的路径AMNB最短的是(假定河的两岸是平行直线,桥要与河岸垂直)()A.B.C.D.解:根据垂线段最短,得出MN是河的宽时,MN最短,即MN⊥直线a(或直线b),只要AM+BN最短就行,即过A作河岸a的垂线AH,垂足为H,在直线AH上取点I,使AI等于河宽.连结IB交河的b边岸于N,作MN垂直于河岸交a边的岸于M点,所得MN即为所求.故选:D.二.填空题(共9小题)7.如图所示,点A在直线a外,点B在直线a上,在直线a上找一点P,使AP+BP 最小的点P有1个,其位置是B点.解:由题意得使AP+BP最小的点P有1个,其位置是B点,故答案为:1,B点.8.如图,∠AOB=45°,OC平分∠AOB,点M为OB上一定点,P为OC上的一动点,N为OB上一动点,当PM+PN最小,∠PMO=45°.解:∵PM=PM′,∴此时PM+PN=PM′+PN′=M′N′,∵点M与点M′关于OC对称,OC平分∠AOB,∴OM=OM′,∵∠AOB=45°,∴∠PM'O=∠AOB=45°,∴∠PMO=∠PM'O=45°,故答案为:45°.9.四边形ABCD中,∠BAD=136°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使三角形AMN周长最小时,则∠AMN+∠ANM的度数为88度.解:延长AB到A′使得BA′=AB,延长AD到A″使得DA″=AD,连接A′A″与BC、CD 分别交于点M、N.∵∠ABC=∠ADC=90°,∴A、A′关于BC对称,A、A″关于CD对称,此时△AMN的周长最小,∵BA=BA′,MB⊥AB,∴MA=MA′,同理:NA=NA″,∴∠A′=∠MAB,∠A″=∠NAD,∵∠AMN=∠A′+∠MAB=2∠A′,∠ANM=∠A″+∠NAD=2∠A″,∴∠AMN+∠ANM=2(∠A′+∠A″),∵∠BAD=136°,∴∠A′+∠A″=180°﹣∠BAD=44°∴∠AMN+∠ANM=2×44°=88°.故答案为:8810.如图,∠AOB=30°,点P是它内部一点,OP=2,如果点Q、点R分别是OA、OB上的两个动点,那么PQ+QR+RP的最小值是2.解:作点P关于OA对称的点P1,作点P关于OB对称的点P2,连接P1P2,与OA 交于点Q,与OB交于点R,此时△PQR的周长最小.从图上可看出△PQR的周长就是P1P2的长,∵∠AOB=30°,∴∠P1OP2=60°.∵OP1=OP2,∴△OP1P2是等边三角形.∴P1P2=OP1=OP=2.∴△PQR周长的最小值是2.即PQ+QR+RP的最小值是2故答案为:2.11.已知:在四边形ABCD中,∠ABC=∠ADC=90°,M、N分别是CD和BC上的点.求作:点M、N,使△AMN的周长最小.作法:如图2,(1)延长AD,在AD的延长线上截取DA´=DA;(2)延长AB,在AB的延长线上截取BA″=BA;(3)连接A′A″,分别交CD、BC于点M、N.则点M、N即为所求作的点.请回答:这种作法的依据是①线段垂直平分线的定义(或线段垂直平分线的判定,或轴对称的性质即对称点的连线段被对称轴垂直平分)②线段垂直平分线上的点到线段两个端点的距离相等(线段垂直平分线的性质);③两点之间线段最短.解:根据线段垂直平分线的性质和两点之间线段最短作图;故答案为:①线段垂直平分线的定义(或线段垂直平分线的判定,或轴对称的性质即对称点的连线段被对称轴垂直平分)②线段垂直平分线上的点到线段两个端点的距离相等(线段垂直平分线的性质);③两点之间线段最短12.如图,在四边形ABCD中,∠DAB=130°,∠D=∠B=90°,点M,N分别是CD,BC上两个动点,当△AMN的周长最小时,∠AMN+∠ANM的度数为100°.解:如图,作点A关于BC的对称点A′,关于CD的对称点A″,连接A′A″与BC、CD的交点即为所求的点M、N,∵∠BAD=130°,∠B=∠D=90°,∴∠A′+∠A″=180°﹣∠130°=50°,由轴对称的性质得:∠A′=∠A′AM,∠A″=∠A″AN,∴∠AMN+∠ANM=2(∠A′+∠A″)=2×50°=100°.故答案为:100°13.如图,△ABC中,∠A=15°,AB是定长.点D,E分别在AB,AC上运动,连结BE,ED.若BE+ED的最小值是2,则AB的长是4.解;作点B关于AC的对称点B',过B作BF⊥AB',∵点B关于AC的对称点B',∴∠B'AE=∠CAB=15°,∵BF⊥AB',∵BF即为BE+ED的最小值,即BF=2,∴AB=4,故答案为:414.如图,∠AOB=30°,∠AOB内有一定点P,且OP=12,在OA上有一点Q,OB上有一点R,若△PQR周长最小,则最小周长是12解:设∠PO A=θ,则∠POB=30°﹣θ,作PM⊥OA与OA相交于M,并将PM延长一倍到E,即ME=PM.作PN⊥OB与OB相交于N,并将PN延长一倍到F,即NF=PN.连接EF与OA相交于Q,与OB相交于R,再连接PQ,PR,则△PQR即为周长最短的三角形.∵OA是PE的垂直平分线,∴EQ=QP;同理,OB是PF的垂直平分线,∴FR=RP,∴△PQR的周长=EF.∵OE=OF=OP=12,且∠EOF=∠EOP+∠POF=2θ+2(30°﹣θ)=60°,∴△EOF是正三角形,∴EF=12,即在保持OP=12的条件下△PQR的最小周长为12.故答案为:12三.解答题(共9小题)15.如图,A,B两村在河L的同侧,A,B到河L的距离分别为1.5km和2km,AB=1.3km,现要在河边建一供水厂,同时向A,B两村供水.若铺设水管的工程费用为每千米1.8万元,问水厂与A村的水平距离为多远时,能使铺设费用最省,并求出总费用约多少万元.解:连接AB,作AF⊥BD于点F,则BF=BD﹣AE=0.5km,∴AF=1.2,作A关于直线L的对称点A′,连接A′B到L交于点C,则C点为水厂所在地,如图,过B作BD⊥L于D,作A′G⊥BD于点G,∵BG=BD+DG=3.5,A′G=AF=1.2,CD=2÷3.5×1.2=,EC=1.2﹣=,∴AC+BC=A′C+BC=A′B=3.7km,∴总费用为3.7×1.8=6.66万元.16.如图,一个人从C点骑马出发到D点,但他必须先到河岸边l1的P1点去让马饮水,然后再到河岸边l2的P2点去,再次让马饮水,最后骑马到D点,他应如何选择饮水点P1,P2.才能使所走的路程CP1+P1P2+P2D最短?解:如图,作点C关于l1的对称点C′,点D关于l2的对称点D′,连接C′D′,交于l1,l2于点P1,点P2,连接CP1,P1P2,P2D,所以路程CP1+P1P2+P2D最短.17.八(二)班举行元旦文艺晚会,桌子摆成两条直线(如图中所示的AO,BO),AO桌面上摆满了桔子,OB桌面上摆满了糖果,坐在C处的小花先拿桔子再拿糖果,然后送给D处的小红,最后回到C处.请你帮助她设计一条行走路线,使其所走的总路程最短(尺规作图,并写出作法,不需说明理由)解:如图所示,小花所走的行走路线为:CM﹣MN﹣ND,所走的总路程最短.18.尺规作图:(1)如图①,江边A,B两个村庄准备集资建造一个自来水厂,请你确定一个厂址,使得从自来水厂到A,B两村所用的水管最短.(2)如图②,P是∠A0B内部一点,试在角的两边上各找一个点E,F,使△PEF 的周长最小.解:(1)如图①,过A点关于江边的对称点C,再连接CB,BC与江边的交点Q 即为自来水厂厂址;(2)如图②,作点P关于OA对称的点M,作点P关于OB对称的点N,连接MN,与OA交于点E,与OB交于点F,此时△PEF的周长最小.19.如图,为了做好2013年沈阳全运会起降的交通安全工作,某交警执勤小队从A处出发,先到公路l1上设卡检查,再到公路l2上设卡检查,最后再到B 地执行任务,他们应如何走才能使总路程最短?【解答】解:如图所示,交警小队沿A→C→D→B走才能使总路程最短.20.如图所示,A、B为公路l同旁的两个村庄,在l上找一点P.(1)当P到A、B等距离时,P在何处?(2)当P到两村距离之和最小时,P在何处?解:(1)因为点P到两个村庄A,B的距离相等,所以P应建在AB的垂直平分线和l的交点处,理由是到线段两个端点距离相等的点在线段的垂直平分线上,如图1:,(2)作点A关于直线l的对称点,连接A′B交直线于点P,点P就是设置的点,如图2:21.如图,A、B两城市之间有一条国道,国道的宽为a,现要在国道上修建一座垂直于国道的立交桥,使通过A、B两城市路程最近,请你设计建桥的位置,并说明理论依据.解:如图,过点B作BC垂直国道,且使BC等于国道宽a,连接AC交国道边缘与M,作MN∥BC即可.理由:两点之间线段最短.22.如图,A和B两地在一条河的两岸,现要在河上造一座桥MN.桥造在何处才能使从A到B的路径AMNB最短?在下图中画出路径,不写画法但要说明理由.(假定河的两岸是平行的直线,桥要与河垂直.)解:如图,作BB'垂直于河岸GH,使BB′等于河宽,连接AB′,与河岸EF相交于M,作MN⊥GH,则MN∥BB′且MN=BB′,于是MNBB′为平行四边形,故NB=MB′.根据“两点之间线段最短”,AB′最短,即AM+BN最短.故桥建立在MN处符合题意.23.如图,平面上有直线a及直线a外的三点A、B、P.(1)过点P画一条直线m,使得m∥a;(2)若直线a、m表示一条河的两岸,现要在这条河上建一座桥(桥与岸垂直),使得从村庄A经桥过河到村庄B的路程最短,试问桥应建在何处?画出示意图.解:(1)如图1所示,(2)如图2,作AA'垂直于河岸a,使AA′等于河宽,连接BA′,与另一条河岸相交于M,作MN⊥直线a,则MN∥AA′且MN=AA′,于是MNAA′为平行四边形,故MA′=NA.根据“两点之间线段最短”,BA′最短,即AN+BM最短.故桥建立在M、N处符合题意.。
八年级数学最短路径题型归纳

八年级数学中的最短路径问题,通常涉及到几何图形中的点、线、面等元素,需要利用一些基本的几何知识和数学原理来求解。
以下是一些常见的最短路径题型及其解题方法:1.两点之间的最短距离:题型描述:在平面上给定两点A和B,求A到B的最短距离。
解题方法:直接连接A和B,线段AB的长度即为最短距离。
2.点到直线的最短距离:题型描述:在平面上给定一点P和一条直线l,求P到l的最短距离。
解题方法:作点P到直线l的垂线,垂足为Q,则PQ的长度即为最短距离。
3.直线到直线的最短距离:题型描述:在平面上给定两条直线l1和l2,求l1到l2的最短距离。
解题方法:如果l1和l2平行,则它们之间的距离即为最短距离;如果l1和l2不平行,则作l1到l2的垂线,垂足所在的线段即为最短4.点到圆的最短距离:题型描述:在平面上给定一点P和一个圆O,求P到圆O的最短距离。
解题方法:如果点P在圆O内,则最短距离为P到圆心的距离减去圆的半径;如果点P在圆O外,则最短距离为P到圆心的距离;如果点P在圆O上,则最短距离为0。
5.圆到圆的最短距离:题型描述:在平面上给定两个圆O1和O2,求O1到O2的最短距离。
解题方法:如果两圆外离,则它们之间的最短距离为两圆的半径之和;如果两圆外切,则它们之间的最短距离为两圆的半径之差;如果两圆相交或内切,则它们之间的最短距离为0;如果两圆内含,则它们之间的最短距离为两圆的半径之差减去两圆半径之和的绝对值。
6.多边形内的最短路径:题型描述:在一个多边形内给定两个点A和B,求A到B的最短解题方法:通常需要将多边形划分为多个三角形,然后利用三角形内的最短路径(即连接两点的线段)来求解。
7.立体几何中的最短路径:题型描述:在立体图形中给定两点A和B,求A到B的最短路径。
解题方法:通常需要将立体图形展开为平面图形,然后利用平面几何中的最短路径原理来求解。
在解决最短路径问题时,需要注意以下几点:准确理解题目要求,确定需要求的是哪两点之间的最短距离。
最短路径知识点总结

最短路径知识点总结最短路径问题的核心思想是通过某种策略找到两个节点之间的最短路径。
在图的表示方法上,最短路径问题通常使用邻接矩阵或邻接表来表示图的结构。
多种最短路径算法也可以适用于不同的图模型,包括有向图、无向图、带权图等。
常用的最短路径算法包括Dijkstra算法、Bellman-Ford算法、Floyd-Warshall算法等。
下面将对这些算法进行介绍和总结。
Dijkstra算法是一种解决单源最短路径问题的贪心算法。
它的核心思想是通过不断地确定距离源点距离最短的顶点来逐步扩展已知的最短路径集合。
具体步骤包括:初始化距离数组,设置起点距离为0,其他顶点距离为无穷大;选择未访问顶点中距离最短的顶点,并将其标记为已访问;更新与该顶点相邻的顶点的距离;不断重复以上步骤直到所有顶点都被访问。
Dijkstra算法的时间复杂度为O(V^2),其中V表示顶点的个数。
当图比较大时,可以使用堆优化的Dijkstra算法,将时间复杂度优化到O((V+E)logV)。
Bellman-Ford算法是一种解决单源最短路径问题的动态规划算法。
它的核心思想是通过对所有边进行松弛操作,不断更新顶点的最短路径估计值。
具体步骤包括:初始化距离数组,设置起点距离为0,其他顶点距离为无穷大;循环遍历所有边,不断进行松弛操作,直到没有发生变化为止。
Bellman-Ford算法的时间复杂度为O(VE),其中V表示顶点的个数,E表示边的个数。
这个算法可以解决包含负权边的图的最短路径问题,而Dijkstra算法则无法处理负权边。
Floyd-Warshall算法是一种解决多源最短路径问题的动态规划算法。
它的核心思想是通过对所有顶点之间的距离进行不断更新,找到所有顶点之间的最短路径。
具体步骤包括:初始化距离矩阵,设置顶点之间的距离为边的权重,若没有直接相连的边则设置为无穷大;循环遍历所有顶点,尝试将每个顶点作为中转点,并尝试更新所有顶点对之间的距离。
(完整)初二最短路径专题.doc
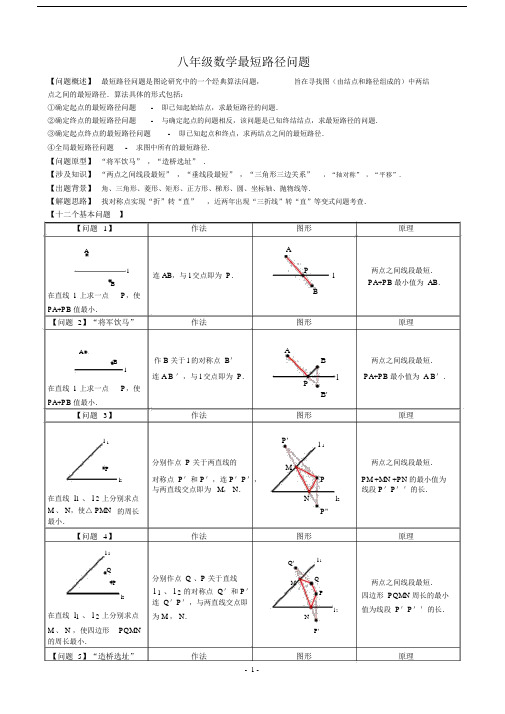
八年级数学最短路径问题【问题概述】最短路径问题是图论研究中的一个经典算法问题,旨在寻找图(由结点和路径组成的)中两结点之间的最短路径.算法具体的形式包括:①确定起点的最短路径问题-即已知起始结点,求最短路径的问题.②确定终点的最短路径问题-与确定起点的问题相反,该问题是已知终结结点,求最短路径的问题.③确定起点终点的最短路径问题-即已知起点和终点,求两结点之间的最短路径.④全局最短路径问题-求图中所有的最短路径.【问题原型】“将军饮马”,“造桥选址”.【涉及知识】“两点之间线段最短”,“垂线段最短” ,“三角形三边关系”,“轴对称” ,“平移”.【出题背景】角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等.【解题思路】找对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题考查.【十二个基本问题】【问题1】作法图形原理A Al连 AB,与 l 交点即为 P.Pl两点之间线段最短.B PA+PB 最小值为 AB.B在直线 l 上求一点P,使PA+PB 值最小.【问题 2】“将军饮马”作法图形原理A AB 作 B 关于 l 的对称点 B' B 两点之间线段最短.l连 A B ',与 l 交点即为 P.l PA+PB 最小值为 A B'.P在直线 l 上求一点P,使B'PA+PB 值最小.【问题3】作法图形原理l 1 P' l1P分别作点 P 关于两直线的M两点之间线段最短.对称点 P'和 P',连 P'P',PM +MN +PN 的最小值为l2 P在直线 l1、 l 2上分别求点与两直线交点即为 M, N.N l2线段 P'P''的长.M 、 N,使△ PMN 的周长P''最小.【问题4】作法图形原理l 1lQ' 1Q分别作点 Q 、P 关于直线P MQ 两点之间线段最短.l 1、 l 2的对称点Q'和P'l2 P 四边形 PQMN 周长的最小连 Q'P',与两直线交点即l 2 值为线段 P'P''的长.在直线 l1、 l 2上分别求点为 M , N.NM 、 N ,使四边形PQMN P'的周长最小.AM Nmn将点 A 向下平移 MN 的长度单位得 A',连 A'B,交 nAA' M 两点之间线段最短.mB直线 m ∥ n ,在 m 、 n ,上分别求点 M 、N,使 MN ⊥m ,且 AM+ MN+ BN 的值最小.【问题 6】ABlM a N在直线 l 上求两点M、N(M 在左),使 MN a ,并使AM + MN+ NB 的值最小.【问题 7】l1Pl 2在l 1上求点A,在 l 2上求点 B,使 PA+ AB 值最小.于点 N,过 N 作 NM ⊥ m 于M.作法将点A 向右平移a 个长度单位得 A',作 A '关于l的对称点 A',连 A'B,交直线l 于点N,将N点向左平移a 个单位得 M.作法作点 P 关于l1的对称点P ',作 P'B⊥l2于 B,交l2于A.AM +MN +BN 的最小值为NnA'B+MN .B图形原理A A'B两点之间线段最短.lM N AM +MN +BN 的最小值为A'B+ MN.A''图形原理l1P'P 点到直线,垂线段最短.APA+ AB 的最小值为线段P'l 2 B的长.B【问题 8】作法l 1NAMl2 作点 A 关于l2的对称点BA ',作点B 关于l1的对称A 为l1上一定点,B 为l2上点 B',连 A'B'交l2于 M,一定点,在 l 2上求点M,交 l 1 于 N.在 l 1 上求点N ,使AM + MN+ NB 的值最小.【问题 9】作法图形原理B'l 1N两点之间线段最短.AAM +MN +NB 的最小值为M B l 2线段 A'B'的长.A'图形原理ABl在直线l 上求一点 P,使 PA PB 的值最小.连AB ,作 AB 的中垂线与直线 l 的交点即为 P.A垂直平分上的点到线段两B端点的距离相等.lP PA PB = 0.ABAl 作直线 AB,与直线 l 的交 B点即为 P.l 在直线 l 上求一点P,使PPA PB 的值最大.【问题 11】作法图形AAl 作 B 关于 l 的对称点 B'B'B 作直线 A B',与 l 交点即lP在直线 l 上求一点P,使为 P. BPA PB 的值最大.三角形任意两边之差小于第三边.PA PB ≤AB.PA PB 的最大值= AB.原理三角形任意两边之差小于第三边.PA PB ≤ AB'.PA PB 最大值= AB'.【精品练习】作图题:【例 1】已知:如图,A, B在直线 L 的两侧,在L 上求一点P,使得 PA+PB最小。
中考专题复习——最短路径问题

word专业资料-可复制编辑-欢迎下载A B C DABABL A BCDDO CP中考专题复习——路径最短问题一、具体内容包括:蚂蚁沿正方体、长方体、圆柱、圆锥外侧面吃食问题;线段(之和)最短问题;二、原理:两点之间,线段最短;垂线段最短。
(构建“对称模型”实现转化)三、例题:例1、①如右图是一个棱长为4的正方体木块,一只蚂蚁要从木块的点A沿木块侧面爬到点B处,则它爬行的最短路径是。
②如右图是一个长方体木块,已知AB=3,BC=4,CD=2,假设一只蚂蚁在点A处,它要沿着木块侧面爬到点D处,则蚂蚁爬行的最短路径是。
例2、①如图,要在河边修建一个水泵站,分别向张村、李庄送水,水泵站修在河边什么地方可使所用的水管最短。
②如图,直线L同侧有两点A、B,已知A、B到直线L的垂直距离分别为1和3,两点的水平距离为3,要在直线L上找一个点P,使PA+PB的和最小。
请在图中找出点P的位置,并计算PA+PB的最小值。
③要在河边修建一个水泵站,向张村、李庄铺设管道送水,若张村、李庄到河边的垂直距离分别为1Km和3Km,张村与李庄的水平距离为3Km,则所用水管最短长度为。
四、练习题(巩固提高)(一)1、如图是一个长方体木块,已知AB=5,BC=3,CD=4,假设一只蚂蚁在点A 处,它要沿着木块侧面爬到点D处,则蚂蚁爬行的最短路径是。
2、现要在如图所示的圆柱体侧面A点与B点之间缠一条金丝带(金丝带的宽度忽略不计),圆柱体高为6cm,底面圆周长为16cm,则所缠金丝带长度的最小值为。
3、如图是一个圆柱体木块,一只蚂蚁要沿圆柱体的表面从A点爬到点B处吃到食物,知圆柱体的高为5 cm,底面圆的周长为24cm,则蚂蚁爬行的最短路径为。
4、正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上的一动点,DN第2题张村李庄张村李庄AABB第1题第3题图(2)EBDACP+MN 的最小值为 。
第4题 第5题 第6题 第7题 5、在菱形ABCD 中,AB=2, ∠BAD=60°,点E 是AB 的中点,P 是对角线AC 上的一个动点,则PE+PB 的最小值为 。
初中数学中考复习专题 最短路径问题 (24张PPT)

【例题分层探究】 问题 1:边 CD 是定值,此问题可转化为计算 CE+DE 的最小值问题. 问题 2:线段 CD,EF 均为定值,此问题可借助轴对称 求最短路径的方法计算出 DE+CF 的最小值.
初中数学中考复习专题 最短路径问题 (24张PPT)
初中数学中考复习专题 最短路径问题 (24张PPT) 初中数学中考复习专题 最短路径问题 (24张PPT)
∵C(0,-5) ∴C′(0,5) ∴直线C′D为y=-7x+5
D(2,-9)
ME
x
AO
B
∴y=0 , 即-7x+5=0 ∴m=5 ∕ 7
∴x=5 ∕ 7
C D
初中数学中考复习专题 最短路径问题 (24张PPT)
初中数学中考复习专题 最短路径问题 (24张PPT)
中考链接
24 如图 Z8-3,在平面直角坐标系中,矩形 OACB 的
A
B l
在直线l上求一 点P,使 PA+PB值最小
作B关于l 的对称点 B',连A B'与l交 点即为P
图形
原理
两点之间线段 最短
PA+PB最小值 为AB
原理
两点之间线段 最短
PA+PB最小值 为AB
问题3
作法
l1
P
分别作点P关于
l2
两直线的对称
在直线l1、l2上 点P'和P",连 分别求点M P'P"与两直线
AM+MN+NB的 值最小.
作点A关于l2的 对称点A',作 点B关于l1的对 称点B',连A 'B'交l2于M
,交l1于N.
图形
原理
两点之间线段 最短.
AM+MN+NB 的最小值为线 段A'B'的
【配套K12】中考数学 专题复习六 求最短路径问题

中考数学专题复习学案六求最短路径问题【专题思路剖析】知识点:“两点之间线段最短”,“垂线段最短”,“点关于线对称”,“线段的平移”。
“饮马问题”,“造桥选址问题”。
考的较多的还是“饮马问题”,出题背景变式有角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等。
这类问题在中考中出现的频率很高,一般与垂线段最短、两点之间线段最短关系密切解题总思路:找点关于线的对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题考查。
在解决最短路径问题时,我们通常利用轴对称、平移等变换把不在一条直线上的两条线段转化到一条直线上,从而作出最短路径的方法来解决问题.【典型例题赏析】类型1 利用“垂线段最短”求最短路径问题例题1:(2015•辽宁省盘锦,第15题3分)如图,菱形ABCD的边长为2,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P,使△PBE的周长最小,则△PBE的周长的最小值为.考点:轴对称-最短路线问题;菱形的性质.分析:连接BD,与AC的交点即为使△PBE的周长最小的点P;由菱形的性质得出∠BPC=90°,由直角三角形斜边上的中线性质得出PE=BE,证明△PBE是等边三角形,得出PB=BE=PE=1,即可得出结果.解答:解:连接BD,与AC的交点即为使△PBE的周长最小的点P;如图所示:∵四边形ABCD是菱形,∴AC⊥BD,AB=BC=CD=DA=2,∴∠BPC=90°,∵E为BC的中点,∴BE=BC=1,PE=BC=1,∴PE=BE,∵∠DAB=60°,∴∠ABC=120°,∴∠PBE=60°,∴△PBE是等边三角形,∴PB=BE=PE=1,∴PB+BE+PE=3;故答案为:3.点评:本题考查了菱形的性质、轴对称以及最短路线问题、直角三角形斜边上的中线性质;熟练掌握菱形的性质,并能进行推理计算是解决问题的关键.【方法点评】本题易错误的利用两点之间线段最短解决,解答时需要准确识图,找到图形对应的知识点.【变式练习】(2015•福建第16题 4分)如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB边上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则B′A 长度的最小值是.考点:翻折变换(折叠问题)..分析:首先由勾股定理求得AC的长度,由轴对称的性质可知BC=CB′=3,当B′A有最小值时,即AB′+CB′有最小值,由两点之间线段最短可知当A、B′、C三点在一条直线上时,AB′有最小值.解答:解:在Rt△ABC中,由勾股定理可知:AC===4,由轴对称的性质可知:BC=CB′=3,∵CB′长度固定不变,∴当AB′+CB′有最小值时,AB′的长度有最小值.根据两点之间线段最短可知:A、B′、C三点在一条直线上时,AB′有最小值,∴AB′=AC﹣B′C=4﹣3=1.故答案为:1.点评:本题主要考查的是轴对称的性质、勾股定理和线段的性质,将求B′A的最小值转化为求AB′+CB′的最小值是解题的关键.类型2 利用“两点之间线段最短”求最短路径问题例题2:(2015•四川凉山州第26题5分)菱形ABCD在平面直角坐标系中的位置如图所示,顶点B(2,0),∠DOB=60°,点P是对角线OC上一个动点,E(0,﹣1),当EP+BP最短时,点P的坐标为.考点:菱形的性质;坐标与图形性质;轴对称-最短路线问题..分析:点B的对称点是点D,连接ED,交OC于点P,再得出ED即为EP+BP最短,解答即可.解答:解:连接ED,如图,∵点B的对称点是点D,∴DP=BP,∴ED即为EP+BP最短,∵四边形ABCD是菱形,顶点B(2,0),∠DOB=60°,∴点D的坐标为(1,),∴点C的坐标为(3,),∴可得直线OC的解析式为:y=x,∵点E的坐标为(﹣1,0),∴可得直线ED的解析式为:y=(1+)x﹣1,∵点P是直线OC和直线ED的交点,∴点P的坐标为方程组的解,解方程组得:,所以点P的坐标为(),故答案为:().点评:此题考查菱形的性质,关键是根据一次函数与方程组的关系,得出两直线的解析式,求出其交点坐标.【方法点评】“两点(直线同侧)一线型”在直线上求一点到两点的和最短时,利用轴对称的知识作一点关于直线的对称点,连接对称点与另一点与直线的交点就是所求的点;“一点两线型”求三角形周长最短问题,作点关于两直线的对称点,连接两个对称点与两直线分别有两个交点,顺次连接所给的点与两交点即可得三角形;“两点两线型”求四边形的周长最短类比“一点两线型”即可.【变式练习】(2015•营口,第10题3分)如图,点P是∠AOB内任意一点,OP=5cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是5cm,则∠AOB的度数是()A.25° B.30° C.35° D.40°考点:轴对称-最短路线问题.分析:分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OC、OD、PM、PN、MN,由对称的性质得出PM=CM,OP=OC,∠COA=∠POA;PN=DN,OP=OD,∠DOB=∠POB,得出∠AOB=∠COD,证出△OCD是等边三角形,得出∠COD=60°,即可得出结果.解答:解:分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OC、OD、PM、PN、MN,如图所示:∵点P关于OA的对称点为C,关于OB的对称点为D,∴PM=CM,OP=OC,∠COA=∠POA;∵点P关于OB的对称点为D,∴PN=DN,OP=OD,∠DOB=∠POB,∴OC=OP=OD,∠AOB=∠COD,∵△PMN周长的最小值是5cm,∴PM+PN+MN=5,∴CM+DN+MN=5,即CD=5=OP,∴OC=OD=CD,即△OCD是等边三角形,∴∠COD=60°,∴∠AOB=30°;故选:B.点评:本题考查了轴对称的性质、最短路线问题、等边三角形的判定与性质;熟练掌握轴对称的性质,证明三角形是等边三角形是解决问题的关键.类型3、求圆上点,使这点与圆外点的距离最小的方案设计在此问题中可根据圆上最远点与最近点和点的关系可得最优设计方案。
(完整版)初二数学最短路径问题知识归纳+练习
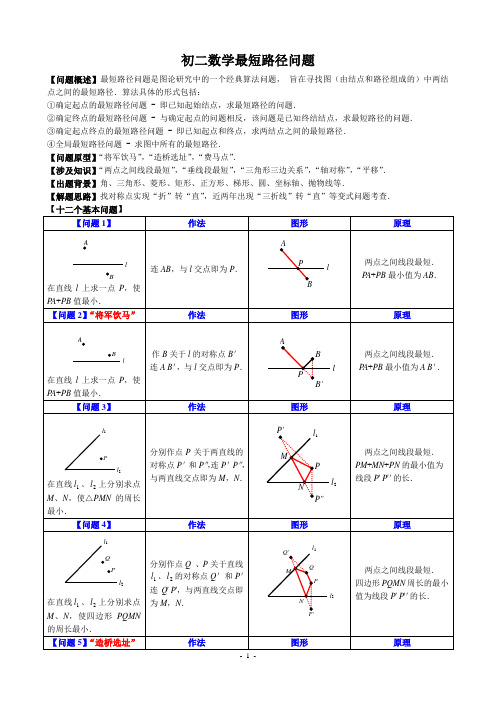
初二数学最短路径问题【问题概述】最短路径问题是图论研究中的一个经典算法问题,旨在寻找图(由结点和路径组成的)中两结点之间的最短路径.算法具体的形式包括:①确定起点的最短路径问题 - 即已知起始结点,求最短路径的问题.②确定终点的最短路径问题 - 与确定起点的问题相反,该问题是已知终结结点,求最短路径的问题.③确定起点终点的最短路径问题 - 即已知起点和终点,求两结点之间的最短路径.④全局最短路径问题 - 求图中所有的最短路径.【问题原型】“将军饮马”,“造桥选址”,“费马点”.【涉及知识】“两点之间线段最短”,“垂线段最短”,“三角形三边关系”,“轴对称”,“平移”.【出题背景】角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等.【解题思路】找对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题考查.在直线l 上求一点P ,使PB PA -的值最大.作直线AB ,与直线l 的交点即为P .三角形任意两边之差小于第三边.PB PA -≤AB .PB PA -的最大值=AB .【问题11】 作法图形 原理在直线l 上求一点P ,使PB PA -的值最大.作B 关于l 的对称点B '作直线A B ',与l 交点即为P .三角形任意两边之差小于第三边.PB PA -≤AB '. PB PA -最大值=AB '.【问题12】“费马点” 作法图形 原理△ABC 中每一内角都小于120°,在△ABC 内求一点P ,使P A +PB +PC 值最小.所求点为“费马点”,即满足∠APB =∠BPC =∠APC =120°.以AB 、AC 为边向外作等边△ABD 、△ACE ,连CD 、BE 相交于P ,点P 即为所求.两点之间线段最短. P A +PB +PC 最小值=CD .【精品练习】1.如图所示,正方形ABCD 的面积为12,△ABE 是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P ,使PD +PE 的和最小,则这个最小值为( )A .3B .26C .3D 62.如图,在边长为2的菱形ABCD 中,∠ABC =60°,若将△ACD 绕点A 旋转,当AC ′、AD ′分别与BC 、CD 交于点E 、F ,则△CEF 的周长的最小值为( ) A .2B .32C .32+D .4lBAlPABl ABlBPAB'ABCPEDCBAADEPB C3.四边形ABCD 中,∠B =∠D =90°,∠C =70°,在BC 、CD 上分别找一点M 、N ,使△AMN 的周长最小时,∠AMN +∠ANM 的度数为( )A .120°B .130°C .110°D .140°4.如图,在锐角△ABC 中,AB =42,∠BAC =45°,∠BAC 的平分线交BC 于点D ,M 、N 分别是AD 和AB 上的动点,则BM +MN 的最小值是 .5.如图,Rt △ABC 中,∠C =90°,∠B =30°,AB =6,点E 在AB 边上,点D 在BC 边上(不与点B 、C 重合), 且ED =AE ,则线段AE 的取值范围是 .6.如图,∠AOB =30°,点M 、N 分别在边OA 、OB 上,且OM =1,ON =3,点P 、Q 分别在边OB 、OA 上,则MP +PQ +QN 的最小值是_________.(注“勾股定理”:直角三角形中两直角边的平方和等于斜边的平方,即Rt △ABC 中,∠C =90°,则有222AB BC AC =+)7.如图,三角形△ABC 中,∠OAB =∠AOB =15°,点B 在x 轴的正半轴,坐标为B (36,0).OC 平分∠AOB ,点M 在OC 的延长线上,点N 为边OA 上的点,则MA +MN 的最小值是______. DEABCD MABMN8.已知A (2,4)、B (4,2).C 在y 轴上,D 在x 轴上,则四边形ABCD 的周长最小值为 ,此时 C 、D 两点的坐标分别为 .9.已知A (1,1)、B (4,2).(1)P 为x 轴上一动点,求PA +PB 的最小值和此时P 点的坐标;(2)P 为x 轴上一动点,求PB PA 的值最大时P 点的坐标;(3)CD 为x 轴上一条动线段,D 在C 点右边且CD =1,求当AC +CD +DB 的最小值和此时C 点的坐标;10.点C 为∠AOB 内一点.(1)在OA 求作点D ,OB 上求作点E ,使△CDE 的周长最小,请画出图形;(2)在(1)的条件下,若∠AOB =30°,OC =10,求△CDE 周长的最小值和此时∠DCE 的度数.图①12.荆州护城河在CC'处直角转弯,河宽相等,从A处到达B处,需经过两座桥DD'、EE',护城河及两桥都是东西、南北方向,桥与河岸垂直.如何确定两座桥的位置,可使A到B点路径最短?。
【初中数学】最短路径模型及例题解析

【初中数学】最短路径模型及例题解析一、最短路径模型简介在日常生活中,我们常常会遇到寻找从一个地点到另一个地点的最短路径问题。
例如,从家到学校、从甲地到乙地等。
在数学领域,最短路径问题属于图论的研究范畴,是图论中的一个基本问题。
最短路径模型就是用来解决这类问题的一种数学方法。
最短路径模型主要包括以下几个要素:1. 图:由顶点(地点)和边(路径)组成的集合。
2. 距离:表示两个顶点之间的距离或权重。
3. 路径:从一个顶点到另一个顶点经过的边的序列。
4. 最短路径:在所有路径中,长度最小的路径。
二、最短路径模型的求解方法1. 枚举法:枚举所有可能的路径,然后从中选择长度最小的路径。
这种方法适用于顶点数量较少的简单图。
2. Dijkstra算法:适用于带权重的有向图,通过逐步求解,找到从源点到其他所有顶点的最短路径。
3. Floyd算法:适用于求解任意两个顶点之间的最短路径,通过动态规划的方法,求解所有顶点对之间的最短路径。
三、例题解析【例题1】某城市有6个主要交通枢纽,分别用A、B、C、D、E、F表示。
下面是这6个交通枢纽之间的距离表(单位:千米):```A B C D E FA 0 5 7 8 9 10B 5 0 6 7 8 9C 7 6 0 4 5 6D 8 7 4 0 3 4E 9 8 5 3 0 2F 10 9 6 4 2 0```求从A到F的最短路径。
【解析】这是一个典型的最短路径问题,我们可以使用Dijkstra算法求解。
1. 初始化:将所有顶点的距离设置为无穷大,源点A的距离设置为0。
2. 选取距离最小的顶点,标记为已访问。
此时,A为已访问顶点。
3. 更新相邻顶点的距离:从A出发,更新B、C、D、E、F的距离。
此时,B、C、D、E、F的距离分别为5、7、8、9、10。
4. 重复步骤2和3,直到所有顶点都被访问。
最后得到的最短路径为A→B→E→F,长度为14千米。
【例题2】某城市有5个公园,分别用P1、P2、P3、P4、P5表示。
初二数学最短路径问题知识归纳+练习
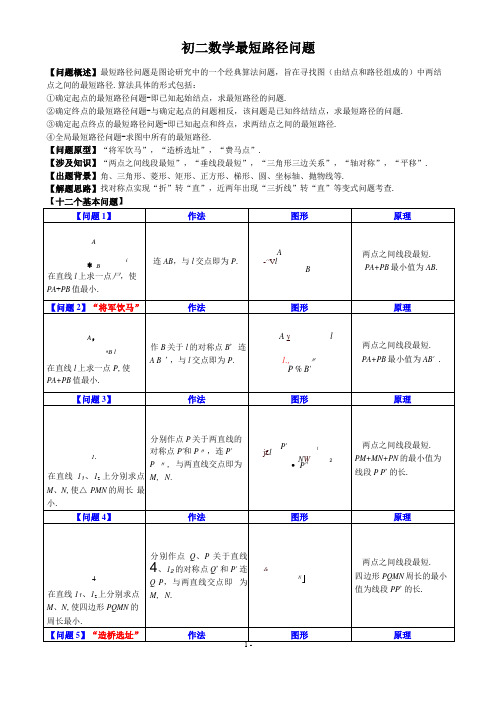
初二数学最短路径问题【问题概述】最短路径问题是图论研究中的一个经典算法问题,旨在寻找图(由结点和路径组成的)中两结点之间的最短路径.算法具体的形式包括:①确定起点的最短路径问题-即已知起始结点,求最短路径的问题.②确定终点的最短路径问题-与确定起点的问题相反,该问题是已知终结结点,求最短路径的问题.③确定起点终点的最短路径问题-即已知起点和终点,求两结点之间的最短路径.④全局最短路径问题-求图中所有的最短路径.【问题原型】“将军饮马”,“造桥选址”,“费马点”.【涉及知识】“两点之间线段最短”,“垂线段最短”,“三角形三边关系”,“轴对称”,“平移”.【出题背景】角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等.【解题思路】找对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题考查.【十二个基本问题】A・*B l在直线l上求一点P,使|PA—PB|的值最大. 作直线AB,与直线l的交点即为P.--^^lP三角形任意两边之差小于第三边.pA^i - PB W AB.|PA- PB|的最大值一AB .【问题11]作法图形原理Al■B在直线l上求一点P,使|PA—PB|的值最大. 作B关于l的对称点B' 作直线A B"与l交点即为P.—r^lB三角形任意两边之差小于第三边.pA^i - PB\ W AB ;|PA—PB| 最大值一AB【问题12]“费马点”作法图形原理A zAB C△ ABC中每一内角都小于120°,在4ABC内求一点P,使PA+PB+PC值最小. 所求点为“费马点”,即满足N APB =N BPC =NAPC =120° .以AB、AC 为边向外作等边^ ABD、△ACE,连CD、BE相交于P,点P即为所求.D"一B C两点之间线段最短.PA+PB+PC最小值一CD.【精品练习】1.如图所示,正方形ABCD的面积为12,八ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点尸,使PD+PE的和最小,则这个最小值为()A. 2V3B.2V16C. 3D. v162.如图,在边长为2的菱形ABCD中,N ABC=60°, 交于点E、F,则△ CEF的周长的最小值为()A. 2B. 2t3C. 2 + J3D. 4若将^ACD绕点A旋转,当AC、AD,分别与BC、CD3.四边形ABCD 中,N B =/D = 90°,N C =70°,在BC 、CD 上分别找一点M 、乂使^ AMN 的周长最小时,上的动点,则BM +MN 的最小值是5 .如图,Rt △ ABC 中,N C =90°,N B = 30°, AB = 6,点E 在AB 边上,点D 在BC 边上(不与点B 、C 重合),且ED =AE ,则线段AE 的取值范围是6 .如图,N AOB = 30°,点M 、N 分别在边OA 、OB 上,且OM =1, ON =3,点P 、Q 分别在边OB 、OA 上, 则MP +PQ + QN 的最小值是.(注”勾股定理”:直角三角形中两直角边的平方和等于斜边的平方,即 Rt △ ABC 中,N C =90°,则有 AC 2 + BC 2 = AB 2 )7 .如图,三角形"BC 中,N OAB =N AOB = 15°,点B 在%轴的正半轴,坐标为B (6<3 , 0).OC 平分N AOB ,点M 在OC 的延长线上,点N 为边OA 上的点,则MA +MN 的最小值是/AMN +N ANM 的度数为( A . 120°B . 130°)C . 110°D . 140°4.如图,在锐角^ABC 中,AB = 4v2 ,N BAC =45°,N BAC 的平分线交BC 于点D , M 、N 分别是AD 和AB8.已知A (2, 4)、B (4, 2). C在y轴上,D在%轴上,则四边形ABCD的周长最小值为此时C、D两点的坐标分别为9.已知A (1, 1)、B (4, 2).(1)P为%轴上一动点,求PA+PB的最小值和此时P点的坐标;(2)P为%轴上一动点,求|PA PB|的值最大时P点的坐标;(3)CD为%轴上一条动线段,D在C点右边且CD =1,求当AC + CD+DB的最小值和此时C点的坐标;10.点C为N AOB内一点.(1)在OA求作点D, OB上求作点E,使△ CDE的周长最小,请画出图形;(2)在(1)的条件下,若N AOB = 30°, OC =10,求4CDE周长的最小值和此时N DCE的度数.如图①,△ ABD 和^ACE 均为等边三角形,BE 、CE 交于凡连AF ,求证:AF +BF + CF = CD ;在^ABC 中,N ABC =30°, AB = 6, BC =8,N A ,N C 均小于 120°,求作一点尸,使 PA+PB+PC 的12.荆州护城河在CC '处直角转弯,河宽相等,从A 处到达B 处,需经过两座桥DD '、EE ',护城河及两桥 都是东西、南北方向,桥与河岸垂直.如何确定两座桥的位置,11. (1) (2) 值最小, 试求出最小值并说明理由.图①。
人教版八年级下册数学专题复习及练习(含解析):最短路径问题

专题13.4最短路径问题1.最短路径问题(1)求直线异侧的两点与直线上一点所连线段的和最小的问题,只要连接这两点,与直线的交点即为所求. 如图所示,点川,万分别是直线2异侧的两个点,在2上找一个点G使CA^CB最短,这时点Q是直线』与初的交点.⑵求直线同侧的两点与直线上一点所连线段的和最小的问题,只要找到其中一个点关于这条宜线的对称点, 连接对称点与另一个点,则与该直线的交点即为所求.如图所示,点月,万分别是直线2同侧的两个点,在』上找一个点G使CA+CB最短,这时先作点〃关为了证明点C的位置即为所求,我们不妨在直线上另外任取一点C',连接EG、BC「、证明M -\-CB<AC f +C* 3 如下:证明:由作图可知,点万和万‘关于直线/对称,所以直线/是线段宓’的垂直平分线.因为点Q与C'在直线上,所以BC=B' G BC =B f r C f・在G 中,AB' <AC r +B f C ,所以AC+B' C<AC r +B f C ,所以AC+BC<AC f+C‘ B.2.运用轴对称解决距离最短问题运用轴对称及两点之间线段最短的性质,将所求线段之和转化为一条线段的长,是解决距离之和最小问题的基本思路,不论题目如何变化,运用时要抓住直线同旁有两点,这两点「到直线上某点的距离和最小越个核心,所有作法都相同.利用轴对称解决最值问题应注意题目要球根据轴对称的性质、利用三角形的三边关系,通过比较来说明最值问题是常用的一种方法.解决这类最值问题时,要认真审题,不要只注意图形而忽略题意要求,「审题不淸导致答非所问.3.利用平移确左最短路径选址选址问题的关键是把各条线段转化到一条线段上.如果两点在一条直线的同侧时,过两点的直线与原直线的交点处构成线段的差最大,如果两点在一条直线的异侧时,过两点的直线与原直线的交点处构成的线段的和最小,都可以用三角形三边关系来推理说明,通常根据最大值或最小值的情况取其中一个点的对称点来解决.解决连接河两岸「的两个点的最短路径问题时,可以通过平移河岸的方法使河的宽度变为零,转化为求直线异侧的两点到直线上一点所连线段的和最小的问题.在解决最短路径问题时,我们通常利用轴对称、平移等变换把不在一条直线上的两条线段转化到一条直线上,从而作出最短路径的方法来解决问题.4.生活中的距离最短问题由两点之间线段最短(或三角形两边之和大于第三边)可知,求距离之和最小问题,就是运用等量代换的方式,把几条线段的和想办法转化在一条线段上,从而解决这个问题,运用轴对称性质,能将两条线段通过类似于镜而反射的方式转化成一条线段,如图,AO+BO=AC的长.所以作已知点关于某直线的对称点是解决这类问题的基本方法.Cy __-7 B5.运用轴对称解决距离之差最大问题利用轴对称和三角形的三边关系是解决几何中的最大值问题的关键.先做出其中一点关于对称轴的对称点,然后连接对称点和另一个点,所得直线与对称轴的交点,即为所求.根据垂直平分线的性质和三角形中两边之差小于第三边易证明这就是最大值.破疑点解决距离的最值问题的关键运用轴对称变换及三角形三边关系是解决一些距离的最值问题的有效方法.对点例题解析【例题1】在图中直线/上找到一点M使它到儿万两点的距离和最小.A【例题2】如图,小河边有两个村庄出B.要在河边建一自来水厂向川村与万村供水.(1)若要使厂部到心万村的距离相等,则应选择在哪建厂?(2)若要使厂部到川,万两村的水管最短,应建在什么地方?【例题3】如图,从川地到万地经过一条小河(河岸平行),今欲在河上建一座与两岸垂直的桥,应如何选择桥的位置才能使从A地到万地的路程最短?【例题4】如图所示,A, 3两点在直线2的两侧,在/上找一点G使点C到点月、万的距离之差最大.如JII练题1 •直线』左侧有两点只Q,试在直线上确左一点Q使得防%最短.2•如图,△月氏与△处关于某条直线对称,请画岀对称轴.A DC F3•如图,A.万为重庆市内两个较大的商圈,现需要在主要交通干道』上修建一个轻轨站只问如何修建,4•如图,四边形ABCD 中,ZBAD=120° , ZB=ZD=90°,在BC、CD ±分别找一点M、N,使Z\AMN 周长最小时,则ZAMN+ZANM的度数为()C. 110°D. 100°5•如图,两条公路0A. 0B相交,在两条公路的中间有一个汕库,设为点P,如在两条公路上各设置一个加油站,,请你设计一个方案,把两个加油站设在何处,可使运汕车从油库出发,经过一个加油站,再到另一个加汕站,最后回到汕库所走的路程最短.专题13.4最短路径问题1.最短路径问题(1)求直线异侧的两点与直线上一点所连线段的和最小的问题,只要连接这两点,与直线的交点即为所求. 如图所示,点川,万分别是直线2异侧的两个点,在2上找一个点G使CA^CB最短,这时点Q是直线』与初的交点.⑵求直线同侧的两点与直线上一点所连线段的和最小的问题,只要找到其中一个点关于这条宜线的对称点, 连接对称点与另一个点,则与该直线的交点即为所求.如图所示,点月,万分别是直线2同侧的两个点,在』上找一个点G使CA+CB最短,这时先作点〃关为了证明点C的位置即为所求,我们不妨在直线上另外任取一点C',连接EG、BC「、证明M -\-CB<AC f +C* 3 如下:证明:由作图可知,点万和万‘关于直线/对称,所以直线/是线段宓’的垂直平分线.因为点Q与C'在直线上,所以BC=B' G BC =B f r C f・在G 中,AB' <AC r +B f C ,所以AC+B' C<AC r +B f C ,所以AC+BC<AC f+C‘ B.2.运用轴对称解决距离最短问题运用轴对称及两点之间线段最短的性质,将所求线段之和转化为一条线段的长,是解决距离之和最小问题的基本思路,不论题目如何变化,运用时要抓住直线同旁有两点,这两点「到直线上某点的距离和最小越个核心,所有作法都相同.利用轴对称解决最值问题应注意题目要球根据轴对称的性质、利用三角形的三边关系,通过比较来说明最值问题是常用的一种方法.解决这类最值问题时,要认真审题,不要只注意图形而忽略题意要求,「审题不淸导致答非所问.3.利用平移确左最短路径选址选址问题的关键是把各条线段转化到一条线段上.如果两点在一条直线的同侧时,过两点的直线与原直线的交点处构成线段的差最大,如果两点在一条直线的异侧时,过两点的直线与原直线的交点处构成的线段的和最小,都可以用三角形三边关系来推理说明,通常根据最大值或最小值的情况取其中一个点的对称点来解决.解决连接河两岸「的两个点的最短路径问题时,可以通过平移河岸的方法使河的宽度变为零,转化为求直线异侧的两点到直线上一点所连线段的和最小的问题.在解决最短路径问题时,我们通常利用轴对称、平移等变换把不在一条直线上的两条线段转化到一条直线上,从而作出最短路径的方法来解决问题.4.生活中的距离最短问题由两点之间线段最短(或三角形两边之和大于第三边)可知,求距离之和最小问题,就是运用等量代换的方式,把几条线段的和想办法转化在一条线段上,从而解决这个问题,运用轴对称性质,能将两条线段通过类似于镜而反射的方式转化成一条线段,如图,AO+BO=AC的长.所以作已知点关于某直线的对称点是解决这类问题的基本方法.Cy __-7 B5.运用轴对称解决距离之差最大问题利用轴对称和三角形的三边关系是解决几何中的最大值问题的关键.先做出其中一点关于对称轴的对称点,然后连接对称点和另一个点,所得直线与对称轴的交点,即为所求.根据垂直平分线的性质和三角形中两边之差小于第三边易证明这就是最大值.破疑点解决距离的最值问题的关键运用轴对称变换及三角形三边关系是解决一些距离的最值问题的有效方法.对点例题解析【例题1】在图中直线/上找到一点M使它到儿万两点的距离和最小.A【答案】见解析。
初中数学中考复习专题 最短路径问题 24张
●
A' ●
P
B ● l
最短路径问题是初中阶段图论研究中的经典算 法问题,旨在寻找图(有结点和路径组成的)中两 结点之间的最短路径算法形式包括:
一、确定起点的最短路径问题
二、确定终点的最短路径问题
三、确定起点、终点的最短路径问题
四、全局最短路径问题
问题原型 “将军饮马”,“造桥选址”,“费马点”
作B关于l 的对称点B ',作直线 A B'与l 交点即为P
.
图形
原理
三角形任意两边 之差小于第三边 ︱PA-PB︱≤AB'. ︱PA-PB︱最大值 =AB'
问题12 “费马点”
作法
图形
原理
所求点为“费马点”,
既满足
△ABC中每一 内角都小于
∠APB=∠BPC=∠ APC=1200.以AB、
1200,在 △ABC内求一
AM+MN+NB的 值最小.
作点A关于l2的 对称点A',作 点B关于l1的对 称点B',连A 'B'交l2于M
,交l1于N.
图形
原理
两点之间线段 最短.
AM+MN+NB 的最小值为线 段A'B'的
长
问题9
作法
A
B l
在直线l上求一 点P,使︱PAPB︱的值最小
连AB, 作AB的 中垂线与 直线l的交 点即为P
AC为边向外作等边 △ABD、△ACE,连
点P,使
CD、BE相交于P,
PA+PB+PC最 点P即为所求点.
小.
两点之间 线段最
短.PA+PB+ PC最小值
=CD.
随堂练习一
如图,已知正方形ABCD,点M为BC边的中点,
专题复习--线段之和最短的问题

A B 、
2 17
17
8 、17
17
C、 4 17 17
D、3
四、能力拓展 如图,D是∠ABC内的一点,在AB上找 一点E,在AC上找一点F,使△EFD的 周长最短.
A
EF
D
B
C
课堂小结
本节课我们学习了 两线段和的最小值 问题,
这类问题的解题方法是怎样的?
不管在什么背景下,有关两线段之和最小问题, 总是化归到“两点之间的所有连线中,线段最 短”,而转化的方法大都是借助于“轴对称 点”,实现“折”化“直”
a
b
B
-----垂线段最短”
3.相传,古希腊有一位久负盛名 的学者,名叫海伦.有一天,一 位将军专程拜访海伦,求教一个 百思不得其解的问题:
从图中的A 地出发,到一条 笔直的河边l 饮马,然后到B 地.到河边什么地方饮马可使 他所走的路线全程最短?
B A
l
一、基本要求:
在直线 a外同侧有两个点A、B,在直线 a 上找一点P,使点P到A、B两个点的距离之 和最短 .
ABCD
(1)求C、M两点坐标; D
C
(2)在x轴上是否存在 一点Q,使得的△QMC 周长最小?若存在,
求出点Q的坐标; 若不存在,说明理由.
M
AO P
B
5、如图,已知二次函数y=ax2-4x+c 的图象
与坐标轴交于点A(-1, 0)和点B(0,-5).
(1)求该二次函数的解析式;y x 2 4x 5
将实际问题中A,B两地与 笔直的河L抽象成点A.点B 和直线a,b如图8
A
M
b
NB
图8
③作图过程:
将A点往直线a的垂直方向平移MN个单位后到 A′,连结A′,B,与直线b相交的一点为N点,再过N点 作NM⊥ a,与直线a的交点为M. 即MN为所求 AM+MN+NB最短的位置(如图).
专题复习——最短路径问题+课件2024-2025学年华东师大版数学八年级上册

A.6㎝ B.12 ㎝ C.13 ㎝ D.16 ㎝ 解:圆柱体的底面周长为24cm,则DE=12ຫໍສະໝຸດ m,根据两点之间线段最短,
CD=
=4
≈13cm
而走B﹣D﹣C的距离更短, ∵,BD=4,BC= ∴BD+BC≈11.64≈12.
挑战自我
如图,圆柱的底面周长为6cm,AC是底面圆的直径, 高BC=6cm,点P是母线BC上一点,且PC= BC. 求蚂蚁从A点出发沿着圆柱体的表面爬行到点P的 最短距离是
探索4:蚂蚁在圆锥上爬行
4.如图,一圆锥的底面半径为2,母线PB的长为6, D为PB的中点.一只蚂蚁从点A出发, 沿着圆锥的侧面爬行到点D,求蚂蚁爬行的最短路程
方法点拨:圆锥的侧面展开图是一个扇形,本题 就是把圆锥的侧面展开成扇形,“化曲面为平面”, 用勾股定理解决.
数学与生活:蚂蚁在台阶中爬行
B
B
B
5 13
A
A
A
A
2.有一圆柱,底面圆的周长为12cm,高为5cm, 在圆柱的下底面A点处有一只蚂蚁,
它想绕圆柱体一周爬行到它的顶端B点处, 它爬行的最短路线长为多少?
变式:
3.如图A,一圆柱体的底面周长为24cm,高BD为4cm, BC是直径,一只蚂蚁从点D出发沿着圆柱的表面爬行到 点C的最短路程大约是( )
如图是一个三级台阶,它的每一级的长宽和高分别为
20dm、3dm、2dm,A和B是这个台阶两个相对的端点,
A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁
沿着台阶面爬到B点最短路程是多少?
A
20
C
A
20
3
23
2
3
2
B
3
2 B
专题最短路径问题复习 ppt课件

2020/12/2
1
1.最短路径问题的类型
(一)两点一线型的线段和最小值问题;
①两点在直线异侧 ②两点在直线同侧
(二)两线一点型线段和最小值问题;
(三)两点两线型的线段和最小值问题;
(四)造桥选址问题. 2020/12/2
2 如果老师最后没有总结一节课的重点的难点,你 是否会认为老师的教学方法需要改进?
小河边去饮水,然后回家(即图中的小屋B). 问:马牵到小河边什么地方饮 水,然后回家所走的路程最短?请在图中画出河边马饮水的位置.
A'
C
2020/12/2
练习3. 如图,已知点D、点E分别是等边三角形ABC中BC、
AB边的中点,AD=5,点F是AD边上的动点,则BF+EF的最小
值为( B )
A.7.5
C
E F
∟
A
M
B
D
2020/12/2
16
知识点一:利用轴对称解决最短路径问题
典例讲评
两线两点型
某中学八(12)班举行文艺晚会, C 桌子摆成如图所示两直排(图中的AO, A
MO
BO),AO桌面上摆满了橘子,OB桌面
C
N
上摆满了糖果,站在C处的学生小明先 拿橘子再拿糖果,然后到D处座位上, 请你帮助他设计一条行走路线,使其所
B.5
C.4
D.不能确定
解析:△ABC为等边三角形,点D是BC边的中点,即点B与点C关于直线 AD对称.∵点F在AD上,故BF=CF.即BF+EF的最小值可转化为求CF+EF的 最小值,故连接CE即可,线段CE的长即为BF+EF的最小值.
2020/12/2
变式.如图,△ABC是等边三角形,高AD=3,点E是AB上
初二数学专题:最短路径问题

初二数学专题:最短路径问题问题概述】最短路径问题是图论研究中的一个经典算法问题,旨在寻找图中两结点之间的最短路径。
算法包括确定起点的最短路径问题、确定终点的最短路径问题、确定起点和终点的最短路径问题以及全局最短路径问题。
问题原型】最短路径问题有“将军饮马”、“造桥选址”、“费马点”等原型。
涉及知识】解决最短路径问题需要掌握“两点之间线段最短”、“垂线段最短”、“三角形三边关系”、“轴对称”、“平移”等知识。
此外,角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等也可能涉及到该问题。
解题思路】解决最短路径问题的思路包括找对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题。
十二个基本问题】问题1】已知点A、B和直线l,求在直线l上距离点A和点B之和最小的点P。
作法:在直线l上找到与AB连线垂直的交点P。
问题2】“将军饮马”已知点A、B和直线l,求在直线l上距离点A和点B之和最小的点P。
作法:将点B关于直线l对称得到点B',连接AB',在直线l上找到与AB'连线垂直的交点P。
问题3】已知两条直线l1、l2和点P,求在直线l1、l2上距离点P之和最小的两个点M、N。
作法:在直线l1、l2上找到与点P对称的点P'、P'',连接P'P'',在直线l1、l2上找到与P'、P''连线垂直的交点M、N。
问题4】已知两条直线l1、l2和点Q、P,求在直线l1、l2上距离点Q、P之和最小的两个点M、N。
作法:将点Q、P分别关于直线l1、l2对称得到点Q'、P',连接Q'P',在直线l1、l2上找到与Q'、P'连线垂直的交点M、N。
问题5】“造桥选址”已知点A、B和线段MN,求在点A向下平移MN长度单位后,在直线m上距离点A和点B之和最小的点N,以及在直线n上与N连线垂直的交点M。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
CD 图(2)图(3)专题复习最短路径(一)1、如图是一个长方体木块,已知AB=5,BC=3,CD=4,假设一只蚂蚁在点A 处,它要沿着木块侧面爬到点D 处,则蚂蚁爬行的最短路径是 。
2、现要在如图所示的圆柱体侧面A 点与B 点之间缠一条金丝带(金丝带的宽度忽略不计),圆柱体高为6cm ,底面圆周长为16cm ,则所缠金丝带长度的最小值为 。
3、如图是一个圆柱体木块,一只蚂蚁要沿圆柱体的表面从A 点爬到点B 处吃到食物,知圆柱体的高为5 cm ,底面圆的周长为24cm ,则蚂蚁爬行的最短路径为 。
4、正方形ABCD 的边长为8,M 在DC 上,且DM =2,N 是AC 上的一动点,DN +MN 的最小值为 。
第4题 第5题 第6题 第7题5、在菱形ABCD 中,AB=2, ∠BAD=60°,点E 是AB 的中点,P 是对角线AC 上的一个动点,则PE+PB 的最小值为 。
6、如图,在△ABC 中,AC =BC =2,∠ACB =90°,D 是BC 边的中点,E 是AB 边上一动点,则EC +ED 的最小值为____ ___。
第2题ABB第1题第3题⌒⌒⌒7、AB 是⊙O 的直径,AB=2,OC 是⊙O 的半径,OC ⊥AB ,点D 在AC 上,AD = 2CD ,点P 是半径OC 上的一个动点,则AP+PD 的最小值为____ ___。
(二)8、如图,点P 关于OA 、OB 的对称点分别为C 、D ,连接CD ,交OA 于M ,交OB于N ,若CD =18cm ,则△PMN 的周长为________。
9、已知,如图DE 是△ABC 的边AB 的垂直平分线,D 为垂足,DE 交BC 于E ,且AC =5,BC =8,则△AEC 的周长为__________。
10、已知,如图,在△ABC 中,AB <AC ,BC 边上的垂直平分线DE 交BC 于点D ,交AC 于点E ,AC =8,△ABE 的周长为14,则AB 的长 。
11、如图,在锐角△ABC 中,AB =42,∠BAC =45°,∠BAC 的平分线交BC 于点D ,M 、N 分别是AD 和AB 上的动点,则BM+MN 的最小值是____.12、在平面直角坐标系中,有A (3,-2),B (4,2)两点,现另取一点C (1,n ),当n = 时,AC + BC 的值最小.C第11题 第14题 第15题13、△ABC 中,∠C = 90°,AB = 10,AC=6,BC=8,过AB 边上一点P 作PE ⊥AC 于E ,PF⊥BC于 F,E、F是垂足,则EF的最小值等于.14、如图,菱形ABCD中,AB=2, ∠BAD=60°,点E、F、P分别是AB、BC、AC上的动点,则PE+PF的最小值为___________.15、如图,村庄A、B位于一条小河的两侧,若河岸a、b彼此平行,现在要建设一座与河岸垂直的桥CD,问桥址应如何选择,才能使A村到B村的路程最近?16、一次函数y=kx+b的图象与x、y轴分别交于点A(2,0),B(0,4).(1)求该函数的解析式;(2)O为坐标原点,设OA、AB的中点分别为C、D,P为OB上一动点,求PC+PD的最小值,并求取得最小值时P点坐标.(三)16、如图,已知∠AOB内有一点P,试分别在边OA和OB上各找一点E、F,使得△PEF的周长最小。
试画出图形,并说明理由。
17、如图,直线l是第一、三象限的角平分线.实验与探究:(1)由图观察易知A(0,2)关于直线l的对称点A′的坐标为(2,0),请在图中分别标明B(5,3)、C(-2,5)关于直线l的对称点B′、C′的位置,并写出他们的坐标:B′、C′;归纳与发现:(2)结合以上三组点的坐标,你会发现:坐标平面内任一点P (a ,b )关于第一、三象限的角平分线l 的对称点P ′的坐标为 ; 运用与拓广:(3)已知两点D (1,-3)、E (-1,-4),试在直线l 上确定一点Q ,使点Q 到D 、E 两点的距离之和最小,并求出Q 点坐标.18、几何模型:条件:如图,A 、B 是直线L 同旁的两个定点.问题:在直线L 上确定一点P ,使PA+PB 的值最小.方法:作点A 关于直线l 的对称点A ',连结A B '交l 于点P ,则PA PB A B '+=的值最小(不必证明). 模型应用:(1)如图1,正方形ABCD 的边长为2,E 为AB 的中点,P 是AC 上一动点.连结BD ,由正方形对称性可知,B 与D 关于直线AC 对称.连结ED 交AC 于P ,则PB PE +的最小值是___________;(2)如图2,O ⊙的半径为2,点A B C 、、在O ⊙上,OA OB ⊥,60AOC ∠=°,P 是OB 上一动点,求PA PC +的最小值;(3)如图3,∠AOB=45°,P 是∠AOB 内一点,PO=10,Q 、R 分别是OA 、OB 上的动点,求△PQR 周长的最小值.19、问题探究(1)如图①,四边形ABCD 是正方形, 10AB cm =,E 为边BC 的中点,P 为BD 上的一个动点,求PC PE +的最小值;(2)如图②,若四边形ABCD 是菱形, 10AB cm =,45ABC ∠=°,E 为边BC 上的一个动点,P 为BD 上的一个动点,求PC PE +的最小值;问题解决(3)如图③,若四边形ABCD 是矩形, 10AB cm =,20BC cm =,E 为边BC 上的一个动点,P 为BD 上的一个动点,求PC PE +的最小值;O AB P R Q 图3 A B EC B 图1O AB C图2P A B A 'P lA DBCADBCEP20.如图,在直角坐标系中,点A 的坐标为(-2,0),连结0A ,将线段OA 绕原点O 顺时针旋转120。
,得到线段OB. (1)求点B 的坐标;(2)求经过A 、O 、B 三点的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C ,使△BOC 的周长最小?若存在,求出点C 的坐标;若不存在,请说明理由.(注意:本题中的结果均保留根号) 解:(1)过点B 作BD ⊥x 轴于点D ,由已知可得:OB=OA=2,∠BOD=60。
.在Rt △OBD 中,∠ODB=90。
,∠OBD=30。
. ∴OD=1,∴点B 的坐标是(1,.(2)设所求抛物线的解析式为2y ax bx c =++,由已知可得:0420c a b c a b c =⎧⎪++=⎨⎪-+=⎩解得:,0.33a b c ===∴所求抛物线解析式为2.33y x x =+ (3)存在.由233y x x =+配方后得:()2133y x =+-∴抛物线的对称轴为x =-1.(也写用顶点坐标公式求出)∵OB=2,要使△BOC 的周长最小,必须BC+CO 最小. ∵点O 与点A 关于直线x =-1对称,有CO=CA. △ BOC 的周长=OB+BC+CO=OB+BC+CA.∴当A 、C 、B 三点共线,即点C 为直线AB 与抛物线对称轴的交点时,BC+CA 最小,此时△BOC 的周长最小.设直线AB的解析式为,:20k b y kx b k b ⎧+=⎪=+⎨-+=⎪⎩则有解得:k b == ∴直线AB的解析式为y x =+ 当x =-1时,3y =∴所求点C 的坐标为(-1,3). 21、如图,抛物线2y ax bx c =++的顶点P的坐标为13⎛⎫- ⎪ ⎪⎝⎭,,交x 轴于A 、B 两点,交y轴于点(0C ,. (1)求抛物线的表达式.(2)把△ABC 绕AB 的中点E 旋转180°,得到四边形ADBC判断四边形ADBC 的形状,并说明理由.(3)试问在线段AC 上是否存在一点F ,使得△FBD 若存在,请写出点F 的坐标;若不存在,请说明理由. 解:(1)由题意知解得3a =,3b =- -------------3分 (列出方程组给1分,解出给2分)∴抛物线的解析式为2y x x =-- -----------4分 (2)设点A (1x ,0),B (2x ,0)20x x -=, 解得1213x x =-=, -------------5分 ∴∣OA ∣=1,∣OB ∣=3.又∵tan ∠OCB=||||OB OC = ∴∠OCB =60°,同理可求∠OCA =30°.∴∠ACB =90° ----------6分 由旋转性质可知AC =BD ,BC =AD∴四边形ADBC 是平行四边形 ----------------------------7分 又∵∠ACB =90°.∴四边形ADBC 是矩形 --------------------------8分 (3)延长BC 至N ,使CN CB =.假设存在一点F ,使△FBD 的周长最小.即FD FB DB ++最小.∵DB 固定长.∴只要FD +FB 最小.又∵CA ⊥BN ∴FD +FB =FD +FN .∴当N 、F 、D 在一条直线上时,FD +FB 最小 .---------------------10分又∵C 为BN 的中点, ∴12FC AC =(即F 为AC 的中点).又∵A (-1,0),C (0,-3) ∴ 点F 的坐标为F (12-,2-∴ 存在这样的点F (12-,-,使得△FBD 的周长最小.---12分22. 已知:直线112y x =+与y 轴交于A ,与x 轴交于D ,抛物线212y x bx c =++与直线交于A 、E 两点,与x 轴交于B 、C 两点,且B 点坐标为 (1,0).(1)求抛物线的解析式;(2)动点P 在x 轴上移动,当△PAE 是直角三角形且以P 为直角顶点时,求点P 的坐标. (3)在抛物线的对称轴上找一点M ,使||AM MC -的值最大,求出点M 的坐标.答案:(1)将A (0,1)、B (1,0)坐标代入212y x bx c =++得 1102c b c =⎧⎪⎨=++⎪⎩ 解得321b c ⎧=-⎪⎨⎪=⎩ ∴抛物线的解折式为213122y x x =-+. 3分 (2)设点E 的横坐标为m ,则它的纵坐标为213122m m -+,则E (m ,213122m m -+).又∵点E 在直线112y x =+上,∴21311122m m m -+=+.解得10m =(舍去),24m =.∴E 的坐标为(4,3). 4分 过E 作EF x ⊥轴于F ,设P(b,0). 由90OPA FPE ∠+∠=°,得OPA FEP ∠=∠.Rt Rt AOP PFE △∽△. 由AO OP PF EF =得143bb =-.解得11b =,23b =.∴此时的点P 的坐标为(1,0)或(3,0). 6分 (3)抛物线的对称轴为32x =. ∵B 、C 关于x =23对称,∴MC MB =. 要使||AM MC -最大,即是使||AM MB -最大. 8分由三角形两边之差小于第三边得,当A 、B 、M 在同一直线上时||AM MB -的值最大. 易知直线AB 的解折式为1y x =-+.∴由132y xx=-+⎧⎪⎨=⎪⎩得3212xy⎧=⎪⎪⎨⎪=-⎪⎩∴M(23,-21). 10分。
