初二最短路径问题归纳
八年级数学最短路径题型归纳

八年级数学中的最短路径问题,通常涉及到几何图形中的点、线、面等元素,需要利用一些基本的几何知识和数学原理来求解。
以下是一些常见的最短路径题型及其解题方法:1.两点之间的最短距离:题型描述:在平面上给定两点A和B,求A到B的最短距离。
解题方法:直接连接A和B,线段AB的长度即为最短距离。
2.点到直线的最短距离:题型描述:在平面上给定一点P和一条直线l,求P到l的最短距离。
解题方法:作点P到直线l的垂线,垂足为Q,则PQ的长度即为最短距离。
3.直线到直线的最短距离:题型描述:在平面上给定两条直线l1和l2,求l1到l2的最短距离。
解题方法:如果l1和l2平行,则它们之间的距离即为最短距离;如果l1和l2不平行,则作l1到l2的垂线,垂足所在的线段即为最短4.点到圆的最短距离:题型描述:在平面上给定一点P和一个圆O,求P到圆O的最短距离。
解题方法:如果点P在圆O内,则最短距离为P到圆心的距离减去圆的半径;如果点P在圆O外,则最短距离为P到圆心的距离;如果点P在圆O上,则最短距离为0。
5.圆到圆的最短距离:题型描述:在平面上给定两个圆O1和O2,求O1到O2的最短距离。
解题方法:如果两圆外离,则它们之间的最短距离为两圆的半径之和;如果两圆外切,则它们之间的最短距离为两圆的半径之差;如果两圆相交或内切,则它们之间的最短距离为0;如果两圆内含,则它们之间的最短距离为两圆的半径之差减去两圆半径之和的绝对值。
6.多边形内的最短路径:题型描述:在一个多边形内给定两个点A和B,求A到B的最短解题方法:通常需要将多边形划分为多个三角形,然后利用三角形内的最短路径(即连接两点的线段)来求解。
7.立体几何中的最短路径:题型描述:在立体图形中给定两点A和B,求A到B的最短路径。
解题方法:通常需要将立体图形展开为平面图形,然后利用平面几何中的最短路径原理来求解。
在解决最短路径问题时,需要注意以下几点:准确理解题目要求,确定需要求的是哪两点之间的最短距离。
(word完整版)初二数学最短路径问题知识归纳+练习,推荐文档
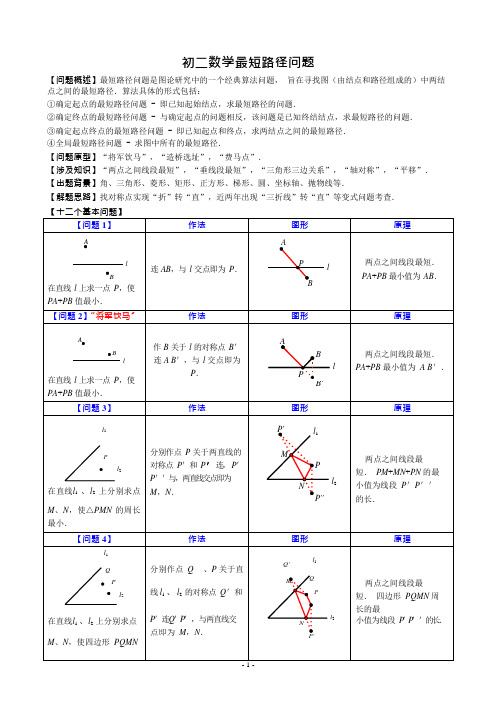
初二数学最短路径问题【问题概述】最短路径问题是图论研究中的一个经典算法问题,旨在寻找图(由结点和路径组成的)中两结点之间的最短路径.算法具体的形式包括:①确定起点的最短路径问题 - 即已知起始结点,求最短路径的问题.②确定终点的最短路径问题 - 与确定起点的问题相反,该问题是已知终结结点,求最短路径的问题.③确定起点终点的最短路径问题 - 即已知起点和终点,求两结点之间的最短路径.④全局最短路径问题 - 求图中所有的最短路径.【问题原型】“将军饮马”,“造桥选址”,“费马点”.【涉及知识】“两点之间线段最短”,“垂线段最短”,“三角形三边关系”,“轴对称”,“平移”.【出题背景】角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等.【解题思路】找对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题考查.【问题1】作法图形原理AlB在直线l 上求一点P,使PA+PB 值最小.连AB,与l 交点即为P.AP lB两点之间线段最短.PA+PB 最小值为AB.【问题2】“将军饮马”作法图形原理ABl在直线l 上求一点P,使PA+PB 值最小.作B 关于l 的对称点B'连A B',与l 交点即为P.ABlP两点之间线段最短.PA+PB 最小值为A B'.B'【问题3】作法图形原理l1Pl2在直线l1、l2上分别求点M、N,使△PMN 的周长最小.分别作点P 关于两直线的对称点P'和P'连,P'P''与,两直线交点即为M,N.P' l1MPNl2P''两点之间线段最短.PM+MN+PN 的最小值为线段P'P''的长.【问题4】作法图形原理l1QPl2在直线l1、l2上分别求点M、N,使四边形PQMN 分别作点Q 、P 关于直线l1、l2的对称点Q'和Q'l1M QP两点之间线段最短.四边形PQMN 周长的最P'连Q'P',与两直线交l2N 小值为线段P'P''的长.点即为M,N.P'PE3在直线 l 上求一点 P ,使 直线 l 的交点即为 P .端点的距离相等.PA - PB =0.PA - PB 的值最小.【问题 10】作法图形原理ABl在直线 l 上求一点 P ,使PA - PB 的值最大.作直线 AB ,与直线 l 的交点即为 P .ABPl三角形任意两边之差小于第三边. PA - PB ≤AB .PA - PB 的最大值=AB .【问题 11】作法图形原理AlB在直线 l 上求一点 P ,使PA - PB 的值最大.三角形任意两边之差小于A第三作 B 关于 l 的对称点 B ' 作直线 A B ',与 l 交点B'Pl边. PA - PB ≤AB '.即为 P .BPA - PB 最大值=AB '.【问题 12】“费马点”作法 图形原理A所求点为“费马点”,即满足DBC∠APB =∠BPC =∠APC=120°.以 AB 、AC 为APE两点之间线段最短. PA +PB +PC 最小值△ABC 中每一内角都小于 边向外作等边△ABD 、△ BC=CD .120°,在△ABC 内求一 ACE ,连 CD 、BE 相交于 点 P ,使 PA +PB +PC 值最 P ,点 P 即为所求.小.【精品练习】1. 如图所示,正方形 ABCD 的面积为 12,△ABE 是等边三角形,点 E 在正方形 ABCD 内,在对角线 AC 上有一点 P ,使 PD +PE 的和最小,则这个最小值为( )A. 2B. 2 ADC .3D .BC2. 如图,在边长为 2 的菱形 ABCD 中,∠ABC =60°,若将△ACD 绕点 A 旋转,当 AC ′、AD ′分别与 BC 、CD- 3 -662 EDM3交于点 E 、F ,则△CEF 的周长的最小值为()A .2B . 2C . 2 +D .43. 四边形 ABCD 中,∠B =∠D =90°,∠C =70°,在 BC 、CD 上分别找一点 M 、N ,使△AMN 的周长最小时,∠AMN +∠ANM 的度数为()A .120°B .130°C .110°D .140°A DBNC4. 如图,在锐角△ABC 中,AB =4 ,∠BAC =45°,∠BAC 的平分线交 BC 于点 D ,M 、N 分别是 AD 和AB 上的动点,则 BM +MN 的最小值是 .A5. 如图,Rt △ABC 中,∠C =90°,∠B =30°,AB =6,点 E 在 AB 边上,点 D 在 BC 边上(不与点 B 、C 重合),且 ED =AE ,则线段 AE 的取值范围是 .ACB6. 如图,∠AOB =30°,点 M 、N 分别在边 OA 、OB 上,且 OM =1,ON =3,点 P 、Q 分别在边 OB 、OA 上,则 MP +PQ +QN 的最小值是 .(注“勾股定理”:直角三角形中两直角边的平方和等于斜边的平方,即 Rt △ABC 中,∠C =90°,则有 AC 2 + BC 2 = AB 2 )- 4 -D M33 yABOxyBA OCDx7. 如图,三角形△ABC 中,∠OAB =∠AOB =15°,点 B 在 x 轴的正半轴,坐标为 B ( 6 ,0).OC 平分∠AOB ,点 M 在 OC 的延长线上,点 N 为边 OA 上的点,则 MA +MN 的最小值是.8. 已知 A (2,4)、B (4,2).C 在 y 轴上,D 在 x 轴上,则四边形 ABCD 的周长最小值为,此时 C 、D 两点的坐标分别为.9.已知 A (1,1)、B (4,2).(1)P 为 x 轴上一动点,求 PA +PB 的最小值和此时 P 点的坐标;(2)P 为 x 轴上一动点,求 PA PB 的值最大时 P 点的坐标;(3)CD 为 x 轴上一条动线段,D 在 C 点右边且 CD =1,求当 AC +CD +DB 的最小值和此时 C 点的坐标;10. 点 C 为∠AOB 内一点.(1) 在 OA 求作点 D ,OB 上求作点 E ,使△CDE 的周长最小,请画出图形;(2) 在(1)的条件下,若∠AOB =30°,OC =10,求△CDE 周长的最小值和此时∠DCE 的度数.A- 5 -yBA OxyBA OxCO BAF11.(1)如图①,△ABD 和△ACE 均为等边三角形,BE 、CE 交于 F ,连 AF ,求证:AF +BF +CF =CD ;(2)在△ABC 中,∠ABC =30°,AB =6,BC =8,∠A ,∠C 均小于 120°,求作一点 P ,使 PA +PB +PC 的值最小,试求出最小值并说明理由.DEBC① ①① ①12.荆州护城河在 CC '处直角转弯,河宽相等,从 A 处到达 B 处,需经过两座桥 DD '、EE ',护城河及两桥都是东西、南北方向,桥与河岸垂直.如何确定两座桥的位置,可使 A 到 B 点路径最短?- 6 -- 7 -“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。
八年级最短路径问题归纳

八年级最短路径问题归纳最短路径问题是图论中的一个经典问题,也是计算机科学中的重要研究领域之一。
在八年级的学习中,我们也会接触到最短路径问题,并且通过一些简单的算法来解决这个问题。
本文将对八年级最短路径问题进行归纳总结,希望能够帮助大家更好地理解和应用这个问题。
一、最短路径问题的定义最短路径问题是指在一个给定的图中,找出两个顶点之间的最短路径,即路径上的边权之和最小。
其中,图由顶点和边组成,顶点表示路径中的点,边表示路径中的通路或连接。
二、最短路径问题的应用最短路径问题在生活中有着广泛的应用,比如导航系统中的最短路径规划、货物运输中的最短路径选择等等。
通过寻找最短路径,可以帮助我们节省时间和资源,提高效率。
三、最短路径问题的解决方法1. 迪杰斯特拉算法迪杰斯特拉算法是解决最短路径问题的一种常用算法。
该算法通过不断更新起点到各个顶点的最短路径,直到找到终点的最短路径为止。
迪杰斯特拉算法的具体步骤如下:- 初始化起点到各个顶点的距离为无穷大,起点到自身的距离为0;- 选择一个未访问的顶点,更新起点到其他顶点的距离;- 重复上述步骤,直到找到终点的最短路径或所有顶点都被访问过。
2. 弗洛伊德算法弗洛伊德算法是解决最短路径问题的另一种常用算法。
该算法通过不断更新任意两个顶点之间的最短路径,直到更新完所有顶点对之间的最短路径为止。
弗洛伊德算法的具体步骤如下:- 初始化任意两个顶点之间的距离,如果两个顶点之间有直接的边,则距离为边的权值,否则距离为无穷大;- 选择一个顶点作为中转点,更新任意两个顶点之间的距离;- 重复上述步骤,直到更新完所有顶点对之间的最短路径。
四、最短路径问题的注意事项在解决最短路径问题时,需要注意以下几点:1. 图的表示方式:可以使用邻接矩阵或邻接表来表示图,根据具体的问题选择合适的表示方式。
2. 边的权值:边的权值可以表示两个顶点之间的距离、时间、花费等等,根据具体的问题选择合适的权值。
初二数学最短路径问题知识归纳+练习

初二数学最短路径问题【问题概述】最短路径问题是图论研究中的一个经典算法问题,旨在寻找图(由结点和路径组成的)中两结点之间的最短路径.算法具体的形式包括:-①确定起点的最短路径问题即已知起始结点,求最短路径的问题.-②确定终点的最短路径问题与确定起点的问题相反,该问题是已知终结结点,求最短路径的问题.-③确定起点终点的最短路径问题即已知起点和终点,求两结点之间的最短路径.④全局最短路径问题-求图中所有的最短路径.【问题原型】.“将军饮马”,“造桥选址”,“费马点”【涉及知识】“两点之间线段最短”,“垂线段最短”,“三角形三边关系”,“轴对称”,“平移”.【出题背景】角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等.【解题思路】找对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题考查.】【十二个基本问题】1作法图形【问题原理A A两点之间线段最短.P l.交点即为P连AB,与l l PA+PB 最小值为AB.BB,使上求一点P在直线l值最小.PA+PB【问题2】“将军饮马”作法图形原理A AB'B关于作B l 的对称点两点之间线段最短.Bl l PA+PB 最小值为 A B P.'.连A B ',与l 交点即为P,使P在直线l 上求一点B'PA+PB 值最小.3】作法图形原理【问题P'l 1l 1分别作点P 关于两直线的两点之间线段最短.M PPM +MN +PN 的最小值为对称点P'和P',连P'P',P ll l 、上2.M,P'''的长.N与两直线交点即为线段P分别求点在直线l212NM 、N,使△PMN的周长P''最小.4】作法【问题图形原理l 1l1Q'Q关于直线分别作点Q 、P Q两点之间线段最短.MPl 、l P'Q'和的对称点21P周长的最小四边形PQMN l2',与两直线交点即Q连'P值为线段P'P''的长.l 2、l l 上分别求点在直线.,N为M21N,使四边形N 、M PQMN P'的周长最小.【问题5】“造桥选址”作法图形原理范文A A M m将点A 向下平移MN 的长度两点之间线段最短.n A'M n'B,交单位得A',连A N m AM +MN +BN 的最小值为B于m N 作NM ⊥于点N,过n N,n ,在m 、n 直线m ∥A'B+MN ..M B MN、N,使上分别求点M 的,且AM+ MN+ BN ⊥m 值最小.【问题6】作法图形原理A A'A将点A 向右平移a 个长度单B B l两点之间线段最短.的对',作 A '关于位得A l a N l M,交直线称点A',连A'B AM +MN +BN 的最小值为MN l MM(上求两点、N在直线l 点向左平,将于点NNA'B+ MN.A''MN a 移 a 个单位得M.在左),使,并使的值最小.AM + MN+ NB 】【问题7作法图形原理l l1 1 P'P P l点到直线,垂线段最短.',的对称点作点P 关于P 1A ll 于B⊥,交作P'B22PA+ AB 的最小值为线段P'l 2于A.l B的长.2l l 上求A上求点在,在21B,使PA+ AB 值最小.点B图形原理】【问题8作法l 1B'NAl 1l的对称点关于 A 作点2l2两点之间线段最短.MB l 的对称A ',作点 B 关于N1A AM +MN +NB 的最小值为lll,于B'交M 为上点B',连A'A 为上一定点,B 212线段A'B'的长.l 2BM l l ,一定点,在上求点交M.N 于21A'l 在使,N 点上求1的值最小.AM + MN+ NB图形原理】【问题9作法A A垂直平分上的点到线段两B端点的距离相等.B的中垂线与AB ,作连AB l l.l 直线的交点即为P PA PB =0.P PA 上求一点l P,使在直线的值最小.PB【问题10】作法图形原理范文A三角形任意两边之差小于A B作直线AB,与直线l 的交第三边.PA PB ≤AB.l Bl .点即为P P,使l 上求一点P在直线PA PB 的最大值=AB.PA PB 的值最大.【问题11】作法图形原理A三角形任意两边之差小于A作B 关于l 的对称点B'l B'第三边.PA PB ≤AB'.l交点即l 作直线 A B',与B P为P.B PA PB 最大值=AB'.,使l 上求一点P在直线PA PB 的值最大.【问题12】“费马点”作法图形原理A所求点为“费马点”,即满D APB=∠BPC=∠足∠A两点之间线段最短.E AC°.以AB、APC=120 C B、ABD 为边向外作等边△PA+ PB+ PC 最小值=CD .P△ABC 中每一内角都小于△ACE,连CD 、BE 相交CB于P ,点P 即为所求.,ABC 内求一点P120°,在△值最小.PA+PB+PC 使【精品练习】1 的面积为.如图所示,正方形ABCD12,△ABE 是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P,使PD +PE 的和最小,则这个最小值为()AD62 62 3B..C.3D A.PEBC2.如图,在边长为2 的菱形ABCD 中,∠ABC =60 °,若将△ACD 绕点 A 旋转,当AC ′、AD ′分别与BC 、CD)交于点E、F ,则△CEF 的周长的最小值为(A.2B.2 3C.23D.4范文3.四边形ABCD 中,∠B=∠D =90°,∠C=70 °,在BC 、CD 上分别找一点M、N,使△AMN 的周长最小时,∠AMN + ∠ANM 的度数为()AD°110°D.140CA.120°B.130°.N BM4.如图,在锐角△ABC 中,AB =42 ,∠BAC=45 °,∠BAC 的平分线交BC 于点D,M、N 分别是AD 和ABC 的最小值是上的动点,则BM +MN .D MAN B5.如图,Rt△ABC 中,∠C=90 °,∠B=30 °,AB=6,点E 在AB 边上,点D 在BC 边上重合),、C (不与点B.的取值范围是且ED =AE,则线段AEA ECD B6.如图,∠AOB=30°,点M、N 分别在边OA、OB 上,且OM =1,ON=3,点P、Q 分别在边OB、OA 上,则MP +PQ+QN 的最小值是_________.(注“勾股定理”:直角三角形中两直角边的平方和等于斜边的平方,222BC AC AB°,则有=90 C即Rt△ABC 中,∠)7.如图,三角形△ABC中,∠OAB=∠AOB=15°,点B 在x轴的正半轴,坐标为B( 63 ,0).OC 平分∠AOB ,点M 在OC 的延长线上,点N 为边OA 上的点,则MA +MN 的最小值是______.范文y轴上,D 在在x 轴上,则四边形4)、B (4,2).C 8.已知A(2,ABCD 的周长最小值为,两点的坐标分别为D 此时C、.yABOx.已知9).,2 1,1)、B(4A(y点的坐标;轴上一动点,求PA+PB 的最小值和此时P (1)P 为xBAOx点的坐标;P 的值最大时x 轴上一动点,求PA PB )(2 P 为y BAOx(3)CD 为x 轴上一条动线段, D 在 C 点右边且CD =1,求当AC+ CD+ DB 的最小值和此时C 点的坐标;yBAOxC D10 .点C 为∠AOB 内一点.(1)在OA 求作点 D ,OB 上求作点E ,使△CDE 的周长最小,请画出图形;(2)在(1)的条件下,若∠AOB =30°,OC=10,求△CDE 周长的最小值和此时∠DCE 的度数.ACB O范文11.(1)如图①,△ABD 和△ACE 均为等边三角形,BE、CE 交于F,连AF,求证:AF +BF +CF =CD ;(2)在△ABC 中,∠ABC =30°,AB=6,BC=8,∠ A ,∠C 均小于120°,求作一点P,使PA+PB+PC 的值最小,试求出最小值并说明理由.DA A EC B F图②C B图①处,需经过两座桥处到达 B A '处直角转弯,河宽相等,从12 .荆州护城河在CC',护城河及两桥EE '、DD点路径最短?到都是东西、南北方向,桥与河岸垂直.如何确定两座桥的位置,可使B A范文。
八年级最短路径问题归纳小结

八年级数学最短路径问题【问题概述】 最短路径问题是图论研究中的一个经典算法问题, 旨在寻找图(由结点和路径组成的)中两结点之间的最短路径•算法具体的形式包括: ① 确定起点的最短路径问题 - ② 确定终点的最短路径问题- ③ 确定起点终点的最短路径问题 即已知起始结点,求最短路径的问题.与确定起点的问题相反,该问题是已知终结结点,求最短路径的问题.-即已知起点和终点,求两结点之间的最短路径. ④全局最短路径问题-求图中所有的最短路径.【问题原型】“将军饮马”,“造桥选址”,“费马点”.【涉及知识】“两点之间线段最短”,“垂线段最短”,“三角形三边关系”,“轴对称”,“平移” 【出题背景】 角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等.【解题思路】 找对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题考查.【十二个基本问题】A在直线丨上求一点 P ,使 PA+PB 值最小.|【问题2】“将军饮马” 在直线I A 上求一点 P ,使 PA+PB 值最小.*Bl【问题3】在直线l i 、I 2上分别求点M 、N ,使△ PMN 的周长 最小.P 【问题4】12l ila 上分别求点】边形 PQMN P----------------------------=-4a ------------------【问题5】“造桥选址”A直线m 产n ,在m 、n , 上分别求点 M * N :使MN 丄 m ,且 AM+MN + BN 的N值最小.*B【问题6】A在直线1上求两点.B M 、N ( M 在左)半M4=a ,并使M a NAM + MN + NB 的值最小.【问题7】作法作B 关于l 的对称点B / 连AB /,与l 交点即为P .作法分别作点P 关于两直线的 对称点P /和P 〃,连P / P 〃,与两直线交点即为 M , N .作法分别作点Q 、P 关于直线l i 、l a 的对称点Q /和P / 连QP ,与两直线交点即 为 M , N .作法 将点A 向下平移MN 的长 度单位得A ,,连A/B,交n 于点N ,过N 作NM 丄m 于 M .作法将点A 向右平移a 个长度 单位得A ,,作A /关于I 的 对称点A 〃,连A 〃B ,交直线 l 于点N ,将N 点向左平 移a 个单位得M .作法作点P 关于l i 的对称点 两点之间线段最短.FA + PB 最小值为AB .原理两点之间线段最短. PA+PB 最小值为A B ,.原理两点之间线段最短.PM +MN + PN 的最小值为线段PP /的长.原理两点之间线段最短. 四边形PQMN 周长的最小 值为线段P Z P Z/的长.原理两点之间线段最短. AM +MN + BN 的最小值为A B+MN .两点之间线段最短. AM +MN + BN 的最小值为 A 〃B+MN .【问题1】 作法图形原理Rl 2在直线l 1、M 、N ,使四的周长最小. 连AB ,与l 交点即为P .原理原理点到直线,垂线段最短.A B在l i 上求点A ,在12上求 点B ,使PA+AB 值最小.P /,作PB 丄丨2于B ,交丨2 于A .PA+AB 的最小值为线段 P B 的长.【问题8】作法图形原理l iA 为l 1上一定点为l 2上 一定点,在双求点 M , 在上求点B N ,|2使AM + MN + NB 的值最小.作点A 关于|2的对称点 A /,作点B 关于l i 的对称 点B /,连A B 交|2于M , 交l i 于N .B'*\ 11两点之间线段最短. AM +MN + NB 的最小值为 线段A B 的长.【问题9】作法 亍图形 B 2A原理A在直线Al 上求一点 |PA—PB|的值最小 .P ,使 连AB ,作AB 的中垂线与 直线l 的交点即为P . A\>B l」P 垂直平分上的点到线段两 端点的距离相等.PA-PB = 0.【问题10】 作法/图形原理在直线l A 上求一点P ,使 |PA —PB|的值最大.1作直线AB ,与直线l 的交 点即为P .A ^^B 一lP三角形任意两边之差小于第三边.PA —PB < AB .PA — PB|的最大值 =AB . 【问题11】作法 图形原理在直线l 上求一点P ,使 |PA —PB|的值最大.l*B作B 关于l 的对称点B / 作直线A B/,与l 交点即为P .A---------------- l B三角形任意两边之差小于 第三边.PA —PB <AB /.PA —PB 最大值=AB Z .【问题12】“费马点”作法图形原理A△ ABC 中每一小于 120 °,在X ABC 内求一点 P ,使虫+PB + PC 值最小.所求点为“费马点”,即满 足/ APB = Z BPC = Z APC = 120 ° .以 AB 、AC 为边向外作等边厶ABD 、 △ ACE ,连 CD 、BE 相交于P ,点P 即为所求.ABC两点之间线段最短. PA+PB+PC 最小值=CD .1如图所示,正方形 ABCD 的面积为12,^ ABE 是等边三角形,点 E 在正方形ABCD 内,在对角线 AC 上有 一点P ,使PD+PE 的和最小,则这个最小值为( )A . 2'3B . 2 6C . 3D .62•如图,在边长为 2的菱形 ABCD 中,/ ABC = 60 °若将 交于点E 、F ,则△ CEF 的周长的最小值为( )A . 2B . 2.3C . 2D . 43.四边形 ABCD 中,/ B = Z D = 90 ° / C = 70 ° 在 BC 、2 / 3A _______________ D/ AMN+ / ANM 的度数为( A . 120 °B . 130 °)C .110 °D . 140 ° 4.如图,在锐角厶 ABC 中, AB = 4罷,/ BAC = 45 ° / BAC 的平分线交 BC 于点D , M 、N 分别是 AD 和ABC 上的动点,贝U BM+MN 的最小值是 5.如图,Rt △ ABC 中,/ C = 90 ° / B = 30 ° AB = 6,点E 在AB 边上,点D 在BC 边上(不与 且ED = AE ,则线段AE 的取值范围是 A 6 .如图,/ AOB = 30。
【初二】最短路径问题归纳

最短路径问题专题学习【基本问题】一定点,在2l 上求点M ,在1l 上求点N ,使AM +MN +NB 的值最小.【问题9】 作法图形 原理在直线l 上求一点P ,使PB PA -的值最小.连AB ,作AB 的中垂线与直线l 的交点即为P .垂直平分上的点到线段两端点的距离相等.PB PA -=0.【问题10】 作法图形 原理在直线l 上求一点P ,使PB PA -的值最大.作B 关于l 的对称点B '作直线A B ',与l 交点即为P .三角形任意两边之差小于第三边.PB PA -≤AB '. PB PA -最大值=AB '.【精品练习】1.如图所示,正方形ABCD 的面积为12,△ABE 是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P ,使PD +PE 的和最小,则这个最小值为( )A .3.6 C .3 D 62.如图,在边长为2的菱形ABCD 中,∠ABC =60°,若将△ACD 绕点A 旋转,当AC ′、AD ′分别与BC 、CD 交于点E 、F ,则△CEF 的周长的最小值为( )A .2B .32C .32+D .4lBAl ABDEABC ADEPB CDAMABMN3.四边形ABCD 中,∠B =∠D =90°,∠C =70°,在BC 、CD 上分别找一点M 、N ,使△AMN 的周长最小 时,∠AMN +∠ANM 的度数为( )A .120°B .130°C .110°D .140°4.如图,在锐角△ABC 中,AB =42,∠BAC =45°,∠BAC 的平分线交BC 于点D ,M 、N 分别是AD和AB 上的动点,则BM +MN 的最小值是 .5.如图,Rt △ABC 中,∠C =90°,∠B =30°,AB =6,点E 在AB 边上,点D 在BC 边上(不与点B 、C 重合),且ED =AE ,则线段AE 的取值范围是 .6.如图,∠AOB =30°,点M 、N 分别在边OA 、OB 上,且OM =1,ON =3,点P 、Q 分别在边OB 、OA 上,则MP +PQ +QN 的最小值是_________.7.如图,三角形△ABC 中,∠OAB =∠AOB =15°,点B 在x 轴的正半轴,坐标为B (36,0).OC 平分∠AOB ,点M 在OC 的延长线上,点N 为边OA 上的点,则MA +MN 的最小值是______.8.已知A (2,4)、B (4,2).C 在y 轴上,D 在x 轴上,则四边形ABCD 的周长最小值为 ,此时 C 、D 两点的坐标分别为 .9.已知A (1,1)、B (4,2).(1)P 为x 轴上一动点,求PA +PB 的最小值和此时P 点的坐标;yxBOAyxBAO第2题 第3题 第4题 第5题第6题 第7题(2)P 为x 轴上一动点,求PB PA 的值最大时P 点的坐标;(3)CD 为x 轴上一条动线段,D 在C 点右边且CD =1,求当AC +CD +DB 的最小值和此时C 点的坐标;10.点C 为∠AOB 内一点.(1)在OA 求作点D ,OB 上求作点E ,使△CDE 的周长最小,请画出图形;(2)在(1)的条件下,若∠AOB =30°,OC =10,求△CDE 周长的最小值和此时∠DCE 的度数.。
(精编)八年级最短路径问题归纳小结

八年级数学最短路径问题【问题概述】最短路径问题是图论研究中 的一个经典算法问题,旨在寻找图(由结点和路径组成 的)中两结点之间 的最短路径.算法具体 的形式包括: ①确定起点 的最短路径问题 ②确定终点 的最短路径问题③确定起点终点 的最短路径问题 -即已知起始结点,求最短路径 的问题.-与确定起点 的问题相反,该问题是已知终结结点,求最短路径 的问题.-即已知起点和终点,求两结点之间 的最短路径.④全局最短路径问题-求图中所有 的最短路径.【问题原型】“将军饮马”,“造桥选址”,“费马点”.【涉及知识】“两点之间线段最短”,“垂线段最短”,“三角形三边关系”,“轴对称”,“平移”. 【出题背景】角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等.【解题思路】找对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题考查. 【十二个基本问题】【问题 1】作法连 AB ,与 l 交点即为 P .作法图形 原理AA两点之间线段最短. l P lBPA+PB 最小值为 AB .B在直线 l 上求一点 P ,使 PA+PB 值最小.【问题 2】“将军饮马”图形 原理AABl作 B 关于 l 的对称点 B ' 连 A B ',与 l 交点即为 P .B 两点之间线段最短. lPA+PB 最小值为 A B '.P在直线 l 上求一点 P ,使 PA+PB 值最小.B'【问题 3】作法图形原理l 1P'l 1分别作点 P 关于两直线 的两点之间线段最短. PM对称点 P '和 P '',连 P 'P '',PM +MN+PN 的最小值为 P l 2与两直线交点即为 M ,N .线段 P 'P '' 的长.l 2在直线 l 、 l 1上分别求点 2 NM 、N ,使△ PMN 的周长 P''最小.【问题 4】作法图形原理l 1 l 1 Q'Q 分别作点 Q 、P 关于直线Q P M两点之间线段最短. 四边形 PQMN 周长 的最小 值为线段 P 'P '' 的长.l 1、 l 的对称点 Q '和 P '2P l 2连 Q 'P ',与两直线交点即 l 2N 在直线 l 、 l 1为 M , N .上分别求点 2P'M 、N ,使四边形 PQMN的周长最小.【问题 5】“造桥选址” 作法图形 原理AAM Nm n将点 A 向下平移 MN 的长 度单位得 A ',连 A 'B ,交 n 于点 N ,过 N 作 NM ⊥ m 于 M .A'两点之间线段最短.AM +MN+BN 的最小值为 A 'B+MN .Mm n B直线 m ∥ n ,在 m 、 n , 上分别求点 M 、N ,使 MN ⊥ m ,且 AM+ MN+ BN 的 值最小.NB【问题 6】作法图形原理AAA'将点 A 向右平移 a 个长度单位得 A ',作 A '关于 l 的 对称点 A '',连 A ''B ,交直线 BB两点之间线段最短. la M NlAM +MN+BN 的最小值为 M N在直线 l 上求两点 M 、N (M 在左),使 MN a ,并使 l 于点 N ,将 N 点向左平 A ''B+ MN .A''移 a 个单位得 M .AM+MN+ NB 的值最小.【问题 7】作法 图形原理l 1l 1 P'P作点 P 关于 l 1 的对称点 点到直线,垂线段最短. PAP ',作 P 'B ⊥ l 于 B ,交 l 2 2PA+AB 的最小值为线段 P ' l 2于 A .B 的长.l 2在 l 1 A ,在 l上求2上求点 B点 B ,使 PA+AB 值最小. 【问题 8】作法 图形原理l 1B'NAl 1l 2作点 A 关于 l 2 的对称点 MB两点之间线段最短. A ',作点 B 关于 l 的对称N 1 AAM +MN+NB 的最小值为线段 A 'B ' 的长.A 为 l 上一定点,B 为 l 上点 B ',连 A 'B '交l 于 M ,2 1 2 l 2M B一定点,在 l 2上求点 M ,交 l 1 于 N . A'在 l 1 N ,使上求点AM+MN+ NB 的值最小.【问题 9】作法图形 原理AA垂直平分上 的点到线段两端点 的距离相等.Bl连 AB ,作 AB 的中垂线与 直线 l 的交点即为 P .BlPPA PB =0.在直线 l 上求一点 P ,使 PA PB 的值最小.【问题 10】 作法图形 原理A 三角形任意两边之差小于ABl 作直线 AB,与直线 l 的交点即为 P.第三边.PA PB≤ AB.BlP在直线 l上求一点 P,使PA PB 的值最大.【问题 11】PA PB 的最大值=AB.作法图形原理AA 三角形任意两边之差小于l 作 B关于 l 的对称点 B'作直线 A B',与 l交点即为 P.B'第三边. PA PB≤ AB'.lBPB在直线 l上求一点 P,使PA PB 的值最大.【问题 12】“费马点”APA PB最大值= AB'.作法图形原理所求点为“费马点”,即满D足∠ APB=∠ BPC=∠AEAPC=120°.以 AB、AC为边向外作等边△ ABD、△ACE,连 CD、BE相交于 P,点 P即为所求.两点之间线段最短.B CPA+PB+PC最小值=CD.P△ABC中每一内角都小于120°,在△ ABC内求一点P,使 PA+PB+PC值最小.B C【精品练习】1.如图所示,正方形ABCD 的面积为 12,△ ABE是等边三角形,点E在正方形 ABCD内,在对角线 AC上有一点 P,使 PD +PE 的和最小,则这个最小值为()A D A.2 3 B.2 6 C.3 D. 6PEB C2.如图,在边长为 2 的菱形 ABCD中,∠ ABC=60°,若将△ACD绕点 A旋转,当 AC′、AD′分别与 BC、CD 交于点 E、F,则△ CEF 的周长的最小值为()A. 2 C. 2B. 2 3D.433.四边形 ABCD中,∠ B=∠ D=90°,∠ C= 70°,在 BC、CD上分别找一点 M、 N,使△ AMN 的周长最小时,∠ AMN+∠ANM 的度数为(A.120° B.130°)A D C.110°D.140°NBMC4.如图,在锐角△ ABC中, AB=4 2,∠ BAC= 45°,∠ BAC 的平分线交 BC于点 D,M、N分别是 AD和 ABC上的动点,则 BM +MN 的最小值是.DMA BN5.如图, Rt△ABC中,∠ C=90°,∠ B=30°,AB=6,点 E在 AB边上,点 D在 BC边上(不与点 B、C重合),且 ED= AE,则线段 AE 的取值范围是.AEBC D6.如图,∠ AOB=30°,点 M、N分别在边 OA、OB上,且 OM=1,ON=3,点 P、Q分别在边 OB、OA上,则 MP+PQ+QN 的最小值是 _________.(注“勾股定理”:直角三角形中两直角边的平方和等于斜边的平方,即 Rt△ABC中,∠ C= 90°,则有AC 2 BC 2 AB2 )7.如图,三角形△ABC中,∠ OAB=∠ AOB=15°,点 B在 x轴的正半轴,坐标为B( 6 3,0).OC平分∠ AOB,点 M在 OC 的延长线上,点 N为边 OA上的点,则 MA+MN 的最小值是 ______.8.已知 A( 2,4)、B(4,2).C在y轴上, D在 x轴上,则四边形 ABCD 的周长最小值为,此时 C、D两点的坐标分别为.yABxO9.已知 A( 1,1)、B(4,2).y(1)P为 x轴上一动点,求 PA+PB 的最小值和此时 P点的坐标;BAO y x(2)P为 x轴上一动点,求PA PB 的值最大时 P点的坐标;BAO x (3)CD为 x轴上一条动线段, D在 C点右边且 CD=1,求当 AC+ CD+ DB 的最小值和此时 C点的坐标;yBAO xC D10.点 C为∠ AOB内一点.(1)在 OA求作点 D,OB上求作点 E,使△ CDE 的周长最小,请画出图形;(2)在( 1)的条件下,若∠ AOB=30°, OC=10,求△ CDE周长的最小值和此时∠DCE 的度数.ACO B11.(1)如图①,△ ABD和△ ACE均为等边三角形, BE、CE交于 F,连 AF,求证: AF+BF +CF=CD;(2)在△ ABC中,∠ ABC=30°,AB=6,BC=8,∠ A,∠ C均小于 120°,求作一点 P,使 PA+PB+PC 的值最小,试求出最小值并说明理由.DAAEF B C图②B C图①12.荆州护城河在 CC'处直角转弯,河宽相等,从A处到达 B处,需经过两座桥DD'、EE',护城河及两桥都是东西、南北方向,桥与河岸垂直.如何确定两座桥的位置,可使A到 B点路径最短?。
(完整版)八年级最短路径问题归纳小结.doc
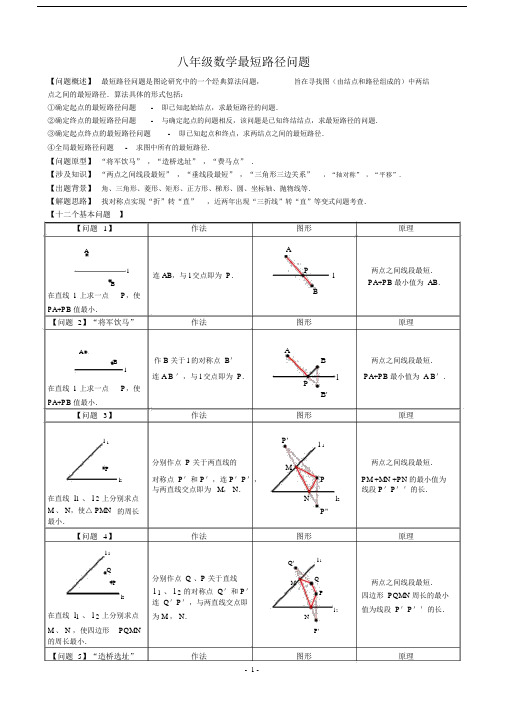
八年级数学最短路径问题【问题概述】最短路径问题是图论研究中的一个经典算法问题,旨在寻找图(由结点和路径组成的)中两结点之间的最短路径.算法具体的形式包括:①确定起点的最短路径问题-即已知起始结点,求最短路径的问题.②确定终点的最短路径问题-与确定起点的问题相反,该问题是已知终结结点,求最短路径的问题.③确定起点终点的最短路径问题-即已知起点和终点,求两结点之间的最短路径.④全局最短路径问题-求图中所有的最短路径.【问题原型】“将军饮马”,“造桥选址” ,“费马点”.【涉及知识】“两点之间线段最短”,“垂线段最短” ,“三角形三边关系”,“轴对称” ,“平移”.【出题背景】角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等.【解题思路】找对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题考查.【十二个基本问题】【问题1】作法图形原理A Al连 AB,与 l 交点即为 P.Pl两点之间线段最短.B PA+PB 最小值为 AB.B在直线 l 上求一点P,使PA+PB 值最小.【问题 2】“将军饮马”作法图形原理A AB 作 B 关于 l 的对称点 B' B 两点之间线段最短.l连 A B ',与 l 交点即为 P.l PA+PB 最小值为 A B'.P在直线 l 上求一点P,使B'PA+PB 值最小.【问题3】作法图形原理l 1 P' l1P分别作点 P 关于两直线的M两点之间线段最短.对称点 P'和 P',连 P'P',PM +MN +PN 的最小值为l2 P在直线 l1、 l 2上分别求点与两直线交点即为 M, N.N l2线段 P'P''的长.M 、 N,使△ PMN 的周长P''最小.【问题4】作法图形原理l 1lQ' 1Q分别作点 Q 、P 关于直线P MQ 两点之间线段最短.l 1、 l 2的对称点Q'和P'l2 P 四边形 PQMN 周长的最小连 Q'P',与两直线交点即l 2 值为线段 P'P''的长.在直线 l1、 l 2上分别求点为 M , N.NM 、 N ,使四边形PQMN P'的周长最小.【问题 5】“造桥选址”作法图形原理- 1 -AM Nmn将点 A 向下平移MN 的长度单位得A',连 A'B,交 nAA' M 两点之间线段最短.mB直线 m ∥ n ,在 m 、 n ,上分别求点 M 、N,使 MN ⊥m ,且 AM+ MN+ BN 的值最小.【问题 6】ABlM a N在直线 l 上求两点M、N(M 在左),使 MN a ,并使AM + MN+ NB 的值最小.【问题 7】l1Pl 2在l 1上求点A,在 l 2上求点 B,使 PA+ AB 值最小.于点 N,过 N 作 NM ⊥ m 于M.作法将点 A 向右平移 a 个长度单位得 A',作 A'关于l的对称点 A',连 A'B,交直线l 于点N,将N点向左平移a 个单位得 M.作法作点 P 关于l1的对称点P ',作 P'B⊥l2于 B,交l2于A.AM +MN +BN 的最小值为NnA'B+MN .B图形原理A A'B两点之间线段最短.lM N AM +MN +BN 的最小值为A'B+ MN.A''图形原理l1P'P 点到直线,垂线段最短.APA+ AB 的最小值为线段P'l 2 B的长.B【问题 8】作法l 1NAMl2 作点 A 关于l2的对称点BA ',作点B 关于l1的对称A 为l1上一定点,B 为l2上点 B',连 A'B'交l2于 M,一定点,在 l 2上求点M,交 l 1 于 N.在 l 1 上求点N ,使AM + MN+ NB 的值最小.【问题 9】作法图形原理B'l 1N两点之间线段最短.AAM +MN +NB 的最小值为M B l 2线段 A'B'的长.A'图形原理ABl在直线l 上求一点 P,使 PA PB 的值最小.连AB ,作 AB 的中垂线与直线 l 的交点即为 P.A垂直平分上的点到线段两B端点的距离相等.lP PA PB = 0.【问题 10】作法图形原理- 2 -A三角形任意两边之差小于A Bl作直线 AB ,与直线 l 的交第三边. PA PB ≤AB .B点即为 P .l在直线 l 上求一点 P ,使PPA PB 的最大值 = AB .PA PB 的值 最大 .【问题 11】作法 图形原理AAl 作 B 关于 l 的对称点 B ' B'B作直线 A B ',与 l 交点即lP为 P .B在直线 l 上求一点 P ,使PA PB 的值 最大 .三角形任意两边之差小于第三边. PA PB ≤ AB '.PA PB 最大值 = AB '.【问题 12】“费马点”作法图形原理ABC所求点为“费马点” ,即满足∠ APB =∠ BPC =∠APC = 120 °.以 AB 、 ACDAE两点之间线段最短.为边向外作等边△ ABD 、PPA+ PB+ PC 最小值 = CD .△ ABC 中每一内角都小于120°,在△ ABC 内求一点P ,使 PA+PB+PC 值最小.△ ACE ,连 CD 、 BE 相交于 P ,点 P 即为所求.BC【精品练习 】 1.如图所示,正方形ABCD 的面积为 12,△ ABE 是等边三角形,点一点 P ,使 PD +PE 的和最小,则这个最小值为( )A . 23 B . 2 6C . 3D . 62.如图,在边长为 2 的菱形 ABCD 中,∠ ABC = 60 °,若将 △ ACD交于点 E 、 F ,则 △ CEF 的周长的最小值为( )E 在正方形 ABCD 内,在对角线 AC 上有ADPEB C绕点 A 旋转,当 AC ′、 AD ′分别与 BC 、 CDA . 2B . 2 3C . 2 3D . 4- 3 -3.四边形 ABCD 中,∠ B=∠ D = 90 °,∠ C= 70 °,在 BC 、 CD 上分别找一点M、 N,使△ AMN 的周长最小时,∠ AMN + ∠ ANM 的度数为()A DA . 120°B. 130°C.110 °D. 140 °NBMC 4.如图,在锐角△ ABC 中, AB = 4 2 ,∠ BAC = 45 °,∠ BAC 的平分线交 BC 于点D , M、 N 分别是 AD 和 AB上的动点,则 BM +MN 的最小值是C.DMAN B5.如图, Rt△ ABC 中,∠ C= 90 °,∠ B= 30 °,AB= 6,点 E 在 AB 边上,点 D 在 BC 边上(不与点B、C 重合),且 ED = AE,则线段AE 的取值范围是.AEC D B 6.如图,∠AOB = 30 °,点 M、 N 分别在边OA、 OB 上,且OM = 1, ON= 3,点 P 、 Q 分别在边OB、 OA 上,则 MP + PQ+ QN 的最小值是_________.(注“勾股定理”:直角三角形中两直角边的平方和等于斜边的平方,即 Rt△ABC 中,∠ C= 90°,则有AC 2BC 2AB2)7.如图,三角形△ ABC中,∠OAB=∠AOB=15°,点B在x轴的正半轴,坐标为B( 6 3 , 0).OC 平分∠ AOB ,点 M 在 OC 的延长线上,点N 为边 OA 上的点,则MA + MN 的最小值是 ______.- 4 -8.已知 A( 2, 4)、 B (4, 2). C 在y轴上, D 在 x 轴上,则四边形ABCD 的周长最小值为,此时 C、 D 两点的坐标分别为.yABO x 9.已知A( 1, 1)、 B (4, 2).y( 1) P 为 x 轴上一动点,求PA+PB 的最小值和此时P 点的坐标;BAO x( 2) P 为 x 轴上一动点,求PA PB 的值最大时P 点的坐标;yBAO x( 3) CD 为 x 轴上一条动线段, D 在 C 点右边且CD = 1,求当AC+ CD+ DB 的最小值和此时 C 点的坐标;yBAO C D x10 .点 C 为∠ AOB 内一点.( 1)在 OA 求作点 D , OB 上求作点 E ,使△ CDE 的周长最小,请画出图形;( 2)在( 1)的条件下,若∠AOB = 30°, OC= 10,求△ CDE 周长的最小值和此时∠DCE 的度数.ACO B- 5 -11.( 1)如图①,△ ABD 和△ ACE 均为等边三角形,BE、 CE 交于 F,连 AF,求证: AF +BF +CF = CD ;( 2)在△ ABC 中,∠ ABC = 30°, AB= 6, BC= 8,∠ A ,∠ C 均小于 120°,求作一点 P,使 PA+PB+PC 的值最小,试求出最小值并说明理由.DAAEFB C图①B C图②12 .荆州护城河在CC'处直角转弯,河宽相等,从 A 处到达 B 处,需经过两座桥DD '、 EE ',护城河及两桥都是东西、南北方向,桥与河岸垂直.如何确定两座桥的位置,可使 A 到 B 点路径最短?- 6 -。
最新八年级最短路径问题归纳小结
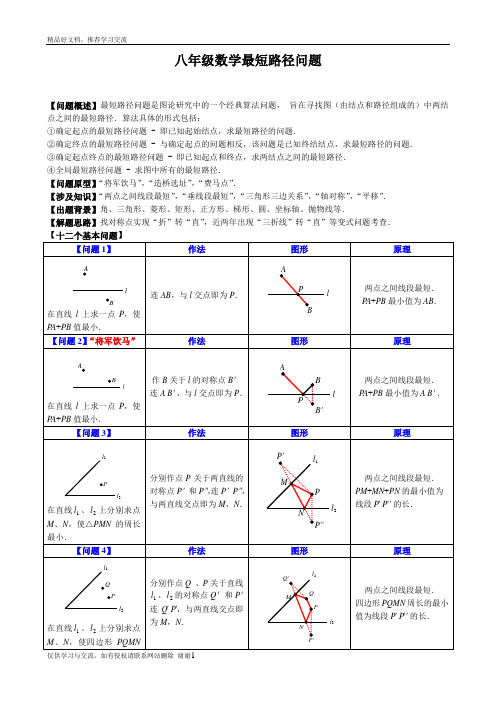
八年级数学最短路径问题【问题概述】最短路径问题是图论研究中的一个经典算法问题,旨在寻找图(由结点和路径组成的)中两结点之间的最短路径.算法具体的形式包括:①确定起点的最短路径问题 - 即已知起始结点,求最短路径的问题.②确定终点的最短路径问题 - 与确定起点的问题相反,该问题是已知终结结点,求最短路径的问题.③确定起点终点的最短路径问题 - 即已知起点和终点,求两结点之间的最短路径.④全局最短路径问题 - 求图中所有的最短路径.【问题原型】“将军饮马”,“造桥选址”,“费马点”.【涉及知识】“两点之间线段最短”,“垂线段最短”,“三角形三边关系”,“轴对称”,“平移”.【出题背景】角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等.【解题思路】找对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题考查.【问题10】 作法图形 原理在直线l 上求一点P ,使PB PA -的值最大.作直线AB ,与直线l 的交点即为P .三角形任意两边之差小于第三边.PB PA -≤AB .PB PA -的最大值=AB .【问题11】 作法图形 原理在直线l 上求一点P ,使PB PA -的值最大.作B 关于l 的对称点B '作直线A B ',与l 交点即为P .三角形任意两边之差小于第三边.PB PA -≤AB '. PB PA -最大值=AB '.【问题12】“费马点” 作法图形 原理△ABC 中每一内角都小于120°,在△ABC 内求一点P ,使P A +PB +PC 值最小.所求点为“费马点”,即满足∠APB =∠BPC =∠APC =120°.以AB 、AC 为边向外作等边△ABD 、△ACE ,连CD 、BE 相交于P ,点P 即为所求.两点之间线段最短. P A +PB +PC 最小值=CD .【精品练习】1.如图所示,正方形ABCD 的面积为12,△ABE 是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P ,使PD +PE 的和最小,则这个最小值为( )A .3B .26C .3D 62.如图,在边长为2的菱形ABCD 中,∠ABC =60°,若将△ACD 绕点A 旋转,当AC ′、AD ′分别与BC 、CD 交于点E 、F ,则△CEF 的周长的最小值为( ) A .2B .32C .32+D .4lBAlPABl ABlBPAB'ABCPEDCBAADEPB C3.四边形ABCD 中,∠B =∠D =90°,∠C =70°,在BC 、CD 上分别找一点M 、N ,使△AMN 的周长最小时,∠AMN +∠ANM 的度数为( )A .120°B .130°C .110°D .140°4.如图,在锐角△ABC 中,AB =42,∠BAC =45°,∠BAC 的平分线交BC 于点D ,M 、N 分别是AD 和AB 上的动点,则BM +MN 的最小值是 .5.如图,Rt △ABC 中,∠C =90°,∠B =30°,AB =6,点E 在AB 边上,点D 在BC 边上(不与点B 、C 重合), 且ED =AE ,则线段AE 的取值范围是 .6.如图,∠AOB =30°,点M 、N 分别在边OA 、OB 上,且OM =1,ON =3,点P 、Q 分别在边OB 、OA 上,则MP +PQ +QN 的最小值是_________.(注“勾股定理”:直角三角形中两直角边的平方和等于斜边的平方,即Rt △ABC 中,∠C =90°,则有222AB BC AC =+)7.如图,三角形△ABC 中,∠OAB =∠AOB =15°,点B 在x 轴的正半轴,坐标为B (36,0).OC 平分∠AOB ,点M 在OC 的延长线上,点N 为边OA 上的点,则MA +MN 的最小值是______. DEABCD CMABMN8.已知A (2,4)、B (4,2).C 在y 轴上,D 在x 轴上,则四边形ABCD 的周长最小值为 ,此时 C 、D 两点的坐标分别为 .9.已知A (1,1)、B (4,2).(1)P 为x 轴上一动点,求PA +PB 的最小值和此时P 点的坐标;(2)P 为x 轴上一动点,求PB PA 的值最大时P 点的坐标;(3)CD 为x 轴上一条动线段,D 在C 点右边且CD =1,求当AC +CD +DB 的最小值和此时C 点的坐标;10.点C 为∠AOB 内一点.(1)在OA 求作点D ,OB 上求作点E ,使△CDE 的周长最小,请画出图形;(2)在(1)的条件下,若∠AOB =30°,OC =10,求△CDE 周长的最小值和此时∠DCE 的度数.图①12.荆州护城河在CC'处直角转弯,河宽相等,从A处到达B处,需经过两座桥DD'、EE',护城河及两桥都是东西、南北方向,桥与河岸垂直.如何确定两座桥的位置,可使A到B点路径最短?什么是主语、谓语、宾语、宾补、状语、定语?主语是一个句子中所要表达,描述的人或物,是句子叙述的主体。
(完整版)初二数学最短路径问题知识归纳+练习
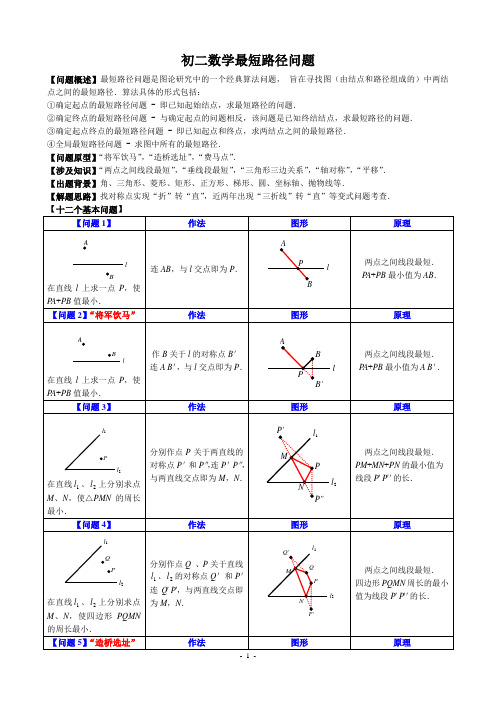
初二数学最短路径问题【问题概述】最短路径问题是图论研究中的一个经典算法问题,旨在寻找图(由结点和路径组成的)中两结点之间的最短路径.算法具体的形式包括:①确定起点的最短路径问题 - 即已知起始结点,求最短路径的问题.②确定终点的最短路径问题 - 与确定起点的问题相反,该问题是已知终结结点,求最短路径的问题.③确定起点终点的最短路径问题 - 即已知起点和终点,求两结点之间的最短路径.④全局最短路径问题 - 求图中所有的最短路径.【问题原型】“将军饮马”,“造桥选址”,“费马点”.【涉及知识】“两点之间线段最短”,“垂线段最短”,“三角形三边关系”,“轴对称”,“平移”.【出题背景】角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等.【解题思路】找对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题考查.在直线l 上求一点P ,使PB PA -的值最大.作直线AB ,与直线l 的交点即为P .三角形任意两边之差小于第三边.PB PA -≤AB .PB PA -的最大值=AB .【问题11】 作法图形 原理在直线l 上求一点P ,使PB PA -的值最大.作B 关于l 的对称点B '作直线A B ',与l 交点即为P .三角形任意两边之差小于第三边.PB PA -≤AB '. PB PA -最大值=AB '.【问题12】“费马点” 作法图形 原理△ABC 中每一内角都小于120°,在△ABC 内求一点P ,使P A +PB +PC 值最小.所求点为“费马点”,即满足∠APB =∠BPC =∠APC =120°.以AB 、AC 为边向外作等边△ABD 、△ACE ,连CD 、BE 相交于P ,点P 即为所求.两点之间线段最短. P A +PB +PC 最小值=CD .【精品练习】1.如图所示,正方形ABCD 的面积为12,△ABE 是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P ,使PD +PE 的和最小,则这个最小值为( )A .3B .26C .3D 62.如图,在边长为2的菱形ABCD 中,∠ABC =60°,若将△ACD 绕点A 旋转,当AC ′、AD ′分别与BC 、CD 交于点E 、F ,则△CEF 的周长的最小值为( ) A .2B .32C .32+D .4lBAlPABl ABlBPAB'ABCPEDCBAADEPB C3.四边形ABCD 中,∠B =∠D =90°,∠C =70°,在BC 、CD 上分别找一点M 、N ,使△AMN 的周长最小时,∠AMN +∠ANM 的度数为( )A .120°B .130°C .110°D .140°4.如图,在锐角△ABC 中,AB =42,∠BAC =45°,∠BAC 的平分线交BC 于点D ,M 、N 分别是AD 和AB 上的动点,则BM +MN 的最小值是 .5.如图,Rt △ABC 中,∠C =90°,∠B =30°,AB =6,点E 在AB 边上,点D 在BC 边上(不与点B 、C 重合), 且ED =AE ,则线段AE 的取值范围是 .6.如图,∠AOB =30°,点M 、N 分别在边OA 、OB 上,且OM =1,ON =3,点P 、Q 分别在边OB 、OA 上,则MP +PQ +QN 的最小值是_________.(注“勾股定理”:直角三角形中两直角边的平方和等于斜边的平方,即Rt △ABC 中,∠C =90°,则有222AB BC AC =+)7.如图,三角形△ABC 中,∠OAB =∠AOB =15°,点B 在x 轴的正半轴,坐标为B (36,0).OC 平分∠AOB ,点M 在OC 的延长线上,点N 为边OA 上的点,则MA +MN 的最小值是______. DEABCD MABMN8.已知A (2,4)、B (4,2).C 在y 轴上,D 在x 轴上,则四边形ABCD 的周长最小值为 ,此时 C 、D 两点的坐标分别为 .9.已知A (1,1)、B (4,2).(1)P 为x 轴上一动点,求PA +PB 的最小值和此时P 点的坐标;(2)P 为x 轴上一动点,求PB PA 的值最大时P 点的坐标;(3)CD 为x 轴上一条动线段,D 在C 点右边且CD =1,求当AC +CD +DB 的最小值和此时C 点的坐标;10.点C 为∠AOB 内一点.(1)在OA 求作点D ,OB 上求作点E ,使△CDE 的周长最小,请画出图形;(2)在(1)的条件下,若∠AOB =30°,OC =10,求△CDE 周长的最小值和此时∠DCE 的度数.图①12.荆州护城河在CC'处直角转弯,河宽相等,从A处到达B处,需经过两座桥DD'、EE',护城河及两桥都是东西、南北方向,桥与河岸垂直.如何确定两座桥的位置,可使A到B点路径最短?。
初二数学最短路径问题知识归纳+练习

初二数学最短路径问题【问题概述】最短路径问题是图论研究中的一个经典算法问题,旨在寻找图(由结点和路径组成的)中两结点之间的最短路径.算法具体的形式包括:①确定起点的最短路径问题 - 即已知起始结点,求最短路径的问题.②确定终点的最短路径问题 - 与确定起点的问题相反,该问题是已知终结结点,求最短路径的问题.③确定起点终点的最短路径问题- 即已知起点和终点,求两结点之间的最短路径.④全局最短路径问题- 求图中所有的最短路径.【问题原型】“将军饮马”,“造桥选址”,“费马点”.【涉及知识】“两点之间线段最短”,“垂线段最短”,“三角形三边关系”,“轴对称”,“平移”.【出题背景】角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等.【解题思路】找对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题考查.【十二个基本问题】【问题1】作法图形原理在直线l 上求一点P ,使PA+PB 值最小.连AB ,与l 交点即为P .两点之间线段最短.P A+PB 最小值为AB .【问题2】“将军饮马”作法图形原理在直线l 上求一点P ,使PA+PB 值最小.作B 关于l 的对称点B '连A B ',与l 交点即为P .两点之间线段最短.P A+PB 最小值为 A B '.【问题3】作法图形原理在直线1l 、2l 上分别求点M 、N ,使△PMN 的周长最小.分别作点P 关于两直线的对称点P '和P '',连P 'P '',与两直线交点即为M ,N .两点之间线段最短.PM +MN +PN 的最小值为线段P 'P ''的长.【问题4】作法图形原理在直线1l 、2l 上分别求点M 、N ,使四边形PQMN的周长最小.分别作点Q 、P 关于直线1l 、2l 的对称点Q '和P '连Q 'P ',与两直线交点即为M ,N .两点之间线段最短.四边形PQMN 周长的最小值为线段P 'P ''的长.【问题5】“造桥选址”作法图形原理l ABlP BAlBAlPB'AB l 1l 2Pl 1l 2NMP''P'P l 1l 2N MP'Q'Q P l 1l 2P Q直线m ∥n ,在m 、n ,上分别求点M 、N ,使MN⊥m ,且AM+MN+BN 的值最小.将点A 向下平移MN 的长度单位得A ',连A 'B ,交n 于点N ,过N 作NM ⊥m 于M .两点之间线段最短.AM +MN +BN 的最小值为A 'B+MN .【问题6】作法图形原理在直线l 上求两点M 、N (M 在左),使a MN,并使AM +MN+NB 的值最小.将点A 向右平移a 个长度单位得A ',作A '关于l 的对称点A '',连A ''B ,交直线l 于点N ,将N 点向左平移a 个单位得M .两点之间线段最短.AM +MN +BN 的最小值为A ''B+MN .【问题7】作法图形原理在1l 上求点A ,在2l 上求点B ,使PA+AB 值最小.作点P 关于1l 的对称点P ',作P 'B ⊥2l 于B ,交2l 于A .点到直线,垂线段最短.PA+AB 的最小值为线段P 'B 的长.【问题8】作法图形原理A 为1l 上一定点,B 为2l 上一定点,在2l 上求点M ,在1l 上求点N ,使AM +MN+NB 的值最小.作点A 关于2l 的对称点A ',作点B 关于1l 的对称点B ',连A 'B '交2l 于M ,交1l 于N .两点之间线段最短.AM +MN +NB 的最小值为线段A 'B '的长.【问题9】作法图形原理在直线l 上求一点P ,使PB PA的值最小.连AB ,作AB 的中垂线与直线l 的交点即为P .垂直平分上的点到线段两端点的距离相等.PB PA=0.【问题10】作法图形原理m n MNA'BAla ABM Nm n ABMNlA''A'BAMNl 1l 2ABP'Pl 1l 2Pl 2l 1ABNMl 2l 1M NA'B'A BlBAlPBA在直线l 上求一点P ,使PB PA的值最大.作直线AB ,与直线l 的交点即为P .三角形任意两边之差小于第三边.PB PA≤AB .PB PA 的最大值=AB .【问题11】作法图形原理在直线l 上求一点P ,使PB PA的值最大.作B 关于l 的对称点B '作直线 A B ',与l 交点即为P .三角形任意两边之差小于第三边.PB PA ≤AB '.PB PA 最大值=AB '.【问题12】“费马点”作法图形原理△ABC 中每一内角都小于120°,在△ABC 内求一点P ,使P A+PB+PC 值最小.所求点为“费马点”,即满足∠APB =∠BPC =∠APC =120°.以AB 、AC 为边向外作等边△ABD 、△ACE ,连CD 、BE 相交于P ,点P 即为所求.两点之间线段最短.PA+PB+PC 最小值=CD .【精品练习】1.如图所示,正方形ABCD 的面积为12,△ABE 是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P ,使PD +PE 的和最小,则这个最小值为()A .23B .26C .3D .62.如图,在边长为2的菱形ABCD 中,∠ABC =60°,若将△ACD 绕点A 旋转,当AC ′、AD ′分别与BC 、CD交于点E 、F ,则△CEF 的周长的最小值为()A .2B .32C .32D .4lBAlPABl ABlBP AB'ABCPEDCBAADEPBC3.四边形ABCD 中,∠B =∠D =90°,∠C =70°,在BC 、CD 上分别找一点M 、N ,使△AMN 的周长最小时,∠AMN +∠ANM 的度数为()A .120°B .130°C .110°D .140°4.如图,在锐角△ABC 中,AB =42,∠BAC =45°,∠BAC 的平分线交BC 于点D ,M 、N 分别是AD 和AB上的动点,则BM +MN 的最小值是.5.如图,Rt △ABC 中,∠C =90°,∠B =30°,AB =6,点E 在AB 边上,点D 在BC 边上(不与点B 、C 重合),且ED =AE ,则线段AE 的取值范围是.6.如图,∠AOB =30°,点M 、N 分别在边OA 、OB 上,且OM =1,ON =3,点P 、Q 分别在边OB 、OA 上,则MP +PQ +QN 的最小值是_________.(注“勾股定理”:直角三角形中两直角边的平方和等于斜边的平方,即Rt △ABC 中,∠C =90°,则有222AB BC AC )7.如图,三角形△ABC 中,∠OAB =∠AOB =15°,点B 在x 轴的正半轴,坐标为B(36,0).OC 平分∠AOB ,点M 在OC 的延长线上,点N 为边OA 上的点,则MA +MN 的最小值是______.DEABCDABCMNCADBMN8.已知A (2,4)、B (4,2).C 在y 轴上,D 在x 轴上,则四边形ABCD 的周长最小值为,此时C 、D 两点的坐标分别为.9.已知A (1,1)、B (4,2).(1)P 为x 轴上一动点,求PA+PB 的最小值和此时P 点的坐标;(2)P 为x 轴上一动点,求PB PA 的值最大时P 点的坐标;(3)CD 为x 轴上一条动线段,D 在C 点右边且CD =1,求当AC+CD+DB 的最小值和此时C 点的坐标;10.点C 为∠AOB 内一点.(1)在OA 求作点D ,OB 上求作点E ,使△CDE 的周长最小,请画出图形;(2)在(1)的条件下,若∠AOB =30°,OC =10,求△CDE 周长的最小值和此时∠DCE 的度数.yxBOA CDyxBOA yxBOA COBAyxBAO11.(1)如图①,△ABD 和△ACE 均为等边三角形,BE 、CE 交于F ,连AF ,求证:AF +BF +CF =CD ;(2)在△ABC 中,∠ABC =30°,AB =6,BC =8,∠A ,∠C 均小于120°,求作一点P ,使PA+PB+PC 的值最小,试求出最小值并说明理由.12.荆州护城河在CC '处直角转弯,河宽相等,从A 处到达B 处,需经过两座桥DD '、EE ',护城河及两桥都是东西、南北方向,桥与河岸垂直.如何确定两座桥的位置,可使A 到B 点路径最短?图②ACB图①FEDBAC。
【初二】最短路径问题归纳

最短路径问题专题学习【基本问题】PB PA -的值最大.【精品练习】1.如图所示,正方形ABCD 的面积为12,△ABE 是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P ,使PD +PE 的和最小,则这个最小值为( )A .23B .26C .3D .62.如图,在边长为2的菱形ABCD 中,∠ABC =60°,若将△ACD 绕点A 旋转,当AC ′、AD ′分别与BC 、CD 交于点E 、F ,则△CEF 的周长的最小值为( )A .2B .32C .32+D .43.四边形ABCD 中,∠B =∠D =90°,∠C =70°,在BC 、CD 上分别找一点M 、N ,使△AMN 的周长最小时,∠AMN +∠ANM 的度数为( )A .120°B .130°C .110°D .140°4.如图,在锐角△ABC 中,AB =42,∠BAC =45°,∠BAC 的平分线交BC 于点D ,M 、N 分别是AD和AB 上的动点,则BM +MN 的最小值是 .5.如图,Rt △ABC 中,∠C =90°,∠B =30°,AB =6,点E 在AB 边上,点D 在BC 边上(不与点B 、C 重合),且ED =AE ,则线段AE 的取值范围是 .6.如图,∠AOB =30°,点M 、N 分别在边OA 、OB 上,且OM =1,ON =3,点P 、Q 分别在边OB 、OA上,则MP +PQ +QN 的最小值是_________.DEABC ADE PBCDACMABMN第2题 第3题 第4题 第5题7.如图,三角形△ABC 中,∠OAB =∠AOB =15°,点B 在x 轴的正半轴,坐标为B (36,0). OC 平分∠AOB ,点M 在OC 的延长线上,点N 为边OA 上的点,则MA +MN 的最小值是______.8.已知A (2,4)、B (4,2).C 在y 轴上,D 在x 轴上,则四边形ABCD 的周长最小值为 , 此时 C 、D 两点的坐标分别为 .9.已知A (1,1)、B (4,2).(1)P 为x 轴上一动点,求P A +PB 的最小值和此时P 点的坐标;(2)P 为x 轴上一动点,求PB PA 的值最大时P 点的坐标;(3)CD 为x 轴上一条动线段,D 在C 点右边且CD =1,求当AC +CD +DB 的最小值和此时C 点的坐标;10.点C 为∠AOB 内一点.(1)在OA 求作点D ,OB 上求作点E ,使△CDE 的周长最小,请画出图形;(2)在(1)的条件下,若∠AOB =30°,OC =10,求△CDE 周长的最小值和此时∠DCE 的度数. 第6题 第7题。
【初二】最短路径问题归纳
最短路径问题专题学习(【问题10】 作法图形 原理】在直线l 上求一点P ,使PB PA -的值最大.作B 关于l 的对称点B '作直线A B ',与l 交点即为P .三角形任意两边之差小于第三边.PB PA -≤AB '.PB PA -最大值=AB '.【精品练习】1.如图所示,正方形ABCD 的面积为12,△ABE 是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P ,使PD +PE 的和最小,则这个最小值为( )A .23B .6C .3D 62.如图,在边长为2的菱形ABCD 中,∠ABC =60°,若将△ACD 绕点A 旋转,当AC ′、AD ′分别与BC 、CD 交于点E 、F ,则△CEF 的周长的最小值为( )A .2B .32C .32+D .4。
3.四边形ABCD 中,∠B =∠D =90°,∠C =70°,在BC 、CD 上分别找一点M 、N ,使△AMN 的周长最小 时,∠AMN +∠ANM 的度数为( )A .120°B .130°C .110°D .140°4.如图,在锐角△ABC 中,AB =42,∠BAC =45°,∠BAC 的平分线交BC 于点D ,M 、N 分别是AD和AB 上的动点,则BM +MN 的最小值是 .5.如图,Rt △ABC 中,∠C =90°,∠B =30°,AB =6,点E 在AB 边上,点D 在BC 边上(不与点B 、C 重l ABDEABC AD ~E PB CDAMABMN第2题 第3题 第4题 第5题合),且ED =AE ,则线段AE 的取值范围是 .6.如图,∠AOB =30°,点M 、N 分别在边OA 、OB 上,且OM =1,ON =3,点P 、Q 分别在边OB 、OA 上,则MP +PQ +QN 的最小值是_________.~7.如图,三角形△ABC 中,∠OAB =∠AOB =15°,点B 在x 轴的正半轴,坐标为B (36,0). OC 平分∠AOB ,点M 在OC 的延长线上,点N 为边OA 上的点,则MA +MN 的最小值是______.#8.已知A (2,4)、B (4,2).C 在y 轴上,D 在x 轴上,则四边形ABCD 的周长最小值为 , 此时 C 、D 两点的坐标分别为 .9.已知A (1,1)、B (4,2).(1)P 为x 轴上一动点,求PA +PB 的最小值和此时P 点的坐标;,(2)P 为x 轴上一动点,求PB PA 的值最大时P 点的坐标;(3)CD 为x 轴上一条动线段,D 在C 点右边且CD =1,求当AC +CD +DB 的最小值和此时C 点的坐标;yx BO A C DyxBOA yx B OA yxBAO第6题 第7题10.点C为∠AOB内一点.(1)在OA求作点D,OB上求作点E,使△CDE的周长最小,请画出图形;(2)在(1)的条件下,若∠AOB=30°,OC=10,求△CDE周长的最小值和此时∠DCE的度数.。
八年级最短路径问题归纳小结

八年级数学最短路径问题【问题概述】最短路径问题是图论研究中的一个经典算法问题,旨在寻找图(由结点和路径组成的)中两结点之间的最短路径•算法具体的形式包括:①确定起点的最短路径问题-即已知起始结点,求最短路径的问题.②确定终点的最短路径问题-与确定起点的问题相反,该问题是已知终结结点,求最短路径的问题.③确定起点终点的最短路径问题-即已知起点和终点,求两结点之间的最短路径.④全局最短路径问题-求图中所有的最短路径.【问题原型】“将军饮马”,“造桥选址”,“费马点”.【涉及知识】“两点之间线段最短”,“垂线段最短”,“三角形三边关系”,“轴对称”,“平移”.【出题背景】角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等.【解题思路】找对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题考查.十二个基本问题】E 在正方形ABCD 内,在对角线 AC 上有A ■.B lP ,使作直线AB ,与直线l 的交 点即为P .A三角形任意两边之差小于 第三边.PA _PB PA_PB 的最大值 < AB .=AB .在直线丨上求一点|PA —PB|的值最大.甘IP【问题11】作法图形 原理AA•k..三角形任意两边之差小于l作B 关于l 的对称点B /、-.l第三边. PA —PB < AB /.*B作直线A B/,与l 交点即为P .B在直线丨上求一点 P ,使|PA —PB|最大值= AB Z .|PA —PB 的值最大.【问题12】“费马点”作法图形原理A所求点为“费马点”,即满/\足/ APB = Z BPC = Z D 1 V FXAPC = 120 ° .以 AB 、ACI;■AE人两点之间线段最短B ----------------------- Cx7\ • • • /为边向外作等边厶ABD 、PA+PB+PC 最小值 =CD .△ ABC 中每一内角都小于 △ ACE ,连 CD 、BE 相交 wBC120 °,在厶ABC 内求一点于P ,点P 即为所求.P ,使 FA+PB + PC 值最小.【精品练习】1如图所示,正方形 ABCD 的面积为12,^ ABE 是等边三角形,点 一点P ,使PD+PE 的和最小,则这个最小值为( )A . 2 3B . 2 6C . 3D . 、一 62•如图,在边长为 2的菱形 ABCD 中,/ ABC = 60 °若将△ ACD 绕点A 旋转,当 AC'、AD '分别与BC 、CD 交于点E 、F ,则△ CEF 的周长的最小值为( )A . 2B . 2.3C . 2 3D . 4A. 120 °B. 130C. 110 ° D . 1404.如图,在锐角厶ABC中,AB = 4^2,/ BAC = 45 ° / BAC的平分线交BC于点D , M、N分别是AD和AB 上的动点,贝U BM+MN的最小值是_____________________且ED = AE,则线段AE的取值范围是______________________则MP + PQ + QN的最小值是 __________ •(注“勾股定理”即Rt△ ABC 中,/ C= 90°,则有AC2 BC^AB2):直角三角形中两直角边的平方和等于斜边的平方,3.四边形ABCD中,/ B = Z D = 90 ° / C= 70 °在BC、CD上分别找一点M、”,使厶AMN的周长最小时,/ AMN+ / ANM的度数为()5•如图,Rt△ ABC中,/ C = 90 ° / B= 30 ° AB = 6,点E在AB边上,点D在BC边上(不与点B、C重合),6 .如图,/ AOB = 30。
【初二】最短路径问题归纳

【基本问题 】【问题 1】 作法 图形 原理两点之间线段最短.连 AB ,与 l 交点即为P .PA+PB 最小值为 AB .在直线 l 上求一点 P ,使 PA+PB 值最小.【问题 2】“将军饮马” 作法 图形 原理作 B 对于 l 的对称点 B '两点之间线段最短. 连 A B ',与 l 交点即为 P .PA+PB 最小值为 A B '.在直线 l 上求一点 P ,使 PA+PB 值最小.【问题 3】 作法 图形 原理分别作点 P 对于两直线的两点之间线段最短. 对称点 P '和 P ',连 P 'P ', PM +MN +PN 的最小值为 与两直线交点即为 M , N .线段 P 'P ''的长.在直线 l 1 、 l 2 上分别求点 M 、 N ,使△ PMN 的周长 最小.【问题 4】 作法 图形 原理分别作点 Q 、P 对于直线 两点之间线段最短.l 1 、 l 2 的对称点 Q '和 P '四边形 PQMN 周长的最小连 Q 'P ',与两直线交点即值为线段 P 'P ''的长.在直线 l 1 、 l 2 上分别求点 为 M , N .M 、 N ,使四边形 PQMN 的周长最小.【问题 5】“造桥选址” 作法 图形 原理将点 A 向下平移 MN 的长两点之间线段最短.度单位得 A ',连 A 'B ,交 nAM +MN +BN 的最小值为于点 N ,过 N 作 NM ⊥ m 于直线 m ∥ n ,在 m 、 n ,A 'B+MN .上分别求点 M .M 、N ,使 MN⊥ m ,且 AM+ MN+ BN 的值最小.【问题 6】 作法图形 原理将点 A 向右平移 a 个长度两点之间线段最短.- 1 -单位得 A',作 A '对于 l 的AM +MN +BN 的最小值为对称点 A',连 A'B,交直线A'B+ MN.l 于点 N,将 N 点向左平在直线 l 上求两点 M 、N( M移 a 个单位得M.在左),使 MN a ,并使AM + MN+ NB 的值最小.【问题 7】作法图形原理作点 P 对于 l 1的对称点点到直线,垂线段最短.P ',作 P'B⊥ l 2于 B,交 l 2PA+ AB 的最小值为线段P'于 A.B的长.在 l 1上求点 A,在 l 2上求点 B,使 PA+ AB 值最小.【问题 8】作法图形原理作点 A 对于 l 2的对称点两点之间线段最短.A ',作点B 对于 l1的对称A 为 l 1上必定点, B 为 l 2上AM +MN +NB 的最小值为点 B',连 A'B'交l 2于 M,必定点,在 l 2上求点 M ,交 l 1于 N.线段 A'B'的长.在l 1上求点N ,使AM + MN+ NB 的值最小.【问题 9】作法图形原理垂直均分上的点到线段两连 AB ,作 AB 的中垂线与端点的距离相等.直线 l 的交点即为P.PA PB =0.在直线l 上求一点P,使PA PB 的值最小.【问题 10】作法图形原理三角形随意两边之差小于作 B 对于 l 的对称点B'作直线 A B',与 l 交点即为 P.在直线l 上求一点P,使第三边.PA PB ≤AB'.PA PB 最大值=AB'.PA PB 的值最大.【精选练习】1.如下图,正方形ABCD 的面积为12,△ ABE 是等边三角形,点 E 在正方形ABCD 内,在对角线AC- 2 -上有一点 P,使 PD+PE 的和最小,则这个最小值为()A .23B.26C.3 D .62.如图,在边长为 2 的菱形 ABCD 中,∠ ABC= 60°,若将△ACD 绕点 A 旋转,当AC′、 AD ′分别与 BC、CD 交于点 E、 F ,则△ CEF 的周长的最小值为()A .2B . 2 3C. 23 D . 43.四边形ABCD 中,∠ B=∠ D= 90°,∠ C= 70°,在 BC、 CD 上分别找一点M、 N,使△ AMN 的周长最小时,∠ AMN +∠ ANM 的度数为()A .120°B .130°C. 110°D. 140°4.如图,在锐角△ABC 中, AB= 4 2 ,∠BAC=45°,∠BAC的均分线交BC 于点 D , M、N 分别是 AD 和 AB 上的动点,则BM +MN 的最小值是.5.如图, Rt△ ABC 中,∠ C= 90°,∠ B= 30°, AB= 6,点 E 在 AB 边上,点 D 在 BC 边上(不与点B、 C 重合),且 ED = AE,则线段 AE 的取值范围是.6.如图,∠ AOB= 30°,点 M、 N 分别在边OA、OB 上,且 OM = 1,ON= 3,点 P、Q 分别在边 OB、OA上,则 MP+ PQ+ QN 的最小值是 _________.7.如图,三角形△ABC中,∠ OAB=∠ AOB=15°,点B在x轴的正半轴,坐标为B( 6 3 , 0).OC 均分∠ AOB,点 M 在 OC 的延伸线上,点N 为边 OA 上的点,则MA+ MN 的最小值是 ______.- 3 -8.已知 A( 2,4)、B( 4,2).C 在 y 轴上, D 在 x 轴上,则四边形 ABCD 的周长最小值为,此时C、 D 两点的坐标分别为.9.已知 A( 1, 1)、 B( 4, 2).( 1) P 为 x 轴上一动点,求PA+PB 的最小值和此时P 点的坐标;( 2) P 为 x 轴上一动点,求PA PB 的值最大时P 点的坐标;( 3) CD 为 x 轴上一条动线段, D 在 C 点右侧且 CD = 1,求当 AC+CD +DB 的最小值和此时 C 点的坐标;10.点 C 为∠ AOB 内一点.( 1)在 OA 求作点 D, OB 上求作点E,使△ CDE 的周长最小,请画出图形;( 2)在( 1)的条件下,若∠AOB= 30°, OC=10,求△ CDE 周长的最小值和此时∠DCE 的度数.- 4 -。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最短路径问题专题学习
【精品练习】
1.如图所示,正方形ABCD 的面积为12,△ABE 是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P ,使PD +PE 的和最小,则这个最小值为( )
A .23
B .26
C .3
D .6
2.如图,在边长为2的菱形ABCD 中,∠ABC =60°,若将△ACD 绕点A 旋转,当AC ′、AD ′分别与BC 、CD 交于点E 、F ,则△CEF 的周长的最小值为( )
A .2
B .32
C .32
D .4
3.四边形ABCD 中,∠B =∠D =90°,∠C =70°,在BC 、CD 上分别找一点M 、N ,使△AMN 的周长最小
时,∠AMN +∠ANM 的度数为( )
A .120°
B .130°
C .110°
D .140°
4.如图,在锐角△ABC 中,AB =42,∠BAC =45°,∠BAC 的平分线交BC 于点D ,M 、N 分别是AD
和AB 上的动点,则BM +MN 的最小值是 .
5.如图,Rt △ABC 中,∠C =90°,∠B =30°,AB =6,点E 在AB 边上,点D 在BC 边上(不与点B 、C 重
合),且ED =AE ,则线段AE 的取值范围是 .
6.如图,∠AOB =30°,点M 、N 分别在边OA 、OB 上,且OM =1,ON =3,点P 、Q 分别在边OB 、OA
上,则MP +PQ +QN 的最小值是_________.
D
E
A
B
C A
D
E P
B
C
D
A
M
A
B
M
N
第2题 第3题 第4题 第5题
7.如图,三角形△ABC 中,∠OAB =∠AOB =15°,点B 在x 轴的正半轴,坐标为B (36,0). OC 平分∠AOB ,点M 在OC 的延长线上,点N 为边OA 上的点,则MA +MN 的最小值是______.
8.已知A (2,4)、B (4,2).C 在y 轴上,D 在x 轴上,则四边形ABCD 的周长最小值为 , 此时 C 、D 两点的坐标分别为 .
9.已知A (1,1)、B (4,2).
(1)P 为x 轴上一动点,求P A +PB 的最小值和此时P 点的坐标;
(2)P 为x 轴上一动点,求PB PA 的值最大时P 点的坐标;
(3)CD 为x 轴上一条动线段,D 在C 点右边且CD =1,求当AC +CD +DB 的最小值和此时C 点的坐标;
10.点C 为∠AOB 内一点.
(1)在OA 求作点D ,OB 上求作点E ,使△CDE 的周长最小,请画出图形;
(2)在(1)的条件下,若∠AOB =30°,OC =10,求△CDE 周长的最小值和此时∠DCE 的度数.
第6题 第7题。
