物理2-25量子3
量子力学试题及答案

量子力学试题及答案一、选择题(每题2分,共20分)1. 量子力学的基本原理之一是:A. 牛顿运动定律B. 薛定谔方程C. 麦克斯韦方程组D. 热力学第二定律2. 波函数的绝对值平方代表:A. 粒子的动量B. 粒子的能量C. 粒子在某一位置的概率密度D. 粒子的波长3. 以下哪个不是量子力学中的守恒定律?A. 能量守恒B. 动量守恒C. 角动量守恒D. 电荷守恒4. 量子力学中的不确定性原理是由哪位物理学家提出的?A. 爱因斯坦B. 波尔C. 海森堡D. 薛定谔5. 在量子力学中,一个粒子的波函数可以表示为:B. 一个复数C. 一个向量D. 一个矩阵二、简答题(每题10分,共30分)1. 简述海森堡不确定性原理,并解释其在量子力学中的意义。
2. 解释什么是量子纠缠,并给出一个量子纠缠的例子。
3. 描述量子隧道效应,并解释它在实际应用中的重要性。
三、计算题(每题25分,共50分)1. 假设一个粒子在一维无限深势阱中,其波函数为ψ(x) = A *sin(kx),其中A是归一化常数。
求该粒子的能量E。
2. 考虑一个二维电子在x-y平面上的波函数ψ(x, y) = A * e^(-αx) * cos(βy),其中A是归一化常数。
求该电子的动量分布。
答案一、选择题1. B. 薛定谔方程2. C. 粒子在某一位置的概率密度3. D. 电荷守恒4. C. 海森堡二、简答题1. 海森堡不确定性原理指出,粒子的位置和动量不能同时被精确测量,其不确定性关系为Δx * Δp ≥ ħ/2,其中ħ是约化普朗克常数。
这一原理揭示了量子世界的基本特性,即粒子的行为具有概率性而非确定性。
2. 量子纠缠是指两个或多个量子系统的状态不能独立于彼此存在,即使它们相隔很远。
例如,两个纠缠的电子,无论它们相隔多远,测量其中一个电子的自旋状态会即刻影响到另一个电子的自旋状态。
3. 量子隧道效应是指粒子在经典物理中无法穿越的势垒,在量子物理中却有一定概率能够穿越。
人教版高中物理必修3课程目录与教学计划表

人教版高中物理必修3课程目录与教学计
划表
课程目录
1. 第一章光的直线传播
- 1.1 光的直线传播特性
- 1.2 光的反射
- 1.3 镜子中的像
- 1.4 光的折射
- 1.5 细棱镜光的偏转和分光
- 1.6 选择折射率规律
- 1.7 光的全反射
- 1.8 光的色散与衍射
- 1.9 眼镜和光仪器
2. 第二章光的波动性及其应用
- 2.1 单色光
- 2.2 光的干涉
- 2.3 论干涉条纹
- 2.4 干涉仪
- 2.5 光的衍射
- 2.6 论衍射条纹
- 2.7 哈密顿原理及其应用
- 2.8 光波的多普勒效应
- 2.9 光的偏振
3. 第三章量子物理学原理
- 3.1 稳定原子模型及能级图
- 3.2 光电效应
- 3.3 单色光的能量量子化
- 3.4 X射线的产生及应用
- 3.5 康普顿效应
- 3.6 德布罗意波
- 3.7 玻尔原子模型和玻尔频率条件- 3.8 原子能级和光谱
教学计划表
以上为人教版高中物理必修3课程目录与教学计划表,共计28个课时。
注:每个课时的重点、难点和教学时长仅供参考,根据实际教学情况有所调整。
量子力学中的自旋角动量和轨道角动量的叠加-概述说明以及解释

量子力学中的自旋角动量和轨道角动量的叠加-概述说明以及解释1.引言1.1 概述量子力学是描述微观领域的物理学理论,它在20世纪初由一些杰出的科学家如普朗克、爱因斯坦等人奠定了基础。
在量子力学中,自旋角动量和轨道角动量是两个重要的概念。
自旋角动量是粒子固有的属性,类似于物体的自转。
它与粒子的旋转对称性有关,可以用半整数来表示。
经过实验证明,自旋角动量在微观领域中起着非常重要的作用,并且与一些基本粒子的特性紧密相关。
自旋角动量的量子化使得粒子的行为在某些情况下表现出了奇特的性质,例如自旋相互作用和贝尔不等式等。
轨道角动量是粒子的运动轨道引起的角动量,与粒子的运动速度和轨道形状有关。
它可以用整数来表示。
轨道角动量在描述粒子围绕某一点或某一轴旋转的过程中的动力学性质时非常有用。
例如,在原子物理学中,轨道角动量可以解释电子在原子轨道中的分布和运动方式。
在量子力学中,自旋角动量和轨道角动量可以进行叠加,形成新的总角动量。
这种叠加有一些独特的规则和性质,例如自旋角动量和轨道角动量相互作用会导致总角动量的取值范围发生变化。
这种角动量的叠加在理论和实验研究中非常常见,对于理解粒子行为和物理现象具有重要意义。
本文将通过介绍自旋角动量和轨道角动量的定义和性质,探讨它们在量子力学中的叠加规律和重要性。
此外,我们还将讨论量子力学中自旋角动量和轨道角动量的一些应用,并对文章进行总结和结论。
这样的研究不仅有助于深入理解量子力学的基本概念和原理,还为未来的量子技术和量子计算领域的发展提供了理论基础和实验指导。
1.2文章结构文章结构部分的内容可以包括以下内容:文章的结构是为了让读者更好地理解和组织文章内容,使其逻辑清晰、层次分明。
本文将按照以下结构展开讨论:2.正文:本部分将详细介绍自旋角动量和轨道角动量的定义和性质,并探讨它们的叠加效应。
具体包括以下几个方面的内容:2.1 自旋角动量的定义和性质:介绍自旋角动量的概念和定义,包括自旋角动量的量子化、自旋的本质和自旋之间的相关性质等内容。
25个物理常数

25个物理常数篇一:标题: 25个物理常数(创建与标题相符的正文并拓展)正文:物理学是研究自然现象的科学,其基础是一些基本常数。
这些常数是通过对自然界的观察和实验得出的,它们对物理学的理论和实践具有至关重要的影响。
本文将介绍25个基本的物理学常数,包括它们的值、定义和意义。
1. 开尔文(k)开尔文(k)是一个常量,它的值为1.19264×10-19J/(K·K)。
它是电离常数,用于描述电解质的电离程度。
2. 普朗克常数(h)普朗克常数(h)是一个基本的物理学常数,它的值为6.626176×10-35J/(K·s)。
它是热力学中的基本常数,用于描述能量和热量之间的关系。
3. 光速(c)光速(c)是一个基本的物理学常数,它的值为299,792,458米/秒。
它是真空中光的速度,也是宇宙中最基本的速度。
4. 磁感应强度(B)磁感应强度(B)是一个物理学常数,用于描述磁场的强度。
它的值通常在0到1000特斯拉之间,磁感应强度越大,磁场越强。
5. 电容(C)电容(C)是一个物理学常数,用于描述电容器的电容值。
它的值通常在0到1特斯拉之间,电容器的电容值越大,电容器的储存电能的能力越强。
6. 电阻(R)电阻(R)是一个物理学常数,用于描述导体的电阻值。
它的值通常在0到无穷大之间,电阻值越大,导体的电阻能力越强。
7. 温度(T)温度(T)是物理学中的基本常数,用于描述物体的状态。
它的值通常在0到开尔文之间,温度越高,物体的状态越热。
8. 引力(G)引力(G)是物理学中的基本常数,用于描述物体之间的引力大小。
它的值通常在6.6743×10-11N·(m/kg)^2。
9. 电磁场频率(E)电磁场频率(E)是物理学常数,用于描述电磁场的传播速度。
它的值通常在真空中约为3×10^10米/秒。
10. 质能关系(E=mc2)质能关系(E=mc2)是物理学中的一个重要公式,用于描述质量和能量之间的关系。
量子物理物理课件.ppt

1927年获诺贝尔奖
例:波长为 2.0A0 的X射线射到碳块上,由于康普顿 散射 ,频率改变 0.04%。求: (1)该光子的散射角 (2) 反冲电子的动能
解:(1)
解出
(2)
0.04%
第 25 章 玻尔的原子量子理论
§25—1 氢原子光谱的实验规律
2、频率跃迁假设:当原子能级 跃迁时,才发射(或吸收)光子,
3、量子化条件:稳态时电子角动量应等于 的整数倍。
)
1,2,
(n
2
L
h
=
p
=
=
h
n
n
L
h
E
E
k
n
-
=
n
其频率为
+
-
E E3 E2 E1
1913发表‘论原子分子结构’
E1 , E2 , E3 …… En (定态)
2、量子理论的成功:
光子与束缚电子作弹性碰撞时,不改变能量,故 不变 , 不变。
解释实验现象( 有 、 ’, ’> )
光子与自由电子作弹性碰撞时,要传 一 部分能量给 电子
n
=
=
l
c
cT
如何解释实验规律?
n
=
l
c
频率为 的 X射线,是 能量为 = h 的光子流
一、卢瑟福原子模型(原子的有核模型)
严重的问题:
原子的稳定性问题?
原子分立的线状光谱?
)
1
1
(
2
2
n
k
Rc
-
=
n
广义的巴尔末公式
2
2
n
量子力学第二版周世勋1PDF

1 Quantum mechanism Quantum mechanism 宝鸡文理学院物理与信息技术系1.《量子力学教程》曾谨言著 科学出版社2003年第一版 普通高等教育十五国家级规划教材 2.《量子力学导论》曾谨言著 北京大学出版社 1998年第二版 3.《量子力学导论》熊钰庆主编 广东高等教育出版社 2000年第一版 《量子力学教程》周世勋编 高等教育出版社参考书及学习网站4.《量子力学基础》关洪 高等教育出版社 1999年第一版 5.《量子力学》汪德新 湖北科学技术出版社出版 2000年第一版 6.《量子力学教程习题剖析》孙婷雅编 科学出版社出版 2004年第一版 7. 宝鸡文理学院陕西省精品课程《量子力学》http://218.195.112.45/jpkc/liangzi/kc_web/ Content Content 第一章绪论Ch1. The basic concepts of quantum mechanism 第二章波函数和薛定谔方程Ch2. The wave function and Schr??dinger’s equation 第三章量子力学中的力学量Ch3. The Dynamical variable in Quantum Mechanism 第四章态和力学量的表象Ch4. The representation of the states and operators 第五章微扰理论Ch5. Perturbation theory第六章散射Ch6. The general theory of scattering 第七章自旋与全同粒子Ch7. Spin and identity of particles The birth of quantum mechanismThe birth of quantum mechanism Chap.1.绪论The birth of quantum mechanism Chap.1.绪论The birth of quantum mechanism 6 1.1 经典物理学的困难The difficult in classical physics 1.2 光的波粒二象性The duality of light between wave and particle 1.3 微粒的波粒二象性The duality of small particles between wave and particle Chap.1.绪论The birth of quantum mechanism Chap.1.绪论The birth of quantum mechanism 7 近几十年来 在不同领域相继发现了宏观量子效应 如超导现象 超流现象 乃至一些天体现象表明宏观世界的物质运动也遵循量子力学规律 人们所熟知的经典力学规律只是量子力学规律在特定条件下的一个近似。
现代物理基础丛书

现代物理基础丛书1《现代声学理论基础》马大猷著2《物理学家用微分几何》(第二版)侯伯元、侯伯宇著3《数学物理方程及其近似方法》程建春编著4《计算物理学》马文淦编著5《相互作用的规范理论》(第二版)戴元本著6《理论力学》张建树、孙秀泉、张正军编著7《微分几何入门与广义相对论》(上册)(第二版)梁灿彬、周彬著8《物理学中的群论》(第二版)马中骐著9《辐射和光场的量子统计理论》曹昌祺著10《实验物理中的概率和统计》(第二版)朱永生著11《声学理论与工程应用》何琳、朱海潮、邱小军、杜功焕编著12《高等原子分子物理学》(第二版)徐克尊著13《大气声学》(第二版)杨训仁、陈宇著14《输运理论》(第二版)黄祖洽、丁鄂江著15《量子统计力学》(第二版)张先蔚编著16《凝聚态物理的格林函数理论》王怀玉著17《激光光散射谱学》张明生著18《量子非阿贝尔规范场论》曹昌祺著19《狭义相对论》(第二版)刘辽、费保俊、张允中编著20《经典黑洞和量子黑洞》王永久著21《路径积分与量子物理导引-现代高等量子力学初步》侯伯元、云国宏、杨战营编著22《量子光学导论》(第二版)谭维翰著23《全息干涉计量——原理和方法》熊秉衡、李俊昌编著24《实验数据多元统计分析》朱永生编著25《微分几何入门与广义相对论》(中册)(第二版)梁灿彬、周彬著26《中子引发轻核反应的统计理论》张竞上著27《工程电磁理论》张善杰著28《微分几何入门与广义相对论》(下册)(第二版)梁灿彬、周彬著29《经典电动力学》曹昌祺著30《经典宇宙和量子宇宙》王永久著31《高等结构动力学》(第二版)李东旭编著32《粉末衍射法测定晶体结构(上册)X射线衍射结构晶体学基础》(第二版)梁敬魁编著32《粉末衍射法测定晶体结构(下册)X射线衍射在材料科学中的应用》(第二版)梁敬魁编著33《量子计算与量子信息原理》[意] Giuliano Benenti、Giulio Casati、Giuliano Strini 著王文阁李保文译34《近代晶体学》(第二版)张克从著35《引力理论》王永久著36《低温等离子体—-等离子体的产生、工艺、问题及前景》[俄]В. М。
《机械工程》专业攻读博士学位课程
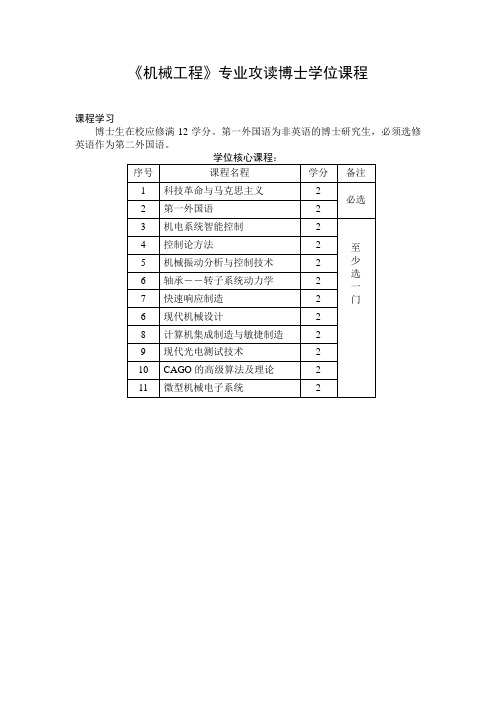
《机械工程》专业攻读博士学位课程课程学习博士生在校应修满12学分。
第一外国语为非英语的博士研究生,必须选修英语作为第二外国语。
《仪器科学与技术》专业攻读博士学位课程课程学习博士生在校学习阶段包括课程学习及必修环节两部分,修满至少12学分。
第一外国语为非英语的博士研究生,必须选修英语作为第二外国语。
必修环节2学分:讲座选听1学分;学位论文选题报告1学分。
《材料科学与工程》专业攻读博士学位课程课程学习博士学位核心课程:1、科技革命与马克思主义2、第一外国语3、材料研究创新学4、材料热力学5、材料力学行为6、材料表面工程7、非金属材料的设计与优化8、高新技术材9、材料科学前沿10、材料物理11、材料化学12、现代凝固学13、传输原理14、焊接传热传质15、焊接物理冶金16、结合力学分析17、焊接过程数值分析学分要求:学位课程至少10学分,其中科技革命与马克思主义、第一外国语、材料科学前沿为必选课程。
总学分为12学分,10学分(课程学习环节)+2学分(必修环节)《动力工程及工程热物理》专业攻读博士学位课程课程学习1、博士生在校学习阶段包括课程学习及必修环节两部分,修满至少12学分,其中学位必修课4学分,必修环节2学分,其他为学位选修课。
第一外国语为非英语的博士生必须选英语为第二外国语,第二外国语在必修的12学分外记2学分。
2、学位必修课4学分包括:(1)第一外国语:2学分(其中:基础部分1学分,专业部分1学分)(2)科技革命与马克思主义:2学分3、必修环节2学分包括:讲座选听 1学分学位论文选题报告1学分4、博士学位核心课程1.流体力学的近代进展2.燃烧学的近代进展3.多相流及其进展4.计算传热学的近代进展5.偏微分方程的现代数值解法6.制冷、空调、热泵中的CFCs的替代7.洁净燃烧及污染防治进展8.热力学的近代进展9.低温机械与系统的工作过程10.流体机械计算流体动力学11.压缩机现代理论方法12.叶轮机械气动热力学13.多相流动力学基础14.化工过程综合与优化《核科学与工程》专业攻读博士学位课程课程学习博士生在校学习阶段包括课程学习及必修环节两部分,修满至少12学分,其中学位必修课4学分,必修环节2学分,其他这学位选修课。
【精选】量子物理在生活中的应用

量子物理在生活中的应用——太阳能电池1.量子力学量子概念是1900年普朗克首先提出的,到今天已经一百多年了。
经过玻尔、德布罗意、玻恩、海森柏、薛定谔、狄拉克、爱因斯坦等许多物理大师的创新努力,到20世纪30年代,初步建立了一套完整的量子力学理论。
量子物理是描述微小世界——即原子和亚原子领域的物理学,它不同于描述我们所熟悉的日常世界的“经典物理”学。
经典物理与我们的常识是一致的,而这些常识又是基于我们的感觉的。
量子物理则不同,它违背常识。
尽管量子力学是为描述远离我们的日常生活经验的抽象原子世界而创立的,但它对日常生活的影响无比巨大。
没有量子力学作为工具,就不可能有化学、生物、医学以及其他每一个关键学科的引人入胜的进展。
没有量子力学就没有全球经济可言,因为作为量子力学的产物的电子学革命将我们带入了计算机时代。
同时,光子学的革命也将我们带入信息时代。
量子物理的杰作改变了我们的世界,科学革命为这个世界带来了的福音,也带来了潜在的威胁。
2.太阳能太阳能(Solar Energy),一般是指太阳光的辐射能量,是一种清洁的可再生能源,在现代一般用作发电。
自地球形成生物就主要以太阳提供的热和光生存,而自古人类也懂得以阳光晒干物件,并作为保存食物的方法,如制盐和晒咸鱼等。
但在化石燃料减少下,才有意把太阳能进一步发展。
太阳能的利用有被动式利用(光热转换)和光电转换两种方式。
太阳能发电一种新兴的可再生能源。
广义上的太阳能是地球上许多能量的来源,如风能,化学能,水的势能等等。
3.太阳能电池的工作原理太阳光照在半导体p-n结上,形成新的空穴-电子对,在p-n结电场的作用下,光生空穴由n区流向p区,光生电子由p区流向n区,接通电路后就形成电流。
这就是光电效应太阳能电池的工作原理。
太阳能发电有两种方式,一种是光—热—电转换方式,另一种是光—电直接转换方式。
3.1光—热—电转换光—热—电转换方式通过利用太阳辐射产生的热能发电,一般是由太阳能集热器将所吸收的热能转换成工质的蒸气,再驱动汽轮机发电。
普朗克能量子假说

德国物理学家,量子物理 学的开创者和奠基人。 普朗克的伟大成就,就是 创立了量子理论,1900年12月 14日他在德国物理学会上,宣 读了以《关于正常光谱中能量 分布定律的理论》为题的论文, 提出了能量的量子化假设。这 是物理学史上的一次巨大变革。 从此结束了经典物理学一统天 下的局面。劳厄称这一天为 “量子论的诞生日”。
二、爱因斯坦光子论
1、光电效应的实验规律
当光照射到金属表面 时,金属中有电子逸出的 现象叫光电效应。 A
实验装置 K
G
如将K接正极、A接负极, 则光电子离开K后,将受到 电场的阻碍作用。当K、A 之间的反向电势差等于U0时, 从K逸出的动能最大的电子 刚好不能到达A,电路中没 有电流,U0叫遏止电压。
弗兰克-赫兹实验
实验装置 ——证明原子能级的存在
F V G P A 管内充满低压汞蒸汽,电 子从加热的灯丝F发射, + 在加速电压U0作用下电子 被加速,向栅极G运动, 在GP之间加反向电压Ur (0.5V左右),电子穿过栅 极G到达P,在电路中可 看出电流IP。
300 IP 200 100
+
9.8 4.9
U
Ek max eU0
实验现象
(1)饱和光电流:饱和光电流强度与入射光强度成正比。 I (2)存在截止频率:对某一种金属来说,只有
当入射光的频率大于某一频率n0时,电子才能 从金属表面逸出,电路中才有光电流,这个频 率n0叫做截止频率——红限.
IS
2 1 0
3
(3)线性性:用不同频率的光照射金属K的表 面时,只要入射光的频率大于截止频率,遏 止电势差与入射光频率具有线性关系。
丹麦理论物 理学家,现 代物理学的 创始人之一
高校化工专业课件第25章量子力学基础(分析化学)

解: 电子横向位置的不确定量
x
2mx
1.051034 J s 29.111031 kg1104 m
0.58 m s
x 0.01cm
eU 1 mv2 2
v 6107 m / s
n E E 以,经典物理可以看作是量子物理中量子数 n
时的极限情况。
n
n
一维无限深势阱
例题: 试求在一维无限深势阱中粒子概率密度的最大 值的位置。
高校化工专业课件第25章量子力学基 础(分析化学)
§25-1 德布罗意假设 波-粒二象性
1. 德布罗意假设
德布罗意在光的波粒二象性的启发下,提出了实物粒子(如电子、质子等)也 具有波-粒二象性的假设。
E mc2 h
p mv h
——德布罗意公式
与实物粒子相联系的波 —— 德布罗意波(物质波)
1927年德国物理学家海森伯(W.Heisenberg)根据量子力学 推出微观粒子在位置与动量两者不确定量间的关系
在某一方向(如x方向)粒子的位置不确定量x和该方向上的动量的不确定量 px有
xpx / 2 h 1.051034 J s
2
二. 简单推导 x
电子束v x
电子的单缝衍射
px
p
2
——概率密度
表示在某一时刻在某点处单位体积内粒子出现的概率。
3. 波函数的归一化条件 粒子在任意时刻在整个空间出现的概率等于1
2dV 1
——波函数的归一化条件 4. 波函数的标准条件
单值, 有限, 连续, 归一化
三. 薛定锷方程
物理学中的25个难题

物理学中的25个难题世界著名理论物理学家、2004年诺贝尔物理学奖获得者、美国Kavli理论物理研究所所长大卫·格罗斯(David Gross)教授在2005年2月27日中国科学院理论物理所作了题为“The future of physics--物理学的将来”的科学报告。
格罗斯教授的“The Future of Physics”报告,讨论了当前物理学面临的25个问题及它们如何引导物理学未来25年的发展。
格罗斯说,过去25年到35年中,物理学取得了巨大进展,但同时人们面临的未知事物同样增多。
他将这些“未知”归纳为当前物理学面临的25个问题,认为它们将引导物理学下一个25年的发展。
分属宇宙论、天体物理学、凝聚态物理学、粒子物理学、弦理论、生物物理学和科学政策及社会学七大领域的这25个问题,广泛涉及宇宙起源、暗物质、暗能量、星体形成、广义相对论、量子力学、复杂性、量子计算机、理论生物学、基因组学和计算物理学等。
2005年2月27日,格罗斯教授在“前沿科学论坛”上发表演讲的具体问题包括:1.宇宙起源:宇宙学观测表明宇宙是膨胀着的。
通过对微波背景辐射和宇宙大尺度结构等的观测,宇宙的历史可以追溯到极早期发生的大爆炸。
我们所知的基本物理,比如广义相对论和粒子物理标准模型,在那里都不适用。
为理解宇宙起源,需要了解大爆炸时期的基本物理。
2.暗物质的本质:现代宇宙学观测表明宇宙中存在暗物质和暗能量。
但是它们的起源仍然是个谜。
3.暗能量的本质4.恒星、行星的形成:天体的形成是天体物理学中的重要问题。
适合生物存在的行星,在银河系中出现的几率到底是多少?5.广义相对论:广义相对论在所有尺度上都是正确的吗?6.量子力学:量子力学取得了巨大成功,但它描述的是自然的最终理论吗?也许它会在很小的距离上和非常复杂的系统中失效,是否可用来描绘整个宇宙也还值得探讨。
7.标准模型:粒子物理标准模型无疑极为成功,但人们并没有理解夸克和轻子的质量混合的物理起源和中微子的质量等。
2024版年度物理(中职通用版)全套教学课件

2024/2/3
1
目录
• 物理学科概述 • 力学基础知识 • 热学基础知识 • 电磁学基础知识 • 光学基础知识 • 现代物理初步知识
2024/2/3
2
01
物理学科概述
2024/2/3
3
物理学科定义与特点
2024/2/3
定义
物理学是研究物质的基本结构、相 互作用和运动规律的自然科学。
特点
实验为基础,理论为指导,注重定 量分析和科学思维。
4
物理学科发展历史
01
02
03
古代物理学
以自然哲学为主,探讨自 然现象的本质。
2024/2/3
近代物理学
以实验为基础,建立了经 典力学、热力学和电磁学 等理论体系。
现代物理学
以相对论和量子力学为代 表,揭示了微观和宏观世 界的奥秘。
5
物理学科在中职教育中地位
21
电磁波产生、传播和接收
电磁波的产生
电磁波是由变化的电场和磁场相互 激发而产生的波动现象。
电磁波的传播
电磁波可以在真空中传播,其传播 速度等于光速,具有波粒二象性。
2024/2/3
电磁波的接收
电磁波可以通过天线等设备接收并 转换为电信号进行处理和应用。
电磁波的应用与防护
电磁波在通信、广播、雷达等领域 有广泛应用,但过强的电磁波也会 对人体和环境产生危害,因此需要
光的干涉 两列或多列光波在空间某些区域相遇时相互叠加,在某些 区域始终加强,在另一些区域始终减弱,形成稳定的强弱 分布的现象。
光的衍射
光在传播过程中遇到障碍物或小孔时,偏离直线传播的途 径而绕到障碍物后面传播的现象。
物理学经典名言

物理学经典名言1. “如果我比别人看得更远,那是因为我站在巨人的肩膀上。
”——牛顿这句话充分体现了科学研究的传承性,牛顿也借此表达了对前人研究成果的尊重和借鉴!2. “能量既不会凭空产生,也不会凭空消失,它只会从一种形式转化为另一种形式,或者从一个物体转移到其它物体,而能量的总量保持不变。
”——迈尔哇塞,这真的让我们深刻理解到能量守恒的神奇和永恒!3. “电和磁的实验中最明显的现象是,处于彼此距离相当远的物体之间的相互作用。
因此,把这些现象化为科学的第一步就是,确定物体之间作用力的大小和方向。
”——麦克斯韦瞧瞧,这不就为电磁学的研究指明了方向嘛!4. “给我一个支点,我就能撬起地球。
”——阿基米德这是多么大胆而又充满想象力的宣言呀!5. “所有的科学不是物理学,就是集邮。
”——卢瑟福哎呀,这凸显了物理学在科学领域的重要地位!6. “物理学的任务是发现普遍的自然规律。
因为这样的规律的最简单的形式之一表现为某种物理量的不变性,所以对于守恒量的寻求不仅是合理的,而且也是极为重要的研究方向。
”——劳厄可不是嘛,这让我们明白守恒量在物理学中的关键作用!7. “实验可以推翻理论,而理论永远无法推翻实验。
”——丁肇中哇哦,强调了实验对于物理学的决定性作用!8. “自然界没有跳跃。
”——莱布尼茨这表明了自然界变化的连续性,在物理学中多么重要!9. “方程式之美,远比符合实验结果更重要。
”——狄拉克呀,让我们看到了物理学中理论之美的独特魅力!10. “物理定律不能单靠思维来获得,还应致力于观察和实验。
”——普朗克没错没错,观察和实验可是物理学的基石呀!11. “发现的艺术就是正确概括的艺术。
”——玻尔这告诉我们在物理学中概括总结的重要性哟!12. “我可以很确定地说,没有人真正理解量子力学。
”——费曼哈哈,是不是让我们对量子力学充满了好奇和敬畏!13. “科学是一种方法,它教导人们:一些事物是如何被了解的,不了解的还有些什么,对于了解的,现在又了解到什么程度。
曾谨严量子力学习题第二章

= = 用高斯定理: = 中间一式的第一项是零,因为假定满足平方可积条件,因而因此 ,能让能量 平均值 因此令(本征态)则而
得证 # [9]设粒子在势场中运动 (1)证明其能量的平均值是: (1) 其中W是能量密度 (2)证明能量守恒公式
利用积分 :
写出共轭函数(前一式变号):
本题也可以用Fresnel积分表示,为此可将(6)式积分改为: 用课本公式得,两者相乘,可得相同的结果。 #
[14]在非定域势中粒子的薛定谔方程式是: (1)
求几率守恒对非定域势的要求。此时,只依赖于波函数在空间一点的几 率波是否存在?
[解]按题意,是要求写出几率守恒的条件,从这个条件寻出应当遵 守的要求。几率守恒的条件是:
(6) 故相速度(物质波的)应当超过光速。 最后找出和的关系,将(1)(2)相除,再运用德氏波假设:
, (7) # [6](1)试用Fermat最小光程原理导出光的折射定律
(2)光的波动论的拥护者曾向光的微粒论者提出下述非难: 如认为光是粒子,则其运动遵守最小作用量原理 认为则这将导得下 述折射定律 这明显违反实验事实,即使考虑相对论效应,则对自由粒子:仍就 成立,E是粒子能量,从一种媒质到另一种媒质E仍不变,仍有,你怎 样解决矛盾?
(解)甲法:光线在同一均匀媒质中依直线传播,因此自定点A到定 点B的路径是两段直线:光程
设A,B到界面距离是a,b(都是常量)有 又AB沿界面的投影c也是常数,因而,存在约束条件:
(2) 求(1)的变分,而将,看作能独立变化的,有以下极值条件 (3) 再求(2)的变分
(3)与(4)消去和得 (5)
(1)
量子的原理特性

量子的原理特性
1、量子测不准。
也称为不确定性原理,即观察者不可能同时知道一个粒子的位置和它的速度,粒子位置的总是以一定的概率存在某一个不同的地方,而对未知状态系统的每一次测量都必将改变系统原来的状态。
也就是说,测量后的微粒相比于测量之前,必然会产生变化。
2、量子不可克隆。
量子不可克隆原理,即一个未知的量子态不能被完全地克隆。
在量子力学中,不存在这样一个物理过程:实现对一个未知量子态的精确复制,使得每个复制态与初始量子态完全相同。
3、量子不可区分。
量子不可区分原理,即不可能同时精确测量两个非正交量子态。
事实上,由于非正交量子态具有不可区分性,无论采用任何测量方法,测量结果的都会有错误。
25 力学量的平均值、算符表示 平均值
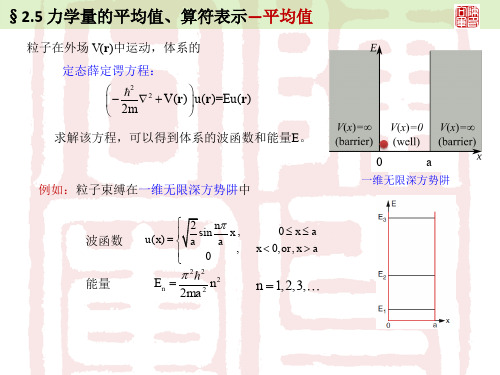
§2.5 力学量的平均值、算符表示—算符表示
Cartesian coordinates
Spherical coordinates
( x, y, z )
(r , , )
x r sin cos y r sin sin z r cos
r x2 y 2 z 2 z arccos x2 y 2 z 2 y arctan x
i
p r
d
( p, t )
2
表示平面波
e
pr
的所占的比重,即粒子动量取为 p 的概率。
(p,符表示—平均值
所以,动量的平均值
p
p ( p, t ) dp * ( p, t ) p ( p, t )dp
定态薛定谔方程:
2 2 V (r ) u (r )=Eu (r ) 2m
ˆ (r)=Eu(r) Hu
§2.5 力学量的平均值、算符表示—算符表示
量子力学中,描述微观粒子的力学量均有对应的算符
(1) 位矢 r r (2) 势能 V(r) V(r) (3) 动量 p
r x2 y 2 z 2 z arccos x2 y 2 z 2 y arctan x
§2.6 单电子(H)原子—中心力场薛定谔方程
From
求解中心力场中的薛定谔方程,球坐标系是自然的选择
ˆ ˆ z zp ˆ y i Lx yp ˆ ˆ x xp ˆ z i Ly zp ˆz xp ˆ y yp ˆ x i L
y z y z z x z x x y x y
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
L
威尔孙云室观察到 的“轨道”仍有意 义!
例:试估算氢原子可能具有的最低能量.
电子被束缚在半径为r的球内,所以 x r
按不确定关系 p ~ / r
2
p p / r
若不计核的运动,氢原子的能量就是电子的能量:
2 p e E Ek E p 2me 4 o r
h 6.63 10 0.15nm 27 m n v 1.67 10 2700
34
例:设电子的总能量E=Ek+m0c2,试推出物质波波长的公式.
1 2 2 E k 2m 0 c E k c ch h 2 2 p E k 2m 0 c E k h 2 当v c,略去 E k 应用此式,上两例 2m 0 E k
v ~ 10
18
m s
1
远远小于测量速度的误差,完全可以忽略!
对于宏观粒子,不确定度关系没有限制作用!
例:试求原子中电子速度的不确定量,
取原子的线度为10–10 m. 10 解: r ~ x 10 m
1.05 10 v x 31 10 2mr 2 9.11 10 10
7个电子
100个电子
3000
20000
70000
底片上出现一个一个的点子 电子具有粒子性。 随着电子增多,逐渐形成衍射图样 来源于 而不是电子间相 ―一个电子”所具有的波动性, 互作用的结果。
微观粒子的波粒二象性:
(1) 粒子性 • ―原子性”或“整体性” • 不是经典的粒子,抛弃了“轨道”概念 (2) 波动性
B D
d
O
p
1
A C
y
h dp d( ) 2 d
h
x d
B
p
1
D
O
x=d A
px
C
y
电子衍射中央明纹旁第一级暗纹衍射角1
sin 1
d
中央明纹内对应动量x分量有:
h h h 可见 p x p sin 1 x p x h d d x
实验表明: 1.原子具有线状光谱; 2.各谱线间具有一定的关系
3.每一谱线的波数都可表达为两个光谱项之差。
玻尔的氢原子理论
1913年玻尔从好友那里得知氢原 子光谱的经验公式时,他立即获得 了他理论“七巧板中的最后一块”。 正如他后来常说的:
“我一看到巴耳末公式,整个问 题对我来说就全部清楚了。”
h
(3)轨道量子化条件:定态下电子的轨道运动角动量 是量子化的. h
Ln
2
则
n 1,2,3,
h 令 2
L n
n 1,2,3,
氢原子轨道半径和能量的计算
利用库仑定律、牛顿定律和玻尔的量子假设
e2 4 0 r
2
h 根据角动量量子化条件 L mvr n n 1,2,3, 2 2 2 0h ) n 1,2,3, 根据以上二式解得 rn n ( 2 me 2 0h 0.529 10 10 m 当n=1时 r1 me 2 ?
2 2 2 4 12 0 2
能级的自然宽度和寿命: Et 2 设体系处于某能量状态的寿命为 , 则该状态能量的不确定程度E(能级自然宽 度)为:
/ 2 3.310 16 (eV s) E 2t ( s) 假定原子中某一激发态的寿命 ~ 10-8 s
考虑到其他高级次衍射条纹.
0 p x p sin 1
h p
同理
y p y h
x px h z pz h
由量子力学严格推导的结论:
不确定关系的物理意义: 当粒子位臵的不确定度x小时,动量的不确定度p就大, 反之亦然.即微观粒子不可能同时具有确定的位臵和动量. 特别是当 p 0; x 对于理想的单色平面波 p 0 x 共轭物理量 不确定关系不仅存在于位臵、动量之间.
它能解释谱线的自然宽度
17-1-4 氢原子光谱
氢原子光谱的规律性
氢原子的可见光光谱:
玻尔的氢原子理论
4340.5Å 6562.8Å 4861.3Å 紫 红 蓝 。 ‥ 1853年瑞典人埃格斯特朗(A.J.Angstrom) 。 测得氢可见光光谱的红线, A即由此得来。 到1885年, 观测到的氢原子光谱线已有14条,
则其能级宽度为: E ~ 3.310 8 eV 理论上计算平均寿命 估计能级宽度 实验上测量能级宽度估计不稳态的寿命
例: 对于宏观粒子, m=10 –10kg的微小尘埃,测定它的位 臵不难准确到 x 106 m
由 x p x x m v x 2 2 34 6.63 10 18 1 0.53 10 m s v x 10 6 2mx 4 10 10
光(电磁辐射)的波粒二象性
2 狭义相对论的动量和能量的关系 E 2 p 2 c 2 E0 因为没有静止的光子, 所以光子的静能量 E0 0
E h h m c 光子的动量 p c c E h
光子的质量
c c2 质量、动量描述光的粒子性; h m.p 频率、波长描述波动性.
不同的 k 对应为莱曼系、帕邢系、布喇系、...
656.3nm
~ 1 R( 1 1 ) 赖曼系 12 n 2 ~ 1 R( 1 1 ) 帕邢系 32 n2
n 2,3,4,
n 4,5,6,
~ 1 R( 1 1 ) n 5,6,7, 布喇开系 42 n2 ~ 1 R( 1 1 ) n 6,7,8, 普丰德系 52 n2
34
5.8 10 m s
6
1
2
v m 由玻尔的氢原子理论 2 4 0 r r
e
2
e 6 1 v~ ~ 10 m s 4 0 mr1
―轨道”已失去意义!
2
对于微观粒子不确定 度关系的限制显著,不 能用经典力学量描述 原子内电子的运动!
例:讨论电视显象管中的电子
v ~ 10 ms
不确定度
Werner Karl Heisenberg 德国人 1901-1976
获1932年诺贝尔 物理学奖
Uncertainty relation
问题引入: 测量波长 x n x 计数的偏差可以 1 n x x n n1 n1 则
即
x ~ n x
北京交通大学工科物理基地
本章主要内容:
§17.1 物质波
§17.2 态函数 薛定谔方程
§17.3 力学量的本征值问题 力学量的平均值 §17.4 原子 §17.5 分子
§17.1
主要内容:
物质波
光的粒子性
17-1-1 光的量子性 17-1-2 德布罗意波
粒子的波动性
17-1-3 海森伯不确定关系
若合理地假定
5 1
v 10 ms p mv p mv 使得 6 由不确定度关系 x 5.8 10 m 2 m v
显象管的尺寸 L 0.4 m x
1
电子的物质波波长 h 7.4 10 9 m
p x ~ 10 5 足够精确! L
x p x ; y p y ; z pz 2 2 2
角位置与角动量的不确定关系:
时间与能量的不确定关系: E t 2
L
在微观问题中,不确定关系常被用来作数量级估算
2
E t 2
推导如下:
E ( p c m c ) mc 1 2 2 2 4 1 2 2 E ( p c m0 c ) 2 pc p 2 2 pc p pp vp E m Et pvt x p 2
t E 2 E h
c 2
t E 2 E h
632.8 nm 14 1 4.741 10 s
谱线的 自然宽度
Байду номын сангаас
3 108 1.59 107 2.12 1014 m 14 2 (4.741 10 )
光子的本质: 光既具有波动性,又具有粒子性
m
2
例:估算热中子的德布罗意波长。
(T=300K。mn=1.6710-27kg) 3 3 解: kT 1.38 10 23 300 2 2
6.21 1021 J 0.038 eV
1 2 mv 2 1 v 2 m n 2700m s
n1
~
2
2
n 对频率 t
1 ~ x ( ) ~ 1 n1 n 1 t t t
t ~ 1
微观粒子的波动性表现在 位臵,动量等力学量测量中. 位臵不确定量:x、y、z. 动量不确定量:p 来源于波长的非单色性
海森堡 位置与动量不确定关系: xpx , yp y , zpz 2 2 2 x
E p c m c 1 1 1 2 1 2 4 2 2 2 2 4 2 p ( E m0 c ) [( Ek m0c ) m0 c ] c c
解:
2 2 2 2 4 0
1
h 2m 0 E k
6.63 10
34
1 2 2 0.05 0.05 300 2
35
4.42 10 m
(4.4 1035 m )
2
h 2m 0 E k
1.45 10
10
m 0.145nm
(0.15nm )
对于宏观低速物体
h 2m 0 E k
具有普遍意义!
