方程不等式与一次函数专题(实际应用)
中考数学复习攻略 专题6 方程与不等式的实际应用(含答案)

专题六 方程与不等式的实际应用解决方程与不等式的实际应用题的一般步骤:①认真审题,理解题意,弄清题中的已知量、未知量以及它们之间的关系;②设未知数(合理地选择未知数是解题的关键);③列方程(组)或不等式;④解方程(组)或不等式(注意:解分式方程时必须要有“验根”这一步);⑤检验,对所求结果进行检验,看是否符合题意;⑥作答.解决方程与不等式的实际应用题时,首先要认真审题,从题中找出已知量与未知量之间的关系,然后根据题意列出关系式,进而解决相关问题.在解决问题的过程中要注意方程与不等式的解是否符合题意,涉及函数要检验自变量的取值范围,当题干中出现方案设计问题或最值问题时,往往需要根据题干中的已知条件和函数的增减性来解决方案设计或最值问题.中考重难点突破一次方程(组)的实际应用【例1】(2021·陕西中考)一家商店在销售某种服装(每件的标价相同)时,按这种服装每件标价的8折销售10件的销售额,与按这种服装每件的标价降低30元销售11件的销售额相等.求这种服装每件的标价.【解析】设这种服装每件的标价是x 元,根据“这种服装每件标价的8折销售10件的销售额,与按这种服装每件的标价降低30元销售11件的销售额相等”列出方程,然后解方程即可求解.【解答】解:设这种服装每件的标价是x 元.根据题意,得10×0.8x =11(x -30).解得x =110.答:这种服装每件的标价为110元.1.现有一条长度为359 mm 的铜管料,把它锯成长度分别为39 mm 和29 mm 的两种不同规格的小铜管(要求没有余料).每锯一次损耗1 mm 的铜管料.为了使铜管料损耗最少,应分别锯成39 mm 的小铜管__6__段,29 mm 的小铜管__4__段.2.某中学组织七年级全体学生参加社会实践,若只调配45座客车若干辆,则有15人没有座位;若只调配30座客车,则用车数量将增加3辆,且空出15个座位.(1)该学校七年级总共有多少学生?(2)若同时调配45座和30座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?解:(1)设只调配45座客车x 辆,则该学校七年级共有学生(45x +15)人,只调配30座客车需要(x +3)辆.由题意,得30(x +3)-(45x +15)=15.解得x =4.∴45x +15=45×4+15=180+15=195.答:该学校七年级共有学生195人;(2)设需要调配45座客车m 辆,30座客车n 辆,由题意,得45m +30n =195.∴n =13-3m 2. 又∵m ,n 均为正整数,∴⎩⎪⎨⎪⎧m =1,n =5 或⎩⎪⎨⎪⎧m =3,n =2. 答:需调配45座客车1辆,30座客车5辆或调配45座客车3辆,30座客车2辆.分式方程的实际应用【例2】(2021·常州中考)为落实节约用水的政策,某旅游景点进行设施改造,将手拧水龙头全部更换成感应水龙头.已知该景点在设施改造后,平均每天用水量是原来的一半,20 t 水可以比原来多用5天.该景点在设施改造后平均每天用水多少吨?【解析】本题考查了分式方程的应用,读懂题意,找到合适的等量关系是解决问题的关键.设该景点在设施改造后平均每天用水x t ,则在改造前平均每天用水2x t ,根据“20 t 水可以比原来多用5天”列出方程并解答.【解答】解:设该景点在设施改造后平均每天用水x t ,则在改造前平均每天用水2x t.根据题意,得20x -202x=5. 解得x =2.经检验,x =2是原方程的解,且符合题意.答:该景点在设施改造后平均每天用水2 t .3.(2021·徐州中考)某网店开展促销活动,其商品一律按8折销售,促销期间用400元在该网店购得某商品的数量较打折前多出2件.问:该商品打折前每件多少元?解:设该商品打折前每件x 元,则打折后每件0.8x 元.根据题意,得400x +2=4000.8x. 解得x =50.经检验,x =50是原方程的解,且符合题意.答:该商品打折前每件50元.方程与不等式的综合应用【例3】某学校为丰富同学们的课余生活,购买了一批数量相等的象棋和围棋供兴趣小组使用,其中购买象棋用了420元,购买围棋用了756元,已知每副围棋比每副象棋贵8元.(1)求每副围棋和象棋各是多少元?(2)若该校决定再次购买同种围棋和象棋共40副,且再次购买的费用不超过600元,则该校最多可再购买多少副围棋?【解析】(1)设每副围棋x 元,则每副象棋(x -8)元,根据“420元购买象棋数量=756元购买围棋数量”列出方程求解即可;(2)设购买围棋m 副,则购买象棋(40-m )副,根据题意列出不等式求解即可.【解答】解:(1)设每副围棋x 元,则每副象棋(x -8)元.根据题意,得420x -8=756x .解得x =18. 经检验,x =18是原方程的解,且符合题意.∴x -8=10.答:每副围棋18元,每副象棋10元;(2)设该校购买m 副围棋,则购买(40-m )副象棋.根据题意,得18m +10(40-m )≤600.解得m ≤25.∵m 为正整数,∴m 的最大值是25.答:该校最多可再购买25副围棋.4.(2021·玉林中考)某市垃圾处理厂利用焚烧垃圾产生的热能发电.有A ,B 两个焚烧炉,每个焚烧炉每天焚烧垃圾均为100 t ,每焚烧一吨垃圾,A 焚烧炉比B 焚烧炉多发电50度,A ,B 焚烧炉每天共发电55 000度.(1)求焚烧一吨垃圾,A 焚烧炉和B 焚烧炉各发电多少度?(2)若经过改进工艺,与改进工艺之前相比每焚烧一吨垃圾,A 焚烧炉和B 焚烧炉的发电量分别增加a %和2a %,则A ,B 焚烧炉每天共发电至少增加(5+a )%,求a 的最小值.解:(1)设焚烧一吨垃圾,A 焚烧炉发电m 度,B 焚烧炉发电n 度.根据题意,得⎩⎪⎨⎪⎧m -n =50,100(m +n )=55 000. 解得⎩⎪⎨⎪⎧m =300,n =250.答:焚烧一吨垃圾,A 焚烧炉发电300度,B 发焚烧炉发电250度;(2)由题意,得改进工艺后每焚烧一吨垃圾A 焚烧炉发电300(1+a %)度,则B 焚烧炉发电250(1+2a %)度,由题意,得100×300(1+a %)+100×250(1+2a %)≥55 000[1+(5+a )%].整理,得5a ≥55.解得a ≥11.∴a 的最小值为11.一元二次方程的实际应用【例4】(2021·烟台中考)直播购物逐渐走进了人们的生活.某电商在抖音上对一款成本价为40元的小商品进行直播销售,如果按每件60元销售,每天可卖出20件.通过市场调查发现,每件小商品售价每降低5元,日销售量增加10件.(1)若日利润保持不变,商家想尽快销售完该款商品,每件售价应定为多少元?(2)小明的线下实体商店也销售同款小商品,标价为每件62.5元.为提高市场竞争力,促进线下销售,小明决定对该商品实行打折销售,使其销售价格不超过(1)中的售价,则该商品至少需打几折销售?【解析】(1)根据日利润=每件利润×日销售量,可求出售价为60元时的原利润,设售价应定为x 元,则每件的利润为(x -40)元,日销售量为20+10(60-x )5=(140-2x )件,根据日利润=每件利润×日销售量,即可得出关于x 的一元二次方程,解之取其较小值即可得出结论;(2)设该商品需要打a 折销售,根据销售价格不超过50元,列出不等式求解即可.【解答】解:(1)设售价应定为x 元,则每件的利润为(x -40)元,日销售量为20+10(60-x )5=(140-2x )件. 由题意,得(x -40)(140-2x )=(60-40)×20.整理,得x 2-110x +3 000=0.解得x 1=50,x 2=60(舍去).答:每件售价应定为50元;(2)设该商品需要打a 折销售.由题意,得62.5×a 10≤50. 解得a ≤8.答:该商品至少需打8折销售.5.列方程(组)解应用题:某驻村工作队,为带动群众增收致富,巩固脱贫攻坚成效,决定在该村山脚下,围一块面积为600 m 2的矩形试验茶园,便于成功后大面积推广.如图,茶园一面靠墙,墙长35 m ,另外三面用69 m 长的篱笆围成,其中一边开有一扇1 m 宽的门(不包括篱笆).求这个茶园的长和宽.解:设茶园AB 边的长为x m ,则BC 边的长为(69+1-2x ) m .根据题意,得x (69+1-2x )=600.整理,得x 2-35x +300=0.解得x 1=15,x 2=20.当x =15时,70-2x =40>35,不符合题意,舍去;当x =20时,70-2x =30<35,符合题意.答:这个茶园的长和宽分别为30 m ,20 m .6.如图,某城建部门计划在新建的城市广场的一块长方形空地上修建一个面积为1 200 m 2的停车场,将停车场四周余下的空地修建成同样宽的通道,已知整个长方形空地的长为50 m ,宽为40 m.(1)求四周通道的宽度;(2)某建筑公司希望用80万元的承包金额承揽这项工程,城建部门认为金额太高需要降价,经过两次协商,最终以51.2万元达成一致,若两次降价的百分率相同,求每次降价的百分率.解:(1)设四周通道的宽度为x m ,则停车场的长为(50-2x ) m ,宽为(40-2x ) m.由题意,得(50-2x )(40-2x )=1 200.整理,得x 2-45x +200=0.解得x 1=5,x 2=40.当x =5时,40-2x =40-2×5=30,符合题意;当x =40时,40-2x =40-2×40=-40<0,不符合题意,舍去.答:四周通道的宽度为5 m ;(2)设每次降价的百分率为a .由题意,得80(1-a )2=51.2.解得a 1=0.2=20%,a 2=1.8(不合题意,舍去).答:每次降价的百分率为20%.中考专题过关1.(2021·吉林中考)港珠澳大桥是世界上最长的跨海大桥,它由桥梁和隧道两部分组成,桥梁和隧道全长共55 km.其中桥梁长度比隧道长度的9倍少4 km.求港珠澳大桥的桥梁长度和隧道长度.解:设港珠澳大桥隧道长度为x km ,桥梁长度为y km.由题意,得⎩⎪⎨⎪⎧x +y =55,y =9x -4. 解得⎩⎪⎨⎪⎧x =5.9,y =49.1. 答:港珠澳大桥的桥梁长度和隧道长度分别为49.1 km 和5.9 km.2.(2021·郴州中考)“七·一”建党节前夕,某校决定购买A ,B 两种奖品,用于表彰在“童心向党”活动中表现突出的学生.已知A 奖品比B 奖品每件多25元,预算资金为1 700元,其中800元购买A 奖品,其余资金购买B 奖品,且购买B 奖品的数量是A 奖品的3倍.(1)求A ,B 奖品的单价;(2)购买当日,正逢该店搞促销活动,所有商品均按原价八折销售,故学校调整了购买方案:不超过预算资金且购买A 奖品的资金不少于720元,A ,B 两种奖品共100件,求购买A ,B 两种奖品的数量,有哪几种方案?解:(1)设A 奖品的单价为x 元,则B 奖品的单价为(x -25)元.由题意,得800x ×3=1 700-800x -25. 解得x =40.经检验,x =40是原方程的解,且符合题意.∴x -25=15.答:A 奖品的单价为40元,B 奖品的单价为15元;(2)设购买A 奖品的数量为m 件,则购买B 奖品的数量为(100-m )件.由题意,得⎩⎪⎨⎪⎧40×0.8×m ≥720,40×0.8×m +15×0.8×(100-m )≤1 700. 解得22.5≤m ≤25.∵m 为正整数,∴m 的值为23,24,25.∴有三种方案:①购买A 奖品23件,B 奖品77件;②购买A 奖品24件,B 奖品76件;③购买A 奖品25件,B 奖品75件.3.(2021·朝阳中考)某商场以每件20元的价格购进一种商品,规定这种商品每件售价不低于进价,又不高于38元,经市场调查发现:该商品每天的销售量y (件)与每件售价x (元)之间符合一次函数关系,如图所示.(1)求y 与x 之间的函数关系式;(2)该商场销售这种商品要想每天获得600元的利润,每件商品的售价应定为多少元?(3)设商场销售这种商品每天获利w (元),当每件商品的售价定为多少元时,每天销售利润最大?最大利润是多少?解:(1)设y 与x 之间的函数关系式为y =kx +b (k ≠0).由所给函数图象可知,⎩⎪⎨⎪⎧25k +b =70,35k +b =50. 解得⎩⎪⎨⎪⎧k =-2,b =120. ∴y 与x 之间的函数关系式为y =-2x +120(20≤x ≤38);(2)根据题意,得(x -20)(-2x +120)=600.整理,得x 2-80x +1 500=0.解得x =30或x =50(不合题意,舍去).答:每件商品的售价应定为30元;(3)∵y =-2x +120,∴w =(x -20)y=(x -20)(-2x +120)=-2x 2+160x -2 400=-2(x -40)2+800.∵-2<0,20≤x ≤38,∴当x =38时,w 最大=792.∴当每件商品的售价定为38元时,每天销售利润最大,最大利润是792元.。
一次函数与方程、不等式详细教案

一次函数与方程、不等式详细教案第一章:一次函数的概念与性质1.1 一次函数的定义介绍一次函数的定义:形式为y = kx + b(k、b为常数,k≠0)的函数。
强调一次函数的图像为直线。
1.2 一次函数的斜率与截距解释斜率k的意义:直线的倾斜程度。
解释截距b的意义:直线与y轴的交点。
1.3 一次函数的图像特点描述一次函数图像的形状、方向和位置。
第二章:一次函数的图像与解析式2.1 一次函数图像的绘制利用斜率和截距绘制一次函数的图像。
2.2 一次函数解析式的求解介绍求解一次函数解析式的方法:观察图像或给定的点。
2.3 一次函数图像与解析式的关系解释图像与解析式之间的联系。
第三章:一次函数的应用3.1 线性方程的解法介绍解线性方程的方法:代入法、消元法等。
3.2 实际问题中的一元一次方程举例说明一元一次方程在实际问题中的应用。
3.3 一次函数与不等式介绍一次函数与不等式的关系:图像与解集。
第四章:一元一次不等式的解法4.1 不等式的基本性质介绍不等式的加减乘除性质。
4.2 一元一次不等式的解法介绍解一元一次不等式的方法:同解变形、图像法等。
4.3 不等式的应用举例说明一元一次不等式在实际问题中的应用。
第五章:一次函数与方程的综合应用5.1 实际问题中的一次函数与方程组举例说明一次函数与方程组在实际问题中的应用。
5.2 一次函数与方程的综合解法介绍一次函数与方程的综合解法:代入法、图像法等。
5.3 一次函数与方程的拓展应用探讨一次函数与方程在其他领域的应用。
第六章:一次函数的图像与几何性质6.1 一次函数图像的交点介绍如何求出两条一次函数图像的交点。
强调交点在解析几何中的应用。
6.2 一次函数图像与坐标轴的交点解释一次函数与x轴、y轴的交点求解方法。
6.3 一次函数图像的距离和角度介绍如何利用一次函数图像求解两点间的距离和角度。
第七章:一次函数图像的变换7.1 一次函数图像的平移介绍如何对一次函数图像进行上下、左右平移。
专题:一次函数与方程、不等式【精品】

A
B
C
D
12.若以二元一次方程x+2y-b=0的解为坐标的点(x,y)都在直线y=-0.5x+b-1
上,则常数b等于( B )
A.0.5
B.2
C.-1
D.1
知识点4 一次函数与二元一次方程组
13.如图,直线y=ax-b与直线y=mx+1交于点A(2,3),则方程组maxxyyb1
的解为( A )
解:(1)x=-0.5.
(2)x=1.
(3)x<-0.5.
(4)0<x<2.
知识点3 一次函数与二元一次方程
10.直线l是以二元一次方程8x-4y=5的解为坐标所构成的直线,则该直线不经过的
象限是( B )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
11.下面四条直线,其中直线上每个点的坐标都是二元一次方程2x-y=2的解的
2.已知方程kx+b=0的解是x=3,则函数y=kx+b的图象可能是( C )
A
B
C
D
3.已知关于x的方程mx+n=0的解为x=-3,则直线y=mx+ n与x轴的交点坐标是 (-3,0) . 4.如图所示,已知直线y=ax-b,则关于x的方程 ax-b=1的解是 x=4 .
5.如图所示是一次函数y=kx+b在平面直角坐标系
14.若关于x,y的二元一次方程组
y=kx+b y=mx+n
的解为
x=1 y=2
则一次函数y=kx+b与y=mx+n的图象的交点坐标为( A )
A.(1,2) B.(2,1) C.(2,3) D.(1,3)
15.如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).
(1)求b的值;
中考方程(组)不等式(组)一次函数求最值的综合应用

专题8 一次函数的应用(即方程(组)不等式(组)和一次函数的综合应用)一次函数求最值,不同于二次函数求最值,它一般分三步:1.根据题目中的等式条件,建立一次函数关系式,确定其增减性;2.根据题目中的不等式条件,列不等式(组),求出自变量的取值范围;3.根据一次函数的增减性,恰当选取自变量的值,求函数的最值。
1.某商场同时购进甲、乙两种商品共200件,其进价和售价如下表,设其中甲种商品购进x件(1)若该商场购进这200件商品恰好用去17900元,求购进甲、乙两种商品各多少件?(2)若设该商场售完这200件商品的总利润为y元.①求y与x的函数关系式;②该商品计划最多投入18000元用于购买这两种商品,则至少要购进多少件甲商品?若售完这些商品,则商场可获得的最大利润是多少元?(3)实际进货时,生产厂家对甲种商品的出厂价下调a元(50<a<70)出售,且限定商场最多购进120件,若商场保持同种商品的售价不变,请你根据以上信息及(2)中的条件,设计出使该商场获得最大利润的进货方案.2.某销售商准备采购A、B两种型号的空气净化器,经调查,采购2台A型净化器和3台B型净化器共需花费11500元,且采购5台A型净化器和购进4台B型净化器所需的费用相等.(1)求每台A型、B型净化器的进价各是多少?(2)若销售商购进A型、B型净化器共50台,其中A型的台数不大于B型的台数,且不少于15台,设购进A型净化器a台.①求a的的取值范围;②已知A型的售价是2600元/台,B型的售价是3200元/台,设销售商售完50台净化器获得的利润为w,求w的最大值.3.某商场筹集资金12.8万元,一次性购进空调、彩电共30台,已知购买3台空调和2台彩电花费2.32万元,购买2台空调和4台彩电需花费2.48万元。
(1)求每台空调与彩电的进价分别是多少元?(2)已知每台空调的售价为6100元,每台彩电的售价为3900元,设商场计划购进空调x台,空调和彩电全部销售后商场获得的利润为y元,试求出y与x的函数关系式;(3)根据市场需要,这些空调、彩电很快全部售出,商场计划再次筹集资金12.8万元,一次性购买空调、彩电共30台,且可全部售出,在(2)的条件下,商场如何进货可获得最大利润,最大利润是多少元?4.某超市计划购进甲、乙两种玩具若干件,已知5件甲种玩具与3件乙种玩具的进价之和为231元,2件甲种玩具的进价与3件乙种玩具的进价之和为141元.(1)求每件甲种玩具和每件乙种玩具的进价分别是多少?(2)如果购进甲种玩具有优惠,优惠方法:购进甲种玩具超过20件,超出部分可以享受7折优惠,若购进x(x>0,且x为整数)件甲种玩具需花费y元,请求出y与x的函数关系式;(3)在(2)的条件下,超市决定在甲、乙两种玩具中选购其中一种,且数量超过20件,超市应选择购进哪种玩具最省钱.5.学校打算购进一批甲、乙两种办公桌若干张,若学校购进15张甲办公桌和10张乙办公桌共花费15500元,购进8张甲种办公桌的费用与购买5张乙办公桌的费用相等.(1)求甲、乙两种办公桌每张各多少元?(2)若学校购进甲、乙两种办公桌共30张,且甲种办公桌不多于乙种办公桌数量的2倍,请你设计一种费用最少的方案,并求出该方案所需费用.6.某服装公司招工广告承诺:熟练工人每月工资至少3000元.每天工作8小时,一个月工作25天.月工资底薪800元,另加计件工资.加工1件A型服装计酬16元,加工1件B型服装计酬12元.在工作中发现一名熟练工加工1件A型服装和2件B型服装需4小时,加工3件A型服装和1件B型服装需7小时.(工人月工资=底薪+计件工资)(1)一名熟练工加工1件A型服装和1件B型服装各需要多少小时?(2)一段时间后,公司规定:“每名工人每月必须加工A,B两种型号的服装,且加工A型服装数量不少于B型服装的一半”.设一名熟练工人每月加工A型服装a件,工资总额为W元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?7.某地新建的一个企业,每月产生1960吨污水,为保护环境,该企业计划购置污水处理器,并在如下两个型号中选择:已知商家售出的2台A型污水处理器和3台B型污水处理器的总价为44万元,售出的1台A型污水处理器和4台B型污水处理器的总价为42万元.(1)求每台A型污水处理器和B型污水处理器的价格分别是多少万元?(2)为确保将每月产生的污水全部处理完,该企业决定购买上述的两种污水处理器共10台,请你设计出最省钱的购买方案,请求出最低费用.答案自我诊断1.考点:一次函数的应用.分析:(1)甲种商品购进x件,乙种商品购进了200﹣x件,由总价=甲单价×甲商品数量+乙单价×乙商品数量,可得出关于x的一元一次方程,解出方程即可得出结论;(2)①根据利润=甲商品单件利润×数量+乙商品单件利润×数量,即可得出y关于x的函数解析式;②根据总价=甲单价×甲数量+乙单价×乙数量,列出关于x的一元一次不等式,解不等式即可得出x的取值范围,再根据y关于x函数的增减性即可解决最值问题;(3)根据利润=甲单件利润×数量+乙单件利润×数量,可得出y关于x的函数解析式,分x的系数大于0、小于0以及等于0三种情况考虑即可得出结论.解:(1)甲种商品购进x件,乙种商品购进了200﹣x件,由已知得:80x+100(200﹣x)=17900,解得:x=105,200﹣x=200﹣105=95(件).答:购进甲种商品105件,乙种商品95件.(2)①由已知可得:y=(160﹣80)x+(240﹣100)(200﹣x)=﹣60x+28000(0≤x≤200).②由已知得:80x+100(200﹣x)≤18000,解得:x≥100,∵y=﹣60x+28000,在x取值范围内单调递减,∴当x=100时,y有最大值,最大值为﹣60×100+28000=22000.故该商场获得的最大利润为22000元.(3)y=(160﹣80+a)x+(240﹣100)(200﹣x),即y=(a﹣60)x+28000,其中100≤x≤120.①当50<a<60时,a﹣60<0,y随x的增大而减小,∴当x=100时,y有最大值,即商场应购进甲、乙两种商品各100件,获利最大.②当a=60时,a﹣60=0,y=28000,即商场应购进甲种商品的数量满足100≤x≤120的整数件时,获利都一样.③当60<x<70时,a﹣60>0,y岁x的增大而增大,∴当x=120时,y有最大值,即商场应购进甲种商品120件,乙种商品80件获利最大.点评:本题考查了一次函数的应用、一元一次不等式的应用以及一元一次方程的应用,解题的关键是:(1)根据数量关系列出关于x的一元一次方程;(2)根据数量关系找出y关于x的函数关系式;(3)根据一次函数的系数分类讨论.本题属于中档题,难度不大,但过程比较繁琐,因此再解决该题是一定要细心.4.考点:一次函数的应用;二元一次方程组的应用;一元一次不等式的应用.分析:(1)设熟练工加工1件A型服装需要x小时,加工1件B型服装需要y小时,根据“一名熟练工加工1件A型服装和2件B型服装需4小时,加工3件A型服装和1件B型服装需7小时”,列出方程组,即可解答.(2)当一名熟练工一个月加工A型服装a件时,则还可以加工B型服装(25×8﹣2a)件.从而得到W=﹣8a+3200,再根据“加工A型服装数量不少于B型服装的一半”,得到a≥50,利用一次函数的性质,即可解答.解:(1)设熟练工加工1件A型服装需要x小时,加工1件B型服装需要y小时.由题意得:,解得:答:熟练工加工1件A型服装需要2小时,加工1件B型服装需要1小时.(2)当一名熟练工一个月加工A型服装a件时,则还可以加工B型服装(25×8﹣2a)件.∴W=16a+12(25×8﹣2a)+800,∴W=﹣8a+3200,又∵a≥,解得:a≥50,∵﹣8<0,∴W随着a的增大则减小,∴当a=50时,W有最大值2800.∵2800<3000,∴该服装公司执行规定后违背了广告承诺.。
人教版中考数学考点系统复习 第二章 方程(组)与不等式(组) 第一节 一次方程(组)及其应用

∴原方程组的解为y=1,将y=1 代入 2kx-3y<5 得 2×k×2-3<5,解得 k<2.
命题点 2:一次方程(组)的应用(近 3 年考查 15 次)
7.(数学文化)(2021·武汉第 7 题 3 分)我国古代数学名著《九章算术》
中记载:“今有共买物,人出八,盈三;人出七,不足四,问人数,物价
32 人.2 艘大船与 1 艘小船一次共可以满载游客 46 人.则 1 艘大船与 1
艘小船一次共可以满载游客的人数为
( B)
A.30
B.26
C.24
D.22
11.★(2022·武汉第 10 题 3 分)幻方是古老的数学问题,我国古代的《洛 书》中记载了最早的幻方——九宫格.将 9 个数填入幻方的空格中,要 求每一横行、 每一竖列以及两条对角线上的 3 个数之和相等,例如图① 就是一个幻方.图②是一个未完成的幻方,则 x 与 y 的和是 ( D ) A.9 B.10 C.11 D.12
14.(2020·仙桃第 12 题 3 分)篮球联赛中,每场比赛都要分出胜负,每 队胜 1 场得 2 分,负 1 场得 1 分.某队 14 场比赛得到 23 分,则该队胜 了__99__场.
15.(2020·黄冈第 19 题 6 分)为推广黄冈各县市名优农产品,市政府组 织创办了“黄冈地标馆”,一顾客在“黄冈地标馆”发现,如果购买 6 盒 羊角春牌绿茶和 4 盒九孔牌藕粉,共需 960 元,如果购买 1 盒羊角春牌 绿茶和 3 盒九孔牌藕粉共需 300 元,请问每盒羊角春牌绿茶和每盒九孔 牌藕粉分别需要多少元?
【分层分析】设购进创意文具袋 x 个,由题干信息①得购进笔记本为
((2x2+x+10)个,由题干信息②可列方程为 xx++(2(x2+x1+0)1=0)190.
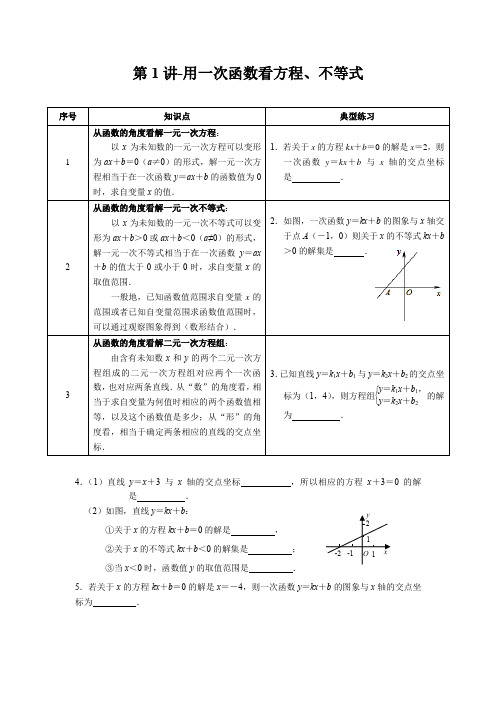
第1讲-用一次函数看方程、不等式
y2 1 1 O -2 -1x第1讲-用一次函数看方程、不等式序号知识点典型练习1从函数的角度看解一元一次方程:以x 为未知数的一元一次方程可以变形为ax +b =0(a ≠0)的形式,解一元一次方程相当于在一次函数y =ax +b 的函数值为0时,求自变量x 的值.1.若关于x 的方程kx +b =0的解是x =2,则一次函数y =kx +b 与x 轴的交点坐标是 .2从函数的角度看解一元一次不等式:以x 为未知数的一元一次不等式可以变形为ax +b >0或ax +b <0(a ≠0)的形式,解一元一次不等式相当于在一次函数y =ax+b 的值大于0或小于0时,求自变量x 的取值范围.一般地,已知函数值范围求自变量x 的范围或者已知自变量范围求函数值范围时,可以通过观察图象得到(数形结合). 2.如图,一次函数y =kx +b 的图象与x 轴交于点A (-1,0)则关于x 的不等式kx +b >0的解集是 .3从函数的角度看解二元一次方程组: 由含有未知数x 和y 的两个二元一次方程组成的二元一次方程组对应两个一次函数,也对应两条直线.从“数”的角度看,相当于求自变量为何值时相应的两个函数值相等,以及这个函数值是多少;从“形”的角度看,相当于确定两条相应的直线的交点坐标. 3.已知直线y =k 1x +b 1与y =k 2x +b 2的交点坐标为(1,4),则方程组⎩⎨⎧y =k 1x +b 1,y =k 2x +b 2的解为 .4.(1)直线y =x +3与x 轴的交点坐标 ,所以相应的方程x +3=0的解是 .(2)如图,直线y =kx +b :①关于x 的方程kx +b =0的解是 , ②关于x 的不等式kx +b <0的解集是 ; ③当x <0时,函数值y 的取值范围是 .5.若关于x 的方程kx +b =0的解是x =-4,则一次函数y =kx +b 的图象与x 轴的交点坐标为 .-21O yx-3Oxy -6 y 1=kx yy 2=ax+bx -2O -4 P6.已知一次函数y =kx +b 的图象,如图所示,当x <0时,y 的取值范围是( ).A .y >0B .y <0C .-2<y <0D .y <-27.如图,已知一次函数图象y =-2x -6,利用图象回答: (1)不等式-2x -6>0解集是 ,不等式-2x -6<0解集是 ;(2)函数图象与坐标轴围成的三角形的面积为 ; (3)当y =-4时,则x = ,当y =2时,则x = ;(4)如果y 的取值范围-4<y ≤2,则x 的取值范围 ;(5)如果x 的取值范围-3≤x ≤3,则y 的最大值是 ,最小值是 ; (6)若直线y =3x +4和直线y =-2x -6交于点A ,则点A 的坐标 .8.如图所示,已知直线y 2=ax +b 和直线y 1=kx 的图象交于点P ,利用图象回答:(1)关于二元一次方程组⎩⎨⎧y =ax+b ,y =kx的解是 ,则两直线的交点坐标是 ;(2)当y 2<y 1时,则x 的取值范围是 ; (3)当ax +b ≥kx 时,则x 的取值范围是 ; (4)当ax ≤kx -b 时,则x 的取值范围是 .9.(15海珠期末)直线y =x +1与直线y =-2x +a 的交点在第一象限,则a 的取值可以是( ). A .2B .1C .0D .-110.(15一中期末)如图,已知函数y1=3x+b和y2=ax-3的图象交于点P(-2,-5),则不等式3x+b>ax-3的解集为.11.(13太原期末改编)如图,直线l1:y1=x+1与直线l2:y2=mx+n相交于点P(1,b),直线y2与x轴交于点A(4,0).(1)求b的值并直接写出关于x,y的方程组1y xy mx n=+⎧⎨=+⎩的解;(2)求直线l2的表达式;(3)判断直线l3:y3=nx+m是否也经过点P?请说明理由.(4)若y3>y2>0,则x的取值范围是________________.12.已知一次函数y =kx+b的图象,如图所示,当y<0时,x的取值范围是().A.x>0B.x<0C.0<x<1D.x<113.(11广州)当实数x的取值使得x-2有意义时,函数y=4x+1中y的取值范围是().A.y≥-7B.y≥9 C.y>9D.y≤9 14.(15海珠期末)如图,直线y1=x+b与y2=kx-1相交于点P,点P的横坐标为-1,则关于x的不等式x+b>kx-1的解集在数轴上表示正确的是().A.B.C.D.15.如图,1l反映了某公司的销售收入与销售量的关系,2l反映了该公司产品的销售成本与销售量的关系,当该公司盈利(收入大于成本)时,销售量().A.小于3t B.大于3t C.小于4t D.大于4t第14题第15题16.(16天河期末)一次函数y1=kx+b与y2=x+a的图象如图,则下列结论①k<0;②a>0;③当x<4时,y1<y2;④b<0.其中正确的结论的个是().A.4个B.3个C.2个D.1个-2yO1x17.(16南充)小朱和爸爸从家步行去公园,爸爸先出发一直匀速前行,小朱后出发.家到公园的距离为2500m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象.(1)直接写出小朱所走路程s与时间t的函数关系式;(2)小朱出发多少时间与爸爸第三次相遇?(3)在速度都不变的情况下,小朱希望比爸爸早20min到达公园,则小朱在步行过程中停留的时间需作怎样的调整?18.(15衢州)高铁的开通,给衢州市民出行带来了极大的方便,“五一”期间,小卓卓和小越越相约到杭州市的某游乐园游玩,小卓卓乘私家车从衢州出发1小时后,小越越乘坐高铁从衢州出发,先到杭州火车站,然后再转出租车去游乐园(换车时间忽略不计),两人恰好同时到达游乐园,他们离开衢州的距离y(千米)与乘车时间t(小时)的关系如图所示.请结合图象解决下面问题:(1)高铁的平均速度是每小时多少千米?(2)当小越越达到杭州火车东站时,小卓卓距离游乐园还有多少千米?(3)若小卓卓要提前18分钟到达游乐园,问私家车的速度必须达到多少千米/小时?y (千米)游乐园t(小时)19.(14海珠期末)今年龙舟赛甲乙两队同时出发,其中甲、乙两队在比赛时,路程y (千米)与时间x (小时)的函数关系如图所示.甲队在出发2.5小时到达终点.(假设乙队速度不变)(1)写出比赛全程多少千米?谁先到达终点?乙队花多少时间到达终点? (2)求乙队何时追上甲队?(3)求在比赛过程中,甲乙两队何时相距最远?20.(1)(12恩施州)如图,直线y =kx +b 经过A (3,1)和B (6,0)两点,则不等式组0<kx +b<13x 的解集为 .(1) (2)(2)如图,直线y =kx +b 经过A (2,1),B (-1,-2)两点,则不等式组12x >kx +b >-2的解集为 .21.(15广雅期末)若直线y =-2x +m 与直线y =2x -1的交点在第四象限,则m 的取值范围是( ). A .m >-1 B .m <1C .-1<m <1D .-1≤m ≤1yA 2 1 xB 0 -1 -2 -3 -2-1 1 2 322.依照题意,解答下列问题:(1)如图①,已知直线y =2x +4与x 轴,y 轴分别交于A ,B 两点,请在图①中画出直线y =-12x +4,并探究两函数的图象与x 轴围成的三角形的特点;(2)如图②,已知点M 和点N 的坐标分别为(3,4)和(-2,-1),问在y 轴上是否存在一点P ,使△MNP 是以点M 或点N 为直角顶点的直角三角形?若存在,请求出P 的坐标;若不存在,请说明理由.y xB AO(图①))yx MN O(图②))第一讲-参考答案1.(2,0) 2.x >-13.⎩⎨⎧x =1,y =44.(1)(-3,0),x =-3; (2)①x =-2;②x <-2;③y <1. 5.(-4,0)6.D 7.(1)x <-3,x >-3; (2)9;(3)-1,-4; (4)-4≤x <-1;(5)0,-12;(6)(-2,-2).8.(1)⎩⎨⎧x =-4,y =-2,(-4,-2);(2)x >-4;(3)x ≤-4;(4)x ≥-4.9.A10.x >-211.(1)b =2,12x y =⎧⎨=⎩; (2)2833y x =-+;(3)由(2)可知m =23-,n =83,∴ y =83x -23,当x =1时,y =2.∴直线l 3:y =nx +m 也经过点P . (4)1<x <4.12.D 13.B 14.A 15.D 16.D17.解:(1)s =50(020)1000(2030)50500(3060)t t t t t ⎧⎪⎨⎪-⎩≤≤<≤<≤;(2)设小朱的爸爸所走的路程s 与步行时间t 的函数关系式为:s =kt +b ,则251000250k b b +=⎧⎨=⎩,解得30250k b =⎧⎨=⎩,则小朱的爸爸所走的路程与步行时间的关系式为:s =30t +250, 当50t -500=30t +250,即t =37.5min 时,小朱与爸爸第三次相遇; (3)30t +250=2500,解得,t =75,则小朱的爸爸到达公园需要75min , ∵小朱到达公园需要的时间是60min ,∴小朱希望比爸爸早20min 到达公园,则小朱在步行过程中停留的时间需减少5min .18.解:(1)v =2402-1=240(km/h ).答:高铁的平均速度是每小时240千米; (2)设乘坐高铁时路程与时间的关系式为y =kt +b ,当t =1时,y =0,当t =2时,y =240,得:⎩⎨⎧0=k +b 240=2k +b ,解得:⎩⎨⎧k =240b =-240,故把t =1.5代入y =240t -240,得y =120, 设乘坐私家车时路程与时间的关系式为y =at , 当t =1.5,y =120,得a =80,∴y =80t , 当t =2,y =160,216-160=56(千米), ∴小卓卓距离游乐园还有56千米; (3)把y =216代入y =80t ,得t =2.7,2.7-1860=2.4(小时),216 2.4=90(千米/时).∴小卓卓要提前18分钟到达游乐园,私家车的速度必须达到90千米/小时.19.解:(1)35千米;乙;3516小时; (2)对于乙队,x =1时,y =16,所以y =16x ,对于甲队,出发1小时后,设y 与x 关系为y =kx +b ,把x =1,y =20和x =2.5,y =35代入,得⎩⎨⎧20=k +b35=2.5k +b,则y =10x +10.联立方程组,⎩⎨⎧y =16x y =10x +10,得x =53,即:出发1小时40分钟后,乙队追上甲队; (3)1小时之内,两队相距最远距离是4千米,即当x =3516时,y 甲=10×3516+10=31.875,y 乙=35,y 甲-y 乙=35-31.875=3.125; 当x =1时,y 甲-y 乙=20-16=4;∵3.125<4,所以比赛过程中,甲、乙两队在出发后1小时相距最远.20.(1)3<x <6;(2)-1<x <2. 21.C22.(1)图略;用勾股定理的逆定理可以证明两函数与x 轴围成的三角形是一个直角三角形; (2)设P (0,y ),①当PM为斜边时,PN2+MN2=PM2,即(-2)2+(-1-y)2+25+25=32+(4-y)2,解得:y=-3,即P为(0,-3);②当PN为斜边时,PM2+MN2=PN2,即32+(4-y)2+25+25=(-2)2+(-1-y)2,解得:y=7,即P为(0,7);综上所述,在y轴上存在一点P,使△MNP是直角三角形,P为(0,-3)或(0,7).。
一次函数与方程、不等式

第9讲一次函数与方程、不等式考点·方法·破译1.一次函数与一元一次方程的关系:任何一元一次方程都可以转化成kx+b=0(k、b 为常数,k≠0)的形式,可见一元一次方程是一次函数的一个特例.即在y=kx+b中,当y =0时则为一元一次方程.2.一次函数与二元一次方程(组)的关系:⑴任何二元一次方程ax+by=c(a、b、c为常数,且a≠0,b≠0)都可以化为y=a cxb b -+的形式,因而每个二元一次方程都对应一个一次函数;⑵从“数”的角度看,解方程组相当于求两个函数的函数值相等时自变量的取值,以及这个函数值是什么;从“形”的角度看,解方程组相当于确定两个函数图像交点的坐标.3.一次函数与一元一次不等式的关系:由于任何一元一次不等式都可以转化成ax+b >0或ax+b<0(a、b为常数,a≠0)的形式,所以解一元一次不等式可以看成是当一次函数的函数值大于或小于0时,求相应自变量的取值范围.经典·考题·赏析【例1】直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b>k2x的解为()A.x>-1 B.x<-1 C.x<-2 D.无法确定【解法指导】由图象可知l1与l2的交点坐标为(-1,-2),即当x=-1时,两函数的函数值相等;当x>-1时,l2的位置比l1高,因而k2x>k1x+b;当当x<-1时,l1的位置比l2高,因而k2x<k1x+b.因此选A.【变式题组】01.(咸宁)直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x>k1x+b的解集为________.第1题图第2题图第3题图第4题图02.(浙江金华)一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a >0;③当x<3时,y1<y2中,正确的个数是()A.0 B.1 C.2 D.3 03.如图,已知一次函数y=2x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得不等式2x+b>ax-3的解集是________.04.(武汉)如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式12x>kx+b>-2的解集为_________.【例2】若直线l1:y=x-2与直线l2:y=3-mx在同一平面直角坐标系的交点在第一象限,求m的取值范围.【解法指导】直线交点坐标在第一象限,即对应方程组的解满足00x y >⎧⎨>⎩,从而求出m 的取值范围.解:23y x y mn =-⎧⎨=-⎩,∴51321x m m y m ⎧=⎪⎪+⎨-⎪=⎪+⎩,∵00x y >⎧⎨>⎩,∴5013201mm m⎧>⎪⎪+⎨-⎪>⎪+⎩,即10320m m +>⎧⎨->⎩,∴-1<m <32.【变式题组】01. 如果直线y =kx +3与y =3x -2b 的交点在x 轴上,当k =2时,b 等于( )A .9B .-3C .32-D .94-02. 若直线122y x =-与直线14y x a =-+相较于x 轴上一点,则直线14y x a =-+不经过( )A .第四象限B .第三象限C .第二象限D .第一象限 03. 两条直线y 1=ax +b ,y 2=cx +5,学生甲解出它们的交点坐标为(3,-2),学生乙因抄错了c 而解出它们的交点坐标为(34,14),则这两条直线的解析式为____________. 04. 已知直线y =3x 和y =2x +k 的交点在第三象限,则k 的取值范围是________.【例3】(四川省初二数学联赛试题)在直角坐标系中,若一点的纵横坐标都是整数,则称该点为整点,设k 为整数,当直线y =x -2与y =kx +k 的交点为整点时,k 的取值可以取( )A .4个B .5个C .6个D .7个 【解法指导】两直线的交点为整点即对应方程组的解均为整数.解:由2y x y kx k =-⎧⎨=+⎩得21221k x kk y k +⎧=⎪⎪-⎨+⎪=-⎪-⎩,∵两直线交点为整数, ∴x 、y 均为整数,又当x 为整数时,y 为整数, ∴21k k +-为整数即可,2213311111k k k k k k k ++-+=-=-=------, ∵k -1是整数,∴k -1=±1,±3时,x 、y 为整数, ∴k =-2,0,2,4. 所以选A .【变式题组】01. (广西南宁)从2,3,4,5这四个数中,任取两个数p 和q (p ≠q ),构成函数y =px -2和y =x +q ,并使这两个函数图象的交点在直线x =2的右侧,则这样的有序数对(p ,q )共有( ) A .12对 B .6对 C .5对 D .3对 02. (浙江竞赛试题)直线l :y =px (p 是不等于0的整数)与直线y =x +10的交点恰好是整点(横坐标和纵坐标都是整数),那么满足条件的直线l 有( ) A .6条 B .7条 C .8条 D .无数条 03. (荆州竞赛试题)点A 、B 分别在一次函数y =x ,y =8x 的图像上,其横坐标分别是a 、b (a >0,b >0).若直线AB 为一次函数y =kx +m 的图象,则当ba是整数时,求满足条件的整数k 的值. 【例4】已知x 、y 、z 都为非负数,满足x +y -z =1,x +2y +3z =4,记ω=3x +2y +z .求ω的最大值与最小值.【解法指导】将x 、y 、z 中的三个未知量选定一个看成已知,则关于x 、y 、z 的三元方程可变成关于x 、y 的二元方程,从而求出x 与y ,然后代入ω=3x +2y +z 中,可得ω与z 的一次函数关系式,然后再求出z 的取值范围,即可求出ω的最大值与最小值.解:由已知得:1243x y z x y z +=+⎧⎨+=-⎩,∴5234x z y z =-⎧⎨=-⎩,∴ω=3x +2y +z =3(5z -2)+2(3-4z )+z =8z .∵x 、y 、z 都为非负数,∴5203400z z z -⎧⎪-⎨⎪⎩≥≥≥,∴2354z ≤≤,∴ω的最大值为8×34=6,ω的最小值为8×25=165.【变式题组】01. (荆州竞赛试题)已知x 满足不等式:31752233x xx -+--≥,|x -3|-|x +2|的最大值为p ,最小值为q ,则pq 的值是( )A .6B .5C .-5D .-102. 已知非负数a 、b 、c 满足条件:3a +2b +c =4,2a +b +3c =5.设S =5a +4b +7c 的最大值为m ,最小值为n ,则n -m =________.03. (黄冈竞赛试题)若x +y +z =30,3x +y -z =50,x 、y 、z 均为非负数,则M =5x +4y+2z 的取值范围是( ) A .100≤M ≤110 B .110≤M ≤120 C .120≤M ≤130 D .130≤M ≤140【例5】已知直线l 1经过点(2,5)和(-1,-1)两点,与x 轴的交点是点A ,将直线y =-6x +5的图象向上平移4个单位后得到l 2,l 2与l 1的交点是点C ,l 2与x 轴的交点是点B ,求△ABC 的面积.【解法指导】设直线l 1的解析式为y =kx +b ,∵l 1经过(2,5),(-1,-1)两点, ∴251k b k b +=⎧⎨-+=-⎩,解得21k b =⎧⎨=⎩,∴y =2x +1,∴当y =0时,2x +1=0,x =12-,∴A (12-,0).又∵y =-6x +5的图象向上平移4个单位后得l 2,∴l 2的解析式为y =-6x +9, ∴当y =0时,-6x +9=0,x =32,∴B (32,0).∴2169y x y x =+⎧⎨=-+⎩,∴13x y =⎧⎨=⎩,∴C (1,3),∴AB =32-(12-)=2,∴S △ABC =12×2×3=3.演练巩固·反馈提高01. 已知一次函数y =32x +m ,和y =12-x +n 的图象交点A (-2,0),且与y 轴分别交于B 、C 两点,那么△ABC 的面积是( )A .2B .3C .4D .602. 已知关于x 的不等式ax +1>0(a ≠0)的解集是x <1,则直线y =ax +1与x 轴的交点是( )A .(0,1)B .(-1,0)C .(0,-1)D .(1,0)第3题图 第6题图03. 如图,直线y =kx +b 与x 轴交于点A (-4,0),则y >0时,x 的取值范围是( )A .x >-4B .x >0C .x <-4D .x <0 04. 直线kx -3y =8,2x +5y =-4交点的纵坐标为0,则k 的值为( )A .4B .-4C .2D .-205. 直线y =kx +b 与坐标轴的两个交点分别为A (2,0)和B (0,-3).则不等式kx +b +3≥0的解集为( ) A .x ≥0 B .x ≤0 C .x ≥2 D .x ≤206. 如图是在同一坐标系内作出的一次函数y 1、y 2的图象l 1、l 2,设y 1=k 1x +b 1,y 2=k 2x+b 2,则方程组111222y k x b y k x b ⎧⎨⎩=+,=+的解是( )A .22x y =-⎧⎨=⎩B .23x y =-⎧⎨=⎩C .33x y =-⎧⎨=⎩D .34x y =-⎧⎨=⎩07. 若直线y =ax +7经过一次函数y =4-3x 和y =2x -1的交点,则a =_________. 08. 已知一次函数y =2x +a 与y =-x +b 的图象都经过A (-2,0),且与y 轴分别交于B 、C 两点,则S △ABC =_________.09. 已知直线y =2x +b 和y =3bx -4相交于点(5,a ),则a =___________. 10.已知函数y =-x +m 与y =mx -4的图象交点在x 轴的负半轴上,则m 的值为__________.11.直线y =-2x -1与直线y =3x +m 相交于第三象限内一点,则m 的取值范围是___________. 12.若直线122a y x =-+与直线31544y x =-+的交点在第一象限,且a 为整数,则a =_________.13.直线l 1经过点(2,3)和(-1,-3),直线l 2与l 1交于点(-2,a ),且与y 轴的交点的纵坐标为7.⑴求直线l2、l1的解析式;⑵求l2、l1与x轴围成的三角形的面积;⑶x取何值时l1的函数值大于l2的函数值?14.(河北)如图,直线l1的解析式为y=-3x+3,l1与x轴交于点D,直线l2经过点A(4,0),B(3,32 ).⑴求直线l2的解析式;⑵求S△ADC;⑶在直线l2上存在异于点C的另一点P,使得S△ADP=S△ADC,求P点坐标.l2第14题图。
一次函数与一元一次方程和不等式的应用

龙文教育一对一个性化辅导教案学生林菁华学校年级年级次数第23次科目数学教师日期2016-5-6 时段19-21 课题一次函数与方程、不等式综合运用教学重点会根据已知条件确定一次函数的解析式;会根据一次函数的解析式求其图象与坐标轴的交点坐标;能根据一次函数的图象求二元一次方程组的近似解教学难点会根据已知条件确定一次函数的解析式;会根据一次函数的解析式求其图象与坐标轴的交点坐标;能根据一次函数的图象求二元一次方程组的近似解教学目标会根据已知条件确定一次函数的解析式;会根据一次函数的解析式求其图象与坐标轴的交点坐标;能根据一次函数的图象求二元一次方程组的近似解教学步骤及教学内容一、课前热身:1、检查学生的作业,及时指点;2、通过沟通了解学生的思想动态和了解学生的本周学校的学习内容。
3、课前小测二、内容讲解:三、课堂小结:带领学生对本次课授课内容进行回顾、总结四、作业布置:布置适量的作业学生课外进行巩固管理人员签字:日期:年月日作业布置1、学生上次作业评价:○好○较好○一般○差备注:2、本次课后作业:课堂小结家长签字:日期:年月日知识重现一、一次函数与一元一次方程的关系直线y b k 0kx =+≠()与x 轴交点的横坐标,就是一元一次方程b 0(0)kx k +=≠的解。
求直线y b kx =+与x 轴交点时,可令0y =,得到方程b 0kx +=,解方程得x bk=-,直线y b kx =+交x 轴于(,0)b k -,bk -就是直线y b kx =+与x 轴交点的横坐标。
二、一次函数与一元一次不等式的关系任何一元一次不等式都可以转化为a b 0x +>或a b 0x +<(b a 、为常数,0a ≠)的形式,所以解一元一次不等式可以看作:当一次函数值大(小)于0时,求自变量相应的取值范围。
三、一次函数与二元一次方程(组)的关系一次函数的解析式y b k 0kx =+≠()本身就是一个二元一次方程,直线y b k 0kx =+≠()上有无数个点,每个点的横纵坐标都满足二元一次方程y b k 0kx =+≠(),因此二元一次方程的解也就有无数个。
初二数学-一次函数、方程(组)及不等式的综合应用

不等式在实际问题中的应用
方案优选问题 在多种方案中选择最优方案,可以通过建立和解决不等式来比较各种方案的优劣。 最大值最小值问题 在生产、生活中,经常需要求某个量的最大值或最小值,可以通过建立不等式来解决。 经济问题 在经济学中,价格、成本、利润等变量之间存在不等关系,可以通过建立和解决不等式来分析经济问题。
建立实际问题与数学模型的联系
实际问题的数学建模与解决
通过分析实际问题,将问题转化为数学模型,如线性方程、不等式或函数表达式。
利用数学知识和方法求解数学模型,得出实际问题的解决方案。
实际问题的数学解决方案
将数学解决方案应用到实际问题中,验证其可行性和有效性。
实际问题的应用与验证
综合应用题的解题思路与技巧
方程组在实际问题中的应用
在经济学中,方程组被用来描述和解决各种问题,如供需关系、成本和收益等。
经济问题
在解决物理问题时,经常需要建立和解决方程组,例如在力学、电磁学和热力学等领域。
物理问题
在航天工程中,需要建立复杂的方程组来描述和解决飞行器的轨道、速度和加速度等问题。
航天工程
PART THREE
初二数学-一次函数、方程(组)及不等式的综合应用
答辩学生:XXX 指导老师:XXX
Contents
目 录
目录
绪论
研究 方法
PART ONE
一次函数的应用
3.1关键技术 3.2技术难点 3.3案例分析
一次函数的定义与性质
一次函数是形如$y=kx+b$的函数,其中$k$和$b$是常数,且$k neq 0$。 一次函数的图像是一条直线,其斜率为$k$,截距为$b$。 一次函数的性质包括单调性、奇偶性等,这些性质在解决实际问题中具有重要意义。
八上 一次函数与方程组、不等式 知识点+例题+练习 (非常好 分类全面)
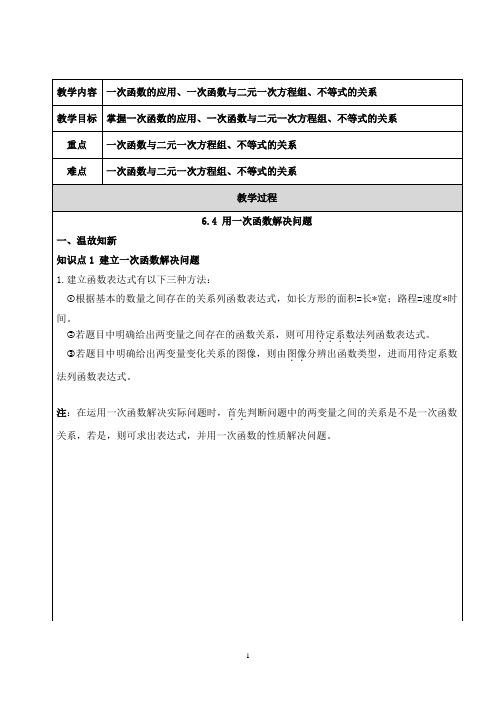
例1 从2014年起,中国的鞋号已“变脸”,新的国家标准要求鞋号用毫米数标注.据了解大多数市民还不了解此新标准,小明对新旧鞋号的标注变化进行了对比研究,发现新标准鞋子毫米数y与旧鞋号x之间存在着一次函数关系,并得到相关数据如下:旧鞋号 x 36 38 40新标准毫米数y230 240 250(1)请你帮助小明根据上述数据归纳出新标准毫米数与旧鞋号标注之间的换算关系式,并用一句简明的数学语言来表示;(2)如果小明的爸爸穿的一双42号凉鞋坏了,准备买一双同样尺寸的新凉鞋,那么应买一双多少毫米数的新凉鞋?例2 某种拖拉机的油箱可储油40L,加满油并开始工作后,•油箱中的余油量y(L)与工作时间x(h)之间为一次函数关系,如图所示.(1)求y与x的函数解析式.(2)一箱油可供拖位机工作几小时?知识点2 图像法解决实际问题注:读图时一定要明确横纵坐标表示的量所代表的意义。
例3 某公司推销一种产品,设x(件)是推销产品的数量,y(元)是推销费,如图表示了公司每月付给推销员推销费的两种方案,看图解答下列问题:(1)求yl 与y2的函数表达式;(2)解释图中表示的两种方案是如何付推销费的;(3)如果你是推销员,应如何选择付费方案.二、典型例题题型1 运用一次函数的关系解决生活中的实际问题例 1 如图,两摞相同规格的饭碗整齐地叠放在桌面上,请根据图中给的数据信息,解答下列问题:(1)求整齐摆放在桌面上饭碗的高度y(cm)与饭碗数x(个)之间的一次函数表达式;(2)若桌面上有12个饭碗,整齐叠放成一摞,求出它的高度;(3)若桌面上有若干个饭碗,整齐叠放成一摞,已测得它的高度为37.5cm,你能求出此时有多少个饭碗吗?题型2利用图表信息解决实际问题例2 某厂家生产两种款式的布质环保购物袋,每天共生产4500个,两种购物袋的成本和售价如下表,设每天生产A种购物袋x个,每天共获利y元.(1)求y与x的函数关系式;(2)如果该厂每天最多投入成本10000元,那么每天最多获利多少元?题型3 建立一次函数模型解决实际问题例3 某下岗职工购进一批苹果到农贸市场零售,已知买出的苹果数量x(kg)与收入y(元)的关系如下表:在平面直角坐标系中描点,观察点的分布情况,探求收入y(元)与买出数量x(kg)之间的函数关系式。
一次函数与一元一次方程、不等式

2
易错小结
-1<x<2
易错点:利用函数图象解不等式时,对函数值和点的坐 标的关系不理解导致出错(数形结合思想).
例1
利用函数图象解出x:3x-2=x+4.
先将方程化为ax+b=0的形式, 再在坐标系中画出函数y=ax+ b的图象,然后观察出直线y= ax+b与x轴的交点坐标,从而 取定所求x的值.
导引:
由3x-2=x+4得2x-6=0画函 数y=2x-6的图象,如图所示, 由图可知,直线y=2x-6与x轴的交点为(3,0), 所以x=3.
3
C
已知一次函数y=2x+n的图象如图所示,则方程2x+n=0的解可能是( ) A.x=1 B.x= C.x=- D.x=-1
4
C
【2017·湘潭】一次函数y=ax+b的图象如图所示,则不等式ax+b≥0的解集是( ) A.x≥2 B.x≤2 C.x≥4 D.x≤4
5
B
【2017·菏泽】如图,函数y1=-2x与y2=ax+3的图象相交于点A(m,2),则关于x的不等式-2x>ax+3的解集是( ) A.x>2 B.x<2 C.x>-1 D.x<-1
D
【中考·合肥】已知方程 x+b=0的解是x= -2,下列可能为直线y= x+b的图象的是 ( )
2
C
如图,若一次函数y=-2x+b的图象交y轴于点A(0,3),则不等式-2x+b>0的解集为( ) A.x> B.x>3 C.x< D.x<3
2
已知小刚从家出发7分钟时与家的距离是1 200米, 从上公交车到他到达学校共用10分钟.下列说法: ①公交车的速度为400米/分钟; ②小刚从家出发5分钟时乘上公交车; ③小刚下公交车后跑向学校的速度是100米/分钟; ④小刚上课迟到了1分钟.其中正确的有( ) A.4个 B.3个 C.2个 D.1个
一次函数与一元一次方程和不等式同步辅导(含答案)--绝对经典

11.3.1 -11.3.2 一次函数与一元一次方程和不等式重点知识讲解1.一元一次方程ax+b=0(a≠0)与一次函数y=ax+b(a≠0)的关系(1)一元一次方程ax+b=0(a≠0)是一次函数y=ax+b(a≠0)的函数值为0时的特殊情形.(2)直线y=ax+b与x轴交点的横坐标就是一元一次方程ax+b=0的解x=-ba。
2.一元一次不等式与一次函数的关系(1)一元一次不等式ax+b>0或ax+b<0(a≠0)是一次函数y=ax+b(a≠0)•的函数值不等于0的情形.(2)直线y=ax+b上使函数值y>0(x轴上方的图像)的x的取值范围是ax+b>0的解集;使函数值y<0(x 轴下方的图像)的x的取值范围是ax+b<0的解集.经验与方法技巧1.利用一次函数求一元一次方程的解题步骤(1)将一元一次方程化成ax+b=0的形式.(2)画出y=ax+b的图像,确定其与x轴交点的横坐标.2.利用一次函数求一元一次不等式的解集的技巧根据不等式的特点,灵活采用求解方法:(1)利用一个一次函数;(2)•利用两个一次函数.典型例题例1画出y=-3x+5的图象,利用图像求方程-3x+5=0的解.解析取点(0,5),(53,0),图像如图所示.∵直线y=-3x+5与x轴交点的横坐标为53,∴方程-3x+5=0的解为x=53。
评注画函数图像时要准确,求出直线y=-3x+5与x•轴交点的横坐标即为方程的解.例2画出函数y=-3x+12的图像,利用图像求:(1)不等式-3x+12>0的解集.(2)不等式-3x+12≤0的解集.(3)如果y的值在-6≤y≤6的范围内,那么相应的x的值在什么范围内?解析取点(0,12),(4,0),作出函数图像,如图所示,由图像可以看出:(1)当y>0时,x的取值范围为x<4,∴不等式-3x+12>0的解集为x<4.(2)当y≤0时,x的取值范围为x≥4.∴不等式-3x+12≤0的解集为x≥4.(3)当-6≤y≤6时,x的取值范围为2≤x≤6.评注借助图像求不等式的解集,关键是要清楚以下几点:①y>0时,x•的取值范围就是x轴上方的图像所对应的x的取值范围.②y<0时,x的取值范围就是x•轴下方的图像所对应的x的取值范围.③y=0时,x的值就是图像与x轴交点的横坐标.④当y>a或y<a(a≠0)时,应先确定当y=a时对应的x值,然后再进一步确定x的取值范围.例3若y1=-x+3,y2=3x-4,当x取何值时,y1<y2?解析∵y1<y2,∴-x+3<3x-4,解得x>74,∴当x>74时,y1<y2.评注此题是两个一次函数之间的关系,可以直接借助一元一次不等式求出x的取值范围.教材例题习题的变形题例(P41例2)用画图像的方法解下列各题:- 1 -(1)解不等式:5x+4>2x+10.(2)解方程:5x+4=2x+10.解析(1)如图,原不等式可化为3x-6>0,画出直线y=3x-6,由图像可以看出,当x>2时,这条直线上的点在x轴的上方,即这时y=3x-6>0,所以不等式的解集为x>2.(2)原方程可化为3x-6=0.由图像可以看出,y=3x-6与x轴交点的横坐标为2,所以原方程的解为x=2.评注①从函数的角度看问题,能发现一次函数与一元一次不等式、•一元一次方程之间的联系,体现了数形结合的思想.②本题求不等式的解集时,还可将不等式的两边分别看作两个一次函数,画出两条直线,比较直线上点的位置的高度,也可求得不等式的解集.学科内综合题例1甲、乙两辆摩托车分别从相距20km的A,B两地出发,相向而行,图中的L1,L2分别表示甲、乙两辆摩托车离开A地的距离s(km)与行驶时间t(h)•之间的函数关系.(1)哪辆摩托车的速度较快?(2)经过多长时间,甲摩托车行驶到A,B两地的中点?解析(1)由图像可以看出,甲摩托用了0.6h行驶了20km,而乙摩托车用了0.•5h行驶了20km,所以乙摩托车的速度较快.(2)设L1的关系式为y=kx,把x=0.6,y=20代入,得20=0.6k,解得k=1003,∴y=1003x.当y=10时,10=1003x.所以经过0.3h,甲摩托车行驶到A,B两地的中点.评注本题第(1)题是比较速度的大小,这一点可以通过图像提供的数量直接分析出来.第(2)题的关键是要分析出甲摩托车行驶到中点时所行驶的路程为10km.例2已知y=12x-2.(1)x取何值时,y>0?(2)x取何值时,y<0?(3)当x>4时,求y的取值范围.解析作出y=12x-2的图像,如图所示.(1)当x>4时,y>0.(2)当x<4时,y<0.(3)当x>4时,y的取值范围是y>0.评注本题可以通过图像直观地得出结论.综合应用题例1某单位计划在新年期间组织员工到某地旅游,参加旅游的人数估计为10~20人,甲、乙两家旅行社的服务质量相同,且报价都是每人200元.经过协商,•甲旅行社表示可给予每位游客七五折优惠;乙旅行社表示可先免去一位游客的旅游费用,再给其余游客八折优惠.该单位选择哪一家旅行社支付的旅游费用较少?解析设该单位参加这次旅游的人数是x人,选择甲旅行社时所需的费用为y1元,选择乙旅行社时所需的费用为y2元,则y1=200×0.75x,即y1=150x;y2=200×0.8(x-1),即y2=160x-160.由y1=y2,得150x=160x-160,解得x=16;- 2 -由y1>y2,得150x>160x-160,解得x<16;由y1<y2,得150x<160x-160,解得x>16.因为参加旅游的人数估计为10~20人,所以,当x=16时,甲、•乙两家旅行社的收费相同;当17≤x≤20时,选择甲旅行社费用较少;当10≤x≤15时,选择乙旅行社费用较少.评注已知前提条件,设计方案是解决实际问题的一种常见形式.明确每一种收费方式占优势时对应的自变量的取值范围是解决此类问题的关键,•借助不等式就可确定自变量的取值范围.例2兄弟俩赛距,哥哥先让弟弟跑9m,然后自己才开始跑.已知弟弟每秒跑3m,•哥哥每秒跑4m.列出函数关系式,作出函数图像,观察图像回答下列问题:(1)何时弟弟跑在哥哥前面?(2)何时哥哥跑在弟弟前面?(3)谁先跑过20m?谁先跑过100m?解析设哥哥跑了ts,则哥哥所跑的路程与时间的关系式为s1=4t;弟弟所跑的路程与时间的关系为s2=3t+9.图像如图所示.当s1=s2时,4t=3t+9,t=9.(1)当0≤t<9时,弟弟跑在哥哥的前面.(2)当t>9时,哥哥跑在弟弟的前面.(3)∵20<36,∴弟弟先跑过20m.∵100>36,∴哥哥先跑过100m.评注本题可以从时间或路程两个角度进行分析.在同一时间内,谁跑的路程远,谁就在前面,谁就先跑过20m,100m.也可比较他们各自所用的时间,谁用的时间短,•谁就先跑过.本题既可以通过计算来进行比较,也可通过图像直观地进行判断.创新题例(探究题)我边防局接到情报,在离海岸5海里处有一可疑船只A•正向公海方向行驶,边防局迅速派出快艇B追赶.图中L1,L2分别表示两船相对于海岸的距离s(海里)与追赶时间t(min)之间的关系.(1)A,B哪一个的速度快?(2)至少要用多长时间才能追上可疑船只A?解析由图像可确定L表示快艇B的图像,L表示可疑船只A的图像.(1)快艇10min行驶了5海里,所以其速度为5÷10=0.5(海里/min).可疑船只10min行驶了7-5=2(海里),所以其速度为2÷10=0.2(海里/min).所以快艇B的速度快.(2)设L1的关系式为y1=kx,把(10,5)代入,得5=10k,解得k=0.5,∴y1=0.5x.设L2的关系式为y2=kx+5,把(10,7)代入,得7=10k+5,解得k=0.2,∴y2=0.2x+5.当y1≥y2,即0.5x≥0.2x+5时,0.3x≥5,x≥503.所以至少需要503min,快艇才能追上可疑船只.中考题例(2004年苏州卷)如图,平面直角坐标系中画出了函数y=kx+b的图像.(1)根据图像,求k和b的值.(2)在图中画出函数y=-2x+2的图像.(3)求x的取值范围,使函数y=kx+b的函数值大于函数y=-2x+2的函数值.解析(1)∵直线y=kx+b经过点(-2,0),(0,2).- 3 -- 4 -∴02,20,k b b =-+⎧⎨=+⎩ 解得1,2,k b =⎧⎨=⎩ ∴y=x+2.(2)y=-2x+2经过(0,2),(1,0),图像如图所示.(3)当y=kx+b 的函数值大于y=-2x+2的函数值时,也就是x+2>-2x+2,解得x>0,•即x 的取值范围为x>0.11.3.1 一次函数与一元一次方程同步练习[要点再现]1.由于任何一元一次方程都可以转化为 的形式,所以解一元一次方程可以转化为:当 时,求 的值。
培优专题(四) 一次函数与方程、不等式的实际应用问题
数学
人教版八年级下册
课件目录
首
页
末
页
2.某市出租车计费方法如图1所示,x(km)表示行驶里程,y(元)表 示车费,请根据图象回答下列问题:
图1 (1)出租车的起步价是多少元?当x>3时,求y关于x的函数解析 式;
数学
人教版八年级下册
课件目录
首
页
末
页
(2)若某乘客有一次乘出租车的车费为32元,求这位乘客乘车的 里程.
数学
人教版八年级下册
课件目录 首 页 末 页
8.[2014· 番禺]某化妆品公司每月付给销售人员的工资有两种方 案. 方案一:没有底薪,只拿销售提成; 方案二:底薪加销售提成. 已知每件商品的销售提成方案二比方案一少7元.设销售人员 月销售x件商品时的月工资为y元.如图4,l1表示方案一中y与x
函数关系的图象,l2表示方案二中y与x函数关系的图象.解答
(2)若某人计划在商场购买价格为5880元的电视机一台,请分析选 哪种方案更省钱. 解:(1)方案一:y=0.95x;方案二:y=0.9x+300; (2)∵0.95×5880=5586(元),0.9×5880+300=5592(元),∴选择方
案一更省钱.
数学
人教版八年级下册
课件目录 首 页 末 页
12
22
30
设按计划全部售出后的总利润为y百元,其中批发量为x吨,且 加工销售量为15吨.
(1)求y与x之间的函数关系式;
(2)若零售量不超过批发量的4倍,求该生产基地按计划全部售 完荸荠后获得的最大利润.
数学
人教版八年级下册
课件目录 首 页 末 页
解: (1)依题意可知零售量为 (25- x)吨,则 y= 12x+ 22(25- x)+ 30×15, ∴ y=- 10x+ 1 000; (2)依题意有: x≥ 0, 25- x≥0, 解得:5≤x≤25, 25- x≤4x, ∵- 10< 0,∴ y 随 x 的增大而减小. ∴当 x= 5 时, y 有最大值,且 y 最大值= 950. ∴最大利润为 950 百元.
中考数学 精讲篇 考点系统复习 第二章 方程(组)与不等式(组) 第一节 一次方程(组)及其应用

5.(数学文化)《九章算术》是中国古代数学著作之一,书中有这样的一 个问题:五只雀、六只燕共重一斤,雀重燕轻,互换一只,恰好一样重.问: 每只雀、燕的质量各为多少?设一只雀的质量为 x 斤,一只燕的质量为 y
5x+6y=1, 斤,则可列方程组为__4x+y=5y+__x.
【考情分析】广西近 6 年主要考查解一元一次方程或二元一次方程组, 应用一元一次方程或二元一次方程组解决简单的实际问题,难度小,分 值 3-10 分,常在解答题中与不等式、一次函数的实际应用结合考查.
x=1, 则方程组的解为y=-1.
x-3y=-2, 5.(2020·玉林第 20 题 6 分)解方程组:2x+y=3.
x-3y=-2①, 解:2x+y=3②. ①+②×3 得 x+6x=-2+3×3, 解得 x=1, 将 x=1 代入②得 2+y=3, 解得 y=1.
x=1, 则方程组的解为y=1.
根据题意可列方程组为
y=3x-2, A.y=2x+9
y=3x-2, C.y=2x-9
y=3(x-2), B.y=2x+9
y=3(x-2), D.y=2x-9
( B)
7.(2021·桂林第 24 题 8 分)为了美化环境,建设生态桂林,某社区需 要进行绿化改造,现有甲、乙两个绿化工程队可供选择,已知甲队每天 能完成的绿化改造面积比乙队多 200 m2,甲队与乙队合作一天能完成 800 m2 的绿化改造面积. (1)甲、乙两工程队每天各能完成多少 m2的绿化改造面积? (2)该社区需要进行绿化改造的区域共有 12 000 m2,甲队每天的施工费 用为 600 元,乙队每天的施工费用为 400 元,比较以下三种方案: ①甲队单独完成;②乙队单独完成;③甲、乙两队全程合作完成. 哪一种方案的施工费用最少?
专题4 一次函数与方程、不等式的关系-重难点题型(举一反三)(浙教版)(解析版)

专题5.4 一次函数与方程、不等式的关系-重难点题型【浙教版】【知识点1 一次函数与一元一次方程、不等式的关系】【例1】(2020秋•包河区期中)根据一次函数y=kx+b的图象,直接写出下列问题的答案:(1)关于x的方程kx+b=0的解;(2)代数式k+b的值;(3)关于x的方程kx+b=﹣3的解.【解题思路】(1)利用函数图象写出函数值为0时对应的自变量的值即可;(2)利用函数图象写出x=1时对应的函数值即可(3)利用函数图象写出函数值为﹣3时对应的自变量的值即可.【解答过程】解:(1)当x=2时,y=0,所以方程kx+b=0的解为x=2;(2)当x=1时,y=﹣1,所以代数式k+b的值为﹣1;(3)当x=﹣1时,y=﹣3,所以方程kx+b=﹣3的解为x=﹣1.【变式1-1】(2021秋•泰兴市校级期末)已知一次函数y=kx+1与y=−12x+b的图象相交于点(2,5),求关于x的方程kx+b=0的解.【解题思路】首先将(2,5)点代入一次函数解析式求出k,b的值,进而解方程得出答案.【解答过程】解:∵一次函数y=kx+1与y=−12x+b的图象相交于点(2,5),∴5=2k+1,5=−12×2+b,解得:k=2,b=6,则kx+b=0为:2x+6=0,解得:x=﹣3.【变式1-2】一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x的方程kx+b=4的解为多少?【解题思路】先求出函数的解析式,再把y=4代入,即可求出x.【解答过程】解:把(0,1)和(2,3)代入y=kx+b得:{b=12k+b=3,解得:k=1,b=1,即y=x+1,当y=4时,x+1=4,解得:x=3,∴方程kx+b=4的解为x=3.【变式1-3】已知一次函数y=kx﹣6的图象如图(1)求k的值;(2)在图中的坐标系中画出一次函数y=﹣3x+3的图象(要求:先列表,再描点,最后连线);(3)根据图象写出关于x的方程kx﹣6=﹣3x+3的解.【解题思路】(1)将点(4,0)代入y=kx﹣6,利用待定系数求出k的值;(2)利用描点法画出一次函数y=﹣3x+3的图象;(3)根据图象写出它们的交点坐标,即可得到关于x的方程kx﹣6=﹣3x+3的解.【解答过程】解:(1)∵一次函数y=kx﹣6的图象过点(4,0),∴4k﹣6=0,∴k=3 2;(2)列表:描点:在平面直角坐标系中描出两点(0,3)、(1,0),连线:过点(0,3)、(1,0)画直线,得出一次函数y=﹣3x+3的图象;(3)一次函数y=kx﹣6与y=﹣3x+3的图象交于点(2,﹣3),则关于x的方程kx﹣6=﹣3x+3的解为x=2.【题型2 一次函数的与一元一次不等式(数形结合)】【例2】(2021春•高明区期末)一次函数y1=ax+b与y2=cx+d的图象如图所示,下列说法:①对于函数y1=ax+b来说,y随x的增大而增大;②函数y=ax+d不经过第二象限;③不等式ax﹣d≥cx﹣b的解集是x≥4;④a﹣c=14(d﹣b),其中正确的是()A.①②③B.①③④C.②③④D.①②④【解题思路】根据题意和函数图象中的数据,可以判断各个小题中的结论是否成立,从而可以解答本题.【解答过程】解:由图象可得,对于函数y=ax+b来说,y随x的增大而增大,故①正确;a>0,d>0,则函数y=ax+d经过第一、二、三象限,不经过第四象限,故②不正确;由ax﹣d≥cx﹣b可得ax+b≥cx+d,故不等式ax﹣d≥cx﹣b的解集是x≥4,故③正确;4a+b=4c+d可以得到a﹣c=14(d﹣b),故④正确;故选:B.【变式2-1】(2021•安徽模拟)已知一次函数y1=kx+3(k为常数,且k≠0)和y2=x﹣3.当x<2时,y1>y2,则k的取值范围是()A.﹣2≤k≤1且k≠0B.k≤﹣2C.k≥1D.﹣2<k<1且k≠0【解题思路】解不等式kx+3>x﹣3,根据题意得出k﹣1<0且−6k−1≥2且k≠0,解此不等式即可.【解答过程】解:∵一次函数y1=kx+3(k为常数,且k≠0)和y2=x﹣3,当x<2时,y1>y2,∴kx+3>x﹣3,∴kx﹣x>﹣6,∴k﹣1<0且−6k−1≥2且k≠0,当k﹣1<0时,−6k−1≥2时,k≥﹣2,所以不等式组的解集为﹣2≤k<1且k≠0;当k=1时,也成立,故k的取值范围是﹣2≤k≤1且k≠0,故选:A .【变式2-2】(2021春•盐湖区校级期末)我们知道,若ab >0.则有{a >0b >0或{a <b <0.如图,直线y =kx +b 与y =mx +n 分别交x 轴于点A (﹣0.5,0)、B (2,0),则不等式(kx +b )(mx +n )>0的解集是( )A .x >2B .﹣0.5<x <2C .0<x <2D .x <﹣0.5或x >2【解题思路】由若不等式(kx +b )(mx +n )>0,则{kx +b >0mx +n >0或{kx +b <0mx +n <0,然后分类讨论,分别根据函数图象求得解集.【解答过程】解:∵若ab >0.则有{a >0b >0或{a <0b <0,∴若不等式(kx +b )(mx +n )>0,则{kx +b >0mx +n >0或{kx+b <0mx +n <0.当{kx +b >0mx +n >0,由图得:{x <−0.5x >2,此时该不等式无解.当{kx +b <0mx +n <0,由图得:{x >−0.5x <2,此时不等式组的解集为﹣0.5<x <2.综上:﹣0.5<x <2.故选:B .【变式2-3】(2021春•中山市期末)一次函数y 1=ax +b 与y 2=cx +d 的图象如图所示,下列说法:①对于函数y 1=ax +b 来说,y 随x 的增大而减小;②函数y =ax +d 的图象不经过第一象限;③不等式ax +b >cx +d 的解集是x >3;④d ﹣b =3(a ﹣c ).其中正确的有( )A .①③B .②③④C .①②④D .②③【解题思路】仔细观察图象:①根据函数图象直接得到结论;②观察函数图象可以直接得到答案;③以两条直线的交点为分界,哪个函数图象在上面,则哪个函数值大;④根据两直线交点可以得到答案.【解答过程】解:由图象可得:对于函数y 1=ax +b 来说,y 随x 的增大而减小,故①说法正确;由于a <0,d <0,所以函数y 2=ax +d 的图象经过第二,三,四象限,即不经过第一象限,故②说法正确,由图象可得当x <3时,一次函数y 1=ax +b 图象在y 2=cx +d 的图象上方,∴ax +b >cx +d 的解集是x <3,故③说法不正确;∵一次函数y 1=ax +b 与y 2=cx +d 的图象的交点的横坐标为3,∴3a +b =3c +d∴3a ﹣3c =d ﹣b ,∴d ﹣b =3(a ﹣c ).故④说法正确,故选:C .【题型3 一次函数的与一元一次不等式(取值范围)】【例3】(2021春•海淀区期末)在平面直角坐标系xOy 中,直线l :y 1=x +1与直线l 2:y 2=2x ﹣2交于点A .(1)求点A 的坐标;(2)当y 1>y 2时,直接写出x 的取值范围;(3)已知直线l 3:y 3=kx +1,当x <3时,对于x 的每一个值,都有y 3>y 2,直接写出k 的取值范围.【解题思路】(1)由直线l :y 1=x +1与直线l 2:y 2=2x ﹣2交于点A ,故可联立方程组:{y =x +1,y =2x −2.得{x =3y =4,故A (3,4).(2)根据函数图象,可知:当y 1>y 2时,x <3.(3)当x <3时,对于x 的每一个值,都有y 3>y 2,故当x <3,y 3﹣y 2>0恒成立,得1≤k ≤2.【解答过程】解:(1)由题意得:{y =x +1,y =2x −2.解得:{x =3,y =4.∴A (3,4).(2)如图,当y 1>y 2时,x <3.(3)当x <3,y 3>y 2恒成立,则x <3,y 3﹣y 2>0恒成立.∵y 3=kx +1,y 2=2x ﹣2,∴y 3﹣y 2=(kx +1)﹣(2x ﹣2)=(k ﹣2)x +3.∴若x <3,y 3﹣y 2>0恒成立,则[(k ﹣2)x +3]min >0.当k ﹣2=0,即k =2,[(k ﹣2)x +3]min =3>0.当k ﹣2>0,即k >2,[(k ﹣2)x +3]min 不存在.当k ﹣2<0,即k <2,[(k ﹣2)x +3]min =3(k ﹣2)+3≥0,故k ≥1.综上:1≤k ≤2.【变式3-1】(2021春•茌平区期末)已知:如图一次函数y 1=﹣x ﹣2与y 2=x ﹣4的图象相交于点A .(1)求点A 的坐标;(2)若一次函数y 1=﹣x ﹣2与y 2=x ﹣4的图象与x 轴分别相交于点B 、C ,求△ABC 的面积.(3)结合图象,直接写出y 1≥y 2时x 的取值范围.【解题思路】(1)将两个函数的解析式联立得到方程组{y =−x −2y =x −4,解此方程组即可求出点A 的坐标;(2)先根据函数解析式求得B 、C 两点的坐标,可得BC 的长,再利用三角形的面积公式可得结果;(3)根据函数图象以及点A 坐标即可求解.【解答过程】解:(1)解方程组{y =−x −2y =x −4,得{x =1y =−3,所以点A坐标为(1,﹣3);(2)当y1=0时,﹣x﹣2=0,x=﹣2,则B点坐标为(﹣2,0);当y2=0时,x﹣4=0,x=4,则C点坐标为(4,0);∴BC=4﹣(﹣2)=6,∴△ABC的面积=12×6×3=9;【变式3-2】(2021春•海珠区期末)已知一次函数y1=ax+b的图象交x轴和y轴于点B和D;另一个一次函数y2=bx+a的图象交x轴和y轴于点C和E,且两个函数的图象交于点A(1,4)(1)当a,b为何值时,y1和y2的图象重合;(2)当0<a<4,且在x<1时,则y1>y2成立.求b的取值范围;【解题思路】(1)把A(1,4)代入y1=ax+b求得a+b=4,得到b=4﹣a,于是得到结论;(2)根据题意列不等式即可得到结论;【解答过程】解:(1)∵y1=ax+b的图象过点A(1,4),∴a+b=4,∴b=4﹣a,∴y1=ax+(4﹣a),y2=(4﹣a)x+a,∵y1和y2的图象重合,∴a=4﹣a,∴a=2,b=2;即当a=2,b=2时,y1和y2的图象重合;(2)∵a+b=4,如图1,∴a=4﹣b,∴y1=(4﹣b)x+b,y2=bx+(4﹣b),∵0<a<4,0<4﹣b<4且x<1时,y1>y2成立,∴由图象得4﹣b<b,∴2<b<4;【变式3-3】(2020春•赣县区期末)如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象经过点A(﹣2,4),且与正比例函数y=−23x的图象交于点B(a,2).(1)求a的值及一次函数y=kx+b的解析式;(2)若一次函数y=kx+b的图象与x轴交于点C,且正比例函数y=−23x的图象向下平移m(m>0)个单位长度后经过点C,求m的值;(3)直接写出关于x 的不等式0<−23x <kx +b 的解集.【解题思路】(1)先确定B 的坐标,然后根据待定系数法求解析式;(2)先求得C 的坐标,然后根据题意求得平移后的直线的解析式,把C 的坐标代入平移后的直线的解析式,即可求得M 的值;(3)找出直线y =−23x 落在y =kx +b 的下方且在x 轴上方的部分对应的x 的取值范围即可.【解答过程】解:(1)∵正比例函数y =−23x 的图象经过点B (a ,2),∴2=−23a ,解得,a =﹣3,∴B (﹣3,2),∵一次函数y =kx +b 的图象经过点A (﹣2,4),B (﹣3,2),∴{−2k +b =4−3k +b =2,解得{k =2b =8,∴一次函数y =kx +b 的解析式为y =2x +8;(2)∵一次函数y =2x +8的图象与x 轴交于点C ,∴C (﹣4,0),∵正比例函数y =−23x 的图象向下平移m (m >0)个单位长度后经过点C ,∴平移后的函数的解析式为y =−23x ﹣m ,∴0=−23×(﹣4)﹣m ,解得m =83;(3)∵一次函y =kx +b 与正比例函数y =−23x 的图象交于点B (﹣3,2),且一次函数y =2x +8的图象与x 轴交于点C (﹣4,0),∴关于x 的不等式0<−23x <kx +b 的解集是﹣3<x <0.【题型4 一次函数与一元一次不等式(面积问题)】【例4】(2021春•诸城市期末)如图,直线y=kx+b分别与x轴、y轴交于点A(﹣2,0),B(0,3);直线y=1﹣mx分别与x轴交于点C,与直线AB交于点D,已知关于x的不等式kx+b>1﹣mx的解集是x>−4 5.(1)分别求出k,b,m的值;(2)求S△ACD.【解题思路】(1)首先利用待定系数法确定直线的解析式,然后根据关于x的不等式kx+b>1﹣mx的解集是x>−45得到点D的横坐标为−45,再将x=−45代入y=32x+3,得:y=95,将x=−45,y=95代入y=1﹣mx求得m=1即可;(2)先确定直线与x轴的交点坐标,然后利用三角形的面积公式计算即可.【解答过程】解:(1)∵直线y=kx+b分别与x轴、y轴交于点A(﹣2,0),B(0,3),{−2k+b=0b=3,解得:k=32,b=3,∵关于x的不等式kx+b>1﹣mx的解集是x>−4 5,∴点D的横坐标为−4 5,将x=−45代入y=32x+3,得:y=95,∴D(−45,95),将x=−45,y=95代入y=1﹣mx,解得:m=1;(2)如图,过点D作DH⊥AC于H,则DH=9 5对于y =1﹣x ,令y =0,得:x =1,∴点C 的坐标为(1,0),∴S △ACD =12•AC •DH =12×[1﹣(﹣2)]×95=2710.【变式4-1】(2021春•东辽县期末)已知直线y =kx +5交x 轴于A ,交y 轴于B 且A 坐标为(5,0),直线y =2x ﹣4与x 轴于D ,与直线AB 相交于点C .(1)求点C 的坐标;(2)根据图象,写出关于x 的不等式2x ﹣4>kx +5的解集;(3)求△ADC 的面积.【解题思路】(1)根据点A 的坐标利用待定系数法可求出直线AB 的解析式,联立直线AB 、CD 的解析式成方程组,通过解方程组即可求出点C 的坐标;(2)根据直线AB 、CD 的上下位置关系结合点C 的坐标,即可得出不等式2x ﹣4>kx +5的解集;(3)利用一次函数图象上点的坐标特征可求出点D 的坐标,再根据三角形的面积公式即可求出△ADC 的面积.【解答过程】解:(1)∵直线y =kx +5经过点A (5,0),∴5k +5=0,解得:k =﹣1,∴直线AB 的解析式为y =﹣x +5.联立直线AB 、CD 的解析式成方程组,{y =−x +5y =2x −4,解得:{x =3y =2,∴点C 的坐标为(3,2).(2)观察函数图象可知:当x >3时,直线y =2x ﹣4在直线y =﹣x +5的上方, ∴不等式2x ﹣4>kx +5的解集为x >3.(3)当y =2x ﹣4=0时,x =2,∴点D 的坐标为(2,0),∴S △ACD =12(x A ﹣x D )•y C =12×(5﹣2)×2=3.【变式4-2】(2020春•宁化县校级月考)如图,直线l1:y=2x与直线l2:y=kx+3在同一平面直角坐标系内交于点P(a,2).(1)求出不等式2x≤kx+3的解集;(2)求出△OAP的面积.【解题思路】(1)利用一次函数图象上点的坐标特征先求出a的值,然后观察函数图象,写出直线y=kx+3在直线y=2x上方所对应的自变量的取值范围即可;(2)先求出直线l2的解析式,再求出A点坐标,然后利用三角形面积公式求解.【解答过程】解:(1)把P(a,2)代入y=2x得2a=2,解得a=1,则P(1,2),当x≤1时,2x≤kx+3,所以不等式2x≤kx+3的解集为x≤1;(2)把P(1,2)代入y=kx+3得k+3=2,解得k=﹣1,所以直线l2的解析式为y=﹣x+3,当y=0时,﹣x+3=0,解得x=3,则A(3,0),所以△OAP的面积=12×2×3=3.【变式4-3】已知一次函数y1=﹣2x﹣3与y2=12x+2.(1)在同一平面直角坐标系中,画出这两个函数的图象;(2)根据图象,不等式﹣2x﹣3>12x+2的解集为x<﹣2;(3)求两图象和y轴围成的三角形的面积.【解题思路】(1)先求出直线y1=﹣2x﹣3,y2=12x+2与x轴和y轴的交点,再画出两函数图象即可;(2)直线y1=﹣2x﹣3的图象落在直线y2=12x+2上方的部分对应的x的取值范围就是不等式﹣2x﹣3>12x+2的解集;(3)根据三角形的面积公式求解即可.【解答过程】解:(1)函数y1=﹣2x﹣3与x轴和y轴的交点分别是(﹣1.5,0)和(0,﹣3),y2=12x+2与x轴和y轴的交点分别是(﹣4,0)和(0,2),其图象如图:(2)观察图象可知,函数y1=﹣2x﹣3与y2=12x+2交于点(﹣2,1),当x<﹣2时,直线y1=﹣2x﹣3的图象落在直线y2=12x+2的上方,即﹣2x﹣3>12x+2,所以不等式﹣2x﹣3>12x+2的解集为x<﹣2;故答案为x<﹣2;(3)∵y1=﹣2x﹣3与y2=12x+2与y轴分别交于点A(0,﹣3),B(0,2),∴AB=5,∵y1=﹣2x﹣3与y2=12x+2交于点C(﹣2,1),∴△ABC的边AB上的高为2,∴S△ABC=12×5×2=5.【题型5 一次函数的与一元一次不等式(求点的坐标)】【例5】如图,直线y=kx+b与坐标轴相交于点M(3,0),N(0,4),且MN=5.(1)求直线MN的解析式;(2)根据图象,写出不等式kx+b≥0的解集;(3)若点P 在x 轴上,且点P 到直线y =kx +b 的距离为125,直接写出符合条件的点P的坐标.【解题思路】(1)把点M 、N 的坐标分别代入一次函数解析式,列出关于系数k 、b 的方程组,通过解方程组求得它们的值;(2)直线y =kx +b 在x 轴及其上方的部分对应的x 的取值范围即为所求;(3)作△OMN 的高OA .根据三角形的面积公式求出OA =OM⋅ON MN =3×45=125,则点P 的坐标是(0,0);在x 轴上作O 关于M 的对称点为(6,0),易得(6,0)到直线y =kx +b 的距离也为125.【解答过程】解:(1)∵直线y =kx +b 与坐标轴相交于点M (3,0),N (0,4), 所以{3k +b =0b =4,解得:{k =−43b =4, ∴直线MN 的解析式为:y =−43x +4;(2)根据图形可知,当x ≤3时,y =kx +b 在x 轴及其上方,即kx +b ≥0,则不等式kx +b ≥0的解集为x ≤3;(3)如图,作△OMN 的高OA .∵S △OMN =12MN •OA =12OM •ON ,∴OA =OM⋅ON MN =3×45=125,∴点P 的坐标是(0,0);在x 轴上作O 关于M 的对称点为(6,0),易得(6,0)到直线y =kx +b 的距离也为125,所以点P 的坐标是(0,0)或(6,0).【变式5-1】(2021春•顺德区期末)一次函数y 1=kx +b 和y 2=﹣4x +a 的图象如图所示,且A (0,4),C (﹣2,0).(1)由图可知,不等式kx +b >0的解集是 x >﹣2 ;(2)若不等式kx +b >﹣4x +a 的解集是x >1.①求点B 的坐标;②求a 的值.【解题思路】(1)根据函数图象和题意可以直接写出不等式kx +b >0的解集;(2)①由题意可以求得k 、b 的值,然后将x =1代入y 1=kx +b 即可求得点B 的坐标; ②根据点B 也在函数y 2=﹣4x +a 的图象上,从而可以求得a 的值.【解答过程】解:(1)∵A (0,4),C (﹣2,0)在一次函数y 1=kx +b 上,∴不等式kx +b >0的解集是x >﹣2,故答案为:x >﹣2;(2)①∵A (0,4),C (﹣2,0)在一次函数y 1=kx +b 上,∴{b =4−2k +b =0,得{k =2b =4,∴一次函数y 1=2x +4,∵不等式kx +b >﹣4x +a 的解集是x >1,∴点B 的横坐标是x =1,当x =1时,y 1=2×1+4=6,∴点B 的坐标为(1,6);②∵点B (1,6),∴6=﹣4×1+a ,得a =10,即a 的值是10.【变式5-2】(2020秋•南京期末)已知直线y =kx +b 经过点A (5,0),B (1,4).(1)求直线AB 的函数关系式;(2)若直线y =2x ﹣4与直线AB 相交于点C ,求点C 的坐标;(3)根据图象,直接写出当x 在什么范围内,不等式2x ﹣4>kx +b .【解题思路】(1)利用待定系数法即可求得函数的解析式;(2)解两个函数解析式组成方程组即可求解;(3)关于x 的不等2x ﹣4>kx +b 的解集就是函数y =kx +b 的图象在下边的部分自变量的取值范围.【解答过程】解:(1)根据题意得{5k +b =0k +b =4,解得{k =−1b =5,则直线AB 的解析式是y =﹣x +5;(2)根据题意得{y =−x +5y =2x −4,解得:{x =3y =2,则C 的坐标是(3,2);(3)根据图象可得不等式的解集是x >3.【变式5-3】在平面直角坐标系中,直线y =﹣2x +1与y 轴交于点C ,直线y =x +k (k ≠0)与y 轴交于点A ,与直线y =﹣2x +1交于点B ,设点B 的横坐标为﹣2.(1)求点B 的坐标及k 的值;(2)求直线y =﹣2x +1、直线y =x +k 与y 轴所围成的△ABC 的面积;(3)根据图象直接写出不等式﹣2x +1>x +k 的解集.【解题思路】(1)对于y =﹣2x +1,计算自变量为﹣2时的函数值可得到B 点坐标,然后把B 点坐标代入y =x +k 可得到k 的值;(2)先确定两直线与y 轴的交点A 、C 的坐标,然后利用三角形面积公式求解;(3)观察函数图象,写出直线y =﹣2x +1在直线y =x +k 上方所对应的自变量的范围即可.【解答过程】解:(1)当x =﹣2时,y =﹣2×(﹣2)+1=5,则B (﹣2,5). 把B (﹣2,5)代入y =x +k 得﹣2+k =5,解得k =7;(2)当x =0时,y =﹣2x +1=1,则C (0,1);当x =0时,y =x +7=7,则A (0,7)所以AC =7﹣1=6,所以S △ABC =12×6×2=6;(3)x <﹣2.【例6】(2021•济南二模)中国古代数学专著《九章算术》“方程”一章记载用算筹(方阵)表示二元一次方程组的方法,发展到现代就是用矩阵式(a 1b 1a 2b 2)(x y )=(c 1c 2)来表示二元一次方程组{a 1x +b 1y =c 1a 2x +b 2y =c 2,而该方程组的解就是对应两直线(不平行)a 1x +b 1y =c 1与a 2x +b 2y =c 2的交点坐标P (x ,y ).据此,则矩阵式(4−1−31)(x y )=(3−1)所对应两直线交点坐标是 (2,5) .【解题思路】根据题意得出方程组,求出方程组的解,再得出答案即可.【解答过程】解:根据题意得:{4x −y =3①−3x +y =−1②,①+②,得x =2,把x =2代入①,得8﹣y =3,解得:y =5,所以方程组的解为{x =2y =5,∴两直线交点坐标是(2,5),故答案为:(2,5).【变式6-1】如图,直线y =﹣2x +6与直线y =mx +n 相交于点M (p ,4).(1)求p 的值;(2)直接写出关于x ,y 的二元一次方程组{y =−2x +6y =mx +n 的解;(3)判断直线y =3nx +m ﹣2n 是否也过点M ?并说明理由.【解题思路】(1)根据直线y =﹣2x +6经过点M ,即可求出p .(2)由图象可知交点的坐标就是方程组的解.(3)先求出m +n =4,用代入法可以解决.【解答过程】解:(1)∵直线y =﹣2x +6经过点M (p ,4),∴4=﹣2p +6,∴p =1.(2)由图象可知方程组的解为{x =1y =4,(3)结论:直线y =3nx +m ﹣2n 经过点M ,理由如下:∵点M (1,4)在直线y =mx +n 上,∴m +n =4,∴当x =1,时,y =3nx +m ﹣2n =m +n =4,∴直线y =3nx +m ﹣2n 经过点M .【变式6-2】(2021秋•文成县期末)如图,l 1,l 2分别表示两个一次函数的图象,它们相交于点P ,(1)求出两条直线的函数关系式;(2)点P 的坐标可看作是哪个二元一次方程组的解;(3)求出图中△APB 的面积.【解题思路】(1)由图可得两函数与坐标轴的交点坐标,用待定系数法可求出它们的函数解析式;(2)联立两个一次函数的解析式,所得方程组的解即为P 点坐标.(3)△ABP 中,以AB 为底,P 点横坐标的绝对值为高,可求出△ABP 的面积.【解答过程】解:(1)设直线l 1的解析式是y =kx +b ,已知l 1经过点(0,3),(1,0), 可得:{b =3k +b =0,解得{b =3k =−3,则函数的解析式是y =﹣3x +3;同理可得l 2的解析式是:y =x ﹣2.(2)点P 的坐标可看作是二元一次方程组{y =−3x +3y =x −2的解.(3)易知:A (0,3),B (0,﹣2),P (54,−34);∴S △APB =12AB •|x P |=12×5×54=258.【变式6-3】(2020秋•西安期末)学校准备五一组织老师去隆中参加诸葛亮文化节,现有甲、乙两家旅行社表示对老师优惠,设参加文化节的老师有x 人,甲、乙两家旅行社实际收费为y 1、y 2,且它们的函数图象如图所示,根据图象信息,请你回答下列问题:(1)当参加老师的人数为多少时,两家旅行社收费相同?(2)当参加老师的人数为多少人时,选择甲旅行社合算?(3)如果全共有50人参加时,选择哪家旅行社合算?【解题思路】(1)当两函数图象相交时,两家旅行社收费相同,由图象即可得出答案.(2)由图象比较收费y 1、y 2,即可得出答案.(3)当有50人时,比较收费y1、y2,即可得出答案.【解答过程】解:(1)当两函数图象相交时,两家旅行社收费相同,由图象知为30人;(2)由图象知:当有30人以下时,y1<y2,所以选择甲旅行社合算;(3)由图象知:当有50人参加时,y1>y2,所以选择乙旅行社合算;。
专题06 方程与不等式的实际运用【考点巩固】(解析版)

专题06 方程与不等式的实际运用题型1:工程问题1.九龙坡区某工程公司积极参与“精美城市,幸福九龙坡建设,该工程公司下属的甲工程队、乙工程队别 承包了杨家坪地区的A 工程、B 工程,甲工程队晴天需要14天完成,雨天工作效率下降30%,乙工程队晴 天需15天完成,雨天工作效率下降20%,实际上两个工程队同时开工,同时完工.两工程队各工作了 天.【分析】根据题意找出两个等量关系:①甲工程队晴天所做的工程量+雨天所做的工程量=总工程量;①乙工程队晴天所做的工程量+雨天所做的工程量=总工程量.设工程总量为1,则甲工程队晴天工作效率为114,雨天工作效率为1−30%14;乙工程队晴天工作效率为115,雨天工作效率为1−20%15,根据等量关系列出方程组求解即可.【详解】解:设两工程队各工作了x 天,在施工期间有y 天有雨,由题意得:{114(x −y)+1−30%14y =1115(x −y)+1−20%15y =1, 解得:{x =17y =10.即两工程队各工作了17天. 故答案为:17.2.(2021·湖南中考真题)为了改善湘西北地区的交通,我省正在修建长(沙)-益(阳)-常(德)高铁,其中长益段将于2021年底建成.开通后的长益高铁比现在运行的长益城际铁路全长缩短了40千米,运行时间为16分钟;现乘坐某次长益城际列车全程需要60分钟,平均速度是开通后的高铁的1330. (1)求长益段高铁与长益城际铁路全长各为多少千米?(2)甲、乙两个工程队同时对长益段高铁全线某个配套项目进行施工,每天对其施工的长度比为7:9,计划40天完成.施工5天后,工程指挥部要求甲工程队提高工效,以确保整个工程提早3天以上(含3天)完成,那么甲工程队后期每天至少施工多少千米?【答案】(1)长益段高铁全长为64千米,长益城际铁路全长为104千米;(2)0.85千米. 【分析】(1)设开通后的长益高铁的平均速度为x 千米/分钟,从而可得某次长益城际列车的平均速度为1330x 千米/分钟,再根据“路程=速度⨯时间”、“开通后的长益高铁比现在运行的长益城际铁路全长缩短了40千米”建立方程,解方程即可得;(2)先求出甲、乙两个工程队每天对其施工的长度,再设甲工程队后期每天施工y 千米,根据“整个工程提早3天以上(含3天)完成”建立不等式,解不等式即可得. 【详解】解:(1)设开通后的长益高铁的平均速度为x 千米/分钟,则某次长益城际列车的平均速度为1330x 千米/分钟,由题意得:1360164030x x ⨯-=, 解得4x =,则16464⨯=(千米),1313606041043030x ⨯=⨯⨯=(千米), 答:长益段高铁全长为64千米,长益城际铁路全长为104千米; (2)由题意得:甲工程队每天对其施工的长度为7647794010⨯=+(千米), 乙工程队每天对其施工的长度9649794010⨯=+(千米), 设甲工程队后期每天施工y 千米, 则979(4053)()64()5101010y --+≥-+⨯, 解得1720y ≥, 即0.85y ≥,答:甲工程队后期每天至少施工0.85千米. 题型2:行程问题3.某体育场的环形跑道长400m ,甲、乙分别以一定的速度练习长跑和自行车,如果反向而行,他们每隔 30s 相遇一次.如果同向而行,那么每隔80s 乙就追上甲一次.则甲的速度是 m /s .【分析】设甲的速度为xm /s ,乙的速度为ym /s ,根据“某体育场的环形跑道长400m ,如果反向而行,他们每隔30s 相遇一次.如果同向而行,那么每隔80s 乙就追上甲一次”,即可得出关于x ,y 的二元一次方程组,解之即可得出结论.【解答】解:设甲的速度为xm /s ,乙的速度为ym /s , 依题意,得:{30x +30y =40080y −80x =400,解得:{x =256y =556.故答案为:256.4.(2021·山西中考真题)太原武宿国际机场简称“太原机场”,是山西省开通的首条定期国际客运航线.游客从太原某景区乘车到太原机场,有两条路线可供选择,路线一:走迎宾路经太输路全程是25千米,但交通比较拥堵;路线二:走太原环城高速全程是30千米,平均速度是路线一的53倍,因此到达太原机场的时间比走路线一少用7分钟,求走路线一到达太原机场需要多长时间.【答案】25分钟 【分析】设走路线一到达太原机场需要x 分钟,用含x 的式子表示路线一、二的速度,再根据路线二平均速度是路线一的53倍列等式计算即可. 【详解】解:设走路线一到达太原机场需要x 分钟. 根据题意,得5253037x x ⨯=-.解得:25x =.经检验,25x =是原方程的解.答:走路线一到达太原机场需要25分钟.5.(2021·湖南岳阳市·中考真题)星期天,小明与妈妈到离家16km 的洞庭湖博物馆参观.小明从家骑自行车先走,1h 后妈妈开车从家出发,沿相同路线前往博物馆,结果他们同时到达.已知妈妈开车的平均速度是小明骑自行车平均速度的4倍,求妈妈开车的平均速度.【答案】妈妈开车的平均速度是48km/h . 【分析】设妈妈开车的平均速度为x km/h ,根据小明行驶的时间比妈妈多用1小时列出方程,求解并检验可得结论. 【详解】解:设妈妈开车的平均速度为x km/h ,则小明的速度为4xkm/h ,根据题意得, 161614x x -= 解得,48x =经检验,48x =是原方程的根, 答:妈妈开车的平均速度是48km/h .题型3:历史文献问题6.(2021·甘肃武威市·中考真题)我国古代数学著作《孙子算经》有“多人共车”问题:“今有三人共车,二车空;二人共车,九人步.问:人与车各几何?”其大意如下:有若干人要坐车,如果每3人坐一辆车,那么有2辆空车;如果每2人坐一辆车,那么有9人需要步行,问人与车各多少?设共有x 人,y 辆车,则可列方程组为( ) A .3(2)29y xy x-=⎧⎨-=⎩B .3(2)29y xy x+=⎧⎨+=⎩C .3(2)29y xy x-=⎧⎨+=⎩D .3(2)29y xy x -=⎧⎨+=⎩【答案】C 【分析】设共有x 人,y 辆车,由每3人坐一辆车,有2辆空车,可得()32,y x -= 由每2人坐一辆车,有9人需要步行,可得:29,y x += 从而可得答案. 【详解】解:设共有x 人,y 辆车,则3(2)29y xy x -=⎧⎨+=⎩故选:.C7.(2021·浙江绍兴市·中考真题)我国明代数学读本《算法统宗》有一道题,其题意为:客人一起分银子,若每人7两,还剩4两;若每人9两,则差8两,银子共有_______两.(注:明代时1斤=16两) 【答案】46 【分析】题目中分银子的人数和银子的总数不变,有两种分法,根据银子的总数一样建立等式,进行求解. 【详解】解:设有x 人一起分银子,根据题意建立等式得,7498x x +=-,解得:6x =,∴银子共有:67446⨯+=(两)故答案是:46.8.(2021·湖南邵阳市·中考真题)《九章算术》中有一道阐述“盈不足术”的问题,原文如下:今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?意思是:几个人一起去购买某物品,如果每人出8钱,则多了3钱;如果每人出7钱,则少了4钱.问有多少人,物品的价值是多少?该问题中物品的价值是______钱. 【答案】53 【分析】设人数为x ,再根据两种付费的总钱数一样即可求解. 【详解】 解:设一共有x 人 由题意得:8374x x -=+ 解得:7x =所以价值为:78353⨯-=(钱) 故答案是:53. 题型4:数字问题9.(2021·山西中考真题)2021年7日1日建党100周年纪念日,在本月日历表上可以用一个方框圈出4个数(如图所示),若圈出的四个数中,最小数与最大数的乘积为65,求这个最小数(请用方程知识解答).【答案】5 【分析】根据日历上数字规律得出,圈出的四个数最大数与最小数的差值为8,设最小数为x ,则最大数为+8x ,结合已知,利用最大数与最小数的乘积为65列出方程求解即可. 【详解】解:设这个最小数为x . 根据题意,得()865x x +=.解得15=x ,213x =-(不符合题意,舍去). 答:这个最小数为5.题型5:增长率问题10.(2021·内蒙古通辽市·中考真题)随着互联网技术的发展,我国快递业务量逐年增加,据统计从2018年到2020年,我国快递业务量由507亿件增加到833.6亿件,设我国从2018年到2020年快递业务量的年平均增长率为x ,则可列方程为( ) A .()50712833.6x += B .()50721833.6x ⨯+=C .()25071833.6x += D .()()250750715071833.6x x ++++=【答案】C 【分析】根据题意,业务量由507亿件增加到833.6亿件,2020年快递业务量为833.6亿件,逐年分析即可列出方程. 【详解】设从2018年到2020年快递业务量的年平均增长率为x ,2018年我国快递业务量为:507亿件,2019年我国快递业务量为:507507x +=507(1)x +亿件, 2020年我国快递业务量为:507(1)x ++2507(1)=507(1)x x x ++, 根据题意,得:()25071833.6x += 故选C .11.(2021·四川宜宾市·中考真题)据统计,2021年第一季度宜宾市实现地区生产总值约652亿元,若使该市第三季度实现地区生产总值960亿元,设该市第二、三季度地区生产总值平均增长率为x ,则可列方程__________.【答案】()26521960x += 【分析】根据题意,第一季度地区生产总值(1⨯+平均增长率2)=第三季度地区生产总值,按照数量关系列方程即可得解. 【详解】解:根据题意,第一季度地区生产总值(1⨯+平均增长率2)=第三季度地区生产总值列方程得:()26521960x +=, 故答案为:()26521960x +=.题型6:几何图形问题12.在一幅长50cm ,宽40cm 的矩形风景画的四周镶一条外框,制成一幅矩形挂图(如图所示),如果要使整个挂图的面积是3000cm 2,设边框的宽为x cm ,那么x 满足的方程是( )A .(50﹣2x )(40﹣2x )=3000B .(50+2x )(40+2x )=3000C .(50﹣x )(40﹣x )=3000D .(50+x )(40+x )=3000【答案】B【详解】解:设边框的宽为x cm,所以整个挂画的长为(50+2x)cm,宽为(40+2x)cm,根据题意,得:(50+2x)(40+2x)=3000,故选:B.13.如图,某农户准备建一个长方形养鸡场,养鸡场的一边靠墙,若墙长为18m,另三边用竹篱笆围成,篱笆总长35m,围成长方形的养鸡场四周不能有空隙.(1)要围成养鸡场的面积为150m2,则养鸡场的长和宽各为多少?(2)围成养鸡场的面积能否达到200m2?请说明理由.【答案】(1)养鸡场的宽是10m,长为15m;(2)围成养鸡场的面积不能达到200m2,见解析【详解】解:(1)设养鸡场的宽为x m,根据题意得:x(35﹣2x)=150,解得:x1=10,x2=7.5,当x1=10时,35﹣2x=15<18,当x2=7.5时35﹣2x=20>18,(舍去),则养鸡场的宽是10m,长为15m.(2)设养鸡场的宽为x m,根据题意得:x(35﹣2x)=200,整理得:2x2﹣35x+200=0,①=(﹣35)2﹣4×2×200=1225﹣1600=﹣375<0,因为方程没有实数根,所以围成养鸡场的面积不能达到200m2.题型7:方案问题14.(2021·江苏无锡市·中考真题)为了提高广大职工对消防知识的学习热情,增强职工的消防意识,某单位工会决定组织消防知识竞赛活动,本次活动拟设一、二等奖若干名,并购买相应奖品.现有经费1275元用于购买奖品,且经费全部用完,已知一等奖奖品单价与二等奖奖品单价之比为4①3.当用600元购买一等奖奖品时,共可购买一、二等奖奖品25件.(1)求一、二等奖奖品的单价;(2)若购买一等奖奖品的数量不少于4件且不超过10件,则共有哪几种购买方式?【答案】(1)一、二等奖奖品的单价分别是60元,45元;(2)共有3种购买方案,分别是:一等奖品数4件,二等奖品数23件;一等奖品数7件,二等奖品数19件;一等奖品数10件,二等奖品数15件.【分析】(1)设一、二等奖奖品的单价分别是4x,3x,根据等量关系,列出分式方程,即可求解;(2)设购买一等奖品的数量为m件,则购买二等奖品的数量为8543m-件,根据4≤m≤10,且8543m-为整数,m为整数,即可得到答案.【详解】解:(1)设一、二等奖奖品的单价分别是4x,3x,由题意得:60012756002543x x-+=,解得:x=15,经检验:x=15是方程的解,且符合题意,①15×4=60(元),15×3=45(元),答:一、二等奖奖品的单价分别是60元,45元;(2)设购买一等奖品的数量为m件,则购买二等奖品的数量为127560854453m m--=件,①4≤m≤10,且8543m-为整数,m为整数,①m=4,7,10,答:共有3种购买方案,分别是:一等奖品数4件,二等奖品数23件;一等奖品数7件,二等奖品数19件;一等奖品数10件,二等奖品数15件.15.(2021·黑龙江鹤岗市·中考真题)“中国人的饭碗必须牢牢掌握在咱们自己手中”.为扩大粮食生产规模,某粮食生产基地计划投入一笔资金购进甲、乙两种农机具,已知购进2件甲种农机具和1件乙种农机具共需3.5万元,购进1件甲种农机具和3件乙种农机具共需3万元.(1)求购进1件甲种农机具和1件乙种农机具各需多少万元?(2)若该粮食生产基地计划购进甲、乙两种农机具共10件,且投入资金不少于9.8万元又不超过12万元,设购进甲种农机具m件,则有哪几种购买方案?哪种购买方案需要的资金最少,最少资金是多少?(3)在(2)的方案下,由于国家对农业生产扶持力度加大,每件甲种农机具降价0.7万元,每件乙种农机具降价0.2万元,该粮食生产基地计划将节省的资金全部用于再次购买甲、乙两种农机具(可以只购买一种),请直接写出再次购买农机具的方案有哪几种?【答案】(1)购进1件甲种农机具需1.5万元,购进1件乙种农机具需0.5万元;(2)有三种方案:方案一:购买甲种农机具5件,乙种农机具5件;方案二:购买甲种农机具6件,乙种农机具4件;方案三:购买甲种农机具7件,乙种农机具3件;方案一需要资金最少,最少资金是10万元;(3)节省的资金再次购买农机具的方案有两种:方案一:购买甲种农机具0件,乙种农机具15件;方案二:购买甲种农机具3件,乙种农机具7件 【分析】(1)设购进1件甲种农机具需x 万元,购进1件乙种农机具需y 万元,根据题意可直接列出二元一次方程组求解即可;(2)在(1)的基础之上,结合题意,建立关于m 的一元一次不等式组,求解即可得到m 的范围,从而根据实际意义确定出m 的取值,即可确定不同的方案,最后再结合一次函数的性质确定最小值即可; (3)结合(2)的结论,直接求出可节省的资金,然后确定降价后的单价,再建立二元一次方程,并结合实际意义进行求解即可. 【详解】解:(1)设购进1件甲种农机具需x 万元,购进1件乙种农机具需y 万元.根据题意,得2 3.533x y x y +=⎧⎨+=⎩,解得: 1.50.5x y =⎧⎨=⎩,答:购进1件甲种农机具需1.5万元,购进1件乙种农机具需0.5万元. (2)根据题意,得 1.50.5(10)9.81.50.5(10)12m m m m +-≥⎧⎨+-≤⎩,解得:4.87m ≤≤, ①m 为整数, ①m 可取5、6、7, ①有三种方案:方案一:购买甲种农机具5件,乙种农机具5件; 方案二:购买甲种农机具6件,乙种农机具4件; 方案三:购买甲种农机具7件,乙种农机具3件. 设总资金为W 万元,则()1.50.5105W m m m =+-=+,①10k =>,①W 随m 的增大而增大,①当5m =时,5510W =+=最小(万元),①方案一需要资金最少,最少资金是10万元.(3)由(2)可知,购买甲种农机具5件,乙种农机具5件时,费用最小,根据题意,此时,节省的费用为50.750.2 4.5⨯+⨯=(万元),降价后的单价分别为:甲种0.8万元,乙种0.3万元,设节省的资金可购买a 台甲种,b 台乙种,则:0.80.3 4.5a b +=,由题意,a ,b 均为非负整数,①满足条件的解为:015a b =⎧⎨=⎩或37a b =⎧⎨=⎩, ①节省的资金再次购买农机具的方案有两种:方案一:购买甲种农机具0件,乙种农机具15件;方案二:购买甲种农机具3件,乙种农机具7件.16.(2021·黑龙江中考真题)“中国人的饭碗必须牢牢掌握在咱们自己手中”.为扩大粮食生产规模,某粮食生产基地计划投入一笔资金购进甲、乙两种农机具,已知购进2件甲种农机具和1件乙种农机具共需3.5万元,购进1件甲种农机具和3件乙种农机具共需3万元.(1)求购进1件甲种农机具和1件乙种农机具各需多少万元?(2)若该粮食生产基地计划购进甲、乙两种农机具共10件,且投入资金不少于9.8万元又不超过12万元,设购进甲种农机具m 件,则有哪几种购买方案?(3)在(2)的条件下,哪种购买方案需要的资金最少,最少资金是多少?【答案】(1)购进1件甲种农机具需1.5万元,购进1件乙种农机具需0.5万元;(2)购进甲种农机具5件,乙种农机具5件;购进甲种农机具6件,乙种农机具4件;购进甲种农机具7件,乙种农机具3件;(3)购进甲种农机具5件,乙种农机具5件所需资金最少,最少资金为10万元.【分析】(1)设购进1件甲种农机具需x 万元,购进1件乙种农机具需y 万元,然后根据题意可得2 3.533x y x y +=⎧⎨+=⎩,进而求解即可;(2)由(1)及题意可得购进乙种农机具为(10-m )件,则可列不等式组为()9.8 1.50.51012m m ≤+-≤,然后求解即可;(3)设购买农机具所需资金为w 万元,则由(2)可得5w m =+,然后结合一次函数的性质及(2)可直接进行求解.【详解】解:(1)设购进1件甲种农机具需x 万元,购进1件乙种农机具需y 万元,由题意得:2 3.533x y x y +=⎧⎨+=⎩, 解得: 1.50.5x y =⎧⎨=⎩, 答:购进1件甲种农机具需1.5万元,购进1件乙种农机具需0.5万元.(2)由题意得:购进乙种农机具为(10-m )件,①()9.8 1.50.51012m m ≤+-≤,解得:4.87m ≤≤,①m 为正整数,①m 的值为5、6、7,①共有三种购买方案:购进甲种农机具5件,乙种农机具5件;购进甲种农机具6件,乙种农机具4件;购进甲种农机具7件,乙种农机具3件;.(3)设购买农机具所需资金为w 万元,则由(2)可得5w m =+,①1>0,①w 随m 的增大而增大,①当m =5时,w 的值最小,最小值为w=5+5=10,答:购进甲种农机具5件,乙种农机具5件所需资金最少,最少资金为10万元.题型8:利润问题17.(2021·四川遂宁市·中考真题)某服装店以每件30元的价格购进一批T 恤,如果以每件40元出售,那么一个月内能售出300件,根据以往销售经验,销售单价每提高1元,销售量就会减少10件,设T 恤的销售单价提高x 元.(1)服装店希望一个月内销售该种T 恤能获得利润3360元,并且尽可能减少库存,问T 恤的销售单价应提高多少元?(2)当销售单价定为多少元时,该服装店一个月内销售这种T 恤获得的利润最大?最大利润是多少元?【答案】(1)2元;(2)当服装店将销售单价50元时,得到最大利润是4000元【分析】(1)根据题意,通过列一元二次方程并求解,即可得到答案;(2)设利润为M 元,结合题意,根据二次函数的性质,计算得利润最大值对应的x 的值,从而得到答案.【详解】(1)由题意列方程得:(x +40-30) (300-10x )=3360解得:x 1=2,x 2=18①要尽可能减少库存,①x 2=18不合题意,故舍去①T 恤的销售单价应提高2元;(2)设利润为M 元,由题意可得:M =(x +40-30)(300-10x )=-10x 2+200x +3000=()210104000x --+①当x =10时,M 最大值=4000元①销售单价:40+10=50元①当服装店将销售单价50元时,得到最大利润是4000元.18.(2021·浙江中考真题)今年以来,我市接待的游客人数逐月增加,据统计,游玩某景区的游客人数三月份为4万人,五月份为5.76万人.(1)求四月和五月这两个月中,该景区游客人数平均每月增长百分之几;(2)若该景区仅有,A B 两个景点,售票处出示的三种购票方式如表所示:据预测,六月份选择甲、乙、丙三种购票方式的人数分别有2万、3万和2万.并且当甲、乙两种门票价格不变时,丙种门票价格每下降1元,将有600人原计划购买甲种门票的游客和400人原计划购买乙种门票的游客改为购买丙种门票.①若丙种门票价格下降10元,求景区六月份的门票总收入;①问:将丙种门票价格下降多少元时,景区六月份的门票总收入有最大值?最大值是多少万元?【答案】(1)20%;(2)①798万元,①当丙种门票价格降低24元时,景区六月份的门票总收人有最大值,为817.6万元【分析】(1)设四月和五月这两个月中,该景区游客人数的月平均增长率为x ,则四月份的游客为()41x +人,五月份的游客为()241x +人,再列方程,解方程可得答案;(2)①分别计算购买甲,乙,丙种门票的人数,再计算门票收入即可得到答案;①设丙种门票价格降低m 元,景区六月份的门票总收人为W 万元,再列出W 与m 的二次函数关系式,利用二次函数的性质求解最大利润即可得到答案.【详解】解:(1)设四月和五月这两个月中,该景区游客人数的月平均增长率为x ,由题意,得24(1) 5.76x += ()21 1.44,x ∴+=解这个方程,得120.2, 2.2x x ==-(舍去)答:四月和五月这两个月中,该景区游客人数平均每月增长20%.(2)①由题意,丙种门票价格下降10元,得:购买丙种门票的人数增加:0.6+0.4=1(万人),购买甲种门票的人数为:20.6 1.4-=(万人),购买乙种门票的人数为:30.4 2.6-=(万人),所以:门票收入问; ()()100 1.480 2.61601021⨯+⨯+-⨯+798=(万元)答:景区六月份的门票总收入为798万元.①设丙种门票价格降低m 元,景区六月份的门票总收人为W 万元,由题意,得()()()()10020.068030.0416020.060.04W m m m m m =-+-+-++化简,得20.1(24)817.6W m =--+,0.10-<,①当24m =时,W 取最大值,为817.6万元.答:当丙种门票价格降低24元时,景区六月份的门票总收人有最大值,为817.6万元.题型9:一般问题19.(2021·辽宁本溪市·中考真题)某班计划购买两种毕业纪念册,已知购买1本手绘纪念册和4本图片纪念册共需135元,购买5本手绘纪念册和2本图片纪念册共需225元.(1)求每本手绘纪念册和每本图片纪念册的价格分别为多少元?(2)该班计划购买手绘纪念册和图片纪念册共40本,总费用不超过1100元,那么最多能购买手绘纪念册多少本?【答案】(1)每本手绘纪念册35元,每本图片纪念册25元;(2)最多能购买手绘纪念册10本.【分析】(1)设每本手绘纪念册x 元,每本图片纪念册y 元,根据题意列出二元一次方程组,求解即可;(2)设购买手绘纪念册a 本,则购买图片纪念册()40a -本,根据题意列出不等式,求解不等式即可.【详解】解:(1)设每本手绘纪念册x 元,每本图片纪念册y 元,根据题意可得:413552225x y x y +=⎧⎨+=⎩, 解得3525x y =⎧⎨=⎩,答:每本手绘纪念册35元,每本图片纪念册25元;(2)设购买手绘纪念册a 本,则购买图片纪念册()40a -本,根据题意可得:()3525401100a a +-≤,解得10a ≤,①最多能购买手绘纪念册10本.20.(2021·江苏常州市·中考真题)为落实节约用水的政策,某旅游景点进行设施改造,将手拧水龙头全部更换成感应水龙头.已知该景点在设施改造后,平均每天用水量是原来的一半,20吨水可以比原来多用5天,该景点在设施改造后平均每天用水多少吨?【答案】该景点在设施改造后平均每天用水2吨.【分析】设该景点在设施改造后平均每天用水x 吨,则原来平均每天用水2x 吨,列出分式方程,即可求解.【详解】解:设该景点在设施改造后平均每天用水x 吨,则原来平均每天用水2x 吨, 由题意得:202052x x-=,解得:x =2, 经检验:x =2是方程的解,且符合题意,答:该景点在设施改造后平均每天用水2吨.21.某商店销售一款工艺品,每件的成本是30元,为了合理定价,投放市场进行试销:据市场调查,销售单价是40元时,每天的销售量是80件,而销售单价每提高1元,每天就少售出2件,但要求销售单价不得超过55元.(1)若销售单价为每件45元,求每天的销售利润.(2)要使每天销售这种工艺品盈利1200元,那么每件工艺品售价应为多少元?【答案】(1)1050元;(2)50元【详解】解:(1)(4530)[80(4540)2]1050-⨯--⨯=(元).答:每天的销售利润为1050元.(2)设每件工艺品售价为x 元,则每天的销售量是[802(40)]x --件,依题意,得(30)[802(40)]1200x x ---=,整理,得2x 110x 30000-+=,解得1250,60x x ==(不合题意,舍去).答:每件工艺品售价应为50元.题型10:分段收费22.为建设资源节约型社会,醴陵市自2012年以来就对家庭用电收费实行阶梯电价,即每月对每户居民的用电量分为三个档级收费,第一档为用电量在180度及(含180度)以内的部分,执行基本价格;第二档为用电量在180度以上到450度时(含450度时)的部分,实行提高电价;第三档为用电量超出450度时的部分,执行市场调节价格.经统计,我市小军同学家今年2月份用电200度,电费为119元,3月份用电210度时,电费为125.4元.(1)请根据小军家的用电量和电费情况,求出第一档的电价和第二档的电价分别是多少元/度.(2)已知小军同学家今年4、5月份的家庭用电量分别为160度和230度,请问小军家4、5月份的电费分别为多少元?【分析】(1)设第一档的电价为x 元/度,第二档的电价为y 元/度,根据“小军同学家今年2月份用电200度,电费为119元,3月份用电210度时,电费为125.4元”,即可得出关于x ,y 的二元一次方程组,解之即可得出结论;(2)利用小军家4月份的电费=第一档电价×4月份的用电量和小军家5月份的电费=第一档电价×180+第二档电价×(5月份的用电量﹣180),即可求出结论.【解答】解:(1)设第一档的电价为x 元/度,第二档的电价为y 元/度,依题意,得:{180x +(200−180)y =119180x +(210−180)y =125.4, 解得:{x =0.59y =0.64. 答:第一档电价为0.59元/度,第二档的电价为0.64元/度.(2)0.59×160=94.4(元),0.59×180+0.64×(230﹣180)=138.2(元).答:小军家4月份的电费为94.4元,5月份的电费为138.2元.23.为鼓励市民节约用水,某市居民生活用水按阶梯式水价计费.下表是该市居民“一户一表”生活用水阶梯式计费价格表的部分信息,请解答:自来水销售价格每户每月用水量单位:元/吨 15吨及以下a 超过15吨但不超过25吨的部分b 超过25吨的部分 5(1)小王家今年3月份用水20吨,要交水费 元;(用a ,b 的代数式表示)(2)小王家今年4月份用水21吨,交水费48元;邻居小李家4月份用水27吨,交水费70元,求a ,b 的值.(3)在第(2)题的条件下,小王家5月份用水量与4月份用水量相同,却发现要比4月份多交9.6元钱水费,小李告诉小王说:“水价调整了,表中表示单位的a ,b 的值分别上调了整数角钱(没超过1元),其他都没变.”到底上调了多少角钱呢?请你帮小王求出符合条件的所有可能情况.【分析】(1)根据题意列出代数式即可;(2)根据题意列方程组,即可得到结论;。
第09讲 一次函数及方程不等式+专题:一次函数的应用

一、一次函数与方程、不等式的关系知识点一:二元一次方程组的图像解法(1)一般地,一次函数y=kx+b 的图像上的任意一点的 都是二元一次方程kx —y+b=0的 ;,以二元一次方程kx —y+b=0的 为 的点都在一次函数y=kx+b 的图像上。
(2)一般地,如果2个一次函数的图像有 ,那么 就是相应的二元一次方程组的解。
(3)求直线y=k 1x+b 1(k 1≠0) 与直线y=k 2x+b 2(k 2≠0)的交点坐标只要求出 即可。
【例1】方函数y=-2x+1与y=3x -9的图象交点坐标为 ,这对数是方程组 ___________的解。
【例2】已知直线1l :33y x =-和直线2l :362y x =-+相交于点A 。
(1)求点A 坐标;(2)若1l 与x 轴交于点B ,2l 与x 轴交于点C ,求△ABC 面积;(3)若点D 与点A 、B 、C 能构成平行四边形,试写出点D 坐标。
(只需写出坐标,不必写解答过程)精讲精练第九讲、一次函数及方程不等式+专题:一次函数的应用知识点二:一次函数与不等式(组)【例3】已知一次函数25y x=-+.(1)画出它的图象;(2)求出当32x=时,y的值;(3)求出当3y=-时,x的值;(4)观察图象,求出当x为何值时,0y>,0y=,0y<【例4】直线11:l y k x b=+与直线22:l y k x=在同一平面直角坐标系中的图象如图所示,则关于x的不等式21k x k x b>+的解集为______.一次函数与方程习题1.如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,二元一次方程组⎩⎨⎧=+=,,kxybaxy的解是________.2.一次函数421-=xy和y=-3x+3的图象的交点坐标是________.l2l13-1Oyx对应练习3.将方程x +3y =7全部的解写成坐标(x ,y )的形式,那么用全部的坐标描出的点都在直线( )上. A .3731-=x yB .3731+=x y C .3731+-=x yD .3731--=x y4.如图所示,图中两条直线l 1、l 2的交点坐标可以看做是方程组( )的解.A .⎩⎨⎧=-=+42,2y x y xB .⎩⎨⎧=-=-42,2y x y xC .⎩⎨⎧=-=-42,2x y y xD .⎩⎨⎧-=-=+42,2y x y x5.已知:直线.221--=x y(1)求直线221--=x y 与x 轴的交点B 的坐标;(2)若过y 轴上一点A (0,3)作与x 轴平行的直线l ,求它与直线221--=x y 的交点M 的坐标; (3)若过x 轴上一点C (3,0)作与x 轴垂直的直线m ,求它与直线221--=x y 的交点N 的坐标.6.两个一次函数的图象如图所示, (1)分别求出两个一次函数的解析式; (2)求出两个一次函数图象的交点坐标; (3)求这两条直线与y 轴围成三角形的面积.一次函数与不等式1.如图1,直线y=kx+b与x轴交于点(-4,0),则y>0时,x的取值范围是______.图1 图22.如图2,直线y=kx+b与y轴交于(0,3),则当x<0时,y的取值范围是______.3.一次函数y=kx+b的图象如图3,则当x______时,y<4.4.一次函数y1=k1x+b1与y2=k2x+b2的图象如图4所示,则当x______时,y1<y2;当x______时,y1=y2;当x______时,y1>y2.图3 图45.已知:如图5,一次函数y=kx+b的图象与x轴交于点M,则点M的横坐标x M=_____.(1)若k>0,则当x<x M时,y______0;当x>x M时,y______0;(2)若k<0,则当x<x M时,y_____0;当x>x M时,y______0.图56.函数y=kx+b的图象如图6所示,则关于x的不等式kx+b<0的解集是()A.x>0 B.x<0C.x>2 D.x<2图67.已知:一次函数y=-2x+3.(1)在平面直角坐标系中,画出此函数的图象;(2)当x为何值时,y>0?(3)当x为何值时,y≤1?(4)当-2≤x≤3时,求y的变化范围,并指出当x为何值时,y有最大值?(5)当1<y<5时,求x的变化范围.专题二:一次函数综合应用1.如图,直线y=x﹣4分别与x轴、y轴交于点A和点B,点C、D分别是线段OA、AB的中点,点P为OB上一动点,当PC+PD取最小值时点P的坐标是()A.(0,﹣1)B.(0,﹣2)C.(0,﹣3)D.(0,﹣4)2.如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x﹣6上时,线段BC扫过的面积为________cm2.3.小明和小红两人周末去爬山,小红先出发,中间休息了一段时间,然后按休息前的进度继续前进,最后比小明迟到达山顶.设他们俩从山脚出发后所用的时间t(分钟)与所走的路程S(米)之间的函数关系如图所示:(1)根据图象小明登山的速度为米/分,小红的登山速度为米/分.(2)求出BC段图象的函数关系式,并写出自变量的取值范围.(3)小明到达山顶后,小红还有多少米到山顶?精讲精练4.“日啖荔枝三百颗,不辞长作岭南人”,广东的夏季盛产荔枝,桂味、糯米糍是荔枝的品种之一.佳佳同学先用52元购买2千克桂味和1千克糯米糍;几天后,他用76元购买1千克桂味和3千克糯米糍.(前后两次两种荔枝的售价不变) (1)求桂味、糯米糍的售价分别是每千克多少元?(2)若佳佳同学用y 元买了这两种荔枝共中10千克,设买了x 千克桂味. ①写出y 与x 的函数关系式.②若要求糯米糍的重量不少于桂味重量的3倍,请帮佳佳同学设计一个购买方案,使所需的费用最少,并求出最少费用.一、选择题1.判断下列变化过程中,两变量存在函数关系的是( ). A.x ,y 是变量,y =±3xB.人的身高与年龄C.三角形的底边长与面积D.速度一定的汽车所行驶的路程与时间 2.下列函数是一次函数的是( ).A .B .C .D .y =3x3. 若点(3,1)在一次函数的图象上,则k 的值是( ). A.5 B .4 C .3 D .12302x y -+=241y x =-2y x =y kx 2(k 0)=-≠课后作业4.如图,小红居住的小区内有一条笔直的小路,小路的正中间有一路灯,晚上小红由A 处径直走到B 处,她在灯光照射下的影长l 与行走的路程s 之间的变化关系用图象刻画出来,大致图象是( ).5.若一次函数y =(2-m )x -2的函数值y 随x 的增大而减小,则m 的取值范围是( ). A.m <0 B.m >0 C.m <2 D.m >26.已知函数y = −2x +3,当自变量x 增加1时,则其对应的函数值( ). A .增加1 B .减少 1 C .增加2 D .减少27.如果直线y =3x +6与y =2x -4交点坐标为(a ,b ),则,x a y b =⎧⎨=⎩是下列哪个方程组的解( ). A.36,24y x x y -=⎧⎨-=⎩ B.36,24y x x y -=⎧⎨-=-⎩ C.36,24x y x y +=⎧⎨-=⎩ D.36,24x y x y -=⎧⎨-=-⎩8.小敏从A 地出发向B 地行走,同时小聪从B 地出发向A 地行走,如图2所示,相交于点P 的两条线段l 1、l 2分别表示小敏、小聪离B 地的距离y (km)与已用时间x (h)之间的关系,则小敏、小聪的速度分别是( ).图2A.3km/h 和4km/hB.3km/h 和3km/hC.4km/h 和4km/hD.4km/h和3km/h9. 如图3,直线l 经过第二,三,四象限,l 的解析式是,则m 的取值范围则数轴上表示为( )图310. 函数y =ax +b 与y =bx +a 的图象在同一坐标系内的大致位置可能是( ).A B C D二、填空题11.若是正比例函数,则b=_________.12. 市场上一种豆子每千克售2元,即单价是2元/千克,豆子总的售价(元)与所售豆子的数量kg 之间的关系为_______,当售出豆子5kg 时,豆子总售价为______元;当售出豆子10kg 时,豆子总售价为______元.13. 如图4所示是计算机程序计算,若输入x =-1,则最后输出结果是______.图414. 在平面直角坐标系中,已知一次函数的图像经过,两点,若,则 (填“>”,“<”或“=”).15. 将直线y =3x 向下平移5个单位,得到直线 ;将直线y =-x -5向上平移5个单位,得到直线 .()ym 2x n =-+23yx b =+-y x y 2x 1=+111P (x ,y )222P (x ,y )12x x <1y 2y16. 过点(-1,7)的一条直线与x轴,y轴分别相交于点A,B,且与直线平行.则在线段AB上,横、纵坐标都是整数的点的坐标是.三、解答题17. △ABC的底边BC=10cm,当BC边上的高线AD从小到大变化时,△ABC的面积也随之变化.(1)在这个变化过程中,自变量和因变量各是什么?(2)△ABC的面积S(cm2)与高线h(cm)之间的关系式是什么?18. 已知y与x成正比例,当x=1时,y=2,求y与x的函数关系式.19. 直线y=2x+b经过点(3,5),求关于x的不等式2x+b≥0的解集.20. 如图5,已知函数y=kx+3与y=mx的图象相交于点P(2,1).求:(1)这两个函数的解析式;(2)图中阴影部分的面积.3y x12=-+21. 为了增强居民的节约用水的意识,某市制定了新的水费标准:每户每月用水量不超过5吨的部分,自来水公司按每吨2元收费;超过5吨的部分,按每吨2.6元收费.设某用户月用水量x 吨,自来水公司的应收水费为y元.(1)试写出y(元)与x(吨)之间的函数关系式;(2)该户今年5月份的用水量为8吨,自来水公司应收水费多少元?22. 已知函数y=(8-2m)x+m-2.(1)若函数图象经过原点,求m的值;(2)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围;(3)若这个函数是一次函数,且图象经过一、二、三象限,求m的取值范围.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
方程、不等式与一次函数专题练习(实际应用)题型一:方程、不等式的直接应用典型例题1:(2009,株洲)初中毕业了,孔明同学准备利用暑假卖报纸赚取140~200元钱,买一份礼物送给父母.已知:在暑假期间,如果卖出的报纸不超过1000份,则每卖出一份报纸可得0.1元;如果卖出的报纸超过1000份,则超过部分....每份可得0.2元. (1)请说明:孔明同学要达到目的,卖出报纸的份数必须超过1000份.(2)孔明同学要通过卖报纸赚取140~200元,请计算他卖出报纸的份数在哪个范围内.典型例题2:(2007,福州,10分)李晖到“宁泉牌”服装专卖店做社会调查.了解到商店为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息: 假设月销售件数为x 件,月总收入为y 元,销售1件奖励a 元,营业员月基本工资为b 元. (1)求a ,b 的值;(2)若营业员小俐某月总收入不低于1800元,则小俐当月至少要卖服装多少件?配套练习:3、(2009,益阳)开学初,小芳和小亮去学校商店购买学习用品,小芳用18元钱买了1支钢笔和3本笔记本;小亮用31元买了同样的钢笔2支和笔记本5本.(1)求每支钢笔和每本笔记本的价格;(2)校运会后,班主任拿出200元学校奖励基金交给班长,购买上述价格的钢笔和笔记本共48件作为奖品,奖给校运会中表现突出的同学,要求笔记本数不少于钢笔数,共有多少种购买方案?请你一一写出.4、(2009,济南)自2008年爆发全球金融危机以来,部分企业受到了不同程度的影响,为落实“促民生、促经济”政策,济南市某玻璃制品销售公司今年1月份调整了职工的月工资分配方案,调整后月工资由基本保障工资和计件奖励工资两部分组成(计件奖励工资=销售每件的奖励金额×销售的件数).下表是甲、乙两位职工今年五月份的工资情况信息:(1)试求工资分配方案调整后职工的月基本保障工资和销售每件产品的奖励金额各多少元?(2)若职工丙今年六月份的工资不低于2000元,那么丙该月至少应销售多少件产品?5、(2009,青岛)北京奥运会开幕前,某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.(1)该商场两次共购进这种运动服多少套?(2)如果这两批运动服每套的售价相同,且全部售完后总利润率不低于20%,那么每套售价至少是多少元?(利润率100%=⨯利润成本)题型二:方案设计典型例题6、(2009,深圳)迎接大运,美化深圳,园林部门决定利用现有的3490盆甲种花卉和2950盆乙种花卉搭配A 、B 两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个A 种造型需甲种花卉80盆,乙种花卉40盆,搭配一个B 种造型需甲种花卉50盆,乙种花卉90盆.(1)某校九年级(1)班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来.(2)若搭配一个A 种造型的成本是800元,搭配一个B 种造型的成本是960元,试说明(1)中哪种方案成本最低?最低成本是多少元?典型例题7:(2008、湖北咸宁)“5、12”四川汶川大地震的灾情牵动全国人民的心,某市A 、B 两个蔬菜基地得知四川C 、D 两个灾民安置点分别急需蔬菜240吨和260吨的消息后,决定调运蔬菜支援灾区。
已知A 蔬菜基地有蔬菜200吨,B 蔬菜基地有蔬菜300吨,现将这些蔬菜全部调往C 、D 两个灾民安置点。
从A 地运往C 、D 两处的费用分别为每吨20元和25元,从B 地运往C 、D 两处的费用分别为每吨15元和18元。
设从地运往处的蔬菜为x 吨。
x 的值;⑵、设A 、B 两个蔬菜基地的总运费为w 元,写出w 与x 之间的函数关系式,并求总运费最小的调运方案;⑶、经过抢修,从B 地到C 地的路况得到进一步改善,缩短了运输时间,运费每吨减少m 元(m >0),其余路线的运费不变,试讨论总运费最小的调运方案。
配套练习:8.(2009,牡丹江)某冰箱厂为响应国家“家电下乡”号召,计划生产A、B两种型号的冰箱100台.经预算,两种冰箱全部售出后,可获得利润不低于4.75万元,不高于4.8万元,两种型号的冰箱生产成本和售价如下表:(1)冰箱厂有哪几种生产方案?(2)该冰箱厂按哪种方案生产,才能使投入成本最少?“家电下乡”后农民买家电(冰箱、彩电、洗衣机)可享受13%的政府补贴,那么在这种方案下政府需补贴给农民多少元?(3)若按(2)中的方案生产,冰箱厂计划将获得的全部利润购买三种物品:体育器材、实验设备、办公用品支援某希望小学.其中体育器材至多买4套,体育器材每套6000元,实验设备每套3000元,办公用品每套1800元,把钱全部用尽且三种物品都购买的情况下,请你直接写出实验设备的买法共有多少种.9.光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台.•现将这50台联合收割机派往A,B两地区收割小麦,其中30台派往A地区,20台派往B地区.每台甲型收割机的租金每台乙型收割机的租金A地区1800元1600元B地区1600元1200元(1)设派往A地区x台乙型联合收割机,农机租赁公司这50台联合收割机一天获得的租金为y(元),求y与x之间的函数关系式,并写出x的取值范围;(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79600元,•说明有多少种分派方案,并将各种方案设计出来;(3)如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提出一条合理建议。
10.(2009,抚顺)某食品加工厂,准备研制加工两种口味的核桃巧克力,即原味核桃巧克力和益智核桃巧克力.现有主要原料可可粉410克,核桃粉520克.计划利用这两种主要原料,研制加工上述两种口味的巧克力共50块.加工一块原味核桃巧克力需可可粉13克,需核桃粉4克;加工一块益智核桃巧克力需可可粉5克,需核桃粉14克.加工一块原味核桃巧克力的成本是1.2元,加工一块益智核桃巧克力的成本是2元.设这次研制加工的原味核桃巧克力x块.(1)求该工厂加工这两种口味的巧克力有哪几种方案?(2)设加工两种巧克力的总成本为y元,求y与x的函数关系式,并说明哪种加工方案使总成本最低?总成本最低是多少元?题型三:不等式与一次函数的实际应用典型例题11:(南充市2009)某电信公司给顾客提供了两种手机上网计费方式:方式A以每分钟0.1元的价格按上网时间计费;方式B除收月基费20元外,再以每分钟0.06元的价格按上网时间计费.假设顾客甲一个月手机上网的时间共有x分钟,上网费用为y元.(1)分别写出顾客甲按A、B两种方式计费的上网费y元与上网时间x分钟之间的函数关系式,并在图7的坐标系中作出这两个函数的图象;(2)如何选择计费方式能使甲上网费更合算?典型例题12:(2009,朝阳)某学校计划租用6辆客车送一批师生参加一年一度的哈尔滨冰雕节,感受冰雕艺术的魅力.现有甲、乙两种客车,它们的载客量和租金如下表.设租用甲种客车x辆,租车总费用为y元.(1)求出y(元)与x(辆)之间的函数关系式,指出自变量的取值范围;(2)若该校共有240名师生前往参加,领队老师从学校预支租车费用1650元,试问预支的租车费用是否可以结余?若有结余,最多可结余多少元?典型例题13:(2009、唐山)送家电下乡活动开展后,某家电经销商计划购进A、B、C三种家电共70台,每种家电至少要购进8台,且恰好用完资金45000元。
设购进A种家电x台,B种家电y台。
三种家电的进价和预售价如下表:⑴、用含x,y的式子表示购进C种家电的台数;⑵、求出y与x之间的函数关系式;⑶、假设所购进家电全部售出,综合考虑各种因素,该家电经销商在购销这批家电过程中需另外支出各种费用共1000元。
①、求出预估利润P(元)与x(台)的函数关系式;型号A型B型成本(元/台)2200 2600售价(元/台)2800 3000甲种客车乙种客车载客量(人/辆)45 30租金(元/辆)280 200②、求出预估利润的最大值,并写出此时购进三种家电各多少台。
典型例题14:.(2009年河北)某公司装修需用A型板材240块、B型板材180块,A型板材规格是60 cm×30 cm,B型板材规格是40 cm×30 cm.现只能购得规格是150 cm×30 cm的标准板材.一张标准板材尽可能多地裁出A型、B型板材,裁法一裁法二裁法三A型板材块数 1 2 0B型板材块数 2 m n设所购的标准板材全部裁完,其中按裁法一裁x张、按裁法二裁y张、按裁法三裁z张,且所裁出的A.B两种型号的板材刚好够用.(1)上表中,m = ,n = ;(2)分别求出y与x和z与x的函数关系式;(3)若用Q表示所购标准板材的张数,求Q与x的函数关系式,并指出当x取何值时Q最小,此时按三种裁法各裁标准板材多少张?【关键词】函数的运用配套练习:15、(2009、保定)水果经销商计划将一批苹果从我市运往某地销售,有汽车、火车两种运输工具可供选择,两种运输工具的主要参考数据如下:设我市到某地的路程为x千米,这批水果在途中的损耗为150元/时,若选用汽车运输,其总费用为y1元,若选用火车运运输工具途中平均速度途中平均费用装卸费用汽车75 8 1000火车100 6 2000⑴、分别写出y1,y2与x之间的函数关系式;⑵、请你为水果经销商设计省钱的运输方案,并说明理由。
16、(2009,莆田)某工厂计划招聘A、B两个工种的工人共120人,A、B两个工种的工人月工资分别为800元和1000元.(1)若某工厂每月支付的工人工资为ll000O元,那么A、B两个工种的工人各招聘多少人?设招聘A工种的工人x人。
根据题设完成下列表格,并列方程求解.项目工种工人每月工资(元)招聘人数工厂应付工人的月工资(元)A xB(2)若要求B工种的人数不少于A工种人数的2倍,那么招聘A工种的工人多少人时,可使工厂每月支付的工人工资最少?17、(2009,清远)某饮料厂为了开发新产品,用A种果汁原料和B种果汁原料试制新型甲、乙两种饮料共50千克,设甲种饮料需配制x千克,两种饮料的成本总额为y元.(1)已知甲种饮料成本每千克4元,乙种饮料成本每千克3元,请你写出y与x之间的函数关系式.(2)若用每千克饮料果汁含量果汁甲乙A 0.5千克0.2千克B 0.3千克0.4千克请你列出关于x且满足题意的不等式组,求出它的解集,并由此分析如何配制这两种饮料,可使y值最小,最小值是多少?18、(2009,铁岭)为迎接国庆六十周年,某校团委组织了“歌唱祖国”有奖征文活动,并设立了一、二、三等奖.学校计划派人根据设奖情况买50件奖品,其中二等奖件数比一等奖件数的2倍还少10件,三等奖所花钱数不超过二等奖所花钱数的1.5倍.各种奖品的单价如下表所示.如果计划一等奖买x件,买50件奖品的总钱数是w元.(1)求w与x的函数关系式及自变量x的取值范围;(2)请你计算一下,如果购买这三种奖品所花的总钱数最少?最少是多少元?5、(2009,梧州)某工厂要招聘甲、乙两种工种的工人150人,甲、乙两种工种的工人的月工资分别为600元和1000元.(1)设招聘甲种工种工人x人,工厂付给甲、乙两种工种的工人工资共y元,写出y(元)与x(人)的函数关系式;(2)现要求招聘的乙种工种的人数不少于甲种工种人数的2倍,问甲、乙两种工种各招聘多少人时,可使得每月所付的工资最少?19、(2009、河南)某家电商场计划用32400元购进“家电下乡”指定产品中的电视机、冰箱、洗衣机共15台。
