pn结电容第九次课.ppt
合集下载
PN结原理及制备工艺ppt课件

❖当温度一定时,少子浓度一定,反向电流几乎不随 外加电压而变化,故称为 反向饱和电流 。
15
PN结正偏时呈导通 状态,正向电阻很小, 正向电流很大;
PN结反偏时呈截止 状态,反向电阻很大, 反向电流很小。 —— PN结的单向导电 性
16
半导体二极管的结构和类型
在一个PN结的两端,各引一根电极引线,并用外壳封装起来就 构成了半导体二极管,(或称晶体二极管,简称二极管。 由P区引出的电极称为阳极(正极) 由N区引出的电极称为阴极(负极)
8
说明 ❖杂质半导体呈电中性,任一空间的正负电荷数相等
N型半导体:电子+正离子 P型半导体:空穴+负离子 ❖多子主要由掺杂形成,少子本征激发形成
9
PN结的形成
载流子的扩散运动
★PN结:
P区
- ---- ---- ----
+ ++++ + ++++
+ + + + + N区
建立内电场
扩散运动和 漂移运动达到
12
综上所述,PN结中存在着两种载流子的运 动。一种是多子克服电场的阻力的扩散运 动;另一种是少子在内电场的作用下产生 的漂移运动。因此,只有当扩散运动与漂 移运动达到动态平衡时,空间电荷区的宽 度和内建电场才能相对稳定。由于两种运 动产生的电流方向相反,因而在无外电场 或其他因素激励时,PN结中无宏观电流。
做为扩散的掩蔽膜。 4、氧化层的厚度需要大于设计的厚度,为2什2 么
(2) 涂胶
photoresist
问题: 1、涂胶.avi过程 2、光刻胶分类,作用,常用的光刻胶?
聚乙烯醇肉桂酸酯光刻胶 3、涂胶后,曝光前,有一个对光刻胶加固的过程叫做??
15
PN结正偏时呈导通 状态,正向电阻很小, 正向电流很大;
PN结反偏时呈截止 状态,反向电阻很大, 反向电流很小。 —— PN结的单向导电 性
16
半导体二极管的结构和类型
在一个PN结的两端,各引一根电极引线,并用外壳封装起来就 构成了半导体二极管,(或称晶体二极管,简称二极管。 由P区引出的电极称为阳极(正极) 由N区引出的电极称为阴极(负极)
8
说明 ❖杂质半导体呈电中性,任一空间的正负电荷数相等
N型半导体:电子+正离子 P型半导体:空穴+负离子 ❖多子主要由掺杂形成,少子本征激发形成
9
PN结的形成
载流子的扩散运动
★PN结:
P区
- ---- ---- ----
+ ++++ + ++++
+ + + + + N区
建立内电场
扩散运动和 漂移运动达到
12
综上所述,PN结中存在着两种载流子的运 动。一种是多子克服电场的阻力的扩散运 动;另一种是少子在内电场的作用下产生 的漂移运动。因此,只有当扩散运动与漂 移运动达到动态平衡时,空间电荷区的宽 度和内建电场才能相对稳定。由于两种运 动产生的电流方向相反,因而在无外电场 或其他因素激励时,PN结中无宏观电流。
做为扩散的掩蔽膜。 4、氧化层的厚度需要大于设计的厚度,为2什2 么
(2) 涂胶
photoresist
问题: 1、涂胶.avi过程 2、光刻胶分类,作用,常用的光刻胶?
聚乙烯醇肉桂酸酯光刻胶 3、涂胶后,曝光前,有一个对光刻胶加固的过程叫做??
医学影像学精-PN结ppt课件

.
PN结单向导电性引言:
PN结具有单向导电性,若外加电压使电流从P 区流到N区,PN结呈低阻性,所以电流大;反 之是高阻性,电流小。
如果外加电压使: PN结P区的电位高于N区的电位称为加正向 电压,简称正偏; PN结P区的电位低于N区的电位称为加反向 电压,简称反偏。
.
2、PN结的单向导电性
1)PN结加正向电压时:P区接电源正端,N区接
UB
.
4、PN结的击穿 当反向电压超过一定值时,PN结会出现击穿,此时 反向电流剧增,反向电流开始剧增的电压称为
反向击穿电压. 1)齐纳击穿: 内电场的强作用下,束缚电子被直接从 共价键中拉出来,形成电子空穴对,而产生大量的载 流子,加强了漂移运动,出现击穿.本质是场致激发.<5 2)雪崩击穿: 内电场的强作用下,在结内作漂移运动的少
外电路形成极小 反向电流反向饱
和电流 I
反偏总结:外加的反向电压有一部分降落在PN 结区,方向与PN结内电场方向相同,加强了内 电场。内电场对多子扩散运动的阻碍增强,扩 散电流大大减小。此时PN结区的少子在内电场 作用下形成的漂移电流大于扩散电流,可忽略 扩散电流,PN结呈现高阻性。
在一定的温度条件下,由本征激发决定的少子浓度
电源负端
动画演示
PN结正偏
P
耗尽层
N 内电场 减弱
耗尽层 变窄
扩散运动 加强
漂移运动 减弱
外电场
内电场
结平衡 破坏
.
2、 PN 结 的 单 向 导 电 性
.
2)PN结加反向电压时:P区接电源负端,N区接
电源正端 动画演示
耗尽层
PN结反偏
内电场 外电场
.
内电场 耗尽层 扩散运动
PN结单向导电性引言:
PN结具有单向导电性,若外加电压使电流从P 区流到N区,PN结呈低阻性,所以电流大;反 之是高阻性,电流小。
如果外加电压使: PN结P区的电位高于N区的电位称为加正向 电压,简称正偏; PN结P区的电位低于N区的电位称为加反向 电压,简称反偏。
.
2、PN结的单向导电性
1)PN结加正向电压时:P区接电源正端,N区接
UB
.
4、PN结的击穿 当反向电压超过一定值时,PN结会出现击穿,此时 反向电流剧增,反向电流开始剧增的电压称为
反向击穿电压. 1)齐纳击穿: 内电场的强作用下,束缚电子被直接从 共价键中拉出来,形成电子空穴对,而产生大量的载 流子,加强了漂移运动,出现击穿.本质是场致激发.<5 2)雪崩击穿: 内电场的强作用下,在结内作漂移运动的少
外电路形成极小 反向电流反向饱
和电流 I
反偏总结:外加的反向电压有一部分降落在PN 结区,方向与PN结内电场方向相同,加强了内 电场。内电场对多子扩散运动的阻碍增强,扩 散电流大大减小。此时PN结区的少子在内电场 作用下形成的漂移电流大于扩散电流,可忽略 扩散电流,PN结呈现高阻性。
在一定的温度条件下,由本征激发决定的少子浓度
电源负端
动画演示
PN结正偏
P
耗尽层
N 内电场 减弱
耗尽层 变窄
扩散运动 加强
漂移运动 减弱
外电场
内电场
结平衡 破坏
.
2、 PN 结 的 单 向 导 电 性
.
2)PN结加反向电压时:P区接电源负端,N区接
电源正端 动画演示
耗尽层
PN结反偏
内电场 外电场
.
内电场 耗尽层 扩散运动
半导体pn结异质结和异质结构ppt课件

“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
PN结的正向导电性
在PN结上外加一电压 ,如果P 型一边接正极 ,N型一边接负极,电流便 从P型一边流向N型一边,空穴和电子都向 界面运动,使空间电荷区变窄,甚至消失,
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
若干半导体杂质掺杂的一些考虑
杂质半导体ni,电子浓度n,空穴浓度p 之间的关系
n = ni e^(Ef-Ei)/kT, P = ni e^(Ei-Ef)/kT, ni^2 = n p Ei本征费米能级 Ef杂质费米能, 在n型半导体中,n>p,因此, Ef>Ei 在p型半导体中, p>n,因此, Ei>Ef
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
几个重要参数和概念 • 接触电位差:
由于空间电荷区存在电场,方向由N到P,因 此N区电位比P区高,用V表示,称作接触电位 差,它与半导体的类型(禁带宽度),杂质掺杂 浓度,环境温度等密切相关,一般为0.几V到 1.几V • 势垒高度:
pn结基础(共91张)

]2
N A (1 N A ND )
xn
[ 2r0
q
Vbi ND (1 ND
1
]2 NA)
xm
xn
xp
[ 2r0
q
1 ( NA
1 ND
1
)Vbi ]2
第15页,共91页。
② 有外加偏压时的突变(tūbiàn)结(非平衡突变(tūbiàn)结)
假设外加偏压V全部降落在耗尽层上
可忽略压降 (小注入)
p
p
0 p
p
p
0 p
n n0p n n
n nn0 n nn0 p p0p p p
p
n
xp xn
第25页,共91页。
非平衡(pínghéng)pn结-能带图
EC
EC
EC
E
p f
EC
E
n f
E
p f
q(Vbi V f )
EC
E
p f
E
n f
EV
EV
EV
EV
EV
外加偏压使电子和空穴不再有统一的费米能级
N ( x)
0
N
(
x
)
N N
A D
x xj x xj
xj
x
单边突变结(p+n结或n+p
结):一边的杂质浓度远大 于另一边
线性缓变结杂质分布的特 点:在结附近两侧杂质浓 度随距离线性变化,杂质 浓度梯度aj为常数。
N (x)
0
N(x) j (x xj )
xj
x
j
dN ( dx )xxj
突变结和线性缓变结是实际结杂 质浓度分布的两个极端近似。突 变结适用于表面浓度较高结深较 浅的结,线性缓变结适用于表面 浓度较低结深较深的缓变结。
N A (1 N A ND )
xn
[ 2r0
q
Vbi ND (1 ND
1
]2 NA)
xm
xn
xp
[ 2r0
q
1 ( NA
1 ND
1
)Vbi ]2
第15页,共91页。
② 有外加偏压时的突变(tūbiàn)结(非平衡突变(tūbiàn)结)
假设外加偏压V全部降落在耗尽层上
可忽略压降 (小注入)
p
p
0 p
p
p
0 p
n n0p n n
n nn0 n nn0 p p0p p p
p
n
xp xn
第25页,共91页。
非平衡(pínghéng)pn结-能带图
EC
EC
EC
E
p f
EC
E
n f
E
p f
q(Vbi V f )
EC
E
p f
E
n f
EV
EV
EV
EV
EV
外加偏压使电子和空穴不再有统一的费米能级
N ( x)
0
N
(
x
)
N N
A D
x xj x xj
xj
x
单边突变结(p+n结或n+p
结):一边的杂质浓度远大 于另一边
线性缓变结杂质分布的特 点:在结附近两侧杂质浓 度随距离线性变化,杂质 浓度梯度aj为常数。
N (x)
0
N(x) j (x xj )
xj
x
j
dN ( dx )xxj
突变结和线性缓变结是实际结杂 质浓度分布的两个极端近似。突 变结适用于表面浓度较高结深较 浅的结,线性缓变结适用于表面 浓度较低结深较深的缓变结。
《半导体PN结》PPT课件

本征半导体的导电能力取决于载流子的浓度。
温度越高,载流子的浓度越高。因此本征半
导体的导电能力越强,温度是影响半导体性
能的一个重要的外部因素,这是半导体的一
大特点。
精选课件ppt
12
总结
西安电子科技大学计算机学院吴自力 2012--2
本征激发:在室温或光照下价电子获得足够能键中留
因无共价键束缚而很容易被激发而成为自由电子。
在N型半导体中自由电子是多数载流子,它主要由 杂质原子提供;空穴是少数载流子, 由热激发形成。
提供自由电子的五价杂质原子因带正电荷而成为 正离子,因此五价杂质原精选子课件也ppt称为施主杂质。
15
西安电子科技大学计算机学院吴自力 2012--2
N 型半导体
而空穴的迁移相当于
+4
+4
正电荷的移动,因此
可以认为空穴是载流
子。
精选课件ppt
11
西安电子科技大学计算机学院吴自力 2012--2
自由电子的定向运动形成了电子电流,空穴的定 向运动也可形成空穴电流,它们的方向相反。
空穴的运动 = 相邻共价键中的价电子反向依次填补空穴位来实现的
本征半导体中电流由两部分组成: 1. 自由电子移动产生的电流。 2. 空穴移动产生的电流。
1
西安电子科技大学计算机学院吴自力 2012--2
§1.1 半导体的基本知识
1.1.1 本征半导体 1)导体、半导体和绝缘体
根据物体导电能力(电阻率)的不同,来划分导 体、绝缘体和半导体。
导体:自然界中很容易导电的物质称为导体,金属 一般都是导体。
绝缘体:有的物质几乎不导电,称为绝缘体,如橡皮、 陶瓷、塑料和石英。
精选课件ppt
温度越高,载流子的浓度越高。因此本征半
导体的导电能力越强,温度是影响半导体性
能的一个重要的外部因素,这是半导体的一
大特点。
精选课件ppt
12
总结
西安电子科技大学计算机学院吴自力 2012--2
本征激发:在室温或光照下价电子获得足够能键中留
因无共价键束缚而很容易被激发而成为自由电子。
在N型半导体中自由电子是多数载流子,它主要由 杂质原子提供;空穴是少数载流子, 由热激发形成。
提供自由电子的五价杂质原子因带正电荷而成为 正离子,因此五价杂质原精选子课件也ppt称为施主杂质。
15
西安电子科技大学计算机学院吴自力 2012--2
N 型半导体
而空穴的迁移相当于
+4
+4
正电荷的移动,因此
可以认为空穴是载流
子。
精选课件ppt
11
西安电子科技大学计算机学院吴自力 2012--2
自由电子的定向运动形成了电子电流,空穴的定 向运动也可形成空穴电流,它们的方向相反。
空穴的运动 = 相邻共价键中的价电子反向依次填补空穴位来实现的
本征半导体中电流由两部分组成: 1. 自由电子移动产生的电流。 2. 空穴移动产生的电流。
1
西安电子科技大学计算机学院吴自力 2012--2
§1.1 半导体的基本知识
1.1.1 本征半导体 1)导体、半导体和绝缘体
根据物体导电能力(电阻率)的不同,来划分导 体、绝缘体和半导体。
导体:自然界中很容易导电的物质称为导体,金属 一般都是导体。
绝缘体:有的物质几乎不导电,称为绝缘体,如橡皮、 陶瓷、塑料和石英。
精选课件ppt
(完整版)PN结结电容

PN结结电容
PN结:
1)在外加正向电压时,电压大小的变化,引起空间电荷区(耗尽层)宽窄的变化,即空间电荷区正负电荷多少的变化,类似于电容充放电时极板电荷的变化,这种电容效应称之为“势垒电容”,Cb。
受主原子施主原子变成带电离子的数量变化
当PN结加反向电压时,Cb明显随u的变化而变化,利用这一特性制成变容二极管。
2)在外加正向电压大小变化时,引起耗尽层载流子(少子)浓度及数量的变化,这种电容效应称之为“扩散电容”,Cd。
3)PN结电容Cj=Cb+Cd
结面积小的为1pF左右,结面积大的为几十至几百pF,对于低频信号呈现出很大的容抗,其作用可忽略不计,因而只有在高频时才考虑结电容的作用。
PN结电容和雪崩二极管PPT课件

• 在这里,Xm相当于平行板电容器两极板的 间距.
.
6
• PN结势垒电容与平行板电容器的主要区别 在于:平行板电容器两极板间的距离d是一个 常数,它不随电压V变化,而空间电荷宽度 Xm不是一个常数,而是随电压V变化 的.因此平行板电容器的电容是常数,而 PN结的势垒电容是偏压V的函数.通常所 说的PN结电容是指在一定的直流外加偏压 下,当电压有一微小变化σV时,相应的电 荷变化量σQ与σV的比值,一般称它为微分 电容.
.
19
此外,雪崩二极管具有和 齐纳二极管相似的伏安特 性曲线,在击穿状态时, 电流在很宽的范围内变化时, 二级管两端电压保持稳定。 因此,雪崩二极管亦可用于 稳压电源电路中。
雪崩二极管用于稳压
.
20
Thanks
.
21
.
9
• 所以外加电压变化时,n区扩散区内积累的 非平衡空穴也增加.与它保持电中性的电 子也相应增加。
• 同样,p区扩散区内积累的非平衡电子和与它 保持电中性的空穴也要增加。
• 这种由于扩散区的电荷数量随外加电压的 变化所产生的电容效应.称为p—n结的扩 散电容。
.
10
• 实验发现,PN结的势垒电容和扩散电容都 随外加电压而变化,表明它们是可变电容。 因此,引入微分电容的概念来表示PN结的 电容。
• 这些电子和空穴在高压作用下又去碰撞其他的原 子,产生更多的电子-空穴对。如此链锁反应, 一下子就会产生出大量的电子-空穴对,以致通 过PN结的反向电流猛增,于是出现PN结击穿现 象。
.
ห้องสมุดไป่ตู้13
PN结雪崩击穿示意图
因为这种击穿现 象发生时,电流 的猛增象雪崩一 样,所以常称为 雪崩击穿。
.
.
6
• PN结势垒电容与平行板电容器的主要区别 在于:平行板电容器两极板间的距离d是一个 常数,它不随电压V变化,而空间电荷宽度 Xm不是一个常数,而是随电压V变化 的.因此平行板电容器的电容是常数,而 PN结的势垒电容是偏压V的函数.通常所 说的PN结电容是指在一定的直流外加偏压 下,当电压有一微小变化σV时,相应的电 荷变化量σQ与σV的比值,一般称它为微分 电容.
.
19
此外,雪崩二极管具有和 齐纳二极管相似的伏安特 性曲线,在击穿状态时, 电流在很宽的范围内变化时, 二级管两端电压保持稳定。 因此,雪崩二极管亦可用于 稳压电源电路中。
雪崩二极管用于稳压
.
20
Thanks
.
21
.
9
• 所以外加电压变化时,n区扩散区内积累的 非平衡空穴也增加.与它保持电中性的电 子也相应增加。
• 同样,p区扩散区内积累的非平衡电子和与它 保持电中性的空穴也要增加。
• 这种由于扩散区的电荷数量随外加电压的 变化所产生的电容效应.称为p—n结的扩 散电容。
.
10
• 实验发现,PN结的势垒电容和扩散电容都 随外加电压而变化,表明它们是可变电容。 因此,引入微分电容的概念来表示PN结的 电容。
• 这些电子和空穴在高压作用下又去碰撞其他的原 子,产生更多的电子-空穴对。如此链锁反应, 一下子就会产生出大量的电子-空穴对,以致通 过PN结的反向电流猛增,于是出现PN结击穿现 象。
.
ห้องสมุดไป่ตู้13
PN结雪崩击穿示意图
因为这种击穿现 象发生时,电流 的猛增象雪崩一 样,所以常称为 雪崩击穿。
.
PN结工作原理-动态图画ppt课件
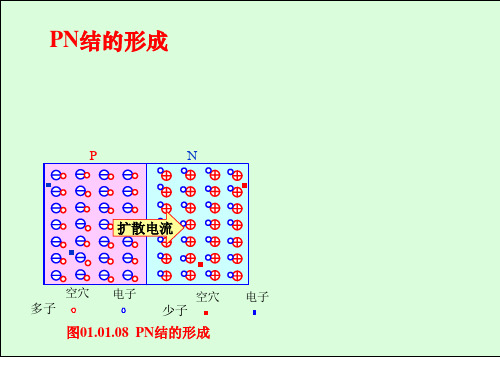
因浓度差
多子的扩散运动由杂质离子形成空间电荷区
空间电荷区形成内电场
内电场促使少子漂移
内电场阻止多子扩散
扩散电流 = 漂移电流
PN加正向电压时的导电情况
P
PN结
N
内内电电场场
外电场
R
IF
E
图01.01.11 PN结加正向电压
PN结加反向电压时的导电情况
P
PN结
N
内内电电场场
外电场 R
E IS
图01.01.12 PN结加反向电压
势垒电容CB
P
N
CB
U
反向区
U
U 0
图 01.01.13 势垒电容示意图
扩散电容CD
少子浓度
pn
np
1
2
2 1
+
-
U U
图 01.01.14 扩散电容示意图
PN结的形成
P
N
扩散电流
空穴 电子
空穴 电子
多子
少子
图01.01.08 PN结的形成
P
N
内电场
漂移电流 扩散电流
空穴 电子
多子
空穴
少子
电子
图01.01.08 PN结的形成
P
N
内电场
漂移电流 扩散电流
空穴
多子
电子
空穴
少子
电子
图01.01.08 PN结的形成
以上在N型半导体和P型半导体结合面上形成的物理过程 过程概括如下:
PN结——电容特性优秀课件

的电子电流一定;半导体流向金
-
属的电子电流因电位增加而降低,
故有半导体→金属反向电流(恒
定)。
金属半导体接触I-U特性类似于pn结的伏安特性
I
正向特性
VD
反向特性
肖特基二极管
利用金属—半导体整流接触特性制成的二极管称 为肖特基二极管。
肖特基二极管与pn二极管的比较
相同:单向导电性 不同:
1 反向电流产生机制不同: ➢肖特基二极管为多数载流子工作 ➢pn接面二极管为少数载流子工作 ➢结果:肖特基二极管的饱和电流要 大得多,起始电流也较大。
P
△U变化时,P区 积累的非平衡少 子浓度分布图
3 1
2
电子浓度
1 ΔU=0
2 ΔU<0
x 3 ΔU>0
U ΔU
N
+ +
+ +
....................................
. ..
.
.
P
PN结正向偏置电压越高,积累的非平衡少子越多。
这种电容效应用扩散电容CD表征。
CD Q U
PN结正偏时,由N区扩 散到P区的电子(非平衡少 子),堆积在 P 区内紧靠 PN结的附近,到远离交界 面处,形成一定的浓度梯 度分布曲线。电压增大, 正向(扩散)电流增大。
扩散电容示意图
U ΔU
N
+ +
+ +
....................................
. . .
..
C1 L
Байду номын сангаасDC
R
+ UD –
p-n结电容-第九次课

1
CT =
d QT dV
=[
ε sε 0 q N D N A
2 ND + N A
1 −1 2
(VD + V ) ] =
1 −1 2
ε sε 0
xD
单边突变结:p + n结N A >> N D CT = [
ε sε 0 qN D
2
1 ε sε 0 qN D (VD + V ) ] ⇒ 2 = (VD + V ) CT 2
•
• 求解空间电荷区的电场、电位分布时,我们得 到:
N D xTn = N A xTp ...............................电场在x = 0处连续 V = q ( N x 2 + N x 2 )...........电位在x = 0处连续 A Tp D Tn D 2ε ε 0 s
ε (0) = ε max =
qN A xTp
ε 0ε s
=
qN D xTn
ε 0ε s
2)突变结的电位分布
dV = −ε ( x) ⇒ V ( x) = ∫ ε ( x)dx + D dx
同样,求解需要分成两个区域: 同样,求解需要分成两个区域:( -xTp , 0)和(0 , xTn ) )
• (− xTp ,0) :
qN A 2 qN A ε 1 ( x) = − x + xTp x + D1 ( x + xTp ) ⇒ V1 ( x) = ∫ ε 1 ( x)dx + D1 = ε 0ε S ε 0ε S 2ε 0ε S 边界条件:V1 x = − x = 0 Tp qN A 2 qN A 2 ⇒ V1 ( x) = ( x + xTp ) + xTp x 2ε 0ε S ε 0ε S qN A (0, xTn ) : qN D 2 qN A ( x − xTn ) ⇒ V2 ( x) = ∫ ε 2 ( x)dx + D2 = − x + xTn x + D2 ε 2 ( x) = 2ε 0ε S ε 0ε S ε 0ε S 边界条件:V2 x = x = VD
CT =
d QT dV
=[
ε sε 0 q N D N A
2 ND + N A
1 −1 2
(VD + V ) ] =
1 −1 2
ε sε 0
xD
单边突变结:p + n结N A >> N D CT = [
ε sε 0 qN D
2
1 ε sε 0 qN D (VD + V ) ] ⇒ 2 = (VD + V ) CT 2
•
• 求解空间电荷区的电场、电位分布时,我们得 到:
N D xTn = N A xTp ...............................电场在x = 0处连续 V = q ( N x 2 + N x 2 )...........电位在x = 0处连续 A Tp D Tn D 2ε ε 0 s
ε (0) = ε max =
qN A xTp
ε 0ε s
=
qN D xTn
ε 0ε s
2)突变结的电位分布
dV = −ε ( x) ⇒ V ( x) = ∫ ε ( x)dx + D dx
同样,求解需要分成两个区域: 同样,求解需要分成两个区域:( -xTp , 0)和(0 , xTn ) )
• (− xTp ,0) :
qN A 2 qN A ε 1 ( x) = − x + xTp x + D1 ( x + xTp ) ⇒ V1 ( x) = ∫ ε 1 ( x)dx + D1 = ε 0ε S ε 0ε S 2ε 0ε S 边界条件:V1 x = − x = 0 Tp qN A 2 qN A 2 ⇒ V1 ( x) = ( x + xTp ) + xTp x 2ε 0ε S ε 0ε S qN A (0, xTn ) : qN D 2 qN A ( x − xTn ) ⇒ V2 ( x) = ∫ ε 2 ( x)dx + D2 = − x + xTn x + D2 ε 2 ( x) = 2ε 0ε S ε 0ε S ε 0ε S 边界条件:V2 x = x = VD
PN结的形成及特性PPT课件

- - - - - - + ++ +++
- - - - - - + ++ +++
- - - - - -+ ++ +++
少子(自由电子)
P
N
少子(空穴)
N区有许多自由电子(多数载流子)和几个由于热产生的空穴 (少数载流子),而P区有许多空穴(多数载流子)和几个由于热产生 的自由电子(少数电子)。PN结构成了基本的二极管。二极管是只允 许电流往一个方向流动的元件。
P
N
第2页/共44页
P 型半导体
N 型半导体
- - - - - - + ++ +++
- - - - - - + ++ +++
- - - - - - + ++ +++
- - - - - - + ++ +++
- - - - - - + ++ +++
- - - - - -+ ++ +++
少子(自由电子)
P
N
第6页/共44页
- - - - - - + ++ +++
- - - - - - + ++ +++
- - - - - - + ++ +++
模电PN结电容PPT学习教案

2021/7/1
id
CD id
rd
CT 当频率很高时
第3页/共6页
如果使二极管反偏,这时CD=0 反向电阻rd很大,反偏二极管在高频 时可以 当作电 容器来 使用,
CT
CT (0) (1 uD )
U
Uφ为PN结内建电压,CT (0)是反向偏压UD=0V时的势垒电容。γ 称为变 容指数
CT
变容二极管
id id
CD
rd CT
CT -U+
CT(0)
UD UΦ 变容管的压控特性曲线
变容管广泛应用于高频电路
变容管的电路符号
第4页/共6页
2021/7/1
特殊二极管
1.光敏二极管
2 . 发光二极管
I/μA
光敏二极管的符号
- -8 -4 12
UD / V
E=200lx
E=400lx -
光电二极管的P50N结特性曲线
模电PN结电容
会计学
1
1.势垒电容CT
CT
dQ dUD
Q U D
当反偏电压UD增大ΔUD时
相当于对PN结充电
同理,当UD减小ΔUD时
相当于PN结放电
CT
dQ dUD
Q U D
可见,势垒电容可等效为一个极板距 离随外 加电压 变化的 平行板 电容, 极板距 离就相 当于空 间电荷 区的宽 度。
2021/7/1
第2页/共6页
2021/7/1
3 变容二极管
PN结总电容CJ = CT +CD,称CJ为的结电容 正偏二极管的扩散电容CD比势垒电容 CT大,CJ以C D为主 加反向偏压时,CD=0,CJ以CT为主 二极管高频小信号模型 一般当信号角频率ω较低时,rd<< l/(ωCJ) ,CD和CT的容抗很大,相当于开路,二 极管的 小信号 模型中 只有rd
id
CD id
rd
CT 当频率很高时
第3页/共6页
如果使二极管反偏,这时CD=0 反向电阻rd很大,反偏二极管在高频 时可以 当作电 容器来 使用,
CT
CT (0) (1 uD )
U
Uφ为PN结内建电压,CT (0)是反向偏压UD=0V时的势垒电容。γ 称为变 容指数
CT
变容二极管
id id
CD
rd CT
CT -U+
CT(0)
UD UΦ 变容管的压控特性曲线
变容管广泛应用于高频电路
变容管的电路符号
第4页/共6页
2021/7/1
特殊二极管
1.光敏二极管
2 . 发光二极管
I/μA
光敏二极管的符号
- -8 -4 12
UD / V
E=200lx
E=400lx -
光电二极管的P50N结特性曲线
模电PN结电容
会计学
1
1.势垒电容CT
CT
dQ dUD
Q U D
当反偏电压UD增大ΔUD时
相当于对PN结充电
同理,当UD减小ΔUD时
相当于PN结放电
CT
dQ dUD
Q U D
可见,势垒电容可等效为一个极板距 离随外 加电压 变化的 平行板 电容, 极板距 离就相 当于空 间电荷 区的宽 度。
2021/7/1
第2页/共6页
2021/7/1
3 变容二极管
PN结总电容CJ = CT +CD,称CJ为的结电容 正偏二极管的扩散电容CD比势垒电容 CT大,CJ以C D为主 加反向偏压时,CD=0,CJ以CT为主 二极管高频小信号模型 一般当信号角频率ω较低时,rd<< l/(ωCJ) ,CD和CT的容抗很大,相当于开路,二 极管的 小信号 模型中 只有rd
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0
XD 0
2
q
j xdx
q j xD2
8
xD
QT
[120 s q j
(VD
1
VR )]3
q
8
j
[120 s q j
(VD
2
VR )]3
CT
d QT dVR
[
02
2 s
q j
1
]3
0 s
12 VD VR
xD
讨论:
CT是微分电容,随反向偏压的增加,xD增加, CT下降。
无论突变结,缓变结,其ln CT与lnV之间都是线性关系:
x3 q j 8 0 S
xD x
线性缓变结的接触电势电位分布差:
VD
V ( xD 2
)
V (
xD 2
)
q j xD3
12
•
线性缓变结情况
在前面的内容,求空间电荷区电场、电位分布时得出
VD
q (
12
j xD3 )
在外加电压V 下,有:
VD
VR
q 12
(
j
xD3
)
QT
XD
2 (x)dx
qVF
e k0T
在P 型侧,从过剩载流子分布入手:
x xTp
n(x) [ p(xTp ) n0 p ]e Ln
QDp
q
xTp
n( x)dx
q[n(xTp ) n0 p ]Ln
qVF
qn0 p (e k0T 1)Ln
CDp
dQDp dVF
q2n0 p Ln kT
qVF
e k0T
总扩散电容CD 是P 型侧和N 型侧之和
0处连续 0处连续
• 当存在外加电压V 时,上式变为:
N AxTp ND xTn QT / q
VD
V
q
2 s0
(N A xT2p
ND xT2n )
• 求得:
QT
[2 s0q
ND NA NDNA
(VD
V
1
)]2
xD
xTn
xTp
[ 2 s0
q
ND NA NDNA
1
(VD V )]2
CT
(x)dx D
同样,求解需要分成两个区域:( -xTp , 0)和(0 , xTn )
•
(xTp ,0) :
1 ( x)
qN A
0 S
(x
xTp
)
V1 ( x)
1(x)dx D1
qN A
2 0 S
x2
qNA
0 S
xTp
x
D1
边界条件:V1 xxTp 0
V1(x)
qN A
2 0 S
CD
CDn
CDp
q2 (n0 p Ln kT
p0n Lp )
qVF
e k0T
讨论
CD 随正向偏压的增加而增加; 需要指出的是:这里计算的CT 、CD的表达式都是单位面
积的电容值,它们的单位都是F/m2,在实际计算中,应 再乘上结面积,得出实际的电容值,即:
CD’=A CD, CT’=A CT
突变结,斜率为-1/2,
CT
[0s
2
NDNA ND ND
(VD
1
V )1]2
缓变结,斜率为-1/3,
CT
[02 s2
12
q j
1
]3
VD V
据此,可以区分出这两种结的类型。由x轴和y轴截距,分别 可以求出掺杂浓度或浓度梯度及接触电势差VD
二、扩散电容CD 扩散电容CD 是两电容的并联—— N 型侧的过剩载流子电容
一、势垒电容CT
• 势垒电容的定义为: CT
d QT dV
其中:QT 为势垒区中正电荷或负电荷量,V 为外加电压。 突变结情况
pn结中电场、电位分布与pn结能带图
探讨电场、电位分布,从三组基本方程中的泊松方程着
手。
(
x)
d (x)
dx 0 s
(x) dV (x)
dx
q[nD (x)
d QT dV
[s0q
2
NDNA ND NA
(VD
1
V )1]2
s 0
xD
单边突变结:pn结N A ND
CT
[s0qND
2
(VD
1
V )1]2
1 CT2
s 0qN D
2
(VD
V)
•
线性缓变结的电位分布:
dV (x) dx
(x)
V
(x)
(x)dx
D
V 0 x0
V (x) q j 6 0 S
(x2
xT2p )
qN A
0 S
xTp x
(0, xTxTn
)
V2 (x)
2 (x)dx D2
qND
2 0 S
x2
qNA
0 S
xTn x D2
边界条件:V2 xxTn VD
V2 (x)
VD
qN A
2 0 S
(x2
xT2n )
qN A
0 S
0
x xTp , x xTn
(xTp ,0) :
d1
dx
qNA
0 S
1(x)
qN A
0 S
0 1 x xTp
x
c1
1
(
x)
qNA
0 S
(x
xTp )
(0, xTn ) :
d 2
dx
qND
0 S
2(x)
0 2 xxTn
qND
0 S
x
c2
2
(
x)
qND
0 S
(x xTn )
讨论
在x = 0 点,电场是连续的,即:
1(0) = 2(0), ND .xTN = NA .xTP (此式的意义是空间电荷区中正负电荷数相等)。
在空间电荷区中,电场最强点在x = 0 点,其值为:
(0)
max
qN A xTp
0 s
qND xTn
0 s
2)突变结的电位分布
dV dx
(x) V (x)
CDN 与P 型侧的过剩载流子电容CDP 的并联。 在N 型侧:从过剩载流子分布入手:
x xTn
p(x) [ p(xTn ) p0n ]e Lp
QDn q xTn p(x)dx q[ p(xTn ) p0n ]Lp
qVF
qp0n (e k0T 1)Lp
CDn
dQDn dVF
q2 p0n Lp kT
q
ND
1
)2
NA(NA ND)
xD
xTN
xTP
[ 20SVD
q
1 ( NA
1 ND
1
)] 2
PN结的空间电荷区宽度,主要由掺杂浓度低的一边决定。
势垒高坡阻止了电子的扩散趋势,使之达到平衡
•
• 求解空间电荷区的电场、电位分布时,我们得 到:
VNDDxTn2q0Ns
AxTp ..............................电. 场在x (N AxT2p ND xT2n )...........电位在x
p
A
(
x)
p
(
x)
n(
x)]
• 在空间电荷区中做以下近似:
1、耗尽层近似:在(-xTp, xTn)中,n(x)=0,p(x)=0; 在(-xTp, xTn)外,n(x)=n0,p(x)=p0;
2、假定杂质全部电离nD+=ND,pA-=NA
突变结:
1)突变结的电场分布
(x) qqNNDA
xTp x 0 0 x xTn
xTn x
讨论: 在x=0点,电势连续,即:
V1 (0)
V2 (0) :VD
q
20 S
(N A xT2p
N D xT2n )
此式连同电场在x=0点连续的结果: ND .xTN = NA .xTP,可以解出 xTN,xTP的具体数值
xTN
( 20SVD
q
N
D
(
N NA
A
N
D
)
)
1 2
,
xTP
( 20SVD
• §6.4 pn 结电容
• 电容:两极板上的电荷随电压的变化关系可用电容表示。在 交流信号作用下,pn结会失去单向导电性,说明有电容作用。
• 在pn结中,有两类电荷会随外加电压变化:
• 势垒区中的杂质离子电荷是随着外加偏置电压而变化的,由 此引起的电容效应称为势垒电容,以CT 表示;
pn在偏置下,在结两侧的扩散区内,各存在着两组过剩载 流子,它们的数量也随着外加电压的变化而变化。这种电 容效应称为扩散电容,以CD表示。
XD 0
2
q
j xdx
q j xD2
8
xD
QT
[120 s q j
(VD
1
VR )]3
q
8
j
[120 s q j
(VD
2
VR )]3
CT
d QT dVR
[
02
2 s
q j
1
]3
0 s
12 VD VR
xD
讨论:
CT是微分电容,随反向偏压的增加,xD增加, CT下降。
无论突变结,缓变结,其ln CT与lnV之间都是线性关系:
x3 q j 8 0 S
xD x
线性缓变结的接触电势电位分布差:
VD
V ( xD 2
)
V (
xD 2
)
q j xD3
12
•
线性缓变结情况
在前面的内容,求空间电荷区电场、电位分布时得出
VD
q (
12
j xD3 )
在外加电压V 下,有:
VD
VR
q 12
(
j
xD3
)
QT
XD
2 (x)dx
qVF
e k0T
在P 型侧,从过剩载流子分布入手:
x xTp
n(x) [ p(xTp ) n0 p ]e Ln
QDp
q
xTp
n( x)dx
q[n(xTp ) n0 p ]Ln
qVF
qn0 p (e k0T 1)Ln
CDp
dQDp dVF
q2n0 p Ln kT
qVF
e k0T
总扩散电容CD 是P 型侧和N 型侧之和
0处连续 0处连续
• 当存在外加电压V 时,上式变为:
N AxTp ND xTn QT / q
VD
V
q
2 s0
(N A xT2p
ND xT2n )
• 求得:
QT
[2 s0q
ND NA NDNA
(VD
V
1
)]2
xD
xTn
xTp
[ 2 s0
q
ND NA NDNA
1
(VD V )]2
CT
(x)dx D
同样,求解需要分成两个区域:( -xTp , 0)和(0 , xTn )
•
(xTp ,0) :
1 ( x)
qN A
0 S
(x
xTp
)
V1 ( x)
1(x)dx D1
qN A
2 0 S
x2
qNA
0 S
xTp
x
D1
边界条件:V1 xxTp 0
V1(x)
qN A
2 0 S
CD
CDn
CDp
q2 (n0 p Ln kT
p0n Lp )
qVF
e k0T
讨论
CD 随正向偏压的增加而增加; 需要指出的是:这里计算的CT 、CD的表达式都是单位面
积的电容值,它们的单位都是F/m2,在实际计算中,应 再乘上结面积,得出实际的电容值,即:
CD’=A CD, CT’=A CT
突变结,斜率为-1/2,
CT
[0s
2
NDNA ND ND
(VD
1
V )1]2
缓变结,斜率为-1/3,
CT
[02 s2
12
q j
1
]3
VD V
据此,可以区分出这两种结的类型。由x轴和y轴截距,分别 可以求出掺杂浓度或浓度梯度及接触电势差VD
二、扩散电容CD 扩散电容CD 是两电容的并联—— N 型侧的过剩载流子电容
一、势垒电容CT
• 势垒电容的定义为: CT
d QT dV
其中:QT 为势垒区中正电荷或负电荷量,V 为外加电压。 突变结情况
pn结中电场、电位分布与pn结能带图
探讨电场、电位分布,从三组基本方程中的泊松方程着
手。
(
x)
d (x)
dx 0 s
(x) dV (x)
dx
q[nD (x)
d QT dV
[s0q
2
NDNA ND NA
(VD
1
V )1]2
s 0
xD
单边突变结:pn结N A ND
CT
[s0qND
2
(VD
1
V )1]2
1 CT2
s 0qN D
2
(VD
V)
•
线性缓变结的电位分布:
dV (x) dx
(x)
V
(x)
(x)dx
D
V 0 x0
V (x) q j 6 0 S
(x2
xT2p )
qN A
0 S
xTp x
(0, xTxTn
)
V2 (x)
2 (x)dx D2
qND
2 0 S
x2
qNA
0 S
xTn x D2
边界条件:V2 xxTn VD
V2 (x)
VD
qN A
2 0 S
(x2
xT2n )
qN A
0 S
0
x xTp , x xTn
(xTp ,0) :
d1
dx
qNA
0 S
1(x)
qN A
0 S
0 1 x xTp
x
c1
1
(
x)
qNA
0 S
(x
xTp )
(0, xTn ) :
d 2
dx
qND
0 S
2(x)
0 2 xxTn
qND
0 S
x
c2
2
(
x)
qND
0 S
(x xTn )
讨论
在x = 0 点,电场是连续的,即:
1(0) = 2(0), ND .xTN = NA .xTP (此式的意义是空间电荷区中正负电荷数相等)。
在空间电荷区中,电场最强点在x = 0 点,其值为:
(0)
max
qN A xTp
0 s
qND xTn
0 s
2)突变结的电位分布
dV dx
(x) V (x)
CDN 与P 型侧的过剩载流子电容CDP 的并联。 在N 型侧:从过剩载流子分布入手:
x xTn
p(x) [ p(xTn ) p0n ]e Lp
QDn q xTn p(x)dx q[ p(xTn ) p0n ]Lp
qVF
qp0n (e k0T 1)Lp
CDn
dQDn dVF
q2 p0n Lp kT
q
ND
1
)2
NA(NA ND)
xD
xTN
xTP
[ 20SVD
q
1 ( NA
1 ND
1
)] 2
PN结的空间电荷区宽度,主要由掺杂浓度低的一边决定。
势垒高坡阻止了电子的扩散趋势,使之达到平衡
•
• 求解空间电荷区的电场、电位分布时,我们得 到:
VNDDxTn2q0Ns
AxTp ..............................电. 场在x (N AxT2p ND xT2n )...........电位在x
p
A
(
x)
p
(
x)
n(
x)]
• 在空间电荷区中做以下近似:
1、耗尽层近似:在(-xTp, xTn)中,n(x)=0,p(x)=0; 在(-xTp, xTn)外,n(x)=n0,p(x)=p0;
2、假定杂质全部电离nD+=ND,pA-=NA
突变结:
1)突变结的电场分布
(x) qqNNDA
xTp x 0 0 x xTn
xTn x
讨论: 在x=0点,电势连续,即:
V1 (0)
V2 (0) :VD
q
20 S
(N A xT2p
N D xT2n )
此式连同电场在x=0点连续的结果: ND .xTN = NA .xTP,可以解出 xTN,xTP的具体数值
xTN
( 20SVD
q
N
D
(
N NA
A
N
D
)
)
1 2
,
xTP
( 20SVD
• §6.4 pn 结电容
• 电容:两极板上的电荷随电压的变化关系可用电容表示。在 交流信号作用下,pn结会失去单向导电性,说明有电容作用。
• 在pn结中,有两类电荷会随外加电压变化:
• 势垒区中的杂质离子电荷是随着外加偏置电压而变化的,由 此引起的电容效应称为势垒电容,以CT 表示;
pn在偏置下,在结两侧的扩散区内,各存在着两组过剩载 流子,它们的数量也随着外加电压的变化而变化。这种电 容效应称为扩散电容,以CD表示。
