化学反应工程 101 - CSTR停留时间分布计算87页PPT
化学反应工程第五章课件

m
C A0
0
xAf
xA
0
xAf
xA
m P Vm VP
m 比较 P
1 (rA )
Chemical Reaction Engineering
xA
n =0 n=1
n=2
0.9
1
4
10
0.99
1
22 100
1
n=2
(rA )
P
n=1
CA0
0
xAf 1
xAf 2
xA
xA越大,相差越大
0
xAf
xA
反应移到一个管内径为125mm 的理想管式反应器中
进行,仍维持 75℃等温操作,且处理量和所要求转化 率相同,求所需反应器的管长。
Chemical Reaction Engineering
解:由于CA0 CB0 ,且是等摩尔反应,所以反应速率方程为
(rA )
kCACB
kC
2 A
此反应在理想间歇反应器中达到要求转化率所需反应时间为
基本方程
cA0 cAf
(rA )
cA0 xAf kcAn0 (1 xAf
)n
cAn 01k
xAf (1 xAf
)n
反应器型式 反应级数
一级
二级
零级
PFR
k ln 1 或 1 xA
C A e k C A0
C A0 k
1
xA xA
或
CA 1 C A0 1 C A0 k
k
CA0
xA
1
C A 1 k
Chemical Reaction Engineering
第五章 连续流动釜式反应器(CSTR) (Continuous Stirred Tank Reactor)
化学反应工程陈甘棠第四章课件

cA 81.3333
c A dt
0
2019/10/29
Et 4 0.0492
t5 81.3333
t
Ft Etdt
0
F t
5
t5 E t
0
dt
15 81.33330
cAdt
77 81.3333
0.9467
tc A dt
o
留在系统中的量 VRCA00tI(t)dt
2019/10/29
t
t
v0cA01Ftd tVRcA0Itdt
0
0
1 F t It tIt EtdIt
dt
有时采用
强度函数
t1
Et It
表示两者的关系:
t1
t t 2 E t dt t 2 0
t
t
2
Etdt
t2Etdtt2
E t dt
0
0
0
2019/10/29
令:无因次时间: t t
则: 无因次平均停留时间 t 1
t
Ed1Etdt
0
0
E()dE(t)dt t
t
EEt EtEt
t
FFt dF dF t
2019/10/29
若以
2
表示以为自变量的方差,则它与
2 t
的关系为:
2 12Ed
0
0
t t
2
1
Ed
t
0
0 dt
F t 0
反应工程 停留时间分布分析

无因次停留时间(对比时间) • 对比停留时间 t θ
• 对比停留时间的数学期望 • 对比停留时间的方差
2 t 2 0
1
2 2
(t ) E (t )dt ( 1)
0
E ( )
d
2
0
( 1) 2 E ( )d 2 2
两种理想反应器的方差
• 全混流反应器
σ t2 t 2 E (t )dt 2 t 2
0 0
1
e dt 2 2
-
t
2 1
2
σ
2 t 2
2
• 平推流反应器
σ σ 0
2 t 2பைடு நூலகம்
用脉冲信号法测定某反应器的停留时间分布,得 到不同时刻反应器出口示踪剂浓度如下所列。
时间t/min 出口示踪剂浓度c/(g/L) 0 0 5 3 10 5 15 5 20 4 25 2 30 1 35 0
利用上述数据标绘该反应器的E曲线,并计算反应 器的平均停留时间,停留时间分布的方差t 2和2。
• 平均停留时间
ci(t) ti ci(t)ti ti ci(t) ti Ei (t )ti ti ti ci (t )ti ci (t )ti ci (t ) • 方差 2 2 c (t) t c (t) t t 2 2 2 2 i i i i i ci(t) σ t ti ti 2 ci (t )ti ci (t )ti ci (t )
停留时间分布
3月19日
停留时间分布曲线应用
• • • • 判断反应器中的流动状况 判断反应器的不良状况 实际反应器与理想反应器的偏差定量化 用于反应器的计算
化学反应工程第五章

5.2.1 停留时间(寿命)分布密度函数E(t)
• 如图5.2-1所示,t=0时瞬间进入的N个流体质点 中,寿命介于t →t+dt之间的质点数dN所占总质 点数N的分率dN/N=E(t)dt,E(t)dt为一微分的分 率,E(t)= dN/N dt,其量纲为[时间]-1,称为停 留时间(寿命)分布密度函数。
• 当t→∞时,t→0同时进入反应器的N个质点全 部流出反应器,故有:
F (t ) t E (t )dt 1
0
dF (t ) E (t ) dt
或
dF (t ) E (t )dt
• 停留时间分布积累函数F(t)有以下性质: • t=0时,F(t)=0;t=∞时,F(t)=1,所以, 0≤F(t)≤1,即,F(t)是一个单调不减函数; • dF(t)/dt=E(t) ,F(t)为一无因次数
t 0
• 例如某一次的考试成绩分布如下:
则平均成绩 M=∑MiXi=60*5%+70*15%+80*65%+90*15%=79 可见平均成绩是各级成绩的加权平均值。
• 流体质点在反应器中的停留时间可能值为0→∞, 停留时间为t的流体质点所占的分率为E(t)dt, 故: 平均停留时间 t 0 tE (t )dt tE (t )t 0 为避免实验结果带来的系统误差,对于离散型 数据可以除于 E (t )t i
t
tE (t )t E (t )t
0 0
0
i
ti 相同
tE (t ) E (t )
0 0
脉冲示踪法
tC (t ) C (t )
0 0
i
化学反应工程基础连续流动反应器的停留时间分布

1.阶跃示踪法
阶跃讯号响应曲线
待测定系统稳定后,将 原来反应器中流动的流休切 换为另一种含有示踪剂的流 体。一直保侍到实验结束, 并保诗切换而后流体流量不 变。
开始时,出口流体中有示踪剂流体的分率很小,随着时间的推延, 有示踪剂流体在出口流体中的分率不断增加,当t→∞时,分率趋于1。
,以C t v0
Q
对τ作图即可得停留时间分布密度函
数曲线。
▪ 脉冲示踪法要求进料瞬间完成,技术要求较高,可在生产中在线测定。
连续流动反应器的停留时间分布
停留时间分布的数字特征
由于停留时间分布密度函数E(t)对单个流体微元来讲, 就是随机变量——停留时间的概率密度函数,因此也可用 这些函数的特征值作为随机变量的比较基准来进行定量比 铰,而无需对分布曲线本身进行比较。
0
t
2
1
t
dt
2
0
2 2 2
2
无因次方差:
2
2
1
2
流动模型
理想混合流的E(t)和F(t)曲线图
t=0时,F(t)=0,E(t)= 1 ;此时E(t)取得极大值。
t=τ时,F(τ)=1-e-1 = 0.623
流动模型
非理想流动模型
1.多级理想混合模型 把实际反应器中无序的返混程度等效于N个等体积的理想混合流反
反应器内流体的返混 对化学反应的影响
和容积效率相关的因素: 1. 反应器的类型
对于同一简单反应,在相同的工艺条件下,为达到相同的转化率,平 推流反应器所需体积最小,理想混合流所需的反应器体积最大。
2. 化学反应的级数及化学反应控制的转化率 如实际反应器都选用理想混合反应器,不同反应级数的容积效率:
化学反应工程 101 - CSTR停留时间分布计算

(θ ) E( )dθ
2 2 0
0
t t t E(t)d
2
2 t 2 ( t t ) 2 E(t)dt 2 0 2 无因次方差 和无因次时间θ的关系:
4.1.1 停留时间分布的定量描述
4.1.2 停留时间分布的函数表达式 1. 停留时间分布密度函数 2. 停留时间分布函数 4.1.3 停留时间的实验测定 1. 脉冲示踪法 2. 阶跃示踪法 4.1.4 停留时间分布函数的数字特征
4.1.1 停留时间分布的定量描述
停留时间:反应物料从反应器入口到出口所经历的时间
(4)计算结果列表
c
0
i
A
t
t c A
0
i
100
100
4.1.3 停留时间分布的实验测定
—— 脉冲示踪法
4.1.3 停留时间分布的实验测定
—— 阶跃示踪法
1. 操作:输入采用切换的方法
含示踪剂流体V ↓ 主流体V 系统 V 检测示踪剂
c0(t) c (∞) 升阶法 t =0 (a)
0 0
m 80 100 V 0.8
0
m c A (t)dt 100 V
4.1.3 停留时间分布的实验测定
—— 脉冲示踪法
(2)E(t)的计算
由E(t)的计算式: E(t) (3)F(t)的计算
t t
cA (t) cA (t) m 100 V
c A (t) V t F(t) Et dt dt ct dt 0 0 m m 0 V
(1) 停留时间分布函数F(t)
【精编】化学反应工程第三章.PPT课件

VR
V0 ( xAf kCA0 1 xAf
)
VR
V0 SkCA0
ln 1SxAf (1S)(1xAf
)
xAf
CA0k 1 CA0k
xAf
(1(1SS)()eeCCAA00kk
1) 1
r kC A
n A
VRk(nV10)CA n 01[1(1( 1xA xfA)fn)n11]
1级反应:CA CA0ekt
C A 随 t 较缓慢下降;
2级反应:CA
CA0 1 CA0kt
C A 随 t 缓慢下降。
对于一级或二级不可逆反应,在反应后期,CA的下降 速率,即xA的上升速率相当缓慢。若追求过低的残余 浓度,即过高的转化率,则在反应后期要花费大量的
反应时间。(见书上例3-1)
例 3-1 在间歇反应器中进行等温二级反应 A→B 反应速率 r0 .0C 1 A 2 m/o l(s)l
平推流反应器
VR/V0 CA0
xAf 0
dxA rA
tmV VR 0
CA0
xAf 0
dxA rA
ห้องสมุดไป่ตู้
式中rAkCAn ; CACA0(1xA)
间歇反应器
t CA0
xAf 0
dxA rA
间歇反应器中的结论完全适用于平推流反应器。
三. 等温平推流反应器的计算
等温平推流反应器是指反应物料温度相同,不随
1.CA0→(VR1 ,T1 )→ CA1 → (VR2 ,T2 ) → CAf
2. CA0→ (VR2 ,T2 ) → CA2 → (VR1 ,T1 ) → CAf
第三节 连续流动釜式反应器
(全混流反应器)
[化学反应工程原理]第十章__停留时间分布-数学期望及方差
![[化学反应工程原理]第十章__停留时间分布-数学期望及方差](https://img.taocdn.com/s3/m/7b781c5465ce0508763213e1.png)
tm
tE(t)dt
0
E (t )dt
tE(t)dt
0
0
它是指整个物料在设备内的停留时间,而不是个别质点的 停留时间。 不管设备型式和个别质点的停留时间,只要反应体积与物 料体积流量比值相同,平均停留时间就相同。
➢在实验中得到的是离散情况(即各个别时间)下的E(t),可用 下式计算:
tm
dC dt
V VR
C0C1 tmC0CdC 1
dt
C0 C tm
积分上式:ln C0 C t C F (t) 1 et /tm
C0
tm C0
F ( ) 1 e
E(t) dF(t) 1 exp( t )
dt tm
tm
方差为
2
1,
2 t
tm2
全混流反应器的F(t)和E(t)函数的曲线如图示。
ci
cn
②轴向扩散模型
轴向扩散
N
Dx
dc dx
c c+dc
dx
一、多釜串联模型(N为模型参数)
多釜串联模型是用N个全混釜串联来模拟一个实 际的反应器。N为模型参数。
1.模型假定条件: ① 每一级内为全混流; ② 级际间无返混; ③ 各釜体积相同
2.多釜串联模型的停留时间分布
设反应器总体积为Vr,并假想由N个体积相等的全混釜串联组 成,釜间无任何返混。若对系统施加脉冲示踪后,作示踪剂
F(t)
阶跃输入 出口响应
0
t
阶跃法所得输入—响应曲线
由图可知,在t=0时,C=0;t↑, C→ C0
阶跃示踪法测得的是停留时间分布函数F(t)
时间为t时,出口物料中示踪剂浓度为C(t),物料流量为 V,所以示踪剂流出量为V C(t),又因为在时间为t时流出 的示踪剂,也就是反应器中停留时间小于t的示踪剂,按 定义,物料中停留时间小于t的粒子所占的分率为F(t),因 此,当示踪剂入口流量为VC0时,出口流量VC0 F(t),所 以有:
《化学反应工程》阶段辅导连续流动釜式反应器(CSTR)

f
(t)
0
t t
t t
F(t)
0
t t
1 t t
20
CSTR中的停留时间分布
f (t) 1e tt t
t
F(t)1e t
0.632
2
2 t
t2
1
《化学反应工程》阶段辅
导连续流动釜式反应器
[例 ] 有 一 全 混 釜 反 应 器 ,已 知 反 应 器 体 积 为 10l0 ,流 量 为 1l0 /min,试 估 计 离 开
v0
CA1 (rA)
(1 R)
CAf CA0 RCAf
1R
dCA (rA)
所以: (1R)'
《化学反应工程》阶段辅 导连续流动釜式反应器
返混的分析讨论
返混—重要的工程因素
⑴返混是连续化过程的伴生结果
Batch Reactor
CSTR
⑵返混与反应器型式无关,与操作方式有关。
间歇反应釜
连续CSTR
C A0
C A0
CSTR
k x A 或 1 xA
CA 1 C A0 1 k
C
A0 k
xA (1 xA
)2
或
C A 1 4C A0k 1
C A0
2C A0k
k CA0 xA 1
C A 1 k
C A0
C A0
需记忆积分结果
《化学反应工程》阶段辅 导连续流动釜式反应器
由基本方程导出
图解法
导连续流动釜式反应器
RTD的数字特征
•数学期望 t —物料的平均停留时间
f (t)
tf(t)dt
t
0
f (t)dt
化工专业实验:停留时间分布的测定
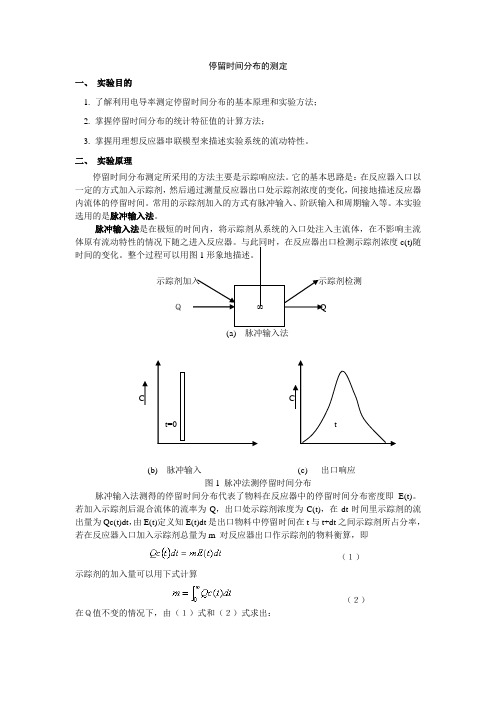
停留时间分布的测定一、实验目的1. 了解利用电导率测定停留时间分布的基本原理和实验方法;2. 掌握停留时间分布的统计特征值的计算方法;3. 掌握用理想反应器串联模型来描述实验系统的流动特性。
二、实验原理停留时间分布测定所采用的方法主要是示踪响应法。
它的基本思路是:在反应器入口以一定的方式加入示踪剂,然后通过测量反应器出口处示踪剂浓度的变化,间接地描述反应器内流体的停留时间。
常用的示踪剂加入的方式有脉冲输入、阶跃输入和周期输入等。
本实验选用的是脉冲输入法。
脉冲输入法是在极短的时间内,将示踪剂从系统的入口处注入主流体,在不影响主流体原有流动特性的情况下随之进入反应器。
与此同时,在反应器出口检测示踪剂浓度c(t)随时间的变化。
整个过程可以用图1形象地描述。
示踪剂加入示踪剂检测Q∞Q(a) 脉冲输入法C Ct=0 t(b) 脉冲输入(c) 出口响应图1 脉冲法测停留时间分布脉冲输入法测得的停留时间分布代表了物料在反应器中的停留时间分布密度即E(t)。
若加入示踪剂后混合流体的流率为Q,出口处示踪剂浓度为C(t),在dt时间里示踪剂的流出量为Qc(t)dt,由E(t)定义知E(t)dt是出口物料中停留时间在t与t+dt之间示踪剂所占分率,若在反应器入口加入示踪剂总量为m 对反应器出口作示踪剂的物料衡算,即(1)示踪剂的加入量可以用下式计算(2)在Q值不变的情况下,由(1)式和(2)式求出:(3)关于停留时间的另一个统计函数是停留时间分布函数F(t),即(4)用停留时间分布密度函数E(t)和停留时间分布函数F(t)来描述系统的停留时间,给出了很好的统计分布规律。
但是为了比较不同停留时间分布之间的差异,还需要引入另外两个统计特征值,即数学期望和方差。
数学期望对停留时间分布而言就是平均停留时间_t ,即 (5)方差是和理想反应器模型关系密切的参数,它的定义是:(6) 若采用无因次方差2Θσ则有222/t t σσΘ=对活塞流反应器02=Θσ,而对全混流反应器12=Θσ;对介于上述两种理想反应器之间的非理想反应器可以用多釜串联模型描述。
停留时间分布的实验测定ppt实用资料

图中曲线下微小面积E(t)dt表示停 留时间在t和t+dt之间的物料占t=0 时进料的分率。
t t+dt
t
停留时间分布的数学描述
• 停留时间分布密度E(t):同时进入反应器的N个 流体质点中,停留时间介于t与t+dt间的质点所 占分率dN/N为E(t)dt。
E(t)dF(t)dC(t)
dt C0dt
F(t)
t
t
F(t) C(t)dt 0
C(t)dt
0
C(t)dt
0
可直接测得
几种流型的停留时间分布函数 与分布密度
t20 (t E t)(2 t) E d (t)d t t0 (t t)2E (t)d t0 t2E (t)d t t2 0
• 方差是停留时间分布离散程度的量度 • 方差越小,越接近平推流
tt
• 对平推流,各物料质点的停留时间相等,故
方差为零。
停留时间分布的数学描述
• 如果是离散型数据,将积分改为加和:
t2
t2E(t)t t2
0
• 取样为等时间间隔时:
t 2
(t t)2 E (t) t
E (t) t
t2 E (t) t 2 t
E (t) t
t2 E (t) 2 t
E (t)
停留时间分布的数学描述
❖ 对比时间(无因次时间):
t tm
t
t
❖平均对比时间: t t 1
停留时间分布的数学描述
一、分布密度与分布函数
全混流反应器:机械混合最大
《化学反应工程》课件-第五章-1

c0
P N,
F (t)
cN
(t)
1 e
t
N
c0
P1
t P1
p 1!
非理想流动模型和非理想反应器的计算
3. 多釜串联模型
数学模型:
F (
)
1
e N
N
P1
N P1 p 1!
E( )
dF( ) d( )
NN
N 1!
N 1eN
E( )d
N N N eN
N 1!
d
1
0
0
2
0
测反应器的停留时间分布,求出
2
根据
2
2 Pe
2 Pe2
1 ePe
,求出模型参数
Pe
解反应模型求转化率。
反应模型方程 (关键组分A)
Da
d 2cA dZ 2
u
dc dZ
RA
0
c t
Da
2c Z 2
u
c Z
若轴向扩散项 为零,则化简 为活塞流模型
非理想流动模型和非理想反应器的计算
3. 轴向扩散模型
小结:用轴向扩散模型进行反应器计算步骤
测反应器的停留时间分布,求出
2
根据
2
2 Pe
2 Pe2
1 ePe
,求出模型参数
Pe
解反应模型求转化率。
反应模型方程求解方法
若:r kcA
Z
0, ucA0
ucA
Da
dcA dZ
0
Z
Lr
,
dcA dZ
Lr
0
适用:微观流体
cA
4
cA0
一级反应与停留时间的分布

一级反应与停留时间的分布1. 停留时间分布是指物料质点从进入反应器开始,到离开为止,在反应器中总共停留的时间,这个时间也就是质点的寿命,固体粒子停留时间测量方法有间接法和直接法两种,间接的测量是基于总的固体相速度和相分率,而直接法大多借助示踪剂进行测量.2. 速率常数 k 的单位为时间的负一次方,时间 t 可以是秒(s),分(min),小时(h),天(d)和年(a)等。
半衰期t 1/2 是一个与反应物起始浓度无关的常数In(a -x)与时间 t 呈线性关系。
引申的特点:(1) 所有分数衰期都是与起始物浓度无关的常数。
(2) (3) 反应间隔 t 相同有定值。
3. 仪器的连续运转,返混由于材料的装置,同时各部分材料进入装置,可分别采取不同的流动路径,停留时间内的设备是不一样的,所以一定的分布是由统计规律。
1/21ln 2/t k =1/23/47/8::1:2:3t t t =1e k t a x a --=一批式反应器,问题是比较简单的,因为反应材料加载一次,所以在任何时刻,所有材料在反应器中的停留时间是一样的。
停留时间分布不存在问题。
流动反应器,由于液体不断流入系统和连续流动的系统,由于不均匀的速度分布系统中的流体,分子扩散的流体,湍流扩散,搅拌所造成的强对流,以及设备安装不良死区,窜流,短路,和其他原因,流体粒子的停留时间在系统必须是长或短,有的很快离开,而其他人经历了一段漫长的时间离开之前形成的停留时间分布。
长度的停留时间直接影响反应速率(如影响的程度,反应)更长,更完整的反应的进行,粒子在出口时,反应速率高,能见度研究反应停留时间的材料在反应器中具有非常重要的意义。
由于停留时间分布的物质在反应完全是随机的,因此可以被概念的基础上,概率分布的材料,反应器内的停留时间分布的定性描述。
停留时间分布函数与分布密度停留时间分布密度电子(吨)的定义是。
粒子的定义:在稳定的连续流动系统,在进入反应器,停留时间不~吨+驱动部分的颗粒的总粒子数的部分称为:停留时间分布密度函数停留时间分布停留时间分布实验测定停留时间分布的实验测定采用信号响应法。
化学反应工程第五章

Q Q 1 Q E (t )dt QE(t )dt C (t )dt C (t )dt
0 0 0 0
所以
式中
0
C (t )dt 用于表示C(t)~t连续型数据
在实验中,可以用水为流体,流经一容器,向其 入口处注入KCL溶液,立刻在出口处测定流出液 的电导值,在电导仪中转变成电信号,通过记录 仪记录电导率随时间的变化曲线,因为在低浓度 时电导率与示踪剂KCL浓度成正比,而后者又与 E(t)值成正比,故电导率曲线即相当于E(t)曲线, 由此曲线也可求得F(t)曲线。
VR
t 0
[1 F (t )]dt I (t )dt I (t ) [1 F (t )] 1
由实验测得F(t)~t曲线后, 可由此式求得I(t)~t的对应 值,给出I(t)~t曲线后,可 以进一步用积分法求得年 龄分布积累函数Y(t)~t曲线。 故不论用脉冲法或阶跃法 示踪法均可以测得4个停留 时间分布函数。
5.2.1 停留时间(寿命)分布密度函数E(t)
• 如图5.2-1所示,t=0时瞬间进入的N个流体质点 中,寿命介于t →t+dt之间的质点数dN所占总质 点数N的分率dN/N=E(t)dt,E(t)dt为一微分的分 率,E(t)= dN/N dt,其量纲为[时间]-1,称为停 留时间(寿命)分布密度函数。
t 0
• 例如某一次的考试成绩分布如下:
则平均成绩 M=∑MiXi=60*5%+70*15%+80*65%+90*15%=79 可见平均成绩是各级成绩的加权平均值。
• 流体质点在反应器中的停留时间可能值为0→∞, 停留时间为t的流体质点所占的分率为E(t)dt, 故: 平均停留时间 t 0 tE (t )dt tE (t )t 0 为避免实验结果带来的系统误差,对于离散型 数据可以除于 E (t )t i
停留时间分布-01

◆ 停留时间分布的分类
• 寿命分布: 是指流体粒子从进入系统起到离开系统 止,在系统停留的时间。是指反应器出 口流出流体的停留时间。 • 年龄分布: 是对存留在系统中的流体粒子而言,从 进入系统算起在系统中的停留时间。 • 更有实际意义的是受命分布。
◆ 研究停留时间分布的系统
• 系统有闭式系统和开式系统之分。 闭式系统具有闭式边界,即进口和出口 没有返混(即在入口和出口处设置有单 向阀)。反之,则为开式边界。 • 停留时间分布研究的系统为闭式系统。
在某瞬间t=0,将流入系统的流体切换 为含有示踪剂A的浓度CA0的第二流体, 切换后应保持系统流动模式不变。
做物料衡算
C A v0 v0 C A0 F (t )
F (t ) CA C A0
这样可以通过CA—t曲线获得F(t)曲线。 阴影面积
Ac
CA
0
0
tdCA C A0 tdF (t ) C A0 tE(t )dt C A0 t
停留时间范 围 t→t+△t 出口流中的 红色粒子数 分率△N/N
0-2 2-3 3-4 4-5 5-6 6-7 7-8 8-9 9-10 10-11 11-12 1214
0
2
6
12
18
22
17
12
6
4
1
0
0
0.02
0.06
0.12
0.18
0.22
0.170.12源自0.060.040.01
0
• 如果假定红色粒子和主流体之间除了颜色的差别以外,其余所有性质 都完全相同,那么就可以认为这100个粒子的停留时间分布就是主流 体的停留时间分布。
2 2 2 0 0 0
停留时间分布及其方差偏度一.工业背景停留时间分布是指反应物从进入

停留时间分布及其方差偏度一.工业背景停留时间分布是指反应物从进入反应器开始到出反应器所经历的时间。
停留时间分布的测定除了可以确定产物的定量分布,用于计算其他变化量,并作为物料、热量衡算的基础之外,还可以用来分析现有设备的工作情况,例如,可通过停留时间分布的测定来检查填料塔或固定床反应器是否存在死区或短路等现象,通过分析提出改进操作性能的方程。
描述停留时间分布的函数有停留时间分布密度函数和停留时间分布函数。
二.停留时间分布及描述1.停留时间分布密度函数定义:在稳定态流动下,某瞬间t=0时进入反应器的物料,如果停留时间在(t~t+d t)区间内的物料质点占总物料的分率为E(t)d t,那么E(t)即为停留时间分布密度函数,即其中E(t)为停留时间分布密度函数,单位:2.停留时间分布函数定义:在稳定态流动下,于瞬间t=0时进入反应器的物料中,停留时间小于t的物料质点占总物料的分率,即F(t)为停留时间分布函数3.E(t)和F(t)之间的关系由图可知,(1)停留时间分布曲线为单调递增曲线(2)F(0)=0(3)(4)E(t)单位为,F(t)无因次三.停留时间分布的测定1.停留时间分布通常采用实验测定,由于物料质点彼此之间很难区分,所以测定物料在反应器中的停留时间通常借助示踪剂。
2.脉冲法定义:在极短时间内将一定量的示踪剂迅速注入反应器进料中,然后分析出口流量中示踪剂的浓度随时间变化情况。
t~t+Δt间示踪剂的量为:;停留时间介于t~t+Δt的示踪剂所占分率:;根据停留时间分布密度函数的定义:;,,经过足够长的时间,所有示踪剂都会流出系统代入得。
4.阶跃示踪法阶跃法测定停留时间分布的装置和脉冲法相同,具体步骤如下:物料保持稳定流动,在测定过程中一直保持稳定流动,物料的流况不变。
在时间为t时,如果出口示踪剂浓度为,则单位时间时间内示踪剂的流出量为,又因为此时流出的物料质点的停留时间均小于t,所以占单位时间内进入系统的总物料的分率为F(t),,由此可以看出,采用阶跃法测得的是停留时间分布函数。
