2012年中考数学压轴题预测100题精选
2012年中考数学压轴题精选附答案
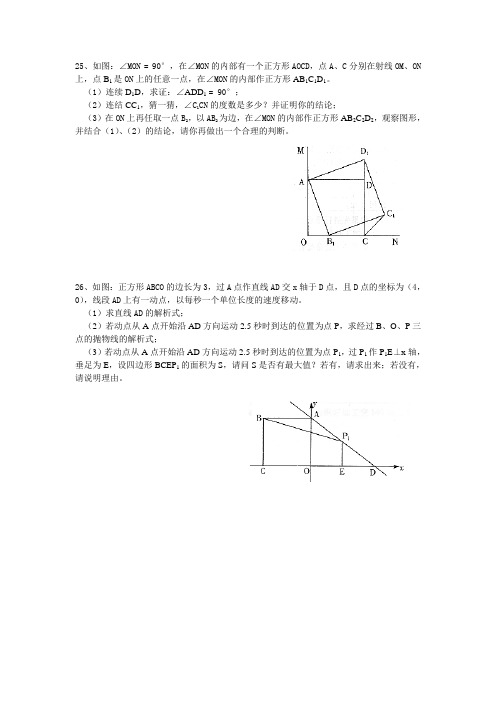
25、如图:∠MON = 90°,在∠MON的内部有一个正方形AOCD,点A、C分别在射线OM、ON 上,点B1是ON上的任意一点,在∠MON的内部作正方形AB1C1D1。
(1)连续D1D,求证:∠ADD1= 90°;(2)连结CC1,猜一猜,∠C1CN的度数是多少?并证明你的结论;(3)在ON上再任取一点B2,以AB2为边,在∠MON的内部作正方形AB2C2D2,观察图形,并结合(1)、(2)的结论,请你再做出一个合理的判断。
26、如图:正方形ABCO的边长为3,过A点作直线AD交x轴于D点,且D点的坐标为(4,0),线段AD上有一动点,以每秒一个单位长度的速度移动。
(1)求直线AD的解析式;(2)若动点从A点开始沿AD方向运动2.5秒时到达的位置为点P,求经过B、O、P三点的抛物线的解析式;(3)若动点从A点开始沿AD方向运动2.5秒时到达的位置为点P1,过P1作P1E⊥x轴,垂足为E,设四边形BCEP1的面积为S,请问S是否有最大值?若有,请求出来;若没有,请说明理由。
24.如图,以BC为直径的⊙O交△CFB的边CF于点A,BM平分∠ABC交AC于点M,AD⊥3,AD=12.BC于点D,AD交BM于点N,ME⊥BC于点E,AB2=AF·AC,cos∠ABD=5⑴求证:△ANM≌△ENM;⑵求证:FB是⊙O的切线;⑶证明四边形AMEN是菱形,并求该菱形的面积S.7),且顶点C的横坐标为4,该图象在x 轴上截25.如图,二次函数的图象经过点D(0,39得的线段AB的长为6.⑴求二次函数的解析式;⑵在该抛物线的对称轴上找一点P,使PA+PD最小,求出点P的坐标;⑶在抛物线上是否存在点Q,使△QAB与△ABC相似?如果存在,求出点Q的坐标;如果不存在,请说明理由.七、(本大题8分)20.如图8,半圆的直径10AB =,点C 在半圆上,6BC =. (1)求弦AC 的长;(2)若P 为AB 的中点,PE AB ⊥交AC 于点E ,求PE 的长.21.如图9,已知正比例函数和反比例函数的图象都经过点(33)A ,. (1)求正比例函数和反比例函数的解析式;(2)把直线O A 向下平移后与反比例函数的图象交于点(6)B m ,,求m 的值和这个一次函数的解析式;(3)第(2)问中的一次函数的图象与x 轴、y 轴分别交于C 、D ,求过A 、B 、D 三点的二次函数的解析式;(4)在第(3)问的条件下,二次函数的图象上是否存在点E ,使四边形O ECD 的面积1S 与四边形O ABD 的面积S 满足:123S S =?若存在,求点E 的坐标;若不存在,请说明理由.P BC EA (图8)23.(本小题9分)如图,AB 是⊙O 的直径,C 是AB 延长线上一点,CD 与⊙O 相切于点E ,AD ⊥CD (1)求证:AE 平分∠DAC ; (2)若AB=3,∠ABE=60°,①求AD 的长;②求出图中阴影部分的面积。
2012年全国各地中考数学压轴题精选(解析版...

2012年全国各地中考数学压轴题精选(解析版二)11.(2012•重庆)已知:如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=6,AB=3.E为BC边上一点,以BE为边作正方形BEFG,使正方形BEFG和梯形ABCD在BC的同侧.(1)当正方形的顶点F恰好落在对角线AC上时,求BE的长;(2)将(1)问中的正方形BEFG沿BC向右平移,记平移中的正方形BEFC为正方形B′EFG,当点E与点C重合时停止平移.设平移的距离为t,正方形B′EFG的边EF与AC交于点M,连接B′D,B′M,DM,是否存在这样的t,使△B′DM是直角三角形?若存在,求出t的值;若不存在,请说明理由;(3)在(2)问的平移过程中,设正方形B′EFG与△ADC重叠部分的面积为S,请直接写出S与t之间的函数关系式以及自变量t的取值范围.解题思路:(1)首先设正方形BEFG的边长为x,易得△AGF∽△ABC,根据相似三角形的对应边成比例,即可求得BE的长;(2)首先利用△MEC∽△ABC与勾股定理,求得B′M,DM与B′D的平方,然后分别从若∠DB′M=90°,则DM2=B′M2+B′D2,若∠DB′M=90°,则DM2=B′M2+B′D2,若∠B′DM=90°,则B′M2=B′D2+DM2去分析,即可得到方程,解方程即可求得答案;(3)分别从当0≤t≤时,当<t≤2时,当2<t≤时,当<t≤4时去分析求解即可求得答案.解答:解:(1)如图①,设正方形BEFG的边长为x,则BE=FG=BG=x,∵AB=3,BC=6,∴AG=AB﹣BG=3﹣x,∵GF∥BE,∴△AGF∽△ABC,∴,即,解得:x=2,即BE=2;(2)存在满足条件的t,理由:如图②,过点D作DH⊥BC于H,则BH=AD=2,DH=AB=3,由题意得:BB′=HE=t,HB′=|t﹣2|,EC=4﹣t,∵EF∥AB,∴△MEC∽△ABC,∴,即,∴ME=2﹣t,在Rt△B′ME中,B′M2=ME2+B′E2=22+(2﹣t)2=t2﹣2t+8,在Rt△DHB′中,B′D2=DH2+B′H2=32+(t﹣2)2=t2﹣4t+13,过点M作MN⊥DH于N,则MN=HE=t,NH=ME=2﹣t,∴DN=DH﹣NH=3﹣(2﹣t)=t+1,在Rt△DMN中,DM2=DN2+MN2=t2+t+1,(Ⅰ)若∠DB′M=90°,则DM2=B′M2+B′D2,即t2+t+1=(t2﹣2t+8)+(t2﹣4t+13),解得:t=,(Ⅱ)若∠B′MD=90°,则B′D2=B′M2+DM2,即t2﹣4t+13=(t2﹣2t+8)+(t2+t+1),解得:t1=﹣3+,t2=﹣3﹣(舍去),∴t=﹣3+;(Ⅲ)若∠B′DM=90°,则B′M2=B′D2+DM2,即:t2﹣2t+8=(t2﹣4t+13)+(t2+t+1),此方程无解,综上所述,当t=或﹣3+时,△B′DM是直角三角形;(3)①如图③,当F在CD上时,EF:DH=CE:CH,即2:3=CE:4,∴CE=,∴t=BB′=BC﹣B′E﹣EC=6﹣2﹣=,∵ME=2﹣t,∴FM=t,当0≤t≤时,S=S△FMN=×t×t=t2,②当G在AC上时,t=2,∵EK=EC•tan∠DCB=EC•=(4﹣t)=3﹣t,∴FK=2﹣EK=t﹣1,∵NL=AD=,∴FL=t﹣,∴当<t≤2时,S=S△FMN﹣S△FKL=t2﹣(t﹣)(t﹣1)=﹣t2+t﹣;③如图⑤,当G在CD上时,B′C:CH=B′G:DH,即B′C:4=2:3,解得:B′C=,∴EC=4﹣t=B′C﹣2=,∴t=,∵B′N=B′C=(6﹣t)=3﹣t,∵GN=GB′﹣B′N=t﹣1,∴当2<t≤时,S=S梯形GNMF﹣S△FKL=×2×(t﹣1+t)﹣(t﹣)(t﹣1)=﹣t2+2t﹣,④如图⑥,当<t≤4时,∵B′L=B′C=(6﹣t),EK=EC=(4﹣t),B′N=B′C=(6﹣t)EM=EC=(4﹣t),S=S梯形MNLK=S梯形B′EKL﹣S梯形B′EMN=﹣t+.综上所述:当0≤t≤时,S=t2,当<t≤2时,S=﹣t2+t﹣;当2<t≤时,S=﹣t2+2t﹣,当<t≤4时,S=﹣t+.12.(2012•泰安)如图,半径为2的⊙C与x轴的正半轴交于点A,与y轴的正半轴交于点B,点C的坐标为(1,0).若抛物线y=﹣x2+bx+c过A、B两点.(1)求抛物线的解析式;(2)在抛物线上是否存在点P,使得∠PBO=∠POB?若存在,求出点P的坐标;若不存在说明理由;(3)若点M是抛物线(在第一象限内的部分)上一点,△MAB的面积为S,求S的最大(小)值.解题思路:(1)利用待定系数法求抛物线的解析式.因为已知A(3,0),所以需要求得B点坐标.如答图1,连接OB,利用勾股定理求解;(2)由∠PBO=∠POB,可知符合条件的点在线段OB的垂直平分线上.如答图2,OB的垂直平分线与抛物线有两个交点,因此所求的P点有两个,注意不要漏解;(3)如答图3,作MH⊥x轴于点H,构造梯形MBOH与三角形MHA,求得△MAB面积的表达式,这个表达式是关于M点横坐标的二次函数,利用二次函数的极值求得△MAB面积的最大值.解答:解:(1)如答图1,连接OB.∵BC=2,OC=1∴OB==∴B(0,)将A(3,0),B(0,)代入二次函数的表达式得,解得,∴y=﹣x2+x+.(2)存在.如答图2,作线段OB的垂直平分线l,与抛物线的交点即为点P.∵B(0,),O(0,0),∴直线l的表达式为y=.代入抛物线的表达式,得﹣x2+x+=;解得x=1±,∴P(1±,).(3)如答图3,作MH⊥x轴于点H.设M(x m,y m),则S△MAB=S梯形MBOH+S△MHA﹣S△OAB=(MH+OB)•OH+HA•MH﹣OA•OB =(y m+)x m+(3﹣x m)y m﹣×3×=x m+y m﹣∵y m=﹣x m2+x m+,∴S△MAB=x m+(﹣x m2+x m+)﹣=x m2+x m=(x m﹣)2+∴当x m=时,S△MAB取得最大值,最大值为.13.(2012•铜仁地区)如图已知:直线y=﹣x+3交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C (1,0)三点.(1)求抛物线的解析式;(2)若点D的坐标为(﹣1,0),在直线y=﹣x+3上有一点P,使△ABO与△ADP相似,求出点P的坐标;(3)在(2)的条件下,在x轴下方的抛物线上,是否存在点E,使△ADE的面积等于四边形APCE的面积?如果存在,请求出点E的坐标;如果不存在,请说明理由.解题思路:(1)首先确定A、B、C三点的坐标,然后利用待定系数法求抛物线的解析式;(2)△ABO为等腰直角三角形,若△ADP与之相似,则有两种情形,如答图1所示.利用相似三角形的性质分别求解,避免遗漏;(3)如答图2所示,分别计算△ADE的面积与四边形APCE的面积,得到面积的表达式.利用面积的相等关系得到一元二次方程,将点E是否存在的问题转化为一元二次方程是否有实数根的问题,从而解决问题.需要注意根据(2)中P点的不同位置分别进行计算,在这两种情况下,一元二次方程的判别式均小于0,即所求的E点均不存在.解答:解:(1)由题意得,A(3,0),B(0,3)∵抛物线经过A、B、C三点,∴把A(3,0),B(0,3),C(1,0)三点分别代入y=ax2+bx+c,得方程组…3分解得:∴抛物线的解析式为y=x2﹣4x+3 …5分(2)由题意可得:△ABO为等腰三角形,如答图1所示,若△ABO∽△AP1D,则∴DP1=AD=4,∴P1(﹣1,4)…7分若△ABO∽△ADP2 ,过点P2作P2 M⊥x轴于M,AD=4,∵△ABO为等腰三角形,∴△ADP2是等腰三角形,由三线合一可得:DM=AM=2=P2M,即点M与点C重合,∴P2(1,2)…10分(3)如答图2,设点E(x,y),则S△ADE=①当P1(﹣1,4)时,S四边形AP1CE=S△ACP1+S△ACE==4+|y|…11分∴2|y|=4+|y|,∴|y|=4∵点E在x轴下方,∴y=﹣4,代入得:x2﹣4x+3=﹣4,即x2﹣4x+7=0,∵△=(﹣4)2﹣4×7=﹣12<0∴此方程无解…12分②当P2(1,2)时,S四边形AP2CE=S△ACP2+S△ACE==2+|y|,∴2|y|=2+|y|,∴|y|=2∵点E在x轴下方,∴y=﹣2,代入得:x2﹣4x+3=﹣2,即x2﹣4x+5=0,∵△=(﹣4)2﹣4×5=﹣4<0∴此方程无解综上所述,在x轴下方的抛物线上不存在这样的点E.…14分14.(2012•温州)如图,经过原点的抛物线y=﹣x2+2mx(m>0)与x轴的另一个交点为A.过点P(1,m)作直线PM⊥x轴于点M,交抛物线于点B.记点B关于抛物线对称轴的对称点为C(B、C不重合).连接CB,CP.(1)当m=3时,求点A的坐标及BC的长;(2)当m>1时,连接CA,问m为何值时CA⊥CP?(3)过点P作PE⊥PC且PE=PC,问是否存在m,使得点E落在坐标轴上?若存在,求出所有满足要求的m的值,并定出相对应的点E坐标;若不存在,请说明理由.解题思路:(1)把m=3,代入抛物线的解析式,令y=0解方程,得到的非0解即为和x轴交点的横坐标,再求出抛物线的对称轴方程,进而求出BC的长;(2)过点C作CH⊥x轴于点H(如图1)由已知得∠ACP=∠BCH=90°,利用已知条件证明△AGH∽△PCB,根据相似的性质得到:,再用含有m的代数式表示出BC,CH,BP,代入比例式即可求出m的值;(3)存在,本题要分当m>1时,BC=2(m﹣1),PM=m,BP=m﹣1和当0<m<1时,BC=2(1﹣m),PM=m,BP=1﹣m,两种情况分别讨论,再求出满足题意的m值和相对应的点E坐标.解答:解:(1)当m=3时,y=﹣x2+6x令y=0得﹣x2+6x=0∴x1=0,x2=6,∴A(6,0)当x=1时,y=5∴B(1,5)∵抛物线y=﹣x2+6x的对称轴为直线x=3又∵B,C关于对称轴对称∴BC=4.(2)过点C作CH⊥x轴于点H(如图1)由已知得∠ACP=∠BCH=90°∴∠ACH=∠PCB又∵∠AHC=∠PBC=90°∴△AGH∽△PCB,∴,∵抛物线y=﹣x2+2mx的对称轴为直线x=m,其中m>1,又∵B,C关于对称轴对称,∴BC=2(m﹣1),∵B(1,2m﹣1),P(1,m),∴BP=m﹣1,又∵A(2m,0),C(2m﹣1,2m﹣1),∴H(2m﹣1,0),∴AH=1,CH=2m﹣1,∴,∴m=.(3)∵B,C不重合,∴m≠1,(I)当m>1时,BC=2(m﹣1),PM=m,BP=m﹣1,(i)若点E在x轴上(如图1),∵∠CPE=90°,∴∠MPE+∠BPC=∠MPE+∠MEP=90°,PC=EP,∴△BPC≌△MEP,∴BC=PM,∴2(m﹣1)=m,∴m=2,此时点E的坐标是(2,0);(ii)若点E在y轴上(如图2),过点P作PN⊥y轴于点N,易证△BPC≌△NPE,∴BP=NP=OM=1,∴m﹣1=1,∴m=2,此时点E的坐标是(0,4);(II)当0<m<1时,BC=2(1﹣m),PM=m,BP=1﹣m,(i)若点E在x轴上(如图3),易证△BPC≌△MEP,∴BC=PM,∴2(1﹣m)=m,∴m=,此时点E的坐标是(,0);(ii)若点E在y轴上(如图4),过点P作PN⊥y轴于点N,易证△BPC≌△NPE,∴BP=NP=OM=1,∴1﹣m=1,∴m=0(舍去),综上所述,当m=2时,点E的坐标是(0,2)或(0,4),当m=时,点E的坐标是(,0).15.(2012•成都)如图,在平面直角坐标系xOy中,一次函数(m为常数)的图象与x轴交于点A(﹣3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A,C两点,并与x轴的正半轴交于点B.(1)求m的值及抛物线的函数表达式;(2)设E是y轴右侧抛物线上一点,过点E作直线AC的平行线交x轴于点F.是否存在这样的点E,使得以A,C,E,F为顶点的四边形是平行四边形?若存在,求出点E的坐标及相应的平行四边形的面积;若不存在,请说明理由;(3)若P是抛物线对称轴上使△ACP的周长取得最小值的点,过点P任意作一条与y轴不平行的直线交抛物线于M1(x1,y1),M2(x2,y2)两点,试探究是否为定值,并写出探究过程.题思路:(1)首先求得m的值和直线的解析式,根据抛物线对称性得到B点坐标,根据A、B点坐标利用交点式求得抛物线的解析式;(2)存在点E使得以A、C、E、F为顶点的四边形是平行四边形.如答图1所示,过点E作EG⊥x轴于点G,构造全等三角形,利用全等三角形和平行四边形的性质求得E点坐标和平行四边形的面积.注意:符合要求的E点有两个,如答图1所示,不要漏解;(3)本问较为复杂,如答图2所示,分几个步骤解决:第1步:确定何时△ACP的周长最小.利用轴对称的性质和两点之间线段最短的原理解决;第2步:确定P点坐标P(1,3),从而直线M1M2的解析式可以表示为y=kx+3﹣k;第3步:利用根与系数关系求得M1、M2两点坐标间的关系,得到x1+x2=2﹣4k,x1x2=﹣4k﹣3.这一步是为了后续的复杂计算做准备;第4步:利用两点间的距离公式,分别求得线段M1M2、M1P和M2P的长度,相互比较即可得到结论:=1为定值.这一步涉及大量的运算,注意不要出错,否则难以得出最后的结论.答:解:(1)∵经过点(﹣3,0),∴0=+m,解得m=,∴直线解析式为,C(0,).∵抛物线y=ax2+bx+c对称轴为x=1,且与x轴交于A(﹣3,0),∴另一交点为B(5,0),设抛物线解析式为y=a(x+3)(x﹣5),∵抛物线经过C(0,),∴=a•3(﹣5),解得a=,∴抛物线解析式为y=x2+x+;(2)假设存在点E使得以A、C、E、F为顶点的四边形是平行四边形,则AC∥EF且AC=EF.如答图1,(i)当点E在点E位置时,过点E作EG⊥x轴于点G,∵AC∥EF,∴∠CAO=∠EFG,又∵,∴△CAO≌△EFG,∴EG=CO=,即y E=,∴=x E2+x E+,解得x E=2(x E=0与C点重合,舍去),∴E(2,),S▱ACEF=;(ii)当点E在点E′位置时,过点E′作E′G′⊥x轴于点G′,同理可求得E′(+1,),S▱ACE′F′=.(3)要使△ACP的周长最小,只需AP+CP最小即可.如答图2,连接BC交x=1于P点,因为点A、B关于x=1对称,根据轴对称性质以及两点之间线段最短,可知此时AP+CP最小(AP+CP最小值为线段BC的长度).∵B(5,0),C(0,),∴直线BC解析式为y=x+,∵x P=1,∴y P=3,即P(1,3).令经过点P(1,3)的直线为y=kx+3﹣k,∵y=kx+3﹣k,y=x2+x+,联立化简得:x2+(4k﹣2)x﹣4k﹣3=0,∴x1+x2=2﹣4k,x1x2=﹣4k﹣3.∵y1=kx1+3﹣k,y2=kx2+3﹣k,∴y1﹣y2=k(x1﹣x2).根据两点间距离公式得到:M1M2==== ∴M1M2===4(1+k2).又M1P===;同理M2P=∴M1P•M2P=(1+k2)•=(1+k2)•=(1+k2)•=4(1+k2).∴M1P•M2P=M1M2,∴=1为定值.16.(2012•梅州)如图,矩形OABC中,A(6,0)、C(0,2)、D(0,3),射线l过点D且与x轴平行,点P、Q分别是l和x轴正半轴上动点,满足∠PQO=60°.(1)①点B的坐标是(6,2);②∠CAO=30度;③当点Q与点A重合时,点P的坐标为(3,3);(直接写出答案)(2)设OA的中心为N,PQ与线段AC相交于点M,是否存在点P,使△AMN为等腰三角形?若存在,请直接写出点P的横坐标为m;若不存在,请说明理由.(3)设点P的横坐标为x,△OPQ与矩形OABC的重叠部分的面积为S,试求S与x的函数关系式和相应的自变量x的取值范围.解题思路:(1)①由四边形OABC是矩形,根据矩形的性质,即可求得点B的坐标;②由正切函数,即可求得∠CAO的度数,③由三角函数的性质,即可求得点P的坐标;(2)分别从MN=AN,AM=AN与AM=MN去分析求解即可求得答案;(3)分别从当0≤x≤3时,当3<x≤5时,当5<x≤9时,当x>9时去分析求解即可求得答案.解答:解:(1)①∵四边形OABC是矩形,∴AB=OC,OA=BC,∵A(6,0)、C(0,2),∴点B的坐标为:(6,2);②∵tan∠CAO===,∴∠CAO=30°;③如下图:当点Q与点A重合时,过点P作PE⊥OA于E,∵∠PQO=60°,D(0,3),∴PE=3,∴AE==3,∴OE=OA﹣AE=6﹣3=3,∴点P的坐标为(3,3);故答案为:①(6,2),②30,③(3,3);(2)情况①:MN=AN=3,则∠AMN=∠MAN=30°,∴∠MNO=60°,∵∠PQO=60°,即∠MQO=60°,∴点N与Q重合,∴点P与D重合,∴此时m=0,情况②,如图AM=AN,作MJ⊥x轴、PI⊥x轴;MJ=MQ•sin60°=AQ•sin60°=(OA﹣IQ﹣OI)•sin60°=(3﹣m)=AM=AN=,可得(3﹣m)=,解得:m=3﹣,情况③AM=NM,此时M的横坐标是4.5,过点P作PI⊥OA于I,过点M作MG⊥OA于G,∴MG=,∴QK===3,GQ==,∴KG=3﹣0.5=2.5,AG=AN=1.5,∴OK=2,∴m=2,(3)当0≤x≤3时,如图,OI=x,IQ=PI•tan60°=3,OQ=OI+IQ=3+x;由题意可知直线l∥BC∥OA,可得,EF=(3+x),此时重叠部分是梯形,其面积为:S梯形=(EF+OQ)•OC=(3+x),当3<x≤5时,S=S梯形﹣S△HAQ=S梯形﹣AH•AQ=(3+x)﹣(x﹣3)2,当5<x≤9时,S=(BE+OA)•OC=(12﹣x),当9<x时,S=OA•AH=.17.(2012•株洲)如图,一次函数分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.(1)求这个抛物线的解析式;(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN有最大值?最大值是多少?(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.解题思路:(1)首先求得A、B点的坐标,然后利用待定系数法求抛物线的解析式;(2)本问要点是求得线段MN的表达式,这个表达式是关于t的二次函数,利用二次函数的极值求线段MN的最大值;(3)本问要点是明确D点的可能位置有三种情形,如答图2所示,不要遗漏.其中D1、D2在y轴上,利用线段数量关系容易求得坐标;D3点在第一象限,是直线D1N和D2M的交点,利用直线解析式求得交点坐标.解答:解:(1)∵分别交y轴、x轴于A、B两点,∴A、B点的坐标为:A(0,2),B(4,0)…(1分)将x=0,y=2代入y=﹣x2+bx+c得c=2…(2分)将x=4,y=0代入y=﹣x2+bx+c得0=﹣16+4b+2,解得b=,∴抛物线解析式为:y=﹣x2+x+2…(3分)(2)如答图1,设MN交x轴于点E,则E(t,0),BE=4﹣t.∵tan∠ABO===,∴ME=BE•tan∠ABO=(4﹣t)×=2﹣t.又N点在抛物线上,且x N=t,∴y N=﹣t2+t+2,∴MN=y N﹣ME=﹣t2+t+2﹣(2﹣t)=﹣t2+4t…(5分)∴当t=2时,MN有最大值4…(6分)(3)由(2)可知,A(0,2),M(2,1),N(2,5).以A、M、N、D为顶点作平行四边形,D点的可能位置有三种情形,如答图2所示.…(7分)(i)当D在y轴上时,设D的坐标为(0,a)由AD=MN,得|a﹣2|=4,解得a1=6,a2=﹣2,从而D为(0,6)或D(0,﹣2)…(8分)(ii)当D不在y轴上时,由图可知D为D1N与D2M的交点,易得D1N的方程为y=x+6,D2M的方程为y=x﹣2,由两方程联立解得D为(4,4)…(9分)故所求的D点坐标为(0,6),(0,﹣2)或(4,4)…(10分)18.(2012•南充)如图,⊙C的内接△AOB中,AB=AO=4,tan∠AOB=,抛物线y=ax2+bx经过点A(4,0)与点(﹣2,6).(1)求抛物线的函数解析式;(2)直线m与⊙C相切于点A,交y轴于点D.动点P在线段OB上,从点O出发向点B运动;同时动点Q在线段DA上,从点D出发向点A运动;点P的速度为每秒一个单位长,点Q的速度为每秒2个单位长,当PQ⊥AD 时,求运动时间t的值;(3)点R在抛物线位于x轴下方部分的图象上,当△ROB面积最大时,求点R的坐标.解题思路:(1)根据抛物线y=ax2+bx经过点A(4,0)与点(﹣2,6),利用待定系数法求抛物线解析式;(2)如答图1,由已知条件,可以计算出OD、AE等线段的长度.当PQ⊥AD时,过点O作OF⊥AD于点F,此时四边形OFQP、OFAE均为矩形.则在Rt△ODF中,利用勾股定理求出DF的长度,从而得到时间t的数值;(3)因为OB为定值,欲使△ROB面积最大,只需OB边上的高最大即可.按照这个思路解决本题.如答图2,当直线l平行于OB,且与抛物线相切时,OB边上的高最大,从而△ROB的面积最大.联立直线l和抛物线的解析式,利用一元二次方程判别式等于0的结论可以求出R点的坐标.解答:解:(1)∵抛物线y=ax2+bx经过点A(4,0)与点(﹣2,6),∴,解得∴抛物线的解析式为:y=x2﹣2x.(2)如答图1,连接AC交OB于点E,由垂径定理得AC⊥OB.∵AD为切线,∴AC⊥AD,∴AD∥OB.∵tan∠AOB=,∴sin∠AOB=,∴AE=OA•sin∠AOB=4×=2.4,OD=OA•tan∠OAD=OA•tan∠AOB=4×=3.当PQ⊥AD时,OP=t,DQ=2t.过O点作OF⊥AD于F,则在Rt△ODF中,OD=3,OF=AE=2.4,DF=DQ﹣FQ=DQ﹣OP=2t﹣t=t,由勾股定理得:DF===1.8,∴t=1.8秒;(3)如答图3,设直线l平行于OB,且与抛物线有唯一交点R(相切),此时△ROB中OB边上的高最大,所以此时△ROB面积最大.∵tan∠AOB=,∴直线OB的解析式为y=x,由直线l平行于OB,可设直线l解析式为y=x+b.∵点R既在直线l上,又在抛物线上,∴x2﹣2x=x+b,化简得:2x2﹣11x﹣4b=0.∵直线l与抛物线有唯一交点R(相切),∴判别式△=0,即112+32b=0,解得b=,此时原方程的解为x=,即x R=,而y R=x R2﹣2x R=∴点R的坐标为R(,).19.(2012•凉山州)如图,在平面直角坐标系中,直线y=x+4与x轴、y轴分别交于A、B两点,抛物线y=﹣x2+bx+c 经过A、B两点,并与x轴交于另一点C(点C点A的右侧),点P是抛物线上一动点.(1)求抛物线的解析式及点C的坐标;(2)若点P在第二象限内,过点P作PD⊥轴于D,交AB于点E.当点P运动到什么位置时,线段PE最长?此时PE等于多少?(3)如果平行于x轴的动直线l与抛物线交于点Q,与直线AB交于点N,点M为OA的中点,那么是否存在这样的直线l,使得△MON是等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.题思路:(1)首先求得A、B点的坐标,然后利用待定系数法求抛物线的解析式,并求出抛物线与x轴另一交点C的坐标;(2)关键是求出线段PE长度的表达式,设D点横坐标为t,则可以将PE表示为关于t的二次函数,利用二次函数求极值的方法求出PE长度的最大值;(3)根据等腰三角形的性质和勾股定理,将直线l的存在性问题转化为一元二次方程问题,通过一元二次方程的判别式可知直线l是否存在,并求出相应Q点的坐标.注意“△MON是等腰三角形”,其中包含三种情况,需要逐一讨论,不能漏解.答:解:(1)∵直线y=x+4与x轴、y轴分别交于A、B两点,∴A(﹣4,0),B(0,4)抛物线y=﹣x2+bx+c经过A、B两点,可得,解得,∴抛物线解析式为y=﹣x2﹣3x+4.令y=0,得﹣x2﹣3x+4=0,解得x1=﹣4,x2=1,∴C(1,0).(2)如答图1所示,设D(t,0).∵OA=OB,∴∠BAO=45°,∴E(t,t),P(t,﹣t2﹣3t+4).PE=y P﹣y E=﹣t2﹣3t+4﹣t=﹣t2﹣4t=﹣(t+2)2+4,∴当t=﹣2时,线段PE的长度有最大值4,此时P(﹣2,6).(3)存在.如答图2所示,过N点作NH⊥x轴于点H.设OH=m(m>0),∵OA=OB,∴∠BAO=45°,∴NH=AH=4﹣m,∴y Q=4﹣m.又M为OA中点,∴MH=2﹣m.△MON为等腰三角形:①若MN=ON,则H为底边OM的中点,∴m=1,∴y Q=4﹣m=3.由﹣x Q2﹣3x Q+4=3,解得x Q=,∴点Q坐标为(,3)或(,3);②若MN=OM=2,则在Rt△MNH中,根据勾股定理得:MN2=NH2+MH2,即22=(4﹣m)2+(2﹣m)2,化简得m2﹣6m+8=0,解得:m1=2,m2=4(不合题意,舍去)∴y Q=2,由﹣x Q2﹣3x Q+4=2,解得x Q=,∴点Q坐标为(,2)或(,2);③若ON=OM=2,则在Rt△NOH中,根据勾股定理得:ON2=NH2+OH2,即22=(4﹣m)2+m2,化简得m2﹣4m+6=0,∵△=﹣8<0,∴此时不存在这样的直线l,使得△MON为等腰三角形.综上所述,存在这样的直线l,使得△MON为等腰三角形.所求Q点的坐标为(,3)或(,3)或(,2)或(,2).20.(2012•衢州)如图,把两个全等的Rt△AOB和Rt△COD分别置于平面直角坐标系中,使直角边OB、OD在x 轴上.已知点A(1,2),过A、C两点的直线分别交x轴、y轴于点E、F.抛物线y=ax2+bx+c经过O、A、C三点.(1)求该抛物线的函数解析式;(2)点P为线段OC上一个动点,过点P作y轴的平行线交抛物线于点M,交x轴于点N,问是否存在这样的点P,使得四边形ABPM为等腰梯形?若存在,求出此时点P的坐标;若不存在,请说明理由.(3)若△AOB沿AC方向平移(点A始终在线段AC上,且不与点C重合),△AOB在平移过程中与△COD重叠部分面积记为S.试探究S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.解题思路:(1)抛物线y=ax2+bx+c经过点O、A、C,利用待定系数法求抛物线的解析式;(2)根据等腰梯形的性质,确定相关点的坐标以及线段长度的数量关系,得到一元二次方程,求出t的值,从而可解.结论:存在点P(,),使得四边形ABPM为等腰梯形;(3)本问关键是求得重叠部分面积S的表达式,然后利用二次函数的极值求得S的最大值.解答中提供了三种求解面积S表达式的方法,殊途同归,可仔细体味.解答:解:(1)∵抛物线y=ax2+bx+c经过点O、A、C,可得c=0,∴,解得a=,b=,∴抛物线解析式为y=x2+x.(2)设点P的横坐标为t,∵PN∥CD,∴△OPN∽△OCD,可得PN=∴P(t,),∵点M在抛物线上,∴M(t,t2+t).如解答图1,过M点作MG⊥AB于G,过P点作PH⊥AB于H,AG=y A﹣y M=2﹣(t2+t)=t2﹣t+2,BH=PN=.当AG=BH时,四边形ABPM为等腰梯形,∴t2﹣t+2=,化简得3t2﹣8t+4=0,解得t1=2(不合题意,舍去),t2=,∴点P的坐标为(,)∴存在点P(,),使得四边形ABPM为等腰梯形.(3)如解答图2,△AOB沿AC方向平移至△A′O′B′,A′B′交x轴于T,交OC于Q,A′O′交x轴于K,交OC于R.求得过A、C的直线为y AC=﹣x+3,可设点A′的横坐标为a,则点A′(a,﹣a+3),易知△OQT∽△OCD,可得QT=,∴点Q的坐标为(a,).解法一:设AB与OC相交于点J,∵△ARQ∽△AOJ,相似三角形对应高的比等于相似比,∴=∴HT===2﹣a,KT=A′T=(3﹣a),A′Q=yA′﹣yQ=(﹣a+3)﹣=3﹣a.S四边形RKTQ=S△A′KT﹣S△A′RQ=KT•A′T﹣A′Q•HT=••(3﹣a)﹣•(3﹣a)•(﹣a+2)=a2+a﹣=(a﹣)2+由于<0,∴在线段AC上存在点A′(,),能使重叠部分面积S取到最大值,最大值为.解法二:过点R作RH⊥x轴于H,则由△ORH∽△OCD,得①由△RKH∽△A′O′B′,得②由①,②得KH=OH,OK=OH,KT=OT﹣OK=a﹣OH ③由△A′KT∽△A′O′B′,得,则KT=④由③,④得=a﹣OH,即OH=2a﹣2,RH=a﹣1,所以点R的坐标为R(2a﹣2,a﹣1)S四边形RKTQ=S△QOT﹣S△ROK=•OT•QT﹣•OK•RH=a•a﹣(1+a﹣)•(a﹣1)=a2+a﹣=(a﹣)2+由于<0,∴在线段AC上存在点A′(,),能使重叠部分面积S取到最大值,最大值为.解法三:∵AB=2,OB=1,∴tan∠O′A′B′=tan∠OAB=,∴KT=A′T•tan∠O′A′B′=(﹣a+3)•=a+,∴OK=OT﹣KT=a﹣(a+)=a﹣,过点R作RH⊥x轴于H,∵tan∠OAB=tan∠RKH==2,∴RH=2KH又∵tan∠OAB=tan∠ROH===,∴2RH=OK+KH=a﹣+RH,∴RH=a﹣1,OH=2(a﹣1),∴点R坐标R(2a﹣2,a﹣1)S四边形RKTQ=S△A′KT﹣S△A′RQ=•KT•A′T﹣A′Q•(xQ﹣xR)=••(3﹣a)﹣•(3﹣a)•(﹣a+2)=a2+a﹣=(a﹣)2+由于<0,∴在线段AC上存在点A′(,),能使重叠部分面积S取到最大值,最大值为.。
2012年中考数学压轴题100题精选(71-80题)答案

2012年中考数学压轴题100题精选(71-80题)答案2 ba【071】解:(1)由题意得,解得13 2a 4 9a 3b c 0∴此抛物线的解析式为3b 3c 2 c 2 242分 y x 2x 33(2)连结、.因为的长度一定,所以周长最小,就是使最ACBCBC△PBCPC PB小.点关于对称轴的对称点是点,与对称轴的交点即为所求的点. ACx 1BAP y 设直线的表达式为ACy kx b E,k A O B x 则解得3 D2 3k b 0∴此直线的表达式为……5分b 2 b 2 P 2 C.344 (第24题图)把代入得∴点的坐标y x 2, 33 (3)为······································ 6分 ·x 1y P 1存在最大值·························································································7分S理由:∵即DE∥PC,DE∥AC.ODOE2 mOE∴∴即△OED∽△OAC. , .OCOA2333∴OE 3 mm,AE 3,OE 22方法一:OP连结△OED△POE△POD△OED四边形S S S S S SPDOE134113= 3 m 2 m 1 3 m 2 m·················································223222 332= ···········································8分m m423333m 1∵,∴当最大4424时, ·········································· 9分 0S方法二:S S S S S△OAC△OED△AEP△PCD1131341 =13 2 3 m 2 m m m2222232 33332 2= (8)分 m m m 1 424433∵,∴当时,··························································9分m 1 0S 最大448【072】解:(1)①,,,S=12 OC 4OA 4AB 2OABC梯形2②当时,直角梯形OABC被直线扫过的面积=直角梯形OABC面积-直角三角开DOE面积2 t 4l1228 (2)存S 12 (4 t) 2( 4t )t t8 4在,,4),P(4,4),P(8,4)P( 12,4),P( 4,4),P( 451233对于第(2)题我们提供如下详细解答(评分无此要求).下面提供参考解法二:① 以点D为直角顶点,作轴PP x1 设.(图示阴影), 在Rt OD E中,OE 2OD, OD b,OE 2bRt ODE Rt PPD1,在上面二图中分别可得到点的生标为P(-12,4)、P(-4,4)E点在0点 b ,2b 8P与A点之间不可能;② 以点E为直角顶点8同理在②二图中分别可得点的生标为P(-,4)、P(8,4)E点在0点下方不可能. P3③ 以点P为直角顶点同理在③二图中分别可得点的生标为P(-4,4)(与①情形二重合舍去)、P(4,4),PE点在A点下方不可能. 8综上可得点的生标共5个解,分别为P(-12,4)、P(-4,4)、P(-,4)、P3P(8,4)、P (4,4).下面提供参考解法二:以直角进行分类进行讨论(分三类):第一类如上解法⑴中所示图此时D(-b,o),E(O,2b) P为直角:设直线DE:y 2x 2b,b1b3b,直线的中垂线方程:,令得.由的中点坐标为(-,b)y b (x )P( 8,4)DEy 4 2222 3 222222 (b 8) (4 2b) b 4b 已知可得即化简得解2PE DE3b 32b 64 0283b 得 ; P( 4,4)b 8,b 将之代入P (-8,4) P (4,4)、 121232 第二类如上解法②中所示图此时D (-b,o),E(O,2b) E 为直角:设直线DE :y 2x 2b ,1,直线的方程:,令得.由已知可得即y x 2bPEPE DEP(4b 8,4)y 4 2 222222化简得解之得 ,(4b 8) (4 2b) b 4bb (2b 8)48 b 4,b ,4)将之代入P (4b-8,4) P (8,4)、P( 123433 第三类如上解法③中所示图此时D (-b,o),E(O,2b) D 为直角:设直线DE :y 2x 2b ,1,直线的方程:,令得.由已知可得即y (x b)PDPD DEP( b 8,4)y 4 2 2222 解得8 4 b 4b (-b-8,4) P (-12,4)、b 4,b 4将之代入P512. (与重合舍去)P( 4,4)P( 4,4)P6628综上可得点的生标共5个解,分别为P (-12,4)、P (-4,4)、P (-,4)、 P 3P (8,4)、P (4,4). 事实上,我们可以得到更一般的结论: b a 如果得出设,则P 点的情形如下 AB a 、OC b 、OA h 、k h 直角分类情形 k 1k 1 P(h,h)1 P( h,h) P 为直角1 P( h,h)2hk P( ,h)3h1 k P( ,h) E 为直角2hk2 P(,h)4k 1 P( h(k 1),h)P(0,h)53 D 为直角 P( 2h,h)P( h(k 1),h)46 【073】(1)∵∠A 、∠C 所对的圆弧相同,∴∠A =∠C . APPD ∴Rt △APD ∽Rt △CPB ,∴,∴PA·PB =PC·PD ;………………………3分 CPPB(2)∵F 为BC 的中点,△BPC 为Rt △,∴FP=FC,∴∠C=∠CPF.又∠C=∠A,∠DPE=∠CPF,∴∠A=∠DPE.∵∠A+∠D=90°,∴∠DPE+∠D=90°.∴EF⊥AD.(3)作OM⊥AB于M,ON⊥CD于N,同垂径定理:222222∴OM=(2)-4=4,ON=(2)-3=11 55 y 又易证四边形MONP是矩形, O l 3O P 2O 2260°∴OP= OM ON 151 B D D x O A 1 C (第22题答图)点坐标为.在中,,Rt△AOC OAC 60° A ( 12,【074】(1)解:由题意得,OA | 4| |8| 12设直线的解析式为,由过两点的坐标为. C(0, 123) 123 b0) OC OAtan OAC 12 tan60° 123b 123 解得直线的解析式为:. ly 3x 123 k 3 点,得 A、Clly kx b 0 12k b(2)如图,设平移秒后到处与第一次外切于点,⊙O⊙O⊙O t P231与轴相切于点,连接.则x OO OP PO 8 5 13在⊙ODOO,OD1313113313轴,, OD⊥x OD 531312222OD OO OD 13 5 12中,.····································6分Rt△OOD111331131,,(秒)平移的时间为5OD OO OD 4 13 17 DD OD OD 17 12 51111115秒. ····························································· 8分 ⊙O t 521【075】解:(1)对称轴是直线:, x 1点A的坐标是(3,0).···························································· 2分(说明:每写对1个给1分,“直线”两字没写不扣分)(2)如∵点ADC的坐标分别图11,连接AC、AD,过D作于点M,DM y 轴△AOC∽△CMD解法一:利用、、、, a b b是 A (3,0),D(1,)C(0),AOOC3b3 ab 0∴AO=3,MD=1.由得∴·············································3分∴函数解析式0 2CMMDa13 ab 0a 1 2又∵∴由得0 a ( 1) 2a ( 1) b b 33a b为: ·········································································· 6分 y x 2x 3解法二:利用以AD为直径的圆经过点C ∵点A、D的坐标分别是A (3,0)、D(1,)、C(0,), a b b222222∴,,∵∴…① 又AC 9 bCD 1 aAD 4 ( a b)AC CD AD2∵…②···········································4分由①、②得∴函数解析式3 ab 00 a ( 1) 2a ( 1) b2为:·······························6分a 1,b 3y x 2x 3(3)如图所示,当BAFE为平行四边形时,则∥,并且=. BAEFBAEF ∵=4,∴=4 ,由于对称为,∴点F的横坐标为5. ·························· 7分 x 1BAEF2 E 将根据抛物线的对称代入得,∴F(5,12). F x 5y x 2x 3y 12 y性可知,在对称轴的左侧抛物线上也存在点F,使得四边形BAEF是平行四边形,此时点F坐标为(,12). 3当四边形BEAF是平行四边形时,点F即为点D,此时点F的坐标为(1,). 4综上所述,点F的坐标为(5,12), O A B x (,12)或(1,). 3 4【076】解:(1)∵四边形OBHC为矩形,∴CD∥AB, C 又D(5,2),∴C(0,2),OC=2 .图11 ∴解得 2 1 2 5 5 m n 2 D 5n 2 mn 22 152 ∴抛物线的解析式为:…… 4分y x x 222(2)点E落在抛物线上. 理由如下:……… 5分152由y = 0,得. 解得x=1,x=4.∴A(4,0),B(1,0). x x 2 01222 ∴OA=4,OB=1. 由矩形性质知:CH=OB=1,BH=OC=2,∠BHC=90°,由旋转、轴对称性质知:EF=1,BF=2,∠EFB=90°,∴点E的坐标为(3,-1). 151522把x=3代入,得,2222(3)法一:∴点E在抛物线上. y x x 2y 3 3 2 1存在点P(a,0),延长EF交CD于点G,易求OF=CG=3,PB=a-1. S=5,S= 3,记S= S,S= S, BCGF ADGF BCQP 1ADQP 2梯形梯形梯形梯形1 下面分两种情形:①当S∶S=1∶3时,,S (5 3)2 512 14PFEF1此时点P在点F(3,0)的左侧,则PF = 3-a,由△EPF∽△EQG,得,则QG=9 QGEG319-3a,∴CQ=3-(9-3a) =3a -6,由S=2,得,解得;(3a 6 a 1) 2 2a 1243②当S∶S=3∶1时,此时点P在点F(3,0)的右侧,则PF = a-S (5 3) 6 51214,3,由△EPF∽△EQG,得QG = 3a-9,∴CQ = 3 +(3 a-9)= 3 a-6,913113由S= 6,得,解得,综上所述:所求点P的坐标为24440)……… 14分(,0)或(,(3a 6 a 1) 2 6a 1法二:存在点P(a,0). 记S= S,S= S,易求S= 8. BCQP 1ADQP 2ABCD 梯形梯形梯形当PQ经过点F(3,0)时,易求S=5,S= 3,此时S∶S不符合条件,故a≠3. 12 121 k,则,解得设直线PQ的解3k b 1 a 3k≠0 y = kx+b()析式为, aak b 0 b∴. 由y = 2得xa 3 1a= 3a-6,∴Q(3a-6,2)……… 10分 y x a 3a 31∴CQ1211= 2;= 3a-6,BP = a-1,. (3a 6 a 1) 2 4a 7S下面分两种情形:①当S∶S= 1∶3时,S 8S 12 1梯形ABCD449-∴4a7 = 2,解得; (12)分a 43313-②当S∶S= 3∶1时,;∴4a7 = 6,解得;1梯形ABCD444913,0)………… 14分综上S 8 6S a 12所述:所求点P的坐标为(,0)或(44913[说明:对于第(3)小题,只要考生能求出或两个答案,就给6分. ] a a 443【077】解:(1)把B(0,6)代入,得=6 (1)分my m43 把=0代入,得=8 xy 6y4∴点A 的坐标为(8,0)…………… 3分 B'PCP(2)在矩形OACB中,AC =OB=6,BC=OA=8,∠C=90°GDQ∴AB=FIE'JM∵PD⊥AB∴∠PDB=∠C=2222AC BC 6 8 1090° OMEABDBD8BC,∴∴cos CBA BPa10BA 44∴BD aAD 10 a55又∵BC∥AE,∴△PBD∽△EAD4a10 AEAEAD54a5∴,即,∴ AE (10 ) 12.5 a 4aaBPBD45511∵,∴梯形PEAC22S (PC AE)ACs (8 a 12.5 a)6 6a 61.5()……………………………7分(注:写成不扣分) o a 8o a 8② ⊙Q是△OAB的内切圆,可设⊙Q的半径为r 11∵,解得OAB22、、r=2.………………………………………8分 S (6 8 10)r 6 8设⊙Q与OBABOA分别切于点F、G、H 可知,OF=2∴BF=BG=OB-OF=6-2=4,设直线PD与⊙Q交于点I、J ,过Q作QM⊥IJ于点1M,连结IQ、QG,∵QI=2, IM IJ 1.2222 ∴∴在∴BD=矩形GQMD中,GD=QM=1.6 QM QI IM 1.6BDBC85BG+GD=4+1.6=5.6,由,得 cos CBA BP BD 7 BPBA104∴点P的坐标为(7,6)…………………………………………………………………11分当PE在圆心Q的另一侧时,同理可求点P的坐标为(3,6)………………………12分综上,P点的坐标为(7,6)或(3,6).………………………………………………13分。
2012中考数学 压轴题精选精析(91-100例)

2012中考数学压轴题精选精析(91-100例)19.(2011·某某某某·模拟9)化工商店销售某种新型化工原料,其市场指导价是每千克160元(化工商店的售价还可以在市场指导价的基础上进行浮动),这种原料的进货价是市场指导价的75%.(1)为了扩大销售量,化工商店决定适当调整价格,调整后的价格按八折销售,仍可获得实际售价的20%的利润.求化工商店调整价格后的标价是多少元?打折后的实际售价是多少元?(2)化工商店为了解这种原料的月销售量y(千克)与实际售价x(元/千克)之间的关系,每个月调整一次实际售价,试销一段时间后,部门负责人把试销情况列成下表:实际售价x(元/千克)…150 160 168 180月销售量y(千克)…500 480 464 440 …①请你在所给的平面直角坐标系中,以实际售价x(元/千克)为横坐标,月销售量y(千克)为纵坐标描出各点,观察这些点的发展趋势,猜想y与x之间可能存在怎样的函数关系;②请你用所学过的函数知识确定一个满足这些数据的y与x之间的函数表达式,并验证你在①中的猜想;③若化工商店某月按同一实际售价共卖出这种原料450千克,请你求出化工商店这个月销售这种原料的利润是多少元?第24题答案:解:(1)依题意,每千克原料的进货价为160×75%=120(元) --------------2分设化工商店调整价格后的标价为x元,则0.8x-120=0.8x×20%解得x=187.5187.5×0.8=150(元)----------------------------------------------------------------------2分∴调整价格后的标价是187.5元,打折后的实际售价是150元.----------1分(2)①描点画图,观察图象,可知这些点的发展趋势近似是一条直线,所以猜想y与x之间存在着一次函数关系.--------------------------------------------------------------2分②根据①中的猜想,设y 与x 之间的函数表达式为y =kx +b ,将点(150,500)和(160,480)代入表达式,得⎩⎪⎨⎪⎧500=150k +b 480=160k +b 解得⎩⎪⎨⎪⎧k =-2b =800∴y 与x 的函数表达式为y =-2x +800---------------------------------------------2分将点(168,464)和(180,440)代入y =-2x +800均成立,即这些点都符合y =-2x +800的发展趋势.∴①中猜想y 与x 之间存在着一次函数关系是正确的.---------------------------1分③设化工商店这个月销售这种原料的利润为w 元,当y =450时,x =175∴w =(175-120)×450=24750(元)答:化工商店这个月销售这种原料的利润为24750元.---------------------------2分20.(2011·某某某某·模拟10)如图,抛物线的顶点坐标是⎪⎭⎫ ⎝⎛8925,-,且经过点) 14 , 8 (A .(1)求该抛物线的解析式;(2)设该抛物线与y 轴相交于点B ,与x 轴相交于C 、D 两点(点C 在点D 的左边),试求点B 、C 、D 的坐标;(3)设点P 是x 轴上的任意一点,分别连结AC 、BC . 试判断:PB PA +与BC AC +的大小关系,并说明理由.答案:(1)(4分)设抛物线的解析式为89252-⎪⎭⎫ ⎝⎛-=x a y ………………………1分∵抛物线经过)14,8(A ,∴89258142-⎪⎭⎫ ⎝⎛-a =,解得:21=a …………2分∴8925212-⎪⎭⎫ ⎝⎛-=x y (或225212+-=x x y ) …………………………1分(2)(4分)令0=x 得2=y ,∴)2,0(B ……………………………………1分 令0=y 得0225212=+-x x ,解得11=x 、42=x ………………………2分 ∴)0 , 1(C 、) 0, 4(D …………………………………………………………1分 (3)(4分)结论:BC AC PB PA +≥+…………………………………1分 理由是:①当点CP 与点重合时,有BC AC PB PA +=+………………………………1分②当时异于点点C P ,∵直线AC 经过点)14,8(A 、)0,1(C ,∴直线AC 的解析式为22-=x y ………3分DAO xyCB . (第24题图)C xyAB DO P .设直线AC 与y 轴相交于点E ,令0=x ,得2-=y , ∴)2,0(-E ,则)2,0()2,0(B E 与点-关于x 轴对称 ∴EC BC =,连结PE ,则PB PE =, ∴AE EC AC BC AC =+=+,∵在APE ∆中,有AE PE PA >+∴BC AC AE PE PA PB PA +=>+=+…………………………………1分 综上所得BC AC BP AP +≥+21.(2011·某某某某·模拟11) 如图,以O 为原点的直角坐标系中,A 点的坐标为(0,1),直线x=1交x 轴于点B 。
2012年中考数学压轴题70题

2012年中考数学压轴题70题精选【001】如图,已知抛物线2(1)y a x=-+a≠0)经过点(2)A-,0,抛物线的顶点为D,过O作射线OM AD∥.过顶点D平行于x轴的直线交射线OM于点C,B在x轴正半轴上,连结BC.(1)求该抛物线的解析式;(2)若动点P从点O出发,以每秒1个长度单位的速度沿射线OM运动,设点P运动的时间为()t s.问当t为何值时,四边形DAOP分别为平行四边形?直角梯形?等腰梯形?(3)若OC OB=,动点P和动点Q分别从点O和点B同时出发,分别以每秒1个长度单位和2个长度单位的速度沿OC和BO运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为t()s,连接PQ,当t为何值时,四边形BCPQ的面积最小?并求出最小值及此时PQ的长.【002】如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)、C(8,0)、D (8,8).抛物线y=ax2+bx过A、C两点.(1)直接写出点A的坐标,并求出抛物线的解析式;(2)动点P从点A出发.沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动.速度均为每秒1个单位长度,运动时间为t秒.过点P作PE⊥AB交AC于点E,①过点E作EF⊥AD于点F,交抛物线于点G.当t为何值时,线段EG最长?②连接EQ.在点P、Q运动的过程中,判断有几个时刻使得△CEQ是等腰三角形?请直接写出相应的t值。
【003】如图13,二次函数)0(2<++=p q px x y 的图象与x 轴交于A 、B 两点,与y 轴交于点C (0,-1),ΔABC 的面积为45。
(1)求该二次函数的关系式;(2)过y 轴上的一点M (0,m )作y 轴的垂线,若该垂线与ΔABC 的外接圆有公共点,求m 的取值范围;(3)在该二次函数的图象上是否存在点D ,使四边形ABCD 为直角梯形?若存在,求出点D 的坐标;若不存在,请说明理由。
2012年中考数学压轴题100题精选(21-30题)答案

2012年中考数学压轴题100题精选(21-30题)答案【021】解:(1);… ………………………………3分21(2)①EF∥AB.……………………………………4分,.证明:如图,由题意可得A(–4,0),B(0,3),34kk∴PA=3,PE=,PB=4,PF=.34PA312PB412∴,k∴.………………………… 6分PEPF又∵∠APB=∠EPF.∴△APB ∽△EPF,∴∠PAB=∠PEF.∴EF∥AB.…………………………… 7分②S没有最小值,理由如下:2过E作EM⊥y轴于点M,过F作FN⊥x轴于点N,两线交于点Q.由上知M(0,),N(,0),Q(,).……………… 8分4334-而S= S,∴S=SS=S-S=S+S+SEFQPEF2PEFOEFEFQOEFEOMFONOMQN △△△△△△△△矩形==2222.………………………… 10分6当时,S的值随k的增大而增大,而0<k<12.…………… 11分 2222∴0<S<24,s没有最小值.…………………………… 12分 22、说明:1.证明AB∥EF时,还可利用以下三种方法.方法一:分别求出经过AB两点和经过、EF两点的直线解析式,利用这两个解析式中x的系数相等来证明AB∥EF;方法二:tantan、,PAB利用=来证明AB∥EF;方法三:连接AFBE利用S=SAEFBFE△△、、得到点A点B到直线EF的距离相等,再由AB两点在直线EF同侧可得到AB∥EF.2.求S的值时,还可进行如下变形:2S=S-S=S-(S-S)=2 S-S,再利用第(1)2PEFOEFPEFPEOFPEFPEFPEOF△△△四边形△△四边形题中的结论.2【022】解:(1)设抛物线的解析式为:y=a(x-m+2)(x-m-2)=a(x-m)-4a.……2分∵AC⊥BC,由抛物线的对称性可知:△ACB是等腰直角三角形,又AB=4,112∴C(m,-2)代入得a=.∴解析式为:y=(x-m)-2.………………………5分22(亦可求C点,设顶点式)(2)∵m为小于零的常数,∴只需将抛物线向右平移-m个单位,再向上平移2个单位,可以使抛12物线y=(x-m)-2顶点在坐标原点. (7)分212m-2),设存在实数m,使得△BOD为等腰三角形.(3)由(1)得D(0,2∵△BOD为直角三角形,∴只能OD=OB.……………………………………………9分12∴m-2=|m +2|,当m+2>0时,解得m=4或m=-2(舍).2当m +2<0时,解得m=0(舍)或m=-2(舍);当m+2=0时,即m=-2时,B、O、D三点重合(不合题意,舍) 综上所述:存在实数m=4,使得△BOD为等腰三角形.……………………………12分△MBC【023】(1)证明:∵是等边三角形,∠∠D ∴∥BC∵是中点∴∵∠∠∠∠,∴△AMB≌△∴∴∴梯形是等腰梯形.△MBC(2)解:在等边中,60°Q,∠∠, B C P∠∠∠∠∠∴∠∠QPC△BMP∽△CQP∴∴∴··································5分,,∵∴················································6分∴∴ (7)分,BPMDBP∥∥(3)解:①当时,则有则四边形和四边形均为平行四边形∴,PCMDPC∥∥当时,则有,则四边形和四边形均为平行四边形∴441313,,、、、、∴当或时,以PM和ABC D中的两个点为顶点的四44边形是平行四边形.此时平行四边形有4个.△PQCy∴当取最小值时,为直角三角形∵4PB,∠,∠,∠∴是的中点,而∴∴BC【024】(1)由可知,,又△ABC为等腰直角三角形,∴,,所以点A的坐标是().D(2)∵∴,则点的坐标是().又抛物线顶点为,且过点、,所以可设抛物线的解析式为:,得:解得∴抛物线的解析式为………7分M(3)过点作于点,过点作于点,设点的坐标是,则,.PQM∵∴∽∴即,得∵BQN∴∽∴即,得又∵∴即为定值8. 【025】解:(1)设点M的横坐标为x,则点M的纵坐标为-x+4(0<x<4,x>0,-x+4>0);则:MC=∣-x+4∣=-x+4,MD=∣x∣=x;∴C=2(MC+MD)=2(-x+4+x)=8 OCMD四边形∴当点M在AB上运动时,四边形OCMD的周长不发生变化,总是等于8;22(2)根据题意得:S=MC·MD=(-x+4)·x=-x+4x=-(x-2)+4 OCMD四边形∴四边形OCMD的面积是关于点M的横坐标x(0<x<4)的二次函数,并且当x=2,即当点M运动到线段AB的中点时,四边形OCMD的面积最大且最大面积为4;(3)如图10(2),当时,;如图10(3),当时,;22a∴S与的函数的图象如下图所示: S 14·2(2·12(·a0 2 4 22【026】解:(1)∵AH∶AC=2∶3,AC=6∴AH=AC=×6=433又∵HF∥DE,∴HG∥CB,∴△AHG∽△ACB…………………………1分AHHG4HG16∴=,即=,∴HG=…………………………………2分63ACBC8111632...........................................∴S=AHHG=×4×=3分△AHG2233(2)①能为正方形...........................................................................4分′′∵HH′∥CD,HC∥HD,∴四边形CDHH为平行四边形′又∠C=90°,∴四边形CDHH为矩形.......................................5分又CH=AC-AH=6-4=2′∴当CD=CH=2时,四边形CDHH为正方形′此时可得t=2秒时,四边形CDHH为正方形 (6)分②(Ⅰ)∵∠DEF=∠ABC,∴EF∥∴当t=4秒时,直角梯形的腰EF与BA重合.′当0≤t≤4时,重叠部分的面积为直角梯形DEFH的面积.…………7分FMAC63过F作FM⊥DE于M,=tan∠DEF=tan∠ABC=== BC84ME44884FM=×2=,HF=DM=DE-ME=4-=∴ME= 33333141616∴直角梯形DEFH′的面积为(4+)×2=∴y= 23331′(Ⅱ)∵当4<t≤5时,重叠部分的面积为四边形CBGH的面积-矩形CDHH的面积.而S边形31324040×8×6-==2t∴y=-=S-S=矩形′△△CDHHCBGHABCAHG233331PD′(Ⅲ)当5<t≤8时,如图,设HD交AB于P.=8-又=tan∠ABC=43DB33∴PD=DB=(8-t)∴重叠部分的面积y=S , 443331122·PDDB=·(8-t)(8-t)=(8-t)=t-△PDB=48822∴重叠部分面积y与t的函数关系式:3(0≤t≤4)16401 -2t(4<t≤5)33312t-6t+24(5<t≤8)【027】解:(1)设抛物线的解析式为:, 把A(3,0)代入解析式求得所以,设直线AB的解析式为:由求得B点的坐标为把,代入中解得:所以 6分2(2)因为C点坐标为(1,4) ,所以当x=1时,y=4,y=2所以CD=4-2=2 8分平方单位) 假设存在符合条件的点P,设P点的横坐标为x,△PAB的铅垂高为h,则,由S=CABPAB△△12819322得:,化简得:解得,将代入中,解得P点坐标为1224y【028】解:(1)(5′) ∵抛物线与轴交于点(0,3),∴设抛物线解析式为(1′) 根据题意,得,解得∴抛物线的解析式为(5′) (2)(5′)由顶点坐标公式得顶点坐标为(1,4)(2′) 设对称轴与x轴的交点为∴四边形ABDE的面积梯形(5′)222(3)(2′)相似如图,BD=∴BE= ;∴即: ,所以是直角三角形∴,且, ∴∽′【029】解(1)因为△= 所以不论a为何实数,此函数图象与x轴总有两个交点。
2012中考数学压轴题精选精析(81-90例)

2012中考数学压轴题精选精析(81-90例)一、解答题1、(2011年湖北随州十校联考数学试题)如图所示,在平面直角坐标系中.二次函数y=a(x-2)2-1图象的顶点为P,与x轴交点为 A、B,与y轴交点为C.连结BP并延长交y轴于点D. 连结AP,△APB为等腰直角三角形。
(1)求a的值和点P、C、D的坐标;(2)连结BC、AC、AD。
将△BCD绕点线段CD上一点E逆时针方向旋转90°,得到一个新三角形.设该三角形与△ACD重叠部分的面积为S。
①当点E在(0,1)时,在图25—1中画出旋转后的三角形,并出求S.②当点E在线段CD(端点C、D除外)上运动时,设E(0,b),用含b的代数式表示S,并判断当b为何值时,重叠部分的面积最大?写出最大值.解:(1)a=1 P(2,-1) C(0,3) D(0,-3),(各1分,共4分)(2)画出图形(1分)可用相似三角形的面积求S=23(2分)(3)当b≥0如图,可用相似三角形的面积求21(3)6s b=-(2分)当b=0时,S=32(1分)当b<0时 BD旋转后经过A时,b=-1①-1<b≤0时,(2分)②b<-1时(2分)2、(2011年重庆一中摸底试卷)如图等腰直角三角形纸片ABC中,AC=BC=4,90oACB∠=直角边AC在x轴上,B点在第二象限,A(1,0),AB交y轴于E,将纸片过E点折叠使BE与EA所在直线重合,得到折痕EF(F在x轴上),再展开还原沿EF剪开得到四边形BCFE,然后把四边形BCFE从E点开始沿射线EA平移,至B点到达A点停止.设平移时间为t(s),移动速度为每秒1个单位长度,平移中四边形BCFE与AEF∆重叠的面积为S.(1)求折痕EF的长;(2)是否存在某一时刻t使平移中直角顶点C经过抛物线342++=xxy的顶点?若存在,求出t值;若不存在,请说明理由;(3)直接写出....S与t的函数关系式及自变量t的取值范围.解:(1)折痕2EF=(2)2t=(s)(3)212,(02).2s t t t=-+≤≤1,(222).s t=≤≤2121,(2232).4s t t t=-+-≤≤21228,(3242).4s t t t=-+≤≤3、(2011泰兴市济川实验初中初三数学阶段试题)如图,矩形A’B’C’D’是矩形OABC(边OA 在x 轴正半轴上,边OC 在y 轴正半轴上)绕B 点逆时针旋转得到的,O ’点在x 轴的正半轴上,B 点的坐标为(1,3).O’C’与AB 交于D 点.(1)如果二次函数2y ax bx c =++(0a ≠)的图象经过O ,O ’两点且图象顶点M 的纵坐标为1-,求这个二次函数的解析式;(2)求D 点的坐标.(3)若将直线OC 绕点O 旋转α度(0<α<90)后与抛物线的另一个 交点为点P ,则以O 、O’、B 、P 为顶点的四边形能否是平行 四边形?若能,求出αtan 的值;若不能,请说明理由.解:(1)x x y 22-= ……3 分(2)D(1,34) ……7分 (3)tan α=1或31……12分(求出一个得3分,求两个得5分)4、(2011年山东三维斋一模试题)如图所示,已知抛物线21y x =-与x 轴交于A 、B 两点,与y 轴交于点C .(1)求A 、B 、C 三点的坐标.(2)过点A 作AP ∥CB 交抛物线于点P ,求四边形ACBP 的面积. (3)在x 轴上方的抛物线上是否存在一点M ,过M 作MG ⊥x 轴于点G ,使以A 、M 、G 三点为顶点的三角形与∆PCA 相似. 若存在,请求出M 点的坐标;否则,请说明理由. 解:(1)令0y =,得210x -= 解得1x =±令0x =,得1y =-∴ A (1,0)- B (1,0) C (0,1)- ··· (2分)(2)∵O A =O B =O C =1 ∴∠BAC =∠AC O=∠BC O=45∵A P ∥CB , ∴∠P AB =45过点P 作P E ⊥x 轴于E ,则∆A P E 为等腰直角三角形令O E =a ,则P E =1a + ∴P (,1)a a +∵点P 在抛物线21y x =-上 ∴211a a +=- 解得12a =,21a =-(不合题意,舍去)∴P E =3 ··························································································· 4分)∴四边形ACB P 的面积S =12AB •O C +12AB •P E =112123422⨯⨯+⨯⨯= ······································ 6分) (3)假设存在∵∠P AB =∠BAC =45 ∴P A ⊥AC∵MG ⊥x 轴于点G , ∴∠MG A =∠P AC =90 在Rt △A O C 中,O A =O C =1 ∴AC =2在Rt △P AE 中,AE =P E =3 ∴A P= 32 ··············································· 7分) 设M 点的横坐标为m ,则M 2(,1)m m -①点M 在y 轴左侧时,则1m <-(ⅰ) 当∆A MG ∽∆P CA 时,有AG PA =MG CA∵A G=1m --,MG=21m -即211322m m ---= 解得11m =-(舍去) 223m =(舍去)(ⅱ) 当∆M A G ∽∆P CA 时有AG CA =MGPA即 211232m m ---= A BC 'MA 'O xyO ' CD第28题图CPByAoxEyPAoGMC ByPAox解得:1m =-(舍去) 22m =-∴M (2,3)- ··········································································· (10分)② 点M 在y 轴右侧时,则1m > (ⅰ) 当∆A MG ∽∆P CA 时有AG PA =MGCA∵A G=1m +,MG=21m -∴ 211322m m +-= 解得11m =-(舍去) 243m =∴M 47(,)39(ⅱ) 当∆M A G ∽∆P CA 时有AG CA =MGPA即 211232m m +-= 解得:11m =-(舍去) 24m = ∴M (4,15)∴存在点M ,使以A 、M 、G 三点为顶点的三角形与∆P CA 相似M 点的坐标为(2,3)-,47(,)39,(4,15) ·································· (12分)5、(2011年深圳市数学模拟试卷)如图13,已知二次函数y=ax 2+bx +c 的象经过A (-1,0)、B (3,0)、N (2,3)三点,且与y 轴交于点C . (1)(3分)求顶点M 及点C 的坐标;(2)(3分)若直线y =kx +d 经过C 、M 两点,且与x 轴交于点D ,试证明四边形CDAN 是平行四边形;(3)(4分)点P 是这个二次函数的对称轴上一动点,请探索:是否存在这样的点P ,使以点P 为圆心的圆经过A 、B 两点,并且与直线CD 相切,如果存在,请求出点P 的坐标;如果不存在,请说明理由. 解:解:(1)因为二次函数y=ax 2+bx +c 的图象经过点A (-1,0)、B (3,0)、N (2,3)所以,可建立方程组:⎪⎩⎪⎨⎧++=++=+-=c b a c b a c b a 2433900,解得:⎪⎩⎪⎨⎧==-=321c b a所以,所求二次函数的解析式为y=-x 2+2x +3,所以,顶点M (1,4),点C (0,3) -------2分(2)直线y=kx+d 经过C 、M 两点,所以⎩⎨⎧=+=43d k d ,即k =1,d =3,直线解析式为y =x +3令y =0,得x =-3,故D (-3,0)∴ CD =23,AN =23,AD =2,CN =2∴CD =AN ,AD =CN∴ 四边形CDAN 是平行四边形(3)假设存在这样的点P ,使以点P 为圆心的圆经过A 、B 两点,并且与直线CD 相切,因为这个二次函数的对称轴是直线x =1,故可设P (1,0y ),则PA 是圆的半径且PA 2=y 02+22,过P 作直线CD 的垂线,垂足为Q ,则PQ =PA 时以P 为圆心的圆与直线CD 相切。
2012中考数学压轴题及答案40例(6)

2012中考数学压轴题及答案40例(6)21.如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)、C(8,0)、D(8,8).抛物线y=ax2+bx过A、C两点.(1)直接写出点A的坐标,并求出抛物线的解析式;(2)动点P从点A出发,沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动,速度均为每秒1个单位长度,运动时间为t秒.过点P作PEAB交AC于点E.①过点E作EFAD于点F,交抛物线于点G.当t为何值时,线段EG最长?②连接EQ,在点P、Q运动的过程中,判断有几个时刻使得△CEQ 是等腰三角形?请直接写出相应的t值.解:(1)点A的坐标为(4,8).1分将A(4,8)、C(8,0)两点坐标分别代入y=ax2+bx,得解得a=-,b=4.抛物线的解析式为y=-x2+4x.3分(2)①在Rt△APE和Rt△ABC中,tanPAE==,即==.PE=AP=t,PB=8-t.点E的坐标为(4+t,8-t).2点G的纵坐标为-(4+t)2+4(4+t)=-t2+8.5分EG=-t2+8-(8-t)=-t2+t∵-0,当=4时,线段EG最长为2.7分②共有三个时刻.8分t1=,t2=,t3=40-.11分22.如图,抛物线y=-x2+2x+3与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.(1)直接写出A、B、C三点的坐标和抛物线的对称轴;(2)连结BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m.①用含m的代数式表示线段PF的长,并求出当m为何值时,四边形PEDF为平行四边形?②设△BCF的面积为S,求S与m的函数关系式.解:(1)A(-1,0),B(3,0),C(0,3).2分抛物线的对称轴是:x=1.3分(2)①设直线BC的解析式为:y=kx+b.将B(3,0),C(0,3)分别代入得:解得直线BC的解析式为y=-x+3.当x=1时,y=-1+3=2,E(1,2).当x=m时,y=-m+3,P(m,-m+3).4分将x=1代入y=-x2+2x+3,得y=4,D(1,4).将x=m代入y=-x2+2x+3,得y=-m2+2m+3.F(m,-m2+2m+3).5分线段DE=4-2=2,线段PF=-m2+2m+3-(-m+3)=-m2+3m6分∵PF∥DE,当PF=DE时,四边形PEDF为平行四边形.由-m2+3m=2,解得:m1=2,m2=1(不合题意,舍去).当m=2时,四边形PEDF为平行四边形.7分②设直线PF与x轴交于点M.由B(3,0),O(0,0),可得:OB=OM+MB=3.则S=S△BPF+S△CPF8分=PFBM+PFOM=PFOB=(-m2+3m)3=-m2+m(03)即S与m的函数关系式为:S=-m2+m(03).9分23.如图,在矩形OABC中,已知A、C两点的坐标分别为A(4,0)、C(0,2),D为OA的中点.设点P是AOC平分线上的一个动点(不与点O重合).(1)试证明:无论点P运动到何处,PC总与PD相等;(2)当点P运动到与点B的距离最小时,试确定过O、P、D三点的抛物线的解析式;(3)设点E是(2)中所确定抛物线的顶点,当点P运动到何处时,△PDE的周长最小?求出此时点P的坐标和△PDE的周长;(4)设点N是矩形OABC的对称中心,是否存在点P,使CPN=90?若存在,请直接写出点P的坐标.解:(1)∵点D是OA的中点,OD=2,OD=OC.又∵OP是COD的角平分线,POC=POD=45.△POC≌POD,PC=PD;3分(2)如图,过点B作AOC的平分线的垂线,垂足为P,点P即为所求.易知点F的坐标为(2,2),故BF=2,作PMBF.∵△PBF是等腰直角三角形,PM=BF=1.点P的坐标为(3,3).∵抛物线经过原点可设抛物线的解析式为y=ax2+bx.又∵抛物线经过点P(3,3)和点D(2,0)解得过O、P、D三点的抛物线的解析式为y=x2-2x;7分(3)由等腰直角三角形的对称性知D点关于AOC的平分线的对称点即为C点.连接EC,它与AOC的平分线的交点即为所求的P点(因为PE+PD=EC,而两点之间线段最短),此时△PED的周长最小.∵抛物线y=x2-2x的顶点E的坐标(1,-1),C点的坐标(0,2) 设CE所在直线的解析式为y=kx+b则解得CE所在直线的解析式为y=-3x+2.联立,解得,故点P的坐标为(,).△PED的周长即是CE+DE=;11分(4)存在点P,使CPN=90,其坐标为(,)或(2,2).14分24.如图1,已知抛物线经过坐标原点O和x轴上另一点E,顶点M的坐标为(2,4);矩形ABCD的顶点A与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3.(1)求该抛物线所对应的函数关系式;(2)将矩形ABCD以每秒1个单位长度的速度从图1所示的位置沿x轴的正方向匀速平行移动,同时一动点P也以相同的速度从点A 出发向B匀速移动,设它们运动的时间为t秒(03),直线AB与该抛物线的交点为N(如图2所示).①当t=时,判断点P是否在直线ME上,并说明理由;②设以P、N、C、D为顶点的多边形面积为S,试问S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.解:(1)∵因所求抛物线的顶点M的坐标为(2,4)可设其对应的函数关系式为y=a(x-2)2+4.1分又抛物线经过坐标原点O(0,0),a(0-2)2+4=0.2分解得a=-1.3分所求函数关系式为y=-(x-2)2+4,即y=-x2+4x.4分(2)①点P不在直线ME上,理由如下:5分根据抛物线的对称性可知E点的坐标为(4,0).设直线ME的解析式为y=kx+b,将M(2,4),E(4,0)代入,得解得.直线ME的解析式为y=-2x+8.6分当t=时,OA=AP=,P(,).7分∵点P的坐标不满足直线ME的解析式y=-2x+8当t=时,点P不在直线ME上.8分②S存在最大值,理由如下:9分∵点A在x轴的非负半轴上,且N在抛物线上,OA=AP=t.P(t,t),N(t,-t2+4t),AN=-t2+4t(03)PN=AN-AP=-t2+4t-t=-t2+3t=t(3-t)010分(ⅰ)当PN=0,即t=0或t=3时,以点P,N,C,D为顶点的多边形是三角形,此三角形的高为AD.S=DCAD=32=3.11分(ⅱ)当PN0时,以点P,N,C,D为顶点的多边形是四边形.∵PN∥CD,ADCD.S=(CD+PN)AD=(3-t2+3t)2=-t2+3t+3=-(t-)2+(0当t=时,S最大=.12分综上所述,当t=时,以点P,N,C,D为顶点的多边形面积S 有最大值,最大值为.13分说明:(ⅱ)中的关系式,当t=0和t=3时也适合.25.如图1,已知抛物线y=ax2-2ax-3与x轴交于A、B两点,其顶点为C,过点A的直线交抛物线于另一点D(2,-3),且tanBAD=1.(1)求抛物线的解析式;(2)连结CD,求证:AD(3)如图2,P是线段AD上的动点,过点P作y轴的平行线交抛物线于点E,求线段PE长度的最大值;(4)点Q是抛物线上的动点,在x轴上是否存在点F,使以A,D,F,Q为顶点的四边形是平行四边形?若存在,直接写出点F的坐标;若不存在,请说明理由.解:(1)如图1,过点D作DHx轴于H,则OH=2,DH=3.∵tanBAD=1,AH=DH=3,AO=3-2=1.1分A(-1,0).2分把A(-1,0)代入y=ax2-2ax-3,得a+2a-3=0.a=1.3分抛物线的解析式为y=x2-2x-3.4分(2)∵y=x2-2x-3=(x-1)2-4C(1,-4).5分连结AC,则AD2=32+32=18,CD2=(2-1)2+(-3+4)2=2,AC2=(1+1)2+42=20.AD2+CD2=AC2,△ACD是直角三角形,且ADC=90.7分ADCD.8分(3)设直线AD的解析式为y=kx+b,把A(-1,0),D(2,-3)代入求得直线BC的解析式为y=-x-1.9分设点P的横坐标为x,则P(x,-x-1),E(x,x2-2x-3).∵点P在点E的上方EP=(-x-1)-(x2-2x-3)=-x2+x+2=-(x-)2+10分当x=时,线段PE长度的最大值=.12分(4)存在,点F的坐标分别为F1(-3,0),F2(1,0),F3(,0),F4(,0).16分关于点F坐标的求解过程(原题不作要求,本人添加,仅供参考) 如图3①若四边形ADQ1F1为平行四边形,则AF1=DQ1,DQ1∥AF1.点Q1的纵坐标为-3,代入y=x2-2x-3,得x2-2x-3=-3,x1=0,x2=2.∵D(2,-3),Q1(0,-3),DQ1=2,AF1=2.F1(-3,0).②若四边形AF2DQ2为平行四边形,同理可得F2(1,0).③若四边形AQ3F3D为平行四边形,则AQ3=DF3.点Q3的纵坐标为3,代入y=x2-2x-3,得x2-2x-3=3,x3=,x4=.-1-()=,OF3=2-()=.F3(,0).④若四边形AQ4F4D为平行四边形,则OF4=()-()+()=F4(,0).26.已知二次函数y=ax2+bx+c(a0)的图象经过点A(1,0),B(2,0),C(0,-2),直线x=m(m2)与x轴交于点D.(1)求二次函数的解析式;(2)在直线x=m(m2)上有一点E(点E在第四象限),使得E、D、B为顶点的三角形与以A、O、C为顶点的三角形相似,求E点坐标(用含m的代数式表示);(3)在(2)成立的条件下,抛物线上是否存在一点F,使得四边形ABEF为平行四边形?若存在,请求出m的值及四边形ABEF的面积;若不存在,请说明理由.解:(1)∵二次函数y=ax2+bx+c的图象经过点A(1,0),B(2,0),C(0,-2)解得二次函数的解析式y=-x2+3x-2.2分(2)当△EDB∽△AOC时,有=或=∵AO=1,CO=2,BD=m-2.当=时,得=,ED=.∵点E在第四象限,E1(m,).4分当=时,得=,ED=2m-4.∵点E在第四象限,E2(m,4-2m).6分(3)假设抛物线上存在一点F,使得四边形ABEF为平行四边形,则EF=AB=1,点F的横坐标为m-1.当点E1的坐标为(m,)时,点F1的坐标为(m-1,).∵点F1在抛物线的图象上,=-(m-1)2+3(m-1)-2.2m2-11m+14=0,解得m1=,m2=2(不合题意,舍去).F1(,-).S□ABEF=1=.9分当点E2的坐标为(m,4-2m)时,点F2的坐标为(m-1,4-2m).∵点F2在抛物线的图象上,4-2m=-(m-1)2+3(m-1)-2.m2-7m+10=0,解得m1=5,m2=2(不合题意,舍去).F2(4,-6).S□ABEF=16=6.12分注:其它解法可参照评分标准给分.27.已知:t1,t2是方程t2+2t-24=0,的两个实数根,且t1(1)求这个抛物线的解析式;(2)设点P(x,y)是抛物线上一动点,且位于第三象限,四边形OPAQ是以OA为对角线的平行四边形,求□OPAQ的面积S与之间的函数关系式,并写出自变量的取值范围;(3)在(2)的条件下,当□OPAQ的面积为24时,是否存在这样的点P,使□OPAQ为正方形?若存在,求出P点的坐标;若不存在,说明理由.解:(1)由t2+2t-24=0,解得t1=-6,t2=4.1分∵t1∵抛物线y=x2+bx+c的图象经过点A,B两点解得这个抛物线的解析式为y=x2+x+4.4分(2)∵点P(x,y)在抛物线上,且位于第三象限,y0,即-y0.又∵S=2S△APO=2|O A||y|=|OA||y|=6|y|S=-6y.6分=-6(x2+x+4)=-4(x2+7x+6)=-4(x+)2+25.7分令y=0,则x2+x+4=0,解得x1=-6,x2=-1.抛物线与x轴的交点坐标为(-6,0)、(-1,0)x的取值范围为-6(3)当S=24时,得-4(x+)2+25=24,解得:x1=-4,x2=-3.9分代入抛物线的解析式得:y1=y2=-4.点P的坐标为(-3,-4)、(-4,-4).当点P为(-3,-4)时,满足PO=PA,此时,□OPAQ是菱形.当点P为(-4,-4)时,不满足PO=PA,此时,□OPAQ不是菱形.10分要使□OPAQ为正方形,那么,一定有OAPQ,OA=PQ,此时,点的坐标为(-3,-3),而(-3,-3)不在抛物线y=x2+x+4上,故不存在这样的点P,使□OPAQ为正方形.12分精心整理,仅供学习参考。
2012年中考数学压轴题100题精选(11-20题)答案

2012 年中考数学压轴题100题优选(11-20题)答案【011】解:(1)证明:在Rt△FCD中,∵G为D F 的中点,∴CG= FD.⋯⋯⋯ 1分同理,在Rt△DEF 中,EG= FD .⋯⋯⋯⋯ 2分∴CG=EG.⋯⋯⋯⋯⋯⋯⋯ 3分(2 )(1 )中结论仍然成立,即EG=CG.⋯⋯⋯⋯⋯⋯⋯⋯⋯分⋯4证法一:连结AG,过G点作MN⊥AD 于M ,与EF 的延伸线交于N 点.在△DAG 与△DCG 中,∵AD=CD,∠ADG=∠CDG ,DG=DG ,∴△DAG≌△DCG .∴AG=CG.⋯⋯⋯⋯⋯⋯⋯⋯分⋯5在△DMG 与△FNG中,∵∠DGM=∠FGN,FG=DG,∠MDG=∠NFG,∴△DMG≌△FNG.∴MG=NG 在矩形AENM 中,AM=EN.⋯⋯⋯⋯⋯分6在R t△AMG 与Rt△ENG 中,∵AM=EN,MG=NG ,∴△AMG≌△ENG .∴AG=EG .∴EG=CG.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯分⋯证8法二:延伸CG至M,使MG=CG,连结MF,ME,E C,⋯⋯⋯⋯⋯⋯⋯⋯分4在△DCG 与△FMG 中,∵FG=DG,∠MGF=∠CGD,MG=CG,∴△DCG ≌△FMG.∴MF=CD,∠FMG=∠DCG.∴MF∥CD∥AB.⋯⋯⋯⋯⋯⋯⋯⋯分⋯∴5在Rt△MFE与Rt△CBE 中,∵MF=CB,EF=BE,∴△MFE ≌△CBE.∴∠MEC=∠MEF+∠FEC=∠CEB+∠CEF=90°.∴△MEC为直角三角形.∵MG = CG,∴EG= MC.⋯⋯⋯ 8分(3)(1)中的结论仍旧建立,即EG=CG.其余的结论还有:EG⊥CG.⋯⋯10分OO【012】解:(1)圆心在座标原点,圆的半径为1,A、B、C、D0)B(0,1、) C(1,、0)D(0,1)A( 1,、点的坐标分别为AM、NMA、NCOC y 抛x 物线与直线交于点,且分别与圆相切于点和点,、DM 、N 1、) N(11),D(01),、M( 1,1、) N(11),M( 1 ,.点在抛物线上,将的坐标代入c 1a 1 2 1 a b cb 1,y 得:ax b解x之,c得:1 a b cc 12 y x x1·············:.·····································4 分抛物线的分析式为215 2y x x 1 x( 2 )24 1x 抛物线的对称轴为, 2115 OE ,DE 1.······················6 分242 yBF ,BFD 90连°结, D NDEOD △BFD∽△EOD,,DBFD E A O x C5 F DE ,OD ,1DB 2又,P M 2 B45 FD , 545535 EF FD DE .···············································································8 分5210P(3)点在抛物线上.·············································································b过点的直································9 分D、Cy kx设线为:,k ,1b ,1、0)D(01),y kx bC的(1坐标代入,得:,将点DCy x 1·························································10 分直线为:.·xBBPPOy过1点作圆的切线与轴平行,点的纵坐标为,x 2y 1y x将代1 入,得:.22 Px 2y x x 1 2 2 1 1 (2,,当时,,点的坐标为2Py x x 因此1 ,点在抛物线上.·············································································0该抛物线·12 分 2 y ax bx 2 ,,2)可C(设的分析式为.【013】解:(1)该抛物线过点0)B(1,0)A(4,,代入,将1 a ,16a 4b2 ,0 2得解得5a b 2.0 b .2152y x x 2 ······························(3 分)此抛物线的分析式为.·22(2)存在.··························································································································(4 分)m P 如图,设点的横坐标为,152 m m则2P点的纵坐标为,22 y1 m 4 当时,P D152PM m m 2AM ,4.m A B 22 M 1 xO 4 COA PMA 又9,0 ° E AMAO2 2时,①当 C PMOC1(第26题图)△APM∽△ACO ,15 24 m 2 m m 2 即.22 m ,2m 41) P (,2.·解得,····································································(6 分)(舍去)12AMOC1152 2(4 m) m △mA PM2∽△CAO②当时,,即.PMOA222m 4m 解5 得,(均不合题意,舍去)12 1 m 41),P.(2 ······················································,·······································(7 分)当时m 4 2)P(5,.·近似地可求出当时,·········································································(8 分)m 1 14)P( ,.3 当时,P1) 14)( ,3(2,(5,2)或.·或综上所述,符合条件的点为·································(9 分)152t t 2 DDt(0 t.(4) 3)如图,设点的横坐标为,则点的纵坐标为221y x 2DEACAC过y作轴的平行线交于.由题意可求得直线的分析式为.(10 分)215111 22 Et ,t 2 DE t t 2 t 2 点t 的2 t坐标为..·(11 分)2222211 222 S t 2t 4 t 4t .(t 2) 422 t 2△DAC1) D(2,···············································△DAC,面积最大.045AOAy x【014】(1)···········(13 分).·当时解:∵点第一次落在直线上时停止旋转,∴旋转了.2 45 2O A. ⋯⋯⋯⋯⋯分4∴在旋转过程中所扫过的面积为3602MNAC BMN BAC 45 BNM B C(A 2 4)5解:∵∥,∴,. BMN BNMBM BNBA BCAM∴.∴又∵,∴.OAOC OAM OCN OAM A O O C M N CON 又∵,,∴.∴.∴1 AOM (90 45 OABC. MNAC 过程中,当和平行时,正方形旋转的度∴旋转245 数为.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯分⋯⋯0⋯ 8AOE 45 AOMBAEpy(3 )答:值无变化.证明:延伸交轴于点,则,000 AOE CON 90 45 AOM 45 AO M ,∴. 又∵,000 OAE 180 90 90 OCN OAE OCNOE ON,AE CN.∴.∴. 0OM OM OME OMN MOE MO y N又45 ∵,, ∴. y x E MN ME AM AEMN AM ∴.∴C N, AM p MN BN BM AM CN BN BM AB∴. B C B 4 OABCp∴在旋转正方形的过程中,值无变化. ⋯⋯⋯⋯⋯分12 xN O C (第26题)72【015】⑴设二次函数的分析式为:y=a(x-h)+k∵极点C 的横坐标为4 ,且过点(0 ,)3972∴y=a(x-4)+k ⋯⋯⋯⋯⋯3⋯①16a k又9 ∵对称轴为直线x=4,图象在x轴上截得的线段长为6 ∴A(1,0),B(7,0)332 ∴0=9a+k ⋯⋯⋯⋯⋯⋯②由①②解得a=,k=∴二次函数的分析式为:y=(x-4)--33 99⑵∵点A、B 对于直线x=4对称∴PA=PB∴PA+PD=PB+PD≥ D B∴当点P 在线段DB上时P A+PD获得最小值∴DB与对称轴的交点即为所求点P设直线x=4 与x轴交于点M∵PM∥OD ,∴∠BPM=∠BDO ,又∠PBM=∠DBO 73 3 PMBM339∴点P 的坐标为(4 ,)∴△BPM∽△BDO∴∴PM DOBO373 3 ⑶由⑴知点C(4,) ,又∵AM=3 ,∴在Rt△AMC 中,cot∠ACM= , 3 3oo∴∠ACM=60 ,∵AC=BC,Q作QN⊥x,过∴∠ACB=120 ①当点Q 在x轴上方时轴于N 假如AB=BQ,由△ABC∽△ABQ有oo BQ=6,∠QBN=60∴QN=3,BN=3,ON=10,此∠ABQ=120,则时点Q(10,),333 假如AB=AQ,由对称性知Q(-2,)33 ②当点Q 在x轴下方时,△QAB就是△ACB,此时点Q 的坐标是( 4,),3经查验,点(10,)与(-2,)都在抛物线上3333综上所述,存在这样的点Q,使为(10,)或(-2,)或△QAB∽△ABC 点Q 的坐标(4,).3333 3 y kx(k 【0)016】解:(1)设正比例函数的分析式为,11k 1y kx3 3k3),A,(3因此,解得.由于的图象过点111y x这个正比率函数的分析式为.·················································································(1 分)kk22y (k 0)y ,A(3)设反比率函数的分析式为.由于的图象过点,因此2xxk923 y k ,解9得.这个反比例函数的解析式为.········································(2 分)23x9933 y m ,B m(6)B6,(2 )由于点在的图象上,所以,则点.········(3 分)x622 y kx b(k 0)y kx设b一y次函x数分析式为.因为的图象是由平移获得的,3333 k 1y x by x,因此bB,6即.又由于的图象过点,所以32 399 6 bb y ,x 解得,一次函数的解析式为.·································(4 分)22299 y x ,DD0 (y3)由于的图象交轴于点,所以的坐标为.22 2y ax bx c(a设二0)次函数的解析式为.39 2Dy ax bx ,c 3B)6A,(3 0 ,、、和由于的图象过点,22 1 9a 3b,a c3, 2 3 b ,436a 6b c ,所以·····················(5 分)解得 2 99 c. c .2 2192y x这4x个二次函数的分析式为.····························································(6 分)2299 x y x CC,0(4)交轴于点,点的坐标是,22 151131 y6 6 6 3 3 如图3所S示,22222 A 99 3 45 18 B E4281 .O 6 3 C x 4281227 S S ,E y()x假定存在点,使.1003432 Dy x0 ECDOE,四边形的极点只能在轴上方,019919819 y y .S S001S△OCD△OCE2222284819273 y y E(x ,y) ,.在二次函数的图象上,000084221932 x 4x x .2解x 得或6.00002223 x 6x 6BCD,O E当E时6,点与点重合,这时不是四边形,故舍去,002 3 ,点E的2坐标为.(8 分)2 2y b x x c,,0)B(0 ,2)A(1 ,【017 】解:(1 )已知抛物线经过0 1 b cb 3 解得2 0 0 cc 2 2 y x 3x2··················分··所····2·······求抛物线的分析式为.·OA ,1OB 2,0)B(0,2) A(1,,(2)C(31),可得旋转后点的坐标为·································································································3 分·2x 3y x 3x 2y 2当时,由得,2y x 3x 22,)(3 可知抛物线过点Cy将原抛物线沿轴向下平移 1 个单位后过点. 2 y x 3x 1·····················分·5·平·移·后·的·抛·物·线·解·析·式············为:.·22 NNy x3x 1(x,x 3x 1() 3 )点在上,可设点坐标为0002335 2x y x 3x 1y将配x方得,其对称轴为.··································6 分224 3 y 0 x ①当时,如图①,02 S 2S △NBB△NDD B11113 1 x 2 1 00 A 222 1 O x D N D 1图①x 1 02x 3x 1 此时1 00 N(1,1) 点的坐标为·········································································································8 分.·y 3x ②当时,如图②02113 B 1 x 2 同理x 可得00222 N B C 1 A x 3 O x D 0D12x 3x 1 此1时00图②N,(31).点的坐标为N,1)(1(31) ,或综上,点的坐标为 (10)分.·2 y ax bx ,40a)C(0,4)A( 1,两点,【018】解:(1)抛物线经过a b 4a ,0a,1解得4a 3. 2 y x 3x 抛物线的分析式为. 2 m 1 m 3m 4,D(mm 1)( 2 )点在抛物线上,,y2 m 1m 3m 2m 即3,或0. D CDD 4)(,3 .点在第一象限,点的坐标为CBA 45°O A,.O B由(1)知 E DEBC设点对于直线的对称点为点. A B x C∥D ABCD 3 C,(04) O ,,且,ECB DCB,45°ECE CD 3y点在轴上,且.OE 1 ,E(10),.DBC即点对于直线对称的点的坐标为(0,1).PF⊥ABFEDE⊥BC(3 )方法一:作于,于.y OBC 4 5°OB OC,,4由(1)有:DBP 45,°CBD P.BA D C∥D OBCD 3 C,(,0 4)D(3,4) C ,且.P EDCE CBO,4 53°2 A B DE CE.xF O 2 52 BC 42 OB OC 4 C B E C E B,,,2DE3 tan PBF tan C.BD BE5PF 3tBF 5tOF 5t设4,则,,P( 5t ,43t).P点在抛物线上, 2 3t ( 5t 4) 3( 5t ,4) 4 22266 t t 0 ,(P 舍去)或,.25525 DBDPBD⊥D HxHQG⊥DHQQ 方法二:过点作的垂线交直线于点,过点作轴于.过点作G 于.yPBD ,45°QD D.B 90°QDG ,BDHD C Q G P DQG QDG 90°DQG BDH 又,. A BDG BH 1△QDG≌△DBH QG DH ,,4.x OH 4) Q( 1,3)D(3 ,,.由( 2 )知312y x BP ,0B)(,4直线的分析式为.552 2 x ,y x 3x ,4 x 4,2 5解1方程组得312y;606y x,1y 55. 2 25 266 P ,点的坐标为.525 【019】(1)EO>EC,原因以下:由折叠知,EO=EF,在Rt△EFC中,EF为斜边,∴EF>EC,故EO>EC ⋯ 2 分(2 )m为定值22222∵S=CF=EF -EC=EO -EC=(EO+EC)(EO―EC)=CO·(EO―E C C F)G H四边形S=CM·CO=|CE―EO|·CO=(EO―E·C C)O C M N O四边形S四边形CFGHm ∴1⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯分⋯⋯⋯ 4 S 四边形CMNO12121 QFC,E QF∴EF=EO= ( 3 )∵CO=1 ,33331∴cos∠FEC=∴∠FEC=60°, 2180 60 60 ,O E E A A O30 FEA三角等边∴22EQ ∴△EFQ为形,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯分⋯5 31133EQ EQ 作QI⊥EO 于I,EI=,IQ= 2323 21131 ∴(,)IO=∴Q 点坐标为⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯分⋯⋯336333 312(,)∵抛物线y=mx+bx+c过点C(0,1),Q,m=1 33b ∴3可求得,c=1 2y x 3x ∴抛1 物线分析式为⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯分⋯⋯ 7 2 AO 3EO 3 (4)由(3),3 2221 2x 3y (3) 3 3 当1时,<AB 3333231(,)∴P 点坐标为⋯⋯⋯⋯⋯⋯⋯分833121 ∴BP=AO 33 方法1:若△PBK 与△AEF相像,而△AEF≌△AEO,则分状况以下: 2 234383 B K BK (,1)(,1)时①,∴K点坐标为或 3 999 223 332 2343BK (,1)(0,1) BK②时,∴K 点坐标为或⋯⋯⋯⋯1分0 333 223 3 3 故直线K P 与y轴交点T 的坐标为571(0, 或) (0,)或(0, 或)(0,1) ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯分⋯⋯333 12 方法2:若△BPK与△AEF相像,由(3)得:P作PR⊥y轴于R,则∠RTP=60°或30°23 RT 3 2当①∠RTP=30°∠BPK=3°0或60°,过时, 3 232 3 RT 当②∠RTP=60°时,33 175T(0,),T(0, ,) T(0, ,)T(0,1) ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯分⋯∴112234333【020】解:(1)①CF⊥BD,CF=BD ②建立,理由以下:∵∠FAD=∠BAC=9°0∴∠BAD=∠CAF又BA=CA ,AD=AF ∴△BAD≌△CAF∴CF=BD∠ACF=∠ACB=4°5∴∠BCF=90°∴CF⊥BD (1 分)(⋯2⋯)当∠ACB=4°5时可得CF⊥BC,原因以下:如图:过点 A 作AC 的垂线与CB 所在直线交于G则∵∠ACB=4°5∴AG=AC ∠AGC=∠ACG=4°5 ∵AG=AC AD=AF ⋯(⋯1⋯分)∴△GAD≌△CAF(SAS)∴∠ACF=∠AGD=4°5 ∴∠GCF=∠GCA+∠ACF=90°∴CF⊥BC ⋯(⋯⋯2分⋯)(3)如图:作AQBC 于Q ∵∠ACB=4°5AC=4 ∴CQ=AQ=4 2∵∠PCD=∠ADP=90°∴∠ADQ+∠CDP=∠CDP+∠CPD=90°∴△ADQ∽△DPC ⋯(1 分)PCCD∴= DQAQ 设CD为x(0 <x < 3 )则D Q=CQ -CD=4 -x 则xPC= ⋯⋯⋯⋯(1 分)44 x1212∴PC=(-x+4x)=-(x-2)+1≥1 44 当x=2时,PC最长,此时P C=1 ⋯⋯⋯(1 分)。
2012年中考数学模拟压轴题100题精选(91-100题)答案

2012年中考数学模拟压轴题100题精选(91-100题)答案【091】(1)解:法1:由题意得⎩⎨⎧n =2+c ,2n -1=2+c . ……1分解得⎩⎨⎧n =1,c =-1.……2分法2:∵ 抛物线y =x 2-x +c 的对称轴是x =12,且 12-(-1) =2-12 A 、B 两点关于对称轴对称.∴ n =2n -1 ……1分 ∴ n =1,c =-1. ……2分∴ 有 y =x 2-x -1 ……3分 =(x -12)2-54.∴ 二次函数y =x 2-x -1的最小值是-54. ……4分(2)解:∵ 点P (m ,m )(m >0),∴ PO =2m .∴ 22≤2m ≤2+2.∴ 2≤m ≤1+2. ……5分 法1: ∵ 点P (m ,m )(m >0)在二次函数y =x 2-x +c 的图象上, ∴ m =m 2-m +c ,即c =-m 2+2m . ∵ 开口向下,且对称轴m =1,∴ 当2≤m ≤1+2 时,有 -1≤c ≤0. ……6分 法2:∵ 2≤m ≤1+2, ∴ 1≤m -1≤2. ∴ 1≤(m -1)2≤2.∵ 点P (m ,m )(m >0)在二次函数y =x 2-x +c 的图象上, ∴ m =m 2-m +c ,即1-c =(m -1)2.∴ 1≤1-c ≤2.∴ -1≤c ≤0. ……6分 ∵ 点D 、E 关于原点成中心对称, 法1: ∴ x 2=-x 1,y 2=-y 1.∴ ⎩⎨⎧y 1=x 12-x 1+c ,-y 1=x 12+x 1+c .∴ 2y 1=-2x 1, y 1=-x 1. 设直线DE :y =kx . 有 -x 1=kx 1.由题意,存在x 1≠x 2.∴ 存在x 1,使x 1≠0. ……7分∴ k =-1.∴ 直线DE : y =-x . ……8分 法2:设直线DE :y =kx .则根据题意有 kx =x 2-x +c ,即x 2-(k +1) x +c =0. ∵ -1≤c ≤0, ∴ (k +1)2-4c ≥0.∴ 方程x 2-(k +1) x +c =0有实数根. ……7分 ∵ x 1+x 2=0, ∴ k +1=0. ∴ k =-1.∴ 直线DE : y =-x . ……8分 若 ⎩⎪⎨⎪⎧y =-x ,y =x 2-x +c +38.则有 x 2+c +38=0.即 x 2=-c -38. ① 当 -c -38=0时,即c =-38时,方程x 2=-c -38有相同的实数根,即直线y =-x 与抛物线y =x 2-x +c +38有唯一交点. ……9分② 当 -c -38>0时,即c <-38时,即-1≤c <-38时,方程x 2=-c -38有两个不同实数根,即直线y =-x 与抛物线y =x 2-x +c +38有两个不同的交点. ……10分③ 当 -c -38<0时,即c >-38时,即-38<c ≤0时,方程x 2=-c -38没有实数根,即直线y =-x 与抛物线y =x 2-x +c +38没有交点. ……11分【092】解:(1)如图,在坐标系中标出O ,A ,C∵∠AO C≠90°, ∴∠ABC =90°,故BC ⊥OC , BC ⊥AB ,∴B (72,1).(1分,)即s =72,t =1.直角梯形如图所画.(2分)(大致说清理由即可)(2)由题意,y =x 2+mx -m 与 y =1(线段AB )相交,得,12y =x mx m,y =.+-⎧⎨⎩ (3分)∴1=x 2+mx -m ,由 (x -1)(x +1+m )=0,得121,1x x m ==--.∵1x =1<32,不合题意,舍去. (4分)∴抛物线y =x 2+mx -m 与AB 边只能相交于(2x ,1), ∴32≤-m -1≤72,∴9252m --≤≤ . ①(5分)又∵顶点P (2424,m m m+--)是直角梯形OABC 的内部和其边上的一个动点,∴7022m ≤-≤,即7m -≤≤ . ② (6分)∵2224(2)4(1)44211m mm m ++-+-=-=-+≤,(或者抛物线y =x 2+mx -m 顶点的纵坐标最大值是1) ∴点P 一定在线段AB 的下方. (7分) 又∵点P 在x 轴的上方, ∴2440m m+-≥,(4)0,m m +≤∴0,0,4040m m m m ≤≥+≥+≤⎧⎧⎨⎨⎩⎩或者. (*8分) 4(9)0. m ∴-≤≤分③(9分)又∵点P 在直线y =23x 的下方,∴242()432m mm +-≤⨯-,(10分)即(38)0.m m +≥0,0,380380.m m m m ≤≥+≤+≥⎧⎧⎨⎨⎩⎩或者 (*8分处评分后,此处不重复评分) 80.3m m ∴≤-≥(11分),或 ④由①②③④ ,得4-≤83m ≤-.(12分)说明:解答过程,全部不等式漏写等号的扣1分,个别漏写的酌情处理.【093】解:(1)连结BO 与A C 交于点H ,则当点P 运动到点H 时,直线DP 平分矩形O ABC 的面积.理由如下:∵矩形是中心对称图形,且点H 为矩形的对称中心.又据经过中心对称图形对称中心的任一直线平分此中心对称图形的面积,因为直线DP 过矩形O ABC的对称中心点H ,所以直线DP 平分矩形O ABC 的面积.…………2分由已知可得此时点P 的坐标为3(2)2P ,.设直线DP 的函数解析式为y kx b =+.则有503 2.2k b k b -+=⎧⎪⎨+=⎪⎩,解得413k =,2013b =.所以,直线DP 的函数解析式为:4201313y x =+.··················································· 5分(2)存在点M 使得D O M △与A B C △相似.如图,不妨设直线DP 与y 轴的正半轴交于点(0)m M y ,. 因为D O M ABC ∠=∠,若△DOM 与△ABC 相似,则有O M BC O DAB=或O M AB O DBC=.当O M BC O D AB=时,即354m y =,解得154m y =.所以点115(0)4M ,满足条件.当O M AB O DBC=时,即453m y =,解得203m y =.所以点220(0)3M ,满足条件.由对称性知,点315(0)4M -,也满足条件.综上所述,满足使D O M △与A B C △相似的点M 有3个,分别为115(0)4M ,、220(0)3M ,、315(0)4M -,. ·············································································································· 9分(3)如图 ,过D 作DP ⊥AC 于点P ,以P 为圆心,半径长为52画圆,过点D 分别作P 的切线DE 、DF ,点E 、F 是切点.除P 点外在直线AC 上任取一点P 1,半径长为52画圆,过点D 分别作P 的切线DE 1、DF 1,点E 1、F 1是切点.在△DEP 和△DFP 中,∠PED =∠PFD ,PF =PE ,PD =PD ,∴△DPE ≌△DPF . ∴S四边形DEPF =2S△DPE =2×1522DE PE DE PE DE⨯⋅=⋅=.∴当DE 取最小值时,S四边形DEPF 的值最小. ∵222D E D P P E =-,2221111DE DP P E =-,∴222211DE DE DP DP -=-. ∵1DP DP >,∴2210DE DE ->. ∴1DE DE >.由1P 点的任意性知:DE 是D点与切点所连线段长的最小值. (12)在△ADP 与△AOC 中,∠DPA =∠AOC , ∠DAP =∠CAO , ∴△ADP ∽△AOC .x∴DP CO DACA=,即485D P =.∴325D P =.∴10D E ==.∴S四边形DEPF=44·····································································14分(注:本卷中所有题目,若由其它方法得出正确结论,请参照标准给分.) 【094】解:(1)令二次函数2y ax bx c =++,则16402a b c a b c c -+=⎧⎪++=⎨⎪=⎩········································································································· 1分 12322a b c ⎧=-⎪⎪⎪∴=-⎨⎪=⎪⎪⎩··················································································································· 2分∴过A B C ,,三点的抛物线的解析式为213222y x x =--+ ······································· 4分(2)以A B 为直径的圆圆心坐标为302O ⎛⎫' ⎪⎝⎭,52O C '∴=32O O '=································································································· 5分C D 为圆O '切线 O C C D '∴⊥ ··············································································· 6分 90O C D D C O '∴∠+∠=°90C O O O C O ''∠+∠=° C O O D C O'∴∠=∠ O C O C D O '∴△∽△ //O O O C O C O D '=······························································ 8分 3/22/2O D = 83O D ∴=D ∴坐标为803⎛⎫⎪⎝⎭, ······································································································· 9分(3)存在 ····················································································································10分 抛物线对称轴为32X =-设满足条件的圆的半径为r ,则E 的坐标为3()2r r -+,或3()2F r r --,而E 点在抛物线213222y x x =--+上21333()()22222r r r ∴=--+--++112r ∴=-+212r =--故在以E F 为直径的圆,恰好与x轴相切,该圆的半径为12-+,12+···········12分注:解答题只要方法合理均可酌情给分 【095】(1)B (4,0),(02)C -,.··········································································· 2分213222y x x =--. ···································································································· 4分 (2)A B C △是直角三角形. ······················································································ 5分 证明:令0y =,则2132022x x --=.1214x x ∴=-=,.(10)A ∴-,. ················································································································ 6分解法一:5AB AC BC ∴===,. ······························································ 7分22252025AC BC AB ∴+=+==.A B C ∴△是直角三角形. ····························································································· 8分 解法二:11242C O A O A O C O B O B OO C===∴== ,,,90A O C C O B ∠=∠= °,A O C C OB ∴△∽△. ································································································· 7分 AC O C B O ∴∠=∠. 90C B O B C O ∠+∠= °,90A C O B C O ∴∠+∠=°.即90A C B ∠=°.A B C ∴△是直角三角形. ····························································································· 8分(3)能.①当矩形两个顶点在A B 上时,如图1,C O 交G F 于H .G F A B ∥,C G F C A B ∴△∽△. G F C H A B C O∴=. ························································ 9分 解法一:设G F x =,则D E x =,25C H x =,225D G O H O C C H x ==-=-.2222255D EFG S x x x x ⎛⎫∴=-=-+ ⎪⎝⎭矩形·图1522⎝⎭当52x =时,S 最大.512D E D G ∴==,.A D G A O C △∽△, 11222A D D G A D O D O E A OO C∴=∴=∴==,,,.102D ⎛⎫∴- ⎪⎝⎭,,(20)E ,. ····························································································11分 解法二:设D G x =,则1052xD E G F -==.221055555(1)2222D E F G xS x x x x -∴==-+=--+矩形·. ···········································10分∴当1x =时,S 最大.512D G D E ∴==,.A D G A O C △∽△, 11222A D D G A D O D O E A OO C∴=∴=∴==,,,.102D ⎛⎫∴- ⎪⎝⎭,,(20)E ,. ····························································································11分 ②当矩形一个顶点在A B 上时,F 与C 重合,如图2, D G BC ∥, A G D A C B ∴△∽△. G D A G B CA F∴=.解法一:设G D x =,AC BC ∴==2x G F A C A G ∴=-=.∴2122D EFG x S x x ⎫=-=-+⎪⎭矩形·=(21522x --+. ··································································································12分当x =S 最大.2G D AG ∴==,52A D ∴==.32O D ∴=图22⎝⎭解法二:设D E x =,AC = ,BC =G C x ∴=,AG x =-.2GD x ∴=.()222D EFG S x x x ∴==-+矩形·=25222x ⎛⎫--+ ⎪ ⎪⎝⎭·····································································································12分∴当2x =时,S 最大,2G D AG ∴==.52A D ∴==.3.2O D ∴=∴302D ⎛⎫⎪⎝⎭,·················································································································13分 综上所述:当矩形两个顶点在A B 上时,坐标分别为102⎛⎫-⎪⎝⎭,,(2,0); 当矩形一个顶点在A B 上时,坐标为302⎛⎫⎪⎝⎭, ·································································14分 【096】(1)因所求抛物线的顶点M 的坐标为(2,4),故可设其关系式为()224y a x =-+ ………………(1分) 又抛物线经过O (0,0),于是得()20240a -+=, ………………(2分) 解得 a=-1 ………………(3分)∴ 所求函数关系式为()224y x =--+,即24y x x =-+. ……………(4分)(2)① 点P 不在直线ME 上. ………………(5分)根据抛物线的对称性可知E 点的坐标为(4,0), 又M 的坐标为(2,4),设直线ME 的关系式为y=kx +b . 于是得⎩⎨⎧=+=+4204b k b k ,解得⎩⎨⎧=-=82b k所以直线ME 的关系式为y=-2x +8. ……(6分) 由已知条件易得,当t 25=时,OA=AP 25=,⎪⎭⎫⎝⎛∴25,25P ……………(7分)∵ P 点的坐标不满足直线ME 的关系式y=-2x +8. ∴ 当t 25=时,点P 不在直线ME 上. ………………(8分)② S 存在最大值. 理由如下: ………………(9分)∵ 点A 在x 轴的非负半轴上,且N 在抛物线上, ∴ OA=AP=t .∴ 点P ,N 的坐标分别为(t ,t )、(t ,-t 2+4t ) ∴ AN=-t 2+4t (0≤t ≤3) , ∴ AN -AP=(-t 2+4 t )- t=-t 2+3 t=t (3-t )≥0 , ∴ PN=-t 2+3 t …(10分)(ⅰ)当PN=0,即t=0或t =3时,以点P ,N ,C ,D 为顶点的多边形是三角形,此三角形的高为AD ,∴ S=21DC ·AD=21×3×2=3. ………………(11分)(ⅱ)当PN ≠0时,以点P ,N ,C ,D 为顶点的多边形是四边形∵ PN ∥CD ,AD ⊥CD ,∴ S=21(CD+PN )·AD=21[3+(-t 2+3 t )]×2=-t 2+3 t +3=421232+⎪⎭⎫ ⎝⎛--t 其中(0<t <3),由a=-1,0<23<3,此时421=最大S . …………(12分)综上所述,当t 23=时,以点P ,N ,C ,D 为顶点的多边形面积有最大值,这个最大值为421. ………………(13分)说明:(ⅱ)中的关系式,当t=0和t=3时也适合.【097】解:(1)点D 的坐标为(43)-,. ······························································ (2分) (2)抛物线的表达式为23984y x x =-. ······························································ (4分)(3)抛物线的对称轴与x 轴的交点1P 符合条件. ∵O A C B ∥, ∴1P O M C D O ∠=∠.∵190O P M D C O ∠=∠=°,∴1R t R t P O M C D O △∽△.··························· (6∵抛物线的对称轴3x =,∴点1P 的坐标为1(30)P ,. ····················································································· (7分)过点O 作O D 的垂线交抛物线的对称轴于点2P . ∵对称轴平行于y 轴, ∴2P M O D O C ∠=∠. ∵290P OM DCO ∠=∠=°,∴21Rt Rt P M O DOC △∽△. ············································································· (8分)∴点2P 也符合条件,2O P M O D C ∠=∠.∴121390P O C O P P O D C O ==∠=∠=,°,∴21R t R t P P O D C O △≌△. ··············································································· (9分) ∴124P P C D ==. ∵点2P 在第一象限, ∴点2P 的坐标为2P (34),,∴符合条件的点P 有两个,分别是1(30)P ,,2P (34),.········································(11分) 【098】解:(1)当t =4时,B (4,0) 设直线AB 的解析式为y = kx +b . 把 A (0,6),B (4,0) 代入得:⎩⎨⎧b =64k +b =0, 解得:⎩⎨⎧k =-32b =6, ∴直线AB 的解析式为:y =-32x +6.………………………………………4分(2) 过点C 作CE ⊥x 轴于点E由∠AOB =∠CEB =90°,∠ABO =∠BCE ,得△AOB ∽△BEC . ∴12B EC E B C A OB OA B===,∴BE = 12AO =3,CE = 12OB = t2,∴点C 的坐标为(t +3,t2).…………………………………………………………2分方法一:S 梯形AOEC = 12O E ·(AO +EC )= 12(t +3)(6+t 2)=14t 2+154t +9,S △ AOB = 12AO ·OB = 12×6·t =3t ,S △ BEC = 12BE ·CE = 12×3×t 2= 34,∴S △ ABC = S 梯形AOEC - S △ AOB -S △ BEC= 14t 2+154t +9-3t -34t = 14t 2+9. 方法二:∵AB ⊥BC ,AB =2BC ,∴S △ ABC = 12AB ·BC = BC 2.在R t △ABC 中,BC 2= CE 2+ BE 2= 14t 2+9,即S △ ABC = 14t 2+9.…………………………………………………………2分(3)存在,理由如下: ①当t ≥0时. Ⅰ.若AD =BD . 又∵BD ∥y 轴∴∠OAB =∠ABD ,∠BAD =∠ABD , ∴∠OAB =∠BAD . 又∵∠AOB =∠ABC , ∴△ABO ∽△ACB , ∴12O BB C A OA B==,∴t 6 = 12, ∴t =3,即B (3,0).Ⅱ.若AB =AD .延长AB 与CE 交于点G , 又∵BD ∥CG ∴AG =AC过点A 画AH ⊥CG 于H . ∴CH =HG =12 CG由△AOB ∽△GEB , 得GE BE =AO OB , ∴GE =18t. 又∵HE =AO =6,CE =t2∴18t +6=12 ×(t 2+18t ) ∴t 2-24t -36=0解得:t =12±6 5. 因为 t ≥0,所以t =12+65,即B(12+65,0).Ⅲ.由已知条件可知,当0≤t <12时,∠ADB 为钝角,故BD ≠ AB . 当t ≥12时,BD ≤CE <BC<AB . ∴当t ≥0时,不存在BD =AB 的情况.②当-3≤t <0时,如图,∠DAB 是钝角.设AD =AB , 过点C 分别作CE ⊥x 轴,CF ⊥y 轴于点E ,点F . 可求得点C 的坐标为(t +3,t2),∴CF =OE =t +3,AF =6-t2,由BD ∥y 轴,AB =AD 得,∠BAO =∠ABD ,∠FAC =∠BDA ,∠ABD =∠ADB ∴∠BAO =∠FAC ,又∵∠AOB =∠AFC =90°, ∴△AOB ∽△AFC , ∴B O A OC FA F= , ∴6362t t t -=+-, ∴t 2-24t -36=0解得:t =12±6 5.因为-3≤t <0, 所以t =12-65,即B (12-65,0).③当t <-3时,如图,∠ABD 是钝角.设AB =BD , 过点C 分别作CE ⊥x 轴,CF ⊥y 轴于点E ,点F , 可求得点C 的坐标为(t +3,t2),∴CF = -(t +3),AF =6-t2,∵AB =BD , ∴∠D =∠BAD . 又∵BD ∥y 轴, ∴∠D =∠CAF , ∴∠BAC =∠CAF .又∵∠ABC =∠AFC =90°,AC =AC , ∴△ABC ≌△AFC , ∴AF =AB ,CF =BC ,∴AF =2CF ,即6-t2=-2(t +3),解得:t =-8,即B (-8,0).综上所述,存在点B 使△ABD 为等腰三角形,此时点B 坐标为:B 1 (3,0),B 2 (12+65,0),B 3 (12-65,0),B 4(-8,0). ………………………4分【099】解:(1) 弦(图中线段AB )、弧(图中的ACB 弧)、弓形、求弓形的面积(因为是封闭图形)等.(写对一个给1分,写对两个给2分)(2) 情形1 如图21,AB 为弦,CD 为垂直于弦AB 的直径. …………………………3分 结论:(垂径定理的结论之一). …………………………………………………………………………4分 证明:略(对照课本的证明过程给分). ……………………………………………………………7分 情形2 如图22,AB 为弦,CD 为弦,且AB 与CD 在圆内相交于点P . 结论:PD PC PB PA ⋅=⋅.证明:略.情形3 (图略)AB 为弦,CD 为弦,且m 与n 在圆外相交于点P . 结论:PD PC PB PA ⋅=⋅. 证明:略.情形4 如图23,AB 为弦,CD 为弦,且AB ∥CD . = .证明:略.(上面四种情形中做一个即可,图1分,结论1分,证明3分;其它正确的情形参照给分;若提出的是错误的结论,则需证明结论是错误的)(3) 若点C 和点E 重合,则由圆的对称性,知点C 和点D 关于直径AB 对称. …………………………………………8分 设x BAC=∠,则x BAD =∠,x ABC -︒=∠90.…………………………………………9分 又D 是的中点,所以ABC ACD CAD CAD ∠-︒=+∠=∠1802, 即)90(18022x x -︒-︒=⋅.………………………………………………………………………………10分 解得︒=∠=30BAC x .………………………………………………………………………………………11分 (若求得AC AB 23=或FB AF ⋅=3等也可,评分可参照上面的标准;也可以先直觉猜测点B 、C 是圆的十二等分点,然后说明)【100】解:(1)令0))((4)2(2=+--=∆a m a m b 得222m b a =+ 由勾股定理的逆定理和抛物线的对称性知△ABM 是一个以a 、b 为直角边的等腰直角三角形 (2)设1)2(2-+=x a y ,∵△ABM 是等腰直角三角形∴斜边上的中线等于斜边的一半,又顶点M(-2,-1) ∴121=AB ,即AB =2,∴A(-3,0),B(-1,0)将B(-1,0) 代入1)2(2-+=x a y 中得1=a∴抛物线的解析式为1)2(2-+=x y ,即342++=x x y (3)设平行于x 轴的直线为k y = 解方程组⎩⎨⎧++==342x x y ky 得121++-=k x ,122+--=k x ()1->k∴线段CD 的长为12+k ,∵以CD 为直径的圆与x 轴相切,据题意得kk =+1,ABC A B 第25题图3第25题图22第25题图23m。
2012年中考数学压轴题及解析分类汇编

中考数学压轴题:函数相似三角形问题(一)例1直线113y x =-+分别交x 轴、y 轴于A 、B 两点,△AOB 绕点O 按逆时针方向旋转90°后得到△COD ,抛物线y =ax 2+bx +c 经过A 、C 、D 三点.(1) 写出点A 、B 、C 、D 的坐标;(2) 求经过A 、C 、D 三点的抛物线表达式,并求抛物线顶点G 的坐标;(3) 在直线BG 上是否存在点Q ,使得以点A 、B 、Q 为顶点的三角形与△COD 相似?若存在,请求出点Q 的坐标;若不存在,请说明理由.例2 Rt △ABC 在直角坐标系内的位置如图1所示,反比例函数(0)ky k x=≠在第一象限内的图像与BC 边交于点D (4,m ),与AB 边交于点E (2,n ),△BDE 的面积为2.(1)求m 与n 的数量关系; (2)当tan ∠A =12时,求反比例函数的解析式和直线AB 的表达式; (3)设直线AB 与y 轴交于点F ,点P 在射线FD 上,在(2)的条件下,如果△AEO 与△EFP 相似,求点P 的坐标.图12012中考数学压轴题函数相似三角形问题(二)例3 如图1,已知梯形OABC,抛物线分别过点O(0,0)、A(2,0)、B(6,3).(1)直接写出抛物线的对称轴、解析式及顶点M的坐标;(2)将图1中梯形OABC的上下底边所在的直线OA、CB以相同的速度同时向上平移,分别交抛物线于点O1、A1、C1、B1,得到如图2的梯形O1A1B1C1.设梯形O1A1B1C1的面积为S,A1、B1的坐标分别为(x1,y1)、(x2,y2).用含S的代数式表示x2-x1,并求出当S=36时点A1的坐标;(3)在图1中,设点D的坐标为(1,3),动点P从点B出发,以每秒1个单位长度的速度沿着线段BC运动,动点Q从点D出发,以与点P相同的速度沿着线段DM运动.P、Q两点同时出发,当点Q到达点M时,P、Q两点同时停止运动.设P、Q两点的运动时间为t,是否存在某一时刻t,使得直线PQ、直线AB、x轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似?若存在,请求出t的值;若不存在,请说明理由.图1 图2例4 如图1,已知点A (-2,4) 和点B (1,0)都在抛物线22=++上.y mx mx n (1)求m、n;(2)向右平移上述抛物线,记平移后点A的对应点为A′,点B的对应点为B′,若四边形A A′B′B为菱形,求平移后抛物线的表达式;(3)记平移后抛物线的对称轴与直线AB′的交点为C,试在x轴上找一个点D,使得以点B′、C、D为顶点的三角形与△ABC相似.图12012中考数学压轴题函数相似三角形问题(三) 例5 如图1,抛物线经过点A(4,0)、B(1,0)、C(0,-2)三点.(1)求此抛物线的解析式;(2)P是抛物线上的一个动点,过P作PM⊥x轴,垂足为M,是否存在点P,使得以A、P、M为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;(3)在直线AC上方的抛物线是有一点D,使得△DCA的面积最大,求出点D的坐标.,图1例6 如图1,△ABC 中,AB =5,AC =3,cos A =310.D 为射线BA 上的点(点D 不与点B 重合),作DE //BC 交射线CA 于点E ..(1) 若CE =x ,BD =y ,求y 与x 的函数关系式,并写出函数的定义域; (2) 当分别以线段BD ,CE 为直径的两圆相切时,求DE 的长度;(3) 当点D 在AB 边上时,BC 边上是否存在点F ,使△ABC 与△DEF 相似?若存在,请求出线段BF 的长;若不存在,请说明理由.图1 备用图 备用图例 7 如图1,在直角坐标系xOy 中,设点A (0,t ),点Q (t ,b ).平移二次函数2tx y -=的图象,得到的抛物线F 满足两个条件:①顶点为Q ;②与x 轴相交于B 、C 两点(∣OB ∣<∣OC ∣),连结A ,B .(1)是否存在这样的抛物线F ,使得OC OB OA ⋅=2?请你作出判断,并说明理由;(2)如果AQ ∥BC ,且tan ∠ABO =23,求抛物线F 对应的二次函数的解析式.图12012中考数学压轴题函数等腰三角形问题(一)例1 如图1,已知正方形OABC 的边长为2,顶点A 、C 分别在x 、y 轴的正半轴上,M 是BC 的中点.P (0,m )是线段OC 上一动点(C 点除外),直线PM 交AB 的延长线于点D .(1)求点D 的坐标(用含m 的代数式表示); (2)当△APD 是等腰三角形时,求m 的值;(3)设过P 、M 、B 三点的抛物线与x 轴正半轴交于点E ,过点O 作直线ME 的垂线,垂足为H (如图2).当点P 从O 向C 运动时,点H 也随之运动.请直接写出点H 所经过的路长(不必写解答过程).图1 图2例2 如图1,已知一次函数y =-x +7与正比例函数43y x 的图象交于点A ,且与x 轴交于点B .(1)求点A 和点B 的坐标;(2)过点A作AC⊥y轴于点C,过点B作直线l//y轴.动点P从点O出发,以每秒1个单位长的速度,沿O—C—A的路线向点A运动;同时直线l从点B出发,以相同速度向左平移,在平移过程中,直线l交x轴于点R,交线段BA或线段AO于点Q.当点P到达点A时,点P和直线l都停止运动.在运动过程中,设动点P运动的时间为t秒.①当t为何值时,以A、P、R为顶点的三角形的面积为8?②是否存在以A、P、Q为顶点的三角形是等腰三角形?若存在,求t的值;若不存在,请说明理由.图12012中考数学压轴题函数等腰三角形问题(二)例3 如图1,在直角坐标平面内有点A(6, 0),B(0, 8),C(-4, 0),点M、N 分别为线段AC和射线AB上的动点,点M以2个单位长度/秒的速度自C向A方向作匀速运动,点N以5个单位长度/秒的速度自A向B方向作匀速运动,MN交OB于点P.(1)求证:MN∶NP为定值;(2)若△BNP与△MNA相似,求CM的长;(3)若△BNP是等腰三角形,求CM的长.图1例4 如图1,在矩形ABCD 中,AB =m (m 是大于0的常数),BC =8,E 为线段BC 上的动点(不与B 、C 重合).连结DE ,作EF ⊥DE ,EF 与射线BA 交于点F ,设CE =x ,BF =y .(1)求y 关于x 的函数关系式;(2)若m =8,求x 为何值时,y 的值最大,最大值是多少? (3)若12y m,要使△DEF 为等腰三角形,m 的值应为多少?图12012中考数学压轴题函数相似三角形问题(三)例5 已知:如图1,在平面直角坐标系xOy 中,矩形OABC 的边OA 在y 轴的正半轴上,OC 在x 轴的正半轴上,OA =2,OC =3,过原点O 作∠AOC 的平分线交AB 于点D ,连接DC ,过点D 作DE ⊥DC ,交OA 于点E .(1)求过点E 、D 、C 的抛物线的解析式;(2)将∠EDC 绕点D 按顺时针方向旋转后,角的一边与y 轴的正半轴交于点F ,另一边与线段OC 交于点G .如果DF 与(1)中的抛物线交于另一点M ,点M 的横坐标为56,那么EF =2GO 是否成立?若成立,请给予证明;若不成立,请说明理由; (3)对于(2)中的点G ,在位于第一象限内的该抛物线上是否存在点Q ,使得直线GQ 与AB 的交点P 与点C 、G 构成的△PCG 是等腰三角形?若存在,请求出点Q 的坐标;若不存在成立,请说明理由.图1例6 在平面直角坐标系内,O为原点,点A的坐标为(1,0),点C的坐标为(0,4),直线CM//x轴(如图1所示).点B与点A关于原点对称,直线y=x+b(b为常数)经过点B,且与直线CM相交于点D,联结OD.(1)求b的值和点D的坐标;(2)设点P在x轴的正半轴上,若△POD是等腰三角形,求点P的坐标;(3)在(2)的条件下,如果以PD为半径的圆与圆O外切,求圆O的半径.图12012中考数学压轴题函数直角三角形问题(一)例1 如图1,已知抛物线y=x2+bx+c与x轴交于A、B两点(点A在点B 左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.(1)求抛物线的函数表达式;(2)求直线BC的函数表达式;(3)点E为y轴上一动点,CE的垂直平分线交CE于点F,交抛物线于P、Q两点,且点P在第三象限.①当线段34PQ AB =时,求tan ∠CED 的值;②当以C 、D 、E 为顶点的三角形是直角三角形时,请直接写出点P 的坐标. 温馨提示:考生可以根据第(3)问的题意,在图中补出图形,以便作答.图1例2 设直线l 1:y =k 1x +b 1与l 2:y =k 2x +b 2,若l 1⊥l 2,垂足为H ,则称直线l 1与l 2是点H 的直角线.(1)已知直线①122y x =-+;②2y x =+;③22y x =+;④24y x =+和点C (0,2),则直线_______和_______是点C 的直角线(填序号即可);(2)如图,在平面直角坐标系中,直角梯形OABC 的顶点A (3,0)、B (2,7)、C (0,7),P 为线段OC 上一点,设过B 、P 两点的直线为l 1,过A 、P 两点的直线为l 2,若l 1与l 2是点P 的直角线,求直线l 1与l 2的解析式.图12012中考数学压轴题函数直角三角形问题(三)例 5 如图1,直线434+-=x y 和x 轴、y 轴的交点分别为B 、C ,点A 的坐标是(-2,0).(1)试说明△ABC 是等腰三角形;(2)动点M 从A 出发沿x 轴向点B 运动,同时动点N 从点B 出发沿线段BC 向点C 运动,运动的速度均为每秒1个单位长度.当其中一个动点到达终点时,他们都停止运动.设M 运动t 秒时,△MON 的面积为S .① 求S 与t 的函数关系式;② 设点M 在线段OB 上运动时,是否存在S =4的情形?若存在,求出对应的t 值;若不存在请说明理由;③在运动过程中,当△MON 为直角三角形时,求t 的值.图1例6 已知Rt △ABC 中,︒=∠90ACB ,CB CA =,有一个圆心角为︒45,半径的长等于CA 的扇形CEF 绕点C 旋转,且直线CE ,CF 分别与直线AB 交于点M ,N .(1)当扇形CEF 绕点C 在ACB ∠的内部旋转时,如图1,求证:222BN AM MN +=;思路点拨:考虑222BN AM MN +=符合勾股定理的形式,需转化为在直角三角形中解决.可将△ACM 沿直线CE 对折,得△DCM ,连DN ,只需证BN DN =,︒=∠90MDN 就可以了.请你完成证明过程.(2)当扇形CEF 绕点C 旋转至图2的位置时,关系式222BN AM MN +=是否仍然成立?若成立,请证明;若不成立,请说明理由.图1 图2图5 图6 图72012中考数学压轴题函数平行四边形问题(一)例 1 已知平面直角坐标系xOy (如图1),一次函数334y x =+的图像与y 轴交于点A ,点M 在正比例函数32y x =的图像上,且MO =MA .二次函数y =x 2+bx +c 的图像经过点A 、M .(1)求线段AM 的长;(2)求这个二次函数的解析式;(3)如果点B 在y 轴上,且位于点A 下方,点C 在上述二次函数的图像上,点D 在一次函数334y x =+的图像上,且四边形ABCD 是菱形,求点C 的坐标.图1例2将抛物线c 1:2y =x 轴翻折,得到抛物线c 2,如图1所示.(1)请直接写出抛物线c 2的表达式;(2)现将抛物线c1向左平移m个单位长度,平移后得到新抛物线的顶点为M,与x轴的交点从左到右依次为A、B;将抛物线c2向右也平移m个单位长度,平移后得到新抛物线的顶点为N,与x轴的交点从左到右依次为D、E.①当B、D是线段AE的三等分点时,求m的值;②在平移过程中,是否存在以点A、N、E、M为顶点的四边形是矩形的情形?若存在,请求出此时m的值;若不存在,请说明理由.图12012中考数学压轴题函数平行四边形问题(二)例3 如图1,在平面直角坐标系中,已知抛物线经过A(-4,0)、B(0,-4)、C(2,0)三点.(1)求抛物线的解析式;(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△MAB的面积为S,求S关于m的函数关系式,并求出S的最大值;(3)若点P是抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.图1 图2例4在直角梯形OABC中,CB//OA,∠COA=90°,CB=3,OA=6,BA=别以OA、OC边所在直线为x轴、y轴建立如图1所示的平面直角坐标系.(1)求点B的坐标;(2)已知D、E分别为线段OC、OB上的点,OD=5,OE=2EB,直线DE交x轴于点F.求直线DE的解析式;(3)点M是(2)中直线DE上的一个动点,在x轴上方的平面内是否存在另一点N,使以O、D、M、N为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由.图1 图22012中考数学压轴题函数平行四边形问题(三)例 5 如图1,等边△ABC的边长为4,E是边BC上的动点,EH⊥AC于H,过E作EF∥AC,交线段AB于点F,在线段AC上取点P,使PE=EB.设EC=x(0<x≤2).(1)请直接写出图中与线段EF相等的两条线段(不再另外添加辅助线);(2)Q是线段AC上的动点,当四边形EFPQ是平行四边形时,求平行四边形EFPQ 的面积(用含x的代数式表示);(3)当(2)中的平行四边形EFPQ面积最大值时,以E为圆心,r为半径作圆,根据⊙E与此时平行四边形EFPQ四条边交点的总个数,求相应的r的取值范围.图1例6 如图1,抛物线322++-=x x y 与x 轴相交于A 、B 两点(点A 在点B 的左侧),与y 轴相交于点C ,顶点为D .(1)直接写出A 、B 、C 三点的坐标和抛物线的对称轴;(2)连结BC ,与抛物线的对称轴交于点E ,点P 为线段BC 上的一个动点,过点P 作PF //DE 交抛物线于点F ,设点P 的横坐标为m .①用含m 的代数式表示线段PF 的长,并求出当m 为何值时,四边形PEDF 为平行四边形?②设△BCF 的面积为S ,求S 与m 的函数关系.图1例 7 如图,在平面直角坐标系xOy 中,直线1y x =+与334y x =-+交于点A ,分别交x 轴于点B 和点C ,点D 是直线AC 上的一个动点.(1)求点A 、B 、C 的坐标.(2)当△CBD 为等腰三角形时,求点D 的坐标.(3)在直线AB上是否存在点E,使得以点E、D、O、A为顶点的四边形是平行四边形?如果存在,直接写出BECD的值;如果不存在,请说明理由.图12012中考数学压轴题函数梯形问题(一)例1 已知平面直角坐标系xOy中,抛物线y=ax2-(a+1)x与直线y=kx的一个公共点为A(4,8).(1)求此抛物线和直线的解析式;(2)若点P在线段OA上,过点P作y轴的平行线交(1)中抛物线于点Q,求线段PQ长度的最大值;(3)记(1)中抛物线的顶点为M,点N在此抛物线上,若四边形AOMN恰好是梯形,求点N的坐标及梯形AOMN的面积.备用图图1 图2例 2 已知二次函数的图象经过A (2,0)、C (0,12) 两点,且对称轴为直线x =4,设顶点为点P ,与x 轴的另一交点为点B .(1)求二次函数的解析式及顶点P 的坐标;(2)如图1,在直线 y =2x 上是否存在点D ,使四边形OPBD 为等腰梯形?若存在,求出点D 的坐标;若不存在,请说明理由;(3)如图2,点M 是线段OP 上的一个动点(O 、P 两点除外),以每秒2个单位长度的速度由点P 向点O 运动,过点M 作直线MN //x 轴,交PB 于点N . 将△PMN 沿直线MN 对折,得到△P 1MN . 在动点M 的运动过程中,设△P 1MN 与梯形OMNB 的重叠部分的面积为S ,运动时间为t 秒,求S 关于t 的函数关系式.图1 图22012中考数学压轴题函数梯形问题(二)例3 如图1,在平面直角坐标系xOy 中,抛物线的解析式是y =2114x ,点C 的坐标为(–4,0),平行四边形OABC 的顶点A ,B 在抛物线上,AB 与y 轴交于点M ,已知点Q (x ,y )在抛物线上,点P (t ,0)在x 轴上.(1) 写出点M 的坐标;(2) 当四边形CMQP 是以MQ ,PC 为腰的梯形时.① 求t 关于x 的函数解析式和自变量x 的取值范围;② 当梯形CMQP 的两底的长度之比为1∶2时,求t 的值.图1例 4 已知,矩形OABC 在平面直角坐标系中位置如图1所示,点A 的坐标为(4,0),点C 的坐标为)20(-,,直线x y 32-=与边BC 相交于点D . (1)求点D 的坐标;(2)抛物线c bx ax y ++=2经过点A 、D 、O ,求此抛物线的表达式;(3)在这个抛物线上是否存在点M ,使O 、D 、A 、M 为顶点的四边形是梯形?若存在,请求出所有符合条件的点M 的坐标;若不存在,请说明理由.图12012中考数学压轴题函数平行四边形问题(三)例 5 如图1,等边△ABC 的边长为4,E 是边BC 上的动点,EH ⊥AC 于H ,过E 作EF ∥AC ,交线段AB 于点F ,在线段AC 上取点P ,使PE =EB .设EC =x (0<x ≤2).(1)请直接写出图中与线段EF 相等的两条线段(不再另外添加辅助线);(2)Q 是线段AC 上的动点,当四边形EFPQ 是平行四边形时,求平行四边形EFPQ 的面积(用含x 的代数式表示);(3)当(2)中 的平行四边形EFPQ 面积最大值时,以E 为圆心,r 为半径作圆,根据⊙E 与此时平行四边形EFPQ 四条边交点的总个数,求相应的r 的取值范围.图1例6 如图1,抛物线322++-=x x y 与x 轴相交于A 、B 两点(点A 在点B 的左侧),与y 轴相交于点C ,顶点为D .(1)直接写出A 、B 、C 三点的坐标和抛物线的对称轴;(2)连结BC ,与抛物线的对称轴交于点E ,点P 为线段BC 上的一个动点,过点P 作PF //DE 交抛物线于点F ,设点P 的横坐标为m .①用含m 的代数式表示线段PF 的长,并求出当m 为何值时,四边形PEDF 为平行四边形?②设△BCF 的面积为S ,求S 与m 的函数关系.图1例 7 如图,在平面直角坐标系xOy 中,直线1y x =+与334y x =-+交于点A ,分别交x 轴于点B 和点C ,点D 是直线AC 上的一个动点.(1)求点A 、B 、C 的坐标.(2)当△CBD 为等腰三角形时,求点D 的坐标.(3)在直线AB 上是否存在点E ,使得以点E 、D 、O 、A 为顶点的四边形是平行四边形?如果存在,直接写出BE CD的值;如果不存在,请说明理由.图12012中考数学压轴题函数面积问题(一)例 1 如图1,直线l 经过点A (1,0),且与双曲线m y x=(x >0)交于点B (2,1).过点(,1)P p p -(p >1)作x 轴的平行线分别交曲线m y x =(x >0)和m y x=-(x <0)于M 、N 两点.(1)求m 的值及直线l 的解析式;(2)若点P 在直线y =2上,求证:△PMB ∽△PNA ;(3)是否存在实数p ,使得S △AMN =4S △AMP ?若存在,请求出所有满足条件的p 的值;若不存在,请说明理由.图1例2 如图1,在平面直角坐标系xOy 中,直角梯形OABC 的顶点O 为坐标原点,顶点A 、C 分别在x 轴、y 轴的正半轴上,CB ∥OA ,OC =4,BC =3,OA =5,点D 在边OC 上,CD =3,过点D 作DB 的垂线DE ,交x 轴于点E .(1)求点E的坐标;(2)二次函数y=-x2+bx+c的图像经过点B和点E.①求二次函数的解析式和它的对称轴;②如果点M在它的对称轴上且位于x轴上方,满足S△CEM=2S△ABM,求点M的坐标.图12012中考数学压轴题函数面积问题(二)例3 如图1,四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1).点D是线段BC上的动点(与端点B、C不重合),过点D作直线12y x b=-+交折线OAB于点E.(1)记△ODE的面积为S,求S与b的函数关系式;(2)当点E在线段OA上时,若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1,试探究四边形O1A1B1C1与矩形OABC的重叠部分的面积是否发生变化?若不变,求出重叠部分的面积;若改变,请说明理由.例 4 如图1,在△ABC中,∠C=90°,A C=3,BC=4,CD是斜边AB上的高,点E在斜边AB上,过点E作直线与△ABC的直角边相交于点F,设AE=x,△AEF的面积为y.(1)求线段AD的长;(2)若EF⊥AB,当点E在斜边AB上移动时,①求y与x的函数关系式(写出自变量x的取值范围);②当x取何值时,y有最大值?并求出最大值.(3)若点F在直角边AC上(点F与A、C不重合),点E在斜边AB上移动,试问,是否存在直线EF将△ABC的周长和面积同时平分?若存在直线EF,求出x的值;若不存在直线EF,请说明理由.图1 备用图2012中考数学压轴题函数面积问题(三)例5 如图1,正方形ABCD中,点A、B的坐标分别为(0,10),(8,4),点C在第一象限.动点P在正方形ABCD的边上,从点A出发沿A→B→C→D匀速运动,同时动点Q以相同速度在x轴上运动,当P点到D点时,两点同时停止运动,设运动的时间为t秒.(1)当P点在边AB上运动时,点Q的横坐标x(长度单位)关于运动时间t(秒)的函数图象如图2所示,请写出点Q开始运动时的坐标及点P运动速度;(2)求正方形边长及顶点C的坐标;(3)在(1)中当t为何值时,△OPQ的面积最大,并求此时P点的坐标.(4)如果点P、Q保持原速度速度不变,当点P沿A→B→C→D匀速运动时,OP 与PQ能否相等,若能,写出所有符合条件的t的值;若不能,请说明理由.图1 图2例6 在直角坐标系中,抛物线c=2经过点(0,10)和点(4,2).+y+xbx(1)求这条抛物线的解析式.(2)如图1,在边长一定的矩形ABCD中,CD=1,点C在y轴右侧沿抛物线=2滑动,在滑动过程中CD∥x轴,AB在CD的下方.当点D在y轴上时,y++cbxxAB落在x轴上.①求边BC的长.②当矩形ABCD在滑动过程中被x轴分成两部分的面积比为1:4时,求点C的坐标.。
2012中考数学压轴题及答案40例(2)

2012中考数学压轴题及答案40例(2)5.如图,在直角坐标系xOy 中,点P 为函数214y x =在第一象限内的图象上的任一点,点A 的坐标为(01),,直线l 过(01)B -,且与x 轴平行,过P 作y 轴的平行线分别交x 轴,l 于C Q ,,连结AQ 交x 轴于H ,直线PH 交y 轴于R .(1)求证:H 点为线段AQ 的中点; (2)求证:①四边形APQR 为平行四边形;②平行四边形APQR 为菱形;(3)除P 点外,直线PH 与抛物线214y x =有无其它公共点?并说明理由. (08江苏镇江28题解析)(1)法一:由题可知1AO CQ ==.90AOH QCH ∠=∠=,AHO QHC ∠=∠,AOH QCH ∴△≌△. ····················································································· (1分)OH CH ∴=,即H 为AQ 的中点. ································································· (2分) 法二:(01)A ,,(01)B -,,OA OB ∴=. ······················································ (1分)又BQ x ∥轴,HA HQ ∴=. ·········································································· (2分) (2)①由(1)可知AH QH =,AHR QHP ∠=∠,AR PQ ∥,RAH PQH ∴∠=∠,RAH PQH ∴△≌△. ····················································································· (3分) AR PQ ∴=,又AR PQ ∥,∴四边形APQR 为平行四边形. ··············································· (4分)②设214P m m ⎛⎫ ⎪⎝⎭,,PQ y ∥轴,则(1)Q m -,,则2114PQ m =+.过P 作PG y ⊥轴,垂足为G ,在Rt APG △中,22222222111111444AP AG PG m m m m PQ ⎛⎫⎛⎫=+=-+=+=+= ⎪ ⎪⎝⎭⎝⎭.∴平行四边形APQR 为菱形. ·········································································· (6分)(3)设直线PR 为y kx b =+,由OH CH =,得22m H ⎛⎫⎪⎝⎭,,214P m m ⎛⎫ ⎪⎝⎭,代入得: 2021.4m k b km b m ⎧+=⎪⎪⎨⎪+=⎪⎩, 221.4m k b m ⎧=⎪⎪∴⎨⎪=-⎪⎩,∴直线PR 为2124m y x m =-. ······················ (7分) 设直线PR 与抛物线的公共点为214x x ⎛⎫ ⎪⎝⎭,,代入直线PR 关系式得:22110424m x x m -+=,21()04x m -=,解得x m =.得公共点为214m m ⎛⎫ ⎪⎝⎭,. 所以直线PH 与抛物线214y x =只有一个公共点P . ········································ (8分) 6.如图13,已知抛物线经过原点O 和x 轴上另一点A ,它的对称轴x =2 与x 轴交于点C ,直线y =-2x -1经过抛物线上一点B (-2,m ),且与y 轴、直线x =2分别交于点D 、E . (1)求m 的值及该抛物线对应的函数关系式; (2)求证:① CB =CE ;② D 是BE 的中点;(3)若P (x ,y )是该抛物线上的一个动点,是否存在这样的点P ,使得PB =PE ,若存在,试求出所有符合条件的点P 的坐标;若不存在,请说明理由.(1)∵ 点B (-2,m )在直线y =-2x -1上,∴ m =-2×(-2)-1=3. ………………………………(2分) ∴ B (-2,3)∵ 抛物线经过原点O 和点A ,对称轴为x =2, ∴ 点A 的坐标为(4,0) .设所求的抛物线对应函数关系式为y =a (x -0)(x -4). ……………………(3分) 将点B (-2,3)代入上式,得3=a (-2-0)(-2-4),∴ 41=a . ∴ 所求的抛物线对应的函数关系式为)4(41-=x x y ,即x x y -=241. (6分)(2)①直线y =-2x -1与y 轴、直线x =2的交点坐标分别为D (0,-1) E (2,-5). 过点B 作BG ∥x 轴,与y 轴交于F 、直线x =2交于G , 则BG ⊥直线x =2,BG =4.在Rt △BGC 中,BC =522=+BG CG .∵ CE =5,∴ CB =CE =5. ……………………(9分) ②过点E 作EH ∥x 轴,交y 轴于H , 则点H 的坐标为H (0,-5).又点F 、D 的坐标为F (0,3)、D (0,-1), ∴ FD =DH =4,BF =EH =2,∠BFD =∠EHD =90°.∴ △DFB ≌△DHE (SAS ),∴ BD =DE .即D 是BE 的中点. ………………………………(11分)(3) 存在. ………………………………(12分) 由于PB =PE ,∴ 点P 在直线CD 上,∴ 符合条件的点P 是直线CD 与该抛物线的交点.设直线CD 对应的函数关系式为y =kx +b .将D (0,-1) C (2,0)代入,得⎩⎨⎧=+-=021b k b . 解得 1,21-==b k . A BCODExy x =2 G FH∴ 直线CD 对应的函数关系式为y =21x -1.∵ 动点P 的坐标为(x ,x x -241),∴21x -1=x x -241. ………………………………(13分) 解得 531+=x ,532-=x . ∴ 2511+=y ,2511-=y . ∴ 符合条件的点P 的坐标为(53+,251+)或(53-,251-).…(14分) (注:用其它方法求解参照以上标准给分.)7.如图,在平面直角坐标系中,抛物线y =-32x 2+b x +c 经过A (0,-4)、B (x 1,0)、 C (x 2,0)三点,且x 2-x 1=5. (1)求b 、c 的值;(4分)(2)在抛物线上求一点D ,使得四边形BDCE 是以BC 为对 角线的菱形;(3分)(3)在抛物线上是否存在一点P ,使得四边形B P O H 是以OB 为对角线的菱形?若存在,求出点P 的坐标,并判断这个菱形是否为正方形?若不存在,请说明理由.(3分)解: (解析)解:(1)解法一: ∵抛物线y =-32x 2+b x +c 经过点A (0,-4),∴c =-4 ……1分又由题意可知,x 1、x 2是方程-32x 2+b x +c =0的两个根, ∴x 1+x 2=23b , x 1x 2=-23c =6 ······························································· 2分 由已知得(x 2-x 1)2=25 又(x 2-x 1)2=(x 2+x 1)2-4x 1x 2=49b 2-24 ∴49b 2-24=25 解得b =±314 ····································································································· 3分 当b =314时,抛物线与x 轴的交点在x 轴的正半轴上,不合题意,舍去. ∴b =-314. ···································································································· 4分解法二:∵x 1、x 2是方程-32x 2+b x +c=0的两个根, 即方程2x 2-3b x +12=0的两个根. ∴x =4969b 32-±b , ······································································· 2分∴x 2-x 1=2969b 2-=5,解得 b =±314 ·························································································· 3分 (以下与解法一相同.)(2)∵四边形BDCE 是以BC 为对角线的菱形,根据菱形的性质,点D 必在抛物线的对称轴上, ························································································· 5分 又∵y =-32x 2-314x -4=-32(x +27)2+625····························· 6分∴抛物线的顶点(-27,625)即为所求的点D . ································· 7分 (3)∵四边形BPOH 是以OB 为对角线的菱形,点B 的坐标为(-6,0),根据菱形的性质,点P 必是直线x =-3与 抛物线y =-32x 2-314x -4的交点, ······················································· 8分∴当x =-3时,y =-32×(-3)2-314×(-3)-4=4, ∴在抛物线上存在一点P (-3,4),使得四边形BPOH 为菱形. ·········· 9分 四边形BPOH 不能成为正方形,因为如果四边形BPOH 为正方形,点P 的坐标只能是(-3,3),但这一点不在抛物线上. ········································· 10分8.已知:如图14,抛物线2334y x =-+与x 轴交于点A ,点B ,与直线34y x b =-+相交于点B ,点C ,直线34y x b =-+与y 轴交于点E . (1)写出直线BC 的解析式. (2)求ABC △的面积.(3)若点M 在线段AB 上以每秒1个单位长度的速度从A 向B 运动(不与A B ,重合),同时,点N 在射线BC 上以每秒2个单位长度的速度从B 向C 运动.设运动时间为t 秒,请写出MNB △的面积S 与t 的函数关系式,并求出点M 运动多少时间时,MNB △的面积最大,最大面积是多少?(解析)解:(1)在2334y x =-+中,令0y = 23304x ∴-+=12x ∴=,22x =-(20)A ∴-,,(20)B ,············································· 1分又点B 在34y x b =-+上 302b ∴=-+32b =BC ∴的解析式为3342y x =-+ ·········································································· 2分 (2)由23343342y x y x ⎧=-+⎪⎪⎨⎪=-+⎪⎩,得11194x y =-⎧⎪⎨=⎪⎩ 2220x y =⎧⎨=⎩················································· 4分 914C ⎛⎫∴- ⎪⎝⎭,,(20)B ,4AB ∴=,94CD =·························································································· 5分 1994242ABC S ∴=⨯⨯=△ ····················································································· 6分 (3)过点N 作NP MB ⊥于点PEO MB ⊥ NP EO ∴∥BNP BEO ∴△∽△ ··························································································· 7分 BN NP BE EO∴=····································································································· 8分 由直线3342y x =-+可得:302E ⎛⎫ ⎪⎝⎭, ∴在BEO △中,2BO =,32EO =,则52BE = 25322t NP∴=,65NP t ∴= ··················································································· 9分 16(4)25S t t ∴=- 2312(04)55S t t t =-+<< ················································································ 10分2312(2)55S t =--+ ························································································· 11分 此抛物线开口向下,∴当2t =时,125S =最大 ∴当点M 运动2秒时,MNB △的面积达到最大,最大为125. ······················ 12分。
2012中考数学压轴题及答案40例

2012中考数学压轴题及答案40例(1)1.如图:抛物线经过A (-3,0)、B (0,4)、C (4,0)三点. (1) 求抛物线的解析式.(2)已知AD = AB (D 在线段AC 上),有一动点P 从点A 沿线段AC 以每秒1个单位长度的速度移动;同时另一个动点Q 以某一速度从点B 沿线段BC 移动,经过t 秒的移动,线段PQ 被BD 垂直平分,求t 的值;(3)在(2)的情况下,抛物线的对称轴上是否存在一点M ,使MQ+MC 的值最小?若存在,请求出点M 的坐标;若不存在,请说明理由。
(注:抛物线2y ax bx c =++的对称轴为2b x a=-)解:设抛物线的解析式为2(0)y ax bx c a =++≠,依题意得:c=4且934016440a b a b -+=⎧⎨++=⎩ 解得1313a b ⎧=-⎪⎪⎨⎪=⎪⎩所以 所求的抛物线的解析式为211433y x x =-++(2)连接DQ ,在Rt △AOB 中,2222345AB AO BO=+=+=所以AD=AB= 5,AC=AD+CD=3 + 4 = 7,CD = AC - AD = 7 – 5 = 2 因为BD 垂直平分PQ ,所以PD=QD ,PQ ⊥BD ,所以∠PDB=∠QDB 因为AD=AB ,所以∠ABD=∠ADB ,∠ABD=∠QDB ,所以DQ ∥AB 所以∠CQD=∠CBA 。
∠CDQ=∠CAB ,所以△CDQ ∽ △CABD Q C D A BC A= 即210,577D Q D Q ==所以AP=AD – DP = AD – DQ=5 –107=257,2525177t =÷=所以t 的值是257(3)答对称轴上存在一点M ,使MQ+MC 的值最小 理由:因为抛物线的对称轴为122b x a =-=所以A (- 3,0),C (4,0)两点关于直线12x =对称连接AQ 交直线12x =于点M ,则MQ+MC 的值最小过点Q 作QE ⊥x轴,于E ,所以∠QED=∠BOA=90 DQ ∥AB ,∠ BAO=∠QDE , △DQE ∽△ABOQ E D QD E B OA BA O== 即107453Q E D E ==所以QE=87,DE=67,所以OE =OD + DE=2+67=207,所以Q (207,87)设直线AQ 的解析式为(0)y kx m k =+≠则2087730k m k m ⎧+=⎪⎨⎪-+=⎩由此得8412441k m ⎧=⎪⎪⎨⎪=⎪⎩ 所以直线AQ 的解析式为8244141y x =+ 联立128244141x y x ⎧=⎪⎪⎨⎪=+⎪⎩ 由此得128244141x y x ⎧=⎪⎪⎨⎪=+⎪⎩ 所以M 128(,)241则:在对称轴上存在点M 128(,)241,使MQ+MC的值最小。
2012年中考数学压轴题精选精析

2012年各地中考数学压轴题精选精析(1.2012黄石) 25.(本小题满分10分)已知抛物线1C 的函数解析式为23(0)y ax bx a b =+-<,若抛物线1C 经过点(0,3)-,方程230ax bx a +-=的两根为1x ,2x ,且124x x -=。
(1)求抛物线1C 的顶点坐标. (2)已知实数0x >,请证明:1x x +≥2,并说明x 为何值时才会有12x x+=. (3)若抛物线先向上平移4个单位,再向左平移1个单位后得到抛物线2C ,设1(,)A m y ,2(,)B n y 是2C 上的两个不同点,且满足:090AOB ∠=,0m >,0n <.请你用含有m 的表达式表示出△AOB 的面积S ,并求出S 的最小值及S 取最小值时一次函数OA 的函数解析式。
(参考公式:在平面直角坐标系中,若11(,)P x y ,22(,)Q x y ,则P ,Q 两点间的距离【考点】二次函数综合题. 【专题】压轴题;配方法.【分析】(1)求抛物线的顶点坐标,需要先求出抛物线的解析式,即确定待定系数a 、b 的值.已知抛物线图象与y 轴交点,可确定解析式中的常数项(由此得到a 的值);然后从方程入手求b 的值,题干给出了两根差的绝对值,将其进行适当变形(转化为两根和、两根积的形式),结合根与系数的关系即可求出b 的值. (2)11x x +=,因此将1x x+配成完全平方式,然后根据平方的非负性即可得证.(3)结合(1)的抛物线的解析式以及函数的平移规律,可得出抛物线C 2的解析式;在Rt △OAB 中,由勾股定理可确定m 、n 的关系式,然后用m 列出△AOB 的面积表达式,结合不等式的相关知识可确定△OAB 的最小面积值以及此时m 的值,进而由待定系数法确定一次函数OA 的解析式.【解答】解:(1)∵抛物线过(0,-3)点,∴-3a =-3∴a =1 ……………………………………1分 ∴y=x 2+bx -3∵x 2+bx -3=0的两根为x 1,x 2且21x -x =4∴21221214)(x x x x x x -+=-=4且b <0∴b =-2 ……………………1分 ∴y=x 2-2x -3=(x -1)2-4∴抛物线C1的顶点坐标为(1,-4) ………………………1分 (2)∵x >0,∴0)1(21≥-=-+xx x x ∴,21≥+x x 显然当x =1时,才有,21=+xx ………………………2分 (3)方法一:由平移知识易得C2的解析式为:y =x 2 ………………………1分∴A(m ,m 2),B (n ,n 2) ∵ΔAOB 为Rt Δ ∴OA 2+OB 2=AB 2∴m 2+m 4+n 2+n 4=(m -n )2+(m 2-n 2)2化简得:m n =-1 ……………………1分 ∵SΔAOB =OB OA ∙21=424221n n m m +∙+ ∵m n =-1∴SΔAOB =22221221221mm n m ++=++ =1221121)1(212=∙≥⎪⎭⎫ ⎝⎛+=+m m m m ∴SΔAOB 的最小值为1,此时m =1,A(1,1) ……………………2分 ∴直线OA 的一次函数解析式为y=x ……………………1分方法二:由题意可求抛物线2C 的解析式为:2y x = ··········································· (1分)∴2(,)A m m ,2(,)B n n过点A 、B 作x 轴的垂线,垂足分别为CAOC BOD ACDB S S S S =-- 梯形2222111()()222m n m n m m n n =+--⋅-⋅ 1()2mn m n =--由BOD △ ∽OAC △得 BD ODOC AC=即22n n m m-= ∴1mn =- ········································································································· (1分)∴1n m =-∴1()2S mn m n =--11()2m m=+由(2)知:12m m+≥∴111()2122S m m =+≥⨯=当且仅当1m =,S 取得最小值1此时A 的坐标为(1,1) ·········································································· (2分) ∴一次函数OA 的解析式为y x = ································································· (1分)【点评】该题考查了二次函数解析式的确定、函数图象的平移、不等式的应用等知识,解题过程中完全平方式的变形被多次提及,应熟练掌握并能灵活应用.(2.2012滨州)24.如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣2,﹣4),O(0,0),B(2,0)三点.(1)求抛物线y=ax2+bx+c的解析式;(2)若点M是该抛物线对称轴上的一点,求AM+OM的最小值.考点:二次函数综合题。
2012年中考数学压轴题精选(含答案)

(2012年北京市)24、在△ABC 中,BA =BC ,∠BAC =α,M 是AC 的中点,P 是线段BM 上的动点,将线段PA 绕点P 顺时针旋转2α得到线段PQ 。
(1)若α=60°且点P 与点M 重合(如图1),线段CQ 的延长线交射线BM 于点D ,请补全图形,并写出∠CDB 的度数;(2)在图2中,点P 不与点B 、M 重合,线段CQ 的延长线于射线BM 交于点D ,猜想∠CDB 的大小(用含α的代数式表示),并加以证明;(3)对于适当大小的α,当点P 在线段BM 上运动到某一位置(不与点B 、M 重合)时,能使得线段CQ 的延长线与射线BM 交于点D ,且PQ =DQ ,请直接写出α的范围。
图1QM(P)C B APM图2QCBA(答案)(1)o CDB 30=∠ (2)α-=∠o CDB 90 (3)o o 6045<<α (2012年北京市)25、在平面直角坐标系xOy 中,对于任意两点P 1(x 1,y 1)与P 2(x 2,y 2)的“非常距离”,给出如下定义:若|x 1-x 2|≥|y 1-y 2|,则点P 1与点P 2的“非常距离”为|x 1-x 2|; 若|x 1-x 2|<|y 1-y 2|,则点P 1与点P 2的“非常距离”为|y 1-y 2|。
例如:点P 1(1,2),点P 2(3,5),因为|1-3|<|2-5|,所以点P 1与点P 2的“非常距离”为|2-5|=3,也就是图1中线段P 1Q 与线段P 2Q 长度的较大值(点Q 为垂直于y 轴的直线P 1Q 与垂直于x 轴的直线P 2Q 的交点)。
(1)已知点A(-12,0),B 为y 轴上的一个动点,①若点A 与点B 的“非常距离”为2,写出一个满足条件的点B 的坐标; ②直接写出点A 与点B 的“非常距离”的最小值;(2)已知C 是直/线y =34x +3上的一个动点,①如图2,点D 的坐标是(0,1),求点C 与点D 的“非常距离”的最小值及相应的点C 的坐标;②如图3,E 是以原点O 为圆心,1为半径的圆上的一个动点,求点C 与点E 的“非常距离”的最小值及相应的点E 和点C 的坐标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012年中考数学压轴题预测100题精选(1-10题)答案【001】解:(1) 抛物线2(1)33(0)y a x a =-+≠经过点(20)A -,, 309333a a ∴=+∴=-1分∴二次函数的解析式为:232383333y x x =-++ 3分(2)D 为抛物线的顶点(133)D ∴,过D 作DN OB ⊥于N ,则33DN =, 2233(33)660AN AD DAO =∴=+=∴∠=,°4分OM AD ∥①当AD OP =时,四边形DAOP 是平行四边形 66(s)OP t ∴=∴= 5分②当DP OM ⊥时,四边形DAOP 是直角梯形过O 作OH AD ⊥于H ,2AO =,则1AH =(如果没求出60DAO ∠=°可由Rt Rt OHA DNA △∽△求1AH =)55(s)OP DH t ∴=== 6分③当PD OA =时,四边形DAOP 是等腰梯形 26244(s)OP AD AH t ∴=-=-=∴=综上所述:当6t =、5、4时,对应四边形分别是平行四边形、直角梯形、等腰梯形. 7分(3)由(2)及已知,60COB OC OB OCB ∠==°,,△是等边三角形 则6262(03)OB OC AD OP t BQ t OQ t t =====∴=-<<,,,过P 作PE OQ ⊥于E ,则32PE t=8分113633(62)222BCPQS t t ∴=⨯⨯-⨯-⨯=233633228t ⎛⎫-+ ⎪⎝⎭ 9分当32t =时,BCPQ S 的面积最小值为633810分xyM CDPQO AB N E H∴此时3339333324444OQ OP OE QE PE ==∴=-==,=,222233933442PQ PE QE ⎛⎫⎛⎫∴=+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭11分【002】解:(1)1,85;(2)作QF ⊥AC 于点F ,如图3, AQ = CP= t ,∴3AP t =-.由△AQF ∽△ABC ,22534BC =-=,得45QF t =.∴45QF t =. ∴14(3)25S t t=-⋅, 即22655S t t=-+. (3)能. ①当DE ∥QB 时,如图4.∵DE ⊥PQ ,∴PQ ⊥QB ,四边形QBED 是直角梯形. 此时∠AQP=90°.由△APQ ∽△ABC ,得AQ APAC AB =, 即335t t -=. 解得98t =. ②如图5,当PQ ∥BC 时,DE ⊥BC ,四边形QBED 是直角梯形.此时∠APQ =90°.由△AQP ∽△ABC ,得AQ APAB AC =, 即353t t -=. 解得158t =. (4)52t =或4514t =.【注:①点P 由C 向A 运动,DE 经过点C . 方法一、连接QC ,作QG ⊥BC 于点G ,如图6.PC t =,222QC QG CG =+2234[(5)][4(5)]55t t =-+--. 由22PC QC =,得22234[(5)][4(5)]55t t t =-+--,解得52t =.方法二、由CQ CP AQ ==,得QAC QCA ∠=∠,进而可得 B BCQ ∠=∠,得CQ BQ =,∴52AQ BQ ==.∴52t =.②点P 由A 向C 运动,DE 经过点C ,如图7.A CB PQ ED图4 A CBP QD图3 EF ACBP Q E D 图5A C(E)B PQ D 图6 GA C(E)B PQ D图7G22234(6)[(5)][4(5)]55t t t -=-+--,4514t =】【003】解.(1)点A 的坐标为(4,8) …………………1分将A (4,8)、C (8,0)两点坐标分别代入y=ax2+bx 8=16a+4b得 0=64a+8b得a=-12,b=4解∴抛物线的解析式为:y=-12x2+4x …………………3分 (2)①在Rt △APE 和Rt △ABC 中,tan ∠PAE=PE AP =BC AB ,即PE AP =48 ∴PE=12AP=12t .PB=8-t . ∴点E的坐标为(4+12t ,8-t ).∴点G 的纵坐标为:-12(4+12t )2+4(4+12t )=-18t2+8. …………………5分 ∴EG=-18t2+8-(8-t) =-18t2+t.∵-18<0,∴当t=4时,线段EG 最长为2. …………………7分②共有三个时刻. …………………8分t1=163, t2=4013,t3= 8525+. …………………11分【004】(1)解:由28033x +=,得4x A =-∴.点坐标为()40-,.由2160x -+=,得8x B =∴.点坐标为()80,.∴()8412AB =--=.(2分)由2833216y x y x ⎧=+⎪⎨⎪=-+⎩,.解得56x y =⎧⎨=⎩,.∴C 点的坐标为()56,.(3分)∴111263622ABC C S AB y ==⨯⨯=△·.(4分)(2)解:∵点D 在1l 上且2888833D B D x x y ==∴=⨯+=,. ∴D 点坐标为()88,.(5分)又∵点E 在2l 上且821684E D E E y y x x ==∴-+=∴=,..∴E 点坐标为()48,.(6分)∴8448OE EF =-==,.(7分)(3)解法一:①当03t <≤时,如图1,矩形DEFG 与ABC △重叠部分为五边形CHFGR (0t =时,为四边形CHFG ).过C 作CM AB ⊥于M ,则Rt Rt RGB CMB △∽△.∴BG RG BM CM =,即36t RG=,∴2RG t =.Rt Rt AFH AMC △∽△, ∴()()11236288223ABC BRG AFH S S S S t t t t =--=-⨯⨯--⨯-△△△.即241644333S t t =-++.(10分) 【005】(1)如图1,过点E 作EG BC ⊥于点G . 1分 ∵E 为AB 的中点,∴122BE AB ==.在Rt EBG △中,60B =︒∠,∴30BEG =︒∠. 2分∴22112132BG BE EG ===-=,.即点E 到BC 的距离为3. 3分A DB EO RF xy1l 2l M (图3)G CA DB EO CF x y1l 2lG (图1)RM A D B EO CF xy1l 2l G (图2)RM 图1AD E BF CG(2)①当点N 在线段AD 上运动时,PMN △的形状不发生改变. ∵PM EF EG EF ⊥⊥,,∴PM EG ∥. ∵EF BC ∥,∴EP GM =,3PM EG ==. 同理4MN AB ==. 4分如图2,过点P 作PH MN ⊥于H ,∵MN AB ∥, ∴6030NMC B PMH ==︒=︒∠∠,∠.∴1322PH PM ==.∴3cos302MH PM =︒= .则35422NH MN MH =-=-=.在Rt PNH △中,222253722PN NH PH ⎛⎫⎛⎫=+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭.∴PMN △的周长=374PM PN MN ++=++. 6分②当点N 在线段DC 上运动时,PMN △的形状发生改变,但MNC △恒为等边三角形. 当PM PN =时,如图3,作PR MN ⊥于R ,则MR NR =.类似①,32MR =.∴23MN MR ==. 7分∵MNC △是等边三角形,∴3MC MN ==.此时,6132x EP GM BC BG MC ===--=--=.8分图2A D E BFCPNMG H当MP MN =时,如图4,这时3MC MN MP ===. 此时,61353x EP GM ===--=-.当NP NM =时,如图5,30NPM PMN ==︒∠∠. 则120PMN =︒∠,又60MNC =︒∠, ∴180PNM MNC +=︒∠∠.因此点P 与F 重合,PMC △为直角三角形.∴tan301MC PM =︒= .此时,6114x EP GM ===--=. 综上所述,当2x =或4或()53-时,PMN △为等腰三角形.【006】解:(1)OC=1,所以,q=-1,又由面积知0.5OC ×AB=45,得AB=52,设A (a,0),B(b,0)AB=b -a=2()4a b ab +-=52,解得p=32±,但p<0,所以p=32-。
所以解析式为:2312y x x =--(2)令y=0,解方程得23102x x --=,得121,22x x =-=,所以A(12-,0),B(2,0),在直角三角形AOC 中可求得AC=52,同样可求得BC=5,显然AC2+BC2=AB2,得△ABC 是直角三角形。
AB 为斜边,所以外接圆的直径为AB=52,所以5544m -≤≤。
(3)存在,AC ⊥BC ,①若以AC 为底边,则BD//AC,易求AC 的解析式为y=-2x-1,可设BD 的解析式图3A D E BFCPN M 图4AD EB F CPM N 图5A D EB F (P ) CMN GGRG为y=-2x+b,把B(2,0)代入得BD解析式为y=-2x+4,解方程组231224y x xy x⎧=--⎪⎨⎪=-+⎩得D(52-,9)②若以BC为底边,则BC//AD,易求BC的解析式为y=0.5x-1,可设AD的解析式为y=0.5x+b,把A(12-,0)代入得AD解析式为y=0.5x+0.25,解方程组23120.50.25y x xy x⎧=--⎪⎨⎪=+⎩得D(53,22) 综上,所以存在两点:(52-,9)或(53,22)。
【007】∴∠1与∠3互余,∠2与∠3互余,∴△BAD≌△CBE…………………………………………2分∴AD=BE……………………………………………………3分(2)∵E 是AB 中点,∴EB=EA 由(1)AD=BE 得:AE=AD ……………………………5分 ∵AD ∥BC ∴∠7=∠ACB=45°∵∠6=45°∴∠6=∠7 由等腰三角形的性质,得:EM=MD ,AM ⊥DE 。
即,AC 是线段ED 的垂直平分线。
……………………7分 (3)△DBC 是等腰三角(CD=BD )……………………8分 理由如下:由(2)得:CD=CE 由(1)得:CE=BD ∴CD=BD ∴△DBC 是等腰三角形。
……………………………10分 【009】解:(1)①AC x ⊥轴,AE y ⊥轴,∴四边形AEOC 为矩形. BF x ⊥轴,BD y ⊥轴,∴四边形BDOF 为矩形.AC x ⊥轴,BD y ⊥轴,∴四边形AEDK DOCK CFBK ,,均为矩形. 1分 1111OC x AC y x y k === ,,,∴11AEOC S OC AC x y k === 矩形 2222OF x FB y x y k === ,,, ∴22BDOF S OF FB x y k === 矩形. ∴AEOC BDOF S S =矩形矩形.AEDK AEOC DOCK S S S =-矩形矩形矩形,C F B K BD O F D S S S=-矩形矩形矩形,∴AEDK CFBK S S =矩形矩形. 2分②由(1)知AEDK CFBKS S =矩形矩形.∴AK DK BK CK =. ∴AK BK CK DK =. 4分90AKB CKD ∠=∠=°,O C F MDE NKy xAB 图1∴AKB CKD △∽△. 5分∴CDK ABK ∠=∠. ∴AB CD ∥. 6分 AC y ∥轴,∴四边形ACDN 是平行四边形. ∴AN CD =. 7分同理BM CD =.AN BM ∴=. 8分(2)AN 与BM 仍然相等.9分AEDK AEOC ODKC S S S =+矩形矩形矩形,BKCF BDOF ODKCS S S =+矩形矩形矩形,又AEOC BDOF S S k==矩形矩形,∴AEDK BKCF S S =矩形矩形. 10分 ∴AK DK BK CK =. ∴CK DKAK BK =.K K ∠=∠,∴CDK ABK △∽△. ∴CDK ABK ∠=∠. ∴AB CD ∥. 11分 AC y ∥轴,∴四边形ANDC 是平行四边形. ∴AN CD =.OC D KF E N yxABM图2同理BM CD =.∴AN BM =. 12分【010】解:(1)根据题意,得34231.2a a b b a -=+-⎧⎪⎨-=⎪⎩, 2分 解得12.a b =⎧⎨=-⎩,∴抛物线对应的函数表达式为223y x x =--. 3分(2)存在.在223y x x =--中,令0x =,得3y =-. 令0y =,得2230x x --=,1213x x ∴=-=,.(10)A ∴-,,(30)B ,,(03)C -,.又2(1)4y x =--,∴顶点(14)M -,. 5分 容易求得直线CM 的表达式是3y x =--. 在3y x =--中,令0y =,得3x =-.(30)N ∴-,,2AN ∴=. 6分在223y x x =--中,令3y =-,得1202x x ==,.2CP AN CP ∴=∴=,.AN CP ∥,∴四边形ANCP 为平行四边形,此时(23)P -,. 8分(3)AEF △是等腰直角三角形.理由:在3y x =-+中,令0x =,得3y =,令0y =,得3x =.∴直线3y x =-+与坐标轴的交点是(03)D ,,(30)B ,. OD OB ∴=,45OBD ∴∠=°. 9分又 点(03)C -,,OB OC ∴=.45OBC ∴∠=°. 10分 由图知45AEF ABF ∠=∠=°,45AFE ABE ∠=∠=°. 11分90EAF ∴∠=°,且AE AF =.AEF ∴△是等腰直角三角形.12分y xEDNOA CMPN1F (第26题图)(4)当点E 是直线3y x =-+上任意一点时,(3)中的结论成立. 14分。
