清华大学贾仲孝老师(贾哥)高等数值分析证明题汇总

合集下载

数值分析简明教程课后习题答案

比较详细的数值分析课后习题答案0.1算法1、（p.11，题1）用二分法求方程013=--x x 在[1,2]内的近似根，要求误差不超过10-3.【解】由二分法的误差估计式311*10212||-++=≤=-≤-εk k k a b x x ，得到100021≥+k .两端取自然对数得96.812ln 10ln 3≈-≥k ，因此取9=k ，即至少需2、（p.11，题2）证明方程210)(-+=x e x f x在区间[0,1]内有唯一个实根；使用二分法求这一实根，要求误差不超过21021-⨯。

【解】由于210)(-+=x e x f x，则)(x f 在区间[0,1]上连续，且012010)0(0<-=-⨯+=e f ，082110)1(1>+=-⨯+=e e f ，即0)1()0(<⋅f f ，由连续函数的介值定理知，)(x f 在区间[0,1]上至少有一个零点.又010)('>+=x e x f ，即)(x f 在区间[0,1]上是单调的，故)(x f 在区间[0,1]内有唯一实根.由二分法的误差估计式211*1021212||-++⨯=≤=-≤-εk k k a b x x ，得到1002≥k .两端取自然对数得6438.63219.322ln 10ln 2=⨯≈≥k ，因此取7=k ，即至少需二分0.2误差1．（p.12，题8）已知e=2.71828…，试问其近似值7.21=x ，71.22=x ，x 2=2.71，718.23=x 各有几位有效数字？并给出它们的相对误差限。

【解】有效数字：因为11102105.001828.0||-⨯=<=- x e ，所以7.21=x 有两位有效数字；因为12102105.000828.0||-⨯=<=- x e ，所以71.22=x 亦有两位有效数字；因为3310210005.000028.0||-⨯=<=- x e ，所以718.23=x 有四位有效数字；%85.17.205.0||111=<-=x x e r ε； %85.171.205.0||222=<-=x x e r ε； %0184.0718.20005.0||333=<-=x x e r ε。

数值分析试题及答案汇总

数值分析试题及答案汇总TTA standardization office【TTA 5AB- TTAK 08- TTA 2C】数值分析试题一、填空题（2 0×2′） 1.⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡-=32,1223X A 设x =是精确值x *=的近似值，则x 有 2 位有效数字。

2. 若f (x )=x 7－x 3＋1，则f [20,21,22,23,24,25,26,27]= 1 ， f [20,21,22,23,24,25,26,27,28]=0 。

3. 设，‖A ‖∞＝___5 ____，‖X ‖∞＝__ 3_____，‖AX ‖∞≤_15_ __。

4. 非线性方程f (x )=0的迭代函数x =(x )在有解区间满足 |’(x )| <1 ，则使用该迭代函数的迭代解法一定是局部收敛的。

5. 区间[a ,b ]上的三次样条插值函数S (x )在[a ,b ]上具有直到 2 阶的连续导数。

6. 当插值节点为等距分布时，若所求节点靠近首节点，应该选用等距节点下牛顿差商公式的前插公式，若所求节点靠近尾节点，应该选用等距节点下牛顿差商公式的后插公式；如果要估计结果的舍入误差，应该选用插值公式中的拉格朗日插值公式。

7. 拉格朗日插值公式中f (x i )的系数a i (x )的特点是：=∑=ni i x a 0)( 1 ；所以当系数a i (x )满足 a i (x )>1 ，计算时不会放大f (x i )的误差。

8. 要使20的近似值的相对误差小于%，至少要取 4 位有效数字。

9. 对任意初始向量X (0)及任意向量g ，线性方程组的迭代公式x (k +1)=Bx (k )+g (k =0,1,…)收敛于方程组的精确解x *的充分必要条件是 (B)<1 。

10. 由下列数据所确定的插值多项式的次数最高是 5 。

11. 牛顿下山法的下山条件为 |f(xn+1)|<|f(xn)| 。

数值分析试题与答案

一. 填空题（本大题共4小题，每小题4分，共16分）1.设有节点012,,x x x ，其对应的函数()y f x =的值分别为012,,y y y ，则二次拉格朗日插值基函数0()l x 为。

2.设()2f x x =，则()f x 关于节点0120,1,3x x x ===的二阶向前差分为。

3.设110111011A -⎡⎤⎢⎥=--⎢⎥⎢⎥-⎣⎦，233x ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦，则1A ＝，1x = 。

4. 1n +个节点的高斯求积公式的代数精确度为。

二．简答题（本大题共3小题，每小题8分，共24分）1. 哪种线性方程组可用平方根法求解？为什么说平方根法计算稳定？2. 什么是不动点迭代法？()x ϕ满足什么条件才能保证不动点存在和不动点迭代序列收敛于()x ϕ的不动点？3. 设n 阶矩阵A 具有n 个特征值且满足123n λλλλ>≥≥≥，请简单说明求解矩阵A 的主特征值和特征向量的算法及流程。

三．求一个次数不高于3的多项式()3P x ，满足下列插值条件：i x 1 2 3 i y 2 4 12 i y '3并估计误差。

（10分）四．试用1,2,4n =的牛顿-科特斯求积公式计算定积分1011I dx x=+⎰。

（10分）五．用Newton 法求()cos 0f x x x =-=的近似解。

（10分）六．试用Doolittle 分解法求解方程组：12325610413191963630x x x -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦⎣⎦ （10分）七．请写出雅可比迭代法求解线性方程组123123123202324812231530x x x x x x x x x ++=⎧⎪++=⎨⎪-+=⎩ 的迭代格式，并判断其是否收敛？（10分）八．就初值问题0(0)y yy y λ'=⎧⎨=⎩考察欧拉显式格式的收敛性。

（10分）《数值分析》（A ）卷标准答案（2009－2010－1）一．填空题（每小题3分，共12分） 1. ()1200102()()()()x x x x l x x x x x --=--； 2.7；3. 3，8；4. 2n+1。

数值分析课后部分习题答案

解
x * = 2.00021 = 0.200021 × 101 ，即 m = 1
1 1 × 10m − n = × 10−3 ， 2 2
由有效数字与绝对误差的关系得即
m − n = −3 ，所以， n = 2 ； y* = 0.032 = 0.32 × 101 ，即 m = 1
由有效数字与绝对误差的关系得即
m − n = −3 ，所以， n = 4 ； z * = 0.00052 = 0.52 × 10−3 ，即 m = −3
1 1 × 10m − n = × 10−3 ， 2 2
由有效数字与绝对误差的关系得即
m − n = −3 ，所以， n = 0 .
1 1 × 10m − n = × 10−3 ，Fra bibliotek2 2=
f [x1 , x2 ,⋯ , x n ]-f [ x0 , x1 ,⋯ , x n−1 ] g[ x1 , x2 ,⋯ , x n ] − g[ x0 , x1 ,⋯ , x n−1 ] + x n − x0 x n − x0
( x − 1)( x − 2)( x − 3) 1 =- ( x − 1)( x − 2)( x − 3) ， (0 − 1)(0 − 2)(0 − 3) 6
x ( x − 2)( x − 3) 1 = x ( x − 2)( x − 3) ， (1 − 0)(1 − 2)(1 − 3) 2 x( x − 1)( x − 3) 1 =- x( x − 1)( x − 3) ， (2 − 0)(2 − 1)(2 − 3) 2 x( x − 1)( x − 2) 1 = x ( x − 1)( x − 2) ， (3 − 0)(3 − 1)(3 − 2) 6

数值分析习题（含答案）

数值分析习题（含答案）第一章绪论姓名学号班级习题主要考察点：有效数字的计算、计算方法的比较选择、误差和误差限的计算。

1 若误差限为5105.0-?,那么近似数0.003400有几位有效数字？（有效数字的计算）解：2*103400.0-?=x ，325*10211021---?=?≤-x x 故具有3位有效数字。

2 14159.3=π具有4位有效数字的近似值是多少？（有效数字的计算）解：10314159.0?= π，欲使其近似值*π具有4位有效数字，必需41*1021-?≤-ππ，3*310211021--?+≤≤?-πππ，即14209.314109.3*≤≤π即取（3.14109 , 3.14209）之间的任意数，都具有4位有效数字。

3 已知2031.1=a ，978.0=b 是经过四舍五入后得到的近似值，问b a +，b a ?有几位有效数字？（有效数字的计算）解：3*1021-?≤-aa ，2*1021-?≤-b b ，而1811.2=+b a ，1766.1=?b a 2123****102110211021)()(---?≤?+?≤-+-≤+-+b b a a b a b a故b a +至少具有2位有效数字。

2123*****10210065.01022031.1102978.0)()(---?≤=?+?≤-+-≤-b b a a a b ba ab 故b a ?至少具有2位有效数字。

4 设0>x ，x 的相对误差为δ，求x ln 的误差和相对误差？（误差的计算）解：已知δ=-**xx x ，则误差为δ=-=-***ln ln xx x x x则相对误差为******ln ln 1ln ln ln xxx x xxx x δ=-=-5测得某圆柱体高度h 的值为cm h 20*=，底面半径r 的值为cm r 5*=，已知cm h h 2.0||*≤-，cm r r 1.0||*≤-，求圆柱体体积h r v2π=的绝对误差限与相对误差限。

清华大学高等数值分析实验设计及答案

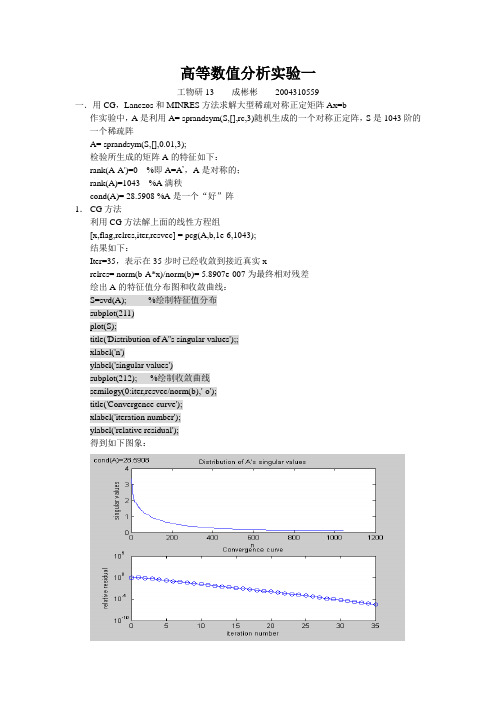
高等数值分析实验一工物研13 成彬彬2004310559一．用CG，Lanczos和MINRES方法求解大型稀疏对称正定矩阵Ax=b作实验中，A是利用A= sprandsym(S,[],rc,3)随机生成的一个对称正定阵，S是1043阶的一个稀疏阵A= sprandsym(S,[],0.01,3);检验所生成的矩阵A的特征如下：rank(A-A')=0 %即A=A’，A是对称的；rank(A)=1043 %A满秩cond(A)= 28.5908 %A是一个“好”阵1．CG方法利用CG方法解上面的线性方程组[x,flag,relres,iter,resvec] = pcg(A,b,1e-6,1043);结果如下：Iter=35，表示在35步时已经收敛到接近真实xrelres= norm(b-A*x)/norm(b)= 5.8907e-007为最终相对残差绘出A的特征值分布图和收敛曲线：S=svd(A); %绘制特征值分布subplot(211)plot(S);title('Distribution of A''s singular values');;xlabel('n')ylabel('singular values')subplot(212); %绘制收敛曲线semilogy(0:iter,resvec/norm(b),'-o');title('Convergence curve');xlabel('iteration number');ylabel('relative residual');得到如下图象：为了观察CG方法的收敛速度和A的特征值分布的关系，需要改变A的特征值：(1).研究A的最大最小特征值的变化对收敛速度的影响在A的构造过程中，通过改变A= sprandsym(S,[],rc,3)中的参数rc(1/rc为A的条件数)，可以达到改变A的特征值分布的目的：通过改变rc=0.1，0.0001得到如下两幅图以上三种情况下，由收敛定理2.2.2计算得到的至多叠代次数分别为：48，14和486，由于上实验结果可以看出实际叠代次数都比上限值要小较多。

数值分析习题解二三章

数值分析习题解⼆三章12. 设()k T x 是k 次Chebyshev 多项式，证明（1）()()m n mn T T x T x =；（2）()()()()2m n m n m n T x T x T x T x +-+=. 证明：由Chebyshev 多项式的定义，()()()()()()cos arccos cos arccos cos arccos m n mn T T x m n x m n x T x ==??=()()()()()()()()()()cos arccos cos arccos 2cos arccos cos arccos 2m n m n m n T x T x m n x m n x m x n x T x T x +-+=+?+-?=??= 13. 求函数()f x =[]0,1上的⼀次最佳平⽅逼近多项式。

解：⽅法⼀（⽤多项式21,,,x x 作基底）令()01x ?=，()1x x ?=，设所求多项式为()*01S x a a x =+。

因为()12000,1d 1x ??==?，()()1011001,,d 2x x ===?，()121101,d 3x x ??==?，()(001,ln 122f x ?==++?，()()1101,13f x ?==?所以关于0a 和1a 的法⽅程为(()0011111ln 1=0.9343222110.4269511233a a a a ??+?=?=因此所求最佳平⽅逼近多项式 ()*0.934320.42695S x x =+。

⽅法⼆（⽤Legendre 正交多项式()01P x =, ()1P x x =, ()()221 31P x x =-, 因为[][]0,11,1≠-，令()[]11,1,12x t t =+∈-，则()()f x F t ==令()()001t P t ?==，()()11t P t t ?==，则()0,,2,21i j i ji j i ??≠??=?=?+?。

高等数值分析第二章答案

第二章习题参考答案1.解：由于20Ax b−≥，极小化2b Ax −与极小化22Ax b −是等价的。

令22()(,)(,)2(,)x Ax b Ax Ax b b Ax b ϕ=−=+−，对于任意的n R y x ∈,和实数α，)()(),()()(,*222*2****x Ay a x Ay Ay a x ay x b Ax x ϕϕϕϕ≥+=+=+=则有满足若这表示处达到极小值。

在*)(x x ϕ反之，若必有处达到极小，则对任意在nR y x ay x ∈+*)(ϕ0),(2),(2),(20)(**0*=−=+−=+=Ay b Ax Ay Ay a Ay b Ax daay x d a 即ϕ故有 b Ax =*成立。

以上证明了求解,22b Ax b Ax −=等价于极小化即。

等价于极小化2b Ax b Ax −= 推导最速下降法过程如下：),/(),(0),(),(,0),,2)(222)()(11k T k T k T k k T k T k T k k T k k k T k k kT k T k T T x x k r AA r AA r AA r a r AA r AA a r AA r r aA x da dx a r aA x x r A Ax b A Ax A b A x grad x x k==+−=++==−=−=−++=最终得到得出（由取得极小值。

使求出取的负梯度方向，且下降最快的方向是该点在ϕϕϕ给出的算法如下：1）)(000Ax b A r A R x T T n −=∈，计算给定； 2）L ,2,1,0=k 对于）转到否则数。

为一事先给定的停机常则停止；其中若2),/(),(10,11kT k k k k T k k k k k k k k k r A p Ax b r r A a x x Ap Ap p p a k k r =−=+==+=>≤−−εε2.证明 1）正定性由对称正定矩阵的性质，(),0x Ax ≥（当且仅当x ＝0时取等号），所以 ()12,0Axx Ax =≥（当且仅当x ＝0时取等号）2）齐次性()()()121122,(),,AA xx A x x Ax x Ax x αααααα⎡⎤====⎣⎦3）o1方法（一）A 是对称正定矩阵，得到(,())0x y A x y λλ++≥，把它展开如下2(,)(,)(,)(,)0y Ay x Ay y Ax x Ax λλλ+++≥考虑到(,)(,)(,)x Ay Ax y y Ax ==，把上式看成关于λ的一元二次方程，则式子等价于24(,)4(,)(,)0x Ay x Ax y Ay ∆=−≤因此1/21/2(,)(,)(,)x Ay x Ax y Ay ≤所以1/21/221/21/2((,)(,))(,)(,)2(,)(,)(,)(,)2(,)(,)(,)(,)(,)((),())x Ax y Ay x Ax y Ay x Ax y Ay x Ax y Ay x Ay x Ax y Ay x Ay y Ax x y A x y +=++≥++=+++=++两边开平方即可得到AA A x yx y +≤+因此，1/2(,)A x Ax x =是一种向量范数。

数值分析试题与答案

试题__2009___年~__2010___年第一学期课程名称：数值分析专业年级： 2009级（研究生）考生学号：考生姓名：试卷类型： A 卷 √ B 卷 □ 考试方式: 开卷 √ 闭卷 □………………………………………………………………………………………………………一. 填空题（本大题共4小题，每小题4分，共16分）1.设有节点012,,x x x ，其对应的函数()y f x =的值分别为012,,y y y ，则二次拉格朗日插值基函数0()l x 为。

2.设()2f x x =，则()f x 关于节点0120,1,3x x x ===的二阶向前差分为。

3.设110111011A -⎡⎤⎢⎥=--⎢⎥⎢⎥-⎣⎦，233x ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦，则1A ＝，1x = 。

4. 1n +个节点的高斯求积公式的代数精确度为。

三．求一个次数不高于3的多项式()3P x ，满足下列插值条件：i x 1 2 3 i y 2 4 12 i y '3并估计误差。

（10分）四．试用1,2,4n =的牛顿-科特斯求积公式计算定积分1011I dx x=+⎰。

（10分）五．用Newton 法求()cos 0f x x x =-=的近似解。

高等数值分析第二次实验作业(贾忠孝)

3. 对 1 中的例子固定特征值的实部, 变化虚部, 比较收敛性. A 矩阵每个小块有如下形式：
A i i
其特征值为
i i
i ii ，对其次对角元素 i 做如下处理：
i ' k i
其特征值变为果：
i ik i 。在本题中分别设定 k 的取值为 0.5，1，2，4。可以得到下面的结
结果分析：（1）当 k 越大，既即特征根虚部越大时，基本 Arnoldi 方法和 GMRES 方法的收敛速度会越来越慢，Arnoldi 方法的振荡程度会随着 k 值的增大而增大，振荡范围也增大。当 k 大到 10 或者 10 以上时，两法都只在最后一步（第 1000 步）收敛，而且都是急剧收敛。（2） GMRES 法的残量一直比 Arnoldi 法的残量小，且相对残差的曲线平滑。.
GMRES算法计算 m个特征向量组成的 b的收敛曲线 4 2 0 -2 GMRES, GMRES, GMRES, GMRES, m m m m = = = = 10 50 100 1000
log(||rk||)
-4 -6 -8 -10 -12 -14
0
50 Iteration Times
100
150
结果分析：（1）当 m 较小时，收敛速度很快，但其随着 m 值的增大而慢慢变小。但是一直到最后一步之前，收敛的幅度都不大，往往是在最后一步急剧收敛；（2）当 m 较大时，收敛的速度随 m 的增大而微弱减小，而且其在步数比较小的时候，收敛速度较快，越往后走反而慢。（3） Arnoldi 法比 GMRES 法收敛曲线的趋势是基本一样的，而且 Arnoldi 法收敛比 GMRES 法要快，相对残量： 1.构造例子特征值全部在右半平面时,观察基本的 Arnoldi 方法和 GMRES 方法的数值性态,和相应重新启动算法的收敛性. 解：构造 1000 阶符合条件的矩阵 A。根据实 Schur 分解，构造如下形式的矩阵：

清华大学高等数值分析(李津)所有作业答案合集

20130917题目求证：在矩阵的LU 分解中，111n n Tn ij i j j i j L I e e α-==+⎛⎫=- ⎪⎝⎭∑∑证明：在高斯消去过程中，假设0jj a ≠ ，若a=0，可以通过列变换使得前面的条件成立，这里不考虑这种情况。

对矩阵A 进行LU 分解，()()()()()1111111L M n M M M n ---=-=∙∙-………… ，其中()1n Tn ij i j i j M j I e e α=+⎛⎫=+ ⎪⎝⎭∑ ，i e 、j e 为n 维线性空间的自然基。

()M j 是通过对单位阵进行初等变换得到，通过逆向的变换则可以得到单位阵，由此很容易得到()M j 的逆矩阵为1n Tn ij i j i j I e e α=+⎛⎫- ⎪⎝⎭∑。

故111n n T n ij i j n j i j L I e e I α-==+⎛⎫⎛⎫=- ⎪ ⎪ ⎪⎝⎭⎝⎭∏∑上式中的每一项均是初等变换，从右向左乘，则每乘一次相当于对右边的矩阵进行一次向下乘法叠加的初等变换。

由于最初的矩阵为单位阵，变换从右向左展开，因而每一次变换不改变已经更新的数据，既该变换是从右向左一列一列更新数据，故11nn Tn ij i j j i j L I e e α==+⎛⎫=- ⎪⎝⎭∑∑。

数学证明：1nTi j i ji j ee α=+⎛⎫ ⎪⎝⎭∑具有,000n j jA -⎛⎫ ⎪⎝⎭ 和1,1000n j n j B -+-+⎛⎫⎪⎝⎭ 的形式，且有+1,-11,10000=000n j j n j n j AB --+-+⎛⎫⎛⎫⎪⎪⎝⎭⎝⎭ 而11n n T ij i j j k i j e e α-==+⎛⎫ ⎪⎝⎭∑∑具有1,1000n k n k B -+-+⎛⎫⎪⎝⎭的形式，因此：1311111211121==n n n n n n T T T n ij i j n ij i j n ik i k j i j j i j k n i k n n T n i i n ik i i i k L I e e I e e I e e I e e I e ααααα---==+==+=-=+==+⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=---⎢⎥ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎛⎫⎛⎫⎛⎫=-- ⎪ ⎪ ⎝⎭⎝⎝⎭∏∑∏∑∑∑∑∑……11211n n n T Tk n ik i kk k i k e I e e α--===+⎛⎫⎛⎫=- ⎪⎪ ⎪⎭⎝⎭⎝⎭∑∑∑#20130924题目一问：能否用逐次householder 相似变换变实矩阵A 为上三角矩阵，为什么？解：不能用逐次householder 相似变换变A 为上三角矩阵，原因如下：A 记作：()12=,,n A a a a ……，，存在householder 阵1H s.t. 1111H a e α= ，则()()()111111111111111111111,,,0T Th H AH H a A H e H A H e H A H h H A H ααα⎛⎫'''=== ⎪⎪'⎝⎭⎛⎫''=+ ⎪ ⎪⎝⎭11H A H ''第一列的元素不能保证为1e 的倍数，故无法通过householder 变换实现上三角化。

贾忠孝历年考题

2012高等数值分析（贾仲孝老师）
首先庆贺自己研究生的第一门也是最后一门考试顺利结束，哦也，再也没有考试啦！
贾哥延续了考题沿用往年题的优良传统，详情见拍照，全部是历年考题，基本上是按着去年考题来的，只有一道题第二个小问号改了一下而已。

1. 用householder和givens变换做QR分解，由于矩阵特殊，非常简单。

如果拿不准，不妨用GS方法做一遍验证一下，因为不同的QR分解只是符号有差异而已，GS还是比householder简单很多的。

2.1证明rayleigh商最大值等于A的最大特征值，将x拆成各个特征向量之和就容易证。

2.2幂法求一个特征值，一步收敛
3. 第三次作业第三题，也是去年的原题，基本上都不用想，直接默写就行了
4.1 去年考题。

注意到Ak*R（k-1）=R（k-1）*A（k-1），那么就类似冒泡算法把Ak移到最右边变成一个A
4.2 有点小恶心，去年这个问号问的是Qk第一列是特征向量x1，只需要两边同乘以e1即可，但今年问的是最后一行是特征向量xn，顿时就不会证了，当时打眼一看觉得貌似A也不能说明是可逆的，就没往反幂法这个方向去，但是后来想想其实最多也就是lamdaN=0，其他不为0，也许可以分情况讨论下？后来有同学说假设可逆用了反幂法也没得到什么结论...不知道...还好就是5分，丢了就丢了吧
5 考过多年的经典背诵题，默写rayleigh ritz方法和贾哥定理，以及Arnolid和精化Arnolid算法。

贾哥高等数值分析报告第一次实验

高等数值分析第一次实验第一题：构造例子说明CG的数值形态。

当步数 = 阶数时CG的解如何？当A的最大特征值远大于第二个最大特征值，最小特征值远小于第二个最小特征值时，方法的收敛性如何？解：用Housholder变换和对角阵构造1000阶正定对称矩阵A：1）构造对角阵D = diag( linspace(1, 1000, 1000) )；2）构造Householder阵H。

取单位向量w=[1,0,0,.....0]T，I为1000阶单位矩阵，H = I –w T w。

3）构造对称正定矩阵A。

A = H T DH。

由于D是对角阵，H是对称的，所以A对称；且A与D 具有相同的特征值linspace(1, 1000, 1000) > 0，因此A对阵正定。

4）b=rand(1000,1);取初始解x0=zeros(1000,1);1.计算Ax = b利用matlab编程实现CG算法。

由于实际计算存在机器误差，因此迭代1000步后的残差不等于0，因此不能用rk=0作为停机准则，否则matlab会无休止地计算下去。

本例采用停机准则为：迭代步数=1000步。

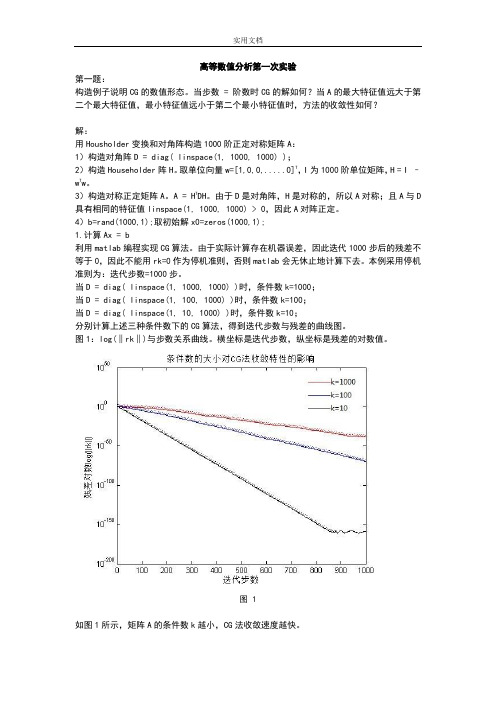
当D = diag( linspace(1, 1000, 1000) )时，条件数k=1000；当D = diag( linspace(1, 100, 1000) )时，条件数k=100；当D = diag( linspace(1, 10, 1000) )时，条件数k=10；分别计算上述三种条件数下的CG算法，得到迭代步数与残差的曲线图。

图1：log(‖rk‖)与步数关系曲线。

横坐标是迭代步数，纵坐标是残差的对数值。

图 1如图1所示，矩阵A的条件数k越小，CG法收敛速度越快。

附matlab程序1-1：clear allclc%条件数k=1000D=diag(linspace(1,1000,1000)); w=eye(1,1000);I=eye(1000);H=I-w*w';A=H'*D*H;%生成1000阶的对称矩阵b=rand(1000,1);x=zeros(1000,1);%初始解r=b-A*x;%初始残量p=r;%初始搜索方向k=0;semilogy(0,norm(r),'r-');hold on;while k<1000alpha = r'*p/(p'*A*p);x = x+alpha*p;rold = r;r = rold-alpha*A*p;beta = r'*r/(rold'*rold); p = r+beta*p;semilogy(k,norm(r),'r-'); hold on;k=k+1;end%条件数k=100clear allD=diag(linspace(1,100,1000));w=eye(1,1000);I=eye(1000);H=I-w*w';A=H'*D*H;%生成1000阶的对称矩阵b=rand(1000,1);x=zeros(1000,1);%初始解r=b-A*x;%初始残量p=r;%初始搜索方向k=0;semilogy(0,norm(r),'b-');hold on;while k<1000alpha = r'*p/(p'*A*p);x = x+alpha*p;rold = r;r = rold-alpha*A*p;beta = r'*r/(rold'*rold);p = r+beta*p;semilogy(k,norm(r),'b-');hold on;k=k+1;end%条件数k=10clear allD=diag(linspace(1,10,1000));w=eye(1,1000);I=eye(1000);H=I-w*w';A=H'*D*H;%生成1000阶的对称矩阵b=rand(1000,1);x=zeros(1000,1);%初始解r=b-A*x;%初始残量p=r;%初始搜索方向k=0;semilogy(0,norm(r),'black-');hold on;while k<1000alpha = r'*p/(p'*A*p);x = x+alpha*p;rold = r;r = rold-alpha*A*p;beta = r'*r/(rold'*rold);p = r+beta*p;semilogy(k,norm(r),'black-');hold on;k=k+1;endtitle('条件数的大小对CG法收敛特性的影响');xlabel('迭代步数')ylabel('残差对数log(||rk||)')2.构造特殊特征值分布构造对称正定矩阵A1和A2。

清华大学贾仲孝老师贾哥高等数值分析证明题汇总

pPk ,p(0)1 1i k
p(i )
可取pk
(t )
(t
1 j k
j
)
(1)k
1 j k
(
j
)
min Xp()y pPk ,p(0)1
则max 1i n
p(i )
=0
rk 0，即 rk =0
证毕！
对于 MINRES，同理可证。
3. 证 Arnoldi 过程中断时不会发生方法中断。
AVm
VmHm
min
pPk ,p(0)1
p()-1r0
n
取r0
i 1
i
xi
Xy,其中y=(1, 2, 3 k-1, k ,0,00,0)T
则 rk
min pPk ,p(0)1
p()-1r0
= min pPk ,p(0)1
Xp()X 1Xy
即 rk
X
min p()y
pPk ,p(0)1
rk X
y
min max
(t
1 j k
j
)
(1)k
1 j k
(
j
)
则max 1i n
p(i )
=0
rk 0，即 rk =0
证毕！
对于 MINRES，() =1，同理可证。
2. 若 A 可对角化，A 有 n 个不同的特征值，r0 是由 k 个不同特征值的特征向量构成。证明 GMERES 和 MINRES 至多 k 步收敛。
3/6
Tn1 Qn1A1Qn 又因为：r0 e1 Tn yn
yn Tn1 r0 e1
则又因为Xn X0 Qn yn X0 QnQn1A1Qn r0 e1 X0 A1r0

清华大学贾仲孝高等数值分析第二次作业

1. 解：由于求解Ax b =等价于极小化2Ax b -，相当于极小化泛函：()()1,2x Ax b Ax b ϕ=-- 从任一k x 出发，沿着()x ϕ在k x 点下降最快的方向搜索下一个近似点1k x +，使得()1k x ϕ+在该方向上达到极小值，最速下降方向为：()()T T k k x A Ax b A r ϕ-∇=--=令1,T k k k k k k p A r x x p α+==+，需要寻找合适的k α使得()()11min k k Rx x αϕϕ++∈=，则()()()()()()1,=T T T T k k k k k k k k d x x p p A A x p b p A p r d ϕϕααα+=∇=+-- 令()0d x d ϕα=，可得： ()()()(),,,,k k k k k k k k k Ap r p p Ap Ap Ap Ap α==则()22,0k k d Ap Ap d ϕα=>，因此上式的k α即为所求于是得到极小化泛函()()1,2x Ax b Ax b ϕ=--的最速下降法： 1) 选取初值0n x R ∈，计算00r b Ax =-2) k=0,1,2,……若k r ε≤，则停止；ε为事先给定的停机场数；否则，k=k+1()()11;,;,;;T k k k k k k k k k k k k k k k p A r p p Ap Ap x x p r r Ap ααα++===+=-2. 解：()()111k k k k AAAx x x r x p A x x α***----=+-=-其中()1p A A α=-，设A 的特征根为120n λλλ≥≥≥> ，则有()11max k i k AAi nx x p x x λ**-≤≤-≤-当120αλ<<时，()1max 1i i np λ≤≤<，因此此方法收敛当()111n αλαλ-=--即12n αλλ=+时，()1max i i n p λ≤≤取最小值11n nλλλλ-+，此时收敛最快3. 解：设x *为方程组Ax b =精确解，k k e x x *=-，则()1,TT Tk k k E e e -=，则原迭代法等价于()110k k I A I E E I βαβ+⎡++-⎤=⎢⎥⎣⎦令()10I A I B I βαβ⎡++-⎤=⎢⎥⎣⎦，则迭代法收敛等价于()1B ρ<，即()1,1i B i nλ<≤≤，令0B I λ-=，即 ()10n I A ββλαλλ⎛⎫+--+-= ⎪⎝⎭ 当0λ≠时，则有10I A ββλαλ⎛⎫+--+= ⎪⎝⎭设120n μμμ≥≥≥> 是A 的特征根，则有()210101112i i i ββλαμλλβαμλβλβαμβ+--+=-+++=<⇔++<+<则有：()()()11112,1211,0,1211,0i i B i ni n ρβαμβββαμββαμ<⇔++<+<≤≤+⇔<-<<≤≤+⇔<-<< 4.5. 证明：反证法。

清华大学贾仲孝老师高等数值分析报告第二次实验

高等数值分析第二次实验作业T1.构造例子特征值全部在右半平面时, 观察基本的Arnoldi 方法和GMRES 方法的数值性态, 和相应重新启动算法的收敛性. Answer:（1）构造特征值均在右半平面的矩阵A ：根据实Schur 分解，构造对角矩阵D 由n 个块形成，每个对角块具有如下形式，对应一对特征值i i i αβ±ii i i i S αββα-⎛⎫= ⎪⎝⎭这样D=diag(S 1,S 2,S 3……S n )矩阵的特征值均分布在右半平面。

生成矩阵A=U TAU ，其中U 为正交阵，则A 矩阵的特征值也均在右半平面。

不妨构造A 如下所示：2211112222/2/2/2/2N NA n n n n ⨯-⎛⎫⎪ ⎪ ⎪- ⎪= ⎪ ⎪ ⎪- ⎪ ⎪⎝⎭ 由于选择初值与右端项：x0=zeros(2*N,1);b=ones(2*N,1);则生成矩阵A 的过程代码如下所示：N=500 %生成A 为2N 阶 A=zeros(2*N); for a=1:NA(2*a-1,2*a-1)=a; A(2*a-1,2*a)=-a; A(2*a,2*a-1)=a; A(2*a,2*a)=a; endU = orth(rand(2*N,2*N)); A1 = U'*A*U;（2）观察基本的Arnoldi 和GMRES 方法编写基本的Arnoldi 函数与基本GMRES 函数，具体代码见附录。

function [x,rm,flag]=Arnoldi(A,b,x0,tol,m) function [x,rm,flag]=GMRES(A,b,x0,tol,m)输入:A 为方程组系数矩阵，b 为右端项，x0为初值，tol 为停机准则，m 为人为限制的最大步数。

输出:x 为方程的解，rm 为残差向量，flag 为解是否收敛的标志。

外程序如下所示： e=1e-6; m=700;tic[xA,rmA,flagA]=Arnoldi(A1,b,x0,e,m);toctic[xG,rmG,flagG]=GMRES(A1,b,x0,e,m);tocsubplot(1,2,1);semilogy(rmA)title('ArnoldiÊÕÁ²ÇúÏß')xlabel('µü´ú²½Êýk')ylabel('log(||rk||)')subplot(1,2,2);semilogy(rmG)title('GMRESÊÕÁ²ÇúÏß')xlabel('µü´ú²½Êýk')ylabel('log(||rk||)')得到：得到两种方法的收敛曲线如上所示，将计算结果整理在下表中：结果讨论：1.从图中可以看出，基本的Arnoldi方法经过546步收敛，基本的GMRES方法经过526步收敛，基本的GMRES收敛速度会略快于基本的Arnoldi方法。

清华大学高等数值分析_第三次作业答案

得如下算法： (1) 选初始 x0 ∈ Rn , 计算初始残差 r0 = b − Ax0 , ε > 0 为停机准则； (2) 对 k = 1, 2, . . .直到 rk < ε
T 求解 (D1 D1 + E T E )y1 = (AT rk−1 )(1 : m) ; T 求解 (D2 D2 + F T F )y2 = (AT rk−1 )(m + 1 : n) ;
1 0 0 0 √ √ 3 2 − 2 / 6 0 H= √ √ 0 2/ 6 1/2 − 3/6 √ 0 0 3/6 −1/2
1 1 7. 取上题中的矩阵 A 以及 b = , m = 2, x0 = 0, 完成求解 Ax = 1 1 G b 的 Arnoldi 和 GMRES 算法, 得出 xA 2 和 x2 . 8. 分别取 A1 = (aij ) = ( 2 1 ), i+j−1 1
?1102??????????nna3?????????????????????????2?112?1
高等数值分析第三章作业参考答案
1. 考虑线性方程组 Ax = b, 其中 A 是对称正定矩阵. 用 Galerkin 原理求解方程 K = L = Span(v ), 这里 v 是一个固定的向量. e0 = x∗ − x0 , e1 = x∗ − x1 证明 (e1 , Ae1 ) = (e0 , Ae0 ) − (r, v )2 /(Av, v ), 其中 r = b − Ax0 . v 应当取哪个向量在某种意义上是最佳的? (∗)
证明. 令 x1 = x0 + αv , 那么 r1 = r − αAv, e1 = e0 − αv . 由 Galerkin 原