框架在竖向荷载作用下内力计算解析
土木工程毕业设计 第六章 竖向荷载(恒载 活载)作用下框架内力计算讲解
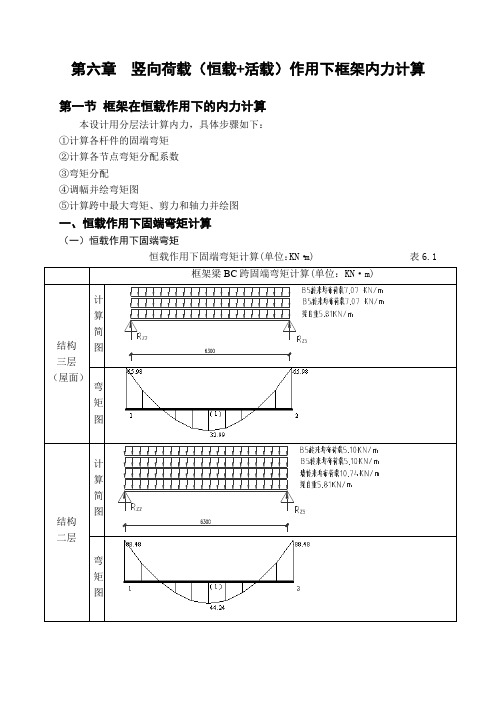
第六章竖向荷载(恒载+活载)作用下框架内力计算第一节框架在恒载作用下的内力计算本设计用分层法计算内力,具体步骤如下:①计算各杆件的固端弯矩②计算各节点弯矩分配系数③弯矩分配④调幅并绘弯矩图⑤计算跨中最大弯矩、剪力和轴力并绘图一、恒载作用下固端弯矩计算(一)恒载作用下固端弯矩恒载作用下固端弯矩计算(单位:KN·m) 表6.1弯矩图恒载作用下梁固端弯矩计算统计表6.2(二)计算各节点弯矩分配系数用分层法计算竖向荷载,假定结构无侧移,计算时采用力矩分配法,其计算要点是:①计算各层梁上竖向荷载值和梁的固端弯矩。
②将框架分层,各层梁跨度及柱高与原结构相同,柱端假定为固端。
③计算梁、柱线刚度。
对于柱,假定分层后中间各层柱柱端固定与实际不符,因而,除底层外,上层柱各层线刚度均乘以0.9修正。
有现浇楼面的梁,宜考虑楼板的作用。
每侧可取板厚的6倍作为楼板的有效作用宽度。
设计中,可近似按下式计算梁的截面惯性矩:一边有楼板:I=1.5Ir两边有楼板:I=2.0Ir④计算和确定梁、柱弯矩分配系数和传递系数。
按修正后的刚度计算各结点周围杆件的杆端分配系数。
所有上层柱的传递系数取1/3,底层柱的传递系数取1/2。
⑤按力矩分配法计算单层梁、柱弯矩。
⑥将分层计算得到的、但属于同一层柱的柱端弯矩叠加得到柱的弯矩。
(1)计算梁、柱相对线刚度图6.1 修正后梁柱相对线刚度(2)计算弯矩分配系数结构三层=5.37÷(5.37+1.18)=0.820①梁μB3C3μ=5.37÷(5.37+3.52+1.18)=0.533C3B3=3.52÷(5.37+3.52+1.18)=0.350μC3D3=3.52÷(3.52+1.18)=0.749μD3C3=1.18÷(5.37+1.18)=0.180②柱μB3B2=1.18÷(5.37+3.52+1.18)=0.117μC3C2=1.18÷(3.52+1.18)=0.251μD3D2结构二层①梁μ=5.37÷(1.18+1.18+5.37)=0.695B2C2=5.37÷(1.18+1.18+5.37+3.52)=0.477μC2B2μ=3.52÷(1.18+1.18+5.37+3.52)=0.313 C2D2=3.52÷(1.18+1.18+3.52)=0.5986 μD2C2=1.18÷(1.18+1.18+5.37)=0.1525②柱μB2B3μ=1.18÷(1.18+1.18+5.37)=0.1525B2B1=1.18÷(1.18+1.18+5.37+3.52)=0.105 μC2C3μ=1.18÷(1.18+1.18+5.37+3.52)=0.105 C2C1=1.18÷(1.18+1.18+3.52)=0.2007 μD2D3μ=1.18÷(1.18+1.18+3.52)=0.2007D2D1结构一层=5.37÷(1.18+1+5.37)=0.711①梁μB1C1=5.37÷(1.18+1+5.37+3.52)=0.485 μC1B1=3.52÷(1.18+1+5.37+3.52)=0.318 μC1D1=3.52÷(1.18+1+3.52)=0.618μD1C1=1.18÷(1.18+1+5.37)=0.156②柱μB1B2=1÷(1.18+1+5.37)=0.133μB1B0=1.18÷(1.18+1+5.37+3.52)=0.107μC1C2=1÷(1.18+1+5.37+3.52)=0.090μC1C0μ=1.18÷(1.18+1+3.52)=0.207D1D2μ=1÷(1.18+1+3.52)=0.175D1D0(三)分层法算恒载作用下弯矩恒载作用下结构三层弯矩分配表6.3B C D上柱偏心弯矩分配系数0固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次分配14.650 -13.883 226.915 20.861 -251.346 84.509 -112.810 二次分配14.512 -14.512 228.818 21.278 -250.096 105.707 -105.707恒载作用下结构二层弯矩分配表6.40.768 12.717 -28.301↑↑↑B C D偏心弯矩分配系数固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次分配 6.931 4.431 -4.607 308.811 46.295 47.232 -385.113 169.804 -113.072 -92.837二次分配 5.901 3.401 -9.302 300.595 44.486 45.423 -390.504 191.416 -105.826 -85.591恒载作用下结构一层弯矩分配表6.52.127 9.081 -7.935↑↑↑B C D偏心弯矩分配系数固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次二次7.030 5.338 -12.368 267.469 35.352 22.097 -324.919 357.349 -46.247 -15.172 -295.930图6.2 弯矩再分配后恒载作用下弯矩图(KN·m)(四)框架梁弯矩塑性调幅为了减少钢筋混凝土框架梁支座处的配筋数量,在竖向荷载作用下可以考虑竖向内力重分布,主要是降低支座负弯矩,以减小支座处的配筋,跨中则应相应增大弯矩。
框架在竖向荷载作用下内力计算

Mik MiFk 2Mi'k Mk' i
…3.6.4
或
Mik MiFk Mi'k (Mi'k Mk' i ) …3.6.5
➢ 根据算得的各杆端弯矩值,作最后的弯矩图并求得 相应的剪力图和轴力图。
例题:
0.463
A2
结点B2与结点A2分配系数相同
(2)计算固端弯矩:
mA2B2
1 12
q2l 2
1 12
10
82
53.333kN
gm
mB2 A2
1 12
q2l 2
1 12
10 82
53.333kN gm
(3)循环过程B2
A2
4、还原-叠加、结点不平衡弯矩再分配一次
6、计算框架梁其他截面的弯矩 计算框架梁截面的剪力 计算框架柱的轴力
结点A1:
S A1A2 4(0.9ic2 ) S A1A0 4ic1
S A1B1 4ib
S 4(ic1 0.9ic2 ib ) 4 2.478
A1
A1A2
S A1A2 S
4 0.9 1 0.363 4 2.478
A1
A1A0
S A1A0 S
4 0.801 4 2.478
1 0.0133E 12
ic 2
EIc H2
1 1 0.0666E 4 12
1 0.0166E 12
ib
EIb L
1 1 0.1029E 8Βιβλιοθήκη 121 0.0129E 12
相对线刚度: 设:ic2 1
则 ic1 0.801
ib 0.777
2、把框架以按层拆为两个开口框架
H2=4000
框架施工图—内力分析及侧移计算(建筑构造)

(2) 侧移刚度d的确定 侧移刚度d表示柱上下两端有单位侧移时在柱中产生的 剪力。根据假定(1),梁柱线刚度之比无穷大,则各 柱端转角为零,由结构力学的两端无转角但有单位水平 位移时杆件的杆端剪力方程,柱的侧移刚度d可写成:
V 12 i
d= =
c
D
h2
EI
i=
c
h
内力分析及侧移计算
(3)同层各柱剪力的确定
(5
柱端弯矩确定以后,根据节点平衡条件可确定梁的弯矩。
对于边柱节点(图(a)),有Mb=Mc1+Mc2 对于中柱节点(图1(b))
Mb1=ib1/(ib1+ib2)(Mc1+Mc2 Mb2=ib2/(ib1+ib2)(Mc1+Mc2)
内力分析及侧移计算
如图所示,从框架中任取一柱AB,根据转角位移方
内力分析及侧移计算
分层法
认为某层框架梁上的荷载只给本层梁及与本层梁相连的框架产 生剪力和弯矩
进行弯矩分配后叠加,叠加后的不平衡弯矩再分配但不传递
内力分析及侧移计算
2 框架在水平荷载作用下内力的近似计算——反弯点法和D值法
A 反弯点法 反弯点法基本假定: (1) 在进行各柱间的剪力分配时,假定梁与柱的线
(2) 在确定各柱的反弯点位置时,假定除底层柱以
多层多跨框架所受水平荷载主要是风荷载及水平 地震作用。一般可简化为作用在框架节点上的集中 荷载,其弯矩图如图(a)所示。它的特点是,各杆的 弯矩图都是直线形,每杆都有一个零弯矩点,称为 反弯点。框架在水平荷载作用下的变形情况如图(b) 所示
内力分析及侧移计算
程,柱两端剪力为:
V
=
12ic h2
6ic h
12.4多层框架结构在竖向荷载下的内力计算方法

12.4竖向荷载作用下的内力近似计算
第十二章 多层框架结构房屋
2.计算模型的确定 在计算简图中,框架节点多为刚接,柱子下端在基础顶面,也按刚接 考虑。杆件用轴线表示,梁柱的连接区用节点表示。等截面轴线取截面形 心位置,当上下柱截面尺寸不同时,则取上层柱形心线作为柱轴线。跨度 取柱轴线间的距离。计算简图中的柱高,对楼层取层高;对底层柱,现浇 楼板取基础顶面与二层楼板顶面之间的高度。 当各跨跨度不等但相差不超过10%时,可当作具有平静跨度的等跨框架。
12.4竖向荷载作用下的内力近似计算
第十二章 多层框架结构房屋
4.荷载计算
作用在多、高层建筑结构上的荷载有竖向荷载和水平荷载。竖向 荷载包括恒载和楼(屋)面活荷载、雪荷载,水平荷载包括风荷载和 水平地震作用。 活荷载大小见《建筑结构荷载规范》GB50009-2012第5.1.1条。
12.4竖向荷载作用下的内力近似计算
12.4竖向荷载作用下的内力近似计算
第十二章 多层框架结构房屋
由于计算时假定柱的远端为固定端,实际上除底层柱在基础处为固定 端外,其余各住的远端均有转角而非固定端。为减少由此引起的误差,除 底层柱外,其他各层柱的线刚度均乘以折减系数0.9,并取传递系数为1/3; 底层柱及梁的传递系数仍为1/2。 例12-2 用分层法计算例12-1框架的弯矩,并绘制弯矩图。
1转动刚度第十二章多层框架结构房屋124竖向荷载作用下的内力近似计算2分配系数第十二章多层框架结构房屋124竖向荷载作用下的内力近似计算3传递系数第十二章多层框架结构房屋124竖向荷载作用下的内力近似计算4杆端弯矩第十二章多层框架结构房屋124竖向荷载作用下的内力近似计算例121三跨二层钢筋混凝土框架各层框架梁所承受的竖向荷载设计值如图所示图中括号内数值为各杆件的相对线刚度
框架结构竖向荷载作用下的内力计算

第6章竖向荷载作用下内力计算§框架结构的荷载计算§6.1.1.板传荷载计算计算单元见下图所示:因为楼板为整体现浇,本板选用双向板,可沿四角点沿45°线将区格分为小块,每个板上的荷载传给与之相邻的梁,板传至梁上的三角形或梯形荷载可等效为均布荷载。
图6-1 框架结构计算单元图6-2 框架结构计算单元等效荷载一.B ~C, (D ~E)轴间框架梁:屋面板传荷载:恒载:2226.09KN/m 1.5m [1-2(1.5/6)(1.5/6)]2=17.128KN/m ⨯⨯+⨯活载:2222.0KN/m 1.5m [1-2(1.5/6)(1.5/6)]2=5.625KN/m ⨯⨯⨯+⨯楼面板传荷载:恒载:2223.83KN/m 1.5m [1-2(1.5/6)(1.5/6)]2=10.772KN/m ⨯⨯⨯+⨯活载:2222.0KN/m 1.5m [1-2(1.5/6)(1.5/6)]2=5.625KN/m ⨯⨯⨯+⨯梁自重:mB ~C, (D ~E)轴间框架梁均布荷载为:屋 面 梁:恒载=梁自重+板传荷载= KN/m+ KN/m= KN/m活载=板传荷载= KN/m楼面板传荷载:恒载=梁自重+板传荷载= KN/m+ KN/m= KN/m活载=板传荷载= KN/m二. C ~D 轴间框架梁:屋面板传荷载:恒载:2⨯⨯⨯6.09KN/m 1.2m5/82=9.135KN/m活载:22.0KN/m 1.5m5/82=3KN/m⨯⨯⨯楼面板传荷载:恒载:23.83KN/m 1.25/82=5.745KN/m⨯⨯⨯活载:2⨯⨯⨯2.0KN/m 1.2m5/82=3.75KN/m梁自重:mC~D轴间框架梁均布荷载为:屋面梁:恒载=梁自重+板传荷载= KN/m+ KN/m= KN/m活载=板传荷载=3 KN/m楼面板传荷载:恒载=梁自重+板传荷载= KN/m+m=m活载=板传荷载= KN/m三.B轴柱纵向集中荷载计算:顶层柱:女儿墙自重:(做法:墙高900㎜,100㎜的混凝土压顶)33⨯⨯+⨯⨯+m m kn m KN m m m0.240.918/25/0.10.24()⨯+⨯=m m m KN m1.220.240.5 5.806/顶层柱恒载=女儿墙+梁自重+板传荷载=5.806/6 3.975/(60.6)KN m KN m m m ⨯+⨯-⨯()()2212 1.5/6 1.5/66/42 6.09/ 1.55/832123.247KN m m KN ⎡⎤-⨯+⨯⨯+⨯⨯⨯⨯=⎣⎦顶层柱活载=板传荷载=()()222.0/ 1.512 1.5/6 1.5/66/42KN m m ⎡⎤⨯⨯-⨯+⨯⨯+⎣⎦2.0/ 1.55/83219.688KN m m KN ⨯⨯⨯⨯=标准层柱恒载=墙自重+梁自重+板荷载=7.794/(60.6) 3.975/(60.6) 3.83/ 1.55/832KN m KN m KN m m ⨯-+⨯-+⨯⨯⨯⨯ (2.332311.52)61/42 2.3325/61/42KN m ++⨯⨯⨯+⨯⨯⨯+()()223.83 1.512 1.5/6 1.5/66/42124.172m m KN ⎡⎤⨯⨯-⨯+⨯⨯=⎣⎦标准层柱活载=板传荷载=()()222.0 1.512 1.5/6 1.5/63 2.0 1.55/83219.688m m m m KN ⎡⎤⨯⨯-⨯+⨯+⨯⨯⨯⨯=⎣⎦基础顶面荷载=底层外纵墙自重+基础自重=9.738/(60.6) 2.5/(60.6)16.085KN m m m KN m m m KN ⨯-+⨯-=四.C 柱纵向集中力计算:顶层柱荷载=梁自重+板传梁荷载=3.975/(90.9) 2.349/(1.20.3) 6.09/ 1.55/832KN m m KN m m KN m m ⨯-+⨯-+⨯⨯⨯⨯ 6.09/ 1.25/8 1.22(2.3323/11.52/)61/42KN m m KN m KN m m +⨯⨯⨯⨯++⨯⨯⨯ 154.318KN =顶层柱活载=板传荷载=()()222.0 1.512 1.5/6 1.5/63m m ⎡⎤⨯⨯-⨯+⨯+⎣⎦()()222.0 1.212 1.2/6 1.2/63 2.0 1.2m m m m ⎡⎤⨯⨯-⨯+⨯+⨯⎣⎦5/8 1.22 2.0 1.55/83239.272m m KN ⨯⨯⨯+⨯⨯⨯⨯=标准柱恒载=墙+梁自重+板传荷载=11.52/(30.6)15.12/(30.6)15.12/(30.6)KN m m KN m m KN m m ⨯-+⨯-+⨯-+2.349/(1.20.3)3.975/(60.6) 6.09/ 1.55/832KN m m KN m m KN m m ⨯-+⨯-+⨯⨯⨯⨯+26.09/61/21/2 2.67/ 2.4/26 3.83/36200.173KN m m KN m m KN m m m KN ⨯⨯⨯+⨯⨯+⨯⨯=标准层活载=板传荷载=222.0/36 2.5/ 1.2654KN m m m KN m m m KN ⨯⨯+⨯⨯=基础顶面恒载=底层外纵墙自重+基础自重9.738/(60.6) 2.5/(60.6)66.085KN m m m KN m m m KN ⨯-+⨯-=(3).框架柱自重:柱自重: 底层:×0.6m ×0.6m ×253/KN m ×4.55m=其余柱:×0.6m ×0.6m ×253/KN m ×3.6m=§恒荷载作用下框架的内力§6.2.1.恒荷载作用下框架的弯矩计算一.恒荷载作用下框架可按下面公式求得:21/12ab M ql =- (61)-21/12ba M ql = (62)-故:2771/1221.03663.09.B C M KN m =-⨯⨯=-7763.09.C B M KN m =2771/1211.4846 5.512.C D M KN m =-⨯⨯=-77 5.512.C D M KN m =2661/1214.747644.241.B C M KN m =-⨯⨯=-6644.241.C B M KN m =2661/128.096 3.883.C D M KN m =-⨯⨯=-66 3.883.D C M KN m =恒荷载作用下框架的受荷简图如图6-3所示:注:1.图中各值的单位为KN2.图中数值均为标准值3.图中括号数值为活荷载图6-4:恒载作用下的受荷简图(2).根据梁,柱相对线刚度,算出各节点的弯矩分配系数ij μ:/()ij c b i i i μ=∑+∑ (63)-分配系数如图6-5 , 图6-6所示:图6-5 B 柱弯矩各层分配系数简图B 柱:底层:0.801/(0.8010.609 1.0)0.332i ++=下柱=1.0/(0.8010.609 1.0)0.415i ++=上柱=0.609/(0.8010.609 1.0)0.253i ++=左梁=标准层: 1.0/(0.609 1.0 1.0)0.383i ++=上柱=1.0/(0.609 1.0 1.0)0.383i ++=下柱=0.609/(0.609 1.0 1.0)0.234i ++=左梁=顶层: 1.0/(0.609 1.0)0.622i +=下柱=0.609/(0.609 1.0)0.622i +=左梁=图6-6 C 柱弯矩各层分配系数简图C 柱: 0.609/(0.609 1.00.2110.801)0.232i +++=右梁=1.0/(0.609 1.00.2110.801)0.382i +++=上柱= 0.801/(0.609 1.00.2110.801)0.306i +++=下柱= 0.211/(0.609 1.00.2110.801)0.081i +++=左梁=标准层: 1.0/(0.609 1.00.2110.801)0.355i +++=下柱=1.0/(0.609 1.00.2110.801)0.355i +++=上柱=0.609/(0.609 1.00.2110.801)0.216i +++=右梁=0.211/(0.609 1.00.2110.801)0.074i +++=左梁=顶层: 1.0/(0.609 1.00.211)0.549i ++=下柱=0.211/(0.609 1.00.211)0.116i ++=左梁=0.609/(0.609 1.00.211)0.335i ++=右梁=三.恒荷载作用下的弯矩剪力计算,根据简图(6-4)梁:A M 0∑= 21/2.0A B B M M ql Q l ---=/1/2B A B Q M M l ql =--B M 0∑= 21/2.0A B A M M ql Q l -+-=/1/2A A B Q M M l ql =-+ (6-4) 柱:C M 0∑= .0C D D M M Q h ---=()/D C D Q M M h =-+D M 0∑= .0C D C M M Q h ---=()/C C D Q M M h =-+ (6-5)四.恒荷载作用下的边跨框架的轴力计算,包括连梁传来的荷载及柱自重.7123.24721.1036/2186.556N KN=+⨯=67124.17214.7476/238.88393.849N N KN =++⨯+=56124.17214.7476/238.88601.142N N KN =++⨯+=45124.17214.7476/238.88808.435N N KN =++⨯+=34124.17214.7476/238.881015.728N N KN =++⨯+=23124.17214.7476/238.881223.021N N KN =++⨯+=12124.17214.7476/238.881382.487N N KN =++⨯+= 恒荷载作用下的中跨框架的轴力计算:7154.31811.484 2.4/2168.099N KN=+⨯=67200.1738.09 2.4/238.88416.88N N KN =++⨯+=56200.1738.09 2.4/238.88665.621N N KN =++⨯+=45200.1738.09 2.4/238.88808.435N N KN =++⨯+=34200.1738.09 2.4/238.881015.728N N KN =++⨯+=23200.1738.09 2.4/238.881223.021N N KN =++⨯+=12200.1738.09 2.4/238.881382.487N N KN =++⨯+=图6-5 恒荷载作用下的计算简图五.弯矩分配及传递弯矩二次分配法比分层法作了更进一步的简化。
4_竖向荷载作用下框架内力计算

4_竖向荷载作用下框架内力计算在结构设计过程中,框架结构是一种常见的结构形式。
在实际工程中,框架结构会受到各种荷载的作用。
竖向荷载是一种重要的荷载形式,常见的竖向荷载包括自重、活荷载和附加荷载等。
在框架结构内力计算中,需要首先确定结构的几何特征,包括框架的截面形状、材料参数和受力情况等。
然后根据几何特征和力学原理,分析结构的受力平衡和变形情况,最终得到内力的计算结果。
下面将以一个简单的框架结构为例,介绍竖向荷载作用下框架内力计算的基本步骤。
1.框架结构的受力分析首先,需要绘制框架的受力图。
在竖向荷载作用下,框架的受力主要包括竖向荷载的作用力、支座反力和框架内部的轴力、剪力和弯矩等。
通过受力分析,可以将框架结构简化为若干个矩形梁和柱,以便进行进一步的计算。
2.框架结构的力学模型化将框架结构进行力学模型化,即将结构划分为若干个杆件和节点,并确定节点的受力情况。
杆件的长度、截面形状和材料参数等需要根据实际情况进行设定,以便计算杆件的受力。
3.杆件的受力计算根据竖向荷载作用下杆件的受力平衡和变形情况,可以得到杆件的轴力、剪力和弯矩等。
对于轴力,可以利用静力平衡原理进行计算。
对于剪力和弯矩,可以根据杆件的受力分布和形状进行计算,常用的方法包括截面法和弯矩传递法等。
4.框架结构的内力计算根据杆件的受力计算结果,可以得到框架结构内各个节点的内力情况。
根据节点的受力平衡条件,可以计算出节点上的轴力、剪力和弯矩等。
此外,还需要考虑支座反力的作用,以及与其他荷载(如横向荷载)的叠加效应。
5.内力的承载能力和设计校核根据内力计算结果,可以对框架结构的承载能力进行评估和校核。
根据设计规范和材料参数,结合强度和稳定性要求,进行构件的截面尺寸校核。
如果结构的承载能力满足要求,则结构设计合理;否则,需要进行后续的调整和优化。
总的来说,竖向荷载作用下框架内力计算是结构设计中的重要环节。
通过合理的受力分析和计算,能够得到准确的内力计算结果,从而为结构设计和施工提供科学的依据。
框架结构竖向荷载作用下的内力计算

框架结构竖向荷载作用下的内力计算框架结构是由梁柱等构件组成的,在受到竖向荷载作用下,会引起构件内力的产生。
了解框架结构竖向荷载作用下的内力计算对于结构的设计和分析非常重要。
下面将详细介绍框架结构竖向荷载作用下的内力计算方法。
首先,通过建立结构模型来描述框架结构。
结构模型中包括构件、节点和连接关系。
构件可以是梁或柱,节点是构件之间的连接点,连接关系表示构件之间的刚性约束。
在竖向荷载作用下,框架结构的内力主要有两种情况:梁内力和柱内力。
1.梁内力计算:在竖向荷载作用下,梁会产生弯矩和剪力。
根据梁的基本理论,可以得出计算弯矩和剪力的公式。
-弯矩计算:弯矩是由竖向荷载作用在梁上引起的。
根据弯矩的定义,弯矩M等于施加在梁上的力乘以力臂。
当梁需要承受重力荷载时,弯矩的计算公式为M=w*l^2/8,其中w为荷载大小,l为梁的跨度。
-剪力计算:剪力是由竖向荷载作用在梁上引起的。
根据剪力的定义,剪力V等于施加在梁上的力。
当梁需要承受重力荷载时,剪力的计算公式为V=w*l/2,其中w为荷载大小,l为梁的跨度。
2.柱内力计算:在竖向荷载作用下,柱会产生压力和拉力。
根据柱的基本理论,可以得出计算压力和拉力的公式。
-压力计算:压力是由竖向荷载作用在柱上引起的。
根据力学平衡原理,压力P等于施加在柱上的荷载之和。
当柱需要承受多个重力荷载时,压力的计算公式为P=∑w,其中w为荷载大小。
-拉力计算:拉力是由竖向荷载作用在柱上引起的。
和压力类似,拉力T等于施加在柱上的荷载之和。
在实际计算过程中,需要考虑梁和柱的截面形状和材料性质,以及节点和连接部位的刚性约束等因素。
同时,还需要考虑结构的整体平衡条件和节点处的力的平衡条件。
在计算过程中,可以使用静力平衡原理和弹性力学理论来进行分析。
通过平衡方程和应变-位移关系等基本原理,可以建立结构方程组,并通过求解方程组得到内力的值。
总结起来,框架结构竖向荷载作用下的内力计算是一个复杂的过程,需要考虑多个因素和使用多种方法。
第七章 竖向荷载作用下框架内力计算
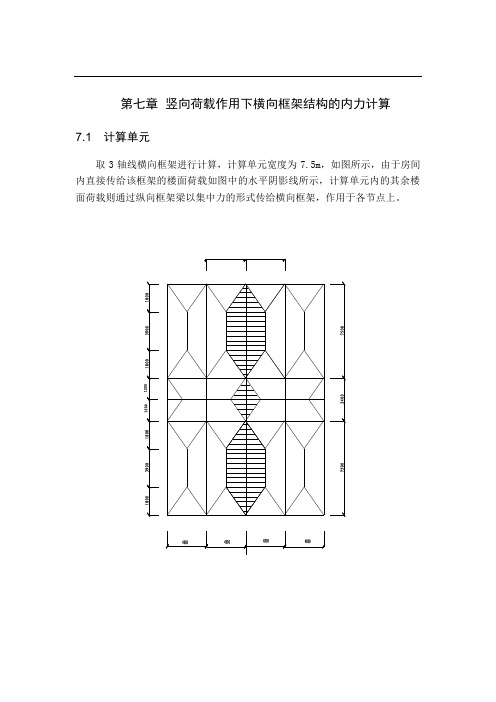
第七章 竖向荷载作用下横向框架结构的内力计算7.1 计算单元取3轴线横向框架进行计算,计算单元宽度为7.5m ,如图所示,由于房间内直接传给该框架的楼面荷载如图中的水平阴影线所示,计算单元内的其余楼面荷载则通过纵向框架梁以集中力的形式传给横向框架,作用于各节点上。
7.2 荷载计算节点集中荷载1P : 边纵梁传来:(a)屋面自重(三角形部分):N k 78.56298.423.3.26.3=⨯⨯⨯(b)边纵梁自重: 5.709⨯6.0=43.73kN 女儿墙自重: kN 87.330.6312.3=⨯合计: 1P = 154.32kN节点集中荷载2P :纵梁传来(a )屋面自重(三角形部分):KN 12.27298.40.326.3=⨯⨯⨯(b )走道屋面板自重0.5⨯(6.0+6.0-3)⨯1.5⨯4.98=58.79KN纵梁自重: 5.709⨯6.0=43.73kN合计: 2P = 170.55kN对于1~4层,计算的方法基本与第五层相同,计算过程如下: 1 5.709/q kN m =1q '=3.46/kN/mm KN q /99.103.333.32=⨯= m KN q /99.74.233.32=⨯=节点集中荷载1P :纵梁自重: 5.709⨯6.0=43.73kN外墙自重:()88.76KN 68.37.03.3225.00.6=⨯-⨯⨯-)( 来纵梁传楼面自重(三角形部分): (0.5 3.60.5 3.6 3.33)221.58kN ⨯⨯⨯⨯⨯= 扣窗面积墙重加窗重: 2 2.4 2.0 3.682 2.1631.01kN -⨯⨯⨯+⨯=-合计: 174.24kN节点集中荷载2P :纵梁自重: 5.709⨯7.2=41.10kN 内墙自重: 71.50kN 纵梁传来(a)楼面自重(三角形部分):()KN5.0=⨯0.3⨯⨯5.0⨯⨯66.233.3780.3(b)走道楼面板自重(梯形部分)()KN⨯5.0=⨯5.7⨯+-48.9333.30.38.15.7扣窗面积墙重加窗重: 2.412 3.6820.4816.10kN-⨯⨯⨯+⨯=-合计: 152.58kN 7.2.2活荷载计算:活荷载作用下各层框架梁上的荷载分布如图:合计: 7.99KNP:节点集中荷载2屋面活载(三角形部分):2⨯(0.5⨯3.0⨯0.5⨯3.0⨯0.5)=2.72KN走道传来屋面荷载(梯形部分): ()KN 05.45.05.14.20.60.621=⨯⨯-+合计: 12.04KN 对于1~4层,m KN /6.60.30.2q 2=⨯= m KN q /64.25.2'2=⨯= 节点集中荷载1P : 楼面活载(三角形部分):2⨯(0.5⨯3.30.5⨯3.3⨯2)=10.89KN合计: 31.97KN中节点集中荷载2P : 楼面活载(三角形部分):2⨯(0.5⨯3.30.5⨯3.3⨯2)=10.89KN走道传来屋面荷载(梯形部分):()KN 25.205.25.14.20.60.621=⨯⨯-+ 纵梁传来的屋面活载(梯形部分):()KN 08.2128.10.35.75.75.0=⨯⨯-+⨯ 合计: 52.22KN7.2.3.屋面雪荷载标准值:同理,在屋面雪荷载作用下KN/m 16.10.335.0q 2=⨯= m KN q /84.04.235.0'2=⨯=节点集中荷载1P : 屋面雪载(三角形部分):2⨯(0.5⨯3.3⨯0.5⨯3.3⨯0.35)=2.08KN纵梁传来的屋面雪载(梯形部分)()KN 69.335.08.16.35.75.75.0=⨯⨯-+⨯ 合计: 5.77KN中节点集中荷载2P : 屋面雪载(三角形部分):2⨯(0.5⨯3.3⨯0.5⨯3.3⨯0.35)=2.08KN走道传来屋面雪载(梯形部分): ()KN 835.235.05.14.25.75.721=⨯⨯-+纵梁传来的屋面雪载(梯形部分): 3.97KN 合计: 8.72KN 1~4层,雪荷载作用下的节点集中力同屋面活荷载作用下的。
土木工程毕业设计 第六章 竖向荷载作用下框架内力计算

第六章竖向荷载(恒载+活载)作用下框架内力计算第一节框架在恒载作用下的内力计算本设计用分层法计算内力,具体步骤如下:①计算各杆件的固端弯矩②计算各节点弯矩分配系数③弯矩分配④调幅并绘弯矩图⑤计算跨中最大弯矩、剪力和轴力并绘图一、恒载作用下固端弯矩计算(一)恒载作用下固端弯矩恒载作用下固端弯矩计算(单位:KN·m) 表恒载作用下梁固端弯矩计算统计表(二)计算各节点弯矩分配系数用分层法计算竖向荷载,假定结构无侧移,计算时采用力矩分配法,其计算要点是:①计算各层梁上竖向荷载值和梁的固端弯矩。
②将框架分层,各层梁跨度及柱高与原结构相同,柱端假定为固端。
③计算梁、柱线刚度。
对于柱,假定分层后中间各层柱柱端固定与实际不符,因而,除底层外,上层柱各层线刚度均乘以修正。
有现浇楼面的梁,宜考虑楼板的作用。
每侧可取板厚的6倍作为楼板的有效作用宽度。
设计中,可近似按下式计算梁的截面惯性矩:一边有楼板:I=两边有楼板:I=④计算和确定梁、柱弯矩分配系数和传递系数。
按修正后的刚度计算各结点周围杆件的杆端分配系数。
所有上层柱的传递系数取1/3,底层柱的传递系数取1/2。
⑤按力矩分配法计算单层梁、柱弯矩。
⑥将分层计算得到的、但属于同一层柱的柱端弯矩叠加得到柱的弯矩。
(1)计算梁、柱相对线刚度图修正后梁柱相对线刚度(2)计算弯矩分配系数结构三层=÷+=①梁μB3C3μ=÷++=C3B3=÷++=μC3D3μ=÷+=D3C3=÷+=②柱μB3B2μ=÷++=C3C2μ=÷+=D3D2结构二层=÷++=①梁μB2C2μ=÷+++=C2B2=÷+++=μC2D2μ=÷++=D2C2②柱μ=÷++=B2B3=÷++=μB2B1=÷+++=μC2C3=÷+++=μC2C1=÷++=μD2D3μ=÷++=D2D1结构一层=÷+1+=①梁μB1C1=÷+1++=μC1B1=÷+1++=μC1D1=÷+1+=μD1C1=÷+1+=②柱μB1B2=1÷+1+=μB1B0=÷+1++=μC1C2=1÷+1++=μC1C0μ=÷+1+=D1D2μ=1÷+1+=D1D0(三)分层法算恒载作用下弯矩恒载作用下结构三层弯矩分配表B C D上柱偏心弯矩分配系数0固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次分配二次分配恒载作用下结构二层弯矩分配表↑↑↑B C D偏心弯矩分配系数固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次分配二次分配恒载作用下结构一层弯矩分配表↑↑↑B C D偏心弯矩分配系数固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次二次图弯矩再分配后恒载作用下弯矩图(KN·m)(四)框架梁弯矩塑性调幅为了减少钢筋混凝土框架梁支座处的配筋数量,在竖向荷载作用下可以考虑竖向内力重分布,主要是降低支座负弯矩,以减小支座处的配筋,跨中则应相应增大弯矩。
竖向荷载作用下内力分析 (2)

5.6 竖向荷载作用下内力分析: 5.6.1 计算单元及计算简图的确定:仍取④轴线横向框架和⑤⑥轴线间的横向剪力墙进行计算,由于楼面荷载均匀分布,故取两轴线中线之间的长度为计算单元宽度,计算简图如下图所示:图1-35 竖向荷载计算单元 5.6.2 荷载计算(标准值): 5.6.2.1框架荷载计算: (1)恒荷载作用情况下:0q 包括梁重(扣除板重)和隔墙重,由前面的相关数据得:1~8F :()()32025/0.80.10.4 1.88/ 3.60.8q KN m m m m KN m m =⨯-⨯+⨯-7/ 5.828/12.828/KN m KN m KN m =+= 9F : 0 6.7/q K N m =(注:0'7.0/q KN m =)12,q q 为板自重传给横梁的荷载峰值:1~8F :2122 3.8/ 4.215.96/3.8/ 4.215.96/q KN m m KN m q KN m m KN m=⨯==⨯=9F :2122 6.84/ 4.228.728/6.84/ 4.228.728/q K N m m K N m q K N m m K N m =⨯==⨯=1P 为纵梁传给○A 柱的板自重、梁自重(扣除板厚)和外隔墙重:1~5F :()()21 2.1 4.2 2.113.8/ 4.2 2.127/8.40.6522P KN m KN m m m +⨯⎡⎤=⨯⨯⨯+⨯+⨯-⎢⎥⎣⎦()()22.21/3.90.88.40.65K N m m m m m +⨯-⨯- 198.317KN = 6~8F :()()()190.972 2.21/ 3.90.878.40.55P KN KN m m =+⨯-⨯8.4-0.55+⨯- 199.702KN =9F :()21 6.84/11.972 6.7216.35P KN m KN =⨯⨯+⨯8.4-0.55=1M 为1P 对上柱形心轴产生的偏心矩:1~5F :1198.3170.07514.874M KN m KM m =-⨯=- 6~8F :1199.7020.025 4.993M KN m KM m =-⨯=-9F : 1216.350.025 5.409M K N m K M m=-⨯=- 此外,2P 、3P 、4P 分别为纵梁传给○B 轴、○C 轴、○D 轴柱的板自重、梁自重(扣除板厚)和外隔墙重,4M 为4P 对上柱形心轴产生的偏心矩,计算方法如上所述,计算过程从略,计算结果见表1-31 。
第六章-框架在竖向荷载作用下的内力分析
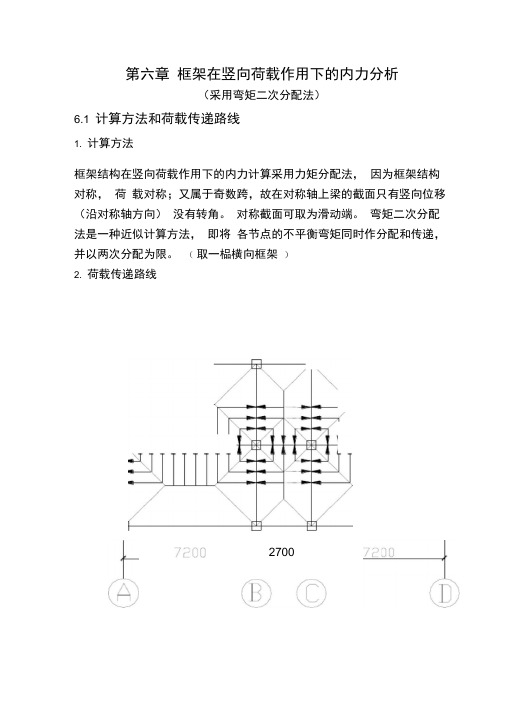
第六章框架在竖向荷载作用下的内力分析(采用弯矩二次分配法)6.1 计算方法和荷载传递路线1. 计算方法框架结构在竖向荷载作用下的内力计算采用力矩分配法,因为框架结构对称,荷载对称;又属于奇数跨,故在对称轴上梁的截面只有竖向位移(沿对称轴方向)没有转角。
对称截面可取为滑动端。
弯矩二次分配法是一种近似计算方法,即将各节点的不平衡弯矩同时作分配和传递,并以两次分配为限。
(取一榀横向框架)2. 荷载传递路线2700对于边跨板,为7.2 m×4.5m,由于7.2/4.5<3.0 所以按双向板计算对于中跨板,为 4.5m×2. 7m,由于 4.5/2.7 〈3.0 所以按双向板计算6.2 竖向荷载计算5.2.1 A-B(C-D) 轴间框架梁板传至梁上的三角形或梯形荷载等效为均布荷载。
1. 屋面板传载恒载: 5.0 ×4.5/2 ×(1-2 ×0.312+0.313) ×2=18.85kN/m活载:0.5 ×4.5/2 ×(1-2 ×0.312+0.313) ×2=1.89kN/m2. 楼面板传荷载恒载: 3.99 ×4.5/2 ×(1-2 × 0.31 2+0.31 3) ×2=15.08kN/m活载: 2.0 ×4.5/2 ×(1-2 ×0.312+0.313) ×2=7.56kN/m3. 梁自重: 5.46 kN/mA-B(C-D) 轴间框架梁均布荷载为:屋面梁:恒载=梁自重+板传荷载=5.46 kN/m+18.85 kN/m=24.31 kN/m 活载=板传荷载=1.89 kN/m楼面梁:恒载=梁自重+板传荷载=5.46 kN/m+15.08 kN/m=20.54 kN/m 活载=板传荷载=7.56 kN/m5.2.2 B-C 轴间框架梁1. 屋面板传载恒载: 5.0 ×2.4/2 ×5/8 ×2=8.44kN/m活载:0.5 ×2.7/2 ×5/8 ×2=0.84kN/m2. 楼面板传荷载恒载: 3.99 ×2.7/2 ×5/8 ×2=6.73kN/m活载: 2.0 ×2.7/2 ×5/8 ×2=4.22kN/m3. 梁自重: 3.9kN/mB-C 轴间框架梁均布荷载为:屋面梁:恒载=梁自重+板传荷载=3.9 kN/m+8.44kN/m=12.34kN/m 活载=板传荷载=0.84kN/m楼面梁:恒载=梁自重+板传荷载=3.9 kN/m+6.73kN/m=10.63kN/m 活载=板传荷载=4.22kN/m6.3 框架计算简图g=24.31KN/m g=12.34KN/m g=24.31KN/m(q=1.89KN/m)2700框架计算简图6.4. 梁固端弯矩梁端弯矩以绕杆端顺时针为正,反之为负。
竖向荷载作用下框架结构的内力计算
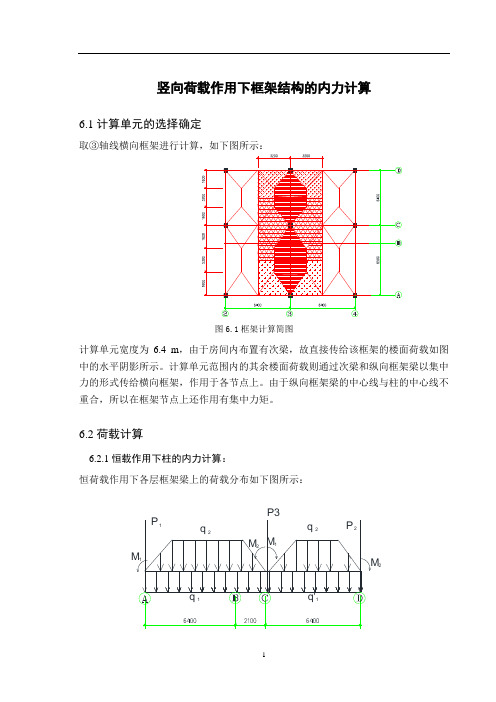
竖向荷载作用下框架结构的内力计算6.1计算单元的选择确定取③轴线横向框架进行计算,如下图所示:图6.1框架计算简图计算单元宽度为6.4 m,由于房间内布置有次梁,故直接传给该框架的楼面荷载如图中的水平阴影所示。
计算单元范围内的其余楼面荷载则通过次梁和纵向框架梁以集中力的形式传给横向框架,作用于各节点上。
由于纵向框架梁的中心线与柱的中心线不重合,所以在框架节点上还作用有集中力矩。
6.2荷载计算6.2.1恒载作用下柱的内力计算:恒荷载作用下各层框架梁上的荷载分布如下图所示:2图6.2恒荷载作用下各层框架梁上的荷载分布图(1)、对于顶层屋面,q1、q1'代表横梁自重,为均布荷载形式。
q1=0.3×0.75×25=5.625kN/mq1'=0.3×0.75×25=5.625kN/mq2为屋面板传给横梁的梯形荷载。
q2=5.29×3.2=16.928kN/mP1、P2分别由边纵梁、中纵梁直接传给柱的恒载,它包括主梁自重、次梁自重、楼板重等重力荷载,计算如下:P1=6.4*0.3*0.75*25+8.5/2*0.25*0.6*25+5.29*3.2*1.6+(5.3+8.5)*1.6*5.29/4=108.223KN P2=6.4*0.3*0.75*25+6.4/2*0.25*0.6*25+5.29*3.2*1.6 +(3.2+6.4)*1.6*5.29/4=95.398KN P3=6.4*0.3*0.75*25+(8.5+6.4)*0.5*0.25*0.6*25+5.29*3.2*1.6*2++(3.2+6.4)*1.6*5.29/4= 190.64KN集中力矩M1=P1e1=108.223×(0.6 -0.3)/2=16.23kN·mM2=P2e2=147.23×(0.6 -0.3)/2=14.31kN·m(2)、对于3层,包括梁自重和其上横墙自重,为均布荷载,其它荷载的计算方法同第顶层。
竖向荷载作用下框架结构采用分层法进行内力计算举例

竖向荷载作用下框架结构采用分层法进行内力计算举例
例,某8层框架,底层层高5.0m ,其余层层高3.2 m ,各层横梁竖向均布荷载为12kN/m ,各层梁柱的相对线刚度如下图所示,用分层法计算此框架在竖向荷载作用下的弯矩。
梁柱相对线刚度图
解:分层法采用力矩分配法计算,具体过程见以下各图,各杆的分配系数写在方框内。
带*号的数值是固端弯矩,各结点均分配两次,次序为先两边结点,后中间结点。
固端弯矩分配时要变号,弯矩传递不变号。
梁端弯矩传递系数为1/2,顶层和中间层各柱远端弯矩等于各柱近梁端弯矩的1/3(即传递系数为1/3),底层各柱远端弯矩等于各柱近梁端弯矩的1/2(即传递系数为1/2)。
最下一行数字为分配后各杆端弯矩。
12
-2
ql M =均载固, Fe M -=集中荷载固, 集中荷载均载梁固端M M M +=
顶层框架力矩分配过程
顶层弯矩图
中间层框架力矩分配过程
中间层弯矩图
底层框架力矩分配过程
底层弯矩图
各层柱端弯矩叠加,不平衡弯矩可再进行一次分配,得到框架弯矩总图(略)。
梁剪力可采用结构力学取脱离体的方法。
某框架顶层受荷图
完成顶层框架力矩分配过程。
计算竖向荷载作用下的框架结构的方法

计算竖向荷载作用下的框架结构的方法框架结构是一种常见的建筑结构,它由柱子和梁组成。
竖向荷载是作用在结构的垂直方向上的力,包括自重、楼层荷载、雨水荷载、雪荷载等。
为了确保框架结构的安全性和承载能力,需要进行竖向荷载的计算和分析。
在计算竖向荷载作用下的框架结构时,一般采用结构分析的方法,包括静力分析和动力分析。
静力分析是指在结构不考虑振动和位移的情况下进行的力学分析。
它主要采用受力平衡方程来计算结构的内力和变形。
对框架结构来说,可以采用刚度法、位移法和力法等方法进行分析。
1. 刚度法:刚度法是一种常用的静力分析方法。
它基于结构刚度和受力平衡原理,将结构划分为单元,通过计算单元的刚度矩阵和节点位移来求解结构的内力和变形。
刚度法适用于简单框架结构的分析,通过构建刚度方程组,可以求解出结构的内力和位移。
2. 位移法:位移法是一种将结构的位移作为主要未知量的静力分析方法。
它基于受力平衡原理和位移相容条件,将结构划分为单元,在每个单元内根据位移的连续性和力的平衡关系建立方程。
通过求解位移方程组,可以得到结构的内力和位移。
3. 力法:力法是一种以力作为主要未知量的静力分析方法。
它基于受力平衡原理和材料力学性质,通过构建力的平衡方程组和力的变形关系式,求解出结构的内力和位移。
力法适用于结构相对复杂,难以直接建立刚度方程的情况。
动力分析是指考虑结构的振动和变形对受力和稳定性的影响进行分析。
在竖向荷载作用下的框架结构中,垂直地震荷载是最常见且重要的动力荷载。
动力分析一般分为静态分析和动态分析。
1. 静态分析:静态分析是指在地震作用下无需考虑结构的动力响应,主要考虑的是结构的受力和变形。
通过采用静态等效荷载法,将地震荷载转化为与之等效的静态荷载进行分析。
静态分析适用于低层次、简单结构,不涉及结构的动力特性。
2. 动态分析:动态分析是指考虑结构的动力响应,对地震荷载进行全面分析。
动态分析可以细分为线性动力分析和非线性动力分析。
竖向荷载作用下框架结构的内力计算计算书3:正文6-11章

第6章竖向荷载作用下框架结构的内力计算6.1计算单元的确定取7轴线横向框架进行计算,计算单元宽度为2.75m,如图6.1所示。
传给该框架的楼面荷载如图中的水平阴影线所示,计算单元范围内的其余楼面荷载则通过次梁和纵向框架梁以集中力的形式传给横向框架,作用于各节点上。
由于纵向框架的中心线与柱的中心线不重合,因此在框架节点上还作用有集中力矩。
图6.1 计算单元6.2 竖向荷载计算6.2.1恒荷计算1.1-5层荷载计算:梁自重:梁AB=2.1kN/m梁BD=2.1kN/m梁DE=2.1kN/m挑梁=0.525kN/m板传递给梁的梯形及三角形荷载:板AB(左)=3.742kN/m×1.35m=5.05kN/m板AB(右)=3.742kN/m×1.5m=5.61kN/m板BD(左)=3.742kN/m×1.95m=7.29kN/m板BD(右)=3.742kN/m×2.1m=7.85kN/m板DE(左)=3.742kN/m×1.35m=5.05kN/m板DE(右)=3.742kN/m×1.4m=5.24kN/m悬挑部分的板为单向板,所以直接传递给梁的恒荷载为零墙自重:墙AB =2.12×2.4=5.09kN/m墙BD =2.12×2.4=5.09kN/m墙DE =2.12×2.4=5.09kN/m墙悬挑=2.12×2.6=5.51kN/m恒载:梁自重+板传荷载+墙自重挑梁=梁自重+墙自重柱的集中力:A 3.740.50.5 2.71.350.531.5 2.850.525 2.375 2.6 2.8526.78kNP=⨯⨯⨯⨯+⨯⨯⨯⨯⨯=()++B 3.740.50.5 2.7 1.350.53 1.5 2.850.5250.5 3.743.150.750.50.5 1.95 1.950.5 2.1 3.9 2.12 2.6 2.8538.31k NP =⨯⨯⨯⨯+⨯⨯⨯⨯⨯⨯⨯+⨯⨯+⨯⨯+⨯⨯=()++() D 3.740.50.5 2.71.350.5 2.81.4 2.750.5250.5 3.743.150.750.50.5 1.951.950.5 2.1 3.5 2.12 2.6 2.7536.31kNP =⨯⨯⨯⨯+⨯⨯⨯⨯⨯⨯⨯+⨯⨯+⨯⨯+⨯⨯=()++() E 3.740.50.5 2.71.350.5 2.81.4 2.750.5250.5 3.740.65 5.52.375 2.6 2.8532.8kNP =⨯⨯⨯⨯+⨯⨯⨯⨯⨯⨯+⨯⨯=()++E 0.5 3.740.65 5.5 2.750.525 2.375110.5kN P -=⨯⨯⨯⨯+⨯=+柱所受集中力产生的弯矩:A 26.78(0.450.2)/2 3.35kN m M =⨯-=⋅B 0kN m M =⋅D 36.31(0.450.2)/2 4.45kN m M =⨯-=⋅E 32.8(0.450.2)/2 4.1kN m M =⨯-=⋅ 2.6层荷载计算:梁自重:梁AB=2.1kN/m梁BD=2.1 kN/m 梁DE=2.1kN/m挑梁=0.525 kN/m板传递给梁的梯形及三角形荷载: 板AB (左)=3.742kN/m ×1.35m=5.05kN/m 板AB (右)=3.742kN/m ×1.5m=5.61kN/m 板BD (左)=3.742kN/m ×1.95m=7.29kN/m 板BD (右)=3.742kN/m ×2.1m=7.85kN/m 板DE (左)=3.742kN/m ×1.35m=5.05kN/m 板DE (右)=3.742kN/m ×1.4m=5.24kN/m 悬挑部分的板为单向板,所以直接传递给梁的恒荷载为零 墙自重: 墙AB =2.12×1.925=4.081kN/m墙BD =2.12×3.36=7.12kN/m 墙DE =2.12×1.725=3.657kN/m恒载:梁自重+板传荷载+墙自重挑梁=梁自重 柱的集中力 A 3.740.50.5 2.71.350.531.5 2.850.525 2.3750.6 2.8513.17kN P =⨯⨯⨯⨯+⨯⨯⨯⨯⨯=()++ B 3.740.50.5 2.71.350.531.5 2.850.5250.5 3.74 3.150.750.50.51.951.950.5 2.1 3.922.6kN P =⨯⨯⨯⨯+⨯⨯⨯⨯⨯⨯⨯+⨯⨯+⨯⨯=()++() D 3.740.50.5 2.71.350.5 2.81.4 2.750.5250.5 3.74 3.150.750.50.51.951.950.5 2.1 3.521.15kN P =⨯⨯⨯⨯+⨯⨯⨯⨯⨯⨯⨯+⨯⨯+⨯⨯=()++() E 3.740.50.5 2.71.350.5 2.81.4 2.750.5250.5 3.740.65 5.5 2.375 0.6 2.8519.26 kNP =⨯⨯⨯⨯+⨯⨯⨯⨯⨯⨯+⨯⨯=()++-E 0.5 3.740.65 5.5 2.750.5258.13kN P =⨯⨯⨯⨯=+柱所受集中力产生的弯矩:A 13.17(0.450.2)/2 1.65kN m M =⨯-=⋅B 0kN m M =⋅D 21.15(0.450.2)/2 2.64kN m M =⨯-=⋅E 19.26(0.450.2)/2 2.41kN m M =⨯-=⋅ 3.顶层荷载计算:梁自重:梁AB=2.35 kN/m 梁BD=2.35 kN/m 梁DE=2.35 kN/m板传递给梁的梯形及三角形荷载: 板AB (左)=5.192kN/m ×1.35m=7.01kN/m 板AB (右)=5.192kN/m ×1.5m=7.79kN/m 板BD (左)= 5.192kN/m ×1.95m=7.29kN/m 板BD (右)= 5.192kN/m ×2.1m=10.9kN/m 板DE (左)= 5.192kN/m ×1.35m=7.01kN/m 板DE (右)= 5.192kN/m ×1.4m=7.27kN/m 悬挑部分的板为单向板,所以直接传递给梁的恒荷载为零柱的集中力: A 5.190.50.5 2.71.350.531.5 2.850.5251.1212.24kN P =⨯⨯⨯⨯+⨯⨯⨯⨯=()+ B 5.190.50.5 2.7 1.350.53 1.5 2.850.525 1.120.55.19 3.15 0.750.50.51.951.950.5 2.1 3.915.83kN P =⨯⨯⨯⨯+⨯⨯⨯⨯⨯⨯⨯⨯+⨯⨯+⨯⨯=()++() D 5.190.50.5 2.71.350.5 2.81.4 2.750.5251.120.5 5.19 3.150.750.50.51.951.950.5 2.1 3.528.97kNP =⨯⨯⨯⨯+⨯⨯⨯⨯⨯⨯⨯⨯+⨯⨯+⨯⨯=()++() E 5.190.50.5 2.7 1.350.5 2.8 1.49.82k NP =⨯⨯⨯⨯+⨯⨯=()柱所受集中力产生的弯矩:A 12.24(0.450.2)/2 1.53kN m M =⨯-=⋅B 0kN m M =⋅ D 28.97(0.450.2)/2 3.62kN m M =⨯-=⋅ E 9.82(0.450.2)/2 1.23kN m M =⨯-=⋅6.2.2 活荷载计算活荷载作用下各层框架梁上活载为板传递给梁的荷载。
在竖向荷载作用下框架结构内力计算的独立柱法

在竖向荷载作用下框架结构内力计算的独立
柱法
独立柱法(Independent column method)是一种用于计算框架结
构内力的方法。
该方法假定每个柱子自行承担着水平力和垂直力,而
不会在柱与梁交接处转移或者共同承担力。
这种假设是为了简化计算、降低复杂度,以及实现直观清晰的用图。
在竖向荷载作用下,独立柱法的基本流程如下:
1. 选择独立柱:首先,需要找到框架结构中具有独立性的柱子。
这些柱子不会受到其他柱子影响,而是自行承担全部荷载。
一般而言,独立柱一般位于框架结构的边缘或角落处。
2. 画高度分块图:将框架结构按水平方向分成若干段,并在每段
上标注高度分块图。
高度分块图指的是每段内荷载分别作用的高度分
布情况。
3. 分别计算每段内的内力:对于每个高度分块,需要按照作用在
该块上的荷载大小和作用位置,结合高度分块的边界条件计算出该段
内的各个柱子和梁的内力。
4. 检查结构的均衡性:根据计算结果,检查整个框架结构是否处
于静态均衡状态,即荷载是否平衡、荷载反力大小是否与荷载大小等
比例,以及结构中每个柱子和梁是否都满足受力平衡。
5. 进行调整和修正:如有必要,可通过对独立柱、高度分块等参
数进行调整和修正,重新计算内力直到满足均衡条件。
总之,独立柱法是一种通过分析框架结构内各部分的受力情况,
来计算出结构整体受力状态的方法。
虽然存在简化和理论假设的缺陷,但该方法依然具有较高的实用价值。
第五章.竖向荷载作用下的框架内力计算

第五章.竖向荷载作⽤下的框架内⼒计算5.1 计算单元的确定取6号轴线⼀榀框架进⾏计算,计算宽度为(6.6+6.6)/2=6.6m 。
如图下图所⽰横向框架荷载传递图5.2 荷载计算5.2.1 恒荷载的计算 1、五层、(1)q 、q 0、q 0′、q 0″分别为⼥⼉墙、边跨横梁(⾛道纵梁)、⾛道横梁、次梁⾃重(扣除板⾃重),为均布荷载形式;β为考虑梁粉刷⾃重时的放⼤系数,取β=1.05。
⼥⼉墙:q=3.47×0.9=3.12 kN/m 边跨横梁(⾛道纵梁):q 0=1.05×0.3×(0.6-0.1)×25=3.94kN/m ⾛道横梁:q 0′=1.05×0.3×(0.4-0.1)×25=2.36kN/m 次梁:q 0″=1.05×0.2×(0.5-0.1)×25=2.1kN/m(2)q 1、q 1′分别为屋⾯板⾃重传给横梁的梯形和三⾓形荷载等效为均布荷载值 q 1=[1-2×(3.3/6.6×2) 2+(3.3/6.6×2)3]×4.38×3.3/2=6.44kN/mq 1′=85×4.38×3.0/2=4.11kN/m(3)q 2、q 2′分别为屋⾯板⾃重传给纵梁上的梯形和三⾓形荷载等效为均布荷载值梯形:q 2=[1-2×(3.0/6.6×2) 2+(3.0/6.6×2)3]×4.38×3.0/2=5.96kN/m三⾓形:q 2′=85×4.38×3.3/2=4.52kN/mP 1为由板传给次梁及次梁⾃重传给纵梁的集中⼒ P 1= q 1×6.6+ q 0″×6.6/2=49.43kNP 2为由板传给外纵梁及外纵梁、⼥⼉墙⾃重传给柱⼦的集中⼒ P 2=( q 2′+ q 0+q )×3.3×2=76.42 kNP 3为由板传给内纵梁及内纵梁⾃重传给柱⼦的集中⼒。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
行分配和传递,直到完成一个完整的循环;一般要进行两到三 个循环。
4、还原:分层计算得到的梁端弯矩即为其最后弯矩;除底层 柱外,每根柱弯矩需由上、下两层计算所得的弯矩叠加得到。 5、结点处弯矩常不为零,如需修正可将结点不平衡力矩再做 一次弯矩分配。
A2
ic2 1
A1
q1=10kN/m
B2
ib 0.777 ic2 1
B1
8000
H2=4000
A2
B2
ic2 1
A1
q1=8kN/m
ic2 1
B1
ic1 0.801
A0
ib 0.777
ic1 0.801
B0
8000
H1=5000
3、用力矩分配法计算第二层开口框架
(1)计算分配系数:
(1)分层法
▪ 分层法计算框架的内力的思路
以求解框架梁端与柱端弯矩为目标进行的,在求出 框架梁端和柱端弯矩后,即可求出梁其他截面的弯矩; 然后再求出梁的剪力和柱的轴力。
▪ 基本假定:
➢ 忽略垂直荷载作用下框架结构的侧移; ➢ 每层梁上的荷载只在本层梁及与其相连的上、下层柱
产生内力,不在其他层梁和其他层柱上产生内力。
根据以上假定,多、高层框架可分层作为若干 个彼此互不关连的且柱端为完全固定的简单刚架进 行近似计算。简单刚架可用弯矩分配法计算,一般 循环2次。
分层法计算示意图
注意事项:
➢ 由于除底层外上层各柱的柱端实际为弹性固定,计算简 图中假定为完全嵌固,为减少计算误差,除底 层柱外, 上层各柱的线刚度乘以0.9的修正系数。
不平衡力矩再作一次弯矩分配。
直捷分层法
对上述分层法再简化
• 远端刚接柱的线刚度不再乘以折减系数0.9; • 除柱脚固定支承的底层柱从上端以1/2的传递系数将弯矩
传给柱脚外,其他各层柱在上、下端不再传递弯矩。
柱端弯矩也无需从相邻两层的分析中叠加。
用分层法计算框架内力的步骤:
1、计算梁柱线刚度 2、把框架以按层拆为若干个开口框架 3、用力矩分配法分别计算每层框架的内力
0.323
A1
结点B1:
与结点A1分配系数相同
A1B1
S A1B1 S
A1
4 0.777 4 2.478
0.314
(2)计算固端弯矩:
1 882 12
42.667kN
m
mB1A1
1 12
q1l
2
1 882 12
42.667kN
m
(3)循环过程:A1
B1
用力矩分配法计算顶层开口框架
A2
结点B2与结点A2分配系数相同
(2)计算固端弯矩:
mA2B2
1 12
q2l
2
1 1082 12
53.333kN
m
mB2 A2
1 12
q2l 2
1 1082 12
53.333kN
m
(3)循环过程B2
A2
4、还原-叠加、结点不平衡弯矩再分配一次
6、计算框架梁其他截面的弯矩 计算框架梁截面的剪力 计算框架柱的轴力
6、计算梁跨中弯矩,计算梁剪力,绘制框架M、V图
例题:
用分层法计算 图示框架的内力
1、计算梁柱线刚度
Ic
bh3 12
1 0.4 0.553 12
1 0.0666 12
Ib
bh3 12
1 0.3 0.73 12
1 0.1029 12
ic1
EIc H1
1 1 0.0666E 5 12
(1)计算分配系数:
A2结点
S A2 A1 4(0.9ic2 )
S A2B2 4ib
S 4(0.9ic2 ib ) 4 1.677
A2
A2 A1
S A2 A1 S
4 0.9 1 4 1.677
0.537
A2
A2B2
S A2 B 2 S
4 0.777 4 1.677
0.463
结点A1:
S A1A2 4(0.9ic2 ) S A1A0 4ic1
S A1B1 4ib
S 4(ic1 0.9ic2 ib ) 4 2.478
A1
A1A2
S A1A2 S
4 0.9 1 0.363 4 2.478
A1
A1A0
S A1A0 S
4 0.801 4 2.478
➢ 按下式计算每一杆件的近端转角弯矩M’ik,即
Mi'k
' M F
ik
i
M ' ki
i
式中,
M
' ki
——汇交于节点i各杆的远端转角弯矩
i
之和,最初可假定为0。
注:按上述公式计算时,一般选择不平衡弯矩较大的节点开始计 算循环若干轮,直到全部节点的弯矩值达到要求的精度为止。
➢ 按下式计算每一杆端的最后弯矩值,即
1 0.0133E 12
ic 2
EIc H2
1 1 0.0666E 4 12
1 0.0166E 12
ib
EIb L
1 1 0.1029E 8 12
1 0.0129E 12
相对线刚度: 设:ic2 1
则 ic1 0.801
ib 0.777
2、把框架以按层拆为两个开口框架
H2=4000
绘出弯矩图、剪力图
(2)迭代法
不考虑框架侧移时
基本步骤: ➢ 绘出结构的计算简图,在每个节点上绘两个框;
➢ 计算汇交于每一节点各杆的转角分配系数,并检查是否
满足
i'k
1 2
,以作校核;
i'k
1 2
iik iik
(i)
➢ 计算荷载作用下各杆端产生的固端弯矩MFik,并写在相 应的各杆端部,求出汇交于每一节点的各杆固端弯矩之 和MFi,把它写在该节点的内框中;
多层与高层房屋结构设计
多层与高层框架结构设计
Multi-story Frame Structures and Tall Frame Structures
第五讲
——框架在竖向荷载作用下内力的近似计算方法
竖向荷载下的内力计算的弹性分析方法
在竖向荷载(vertical load)作用下,多、高层框架结构的 内力可用力法、位移法等结构力学方法计算。工程设计中,如 采用手算,可采用分层法、迭代法、力矩分配法、弯矩二次分 配法及系数法等近似方法计算
线刚度修正
➢ 考虑除支座外,框架各节点为弹性固定,因此底层柱 的弯矩传递系数取1/2,其他各层柱的矩传递系数1/3; 传递系数修正
➢ 分层法计算的各梁弯矩为最终弯矩 ➢ 每一柱弯矩需由上、下两层计算所得的弯矩叠加而成 ➢ 在内力与位移计算中,所有构件均可采用弹性刚度。 ➢ 叠加后框架节点处弯矩常不为零,如需修正可将节点
