上海教育版数学七下12.2《数的开方》word教案4
春上海教育版七下第2节《数的开方》word学案

第11章数的开方—11.1平方根与立方根第1课时平方根【学习目标】:1.掌握平方根与算术平方根的概念,并能正确的用符号表示, 2.能归纳理解并能运用平方根的性质 3.能求出一个数的平方根与算术平方根。
【学习重点】:平方根与算术平方根的概念以及开方运算【学习难点】:平方根性质的理解与运用【合作探究】:作__________________.例题1:求81,925的平方根变式练习:(口答)快速说出下列各数的平方根4, 36 ,0, 0.49 ,1思考:—4有没有平方根?为什么?合作探究二:平方根性质的理解与运用请你仔细观察例题1的计算结果归纳总结平方根的性质:(1)一个正数有______个平方根,它们互为_______;(2)0有____个平方根,是___;(3)负数______平方根(因此0a≥)例题1:下列各式中哪些有意义?哪些无意义?(1),(2)(3)(4)(5) (6)例题2:如果一个正数有两个平方根分别是m+3与2m-15,(1)求m的值.(2)求这个数合作探究三:算术平方根的认识(看书3页完成下列填空)算术平方根的定义:_____________________叫做a 算术平方根,记作__________,读作_____________,另一个平方根是它的相反数,即温馨提示:算术平方根a 具有双重非负性:(1)被开方数a 是非负数,即a ≥0. (2) 算术平方根a 本身是非负数,即a ≥0。
例题:先说明下列各数表示的意义.再求下列各式的值,:(1) (2) (3) (4) (5)温馨提示:a 的平方根记作“【知识运用】:求一个非负数的平方根的运算,叫做________________.求一个正数开 方的关键是找出它的算术平方根。
例题1:将下列各数开平方(1)25 (2)641(3) 0.01变式:你能快速说出下列各数的平方根吗?9, 16, 64, 121, 144, 225【课后检测】 一.填空题:(1)1的平方根=______.1000平方根是__________,2的平方根是__________(4)若x 2=6,则x =_________(5).若a 的平方根是±3,那么a=_______(6)、平方根等于本身的数有_______,算术平方根等于本身的数是______ 二、选择题1.下列计算正确的是( ) A.±2)3(-=±3B.±25=5C. -2)1(-=1D.2)2(-=-22.下列说法正确的是( )A.7是49的平方根,49的平方根是7。
沪教版数学七年级下册12.2《数的开方》教学设计1

沪教版数学七年级下册12.2《数的开方》教学设计1一. 教材分析《数的开方》是沪教版数学七年级下册12.2章节的内容,本节内容是在学生已经掌握了有理数的乘方、平方根等知识的基础上进行学习的。
数的开方是数学中的一个基本运算,它不仅可以解决一些实际问题,而且是学习更高深数学知识的基础。
本节课的教学内容主要包括平方根的定义、求一个数的平方根的方法以及平方根的性质等。
二. 学情分析学生在学习本节课之前,已经掌握了有理数的乘方、平方根等知识,具备了一定的数学基础。
但是,对于平方根的性质和求法,学生可能还不够熟悉。
此外,学生可能对数的开方在实际生活中的应用还不够了解。
三. 教学目标1.知识与技能:理解平方根的定义,掌握求一个数的平方根的方法,理解平方根的性质。
2.过程与方法:通过自主学习、合作交流的方式,培养学生的数学思维能力和解决问题的能力。
3.情感态度与价值观:激发学生对数学的兴趣,培养学生积极思考、勇于探索的精神。
四. 教学重难点1.重点:平方根的定义,求一个数的平方根的方法,平方根的性质。
2.难点:平方根的性质的理解和应用。
五. 教学方法1.自主学习:引导学生自主探究平方根的定义和求法,培养学生的自主学习能力。
2.合作交流:学生进行小组讨论,分享学习心得,提高学生的合作交流能力。
3.实例讲解:通过具体例子,讲解平方根的性质和应用,帮助学生理解和掌握知识。
六. 教学准备1.教学PPT:制作包含平方根的定义、求法、性质等内容的教学PPT。
2.练习题:准备一些有关平方根的练习题,用于巩固所学知识。
3.教学工具:准备黑板、粉笔等教学工具。
七. 教学过程1.导入(5分钟)教师通过提问方式引导学生回顾平方根的定义和求法,为新课的学习做好铺垫。
2.呈现(10分钟)教师通过PPT展示平方根的性质,引导学生初步理解平方根的性质。
3.操练(10分钟)教师提出一些有关平方根性质的题目,让学生在课堂上进行练习,巩固所学知识。
春上海教育版数学七下12.2《数的开方》word教案4

平方根与立方根练习卷一、填空题:1、144的算术平方根是 ,16的平方根是 ;2、327= , 64-的立方根是 ;3、7的平方根为 ,21.1= ;4、一个数的平方是9,则这个数是 ,一个数的立方根是1,则这个数是 ;5、平方数是它本身的数是 ;平方数是它的相反数的数是 ;6、当x= 时,13-x 有意义;当x= 时,325+x 有意义;7、若164=x ,则x= ;若813=n,则n= ; 8、若3x x =,则x= ;若x x -=2,则x ;9、若0|2|1=-++y x ,则x+y= ;10、计算:381264273292531+-+= ;二、选择题11、若a x =2,则( )A 、x>0B 、x≥0C 、a>0D 、a≥012、一个数若有两个不同的平方根,则这两个平方根的和为( ) A 、大于0 B 、等于0 C 、小于0 D 、不能确定 13、一个正方形的边长为a ,面积为b ,则( ) A 、a 是b 的平方根 B 、a 是b 的的算术平方根 C 、b a±= D 、a b =14、若a≥0,则24a 的算术平方根是( ) A 、2a B 、±2a C 、a 2 D 、| 2a |15、若正数a 的算术平方根比它本身大,则( ) A 、0<a<1 B 、a>0 C 、a<1 D 、a>1 16、若n 为正整数,则121+-n 等于( )A 、-1B 、1C 、±1D 、2n+117、若a<0,则aa 22等于( )A 、21 B 、21- C 、±21 D 、0 18、若x-5能开偶次方,则x 的取值范围是( ) A 、x≥0 B 、x>5 C 、x≥5 D 、x≤5 三、计算题 19、2228-+ 20、49.0381003⨯-⨯21、914420045243⨯⨯⨯ 22、83122)10(973.0123+--⨯-四、解答题 23、解方程:0324)1(2=--x 24、解方程:x x 1225)32(2-=-25、若312-a 和331b -互为相反数,求ba的值。
12章数的开方全章教案_Microsoft_Word_文档

12章数的开方全章教案_Microsoft_Word_文档§12.1.1平方根【教学目标】一、知识目标1.了解开平方、平方根、算术平方根的意义,了解平方根、算术平方根的表示方法.2.理解开平方与平方运算是互为逆运算.3.会用平方求已知数的平方根,会利用平方运算验证一个数的平方根。
4.了解平方根、算术平方根的性质.5.会用计算器求一个非负数的算术平方根。
.二、能力目标1、经历探索开方运算与乘方运算是互为逆运算的过程,学会利用转化的思想方法解决新问题;2、经历运用数学符号描述开方运算的过程,建立初步数学符号感,发展抽象思维能力三、情感态度目标通过创设问题情境,让学生体会到数学来源于社会生活实际,并为社会实践服务,认识到客观世界是一个对立的统一体.【重点难点】重点:求已知数的平方根难点:平方根与算术平方根的联系和区别。
疑点:利用平方运算解决简单问题。
【教学设想】教学思路:情境质疑-数学建模-解释应用-巩固提高。
【课时安排】2课时平方根(11)第1课时平方根(【教学目标】1、了解开平方、平方根和算术平方根的意义及其表示方法.2、理解平方运算与开平方运算是互逆运算的关系.3、会用平方运算求非负数的平方根与算术平方根,。
【教学过程】1、情境导入:问题:要剪出一块面积为25cm的正方形纸片,纸片的边长应是多少?你能用方程表示这个问题吗?试试看.2.课前热身:根据上述提出的间题,请同学们作如下讨论:(1)这种运算(2x =25)是已知什么?求什么?(2)这种运算与平方运算之间存在怎样的关系?3、合作探究(1)整体感知数学来源于社会生活,并为社会生活服务,为了解决课本开始提出的问题,这节课我们开始学习一种新的运算---开平方运算。
(2)师生互动:互动1:师:先填空,再观察两种运算的结构特点,回答问题。
平方运算是已知,求;后面的运算是已知,这节课我们开始学习一种新的运算是。
生:先动手操作尝试,再在相互交流的基础上逐个举手回答提出的问题,不断补充完善,达成共识。
沪教版(上海)七年级下册 12.2 平方根和开平方 教案设计

平方根和开平方【教学目标】一、知识目标掌握平方根与算术平方根的概念与性质,能及时通过开方运算求一个非负数的平方根及算术平方根,理解平方根与开平方互为逆运算。
二、能力目标通过对平方根概念及性质的探究,渗透分类讨论和数形结合的数学思想方法,提高数学探究能力和归纳表达能力。
三、情感目标鼓励学生积极主动地参与教与学的整个过程,激发学生求知的欲望,增加学生学习数学的兴趣与信心。
【教学重难点】1.平方根与算术平方根的概念和性质。
2.平方根与算术平方根的区别与联系。
【教学过程】一、创设情景、感悟新知首先,呈现三个问题:(1)一个正方形桌面的边长是3m,求这个桌面的面积是多少平方米?(2)已知一个正方形的面积是9cm2,求它的边长。
(3)如果一个正方形展厅的地面面积为50平方米,求它的边长。
解:(1)32=9;(2)设正方形的边长为a cm,有:a2=9;a=3或a=-3(舍去)。
(3)设正方形的边长为a cm,有:a2=50;解得a=?这就要用到这节课所学的内容,即平方根。
二、合作交流、解读探究平方根的概念。
首先安排练习1,求已知数的平方。
练习1:计算:(1)22;(2)29.0;(3)24-)( (4)243⎪⎭⎫ ⎝⎛; (5)243-⎪⎭⎫ ⎝⎛; (6)20。
接着安排了练习2,逆向设问,已知某数的平方,求该数。
练习2:填空:(1)()42=; (2)()81.02=; (3)()1692=; (4)()02=。
通过观测、比较练习1、练习2,引导学生发现前者是平方运算,后者是平方运算的逆运算。
自然地引出平方根和开平方的概念。
平方根的概念:一般地,如果一个数的平方等于a ,那么这个数叫做a 的平方根或二次方根,即若a x =2,则x 叫做a 的平方根。
开平方运算:求一个数a 的平方根的运算,叫做开平方。
练习3:求x :(1)812=x ;(2)02=x ;(3)42-=x ;(4)36.02=x ;(5)492-=x ;(6)1212=x 。
沪教版数学七年级下册12.2《数的开方》教学设计4

沪教版数学七年级下册12.2《数的开方》教学设计4一. 教材分析《数的开方》是沪教版数学七年级下册12.2章的教学内容。
本节内容是在学生已经掌握了有理数、分数、乘方等知识的基础上,进一步学习数的开方运算。
数的开方是数学中的基本运算之一,对于学生来说,理解并掌握开方的概念、法则和运算方法是十分重要的。
二. 学情分析学生在学习本节内容之前,已经掌握了有理数、分数、乘方等知识,具备了一定的数学基础。
但学生在学习数的开方时,可能会对负数的开方、无理数等概念产生困惑。
因此,在教学过程中,需要关注学生的学习需求,针对学生的实际情况进行教学。
三. 教学目标1.理解数的开方的概念,掌握数的开方的法则和运算方法。
2.能够进行数的开方运算,解决实际问题。
3.培养学生的逻辑思维能力,提高学生的数学素养。
四. 教学重难点1.数的开方的概念和法则。
2.负数的开方、无理数的理解。
3.数的开方在实际问题中的应用。
五. 教学方法1.采用问题驱动的教学方法,引导学生主动探究数的开方的概念和法则。
2.利用多媒体教学,直观展示数的开方过程,帮助学生理解。
3.采用实例分析法,让学生通过解决实际问题,巩固数的开方运算。
4.小组讨论,培养学生的合作意识和团队精神。
六. 教学准备1.多媒体教学设备。
2.教学课件。
3.练习题。
七. 教学过程1.导入(5分钟)利用多媒体展示一些生活中的实例,如立方体的体积计算等,引导学生思考这些实例与数的开方之间的关系。
2.呈现(10分钟)介绍数的开方的概念、法则和运算方法。
通过示例,让学生了解负数的开方、无理数等概念。
3.操练(10分钟)让学生进行数的开方运算,解决实际问题。
教师巡回指导,解答学生的疑问。
4.巩固(10分钟)学生进行小组讨论,分享彼此的解题心得。
教师点评学生的解题过程,指出不足之处,给予指导。
5.拓展(5分钟)引导学生思考数的开方在实际生活中的应用,如建筑设计、物理等领域。
6.小结(5分钟)教师总结本节课的主要内容,强调数的开方的概念、法则和运算方法。
沪教版数学七年级下册12.2《数的开方》教学设计4

沪教版数学七年级下册12.2《数的开方》教学设计4一. 教材分析《数的开方》是沪教版数学七年级下册的教学内容,本节课主要介绍实数的开方运算。
通过学习,学生能够理解开方的概念,掌握开方运算的法则,并能够熟练地进行实数的开方运算。
教材中安排了丰富的例题和练习题,有助于学生巩固所学知识。
二. 学情分析学生在学习本节课之前,已经掌握了有理数的运算、平方根的概念等相关知识。
但部分学生对于实数的开方运算可能存在理解上的困难,需要教师在教学中进行针对性的引导和辅导。
三. 教学目标1.知识与技能:使学生理解数的开方的概念,掌握数的开方运算的法则,能够熟练地进行实数的开方运算。
2.过程与方法:通过探究、实践,培养学生运用数学知识解决实际问题的能力。
3.情感态度与价值观:激发学生学习数学的兴趣,培养学生的自主学习能力。
四. 教学重难点1.重点:数的开方的概念,数的开方运算的法则。
2.难点:理解并掌握实数的开方运算,能够灵活运用开方运算解决实际问题。
五. 教学方法采用问题驱动法、案例教学法、小组合作学习法等,引导学生主动探究,合作交流,实践操作,从而达到对知识的深入理解。
六. 教学准备1.教学课件:制作数的开方教学课件,展示相关概念、例题和练习题。
2.教学素材:准备一些实际问题,用于引导学生运用开方运算解决实际问题。
3.学具:为学生准备纸笔等学习用品,方便学生进行练习和记录。
七. 教学过程1.导入(5分钟)利用数学故事、实际问题等方式,引导学生回顾平方根的概念,为新课的学习做好铺垫。
2.呈现(10分钟)介绍数的开方的概念,引导学生通过观察、思考,发现开方运算的法则,并进行总结。
3.操练(10分钟)出示一些例题,让学生独立进行解答,教师进行讲解和指导。
在此过程中,注重引导学生运用开方运算的法则,提高运算速度和准确性。
4.巩固(10分钟)出示一些练习题,让学生进行巩固练习,教师进行讲解和指导。
在此过程中,注重引导学生运用开方运算解决实际问题,提高学生的应用能力。
沪教版(上海)七年级下册 12.3 立方根和开立方-教案设计

立方根和开立方【教学目标】一、知识与技能1.了解立方根的概念,初步学会用根号表示一个数的立方根,让学生体会一个数的立方根的唯一性。
2.了解开立方与立方互为逆运算,会用立方运算求某些数的立方根,分清一个数的立方根与平方根的区别。
3.能用有理数估计一个无理数的大致范围,使学生形成估算的意识,培养学生的估算能力。
二、情感、态度与价值观1.通过立方根的学习,认识数学与人类生活的密切联系,激发学生的学习兴趣。
2.通过探究活动,锻炼克服困难的意志,增强自信心,激发学生的探索热情。
【教学重难点】1.了解数的立方根的概念和性质,会用三次根号表示数的立方根,用立方运算求一个数的立方根。
2.用立方运算求一个数的立方根,认识平方根与立方根的区别。
【教学过程】一、复习师:请同学们回忆上节课我们是怎样定义平方根的?它的符号怎么表示?生:如果a x =2,那么x 叫做a 的平方根(或二次方根)。
符号表示:“a ±”其中0≥a (教师板书)。
师:我们还学习了一种新的运算,是什么运算呢?它是怎么定义的?生:开平方:求一个数a 的平方根的运算,叫做开平方。
(与平方互为逆运算)。
设计意图:通过对平方根的复习,可以增加学生对平方根的印象,同时,教师也能通过学生复习过程的表现,间接了解学生对知识的掌握程度,也能让学生再学习完立方根的新知识后,更好的对这两个概念进行比较。
二、设计情境,导入新课问题1:要制作一种容积为327m 的正方体形状的包装箱,这种包装箱的棱长应该是多少?你是怎么知道的?设这种包装箱的棱长为m x ,则3x =27,这就是求一个数,使它的立方等于27。
因为33=27,所以x=3。
即这种包装箱的边长应为3 m 。
加问:如果把容积改为500,棱长应该是多少呢?本题是已知一个数x 的立方,求这个数的值,而平方根是已知一个数的平方,求这个数,从而学生可以类比平方根的概念归纳出立方根的概念。
师:对比平方根的定义,你能归纳出立方根的定义是什么吗?学生谈论思考,教师引导归纳概念:概念归纳:如果一个数的立方等于a ,这个数叫做a 的立方根(也叫做三次方根),即如果3x a =,那么x 叫做a 的立方根(教师板书)。
数的开方教案

数的开方教案教案标题:数的开方教案教学目标:1. 理解数的开方的概念和意义。
2. 学会使用数的开方运算符号。
3. 掌握求解简单数的开方运算。
教学准备:1. 教师准备一些平方数的卡片,如1、4、9、16等。
2. 学生准备纸和铅笔。
教学过程:引入活动:1. 教师出示一些平方数的卡片,让学生观察并思考:这些数有什么特点?它们和其他数有什么不同?2. 引导学生回顾平方数的定义:平方数是某个数与自身相乘的结果。
例如,2的平方是4,3的平方是9等。
探究活动:1. 教师引导学生思考:如果给你一个数,你如何求这个数的平方根呢?请尝试一下。
2. 学生独立尝试求解一些简单数的平方根,如1的平方根是多少?4的平方根是多少?3. 学生互相交流并分享自己的解答,教师引导学生总结出求解平方根的方法。
概念讲解:1. 教师通过示例,向学生讲解数的开方运算符号√的意义和使用方法。
例如,√9表示求9的平方根。
2. 教师解释平方根的定义:对于一个非负数a,如果存在一个非负数b,使得b 的平方等于a,那么b就是a的平方根。
练习活动:1. 学生进行一些简单的数的开方计算练习,如√16、√25等。
2. 学生互相交流并核对答案。
3. 教师提供一些挑战性的开方问题,如√2、√7等,鼓励学生尝试解答。
拓展活动:1. 学生自主选择一些数,计算它们的平方根,并绘制一个数的开方表格。
2. 学生互相交流并分享自己的表格,讨论不同数的平方根的特点和规律。
总结活动:1. 教师引导学生总结本节课学到的知识点和方法。
2. 学生回答教师提出的问题,巩固对数的开方的理解。
评估活动:教师布置一些练习题,让学生独立完成并交卷,检验学生对数的开方的掌握程度。
教学延伸:对于高年级学生,可以引入负数的开方概念,并进行相关的拓展讨论。
注意事项:1. 在引入活动中,教师要引导学生主动思考和发现数的开方的规律。
2. 在概念讲解中,教师要结合具体的示例进行解释,让学生更好地理解数的开方的概念。
沪教版(五四学制)七年级数学下册教案:12.2 n次方根

课题n次方根教学目标1.理解n次方根、开n次平方运算、被开方数、根指数的概念和意义;2.掌握“一个数的偶次方根和奇次方根”的区别;3.掌握n次方根的符号表示方法.重点、难点重点:n次方根的概念,求一个数的n次方和n次方根的互逆运算;难点:根据n的奇偶性对n次方根的影响,用符号正确表示不同实数的n次方根.教学内容一、【课前引导】1、求下列各式的值:16的平方根是,16的平方根是。
课前练习二2、平方根的特征:正数有个平方根,这两个平方根是;负数有个平方根;零的平方根是。
3、立方根的特征:正数有个的立方根;负数有个的立方根;零的立方根是。
1.正数有一个正的奇次方根,负数也有一个负的奇次方根,零的奇次方根是零。
正数有两个偶次方根,它们互为相反数;负数没有偶次方根,零的偶次方根是零。
2. 实数a 的奇次方根有且只有一个,表示为n a 。
其中被开方数a 是任意一个实数,根指数n 是大于1的奇数。
正数a 的偶次方根有两个,它们互为相反数,表示为±n a 。
其中被开方数a >0,根指数n 是正偶数(当n=2时,在±n a 中省略n )。
负数的偶次方根不存在。
零的n 次方根等于零,表示为00=n 。
本课小结1. n 次方根;如果一个数(x )的n 次方(n 是大于1的整数)等于a ,那么这个数(x )叫做a 的n 次方根。
当n 为奇数时,a 的n 次方根表示为n a ;当n 为偶数时,正数a 的n 次方根表示为±n a 。
2. 开方:求一个数a 的n 次方根的运算叫做开才n 次方,简称开方。
3. n 次方根的特征:实数a 的奇次方根有且只有一个。
正数a 的偶次方根有两个,它们互为相反数。
负数的偶次方根不存在。
零的n 次方根等于零。
新课探索三⑴求24332-的5次方根; ⑵求1024的10次方根; ⑶求2)8(-的6次方根。
课内练习一1. 求下列各数的四次方根:⑴ 161; ⑵ 81; ⑶ 1; ⑷ 0.课内练习二2. 求下列各数的五次方根:⑴ 321; ⑵ -32; ⑶ -1; ⑷ 0.课内练习三3. 求值:⑴ 4625; ⑵ 41615; ⑶62)81(-. 课内练习四4. 用计算器,求近似值(保留三位小数):⑴ 41000; ⑵5640-;⑶6518-课内练习五5.用计算器,求近似值(保留三位小数):⑴5532-;1. 求值:2. 下列说法中,正确的是( )(A )1的任何次方根都是1;(B )0的任何次方根都是0;(C )负数没有方根;(D )正数的方根互为相反数。
沪教版(上海)七年级下册 12.2 平方根和开平方-教案设计

平方根和开平方【教学目标】1.理解平方根产生的背景和平方根的概念及其符号表示;2.知道正平方根与平方根的区别,理解正数的两平方根之间的关系及实数范围内负数没有平方根;3.会根据平方根、开平方的意义和运算性质,求完全平方数的平方根。
【教学重难点】理解开平方和平方运算的互逆关系,运用平方根的运算性质求完全平方数的平方根。
【教学过程】一、问题导入1.问题:小丽家有一张方桌,桌面是面积为64平方分米的正方形,这个正方形桌面的边长是多少?2.解答:设正方形桌面的边长为x 分米,则可得:x 2=64,因为x>0,所以x=8.3.思考:上述问题可以归结为“已知一个数的平方,求这个数”。
在解决问题时,我们联想到了哪一种运算?二、学习新课1.概念辨析(1)已知一个数的平方等于a ,那么这个数叫做a 的平方根,即x 2=a ,我们把x 叫做a 的平方根,a 叫做被开方数。
(2)求一个数a 的平方根的运算叫做开平方运算。
例如,求64的平方根,就要对64进行“开平方”的运算,64是被开放数,这就要找出满足642=x 的数x ,因为64)8(,64822=-=,所以64的平方根是±8.在平方根概念中,涉及到平方运算。
我们规定无理数的平方遵循同有理数一样的符号运算。
【强调】平方运算和开平方运算互为逆运算。
2.例题分析求下列各数的平方根,并根据你的解答过程总结:正数、0、负数的平方根有什么不同?(1)0.16; (2)-259; (3)0. 解:(1)因为(±0.4)2=0.16,所以0.16的平方根是±0.4.(2)因为不存在一个实数的平方根为-259,所以-259无平方根。
(3)因为02=0,所以0的平方根为0.3.性质归纳(1)因为任何一个实数的平方都是非负的,所以负数没有平方根;(2)因为任何一对非零相反数的平方都是同一个正数,因此正数a 有2个不同的平方根,记作“±a ”,它们互为相反数,其中“a ”表示正的平方根(也可以称算术平方根),读作“根号a ”。
沪教版数学七年级下册12.2《数的开方》教学设计2

沪教版数学七年级下册12.2《数的开方》教学设计2一. 教材分析数的开方是初中数学中的重要内容,也是学习更高深数学的基础。
沪教版数学七年级下册12.2《数的开方》一章,主要介绍了实数的开方运算。
通过这一章节的学习,学生能够理解并掌握数的开方运算的方法,能够运用开方运算解决实际问题。
教材通过丰富的例题和练习题,帮助学生巩固开方运算的知识。
二. 学情分析学生在学习数的开方之前,已经学习了有理数的运算,对实数的概念有了初步的认识。
但是,学生可能对数的开方运算的理解不够深入,需要通过实例和练习来进一步理解和掌握。
同时,学生可能对数的开方运算的运用还不够熟练,需要通过大量的练习来提高运算速度和准确度。
三. 教学目标1.知识与技能目标:学生能够理解数的开方的概念,掌握数的开方运算的方法,能够运用数的开方解决实际问题。
2.过程与方法目标:通过实例和练习,学生能够深入理解数的开方运算的原理,提高运算速度和准确度。
3.情感态度与价值观目标:学生能够积极参与数的开方的学习,培养对数学的兴趣和好奇心,提高学习数学的积极性。
四. 教学重难点1.教学重点:数的开方的概念,数的开方运算的方法。
2.教学难点:数的开方运算的运用,提高运算速度和准确度。
五. 教学方法1.实例教学法:通过具体的实例,让学生理解数的开方的概念和运算方法。
2.练习教学法:通过大量的练习,提高学生对数的开方运算的掌握程度。
3.小组合作学习法:学生分组进行讨论和练习,培养学生的合作能力和团队精神。
六. 教学准备1.教学课件:制作数的开方的教学课件,包括数的开方的概念、运算方法、实例和练习题。
2.教学练习题:准备大量的练习题,包括基础题和提高题,以满足不同学生的学习需求。
3.教学工具:准备黑板、粉笔、投影仪等教学工具。
七. 教学过程1.导入(5分钟)利用实例引入数的开方的概念,让学生初步了解数的开方运算。
2.呈现(15分钟)讲解数的开方的运算方法,通过具体的实例,让学生深入理解数的开方运算的原理。
沪教版数学七年级下册12.2《数的开方》教学设计2

沪教版数学七年级下册12.2《数的开方》教学设计2一. 教材分析《数的开方》是沪教版数学七年级下册12.2章节的内容,本节内容是在学生已经掌握了有理数的乘方、平方根和立方根的基础上进行学习的。
本节主要介绍实数的开方,包括正数的开方、负数的开方和零的开方,以及开方与乘方的关系。
教材通过具体的例子引导学生探究和发现开方的性质和规律,进一步培养学生的逻辑思维能力和数学素养。
二. 学情分析学生在学习本节内容之前,已经掌握了有理数的乘方、平方根和立方根的知识,具备了一定的数学基础。
但学生在学习过程中可能对负数的开方和零的开方存在一定的困惑,因此,在教学过程中,教师需要耐心引导,让学生充分理解和掌握开方的概念和方法。
三. 教学目标1.理解实数的开方概念,掌握正数、负数和零的开方方法。
2.掌握开方与乘方的关系,能够运用开方解决实际问题。
3.培养学生的逻辑思维能力和数学素养,提高学生的数学思维水平。
四. 教学重难点1.重难点:实数的开方方法,特别是负数和零的开方。
2.易错点:学生可能对负数和零的开方存在误解,认为负数没有平方根和零没有平方根。
五. 教学方法1.启发式教学法:教师通过提问、引导学生思考,激发学生的学习兴趣和探究欲望。
2.实例教学法:教师通过具体的例子,让学生直观地理解开方的概念和方法。
3.小组合作学习:学生分组讨论,共同探究开方的问题,培养学生的合作意识和团队精神。
六. 教学准备1.教学PPT:制作有关开方的PPT,内容包括开方的定义、方法以及相关实例。
2.教学素材:准备一些有关开方的实际问题,用于巩固和拓展学生的知识。
3.黑板和粉笔:用于板书和讲解。
七. 教学过程1.导入(5分钟)教师通过提问方式引导学生回顾平方根和立方根的概念,为新课的学习做好铺垫。
2.呈现(10分钟)教师通过PPT展示实数的开方概念,引导学生观察和思考正数、负数和零的开方方法。
3.操练(10分钟)教师给出一些有关开方的实际问题,让学生分组讨论,共同探究解决问题的方法。
上海教育版七下第2节《数的开方》word学案

第11章数的开方—11.1平方根与立方根第1课时平方根【学习目标】:1.掌握平方根与算术平方根的概念,并能正确的用符号表示, 2.能归纳理解并能运用平方根的性质 3.能求出一个数的平方根与算术平方根。
【学习重点】:平方根与算术平方根的概念以及开方运算【学习难点】:平方根性质的理解与运用【自主学习】:【合作探究】:合作探究一:平方根的认识与理解(看书第2页试一试上面的内容,完成下列填空)读作__________________.例题1:求81,925的平方根变式练习:(口答)快速说出下列各数的平方根4, 36 ,0, 0.49 ,1思考:—4有没有平方根?为什么?合作探究二:平方根性质的理解与运用请你仔细观察例题1的计算结果归纳总结平方根的性质:(1)一个正数有______个平方根,它们互为_______;(2)0有____个平方根,是___;(3)负数______平方根(因此0a≥)例题1:下列各式中哪些有意义?哪些无意义?(1),(2)(3)(4)(5)例题2:如果一个正数有两个平方根分别是m+3与2m-15,(1)求m的值.(2)求这个数合作探究三:算术平方根的认识(看书3页完成下列填空)算术平方根的定义:_____________________叫做a 算术平方根,记作__________,读作_____________,另一个平方根是它的相反数,即 温馨提示:算术平方根a 具有双重非负性:(1)被开方数a 是非负数,即a ≥0. (2) 算术平方根a 本身是非负数,即a ≥0。
例题:先说明下列各数表示的意义.再求下列各式的值,:(1) (2) (3) (4) (5)温馨提示:a 的平方根记作“【知识运用】:求一个非负数的平方根的运算,叫做________________.求一个正数开 方的关键是找出它的算术平方根。
例题1:将下列各数开平方(1)25 (2)641(3) 0.01变式:你能快速说出下列各数的平方根吗?9, 16, 64, 121, 144, 225【课后检测】 一.填空题:(1)1的平方根=______.1000平方根是__________,2的平方根是__________(4)若x 2=6,则x =_________(5).若a 的平方根是±3,那么a=_______(6)、平方根等于本身的数有_______,算术平方根等于本身的数是______ 二、选择题1.下列计算正确的是( )A.±2)3(-=±3B.±25=5C. -2)1(-=1D.2)2(-=-2 2.下列说法正确的是( )A.7是49的平方根,49的平方根是7。
沪教版(上海)数学七年级第二学期12.2 平方根和开平方(1) 教案
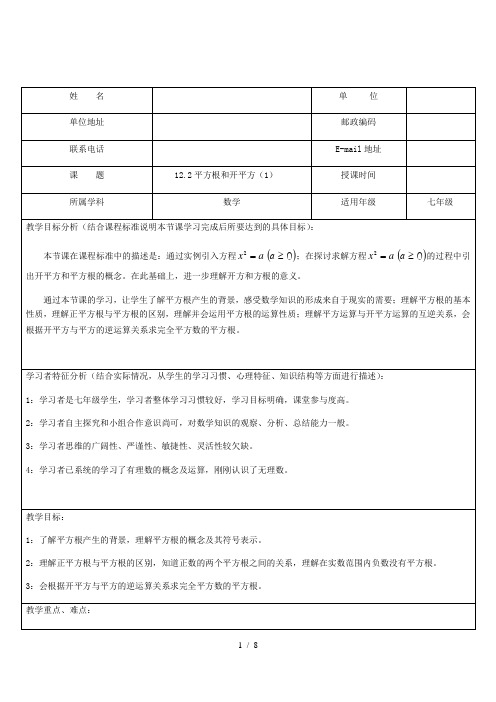
3:根据概念求平方根: 例题1:求下列各数的平方根(1)0.16; (2)259; (3)0. (4)-4()4.016.016.04.0,16.04.0122±∴=-=的平方根是)解((教师以第(1)小题为例引导学生理解平方根的概念并指导学生书写规范)运算。
5325925953-25953222±∴=⎪⎭⎫⎝⎛=⎪⎭⎫⎝⎛的平方根是,)解( 没有平方根。
都不可能为负数,任何一个数的平方)(的平方根是)(4-4.000032∴∴= 能利用概念求平方根。
此题分别设置了求正数,零和负数的平方根问题,为目标二的研究奠定了基础。
新课探索二:目标二:平方根的性质(在实数范围内) 1:讨论归纳平方根的基本性质:(讨论:在实数范围内平方根具有什么性质? 教师引导学生理解平方根的概念和例题1显示的结果,进而把实数分为正数,零和负数三种情况来总结;【说明】1:“a ”是一个数学符号,其意义是:非负数a 的算术平方根;同时它也表示一个数,这个数的平方等于a ,即()a a =22:负数的平方根问题在高中数学中将进一步研究。
)1:(1)因为任何一对非零相反数的平方都是同一个 ,因此正数a 有 个平方根,它们互为 ,记作“ ”,其中“a ”表示a 的正的平方根(又叫算术平方根),读作“根号a ”, “a -”表示a 的负的平方根,读作“负根号a ”.(2)因为0的平方等于 ,所以0的平方根就是 ,即: .(3)因为任何一个实数的平方都是 的,所以 ;教师引导学生总结,培养学生分析问题,总结问题的能力。
能力提升1:若2<x ,化简x x -+-3)2(2的正确结果是( )A 、1-B 、1C 、25x - D 、52x -22011,2012-2011:2-=-+a a a a a 求满足已知数此部分根据学生课堂实际学习情况灵活选择。
课堂小结1:本节课你有哪些收获?2:你认为我们在做题时要注意什么细节,或者你在学习的过程中预测到我们在做题时容易出什么错?第一个问题主要是让学生养成总结的习惯,让所学知识不断系统化;第二的问题是提醒学生在做题的过程要注重细节,对于容易出错的地方要重视。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平方根与立方根练习卷
一、填空题:
1、144的算术平方根是 ,16的平方根是 ;
2、327= , 64-的立方根是 ;
3、7的平方根为 ,21.1= ;
4、一个数的平方是9,则这个数是 ,一个数的立方根是1,则这个数是 ;
5、平方数是它本身的数是 ;平方数是它的相反数的数是 ;
6、当x= 时,13-x 有意义;当x= 时,325+x 有意义;
7、若164=x ,则x= ;若813=n ,则n= ;
8、若3x x =,则x= ;若x x -=2,则x ;
9、若0|2|1=-++y x ,则x+y= ;
10、计算:38126427
32925
31+-+= ;
二、选择题
11、若a x =2,则( )
A 、x>0
B 、x≥0
C 、a>0
D 、a≥0
12、一个数若有两个不同的平方根,则这两个平方根的和为( )
A 、大于0
B 、等于0
C 、小于0
D 、不能确定
13、一个正方形的边长为a ,面积为b ,则( )
A 、a 是b 的平方根
B 、a 是b 的的算术平方根
C 、b a ±=
D 、a b = 14、若a≥0,则24a 的算术平方根是( )
A 、2a
B 、±2a
C 、a 2
D 、| 2a |
15、若正数a 的算术平方根比它本身大,则( )
A 、0<a<1
B 、a>0
C 、a<1
D 、a>1
16、若n 为正整数,则121+-n 等于( )
A 、-1
B 、1
C 、±1
D 、2n+1
17、若a<0,则a a 22
等于( )
A 、21
B 、21
- C 、±21
D 、0
18、若x-5能开偶次方,则x 的取值范围是( )
A 、x≥0
B 、x>5
C 、x≥5
D 、x≤5
三、计算题
19、2228-+ 20、49.0381003⨯-⨯
21、914420045243⨯
⨯⨯ 22、83122)10(973.0123+--⨯-
四、解答题
23、解方程:0324)1(2=--x 24、解方程:x x 1225)32(2-=-
25、若312-a 和331b -互为相反数,求b
a 的值。
