第07章 数 组
NO.07 第七章--测量与量表

明了物体拥有一些特性的相对程度。定序尺度之间可进行“=”或 “≠” ,还可进行“<”或“>”运算。
等距尺度(interval scale):尺度上数字相等的距离代表被测特性
的相等值,又称间隔尺度、区间尺度。其尺度间可进行“=”或 “≠” ,“<”或“>”和“+”或“-”的运算。
31
当要评价的对象的个数不多时,成对比较法是 有用的。但如果要评价的对象超过10个,这种 方法就太麻烦了。另外一个缺点是“可传递性” 的假设可能不成立,在实际研究中这种情况常 常发生。同时对象列举的顺序可能影响受测者, 造成顺序反应误差。而且这种“二中选一”的 方式和实际生活中作购买选择的情况也不太相 同,受访者可能在A、B两种品牌中对A要略为 偏爱些,但实际上却两个品牌都不喜欢。
第二节 比较量表技术
20
一、等级顺序量表
等级顺序量表是一种顺序量表,它是将许多研 究对象同时展示给受测者,并要求他们根据某 个标准对这些对象排序或分成等级。例如,要 求受访者根据总体印象对不同品牌的商品进行 排序。典型地,这种排序要求受测者对他们认 为最好的品牌排“1”号,次好的排“2”号,依 次类推,直到量表中列举出的每个品牌都有了 相应的序号为止。一个序号只能用于一种品牌。
量表,也称标度、计量,涉及到产生一个 将被测量物体定位的连续统一体。
3
测量分三个步骤
第一步,选取被测事物; 第二步,利用数字或符号代表事物的特征; 第三步,运用预先设定的准则给事物一个符号或数字,
以代表其评价。
• 例如,将“对于某商场的态度”这一态度变量的可
能取值,用不同的数字来代表:“1”代表“喜欢”, “2”代表“无所谓”,“3”代表“不喜欢”;然后, 根据受访者是回答“喜欢”、“无所谓”和“不喜 欢”填写调查问卷或调查表。这就是一个典型的三 等级量表。
初中数学课程与教学第07章 “统计与概率”的学与教(自测题参考答案)

第七章 统计与概率一、选择题1.在统计中,样本的方差可以近似地反映总体的( )A.平均状态B.波动大小C.分布规律D.最大值和最小值2.在方差计算公式])20()20()20[(10121022212-++-+-=x x x s 中,数字10和20分别表示( )A.数据的个数和方差B.平均数和数据的个数C.数据的个数和平均数D.数据组的方差和平均数3.将一组数据中每个数据的值都减去同一个常数,那么下列结论成立的是( )A.平均数不变B.方差和标准差都不变C.方差改变D.方差不变但标准差改变 二、填空题1.一组数据中出现次数最多的数据称为 .2. 数据98,100,101,102,99的样本标准差是. 3. 为了估计鱼塘里有多少条鱼,我们从鱼塘里捕上100条鱼做上标记,然后放回鱼塘里去,待带标记的鱼完全混合于鱼群后,再捕第二次样品鱼200条,其中带标记的鱼有25条,试估计鱼塘里约有鱼 条.三、名词解释1. 随机现象2. SOLO 分类法四、简答题1. 7-9年级“统计与概率”教学要注意哪几个方面?2. 请简述7-9年级“统计与概率”学习中的用样本估计总体的思想方法.五、论述题:请谈谈学生对概率统计的认知发展的阶段.六、案例分析:以下是一节“频率与概率”课的教学,请根据该案例回答后面的问题.【教学案例:频率与概率】第一板块:试验猜想扑克牌的红桃A 、红桃2和方块A 、方块2,把红桃A 、红桃2作为一组,把方块A 、方块2作为另一组,从每组牌中各摸出一张每组拿出准备的,称为一次试验。
1.一次试验中两张牌的牌面数字之和可能是哪些值?2.每人做30次试验,依次记录每次摸得的牌面数字,根据试验结果填写下面表格:3.根据上表,制作频数分布直方图。
4.你认为哪种情况的频率最大?5.八个小组组成一个大组,分别汇总其中两小组、三小组、……、八小组的试验数据,相应得出60次、90次、120次、……、240次时两张牌的牌面数字和等于3的频率,填写下表,并绘制相应的折线图。
市北资优六年级分册 第07章 7.8 一次方程组的应用+滕小红

7.8 一次方程组的应用【例1】小明去年2月在小卖店买了3本练习本和5包盐正好用去5元钱,今年3月,他又带5元钱去该店买同样的练习本和食盐,因为练习本每本比去年涨价1角,食盐每包涨价5分,小明就只好买了3本练习本和4包盐,结果找回2角钱,那么去年2月每本练习本多少钱,每包食盐多少钱? 【分析】根据题意,可以得到两个等式:去年2月3本练习本的钱+5包食盐的钱=5元;今年3月3本练习本的钱+4包食盐的钱=5元-0.2元.【解】设去年2月练习本每本x 元,食盐每包y 元,则今年3月练习本每本(x +0.1)元,食盐每包(y +0.05)元.根据题意,得355,3(0.1)4(0.05)50.2.x y x y +=⎧⎨+++=-⎩①②②化简得,3x +4y =4.3,③①-③得,y =0.7. 把y =0.7代入①,得x =0.5. 所以,这个方程组的解为0.5,0.7.x y =⎧⎨=⎩答:去年2月练习本每本5角,食盐每包7角.【例2】一批货物要运往某地,货主准备租用汽车运输公司的甲、乙两种货车,已知过去两次租用这两种货车情况如下表:30元计算,问:货主应付运费多少元? 【分析】由图表可知:甲种货车第一次运输货物的总重量+乙种货车第一次运输货物的总重量=15.5; 甲种货车第二次运输货物的总重量+乙种货车第二次运输货物的总重量=35. 【解】设甲、乙两种货车的载重量各为x 吨、y 吨,依题意,有2315.5,5635.x y x y +=⎧⎨+=⎩解这个方程组,得4,2.5.x y =⎧⎨=⎩ 30×(4×3+2.5×5)=735(元) .答:货主应付运费735元.【例3】甲对乙说:“当我的岁数是你现在的岁数时,你才4岁.”乙对甲说:“当我的岁数是你的岁数时,你将61岁.”那么甲与乙现在的年龄分别是多少岁? 【分析】由题意,可以得到以下等式:甲的年龄-乙的年龄=乙的年龄-4=61-甲的年龄. 【解】设甲、乙现在的年龄分别为x 岁、y 岁,根据题意,得4,61.x y y x y x -=-⎧⎨-=-⎩解这个方程组,得42,23.x y =⎧⎨=⎩答:甲现在42岁,乙现在23岁.练习7.8(1)1.一张方桌由一个桌面和四条腿组成.如果1立方米木料可制成方桌的桌面50个,或制作桌腿300条.现有5立方米木料,怎样分工能使木料全部用完,并且桌面与桌腿都能配成套?某人在该周内持有甲、乙两种股票,若按照两种股票每天收盘价计算(不计手续费、税费等),该人账户上星期二相比星期一获利200元,星期三相比星期二获利1300元,试问该人持有甲、乙股票各多少股?3.某杂志月刊,全年共出12期,每期定价2.50元,某中学六年级组织集体订阅,有些学生订半年而另一些学生订全年,共需订费1320元.求该中学六年级订阅该杂志的学生人数.4.某厂去年总产值比总支出多500万元,而今年计划的总产值比总支出多950万元.已知今年计划总产值比去年增加15%,而计划总支出比去年减少10%,求今年计划的总产值与总支出分别为多少万元?5.甲、乙两人在一条与铁路平行的笔直的小路上,同时同地背向而行.当一列火车开过来时,两人在行进中各自测出整列火车通过的时间分别为42秒和34秒,且在整列火车通过时各自走了68米和44米,求火车的速度.练习7.8(1)答案:1.3立方米木料作桌面,2立方米木料作桌腿,恰好配成方桌150张。
07第七章 IT服务持续改进
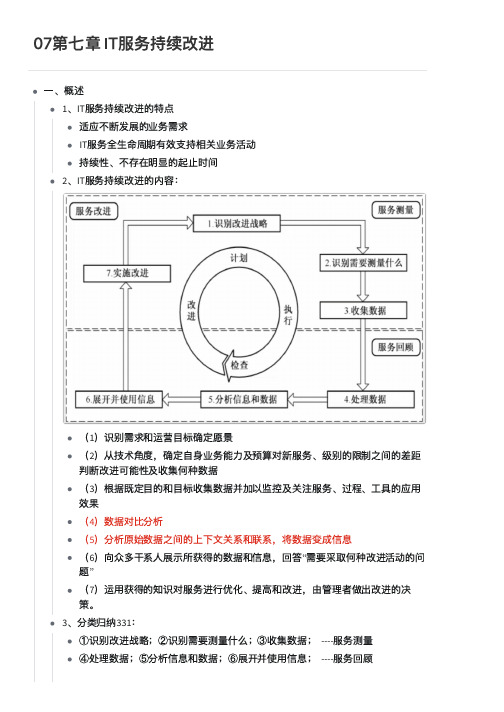
07第七章 IT服务持续改进⼀、概述1、IT服务持续改进的特点适应不断发展的业务需求IT服务全⽣命周期有效⽀持相关业务活动持续性、不存在明显的起⽌时间2、IT服务持续改进的内容:(1)识别需求和运营⽬标确定愿景(2)从技术⻆度,确定⾃身业务能⼒及预算对新服务、级别的限制之间的差距判断改进可能性及收集何种数据(3)根据既定⽬的和⽬标收集数据并加以监控及关注服务、过程、⼯具的应⽤效果(4)数据对⽐分析(5)分析原始数据之间的上下⽂关系和联系,将数据变成信息(6)向众多⼲系⼈展示所获得的数据和信息,回答“需要采取何种改进活动的问题”(7)运⽤获得的知识对服务进⾏优化、提⾼和改进,由管理者做出改进的决策。
3、分类归纳331:①识别改进战略;②识别需要测量什么;③收集数据; ----服务测量④处理数据;⑤分析信息和数据;⑥展开并使⽤信息; ----服务回顾⑦实施改进; ----服务改进⼆、服务测量1、测量指标的类型:(1)技术指标:基于IT组件和应⽤的测量,如可⽤性、性能。
(2)过程指标:通常以KPI表示,反映服务管理过程的运⾏或健康状况。
KPI有助于回答4个关键问题:过程的质量、绩效、价值和符合性,持续服务改进利⽤这些KPI识别对各过程的改进机会。
(3)服务指标:对端到端的服务绩效的测量,通过技术和过程指标加以计算。
2、服务测量的活动(1)服务⼈员的测量⼈员是提供IT服务的基础,因此服务⼈员测量单独作为服务测量的⼀个测量项,并没有作为服务资源的内容。
①识别备份⼯程师的满⾜度和可⽤性(现有备份的);②测量⼈员招聘需求的匹配度(预计招聘的);③收集培训的应⽤情况;④⼈员能⼒测量;⑤服务⼯作量测量(⼯作配⽐预测);⑥岗位职责更新情况;⑦⼈员绩效考核分配机制测量;⑧实时监控团队⼯作状态。
(2)服务资源的测量:⼯具:①测量⼯具的功能与服务管理过程是否有效匹配(⼯具针对性)②周期性识别相关⼯具的使⽤⼿册是否有效并进⾏相关验证(⼯具可操作性)③监控IT服务运维⼯具的健康状态(⼯具可⽤性及准确性)服务台:⽐如接听率、派单准确率、录单率、平均通话时间备件库:⽐如盘点备件资产、统计备件损坏率、统计备件命中率、统计备件复⽤率知识库:收集知识的积累数量、知识的利⽤率、知识的更新率、知识的完整性、各类知识的⽐重、知识新增数量与事件和问题发⽣数量的对⽐关系(3)技术的测量:①识别研发规划②识别研发成果③技术⼿册及SOP统计④应急预案实施统计⑤监控点和阈值统计(4)过程的测量:服务过程测量活动是分层次的,⾄少有服务管控和服务执⾏两个层次。
第07讲一次函数-—图象与性质(教案)

-一次函数图象的变换与识别
4.练习与巩固
-判断一次函数的增减性
-根据斜率和截距绘制一次函数图象
-解答与一次函数相关的问题,运用图象分析解决实际问题
二、核心素养目标
1.培养学生的数感与符号意识,通过一次函数的学习,使学生能够理解数学符号表示的实际意义,提高运用符号进行表达和交流的能力。
-图象的变换:难点在于掌握一次函数图象的平移、压缩、拉伸等变换规律,以及这些变换对斜率和截距的影响。
-例如:当一次函数图象进行平移时,斜率k保持不变,截距b发生变化,学生需要理解这种变换背后的数学原理。
四、教学流程
(一)导入新课(用时5分钟)
同学们,今天我们将要学习的是《一次函数—图象与性质》这一章节。在开始之前,我想先问大家一个问题:“你们在日常生活中是否遇到过物体以固定速度移动的情况?”(如骑自行车匀速前进)。这个问题与我们将要学习的一次函数密切相关。通过这个问题,我希望能够引起大家的兴趣和好奇心,让我们一同探索一次函数图象与性质的奥秘。
2.教学难点
-一次函数图象的理解:难点在于理解一次函数图象的几何意义,如何从图象中获取信息,以及如何将实际问题转化为一次函数图象。
-例如:学生可能难以理解图象上某点的坐标如何对应实际问题中的具体情境。
-一次函数性质的深入理解:难点在于理解斜率和截距对一次函数图象的精确影响,以及如何通过性质预测图象的形态。
3.重点难点解析:在讲授过程中,我会特别强调一次函数的斜率和截距这两个重点。对于难点部分,如斜率的意义和截距的物理含义,我会通过举例和图象分析来帮助大家理解。
(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与一次函数相关的实际问题,如物体的匀速运动。
07第七章 市场调查资料的整理和基础分析

表7-5 态度测 评选项 大学以下
被调查者对空调维修服务满意度测评汇总表 男 大学以上 小计 大学以下 女 大学以上 小计 合计
很满意
较满意 一般 不满意 很不满意
135
126 124 196 180
116
48 52 46 12
251
174 176 242 192
124
141 136 170 195
(一)集中趋势分析指标 1.众数
【例7-6】1,2,3,3,4的众数是3。但是,如果有两个或 两个以上个数出现次数都是最多的,那么这几个数都是这 组数据的众数。例如:1,2,2,3,3,4的众数是2和3。 还有,如果所有数据出现的次数都一样,那么这组数据没 有众数。例如:1,2,3,4,5没有众数。
第一节 市场调查资料整理的内容和程序 第二节 原始资料的整理 第三节 二手资料的整理 第四节 市场调查资料基础分析
引入
第一节 市场调查资料整理的内容和程序
一、市场调查资料整理的内容 (1)数据确认 (2)数据处理 (3)数据陈示
二、市场调查资料整理的程序 1.确认数据资料 2.对数据进行编码和录入 3.对数据进行初步分析
噪声大小
115
230
680
365
310
1 700
表7-4
文化程度 性别 小学以下
被调查者性别与文化程度分布(单位:人)
男 6
女 4
合计 10
初中 高中高职
专科 大学本科 硕士博士 合 计
210 297
248 226 48 1 035
176 321
265 177 22 965
迈达斯学习第07章结果.doc

无私分享无私分享无私分享无私分享无私分享无私分享无私分享第七章“结果”中的常见问题 (3)7.1 施工阶段分析时,自动生成的“CS:恒荷载”等的含义? (3)7.2 为什么“自动生成荷载组合”时,恒荷载组合了两次? (3)7.3 为什么“用户自定义荷载”不能参与自动生成的荷载组合? (4)7.4 为什么在自动生成的正常使用极限状态荷载组合中,汽车荷载的组合系数不是0.4或0.7? (5)7.5 为什么在没有定义边界条件的节点上出现了反力? (5)7.6 为什么相同的两个模型,在自重作用下的反力不同? (6)7.7 为什么小半径曲线梁自重作用下内侧支反力偏大? (6)7.8 为什么移动荷载分析得到的变形结果与手算结果不符? (7)7.9 为什么考虑收缩徐变后得到的拱顶变形增大数十倍? (8)7.10 为什么混凝土强度变化,对成桥阶段中荷载产生的位移没有影响? (8)7.11 为什么进行钢混叠合梁分析时,桥面板与主梁变形不协调? (9)7.12 为什么悬臂施工时,自重作用下悬臂端发生向上变形? (10)7.13 为什么使用“刚性连接”连接的两点,竖向位移相差很大? (11)7.14 为什么连续梁桥合龙后变形达上百米? (12)7.15 为什么主缆在竖直向下荷载作用下会发生上拱变形? (13)7.16 为什么索单元在自重荷载作用下转角变形不协调? (14)7.17 为什么简支梁在竖向荷载下出现了轴力? (14)7.18 为什么“移动荷载分析”时,车道所在纵梁单元的内力远大于其它纵梁单元的内力?157.19 如何在“移动荷载分析”时,查看结构同时发生的内力? (15)7.20 空心板梁用单梁和梁格分析结果相差15%? (17)7.21 为什么徐变产生的结构内力比经验值大上百倍? (17)7.22 如何查看板单元任意剖断面的内力图? (18)7.23 为什么相同荷载作用下,不同厚度板单元的内力结果不一样? (19)7.24 为什么无法查看“板单元节点平均内力”? (21)7.25 如何一次抓取多个施工阶段的内力图形? (21)7.26 如何调整内力图形中数值的显示精度和角度? (22)7.27 为什么在城-A车道荷载作用下,“梁单元组合应力”与“梁单元应力PSC”不等?257.28 为什么“梁单元组合应力”不等于各分项正应力之和? (25)7.29 为什么连续梁在整体升温作用下,跨中梁顶出现压应力? (25)7.30 为什么PSC截面应力与PSC设计结果的截面应力不一致? (26)7.31 为什么“梁单元应力PSC”结果不为零,而“梁单元应力”结果为零? (26)7.32 如何仅显示超过某个应力水平的杆件的应力图形? (27)7.33 为什么“水化热分析”得到的地基温度小于初始温度? (29)7.34 “梁单元细部分析”能否查看局部应力集中? (30)7.35 为什么修改自重系数对“特征值分析”结果没有影响? (30)7.36 为什么截面偏心会影响特征值计算结果? (31)7.37 为什么“特征值分析”没有扭转模态结果? (32)7.38 “屈曲分析”时,临界荷载系数出现负值的含义? (32)7.39 “移动荷载分析”后自动生成的MVmax、MVmin、MVall工况的含义? (33)7.40 为什么“移动荷载分析”结果没有考虑冲击作用? (33)7.41 如何得到跨中发生最大变形时,移动荷载的布置情况? (34)7.42 为什么选择影响线加载时,影响线的正区和负区还会同时作用有移动荷载?357.43 为什么移动荷载分析得到的结果与等效静力荷载分析得到结果不同? (35)7.44 如何求解斜拉桥的最佳初始索力? (36)7.45 为什么求斜拉桥成桥索力时,“未知荷载系数”会出现负值? (38)7.46 为什么定义“悬臂法预拱度控制”时,提示“主梁结构组出错”? (38)7.47 如何在预拱度计算中考虑活载效应? (38)7.48 桥梁内力图中的应力、“梁单元应力”、“梁单元应力PSC”的含义? (39)7.49 由“桥梁内力图”得到的截面应力的文本结果,各项应力结果的含义? (40)7.50 为什么定义查看“结果>桥梁内力图”时,提示“设置桥梁主梁单元组时发生错误!”? (41)7.51 为什么无法查看“桥梁内力图”? (41)7.52 施工阶段分析完成后,自动生成的“POST:CS”的含义? (42)7.53 为什么没有预应力的分析结果? (42)7.54 如何查看“弹性连接”的内力? (44)7.55 为什么混凝土弹性变形引起的预应力损失为正值? (44)7.56 如何查看预应力损失分项结果? (45)7.57 为什么定义了“施工阶段联合截面”后,无法查看“梁单元应力”图形? . 46 7.58 为什么拱桥计算中出现奇异警告信息? (47)7.59 如何在程序关闭后,查询“分析信息”的内容? (48)第七章“结果”中的常见问题7.1施工阶段分析时,自动生成的“CS:恒荷载”等的含义?具体问题进行施工阶段分析,程序会自动生成CS:恒荷载、CS:施工荷载、CS:收缩一次、CS:收缩二次、CS:徐变一次、CS:徐变二次、CS:钢束一次、CS:钢束二次、CS:合计,这些荷载工况各代表什么含义?在结果查看时有哪些注意事项?相关命令——问题解答MIDAS在进行施工阶段分析时,自动将所有施工阶段作用的荷载组合成一个荷载工况“CS:恒荷载”;如果想查看某个或某几个施工阶段恒荷载的效应,可以将这些荷载工况从“CS:恒荷载”分离出来,生成荷载工况“CS:施工荷载”;钢束预应力、收缩徐变所产生的直接效应程序自动生成荷载工况“CS:钢束一次”、“CS:收缩一次”、“CS:徐变一次”,由于结构超静定引起的钢束预应力二次效应、收缩徐变二次效应,程序自动生成荷载工况“CS:钢束二次”、“CS:收缩二次”、“CS:徐变二次”;“CS:合计”表示所有施工荷载的效应。
市北资优六年级分册 第07章 7.1 方程与方程的解+胡敏

例1判断下列各式那些是方程,哪些不是方程:
(1) ;(2) ;(3) ;(4) ;(5)
分析方程有两个必备条件,未知数、等式是用来作为判断是不是方程的标准.
解(1)、(2)、(4)是方程,(3)(5)不是方程.
例2根据下列条件,列出方程:
4、若 、 都是质数,以 为未知数的方程 的解是1,求 的值.
6、若 ,则关于 的方程 必有一个解是.
练习7.1答案
1、1998.提示:由题意得, ,因此原式=1998.
2、0.提示:原式
3、 .提示:将 代入方程 ,可得 .当 时,
原式 .
4、15.提示:把 代入方程 ,得 ,故 与 中必有一个数为偶数.①若 ,则 , ;② 若 为偶数,则 ,而87不是质数,与题设矛盾,舍去, .
想一想方程 还有别的根吗?
是方程 的解吗?
例3检验下列各数是不是方程 的解.
(1) (2)
分析检验一个数是否为某个方程的解,只需要把这个数分别代入方程的左边和右边,如果左右两边的值相等,那么这个数就是方程的解,否则就不是方程的解.
解(1)检验:把 分别代入方程的左边和右边,得左边 右边
因为左边 右边,所以 不是方程 的解.
5、2.提示:因为 , 、 均为质数, ,所以 必为2,(否则 、 同为奇数,不满足 ).
6、 .提示:由题意得, ,则 必是原方程的一个解.
(1)50千克含糖 的糖水,现在要把它的浓度提高到含糖15%,需加糖 千克;
(2)商店对某种商品调价,按原价的8折出售,此时商店的利润率是15%,此商品的原价为300元,商店的进价是 元.
解(1)所列方程为 ;
第07章 原子结构 习题解答

第07章习题解答第07章(02484)原子轨道就是原子核外电子运动的轨道,这与宏观物体运动轨道的含义相同。
()。
解:错第07章(02485)以电子概率(几率)密度表示的空间图象即为原子轨道,波函数的空间图象即为电子云。
()解:错第07章(02486)电子云是核外电子分布概率(几率)密度的空间图象。
.()解:对第07章(02487)波函数ψ表明微观粒子运动的波动性,其数值可大于零也可小于零,∣ψ∣2表示电子在原子核外空间出现的概率(几率)密度。
.()解:对第07章(02488)所谓某原子轨道是指.()。
(A)一定的电子云;(B)核外电子出现的概率(几率);(C)一定的波函数;(D)某个径向分布函数。
解: C第07章(02489)与波函数视为同义语的是()。
(A)概率(几率)密度;(B)电子云;(C)原子轨道;(D)原子轨道的角度分布图。
解: C第07章(02490)氢原子的原子轨道能量取决于量子数()。
(A)n;(B)n和l;(C)l;(D)m。
解: A第07章(02491)下列有关电子云的叙述中,错误的是()。
(A)电子云形象地表示了电子在核外某处单位微体积内出现的概率(几率);(B)电子云形象化地表示了电子在核外空间某处出现的概率(几率)密度;(C)1s电子云界面图是一个球面,表示在这个球面以外,电子出现的概率(几率)为零;(D)电子云是电子运动的统计结果,它好象形成了一团带负电荷的云,包围在原子核的外边。
解: C第07章(02492)某原子轨道用波函数表示时,下列表示中正确的是()。
(A)ψn;(B)ψn,l;(C)ψn,l,m;(D)ψn,l,m,ms解: C第07章(02493)在氢原子光谱的能量关系式中,当处于基态时n1=______________,当核外电子电离时,n2=______________。
解:1;∞。
第07章(02494)氢原子光谱在可见光区有__________条谱线,可表示为_________________。
遗传学:07-第七章 染色体数目变异

二倍体西瓜 (2n=2x=22=11 II)
加倍
同源四倍体
二倍体西瓜
(2n=4x=11 IV) × (2n=2x=22=11 II)
三倍体西瓜(2n=3x=11 III)
三倍体无籽西瓜
3x = 33 = 11 Ⅲ
····· ·
··· (1/2)11×2 ···
四. 同源四倍体基因分离规律
杂合基因型 AAAa AAaa Aaaa 假定只发生2/2式分离
1. 基因的染色体随机分离 (基因距离着丝点较近)
配子类型及比例 AA :Aa : aa = 2 : 8 :2
例如,同源四倍体的三式基因型(AAAa),在染色体 随机分离的情况下,不能产生aa基因型的配子,在 染色单体随机分离的情况下,可以产生aa配子
第三节 异源多倍体
C
1 2
-2
=10
aa
2
C10 : 1
(13AA + 10Aa + 1aa )2
AAAA : AAAa : AAaa : Aaaa : aaaa =169 : 260 : 126 : 20 : 1
[A] : [a] = 575 : 1
在染色单体不完全随机分离的情况下,同一 染色体的两条姊妹染色单体或其姊妹区段可 以进入同一配子;而染色体随机分离不能
其余n为21—24 或 14—19 小孢子0.8 4.5 复8式.5 14单.5式22.9 30.8 18.
大孢4x子 AAA3.A5 AA9.A0 a 1A4A. a2a1.A5 aa3a4.5aaa1a7.5 三式 复式 单式
第07章-C++程序设计教程(第3版)(通用版)-钱能-清华大学出版社

数组是一定元素个数的连续空间整体
为了性能,C/C++拒绝传递数组整体
传递数组需传两个参数:数组首址和元素个数
int a[100],b[100]; void f(int* x, int* y, int n){
for(int i=0; i<n; i++)
x[i]=y[i];
}
void g(){
f(a,b,100);
if(grade[i]>max) max=grade[i];
return max; //返回最大成绩 } int main(){
int sg[3][4]={{68,77,73,86},{87,96,78,89},{90,70,81,86}}; cout<<"the max grade is "<<maxi(*sg,12)<<“\n”; }
int b[3][3]={ 1,2,3,4,5,6,7,8,9 }; //亦可
int b[2][3]={ {1,2},{4} };
//缺处补0
int b[3][3]={ 1,2,3,4,5,6 }; //缺处补0
int b[3][3]={ {1,2},{4} };
//亦可,缺处补0
int b[3][3]={ 1,2,3,{4,5,6} }; //不可
if(grade[i][j]>max) max=grade[i][j];
return max; //返回最大成绩 } int main(){
int sg[3][4]={{68,77,73,86},{87,96,78,89},{90,70,81,86}}; cout<<"the max grade is "<<maxi(sg,3,4)<<“\n”; }
07第七章 染色体数目变异

(1) 同源多倍体形态特征
染色体的同源倍数越多, 染色体的同源倍数越多,核体积和细胞体积越大 气孔和保卫细胞比二倍体大, 气孔和保卫细胞比二倍体大,单位面积的气孔数少 多数同源多倍体叶片大小、花朵大小, 多数同源多倍体叶片大小、花朵大小,茎粗和叶片 厚度随着染色体数目的增加而增加, 厚度随着染色体数目的增加而增加,成熟期则延迟 同源多倍体基因剂量远比二倍体大, 同源多倍体基因剂量远比二倍体大,这对同源多倍 体的生长和发育是会有影响的
农作物: 农作物:栽培的小 燕麦、棉花、 麦、燕麦、棉花、 烟草、甘蔗、油菜、 烟草、甘蔗、油菜、 马铃薯等 果树:苹果、 果树:苹果、梨、 樱桃、草莓等; 樱桃、草莓等; 花卉:菊花, 花卉:菊花,大 理菊、水仙、 理菊、水仙、郁 金香等
异源多倍体的特点: 异源多倍体的特点:
•异源多倍体具有与二倍体相同的性状遗传规 异源多倍体具有与二倍体相同的性状遗传规 律,但表现型可能比二倍体复杂的多 •异源多倍体在形成的初期表现不稳定,容易 异源多倍体在形成的初期表现不稳定, 异源多倍体在形成的初期表现不稳定 发生染色体重排或丢失。 发生染色体重排或丢失。
(2)异源多倍体的起源途径 异源多倍体的起源途径 A. 异源六倍体小麦的起源途径
Triticum monococcum 野生一粒小麦 AA(2n=14)
×பைடு நூலகம்
↓
Aegilops speltoides 拟斯尔脱山羊草 2n=2x=BB=14=7II
第七章 染色体数目变异
一、染色体组与染色体的倍性 1. 染色体组
染色体组(genome):指每一物种特有的、维持其生命 :指每一物种特有的、 染色体组 活动所必需的一套基本染色体 遗传学上常把一个正常配子的染色体称为一个染色体组, 遗传学上常把一个正常配子的染色体称为一个染色体组, 上常把一个正常配子的染色体称为一个染色体组 用n表示。 表示。 表示 体细胞中具有两套染色体组, 表示,自然界中存在的 体细胞中具有两套染色体组,用2n表示 自然界中存在的 中具有两套染色体组 表示 生物大都为二倍体. 生物大都为二倍体 体细胞中含有3个以上染色体组的生物称为多倍体 体细胞中含有 个以上染色体组的生物称为多倍体。 个以上染色体组的生物称为多倍体。
2021年数理方法课件 精美PPT 07第7章 一维波动方程的傅里叶解

两边除以 ρΔx, 然后取极限Δx→0:
utt ( x, t) =
T0
uxx(x, t) +
f
( x, t )
➢ 弦振动的泛定方程 ut t = a2ux x + f
u(x,t) ➔ x 处的质元在 t 时刻相对平衡位置的位移 f(x,t) ➔ t 时刻 x 处单位质量所受的横向外力
a = T0 / : 弦中横波的波速 T0 ➔ 初始张力,ρ➔质量线密度
• 整个系统初始状况的表达式称为初始条件 • 对弦振动,泛定方程为 ut t = a2 2u + f
需给出弦在初始时刻 t=0 的位移和速度: u( x,0) = ( x), ut ( x,0) = ( x)
• 泛定方程出现时间的 n 阶偏导数时需要 n 个初始条件
• 对物理量的稳态分布,无初始条件
lxntalnbtalnatxunnn??????sinsincos1??????????????lndxlxnxula0sin02??lxnblanxunnt????sin001????????????????202sincos14ldxlxnxnlh??????????????????????lxlxlhhlxxlhxu22220200ll2xux0h分离变量法得出解的一般形式bn0lxntalnnnhtxun????????sincossin????????12228222sincos14lnnnlhan??????????????????2020cos1coslldxlxnlnxlnlxni????????????20sinldxlxnxi??对奇数n计算积分202sin2cos2llnlxnnlnl??????????????22sinlnn??????2sin822????nnh???回顾
市北资优六年级分册 第07章 7.7 三元一次方程组及其解法+黄启胜

7.7 三元一次方程组及其解法问题在大楼底层有一控制室,用三条导线和楼上某电器相连.这三条导线的颜色分别为红色、黄色、蓝色.大楼要重新设计线路,需要知道这三条导线的电阻.但由于手头没有测量电阻的工具,只有一份书面资料,上面记载着:红色导线与黄色导线电阻之和0.8欧姆(欧姆为电阻的单位),红色导线与蓝色导线电阻之和0.6欧姆,黄色导线与蓝色导线电阻之和1欧姆.请你设计一种数学方法求这三根导线的电阻.可以设红色导线的电阻为x 欧姆,黄色导线的电阻为y 欧姆,蓝色导线的电阻为z 欧姆,则可列出方程:x +y =0.8,x +z =0.6,y +z =1.x 、y 、z 的值应当同时满足以上三个方程,我们可以把这三个方程合在一起,写成0.80.61x y x z y z ⎧⎪⎨⎪⎩+=,+=,+=. 方程组中含有三个未知数,且含未知数的项的次数都是一次,这样的方程组叫做三元—次方程组.例如,方程组261218x y z x y x z y ⎧⎪-⎨⎪+-⎩++=,=,=.也是三元一次方程组.回忆一下,二元一次方程组是如何解的呢?那如何解三元一次方程组呢?可以通过消元,将三元一次方程组化为二元一次方程组,进而再解二元一次方程组.然后再求出被消去的未知数的值即可.例1 解方程组26, 1, 218. x y z x y x z y ++=⎧⎪-=⎨⎪+-=⎩①②③解:由②得,x =y +1.④把④代入①,得,2y +z =25,⑤把④代入③,得,y +z =16.⑥⑤-⑥,得,y =9.把y =9代入⑥,得,z =7.把y =9代入④,得,x =10.所以,原方程组的解为10,9,7.x y z =⎧⎪=⎨⎪=⎩先消哪个元比较好?例2 解方程组2338, 32456, 4566. x y zx y zx y z++=⎧⎪++=⎨⎪++=⎩①②③解:③-①得,x+z=14.④①×2,得,4x+2y+6z=76,⑤⑤-②,得,x+2z=20.⑥⑥-④,得,z=6.把z=6代入④,得,x=8.把x=8,z=6代入①,得,y=4.所以,原方程组的解为8,4,6. xyz=⎧⎪=⎨⎪=⎩例3 解方程组27, 32316,3213.x y zx y zx y z++=⎧⎪++=⎨⎪++=⎩①②③解:①+②+③得,x+y+z=6.④①-④,得,x=1,④×3-②,得,y=2,把x=1,y=2代入①,得,z=3.所以,原方程组的解为1,2,3. xyz=⎧⎪=⎨⎪=⎩回到本节开头的问题,现在你知道红、黄、蓝三条导线的电阻分别是多少了吗?解方程组的主要思想方法是什么?消元消元练习7.71.解方程组, 2355, 3 2. z x yx y zx y z=+⎧⎪-+=⎨⎪+-=⎩2.解方程组3521, 545, 35 2. x y zy z xz x y-+=⎧⎪-+=⎨⎪+-=-⎩3.解方程组29x y z-+=2310x y z++=323x y z+-=1.4.解方程组1232343454515125,1,5,3,2. x x xx x xx x xx x xx x x++=⎧⎪++=⎪⎪++=-⎨⎪++=-⎪⎪++=⎩答案:练习7.71.1,1,0.xyz=⎧⎪=-⎨⎪=⎩2.1,0,1.xyz=⎧⎪=⎨⎪=-⎩3.3,2,2.xyz=⎧⎪=-⎨⎪=⎩4.123452,3,0,2,3.xxxxx=⎧⎪=⎪⎪=⎨⎪=-⎪⎪=-⎩7.7《三元一次方程组及其解法》练习练习7.71.解方程组2636, 31576, 4949.x y zx y zx y z++=⎧⎪++=⎨⎪-+=⎩2.解方程组3564, 2235, 234 4. x y zx y zx y z--=⎧⎪--=⎨⎪--=⎩3.解方程组3413, 535,3.x y zx y zx y z+-=⎧⎪-+=⎨⎪+-=⎩4.解方程组123123123 24,22,2 6. R R RR R RR R R++=⎧⎪++=⎨⎪++=⎩5.解方程组()51118x y--=5629y x-+=3476x y++.6.解方程组25,28,211,2 6.x yy zz uu x+=⎧⎪+=⎪⎨+=⎪⎪+=⎩①②③④答案:练习7.71.5,1,32.xyz=⎧⎪⎪=⎨⎪⎪=-⎩2.2,4,3.xyz=⎧⎪=⎨⎪=-⎩3.2,1,2.xyz=⎧⎪=-⎨⎪=-⎩4.1231,1,3.RRR=⎧⎪=-⎨⎪=⎩5.1,2.xy=-⎧⎨=⎩提示:原方程可化为()51113478656234796x y x yy x x y--⎧++=⎪⎪⎨-+++⎪=⎪⎩化简得31731,21217.x yx y+=⎧⎨+=-⎩解得1,2.xy=-⎧⎨=⎩6.1,2,3,4.xyzu=⎧⎪=⎪⎨=⎪⎪=⎩提示:由④得u=6-2x代入③,得z=4x-1代入②,得y=10-8x代入①得x=1,再依次代。
C++程序设计教程修订版_第07章_数组

2、访问数组元素
•数组中特定的元素通过下标访问。 •为整个数组赋值时,必须一个一个元素逐个访问。
int main() { int iArray[10]; iArray[0] = 1; iArray[1] = 1; iArray[2] = 2; //........ iArray[9] = 55;
}
在定义时也可以只对部分元素赋初值而省略第一维的长度,但 应分行赋初值。如 0 0 3 0 int a[ ][4]={{0,0,3},{ },{0,10}}; 0 0 0 0 0 10 0 0
5、二维数组
作为参数传递一个二维数组给函数,其意义也为内存地址:
//********************* //** ch7_7.cpp ** //********************* #include <iostream.h> int maximum(int[ ][4],int,int); void main() { int sg[3][4]={{68,77,73,86}, {87,96,78,89}, {90,70,81,86}}; int maximum(int grade[][4],int pupils,int tests) { int max=0; for(int i=0; i<pupils; i++) for(int j=0; j<tests; j++) if(grade[i][j]>max) max=grade[i][j];
– int a[500]; – memset(a,0,500*sizeof(int));
• 数组名称 a 代表整个数组的起始(第一个元素)的地址
4、向函数传递参数
• 传给自定义函数
07第7章_三相异步电动机的基本工作原理和结构[1]
![07第7章_三相异步电动机的基本工作原理和结构[1]](https://img.taocdn.com/s3/m/68c90faa80eb6294dc886c51.png)
二、转差率
定义: s n1 n 即同步转速与转子转速之差(称为转差)与同步转速之比。 n1
转差率s是异步电机的一个基本物理量,它能反映异步电机的各种运行状况。
起动瞬间:n = 0, s = 1
空载运行:n≈n1,s≈0 即空载运行时,可以近似认为转子转速等于同步转速。
额定运行: n 略低于n1 ,s = 0.01~0.06
二、单层交叉式绕组
单层交叉式绕组由线圈数和节距不相同的两种线圈组构成,同一组线圈的 形状、几何尺寸和节距均相同,各线圈组的端部互相交叉。
交叉式绕组由两大一 小线圈交叉布置。线圈端部 连线较短,有利于节省材料, 并且省铜。广泛用于q>1的 且为奇数的小型三相异步电 动机。
三、单层同心式绕组 同心式绕组由几个几何尺寸和节距不等的线圈连成同心形状的线圈组构成。
因此任意对调三相异步电动机的两根电源线,便可使电动机反转。 (2) 异步电动机的转速恒小于同步转速
n < n1时,转子与定子磁场间有相对运动,转子才会受到电磁转矩作用。 n = n1时,转子与定子磁场间无相对运动,转子不感应电流不产生转矩。 由于电动机转速n与旋转磁场转速n1不同步,故称为异步电动机。 因为电动机转子电流是通过电磁感应作用产生的,所以又称为感应电动机。
n<0, s >1,电磁转矩为制动转矩,吸收电能和机械能,全部转变成电机损耗。
异步电机主要是工作在电动机运行状态,作为各种生产机械的动力设备。
电动机的标识
三相电动机的铭牌
型号 Y160 – 4 电压 380V 转速 1460r/min 防护等级 IP144 功率因数 0.88
电机厂编号 × × × ×
2. 定子绕组
是电机的电路部分。 定子绕组为按一定规律连接而成的三 相对称绕组,嵌放在定子铁心槽内。
市北资优六年级分册 第07章 7.12 可化为一次方程组的含绝对值符号的方程组+栗小妮

7.12可化为一次方程组的含绝对值符号的方程组例1 解方程组:⎪⎩⎪⎨⎧=++=-+223127213y x y x 解:令a x =+1 ,b y =.则原方程组化为⎪⎩⎪⎨⎧=+=-②①2232723b a b a 由①×3,②×2,得⎪⎩⎪⎨⎧=+=-④③44642169b a b a 由③+④,得13a =65,a =5把a =5代入①,得b =4. 所以⎪⎩⎪⎨⎧==+451y x 可得,⎩⎨⎧==+451y x ,⎩⎨⎧-==+451y x ,⎩⎨⎧=-=+451y x ,⎩⎨⎧-=-=+451y x 所以原方程组的解是⎩⎨⎧==44y x ,⎩⎨⎧-==44y x ,⎩⎨⎧=-=46y x ,⎩⎨⎧-=-=46y x 例2 解方程组:⎪⎩⎪⎨⎧=+=-321y x y x 解:⎪⎩⎪⎨⎧=+=-②①321y x y x 由①得:1=-y x 或1-=-y x与②结合得方程组:(I )⎩⎨⎧=+=-321y x y x ;或(II )⎩⎨⎧=+-=-321y x y x 解(I ):把1+=y x 代入32=+y x ,得321=++y y , 去绝对值符号,解得:32=y 或34-=y 再将y 值代入1+=y x ,解得方程组(I )的解为⎪⎪⎩⎪⎪⎨⎧-=-=3431y x 或⎪⎪⎩⎪⎪⎨⎧==3235y x同理,解得方程组(II )的解为⎪⎪⎩⎪⎪⎨⎧-=-=3235y x 或⎪⎪⎩⎪⎪⎨⎧==3431y x 所以原方程组的解为⎪⎪⎩⎪⎪⎨⎧-=-=3431y x 或⎪⎪⎩⎪⎪⎨⎧==3235y x 或⎪⎪⎩⎪⎪⎨⎧==3235y x 或⎪⎪⎩⎪⎪⎨⎧==3431y x 例3 解方程组:⎪⎩⎪⎨⎧+=+-+=-22x y x y x y x 解:⎪⎩⎪⎨⎧+=+-+=-②①22x y x y x y x 由①得:2+-=+y x y x , 因为0≥-y x ,所以0>+y x , 所以y x y x +=+③把③代入②有2+=+x y x ,所以2=y .将2=y 代入①得:x x =-2,所以x x =-2,④或x x -=-2⑤由无解,由⑤解得1=x ,所以原方程组的解为⎩⎨⎧==21y x练习7.121.解方程组:⎪⎩⎪⎨⎧=-+=--10123612y x y x2.解方程组:()⎪⎩⎪⎨⎧-=+=-++141511y x y x3.解方程组:⎪⎩⎪⎨⎧=+=+21y x y x练习7.12答案1.无解。
离散数学07抽象代数

7.2 代数结构及其性质
定义7.1 设S是一个非空集合。如果有一 个法则, 它对S中任意两个有序元素a与b, 在S中都有一个惟一确定的元素c与它们 对应, 则称这个法则是集合S中一个二元 代数运算。
7.2 代数结构及其性质
一般地,容易得到n元运算的定义:
设S是一个非空集合。如果有一个法则,它 对S中任意n个有序元素a1, a2, „, an, 在S中 都有一个惟一确定的元素d与它们对应, 则称这 个法则是集合S中一个n元代数运算。
7.2 代数结构及其性质
例7.3 设*是定义在集合A上的一个n元运算, S1和S2是在A上运算*下封闭的A的子集, 则 S1∩S2在*下也是封闭的。 证明 对任一组元素a1, a2, „, an∈S1∩S2, 因为a1, a2, „, an∈S1, 且S1在运算*下是 封闭的, 所以, *(a1, a2, „, an)∈S1, 又 因为a1, a2, „, an∈S2, 且S2在运算*下也是 封闭的, 所以有*(a1, a2, „, an)∈S2, 由 此得知*(a1, a2, „, an)∈S1∩S2。即: S1∩S2在*下也是封闭的。
7.2 代数结构及其性质
练习1 通常数的乘法运算是否可看作下
列集合上的二元运算?请说明理由。
(1)A={1,2}
(2)B={x|x是素数}
(3)C={x|x是偶数}
(4)D={2n|n∈N}
7.2 代数结构及其性质
定义7.2 设S上有n元运算*(n为正整数), S′S, 若对任意 a1, a2, „, an∈S′,有 *(a1, a2, „, an)∈S′, 则称S上的*运算对 S′封闭,或称为S′在*下是封闭的。
例7.4
(1)设A={1, 2, „, m}, m是一个正整数。A2 到A的映射定义为:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数组a[4][3]表示矩阵A:a[0][0],a[0][1],……,a[3][2]
返回
2013-10-23 5
7.2 一维数组
1.一维数组的定义: 类型 数组名[数组长度]; 例:int a[6]; 数组长度:用常量表达式来表示数组元 素的个数。 2.一维数组元素的使用: 数组名[下标] 例:a[0]=100;
2013-10-23 17
[例7.8]输入一个3*3的数组,将其行和列互换。 main() { int i,j,b[3][3]; static int a[3][3]={{1,2,3},{4,5,6},{7,8,9}}; for(i=0;i<=2;i++) for(j=0;j<=2;j++) b[j][i]=a[i][j]; 1 4 7 2 5 8 for(i=0;i<=2;i++) 3 6 9 { for(j=0;j<=2;j++) printf("%d ",b[i][j]); printf("\n"); } }
列数
0 1 2 3 4 5 6 7 8
数组长度=常量表达式1*常量表达式2 逻辑结构:
a[0] a[0][0] a[1] a[1][0] a[2] a[2][0]
行名
a[0][1] a[1][1] a[2][1]
a[0][2] a[1][2] a[2][2]
a[0][3] a[1][3] a[2][3]
2013-10-23
8
[例7.3]整数数组的初始化。 int a[]={0,1,0,0,1}; main() { int i; for (i=0;i<5;i++) printf("%d ",a[i]); }
01001
2013-10-23
9
[例7.4]冒泡法从小到大排序程序。
main() 排序过程:设有n个数据,存放到a1到an的n个数组元素中。 { int i,j,t,a[6]={1,0,-8,23,76,-6}; printf("\n"); (1) 从a1到an,依次把两个相邻元素两两比较,即a1与a2比,a2与a3 for (j=1;j<5;j++) for (i=0;i<6-j;i++) 比,…,an-1与an比; if(a[i]>a[i+1]) (2) 每次两相邻元素比较后,若前一个元素值比后一个元素值 {t=a[i];a[i]=a[i+1];a[i+1]=t;} printf("the sorted numbers : \n"); 大,则交换两元素值;否则,不交换。 for (i=0;i<6;i++) printf("%d ",a[i]); } (3)重复上述算法,把a1到an中的最大值换到an ,再把a1到an-1中
2013-10-23
2
7.1 数组和数组元素 7.2 一维数组 7.3 多维数组 7.4 字符数组
退出
2013-10-23 3
7.1 数组和数组元素
数 组 是一种数据结构,处于这种结 数组元素(下标变量) 构中的变量具有相同的性质, 数组中的每个分量,用下标来表示其 数组名 并按一定的顺序排列。 所处位置,各分量排列有序且数据类 表示数组存储区域的首地址,数组的 型相同。 下 标
返回
2013-10-23 16
7.3.2 二维数组的初始化
多维数组的初始化有两种方式: 直述型:将所有常量写在一个花括号内,各个常量之间 用逗号分开,按数组元素存储的顺序对各元素赋初值。 int a[3][4]={1,2,3,4,5,6,7,8,9,10,11,12}; 分列型:用花括号嵌套,即每一组一维数组的初值数据 再用一对花括号括起。 int a[3][4]={{1,2,3,4},{5,6,7,8},{9,10,11,12}}; int a[3][4]={{1},{5},{9}}; 注:若对全部元素都赋初值,第一维长度可省略,但 第二维长度不能省。 int a[][4]={1,2,3,4,5,6,7,8,9,10,11,12};
最大值换到an-1 ,……最后把a1到a2中最大值换到a2中,即完成
排序。
2013-10-23
10
[例7.5]比较交换法从大到小排序程序。
#define N 6 排序过程: main() { int i,j,t,a[N]={1,0,-8,23,76,-6}; (1)通过比较交换将数组元素a1到an中的最大值放入a1中; printf("\n"); for(i=0;i<N-1;i++) (2)再次比较交换将数组元素a2到an中的最大值放入a2中; for(j=i+1;j<=N-1;j++) if(a[i]<a[j]) (3)以此类推,将ai到an中的最大值存入到ai中,直到最后二个元素 {t=a[i];a[i]=a[j];a[j]=t;} printf("the sorted numbers : \n"); an-1与an进行一次比较,依条件交换,较大值存入an-1中,即达到了 for(i=0;i<N;i++) printf("%d ",a[i]); } 按从大到小的排序。
2.二维数组元素的使用
二维数组元素的使用: 数组名[下标1][下标2]
行号 列号
0 1 2 3 4 5 6 7 ………...
二维数组名的使用:是该数组的首地址。
2013-10-23
20 21 22 23
b[0][0][0] b[0][0][1] b[0][0][2] b[0][0][3] b[0][1][0] b[0][1][1] b[0][1][2] b[0][1][3] b[0][2][0] b[0][2][1] b[0][2][2] b[0][2][3] b[1][0][0] b[1][0][1] b[1][0][2] b[1][0][3] b[1][1][0] b[1][1][1] b[1][1][2] b[1][1][3] b[1][2][0] b[1][2][1] b[1][2][2] b[1][2][3]
00 01 02
D (d 0 , d1 , d 2 , d 3 , d 4 , d 5 , d 6 , d 7 , d8 , d 9 )
11 12 A 10 a a21 a22 20 a a31 a32 30
数组d[10]表示向量D: d[0],d[1],d[2],d[3],d[4],d[5],d[6],d[7],d[8],d[9]
1 2 3 4 5 6 a[0][0]=1 addr=0x ffd2 a[0][1]=2 addr=0x ffd4 a[0][2]=3 addr=0x ffd6 addr= %x\n”,i,j,a[i][j],&a[i][j]); a[1][0]=4 addr=0x ffd8 a[1][1]=5 addr=0x ffda a[1][2]=6 addr=0x ffdc
返回
2013-10-23 12
7.3 多维数组
7.3.1 二维数组的定义和使用 7.3.2 二维数组的初始化 7.3.3 二维数组程序举例
返回
2013-10-23 13
7.3.1 二维数组的定义和使用
1.二维数组的定义
类型 数组名[常量表达式1][常量表达式2];
例:int a[3][4];
行数
0 1 2 3 4 5
2013-10-23
4
一维数组:带有一个方括号的数组。a[6] 二维数组:带有两个方括号的数组。data[3][4] 多 维 三维数组:带有三个方括号的数组。c[3][4][5] …… 数 [例7.1] 用数组表示向量D和矩阵A a a a 组 n 维数组: 带有n个方括号的数组。b[4] …[4] a a a
a
a[0] a[1] a[2] a[3] a[4] a[5]
首地址也就是第一个元素的地址,是 用来表示该数组元素在数组中的相 数组的定义: 数组元素的表示: 一个地址常量,不能向它赋值。 对位置,是整型常量,最小值为0,最 数据类型 数组名[数组长度]; 数组名[下标] 大值为数组长度-1。 例:a或&a[0] 例:a[3], data[3][4] 例: a[3]中的下标3 a[6]; int
显示器
2013-10-23
19
[例7.10]求矩阵A与B乘积C。
main() { int i,j,k,m=2,n=3,p=2; static int a[2][3]={ {6,8,7}, {3,4,5} }; static int b[3][2]={ {1,2}, {2,1}, {-1,0} }; static int c[2][2]={ {0,0}, {0,0}}; for(i=0;i<m;i++) for(j=0;j<p;j++) 15 20 6 10 { c[i][j]=0; for(k=0;k<n;k++) c[i][j]=c[i][j]+a[i][k]*b[k][j]; } for(i=0;i<m;i++) { for(j=0;j<p;j++) printf("%d ",c[i][j]); printf("\n"); } }
存储结构:以行为主序方式存放。
2013-10-23
9 10 11
a[0][0] a[0][1] a[0][2] a[0][3] a[1][0] a[1][1] a[1][2] a[1][3] a[2][0] a[2][1] a[2][2] a[2][3]
